Abstract
We investigate hydrodynamic cavitation to inactivate commonly employed Saccharomyces cerevisiae yeast strains in an aqueous solution using different reactors and hydraulic circuit selected to demonstrate the process feasibility on the industrial scale. The target to achieve an useful lethality of the yeast at lower temperature when compared with standard thermal and even with other cavitation processes was achieved, with 90% yeast strains lethality at lower temperature (6.3–9.5°C), and about 20% lower energy input. A separate model simulating the combined thermal and cavitational effects on yeast lethality allows to accommodate the data into a comprehensive framework providing a tool to design further targeted experiments and to predict results when changing the process parameters.
Introduction
Saccharomyces cerevisiae (SC) is the yeast which is most commonly used in the food industry for the fermentation of wine and beer, as well as it is responsible for spoilage in fruit juices and milk [1]. Its inactivation is traditionally performed mostly by means of thermal pasteurization, even though extensive research was aimed at developing alternative methods to achieve a sufficient lethality of SC while keeping temperatures as low as possible [2].
Lower pasteurization temperatures would lead at least in principle to a double advantage: preserving superior nutritive and organoleptic qualities of the food liquids, as well as saving thermal energy, the latter provided that the alternative techniques are sufficiently energy effective.
Beer production, for example, which need a costly thermal pasteurization stage after fermentation in order to avoid further fermentation after bottling as well as to obtain a safe product before release to the market, could benefit from the adoption of new more efficient pasteurization techniques.
Unfortunately, improving lethality and inactivation of SC over standard thermal methods using lower temperatures is quite challenging due to the intrinsic resilience of such microorganisms eventually stopping their reproduction and remaining in a latent state until nutrients restore or environmental conditions turn again favorable [3, 4].
Interest in cavitation processes in liquid media, particularly for food treatment and water processing, has been growing in recent years due to unique features such as scalability, stability and localized release of high-density energy [5, 6]. A myriad of microscopic hot spots characterized by high to extreme density thermal energy, with temperatures up to 10,000 K, and mechanical energy, with pressure waves up to 5000 bar activate or accelerate specific chemical reactions as well as advanced oxidation processes by means of the generation of extremely reactive species such as hydroxyl radicals that can lead to degradation of organic and inorganic chemicals and pollutants [7-9].
Proposed applications of cavitation in liquid media cover a wide range of technological fields, with serious perspectives for industry in the area of biochemical engineering and biotechnology, including microbial cell disruption and disinfection [10]. Coupling with other methods and components stimulating or enhancing oxidation processes, such as Fenton chemistry, hydrogen peroxide, etc., was proven to be advantageous in industrial wastewater treatment applications [11-15].
Nevertheless, in applications concerning liquid foods, oxidation is not desirable as it is harmful to the quality of the food [2]. Remarkably, the shock waves generated by bubbles implosion in hydrocavitation were identified as the dominant factor responsible the disruption of microorganisms [16], which represents a significant motivation to further investigate the applicability of cavitation techniques to yeast inactivation in liquid foods and its feasibility at the industrial scale.
A further practical advantage of cavitation in liquids is the heating occurs directly within the liquid without exchange with hot surfaces or pipes, thereby dramatically reducing heat losses due to internal friction, pressure loss downstream of nozzles, curves, and so forth [17]. As a consequence, in the cavitation treatment of liquid food, thermal gradients are minimized and undesired phenomena such as sugar caramelization are prevented; moreover, the cavitation-induced turbulence enhances the liquid homogenization, thereby accomplishing a further task normally required in liquid food treatment.
Research on cavitation processes aimed at improving sanification of liquid foods has focused on the two main cavitation sources, namely, acoustic (ultrasonic) sources and hydrodynamic (mechanical) reactors. Gogate and coworkers have repeatedly shown that hydrodynamic cavitation (HC) allows to achieve up to two orders of magnitude higher energy efficiency when compared to acoustic cavitation [18], with clear advantages as reduced energy consumption, achievement of microbial lethality at reduced temperatures, and maintenance of fresh-like product quality during processing [5].
Recently, the outperformance of HC over acoustic cavitation and other conventional methods by about two orders of magnitude in terms of energy yield was convincingly proved in the technical field of the synthesis of biodiesel based on the interesterification of waste cooking oil [19], thereby suggesting that such figure could be a broad rule.
This study is mainly aimed at assessing the comparative advantages of the synergistic addition of HC processes to the usual thermal treatment to inactivate the SC in terms of processing temperatures and energy saving. A set of measurements is identified, allowing to perform a significant diagnosis of cavitation yield which is practically feasible in industrial processing, as well as a model is provided to enable the assessment and prediction of the benefits of HC processes on the basis of measurements of bulk properties of a liquid sample and of cavitation parameters. The model is general and can be extended to other yeasts, microorganisms, bacteria, fungi, and spores, as well as to other liquid foods.
The specific substance used in the experiments, namely, a water–sugar solution, makes the results directly applicable to the brewing processes and in particular to beer pasteurization, representing a novelty for both the specific application area and the demonstration of feasibility at the industrial scale.
Theoretical and Experimental Background
HC reactors invariably include some nozzles in order to locally accelerate the liquid, thus lowering its pressure due to the Bernoulli equation [20] and in turn creating countless void, plasma- and vapor-filled bubbles that, under the average pressure of the downstream undisturbed medium, collapse after few milliseconds [21].
The cavitation process is generally represented in terms of bubble density as well as collapse intensity by means of the cavitation number, hereinafter indicated as CN or σ:
|
|
(1) |
where P0 is the downstream average pressure, Pv is the liquid vapor pressure, in turn a function of the average temperature for any given liquid, ρ is the liquid density, and u is the flow velocity [22].
The relationships between features of the cavitation bubbles and the CN σ, in particular the inverse relationship of their density and the direct relationship of the intensity of their collapse, has been known for a long time [23]. More recently, the strongly nonlinear relationship between HC efficiency and CN was clearly shown in terms of production of the hydroxyl radicals [9].
Static HC reactors crossed by the liquid flow are easy to assemble with commonly available commercial electromechanical components, generally with two configuration: orifice plates and Venturi tubes [5, 6]. Venturi tubes show an obvious practical advantage over orifice plates with liquids including solid residues and/or high viscosity components potentially occluding smaller holes [24]. On the other hand, orifice plates allow more flexibility resulting from the different possible geometric arrangement, number, and morphology of the holes, increasing the chance to enhance the cavitation process due to the downstream turbulent interaction of the various jets. The latter effect was translated into a modified CN σmax [23]:
|
|
(2) |
where Σph is the sum of perimeters of the plate holes and pmp is the inner perimeter of the main pipe downstream of the orifice plate.
Assessment of yeast concentration from bulk properties of processed samples
SC yeast consumes sugar contained in a liquid substance according to the general alcoholic fermentation reaction C6H12O6 ⟹ 2 C2H5OH + 2 CO2 [25], therefore the evolution of sugar concentration is a clear marker of the yeast concentration and vitality.
To quantitatively assess the SC concentration, we developed and applied to the postprocessing phase (i.e., after any thermal and/or cavitation treatment) a simple bulk model built upon basic principles of ecological resource–population dynamics [26, 27], the resource being sugar in solution and population being the SC yeast.
The sugar concentration depletion rate at any given time is assumed to be proportional to the product of yeast and sugar concentrations at the same time, so that, in the event the yeast concentration were constant, the sugar concentration would decrease exponentially over time:
|
|
(3) |
where CS(t) is the sugar concentration, NSC(t) is the SC (yeast) concentration, k is a constant that, in the event NSC were constant over time, after its multiplication by NSC can be interpreted as the reciprocal of the time constant in the exponential decay function describing the sugar concentration tendency. Since NSC(t) is actually changing with time, generally equation (3) can be solved only numerically.
In turn, the yeast concentration NSC(t) is assumed to change as a combined result of growth by self-duplication [4] and decay produced by the depletion of sugar. Rigorously, a balance of growth with death rate induced by the toxic metabolites produced during the multiple duplications should be taken into account, but the latter process is assumed to work effectively only over longer time scales, when the liquid has been eventually spoiled. Moreover, although different choices are possible, an arctangent function of the ratio between sugar and yeast concentration, normalized between the extreme values −1 and 1, was deemed to be sufficiently flexible to allow for an accurate description of both yeasts growth and decay rates. The relevant equation reads as follows:
|
|
(4) |
where λ is a constant that, in the event the arctangent function equaled 1 (high values of the sugar to the yeast concentration ratio), can be interpreted as the reciprocal of the time constant in the exponential growth function describing the yeast concentration tendency; aSC and bSC are further constants allowing to describe the yeast concentration decay at low sugar concentration and to appropriately scale the ratio of sugar to yeast concentration, respectively.
All parameters k, λ, aSC, and bSC were estimated on the basis of the first and most unaffected liquid sample extracted at the beginning of the only experiment carried out without any cavitation reactor (hereinafter “blank experiment”), as described in section 'Experiments and estimation of model parameters'. The parameter estimation method along with the respective assumptions, as well as the solution method for the coupled equations (3) and (4), is discussed in the Appendix.
SC inactivation rate from combined thermal and cavitation treatments
The second model is aimed at quantitatively relating the lethality and permanent inactivation induced on SC by a thermal or combined thermal and cavitation process.
First, a model is proposed to simulate the lethality rate induced by a purely thermal treatment, that is, by heating the liquid including the yeast. It should take into account both temperature and residence time; however, the large thermal inertia of the industrial scale experimental installation allows to discard such residence time as a controlling parameter.
Although different choices are possible, in analogy with the bulk model described in section 'Assessment of yeast concentration from bulk properties of processed samples', we represent the ratio between the SC concentration at some time during the process to its initial value by means of the inverse of an arctangent function of the temperature, normalized between the extreme values 0 and 1. The relevant equation reads as follows:
|
|
(5) |
where tp is the heating process time starting from tp = 0, T(tp) is temperature at time tp during the process, AT is a constant regulating the “sharpness” of the arctangent function, Tc is the temperature value at which FT = 1/2. It is worth noting that the function FT cannot be allowed to decrease in the course of a process, regardless of possible short transient cooling phases due to technical needs such as sampling, because inactivation or lethality are irreversible on such short time scales.
The parameters AT and Tc were estimated from the blank experiment, when the liquid treatment was limited to heating, by matching the ratios NSC(tp)/NSC(0) derived from equation (5) with the respective values computed as explained in the Appendix. Moreover, normalizing the FT function in equation (5) enables to fit the interval between null and maximum lethality. It should be noted that the same matching could be performed with observed values of the ratios of the SC concentration. The estimated values of AT and Tc are shown in the Appendix.
The model represented by equation (1) is now generalized to include the additional effect of HC upon the yeasts lethality. In order to keep the model as simple as possible, the additional lethality induced by cavitation is accounted for by multiplying the “thermal” function FT(T) in equation (5) by the integral over the process time of a further “cavitation” function FC; such function FC depends on the CN σ, as per equation (1) or, in the modified form, equation (2), on the frequency of cavitation processes, that is, the number of passages of each fluid parcel through the cavitation reactor per unit time, and again on the temperature, due to the observed strongly synergistic effect of temperature and cavitation [1].
The dependence of FC on the CN σ was chosen such that, all other quantities held constant, it produces up to two local maxima at some values σ = σ1−max and σ = σ2−max with 0 < σ1−max < σ2−max, and falls to zero at both σ = 0 and σ → ∞, where no cavitation occurs. The choice to allow up to two local maxima derives from the consideration that in low CN cavitation regimes more bubbles are generated and their collapse is moderate, while in higher CN cavitation regimes less bubbles are generated and their collapse is more violent; a square dependence on the CN was chosen in order to get more pronounced local maxima in the range of CN of interest.
The relevant equation reads as follows:
|
|
(6) |
where Bc is a “scaling” constant factor, Ncav is the frequency of cavitation processes, that is, the number of passages of each fluid parcel through the cavitation reactor per unit time. In other words, the dependence of FC on the cavitation frequency is kept linear, while an exponential growth function of the temperature is used to represent the observed sharp changes of the cavitation efficiency with temperature itself.
The parameter Tc is chosen as the same temperature value as in equation (5) in order to avoid the introduction of a new parameter. Usually, the quantities Ncav and σ change during any process due to the observed weak dependence of the liquid flow rate and its speed on the actual temperature, which in turn affects the liquid internal friction, therefore their average values are computed.
The equation describing the synergistic effects of the thermal and cavitation processes on the yeast concentration reads as follows:
|
|
(7) |
The parameters Bc, σ1−max, and σ2−max in equation (6) are estimated from the combined thermal and cavitation experiments by matching the ratios NSC(tp)/NSC(0) derived from equation (7) with the respective values computed as in the Appendix, corresponding to samples extracted at different stages of the process.
Again, the same value matching could be performed with observed values of the ratios of the SC concentration, should such measurements be available. The estimated values of Bc, σ1−max, and σ2−max are displayed in the Appendix.
Materials and Methods
Experimental stand
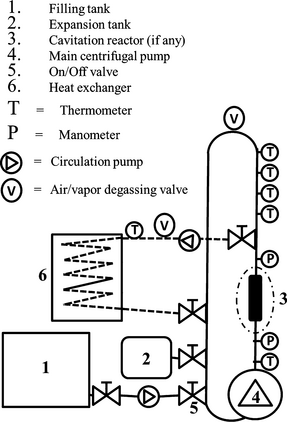
The experimental stand consisted of a closed hydraulic circuit equipped with a main centrifugal pump of nominal mechanical power 4 kW (Lowara SHE 40-160/40); a filling tank where the mixture of water, sugar, SC yeast, and nutrients was prepared before entering the circuit with the help a smaller pump; an expansion tank used to regulate the hydraulic pressure downstream of the cavitation reactor; the cavitation reactor; a secondary circuit to the heat exchanger supplied with a small 100 W circulation pump; On/Off valves to manage filling; and a secondary circuits as well as expansion tank (Fig. 1).
|
|
|
Figure 1. Experimental stand: general scheme with identification of main components. |
The main hydraulic circuit including the cavitation reactor consists of a food quality “AISI 304” stainless steel pipe with internal diameter 97.6 mm, and of a vertical extent slightly taller than 5 m starting from the main pump exit (volume = 90 L). The secondary circuit consists of a one inch (about 25.4 mm) diameter steel pipe connected to the heat exchanger, with a volume about 25 L. The total volume including both the main and the secondary circuit was therefore about 115 L.
The only energy source is electricity powering the main pumps motor. Any heating of the circulating liquid is the result of the conversion of the pumps rotor mechanical energy into heat in the closed hydraulic circuit. Moreover, the HC-induced bulk heating is an energy-intensive process, especially when a vertical geometry of the hydraulic circuit is used [17].
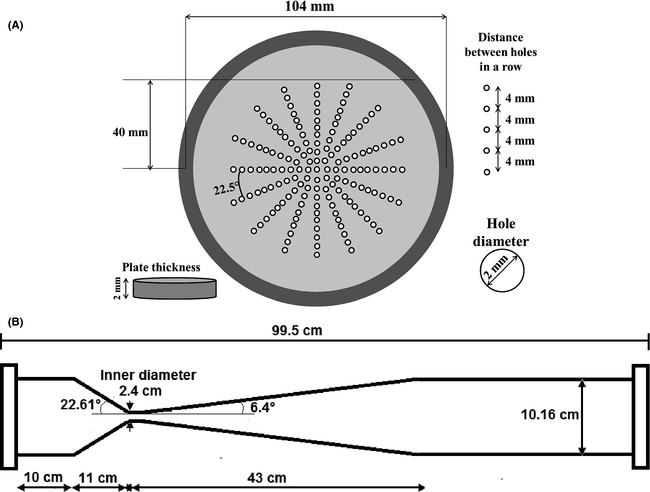
The cavitation reactors used for the experiments were an orifice plate equipped with 156 holes (each having an internal diameter 2 mm) and a Venturi tube (Fig. 2A and B). Both are upscale models of effective configurations used in laboratory scale experiments by researchers in India [23, 28]. The orifice plate total opening was 490 mm2 (6.55% of the main pipes inner section). The corresponding value for the opening of the Venturi tubes nozzle was 452 mm2 (6.05% of the pipes section).
|
|
|
Figure 2. Cavitation reactors: (A) orifice plate and (B) Venturi tube. |
The preparation of the yeast before each experiment, as well as the measurement methods, is described in the Appendix.
Experiments and estimation of model parameters
The main structural and operational features of the performed experiments are listed in Table 1.
| Experiment ID | Cavitation reactor | Volume (L) | Temperature range and samples’ extraction temperature (°C) | Range of cavitation numbera | Range of cavitation frequencyb (min−1) | Processing timec (min) |
|---|---|---|---|---|---|---|
| ||||||
| THERMAL testd | None | 115 |
26.0–73.9 S0–32.8 S1–41.7 S2–53.7 S3–61.5 S4–73.9
|
N/A | N/A | 440 |
| PLATE test | Orifice plate | 115 |
20.2–74.3 S0–25.5 S1–41.0 S2–52.0 S3–62.0 S4–74.3
|
0.14–0.21e 0.44–0.67a
|
7.0–8.6 | 484 |
| VENTURI test #1 | Venturi tube | 115 |
26.3–62.0 S0–33.5 S1–45.8 S2–52.1 S3–57.1 S4–62.0
|
0.64–0.72 | 9.3–10.2 | 263 |
| VENTURI test #2 | Venturi tube | 115 |
25.5–51.8 S0–35.6 S1–51.8
|
0.94–1.18 | 8.8–9.8 | 159 |
| VENTURI test #3_flashf | Venturi tube | 90 |
25.9–72.0 S0–30.5 S1–53.0 S2–62.5 S3–72.0
|
0.84–1.02 | 11.6–13.4 | 75 |
| VENTURI test #4 | Venturi tube | 115 |
27.8–62.5 S0–30.8 S1–42.0 S2–55.5 S3–62.5
|
0.87–1.15 | 9.7–11.8 | 211 |
| VENTURI test #5_flashf | Venturi tube | 90 |
22.8–61.1 S0–32.6 S1–51.7 S2–57.3 S3–61.1
|
0.29–0.44 | 11.7–14.4 | 58 |
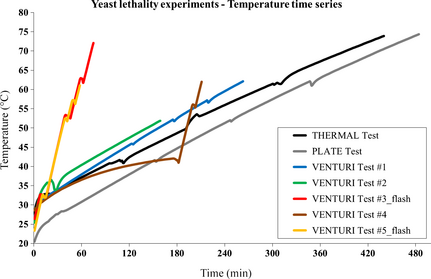
Figure 3 shows the time series of the liquid average temperature for all the performed yeast lethality experiments.
|
|
|
Figure 3. Liquid average temperature time series for all the performed yeast lethality experiments. |
The temperature curves for the VENTURI test #3_flash and VENTURI test #5_flash differ from all the others because those were the only processes carried out without heat exchange, that is, semi-adiabatically (unless unavoidable heat losses due to practical limitations to the thermal insulation). The last phase of the experiment VENTURI test #4 was carried out without heat exchange too, with most of the temperature rise occurring in that phase. The estimated values of the parameters included in the models described in sections 'Assessment of yeast concentration from bulk properties of processed samples' and 'SC inactivation rate from combined thermal and cavitation treatments' are shown in Table A1 in the Appendix.
The temperature curves for the VENTURI test #3_flash and VENTURI test #5_flash differ from all the others because those were the only processes carried out without heat exchange, that is, semi-adiabatically (unless unavoidable heat losses due to practical limitations to the thermal insulation). The last phase of the experiment VENTURI test #4 was carried out without heat exchange too, with most of the temperature rise occurring in that phase. The estimated values of the parameters included in the models described in sections 'Assessment of yeast concentration from bulk properties of processed samples' and 'SC inactivation rate from combined thermal and cavitation treatments' are shown in Table A1 in the Appendix.
Results and Discussion
As explained in section 'Assessment of yeast concentration from bulk properties of processed samples' the initial postprocessing SC yeast concentration for each sample of any experiment listed in Table 1, indicated with NSC(t0), can be retrieved after matching the respective observed sugar concentration time series with the same series predicted on the basis of the model represented by equations (3) and (4) with the parameter values shown in Table A1 in the Appendix.
THERMAL test: the benchmark experiment
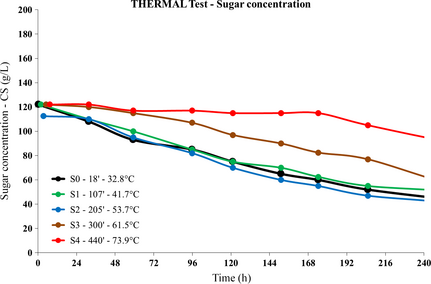
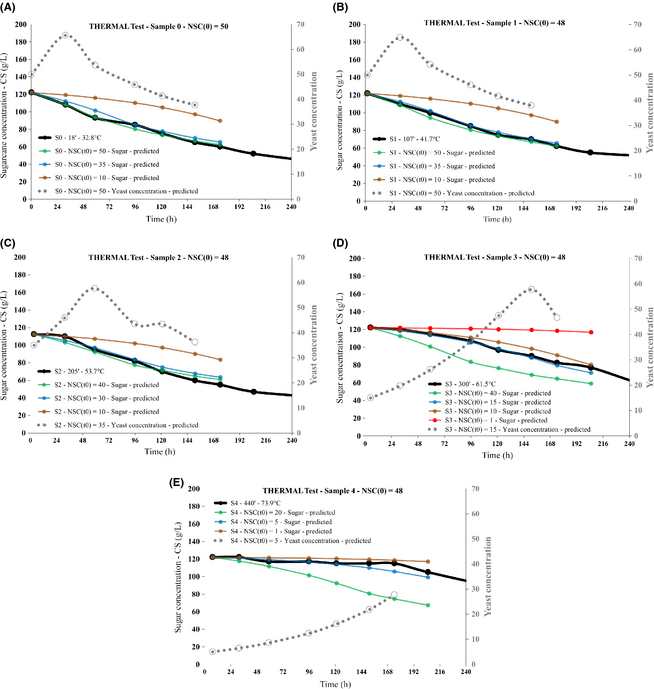
Due to its own relevance as the reference experiment for the calibration of model parameters as well as a “benchmark” for all other experiments, the results for the THERMAL test are shown in full detail. Figure 4 shows the sugar concentration time series for all the samples extracted during the process.
|
|
|
Figure 4. THERMAL test: postprocessing sugar concentration versus time series for all samples. |
Given the measurement error on the order at most of 5 g/L, the differences among the tendencies shown by the time series associated with the first three samples (S0, S1, and S2), the fourth (S3), and the fifth (S4) in Figure 4 are quite significant, showing that a relevant effect upon the yeast activity occurs at 54°C < T < 61°C. A small drop in the sugar concentration occurs even in the S4 sample (heating up to 73.9°C) about 48 h after its extraction.
Charts in Figure 5 show the observed and simulated sugar concentration time series for all samples, along with the predicted yeast concentration time series associated with the best simulated sugar concentration curve.
|
|
|
Figure 5. THERMAL test: observed (black) and model-simulated (colored) sugar concentration, model predicted yeast concentration (dotted gray) versus time series for all samples, each chart (A-E) concerning a specific sample. Time and temperature of any sample during the process are indicated. The postprocessing initial yeast concentration (first point in its time series) is indicated too. |
As explained in the Appendix, the identification of the simulated sugar concentration curve best matching the observed one was performed computing the respective average square distances during the earliest 72 h after sampling.
The initial postprocessing SC yeast concentration NSC(t0) appears to change from the preprocessing value of 50 for samples S0 and S1, to 35 for sample S2, then to 15 for sample S3, and 5 for sample S4, the latter (Fig. 5E) showing a lethality rate around 90% at T = 73.9°C.
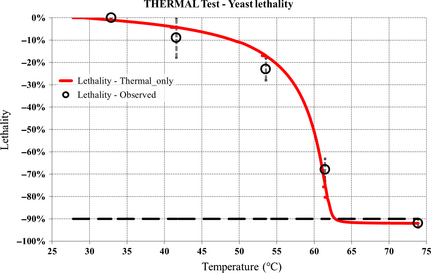
Figure 6 shows the model reconstruction of the yeast lethality rate for the THERMAL test on the basis of equation (5). The error bars on the observed data derive from the uncertainty of the identification of the simulated sugar concentration curve which best matches the observed one.
|
|
|
Figure 6. THERMAL test: model reconstruction of the yeast lethality rate. |
According to the model, the simulated threshold lethality rate of 90% occurs at T = 62.8°C, which is the most important benchmark figure for all other experiments.
Comparative analysis of yeast lethality rates in the cavitation experiments
The lethality rates estimated for each sample collected in the course of the six cavitation experiments listed in Table 1 are compared with the benchmark values of the same quantity retrieved from the THERMAL test in section 'THERMAL test: the benchmark experiment'.
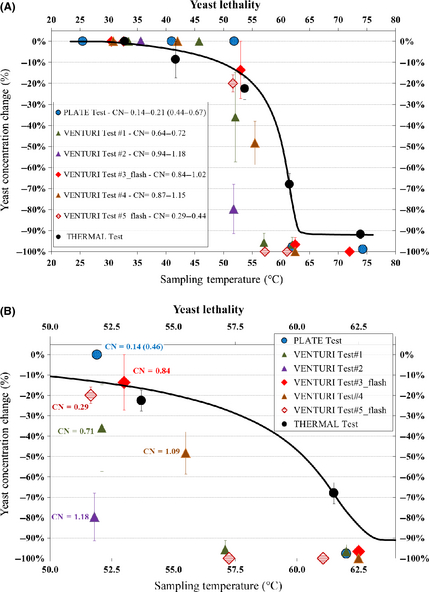
Figure 7 shows the whole set of lethality rates, as well as a focus over the temperature range with the steepest increase of the lethality rate, that is, 50–63°C.
|
|
|
Figure 7. Whole set of lethality rates (A) and focus over the temperature range with the steepest increase of the lethality rate, including labels highlighting the cavitation number occurred before any sampling (B); for the PLATE test, the modified CN is shown, along with the ordinary CN in brackets. |
Figure 7A shows that all lethality rates data points derived from the cavitation tests lie below the THERMAL test lethality curve when both the following conditions are fulfilled: temperature higher than 50°C and lethality rate greater than 15%; moreover, the 90% threshold of the lethality rate is achieved, within the represented uncertainty, at temperatures up to 10°C lower than in the THERMAL test, that is, around 52°C.
Figure 7B, focused on the temperature range where changes of the lethality rate are steepest, shows as well the CN associated with samples collected during all processes, computed at the time of sampling. Although the picture is quite complex, it appears that the best result, namely, the lowest temperature at the 90% lethality rate is achieved with the highest CN (CN = 1.18 in VENTURI test #2).
The semi-adiabatic tests, that is, VENTURI test #3_flash and VENTURI test #5_flash, show approximately the same values for the cavitation frequency and the processing time at any temperature (Table 1), but very different CN (CN = 0.84 and CN = 0.29 for the considered samples extracted from the VENTURI test #3_flash and the VENTURI test #5_flash, respectively, allowing to conclude that the lethality rate is greater when the CN is smaller, that is, in VENTURI test #5_flash).
The other two tests carried out by means of Venturi tube reactor, namely, VENTURI test #1 (CN = 0.71) and VENTURI test #4 (CN = 1.09), the first one with a little longer processing time (Table 1), show a comparable behavior, close to the best of the two flash tests but after much longer processing times.
A tentative conclusion from Venturi tube experiments, within the limits of the cavitation regimes under study, could be that the impact of cavitation processes on the lethality rate shows a local peak at low CNs, around CN = 0.29, decreases as the CN increases up to a little more than 1, after that it increases very sharply, therefore adding confidence to the “two-peak” yeast lethality model represented by equation (6).
Last, the PLATE test, showing a modified CN = 0.14 and CN = 0.46, shows the worst efficiency in terms of lethality, this conclusion being supported by its processing time which is by far the longest among the other cavitation experiments (and close to the processing time of the THERMAL test). Whether this is due to the values of its CN, modified CN, lower cavitation frequency, or other specific features of the reactor configuration, remains so far unclear.
Assuming that the cavitation regime of the PLATE test corresponds to an effective CN somewhere between 0.14 and 0.46, therefore close to that of VENTURI test #5_flash, the important recommendation arises that, in addition to the practical advantages discussed in section 'Theoretical and Experimental Background', the Venturi tube configuration is to be preferred over the orifice plate in order to boost the lethality rate.
This finding could even be more general: Venturi tubes were recently found to outperform orifice plates as cavitation reactors in the fields of degradation of recalcitrant pollutants in aqueous solutions by means of hybrid cavitation and chemical processes [29, 30], as well as in the field of the synthesis of biodiesel based on the interesterification of waste cooking oil [19].
Considering the deviation of the results of the PLATE test from the other ones, the calibration of the cavitation-related parameters included in equation (6) was performed only over the VENTURI experiments, turning out in the identification of two local peaks of the cavitation effect at the CNs σ = σ1-max = 0.3 and σ = σ2-max = 1.7, as shown in Table A1 in the Appendix. It should be stressed here that while the first peak at low CN falls in the range of the performed experiments, the second peak at σ = σ2-max = 1.7 falls well beyond that range, thus pointing to the need for further research by means of equipment able to sustain higher hydraulic pressures (the maximum practicable pressure was around 7.5 bar).
Complex nonlinear behavior of the HC efficiency was found in other works; for example, using an orifice plate as cavitation reactor, the degradation of dichlorvos in aqueous solution showed a sharp peak at high inlet pressure and low temperature [31]; similar results were found in other works using Venturi tubes and dealing with different pollutants such as rhodamine B and p-nitrophenol [29, 30]. The problem in those works is that, increasing the inlet pressure, both liquid circulation velocity and downstream recovery pressure increase, which can partially compensate each other in terms of CN; therefore, it cannot be excluded that more peaks exist over a wide enough range of cavitation regimes.
Microbiological validation of the bulk model
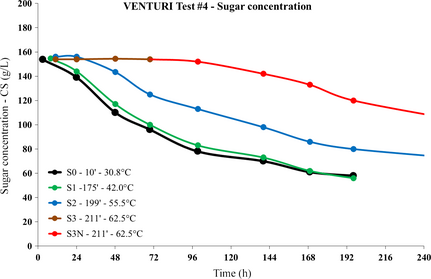
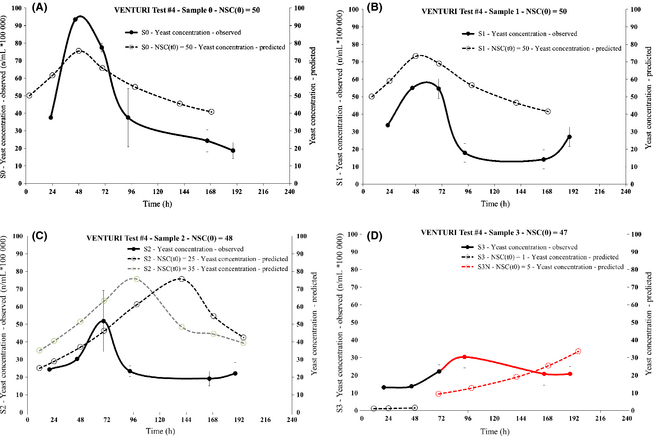
In order to validate the bulk model built upon equations (3) and (4), at least in a qualitative sense, the SC yeast concentration in the samples extracted from the VENTURI test #4 was measured along with the usual sugar concentration. Figure 8 shows the sugar concentration time series for all samples extracted during the process of VENTURI test #4.
|
|
|
Figure 8. VENTURI test #4: postprocessing sugar concentration versus time series for all samples |
A relevant impact on the yeast activity is apparent already at T = 55.5°C. A clearly constant sugar concentration is revealed for the sample S3 extracted at the temperature of 62.5°C.
After 72 h, once the sugar concentration in sample S3 was verified to be constant, further nutrients were added to the same sample and with the same proportion of the liquid initially loaded into the circuit, in order to investigate possible recovery of the yeast cells. The same sample was renamed as “S3N” after the addition of nutrients.
On the basis of the sugar concentration time series shown in Figure 8 for the S3N sample, the yeast recovery was quite slow and limited in extent.
Selected portions of each sample extracted during the VENTURI test #4 process were used to measure the yeast cells concentration according to the methods described in the Appendix.
Charts in Figure 9 show the direct comparison of the observed and model-simulated yeast concentration time series, the latter associated with the best matching of the observed and simulated sugar concentration curves. Error bars representing the standard deviations are based upon the analysis of at least five microbiological samples at all the observed data points except the first two, for which only one sample was available.
|
|
|
Figure 9. VENTURI test #4: observed and model-simulated yeast concentration time series, each chart (A-D) concerning a specific sample. The observation data points are in units of number of yeast cells per mL, divided by 105. |
The simulated steep fall of the initial postprocessing yeast concentration (i.e., the quantity NSC(t0)) going from sample S1 (Fig. 9B) to sample S2 (Fig. 9C) and the even larger decrease going from S2 (Fig. 9C) to S3 (Fig. 9D) are qualitatively very well reproduced by the experimental data. The overall evolution of the postprocessing yeast concentration is also reproduced with fair accuracy at least up to 96 h after sampling, especially for samples S0 (Fig. 9A) and S1 (Fig. 9B).
Therefore, the microbiological analysis offers a qualitative validation of the proposed model and of the overall results of the research, even though the discrepancy of the predicted and observed peak concentration values in samples S2 and S3, as shown in Figure 9C and D, respectively, could suggest that the yeast tendency model as represented by equation (4) is oversimplified and needs further development.
Summary results and energy efficiency considerations
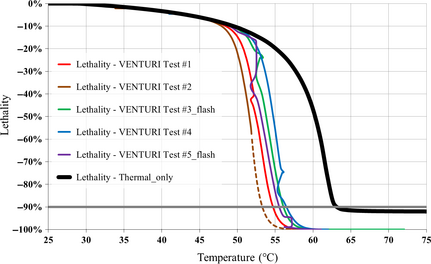
The yeast lethality curves simulated for all the Venturi tube experiments on the basis of equation (7) are shown in Figure 10, along with the same curve derived in the absence of any cavitation process (THERMAL test).
|
|
|
Figure 10. Yeast lethality curves for all VENTURI tests; the dashed portion of the brown curve highlights the extrapolation beyond the maximum temperature achieved in the VENTURI test #2; the thick black curve represents the yeast lethality simulated in the absence of any cavitation process. |
The agreement of the simulated yeast lethality curves with the available observations, which are not shown here, is very good for all experiments, with a limited overestimation of the lethality rate only for the VENTURI test #4 (blue curve in Fig. 10), which could derive from its unique features such as the break of the heat exchange regime (slow warming) after about 3 h of processing, followed by a flash heating, as shown in Figure 3.
Relying on this agreement between simulations and observations, both the temperature associated with the 90% yeast lethality threshold and the difference with regard to the THERMAL test can be inferred for any VENTURI experiment; these results are shown in Table 2.
| Experiment ID | 90% Lethality threshold temperature (°C) | 90% Lethality threshold temperature difference with respect to THERMAL test (°C) |
|---|---|---|
| THERMAL test | 62.8 | |
| VENTURI test #1 | 54.7 | −8.1 |
| VENTURI test #2 | 53.3 | −9.5 |
| VENTURI test #3_flash | 56.4 | −6.4 |
| VENTURI test #4 | 56.5 | −6.3 |
| VENTURI test #5_flash | 55.4 | −7.4 |
The 90% lethality threshold temperature differences span the range −6.3°C to −9.5°C; limited to the flash tests, the best result is −7.4°C, achieved within the VENTURI test #5_flash.
The achievement of the 90% threshold of the yeast lethality rate at lower temperatures can lead both to a significant improvement of the organoleptic and nutritional qualities of the food liquid, and to some energy saving arising from the reduction of the energy requirements for heating.
The experiment VENTURI test #5_flash will be considered for the assessment of the energy saving because it was performed in semiadiabatic conditions, that is, the heat exchanger shown in Figure 1 was disconnected from the main circuit and the deviations from an adiabatic heating process was reduced to the unavoidable heat loss due to the practical limits affecting the thermal insulation. Table 2 shows the difference of the temperature at which the 90% lethality rate was achieved in the VENTURI test #5_flash experiment and the THERMAL test, namely, −7.4°C.
Moreover, in the THERMAL test, the initial temperature was 26.0°C (Table 1), and the temperature at which the 90% lethality was achieved was 62.8°C (Table 2). Assuming that the energy requirements to heat the water–sugar solution is independent of the temperature and proportional to both the mass of the substance and to the change of temperature, the relative energy saving attributable to the cavitation process can be simply estimated from the following ratio: 7.4/(62.8 − 26.0) = 0.20 (20%), which means a relative energy saving per unit temperature decrease with regard to the purely thermal treatment on the order of 2.7%/°C.
The digital Watt-meter mentioned in the Appendix provided the direct measurements of the grid electricity consumed to bring the water–sugar solution from the initial temperature of VENTURI test #5_flash experiment, that is, 22.8°C (Table 1), to the temperature at which the 90% yeast lethality rate is achieved, namely, 55.4°C (Table 2), resulting in approximately 3.1 kWh (11,160 kJ).
Given the water–sugar solution volume of 90 L, a specific energy consumption in the VENTURI test #3_flash equal to 11,160/[90 × (55.4 − 22.8)] = 3.804 kJ/kg °C is estimated, therefore the absolute specific energy saving can be computed as follows: 7.4 × 3.804 = 28.15 kJ/kg.
It should be noted that, in comparison with previous work dealing with cavitation-induced lethality on SC by means of laboratory-scale devices [1, 32], the values of energy consumption reported in this study are lower by nearly one order of magnitude.
Achieving even lower temperatures corresponding to the 90% yeast lethality rate, therefore energy savings well above 20%, is thought to be feasible by at least two different developments; first, placing more than one cavitation reactor in series along the main circuit in order to increase the frequency of occurrence of cavitation processes for each liquid parcel, that is, the factor Ncav in equation (6); second, optimizing the cavitation regimes, for example, exploring higher CN regimes (in turn achievable mainly after increasing the hydraulic pressure) where a local peak of the cavitation function FC expressed in equation (6) was predicted, as shown in Table A1 in the Appendix.
Perspectives and Conclusions
Using a preindustrial scale installation and relying over basic and general principles of resource–population dynamics, we have assessed the comparative advantages of adding HC processes to the usual thermal treatment to inactivate SC in an aqueous solution, in terms of processing temperatures and energy efficiency.
The sugar and SC yeast concentration model represented by equation (3) and equation (4) reproduces fairly well the observational data collected in the course of few targeted experiments. Furthermore, a qualitative microbiological validation of the model confirms the specific trends of yeast concentration.
An original model simulating the yeast lethality rate as a function of temperature and cavitation parameters, represented by equations (5), (6), and (7), and calibrated over the experimental data, allows to interpolate between the sparse data points as well as to extrapolate at least within the range of the observed temperatures.
The impact of the cavitation processes upon the yeast cells lethality has been clearly detected and quantified beyond the purely thermal resistance effects, resulting in a remarkable decrease of the maximum process temperature for the same high lethality threshold. Moreover, the existence of a local peak for the impact upon the yeast lethality at a cavitation regime far beyond the observational data was predicted, pointing to the need for further experiments by means of new equipment.
In conclusion, the following general findings and recommendations arise from this study:
- The synergistic application of thermal and cavitational processes allows to lower the temperature associated with high yeast lethality in an aqueous solution by several degrees.
- Beyond the clear benefits in terms of liquid food quality, energy saving is quite significant: at least 2.7% for every 1°C of decrease of the process maximum temperature.
- Among HC reactors, Venturi tubes outperform orifice plates in terms of yeast lethality.
- The cavitation regimes associated with CNs as low as 0.3 and as high as 1.2 show similar peak performances; nevertheless, the efficiency could further improve with higher CNs.
- The cavitation frequency, that is, the number of passages of each liquid parcel through the reactor, is important; therefore, placing further reactors in series could significantly improve the overall performance.
- Cavitation significantly affects the yeast lethality starting from a definite temperature (51 ± 1°C for a water–sugar solution). Therefore, energy sources cheaper than electricity, such as solar thermal energy, could be used to heat the liquid up to said threshold temperature.
Acknowledgments
This article is dedicated to the memory of Francesco Foresta (1965–2014) for all he has done to advance journalism in Sicily and in Italy. L. A. and F. M. gratefully acknowledge Dr. A. Raschi (CNR) for fruitful discussions and continuous support. This research was partially funded under the project T.I.L.A. (Innovative Technology for Liquid Foods) of Tuscany Regional Government (Decree No. 6107 – 13 December 2013). Selected results of this research were first presented at the Sun New Energy Conference SuNEC 2014 (Santa Flavia, Sicily, Italy, 8–9 September 2014). Two anonymous reviewers are gratefully acknowledged for their valuable comments and suggestions.
Conflict of Interest
None declared.
Appendix
Bulk Model: Parameter Estimation Method
The parameter estimation method for the bulk model described in section 'Assessment of yeast concentration from bulk properties of processed samples' along with the respective assumptions, is discussed in the following:
- a series of values for CS(t) are known from measurements taken at different times, for example, at the initial time t0 and at later times t1, t2, and so forth;
- a value of NSC(t0) just after the sample extraction is assumed arbitrarily, because the ratio of initial yeast concentrations for different experiments is known;
- the value of parameter k is computed from equation (3), according to the following equation:
(A1) - again from equation (3), any value for NSC(t > t0) can be computed assuming the value for parameter k as per equation (A1) as well as measurements for CS(t > t0), according to the following equation:
(A2) - at the initial time t = t0, it is assumed that the ratio CS(t0)/NSC(t0) is high enough so that equation (4) simplifies to: , hence the parameter λ can be retrieved as follows:
(A3) - the parameters aSC and bSC of the arctangent function in equation (4) can finally be estimated from the same equation since the other parameters k and λ are known from equations (A1) and (A3), respectively, CS(t) is measured at any time and NSC(t) is computed by means of equation (A2); using for CS(t) and NSC(t) the first three available values following the sample extraction in order to minimize any deviation of the respective tendencies from the herein described model, the following simple equation system can be written:
(A4)
The estimation of parameters k, λ, aSC, and bSC was therefore fairly objective, although based upon an only liquid sample from the THERMAL test described in Table 1.
Bulk Model: Solution Method
The main objective of the model described in section 'Assessment of yeast concentration from bulk properties of processed samples' is the assessment of the initial value of the yeast concentration NSC(t0) in any sample extracted during a specific process, as a fraction of the yeast concentration before that same process. When dealing with any experiment different from the blank one, the initial value of the yeast concentration before a process is expressed as a fraction (lower or greater than unity, depending on the volume of the processed liquid substance) of the arbitrary value attributed to the first liquid sample extracted at the beginning of the blank experiment, multiplied by the latter value, while the sugar concentration CS(t) is measured at any time.
However, since the value of NSC(t0) is unknown, only the first value of the sugar concentration CS(t0) is assumed to be known, then different first values of the yeast concentration NSC(t0) are used to produce a bundle of curves for CS(t) by solving the coupled equations (3) and (4) with a simple finite differences “forward in time” scheme [33], which, for the first two time steps, reads as follows:
|
|
(A5) |
Finally, the series of measured values for sugar concentration are compared with the respective computed values for the same quantity based on the system of equation (A5), in order to identify the first value of the yeast concentration NSC(t0) originating the computed series, which shows the best matching with the observed tendency during the earlier 72 h after sampling (such time period being chosen as a compromise between the need to avoid significant effects from yeast cells death rate as well as contamination by different microorganisms, on one hand, and allow for recovery of SC cells temporarily inactivated during the experimental processes). The ratio of such NSC(t0) to the initial value of the yeast concentration before a specific process finally gives the measure of the lethality induced by that process on the Saccharomyces cerevisiae (SC).
SC Inactivation Model: Parameter Estimation Method
The parameters AT and Tc of the SC inactivation rate model described in section 'SC inactivation rate from combined thermal and cavitation treatments' were estimated from all the five samples extracted in the course of the THERMAL test too, according to the best qualitative matching of the lethality curves reconstructed from equation (5) with the respective values computed as explained above in this Appendix.
Finally, the parameters Bc and σmax in equation (6) were estimated the same way as AT and Tc and assuming the values of the latter as known, except that the reference experiments were the five ones involving a cavitation reactor as described in Table 1 and equation (7) was used.
Preparation of the Yeast
The SC yeast was prepared before each experiment by supplying nutrients along with water heated to about 40°C. Nutrients are composed of a mix of APA, vitamins and minerals; the APA, composed of ammoniacal nitrogen, amino acids and polypeptides, is instrumental for cell multiplication and for the biosynthesis of proteins. The vitamins (thiamin, biotin, and pantothenic acid) regulate and limit the production of sulfur compounds and fatty acids, as well as are instrumental in the biosynthesis of amino acids and proteins and are important in cell proliferation and resistance to stress. The mineral salts (manganese, magnesium, zinc, copper, potassium, calcium) regulate cell growth, the formation of alcohols and esters, tolerance to ethanol and the temperature also act as enzyme cofactors.
Measurement Methods
The temperature of the circulated liquid was measured every 10 sec and recorded as minute averages by means of a set of five thermocouples in contact with the liquid itself, from which the average value is directly computed. Pressure gauges (manometers) both upstream and downstream of the cavitation reactor, if any, are used for visual inspection, the first mainly for safety reasons, the second in order to check that the pressure regulated by means of the expansion tank corresponds to the downstream pressure, sometimes referred to as “recovery pressure” too, meaning the pressure “recovered” by the liquid flow shortly after passing through the reactor nozzle, which in turn modulates the collapse of the cavitation bubbles. Thermocouples and manometers are placed as shown in Figure 1.
The other relevant physical measurement concerns the water flow: it is assessed from the characteristic curves of the main centrifugal pump supplied by the manufactured, which relate the liquid flow to its power absorption, the latter in turn measured by means of a commercial digital Watt-meter. Once the water flow is known, the liquid speed through the cavitation reactor nozzle is computed simply dividing the water flow itself by the total nozzle opening surface.
The sugar concentration in water solution was measured by means of a simple “Guyot” analogical gauge combining liquid density and temperature, with an estimated maximum error around 5 g/L.
The microbiological measurements were performed after diluting a small sample of processed liquid with methylene blue, which is a basic dye because the methylene chloride salt dissociates in water in the positively charged blue methylene ion and the negatively charged colorless chloride ion. Because of their chemical nature, cytoplasms of any bacterial cells have a weak negative charge therefore the microorganism shall get directly colored. Of course, such coloring process can happen before the cell gets completely destroyed, that is, only early after its death, therefore counting the absolute number of alive cells is needed for a proper balance as much as identifying the dead and alive.
Figure A1 shows the Buerker counting chamber used to count the alive (white) and dead (blue colored) cells by means of a “biological” 600× microscope equipped with a digital camera.
|
|
|
Figure A1. Buerker counting chamber |
Estimated Values for All the Models’ Parameters
All the parameters were quantitatively estimated assuming an arbitrary value equal to 50 for the initial, preprocessing yeast concentration for the THERMAL test and scaling the yeast initial concentration values for the other experiments according to the ratio of their respective volumes to the THERMAL test one, since the same absolute quantity of yeast, equal to 50 g, was used for each experiment; therefore, on the basis of the volume data in Table 1, the initial yeast concentration was equal to 50 for all experiments except for the “VENTURI test #3_flash” with about 64 g.
On the basis of the above written, remembering that for different reasons all the values of the models’ parameters should be considered as first guesses until further experiments will allow to perform more robust assessment of their central values and uncertainties by means of objective estimation methods, the preliminary estimated values of the parameters are shown in Table A1.
| Parameter | Estimated valuea | Relevant equation |
|---|---|---|
| ||
| k | 0.000073 | Equation (3) |
| λ | 0.0121 | Equation (4) |
| aSC | −10.9 | Equation (4) |
| bSC | 5.9 | Equation (4) |
| AT | 1.6 | Equation (5) |
| Tc | 62°C | Equation (5) |
| Bc | 50 | Equation (6) |
| σ1-max | 0.3 | Equation (6) |
| σ2-max | 1.7 | Equation (6) |
References
- Milly, P. J., R. T. Toledo, W. L. Kerr, and D. Armstead. 2008. Hydrodynamic cavitation: characterization of a novel design with energy considerations for the inactivation of Saccharomyces cerevisiae in apple juice. J. Food Sci.73:M298–M303.
- Ngadi, M. O., M. B. Latheef, and L. Kassama. 2012. Emerging technologies for microbial control in food processing. Pp. 363–411inJ. I. Boye and Y. Arcand, eds. Green technologies in food production and processing. Springer, Boston, MA.
- Guth, E., T. Hashimoto, and S. F. Conti. 1972. Morphogenesis of ascospores in Saccharomyces cerevisiae. J. Bacteriol.109:869–880.
- Neiman, A. M.2005. Ascospore formation in the yeast Saccharomyces cerevisiae. Microbiol. Mol. Biol. Rev.69:565–584.
- Gogate, P. R.2011. Hydrodynamic cavitation for food and water processing. Food Bioprocess Technol.4:996–1011.
- Gogate, P. R., and A. B. Pandit. 2001. Hydrodynamic cavitation reactors: a state of the art review. Rev. Chem. Eng.17:1–85.
- Batoeva, A. A., D. G. Aseev, M. R. Sizykh, and I. N. Vol'nov. 2011. A study of hydrodynamic cavitation generated by low pressure jet devices. Russ. J. Appl. Chem.84:1366–1370.
- Capocelli, M., M. Prisciandaro, A. Lancia, and D. Musmarra. 2014. Hydrodynamic cavitation of p-nitrophenol: a theoretical and experimental insight. Chem. Eng. J.254:1–8.
- Capocelli, M., D. Musmarra, and M. Prisciandaro. 2014. Chemical effect of hydrodynamic cavitation: simulation and experimental comparison. AIChE J.60:2566–2572.
- Gogate, P. R., and A. M. Kabadi. 2009. A review of applications of cavitation in biochemical engineering/biotechnology. Biochem. Eng. J.44:60–72.
- Bagal, M. V., and P. R. Gogate. 2014. Wastewater treatment using hybrid treatment schemes based on cavitation and Fenton chemistry: a review. Ultrason. Sonochem.21:1–14.
- Chand, R., D. H. Bremner, K. C. Namkung, P. J. Collier, and P. R. Gogate. 2007. Water disinfection using the novel approach of ozone and a liquid whistle reactor. Biochem. Eng. J.35:357–364.
- Gogate, P. R., S. Mededovic-Thagard, D. McGuire, G. Chapas, J. Blackmon, and R. Cathey. 2014. Hybrid reactor based on combined cavitation and ozonation: from concept to practical reality. Ultrason. Sonochem.21:590–598.
- Gogate, P. R.2007. Application of cavitational reactors for water disinfection: current status and path forward. J. Environ. Manage.85:801–815.
- Chakinala, A. G., D. H. Bremner, P. R. Gogate, K.-C. Namkung, and A. E. Burgess. 2008. Multivariate analysis of phenol mineralisation by combined hydrodynamic cavitation and heterogeneous advanced Fenton processing. Appl. Catal. B Environ.78:11–18.
- Yusaf, T., and R. A. Al-Juboori. 2014. Alternative methods of microorganism disruption for agricultural applications. Appl. Energy114:909–923.
- Baurov, Y. A., F. Meneguzzo, A. Y. Baurov, and A. Y. J. Baurov. 2012. Plasma vacuum bubbles and a new force of nature, the experiments. Int. J. Pure Appl. Sci. Technol.11:34–44.
- Gogate, P. R., and A. B. Pandit. 2011. Cavitation generation and usage without ultrasound: hydrodynamic cavitation. Pp. 69–106inD. S. Pankaj and M. Ashokkumar, eds. Theoretical and experimental sonochemistry involving inorganic system. Springer, Dordrecht–Heidelberg–London–New York.
- Maddikeri, G. L., P. R. Gogate, and A. B. Pandit. 2014. Intensified synthesis of biodiesel using hydrodynamic cavitation reactors based on the interesterification of waste cooking oil. Fuel137:285–292.
- Braeutigam, P., M. Franke, Z.-L. Wu, and B. Ondruschka. 2010. Role of different parameters in the optimization of hydrodynamic cavitation. Chem. Eng. Technol.33:932–940.
- Gogate, P. R.2011. Theory of cavitation and design aspects of cavitational reactors. Pp. 31–68inD. S. Pankaj and M. Ashokkumar, eds. Theoretical and experimental sonochemistry involving inorganic system. Springer, Dordrecht–Heidelberg–London–New York.
- Gogate, P. R.2011. Application of hydrodynamic cavitation for food and bioprocessing. Pp. 141–173inH. Feng, G. Barbosa-Canovas, and J. Weiss, eds. Ultrasound technologies for food bioprocessing. Springer Science + Business Media, LLC, New York, NY.
- Vichare, N. P., P. R. Gogate, and A. B. Pandit. 2000. Optimization of hydrodynamic cavitation using a model. Chem. Eng. Technol.23:683–690.
- Arrojo, S., Y. Benito, and A. M. Tarifa. 2008. A parametrical study of disinfection with hydrodynamic cavitation. Ultrason. Sonochem.15:903–908.
- Carrascosa Santiago, A. V., R. Munoz, and R. G. Garcia. 2011. Molecular wine microbiology. Academic Press, London, UK.
- Gallopin, G. C.1971. A generalized model of a resource-population system. Oecologia7:382–413.
- Gallopin, G. C.1971. A generalized model of a resource-population system II. Stability analysis. Oecologia7:414–432.
- Kumar, P. S., and A. B. Pandit. 1999. Modeling hydrodynamic cavitation. Chem. Eng. Technol.22:1017–1027.
- Pradhan, A. A., and P. R. Gogate. 2010. Removal of p-nitrophenol using hydrodynamic cavitation and Fenton chemistry at pilot scale operation. Chem. Eng. J.156:77–82.
- Mishra, K. P., and P. R. Gogate. 2010. Intensification of degradation of Rhodamine B using hydrodynamic cavitation in the presence of additives. Sep. Purif. Technol.75:385–391.
- Joshi, R. K., and P. R. Gogate. 2012. Degradation of dichlorvos using hydrodynamic cavitation based treatment strategies. Ultrason. Sonochem.19:532–539.
- Yusaf, T.2013. Experimental study of microorganism disruption using shear stress. Biochem. Eng. J.79:7–14.
- Quarteroni, A., and A. Valli. 2008. Numerical approximation of partial differential equations. Springer, Berlin/Heidelberg.
Document information
Published on 01/06/17
Submitted on 01/06/17
Licence: Other
Share this document
Keywords
claim authorship
Are you one of the authors of this document?