Theoretical investigation about the optical characterization of cone-shaped pin-Si nanowire for top cell application

Abstract

Cone-shaped semiconductor silicon nanowires (CS-Si-NWs) grown in vapor liquid solid mode are promising for the fabrication of low-cost high-performance solar cells because of their low processing cost and lower use of Si materials, as compared to planar devices. In this article, the effect of injected charge carriers on the refractive indices and extinction coefficient values in a cone-shaped pin Si NW (CS-pin-Si NW) were considered. Then, the influence of top diameters and periods on the optical absorption was investigated using a finite difference time-domain (FDTD) modeling method. The absorption increased when we decreased the period from 300 to 150 nm for a light wave with a wavelength of 700 nm. However, in the case of incident light at a wavelength of 500 nm, the absorption significantly increased by up to 100% and was found to be independent of the period. On the other hand, we varied the period and the top diameter of the NWs with a fixed bottom diameter. In this case, we found that the period did not significantly affect the absorption value. A high value of the short circuit current density of 19.5 mA/cm² was found in the case of NWs with a top diameter of 110 nm and a period of 150 nm. Combined with the analysis of the ultimate photocurrents, an optimum geometric structure with a top diameter of 70 nm and a period of 150 nm for a CS-pin-Si NW-based top cell for tandem solar cell applications was proposed.

Introduction

Global energy demand will more than double (or more) by 2050, which is particularly worrisome if we do not efficiently use solar irradiance in the near future [1]. The average intensity of solar irradiance that is available on Earth in 1 hour is equal to 4.3 × 10²⁰ J energy, which is equivalent to the energy we consume in 1 year [2], that is, 13 TW. According to Lewis [3], covering 0.16% of the planet with 10% efficient solar cells could provide 20 TW of power. This result indicates that we can produce more power than the annual global requirement by covering <0.16% of the Earth using more efficient low-cost solar cells with an efficiency of more than 25%. Light trapping or confinement in the 3–4 nm diameter structure is quite challenging and must consider different structures and textures [4]. We must increase the supply of Si materials and reduce the cost of photovoltaic device fabrication processes.

One improvement method is to use less Si and low-cost processing methods to create high-efficiency tandem solar cells using Si nanowire (NW) based heterojunction solar cells [4-6]. Another method is to choose cheap and simple growth processes to reduce the fabrication cost of photovoltaic devices. In principle, Si nanostructures can absorb light and directly generate electrons and holes, if they have the same wavelength as the size of the energy gap [5, 7]. There are several unique advantages of Si NWs, that is, the band gap in Si NWs can be transformed from an indirect into a direct-induced band gap via quantum size effects, high crystallinity, self-assembly, high surface-to-volume ratios, and slow electron–hole recombination as compared to the bulk or thin films [5, 6, 8-19]. Si NWs developed using the top-to-bottom approach were explained by Li et al. [20], who showed that power conversion efficiency has made huge progress (to nearly 12%) in <10 years. Wallentin et al. fabricated an InP NW photovoltaic (PV) device, for which 13.8% conversion efficiency was achieved [21, 22]. Si NW-based solar cells are promising for facilitating carrier collection due to the nanostructure size of vertically aligned and ordered arrays of Si NWs. In this way, we can offer straight pathways for carrier collection to escape the device as quickly as possible before recombining in the Si NW-based photovoltaic device [23].

Among bottom-up Si NW growth methods, vapor liquid solid (VLS) mode-based Si NW growth is getting a great deal of attention because of its low-cost processing technique [24]. There have been many reports of bottom-up Si NW growth methods using various materials as a catalyst, such as Au, Al, Ga, In, Pb, Sn, and Zn, via VLS mechanisms [7, 9, 10, 25-33]. Au-catalyzed Si NWs grown using VLS might not be useful for solar cell applications because they create a deep acceptor level at 0.54 eV in the Si band gap, whereas the In catalyst creates a shallow accepter level at 0.16 eV in the Si band gap and can suppress the degradation of minority carrier lifetime [32]. Recently, we successfully controlled the verticality of Si NWs with good crystalline quality. In-catalyzed based Si NWs grown using the VLS mode produced cone-shaped Si NWs because of catalyst trapping by the NWs [32, 33]. Ball et al. [34], investigated the optical characteristics of conical Si NWs and focused on the influence of the Sn catalyst thickness layer and NWs densities on the optical characteristics.

The cone-shaped (CS) pin-Si NW structure could provide a promising path toward cost-effective, Si-based nano-devices including tandem solar cells grown using the VLS growth mode because of the efficient absorption of photons [35-41]. There are several reports available on the optical modeling and simulation of different geometrical shapes, sizes, and materials. [42-51]. Few years ago, optical properties of c-Si nanohole array structures for solar photovoltaic applications were investigated [42] and it was found that the nanohole absorption is better than nanorod arrays for solar cells application. Foldyna et al. [43], found that when double-diameter nanowire arrays were used for solar cell, then J_sc were increased up to 10% using optical simulation model. Recently, shape-dependent power conversion efficiency (PCE) of Si NW, solar cells with polygonal cross-sectional shapes, including trigon, tetragon, hexagon, and circle, were investigated [44] based on the atomic-bond-relaxation (ABR) approach and detailed balance principle. In this investigation, one claim was made that the classical detailed balance principle can be extended to the nanometer scale through ABR consideration, which considers the effect originated from the end relaxation, including surface and edge parts of the NWs [44]. Moreover, five different shapes (cylindrical, truncated conical, convex conical, conical, and concave conical) of silicon NW arrays arranged in a square are studied [45], and, if the cross section of silicon NW is changed into a square, both light trapping and effective light absorption are enhanced, and the Eiffel Tower-shaped NW arrays have optimal effective light absorption [45]. Geng et al. [46], used FDTD simulation model, and found that the absorption efficiency of optimized random Si NW radial p-n junction array reaches 27.8% compared with a value of ordered Si NWs radial p-n junction array, which is 19.9%. The influence of assembly structure and monotonic grating structures on the optical absorption were also investigated here [47]. And it was found that the assembly structure yields a higher spectral absorptance and conversion efficiency of solar cells as compared to the monotonic grating and nanorod structures because of the combined effects of nanorod and grating components [47]. One interesting research problem about tuning the UV emission of the ZnO–ZnS core–shell nanorod arrays by changing the index of the substrate were investigated [48], and it was concluded that the introduction of active host medium is responsible for the optical absorption, which was greater than the expected Lambert–Beer law [48]. Michallon et al. [49], rigorously investigated the optical behavior of extremely thin absorber solar cells based on ZnO/CdTe core–shell nanowire (NW) arrays with square, hexagonal, or triangular arrangements, using three-dimensional rigorous coupled wave analysis (RCWA). It was concluded that the light absorption is more efficient in the NW square arrangement than in the hexagonal and triangular arrangements [49]. The same author undertook the comparative studies of optical properties of Si and ZnO/CdTe core/shell nanowire arrays and it was revealed that core–shell nanowire arrays made of ZnO/CdTe can more efficiently absorb light than that of the Si [50]. Li et al., found that the silicon nanocube (SiNC) base diameter should be equal to the array periodicity for efficient solar energy harvesting, and the optimized light absorption could be realized when the SiNC height reaches ~400 nm [51].

Theoretically speaking, the optical properties of silicon can be strongly affected by injection of charge carriers (ΔN) into an undoped sample. However, there is no experimental report in the Si literature on spectral changes via free carrier injection/depletion. On the other hand, there are few references that show the effects of impurity doping on the optical properties of bulk silicon (Si) film [52, 53]. The influence of density N_i of impurity atoms on the variation of absorption spectrum, in the bulk crystal is experimentally known [52]. There are no reports on the optical simulation model of CS-pin-Si NW that consider the influence of refractive indices on the absorption due to the charge carrier injection into the pin region of cone-shaped NWs. Therefore, in this research article, the influence of top diameter and periods (in the context of charge carrier injection into the doped region of CS-pin-Si NW solar cells) on the optical absorption were investigated using the FDTD modeling method. The reason why we choose FDTD will be explained in the next section.

Methods

The simulation model should be as realistic as possible, so that it can be correlated with the experimental application of the desired photovoltaic device structure, including CS-pin-Si NWs solar applications. For reliable modeling, it is essential to obtain the electromagnetic field with high accuracy such that near-field effects, which have a strong influence on the final value of light absorption in the NWs, can be evaluated. In line with this point of view, some approximations such as coupled-mode theory do not give us more reliable and accurate information about absorption in NW-based top cells for tandem structure applications because coupled mode theory does not take into account the contribution of the near-field effects [40, 41].

Using numerical methods, we can solve Maxwells equations in the time-domain (such as using FDTD) or in the frequency domain [such as using the finite element method (FEM), RCWA, the FDFD method, or the multiple multipole method (MMP)]. FEM and FDTD methods have been extensively used in the literature to model the optical characterization of photovoltaic device structures including Si NWs Solar cells [46, 47]. However, the FDTD method is vulnerable to numerical errors such as numerical dispersion, and special care is needed during the implementation of the scheme.

In the FDTD method, the grid size might restrict the time-step duration; therefore, a finer mesh indicates a slower simulation. This disadvantage is even more pronounced when dispersive materials are used. If special care is taken, then the usefulness of using the FDTD method is that one can simulate a wide range of wavelengths in one run, which is a great advantage over other available numerical schemes. FDTD can also take into account the near-field effect.

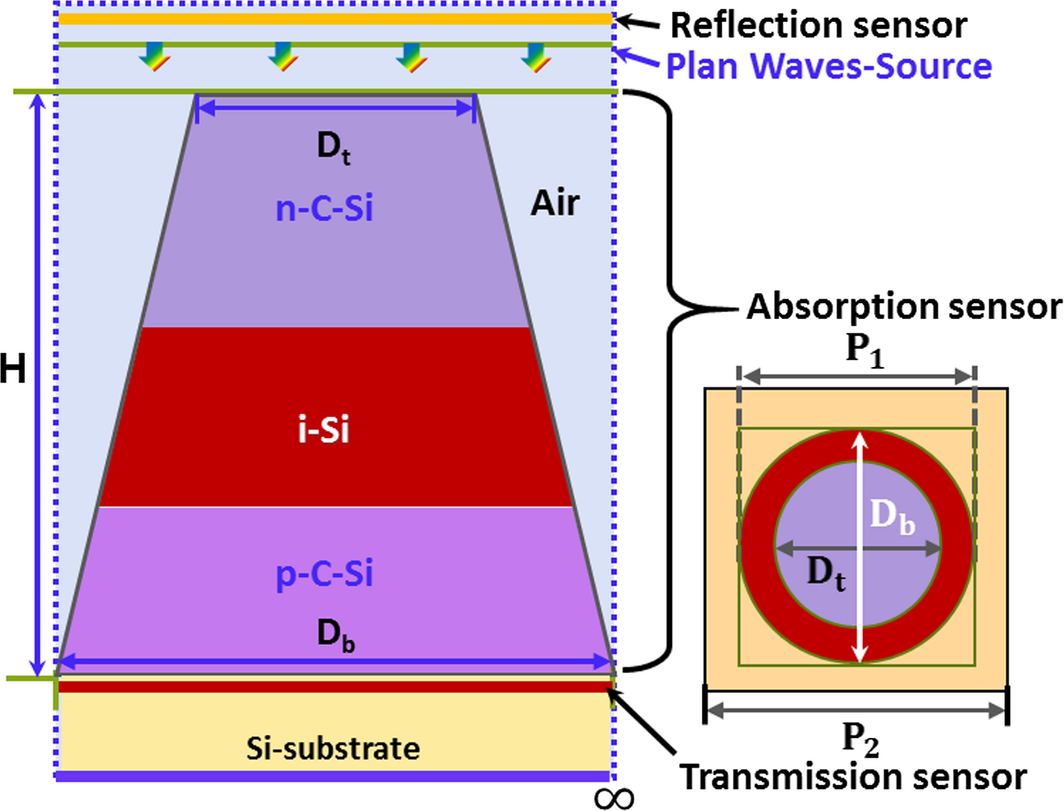
Therefore, we choose an FDTD numerical method and used a fine mesh of roughly 2 nm to simulate the three-dimensional (3D) CS-pin-Si NW, as shown in Figure 1. In the remainder of the article, we will refer to the CS-pin-Si NW simply as NW.

Figure 1. 3D simulated unit CS-pin-Si NW top cell with periods P1 and P2. The geometrical parameters in the x-z plane and y direction are directed into the page.

The absorption that may occur for photon energies smaller than the bandgap is mainly due to the free carrier absorption and it is known fact that the free carrier absorption coefficient is proportional to the local carrier concentration [52]. And therefore the degree of optical confinement might be having strong influence on the spectral absorption factor for photons with an energy smaller than the bandgap, that is, for the case of long wavelength solar irradiance.

The cone-shaped axial NWs for PV cell can be represented by a multilayer structure (pin), each layer being characterized by a complex refractive index,

$N\quad =\quad n-ik$

(1)

where both the real refractive index n and the extinction coefficient k, which are the functions of λ, can be found in the literature [54, 55]. Note that the absorption coefficient α and the extinction coefficient k are related as:

$\alpha ={\frac {4\pi k}{\lambda }}.$

(2)

It is obvious from equation (2) that α decreases strongly with increasing wavelength [52]. Short wavelength photons (λ < 1000 nm) have an energy larger than the bandgap, and therefore are able to create electron–hole pairs and can readily be absorbed by the crystalline silicon (c-Si). However, long wavelength photons (λ > 1200 nm) cannot generate electron–hole pairs and are hardly absorbed by c-Si. Photons in the transition region (1000 nm < λ < 1200 nm) are weakly absorbed, that is, are only absorbed after having traveled some distance in the c-Si material.

Therefore, n- or p-type doping in to a semiconductor means that “free” electrons or holes are introduced. These free charge carriers can also absorb photons (but electron–hole pairs are not generated). Hence, the absorption coefficient of silicon depends on n- and p-type doping concentration c_n and c_p [52, 53].

Soref and Bennett have experimentally found that the optical properties of Si can strongly be affected by the injection of charge carriers (ΔN) into the undoped sample or by the removal of free carriers (−ΔN) from a doped sample [52]. And it was assumed that the free carrier concentration (FCI) is equal to the dopant concentration. The influence of the refractive index change (Δn) of crystalline Si (c-Si) produced by an applied electric field (E) or by a change in the concentration of charge carriers (ΔN) has been determined. The influence of a density N_i of impurity atoms on the variation of absorption spectrum in the bulk crystal has already been experimentally found. Changes in the optical absorption coefficient of the material (Δα) at the wavelength of interest were observed and low-loss propagation were reported [52]. The refractive index change Δn calculated from the spectrum is assumed to be the value of Δn that arises from ΔN. The following well-known formulas for refraction and absorption due to free electrons and free holes, respectively, were used to calculate the refractive index (n), the extinction coefficient (k) values for the p-type c-Si, i-type c-Si, and n-type c-Si layers of the pin structure of the NW as shown in Figure 1:

$\Delta n\quad =\quad -e^{2}{\lambda }^{2}/8{\pi }^{2}c^{2}{\epsilon }_{o}\left({\frac {\Delta N_{e}}{m^{_{\ast }}{}_{ce}}}+\right.$$\left.{\frac {\Delta N_{h}}{m^{_{\ast }}{}_{ch}}}\right)$

(3)

$\Delta \alpha \quad =\quad e^{3}{\lambda }^{2}/4{\pi }^{2}c^{3}{\epsilon }_{o}\left({\frac {\Delta N_{e}}{m^{{_{\ast }}2}{}_{ce}{\mu }_{e}}}+\right.$$\left.{\frac {\Delta N_{h}}{m^{{_{\ast }}2}{}_{ch}{\mu }_{h}}}\right)$

(4)

where e is the electronic charge, ${\textstyle {\epsilon }_{o}}$ is the permittivity of free space, n is the refractive index of unperturbed c-Si, ${\textstyle m^{_{\ast }}{}_{ce}}$ is the conductivity effective mass of electrons, ${\textstyle m^{_{\ast }}{}_{ch}}$ is the conductivity effective mass of holes, ${\textstyle {\mu }_{e}}$ is the electron mobility, and ${\textstyle {\mu }_{h}}$ is the hole mobility. The impurity of electron density, ${\textstyle \Delta N_{e}={10}^{19}\quad {\mbox{cm}}^{-3}}$, and hole density, ${\textstyle \Delta N_{h}={10}^{19}\quad {\mbox{cm}}^{-2}}$, were used in equations (3) and (4), respectively.

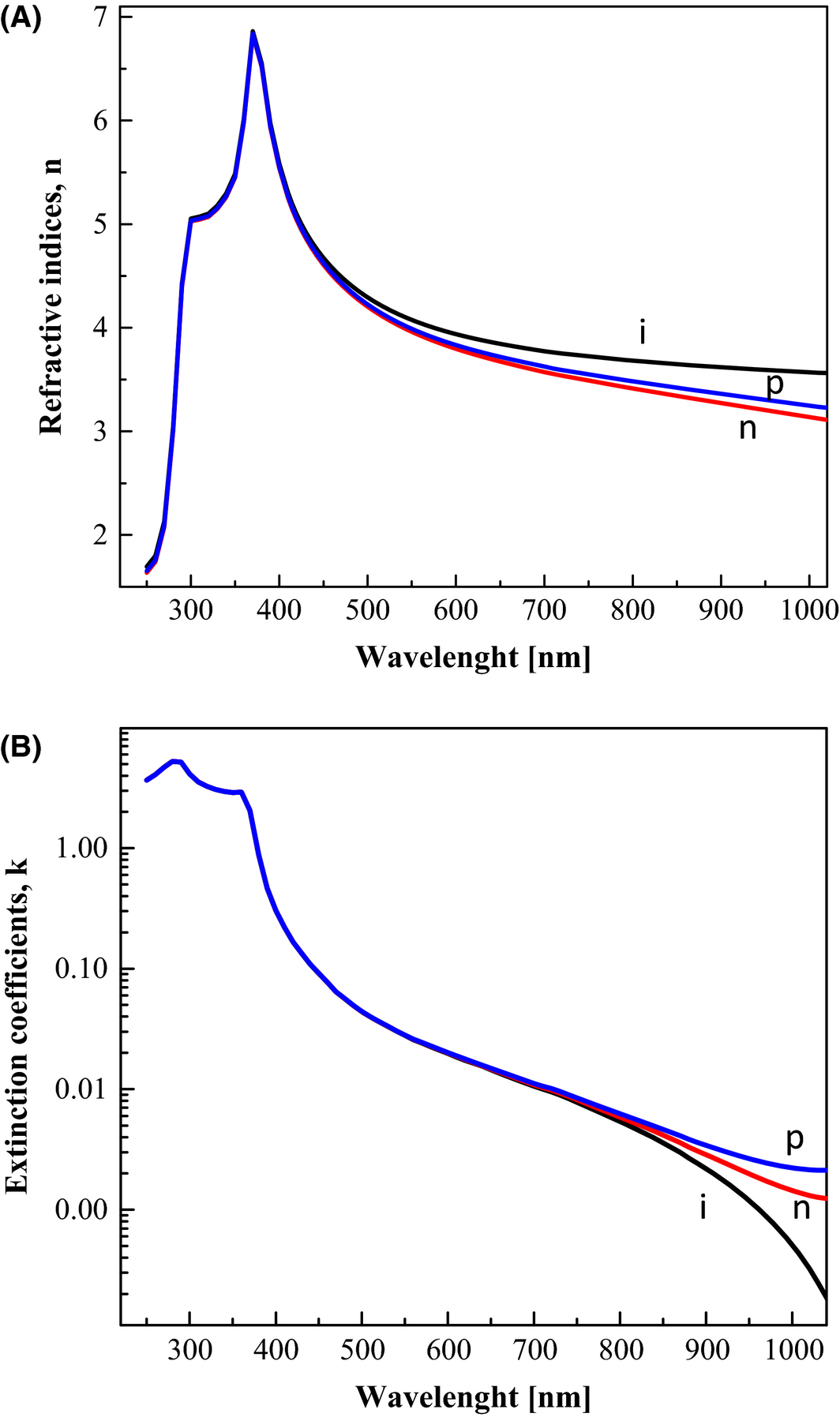
Then, the n and k values of the i-type c-Si, n-type c-Si, and p-type c-Si-layer were calculated, which are shown in Figure 2(A and B). These n and k values were used in this model to investigate the influence of injected charge in the pin junction of the NWs. The detailed structure of the simulated NW-based top cell is shown in Figure 1, where the height of the NW was chosen to be 5 μm, and the bottom diameter D_b = 150 nm was kept fixed, with two different periods, that is, P1 = D_b = 150 nm and P2 = 2D_b = 300 nm. In this model, the top diameter D_t of the NWs was varied from 70 nm to 110 nm and a periodic boundary condition was set along the x direction and the perfectly matched layer (PML) boundary condition was set along the z direction.

Figure 2. (A) Refractive indices, n, and (B) extinction coefficients, k, data versus wavelength of the p-type c-Si, n-type c-Si, and i-Si layers of CS-pin-Si NW top cells as obtained from given theoretical data [43].

The AM 1.5 condition was used to calculate the short circuit current density (J_sc) in this model. It is well-known that sunlight is composed of both transverse electric (TE) and transverse magnetic (TM) modes, where TE is equivalent to TM because of the structural symmetry in NW. Therefore, we choose only the TE mode to investigate optical confinement in the NW. Air was taken as a background material for the NW, where the TE mode polarizes the incoming light such that the electric field is in the x direction, E_x, and the magnetic field is in the y direction, H_y. The wires have the same width and period in the x and y directions. The periodic boundary condition is also set in the y direction. The simulated region of Si NWs is represented by a cone-shaped frame in which PML boundary conditions and the source were assigned to the top and bottom, respectively. The reflectance and transmission sensor were placed at the top and bottom, respectively, of the NWs, as shown in Figure 1.

The optical generation rates and ultimate photocurrents were also calculated by using equation (5) after plugging the value of EQE (external quantum efficiency) and solar spectral irradiance. It is well-known that the photocurrent is an accumulative sum of the electron–hole pairs (EHPs) generated by the incident photons at different wavelengths of the solar spectrum. When the photons are absorbed in the active layer of the NWs, then they can completely contribute to the photocurrent, that is, if all of them generate EHPs and all of these EHPs are collected (assuming that the absorption in the other layers of the solar cell do not contribute to the photocurrent and under the perfect carrier extraction condition), then the short circuit current density of the solar cell can be written as:

$J_{sc}\quad =\quad q{\int }_{\Delta \lambda }{\frac {\lambda }{hc}}\Phi \left(\lambda \right)\cdot EQE\left(\lambda \right)d\lambda$

(5)

where λ is the wavelength of the incident photon, h is Plancks constant, c is the speed of light in air, q is the electron charge, Φ is solar spectral irradiance, and EQE is the external quantum efficiency of the solar cell. In simpler terms, EQE indicates how much of the energy of the incident light is converted into electrical energy at each wavelength.

In this article, the influence of top diameter variation of the NWs and the period variation of the NWs regarding optical absorption in the NW top cell were investigated in the wavelength range between 300 and 1000 nm. The influence of the refractive index n (wavelength variation was between 600 and 1000 nm for p-type c-Si, i-Si, and n-type c-Si, of axial pin structure NWs) on the light absorption was evaluated.

Results and Discussion

Absorption, reflection, and transmission were theoretically investigated for periods P1 and P2 for the wavelength range from 300 to 1000 nm as a function of D_t of the NWs. The absorption was normalized by the entire incident light that irradiated both the NWs and air as a medium. When we used the absorption in the range of wavelengths shorter than 400 nm, we encountered large calculation errors in FDTD, and therefore, we used “absorption = 1–reflectance (R) – transmittance (T)” data for absorption in the range of wavelengths shorter than 400 nm.

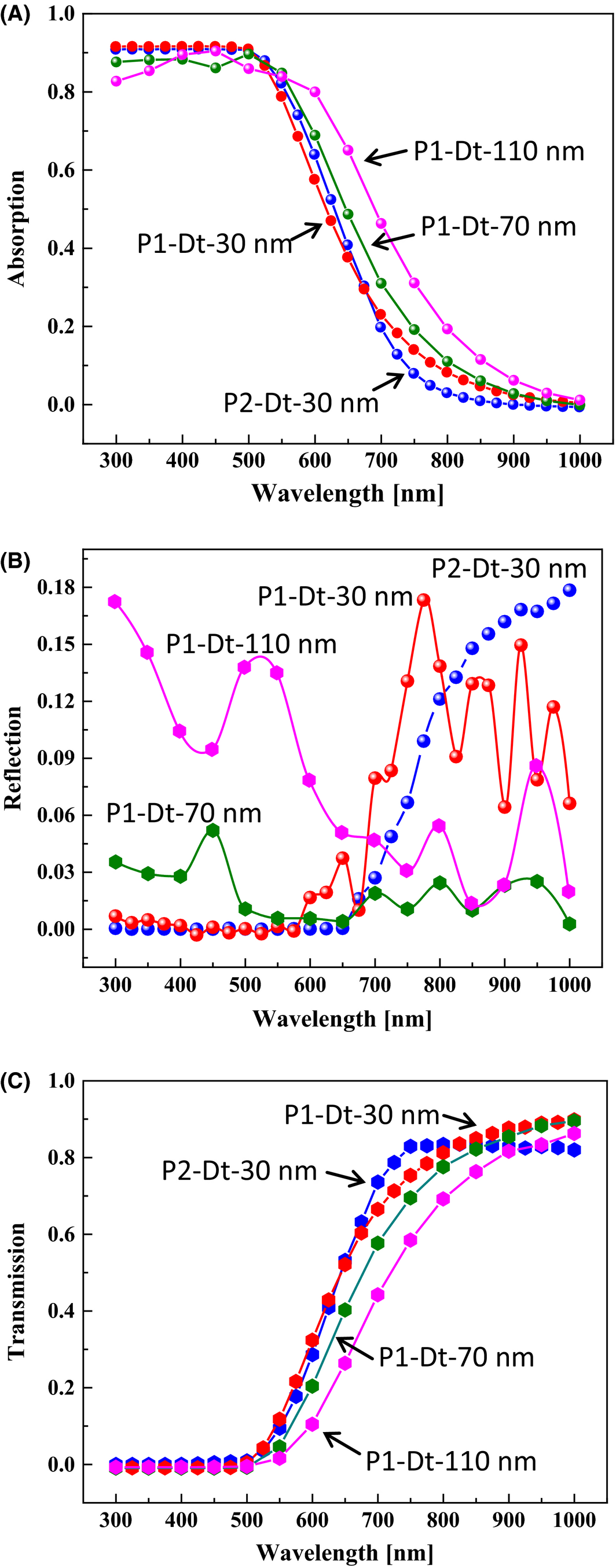
Figure 3(A–C) gives the simulated optical properties of the NW-based solar cells. In the shorter wavelength region (<600 nm), the absorption is independent of period but strongly depends on the top diameter of the NWs, as shown in Figure 3(A). On the other hand, in the long wavelength region (>600 nm), the absorption increases with the increase of top diameter D_t = 110 nm for period P1, which can be attributed to both the relatively small diameter and the periods for successive internal reflection. The highest absorption shoulder trend toward long wavelength was found at D_t = 110 nm, as shown in Figure 3(A). This trend of absorption is attributed to the reflectance behavior shown in Figure 3(B) in the same wavelength region. Furthermore, on the basis of our result, we realized that the exposed area of the NWs and the angle of incident light depend on the top diameter of the NWs, which might be responsible for causing enhancement of absorption value for D_t = 110 nm for period P1. We found that the absorption for period P1 and period P2 with D_t = 30 nm is almost the same as that in the low wavelength region (<600 nm), as shown in Figure 3(A); the same phenomenon is seen in the reflectance behavior, as shown in Figure 3(B). Note that the period, or optimization of the period, could cause enhanced absorption and suppressed reflection because of successive internal reflection from the neighboring NWs during efficient absorption. The reflectance of NWs with D_t = 30 nm for period P1 gives a reasonable value of <3% in the wavelength range between 300 and 600 nm; one abrupt peak was observed near 790 nm, as shown in Figure 3(B), which might be caused by the interference of light waves. Figure 3(C) gives the transmission behavior of NWs; relatively high transmission behavior was found in NWs with D_t = 30 nm for period P2 = 300 nm, than the NW with D_t = 110 nm and period P1 = 150 nm, in the high wavelength region (>500 nm). Furthermore, at wavelengths longer than 650 nm, the n and k values of n-type c-Si and p-type c-Si layers of Si NWs are relatively large and interference effects can be reduced because of the oscillation of reflectance and transmittance.

Figure 3. Optical characterization of the CS-pin-Si NW top cell with varying top diameters Dt in the range of 30–70 nm, and with periods P1 and P2, for (A) absorption, (B) reflection, and (C) transmission.

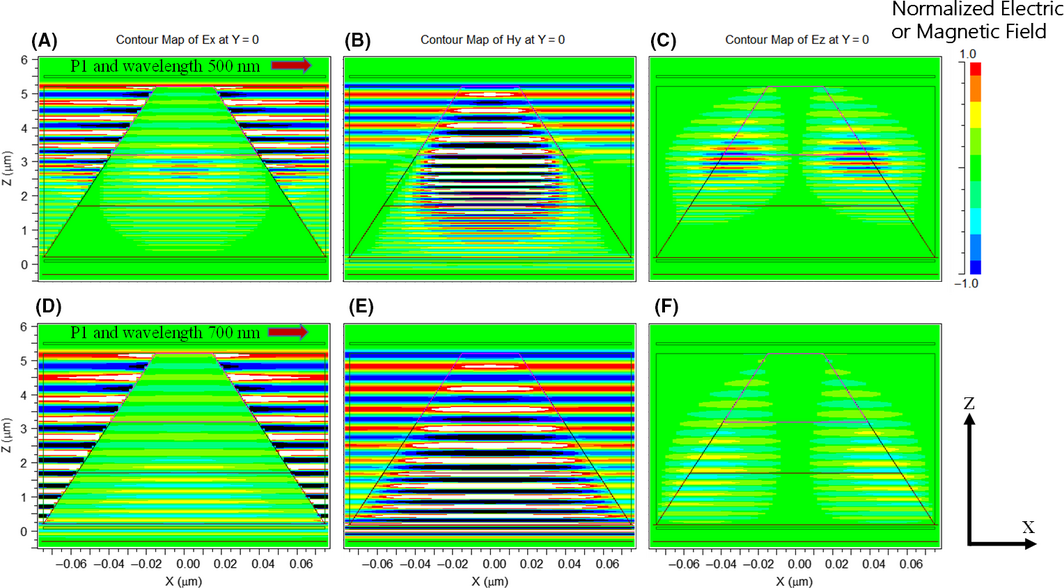
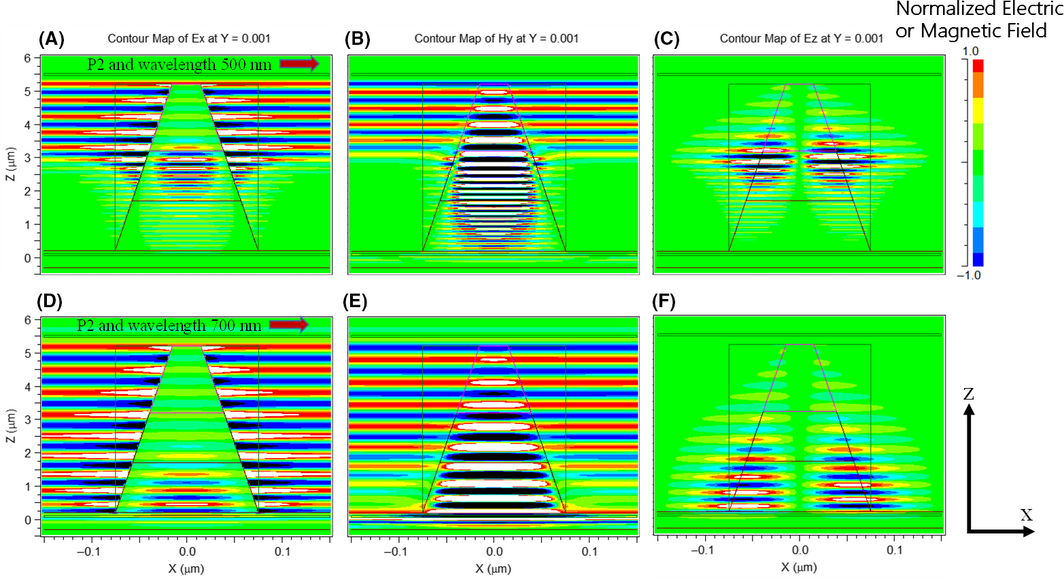
The mapping in Figure 4 shows the distribution of the normalized electric field E_x and E_z, and the normalized magnetic field, H_y, of the TE mode at irradiated light wavelengths of 500 nm and 700 nm for the period P1 = 150 nm with a top diameter D_t = 30 nm. Figure 4(A–C) shows the results with period P1 = 150 nm at a wavelength of 500 nm. Figure 4(D–F) shows the results with same period P1 at a wavelength of 700 nm. The cone shapes in the center of Figure 4(A–F) represent the pin structure of crystalline silicon solar cells. E_x is concentrated in a very small area of the NWs, but occupies a large area of the air as a background, as shown in Figure 4(A). E_z is confirmed to be at the edge of the NWs, as shown in Figure 4(C), which means that the incoming light is refracted toward the high refractive index (n) material, that is, doped Si or undoped Si. On the other hand, as shown in Figure 4(B), the magnetic field is distributed uniformly near the top of the NWs both in air and in the NWs for the case of period P1, at 500 nm in wavelength. These behaviors of the electromagnetic field might be due to the boundary condition between the two different media and the top diameter in the context of the n value of the n-type c-Si layer. The influence of refractive index variation on n-type c-Si layers at 500 nm caused by free carrier injection is negligible, as shown in Figure 2(A). The parallel magnetic field and vertical electric flux density of the material interface are continuous until the n-type c-Si layer is reached. Thus, when the diameter is smaller than the wavelength of the irradiated light, then the H_y density distribution was found to be concentrated in the area near the NW and probably gives rise to the enhanced absorption at the wavelength of 500 nm.

Figure 4. Electric and magnetic fields of the electromagnetic waves in each direction of CS-pin-Si NW for the case of period P1, with top diameter Dt = 30 nm (A) Ex at a wavelength of 500 nm, (B) Hy at a wavelength of 500 nm, and (C) Ez of Si NW at a wavelength of 500 nm, (D) Ex of Si NW at a wavelength of 700 nm, (E) Hy of Si NW at a wavelength of 700 nm, and (F) Ez of Si NW at a wavelength of 700 nm. [Colour figure can be viewed at wileyonlinelibrary.com].

For the NW arrangement with period P1 where the irradiated light has a wavelength of 700 nm was used, weak E_x is concentrated in the p-layer of the NWs (bottom side of the NWs), and most of E_x was concentrated in the air region, as shown in Figure 4(D). Some contribution of E_z is confirmed at the edge of the NWs, as shown in Figure 4(F). The influence of refractive index variation on the p-type c-Si layer at 700 nm caused by free carrier injection is important, as shown in Figure 2(A), which shows a higher refractive index value at 700 nm as compared to both the i-Si layer and the p-type c-Si layer. Therefore, we speculate that a small contribution of absorption may be caused by the high refractive index values of the p-type c-Si layer of the pin structure of NWs in the wavelength range of roughly 700 nm. On the other hand, H_y is concentrated uniformly over the entire area of NWs and in the region of air, for the case of period P1 at 700 nm in wavelength, as shown in Figure 4(E). This result further shows that H_y is distributed over a large area at 700 nm in wavelength and confirms higher transmission and low absorption. If we compare this result with the case in Figure 4(B), H_y is concentrated in the area near the NWs for the case of period P1 and a wavelength of 500 nm, which is probably caused by the parallel magnetic field density. The light at 500 nm in wavelength would not likely reach the flat space between each NW, as shown in Figure 4(A–F); therefore, the light shows high absorption (nearly 100% absorption) in this case.

The mapping in Figure 5 shows the distribution of the normalized electric field E_x, E_z, and the normalized magnetic field, H_y, of the TE mode at a wavelength of 500 nm and 700 nm, respectively, for a period P2 of 300 nm and a D_t value of 30 nm. Figure 5(A–C) show the results at a wavelength of 500 nm. Figure 5(D–F) show the results at a wavelength of 700 nm. E_x is concentrated only in a very small area of the i-Si layer; however, highly concentrated distributions were found in the air region, as shown in Figure 5(A) and weak E_z was confirmed at the edge of the NWs, as shown in Figure 5(C). On the other hand, as shown in Figure 5(B), H_y is distributed uniformly, around the top of the n-type c-Si NWs both in air and in the NWs, at 500 nm in wavelength. A significant concentration of H_y was observed throughout the NW layer, which, in this case, was without transmission.

Figure 5. Electric and magnetic fields of the electromagnetic waves in each direction of CS-pin-Si NWs for the case of period P2, with Dt = 30 nm (A) Ex, (B) Hy, and (C) Ez of Si NW at a wavelength 500 nm. (D) Ex, (E) Hy, and (F) Ez of Si NW at a wavelength 700 nm. [Colour figure can be viewed at wileyonlinelibrary.com].

For the case of light with a wavelength of 700 nm, with P2 relatively high, E_x is concentrated in the p-layer of the NWs (bottom side of the NWs), and most of E_x was concentrated in the air region, as shown in Figure 5(D), and a small contribution of E_z was confirmed at the edge of the p-type c-Si NWs, as shown in Figure 5(F). On the other hand, as shown in Figure 5(E), H_y is uniformly distributed over the entire area of the NWs and the air region at 700 nm in wavelength. This figure further shows that H_y is distributed over a large area at 700 nm in wavelength and confirms a higher transmission and low absorption as compared to the case in Figure 5(B), where H_y is concentrated in the nearby region in the NW, for the case of period P2 at 500 nm in wavelength.

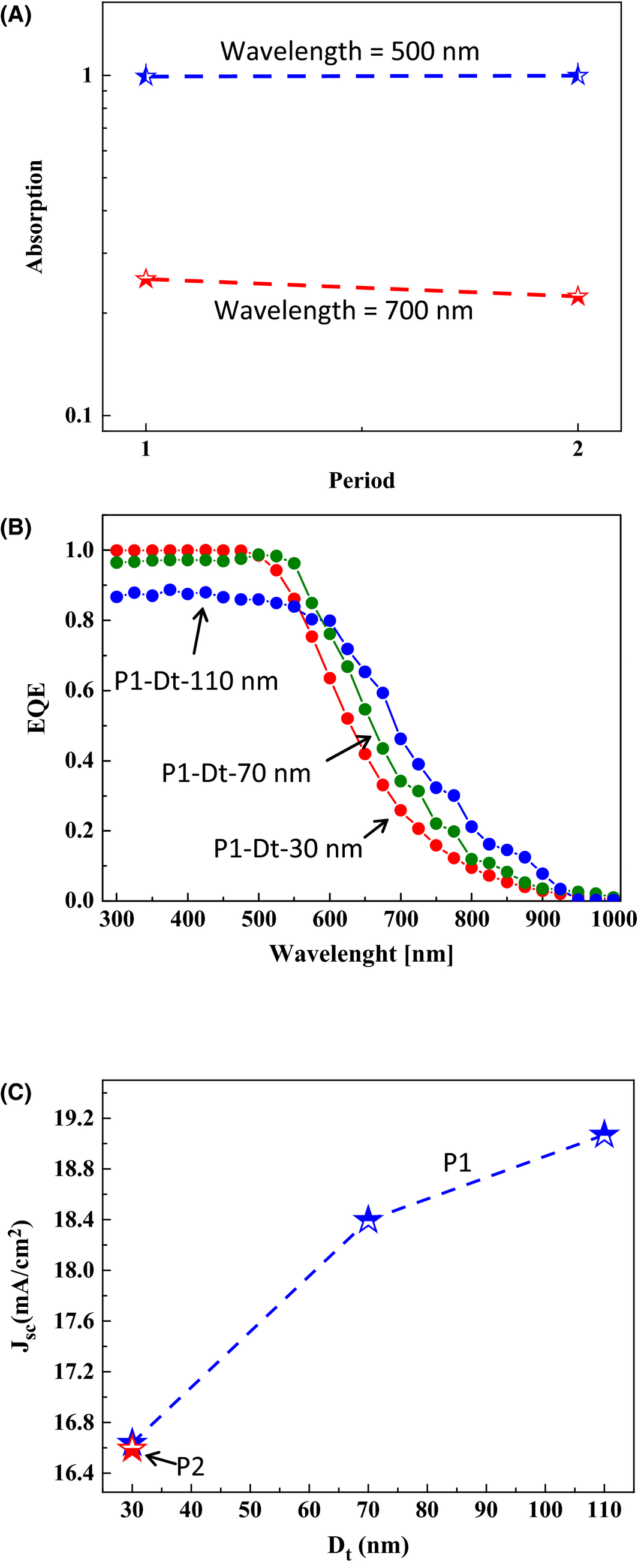
The light absorption at specific wavelengths of interest, such as 500 nm and 700 nm, were also investigated for the case of periods P1 and P2, respectively. In the case of a wavelength of 500 nm, the absorption significantly increased and was found to be independent of the period (P1 or P2), as shown in Figure 6(A); however, the absorption increased slightly when we decreased the period from 300 to 150 nm at a wavelength of 700 nm. The same behavior was confirmed in the mapping of E_x, E_z, and H_y, as shown in Figure 4.

Figure 6. (A) Absorption as a function of periods (P1 and P2) in the wavelength regime from 500 nm to 700 nm with Dt = 30 nm. (B) QE versus wavelength for a period P1 with Dt = 30, 70, and 110 nm, of CS-pin-Si NWs solar cells and (C) Jsc versus Dt of the Si NW for the case of periods P1 and P2.

Perfect carrier extraction was assumed, and therefore, the EQE was assumed to be equal to the absorption. EQE for periods P1 and P2 for D_t = 30 nm were calculated; almost 100% values were observed below 550 nm in wavelength, as shown in Figure 6(B). Good light scattering was observed in the NW arrangement with period P1, as compared to P2 or bulk Si, because of the high value of successive internal reflections from the neighboring NWs. Additionally, a significant change of absorption between the short wavelength side and the long wavelength side were found for a top diameter D_t of 70 nm, with period P1 = 150 nm for the NWs. The highest values of EQE were observed for period P1 with D_t = 30 nm in the wavelength region of <550 nm, as shown in Figure 6(B). Relatively high EQE values were observed in the wavelength region of >600 nm for the D_t = 110 nm for period P1 in the NWs, which can be attributed to both the large value of the top diameter, and the high refractive index values in the p-type c-Si layer of the NWs. In practical applications, we must consider the influence of the interface condition and the good quality of the pin structure growth of NWs on EQE enhancement.

Short circuit current density for period P1 and P2 were calculated as a function of D_t using equation (5). The J_sc values were enhanced to as high as 19.2 mA/cm² when we reduce the period from 300 to 150 nm and increase D_t up to 110 nm, as shown in Figure 6(C). However, J_sc values of roughly 18.4 mA/cm² were achieved in the case of D_t = 70 nm with period P1 for a single NW. Note that the presence of cone-shaped NWs improves the photocurrent J_sc, in TE, which is observed when only one wire is present per period because of the difference of the effect of the NWs on J_sc in the TE polarizations, and also because sunlight is not naturally polarized. One possible concern regarding the NWs is that they may interfere with carrier collection. This phenomenon can occur in different scenarios. First, the formation of voids/defects around the particle and poor material quality at the particle interface may create a high interface defect state density, thus causing problems for carrier collection. Second, voids or defects can reduce the influence of the internal electric field on the generated carriers and deviated carrier transform inside the NW solar cell. In the near future, these issues will be addressed in the context of CS-Si NW top cells for tandem solar cell applications.

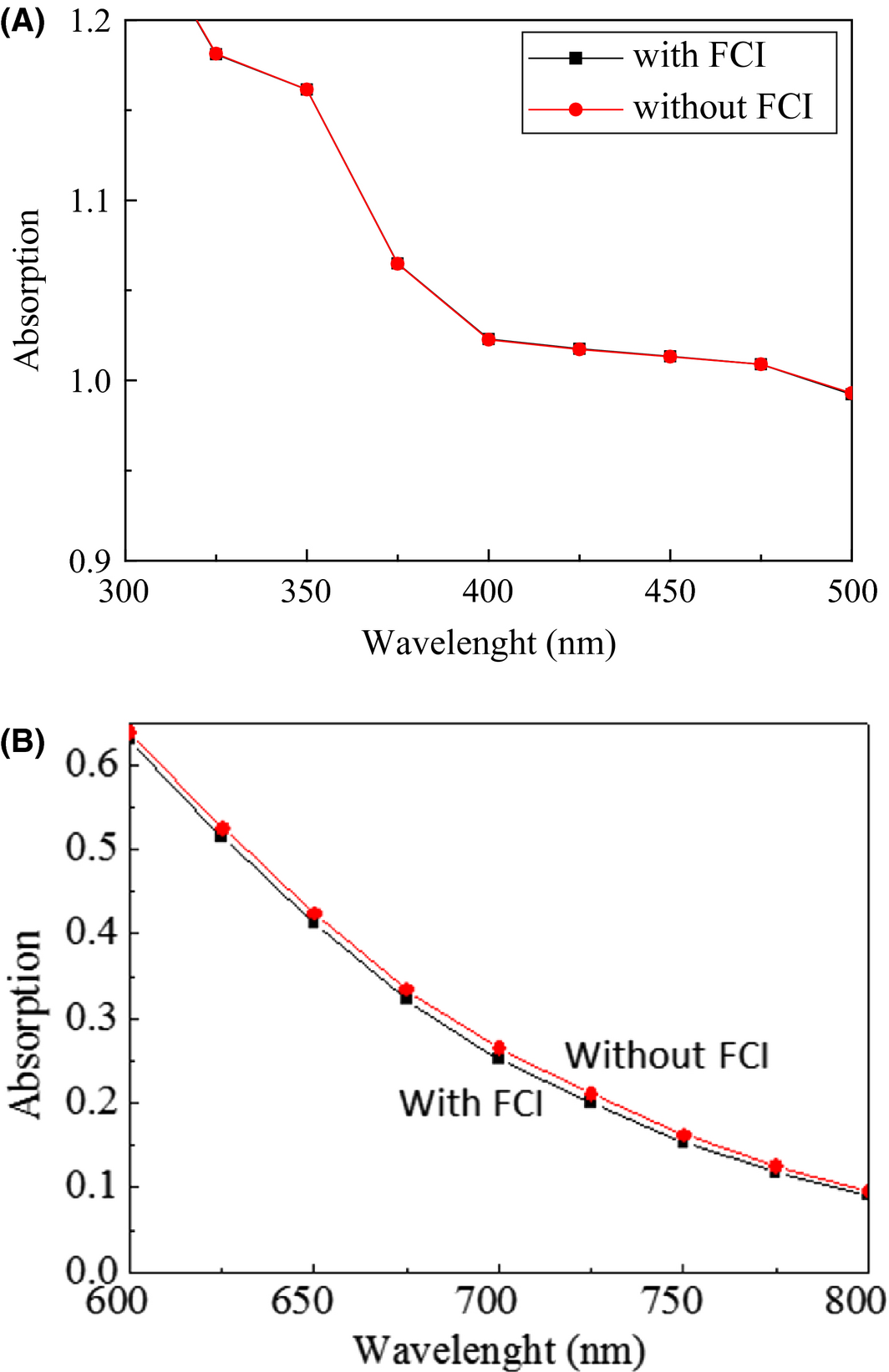
In this part, the influence of the free carrier injection (FCI) on the absorption in CS-pin-SiNW for case with D_t = 30 nm and P1, were discussed as shown in Figure 7(A and B), where the free carrier concentration (FCI) is equal to dopant concentration. The Figure 7(A) gives the absorption for both the cases (with FCI and without FCI) for the wavelength range (600 < λ < 900 nm). In this case, we found that the absorption was enhanced slightly for the case of without FCI than the case with FCI in p-type and n-type region of NW, respectively. Similarly, we also focused on the absorption for both the cases (with FCI and without FCI) for the wavelength range (300 < λ < 600 nm in Figure 7(B) for NW. In this region of wavelength (300–600 nm) for NWs, the absorption was found to be independent of doping. However, small influence of free carrier absorption, on the absorption factor were realized in the 600 nm < λ < 900 nm. And we also realize that it can be unexpectedly large in the long wavelength side due to the higher k-values as a function of n-type impurity doping in NWs as depicted from Figure 2(B). We need to investigate in detail the influence of doping on the absorption beyond the wavelength 1200 nm in the near future for the small band gap materials like Si_0.80Ge_0.20 NWs (band gap≃1.0-0.98 eV) to exploit the solar irradiance on the long wavelength side.

Figure 7. (A) The behavior of the free carrier injection (FCI) on the absorption in NW with Dt = 30 nm and P1, (for the case with FCI and without FCI) for the wavelength range (300 < λ < 600 nm) and (B) The behavior of the free carrier injection (FCI) on the absorption in NW with Dt = 30 nm and P1, (for the case with FCI and without FCI) for the wavelength range (600 < λ < 800 nm).

Conclusion

In this article, the influence of free carrier injection into the doped region of CS-pin Si NWs for solar cell applications (as a function of top diameter and periods) on the optical absorption was successfully evaluated. However, the small influence of free carrier absorption, on the absorption factor were realized in the 600 nm < λ < 900 nm, but we realize that it can be unexpectedly large in the long wavelength side due to the higher k-values as a function of impurity doping in NWs. We found that light scattering caused by the cone-shaped Si NW structure with a period of 150 nm and a top diameter of 70 nm improves the optical confinement for solar cells applications grown using the VLS mode. The absorption increased when we decreased the period from 300 to 150 nm for a wavelength of 700 nm. In the case of a wavelength of 500 nm, the absorption significantly increased by up to 100% and was found to be independent of the period. EQE for a period of 150 nm and top diameter of 30 nm reached almost 100% of the value at 550 nm in wavelength. The calculated J_sc values were found to be as high as 19.2 mA/cm² in the case of a top diameter of 110 nm at a period of 150 nm. A reasonable J_sc value of roughly 18.4 mA/cm² in the case of a top diameter of 70 nm with a period of 150 nm. These findings can play a significant role in realizing practical applications of CS-pin junction Si NW-based solar cells grown using the VLS mode for tandem solar cell applications.

Acknowledgments

This work was supported by the MEXT, Japan, FUTURE PV-Innovation Project. We thank Toshio Hama for his valuable comments on the results of optical simulation and D. Kanematsu for his fruitful discussions and valuable comments on the results of optical simulations.

Conflict of Interest

None declared.

References

1. Jha, A. R.2010. P. 6Solar cell technology and applications. CRC Press, Taylor and Francis Group, LLC, Boca Raton, Fla, USA.
2. Sze, S. M.2002. P. 319Semiconductor devices, 2nd ed. Physics and Technology, Wiley Interscience, New York.
3. Lewis, N. S.2007. Toward cost-effective solar energy use. Science315:798.
4. Kanematsu, D., S. Yata, A. Terakawa, M. Tanaka, and M. Konagai. 2015. Effective light trapping by modulated quantum structures for Si nanowire/wall solar cells. Jpn. J. Appl. Phys.54:102301.
5. Chutinan, A., and S. John. 2008. Light trapping and absorption optimization in certain thin-film photonic crystal architectures. Phys. Rev. A78:023825.
6. Tsakalakos, L., J. Balch, J. Fronheiser, and B. A. Korevaar. 2007. Silicon nanowire solar cells. Appl. Phys. Lett.91:233117.
7. Al-Taay, H. F.2014. Growth and characterization of silicon nanowires for solar cell applications. [Ph.D. thesis], Murdoch University, Perth, Australia, p. 14.
8. Feynman, R. P.1960. Theres Plenty of Room at the Bottom. Eng. Sci.23:22.
9. Srivastava, S. K., D. Kumar, P. K. Singh, and V. Kumar. 2009. Silicon nanowire arrays based “black silicon” solar cells. P. 1851in Proceedings of 34th IEEE Photovoltaic Specialists Conference. IEEE, Philadelphia, PA, USA.
10. Wagner, R. S., and W. C. Ellis. 1964. Vapor-liquid-solid mechanism of single crystal growth. Appl. Phys. Lett.4:89.
11. Iijima, S.1991. Helical microtubules of graphitic carbon. Nature354:56.
12. Sattler, K. D.2011. P. 12Handbook of nanophysics- nanotubes and nanowires. CRC Press, Taylor and Francis Group, an informa business, Boca Raton London New York.
13. Pavesi, L.2009. Optical gain and lasing in low dimensional silicon. P. 104inD. J. Lockwood and N. Koshida, eds. Device applications of silicon nanocrystals and nanostructures. Springer, Science + Business Media, LLC, New York, USA.
14. Honsberg, C. B., A. M. Barnett, and D. Kirkpatrick. 2006. Nanostructured Solar Cells for High Efficiency Photovoltaics. P. 2565in Proceedings of 4th IEEE World Conference on Photovoltaic Energy 2. IEEE, WCPEC-4-Waikoloa, HI, USA.
15. Ma, D. D., C. S. Lee, F. C. Au, S. Y. Tong, and S. T. Lee. 2003. Small-diameter silicon nanowire surfaces. Science299:1874.
16. Baxter, J. B., and E. S. Aydil. 2005. Nanowire-based dye-sensitized solar cells. Appl. Phys. Lett.86:053114.
17. Law, M., L. E. Greene, J. C. Johnson, R. J. Saykally, and P. Yang. 2005. Nanowire dye-sensitized solar cells. Nat. Mater.4:455.
18. Huynh, W. U., J. J. Dittmer, and A. P. Alivisatos. 2002. Hybrid nanorod-polymer solar cells. Science295:2425.
19. Thony, P., R. Delsol, C. Jaussaud, N. Rondel, E. Rouvière, S. Poncet, et al. 2008. Silicon Solar Cell, Silicon Nanowires, Vapour-Liquid-Solid (VLS) Growth. P. 670in Proceedings of 23rd European Photovoltaic Solar Energy Conference and Exhibition.
20. Li, Y., Q. Chen, D. He, and J. Li. 2014. Radial junction Si micro/nano-wire array photovoltaics: recent progress for theoretical investigation to experimental realization. Nano Energy7:10.
21. Borgström, M. T., J. Wallentin, J. Trägårdh, P. Ramvall, M. Ek, L. R. Wallenberg, et al. 2010. In situ etching for total control over axial and radial nanowire growth. Nano Res.3:264.
22. Wallentin, J., N. Anttu, D. Asoli, M. Huffman, I. Åberg, M. H. Magnusson, et al. 2013. InP nanowire array solar cells achieving 13.8% efficiency by exceeding the ray optics limit. Science339:1057.
23. Huang, J.-S., C.-Y. Hsiao, S.-J. Syu, J.-J. Chao, and C.-F. Lin. 2009. Well-aligned single-crystalline silicon nanowire hybrid solar cells on glass. Sol. Energy Mater. Sol. Cells93:621.
24. Zheng, M., K. Horowitz, M. Woodhouse, C. Battaglia, R. Kapadia, and A. Javey. 2016. III-Vs at scale: a PV manufacturing cost analysis of the thin film vapor–liquid–solid growth mode. Prog. Photovolt. Res. Appl.24:871–878.
25. Olesinski, R. W., and G. J. Abbaschian. 1984. The Si-Sn (Silicon-Tin) system. Bull. Alloy Phase. Diag.5:273.
26. Givargizov, E. I.1975. Fundamental aspects of VLS growth. J. Cryst. Growth31:20.
27. Wang, Y., V. Schmidt, S. Senz, and U. Gösele. 2006. Epitaxial growth of silicon nanowires using an aluminium catalyst. Nat. Nanotechnol.1:186.
28. Sunkara, M. K., S. Sharma, R. Miranda, G. Lian, and E. C. Dickey. 2001. Bulk synthesis of silicon nanowires using a low-temperature vapor–liquid–solid method. Appl. Phys. Lett.79:1546.
29. Zhang, J., F. Jiang, Y. Yang, and J. Li. 2007. Molten Pb as a catalyst for large-scale growth of highly aligned silicon oxide nanowires. J. Cryst. Growth307:76.
30. Jeon, M., H. Uchiyama, and K. Kamisako. 2009. Characterization of Tin-catalyzed silicon nanowires synthesized by the hydrogen radical-assisted deposition method. Mater. Lett.63:246.
31. Yu, J.-Y., S.-W. Chung, and J. R. Heath. 2000. Silicon nanowires: preparation, device fabrication, and transport properties. J. Phys. Chem. B104:11864.
32. Ajmal Khan, M., Y. Ishikawa, I. Kita, K. Fukunaga, T. Fuyuki, and M. Konagai. 2015. Control of verticality and (111) orientation of In-catalyzed silicon nanowires grown in the vapour–liquid–solid mode for nanoscale device applications. J. Mater. Chem. C3:11577.
33. Ajmal Khan, M., Y. Ishikawa, I. Kita, A. Tani, H. Yano, T. Fuyuki, et al. 2016. Investigation of crystallinity and planar defects in the Si nanowires grown by vapor-liquid-solid mode using indium catalyst for solar cell applications. Jpn. J. Appl. Phys.55:01AE03.
34. Ball, J., A. Centeno, B. G. Mendis, H. S. Reehal, and N. Alford. 2012. Optical characteristics of silicon nanowires grown from tin catalyst layers on silicon coated glass. Opt. Express20:20266.
35. Hu, L., and G. Chen. 2007. Analysis of optical absorption in silicon nanowire arrays for photovoltaic applications. Nano Lett.7:3249.
36. Sivakov, V., G. Andrä, A. Gawlik, A. Berger, J. Plentz, F. Falk, et al. 2009. Silicon nanowire-based solar cells on glass: synthesis, optical properties, and cell parameters. Nano Lett.9:1549.
37. Muskens, O. L., J. G. Rivas, R. E. Algra, E. P. A. M. Bakkers, and A. Lagendijk. 2008. Design of light scattering in nanowire materials for photovoltaic applications. Nano Lett.8:2638.
38. Muskens, O. L., S. L. Diedenhofen, B. C. Kaas, R. E. Algra, E. P. A. M. Bakkers, J. G. Rivas, et al. 2009. Large photonic strength of highly tunable resonant nanowire materials. Nano Lett.9:930.
39. Garnett, E., and P. Yang. 2010. Light trapping in silicon nanowire solar cells. Nano Lett.10:1082.
40. Haus, H. A., W. P. Huang, S. Kawakami, and N. A. Whitaker. 1987. Coupled- mode theory of optical waveguides. J. Lightwave Technol.5:16.
41. Haus, H. A.1984. Waves and fields in optoelectronics. Prentice Hall, Englewood Cliffs, NJ.
42. Han, S. E., and G. Chen. 2010. Optical absorption enhancement in silicon nanohole arrays for solar photovoltaics. Nano Lett.10:1012–1015.
43. Foldyna, M., L. Yu, and P. R. Cabarrocas. 2013. Theoretical short-circuit current density for different geometries and organizations of silicon nanowires in solar cells. Sol. Energy Mater. Sol. Cells117:645–651.
44. He, Y., W. Yu, and G. Ouyan. 2016. Shape-dependent conversion efficiency of Si nanowire solar cells with polygonal cross-sections. J. Appl. Phys.119:225101.
45. Duan, Z., M. Li, T. Mwenya, P. Fu, Y. Li, and D. Song. 2016. Effective light absorption and its enhancement factor for silicon nanowire-based solar cell. Appl. Opt.55:117–121.
46. Geng, C., et al. 2016. Optical design of nanowire array on silicon thin film solar cell. Acta Phys. Sinica65:Article number 070201.
47. Jia, Z., et al. 2016. Optical properties of a grating-nanorod assembly structure for solar cells. Optics Commun.376:14–20.
48. Jule, L., et al. 2016. Enhancing absorption in coated semiconductor nanowire/nanorod core-shell arrays using active host matrices. Optics Commun.380:186–194.
49. Michallon, J., et al. 2015. Light absorption processes and optimization of ZnO/CdTe core-shell nanowire arrays for nanostructured solar cells. Nanotechnology26:Article number 075401.
50. Michallon, J., et al. 2013. Comparison of optical properties of Si and ZnO/CdTe core/shell nanowire arrays. Mater. Sci. Eng., B178:665–669.
51. Li, J., H. Yu, S. M. Wong, G. Zhang, G.-Q. Lo, and D.-L. Kwong. 2010. Si nanocone array optimization on crystalline Si thin films for solar energy harvesting. J. Phys. D: Appl. Phys.43:255101.
52. Soref, R. A., and B. R. Bennett. 1987. Electrooptical effects in silicon. IEEE J. Quantum Electron.23:123.
53. Green, M. A.1995. Pp. 46–48Silicon solar cells: advanced principles & practice. University of New South Wales, Sydney, NSW.
54. Palik, E. D.1985. Pp. 397–401Handbook of optical constants of solids. ACADEMIC PRESS, INC. Harcourt Brace Jovanovich, Publishers New York London Sydney Tokyo Toronto.
55. Rubin, M.1985. Soda lime silica glasses. Sol. Energy Mater.12:275.