Test case minimization approach using fault detection and combinatorial optimization techniques for configuration-aware structural testing

Abstract

This paper presents a technique to minimize the number of test cases in configuration-aware structural testing. Combinatorial optimization is used first to generate an optimized test suite by sampling the input configuration. Second, for further optimization, the generated test suite is filtered based on an adaptive mechanism by using a mutation testing technique. The initialized test suite is optimized using cuckoo search (CS) along with combinatorial approach, and mutation testing is used to seed different faults to the software-under-test, as well as to filter the test cases based on the detected faults. To measure the effectiveness of the technique, an empirical study is conducted on a software system. The technique proves its effectiveness through the conducted case study. The paper also shows the application of combinatorial optimization and CS to the software testing.

Keywords

Combinatorial testing ; Test case design ; Fault seeding ; Software mutation testing ; Software structural testing ; Cuckoo search algorithm

1. Introduction

Similar to any other engineering process, software development is subjected to cost. Nowadays, software testing (as a process of the software development life cycle) consumes most of the time and cost spent on software development. This cost may decrease rapidly as testing time decreases. Most of the time, a software may be released without being tested sufficiently because of marketing pressure as well as the intention to save time and cut costs. However, releasing low-quality software products to the market is no longer acceptable because it may cause loss of revenue or even loss of life. Thus, software testers should design high-quality test cases that catch most of the faults in the software without taking more than the scheduled time for testing. Thus, test case minimization mechanisms play a major role in reducing the number of test cases without affecting their quality. However, reducing the number of test cases especially in configurable software systems is a major problem.

In recent years, configurable software systems have gained paramount importance in the market because of their ability to alter software behavior through configuration. Traditional test design techniques are useful for fault discovery and prevention but not for fault elimination because of the combinations of input components and configurations [1] . We consider that all configuration combinations lead to exhaustive testing, which is impossible because of time and resource constraints [2]  and [3] . The number of test cases could be minimized by designing effective test cases that have the same effect as exhaustive testing.

Strategies have been developed in the last 20 years to solve the aforementioned problem. Among these strategies, combinatorial testing strategies are the most effective in designing test cases for the problem. These strategies help search and generate a set of tests, thereby forming a complete test suite that covers the required combinations in accordance with the strength or degree of combination. This degree starts from two (i.e., d  = 2, where d is the degree of combinations).

We consider that all combinations in a minimized test suite is a hard computational optimization problem [4] , [5]  and [6] because searching for the optimal set is a nondeterministic polynomial time (NP)-hard problem [5] , [6] , [7] , [8]  and [9] . Thus, searching for an optimum set of test cases can be a difficult task, and finding a unified strategy that generates optimum results is challenging. Two directions can be followed to solve this problem efficiently and to find a near-optimal solution. The first uses computational algorithms with a mathematical arrangement; the other uses nature-inspired meta-heuristic algorithms [10] .

Using nature-inspired meta-heuristic algorithms can generate more efficient results than computational algorithms with a mathematical arrangement [10]  and [11] . In addition, this approach is more flexible than others because it can construct combinatorial sets with different input factors and levels. Thus, its outcome is more applicable because most real-world systems have different input factors and levels.

Developed by Xin-She Yang and Suash Deb [12] , the cuckoo search (CS) algorithm is a new algorithm that can be used to efficiently solve global optimization problems [13] . CS can solve NP-hard problems that cannot be solved by exact solution methods [14] . This algorithm is applicable and efficient in various practical applications [9] , [13] , [15] , [16]  and [17] . Recent evidence shows that CS is superior to other meta-heuristic algorithms in solving NP-complete problems [9] , [13] , [16]  and [17] .

Although combinatorial testing proves its effectiveness in many researches in the literature, evidence showed that there are weak points in this testing technique [18] . It supposes that the input factors have the same impact of the system. However, practically the test cases have different impact and some of the test cases may not detect any fault. In other words, most of the faults may be detected by a fraction of the test suite. Hence, there should be a mechanism to filter the test suite based on the fault detection strength of each test case. Success to do so will lead to further optimize the generated test suite by the combinatorial strategy. This paper presents a technique to overcome this problem systematically. It should be noted that there could be constraints among the input configuration of the software-under-test. This is out of the scope of this paper; however, the method could be applicable for this issue too.

The rest of the paper is organized as follows: Section 2 presents the mathematical notations, definitions, and theories behind the combinatorial testing. Section 3 illustrates a practical model of the problem using a real-world case study. Section 4 summarizes recent related works and reviews the existing literature. Section 5 discusses the methodology of the research and implementation. The section reviews CS in detail and discusses how the combinatorial test suites are generated using such an algorithm. Section 6 contains the evaluation results. Section 7 gives threats to validity for the experiments and case study. Finally, Section 8 concludes the paper.

2. Combinatorial optimization and its mathematical representation

A future move toward combinatorial testing involves the use of a sampling strategy derived from a mathematical object called covering array (CA) [19] . In combinatorial testing, a CA can be demonstrated simply through a table that contains the designed test cases. Each row of the table represents a test case, and each column is an input factor for the software-under-test.

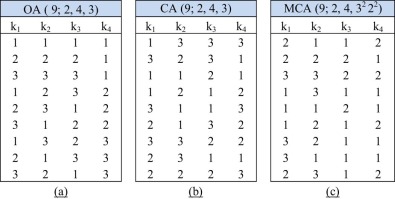
This mathematical object originates essentially from another object called orthogonal array (OA) [20] . An OA_λ (N ; d , k , v ) is an N  ×  k array, where for every N  ×  d sub-array, each d -tuple occurs exactly λ times, where λ  =  N/v^d ; d is the combination strength; k is the number of factors (k  ≥  d ); and v is the number of symbols or levels associated with each factor. In covering all the combinations, each d -tuple must occur at least once in the final test suite [21] . When each d -tuple occurs exactly once, λ  = 1, and it can be unmentioned in the mathematical syntax, that is, OA (N ; d , k , v ). As an example, OA (9; 2, 4, 3) contains three levels of value (v ) with a combination degree (d ) equal to two, and four factors (k ) can be generated by nine rows. Fig. 1 (a) illustrates the arrangement of this array.

Fig. 1. Three different examples to illustrate OA, CA, and MCA.

The main drawback of OA is its limited usefulness in this application because it requires the factors and levels to be uniform, and it is more suitable for small-sized test suites [22]  and [23] . To address this limitation, CA has been introduced.

CA is another mathematical notation that is more flexible in representing test suites with larger sizes of different parameters and values. In general, CA uses the mathematical expression CA_λ (N ; d , k , v ) [24] . A CA_λ (N ; d , k , v ) is an N  ×  k array over (0, …, v    − 1) such that every ${\textstyle B=\left\{b_{0}{\mbox{​}},{\mbox{ }}\ldots {\mbox{ }},{\mbox{ }}b_{d-1}\right\}\in \left({\begin{array}{c}\left\{0,{\mbox{ }}\ldots {\mbox{ }},{\mbox{ }}k-1\right\}d\\d\end{array}}\right)}$ is λ -covered and every N  ×  d sub-array contains all ordered subsets from v values of size d at least λ times [25] , where the set of column B  =  {b₀ , …, b _d-1 }  ⊇  {0, …, k − 1 }.To ensure optimality, we normally want d -tuples to occur at least once. Thus, we consider the value of λ  =  1 , which is often omitted. The notation becomes CA (N ; d , k , v ) [26] . We assume that the array has size N , combination degree d , k factors, v levels, and index λ . Given d , k , v , and λ , the smallest N for which a CA_λ (N ; t , k , v ) exists is denoted as CAN_λ(d , k , v ). A CA_λ (N ; d , k , v ) with N = CAN_λ (d , k , v ) is said to be optimal as shown in Eq. 1 [27] . Fig. 1 (b) shows a CA with size 9, which has 4 factors each having 3 levels with a combination degree equal to 2.

${\mbox{CAN}}{\mbox{ }}\left(d,{\mbox{ }}k,{\mbox{ }}v\right)=$$min\left\{N{\mbox{ }}:{\mbox{ }}\ni {\mbox{CA}}{\mbox{ }}\left(N,{\mbox{ }}d,{\mbox{ }}k,{\mbox{ }}v\right)\right\}$

( 1)

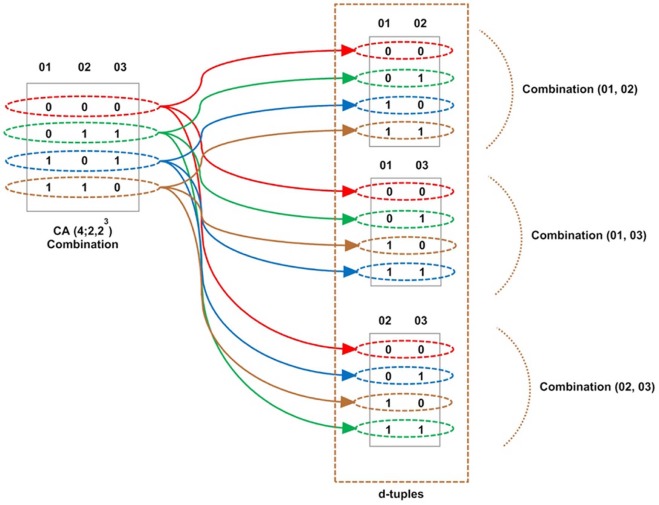
CA is suitable when the number of levels v is equal for each factor in the array. When factors have different numbers of levels, mixed covering array (MCA) is used. MCA is notated as MCA (N , d , k , (v₁ , v₂ , v₃ ………. v_k )). It is an N  ×  k array on v levels and k factors, where the rows of each N  ×  d sub-array cover all d -tuples of values from the d columns at least once [2] . For more flexibility in the notation, MCA can be represented as MCA (N ; d , v ^k )) and can be used for a fixed-level CA such as CA (N ; d , v ^k ) [8].Fig. 1 (c) illustrates an MCA with size 9 that has 4 factors: 2 of them having 3 levels each and the other 2 having 2 values each. In addition, Fig. 2 shows an example CA (4; 2, 2³ ) of the way the d -tuples are generated and covered using CA.

Fig. 2. Illustration of the way the d -tuples are covered by the CA.

3. Problem definition through a practical example

With the development of communication systems, mobile phones are among the latest industry innovations and a common mode of communication among humans. Various operating systems have been developed for these devices as platforms for performing basic tasks, such as recognizing inputs, sending outputs, keeping track of files, and controlling peripheral devices. This development has paved the way for the emergence of smart phones. Smart phone applications or “apps” installed on mobile platforms perform useful tasks. Android is an important platform that includes a specialized operating system and an open-source development environment.

In controlling the behavior of a smart phone, many configuration options must be adjusted in the Android unit. In executing the running apps on a variety of hardware and software platforms, this adjustment of options plays an important role. Some smart phones, for example, have a physical keyboard, whereas others have a soft keyboard. Fig. 3 shows a sample of the resource configuration file “configuration.java” source code for Android. The numerous configuration factors in the code are highlighted and they must be adjusted.

Fig. 3. Android resource configuration file.

Fig. 3 shows that each factor has different options or levels. For example, the NAVIGATION factor has five levels, which are DPAD, NONAV, TRACKBALL, UNDEFINED, and WHEEL. Table 1 summarizes these parameters and their possible values.

Table 1. Android resource configuration factors and levels.

Factors	No. of levels	Actual values
SCREENLAYOUT_SIZE	5	LARGE, MASK, NORMAL, SMALL, UNDEFINED
SCREENLAYOUT_LONG	4	MASK, NO, UNDEFINED, YES
TOUCHSCREEN	4	FINGER, NOTOUCH, STYLUS, UNDEFINED
KEYBOARD	4	12KEY, NOKEYS, QWERTY, UNDEFINED
KEYBOARDHIDDEN	3	NO, UNDEFINED, YES
HARDKEYBOARDHIDDEN	3	NO, UNDEFINED, YES
NAVIGATION	5	DPAD, NONAV, TRACKBALL, UNDEFINED, WHEEL
NAVIGATIONHIDDEN	3	NO, UNDEFINED, YES
ORIENTATION	4	LANDSCAPE, PORTRAIT, SQUARE, UNDEFINED

Testing any application on the device by applying a set of designed test cases may expose a set of faults. However, evidence shows that applying the same set of test cases but with different configurations may result in different faults [28]  and [29] , which in turn lead us to consider different configurations for the same software-under-test (i.e., configuration-aware testing). In addition, evidence shows that considering the interaction between the configurations (i.e., combination of configurations) will also lead us to detect new faults [30] . In this case, the tester may test the app against all the configurations, which is called exhaustive testing. However, this testing leads to an enormous amount of test cases, which make the testing process intractable.

Around 35 options must be set in the app configuration file. To test the entire configuration exhaustively, we need to test 3³ 4⁴ 5² , which translates to 172,800 configurations. However, this number of test cases requires a significant amount of time and resources.

Using the combinatorial testing approach, a tester can test the combination of configurations. In addition to the benefit of testing unexpected combinations among the individual factors, this technique is an alternative to exhaustive testing. The use of combinatorial testing reduces the exhaustive test cases based on the combination degree (d ), which depends mainly on the CA notations and mathematical models. For example, d  = 2 represents the combination of two factors. Here, instead of 172,800 test cases, 29 test cases are taken. Table 2 shows an example of the way this technique reduces the exhaustive test cases based on d .

Table 2. Number of test cases and its reduction percentage compared to exhaustive testing.

d	No. of tests	% Reduction
2	29	99.98
3	139	99.91
4	632	99.63
5	2533	98.53
6	9171	94.69

Evidence shows that taking the combinations of two and three is appropriate for many applications. However, we still need higher interactions for many other applications, especially for 2 ≤ d ≤ 6.

4. Related work and review of literature

Although the problem of CA generation is an NP-hard problem, researchers have attempted to solve it using various methods. This section focuses on the general techniques and tools that have been developed by researchers. Some of these tools are freely available, whereas others are presented only as evidence in the literature.

4.1. Test suite generation strategies

To date, many software tools and strategies have been developed for test suite generations. The first attempt of researchers started from the algebraic approach and the OA that is derived from mathematical functions. This way requires the input factors and levels to be constructed by predefined rules without requiring any details of combinations. This approach is performed directly by calculating a mathematical purpose for the value [8] . Despite its usefulness, OA is too restrictive because it exploits mathematical properties, thereby requiring the parameters and values to be uniform. To overcome this limitation, the mutual orthogonal array (MOA) [31] has been introduced to support non-uniform values. However, a major drawback exists for MOA and OA, that is, a feasible solution is available only for certain configurations [8]  and [31] .

Another approach from the literature is the computational approach that uses one-factor-at-time (OFAT) and one-test-at-time (OTAT). In this strategy, a single test or a set of completed test cases is a candidate for every iteration, after which the algorithm searches for the test case that covers the most uncovered d -tuples to be added to the final test suite. Based on this approach, several tools and strategies have been developed in previous studies. Different well-known strategies were developed in this approach, such as automatic efficient test generator (AETG) by [32] , classification-tree editor eXtended logics (CTE-XL) developed by [33] , test vector generator (TVG) by [34] , and test configuration (TConfig) by [35] . AETG has been modified later to mAETG by [36] . In addition, Jenny [37] , pairwise independent combinatorial testing (PICT) [38] , constrained array test system (CATS) [39] , and intelligent test case handler (ITCH) [10] were developed successfully. Tai and Lie [4] tried to use a different and faster algorithm in this approach by developing in-parameter order (IPO), as well as its variant tools IPOG and IPOG-D [8]  and [40] .

Various tools and strategies are still being developed to generate minimal combinatorial test suites. A few of them are available as freeware on the Internet [41] . Each strategy has its own features and advantages. None of them is the best for all input configurations. Sometimes, they are used together, and then the best result is chosen.

Most recently, important efforts have been made to implement artificial intelligence (AI)-based strategies for the combinatorial test suite generations. So far, genetic algorithm (GA) [42] , [43]  and [44] , simulated annealing (SA) implemented in CASA tool [45] , tabu search (TS) [46] , ant colony algorithm (ACA) [47] , and particle swarm optimization (PSO) implemented in PSTG tool [48]  and [49] have been developed and successfully implemented for small-scale combination degrees [10] .

On the one hand, in constructing combinatorial test suites, GA, SA, and TS have been implemented by [50] . The implementation supports small combinations of input factors d  = 2 (i.e., pairwise). The results confirm that GA has been the least efficient compared with SA and TS. In addition, TS is effective for small search spaces, whereas SA performs with better results for large search spaces. When the combinations had been increased by three and greater, Cohen [36] developed and implemented SA for d  = 3 when a large search space for this case was generated. The result confirms that SA performed with better outcomes to find the optimal solution.

On the other hand, Shiba et al. [51] have developed two artificial methods GA and ACA combined with the compaction algorithm. The results show that the generated CA is usually small. However, they are not always optimal in size for the combination degree 2 ≤ d  ≤ 3. Another technique in constructing CA is the particle swarm-based test generator (PSTG) developed by [30] . This technique shows that PSO supports a high combination between the input factors 2 ≤ d  ≤ 6, which means that it obtains large search spaces. The result shows that PSO has more effective roles than the other techniques. However, the problem with the conventional PSO is the reduction of convergence speed with the increase in the number of iterations, which affects the particles in achieving the best value [52] . PSO also appears to have the problem of parameter tuning because of the varying performance of different parameter values. In fact, most of the meta-heuristic algorithms use local search and global search with a generated random initial population [11] . Gaining an optimal combinatorial test suite every time is next to impossible because of its NP-completeness.

4.2. A brief review of generation tools

As mentioned previously, the two basic directions of generating combinatorial test suites are computational and AI-based strategies. In this section, attention is paid to the recapitulation of the tools using computational and AI-based approaches.

The implementations of the computational approach mainly use two directions of algorithms: sequential and parallel implementation algorithms. Sequential implementation builds the test case individually until completion. Parallel implementation consists of multiple processing units that together construct the final test suite. Here, a sequential algorithm functions better than the parallel algorithm because a sequential algorithm is less difficult to implement. However, the sequential algorithm tends to consume more time than the parallel implementation, especially for large input factors and configurations [53] .

As mentioned, some of the tools that have been implemented by many developers are now available for generating test suites. Many tools have been developed in the literature, such as AETG, mAETG, PICT, CTE-XL, TVG, Jenny, TConfig, ITCH, IPO, IPOG, and IPOG-D.

The AETG strategy uses OTAT and supports only uniform degrees of interaction [32] . It initializes by generating some candidate test cases and then selects one of them as a final solution that covers most tuples. Thereafter, it randomly selects another case from the remaining input factors. For each remaining input factor, choosing values that cover the most uncovered d -tuples is necessary [32]  and [53] . From the inability of this strategy to be evaluated, Cohen [36] implements it again with modifications in a tool called mAETG.

The PICT strategy uses the greedy algorithm and OTAT. PICT contains two main phases: preparation and generation. The first phase computes all the information needed for the second phase. The generation process starts by marking the first uncovered tuples from the uncovered tuples list, and then the “don't care” values are filled iteratively by the value that covers the most uncovered tuples [38] . Although PICT formulates pseudo-random choices, it is always initialized with the same seed value (except when the user specifies otherwise). As a result, two executions with the same input construct the same output [53] .

The TVG algorithm uses OTAT and generates test cases for each execution with different results for the same inputs. TVG supports all types of interaction degrees. It has been implemented as a Java program with a GUI that covers d -tuples, where d is specified by the tester [53] .

The Jenny strategy uses OTAT that starts generating with 1-tuple and then extends to cover 2-tuples until it covers all d -tuples (where d is specified by the tester). Jenny only supports uniform combination degrees. It covers most of the combinations with fewer test cases than other strategies [37]  and [53] .

TConfig is another test-suite generation strategy that uses OTAT and OPAT. It is dependent on two main methods: recursive block and IPO. The first method is used to generate the pairwise test suite, and the second method is used for higher uniform degrees of combinations. The recursive block method uses the algebraic approach to generate a test suite based on OA. It has been used as initial blocks for the larger CA including all d -combinations that can be generated by building CA from orthogonal arrays [53] .

The IPO strategy uses OFAT, which begins the generation process from 2-combinations and then extends by adding one parameter at a time based on horizontal extension. To ensure the coverage of all d-tuples, a new test case may be added from time to time based on vertical extension [4] . Based on this idea, the technique generalizes the IPO strategy from pairwise testing to multi-way testing and produces the modern strategy called IPOG by [40] . However, multi-way testing has time and space requirements because the number of combinations is frequently very large. For this purpose, based on the IPOG strategy [8] , a new strategy named IPOG-D is introduced, which is sometimes called doubling construct. The doubling construct algorithm is used to raise the initial test suite size. Thus, the number of horizontal and vertical extensions needed by the IPOG-D strategy can be efficiently reduced as compared to IPOG, which results in reduced execution time [53] .

In addition to the aforementioned strategies and algorithms, several attempts have been made to develop combinatorial strategies based on AI (i.e., AI procedure). So far, the GA, ACA, SA, TS, and PSTG AI-based techniques have been implemented successfully to generate combinatorial test suites. In general, these techniques are used to find the optimal solution among a finite number of solutions. Each technique starts by initializing random populations and then iteratively updates the population according to specific algorithms and update roles.

GA is a heuristic search technique that has been widely used in solving problems ranging from optimization to machine learning [6] . It is initialized with random solutions that denote chromosomes. Thereafter, it formulates a new solution by exchanging and swapping two good candidates. The procedure swapping has been applied by specific processes, such as the mutation and crossover processes. Finally, it chooses the best solution among the solutions and adds to the final test suite.

In ACA, an individual ant makes candidate solutions in the first round with an empty solution and then iteratively adds solution components until the generated solutions are completed. After building the completed solutions, the ants offer feedback on the solutions, and better solutions are used by many ants [54] . The searching operation is performed by a number of ants. The best path implies the best value for a test case because ants travel from one position to another to find the best path [53] .

Most recently, SA is implemented in CASA tool. The search progress in SA consists of two main parts that take on search procedures. The first part is the acceptance probability of the current solution, and the second one is differences in objective value between the current solution and the neighboring solution. It allows for fewer restricted movements through the search space, and probability of the search attractive stuck in local optima [11] . This algorithm starts randomly, and after that it applies to a number of transformations according to probability equation. The probability equation depends greatly on input-factors [53] .

The progresses in TS identify neighbors or a set of moves that may be useful to a given solution to make a new one. It stores more accurately and moves in a data structure that is called tabu-list. It records information regarding a solution attribute that is useful for modification of movement from one solution to another. Selecting good solution is done by using adapted evaluation strategies that help the introduction of current solution [54] .

PSTG strategy uses PSO algorithm to initialize random population in the beginning and that each solution has its velocity. The whole population is named swarm, and each solution is the swarm called particle. The fitness function is defined based on the coverage of d-tuples here. Each solution becomes a good candidate when it covers most of the d-tuples combinations. The algorithm updates the search space periodically based on the update role and velocity of the particle. Here, the role is based on parameters to adjust the movement of the particles and their speed of convergence. These parameters must be tuned carefully to get optimal solution and not to get stuck to the local minima [30]  and [55] .

5. Cuckoo search for combinatorial testing

As shown in the literature, the nature-inspired and AI-based algorithms and strategies can achieve more efficient results compared with the other algorithms and methods. The AI-based algorithms require greater computation time to generate final combinatorial sets because of the heavy computation of the search process for covering d -tuples.

PSO attempts to solve this problem by using lighter weight computation in the update and search processes as compared to the other algorithms. Evidence in the literature shows better results of PSO in most cases as compared to the other methods [30] . In fact, PSO is not deprived of problems and drawbacks.

The performance of PSO generally depends on the values of the tuning parameters. In other words, PSO combines two roles of searching mechanisms: exploration and exploitation. In the former mechanism, PSO performs global optimum solution searching, and in the latter mechanism it seeks more accurate optimum solutions by converging the search around a promising candidate. For instance, selecting the right values for these parameters should be based on the compromise between local and global explorations that would facilitate faster convergence. Evidence shows that depending on the complexity of the problem, different values of these parameters are required to achieve the optimum required solution [56]  and [57] . Moreover, the search process in this algorithm becomes stuck in the local optima. Thus, finding the best solution becomes difficult after a certain number of iterations. In solving this issue, new algorithms that contain few parameters to be tuned and do not have drawbacks are more effective.

CS was developed by Yang and Deb [58] in 2009. It is one of the newest nature-inspired meta-heuristic algorithms used to solve global optimization problems [13] . Most recently, CSA enhanced by the so-called Lévy flight method was used instead of simple random walks [13]  and [55] .

The algorithm is mainly based on the nature-inspired behavior of cuckoo birds. A species of cuckoo lays eggs in other nests. If a host bird determines that the eggs are not its own, then it will either throw these alien eggs away or simply abandon its nest and build a new nest elsewhere. The main idealized roles of CSA show that each cuckoo lays one egg at a time and dumps its egg in a randomly chosen nest. The best nests with high-quality eggs carry over to the next generations, and the number of available host nest is fixed. Thus, an egg that is laid by a cuckoo bird is discovered by the host bird with a probability between 0 and 1. In addition, CS can work with NP-hard problems and can obtain the best solution among several solutions [9]  and [14] .

Based on these prospects, the hypothesis of this research supposes that this algorithm could perform well to solve the combinatorial optimizations problems.

This section provides the necessary details for the developed strategy. Section 5.1 presents the necessary background and illustrates the essential details of CS and its mechanism. Section 5.2 presents the details of the “d-tuples generation” algorithm. Then, Section 5.3 presents the CS used for combinatorial testing and its optimization process and implementation.

5.1. Cuckoo search (CS)

CS is one of the newest and the most modern strategies applied in solving optimization problems. The algorithm is mainly used to solve NP-hard problems that need global search techniques [13]  and [58] . Fig. 4 shows the pseudocode that illustrates the general steps of this algorithm.

Fig. 4. Pseudocode of CS [58] .

The rules of CSA are as follows. (1) Each cuckoo randomly selects a nest to lay an egg in it, in which the egg represents a solution in a set of solutions. (2) Part of the nest contains the best solutions (eggs) that will survive for the next generation. (3) The probability of the host bird finding the alien egg in a fixed number of nests is p_a  ∈ [0,1] [59] . If the host bird discovers an alien egg with this probability, then the bird either discards the egg or abandons the nest to build a new one. Thus, we assume that a part of p_a with n nest is replaced by new nests.

Lévy flight is used in CSA to conduct local and global searches [60] . The rule of Lévy flight is used successfully in stochastic simulations of different applications, such as biology and physics. Lévy flight is a random path of walking that takes a sequence of jumps, which are selected from a probability function. A step can be represented by the following equation for the solution x^(t+1) of cuckoo i :

$x_{i}^{t+1}=x_{i}^{\left(t\right)}+\alpha \oplus L{\mbox{ }}{\acute {e}}{\mbox{ }}{\mbox{vy}}{\mbox{ }}\left(\lambda \right)$

( 2)

where ${\textstyle \alpha }$ the size of each step, in which ${\textstyle \alpha >0}$ and depends on the optimization problem scale. The product ${\textstyle \oplus }$ is the entrywise multiplication, and ${\textstyle L{\mbox{ }}{\acute {e}}{\mbox{ }}{\mbox{vy}}{\mbox{ }}\left(\lambda \right)}$ is the Lévy distribution. The algorithm continues to move the eggs to another position if the objective function finds better positions. This can be noticed clearly in Fig. 4 when F_i is replaced with F_j where j is the indication of a new solution generated after update.

Another advantage of CSA over other stochastic optimization algorithms, such as PSO and GA, is its lack of many parameters for tuning. The only parameter for tuning is p_a . Yang and Deb [15]  and [58] obtained evidence from the literature and showed that the generated results were independent of the value of this parameter and could be fit to a proposed value p_a   =  0.25.

In using the algorithm for combinatorial test suite generation, adapting the algorithm to the generation strategy is essential. Here, the fitness function plays an important role in the adaptation and application of CS. In this paper, after the population is initialized, the CS takes the number of covered d -tuples in each nest in the population as a fitness function. This function selects the best rows that cover most of the combinations in the d -tuples list.

5.2. The d-tuples generation algorithm

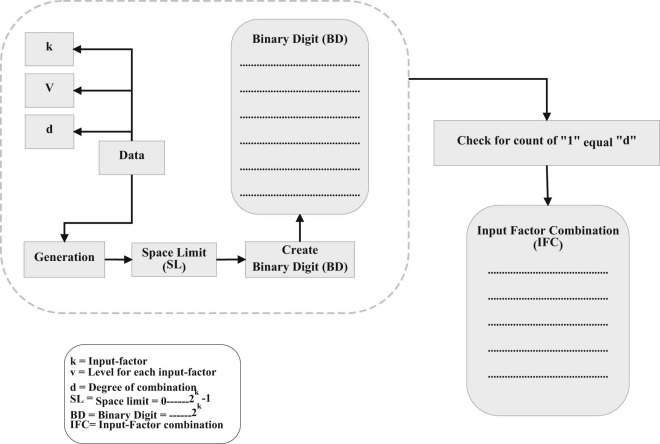
Generating the all-combination-list (i.e., d -tuples list) is essential in calculating the fitness function F_i   = f (x_i ). The d -tuples list contains all possible combinations of input factors k . This algorithm mainly takes three inputs: number of input factors (k ), level of each input factor (v ), and degree of combination (d ). To generate the d -tuples list, the strategy first generates a binary digit (BD) list that contains binary digits; this BD list starts from zero to space limit (SL). SL is calculated by Eq. 3.

The BD list can be filled by binary digits, and the total number of elements of the BD list is equal to (2^k ).

$SL=\left(2^{k}\right)-1{\mbox{ }}\left(k{\mbox{ }}numbers{\mbox{ }}of{\mbox{ }}input-\right.$$\left.factor\right)$

( 3)

$C_{d}^{k}={\frac {k!}{d!{\mbox{ }}\times {\mbox{ }}\left(k-d\right)!}}$

( 4)

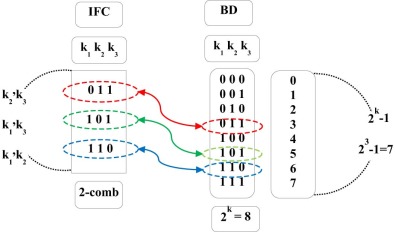
When the BD list is created, an algorithm filters the BD list based on the combination degree. The algorithm counts the number of 1s in each binary number and passes only those binary numbers that meet the combinatorial degree specified in the input at the beginning. Fig. 5 shows the creation of BD and IFC. Basing on the specified degree of combination, the check point compares each element in the BD list to a degree number (d   ). The summation repeats 1 for each row element in the BD list that has the same degree number (i.e., ${\textstyle \sum repeated{\mbox{ }}''1''=d}$ ). For example, if d  = 2, then each binary digit must contain two 1s, in which (011), (101), and (110) pass the filter. The IFC is a list that represents input factor combinations. Here, for each position that contains 0, a “don't care” value of the input factor is inserted. However, the 1s in the same binary element are replaced by a level for that particular input factor. For example, (011) represents three input factors (k₁ , k₂ , and k₃ ). In this case, the first input factor (k₁  = 0) is counted as a “don't care,” whereas the combination is between the second and third factors.

Fig. 5. IFC algorithm diagram.

Here, the algorithm neglects elements in the BD list that do not satisfy the combination degree conditions and adds the rest of the elements to the IFC list. Fig. 6 illustrates a running example of this algorithm through a simple diagram. The diagram shows an example with d  = 2 and k  = 3. Thus, SL = ((2 × 2 × 2) − 1) = 7, which in turn counts binary numbers from 0 to 7. The outcome of the algorithm satisfies the results in Eq. 4, where the (c) represents the combinations [61] , that is, the number of combinations is equal to three elements in IFC.

Fig. 6. The IFC and BD for d  = 2, k = 3.

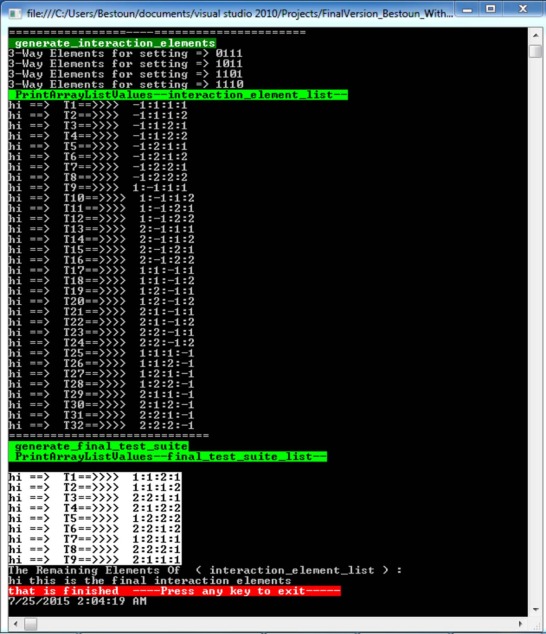
The output list of this algorithm can be noted clearly in the output screen of the strategy shown in Fig. 7 for a system with CA (4; 2, 2⁴ ).

Fig. 7. Output screen shot of the strategy.

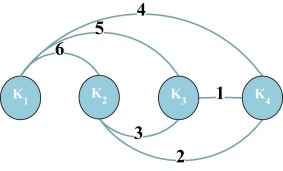
An algorithm is used to assess the search process for the combinations efficiently. In this paper, the rows in the d -tuples list are stored in groups. Each group is assigned with an index number that indicates its position in the list. The groups are selected based on the combination of factors. The number of input factors equals four (k₁ , k₂ , k₃ , and k₄ ), and each input factor has two levels (v_i  = 2, 2, 2, 2) when the degree of combination equals two (d  = 2). According to Eq. 4, the number of input factor combinations can be determined as follows:

$C_{2}^{4}={\frac {4!}{2!{\mbox{ }}\times {\mbox{ }}\left(4-2\right)!}}=$${\frac {4\times 3\times 2\times 1}{2\times 1\times 2\times 1}}=$${\frac {24}{4}}=6$

According to the results, six combinations are possible, as shown in Fig. 8 .

Fig. 8. Combination paths.

For each path, multiplying the levels can be combined [(k₃ , k₄ ), (k₂ , k₄ ), (k₂ , k₃ ), (k₁ , k₄ ), (k₁ , k₃ ), (k₁ , k₂ )], and then the results are equal to [(2 × 2 = 4), (2 × 2 = 4), (2 × 2 = 4), (2 × 2 = 4), (2 × 2 = 4), (2 × 2 = 4)], respectively.

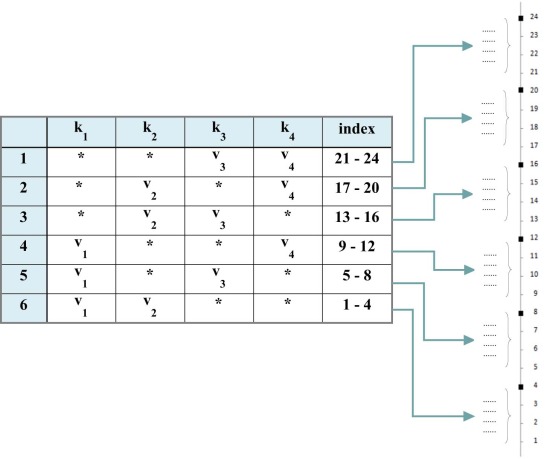
According to these results, the search space is divided into six partitions, and an indexing for each partition is created by considering the summation of each combination [(4), (4 + 4 = 8), (8 + 4 = 12), (12 + 4 = 16), (16 + 4 = 20), (20 + 4 = 24)]. Thus, six categories are created dynamically by the strategy, such as [(1–4), (5–8), (9–12), (13–16), (15–20), (21–24)]. Fig. 9 illustrates this mechanism in detail for the given example.

Fig. 9. Indexing of the search space.

The advantage of this mechanism is the speedup of the search process because the strategy searches only for related tuples in the given index number. The index changes dynamically as the best test case is found because the related tuples in the search space are deleted immediately.

5.3. Optimization process with CS

After the d -tuples list is generated, the CS starts. In this paper, the CS is modified to solve the current problem. The fitness function is used to derive the better solution among a set of solutions. In this paper, a row with higher fitness weight is defined as a row that can cover a higher number of rows in the d -tuples list. Fig. 10 shows the pseudocode of combinatorial test suite generation, in which CS is modified for this purpose.

Fig. 10. Pseudocode of combinatorial test suite generation with CS.

The strategy starts by considering the input configuration. Then, the d -tuples list is generated. The CS starts by initializing a random population that contains a number of nests. Given that the number of levels for each input factor is a discrete number, the initialized population is discrete, not an open interval. Thus, the population is initialized with a fixed interval between 0 and v_i . In this paper, a system has different factors in which a test case is a composite of more than two factors that form a row in the final test suite. As a result of such an arrangement, each test case is treated as a vector x_i that has dimensions equal to the number of input factors of the system. In addition, the levels for each input factor are basically an integer value. As a result, each dimension in the vector-initialized population must be an integer value.

Although the initial population is initialized in a discrete interval, the algorithm can produce out-of-the-bound levels for the input factors. Thus, the vector must be restricted with lower and upper bounds. The rationale for this restriction is that the cuckoo lays its eggs in the nests that are recognized by its eyes.

When the CSA iterates, it uses Lévy flight to walk toward the optimum solution. The Lévy flight is a walk that uses random steps, in which the length of each step is determined by Lévy distribution. The generation of random steps in the Lévy flight consists of two steps [62] , namely generating the steps and choosing a random direction. The generation of direction normally follows a uniform distribution. However, in the literature, the generation of steps follows a few methods. This paper follows the Mantegna algorithm, which is the most efficient and effective step-generation method [62] . In this algorithm, a step length s can be defined as follows:

$s={\frac {u}{{\vert v\vert }^{\frac {1}{\beta }}}}$

( 5)

where u and v are derived from the normal distribution in which

$u\sim N\left(0,{\mbox{ }}{\sigma }_{u}^{2}\right),{\mbox{ }}v\sim N\left(0,{\mbox{ }}{\sigma }_{u}^{2}\right)$

( 6)

${\sigma }_{u}={\left\{{\frac {\Gamma \left(1+\beta \right)sin\left({\frac {\pi \beta }{2}}\right)}{\Gamma \left[{\frac {1+\beta }{2}}\right]\beta 2^{\frac {\beta -1}{2}}}}\right\}}^{1/\beta }{\mbox{​}},{\mbox{ }}{\sigma }_{v}=$$1$

( 7)

Based on the aforementioned design constraints, the complete strategy steps, including the CSA, are summarized in Fig. 10 .

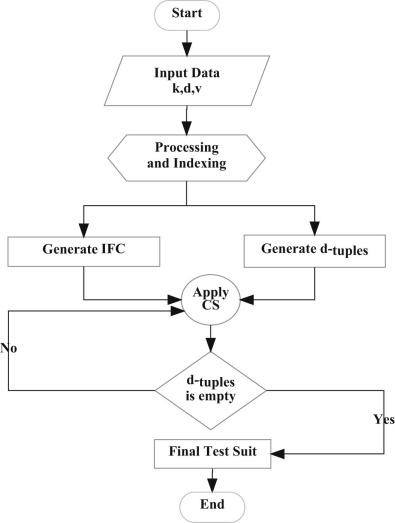
As mentioned, the strategy starts by considering the input configuration (Step 1). Normally, the input is a composite input with factors, levels, and desired combination degree d . The combination degree is d  > 1, which is less than or equal to the number of input factors. Through the all-combination-list generation algorithm described previously, the d -tuples list is generated (Step 1). Thereafter, the strategy uses the CSA, which starts by initializing a population with m nests, with each nest consisting of dimensional vectors equal to the number of factors with a number of levels (Step 2). From a practical point of view, each nest contains a candidate test case for the final test suite (FTS). Thereafter, the CSA assesses each nest by evaluating its coverage capability of the d -tuples (Steps 3-5). For example, a nest that can cover 4-tuples has a weight of coverage of 4. The strategy uses a special mechanism described previously ( Section 5.2 ) to determine the number of covered tuples and to verify the weight. Using the results of coverage for all nests, the strategy sorts the nests again in the search space based on the highest coverage (Step 10). The lowest coverage in the search space is abandoned. For the abandoned nests, a Lévy flight is conducted to verify the availability of better coverage (Step 13). If better coverage is obtained for a specific nest, then the nest is replaced by the content of the current nest. Thereafter, for the better nests, a Lévy flight is conducted to search for the best local nests (Step 20). If better coverage is obtained after the Lévy flight for a specific nest, then the nest is replaced with the ones with better coverage (Steps 21 to 24). These steps (Steps 7 to 28) in the CSA update the search space for each iteration.

Two stopping criteria are defined for the CSA. First, if the nest reaches the maximum coverage, then the loop stops and the algorithm adds this test case to the FTS and removes its related tuples in the n -tuples list. Second, if the d -tuples list is empty, then no combinations are covered. If the iteration reaches the final iteration, then the algorithm selects the best coverage nest to be added to the FTS (Step 27) and removes the related tuples in the d -tuples list (Step 28). This mechanism continues as long as n -tuples remain in the list. Fig. 11 presents the general procedure of the strategy.

Fig. 11. Flow chart of the CS strategy.

6. Evaluation results and discussion

To evaluate the effectiveness of the generated test suite, the strategy is evaluated by adopting a case study on a reliable artifact program to prove the applicability and correctness of the strategy for a real-world software testing problem. The generated test suite in the first stage does not consider the internal structure of the artifact program. However, after the generation, the test suite is filtered based on structural testing methods and detected faults. In making a fair comparison, the generation efficiency of the first stage (i.e., without filtering) is compared with that of other strategies.

Some strategies are available publicly as tools to be downloaded and installed, whereas other strategies are unavailable publicly. Having all the tools installed in the same environment is essential to ensuring a fair comparison. The proposed strategy is compared with seven well-known strategies, namely Jenny, TConfig, PICT, TVG, IPOG, IPOG-D, and PSO. The experimental environment consists of a desktop PC with Windows 7 operating system, 64-bit, 2.5 GHz, Intel Core i5 CPU, and 6 GB of RAM. The algorithms are coded and implemented in C#.

6.1. The CS efficiency evaluation experiments

Efficiency of generation is measured by the size of the constructed test suites. All results are compared with those strategies published in the literature and those available freely for download. In addition to the input configuration of the selected artifact used for case study, different benchmarks are selected from literature for better evaluation. The procedure of the comparison categorizes the experiments into different sets. Since the test suite basic components are input factors (k), the levels of these factors (v) and the combination degree, the experiments are taking these components as bases. The first set of experiment is the artifact program used for case study.

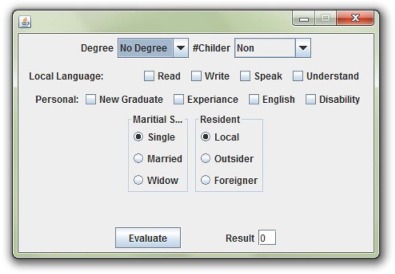
Here, an artifact program is selected as the object of the empirical case study. The program is used to evaluate the personal information of new applicants for officer positions. The program consists of various GUI components that represent personal information and criteria to be converted into a weighted number. Each criterion has an effect on the final result, which decides the rank and monthly wage of the officer. The final number is the resulting point. The program is selected because it has a nontrivial code base and different configurations. Fig. 12 shows the main window of the program.

Fig. 12. Main window of the empirical study program.

The program regards different configurations as input factors. Each input factor has different levels. For example, the user can choose “No Degree,” “Primary,” “Secondary,” “Diploma,” “Bachelor,” “Master,” and “Doctorate” levels for the “Degree” factor. Table 3 summarizes the factors and levels for the program.

Table 3. Summary of the input factors and levels for the case study program.

No.	Factors	Levels
1	Degree	[No Degree, Primary, Secondary, Diploma, Bachelor, Master, Doctor]
2	Children	[Non, 1, 2, 3, 4, More_than_4]
3	Read	[Checked, unchecked]
4	Write	[Checked, unchecked]
5	Speak	[Checked, unchecked]
6	Understand	[Checked, unchecked]
7	New graduate	[Checked, unchecked]
8	Experience	[Checked, unchecked]
9	English	[Checked, unchecked]
10	Disability	[Checked, unchecked]
11	Marital status	[Single, Married, Widow]
12	Resident	[Local, Outsider, Foreigner]

To this end, the input configuration of the program can be represented by one factor with seven levels, one factor with six levels, eight factors with two levels each, and two factors with three levels each. Thus, this input configuration can be notated in an MCA notation as MCA (N ; d , 7¹ 6¹ 2⁸ 3² ). We need 96,768 test cases to test the program with exhaustive configuration testing. In this paper, a combinatorial test suite is generated by considering the input configuration to minimize the number of test cases. Table 4 shows the size of each test suite generated by CS strategy as well as the time in seconds of generation, considering the combination degree compared with other strategies. The best results for each configuration in the table are shown in bold numbers.

Table 4.

Comparison of the test suite size generated and time of generation by different strategies for the case study.

Comb. degree (d)	PICT	IPOG	IPOG-D	Jenny	TVG	PSO	CS
	Size/Time	Size/Time	Size/Time	Size/Time	Size/Time	Size/Time	Size/Time
2	310/3.47	42 /0.43	57/0.25	42/0.18	42 /3.79	42 /5.32	42/ 18.3
3	1793/8.36	141/2.45	195/0.76	156/1.54	144/9.43	139/25.82	136/ 21.65
4	6652/40.32	505/20.89	926/13.65	477/24.47	497/92.32	459/97.49	446/ 73.69
5	23014/475.22	1485/105.76	2811/24.65	1240/63.78	1234/204.81	1225/406.52	1205/ 203.52
6	46794/782.12	3954/187.54	7243/58.32	3041/92.13	3218/542.03	3078/865.37	2886/ 612.74

Table 4 shows the size of the smallest generated sizes for the combinatorial test suite when 2 ≤ d  ≤ 6. In addition, the table shows the time of generation for these configurations. The table shows that PICT can generate the largest sizes and time in all cases as compared to the other competitors. IPOG and IPOG-D perform effectively in all configurations. However, IPOG and IPOG-D fail to generate optimized results of size in most of the cases. However, they are very fast for test suite generation. IPOG-D is the fastest strategy for generation, although its size of generation is not superior. Jenny and TVG can generate better results than IPOG and IPOG-D in term of size. However, Jenny is faster than TVG, and in some cases it can beat IPOG-D. TVG can generate better results than Jenny in most cases in term of size. Aside from CSA, PSO generates better results for most configurations. Similarly, CS can achieve better results for all configurations and can achieve better results in terms of size as compared with PSO. However, due to its light weight, CS is faster than PSO. Notably, the size of the CA depends on the values and degrees of combinations, which can be interpreted by the equation of the growth of size published in the literature as O (v^t log p ) [40] .

To make a fare comparison and to get better indication of the test generation efficiency, benchmarks are considered from [4] , [42]  and [63] . Table 5  and Table 6 show the best size and execution time of each test suite generated by CSA strategy compared with other strategies considering the combination degree equal to 2 for Table 5 and mixed between 2 and 3 in Table 6 . For those strategies that are not available freely for download, only the size of the generation is presented in the table. The best results are represented in bold numbers, while NA indicates that the results are not available for that configuration.

Table 5. Comparison of the test suite size generated by different strategies.

Configuration	AETG	PairTest	TConfig	Jenny	DDA	CASA	AllPairs	PICT	CSA
	Size	Size	Size/Time	Size/Time	Size	Size/Time	Size	Size/Time	Size/Time
34	9	9	9/ 0.11	11/0.09	NA	9/ 0.22	9	9/ 0.21	9/ 0.13
313	15	17	15/ 25.12	18/18.34	18	16/38.45	17	18/25.57	15/ 22.45
415 317 220	41	34	40/722.43	38/342.53	35	34/483.23	34	37/372.51	33/ 942.18
41 339 235	28	26	30/1534.26	28/1276.37	27	22/ 1638.22	26	27/1348.53	25/1749.12
2100	10	15	14/2437.56	16/1754.36	15	12/1734.45	14	15/1567.34	16/2367.23
1020	180	212	231/3890.43	193/2542.12	201	NA	197	210/2934.5	210/3950.2

Table 6. Comparison with existing meta-heuristic algorithms for different configurations.

Configuration	AETG	mATEG	GA	CASA	ACA	PSO	CSA
	Size	Size	Size	Size/Time	Size	Size/Time	Size/Time
CA(N; 2, 34 )	9	9	9	9/ 0.15	9	9/0.14	9/0.14
CA(N; 2, 313 )	15	17	17	16/19.54	17	17/18.45	20/25.34
MCA(N; 2, 51 38 22 )	19	20	15	15/ 12.43	16	21/17.34	21/16.51
MCA(N; 2, 61 51 46 38 23 )	34	35	33	30/ 18.52	32	39/120.37	43/147.29
MCA(N; 2, 71 61 51 46 38 23 )	45	44	42	42/ 28.34	42	48/136.32	51/132.61
CA(N; 3, 36 )	47	38	33	33/ 8.43	33	42/9.32	43/8.37
CA(N; 3, 46 )	105	77	64	64/ 69.52	64	102/115.33	105/110.11

In these configurations from Table 5  and Table 6 , the results for GA, ACA, and CASA perform more efficient than the other strategies and generate better sizes than the others in Table 6 . However, CSA is able to generate better results most of the time in Table 5 . PSO, AETG, mAETG, and CSA are producing comparative results in these configurations. However, they are failed to produce best results for most of these configurations. Although the reported results for GA and ACA are showing better results, these algorithms are using “compaction algorithm,” which optimizes the output of the GA and ACA by further optimization of combining the rows of the constructed CAs. As a result, the reported results do not show the actual efficiency GA and ACA. CASA can generate best results in different configurations. However, it can be noted that when the degree of combination or the input factors with levels get higher in values, it either fails to generate the final array or takes too long time for generation due to the heavy weight of the algorithm. CS performs well for these configurations; however, there is few evidence reported by these algorithms to investigate and evaluate CS against them since they are not freely available.

6.2. The CSA effectiveness evaluation through an empirical case study

After the test suite is generated, it is further optimized by using feedback from the software-under-test. In evaluating this approach, the software-under-test has been injected with various types of transition mutations (faults) using MuClipse [64] to verify the effectiveness of the proposed strategy. MuClipse is a mutation injection software that uses muJava as a mutation tool. MuClipse creates various types of faults within the original program to test the effectiveness of the generated test suites in detecting these faults.

In general, mutation testing has two advantages on the test suites obtained from the strategy. The first is that it verifies the contribution of different methods and variables defined in the class on the calculation process within the class. The second is that it determines whether any similar behavior or reaction exists between the test cases. Deriving similar test cases and reducing the number of cases used in the FTS are important.

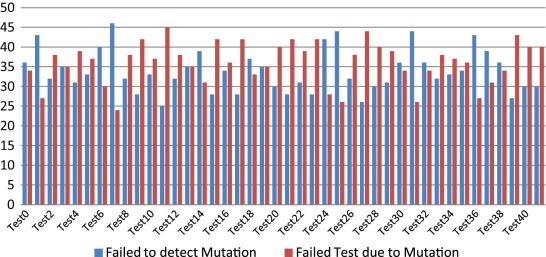
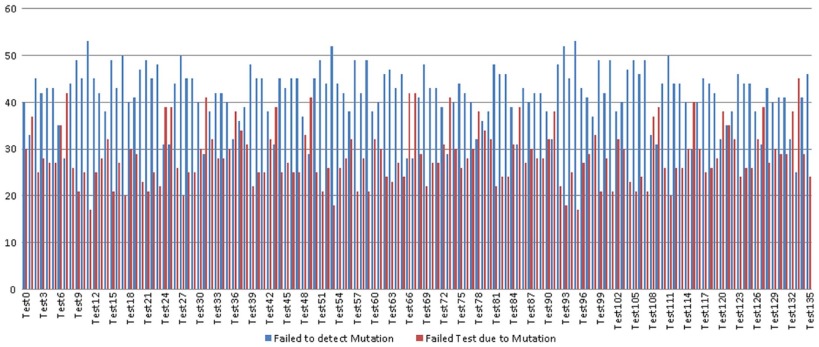
As shown in Table 4 , when the combination degree is 2, 42 test cases are generated from the optimization algorithm, which covers the entire code. muJava generates 278 mutation classes, which are then reduced to 70 mutation classes as a result of similarities in the mutation concept generating the same effect. Fig. 13 shows the reaction of these test cases to the 70 mutation classes.

Fig. 13. Reaction of the test cases with the configuration for the number of mutations detected when d  = 2.

The blue strips in Fig. 13 represent the number of mutation classes that achieve a correct result. In this case, the test case is not affected by the injected mutation because the mutation has no effect on the class calculation and the final result. By contrast, the red strips represent the number of failed test cases that resulted from the effect of the injected mutation. In this case, the mutation has a direct effect on the calculated result and thus achieves an incorrect result. In this study, when d  = 2, 12 faults are not detected during the 42 tests.

The number of failed test cases with various mutation classes is used to determine the test cases with the same response. The cases with the same number of failed tests are compared to detect any behavioral similarity toward the mutations. From the obtained results, test cases 22 and 29 exhibit the same response for all mutation classes. As a result, test case 29 is an excess to the test cases and can be deleted. Meanwhile, the remaining test cases respond differently to the mutation classes and are thus retained.

When the combination degree is 2, 136 test cases are obtained from the program-testing strategy. Fig. 14 shows the reaction to the same 70 mutation classes used when the combination degree is 2.

Fig. 14. Reaction of the test cases with the configuration for the number of mutations detected when d  = 3.

As shown in Fig. 14 , the 136 test cases are applied to verify similarity in the same manner as in the previous case. The test cases with the same response to the mutation are deleted to further optimize the FTS. Notably, many tests cannot detect many mutations at once. However, the overall test cases successfully detect all the mutations, including the 12 faults that are not detected by the test suite with a combination degree of 2. The higher combination degree (i.e., the test suites for d  > 3) is also able to detect the faults. However, as far as all the faults detected by the test suite of d  = 3 are concerned; the results are not reported in this study to avoid redundancy.

For further inspection of the results, the plot of fault detection density for each test case is shown in the bubble charts in Fig. 15  and Fig. 16 for the case when d = 2 and d = 3, respectively.

Fig. 15  and Fig. 16 show the fault density when d = 2 and 3. Bubble chart is useful to show the density of fault detection. Here the size of the bubbles represents the density of fault detection. In other words, for a given test case, when the size of the bubble is bigger than other test case, this means that the fault detection density of the former test case is better than the latter one. For better inspection and illustration, the graphs are divided into parts. In Fig. 15 , the graph is divided into two parts. In the same way, Fig. 16 is divided into four parts because of the large number of test cases when d  = 3. The X-axis represents the test case number and the Y-axis represents the number of detected faults that have been injected. Different color is used for each test case to differentiate between the cases.

Fig. 15. Fault detection density for each test case when d  = 2.

Fig. 16. Fault detection density for each test case when d  = 3.

The graphs show that the density of fault detection varies depending on the test case. Some of the test cases have low density, and they can detect faults that have been detected already by other test cases. Thus, this test case can be omitted from the test suite.

The graph also reveals that the variation of the combination degree may produce new faults. To this end, when the combination degree grows to three, the undetected faults by the lower degree can be detected successfully. However, for this application, using a higher degree does not lead to new faults because 70 faults have been injected into the program manually, and they have been detected. For better inspection, the code coverage is measured during the testing process for each test suite. The results showed that the code coverage is 84.57% when combination degree is equal to two, whereas the code coverage is 99.36% when the combination degree is equal to three. This finding in turn interprets the results clearly.

In considering the aforementioned discussion, the generated test suite is optimized further by omitting low density test cases and ensuring the detection of those faults detected by the other test cases. The new sizes are 36 and 112 when d = 2 and d = 3, respectively.

7. Threats to validity

This paper faces different threats to validity as in the case of other studies. Attention focuses on reducing these threats by designing and running different experiments. However, the threats must still be addressed. First, because of the lack of results for the meta-heuristic algorithms, more experiments are needed to further evaluate the strengths and weaknesses of different algorithms. Second, only one program is considered as a case study. Although the program is an ideal artifact for functional testing, more case studies and evidence can show the effectiveness of the approach. In addition, the faults injected in the current program can be detected when the test suite has a combination degree equal to three. However, other kinds of faults that can be detected by a higher degree of combination can exist within the same case study.

8. Conclusion

In this paper, a technique is presented to detect the “configuration-aware” faults in software. The technique is based on combinatorial optimization and sampling. Through combinatorial optimization, the input configurations are sampled systematically to generate an optimized test set. CS is used to optimize and search for an optimal solution by covering the d -tuples list. For the purpose of evaluation, a user-configurable system is used as a case study. In addressing the usefulness of the study more effectively, different faults were seeded in the software-under-test through mutation-testing techniques. The evaluation results show that using CS to optimize the combinatorial test suites can generate better results most of the time. The strategy proved its effectiveness in detecting faults in programs by using the functional testing approach. The proposed strategy can be useful for different testing techniques as long as test case design and minimization are used. For example, regression testing can be useful for the test suite used for different versions of the same program. It can also be useful for test case prioritization for prioritizing the test case base on the fault density.

Several directions for future research are available. First, the performance could be significantly improved in the future by designing more efficient and effective data structures to hasten the search process, which may help the strategy to support combination degrees higher than 6. Extending the strategy is possible to support different degrees of combination, including variable degree, as well as to support the seeding and constraints of combination. The approach also opens new research directions in mobile application testing and characterization.

Acknowledgments

The author would like to thank “Dr. Mouayad A. Sahib” for his time and advice during the writing of the paper. It is also worth mentioning the IDSIA Institute and Swiss Excellence Scholarship for hosting and supporting this research.

References

1. [1] M.B. Cohen, M.B. Dwyer, J. Shi; Interaction testing of highly-configurable systems in the presence of constraints; International Symposium on Software Testing and Analysis (2007), pp. 129–139 London, United Kingdom
2. [2] Q. Xiao, M.B. Cohen, K.M. Woolf; Combinatorial interaction regression testing: a study of test case generation and prioritization; Software Maintenance, 2007. ICSM 2007. IEEE International Conference on (2007), pp. 255–264
3. [3] D.S. Hoskins, C.J. Colbourn, D.C. Montgomery; Software performance testing using covering arrays: efficient screening designs with categorical factors; presented at the; Proceedings of the 5th International Workshop on Software and Performance, Palma, Illes Balears, Spain  (2005)
4. [4] K.C. Tai, Y. Lie; In-parameter-order: a test generation strategy for pairwise testing; 3rd IEEE International Symposium on High-Assurance Systems Engineering (1998), pp. 254–261 Washington, DC, USA
5. [5] C. Yilmaz, M.B. Cohen, A. Porter; Covering arrays for efficient fault characterization in complex configuration spaces; presented at the ACM SIGSOFT Software Engineering Notes  (2004)
6. [6] V.V. Kuliamin, A. Petoukhov; A survey of methods for constructing covering arrays; Programming and Computer Software, 37 (2011), pp. 121–146
7. [7] S. Maity, A. Nayak, M. Zaman, N. Bansal, A. Srivastava; An improved test generation algorithm for pair-wise testing; International Symposium on Software Reliability Engineering (ISSRE)  (2003)
8. [8] Y. Lei, R. Kacker, D.R. Kuhn, V. Okun, J. Lawrence; IPOG-IPOG-D: efficient test generation for multi-way combinatorial testing; Softw. Test. Verif. Reliab, 18 (2008), pp. 125–148
9. [9] A. Ouaarab, B. Ahiod, X.-S. Yang; Discrete cuckoo search algorithm for the travelling salesman problem; Neur. Comput. Appl, 24 (2014)
10. [10] C. Nie, H. Leung; A survey of combinatorial testing; ACM Comput. Surv, 43 (2011), pp. 1–29
11. [11] P. McMinn; Search-based software test data generation: a survey: research Articles; Softw. Test. Verif. Reliab, 14 (2004), pp. 105–156
12. [12] X.-S. Yang, S. Deb; Cuckoo search via Levy flights; Nature & Biologically Inspired Computing (NaBIC) 2009 (2009), pp. 210–214
13. [13] X.-S. Yang, S. Deb; Cuckoo search: recent advances and applications; Neur. Comput. Appl, 24 (2014), pp. 169–174
14. [14] S. Dejam, M. Sadeghzadeh, S.J. Mirabedini; Combining cuckoo and tabu algorithms for solving quadratic assignment problems; Journal of Academic and Applied Studies, 2 (2012), pp. 1–8
15. [15] X.-S. Yang, S. Deb; Engineering optimisation by cuckoo search; International Journal of Mathematical Modelling and Numerical Optimisation, 1 (2010), pp. 330–343
16. [16] R. Rajabioun; Cuckoo optimization algorithm; Appl. Soft Comput, 11 (2011), pp. 5508–5518
17. [17] S. Kamat, A.G. Karegowda; A brief survey on cuckoo search applications; Int. J. Innov. Res. Comput. Commun. Eng, 2 (2014)
18. [18] C. Nie, H. Leung; The minimal failure-causing schema of combinatorial testing; ACM Trans. Softw. Eng. Methodol, 20 (2011), pp. 1–38
19. [19] S. Fouch, M.B. Cohen, A. Porter; Towards incremental adaptive covering arrays; presented at; The 6th Joint Meeting on European Software Engineering Conference and the ACM SIGSOFT Symposium on the Foundations of Software Engineering: companion papers, Dubrovnik, Croatia  (2007)
20. [20] B.S. Ahmed, K.Z. Zamli; A variable strength interaction test suites generation strategy using particle swarm optimization; J. Syst. Softw, 84 (2011), pp. 2171–2185
21. [21] D. Hoskins, R.C. Turban, C.J. Colbourn; Experimental designs in software engineering: d-optimal designs and covering arrays; ACM workshop on interdisciplinary software engineering research (2004), pp. 55–66 Newport Beach, CA, USA
22. [22] R.S. Pressman, B.R. Maxim; Software Engineering: A Practitioners Approach; (eighth ed.)McGraw-Hill (2015)
23. [23] A.H. Ronneseth, C.J. Colbourn; Merging covering arrays and compressing multiple sequence alignments; Discr. Appl. Mathemat, 157 (2009), pp. 2177–2190
24. [24] R.N. Kacker, D. Richard Kuhn, Y. Lei, J.F. Lawrence; Combinatorial testing for software: an adaptation of design of experiments; Measurement, 46 (2013), pp. 3745–3752
25. [25] C. Yilmaz, S. Fouche, M.B. Cohen, A. Porter, G. Demiroz, U. Koc; Moving forward with combinatorial interaction testing; Computer, 47 (2014), pp. 37–45
26. [26] A. Hartman, L. Raskin; Problems and algorithms for covering arrays; Discrete Mathematics, 284 (2004), pp. 149–156
27. [27] M. Chateauneuf, D.L. Kreher; On the state of strength-three covering arrays; J. Combinat. Des, 10 (2002), pp. 217–238
28. [28] X. Qu; Testing of configurable systems; Chapter 4 M. Atif (Ed.), Advances in Computers, vol. 89, Elsevier (2013), pp. 141–162
29. [29] X. Qu, M.B. Cohen, G. Rothermel; Configuration-aware regression testing: an empirical study of sampling and prioritization; 2008 International Symposium on Software Testing and Analysis (2008), pp. 75–86 Seattle, WA, USA
30. [30] B.S. Ahmed, K.Z. Zamli, C.P. Lim; Application of particle swarm optimization to uniform and variable strength covering array construction; Appl. Soft Comput, 12 (2012), pp. 1330–1347
31. [31] C.S. Cheng; Orthogonal arrays with variable numbers of symbols; Ann. Statist, 8 (1980), pp. 447–453
32. [32] D.M. Cohen, S.R. Dalal, M.L. Fredman, G.C. Patton; The AETG system: an approach to testing based on combinatorial design; IEEE Trans. Softw. Eng, 23 (1997), pp. 437–444
33. [33] E. Lehmann, J. Wegener; Test case design by means of the CTE XL; 8th European International Conference on Software Testing, Analysis & Review (EuroSTAR 2000) (2000), pp. 1–10 Copenhagen, Denmark
34. [34] J. Arshem; http://sourceforge.net/projects/tvg/ (2000) accessed 03.01.15
35. [35] A.W. Williams; Determination of test configurations for pair-wise interaction coverage; 13th International Conference on Testing Communicating Systems: Tools and Techniques (2000), pp. 59–74 Deventer, The Netherlands
36. [36] M.B. Cohen; Designing test suites for software interaction testing; Doctor of Philosophy PhD thesis; University of Auckland  (2004)
37. [37] B. Jenkins; http://burtleburtle.net/bob/math/jenny.html (2005) accessed 03.01.15
38. [38] J. Czerwonka; Pairwise testing in real world. Practical extensions to test case generators; Proceedings of the 24th Pacific Northwest Software Quality Conference (2006), pp. 419–430 Portland, Oregon
39. [39] G.B. Sherwood, S.S. Martirosyan, C.J. Colbourn; Covering arrays of higher strength from permutation vectors; J. Combinat. Des, 14 (2006), pp. 202–213
40. [40] Y. Lei, R. Kacker, D.R. Kuhn, V. Okun, J. Lawrence; IPOG: a general strategy for t-way software testing; 4th Annual IEEE International Conference and Workshops on the Engineering of Computer-Based Systems (2007), pp. 549–556 Tucson, Arizona
41. [41] J. Czerwonka; Available tools; http://www.pairwise.org/tools.asp (2015) accessed 07.03.15
42. [42] T. Shiba, T. Tsuchiya, T. Kikuno; Using artificial life techniques to generate test cases for combinatorial testing; 28th Annual International Computer Software and Applications Conference, vol. 1 (2004), pp. 72–77 Hong Kong
43. [43] R.P. Pargas, M.J. Harrold, R.R. Peck; Test-data generation using genetic algorithms; Softw. Test. Verif. Reliab, 9 (1999), pp. 263–282
44. [44] S. Huang, M.B. Cohen, A.M. Memon; Repairing GUI test suites using a genetic algorithm; 3rd IEEE International Conference on Software Testing, Verification and Validation (2010), pp. 245–254 Washington, DC, USA
45. [45] B.J. Garvin, M.B. Cohen, M.B. Dwyer; An improved meta-heuristic search for constraints interaction testing; International Symposium on Search-based Software Engineering (SBSE) (2009)
46. [46] K.J. Nurmela; Upper bounds for covering arrays by tabu search; Discr. Appl. Mathemat, 138 (2004), pp. 143–152
47. [47] X. Chen, Q. Gu, A. Li, D. Chen; Variable strength interaction testing with an ant colony system approach; 16th Asia-Pacific Software Engineering Conference (2009), pp. 160–167 Penang, Malaysia
48. [48] B.S. Ahmed, M.A. Sahib, M.Y. Potrus; Generating combinatorial test cases using simplified swarm optimization (SSO) algorithm for automated GUI functional testing; Engineering Science and Technology, an International Journal, 17 (2014), pp. 218–226
49. [49] T. Mahmoud, B.S. Ahmed; An efficient strategy for covering array construction with fuzzy logic-based adaptive swarm optimization for software testing use; Exp. Syst. Appl, 42 (2015), pp. 8753–8765
50. [50] J. Stardom; Metaheuristics and the search for covering and packing arrays; Masters thesis Simon Fraser University (2001)
51. [51] T. Shiba, T. Tsuchiya, T. Kikuno; Using artificial life techniques to generate test cases for combinatorial testing; 28th Annual International Computer Software and Applications Conference (2004), pp. 72–77 Hong Kong
52. [52] H. Liu, A. Abraham, W. Zhang; A fuzzy adaptive turbulent particle swarm optimisation; Int. J. Innov. Comput. Appl, 1 (2007), pp. 39–47
53. [53] R.R. Othman, K.Z. Zamli, S.M.S. Mohamad; T-way testing strategies: a critical survey and analysis; Int. J. Dig. Cont. Technol. Appl, 7 (2013), pp. 22–235
54. [54] H.M. Nehi, S. Gelareh; A survey of meta-heuristic solution methods for the quadratic assignment problem; Applied Mathematical Sciences, 1 (2007), pp. 2293–2312
55. [55] X.-S. Yang; Metaheuristic optimization; Scholarpedia, 6 (2011)
56. [56] W. Huimin, G. Qiang, Q. Zhaowei; Parameter tuning of particle swarm optimization by using Taguchi method and its application to motor design; 4th IEEE International Conference on Information Science and Technology (ICIST) (2014), pp. 722–726
57. [57] G. Xu; An adaptive parameter tuning of particle swarm optimization algorithm; Appl. Mathemat. Comput, 219 (2013), pp. 4560–4569
58. [58] X.-S. Yang, S. Deb; Cuckoo search via Lévy flights; Nature & Biologically Inspired Computing, 2009. NaBIC 2009. World Congress on (2009), pp. 210–214
59. [59] X. Li, M. Yin; Modified cuckoo search algorithm with self adaptive parameter method; Inf. Sci. (Ny), 298 (2015), pp. 80–97
60. [60] T.T. Nguyen, D.N. Vo; Modified cuckoo search algorithm for short-term hydrothermal scheduling; Int. J. Elec. Power Energ. Syst, 65 (2015), pp. 271–281
61. [61] D.J. Velleman, G.S. Call; Permutations and combination locks; Mathematics Magazine, 68 (1995), pp. 243–253
62. [62] X.-S. Yang; Nature-Inspired Metaheuristic Algorithms; (second ed.)Luniver Press (2010)
63. [63] J. Czerwonka; Pairwise testing in real world: practical extensions to test case generator; 24th Pacific Northwest Software Quality Conference (2006), pp. 419–430 Portland, Oregon, USA
64. [64] MuClipse; MuClipse development web page; http://muclipse.sourceforge.net/ (2015)