1 Introducción
Todas las instalaciones que estén expuestas a algún tipo de radiación necesitan ser protegidas, ya no solo por el daño que pueden sufrir los equipos sino fundamentalmente por el daño en los seres humanos.
Las radiaciones se diferencian unas de otras por su interacción con la materia y, en consecuencia, por la penetración en ella. Así, una radiación alfa puede ser parada por una hoja de papel, mientras que una beta ya necesita una lámina de alumnio. En el caso de los rayos X y la radiación gamma se usan placas de plomo, aunque la naturaleza de estas radiaciones no son iguales, la energía se emite en forma de fotones. La relación entre la energía del fotón y la longitud de onda de la radiacción λ, viene dada por la ecuación de Plank (ecuación 1), donde h es la constante de Plank (6,62 x 10-27 erg.s) y c la velocidad de la luz (3,00 x 1010 cm/s).
E=h·c/ʎ (1)
Una de las primeras aplicaciones de la radiación se encuentran los rayos X de baja energía, usados para determinar la estructura de los materiales y en medicina. Posteriormente, surgieron fuentes de mayor energía y voltaje, y consecuentemente hubo que estudiar los problemas ocasionados por la radiación en los materiales [1], centrando su atención en los poliméros por la reducción de peso que originan.
Los electrones, como toda partícula cargada, también pierden energía al penetrar en la materia realizando un camino muy sinuoso debido a que su masa es muy pequeña relativa a la masa atómica. Las grandes desviaciones que se producen son debidas a que interactúan mayormente con otros electrones ligados en el material. Por otro lado, también pueden colisionar con los núcleos, lo que hace que el electrón cambie bruscamente de dirección [2]. La pérdida de energía del electrón se debe a dos fenómenos:
- 1- por colisiones con los electrones y núcleos del material,
- 2- por emisión de radiación electromagnética o radiación de enfrenamiento (bremsstrahlung)
La pérdida por radiación electromagnética es más importante para energías del electrón muy altas (varios MeV) o para material absorbente con alto número atómico.
La pérdida de energía de las partículas beta por radiación de enfrenamiento, por centímetro de trayectoria, es aproximadamente proporcional al cuadrado del número atómico del absorbente y a la energía de las partículas. Por lo que el enfrenamiento se acentúa en los elementos de número atómico elevado. El espesor de absorbente capaz de reducir a cero la ionización producida por partículas beta, viene definido por la ecuación 2, donde R es el alcance de las partículas y ρ la densidad del material
En su trayectoria dentro de un absorbente, la partícula cargada disminuye progresivamente su energía hasta llegar al reposo después de atravesar cierto espesor. Se define como alcance, al espesor mínimo de absorbente que resulte suficiente para que la partícula pierda totalmente su energía en él. Este alcance está sujeto a una fluctuación estadística que hace que partículas con igual energía inicial tengan distinto alcance [3].
En el intervalo de energías de las partículas beta se ha visto que hay una variación lineal entre 0,5 y 3 MeV, obteniéndose la ecuación 3 como ecuación de la recta densidad superficial de aluminio frente a la energía de las partículas beta.
Cuando una radiación gamma atraviesa la materia, la desaparición de fotones produce un decaimiento exponencial de la intensidad. Así se puede aplicar la ecuación 4, donde dx, diferencial del espesor de absorbente, es proporcionar a la intensidad de la radiación (I) en un punto dado, siendo μ el coeficiente de atenuación lineal de absorbente, expresado en cm-1
Para energías de fotones por debajo de 1000 keV, los principales procesos de interacción son: dispersión incoherente (Compton), dispersión coherente (Rayleigh) y absorción de efectos fotoeléctricos atómicos. Para energías de fotones por encima de 1000 keV, se debe incluir la producción de pares de campos nucleares y la producción de campos atómicos (tripletes) [2].
Debido al alto contenido de átomos de H, el agua tiene una buena capacidad de protección para los neutrones. Pero el problema es que se encuentra en estado líquido a temperatura ambiente. Los polímeros y los materiales plásticos son ricos en átomos de H, se encuentran en estado sólido a temperatura ambiente, tienen baja densidad en comparación con los materiales de protección convencionales, como el plomo y el hormigón [4]. Además, pueden ser transformados en láminas delgadas fácilmente. Por otro lado, los rayos X están considerados como radiación de baja densidad de ionización [5], este tipo de radiación es la más utilizada en el campo de irradiación de polímeros, siendo los cambios producidos en ellos usados en aplicaciones industriales. Estos cambios dependen del peso molecular del polímero. La radiación de baja densidad puede producir ionización y excitación, siendo más fácil romper enlaces C-H que enlaces C-C.
El boro tiene una sección transversal con alta absorción de neutrones, 767 barn en la región de energía térmica debido al isótopo 10B. Esto lo convierte en un material valioso para fines de blindaje y como moderador de neutrones. Soltani et al. 6] demostraron que la disminución de la partícula de carburo de boro permite disminuir el espesor de la capa de blindaje y aumenta la probabilidad de las colisiones.
Como apantallante de neutrones se emplean también estructuras multicapa con polímeros y materiales compuestos con boro y otros cerámicos como el sulfato de bario. Zhang et al. [7] encontraron que la probabilidad de colisión entre fotones incidentes y partículas en forma de escamas se mejoró por la alineación de partículas BN.
El propósito de esta contribución es estudiar el porcentaje de boro a añadir para mejorar la capacidad de protección de materiales compuestos basados en polímeros hidrogenados de baja densidad y boro para rayos X.
Aunque existen programas de calculo que permiten calcular parámetros como coeficiente de atenuación líneal o coeficiente de atenuación másica, entre el que se encuentra el kit de herramientas GRIC o el software WinX-Com usados por otros investigadores en estudios similares [8], en este trabajo se ha realizado un primer estudio con cálculos manuales para seleccionar el material más eficiente.
2 Procedimiento Experimental
2.1 Materiales
LDPE (polietileno de baja densidad) y sus composites se prepararon usando polvo de LDPE comercial (0.92 g/cm3 de densidad) suministrado por Dow Europe GmbH (Suiza). El polvo de boro (B) amorfo (2.34-2.37 g/cm3 de densidad), fue suministrado por Strem Chemicals Inc. Bischheim-France. En el estudio de la morfología de las partículas de boro (Figura 1) se encuentran numerosos aglomerados, pese a tener una distribución granulométrica muy fina (d50 = 95 nm).
2.2 Fabricación de materiales compuestos
El LDPE y las partículas de boro se mezclaron en un reómetro Rheodrive 5000 (Haake Fision). Se prepararon tres concentraciones diferentes de B (15, 30 y 60 % en peso), para realizar las mezclas se usó una temperatura de 130 ºC a una velocidad de 50 rpm durante 6 min. Los precursores fueron moldeados por compresión en una prensa de platos calientes a 170º C y 5.5 MPa (Remtex, Barcelona, Spain). Para cada formulación se obtuvo una plancha de 150 mm de diámetro con un espesor entre 0.1 y 0.2 mm. Se fabricó también una plancha igual de LDPE, para comparar con los composites.
2.3 Rayos X
Se ha utilizado un difractómetro automático Philips X’Pert, operando a 40 kV y una intensidad de 40mA. La radiación utilizada ha sido la Kα del cobre (λ=1,5406 Å) filtrada con un monocromador de grafito. La recogida de datos se realizó mediante un barrido automático por pasos entre 2θ = 20-100 º, con un tamaño de paso goniométrico de 0.02º y un tiempo de contaje de 1.5 s por paso.
Primero se hizo un difractograma sobre un pin de aluminio y después se fueron interponiendo fims de polietileno y de material compuesto para ver el apantallamiento producido, teniendo en cuenta el área del pico principal del aluminio, situado a 44.7º. De todos los materiales se hicieron tres grosores diferentes de films.
3 Resultados
Teniendo en cuenta que la energía de la fuente es de 40 keV (0.04 MeV), aplicando la ecuación 1 y cambiando los ergios a MeV, la longitud de onda resultante es 3.13 x 10-9 cm. Los rayos gamma poseen energías comprendidas entre 0.1 a 10 MeV, estando sus longitudes de onda entre la región de 10-9 a 10-11 cm. En el caso estudiado la longitud de onda se encuentra en esta región, por lo que la radiación gamma se produce. Los rayos gamma se emiten en forma de fotones y su energía es igual a la diferencia de energías entre los dos estados que intervienen en la transición.
Para calcular el efecto absorbente de los materiales usados en este estudio, se parte de las ecuaciones 2 y 3. En este estudio en un principio se intentó suponer que para la energía de rayos X usada de 40 keV también se va a cumplir la ecuación 3, y se hace una aproximación del alcance (R) para los diferentes materiales usados, teniendo en cuenta la densidad teórica (Tabla 1) calculada para estos materiales, siendo la densidad del boro 2.35 g/cm3. También está admitido, de forma general, que el espesor de absorción es independiente de la naturaleza del material absorbente.
| LDPE | LDPE15B | LDPE30B | LDPE60B | |
| Densidad (g/cm3) | 0.92 | 1.01 | 1.13 | 1.45 |
Sin embargo, a partir de la ecuación 3 no se pudieron calcular los alcances máximo, ya que el valor de R (cm) obtenido es negativo por lo que la aproximación no es válida para estos materiales y la energía de 0.04 MeV usada. Por lo que se integraron los picos de los espectros de rayos X obtenidos interponiendo 0.1 mm de material compuesto con diferentes porcentajes de boro o de polietileno sin boro. En la Tabla 2 se puede observar como al aumentar el porcentaje de boro aumenta el apantallamiento y como al interponer dos capas de 0.1 mm en lugar de una, también el apantallamiento del aluminio aumenta, aunque la proporción de aumento es más baja ya que solo se aumenta el apantallamiento en un 8.28%.
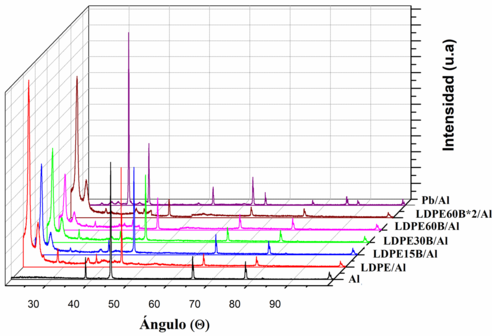
La Figura 2 muestra todos los difractogramas realizados. Se puede observar como para el LDPE y sus composites hay una parte cristalina correspondiente al polietileno, ya que hay unos picos entre 20 y 25º, que no se ven en el aluminio y en el plomo. Si se tiene en cuenta el pico más alto del aluminio, en torno a 44.7º, se observa cómo va disminuyendo conforme aumenta el porcentaje de boro. Al observar el difractograma del plomo (se interpuso una lámina de 0.05 mm) ya no se ve el pico del aluminio. Esto está verificando su alto poder de apantallamiento.
| Ángulo “Al” (θ) | Área pico | % pico apantallado | |
| Al (porta) | 44.67 | 780.13 | |
| LDPE/Al | 44.39 | 293.94 | 14.00 |
| LDPE15B/Al | 44.51 | 511.81 | 20.97 |
| LDPE30B/Al | 44.45 | 423.96 | 24.95 |
| LDPE60B/Al | 44.51 | 226.29 | 51.82 |
| LDPE60B*2/AL | 44.39 | 137.81 | 60.10 |
En la Tabla 2, se puede ver más claramente el efecto de disminución que se produce en el pico de mayor intensidad del aluminio, llegando a apantallar el 50 % con la lámina de 0.1 mm del composite con el 60 % de boro. Si en lugar de la lámina se ponen dos del composite más apantallante el apantallamiento no aumenta considerablemente, ni siquiera por aumento del espesor.
Si en la ecuación 4, se asimila la intensidad (I) al área de pico del aluminio que se está viendo, es posible calcular μ (coeficiente de atenuación linear) del absorbente. Cuando la ecuación 4 se integra se obtiene la ecuación 5,
siendo I0 el área del pico del aluminio sin apantallar y Ix el área apantallada. La ecuación 5 se puede escribir como la ecuación de una recta (ecuación 6)
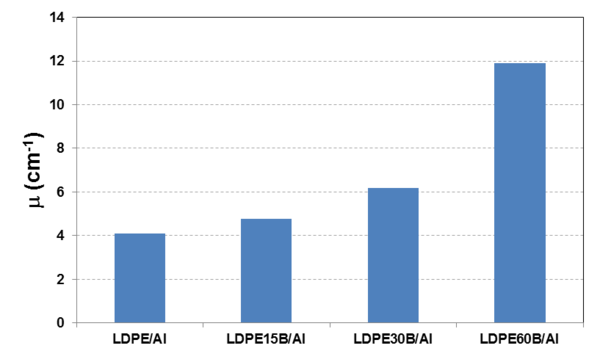
Cuando se representan las rectas para distintos espesores, de acuerdo a la ecuación 6 y se calcula μ de la pendiente de la recta, se observa como aumenta con el porcentaje de boro. Este coeficiente es de 12 cm-1 en el caso del material compuesto con el 60% de boro
En teoría el carácter exponencial de la atenuación de rayos gamma quiere decir que si bien la cantidad de radiación absorbida por un determinado espesor de material es proporcional a la intensidad inicial, la fracción absorbida es independiente de esta intensidad. Por otro lado también implica que se necesitaría un espesor infinito de material para absorber completamente la radiación gamma, es decir para hacer Ix = 0. En el caso del material compuesto con el 60% de boro, un espesor de un 1 mm haría el Log Ix igual a cero y por lo tanto Ix sería igual 1.
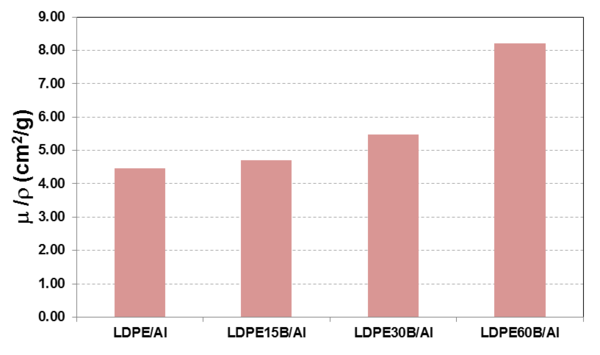
Si se tiene en cuenta la densidad del material se puede calcular el coeficiente de atenuación másico, este coeficiente es importante en intervalos de energía donde predomina el efecto Compton (un fotón gamma realiza una colisión elástica con un electrón externo de un átomo del material absorbente). En la Figura 4 se muestran los coeficientes de atenuación másico dependiendo de la cantidad de boro. Evidentemente el que más disminuye, en relación con el coeficiente de atenuación lineal, es el que contiene el 60% de boro por su mayor densidad.
4 Conclusiones
En este trabajo se ha estudiado el efecto apantallante que realiza el polietileno y los materiales compuestos de polietileno con 15, 30 y 60 % de Boro en peso, ante una energía de 40 keV.
Se ha podido comprobar que al aumentar el porcentaje de boro aumenta el coeficiente de atenuación lineal y aunque la densidad del material compuesto con el 60 % de boro es mayor, también presenta el mayor coeficiente de atenuación másico.
Una lámina con un espesor de 1 mm podría absorber prácticamente en su totalidad un haz de fotones de 40 keV.
Referencias
[1] A.Charlesby. Nuclear Instruments and Methods in Physics Research Section B; 105, pág. 217-224 (1995) https://doi.org/10.1016/0168-583X(95)00627-3
[2] S.Glasstone, A.Sesonske. Ingeniería de Reactores Nucleares. Ed. Reverté, S.A. Barcelona (1990)
[3] H.E. Bosch. Elementos de física nuclear. CAESE Buenos Aires (1970)
[4] E. Gallego, A. Lorente, H. R. Vega-Carrillo. Nuclear Technology; 168, pág 399–404 (2009) https://doi.org/10.13182/NT09-A9216
[5] A. Chapiro. Nuclear Instruments and Methods in Physics Research Section B; 105, pág 5-7 (1995) https://doi.org/10.1016/0168-583X(95)00861-6
[6] Z. Soltani, A. Beigzadeh, F. Ziaie , E. Asadi. Radiation Physics and Chemistry, 127, pág.182–187 (2016) http://dx.doi.org/10.1016/j.radphyschem.2016.06.027
[7] X. Zhang, M. Yang, X. Zhang, H. Wu, S. Guo, Y. Wang. Composites Science and Technology, 150, pág. 16-23 (2017) http://dx.doi.org/10.1016/j.compscitech.2017.06.007
[8] K.S. Mann, A. Rani, M. S. Heer. Radiation Physics and Chemistry, 106, pág. 247–254 (2015) http://dx.doi.org/10.1016/j.radphyschem.2014.08.005
Document information
Published on 01/06/22
Accepted on 01/06/22
Submitted on 28/05/22
Volume 04 - Comunicaciones Matcomp19 (2020), Issue Núm. 1 - Avances en Materiales Compuestos. Nuevos Campos de Aplicación., 2022
DOI: 10.23967/r.matcomp.2022.06.002
Licence: Other
Share this document
Keywords
claim authorship
Are you one of the authors of this document?