Abstract
In the present investigation, an oscillating motion of unsteady Burgers fluid in a circular cylinder was modeled with different pressure waveforms. Three different waveforms are considered: the case of a trapezoidal, triangular and sinusoidal waveform. Analytical solutions of velocity and temperature distribution are obtained for an oscillating laminar flow, which can be used to analyze the effects of flow type on the heat transfer performance. The limiting cases have been considered to examine the heat transfer performance of four different non-Newtonian fluids. Results show that the heat transfer of the oscillating flow depends on the fluid material parameter, Prandtl number, amplitude oscillating waveform and radial coordinate. The trapezoidal and sinusoidal waveforms of oscillating motion can result in a higher heat transfer performance.
Keywords
Trapezoidal waveform ; Triangular waveform ; Sinusoidal waveform ; Transient flow ; Analytical solution
Nomenclature
An- Constant defined by Eq. (23)
- Revlin-Ericksen tensors
Bn- Constant defined by Eq. (24)
Cn- Constant defined by Eq. (42)
cp- Specific heat at constant pressure
- Material time derivative
Dn- Constant defined by Eq. (43)
- Constant defined by Eq. (44)
- Constant defined by Eq. (45)
F- Eigenfunction
H- Constant defined by Eq. (25)
H1- Function defined by Eq. (26)
H2- Function defined by Eq. (27)
I- Identity tensor
Jn- Bessel function of order n
k- Thermal conductivity, W/mK
k0 ,…, k3- Real constants
p- Pressure, N/m2
Pr- Prandtl number
q- Heat flux, W/m2
r- Radius, m
sm , sq , - Eigenvalues
S- Extra-stress tensor
Re- Reynolds number
t- Time, s
T- Cauchy stress tensor
u- Velocity, m/s
z- Axial position, m
Greek letters
γ- Amplitude of pressure fluctuation, m
λ1- Relaxation time
λ2- Material constant of Burgers' fluid
λ3- Retardation time
µ- Dynamic viscosity, N-s/m2
ν- Kinematic viscosity, N-s-m/kg
ρ- Density, kg/m3
ω- Angular velocity, rad/s
Θ- Temperature, K
Superscripts
- - Dimensional conditions
Subscripts
s- Steady state
t- Transient state
w- Wall
1. Introduction
Ruckmongathan [1] showed that besides the multisteps, other waveforms like trapezoidal and triangular exist in electronics for reducing power dissipation in liquid crystal displays. Most of the electronic components and systems continue reduction in size while growing in energy density resulting in the need for more efficient thermal management. Oscillating heat cylinder occurs in many electronic devices, and most of the interest in this subject is the ability to establish extra-high effective thermal and manage high energy rich in heat fluxes [2] , [3] , [4] , [5] and [6] . Yu et al. [7] developed an analytical solution to determine pulsating laminar heat convection in a circular tube with constant heat flux. The results show that both the temperature profile and the Nusselt number fluctuate periodically about the solution for steady laminar convection, with the fluctuation amplitude depending on the dimensionless pulsation frequency, the amplitude of the pressure, and the Prandtl number. Wang and Zhang [8] analyzed convection heat transfer of pulsing turbulent flow in a pipe with constant wall temperature and high velocity oscillating amplitudes. Their results showed that the heat transfer enhancement is principally impacted by Womersley number and velocity oscillation amplitude. Pendyala et al. [9] conducted experimental studies on the oscillation flow and heat transfer in a vertical tube with a constant amplitude. The results indicated that the influence of an externally imposed periodic oscillation on the heat transfer is stronger at lower flow rates. Akdag and Ozguc [10] analyzed experimentally the heat transfer flow with constant heat flux and oscillating flow inside a vertical annular liquid column. The results demonstrated that heat transfer increases with increasing both the amplitude of the oscillation and frequency. Liu et al. [11] solved the energy equation of circular micro-channels, which considers axial heat conduction, velocity slip, temperature jump, viscous dissipation and thermal entrance effect. The design criterion for whether the axial heat conduction and viscous dissipation should be considered in engineering is given by studying their contributions to average Nusselt number.
Yin and Ma [12] reported the analytical result on an oscillating capillary tube in Newtonian laminar pulsating flows driven by a sinusoidal waveform. Their results show that the oscillating frequency, amplitude, and Prandtl number, are significant factors affecting the heat transfer performance of an oscillating flow in a capillary tube. Yin and Ma [13] investigated Newtonian flow in a tube driven by a triangular pressure waveform and showed how the oscillating flow could result in a different heat transfer coefficient with the corresponding result of a sinusoidal pressure waveform. Abdulhameed et al. [14] proposed the mathematical modeling of unsteady second grade fluid flowing in a capillary tube with sinusoidal pressure waveform and non-homogenous boundary conditions. Exact analytical solutions for the velocity profiles have been obtained in explicit forms using finite Hankel transform. The solutions are written as the sum of the steady and transient solutions for small and large times. For large value of times, the starting solution reduces to the well-known periodic solution that coincides with the corresponding solution of a Newtonian fluid. Khalid et al. [15] studied the problem of unsteady MHD free convection flow of Casson fluid past over an oscillating vertical plate embedded in a porous medium. The governing equations were solved using the Laplace transform technique and exact solutions for velocity and energy are obtained. Gul et al. [16] analyzed the problem of unsteady thin film flow of a second grade fluid over a vertical oscillating belt. The governing equation for velocity field was solved analytically using Adomian decomposition method (ADM) and Optimal asymptotic method (OHAM).
As mentioned above, the previous literature have focused on the Newtonian and second-grade fluids at a sinusoidal and triangular waveform effect on the heat transfer performance of oscillating flow in a capillary tube. The oscillating flow non-Newtonian Burgers' fluid at a trapezoidal, triangular and sinusoidal waveform has not been investigated before. It has been demonstrated that the oscillating heat tube using the thermally excited oscillating motion can significantly enhance the heat transfer performance (Yin and Ma [13] ). The unanswered questions regarding trapezoidal, triangular and sinusoidal waveforms in Burgers' fluid made it necessary to study the effect of oscillating motion on the heat transfer performance of oscillating flow in a circular cylinder. In the current investigation, a Burgers' fluid of an oscillating flow with trapezoidal, triangular and sinusoidal waveforms is modeled using an infinite Fourier series. Using the constant heat flux boundary condition, analytical solutions of velocity and temperature distribution have been obtained. The effects of waveform frequency, waveform amplitude, and Pr number on the heat transfer performance of oscillating flow are analyzed. To demonstrate the unique feature of trapezoidal waveform effect, the sinusoidal waveform and triangular effect on the temperature of the oscillating flow are presented as well.
2. Governing equation of Burgers' fluid
Burgers' model has the ability in successfully capturing various non-Newtonian strange features, e.g. shear thinning/thickening and display of elastic effects. Therefore, it has been the subject of many investigations covering various facets [17] , [18] , [19] , [20] and [21] .
The constitutive equations for an incompressible homogeneous Burgers' fluid are given by:
|
|
( 1) |
where
|
|
( 2) |
where T is the Cauchy stress tensor, − pI is the indeterminate spherical stress, S is the extra-stress tensor, λ1 is the relaxation time, λ2 is the material constant of Burgers' fluid, is the material time differentiation, L is the velocity gradient, T is the transpose operator, µ is the dynamic viscosity, A is the first Rivlin-Ericksen tensor and λ3 is the retardation time.
The above model includes special cases, the Oldroid-B model , the Maxwell model , the second-grade model and the linear viscous model .
The flow is incompressible and the surface tension effect is not considered
|
|
( 3) |
where the velocity and temperature fields are assumed to be of the form:
|
|
( 4) |
Under the above considerations, Eq. (3) gives the following dimensional governing equations
|
|
( 5) |
|
|
( 6) |
The boundary conditions corresponding to Eqs. (5) and (6) are
|
|
( 7) |
|
|
( 8) |
3. Trapezoidal pressure waveform
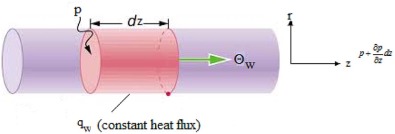
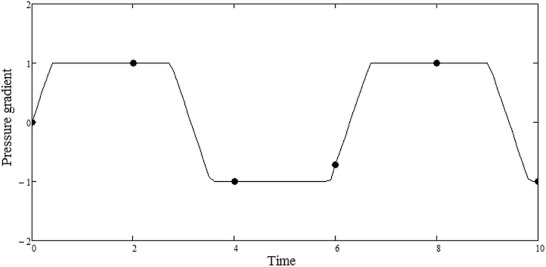
The oscillating Burgers' flow shown in Fig. 1 is driven by pressure difference with a trapezoidal waveform as in Fig. 2 of amplitude γ and frequency ω , i.e.
|
|
( 9) |
|
|
|
Fig. 1. The physical model configuration. |
|
|
|
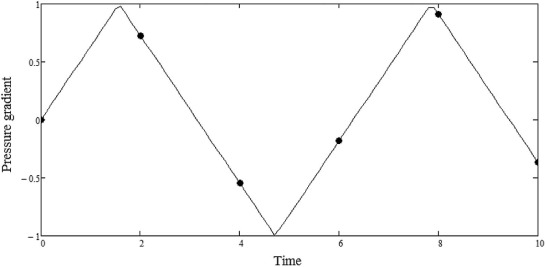
Fig. 2. Triangular pressure waveform configuration. |
Here, we need to solve Eqs. (5) and (6) subject to Eqs. (7) and (8) in the case where pressure gradient is given by Eq. (9) .
Consider the following nondimensional quantities
|
|
( 10) |
Using Eq. (10) in Eqs. (5) and (6) , the dimensionless momentum and energy equations (after dropping the * notation):
|
|
( 11) |
|
|
( 12) |
while the boundary conditions in dimensionless form are
|
|
( 13) |
|
|
( 14) |
Consider the fluid velocity into two components: a steady us , and transient ut parts i.e.
|
|
( 15) |
Using Eq. (15) into Eq. (11) , we obtained steady and transient components:
|
|
( 16) |
|
|
( 17) |
The steady solution of Eq. (16) is followed as
|
|
( 18) |
Applying the Bessel transform [22] , [23] and [24] to Eq. (17) , we obtain
|
|
( 19) |
where , , Denote , then Eq. (19) becomes
|
|
( 20) |
Assuming the solution of Eq. (20) of the form:
|
|
( 21) |
then Eq. (20) after rearranging yields:
|
|
( 22) |
The expression for An and Bn could be obtained as:
|
|
( 23) |
|
|
( 24) |
where
|
|
( 25) |
|
|
( 26) |
|
|
( 27) |
Hence, the expression for can be written as:
|
|
( 28) |
Applying the inverse Bessel transform:
|
|
( 29) |
where J1 is the Bessel function of first kind of order one and sm is the eigenvalue of the Bessel function of first kind of order zero.
Consider the temperature field in two components:
|
|
( 30) |
where is the steady and is the transient components.
Substituting Eqs. (15) and (30) into Eq. (12) and separating the result into steady and transient components:
|
|
( 31) |
|
|
( 32) |
Assuming and using the expression in Eq. (18) , Eq. (31) transformed as:
|
|
( 33) |
and this can be separated into two components as:
|
|
( 34) |
|
|
( 35) |
where k0 is the separation constant.
Integrating Eqs. (34) and (35) yields:
|
|
( 36) |
|
|
( 37) |
Using the boundary conditions (13) and (14) , it followed that k0 = 1, k1 = k2 = 0 and . Hence, the solution of the steady temperature is obtained as:
|
|
( 38) |
Plugging Eqs. (38) and (29) into Eq. (32) and apply the Bessel transform:
|
|
( 39) |
where . If , N = 2n − 1, Eq. (39) can be expressed as:
|
|
( 40) |
|
|
( 41) |
Solving Eqs. (40) and (41) for Cn and Dn gives:
|
|
( 42) |
|
|
( 43) |
where
|
|
( 44) |
|
|
( 45) |
The solution of temperature distribution is expressed as:
|
|
( 46) |
Applying the inverse Bessel transform:
|
|
( 47) |
4. Triangular pressure waveform
Here, we consider a triangular pressure waveform given by Fig. 3 of amplitude γ and frequency ω is:
|
|
( 48) |
|
|
|
Fig. 3. Trapezoidal pressure waveform configuration. |
Using the same methodology in the preceding analysis, we obtain the velocity field and temperature distribution for triangular waveform as:
|
|
( 49) |
and
|
|
( 50) |
Letting λ1 = λ2 = λ3 = 0, into Eqs. (25) , (26) and (27) , the case of Newtonian fluid, Eqs. (49) and (50) becomes identical with that obtained by Yin and Ma [13] .
5. Sinusoidal pressure waveform
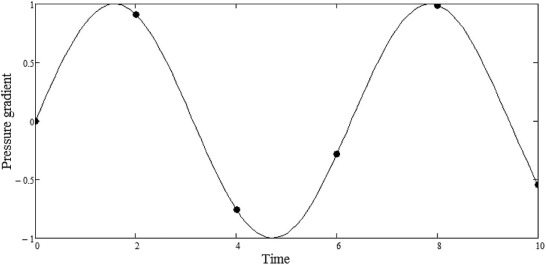
In this section, the oscillating Burgers' flow is driven by pressure difference with a sinusoidal waveform given in Fig. 4 of amplitude γ and frequency ω , i.e.,
|
|
( 51) |
|
|
|
Fig. 4. Sinusoidal pressure waveform configuration. |
Applying the same methodology in the preceding analysis, the velocity and temperature distribution for sinusoidal waveform:
|
|
( 52) |
and
|
|
( 53) |
Making λ1 = λ2 = λ3 = 0, into Eqs. (25) , (26) and (27) , the case of Newtonian fluid, Eqs. (52) and (53) becomes identical with that obtained by Yin and Ma [12] .
6. Results and discussion
In this section, we analyzed the transient temperature distribution for various types of fluids namely, a Newtonian fluid for which λ1 = λ2 = λ3 = 0, a Maxwell fluid for which λ1 ≠ 0, λ2 = λ3 = 0, an Oldroyd-B fluid for which λ1 ≠ 0, λ2 = 0, λ3 ≠ 0, and a Burgers' fluid.
Table 1 shows numerical values for different pressure waveforms at r = 0.00, λ1 = 0.25, λ2 = 0.25, λ3 = 0.25, and ω = 1. As can be seen, the performance of the transient temperature distribution is higher for trapezoidal pressure waveform in comparison with triangular and sinusoidal pressure waveforms. It is obvious that the peak of the transient temperature only achieves less compared with trapezoidal and sinusoidal.
Table 1.
Numerical values of the peak of the transient temperature distribution with different pressure waveforms.
|
t |
|
| |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.00 | 0.0000 | 0.0000 | 0.000 | |||||||||
| 0.20 | 0.507 | 0.127 | 0.199 | |||||||||
| 0.40 | 0.995 | 0.255 | 0.389 | |||||||||
| 0.60 | 1.000 | 0.382 | 0.565 | |||||||||
| 0.80 | 0.999 | 0.509 | 0.717 | |||||||||
| 1.00 | 0.999 | 0.637 | 0.841 | |||||||||
| 1.20 | 0.999 | 0.764 | 0.932 | |||||||||
| 1.40 | 1.000 | 0.891 | 0.985 | |||||||||
| 1.60 | 1.000 | 0.982 | 1.000 | |||||||||
| 1.80 | 1.000 | 0.854 | 0.974 | |||||||||
| 2.00 | 1.000 | 0.727 | 0.909 |
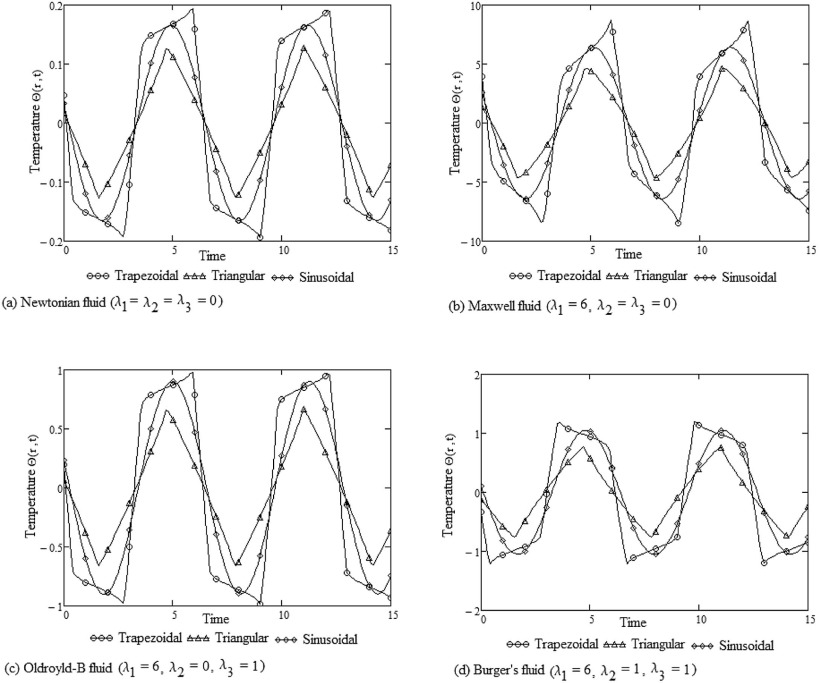
The effects of physical parameters, such as the Prandtl number, Pr , amplitude of pressure fluctuation, γ , and radial coordinate, r , on the transient temperature distribution for all four types of fluid have been shown in Fig. 5 , Fig. 6 , Fig. 7 and Fig. 8 . In all these figures, waveforms profiles are shown for both trapezoidal, triangular and sinusoidal pressure waveforms. Also, from these figures, it is observed that the variation for waveform effects with the classical Newtonian, Maxwell, Oldroyd-B and Burgers' fluids are distinct. Maxwell fluid has the maximum waveform effect as compared with Burgers' fluid. The waveform effect of an Oldroyd-B fluid is smaller than those for a Burgers' fluid. The Newtonian fluid has the lowest waveform effect.
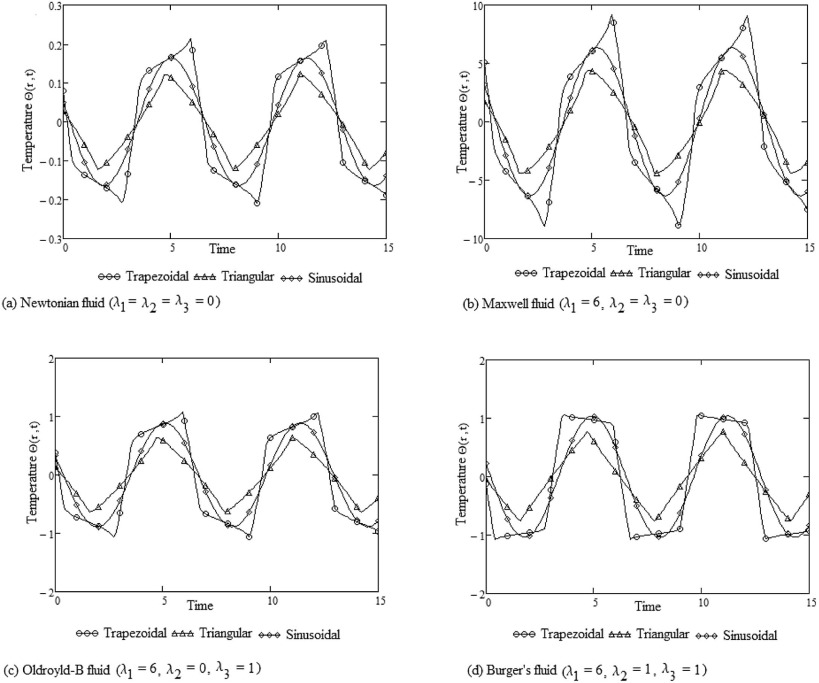
Fig. 5 (a)–(d) shows the waveform effect on transient temperature distribution of an oscillating motion at Pr = 0.1, γ = 0.01, and ω = 1.0. As shown in Fig. 5 (a)–(d), when the oscillating flow is driven by a trapezoidal waveform pressure difference, the peak of the transient temperature distribution can reach the same level as when is driven by sinusoidal waveform difference. However, when the pressure waveform is triangular with the same frequency and same amplitude, the peak of the transient temperature only achieves less compared with trapezoidal and sinusoidal. This indicates that for an oscillating flow with trapezoidal and sinusoidal waveforms, an optimum frequency and an amplitude exist which can significantly increase the heat transfer performance. When the Prandtl number Pr increases from 0.1 to 1.0, keeping amplitude and frequency fixed, i.e., γ = 0.01 and ω = 1.0, the influence of Pr on transient temperature becomes negligibly small as shown in Fig. 6 (a)–(d).
|
|
|
Fig. 5. Waveform effects on temperature distribution at Pr = 0.1 when γ = 0.01, ω = 1.0 and r = 0.0. |
|
|
|
Fig. 6. Waveform effects on temperature distribution at Pr = 1.0 when γ = 0.01, ω = 1.0 and r = 0.0. |
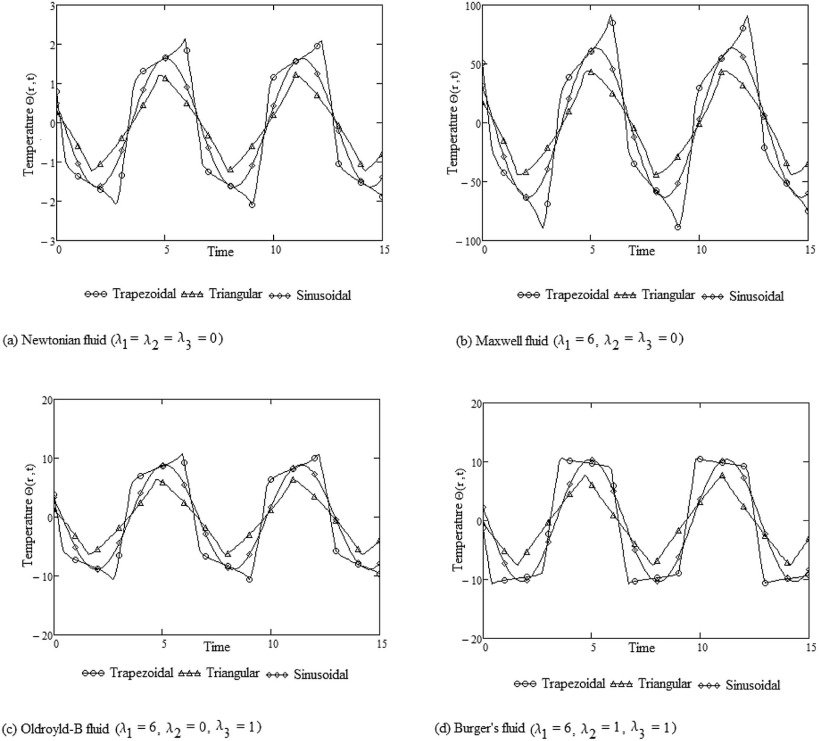
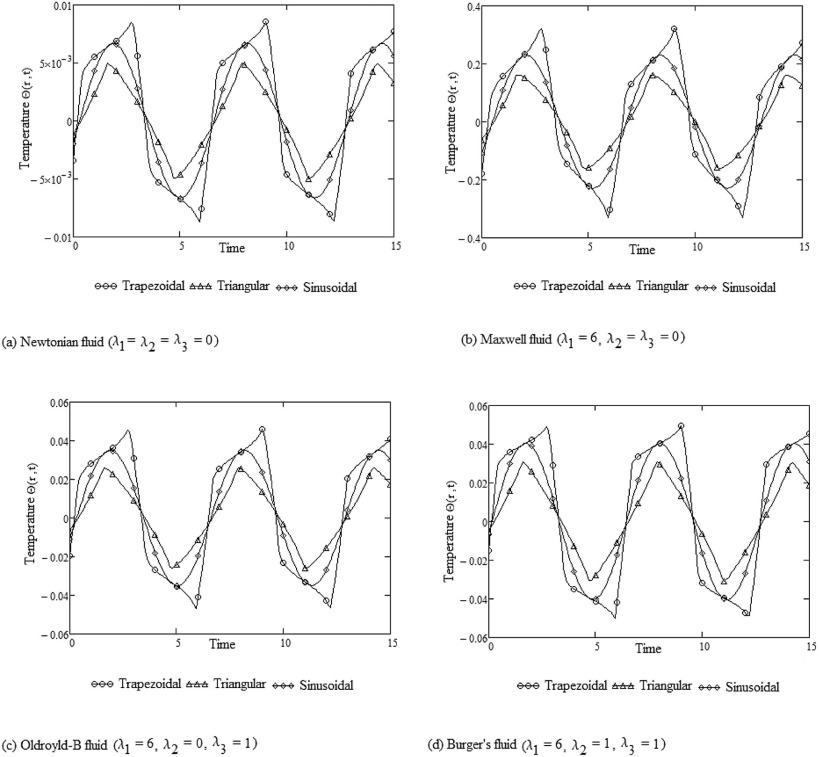
The effect of waveform amplitude is shown in Fig. 7 (a)–(d). It demonstrates that when the pressure oscillating amplitude increases to γ = 0.1, keeping the Prandtl number and dimensionless frequency fixed, i.e. Pr = 1 and ω = 1.0, the peak transient temperature increases as compared with Fig. 6 (a)–(d) when γ = 0.01. These results indicate that maximizing the oscillating amplitude can enhance heat transfer for trapezoidal, triangular and sinusoidal pressure waveforms. It is also interesting to observe that the waveform effect in Fig. 7 (a)–(d) is equal to 10 times as that in Fig. 7 (a)–(d). If the radial coordinate is increased, i.e. r = 0.5, keeping other conditions fixed, i.e. Pr = 1.0, γ = 0.01 and ω = 1.0, as shown in Fig. 8 (a)–(d), it can be found that the peak transient temperature decreases significantly. This indicates that the transient temperature is at the maximum at the surface of the cylinder and it decreases on increasing radial coordinate r to approach constant heat flux.
|
|
|
Fig. 7. Waveform effects on temperature distribution at γ = 0.1 when Pr = 1.0, ω = 1.0 and r = 0.0. |
|
|
|
Fig. 8. Waveform effects on temperature distribution at γ = 0.1 when Pr = 1.0, ω = 1.0 and r = 0.5. |
7. Conclusions
Analytical solutions of velocity and temperature distributions of a laminar oscillating flow of Burgers' fluid driven by trapezoidal, triangular and sinusoidal pressure waveforms are obtained in explicit form. The models of Newtonian, Maxwell and Oldroyd-B are obtained from the present analysis as the limiting cases. Results show that the peak temperature for trapezoidal and sinusoidal pressure waveforms is very different from triangular pressure waveform. For an oscillating flow that was driven by a trapezoidal waveform, when the radial coordinate decreases or when the amplitude increases, the oscillating motion can enhance heat transfer. However, for small pulsating frequencies, e.g. ω = 0.1, the influence of Pr on transient temperature becomes negligibly small.
Acknowledgments
We are thankful for the constructive comments and suggestions of the reviewers that help the authors a lot to improve the manuscript quality. The third author acknowledges the Ministry of Higher Education Malaysia (MOHE ) and the Research Management Centre-UTM for the financial support through vote numbers 06H67 and 4F255 .
References
- [1] T.N. Ruckmongathan; Techniques for reducing the hardware complexity and the power consumption of drive electronics; Preceding Asian Symposium on Information Display ( ), October 812 (2006), pp. 115–120
- [2] E.G. Richardson, E. Tyler; The transverse velocity gradient near the mouths of pipes in which an alternating or continuous flow of air is established; Proc. Phys. Soc, 42 (1929), pp. 1–15
- [3] T. Zhao, P. Cheng; A numerical solution of laminar forced convection in a heated pipe subjected to a reciprocating flow; Int. J. Heat Mass Tran, 38 (1995), pp. 3011–3022
- [4] T. Moschandreou, M. Zamir; Heat transfer in a tube with pulsating flow and constant heat flux; Int. J. Heat Mass Tran, 40 (1997), pp. 2461–2466
- [5] Z.X. Guo, H.J. Sung; Analysis of the Nusselt number in pulsating pipe flow; Int. J. Heat Mass Tran, 40 (1997), pp. 2486–2489
- [6] H.N. Hemida, M.N. Sabry, A. Abdel-Rahim, H. Mansour; Theoretical analysis of heat transfer in laminar pulsating flow; Int. J. Heat Mass Tran, 45 (2002), pp. 1767–1780
- [7] J.C. Yu, Z.X. Li, T.S. Zhao; An analytical study of pulsating laminar heat convection in a circular tube with constant heat flux; Int. J. Heat Mass Tran, 47 (2004), pp. 5297–5301
- [8] X.F. Wang, N.L. Zhang; Numerical analysis of heat transfer in pulsating turbulent flow in a pipe; Int. J. Heat Mass Tran, 48 (2005), pp. 3957–3970
- [9] R. Pendyala, S. Jayanti, A.R. Balakrishnan; Convective heat transfer in single-phase flow in a vertical tube subjected to axial low frequency oscillations; Heat Mass Transfer, 44 (2008), pp. 857–864
- [10] U. Akdag, A.F. Ozguc; Experimental investigation of heat transfer in oscillating annular flow; Int. J. Heat Mass Tran, 52 (2009), pp. 2667–2672
- [11] H.L. Liu, X.D. Shao, J.Y. Jia; Effects of axial heat conduction and viscous dissipation on heat transfer in circular micro-channels; Int. J. Therm. Sci, 66 (2013), p. 3441
- [12] D. Yin, H.B. Ma; Analytical solution of oscillating flow in a capillary tube; Int. J. Heat Mass Tran, 66 (2013), pp. 699–705
- [13] D. Yin, H.B. Ma; Analytical solution of heat transfer of oscillating flow at a triangular pressure waveform; Int. J. Heat Mass Tran, 70 (2014), pp. 46–53
- [14] M. Abdulhameed, D. Vieru, R. Roslan, S. Shafie; Exact solution of unsteady flow generated by sinusoidal pressure gradient in a capillary tube; Alex. Eng. J., 54 (2015), pp. 935–939
- [15] A. Khalid, I. Khan, A. Khan, S. Shafie; Unsteady MHD free convection flow of Casson fluid past over an oscillating vertical plate embedded in a porous medium; Eng. Sci. Technol. Int. J., 18 (2015), pp. 309–317
- [16] T. Gul, S. Islam, R.A. Shah, I. Khan, S. Shafie, M.A. Khan; Analysis of thin film flow over a vertical oscillating belt with a second grade fluid; Eng. Sci. Technol. Int. J., 18 (2015), pp. 207–217
- [17] T. Hayat, C. Fetecau, S. Asghar; Some simple flows of a Burgers' fluid; Int. J. Eng. Sci, 44 (2006), pp. 1423–1431
- [18] M. Khan, S.H. Ali, C. Fetecau; Exact solutions of accelerated flows for a Burgers' fluid. I. The case ; Appl. Math. Comput, 203 (2008), pp. 881–894
- [19] H.K. Xin, P. Jie, Z.K. Qin; The linear stability of plane Poiseuille flow of Burgers fluid at very low Reynolds numbers; J. Non-Newton Fluid, 167 (2012), pp. 87–94
- [20] M. Javed, T. Hayat, A. Alsaedi; Peristaltic flow of Burgers' fluid with compliant walls and heat transfer; Appl. Math. Comput, 244 (2014), pp. 654–671
- [21] J. Hron, K.R. Rajagopal, K. Tuma; Flow of a Burgers fluid due to time varying loads on deforming boundaries; J. Non-Newton Fluid, 210 (2014), pp. 66–77
- [22] M. Garg, A. Rao, S.L. Kalla; On a generalized finite Hankel transform; Appl. Math. Comput, 190 (2007), pp. 705–711
- [23] W.N. Everitt, H. Kalf; The Bessel differential equation and the Hankel transform; J. Comput. Appl. Math, 208 (2007), pp. 3–19
- [24] X.J. Li; On the Hankel transformation of order zero; J. Math. Anal. Appl, 335 (2007), pp. 935–940
Document information
Published on 10/04/17
Licence: Other
Share this document
Keywords
claim authorship
Are you one of the authors of this document?