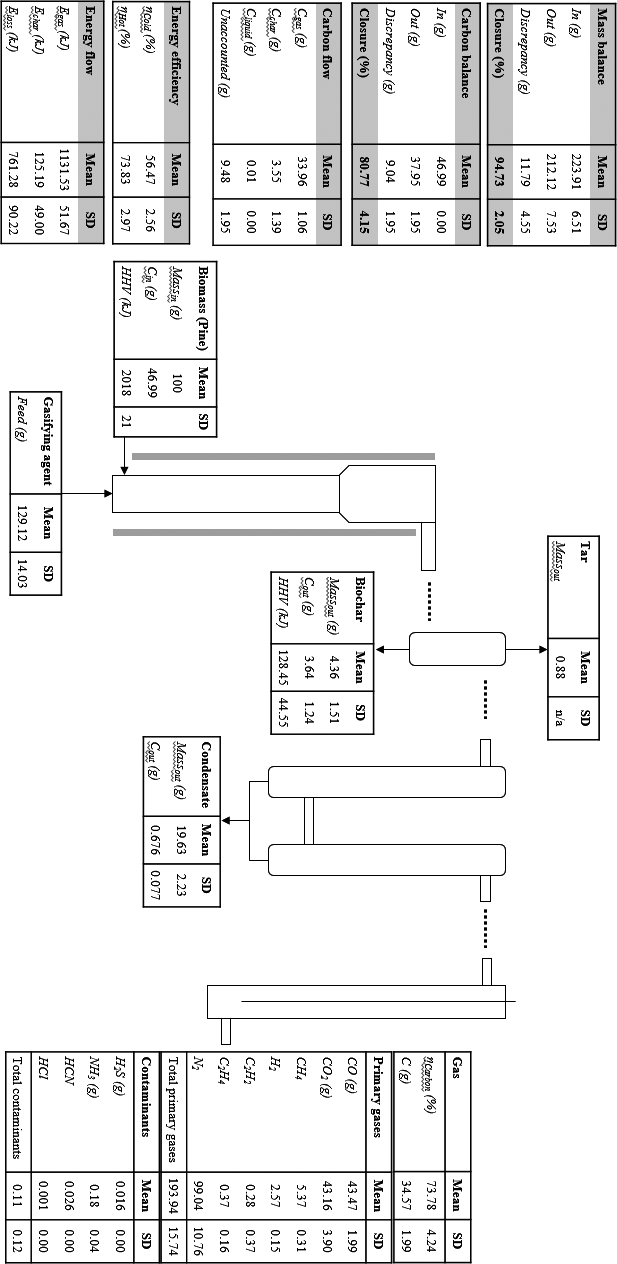
Abstract
The purpose of this study was to evaluate the effects of temperature and equivalence ratios (ERs) on the distribution of products (primary gases carbon monoxide [CO], H2, CH4, CO2), gas phase contaminants (tar, NH3, HCN, H2S, HCl), char, carbon, and inorganics), and energy flows on an oxygen-blown bubbling fluidized bed gasifier system using loblolly pine. The goal and value of this study was to provide quantitative and qualitative performance analysis and data for process engineering and optimization of these fledgling biomass conversion systems. As temperature and ER increased, mass balance closures also increased from 94.73% to 96.72% for temperature and 89.82–96.93% for ER. In addition, the carbon closures ranged from 80.77% to 92.29% and from 79.09% to 87.13% as temperature and ER increased, respectively. Carbon conversion efficiency to gas product ranged from 72.26% to 84.32% as temperature increased and from 72.26% to 84.66% as ER increased. Carbon flow analysis showed that the char product streams retained 10.26–6.94% and 8.82–2.13% of the carbon fed to the gasifier as temperature and ER increased, respectively. The carbon content in the liquid condensate was minimal compared to the carbon in other product streams and accounted for less than 0.1% of the carbon input to the gasifier at all conditions. The cold and hot gas efficiencies increased from 56.12% to 67.45% and from 67.51% to 83.83% as temperature increased due to higher production of CO and hydrogen (H2). In contrast, cold and hot gas efficiencies decreased from 63.85% to 52.84% and from 78.06% to 73.00% as ER increased, respectively, due to enhanced oxidation of gas products resulting in a net decrease in heating value.
Introduction
Biomass conversion into energy, fuel, and products has attracted significant interest in recent years due to concerns over the harmful effect of greenhouse gas emissions and national security [1]. In particular, biomass conversion into biofuel, energy, and bioproducts through gasification is particularly very interesting due to the possibility to produce a wide variety of biofuels, energy, and intermediate products [2]. During gasification, biomass is converted at high temperatures (650–1200°C) and limited oxygen into char and producer gas. In industrial-scale applications, char generated during gasification is further combusted to generate and recirculate the heat required for the process, thereby improving the process efficiency. On the other hand, species in the producer gas, in particular carbon monoxide (CO) and H2, are essential building blocks for fuel and chemical synthesis, and for power generation. However, the presence of harmful contaminants (tar, NH3, HCN, H2S, COS, HCl, HF, trace metals etc.) species can hinder the utilization of valuable species by deactivating catalysts in downstream processes [3], corroding and fouling equipment [4], and leading to increasing emissions of regulated and harmful pollutants [5].
In evaluating the technical and economic viability of gasification applications, it is important to have usable process data in order to properly select and size ancillary equipment [6, 7]. While there is an abundance of information on primary gas constituents of producer gas (CO, H2, CO2, CH4, and H2O), comprehensive studies of material and energy flows in gasification systems and distribution of contaminants are sparingly presented and are often guarded proprietary information by companies. Such studies are of great importance because they provide quantitative and qualitative data necessary in preliminary process engineering and optimization as well as validation data for models not solely focused on predicting primary gas constituents.
In recent years, several studies have reported information that provide a partial snapshot of product distribution during gasification at various process conditions. Carpenter et al.[8] investigated steam gasification of various biomass feedstocks and reported on the impact of temperature and steam-to-biomass (S/B) on primary gases, select contaminants (tar, H2S, COS), and performance (carbon balance, cold gas efficiency etc.). However, the study did not address inorganic and nitrogenous contaminants nor did it present a distribution of products in output streams. Aljbour and Kawamoto [9] reported on the effect of temperature, equivalence ratio (ER) and S/B on primary gases and major contaminants. Seldom do studies provide a comprehensive report that includes detailed gas composition including major contaminants, process performance indicators (carbon conversion, cold and hot gas efficiencies) as well as detailed material and energy flow in the process. Consequently, the aim of this paper was to provide comprehensive snapshots of relevant and important process information as affected by temperature (790, 934, and 1078°C) and ERs (0.15, 0.25, and 0.35) during oxygen gasification of loblolly pine hereafter referred to as pine. The objectives of the study are to perform a process analysis through mass and energy balance and to establish the distribution of major products and contaminants throughout the process. The temperature and ER ranges were selected to cover most commonly used experimental conditions used in the literature. The process snapshots include information on the distribution of products primary gases (CO, H2, CH4, CO2), gas phase contaminants (tar, NH3, HCN, H2S, HCl), char, carbon, and inorganics and energy flows on an oxygen-blown bubbling fluidized bed gasifier system.
Materials and Methods
Experimental setup and product sampling
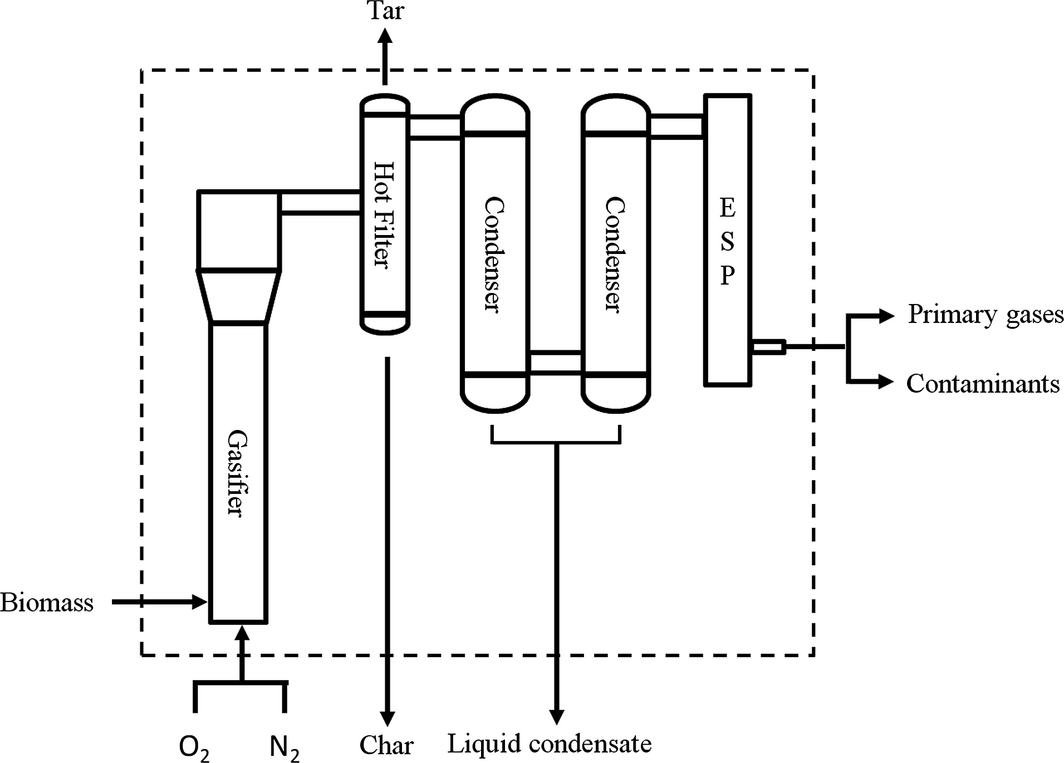
The control volume, the input and output streams considered for material balance and energy analysis in this study are shown in Figure 1. Further details of the gasification experimental setup can be found in an earlier study [10]. Materials enter the systems in the form of biomass as pine sawdust, gasifying agent as oxygen (O2), and fluidization gas as nitrogen (N2). Materials exit the system in the form of biomass residue as char, liquid condensate, noncondensable gaseous products (primary gases and contaminants), and condensable tar compounds.
|
|
|
Figure 1. Material balance and energy analysis control volume with input and output streams. The hot filter was maintained at ~350°C while the condensers were maintained between 0 and −5°C. The electrostatic precipitator was supplied with 20 kV to induce aerosol condensation. |
In this study, O2 and N2 are supplied separately, the first as the oxidizing medium and the second as the fluidization medium. This approach was taken to decouple fluidization, essential to avoid feeding issues, and gasification which requires an oxidizing agent. Based on preliminary experimental trials, it was established that the suitable nitrogen flow rate for proper fluidization and biomass feeding was near 16.5 L/min. This nitrogen flow rate was thus maintained constant in subsequent experiments, while oxygen flow rate was varied to obtain the desired ER. The composition of oxygen and nitrogen varied from 5.25 wt% to 94.75 wt% at 0.15 ER and 9.52–90.48 wt% at 0.35 ER, respectively. This resulted in a nitrogen enriched gasifying agent and a higher than typical nitrogen content in the exit gas when compared to typical air gasification. In order to eliminate this ambiguity and allow for comparison with the reported results for air gasification, the inert nitrogen was adjusted to achieve a normal O2/N2 (i.e., 23/77 wt%) composition in air. This approach does not affect the material balance since nitrogen, being inert in the process, simply enters and exits the control volume. However, in order to enable easy comparison with published results, the excess nitrogen has been discounted and results are reported on an adjusted air equivalent basis.
Material characterization
Loblolly pine was secured from a local wood chipping facility in Opelika, AL. Given our geographical location and our institutions mission to service the southeastern region of the US, loblolly pine was selected because it is the most abundant woody biomass in our region [11]. Nonetheless, the outcomes of this study are applicable to other woody biomass feedstocks provided their chemical compositions are similar. The loblolly pine wood chips were air-dried, ground, and sieved through a 850-μm screen opening prior to any characterization. Ultimate and proximate analyses were performed for raw pine wood. Ultimate analysis was carried out by a CHNS/O elemental analyzer (PerkinElmer, Model 2400, Waltham, MA) while the higher heating value (HHV) of pine (HHVpine) was determined with a bomb calorimeter (IKA Bomb Calorimeter, Model C-200, Wilmington, NC). The elemental composition of char product stream was determined using a CHNS/O analyzer while the carbon content in the liquid condensate was determined using a total organic carbon (TOC) analyzer (TOC-L Analyzer, Shimadzu Scientific Instruments Inc., Columbia, MD). As elemental analysis on char samples with high ash content was challenging due to rapid deactivation of CHNS oxidation columns, presumably due to catalyst poisoning by char inorganic elements, only the samples with lowest ash content at each conditions (temperature and ER) were analyzed to avoid this issue. The HHV of char (HHVchar) was determined using the Milne equation as depicted below in equation (1).
|
|
(1) |
where C, H, N, O, S, and ash are the mass and the ash fractions in wt% of dry material and HHVMilne, dry was the heating value for dry material in MJ/kg.
The primary gas concentrations were determined using a gas analyzer equipped with nondispersive infrared and thermal conductivity detectors (NOVA, Niagara Falls, NY). Noncondensable gas contaminants were measured with an FTIR gas analyzer fitted with a 4 m gas cell and a liquid nitrogen cooled Mercury cadmium telluride detector (IMAAC, Austin, TX). For all noncondensable gases, only steady-state concentrations were considered. Due to its condensable nature and its significance in biomass gasification, tar was measured using a slip stream out of the hot gas filter. The gas slip stream was scrubbed through five impinger bottles, each containing 50 mL of isopropanol at a flow rate of 2 L/min (STP) and the tar content was determined gravimetrically.
Performance analysis
The material and energy balance was conducted using 100 g as the basis of calculation. This is an arbitrary value selected for convenience and all values can be scaled up or down throughout the system by applying a factor to this basis. A detailed sample calculation is presented in the Data S1.
Mass and carbon balance
The material and carbon flows for all input and output streams were considered for this mass balance. Using the law of conservation of mass, shown in equation (2), material balances were carried out for all process conditions.
|
|
(2) |
where min and mout are the mass of input and output streams, respectively. In addition, the carbon flow and balance was also carried. The application of the law of mass conservation to the control volume results in the following mass and carbon balance equations shown by equations (3) and (4) below:
|
|
(3) |
|
|
(4) |
where , , represent the mass input in grams of pine, oxygen and nitrogen to the system, , , , represent the mass output of gas, total contaminants including tar, char and liquid condensate, represents the mass input in grams of carbon from pine and , and represent the mass output in grams of carbon in the gas, char, and liquid condensate streams. For the input streams, pine is the only source of carbon input, and therefore, only this stream was considered. For the output streams, the carbon input from pine is partitioned into all product streams. For the gas product stream, only carbon from the primary gases was considered. It is noteworthy to indicate that carbon present in tar is not accounted for in the carbon balance as the tar carbon fraction is unknown due to challenges in accurately quantifying all carbon bearing species in the tar scrubbing solutions. However, this omission should not significantly impact the carbon balance accuracy as tar only accounts for 0.83 g/100 g biomass, at most, in this study.
In material balance analysis, it is possible to have a discrepancy due to measurement error. The accuracy in input and output measurements is assessed by the mass and carbon balance closures, the mass ratio of output to input is represented by the equations (5) and (6) below:
|
|
(5) |
|
|
(6) |
where ∅mass and ∅c represent mass and carbon balance closures, i and j represent input and output streams, respectively.
Carbon conversion efficiency
In addition to the mass and carbon balance, the carbon conversion efficiency to primary gases was also determined as it is a widely reported parameter in gasification studies. The carbon conversion efficiency, ηc, is defined as the mass of carbon in the primary gases over the mass of carbon from biomass (i.e., pine) supplied to the gasifier as shown in equation (7).
|
|
(7) |
where , defined in equation (8) is the mass fraction of carbon-bearing species (s = CO, CO2, CH4, C2H2, and C2H4) and is the mass output of the corresponding species in the primary gas output stream.
|
|
(8) |
where n and MWs are the number of carbon and molecular weight of gas species s. , , , and are 0.43, 0.27, 0.75, 0.92, and 0.86, respectively.
Energy analysis
The energy analysis in this study examines the flow of HHV from pine into the product streams of the control volume. The expression of the energy analysis is represented by equation (9) below:
|
|
(9) |
where is the heating value of pine and and represent the heating value of the gas and char output streams and represents the energy unrecovered into valuable products expressed in kJ. Using the specific heating values of pine and char gives rise to the following expressions:
|
|
(10) |
|
|
(11) |
|
|
(12) |
where HHVs represents the specific HHV of gas species (s = CO, H2, CH4, C2H2, and C2H4) and are reported in Table S2.
Cold and hot gas efficiencies and volumetric gas heating value
Cold and hot gas efficiencies are widely reported in gasification studies and are therefore calculated in this study. The cold gas efficiency () and hot gas efficiency () are expressed by the equations (13) and (14).
|
|
(13) |
|
|
(14) |
where , expressed in equation (15), is the sensible heat of the primary gas output in kJ.
|
|
(15) |
where Cp,s, primary gas (kJ/g K) is the individual specific heat of the primary gas species s (s = CO, CO2, CH4, H2, N2) and Tout (K) is the exit gas temperature. The specific heat capacity was determined using the Shomate equation as illustrated below in equation (16).
|
|
(16) |
with the coefficients A, B, C, D, and E taken from the National Institute of Standards and Technology database [12] and T’ is defined as. The coefficients of the Shomate equations are listed in Table S1. In addition to the energy efficiencies, the volumetric producer gas energy content is also commonly determined in experimental studies and is therefore evaluated as expressed in equation (17).
|
|
(17) |
where is the volumetric heating value of the producer gas and ρs is the density of gas species is listed in Table S2. In addition, a sample mass and energy balance calculations are provided in Data S1.
Results and Discussion
Effect of temperature and ER on products
The products from the main output streams were quantified at the three temperatures and ERs and summarized in Tables 1 and 2 to indicate the effect of temperature and ER. These results indicate that pine is predominantly converted to product gas (>73 wt%). As expected, the mass of carbon from pine transferred to the gas product increased as temperature and ER increased as evidenced by increasing concentrations of carbon-bearing compounds [8-10]. The TOC analysis of the liquid condensate showed that minimal carbon is contained in this product stream. The carbon concentrations are 0.29, 0.49, and 0.91 mg C/g condensate for 0.15, 0.25, and 0.35 ERs and 1.93, 0.49, and 0.15 mg C/g condensate for 790, 934, and 1078°C, respectively.
| Means (SD) | Temperature°C | ||
|---|---|---|---|
| 790 | 934 | 1078 | |
| |||
| Primary gases (g/100 g pine)a | |||
| CO | 37.96 (3.25) | 43.47 (1.99) | 64.70 (11.92) |
| CO2 | 46.40 (2.52) | 43.16 (3.90) | 31.18 (2.81) |
| CH4 | 8.58 (1.67) | 5.37 (0.31) | 2.92 (0.40) |
| H2 | 1.75 (0.34) | 2.57 (0.15) | 4.27 (0.11) |
| C2H2 | 0.61 (0.14) | 0.70 (0.04) | 0.44 (0.05) |
| C2H4 | 5.20 (1.24) | 3.73 (1.57) | 1.37 (0.47) |
| Char(g/100 g pine) | 6.07 (1.20) | 3.65 (1.27) | 4.09 (2.02) |
| Liquid condensate (g/100 g pine) | 20.87 (1.20) | 16.93 (3.08) | 11.75 (0.67) |
| Mean (SD) | ER | ||
|---|---|---|---|
| 0.15 | 0.25 | 0.35 | |
| |||
| Primary gas (g/100 g)a | |||
| CO | 51.90 (4.44) | 43.47(1.99) | 46.06 (6.10) |
| CO2 | 26.68 (2.98) | 43.16 (3.90) | 59.19 (4.48) |
| CH4 | 4.68 (0.20) | 5.37 (0.31) | 4.93 (0.85) |
| H2 | 3.56 (0.35) | 2.57 (0.15) | 2.40 (0.37) |
| C2H2 | 0.78 (0.01) | 0.70 (0.04) | 0.67 (0.07) |
| C2H4 | 7.43 (2.07) | 3.73 (1.57) | 4.33 (1.63) |
| Char (g/100 g pine) | 5.03 (0.77) | 3.65 (1.27) | 1.21 (0.32) |
| Liquid condensate (g/100 g pine) | 9.30 (0.58) | 16.93 (3.08) | 18.17 (4.42) |
The char samples collected from each condition were fully characterized to determine how the content of organic and inorganic constituents varies with temperature and ER. The effect of the temperature and ER on the ultimate and proximate analyses on char samples are summarized in Tables 3 and 4 for char samples with the lowest ash content. However, overall, it was observed that ash content of char samples varied widely from 4.47 wt% to 64.63 wt%, as received for all samples. For reference, the ash content in pine was only 0.34 wt%. This increase in char ash content is due to two primary reasons: ash accumulation in char stream as biomass is decomposed into gas products and fine bed material (sand) entrainment into char filter. However, as the mass of sand used for fluidization is always deducted from the reported values, it stands to reason that the increase in ash content in char observed is solely due to ash accumulation. While this observation is expected, it is nonetheless important to quantify this behavior as char has many applications that might be adversely or positively affected by the ash content [13, 14].
| Mean (SD) | Pine | Temperature°C | ||
|---|---|---|---|---|
| 790 | 934 | 1078 | ||
| ||||
| Elements, wt% dry | ||||
| C | 47.14 (0.18) | 82.87 (1.60) | 85.38 (3.64) | 81.56 (1.16) |
| H | 6.52 (0.04) | 1.33 (0.04) | 0.34 (0.02) | 0.96 (0.11) |
| N | 0.44 (0.10) | 0.42 (0.03) | 0.31 (0.02) | 0.35 (0.03) |
| S | 0.10 | n/a | n/a | n/a |
| Oa | 45.46 (0.24) | 9.15 (1.63) | 4.38 (3.65) | 1.37 (0.88) |
| Ash, wt% dry | 0.34 (0.01) | 6.22 (0.0045) | 9.59 (0.01) | 15.75 (0.35) |
| HHV, MJ/kg dry basis | 20.18 (0.21) | 28.78 (0.79)b | 28.86 (1.66)b | 28.63 (0.39)b |
| Mean (SD) | Pine | ER | ||
|---|---|---|---|---|
| 0.15 | 0.25 | 0.35 | ||
| ||||
| Elements, wt% dry | ||||
| C | 47.14 (0.18) | 84.12 (3.39) | 85.38 (3.65) | 81.24 (3.7) |
| H | 6.52 (0.04) | 0.37 (0.12) | 0.34 (0.02) | 0.42 (0.2) |
| N | 0.44 (0.10) | 0.24 (0.06) | 0.31 (0.02) | 0.2 (0.05) |
| S | 0.10 | n/a | n/a | n/a |
| Oa | 45.46 (0.24) | 9.87 (4.15) | 4.38 (3.65) | 8.26 (3.56) |
| Ash, wt% dry | 0.34 (0.01) | 5.43 (1.21) | 9.59 (0.01) | 9.91 (0.04) |
| HHV, MJ/kg dry basis | 20.18 (0.21) | 27.87 (1.70)b | 28.86 (1.66)b | 27.08 (1.60)b |
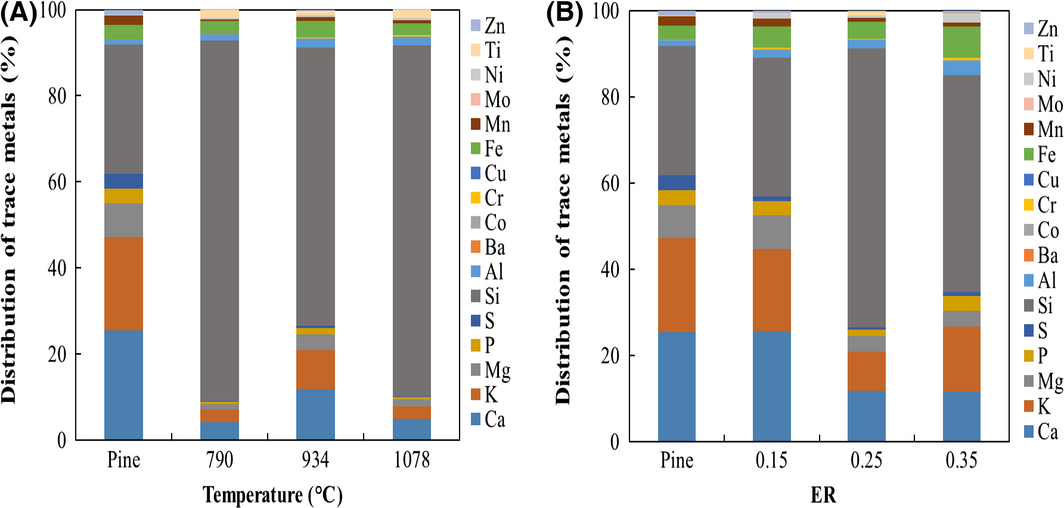
The elemental composition of char at different temperatures and ERs did not show any clear trend. All samples have higher carbon content (>80 wt%, dry basis) while other elements, oxygen in particular, are significantly lower relative to their initial concentration in pine resulting in a corresponding increase in energy content. The elemental compositions as well as the HHVs, determined using the Milne formula, are similar to values reported in the Energy Research Center of the Netherlands (ECN) Phyllis2 database for various biomass char samples [15]. As illustrated in Figure 2A and B, temperature and ER have noticeably altered the distribution of trace metals in the char samples. In general, when compared to that of pine, all elements in char samples increase in concentration as temperature and ER increase. Interestingly, several catalytically active elements (Co, Ni, Fe, Ca, and Mg) significantly increase in the char samples as compared to raw pine. This finding supports the well-accepted claim that inorganic elements of biochar catalyze reactions in bio-oil leads to increasing instability [13].
|
|
|
Figure 2. Distribution of trace metal elements in pine and char over (A) temperature (790, 934, and 1078°C) and (B) equivalence ratio (ER) (0.15, 0.25, and 0.35 ERs). |
Effect of temperature and ER on mass and carbon balance
The mass and carbon balances were determined for all process conditions by accounting for mass input and output from all streams. The mass balance closure was 97.47, 94.73, and 96.72% for 790, 934, and 1078°C and 89.82, 94.73, and 96.93% for 0.15, 0.25, and 0.35 ER, respectively. These mass balance closures are similar to mass balance closure results reported by other investigators [8, 16, 17]. Additionally, carbon closures were 87.29, 80.77, and 92.29% for 790, 934, and 1078°C and 79.096, 80.77, and 87.13% for 0.15, 0.25, and 0.35 ER, respectively. Other studies have reported similarly carbon balance closures [8, 16] although higher closures have been reported by van der Drift and coworkers when carbon-rich light hydrocarbons were included in the carbon balance.
Among all product streams, producer gas accounted for the highest proportion of carbon relative to the carbon input from biomass. The carbon conversion efficiency to product gas was 76.06, 72.26, and 84.32% for 790, 934, and 1078°C and 74.10, 72.26, and 84.66% for ER of 0.15, 0.25, and 0.35, respectively. The overall increase in carbon conversion efficiencies as temperature and ER increased is due to the greater conversion of biomass to noncondensable gas product through the Boudouard and water gas reaction as well as carbon oxidation reactions [9, 10].
|
|
(R1) |
|
|
(R2) |
|
|
(R3) |
|
|
(R4) |
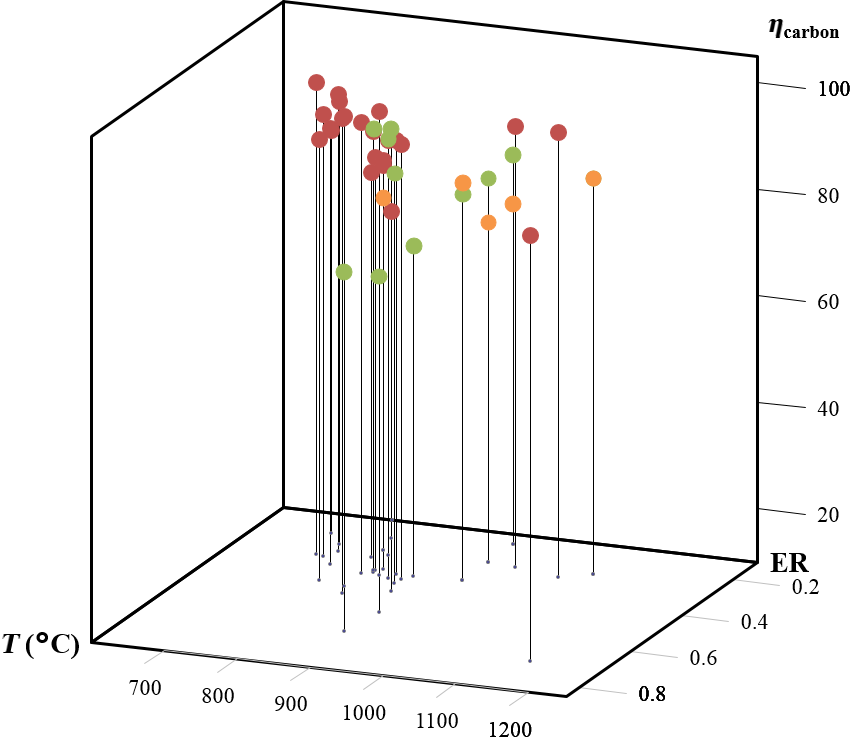
Figure 3 shows a comparison of the carbon conversion efficiencies achieved in this study and values reported by various authors for air-blown fluidized bed gasifiers. The results from this study are within the range of values reported for bubbling fluidized bed reactors [16, 18, 19] but lower than circulating fluidized bed reactors which typically achieve higher carbon conversion efficiency.
|
|
|
Figure 3. Carbon conversion efficiency in this study compared with several reports in woody biomass air gasification in bubbling fluidized bed reactors. Orange points represent data from this study, green points data for bubbling fluidized bed, and red points data for circulating fluidized bed [16-19, 23, 24]. |
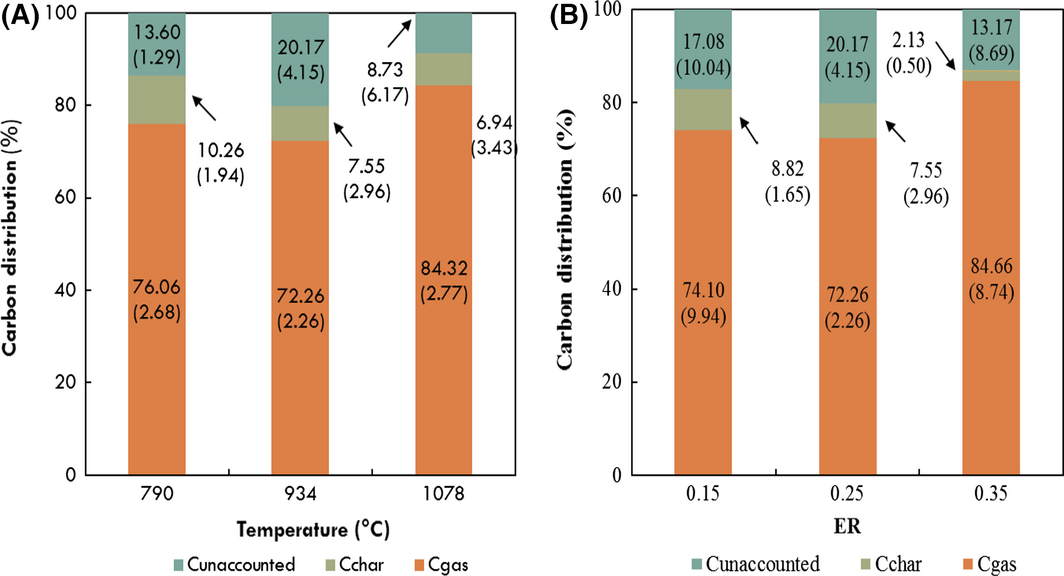
Carbon distribution in the product streams is shown in Figure 4A and B for temperature and ER, respectively. For both temperature and ER, carbon in the gas stream accounted for the largest percentage (74–85%) of carbon fed to the gasifier, followed by carbon in the char stream. Carbon in liquid condensate is minor with less than 0.1% of feed carbon for all conditions. The carbon unaccounted for in the carbon balance ranged from 18.45% to 8.73% and 18.45–13.17% for temperature and ER, respectively. The unaccounted carbon is likely present as uncollected product from the gasifier, carbon in the tar product stream, which is not included in the carbon balance, as well as in other carbon-bearing gas species such as C2–C6 compounds, which are not measured in this study. As exhaustive characterization of noncondensable gases, tar compounds, and other contaminants is challenging and unrealistic given the plethora of compounds, such carbon balance discrepancies are not unreasonable [8]. Figure 5 illustrates the mass and carbon balance of the process at 934°C and 0.25 ER. For the sake of brevity, mass and energy balance diagrams of all other temperature and ER conditions are shown in Figures S1, S2, S3, and S4 in the Data S1.
|
|
|
Figure 4. Effect of (A) temperature and (B) equivalence ratio on carbon distribution in product streams. Values in parentheses represent standard deviations. Carbon in liquid condensate product (<0.5% of carbon in raw pine) is not shown here. |
|
|
|
Figure 5. Process mass, carbon, and energy balance diagram at 934°C and 0.25 equivalence ratio. |
Effect of temperature and ER on energy analysis
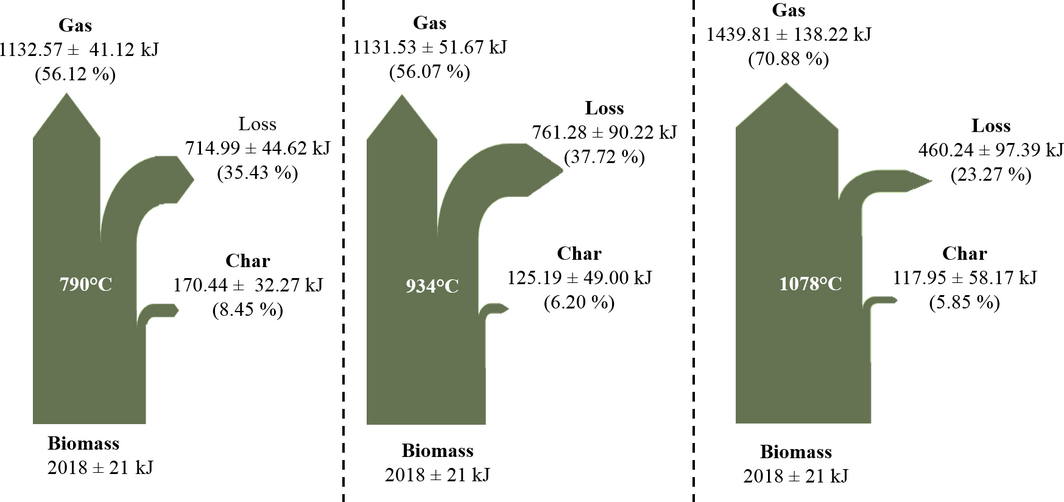
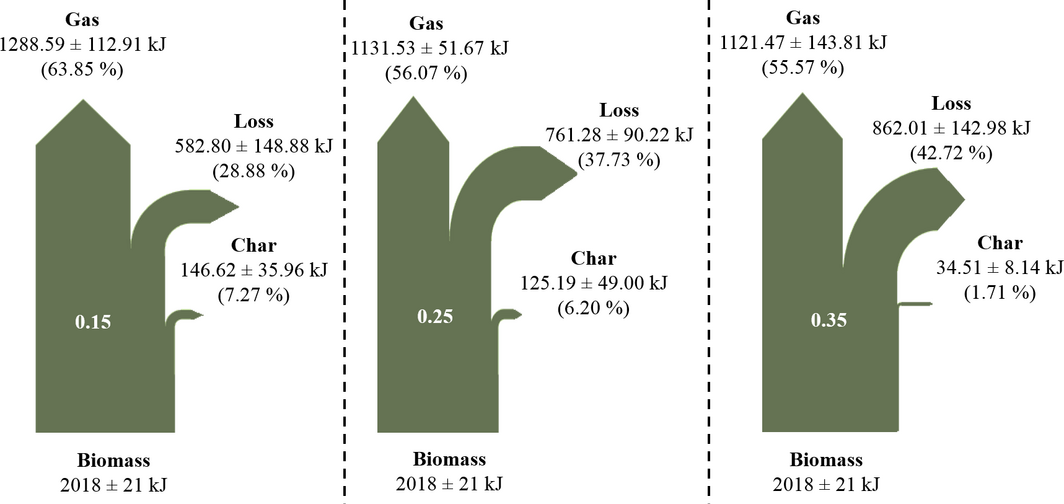
Energy analysis of the process at all conditions was carried out by considering the energy distribution in the product streams, the energy efficiencies (ηcold gas and ηhot gas) and the heating value of the producer. The process energy flows are shown in Figures 6 and 7. As temperature and ER increased, the char energy output decreases from 170.44 kJ to 117.95 kJ and from 146.62 kJ to 34.51 kJ. The decrease in char energy flow is due to the decrease in char yield as both temperature and ERs are increased due to greater biomass decomposition and thus lower char production.
|
|
|
Figure 6. Effect of temperature on energy flow illustrated by Shankey diagrams. |
|
|
|
Figure 7. Effect of equivalence ratio on energy flow illustrated by Shankey diagrams. |
The total producer gas energy output varied from 1132.57 kJ to 1439.81 kJ as temperature increased and from 1288.59 kJ to 1121.47 kJ as ER increased. The increase in producer gas energy output is due to the increase in CO and H2 and decrease in CO2 as temperature is increased as observed in several studies [20]. In contrast, the producer gas energy output decreased as ER is increased due to increased oxidation of CO and H2 to CO2 and H2O [9, 10].
The energy loss represents unrecovered energy into valuable products and includes heat loss from the systems as well as energy contained in contaminants as well as other gaseous species was not measured. The energy losses vary from 37.72% to 23.27% and 28.88–42.72% of the total biomass energy content as temperature and ER increased, respectively. The decrease in energy loss as temperature is increased is due to the increase in gas energy flow. In contrast, the energy loss increases with ER due to the reduction in the concentrations of CO and H2, the increase in CO2 concentration, the increase in liquid condensate, and the decrease in the char energy. The energy loss at 790°C is similar to figures reported at similar conditions by Lim et al.[21].
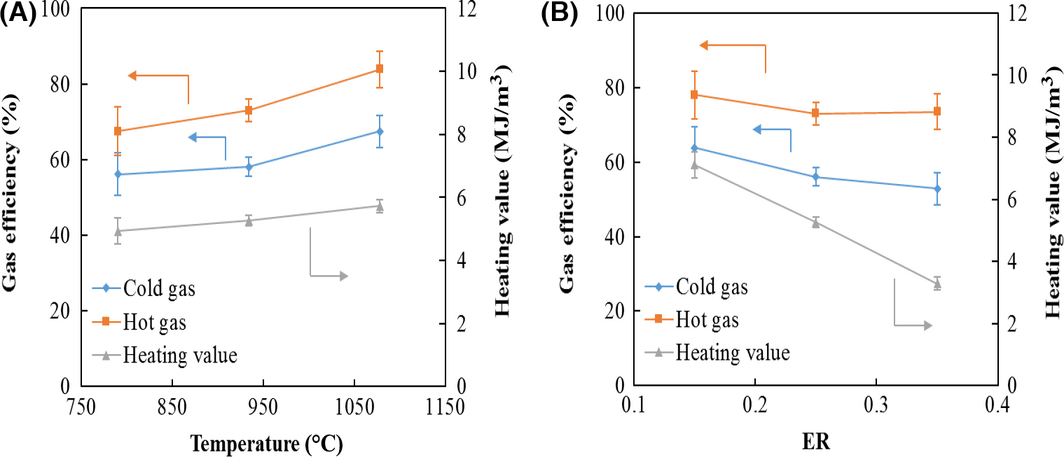
Cold and hot gas efficiencies are two common thermodynamic efficiencies utilized to access the performance of gasification. Figure 8A and B show the effect of temperature and ER on the cold and hot gas efficiencies as well as on the heating value of the producer. As temperature is increased, both cold gas and hot gas efficiencies increase in a similar fashion from 56.12% to 67.45 and from 67.51% to 83.83%, respectively. The increase in gas efficiencies as temperature is increased is due to the increase in CO and decrease in CO2 concentrations over the same range of temperature [8-10, 16, 17].
|
|
|
Figure 8. Effect of (A) temperature and (B) equivalence ratio on cold and hot gas efficiencies and heating value of producer gas. |
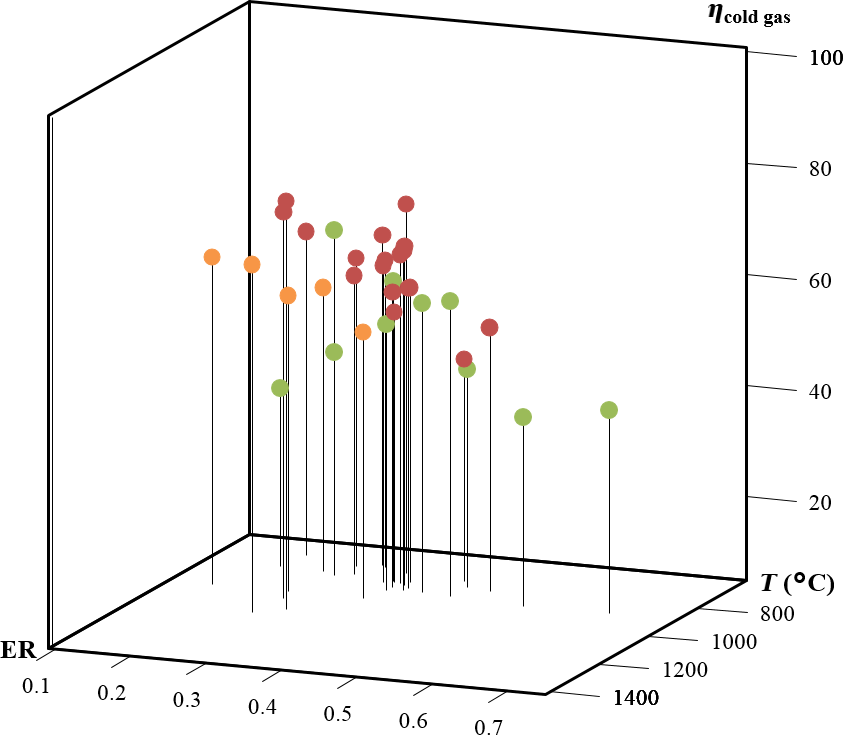
The cold and hot gas efficiencies in this study fall in the range of values reported in other studies as illustrated in Figure 8. The heating value of the producer gas increased slightly from 4.93, 5.26, and 5.73 MJ/m3 for 790, 934, and 1078°C and 7.11, 5.26, and 3.28 MJ/m3 for 0.15, 0.25, and 0.35 ER, respectively. In this case also, the increase in heating value of the syngas is due to the increase in CO and H2 as temperature is increased. In contrast, CO and H2 decrease as ER increases while CO2 increases, thus decreasing the heating value of the gas product. The producer gas heating values in this study are similar to values reported for air gasification where energy content ranges from 2.93 MJ/m3 [19] to 6.3 MJ/m3 [22] (Fig. 9).
|
|
|
Figure 9. Cold gas efficiency in this study compared with several reports in woody biomass air gasification in fluidized bed reactors. Orange points represent data from this study, green points data for bubbling fluidized bed gasifiers, and red points data for circulating fluidized bed gasifiers [16-19, 23, 24]. |
Conclusions
This study presents an extensive performance analysis over a wide range of conditions and could provide guidance in process engineering decisions by (1) providing an reasonable estimate of the effect of changes in primary conditions (temperature and ER) on syngas quality, product distribution, and process efficiencies; (2) providing valuable data for process modeling activities; and (3) providing basic data required in process design. The mass and energy balance of pine was analyzed at three temperatures (790, 934, and 1078°C) and ER (0.15, 0.25, and 0.35) during biomass gasification. Mass balance closures were 97.47, 94.73, and 96.72% and 89.82, 94.73, and 96.93% as temperature and ER increased. In addition, the carbon closures were 87.29, 80.77, and 92.29% and 79.09, 80.77, and 87.13% as temperature and ER increased. Carbon conversion efficiencies to gaseous products ranged from 72.26% to 84.32% as temperature increased and from 72.26% to 84.66% as ER increased. Carbon flow analysis showed that the char product streams retained 10.26–6.94% and 8.82–2.13% of the carbon feed to the gasifier as temperature and ER increases, respectively. The carbon content in the liquid condensate was minimal compared to the carbon in other product streams and accounted for less than 0.1% of the carbon input to the gasifier at all conditions.
The cold and hot gas efficiencies increase from 56.12% to 67.45% and from 67.51% to 83.83% as temperature is increased primarily due to an increase in CO and H2 concentrations enhanced by the Boudouard reaction. In contrast, cold and hot gas efficiencies decreased as ER increased due to the decrease in CO and H2 concentrations. This decrease is due to greater oxidation of CO to CO2 and H2 to H2O as oxygen availability is increased. The heating value of producer gas increased with increasing temperature and decreased with increasing ER for similar reasons as the cold and hot gas efficiencies.
Nomenclature
| Symbol | Units | Description |
|---|---|---|
| g | Mass input of pine to the control volume | |
| g | Mass input of oxygen to the control volume | |
| g | Mass input of nitrogen to the control volume | |
| g | Mass output of primary gas from the control volume | |
| g | Mass output of contaminants from the control volume | |
| g | Mass output of char from the control volume | |
| g | Mass output of liquid condensate from the control volume | |
| c | Subscript denotation for carbon | |
| g | Mass input of carbon from pine | |
| , | g | Mass output of carbon from primary gases |
| g | Mass output of carbon from char | |
| g | Mass output of carbon from liquid condensate | |
| g | Mass output of the gas species s in primary gas | |
| g | Mass output of carbon for carbon-bearing species s (s = CO, CO2, CH4, C2H2 and C2H4) | |
| % | Mass balance closure for control volume | |
| % | Carbon balance closure for control volume | |
| s | Gas species in primary gas (CO, CO2, CH4, C2H2 and C2H4) | |
| Mass fraction of carbon-bearing species (s = CO, CO2, CH4, C2H2 and C2H4) | ||
| N | Number of carbon in carbon-bearing species | |
| MWs | g/gmol | Molecular weight of gas species s |
| kJ | Higher heating value of pine input stream | |
| kJ/g | Specific higher heating value of pine | |
| kJ/g | Specific higher heating value of char | |
| kJ/g | Specific higher heating value of gas species s where s = CO, CO2, CH4, C2H2 and C2H4 | |
| kJ | Higher heating value of the primary gas output stream | |
| kJ | Higher heating value of char output stream | |
| kJ | Higher heating value unaccounted | |
| % | Carbon conversion efficiency | |
| % | Cold gas efficiency | |
| % | Hot gas efficiency | |
| kJ | Sensible heat of the primary gas output | |
| kJ | Sensible heat of species s in primary gas | |
| K | Exit gas temperature | |
| A, B, C, D and E | Coefficients of Shomate specific heat capacity equation | |
| T′ | K/1000 | Temperature in the Shomate specific heat capacity equation |
| kJ/g K | Specific heat capacity of gas species s | |
| MJ/m3 | Volumetric heating value of primary gas, reported on an air equivalent basis | |
| g/cm3 | Density of the primary gas species s | |
| gC/g pine | Carbon mass fraction of pine as determined by ultimate analysis | |
| gC/g char | Carbon mass fraction of char as determined by ultimate analysis | |
| mgC/g liquid | Carbon mass fraction of liquid condensate as determined by total organic carbon (TOC) analysis |
Acknowledgements
Authors thank the United States Department of Agriculture-National Institute of Food and Agriculture (USDA-NIFA) for providing funding for this research through the Integrated Biomass Supply Systems (IBSS) project (2011-68005-30410).
Conflict of Interest
None declared.
References
- Escobar, J. C., E. S. Lora, O. J. Venturini, E. E. Yáñez, E. F. Castillo, and O. Almazan. 2008. Biofuels: environment, technology and food security. Renew. Sustain. Energy Rev.13:1275–1287.
- Huber, G. W., S. Iborra, and A. Corma. 2006. Synthesis of transportation fuels from biomass: chemistry, catalysts, and engineering. Chem. Rev.106:4044–4098.
- Boldrin, P., M. Millan-Agorio, and N. P. Brandon. 2014. Effect of sulfur- and tar-contaminated Syngas on solid oxide fuel cell anode materials. Energy Fuels29:442–446.
- Heyne, S., T. Liliedahl, and M. Marklund. 2013. Biomass gasification – A synthesis of technical barriers and current research issues for deployment at large scale. The Swedish Knowledge Centre for Renewable Transportation Fuels, Göteborg, Sweden.
- Cui, H., S. Q. Turn, V. Keffer, D. Evans, T. Tran, and M. Foley. 2010. Contaminant estimates and removal in product gas from biomass steam gasification. Energy Fuels24:1222–1233.
- Abdoulmoumine, N., A. Kulkarni, S. Adhikari, S. Taylor, and E. Loewenstein. 2012. Economic analysis of municipal power generation from gasification of urban green wastes: case study of Fultondale, Alabama, USA. Biofuels, Bioprod. Biorefin.6:521–533.
- Lysenko, S., S. Sadaka, and R. C. Brown. 2012. Comparison of the cost of hydrogen from air-blown and thermally ballasted gasifiers. Biofuels, Bioprod. Biorefin.6:673–685.
- Carpenter, D. L., R. L. Bain, R. E. Davis, A. Dutta, C. J. Feik, K. R. Gaston, et al. 2010. Pilot-scale gasification of corn stover, switchgrass, wheat straw, and wood: 1. parametric study and comparison with literature. Ind. Eng. Chem. Res.49:1859–1871.
- Aljbour, S. H., and K. Kawamoto. 2013. Bench-scale gasification of cedar wood – Part I: effect of operational conditions on product gas characteristics. Chemosphere90:1495–1500.
- Abdoulmoumine, N., A. Kulkarni, and S. Adhikari. 2014. Effects of temperature and equivalence ratio on pine Syngas primary gases and contaminants in a Bench-Scale Fluidized Bed Gasifier. Ind. Eng. Chem. Res.53:5767–5777.
- Perlack, R. D., and B. J. Stokes. 2011. U.S. Billion-Ton update: biomass supply for a bioenergy and bioproducts industry. Oak Ridge National Laboratory, Oak Ridge, TN. U.S. Department of Energy, 2011 Contract No.: ORNL/TM-2011/224.
- Burgess, D. R., H. Y. Afeefy, J. F. Liebman, and S. E. Stein. 2005. Gas phase thermochemistry data. inW. G. Mallard and P. J. Linstrom, eds. NIST chemistry WebBook. National Institute of Standards and Technology, Gaithersburg, MD.
- Agblevor, F., and S. Besler. 1996. Inorganic compounds in biomass feedstocks. 1. Effect on the quality of fast pyrolysis oils. Energy Fuels10:293–298.
- Oasmaa, A., and C. Peacocke. 2010. Properties and fuel use of biomass-derived fast pyrolysis liquids – A guide. VTT Technical Research Centre of Finland, Otaniemi, Espoo, Finland. Contract No.: VTT Publications 731.
- Phyllis2 Database for biomass and waste [Internet]. Energy Research Center of the Netherlands. (accessed 23 April 2014).
- Campoy, M., A. Gómez-Barea, F. B. Vidal, and P. Ollero. 2009. Air–steam gasification of biomass in a fluidised bed: process optimisation by enriched air. Fuel Process. Technol.90:677–685.
- van der Drift, A., J. van Doorn, and J. W. Vermeulen. 2001. Ten residual biomass fuels for circulating fluidized-bed gasification. Biomass Bioenergy20:45–56.
- Campoy, M., A. Gómez-Barea, A. L. Villanueva, and P. Ollero. 2008. Air−steam gasification of biomass in a fluidized bed under simulated autothermal and adiabatic conditions. Ind. Eng. Chem. Res.47:5957–5965.
- Cao, Y., Y. Wang, J. T. Riley, and W.-P. Pan. 2006. A novel biomass air gasification process for producing tar-free higher heating value fuel gas. Fuel Process. Technol.87:343–353.
- Zhou, J., S. M. Masutani, D. M. Ishimura, S. Q. Turn, and C. M. Kinoshita. 2000. Release of fuel-bound nitrogen during biomass gasification. Ind. Eng. Chem. Res.39:626–634.
- Lim, M. T., and Z. Alimuddin. 2008. Bubbling fluidized bed biomass gasification–performance, process findings and energy analysis. Renewable Energy33:2339–2343.
- Narvaez, I., A. Orio, M. P. Aznar, and J. Corella. 1996. Biomass gasification with air in an atmospheric bubbling fluidized bed. Effect of six operational variables on the quality of the produced raw gas. Ind. Eng. Chem. Res.35:2110–2120.
- Bingyan, X., L. Zengfan, W. Chungzhi, H. Haitao, and Z. Xiguang. 1994. Integrated energy systems in China – the cold northeastern region experience – circulating fluidized bed gasifier for biomass. Natural Resources Management and Environment Department, United Nation Food and Agricultural Organization, Rome, Italy. Report No. (accessed 28 November 2013).
- Li, X. T., J. R. Grace, C. J. Lim, A. P. Watkinson, H. P. Chen, and J. R. Kim. 2004. Biomass gasification in a circulating fluidized bed. Biomass Bioenergy26:171–193.
Document information
Published on 01/06/17
Submitted on 01/06/17
Licence: Other
Share this document
Keywords
claim authorship
Are you one of the authors of this document?