A Utilization-based Genetic Algorithm for Solving the University Timetabling Problem (UGA)

Abstract

Building university timetables is a complex process that considers varying types of constraints and objectives from one institution to another. The problem solved in this paper is a real one featuring a number of hard and soft constraints that are not very conventional. The pursued objective is also novel and considers maximizing resource utilization. This paper introduces a genetic algorithm that uses some heuristics to generate an initial population of feasible good quality timetables. The algorithm uses a simple weighted sum formula to respect professors’ preferences and handle conflicts. In order to reduce waste, a crossover type focusing on the utilization rates of learning spaces is introduced. A targeted mutation operator that uses a local search heuristic is also employed. The algorithm applies a composite fitness function that considers space utilization, gaps between events and a maximum number of lectures per day. A large dataset with real data from the Faculty of Commerce, Alexandria University in Egypt was used to test the contributed algorithm. The algorithm was also tested against two difficult benchmark problems from the literature. Testing proved that the developed algorithm is an effective tool for managing timetables and resources in universities. It performed remarkedly well on the large datasets of the two benchmark problems and it also respected more constraints than those stated in the initial problem statement of the two benchmark datasets.

Keywords

University timetabling; Resource management; Space utilization; Genetic algorithms; Higher education problems; Egypt

1. Introduction

Timetabling is an NP-hard optimization problem [1], [2] and [3], for which a good solution needs to be found among a set of complex variables and constraints. The problem is to assign a feasible tuple of variables which optimizes a set of metrics and indicators such as minimizing time gaps, maximizing space utilization, and minimizing cost relevant to the use of resources [4]. Finding an efficient algorithm for such problems is hard and complex especially when the problem gets larger. According to Tovey [5], good solutions can be provided when the problem is better understood in terms of its hardness or simplicity. Organizations such as educational institutions use timetables to schedule classes and/or lectures by assigning times and places to future events in a way that makes optimal use of the available resources [6], [7], [8], [9] and [10]. Universities increasingly deal with a large number of courses, groups and professors. Poorly designed timetables are not only inconvenient, but also result in significant losses in terms of time, effort and money.

Allocation of spaces inside university campuses is growing more and more important. Spaces inside universities include rooms, halls, amphitheatres, offices, parking lots. The increasing number of students flowing every year increases the need for managing and utilizing these spaces. Space allocation problems are also NP-Hard as timetabling problems. There exists P^E ways of allocating E events to P places when searching for an optimal solution [11]. This implies that no efficient algorithm exists to solve large instances of these problems in a reasonable time [12]. Variations in the size of the problem, its constraints and objectives will also affect the time required to perform space allocation while guaranteeing good utilization levels of spaces [13].

In her report “The black holes of space economics”, Shove [14] has pointed out the interdependent and conflicting interests of students, lecturers, timetablers and administrators. She highlighted that each has his own interest in utilizing spaces and his own definition of what effective space management means. Shove explained that overestimating the need for more spaces is a rational response to uncertainty. She confirmed that this is the case when space is being viewed as a free good in the absence of a proper plan and vision to target good utilization levels. Poor space allocation can force the decision maker to provision unneeded resources. When solving the space allocation problem in higher education, the different spaces available, the different uses of each space, the timeslots in which it is available and all other constraints need to be identified. In academic institutions, manual approaches to solve resource allocation problems may result in wasting a large number of resources that could be better managed and utilized.

A key aspect that motivated this research is that previous studies focused much on the computational time of the algorithms proposed [15], [16], [17], [18], [19] and [20], even when considering a small problem instance and few constraints. In contrast, the reality of the Egyptian public universities, with the limited resources available and the large numbers of students and professors they have, forces us to assign priority to the real problems together with their relevant constraints. In fact, the computational time and power should no longer be the focus for this type of problems, where solutions are not instantly needed. Even if the developed algorithms take relatively longer time, they would at least be capable of the following: (i) responding to a real problem with its constraints, (ii) addressing big size problem instances and (iii) taking less time than the manual process because constructing timetables starts a long time before they are actually needed [21] and [22].

This paper presents a genetic algorithm for solving a university course-timetabling problem. The studied case is of the Faculty of Commerce, Alexandria University, Egypt, where building undergraduate semester timetables start six weeks before the academic semester begins.

This paper is organized as follows: Section 2 reviews the related work on the timetabling and space allocation problems. Section 3 describes the contributed solution methodology. Testing and results are presented in Section 4. Section 5 includes the conclusion and future work and an acknowledgment is made in last section.

2. Related work

University course timetabling problems are defined by Carter and Laporte [23] as multi-dimensional problems, in which a number of students and professors are assigned to lectures and events. An event is a pair of a suitable room and timeslot [24]. In [25], the author stated that rooms and space allocation decisions are problems associated with the timetabling procedures inside institutions. Burke and Varley [26] also agreed that space allocation and timetabling problems in academic institutions are strongly correlated. Schaerf [27] conducted a survey to collect necessary information to understand the different timetabling problems and the different methods and approaches used to solve them. He claimed that the basic concept behind all the approaches used relies on “scheduling the most constrained lectures first”, and the thing that differentiates one from another is how the expression “most constrained” is defined in the different problems being solved. Space allocation in universities and academic institutions is the assignment of a set of lectures or meetings to a set of rooms and timeslots [26], [28] and [29].

Burke and Varley [26] made many efforts toward defining and discovering the different dimensions and requirements of the space allocation problem inside ninety-six universities and academic institutions in the United Kingdom. They collected the information from universities using questionnaires. The questionnaires stressed on three main aspects: the size and diversity of the space allocation process, the tools used to automate the space allocation process and the constraints considered when allocating these spaces. The main purpose of this survey was to discover whether a generic solution to the problem could be articulated or the variance among universities will prohibit such approach. They have concluded that a generic system for the space allocation must be able to satisfy all the requirements specified by a university.

Different approaches that were used in solving the space allocation problems were also used in solving the timetabling problems. These include simulated annealing [30], [31] and [32], tabu search [15], [33], [34] and [35], integer programming [36] and genetic algorithms [37], [38] and [39]. Some contributions are as follows.

Sutar and Bichkar [16] introduced a genetic algorithm to solve a real university timetabling problem in India. An initial population is randomly generated and parents are selected for crossover based on their fitness values. All the produced offsprings from crossover are subject to mutation; however, the crossover and mutation operators’ implementation applied were not clear in their work. In the set of hard and soft constraints, learning space capacities were not mentioned. Lectures’ timeslot availabilities were not prioritized but minimum and maximum limits of weekly working hours for each were set.

Rakesh and Gupta [40] built a university course timetable using a hybrid algorithm. They used the genetic algorithm and iterated local search to avoid getting trapped in local optima. The objective of their approach was to satisfy the set of hard constraints and minimize the violation of the soft constraints. The hard constraints include having students attend one event at any timeslot, assigning all events to suitable spaces with adequate number of seats, and assigning only one event to any one room in any timeslot. The soft constraints were about avoiding scheduling events in the last day slots, avoiding scheduling more than two consecutive events in a day for students, and ensuring scheduling more than one event in a day for all students. Their hybrid algorithm did not take into account the utilization rate in the proposed objective function.

El-Sherbiny et al. [41] proposed a combination of a hill climbing optimization and genetic algorithm to build a university course timetable. The objective of the authors was to minimize violating any of the soft constraints. The set of the hard constraints respects that teachers or professors must not be assigned to more than one class in any timeslot, a class could not be assigned to more than one teacher in a timeslot, and the room cannot be allocated more than once at any given timeslot. Additionally, the algorithm should respect a certain number of timeslots per week and a class should attend a certain number of lectures per week. The utilization of spaces was considered in the set of soft constraints represented in a cost function. The cost function aims to minimize the difference between the number of students attending and the capacity of the learning space.

Socha et al. [42] proposed two ant systems for solving university course timetabling: the ant colony system (ACS) and the MAX–MIN ant system. Their objective was to minimize the number of soft constraint violations in feasible timetables. These constraints included the following: minimizing the number of classes students can take in end of day slots and minimizing the probability of a student having more than one class per day. Both algorithms start with a population of ants, where each ant starts building a timetable by assigning all the events to timeslots. Ants choose timeslots probabilistically based on heuristic information and a matrix of pheromone values. However, the two proposed algorithms differ in their ways of updating pheromone values. The MAX–MIN ant system uses a global update rule that sets upper and lower bounds to control the maximum difference between the highest and lowest pheromone levels. On the other hand, the ACS adds to the global update rule a special local update rule. This local update is applied to the selected element in the pheromone matrix, corresponding to a certain timeslot (t) for an event (e), to decrease the probability of other ants to choose the same timeslot for the same event and to encourage them to choose other timeslots. After assigning all events to timeslots, rooms are assigned and a hill climbing local search heuristic is applied to improve the solution produced. Space capacities and the numbers of students attending were taken into account as hard constraints.

Lü and Hao [15], developed an adaptive tabu search, in which an initial timetable was constructed using a greedy search heuristic. This greedy search starts with an empty schedule and starts assigning lectures by selecting an unassigned lecture and a suitable period-room event. However, greedy search heuristics tend to work efficiently at the beginning of the timetable construction process while causing conflicts in assigning later events [32]. The objective of the method was to minimize the number of soft constraint violations in a feasible timetable. Although teachers’ timeslot availabilities were considered a main hard constraint, no prioritization approaches were incorporated to handle this issue if the number of available slots for more than one teacher is the same.

Sabar et al. [18], introduced a honeybee mating optimization algorithm (HBMO) to solve examination and course timetabling problems. The objective was to satisfy the set of hard constraints and to minimize the number of students affected when a soft constraint is violated. Sabar et al. [18] used the least saturation degree first (SD), the largest degree first (LD) and largest enrollment first (LE) heuristics with the honeybee algorithm to create initial feasible timetables. The crossover employed is done through selecting two random genes (timeslots) from the queen and a drone and moving all the events from timeslot1 (T1), for example, in the queen to timeslot2 (T2) in the drone. A successful move takes place if an event does not conflict with the events in the new timeslot or if it does not already exist in that new timeslot. A mutation operator that swaps a subset of events between two timeslots is applied for preventing a drone’s sperm from being used again in another mating flight. The authors show that the honeybee mating optimization algorithm is a promising approach in solving educational timetabling problems. The set of hard constraints is very much similar to those of previous contributions. This set includes allocating events according to room capacities. Professors’ availability timeslots and preferences are neither considered hard nor soft constraints.

Chen and Shih [20] used two Particle Swarm Optimization (PSO) types: the inertia weight and constriction versions to construct university timetables. The objective was to respect as much soft constraints as possible to increase teachers’ and classes’ satisfaction. In the set of soft constraints, teachers’ preferences as well as students were respected. Teachers’ preferences were collected through questionnaires that ranked timeslots in numbers from 1 to 5 from the least favorable to the most favorable timeslot by a teacher and number −10 for impossible-to-schedule timeslots. However, no hard or soft constraint mentioned the importance of respecting room capacities. Chen and Shih concluded that prioritizing teachers is an effective factor with significant effect on timetables quality [20]. This aspect is considered in the research presented in this paper.

Genetic algorithms were chosen to solve the problem of this paper because they are known for their robustness [43] and [44] in solving complex combinatorial problems. Genetic algorithms are characterized by their flexibility and ability to search in complex, large spaces [45]. They are considered one of the most powerful tools in solving course and exam timetabling problems [46], [47] and [48]. Moreover, genetic algorithms have the advantage of being adaptive search algorithms [49].

3. Methodology

Developments made in the area of timetabling resulted in launching the Practice and Theory of Automated Timetabling (PATAT) series of conferences, which sponsors the International Timetabling Competition (ITC) [50]. This competition aims at encouraging research in the area of timetabling to bridge the gap between theory and practice in real-world applications. This paper proposes a novel approach to tackle a real world big size timetabling problem. Due to the complexity of the timetabling problems, a wide range of heuristics is used to find feasible solutions [4], [18] and [50]. This paper contributes to a genetic algorithm approach that allocates teaching events to spaces and timeslots. It uses a number of heuristics to find initial feasible solutions and it considers the following set of hard and soft constraints:

• Hard constraints
• Professors are assigned timeslots of their preferences according to a certain priority measure.
• Number of students is compatible with room capacities.
• Professors are not assigned to different rooms at the same timeslot.
• Student groups are not assigned to different rooms at the same timeslot.
• Fridays and end of day slots are not permitted (weeks start Saturday and end Wednesday).
• All timetables should include all the lectures.
• Soft constraints
• No more than two lectures per day for every professor.
• No more than two lectures per day for every group.
• No gaps between lectures for a group.
• No gaps between lectures for a professor
• Occupancy rate of each event either is not less than 75% or equals to 0%.

Most of the studies conducted to construct university timetables did not consider timeslot availability for each professor as a hard constraint [51], [52], [53], [54], [55] and [56]. Some others did not consider it even as a soft constraint [18]. The main focus is often directed toward avoiding the infeasibility of having two lectures at the same time; for a professor or a group, the capacity of rooms is considered based on a predicted number of attendees [57], [29], [58] and [9] without encompassing more real life hard constraints such as professors’ preferences and their timeslot availabilities. Few contributions considered professors’ preferences as a soft constraint [60], [61], [52] and [16]. Badri [60] constructed a departmental timetable that considered professors’ preferences in two phases: first, a matrix that maximizes the faculty member’s preference for courses; and second, he maximizes the faculty member’s preferences for timings of the lectures at the University of United Arab Emirates. Some researchers suggested the introduction of utility functions for professors’ preferences that can help in building timetables [62], [63], [64] and [65]. Schniederjans and Kim [66] argued that building such functions requires a lot of effort and time that can practically be an obstacle. Aljarah et al. [55] considered professors’ preferences and adopted a mining technique only to substitute the process of collecting information from every professor at the beginning of every semester. To avoid using complex functions and mining algorithms, this paper considers a simple to implement and a practical weighted sum formula to prioritize professors’ preferences. Respecting professors’ preferences aims at reducing the effort needed to reallocate assignments in later stages and to make major timetable modifications more than once over few days.

In the following subsections, the authors introduce a genetic algorithm by examining its representation, the selection process of chromosomes, its fitness function and the crossover and mutation operators.

3.1. Representation

Representations play a role in the performance of the algorithm during the search process [67]. Different chromosome representations are used to represent course timetables [68], [53], [69] and [56]. Montana et al. [45] suggested that the best representation of a chromosome differs from a problem to another depending heavily on the constraints and requirements of each problem. For simplicity purposes, some researchers represent timetables in the form of binary strings [43]. Dhande et al. [48] stressed that this simple representation is not an ideal approach and that there is no clear alternative to it.

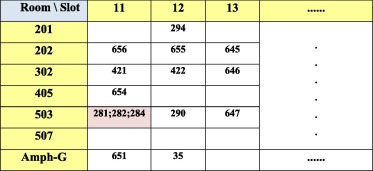
The authors introduce a generic two-dimensional chromosome representation that can easily fit with different university course timetabling problems (see Fig. 1). A list of all the rooms is presented in the first column. The first row of the chromosome represents all the timeslots. Timeslots consist of two main parts: the day and the timeslot order in that day represented in the form of two numeric values. For example, Saturdays are assigned number “1” because it is the first day in the week. Events are scheduled over only 10 h. Lecture durations can be of two or three hours. Each day consists of a maximum of five timeslots in case only two hours lectures are scheduled and a maximum of three slots in case only three hours lectures are scheduled. The two-hour duration lectures are assigned to a subset of the large rooms. Smaller rooms are dedicated to the three-hour duration lectures. This is because large rooms at the Faculty of Commerce are few and frequently needed. Each timeslot is given an ID. If a slot ID is “11”, this means it is the first timeslot (from 8.00 AM to 11.00 AM) on “Saturday”; an ID of “12” refers to the second timeslot (11.00 AM–2.00 PM) on Saturday and so on. The numbering system also continues to represent the two hour duration slots.

Figure 1. Example of chromosome representation.

In Fig. 1, intersections between rooms and timeslots represent the potential combinations where events can be assigned. Intersections are filled with the event ID. Event IDs are composite attributes that represent three aspects at a time: the group ID to be assigned, the professor ID involved in teaching this group and the course ID the professor teaches to this group. For example, event ID “294”, in the intersecting cell between room “201” and timeslot “12” represents professor ID “7” who teaches group ID “33” the course ID “66”. Having more than one event ID in a cell like the intersecting cell of room “503” and timeslot “11” means that a number of event IDs share the same course and professor and should be scheduled together. In reality, this corresponds to two or more groups, maybe from different departments, who attend the same lecture. Room capacity constraints are respected in this case.

3.2. Selection

Genetic algorithms are population-based metaheuristics that start with a pool of solutions to select from [9]. Creating an initial population starts with an empty timetable. Most of the solutions proposed in the literature rely on random assignment of events to create an initial population [10]. However, [71], [58], [72] and [55] suggested that random generation methods do not, in many cases, guarantee producing good quality or even feasible solutions. A set of feasible as well as infeasible solutions are obtained when randomly generating an initial population. In some cases, the set of infeasible solutions is discarded and the remaining set of feasible solutions is used to produce upcoming generations [24]. In other cases, the set of infeasible solutions is not discarded but repaired to turn them to feasible solutions using some heuristics [42], which requires more computational time. An advantage of starting with good initial feasible solutions is increasing the probability of directing the search toward better regions of the search space to help further convergence toward better solutions [18]. In this work, the authors use some heuristics to generate initial good quality feasible timetables that do not violate any of the hard constraints. A combination of some heuristics suggested by [18] is applied with the objective of narrowing the search space and reducing the probability of getting infeasible solutions [73]. These heuristics are presented in Sections 3.2.1 and 3.2.2.

3.2.1. Largest degree first (LD) heuristic

Sabar et al. [18] recommended creating initial solutions by assigning the most conflicting events first. Conflicting events differ from institution to another as the set of hard and soft constraints differs. In this paper’s problem, professors’ preferences are considered when constructing timetables. The most conflicting events are the events for which professors have very few numbers of available suitable timeslots. This means that if a professor has only one available timeslot to deliver the lecture, it will be infeasible to assign him/her to any other timeslot. In the “Largest Degree First” (LD) heuristic, events are ordered, in a decreasing order by the number of conflicts they have with all other events. The authors use this heuristic to order the list of events in an ascending order by their professors’ availability timeslots to start the assignment of professors with least availabilities.

The studied problem size is large. The number of professors involved is 131 and there can be more than two professors with similar few numbers of available timeslots. As a result, prioritization among professors is considered in order to determine which event is to be assigned first and to avoid conflicts. This is achieved by implementing a weighted sum approach that assigns weights to professors according to the factors in Table 1.

Table 1. Factors based on which weights are calculated.

Factor	Weight
Part-timer	0.5
Academic rank	0.3
No. of groups taught per professor	0.2
Age (50–75 years old)	0.1

The table shows the factors and the weights of each factor based on which a weighted sum is calculated for every professor. The first factor is whether the professor is a part-timer, who comes to campus only for teaching the course at the faculty but not a member of the Faculty of Commerce staff. This factor is assigned the highest weight (0.5), due to the inflexibility of finding alternative timeslots for part-timers. Secondly, the number of groups each professor teaches is examined. In year 2012–2013 in the first semester at the Faculty of Commerce, the minimum number of groups a professor was assigned to was one group and the maximum number was nine groups. Taking the average of both, gives us a number of five groups. Thus, if the number of groups a professor will teach is five or greater, he/she is given priority relative to a professor with a less number of groups and a weight of 0.3 is assigned. Thirdly, the academic rank of a professor is considered. If the professor is an associate professor or higher, a weight of 0.2 is given. The age of the professor is another important factor where elder professors’ preferences are a priority. If the age of the professor is between 50 and 75 years old, a weight of 0.1 is added. Since, no weighted sum approaches for prioritization were proposed in the literature, the weights assigned to the factors in this work are proposed based on their level of significance as concluded by the authors from the practices followed in building timetables at the Faculty of Commerce, Alexandria University. These weights are thus adjustable according to the problem under study. It is also possible in following semesters that weights change in their level of significance for the same faculty.

In the proposed methodology, professors whose summed weights were 0.4 or greater are referred to as “high weight”. Population initialization starts with this list of high weight professors, who require priority assignments. This list is then sorted in a descending order based on the weights. If two professors have the same weight, the number of their available timeslots is compared so that the professor with less availability is selected first. If the number of available timeslots for both is the same, their academic ranks are then compared. If the academic rank of one professor is greater than the other, his preference is considered first. If both ranks are the same, the number of groups each professor teaches are then compared using the “Largest Enrollment First” (LE) heuristic [18]. In the case where both share the same number of groups, the age is checked so that the oldest is selected.

This assignment process is repeated until all high weight professors are assigned. Afterward, the rest of professors with weights less than 0.4 and more available timeslots are assigned.

3.2.2. Largest enrollment first (LE) heuristic

The largest enrollment first (LE) heuristic deals with the number of groups each professor teaches. Accordingly, professors with the greatest number of groups are given priority in assignment. By applying this, the authors are able to narrow the search space and deal with the assignments that might increase the chance of getting an infeasible solution.

When scheduling an event, the search process starts with a list of suggested rooms identified by their capacities so that best fit room capacities are suggested. For example; if the number of attendees in a group is 300, the list of suggested rooms will be those with capacities between 300 and 400 maximum, while, greater capacities (500–600) will not be proposed to ensure efficient resource utilization. When a suitable room is found, the search space is then explored for a timeslot that matches the professor’s preference. If none of the suggested rooms is available at any suitable timeslot, greater room capacities can then be proposed. The genetic algorithm proposed is illustrated by the pseudo-code in Table 2.

Table 2. UGA Pseudo-code.

1.	Input: A problem instance I
2.	Set the maximum number of iterations (Iter) as a stopping criteria, Iter = T
3.	Set the maximum population size (Y)
4.	Set the maximum number of crossover iterations (C), C = Y/2(Y/2-1)
5.	The number of mutation iterations (Iter_M) = the number of underutilized rooms (U) in the chromosome on hand. Iter_M = U
6.	Generate initial population of chromosomes = Y using LD and LE heuristic
7.	Evaluate the fitness value of each individual
8.	Sort individuals descending based on their fitness values
9.	Select the best individual as the best solution so far
10.	While (Iter <= T)
11.	Select (Y/2) number of the first best individuals from the previous population
12.	For i = 1 to C
13.	Perform utilization crossover among the best-chosen chromosomes and add the produced chromosomes to the (Y/2) individuals
14.	Evaluate fitness value of the new population chromosomes
15.	Select the best (Y) number of chromosomes as parents for the next generation and discard the rest
16.	Select the one best chromosome so far from the (Y) chromosomes
17.	Compare its fitness value with the best chromosome so far on hand
18.	If (new best individual fitness > on hand old best individual fitness)
19.	Replace the old best chromosome with the new one
20.	End if
21.	End for
22.	While (Iter_M <= U)
23.	Apply targeted mutation using (Simple Descent) to improve the best chromosome on hand
24.	Evaluate fitness value of the new child
25.	If (new best individual fitness from mutation > old best individual fitness)
26.	Replace the old best chromosome by the new one produced from the current mutation
27.	End if
28.	End while
29.	End while
30.	Output: The best chromosome achieved for the problem instance I

In line (6), the algorithm uses the largest enrollment (LE) and the largest degree (LD) heuristics to generate a predetermined number of chromosomes (Y) to form the population. In line (7), fitness values of the chromosomes produced are calculated and the best half of the chromosomes (Y/2) are selected for crossover, while discarding low fitness value chromosomes. In line (13), crossover takes place between two chromosomes to produce new two offsprings. The old parents are also added to the new population. Then, their fitness values are sorted in a descending order to choose the first chromosomes with highest fitness values and exclude the rest. The new generation of chromosomes becomes the input for creating the next population following the same steps.

After each crossover, a mutation operator is applied to the best solution found so far to obtain a better fitness value. The number of mutations in a chromosome depends on the number of the underutilized events in the solution. This process is repeated until the maximum number of iterations (Iter) is reached.

3.3. Fitness function

Fitness functions are functions calculated for every candidate solution to measure how “fit” or “good” it is [74], [43] and [75]. This function is problem-specific and does not have a standard formula of calculation [58]. In university timetabling problems, common fitness functions are based on calculating the number of unscheduled events [76] and [59]. This calculation is too simplistic and involves that some events may remain unscheduled which violates the hard constraints. In this paper, a feasible solution is one that does not include any unscheduled event. Erben and Kepplar [37] calculated the fitness value based on the violation of soft constraints assuming that they accept only feasible solutions with zero unscheduled events. This was also done by [16] and [70]. In [18], the objective was to satisfy all the hard constraints and to minimize the number of students affected by the violation of any soft constraint. Lewis and Paechter [58] created a function that calculates the number of extra timeslots used than the number planned to be used, in addition to, the number of events contained inside each extra timeslot. According to [77] and [35], the fitness function is a weighted sum calculated based on the violation of soft constraints.

Space utilization rate measures are used to calculate the fitness function of the problem studied in this paper. Space utilization rates are used to measure the efficiency in using a certain space relative to its capacity as well as its availability. Utilization rates (see Eq. (1)) are the product of two other rates called the frequency rate and the occupancy rate [78]. Frequency rates are rates that measure how often a room is used relative to the total number of hours during which it is available (see Eq. (2)) [28], [79] and [28]. On the other hand, occupancy rates are rates that measure the extent to which a room is fully occupied relative to its total capacity (see Eq. (3)) [80].

Utilization rate/room

$\left({\mbox{Freq}}.\quad {\mbox{Rate}}/{\mbox{Room}})\ast ({\mbox{Occup}}.\quad {\mbox{Rate}}/{\mbox{Room}}\right)$

(1)

Frequency rate/room

${\mbox{Total hours used}}/{\mbox{Total No. of hours the room is available}}$

(2)

Occupancy rate/room

${\mbox{No. of occupied seats}}/{\mbox{Total capacity of the room}}$

(3)

According to the Higher Education benchmark standards used by the universities of Wisconsin; Singapore; New Zealand; Australia and Hong Kong, a percentage of 56 or higher is the benchmark used to represent good utilization rates of a space and a percentage of 75 or higher is used for representing good frequency and occupancy rates for rooms. In this paper, the authors followed the same standard rates as the previously mentioned universities.

To get the utilization rate of a room in a day, the averages of both the frequency and occupancy rates of that day are multiplied. Similarly, when calculating the utilization rate of a room in a week, the averages of the frequency and occupancy rates of that week are multiplied. In this work, the fitness function is a composite function that calculates the fitness of a certain chromosome based on a number of important factors. These factors are as follows:

• No of events with best occupancy rates.
• No of rooms with best frequency rates.
• Any gap between two lectures per day for a professor or a group.
• Assigning more than two lectures per day for a professor or a group.

During the algorithm-testing phase, the authors discovered that the fitness values of some of the generated timetables were the same while the table structure of one could be better than the other. Then, the authors decided to assign weights to the factors they consider more significant and to calculate a corresponding weighted sum. The weights assigned to the factors are shown in Table 3.

Table 3. Weights assigned to each factor used to calculate the fitness function.

Factor	Weight assigned
No of events with best occupancy rates (⩾75% or zero)	4
No of rooms with best frequency rates (⩾75%)	3
Any gap between two lectures per day for a Prof. or a Group	2 (penalty)
Assigning more than two lectures per day for a Prof. or a Group	1 (penalty)

From Table 3, both occupancy rates and frequency rates are included in the calculation of the fitness function because they are used to calculate utilization rates. However, the weight assigned to the events with best occupancy rates (equals to 4) is greater than the frequency rates (equals to 3), because the efficient utilization of spaces is more important than the frequent usage of rooms. Finding gaps between two lectures for a professor or a group is given a penalty of two. Finally, assigning more than two lectures per day for a professor or a group is given a penalty of 1. The factors and the weights can be changed if the level of significance of any of the factors changes. This is calculated by the equation mentioned below:

${\mbox{Fitness}}\quad (C)=\sum _{i=1}^{4}w_{i}k_{i}$

(4)

where (C) refers to a chromosome (candidate solution), and (w) refers to the weight assigned to the factor (k), where (k) refers to any of the factors from 1 to 4 in Table 3. The weight (w) takes a positive value for factors 1 and 2 and takes a negative value (penalty) for factors 3 and 4.

3.4. Crossover

There is no one unified standard method of crossover. It has various types and forms [53], [81], [16] and [70]. Some population-based algorithms do not employ the crossover operator [82] and [83]. The reason behind this may be due to the complexity of its application while keeping the solution feasible [18]. Simply, crossover means; recombining parts from two parent chromosomes in order to form new offsprings that may have better fitness values than the two parents [35]. A common crossover strategy followed by many researchers is the point crossover method [43], [45] and [48]. In point crossover, a chromosome is split at a point (gene), that is usually randomly selected [8] and [10] and exchanged by the same split part of the second chromosome to swap the two parts together [84]. Crossover techniques also differ according to the representation of the chromosome itself.

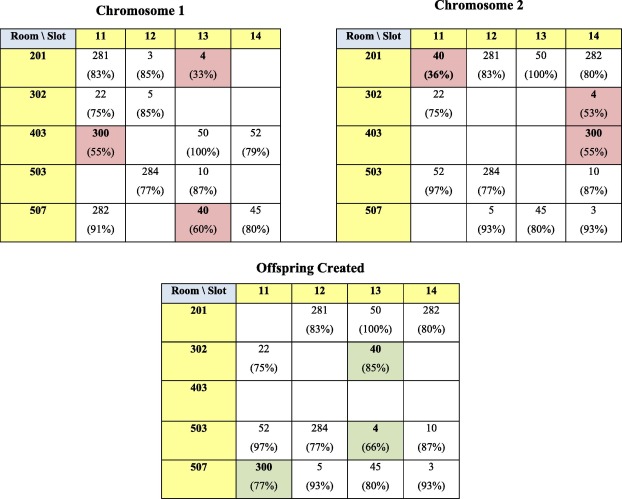
The authors introduce a crossover type that they named “utilization crossover”. This crossover focuses on the utilization rates of teaching spaces. Observations from running the algorithm revealed that, in many cases, chromosomes hold close utilization rates of some events although they differ in their placements in the timetable from a chromosome to another. Utilization crossover aims at reducing the number of the under/over-utilized events (with occupancy rates less than 75% and greater than 100%, respectively) as much as possible to increase the number of well-utilized events in a chromosome. This is achieved through obtaining a list of all the underutilized and over-utilized events from one chromosome and randomly selecting 50 percent of the events from this list to be assigned to other random rooms, within the same timeslot, in the other chromosome. When selecting any event, its utilization rate, in the other chromosome, is obtained so that an accepted move takes place if the utilization rate of the moved event is improved in the new place without violating any hard constraint. If a successful move takes place, the event is then removed from its old place in the new chromosome to avoid duplication (see Fig. 2).

Figure 2. Chromosomes’ snapshots to illustrate utilization crossover logic.

From Fig. 2, three underutilized events with the IDs (4, 40 and 300) were detected in chromosome one. In the second chromosome, these events’ occupancy rates were found to be underutilized as well. Thus, random suggested rooms were introduced aiming at achieving improved rates without violating the event’s professor timeslot preference. Successful moves took place for event ID (40) from room 201 with 36% occupancy rate to 85% in room 302. Similarly, this happened for event IDs (4 and 300) where occupancy rates have improved from 53% in room 302 to 66% in room 503 for ID (4) and from 55% in room 403 to 77% in room 507 for event ID (300).

3.5. Mutation

Mutation is the last step of improving a chromosome [43], [50] and [16]. Mutation is similar to crossover except that it makes changes in a chromosome itself. Most of the mutation strategies follow a random selection approach (e.g. roulette wheel) to make modifications in a chromosome [10], in which it randomly selects a timeslot and a room for a certain course or lecture to be assigned to.

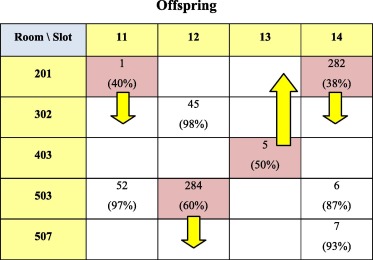
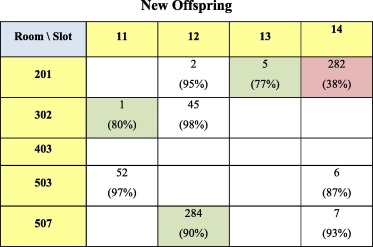
The mutation operator used is “targeted mutation” [67] which focuses on targeted parts of the chromosome and not on random selections. Therefore, to reach more efficient utilization rates of spaces, the targeted parts for the mutation process are the events with low occupancy rates. A simple descent search heuristic is applied as a local search to improve the chromosome. A list of the underutilized events (with occupancy rates less than 75%) is obtained. In order to improve the best solution obtained, random events are chosen from the list and the simple descent examines their neighborhoods. A neighborhood is obtained by moving one event from its current room to another randomly selected room within the same timeslot in order to respect professors’ preferences while improving utilization. This is unlike [18] and [85], where the neighborhood of a solution is obtained by moving an event from one slot to another random slot within the same room. A successful move takes place when no hard constraint is violated and the new solution replaces the old if its fitness value is better; otherwise things are left unchanged (see Offspring snapshot before mutation Figure 3 and Figure 4). The algorithmic parameters used in the proposed approach are presented in Appendix A.

Figure 3. Offspring snapshot before mutation.

Figure 4. New offspring snapshot after mutation.

From the figures aforesaid, it is clear that three events made successful movements out of four. The reason behind leaving the event ID (282) unchanged is either due to violating any of the hard constraints or due to resulting in an unchanged or worse occupancy rate.

4. Testing and results

This section investigates the proposed methodology. It is divided into four subsections. The first is on the description and the evaluation of the case of the Faculty of Commerce in Alexandria University, which is an important real complex problem rich with constraints that motivated the work presented in this paper. The second subsection demonstrates the solution of the problem using the UGA contributed in this paper. The third subsection discusses the applicability of the UGA to other problems including other soft and hard constraints. Lastly, testing UGA against benchmark problems, to prove its generality and capability to deal with the hardest timetabling problems, is presented in the last subsection.

4.1. Current case evaluation

The studied case is of the Faculty of Commerce-Alexandria University, Egypt, where building undergraduate semester timetables starts six weeks before the academic semester begins. Personnel build the timetable based on a semester course plan communicated by the academic departments. There are four main divisions at the bachelor level inside the faculty: the Arabic (AR) division, the Affiliated Arabic division (AA), where students are evaluated using different methods, the English (E) division and the French (F) division. Each division can study in seven specialties starting from the third academic year in a four-year based education system where the academic year consists of two semesters. In the first semester for year 2012–2013, the number of professors involved in teaching was 131 and the number of courses taught was 150 (including courses taught in the three different languages). Thirty-two learning spaces were available and 337 events were considered to construct a timetable over a seven-day week. The academic week starts on Saturdays and the number of lecturing hours per day is 12 from 8:00 a.m to 8:00 p.m. The faculty builds the timetable centrally for the seven departments and all the student groups. The Faculty of Commerce is one with a very large number of students (between 10 and 2650 per group in year 2012–2013) and a total of 57 groups (see Table 4). Hard constraints include assigning professors to timeslots of their preferences, respecting room capacities, avoiding lectures’ conflicts for professors and groups, excluding Fridays and end of day timeslots, and assigning all the lectures to the timetable. Professors’ preferences are collected from professors before the semester begins. The set of soft constraints includes respecting a maximum number of lectures per professor and per group in one day, decreasing gaps between lectures for a professor and for a group and targeting either no less than 75% or 0% occupancy rate for each allocated event. The objective pursued in the paper is reflected in the fitness function that considers the soft constraints together with the best frequency rates for a room per day. Occupancy and frequency rates are defined in Section 3.3.

Table 4. Description of the actual problem instance in 2012–2013 at faculty of commerce.

Item	Data
No. of lecturers	131
No. of courses	150
No. of departments	7
No. of students	Between 10 and 2650
No. of groups	57
No. of rooms	32
No. of events	337
No. of days	7
No. of hrs to schedule/day	12

The described case was selected for a number of reasons:

• The faculty does not follow any automated approach when constructing timetables. Thus, it was a fresh ground to test the contributed approach.
• The problem size is very large and complex in terms of the following: the number of students enrolled each year, the number of groups, the number of departments, the number of professors, and the limited number of teaching spaces.
• The large number of common lectures among student groups from different departments.
• The faculty works seven days a week including Fridays to be able to find a room to assign events.
• Lectures’ time durations are not standardized; some are three-hour and others are two-hour duration. This makes it harder to assign events while avoiding intersections.

Starting with the manual solution applied by the university, in 2012–2013 timetables, a number of events were inefficiently scheduled to incompatible rooms in the faculty. The actual problem description of the Faculty of Commerce in semester one for year 2012–2013 is illustrated in Table 4.

Average occupancy rates for rooms per day in year 2012–2013 determined by the manually developed timetable are shown in Table 5 and Table 6.

Table 5. Manual avg. occupancy room rates per day in semester one for year 2012–2013.

Room/day	Sat (%)	Sun (%)	Mon (%)	Tue (%)	Wed (%)	Thu (%)	Fri (%)
201	33	0	17	0	67	3	0
202	87	8	33	42	4	2	0
203	83	0	0	0	89	0	0
301	11	0	20	31	22	14	0
302	127	87	67	50	53	33	0
303	8	0	2	3	12	1	0
401	27	35	40	13	0	0	0
403	32	40	40	8	13	35	0
405	48	40	21	27	27	48	0
407	33	6	13	2	18	6	0
501	1	60	2	0	47	93	0
503	47	0	0	0	80	0	0
506	1	0	2	1	0	0	0
507	12	73	7	13	0	13	0
601	6	15	27	167	3	87	0
603	4	0	27	0	6	12	0
605	7	3	7	33	0	0	0
705	27	3	17	0	87	0	0
707	0	0	0	0	0	0	0
91	0	0	0	0	0	0	0
92	0	0	0	0	0	0	0
93	0	0	0	0	0	0	0
94	0	0	0	0	0	0	0
95	0	0	0	0	0	0	0
1	7	0	0	13	0	0	0
2	24	17	11	7	16	13	0
3	32	30	43	0	30	0	0
4	190	404	0	7	404	9	0
5	1	64	3	0	43	0	0
6	90	150	120	83	74	65	30
7	88	45	128	0	95	139	32
8	7	333	0	0	40	27	0

Table 6. Summary results of Table 5.

No. of room days with avg_occ_rates <75% per day	No. of room days with avg_occ_rates between 75% and 100%	No. of room days with avg_occ_rates = 0%	No. of room days with avg_occ_rates >100%	Total
99	12	103	10	224

It is obvious from Table 6 that the number of events with poor occupancy rates (less than 75%) is 99 events compared to the number of events with good occupancy rates that are 12 only. There are 10 events with occupancy rates that exceeded 100%. This means that the corresponding rooms were overutilized. The number of events left idle and unoccupied is 103 events.

4.2. Testing using UGA

The data for the case tested using UGA are presented in Table 7. The same parameters of the manual case were used. However, a five days week was considered as well as shorter working day. The solution obtained used less rooms.

Table 7. Description of the solved problem instance in 2012–2013 at faculty of commerce.

Item	Data
No. of lecturers	131
No. of courses	150
No. of departments	7
No. of students	Between 10 and 2650
No. of groups	57
No. of rooms	32
No. of events	337
No. of days	5
No. of hrs to schedule/day	10

From Table 7, it is clear that the number of working days was reduced to five instead of seven. This does not contradict the professors’ preferences as professors may have Thursdays off or use them in other activities. This also means that there are still two more working days to assign more lectures if needed. After applying and running UGA, the utilization rates obtained (see Table 8 and Table 9).

Table 8. Avg. occupancy room rates per days using UGA on the faculty of commerce dataset.

Room/day	Sat (%)	Sun (%)	Mon (%)	Tue (%)	Wed (%)
201	0	0	0	0	0
202	0	0	71	76	0
203	0	0	0	0	0
301	0	0	83	83	0
302	0	0	0	58	0
303	0	0	0	0	0
401	0	0	0	0	0
403	0	0	0	0	0
405	0	0	0	0	0
407	91	0	89	91	93
501	0	0	0	0	0
503	0	0	0	0	0
506	0	0	0	0	0
507	50	0	0	0	67
601	92	83	76	86	83
603	0	0	100	79	0
605	83	75	80	79	75
705	0	0	0	0	0
707	0	0	0	0	0
91	91	93	96	93	93
92	0	0	0	0	0
93	100	88	93	96	85
94	0	0	0	0	0
95	100	80	100	80	100
1	88	61	80	66	0
2	50	0	100	56	0
3	0	0	0	56	0
4	0	0	0	80	0
5	89	98	100	98	97
6	83	83	83	83	83
7	97	96	97	100	100
8	72	53	56	46	59

Table 9. Summary results of Table 8.

No. of room days with avg_occ_rates <75% per day	No. of room days with avg_occ_rates between 75% and 100%	No. of room days with avg_occ_rates = 0%	No. of room days with avg_occ_rates >100%	Total
16	60	148	0	224

A comparison between the change in rates between the old timetable constructed in year 2012–2013 and the timetable constructed using UGA algorithm is summarized in Table 10.

Table 10. Old and new timetable occupancy rates comparison.

Rate Range	Manual Approach	UGA
No. of rooms with avg. Occ_Rates <75%	99	18
No. of rooms with avg. Occ_Rates ⩾75%	12	61
No. of rooms with avg. Occ_Rates = 0%	103	145
No. of rooms with avg. Occ_Rates >100%	10	0

According to Table 11, it is obvious that approximately 41% of the rooms available were saved instead of 19% in the old approach. Forty percent (40%) of the total working hours available weekly to build the schedule were saved as well. Applying UGA also excluded two days for a weekend (Thursdays and Fridays) when building timetables and reduced the number of potential lecture periods per days to five instead of six.

Table 11. No. of resources saved by applying UGA.

Item	Old approach	New approach
Total no. of rooms saved out of 32 rooms	6	13
Total working hours available weekly to build the schedule	84	50
Total no. of hours saved relevant to the max. timeslots allowed	0	34
No. of days worked	7	5
No. of days saved relevant to the max. days allowed	0	2
Max. no. of lecture periods/day	6	5

4.3. Testing UGA on other problems

The UGA contributed in this paper is intended to solve university course timetabling problems where the objective is space utilization optimization. It was applied on the Faculty of Commerce dataset where the real problem under study was identified and motivated this work. Although the developed algorithm was used to solve a complex case study compared to those reported in the literature, it is important to demonstrate how generic and robust the proposed algorithm is in solving other university course timetabling problems. Other tests were done on two benchmark datasets selected from the third track of the International Timetabling Competition (ITC) 2007, which is the curriculum-timetabling track, that considers the course timetabling problem and applies to the University of Udine in Italy [73] and [86].

In the original formulation of the two chosen datasets some constraints of the problem studied in this paper were not included. These are as follows:

• Rooms might not be available in certain periods, and they must not be suitable for specific lectures. In comparison with the studied case, these are considered hard constraints.
• Rooms have the same capacities. In comparison with the studied case, rooms had different capacities and they have to be matched against the number of attendees in a lecture.
• Teacher preferences on periods and rooms are only included as soft constraints. In comparison with the studied case, preferences for periods are considered hard constraints.

In order to maintain the same level of problem complexity when testing the algorithm, the authors added these removed features as hard constraints. Additionally, they assumed that all rooms are available in all the allowed time periods. The maximum number of students in a lecture was set to be 600 when testing with these datasets because nothing was mentioned about the number of students in the original formulation of the benchmark problems. The authors did not assume that rooms are of similar capacities, but rather used the different capacities of the Faculty of Commerce’s spaces, which makes the problem harder to solve and requires more computational time. The proposed composite fitness function that focuses on the utilization rates of spaces was used to evaluate the solution quality. Details about solving the two-benchmark datasets are shown in Table 12, Table 13, Table 14, Table 15 and Table 16.

Table 12. Problem description of faculty of commerce, in year 2012–2013 and datasets 1 and 2.

Item	Case dataset (faculty of commerce)	Dataset 1	Dataset 2
No. of lecturers	131	47	95
No. of courses	150	54	121
Max. no. of students	600	600	600
No. of rooms	32	9	19
No. of events	337	152	390
No. of days	5	6	5
Max. no. of periods/day	5	6	5

Table 13. Avg. occupancy room rates per days using UGA (dataset 1).

Room/day	Sat (%)	Sun (%)	Mon (%)	Tue (%)	Wed (%)	Thus (%)
201	0	0	0	0	0	0
202	83	70	76	83	74	0
203	0	0	0	0	0	0
301	0	0	0	0	0	0
302	0	0	0	0	0	0
303	0	0	0	0	0	0
401	0	0	0	0	0	0
403	0	0	0	0	0	0
405	0	0	0	0	0	0
407	0	0	93	89	90	89
501	0	0	0	0	0	0
503	0	0	0	0	0	0
506	0	0	0	0	0	0
507	72	33	50	67	67	83
601	83	83	100	91	94	83
603	0	0	0	0	0	0
605	0	0	0	0	0	0
705	0	0	0	0	0	0
707	0	0	0	0	0	0
91	91	93	96	93	93	93
92	0	0	0	0	0	0
93	93	95	96	100	100	100
94	0	0	0	0	0	0
95	0	0	0	0	0	0
1	100	83	100	75	100	0
2	0	0	0	0	0	0
3	0	0	0	0	0	0
4	0	0	0	0	0	0
5	0	0	0	0	0	0
6	83	83	83	83	83	0
7	100	100	100	100	100	100
8	0	0	0	0	0	0

Table 14. Summary results of Table 13.

No. of room days with avg_occ_rates <75% per day	No. of room days with avg_occ_rates between 75% and 100%	No. of room days with avg_occ_rates = 0%	No. of room days with avg_occ_rates >100%	Total
7	42	175	0	224

Table 15. Avg. occupancy room rates per days using UGA (dataset 2).

Room/day	Sat (%)	Sun (%)	Mon (%)	Tue (%)	Wed (%)
201	0	0	0	0	0
202	75	75	78	83	65
203	0	0	0	0	0
301	0	0	0	0	0
302	80	78	77	78	83
303	0	0	0	0	0
401	97	97	97	83	100
403	0	0	0	0	0
405	0	0	0	0	0
407	80	93	76	80	56
501	0	0	0	0	0
503	0	0	0	0	0
506	0	0	0	0	0
507	45	0	50	63	58
601	83	83	83	81	83
603	0	0	0	91	91
605	0	0	0	0	0
705	0	0	0	0	0
707	0	0	0	0	0
91	91	93	96	93	93
92	0	0	0	0	0
93	99	96	95	88	91
94	0	0	0	0	0
95	96	88	92	96	84
1	68	61	80	65	80
2	65	66	66	76	60
3	90	98	59	98	75
4	100	97	96	98	96
5	90	98	97	93	99
6	77	81	74	82	80
7	98	100	100	100	100
8	59	46	54	63	51

Table 16. Summary results of Table 15.

No. of room days with avg_occ_rates <75% per day	No. of room days with avg_occ_rates between 75% and 100%	No. of room days with avg_occ_rates = 0%	No. of room days with avg_occ_rates >100%	Total
20	66	138	0	224

Additionally, a comparison has been made between the computational time required to run the two datasets using UGA and the BWAS and BWACS algorithms developed in [73] including LS1 and LS2. For a fair comparison, the number of iterations considered was 45 iterations with 20 solutions produced in each iteration to eventually get 900 solutions. However, it was noticed that after the fourth or the fifth iteration no improvement to the solution takes place. This means that increasing the number of iterations might not be useful in all cases, but only consumes additional computational time. A stopping criterion was then used when the solution does not change after a number of iterations. The performance comparison is better illustrated in Table 17.

Table 17. Computational time comparison (in hours) between UGA and the BWAS and BWACS.

Algorithm${\textstyle \setminus }$dataset	Dataset 1	Dataset 2
UGA	4.5	11.1
BWAS	3.9	13
BWACS	3.4	12.2

All the previously presented tests were done on a personal computer Core i5 2.40 GHz CPU and 6 GB RAM using Java 6 as a programming language and PostgresSQL 9.3 as a database management system. It is obvious from testing the algorithm on different datasets, that UGA algorithm is a robust generic algorithm that generates good utilization rates for the allocated spaces. However, the computational time required by UGA algorithm to test dataset 1 was slightly longer than BWAS and BAWCS, and it consumed less time in dataset 2. This is still acceptable because constructing timetables is not a problem solved every day. It is a process that takes place long before academic semesters begin. Additionally, the authors have tested the benchmarks based on constraints that are more complex and with a more elaborate objective that were not taken into consideration in their original problem formulation.

5. Conclusion and future work

University timetabling is a hard to solve problem, especially, in large universities. Constructing timetables is an important task that consumes time and effort of the involved personnel. This paper reviewed some of the work related to timetabling and space allocation problems. It was obvious that different evolutionary algorithms were developed aiming at reducing the computational time required to solve these problems without considering much of the real-world constraints. It was also reported that genetic algorithms have proven success in solving many timetabling problems. In this work, a utilization-based genetic algorithm is proposed to solve a real course timetabling problem with a number of soft and hard constraints including professors’ preferences, which is considered a novel contribution overlooked by the previous literature. A simple weighted sum formula is used to prioritize professors according to their availabilities. The authors developed a new utilization-based crossover type that aims at reducing the number of underutilized/over-utilized events in a timetable. Moreover, a mutation operator that targets under/over-utilized events was integrated with a simple descent local search heuristic to improve the solution. The fitness function developed in this work considers utilization rates along with other factors to evaluate the fitness of chromosomes. Weights are assigned to each of the factors used in calculating the fitness value based on each factor’s level of significance to the institution constructing the timetable.

The case study used to test the algorithm was of the Faculty of Commerce, Alexandria University in Egypt. This case study was chosen because of its big problem size and the limited resources available. A comparison between the timetable generated by the old manual approach and the timetable generated using UGA was made to highlight the number of resources saved. The results showed that applying UGA enhanced the occupancy rates of the allocated events and saved many resources. Moreover, to prove the robustness of the developed algorithm, it was tested against two medium and big size benchmark datasets. Results of the testing showed that UGA took less computational time for solving the big size problem and slightly more time was required with the medium sized benchmark dataset. However, testing the two datasets was not on their original simplified formulations since the constraints defined in the Faculty of Commerce case study were incorporated. This shows that UGA outperforms the previously contributed approaches to solve these problems even with slightly more computational time for the medium sized dataset. The overall performance of UGA with the constraints elaborated in the paper and the objective proposed prove that it is an effective tool for generating timetables in big universities.

Future research will focus on applying UGA with flow optimization considerations inside campuses. This means that it is better to allocate consecutive events for a group to the same room or to rooms that are close to each other to avoid logistical problems inside academic institutions. Another avenue of research that seems very promising is the use of emerging technologies in order to be able to report actual numbers of students attending lectures and to avoid predicted numbers in calculating utilization rates. Attendance patterns vary a lot in Egyptian public universities and the number of attendees needs to be tracked in order to be able to calculate accurate utilization rates. Revealing such information will help dynamically improving the initially constructed timetables and freeing unneeded resources.

Acknowledgment

Special thanks are due to Professor Saleh El Shehaby for his recommendations and constructive opinions on an earlier version of this paper.

Appendix A

UGA algorithmic parameters.

Parameter	Value/name
Chromosome generation method	Generated by (LD + LE)
Population size	20
Crossover type	Utilization crossover
Mutation typeLocal search used with mutation	Targeted Mutation (targeting utilization rates)Simple descent
Fitness function	Composite function (incorporating utilization rates)

References

1. [1] M. Garey, D. Johnson; Computers and Intractability: A Guide to The Theory of NP-Completeness; Freeman and Company, New York (1979)
2. [2] A. Mahiba, C. Durai; Genetic algorithm with search bank strategies for university course timetabling problem; Int. Conf. Model Optim. Comput. (ICMOC 2012), 38 (2012), pp. 253–263
3. [3] M. Abbaszadeh, S. Saeedv; A fast genetic algorithm for solving university scheduling problem; Int. J. Artif. Intell. (IJAI), 3 (1) (2014), pp. 7–15
4. [4] S. Brailsford, C. Potts, B. Smith; Constraint satisfaction problems: algorithms and applications; Eur. J. Oper. Res., 119 (1999), pp. 557–581
5. [5] C. Tovey; Tutorial on computational complexity; Interfaces, 32 (3) (2002), pp. 30–61
6. [6] E. Burke, J. Kingston, K. Jackson, R. Weare; Automated university timetabling: the state of the art; Comput. J., 40 (9) (1997), pp. 565–571
7. [7] S. Abdullah, H. Turabieh, B. McCollum, E. Burke; An investigation of a genetic algorithm and sequential local search approach for curriculum-based course timetabling problems; Multidisciplinary Int. Conf. Scheduling: Theory Appl. (2009), pp. 727–731
8. [8] N. Al-Milli; Hybrid genetic algorithms with simulating annealing for university course timetabling problems; J. Theor. Appl. Inf. Technol., 29 (2) (2011), pp. 100–106
9. [9] M. Al-Betar, A. Khader; A harmony search algorithm for university course timetabling; Ann. OR, 194 (1) (2012), pp. 3–31
10. [10] S. Asiyaban, Z. Mousavinasab; University course timetabling using multi-population genetic algorithm guided with local search and fuzzy logic; J. Council Innovative Res. (CIR), 11 (10) (2013), pp. 3043–3050
11. [11] K. Tindell, A. Burns, A. Wellings; Allocating hard real time tasks (an np-hard problem made easy; Real-Time Syst. J., 4 (2) (1992), pp. 145–165
12. [12] J. Hansen, S. Raut, S. Swami; Retail shelf allocation: a comparative analysis of heuristic and meta-heuristic approaches; J. Retail., 86 (1) (2010), pp. 94–105
13. [13] H. Cambazard, F. Demazeau, Interactively solving school timetabling problems using extensions of constraint programming, in: Proceedings of the 5th International Conference on the Practice and Theory of Automated Timetabling (PATAT-2004), 2004, pp. 190–207.
14. [14] E. Shove, The Black Holes of Space Economics: A Discussion of Space Utilization and Space Charging in Higher Education. Internal Report for the University of Sunderland, 1993.
15. [15] Z. Lü, J. Hao; Adaptive tabu search for course timetabling; Eur. J. Oper. Res., 200 (2010), pp. 235–244
16. [16] S. Sutar, R. Bichkar; University timetabling based on hard constraints using genetic algorithm; Int. J. Comput. Appl., 42 (15) (2012), pp. 1–5
17. [17] N. Sabar, M. Ayob, R. Qu, G. Kendall; A graph coloring constructive hyper-heuristic for examination timetabling problems; Appl. Intell., 37 (1) (2012), pp. 1–11
18. [18] N. Sabar, M. Ayob, G. Kendall, R. Qu; A honey-bee mating optimization algorithm for educational timetabling problems; Eur. J. Oper. Res., 216 (3) (2012), pp. 533–543
19. [19] S. Abdullah, H. Turabieh, Generating university course timetable using genetic algorithm and local search, in: Proceeding of the 3rd Int. Conference on Hybrid Information Technology, 2008, pp. 254–260.
20. [20] R. Chen, H. Shih; Solving university course timetabling problems using constriction particle swarm optimization with local search; Algorithms J., 6 (2013), pp. 227–244
21. [21] E. Burke, A. Eckersley, B. McCollum, S. Petrovic, R. Qu; Hybrid variable neighbourhood approaches to university exam timetabling; Eur. J. Oper. Res., 206 (2010), pp. 46–53
22. [22] D. Mittal, H. Doshi, M. Sunasra, R. Nagpure; Automatic timetable generation using genetic algorithm; Int. J. Adv. Res. Comput. Commun. Eng., 4 (2) (2015), pp. 245–248
23. [23] M. Carter, G. Laporte, Recent developments in practical course timetabling, in: Proc. of the 2nd Int. Conf. on Practice and Theory of Automated Timetabling, LNCS 1408, 1998, pp. 3–19.
24. [24] S. Jat, S. Yang, A guided search genetic algorithm for the university course timetabling problem, in: Multidisciplinary Intl. Conf. on Scheduling: Theory and Applications (MISTA 2009), 2009, pp. 180–191.
25. [25] L. Reis, E. Oliveira, A language for specifying complete timetabling problems, in: Third Int. Conf. on Practice and Theory of Automated Timetabling III, 1998, pp. 322–341.
26. [26] E. Burke, D. Varley, Space allocation: an analysis of higher education requirements, in: Selected Papers from the 2nd Int. Conf. on Practice and Theory of Automated Timetabling II, 1997, pp. 20–36.
27. [27] A. Schaerf; A survey of automated timetabling; Artif. Intell. Rev., 13 (2) (1999), pp. 87–127
28. [28] C. Beyrouthy, E. Burke, D. Landa-Silva, B. McCollum, P. McMullan, A. Parkes, The teaching space allocation problem with splitting, in: Proceedings of the 6th International Conference on the Practice and Theory of Automated Timetabling (PATAT ’06), Brno, August 2006, pp. 103–122, ISBN 80-210-3726-1.
29. [29] C. Beyrouthy, E. Burke, D. Landa-Silva, B. McCollum, P. McMullan, A. Parkes; Towards improving the utilization of university teaching space; J. Operational Res. Soc., 60 (1) (2007), pp. 130–143
30. [30] L. Chwif, M. Barretto, L. Moscato; A solution to the facility layout problem using simulated annealing; Comput. Ind., 36 (1–2) (1998), pp. 125–132
31. [31] K. Dowsland, E. Soubeiga, E. Burke; A simulated annealing hyper-heuristic for determining shipper sizes; Eur. J. Oper. Res., 179 (2005), pp. 759–774
32. [32] S. Ceschia, L. Gaspero, A. Schaerf; Design, engineeering and experimental analysis of a simulated annealing approach to the post-enrollment course timetabling problem; J. Comput. Oper. Res., 39 (2012), pp. 1615–1624
33. [33] D. Costa; A tabu search for computing an operational timetable; Eur. J. Oper. Res., 76 (1994), pp. 98–110
34. [34] A. McKendall, J. Jaramillo; Improved tabu search heuristics for the dynamic space allocation problem; Comput. Oper. Res., 35 (2008), pp. 3347–3359
35. [35] S. Jat, S. Yang; A hybrid genetic algorithm and tabu search approach for post enrolment course timetabling; J. Sched., 14 (6) (2011), pp. 617–637
36. [36] O. Ülker, D. Landa-Silva; A 0/1 integer programming model for the office space allocation problem; Electron. Notes Discrete Math., 36 (2010), pp. 575–582
37. [37] W. Erben, J. Keppler, A genetic algorithm solving a weekly course-timetabling problem, in: E. Burke, P. Ross (Eds.), The Practice and Theory of Automated Timetabling: Selected Papers. Lecture Notes in Computer Science, vol. 1153, 1998, pp. 198–211.
38. [38] K. Ellingsen, M. Penaloza, A genetic algorithm approach for finding a good course schedule, Technical Report, South Dakota School of Mines and Technology, USA, 2003.
39. [39] S. Ghaemi, M. Vakili, A. Aghagolzadeh; Using a genetic algorithm optimizer tool to solve university timetable scheduling problem; IEEE Int. Symp. Signal Process. Appl., 2007 (2007), pp. 1–4
40. [40] B. Rakesh, D. Gupta; A hybrid algorithm for university course timetabling problem; Innovative Syst. Des. Eng., 6 (2) (2015), pp. 60–66
41. [41] M. El-Sherbiny, R. Zeineldin, A. El-Dhshan; Genetic algorithm for solving course timetable problems; Int. J. Comput. Appl., 124 (10) (2015), pp. 1–7
42. [42] K. Socha, M. Samples, M. Manfrin, Ant algorithms for the university course timetabling problem with regard to the state-of-the-art, Evolutionary Computation in Combinatorial Optimization (EvoCOP 2003), vol. 2611, Lecture Notes in Computer Science, 2003, pp. 334–345.
43. [43] M. Pelikan, Genetic Algorithms, Missouri Estimation of Distribution Algorithms Laboratory, MEDAL Report No. 2010007, 2010.
44. [44] H. Sani, M. Yabo; Solving timetabling problems using genetic algorithm technique; Int. J. Comput. Appl., 134 (15) (2016), pp. 33–38
45. [45] D. Montana, M. Brinn, S. Moore, G. Bidwell, Genetic algorithms for complex, real-time scheduling, in: Proc. of the 1998 IEEE Int. Conf. on Systems, Man, and Cybernetics, 1998, pp. 2213–2218.
46. [46] P. Ross, D. Corne, H. Fang; Improving evolutionary timetabling with delta evaluation and directed mutation; LNCS: Parallel Problem Solving from Nature—PPSN III, vol. 866, Springer, Berlin (1994), pp. 556–565
47. [47] M. Hosny, S. Fatima; A survey of genetic algorithms for the university timetabling problem; Int. Conf. Future Inf. Technol. IPCSIT, 13 (2011), pp. 34–39
48. [48] A. Dhande, S. Ladhake, S. Dhande; Genetic algorithm – an effective approach to solve real application problem; Int. J. Adv. Res. Comput. Sci. Software Eng., 2 (2) (2012)
49. [49] Y. Juang, S. Lin, H. Kao; An adaptive scheduling system with genetic algorithms for arranging employee training programs; Expert Syst. Appl., 33 (2007), pp. 642–651
50. [50] O. Arogundade, A. Akinwale, O. Aweda; A genetic algorithm approach for a real-world university examination timetabling problem; Int. J. Comput. Appl., 12 (5) (2010), pp. 1–4
51. [51] J. Blanco, I. Khatib, Course scheduling as a constraint satisfaction problem, in: Proceedings of PACT98 – The Fourth Int. Conf. and Exhibition on the Practical Application of Constraint Technology, London, England, 1998.
52. [52] S. Daskalaki, T. Birbas, E. Housos; An integer programming formulation for a case study in university timetabling; Eur. J. Oper. Res., 153 (2004), pp. 117–135
53. [53] S. Kazarlis, Solving university timetabling problems using advanced genetic algorithms, in: The 5th Int. Conf. on Technology and Automation (ICTA’05), 2005.
54. [54] A. Gunawan, K. Ng, K. Poh; An improvement heuristics for the timetabling problem; Int. J. Comput. Sci., 1 (2) (2007), pp. 162–178
55. [55] I. Aljarah, A. Salhieh, H. Faris; An automatic course scheduling approach using instructors’ preferences; IJET, 7 (1) (2012), pp. 24–32
56. [56] D. Suryadi, R. Pilipus, Genetic algorithm for university timetable planning in FTI, in: Proc. Of the 2012 Int. Conf. on Industrial Engineering and Operations Management, 2012, pp. 656–664.
57. [57] S. Daskalaki, T. Birbas; Efficient solutions for a university timetabling problem through integer programming; Eur. J. Oper. Res., 160 (2005), pp. 106–120
58. [58] R. Lewis, B. Paechter; Finding feasible timetables using group-based operators; IEEE Trans. Evol. Comput., 11 (2007), pp. 397–413
59. [59] D. Qaurooni, M. Akbarzadeh-T; Course timetabling using evolutionary operators; Appl. Soft Comput., 13 (5) (2013), pp. 2504–2514
60. [60] M. Badri; A two-stage multiobjective scheduling model for [faculty-course-time] assignments; Eur. J. Oper. Res., 94 (1996), pp. 16–28
61. [61] W. Faber, N. Leone, G. Pfeifer, Representing school timetabling in a disjunctive logic programming language, in: Proc. of the 13th Workshop on Logic Programming (WLP ’98), 1998, pp. 1–8.
62. [62] G. Harwood, R. Lawless; Optimizing faculty teaching schedules; Decis. Sci., 6 (1975), pp. 513–524
63. [63] J. Bristle; A linear programming solution to the faculty assignment problem; Socio-Econ. Plann. Sci., 10 (1976), pp. 227–230
64. [64] W. Shih, J. Sullivan; Dynamic course scheduling for college faculty via zero-one programming; Decis. Sci., 8 (4) (1977), pp. 711–721
65. [65] R. McClure, C. Wells; A mathematical programming model for faculty course assignments; Decis. Sci., 15 (3) (1984), pp. 409–420
66. [66] M. Schniederjans, G. Kim; A goal programming model to optimize departmental preference in course assignments; Comput. Oper. Res., 14 (2) (1987), pp. 87–96
67. [67] B. Paechter, A. Cumming, H. Luchian, M. Petriuc; Two solutions to the general timetable problem using evolutionary methods; Proc. First IEEE Conf. Evolutionary Comput., 1994 (1994), pp. 301–305
68. [68] B. Wall, A Genetic Algorithm for Resource-Constrained Scheduling, Ph.D. Thesis, MIT, <http://lancet.mit.edu/ga>, 1996.
69. [69] J. Mendes, J. Goncalves, M. Resende, Random key based genetic algorithm for the resource constrained project scheduling problem, AT&T Labs Research Technical Report TD-6DUK2C, 2005.
70. [70] O. Obaid, M. Ahmad, S. Mostafa, M. Mohammed; Comparing performance of genetic algorithm with varying crossover in solving examination timetabling problem; J. Emerg. Trends Comput. Inf. Sci., 3 (10) (2012), pp. 1427–1434
71. [71] R. Qu, E. Burke; Hybridisations within a graph based hyper-heuristic framework for university timetabling problems; J. Operational Res. Soc. (JORS), 60 (2009), pp. 1273–1285
72. [72] N. Sabar, M. Ayob, G. Kendall, Solving examination timetabling problems using honey-bee mating optimization (ETP-HBMO), in: Multidisciplinary International Conf. on Scheduling: Theory and Applications (MISTA 2009), 2009, pp. 399–408.
73. [73] T. Thepphakorn, P. Pongcharoen, C. Hicks; An ant colonybased timetabling tool; Int. J. Prod. Econom., 149 (2014), pp. 131–144
74. [74] A. Colorni, M. Dorigo, V. Maniezzo, A genetic algorithm to solve the timetable problem, Technical Report No. 90–060, Politecnico di Milano, Italy, 1990.
75. [75] S. Yang, S. Jat; Genetic algorithms and local search strategies for university course timetabling; IEEE Trans. Syst. Man Cybern. Part C Appl. Rev., 41 (1) (2011), pp. 93–106
76. [76] G. Lach, M. Lübbecke; Curriculum based course timetabling: new solutions to Udine benchmark instances; Ann. Opr. Res., 194 (1) (2012), pp. 255–272
77. [77] A. Chaudhuri, K. De; Fuzzy genetic heuristic for university course timetable problem; Int. J. Adv. Soft Comput. Appl., 2 (1) (2010), pp. 100–123
78. [78] Space Management Group (SMG), Space Utilization: Practice Performance and Guidelines, UK Higher Education Space Management Project, 2009.
79. [79] Tertiary Education Facilities Management Association, TEFMA “Space Planning Guidelines: Edition 3”, <http://www.tefma.com/uploads/content/26-TEFMA-SPACE-PLANNING-GUIDELINES-FINAL-ED3-28-AUGUST-09.pdf>, 2009.
80. [80] S. Abdullah, H. Ali, I. Sipan; Benchmarking space usage in higher education institutes: attaining efficient use; J. Techno-Soc., 4 (1) (2012), pp. 11–20
81. [81] A. Jain, S. Jain, P. Chande; Formulation of genetic algorithm to generate good quality course timetable; Int. J. Innovation, Manage. Technol., 1 (3) (2010), pp. 248–251
82. [82] P. Cote, R. Sabourin, A hybrid multi-objective evolutionary algorithm for the uncapacitated exam proximity problem, in: E.K. Burke, M. Trick (Eds.), Selected Papers from the 5th International Conf. on the Practice and Theory of Automated Timetabling. Springer Lecture, Notes in Computer Science, vol. 3616, 2005, pp. 294–312.
83. [83] D. Landa-Silva, J. Obit; Evolutionary non-linear great deluge for university course timetabling; Proceeding of 2009 Int. Conf. on Hybrid Artificial Intelligent HAIS09, Springer-Verlag, Berlin Heidelberg (2009), pp. 269–276 LNAI 5572
84. [84] D. Beasley, D. Bull, R. Martin; An overview of genetic algorithms: part 2, research topics; University Computing, 15 (4) (1993), pp. 170–181
85. [85] O. Rossi-Doria, M. Sampels, M. Birattari, M. Chiarandini, M. Dorigo, L. Gambardella, J. Knowles, M. Manfrin, M. Mastrolilli, B. Paechter, L. Paquete; A comparison of the performance of different metaheuristics on the timetabling problem; Proceedings of the 4th Int. Conf. of the Practice and Theory of Automated Timetabling (PATAT-2002), vol. 2740, Springer, Berlin Heidelberg (2002), pp. 329–351
86. [86] L. Di Gaspero, S. Mizzaro, A. Schaerf, A multiagent architecture for distributed course timetabling, in: Proceedings of the 5th Int. Conf. on the Practice and Theory of Automated Timetabling (PATAT-2004), 2004, pp. 471–474.