Rotation effect on peristaltic transport of a Jeffrey fluid in an asymmetric channel with gravity field

Abstract

In this paper, the peristaltic flow of a Jeffrey fluid in an asymmetric rotating channel is studied under long wavelength and low Reynolds number assumptions are investigated. Closed form expressions for the pressure gradient, pressure rise, stream function, axial velocity and shear stress on the channel walls have been computed numerically. The effects of the ratio of relaxation to retardation times, time-mean flow, rotation, the phase angle and the gravity field on the pressure gradient, pressure rise, streamline, axial velocity and shear stress are discussed in detail and shown graphically. The results indicate that the effect of the ratio of relaxation to retardation times, time-mean flow, rotation, the phase angle and the gravitational field are very pronounced in the phenomena. Comparison was made with the results obtained in the asymmetric channel and symmetric channel.

Keywords

Jeffrey fluid; Rotation; Peristaltic; Asymmetric channel; Gravity field

1. Introduction

A variety of complex rheological fluids can easily be transported from one place to another place with a special type of pumping known as Peristaltic pumping. This pumping principle is called peristalsis. The mechanism includes involuntary periodic contraction followed by relaxation or expansion of the ducts the fluids move through. This leads to the rise in pressure gradient that eventually pushes the fluid forward. This type of pumping is first observed in physiology where the food moves through the digestive tract, urine transports from the kidney to the bladder through ureters, semen moves through the vas deferens, lymphatic fluids moves through lymphatic vessels, bile flows from the gall bladder into the duodenum, spermatozoa move through the ductus efferentes of the male reproductive tract and cervical canal, ovum moves through the fallopian tube, and blood circulates in small blood vessels. Historically, however, the engineering analysis of peristalsis was initiated much later than in physiological studies. Applications in industrial fluid mechanics are like aggressive chemicals, high solid slurries, noxious fluid (nuclear industries) and other materials that are transported by peristaltic pumps. Roller pumps, hose pumps, tube pumps, finger pumps, heart–lung machines, blood pump machines, and dialysis machines are engineered on the basis of peristalsis. The study of the peristaltic transport of a fluid in the presence of an external magnetic field and rotation is of great importance with regard to certain problems involving the movement of conductive physiological fluids, e.g. blood and saline water. Abd-Alla et al. [1] investigated the effect of rotation on peristaltic flow of a micropolar fluid through a porous medium with an external magnetic field. Akram et al. [2] studied the numerical and analytical treatment on peristaltic flow of Williamson fluid in the occurrence of induced magnetic. Akram and Nadeem [3] discussed the influence of induced magnetic field and heat transfer on the peristaltic motion of a Jeffrey fluid in an asymmetric channel: Closed form solution field. Abd-Alla et al. [4] studied the effects of rotation and initial stress on peristaltic transport of fourth grade fluid with heat transfer and induced magnetic field. Hayat et al. [5] discussed the influence of compliant wall properties and heat transfer on the peristaltic flow of an incompressible viscous fluid in an curved channel. Bhargava et al. [6] have studied finite element study of nonlinear two-dimensional deoxygenated biomagnetic micropolar flow. Ali et al. [7] discussed the peristaltic motion of a non-Newtonian fluid in a channel having compliant boundaries. Abd-Alla et al. [8] studied the effects of rotation and magnetic field on nonlinear peristaltic flow of second-order fluid in an asymmetric channel through a porous medium. Hayat et al. [9] analyzed the effect of an induced magnetic field on the peristaltic flow of an incompressible Carreau fluid in an asymmetric channel. Pandey et al. [10] concerned with the theoretical study of two-dimensional peristaltic flow of power-law fluids in three layers with different viscosities. Jiménez-Lozano and Sen [11] investigated the streamline patterns and their local and global bifurcations in a two-dimensional planar and axisymmetric peristaltic flow for an incompressible Newtonian fluid. Hayat et al. [12] analyzed the effect of an induced magnetic field on the peristaltic flow of an incompressible Carreau fluid in an asymmetric channel. Srinivas and Kothandapani [13] investigated the effects of heat and mass transfer on peristaltic transport in a porous space with compliant walls. Abd-Alla et al. [14] discussed the Effects of an endoscope and rotation on peristaltic flow in a tube with long wavelength. Abd-Alla et al. [15] investigated the peristaltic flow in a tube with an endoscope subjected to magnetic field. Hayat and Noreen [16] discussed the influence of an induced magnetic field on the peristaltic flow of an incompressible fourth grade fluid in a symmetric channel with heat transfer. Nadeem and Akbar [17] investigated the peristaltic flow of an incompressible MHD Newtonian fluid in a vertical annulus. Abd-Alla et al. [18] investigated the peristaltic flow in cylindrical tubes with an endoscope subjected to effect of rotation and magnetic field. Nadeem et al. [19] studied the concentrates on the heat transfer characteristics and endoscope effects for the peristaltic flow of a third order fluid. Abd-Alla and Abo-Dahab [20] studied the magnetic field and rotation effects on peristaltic transport of a Jeffrey fluid in an asymmetric channel. Abd-Alla et al. [21] investigated the effect of the rotation, magnetic field and initial stress on peristaltic motion of micropolar fluid. Mahmoud et al. [22] discussed the effect of the rotation on wave motion through cylindrical bore in a micropolar porous medium. The dynamic behavior of a wet long bone that has been modeled as a piezoelectric hollow cylinder of crystal class 6 is investigated by Abd-Alla et al. [23]. Vajravelu et al. [27] investigated the peristaltic transport of a conducting Jeffrey fluid in an inclined asymmetric channel. The extensive literature on the topic is now available and we can only mention a few recent interesting investigations in Refs. [28], [29], [30], [31], [32], [33], [34], [35], [36], [37] and [38].

The aim of this paper was to study the effect of rotation and gravity field on the peristaltic transport of Jeffrey type in asymmetric channel. Here the governing equations are nonlinear in nature; we used infinitely long wavelength assumption to obtain linear zed system of coupled differential equations which are then solved analytically. Results have been discussed for pressure gradient, pressure rise, streamline and axial velocity to observe the ratio of relaxation to retardation times, time-mean flow, rotation, the phase angle and the gravity field effect. The numerical result displayed by figures and the physical meaning is explained. The results and discussions presented in this study may be helpful to further understand peristaltic motion for non-Newtonian fluids in an asymmetric channel and a symmetric channel.

2. Formulation of the problem

Let us consider the peristaltic transport of an incompressible viscous fluid in a two-dimensional channel of width d₁ + d₂. The channel walls are inclined at angles α. The flow is induced by sinusoidal wave trains propagating with constant speed c along the channel walls.

The geometry of the wall surfaces is

${\overline {h}}_{1}({\overline {X}}{\mbox{,}}{\overline {t}})=$$d_{1}+a_{1}cos\left[{\frac {2\pi }{\lambda }}({\overline {X}}-\right.$$\left.c{\overline {t}})\right]{\mbox{,}}\quad {\mbox{at upper wall,}}$

(1a)

${\overline {h}}_{2}({\overline {X}}{\mbox{,}}{\overline {t}})=$$-d_{2}-b_{1}cos\left[{\frac {2\pi }{\lambda }}({\overline {X}}-\right.$$\left.c{\overline {t}})+\phi \right]{\mbox{,}}\quad {\mbox{at lower wall,}}$

(1b)

where a₁ and b₁ are the amplitudes of the waves, ${\textstyle \lambda }$ is the wavelength, c is the wave speed, ${\textstyle \phi \quad (0\leqslant \phi \leqslant \pi )}$ is the phase difference, ϕ = 0 corresponds to symmetric channel with waves out of phase and ϕ = π the waves are in phase, and further a₁, b₁, d₁, d₂ and ϕ satisfy the condition.

$a_{1}^{2}+b_{1}^{2}+2a_{1}b_{1}cos\quad \phi \quad \preccurlyeq \quad {\left(d_{1}+d_{2}\right)}^{2}{\mbox{.}}$

(2)

The Cauchy ${\textstyle \left({\overline {T}}\right)}$ and extra ${\textstyle \left({\overline {S}}\right)}$ stress tensors are

${\overline {T}}=-{\overline {p}}{\overline {I}}+{\overline {S}}{\mbox{,}}$

${\overline {S}}={\frac {\mu }{1+{\lambda }_{1}}}\left({\overline {\overset {\cdot }{\gamma }}}+\right.$$\left.{\lambda }_{2}{\overline {\ddot {\gamma }}}\right){\mbox{,}}$

(3)

where ${\textstyle {\overline {p}}}$ is the pressure, ${\textstyle {\overline {I}}}$ is the identity tensor, ${\textstyle {\lambda }_{1}}$ is the ratio of relaxation to retardation times, ${\textstyle {\lambda }_{2}}$ is the retardation time, and ${\textstyle {\overset {\cdot }{\gamma }}}$ is the shear rate.

In laboratory frame, the following set of pertinent field equations governing the flow is as follows:

$\rho \left[{\frac {\partial }{\partial t}}+{\overline {U}}{\frac {\partial }{\partial {\overline {X}}}}+\right.$$\left.{\overline {V}}{\frac {\partial }{\partial {\overline {Y}}}}\right]{\overline {U}}-$$2\rho \Omega {\overline {V}}=-{\frac {\partial {\overline {P}}}{\partial {\overline {X}}}}+$${\frac {\partial }{\partial {\overline {X}}}}\left({\overline {S}}_{{\overline {X}}{\overline {X}}}\right)+$${\frac {\partial }{\partial {\overline {Y}}}}\left({\overline {S}}_{{\overline {X}}{\overline {Y}}}\right)+$$\rho {\overline {g}}sin\quad \alpha {\mbox{,}}$

(4)

$\rho \left[{\frac {\partial }{\partial t}}+{\overline {U}}{\frac {\partial }{\partial {\overline {X}}}}+\right.$$\left.{\overline {V}}{\frac {\partial }{\partial {\overline {Y}}}}\right]{\overline {V}}+$$2\rho \Omega {\overline {U}}=-{\frac {\partial {\overline {P}}}{\partial {\overline {Y}}}}+$${\frac {\partial }{\partial {\overline {X}}}}\left({\overline {S}}_{{\overline {X}}{\overline {Y}}}\right)+$${\frac {\partial }{\partial {\overline {Y}}}}\left({\overline {S}}_{{\overline {Y}}Y}\right)-$$\rho {\overline {g}}cos\quad \alpha$

(5)

${\frac {\partial {\overline {U}}}{\partial {\overline {X}}}}+$${\frac {\partial {\overline {V}}}{\partial {\overline {Y}}}}=$$0{\mbox{,}}$

(6)

${\overline {P}}={\overline {p}}-{\frac {1}{2}}\rho {\Omega }^{2}{\overline {R}}^{2}{\mbox{.}}$

(6a)

in which ${\textstyle {\overline {U}}}$ and ${\textstyle {\overline {V}}}$ are the velocity components in the ${\textstyle {\overline {X}}}$ and ${\textstyle {\overline {Y}}}$ – directions, respectively, ${\textstyle {\overset {\rightarrow }{\Omega }}=\Omega {\underline {k}}}$, k   is the unit vector, ${\textstyle {\overset {\rightarrow }{\Omega }}=(0{\mbox{,}}0{\mbox{,}}\Omega )}$ is the rotation vector, ${\textstyle {\overline {R}}}$ is given by ${\textstyle {\overline {R}}^{2}={\overline {X}}^{2}+{\overline {Y}}^{2}}$, ${\textstyle {\overline {P}}}$ is the modified pressure, and the equations of motion in the rotating frame have two additional terms ${\textstyle \rho ({\overset {\rightarrow }{\Omega }}\wedge ({\overset {\rightarrow }{\Omega }}\wedge {\overset {\rightarrow }{R}})}$ is the centrifugal force, ${\textstyle 2\rho ({\overset {\rightarrow }{\Omega }}\wedge {\overset {\rightarrow }{V}})}$ is the Coriolis force, ${\textstyle {\overset {\rightarrow }{R}}=({\overline {X}}{\mbox{,}}{\overline {Y}}{\mbox{,}}0)}$, ${\textstyle {\overset {\rightarrow }{V}}=({\overline {U}}{\mbox{,}}{\overline {V}}{\mbox{,}}0)}$ is the velocity vector and ρ is the density.

The flow is inherently unsteady in the laboratory frame ${\textstyle \left({\overline {X}}{\mbox{,}}{\overline {Y}}\right)}$. However, the flow becomes steady in a wave frame ${\textstyle \left({\overline {x}}{\mbox{,}}{\overline {y}}\right)}$ moving away from the laboratory frame with speed c in the direction of propagation of the wave. Taking u and v the velocity component in x and y  -directions, the transformation from the laboratory frame to the wave frame is given by ${\textstyle {\overline {x}}={\overline {X}}-c{\overline {t}}}$, ${\textstyle {\overline {y}}={\overline {Y}}}$, ${\textstyle {\overline {u}}={\overline {U}}-c{\mbox{,}}}$

${\overline {v}}={\overline {V}}{\mbox{,}}\quad {\overline {p}}({\overline {x}})=$${\overline {P}}({\overline {X}}{\mbox{,}}{\overline {t}}){\mbox{,}}$

(7)

where ${\textstyle {\overline {u}}}$ and ${\textstyle {\overline {v}}}$ are the velocity components in the wave frame ${\textstyle \left({\overline {x}}{\mbox{,}}{\overline {y}}\right)}$, ${\textstyle {\overline {p}}}$ and ${\textstyle {\overline {P}}}$ are pressure in wave and fixed frame of references, respectively.

The appropriate non-dimensional variables for the flow are defined as follows:

$x={\frac {2\pi {\overline {x}}}{\lambda }}{\mbox{,}}\quad y=$${\frac {\overline {y}}{d_{1}}}{\mbox{,}}\quad u={\frac {\overline {u}}{c}}{\mbox{,}}\quad v=$${\frac {\overline {v}}{c\delta }}{\mbox{,}}\quad \delta =$${\frac {2\pi d_{1}}{\lambda }}{\mbox{,}}$ $p={\frac {2\pi d_{1}^{2}{\overline {p}}}{\mu c\lambda }}{\mbox{,}}\quad t=$${\frac {2\pi c{\overline {t}}}{\lambda }}{\mbox{,}}\quad h_{1}=$${\frac {{\overline {h}}_{1}}{d_{1}}}{\mbox{,}}\quad h_{2}={\frac {{\overline {h}}_{2}}{d_{1}}}{\mbox{,}}\quad s=$${\frac {d_{1}}{\mu c}}{\overline {s}}{\mbox{,}}$ $d={\frac {d_{2}}{d_{1}}}{\mbox{,}}\quad a={\frac {a_{1}}{d_{1}}}{\mbox{,}}\quad b=$${\frac {b_{1}}{d_{1}}}{\mbox{,}}\quad \Omega ={\frac {{\overline {\Omega }}a_{1}^{2}}{\mu }}{\mbox{.}}$

(8a)

Introducing the dimensionless stream function ψ(x, y) such that,

$u={\frac {\partial \psi }{\partial y}}{\mbox{,}}\quad v=$$-\delta {\frac {\partial \psi }{\partial x}}{\mbox{.}}$

(8b)

Using Eqs. (7), (8a) and (8b) into Eqs. (3), (4) and (5) and eliminating pressure by cross differentiation, we get

$\delta Re\left[\left({\frac {\partial \psi }{\partial y}}{\frac {\partial }{\partial x}}-\right.\right.$$\left.\left.{\frac {\partial \psi }{\partial x}}{\frac {\partial }{\partial y}}\right){\nabla }^{2}\psi \right]=$$\left[\left({\frac {{\partial }^{2}}{\partial y^{2}}}-{\delta }^{2}{\frac {{\partial }^{2}}{\partial x^{2}}}\right)s_{xy}\right]+$$\delta \left[{\frac {{\partial }^{2}}{\partial x\partial y}}\left(s_{xx}-\right.\right.$$\left.\left.s_{xy}\right)\right]+{\frac {\rho \mu \Omega }{a_{1}^{2}}}{\frac {{\partial }^{2}\psi }{\partial y^{2}}}+$${\frac {{gc}^{2}}{d_{1}}}sin\alpha {\mbox{,}}$

(9)

in which

$s_{xx}={\frac {2\delta }{1+{\lambda }_{1}}}\left[1+{\frac {\delta {\lambda }_{2}c}{d_{1}}}\left({\frac {\partial \psi }{\partial y}}{\frac {\partial }{\partial x}}+\right.\right.$$\left.\left.{\frac {\partial \psi }{\partial x}}{\frac {\partial }{\partial y}}\right)\right]{\frac {{\partial }^{2}\psi }{\partial x\partial y}}{\mbox{,}}$

(10)

$s_{xy}={\frac {1}{1+{\lambda }_{1}}}\left[1+{\frac {\delta {\lambda }_{2}c}{d_{1}}}\left({\frac {\partial \psi }{\partial y}}{\frac {\partial }{\partial x}}-\right.\right.$$\left.\left.{\frac {\partial \psi }{\partial x}}{\frac {\partial }{\partial y}}\right)\right]\left({\frac {{\partial }^{2}\psi }{\partial y^{2}}}-\right.$$\left.{\delta }^{2}{\frac {{\partial }^{2}\psi }{\partial x^{2}}}\right){\mbox{,}}$

(11)

$s_{yy}=-{\frac {2\delta }{1+{\lambda }_{1}}}\left[1+{\frac {\delta {\lambda }_{2}c}{d_{1}}}\left({\frac {\partial \psi }{\partial y}}{\frac {\partial }{\partial x}}-\right.\right.$$\left.\left.{\frac {\partial \psi }{\partial x}}{\frac {\partial }{\partial y}}\right)\right]{\frac {{\partial }^{2}\psi }{\partial x\partial y}}{\mbox{,}}$

(12)

${\nabla }^{2}={\delta }^{2}{\frac {{\partial }^{2}\psi }{\partial x^{2}}}+$${\frac {{\partial }^{2}\psi }{\partial y^{2}}}{\mbox{,}}\quad \delta =$${\frac {2\pi d_{1}}{\lambda }}{\mbox{,}}$

where

$Re={\frac {\rho {cd}_{1}}{\mu }}\quad {\mbox{is the Reynolds number.}}$

(13)

Under the long wavelength approximation ${\textstyle \left({\mbox{i}}.{\mbox{e}}.\lambda \gg a\right)}$, we have δ → 0 and along with low-Reynolds number in our analysis.

In view of these approximations, Eqs. (9) and (11) reduce to the following:

${\frac {{\partial }^{2}}{\partial y^{2}}}\left[{\frac {1}{\left(1+{\lambda }_{1}\right)}}{\frac {{\partial }^{2}\psi }{\partial y^{2}}}\right]-$$\left({\frac {\rho a^{2}\Omega }{\mu }}\right){\frac {{\partial }^{2}\psi }{\partial y^{2}}}+$${\frac {{gd}_{1}}{c^{2}}}sin\quad \alpha =0{\mbox{.}}$

(14)

The boundary conditions for the stream functions in the wave frame are

$\psi ={\frac {q}{2}}{\mbox{,}}\quad h_{1}=1+acos[x]{\mbox{,}}$

(15)

$\psi =-{\frac {q}{2}}\quad {\mbox{at}}\quad y=h_{2}(x)=-d-$$bcos\left[{\frac {2\pi }{\lambda }}(x)+\phi \right]{\mbox{,}}$

(16)

${\frac {\partial \psi }{\partial y}}=-1\quad {\mbox{at}}\quad y=$$h_{1}\quad {\mbox{and}}\quad y=h_{2}{\mbox{,}}$

(17)

where q is the flux in the wave frame and a, b, ϕ and d satisfy the relation

$a^{2}+b^{2}+2ab\quad cos\quad \phi \leqslant {\left(1+d\right)}^{2}{\mbox{.}}$

(18)

3. Solution of the problem

The solutions of Eq. (14) subject to the boundary conditions (15), (16) and (17) are given as

$\psi ={\frac {(h_{1}+h_{2})\left[Nq+2tanh\left[{\frac {N(h_{1}-h_{2})}{2}}\right]\right]}{2N(h_{2}-h_{1})+4tanh\left[{\frac {N(h_{1}-h_{2})}{2}}\right]}}+$${\frac {Nq+2tanh\left[{\frac {N(h_{1}-h_{2})}{2}}\right]}{N(h_{1}-h_{2})-2tanh\left[{\frac {N(h_{1}-h_{2})}{2}}\right]}}y+$${\frac {(q+h_{1}-h_{2}){\mbox{sech}}\left[{\frac {N(h_{1}-h_{2})}{2}}\right]sinh\left[{\frac {N(h_{1}-h_{2})}{2}}\right]}{N(h_{1}-h_{2})-2tanh\left[{\frac {N(h_{1}-h_{2})}{2}}\right]}}\times cosh(Ny)+$${\frac {(q+h_{1}-h_{2}){\mbox{sech}}\left[{\frac {N(h_{1}-h_{2})}{2}}\right]cosh\left[{\frac {N(h_{1}-h_{2})}{2}}\right]}{N(h_{1}-h_{2})+2tanh\left[{\frac {N(h_{1}-h_{2})}{2}}\right]}}\times sinh(Ny)-$${\frac {{gd}_{1}}{2N^{2}c^{2}}}y^{2}{\mbox{,}}$

(19)

where ${\textstyle N^{2}={\frac {\rho a^{2}{\Omega }^{2}}{\mu }}(1+{\lambda }_{1})}$.

The flux at any axial station in the fixed frame is

$Q={\int }_{h_{2}}^{h_{1}}\left({\frac {\partial \psi }{\partial y}}+\right.$$\left.1\right)dy=h_{1}-h_{2}+q{\mbox{.}}$

(20)

The time-mean flow over a period T   at a fixed position ${\textstyle {\overline {X}}}$ is defined as

$\Theta ={\frac {1}{T}}{\int }_{0}^{T}Q\quad dt={\frac {1}{T}}{\int }_{0}^{T}(q+$$h_{1}-h_{2})dt=q+1+d{\mbox{.}}$

(21)

The pressure gradient is obtained from the dimensionless momentum equation for the axial velocity as

${\frac {dp}{dx}}={\frac {1}{1+{\lambda }_{1}}}\left[{\frac {N^{3}(q+h_{1}-h_{2})}{N(h_{2}-h_{1})+2tanh\left[{\frac {N(h_{1}-h_{2})}{2}}\right]}}\right]+$${\frac {\rho {gd}_{1}^{2}}{c\mu }}sin\quad \alpha {\mbox{.}}$

(22)

The non-dimensional expression for the pressure rise per wavelength ${\textstyle \Delta p_{\lambda }}$ and frictional forces on the lower ${\textstyle \left(F_{\lambda }^{l}\right)}$ and upper ${\textstyle \left(F_{\lambda }^{u}\right)}$ walls on the lower is defined as follows:

$\Delta p_{\lambda }={\int }_{0}^{2\pi }\left({\frac {dp}{dx}}\right)dx{\mbox{,}}$

(23)

$F_{\lambda }^{l}={\int }_{0}^{1}h_{2}^{2}\left(-{\frac {dp}{dx}}\right)dx{\mbox{,}}$

(24)

$F_{\lambda }^{u}={\int }_{0}^{1}h_{1}^{2}\left(-{\frac {dp}{dx}}\right)dx{\mbox{.}}$

(25)

The non-dimensional shear stress (11) at the upper wall of the channel is reduced to

$S_{xy}={\frac {1}{1+{\lambda }_{1}}}{\frac {{\partial }^{2}\psi }{\partial y^{2}}}=$${\frac {N^{2}(q+h_{1}-h_{2}){\mbox{sech}}\left[{\frac {N(h_{1}-h_{2})}{2}}\right]}{(1+{\lambda }_{1})\left\{N(h_{1}-h_{2})-2tanh\left[{\frac {N(h_{1}-h_{2})}{2}}\right]\right\}}}\times \left\{sinh\left[{\frac {N(h_{1}-h_{2})}{2}}\right]cosh{Mh}_{1}\right\}{\mbox{.}}$

(26)

Expression for wave shape: we can deduce the asymmetric channel into symmetric channel by taking ${\textstyle a=b{\mbox{,}}\quad d=1\quad {\mbox{and}}\quad \phi =0}$.

4. Numerical results and discussion

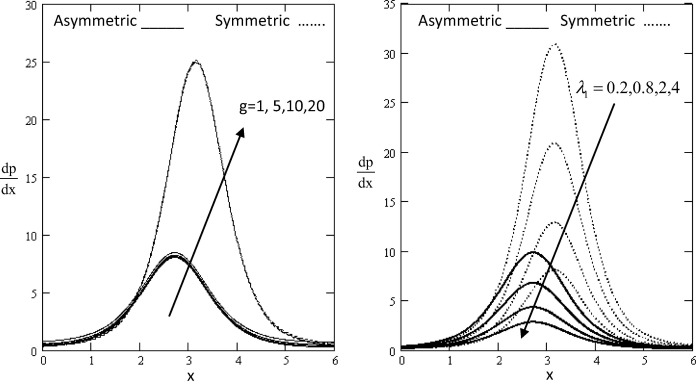
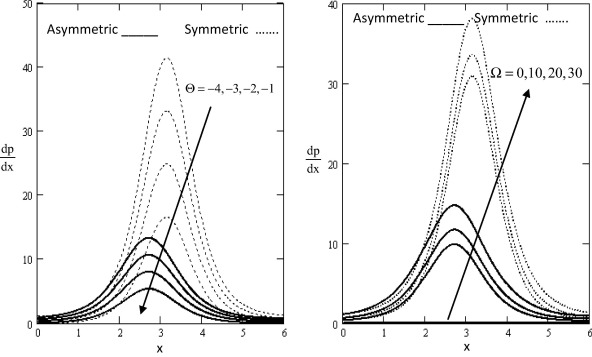
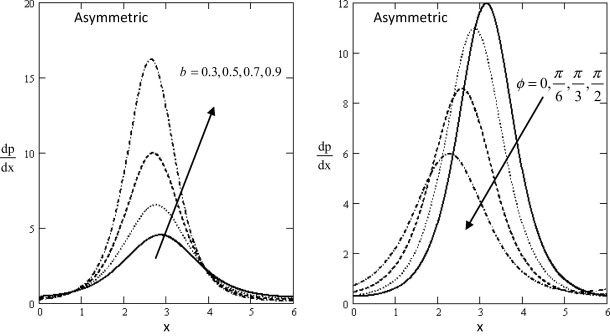
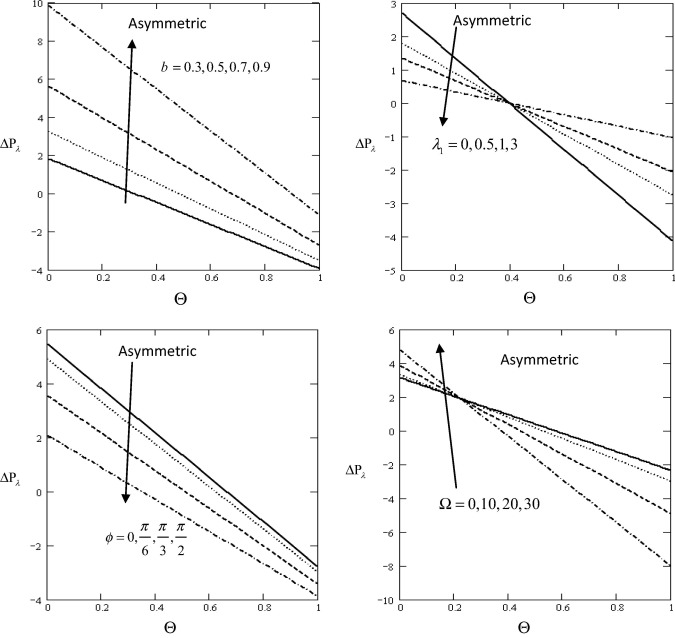
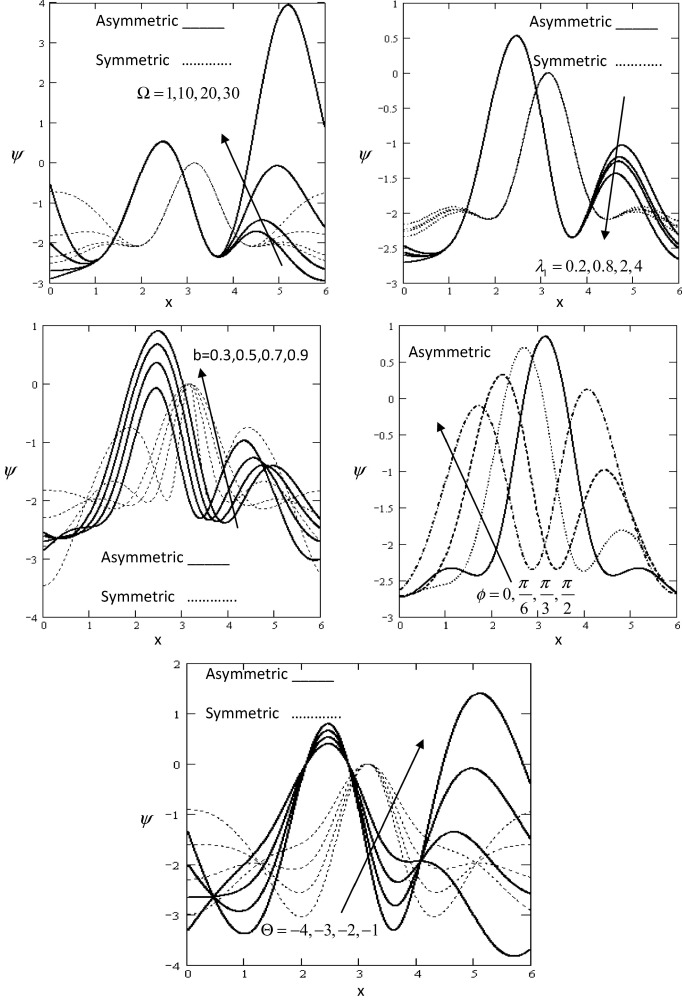
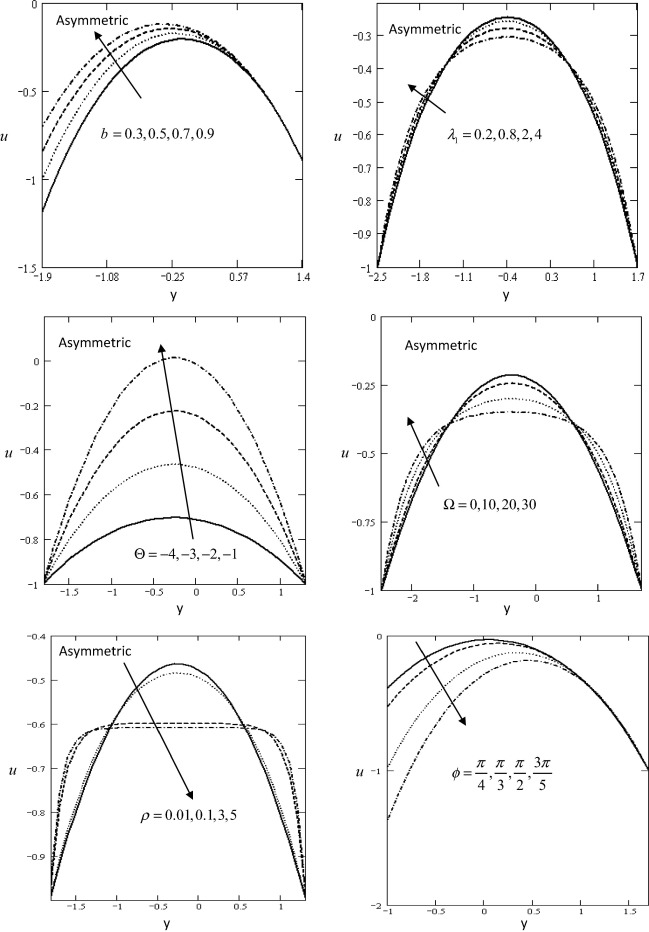
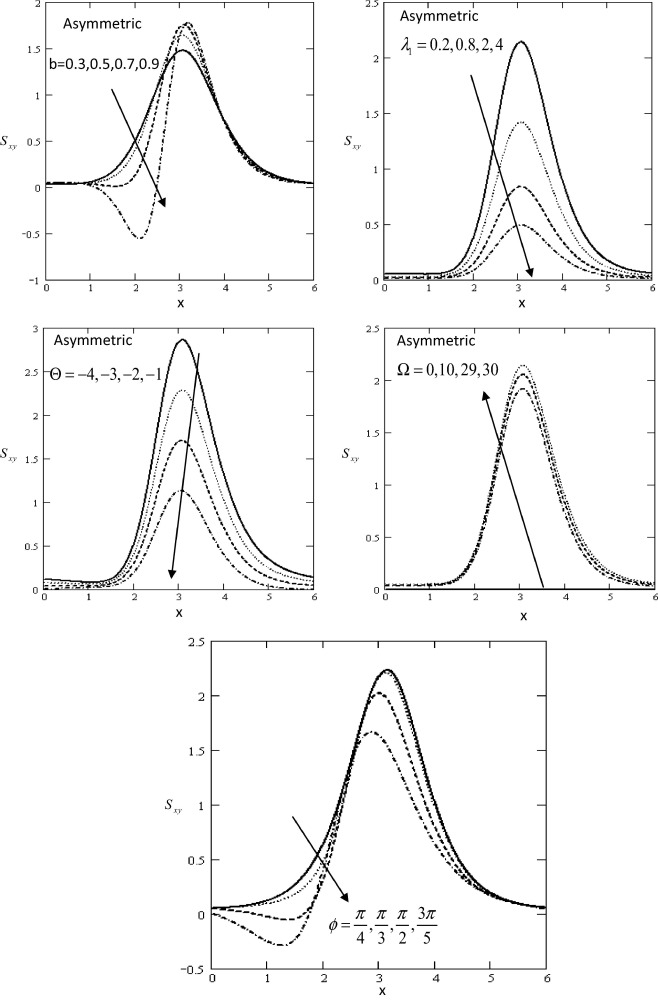
In order to gain physical insight the pressure gradient ${\textstyle {\frac {dp}{dx}}}$, pressure rise ${\textstyle \Delta p_{\lambda }}$, streamline ψ, velocity u, and shear stress S_xy have been discussed by assigning numerical values to the parameter encountered in the problem in which the numerical results are displayed with the graphic illustrations. The variations are shown in Figure 1, Figure 2, Figure 3, Figure 4, Figure 5, Figure 6 and Figure 7 respectively.

Figure 1. Variation of ${\textstyle {\frac {dp}{dx}}}$ with influence of g   and ${\textstyle {\lambda }_{1}}$ with respect to x.

Figure 2. Variation of ${\textstyle {\frac {dp}{dx}}}$ with influence of Θ and Ω with respect to x.

Figure 3. Variation of ${\textstyle {\frac {dp}{dx}}}$ with influence of b and ϕ for asymmetric with respect to x.

Figure 4. Variation of ${\textstyle \Delta P_{\lambda }}$ with influence of ${\textstyle M{\mbox{,}}\quad {\lambda }_{1}{\mbox{,}}\quad \phi {\mbox{,}}\quad \Omega {\mbox{,}}\quad b}$ with respect to Θ.

Figure 5. Variation of ψ   with influence of ${\textstyle \Omega {\mbox{,}}\quad {\lambda }_{1}{\mbox{,}}\quad b{\mbox{,}}\quad \phi {\mbox{,}}\quad \Theta }$ with respect to x.

Figure 6. Variation of u   with influence of ${\textstyle b{\mbox{,}}\quad {\lambda }_{1}{\mbox{,}}\quad \Theta {\mbox{,}}\quad \Omega {\mbox{,}}\quad \rho {\mbox{,}}\quad \phi }$ with respect to y.

Figure 7. Variation of Sxy   with influence of ${\textstyle b{\mbox{,}}\quad {\lambda }_{1}{\mbox{,}}\quad \Theta {\mbox{,}}\quad \Omega {\mbox{,}}\quad \phi }$ with respect to x.

Figure 1, Figure 2 and Figure 3 show the variations of the axial pressure gradient ${\textstyle {\frac {dp}{dx}}}$ with respect to the axial x in which it has oscillatory behavior in the whole range of the x  -axis for different values of the gravity field, the ratio of relaxation to retardation times ${\textstyle {\lambda }_{1}{\mbox{,}}}$, time-mean flow Θ, rotation Ω, the non-dimensional amplitude of wave b in asymmetric and the phase angle ϕ. In both figures, it is clear that the pressure gradient has a nonzero value only in a bounded region of space. The effect of gravity field, the ratio of relaxation to retardation times, time-mean flow, rotation, the non-dimensional amplitude of wave and the phase angle decrease and increase gradually. It is observed that the pressure gradient increases with increase in gravity field, rotation and the non-dimensional amplitude of wave, while it decreases with increase in the time-mean flow, the ratio of relaxation to retardation times and the phase angle. It is noticed the axial pressure gradient when compared to the case of asymmetric and symmetric channel. The pressure gradient in case of symmetric channel exceeds in magnitude when compared with asymmetric channel. Moreover, it can be noticed that on the one hand, in the wider part of channel x ∊ [0, 2] and [3, 5, 6], the pressure gradient is relatively small, i.e., the flow can easily pass without imposition of a large pressure gradient. On the other hand, in a narrow part of the channel x ∊ [2, 3.5] a much pressure gradient is required to maintain the flux to pass it especially near x = 2.7.

Fig. 4 shows that the variations of the pressure rise ${\textstyle \Delta p_{\lambda }}$ with respect to the time mean flow Θ for different values of the non-dimensional amplitude of wave b  , the ratio of relaxation to retardation times ${\textstyle {\lambda }_{1}}$, the phase difference ϕ and rotation Ω  . In both figures, it is clear that the pressure rise has a nonzero value only in a bounded region of space. It is observed that the pressure rise increases with increase in the non-dimensional amplitude of wave and rotation, while it decreases with increasing the ratio of relaxation to retardation times and the phase difference. The graph is sectored so that the upper right-hand quadrant (I) denotes the region of the peristaltic pumping ${\textstyle \left(\Theta >0{\mbox{,}}\quad \Delta p_{\lambda }>0\right)}$. Quadrant (II) is designated as augmented flow when ${\textstyle \Theta >0{\mbox{,}}\quad \Delta p_{\lambda }<0}$. Quadrant (IV) such that ${\textstyle \Theta <0{\mbox{,}}\quad \Delta p_{\lambda }>0}$ is called retrograde or backward pumping.

Fig. 5 shows the variations of the streamlines ψ with respect to the axial x in which it has oscillatory behavior in the whole range of the x-axis for different values of the rotation Ω  , the ratio of relaxation to retardation times ${\textstyle {\lambda }_{1}}$, the non-dimensional amplitude of wave b, the phase angle ϕ and time-mean flow Θ in asymmetric and symmetric channel. In both figures, it is clear that the streamlines have a nonzero value only in a bounded region of space. The effect of rotation, the ratio of relaxation to retardation times, the non-dimensional amplitude of wave, the phase difference and time-mean flow decrease and increase gradually.

It is observed that the streamline increases with increase in the rotation, the non-dimensional amplitude of wave, phase angle and time-mean flow, while it decreases with increase in the ratio of relaxation to retardation times. It is noticed the streamlines when compared to the case of asymmetric and symmetric channel. The streamlines in case of symmetric channel exceed in magnitude when compared with asymmetric channel. The streamlines near the channel walls do nearly strictly follow the wall waves, which are mainly engendered by the relative movement of the walls.

Fig. 6 shows the variations of the axial velocity u with respect to the axial y in which it has oscillatory behavior in the whole range of the y-axis for different values of the non-dimensional amplitude of wave b  , ratio of relaxation to retardation times ${\textstyle {\lambda }_{1}}$, time-mean flow Θ, rotation Ω, density ρ and the phase angle ϕ in asymmetric channel. In both figures, it is clear that the axial velocity have a nonzero value only in a bounded region of space. The effect of the non-dimensional amplitude of wave, the ratio of relaxation to retardation times, time-mean flow, rotation, the density and the phase angle decrease and increase gradually. It is observed that the axial velocity increases with increase in the non-dimensional amplitude of wave, ratio of relaxation to retardation times, the time-mean flow and rotation, while it decreases with increase in the density and the phase angle.

Fig. 7 displays the variations of the value of axial shear stress S_xy with respect to the axial x in which it has oscillatory behavior which may be due to peristalsis in the whole range of the x-axis for different values of the non-dimensional amplitude of wave b  , the ratio of relaxation to retardation times ${\textstyle {\lambda }_{1}}$, time-mean flow Θ, rotation Ω and the phase angle ϕ in asymmetric channel. In both figures, it is clear that the value of shear stress has a nonzero value only in a bounded region of space. The effect of the non-dimensional amplitude of wave, the ratio of relaxation to retardation times, time-mean flow, rotation, and the phase angle decrease and increase gradually. It is observed that the shear stress increases with increase in the rotation, while it decreases with increase in the non-dimensional amplitude of wave, the ratio of relaxation to retardation times, time-mean flow and phase angle. Moreover the values of shear stress are larger in case of a Jeffery fluid when compared with Newtonian fluid.

5. Conclusion

Due to the complicated nature of the governing equations for the pertinent field equations governing the peristaltic transport of Jeffery fluid, the work done in this field is unfortunately limited in number. The method used in this study provides a quite successful in dealing with such problems. This method gives exact solutions in the peristaltic transport without any assumed restrictions on the actual physical quantities that appear in the governing equations of the problem considered. Important phenomena are observed in all these computations:

• If ${\textstyle {\lambda }_{1}=0{\mbox{,}}\quad \Omega =0{\mbox{,}}\quad g=}$$0$, our results are in agreement with Refs. ([24], [25] and [26]) and Mishra and Rao [28].
• It was found that for large values of the non-dimensional amplitude of wave b  , the ratio of relaxation to retardation times ${\textstyle {\lambda }_{1}}$, time-mean flow Θ, rotation Ω, the phase angle ϕ and the gravity field g in asymmetric and symmetric channel. The solution is obtained in the context of the peristaltic transport of fluid.
• By comparing Figure 1, Figure 2, Figure 3, Figure 4, Figure 5, Figure 6 and Figure 7 for the peristaltic transport of fluid with figures without gravity field and rotation, it was found the same behavior in the same field.
• The magnitude of pressure gradient at the upper wall in a symmetric channel is greater than in an asymmetric channel.
• The results presented in this paper should be proved useful for researchers in scientific and engineering, as well as for those working on the development of fluid mechanics. Study of the phenomenon of the non-dimensional amplitude of wave, the ratio of relaxation to retardation times, time-mean flow, rotation, the phase angle and the gravity field in asymmetric and symmetric channel influence and operations are also used to improve the conditions of peristaltic motion.

References

1. [1] A.M. Abd-Alla, S.M. Abo-Dahab, R.D. Al-Simery; Effect of rotation on peristaltic flow of a micropolar fluid through a porous medium with an external magnetic field; J. Magn. Magn. Mater., 348 (2013), pp. 33–43
2. [2] S. Akram, S. Nadeem, M. Hanif; Numerical and analytical treatment on peristaltic flow of Williamson fluid in the occurrence of induced magnetic field; J. Magn. Magn. Mater., 346 (2013), pp. 142–151
3. [3] Safia Akram, S. Nadeem; Influence of induced magnetic field and heat transfer on the peristaltic motion of a Jeffrey fluid in an asymmetric channel: closed form solutions; J. Magn. Magn. Mater., 328 (2013), pp. 11–20
4. [4] A.M. Abd-Alla, S.M. Abo-Dahab, H.D. El-Shahrany; Effects of rotation and initial stress on peristaltic transport of fourth grade fluid with heat transfer and induced magnetic field; J. Magn. Magn. Mater., 349 (2014), pp. 268–280
5. [5] T. Hayat, M. Javed, A.A. Hendi; Peristaltic transport of viscous fluid in a curved channel with compliant walls; Int. J. Heat Mass Transf., 54 (2011), pp. 1615–1621
6. [6] R. Bhargava, O.A. Bég, S. Sharma, J. Zueco; Finite element study of nonlinear two-dimensional deoxygenated biomagnetic micropolar flow; Nonlinear Sci. Numer. Simul., 15 (2010), pp. 1210–1223
7. [7] N. Ali, T. Hayat, S. Asghar; Peristaltic flow of a Maxwell fluid in a channel with compliant walls; Chaos, Solitons Fractals, 39 (2009), pp. 407–416
8. [8] A.M. Abd-Alla, S.M. Abo-Dahab, H.D. El-Shahrany; Effects of rotation and magnetic field on nonlinear peristaltic flow of second-order fluid in an asymmetric channel through a porous medium; Chin. Phys. B, 22 (2013), pp. 325–352
9. [9] T. Hayat, N. Saleem, N. Ali; Effect of induced magnetic field on peristaltic transport of a Carreau fluid; Nonlinear Sci. Numer. Simul., 15 (2010), pp. 2407–2423
10. [10] S.K. Pandey, M.K. Chaube, D. Tripathi; Peristaltic transport of multilayered power-law fluids with distinct viscosities: a mathematical model for intestinal flows; J. Theor. Biol., 278 (2011), pp. 11–19
11. [11] J. Jimé nez-Lozano, M. Sen; Streamline topologies of two-dimensional peristaltic flow and their bifurcations; Chem. Eng. Process., 49 (2010), pp. 704–715
12. [12] T. Hayat, N. Saleem, S. Asghar, M.S. Alhothuali, A. Alhomaidan; Influence of induced magnetic field and heat transfer on peristaltic transport of a Carreau fluid; Nonlinear Sci. Numer. Simul., 16 (2011), pp. 3559–3577
13. [13] S. Srinivas, M. Kothandapani; The influence of heat and mass transfer on MHD peristaltic flow through a porous space with compliant walls; Appl. Math. Comput., 213 (2009), pp. 197–208
14. [14] A.M. Abd-Alla, S.M. Abo-Dahab, H.D. El-Shahrany; Effects of an endoscope and rotation on peristaltic flow in a tube with long wavelength; J. Comput. Theor. Nanosci., 11 (2014), pp. 1055–1065
15. [15] A.M. Abd-Alla, S.M. Abo-Dahab, R.D. El-Semiry; Long wavelength peristaltic flow in a tubes with an endoscope subjected to magnetic field; Korea–Australia Rheol. J., 25 (2013), pp. 107–118
16. [16] T. Hayat, S. Noreen; Peristaltic transport of fourth grade fluid with heat transfer and induced magnetic field; Comptes Rendus Mécanique, 338 (2010), pp. 518–528
17. [17] S. Nadeem, N.S. Akbar; Influence of radially varying MHD on the peristaltic flow in an annulus with heat and mass transfer; J. Taiwan Inst. Chem. Eng., 41 (2010), pp. 286–294
18. [18] A.M. Abd-Alla, S.M. Abo-Dahab, R.D. El-Semiry; Peristaltic flow in cylindrical tubes with an endoscope subjected to effect of rotation and magnetic field; J. Comput. Theor. Nanosci., 11 (2014), pp. 1040–1050
19. [19] S. Nadeem, T. Hayat, N. Sher Akbar, M.Y. Malik; On the influence of heat transfer in peristalsis with variable viscosity; Int. J. Heat Mass Transf., 52 (2009), pp. 4722–4730
20. [20] A.M. Abd-Alla, S.M. Abo-Dahab; Magnetic field and rotation effects on peristaltic transport of a Jeffrey fluid in an asymmetric channel; J. Magn. Magn. Mater., 374 (2015), pp. 680–689
21. [21] A.M. Abd-Alla, G.A. Yahya, S.R. Mahmoud, H.S. Alosaimi; Effect of the rotation, magnetic field and initial stress on peristaltic motion of micropolar fluid; Meccanica, 47 (2012), pp. 1455–1465
22. [22] S.R. Mahmoud, A.M. Abd-Alla, M.A. El-Sheikh; Effect of the rotation on wave motion through cylindrical bore in a micropolar porous medium; Int. Mod. Phys. B, 25 (2011), pp. 2713–2728
23. [23] A.M. Abd-Alla, S.M. Abo-Dahab, S.R. Mahmoud; Wave propagation modeling in cylindrical human long wet bones with cavity; Meccanica, 46 (6) (2011), pp. 1413–1428
24. [24] A.M. Siddiqui, W.H. Schehawey; Peristaltic flow of a second-order fluid in tubes; J. Non-Newtonian Fluid Mech., 53 (1994), pp. 257–284
25. [25] A.H. Shapiro, M.Y. Jaffrin, S.L. Weinberg; Peristaltic pumping with long wavelengths at low Reynolds number; J. Fluid Mech., 37 (1969), pp. 799–825
26. [26] J.B. Shukla, R.S. Parihar, S.P. Gupta; Effects of peripheral-layer viscosity on peristaltic transport of a bio-fluid; J. Fluid Mech., 97 (1980), pp. 225–237
27. [27] K. Vajravelu, S. Sreenadh, G. Sucharitha, P. Lakshminarayana; Peristaltic transport of a conducting Jeffrey fluid in an inclined asymmetric channel; Int. J. Biomath., 7 (2014), pp. 45–64
28. [28] M. Mishra, A. Ramachandra Rao; Peristaltic transport of a Newtonian fluid in an asymmetric channel; ZAMP, 54 (2003), pp. 532–550
29. [29] A.M. Abd-Alla, S.M. Abo-Dahab, Maram M. Albalawi; Radially varying magnetic field on the peristaltic flow in a tube with an endoscope under the effect of rotation; J. Comput. Theor. Nanosci., 12 (2015), pp. 3066–3075
30. [30] A.M. Abd-Alla, S.M. Abo-Dahab, Mram Albalawi; Effect of variable viscosity on peristaltic flow of second order fluid with heat and mass transfer; J. Comput. Theor. Nanosci., 12 (2015), pp. 3110–3117
31. [31] M. Sheikholeslami, M.M. Rashidi; Ferrofluid heat transfer treatment in the presence of variable magnetic field; Eur. Phys. J. Plus, 130 (2015), pp. 115–130
32. [32] M. Sheikholeslami, R. Ellahi; Three dimensional mesoscopic simulation of magnetic field effect on natural convection of nanofluid; Int. J. Heat Mass Transf., 89 (2015), pp. 799–808
33. [33] A.M. Abd-Alla, S.M. Abo-Dahab; Effect of an endoscope and rotation on the peristaltic flow involving a Jeffrey fluid with magnetic field; J. Braz. Soc. Mech. Sci. Eng., 37 (2015), pp. 1277–1289
34. [34] M.S. Kandelousi; KKL correlation for simulation of nanofluid flow and heat transfer in a permeable channel; Phys. Lett. A, 378 (2014), pp. 3331–3339
35. [35] M. Sheikholeslami, S. Abelman; Two-phase simulation of nanofluid flow and heat transfer in an annulus in the presence of an axial magnetic field; IEEE Trans. Nanotechnol., 14 (2015), pp. 561–569
36. [36] A.M. Abd-Alla, S.M. Abo-Dahab, A. Kilicman; Peristaltic flow of a Jeffrey fluid under the effect of radially varying magnetic field in a tube with an endoscope; J. Magn. Magn. Mater., 384 (2015), pp. 79–86
37. [37] A.M. Abd-Alla, S.M. Abo-Dahab, A. Kilicman, R.D. El-Semiry; Effect of heat and mass transfer and rotation on peristaltic flow through a porous medium with compliant walls; Multidiscipline Model. Mater. Struct., 10 (2014), pp. 399–415
38. [38] M. Sheikholeslami, D.D. Ganji, M.Y. Javed, R. Ellahi; Effect of thermal radiation on magnetohydrodynamics nanofluid flow and heat transfer by means of two phase model; J. Magn. Magn. Mater., 374 (2015), pp. 36–43