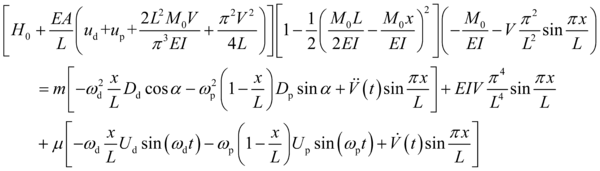Revision as of 08:34, 7 June 2019

Abstract: In this work, based on dynamic characteristics of radial gates, a nonlinear differential equation of motion for the radial gate arm is established. Excitation conditions of principal parametric resonance and subharmonic parametric resonance are obtained by using multi-scale method and numerical method. The parameter analysis shows that: comparing with traditional calculation method of dynamic instability region division, the presented method is more suitable to analysis of parametric vibration for radial gates as considering the end moment, vibration duration and amplitude. The vibration amplitudes of arm increase with the increase of its length and excitation amplitude, as well as the decrease of arm inclination angle. Moreover, the parametric resonance is easier to be excited and its resonance region become wider with the initial end moment increasing. Since the vibration response of the arm is influenced by the nonlinear term in the equation, the damping effect is limited. Thus, energy transfer method (e.g. tuned mass damper) can be adopted to achieve vibration control.

Keywords: Radial gate; parametric vibration; multi-scale method; parameter analysis

1. Introduction

The radial gate is a main regulating structure in hydraulic engineering, and its stability is directly related to the safe operation of reservoir. However, the dynamic instability mechanism of radial gates has not been explained clearly up to now, which causes existing structures which are built without proper anti-vibration design at the time of construction are especially vulnerable. Even if they were designed for anti-vibration performance, their design may not comply with current code [1] and thus may have deficient anti-vibration performance. In recent years, multitudes of engineering practices have shown that the radial gates will produce different degrees of vibration and even cause integral instability failure under the flow-induced vibration [2]. Because of their arm is lightness, slenderness and flexibility render this structure more vulnerable to vibrations and dynamic instabilities when subjected to water loads. Consequently, the dynamic stability of the radial gate arm has become a significant problem needs to be solved in both stage of design and operation [3]. According to the excitations like cavity flow, Carmen vortex, special hydrodynamic load and so on, the vibration patterns of gates can be divided into forced vibration, self-excited vibration and parametric vibration. Among them, the parametric vibration only appears in radial gates. The parametric resonance is much more dangerous than standard forced resonance, because its amplitudes increase exponentially. The problem of parametric vibration arises in many branches of physics and engineering has been studied extensively such as cable structure [4], beam structure [5], plate and shell structures [6] and coupled model [7]. In 1980's, Zhang [8] observed the phenomenon of parametric vibration during gate operation in dynamic water and judged it was one of the important reasons for dynamic instability of arm through engineering failure examples, and proposed a concise analytical calculation method. Subsequently, there are fascinating researches which have been carried out on the division of dynamic instability region [9]. However, the dynamic instability region can be used to determine whether parametric resonance occur or not, but it does not yield the response amplitude at arbitrary time. Usually the radial gate is subjected to flow-induced load for a relatively short period of time, and the arm amplitudes remain fluctuating in a narrow range without infinite magnification trend. Thus, the method of dynamic instability region may not be an accurate criterion for defining dynamic instability without time factor. Nowadays, Zhang and Xie [10] investigated the chaotic behaviors of nonlinear systems in the radial gate arm under certain dynamic loads and proved the necessity to analyze the stability of radial gate with excitation amplitude and duration effects.

In this paper, according to the mechanical characteristics of the radial gate, with full considerations of geometric nonlinear factors caused by bending moment and large displacement at the high head, the nonlinear differential equation of motion for the arm is established. The stability of parametric vibration is given by methods of multi-scale method and numerical method. Moreover, the effects of excitation factors (water head, frequency, time, amplitude) and structural elements (angle, length, damping) on the vibration response of arm are quantitatively analyzed.

2. Derivation of the nonlinear differential equation of motion for the radial gate arm

Several basic assumptions are made before establishing the equation of motion for radial gate arms:

(1) The material nonlinearity of the arm is assumed as elastic.

(2) Torsional stiffness and shear stiffness of the arm are not considered.

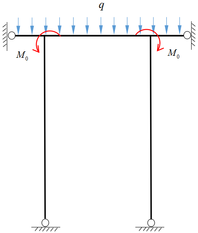
On the premise of the above assumptions, the analytical model of the in-plane main frame is established in Figure 1.

Recently, Zhang et al. [11] proposed a non-moment design method for the out-of-plane main frame of radial gate, but the in-plane layout scheme without bending moment has not been reported up to now. Hu et al. [12] examined that the effect of initial end bending moment M₀ of in-plane radial gate arm can not be ignored by prototype observation. Thus, according to the relationship between the deflection and the moment of the material:

and the arm boundary conditions:

The sag of the arm can be defined as follow：

where EI represents the flexural rigidity, L represents the length of the arm.

Consider a radial gate arm, as depicted in Figure 2, with the longitudinal u(x,t) and transverse displacements v(x,t), earthquake excitation frequency ω_p, flow-induced excitation frequency ω_d, earthquake excitation load D_p, flow excitation load D_d. The equation of motion for this structure is:

where T₀ is tangential hydrostatic pressure, τ is additional tangential hydrodynamic pressure, s is the coordinate by the arc length. m is the mass per unit length of the arm, μ is denoting damping coefficient.

According to the geometric deformation and the stress state of the arm model, the results are obtained:

where H₀ and h represent the axial hydrostatic pressure and the additional axial hydrodynamic pressure, respectively.

By Taylor formula, the equation (5) is expanded at dη/dx=0：

Substituting of equations (5) and (6) into equation (4), the following equation is obtained:

The length variation of micro-segment ds' is assumed as：

Neglecting the longitudinal inertia gives：

as ds≈dx, equation (9) can be rewritten:

The boundary conditions for generalized displacements vector (Figure 2) are：

In this study, the first-order mode is dominated. Hence, the displacement v(x,t) can be expressed as：

where V(t) is the displacement amplitude.

When only the flow-induced vibration is considered, supposing D_p=0, equation (11) can be rewritten as:

The internal force of the arm can be expressed as：

where ${\displaystyle u_{\mbox{d}}=U_{\mbox{d}}cos\left({\omega }_{\mbox{d}}t\right)=}$${\displaystyle D_{\mbox{d}}cos\left(\alpha \right)cos\left({\omega }_{\mbox{d}}t\right)}$ , ${\displaystyle u_{\mbox{p}}=U_{\mbox{p}}cos\left({\omega }_{\mbox{p}}t\right)=}$${\displaystyle D_{\mbox{p}}cos\left(\alpha \right)cos\left({\omega }_{\mbox{p}}t\right)}$ .

Substituting equations (3), (12) and (13) into equation (7) yields:

(14)

Then, according to the Galerkin method,the equation of motion is obtained as follows:

where

${\displaystyle 2\xi {\omega }_{\mbox{a}}={\frac {\mu }{m}}}$ , ${\displaystyle {\omega }_{\mbox{a}}^{2}={\omega }_{0}^{2}\left(1+\lambda \right)}$ , ${\displaystyle {\omega }_{0}^{2}={\frac {{\pi }^{2}H_{0}}{mL_{}^{2}}}+{\frac {EI{\pi }^{4}}{mL_{}^{4}}}}$ ,

${\displaystyle \theta =\left\{\left[{\frac {M_{0}^{2}{\pi }^{2}L}{4E_{}^{2}I_{}^{2}}}\left({\frac {L}{4}}+\right.\right.\right.}$${\displaystyle \left.\left.\left.{\frac {1}{3}}+{\frac {1}{2{\pi }^{2}}}-\right.\right.\right.}$${\displaystyle \left.\left.\left.E\right)\right]H_{0}+{\frac {4M_{0}^{2}AL_{}^{3}}{EI_{}^{2}{\pi }^{4}}}\left({\frac {M_{0}^{2}L_{}^{2}}{4E_{}^{2}I_{}^{2}}}-\right.\right.}$${\displaystyle \left.\left.1\right)\right\}/\left(-{\frac {mL}{2}}\right)}$ ,

${\displaystyle a=\left\{\left[{\frac {M_{0}^{2}{\pi }^{2}L}{4E_{}^{2}I_{}^{2}}}\left({\frac {L}{4}}+\right.\right.\right.}$${\displaystyle \left.\left.\left.{\frac {1}{3}}+{\frac {1}{2{\pi }^{2}}}-\right.\right.\right.}$${\displaystyle \left.\left.\left.E\right)-{\frac {{\pi }^{2}}{2L}}\right]H_{0}+\right.}$${\displaystyle \left.{\frac {4M_{0}^{2}AL_{}^{3}}{E_{}I_{}^{2}{\pi }^{4}}}\left({\frac {M_{0}^{2}L_{}^{2}}{4E_{}^{2}I_{}^{2}}}-\right.\right.}$${\displaystyle \left.\left.1\right)-EI{\frac {{\pi }^{4}}{2L_{}^{3}}}\right\}{\frac {EA}{L}}/\left(-\right.}$${\displaystyle \left.{\frac {mL}{2}}\right)}$ ,

${\displaystyle b=\left\{\left[{\frac {M_{0}^{2}{\pi }^{2}L}{4E_{}^{2}I_{}^{2}}}\left({\frac {L}{4}}+\right.\right.\right.}$${\displaystyle \left.\left.\left.{\frac {1}{3}}+{\frac {1}{2{\pi }^{2}}}-\right.\right.\right.}$${\displaystyle \left.\left.\left.E\right)-{\frac {{\pi }^{2}}{2L}}\right]H_{0}+\right.}$${\displaystyle \left.{\frac {4M_{0}^{2}AL_{}^{3}}{EI_{}^{2}{\pi }^{4}}}\left({\frac {M_{0}^{2}L_{}^{2}}{4E_{}^{2}I_{}^{2}}}-\right.\right.}$${\displaystyle \left.\left.1\right)-{\frac {{\pi }^{4}EI}{2L_{}^{3}}}\right\}{\frac {2L_{}^{2}M_{}A}{{\pi }^{3}}}/\left(-\right.}$${\displaystyle \left.{\frac {mL}{2}}\right)}$ ,

${\displaystyle c=\left\{\left[{\frac {M_{0}^{2}{\pi }^{2}L}{4E_{}^{2}I_{}^{2}}}\left({\frac {L}{4}}+\right.\right.\right.}$${\displaystyle \left.\left.\left.{\frac {1}{3}}+{\frac {1}{2{\pi }^{2}}}-\right.\right.\right.}$${\displaystyle \left.\left.\left.E\right)-{\frac {{\pi }^{2}}{2L}}\right]H_{0}+\right.}$${\displaystyle \left.{\frac {4M_{0}^{2}AL_{}^{3}}{EI_{}^{2}{\pi }^{4}}}\left({\frac {M_{0}^{2}L_{}^{2}}{4E_{}^{2}I_{}^{2}}}-\right.\right.}$${\displaystyle \left.\left.1\right)-EI{\frac {{\pi }^{4}}{2L_{}^{3}}}\right\}{\frac {EA{\pi }^{2}}{4L_{}^{2}}}/\left(-\right.}$${\displaystyle \left.{\frac {mL}{2}}\right)}$ ,

${\displaystyle c_{\mbox{d}}={\frac {4c_{i}}{\pi m}}sin\left({\frac {\pi x_{{\mbox{d}}i}}{L}}\right)}$ , ${\displaystyle d_{\mbox{d}}=\left[{\frac {2AM_{0}}{\pi I}}\left({\frac {M_{0}^{2}L_{}^{2}}{8EI_{}^{2}}}-\right.\right.}$${\displaystyle \left.\left.1\right)-m{\frac {L}{\pi }}v_{\mbox{d}}^{2}\right]/\left(-\right.}$${\displaystyle \left.{\frac {mL}{2}}\right)}$ ,

${\displaystyle e=\left({\frac {M_{0}^{2}L_{}^{2}}{8EI_{}^{2}}}-1\right){\frac {2M_{0}L}{EI\pi }}/\left(-\right.}$${\displaystyle \left.{\frac {mL}{2}}\right)}$ .

where ξ is the damping ratio, ω₀ is the first-order natural frequency, λ is the arm parameter of the end moment.

Compared with the classical parametric vibration models [2, 9-10], this model is more comprehensive and can more accurately reflect the characteristics of the parametric vibration of radial gates.

3. Stability analysis

The multi-scale method will be used to solve the nonlinear equation of motion. Therefore, the following substitutions are made:

where ε is a small dimensionless perturbation parameter. Then, equation (15) can be rewritten to:

where u_e represents excitation load. Suppose that the solution to equation (17) can be expressed as:

where T₀=t, T₁=tε, T₂=t. Substituting equation (18) into equation (17) and equating the coefficients of like powers of ε result in the following differential equations:

The complex solution to equation (19) can be obtained as:

where ${\displaystyle {\overline {A}}}$ is the complex conjugate of A.

Substituting equation (22) into equation (20), one gets:

where cc indicates the complex conjugate part at the right-hand side of equation (23). Eliminating the secular terms in equation (21) leads to:

Substituting equations (22) and (24) into equation (21) lead to:

Here, the subharmonic parametric resonance, ω_e=2ω_a is studied. Therefore, one has:

Eliminating secular term in equation (25), the following is obtained：

Write A in the exponential function form as follows:

where α(t) and θ(t) are real functions. Substituting equation (28) into equation (27) and separating the resulting equation into real and imaginary parts yield:

where γ=ε²σT₀-θ. The stationary solution equation α_s and γ_s can be obtained from equations (29) and (30) by letting ${\displaystyle {\dot {\alpha }}={\dot {\gamma }}=0}$ . The vibration amplitude can be expressed as:

For α_s is a real number, from equation (31), the condition of the structural motion stability can be obtained as follows:

or

From which one can see that many parameters like axial force, length of arms, etc. affect the structural motion stability region.

4. Numerical analysis

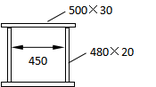
Taking a representative radial gate arm for study. The arm has box section, whose cross-sectional dimensions are shown in Figure 3. Arm length L=16m, mass per unit length m=386kg/m, modulus of elasticity E=210GPa.

In MATLAB, the standard fourth-order Runge-Kutta method is used to solve the numerical solution of equation (15) and the influence of the excitation elements and the structural elements for vibration of the radial gate arm is analyzed.

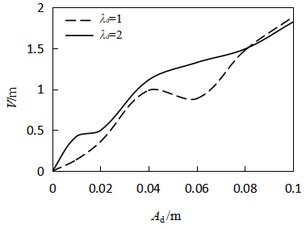
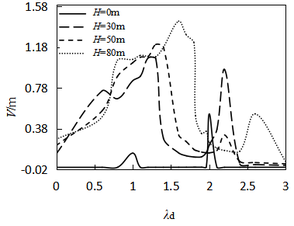
4.1 Effects of water head

When Initial disturbance V(0)=10^-4m, excitation amplitude A_d=0.01m, time t=500s, damping coefficient μ=0 and initial water head H=0, the effects of varying water head on vibration amplitude are shown in Figure 4. Where λ_d denotes the ratio of the external excitation frequency to the natural frequency of the arm. According to the Chinese and American codes, the layout of main beam of radial gate is equal load, and the hydrostatic pressure H₀ is related function of water head. The analysis of water head is shown in Table 1.

When the principal parametric resonance occurs, the amplitude of the arm increases with the increase of the water head, and the maximum displacement reaches 0.57m. In the case of subharmonic parametric resonance, the tendency of change is opposite, and the maximum amplitude is 0.18m. Overall, both types of parametric resonance responses change slowly and the axial hydrostatic pressure of the arm can be assumed to be 80m head in later analysis.

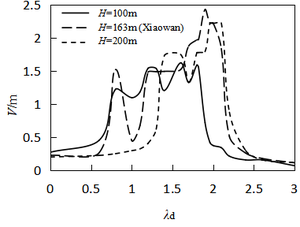
4.2 Effects of excitation frequency ratio and initial end bending moment

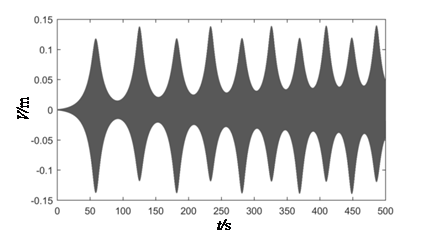
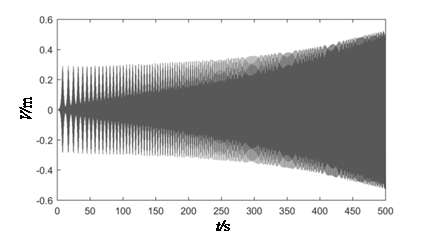
Figure 5 depicts the relationship between the amplitude and the excitation frequency ratio subjected to the initial end bending moment of different water heads. In figures, at H=0, the peak value of parametric resonance only appears at λ_d=1 and λ_d=2. This phenomenon matches the case of Design Code for Steel Gate in Water Resources and Hydropower Projects (SL74-2013) [1]. The Figure 6 shows that when the initial end bending moment is not taken into consideration, the beat vibration phenomenon can be observed, and the beat amplitude value increases over time at the subharmonic parametric resonance. However, take into account intitial end bending moment (Figure 5), the amplitude peak will be shift, and the arm response amplitudes increase with the initial end bending moment level, the resonance region become wider, which makes the parametric resonance more easily excited. The maximum displacements of parametric resonance are 1.44m and 2.2m at dividing point of high head in current code 80m and maximum existing design head 163m (Table 1). Through the above analysis, it is further clarified that the parametric resonance excitation condition mentioned in Chinese code is a special case in the parametric resonance region, which only consider the parametric resonance occur at the near doubled natural frequency. In order to obtain a more accurate response of the arm, the calculation method of instability regions for radial gates should be adopted in this paper.

(a) H<100m	(b) H≥100m

(a) λd=1	(b) λd=2

4.3 Effects of excitation amplitude

Figure 7 demonstrates the relationship between the displacement and the excitation amplitudes. The diagram shows that when parametric resonance occurs, the displacement response is closely related to the excitation amplitude. The response nonlinearly increases with the increase of excitation amplitude. When the excitation amplitude is less than 0.08m, the subharmonic parametric resonance response is greater than the principal parametric resonance response. While as the excitation amplitude is greater than 0.08m, two kinds of parametric resonance responses are almost equal. When the excitation amplitude is less than 0.01m, the arm swings in a smaller range, which makes it difficult to form destructive vibration. Thus, the response of the arm should be fully considered with the factor of excitation amplitudes.

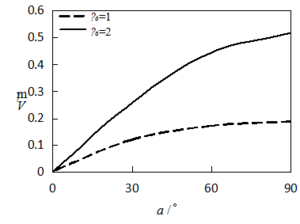
4.4 Effects of inclination angle

The effect of inclination angle of radial gate arm on vibration amplitude is presented in Figure 8. The amplitude displacement increases significantly at subharmonic parametric resonance with the increase of angle. But, at the parametric resonance, when the angle is less than 45 degrees, the amplitude increases rapidly, and then tends to steady. Thus, the inclination should be reasonably arranged in combination with considering displacement constraint in the design of radial gate.

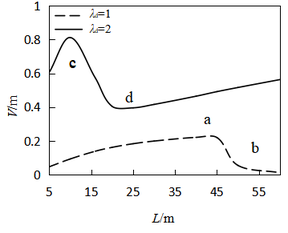
4.5 Effects of arm length and excitation time

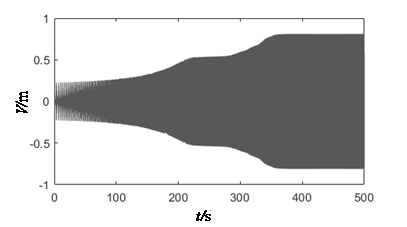
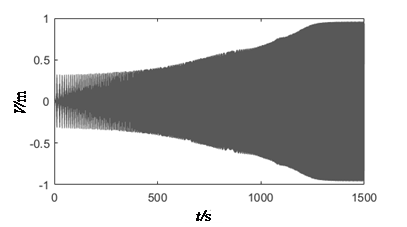
According to the characteristics of traditional radial gate and special planar radial gate as depicted in [13], arm length from 5 to 25m is examined in this paper. The curve of the relationship between the amplitude and length of arm is shown in Figure 9.

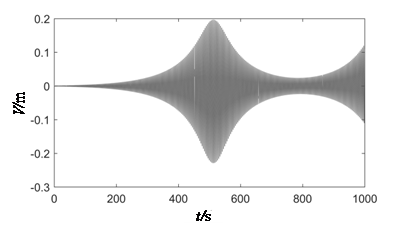
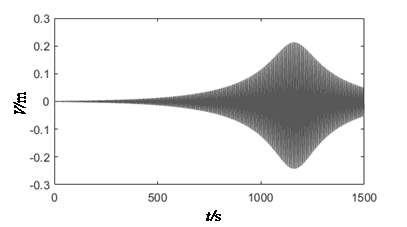
It can be found that the calculated results are not agreement with the description of the traditional unstable regions partition method. In the past review, with the increase of length, the flexibility and response amplitude of the arm should increase correspondingly. However, the inflection point appears in the Figure 9, this dependence of curve is not linear. Then, the time history analysis at a, b, c, d on both sides of the inflection are given in Figure 10. When the arm length is more than 45m and 20m respectively at λ_d=1 and λ_d=2, a longer excitation time is needed to reach peak response. This result proved that the gate may not show strong vibration in the initial stage of local opening operation, while the vibration amplitude will become much stronger over time, until the whole structure reaches integral instability failure. The results also proves that it is not advisable to ignore the time factor in the traditional design.

It can be seen that, from the above analysis, the time factor of local opening should be considered in the initial design stage. Meanwhile, in the stages of completion and operation, the corresponding guidance of local opening range and opening-closing time should be given in detail according to the vibration analysis results in an project. It is more reasonable that the length of radial gate arm is chosen less then 20m in 500s according to the case presented in this article.

(a) λd=1, L=45 (Vmax=0.2291)	(b) λd=1, L=60 (Vmax=0.2427)
(c) λd=2, L=10 (Vmax=0.8116)	(d) λd=2, L=20 (Vmax=0.9604)

4.6 Effects of damping

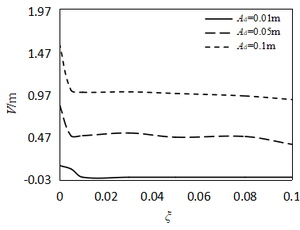
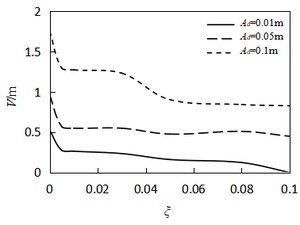
(1) λd=1	(b) λd=2

Figure 11 illustrates the relationship between amplitude and damping ratio under different excitation amplitudes. As can be seen from the diagram, amplitudes nonlinearly decrease with the damping ratio increaseing. Furthermore, the amplitude decreases rapidly at λ_d=1, ξ<0.01, and then tends to steady. The damping decrement at λ_d=2 is slightly higher than λ_d=1. As a whole, the damping effect on the vibration control is relatively insensitive. Once the parametric resonance is excited, the resonance amplitudes are mainly affected by the nonlinear term rather than the damping coefficient. Thus, adopting means of energy transfer (such as tuned dampers), the much more significant damping effect will be achieved.

5 Conclusions

This paper is devoted to nonlinear parametric vibration of radial gates. the nonlinear differential equation of motion for radial gate arm is derived with considering the geometric nonlinear and large displacement. Furthermore, the stability and vibration response of principal parametric resonance and subharmonic parametric resonance are investigated by using multi-scale method and numerical method. At the same time, the above-mentioned methods make up for the defects of the former methods of dividing the dynamic instability zone with not considering effects of response amplitude and time. The results are discussed as follows：

(1) The change of hydrostatic pressure caused by the water head has little effect on the parametric vibration, while the resonance region broaden with increase in the initial bending moment.

(2) The increasing of amplitude response increases both the excitation amplitude and the arm length, moreover, it reduces the inclination angle.

(3) Vibration amplitude will become much stronger over time. Thus, the time factor should be consider in design and operation stages.

(4) The vibration response mainly depends on the coefficient of nonlinear term, while the damping effect is limited. Thus, energy transfer method should be adopted to suppress the vibration.

Data Availability Statement

All data, models, and code generated or used during the study appear in the summitted article.

Acknowledgements

This research is supported by National Natural Science Foundation of China (Grant No. 51179164 and 51478354).

References

[1] CMWR (China Ministry of Water Resources). (2013) Design Code for Steel Gate in Water Resources and Hydropower Projects (SL74-2013). China Water & Power Press, Beijing.

[2] Niu, Z.G., Li, T.C. (2008) Research on Dynamic Stability of Steel Radial Gates. In: Earth and Space. Long Beach. pp. 1-8.

[3] Wang, Z.Z., Zhang, X.C., Liu, J.L. (2017) Advances and developing trends in research of large hydraulic steel gates. J. Hydroelectr. Eng., 36: 1-18.

[4] Demsic, M., Uros, M., Lazarevic, A.J., Lazarevic, D. (2019) Resonance regions due to interaction of forced and parametric vibration of a parabolic cable. J. Sound. Vib., 447: 78-104.

[5] Zhang, X., Peng, J., Wang, L. (2014) Parametric resonances in the two-to-one resonant beams on elastic foundation. Nonlinear Dynam., 77: 339-352.

[6] Franzini, G.R., Pesce, C.P., Gonçalves, R.T., Fujarra, A.L.C., Mendes, P. (2018). An experimental investigation on concomitant vortex-induced vibration and axial top-motion excitation with a long flexible cylinder in vertical configuration. Ocean Engineering, 156: 596-612.

[7] Wei, M.H., Lin, K., Jin,L., Zou, D.J. (2016) Nonlinear dynamics of a cable-stayed beam driven by sub-harmonic and principal parametric resonance. Int. J. Mech. Sci., 110: 78-93.

[8] Zhang, J.G. (1985) Summary on the study of gate vibration in China. Water Power, 11: 38-44.

[9] Liu, J.L., Wang, Z.Z., Fang, X., Fang, H.M. (2011) Dynamic instability mechanism and vibration control of radial gate arms. Appl. Mech. Mater., 50: 309-313.

[10] Zhang, J., Xie, Z.X. (2011) Nonlinear vibration and chaos phenomena of arm structures in radial gate. Water Power, 50: 309-313.

[11] Zhang, X.C., Wang, Z.Z., Sun, D.X. (2018) Research on rational layout of strut arms of tainter gate in vertical frame. Revista Internacional de Métodos Numéricos para Cálculo y Diseño en Ingeniería, 34: 1-6.

[12] Hu, M.S., Yang, Z.Z., Xu, J., Zhang, B. (2015) Modal parameter identification of radial gate based on stochastic subspace method. Water resour. power, 33: 164-167.

[13] Chen, F.Z., Yan, G.H. (2015) The key technology research on Chinese special type sluice. Hohai University Press, Nanjing.