Revision as of 14:30, 9 June 2022 (view source) Rimni (talk | contribs) (→‎2. Proposed scheme) ← Older edit		Revision as of 14:31, 9 June 2022 (view source) Rimni (talk | contribs) Newer edit →
Line 260:		Line 260:
	In the present work it is proposed to use Runge-Kutta <span id='citeF-20'></span>[[#cite-20|[20]]] of 2nd, 3rd, and 4th order, as follows:		In the present work it is proposed to use Runge-Kutta <span id='citeF-20'></span>[[#cite-20|[20]]] of 2nd, 3rd, and 4th order, as follows:
−	==Second-order Runge-Kutta method==	+	===Second-order Runge-Kutta method===
	{| class="formulaSCP" style="width: 100%; text-align: left;"		{| class="formulaSCP" style="width: 100%; text-align: left;"

---

Revision as of 14:31, 9 June 2022

Abstract

One of the greatest challenges in the area of applied mathematics continues to be the design of numerical methods capable of approximating the solution of partial differential equations quickly and accurately. One of the most important equations, due to the hydraulic and transport applications it has, and the large number of difficulties that it usually presents when solving it numerically is the Diffusion Equation.

In the present work, a Method of Lines applied to the numerical solution of the said equation in irregular regions is presented using a scheme of Generalized Finite Differences. The second-order finite difference method uses a central node and 8 neighbor points in order to address the spatial approximation. A series of tests and numerical results are presented, which show the accuracy of the proposed method.

Keywords: Generalized finite differences, method of lines, diffusion equation, irregular regions

1. Introduction

When a substance is been transported with a speed equal to zero, i.e. no flow moves it, then, according to the transport equation [1], the initial profile of the substance should remain the same as time goes by, maintaining the substance concentration at each point in the fluid.

However, in practice, this does not happen due to molecular diffusion; this is due to the molecules being in constant motion, causing collisions and rebounds in different directions. The molecules will tend to separate, or diffuse, within the flow. In general, this movement moves from areas with a higher density of molecules to areas with a lower density; this is called diffusion and can be described by a well-known Partial Differential Equation:

${\displaystyle {\frac {\partial u}{\partial t}}=\nu \nabla ^{2}u}$

(1)

where ${\textstyle \nu }$ represents the diffusion coefficient, which tells how easy a substance diffuses in a medium.

In the past years, many people have worked in different methods to achieve good numerical solutions to this equation, involving a great variety of modern and classical techniques. Nevertheless, even though a large number of numerical methods have been proposed to solve it, a large number of these have a rather limited application to real-world scenarios since they are designed for regular regions.

This is due to the fact that the spatial discretization of the diffusion equation imposes bounds on the time step size in order to achieve numerical stability. However, the use of semidiscretization schemes allows for overcoming many stability issues by using well-known and widely used one-step methods for ordinary initial value problems. For example, in Manshoor et al. [2], a Method of Lines, involving solutions with ${\textstyle a}$ Runge-Kutta method, is presented along with its stability analysis; the results presented show that it is possible to use this kind of method to compute numerical solutions of the equation, yet, the regions where the method is tested are unidimensional regions. On the side of the Generalized Finite Difference methods, Ureña et al. [3] present a scheme to achieve numerical solutions using this method; the results presented in this work show that it is possible to solve different Partial Differential Equations using finite differences over non-regular clouds of points; this work presents that the solutions obtained with this method satisfactorily match with the exact solution of the proposed tests. Some other authors, like Li et al. [4,5,6,7,8,9], and Wang et al. [10] have addressed a large number of applications. Nevertheless, the computational cost of the method as proposed in the aforementioned papers is high, so for each node of the cloud it is required to take up to twenty-six support nodes, even in 2D problems, which increases the computational cost of the implementation.

On the other hand, some variations of the presented generalized finite difference method for several transport equations, which produce satisfactory numerical solutions using a low-cost implementation for the spatial discretization were presented in [11,12,13,14,15]. Even though, the use of several straightforward time integration schemes remained an important issue to take into account.

For the case of interest of this work, it is important to obtain an approximation in generalized finite differences, for the spatial part, to the solution of the problem

${\displaystyle {\frac {\partial }{\partial t}}u(x,y,t)=\nu \left({\frac {\partial ^{2}}{\partial x^{2}}}u(x,y,t)+{\frac {\partial ^{2}}{\partial y^{2}}}u(x,y,t)\right)\Omega \times [0,T]\nu \in I\!\!R,}$ ${\displaystyle u(x,y,0)=g(x,y)(x,y)\in \Omega ,}$ ${\displaystyle u(x,y,t)|_{\partial \Omega }=g(x,y,t)(x,y)\in \Omega t\in [0,T],}$

where ${\textstyle \Omega }$ is a simply connected planar domain, and its boundary, and ${\textstyle \partial \Omega }$ is a positively oriented Jordan polygon, as the domain shown in Figure 1.

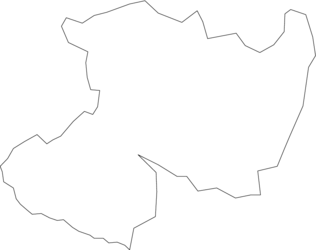
Figure 1. Example of an ${\displaystyle \Omega }$ domain

On the other hand, for the temporal discretization, a Method of Lines (MOL) is proposed [16]. The basic idea of the MOL is to solve a time-dependent Partial Differential Equation (PDE) by discretizing the spatial derivatives and then, integrating the semi-discretized problem as an Ordinary Differential Equations (ODE) system.

2. Proposed scheme

In order to apply a MOL for the case of the diffusion equation

${\displaystyle {\frac {\partial }{\partial t}}u(x,y,t)=\nu \left({\frac {\partial ^{2}}{\partial x^{2}}}u(x,y,t)+{\frac {\partial ^{2}}{\partial y^{2}}}u(x,y,t)\right),}$

it is possible to discretize the spatial derivatives applying a generalized finite differences method, for that it is convenient to considerate the approximation to the second or-er linear operator

${\displaystyle Lu=Au_{xx}+Bu_{xy}+Cu_{yy}+Du_{x}+Eu_{y}+Fu,}$

(2)

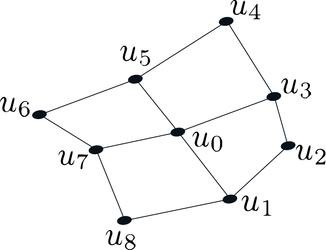
where ${\textstyle A}$, ${\textstyle B}$, ${\textstyle C}$, ${\textstyle D}$, ${\textstyle E}$, and ${\textstyle F}$ are given functions. Within an arbitrary distribution of nodes, like the one presented in Figure 2, it is possible to approximate its value at a node ${\textstyle p_{0}=(x_{0},y_{0})}$ using values of ${\textstyle u}$ at some neighbor nodes ${\textstyle p_{i}=(x_{i},y_{i})}$, ${\textstyle i~=~1,2,\dots ,q}$ [12]. For this work, a finite difference scheme is applied at the node ${\textstyle p_{0}}$, which can be written as a linear combination as

${\displaystyle L_{0}=\Gamma _{0}u(p_{0})+\Gamma _{1}u(p_{1})+...+\Gamma _{q}u(p_{q})=\sum _{i=0}^{q}\Gamma _{i}u(p_{i}).}$

(3)

where ${\textstyle \Gamma _{0},\Gamma _{1},\dots ,\Gamma _{q}}$ are adequate weighs.

Figure 2. Arbitrary distribution of ${\displaystyle p_{0}}$ and its neighbors

According to Strikwerda [17] and Thomas [18], a finite difference scheme ${\textstyle L_{0}}$ is consistent with the linear operator ${\textstyle L}$ if the local truncation error ${\textstyle \tau }$ satisfies that

${\displaystyle \tau =\left[Lu\right]_{p_{0}}-[L_{0}u]_{p_{0}}\to 0}$

(4)

as ${\textstyle p_{1}}$, ${\textstyle p_{2}}$, ${\textstyle \dots }$, ${\textstyle p_{q}\to p_{0}}$.

Using the six first terms of Taylor's series expansion, up to second order, of the consistency condition (4), it is possible to obtain the system

${\displaystyle \left({\begin{array}{lclc}1&1&...&1\\0&\Delta x_{1}&...&\Delta x_{q}\\0&\Delta y_{1}&...&\Delta y_{q}\\0&(\Delta x_{1})^{2}&...&(\Delta x_{q})^{2}\\0&\Delta x_{1}\Delta y_{1}&...&\Delta x_{q}\Delta y_{q}\\0&(\Delta y_{1})^{2}&...&(\Delta y_{q})^{2}\\\end{array}}\right)\left({\begin{array}{l}\Gamma _{0}\\\Gamma _{1}\\\Gamma _{2}\\.\\.\\.\\\Gamma _{q}\\\end{array}}\right)=\left({\begin{array}{l}F(p_{0})\\D(p_{0})\\E(p_{0})\\2A(p_{0})\\B(p_{0})\\2C(p_{0})\\\end{array}}\right),}$

(5)

where ${\textstyle \Delta x_{i}=x_{i}-x_{0}}$ and ${\textstyle \Delta y_{i}=y_{i}-y_{0}}$. In order o solve this linear system, it is possible to separate the first equation of the system (5)

${\displaystyle \sum _{i=0}^{q}\Gamma _{i}-F(p_{0})=0}$

(6)

and then, the problem defined by

${\displaystyle \left({\begin{array}{lcl}\Delta x_{1}&...&\Delta x_{q}\\\Delta y_{1}&...&\Delta y_{q}\\(\Delta x_{1})^{2}&...&(\Delta x_{q})^{2}\\\Delta x_{1}\Delta y_{1}&...&\Delta x_{q}\Delta y_{q}\\(\Delta y_{1})^{2}&...&(\Delta y_{q})^{2}\\\end{array}}\right)\left({\begin{array}{l}\Gamma _{1}\\\Gamma _{2}\\.\\.\\.\\\Gamma _{q}\\\end{array}}\right)=\left({\begin{array}{l}D(p_{0})\\E(p_{0})\\2A(p_{0})\\B(p_{0})\\2C(p_{0})\\\end{array}}\right),}$

(7)

can be solved using the reduced Cholesky factorization of its normal equations, as in [19], namely

${\displaystyle M^{T}M\Gamma =M^{T}\beta ,}$

where

${\displaystyle M=\left({\begin{array}{clc}\Delta x_{1}&...&\Delta x_{q}\\\Delta y_{1}&...&\Delta y_{q}\\(\Delta x_{1})^{2}&...&(\Delta x_{q})^{2}\\\Delta x_{1}\Delta y_{1}&...&\Delta x_{q}\Delta y_{q}\\(\Delta y_{1})^{2}&...&(\Delta y_{q})^{2}\\\end{array}}\right),\quad \Gamma =\left({\begin{array}{l}\Gamma _{1}\\\Gamma _{2}\\.\\.\\.\\\Gamma _{q}\\\end{array}}\right),\quad \beta =\left({\begin{array}{l}D(p_{0})\\E(p_{0})\\2A(p_{0})\\B(p_{0})\\2C(p_{0})\\\end{array}}\right).}$

The value of ${\textstyle \Gamma _{0}}$ is then obtained from (6) assuming, for the case of the diffusion equation, ${\textstyle F(p_{0})=0}$.

Now, the scheme defined by Eq.(7) can be used to approximate the linear operator

${\displaystyle Lu=\nu \left({\frac {\partial ^{2}u}{\partial x^{2}}}+{\frac {\partial ^{2}u}{\partial y^{2}}}\right)}$

taking ${\textstyle A=C=\nu }$, and ${\textstyle B=D=E=0}$. The resulting ${\textstyle \Gamma _{i}}$ coefficients, define the Finite-Difference Scheme

${\displaystyle {\frac {\partial }{\partial t}}u_{i}(t)=\sum _{j=0}^{q}\Gamma _{j}u_{j}(t),}$

(8)

for diffusion equation, where ${\textstyle u_{i}(t)}$ is the approximation to the solution in the point ${\textstyle p_{i}=(x_{i},y_{i})}$, and ${\textstyle p_{j}}$ are the corresponding neighbor nodes of ${\textstyle p_{i}}$.

An important issue to be taken into account is the number of neighbors, ${\textstyle q}$, to use in the scheme. In this paper, 8 neighbor points were taken into account following the stencil shown in Figure 3.

Figure 3. Centered stencil used in the scheme

Once a discretization of the spatial operator is obtained, following the idea presented in [1], the semi-discretized PDE can be rewritten as a linear ODE system in time,

${\displaystyle {\frac {\partial }{\partial t}}u_{i}(t)=\sum _{j=0}^{8}\Gamma _{j}u_{j}(t),i=1,\dots ,m,}$

where ${\textstyle m}$ is the total amount of grid points.

There exist several ways to approximate the solution of this ODE system, for example, it is possible to use a forward Euler method as

${\displaystyle {\frac {u_{i}^{k+1}-u_{i}^{k}}{\Delta t}}=\sum _{j=0}^{8}\Gamma _{j}u_{j}^{k},}$

nevertheless, this kind of implementation has proven to be conditionally stable and, in some cases, the stability conditions are difficult to accomplish.

Another way to solve this system is the Method of Lines, where each ${\textstyle u_{i}(t)}$ is solved for a fixed grid node ${\textstyle p_{i}=(x_{i},y_{i})}$, i.e. it is solved by “lines”. As we are now dealing with a set of ODEs, it is possible to use a Runge-Kutta method, to solve the ODE on each line in order to obtain stable and accurate results.

In the present work it is proposed to use Runge-Kutta [20] of 2nd, 3rd, and 4th order, as follows:

Second-order Runge-Kutta method

${\displaystyle u_{i}^{k}=u_{i}^{k-1}+{\frac {\Delta t}{2}}\left(r_{1}+r_{2}\right),}$

where

${\displaystyle r_{1}=u_{i}^{k-1},}$ ${\displaystyle r_{2}=u_{i}^{k-1}+{\frac {\Delta t}{2}}(r_{1}).}$ ${\displaystyle u_{i}^{k-1}=\sum _{j=0}^{8}\Gamma _{j}u_{j}^{k-1}}$

Third-order Runge-Kutta method

${\displaystyle u_{i}^{k}=u_{i}^{k-1}+{\frac {\Delta t}{6}}\left(r_{1}+4r_{2}+r_{3}\right),}$

where

${\displaystyle r_{1}=u_{i}^{k-1},}$ ${\displaystyle r_{2}=u_{i}^{k-1}+{\frac {\Delta t}{2}}(r_{1}),}$ ${\displaystyle r_{3}=u_{i}^{k-1}+\Delta t(2r_{2}-r_{1}),}$ ${\displaystyle u_{i}^{k-1}=\sum _{j=0}^{8}\Gamma _{j}u_{j}^{k-1}}$

Fourth-order Runge-Kutta method

${\displaystyle u_{i}^{k}=u_{i}^{k-1}+{\frac {\Delta t}{6}}\left(r_{1}+2r_{2}+2r_{3}+r_{4}\right),}$

where

${\displaystyle r_{1}=u_{i}^{k-1},}$ ${\displaystyle r_{2}=u_{i}^{k-1}+{\frac {\Delta t}{2}}(r_{1}),}$ ${\displaystyle r_{3}=u_{i}^{k-1}+{\frac {\Delta t}{2}}(r_{2}),}$ ${\displaystyle r_{4}=u_{i}^{k-1}+\Delta t(r_{3}),}$ ${\displaystyle u_{i}^{k-1}=\sum _{j=0}^{8}\Gamma _{j}u_{j}^{k-1}}$

in all the cases, ${\textstyle k}$ represents the time level.

3 Numerical tests

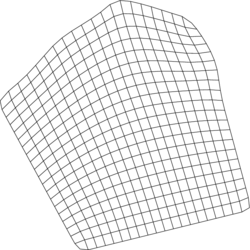
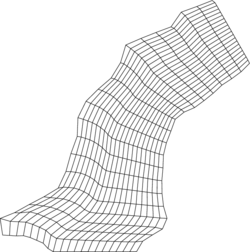
To show the performance of the proposed scheme, the problem of obtaining a numerical solution to the diffusion equation in four different regions was proposed. The first region, denoted as A, corresponds to the unitary square, for comparison reasons, and the other three regions, denoted as B, C, and D, are non-rectangular planar domains. All the regions were scaled to fit on ${\textstyle [0,1]\times [0,1]}$, and meshed with ${\textstyle 21\times {21}}$ nodes, following a variational procedure implemented in UNAMalla [21], then they were subdivided to obtain meshes with ${\textstyle 41\times {41}}$ nodes. The meshes for with ${\textstyle 21\times {21}}$ nodes for each region can be seen in Figure 4

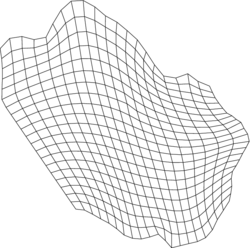
Figure 4: Meshes of the test regions with ${\displaystyle 21\times {21}}$ nodes.

For all the regions, two different tests were performed:

Test 1. Following the same idea as In [22], where a well-known diffusion problem is presented, the initial and boundary conditions were taken from the closed-form solution:

${\displaystyle g(x,y,t)=e^{(-2\pi ^{2}\nu t)}\cos(\pi x)\cos(\pi y).}$

Test 2. For comparison purposes, one of the tests presented in [23], was also taken into account; in this case, the initial and boundary conditions were taken from the closed-form solution:

${\displaystyle g(x,y,t)=e^{(-2\pi ^{2}\nu t)}\sin(\pi x+\pi y).}$

The time interval ${\textstyle [0,1]}$ was subdivided with different discretizations, the number of time steps was chosen to satisfy the classical Courant condition [24]:

${\displaystyle \Delta t={\frac {(\max(\Delta x))^{2}+(\max(\Delta y))^{2}}{2\nu }},}$

where ${\textstyle \Delta x}$ and ${\textstyle \Delta y}$ are the spatial steps on each grid, taken from the meshes with ${\textstyle 41\times {41}}$ nodes, and ${\textstyle \nu =0.2}$.

The norm of the quadratic error, at a ${\textstyle k-}$the time level can be computed as

${\displaystyle \|e^{k}\|_{2}={\sqrt {\sum _{i,j}(u_{i,j}^{k}-U_{i,j}^{k})^{2}A_{i,j}}}}$

where ${\textstyle U_{i,j}^{k}}$ and ${\textstyle u_{i,j}^{k}}$ are the approximated and theoretical solutions, respectively, at the ${\textstyle i,j}$-th grid node, and ${\textstyle A_{i,j}}$ is the area of the polygon defined by the points ${\textstyle P_{i+1,j}}$, ${\textstyle P_{i,j+1}}$, ${\textstyle P_{i-1,j}}$ and ${\textstyle P_{i,j-1}}$.

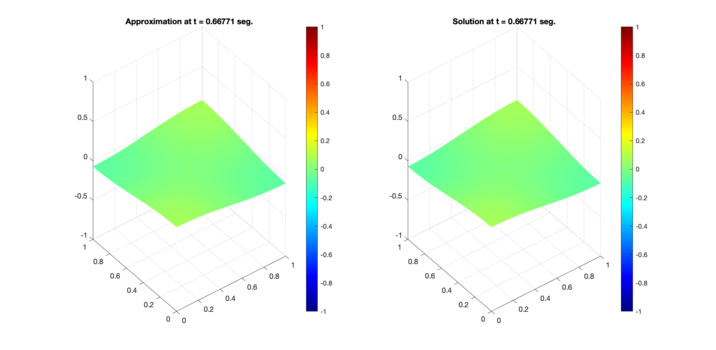
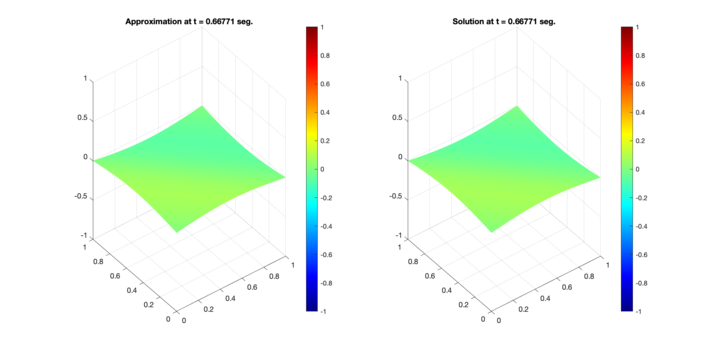
Figure 5 presents a comparison of the numerical results obtained with the proposed scheme using the second-order Runge-Kutta approximation and the exact solutions for the test region A at time ${\textstyle t=0.66}$s. The approximation is presented on the left, and the exact solution on the right.

Figure 5: Comparison between numerical results (left) and exact solution (right) for test region A. Test 1 (Top) and Test 2 (Bottom).

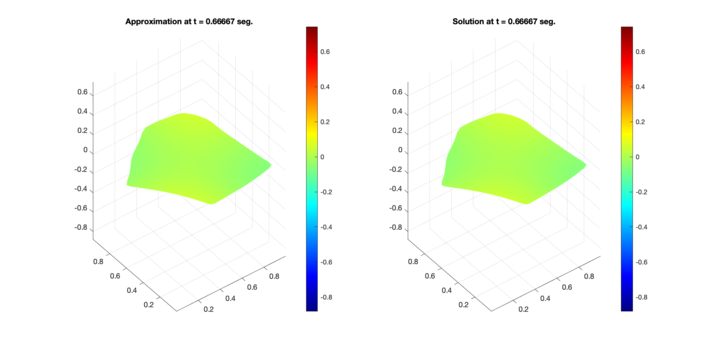
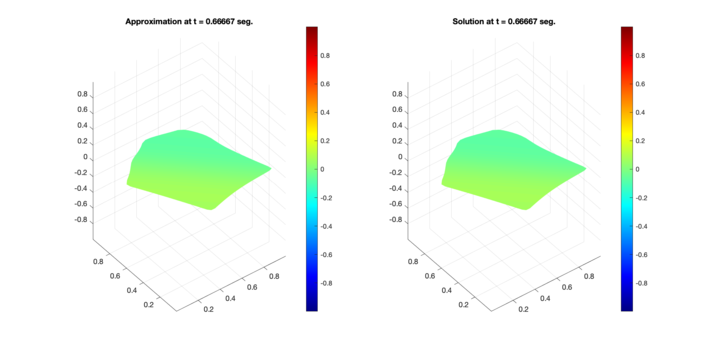
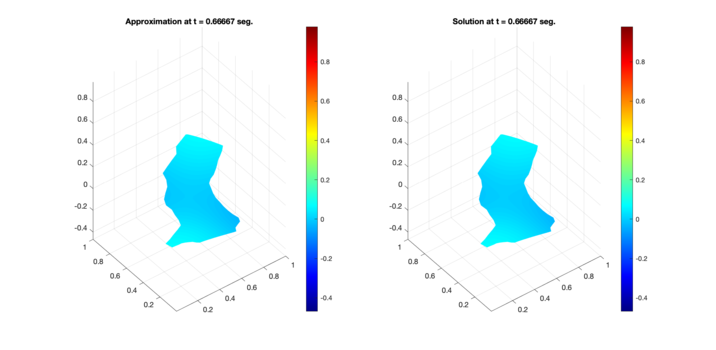
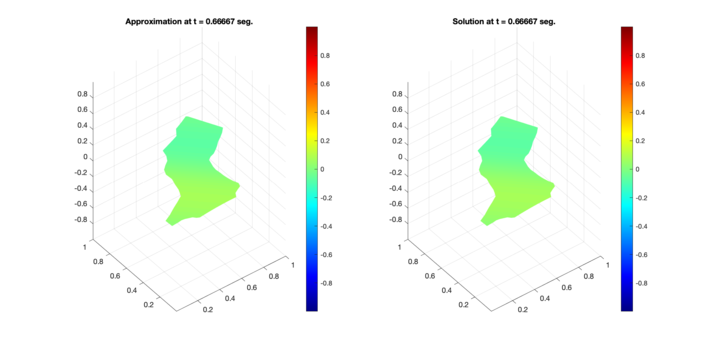
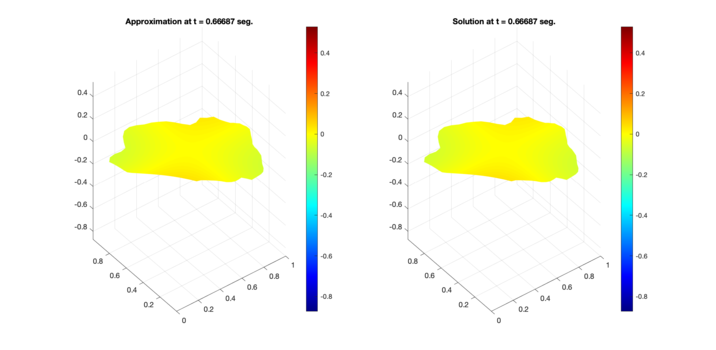
Similarly, Figures 6, 7, and 8 present the respective comparisons for the regions B, C, and D.

¡

Figure 6: Comparison between numerical results (left) and exact solution (right) for test region B. Test 1 (Top) and Test 2 (Bottom).

Figure 7: Comparison between numerical results (left) and exact solution (right) for test region C. Test 1 (Top) and Test 2 (Bottom).

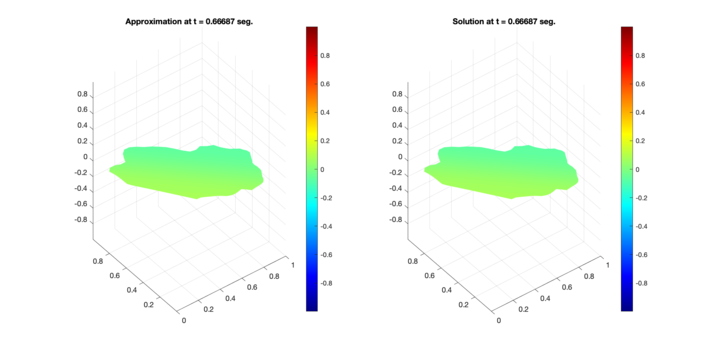
Figure 8: Comparison between numerical results (left) and exact solution (right) for test region D. Test 1 (Top) and Test 2 (Bottom).

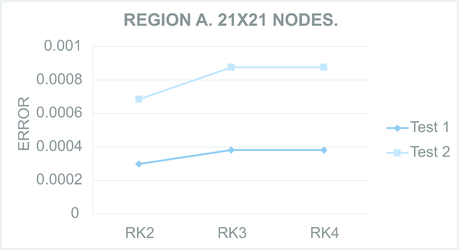
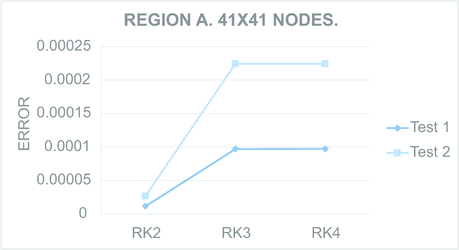
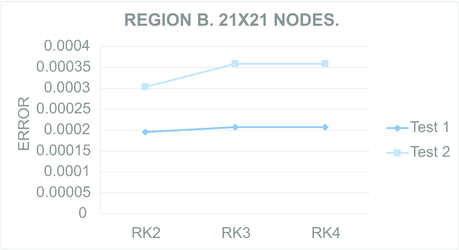
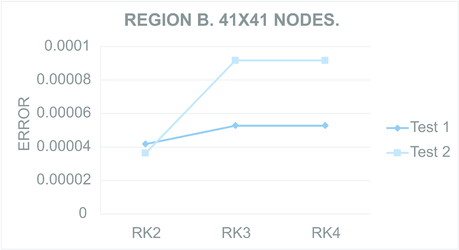
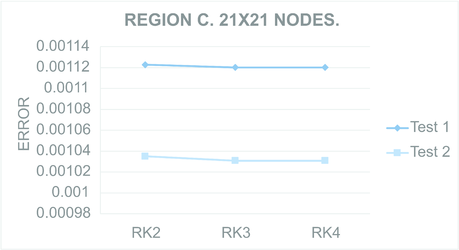
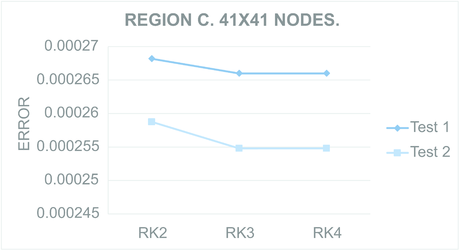
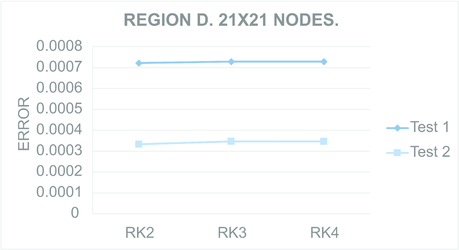
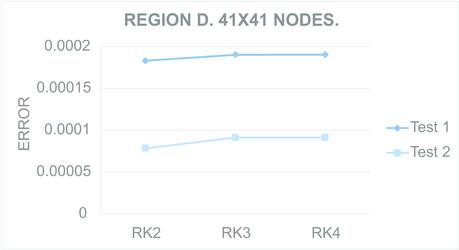
Figures 9 to 12 present the maximum value of the error ${\textstyle \|e^{k}\|_{2}}$ computed for all the regions. For each Figure, both tests were performed in the regions meshed with ${\textstyle 21\times {21}}$ nodes and ${\textstyle 41\times {41}}$ nodes.

Figure 9: Maximum ${\displaystyle \|e^{k}\|_{2}}$ computed for Test region A with ${\displaystyle 21\times {21}}$ nodes (Left) and ${\displaystyle 41\times {41}}$ nodes (Right).

Figure 10: Maximum ${\displaystyle \|e^{k}\|_{2}}$ computed for Test region B with ${\displaystyle 21\times {21}}$ nodes (Left) and ${\displaystyle 41\times {41}}$ nodes (Right).

Figure 11: Maximum ${\displaystyle \|e^{k}\|_{2}}$ computed for Test region C with ${\displaystyle 21\times {21}}$ nodes (Left) and ${\displaystyle 41\times {41}}$ nodes (Right).

Figure 12: Maximum ${\displaystyle \|e^{k}\|_{2}}$ computed for Test region D with ${\displaystyle 21\times {21}}$ nodes (Left) and ${\displaystyle 41\times {41}}$ nodes (Right).

4 Conclusions

The numerical results show that the proposed method of Lines applied to the diffusion equation produces satisfactory numerical solutions. In the tests carried out, no spurious oscillations or instabilities were perceived. In addition, the results show that it is not necessary to “work more” by using higher Runge-Kutta methods; this scheme accomplishes better results when second-order Runge-Kutta is used to solve the Ordinary Differential Equations system.

It is possible to appreciate that with the presented discretizations, even with the fourth-order Runge-Kutta method, acceptable numerical results can be obtained. Additionally, the numerical results shown in Figures 9 to 12 show that a refinement of the spatial mesh can improve the approximations carried out with the method; as expected in these kinds of methods. It is worth mentioning that, for all the tests, a minimum number of time steps was used, taking into account the classical theory for the diffusion equation, which makes the computational cost of this method low, since it does not require making very small temporary discretizations, as in other cases.

Furthermore, the proposed scheme can produce stable results for non-standard initial conditions in highly irregular regions. For example, in the following videos

• https://youtu.be/soUxe5uUY_U
• https://youtu.be/479YeBjqmSs

solutions of the diffusion equation are presented on domains that are geometrical approximations of real geographical locations, where the boundary conditions are fixed as ${\textstyle 0}$ and the initial condition is stated as:

${\displaystyle g(x,y)={\begin{cases}1&x,y{\hbox{ in }}[0.35,0.65]\\0&{\hbox{ All the other cases.}}\end{cases}}}$

It is possible to see that even for these conditions in these regions, the scheme produces stable results that show the expected behavior.

An important remark is that, even when in this work structured convex grids were used, the development of the method doesn't take into account a particular data structure, i.e. this method can be used not only on structured meshes but also as a meshless method, that would be developed as future work.

5 Acknowledgments

We want to thank AULA CIMNE-Morelia and CIC-UMSNH for the financial support for this work. Thanks to Universidad Vasco de Quiroga for lending the facilities to perform the final part of the work done for the paper.

Special thanks to the ``Laboratorio de Matemáticas Aplicadas of the ``Facultad de Ciencias Físico-Matemáticas at ``Universidad Michoacana de San Nicolás de Hidalgo for lending their computational infrastructure.

The authors would also like to thank the reviewers for their valuable feedback and suggestions to improve the present work.

BIBLIOGRAPHY

[1] Gerardo Tinoco-Guerrero and Francisco Javier Domínguez-Mota and José Gerardo Tinoco-Ruiz and Juan Salvador Lucas-Martínez. (2018) "Aproximación de la Ecuación de Advección en Regiones Irregulares Utilizando un Método de Líneas y Diferencias Finitas Generalizadas", Volume 2. Revista Mexicana de Métodos Numéricos 2

[2] Bukhari Manshoor and Hamidon Salleh nad Amir Khalid and Muhammed Abdelfattah Sayed Abdelaal. (2021) "Method of Lines and Runge-Kutta Method in Solving Partial Differential Equation for Heat Equation", Volume 3. Journal of Complex Flow 1 21 - 25

[3] Francisco Ureña Prieto and Juan José Benito Muñoz and Luis Gavete Corvinos. (2011) "Application of the generalized finite difference method to solve the advection-diffusion equation", Volume 235. Journal of Computational and Applied Mathematics 1849 - 1855

[4] Li, Po-Wei and Fan, Chia-Ming and Grabski, Jakub Krzysztof. (2021) "A meshless generalized finite difference method for solving shallow water equations with the flux limiter technique", Volume 131. Elsevier. Engineering Analysis with Boundary Elements 159–173

[5] Zhang, Ting and Lin, Zhen-Huan and Huang, Guan-Yi and Fan, Chia-Ming and Li, Po-Wei. (2020) "Solving Boussinesq equations with a meshless finite difference method", Volume 198. Elsevier. Ocean Engineering 106957

[6] Fu, Zhuo-Jia and Tang, Zhuo-Chao and Zhao, Hai-Tao and Li, Po-Wei and Rabczuk, Timon. (2019) "Numerical solutions of the coupled unsteady nonlinear convection-diffusion equations based on generalized finite difference method", Volume 134. Springer. The European Physical Journal Plus 6 1–20

[7] Zhang, Ting and Ren, Yu-Fei and Yang, Zhi-Qiang and Fan, Chia-Ming and Li, Po-Wei. (2016) "Application of generalized finite difference method to propagation of nonlinear water waves in numerical wave flume", Volume 123. Elsevier. Ocean Engineering 278–290

[8] Li, Po-Wei and Fan, Chia-Ming. (2017) "Generalized finite difference method for two-dimensional shallow water equations", Volume 80. Elsevier. Engineering Analysis with Boundary Elements 58–71

[9] Fu, Zhuo-Jia and Zhang, Jin and Li, Po-Wei and Zheng, Jin-Hai. (2020) "A semi-Lagrangian meshless framework for numerical solutions of two-dimensional sloshing phenomenon", Volume 112. Elsevier. Engineering Analysis with Boundary Elements 58–67

[10] Wang, Qiang and Kim, Pyeoungkee and Qu, Wenzhen. (2022) "A Hybrid Localized Meshless Method for the Solution of Transient Groundwater Flow in Two Dimensions", Volume 10. Mathematics 3

[11] Francisco Javier Domínguez-Mota and Sanzon Mendoza-Armenta and José Gerardo Tinoco-Ruiz. (2011) "Finite Difference Schemes Satisfying an Optimality Condition". IMACS Series in Computational and Applied Mathematics: MASCOT 2010

[12] Gerardo Tinoco-Guerrero and Francisco Javier Domínguez-Mota and José Gerardo Tinoco-Ruiz. (2015) "Numerical Solution of Advection Equations Using Structured Grids on Plane Irregular Regions With a Finite Differences Scheme", Volume 1. Boletín de la Sociedad Mexicana de Computación Científica y Sus Aplicaciones 3 29 - 32

[13] José Gerardo Tinoco-Ruiz and Francisco Javier Domínguez-Mota and Gerardo Tinoco-Guerrero and Pablo Michel Fernández-Valdés and Sanzon Mendoza-Armenta. (2013) "Numerical Solution of Differential Equations in Irregular Plane Regions Using Quality Structured Convex Grids", Volume 4. International Journal of Modeling, Simulation and Scientific Computing 2

[14] Francisco Javier Domínguez-Mota and Juan Salvador Lucas-Martínez and Gerardo Tinoco-Guerrero. (2020) "A Generalized Finite-Differences Scheme Used in Modeling of a Direct and an Inverse Problem of Advection-Diffusion", Volume 33. International Journal of Applied Mathematics 4 599 - 608

[15] Chávez-Negrete, C and Domínguez-Mota, FJ and Santana-Quinteros, D. (2018) "Numerical solution of Richards' equation of water flow by generalized finite differences", Volume 101. Elsevier. Computers and Geotechnics 168–175

[16] William Schiesser. (1991) "The Numerical Method of Lines". San Diego: Academic Press

[17] John C. Strikwerda. (2004) "Finite Difference Schemes and Partial Differential Equations". Society for Industrial and Applied Mathematics

[18] J. W. Thomas. (1995) "Numerical Partial Differential Equations: Finite Difference Methods", Volume 2. Springer

[19] Gerardo Tinoco-Guerrero and Francisco Javier Domínguez-Mota and José Gerardo Tinoco-Ruiz. (2020) "A Study of the Stability for a Generalized Finite-Difference Scheme Applied to the Advection-Diffusion Equation", Volume 176. Mathematics and Computer in Simulations 301 - 311

[20] J. C. Butcher. (1969) "Conference on the Numerical Solution of Differential Equations", Volume 109. Springer 133 - 139

[21] UNAMalla. (2011) "An Automatic Package for Numerical Grid Generation"

[22] José Gerardo Tinoco-Ruiz and Francisco Javier Domínguez-Mota and Juan Salvador Lucas-Martínez and Gerardo Tinoco-Guerrero. (2019) "Study of the Stability of a Generalized Finite Difference Scheme Applied to the Diffusion Equation in Irregular 2D Space Regions Using Convex Grids". IMACS Series in Computational and Applied Mathematics: MASCOT 2018

[23] L.M. Sánchez and F. Ureña and J.J. Benito and L. Gavete. (2009) "Resolución de la ecuación de Difusión en 2-D y 3-D utilizando diferencias finitas generalizadas. Consistencia y Estabilidad". XXI Congreso de Ecuaciones Diferenciales y Aplicaciones 1 - 8

[24] Michael B. Abbott and Andrew D. McCowan and Ian R. Warren. (1984) "Accuracy of Short-Wave Numerical Models", Volume 110. Journal of Hydraulic Engineering 10 1287 - 1301