Integration of game theory and response surface method for robust parameter design

Latest revision as of 15:41, 20 June 2022

Abstract

Robust parameter design (RPD) is to determine the optimal controllable factors that minimize the variation of quality performance caused by noise factors. The dual response surface approach is one of the most commonly applied approaches in RPD that attempts to simultaneously minimize the process bias (i.e., the deviation of the process mean from the target) as well as process variability (i.e., variance or standard deviation). In order to address this tradeoff issue between the process bias and variability, a number of RPD methods are reported in literature by assigning relative weights or priorities to both the process bias and variability. However, the relative weights or priorities assigned are often subjectively determined by a decision maker (DM) who in some situations may not have enough prior knowledge to determine the relative importance of both the process bias and variability. In order to address this problem, this paper proposes an alternative approach by integrating the bargaining game theory into an RPD model to determine the optimal factor settings. Both the process bias and variability are considered as two rational players that negotiate how the input variable values should be assigned. Then Nash bargaining game solution technique is applied to determine the optimal, fair, and unique solutions (i.e., a balanced agreement point) for this game. This technique may provide a valuable recommendation for the DM to consider before making the final decision. This proposed method may not require any preference information from the DM by considering the interaction between the process bias and variability. To verify the efficiency of the obtained solutions, a lexicographic weighted Tchebycheff method which is often used in bi-objective optimization problems is utilized. Finally, in two numerical examples, the proposed method provides non-dominated tradeoff solutions for particular convex Pareto frontier cases. Furthermore, sensitivity analyses are also conducted for verification purposes associated with the disagreement and agreement points.

Keywords: Robust parameter design, lexicographic weighted Tchebycheff, bargaining game, response surface methodology, dual response model

1. Introduction

Due to fierce competition among manufacturing companies and an increase in customer quality requirements, robust parameter design (RPD), an essential method for quality management, is becoming ever more important. RPD was developed to decrease the degree of unexpected deviation from the requirements that are proposed by customers or a DM and thereby helps to improve the quality and reliability of products or manufacturing processes. The central idea of RPD is to build quality into the design process by identifying an optimal set of control factors that make the system impervious to variation [1]. The objectives of RPD are set out to ensure that the process mean is at the desired level and process variability is minimized. However, in reality, a simultaneous realization of those two objectives sometimes is not possible. As Myers et al. [2] stated there are circumstances where the process variability is robust against the effects of noise factors but the mean value is still far away from the target. In other words, a set of parameter values that satisfies these two conflicting objectives may not exist. Hence, the tradeoffs that exist between the process mean and variability are undoubtedly crucial in determining a set of controllable parameters that optimize quality performance.

The tradeoff issue between the process bias and variability can be associated with assigning different weights or priority orders. Weight-based methods assign different weights to the process bias and variability, respectively, to establish their relative importance and transform the bi-objective problem into a single objective problem. The two most commonly applied weight-based methods are the mean square error model [3] and the weighted sum model [4,5]. Alternatively, priority-based methods sequentially assign priorities to the objectives (i.e., minimization of the process bias or variability). For instance, if the minimization of the process bias is prioritized, then the process variability is optimized with a constraint of zero-process bias [6]. Other priority-based approaches are discussed by Myers and Carter [7], Copeland and Nelson [8], Lee et al. [9], and Shin and Cho [10]. In both weight-based and priority-based methods, the relative importance can be assigned by the decision maker’s (DM) preference, which is obviously subjective. Additionally, there are situations in which the DM could be unsure about the relative importance of the process parameters in bi-objective optimization problems.

Therefore, this paper aims to solve this tradeoff problem from a game theory point of view by integrating bargaining game theory into the RPD procedure. First, the process bias and variability are considered as two rational players in the bargaining game. Furthermore, the relationship functions for the process bias and variability are separately estimated by using the response surface methodology (RSM). In addition, those estimated functions are regarded as utility functions that represent players’ preferences and objectives in this bargaining game. Second, a disagreement point, signifying a pair of values that the players expect to receive when negotiation among players breaks down, can be defined by using the minimax-value theory which is often used as a decision rule in game theory. Third, Nash bargaining solution techniques are then incorporated into the RPD model to obtain the optimal solutions. Then, to verify the efficiency of the obtained solutions, a lexicographic weighted Tchebycheff approach is used to generate the associated Pareto frontier so that it can be visually observed if the obtained solutions are on the Pareto frontier. Two numerical examples are conducted to show that the proposed model can efficiently locate well-balanced solutions. Finally, a series of sensitivity analyses are also conducted in order to demonstrate the effects of the disagreement point value on the final agreed solutions.

This research paper is laid out as follows: Section 2 discusses existing literature for RPD and game theory applications. In Section 3, the dual response optimization problem, the lexicographic weighted Tchebycheff method, and the Nash bargaining solution are explained. Next, in Section 4, the proposed model is presented. Then in Section 5, two numerical examples are addressed to show the efficiency of the proposed method, and sensitivity studies are performed to reveal the influence of disagreement point values on the solutions. In Section 6, a conclusion and further research directions are discussed.

2. Literature review

2.1 Robust parameter design

Taguchi proposed both experimental design concepts and parameter tradeoff issues into a quality design process. In addition, Taguchi developed an orthogonal-array-based experimental design and used the signal-to-noise (SN) ratio to measure the effects of factors on desired output responses. As discussed by Leon et al. [11] in some situations, the SN ratio is not independent of the adjustment parameters, so using the SN ratio as a performance measure may often lead to far from the optimal design parameter settings. Box [12] also argued that statistical analyses based on experimental data should be introduced, rather than relying only on the maximization of the SN ratio. The controversy about the Taguchi method is further discussed and addressed by Nair et al. [13] and Tsui [14].

Based on Taguchi’s philosophy, further statistical based methods for RPD have been developed. Vining and Myers [6] introduced a dual response method, which takes zero-process bias as a constraint and minimizes the variability. Copeland and Nelson [15] proposed an alternative method for the dual response problem by introducing a predetermined upper limit on the deviation from the target. Similar approaches related to upper limit concept are further discussed by Shin and Cho [10] and Lee et al. [9] For the estimation phase, Shoemaker et al. [16] and Khattree [17] suggested a utilization of the response surface model approaches. However, when a homoscedasticity assumption for regression is violated, then other methods, such as the generalized linear model, can be applied [18]. Additionally, in cases where there is incomplete data, Lee and Park [19] suggested an expectation-maximization (EM) algorithm to provide an estimation of the process mean and variance, while Cho and Park [20] suggested a weighted least squares (WLS) method. However, Lin and Tu [3] pointed out that the dual response approach had some deficiencies and proposed an alternative method called mean-squared-error (MSE) model. Jayaram and Ibrahim [21] modified the MSE model by incorporating capability indexes and considered the minimization of total deviation of capability indexes to achieve a multiple response robust design. More flexible alternative methods that could obtain Pareto optimal solutions based on a weighted sum model were introduced by many researchers [4,5,22]. In fact, this weighted sum model is more flexible than conventional dual response models, but it cannot be applied when a Pareto frontier is nonconvex [23]. In order to overcome this problem, Shin and Cho [23] proposed an alternative method called lexicographic weighted Tchebycheff by using an ${\textstyle L-\infty }$ norm.

More recently, RPD has become more widely used not only in manufacturing but also in other science and engineering areas including pharmaceutical drug development. New approaches such as simulation, multiple optimization techniques, and neural networks (NN) have been integrated into RPD. For example, Le et al. [24] proposed a new RPD model by introducing a NN approach to estimate dual response functions. Additionally, Picheral et al. [25] estimated the process bias and variance function by using the propagation of variance method. Two new robust optimization methods, the gradient-assisted and quasi-concave gradient-assisted robust optimization methods, were presented by Mortazavi et al. [26]. Bashiri et al. [27] proposed a robust posterior preference method that introduced a modified robust estimation method to reduce the effects of outliers on functions estimation and used non-robustness distance to compare non-dominated solutions. However, the responses are assumed to be uncorrelated. To address the correlation among multiple responses and the variation of noise factors over time, Yang et al. [28] extended offline RPD to online RPD by applying Bayesian seemingly unrelated regression and time series models so that the set of optimal controllable factor values can be adjusted in real-time.

2.2 Game Theory

The field of game theory presents mathematical models of strategic interactions among rational agents. These models can become analytical tools to find the optimal choices for interactional and decision-making problems. Game theory is often applied in situations where the "roles and actions of multiple agents affect each other" [29]. Thus, game theory serves as an analysis model that aims at helping agents to make the optimal decisions, where agents are rational and those decisions are interdependent. Because of the condition of interdependence each agent has to consider other agents’ possible decisions when formulating a strategy. Based on these characteristics of game theory, it is widely applied in multiple disciplines, such as computer science [30], network security and privacy [31], cloud computing [32], cost allocation [33], and construction [34]. Because game theory has a degree of conceptual overlap with optimization and decision-making, three concepts (i.e., game theory, optimization, and decision-making) can often be combined, respectively. According to Sohrabi and Azgom [29], there are three kinds of basic combinations associated with those three concepts as follows: game theory and optimization, game theory and decision-making, game theory, optimization, and decision-making.

The first type of these combinations (i.e., game theory and optimization) further has two possible situations. In the first situation, optimization techniques are used to solve a game problem and prove the existence of equilibrium [35,36]. In the second situation, game theory concepts are integrated to solve an optimization problem. For example, Leboucher et al. [37] used evolutionary game theory to improve the performance of a particle swarm optimization (PSO) approach. Additionally, Annamdas and Rao [38] solved a multi-objective optimization problem by using a combination of game theory and a PSO approach. The second type kind of combination (i.e., game theory and decision-making) integrates game theory to solve a decision-making problem, as discussed by Zamarripa et al. [39] who applied game theory to assist with decision-making problems in supply chain bottlenecks. More recently, Dai et al. [40] attempted to integrate the Stackelberg leadership game into RPD model to solve a dual response tradeoff problem. The third type of combination (i.e., game theory, optimization and decision-making) integrates game theory and optimization to a decision-making problem. For example, a combination of linear programming and game theory was introduced to solve a decision-making problem [41]. Doudou et al. [42] used a convex optimization method and game theory to settle a wireless sensor network decision-making problem.

2.3 Bargaining game

A bargaining game can be applied in a situation where a set of agents have an incentive to cooperate but have conflicting interests over how to distribute the payoffs generated from the cooperation [43]. Hence, a bargaining game essentially has two features: Cooperation and conflict. Because the bargaining game considers cooperation and conflicts of interest as a joint problem, it is more complicated than a simple cooperative game that ignores individual interests and maximizes the group benefit [44]. Typical three bargaining game examples include a price negotiation problem between product sellers and buyers, a union and firm negotiation problem over wages and employment levels, and a simple cake distribution problem.

Significant discussions about the bargaining game can be addressed by Nash [45,46]. Nash [45] presented a classical bargaining game model aimed at solving an economic bargaining problem and used a numerical example to prove the existence of multiple solutions. In addition, Nash [46] extended his research to a more general form and demonstrated that there are two possible approaches to solve a two-person cooperative bargaining game. The first approach, called the negotiation model, is used to obtain the solution through an analysis of the negotiation process. The second approach, called the axiomatic method, is applied to solve a bargaining problem by specifying axioms or properties that the solution should obtain. For the axiomatic method, Nash concluded four axioms that the agreed solution called Nash bargaining solution should have. Based on Nash’s philosophy, many researchers attempted to modify Nash's model and proposed a number of different solutions based on different axioms. One famous modified model replaces one of Nash’s axioms in order to reach a fairer unique solution which is called the Kalai-Smorodinky’s solution [47]. Later, Rubinstein [48] addressed a bargaining problem by specifying a dynamic model which explains a bargaining procedure.

3. Models and methods

3.1 Bi-objective robust design model

A general bi-objective optimization problem involves simultaneous optimization of two conflicting objectives (e.g., $f_{1}({\boldsymbol {\text{x}}})$ and $f_{2}({\boldsymbol {\text{x}}})$ ) that can be described in mathematical terms as $\min[f_{1}({\boldsymbol {\text{x}}}),f_{2}({\boldsymbol {\text{x}}})]$ . The primary objective of PRD is to minimize the deviation of performance of the production process from the target value and the variability of the performance, where this performance deviation can be represented by process bias and the performance variability can be represented by standard deviation or variance. For example, Koksoy [49], Goethals and Cho [50], and Wu and Chyu [51] utilized estimated variance functions to represent process variability. On the other hand, Shin and Cho [10,52], Tang and Xu [53] used estimated standard deviation functions to measure process variability. Steenackers and Guillaume [54] discussed the effect of different response surface expressions on the optimal solutions, and they concluded that both standard deviation and variance can capture the process variability well but can lead to different optimal solution sets. Since it can be infeasible to minimize the process bias and variability simultaneously, a simultaneous optimization of these two process parameters, which are separately estimated by applying RSM, is then transformed into a tradeoff problem between the process bias and variability. This tradeoff problem can be formally expressed as a bi-objective optimization problem [23] as:

$min$	$\left[\left\{{\hat {\mu }}\left({\boldsymbol {\text{x}}}\right)-\tau \right\}^{2},\,{\hat {\sigma }}^{2}({\boldsymbol {\text{x}}})\right]^{T}$
$s.t.$	${\textstyle {\boldsymbol {\text{x}}}\in X\,}$

(1)

where ${\textstyle {\boldsymbol {\text{x}}}}$ , ${\textstyle X}$ , ${\textstyle \tau }$ , ${\textstyle {\left\{{\hat {\mu }}\left({\boldsymbol {\text{x}}}\right)-\tau \right\}}^{2}}$ , and ${\textstyle {\hat {\sigma }}^{2}({\boldsymbol {\text{x}}})}$ represent a vector of design factors, the set of feasible solutions under specified constraints, the target process mean value, and the estimated functions for process bias and variability, respectively.

3.2 Lexicographic weighed Tchebycheff method

A bi-objective robust design problem is generally addressed by introducing a set of parameters, determined by a DM, which represents the relative importance of those two objectives. With the introduced parameters, the bi-objective functions can be transformed into a single integrated function, thus the bi-objective optimization problem can be solved by simply optimizing the integrated function. One way to construct this integrated function is by using the weighted sum of the distance between the optimal solution and the estimated function. Different ways of measuring distance can lead to different solutions, and one of the most common methods is ${\textstyle {L}_{p}}$ metric, where $p=1,2,\,{\mbox{or}}\,\infty$ . When $p=1$ , the metric is called the Manhattan metric, whereas ${\textstyle p=\infty }$ , it is named the Tchebycheff metric [47]. Utopia point represents an initial point to apply $L-\infty$ metric in weighted Tchebycheff method and can be obtained by minimizing each objective function separately. The weak Pareto optimal solutions can be obtained by introducing different weights:

(2)

where ${\textstyle {u}_{i}^{\ast }}$ and ${\textstyle {w}_{i}}$ denote the utopia point values and weights associated with objective functions, respectively. When $p=\infty$ , the above function (i.e., Eq.(2)) will only consider the largest deviation. Although the weighted Tchebycheff method is an efficient approach, its main drawback is that only weak non-dominated solutions can be guaranteed [56], which is obviously not optimal for the DM. So, Steuer and Choo [57] introduced an interactive weighted Tchebycheff method, which can generate every non-dominated point provided that weights are selected appropriately. Shin and Cho [23] introduced the lexicographic weighted Tchebycheff method to the RPD area. This method is proved to be efficient and capable of generating all Pareto optimal solutions when the process bias and variability are treated as a bi-objective problem. The mathematical model is shown below [23]:

$min$	$\left[\,\xi ,\,\left[{\left\{{\hat {\mu }}\left({\boldsymbol {\text{x}}}\right)-t\right\}}^{2}-{u}_{1}^{\ast }\right]+\left[{\hat {\sigma }}^{2}\left({\boldsymbol {\text{x}}}\right)-{u}_{2}^{\ast }\right]\right]$
$s.t.$	$\,\lambda \left[{\left\{{\hat {\mu }}\left({\boldsymbol {\text{x}}}\right)-t\right\}}^{2}-{u}_{1}^{\ast }\right]\leq \xi$
	$\left(1-\lambda \right)\left[{\hat {\sigma }}\left({\boldsymbol {\text{x}}}\right)-{u}_{2}^{\ast }\right]\leq \xi$
	${\boldsymbol {\text{x}}}\in X$

(3)

where $\xi$ and $\lambda$ represent a non-negative variable and a weight term associated with process bias and variability, respectively. The Lexicographic weighed Tchebycheff method is utilized as a verification method in this paper.

3.3 Nash bargaining solution

A two-player bargaining game can be represented by a pair ${\textstyle \,(U,d)}$ , where ${\textstyle U\subset {R}^{2}}$ and ${\textstyle d\subset {R}^{2}}$ . ${\textstyle U=({u}_{1}({\boldsymbol {\text{x}}}){,u}_{2}({\boldsymbol {\text{x}}}))}$ denotes a pair of obtainable payoffs of the two players, where ${\textstyle {u}_{1}({\boldsymbol {\text{x}}})}$ and ${\textstyle {\,u}_{2}\left({\boldsymbol {\text{x}}}\right)\,}$ represent the utility functions for player 1 and 2, respectively, and ${\textstyle {\boldsymbol {\text{x}}}{\,=}{(}{x}_{1},\,{x}_{2})\,}$ denotes a vector of actions taken by players. ${\textstyle d}$ ( ${\textstyle {d=(d}_{1},{d}_{2})}$ ), defined as a disagreement point, represents the payoffs that each player will gain from this game when two players fail to reach a satisfactory agreement. In other words the disagreement point values are the payoffs that each player can expect to receive if a negotiation breaks down. Assuming ${\textstyle {u}_{i}({\boldsymbol {\text{x}}})>{d}_{i}}$ where ${\textstyle {u}_{i}({\boldsymbol {\text{x}}})\in U}$ for ${\textstyle \,i\,=1,2}$ , the set ${\textstyle U\cap \left\{\left({u}_{1}({\boldsymbol {\text{x}}}),{u}_{2}({\boldsymbol {\text{x}}})\right)\in \,{R}^{2}:\,{u}_{1}({\boldsymbol {\text{x}}})\geq {d}_{1};\,{u}_{2}({\boldsymbol {\text{x}}})\geq {d}_{2}\right\}}$ is non-empty. As suggested by the expression of the Nash bargaining game ${\textstyle (U,d)}$ , the Nash bargaining solution is affected by both the reachable utility range ( ${\textstyle U}$ ) and disagreement point value ( ${\textstyle d}$ ). Since ${\textstyle U}$ cannot be changed, rational players will decide a disagreement point value to optimize their bargaining position. According to Myerson [59], there are three possible ways to determine the value of a disagreement point. One standard way is to calculate the minimax value for each player

(4)

To be more specific, Eq.(4) states that, given each possible action for player 2, player 1 has a corresponding best response strategy. Then, among all those best response strategies, player 1 chooses the one that returns the minimum payoff which is defined as a disagreement point value. Following this logic, player 1 can guarantee to receive an acceptable payoff. Another possible way of determining the disagreement point value is to derive the disagreement point value as an effective and rational threat to ensure the establishment of an agreement. The last possibility is to set the disagreement point as the focal equilibrium of the game.

Nash proposed four possible axioms that should be possessed by the bargaining game solution [58,59]:

Pareto optimality

Independence of equivalent utility representation (IEUR)

Symmetry

Independence of irrelevant alternatives (IIA)

The first axiom states that the solution should be Pareto optimal, which means it should not be dominated by any other point. If the notation ${\textstyle f\left(U,d\right)=\left({f}_{1}\left(U,d\right),\,{f}_{2}\left(U,d\right)\right)\,}$ stands for the Nash bargaining solution to the bargaining problem ${\textstyle (U,d)}$ , then the solution ${\textstyle {u}^{\ast }=}$ $\left({u}_{1}\left({\boldsymbol {\text{x}}}^{\mathit {\boldsymbol {\ast }}}\right),{u}_{2}\left({\boldsymbol {\text{x}}}^{\boldsymbol {\ast }}\right)\right)$ can be Pareto efficient if and only if there exists no other point ${\textstyle {u}^{'}=}$ $\left({u}_{1}\left({\boldsymbol {\text{x}}}^{\mathit {\boldsymbol {'}}}\right),\,{u}_{2}\left({\boldsymbol {\text{x}}}^{\boldsymbol {'}}\right)\right)\in U$ such that ${\textstyle {u}_{1}\left({\boldsymbol {\text{x}}}^{\boldsymbol {'}}\right)>{u}_{1}\left({\boldsymbol {\text{x}}}^{\boldsymbol {\ast }}\right);{u}_{2}\left({\boldsymbol {\text{x}}}^{\mathit {\boldsymbol {'}}}\right)\geq {u}_{2}\left({\boldsymbol {\text{x}}}^{\boldsymbol {\ast }}\right)}$ or ${\textstyle {\,u}_{1}\left({\boldsymbol {\text{x}}}^{\boldsymbol {'}}\right)\geq {u}_{1}\left({\boldsymbol {\text{x}}}^{\boldsymbol {\ast }}\right);}$ ${\textstyle {u}_{2}\left({\boldsymbol {\text{x}}}^{\boldsymbol {'}}\right)>{u}_{2}\left({\boldsymbol {\text{x}}}^{\boldsymbol {\ast }}\right)}$ . This implies that there is no alternative feasible solution that is better for one player without worsening the payoff for other players.

The second axiom, IEUR also referred to as scale covariance, states that the solution should be independent of positive affine transformations of utilities.In other words, if a new bargaining game ${\textstyle (G,w)}$ exists, where $G=\left\{{\alpha }_{1}{u}_{1}({\boldsymbol {\text{x}}})+{\beta }_{1},{\alpha }_{2}{u}_{2}({\boldsymbol {\text{x}}})+{\beta }_{2}\right\}$ and $w=\left({\alpha }_{1}{d}_{1}+{\beta }_{1},{\alpha }_{2}{d}_{2}+{\beta }_{2}\right)\,$ and where $\left({u}_{1}({\boldsymbol {\text{x}}}),{u}_{2}({\boldsymbol {\text{x}}})\right)\in U$ and ${\alpha }_{1}>0,{\alpha }_{2}>0$ , then the solution for this new bargaining game (i.e., ${\textstyle f(G,w)}$ ) can be obtained by applying the same transformations, which is demonstrated by Eq.(5) and Figure 1:

(5)

Figure 1. Explanation of IEUR axiom

The third axiom “symmetry” represents that the solutions should be symmetric when the bargaining positions of the two players are completely symmetric. This axiom can be explained as if there is no information that can be used to distinguish one player from the other, then the solutions should also be indistinguishable between players [46].

As shown in Figure 2, the last axiom states that if ${\textstyle {U}_{1}\subset {U}_{2}}$ and ${\textstyle f({U}_{2},d)}$ is located within the feasible area ${\textstyle {U}_{1}}$ , then ${\textstyle f\left({U}_{1,}d\right)=}$ $f({U}_{2},d)$ [59].

Figure 2. Explanation of IIA axiom

The solution function introduced by Nash [46] that satisfies all the four axioms as identified before can be defined as follows:

(6)

where ${\textstyle {u}_{i}({\boldsymbol {\text{x}}})>{d}_{i},\,i=1,2}$ . Intuitively, this function is trying to find solutions that maximize each player’s difference in payoffs between the cooperative agreement point and the disagreement point. In simpler terms, Nash selects an agreement point ${\textstyle ({u}_{1}\left({\boldsymbol {\text{x}}}^{\ast }\right),{u}_{2}({\boldsymbol {\text{x}}}^{\ast }))}$ that maximizes the product of utility gains from the disagreement point ${\textstyle \,({d}_{1},{d}_{2})}$ .

4. The proposed model

The proposed method attempts to integrate bargaining game concepts into the tradeoff issue between the process bias and variability, so that not only the interaction between process bias and variability can be incorporated but also a unique optimal solution can be obtained. The detailed procedure includes problem description, calculation for response functions and disagreement points, bargaining game based RPD model, and verification can be illustrated in Figure 3. As illustrated in Figure 3, the objective of the proposed method is to address the tradeoff between process bias and variability. In the calculation phase, a utopia point can be calculated based on separately estimated functions for the process bias and variability. However, this utopia point is in an infeasible region, which means that a simultaneous minimization of the process bias and variability is unachievable. The disagreement point is calculated by first, optimizing only one of the objective functions (i.e., the estimated process variability or the process bias function) and obtaining a solution set, and second, inserting the obtained solution set into the other objective function to generate a corresponding value. In the proposed model, based on the obtained disagreement point, the Nash bargaining solution concept is applied to solve the bargaining game. While in the verification phase, the lexicographic weighted tchebycheff is applied to generate the associated Pareto frontier, so that the obtained game solution can be compared with other efficient solutions.

Figure 3. The proposed procedure by integrating of bargaining game into RPD

An integration of the Nash bargaining game model involves three steps. First step, the two players and their corresponding utility function should be defined. The process bias can be defined as player A, and variability can be regarded as player B. The RSM-based estimated functions of both responses will be regarded as the players’ utility functions in this bargaining game (i.e., ${\textstyle u_{A}({\boldsymbol {\text{x}}})}$ and ${\textstyle u_{B}({\boldsymbol {\text{x}}})}$ ) where ${\boldsymbol {\text{x}}}$ stands for a vector of controllable factors. Then, the goal of each player is to choose a set of controllable factors while minimizing each individual utility function. Second step, a disagreement point can be determined by applying a minimax-value theory as identified in Equation 7. Based on the tradeoff between the process bias and variability, the modified disagreement point functions can be defined as follows:

(7)

In this way, both player A (i.e., the process bias) and player B (i.e., the process variability) are guaranteed to receive the worst acceptable payoffs. In that case, the disagreement point, defined as the maximum minimum utility value, can be calculated by minimizing only one objective (process variability or bias). The computational functions for the disagreement point values can be formulated as:

(8)

and

(9)

Thus, the idea of the proposed method to find the optimal solutions is to continuously perform bargaining games from the specified disagreement point ${\textstyle ({d}_{A},\,{d}_{B})}$ to Pareto frontier as illustrated in Figure 4. To be more specific, as demonstrated in Figure 4, if the convex curve represents all Pareto optimal solutions, then each point on the curve can be regarded as a minimum utility value for one of the two process parameters (i.e., the process variability or bias). For example, at point A, when the process bias is minimized within the feasible area, the corresponding variability value is the minimum utility value for the process variability, since other utility values would be either dominated or infeasible. These solutions may provide useful insight for a DM when the relative importance between process bias and variability is difficult to identify.

Figure 4. Solution concepts for the proposed bargaining game based RPD method
by integrating trafeoff between both process bias and variability

In the final step, the Nash bargaining solution function ${\textstyle Max\left({u}_{A}({\boldsymbol {\text{x}}})-{d}_{A}\right)\left({u}_{B}({\boldsymbol {\text{x}}})-{d}_{B}\right)}$ is utilized. In an RPD problem, the objective of this problem is to minimize both process bias and variability, so a constraint of ${\textstyle {u}_{i}({\boldsymbol {\text{x}}})}$ < ${\textstyle {d}_{i},\,i=}$ $A,B$ is applied. After the players, utility functions and the disagreement point are identified, the Nash bargaining solution function is applied as below:

$\max$	${\textstyle \left({u}_{A}({\boldsymbol {\text{x}}})-{d}_{A}\right)\left({u}_{B}({\boldsymbol {\text{x}}})-\right.\left.{d}_{B}\right)}$
$s.t.$	${u}_{A}({\boldsymbol {\text{x}}})\leq {d}_{A},{u}_{B}({\boldsymbol {\text{x}}})\leq {d}_{B},\qquad {\mbox{and}}\qquad {\boldsymbol {\text{x}}}\in \,X$

(10)

where

and, where

{\textstyle {\boldsymbol {\text{x}}}=\left[\,{\begin{matrix}{x}_{1}\\{x}_{2}\\\,{\begin{matrix}\vdots \\{x}_{n-1}\\{x}_{n}\end{matrix}}\end{matrix}}\right],\,{\mathit {\boldsymbol {\alpha }}}_{\mathit {\boldsymbol {1}}}=\left[\,{\begin{matrix}{\hat {\alpha }}_{1}\\{\hat {\alpha }}_{2}\\\,{\begin{matrix}\vdots \\{\hat {\alpha }}_{n-1}\\{\hat {\alpha }}_{n}\end{matrix}}\end{matrix}}\right],\,{\mathit {\boldsymbol {\beta }}}_{\mathit {\boldsymbol {1}}}=\,\left[{\begin{matrix}{\hat {\beta }}_{1}\\{\begin{matrix}{\hat {\beta }}_{2}\\\vdots \end{matrix}}\\{\begin{matrix}{\hat {\beta }}_{n-1}\\{\hat {\beta }}_{n}\end{matrix}}\end{matrix}}\right],\,{\mathit {\boldsymbol {\gamma }}}_{\mathit {\boldsymbol {1}}}=\,\left[{\begin{matrix}{\hat {\gamma }}_{1}\\{\begin{matrix}{\hat {\gamma }}_{2}\\\vdots \end{matrix}}\\{\begin{matrix}{\hat {\gamma }}_{n-1}\\{\hat {\gamma }}_{n}\end{matrix}}\end{matrix}}\right],\quad {\mbox{and}}\quad {\boldsymbol {\Gamma }}=\,\left[{\begin{matrix}{\begin{matrix}{\hat {\alpha }}_{11}&{\hat {\alpha }}_{12}/2\\{\hat {\alpha }}_{12}/2&{\hat {\alpha }}_{22}\end{matrix}}&\cdots &{\begin{matrix}{\hat {\alpha }}_{1n}/2\\{\hat {\alpha }}_{2n}/2\end{matrix}}\\\vdots &\ddots &\vdots \\{\begin{matrix}{\hat {\alpha }}_{1n}/2&{\hat {\alpha }}_{2n}/2\end{matrix}}&\cdots &{\hat {\alpha }}_{nn}\end{matrix}}\right]}

{\boldsymbol {\Delta }}=\,\left[{\begin{matrix}{\begin{matrix}{\hat {\beta }}_{11}&{\hat {\beta }}_{12}/2\\{\hat {\beta }}_{12}/2&{\hat {\beta }}_{22}\end{matrix}}&\cdots &{\begin{matrix}{\hat {\beta }}_{1n}/2\\{\hat {\beta }}_{2n}/2\end{matrix}}\\\vdots &\ddots &\vdots \\{\begin{matrix}{\hat {\beta }}_{1n}/2&{\hat {\beta }}_{2n}/2\end{matrix}}&\cdots &{\hat {\beta }}_{nn}\end{matrix}}\right],\quad {\mbox{and}}\quad {\boldsymbol {\mathrm {E} }}=\,\left[{\begin{matrix}{\begin{matrix}{\hat {\gamma }}_{11}&{\hat {\gamma }}_{12}/2\\{\hat {\gamma }}_{12}/2&{\hat {\gamma }}_{22}\end{matrix}}&\cdots &{\begin{matrix}{\hat {\gamma }}_{1n}/2\\{\hat {\gamma }}_{2n}/2\end{matrix}}\\\vdots &\ddots &\vdots \\{\begin{matrix}{\hat {\gamma }}_{1n}/2&{\hat {\gamma }}_{2n}/2\end{matrix}}&\cdots &{\hat {\gamma }}_{nn}\end{matrix}}\right]

where $(d_{A},d_{B})$ , $u_{A}({\boldsymbol {\text{x}}})$ , $u_{B}({\boldsymbol {\text{x}}})$ , ${\hat {\mu }}({\boldsymbol {\text{x}}})$ , ${\hat {\sigma }}^{2}({\boldsymbol {\text{x}}})$ , ${\hat {\sigma }}({\boldsymbol {\text{x}}})$ , $\tau$ , $X$ and ${\bf {x}}$ represent a disagreement point, utility functions for player A and B, an estimated process mean function, process variance function, and standard deviation function, the target value, the feasible area, the vector of controllable factors, respectively. In Eq.(10), ${\boldsymbol {\alpha _{1}}}$ , ${\boldsymbol {\beta _{1}}}$ , ${\boldsymbol {\gamma _{1}}}$ , ${\boldsymbol {\Gamma }}$ , ${\boldsymbol {\Delta }}$ , and ${\boldsymbol {\mathrm {E} }}$ denote vectors and matrixes of estimated regression coefficients for the process mean, variance, and standard deviation, respectively. Here, the constraint $u_{i}({\boldsymbol {\text{x}}})\leq d_{i}$ , where $i=A,B$ , ensures that the obtained agreement point payoffs will be at least as good as the disagreement point payoffs. Otherwise, there is no reason for players to participate in the negotiation.

5. Numerical illustrations and sensitivity analysis

5.1 Numerical example 1

Two numerical examples are conducted to demonstrate the efficiency of the proposed method. As explained in section 3.1, the process variability can be measured in terms of both the estimated standard deviation and variance functions, but the optimal solutions can be different if different response surface expressions are used. Therefore, the equations estimated in the original example were utilized for better comparison. Example 1 investigates the relationship between the coating thickness of bare silicon wafers ( $y$ ) and three controller variables: mould temperature ${\textstyle ({x}_{1})}$ , injection flow rate ${\textstyle ({x}_{2})}$ , and cooling rate ${\textstyle {(x}_{3})}$ [10]. A central composite design and three replications were conducted, and the detailed experimental data with coded values can be shown in Table 1.

Table 1. Data for numerical example 1

Experiments number	$x_{1}$	$x_{2}$	$x_{3}$	$y_{1}$	$y_{2}$	$y_{3}$	$y_{4}$	${\overline {\mathit {y}}}$	${\mathit {\sigma }}$
1	-1	-1	-1	76.30	80.50	77.70	81.10	78.90	2.28
2	1	-1	-1	79.10	81.20	78.80	79.60	79.68	1.07
3	-1	1	-1	82.50	81.50	79.50	80.90	81.10	1.25
4	1	1	-1	72.30	74.30	75.70	72.70	73.75	1.56
5	-1	-1	1	70.60	72.70	69.90	71.50	71.18	1.21
6	1	-1	1	74.10	77.90	76.20	77.10	76.33	1.64
7	-1	1	1	78.50	80.00	76.20	75.30	77.50	2.14
8	1	1	1	84.90	83.10	83.90	83.50	83.85	0.77
9	-1.682	0	0	74.10	71.80	72.50	71.90	72.58	1.06
10	1.682	0	0	76.40	78.70	79.20	79.30	78.40	1.36
11	0	-1.682	0	79.20	80.70	81.00	82.30	80.80	1.27
12	0	1.682	0	77.90	76.40	76.90	77.40	77.15	0.65
13	0	0	-1.682	82.40	82.70	82.60	83.10	82.70	0.29
14	0	0	1.682	79.70	82.40	81.00	81.20	81.08	1.11
15	0	0	0	70.40	70.60	70.80	71.10	70.73	0.30
16	0	0	0	70.90	69.70	69.00	69.90	69.88	0.78
17	0	0	0	70.70	71.90	71.70	71.20	71.38	0.54
18	0	0	0	70.20	71.00	71.50	70.40	70.78	0.59
19	0	0	0	71.50	71.10	71.20	70.00	70.95	0.66
20	0	0	0	71.00	70.40	70.90	69.90	70.55	0.51

The fitted response functions for the process bias and standard deviation of the coating thickness are estimated by using LSM through MINITABsoftware package as:

(11)

where

(12)

where

Based on the proposed RPD procedure as described in Figure 3, those two functions (i.e., process bias and standard deviation) as shown in Eqs.(11) and (12) are regarded as two players and also their associated utility functions in the bargaining game. The disagreement point as shown in Figure 4 can be computed as ${\textstyle d=({d}_{A},{d}_{B})=(1.2398,3.1504)}$ by using Eqs.(8) and (9). Then, the optimization problem can be solved by applying Eq.(10) under an additional constraint, ${\textstyle \sum _{l=1}^{3}{{x}_{l}}^{2}\leq 3}$ . which represents a feasible experiment region.

The solution (i.e., ${\textstyle \left({\hat {\mu }}({\bf {x}}^{*})-\tau \right)^{2}=0.2967}$ and ${\textstyle {\hat {\sigma }}({\bf {x}}^{*})=2.6101}$ ) are calculated by using a MATLAB software package. To perform a comparative study, the optimization results of the proposed method and the conventional dual response approach are summarized in Table 2. Based on Table 2, the proposed method provides slightly better MSE results in this particular numerical example. To check the efficiency of the obtained results, the lexicographic weighted Tchebycheff approach is adopted to procure an associated Pareto frontier which is shown in Figure 5.

Table 2. The optimization results of example 1

	${x}_{1}^{\ast }$	${x}_{2}^{\ast }$	${x}_{3}^{\ast }$	${\left({\hat {\mu }}\left({\bf {x}}^{*}\right)-\tau \right)}^{2}$	${\hat {\sigma }}^{2}({\bf {x}}^{*})$	MSE
Dual response model with WLS	-1.4561	-0.1456	0.5596	0	3.0142	9.0854
Proposed model	-0.8473	0.0399	0.2248	0.2967	2.6101	7.1093

Figure 5. The optimization results plot with the Pareto frontier of example 1

As exhibited in Figure 5, the obtained Nash bargaining solution, which is plotted as a star, is on the Pareto frontier. By using the concept of bargaining game theory, the interaction between process bias and variability can be incorporated while identifying a unique tradeoff result. As result, this proposed method might provide well-balanced optimal solutions associated with the process bias and variability in this particular example.

5.2 Sensitivity analysis for numerical example 1

Based on the optimization results, sensitivity analysis for different disagreement point values are then conducted for verification purposes as shown in Table 3. While changing $d_{B}$ values by both 10% increment and decrement with fixed $d_{A}$ value at 3.1504, the changing patterns of the process bias and variability values are investigated in this sensitivity analysis.

Table 3. Sensitivity analysis results for numerical example 1 by changing

${d}_{A}$	${d}_{B}$	$\left(\left({\hat {\mu }}({\bf {x}})-\tau \right)^{2}-{d}_{A}\right)\ast \left({\hat {\sigma }}({\bf {x}})-{d}_{B}\right)$	$x$	$\left(\mu ({\bf {x}}^{*})-\tau \right)^{2}$	$\sigma ({\bf {x}}^{*})$
0.6589	3.1504	0.2218	[-1.0281 -0.0159 0.3253]	0.157	2.7085
0.7321	3.1504	0.2547	[-1.0017 -0.0078 0.3107]	0.1753	2.6930
0.8134	3.1504	0.2925	[-0.9739 0.0007 0.2953]	0.1953	2.6771
0.9038	3.1504	0.3361	[-0.9445 0.0098 0.2790]	0.2174	2.6608
1.0042	3.1504	0.3861	[-0.9137 0.0193 0.2619]	0.2416	2.6441
1.1158	3.1504	0.4435	[-0.8813 0.0293 0.2438]	0.2680	2.6272
1.2398	3.1504	0.5095	[-0.8473 0.0399 0.2248]	0.2967	2.6101
1.3638	3.1504	0.5775	[-0.8153 0.0499 0.2069]	0.3248	2.5946
1.5002	3.1504	0.6543	[-0.7820 0.0603 0.1881]	0.3549	2.5791
1.6502	3.1504	0.7412	[-0.7475 0.0711 0.1687]	0.3869	2.5637
1.8152	3.1504	0.8393	[-0.7120 0.0824 0.1486]	0.4209	2.5484
1.9967	3.1504	0.9499	[-0.6754 0.0939 0.1278]	0.4567	2.5335
2.1964	3.1504	1.0746	[-0.6381 0.1058 0.1065]	0.4942	2.5191
2.4160	3.1504	1.2148	[-0.6002 0.1180 0.0847]	0.5331	2.5052

As shown in Table 3, if only ${\textstyle {d}_{A}}$ increases, the optimal squared bias ${\textstyle ({\hat {\mu }}({\bf {x}}^{*})-\tau )^{2}}$ increases while the process variability ${\textstyle {\hat {\sigma }}\left({\bf {x}}^{*}\right)}$ decreasing. All of the optimal solutions obtained by using the proposed methods are plotted as circles and compared with the Pareto optimal solutions generated by using the lexicographic weighted Tchebycheff method. Clearly, the obtained solutions are on the Pareto frontier, as shown in Figure 6.

Figure 6. Plot of sensitivity analysis results with the Pareto frontier for numerical example 1 by changing

On the other hand, if ${\textstyle {d}_{A}}$ is considered as a constant and ${\textstyle {d}_{B}}$ is changed by 5% each time, the transformed data is summarized and plotted in Table 4 and Figure 7, respectively.

Table 4. Sensitivity analysis results for numerical example 1 by changing

${d}_{A}$	${d}_{B}$	$\left(\left({\hat {\mu }}({\bf {x}})-\tau \right)^{2}-{d}_{A}\right)\ast \left({\hat {\sigma }}({\bf {x}})-{d}_{B}\right)$	$x$	$\left({\hat {\mu }}({\bf {x}}^{*})-\tau \right)^{2}$	${\hat {\sigma }}({\bf {x}}^{*})$
1.2398	2.4377	0.0076	[-0.2082 0.2495 -0.1539]	0.9764	2.4089
1.2398	2.5660	0.0592	[-0.4198 0.1770 -0.0212]	0.7286	2.4501
1.2398	2.7011	0.1394	[-0.5607 0.1307 0.0618]	0.5746	2.4916
1.2398	2.4832	0.2425	[-0.6726 0.0948 0.1262]	0.4595	2.5324
1.2398	2.9929	0.3664	[-0.7666 0.0651 0.1795]	0.3690	2.5721
1.2398	3.1504	0.5095	[-0.8473 0.0399 0.2248]	0.2967	2.6101
1.2398	3.3079	0.6626	[-0.9141 0.0192 0.2621]	0.2412	2.6444
1.2398	3.4733	0.8316	[-0.9727 0.0011 0.2946]	0.1962	2.6764
1.2398	3.6470	1.0162	[-1.0241 -0.0147 0.3231]	0.1597	2.7061
1.2398	3.8293	1.2159	[-1.0692 -0.0285 0.3480]	0.1303	2.7334
1.2398	4.0208	1.4308	[-1.1088 -0.0406 0.3698]	0.1065	2.7583

Figure 7. Plot of sensitivity analysis results with the Pareto frontier for numerical example 1 by changing

As demonstrated by Table 4, the value of ${\textstyle ({\hat {\mu }}({\bf {x}}^{*})-\tau )^{2}}$ declines while ${\textstyle {\hat {\sigma }}\left({\bf {x}}^{*}\right)}$ grows if ${\textstyle {d}_{B}}$ is increased and ${\textstyle {d}_{A}}$ is kept constant. However, all of the solution points are still on the Pareto frontier, as shown in Figure 7.

5.3 Numerical example 2

In the second example [20], an unbalanced data set is utilized to investigate the relationship between coating thickness ( $y$ ), mould temperature ( ${\textstyle {x}_{1}}$ ) and injection flow rate ( ${\textstyle {x}_{2}}$ ). A 3² factorial design with three levels as -1, 0, and +1 is applied as shown in Table 5.

Table 5. Experimental data for example 2

Experiments number	${\mathit {x}}_{1}$	${\mathit {x}}_{2}$	${\mathit {y}}_{1}$	${\mathit {y}}_{2}$	${\mathit {y}}_{3}$	${\mathit {y}}_{4}$	${\mathit {y}}_{5}$	${\mathit {y}}_{6}$	${\mathit {y}}_{7}$	${\overline {\mathit {y}}}$	${\mathit {\sigma }}^{\mathit {2}}$
1	-1	-1	84.3	57.0	56.5					65.93	253.06
2	0	-1	75.7	87.1	71.8	43.8	51.6			66.00	318.28
3	1	-1	65.9	47.9	63.3					59.03	94.65
4	-1	0	51.0	60.1	69.7	84.8	74.7			68.06	170.35
5	0	0	53.1	36.2	61.8	68.6	63.4	48.6	42.5	53.46	139.89
6	1	0	46.5	65.9	51.8	48.4	64.4			55.40	83.11
7	-1	1	65.7	79.8	79.1					74.87	63.14
8	0	1	54.4	63.8	56.2	48.0	64.5			57.38	47.54
9	1	1	50.7	68.3	62.9					60.63	81.29

Based on Cho and Park [20], a weighted least square (WLS) method was applied to estimate the process mean and variability functions as:

(13)

where

(14)

where

Applying the same logic as utilized in example 1, the ranges for the process bias and variability are calculated by [12.0508, 420.25] and [45.53, 310.39], respectively. The disagreement points are computed as ${\textstyle {d}_{A}=63.0436}$ and ${\textstyle {d}_{B}=112.0959}$ . Applying Eq.(10), the optimal solutions can be obtained as follows: ${\textstyle ({\hat {\mu }}({\bf {x}}^{*})-\tau )^{2}=23.6526}$ and ${\textstyle {\hat {\sigma }}^{2}({\bf {x}}^{*})=58.3974}$ . Based on the optimization results of both the proposed method and the conventional MSE model as demonstrated in Table 6, the optimization results of the proposed method provide a significantly small MSE compared to the conventional MSE model in this particular example.

Table 6. The optimization results of example 2

	${x}_{1}^{\ast }$	${x}_{2}^{\ast }$	$\left\|{\hat {\mu }}({\bf {x}}^{*})-\tau \right\|$	${\hat {\sigma }}^{2}({\bf {x}}^{*})$	MSE
MSE model	0.998	0.998	7.93	45.66	108.48
Proposed model	1.000	0.4440	4.8606	58.3974	82.023

A Pareto frontier including all non-dominated solutions can be obtained by applying a lexicographic weighted Tchebycheff approach. As illustrated by Figure 8, the Nash bargaining solution is on the Pareto frontier, which may clearly verify the efficiency of the proposed method.

Figure 8. The optimization results plot with the Pareto frontier of example 2]]

5.4 Sensitivity analysis for numerical example 2

Applying the same logic for example 2, ${\textstyle {d}_{B}}$ is kept constant as ${\textstyle {d}_{A}}$ is changed by 10%. Table 7 exhibits the effect of changes in ${\textstyle {d}_{A}}$ , and Figure 9 demonstrates the efficiency of the calculated solutions.

Table 7. Sensitivity analysis results for numerical example 2 by changing

${d}_{A}$	${d}_{B}$	$\left(\left({\hat {\mu }}({\bf {x}})-\tau \right)^{2}-{d}_{A}\right)\ast \left({\hat {\sigma }}^{2}({\bf {x}})-{d}_{B}\right)$	$x$	$\left({\hat {\mu }}({\bf {x}}^{*})-\tau \right)^{2}$	${\hat {\sigma }}^{2}({\bf {x}}^{*})$
37.2266	112.0959	790.0487	[ 0.9510 0.3554]	19.9778	66.2928
41.3629	112.0959	986.2591	[0.9813 0.3624]	21.2437	63.0751
45.9588	112.0959	1218.3	[1.0000 0.3751]	22.2248	60.7647
51.0653	112.0959	1482.5	[1.0000 0.3978]	22.6267	59.9662
56.7392	112.0959	1780.6	[1.000 0.4208]	23.0925	59.1766
63.0436	1120959	2116.7	[1.0000 0.4440]	23.6256	58.3974
69.3480	112.0959	2457.5	[1.0000 0.4653]	24.1686	57.7026
76.2828	112.0959	2837.1	[1.0000 0.4867]	24.7721	57.0185
83.9110	112.0959	3259.8	[1.0000 0.5083]	25.4386	56.346
92.3021	112.0959	3730.5	[1.0000 0.5300]	26.1709	55.686
101.5323	112.0959	4254.2	[1.0000 0.5518]	26.9716	55.0393
111.6856	112.0959	4836.8	[1.0000 0.5738]	27.8435	54.407
122.8541	112.0959	5484.6	[1.0000 0.5958]	28.7892	53.7896
135.1396	112.0959	6204.7	[1.0000 0.6179]	29.8115	53.1879

Figure 9. Plot of sensitivity analysis results with the Pareto frontier for numerical example 2 by changing

On the other hand, another sensitivity analysis is conducted by changing ${\textstyle {d}_{B}}$ with 10% increment and decrement while holding ${\textstyle {d}_{A}}$ at a fixed value (63.0436) as shown in Table 8 and plotted in Figure 10.

Table 8. Sensitivity analysis results for numerical example 2 by changing

${d}_{A}$	${d}_{B}$	$\left(\left({\hat {\mu }}({\bf {x}})-\tau \right)^{2}-{d}_{A}\right)\ast \left({\hat {\sigma }}^{2}({\bf {x}})-{d}_{B}\right)$	$x$	$\left({\hat {\mu }}({\bf {x}}^{*})-\tau \right)^{2}$	${\hat {\sigma }}^{2}({\bf {x}}^{*})$
63.0436	48.2536	15.4253	[1.0000 0.9166]	52.7429	46.7561
63.0436	53.6151	102.0493	[1.0000 0.8094]	42.2936	48.6971
63.0436	59.5724	245.6339	[1.0000 0.7284]	36.1567	50.4366
63.0436	66.1915	438.1362	[1.0000 0.6620]	32.0892	52.0372
63.0436	73.5461	677.0693	[1.0000 0.6055]	29.2313	53.5218
63.0436	81.7179	962.4337	[1.0000 0.5567]	27.1579	54.8985
63.0436	90.7977	1295.7	[1.0000 0.5140]	25.6262	56.1698
63.0436	100.8863	1679.3	[1.0000 0.4767]	24.4832	57.3359
63.0436	112.0959	2116.7	[1.0000 0.4440]	23.6256	58.3974
63.0436	123.3066	2562.1	[1.0000 0.4181]	23.0342	59.2691
63.0436	135.6372	3058.4	[1.0000 0.3951]	22.5764	60.0593
63.0436	149.2010	3609.9	[1.0000 0.3748]	22.2214	60.7721
63.0436	164.1211	4223.7	[0.9829 0.3628]	21.3147	62.9025
63.0436	180.5332	4919.9	[0.9512 0.3554]	19.9864	66.2698
63.0436	198.5865	5708.3	[0.9199 0.3472]	18.7938	69.5842

Figure 10. Plot of sensitivity analysis results with the Pareto frontier for numerical example 2 by changing

In general, for both cases, an increase in the value of ${\textstyle {d}_{i}}$ will increase the corresponding bargaining solution value. For example, an increasement of ${\textstyle {d}_{A}}$ will lead to an increase in process bias and a decrease in the variability value. This conclusion also makes sense from the perspective of game theory since it can be explained as disagreement point monotonicity [60] which can be defined as:

For two points, ${\textstyle \,d=\left({d}_{A},\,{d}_{B}\right)}$ and ${\textstyle {d}^{'}=\left({d}_{A}^{'},\,d_{B}^{'}\right)}$ , ${\textstyle {\mbox{if}}\,{d}_{i}^{'}\geq {d}_{i},\,{d}_{j}^{,}={d}_{j},}$ then ${f}_{i}\left(U,{d}^{'}\right)\geq {f}_{i}\left(U,d\right)$ ; $j\not =i$ , and $i,j\in \lbrace A,\,B\rbrace$ , where ${\textstyle {f}_{i}\left(U,{d}^{'}\right)}$ and ${\textstyle {f}_{i}\left(U,d\right)}$ represent the solution payoff for player i after and before the incensement of his disagreement point payoff, respectively. More specifically, the more disagreement point value ( ${\textstyle {d}_{i}}$ ) a player demands for participation in an agreement, the more the player will get. Although, a gain achieved by one player comes at the expense of the other player. This is because if the agreed solution is not an improvement for one player, then the player would not have any incentive to participate in the bargaining game. However, in the RPD case, the objective for a player is to minimize instead of maximize the utility value, so the less ${\textstyle {d}_{i}}$ a player proposes, the higher the requirement the player is actually proposing to participate in a bargaining game.

6. Conclusion and future direction

In a robust design model, when considering the simultaneous minimization of both process bias and variability as a bi-objective problem, there is an intractable tradeoff problem between them. Most existing methods tackle this tradeoff problem by either prioritizing a process parameter or assigning weights to process parameters to indicate the relative importance determined by a DM. However, the DM may struggle with assigning the weights or priority orders to different types and units of responses. Furthermore, the prioritizing or combining response procedure involves a certain degree of subjectivity, as different DMs may have different viewpoints on which process parameter is more important. Thus, in this paper, a bargaining game-based RPD method is proposed to solve this tradeoff problem by integrating Nash bargaining solution techniques and letting the two objectives (e.g., process bias and variability) “negotiate”, so that unique, fair, and efficient solutions can be obtained. These solutions can provide valuable suggestions to the DM, especially when there is no prior information of the relative importance for the process bias and variability. To inspect the efficiency of the obtained solutions, the associated Pareto frontier was generated through applying the lexicographic weighted Tchebycheff method, and thus, the solution position was visually confirmed. As validated by the two numerical examples, compared with the conventional dual response surface method and mean squared error method the proposed method can provide more efficient solutions based on MSE criterion. In addition, a number of sensitivity studies were conducted to investigate the relationship between the disagreement point values ( $d_{i}$ ) and the agreement solutions. This research illustrates the possibility of combining the concept of game theory with an RPD model. For further study, the proposed method will be extended to solve the multiple response optimization problems. The tradeoff issue among multiple responses can be addressed by applying the multilateral bargaining game theory, where each quality response is regarded as a rational player who attempts to reach an agreement with others on which set of control factors to choose. In the game, each response proposes a solution set that optimizes the respective estimated response function and is subject to the expectations of the other responses.

Acknowledgment

This research was a part of the project titled ‘Marine digital AtoN information management and service system development (2/5) (20210650)’, funded by the Ministry of Oceans and Fisheries, Korea.

References

[1] Park G.J., Lee T.H., Lee K.H., Hwang K.H. Robust design: an overview. AIAA Journal, 44(1):181-191, 2006.

[2] Myers W.R., Brenneman W.A., Myers R.H. A dual-response approach to robust parameter design for a generalized linear model. Journal of Quality Technology, 37(2):130-138, 2005.

[3] Lin D.K.J., Tu W. Dual response surface optimization. Journal of Quality Technology, 27:34-39, 1995.

[4] Cho B.R., Philips M.D., Kapur K.C. Quality improvement by RSM modeling for robust design. The 5th Industrial Engineering Research Conference, Minneapolis, 650-655, 1996.

[5] Ding R., Lin D.K.J., Wei D. Dual response surface optimization: A weighted MSE approach. Quality Engineering 16(3):377-385, 2004.

[6] Vining G.G., Myers R.H. Combining Taguchi and response surface philosophies: A dual response approach. Journal of Quality Technology, 22:38-45, 1990.

[7] Myers R.H., Carter W.H. Response surface methods for dual response systems. Technometrics, 15(2):301-307, 1973.

[8] Copeland K.A., Nelson P.R. Dual response optimization via direct function minimization. Journal of Quality Technology, 28(3):331-336, 1996.

[9] Lee D., Jeong I., Kim K. A posterior preference articulation approach to dual-response surface optimization. IIE Transaction, 42(2):161-171, 2010.

[10] Shin S., Cho B.R. Robust design models for customer-specified bounds on process parameters. Journal of Systems Science and Systems Engineering, 15:2-18, 2006.

[11] Leon R.V., Shoemaker A.C., Kackar R.N. Performance measures independent of adjustment: an explanation and extension of Taguchi’s signal-to-noise ratios. Technometrics, 29(3):253-265, 1987.

[12] Box G. Signal-to-noise ratios, performance criteria, and transformations. Technometrics, 30(1):1-17, 1988.

[13] Nair V.N., Abraham B., MacKay J., et al. Taguchi's parameter design: a panel discussion. Technometrics, 34(2):127-161, 1992.

[14] Tsui K.L. An overview of Taguchi method and newly developed statistical methods for robust design. IIE Transactions, 24(5):44-57, 1992.

[15] Copeland K.A., Nelson P.R. Dual response optimization via direct function minimization. Journal of Quality Technology, 28(3):331-336, 1996.

[16] Shoemaker A.C., Tsui K.L., Wu C.F.J. Economical experimentation methods for robust design. Technometrics, 33(4):415-427, 1991.

[17] Khattree R. Robust parameter design: A response surface approach. Journal of Quality Technology, 28(2):187-198, 1996.

[18] Pregibon D. Generalized linear models. The Annals of Statistics, 12(4):1589–1596, 1984.

[19] Lee S.B., Park C. Development of robust design optimization using incomplete data. Computers & Industrial Engineering, 50(3):345-356, 2006.

[20] Cho B.R., Park C. Robust design modeling and optimization with unbalanced data. Computers & Industrial Engineering, 48(2):173-180, 2005.

[21] Jayaram J.S.R., Ibrahim Y. Multiple response robust design and yield maximization. International Journal of Quality & Reliability Management, 16(9):826-837, 1999.

[22] Köksoy O., Doganaksoy N. Joint optimization of mean and standard deviation using response surface methods. Journal of Quality Technology, 35(3):239-252, 2003.

[23] Shin S., Cho B.R. Studies on a biobjective robust design optimization problem. IIE Transactions, 41(11):957-968, 2009.

[24] Le T.H., Tang M., Jang J.H., et al. Integration of functional link neural networks into a parameter estimation methodology. Applied Sciences, 11(19):9178, 2021.

[25] Picheral L., Hadj-Hamou K., Bigeon J. Robust optimization based on the Propagation of Variance method for analytic design models. International Journal of Production Research, 52(24):7324-7338, 2014.

[26] Mortazavi A., Azarm S., Gabriel S.A. Adaptive gradient-assisted robust design optimization under interval uncertainty. Engineering Optimization, 45(11):1287-1307, 2013.

[27] Bashiri M., Moslemi A., Akhavan Niaki S.T. Robust multi‐response surface optimization: a posterior preference approach. International Transactions in Operational Research, 27(3):1751-1770, 2020.

[28] Yang S., Wang J., Ren X., Gao T. Bayesian online robust parameter design for correlated multiple responses. Quality Technology & Quantitative Management, 18(5):620-640, 2021.

[29] Sohrabi M.K., Azgomi H. A survey on the combined use of optimization methods and game theory. Archives of Computational Methods in Engineering, 27(1):59-80, 2020.

[30] Shoham Y. Computer science and game theory. Communications of the ACM, 51(8):74-79, 2008.

[31] Manshaei M.H., Zhu Q., Alpcan T., et al. Game theory meets network security and privacy. ACM Computing Surveys (CSUR), 45(3):1-39, 2013.

[32] Pillai P.S., Rao S. Resource allocation in cloud computing using the uncertainty principle of game theory. IEEE Systems Journal, 10(2):637-648, 2014.

[33] Lemaire J. An application of game theory: cost allocation. ASTIN Bulletin: The Journal of the IAA, 1984; 14(1):61-81, 1984. Published online by Cambridge University Press in 2014.

[34] Barough A.S., Shoubi M.V., Skardi M.J.E. Application of game theory approach in solving the construction project conflicts. Procedia-Social and Behavioral Sciences, 58:1586-1593, 2012.

[35] Gale D., Kuhn H.W., Tucker A.W. Linear programming and the theory of game. Activity analysis of production and allocation, 13:317-335, 1951.

[36] Mangasarian O.L., Stone H. Two-person nonzero-sum games and quadratic programming. Journal of Mathematical Analysis and Applications, 9(3):348-355, 1964.

[37] Leboucher C., Shin H.S., Siarry P., et al. Convergence proof of an enhanced particle swarm optimization method integrated with evolutionary game theory. Information Sciences, 346:389-411, 2016.

[38] Annamdas K.K., Rao S.S. Multi-objective optimization of engineering systems using game theory and particle swarm optimization. Engineering Optimization, 41(8):737-752, 2009.

[39] Zamarripa M.A., Aguirre A.M., Méndez C.A., Espuña A. Mathematical programming and game theory optimization-based tool for supply chain planning in cooperative/competitive environments. Chemical Engineering Research and Design, 91(8):1588-1600, 2013.

[40] Dai L., Tang M., Shin S. Stackelberg game approach to a bi-objective robust design optimization. Revista Internacional de Métodos Numéricos para Cálculo y Diseño en Ingeniería, 37(4), 2021.

[41] Matejaš J., Perić T. A new iterative method for solving multiobjective linear programming problem. Applied Mathematics and Computation, 243:746-754, 2014.

[42] Doudou M., Barcelo-Ordinas J.M., Djenouri D., Garcia-Vidal J., Bouabdallah A., Badache N. Game theory framework for MAC parameter optimization in energy-delay constrained sensor networks. ACM Transactions on Sensor Networks (TOSN), 12(2):1-35, 2016.

[43] Muthoo A. Bargaining theory with applications. Cambridge University Press, 1999.

[44] Goodpaster G. Rational decision-making in problem-solving negotiation: Compromise, interest-valuation, and cognitive error. Ohio St. J. on Disp. Resol., 8:299-360, 1992.

[45] Nash J.F. The bargaining problem. Econometrica, 18(2):155-162, 1950.

[46] Nash J.F. Two-person cooperative games. Econometrica, 21(1):128-140, 1953.

[47] Kalai E., Smorodinsky M. Other solutions to Nash's bargaining problem. Econometrica: Journal of the Econometric Society, 43(3):513-518, 1975.

[48] Rubinstein A. Perfect equilibrium in a bargaining model. Econometrica: Journal of the Econometric Society, 50(1):97-109, 1982.

[49] Köksoy O. A nonlinear programming solution to robust multi-response quality problem. Applied Mathematics and Computation, 196(2):603-612, 2008.

[50] Goethals P.L., Cho B.R. Extending the desirability function to account for variability measures in univariate and multivariate response experiments. Computers & Industrial Engineering, 62(2):457-468, 2012.

[51] Wu F.C., Chyu C.C. Optimization of robust design for multiple quality characteristics. International Journal of Production Research, 42(2):337-354, 2004.

[52] Shin S., Cho B.R. Bias-specified robust design optimization and its analytical solutions. Computers & Industrial Engineering, 48(1):129-140, 2005.

[53] Tang L.C., Xu K. A unified approach for dual response surface optimization. Journal of quality technology, 34(4):437-447, 2002.

[54] Steenackers G., Guillaume P. Bias-specified robust design optimization: A generalized mean squared error approach. Computers & Industrial Engineering, 54(2):259-268, 2008.

[55] Mandal W.A. Weighted Tchebycheff optimization technique under uncertainty. Annals of Data Science, 8:709–731, 2021.

[56] Dächert K., Gorski J., Klamroth K. An augmented weighted Tchebycheff method with adaptively chosen parameters for discrete bicriteria optimization problems. Computers & Operations Research, 39(12):2929-2943, 2012.

[57] Steuer R.E., Choo E.U. An interactive weighted Tchebycheff procedure for multiple objective programming. Mathematical Programming, 26(3):326-344, 1983.

[58] Rausser G.C., Swinnen J., Zusman P. Political power and economic policy: Theory, analysis, and empirical applications. Cambridge University Press, 2011.

[59] Myerson R.B. Game theory: Analysis of conflict. Harvard University Press, Cambridge, MA. London England, 1991.

[60] Thomson W. Chapter 35: Cooperative models of Bargaining. In: Handbook of Game Theory with Economic Applications, 2:1237-1284, 1994.

Latest revision as of 15:41, 20 June 2022

Abstract

1. Introduction

2. Literature review

2.1 Robust parameter design

2.2 Game Theory

2.3 Bargaining game

3. Models and methods

3.1 Bi-objective robust design model

3.2 Lexicographic weighed Tchebycheff method

3.3 Nash bargaining solution

4. The proposed model

5. Numerical illustrations and sensitivity analysis

5.1 Numerical example 1

5.2 Sensitivity analysis for numerical example 1

5.3 Numerical example 2

5.4 Sensitivity analysis for numerical example 2

6. Conclusion and future direction

Acknowledgment

References

Document information

Document Score

Share this document

Keywords

claim authorship

@@ Line 4: / Line 4: @@
 <div class="center" style="width: auto; margin-left: auto; margin-right: auto;">
 ''' Integration of Game theory and Response Surface Method for Robust Parameter Design'''</div>
--->== Abstract ==
+-->
-The basic principle of robust parameter design (RPD) is to determine the optimal values of a set of controllable parameters that minimize the quality performance fluctuations caused by noise factors. The dual response surface method is one of the most widely applied approaches in RPD that tries to simultaneously minimize the deviation of the process mean from target and the process variance. However, there are situations when a compromise between the process mean and process variance is necessary, then the trade-off between them becomes an intractable problem. In order to solve the problem, we introduce a method that attempts to integrate the bargaining game theory concept into RPD to determine the optimal solutions. To verify the efficiency of our proposed method, the lexicographic weighted Tchebycheff method is applied to identify if the calculated solution is on the associated Pareto frontier. Two numerical examples show that our model works well in convex frontier cases. Lastly, several sensitivity analyses are conducted to examine the effect of the disagreement point value on the final solution.
+== Abstract ==
+Robust parameter design (RPD) is to determine the optimal controllable factors that minimize the variation of quality performance caused by noise factors. The dual response surface approach is one of the most commonly applied approaches in RPD that attempts to simultaneously minimize the process bias (i.e., the deviation of the process mean from the target) as well as process variability (i.e., variance or standard deviation). In order to address this tradeoff issue between the process bias and variability, a number of RPD methods are reported in literature by assigning relative weights or priorities to both the process bias and variability. However, the relative weights or priorities assigned are often subjectively determined by a decision maker (DM) who in some situations may not have enough prior knowledge to determine the relative importance of both the process bias and variability. In order to address this problem, this paper proposes an alternative approach by integrating the bargaining game theory into an RPD model to determine the optimal factor settings. Both the process bias and variability are considered as two rational players that negotiate how the input variable values should be assigned. Then Nash bargaining game solution technique is applied to determine the optimal, fair, and unique solutions (i.e., a balanced agreement point) for this game. This technique may provide a valuable recommendation for the DM to consider before making the final decision. This proposed method may not require any preference information from the DM by considering the interaction between the process bias and variability. To verify the efficiency of the obtained solutions, a lexicographic weighted Tchebycheff method which is often used in bi-objective optimization problems is utilized. Finally, in two numerical examples, the proposed method provides non-dominated tradeoff solutions for particular convex Pareto frontier cases. Furthermore, sensitivity analyses are also conducted for verification purposes associated with the disagreement and agreement points.
-'''Keywords''': robust design, lexicographic weighted Tchebycheff, bargaining game, response surface methodology, dual response model
+'''Keywords''': Robust parameter design, lexicographic weighted Tchebycheff, bargaining game, response surface methodology, dual response model
-<span id='bookmark0'></span>
+==1. Introduction==
-=1. INTRODUCTION=
+Due to fierce competition among manufacturing companies and an increase in customer quality requirements, robust parameter design (RPD), an essential method for quality management, is becoming ever more important. RPD was developed to decrease the degree of unexpected deviation from the requirements that are proposed by customers or a DM and thereby helps to improve the quality and reliability of products or manufacturing processes. The central idea of RPD is to build quality into the design process by identifying an optimal set of control factors that make the system impervious to variation [1]. The objectives of RPD are set out to ensure that the process mean is at the desired level and process variability is minimized. However, in reality, a simultaneous realization of those two objectives sometimes is not possible. As Myers et al. [2] stated there are circumstances where the process  variability is robust against the effects of noise factors but the mean value is still far away from the target. In other words, a set of parameter values that satisfies these two conflicting objectives may not exist. Hence, the tradeoffs that exist between the process mean and variability are undoubtedly crucial in determining a set of controllable parameters that optimize quality performance.
-<span id='OLE_LINK4'></span><span id='OLE_LINK5'></span><span id='OLE_LINK6'></span><span id='OLE_LINK7'></span>Due to fierce competition among manufacturing companies and an increase in customer quality requirements, RPD as an essential method for quality management is becoming ever more important. RPD was developed to decrease the degree of unexpected deviation from the requirements and improve product or process quality and reliability. The essential concept of RPD is to build quality into the design process by identifying the optimal set of control factor values that make the system insensitive to variation[[#1|[]]<span id='cite-1'></span>[[#1|1].]]The objectives of RPD are to ensure the process mean is at the desired level and process variance is minimized. However, in reality, a simultaneous realization of those two objectives sometimes is not possible. As Myers ''et al''. [2][[Draft Shin 691882792|<span id="cite-2"></span>]] discussed there are circumstances when the process mean and variance are robust to the effects of noise factors but the mean value is far away from the target. In other words, a set of parameter values that satisfies two conflicting objectives may not exist. Hence, the trade-off between the process mean and variance is undoubtedly crucial.
+The tradeoff issue between the process bias and variability can be associated with assigning different weights or priority orders. Weight-based methods assign different weights to the process bias and variability, respectively, to establish their relative importance and transform the bi-objective problem into a single objective problem. The two most commonly applied weight-based methods are the mean square error model [3] and the weighted sum model [4,5]. Alternatively, priority-based methods sequentially assign priorities to the objectives (i.e., minimization of the process bias or variability). For instance, if the minimization of the process bias is prioritized, then the process variability is optimized with a constraint of zero-process bias [6]. Other priority-based approaches are discussed by Myers and Carter [7], Copeland and Nelson [8], Lee et al. [9], and Shin and Cho [10]. In both weight-based and priority-based methods, the relative importance can be assigned by the decision maker’s (DM) preference, which is obviously subjective. Additionally, there are situations in which the DM could be unsure about the relative importance of the process parameters in bi-objective optimization problems.
-<span id='OLE_LINK2'></span><span id='OLE_LINK22'></span>Currently, the trade-off between process bias, which is the deviation from the target process mean value, and variance is generally based on signing different weights or priority orders to transform a multidimensional problem into a single dimension one. Normally, weight-based methods assign different weights to the process bias and variance, respectively, to imply their relative importance and transform the bi-objective problem into a single objective problem, while priority-based methods prioritize one of the objectives by satisfying one objective first and then moving to the next.  For instance, if the process bias is given priority, then minimizes process bias first and obtains a corresponding feasible solution area, after that, optimizes variance within that area. In both weight-based and priority-based methods, the relative importance is assigned based on the decision maker’s (DM) preference, which is obviously subjective. Additionally, there are situations in which the DM is unsure about relative importance in the bi-objective optimization problem. Therefore, this paper aims to solve the trade-off problem from the game theory point of view by integrating the bargaining game theory into the PRD procedure.  The two objectives (the process bias and variance) are considered as two rational players that negotiate about how the input variable values should be assigned, and the Nash bargaining game solution concept is applied to define a fair, optimal, and unique solution for the game, which should provide a valuable suggestion for DM to make a final decision. To verify the efficiency of our obtained solution, the lexicographic weighted Tchebycheff approach is used to generate the associated Pareto frontier so that we can visually observe if our solution is on the Pareto frontier.  Two numerical examples show that the proposed model can efficiently locate a well-balanced solution. Sensitivity analyses for the effects of the disagreement point value on the final solution are also conducted.
+Therefore, this paper aims to solve this tradeoff problem from a game theory point of view by integrating bargaining game theory into the RPD procedure. First, the process bias and variability are considered as two rational players in the bargaining game. Furthermore, the relationship functions for the process bias and variability are separately estimated by using the response surface methodology (RSM). In addition, those estimated functions are regarded as utility functions that represent players’ preferences and objectives in this bargaining game. Second, a disagreement point, signifying a pair of values that the players expect to receive when negotiation among players breaks down, can be defined by using the minimax-value theory which is often used as a decision rule in game theory. Third, Nash bargaining solution techniques are then incorporated into the RPD model to obtain the optimal solutions. Then, to verify the efficiency of the obtained solutions, a lexicographic weighted Tchebycheff approach is used to generate the associated Pareto frontier so that it can be visually observed if the obtained solutions are on the Pareto frontier. Two numerical examples are conducted to show that the proposed model can efficiently locate well-balanced solutions. Finally, a series of sensitivity analyses are also conducted in order to demonstrate the effects of the disagreement point value on the final agreed solutions.
-This research is laid out as follows: Section 2 discusses the literature on RPD and game theory application. In Section 3, the dual response optimization problem, the lexicographic weighted Tchebycheff method, and Nash bargaining solution are explained. Next, in Section 4, the proposed model is presented. Then in Section 5, two numerical examples are conducted to show the efficiency of the proposed method, and sensitivity studies are performed to reveal the influence of disagreement point values on the solution. In Section 6, a conclusion and further research direction are discussed.
+This research paper is laid out as follows: Section 2 discusses existing literature for RPD and game theory applications. In Section 3, the dual response optimization problem, the lexicographic weighted Tchebycheff method, and the Nash bargaining solution are explained. Next, in Section 4, the proposed model is presented. Then in Section 5, two numerical examples are addressed to show the efficiency of the proposed method, and sensitivity studies are performed to reveal the influence of disagreement point values on the solutions. In Section 6, a conclusion and further research directions are discussed.
-== <span id="_Hlk58849949"></span>2. RELATED RESEARCH ==
+<span id="OLE_LINK4"></span><span id="OLE_LINK5"></span><span id="OLE_LINK6"></span><span id="OLE_LINK7"></span><span id="cite-1"></span>[[Draft Shin 691882792|<span id="cite-2"></span>]]<span id="OLE_LINK2"></span><span id="OLE_LINK22"></span>
+<span id="_Hlk58849949"></span>
+==2.  Literature review ==
 ===2.1 Robust parameter design ===
-Taguchi was the first person to include both experimental concepts and an overarching design philosophy into the quality design process. Taguchi developed an orthogonal array based experimental design and use the signal-to-noise(SN) ratio to measure the effects of factors on desired output responses. Despite the wide acceptance of his philosophy, his method was contentious. As discussed by Leon, Shoemaker, and Kackar[[#3|[]]<span id='cite-3'></span>[[#3|<nowiki>3]</nowiki>]], in some situations, the SN ratio is not independent of the adjustment parameters, so use of the SN ratio as a performance measure can lead to far from optimal design parameter settings. SN ratio as a performance measure is appropriate only when a particular assumption is satisfied. Box [[#4|[]]<span id='cite-4'></span>[[#4|<nowiki>4]</nowiki>]] also argued that statistical analysis based on experimental data should be introduced, rather than relying only on the maximization of the SN ratio. The controversy about the Taguchi method is further discussed and addressed by Nair ''et al.'' [[#5|[]]''<span id="cite-5"></span>''[[#5|<nowiki>5]</nowiki>]] and Tsui [[#6|[]]<span id='cite-6'></span>[[#6|<nowiki>6]</nowiki>]].
+Taguchi proposed both experimental design concepts and parameter tradeoff issues into a quality design process. In addition, Taguchi developed an orthogonal-array-based experimental design and used the signal-to-noise (SN) ratio to measure the effects of factors on desired output responses. As discussed by Leon et al. [11] in some situations, the SN ratio is not independent of the adjustment parameters, so using the SN ratio as a performance measure may often lead to far from the optimal design parameter settings. Box [12] also argued that statistical analyses based on experimental data should be introduced, rather than relying only on the maximization of the SN ratio. The controversy about the Taguchi method is further discussed and addressed by Nair et al. [13] and Tsui [14].
-<span id='_Ref87630774'></span><span id='_Ref76152586'></span>Based on Taguchi's philosophy, further statistics-based methods have been developed. Vining and Myers [[#7|[]]<span id='cite-7'></span>[[#7|<nowiki>7]</nowiki>]] introduced the dual response method, which takes zero-process bias as a constraint and minimizes the variance. Shoemaker ''et al''. [[#8|[]]<span id='cite-8'></span>[[#8|<nowiki>8]</nowiki>]] and Khattree [[#9|[]]<span id='cite-9'></span>[[#9|<nowiki>9]</nowiki>]]  discussed the advantages of using the response surface model approach. The generalized linear model method can be applied when the homoscedasticity assumption for regression is violated [[#10|[]]<span id='cite-10'></span>[[#10|10].]]  Additionally, in cases with incomplete data, Lee and Park [[#11|[]]<span id='cite-11'></span>[[#11|<nowiki>11]</nowiki>]] suggested an expectation-maximization (EM) algorithm for estimation of the process mean and variance, while Cho and Park [[#12|[]]<span id='cite-12'></span>[[#12|<nowiki>12]</nowiki>]] suggested the weighted least squares (WLS) method. However, Lin and Tu [[#13|[]]<span id='cite-13'></span>[[#13|<nowiki>13]</nowiki>]] pointed out that the dual response approach had some deficiencies and proposed an alternative method, the mean-squared-error (MSE) model. Jayaram and Ibrahim [[#14|[]]<span id='cite-14'></span>[[#14|<nowiki>14]</nowiki>]] modified the MSE model by incorporating the capability indexes and considered the minimization of total deviation of the capability indexes to achieve a multiple response robust design. A more flexible alternative method that searched for Pareto optimal solutions based on the weighted-sum model concept was introduced [[#15|[]]<span id='cite-15'></span>[[#15|<nowiki>15]</nowiki>]]. In fact, the weighted sum approach is more flexible than the traditional dual response model, but it cannot be applied when the Pareto frontier is nonconvex, as discussed in detail by Shin and Cho [[#16|[]]<span id='cite-16'></span>[[#16|<nowiki>16]</nowiki>]], instead they proposed a superior method called lexicographic weighted Tchebycheff.
+Based on Taguchi’s philosophy, further statistical based methods for RPD have been developed. Vining and Myers [6] introduced a dual response method, which takes zero-process bias as a constraint and minimizes the variability. Copeland and Nelson [15] proposed an alternative method for the dual response problem by introducing a predetermined upper limit on the deviation from the target. Similar approaches related to upper limit concept are further discussed by Shin and Cho [10] and Lee et al. [9] For the estimation phase, Shoemaker et al. [16] and Khattree [17] suggested a utilization of the response surface model approaches. However, when a homoscedasticity assumption for regression is violated, then other methods, such as the generalized linear model, can be applied [18].  Additionally, in cases where there is incomplete data, Lee and Park [19] suggested an expectation-maximization (EM) algorithm to provide an estimation of the process mean and variance, while Cho and Park [20] suggested a weighted least squares (WLS) method. However, Lin and Tu [3] pointed out that the dual response approach had some deficiencies and proposed an alternative method called mean-squared-error (MSE) model. Jayaram and Ibrahim [21] modified the MSE model by incorporating capability indexes and considered the minimization of total deviation of capability indexes to achieve a multiple response robust design. More flexible alternative methods that could obtain Pareto optimal solutions based on a weighted sum model were introduced by many researchers [4,5,22]. In fact, this weighted sum model is more flexible than conventional dual response models, but it cannot be applied when a Pareto frontier is nonconvex [23]. In order to overcome this problem, Shin and Cho [23] proposed an alternative method called lexicographic weighted Tchebycheff by using an <math display="inline">L-\infty</math> norm.
-More recently, RPD has become more widely used not only in manufacturing but also in the pharmaceutical and engineering fields, etc. New technologies such as simulation, multiple optimization techniques, and neural network (NN) have been applied to RPD.  Shin ''et al.'' [[#17|[]]<span id='cite-17'></span>[[#17|<nowiki>17]</nowiki>]] proposed a new RPD model that applied the NN and Akaike information criterion, and then used the desirability function as feedback in the NN.  Picheral ''et al''. [[#18|[]]<span id='cite-18'></span>[[#18|<nowiki>18]</nowiki>]] calculated process bias and variance using the propagation of variance method. Two new robust optimization methods: gradient-assisted robust optimization and quasi-concave gradient-assisted robust optimization were presented by Mortazavi ''et al''. [[#19|[]]<span id='cite-19'></span>[[#19|<nowiki>19]</nowiki>]].
+More recently, RPD has become more widely used not only in manufacturing but also in other science and engineering areas including pharmaceutical drug development. New approaches such as simulation, multiple optimization techniques, and neural networks (NN) have been integrated into RPD. For example, Le et al. [24] proposed a new RPD model by introducing a NN approach to estimate dual response functions. Additionally, Picheral et al. [25] estimated the process bias and variance function by using the propagation of variance method. Two new robust optimization methods, the gradient-assisted and quasi-concave gradient-assisted robust optimization methods, were presented by Mortazavi et al. [26]. Bashiri et al. [27] proposed a robust posterior preference method that introduced a modified robust estimation method to reduce the effects of outliers on functions estimation and used non-robustness distance to compare non-dominated solutions. However, the responses are assumed to be uncorrelated. To address the correlation among multiple responses and the variation of noise factors over time, Yang et al. [28] extended offline RPD to online RPD by applying Bayesian seemingly unrelated regression and time series models so that the set of optimal controllable factor values can be adjusted in real-time.
 ===2.2 Game Theory ===
-<span id='_Ref76149866'></span><span id='OLE_LINK20'></span><span id='OLE_LINK21'></span>The field of game theory presents mathematical models of strategic interactions among rational agents. These models are analytical tools to find the optimal choices for interactional and decision-making problems. Game theory is often applied when the “roles and actions of multiple agents affect each other”[[#20|[]]<span id='cite-20'></span>[[#20|<nowiki>20]</nowiki>]]. Thus, game theory aims to predict and analyze other agents’ effects on self-interest, and then, based on the analysis, choose the best possible move. Given the characteristics of game theory, it is widely applied in multiple disciplines, such as computer science [[#21|[]]<span id='cite-21'></span>[[#21|<nowiki>21]</nowiki>]], network security and privacy[[#22|[]]<span id='cite-22'></span>[[#22|<nowiki>22]</nowiki>]], cloud computing [[#23|[]]<span id='cite-23'></span>[[#23|<nowiki>23]</nowiki>]], cost allocation [[#24|[]]<span id='cite-24'></span>[[#24|<nowiki>24]</nowiki>]], and construction [[#25|[]]<span id='cite-25'></span>[[#25|<nowiki>25]</nowiki>]]. Because game theory has some degree of conceptual overlap with optimization, game theory and optimization techniques are often combined. According to Sohrabi and Azgom [19]<span id='cite-_Ref76149866'></span>, there are three basic combinations of game theory and optimization. One uses optimization techniques to solve a game problem and prove the existence of equilibrium; this is discussed by a number of researchers [[#26|[]]<span id='cite-26'></span>[[#26|26]],<span id='cite-27'></span>[[#27|<nowiki>27]</nowiki>]]. The second integrates game theoretical concepts to improve an optimization problem, as discussed by Leboucher ''et al.''[[#28|[]]<span id='cite-28'></span>[[#28|<nowiki>28]</nowiki>]], Annamdas and Rao [[#29|[]]<span id='cite-29'></span>[[#29|<nowiki>29]</nowiki>]], Zamarripa ''et al.'' [[#30|[]]<span id='cite-30'></span>[[#30|<nowiki>30]</nowiki>]], and Shi ''et al.'' [[#31|[]]<span id='cite-31'></span>[[#31|<nowiki>31]</nowiki>]]. The last combinatory method is the most common one; it applies game theory and optimization techniques simultaneously to solve a complicated problem. For example, a combination of linear programming and cooperative game method was introduced to solve a decision-making problem [[#32|[]]<span id='cite-32'></span>[[#32|<nowiki>32]</nowiki>]]. Doudou ''et al.''[[#33|[]]<span id='cite-33'></span>[[#33|<nowiki>33]</nowiki>]] used the convex optimization method and non-cooperative game theory to settle the wireless sensor network problem.
+The field of game theory presents mathematical models of strategic interactions among rational agents. These models can become analytical tools to find the optimal choices for interactional and decision-making problems. Game theory is often applied in situations where the "roles and actions of multiple agents affect each other" [29]. Thus, game theory serves as an analysis model that aims at helping agents to make the optimal decisions, where agents are rational and those decisions are interdependent.  Because of the condition of interdependence each agent has to consider other agents’ possible decisions when formulating a strategy. Based on these characteristics of game theory, it is widely applied in multiple disciplines, such as computer science [30], network security and privacy [31], cloud computing [32], cost allocation [33], and construction [34]. Because game theory has a degree of conceptual overlap with optimization and decision-making, three concepts (i.e., game theory, optimization, and decision-making) can often be combined, respectively. According to Sohrabi and Azgom [29], there are three kinds of basic combinations associated with those three concepts as follows: game theory and optimization, game theory and decision-making, game theory, optimization, and decision-making.
-<span id='OLE_LINK16'></span><span id='OLE_LINK17'></span>Many previous studies have attempted to apply game theory in different situations. Indeed, game theory is helpful for any situation in which agents’ interests conflict and interact. The parameter optimization problem or the trade-off between process variance and bias in RD is precisely this type of situation, which is why it is possible to integrate game theory and RD. For example, Dai ''et al''. [[#34|[]]<span id='cite-34'></span>[[#34|<nowiki>34]</nowiki>]] attempted to address the RPD problem by integrating the Stackelberg game. In this paper, we mainly focus on one of the cooperative games – the bargaining game.
+The first type of these combinations (i.e., game theory and optimization) further has two possible situations. In the first situation, optimization techniques are used to solve a game problem and prove the existence of equilibrium [35,36]. In the second situation, game theory concepts are integrated to solve an optimization problem. For example, Leboucher et al. [37] used evolutionary game theory to improve the performance of a particle swarm optimization (PSO) approach. Additionally, Annamdas and Rao [38] solved a multi-objective optimization problem by using a combination of game theory and a PSO approach. The second type kind of combination (i.e., game theory and decision-making) integrates game theory to solve a decision-making problem, as discussed by Zamarripa et al. [39] who applied game theory to assist with decision-making problems in supply chain bottlenecks. More recently, Dai et al. [40] attempted to integrate the Stackelberg leadership game into RPD model to solve a dual response tradeoff problem. The third type of combination (i.e., game theory, optimization and decision-making) integrates game theory and optimization to a decision-making problem. For example, a combination of linear programming and game theory was introduced to solve a decision-making problem [41]. Doudou et al. [42] used a convex optimization method and game theory to settle a wireless sensor network decision-making problem.<span id="_Ref76149866"></span><span id="OLE_LINK20"></span><span id="OLE_LINK21"></span><span id="cite-20"></span><span id="cite-21"></span><span id="cite-22"></span><span id="cite-23"></span><span id="cite-24"></span><span id="cite-25"></span><span id="cite-_Ref76149866"></span><span id="cite-26"></span><span id="cite-27"></span><span id="cite-28"></span><span id="cite-29"></span><span id="cite-30"></span><span id="cite-31"></span><span id="cite-32"></span><span id="cite-33"></span><span id='OLE_LINK16'></span><span id='OLE_LINK17'></span><span id='cite-34'></span>
-===2.3 Bargaining Game===
+===2.3 Bargaining game===
-A problem-solving negotiation also called a bargaining problem is a situation where a set of agents try to reach a unanimous agreement based on their own interests by bargaining[[#35|[]]<span id='cite-35'></span>[[#35|<nowiki>35]</nowiki>]]. Hence, the bargaining game essentially has two features, namely, cooperation and conflict. Because the bargaining problem treats cooperation and conflicts of interest as a joint problem, bargaining problems are much more complicated than simple pure cooperative games that ignore individual interest and seek to maximize the group benefit [[#36|[]]<span id='cite-36'></span>[[#36|<nowiki>36]</nowiki>]]. Typical examples of bargaining problems include negotiation between product seller and buyer, union/firm negotiation over wage and employment level, and simple cake distribution problem.
+A bargaining game can be applied in a situation where a set of agents have an incentive to cooperate but have conflicting interests over how to distribute the payoffs generated from the cooperation [43]. Hence, a bargaining game essentially has two features: Cooperation and conflict. Because the bargaining game considers cooperation and conflicts of interest as a joint problem, it is more complicated than a simple cooperative game that ignores individual interests and maximizes the group benefit [44]. Typical three bargaining game examples include a price negotiation problem between product sellers and buyers, a union and firm negotiation problem over wages and employment levels, and a simple cake distribution problem.
-<span id='OLE_LINK3'></span>All formal discussions about the bargaining game were sparked by the publication of two papers by Nash [[#37|[]]<span id='cite-37'></span>[[#37|37]],<span id='cite-38'></span>[[#38|<nowiki>38]</nowiki>]]. In 1950, Nash [37] presented a classical bargaining model aimed at solving an economic problem (bilateral monopoly). He used a numerical example to prove the existence of multiple solution points. In 1953, Nash [38] extended his research to a more general form and demonstrated that there are two possible approaches to solving a two-person cooperative bargaining game to get a unique solution. The first approach, called the negotiation model, is through the analysis of the negotiation process, while the second is called the axiomatic approach. The basic idea of the axiomatic approach is to set out axioms or properties that the solution function may obtain, then classify and study all functions and find the one that captures those properties. Thus, Nash assumed some axioms that the binding agreement solution should have. Since the 1950s, many scholars have attempted to modify Nash's model and proposed several different solutions based on different axioms. One of the most famous models is called the Rubinstein bargaining model [[#39|[]]<span id='cite-39'></span>[[#39|<nowiki>39]</nowiki>]]. The Rubinstein bargaining model deals with a bargaining game with alternate offerings on an infinite time horizon with consideration of discounting factors (assumption for “delays are costly”). Later, Kalai & Smorodinsky [[#40|[]]<span id='cite-40'></span>[[#40|<nowiki>40]</nowiki>]] introduced an alternative solution to the bargaining problem, known as Kalai-Smorodinky's solution, which replaced one of Nash's axioms in order to reach a fairer unique solution. However, in this paper, only the concept of the Nash demanding theory and Nash bargaining solution will be used.
+Significant discussions about the bargaining game can be addressed by Nash [45,46]. Nash [45] presented a classical bargaining game model aimed at solving an economic bargaining problem and used a numerical example to prove the existence of multiple solutions. In addition, Nash [46] extended his research to a more general form and demonstrated that there are two possible approaches to solve a two-person cooperative bargaining game. The first approach, called the negotiation model, is used to obtain the solution through an analysis of the negotiation process. The second approach, called the axiomatic method, is applied to solve a bargaining problem by specifying axioms or properties that the solution should obtain. For the axiomatic method, Nash concluded four axioms that the agreed solution called Nash bargaining solution should have. Based on Nash’s philosophy, many researchers attempted to modify Nash's model and proposed a number of different solutions based on different axioms. One famous modified model replaces one of Nash’s axioms in order to reach a fairer unique solution which is called the Kalai-Smorodinky’s solution [47]. Later, Rubinstein [48] addressed a bargaining problem by specifying a dynamic model which explains a bargaining procedure. <span id="cite-35"></span><span id="cite-36"></span><span id='OLE_LINK3'></span><span id='cite-37'></span><span id='cite-38'></span><span id='cite-39'></span><span id='cite-40'></span>
-==3. MODELS AND METHODS==
+==3. Models and methods ==
 ===3.1 Bi-objective robust design model===
-Based on the discussion in section 2, the dual response trade-off problem can be formally expressed as a bi-objective problem [16]<span id='cite-_Ref76152586'></span> as:
+A general bi-objective optimization problem involves simultaneous optimization of two conflicting objectives (e.g.,  <math>f_1({\boldsymbol{\text{x}}})</math> and <math>f_2({\boldsymbol{\text{x}}})</math>) that can be described in mathematical terms as <math>\min[f_1({\boldsymbol{\text{x}}}), f_2({\boldsymbol{\text{x}}})]</math>. The primary objective of PRD is to minimize the deviation of performance of the production process from the target value and the variability of the performance, where this performance deviation can be represented by process bias and the performance variability can be represented by standard deviation or variance. For example, Koksoy [49], Goethals and Cho [50], and Wu and Chyu [51]  utilized estimated variance functions to represent process variability. On the other hand, Shin and Cho [10,52], Tang and Xu [53] used estimated standard deviation functions to measure process variability. Steenackers and Guillaume [54] discussed the effect of different response surface expressions on the optimal solutions, and they concluded that both standard deviation and variance can capture the process variability well but can lead to different optimal solution sets. Since it can be infeasible to minimize the process bias and variability simultaneously, a simultaneous optimization of these two process parameters, which are separately estimated by applying RSM, is then transformed into a tradeoff problem between the process bias and variability. This tradeoff problem can be formally expressed as a bi-objective optimization problem [23] as:<span id="cite-_Ref76152586"></span>
 {| class="formulaSCP" style="width: 100%; text-align: center;"
@@ Line 53: / Line 57: @@
 |-
 |<math>min</math>
-| <math display="inline">{\left[ {\left\{ \hat{\mu }\left( \boldsymbol{x}\right) -\tau \right\} }^{2},\, {\hat{\sigma }}^{2}(\boldsymbol{x})\right] }^{T}</math>
+| <math>\left[ \left\{ \hat{\mu }\left( \boldsymbol{\text{x}}\right) -\tau \right\}^{2},\, \hat{\sigma }^{2} (\boldsymbol{\text{x}})\right]^{T}</math>
 |-
 |<math>s.t.</math>
-|<math display="inline"> \boldsymbol{x}\in X\,</math>
+|<math display="inline"> {\boldsymbol{\text{x}}}\in X\,</math>
 |}
 | style="width: 5px;text-align: right;white-space: nowrap;" | (1)
 |}
-where <math display="inline">\boldsymbol{x}</math>''' '''represents a vector of design factors, <math display="inline">X</math> denotes the feasible area, <math display="inline">\tau</math>  indicates the target value. <math display="inline">{\left\{ \hat{\mu }\left( \boldsymbol{x}\right) -\tau \right\} }^{2}</math> and <math display="inline">{\hat{\sigma }}^{2}(\boldsymbol{x})</math> are the estimated functions for process bias and variance, respectively.
+where <math display="inline">{\boldsymbol{\text{x}}}</math>, <math display="inline">X</math>, <math display="inline">\tau</math>, <math display="inline">{\left\{ \hat{\mu }\left( {\boldsymbol{\text{x}}}\right) -\tau \right\} }^{2}</math>, and <math display="inline">{\hat{\sigma }}^{2}({\boldsymbol{\text{x}}})</math> represent a vector of design factors, the set of feasible solutions under specified constraints, the target process mean value, and the estimated functions for process bias and variability, respectively.
-===3.2 Lexicographic weighed Tchebycheff method.===
+===3.2 Lexicographic weighed Tchebycheff method===
-The basic idea of a weighted metrics method is to find the closest feasible solution to the utopia point. Different ways of measuring distance can lead to different solutions. The most common metric is <math display="inline">{L}_{p}</math> metric, where <math>p=1,2,or\, \infty</math>. When <math>p=1</math>, it is called the Manhattan metric, whereas <math display="inline">p=\infty</math> is named the Tchebycheff metric [[#41|[]]<span id='cite-41'></span>[[#41|<nowiki>41]</nowiki>]]. The weakly Pareto optimal solutions can be obtained by introducing different weights.
+A bi-objective robust design problem is generally addressed by introducing a set of parameters, determined by a DM, which represents the relative importance of those two objectives. With the introduced parameters, the bi-objective functions can be transformed into a single integrated function, thus the bi-objective optimization problem can be solved by simply optimizing the integrated function. One way to construct this integrated function is by using the weighted sum of the distance between the optimal solution and the estimated function. Different ways of measuring distance can lead to different solutions, and one of the most common methods is <math display="inline">{L}_{p}</math> metric, where <math>p=1,2,\, \mbox{or}\, \infty</math>. When <math>p=1</math>, the metric is called the Manhattan metric, whereas <math display="inline">p=\infty</math>, it is named the Tchebycheff metric [47]. Utopia point represents an initial point to apply <math>L-\infty</math> metric in weighted Tchebycheff method and can be obtained by minimizing each objective function separately. The weak Pareto optimal solutions can be obtained by introducing different weights: <span id='cite-41'></span>
 {| class="formulaSCP" style="width: 100%; text-align: center;"
@@ Line 72: / Line 76: @@
 {| style="text-align: center; margin:auto;"
 |-
-| ''<math display="inline">\mathrm{min}\,{(\sum _{i=1}^{p}{w}_{i}{\left| {f}_{i}\left( \boldsymbol{x}\right) -{u}_{i}^{\ast }\right| }^{p})}^{\frac{1}{p}}</math>''
+| <math>\mathrm{min}\,\left(\displaystyle\sum _{i=1}^{p}{w}_{i}\left| {f}_{i}\left( \boldsymbol{\text{x}}\right) -{u}_{i}^{\ast }\right| ^{p}\right)^{\frac{1}{p}}</math>
 |}
 | style="width: 5px;text-align: right;white-space: nowrap;" | (2)
 |}
+where <math display="inline">{u}_{i}^{\ast }</math> and <math display="inline">{w}_{i}</math> denote the utopia point values and weights associated with objective functions, respectively. When <math>p=\infty</math>, the above function (i.e., Eq.(2)) will only consider the largest deviation. Although the weighted Tchebycheff method is an efficient approach, its main drawback is that only weak non-dominated solutions can be guaranteed [56], which is obviously not optimal for the DM. So, Steuer and Choo [57] introduced an interactive weighted Tchebycheff method, which can generate every non-dominated point provided that weights are selected appropriately. Shin and Cho [23] introduced the lexicographic weighted Tchebycheff method to the RPD area. This method is proved to be efficient and capable of generating all Pareto optimal solutions when the process bias and variability are treated as a bi-objective problem. The mathematical model is shown below [23]:<span id='cite-42'></span>[[Draft Shin 691882792|<span id="cite-43"></span>]]<span id='cite-_Ref76152586'></span><span id='cite-_Ref76152586'></span>
-where <math display="inline">{u}_{i}^{\ast }</math> is the utopia point and <math display="inline">{w}_{i}</math> is the weight. When <math>p=\infty</math>, the above function will only consider the largest deviation [33]. Although the weighted Tchebycheff method is an efficient approach, its main drawback is that only weak non-dominated solutions can be guaranteed [[#42|[]]<span id='cite-42'></span>[[#42|<nowiki>42]</nowiki>]], which is obviously not optimal for the DM. So, in 1983, Steuer and Choo [[Draft Shin 691882792|[<span id="cite-43"></span><nowiki>43]</nowiki>]] introduced an interactive weighted Tchebycheff method, which can generate every non-dominated point provided that weights are selected appropriately [34]. Shin and Cho [[#_Ref76152586|[15]]]<span id='cite-_Ref76152586'></span> first introduced the lexicographic weighted Tchebycheff method to the RPD area. The method proved to be efficient and capable of generating all Pareto optimal solutions when process bias and variance are treated as a bi-objective problem. The mathematical model is shown below [15]<span id='cite-_Ref76152586'></span>:
 {| class="formulaSCP" style="width: 100%; text-align: center;"
@@ Line 86: / Line 89: @@
 |-
 |<math>min</math>
-| <math display="inline">\mathrm{\, \, \, [\, }\,\xi ,\, \left[ {\left\{ \hat{\mu }\left( \boldsymbol{x}\right) -t\right\} }^{2}-{u}_{1}^{\ast }\right] +[{\hat{\sigma }}^{2}\left( \boldsymbol{x}\right) -{u}_{2}^{\ast }]]</math>
+| <math>\left[\,\xi ,\, \left[ {\left\{ \hat{\mu }\left( {\boldsymbol{\text{x}}}\right) -t\right\} }^{2}-{u}_{1}^{\ast }\right] +\left[{\hat{\sigma }}^{2}\left( {\boldsymbol{\text{x}}}\right) -{u}_{2}^{\ast }\right]\right]</math>
 |-
 |<math>s.t.</math>
-|<math> \, \lambda [{\left\{ \hat{\mu }\left( \boldsymbol{x}\right) -t\right\} }^{2}-{u}_{1}^{\ast }]\leq \xi</math>
+|<math> \, \lambda \left[{\left\{ \hat{\mu }\left( {\boldsymbol{\text{x}}}\right) -t\right\} }^{2}-{u}_{1}^{\ast }\right]\leq \xi</math>
 |-
 |
-|<math>\left( 1-\lambda \right) [\hat{\sigma }\left( \boldsymbol{x}\right) -{u}_{2}^{\ast }]\leq \xi</math>
+|<math>\left( 1-\lambda \right) \left[\hat{\sigma }\left({\boldsymbol{\text{x}}}\right) -{u}_{2}^{\ast }\right]\leq \xi</math>
 |-
 |
-|<math>\boldsymbol{x}\in X</math>
+|<math>{\boldsymbol{\text{x}}}\in X</math>
 |}
 | style="width: 5px;text-align: right;white-space: nowrap;" | (3)
 |}
-where <math>\xi</math> is a non-negative variable and <math display="inline">X</math> denotes the set of feasible solutions under specified constraints. Additionally, <math display="inline">{u}_{i}^{\ast }</math> is the utopia point and <math>\lambda</math> is the weight.
+where <math>\xi</math> and <math>\lambda</math> represent a non-negative variable and a weight term associated with process bias and variability, respectively. The Lexicographic weighed Tchebycheff method is utilized as a verification method in this paper.
 ===3.3 Nash bargaining solution===
-A two-player bargaining game can be represented by a pair <math display="inline">\, (U,d)</math>, where <math display="inline">U\subset {R}^{2}</math>and <math display="inline">d\subset {R}^{2}</math>.  <math display="inline">U</math> is the set of obtainable payoff combinations of the two players through an agreement. <math display="inline">U=</math><math>({u}_{1}(\boldsymbol{x}){,u}_{2}(\boldsymbol{x}))</math> where <math display="inline">{u}_{1}(\boldsymbol{x})</math> and <math display="inline">{\, u}_{2}\left( \boldsymbol{x}\right) \,</math> are the utility payoff functions for player 1 and 2, respectively, and <math display="inline">\boldsymbol{x}\boldsymbol{\, =}\boldsymbol{(}{x}_{1},\, {x}_{2})\,</math> is a vector of actions taken by each player. A disagreement point <math display="inline">d</math> ( <math display="inline">{d=(d}_{1},{d}_{2})</math>) represents the payoff that each player will gain from this game when two players fail to reach a satisfactory agreement [39]. In other words, the disagreement point is the payoff each player would expect to receive if negotiation breaks down. Notice that we assume there exists <math display="inline">{u}_{i}(\boldsymbol{x})\in U</math> where <math display="inline">{u}_{i}(\boldsymbol{x})>{d}_{i}</math> for <math display="inline">\, i\, =</math><math>1,\, 2</math>. In mathematical form: the set <math display="inline">U\cap \left\{ \left( {u}_{1}(\boldsymbol{x}),{u}_{2}(\boldsymbol{x})\right) \in \, {R}^{2}:\, {u}_{1}(\boldsymbol{x})\geq {d}_{1};\, {u}_{2}(\boldsymbol{x})\geq {d}_{2}\right\}</math>  is non-empty. As suggested by the notation, a Nash bargaining solution is affected by both the reachable utility range (<math display="inline">U</math>) and disagreement point value (<math display="inline">d</math>). So, predictably, each rational player will choose the disagreement point that maximizes his own bargaining position. According to Myerson [36], there are three possible ways of determining the value of the disagreement point. One standard method is to choose the minimax value for each player.
+A two-player bargaining game can be represented by a pair <math display="inline">\, (U,d)</math>, where <math display="inline">U\subset {R}^{2}</math> and <math display="inline">d\subset {R}^{2}</math>. <math display="inline">U=({u}_{1}({\boldsymbol{\text{x}}}){,u}_{2}({\boldsymbol{\text{x}}}))</math> denotes a pair of obtainable payoffs of the two players, where <math display="inline">{u}_{1}({\boldsymbol{\text{x}}})</math> and <math display="inline">{\, u}_{2}\left({\boldsymbol{\text{x}}}\right) \,</math> represent the utility functions for player 1 and 2, respectively, and <math display="inline">{\boldsymbol{\text{x}}}{\, =}{(}{x}_{1},\, {x}_{2})\,</math> denotes a vector of actions taken by players. <math display="inline">d</math> (<math display="inline">{d=(d}_{1},{d}_{2})</math>), defined as a disagreement point, represents the payoffs that each player will gain from this game when two players fail to reach a satisfactory agreement. In other words the disagreement point values are the payoffs that each player can expect to receive if a negotiation breaks down. Assuming <math display="inline">{u}_{i}({\boldsymbol{\text{x}}})>{d}_{i}</math> where <math display="inline">{u}_{i}({\boldsymbol{\text{x}}})\in U</math> for <math display="inline">\, i\, =1,2</math>, the set <math display="inline">U\cap \left\{ \left( {u}_{1}({\boldsymbol{\text{x}}}),{u}_{2}({\boldsymbol{\text{x}}})\right) \in \, {R}^{2}:\, {u}_{1}({\boldsymbol{\text{x}}})\geq {d}_{1};\, {u}_{2}({\boldsymbol{\text{x}}})\geq {d}_{2}\right\}</math> is non-empty. As suggested by the expression of the Nash bargaining game <math display="inline">(U, d)</math>, the Nash bargaining solution is affected by both the reachable utility range (<math display="inline">U</math>) and disagreement point value (<math display="inline">d</math>). Since <math display="inline">U</math> cannot be changed, rational players will decide a disagreement point value to optimize their bargaining position. According to Myerson [59], there are three possible ways to determine the value of a disagreement point. One standard way is to calculate the minimax value for each player
-{| class="formulaSCP" style="width: 100%; text-align: center;"
-|
+{| class="formulaSCP" style="width: 100%; text-align: left;"
-|<math>{d}_{1}=\mathrm{min}\,\mathrm{max}\,{u}_{1}({x}_{1},{x}_{2})</math>
-|（4）
 |-
-|and
+|
-| <math>{d}_{2}=\mathrm{min}\,\mathrm{max}\,{u}_{2}({x}_{1},{x}_{2})</math>
+{| style="text-align: center; margin:auto;width: 100%;"
-|
+|-
+| style="text-align: center;" | <math>{d}_{1}=\mathrm{min}\,\mathrm{max}\,{u}_{1}({x}_{1},{x}_{2})\,\quad \mbox{and} \,\quad{d}_{2}=\mathrm{min}\,\mathrm{max}\,{u}_{2}({x}_{1},{x}_{2})</math>
+|}
+| style="width: 5px;text-align: right;white-space: nowrap;" |(4)
 |}
+To be more specific, Eq.(4) states that, given each possible action for player 2, player 1 has a corresponding best response strategy. Then, among all those best response strategies, player 1 chooses the one that returns the minimum payoff which is defined as a disagreement point value. Following this logic, player 1 can guarantee to receive an acceptable payoff. Another possible way of determining the disagreement point value is to derive the disagreement point value as an effective and rational threat to ensure the establishment of an agreement. The last possibility is to set the disagreement point as the focal equilibrium of the game.
-To be more specific, Equation 4 states that, given each possible action for player 2, player 1 has a corresponding best response. Then, among those best response values, player 1 chooses the minimum value. By following this logic, player 1 can guarantee the minimum receivable payoff. Another possible way is to derive the disagreement point value as an effective and rational threat to ensure the establishment of an agreement. The third possibility is to set the disagreement point as the focal equilibrium of the game.
+Nash proposed four possible axioms that should be possessed by the bargaining game solution [<span id='cite-44'></span><span id='cite-45'></span>58,59]:
-Nash proposed four possible axioms that should be possessed by the solution function [<span id='cite-44'></span>44-<span id='cite-45'></span>45]:
 :* Pareto optimality
@@ Line 128: / Line 131: @@
 :* Independence of irrelevant alternatives (IIA)
-The first axiom states that the solution should be Pareto optimal, which means it should not be weakly dominated by any other point. If the notation <math display="inline">f\left( U,d\right) =</math><math>\left( {f}_{1}\left( U,d\right) ,\, {f}_{2}\left( U,d\right) \right) \,</math> stands for the Nash bargaining solution to the bargaining problem (<math display="inline">U,d</math>), then solution <math display="inline">{u}^{\ast }=</math><math>\left( {u}_{1}\left( {\boldsymbol{x}}^{\mathit{\boldsymbol{\ast }}}\right) ,{u}_{2}\left( {\boldsymbol{x}}^{\boldsymbol{\ast }}\right) \right)</math>  is weakly Pareto efficient if and only if there exists no other point  <math display="inline">{u}^{'}=</math><math>\left( {u}_{1}\left( {\boldsymbol{x}}^{\mathit{\boldsymbol{'}}}\right) ,\, {u}_{2}\left( {\boldsymbol{x}}^{\boldsymbol{'}}\right) \right) \in U</math> such that <math display="inline">{u}_{1}\left( {\boldsymbol{x}}^{\boldsymbol{'}}\right) >{u}_{1}\left( {\boldsymbol{x}}^{\boldsymbol{\ast }}\right) ;{u}_{2}\left( {\boldsymbol{x}}^{\mathit{\boldsymbol{'}}}\right) \geq {u}_{2}\left( {\boldsymbol{x}}^{\boldsymbol{\ast }}\right)</math>  or <math display="inline">{\, u}_{1}\left( {\boldsymbol{x}}^{\boldsymbol{'}}\right) \geq {u}_{1}\left( {\boldsymbol{x}}^{\boldsymbol{\ast }}\right) ;</math> <math display="inline">{u}_{2}\left( {\boldsymbol{x}}^{\boldsymbol{'}}\right) >{u}_{2}\left( {\boldsymbol{x}}^{\boldsymbol{\ast }}\right)</math>  This implies that there is no other alternative feasible allocation that is better than the solution for one player without worsening the other player’s payoff.
+The first axiom states that the solution should be Pareto optimal, which means it should not be dominated by any other point. If the notation <math display="inline">f\left( U,d\right) =\left( {f}_{1}\left( U,d\right) ,\, {f}_{2}\left( U,d\right) \right) \,</math> stands for the Nash bargaining solution to the bargaining problem <math display="inline">(U,d)</math>, then the solution <math display="inline">{u}^{\ast }=</math><math>\left( {u}_{1}\left( {{\boldsymbol{\text{x}}}}^{\mathit{\boldsymbol{\ast }}}\right) ,{u}_{2}\left( {{\boldsymbol{\text{x}}}}^{\boldsymbol{\ast }}\right) \right)</math>  can be Pareto efficient if and only if there exists no other point <math display="inline">{u}^{'}=</math><math>\left( {u}_{1}\left( {{\boldsymbol{\text{x}}}}^{\mathit{\boldsymbol{'}}}\right) ,\, {u}_{2}\left( {{\boldsymbol{\text{x}}}}^{\boldsymbol{'}}\right) \right) \in U</math> such that <math display="inline">{u}_{1}\left( {{\boldsymbol{\text{x}}}}^{\boldsymbol{'}}\right) >{u}_{1}\left( {{\boldsymbol{\text{x}}}}^{\boldsymbol{\ast }}\right) ;{u}_{2}\left( {{\boldsymbol{\text{x}}}}^{\mathit{\boldsymbol{'}}}\right) \geq {u}_{2}\left( {{\boldsymbol{\text{x}}}}^{\boldsymbol{\ast }}\right)</math>  or <math display="inline">{\, u}_{1}\left( {{\boldsymbol{\text{x}}}}^{\boldsymbol{'}}\right) \geq {u}_{1}\left( {{\boldsymbol{\text{x}}}}^{\boldsymbol{\ast }}\right) ;</math> <math display="inline">{u}_{2}\left( {{\boldsymbol{\text{x}}}}^{\boldsymbol{'}}\right) >{u}_{2}\left( {{\boldsymbol{\text{x}}}}^{\boldsymbol{\ast }}\right)</math>. This implies that there is no alternative feasible solution that is better for one player without worsening the payoff for other players.
-The second axiom, IEUR also referred to as scale covariance, states that the solution should be independent of positive affine transformations of utilities. For example, for any numbers <math display="inline">\, {\alpha }_{1},\, {\alpha }_{2},\, \, {\beta }_{1},\, \, {\beta }_{2}\, </math> where <math> {\alpha }_{1}>0,{\alpha }_{2}>0</math>, if we have <math>U</math> as the feasible area, <math>d</math> as the disagreement point, and <math>f(U,d)</math> as the solution, with the transformation given below:<span id="OLE_LINK8"></span><span id="OLE_LINK9"></span>
+The second axiom, IEUR also referred to as scale covariance, states that the solution should be independent of positive affine transformations of utilities.In other words, if a new bargaining game <math display="inline">(G,w)</math> exists, where <math>G=\left\{ {\alpha }_{1}{u}_{1}({\boldsymbol{\text{x}}})+ {\beta }_{1},{\alpha }_{2}{u}_{2}({\boldsymbol{\text{x}}})+{\beta }_{2}\right\}</math> and  <math>w=\left({\alpha }_{1}{d}_{1}+{\beta }_{1},{\alpha }_{2}{d}_{2}+{\beta }_{2}\right)\,</math> and where <math>\left({u}_{1}({\boldsymbol{\text{x}}}),{u}_{2}({\boldsymbol{\text{x}}})\right)\in U</math> and <math> {\alpha }_{1}>0,{\alpha }_{2}>0</math>, then the solution for this new bargaining game (i.e., <math display="inline">f(G,w)</math>) can be obtained by applying the same transformations, which is demonstrated by Eq.(5) and [[#img-1|Figure 1]]:
-{| class="formulaSCP" style="width: 100%; text-align: center;"
-|
+{| class="formulaSCP" style="width: 100%; text-align: left;"
-|<math>\, \, G=\lbrace \left( {\alpha }_{1}{u}_{1}(\boldsymbol{x})+\right.\left. {\beta }_{1},{\alpha }_{2}{u}_{2}(\boldsymbol{x})+{\beta }_{2}\, :\left( {u}_{1},{u}_{2}\right) \in U\right\} </math>
-|（5）
 |-
-|and
+|
-| <math>w=({\alpha }_{1}{d}_{1}+{\beta }_{1},{\alpha }_{2}{d}_{2}+{\beta }_{2})\,</math>
+{| style="text-align: center; margin:auto;width: 100%;"
-|
+|-
+| style="text-align: center;" |<math>\, \, f(G,\, w)=({\alpha }_{1}{f}_{1}(U,d)+{\beta }_{1},\, {\alpha }_{2}{f}_{2}(U,\, d)+{\beta }_{2})\,
+</math>
+|}
+| style="width: 5px;text-align: right;white-space: nowrap;" |(5)
 |}
-then the new solution <math display="inline">f(G,w)</math> should be
+<div id='img-1'></div>
+{| style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: auto;max-width: auto;"
+|-
+|style="padding:10px;"| [[File:Dail2.png|450px]]
+|- style="text-align: center; font-size: 75%;"
+| colspan="1" style="padding:10px;"| '''Figure 1'''. Explanation of IEUR axiom
+|}
-<div style="text-align: right; direction: ltr; margin-left: 1em;">
-{| class="formulaSCP" style="width: 100%; text-align: center;"
+The third axiom “symmetry” represents that the solutions should be symmetric when the bargaining positions of the two players are completely symmetric. This axiom can be explained as if there is no information that can be used to distinguish one player from the other, then the solutions should also be indistinguishable between players [46].
-|<math>\, \, f(G,\, w)=({\alpha }_{1}{f}_{1}(U,d)+{\beta }_{1},\, {\alpha }_{2}{f}_{2}(U,\, d)+{\beta }_{2})\,
-</math>
+As shown in [[#img-2|Figure 2]], the last axiom states that if <math display="inline">{U}_{1}\subset {U}_{2}</math> and <math display="inline">f({U}_{2},d)</math> is located within the feasible area <math display="inline">{U}_{1}</math>, then <math display="inline">f\left( {U}_{1,}d\right) =</math><math>f({U}_{2},d)</math> [59].
-|（6）
+<div id='img-2'></div>
+{| style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: auto;max-width: auto;"
+|-
+|style="padding:10px;"| [[File:Draft_Shin_691882792-image2.png|centre|374x374px|]]
+|- style="text-align: center; font-size: 75%;"
+| colspan="1" style="padding:10px;"| '''Figure 2'''. Explanation of IIA axiom
 |}
-</div>
-where'' '' <math display="inline">{\alpha }_{1}</math> and <math display="inline">{\alpha }_{2}</math> are positive numbers.
-[[File:Draft_Shin_691882792-image1.png|centre|294x294px]]
-<div class="center" style="width: auto; margin-left: auto; margin-right: auto;">
+The solution function introduced by Nash [46] that satisfies all the four axioms as identified before can be defined as follows:
-'''FIGURE 1'''   Explanation of IEUR axiom</div>
-As suggested by Figure 1, the solution to the new bargaining problem ''f'' (''G, w'') can be derived from ''f ''(''U, d'') by applying the same transformation.
+{| class="formulaSCP" style="width: 100%; text-align: center;"
+|-
+|
+{| style="text-align: center; margin:auto;"
+|-
+| <math display="inline">f\left( U,\, d\right) =Max\prod _{i=1,2}^{}({u}_{i}({\boldsymbol{\text{x}}})-{d}_{i})=</math><math>Max\, ({u}_{1}({\boldsymbol{\text{x}}})-{d}_{1})({u}_{2}({\boldsymbol{\text{x}}})-{d}_{2})</math>
+|}
+| style="width: 5px;text-align: right;white-space: nowrap;" | (6)
+|}
-The third axiom “symmetry” means, in a bargaining game, where the position of the two players is completely symmetric, the solution should also be symmetric. This means that if there is no information that can be used to distinguish one player from the other, the solution will also be indistinguishable between players,'' '' <math display="inline">{f}_{1}\left( U,d\right) =\ldots =</math><math>{f}_{n}\left( U,d\right)</math>  [42].
+where <math display="inline">{u}_{i}({\boldsymbol{\text{x}}})>{d}_{i},\, i=1,2</math>. Intuitively, this function is trying to find solutions that maximize each player’s difference in payoffs between the cooperative agreement point and the disagreement point. In simpler terms, Nash selects an agreement point <math display="inline">({u}_{1}\left( {{\boldsymbol{\text{x}}}}^{\ast }\right) ,{u}_{2}({{\boldsymbol{\text{x}}}}^{\ast }))</math> that maximizes the product of utility gains from the disagreement point <math display="inline">\, ({d}_{1},{d}_{2})</math>.
-The last axiom is the most contentious. It states that if <math display="inline">{U}_{1}\subset {U}_{2}</math>'' '' and'' '' <math display="inline">f({U}_{2},d)</math> is within the feasible area ( <math display="inline">{U}_{1}</math>), then <math display="inline">f\left( {U}_{1,}d\right) =</math><math>f({U}_{2},d)</math>. The concept is demonstrated in Figure 2.
+== 4. The proposed model ==
-<div class="center" style="width: auto; margin-left: auto; margin-right: auto;">
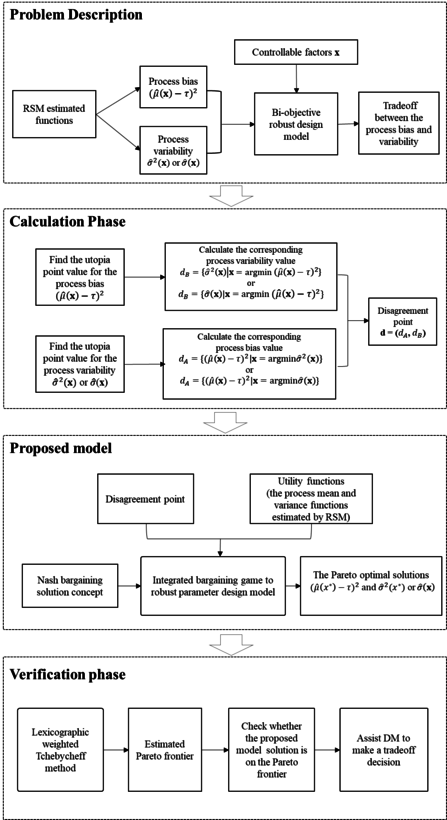
+The proposed method attempts to integrate bargaining game concepts into the tradeoff issue between the process bias and variability, so that not only the interaction between process bias and variability can be incorporated but also a unique optimal solution can be obtained. The detailed procedure includes problem description, calculation for response functions and disagreement points, bargaining game based RPD model, and verification can be illustrated in [[#img-3|Figure 3]]. As illustrated in [[#img-3|Figure 3]], the objective of the proposed method is to address the tradeoff between process bias and variability. In the calculation phase, a utopia point can be calculated based on separately estimated functions for the process bias and variability. However, this utopia point is in an infeasible region, which means that a simultaneous minimization of the process bias and variability is unachievable. The disagreement point is calculated by first, optimizing only one of the objective functions (i.e., the estimated process variability or the process bias function) and obtaining a solution set, and second, inserting the obtained solution set into the other objective function to generate a corresponding value. In the proposed model, based on the obtained disagreement point, the Nash bargaining solution concept is applied to solve the bargaining game. While in the verification phase, the lexicographic weighted tchebycheff is applied to generate the associated Pareto frontier, so that the obtained game solution can be compared with other efficient solutions.
- [[Image:Draft_Shin_691882792-image2.png|308x308px]] </div>
-<div class="center" style="width: auto; margin-left: auto; margin-right: auto;">
+<div id='img-3'></div>
-'''FIGURE 2 '''Explanation of IIA axiom</div>
+{| style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: auto;max-width: auto;"
+|-
+|style="padding:10px;"|  [[File:New2.png|centre|820x820px|]]
+|- style="text-align: center; font-size: 75%;"
+| colspan="1" style="padding:10px;"| '''Figure 3'''. The proposed procedure by integrating of bargaining game into RPD
+|}
-To be more specific, the axiom asserts that an increase or decrease in the number of irrelevant alternative options should not affect the final solution [43].
-Nash [39] introduced a solution function that satisfies all four of the axioms stated above, which has been proven by many researchers:
+An integration of the Nash bargaining game model involves three steps. First step, the two players and their corresponding utility function should be defined. The process bias can be defined as player A, and variability can be regarded as player B. The RSM-based estimated functions of both responses will be regarded as the players’ utility functions in this bargaining game (i.e., <math display="inline">u_{A}({\boldsymbol{\text{x}}})</math> and <math display="inline"> u_{B}({\boldsymbol{\text{x}}})</math>) where <math>{\boldsymbol{\text{x}}}</math> stands for a vector of controllable factors. Then, the goal of each player is to choose a set of controllable factors while minimizing each individual utility function. Second step, a disagreement point can be determined by applying a minimax-value theory as identified in Equation 7. Based on the tradeoff between the process bias and variability, the modified disagreement point functions can be defined as follows:
 {| class="formulaSCP" style="width: 100%; text-align: center;"
@@ Line 179: / Line 203: @@
 {| style="text-align: center; margin:auto;"
 |-
-| <math display="inline">f\left( U,\, d\right) =Max\prod _{i=1,2}^{}({u}_{i}(\boldsymbol{x})-{d}_{i})=</math><math>Max\, ({u}_{1}(\boldsymbol{x})-{d}_{2})({u}_{2}(\boldsymbol{x})-{d}_{2})</math>
+| <math>{d}_{A}=\mathrm{max}\,\mathrm{min}\,{u}_{A}({\boldsymbol{\text{x}}})\,\quad \mbox{and}\,\quad {d}_{B}=\mathrm{max}\,\mathrm{min}\,{u}_{B}({\boldsymbol{\text{x}}})</math>
 |}
 | style="width: 5px;text-align: right;white-space: nowrap;" | (7)
 |}
+In this way, both player A (i.e., the process bias) and player B (i.e., the process variability) are guaranteed to receive the worst acceptable payoffs. In that case, the disagreement point, defined as the maximum minimum utility value, can be calculated by minimizing only one objective (process variability or bias). The computational functions for the disagreement point values can be formulated as:
-where <math display="inline">{u}_{i}(\boldsymbol{x})>{d}_{i},\, i=1,2</math>. The maximization problem has a unique solution. Intuitively, this function is trying to find a solution that maximizes each player’s difference in payoff between the cooperative agreement point and the disagreement point. In simpler terms, Nash selects a pair value of ( <math display="inline">{u}_{1}\left( \boldsymbol{x}\right) ,{u}_{2}(\boldsymbol{x}))</math> that maximizes the product of utility gains from'' d''. The larger the distance between the agreement point ( <math display="inline">{u}_{1}\left( {\boldsymbol{x}}^{\ast }\right) ,{u}_{2}({\boldsymbol{x}}^{\ast }))</math> and the disagreement point <math display="inline">\, ({d}_{1},{d}_{2})</math>, the more motivated the players will be to reach the agreement.
-. Proposed model
-The proposed model tries to integrate a bargaining game concept into the trade-off between process bias and variance, so that we can not only incorporate the interaction between process bias and variance but also obtain a unique answer to help the DM make a final decision.
-An application of the bargaining game model involves several steps, first, the two players and their corresponding utility function should be defined. The process bias can be defined as player A, and variance can be regarded as player B. The response surface method estimated function of each response will be treated as the player’s utility function: <math display="inline">{\, u}_{A}\left( \boldsymbol{x}\right) \,</math> and <math display="inline">{\, u}_{B}\left( \boldsymbol{x}\right)</math>  where <math>\boldsymbol{x}</math> stands for a vector of control factors. The strategy is to choose the control factors’value to minimize the individual objective function. Second, the disagreement point payoff has to be defined. Recall that the disagreement point <math display="inline">d=</math><math>({d}_{A},\, {d}_{B})\,</math> is the payoff that each player will get if they cannot reach an agreement. Generally, the disagreement point is determined by applying the minimax-value theory. However, given the trade-off between the process bias and variance, the objective is minimization instead of utility maximization, so with some modification, we have
 {| class="formulaSCP" style="width: 100%; text-align: center;"
@@ Line 198: / Line 215: @@
 {| style="text-align: center; margin:auto;"
 |-
-| <math display="inline">{d}_{A}=\mathrm{max}\,\mathrm{min}\,{u}_{A}(\boldsymbol{x})</math>
+| <math>\left\{ {d}_{A}={u}_{A}({\boldsymbol{\text{x}}})|{\boldsymbol{\text{x}}}=\arg\min{u}_{B}({\boldsymbol{\text{x}}})\qquad \mbox{and}\qquad {\boldsymbol{\text{x}}}\in X\right\} </math>
 |}
 | style="width: 5px;text-align: right;white-space: nowrap;" | (8)
 |}
 and
@@ Line 211: / Line 227: @@
 {| style="text-align: center; margin:auto;"
 |-
-| <math display="inline">{d}_{B}=\mathrm{max}\,\mathrm{min}\,{u}_{B}(\boldsymbol{x})</math>
+| <math>\left\{ {d}_{B}={u}_{B}({\boldsymbol{\text{x}}})|{\boldsymbol{\text{x}}}=\arg\min{u}_{A}({\boldsymbol{\text{x}}})\qquad \mbox{and}\qquad{\boldsymbol{\text{x}}}\in X\right\} </math>
 |}
 | style="width: 5px;text-align: right;white-space: nowrap;" | (9)
 |}
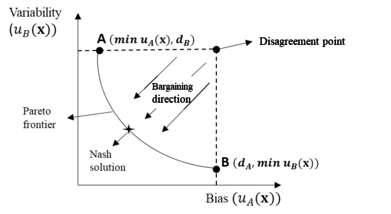
+Thus, the idea of the proposed method to find the optimal solutions is to continuously perform bargaining games from the specified disagreement point <math display="inline">({d}_{A} ,\, {d}_{B})</math> to Pareto frontier as illustrated in [[#img-4|Figure 4]]. To be more specific, as demonstrated in [[#img-4|Figure 4]], if the convex curve represents all Pareto optimal solutions, then each point on the curve can be regarded as a minimum utility value for one of the two process parameters (i.e., the process variability or bias). For example, at point A, when the process bias is minimized within the feasible area, the corresponding variability value is the minimum utility value for the process variability, since other utility values would be either dominated or infeasible. These solutions may provide useful insight for a DM when the relative importance between process bias and variability is difficult to identify.
-<span id='OLE_LINK15'></span>In this way, both the process variance and bias can guarantee the worst acceptable payoff. For example, process bias can take various values when variance is kept constant (e.g. <math display="inline">{\tilde{u}}_{B}(\boldsymbol{x})</math>) because multiple solution sets can result in the same variance value with different bias values. However, the process bias will choose the solution set that gives the smallest bias value, which is defined as the best response. Among the best responses for different situations, bias chooses the maximum as the disagreement point so that even if the agreement breaks down, the selected disagreement point is guaranteed.  As demonstrated by Figure 3, the convex curve represents all of the Pareto optimal solutions. Each point on the curve can be understood as the best response for bias when variance chooses a specific value, and vice versa. For example, when the process bias takes the minimum value at point A, the best response for variance is the corresponding variance value, since other variance values would be either dominated or infeasible. In that case, the disagreement point can be calculated by minimizing only one object (process variance or bias). When the process bias is minimized, a corresponding variance value can be calculated, and vice versa. These calculated values are treated as the disagreement point payoff. In mathematical form, this is:
+<div id='img-4'></div>
+{| style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: auto;max-width: auto;"
+|-
+|style="padding:10px;"|  [[File:New.png|centre|391x391px|]]
+|- style="text-align: center; font-size: 75%;"
+| colspan="1" style="padding:10px;"| '''Figure 4'''. Solution concepts for the proposed bargaining game based RPD method<br> by integrating trafeoff between both process bias and variability
+|}
+In the final step, the Nash bargaining solution function <math display="inline">Max\left( {u}_{A}({\boldsymbol{\text{x}}})- {d}_{A}\right) \left( {u}_{B}({\boldsymbol{\text{x}}})-{d}_{B}\right)</math> is utilized. In an RPD problem, the objective of this problem is to minimize both process bias and variability, so a constraint of <math display="inline">{u}_{i}({\boldsymbol{\text{x}}})</math>< <math display="inline">{d}_{i},\, i=</math><math>A,B</math> is applied. After the players, utility functions and the disagreement point are identified, the Nash bargaining solution function is applied as below:
 {| class="formulaSCP" style="width: 100%; text-align: center;"
@@ Line 224: / Line 250: @@
 {| style="text-align: center; margin:auto;"
 |-
-| <math display="inline">\left\{ {d}_{A}={u}_{A}(\boldsymbol{x})\right\} </math>
+|<math>\max </math>
+| <math display="inline"> \left( {u}_{A}({\boldsymbol{\text{x}}})-{d}_{A}\right) \left( {u}_{B}({\boldsymbol{\text{x}}})-\right.\left. {d}_{B}\right) </math>
+|-
+|<math>s.t. </math>
+|<math>{u}_{A}({\boldsymbol{\text{x}}})\leq {d}_{A},{u}_{B}({\boldsymbol{\text{x}}})\leq {d}_{B}, \qquad \mbox{and} \qquad {\boldsymbol{\text{x}}}\in \,X</math>
 |}
 | style="width: 5px;text-align: right;white-space: nowrap;" | (10)
 |}
+where
-and
+{| style="text-align: center; margin:auto;"
+|-
+|<math>u_A({\boldsymbol{\text{x}}})=\bigl(\widehat{\mu}({\boldsymbol{\text{x}}})-\tau\bigr)^2,\,u_B({\boldsymbol{\text{x}}})=\hat{\sigma}^2({\boldsymbol{\text{x}}})\,or\,\hat{\sigma}({\boldsymbol{\text{x}}})</math>
+|-
+|<math>\hat{\mu}({\boldsymbol{\text{x}}})=\alpha_0+{\boldsymbol{\text{x}}}^T\boldsymbol{\alpha_1}+{\boldsymbol{\text{x}}}^T\boldsymbol{\Gamma}{\boldsymbol{\text{x}}},\quad \mbox{and}\quad \hat{\sigma}^2({\boldsymbol{\text{x}}})=\beta_0+{\boldsymbol{\text{x}}}^T\boldsymbol{\beta_1}+{\boldsymbol{\text{x}}}^T\Delta{\boldsymbol{\text{x}}}</math>
+|-
+|<math>\hat{\sigma}({\boldsymbol{\text{x}}})=\gamma_0+{\boldsymbol{\text{x}}}^T\boldsymbol{\gamma_1}+{\boldsymbol{\text{x}}}^T\Epsilon{\boldsymbol{\text{x}}}</math>
+|}
+and, where
 {| class="formulaSCP" style="width: 100%; text-align: center;"
 |-
@@ Line 237: / Line 275: @@
 {| style="text-align: center; margin:auto;"
 |-
-| <math display="inline">\left\{ {d}_{B}={u}_{B}(\boldsymbol{x})\, \right\} </math>
+| <math display="inline">{\boldsymbol{\text{x}}}=\left[ \, \begin{matrix}{x}_{1}\\{x}_{2}\\\, \begin{matrix}\vdots \\{x}_{n-1}\\{x}_{n}\end{matrix}\end{matrix}\right], \,{\mathit{\boldsymbol{\alpha }}}_{\mathit{\boldsymbol{1}}}=\left[ \, \begin{matrix}{\hat{\alpha }}_{1}\\{\hat{\alpha }}_{2}\\\, \begin{matrix}\vdots \\{\hat{\alpha }}_{n-1}\\{\hat{\alpha }}_{n}\end{matrix}\end{matrix}\right],\,{\mathit{\boldsymbol{\beta }}}_{\mathit{\boldsymbol{1}}}=\, \left[ \begin{matrix}{\hat{\beta }}_{1}\\\begin{matrix}{\hat{\beta }}_{2}\\\vdots \end{matrix}\\\begin{matrix}{\hat{\beta }}_{n-1}\\{\hat{\beta }}_{n}\end{matrix}\end{matrix}\right], \,{\mathit{\boldsymbol{\gamma }}}_{\mathit{\boldsymbol{1}}}=\, \left[ \begin{matrix}{\hat{\gamma }}_{1}\\\begin{matrix}{\hat{\gamma }}_{2}\\\vdots \end{matrix}\\\begin{matrix}{\hat{\gamma }}_{n-1}\\{\hat{\gamma }}_{n}\end{matrix}\end{matrix}\right],\quad \mbox{and}\quad \boldsymbol{\Gamma}=\, \left[ \begin{matrix}\begin{matrix}{\hat{\alpha }}_{11}&{\hat{\alpha }}_{12}/2\\{\hat{\alpha }}_{12}/2&{\hat{\alpha }}_{22}\end{matrix}&\cdots &\begin{matrix}{\hat{\alpha }}_{1n}/2\\{\hat{\alpha }}_{2n}/2\end{matrix}\\\vdots &\ddots &\vdots \\\begin{matrix}{\hat{\alpha }}_{1n}/2&{\hat{\alpha }}_{2n}/2\end{matrix}&\cdots &{\hat{\alpha }}_{nn}\end{matrix}\right] </math>
 |}
-| style="width: 5px;text-align: right;white-space: nowrap;" | (11)
+|-
+|<math>\boldsymbol{\Delta}=\, \left[ \begin{matrix}\begin{matrix}{\hat{\beta }}_{11}&{\hat{\beta }}_{12}/2\\{\hat{\beta }}_{12}/2&{\hat{\beta }}_{22}\end{matrix}&\cdots &\begin{matrix}{\hat{\beta }}_{1n}/2\\{\hat{\beta }}_{2n}/2\end{matrix}\\\vdots &\ddots &\vdots \\\begin{matrix}{\hat{\beta }}_{1n}/2&{\hat{\beta }}_{2n}/2\end{matrix}&\cdots &{\hat{\beta }}_{nn}\end{matrix}\right],\quad \mbox{and}\quad\boldsymbol{\Epsilon}=\, \left[ \begin{matrix}\begin{matrix}{\hat{\gamma }}_{11}&{\hat{\gamma }}_{12}/2\\{\hat{\gamma }}_{12}/2&{\hat{\gamma }}_{22}\end{matrix}&\cdots &\begin{matrix}{\hat{\gamma }}_{1n}/2\\{\hat{\gamma}}_{2n}/2\end{matrix}\\\vdots &\ddots &\vdots \\\begin{matrix}{\hat{\gamma}}_{1n}/2&{\hat{\gamma }}_{2n}/2\end{matrix}&\cdots &{\hat{\gamma }}_{nn}\end{matrix}\right]</math>
 |}
+where <math>(d_A, d_B)</math>, <math>u_A({\boldsymbol{\text{x}}})</math>, <math>u_B({\boldsymbol{\text{x}}})</math>, <math>\hat{\mu}({\boldsymbol{\text{x}}})</math>, <math>\hat{\sigma}^2({\boldsymbol{\text{x}}})</math>, <math>\hat{\sigma}({\boldsymbol{\text{x}}})</math>, <math>\tau</math>, <math>X</math> and <math>\bf x</math> represent a disagreement point, utility functions for player A and B, an estimated process mean function, process variance function, and standard deviation function, the target value, the feasible area, the vector of controllable factors, respectively. In Eq.(10), <math>\boldsymbol{\alpha_1} </math>, <math>\boldsymbol{\beta_1} </math>, <math>\boldsymbol{\gamma_1} </math>, <math>\boldsymbol{\Gamma} </math>, <math>\boldsymbol{\Delta} </math>, and <math>\boldsymbol{\Epsilon} </math> denote vectors and matrixes of estimated regression coefficients for the process mean, variance, and standard deviation, respectively. Here, the constraint <math>u_i({\boldsymbol{\text{x}}})\leq d_i </math>, where <math>i=A,B </math>, ensures that the obtained agreement point payoffs will be at least as good as the disagreement point payoffs. Otherwise, there is no reason for players to participate in the negotiation.
-It is obvious that B ( <math display="inline">{d}_{A}\, ,\, {minu}_{B}(\boldsymbol{x})</math>) and A ( <math display="inline">min{u}_{A}(\boldsymbol{x}),\, {d}_{B})</math> are two Pareto optimal points. Thus, it is intuitively true that starting from the specified disagreement point, two players continue to bargain until an agreement is reached, this agreed solution point, marked as an asterisk, should be able to help the DM make a final decision.
-<div class="center" style="width: auto; margin-left: auto; margin-right: auto;">
- [[Image:Draft_Shin_691882792-image3.png|407x407px]] </div>
-<div class="center" style="width: auto; margin-left: auto; margin-right: auto;">
-'''FIGURE 3 '''Integration of the bargaining game into the trade-off problem between process bias and variance
-</div>
-Finally, the Nash bargaining solution function <math display="inline">Max\left( {u}_{A}(\boldsymbol{x})-\right. </math><math>\left. {d}_{A}\right) \left( {u}_{B}(\boldsymbol{x})-{d}_{B}\right)</math>  is used. In an RPD situation, the objective is to minimize both process bias and variance, so instead of the original constraint <math display="inline">{u}_{i}(\boldsymbol{x})</math>> <math display="inline">{d}_{i},\, i=</math><math>A,B</math>, a new constraint <math display="inline">{u}_{i}(\boldsymbol{x})</math>< <math display="inline">{d}_{i},\, i=</math><math>A,B</math> is assumed. Applying the Nash bargaining solution function gives:
-<div style="text-align: right; direction: ltr; margin-left: 1em;">
-<math display="inline">max\, \, \, \, \left( {u}_{A}(\boldsymbol{x})-{d}_{A}\right) \left( {u}_{B}(\boldsymbol{x})-\right. </math><math>\left. {d}_{B}\right)</math>                                         （12）</div>
-''s.t.        '' <math display="inline">{u}_{A}(\boldsymbol{x})\leq {d}_{A}</math>''                                                                ''（13）
-''   '' <math display="inline">{\quad u}_{B}(\boldsymbol{x})\leq {d}_{B}</math>
-'''                      ''' <math display="inline">\boldsymbol{x}\in \,</math> ''X''
-where                                                   <math display="inline">{u}_{A}\left( \boldsymbol{x}\right) =</math><math>{\left( \hat{\mu }(\boldsymbol{x})-\tau \right) }^{2}</math>
-and                                              <math display="inline">{u}_{B}\left( \boldsymbol{x}\right) =</math><math>{\hat{\sigma }}^{2}(\boldsymbol{x})</math>
-where <math display="inline">\, {d=(d}_{A},{d}_{B})</math> represents the disagreement point which specifies each player’s payoff when no agreement is reached (defined in Equations 10 and 11). <math display="inline">\hat{\mu }\left( \boldsymbol{x}\right)</math>  and <math display="inline">{\hat{\sigma }}^{2}\left( \boldsymbol{x}\right)</math>  are the mean and variance RSM estimated functions (shown in Equation 14 and 15), respectively. <math display="inline">\tau</math>  represents the target value
-<div style="text-align: right; direction: ltr; margin-left: 1em;">
-<math display="inline">\hat{\mu }\left( \boldsymbol{x}\right) \mathit{\boldsymbol{=\, }}{\alpha }_{0}\mathit{\boldsymbol{+\, }}{\boldsymbol{x}}^{T}{\boldsymbol{\alpha }}_{\boldsymbol{1}}\mathit{\boldsymbol{+\, }}{\boldsymbol{x}}^{T}\boldsymbol{A\, x}</math>'''                         '''（14）</div>
-where
-<div class="center" style="width: auto; margin-left: auto; margin-right: auto;">
-<math display="inline">\boldsymbol{x}=\left[ \, \begin{matrix}{x}_{1}\\{x}_{2}\\\, \begin{matrix}\vdots \\{x}_{n-1}\\{x}_{n}\end{matrix}\end{matrix}\right]</math>  , <math display="inline">{\mathit{\boldsymbol{\alpha }}}_{\mathit{\boldsymbol{1}}}=</math><math>\left[ \, \begin{matrix}{\hat{\alpha }}_{1}\\{\hat{\alpha }}_{2}\\\, \begin{matrix}\vdots \\{\hat{\alpha }}_{n-1}\\{\hat{\alpha }}_{n}\end{matrix}\end{matrix}\right]</math> , and <math display="inline">\boldsymbol{A}=</math><math>\, \left[ \begin{matrix}\begin{matrix}{\hat{\alpha }}_{11}&{\hat{\alpha }}_{12}/2\\{\hat{\alpha }}_{12}/2&{\hat{\alpha }}_{22}\end{matrix}&\cdots &\begin{matrix}{\hat{\alpha }}_{1n}/2\\{\hat{\alpha }}_{2k}/2\end{matrix}\\\vdots &\ddots &\vdots \\\begin{matrix}{\hat{\alpha }}_{1n}/2&{\hat{\alpha }}_{2n}/2\end{matrix}&\cdots &{\hat{\alpha }}_{nn}\end{matrix}\right]</math> </div>
-<div style="text-align: right; direction: ltr; margin-left: 1em;">
-and                                     <math display="inline">{\hat{\sigma }}^{2}\left( \boldsymbol{x}\right) \mathit{\boldsymbol{=\, }}{\beta }_{0}\mathit{\boldsymbol{+\, }}{{\boldsymbol{x}}^{\mathit{\boldsymbol{T}}}\mathit{\boldsymbol{\beta }}}_{\mathit{\boldsymbol{1}}}\mathit{\boldsymbol{+\, }}{\boldsymbol{x}}^{\mathit{\boldsymbol{T}}}\boldsymbol{Bx}</math>                            （15）</div>
-where
-<div class="center" style="width: auto; margin-left: auto; margin-right: auto;">
-<math display="inline">\, \boldsymbol{x}=\left[ \, \begin{matrix}{x}_{1}\\{x}_{2}\\\, \begin{matrix}\vdots \\{x}_{n-1}\\{x}_{n}\end{matrix}\end{matrix}\right]</math>  , <math display="inline">{\mathit{\boldsymbol{\beta }}}_{\mathit{\boldsymbol{1}}}=</math><math>\, \left[ \begin{matrix}{\hat{\beta }}_{1}\\\begin{matrix}{\hat{\beta }}_{2}\\\vdots \end{matrix}\\\begin{matrix}{\hat{\beta }}_{n-1}\\{\hat{\beta }}_{n}\end{matrix}\end{matrix}\right]</math> , and <math display="inline">\boldsymbol{B}=</math><math>\, \left[ \begin{matrix}\begin{matrix}{\hat{\beta }}_{11}&{\hat{\beta }}_{12}/2\\{\hat{\beta }}_{12}/2&{\hat{\beta }}_{22}\end{matrix}&\cdots &\begin{matrix}{\hat{\beta }}_{1n}/2\\{\hat{\beta }}_{2n}/2\end{matrix}\\\vdots &\ddots &\vdots \\\begin{matrix}{\hat{\beta }}_{1n}/2&{\hat{\beta }}_{2n}/2\end{matrix}&\cdots &{\hat{\beta }}_{nn}\end{matrix}\right]</math> </div>
-Here, the constraint of <math display="inline">{u}_{i}(\boldsymbol{x})</math>≤ <math display="inline">{d}_{i},\, \, i=</math><math>A,B</math> ensures that the approaching agreement point payoff will be at least as good as the disagreement point payoff. Otherwise, there is no reason for the negotiation. The integrated process is summarized in Figure 4.
-<div class="center" style="width: auto; margin-left: auto; margin-right: auto;">
- [[Image:Draft_Shin_691882792-image4.png|600px]] </div>
-<div class="center" style="width: auto; margin-left: auto; margin-right: auto;">
-'''FIGURE 4:''' Illustration of the integration of bargaining game into RPD</div>
 == 5.  Numerical illustrations and sensitivity analysis ==
@@ Line 298: / Line 287: @@
 ===5.1 Numerical example 1===
-<span id='_Hlk60583940'></span>Two numerical examples are conducted to study the efficiency of our proposed method. Example 1 investigates the relationship between the coating thickness of bare silicon wafers (''y'') and three controller variables, mould temperature <math display="inline">({x}_{1})</math>, injection flow rate <math display="inline">({x}_{2})</math>, and cooling rate <math display="inline">{(x}_{3})</math>. This example was also discussed by Shin and Cho.<span id='cite-46'></span>[[#46|46]]  A central composite design with <math display="inline">{2}^{3}\,</math> factorial design points and three replications was conducted, and details of the experimental data with coded value are shown in Table 1:
+<span id='_Hlk60583940'></span>
+Two numerical examples are conducted to demonstrate the efficiency of the proposed method. As explained in section 3.1, the process variability can be measured in terms of both the estimated standard deviation and variance functions, but the optimal solutions can be different if different response surface expressions are used. Therefore, the equations estimated in the original example were utilized for better comparison. Example 1 investigates the relationship between the coating thickness of bare silicon wafers (<math>y </math>) and three controller variables: mould temperature <math display="inline">({x}_{1})</math>, injection flow rate <math display="inline">({x}_{2})</math>, and cooling rate <math display="inline">{(x}_{3})</math> [10]. A central composite design and three replications were conducted, and the detailed experimental data with coded values can be shown in [[#tab-1|Table 1]].
+<span id='cite-46'></span>
-<div class="center" style="width: auto; margin-left: auto; margin-right: auto;">
+<div class="center" style="width: auto; margin-left: auto; margin-right: auto;font-size: 75%;">
-'''TABLE 1 '''Data for numerical example 1</div>
+'''Table 1'''. Data for numerical example 1</div>
-{| style="width: 100%;margin: 1em auto 0.1em auto;border-collapse: collapse;"
+<div id='tab-1'></div>
+{| class="wikitable" style="margin: 1em auto 0.1em auto;border-collapse: collapse;font-size:85%;width:auto;"
+|-style="text-align:center"
+! Experiments number !! <math>x_1</math> !! <math>x_2</math> !! <math>x_3</math> !! <math>y_1</math> !! <math>y_2</math> !!<math>y_3</math> !! <math>y_4</math> !! <math>\overline{\mathit{y}}</math> !! <math>\mathit{\sigma }</math>
 |-
-|  style="border-top: 1pt solid black;border-bottom: 1pt solid black;text-align: center;vertical-align: top;"|'''Experiments'''
+| style="text-align: center;vertical-align: top;" |1
+| style="text-align: center;" |-1
-'''number'''
+| style="text-align: center;" |-1
-|  style="border-top: 1pt solid black;border-bottom: 1pt solid black;text-align: center;"|<math>{\boldsymbol{x}}_{\mathit{\boldsymbol{1}}}</math>
+| style="text-align: center;" |-1
-|  style="border-top: 1pt solid black;border-bottom: 1pt solid black;text-align: center;"|<math>{\boldsymbol{x}}_{\mathit{\boldsymbol{2}}}</math>
+| style="text-align: center;" |76.30
-|  style="border-top: 1pt solid black;border-bottom: 1pt solid black;text-align: center;"|<math>{\boldsymbol{x}}_{\mathit{\boldsymbol{3}}}</math>
+| style="text-align: center;" |80.50
-|  style="border-top: 1pt solid black;border-bottom: 1pt solid black;text-align: center;"|<math>{\boldsymbol{y}}_{\mathit{\boldsymbol{1}}}</math>
+| style="text-align: center;" |77.70
-|  style="border-top: 1pt solid black;border-bottom: 1pt solid black;text-align: center;"|<math>{\boldsymbol{y}}_{\mathit{\boldsymbol{2}}}</math>
+| style="text-align: center;" |81.10
-|  style="border-top: 1pt solid black;border-bottom: 1pt solid black;text-align: center;"|<math>{\boldsymbol{y}}_{\mathit{\boldsymbol{3}}}</math>
+| style="text-align: center;" |78.90
-|  style="border-top: 1pt solid black;border-bottom: 1pt solid black;text-align: center;"|<math>{\boldsymbol{y}}_{\mathit{\boldsymbol{4}}}</math>
+| style="text-align: center;" |2.28
-|  style="border-top: 1pt solid black;border-bottom: 1pt solid black;text-align: center;"|<math>\overline{\mathit{\boldsymbol{y}}}</math>
-|  style="border-top: 1pt solid black;border-bottom: 1pt solid black;text-align: center;"|<math>\mathit{\boldsymbol{\sigma }}</math>
 |-
-|  style="border-top: 1pt solid black;text-align: center;vertical-align: top;"|1
+| style="text-align: center;vertical-align: top;" |2
-|  style="border-top: 1pt solid black;text-align: center;"|-1
+| style="text-align: center;" |1
-|  style="border-top: 1pt solid black;text-align: center;"|-1
+| style="text-align: center;" |-1
-|  style="border-top: 1pt solid black;text-align: center;"|-1
+| style="text-align: center;" |-1
-|  style="border-top: 1pt solid black;text-align: center;"|76.30
+| style="text-align: center;" |79.10
-|  style="border-top: 1pt solid black;text-align: center;"|80.50
+| style="text-align: center;" |81.20
-|  style="border-top: 1pt solid black;text-align: center;"|77.70
+| style="text-align: center;" |78.80
-|  style="border-top: 1pt solid black;text-align: center;"|81.10
+| style="text-align: center;" |79.60
-|  style="border-top: 1pt solid black;text-align: center;"|78.90
+| style="text-align: center;" |79.68
-|  style="border-top: 1pt solid black;text-align: center;"|2.28
+| style="text-align: center;" |1.07
 |-
-|  style="text-align: center;vertical-align: top;"|2
+| style="text-align: center;vertical-align: top;" |3
-|  style="text-align: center;"|1
+| style="text-align: center;" |-1
-|  style="text-align: center;"|-1
+| style="text-align: center;" |1
-|  style="text-align: center;"|-1
+| style="text-align: center;" |-1
-|  style="text-align: center;"|79.10
+| style="text-align: center;" |82.50
-|  style="text-align: center;"|81.20
+| style="text-align: center;" |81.50
-|  style="text-align: center;"|78.80
+| style="text-align: center;" |79.50
-|  style="text-align: center;"|79.60
+| style="text-align: center;" |80.90
-|  style="text-align: center;"|79.68
+| style="text-align: center;" |81.10
-|  style="text-align: center;"|1.07
+| style="text-align: center;" |1.25
 |-
-|  style="text-align: center;vertical-align: top;"|3
+| style="text-align: center;vertical-align: top;" |4
-|  style="text-align: center;"|-1
+| style="text-align: center;" |1
-|  style="text-align: center;"|1
+| style="text-align: center;" |1
-|  style="text-align: center;"|-1
+| style="text-align: center;" |-1
-|  style="text-align: center;"|82.50
+| style="text-align: center;" |72.30
-|  style="text-align: center;"|81.50
+| style="text-align: center;" |74.30
-|  style="text-align: center;"|79.50
+| style="text-align: center;" |75.70
-|  style="text-align: center;"|80.90
+| style="text-align: center;" |72.70
-|  style="text-align: center;"|81.10
+| style="text-align: center;" |73.75
-|  style="text-align: center;"|1.25
+| style="text-align: center;" |1.56
 |-
-|  style="text-align: center;vertical-align: top;"|4
+| style="text-align: center;vertical-align: top;" |5
-|  style="text-align: center;"|1
+| style="text-align: center;" |-1
-|  style="text-align: center;"|1
+| style="text-align: center;" |-1
-|  style="text-align: center;"|-1
+| style="text-align: center;" |1
-|  style="text-align: center;"|72.30
+| style="text-align: center;" |70.60
-|  style="text-align: center;"|74.30
+| style="text-align: center;" |72.70
-|  style="text-align: center;"|75.70
+| style="text-align: center;" |69.90
-|  style="text-align: center;"|72.70
+| style="text-align: center;" |71.50
-|  style="text-align: center;"|73.75
+| style="text-align: center;" |71.18
-|  style="text-align: center;"|1.56
+| style="text-align: center;" |1.21
 |-
-|  style="text-align: center;vertical-align: top;"|5
+| style="text-align: center;vertical-align: top;" |6
-|  style="text-align: center;"|-1
+| style="text-align: center;" |1
-|  style="text-align: center;"|-1
+| style="text-align: center;" |-1
-|  style="text-align: center;"|1
+| style="text-align: center;" |1
-|  style="text-align: center;"|70.60
+| style="text-align: center;" |74.10
-|  style="text-align: center;"|72.70
+| style="text-align: center;" |77.90
-|  style="text-align: center;"|69.90
+| style="text-align: center;" |76.20
-|  style="text-align: center;"|71.50
+| style="text-align: center;" |77.10
-|  style="text-align: center;"|71.18
+| style="text-align: center;" |76.33
-|  style="text-align: center;"|1.21
+| style="text-align: center;" |1.64
 |-
-|  style="text-align: center;vertical-align: top;"|6
+| style="text-align: center;vertical-align: top;" |7
-|  style="text-align: center;"|1
+| style="text-align: center;" |-1
-|  style="text-align: center;"|-1
+| style="text-align: center;" |1
-|  style="text-align: center;"|1
+| style="text-align: center;" |1
-|  style="text-align: center;"|74.10
+| style="text-align: center;" |78.50
-|  style="text-align: center;"|77.90
+| style="text-align: center;" |80.00
-|  style="text-align: center;"|76.20
+| style="text-align: center;" |76.20
-|  style="text-align: center;"|77.10
+| style="text-align: center;" |75.30
-|  style="text-align: center;"|76.33
+| style="text-align: center;" |77.50
-|  style="text-align: center;"|1.64
+| style="text-align: center;" |2.14
 |-
-|  style="text-align: center;vertical-align: top;"|7
+| style="text-align: center;vertical-align: top;" |8
-|  style="text-align: center;"|-1
+| style="text-align: center;" |1
-|  style="text-align: center;"|1
+| style="text-align: center;" |1
-|  style="text-align: center;"|1
+| style="text-align: center;" |1
-|  style="text-align: center;"|78.50
+| style="text-align: center;" |84.90
-|  style="text-align: center;"|80.00
+| style="text-align: center;" |83.10
-|  style="text-align: center;"|76.20
+| style="text-align: center;" |83.90
-|  style="text-align: center;"|75.30
+| style="text-align: center;" |83.50
-|  style="text-align: center;"|77.50
+| style="text-align: center;" |83.85
-|  style="text-align: center;"|2.14
+| style="text-align: center;" |0.77
 |-
-|  style="text-align: center;vertical-align: top;"|8
+| style="text-align: center;vertical-align: top;" |9
-|  style="text-align: center;"|1
+| style="text-align: center;" |-1.682
-|  style="text-align: center;"|1
+| style="text-align: center;" |0
-|  style="text-align: center;"|1
+| style="text-align: center;" |0
-|  style="text-align: center;"|84.90
+| style="text-align: center;" |74.10
-|  style="text-align: center;"|83.10
+| style="text-align: center;" |71.80
-|  style="text-align: center;"|83.90
+| style="text-align: center;" |72.50
-|  style="text-align: center;"|83.50
+| style="text-align: center;" |71.90
-|  style="text-align: center;"|83.85
+| style="text-align: center;" |72.58
-|  style="text-align: center;"|0.77
+| style="text-align: center;" |1.06
 |-
-|  style="text-align: center;vertical-align: top;"|9
+| style="text-align: center;vertical-align: top;" |10
-|  style="text-align: center;"|-1.682
+| style="text-align: center;" |1.682
-|  style="text-align: center;"|0
+| style="text-align: center;" |0
-|  style="text-align: center;"|0
+| style="text-align: center;" |0
-|  style="text-align: center;"|74.10
+| style="text-align: center;" |76.40
-|  style="text-align: center;"|71.80
+| style="text-align: center;" |78.70
-|  style="text-align: center;"|72.50
+| style="text-align: center;" |79.20
-|  style="text-align: center;"|71.90
+| style="text-align: center;" |79.30
-|  style="text-align: center;"|72.58
+| style="text-align: center;" |78.40
-|  style="text-align: center;"|1.06
+| style="text-align: center;" |1.36
 |-
-|  style="text-align: center;vertical-align: top;"|10
+| style="text-align: center;vertical-align: top;" |11
-|  style="text-align: center;"|1.682
+| style="text-align: center;" |0
-|  style="text-align: center;"|0
+| style="text-align: center;" |-1.682
-|  style="text-align: center;"|0
+| style="text-align: center;" |0
-|  style="text-align: center;"|76.40
+| style="text-align: center;" |79.20
-|  style="text-align: center;"|78.70
+| style="text-align: center;" |80.70
-|  style="text-align: center;"|79.20
+| style="text-align: center;" |81.00
-|  style="text-align: center;"|79.30
+| style="text-align: center;" |82.30
-|  style="text-align: center;"|78.40
+| style="text-align: center;" |80.80
-|  style="text-align: center;"|1.36
+| style="text-align: center;" |1.27
 |-
-|  style="text-align: center;vertical-align: top;"|11
+| style="text-align: center;vertical-align: top;" |12
-|  style="text-align: center;"|0
+| style="text-align: center;" |0
-|  style="text-align: center;"|-1.682
+| style="text-align: center;" |1.682
-|  style="text-align: center;"|0
+| style="text-align: center;" |0
-|  style="text-align: center;"|79.20
+| style="text-align: center;" |77.90
-|  style="text-align: center;"|80.70
+| style="text-align: center;" |76.40
-|  style="text-align: center;"|81.00
+| style="text-align: center;" |76.90
-|  style="text-align: center;"|82.30
+| style="text-align: center;" |77.40
-|  style="text-align: center;"|80.80
+| style="text-align: center;" |77.15
-|  style="text-align: center;"|1.27
+| style="text-align: center;" |0.65
 |-
-|  style="text-align: center;vertical-align: top;"|12
+| style="text-align: center;vertical-align: top;" |13
-|  style="text-align: center;"|0
+| style="text-align: center;" |0
-|  style="text-align: center;"|1.682
+| style="text-align: center;" |0
-|  style="text-align: center;"|0
+| style="text-align: center;" |-1.682
-|  style="text-align: center;"|77.90
+| style="text-align: center;" |82.40
-|  style="text-align: center;"|76.40
+| style="text-align: center;" |82.70
-|  style="text-align: center;"|76.90
+| style="text-align: center;" |82.60
-|  style="text-align: center;"|77.40
+| style="text-align: center;" |83.10
-|  style="text-align: center;"|77.15
+| style="text-align: center;" |82.70
-|  style="text-align: center;"|0.65
+| style="text-align: center;" |0.29
 |-
-|  style="text-align: center;vertical-align: top;"|13
+| style="text-align: center;vertical-align: top;" |14
-|  style="text-align: center;"|0
+| style="text-align: center;" |0
-|  style="text-align: center;"|0
+| style="text-align: center;" |0
-|  style="text-align: center;"|-1.682
+| style="text-align: center;" |1.682
-|  style="text-align: center;"|82.40
+| style="text-align: center;" |79.70
-|  style="text-align: center;"|82.70
+| style="text-align: center;" |82.40
-|  style="text-align: center;"|82.60
+| style="text-align: center;" |81.00
-|  style="text-align: center;"|83.10
+| style="text-align: center;" |81.20
-|  style="text-align: center;"|82.70
+| style="text-align: center;" |81.08
-|  style="text-align: center;"|0.29
+| style="text-align: center;" |1.11
 |-
-|  style="text-align: center;vertical-align: top;"|14
+| style="text-align: center;vertical-align: top;" |15
-|  style="text-align: center;"|0
+| style="text-align: center;" |0
-|  style="text-align: center;"|0
+| style="text-align: center;" |0
-|  style="text-align: center;"|1.682
+| style="text-align: center;" |0
-|  style="text-align: center;"|79.70
+| style="text-align: center;" |70.40
-|  style="text-align: center;"|82.40
+| style="text-align: center;" |70.60
-|  style="text-align: center;"|81.00
+| style="text-align: center;" |70.80
-|  style="text-align: center;"|81.20
+| style="text-align: center;" |71.10
-|  style="text-align: center;"|81.08
+| style="text-align: center;" |70.73
-|  style="text-align: center;"|1.11
+| style="text-align: center;" |0.30
 |-
-|  style="text-align: center;vertical-align: top;"|15
+| style="text-align: center;vertical-align: top;" |16
-|  style="text-align: center;"|0
+| style="text-align: center;" |0
-|  style="text-align: center;"|0
+| style="text-align: center;" |0
-|  style="text-align: center;"|0
+| style="text-align: center;" |0
-|  style="text-align: center;"|70.40
+| style="text-align: center;" |70.90
-|  style="text-align: center;"|70.60
+| style="text-align: center;" |69.70
-|  style="text-align: center;"|70.80
+| style="text-align: center;" |69.00
-|  style="text-align: center;"|71.10
+| style="text-align: center;" |69.90
-|  style="text-align: center;"|70.73
+| style="text-align: center;" |69.88
-|  style="text-align: center;"|0.30
+| style="text-align: center;" |0.78
 |-
-|  style="text-align: center;vertical-align: top;"|16
+| style="text-align: center;vertical-align: top;" |17
-|  style="text-align: center;"|0
+| style="text-align: center;" |0
-|  style="text-align: center;"|0
+| style="text-align: center;" |0
-|  style="text-align: center;"|0
+| style="text-align: center;" |0
-|  style="text-align: center;"|70.90
+| style="text-align: center;" |70.70
-|  style="text-align: center;"|69.70
+| style="text-align: center;" |71.90
-|  style="text-align: center;"|69.00
+| style="text-align: center;" |71.70
-|  style="text-align: center;"|69.90
+| style="text-align: center;" |71.20
-|  style="text-align: center;"|69.88
+| style="text-align: center;" |71.38
-|  style="text-align: center;"|0.78
+| style="text-align: center;" |0.54
 |-
-|  style="text-align: center;vertical-align: top;"|17
+| style="text-align: center;vertical-align: top;" |18
-|  style="text-align: center;"|0
+| style="text-align: center;" |0
-|  style="text-align: center;"|0
+| style="text-align: center;" |0
-|  style="text-align: center;"|0
+| style="text-align: center;" |0
-|  style="text-align: center;"|70.70
+| style="text-align: center;" |70.20
-|  style="text-align: center;"|71.90
+| style="text-align: center;" |71.00
-|  style="text-align: center;"|71.70
+| style="text-align: center;" |71.50
-|  style="text-align: center;"|71.20
+| style="text-align: center;" |70.40
-|  style="text-align: center;"|71.38
+| style="text-align: center;" |70.78
-|  style="text-align: center;"|0.54
+| style="text-align: center;" |0.59
 |-
-|  style="text-align: center;vertical-align: top;"|18
+| style="text-align: center;vertical-align: top;" |19
-|  style="text-align: center;"|0
+| style="text-align: center;" |0
-|  style="text-align: center;"|0
+| style="text-align: center;" |0
-|  style="text-align: center;"|0
+| style="text-align: center;" |0
-|  style="text-align: center;"|70.20
+| style="text-align: center;" |71.50
-|  style="text-align: center;"|71.00
+| style="text-align: center;" |71.10
-|  style="text-align: center;"|71.50
+| style="text-align: center;" |71.20
-|  style="text-align: center;"|70.40
+| style="text-align: center;" |70.00
-|  style="text-align: center;"|70.78
+| style="text-align: center;" |70.95
-|  style="text-align: center;"|0.59
+| style="text-align: center;" |0.66
 |-
-|  style="text-align: center;vertical-align: top;"|19
+| style="text-align: center;vertical-align: top;" |20
-|  style="text-align: center;"|0
+| style="text-align: center;" |0
-|  style="text-align: center;"|0
+| style="text-align: center;" |0
-|  style="text-align: center;"|0
+| style="text-align: center;" |0
-|  style="text-align: center;"|71.50
+| style="text-align: center;" |71.00
-|  style="text-align: center;"|71.10
+| style="text-align: center;" |70.40
-|  style="text-align: center;"|71.20
+| style="text-align: center;" |70.90
-|  style="text-align: center;"|70.00
+| style="text-align: center;" |69.90
-|  style="text-align: center;"|70.95
+| style="text-align: center;" |70.55
-|  style="text-align: center;"|0.66
+| style="text-align: center;" |0.51
-|-
-|  style="border-bottom: 1pt solid black;text-align: center;vertical-align: top;"|20
-|  style="border-bottom: 1pt solid black;text-align: center;"|0
-|  style="border-bottom: 1pt solid black;text-align: center;"|0
-|  style="border-bottom: 1pt solid black;text-align: center;"|0
-|  style="border-bottom: 1pt solid black;text-align: center;"|71.00
-|  style="border-bottom: 1pt solid black;text-align: center;"|70.40
-|  style="border-bottom: 1pt solid black;text-align: center;"|70.90
-|  style="border-bottom: 1pt solid black;text-align: center;"|69.90
-|  style="border-bottom: 1pt solid black;text-align: center;"|70.55
-|  style="border-bottom: 1pt solid black;text-align: center;"|0.51
 |}
-The estimated response functions are:
+The fitted response functions for the process bias and standard deviation of the coating thickness are estimated by using  LSM through MINITABsoftware package as:
-<div style="text-align: right; direction: ltr; margin-left: 1em;">
+{| class="formulaSCP" style="width: 100%; text-align: center;"
-<math display="inline">{\left( \mu \left( \boldsymbol{x}\right) -\tau \right) }^{2}=</math><math>{\left( 72.21+0.59{x}_{1}-0.35{x}_{2}-0.01{x}_{3}+0.28{{x}_{1}}^{2}+1.29{{x}_{2}}^{2}+1.85{{x}_{3}}^{2}+0.09{x}_{1}{x}_{2}+1.66{x}_{1}{x}_{3}+1.51{x}_{2}{x}_{3}-71.14\right) }^{2}</math>                                 （16）</div>
+|-
+|
+{| style="text-align: center; margin:auto;"
+|-
+| <math>\hat{\mu }\left({\bf x}\right) =\,72.21 +\, {\bf x}^{T} \boldsymbol{\alpha }_{1}+{\bf x}^{T}\boldsymbol{\Gamma} {\bf x}</math>
+|}
+| style="width: 5px;text-align: right;white-space: nowrap;" | (11)
+|}
-<math display="inline">\begin{matrix}\sigma \left( \boldsymbol{x}\right) =2.55+0.38{x}_{1}-0.43{x}_{2}+0.56{x}_{3}+0.49{{x}_{1}}^{2}+0.61{{x}_{2}}^{2}+0.85{{x}_{3}}^{2}\\-0.47{x}_{1}{x}_{2}+0.72{x}_{1}{x}_{3}-0.12{x}_{2}{x}_{3}\end{matrix}</math>                            （17）
+where
-First, taking process bias as player A and standard deviation as player B, the utopia points for the two are (0, 3.1504) and (2.3948, 1.2398), respectively. The disagreement point is d= ( <math display="inline">{d}_{\mathit{\boldsymbol{A}}}</math>, <math display="inline">{d}_{\mathit{\boldsymbol{B\, }}})=</math>(1.2398, 3.1504) where <math display="inline">{d}_{A}</math> is calculated by minimizing the standard deviation ( <math display="inline">\sigma (\boldsymbol{x})</math>) and obtaining the corresponding process bias ( <math display="inline">{\left( \hat{\mu }\left( \boldsymbol{x}\right) -\tau \right) }^{2})</math> value as <math display="inline">\, {d}_{A}</math>. Similarly, <math display="inline">{d}_{B\mathit{\boldsymbol{\, }}}</math>is calculated by minimizing the process bias and obtaining the corresponding standard deviation value. Then, the optimization problem can be solved using Formula (12) under the constraints of (13) and   <math display="inline">\sum _{l=1}^{3}{{x}_{l}}^{2}\leq 3</math>.
+{| class="formulaSCP" style="width: 100%; text-align: center;"
-The solution is calculated by using the MATLAB R2016a built-in optimization tool fmincon, and the results are <math display="inline">{\left( \hat{\mu }\left( \boldsymbol{x}\right) -\tau \right) }^{2}=</math><math>0.2967</math> and <math display="inline">\sigma \left( \boldsymbol{x}\right)</math> = 2.6101. The lexicographic weighted Tchebycheff approach is adopted to check the efficiency of the result, and the Pareto frontier result is shown in Figure 5.
-<div class="center" style="width: auto; margin-left: auto; margin-right: auto;">
-<span style="text-align: center; font-size: 75%;"> [[Image:Draft_Shin_691882792-image5.png|378px]] </span></div>
-<div class="center" style="width: auto; margin-left: auto; margin-right: auto;">
-'''FIGURE 5 '''Pareto frontier for example 1 and solution plot of the proposed method</div>
-As shown in Figure 5, our Nash bargaining solution, which is plotted as a star, is on the Pareto frontier. When using the concept from bargaining game theory, the interaction between process bias and variance is incorporated and a unique tradeoff result is identified. This result could provide useful information to help DMs choose from abundant available non-dominated points.
-===5.2 Numerical example 2===
-The second example is from Cho and Park;<span id='cite-47'></span>[[#47|47]] it is an unbalanced data case that studies the relationship between coating thickness (''y''), mould temperature ( <math display="inline">{x}_{1}</math>), and injection flow rate ( <math display="inline">{x}_{2}</math>). The authors used a <math display="inline">{3}^{2}</math> factorial design with three levels, -1, 0, and +1, respectively. The detailed data is shown in Table 2:
-<div class="center" style="width: auto; margin-left: auto; margin-right: auto;">
-'''TABLE 2'''  Data for numerical example 2</div>
-{| style="width: 100%;border-collapse: collapse;"
 |-
-|  style="border-top: 1pt solid black;border-bottom: 1pt solid black;text-align: center;"|'''Experiments'''
+|
+{| style="text-align: center; margin:auto;"
+|-
+|<math>\boldsymbol{\alpha }_{1}=\, \left[ \begin{matrix}0.59\\-0.35\\-0.01\end{matrix}\right],  \qquad \mbox{and}  \qquad \boldsymbol\Gamma =\, \left[ \begin{matrix}0.28&0.045&0.83\\0.045&1.29&0.755\\0.83&0.755&1.85\end{matrix}\right] </math>
+|}
+|}
-'''number'''
+{| class="formulaSCP" style="width: 100%; text-align: center;"
-|  style="border-top: 1pt solid black;border-bottom: 1pt solid black;text-align: center;"|<math>{\mathit{\boldsymbol{x}}}_{\boldsymbol{1}}</math>
-|  style="border-top: 1pt solid black;border-bottom: 1pt solid black;text-align: center;"|<math>{\mathit{\boldsymbol{x}}}_{\boldsymbol{2}}</math>
-|  style="border-top: 1pt solid black;border-bottom: 1pt solid black;text-align: center;"|<math>{\mathit{\boldsymbol{y}}}_{\boldsymbol{1}}</math>
-|  style="border-top: 1pt solid black;border-bottom: 1pt solid black;text-align: center;"|<math>{\mathit{\boldsymbol{y}}}_{\boldsymbol{2}}</math>
-|  style="border-top: 1pt solid black;border-bottom: 1pt solid black;text-align: center;"|<math>{\mathit{\boldsymbol{y}}}_{\boldsymbol{3}}</math>
-|  style="border-top: 1pt solid black;border-bottom: 1pt solid black;text-align: center;"|<math>{\mathit{\boldsymbol{y}}}_{\boldsymbol{4}}</math>
-|  style="border-top: 1pt solid black;border-bottom: 1pt solid black;text-align: center;"|<math>{\mathit{\boldsymbol{y}}}_{\boldsymbol{5}}</math>
-|  style="border-top: 1pt solid black;border-bottom: 1pt solid black;text-align: center;"|<math>{\mathit{\boldsymbol{y}}}_{\boldsymbol{6}}</math>
-|  style="border-top: 1pt solid black;border-bottom: 1pt solid black;text-align: center;"|<math>{\mathit{\boldsymbol{y}}}_{\boldsymbol{7}}</math>
-|  style="border-top: 1pt solid black;border-bottom: 1pt solid black;text-align: center;"|<math>\overline{\mathit{\boldsymbol{y}}}</math>
-|  style="border-top: 1pt solid black;border-bottom: 1pt solid black;text-align: center;"|<math>{\mathit{\boldsymbol{\sigma }}}^{\mathit{\boldsymbol{2}}}</math>
 |-
-|  style="border-top: 1pt solid black;text-align: center;"|1
+|
-|  style="border-top: 1pt solid black;text-align: center;"|-1
+{| style="text-align: center; margin:auto;"
-|  style="border-top: 1pt solid black;text-align: center;"|-1
-|  style="border-top: 1pt solid black;text-align: center;"|84.3
-|  style="border-top: 1pt solid black;text-align: center;"|57.0
-|  style="border-top: 1pt solid black;text-align: center;"|56.5
-|  style="border-top: 1pt solid black;text-align: center;"|
-|  style="border-top: 1pt solid black;text-align: center;"|
-|  style="border-top: 1pt solid black;text-align: center;"|
-|  style="border-top: 1pt solid black;text-align: center;"|
-|  style="border-top: 1pt solid black;text-align: center;"|65.93
-|  style="border-top: 1pt solid black;text-align: center;"|253.06
 |-
-|  style="text-align: center;"|2
+| <math>\hat{\sigma }\left( {\bf x}\right)=\, 2.55\,+ {\bf x}^T\boldsymbol{\gamma}_1+{\bf x}^T \Epsilon {\bf x}</math>
-|  style="text-align: center;"|0
+|}
-|  style="text-align: center;"|-1
+| style="width: 5px;text-align: right;white-space: nowrap;" | (12)
-|  style="text-align: center;"|75.7
+|}
-|  style="text-align: center;"|87.1
-|  style="text-align: center;"|71.8
+where
-|  style="text-align: center;"|43.8
-|  style="text-align: center;"|51.6
+{| class="formulaSCP" style="width: 100%; text-align: left;"
-|  style="text-align: center;"|
-|  style="text-align: center;"|
-|  style="text-align: center;"|66.00
-|  style="text-align: center;"|318.28
 |-
-|  style="text-align: center;"|3
+|
-|  style="text-align: center;"|1
+{| style="text-align: center; margin:auto;width: 100%;"
-|  style="text-align: center;"|-1
-|  style="text-align: center;"|65.9
-|  style="text-align: center;"|47.9
-|  style="text-align: center;"|63.3
-|  style="text-align: center;"|
-|  style="text-align: center;"|
-|  style="text-align: center;"|
-|  style="text-align: center;"|
-|  style="text-align: center;"|59.03
-|  style="text-align: center;"|94.65
 |-
-|  style="text-align: center;"|4
+| style="text-align: center;" |<math>\boldsymbol\gamma_1=\, \left[ \begin{matrix}0.38\\-0.43\\0.56\end{matrix}\right],  \qquad \mbox{and}  \qquad \boldsymbol\mathrm{E}=\, \left[ \begin{matrix}0.49&-0.235&0.36\\-0.235&0.61&-0.06\\0.36&-0.06&0.85\end{matrix}\right] </math>
-|  style="text-align: center;"|-1
+|}
-|  style="text-align: center;"|0
-|  style="text-align: center;"|51.0
-|  style="text-align: center;"|60.1
-|  style="text-align: center;"|69.7
-|  style="text-align: center;"|84.8
-|  style="text-align: center;"|74.7
-|  style="text-align: center;"|
-|  style="text-align: center;"|
-|  style="text-align: center;"|68.06
-|  style="text-align: center;"|170.35
-|-
-|  style="text-align: center;"|5
-|  style="text-align: center;"|0
-|  style="text-align: center;"|0
-|  style="text-align: center;"|53.1
-|  style="text-align: center;"|36.2
-|  style="text-align: center;"|61.8
-|  style="text-align: center;"|68.6
-|  style="text-align: center;"|63.4
-|  style="text-align: center;"|48.6
-|  style="text-align: center;"|42.5
-|  style="text-align: center;"|53.46
-|  style="text-align: center;"|139.89
-|-
-|  style="text-align: center;"|6
-|  style="text-align: center;"|1
-|  style="text-align: center;"|0
-|  style="text-align: center;"|46.5
-|  style="text-align: center;"|65.9
-|  style="text-align: center;"|51.8
-|  style="text-align: center;"|48.4
-|  style="text-align: center;"|64.4
-|  style="text-align: center;"|
-|  style="text-align: center;"|
-|  style="text-align: center;"|55.40
-|  style="text-align: center;"|83.11
-|-
-|  style="text-align: center;"|7
-|  style="text-align: center;"|-1
-|  style="text-align: center;"|1
-|  style="text-align: center;"|65.7
-|  style="text-align: center;"|79.8
-|  style="text-align: center;"|79.1
-|  style="text-align: center;"|
-|  style="text-align: center;"|
-|  style="text-align: center;"|
-|  style="text-align: center;"|
-|  style="text-align: center;"|74.87
-|  style="text-align: center;"|63.14
-|-
-|  style="text-align: center;"|8
-|  style="text-align: center;"|0
-|  style="text-align: center;"|1
-|  style="text-align: center;"|54.4
-|  style="text-align: center;"|63.8
-|  style="text-align: center;"|56.2
-|  style="text-align: center;"|48.0
-|  style="text-align: center;"|64.5
-|  style="text-align: center;"|
-|  style="text-align: center;"|
-|  style="text-align: center;"|57.38
-|  style="text-align: center;"|47.54
-|-
-|  style="border-bottom: 1pt solid black;text-align: center;"|9
-|  style="border-bottom: 1pt solid black;text-align: center;"|1
-|  style="border-bottom: 1pt solid black;text-align: center;"|1
-|  style="border-bottom: 1pt solid black;text-align: center;"|50.7
-|  style="border-bottom: 1pt solid black;text-align: center;"|68.3
-|  style="border-bottom: 1pt solid black;text-align: center;"|62.9
-|  style="border-bottom: 1pt solid black;text-align: center;"|
-|  style="border-bottom: 1pt solid black;text-align: center;"|
-|  style="border-bottom: 1pt solid black;text-align: center;"|
-|  style="border-bottom: 1pt solid black;text-align: center;"|
-|  style="border-bottom: 1pt solid black;text-align: center;"|60.63
-|  style="border-bottom: 1pt solid black;text-align: center;"|81.29
 |}
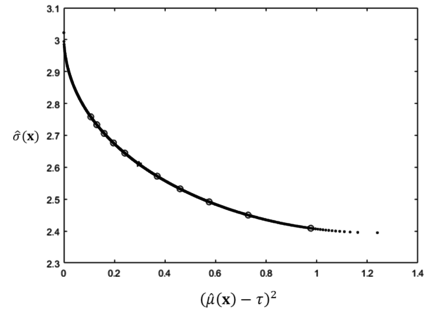
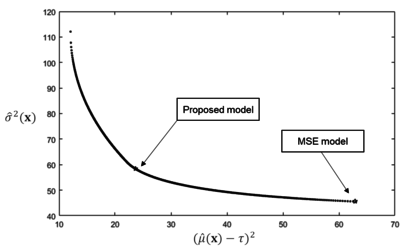
+Based on the proposed RPD procedure as described in [[#img-3|Figure 3]], those two functions (i.e., process bias and standard deviation) as shown in Eqs.(11) and (12) are regarded as two players and also their associated utility functions in the bargaining game.  The disagreement point as shown in [[#img-4|Figure 4]] can be computed as <math display="inline">d=({d}_{A}, {d}_{B})=(1.2398, 3.1504)</math>  by using Eqs.(8) and (9). Then, the optimization problem can be solved by applying Eq.(10) under an additional constraint, <math display="inline">\sum _{l=1}^{3}{{x}_{l}}^{2}\leq 3</math>. which represents a feasible experiment region.
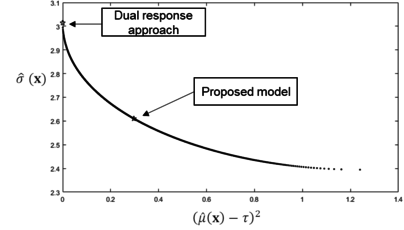
-Cho and Park (2005) used the weighted least square (WLS) method to estimate the mean and variance function, as:
+The solution (i.e., <math display="inline">\left( \hat{\mu }({\bf x}^* ) -\tau \right)^{2}= 0.2967</math> and <math display="inline">\hat\sigma ({\bf x}^*) = 2.6101</math>) are calculated by using a MATLAB software package. To perform a comparative study, the optimization results of the proposed method and the conventional dual response approach are summarized in [[#tab-2|Table 2]]. Based on [[#tab-2|Table 2]], the proposed method provides slightly better MSE results in this particular numerical example. To check the efficiency of the obtained results, the lexicographic weighted Tchebycheff approach is adopted to procure an associated Pareto frontier which is shown in [[#img-5|Figure 5]].
-<div style="text-align: right; direction: ltr; margin-left: 1em;">
-<math display="inline">\hat{\mu }\left( \boldsymbol{x}\right) =55.08-5.76{x}_{1}-</math><math>0.52{x}_{2}+5.51{x}_{1}^{2}+5.47{x}_{2}^{2}-1.84{x}_{1}{x}_{2}</math>                  （18） </div>
-<div style="text-align: right; direction: ltr; margin-left: 1em;">
-<math display="inline">{\hat{\sigma }}^{2}\left( \boldsymbol{x}\right) =154.26-</math><math>39.34{x}_{1}-93.09{x}_{2}-38.31{x}_{1}^{2}+17.81{x}_{2}^{2}+44.14{x}_{1}{x}_{2}</math>      （19）</div>
-Modifying the mean function as squared bias:
-<div style="text-align: right; direction: ltr; margin-left: 1em;">
+<div class="center" style="width: auto; margin-left: auto; margin-right: auto;font-size: 75%;">
-<math display="inline">{(\hat{\mu }(\boldsymbol{x})-\tau )}^{2}={((55.08-5.76{x}_{1}-0.52{x}_{2}+5.51{x}_{1}^{2}+5.47{x}_{2}^{2}-1.84{x}_{1}{x}_{2})-50)}^{2}</math> （20）</div>
+'''Table 2'''. The optimization results of example 1</div>
-Applying the same logic as in example 1, the process bias is player A and variance as player B. First, the ranges for bias and variance are calculated using the built-in optimization tool called fmincon; these are [12.0508, 420.25] and [45.53, 310.39], respectively. Second, the disagreement points are computed as <math display="inline">{d}_{A}</math> =63.0436 and <math display="inline">{d}_{B}</math>=112.0959. Applying function (12) while taking function (13) and <math display="inline">-</math><math>1<{x}_{k}<1,\, k=1,\, 2</math> as constraints gives the ultimate answer, <math display="inline">{(\hat{\mu }(\boldsymbol{x})-\tau )}^{2}</math>=23.6526, <math display="inline">{\hat{\sigma }}^{2}\left( \boldsymbol{x}\right) =</math> 58.3974. When this result is compared with that of Cho and Park<sup> 46</sup> which used a dual response model with WLS estimation method, our result outperforms theirs in terms of MSE (Table 3).
+<div id='tab-2'></div>
+{| class="wikitable" style="margin: 1em auto 0.1em auto;border-collapse: collapse;font-size:85%;width:auto;"
-<div class="center" style="width: auto; margin-left: auto; margin-right: auto;">
+|-style="text-align:center"
-'''TABLE 3''' Optimal solution comparison</div>
+! !! <math>{x}_{1}^{\ast }</math> !! <math>{x}_{2}^{\ast }</math> !! <math>{x}_{3}^{\ast }</math> !! <math>{\left( \hat{\mu }\left( {\bf x}^*\right) -\tau \right) }^{2}</math> !! <math>\hat{\sigma }^{2}({\bf x}^*)</math> !! MSE
-{| style="width: 100%;border-collapse: collapse;"
 |-
-|  style="border: 1pt solid black;text-align: center;"|
+|  style="text-align: left;"|'''Dual response model with WLS'''
-|  style="border: 1pt solid black;text-align: center;vertical-align: top;"|<math>{x}_{1}^{\ast }</math>
+|  style="text-align: center;"|-1.4561
-|  style="border: 1pt solid black;text-align: center;vertical-align: top;"|<math>{x}_{2}^{\ast }</math>
+|  style="text-align: center;"|-0.1456
-|  style="border: 1pt solid black;text-align: center;vertical-align: top;"|<math>\left| \hat{\mu }\mathit{\boldsymbol{(}}\boldsymbol{x}\mathit{\boldsymbol{)-}}\tau \right|</math>
+|  style="text-align: center;"|0.5596
-|  style="border: 1pt solid black;text-align: center;vertical-align: top;"|<math>{\hat{\sigma }}^{2}\mathit{\boldsymbol{(}}\boldsymbol{x}\mathit{\boldsymbol{)}}</math>
+|  style="text-align: center;"|0
-|  style="border: 1pt solid black;text-align: center;vertical-align: top;"|MSE
+|  style="text-align: center;"|3.0142
+|  style="text-align: center;"|9.0854
 |-
-|  style="border: 1pt solid black;text-align: center;"|Dual response model with WLS
+|  style="text-align: left;"|'''Proposed model'''
-|  style="border: 1pt solid black;text-align: center;"|0.998
+|  style="text-align: center;"|-0.8473
-|  style="border: 1pt solid black;text-align: center;"|0.998
+|  style="text-align: center;"|0.0399
-|  style="border: 1pt solid black;text-align: center;"|7.93
+|  style="text-align: center;"|0.2248
-|  style="border: 1pt solid black;text-align: center;"|45.66
+|  style="text-align: center;"|0.2967
-|  style="border: 1pt solid black;text-align: center;"|108.48
+|  style="text-align: center;"|2.6101
-|-
+|  style="text-align: center;"|7.1093
-|  style="border: 1pt solid black;text-align: center;"|Proposed model
-|  style="border: 1pt solid black;text-align: center;"|1.000
-|  style="border: 1pt solid black;text-align: center;"|0.4440
-|  style="border: 1pt solid black;text-align: center;"|4.8606
-|  style="border: 1pt solid black;text-align: center;"|58.3974
-|  style="border: 1pt solid black;text-align: center;"|82.023
 |}
-By applying the lexicographic weighted Tchebycheff approach, we can obtain all non-dominated points that form the Pareto optimal frontier (Figure 6). Again, the Nash bargaining solution is on the Pareto frontier, which may provide a valuable suggestion for the trade-off problem.
+<div id='img-5'></div>
+{| style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: auto;max-width: auto;"
+|-
+|style="padding:10px;"| [[File:News.png|alt=|centre|404x404px|]]
+|- style="text-align: center; font-size: 75%;"
+| colspan="1" style="padding:10px;"| '''Figure 5'''. The optimization results plot with the Pareto frontier of example 1
+|}
-<div class="center" style="width: auto; margin-left: auto; margin-right: auto;">
- [[Image:Draft_Shin_691882792-image6.png|396px]] </div>
-<div class="center" style="width: auto; margin-left: auto; margin-right: auto;">
+As exhibited in [[#img-5|Figure 5]], the obtained Nash bargaining solution, which is plotted as a star, is on the Pareto frontier. By using the concept of bargaining game theory, the interaction between process bias and variability can be incorporated while identifying a unique tradeoff result. As result, this proposed method might provide well-balanced optimal solutions associated with the process bias and variability in this particular example.
-'''     FIGURE 6 '''Pareto frontier for example 2 and solution plot of the proposed method</div>
-===5.3 Sensitivity analysis for numerical example 1===
+=== 5.2 Sensitivity analysis for numerical example 1===
-In this section, the effect of different disagreement point values will be investigated. In example 1, the disagreement point is ''d''= ( <math display="inline">{d}_{A}</math>, <math display="inline">{d}_{B\mathit{\boldsymbol{\, }}})=</math> (1.2398, 3.1504). Now, while the value of <math display="inline">{d}_{B\mathit{\boldsymbol{\, }}}</math>is fixed at 3.1504, the value of <math display="inline">{d}_{A\mathit{\boldsymbol{\, }}}</math> is changed in steps of 10% (both increase and decrease) and the resulting changes in process bias and variance are investigated.
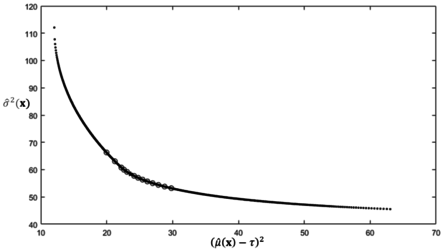
+Based on the optimization results, sensitivity analysis for different disagreement point values are then conducted for verification purposes as shown in [[#tab-3|Table 3]]. While changing  <math>d_B</math> values by both 10% increment and decrement with fixed <math>d_A</math> value at 3.1504, the changing patterns of the process bias and variability values are investigated in this sensitivity analysis.
-<div class="center" style="width: auto; margin-left: auto; margin-right: auto;">
+<div class="center" style="font-size: 75%;">'''Table 3'''. Sensitivity analysis results for numerical example 1 by changing <math display="inline">{d}_{A}</math></div>
-'''TABLE 4''' Example 1 sensitivity analysis; <math display="inline">{d}_{A}</math> is increased and decreased by 10%</div>
-{| style="width: 100%;border-collapse: collapse;"
+<div id='tab-3'></div>
+{| class="wikitable" style="margin: 1em auto 0.1em auto;border-collapse: collapse;font-size:85%;width:auto;"
+|-style="text-align:center"
+!<math>{d}_{A}</math> !! <math>{d}_{B}</math> !! <math>\left(\left( \hat{\mu }({\bf x}) -\tau \right)^2 -{d}_{A}\right)\ast \left( \hat{\sigma }({\bf x}) -{d}_{B}\right)</math> !! <math>x</math> !! <math>\left( \mu ({\bf x}^*) -\tau \right)^2</math> !! <math>\sigma ({\bf x}^*)</math>
 |-
-|  style="border-top: 1pt solid black;text-align: center;"|<math>{d}_{A}</math>
+|  style="text-align: center;"|0.6589
-|  style="border-top: 1pt solid black;text-align: center;"|<math>{d}_{B}</math>
+|  style="text-align: center;"|3.1504
-|  style="border-top: 1pt solid black;text-align: center;"|<math>{\mathit{\boldsymbol{((}}\hat{\mu }\left( \boldsymbol{x}\right) \mathit{\boldsymbol{-}}t\mathit{\boldsymbol{)}}}^{\mathit{\boldsymbol{2}}}-</math><math>{d}_{A}\boldsymbol{)\ast (}\hat{\sigma }\left( \boldsymbol{x}\right) -</math><math>{d}_{B}\mathit{\boldsymbol{)}}</math>
+|  style="text-align: center;"|0.2218
-|  style="border-top: 1pt solid black;text-align: center;"|'''x'''
+|  style="text-align: center;"|[-1.0281  -0.0159  0.3253]
-|  style="border-top: 1pt solid black;text-align: center;"|<math>{\boldsymbol{(}\mu \left( \boldsymbol{x}\right) \boldsymbol{-}\tau \boldsymbol{)}}^{\boldsymbol{2}}</math>
+|  style="text-align: center;"|0.157
-|  style="border-top: 1pt solid black;text-align: center;"|<math>\sigma \left( \boldsymbol{x}\right)</math>
+|  style="text-align: center;"|2.7085
-|-
-|  style="border-top: 1pt solid black;text-align: center;"|0.6589
-|  style="border-top: 1pt solid black;text-align: center;"|3.1504
-|  style="border-top: 1pt solid black;text-align: center;"|0.2218
-|  style="border-top: 1pt solid black;text-align: center;"|[-1.0281  -0.0159  0.3253]
-|  style="border-top: 1pt solid black;text-align: center;"|0.157
-|  style="border-top: 1pt solid black;text-align: center;"|2.7085
 |-
 |  style="text-align: center;"|0.7321
@@ Line 860: / Line 708: @@
 |  style="text-align: center;"|2.5191
 |-
-|  style="border-bottom: 1pt solid black;text-align: center;"|2.4160
+|  style="text-align: center;"|2.4160
-|  style="border-bottom: 1pt solid black;text-align: center;"|3.1504
+|  style="text-align: center;"|3.1504
-|  style="border-bottom: 1pt solid black;text-align: center;"|1.2148
+|  style="text-align: center;"|1.2148
-|  style="border-bottom: 1pt solid black;text-align: center;"|[-0.6002    0.1180    0.0847]
+|  style="text-align: center;"|[-0.6002    0.1180    0.0847]
-|  style="border-bottom: 1pt solid black;text-align: center;"|0.5331
+|  style=text-align: center;"|0.5331
-|  style="border-bottom: 1pt solid black;text-align: center;"|2.5052
+|  style="text-align: center;"|2.5052
 |}
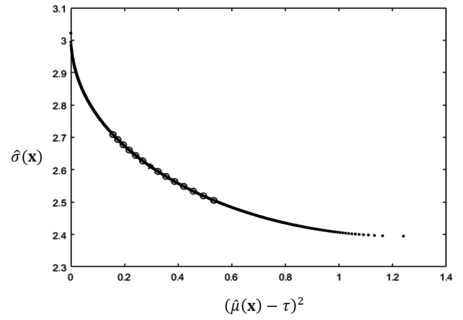
-As shown in Table 4, if only <math display="inline">{d}_{A}</math> increases, the final solution value of <math display="inline">{(\hat{\mu }(\boldsymbol{x})-\tau )}^{2}</math> increases while <math display="inline">\hat{\sigma }\left( \boldsymbol{x}\right)</math>  decreases. All of the calculated results are plotted as circles and compared with the Pareto frontier generated by the lexicographic weighted Tchebycheff method. Clearly, all of the points are on the Pareto frontier, as shown in Figure 7.
+As shown in [[#tab-3|Table 3]], if only <math display="inline">{d}_{A}</math> increases, the optimal squared bias <math display="inline">(\hat{\mu }({\bf x}^*)-\tau )^{2}</math> increases while the process variability <math display="inline">\hat{\sigma }\left( {\bf x}^*\right)</math> decreasing. All of the optimal solutions obtained by using the proposed methods are plotted as circles and compared with the Pareto optimal solutions generated by using the lexicographic weighted Tchebycheff method. Clearly, the obtained solutions are on the Pareto frontier, as shown in [[#img-6|Figure 6]].
-<div class="center" style="width: auto; margin-left: auto; margin-right: auto;">
+<div id='img-6'></div>
-''' [[Image:Draft_Shin_691882792-image7.png|384px]] '''</div>
+{| style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: auto;max-width: auto;"
+|-
+|style="padding:10px;"|  [[File:Draft_Shin_691882792-image7.png|centre|463x463px]]
+|- style="text-align: center; font-size: 75%;"
+| colspan="1" style="padding:10px;"| '''Figure 6'''. Plot of sensitivity analysis results with the Pareto frontier for numerical example 1 by changing <math display="inline">{d}_{A}</math>
+|}
-<div class="center" style="width: auto; margin-left: auto; margin-right: auto;">
-'''FIGURE 7 '''A''' '''plot of all calculated solution points for numerical example 1 when <math display="inline">{d}_{A}</math> is changed by 10%</div>
-On the contrary, if <math display="inline">{d}_{A}</math> is treated as a constant and <math display="inline">{d}_{B}</math> is changed by 5% each time, the data is transformed as summarized in Table 5 and Figure 8.
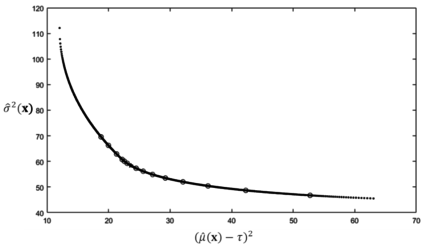
+On the other hand, if <math display="inline">{d}_{A}</math> is considered as a constant and <math display="inline">{d}_{B}</math> is changed by 5% each time, the transformed data is summarized and plotted in [[#tab-4|Table 4]] and [[#img-7|Figure 7]], respectively.
-<div class="center" style="width: auto; margin-left: auto; margin-right: auto;">
+<div class="center" style="font-size: 75%;">'''Table 4'''. Sensitivity analysis results for numerical example 1 by changing <math display="inline">{d}_{B}</math></div>
-'''TABLE 5''' Example 1 sensitivity analysis; <math display="inline">{d}_{B}</math> is increased and decreased by 5%</div>
-{| style="width: 100%;border-collapse: collapse;"
+<div id='tab-4'></div>
+{| class="wikitable" style="margin: 1em auto 0.1em auto;border-collapse: collapse;font-size:85%;width:auto;"
+|-style="text-align:center"
+!<math>{d}_{A}</math> !! <math>{d}_{B}</math> !! <math>\left(\left( \hat{\mu }({\bf x}) -\tau \right)^2 -{d}_{A}\right)\ast \left( \hat{\sigma }({\bf x}) -{d}_{B}\right)</math> !! <math>x</math> !! <math>\left( \hat{\mu} ( {\bf x}^*) -\tau \right)^2</math> !! <math>\hat{\sigma} ({\bf x}^*)</math>
 |-
-|  style="border-top: 1pt solid black;border-bottom: 1pt solid black;text-align: center;"|<math>{d}_{A}</math>
+|  style="text-align: center;"|1.2398
-|  style="border-top: 1pt solid black;border-bottom: 1pt solid black;text-align: center;"|<math>{d}_{B}</math>
+|  style="text-align: center;"|2.4377
-|  style="border-top: 1pt solid black;border-bottom: 1pt solid black;text-align: center;"|<math>{\mathit{\boldsymbol{((}}\hat{\mu }\left( \boldsymbol{x}\right) \mathit{\boldsymbol{-}}t\mathit{\boldsymbol{)}}}^{\mathit{\boldsymbol{2}}}-</math><math>{d}_{A}\boldsymbol{)\ast (}\hat{\sigma }\left( \boldsymbol{x}\right) -</math><math>{d}_{B}\mathit{\boldsymbol{)}}</math>
+|  style="text-align: center;"|0.0076
-|  style="border-top: 1pt solid black;border-bottom: 1pt solid black;text-align: center;"|'''x'''
+|  style="text-align: center;"|[-0.2082    0.2495   -0.1539]
-|  style="border-top: 1pt solid black;border-bottom: 1pt solid black;text-align: center;"|<math>{\boldsymbol{(}\hat{\mu }\left( \boldsymbol{x}\right) \boldsymbol{-}\tau \boldsymbol{)}}^{\boldsymbol{2}}</math>
+|  style="text-align: center;"|0.9764
-|  style="border-top: 1pt solid black;border-bottom: 1pt solid black;text-align: center;"|<math>\hat{\sigma }\left( \boldsymbol{x}\right)</math>
+|  style="text-align: center;"|2.4089
-|-
-|  style="border-top: 1pt solid black;text-align: center;"|1.2398
-|  style="border-top: 1pt solid black;text-align: center;"|2.4377
-|  style="border-top: 1pt solid black;text-align: center;"|0.0076
-|  style="border-top: 1pt solid black;text-align: center;"|[-0.2082    0.2495   -0.1539]
-|  style="border-top: 1pt solid black;text-align: center;"|0.9764
-|  style="border-top: 1pt solid black;text-align: center;"|2.4089
 |-
 |  style="text-align: center;"|1.2398
@@ Line 961: / Line 807: @@
 |  style="text-align: center;"|2.7334
 |-
-|  style="border-bottom: 1pt solid black;text-align: center;"|1.2398
+|  style="text-align: center;"|1.2398
-|  style="border-bottom: 1pt solid black;text-align: center;"|4.0208
+|  style="text-align: center;"|4.0208
-|  style="border-bottom: 1pt solid black;text-align: center;"|1.4308
+|  style="text-align: center;"|1.4308
-|  style="border-bottom: 1pt solid black;text-align: center;"|[-1.1088   -0.0406    0.3698]
+|  style="text-align: center;"|[-1.1088   -0.0406    0.3698]
-|  style="border-bottom: 1pt solid black;text-align: center;"|0.1065
+|  style="text-align: center;"|0.1065
-|  style="border-bottom: 1pt solid black;text-align: center;"|2.7583
+|  style="text-align: center;"|2.7583
 |}
-<div class="center" style="width: auto; margin-left: auto; margin-right: auto;">
+<div id='img-7'></div>
-  [[Image:Draft_Shin_691882792-image8.png|366px]] </div>
+{| style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: auto;max-width: auto;"
+|-
+|style="padding:10px;"|  [[File:Draft_Shin_691882792-image8.png|centre|435x435px]]
+|- style="text-align: center; font-size: 75%;"
+| colspan="1" style="padding:10px;"| '''Figure 7'''. Plot of sensitivity analysis results with the Pareto frontier for numerical example 1 by changing <math display="inline">{d}_{B}</math>
+|}
-<div class="center" style="width: auto; margin-left: auto; margin-right: auto;">
-'''FIGURE 8''' A plot of all calculated solution points for numerical example 1 when <math display="inline">{d}_{B}</math> is changed by 5%</div>
-As demonstrated by Table 5, solution value of <math display="inline">{(\hat{\mu }(\boldsymbol{x})-\tau )}^{2}</math> declines while <math display="inline">\, \hat{\sigma }\left( \boldsymbol{x}\right)</math>  grows if <math display="inline">{d}_{B}</math> is increased and <math display="inline">{d}_{A}</math> is kept constant. However, all of the solution points are still on the Pareto frontier, as shown in Figure 8.
+As demonstrated by [[#tab-4|Table 4]], the value of <math display="inline">(\hat{\mu }({\bf x}^*)-\tau )^{2}</math> declines while <math display="inline">\hat{\sigma }\left( {\bf x}^*\right)</math>  grows if <math display="inline">{d}_{B}</math> is increased and <math display="inline">{d}_{A}</math> is kept constant. However, all of the solution points are still on the Pareto frontier, as shown in [[#img-7|Figure 7]].
-===5.4 Sensitivity analysis for numerical example 2===
+===5.3 Numerical example 2===
-Applying the same logic for example 2, <math display="inline">{d}_{B}</math> is kept constant as <math display="inline">{d}_{A}</math> is changed by 10%. Table 6 exhibits the effect of changes in <math display="inline">{d}_{A}</math>, and Figure 9 demonstrates the efficiency of the calculated solutions.
+In the second example [20], an unbalanced data set is utilized to investigate the relationship between coating thickness (<math>y</math>), mould temperature (<math display="inline">{x}_{1}</math>) and injection flow rate (<math display="inline">{x}_{2}</math>). A 3<sup>2</sup> factorial design with three levels as -1, 0, and +1 is applied as shown in [[#tab-5|Table 5]].
-<div class="center" style="width: auto; margin-left: auto; margin-right: auto;">
+<div class="center" style="font-size: 75%;">'''Table 5'''.  Experimental data for example 2</div>
-'''Table 6''' Example 2 sensitivity analysis; <math display="inline">{d}_{A}</math> is increased and decreased by 10%</div>
-{| style="width: 100%;margin: 1em auto 0.1em auto;border-collapse: collapse;"
+<div id='tab-5'></div>
+{| class="wikitable" style="margin: 1em auto 0.1em auto;border-collapse: collapse;font-size:85%;width:auto;"
+|-style="text-align:center"
+! Experiments number !! <math>{\mathit{{x}}}_{{1}}</math> !! <math>{\mathit{{x}}}_{{2}}</math> !! <math>{\mathit{{y}}}_{{1}}</math> !! <math>{\mathit{{y}}}_{{2}}</math> !! <math>{\mathit{{y}}}_{{3}}</math> !!  <math>{\mathit{{y}}}_{{4}}</math> !! <math>{\mathit{{y}}}_{{5}}</math> !! <math>{\mathit{{y}}}_{{6}}</math> !! <math>{\mathit{{y}}}_{{7}}</math> !! <math>\overline{\mathit{{y}}}</math> !! <math>{\mathit{{\sigma }}}^{\mathit{{2}}}</math>
 |-
-|  style="border-top: 1pt solid black;border-bottom: 1pt solid black;text-align: center;"|<math>{d}_{A}</math>
+|  style="text-align: center;"|1
-|  style="border-top: 1pt solid black;border-bottom: 1pt solid black;text-align: center;"|<math>{d}_{B}</math>
+|  style="text-align: center;"|-1
-|  style="border-top: 1pt solid black;border-bottom: 1pt solid black;text-align: center;"|<math>{\mathit{\boldsymbol{((}}\hat{\mu }\left( \boldsymbol{x}\right) \mathit{\boldsymbol{-}}\tau \mathit{\boldsymbol{)}}}^{\mathit{\boldsymbol{2}}}-</math><math>{d}_{A}\boldsymbol{)\ast (}{\hat{\sigma }}^{2}\left( \boldsymbol{x}\right) -</math><math>{d}_{B}\mathit{\boldsymbol{)}}</math>
+|  style="text-align: center;"|-1
-|  style="border-top: 1pt solid black;border-bottom: 1pt solid black;text-align: center;"|'''x '''
+|  style="text-align: center;"|84.3
-|  style="border-top: 1pt solid black;border-bottom: 1pt solid black;text-align: center;"|<math>{\boldsymbol{(}\hat{\mu }\left( \boldsymbol{x}\right) \boldsymbol{-}\tau \boldsymbol{)}}^{\boldsymbol{2}}</math>
+|  style="text-align: center;"|57.0
-|  style="border-top: 1pt solid black;border-bottom: 1pt solid black;text-align: center;"|<math>{\hat{\sigma }}^{\mathit{\boldsymbol{2}}}\left( \boldsymbol{x}\right)</math>
+|  style="text-align: center;"|56.5
+|  style="text-align: center;"|
+|  style="text-align: center;"|
+|  style="text-align: center;"|
+|  style="text-align: center;"|
+|  style="text-align: center;"|65.93
+|  style="text-align: center;"|253.06
 |-
-|  style="border-top: 1pt solid black;text-align: center;"|37.2266
+|  style="text-align: center;"|2
-|  style="border-top: 1pt solid black;text-align: center;"|112.0959
+|  style="text-align: center;"|0
-|  style="border-top: 1pt solid black;text-align: center;"|790.0487
+|  style="text-align: center;"|-1
-|  style="border-top: 1pt solid black;text-align: center;"|[ 0.9510    0.3554]
+|  style="text-align: center;"|75.7
-|  style="border-top: 1pt solid black;text-align: center;"|19.9778
+|  style="text-align: center;"|87.1
-|  style="border-top: 1pt solid black;text-align: center;"|66.2928
+|  style="text-align: center;"|71.8
+|  style="text-align: center;"|43.8
+|  style="text-align: center;"|51.6
+|  style="text-align: center;"|
+|  style="text-align: center;"|
+|  style="text-align: center;"|66.00
+|  style="text-align: center;"|318.28
+|-
+|  style="text-align: center;"|3
+|  style="text-align: center;"|1
+|  style="text-align: center;"|-1
+|  style="text-align: center;"|65.9
+|  style="text-align: center;"|47.9
+|  style="text-align: center;"|63.3
+|  style="text-align: center;"|
+|  style="text-align: center;"|
+|  style="text-align: center;"|
+|  style="text-align: center;"|
+|  style="text-align: center;"|59.03
+|  style="text-align: center;"|94.65
+|-
+|  style="text-align: center;"|4
+|  style="text-align: center;"|-1
+|  style="text-align: center;"|0
+|  style="text-align: center;"|51.0
+|  style="text-align: center;"|60.1
+|  style="text-align: center;"|69.7
+|  style="text-align: center;"|84.8
+|  style="text-align: center;"|74.7
+|  style="text-align: center;"|
+|  style="text-align: center;"|
+|  style="text-align: center;"|68.06
+|  style="text-align: center;"|170.35
+|-
+|  style="text-align: center;"|5
+|  style="text-align: center;"|0
+|  style="text-align: center;"|0
+|  style="text-align: center;"|53.1
+|  style="text-align: center;"|36.2
+|  style="text-align: center;"|61.8
+|  style="text-align: center;"|68.6
+|  style="text-align: center;"|63.4
+|  style="text-align: center;"|48.6
+|  style="text-align: center;"|42.5
+|  style="text-align: center;"|53.46
+|  style="text-align: center;"|139.89
+|-
+|  style="text-align: center;"|6
+|  style="text-align: center;"|1
+|  style="text-align: center;"|0
+|  style="text-align: center;"|46.5
+|  style="text-align: center;"|65.9
+|  style="text-align: center;"|51.8
+|  style="text-align: center;"|48.4
+|  style="text-align: center;"|64.4
+|  style="text-align: center;"|
+|  style="text-align: center;"|
+|  style="text-align: center;"|55.40
+|  style="text-align: center;"|83.11
+|-
+|  style="text-align: center;"|7
+|  style="text-align: center;"|-1
+|  style="text-align: center;"|1
+|  style="text-align: center;"|65.7
+|  style="text-align: center;"|79.8
+|  style="text-align: center;"|79.1
+|  style="text-align: center;"|
+|  style="text-align: center;"|
+|  style="text-align: center;"|
+|  style="text-align: center;"|
+|  style="text-align: center;"|74.87
+|  style="text-align: center;"|63.14
+|-
+|  style="text-align: center;"|8
+|  style="text-align: center;"|0
+|  style="text-align: center;"|1
+|  style="text-align: center;"|54.4
+|  style="text-align: center;"|63.8
+|  style="text-align: center;"|56.2
+|  style="text-align: center;"|48.0
+|  style="text-align: center;"|64.5
+|  style="text-align: center;"|
+|  style="text-align: center;"|
+|  style="text-align: center;"|57.38
+|  style="text-align: center;"|47.54
+|-
+|  style="text-align: center;"|9
+|  style="text-align: center;"|1
+|  style="text-align: center;"|1
+|  style="text-align: center;"|50.7
+|  style="text-align: center;"|68.3
+|  style="text-align: center;"|62.9
+|  style="text-align: center;"|
+|  style="text-align: center;"|
+|  style="text-align: center;"|
+|  style="text-align: center;"|
+|  style="text-align: center;"|60.63
+|  style="text-align: center;"|81.29
+|}
+Based on Cho and Park [20], a weighted least square (WLS) method was applied to estimate the process mean and variability functions as:
+{| class="formulaSCP" style="width: 100%; text-align: center;"
+|-
+|
+{| style="text-align: center; margin:auto;"
+|-
+| <math display="inline">\hat{\mu }\left(\boldsymbol{\text{x}}\right) =\,55.08\, + \boldsymbol{\text{x}}^{T}\boldsymbol{\alpha }_{1}+\, \boldsymbol{\text{x}}^{T}\boldsymbol\Gamma{\boldsymbol{\text{x}}} </math>
+|}
+| style="width: 5px;text-align: right;white-space: nowrap;" | (13)
+|}
+where
+{| class="formulaSCP" style="width: 100%; text-align: center;"
+|-
+|
+{| style="text-align: center; margin:auto;"
+|-
+<math>\boldsymbol\alpha_1=\, \left[ \begin{matrix}-5.76\\-0.52\\\end{matrix}\right], \qquad \mbox{and} \qquad \boldsymbol\Gamma=\, \left[ \begin{matrix}5.51&-0.92\\-0.92&5.47\\\end{matrix}\right] </math>
+|}
+|}
+{| class="formulaSCP" style="width: 100%; text-align: center;"
+|-
+|
+{| style="text-align: center; margin:auto;"
+|-
+| <math>\hat{\sigma }^{2}( {\bf x})=\, 154.26\,+ \boldsymbol{\text{x}}^{T}\mathit{\boldsymbol{\beta }}_{1}+\, \boldsymbol{\text{x}}^{T}\boldsymbol\Delta\boldsymbol{\text{x}} </math>
+|}
+| style="width: 5px;text-align: right;white-space: nowrap;" | (14)
+|}
+where
+{| class="formulaSCP" style="width: 100%; text-align: center;"
+|-
+|
+{| style="text-align: center; margin:auto;"
+|-
+<math>\boldsymbol\beta_1=\, \left[ \begin{matrix}-39.34\\-93.09\\\end{matrix}\right], \qquad \mbox{and} \qquad\boldsymbol\Delta=\, \left[ \begin{matrix}-38.31&22.07\\22.07&17.81\\\end{matrix}\right] </math>
+|}
+|}
+Applying the same logic as utilized in example 1, the ranges for the process bias and variability are calculated by [12.0508, 420.25] and [45.53, 310.39], respectively. The disagreement points are computed as <math display="inline">{d}_{A} =63.0436</math> and <math display="inline">{d}_{B}=112.0959</math>. Applying Eq.(10), the optimal solutions can be obtained as follows: <math display="inline">(\hat{\mu }({\bf x}^*)-\tau )^{2}=23.6526</math> and <math display="inline">{\hat{\sigma }}^{2}( {\bf x}^*) = 58.3974</math>. Based on the optimization results of both the proposed method and the conventional MSE model as demonstrated in [[#tab-6|Table 6]], the optimization results of the proposed method provide a significantly small MSE compared to the conventional MSE model in this particular example.
+<div class="center" style="font-size: 75%;">'''Table 6'''. The optimization results of example 2</div>
+<div id='tab-6'></div>
+{| class="wikitable" style="margin: 1em auto 0.1em auto;border-collapse: collapse;font-size:85%;width:auto;"
+|-style="text-align:center"
+! !! <math>{x}_{1}^{\ast }</math> !! <math>{x}_{2}^{\ast }</math> !! <math>\left| \hat{\mu }({\bf x}^*)-\tau \right|</math> !! <math>\hat{\sigma }^{2}({\bf x}^*)</math> !! MSE
+|-
+|  style="text-align: left;"|'''MSE model'''
+|  style="text-align: center;"|0.998
+|  style="text-align: center;"|0.998
+|  style="text-align: center;"|7.93
+|  style="text-align: center;"|45.66
+|  style="text-align: center;"|108.48
+|-
+|  style="text-align: left;"|'''Proposed model'''
+|  style="text-align: center;"|1.000
+|  style="text-align: center;"|0.4440
+|  style="text-align: center;"|4.8606
+|  style="text-align: center;"|58.3974
+|  style="text-align: center;"|82.023
+|}
+A Pareto frontier including all non-dominated solutions can be obtained by applying a lexicographic weighted Tchebycheff approach. As illustrated by [[#img-8|Figure 8]], the Nash bargaining solution is on the Pareto frontier, which may clearly verify the efficiency of the proposed method.
+<div id='img-8'></div>
+{| style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: auto;max-width: auto;"
+|-
+|style="padding:10px;"|  [[File:Ty1.png|centre|407x407px|]]
+|- style="text-align: center; font-size: 75%;"
+| colspan="1" style="padding:10px;"| '''Figure 8'''. The optimization results plot with the Pareto frontier of example 2]]
+|}
+===5.4 Sensitivity analysis for numerical example 2===
+Applying the same logic for example 2, <math display="inline">{d}_{B}</math> is kept constant as <math display="inline">{d}_{A}</math> is changed by 10%. [[#tab-7|Table 7]] exhibits the effect of changes in <math display="inline">{d}_{A}</math>, and [[#img-9|Figure 9]] demonstrates the efficiency of the calculated solutions.
+<div class="center" style="font-size: 75%;">'''Table 7'''. Sensitivity analysis results for numerical example 2 by changing <math display="inline">{d}_{A}</math></div>
+<div id='tab-7'></div>
+{| class="wikitable" style="margin: 1em auto 0.1em auto;border-collapse: collapse;font-size:85%;width:auto;"
+|-style="text-align:center"
+!<math>{d}_{A}</math> !! <math>{d}_{B}</math> !! <math>\left(\left( \hat{\mu }({\bf x}) -\tau \right)^2 -{d}_{A}\right)\ast \left( \hat{\sigma }^2({\bf x}) -{d}_{B}\right)</math> !! <math>x</math> !! <math>\left( \hat{\mu} ( {\bf x}^*) -\tau \right)^2</math> !! <math>\hat{\sigma}^2 ({\bf x}^*)</math>
+|-
+|  style="text-align: center;"|37.2266
+|  style="text-align: center;"|112.0959
+|  style="text-align: center;"|790.0487
+|  style="text-align: center;"|[ 0.9510    0.3554]
+|  style="text-align: center;"|19.9778
+|  style="text-align: center;"|66.2928
 |-
 |  style="text-align: center;"|41.3629
@@ Line 1,085: / Line 1,137: @@
 |  style="text-align: center;"|53.7896
 |-
-|  style="border-bottom: 1pt solid black;text-align: center;"|135.1396
+|  style="text-align: center;"|135.1396
-|  style="border-bottom: 1pt solid black;text-align: center;"|112.0959
+|  style="text-align: center;"|112.0959
-|  style="border-bottom: 1pt solid black;text-align: center;"|6204.7
+|  style="text-align: center;"|6204.7
-|  style="border-bottom: 1pt solid black;text-align: center;"|[1.0000    0.6179]
+|  style="text-align: center;"|[1.0000    0.6179]
-|  style="border-bottom: 1pt solid black;text-align: center;"|29.8115
+|  style="text-align: center;"|29.8115
-|  style="border-bottom: 1pt solid black;text-align: center;"|53.1879
+|  style="text-align: center;"|53.1879
 |}
-<div class="center" style="width: auto; margin-left: auto; margin-right: auto;">
+<div id='img-9'></div>
- [[Image:Draft_Shin_691882792-image9.png|438px]] </div>
+{| style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: auto;max-width: auto;"
+|-
+|style="padding:10px;"| [[File:Draft_Shin_691882792-image9.png|centre|445x445px]]
+|- style="text-align: center; font-size: 75%;"
+| colspan="1" style="padding:10px;"| '''Figure 9'''. Plot of sensitivity analysis results with the Pareto frontier for numerical example 2 by changing <math display="inline">{d}_{A}</math>
+|}
-<div class="center" style="width: auto; margin-left: auto; margin-right: auto;">
-'''Figure 9''' A plot of all calculated solution points for numerical example 2 when <math display="inline">{d}_{A}</math> is changed by10%</div>
-Likewise, <math display="inline">{d}_{A}</math> is kept constant while <math display="inline">{d}_{B}</math> is changed by 10%.  The altered data are summarized in Table 7 and plotted in Figure 10.
+On the other hand, another sensitivity analysis is conducted by changing <math display="inline">{d}_{B}</math> with 10% increment and decrement while holding <math display="inline">{d}_{A}</math> at a fixed value (63.0436) as shown in [[#tab-8|Table 8]] and plotted in [[#img-10|Figure 10]].
-<div class="center" style="width: auto; margin-left: auto; margin-right: auto;">
+<div class="center" style="font-size: 75%;">'''Table 8'''. Sensitivity analysis results for numerical example 2 by changing <math display="inline">{d}_{B}</math></div>
-'''Table 7''' Example 2 sensitivity analysis; <math display="inline">{d}_{B}</math> is increased and decreased by 10%</div>
-{| style="width: 100%;border-collapse: collapse;"
+<div id='tab-8'></div>
+{| class="wikitable" style="margin: 1em auto 0.1em auto;border-collapse: collapse;font-size:85%;width:auto;"
+|-style="text-align:center"
+!<math>{d}_{A}</math> !! <math>{d}_{B}</math> !! <math>\left(\left( \hat{\mu }({\bf x}) -\tau \right)^2 -{d}_{A}\right)\ast \left( \hat{\sigma }^2({\bf x}) -{d}_{B}\right)</math> !! <math>x</math> !! <math>\left( \hat{\mu} ( {\bf x}^*) -\tau \right)^2</math> !! <math>\hat{\sigma}^2 ({\bf x}^*)</math>
 |-
-|  style="border-top: 1pt solid black;border-bottom: 1pt solid black;text-align: center;"|<math>{d}_{A}</math>
+|  style="text-align: center;vertical-align: top;"|63.0436
-|  style="border-top: 1pt solid black;border-bottom: 1pt solid black;text-align: center;"|<math>{d}_{B}</math>
+|  style="text-align: center;vertical-align: top;"|48.2536
-|  style="border-top: 1pt solid black;border-bottom: 1pt solid black;text-align: center;"|<math>{\mathit{\boldsymbol{((}}\hat{\mu }\left( \boldsymbol{x}\right) \mathit{\boldsymbol{-}}\tau \mathit{\boldsymbol{)}}}^{\mathit{\boldsymbol{2}}}-</math><math>{d}_{A}\boldsymbol{)\ast (}{\hat{\sigma }}^{\mathit{\boldsymbol{2}}}\left( \boldsymbol{x}\right) -</math><math>{d}_{B}\mathit{\boldsymbol{)}}</math>
+|  style="text-align: center;vertical-align: top;"|15.4253
-|  style="border-top: 1pt solid black;border-bottom: 1pt solid black;text-align: center;"|'''x '''
+|  style="text-align: center;vertical-align: top;"|[1.0000    0.9166]
-|  style="border-top: 1pt solid black;border-bottom: 1pt solid black;"|<math>{\boldsymbol{(}\hat{\mu }\left( \boldsymbol{x}\right) \boldsymbol{-}\tau \boldsymbol{)}}^{\boldsymbol{2}}</math>
+|  style="text-align: center;vertical-align: top;"|52.7429
-|  style="border-top: 1pt solid black;border-bottom: 1pt solid black;text-align: center;"|<math>{\hat{\sigma }}^{\mathit{\boldsymbol{2}}}\left( \boldsymbol{x}\right)</math>
+|  style="text-align: center;vertical-align: top;"|46.7561
-|-
-|  style="border-top: 1pt solid black;text-align: center;vertical-align: top;"|63.0436
-|  style="border-top: 1pt solid black;text-align: center;vertical-align: top;"|48.2536
-|  style="border-top: 1pt solid black;text-align: center;vertical-align: top;"|15.4253
-|  style="border-top: 1pt solid black;text-align: center;vertical-align: top;"|[1.0000    0.9166]
-|  style="border-top: 1pt solid black;text-align: center;vertical-align: top;"|52.7429
-|  style="border-top: 1pt solid black;text-align: center;vertical-align: top;"|46.7561
 |-
 |  style="text-align: center;vertical-align: top;"|63.0436
@@ Line 1,212: / Line 1,262: @@
 |  style="text-align: center;vertical-align: top;"|66.2698
 |-
-|  style="border-bottom: 1pt solid black;text-align: center;vertical-align: top;"|63.0436
+|  style="text-align: center;vertical-align: top;"|63.0436
-|  style="border-bottom: 1pt solid black;text-align: center;vertical-align: top;"|198.5865
+|  style="text-align: center;vertical-align: top;"|198.5865
-|  style="border-bottom: 1pt solid black;text-align: center;vertical-align: top;"|5708.3
+|  style="text-align: center;vertical-align: top;"|5708.3
-|  style="border-bottom: 1pt solid black;text-align: center;vertical-align: top;"|[0.9199    0.3472]
+|  style="text-align: center;vertical-align: top;"|[0.9199    0.3472]
-|  style="border-bottom: 1pt solid black;text-align: center;vertical-align: top;"|18.7938
+|  style="text-align: center;vertical-align: top;"|18.7938
-|  style="border-bottom: 1pt solid black;text-align: center;vertical-align: top;"|69.5842
+|  style="text-align: center;vertical-align: top;"|69.5842
 |}
-<div class="center" style="width: auto; margin-left: auto; margin-right: auto;">
+<div id='img-10'></div>
-  [[Image:Draft_Shin_691882792-image10.png|402px]] </div>
+{| style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: auto;max-width: auto;"
+|-
+|style="padding:10px;"|  [[File:Draft_Shin_691882792-image10.png|centre|423x423px]]
+|- style="text-align: center; font-size: 75%;"
+| colspan="1" style="padding:10px;"| '''Figure 10'''. Plot of sensitivity analysis results with the Pareto frontier for numerical example 2 by changing <math display="inline">{d}_{B}</math>
+|}
+In general, for both cases, an increase in the value of <math display="inline">{d}_{i}</math> will increase the corresponding bargaining solution value. For example, an increasement of <math display="inline">{d}_{A}</math> will lead to an increase in process bias and a decrease in the variability value. This conclusion also makes sense from the perspective of game theory since it can be explained as disagreement point monotonicity [60] which can be defined as:<span id="cite-48"></span>
+For two points, <math display="inline">\, d=\left( {d}_{A},\, {d}_{B}\right)</math>  and <math display="inline"> {d}^{'}=\left( {d}_{A}^{'},\, d_{B}^{'}\right)</math>, <math display="inline">\mbox{if}\, {d}_{i}^{'}\geq {d}_{i},\, {d}_{j}^{,}={d}_{j},</math> then <math>{f}_{i}\left( U,{d}^{'}\right) \geq {f}_{i}\left( U,d\right)</math>; <math>j\not =i</math>, and <math> i,j\in \lbrace A,\, B\rbrace</math>, where <math display="inline">{f}_{i}\left( U,{d}^{'}\right)</math> and <math display="inline">{f}_{i}\left( U,d\right)</math>  represent the solution payoff for player ''i'' after and before the incensement of his disagreement point payoff, respectively. More specifically, the more disagreement point value (<math display="inline">{d}_{i}</math>) a player demands for participation in an agreement, the more the player will get. Although, a gain achieved by one player comes at the expense of the other player. This is because if the agreed solution is not an improvement for one player, then the player would not have any incentive to participate in the bargaining game. However, in the RPD case, the objective for a player is to minimize instead of maximize the utility value, so the less <math display="inline">{d}_{i}</math> a player proposes, the higher the requirement the player is actually proposing to participate in a bargaining game.
+==6. Conclusion and future direction ==
+In a robust design model, when considering the simultaneous minimization of both process bias and variability as a bi-objective problem, there is an intractable tradeoff problem between them. Most existing methods tackle this tradeoff problem by either prioritizing a process parameter or assigning weights to process parameters to indicate the relative importance determined by a DM. However, the DM may struggle with assigning the weights or priority orders to different types and units of responses. Furthermore, the prioritizing or combining response procedure involves a certain degree of subjectivity, as different DMs may have different viewpoints on which process parameter is more important. Thus, in this paper, a bargaining game-based RPD method is proposed to solve this tradeoff problem by integrating Nash bargaining solution techniques and letting the two objectives (e.g., process bias and variability) “negotiate”, so that unique, fair, and efficient solutions can be obtained. These solutions can provide valuable suggestions to the DM, especially when there is no prior information of the relative importance for the process bias and variability. To inspect the efficiency of the obtained solutions, the associated Pareto frontier was generated through applying the lexicographic weighted Tchebycheff method, and thus, the solution position was visually confirmed. As validated by the two numerical examples, compared with the conventional dual response surface method and mean squared error method the proposed method can provide more efficient solutions based on MSE criterion. In addition, a number of sensitivity studies were conducted to investigate the relationship between the disagreement point values (<math>d_i</math>) and the agreement solutions. This research illustrates the possibility of combining the concept of game theory with an RPD model. For further study, the proposed method will be extended to solve the multiple response optimization problems. The tradeoff issue among multiple responses can be addressed by applying the multilateral bargaining game theory, where each quality response is regarded as a rational player who attempts to reach an agreement with others on which set of control factors to choose. In the game, each response proposes a solution set that optimizes the respective estimated response function and is subject to the expectations of the other responses.
+== Acknowledgment ==
+This research was a part of the project titled ‘Marine digital AtoN information management and service system development (2/5) (20210650)’, funded by the Ministry of Oceans and Fisheries, Korea.
+== References ==
+<div class="auto" style="text-align: left;width: auto; margin-left: auto; margin-right: auto;font-size: 85%;">
+[1] Park G.J., Lee T.H., Lee K.H.,  Hwang K.H. Robust design: an overview. AIAA Journal, 44(1):181-191, 2006.
+[2] Myers W.R., Brenneman W.A.,  Myers R.H. A dual-response approach to robust parameter design for a generalized linear model. Journal of Quality Technology, 37(2):130-138, 2005.
+[3] Lin D.K.J., Tu W.  Dual response surface optimization. Journal of Quality Technology, 27:34-39, 1995.
+[4] Cho B.R., Philips M.D., Kapur K.C.  Quality improvement by RSM modeling for robust design. The 5th Industrial Engineering Research Conference, Minneapolis, 650-655, 1996.
+[5] Ding R., Lin D.K.J.,  Wei D. Dual response surface optimization: A weighted MSE approach. Quality Engineering 16(3):377-385, 2004.
-'''FIGURE 10''' A plot of all calculated solution points for numerical example 2 when <math display="inline">{d}_{B}</math> is changed by 10%
+[6] Vining G.G.,  Myers R.H.  Combining Taguchi and response surface philosophies: A dual response approach. Journal of Quality Technology, 22:38-45, 1990.
-<span id='OLE_LINK13'></span><span id='OLE_LINK14'></span>In conclusion, in both cases, an increase in the value of <math display="inline">{d}_{i}</math> will increase the corresponding bargaining solution value. In other words, an increase in <math display="inline">{d}_{A}</math> will increase the process bias result, and an increase in <math display="inline">{d}_{B}</math> will raise the variance. The result also makes sense from the perspective of game theory since it can be explained as disagreement point monotonicity<span id='cite-48'></span>[[#48|48]] which can be defined as:
+[7] Myers R.H.,  Carter W.H.  Response surface methods for dual response systems. Technometrics, 15(2):301-307, 1973.
-For two points, <math display="inline">\, d=\left( {d}_{A},\, {\, d}_{B}\right)</math>  and <math display="inline">\, {d}^{'}=</math><math>\left( {{d}_{A}}^{'},\, {{\, d}_{B}}^{'}\right)</math> , <math display="inline">if\, {d}_{i}^{'}\geq {d}_{i},\, {d}_{j}^{,}=</math><math>{d}_{j},\, then\, {f}_{i}\left( U,{d}^{'}\right) \geq {f}_{i}\left( U,d\right) \, ;\, j\not =i,\, and\, i,j\in \lbrace A,\, B\rbrace</math> .
+[8] Copeland K.A.,  Nelson P.R. Dual response optimization via direct function minimization. Journal of Quality Technology, 28(3):331-336, 1996.
-where <math display="inline">{f}_{i}\left( U,{d}^{'}\right)</math>  and <math display="inline">{f}_{i}\left( U,d\right)</math> is the solution payoff for player ''i'' after and before the incensement of his disagreement point payoff. <math display="inline">\,</math>  More specifically, the more payoff a player demands for participation in an agreement, the more the player will get. Also, a gain achieved by one player comes at the expense of the other player. This is because when the agreement point is not an improvement for one player, any rational player would have no incentive to participate in the bargaining game. In the RPD case, the less <math display="inline">{d}_{i}</math> a player requires to join the agreement, the more the player is actually requiring since the objective is to minimize objective functions in contrast to the general bargaining game which seeks to maximize the payoff.
+[9] Lee D., Jeong I.,  Kim K. A posterior preference articulation approach to dual-response surface optimization. IIE Transaction, 42(2):161-171, 2010.
-==6. CONCLUSION AND FURTHER DIRECTION==
+[10] Shin S.,  Cho B.R.  Robust design models for customer-specified bounds on process parameters. Journal of Systems Science and Systems Engineering, 15:2-18, 2006.
-In the robust design model, when thinking of process bias and variance as a bi-objective problem, there is an intractable trade-off problem between them. In this paper, we proposed a bargaining game based RPD method to solve the trade-off problem by integrating the Nash bargaining solution concept and letting the two objectives (process bias and variance) “negotiate”, a unique, fair and efficient solution can be obtained that may help a DM to make a final choice.  To inspect the efficiency of our obtained solutions the associated Pareto frontier was generated through the lexicographic weighted Tchebycheff method, and solution positions were visually confirmed. Two numerical examples were presented to illustrate the practicality of the proposed model. As solution figures (Figure 5 and 6) showed that our calculated final solution was on the Pareto frontier, which could provide a final solution for DM to solve the trade-off problem. Furthermore, a number of sensitivity studies were conducted to investigate the relationship between <math display="inline">{d}_{i}</math> and the final solution. This research illustrates the possibility of combining the concept of game theory with the process of RPD. In future, we wish to explore the n-player bargaining game and the asymmetry bargaining game to cover more complicated scenarios.
+[11] Leon R.V., Shoemaker A.C., Kackar R.N. Performance measures independent of adjustment: an explanation and extension of Taguchi’s signal-to-noise ratios. Technometrics, 29(3):253-265, 1987.
-==REFERENCE==
+[12] Box G. Signal-to-noise ratios, performance criteria, and transformations. Technometrics, 30(1):1-17, 1988.
-<div id="1"></div>
+[13] Nair V.N., Abraham B., MacKay J., et al. Taguchi's parameter design: a panel discussion. Technometrics, 34(2):127-161, 1992.
-[[#cite-1|1]] Park, G. J., Lee, T. H., Lee, K. H., & Hwang, K. H. Robust design: an overview. AIAA journal, ''44''(1): 181-191, 2006.
-<div id="2"></div>
+[14] Tsui K.L. An overview of Taguchi method and newly developed statistical methods for robust design. IIE Transactions, 24(5):44-57, 1992.
-[[#cite-2|2]] Myers, W. R., Brenneman, W. A., & Myers, R. H. A dual-response approach to robust parameter design for a generalized linear model. Journal of Quality Technology, ''37''(2), 130-138, 2005.
-<div id="3"></div>
+[15] Copeland K.A.,  Nelson P.R.  Dual response optimization via direct function minimization. Journal of Quality Technology, 28(3):331-336, 1996.
-[[#cite-3|3]] Leon R.V., Shoemaker A.C., Kackar R.N. Performance Measures Independent of Adjustment: an Explanation and Extension of Taguchi’s Signal-To-Noise Ratios. Technometrics, 29(3), 253-265, 1987.
-<div id="4"></div>
+[16] Shoemaker A.C., Tsui K.L., Wu C.F.J. Economical experimentation methods for robust design. Technometrics, 33(4):415-427, 1991.
-[[#cite-4|4]] Box G. Signal-to-noise ratios, performance criteria, and transformations. Technometrics, 30(1): 1-17, 1988.
-<div id="5"></div>
+[17] Khattree R. Robust parameter design: A response surface approach. Journal of Quality Technology, 28(2):187-198, 1996.
-[[#cite-5|5]] Nair V N, Abraham B, MacKay J, et al. Taguchi's parameter design: a panel discussion. Technometrics, 34(2): 127-161, 1992.
-<div id="6"></div>
+[18] Pregibon D. Generalized linear models. The Annals of Statistics, 12(4):1589–1596, 1984.
-[[#cite-6|6]] Tsui K L. An overview of Taguchi method and newly developed statistical methods for robust design. IIE Transactions, 24(5): 44-57, 1992.
-<div id="7"></div>
+[19] Lee S.B., Park C.  Development of robust design optimization using incomplete data. Computers & Industrial Engineering, 50(3):345-356, 2006.
-[[#cite-7|7]] Vining G G, Myers R H. Combining Taguchi and response surface philosophies: a dual response approach. Journal of quality technology, 22(1): 38-45, 1990.
-<div id="8"></div>
+[20] Cho B.R., Park C. Robust design modeling and optimization with unbalanced data. Computers & Industrial Engineering, 48(2):173-180, 2005.
-[[#cite-8|8]] Shoemaker A C, Tsui K L, Wu C F J. Economical experimentation methods for robust design. Technometrics'','' 33(4): 415-427, 1991.
-<div id="9"></div>
+[21] Jayaram J.S.R.,  Ibrahim Y.  Multiple response robust design and yield maximization. International Journal of Quality & Reliability Management, 16(9):826-837, 1999.
-[[#cite-9|9]] Khattree R. Robust parameter design: A response surface approach. Journal of Quality Technology, 28(2): 187-198, 1996.
-<div id="10"></div>
+[22] Köksoy O., Doganaksoy N. Joint optimization of mean and standard deviation using response surface methods. Journal of Quality Technology, 35(3):239-252, 2003.
-[[#cite-10|10]] Pregibon, Daryl. Generalized linear models.'' ''The Annals of Statistics, 12(4): 1589–1596, 1984.
-<div id="11"></div>
+[23] Shin S., Cho B.R. Studies on a biobjective robust design optimization problem. IIE Transactions, 41(11):957-968, 2009.
-[[#cite-11|11]] Lee S B, Park C.  Development of robust design optimization using incomplete data.'' ''Computers & industrial engineering, 50(3): 345-356, 2006.
-<div id="12"></div>
+[24] Le T.H., Tang M., Jang J.H., et al. Integration of functional link neural networks into a parameter estimation methodology. Applied Sciences, 11(19):9178, 2021.
-[[#cite-12|12]] Cho B R, Park C. Robust design modeling and optimization with unbalanced data. Computers & industrial engineering, 48(2): 173-180, 2005.
-<div id="13"></div>
+[25] Picheral L., Hadj-Hamou K., Bigeon J.  Robust optimization based on the Propagation of Variance method for analytic design models. International Journal of Production Research, 52(24):7324-7338, 2014.
-[[#cite-13|13]] Lin D K J, Tu W. Dual response surface optimization. Journal of Quality Technology, 27(1): 34-39, 1995.
-<div id="14"></div>
+[26] Mortazavi A., Azarm S., Gabriel S.A. Adaptive gradient-assisted robust design optimization under interval uncertainty. Engineering Optimization, 45(11):1287-1307, 2013.
-[[#cite-14|14]] Jayaram, J.S.R. and Ibrahim, Y.  Multiple response robust design and yield maximization. International Journal of Quality & Reliability Management, 16(9): 826-837, 1999.  [https://doi.org/10.1108/02656719910274308 https://doi.org/10.1108/02656719910274308]
-<div id="15"></div>
+[27] Bashiri M., Moslemi A., Akhavan Niaki S.T. Robust multi‐response surface optimization: a posterior preference approach. International Transactions in Operational Research, 27(3):1751-1770, 2020.
-[[#cite-15|15]] Köksoy O, Doganaksoy N. Joint optimization of mean and standard deviation using response surface methods. Journal of Quality Technology, 35(3): 239-252, 2003.
-<div id="16"></div>
+[28] Yang S., Wang J., Ren X., Gao T. Bayesian online robust parameter design for correlated multiple responses. Quality Technology & Quantitative Management, 18(5):620-640, 2021.
-[[#cite-16|16]] Shin S, Cho B R. Studies on a biobjective robust design optimization problem. IIE Transactions, 41(11): 957-968, 2009.
-<div id="17"></div>
+[29] Sohrabi M.K., Azgomi H. A survey on the combined use of optimization methods and game theory. Archives of Computational Methods in Engineering, 27(1):59-80, 2020.
-[[#cite-17|17]] Shin, S., Hoang, T. T., Le, T. H., & Lee, M. Y.  A new robust design method using neural network.  Journal of Nanoelectronics and Optoelectronics, 11(1): 68-78, 2016.
-<div id="18"></div>
+[30] Shoham Y. Computer science and game theory. Communications of the ACM, 51(8):74-79, 2008.
-[[#cite-18|18]] Picheral L, Hadj-Hamou K, Bigeon J.  Robust optimization based on the Propagation of Variance method for analytic design models.  International Journal of Production Research, 52(24): 7324-7338, 2014.
-<div id="19"></div>
+[31] Manshaei M.H., Zhu Q., Alpcan T., et al. Game theory meets network security and privacy. ACM Computing Surveys (CSUR), 45(3):1-39, 2013.
-[[#cite-19|19]] Mortazavi A, Azarm S, Gabriel S A. Adaptive gradient-assisted robust design optimization under interval uncertainty.'' ''Engineering Optimization, 45(11): 1287-1307, 2013.
-<div id="20"></div>
+[32] Pillai P.S., Rao S. Resource allocation in cloud computing using the uncertainty principle of game theory. IEEE Systems Journal, 10(2):637-648, 2014.
-[[#cite-20|20]] Sohrabi M K, Azgomi H. A survey on the combined use of optimization methods and game theory. Archives of Computational Methods in Engineering'', ''27(1): 59-80, 2020.
-<div id="21"></div>
+[33] Lemaire J. An application of game theory: cost allocation. ASTIN Bulletin: The Journal of the IAA, 1984; 14(1):61-81, 1984. Published online by Cambridge University Press in 2014.
-[[#cite-21|21]] Shoham Y. Computer science and game theory. Communications of the ACM, 51(8): 74-79, 2008.
-<div id="22"></div>
+[34] Barough A.S., Shoubi M.V., Skardi M.J.E. Application of game theory approach in solving the construction project conflicts. Procedia-Social and Behavioral Sciences, 58:1586-1593, 2012.
-[[#cite-22|22]] Manshaei M H, Zhu Q, Alpcan T, et al. Game theory meets network security and privacy. ACM Computing Surveys (CSUR), 45(3): 1-39, 2013.
-<div id="23"></div>
+[35] Gale D., Kuhn H.W., Tucker A.W. Linear programming and the theory of game. Activity analysis of production and allocation, 13:317-335, 1951.
-[[#cite-23|23]] Pillai P S, Rao S. Resource allocation in cloud computing using the uncertainty principle of game theory. IEEE Systems Journal, 10(2): 637-648, 2014.
-<div id="24"></div>
+[36] Mangasarian O.L., Stone H. Two-person nonzero-sum games and quadratic programming. Journal of Mathematical Analysis and Applications, 9(3):348-355, 1964.
-[[#cite-24|24]] Lemaire J. An application of game theory: cost allocation. ASTIN Bulletin: The Journal of the IAA. 1984; 14(1): 61-81, 2014.
-<div id="25"></div>
+[37] Leboucher C., Shin H.S., Siarry P., et al. Convergence proof of an enhanced particle swarm optimization method integrated with evolutionary game theory. Information Sciences, 346:389-411, 2016.
-[[#cite-25|25]] Barough A S, Shoubi M V, Skardi M J E. Application of game theory approach in solving the construction project conflicts. Procedia-Social and Behavioral Sciences'','' 58: 1586-1593, 2012.
-<div id="26"></div>
+[38] Annamdas K.K., Rao S.S. Multi-objective optimization of engineering systems using game theory and particle swarm optimization. Engineering Optimization, 41(8):737-752, 2009.
-[[#cite-26|26]] Gale D, Kuhn H W, Tucker A W. Linear programming and the theory of game. Activity analysis of production and allocation, 13: 317-335, 1951.
-<div id="27"></div>
+[39] Zamarripa M.A., Aguirre A.M., Méndez C.A.,  Espuña A.  Mathematical programming and game theory optimization-based tool for supply chain planning in cooperative/competitive environments. Chemical Engineering Research and Design, 91(8):1588-1600, 2013.
-[[#cite-27|27]] Mangasarian O L, Stone H. Two-person nonzero-sum games and quadratic programming. Journal of mathematical analysis and applications, 9(3): 348-355, 1964.
-<div id="28"></div>
+[40] Dai L., Tang M., Shin S. Stackelberg game approach to a bi-objective robust design optimization. Revista Internacional de Métodos Numéricos para Cálculo y Diseño en Ingeniería, 37(4), 2021.
-[[#cite-28|28]] Leboucher C, Shin H S, Siarry P, et al. Convergence proof of an enhanced particle swarm optimization method integrated with evolutionary game theory. Information Sciences, 346: 389-411, 2016.
-<div id="29"></div>
+[41] Matejaš J., Perić T. A new iterative method for solving multiobjective linear programming problem. Applied Mathematics and Computation, 243:746-754, 2014.
-[[#cite-29|29]] Annamdas K K, Rao S S. Multi-objective optimization of engineering systems using game theory and particle swarm optimization.'' ''Engineering optimization, 41(8): 737-752, 2009.
-<div id="30"></div>
+[42] Doudou M., Barcelo-Ordinas J.M., Djenouri D., Garcia-Vidal J., Bouabdallah A., Badache N. Game theory framework for MAC parameter optimization in energy-delay constrained sensor networks. ACM Transactions on Sensor Networks (TOSN), 12(2):1-35, 2016.
-[[#cite-30|30]] Zamarripa, M. A., Aguirre, A. M., Méndez, C. A., & Espuña, A.  Mathematical programming and game theory optimization-based tool for supply chain planning in cooperative/competitive environments. Chemical Engineering Research and Design, 91(8): 1588-1600, 2013.
-<div id="31"></div>
+[43] Muthoo A. Bargaining theory with applications. Cambridge University Press, 1999.
-[[#cite-31|31]] Shi, Y., Xing, Y., Mou, C., & Kuang, Z. An optimization model based on game theory. Journal of Multimedia, 9(4): 583, 2014.
-<div id="32"></div>
+[44] Goodpaster G. Rational decision-making in problem-solving negotiation: Compromise, interest-valuation, and cognitive error. Ohio St. J. on Disp. Resol., 8:299-360, 1992.
-[[#cite-32|32]] Matejaš J, Perić T. A new iterative method for solving multiobjective linear programming problem. Applied mathematics and computation, 243: 746-754, 2014.
-<div id="33"></div>
+[45] Nash J.F. The bargaining problem.  Econometrica, 18(2):155-162, 1950.
-[[#cite-33|33]] Doudou, M., Barcelo-Ordinas, J. M., Djenouri, D., Garcia-Vidal, J., Bouabdallah, A., & Badache, N. Game theory framework for MAC parameter optimization in energy-delay constrained sensor networks. ACM Transactions on Sensor Networks (TOSN), 12(2), 1-35, 2016.
-<div id="34"></div>
+[46] Nash J.F.  Two-person cooperative games. Econometrica, 21(1):128-140, 1953.
-[[#cite-34|34]] Dai, L., Tang, M., & Shin, S. Stackelberg game approach to a bi-objective robust design optimization. Revista Internacional de Métodos Numéricos para Cálculo y Diseño en Ingeniería, ''37''(4), 2021.
-<div id="35"></div>
+[47] Kalai E., Smorodinsky M. Other solutions to Nash's bargaining problem.  Econometrica: Journal of the Econometric Society, 43(3):513-518, 1975.
-[[#cite-35|35]] Myerson R B.'' ''Game Theory: Analysis of Conflict. Harvard University Press, Cambridge, MA. London England, 1991.
-<div id="36"></div>
+[48] Rubinstein A.  Perfect equilibrium in a bargaining model.  Econometrica: Journal of the Econometric Society, 50(1):97-109, 1982.
-[[#cite-36|36]] Goodpaster G. Rational decision-making in problem-solving negotiation: Compromise, interest-valuation, and cognitive error. Ohio St. J. on Disp. Resol. 8: 299, 1992.
-<div id="37"></div>
+[49] Köksoy O. A nonlinear programming solution to robust multi-response quality problem. Applied Mathematics and Computation, 196(2):603-612, 2008.
-[[#cite-37|37]] Nash, J. F. The Bargaining Problem.  Econometrica, 18(2):155-162, 1950.
-<div id="38"></div>
+[50] Goethals P.L., Cho B.R. Extending the desirability function to account for variability measures in univariate and multivariate response experiments. Computers & Industrial Engineering, 62(2):457-468, 2012.
-[[#cite-38|38]] Nash, J. F. '' ''Two-Person Cooperative Games.  Econometrica, 21(1):128-140, 1953.
-<div id="39"></div>
+[51] Wu F.C., Chyu C.C.  Optimization of robust design for multiple quality characteristics. International Journal of Production Research, 42(2):337-354, 2004.
-[[#cite-39|39]] Rubinstein A.  Perfect equilibrium in a bargaining model.  Econometrica: Journal of the Econometric Society, 97-109, 1982.
-<div id="40"></div>
+[52] Shin S.,  Cho B.R. Bias-specified robust design optimization and its analytical solutions. Computers & Industrial Engineering, 48(1):129-140, 2005.
-[[#cite-40|40]] Kalai E, Smorodinsky M. Other solutions to Nash's bargaining problem. '' ''Econometrica: Journal of the Econometric Society, 513-518, 1975.
-<div id="41"></div>
+[53] Tang L.C., Xu K. A unified approach for dual response surface optimization. Journal of quality technology, 34(4):437-447, 2002.
-[[#cite-41|41]] Mandal W A. Weighted Tchebycheff optimization technique under uncertainty. Annals of Data Science, 1-23, 2020.
-<div id="42"></div>
+[54]  Steenackers G.,  Guillaume P. Bias-specified robust design optimization: A generalized mean squared error approach. Computers & Industrial Engineering, 54(2):259-268, 2008.
-[[#cite-42|42]] Dächert K, Gorski J, Klamroth K. An augmented weighted Tchebycheff method with adaptively chosen parameters for discrete bicriteria optimization problems. Computers & Operations Research, 39(12): 2929-2943, 2012.
-<div id="43"></div>
+[55] Mandal W.A. Weighted Tchebycheff optimization technique under uncertainty. Annals of Data Science, 8:709–731, 2021.
-[[#cite-43|43]] Steuer R E, Choo E U. An interactive weighted Tchebycheff procedure for multiple objective programming. Mathematical programming, 26(3): 326-344, 1983.
-<div id="44"></div>
+[56] Dächert K., Gorski J., Klamroth K. An augmented weighted Tchebycheff method with adaptively chosen parameters for discrete bicriteria optimization problems. Computers & Operations Research, 39(12):2929-2943, 2012.
-[[#cite-44|44]] Rausser G C, Swinnen J, Zusman P. Political power and economic policy: Theory, analysis, and empirical applications''.'' Cambridge University Press, 2011.
-<div id="45"></div>
+[57] Steuer R.E., Choo E.U. An interactive weighted Tchebycheff procedure for multiple objective programming. Mathematical Programming, 26(3):326-344, 1983.
-[[#cite-45|45]] Muthoo A. Bargaining theory with applications. Cambridge University Press, 1999.
-<div id="46"></div>
+[58] Rausser G.C., Swinnen J., Zusman P. Political power and economic policy: Theory, analysis, and empirical applications. Cambridge University Press, 2011.
-[[#cite-46|46]] Shin S, Cho B R. Robust design models for customer-specified bounds on process parameters. Journal of Systems Science and Systems Engineering, 15(1): 2-18, 2006.
-<div id="47"></div>
+[59] Myerson R.B. Game theory: Analysis of conflict. Harvard University Press, Cambridge, MA. London England, 1991.
-[[#cite-47|47]] Cho B R, Park C. Robust design modeling and optimization with unbalanced data. Computers & industrial engineering'','' 48(2): 173-180, 2005.
-<span id='_GoBack'></span><div id="48"></div>
+[60] Thomson W. Chapter 35: Cooperative models of Bargaining. In: Handbook of Game Theory with Economic Applications, 2:1237-1284, 1994.
-[[#cite-48|48]] Thomson W. In: Handbook of game theory with economic applications.'' ''Cooperative models of Bargaining. 2: 1237-1284, 1994.