(Created page with "==1 Title, abstract and keywords<!-- Your document should start with a concise and informative title. Titles are often used in information-retrieval systems. Avoid abbreviatio...") |
m (Move page script moved page Draft Samper 514505331 to Onate et al 2007h) |
||
| (One intermediate revision by one other user not shown) | |||
| Line 1: | Line 1: | ||
| − | + | Published in ''Computers and Fluids'', Vol. 36 (1), pp. 92-112, 2007<br /> | |
| + | DOI: 10.1016/j.compfluid.2005.07.003 | ||
| − | + | ==Abstract== | |
| − | + | A stabilized finite element method (FEM) for the multidimensional steady state advection-diffusion-absorption equation is presented. The stabilized formulation is based on the modified governing differential equations derived via the Finite Calculus (FIC) method. For 1D problems the stabilization terms act as a nonlinear additional diffusion governed by a single stabilization parameter. It is shown that for multidimensional problems an orthotropic stabilizing diffusion must be added along the principal directions of curvature of the solution. A simple iterative algorithm yielding a stable and accurate solution for all the range of physical parameters and boundary conditions is described. Numerical results for 1D and 2D problems with sharp gradients are presented showing the effectiveness and accuracy of the new stabilized formulation. | |
| + | ==1 INTRODUCTION== | ||
| + | Considerable effort has been spent in recent years to derive finite element methods (FEM) <span id='citeF-1'></span>[[#cite-1|1]] for the solution of the advection-diffusion-reaction equation. In this work we will focus on the so called ''exponential regime'' originated by large absorptive (dissipative) reaction terms. Here the solutions are of the form of real exponential functions. Numerical schemes find difficulties to approximating the sharp gradients appearing in the neighborhood of boundary and internal layers due to high Peclet and/or Damköhler numbers. Non physical oscilaltory solution are found with the standard Galerkin FEM unless some stabilization procedure is used. | ||
| + | Stabilized methods to tackle this problem have been based on streamline-upwind/Petrov-Galerkin (SUPG) <span id='citeF-2'></span>[[#cite-2|2]], Galerkin/least-squares <span id='citeF-5'></span>[[#cite-5|5]], Subgrid Scale (SGS) <span id='citeF-5'></span>[[#cite-5|5]] and Residual Free Bubbles <span id='citeF-14'></span>[[#cite-14|14]] finite element methods. While a single stabilization parameter suffices to yield stabilized (and even nodally exact results) for the one-dimensional (1D) advection-diffusion and the diffusion-reaction equations (Vol. 3 in <span id='citeF-1'></span>[[#cite-1|1]] and <span id='citeF-8'></span>[[#cite-8|8]]), this is not the case for the diffusion-advection-reaction equation. Here, in general, ''two stabilization parameters'' are needed in order to ensure a stabilized solution for all range of physical parameters and boundary conditions <span id='citeF-4'></span>[[#cite-4|4]]. As reported in <span id='citeF-12'></span>[[#cite-12|12]] the SUPG, GLS and SGS methods with a single stabilization parameter fail to obtain a stabilized solution for some specific boundary conditions in the exponential regime with negative (absorption) terms when there is a negative streamwise gradient of the solution. | ||
| − | + | Oñate ''et al.'' [18] have recently presented a stabilized FEM for the advection-diffusion absorption equation based on the use of a single stabilization parameter which has the form of a diffusion term. In [18] the formulation is detailed for 1D problems and only a brief introduction to the multidimensional case is given. This paper extends the ideas presented in [18] and provides evidence of the effectiveness and accuracy of the new formulation to deal with multidimensional advection-diffusion-absorption problems with sharp gradients. | |
| − | + | The stabilized formulation is based on the standard Galerkin FEM solution of the modified governing differential equations derived via the ''Finite Calculus'' (FIC) method [19–20]. The FIC equations are obtained by expressing the balance of fluxes in a domain of finite size. This introduces additional stabilizing terms in the differential equations of the infinitessimal theory which are a function of the balance domain dimensions. Although the FIC–FEM formulation here presented is general, we will restrict its application in this work to linear finite element approximations only. | |
| + | The Galerkin FIC-FEM formulation described here introduces naturally an additional nonlinear dissipation term into the discretized equations which is governed by a ''single stabilization parameter''. In the absence of the absorption term the formulation simplifies to the standard Petrov-Galerkin approach for the advection-diffusion problem For the diffusion-absorption case the diffusion-type stabilization term is identical to that recently obtained by Felippa and Oñate using a variational FIC approach <span id='citeF-15'></span>[[#cite-15|15]]. The general nonlinear form of the stabilization parameter is a function of the signs of the solution and its first and second derivatives. This introduces a non-linearity in the solution scheme and a simple iterative algorithm is described. A simpler constant expression of the stabilization parameter is also presented. | ||
| − | + | Details of the 1D formulation and its extension to deal with multidimensional problems are given. For the multidimensional case Oñate ''et al.'' <span id='citeF-27'></span>[[#cite-27|27]] have recently shown that a general form of the stabilization parameters can be found by writting the FIC equations along the principal curvature directions of the solution. The resulting FIC-FEM formulation is equivalent in this case (for linear elements) to adding a stabilizing diffusion matrix to the standard infinitessimal equation. The stabilizing diffusion matrix depends on the signs of the solution and its derivatives and on the velocities along the principal curvature directions of the solution. This introduces a nonlinearity in the solution process. We present a simple iterative scheme based in assuming that the main principal curvature direction at each point is coincident with the gradient vector direction. In the last part of the paper we present a collection of 1D and 2D examples showing the effectiveness and accuracy of the new FIC-FEM formulation for different values of the advective and absorptive terms. | |
| − | + | ==2 FIC FORMULATION OF THE 1D STATIONARY ADVECTION-DIFFUSION-ABSORPTION EQUATION== | |
| + | The governing equation for the 1D stationary advection-diffusion-absorption problem can be written in the FIC formulation as | ||
| − | 2 | + | {| class="formulaSCP" style="width: 100%; text-align: left;" |
| + | |- | ||
| + | | | ||
| + | {| style="text-align: left; margin:auto;" | ||
| + | |- | ||
| + | | style="text-align: center;" | <math>r - \underline{{h\over 2} {dr\over dx}}{h\over 2} {dr\over dx}=0\quad \hbox{in } x \in (0,L) </math> | ||
| + | |} | ||
| + | | style="width: 5px;text-align: right;" | (1) | ||
| + | |} | ||
| − | + | {| class="formulaSCP" style="width: 100%; text-align: left;" | |
| + | |- | ||
| + | | | ||
| + | {| style="text-align: left; margin:auto;" | ||
| + | |- | ||
| + | | style="text-align: center;" | <math>-u\phi + k {d\phi \over dx} +q^p - \underline{{h\over 2} r}{h\over 2} r=0\quad \hbox{on }\Gamma _q </math> | ||
| + | |} | ||
| + | | style="width: 5px;text-align: right;" | (2) | ||
| + | |} | ||
| − | + | {| class="formulaSCP" style="width: 100%; text-align: left;" | |
| + | |- | ||
| + | | | ||
| + | {| style="text-align: left; margin:auto;" | ||
| + | |- | ||
| + | | style="text-align: center;" | <math>\phi -\phi ^p =0 \quad \hbox{on }\Gamma _\phi </math> | ||
| + | |} | ||
| + | | style="width: 5px;text-align: right;" | (3) | ||
| + | |} | ||
| − | + | where | |
| − | + | {| class="formulaSCP" style="width: 100%; text-align: left;" | |
| + | |- | ||
| + | | | ||
| + | {| style="text-align: left; margin:auto;" | ||
| + | |- | ||
| + | | style="text-align: center;" | <math>r =:-u {d\phi \over dx} +{d\over dx} \left(k{d\phi \over dx}\right)- s\phi + Q </math> | ||
| + | |} | ||
| + | | style="width: 5px;text-align: right;" | (4) | ||
| + | |} | ||
| − | + | In above equations <math display="inline">\phi </math> is the state variable, <math display="inline">x \in [0,L]</math> is the problem domain, <math display="inline">L</math> is the domain length, <math display="inline">u</math> is the velocity field, <math display="inline">k\ge 0</math> is the diffusion, <math display="inline">s\ge 0</math> is the absorption, dissipation or destruction source parameter, <math display="inline">Q</math> is a constant source term, <math display="inline">q^p</math> and <math display="inline">\phi ^p</math> are the prescribed values of the total flux and the unknown function at the Neumann and Dirichlet boundaries <math display="inline">\Gamma _q</math> and <math display="inline">\Gamma _\phi </math>, respectively and <math display="inline">h</math> is a ''characteristic length'' which plays the role of a stabilization parameter. In the 1D problem <math display="inline">\Gamma _\phi </math> and <math display="inline">\Gamma _q</math> consist of four combinations at the end points of the problem domain. | |
| + | Eqs.(1) and (2) are obtained by expressing the balance of fluxes in an arbitrary 1D domain of finite size within the problem domain and at the Neumann boundary, respectively. The variations of the transported variables within the balance domain are approximated by Taylor series expansions retaining one order higher terms than in the infinitessimal theory [19,20]. The underlined stabilizing terms in Eqs.(1) and (2) emanate from these higher order expansions. Note that as the characteristic length parameter <math display="inline">h</math> tends to zero the FIC differential equations gradually recover the standard infinitessimal form. | ||
| − | + | Successful applications of the FIC method to a variety of problems in computational mechanics can be found in [19–30,37]. | |
| − | + | ==3 FINITE ELEMENT FORMULATION== | |
| − | + | We will construct a standard finite element discretization <math display="inline">\left\{l^e\right\}</math> of the 1D analysis domain length <math display="inline">L</math> with index <math display="inline">e</math> ranging from 1 to the number of elements <math display="inline">N</math> <span id='citeF-1'></span>[[#cite-1|1]]. The state variable <math display="inline">\phi </math> is approximated by <math display="inline">\bar \phi </math> over the analysis domain. The approximated variable <math display="inline">\bar \phi </math> is interpolated within each element with <math display="inline">n</math> nodes in the standard manner, i.e. | |
| − | + | {| class="formulaSCP" style="width: 100%; text-align: left;" | |
| + | |- | ||
| + | | | ||
| + | {| style="text-align: left; margin:auto;" | ||
| + | |- | ||
| + | | style="text-align: center;" | <math>\phi \simeq \bar \phi \quad \hbox{for}\quad x \in [0,L]</math> | ||
| + | |} | ||
| + | | style="width: 5px;text-align: right;" | (5a) | ||
| + | |} | ||
| − | + | with | |
| − | 1 | + | {| class="formulaSCP" style="width: 100%; text-align: left;" |
| + | |- | ||
| + | | | ||
| + | {| style="text-align: left; margin:auto;" | ||
| + | |- | ||
| + | | style="text-align: center;" | <math>\bar \phi =\sum \limits _{i=1}^n N_i \phi _i</math> | ||
| + | |} | ||
| + | | style="width: 5px;text-align: right;" | (5b) | ||
| + | |} | ||
| − | + | where <math display="inline">N_i</math> are the element shape functions and <math display="inline">\phi _i</math> are nodal values of the approximate function <math display="inline">\bar \phi </math>. Substituting Eq.(5a) into Eqs.(1) and (2) gives | |
| − | 2 | + | {| class="formulaSCP" style="width: 100%; text-align: left;" |
| + | |- | ||
| + | | | ||
| + | {| style="text-align: left; margin:auto;" | ||
| + | |- | ||
| + | | style="text-align: center;" | <math>\bar r - {h\over 2} {d\bar r\over dx} =r_\Omega \quad \hbox{in } x\in (0,L) </math> | ||
| + | |} | ||
| + | |} | ||
| − | + | {| class="formulaSCP" style="width: 100%; text-align: left;" | |
| + | |- | ||
| + | | | ||
| + | {| style="text-align: left; margin:auto;" | ||
| + | |- | ||
| + | | style="text-align: center;" | <math>-u\bar \phi + k {d\bar \phi \over dx} +q^p - {h\over 2} \bar r=r_q\quad \hbox{on }\Gamma _q </math> | ||
| + | |} | ||
| + | | style="width: 5px;text-align: right;" | (6) | ||
| + | |} | ||
| − | + | {| class="formulaSCP" style="width: 100%; text-align: left;" | |
| + | |- | ||
| + | | | ||
| + | {| style="text-align: left; margin:auto;" | ||
| + | |- | ||
| + | | style="text-align: center;" | <math>\bar \phi -\phi ^p =r_\phi \quad \hbox{on }\Gamma _\phi </math> | ||
| + | |} | ||
| + | | style="width: 5px;text-align: right;" | (7) | ||
| + | |} | ||
| − | + | where <math display="inline">\bar r =r(\bar \phi )</math> and <math display="inline">r_\Omega , r_q</math> and <math display="inline">r_\phi </math> are the residuals of the approximate solution in the problem domain and on the Neumann and Dirichlet boundaries <math display="inline">\Gamma _q</math> and <math display="inline">\Gamma _\phi </math>, respectively. | |
| − | + | The weighted residual form of Eqs.(6)–(8) is written as | |
| + | {| class="formulaSCP" style="width: 100%; text-align: left;" | ||
| + | |- | ||
| + | | | ||
| + | {| style="text-align: left; margin:auto;" | ||
| + | |- | ||
| + | | style="text-align: center;" | <math>\int _L W_i \left(\bar r - {h\over 2} {d\bar r\over dx}\right)dx + \left[\hat W_i \left(-u \bar \phi + k {d\bar \phi \over dx} +q_p - {h\over 2} \bar r \right)\right]_{\Gamma _q} =0 </math> | ||
| + | |} | ||
| + | | style="width: 5px;text-align: right;" | (8) | ||
| + | |} | ||
| − | + | where <math display="inline">W_i(x)</math> and <math display="inline">\hat W_i</math> are test functions satisfying <math display="inline">W_i =\hat W_i =0</math> on <math display="inline">\Gamma _\phi </math>. | |
| − | + | Assuming smooth enough solutions and integrating by parts the term involving <math display="inline">h</math> in the first integral gives for <math display="inline">\hat W_i=-W_i</math> | |
| + | {| class="formulaSCP" style="width: 100%; text-align: left;" | ||
| + | |- | ||
| + | | | ||
| + | {| style="text-align: left; margin:auto;" | ||
| + | |- | ||
| + | | style="text-align: center;" | <math>\int _L W_i \bar r d x - \left[W_i \left(-u \bar \phi + k {d\bar \phi \over dx} +q^p \right)\right]_{\Gamma _q} +\sum \limits _e \int _{l^e} {h\over 2} {dW_i\over dx} \bar r dx =0</math> | ||
| + | |} | ||
| + | | style="width: 5px;text-align: right;" | (9) | ||
| + | |} | ||
| + | The third term in Eq.(10) is computed as the sum of the integrals over the element interiors, therefore allowing for the space derivatives of <math display="inline">\bar r</math> to be discontinuous. Also in Eq.(10) <math display="inline">h</math> has been assumed to be constant within each element, (i.e. <math display="inline">\displaystyle{dh\over dx}=0</math> within <math display="inline">l^e</math>). | ||
| + | The weak form is obtained by integrating by parts the advective and diffusive terms within <math display="inline">\bar r</math> in the first integral of Eq.(10). This gives | ||
| − | == | + | {| class="formulaSCP" style="width: 100%; text-align: left;" |
| − | + | |- | |
| + | | | ||
| + | {| style="text-align: left; margin:auto;" | ||
| + | |- | ||
| + | | style="text-align: center;" | <math>\int _L \left[u {dW_i\over dx} \bar \phi - {dW_i\over dx}k {d\bar \phi \over dx}- W_i s \bar \phi + W_i Q\right]dx - [W_i q^p]_{\Gamma _q} - \sum \limits _e \int _{l^e} \left(\beta k {dW_i\over dx} {d\bar \phi \over dx} -{h\over 2} {dW_i\over dx}Q\right)dx =0 </math> | ||
| + | |} | ||
| + | | style="width: 5px;text-align: right;" | (10) | ||
| + | |} | ||
| − | + | with | |
| + | {| class="formulaSCP" style="width: 100%; text-align: left;" | ||
| + | |- | ||
| + | | | ||
| + | {| style="text-align: left; margin:auto;" | ||
| + | |- | ||
| + | | style="text-align: center;" | <math>\beta = \left[{s\bar \phi \over 2k\bar \phi '}+{u\over 2k}-{\bar \phi ''\over 2\bar \phi '} \right]h </math> | ||
| + | |} | ||
| + | | style="width: 5px;text-align: right;" | (11) | ||
| + | |} | ||
| + | where a prime denotes the derivative with respect to the space coordinate. | ||
| + | Wee see clearly that the last term of Eq.(11) introduces within each element an additional diffusion of value <math display="inline">\beta k</math>. | ||
| − | == | + | Substituting expression (5b) into (11) and choosing a Galerkin method with <math display="inline">W_i =N_i</math> within each element gives the discrete system of FE equations written in the standard matrix form as |
| + | {| class="formulaSCP" style="width: 100%; text-align: left;" | ||
| + | |- | ||
| + | | | ||
| + | {| style="text-align: left; margin:auto;" | ||
| + | |- | ||
| + | | style="text-align: center;" | <math>{K}\bar{\boldsymbol \phi } ={f} </math> | ||
| + | |} | ||
| + | | style="width: 5px;text-align: right;" | (12) | ||
| + | |} | ||
| + | where <math display="inline">\bar{\boldsymbol \phi }</math> is the vector of nodal unknowns and the element contributions to matrix '''K''' and vector <math display="inline">f</math> are | ||
| + | {| class="formulaSCP" style="width: 100%; text-align: left;" | ||
| + | |- | ||
| + | | | ||
| + | {| style="text-align: left; margin:auto;" | ||
| + | |- | ||
| + | | style="text-align: right;" | <math>K_{ij}^e\!\! </math> | ||
| + | | style="text-align: center;" | <math>=</math> | ||
| + | | <math>\!\! \int _{l^e} \left(-u {dN_i\over dx} N_j + k(1+\beta ) {dN_i\over dx}{dN_j\over dx}+ sN_i N_j\right)dx</math> | ||
| + | | style="width: 5px;text-align: right;" | (13) | ||
| + | |- | ||
| + | | style="text-align: right;" | <math> f_i^e\!\! </math> | ||
| + | | style="text-align: center;" | <math>=</math> | ||
| + | | <math> \!\! \int _{l^e} \left(N_i + {h\over 2} {dN_i\over dx} \right)Qdx - (N_i q^p)_{\Gamma _q} </math> | ||
| + | | style="width: 5px;text-align: right;" | (14) | ||
| + | |} | ||
| + | |} | ||
| − | + | The amount of balancing diffusion in Eq.(14) clearly depends on the (nonlinear) stabilization parameter <math display="inline">\beta </math>. The element and critical values of <math display="inline">\beta </math> are deduced in the next section for linear two node elements. | |
| − | + | We note that the integral of the term <math display="inline">\displaystyle{h\over 2} \displaystyle{dN_i\over dx}Q</math> in Eq.(15) vanishes after asssembly when <math display="inline">h </math> and <math display="inline">Q</math> are uniform over a patch of linear elements. | |
| − | + | ==4 COMPUTATION OF THE STABILIZATION PARAMETER FOR LINEAR ELEMENTS== | |
| − | + | The matrix <math display="inline">{K}^e</math> and the vector <math display="inline">{f}^e</math> for two node linear elements are (for constant values of <math display="inline">u,k</math>, <math display="inline">s</math> and <math display="inline">Q</math>) | |
| − | [ | + | {| class="formulaSCP" style="width: 100%; text-align: left;" |
| + | |- | ||
| + | | | ||
| + | {| style="text-align: left; margin:auto;" | ||
| + | |- | ||
| + | | style="text-align: center;" | <math>{K}^e = - {u\over 2} \left[\begin{matrix}-1 & -1\\ 1 & 1\\\end{matrix}\right]+ {k\over l^e} (1+\beta ^e) \left[\begin{matrix}1 & -1\\ - 1 & 1\\\end{matrix}\right]+ {sl^e \over 6} \left[\begin{matrix}2 & 1\\ 1 & 2\\\end{matrix}\right]</math> | ||
| + | |} | ||
| + | | style="width: 5px;text-align: right;" | (16a) | ||
| + | |} | ||
| − | [6] | + | {| class="formulaSCP" style="width: 100%; text-align: left;" |
| − | -->== | + | |- |
| + | | | ||
| + | {| style="text-align: left; margin:auto;" | ||
| + | |- | ||
| + | | style="text-align: center;" | <math>{f}^e = {Ql^e\over 2}\left\{\begin{matrix}1 - \displaystyle{h^e\over 2}\\ 1+ \displaystyle{h^e\over 2}\\\end{matrix}\right\}\qquad + \quad \hbox{boundary term}</math> | ||
| + | |} | ||
| + | | style="width: 5px;text-align: right;" | (16a) | ||
| + | |} | ||
| + | |||
| + | In Eqs.(16) index <math display="inline">e</math>denotes element values. | ||
| + | |||
| + | Assuming <math display="inline">Q=0</math>, a typical stencil for elements of equal size <math display="inline">l</math> can be written as | ||
| + | |||
| + | {| class="formulaSCP" style="width: 100%; text-align: left;" | ||
| + | |- | ||
| + | | | ||
| + | {| style="text-align: left; margin:auto;" | ||
| + | |- | ||
| + | | style="text-align: center;" | <math>\begin{array}{r}-\gamma (\bar \phi _{i+1} -\bar \phi _{i-1})-(1+\beta ) \bar \phi _{i-1}+2(1+\beta ) \bar \phi _i - (1+\beta ) \bar \phi _{i+1}+\\ + \displaystyle{w\over 6} (\bar \phi _{i-1}+ 4 \bar \phi _i + \bar \phi _{i+1})=0 \end{array} </math> | ||
| + | |} | ||
| + | | style="width: 5px;text-align: right;" | (17) | ||
| + | |} | ||
| + | |||
| + | where for simplicity a constant value of <math display="inline">\beta </math> across the mesh has been assumed. In Eq.(17) <math display="inline">\gamma ={ul\over 2k}</math> and <math display="inline">w={sl^2\over 4}</math> are the Peclet number and a velocity independent dimensionless number, respectively. | ||
| + | |||
| + | From Eq.(17) we deduce | ||
| + | |||
| + | {| class="formulaSCP" style="width: 100%; text-align: left;" | ||
| + | |- | ||
| + | | | ||
| + | {| style="text-align: left; margin:auto;" | ||
| + | |- | ||
| + | | style="text-align: center;" | <math>\beta = \gamma \left({\bar \phi _{i+1} -\bar \phi _{i-1}\over \bar \phi _{i+1}- 2\bar \phi _i+ \bar \phi _{i-1} }\right)+ {w\over 6} \left({\bar \phi _{i-1} + 4 \bar \phi _i+\bar \phi _{i+1}\over \bar \phi _{i+1}- 2\bar \phi _i+ \bar \phi _{i+1} }\right)-1 </math> | ||
| + | |} | ||
| + | | style="width: 5px;text-align: right;" | (18) | ||
| + | |} | ||
| + | |||
| + | In the vecinity of a sharp gradient zone we can take | ||
| + | |||
| + | {| class="formulaSCP" style="width: 100%; text-align: left;" | ||
| + | |- | ||
| + | | | ||
| + | {| style="text-align: left; margin:auto;" | ||
| + | |- | ||
| + | | style="text-align: center;" | <math>\begin{array}{l}\bar \phi _{i+1} -\bar \phi _{i-1}\simeq \bar \phi _{max} S_1\\ \bar \phi _{i+1} -2\bar \phi _i+ \bar \phi _{i-1}=\bar \phi _{max} S_2\\ \bar \phi _i+4 \bar \phi _i + \bar \phi _{i+1}= \bar \phi _{i+1}S_0 \end{array} </math> | ||
| + | |} | ||
| + | | style="width: 5px;text-align: right;" | (19) | ||
| + | |} | ||
| + | |||
| + | where <math display="inline">\bar \phi _{max}</math> is the maximum value of the approximate function <math display="inline">\bar \phi </math> in the patch of elements adjacent to the sharp gradient zone and | ||
| + | |||
| + | {| class="formulaSCP" style="width: 100%; text-align: left;" | ||
| + | |- | ||
| + | | | ||
| + | {| style="text-align: left; margin:auto;" | ||
| + | |- | ||
| + | | style="text-align: center;" | <math>S_0= \hbox{sign } (\bar \phi ) ,\quad S_1 = \hbox{sign } \left({d\bar \phi \over dx}\right),\quad S_2 = \hbox{sign } \left({d^2 \bar \phi \over dx^2}\right) </math> | ||
| + | |} | ||
| + | | style="width: 5px;text-align: right;" | (20) | ||
| + | |} | ||
| + | |||
| + | where sign <math display="inline">\bar{(\cdot )}</math> denotes the sign of the magnitude within the brackets computed at the patch mid point. | ||
| + | |||
| + | Substituting Eq.(19) into (18) leads to the following expression of the stabilization parameter | ||
| + | |||
| + | {| class="formulaSCP" style="width: 100%; text-align: left;" | ||
| + | |- | ||
| + | | | ||
| + | {| style="text-align: left; margin:auto;" | ||
| + | |- | ||
| + | | style="text-align: center;" | <math>\beta = \left[\left({S_0\over S_2}\right){w\over 6} +\left({S_1\over S_2}\right) \gamma -1\right] </math> | ||
| + | |} | ||
| + | | style="width: 5px;text-align: right;" | (21) | ||
| + | |} | ||
| + | |||
| + | The ''element stabilization parameter'' <math display="inline">\beta ^e</math> is now defined as | ||
| + | |||
| + | {| class="formulaSCP" style="width: 100%; text-align: left;" | ||
| + | |- | ||
| + | | | ||
| + | {| style="text-align: left; margin:auto;" | ||
| + | |- | ||
| + | | style="text-align: center;" | <math>\begin{array}{l}\beta ^e =\beta \quad \hbox{for } \beta >0\\ \beta ^e =0 \quad \hbox{for } \beta \le 0 \end{array} </math> | ||
| + | |} | ||
| + | | style="width: 5px;text-align: right;" | (22) | ||
| + | |} | ||
| + | |||
| + | where <math display="inline">\beta </math> is given by Eq.(21) and the signs <math display="inline">S_0</math>, <math display="inline">S_1</math> and <math display="inline">S_2</math> are computed now at the element mid-point. | ||
| + | |||
| + | It is clear from above that the computation of the stabilization parameter <math display="inline">\beta ^e</math> requires the knowledge of the sign of the numerical solution <math display="inline">\bar \phi </math> and that of the first and second derivatives of <math display="inline">\bar \phi </math> within each element. This necessarily leads to an iterative scheme. A simple algorithm which provides a stabilized and accurate solution in just two steps is presented below. | ||
| + | |||
| + | ===4.1 Critical stabilization parameter and unstability conditions=== | ||
| + | |||
| + | The following constant value of <math display="inline">\beta </math> over the mesh ensures a stabilized solution for all ranges of <math display="inline">\gamma </math> and <math display="inline">w</math> | ||
| + | |||
| + | {| class="formulaSCP" style="width: 100%; text-align: left;" | ||
| + | |- | ||
| + | | | ||
| + | {| style="text-align: left; margin:auto;" | ||
| + | |- | ||
| + | | style="text-align: center;" | <math>\displaystyle{\beta \le \beta _c = {w\over 6} +\vert \gamma \vert -1} </math> | ||
| + | |} | ||
| + | | style="width: 5px;text-align: right;" | (23) | ||
| + | |} | ||
| + | |||
| + | where <math display="inline">\beta _c </math> is the ''critical stabilization parameter''. Note that <math display="inline">\beta _c</math> corresponds to the maximum value of <math display="inline">\beta </math> in Eq.(21) for <math display="inline">{S_0\over S_2}={S_1\over S_2}=1</math>. A mathematical proof of Eq.(23) is given in [18]. | ||
| + | |||
| + | Clearly the value of <math display="inline">\beta _c</math> of Eq.(23) is meaningful only if <math display="inline">\beta _c >0</math> and this can be taken as an indicator of an unstable solution. Conversely, a value of <math display="inline">\beta _c \le 0</math> indicates that no stabilization is needed. | ||
| + | |||
| + | ===4.2 Iterative solution scheme=== | ||
| + | |||
| + | The following two steps iterative scheme is proposed in order to obtain a stabilized and accurate solution. | ||
| + | |||
| + | step step | ||
| + | |||
| + | Compute a first stabilized solution <math display="inline">\bar{\boldsymbol \phi }^1</math> using the critical value <math display="inline">\beta ^e = \beta _c</math> given by Eq.(23). This ensures a stabilized, although sometimes slightly overdiffusive, solution. | ||
| + | |||
| + | ==~ == | ||
| + | |||
| + | step | ||
| + | |||
| + | Compute the signs of the first and second derivatives of <math display="inline">\bar{\boldsymbol \phi }^1</math> within each element. The second derivative field is obtained as follows | ||
| + | |||
| + | {| class="formulaSCP" style="width: 100%; text-align: left;" | ||
| + | |- | ||
| + | | | ||
| + | {| style="text-align: left; margin:auto;" | ||
| + | |- | ||
| + | | style="text-align: center;" | <math>\left({d^2 \bar \phi ^1 \over dx^2}\right)^e= {1\over l^e} \left[\left({d\hat \phi ^1 \over dx}\right)^e_2 - \left({d\hat \phi ^1 \over dx}\right)^e_1\right] </math> | ||
| + | |} | ||
| + | | style="width: 5px;text-align: right;" | (24) | ||
| + | |} | ||
| + | |||
| + | where <math display="inline">({\hat \cdot })_i^e</math> denotes averaged values of the first derivative at node <math display="inline">i</math> of element <math display="inline">e</math>. At the boundary nodes the constant value of the derivative of <math display="inline">\bar \phi </math> within the element is taken in Eq.(24); i.e. <math display="inline">(\hat{\cdot })_i^e = \left({d\bar \phi \over dx}\right)^{(e)} = {\bar \phi _2 - \bar \phi _1 \over l^e}</math>. | ||
| + | |||
| + | Compute the enhanced stabilized solution <math display="inline">{\boldsymbol \phi }^2</math> using the element value of <math display="inline">\beta ^e</math> given by Eq.(22). | ||
| + | |||
| + | In all the 1D examples solved the above two steps have sufficed to obtain a converged stabilized and accurate solution [18]. The reason of this is that the signs of the first and second derivative fields typically do not change any further after the second step over the elements adjacent to high gradient zones. | ||
| + | |||
| + | ==5 EXTENSION TO MULTI-DIMENSIONAL PROBLEMS== | ||
| + | |||
| + | Consider the general steady-state advection-diffusion-reaction equation written for the zero constant source case (<math display="inline">Q=0</math>) as | ||
| + | |||
| + | <span id="eq-25"></span> | ||
| + | {| class="formulaSCP" style="width: 100%; text-align: left;" | ||
| + | |- | ||
| + | | | ||
| + | {| style="text-align: left; margin:auto;" | ||
| + | |- | ||
| + | | style="text-align: center;" | <math>r(\phi ): =- {u}^T {\boldsymbol \nabla } \phi + {\boldsymbol \nabla }^T {D}{\boldsymbol \nabla }\phi - s\phi =0 </math> | ||
| + | |} | ||
| + | | style="width: 5px;text-align: right;" | (25) | ||
| + | |} | ||
| + | |||
| + | For 2D problems | ||
| + | |||
| + | <span id="eq-26"></span> | ||
| + | {| class="formulaSCP" style="width: 100%; text-align: left;" | ||
| + | |- | ||
| + | | | ||
| + | {| style="text-align: left; margin:auto;" | ||
| + | |- | ||
| + | | style="text-align: center;" | <math>{u}=[u,v]^T\quad ,\quad {\boldsymbol \nabla }=\left[{\partial \over \partial x},{\partial \over \partial y}\right]^T\quad ,\quad {D} =k \left[\begin{matrix}1 &0\\ 0&1\\\end{matrix}\right] </math> | ||
| + | |} | ||
| + | | style="width: 5px;text-align: right;" | (26) | ||
| + | |} | ||
| + | |||
| + | are respectively the velocity vector, the gradient vector and the diffusivity matrix, respectively. For simplicity we have assumed an isotropic diffusion matrix. | ||
| + | |||
| + | The FIC form of Eq.([[#eq-25|25]]) is written as | ||
| + | |||
| + | <span id="eq-27"></span> | ||
| + | {| class="formulaSCP" style="width: 100%; text-align: left;" | ||
| + | |- | ||
| + | | | ||
| + | {| style="text-align: left; margin:auto;" | ||
| + | |- | ||
| + | | style="text-align: center;" | <math>r - \underline{{1\over 2} {h}^T {\boldsymbol \nabla }r}{1\over 2} {h}^T {\boldsymbol \nabla }r=0 </math> | ||
| + | |} | ||
| + | | style="width: 5px;text-align: right;" | (27) | ||
| + | |} | ||
| + | |||
| + | where <math display="inline">r</math> is the original infinitessimal differential equation as defined in Eq.([[#eq-25|25]]). | ||
| + | |||
| + | The Dirichlet and boundary conditions of the FIC formulation are | ||
| + | |||
| + | <span id="eq-28"></span> | ||
| + | {| class="formulaSCP" style="width: 100%; text-align: left;" | ||
| + | |- | ||
| + | | | ||
| + | {| style="text-align: left; margin:auto;" | ||
| + | |- | ||
| + | | style="text-align: center;" | <math>\phi - \phi ^p =0 \quad \hbox{on}\quad \Gamma _\phi </math> | ||
| + | |} | ||
| + | | style="width: 5px;text-align: right;" | (28) | ||
| + | |} | ||
| + | |||
| + | <span id="eq-29"></span> | ||
| + | {| class="formulaSCP" style="width: 100%; text-align: left;" | ||
| + | |- | ||
| + | | | ||
| + | {| style="text-align: left; margin:auto;" | ||
| + | |- | ||
| + | | style="text-align: center;" | <math>- {u}^T {n}\phi + {n}^T {D} {\boldsymbol \nabla } \phi + q^p - \underline{{1\over 2} {h}^T {n}r}{1\over 2} {h}^T {n}r=0 \quad \hbox{on}\quad \Gamma _q </math> | ||
| + | |} | ||
| + | | style="width: 5px;text-align: right;" | (29) | ||
| + | |} | ||
| + | |||
| + | where <math display="inline">n</math> is the normal vector to the boundary where the normal flux is prescribed. As usual index <math display="inline">p</math> denotes the prescribed values. | ||
| + | |||
| + | In Eqs.([[#eq-27|27]]) and ([[#eq-29|29]]) <math display="inline">{h}=[h_x,h_y]^T</math> is the characteristic vector of the 2D FIC formulation which components play the role of stabilization parameters. The underlined terms in Eqs.([[#eq-27|27]]) and ([[#eq-29|29]]) introduce the necessary stability in the numerical solution [19,20,21]. | ||
| + | |||
| + | If vector '''h''' is taken to be parallel to the velocity '''u''' the standard SUPG method is recovered [18–23]. The more general form of '''h''' allows to obtain stabilized finite element solutions in the presence of strong gradients of <math display="inline">\phi </math> near the boundaries (boundary layers) and within the analysis domain (internal layers) <span id='citeF-27'></span>[[#cite-27|27]]. The FIC formulation therefore reproduces the best features of the so called shock-capturing or transverse-dissipation schemes <span id='citeF-2'></span>[[#cite-2|2]]. | ||
| + | |||
| + | {| style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 100%;max-width: 100%;" | ||
| + | |- | ||
| + | | | ||
| + | [[File:Draft_Samper_447243531_2415_Fig1.png|600px|]] | ||
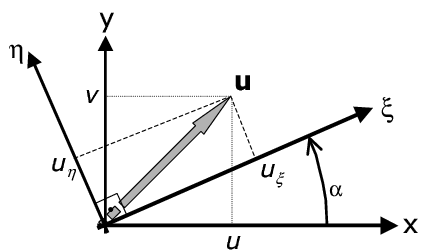
| + | |- style="text-align: center; font-size: 75%;padding:10px;" | ||
| + | | colspan="1" | '''Figure 1'''. Global axes (<math>x,y</math>) and principal curvature axes (<math>\xi ,\eta </math>) | ||
| + | |} | ||
| + | |||
| + | Let us write down the FIC balance equation in the principal curvature axes of the solution <math display="inline">\xi ,\eta </math> (Figure 1). The FIC balance equation is | ||
| + | |||
| + | {| class="formulaSCP" style="width: 100%; text-align: left;" | ||
| + | |- | ||
| + | | | ||
| + | {| style="text-align: left; margin:auto;" | ||
| + | |- | ||
| + | | style="text-align: right;" | | ||
| + | | style="text-align: center;" | | ||
| + | | <math>-u_\xi {\partial \phi \over \partial \xi }-u_\eta {\partial \phi \over \partial \eta }+k \left({\partial ^2\phi \over \partial \xi ^2}+ {\partial ^2\phi \over \partial \eta ^2}\right)-s\phi - {h_\xi \over 2} {\partial \over \partial \xi }\left[-u_\xi {\partial \phi \over \partial \xi }-u_\eta {\partial \phi \over \partial \eta }+ k \left({\partial ^2\phi \over \partial \xi ^2}+ {\partial ^2\phi \over \partial \eta ^2}\right)-s\phi \right]</math> | ||
| + | |- | ||
| + | | style="text-align: right;" | | ||
| + | | style="text-align: center;" | | ||
| + | | <math> - {h_\eta \over 2} {\partial \over \partial \eta } \left[-u_\xi {\partial \phi \over \partial \xi }-u_\eta {\partial \phi \over \partial \eta }+ k \left({\partial ^2\phi \over \partial \xi ^2}+ {\partial ^2\phi \over \partial \eta ^2}\right)-s\phi \right]=0 </math> | ||
| + | |} | ||
| + | | style="width: 5px;text-align: right;" | (30) | ||
| + | |} | ||
| + | |||
| + | where <math display="inline">u_\xi , u_\eta </math> are the velocities along the principal axes of curvature <math display="inline">\xi </math> and <math display="inline">\eta </math>, respectively. | ||
| + | |||
| + | As <math display="inline">\xi </math> and <math display="inline">\eta </math> are the principal curvature axes of the solution then | ||
| + | |||
| + | {| class="formulaSCP" style="width: 100%; text-align: left;" | ||
| + | |- | ||
| + | | | ||
| + | {| style="text-align: left; margin:auto;" | ||
| + | |- | ||
| + | | style="text-align: center;" | <math>{\partial ^2\phi \over \partial \xi \partial \eta }= {\partial ^2\phi \over \partial \eta \partial \xi }=0 </math> | ||
| + | |} | ||
| + | | style="width: 5px;text-align: right;" | (31) | ||
| + | |} | ||
| + | |||
| + | Introducing this simplification into Eq.(30) we can rewrite this equation as | ||
| + | |||
| + | {| class="formulaSCP" style="width: 100%; text-align: left;" | ||
| + | |- | ||
| + | | | ||
| + | {| style="text-align: left; margin:auto;" | ||
| + | |- | ||
| + | | style="text-align: center;" | <math>\begin{array}{l} -u_\xi \displaystyle {\partial \phi \over \partial \xi }-u_\eta {\partial \phi \over \partial \eta }+\left(k + {u_\xi h_\xi \over 2}+ {sh_\xi \over 2} {\partial \phi \over \partial \xi } \left({\partial ^2\phi \over \partial \xi ^2} \right)^{-1} \right){\partial ^2\phi \over \partial \xi ^2} +\\ \displaystyle + \left(k + {u_\eta h_\eta \over 2}+ {sh_\eta \over 2} {\partial \phi \over \partial \eta } \left({\partial ^2\phi \over \partial \eta ^2} \right)^{-1}\right){\partial ^2\phi \over \partial \eta ^2} - s\phi - k \left({h_\xi \over 2}{\partial ^3 \phi \over \partial \xi ^3}+ {h_\eta \over 2} {\partial ^3 \phi \over \partial \eta ^3}\right)=0 \end{array}</math> | ||
| + | |} | ||
| + | | style="width: 5px;text-align: right;" | (32a) | ||
| + | |} | ||
| + | |||
| + | or | ||
| + | |||
| + | {| class="formulaSCP" style="width: 100%; text-align: left;" | ||
| + | |- | ||
| + | | | ||
| + | {| style="text-align: left; margin:auto;" | ||
| + | |- | ||
| + | | style="text-align: center;" | <math> -u_\xi {\partial \phi \over \partial \xi }-u_\eta {\partial \phi \over \partial \eta }+ k(1+\beta _\xi ) {\partial ^2\phi \over \partial \xi ^2} + k (1+\beta _\eta ) {\partial ^2\phi \over \partial \eta ^2} - s\phi -k \left({h_\xi \over 2}{\partial ^3 \phi \over \partial \xi ^3}+ {h_\eta \over 2} {\partial ^3 \phi \over \partial \eta ^3}\right)=0</math> | ||
| + | |} | ||
| + | | style="width: 5px;text-align: right;" | (32b) | ||
| + | |} | ||
| + | |||
| + | We can see clearly from Eq.(33) that the FIC governing equations introduce orthotropic diffusion parameters of values <math display="inline">{\beta _\xi k }</math> and <math display="inline"> { \beta _\eta k}</math> along the <math display="inline">\xi </math> and <math display="inline">\eta </math> axes, respectively with | ||
| + | |||
| + | {| class="formulaSCP" style="width: 100%; text-align: left;" | ||
| + | |- | ||
| + | | | ||
| + | {| style="text-align: left; margin:auto;" | ||
| + | |- | ||
| + | | style="text-align: center;" | <math>\beta _\xi = {u_\xi h_\xi \over 2k} + {sh_\xi \over 2k} {\partial \phi \over \partial \xi } \left({\partial ^2\phi \over \partial \xi ^2} \right)^{-1},\quad \beta _\eta ={u_\xi h_\xi \over 2k} + {sh_\eta \over 2k} {\partial \phi \over \partial \eta } \left({\partial ^2\phi \over \partial \eta ^2} \right)^{-1} </math> | ||
| + | |} | ||
| + | | style="width: 5px;text-align: right;" | (33) | ||
| + | |} | ||
| + | |||
| + | Also note that the last term of Eq.(32b) will vanish after discretization for linear elements. | ||
| + | |||
| + | Eq.(32b) can be rewritten in matrix form (neglecting the last term) as | ||
| + | |||
| + | {| class="formulaSCP" style="width: 100%; text-align: left;" | ||
| + | |- | ||
| + | | | ||
| + | {| style="text-align: left; margin:auto;" | ||
| + | |- | ||
| + | | style="text-align: center;" | <math>- {u}^{\prime T} {\boldsymbol \nabla }^\prime \phi + {\boldsymbol \nabla }^{\prime T} ({D}+\bar {D}^\prime ) {\boldsymbol \nabla }^{\prime }\phi - s\phi =0 </math> | ||
| + | |} | ||
| + | |} | ||
| + | |||
| + | where <math display="inline">{u}^\prime =[u_\xi , u_\eta ]^T</math>, <math display="inline">{\boldsymbol \nabla }^\prime = \left[{\partial \over \partial \xi }, {\partial \over \partial \eta }\right]^T</math>, <math display="inline">D</math> is the “physical” isotropic diffusion matrix and <math display="inline">\bar {D}'</math> is the balancing diffusion matrix in the local axes <math display="inline">\xi </math> and <math display="inline">\eta </math>. The form of this matrix is | ||
| + | |||
| + | {| class="formulaSCP" style="width: 100%; text-align: left;" | ||
| + | |- | ||
| + | | | ||
| + | {| style="text-align: left; margin:auto;" | ||
| + | |- | ||
| + | | style="text-align: center;" | <math>\bar {D}^\prime = \left[\begin{array}{cc}\beta _\xi k& 0\\ 0 &\beta _\eta k \end{array}\right] </math> | ||
| + | |} | ||
| + | | style="width: 5px;text-align: right;" | (34) | ||
| + | |} | ||
| + | |||
| + | The velocities along the principal curvature axes <math display="inline">u_\xi </math> and <math display="inline">u_\eta </math> can be obtained by projecting the cartesian velocities into the principal curvature axes <math display="inline">\xi </math> and <math display="inline">\eta </math> as | ||
| + | |||
| + | {| class="formulaSCP" style="width: 100%; text-align: left;" | ||
| + | |- | ||
| + | | | ||
| + | {| style="text-align: left; margin:auto;" | ||
| + | |- | ||
| + | | style="text-align: center;" | <math>{u}'=\left\{\begin{array}{c}u_\xi \\ u_\eta \end{array}\right\}= {T} {u} \quad \hbox{with}\quad {T}= \left[\begin{array}{cc}c_\alpha & s_\alpha \\ - s_\alpha & c_\alpha \end{array}\right]\quad ,\quad {u}=\left\{\begin{array}{c}u\\v\end{array}\right\} </math> | ||
| + | |} | ||
| + | | style="width: 5px;text-align: right;" | (35) | ||
| + | |} | ||
| + | |||
| + | where <math display="inline">c_\alpha =\cos \alpha </math>, <math display="inline">s_\alpha =\sin \alpha </math> and <math display="inline">\alpha </math> is the angle which the <math display="inline">\xi </math> axis forms with the <math display="inline">x</math> axis (Figure 1). Note that as the solution is continuous the principal curvature directions <math display="inline">\xi </math> and <math display="inline">\eta </math> are orthogonal. | ||
| + | |||
| + | The values of <math display="inline">\beta _\xi </math> and <math display="inline">\beta _\eta </math> are computed by considering the solution of two uncoupled 1D problems along the <math display="inline">\xi </math> and <math display="inline">\eta </math> directions. This gives from Eqs.(21) and (22) | ||
| + | |||
| + | {| class="formulaSCP" style="width: 100%; text-align: left;" | ||
| + | |- | ||
| + | | | ||
| + | {| style="text-align: left; margin:auto;" | ||
| + | |- | ||
| + | | style="text-align: center;" | <math>\beta _\xi = \left[\left({S_0\over S_{\xi _2}}\right){w_\xi \over 6} + \left({S_{\xi _1}\over S_{\xi _2}}\right)\gamma _\xi -1\right]\quad ,\quad \gamma _\xi = {u_\xi l_\xi \over 2k} \quad ,\quad w_\xi = {sl^2_\xi \over k}</math> | ||
| + | |} | ||
| + | | style="width: 5px;text-align: right;" | (37a) | ||
| + | |} | ||
| + | |||
| + | {| class="formulaSCP" style="width: 100%; text-align: left;" | ||
| + | |- | ||
| + | | | ||
| + | {| style="text-align: left; margin:auto;" | ||
| + | |- | ||
| + | | style="text-align: center;" | <math>\beta _\eta = \left[\left({S_0\over S_{\eta _2}}\right){w_\eta \over 6} + \left({S_{\eta _1}\over S_{\eta _2}}\right)\gamma _\eta -1\right]\quad ,\quad \gamma _\eta = {u_\eta l_\eta \over 2k} \quad ,\quad w_\eta = {sl^2_\eta \over k} </math> | ||
| + | |} | ||
| + | | style="width: 5px;text-align: right;" | (37b) | ||
| + | |} | ||
| + | |||
| + | where | ||
| + | |||
| + | {| class="formulaSCP" style="width: 100%; text-align: left;" | ||
| + | |- | ||
| + | | | ||
| + | {| style="text-align: left; margin:auto;" | ||
| + | |- | ||
| + | | style="text-align: center;" | <math>\begin{array}{l}S_0 =\hbox{sign }(\bar \phi ) \quad ,\quad S_{\xi _1}= \hbox{sign } \left(\displaystyle{\partial \bar \phi \over \partial \xi }\right)\quad ,\quad S_{\xi _2}= \hbox{sign } \left(\displaystyle{\partial ^2 \bar \phi \over \partial \xi ^2}\right)\\ S_{\eta _1}= \hbox{sign } \left(\displaystyle{\partial \bar \phi \over \partial \eta }\right)\quad ,\quad S_{\eta _2}= \hbox{sign } \left(\displaystyle{\partial ^2 \bar \phi \over \partial \eta ^2}\right) \end{array} </math> | ||
| + | |} | ||
| + | | style="width: 5px;text-align: right;" | (38) | ||
| + | |} | ||
| + | |||
| + | and <math display="inline">\bar \phi </math> is as usual the approximate solution. | ||
| + | |||
| + | The lengths <math display="inline">l_\xi </math> and <math display="inline">l_\eta </math> are taken as the maximum projection of the velocities <math display="inline">u_\xi </math> and <math display="inline">u_\eta </math> along the element sides (for triangles) and the element diagonals (for quadrilaterals), i.e. | ||
| + | |||
| + | {| class="formulaSCP" style="width: 100%; text-align: left;" | ||
| + | |- | ||
| + | | | ||
| + | {| style="text-align: left; margin:auto;" | ||
| + | |- | ||
| + | | style="text-align: center;" | <math>l_i =\max ({d}_j^T {u}_i)\quad ,\quad i=\xi ,\eta </math> | ||
| + | |} | ||
| + | | style="width: 5px;text-align: right;" | (39a) | ||
| + | |} | ||
| + | |||
| + | with | ||
| + | |||
| + | {| class="formulaSCP" style="width: 100%; text-align: left;" | ||
| + | |- | ||
| + | | | ||
| + | {| style="text-align: left; margin:auto;" | ||
| + | |- | ||
| + | | style="text-align: center;" | <math>\begin{array}{ll}j=1,2,3 \hbox{ (for triangles) and }\\ j=1,2 \hbox{ (for quadrilaterals)}\end{array}</math> | ||
| + | |} | ||
| + | | style="width: 5px;text-align: right;" | (39b) | ||
| + | |} | ||
| + | |||
| + | In Eq.(39a) <math display="inline">{u}_\xi </math> and <math display="inline">{u}_\eta </math> contain the global components of the velocity vectors <math display="inline">\vec u_\xi </math> and <math display="inline">\vec u_\eta </math>, respectively. For triangles <math display="inline">{d}_j</math> are the element side vectors, whereas for quadrilaterals <math display="inline">{d}_j</math> are the element diagonal vectors <span id='citeF-27'></span>[[#cite-27|27]]. | ||
| + | |||
| + | The next step is to transform Eq.(34) to global axes <math display="inline">x,y</math>. The resulting equation is | ||
| + | |||
| + | {| class="formulaSCP" style="width: 100%; text-align: left;" | ||
| + | |- | ||
| + | | | ||
| + | {| style="text-align: left; margin:auto;" | ||
| + | |- | ||
| + | | style="text-align: center;" | <math>-{u}^T {\boldsymbol \nabla }\phi +{\boldsymbol \nabla }^T {D}_G {\boldsymbol \nabla }\phi -s\phi=0 </math> | ||
| + | |} | ||
| + | |} | ||
| + | |||
| + | where the global diffusion matrix <math display="inline">{D}_G</math> is given by | ||
| + | |||
| + | {| class="formulaSCP" style="width: 100%; text-align: left;" | ||
| + | |- | ||
| + | | | ||
| + | {| style="text-align: left; margin:auto;" | ||
| + | |- | ||
| + | | style="text-align: center;" | <math>{D}_G={D}+\bar{D}</math> | ||
| + | |} | ||
| + | | style="width: 5px;text-align: right;" | (41a) | ||
| + | |} | ||
| + | |||
| + | where the global balancing diffusion matrix <math display="inline">\bar{D}</math> is | ||
| + | |||
| + | {| class="formulaSCP" style="width: 100%; text-align: left;" | ||
| + | |- | ||
| + | | | ||
| + | {| style="text-align: left; margin:auto;" | ||
| + | |- | ||
| + | | style="text-align: center;" | <math>\bar {D} = {T}^T \bar {D}^\prime {T}</math> | ||
| + | |} | ||
| + | | style="width: 5px;text-align: right;" | (41b) | ||
| + | |} | ||
| + | |||
| + | ===Remark=== | ||
| + | |||
| + | Similarly as for the 1D problems, a negative value of the parameters <math display="inline">\beta _\xi </math> and <math display="inline">\beta _\eta </math> indicates that no stabilization is needed along the directions <math display="inline">\xi </math> and <math display="inline">\eta </math>, respectively. A zero value of the corresponding stabilization parameter is chosen in this case. | ||
| + | |||
| + | ===Remark=== | ||
| + | |||
| + | The expressions of <math display="inline">\beta _\xi </math> and <math display="inline">\beta _\eta </math> in Eq.(37) can be simplified to | ||
| + | |||
| + | {| class="formulaSCP" style="width: 100%; text-align: left;" | ||
| + | |- | ||
| + | | | ||
| + | {| style="text-align: left; margin:auto;" | ||
| + | |- | ||
| + | | style="text-align: center;" | <math>\begin{array}{l}\beta _\xi \simeq \beta _{\xi _c} =\left[\displaystyle{w_\xi \over 6} +|\gamma _\xi | -1\right]\\ \beta _\eta \simeq \beta _{\eta _c} =\left[\displaystyle{w_\eta \over 6} +|\gamma _\eta | -1\right] \end{array} </math> | ||
| + | |} | ||
| + | | style="width: 5px;text-align: right;" | (42) | ||
| + | |} | ||
| + | |||
| + | This avoids the computation of the sign of the solution and of its first and second derivatives. The expressions of <math display="inline">\beta _{\xi _c}</math> and <math display="inline">\beta _{\eta _c}</math> in Eq.(42) are equivalent to that of the 1D critical stabilization parameter <math display="inline">\beta _c</math> of Eq.(23). The main difference is that the computation of the local directions <math display="inline">\xi </math> and <math display="inline">\eta </math> is still mandatory in the multidimensional case and, therefore, the nonlinearity of the process can not be avoided here. | ||
| + | |||
| + | ===5.1 Computation of the principal curvature axes for linear elements=== | ||
| + | |||
| + | Excellent results have been obtained in our work ''by approximating the main curvature direction <math>\vec \xi </math> by the direction of the gradient vector'' <math display="inline">{\boldsymbol \nabla } \phi </math>. | ||
| + | |||
| + | This simplification allows us to estimate the direction <math display="inline">\vec {\xi }</math> in a very economical manner as the gradient vector <math display="inline">{\boldsymbol \nabla } \bar \phi </math> can be directly computed at any point of a linear element. Direction <math display="inline">\vec {\eta }</math> is taken orthogonal to that of <math display="inline">\vec {\xi }</math> in an anti-clockwise sense. | ||
| + | |||
| + | For linear triangles <math display="inline">{\boldsymbol \nabla }\bar \phi </math> is constant within the element. For four node quadrilaterals <math display="inline">{\boldsymbol \nabla } \bar \phi </math> varies linearly. We have assumed in this case that the direction of <math display="inline">\vec \xi </math> is constant within the element and equal to the direction of vector <math display="inline">{\boldsymbol \nabla } \bar \phi </math> computed at the element center. | ||
| + | |||
| + | The computation of the signs of the second derivative of <math display="inline">\bar \phi </math> in Eq.(38) involves the following steps: 1) recovery of the cartesian first derivative field at the nodes using a nodal averaging procedure; 2) computation of the second derivative tensor at the element center and 3) transformation of this tensor to the local axes <math display="inline">\xi </math> and <math display="inline">\eta </math>. | ||
| + | |||
| + | We note that in problems where positive values of <math display="inline">\bar \phi </math> are prescribed at the Dirichlet boundary, the signs of <math display="inline">S_{\xi _2}</math>, <math display="inline">S_{\eta _2}</math> are positive due to the convexity of the numerical solution. | ||
| + | |||
| + | As mentioned above the dependence of the balancing diffusion matrix <math display="inline">\bar{D}</math> with the principal curvature directions <math display="inline">\vec \xi </math> and <math display="inline">\vec {\eta }</math> introduces a nonlinearity in the solution process. A simple and effective iterative algorithm is described next. | ||
| + | |||
| + | ===5.2 General iterative scheme=== | ||
| + | |||
| + | A stabilized numerical solution can be found by the following algorithm. | ||
| + | |||
| + | '''Step 1''' . For elements in the interior of the domain choose <math display="inline">{}^1{\boldsymbol \xi } ={u}</math>, i.e. the gradient direction is taken coincident with the velocity direction. If <math display="inline">{u}=0</math> then <math display="inline">{}^1{\boldsymbol \xi }</math> is taken coincident with the global <math display="inline">{x}</math> axis. | ||
| + | |||
| + | In elements adjacent to a boundary choose <math display="inline">{}^1{\boldsymbol \xi } ={n }</math> where '''n ''' is the normal to the boundary. | ||
| + | |||
| + | Compute <math display="inline">{}^1{\boldsymbol \eta }, {}^1\bar {D}'</math>, <math display="inline">{}^1\bar {D}</math> and <math display="inline">{}^1{D}_G</math> using the expressions of <math display="inline">\beta _\xi </math> and <math display="inline">\beta _\eta </math> from Eq.(42). | ||
| + | |||
| + | Solve for <math display="inline">{}^1\bar{\boldsymbol \phi }</math>. | ||
| + | |||
| + | Verify that the solution is stable. This implies that there are not undershoots or overshoots in the numerical results with respect to the expected physical values. If the numerical solution is unstable, then go to step 2. | ||
| + | |||
| + | '''Step 2''' . For all elements, compute at the element center <math display="inline">{}^2{\boldsymbol \xi } = {\boldsymbol \nabla }^1\bar \phi </math>. Then compute <math display="inline">{}^2{\boldsymbol \eta } , {}^2\bar{D}'</math>, <math display="inline">{}^2\bar {D}</math> and <math display="inline">{}^2{D}_G</math> using the expressions of <math display="inline">\beta _\xi </math> and <math display="inline">\beta _\eta </math> from Eqs.(37). | ||
| + | |||
| + | Solve for <math display="inline">{}^2\bar{\boldsymbol \phi }</math>. | ||
| + | |||
| + | '''Step 3''' . Estimate the convergence of the process. We have chosen the following convergence norm | ||
| + | |||
| + | {| class="formulaSCP" style="width: 100%; text-align: left;" | ||
| + | |- | ||
| + | | | ||
| + | {| style="text-align: left; margin:auto;" | ||
| + | |- | ||
| + | | style="text-align: center;" | <math>\Vert \phi \Vert = {1\over N\bar \phi _{max}} \left[\sum \limits _{j=1}^n \left({}^{i}\bar \phi _j - {}^{i-1}\bar \phi _j \right)^2 \right]^{1/2} \le \varepsilon </math> | ||
| + | |} | ||
| + | | style="width: 5px;text-align: right;" | (43) | ||
| + | |} | ||
| + | |||
| + | where <math display="inline">N</math> is the total number of nodes in the mesh and <math display="inline">\phi _{max}</math> is the maximum prescribed value at the Dirichlet boundary (if <math display="inline">\bar \phi _{max}=0</math> then <math display="inline">\bar \phi _{max}=1</math>). In above steps the left upper indices denote the iteration number. | ||
| + | |||
| + | In the examples shown in the next section <math display="inline">\varepsilon =10^{-3}</math> has been taken. | ||
| + | |||
| + | If condition (43) is not satisfied, repeat steps 2 and 3 until convergence. | ||
| + | |||
| + | ===Remark=== | ||
| + | |||
| + | For the advective-diffusive problems (i.e. <math display="inline">s=0</math>) the expression of the balancing diffusion matrix in the interior elements for step 1 coincides with the standard (linear) SUPG form <span id='citeF-27'></span>[[#cite-27|27]]. | ||
| + | |||
| + | ===Remark=== | ||
| + | |||
| + | An alternative solution scheme is to use a time relaxation technique based in the solution of a pseudo transient problem with a forward Euler scheme and a diagonal mass matrix. | ||
| + | |||
| + | ==6 1D NUMERICAL EXAMPLES== | ||
| + | |||
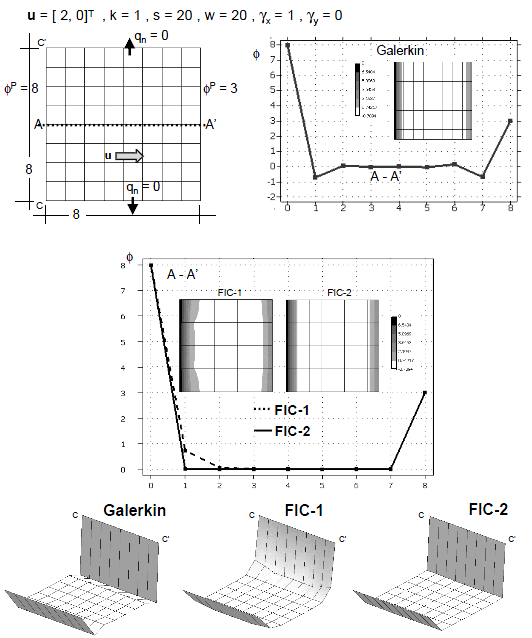
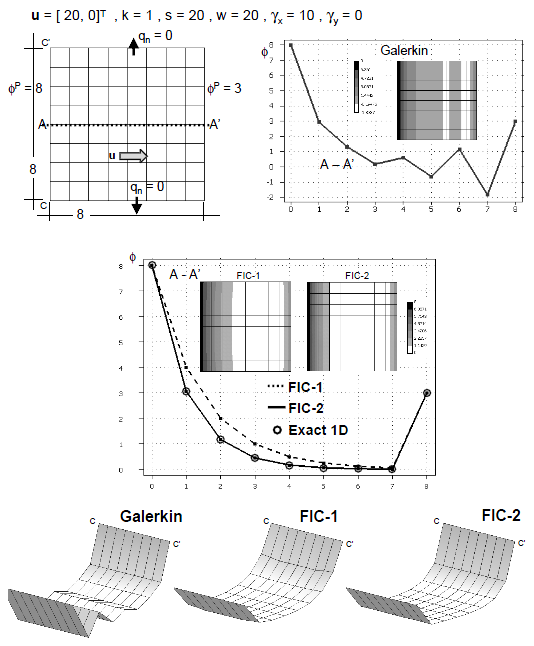
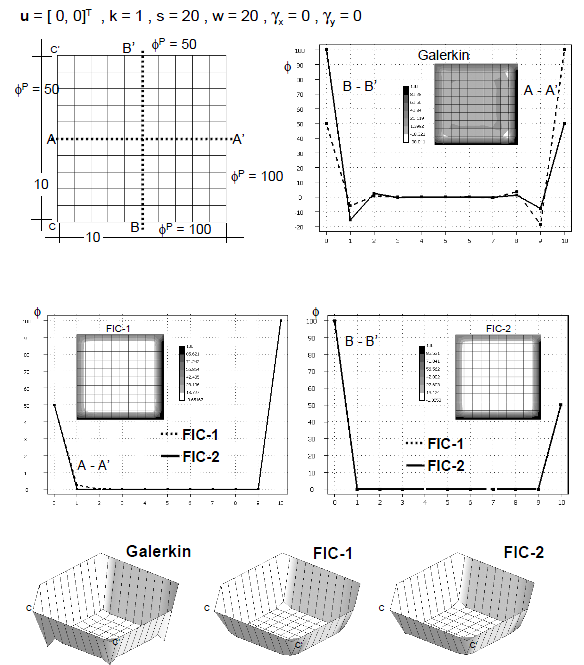
| + | The examples presented in this section are solved in a 1D domain discretized with eight two-node linear elements of unit size. The examples are solved with the same Dirichlet conditions <math display="inline">\phi _1^p =8</math> and <math display="inline">\phi _9^p=3</math> and two different values of <math display="inline">\gamma </math> and <math display="inline">w</math> (<math display="inline">\gamma =1, w=20</math> and <math display="inline">\gamma =10, w=20</math>). We note that for both cases the instability condition (<math display="inline">\beta _c>0</math>) is violated and, hence, the Galerkin solution should yield non-physical results. | ||
| + | |||
| + | Figures 2 and 3 show the numerical results obtained with the standard Galerkin method (<math display="inline">\beta =0</math>) and using the element (<math display="inline">\beta ^e</math>) and critical (<math display="inline">\beta _c</math>) values of the stabilization parameter given by Eqs.(22) and (23), respectively. The exact analytical solution is also shown for comparison. | ||
| + | |||
| + | Table 1 shows the nodal values of the results of the example of Figure 3 for comparison with the 2D solutions presented in the next section. | ||
| + | |||
| + | The following conclusions are drawn from the 1D results. | ||
| + | |||
| + | <ol> | ||
| + | |||
| + | <li>The Galerkin solution (<math display="inline">\beta =0</math>) is unstable for both problems, as expected. </li> | ||
| + | |||
| + | <li>The solution obtained with the critical value <math display="inline">\beta _c</math> is always stable, although it yields slightly overdiffusive results in both cases. </li> | ||
| + | |||
| + | <li>The results obtained with <math display="inline">\beta ^e</math> are less diffusive and more accurate than those obtained with <math display="inline">\beta _c</math>. The explanation is that the sign of the ratio <math display="inline">{S_1/S_2}</math> is negative in the region close to the left end point of the domain. This naturally reduces the value of the stabilizing diffusion parameter <math display="inline">\beta </math> in Eq.(21) with respect to that of <math display="inline">\beta _c</math> in Eq.(23) where the sign effect is not relevant. </li> | ||
| + | |||
| + | <li>The FIC algorithm provides a stabilized solution for Dirichlet problems when there is a negative streamwise gradient of the solution. This is an advantage versus SUPG, GLS and SGS methods using a single stabilization parameter which fail in some cases for these type of problems <span id='citeF-12'></span>[[#cite-12|12]]. </li> | ||
| + | |||
| + | </ol> | ||
| + | |||
| + | Above conclusions have been confirmed in the solution of a wider collection of 1D problems presented in [18]. | ||
| + | {| style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 100%;max-width: 100%;" | ||
| + | |- | ||
| + | |[[Image:draft_Samper_447243531-Fig2.png|450px|]] | ||
| + | |- style="text-align: center;" | ||
| + | | colspan="1" style="text-align: center; font-size: 75%;padding:10px;"| '''Figure 2'''. <math>\phi _1^p=8, \phi _9^p =3, \gamma =1</math> and <math>\omega =20</math>. FIC results for a mesh of 8 linear elements obtained for <math>\beta =0</math> (Galerkin), <math>\beta ^e</math> and <math>\beta _c</math>. Comparison with the analytical solution. | ||
| + | |} | ||
| + | |||
| + | {| style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 100%;max-width: 100%;" | ||
| + | |- | ||
| + | |[[Image:draft_Samper_447243531-Fig6.png|450px|ϕ₁<sup>p</sup>=8, ϕ₉<sup>p</sup>=3, γ=10 and ω=20. FIC results for a mesh of 8 linear elements obtained for β=0 (Galerkin), β<sup>e</sup> and β<sub>c</sub>. Comparison with the analytical solution.]] | ||
| + | |- style="text-align: center;" | ||
| + | | colspan="1" style="text-align: center; font-size: 75%;padding:10px;"| '''Figure 3'''. <math>\phi _1^p =8, \phi _9^p =3, \gamma =10</math> and <math>\omega =20</math>. FIC results for a mesh of 8 linear elements obtained for <math>\beta =0</math> (Galerkin), <math>\beta ^e</math> and <math>\beta _c</math>. Comparison with the analytical solution. | ||
| + | |} | ||
| + | |||
| + | ==7 2D EXAMPLES== | ||
| + | |||
| + | The analysis domain in the first two 2D examples presented is a square of size 8 units. The problems are solved first with relatively coarse meshes of <math display="inline">8\times 8</math> four node bi-linear square elements and <math display="inline">8\times 8\times 2</math> linear triangles. | ||
| + | |||
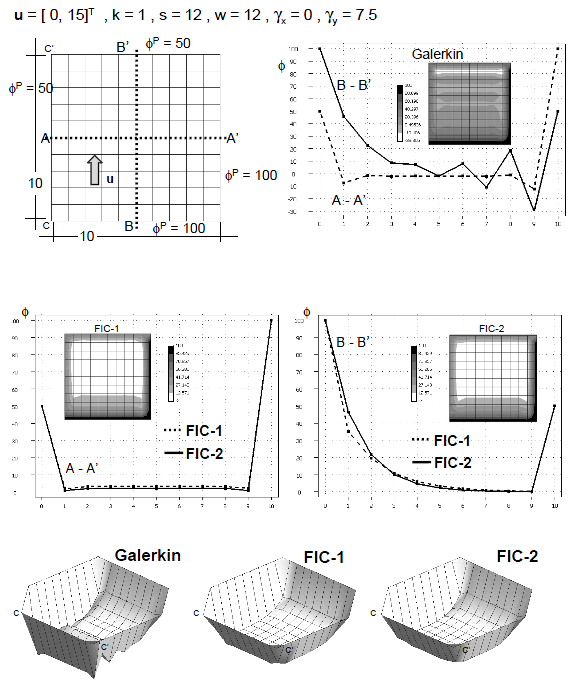
| + | The boundary conditions for both examples are <math display="inline">\phi ^p =8</math> and <math display="inline">\phi ^p =3</math> at the boundaries <math display="inline">x=0</math> and <math display="inline">x=8</math>, respectively and zero normal flux at <math display="inline">y=0</math> and <math display="inline">y=8</math>. This reproduces the condition of the two 1D examples solved in the previous section. The first example is analized for <math display="inline">{u} = [2,0]^T</math>, <math display="inline">k=1</math> and <math display="inline">s=20</math> giving <math display="inline">w=20</math>, <math display="inline">\gamma _x=1</math> and <math display="inline">\gamma _y=0</math> which corresponds to the first 1D example (Figure 2). The correct solution for this problem has a boundary layer in the vecinity of the two sides at <math display="inline">x=0</math> and <math display="inline">x=8</math> where <math display="inline">\phi </math> is prescribed (Figure 4). The numerical results obtained with the standard Galerkin solution are oscillatory as expected. The stabilized FIC formulation elliminates the oscillations and yields the correct physical solution. Good results are obtained for both meshes of linear rectangles and triangles (Figures 4 and 5). | ||
| + | |||
| + | Results labelled as FIC-1 and FIC-2 in the figures correspond to those obtained in the first and second iteration of the algorithm presented in Section 5.2, respectively. We note that the FIC-1 results agree precisely with those obtained in the 1D case for <math display="inline">\beta =\beta _c</math>, whereas the FIC-2 results agree with the more accurate 1D values obtained with the element stabilization parameter <math display="inline">\beta ^e</math> (see Figure 2). | ||
| + | |||
| + | The second example is similar to the first one with <math display="inline">{u} =[20,0]^T</math>, <math display="inline">k=1</math> and <math display="inline">s=20</math> giving <math display="inline">w=20</math>, <math display="inline">\gamma _x =10</math> and <math display="inline">\gamma _y =0</math>. These values correspond to the second 1D problem of the previous section (Figure 3). The Galerkin solution is again oscillatory, whereas the FIC results are physically sound (Figures 6 and 7). Once more the FIC-1 and FIC-2 results are in good agreement with the 1D values shown in Figure 3 for <math display="inline">\beta _c</math> and <math display="inline">\beta _e</math>, respectively for both meshes of square and triangular elements. The coincidence of the 1D and 2D results for this problem can be clearly seen in Table 1. | ||
| + | |||
| + | {| style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 100%;max-width: 100%;" | ||
| + | |- | ||
| + | | | ||
| + | [[File:Draft_Samper_447243531_5062_Fig4.png]] | ||
| + | |- | ||
| + | | colspan="1" style="text-align: center; font-size: 75%;padding:10px;"| '''Figure 4'''. 2D advection-conduction-absorption problem over a square domain of size equal to 8 units. <math>\phi ^p =8</math> at <math>x=0</math>, <math>\phi ^p =3</math> at <math>x=8</math>, <math>q_n =0</math> at <math>y=0</math> and <math>y=8</math>. <math>{u} = [2,0]^T</math>, <math>k=1</math>, <math>s=20</math>, <math>w=20</math>, <math>\gamma _x=1</math> and <math>\gamma _y= 0</math>. Galerkin and FIC solutions for a mesh of <math>8 \times 8</math> four node square elements. | ||
| + | |} | ||
| + | |||
| + | {| style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 100%;max-width: 100%;" | ||
| + | |- | ||
| + | |[[File:Draft_Samper_447243531_5330_Fig5.png]] | ||
| + | |- | ||
| + | | colspan="1" style="text-align: center; font-size: 75%;padding:10px;"| '''Figure 5'''. Solution of problem of Figure 4 with a mesh of <math>8 \times 8\times 2</math> linear triangles. | ||
| + | |} | ||
| + | |||
| + | {| style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 100%;max-width: 100%;" | ||
| + | |- | ||
| + | |[[File:Draft_Samper_447243531_5509_Fig6.png]] | ||
| + | |- | ||
| + | | colspan="1" style="text-align: center; font-size: 75%;padding:10px;"| '''Figure 6'''. 2D advection-conduction-absorption problem over a square domain of size equal to 8 units. <math>\phi ^p =8</math> at <math>x=0</math>, <math>\phi ^p =3</math> at <math>x=8</math>, <math>q_n =0</math> at <math>y=0</math> and <math>y=8</math>. <math>{u} = [20,0]^T</math>, <math>k=1</math>, <math>s=20</math>, <math>w=20</math>, <math>\gamma _x=10</math> and <math>\gamma _y= 0</math>. Galerkin and FIC solutions for a mesh of <math>8 \times 8</math> four node square elements. | ||
| + | |} | ||
| + | |||
| + | {| style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 100%;max-width: 100%;" | ||
| + | |- | ||
| + | |[[File:Draft_Samper_447243531_4066_Fig7.png]] | ||
| + | |- | ||
| + | | colspan="1" style="text-align: center; font-size: 75%;padding:10px;"| '''Figure 7'''. Solution of problem of Figure 5 with a mesh of <math>8 \times 8\times 2</math> linear triangles. | ||
| + | |} | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | |||
| + | {| class="wikitable" style="text-align: center; margin: 1em auto;" | ||
| + | |+ Table. 1 Comparison of 1D and 2D solutions for the advection-diffusion-absorption problem of Figure 3 (<math>\gamma _x =10</math>, <math>w=20</math>) | ||
| + | |- style="border-top: 2px solid;" | ||
| + | | colspan='5' style="border-left: 2px solid;border-right: 2px solid;border-left: 2px solid;border-right: 2px solid;" | '''1D''' | ||
| + | | colspan='4' style="border-left: 2px solid;border-right: 2px solid;border-left: 2px solid;border-right: 2px solid;" | '''2D (nodes along line A-A')''' | ||
| + | |- style="border-top: 2px solid;" | ||
| + | | colspan='5' style="border-left: 2px solid;border-right: 2px solid;border-left: 2px solid;border-right: 2px solid;" | Figure 3 | ||
| + | | colspan='2' style="border-left: 2px solid;border-right: 2px solid;border-left: 2px solid;border-right: 2px solid;" | 4 node quads. (Fig. 6) | ||
| + | | colspan='2' style="border-left: 2px solid;border-right: 2px solid;border-left: 2px solid;border-right: 2px solid;" | 3 node triangles (Fig. 7) | ||
| + | |- style="border-top: 2px solid;" | ||
| + | | style="border-left: 2px solid;border-right: 2px solid;" | Node | ||
| + | | style="border-left: 2px solid;border-right: 2px solid;" | <math>\bar \phi (\beta =0</math>) | ||
| + | | style="border-left: 2px solid;border-right: 2px solid;" | <math>\bar \phi (\beta ^e</math>) | ||
| + | | style="border-left: 2px solid;border-right: 2px solid;" | <math>\bar \phi (\beta _c</math>) | ||
| + | | style="border-left: 2px solid;border-right: 2px solid;" | <math>\phi </math>(exact) | ||
| + | | style="border-left: 2px solid;border-right: 2px solid;" | FIC-1 | ||
| + | | style="border-left: 2px solid;border-right: 2px solid;" | FIC-2 | ||
| + | | style="border-left: 2px solid;border-right: 2px solid;" | FIC-1 | ||
| + | | style="border-left: 2px solid;border-right: 2px solid;" | FIC-2 | ||
| + | |- style="border-top: 2px solid;" | ||
| + | | style="border-left: 2px solid;border-right: 2px solid;" | 1 | ||
| + | | style="border-left: 2px solid;border-right: 2px solid;" | 8,00 | ||
| + | | style="border-left: 2px solid;border-right: 2px solid;" | 8 | ||
| + | | style="border-left: 2px solid;border-right: 2px solid;" | 8 | ||
| + | | style="border-left: 2px solid;border-right: 2px solid;" | 8 | ||
| + | | style="border-left: 2px solid;border-right: 2px solid;" | 8 | ||
| + | | style="border-left: 2px solid;border-right: 2px solid;" | 8 | ||
| + | | style="border-left: 2px solid;border-right: 2px solid;" | 8 | ||
| + | | style="border-left: 2px solid;border-right: 2px solid;" | 8 | ||
| + | |- style="border-top: 2px solid;" | ||
| + | | style="border-left: 2px solid;border-right: 2px solid;" | 2 | ||
| + | | style="border-left: 2px solid;border-right: 2px solid;" | 2,94 | ||
| + | | style="border-left: 2px solid;border-right: 2px solid;" | 3,06 | ||
| + | | style="border-left: 2px solid;border-right: 2px solid;" | 4 | ||
| + | | style="border-left: 2px solid;border-right: 2px solid;" | 3,08 | ||
| + | | style="border-left: 2px solid;border-right: 2px solid;" | 3,99 | ||
| + | | style="border-left: 2px solid;border-right: 2px solid;" | 3,057 | ||
| + | | style="border-left: 2px solid;border-right: 2px solid;" | 4,0 | ||
| + | | style="border-left: 2px solid;border-right: 2px solid;" | 3,059 | ||
| + | |- style="border-top: 2px solid;" | ||
| + | | style="border-left: 2px solid;border-right: 2px solid;" | 3 | ||
| + | | style="border-left: 2px solid;border-right: 2px solid;" | 1,32 | ||
| + | | style="border-left: 2px solid;border-right: 2px solid;" | 1,17 | ||
| + | | style="border-left: 2px solid;border-right: 2px solid;" | 2 | ||
| + | | style="border-left: 2px solid;border-right: 2px solid;" | 1,19 | ||
| + | | style="border-left: 2px solid;border-right: 2px solid;" | 2,00 | ||
| + | | style="border-left: 2px solid;border-right: 2px solid;" | 1,170 | ||
| + | | style="border-left: 2px solid;border-right: 2px solid;" | 2,0 | ||
| + | | style="border-left: 2px solid;border-right: 2px solid;" | 1,167 | ||
| + | |- style="border-top: 2px solid;" | ||
| + | | style="border-left: 2px solid;border-right: 2px solid;" | 4 | ||
| + | | style="border-left: 2px solid;border-right: 2px solid;" | 1,80 | ||
| + | | style="border-left: 2px solid;border-right: 2px solid;" | 0,447 | ||
| + | | style="border-left: 2px solid;border-right: 2px solid;" | 1 | ||
| + | | style="border-left: 2px solid;border-right: 2px solid;" | 0,457 | ||
| + | | style="border-left: 2px solid;border-right: 2px solid;" | 1,00 | ||
| + | | style="border-left: 2px solid;border-right: 2px solid;" | 0,448 | ||
| + | | style="border-left: 2px solid;border-right: 2px solid;" | 1,0 | ||
| + | | style="border-left: 2px solid;border-right: 2px solid;" | 0,452 | ||
| + | |- style="border-top: 2px solid;" | ||
| + | | style="border-left: 2px solid;border-right: 2px solid;" | 5 | ||
| + | | style="border-left: 2px solid;border-right: 2px solid;" | 0,599 | ||
| + | | style="border-left: 2px solid;border-right: 2px solid;" | 0,172 | ||
| + | | style="border-left: 2px solid;border-right: 2px solid;" | 0,5 | ||
| + | | style="border-left: 2px solid;border-right: 2px solid;" | 0,176 | ||
| + | | style="border-left: 2px solid;border-right: 2px solid;" | 0,49 | ||
| + | | style="border-left: 2px solid;border-right: 2px solid;" | 0,172 | ||
| + | | style="border-left: 2px solid;border-right: 2px solid;" | 0,499 | ||
| + | | style="border-left: 2px solid;border-right: 2px solid;" | 0,166 | ||
| + | |- style="border-top: 2px solid;" | ||
| + | | style="border-left: 2px solid;border-right: 2px solid;" | 6 | ||
| + | | style="border-left: 2px solid;border-right: 2px solid;" | -0,633 | ||
| + | | style="border-left: 2px solid;border-right: 2px solid;" | 0,0646 | ||
| + | | style="border-left: 2px solid;border-right: 2px solid;" | 0,25 | ||
| + | | style="border-left: 2px solid;border-right: 2px solid;" | 0,0677 | ||
| + | | style="border-left: 2px solid;border-right: 2px solid;" | 0,248 | ||
| + | | style="border-left: 2px solid;border-right: 2px solid;" | 0,0648 | ||
| + | | style="border-left: 2px solid;border-right: 2px solid;" | 0,2501 | ||
| + | | style="border-left: 2px solid;border-right: 2px solid;" | 0,0681 | ||
| + | |- style="border-top: 2px solid;" | ||
| + | | style="border-left: 2px solid;border-right: 2px solid;" | 7 | ||
| + | | style="border-left: 2px solid;border-right: 2px solid;" | 1,16 | ||
| + | | style="border-left: 2px solid;border-right: 2px solid;" | 0,0264 | ||
| + | | style="border-left: 2px solid;border-right: 2px solid;" | 0,125 | ||
| + | | style="border-left: 2px solid;border-right: 2px solid;" | 0,0261 | ||
| + | | style="border-left: 2px solid;border-right: 2px solid;" | 0,125 | ||
| + | | style="border-left: 2px solid;border-right: 2px solid;" | 0,0255 | ||
| + | | style="border-left: 2px solid;border-right: 2px solid;" | 0,1250 | ||
| + | | style="border-left: 2px solid;border-right: 2px solid;" | 0,0257 | ||
| + | |- style="border-top: 2px solid;" | ||
| + | | style="border-left: 2px solid;border-right: 2px solid;" | 8 | ||
| + | | style="border-left: 2px solid;border-right: 2px solid;" | -1,83 | ||
| + | | style="border-left: 2px solid;border-right: 2px solid;" | 0,0073 | ||
| + | | style="border-left: 2px solid;border-right: 2px solid;" | 0,0625 | ||
| + | | style="border-left: 2px solid;border-right: 2px solid;" | 0,01 | ||
| + | | style="border-left: 2px solid;border-right: 2px solid;" | 0,0615 | ||
| + | | style="border-left: 2px solid;border-right: 2px solid;" | 0,0101 | ||
| + | | style="border-left: 2px solid;border-right: 2px solid;" | 0,0624 | ||
| + | | style="border-left: 2px solid;border-right: 2px solid;" | 0,0072 | ||
| + | |- style="border-top: 2px solid;border-bottom: 2px solid;" | ||
| + | | style="border-left: 2px solid;border-right: 2px solid;" | 9 | ||
| + | | style="border-left: 2px solid;border-right: 2px solid;" | 3 | ||
| + | | style="border-left: 2px solid;border-right: 2px solid;" | 3 | ||
| + | | style="border-left: 2px solid;border-right: 2px solid;" | 3 | ||
| + | | style="border-left: 2px solid;border-right: 2px solid;" | 3 | ||
| + | | style="border-left: 2px solid;border-right: 2px solid;" | 3 | ||
| + | | style="border-left: 2px solid;border-right: 2px solid;" | 3 | ||
| + | | style="border-left: 2px solid;border-right: 2px solid;" | 3 | ||
| + | | style="border-left: 2px solid;border-right: 2px solid;" | 3 | ||
| + | |||
| + | |} | ||
| + | |||
| + | Note that, similarly to the 1D case, the FIC-2 results are more accurate (less diffusive) than those obtained in the first iteration (FIC-1). This is due to the more precise evaluation of <math display="inline">\beta _s</math> and <math display="inline">\beta _\eta </math> in Eqs.(37) accounting for the correct sign of all the terms. | ||
| + | |||
| + | Figures 8–11 show results for the two 2D problems above described solved now with relatively coarse unstructured meshes of linear triangles and quadrilaterals. The effectiveness and accuracy of the FIC iterative scheme is again noticeable in all cases. Note the agreement of the FIC-2 results of Figures 10 and 11 with the exact solution for the equivalent 1D problem of Figure 3. | ||
| + | |||
| + | |||
| + | {| style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 100%;max-width: 100%;" | ||
| + | |- | ||
| + | |[[File:Draft_Samper_447243531_4598_Fig8.png]] | ||
| + | |- | ||
| + | | colspan="1" style="text-align: center; font-size: 75%;padding:10px;"| '''Figure 8'''. Solution of problem of Figure 4 with an unstructured mesh of 209 four node bi-linear quadrilaterals | ||
| + | |} | ||
| + | |||
| + | |||
| + | {| style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 100%;max-width: 100%;" | ||
| + | |- | ||
| + | |[[File:Draft_Samper_447243531_3146_Fig9.png]] | ||
| + | |- | ||
| + | | colspan="1" style="text-align: center; font-size: 75%;padding:10px;" |'''Figure 9'''. Solution of problem of Figure 4 with an unstructured mesh of 176 three node linear triangles | ||
| + | |} | ||
| + | |||
| + | |||
| + | {| style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 100%;max-width: 100%;" | ||
| + | |- | ||
| + | |[[File:Draft_Samper_447243531_4133_Fig10.png]] | ||
| + | |- | ||
| + | | colspan="1" style="text-align: center; font-size: 75%;padding:10px;" |'''Figure 10'''. Solution of problem of Figure 6 with an unstructured mesh of 209 four node bi-linear quadrilaterals | ||
| + | |} | ||
| + | |||
| + | |||
| + | {| style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 100%;max-width: 100%;" | ||
| + | |- | ||
| + | |[[File:Draft_Samper_447243531_5097_Fig11.png]] | ||
| + | |- | ||
| + | | colspan="1" style="text-align: center; font-size: 75%;padding:10px;"| '''Figure 11'''. Solution of problem of Figure 6 with an unstructured mesh of 176 three node triangles | ||
| + | |} | ||
| + | |||
| + | |||
| + | Figure 12 presents the solution of a similar problem where the values of <math display="inline">\phi </math> are prescribed at the four boundaries. The solution domain has now 10 units and the problem is solved first with a mesh of <math display="inline">10\times 10</math> four node square elements. Details of the physical parameters are given in Figure 12. Excellent results are again obtained with the FIC scheme. Similar good results are obtained with a structured mesh of linear triangles (Figure 13) as well as with non structured meshes of linear quadrilateral and triangles (Figures 14 and 15). | ||
| + | |||
| + | {| style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 100%;max-width: 100%;" | ||
| + | |- | ||
| + | |[[File:Draft_Samper_447243531_9361_Fig12.png]] | ||
| + | |- | ||
| + | | colspan="1" style="text-align: center; font-size: 75%;padding:10px;"| '''Figure 12'''. 2D advection-diffusion-absorption problem over a square domain of size equal to 10 units. <math>\phi ^p=50</math> along <math>x=0</math> and <math>y=10</math> and <math>\phi ^p=100</math> along <math>x=10</math> and <math>y=0</math>, <math>{u}= [0,15]^T</math>, <math>k=1</math>, <math>s=12</math>, <math>w=12</math>, <math>\gamma _x=0</math> and <math>\gamma _y= 7.5</math>. Galerkin and FIC solutions for a mesh of <math>10 \times 10</math> four node bi-linear square elements. | ||
| + | |} | ||
| + | |||
| + | {| style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 100%;max-width: 100%;" | ||
| + | |- | ||
| + | |[[File:Draft_Samper_447243531_6440_Fig13.png]] | ||
| + | |- | ||
| + | | colspan="1" style="text-align: center; font-size: 75%;padding:10px;"| '''Figure 13'''. Solution of the problem of Figure 12 with an unstructured mesh of 432 four node bi-linear quadrilaterals | ||
| + | |} | ||
| + | |||
| + | {| style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 100%;max-width: 100%;" | ||
| + | |- | ||
| + | |[[File:Draft_Samper_447243531_3226_Fig14.png]] | ||
| + | |- | ||
| + | | colspan="1" style="text-align: center; font-size: 75%;padding:10px;"| '''Figure 14'''. Solution of problem of Figure 12 with an structured mesh of <math>10\times 10\times 2</math> three node linear triangles | ||
| + | |} | ||
| + | |||
| + | {| style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 100%;max-width: 100%;" | ||
| + | |- | ||
| + | |[[File:Draft_Samper_447243531_6545_Fig15.png]] | ||
| + | |- | ||
| + | | colspan="1" style="text-align: center; font-size: 75%;padding:10px;"| '''Figure 15'''. Solution of problem of Figure 12 with an unstructured mesh of 780 three node triangles | ||
| + | |} | ||
| + | |||
| + | |||
| + | The effectiveness of the FIC scheme for a diffusive-absorptive problem with Dirichlet boundary conditions is shown in Figure 16. The results shown have been obtained with structured meshes of linear quadrilateral and triangles. Note that the four boundary layers are well captured in the first step of the iterative solution. Similar good results have also been obtained with unstructured meshes not shown here. | ||
| + | |||
| + | |||
| + | {| style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 100%;max-width: 100%;" | ||
| + | |- | ||
| + | |[[File:Draft_Samper_447243531_4306_Fig16.png]] | ||
| + | |- | ||
| + | | colspan="1" style="text-align: center; font-size: 75%;padding:10px;"| '''Figure 16'''. Diffusive-absorptive problem over a square domain of size equal to 10 units. <math>\phi ^p=50</math> over <math>x=0</math> and <math>y=10</math> and <math>\phi ^p=100</math> over <math>x=10</math> and <math>y=0</math>, <math>{u}= [0,0]^T</math>, <math>k=1</math>, <math>s=20</math>, <math>w=20</math>, <math>\gamma _x=0</math> and <math>\gamma _y= 0</math>. Galerkin and FIC solutions obtained with structured meshes of four node quadrilaterals and linear triangles. | ||
| + | |} | ||
| + | |||
| + | {| style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 100%;max-width: 100%;" | ||
| + | |- | ||
| + | |[[File:Draft_Samper_447243531_6269_Fig16cont.png]] | ||
| + | |- | ||
| + | | colspan="1" style="text-align: center; font-size: 75%;padding:10px;"| '''Figure 16'''. (cont.) | ||
| + | |} | ||
| + | |||
| + | |||
| + | The final example is a standard benchmark problem of advection-diffusion where sharp layers appear at both the boundary and the interior of the domain. The problem is the advective-diffusive transport of <math display="inline">\phi </math> in a square domain with non uniform Dirichlet conditions, downwards diagonal velocity and zero source terms (i.e. <math display="inline">Q=0</math> and <math display="inline">s=0</math>). Figure 17 displays the SUPG solution and FIC results obtained after two iterations using a structured mesh of <math display="inline">20\times 20</math> linear four node square elements. It is remarkable that the FIC results capture the sharp gradient zones at the boundaries where <math display="inline">\phi </math> is prescribed to zero and at the interior of the domain and elliminate all the spurious oscillations present in the SUPG method. | ||
| + | |||
| + | Similar good results obtained with the FIC method for a wide range of advective-diffusive problems are presented in <span id='citeF-27'></span>[[#cite-27|27]]. Recent applications of the FIC method to incompressible fluid flow problems are reported in [37]. | ||
| + | |||
| + | |||
| + | {| style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 100%;max-width: 100%;" | ||
| + | |- | ||
| + | |[[File:Draft_Samper_447243531_2098_Fig17.png]] | ||
| + | |- | ||
| + | | colspan="1" style="text-align: center; font-size: 75%;padding:10px;"| '''Figure 17'''. Square domain with non uniform Dirichlet conditions, downwards diagonal velocity and zero source. SUPG and FIC solutions obtained with a structured mesh of <math>20\times 20</math> linear four node square elements | ||
| + | |} | ||
| + | |||
| + | ==8 CONCLUSIONS== | ||
| + | |||
| + | The FIC-FEM formulation presented allows to obtain a stabilized and accurate solution for the advection-diffusion-absorption equation. For the 1D problem the formulation is equivalent to adding a non-linear diffusion term to the standard discretized equations which is governed by a single stabilization parameter. The use of the constant critical value of the 1D stabilization parameter provides a stabilized numerical solution in ''a single step''. A more accurate (less diffusive) solution can be obtained using the two step iterative scheme proposed. | ||
| + | |||
| + | The equivalence of the FIC method with a nonlinear stabilizing diffusion term extends naturally to multidimensional problems using structured and unstructured meshes. The key step is to express the governing equations of the FIC formulation in the principal curvature directions of the solution. The resulting FIC equation is equivalent to adding a nonlinear diffusion matrix to the infinitessimal governing equations. The solution process becomes non linear and a simple iterative algorithm has been presented. The approximation of the main principal curvature direction by that of the gradient vector simplifies the computations in the iterative scheme. Excellent results have been obtained for all the 2D problems solved in just two iterations for structured and nonstructured meshes. | ||
| + | |||
| + | It is remarkable that, similarly to the 1D case, good stabilized results are obtained in the first iteration of the scheme proposed (FIC-1 results) and this may be sufficient for many practical cases. More accurate (less diffusive) results are obtained by performing a second iteration at a relatively small additional computational cost. | ||
| + | |||
| + | ==ACKNOWLEDGEMENTS== | ||
| + | |||
| + | The authors also thank Profs. C. Felippa and S.R. Idelsohn for many useful discussions. | ||
| + | |||
| + | This work has been sponsored by the ''Ministerio de Educación y Ciencia of Spain''. Plan Nacional, Project numbers: DPI2001-2193, BIA2003-09078-C02-01, and DPI2004-07410-C03-02. | ||
| + | |||
| + | ==References== | ||
| + | |||
| + | <div id="cite-1"></div> | ||
| + | [[#citeF-1|[1]]] Zienkiewicz O.C. and Taylor R.L. ''The Finite Element Method''. Volume 3. 5th Edition, Butterworth-Heinemann, 2001. | ||
| + | |||
| + | <div id="cite-2"></div> | ||
| + | [[#citeF-2|[2]]] Tezduyar T.E. and Park Y.J. Discontinuity-capturing finite element formulations for nonlinear convection-diffusion-reaction equations. ''Comput. Methods Appl. Mech. Engrg.'', 59, 307–325, 1986. | ||
| + | |||
| + | <div id="cite-3"></div> | ||
| + | [3] Tezduyar T.E., Park Y.J. and Deans H.A. Finite element procedures for time-dependent convection-diffusion-reaction systems. ''Int. J. Num. Meth. Fluids'', 7, 1013–1033, 1987. | ||
| + | |||
| + | <div id="cite-4"></div> | ||
| + | [[#citeF-4|[4]]] Idelsohn S., Nigro N. Storti M. and Buscaglia G. A Petrov-Galerkin formulation for advection-reaction-diffusion problems. ''Comput. Methods Appl. Mech. Engrg.'', 136, 27–46, 1996. | ||
| + | |||
| + | <div id="cite-5"></div> | ||
| + | [[#citeF-5|[5]]] Codina R. Comparison of some finite element methods for solving the diffusion-convection-reaction equation. ''Comput. Methods Appl. Mech. Engrg.'', 156, 186–210, 1998. | ||
| + | |||
| + | <div id="cite-6"></div> | ||
| + | [6] Codina R. On stabilized finite element methods for linear systems of convection-diffusion-reaction equations. ''Comput. Meth. Appl. Mech. Engrg.'', 188, 61–82, 2000. | ||
| + | |||
| + | <div id="cite-7"></div> | ||
| + | [7] Burman E. and Ern A. Nonlinear diffusion and discrete maxium principle for stabilized Galerkin approximations of the convection-diffusion-reaction equation. ''Comput. Meth. Appl. Mech. Engrg.'', 191, 3833–3855, 2002. | ||
| + | |||
| + | <div id="cite-8"></div> | ||
| + | [[#citeF-8|[8]]] Harari I. and Hughes T.J.R. Finite element methods for the Helmholtz equation in an exterior domain: model problems. ''Comput. Meth. Appl. Mech. Engrg.'', 87, 59–96, 1991. | ||
| + | |||
| + | <div id="cite-9"></div> | ||
| + | [9] Harari I. and Hughes T.J.R. Galerkin/least squares finite element methods for the reduced wave equation with non-reflecting boundary conditions in unbounded domains. ''Comput. Meth. Appl. Mech. Engrg.'', 98, 411–454, 1992. | ||
| + | |||
| + | <div id="cite-10"></div> | ||
| + | [10] Harari I. and Hughes T.J.R. Stabilized finite element method for steady advection-diffusion with production. ''Comput. Meth. Appl. Mech. Engrg.'', 115, 165–191, 1994. | ||
| + | |||
| + | <div id="cite-11"></div> | ||
| + | [11] Harari I., Grosh K., Hughes T.J.R., Malhotra M., Pinsky P.M., Stewart J.R. and Thompson L.L. Recent development in finite element methods for structural acoustics. ''Archives of Computational Mechanics in Engineering'', 3, 2-3, 131–309, 1996. | ||
| + | |||
| + | <div id="cite-12"></div> | ||
| + | [[#citeF-12|[12]]] Hauke G. and Garcia-Olivares A. Variational subgrid scale formulations for the advection-diffusion-reaction equation. ''Comput. Methods Appl. Mech. Engrg.'' 2000; 190:6847–6865. | ||
| + | |||
| + | <div id="cite-13"></div> | ||
| + | [13] Hauke G. A simple subgrid scale stabilized method for the advection-diffusion reaction equation. ''Comput. Methods Appl. Mech. Engrg.'' 2002; 191:2925–2947. | ||
| + | |||
| + | <div id="cite-14"></div> | ||
| + | [[#citeF-14|[14]]] Brezzi F., Hauke G., Marin L.D. and Sangalli S. Link-cutting bubbles for the stabilization of convection-diffusion-reaction problems. ''Mathematical Models and Methods in Applied Sciences'', World Scientific Publishing Company, 2002. | ||
| + | |||
| + | <div id="cite-15"></div> | ||
| + | [[#citeF-15|[15]]] Felippa C.A. and Oñate E. Nodally exact Ritz discretization of 1D diffusion-absorption and Helmholtz equations by variational FIC and modified equation methods. Research Report No. PI 237, CIMNE, Barcelona 2004. Submitted to ''Comput. Mechanics''. | ||
| + | |||
| + | <div id="cite-16"></div> | ||
| + | [16] Idelsohn S.R., Heinrich J.C. and Oñate E. Petrov-Galerkin methods for the transient advective-diffusive equation with sharp gradients. ''Int. J. Num. Meth. Engng.'', 39, 1455–1473, 1996. | ||
| + | |||
| + | <div id="cite-17"></div> | ||
| + | [17] Harari I. Stability of semidiscrete advection-diffusion in transient computation. Proceedings of ''6th World Congress on Computational Mechanics'', Beijing, Sept. 2004, Z.H. Yao, M.W. Yuan and W.X. Zhong (Eds.), Tsinghua Univ. Press-Springer. | ||
| + | |||
| + | <div id="cite-18"></div> | ||
| + | [18] Oñate E., Miquel, J. and Hauke, G. Stabilized formulation for the advection-diffusion-reaction equations using finite calculus and linear finite elements. Submittted in ''Comput. Methods Appl. Mech. Engrg.'', March 2005. | ||
| + | |||
| + | <div id="cite-19"></div> | ||
| + | [19] Oñate E. Derivation of stabilized equations for advective-diffusive transport and fluid flow problems. ''Comput. Methods Appl. Mech. Engrg.'', 151 (1-2), 233–267, 1998. | ||
| + | |||
| + | <div id="cite-20"></div> | ||
| + | [20] Oñate E. Possibilities of finite calculus in computational mechanics. ''Int. J. Num. Meth. Engng.'', 60, 255–281, 2004. | ||
| + | |||
| + | <div id="cite-21"></div> | ||
| + | [21] Oñate E., Manzan M. A general procedure for deriving stabilized space-time finite element methods for advective-diffusive problems. ''Int. J. Num. Meth. Fluids'', 31, 203–221, 1999. | ||
| + | |||
| + | <div id="cite-22"></div> | ||
| + | [22] Oñate E., Idelsohn S.R., Zienkiewicz O.C. and Taylor R.L. A finite point method in computational mechanics. Applications to convective transport and fluid flow. ''Int. J. Num. Meth. Engng.'', 39, 3839–3866, 1996. | ||
| + | |||
| + | <div id="cite-23"></div> | ||
| + | [23] Oñate E. A stabilized finite element method for incompressible viscous flows using a finite increment calculus formulation. ''Comput. Methods Appl. Mech. Engrg.'', 182, (1–2), 355–370, 2000. | ||
| + | |||
| + | <div id="cite-24"></div> | ||
| + | [24] Oñate E., García J. A finite element method for fluid-structure interaction with surface waves using a finite calculus formulation. in ''Comput. Methods Appl. Mech. Engrg.'', 191 (6-7), 635-660, 2001. | ||
| + | |||
| + | <div id="cite-25"></div> | ||
| + | [25] Idelsohn S.R., Oñate E. and Del Pin F. A Lagrangian meshless finite element method applied to fluid-structure interaction problems. ''Computers and Structures'', 81, 655–671, 2003. | ||
| + | |||
| + | <div id="cite-26"></div> | ||
| + | [26] Oñate E., Idelsohn S.R., Del Pin F. and Aubry R. The particle finite element method. An overview (PFEM). ''Int. J. Comput. Methods'', 1 (2), 267–307, 2004. | ||
| + | |||
| + | <div id="cite-27"></div> | ||
| + | [[#citeF-27|[27]]] Oñate E., García J. and Idelsohn S.R. Ship Hydrodynamics. ''Encyclopedia of Computational Mechanics'', T. Hughes, R. de Borst and E. Stein (Eds.), Vol. 3, Chapter 18, 579–607, J. Wiley, 2004. | ||
| + | |||
| + | <div id="cite-28"></div> | ||
| + | [28] Oñate E., Taylor R.L., Zienkiewicz O.C. and Rojek J. A residual correction method based on finite calculus. ''Engineering Computations'', 20 (5/6), 629–658, 2003. | ||
| + | |||
| + | <div id="cite-29"></div> | ||
| + | [29] Oñate E., Rojek J., Taylor R.L. and Zienkiewicz O.C. Finite calculus formulation for analysis of incompressible solids using linear triangles and tetrahedra. ''Int. J. Num. Meth. Engng.'', 59 (11), 1473–1500, 2004. | ||
| + | |||
| + | <div id="cite-30"></div> | ||
| + | [30] Oñate E., Zárate F. and Idelsohn S.R. Finite element formulation for convection-diffusion problems with sharp gradients using finite calculus. ''Comput. Meth. Appl. Mech. Engng.'' Submitted Nov. 2004. | ||
| + | |||
| + | <div id="cite-31"></div> | ||
| + | [31] Hughes T.J.R. and Mallet M. A new finite element formulations for computational fluid dynamics: IV. A discontinuity capturing operator for multidimensional advective-diffusive system. ''Comput. Methods Appl. Mech. Engrg.'', 58, 329–336, 1986b. | ||
| + | |||
| + | <div id="cite-32"></div> | ||
| + | [32] Codina R. A discontinuity-capturing crosswind dissipation for the finite element solution of the convection-diffusion equation. ''Comput. Methods Appl. Mech. Engrg.'', 110, 325–342, 1993. | ||
| + | |||
| + | <div id="cite-33"></div> | ||
| + | [33] Hughes T.J.R., Mallet M. and Mizukami A. A new finite element formulation for comptutational fluid dynamics: II Beyond SUPG. ''Comput. Methods Appl. Mech. Engrg.'', 54, 341–355, 1986. | ||
| + | |||
| + | <div id="cite-34"></div> | ||
| + | [34] Galeo A.C. and Dutra do Carmo E.G. A consistent approximate upwind Petrov-Galerkin method for convection-dominated problems. ''Comput. Methods Appl. Mech. Engrg.'', 68, 83–95, 1988. | ||
| + | |||
| + | <div id="cite-35"></div> | ||
| + | [35] Tezduyar T.E. Adaptive determination of the finite element stabilization parameters. ''Proceedings of the ECCOMAS Computational Fluid Dynamics Conference 2001'', Swansea, Wales, UK, CD-Rom, 2001. | ||
| + | |||
| + | <div id="cite-36"></div> | ||
| + | [36] Tezduyar T.E. Computation of moving boundaries and interfaces and stabilization parameters, ''International Journal for Numerical Methods in Fluid'', 43, 555-575, 2003. | ||
| + | |||
| + | <div id="cite-37"></div> | ||
| + | [37] Oñate E., García J., Idelsohn S. and Del Pin F. FIC formulation for finite element analysis of incompressible flows. Eulerian, Lagrangian and ALE approaches. Accepted for publication in ''Computational Methods in Applied Mechanics and Engineering'', 2005. | ||
Latest revision as of 10:56, 10 July 2019
Published in Computers and Fluids, Vol. 36 (1), pp. 92-112, 2007
DOI: 10.1016/j.compfluid.2005.07.003
Abstract
A stabilized finite element method (FEM) for the multidimensional steady state advection-diffusion-absorption equation is presented. The stabilized formulation is based on the modified governing differential equations derived via the Finite Calculus (FIC) method. For 1D problems the stabilization terms act as a nonlinear additional diffusion governed by a single stabilization parameter. It is shown that for multidimensional problems an orthotropic stabilizing diffusion must be added along the principal directions of curvature of the solution. A simple iterative algorithm yielding a stable and accurate solution for all the range of physical parameters and boundary conditions is described. Numerical results for 1D and 2D problems with sharp gradients are presented showing the effectiveness and accuracy of the new stabilized formulation.
1 INTRODUCTION
Considerable effort has been spent in recent years to derive finite element methods (FEM) 1 for the solution of the advection-diffusion-reaction equation. In this work we will focus on the so called exponential regime originated by large absorptive (dissipative) reaction terms. Here the solutions are of the form of real exponential functions. Numerical schemes find difficulties to approximating the sharp gradients appearing in the neighborhood of boundary and internal layers due to high Peclet and/or Damköhler numbers. Non physical oscilaltory solution are found with the standard Galerkin FEM unless some stabilization procedure is used.
Stabilized methods to tackle this problem have been based on streamline-upwind/Petrov-Galerkin (SUPG) 2, Galerkin/least-squares 5, Subgrid Scale (SGS) 5 and Residual Free Bubbles 14 finite element methods. While a single stabilization parameter suffices to yield stabilized (and even nodally exact results) for the one-dimensional (1D) advection-diffusion and the diffusion-reaction equations (Vol. 3 in 1 and 8), this is not the case for the diffusion-advection-reaction equation. Here, in general, two stabilization parameters are needed in order to ensure a stabilized solution for all range of physical parameters and boundary conditions 4. As reported in 12 the SUPG, GLS and SGS methods with a single stabilization parameter fail to obtain a stabilized solution for some specific boundary conditions in the exponential regime with negative (absorption) terms when there is a negative streamwise gradient of the solution.
Oñate et al. [18] have recently presented a stabilized FEM for the advection-diffusion absorption equation based on the use of a single stabilization parameter which has the form of a diffusion term. In [18] the formulation is detailed for 1D problems and only a brief introduction to the multidimensional case is given. This paper extends the ideas presented in [18] and provides evidence of the effectiveness and accuracy of the new formulation to deal with multidimensional advection-diffusion-absorption problems with sharp gradients.
The stabilized formulation is based on the standard Galerkin FEM solution of the modified governing differential equations derived via the Finite Calculus (FIC) method [19–20]. The FIC equations are obtained by expressing the balance of fluxes in a domain of finite size. This introduces additional stabilizing terms in the differential equations of the infinitessimal theory which are a function of the balance domain dimensions. Although the FIC–FEM formulation here presented is general, we will restrict its application in this work to linear finite element approximations only.
The Galerkin FIC-FEM formulation described here introduces naturally an additional nonlinear dissipation term into the discretized equations which is governed by a single stabilization parameter. In the absence of the absorption term the formulation simplifies to the standard Petrov-Galerkin approach for the advection-diffusion problem For the diffusion-absorption case the diffusion-type stabilization term is identical to that recently obtained by Felippa and Oñate using a variational FIC approach 15. The general nonlinear form of the stabilization parameter is a function of the signs of the solution and its first and second derivatives. This introduces a non-linearity in the solution scheme and a simple iterative algorithm is described. A simpler constant expression of the stabilization parameter is also presented.
Details of the 1D formulation and its extension to deal with multidimensional problems are given. For the multidimensional case Oñate et al. 27 have recently shown that a general form of the stabilization parameters can be found by writting the FIC equations along the principal curvature directions of the solution. The resulting FIC-FEM formulation is equivalent in this case (for linear elements) to adding a stabilizing diffusion matrix to the standard infinitessimal equation. The stabilizing diffusion matrix depends on the signs of the solution and its derivatives and on the velocities along the principal curvature directions of the solution. This introduces a nonlinearity in the solution process. We present a simple iterative scheme based in assuming that the main principal curvature direction at each point is coincident with the gradient vector direction. In the last part of the paper we present a collection of 1D and 2D examples showing the effectiveness and accuracy of the new FIC-FEM formulation for different values of the advective and absorptive terms.
2 FIC FORMULATION OF THE 1D STATIONARY ADVECTION-DIFFUSION-ABSORPTION EQUATION
The governing equation for the 1D stationary advection-diffusion-absorption problem can be written in the FIC formulation as
|
|
(1) |
|
|
(2) |
|
|
(3) |
where
|
|
(4) |
In above equations is the state variable, is the problem domain, is the domain length, is the velocity field, is the diffusion, is the absorption, dissipation or destruction source parameter, is a constant source term, and are the prescribed values of the total flux and the unknown function at the Neumann and Dirichlet boundaries and , respectively and is a characteristic length which plays the role of a stabilization parameter. In the 1D problem and consist of four combinations at the end points of the problem domain.
Eqs.(1) and (2) are obtained by expressing the balance of fluxes in an arbitrary 1D domain of finite size within the problem domain and at the Neumann boundary, respectively. The variations of the transported variables within the balance domain are approximated by Taylor series expansions retaining one order higher terms than in the infinitessimal theory [19,20]. The underlined stabilizing terms in Eqs.(1) and (2) emanate from these higher order expansions. Note that as the characteristic length parameter tends to zero the FIC differential equations gradually recover the standard infinitessimal form.
Successful applications of the FIC method to a variety of problems in computational mechanics can be found in [19–30,37].
3 FINITE ELEMENT FORMULATION
We will construct a standard finite element discretization of the 1D analysis domain length with index ranging from 1 to the number of elements 1. The state variable is approximated by over the analysis domain. The approximated variable is interpolated within each element with nodes in the standard manner, i.e.
|
|
(5a) |
with
|
|
(5b) |
where are the element shape functions and are nodal values of the approximate function . Substituting Eq.(5a) into Eqs.(1) and (2) gives
|
|
|
|
(6) |
|
|
(7) |
where and and are the residuals of the approximate solution in the problem domain and on the Neumann and Dirichlet boundaries and , respectively.
The weighted residual form of Eqs.(6)–(8) is written as
|
|
(8) |
where and are test functions satisfying on .
Assuming smooth enough solutions and integrating by parts the term involving in the first integral gives for
|
|
(9) |
The third term in Eq.(10) is computed as the sum of the integrals over the element interiors, therefore allowing for the space derivatives of to be discontinuous. Also in Eq.(10) has been assumed to be constant within each element, (i.e. within ).
The weak form is obtained by integrating by parts the advective and diffusive terms within in the first integral of Eq.(10). This gives
|
|
(10) |
with
|
|
(11) |
where a prime denotes the derivative with respect to the space coordinate.
Wee see clearly that the last term of Eq.(11) introduces within each element an additional diffusion of value .
Substituting expression (5b) into (11) and choosing a Galerkin method with within each element gives the discrete system of FE equations written in the standard matrix form as
|
|
(12) |
where is the vector of nodal unknowns and the element contributions to matrix K and vector are
|
The amount of balancing diffusion in Eq.(14) clearly depends on the (nonlinear) stabilization parameter . The element and critical values of are deduced in the next section for linear two node elements.
We note that the integral of the term in Eq.(15) vanishes after asssembly when and are uniform over a patch of linear elements.
4 COMPUTATION OF THE STABILIZATION PARAMETER FOR LINEAR ELEMENTS
The matrix and the vector for two node linear elements are (for constant values of , and )
|
|
(16a) |
|
|
(16a) |
In Eqs.(16) index denotes element values.
Assuming , a typical stencil for elements of equal size can be written as
|
|
(17) |
where for simplicity a constant value of across the mesh has been assumed. In Eq.(17) and are the Peclet number and a velocity independent dimensionless number, respectively.
From Eq.(17) we deduce
|
|
(18) |
In the vecinity of a sharp gradient zone we can take
|
|
(19) |
where is the maximum value of the approximate function in the patch of elements adjacent to the sharp gradient zone and
|
|
(20) |
where sign denotes the sign of the magnitude within the brackets computed at the patch mid point.
Substituting Eq.(19) into (18) leads to the following expression of the stabilization parameter
|
|
(21) |
The element stabilization parameter is now defined as
|
|
(22) |
where is given by Eq.(21) and the signs , and are computed now at the element mid-point.
It is clear from above that the computation of the stabilization parameter requires the knowledge of the sign of the numerical solution and that of the first and second derivatives of within each element. This necessarily leads to an iterative scheme. A simple algorithm which provides a stabilized and accurate solution in just two steps is presented below.
4.1 Critical stabilization parameter and unstability conditions
The following constant value of over the mesh ensures a stabilized solution for all ranges of and
|
|
(23) |
where is the critical stabilization parameter. Note that corresponds to the maximum value of in Eq.(21) for . A mathematical proof of Eq.(23) is given in [18].
Clearly the value of of Eq.(23) is meaningful only if and this can be taken as an indicator of an unstable solution. Conversely, a value of indicates that no stabilization is needed.
4.2 Iterative solution scheme
The following two steps iterative scheme is proposed in order to obtain a stabilized and accurate solution.
step step
Compute a first stabilized solution using the critical value given by Eq.(23). This ensures a stabilized, although sometimes slightly overdiffusive, solution.
~
step
Compute the signs of the first and second derivatives of within each element. The second derivative field is obtained as follows
|
|
(24) |
where denotes averaged values of the first derivative at node of element . At the boundary nodes the constant value of the derivative of within the element is taken in Eq.(24); i.e. .
Compute the enhanced stabilized solution using the element value of given by Eq.(22).
In all the 1D examples solved the above two steps have sufficed to obtain a converged stabilized and accurate solution [18]. The reason of this is that the signs of the first and second derivative fields typically do not change any further after the second step over the elements adjacent to high gradient zones.
5 EXTENSION TO MULTI-DIMENSIONAL PROBLEMS
Consider the general steady-state advection-diffusion-reaction equation written for the zero constant source case () as
|
|
(25) |
For 2D problems
|
|
(26) |
are respectively the velocity vector, the gradient vector and the diffusivity matrix, respectively. For simplicity we have assumed an isotropic diffusion matrix.
The FIC form of Eq.(25) is written as
|
|
(27) |
where is the original infinitessimal differential equation as defined in Eq.(25).
The Dirichlet and boundary conditions of the FIC formulation are
|
|
(28) |
|
|
(29) |
where is the normal vector to the boundary where the normal flux is prescribed. As usual index denotes the prescribed values.
In Eqs.(27) and (29) is the characteristic vector of the 2D FIC formulation which components play the role of stabilization parameters. The underlined terms in Eqs.(27) and (29) introduce the necessary stability in the numerical solution [19,20,21].
If vector h is taken to be parallel to the velocity u the standard SUPG method is recovered [18–23]. The more general form of h allows to obtain stabilized finite element solutions in the presence of strong gradients of near the boundaries (boundary layers) and within the analysis domain (internal layers) 27. The FIC formulation therefore reproduces the best features of the so called shock-capturing or transverse-dissipation schemes 2.
| Figure 1. Global axes () and principal curvature axes () |
Let us write down the FIC balance equation in the principal curvature axes of the solution (Figure 1). The FIC balance equation is
|
|
(30) |
where are the velocities along the principal axes of curvature and , respectively.
As and are the principal curvature axes of the solution then
|
|
(31) |
Introducing this simplification into Eq.(30) we can rewrite this equation as
|
|
(32a) |
or
|
|
(32b) |
We can see clearly from Eq.(33) that the FIC governing equations introduce orthotropic diffusion parameters of values and along the and axes, respectively with
|
|
(33) |
Also note that the last term of Eq.(32b) will vanish after discretization for linear elements.
Eq.(32b) can be rewritten in matrix form (neglecting the last term) as
|
|
where , , is the “physical” isotropic diffusion matrix and is the balancing diffusion matrix in the local axes and . The form of this matrix is
|
|
(34) |
The velocities along the principal curvature axes and can be obtained by projecting the cartesian velocities into the principal curvature axes and as
|
|
(35) |
where , and is the angle which the axis forms with the axis (Figure 1). Note that as the solution is continuous the principal curvature directions and are orthogonal.
The values of and are computed by considering the solution of two uncoupled 1D problems along the and directions. This gives from Eqs.(21) and (22)
|
|
(37a) |
|
|
(37b) |
where
|
|
(38) |
and is as usual the approximate solution.
The lengths and are taken as the maximum projection of the velocities and along the element sides (for triangles) and the element diagonals (for quadrilaterals), i.e.
|
|
(39a) |
with
|
|
(39b) |
In Eq.(39a) and contain the global components of the velocity vectors and , respectively. For triangles are the element side vectors, whereas for quadrilaterals are the element diagonal vectors 27.
The next step is to transform Eq.(34) to global axes . The resulting equation is
|
|
where the global diffusion matrix is given by
|
|
(41a) |
where the global balancing diffusion matrix is
|
|
(41b) |
Remark
Similarly as for the 1D problems, a negative value of the parameters and indicates that no stabilization is needed along the directions and , respectively. A zero value of the corresponding stabilization parameter is chosen in this case.
Remark
The expressions of and in Eq.(37) can be simplified to
|
|
(42) |
This avoids the computation of the sign of the solution and of its first and second derivatives. The expressions of and in Eq.(42) are equivalent to that of the 1D critical stabilization parameter of Eq.(23). The main difference is that the computation of the local directions and is still mandatory in the multidimensional case and, therefore, the nonlinearity of the process can not be avoided here.
5.1 Computation of the principal curvature axes for linear elements
Excellent results have been obtained in our work by approximating the main curvature direction by the direction of the gradient vector .
This simplification allows us to estimate the direction in a very economical manner as the gradient vector can be directly computed at any point of a linear element. Direction is taken orthogonal to that of in an anti-clockwise sense.
For linear triangles is constant within the element. For four node quadrilaterals varies linearly. We have assumed in this case that the direction of is constant within the element and equal to the direction of vector computed at the element center.
The computation of the signs of the second derivative of in Eq.(38) involves the following steps: 1) recovery of the cartesian first derivative field at the nodes using a nodal averaging procedure; 2) computation of the second derivative tensor at the element center and 3) transformation of this tensor to the local axes and .
We note that in problems where positive values of are prescribed at the Dirichlet boundary, the signs of , are positive due to the convexity of the numerical solution.
As mentioned above the dependence of the balancing diffusion matrix with the principal curvature directions and introduces a nonlinearity in the solution process. A simple and effective iterative algorithm is described next.
5.2 General iterative scheme
A stabilized numerical solution can be found by the following algorithm.
Step 1 . For elements in the interior of the domain choose , i.e. the gradient direction is taken coincident with the velocity direction. If then is taken coincident with the global axis.
In elements adjacent to a boundary choose where n is the normal to the boundary.
Compute , and using the expressions of and from Eq.(42).
Solve for .
Verify that the solution is stable. This implies that there are not undershoots or overshoots in the numerical results with respect to the expected physical values. If the numerical solution is unstable, then go to step 2.
Step 2 . For all elements, compute at the element center . Then compute , and using the expressions of and from Eqs.(37).
Solve for .
Step 3 . Estimate the convergence of the process. We have chosen the following convergence norm
|
|
(43) |
where is the total number of nodes in the mesh and is the maximum prescribed value at the Dirichlet boundary (if then ). In above steps the left upper indices denote the iteration number.
In the examples shown in the next section has been taken.
If condition (43) is not satisfied, repeat steps 2 and 3 until convergence.
Remark
For the advective-diffusive problems (i.e. ) the expression of the balancing diffusion matrix in the interior elements for step 1 coincides with the standard (linear) SUPG form 27.
Remark
An alternative solution scheme is to use a time relaxation technique based in the solution of a pseudo transient problem with a forward Euler scheme and a diagonal mass matrix.
6 1D NUMERICAL EXAMPLES
The examples presented in this section are solved in a 1D domain discretized with eight two-node linear elements of unit size. The examples are solved with the same Dirichlet conditions and and two different values of and ( and ). We note that for both cases the instability condition () is violated and, hence, the Galerkin solution should yield non-physical results.
Figures 2 and 3 show the numerical results obtained with the standard Galerkin method () and using the element () and critical () values of the stabilization parameter given by Eqs.(22) and (23), respectively. The exact analytical solution is also shown for comparison.
Table 1 shows the nodal values of the results of the example of Figure 3 for comparison with the 2D solutions presented in the next section.
The following conclusions are drawn from the 1D results.
- The Galerkin solution () is unstable for both problems, as expected.
- The solution obtained with the critical value is always stable, although it yields slightly overdiffusive results in both cases.
- The results obtained with are less diffusive and more accurate than those obtained with . The explanation is that the sign of the ratio is negative in the region close to the left end point of the domain. This naturally reduces the value of the stabilizing diffusion parameter in Eq.(21) with respect to that of in Eq.(23) where the sign effect is not relevant.
- The FIC algorithm provides a stabilized solution for Dirichlet problems when there is a negative streamwise gradient of the solution. This is an advantage versus SUPG, GLS and SGS methods using a single stabilization parameter which fail in some cases for these type of problems 12.
Above conclusions have been confirmed in the solution of a wider collection of 1D problems presented in [18].
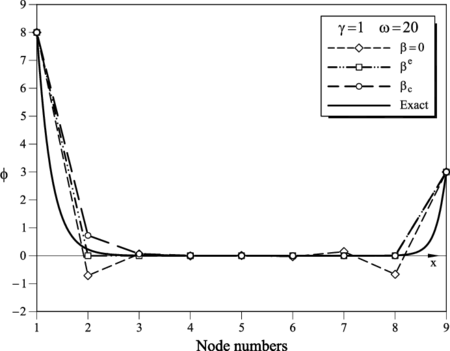
|
| Figure 2. and . FIC results for a mesh of 8 linear elements obtained for (Galerkin), and . Comparison with the analytical solution. |
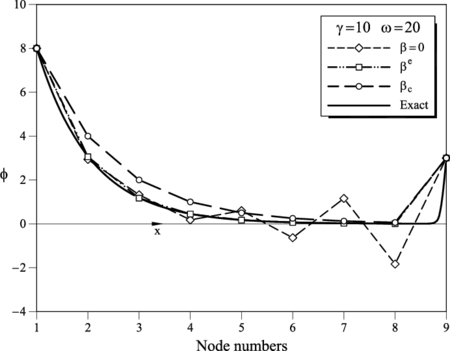
|
| Figure 3. and . FIC results for a mesh of 8 linear elements obtained for (Galerkin), and . Comparison with the analytical solution. |
7 2D EXAMPLES
The analysis domain in the first two 2D examples presented is a square of size 8 units. The problems are solved first with relatively coarse meshes of four node bi-linear square elements and linear triangles.
The boundary conditions for both examples are and at the boundaries and , respectively and zero normal flux at and . This reproduces the condition of the two 1D examples solved in the previous section. The first example is analized for , and giving , and which corresponds to the first 1D example (Figure 2). The correct solution for this problem has a boundary layer in the vecinity of the two sides at and where is prescribed (Figure 4). The numerical results obtained with the standard Galerkin solution are oscillatory as expected. The stabilized FIC formulation elliminates the oscillations and yields the correct physical solution. Good results are obtained for both meshes of linear rectangles and triangles (Figures 4 and 5).
Results labelled as FIC-1 and FIC-2 in the figures correspond to those obtained in the first and second iteration of the algorithm presented in Section 5.2, respectively. We note that the FIC-1 results agree precisely with those obtained in the 1D case for , whereas the FIC-2 results agree with the more accurate 1D values obtained with the element stabilization parameter (see Figure 2).
The second example is similar to the first one with , and giving , and . These values correspond to the second 1D problem of the previous section (Figure 3). The Galerkin solution is again oscillatory, whereas the FIC results are physically sound (Figures 6 and 7). Once more the FIC-1 and FIC-2 results are in good agreement with the 1D values shown in Figure 3 for and , respectively for both meshes of square and triangular elements. The coincidence of the 1D and 2D results for this problem can be clearly seen in Table 1.
| Figure 4. 2D advection-conduction-absorption problem over a square domain of size equal to 8 units. at , at , at and . , , , , and . Galerkin and FIC solutions for a mesh of four node square elements. |
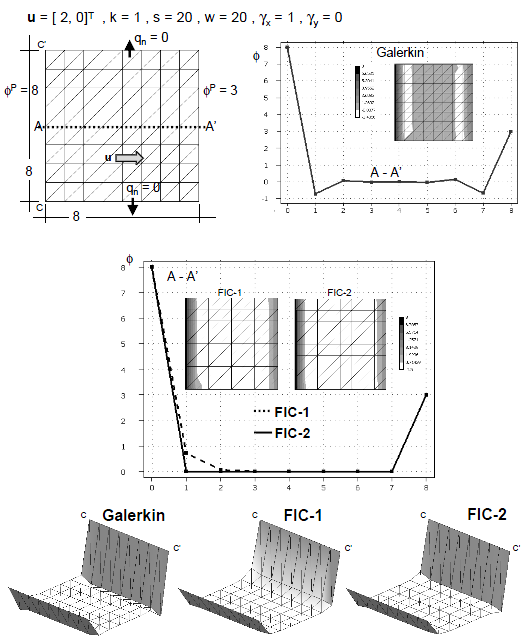
|
| Figure 5. Solution of problem of Figure 4 with a mesh of linear triangles. |
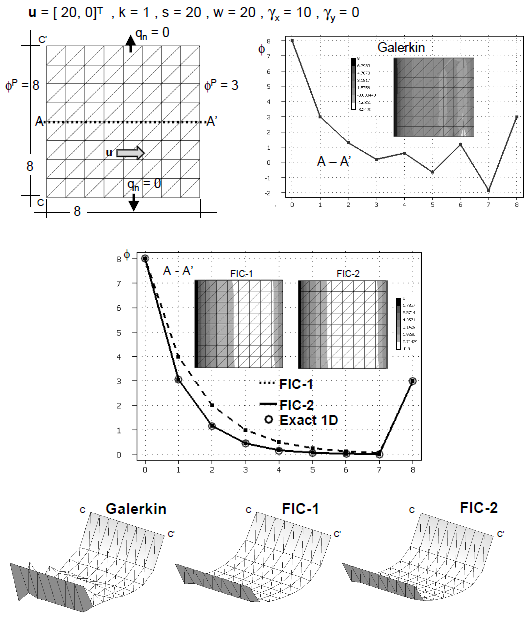
|
| Figure 7. Solution of problem of Figure 5 with a mesh of linear triangles. |
| 1D | 2D (nodes along line A-A') | |||||||
| Figure 3 | 4 node quads. (Fig. 6) | 3 node triangles (Fig. 7) | ||||||
| Node | ) | ) | ) | (exact) | FIC-1 | FIC-2 | FIC-1 | FIC-2 |
| 1 | 8,00 | 8 | 8 | 8 | 8 | 8 | 8 | 8 |
| 2 | 2,94 | 3,06 | 4 | 3,08 | 3,99 | 3,057 | 4,0 | 3,059 |
| 3 | 1,32 | 1,17 | 2 | 1,19 | 2,00 | 1,170 | 2,0 | 1,167 |
| 4 | 1,80 | 0,447 | 1 | 0,457 | 1,00 | 0,448 | 1,0 | 0,452 |
| 5 | 0,599 | 0,172 | 0,5 | 0,176 | 0,49 | 0,172 | 0,499 | 0,166 |
| 6 | -0,633 | 0,0646 | 0,25 | 0,0677 | 0,248 | 0,0648 | 0,2501 | 0,0681 |
| 7 | 1,16 | 0,0264 | 0,125 | 0,0261 | 0,125 | 0,0255 | 0,1250 | 0,0257 |
| 8 | -1,83 | 0,0073 | 0,0625 | 0,01 | 0,0615 | 0,0101 | 0,0624 | 0,0072 |
| 9 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 |
Note that, similarly to the 1D case, the FIC-2 results are more accurate (less diffusive) than those obtained in the first iteration (FIC-1). This is due to the more precise evaluation of and in Eqs.(37) accounting for the correct sign of all the terms.
Figures 8–11 show results for the two 2D problems above described solved now with relatively coarse unstructured meshes of linear triangles and quadrilaterals. The effectiveness and accuracy of the FIC iterative scheme is again noticeable in all cases. Note the agreement of the FIC-2 results of Figures 10 and 11 with the exact solution for the equivalent 1D problem of Figure 3.
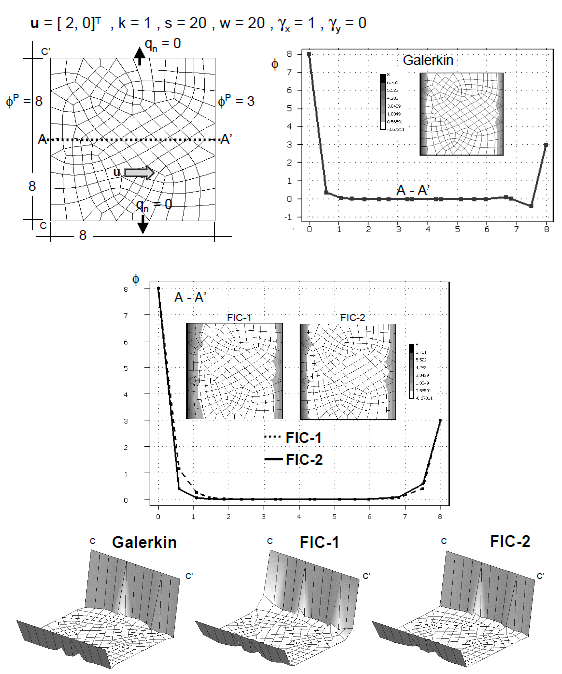
|
| Figure 8. Solution of problem of Figure 4 with an unstructured mesh of 209 four node bi-linear quadrilaterals |
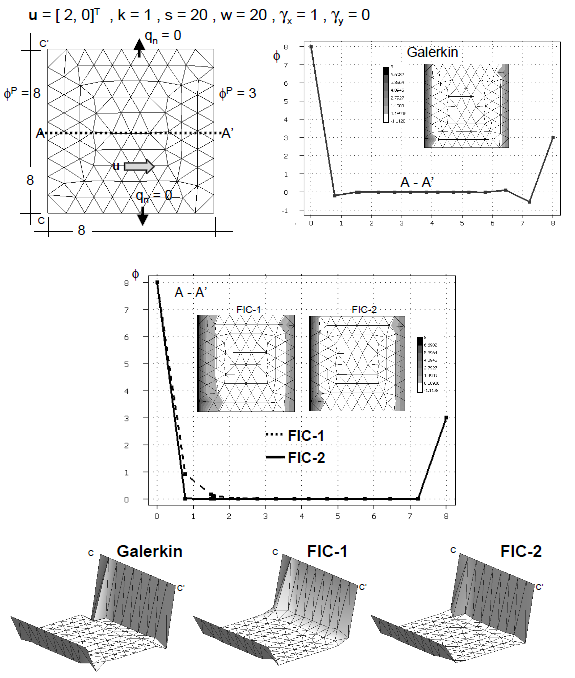
|
| Figure 9. Solution of problem of Figure 4 with an unstructured mesh of 176 three node linear triangles |
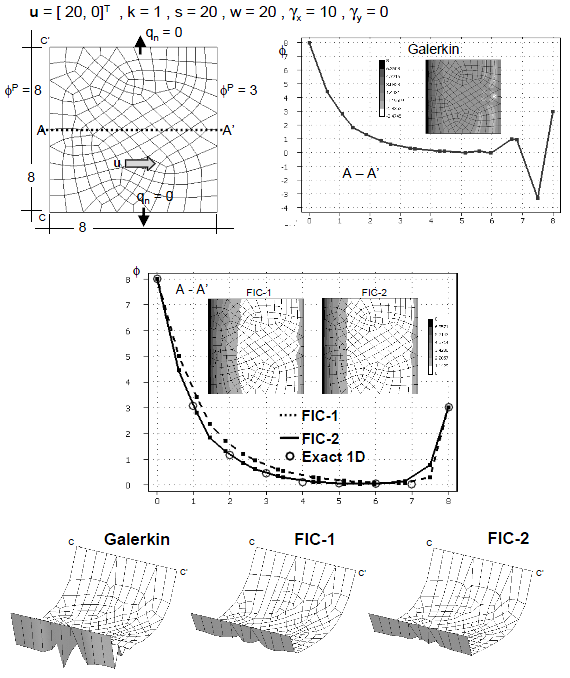
|
| Figure 10. Solution of problem of Figure 6 with an unstructured mesh of 209 four node bi-linear quadrilaterals |
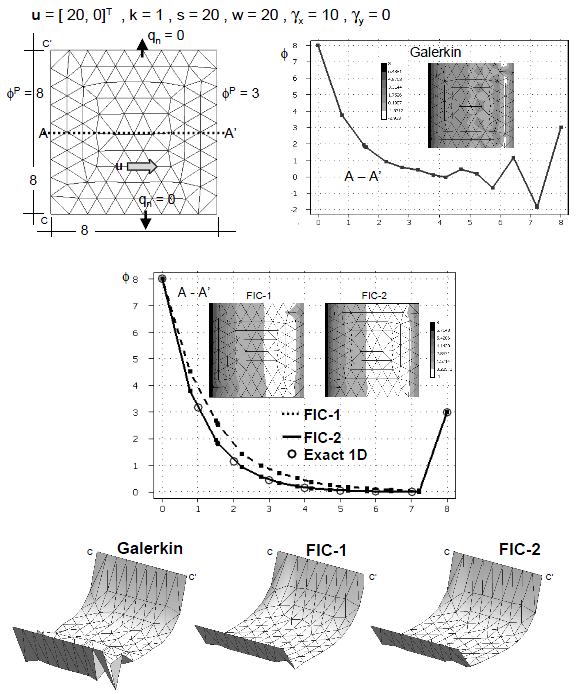
|
| Figure 11. Solution of problem of Figure 6 with an unstructured mesh of 176 three node triangles |
Figure 12 presents the solution of a similar problem where the values of are prescribed at the four boundaries. The solution domain has now 10 units and the problem is solved first with a mesh of four node square elements. Details of the physical parameters are given in Figure 12. Excellent results are again obtained with the FIC scheme. Similar good results are obtained with a structured mesh of linear triangles (Figure 13) as well as with non structured meshes of linear quadrilateral and triangles (Figures 14 and 15).
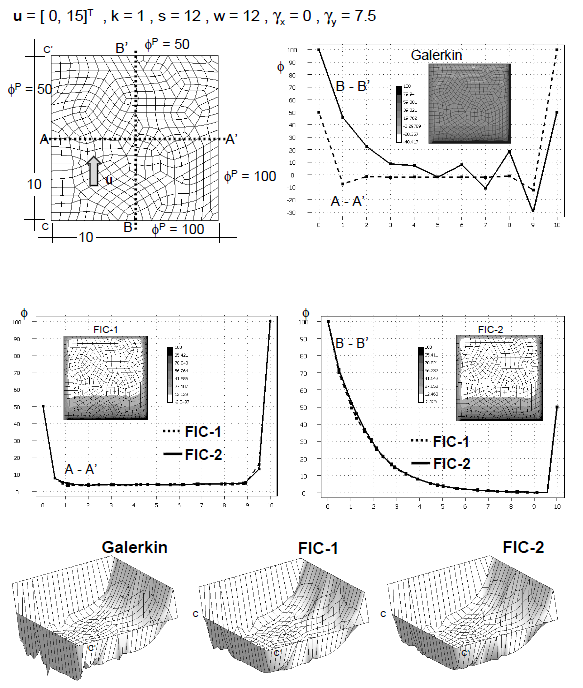
|
| Figure 13. Solution of the problem of Figure 12 with an unstructured mesh of 432 four node bi-linear quadrilaterals |
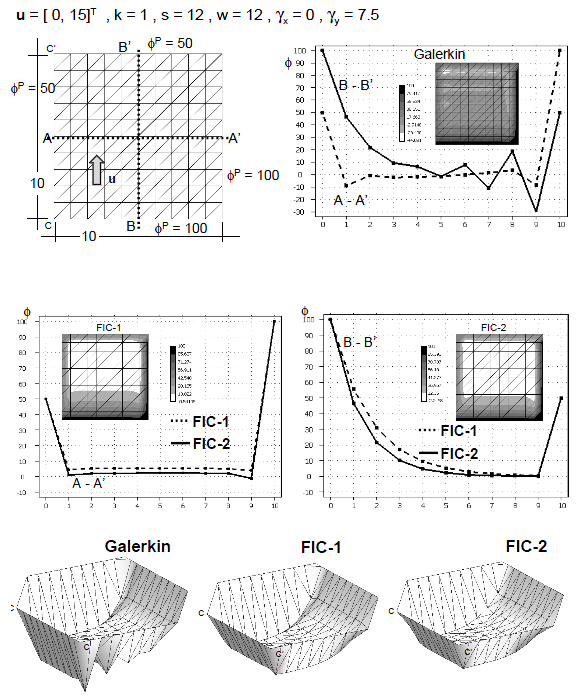
|
| Figure 14. Solution of problem of Figure 12 with an structured mesh of three node linear triangles |
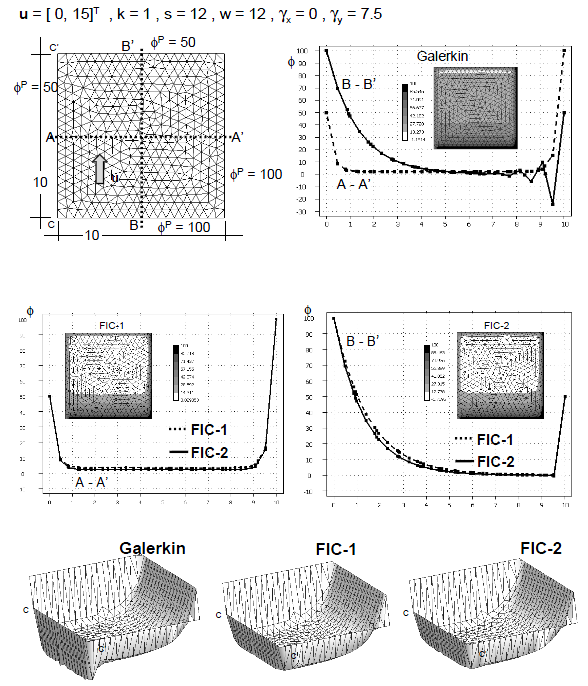
|
| Figure 15. Solution of problem of Figure 12 with an unstructured mesh of 780 three node triangles |
The effectiveness of the FIC scheme for a diffusive-absorptive problem with Dirichlet boundary conditions is shown in Figure 16. The results shown have been obtained with structured meshes of linear quadrilateral and triangles. Note that the four boundary layers are well captured in the first step of the iterative solution. Similar good results have also been obtained with unstructured meshes not shown here.
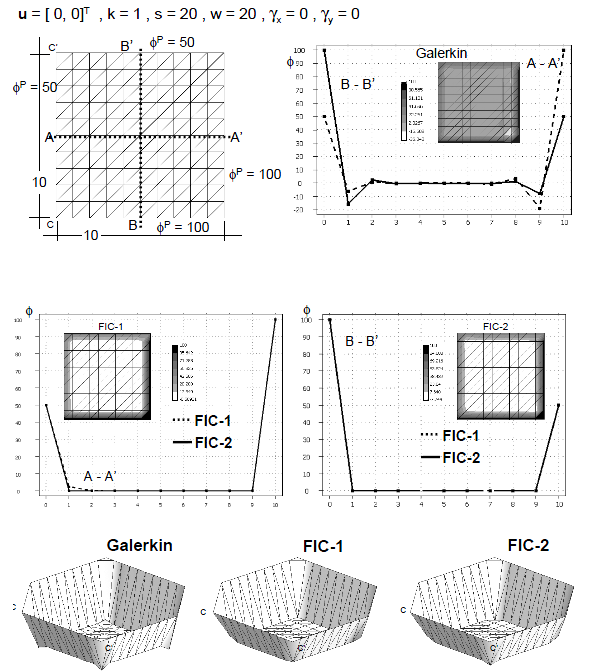
|
| Figure 16. (cont.) |
The final example is a standard benchmark problem of advection-diffusion where sharp layers appear at both the boundary and the interior of the domain. The problem is the advective-diffusive transport of in a square domain with non uniform Dirichlet conditions, downwards diagonal velocity and zero source terms (i.e. and ). Figure 17 displays the SUPG solution and FIC results obtained after two iterations using a structured mesh of linear four node square elements. It is remarkable that the FIC results capture the sharp gradient zones at the boundaries where is prescribed to zero and at the interior of the domain and elliminate all the spurious oscillations present in the SUPG method.
Similar good results obtained with the FIC method for a wide range of advective-diffusive problems are presented in 27. Recent applications of the FIC method to incompressible fluid flow problems are reported in [37].
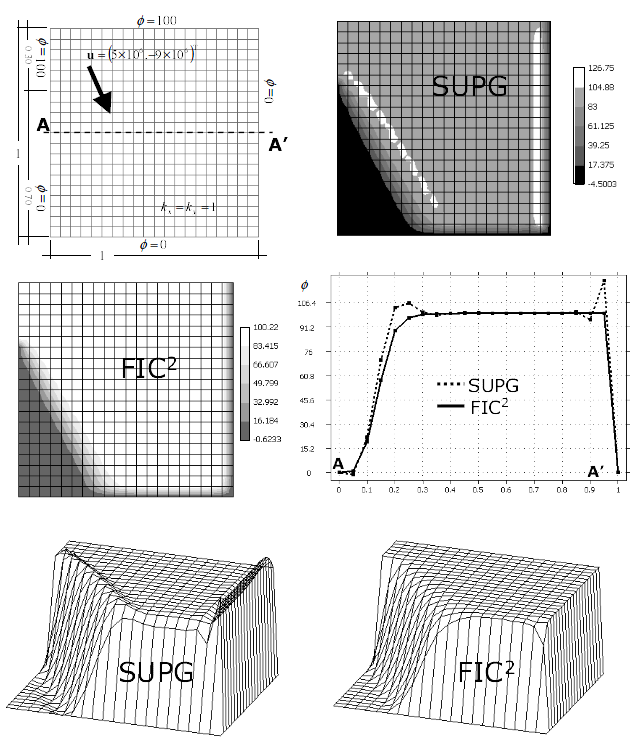
|
| Figure 17. Square domain with non uniform Dirichlet conditions, downwards diagonal velocity and zero source. SUPG and FIC solutions obtained with a structured mesh of linear four node square elements |
8 CONCLUSIONS
The FIC-FEM formulation presented allows to obtain a stabilized and accurate solution for the advection-diffusion-absorption equation. For the 1D problem the formulation is equivalent to adding a non-linear diffusion term to the standard discretized equations which is governed by a single stabilization parameter. The use of the constant critical value of the 1D stabilization parameter provides a stabilized numerical solution in a single step. A more accurate (less diffusive) solution can be obtained using the two step iterative scheme proposed.
The equivalence of the FIC method with a nonlinear stabilizing diffusion term extends naturally to multidimensional problems using structured and unstructured meshes. The key step is to express the governing equations of the FIC formulation in the principal curvature directions of the solution. The resulting FIC equation is equivalent to adding a nonlinear diffusion matrix to the infinitessimal governing equations. The solution process becomes non linear and a simple iterative algorithm has been presented. The approximation of the main principal curvature direction by that of the gradient vector simplifies the computations in the iterative scheme. Excellent results have been obtained for all the 2D problems solved in just two iterations for structured and nonstructured meshes.
It is remarkable that, similarly to the 1D case, good stabilized results are obtained in the first iteration of the scheme proposed (FIC-1 results) and this may be sufficient for many practical cases. More accurate (less diffusive) results are obtained by performing a second iteration at a relatively small additional computational cost.
ACKNOWLEDGEMENTS
The authors also thank Profs. C. Felippa and S.R. Idelsohn for many useful discussions.
This work has been sponsored by the Ministerio de Educación y Ciencia of Spain. Plan Nacional, Project numbers: DPI2001-2193, BIA2003-09078-C02-01, and DPI2004-07410-C03-02.
References
[1] Zienkiewicz O.C. and Taylor R.L. The Finite Element Method. Volume 3. 5th Edition, Butterworth-Heinemann, 2001.
[2] Tezduyar T.E. and Park Y.J. Discontinuity-capturing finite element formulations for nonlinear convection-diffusion-reaction equations. Comput. Methods Appl. Mech. Engrg., 59, 307–325, 1986.
[3] Tezduyar T.E., Park Y.J. and Deans H.A. Finite element procedures for time-dependent convection-diffusion-reaction systems. Int. J. Num. Meth. Fluids, 7, 1013–1033, 1987.
[4] Idelsohn S., Nigro N. Storti M. and Buscaglia G. A Petrov-Galerkin formulation for advection-reaction-diffusion problems. Comput. Methods Appl. Mech. Engrg., 136, 27–46, 1996.
[5] Codina R. Comparison of some finite element methods for solving the diffusion-convection-reaction equation. Comput. Methods Appl. Mech. Engrg., 156, 186–210, 1998.
[6] Codina R. On stabilized finite element methods for linear systems of convection-diffusion-reaction equations. Comput. Meth. Appl. Mech. Engrg., 188, 61–82, 2000.
[7] Burman E. and Ern A. Nonlinear diffusion and discrete maxium principle for stabilized Galerkin approximations of the convection-diffusion-reaction equation. Comput. Meth. Appl. Mech. Engrg., 191, 3833–3855, 2002.
[8] Harari I. and Hughes T.J.R. Finite element methods for the Helmholtz equation in an exterior domain: model problems. Comput. Meth. Appl. Mech. Engrg., 87, 59–96, 1991.
[9] Harari I. and Hughes T.J.R. Galerkin/least squares finite element methods for the reduced wave equation with non-reflecting boundary conditions in unbounded domains. Comput. Meth. Appl. Mech. Engrg., 98, 411–454, 1992.
[10] Harari I. and Hughes T.J.R. Stabilized finite element method for steady advection-diffusion with production. Comput. Meth. Appl. Mech. Engrg., 115, 165–191, 1994.
[11] Harari I., Grosh K., Hughes T.J.R., Malhotra M., Pinsky P.M., Stewart J.R. and Thompson L.L. Recent development in finite element methods for structural acoustics. Archives of Computational Mechanics in Engineering, 3, 2-3, 131–309, 1996.
[12] Hauke G. and Garcia-Olivares A. Variational subgrid scale formulations for the advection-diffusion-reaction equation. Comput. Methods Appl. Mech. Engrg. 2000; 190:6847–6865.
[13] Hauke G. A simple subgrid scale stabilized method for the advection-diffusion reaction equation. Comput. Methods Appl. Mech. Engrg. 2002; 191:2925–2947.
[14] Brezzi F., Hauke G., Marin L.D. and Sangalli S. Link-cutting bubbles for the stabilization of convection-diffusion-reaction problems. Mathematical Models and Methods in Applied Sciences, World Scientific Publishing Company, 2002.
[15] Felippa C.A. and Oñate E. Nodally exact Ritz discretization of 1D diffusion-absorption and Helmholtz equations by variational FIC and modified equation methods. Research Report No. PI 237, CIMNE, Barcelona 2004. Submitted to Comput. Mechanics.
[16] Idelsohn S.R., Heinrich J.C. and Oñate E. Petrov-Galerkin methods for the transient advective-diffusive equation with sharp gradients. Int. J. Num. Meth. Engng., 39, 1455–1473, 1996.
[17] Harari I. Stability of semidiscrete advection-diffusion in transient computation. Proceedings of 6th World Congress on Computational Mechanics, Beijing, Sept. 2004, Z.H. Yao, M.W. Yuan and W.X. Zhong (Eds.), Tsinghua Univ. Press-Springer.
[18] Oñate E., Miquel, J. and Hauke, G. Stabilized formulation for the advection-diffusion-reaction equations using finite calculus and linear finite elements. Submittted in Comput. Methods Appl. Mech. Engrg., March 2005.
[19] Oñate E. Derivation of stabilized equations for advective-diffusive transport and fluid flow problems. Comput. Methods Appl. Mech. Engrg., 151 (1-2), 233–267, 1998.
[20] Oñate E. Possibilities of finite calculus in computational mechanics. Int. J. Num. Meth. Engng., 60, 255–281, 2004.
[21] Oñate E., Manzan M. A general procedure for deriving stabilized space-time finite element methods for advective-diffusive problems. Int. J. Num. Meth. Fluids, 31, 203–221, 1999.
[22] Oñate E., Idelsohn S.R., Zienkiewicz O.C. and Taylor R.L. A finite point method in computational mechanics. Applications to convective transport and fluid flow. Int. J. Num. Meth. Engng., 39, 3839–3866, 1996.
[23] Oñate E. A stabilized finite element method for incompressible viscous flows using a finite increment calculus formulation. Comput. Methods Appl. Mech. Engrg., 182, (1–2), 355–370, 2000.
[24] Oñate E., García J. A finite element method for fluid-structure interaction with surface waves using a finite calculus formulation. in Comput. Methods Appl. Mech. Engrg., 191 (6-7), 635-660, 2001.
[25] Idelsohn S.R., Oñate E. and Del Pin F. A Lagrangian meshless finite element method applied to fluid-structure interaction problems. Computers and Structures, 81, 655–671, 2003.
[26] Oñate E., Idelsohn S.R., Del Pin F. and Aubry R. The particle finite element method. An overview (PFEM). Int. J. Comput. Methods, 1 (2), 267–307, 2004.
[27] Oñate E., García J. and Idelsohn S.R. Ship Hydrodynamics. Encyclopedia of Computational Mechanics, T. Hughes, R. de Borst and E. Stein (Eds.), Vol. 3, Chapter 18, 579–607, J. Wiley, 2004.
[28] Oñate E., Taylor R.L., Zienkiewicz O.C. and Rojek J. A residual correction method based on finite calculus. Engineering Computations, 20 (5/6), 629–658, 2003.
[29] Oñate E., Rojek J., Taylor R.L. and Zienkiewicz O.C. Finite calculus formulation for analysis of incompressible solids using linear triangles and tetrahedra. Int. J. Num. Meth. Engng., 59 (11), 1473–1500, 2004.
[30] Oñate E., Zárate F. and Idelsohn S.R. Finite element formulation for convection-diffusion problems with sharp gradients using finite calculus. Comput. Meth. Appl. Mech. Engng. Submitted Nov. 2004.
[31] Hughes T.J.R. and Mallet M. A new finite element formulations for computational fluid dynamics: IV. A discontinuity capturing operator for multidimensional advective-diffusive system. Comput. Methods Appl. Mech. Engrg., 58, 329–336, 1986b.
[32] Codina R. A discontinuity-capturing crosswind dissipation for the finite element solution of the convection-diffusion equation. Comput. Methods Appl. Mech. Engrg., 110, 325–342, 1993.
[33] Hughes T.J.R., Mallet M. and Mizukami A. A new finite element formulation for comptutational fluid dynamics: II Beyond SUPG. Comput. Methods Appl. Mech. Engrg., 54, 341–355, 1986.
[34] Galeo A.C. and Dutra do Carmo E.G. A consistent approximate upwind Petrov-Galerkin method for convection-dominated problems. Comput. Methods Appl. Mech. Engrg., 68, 83–95, 1988.
[35] Tezduyar T.E. Adaptive determination of the finite element stabilization parameters. Proceedings of the ECCOMAS Computational Fluid Dynamics Conference 2001, Swansea, Wales, UK, CD-Rom, 2001.
[36] Tezduyar T.E. Computation of moving boundaries and interfaces and stabilization parameters, International Journal for Numerical Methods in Fluid, 43, 555-575, 2003.
[37] Oñate E., García J., Idelsohn S. and Del Pin F. FIC formulation for finite element analysis of incompressible flows. Eulerian, Lagrangian and ALE approaches. Accepted for publication in Computational Methods in Applied Mechanics and Engineering, 2005.
Document information
Published on 01/01/2007
DOI: 10.1016/j.compfluid.2005.07.003
Licence: CC BY-NC-SA license
Share this document
claim authorship
Are you one of the authors of this document?