Aolivaresg (talk | contribs) |
|||
| (44 intermediate revisions by 4 users not shown) | |||
| Line 1: | Line 1: | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
==Resumen== | ==Resumen== | ||
| − | + | Los sistemas hidráulicos encargados de la distribución de agua a los usuarios tienen un rol importante en su calidad de vida. Por ello, la determinación de manera precisa del factor de fricción en tuberías, es de gran importancia en el diseño de redes de distribución de agua debido a que influye directamente en el cálculo de caídas de presión (pérdidas de carga) en los sistemas hidráulicos. El objetivo del presente trabajo fue evaluar en forma experimental diferentes correlaciones que describan, mediante una forma explícita, el factor de fricción en una tubería bajo flujo turbulento y la correlación implícita de Colebrook-White. Esto se realizó mediante la comparación de valores numéricos predichos por las correlaciones respecto al valor experimental, encontrándose que la correlación de Colebrook-White predice el factor de fricción con menor porcentaje de error de las 27 correlaciones estudiadas. Para la solución de la ecuación de Colebrook-White se utilizó el método de Newton-Raphson, dado que ésta presenta una estructura recurrente que puede ser llevada a algoritmos y resuelta rápidamente mediante programas computacionales. En este trabajo se desarrolló una herramienta en lenguaje de programación C++ para resolver la ecuación de Colebrook-White.''' | |
| − | '''Palabras clave''': Factor de | + | '''Palabras clave''': Factor de fricción, ecuación de Darcy-Weisbach, ecuación de Colebrook-White, caída de presión en tuberías, correlaciones para evaluar factor de fricción |
| − | + | ||
| − | + | ||
| − | + | ||
==Abstract== | ==Abstract== | ||
| − | + | The hydraulic systems that distribute water to users have an important role in their quality of life. For this reason, the precise determination of the friction factor in pipes is of great importance in the design of water distribution networks because it directly influences the calculation of pressure drop (head losses) in hydraulic systems. The objective of the present work was to evaluate in an experimental manner different correlations that describe, in an explicit form, the friction factor in a pipe under turbulent flow and the implicit Colebrook-White correlation. This was done by comparing the numerical values predicted by the correlations in regard to the experimental value, finding that the Colebrook-White correlation predicts the friction factor with the lowest error percentage among the 27 correlations studied. For the solution of the Colebrook-White equation the Newton-Raphson method was used, given that it presents a recurrent structure that can be taken to algorithms and quickly solved by computer programs. In this work, a tool was developed in the C ++ programming language to solve the Colebrook-White equation. | |
| − | ''' | + | '''Keyvords''': Friction factor, Darcy-Weisbach equation, Colebrook-White equation, pressure drop in pipes, correlation for the friction factor evaluation |
| − | =1. Introducción= | + | ==1. Introducción== |
| − | En la actualidad el manejo de los recursos hídricos es importante, por lo tanto los sistemas hidráulicos que lo distribuyen a las personas, tienen un rol fundamental [1]. En los sistemas hidráulicos, específicamente en las tuberías y diferentes singularidades, siempre ocurre fricción, ocasionando caídas de presión en el flujo a lo largo de su trayectoria. Es importante conocer esta caída de presión, para una apropiada estimación de las presiones de trabajo en los sistemas hidráulicos, por ello se han efectuado diferentes estudios para su determinación y evaluación [2]. Por ello, la determinación de manera precisa del factor de fricción en tuberías es de gran importancia en el diseño de sistemas de conducción y distribución de agua [3]. En el diseño, la longitud de tuberías permanece como parámetro constante e independiente del factor de fricción en los distintos tramos de las redes de agua. En contraste a esto, varios parámetros tales como el diámetro de la tubería y el factor de fricción varían durante la vida útil de las conducciones [4]. Al realizar el análisis de las pérdidas de carga en los sistemas de distribución de agua, se debe tener en cuenta que el factor de fricción es calculado para tres estados del flujo, esto es, flujo laminar, transición y turbulento. Para el flujo laminar el factor de fricción es expresado en forma explícita a través de una simple ecuación (1) | + | En la actualidad el manejo de los recursos hídricos es importante, por lo tanto los sistemas hidráulicos que lo distribuyen a las personas, tienen un rol fundamental [1]. En los sistemas hidráulicos, específicamente en las tuberías y diferentes singularidades, siempre ocurre fricción, ocasionando caídas de presión en el flujo a lo largo de su trayectoria. Es importante conocer esta caída de presión, para una apropiada estimación de las presiones de trabajo en los sistemas hidráulicos, por ello se han efectuado diferentes estudios para su determinación y evaluación [2]. Por ello, la determinación de manera precisa del factor de fricción en tuberías es de gran importancia en el diseño de sistemas de conducción y distribución de agua [3]. En el diseño, la longitud de tuberías permanece como parámetro constante e independiente del factor de fricción en los distintos tramos de las redes de agua. En contraste a esto, varios parámetros tales como el diámetro de la tubería y el factor de fricción varían durante la vida útil de las conducciones [4]. Al realizar el análisis de las pérdidas de carga en los sistemas de distribución de agua, se debe tener en cuenta que el factor de fricción es calculado para tres estados del flujo, esto es, flujo laminar, transición y turbulento. Para el flujo laminar el factor de fricción es expresado en forma explícita a través de una simple ecuación (1) |
{| class="formulaSCP" style="width: 100%; text-align: center;" | {| class="formulaSCP" style="width: 100%; text-align: center;" | ||
| Line 40: | Line 20: | ||
{| style="text-align: center; margin:auto;" | {| style="text-align: center; margin:auto;" | ||
|- | |- | ||
| − | | | + | | <math>f=\frac{64}{\hbox{Re}}</math> |
|} | |} | ||
| style="width: 5px;text-align: right;white-space: nowrap;" | (1) | | style="width: 5px;text-align: right;white-space: nowrap;" | (1) | ||
|} | |} | ||
| − | + | donde <math>f</math> es el factor de fricción de Darcy-Weisbach y el valor Re es el número de Reynolds, que es calculado como se presenta en la ecuación (2): | |
| − | + | ||
{| class="formulaSCP" style="width: 100%; text-align: center;" | {| class="formulaSCP" style="width: 100%; text-align: center;" | ||
| Line 53: | Line 32: | ||
{| style="text-align: center; margin:auto;" | {| style="text-align: center; margin:auto;" | ||
|- | |- | ||
| − | | | + | | <math>\hbox{Re}=\frac{V\cdot D}{\upsilon }</math> |
|} | |} | ||
| style="width: 5px;text-align: right;white-space: nowrap;" | (2) | | style="width: 5px;text-align: right;white-space: nowrap;" | (2) | ||
|} | |} | ||
| − | + | donde <math>V</math>, <math>D</math> y <math>\upsilon</math> corresponden a la velocidad de flujo promedio en la tubería, el diámetro interior de la tubería y la viscosidad cinemática, respectivamente. Colebrook y White (1937) establecieron para el flujo turbulento la relación entre las variables <math>f</math> y Re que es mostrada en la siguiente ecuación (3) no lineal [5]: | |
| − | + | ||
{| class="formulaSCP" style="width: 100%; text-align: center;" | {| class="formulaSCP" style="width: 100%; text-align: center;" | ||
| Line 66: | Line 44: | ||
{| style="text-align: center; margin:auto;" | {| style="text-align: center; margin:auto;" | ||
|- | |- | ||
| − | | | + | | <math>\frac{1}{\sqrt f}=2\hbox{log}\left(\hbox{Re}\sqrt f\right)-0,8</math> |
|} | |} | ||
| style="width: 5px;text-align: right;white-space: nowrap;" | (3) | | style="width: 5px;text-align: right;white-space: nowrap;" | (3) | ||
|} | |} | ||
| − | + | Posteriormente, para flujos en transición y turbulentos, <math>f</math> está relacionado con el valor de Re y <math>\varepsilon /D</math> (rugosidad relativa de la tubería) como se presenta en la ecuación (4) [6]: | |
| − | Posteriormente, para flujos en transición y turbulentos, | + | |
{| class="formulaSCP" style="width: 100%; text-align: center;" | {| class="formulaSCP" style="width: 100%; text-align: center;" | ||
| Line 79: | Line 56: | ||
{| style="text-align: center; margin:auto;" | {| style="text-align: center; margin:auto;" | ||
|- | |- | ||
| − | | [ | + | | <math>\frac{1}{\sqrt f}=-2\hbox{log}\left[\frac{\varepsilon /D}{3,7}+\frac{2,51}{\hbox{Re}\sqrt f}\right]</math> |
|} | |} | ||
| style="width: 5px;text-align: right;white-space: nowrap;" | (4) | | style="width: 5px;text-align: right;white-space: nowrap;" | (4) | ||
|} | |} | ||
| + | Se puede ver claramente que las ecuaciones (3) y (4) son expresiones implícitas que requieren una solución numérica iterativa para estimar de manera precisa el factor de fricción y requiere de la aplicación de métodos numéricos para su solución. En efecto, la ecuación (4) habitualmente es llamada ecuación de Colebrook-White. En este trabajo se ha utilizado el método de Newton–Raphson para resolver dicha ecuación [3,7], que es ampliamente empleado para este tipo de resoluciones. Como alternativa a la resolución de la ecuación implícita, varias investigaciones han sido desarrolladas para aproximar una solución explícita para la ecuación (4). Por ejemplo, Anaya-Durand y colaboradores (2014) evaluaron diferentes correlaciones explícitas que predicen el factor de fricción para un fluido en una tubería, mediante la comparación de valores numéricos de dichos factores respecto a la ecuación de Colebrook-White [2]. Winning y Coole (2013) en su estudio revisaron 28 ecuaciones explícitas para el cálculo del factor de fricción considerando tanto la precisión de la ecuación implícita de Colebrook-White y la eficiencia computacional de las ecuaciones explícitas [8]. Estos métodos numéricos de solución presentan estructuras recurrentes que pueden ser llevadas a algoritmos y resueltas rápidamente mediante programas computacionales. En el presente trabajo se desarrolló un programa en lenguaje C++ para resolver la ecuación de Colebrook-White. El lenguaje C++, fue desarrollado por Bjarne Stroustrup (1990) y es una extensión del lenguaje de programación C, incorporando el concepto de programación orientada a objeto, es por ello que desde el punto de vista de lenguajes de programación orientados a objeto, es un lenguaje híbrido. En dicho sentido el término “C++” significa “incremento de C” y que por lo tanto es una extensión de C [9]. Así, el objetivo del presente trabajo fue efectuar la evaluación experimental de correlaciones para el cálculo del factor de fricción para flujo turbulento en tuberías cilíndricas implementado en laboratorio una experiencia. | ||
| − | + | ==2. Materiales y métodos== | |
| − | =2. | + | ===2.1 Equipo experimental y procedimiento=== |
| − | + | Las mediciones se realizaron en el Laboratorio de Hidráulica del Departamento de Ingeniería en Obras Civiles de la Facultad de Ingeniería de la Universidad de La Serena. En la [[#img-1|Figura 1]] se muestra el sistema para determinar el factor de fricción experimental <math>f_{exp}</math> utilizando la ecuación (6) de Darcy-Weisbach. Este sistema consiste en una bomba centrífuga (REGGIO, STM 50), una tubería de PVC PN-10 de 26 mm de diámetro interior y codos cortos de PVC de 90°, tees de PVC, dos conectores de acero para instalación de las conducciones del manómetro diferencial, válvulas de globo y un estanque graduado de descarga para medir el volumen. También se utilizó un manómetro diferencial (PSE-910) y un cronómetro (KENKO, KK-2802). Se midió el caudal usando el método volumétrico, para lo cual se realizaron 5 mediciones, y en cada una de ellas se verificó el largo o distancia entre los puntos de control de presión (<math>L</math>), junto con el diámetro interior (<math>D</math>) y la rugosidad (<math>\varepsilon</math>) de la tubería. En el estanque acumulador de agua con control de volumen, se midió el tiempo (<math>t</math>) que demoraba en llenar 20 litros. De esta forma con la ecuación (5) se puede determinar la velocidad de escurrimiento al interior de la tubería. | |
| − | + | ||
| − | Las mediciones se realizaron en el Laboratorio de Hidráulica del Departamento de Ingeniería en Obras Civiles de la Facultad de Ingeniería de la Universidad de La Serena. En la | + | |
{| class="formulaSCP" style="width: 100%; text-align: center;" | {| class="formulaSCP" style="width: 100%; text-align: center;" | ||
| Line 98: | Line 74: | ||
{| style="text-align: center; margin:auto;" | {| style="text-align: center; margin:auto;" | ||
|- | |- | ||
| − | | | + | | <math>V=\frac{\left(\frac{\hbox{Vol}}{t}\right)}{\left(\frac{\pi \times D^2}{4}\right)}</math> |
|} | |} | ||
| style="width: 5px;text-align: right;white-space: nowrap;" | (5) | | style="width: 5px;text-align: right;white-space: nowrap;" | (5) | ||
|} | |} | ||
| − | + | donde <math>V</math> es la velocidad de escurrimiento en (m/s), <math>Vol</math> es el volumen igual a 0,02 m<sup>3</sup>, <math>t</math> es el tiempo en (s) que demoró en llenar el volumen antes indicado, <math>D</math> es el diámetro interior de la tubería igual a 0,026 m y π es igual a 3,1416. Al mismo tiempo se midió la diferencia de presión (<math>h</math>) en el manómetro diferencial. Los valores obtenidos se reemplazan en la ecuación (6) para poder determinar <math>f_{exp}</math> | |
| − | < | + | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
{| class="formulaSCP" style="width: 100%; text-align: center;" | {| class="formulaSCP" style="width: 100%; text-align: center;" | ||
| Line 115: | Line 86: | ||
{| style="text-align: center; margin:auto;" | {| style="text-align: center; margin:auto;" | ||
|- | |- | ||
| − | | | + | | <math>f_{\hbox{exp}}=\frac{h\times D\times 2\times g}{L\times V^2}</math> |
|} | |} | ||
| style="width: 5px;text-align: right;white-space: nowrap;" | (6) | | style="width: 5px;text-align: right;white-space: nowrap;" | (6) | ||
|} | |} | ||
| + | donde <math>g</math> es la aceleración de gravedad igual a 9,8 (m/s<sup>2</sup>) y <math>L</math> es la longitud de tubería recta entre los puntos de control de presión correspondiente a 1,0 m. | ||
| + | <div id='img-1'></div> | ||
| + | {| style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: auto;max-width: auto;" | ||
| + | |- | ||
| + | |style="padding:10px;"| [[Image:Draft_Olivares_378270214-image6-c.jpg|600px]] | ||
| + | |- style="text-align: center; font-size: 75%;" | ||
| + | | colspan="1" style="padding-bottom:10px;"| '''Figura 1'''. Esquema del Sistema Experimental para determinar el factor de fricción | ||
| + | |} | ||
| − | + | ===2.2 Correlaciones explícitas para el factor de fricción encontradas en la literatura=== | |
| − | + | ||
| − | ==2.2 Correlaciones explícitas para el factor de fricción encontradas en la | + | |
| − | En la Tabla 1 se presentan varias correlaciones reportadas en la literatura utilizadas para calcular el valor del factor de fricción. | + | En la [[#tab-1|Tabla 1]] se presentan varias correlaciones reportadas en la literatura utilizadas para calcular el valor del factor de fricción. |
| − | Tabla 1 Correlaciones para determinar el factor de fricción | + | <div id='tab-1'></div> |
| + | <div class="auto" style="width: auto; text-align:center;margin-left: auto; margin-right: auto;font-size: 75%;"> | ||
| + | '''Tabla 1''' Correlaciones para determinar el factor de fricción</div> | ||
| − | {| style=" | + | {| style="margin: 1em auto 0.1em auto;border-collapse: collapse;font-size:85%;width:90%;" |
|- | |- | ||
| − | | style="border: 1pt solid black;text-align: center;vertical-align: top;"| | + | | style="border: 1pt solid black;text-align: center;vertical-align: top;"|'''N°''' |
| − | | style="border: 1pt solid black;text-align: center;vertical-align: top;"| | + | | style="border: 1pt solid black;text-align: center;vertical-align: top;"|'''Modelo''' |
| − | | style="border: 1pt solid black;text-align: center;vertical-align: top;"| | + | | style="border: 1pt solid black;text-align: center;vertical-align: top;"|'''Correlación''' |
| − | | style="border: 1pt solid black;text-align: center;vertical-align: top;"| | + | | style="border: 1pt solid black;text-align: center;vertical-align: top;"|'''Rango de Aplicación''' |
|- | |- | ||
| − | | style="border: 1pt solid black;text-align: center;"| | + | | style="border: 1pt solid black;text-align: center;"|1 |
| − | | style="border: 1pt solid black;text-align: center;"| | + | | style="border: 1pt solid black;text-align: center;"|Filonenko [10] |
| − | | style="border: 1pt solid black;text-align: center;"|< | + | | style="border: 1pt solid black;text-align: center;"| <math>f=\left[1,82\;\hbox{log}\left(\hbox{Re}\right)-1,64\right]^{-2}</math> |
| − | | style="border: 1pt solid black;text-align: center;"|< | + | | style="border: 1pt solid black;text-align: center;"| <math>4\times 10^3<\hbox{Re}<1\times 10^8</math> |
| − | + | Tuberías hidráulicamente lisas | |
|- | |- | ||
| − | | style="border: 1pt solid black;text-align: center;"| | + | | style="border: 1pt solid black;text-align: center;"|2 |
| − | | style="border: 1pt solid black;text-align: center;"| | + | | style="border: 1pt solid black;text-align: center;"|Altshul I [2] |
| − | | style="border: 1pt solid black;text-align: center;"|< | + | | style="border: 1pt solid black;text-align: center;"| <math>f=0,11\;\left[\left(\frac{\varepsilon}{D}\right)+\left(\frac{68}{\hbox{Re}}\right)\right]^{0,25}</math> |
| − | | style="border: 1pt solid black;text-align: center;"|< | + | | style="border: 1pt solid black;text-align: center;"| <math>4\times 10^3<\hbox{Re}<1\times 10^8</math> |
| − | < | + | <math>1\times 10^{-6}<\varepsilon /D<0,05</math> |
|- | |- | ||
| − | | style="border: 1pt solid black;text-align: center;"| | + | | style="border: 1pt solid black;text-align: center;"|3 |
| − | | style="border: 1pt solid black;text-align: center;"| | + | | style="border: 1pt solid black;text-align: center;"|Altshul II [2] |
| − | | style="border: 1pt solid black;text-align: center;"|< | + | | style="border: 1pt solid black;text-align: center;"| <math>f=\left\{1,8\;\hbox{log}\left[\frac{\hbox{Re}}{0,135\cdot \hbox{Re}\cdot \left(\frac{\varepsilon}{D}\right)+6,5}\right]\right\}^{-2}</math> |
| − | | style="border: 1pt solid black;text-align: center;"|< | + | | style="border: 1pt solid black;text-align: center;"| <math display="inline">4\times 10^3<\hbox{Re}<1\times 10^8</math> |
| − | < | + | <math display="inline">1\times 10^{-6}<\varepsilon /D<0,05</math> |
|- | |- | ||
| − | | style="border: 1pt solid black;text-align: center;"| | + | | style="border: 1pt solid black;text-align: center;"|4 |
| − | | style="border: 1pt solid black;text-align: center;"| | + | | style="border: 1pt solid black;text-align: center;"|Konakov [11] |
| − | | style="border: 1pt solid black;text-align: center;"|< | + | | style="border: 1pt solid black;text-align: center;"| <math>f=\left[1,8\;\hbox{log}\left(\hbox{Re}\right)-1,5\right]^{-2}</math> |
| − | | style="border: 1pt solid black;text-align: center;"|< | + | | style="border: 1pt solid black;text-align: center;"| <math>4\times 10^3<\hbox{Re}<1\times 10^8</math> |
| − | + | Tuberías hidráulicamente lisas | |
|- | |- | ||
| − | | style="border: 1pt solid black;text-align: center;"| | + | | style="border: 1pt solid black;text-align: center;"|5 |
| − | | style="border: 1pt solid black;text-align: center;"| | + | | style="border: 1pt solid black;text-align: center;"|Shacham I |
| − | | style="border: 1pt solid black;text-align: center;"|< | + | | style="border: 1pt solid black;text-align: center;"| <math>f=\left\{-2\;\hbox{log}\left[\frac{\left(\frac{\varepsilon}{D}\right)}{3,7}-\frac{5,02}{\hbox{Re}}\hbox{log}\left(\frac{\left(\frac{\varepsilon}{D}\right)}{3,7}+\frac{14,5}{\hbox{Re}}\right)\right]\right\}^{-2}</math> |
| − | | style="border: 1pt solid black;text-align: center;"|< | + | | style="border: 1pt solid black;text-align: center;"| <math>4\times 10^3<\hbox{Re}<1\times 10^8</math> |
| − | < | + | <math>1\times 10^{-6}<\varepsilon /D<0,05</math> |
|- | |- | ||
| − | | style="border: 1pt solid black;text-align: center;"| | + | | style="border: 1pt solid black;text-align: center;"|6 |
| − | | style="border: 1pt solid black;text-align: center;"| | + | | style="border: 1pt solid black;text-align: center;"|Shacham II |
| − | | style="border: 1pt solid black;text-align: center;"|< | + | | style="border: 1pt solid black;text-align: center;"| <math>f=\left[\frac{X\;(1-\hbox{ln}X)-\frac{\left(\frac{\varepsilon}{D}\right)}{3,7}}{1,15129X+\frac{2,51}{\hbox{Re}}}\right]^{-2}\hbox{donde}\;X=\frac{\left(\frac{\varepsilon}{D}\right)}{3,7}-\frac{5,02}{\hbox{Re}}\;\hbox{log}\left(\frac{\left(\frac{\varepsilon}{D}\right)}{3,7}+\frac{14,5}{\hbox{Re}}\right)</math> |
| − | | style="border: 1pt solid black;text-align: center;"|< | + | | style="border: 1pt solid black;text-align: center;"| <math>4\times 10^3<\hbox{Re}<1\times 10^8</math> |
| − | < | + | <math>1\times 10^{-6}<\varepsilon /D<0,05</math> |
|- | |- | ||
| − | | style="border: 1pt solid black;text-align: center;"| | + | | style="border: 1pt solid black;text-align: center;"|7 |
| − | | style="border: 1pt solid black;text-align: center;"| | + | | style="border: 1pt solid black;text-align: center;"|Chen [12] |
| − | | style="border: 1pt solid black;text-align: center;"|< | + | | style="border: 1pt solid black;text-align: center;"| <math>\begin{matrix}f=\left[-2\;\hbox{log}\left(\frac{\left(\frac{\varepsilon}{D}\right)}{3,7065}-Y\right)\right]^{-2} \\Y=\frac{5,0452}{\hbox{Re}}\hbox{log}\left[\frac{\left(\frac{\varepsilon}{D}\right)^{1,1098}}{2,8257}+Z\right]\;\;\;y\;\;\;Z=5,8506\;\left(\hbox{Re}\right)^{-0,8981} \end{matrix}</math> |
| style="border: 1pt solid black;text-align: center;"| | | style="border: 1pt solid black;text-align: center;"| | ||
|- | |- | ||
| − | | style="border: 1pt solid black;text-align: center;"| | + | | style="border: 1pt solid black;text-align: center;"|8 |
| − | | style="border: 1pt solid black;text-align: center;"| | + | | style="border: 1pt solid black;text-align: center;"|Churchill [13] |
| − | | style="border: 1pt solid black;text-align: center;"|< | + | | style="border: 1pt solid black;text-align: center;"| <math>f=8\;\left[\left(\frac{8}{\hbox{Re}}\right)^{12}+\;\;\left(A+B\right)^{-\frac{32}{}}\right]^{\frac{1}{12}}</math> |
| − | < | + | <math>A=\;\left[2,457\;\hbox{ln}\left(\frac{1}{\left(\frac{7}{\hbox{Re}}\right)^{0,9}+0.27\;\left(\frac{\varepsilon}{D}\right)}\right)\right]^{16}\;\;\;y\;\;\;B=\left(\frac{37.530}{\hbox{Re}}\right)^{16}</math> |
| style="border: 1pt solid black;text-align: center;"| | | style="border: 1pt solid black;text-align: center;"| | ||
|- | |- | ||
| − | | style="border: 1pt solid black;text-align: center;"| | + | | style="border: 1pt solid black;text-align: center;"|9 |
| − | | style="border: 1pt solid black;text-align: center;"| | + | | style="border: 1pt solid black;text-align: center;"|Swamee and Jain [14] |
| − | | style="border: 1pt solid black;text-align: center;"|< | + | | style="border: 1pt solid black;text-align: center;"| <math>f=\left\{-2\;\hbox{log}\;\left[\frac{\varepsilon }{3,7D}+\frac{5,74}{\hbox{Re}^{0.9}}\right]\right\}^{-2}</math> |
| style="border: 1pt solid black;text-align: center;"| | | style="border: 1pt solid black;text-align: center;"| | ||
|- | |- | ||
| − | | style="border: 1pt solid black;text-align: center;"| | + | | style="border: 1pt solid black;text-align: center;"|10 |
| − | | style="border: 1pt solid black;text-align: center;"| | + | | style="border: 1pt solid black;text-align: center;"|Pavlov [15] |
| − | | style="border: 1pt solid black;text-align: center;"|< | + | | style="border: 1pt solid black;text-align: center;"| <math>f=\left\{-2\;\hbox{log}\;\left[\frac{1}{3,7}\left(\frac{\varepsilon}{D}\right)+\left(\frac{6,81}{\hbox{Re}}\right)^{0,9}\right]\right\}^{-2}</math> |
| − | | style="border: 1pt solid black;text-align: center;"|< | + | | style="border: 1pt solid black;text-align: center;"| <math>4\times 10^3<\hbox{Re}<1\times 10^8</math> |
|- | |- | ||
| − | | style="border: 1pt solid black;text-align: center;"| | + | | style="border: 1pt solid black;text-align: center;"|11 |
| − | | style="border: 1pt solid black;text-align: center;"| | + | | style="border: 1pt solid black;text-align: center;"|Round [16] |
| − | | style="border: 1pt solid black;text-align: center;"|< | + | | style="border: 1pt solid black;text-align: center;"| <math>f=\left\{-1,8\;\hbox{log}\;\left[0,27\;\left(\frac{\varepsilon}{D}\right)+\frac{6,5}{\hbox{Re}}\right]\right\}^{-2}</math> |
| style="border: 1pt solid black;text-align: center;"| | | style="border: 1pt solid black;text-align: center;"| | ||
|- | |- | ||
| − | | style="border: 1pt solid black;text-align: center;"| | + | | style="border: 1pt solid black;text-align: center;"|12 |
| − | | style="border: 1pt solid black;text-align: center;"| | + | | style="border: 1pt solid black;text-align: center;"|Barr [17] |
| − | | style="border: 1pt solid black;text-align: center;"|< | + | | style="border: 1pt solid black;text-align: center;"| <math>f=\left\{-2\;\hbox{log}\;\left[\frac{1}{3,7}\left(\frac{\varepsilon}{D}\right)+\frac{4,518\;\;\hbox{log}\left(\frac{\hbox{Re}}{7}\right)}{\hbox{Re}\left(1+\frac{1}{29}\hbox{Re}^{0,52}\left(\frac{\varepsilon}{D}\right)^{0,7}\right)}\right]\right\}^{-2}</math> |
| style="border: 1pt solid black;text-align: center;"| | | style="border: 1pt solid black;text-align: center;"| | ||
|- | |- | ||
| − | | style="border: 1pt solid black;text-align: center;"| | + | | style="border: 1pt solid black;text-align: center;"|13 |
| − | | style="border: 1pt solid black;text-align: center;"| | + | | style="border: 1pt solid black;text-align: center;"|Zigrang – Sylvester [18] |
| − | | style="border: 1pt solid black;text-align: center;"|< | + | | style="border: 1pt solid black;text-align: center;"| <math>f=\left\{-2\;\hbox{log}\;\left[\frac{1}{3,7}\left(\frac{\varepsilon}{D}\right)-\frac{5,02}{\hbox{Re}}\hbox{log}\left(\frac{1}{3,7}\left(\frac{\varepsilon}{D}\right)-\frac{5,02}{\hbox{Re}}\hbox{log}\left(\frac{1}{3,7}\left(\frac{\varepsilon}{D}\right)+\frac{13}{\hbox{Re}}\right)\right)\right]\right\}^{-2}</math> |
| style="border: 1pt solid black;text-align: center;"| | | style="border: 1pt solid black;text-align: center;"| | ||
|- | |- | ||
| − | | style="border: 1pt solid black;text-align: center;"| | + | | style="border: 1pt solid black;text-align: center;"|14 |
| − | | style="border: 1pt solid black;text-align: center;"| | + | | style="border: 1pt solid black;text-align: center;"|S. E. Haaland [19] |
| − | | style="border: 1pt solid black;text-align: center;"|< | + | | style="border: 1pt solid black;text-align: center;"| <math>f=\left\{-1,8\;\hbox{log}\;\left[\left(\frac{\frac{\varepsilon}{D}}{3,7}\right)^{1,11}+\frac{6,9}{\hbox{Re}}\right]\right\}^{-2}</math> |
| − | | style="border: 1pt solid black;text-align: center;"|< | + | | style="border: 1pt solid black;text-align: center;"| <math>4\times 10^3<\hbox{Re}<1\times 10^8</math> |
| − | < | + | <math>1\times 10^{-6}<\varepsilon /D<0,05</math> |
|- | |- | ||
| − | | style="border: 1pt solid black;text-align: center;"| | + | | style="border: 1pt solid black;text-align: center;"|15 |
| − | | style="border: 1pt solid black;text-align: center;"| | + | | style="border: 1pt solid black;text-align: center;"|Manadilli [20] |
| − | | style="border: 1pt solid black;text-align: center;"|< | + | | style="border: 1pt solid black;text-align: center;"| <math>f=\left\{-2\;\hbox{log}\;\left[\frac{\frac{\varepsilon}{D}}{3,7}+\frac{95}{\hbox{Re}^{0,983}}-\frac{96,82}{\hbox{Re}}\right]\right\}^{-2}</math> |
| − | | style="border: 1pt solid black;text-align: center;"|< | + | | style="border: 1pt solid black;text-align: center;"| <math display="inline">5.235<\hbox{Re}<1\times 10^9</math> |
| − | + | Cualquier valor de ''ε/D'' | |
|- | |- | ||
| − | | style="border: 1pt solid black;text-align: center;"| | + | | style="border: 1pt solid black;text-align: center;"|16 |
| − | | style="border: 1pt solid black;text-align: center;"| | + | | style="border: 1pt solid black;text-align: center;"|Romeo et al. [21] |
| − | | style="border: 1pt solid black;text-align: center;"|< | + | | style="border: 1pt solid black;text-align: center;"| <math>f=\left\{-2\;\hbox{log}\;\left[\frac{\frac{\varepsilon}{D}}{3,7065}-\frac{5,0272}{\hbox{Re}}A\right]\right\}^{-2}</math> |
| − | < | + | <math>A=\hbox{log}\left[\frac{1}{3,827}\left(\frac{\varepsilon}{D}\right)-\frac{4,567}{\hbox{Re}}\hbox{log}\left(\left(\frac{1}{7,7918}\left(\frac{\varepsilon}{D}\right)\right)^{0,9924}+\left(\frac{5,3326}{208,815+\hbox{Re}}\right)^{0,9345}\right)\right]</math> |
| − | | style="border: 1pt solid black;text-align: center;"|< | + | | style="border: 1pt solid black;text-align: center;"| <math>3\times 10^3<\hbox{Re}<1\times 10^8</math> |
| − | < | + | <math>0<\varepsilon /D<0,05</math> |
|- | |- | ||
| − | | style="border: 1pt solid black;text-align: center;"| | + | | style="border: 1pt solid black;text-align: center;"|17 |
| − | | style="border: 1pt solid black;text-align: center;"| | + | | style="border: 1pt solid black;text-align: center;"|Colebrook-White [6] |
| − | | style="border: 1pt solid black;text-align: center;"|< | + | | style="border: 1pt solid black;text-align: center;"| <math>\frac{1}{\sqrt f}=-2\hbox{log}\left[\frac{2,51}{\hbox{Re}\sqrt f}+\frac{\varepsilon /D}{3,7}\right]</math> |
| style="border: 1pt solid black;text-align: center;"| | | style="border: 1pt solid black;text-align: center;"| | ||
|- | |- | ||
| − | | style="border: 1pt solid black;text-align: center;"| | + | | style="border: 1pt solid black;text-align: center;"|18 |
| − | | style="border: 1pt solid black;text-align: center;"| | + | | style="border: 1pt solid black;text-align: center;"|Sonnad and Goudar [22] |
| − | | style="border: 1pt solid black;text-align: center;"|< | + | | style="border: 1pt solid black;text-align: center;"| <math>\frac{1}{\sqrt f}\approx 0,8686\hbox{ln}\left(\frac{0,4587\hbox{Re}}{G^{G/\left(G+1\right)}}\right)</math> |
| − | < | + | <math>G=0,124\hbox{Re}\frac{\varepsilon}{D}+\hbox{ln}\left(0,4587\times \hbox{Re}\right)</math> |
| style="border: 1pt solid black;text-align: center;"| | | style="border: 1pt solid black;text-align: center;"| | ||
|- | |- | ||
| − | | style="border: 1pt solid black;text-align: center;"| | + | | style="border: 1pt solid black;text-align: center;"|19 |
| − | | style="border: 1pt solid black;text-align: center;"| | + | | style="border: 1pt solid black;text-align: center;"|Buzzelli [23] |
| − | | style="border: 1pt solid black;text-align: center;"|< | + | | style="border: 1pt solid black;text-align: center;"| <math>\frac{1}{\sqrt f}=\left(\frac{B_1+2\hbox{log}\left(B_2/\hbox{Re}\right)}{1+\left(2,18/B_2\right)}\right)</math> |
| − | < | + | <math>B_1=\frac{\left(0,774\hbox{ln}\left(\hbox{Re}\right)\right)-1,41}{\left(1+1,32\sqrt{\varepsilon /D}\right)}</math> |
| − | < | + | <math>B_2=\frac{\varepsilon }{3,7D}\hbox{Re}+2,51B_1</math> |
| style="border: 1pt solid black;text-align: center;"| | | style="border: 1pt solid black;text-align: center;"| | ||
|- | |- | ||
| − | | style="border: 1pt solid black;text-align: center;"| | + | | style="border: 1pt solid black;text-align: center;"|20 |
| − | | style="border: 1pt solid black;text-align: center;"| | + | | style="border: 1pt solid black;text-align: center;"|Avci and Karagoz [24] |
| − | | style="border: 1pt solid black;text-align: center;"|< | + | | style="border: 1pt solid black;text-align: center;"| <math>f=\frac{6,4}{\left(\hbox{ln}\left(\hbox{Re}\right)-\hbox{ln}\left(1+0,01\hbox{Re}\frac{\varepsilon D}{}\left(1+10\sqrt{\varepsilon /D}\right)\right)\right)^{2,4}}</math> |
| style="border: 1pt solid black;text-align: center;"| | | style="border: 1pt solid black;text-align: center;"| | ||
|- | |- | ||
| − | | style="border: 1pt solid black;text-align: center;"| | + | | style="border: 1pt solid black;text-align: center;"|21 |
| − | | style="border: 1pt solid black;text-align: center;"| | + | | style="border: 1pt solid black;text-align: center;"|Saeed Samadianfard [25] |
| − | | style="border: 1pt solid black;text-align: center;"|< | + | | style="border: 1pt solid black;text-align: center;"| <math>\begin{matrix}f=\left(\frac{\hbox{Re}^{\varepsilon /D}-0.6315093}{\hbox{Re}^{1/3}+\hbox{Re}\times \varepsilon /D}\right)+0.0275308\left(\frac{6.929841}{\hbox{Re}}+\varepsilon /D\right)^{1.9} \\+\left(\frac{10^{\varepsilon /D}}{\varepsilon /D+4.781616}\right)\left(\sqrt{\varepsilon /D}+\frac{9.99701}{\hbox{Re}}\right) \end{matrix}</math> |
| − | | style="border: 1pt solid black;text-align: center;"|< | + | | style="border: 1pt solid black;text-align: center;"| <math>4\times 10^3<\hbox{Re}<1\times 10^8</math> |
| − | < | + | <math>1\times 10^{-6}<\varepsilon /D<0,05</math> |
|- | |- | ||
| − | | style="border: 1pt solid black;text-align: center;"| | + | | style="border: 1pt solid black;text-align: center;"|22 |
| − | | style="border: 1pt solid black;text-align: center;"| | + | | style="border: 1pt solid black;text-align: center;"|Papaevangelo et al. [26] |
| − | | style="border: 1pt solid black;text-align: center;"|< | + | | style="border: 1pt solid black;text-align: center;"| <math>f_d=\frac{0,2479-0,0000947\times \left(7-\hbox{logRe}\right)^4}{\left[\hbox{log}\left(\frac{\varepsilon }{3,615D}+\frac{7.366}{\hbox{Re}^{0,9142}}\right)\right]^2}</math> |
| − | | style="border: 1pt solid black;text-align: center;"|< | + | | style="border: 1pt solid black;text-align: center;"| <math>1\times 10^4<\hbox{Re}<1\times 10^7</math> |
| − | < | + | <math display="inline">1\times 10^{-5}<\varepsilon /D<0,005</math> |
|- | |- | ||
| − | | style="border: 1pt solid black;text-align: center;"| | + | | style="border: 1pt solid black;text-align: center;"|23 |
| − | | style="border: 1pt solid black;text-align: center;"| | + | | style="border: 1pt solid black;text-align: center;"|Brkic I [27] |
| − | | style="border: 1pt solid black;text-align: center;"|< | + | | style="border: 1pt solid black;text-align: center;"| <math>f_d=\left[-2\hbox{log}\left(10^{-0,4343\beta }+\frac{\varepsilon }{3,71D}\right)\right]^{-2}</math> |
| − | < | + | <math>\beta =\hbox{ln}\frac{\hbox{Re}}{1,816\hbox{ln}\left(\frac{1,1\hbox{Re}}{\hbox{ln}\left(1+1,1\hbox{Re}\right)}\right)}</math> |
| style="border: 1pt solid black;text-align: center;"| | | style="border: 1pt solid black;text-align: center;"| | ||
|- | |- | ||
| − | | style="border: 1pt solid black;text-align: center;"| | + | | style="border: 1pt solid black;text-align: center;"|24 |
| − | | style="border: 1pt solid black;text-align: center;"| | + | | style="border: 1pt solid black;text-align: center;"|Brkic II [27] |
| − | | style="border: 1pt solid black;text-align: center;"|< | + | | style="border: 1pt solid black;text-align: center;"| <math>f_d=\left[-2\hbox{log}\left(\frac{2,18\beta }{\hbox{Re}}+\frac{\varepsilon }{3,71D}\right)\right]^{-2}</math> |
| − | < | + | <math>\beta =\hbox{ln}\frac{\hbox{Re}}{1,816\hbox{ln}\left(\frac{1,1\hbox{Re}}{\hbox{ln}\left(1+1,1\hbox{Re}\right)}\right)}</math> |
| style="border: 1pt solid black;text-align: center;"| | | style="border: 1pt solid black;text-align: center;"| | ||
|- | |- | ||
| − | | style="border: 1pt solid black;text-align: center;"| | + | | style="border: 1pt solid black;text-align: center;"|25 |
| − | | style="border: 1pt solid black;text-align: center;"| | + | | style="border: 1pt solid black;text-align: center;"|Fang et al. [28] |
| − | | style="border: 1pt solid black;text-align: center;"|< | + | | style="border: 1pt solid black;text-align: center;"| <math>f_d=1,613\left\{\hbox{ln}\left[0,234\left(\frac{\varepsilon}{D}\right)^{1,1007}-\frac{60.525}{\hbox{Re}^{1,1105}}+\frac{56.291}{\hbox{Re}^{1,0712}}\right]\right\}^{-2}</math> |
| − | | style="border: 1pt solid black;text-align: center;"|< | + | | style="border: 1pt solid black;text-align: center;"| <math>3\times 10^3<\hbox{Re}<1\times 10^8</math> |
| − | < | + | <math>0<\varepsilon /D<0,05</math> |
|- | |- | ||
| − | | style="border: 1pt solid black;text-align: center;"| | + | | style="border: 1pt solid black;text-align: center;"|26 |
| − | | style="border: 1pt solid black;text-align: center;"| | + | | style="border: 1pt solid black;text-align: center;"|Li et al. [29] |
| − | | style="border: 1pt solid black;text-align: center;"|< | + | | style="border: 1pt solid black;text-align: center;"| <math>\frac{1}{\sqrt{\lambda }}=-2\cdot \hbox{log}_{10}\left(\frac{1,2563}{\hbox{Re}\sqrt{\frac{-0,0015702}{\hbox{ln}\left(\hbox{Re}\right)}+\frac{0,39442031}{\hbox{ln}^2\left(\hbox{Re}\right)}+\frac{2,5341533}{\hbox{ln}^3\left(\hbox{Re}\right)}}}+\frac{\varepsilon }{3,71D}\right)</math> |
| style="border: 1pt solid black;text-align: center;"| | | style="border: 1pt solid black;text-align: center;"| | ||
|- | |- | ||
| − | | style="border: 1pt solid black;text-align: center;"| | + | | style="border: 1pt solid black;text-align: center;"|27 |
| − | | style="border: 1pt solid black;text-align: center;"| | + | | style="border: 1pt solid black;text-align: center;"|Shaikh et al. [30] |
| − | | style="border: 1pt solid black;text-align: center;"|< | + | | style="border: 1pt solid black;text-align: center;"| <math>\lambda =0,25\left[\hbox{log}_{10}\left(\frac{2,51}{\hbox{Re}\cdot \left(1,14-2\cdot \hbox{log}_{10}\left(\frac{\varepsilon D}{}\right)\right)^{\alpha }}+\frac{\varepsilon }{3,71D}\right)\right]^{-2}</math> |
| − | < | + | <math>\alpha =-0,75</math> |
| − | | style="border: 1pt solid black;text-align: center;"|< | + | | style="border: 1pt solid black;text-align: center;"| <math>1\times 10^4<\hbox{Re}<1\times 10^8</math> |
| − | < | + | <math display="inline">1\times 10^{-6}<\varepsilon /D<0,05</math> |
|} | |} | ||
| − | ==2.3 Cálculo del factor de fricción en la | + | ===2.3 Cálculo del factor de fricción en la ecuación implícita de Colebrook-White=== |
| − | La ecuación (4) de Colebrook–White es ampliamente utilizada para determinar el factor de fricción para flujos turbulentos en tuberías rugosas. Se puede apreciar que la ecuación (4) está expresada en forma implícita para | + | La ecuación (4) de Colebrook–White es ampliamente utilizada para determinar el factor de fricción para flujos turbulentos en tuberías rugosas. Se puede apreciar que la ecuación (4) está expresada en forma implícita para <math>f</math> y requiere una solución iterativa para determinar su valor. El método que es adecuado para encontrar una raíz y que ésta sea estable, es el método de Newton–Raphson. La solución aproximada del método se basa en el siguiente algoritmo: |
{| class="formulaSCP" style="width: 100%; text-align: center;" | {| class="formulaSCP" style="width: 100%; text-align: center;" | ||
| Line 323: | Line 302: | ||
{| style="text-align: center; margin:auto;" | {| style="text-align: center; margin:auto;" | ||
|- | |- | ||
| − | | | + | | <math>f_{n+1}=f_n-\frac{g(f_n)}{g'(f_n)}</math> |
|} | |} | ||
| style="width: 5px;text-align: right;white-space: nowrap;" | (7) | | style="width: 5px;text-align: right;white-space: nowrap;" | (7) | ||
| Line 329: | Line 308: | ||
| − | En el método de Newton–Raphson, la ecuación (7) es utilizada para calcular el factor de fricción a partir de un valor inicial dado y que permite estimar el siguiente valor de iteración, con el fin de encontrar la solución a la ecuación (4) del factor de fricción. La ecuación (4) de Colebrook–White puede reordenarse reemplazando el valor de | + | En el método de Newton–Raphson, la ecuación (7) es utilizada para calcular el factor de fricción a partir de un valor inicial dado y que permite estimar el siguiente valor de iteración, con el fin de encontrar la solución a la ecuación (4) del factor de fricción. La ecuación (4) de Colebrook–White puede reordenarse reemplazando el valor de <math>F=1/\surd f</math> y ser expresada mediante una nueva relación <math>g(F)</math> tal como se muestra en la ecuación (8) |
{| class="formulaSCP" style="width: 100%; text-align: center;" | {| class="formulaSCP" style="width: 100%; text-align: center;" | ||
| Line 336: | Line 315: | ||
{| style="text-align: center; margin:auto;" | {| style="text-align: center; margin:auto;" | ||
|- | |- | ||
| − | | [ | + | | <math>g(F)=F+2\hbox{log}\left[\frac{\varepsilon /D}{3,7}+\frac{2,51}{\hbox{Re}}\cdot F\right]</math> |
|} | |} | ||
| style="width: 5px;text-align: right;white-space: nowrap;" | (8) | | style="width: 5px;text-align: right;white-space: nowrap;" | (8) | ||
| Line 342: | Line 321: | ||
| − | Si se asume la ecuación (8) como una función que es siempre continua y diferenciable, se puede obtener la derivada de la función con respecto a | + | Si se asume la ecuación (8) como una función que es siempre continua y diferenciable, se puede obtener la derivada de la función con respecto a <math>F</math>, cuya deducción se presenta en el apéndice y que se muestra en la ecuación (9) |
{| class="formulaSCP" style="width: 100%; text-align: center;" | {| class="formulaSCP" style="width: 100%; text-align: center;" | ||
| Line 349: | Line 328: | ||
{| style="text-align: center; margin:auto;" | {| style="text-align: center; margin:auto;" | ||
|- | |- | ||
| − | | [ | + | | <math>g'(F)=1+\left[\frac{8,06659}{\left(\frac{\varepsilon}{D}\cdot \hbox{Re}+9,287\cdot F\right)}\right]</math> |
|} | |} | ||
| style="width: 5px;text-align: right;white-space: nowrap;" | (9) | | style="width: 5px;text-align: right;white-space: nowrap;" | (9) | ||
| Line 355: | Line 334: | ||
| − | La ecuación (9) tiene capacidad de rápida convergencia, particularmente si hay una estimación adecuada del valor inicial del factor de fricción [7 | + | La ecuación (9) tiene capacidad de rápida convergencia, particularmente si hay una estimación adecuada del valor inicial del factor de fricción [7,3]. En este trabajo la ecuación (4) fue resuelta utilizando el método de Newton–Raphson, mediante un programa computacional desarrollado en lenguaje de programación C++. Esta resolución requiere el ingreso del valor Re y <math>\frac{\varepsilon}{D}</math>, junto con el valor inicial de iteración para <math>F=1/\surd f</math> y el valor de la precisión o error admisible en el desarrollo del proceso iterativo, cuyo diagrama de flujo se encuentra en la [[#img-2|Figura 2]] y el código fuente se presenta en al Apéndice B. |
| − | + | <div id='img-2'></div> | |
| − | == [[Image:Draft_Olivares_378270214-image65.png|534px]] == | + | {| style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: auto;max-width: auto;" |
| − | + | |- | |
| − | Figura 2 | + | |style="padding:10px;"| [[Image:Draft_Olivares_378270214-image65.png|534px]] |
| − | + | |- style="text-align: center; font-size: 75%;" | |
| − | + | | colspan="1" style="padding-bottom:10px;"| '''Figura 2'''. Diagrama de flujo del programa C++ para la resolución de la ecuación de Colebrook–White | |
| − | + | |} | |
| − | + | ||
| − | + | ==3. Resultados y discusión== | |
| − | + | ||
| − | + | La [[#img-3|Figura 3]] muestra el gráfico de caja, que presenta la mediana (línea dentro de la caja), el promedio (cuadrado dentro de la caja), el primer cuartil (25 % de los datos), el tercer cuartil (el 75 % de los datos), el valor mínimo (5% de los datos) y el valor máximo (95% de los datos) del factor de fricción experimental medido en quintuplicado utilizando la ecuación (6), además se calculó su límite de confianza, ecuación (10) | |
| − | Figura 3 | + | |
{| class="formulaSCP" style="width: 100%; text-align: center;" | {| class="formulaSCP" style="width: 100%; text-align: center;" | ||
| Line 376: | Line 352: | ||
{| style="text-align: center; margin:auto;" | {| style="text-align: center; margin:auto;" | ||
|- | |- | ||
| − | | | + | | <math display="inline">L.C.=f_{\hbox{exp,prom}}+\displaystyle\frac{t_{95}\cdot s}{\sqrt n}</math> |
|} | |} | ||
| style="width: 5px;text-align: right;white-space: nowrap;" | (10) | | style="width: 5px;text-align: right;white-space: nowrap;" | (10) | ||
|} | |} | ||
| − | + | donde <math>L.C.</math> corresponde al límite de confianza, <math>f_{\hbox{exp,prom}}</math> al factor de fricción promedio, <math>t_{95}%</math> al valor <math>t</math> de Student para n-1 grados de libertad a un 95% de confianza, <math>s</math> a la desviación estándar y <math>n</math> corresponde al número de réplicas. En este caso el <math>L.C.</math> para un 95% de confianza es igual a 0,022427 ± 0,002190. Cada uno de los valores del factor de fricción obtenido de las correlaciones antes presentadas (Tabla 1) fue evaluado y comparado respecto a su error relativo porcentual con el factor de fricción experimental promedio. El error relativo porcentual se calculó utilizando la ecuación (11) | |
| − | + | ||
{| class="formulaSCP" style="width: 100%; text-align: center;" | {| class="formulaSCP" style="width: 100%; text-align: center;" | ||
| Line 389: | Line 364: | ||
{| style="text-align: center; margin:auto;" | {| style="text-align: center; margin:auto;" | ||
|- | |- | ||
| − | | | + | | <math display="inline">\;E=|\displaystyle\frac{f_{\hbox{exp,prom}}-f_{\hbox{pred}}}{f_{\hbox{exp,prom}}}|\times 100</math> |
|} | |} | ||
| style="width: 5px;text-align: right;white-space: nowrap;" | (11) | | style="width: 5px;text-align: right;white-space: nowrap;" | (11) | ||
|} | |} | ||
| + | donde <math>f_{\hbox{pred}}</math> es el factor de fricción predicho por cada una de las correlaciones indicadas en la Tabla 1, considerando una rugosidad (<math>\varepsilon </math>) de 0,0015 mm para PVC [31] y <math>\varepsilon /D</math> (rugosidad relativa de la tubería) igual a 0,0000576923. En el caso de la correlación de Colebrook-White, el factor de fricción fue obtenido utilizando el método numérico de Newton-Raphson, como fue descrito previamente, para lo cual se desarrolló un programa en C++. La [[#tab-2|Tabla 2]] muestra los resultados obtenidos para el factor de fricción con cada una de las correlaciones evaluadas y el error relativo porcentual respectivo. El estudio se basa en la correlación que arroje el menor porcentaje de error con respecto al valor obtenido de forma experimental, encontrándose que la correlación de Colebrook-White predice el factor de fricción con menor porcentaje de error de las 27 correlaciones estudiadas para un rango de valores de Número de Reynolds comprendido entre <math>37.079 \le Re \le 38.703</math>. | ||
| − | + | <div id='img-3'></div> | |
| + | {| style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: auto;max-width: auto;" | ||
| + | |- | ||
| + | |style="padding:10px;"| [[Image:Draft_Olivares_378270214-image66.png|400px]] | ||
| + | |- style="text-align: center; font-size: 75%;" | ||
| + | | colspan="1" style="padding-bottom:10px;"| '''Figura 3'''. Gráfico de caja del factor de fricción experimental | ||
| + | |} | ||
| − | Tabla 2 Factor de fricción y error relativo porcentual de cada una de las correlaciones estudiadas | + | <div id='tab-2'></div> |
| + | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;font-size:75%;"> | ||
| + | '''Tabla 2'''. Factor de fricción y error relativo porcentual de cada una de las correlaciones estudiadas</div> | ||
| − | {| style=" | + | {| style="margin: 1em auto 0.1em auto;border-collapse: collapse;font-size:85%;width:45%;" |
|- | |- | ||
| − | | style="border: 1pt solid black;text-align: center;"|N° | + | | style="border: 1pt solid black;text-align: center;"|'''N°''' |
| − | | style="border-top: 1pt solid black;border-bottom: 1pt solid black;border-right: 1pt solid black;"|Correlación | + | | style="border-top: 1pt solid black;border-bottom: 1pt solid black;border-right: 1pt solid black;padding-left:5px;"|'''Correlación''' |
| − | | style="border-top: 1pt solid black;border-bottom: 1pt solid black;border-right: 1pt solid black;text-align: center;"|Factor f<br/>Teórico | + | | style="border-top: 1pt solid black;border-bottom: 1pt solid black;border-right: 1pt solid black;text-align: center;"|'''Factor f<br/>Teórico''' |
| − | | style="border-top: 1pt solid black;border-bottom: 1pt solid black;border-right: 1pt solid black;text-align: center;"|% Error Relativo Porcentual | + | | style="border-top: 1pt solid black;border-bottom: 1pt solid black;border-right: 1pt solid black;text-align: center;"|'''% Error Relativo Porcentual''' |
|- | |- | ||
| style="border-left: 1pt solid black;border-bottom: 1pt solid black;border-right: 1pt solid black;text-align: center;vertical-align: bottom;"|1 | | style="border-left: 1pt solid black;border-bottom: 1pt solid black;border-right: 1pt solid black;text-align: center;vertical-align: bottom;"|1 | ||
| − | | style="border-bottom: 1pt solid black;border-right: 1pt solid black;vertical-align: bottom;"|Filonenko | + | | style="padding-left:5px;border-bottom: 1pt solid black;border-right: 1pt solid black;vertical-align: bottom;"|Filonenko |
| style="border-bottom: 1pt solid black;border-right: 1pt solid black;text-align: center;vertical-align: bottom;"|0,0223347 | | style="border-bottom: 1pt solid black;border-right: 1pt solid black;text-align: center;vertical-align: bottom;"|0,0223347 | ||
| style="border-bottom: 1pt solid black;border-right: 1pt solid black;text-align: center;vertical-align: bottom;"|0,4104 | | style="border-bottom: 1pt solid black;border-right: 1pt solid black;text-align: center;vertical-align: bottom;"|0,4104 | ||
|- | |- | ||
| style="border-left: 1pt solid black;border-bottom: 1pt solid black;border-right: 1pt solid black;text-align: center;vertical-align: bottom;"|2 | | style="border-left: 1pt solid black;border-bottom: 1pt solid black;border-right: 1pt solid black;text-align: center;vertical-align: bottom;"|2 | ||
| − | | style="border-bottom: 1pt solid black;border-right: 1pt solid black;vertical-align: bottom;"|Altshul I | + | | style="padding-left:5px;border-bottom: 1pt solid black;border-right: 1pt solid black;vertical-align: bottom;"|Altshul I |
| style="border-bottom: 1pt solid black;border-right: 1pt solid black;text-align: center;vertical-align: bottom;"|0,0228318 | | style="border-bottom: 1pt solid black;border-right: 1pt solid black;text-align: center;vertical-align: bottom;"|0,0228318 | ||
| style="border-bottom: 1pt solid black;border-right: 1pt solid black;text-align: center;vertical-align: bottom;"|1,8062 | | style="border-bottom: 1pt solid black;border-right: 1pt solid black;text-align: center;vertical-align: bottom;"|1,8062 | ||
|- | |- | ||
| style="border-left: 1pt solid black;border-bottom: 1pt solid black;border-right: 1pt solid black;text-align: center;vertical-align: bottom;"|3 | | style="border-left: 1pt solid black;border-bottom: 1pt solid black;border-right: 1pt solid black;text-align: center;vertical-align: bottom;"|3 | ||
| − | | style="border-bottom: 1pt solid black;border-right: 1pt solid black;vertical-align: bottom;"|Altshul II | + | | style="padding-left:5px;border-bottom: 1pt solid black;border-right: 1pt solid black;vertical-align: bottom;"|Altshul II |
| style="border-bottom: 1pt solid black;border-right: 1pt solid black;text-align: center;vertical-align: bottom;"|0,0220010 | | style="border-bottom: 1pt solid black;border-right: 1pt solid black;text-align: center;vertical-align: bottom;"|0,0220010 | ||
| style="border-bottom: 1pt solid black;border-right: 1pt solid black;text-align: center;vertical-align: bottom;"|1,8986 | | style="border-bottom: 1pt solid black;border-right: 1pt solid black;text-align: center;vertical-align: bottom;"|1,8986 | ||
|- | |- | ||
| style="border-left: 1pt solid black;border-bottom: 1pt solid black;border-right: 1pt solid black;text-align: center;vertical-align: bottom;"|4 | | style="border-left: 1pt solid black;border-bottom: 1pt solid black;border-right: 1pt solid black;text-align: center;vertical-align: bottom;"|4 | ||
| − | | style="border-bottom: 1pt solid black;border-right: 1pt solid black;vertical-align: bottom;"|Konakov | + | | style="padding-left:5px;border-bottom: 1pt solid black;border-right: 1pt solid black;vertical-align: bottom;"|Konakov |
| style="border-bottom: 1pt solid black;border-right: 1pt solid black;text-align: center;vertical-align: bottom;"|0,0220148 | | style="border-bottom: 1pt solid black;border-right: 1pt solid black;text-align: center;vertical-align: bottom;"|0,0220148 | ||
| style="border-bottom: 1pt solid black;border-right: 1pt solid black;text-align: center;vertical-align: bottom;"|1,8370 | | style="border-bottom: 1pt solid black;border-right: 1pt solid black;text-align: center;vertical-align: bottom;"|1,8370 | ||
|- | |- | ||
| style="border-left: 1pt solid black;border-bottom: 1pt solid black;border-right: 1pt solid black;text-align: center;vertical-align: bottom;"|5 | | style="border-left: 1pt solid black;border-bottom: 1pt solid black;border-right: 1pt solid black;text-align: center;vertical-align: bottom;"|5 | ||
| − | | style="border-bottom: 1pt solid black;border-right: 1pt solid black;vertical-align: bottom;"|Shacham I | + | | style="padding-left:5px;border-bottom: 1pt solid black;border-right: 1pt solid black;vertical-align: bottom;"|Shacham I |
| style="border-bottom: 1pt solid black;border-right: 1pt solid black;text-align: center;vertical-align: bottom;"|0,0225339 | | style="border-bottom: 1pt solid black;border-right: 1pt solid black;text-align: center;vertical-align: bottom;"|0,0225339 | ||
| style="border-bottom: 1pt solid black;border-right: 1pt solid black;text-align: center;vertical-align: bottom;"|0,4775 | | style="border-bottom: 1pt solid black;border-right: 1pt solid black;text-align: center;vertical-align: bottom;"|0,4775 | ||
|- | |- | ||
| style="border-left: 1pt solid black;border-bottom: 1pt solid black;border-right: 1pt solid black;text-align: center;vertical-align: bottom;"|6 | | style="border-left: 1pt solid black;border-bottom: 1pt solid black;border-right: 1pt solid black;text-align: center;vertical-align: bottom;"|6 | ||
| − | | style="border-bottom: 1pt solid black;border-right: 1pt solid black;vertical-align: bottom;"|Shacham II | + | | style="padding-left:5px;border-bottom: 1pt solid black;border-right: 1pt solid black;vertical-align: bottom;"|Shacham II |
| style="border-bottom: 1pt solid black;border-right: 1pt solid black;text-align: center;vertical-align: bottom;"|0,0224328 | | style="border-bottom: 1pt solid black;border-right: 1pt solid black;text-align: center;vertical-align: bottom;"|0,0224328 | ||
| style="border-bottom: 1pt solid black;border-right: 1pt solid black;text-align: center;vertical-align: bottom;"|0,0269 | | style="border-bottom: 1pt solid black;border-right: 1pt solid black;text-align: center;vertical-align: bottom;"|0,0269 | ||
|- | |- | ||
| style="border-left: 1pt solid black;border-bottom: 1pt solid black;border-right: 1pt solid black;text-align: center;vertical-align: bottom;"|7 | | style="border-left: 1pt solid black;border-bottom: 1pt solid black;border-right: 1pt solid black;text-align: center;vertical-align: bottom;"|7 | ||
| − | | style="border-bottom: 1pt solid black;border-right: 1pt solid black;vertical-align: bottom;"|Chen | + | | style="padding-left:5px;border-bottom: 1pt solid black;border-right: 1pt solid black;vertical-align: bottom;"|Chen |
| style="border-bottom: 1pt solid black;border-right: 1pt solid black;text-align: center;vertical-align: bottom;"|0,0224582 | | style="border-bottom: 1pt solid black;border-right: 1pt solid black;text-align: center;vertical-align: bottom;"|0,0224582 | ||
| style="border-bottom: 1pt solid black;border-right: 1pt solid black;text-align: center;vertical-align: bottom;"|0,1403 | | style="border-bottom: 1pt solid black;border-right: 1pt solid black;text-align: center;vertical-align: bottom;"|0,1403 | ||
|- | |- | ||
| style="border-left: 1pt solid black;border-bottom: 1pt solid black;border-right: 1pt solid black;text-align: center;vertical-align: bottom;"|8 | | style="border-left: 1pt solid black;border-bottom: 1pt solid black;border-right: 1pt solid black;text-align: center;vertical-align: bottom;"|8 | ||
| − | | style="border-bottom: 1pt solid black;border-right: 1pt solid black;vertical-align: bottom;"|Churchill | + | | style="padding-left:5px;border-bottom: 1pt solid black;border-right: 1pt solid black;vertical-align: bottom;"|Churchill |
| style="border-bottom: 1pt solid black;border-right: 1pt solid black;text-align: center;vertical-align: bottom;"|0,0223510 | | style="border-bottom: 1pt solid black;border-right: 1pt solid black;text-align: center;vertical-align: bottom;"|0,0223510 | ||
| style="border-bottom: 1pt solid black;border-right: 1pt solid black;text-align: center;vertical-align: bottom;"|0,3380 | | style="border-bottom: 1pt solid black;border-right: 1pt solid black;text-align: center;vertical-align: bottom;"|0,3380 | ||
|- | |- | ||
| style="border-left: 1pt solid black;border-bottom: 1pt solid black;border-right: 1pt solid black;text-align: center;vertical-align: bottom;"|9 | | style="border-left: 1pt solid black;border-bottom: 1pt solid black;border-right: 1pt solid black;text-align: center;vertical-align: bottom;"|9 | ||
| − | | style="border-bottom: 1pt solid black;border-right: 1pt solid black;vertical-align: bottom;"|Swamee and Jain | + | | style="padding-left:5px;border-bottom: 1pt solid black;border-right: 1pt solid black;vertical-align: bottom;"|Swamee and Jain |
| style="border-bottom: 1pt solid black;border-right: 1pt solid black;text-align: center;vertical-align: bottom;"|0,0223343 | | style="border-bottom: 1pt solid black;border-right: 1pt solid black;text-align: center;vertical-align: bottom;"|0,0223343 | ||
| style="border-bottom: 1pt solid black;border-right: 1pt solid black;text-align: center;vertical-align: bottom;"|0,4125 | | style="border-bottom: 1pt solid black;border-right: 1pt solid black;text-align: center;vertical-align: bottom;"|0,4125 | ||
|- | |- | ||
| style="border-left: 1pt solid black;border-bottom: 1pt solid black;border-right: 1pt solid black;text-align: center;vertical-align: bottom;"|10 | | style="border-left: 1pt solid black;border-bottom: 1pt solid black;border-right: 1pt solid black;text-align: center;vertical-align: bottom;"|10 | ||
| − | | style="border-bottom: 1pt solid black;border-right: 1pt solid black;vertical-align: bottom;"|Pavlov | + | | style="padding-left:5px;border-bottom: 1pt solid black;border-right: 1pt solid black;vertical-align: bottom;"|Pavlov |
| style="border-bottom: 1pt solid black;border-right: 1pt solid black;text-align: center;vertical-align: bottom;"|0,0222177 | | style="border-bottom: 1pt solid black;border-right: 1pt solid black;text-align: center;vertical-align: bottom;"|0,0222177 | ||
| style="border-bottom: 1pt solid black;border-right: 1pt solid black;text-align: center;vertical-align: bottom;"|0,9321 | | style="border-bottom: 1pt solid black;border-right: 1pt solid black;text-align: center;vertical-align: bottom;"|0,9321 | ||
|- | |- | ||
| style="border-left: 1pt solid black;border-bottom: 1pt solid black;border-right: 1pt solid black;text-align: center;vertical-align: bottom;"|11 | | style="border-left: 1pt solid black;border-bottom: 1pt solid black;border-right: 1pt solid black;text-align: center;vertical-align: bottom;"|11 | ||
| − | | style="border-bottom: 1pt solid black;border-right: 1pt solid black;vertical-align: bottom;"|Round | + | | style="padding-left:5px;border-bottom: 1pt solid black;border-right: 1pt solid black;vertical-align: bottom;"|Round |
| style="border-bottom: 1pt solid black;border-right: 1pt solid black;text-align: center;vertical-align: bottom;"|0,0222191 | | style="border-bottom: 1pt solid black;border-right: 1pt solid black;text-align: center;vertical-align: bottom;"|0,0222191 | ||
| style="border-bottom: 1pt solid black;border-right: 1pt solid black;text-align: center;vertical-align: bottom;"|0,9261 | | style="border-bottom: 1pt solid black;border-right: 1pt solid black;text-align: center;vertical-align: bottom;"|0,9261 | ||
|- | |- | ||
| style="border-left: 1pt solid black;border-bottom: 1pt solid black;border-right: 1pt solid black;text-align: center;vertical-align: bottom;"|12 | | style="border-left: 1pt solid black;border-bottom: 1pt solid black;border-right: 1pt solid black;text-align: center;vertical-align: bottom;"|12 | ||
| − | | style="border-bottom: 1pt solid black;border-right: 1pt solid black;vertical-align: bottom;"|Barr | + | | style="padding-left:5px;border-bottom: 1pt solid black;border-right: 1pt solid black;vertical-align: bottom;"|Barr |
| style="border-bottom: 1pt solid black;border-right: 1pt solid black;text-align: center;vertical-align: bottom;"|0,0224172 | | style="border-bottom: 1pt solid black;border-right: 1pt solid black;text-align: center;vertical-align: bottom;"|0,0224172 | ||
| style="border-bottom: 1pt solid black;border-right: 1pt solid black;text-align: center;vertical-align: bottom;"|0,0427 | | style="border-bottom: 1pt solid black;border-right: 1pt solid black;text-align: center;vertical-align: bottom;"|0,0427 | ||
|- | |- | ||
| style="border-left: 1pt solid black;border-bottom: 1pt solid black;border-right: 1pt solid black;text-align: center;vertical-align: bottom;"|13 | | style="border-left: 1pt solid black;border-bottom: 1pt solid black;border-right: 1pt solid black;text-align: center;vertical-align: bottom;"|13 | ||
| − | | style="border-bottom: 1pt solid black;border-right: 1pt solid black;vertical-align: bottom;"|Zigrang - Sylvester | + | | style="padding-left:5px;border-bottom: 1pt solid black;border-right: 1pt solid black;vertical-align: bottom;"|Zigrang - Sylvester |
| style="border-bottom: 1pt solid black;border-right: 1pt solid black;text-align: center;vertical-align: bottom;"|0,0224099 | | style="border-bottom: 1pt solid black;border-right: 1pt solid black;text-align: center;vertical-align: bottom;"|0,0224099 | ||
| style="border-bottom: 1pt solid black;border-right: 1pt solid black;text-align: center;vertical-align: bottom;"|0,0752 | | style="border-bottom: 1pt solid black;border-right: 1pt solid black;text-align: center;vertical-align: bottom;"|0,0752 | ||
|- | |- | ||
| style="border-left: 1pt solid black;border-bottom: 1pt solid black;border-right: 1pt solid black;text-align: center;vertical-align: bottom;"|14 | | style="border-left: 1pt solid black;border-bottom: 1pt solid black;border-right: 1pt solid black;text-align: center;vertical-align: bottom;"|14 | ||
| − | | style="border-bottom: 1pt solid black;border-right: 1pt solid black;vertical-align: bottom;"|S. E. Haaland | + | | style="padding-left:5px;border-bottom: 1pt solid black;border-right: 1pt solid black;vertical-align: bottom;"|S. E. Haaland |
| style="border-bottom: 1pt solid black;border-right: 1pt solid black;text-align: center;vertical-align: bottom;"|0,0222085 | | style="border-bottom: 1pt solid black;border-right: 1pt solid black;text-align: center;vertical-align: bottom;"|0,0222085 | ||
| style="border-bottom: 1pt solid black;border-right: 1pt solid black;text-align: center;vertical-align: bottom;"|0,9734 | | style="border-bottom: 1pt solid black;border-right: 1pt solid black;text-align: center;vertical-align: bottom;"|0,9734 | ||
|- | |- | ||
| style="border-left: 1pt solid black;border-bottom: 1pt solid black;border-right: 1pt solid black;text-align: center;vertical-align: bottom;"|15 | | style="border-left: 1pt solid black;border-bottom: 1pt solid black;border-right: 1pt solid black;text-align: center;vertical-align: bottom;"|15 | ||
| − | | style="border-bottom: 1pt solid black;border-right: 1pt solid black;vertical-align: bottom;"|Manadilli | + | | style="padding-left:5px;border-bottom: 1pt solid black;border-right: 1pt solid black;vertical-align: bottom;"|Manadilli |
| style="border-bottom: 1pt solid black;border-right: 1pt solid black;text-align: center;vertical-align: bottom;"|0,0224538 | | style="border-bottom: 1pt solid black;border-right: 1pt solid black;text-align: center;vertical-align: bottom;"|0,0224538 | ||
| style="border-bottom: 1pt solid black;border-right: 1pt solid black;text-align: center;vertical-align: bottom;"|0,1205 | | style="border-bottom: 1pt solid black;border-right: 1pt solid black;text-align: center;vertical-align: bottom;"|0,1205 | ||
|- | |- | ||
| style="border-left: 1pt solid black;border-bottom: 1pt solid black;border-right: 1pt solid black;text-align: center;vertical-align: bottom;"|16 | | style="border-left: 1pt solid black;border-bottom: 1pt solid black;border-right: 1pt solid black;text-align: center;vertical-align: bottom;"|16 | ||
| − | | style="border-bottom: 1pt solid black;border-right: 1pt solid black;vertical-align: bottom;"|Romeo et al. | + | | style="padding-left:5px;border-bottom: 1pt solid black;border-right: 1pt solid black;vertical-align: bottom;"|Romeo et al. |
| style="border-bottom: 1pt solid black;border-right: 1pt solid black;text-align: center;vertical-align: bottom;"|0,0224568 | | style="border-bottom: 1pt solid black;border-right: 1pt solid black;text-align: center;vertical-align: bottom;"|0,0224568 | ||
| style="border-bottom: 1pt solid black;border-right: 1pt solid black;text-align: center;vertical-align: bottom;"|0,1339 | | style="border-bottom: 1pt solid black;border-right: 1pt solid black;text-align: center;vertical-align: bottom;"|0,1339 | ||
|- | |- | ||
| style="border-left: 1pt solid black;border-bottom: 1pt solid black;border-right: 1pt solid black;text-align: center;vertical-align: bottom;"|17 | | style="border-left: 1pt solid black;border-bottom: 1pt solid black;border-right: 1pt solid black;text-align: center;vertical-align: bottom;"|17 | ||
| − | | style="border-bottom: 1pt solid black;border-right: 1pt solid black;vertical-align: bottom;"|Colebrook-White | + | | style="padding-left:5px;border-bottom: 1pt solid black;border-right: 1pt solid black;vertical-align: bottom;"|Colebrook-White |
| style="border-bottom: 1pt solid black;border-right: 1pt solid black;text-align: center;vertical-align: bottom;"|0,0224321 | | style="border-bottom: 1pt solid black;border-right: 1pt solid black;text-align: center;vertical-align: bottom;"|0,0224321 | ||
| style="border-bottom: 1pt solid black;border-right: 1pt solid black;text-align: center;vertical-align: bottom;"|0,0237 | | style="border-bottom: 1pt solid black;border-right: 1pt solid black;text-align: center;vertical-align: bottom;"|0,0237 | ||
|- | |- | ||
| style="border-left: 1pt solid black;border-bottom: 1pt solid black;border-right: 1pt solid black;text-align: center;vertical-align: bottom;"|18 | | style="border-left: 1pt solid black;border-bottom: 1pt solid black;border-right: 1pt solid black;text-align: center;vertical-align: bottom;"|18 | ||
| − | | style="border-bottom: 1pt solid black;border-right: 1pt solid black;vertical-align: bottom;"|Sonnad and Goudar | + | | style="padding-left:5px;border-bottom: 1pt solid black;border-right: 1pt solid black;vertical-align: bottom;"|Sonnad and Goudar |
| style="border-bottom: 1pt solid black;border-right: 1pt solid black;text-align: center;vertical-align: bottom;"|0,0225639 | | style="border-bottom: 1pt solid black;border-right: 1pt solid black;text-align: center;vertical-align: bottom;"|0,0225639 | ||
| style="border-bottom: 1pt solid black;border-right: 1pt solid black;text-align: center;vertical-align: bottom;"|0,6117 | | style="border-bottom: 1pt solid black;border-right: 1pt solid black;text-align: center;vertical-align: bottom;"|0,6117 | ||
|- | |- | ||
| style="border-left: 1pt solid black;border-bottom: 1pt solid black;border-right: 1pt solid black;text-align: center;vertical-align: bottom;"|19 | | style="border-left: 1pt solid black;border-bottom: 1pt solid black;border-right: 1pt solid black;text-align: center;vertical-align: bottom;"|19 | ||
| − | | style="border-bottom: 1pt solid black;border-right: 1pt solid black;vertical-align: bottom;"|Buzzelli | + | | style="padding-left:5px;border-bottom: 1pt solid black;border-right: 1pt solid black;vertical-align: bottom;"|Buzzelli |
| style="border-bottom: 1pt solid black;border-right: 1pt solid black;text-align: center;vertical-align: bottom;"|0,0224321 | | style="border-bottom: 1pt solid black;border-right: 1pt solid black;text-align: center;vertical-align: bottom;"|0,0224321 | ||
| style="border-bottom: 1pt solid black;border-right: 1pt solid black;text-align: center;vertical-align: bottom;"|0,0238 | | style="border-bottom: 1pt solid black;border-right: 1pt solid black;text-align: center;vertical-align: bottom;"|0,0238 | ||
|- | |- | ||
| style="border-left: 1pt solid black;border-bottom: 1pt solid black;border-right: 1pt solid black;text-align: center;vertical-align: bottom;"|20 | | style="border-left: 1pt solid black;border-bottom: 1pt solid black;border-right: 1pt solid black;text-align: center;vertical-align: bottom;"|20 | ||
| − | | style="border-bottom: 1pt solid black;border-right: 1pt solid black;vertical-align: bottom;"|Avci and Karagoz | + | | style="padding-left:5px;border-bottom: 1pt solid black;border-right: 1pt solid black;vertical-align: bottom;"|Avci and Karagoz |
| style="border-bottom: 1pt solid black;border-right: 1pt solid black;text-align: center;vertical-align: bottom;"|0,0225747 | | style="border-bottom: 1pt solid black;border-right: 1pt solid black;text-align: center;vertical-align: bottom;"|0,0225747 | ||
| style="border-bottom: 1pt solid black;border-right: 1pt solid black;text-align: center;vertical-align: bottom;"|0,6595 | | style="border-bottom: 1pt solid black;border-right: 1pt solid black;text-align: center;vertical-align: bottom;"|0,6595 | ||
|- | |- | ||
| style="border-left: 1pt solid black;border-bottom: 1pt solid black;border-right: 1pt solid black;text-align: center;vertical-align: bottom;"|21 | | style="border-left: 1pt solid black;border-bottom: 1pt solid black;border-right: 1pt solid black;text-align: center;vertical-align: bottom;"|21 | ||
| − | | style="border-bottom: 1pt solid black;border-right: 1pt solid black;vertical-align: bottom;"|Saeed Samadianfard | + | | style="padding-left:5px;border-bottom: 1pt solid black;border-right: 1pt solid black;vertical-align: bottom;"|Saeed Samadianfard |
| style="border-bottom: 1pt solid black;border-right: 1pt solid black;text-align: center;vertical-align: bottom;"|0,0228794 | | style="border-bottom: 1pt solid black;border-right: 1pt solid black;text-align: center;vertical-align: bottom;"|0,0228794 | ||
| style="border-bottom: 1pt solid black;border-right: 1pt solid black;text-align: center;vertical-align: bottom;"|2,0182 | | style="border-bottom: 1pt solid black;border-right: 1pt solid black;text-align: center;vertical-align: bottom;"|2,0182 | ||
|- | |- | ||
| style="border-left: 1pt solid black;border-bottom: 1pt solid black;border-right: 1pt solid black;text-align: center;vertical-align: bottom;"|22 | | style="border-left: 1pt solid black;border-bottom: 1pt solid black;border-right: 1pt solid black;text-align: center;vertical-align: bottom;"|22 | ||
| − | | style="border-bottom: 1pt solid black;border-right: 1pt solid black;vertical-align: bottom;"|Papaevangelou et al. | + | | style="padding-left:5px;border-bottom: 1pt solid black;border-right: 1pt solid black;vertical-align: bottom;"|Papaevangelou et al. |
| style="border-bottom: 1pt solid black;border-right: 1pt solid black;text-align: center;vertical-align: bottom;"|0,0224174 | | style="border-bottom: 1pt solid black;border-right: 1pt solid black;text-align: center;vertical-align: bottom;"|0,0224174 | ||
| style="border-bottom: 1pt solid black;border-right: 1pt solid black;text-align: center;vertical-align: bottom;"|0,0416 | | style="border-bottom: 1pt solid black;border-right: 1pt solid black;text-align: center;vertical-align: bottom;"|0,0416 | ||
|- | |- | ||
| style="border-left: 1pt solid black;border-bottom: 1pt solid black;border-right: 1pt solid black;text-align: center;vertical-align: bottom;"|23 | | style="border-left: 1pt solid black;border-bottom: 1pt solid black;border-right: 1pt solid black;text-align: center;vertical-align: bottom;"|23 | ||
| − | | style="border-bottom: 1pt solid black;border-right: 1pt solid black;vertical-align: bottom;"|Brkic I | + | | style="padding-left:5px;padding-left:5px;border-bottom: 1pt solid black;border-right: 1pt solid black;vertical-align: bottom;"|Brkic I |
| style="border-bottom: 1pt solid black;border-right: 1pt solid black;text-align: center;vertical-align: bottom;"|0,0218275 | | style="border-bottom: 1pt solid black;border-right: 1pt solid black;text-align: center;vertical-align: bottom;"|0,0218275 | ||
| style="border-bottom: 1pt solid black;border-right: 1pt solid black;text-align: center;vertical-align: bottom;"|2,6723 | | style="border-bottom: 1pt solid black;border-right: 1pt solid black;text-align: center;vertical-align: bottom;"|2,6723 | ||
|- | |- | ||
| style="border-left: 1pt solid black;border-bottom: 1pt solid black;border-right: 1pt solid black;text-align: center;vertical-align: bottom;"|24 | | style="border-left: 1pt solid black;border-bottom: 1pt solid black;border-right: 1pt solid black;text-align: center;vertical-align: bottom;"|24 | ||
| − | | style="border-bottom: 1pt solid black;border-right: 1pt solid black;vertical-align: bottom;"|Brkic II | + | | style="padding-left:5px;border-bottom: 1pt solid black;border-right: 1pt solid black;vertical-align: bottom;"|Brkic II |
| style="border-bottom: 1pt solid black;border-right: 1pt solid black;text-align: center;vertical-align: bottom;"|0,0225362 | | style="border-bottom: 1pt solid black;border-right: 1pt solid black;text-align: center;vertical-align: bottom;"|0,0225362 | ||
| style="border-bottom: 1pt solid black;border-right: 1pt solid black;text-align: center;vertical-align: bottom;"|0,4881 | | style="border-bottom: 1pt solid black;border-right: 1pt solid black;text-align: center;vertical-align: bottom;"|0,4881 | ||
|- | |- | ||
| style="border-left: 1pt solid black;border-bottom: 1pt solid black;border-right: 1pt solid black;text-align: center;vertical-align: bottom;"|25 | | style="border-left: 1pt solid black;border-bottom: 1pt solid black;border-right: 1pt solid black;text-align: center;vertical-align: bottom;"|25 | ||
| − | | style="border-bottom: 1pt solid black;border-right: 1pt solid black;vertical-align: bottom;"|Fang et al. | + | | style="padding-left:5px;border-bottom: 1pt solid black;border-right: 1pt solid black;vertical-align: bottom;"|Fang et al. |
| style="border-bottom: 1pt solid black;border-right: 1pt solid black;text-align: center;vertical-align: bottom;"|0,0224542 | | style="border-bottom: 1pt solid black;border-right: 1pt solid black;text-align: center;vertical-align: bottom;"|0,0224542 | ||
| style="border-bottom: 1pt solid black;border-right: 1pt solid black;text-align: center;vertical-align: bottom;"|0,1221 | | style="border-bottom: 1pt solid black;border-right: 1pt solid black;text-align: center;vertical-align: bottom;"|0,1221 | ||
|- | |- | ||
| style="border-left: 1pt solid black;border-bottom: 1pt solid black;border-right: 1pt solid black;text-align: center;vertical-align: bottom;"|26 | | style="border-left: 1pt solid black;border-bottom: 1pt solid black;border-right: 1pt solid black;text-align: center;vertical-align: bottom;"|26 | ||
| − | | style="border-bottom: 1pt solid black;border-right: 1pt solid black;vertical-align: bottom;"|Li et al. | + | | style="padding-left:5px;border-bottom: 1pt solid black;border-right: 1pt solid black;vertical-align: bottom;"|Li et al. |
| style="border-bottom: 1pt solid black;border-right: 1pt solid black;text-align: center;vertical-align: bottom;"|0,0224588 | | style="border-bottom: 1pt solid black;border-right: 1pt solid black;text-align: center;vertical-align: bottom;"|0,0224588 | ||
| style="border-bottom: 1pt solid black;border-right: 1pt solid black;text-align: center;vertical-align: bottom;"|0,1429 | | style="border-bottom: 1pt solid black;border-right: 1pt solid black;text-align: center;vertical-align: bottom;"|0,1429 | ||
|- | |- | ||
| style="border-left: 1pt solid black;border-bottom: 1pt solid black;border-right: 1pt solid black;text-align: center;vertical-align: bottom;"|27 | | style="border-left: 1pt solid black;border-bottom: 1pt solid black;border-right: 1pt solid black;text-align: center;vertical-align: bottom;"|27 | ||
| − | | style="border-bottom: 1pt solid black;border-right: 1pt solid black;vertical-align: bottom;"|Shaikh et al. | + | | style="padding-left:5px;border-bottom: 1pt solid black;border-right: 1pt solid black;vertical-align: bottom;"|Shaikh et al. |
| style="border-bottom: 1pt solid black;border-right: 1pt solid black;text-align: center;vertical-align: bottom;"|0,0213440 | | style="border-bottom: 1pt solid black;border-right: 1pt solid black;text-align: center;vertical-align: bottom;"|0,0213440 | ||
| style="border-bottom: 1pt solid black;border-right: 1pt solid black;text-align: center;vertical-align: bottom;"|4,8280 | | style="border-bottom: 1pt solid black;border-right: 1pt solid black;text-align: center;vertical-align: bottom;"|4,8280 | ||
|} | |} | ||
| − | =4. Conclusiones= | + | ==4. Conclusiones== |
En el presente trabajo se construyó un sistema para determinar el factor de fricción experimental y se comparó con 27 correlaciones utilizadas para obtener de forma teórica el factor de fricción. De estas correlaciones, 26 eran explícitas y una implícita, para la cual se desarrolló un programa en lenguaje C++ que permite el cálculo de factor de fricción utilizando el método de Newton-Raphson. Para este análisis se calculó el error relativo porcentual de cada una de las correlaciones respecto del valor experimental, lo cual permite evaluar la calidad predictiva de cada una de las correlaciones en forma experimental, ya que la mayoría de ellas son propuestas teóricas, siendo las correlaciones de Colebrook-White, Buzzelli y Shacham II las que presentaron el menor error relativo porcentual y la correlación de Shaikh la que presentó el mayor error relativo porcentual. Es importante destacar que la gran mayoría de las correlaciones presenta un error relativo porcentual menor al 1%. Las perspectivas del presente trabajo son desarrollar otras experiencias en el sistema construido para evaluar otras condiciones experimentales, además de entregar el código fuente en lenguaje de programación C++ de la solución de la ecuación de Colebrook-White, el cual permitiría su rápida aplicación en la determinación del factor de fricción y además se podría aplicar a la resolución de otras correlaciones de tipo implícito para el cálculo del factor de fricción. | En el presente trabajo se construyó un sistema para determinar el factor de fricción experimental y se comparó con 27 correlaciones utilizadas para obtener de forma teórica el factor de fricción. De estas correlaciones, 26 eran explícitas y una implícita, para la cual se desarrolló un programa en lenguaje C++ que permite el cálculo de factor de fricción utilizando el método de Newton-Raphson. Para este análisis se calculó el error relativo porcentual de cada una de las correlaciones respecto del valor experimental, lo cual permite evaluar la calidad predictiva de cada una de las correlaciones en forma experimental, ya que la mayoría de ellas son propuestas teóricas, siendo las correlaciones de Colebrook-White, Buzzelli y Shacham II las que presentaron el menor error relativo porcentual y la correlación de Shaikh la que presentó el mayor error relativo porcentual. Es importante destacar que la gran mayoría de las correlaciones presenta un error relativo porcentual menor al 1%. Las perspectivas del presente trabajo son desarrollar otras experiencias en el sistema construido para evaluar otras condiciones experimentales, además de entregar el código fuente en lenguaje de programación C++ de la solución de la ecuación de Colebrook-White, el cual permitiría su rápida aplicación en la determinación del factor de fricción y además se podría aplicar a la resolución de otras correlaciones de tipo implícito para el cálculo del factor de fricción. | ||
| Line 548: | Line 532: | ||
==Referencias== | ==Referencias== | ||
| − | [1] M. S. | + | <div class="auto" style="width: auto; margin-left: auto; margin-right: auto;font-size: 85%;"> |
| + | [1] Ángeles M.S., Chéret I., et al. Manejo integrado de recursos hídricos. Global Water Partnership, Suecia, 2000. | ||
| − | [2] A. I. | + | [2] Anaya-Durand A.I., Cauich-Segovia G.I., Funabazama-Bárcenas O., Gracia-Medrano-Bravo V.A. Evaluación de ecuaciones de factor de fricción explícito para tuberías. Educ. Quim., 25(2):128–134, 2014. |
| − | [3] M. | + | [3] Najafzadeh M., Shiri J., Sadeghi G., Ghaemi A. Prediction of the friction factor in pipes using model tree. ISH J. Hydraul. Eng., 24(1):9–15, 2018. |
| − | [4] M. | + | [4] Özger M., Yildirim G. Determining turbulent flow friction coefficient using adaptive neuro-fuzzy computing technique. Adv. Eng. Softw., 40(4):281–287, 2009. |
| − | [5] C. F. | + | [5] Colebrook C.F., White C.M., Experiments with fluid friction in roughened pipes. Proc. R. Soc. A Math. Phys. Eng. Sci., 161(906):367–381, 1937. |
| − | [6] C. F. | + | [6] Colebrook C.F., et al. Correspondence. Turbulent flow in pipes with particular reference to the transition region between the smooth and rough pipe laws. J. Inst. Civ. Eng., 12(8):393–422, 1939. |
| − | [7] G. L. | + | [7] Augusto G.L., Culaba A.B., Tanhueco R.M.T., Pipe sizing of District cooling distribution network using implicit Colebrook-White equation. J. Adv. Comput. Intell. Intell. Informatics, 20(1):76–83, 2016. |
| − | [8] H. K. | + | [8] Winning H.K., Coole T. Explicit friction factor accuracy and computational efficiency for turbulent flow in pipes. Flow, Turbul. Combust., 90(1):1–27, 2013. |
| − | [9] M. A. | + | [9] Ellis M.A., Stroustrup B. The annotated C++ reference manual. Addison-Wesley, 1990. |
| − | [10] G. | + | [10] Filonenko G. Hydraulic resistance in pipes. Teploenergetika, 1:40–44, 1954. |
| − | [11] V. K. | + | [11] Konakov V.K. New formula for the friction coefficient of smooth tubes. Dokl. Akad. Nauk SSSR, 25(5):14–24, 1950. |
| − | [12] N. H. | + | [12] Chen N.H. An explicit equation for friction factor in pipe. Ind. Eng. Chem. Fundam., 18(3):296–297, 1979. |
| − | [13] S. W. | + | [13] Churchill S.W. Friction-factor equation spans all fluid-flow regimes. Chem. Eng., 84(24):91–92, 1977. |
| − | [14] P. K. | + | [14] Swamee P.K., Jain A.K. Explicit equations for pipe-flow problems. J. Hydraul. Div., 102(5):657–664, 1976. |
| − | [15] K. F. | + | [15] Pávlov K.F., Romankov P.G., Noskov A.A. Problemas y ejemplos para el curso de operaciones básicas y aparatos en tecnología química. Mir, 608 pp., 1981. |
| − | [16] | + | [16] Round G.F. An explicit approximation for the friction factor‐reynolds number relation for rough and smooth pipes. Can. J. Chem. Eng., 58(1):122–123, 1980. |
| − | [17] D. I. H. | + | [17] Barr D.I.H. Solutions of the Colebrook-White function for resistance to uniform turbulent flow. 'Proc. Inst. Civ. Eng., 71(2):529–535, 1981. |
| − | [18] D. J. | + | [18] Zigrang D.J., Sylvester N.D. Explicit approximations to the solution of Colebrook’s friction factor equation. AIChE J., 28(3):514–515, 1982. |
| − | [19] S. E. | + | [19] Haaland S.E. Simple and explicit formulas for the friction factor in turbulent pipe flow. J. Fluids Eng., 105(1):89-90, 1983. |
| − | [20] G. | + | [20] Manadili G. et al. Replace implicit equations with signomial functions. Chem. Eng., 104(8):129-130,132, 1997. |
| − | [21] E. | + | [21] Romeo E., Royo C., Monzón A. Improved explicit equations for estimation of the friction factor in rough and smooth pipes. Chem. Eng. J., 86(3):369–374, 2002. |
| − | [22] J. R. | + | [22] Sonnad J.R., Goudar C.T. Using a mathematically exact alternative to the Colebrook–White equation. J. Hydraul. Eng., 132(8):863–867, 2006. |
| − | [23] D. | + | [23] Buzzelli D. Calculating friction in one step. Mach. Des., 80(12):54–55, 2008. |
| − | [24] A. | + | [24] Avci A., Karagoz I. A novel explicit equation for friction factor in smooth and rough pipes. J. Fluids Eng., 131(6):061203, 2009. |
| − | [25] S. | + | [25] Samadianfard S. Gene expression programming analysis of implicit Colebrook--White equation in turbulent flow friction factor calculation. J. Pet. Sci. Eng., 92:48–55, 2012. |
| − | [26] G. | + | [26] Papaevangelou G., Evangelides C., Tzimopoulos C. A new explicit relation for friction coefficient <math>f</math> in the Darcy-Weisbach equation. PRE10: Prot. Restor. Environ., pp. 166–73, Corfu, 05-09 July, 2010. |
| − | [27] D. | + | [27] Brkić D. Review of explicit approximations to the Colebrook relation for flow friction. J. Pet. Sci. Eng., 77(1):34–48, 2011. |
| − | [28] X. | + | [28] Fang X., Xu Y., Zhou Z. New correlations of single-phase friction factor for turbulent pipe flow and evaluation of existing single-phase friction factor correlations. Nucl. Eng. Des., 241(3):897–902, 2011. |
| − | [29] P. | + | [29] Li P., Seem J.E., Li Y. A new explicit equation for accurate friction factor calculation of smooth pipes. Int. J. Refrig., 34(6):1535–1541, 2011. |
| − | [30] M. M. | + | [30] Shaikh M.M., Massan S.U.R., Wagan A.I. A new explicit approximation to Colebrook’s friction factor in rough pipes under highly turbulent cases. Int. J. Heat Mass Transf., 88: 538–543, 2015. |
| − | [31] L. | + | [31] Neto L., Porto R.D.M. Performance of low-cost ejectors. J. Irrigation and Drainage Engineering, |
| + | 130(2):122–128, 2004. | ||
| + | </div> | ||
==Apéndice A== | ==Apéndice A== | ||
| − | ==Complemento | + | ===Complemento derivada ecuación Colebrook-White=== |
| − | Para la determinación del factor de fricción en flujos turbulentos para tuberías rugosas es utilizada la ecuación (A.1) de Colebrook-White. Esta relación tiene una forma implícita para el valor de | + | Para la determinación del factor de fricción en flujos turbulentos para tuberías rugosas es utilizada la ecuación (A.1) de Colebrook-White. Esta relación tiene una forma implícita para el valor de <math>f</math>, tal como sigue: |
| − | + | {| class="formulaSCP" style="width: 100%; text-align: center;" | |
| + | |- | ||
| + | | | ||
| + | {| style="text-align: center; margin:auto;" | ||
| + | |- | ||
| + | | <math>\displaystyle\frac{1}{\sqrt f}=-2\hbox{log}\left[\displaystyle\frac{2.51}{\hbox{Re}\sqrt f}+\displaystyle\frac{\varepsilon /D}{3.7}\right]</math> | ||
| + | |} | ||
| + | | style="width: 5px;text-align: right;white-space: nowrap;" | (A.1) | ||
| + | |} | ||
| − | + | donde <math>f</math> es el factor de fricción de la tubería, Re es el número de Reynolds y <math>\varepsilon/D</math> es la rugosidad relativa de la tubería. | |
| − | Si se reescribe la ecuación (A.1) reemplazando el valor | + | Si se reescribe la ecuación (A.1) reemplazando el valor <math> F''=''1/\surd f</math> y luego despejando la expresión, se tiene: |
| − | + | {| class="formulaSCP" style="width: 100%; text-align: center;" | |
| + | |- | ||
| + | | | ||
| + | {| style="text-align: center; margin:auto;" | ||
| + | |- | ||
| + | | <math display="inline">g(F)=F+2\hbox{log}\left[\displaystyle\frac{2.51}{\hbox{Re}\sqrt f}+\displaystyle\frac{\varepsilon /D}{3.7}\right]</math> | ||
| + | |} | ||
| + | | style="width: 5px;text-align: right;white-space: nowrap;" | (A.2) | ||
| + | |} | ||
| − | |||
| − | + | Derivando de manera implícita la ecuación (A.2) con respecto a la variable <math> F </math>, se obtiene lo siguiente: | |
| − | + | {| class="formulaSCP" style="width: 100%; text-align: center;" | |
| + | |- | ||
| + | | | ||
| + | {| style="text-align: center; margin:auto;" | ||
| + | |- | ||
| + | | <math display="inline">\displaystyle\frac{d(g(F))}{\hbox{dF}}=g'(F)=\hbox{1+2}\cdot \displaystyle\frac{d}{\hbox{dF}}\left(\hbox{log}\left[\frac{\varepsilon /D}{3,7}+\displaystyle\frac{2,51}{\hbox{Re}}\cdot F\right]\right)</math> | ||
| + | |} | ||
| + | | style="width: 5px;text-align: right;white-space: nowrap;" | (A.3) | ||
| + | |} | ||
| − | + | Utilizando la derivada implícita para <math> F </math> se tiene que: | |
| − | + | {| class="formulaSCP" style="width: 100%; text-align: center;" | |
| + | |- | ||
| + | | | ||
| + | {| style="text-align: center; margin:auto;" | ||
| + | |- | ||
| + | | <math display="inline">\displaystyle\frac{d(\hbox{log}u)}{\hbox{dF}}=\displaystyle\frac{u'u}{\hbox{ln}10}</math> | ||
| + | |} | ||
| + | | style="width: 5px;text-align: right;white-space: nowrap;" | (A.4) | ||
| + | |} | ||
| − | + | Por lo tanto la derivada de la función <math> g(F) </math> con respecto a <math> F </math> es: | |
| + | |||
| + | {| class="formulaSCP" style="width: 100%; text-align: center;" | ||
| + | |- | ||
| + | | | ||
| + | {| style="text-align: center; margin:auto;" | ||
| + | |- | ||
| + | | <math display="inline">g'(F)=\hbox{1+2}\cdot \left[\displaystyle\frac{\displaystyle\frac{2,51}{\hbox{Re}}}{\left(\displaystyle\frac{\varepsilon /D}{3,7}+\displaystyle\frac{2,51}{\hbox{Re}}\cdot F\right)}\displaystyle\frac{1}{\hbox{ln}10}\right]</math> | ||
| + | |} | ||
| + | | style="width: 5px;text-align: right;white-space: nowrap;" | (A.5) | ||
| + | |} | ||
Reescribiendo la expresión anterior se tiene: | Reescribiendo la expresión anterior se tiene: | ||
| − | + | {| class="formulaSCP" style="width: 100%; text-align: center;" | |
| + | |- | ||
| + | | | ||
| + | {| style="text-align: center; margin:auto;" | ||
| + | |- | ||
| + | | <math display="inline">g'(F)=1+\left[\displaystyle\frac{8,06659}{\varepsilon /D\cdot \hbox{Re}+9,287\cdot F}\right]</math> | ||
| + | |} | ||
| + | | style="width: 5px;text-align: right;white-space: nowrap;" | (A.6) | ||
| + | |} | ||
| + | |||
| − | La ecuación (A.6) es la derivada de la función | + | La ecuación (A.6) es la derivada de la función <math> g(F) </math> que ha sido utilizada en el programa desarrollado en lenguaje C++ y que permite iterar y encontrar la solución numérica del factor de fricción para la ecuación (A.1) de Colebrook–White [3,7]. |
==Apéndice B== | ==Apéndice B== | ||
| − | ==Código | + | ===Código fuente programa C++=== |
Para la resolución numérica del factor de fricción de la ecuación implícita de Colebrook-White, se ha programado en lenguaje C++ un código fuente que permite facilitar dicho proceso, para que pueda ser utilizado por otros investigadores. Este código está estructurado de tal forma que permite a cualquier investigador resolver otras ecuaciones modificando incluso el metodo numérico a utilizar. | Para la resolución numérica del factor de fricción de la ecuación implícita de Colebrook-White, se ha programado en lenguaje C++ un código fuente que permite facilitar dicho proceso, para que pueda ser utilizado por otros investigadores. Este código está estructurado de tal forma que permite a cualquier investigador resolver otras ecuaciones modificando incluso el metodo numérico a utilizar. | ||
| − | #include <iostream> | + | #include <iostream> |
| − | #include <math.h> | + | |
| − | #include <fstream> | + | #include <math.h> |
| − | #include <stdlib.h> | + | |
| − | + | #include <fstream> | |
| − | using namespace std; | + | |
| − | + | #include <stdlib.h> | |
| − | double ED, Re, x, xt, error, Precision; | + | |
| − | + | using namespace std; | |
| − | //Despeje de la función G(f)=0 | + | |
| − | //Reemplazo de la variable x=1/RAIZ(f) | + | double ED, Re, x, xt, error, Precision; |
| − | + | ||
| − | double funcG(double x){ | + | //Despeje de la función G(f)=0 |
| − | return x+2*log10(((2.51*x)/Re)+(ED/3.7)); | + | |
| − | } | + | //Reemplazo de la variable x=1/RAIZ(f) |
| − | + | ||
| − | double derivadafuncG(double x){ | + | double funcG(double x){ |
| − | return 1+8.06659/(ED/Re+9.287*x); | + | |
| − | } | + | return x+2*log10(((2.51*x)/Re)+(ED/3.7)); |
| − | + | ||
| − | double friccion(double x){ | + | } |
| − | return pow((1/x),2); | + | |
| − | } | + | double derivadafuncG(double x){ |
| − | + | ||
| − | int main (){ | + | return 1+8.06659/(ED/Re+9.287*x); |
| − | int i=0; | + | |
| − | cout<<"\n\n\tIngrese el Valor de E/D = "; | + | } |
| − | cin>>ED; | + | |
| − | cout<<"\n\tIngrese el Valor de Re = "; | + | double friccion(double x){ |
| − | cin>>Re; | + | |
| − | cout<<"\n\tIngrese Valor inicial 1/SQRT(f) para iterar = "; | + | return pow((1/x),2); |
| − | cin>>x; | + | |
| − | cout<<"\n\tIngrese Valor de precision para el error de iteracion = "; | + | } |
| − | cin>>Precision; | + | |
| − | + | int main (){ | |
| − | //Impresión por pantalla e impresión hacia un archivo en la misma carpet de nombre: resultados.txt | + | |
| − | ofstream salida; | + | int i=0; |
| − | + | ||
| − | salida.open("resultados.txt", ios::out); | + | cout<<"\n\n\tIngrese el Valor de E/D = "; |
| − | if(salida.fail()){ | + | |
| − | cout<<"\nNo se pudo abrir el Archivo"; | + | cin>>ED; |
| − | } | + | |
| − | + | cout<<"\n\tIngrese el Valor de Re = "; | |
| − | salida<<"\n\n\tPrograma para la Determinación del Factor de friccion de Colebrook - White"; | + | |
| − | salida<<"\n\t--------------------------------------------------------------------------"; | + | cin>>Re; |
| − | salida<<"\n\n\n\tDatos ingresados"; | + | |
| − | salida<<"\n\t----------------"; | + | cout<<"\n\tIngrese Valor inicial 1/SQRT(f) para iterar = "; |
| − | salida<<"\n\n\tValor de E/D = "<<ED<<endl; | + | |
| − | salida<<"\n\tValor de Re = "<<Re<<endl; | + | cin>>x; |
| − | salida<<"\n\tValor inicial 1/SQRT(f) para iterar = "<<x<<endl; | + | |
| − | salida<<"\n\tValor de precision para el error de iteracion = "<<Precision<<endl; | + | cout<<"\n\tIngrese Valor de precision para el error de iteracion = "; |
| − | cout<<"\n\n\tResultados del Proceso de Iteracion"; | + | |
| − | salida<<"\n\n\tResultados del Proceso de Iteracion"; | + | cin>>Precision; |
| − | cout<<"\n\t-----------------------------------\n\n"; | + | |
| − | salida<<"\n\t-----------------------------------\n\n"; | + | //Impresión por pantalla e impresión hacia un archivo en la misma carpet de nombre: resultados.txt |
| − | + | ||
| − | do{ | + | ofstream salida; |
| − | xt=x; | + | |
| − | x=x-funcG(x)/derivadafuncG(x); | + | salida.open("resultados.txt", ios::out); |
| − | error=fabs(funcG(x)-funcG(xt)); | + | |
| − | cout<<"\tx"<<i<<" = "<<x<<"\tG("<<i<<") = "<<funcG(x)<<"\t\tError"<<i<<" = "<<error<<endl; | + | if(salida.fail()){ |
| − | salida<<"\tx"<<i<<" = "<<x<<"\tG("<<i<<") = "<<funcG(x)<<"\t\tError"<<i<<" = "<<error<<endl; | + | |
| − | i=i+1; | + | cout<<"\nNo se pudo abrir el Archivo"; |
| − | }while (Precision<error && i<200); | + | |
| − | + | } | |
| − | if (i==200) | + | |
| − | cout<<"\n\nNo hay convergencia"; | + | salida<<"\n\n\tPrograma para la Determinación del Factor de friccion de Colebrook - White"; |
| − | + | ||
| − | else | + | salida<<"\n\t--------------------------------------------------------------------------"; |
| − | cout<<"\n\n\tLa solucion para x = F es igual a "<<x; | + | |
| − | salida<<"\n\n\tLa solucion para x = F es igual a "<<x; | + | salida<<"\n\n\n\tDatos ingresados"; |
| − | cout<<"\n\n\tEl factor de Friccion Colebrook - White es f = "<<friccion(x); | + | |
| − | salida<<"\n\n\tEl factor de Friccion Colebrook - White es f = "<<friccion(x); | + | salida<<"\n\t----------------"; |
| − | salida.close(); | + | |
| − | return 0; | + | salida<<"\n\n\tValor de E/D = "<<ED<<endl; |
| − | } | + | |
| + | salida<<"\n\tValor de Re = "<<Re<<endl; | ||
| + | |||
| + | salida<<"\n\tValor inicial 1/SQRT(f) para iterar = "<<x<<endl; | ||
| + | |||
| + | salida<<"\n\tValor de precision para el error de iteracion = "<<Precision<<endl; | ||
| + | |||
| + | cout<<"\n\n\tResultados del Proceso de Iteracion"; | ||
| + | |||
| + | salida<<"\n\n\tResultados del Proceso de Iteracion"; | ||
| + | |||
| + | cout<<"\n\t-----------------------------------\n\n"; | ||
| + | |||
| + | salida<<"\n\t-----------------------------------\n\n"; | ||
| + | |||
| + | do{ | ||
| + | |||
| + | xt=x; | ||
| + | |||
| + | x=x-funcG(x)/derivadafuncG(x); | ||
| + | |||
| + | error=fabs(funcG(x)-funcG(xt)); | ||
| + | |||
| + | cout<<"\tx"<<i<<" = "<<x<<"\tG("<<i<<") = "<<funcG(x)<<"\t\tError"<<i<<" = "<<error<<endl; | ||
| + | |||
| + | salida<<"\tx"<<i<<" = "<<x<<"\tG("<<i<<") = "<<funcG(x)<<"\t\tError"<<i<<" = "<<error<<endl; | ||
| + | |||
| + | i=i+1; | ||
| + | |||
| + | }while (Precision<error && i<200); | ||
| + | |||
| + | if (i==200) | ||
| + | |||
| + | cout<<"\n\nNo hay convergencia"; | ||
| + | |||
| + | else | ||
| + | |||
| + | cout<<"\n\n\tLa solucion para x = F es igual a "<<x; | ||
| + | |||
| + | salida<<"\n\n\tLa solucion para x = F es igual a "<<x; | ||
| + | |||
| + | cout<<"\n\n\tEl factor de Friccion Colebrook - White es f = "<<friccion(x); | ||
| + | |||
| + | salida<<"\n\n\tEl factor de Friccion Colebrook - White es f = "<<friccion(x); | ||
| + | |||
| + | salida.close(); | ||
| + | |||
| + | return 0; | ||
| + | |||
| + | } | ||
Latest revision as of 11:51, 30 August 2021
Resumen
Los sistemas hidráulicos encargados de la distribución de agua a los usuarios tienen un rol importante en su calidad de vida. Por ello, la determinación de manera precisa del factor de fricción en tuberías, es de gran importancia en el diseño de redes de distribución de agua debido a que influye directamente en el cálculo de caídas de presión (pérdidas de carga) en los sistemas hidráulicos. El objetivo del presente trabajo fue evaluar en forma experimental diferentes correlaciones que describan, mediante una forma explícita, el factor de fricción en una tubería bajo flujo turbulento y la correlación implícita de Colebrook-White. Esto se realizó mediante la comparación de valores numéricos predichos por las correlaciones respecto al valor experimental, encontrándose que la correlación de Colebrook-White predice el factor de fricción con menor porcentaje de error de las 27 correlaciones estudiadas. Para la solución de la ecuación de Colebrook-White se utilizó el método de Newton-Raphson, dado que ésta presenta una estructura recurrente que puede ser llevada a algoritmos y resuelta rápidamente mediante programas computacionales. En este trabajo se desarrolló una herramienta en lenguaje de programación C++ para resolver la ecuación de Colebrook-White.
Palabras clave: Factor de fricción, ecuación de Darcy-Weisbach, ecuación de Colebrook-White, caída de presión en tuberías, correlaciones para evaluar factor de fricción
Abstract
The hydraulic systems that distribute water to users have an important role in their quality of life. For this reason, the precise determination of the friction factor in pipes is of great importance in the design of water distribution networks because it directly influences the calculation of pressure drop (head losses) in hydraulic systems. The objective of the present work was to evaluate in an experimental manner different correlations that describe, in an explicit form, the friction factor in a pipe under turbulent flow and the implicit Colebrook-White correlation. This was done by comparing the numerical values predicted by the correlations in regard to the experimental value, finding that the Colebrook-White correlation predicts the friction factor with the lowest error percentage among the 27 correlations studied. For the solution of the Colebrook-White equation the Newton-Raphson method was used, given that it presents a recurrent structure that can be taken to algorithms and quickly solved by computer programs. In this work, a tool was developed in the C ++ programming language to solve the Colebrook-White equation.
Keyvords: Friction factor, Darcy-Weisbach equation, Colebrook-White equation, pressure drop in pipes, correlation for the friction factor evaluation
1. Introducción
En la actualidad el manejo de los recursos hídricos es importante, por lo tanto los sistemas hidráulicos que lo distribuyen a las personas, tienen un rol fundamental [1]. En los sistemas hidráulicos, específicamente en las tuberías y diferentes singularidades, siempre ocurre fricción, ocasionando caídas de presión en el flujo a lo largo de su trayectoria. Es importante conocer esta caída de presión, para una apropiada estimación de las presiones de trabajo en los sistemas hidráulicos, por ello se han efectuado diferentes estudios para su determinación y evaluación [2]. Por ello, la determinación de manera precisa del factor de fricción en tuberías es de gran importancia en el diseño de sistemas de conducción y distribución de agua [3]. En el diseño, la longitud de tuberías permanece como parámetro constante e independiente del factor de fricción en los distintos tramos de las redes de agua. En contraste a esto, varios parámetros tales como el diámetro de la tubería y el factor de fricción varían durante la vida útil de las conducciones [4]. Al realizar el análisis de las pérdidas de carga en los sistemas de distribución de agua, se debe tener en cuenta que el factor de fricción es calculado para tres estados del flujo, esto es, flujo laminar, transición y turbulento. Para el flujo laminar el factor de fricción es expresado en forma explícita a través de una simple ecuación (1)
|
|
(1) |
donde es el factor de fricción de Darcy-Weisbach y el valor Re es el número de Reynolds, que es calculado como se presenta en la ecuación (2):
|
|
(2) |
donde , y corresponden a la velocidad de flujo promedio en la tubería, el diámetro interior de la tubería y la viscosidad cinemática, respectivamente. Colebrook y White (1937) establecieron para el flujo turbulento la relación entre las variables y Re que es mostrada en la siguiente ecuación (3) no lineal [5]:
|
|
(3) |
Posteriormente, para flujos en transición y turbulentos, está relacionado con el valor de Re y (rugosidad relativa de la tubería) como se presenta en la ecuación (4) [6]:
|
|
(4) |
Se puede ver claramente que las ecuaciones (3) y (4) son expresiones implícitas que requieren una solución numérica iterativa para estimar de manera precisa el factor de fricción y requiere de la aplicación de métodos numéricos para su solución. En efecto, la ecuación (4) habitualmente es llamada ecuación de Colebrook-White. En este trabajo se ha utilizado el método de Newton–Raphson para resolver dicha ecuación [3,7], que es ampliamente empleado para este tipo de resoluciones. Como alternativa a la resolución de la ecuación implícita, varias investigaciones han sido desarrolladas para aproximar una solución explícita para la ecuación (4). Por ejemplo, Anaya-Durand y colaboradores (2014) evaluaron diferentes correlaciones explícitas que predicen el factor de fricción para un fluido en una tubería, mediante la comparación de valores numéricos de dichos factores respecto a la ecuación de Colebrook-White [2]. Winning y Coole (2013) en su estudio revisaron 28 ecuaciones explícitas para el cálculo del factor de fricción considerando tanto la precisión de la ecuación implícita de Colebrook-White y la eficiencia computacional de las ecuaciones explícitas [8]. Estos métodos numéricos de solución presentan estructuras recurrentes que pueden ser llevadas a algoritmos y resueltas rápidamente mediante programas computacionales. En el presente trabajo se desarrolló un programa en lenguaje C++ para resolver la ecuación de Colebrook-White. El lenguaje C++, fue desarrollado por Bjarne Stroustrup (1990) y es una extensión del lenguaje de programación C, incorporando el concepto de programación orientada a objeto, es por ello que desde el punto de vista de lenguajes de programación orientados a objeto, es un lenguaje híbrido. En dicho sentido el término “C++” significa “incremento de C” y que por lo tanto es una extensión de C [9]. Así, el objetivo del presente trabajo fue efectuar la evaluación experimental de correlaciones para el cálculo del factor de fricción para flujo turbulento en tuberías cilíndricas implementado en laboratorio una experiencia.
2. Materiales y métodos
2.1 Equipo experimental y procedimiento
Las mediciones se realizaron en el Laboratorio de Hidráulica del Departamento de Ingeniería en Obras Civiles de la Facultad de Ingeniería de la Universidad de La Serena. En la Figura 1 se muestra el sistema para determinar el factor de fricción experimental utilizando la ecuación (6) de Darcy-Weisbach. Este sistema consiste en una bomba centrífuga (REGGIO, STM 50), una tubería de PVC PN-10 de 26 mm de diámetro interior y codos cortos de PVC de 90°, tees de PVC, dos conectores de acero para instalación de las conducciones del manómetro diferencial, válvulas de globo y un estanque graduado de descarga para medir el volumen. También se utilizó un manómetro diferencial (PSE-910) y un cronómetro (KENKO, KK-2802). Se midió el caudal usando el método volumétrico, para lo cual se realizaron 5 mediciones, y en cada una de ellas se verificó el largo o distancia entre los puntos de control de presión (), junto con el diámetro interior () y la rugosidad () de la tubería. En el estanque acumulador de agua con control de volumen, se midió el tiempo () que demoraba en llenar 20 litros. De esta forma con la ecuación (5) se puede determinar la velocidad de escurrimiento al interior de la tubería.
|
|
(5) |
donde es la velocidad de escurrimiento en (m/s), es el volumen igual a 0,02 m3, es el tiempo en (s) que demoró en llenar el volumen antes indicado, es el diámetro interior de la tubería igual a 0,026 m y π es igual a 3,1416. Al mismo tiempo se midió la diferencia de presión () en el manómetro diferencial. Los valores obtenidos se reemplazan en la ecuación (6) para poder determinar
|
|
(6) |
donde es la aceleración de gravedad igual a 9,8 (m/s2) y es la longitud de tubería recta entre los puntos de control de presión correspondiente a 1,0 m.
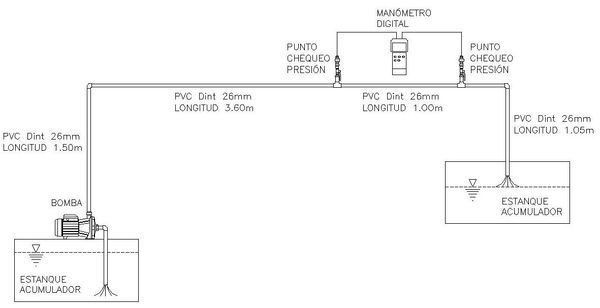
|
| Figura 1. Esquema del Sistema Experimental para determinar el factor de fricción |
2.2 Correlaciones explícitas para el factor de fricción encontradas en la literatura
En la Tabla 1 se presentan varias correlaciones reportadas en la literatura utilizadas para calcular el valor del factor de fricción.
| N° | Modelo | Correlación | Rango de Aplicación |
| 1 | Filonenko [10] |
Tuberías hidráulicamente lisas | |
| 2 | Altshul I [2] |
| |
| 3 | Altshul II [2] |
| |
| 4 | Konakov [11] |
Tuberías hidráulicamente lisas | |
| 5 | Shacham I |
| |
| 6 | Shacham II |
| |
| 7 | Chen [12] | ||
| 8 | Churchill [13] |
|
|
| 9 | Swamee and Jain [14] | ||
| 10 | Pavlov [15] | ||
| 11 | Round [16] | ||
| 12 | Barr [17] | ||
| 13 | Zigrang – Sylvester [18] | ||
| 14 | S. E. Haaland [19] |
| |
| 15 | Manadilli [20] |
Cualquier valor de ε/D | |
| 16 | Romeo et al. [21] |
|
|
| 17 | Colebrook-White [6] | ||
| 18 | Sonnad and Goudar [22] |
|
|
| 19 | Buzzelli [23] |
|
|
| 20 | Avci and Karagoz [24] | ||
| 21 | Saeed Samadianfard [25] |
| |
| 22 | Papaevangelo et al. [26] |
| |
| 23 | Brkic I [27] |
|
|
| 24 | Brkic II [27] |
|
|
| 25 | Fang et al. [28] |
| |
| 26 | Li et al. [29] | ||
| 27 | Shaikh et al. [30] |
|
|
2.3 Cálculo del factor de fricción en la ecuación implícita de Colebrook-White
La ecuación (4) de Colebrook–White es ampliamente utilizada para determinar el factor de fricción para flujos turbulentos en tuberías rugosas. Se puede apreciar que la ecuación (4) está expresada en forma implícita para y requiere una solución iterativa para determinar su valor. El método que es adecuado para encontrar una raíz y que ésta sea estable, es el método de Newton–Raphson. La solución aproximada del método se basa en el siguiente algoritmo:
|
|
(7) |
En el método de Newton–Raphson, la ecuación (7) es utilizada para calcular el factor de fricción a partir de un valor inicial dado y que permite estimar el siguiente valor de iteración, con el fin de encontrar la solución a la ecuación (4) del factor de fricción. La ecuación (4) de Colebrook–White puede reordenarse reemplazando el valor de y ser expresada mediante una nueva relación tal como se muestra en la ecuación (8)
|
|
(8) |
Si se asume la ecuación (8) como una función que es siempre continua y diferenciable, se puede obtener la derivada de la función con respecto a , cuya deducción se presenta en el apéndice y que se muestra en la ecuación (9)
|
|
(9) |
La ecuación (9) tiene capacidad de rápida convergencia, particularmente si hay una estimación adecuada del valor inicial del factor de fricción [7,3]. En este trabajo la ecuación (4) fue resuelta utilizando el método de Newton–Raphson, mediante un programa computacional desarrollado en lenguaje de programación C++. Esta resolución requiere el ingreso del valor Re y , junto con el valor inicial de iteración para y el valor de la precisión o error admisible en el desarrollo del proceso iterativo, cuyo diagrama de flujo se encuentra en la Figura 2 y el código fuente se presenta en al Apéndice B.
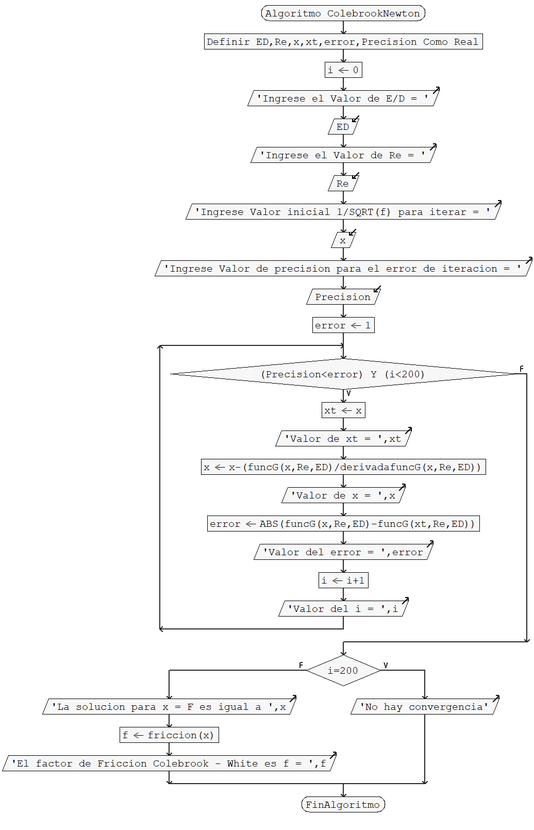
|
| Figura 2. Diagrama de flujo del programa C++ para la resolución de la ecuación de Colebrook–White |
3. Resultados y discusión
La Figura 3 muestra el gráfico de caja, que presenta la mediana (línea dentro de la caja), el promedio (cuadrado dentro de la caja), el primer cuartil (25 % de los datos), el tercer cuartil (el 75 % de los datos), el valor mínimo (5% de los datos) y el valor máximo (95% de los datos) del factor de fricción experimental medido en quintuplicado utilizando la ecuación (6), además se calculó su límite de confianza, ecuación (10)
|
|
(10) |
donde corresponde al límite de confianza, al factor de fricción promedio, al valor de Student para n-1 grados de libertad a un 95% de confianza, a la desviación estándar y corresponde al número de réplicas. En este caso el para un 95% de confianza es igual a 0,022427 ± 0,002190. Cada uno de los valores del factor de fricción obtenido de las correlaciones antes presentadas (Tabla 1) fue evaluado y comparado respecto a su error relativo porcentual con el factor de fricción experimental promedio. El error relativo porcentual se calculó utilizando la ecuación (11)
|
|
(11) |
donde es el factor de fricción predicho por cada una de las correlaciones indicadas en la Tabla 1, considerando una rugosidad () de 0,0015 mm para PVC [31] y (rugosidad relativa de la tubería) igual a 0,0000576923. En el caso de la correlación de Colebrook-White, el factor de fricción fue obtenido utilizando el método numérico de Newton-Raphson, como fue descrito previamente, para lo cual se desarrolló un programa en C++. La Tabla 2 muestra los resultados obtenidos para el factor de fricción con cada una de las correlaciones evaluadas y el error relativo porcentual respectivo. El estudio se basa en la correlación que arroje el menor porcentaje de error con respecto al valor obtenido de forma experimental, encontrándose que la correlación de Colebrook-White predice el factor de fricción con menor porcentaje de error de las 27 correlaciones estudiadas para un rango de valores de Número de Reynolds comprendido entre .
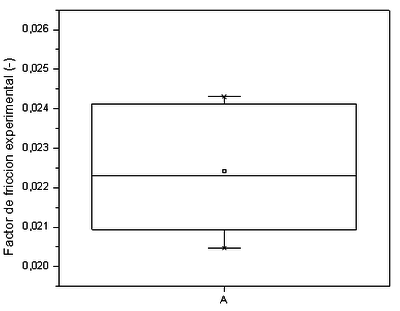
|
| Figura 3. Gráfico de caja del factor de fricción experimental |
| N° | Correlación | Factor f Teórico |
% Error Relativo Porcentual |
| 1 | Filonenko | 0,0223347 | 0,4104 |
| 2 | Altshul I | 0,0228318 | 1,8062 |
| 3 | Altshul II | 0,0220010 | 1,8986 |
| 4 | Konakov | 0,0220148 | 1,8370 |
| 5 | Shacham I | 0,0225339 | 0,4775 |
| 6 | Shacham II | 0,0224328 | 0,0269 |
| 7 | Chen | 0,0224582 | 0,1403 |
| 8 | Churchill | 0,0223510 | 0,3380 |
| 9 | Swamee and Jain | 0,0223343 | 0,4125 |
| 10 | Pavlov | 0,0222177 | 0,9321 |
| 11 | Round | 0,0222191 | 0,9261 |
| 12 | Barr | 0,0224172 | 0,0427 |
| 13 | Zigrang - Sylvester | 0,0224099 | 0,0752 |
| 14 | S. E. Haaland | 0,0222085 | 0,9734 |
| 15 | Manadilli | 0,0224538 | 0,1205 |
| 16 | Romeo et al. | 0,0224568 | 0,1339 |
| 17 | Colebrook-White | 0,0224321 | 0,0237 |
| 18 | Sonnad and Goudar | 0,0225639 | 0,6117 |
| 19 | Buzzelli | 0,0224321 | 0,0238 |
| 20 | Avci and Karagoz | 0,0225747 | 0,6595 |
| 21 | Saeed Samadianfard | 0,0228794 | 2,0182 |
| 22 | Papaevangelou et al. | 0,0224174 | 0,0416 |
| 23 | Brkic I | 0,0218275 | 2,6723 |
| 24 | Brkic II | 0,0225362 | 0,4881 |
| 25 | Fang et al. | 0,0224542 | 0,1221 |
| 26 | Li et al. | 0,0224588 | 0,1429 |
| 27 | Shaikh et al. | 0,0213440 | 4,8280 |
4. Conclusiones
En el presente trabajo se construyó un sistema para determinar el factor de fricción experimental y se comparó con 27 correlaciones utilizadas para obtener de forma teórica el factor de fricción. De estas correlaciones, 26 eran explícitas y una implícita, para la cual se desarrolló un programa en lenguaje C++ que permite el cálculo de factor de fricción utilizando el método de Newton-Raphson. Para este análisis se calculó el error relativo porcentual de cada una de las correlaciones respecto del valor experimental, lo cual permite evaluar la calidad predictiva de cada una de las correlaciones en forma experimental, ya que la mayoría de ellas son propuestas teóricas, siendo las correlaciones de Colebrook-White, Buzzelli y Shacham II las que presentaron el menor error relativo porcentual y la correlación de Shaikh la que presentó el mayor error relativo porcentual. Es importante destacar que la gran mayoría de las correlaciones presenta un error relativo porcentual menor al 1%. Las perspectivas del presente trabajo son desarrollar otras experiencias en el sistema construido para evaluar otras condiciones experimentales, además de entregar el código fuente en lenguaje de programación C++ de la solución de la ecuación de Colebrook-White, el cual permitiría su rápida aplicación en la determinación del factor de fricción y además se podría aplicar a la resolución de otras correlaciones de tipo implícito para el cálculo del factor de fricción.
Referencias
[1] Ángeles M.S., Chéret I., et al. Manejo integrado de recursos hídricos. Global Water Partnership, Suecia, 2000.
[2] Anaya-Durand A.I., Cauich-Segovia G.I., Funabazama-Bárcenas O., Gracia-Medrano-Bravo V.A. Evaluación de ecuaciones de factor de fricción explícito para tuberías. Educ. Quim., 25(2):128–134, 2014.
[3] Najafzadeh M., Shiri J., Sadeghi G., Ghaemi A. Prediction of the friction factor in pipes using model tree. ISH J. Hydraul. Eng., 24(1):9–15, 2018.
[4] Özger M., Yildirim G. Determining turbulent flow friction coefficient using adaptive neuro-fuzzy computing technique. Adv. Eng. Softw., 40(4):281–287, 2009.
[5] Colebrook C.F., White C.M., Experiments with fluid friction in roughened pipes. Proc. R. Soc. A Math. Phys. Eng. Sci., 161(906):367–381, 1937.
[6] Colebrook C.F., et al. Correspondence. Turbulent flow in pipes with particular reference to the transition region between the smooth and rough pipe laws. J. Inst. Civ. Eng., 12(8):393–422, 1939.
[7] Augusto G.L., Culaba A.B., Tanhueco R.M.T., Pipe sizing of District cooling distribution network using implicit Colebrook-White equation. J. Adv. Comput. Intell. Intell. Informatics, 20(1):76–83, 2016.
[8] Winning H.K., Coole T. Explicit friction factor accuracy and computational efficiency for turbulent flow in pipes. Flow, Turbul. Combust., 90(1):1–27, 2013.
[9] Ellis M.A., Stroustrup B. The annotated C++ reference manual. Addison-Wesley, 1990.
[10] Filonenko G. Hydraulic resistance in pipes. Teploenergetika, 1:40–44, 1954.
[11] Konakov V.K. New formula for the friction coefficient of smooth tubes. Dokl. Akad. Nauk SSSR, 25(5):14–24, 1950.
[12] Chen N.H. An explicit equation for friction factor in pipe. Ind. Eng. Chem. Fundam., 18(3):296–297, 1979.
[13] Churchill S.W. Friction-factor equation spans all fluid-flow regimes. Chem. Eng., 84(24):91–92, 1977.
[14] Swamee P.K., Jain A.K. Explicit equations for pipe-flow problems. J. Hydraul. Div., 102(5):657–664, 1976.
[15] Pávlov K.F., Romankov P.G., Noskov A.A. Problemas y ejemplos para el curso de operaciones básicas y aparatos en tecnología química. Mir, 608 pp., 1981.
[16] Round G.F. An explicit approximation for the friction factor‐reynolds number relation for rough and smooth pipes. Can. J. Chem. Eng., 58(1):122–123, 1980.
[17] Barr D.I.H. Solutions of the Colebrook-White function for resistance to uniform turbulent flow. 'Proc. Inst. Civ. Eng., 71(2):529–535, 1981.
[18] Zigrang D.J., Sylvester N.D. Explicit approximations to the solution of Colebrook’s friction factor equation. AIChE J., 28(3):514–515, 1982.
[19] Haaland S.E. Simple and explicit formulas for the friction factor in turbulent pipe flow. J. Fluids Eng., 105(1):89-90, 1983.
[20] Manadili G. et al. Replace implicit equations with signomial functions. Chem. Eng., 104(8):129-130,132, 1997.
[21] Romeo E., Royo C., Monzón A. Improved explicit equations for estimation of the friction factor in rough and smooth pipes. Chem. Eng. J., 86(3):369–374, 2002.
[22] Sonnad J.R., Goudar C.T. Using a mathematically exact alternative to the Colebrook–White equation. J. Hydraul. Eng., 132(8):863–867, 2006.
[23] Buzzelli D. Calculating friction in one step. Mach. Des., 80(12):54–55, 2008.
[24] Avci A., Karagoz I. A novel explicit equation for friction factor in smooth and rough pipes. J. Fluids Eng., 131(6):061203, 2009.
[25] Samadianfard S. Gene expression programming analysis of implicit Colebrook--White equation in turbulent flow friction factor calculation. J. Pet. Sci. Eng., 92:48–55, 2012.
[26] Papaevangelou G., Evangelides C., Tzimopoulos C. A new explicit relation for friction coefficient in the Darcy-Weisbach equation. PRE10: Prot. Restor. Environ., pp. 166–73, Corfu, 05-09 July, 2010.
[27] Brkić D. Review of explicit approximations to the Colebrook relation for flow friction. J. Pet. Sci. Eng., 77(1):34–48, 2011.
[28] Fang X., Xu Y., Zhou Z. New correlations of single-phase friction factor for turbulent pipe flow and evaluation of existing single-phase friction factor correlations. Nucl. Eng. Des., 241(3):897–902, 2011.
[29] Li P., Seem J.E., Li Y. A new explicit equation for accurate friction factor calculation of smooth pipes. Int. J. Refrig., 34(6):1535–1541, 2011.
[30] Shaikh M.M., Massan S.U.R., Wagan A.I. A new explicit approximation to Colebrook’s friction factor in rough pipes under highly turbulent cases. Int. J. Heat Mass Transf., 88: 538–543, 2015.
[31] Neto L., Porto R.D.M. Performance of low-cost ejectors. J. Irrigation and Drainage Engineering, 130(2):122–128, 2004.
Apéndice A
Complemento derivada ecuación Colebrook-White
Para la determinación del factor de fricción en flujos turbulentos para tuberías rugosas es utilizada la ecuación (A.1) de Colebrook-White. Esta relación tiene una forma implícita para el valor de , tal como sigue:
|
|
(A.1) |
donde es el factor de fricción de la tubería, Re es el número de Reynolds y es la rugosidad relativa de la tubería.
Si se reescribe la ecuación (A.1) reemplazando el valor y luego despejando la expresión, se tiene:
|
|
(A.2) |
Derivando de manera implícita la ecuación (A.2) con respecto a la variable , se obtiene lo siguiente:
|
|
(A.3) |
Utilizando la derivada implícita para se tiene que:
|
|
(A.4) |
Por lo tanto la derivada de la función con respecto a es:
|
|
(A.5) |
Reescribiendo la expresión anterior se tiene:
|
|
(A.6) |
La ecuación (A.6) es la derivada de la función que ha sido utilizada en el programa desarrollado en lenguaje C++ y que permite iterar y encontrar la solución numérica del factor de fricción para la ecuación (A.1) de Colebrook–White [3,7].
Apéndice B
Código fuente programa C++
Para la resolución numérica del factor de fricción de la ecuación implícita de Colebrook-White, se ha programado en lenguaje C++ un código fuente que permite facilitar dicho proceso, para que pueda ser utilizado por otros investigadores. Este código está estructurado de tal forma que permite a cualquier investigador resolver otras ecuaciones modificando incluso el metodo numérico a utilizar.
#include <iostream>
#include <math.h>
#include <fstream>
#include <stdlib.h>
using namespace std;
double ED, Re, x, xt, error, Precision;
//Despeje de la función G(f)=0
//Reemplazo de la variable x=1/RAIZ(f)
double funcG(double x){
return x+2*log10(((2.51*x)/Re)+(ED/3.7));
}
double derivadafuncG(double x){
return 1+8.06659/(ED/Re+9.287*x);
}
double friccion(double x){
return pow((1/x),2);
}
int main (){
int i=0;
cout<<"\n\n\tIngrese el Valor de E/D = ";
cin>>ED;
cout<<"\n\tIngrese el Valor de Re = ";
cin>>Re;
cout<<"\n\tIngrese Valor inicial 1/SQRT(f) para iterar = ";
cin>>x;
cout<<"\n\tIngrese Valor de precision para el error de iteracion = ";
cin>>Precision;
//Impresión por pantalla e impresión hacia un archivo en la misma carpet de nombre: resultados.txt
ofstream salida;
salida.open("resultados.txt", ios::out);
if(salida.fail()){
cout<<"\nNo se pudo abrir el Archivo";
}
salida<<"\n\n\tPrograma para la Determinación del Factor de friccion de Colebrook - White";
salida<<"\n\t--------------------------------------------------------------------------";
salida<<"\n\n\n\tDatos ingresados";
salida<<"\n\t----------------";
salida<<"\n\n\tValor de E/D = "<<ED<<endl;
salida<<"\n\tValor de Re = "<<Re<<endl;
salida<<"\n\tValor inicial 1/SQRT(f) para iterar = "<<x<<endl;
salida<<"\n\tValor de precision para el error de iteracion = "<<Precision<<endl;
cout<<"\n\n\tResultados del Proceso de Iteracion";
salida<<"\n\n\tResultados del Proceso de Iteracion";
cout<<"\n\t-----------------------------------\n\n";
salida<<"\n\t-----------------------------------\n\n";
do{
xt=x;
x=x-funcG(x)/derivadafuncG(x);
error=fabs(funcG(x)-funcG(xt));
cout<<"\tx"<<i<<" = "<<x<<"\tG("<<i<<") = "<<funcG(x)<<"\t\tError"<<i<<" = "<<error<<endl;
salida<<"\tx"<<i<<" = "<<x<<"\tG("<<i<<") = "<<funcG(x)<<"\t\tError"<<i<<" = "<<error<<endl;
i=i+1;
}while (Precision<error && i<200);
if (i==200)
cout<<"\n\nNo hay convergencia";
else
cout<<"\n\n\tLa solucion para x = F es igual a "<<x;
salida<<"\n\n\tLa solucion para x = F es igual a "<<x;
cout<<"\n\n\tEl factor de Friccion Colebrook - White es f = "<<friccion(x);
salida<<"\n\n\tEl factor de Friccion Colebrook - White es f = "<<friccion(x);
salida.close();
return 0;
}
Document information
Published on 08/02/19
Accepted on 18/01/19
Submitted on 12/07/18
Volume 35, Issue 1, 2019
DOI: 10.23967/j.rimni.2019.01.001
Licence: CC BY-NC-SA license