The analysis of mode decomposition in interlaminar fracture tests of asymmetric specimens

Revision as of 15:24, 29 April 2022

F.Mujika^a, A. Arrese^a, A.I. Boyano^b, J. De Gracia^b,

^aGRUPO MATERIALES + TECNOLOGÍAS / MECÁNICA DE MATERIALES Departamento de Ingeniería Mecánica. Escuela de Ingeniería de Gipuzkoa.

^bGRUPO MATERIALES + TECNOLOGÍAS / MECÁNICA DE MATERIALES Departamento de Ingeniería Mecánica. Escuela de Ingeniería de Vitoria-Gasteiz

Universidad del País Vasco (UPV/EHU).

Plaza Europa 1, 20018 Donostia-San Sebastián.

Análisis de la descomposición de modos en ensayos de fractura interlaminar asimétricos

Historia del artículo: Recibido 5 de Mayo 2017 En la versión revisada 5 de Mayo 2017 Aceptado 31 de Mayo 2017 Accesible online 21 de Junio 2017	Los ensayos de fractura interlaminar se realizan habitualmente en probetas donde los dos brazos de grieta son simétricos. El ensayo de Viga en Doble Voladizo Asimétrica (ADCB) constituye una excepción, con brazos de distintos espesores con lo que se obtiene modo mixto I/II. La asimetría de ADCB se podría también aplicar a ensayos de Viga con Entalla Final (ENF), con lo que en principio también se obtendrían modos mixtos I/II. La descomposición de modos propuesta por Williams no es válida en el ensayo ADCB y no se han encontrado trabajos relacionados con ensayos de ENF asimétricos en los que se considere la descomposición de modos. En el presente trabajo se desean analizar distintas alternativas para la descomposición de modos en el caso de probetas con brazos asimétricos. La falta de simetría puede deberse a una diferencia de espesores, a una diferencia de materiales o a la combinación de ambos factores. Los resultados obtenidos serán comprobados en primera instancia con los resultados de análisis de descomposición de modos publicados en el caso de ensayos ADCB.
Palabras clave: Fractura interlaminar Descomposición de modos Laminados asimétricos

The analysis of mode decomposition in interlaminar fracture tests of asymmetric specimens.

Keywords: Interlaminar fracture Mode decomposition Asymmetric laminates	Interlaminar failure tests are usually carried out in specimens where crack arms are symmetric. Asymmetric Double Cantiliver Beam (ADCB) is an exception where both crack arms have different thickness in order to get mixed mode I/II. The asymmetry in ADCB specimens could be applied also to te case of End Notched Flexure Tests, obtaining also mixed mode I/II. The decomposition proposed by Williams is not valid in the case of ADCB tests. On the other hand, articles related to asymmetric ENF tests including the mode decompositiion have not been found. The present study deals with the analsys of the mode decomposition in the case of specimens with asymmetric arms. The asymmetry may be related to the different thickness of the crack arms, to different materials or a combination of both factors. The results obtained will be compared with the results of mode decompsition that have been published in the case of ADCB tests.

1 Introducción

Los laminados compuesto que se utilizan en aplicaciones estructurales consisten en muchos casos en laminados constituidos por capas. En cada una de ellas el refuerzo es unidireccional y las propiedades mecánicas del laminado dependen de los materiales de las capas, de la orientación del refuerzo en cada una de ellas, así como del orden en que se apilan las mismas. La ausencia de refuerzo en la dirección perpendicular al laminado está relacionada con la fractura interlaminar, que es una de las limitaciones en la utilización de estos materiales.

Por ejemplo, un impacto de baja energía puede provocar una pequeña deslaminación entre capas. Si una de las partes deslaminadas está sometida a compresión, puede generarse pandeo local que provoca un avance de grieta que puede derivar en el fallo catastrófico del componente.

Para caracterizar la fractura interlaminar, es habitual determinar experimientalmente la tasa crítica de liberación de energía ${\textstyle G}$ , fundamentalmente en modos I, II y modo mixto I/II. Se realizan también ensayos en modo III, que no son objetod del presente trabajo. Las probetas utilizadas tienen geometría de tira y existen diferentes ensayos para determinar ${\textstyle G}$ . Se describirán únicamente los más utilizados. Para determinar GI se utiliza el ensayo de Viga en Doble Voladizo (Double Cantilever Beam, DCB). Para determinar el modo II se utiliza el ensayo de Flexión con Entalla Final (End Notched Flexure, ENF). Para determinar el modo mixto se utiliza el ensayo de flexión en modo mixto (Mixed Mode Bending, MMB) que es una combinación de los dos métodos anteriores.

En los ensayos DCB, ENF y MMB se utilizan probetas que tienen una grieta inicial generada en el proceso de fabricación. Esta grieta está situada en el plano central del laminado, por lo que la configuración de probeta es simétrica en todos los casos. En el ensayo de viga asimétrica en doble voladizo (Asymmetric Double Cantilever Beam, ADCB) los brazos de grieta son de distintos espesores y se produce modo mixto I/II. En la mayoría de los casos los ensayos se realizan en probetas unidireccionales, con la fibra orientada en la longitud de la probeta. Sin embargo, las grietas interlaminares que se producen en servicio ocurren en circunstancias muy distintas a las de los ensayos: distintos espesores de los brazos de grieta, piezas con geometría de placa y distintas orientaciones de la interlámina.

En el presente estudio se aborda la descomposición de modos de probetas con geometría de tira, en la que los brazos de grieta pueden ser de distintos espesores y también de material diferente. Se limita al caso en que el material es ortótropo.

2 Análisis del avance de grieta

2.1 Tasa de liberación de energía

Se analiza un sistema en equilibrio sometido a un sistema de fuerzas independientes ${\textstyle {F}_{i}}$ , siendo ${\textstyle {\delta }_{i}}$ los desplazamientos de los puntos de aplicación de las fuerzas en la misma dirección. El trabajo correspondiente a una variación elemental de los desplazamientos viene dado por:

(1)

Habiéndose utilizado el convenio de índices mudo para suprimir el sumatorio de la ecuación (1).

En un avance infinitesimal de grieta, el balance de energía viene dado por:

(2)

Donde ${\textstyle dU}$ representa la energía interna, ${\textstyle G}$ la energía liberada por unidad de área y ${\textstyle dA}$ el área de la nueva superficie de grieta creada. Si el ancho b es uniforme ${\textstyle dA=}$ $bda$ donde ${\textstyle da}$ es la longitud del avance de grieta.

Según las ecuaciones (1) y (2), la energía interna viene dada por:

(3)

Aun cuando el avance de grieta es un proceso irreversible, se asume que la energía interna es una función de estado, siendo las variables de estado los desplazamientos independientes ${\textstyle {\delta }_{i}}$ y la longitud de grieta ${\textstyle a}$ . Por lo tanto, también puede expresarse como:

(4)

Identificando términos en las ecuaciones (3) y (4) resulta:

(5)

Con lo que se obtienen el primer teorema de Castigliano y la tasa de liberación de energía como liberación de la energía de deformación.

Por otra parte, se define la energía de deformaicón complementaria ${\textstyle C}$ :

(6)

Diferenciando la ecuación (6) y sustituyendo en el balance de energía de la ecuación (3) se obtiene:

(7)

Asumiendo que ${\textstyle C}$ es función de las variables de estado ${\textstyle {F}_{i}}$ y ${\textstyle a}$ :

(8)

Identificando términos en las ecuaciones (7) y (8) se tiene:

(9)

Se obtienen así el primer teorema de Engesser y la tasa de liberación de energía como el incremento de energía de deformación complementaria. En sistemas elásticos lineales el teorema de Engesser se convierte en el teorema de Castigliano, por lo que se denomina a veces teorema de Engesser-Castigliano. Para utilizar este teorema ${\textstyle C}$ se debe expresar en función de las fuerzas aplicadas.

En el caso particular de un sistema elástico lineal sometido a una única carga ${\textstyle F}$ con un desplazamiento asociado ${\textstyle \delta }$ , siendo ${\textstyle \delta =}$ $fF$ se tiene:

(10)

Donde ${\textstyle f}$ representa la flexibilidad del sistema. Utilizando las ecuaciones (5) y (9) resulta en ambos casos que:

(11)

Se ha suprimido el subíndice ${\textstyle F}$ o ${\textstyle \delta }$ indicativo de la derivación parcial, ya que la flexibilidad depende úncamente de la longitud de grieta.

2.2 La integral J y la zona cohesiva

Rice definió la integral J como una integral independiente del camino en una curva cerrada que incluía la punta de grieta:

(12)

Donde ${\textstyle \Gamma }$ es el camino cerrado de integración en sentido anthihorario, ${\textstyle {U}_{0}}$ la densidad de energía de deformación, ${\textstyle {\mathit {\boldsymbol {T}}}}$ el vector tensión y ${\textstyle {\mathit {\boldsymbol {u}}}}$ el vector desplazamiento. Se demuestra además que ${\textstyle J=}$ $G$ en el caso de comportamiento elástico.

Tomando ${\textstyle \Gamma }$ en las cercanías de la punta de grieta ${\textstyle {\mathit {\boldsymbol {T}}}}$ es nulo por lo que la ecuación (12) queda:

(13)

Siendo ${\textstyle \sigma }$ la tensión normal de apertura, ${\textstyle {\Delta }_{n}}$ el desplazamiento relativo asociado, ${\textstyle \tau }$ la tensión cortante y ${\textstyle {\Delta }_{t}}$ el desplazamiento relativo asociado. Por lo tanto, la primera integral de la ecuación representa la contribución del modo I y la segunda integral incluye la contribución de los modos II y III, aunque este último no se considera en el presente trabajo.

Las tensiones y desplazamientos citados corresponden a una zona próxima a la punta de grieta, denominada zona cohesiva. Esta zona está relacionada con diversos factores: plastificación debido a que las tensiones alcanzan el límite elástico, puenteo de fibras en la zona de grieta o aparición de microgrietas. La relación entre las tensiones y los desplazamientos mencionados anteriormente en dicha zona se denomina ley cohesiva y se puede obtener de la siguiente manera: asumiendo que ${\textstyle G}$ es función de los desplazamientos independientes ${\textstyle {\Delta }_{n}}$ y ${\textstyle {\Delta }_{t}}$ , puede escribirse:

(14)

Asumiendo ahora que ${\textstyle G}$ es diferencial exacta:

(15)

Identificando términos en las ecuaciones (14) y (15) resulta:

(16)

En caso de modos puros, únicamente existe un desplazamiento relativo como variable de estado.

Los desplazamientos relativos ${\textstyle {\Delta }_{n}}$ y ${\textstyle {\Delta }_{t}}$ son la suma de los desplazamiento correspondiente a puntos homólogos de cada brazo de grieta, entendiendo como puntos homólogos aquellos que están sometidos a la misma tensión. Por lo tanto, en el caso de que los desplazamientos de los puntos homólogos sean distintos, se podrán descomponer en una parte simétrica que realiza trabajo y una parte antisimétrica que no realiza trabajo y está asociada a un movimiento de sólido rígido.

3 Descomposición de modos

3.1 Avance infinitesimal de grieta

En esta sección se utiliza un procedimiento basado en el estudio de Williams [], determinando directamente la energía complementaria antes y después del avance de grieta sin modificar la carga y utilizando la ecuación (9) para determinar ${\textstyle G}$ .

Se considera un elemento diferencial de longitud ${\textstyle da}$ antes y después del avance de grieta. El brazo superior se denomina 1 y el brazo inferior 2. Ambos brazos pueden ser de material y espersor diferente. Considerando únicamente el efecto de la flexión, la energía complementaria ${\textstyle {C}_{a}}$ antes del avance de grieta viene dada por:

(17)

Donde ${\textstyle D}$ es la rigidez a flexión de toda la sección. Tras el avance de grieta, la energía complementaria ${\textstyle {C}_{d}}$ es:

(18)

Donde ${\textstyle {D}_{1}}$ y ${\textstyle {D}_{2}}$ son las rigideces a flexión de las partes 1 y 2, respectivamente. De acuerdo a la ecuación (9) la tasa crítica de liberación de energía es:

(19)

Donde ${\textstyle {r}_{1}}$ y ${\textstyle {r}_{2}}$ son las relaciones entre rigideces a flexión. Aplicando el principio de superposición los momentos flectores de cada brazo de grieta se descomponen en los correspondientes a los modos de fractura I y II:

(20)

Sustituyendo la ecuación (20) en la ecuación (19) se puede escribir ${\textstyle G}$ en función de los momentos en modo I y II y por lo tanto se obtienen las tasas de liberación de energía correspondientes a cada modo:

{\textstyle {\begin{matrix}{G}_{I}={\frac {1}{2D}}\left[{M}_{1I}^{2}\left({r}_{1}-1\right)+{M}_{2I}^{2}\left({r}_{2}-1\right)-2{M}_{1I}{M}_{2I}\right]\\{G}_{II}={\frac {1}{2D}}\left[{M}_{1II}^{2}\left({r}_{1}-1\right)+{M}_{2II}^{2}\left({r}_{2}-1\right)-2{M}_{1II}{M}_{2II}\right]\end{matrix}}}

(21)

Por otra parte, los términos que contienen productos de momentos en modos I y II deben ser nulos dado que los modos son independientes, es decir:

(22)

Se supone ahora que los momentos de cada modo en ambos brazos de grieta están relacionados según dos parámetros ${\textstyle {c}_{I}}$ y ${\textstyle {c}_{II}}$ , es decir:

(23)

Sustituyendo la ecuación (23) en la ecuación (22):

(24)

Por otra parte, combinando las ecuaciones (20) y (23):

(25)

La determinación de ${\textstyle {c}_{I}}$ y ${\textstyle {c}_{II}}$ se trata en la próxima sección. Conocidos estos parámetros, de las ecuaciones (25) se pueden obtener los momentos en los distintos modos:

{\textstyle {\begin{matrix}{M}_{1I}={\frac {{c}_{II}{M}_{1}-{M}_{2}}{{c}_{II}-{c}_{I}}}\\{M}_{1II}={\frac {{{M}_{2}-c}_{I}{M}_{1}}{{c}_{II}-{c}_{I}}}\end{matrix}}}

(26)

Combinando las ecuaciones (26) con las ecuaciones (21) y (23) pueden determinarse ${\textstyle {G}_{I}}$ y ${\textstyle {G}_{II}}$ .

3.2 Determinación de c_I y c_II

El análisis de Williams está particularizado al caso de único material y distintos espesores. Este investigador estableció que para modo puro I se debía verificar que los momentos fueran opuestos, es decir ${\textstyle {c}_{I}=}$ $-1$ . Por otra parte, para modo puro II estableció la condición de que las curvaturas fueran iguales, con lo que en el caso actual ${\textstyle {c}_{II}=}$ ${\frac {{D}_{2}}{{D}_{1}}}$ . Utilizando estos valores en el caso de igual espesor, la ecuación (24) se satisface idénticamente.

No obstante en el ensayo ADCB, en el que el material es único pero los espesores distintos, los momentos son iguales pero diferentes estudios muestran que existe combinación de modos. Por lo tanto, los valores utilizados en la descomposición de Williams son válidos únicamente en el caso de igual espesor y un único material.

Teniendo en cuenta la ecuación (13) en la que G se obtiene en función de las tensiones y desplazamientos relativos de la zona cohesiva, se puede afirmar que:

1. Las tensiones en puntos homólogos son iguales y opuestas debido al principio de acción y reacción.

2. Los modos puros corresponden a situaciones en las que los desplazamientos de puntos homólogos son iguales y opuestos.

En consecuencia, se pueden probar dos criterios distintos para determinar los parámetros ${\textstyle {c}_{I}}$ y ${\textstyle {c}_{II}}$ :

1. Determinar las condiciones para que los desplazamientos normales a la grieta sean iguales y opuestos en puntos homólogos y aplicar la ecuación (24) como segunda condición.

2. Determinar las condiciones para que los desplazamientos tangenciales en la grieta sean iguales en puntos homólogos y aplicar la ecuación (24) como segunda condición.

Si la hipótesis es correcta, los valores de ${\textstyle {c}_{I}}$ y ${\textstyle {c}_{II}}$ obtenidos en ambos casos deben ser iguales.

No obstante, los desplazamientos normales y tangenciales deben ser calculados teniendo en cuenta todo el sistema, por lo que no pueden relacionarse directamente con los momentos en la punta de grieta. Ello significa que el análisis debe realizarse para cada configuración de ensayo.

Como primera aproximación, puede suponerse que las deformaciones normales correspondientes a modo II son iguales y opuestas en puntos homólogos. Posteriormente, se utiliza la ecuación (24) como segunda condición.

3.3 Ensayo ADCB

En la figura se muestra un ensayo ADCB de una probeta de dimensiones aproximadas a las utilizadas por Mollón et al [2]. Las propiedades del material corresponden al AS4/8552 de Hexcel Composites. La probeta tiene una longitud total de 150 mm, la grieta es de 50 mm, y el espesor de las partes superior e inferior es 1 y 5 mm, respectivamente. Se impone un desplazamiento de 5 mm a la parte superior. Puede apreciarse la inclinación de la probeta debida a la asimetría de los desplazamientos de apertura.

Figura 1. Ensayo ADCB.

Mollón et al. proponen una fórmula para obtener la relación de modos para distintas relaciones de espesores. Dicha fórmula está ajustada a partir de resultados numéricos obtenidos con el Método de Dos Pasos desarrollado por los autores. Los resultados obtenidos a partir de la condición de igualdad de deformaciones mencionada anteriormente concuerdan razonablemente con los obtenidos con la fórmula propuesta.

Conclusiones

La descomposición de modos en probetas de fractura interlaminar con geometría de tira asimétricas está relacionada con los desplazamientos relativos en las cercanías de la punta de grieta. El método de descomposición de Williams sólo es válido en el caso de probetas de un mismo material con la grieta centrada. Las relaciones de modos obtenidas en el caso de ADCB mediante una primera aproximación basada en deformaciones normales concuerdan razonablemente con resultados obtenidos mediante el MEF.

Agradecimientos

Los autores agradecen a la Universidad del País Vasco (UPV/EHU) la financiación del Grupo de Investigación Mecánica de Materiales GIU 16/51 en la convocatoria de 2016.

Referencias

[1] J.G. Williams, International Journal of Fracture 36, pág. 101-119 (1988).

[2] V.Mollón, J. Bonhomme, J. Viña, A. Argüelles, Polymer Testing 29, pág. 766-770 (2010). doi:10.1016/j.polymertesting.2010.04.001

Revision as of 15:24, 29 April 2022

1 Introducción

2 Análisis del avance de grieta

2.1 Tasa de liberación de energía

2.2 La integral J y la zona cohesiva

3 Descomposición de modos

3.1 Avance infinitesimal de grieta

3.2 Determinación de c_I y c_II

3.3 Ensayo ADCB

Conclusiones

Agradecimientos

Referencias

Document information

Document Score

Share this document

Keywords

claim authorship

@@ Line 1: / Line 1: @@
-== Abstract ==
-Interlaminar failure tests are usually carried out in specimens where crack arms are symmetric. Asymmetric Double Cantiliver Beam (ADCB) is an exception where both crack arms have different thickness in order to get mixed mode I/II. The asymmetry in ADCB specimens could be applied also to te case of End Notched Flexure Tests, obtaining also mixed mode I/II.
-The decomposition proposed by Williams is not valid in the case of ADCB tests. On the other hand, articles related to asymmetric ENF tests including the mode decompositiion have not been found.
-The present study deals with the analsys of the mode decomposition in the case of specimens with asymmetric arms. The asymmetry may be related to the different thickness of the crack arms, to different materials or a combination of both factors. The results obtained will be compared with the results of mode decompsition that have been published in the case of ADCB tests.
-== Full document ==
+<div id="_GoBack" class="center" style="width: auto; margin-left: auto; margin-right: auto;">
-<pdf>Media:Draft_Content_633019790native-articles-57.pdf</pdf>
+F.Mujika<sup>a</sup>, A. Arrese<sup>a</sup>, A.I. Boyano<sup>b</sup>, J. De Gracia<sup>b</sup>, </div>
+<div class="center" style="width: auto; margin-left: auto; margin-right: auto;">
+<span style="text-align: center; font-size: 75%;"><sup>a</sup>GRUPO MATERIALES + TECNOLOGÍAS / MECÁNICA DE MATERIALES Departamento de Ingeniería Mecánica. Escuela de Ingeniería de Gipuzkoa.</span></div>
+<div class="center" style="width: auto; margin-left: auto; margin-right: auto;">
+<span style="text-align: center; font-size: 75%;"><sup>b</sup>GRUPO MATERIALES + TECNOLOGÍAS / MECÁNICA DE MATERIALES Departamento de Ingeniería Mecánica. Escuela de Ingeniería de Vitoria-Gasteiz</span></div>
+<div class="center" style="width: auto; margin-left: auto; margin-right: auto;">
+<span style="text-align: center; font-size: 75%;">Universidad del País Vasco (UPV/EHU).</span></div>
+<div class="center" style="width: auto; margin-left: auto; margin-right: auto;">
+<span style="text-align: center; font-size: 75%;">Plaza Europa 1, 20018 Donostia-San Sebastián.</span></div>
+{| style="width: 87%;border-collapse: collapse;"
+|-
+|  colspan='2'  style="vertical-align: top;"|<big>Análisis de la descomposición de modos en ensayos de fractura interlaminar asimétricos </big>
+|-
+|  style="border-bottom: 1pt solid black;vertical-align: top;"|<span style="text-align: center; font-size: 75%;"> [[Image:Mujika_et_al_2017a-image1.png|54px]] </span>
+|  style="vertical-align: top;"|
+|-
+|  style="border-top: 1pt solid black;border-bottom: 1pt solid black;vertical-align: top;"|<span style="text-align: center; font-size: 75%;">Historia del artículo:</span>
+<span style="text-align: center; font-size: 75%;">Recibido 5 de Mayo 2017</span>
+<span style="text-align: center; font-size: 75%;">En la versión revisada 5 de Mayo 2017</span>
+<span style="text-align: center; font-size: 75%;">Aceptado 31 de Mayo 2017</span>
+<span style="text-align: center; font-size: 75%;">Accesible online 21 de Junio 2017</span>
+|  rowspan='4' style="vertical-align: top;"|<span style="text-align: center; font-size: 75%;">Los ensayos de fractura interlaminar se realizan habitualmente en probetas donde los dos brazos de grieta son simétricos. El ensayo de Viga en Doble Voladizo Asimétrica (ADCB) constituye una excepción, con brazos de distintos espesores con lo que se obtiene modo mixto I/II. La asimetría de ADCB se podría también aplicar a ensayos de Viga con Entalla Final (ENF), con lo que en principio también se obtendrían modos mixtos I/II.</span>
+<span style="text-align: center; font-size: 75%;">La descomposición de modos propuesta por Williams no es válida en el ensayo ADCB y no se han encontrado trabajos relacionados con ensayos de ENF asimétricos en los que se considere la descomposición de modos.</span>
+<span style="text-align: center; font-size: 75%;">En el presente trabajo se desean analizar distintas alternativas para la descomposición de modos en el caso de probetas con brazos asimétricos. La falta de simetría puede deberse a una diferencia de espesores, a una diferencia de materiales o a la combinación de ambos factores. Los resultados obtenidos serán comprobados en primera instancia con los resultados de análisis de descomposición de modos publicados en el caso de ensayos ADCB.</span>
+|-
+|  style="border-top: 1pt solid black;vertical-align: top;"|<span style="text-align: center; font-size: 75%;">Palabras clave:</span>
+<span style="text-align: center; font-size: 75%;">Fractura interlaminar</span>
+<span style="text-align: center; font-size: 75%;">Descomposición de modos</span>
+<span style="text-align: center; font-size: 75%;">Laminados asimétricos</span>
+|-
+|  style="border-top: 1pt solid black;vertical-align: top;"|
+|-
+|  colspan='2'  style="vertical-align: top;"|<big>The analysis of mode decomposition in interlaminar fracture tests of asymmetric specimens. </big>
+|-
+|  style="border-bottom: 1pt solid black;vertical-align: top;"|<span style="text-align: center; font-size: 75%;"> [[Image:Mujika_et_al_2017a-image2.png|54px]] </span>
+|  style="vertical-align: top;"|
+|-
+|  style="border-top: 1pt solid black;border-bottom: 1pt solid black;vertical-align: top;"|<span style="text-align: center; font-size: 75%;">Keywords:</span>
+<span style="text-align: center; font-size: 75%;">Interlaminar fracture</span>
+<span style="text-align: center; font-size: 75%;">Mode decomposition</span>
+<span style="text-align: center; font-size: 75%;">Asymmetric laminates</span>
+|  rowspan='2' style="vertical-align: top;"|<span style="text-align: center; font-size: 75%;">Interlaminar failure tests are usually carried out in specimens where crack arms are symmetric. Asymmetric Double Cantiliver Beam (ADCB) is an exception where both crack arms have different thickness in order to get mixed mode I/II. The asymmetry in ADCB specimens could be applied also to te case of End Notched Flexure Tests, obtaining also mixed mode I/II.</span>
+<span style="text-align: center; font-size: 75%;">The decomposition proposed by Williams is not valid in the case of ADCB tests. On the other hand, articles related to asymmetric ENF tests including the mode decompositiion have not been found. </span>
+<span style="text-align: center; font-size: 75%;">The present study deals with the analsys of the mode decomposition in the case of specimens with asymmetric arms. The asymmetry may be related to the different thickness of the crack arms, to different materials or a combination of both factors. The results obtained will be compared with the results of mode decompsition that have been published in the case of ADCB tests.</span>
+|-
+|  style="border-top: 1pt solid black;vertical-align: top;"|
+|}
+==1 Introducción ==
+Los laminados compuesto que se utilizan en aplicaciones estructurales consisten en muchos casos en laminados constituidos por capas. En cada una de ellas el refuerzo es unidireccional y las propiedades mecánicas del laminado dependen de los materiales de las capas, de la orientación del refuerzo en cada una de ellas, así como del orden en que se apilan las mismas. La ausencia de refuerzo en la dirección perpendicular al laminado está relacionada con la fractura interlaminar, que es una de las limitaciones en la utilización de estos materiales.
+Por ejemplo, un impacto de baja energía puede provocar una pequeña deslaminación entre capas. Si una de las partes deslaminadas está sometida a compresión, puede generarse pandeo local que provoca un avance de grieta que puede derivar en el fallo catastrófico del componente.
+Para caracterizar la fractura interlaminar, es habitual determinar experimientalmente la tasa crítica de liberación de energía <math display="inline">G</math>, fundamentalmente en modos I, II y modo mixto I/II. Se realizan también ensayos en modo III, que no son objetod del presente trabajo. Las probetas utilizadas tienen geometría de tira y existen diferentes ensayos para determinar <math display="inline">G</math>. Se describirán únicamente los más utilizados. Para determinar GI se utiliza el ensayo de Viga en Doble Voladizo (Double Cantilever Beam, DCB). Para determinar el modo II se utiliza el ensayo de Flexión con Entalla Final (End Notched Flexure, ENF). Para determinar el modo mixto se utiliza el ensayo de flexión en modo mixto (Mixed Mode Bending, MMB) que es una combinación de los dos métodos anteriores.
+En los ensayos DCB, ENF y MMB se utilizan probetas que tienen una grieta inicial generada en el proceso de fabricación. Esta grieta está situada en el plano central del laminado, por lo que la configuración de probeta es simétrica en todos los casos. En el ensayo de viga asimétrica en doble voladizo (Asymmetric Double Cantilever Beam, ADCB) los brazos de grieta son de distintos espesores y se produce modo mixto I/II. En la mayoría de los casos los ensayos se realizan en probetas unidireccionales, con la fibra orientada en la longitud de la probeta. Sin embargo, las grietas interlaminares que se producen en servicio ocurren en circunstancias muy distintas a las de los ensayos: distintos espesores de los brazos de grieta, piezas con geometría de placa y distintas orientaciones de la interlámina.
+En el presente estudio se aborda la descomposición de modos de probetas con geometría de tira, en la que los brazos de grieta pueden ser de distintos espesores y también de material diferente. Se limita al caso en que el material es ortótropo.
+==2 Análisis del avance de grieta==
+==='''2.1''' Tasa de liberación de energía ===
+Se analiza un sistema en equilibrio sometido a un sistema de fuerzas independientes <math display="inline">{F}_{i}</math>, siendo <math display="inline">{\delta }_{i}</math> los desplazamientos de los puntos de aplicación de las fuerzas en la misma dirección. El trabajo correspondiente a una variación elemental de los desplazamientos viene dado por:
+{| class="formulaSCP" style="width: 100%; text-align: center;"
+|-
+|
+{| style="text-align: center; margin:auto;"
+|-
+| <math display="inline">dW=\sum _{i=1}^{n}{F}_{i}{d\delta }_{i}={F}_{i}{d\delta }_{i}</math>
+|}
+| style="width: 5px;text-align: right;white-space: nowrap;" | (1)
+|}
+Habiéndose utilizado el convenio de índices mudo para suprimir el sumatorio de la ecuación (1).
+En un avance infinitesimal de grieta, el balance de energía viene dado por:
+{| class="formulaSCP" style="width: 100%; text-align: center;"
+|-
+|
+{| style="text-align: center; margin:auto;"
+|-
+| <math display="inline">dW=dU+GdA</math>
+|}
+| style="width: 5px;text-align: right;white-space: nowrap;" | (2)
+|}
+Donde <math display="inline">dU</math> representa la energía interna, <math display="inline">G</math> la energía liberada por unidad de área y <math display="inline">dA</math> el área de la nueva superficie de grieta creada. Si el ancho ''b'' es uniforme <math display="inline">dA=</math><math>bda</math> donde <math display="inline">da</math> es la longitud del avance de grieta.
+Según las ecuaciones (1) y (2), la energía interna viene dada por:
+{| class="formulaSCP" style="width: 100%; text-align: center;"
+|-
+|
+{| style="text-align: center; margin:auto;"
+|-
+| <math display="inline">dU={F}_{i}{d\delta }_{i}-Gbda</math>
+|}
+| style="width: 5px;text-align: right;white-space: nowrap;" | (3)
+|}
+Aun cuando el avance de grieta es un proceso irreversible, se asume que la energía interna es una función de estado, siendo las variables de estado los desplazamientos independientes <math display="inline">{\delta }_{i}</math> y la longitud de grieta <math display="inline">a</math>. Por lo tanto, también puede expresarse como:
+{| class="formulaSCP" style="width: 100%; text-align: center;"
+|-
+|
+{| style="text-align: center; margin:auto;"
+|-
+| <math display="inline">dU={\left( \frac{dU}{{d\delta }_{i}}\right) }_{a}{d\delta }_{i}+</math><math>{\left( \frac{dU}{da}\right) }_{{\delta }_{i}}da</math>
+|}
+| style="width: 5px;text-align: right;white-space: nowrap;" | (4)
+|}
+Identificando términos en las ecuaciones (3) y (4) resulta:
+{| class="formulaSCP" style="width: 100%; text-align: center;"
+|-
+|
+{| style="text-align: center; margin:auto;"
+|-
+| <math display="inline">{\left( \frac{dU}{{d\delta }_{i}}\right) }_{a}={F}_{i}\quad -</math><math>\frac{1}{b}{\left( \frac{dU}{da}\right) }_{{\delta }_{i}}=G</math>
+|}
+| style="width: 5px;text-align: right;white-space: nowrap;" | (5)
+|}
+Con lo que se obtienen el primer teorema de Castigliano y la tasa de liberación de energía como liberación de la energía de deformación.
+Por otra parte, se define la energía de deformaicón complementaria <math display="inline">C</math>:
+{| class="formulaSCP" style="width: 100%; text-align: center;"
+|-
+|
+{| style="text-align: center; margin:auto;"
+|-
+| <math display="inline">C={F}_{i}{\delta }_{i}-U</math>
+|}
+| style="width: 5px;text-align: right;white-space: nowrap;" | (6)
+|}
+Diferenciando la ecuación (6) y sustituyendo en el balance de energía de la ecuación (3) se obtiene:
+{| class="formulaSCP" style="width: 100%; text-align: center;"
+|-
+|
+{| style="text-align: center; margin:auto;"
+|-
+| <math display="inline">dC={\delta }_{i}d{F}_{i}+Gbda</math>
+|}
+| style="width: 5px;text-align: right;white-space: nowrap;" | (7)
+|}
+Asumiendo que <math display="inline">C</math> es función de las variables de estado <math display="inline">{F}_{i}</math> y <math display="inline">a</math>:
+{| class="formulaSCP" style="width: 100%; text-align: center;"
+|-
+|
+{| style="text-align: center; margin:auto;"
+|-
+| <math display="inline">dC={\left( \frac{dC}{{dF}_{i}}\right) }_{a}{dF}_{i}+{\left( \frac{dC}{da}\right) }_{{F}_{i}}da</math>
+|}
+| style="width: 5px;text-align: right;white-space: nowrap;" | (8)
+|}
+Identificando términos en las ecuaciones (7) y (8) se tiene:
+{| class="formulaSCP" style="width: 100%; text-align: center;"
+|-
+|
+{| style="text-align: center; margin:auto;"
+|-
+| <math display="inline">{\left( \frac{dC}{{dF}_{i}}\right) }_{a}={\delta }_{i}\quad \frac{1}{b}{\left( \frac{dC}{da}\right) }_{{F}_{i}}=</math><math>G</math>
+|}
+| style="width: 5px;text-align: right;white-space: nowrap;" | (9)
+|}
+Se obtienen así el primer teorema de Engesser y la tasa de liberación de energía como el incremento de energía de deformación complementaria. En sistemas elásticos lineales el teorema de Engesser se convierte en el teorema de Castigliano, por lo que se denomina a veces teorema de Engesser-Castigliano. Para utilizar este teorema <math display="inline">C</math> se debe expresar en función de las fuerzas aplicadas.
+En el caso particular de un sistema elástico lineal sometido a una única carga <math display="inline">F</math> con un desplazamiento asociado <math display="inline">\delta</math> , siendo <math display="inline">\delta =</math><math>fF</math> se tiene:
+{| class="formulaSCP" style="width: 100%; text-align: center;"
+|-
+|
+{| style="text-align: center; margin:auto;"
+|-
+| <math display="inline">U=\frac{{\delta }^{2}}{2f}\quad C=\frac{f{F}^{2}}{2}</math>
+|}
+| style="width: 5px;text-align: right;white-space: nowrap;" | (10)
+|}
+Donde <math display="inline">f</math> representa la flexibilidad del sistema. Utilizando las ecuaciones (5) y (9) resulta en ambos casos que:
+{| class="formulaSCP" style="width: 100%; text-align: center;"
+|-
+|
+{| style="text-align: center; margin:auto;"
+|-
+| <math display="inline">G=\frac{{F}^{2}}{2b}\left( \frac{df}{da}\right)</math>
+|}
+| style="width: 5px;text-align: right;white-space: nowrap;" | (11)
+|}
+Se ha suprimido el subíndice <math display="inline">F</math> o <math display="inline">\delta</math>  indicativo de la derivación parcial, ya que la flexibilidad depende úncamente de la longitud de grieta.
+==='''2.2''' La integral J y la zona cohesiva===
+Rice definió la integral ''J'' como una integral independiente del camino en una curva cerrada que incluía la punta de grieta:
+{| class="formulaSCP" style="width: 100%; text-align: center;"
+|-
+|
+{| style="text-align: center; margin:auto;"
+|-
+| <math display="inline">J=\int_{\Gamma }^{}\left( {U}_{0}dy-\mathit{\boldsymbol{T}}\frac{\partial \mathit{\boldsymbol{u}}}{\partial x}\, d\Gamma \right)</math>
+|}
+| style="width: 5px;text-align: right;white-space: nowrap;" | (12)
+|}
+Donde <math display="inline">\Gamma</math>  es el camino cerrado de integración en sentido anthihorario, <math display="inline">{U}_{0}</math> la densidad de energía de deformación, <math display="inline">\mathit{\boldsymbol{T}}</math> el vector tensión y <math display="inline">\mathit{\boldsymbol{u}}</math> el vector desplazamiento. Se demuestra además que <math display="inline">J=</math><math>G</math> en el caso de comportamiento elástico.
+Tomando <math display="inline">\Gamma</math>  en las cercanías de la punta de grieta <math display="inline">\mathit{\boldsymbol{T}}</math> es nulo por lo que la ecuación (12) queda:
+{| class="formulaSCP" style="width: 100%; text-align: center;"
+|-
+|
+{| style="text-align: center; margin:auto;"
+|-
+| <math display="inline">J=G=\int_{C}^{}Wdy=\int_{0}^{{\Delta }_{n}}\sigma \, d{\Delta }_{n}+</math><math>\int_{0}^{{\Delta }_{t}}\tau \, d{\Delta }_{t}</math>
+|}
+| style="width: 5px;text-align: right;white-space: nowrap;" | (13)
+|}
+Siendo <math display="inline">\sigma</math>  la tensión normal de apertura, <math display="inline">{\Delta }_{n}</math> el desplazamiento relativo asociado, <math display="inline">\tau</math>  la tensión cortante y <math display="inline">{\Delta }_{t}</math> el desplazamiento relativo asociado. Por lo tanto, la primera integral de la ecuación representa la contribución del modo I y la segunda integral incluye la contribución de los modos II y III, aunque este último no se considera en el presente trabajo.
+Las tensiones y desplazamientos citados corresponden a una zona próxima a la punta de grieta, denominada zona cohesiva. Esta zona está relacionada con diversos factores: plastificación debido a que las tensiones alcanzan el límite elástico, puenteo de fibras en la zona de grieta o aparición de microgrietas. La relación entre las tensiones y los desplazamientos mencionados anteriormente en dicha zona se denomina ley cohesiva y se puede obtener de la siguiente manera: asumiendo que <math display="inline">G</math> es función de los desplazamientos independientes <math display="inline">{\Delta }_{n}</math> y <math display="inline">{\Delta }_{t}</math>, puede escribirse:
+{| class="formulaSCP" style="width: 100%; text-align: center;"
+|-
+|
+{| style="text-align: center; margin:auto;"
+|-
+| <math display="inline">G=\sigma \, d{\Delta }_{n}+\tau \, d{\Delta }_{t}</math>
+|}
+| style="width: 5px;text-align: right;white-space: nowrap;" | (14)
+|}
+Asumiendo ahora que <math display="inline">G</math> es diferencial exacta:
+{| class="formulaSCP" style="width: 100%; text-align: center;"
+|-
+|
+{| style="text-align: center; margin:auto;"
+|-
+| <math display="inline">dG={\left( \frac{dG}{{d\Delta }_{n}}\right) }_{{\Delta }_{t}}{d\Delta }_{n}+</math><math>{\left( \frac{dG}{{d\Delta }_{t}}\right) }_{{\Delta }_{n}}{d\Delta }_{t}</math>
+|}
+| style="width: 5px;text-align: right;white-space: nowrap;" | (15)
+|}
+Identificando términos en las ecuaciones (14) y (15) resulta:
+{| class="formulaSCP" style="width: 100%; text-align: center;"
+|-
+|
+{| style="text-align: center; margin:auto;"
+|-
+| <math display="inline">\sigma ={\left( \frac{dG}{{d\Delta }_{n}}\right) }_{{\Delta }_{t}}\quad \tau =</math><math>{\left( \frac{dG}{{d\Delta }_{t}}\right) }_{{\Delta }_{n}}</math>
+|}
+| style="width: 5px;text-align: right;white-space: nowrap;" | (16)
+|}
+En caso de modos puros, únicamente existe un desplazamiento relativo como variable de estado.
+Los desplazamientos relativos <math display="inline">{\Delta }_{n}</math> y <math display="inline">{\Delta }_{t}</math> son la suma de los desplazamiento correspondiente a puntos homólogos de cada brazo de grieta, entendiendo como puntos homólogos aquellos que están sometidos a la misma tensión. Por lo tanto, en el caso de que los desplazamientos de los puntos homólogos sean distintos, se podrán descomponer en una parte simétrica que realiza trabajo y una parte antisimétrica que no realiza trabajo y está asociada a un movimiento de sólido rígido.
+==3 Descomposición de modos==
+==='''3.1''' Avance infinitesimal de grieta===
+En esta sección se utiliza un procedimiento basado en el estudio de Williams [<span id='cite-'></span>[[#|]]], determinando directamente la energía complementaria antes y después del avance de grieta sin modificar la carga y utilizando la ecuación (9) para determinar <math display="inline">G</math>.
+Se considera un elemento diferencial de longitud <math display="inline">da</math> antes y después del avance de grieta. El brazo superior se denomina 1 y el brazo inferior 2. Ambos brazos pueden ser de material y espersor diferente. Considerando únicamente el efecto de la flexión, la energía complementaria <math display="inline">{C}_{a}</math> antes del avance de grieta viene dada por:
+{| class="formulaSCP" style="width: 100%; text-align: center;"
+|-
+|
+{| style="text-align: center; margin:auto;"
+|-
+| <math display="inline">{C}_{a}=\frac{{\left( {M}_{1}+{M}_{2}\right) }^{2}}{2D}da</math>
+|}
+| style="width: 5px;text-align: right;white-space: nowrap;" | (17)
+|}
+Donde <math display="inline">D</math> es la rigidez a flexión de toda la sección. Tras el avance de grieta, la energía complementaria <math display="inline">{C}_{d}</math> es:
+{| class="formulaSCP" style="width: 100%; text-align: center;"
+|-
+|
+{| style="text-align: center; margin:auto;"
+|-
+| <math display="inline">{C}_{d}=\left( \frac{{M}_{1}^{2}}{2{D}_{1}}+\frac{{M}_{2}^{2}}{2{D}_{2}}\right) da</math>
+|}
+| style="width: 5px;text-align: right;white-space: nowrap;" | (18)
+|}
+Donde <math display="inline">{D}_{1}</math> y <math display="inline">{D}_{2}</math> son las rigideces a flexión de las partes 1 y 2, respectivamente. De acuerdo a la ecuación (9) la tasa crítica de liberación de energía es:
+{| class="formulaSCP" style="width: 100%; text-align: center;"
+|-
+|
+{| style="text-align: center; margin:auto;"
+|-
+| <math display="inline">G=\frac{{C}_{d}-{C}_{a}}{da}=\frac{1}{2D}\left[ {M}_{1}^{2}{r}_{1}+\right. </math><math>\left. {M}_{2}^{2}{r}_{2}-{\left( {M}_{1}+{M}_{2}\right) }^{2}\right]</math>
+|}
+| style="width: 5px;text-align: right;white-space: nowrap;" | (19)
+|}
+Donde <math display="inline">{r}_{1}</math> y <math display="inline">{r}_{2}</math> son las relaciones entre rigideces a flexión. Aplicando el principio de superposición los momentos flectores de cada brazo de grieta se descomponen en los correspondientes a los modos de fractura I y II:
+{| class="formulaSCP" style="width: 100%; text-align: center;"
+|-
+|
+{| style="text-align: center; margin:auto;"
+|-
+| <math display="inline">\begin{matrix}{M}_{1}={M}_{1I}+{M}_{1II}\\{M}_{2}={M}_{2I}+{M}_{2II}\end{matrix}</math>
+|}
+| style="width: 5px;text-align: right;white-space: nowrap;" | (20)
+|}
+Sustituyendo la ecuación (20) en la ecuación (19) se puede escribir <math display="inline">G</math> en función de los momentos en modo I y II y por lo tanto se obtienen las tasas de liberación de energía correspondientes a cada modo:
+{| class="formulaSCP" style="width: 100%; text-align: center;"
+|-
+|
+{| style="text-align: center; margin:auto;"
+|-
+| <math display="inline">\begin{matrix}{G}_{I}=\frac{1}{2D}\left[ {M}_{1I}^{2}\left( {r}_{1}-1\right) +{M}_{2I}^{2}\left( {r}_{2}-1\right) -2{M}_{1I}{M}_{2I}\right] \\{G}_{II}=\frac{1}{2D}\left[ {M}_{1II}^{2}\left( {r}_{1}-1\right) +{M}_{2II}^{2}\left( {r}_{2}-1\right) -2{M}_{1II}{M}_{2II}\right] \end{matrix}</math>
+|}
+| style="width: 5px;text-align: right;white-space: nowrap;" | (21)
+|}
+Por otra parte, los términos que contienen productos de momentos en modos I y II deben ser nulos dado que los modos son independientes, es decir:
+{| class="formulaSCP" style="width: 100%; text-align: center;"
+|-
+|
+{| style="text-align: center; margin:auto;"
+|-
+| <math display="inline">{M}_{1I}{M}_{1II}\left( {r}_{1}-1\right) +{M}_{2I}{M}_{2II}\left( {r}_{2}-\right. </math><math>\left. 1\right) -\left( {M}_{1I}{M}_{2II}+{M}_{1II}{M}_{2I}\right) =0</math>
+|}
+| style="width: 5px;text-align: right;white-space: nowrap;" | (22)
+|}
+Se supone ahora que los momentos de cada modo en ambos brazos de grieta están relacionados según dos parámetros <math display="inline">{c}_{I}</math> y <math display="inline">{c}_{II}</math>, es decir:
+{| class="formulaSCP" style="width: 100%; text-align: center;"
+|-
+|
+{| style="text-align: center; margin:auto;"
+|-
+| <math display="inline">\begin{matrix}{M}_{2I}={{c}_{I}M}_{1I}\\{M}_{2II}={{c}_{II}M}_{1II}\end{matrix}</math>
+|}
+| style="width: 5px;text-align: right;white-space: nowrap;" | (23)
+|}
+Sustituyendo la ecuación (23) en la ecuación (22):
+{| class="formulaSCP" style="width: 100%; text-align: center;"
+|-
+|
+{| style="text-align: center; margin:auto;"
+|-
+| <math display="inline">\left( {r}_{1}-1\right) +{c}_{I}{c}_{II}\left( {r}_{2}-1\right) -</math><math>\left( {c}_{II}+{c}_{I}\right) =0</math>
+|}
+| style="width: 5px;text-align: right;white-space: nowrap;" | (24)
+|}
+Por otra parte, combinando las ecuaciones (20) y (23):
+{| class="formulaSCP" style="width: 100%; text-align: center;"
+|-
+|
+{| style="text-align: center; margin:auto;"
+|-
+| <math display="inline">\begin{matrix}{M}_{1}={M}_{1I}+{M}_{1II}\\{M}_{2}={{c}_{I}M}_{1I}+{{c}_{II}M}_{1II}\end{matrix}</math>
+|}
+| style="width: 5px;text-align: right;white-space: nowrap;" | (25)
+|}
+La determinación de <math display="inline">{c}_{I}</math> y <math display="inline">{c}_{II}</math> se trata en la próxima sección. Conocidos estos parámetros, de las ecuaciones (25) se pueden obtener los momentos en los distintos modos:
+{| class="formulaSCP" style="width: 100%; text-align: center;"
+|-
+|
+{| style="text-align: center; margin:auto;"
+|-
+| <math display="inline">\begin{matrix}{M}_{1I}=\frac{{c}_{II}{M}_{1}-{M}_{2}}{{c}_{II}-{c}_{I}}\\{M}_{1II}=\frac{{{M}_{2}-c}_{I}{M}_{1}}{{c}_{II}-{c}_{I}}\end{matrix}</math>
+|}
+| style="width: 5px;text-align: right;white-space: nowrap;" | (26)
+|}
+Combinando las ecuaciones (26) con las ecuaciones (21) y (23) pueden determinarse <math display="inline">{G}_{I}</math> y <math display="inline">{G}_{II}</math>.
+==='''3.2''' Determinación de c<sub>I</sub> y c<sub>II</sub>===
+El análisis de Williams está particularizado al caso de único material y distintos espesores. Este investigador estableció que para modo puro I se debía verificar que los momentos fueran opuestos, es decir <math display="inline">{c}_{I}=</math><math>-1</math>. Por otra parte, para modo puro II estableció la condición de que las curvaturas fueran iguales, con lo que en el caso actual <math display="inline">{c}_{II}=</math><math>\frac{{D}_{2}}{{D}_{1}}</math>. Utilizando estos valores en el caso de igual espesor, la ecuación (24) se satisface idénticamente.
+No obstante en el ensayo ADCB, en el que el material es único pero los espesores distintos, los momentos son iguales pero diferentes estudios muestran que existe combinación de modos. Por lo tanto, los valores utilizados en la descomposición de Williams son válidos únicamente en el caso de igual espesor y un único material.
+Teniendo en cuenta la ecuación (13) en la que G se obtiene en función de las tensiones y desplazamientos relativos de la zona cohesiva, se puede afirmar que:
+:1. Las tensiones en puntos homólogos son iguales y opuestas debido al principio de acción y reacción.
+:2. Los modos puros corresponden a situaciones en las que los desplazamientos de puntos homólogos son iguales y opuestos.
+En consecuencia, se pueden probar dos criterios distintos para determinar los parámetros <math display="inline">{c}_{I}</math> y <math display="inline">{c}_{II}</math>:
+:1. Determinar las condiciones para que los desplazamientos normales a la grieta sean iguales y opuestos en puntos homólogos y aplicar la ecuación (24) como segunda condición.
+:2. Determinar las condiciones para que los desplazamientos tangenciales en la grieta sean iguales en puntos homólogos y aplicar la ecuación (24) como segunda condición.
+Si la hipótesis es correcta, los valores de <math display="inline">{c}_{I}</math> y <math display="inline">{c}_{II}</math> obtenidos en ambos casos deben ser iguales.
+No obstante, los desplazamientos normales y tangenciales deben ser calculados teniendo en cuenta todo el sistema, por lo que no pueden relacionarse directamente con los momentos en la punta de grieta. Ello significa que el análisis debe realizarse para cada configuración de ensayo.
+Como primera aproximación, puede suponerse que las deformaciones normales correspondientes a modo II son iguales y opuestas en puntos homólogos. Posteriormente, se utiliza la ecuación (24) como segunda condición.
+==='''3.3''' Ensayo ADCB===
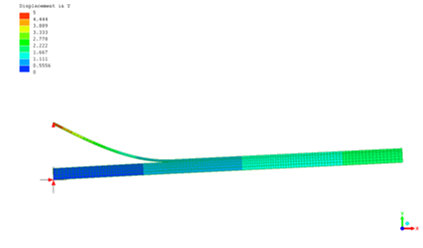
+En la figura se muestra un ensayo ADCB de una probeta de dimensiones aproximadas a las utilizadas por Mollón et al [2]. Las propiedades del material corresponden al AS4/8552 de Hexcel Composites. La probeta tiene una longitud total de 150 mm, la grieta es de 50 mm, y el espesor de las partes superior e inferior es 1 y 5 mm, respectivamente. Se impone un desplazamiento de 5 mm a la parte superior. Puede apreciarse la inclinación de la probeta debida a la asimetría de los desplazamientos de apertura.
+[[Image:Mujika_et_al_2017a-image5-c.png|600px]]
+<div class="center" style="width: auto; margin-left: auto; margin-right: auto;">
+<span style="text-align: center; font-size: 75%;">'''Figura 1.''' Ensayo ADCB.</span></div>
+Mollón et al. proponen una fórmula para obtener la relación de modos para distintas relaciones de espesores. Dicha fórmula está ajustada a partir de resultados numéricos obtenidos con el Método de Dos Pasos desarrollado por los autores. Los resultados obtenidos a partir de la condición de igualdad de deformaciones mencionada anteriormente concuerdan razonablemente con los obtenidos con la fórmula propuesta.
+== Conclusiones==
+La descomposición de modos en probetas de fractura interlaminar con geometría de tira asimétricas está relacionada con los desplazamientos relativos en las cercanías de la punta de grieta. El método de descomposición de Williams sólo es válido en el caso de probetas de un mismo material con la grieta centrada. Las relaciones de modos obtenidas en el caso de ADCB mediante una primera aproximación basada en deformaciones normales concuerdan razonablemente con resultados obtenidos mediante el MEF.
+==Agradecimientos==
+Los autores agradecen a la Universidad del País Vasco (UPV/EHU) la financiación del Grupo de Investigación Mecánica de Materiales GIU 16/51 en la convocatoria de 2016.
+==Referencias==
+<span style="text-align: center; font-size: 75%;">[1]</span> <span style="text-align: center; font-size: 75%;">J.G. Williams, ''International Journal of Fracture'' '''36''', pág. 101-119 (1988). </span>
+<span style="text-align: center; font-size: 75%;">[2]</span> <span style="text-align: center; font-size: 75%;">V.Mollón, J. Bonhomme, J. Viña, A. Argüelles, ''Polymer Testing'' '''29''', pág. 766-770 (2010). doi:10.1016/j.polymertesting.2010.04.001</span>

Revision as of 15:24, 29 April 2022

1 Introducción

2 Análisis del avance de grieta

2.1 Tasa de liberación de energía

2.2 La integral J y la zona cohesiva

3 Descomposición de modos

3.1 Avance infinitesimal de grieta

3.2 Determinación de cI y cII

3.3 Ensayo ADCB

Conclusiones

Agradecimientos

Referencias

Document information

Document Score

Share this document

Keywords

claim authorship

3.2 Determinación de c_I y c_II