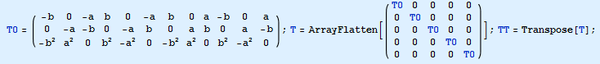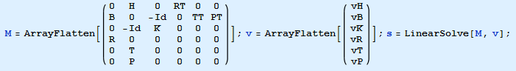Another FEM: Rectangular element of 4 nodes

RESUMEN

Tanto en el tradicional MEF como en la metodología que se propone en este artículo, las Ecuaciones de Compatibilidad se consiguen a partir de las mismas funciones de interpolación, por lo que la matriz Elemental que relaciona las deformaciones en los nodos del elemento con los desplazamientos de dichos nodos es idéntica en ambos procedimientos. Pero, mientras que en aquél se aplica el PTV para la determinación de las Fuerzas Nodales Equivalentes que se han de utilizar para la consecución de las Ecuaciones de Equilibrio de todos los nodos de la estructura, en éste dichas fuerzas se consiguen bajo la hipótesis de que las tensiones en los cuatro lados del rectángulo elemental varían linealmente a lo largo de dichos lados. Además de esto, puesto que el sistema de ecuaciones que en este procedimiento se utiliza viene dado en todas las incógnitas del problema en forma explícita, es posible imponer a cualquiera de dichas incógnitas todo tipo de restricción, por lo que, aparte de las condiciones de apoyo imprescindibles para evitar el movimiento como sólido rígido, se imponen también condiciones de equilibrio a todos y cada uno de los elementos que discretizan la estructura, así como condiciones de tensión normal en el perímetro del dominio. Los ejemplos prácticos que se estudian al final muestran unos resultados un tanto mejorados respecto a los que se obtienen con el tradicional MEF.

Palabras clave: Elemento, matriz, compatibilidad, equilibrio, constitutivas, fuerzas nodales.

SUMMARY

In both of the traditional FEM and the proposed methodology in this article, the compatibility equations are obtained from the same interpolation functions, so the elementary matrix that relates deformations in the nodes of the element with the displacements of that nodes are the same in both procedures. But, whereas in that one the PVW is applied to establish the Equivalent Nodal Forces to be used for the achievement of the equilibrium equations of all the nodes of the structure, in which these forces are obtained from the hypothesis that the stresses on all four sides of the elemental rectangle vary linearly along these sides and are thus to replace said stresses as statically equivalent, concentrated forces. Since the system of equations used in this procedure is given in all the unknowns of the problem explicitly, and it is possible to impose any kind of restriction on any of these unknowns, so that, in addition to the conditions of essential support to avoid movement as a solid rigid, conditions of equilibrium are imposed on every one of the elements that discretize the structure, which is not possible with the usual procedure that, therefore, must resign to be fulfilled in a way such a balance. The practical examples studied at the end show somewhat improved results with respect to the FEM usual procedure.

Keywords: Matrix, element, compatibility, balance, constitutive, nodal forces.

1. Antecedentes.- El cálculo de estructuras por el Método de los Elementos Finitos tradicional (MEF) está fundamentalmente sustentado en, por una parte, la elección de unas determinadas funciones (funciones de interpolación) y, por otra, en la aplicación del Principio de los Trabajos Virtuales (PTV). Pero, comoquiera que dichas funciones no pueden reproducir de forma exacta el comportamiento mecánico de la estructura en estudio y todas las magnitudes involucradas en el proceso de cálculo dependen de forma directa de tales funciones, los resultados que se obtendrán en el cálculo de una estructura (desplazamientos, tensiones, etc.) sólo podrán ser más o menos aproximados; aproximación que además se verá afectada, entre otras causas, por la integración numérica utilizada habitualmente.

Nota: en adelante se hará una distinción entre nodos y nudos, considerando nodos a los vértices de los elementos (que vendrán signados por i, j, k y m para cada elemento e), los cuales estarán sometidos a tensiones y deformaciones, mientras que los nudos (signados por un subíndice numérico en la forma n₁, n₂, etc.) son los puntos donde inciden uno o más nodos y sólo pueden sufrir desplazamientos.

2. Objetivos.- Para el análisis de toda estructura formada por elementos discretos conectados entre sí en unos puntos que llamaremos nudos, es imprescindible el uso de cuatro tipos de ecuaciones básicas: a) Ecuaciones de Equilibrio de fuerzas que inciden en cada nudo, b) Ecuaciones de Compatibilidad que obliguen a que se cumplan unas determinadas relaciones entre los desplazamientos de los nudos y las deformaciones que sufren los elementos, c) Ecuaciones Constitutivas del material, que relacionan las deformaciones con las tensiones y d) Ecuaciones que eviten el movimiento de la estructura como sólido rígido, esto es, las Condiciones Cinemáticas de sustentación. El tratamiento de este último tipo de ecuaciones por el Método de los Multiplicadores de Lagrange permite obtener, junto con los tres tipos anteriores, un sistema en todas las incógnitas involucradas en el análisis de la estructura. Habitualmente se suelen reducir las dimensiones de tal sistema mediante la aplicación del PTV, obteniendo otro menor en las incógnitas de desplazamientos y de Multiplicadores de Lagrange (reacciones con sentido opuesto); sin embargo, en el procedimiento que en este trabajo se presenta, se mantienen de forma explícita todas las ecuaciones mencionadas, lo que permitirá introducir cualquier tipo de restricción a cualquiera de las incógnitas involucradas, por lo que puede obligarse a que se cumpla el equilibrio en cada elemento aislado sin más que añadir al sistema anterior un quinto tipo de ecuaciones: las Condiciones de Restricción Estática interna y, finalmente, un último grupo de ecuaciones que describan el estado tensional del perímetro del dominio: las Condiciones de Restricción estática externa o perimetral.

Es, pues, objetivo de esta investigación el cálculo de estructuras en el espacio 2D, discretizadas mediante elementos finitos rectangulares de 4 nodos, utilizando el sistema de ecuaciones antes descrito (primera diferencia respecto al método clásico, excepto las ecuaciones de compatibilidad, que son idénticas), sistema que contempla el equilibrio de cada elemento aislado (segunda diferencia fundamental) así como el estado tensional del perímetro del dominio (tercera diferencia) y sin la utilización de integración alguna (cuarta diferencia), lo que supone una formulación totalmente distinta a la usada hasta ahora.

3. Herramientas del método.- El procedimiento que aquí se propone es un método matricial, por lo tanto las unidades operativas que maneja son matrices Elementales agrupadas en seis tipos: a) matrices de Fuerzas Nodales, b) matrices de Compatibilidad, c) matrices Constitutivas, d) matrices de Restricciones Cinemáticas (restricciones en aquellos aparatos de apoyo que sustentan a la estructura), e) matrices de Restricciones Estáticas internas (condiciones de equilibrio de cada uno de los elementos finitos con los que se ha discretizado ésta) y f) matrices de Restricciones Estáticas externas (estado tensional del perímetro del dominio).

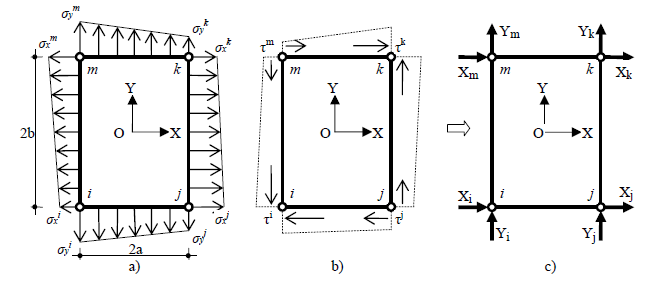
3.1. Matrices Elementales de Fuerzas Nodales.- Son aquellas matrices que permiten determinar las dos componentes de fuerza concentrada (X, Y), en cada uno de los cuatro nodos del elemento, en función de las tensiones existentes en dichos puntos. Coherentemente con las función de interpolación adoptada, las tensiones variarán linealmente a lo largo de cada uno de los lados del rectángulo¹, de dimensiones 2a×2b y espesor t, y por tanto la distribución será entones como se muestra en las Figs. 1 a) y b), donde se ha tomado para dichas tensiones el criterio convencional de signos y se ha supuesto que el elemento no contiene cargas volumétricas ni de superficie.

Fig. 1. Elemento rectangular de 4 nodos aislado: a) Distribución de tensiones normales, b) Tensiones tangenciales, c) Fuerzas Nodales Equivalentes

Signando por i, j, k y m a los nodos del elemento, las componentes de Fuerza Nodal Equivalente en el nodo i (Fig. 1c) podrán obtenerse en la forma^{[1] §7.3.2.}

${\begin{array}{c}X_{i}=-t{\frac {2b}{6}}(2{\sigma }_{x}^{i}+{\sigma }_{x}^{m})-t{\frac {2a}{6}}(2{\tau }^{i}+{\tau }^{j})=-{\frac {t}{3}}(2b{\mbox{ }}{\sigma }_{x}^{i}+b{\mbox{ }}{\sigma }_{x}^{m}+2a{\mbox{ }}{\tau }^{i}+a{\mbox{ }}{\tau }^{j})\\Y_{i}=-t{\frac {2a}{6}}(2{\sigma }_{y}^{i}+{\sigma }_{y}^{j})-t{\frac {2b}{6}}(2{\tau }^{i}+{\tau }^{m})=-{\frac {t}{3}}(2a{\mbox{ }}{\sigma }_{y}^{i}+a{\mbox{ }}{\sigma }_{y}^{j}+2b{\mbox{ }}{\tau }^{i}+b{\mbox{ }}{\tau }^{m})\end{array}}$

(1)

donde X_i e Y_i son, respectivamente, la componente horizontal y vertical de la fuerza concentrada en el nodo i, fuerza que sustituye a las tensiones distribuidas a lo largo de los lados i-j e i-m del elemento. Llamando σ^e al vector columna que contiene las componentes de tensión existentes en los cuatro vértices del elemento (en el orden i, j, k, m), éste vendrá expresado como

$\mathbf {{\mbox{σ}}^{\mbox{e}}} ={\left[{\begin{array}{ccc|ccc|ccc|ccc}{\sigma }_{x}^{i}&{\sigma }_{y}^{i}&{\tau }^{i}&{\sigma }_{x}^{j}&{\sigma }_{y}^{j}&{\tau }^{j}&{\sigma }_{x}^{k}&{\sigma }_{y}^{k}&{\tau }^{k}&{\sigma }_{x}^{m}&{\sigma }_{y}^{m}&{\tau }^{m}\end{array}}\right]}^{T}$

(2)

por lo que las componentes dadas en (1) se podrán escribir matricialmente en la forma

$\left[{\begin{array}{c}X_{i}\\Y_{i}\end{array}}\right]={\frac {t}{3}}\left[{\begin{array}{ccc|ccc|ccc|ccc}-2b&0&-2a&0&0&-a&0&0&0&-b&0&0\\0&-2a&-2b&0&-a&0&0&0&0&0&0&-b\end{array}}\right]\left[\mathbf {{\mbox{σ}}^{\mbox{e}}} \right]$

(3)

y signando por ${\mbox{F}}_{\mbox{i}}^{\mbox{e}},$${\mbox{F}}_{\mbox{j}}^{\mbox{e}},$${\mbox{F}}_{\mbox{k}}^{\mbox{e}}$ y ${\mbox{F}}_{\mbox{m}}^{\mbox{e}}$ a cada uno de los vectores que contienen a las dos componentes de fuerza nodal de los nudos i, j, k y m, respectivamente, la anterior vendrá dada para el nodo i por

$\mathbf {{\mbox{F}}_{\mbox{i}}^{\mbox{e}}} =\mathbf {{\mbox{I}}^{\mbox{e}}} {\mbox{ }}\mathbf {{\mbox{σ}}^{\mbox{e}}}$

(4)

donde se ha llamado

$\mathbf {{\mbox{I}}^{\mbox{e}}} ={\frac {t}{3}}\left[{\begin{array}{ccc|ccc|ccc|ccc}-2b&0&-2a&0&0&-a&0&0&0&-b&0&0\\0&-2a&-2b&0&-a&0&0&0&0&0&0&-b\end{array}}\right]$

(5)

a la matriz de Fuerza Nodal asociada al nodo i, que, como se ha visto, permite calcular las componentes de dicha fuerza en función de las tensiones a las que están sometidos los cuatro nodos del elemento.

Procediendo de la misma forma para los nodos j, k y m, las expresiones para las correspondientes matrices de Fuerza Nodal para estos nodos serán

$\mathbf {{\mbox{J}}^{\mbox{e}}} ={\frac {t}{3}}\left[{\begin{array}{ccc|ccc|ccc|ccc}0&0&-a&2b&0&-2a&b&0&0&0&0&0\\0&-a&0&0&-2a&2b&0&0&b&0&0&0\end{array}}\right]$

(6)

$\mathbf {{\mbox{K}}^{\mbox{e}}} ={\frac {t}{6}}\left[{\begin{array}{ccc|ccc|ccc|ccc}0&0&0&b&0&0&2b&0&2a&0&0&a\\0&0&0&0&0&b&0&2a&2b&a&0&0\end{array}}\right]$

(7)

$\mathbf {{\mbox{M}}^{\mbox{e}}} ={\frac {t}{3}}\left[{\begin{array}{ccc|ccc|ccc|ccc}-b&0&0&0&0&0&0&0&a&-2b&0&2a\\0&0&-b&0&0&0&0&a&0&0&2a&-2b\end{array}}\right]$

(8)

Las expresiones dadas en (5)-(8) son las unidades operativas que llamaremos matrices Elementales de Fuerzas Nodales, con cuyo pertinente ensamblaje se obtendrá una matriz H, matriz de Equilibrio de la Estructura, originándose de esta forma un primer conjunto de ecuaciones lineales simultáneas en las incógnitas de tensiones de todos los nodos de la estructura, que obligará a que se cumpla el equilibrio estático en cada uno sus nudos, siendo el vector de términos independientes de este sistema las acciones que actúan sobre todos ellos, incluidos los que pertenezcan a los aparatos de apoyo.

3.2. Matrices Elementales de Compatibilidad.- Los valores de las deformaciones y de los desplazamientos no pueden ser independientes entre sí, por lo que necesariamente ha de existir un conjunto de ecuaciones que los relacionen. En este trabajo se adoptan las mismas relaciones que habitualmente se han tomado desde la aparición del MEF, las cuales son consecuencia de la adopción de unas determinadas funciones de interpolación con las que se obtienen otras funciones (funciones de forma) de las que se deriva finalmente la conocida expresión

$\mathbf {{\mbox{ε}}_{\mbox{(x,y)}}^{\mbox{e}}} =\mathbf {{\mbox{B}}_{\mbox{(x,y)}}^{\mbox{e}}} {\mbox{ }}\mathbf {{\mbox{d}}_{\mbox{(x,y)}}^{\mbox{e}}}$

(9)

donde $\mathbf {{\mbox{ε}}_{\mbox{(x,y)}}^{\mbox{e}}}$ y $\mathbf {{\mbox{d}}_{\mbox{(x,y)}}^{\mbox{e}}}$ son, respectivamente, los vectores columna de deformación y de desplazamiento de un punto genérico (x,y) del elemento, mientras que la matriz que los relaciona, Matriz de Compatibilidad para el elemento rectangular que nos ocupa, viene dada por la conocida expresión

$\mathbf {{\mbox{B}}_{\mbox{(x,y)}}^{\mbox{e}}} ={\frac {1}{4a{\mbox{ }}b}}\left[{\begin{array}{ccc|ccc|cc}y-b&0&b-y&0&b+y&0&-b-y&0\\0&x-a&0&-a-x&0&a+x&0&a-x\\x-a&y-b&-a-x&b-y&a+x&b+y&a-x&-b-y\end{array}}\right]$

(10)

siendo el origen de coordenadas el centro de gravedad del elemento. Particularizando la expresión (10) para cada uno de los cuatro nodos del elemento, la (9) desarrollada tendrá la forma

$\left[{\begin{array}{c}{\mbox{ε}}_{x}^{i}\\{\mbox{ε}}_{y}^{i}\\{\gamma }^{i}\\{\mbox{ε}}_{x}^{j}\\{\mbox{ε}}_{y}^{j}\\{\gamma }^{j}\\{\mbox{ε}}_{x}^{k}\\{\mbox{ε}}_{y}^{k}\\{\gamma }^{k}\\{\mbox{ε}}_{x}^{m}\\{\mbox{ε}}_{y}^{m}\\{\gamma }^{m}\end{array}}\right]={\frac {1}{2a{\mbox{ }}b}}\left[{\begin{array}{cc|cc|cc|cc}-b&0&b&0&0&0&0&0\\0&-a&0&0&{\mbox{ }}{\mbox{ }}0{\mbox{ }}{\mbox{ }}&{\mbox{ }}{\mbox{ }}0{\mbox{ }}{\mbox{ }}&0&a\\-a&-b&0&b&0&0&a&0\\\hline -b&0&b&0&0&0&0&0\\0&0&0&-a&0&a&0&0\\0&-b&-a&b&a&0&0&0\\\hline 0&0&0&0&b&0&-b&0\\0&0&0&-a&0&a&0&0\\0&0&-a&0&a&b&0&-b\\\hline 0&0&0&0&b&0&-b&0\\0&-a&0&0&0&0&0&a\\-a&0&0&0&0&b&a&-b\end{array}}\right]\left[{\begin{array}{c}u_{i}\\v_{i}\\\hline u_{j}\\v_{j}\\\hline u_{k}\\v_{k}\\\hline u_{m}\\v_{m}\end{array}}\right]{\mbox{ }}{\mbox{ }}{\mbox{ }}{\mbox{ }}{\mbox{ }}{\acute {o}}{\mbox{ }}{\mbox{ }}{\mbox{ }}{\mbox{ }}{\mbox{ }}\mathbf {{\mbox{ε}}^{\mbox{e}}} {\mbox{=}}\mathbf {{\mbox{B}}^{\mbox{e}}} {\mbox{ }}\mathbf {{\mbox{d}}^{\mbox{e}}}$

(11)

que permite el cálculo de las deformaciones ε^e en los cuatro nodos en función de los desplazamientos d^e de ellos. Particionando la matriz B^e anterior se obtienen las expresiones

$\mathbf {{\mbox{i}}^{\mbox{e}}} ={\frac {1}{2a{\mbox{ }}b}}\left[{\begin{array}{cc}-b&0\\0&-a\\-a&-b\\\hline -b&0\\0&0\\0&-b\\\hline 0&0\\0&0\\0&0\\\hline 0&0\\0&-a\\-a&0\end{array}}\right];{\mbox{ }}{\mbox{ }}{\mbox{ }}\mathbf {{\mbox{j}}^{\mbox{e}}} =$${\frac {1}{2a{\mbox{ }}b}}\left[{\begin{array}{cc}b&0\\0&0\\0&b\\\hline b&0\\0&-a\\-a&b\\\hline 0&0\\0&-a\\-a&0\\\hline 0&0\\0&0\\0&0\end{array}}\right];{\mbox{ }}{\mbox{ }}{\mbox{ }}\mathbf {{\mbox{k}}^{\mbox{e}}} =$${\frac {1}{2a{\mbox{ }}b}}\left[{\begin{array}{cc}{\mbox{ }}{\mbox{ }}0{\mbox{ }}{\mbox{ }}&{\mbox{ }}{\mbox{ }}0{\mbox{ }}{\mbox{ }}\\0&0\\0&0\\\hline 0&0\\0&a\\a&0\\\hline b&0\\0&a\\a&b\\\hline b&0\\0&0\\0&b\end{array}}\right];{\mbox{ }}{\mbox{ }}{\mbox{ }}\mathbf {{\mbox{m}}^{\mbox{e}}} =$${\frac {1}{2a{\mbox{ }}b}}\left[{\begin{array}{cc}0&0\\0&a\\a&0\\\hline 0&0\\0&0\\0&0\\\hline -b&0\\0&0\\0&-b\\\hline -b&0\\0&a\\a&-b\end{array}}\right];$

(12)

que llamaremos matrices Elementales de Compatibilidad asociadas a cada uno de los nodos del elemento. La primera de ellas determina las deformaciones que se producirán en los cuatro nodos como consecuencia de los desplazamientos del nodo i, la segunda las deformaciones originadas en dichos nodos debidas a los desplazamientos del j, etc. De forma semejante a las matrices de Fuerzas Nodales deducidas en el apartado anterior, las dadas en (12) no son más que las unidades operativas con cuyo ensamblaje se obtendrá otra matriz B, matriz de Compatibilidad de la Estructura, originándose un segundo conjunto de ecuaciones lineales simultáneas y homogéneas en las incógnitas de desplazamientos d de los nudos y de las deformaciones ε de los nodos que obligarán al cumplimiento de la compatibilidad entre éstas y aquéllos en todo el sistema estructural.

3.3. Matriz Elemental Constitutiva.- Como es bien sabido, la relación existente entre las tensiones y deformaciones en un nodo genérico viene dada por la ley de Hooke generalizada

$\mathbf {{\mbox{σ}}_{\mbox{n}}} =\mathbf {{\mbox{D}}_{\mbox{n}}} {\mbox{ }}\mathbf {{\mbox{ε}}_{\mbox{n}}}$

(13)

donde $\mathbf {{\mbox{σ}}_{\mbox{n}}}$ y $\mathbf {{\mbox{ε}}_{\mbox{n}}}$ son, respectivamente, los vectores columna de tensión y de deformación en dicho nodo y

$\mathbf {{\mbox{D}}_{\mbox{n}}} =E\left[{\begin{array}{ccc}f_{1}&f_{2}&0\\f_{2}&f_{1}&0\\0&0&f_{3}\end{array}}\right];{\mbox{ }}siendo{\mbox{ }}{\mbox{ }}f_{1}=$${\frac {1}{1-{\nu }^{2}}};{\mbox{ }}{\mbox{ }}f_{2}=\nu {\mbox{ }}f_{1};{\mbox{ }}{\mbox{ }}f_{3}=$${\frac {1}{2(1-\nu )}};$

(14)

en donde E es el Módulo de Elasticidad y ν la relación de Poisson del material. Aunque puede operarse con estas expresiones, la introducción del valor numérico de E en la ecuación (13) suele acarrear algún problema de condicionamiento por ser su orden de magnitud muy superior a los del resto de valores involucrados en el proceso de cálculo, por lo que efectuando el cambio de variable ${\mbox{ε}}{\mbox{'}}_{\mbox{n}}=E{\mbox{ }}{\mbox{ε}}_{\mbox{n}}$ la (13) vendrá dada en la forma

$\mathbf {{\mbox{σ}}_{\mbox{n}}} =\mathbf {{\mbox{K}}_{\mbox{n}}} {\mbox{ }}E{\mbox{ }}\mathbf {{\mbox{ε}}_{\mbox{n}}{\mbox{ }}} {\mbox{ }}{\mbox{ }}es{\mbox{ }}{\mbox{ }}decir{\mbox{ }}{\mbox{ }}{\mbox{ }}\mathbf {{\mbox{σ}}_{\mbox{n}}} =$$\mathbf {{\mbox{K}}_{\mbox{n}}} {\mbox{ }}\mathbf {{\mbox{ε}}_{\mbox{n}}^{'}}$

(15)

siendo

$\mathbf {{\mbox{K}}_{\mbox{n}}} =\left[{\begin{array}{ccc}f_{1}&f_{2}&0\\f_{2}&f_{1}&0\\0&0&f_{3}\end{array}}\right]$

(16)

quedando de esta forma eliminado dicho módulo. De acuerdo con esto, y teniendo en cuenta que el elemento que nos ocupa tiene cuatro nodos, llamaremos matriz Elemental Constitutiva K^e a la matriz diagonal por bloques

$\mathbf {K} ^{\mathbf {e} }=\left[{\begin{array}{cccc}\mathbf {K} _{\mathbf {n} }&\mathbf {0} &\mathbf {0} &\mathbf {0} \\\mathbf {0} &\mathbf {K} _{\mathbf {n} }&\mathbf {0} &\mathbf {0} \\\mathbf {0} &\mathbf {0} &\mathbf {K} _{\mathbf {n} }&\mathbf {0} \\\mathbf {0} &\mathbf {0} &\mathbf {0} &\mathbf {K} _{\mathbf {n} }\end{array}}\right]$

(17)

unidad operativa con cuyo ensamblaje se obtendrá una tercera matriz K, matriz Constitutiva de la Estructura, y, por tanto, un tercer sistema de ecuaciones simultáneas lineales, asimismo homogéneas, en las incógnitas de tensiones σ y deformaciones ε' de todos los nodos de la estructura en estudio. Para introducir en la (11) dicho cambio de variable, bastará con multiplicar m.a.m. esta ecuación por E, con lo que la ecuación de compatibilidad para el elemento quedará en la forma

$\mathbf {{\mbox{ε}}{\mbox{'}}^{\mbox{e}}} {\mbox{=}}\mathbf {{\mbox{B}}^{\mbox{e}}} {\mbox{ }}\mathbf {{\mbox{d}}{\mbox{'}}^{\mbox{e}}}$

(18)

donde $\mathbf {{\mbox{ε}}{\mbox{'}}^{\mbox{e}}} =E{\mbox{ }}\mathbf {{\mbox{ε}}^{\mbox{e}}}$ y $\mathbf {{\mbox{d}}{\mbox{'}}^{\mbox{e}}} =E{\mbox{ }}\mathbf {{\mbox{d}}^{\mbox{e}}} .$

3.4. Matrices Elementales de Restricciones Cinemáticas.- Con los tres grupos de ecuaciones indicadas anteriormente se puede formar un sistema de ecuaciones simultáneas y lineales para toda la estructura en las incógnitas de desplazamientos ${\mbox{d'}},$ tensiones σ y deformaciones ${\mbox{ε'}},$ cuya matriz de coeficientes será cuadrada, pero singular, puesto que aún no se han introducido las condiciones de sustentación que eviten el movimiento de la estructura como sólido rígido. Estas condiciones-ecuaciones cinemáticas, que por brevedad supondremos puntuales y homogéneas, aunque pueden ser de cualquier otro tipo, tendrán aquí un tratamiento basado en los Multiplicadores de Lagrange, con lo cual no sólo se evitará la reordenación y eliminación de filas y columnas para proceder a la resolución del sistema resultante, sino que de esta forma se obtendrá directamente el valor de las reacciones en los aparatos de apoyo, pues como se sabe, dichos multiplicadores no son más que éstas con el signo contrario. Aunque las unidades matriciales operativas necesarias para la determinación de tales ecuaciones de restricción pueden ser de varios tipos (piénsese, p.e., en condiciones cinemáticas no concordantes, condiciones multipunto, etc.) en este trabajo nos ceñiremos exclusivamente a las más habituales de desplazamientos nulos en los aparatos de apoyo. Dichas condiciones vendrán dadas en formato matricial por la expresión general (para un nudo genérico n)

$\mathbf {{\mbox{R}}_{\mbox{n}}} {\mbox{ }}\mathbf {{\mbox{d}}_{\mbox{n}}^{'}} ={\mbox{0}}$

(19)

siendo $\mathbf {{\mbox{d}}_{\mbox{n}}^{'}}$ el vector de desplazamientos (multiplicados por E) del nudo restringido n y R_n una de las tres unidades matriciales operativas siguientes, según el tipo de aparato de apoyo en contacto con él

$\mathbf {{\mbox{R}}_{\mbox{n}}} =\left[{\begin{array}{cc}1&0\\0&1\end{array}}\right];{\mbox{ }}\mathbf {{\mbox{R}}_{\mbox{n}}} =\left[{\begin{array}{cc}0&1\end{array}}\right];{\mbox{ }}\mathbf {{\mbox{R}}_{\mbox{n}}} =\left[{\begin{array}{cc}1&0\end{array}}\right]$

(20)

donde el subíndice designará el nudo restringido, correspondiendo la primera de ellas a un apoyo fijo (nulidad de desplazamiento horizontal u_n y vertical v_n), la segunda a un apoyo móvil con plano de rodamiento horizontal (nulidad de desplazamiento vertical v_n) y la tercera a un apoyo móvil con rodamiento vertical (desplazamiento horizontal u_n nulo). El ensamblaje de las matrices Elementales de Restricción Cinemática dadas en (20) proporcionará una matriz R, Matriz de Restricciones Cinemáticas, que genera un primer grupo de restricciones en las incógnitas ${\mbox{d}}_{\mbox{n}}^{'}$ que, junto con las tres anteriores, forman el sistema matricial

$\left[{\begin{array}{ccc|c}\mathbf {0} &\mathbf {H} &\mathbf {0} &\mathbf {R} ^{\mathbf {T} }\\\mathbf {B} &\mathbf {0} &\mathbf {-I} &\mathbf {0} \\\mathbf {0} &\mathbf {-I} &\mathbf {K} &\mathbf {0} \\\hline \mathbf {R} &\mathbf {0} &\mathbf {0} &\mathbf {0} \end{array}}\right]\left[{\begin{array}{c}\mathbf {d'} \\\mathbf {\mbox{σ}} \\\mathbf {\mbox{ε'}} \\\hline {\mbox{ }}{\mbox{ }}{\mathbf {\mbox{λ}} }_{\mathbf {R} }\end{array}}\right]=\left[{\begin{array}{c}\mathbf {v} _{\mathbf {H} }\\\mathbf {0} \\\mathbf {0} \\\hline \mathbf {0} \end{array}}\right]$

(21)

que ahora ya es compatible y determinado, siendo respectivamente $\mathbf {\mbox{d'}}$ , σ, $\mathbf {\mbox{ε'}}$ y λ_R los vectores columna de desplazamientos de nudos (multiplicados por E), tensiones en los nodos, deformaciones en éstos (multiplicadas por E) y Multiplicadores de Lagrange asociados a las restricciones de los apoyos, mientras que v_H es el vector asociado a la matriz H, esto es, el vector de acciones que actúan en todos los nudos de la estructura, incluidos los apoyos. Como puede observarse la matriz de coeficientes no puede ser simétrica -como así ocurre en el Método de la Rigidez para estructuras de barras- debido al incumplimiento de la relación de Contragradiencia; incumplimiento que es consecuencia, por una parte, del carácter aproximado de las funciones de interpolación con las que se ha generado la matriz de Compatibilidad B y, por otra, a la naturaleza también aproximada de la matriz de Equilibrio H, la cual se ha obtenido a partir de la ya comentada hipótesis de variación lineal de las tensiones a lo largo de los lados de los rectángulos elementales que modelizan la estructura.

3.5. Matrices Elementales de Restricciones Estáticas internas.- El sistema (21) tiene, pues, solución, mas en general ésta será inadmisible, pues no está asegurado aún que se cumpla el equilibrio estático de cada uno de los elementos que discretizan a la estructura. Pero, como ya se señaló anteriormente, el procedimiento que aquí se presenta permite obligar a que se cumpla tal condición, es decir, a que las fuerzas nodales que actúan en cada elemento estén en estricto equilibrio²; por lo tanto, se ha de introducir para todo elemento aislado e, por una parte la ecuación matricial de equilibrio de Fuerzas Nodales Equivalentes:

$\mathbf {{\mbox{F}}_{\mbox{i}}^{\mbox{e}}} +\mathbf {{\mbox{F}}_{\mbox{j}}^{\mbox{e}}} +$$\mathbf {{\mbox{F}}_{\mbox{k}}^{\mbox{e}}} +\mathbf {{\mbox{F}}_{\mbox{m}}^{\mbox{e}}} =$$(\mathbf {{\mbox{I}}^{\mbox{e}}} +\mathbf {{\mbox{J}}^{\mbox{e}}} +\mathbf {{\mbox{K}}^{\mbox{e}}} +$$\mathbf {{\mbox{M}}^{\mbox{e}}} ){\mathbf {\mbox{σ}} ^{\mbox{e}}}={\mbox{0}}$

(22)

y por otra el equilibrio de momentos de dichas fuerzas. Tomando, pues, momentos respecto al centro del rectángulo se tiene que cumplir la ecuación matricial, de acuerdo con la Fig. 1c)

$\left[{\begin{array}{cc}b&-a\end{array}}\right]\mathbf {{\mbox{F}}_{\mbox{i}}^{\mbox{e}}} +\left[{\begin{array}{cc}b&a\end{array}}\right]\mathbf {{\mbox{F}}_{\mbox{j}}^{\mbox{e}}} +\left[{\begin{array}{cc}-b&a\end{array}}\right]\mathbf {{\mbox{F}}_{\mbox{k}}^{\mbox{e}}} +\left[{\begin{array}{cc}-b&-a\end{array}}\right]\mathbf {{\mbox{F}}_{\mbox{m}}^{\mbox{e}}} ={\mbox{0}}$

(23)

Sustituyendo en (22) y (23) las expresiones dadas en (5)-(8), operando y simplificando se obtienen finalmente las tres ecuaciones homogéneas de equilibrio para cada elemento e aislado

$\left[{\begin{array}{ccc|ccc|ccc|ccc}-b&0&-a&b&0&-a&b&0&a&-b&0&a\\0&-a&-b&0&-a&b&0&a&b&0&a&-b\\-b^{2}&a^{2}&0&b^{2}&-a^{2}&0&-b^{2}&a^{2}&0&b^{2}&-a^{2}&0\end{array}}\right]\mathbf {{\mbox{σ}}^{\mbox{e}}} =\left[{\begin{array}{c}0\\0\\0\end{array}}\right]$

(24)

y signando por T^e a la matriz de coeficientes, ésta vendrá dada por

$\mathbf {{\mbox{T}}^{\mbox{e}}} =\left[{\begin{array}{ccc|ccc|ccc|ccc}-b&0&-a&b&0&-a&b&0&a&-b&0&a\\0&-a&-b&0&-a&b&0&a&b&0&a&-b\\-b^{2}&a^{2}&0&b^{2}&-a^{2}&0&-b^{2}&a^{2}&0&b^{2}&-a^{2}&0\end{array}}\right]$

(25)

que no es más que la unidad matricial operativa que llamaremos matriz Elemental de Restricciones Estáticas internas, con cuyo ensamblaje se obtendrá otra matriz T, matriz de Restricciones Estáticas internas para toda la estructura y, por tanto, un segundo grupo de restricciones en las incógnitas de tensión σ que obligará a que todos y cada uno de los elementos que la conforman estén en equilibrio estático. Añadiendo, pues, esta última matriz al sistema (21) se obtiene

$\left[{\begin{array}{ccc|cc}\mathbf {0} &\mathbf {H} &{\mbox{0}}&{\mbox{ }}{\mbox{ }}\mathbf {R} ^{\mathbf {T} }&\mathbf {0} \\\mathbf {B} &\mathbf {0} &\mathbf {-I} &\mathbf {0} &\mathbf {T} ^{\mathbf {T} }\\\mathbf {0} &\mathbf {-I} &\mathbf {K} &\mathbf {0} &\mathbf {0} \\\hline \mathbf {R} &\mathbf {0} &\mathbf {0} &\mathbf {0} &\mathbf {0} \\\mathbf {0} &\mathbf {T} &\mathbf {0} &\mathbf {0} &\mathbf {0} \end{array}}\right]\left[{\begin{array}{c}\mathbf {d'} \\\mathbf {\mbox{σ}} \\\mathbf {\mbox{ε'}} \\\mathbf {\mbox{λ}} _{\mathbf {R} }\\\mathbf {\mbox{λ}} _{\mathbf {T} }\end{array}}\right]=\left[{\begin{array}{c}\mathbf {v} _{\mathbf {H} }\\\mathbf {0} \\\mathbf {0} \\\mathbf {0} \\\mathbf {0} \end{array}}\right]$

(26)

sistema que es compatible y determinado, aunque no simétrico.

3.6. Matrices Elementales de Restricciones Estáticas externas o perimetrales.- La resolución del sistema (26) devolverá unos valores de las incógnitas que, si bien mejoran considerablemente a los que se obtienen por el MEF tradicional³, no deben darse como definitivos puesto que, de forma similar a las anteriores restricciones, aún falta por introducir un tercer y último grupo de ellas que describan el estado tensional del contorno del dominio, estado que por brevedad aquí supondremos nulo, como suele ser habitual. La restricción estática de tensión normal nula en los lados i-j ( ${\sigma }_{y}^{i}={\sigma }_{y}^{j}=0$ ) y k-m ( ${\sigma }_{y}^{k}={\sigma }_{y}^{m}=0$ ) de un elemento e perteneciente al perímetro vendrá dada, respectivamente, por las ecuaciones homogéneas

$\mathbf {{\mbox{P}}_{\mbox{i-j}}^{\mbox{e}}} {\mbox{ }}\mathbf {{\mbox{σ}}^{\mbox{e}}} =$${\mbox{0}}{\mbox{ }}{\mbox{ }}{\mbox{ }}{\mbox{ }}{\mbox{ }}y{\mbox{ }}{\mbox{ }}{\mbox{ }}{\mbox{ }}{\mbox{ }}\mathbf {{\mbox{P}}_{\mbox{k-m}}^{\mbox{e}}} {\mbox{ }}\mathbf {{\mbox{σ}}^{\mbox{e}}} =$${\mbox{0}}$

(27)

mientras que la condición de tensión normal nula en lo lados i-m ( ${\sigma }_{x}^{i}={\sigma }_{x}^{m}=0$ ) y j-k ( ${\sigma }_{x}^{j}={\sigma }_{x}^{k}=0$ ) será, de forma similar,

$\mathbf {{\mbox{P}}_{\mbox{i-m}}^{\mbox{e}}} {\mbox{ }}\mathbf {{\mbox{σ}}^{\mbox{e}}} =$${\mbox{0}}{\mbox{ }}{\mbox{ }}{\mbox{ }}{\mbox{ }}{\mbox{ }}y{\mbox{ }}{\mbox{ }}{\mbox{ }}{\mbox{ }}{\mbox{ }}\mathbf {{\mbox{P}}_{\mbox{j-k}}^{\mbox{e}}} {\mbox{ }}\mathbf {{\mbox{σ}}^{\mbox{e}}} =$${\mbox{0}}$

(28)

donde cada una de las matrices de (27) y (28) vienen dadas por

${\begin{array}{c}\mathbf {{\mbox{P}}_{\mbox{i-j}}^{\mbox{e}}} {\mbox{ }}{\mbox{ }}={\mbox{ }}{\mbox{ }}\left[{\begin{array}{ccc|ccc|ccc|ccc}0&1&0&0&0&0&0&0&0&0&0&0\\0&0&0&0&1&0&0&0&0&0&0&0\end{array}}\right]{\mbox{ }}{\mbox{ }}{\mbox{ }}{\mbox{ }}{\mbox{ }}\mathbf {{\mbox{P}}_{\mbox{k-m}}^{\mbox{e}}} =\left[{\begin{array}{ccc|ccc|ccc|ccc}0&0&0&0&0&0&0&1&0&0&0&0\\0&0&0&0&0&0&0&0&0&0&1&0\end{array}}\right]\\\mathbf {{\mbox{P}}_{\mbox{i-m}}^{\mbox{e}}} =\left[{\begin{array}{ccc|ccc|ccc|ccc}1&0&0&0&0&0&0&0&0&0&0&0\\0&0&0&0&0&0&0&0&0&1&0&0\end{array}}\right]{\mbox{ }}{\mbox{ }}{\mbox{ }}{\mbox{ }}{\mbox{ }}\mathbf {{\mbox{P}}_{\mbox{j-k}}^{\mbox{e}}} {\mbox{ }}{\mbox{ }}{\mbox{ }}=\left[{\begin{array}{ccc|ccc|ccc|ccc}0&0&0&1&0&0&0&0&0&0&0&0\\0&0&0&0&0&0&1&0&0&0&0&0\end{array}}\right]\end{array}}$

(29)

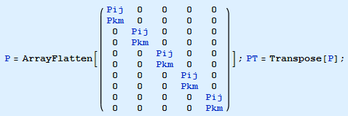
que no son más que las unidades operativas con cuyo ensamblaje se obtendrá una matriz P_, matriz de Restricciones Estáticas perimetrales y, por tanto, un tercer y último grupo de restricciones en las incógnitas de tensión σ que describirá el estado tensional del contorno del dominio en estudio, con lo que el sistema contará ya con la información suficiente para que su resolución pueda devolver unos resultados aceptablemente satisfactorios, sobre todo si la discretización es lo suficientemente tupida.

4. Ensamblaje de las matrices anteriores y del vector de términos independientes.- Como ya se indicó, el método que aquí se propone trata de conseguir mediante una exclusiva manipulación matricial el sistema de ecuaciones de equilibro, compatibilidad y constitutivas, así como unas determinadas condiciones de restricción estática y cinemática, cuya resolución bajo el Método de los Multiplicadores de Lagrange devolverá directamente los valores de todas las incógnitas que describen el comportamiento mecánico del sistema estructural en estudio. Dicho sistema se conseguirá a partir de los correspondientes ensamblajes de las matrices elementales antes deducidas y de los vectores de términos independientes, cada uno de tales ensamblajes se detalla en los siguientes apartados.

4.1. Ensamblaje de la Matriz de Equilibrio (H).- Una vez signados los nodos de cada uno de los elementos por i, j, k y m, de acuerdo con la Fig. 1 y partiendo de un arreglo de tantas filas como nudos n y tantas columnas como elementos e tenga la estructura, el ensamblaje de las matrices elementales dadas en (5)-(8) se podrá abordar por filas o por columnas. En el primer caso se ubicará en la fila f asociada al nudo f las submatrices I^e, J^e, K^e o M^e, correspondientes a los elementos e cuyos vértices incidan en dicho nudo, colocando cada una de ellas en la columna asociada al elemento respectivo. De forma recíproca, se si procede al ensamblaje por columnas, en la columna c, asociada al elemento c, se ubicarán las cuatro submatrices (5)-(8) de dicho elemento en la correspondiente fila (nudo) donde inciden cada uno de los cuatro nodos del mismo.⁴

4.2. Ensamblaje de la Matriz de Compatibilidad (B).- En las estructuras de barras, tanto de nudos rígidos como articulados, es sabido que se cumple la Relación de Contragradiencia, por lo que en estos casos la Matriz de Compatibilidad vendrá dada directamente por H^T, sin necesidad, pues, de proceder a un nuevo ensamblaje para la obtención de B⁵; pero dado el carácter sólo aproximado de las funciones de interpolación que sustentan, como ya se ha dicho, al procedimiento que nos ocupa, no es posible determinar la Matriz de Compatibilidad a partir de la ya calculada matriz H. Será necesario, pues, proceder al pertinente ensamblaje las matrices (12), ensamblaje recíproco del anterior. No obstante, la terminología utilizada en este trabajo (signando con mayúsculas a las matrices elementales de Fuerzas Nodales, expresiones (5)-(8), y con letras minúsculas a las correspondientes matrices de compatibilidad (12)) permite evitar dicho ensamblaje, pues bastará con transponer la matriz de equilibrio H ya ensamblada (antes de que tome sus valores numéricos) y, a continuación, sencillamente cambiar la mayúsculas por las minúsculas para obtener la matriz B.

4.3. Ensamblaje de la Matriz Constitutiva (K).- El ensamblaje de esta matriz es inmediato, pues no es más que un arreglo diagonal por bloques, de dimensiones e×e, donde aquí e es el número de elementos, ubicando la expresión (17) en dicha diagonal.

4.4. Ensamblaje de la Matriz de Restricciones Cinemáticas (R).- Partiendo de un arreglo de tantas filas como aparatos de apoyo tenga la estructura y tantas columnas como nudos totales n tenga ésta, se ubicará en cada una de las filas una de las matrices (20) (según sea el tipo de apoyo con el que se modele la sustentación) y en la columna correspondiente al nudo restringido.

4.5. Ensamblaje de la Matriz de Restricciones Estáticas internas (T).- De la misma forma que la Matriz Constitutiva, esta otra también se obtiene a partir del mismo arreglo diagonal por bloques, en cuya diagonal principal se ha de colocar ahora la matriz elemental dada en (25).

4.6. Ensamblaje de la Matriz de Restricciones Estáticas perimetrales (P).- Partiendo de un arreglo con tantas filas como lados a restringir y tantas columnas como elementos totales tenga la estructura, se ubicarán en cada fila una de las matrices dadas en (29), según sea el lado a restringir, y en la columna correspondiente al elemento al que pertenece dicho lado.

4.7. Ensamblaje del vector de términos independientes (v).- Según todo lo anterior, el vector de términos independientes será un vector cuyas componentes por bloques son todas nulas, excepto el término asociado a las ecuaciones de equilibrio, que contendrá las componentes de acción que actúan en los nudos de la estructura.

5. Sistema Completo.- Ordenando apropiadamente todas las matrices y vectores anteriores, se llega finalmente al Sistema Completo siguiente

${\begin{array}{ccc}{\mbox{ }}&{\begin{array}{ccccccc}{\mbox{ }}&{\underset {\begin{array}{c}\downarrow \\(2n)\end{array}}{\mathbf {d'} }}&{\underset {\begin{array}{c}\downarrow \\(12e)\end{array}}{{\mathbf {\mbox{σ}} }_{}}}&{\underset {\begin{array}{c}\downarrow \\(12e)\end{array}}{\mathbf {\mbox{ε}} \mathbf {'} _{}}}&{\underset {\begin{array}{c}\downarrow \\(?)\end{array}}{{\mathbf {\mbox{λ}} }_{\mathbf {R} }}}&{\underset {\begin{array}{c}\downarrow \\(3e)\end{array}}{{\mathbf {\mbox{λ}} }_{\mathbf {T} }}}&{\underset {\begin{array}{c}\downarrow \\(?)\end{array}}{{\mathbf {\mbox{λ}} }_{\mathbf {P} }}}&{\mbox{ }}\end{array}}&{\mbox{ }}\\{\begin{array}{cc}{\mbox{Ecuaciones de equilibrio (2n)}}&\rightarrow \\{\mbox{ '' de compatibilidad (12e)}}&\rightarrow \\{\mbox{ '' constitutivas (12e)}}&\rightarrow \\{\mbox{Restricciones cinemáticas (?)}}&\rightarrow \\{\mbox{ '' estáticas internas (3e)}}&\rightarrow \\{\mbox{ '' estáticas externas (?)}}&\rightarrow \end{array}}&{\left[{\begin{array}{ccc|ccc}\mathbf {0} &{\mbox{ }}{\mbox{ }}{\mbox{ }}{\mbox{ }}\mathbf {H} &{\mbox{ }}{\mbox{ }}{\mbox{ }}{\mbox{ }}\mathbf {0} &{\mbox{ }}{\mbox{ }}\mathbf {R} ^{\mathbf {T} }&\mathbf {0} &{\mbox{0}}\\\mathbf {B} &{\mbox{ }}{\mbox{ }}{\mbox{ }}{\mbox{ }}\mathbf {0} &{\mbox{ }}{\mbox{ }}{\mbox{ }}{\mbox{ }}\mathbf {-I} &\mathbf {0} &\mathbf {T} ^{\mathbf {T} }&\mathbf {P} ^{\mathbf {T} }\\\mathbf {0} &{\mbox{ }}{\mbox{ }}{\mbox{ }}{\mbox{ }}{\mbox{-I}}&{\mbox{ }}{\mbox{ }}{\mbox{ }}{\mbox{ }}\mathbf {K} &\mathbf {0} &\mathbf {0} &\mathbf {0} \\\hline \mathbf {R} &{\mbox{ }}{\mbox{ }}{\mbox{ }}{\mbox{ }}\mathbf {0} &{\mbox{ }}{\mbox{ }}{\mbox{ }}{\mbox{ }}\mathbf {0} &{\mbox{0}}&{\mbox{0}}&\mathbf {0} \\\mathbf {0} &{\mbox{ }}{\mbox{ }}{\mbox{ }}{\mbox{ }}\mathbf {T} &{\mbox{ }}{\mbox{ }}{\mbox{ }}{\mbox{ }}\mathbf {0} &\mathbf {0} &\mathbf {0} &\mathbf {0} \\\mathbf {0} &{\mbox{ }}{\mbox{ }}{\mbox{ }}{\mbox{ }}\mathbf {P} &{\mbox{ }}{\mbox{ }}{\mbox{ }}{\mbox{ }}\mathbf {0} &\mathbf {0} &\mathbf {0} &\mathbf {0} \end{array}}\right]}&{\left[{\begin{array}{c}\mathbf {d'} \\\mathbf {\mbox{σ}} \\\mathbf {\mbox{ε'}} \\\hline \mathbf {\mbox{λ}} _{\mathbf {R} }\\\mathbf {\mbox{λ}} _{\mathbf {T} }\\\mathbf {\mbox{λ}} _{\mathbf {P} }\end{array}}\right]=\left[{\begin{array}{c}\mathbf {v} _{\mathbf {H} }\\\mathbf {0} \\\mathbf {0} \\\hline \mathbf {0} \\\mathbf {0} \\\mathbf {0} \end{array}}\right]{\acute {o}}{\mbox{ }}\mathbf {M} {\mbox{ }}\mathbf {s=v} }\end{array}}$

(30)

siendo s el vector solución y en donde, para facilitar su lectura, se han colocado a su izquierda la denominación de cada uno de los bloques de ecuaciones con sus respectivas dimensiones y en la parte superior las incógnitas y dimensiones asociadas a cada columna.

6. Sistema Reducido.- Aunque, por compleja que sea la estructura, la capacidad de los actuales (y sobre todo futuros) ordenadores puede ser presumiblemente suficiente para la resolución del Sistema Completo, éste puede reducirse si se desea eliminado las deformaciones, ya que éstas no suelen ser magnitudes fundamentales en el análisis⁶. En efecto, despejando el vector de deformaciones ${\mbox{ε'}}$ del segundo bloque de (30) y sustituyéndolo en el tercero, se obtiene la ecuación matricial

$\mathbf {K} {\mbox{ }}\mathbf {B} {\mbox{ }}\mathbf {d'-I} {\mbox{ }}\mathbf {\mbox{σ+K}} {\mbox{ }}\mathbf {T} ^{\mathbf {T} }{\mathbf {\mbox{λ}} }_{\mathbf {T} }\mathbf {+K} {\mbox{ }}\mathbf {P} ^{\mathbf {T} }{\mathbf {\mbox{λ}} }_{\mathbf {P} }\mathbf {=0}$

(31)

por lo que el Sistema Completo quedará modificado y en la forma siguiente

$\left[{\begin{array}{cc|ccc}\mathbf {0} &{\mbox{ }}{\mbox{ }}{\mbox{ }}{\mbox{ }}\mathbf {H} &{\mbox{ }}{\mbox{ }}\mathbf {R} ^{\mathbf {T} }&\mathbf {0} &{\mbox{0}}\\\mathbf {K} {\mbox{ }}\mathbf {B} &{\mbox{ }}{\mbox{ }}{\mbox{ }}\mathbf {-I} &\mathbf {0} &{\mbox{ }}\mathbf {K} {\mbox{ }}\mathbf {T} ^{\mathbf {T} }&{\mbox{ }}\mathbf {K} {\mbox{ }}\mathbf {P} ^{\mathbf {T} }\\\hline \mathbf {R} &{\mbox{ }}{\mbox{ }}{\mbox{ }}{\mbox{ }}\mathbf {0} &\mathbf {0} &\mathbf {0} &\mathbf {0} \\\mathbf {0} &{\mbox{ }}{\mbox{ }}{\mbox{ }}{\mbox{ }}\mathbf {T} &\mathbf {0} &\mathbf {0} &\mathbf {0} \\\mathbf {0} &{\mbox{ }}{\mbox{ }}{\mbox{ }}{\mbox{ }}\mathbf {P} &\mathbf {0} &\mathbf {0} &\mathbf {0} \end{array}}\right]\left[{\begin{array}{c}\mathbf {d'} \\\mathbf {\mbox{σ}} \\\mathbf {\mbox{λ}} _{\mathbf {R} }\\\mathbf {\mbox{λ}} _{\mathbf {T} }\\\mathbf {\mbox{λ}} _{\mathbf {P} }\end{array}}\right]=\left[{\begin{array}{c}\mathbf {v} _{\mathbf {H} }\\\mathbf {0} \\\mathbf {0} \\\mathbf {0} \\\mathbf {0} \end{array}}\right]$

(32)

que es el Sistema Reducido, habiéndose eliminado, pues, 12e incógnitas y otras tantas ecuaciones, lo cual supone una gran disminución de las dimensiones del sistema, puesto que el número de elementos e generalmente será en la práctica muy elevado.

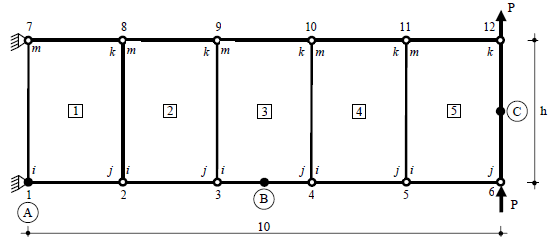
7. Ejemplos prácticos.- La estructura que se muestra en la Fig. 2 es el conocido “Patch test” ⁷ sometido a flexión simple y analizado en las Refs. 2^§6.11, 3^§9.8 y 4^§4.5 con los datos de la Tabla 1 para cada una de ellas:

Fig. 2.- Viga en voladizo Dimensiones, numeración de nudos, de elementos y cargas en el extremo libre

	Tabla 1:Datos para cada Ref.
Autor	h	E	ν	t	P
Ref. 2	2	104	0.3	1	10
Ref. 38	2	1500	0.25	1	150
Ref. 4	1	2×108	0.2	0.1	450

Se pretende calcular la flecha en el punto C y la tensión normal en los puntos A y B utilizando una discretización de sólo 5 elementos rectangulares de 4 nodos. A continuación se expone el desarrollo completo del cálculo con el programa Mathematica 10.0 para los datos de la Ref. 2, evitando por comodidad de escritura subíndices y superíndices en los Input a introducir, habiéndose sombreado éstos para facilitar su lectura.

7.1.- Introducción de datos generales.- De acuerdo con la Fig. 2, la Tabla 1 y la expresión (14):

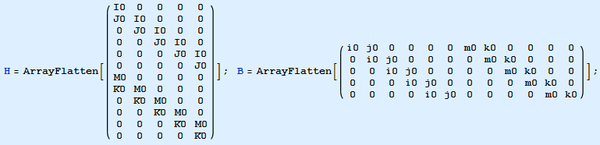
7.2.- Ensamblaje de las matrices de Equilibrio H y de Compatibilidad B⁹.- Puesto que todos los elementos son idénticos, llamando I⁰, J⁰, etc. a las matrices dadas en (5)-(8), del §4.1. y del §4.2.:

y cambiando las mayúsculas por minúsculas en la matriz transpuesta que se obtiene con la anterior orden, el esamblaje de la matriz B viene dado de forma inmediata por:

7.3.- Matrices elementales de Fuerzas Nodales y de Compatibilidad.- De las (5)-(8) y (12):

7.4.- Valores numéricos de las Matrices de Equilibrio H y de Compatibilidad B de la Estructura.- Una vez leídas las anterores matrices, la expresión numérica de las matrices de Equilibrio y Compatibilidad serán:

7.5.- Valor numérico de la Matriz Constitutiva K de la Estructura.- De la (16), (17) y del §4.3:

7.6.- Valor numérico de la Matriz de Restricciones Cinemáticas R.- De la primera de (20) y del §4.4.

7.7.- Valor numérico de la Matriz de Restricciones Estáticas internas T.- De la (25) y del §4.5.:

7.8.- Valor numérico de la Matriz de Restricciones Estáticas perimetrales P.- De (29) y del §4.6., y teniendo en cuenta que los lados a restringir son bordes superior e inferior de la barra, esto es, 10 lados:

7.9.- Vector de términos independientes v.- Llamando v_H, v_B, v_K, v_R, v_T y v_P a los vectores asociados a las respectivas matrices H, B, K, R, T y P e I_d a la matriz identidad, se habrá de escribir, de acuerdo con §4.7.:

7.10.- Ensamblaje del Sistema Completo y cálculo del vector solución s.- Aunque bastaría con tomar el sistema (32), aquí se resolverá el (30), de mayores dimensiones, para que el lector pueda extraer de dicha resolución los valores de todas las incógnitas involucradas en el cálculo de la estructura en estudio, lo que se consigue mediante el Input

y repitiendo el anterior proceso de cálculo para los datos de las demás referencias se obtienen los respectivos vectores solución s, de los que, por motivos de espacio, extraeremos solamente aquéllos valores que se requerían en el enunciado y que se muestran en la Tabla 2, en la que se incluyen, además, los valores teóricamente exactos.

	Tabla 2: Resultados
	Para los datos de la Ref. 2			Para los datos de la Ref. 3			Para los datos de la Ref. 4
	Flecha en C	Tensión σxen A	Tensión σxen B	Flecha en C	Tensión σxen A	Tensión σxen B	Flecha en C	Tensión σxen A	Tensión σxen B
Valores exactos	1.031	300	150	103	4500	2250	0.18	5.40×105	2.70×105
MEF tradicional	0.693	200	111	70.14	2945.45	1636.36	0.067	1.90×105	1.04×105
Método propuesto	1.016	270	150	101.5	4050	2250	0.179	4.86×105	2.70×105

Como puede observarse en dicha Tabla, los resultados dados por el MEF tradicional son altamente inexactos debido, entre otras cosas, a la grosera modelización adoptada, sobre todo para los datos de la Ref. 4 en la que los errores se disparan debido a un valor mayor de la relació a/b¹⁰; de ahí que Babuška y Rheinboldt en 1970, y más recientemente en las referencias 3, 4 y 5, se propongan procedimientos alternativos que, aunque con un mayor número de elementos, consiguen unos resultados que pueden considerarse totalmente aceptables. Concretamente, en la Ref. 4 figuran unos resultados muy similares a los que se obtienen con el procedimiento que en este trabajo se propone, aunque en éste el número de elementos es de 5, mientras que en aquél son necesarios al menos 1192. Por último, se resumen en la Tabla 3 los errores relativos en % para cada uno de los tres ejercicios propuestos.

	Tabla 3: Errores relativos en %
	Ejercicio de la Ref. 2			Ejercicio de la Ref. 3			Ejercicio de la Ref. 4
	Flecha en C	Tensión σxen A	Tensión σxen B	Flecha en C	Tensión σxen A	Tensión σxen B	Flecha en C	Tensión σxen A	Tensión σxen B
MEF tradicional	33	33	26	32	34	27	63	65	61
Método propuesto	1.4	10	0	1.4	10	0	0.56	10	0

Nota.- Si se repitiesen los cálculos anteriores con el método propuesto y una discretización de 10 elementos en vez de 5, los errores se reducirían a la mitad de los que figuran en la última línea de la Tabla 3, excepto el error en la flecha para el ejercicio de la Ref. 4, que sería prácticamente nulo.

1. ¹ Esto no se cumplirá, en general, para las tensiones tangenciales, por lo que se ha de asumir un cierto grado de imprecisión.
2. ² Naturalmente bajo la hipótesis adoptada de variación lineal de las tensiones a lo largo de los lados del elemento.
3. ³ Por motivos de espacio aquí no se muestra este extremo, aunque puede comprobarse resolviendo este sistema para los ejemplos que figuran al final de este trabajo.
4. ⁴ Los ejemplos que más adelante se presentan aclarará mejor dicho ensamblaje.
5. ⁵ O, recíprocamente, ensamblar B y obtener H por transposición de B.
6. ⁶ Lo que en absoluto ha de significar la renuncia a su cálculo, pues éste puede hacerse a posteriori.
7. ⁷ Considerar dos apoyos fijos parece ser lo más coherente para modelizar el empotramiento, aunque algunos autores prefie-ren suponer uno de ellos móvil.
8. ⁸ Aunque estos datos no aparecen de forma explícita en la referencia, los resultados que figuran en ella concuerdan con los valores de la Tabla.
9. ⁹ Compárese la densidad de estos arreglos con elque se obtiene al ensamblar la Matriz de Rigidez tradicional.
10. ¹⁰ Relación que no afecta negativamente a los valores obtenidos por el método propuesto, sino más bien al contrario, como puede observarse comparando los valores de la última fila de las Tablas 2 y 3.

8. Epílogo.- La nota anterior y los valores que se muestran en la Tabla 3 son lo suficientemente explícitos como para inferir que, al menos en los ejemplos analizados, la metodología que en este trabajo se ha expuesto consigue unos resultados más precisos que los que se obtienen por el procedimiento habitual del MEF; faltaría, pues, por comprobar si estas ventajas se mantendrán para estructuras más complejas.

Agradecimientos.- Agradezco la generosa colaboración del delineante J. Antonio Muñoz por los dibujos y la de mi colega J. Lázaro Bailón por la redacción del ABSTRACT en inglés.

Referencias:

[1] Carlos A. Felippa. “Introduction to Finite Element Methods”. Department of Aerospace Engineering Sciences and Center for Aerospace Structures University of Colorado, Boulder, Colorado 80309-0429, USA, (2004).

[2] Robert D. Cook, David S. Malkus, Michael E. Plesha, Robert J. Witt. “Concepts and application of Finite Element Analisis”, 4ª Ed. University of Wisconsin-Madison. JOHN WILEY & SONS, INC. (2002).

[3] O.C. Zienkiewicz, R.L. Taylor, J.Z. Zhu “The Finite Element Method: Its Basis & Fundamentals” 7ª Ed. ELSEVIER (2013).

[4] Eugenio Oñate. “Structural Analysis with the Finite Element Method. Linear Statics” Volume 1. Basis and Solids. CINE (2009).

[5] Juan José Ródenas y otros. “Sobre la necesidad de controlar el error de discretización de elementos finitos en optimización de forma estructural con algoritmos evolutivos”. Revista Internacional de Métodos Numéricos para Cálculo y Diseño en Ingeniería. (2011).