| (35 intermediate revisions by the same user not shown) | |||
| Line 63: | Line 63: | ||
The fly ash mainly has the micro-aggregate effect on the pumpability of the paste backfill slurry. It can significantly improve the workability of the paste backfill slurry and fully allow lubricating ball effect of its spherical particles to improve the fluidity of the newly mixed paste, reduce bleeding, and prevent from segregation [19,20]. | The fly ash mainly has the micro-aggregate effect on the pumpability of the paste backfill slurry. It can significantly improve the workability of the paste backfill slurry and fully allow lubricating ball effect of its spherical particles to improve the fluidity of the newly mixed paste, reduce bleeding, and prevent from segregation [19,20]. | ||
| − | [[#img-4|Figure 4]] demonstrates the strength (28d,8h) and slump for different fly ash-cement ratio (2.0,3.0,4.0,5.0,6.0). As shown in Figure 4, with other conditions unchanged, the higher the fly ash-cement ratio, the greater the slump, the better the fuildity, and the lower the compressive strength is. The reason is that the fine particles of fly ash evenly distributed in the cement particles has the micro-aggregate effect to prevent adhesive aggregation of the cement particles, and release some of the residual mixing water between the cement particles, thus improving the slump and fluidity of the paste slurry. | + | [[#img-4|Figure 4]] demonstrates the strength (28d,8h) and slump for different fly ash-cement ratio (2.0,3.0,4.0,5.0,6.0). As shown in [[#img-4|Figure 4]], with other conditions unchanged, the higher the fly ash-cement ratio, the greater the slump, the better the fuildity, and the lower the compressive strength is. The reason is that the fine particles of fly ash evenly distributed in the cement particles has the micro-aggregate effect to prevent adhesive aggregation of the cement particles, and release some of the residual mixing water between the cement particles, thus improving the slump and fluidity of the paste slurry. |
<div id='img-4'></div> | <div id='img-4'></div> | ||
| Line 144: | Line 144: | ||
{| style="text-align: left; margin:auto;width: 100%" | {| style="text-align: left; margin:auto;width: 100%" | ||
|- | |- | ||
| − | | style="text-align: | + | | style="text-align: center;" | <math>H(t)=-\partial E/\partial w_{ij}(t),H^{{'}}(t)=-\partial E/\partial {w^{{'}}}_{jk}(t)</math> |
|} | |} | ||
| − | |||
|} | |} | ||
| − | |||
{| class="formulaSCP" style="width: 100%; text-align: left;" | {| class="formulaSCP" style="width: 100%; text-align: left;" | ||
|- | |- | ||
| Line 154: | Line 152: | ||
{| style="text-align: left; margin:auto;width: 100%" | {| style="text-align: left; margin:auto;width: 100%" | ||
|- | |- | ||
| − | | style="text-align: | + | | style="text-align: center;" | <math>E=\frac{1}{2}\sum_{p=1}^M\sum_{k=1}^m{\left(o_k^p-z_k^p\right)}^2</math> |
|} | |} | ||
| − | |||
|} | |} | ||
| − | where | + | where <math>o_k^p</math>, <math>z_k^p</math> are the network output and expected value of the sample <math>p</math>, respectively. <math display="inline">M</math> is the number of training sample. |
'''Step 4'''. Modified Threshold value. | '''Step 4'''. Modified Threshold value. | ||
| Line 244: | Line 241: | ||
{| style="text-align: left; margin:auto;width: 100%" | {| style="text-align: left; margin:auto;width: 100%" | ||
|- | |- | ||
| − | | style="text-align: | + | | style="text-align: center;" | <math>\begin{array}{c} |
If\mbox{ }f(w_{1,l+1},w_{2,l+1},...,w_{l,l+1})<f^{{'}}\mbox{ }\\ | If\mbox{ }f(w_{1,l+1},w_{2,l+1},...,w_{l,l+1})<f^{{'}}\mbox{ }\\ | ||
\mbox{ }then\mbox{ }{w^{{'}}}_i=w_{i,l+1},f^{{'}}=f\mbox{ }(w_{1,l+1},w_{2,l+1},...,w_{l,l+1})\\ | \mbox{ }then\mbox{ }{w^{{'}}}_i=w_{i,l+1},f^{{'}}=f\mbox{ }(w_{1,l+1},w_{2,l+1},...,w_{l,l+1})\\ | ||
| Line 252: | Line 249: | ||
\end{array}</math> | \end{array}</math> | ||
|} | |} | ||
| − | |||
|} | |} | ||
| Line 263: | Line 259: | ||
==4. COBPNN modeling and evaluation== | ==4. COBPNN modeling and evaluation== | ||
| − | ===4.1 Modeling | + | ===4.1 Modeling principle=== |
The COBPNN model combines the advantages and disadvantages of the CO and BPNN, and make the best of their strong points to improve the prediction quality of the model. The process is shown in [[#img-5|Figure 5]]. | The COBPNN model combines the advantages and disadvantages of the CO and BPNN, and make the best of their strong points to improve the prediction quality of the model. The process is shown in [[#img-5|Figure 5]]. | ||
| Line 279: | Line 275: | ||
A massive volume of measured data and theoretical studies have shown that the factors affecting the mass of paste slurry in backfilling mining with the paste of coal mine include the slurry mass concentration, solid-cement ratio and fly ash-cement ratio. Taking into account both the integrity of relevant factors and adequacy of the data samples, the above three main factors are chosen as the input parameters of the model. Among them, the paste slump refers to the paste workability, i.e. the capability of ensuring normal backfilling, including water retention, fluidity and cohesiveness of the paste. The slump, initial strength (8h) and later strength (28d) are used as outputs of the model. | A massive volume of measured data and theoretical studies have shown that the factors affecting the mass of paste slurry in backfilling mining with the paste of coal mine include the slurry mass concentration, solid-cement ratio and fly ash-cement ratio. Taking into account both the integrity of relevant factors and adequacy of the data samples, the above three main factors are chosen as the input parameters of the model. Among them, the paste slump refers to the paste workability, i.e. the capability of ensuring normal backfilling, including water retention, fluidity and cohesiveness of the paste. The slump, initial strength (8h) and later strength (28d) are used as outputs of the model. | ||
| − | In the modeling research, based on previous experiences in proportioning, the mass ratios of fly ash to binder and coal gangue to binder take 2~9 and 4~10 respectively, and the mass concentration is 73%~83%. 30 sets of measured data obtained in the orthogonal test are taken as the samples, of which the first 26 sets are used for model learning, and the other 4 for prediction. See Table 1 for details. | + | In the modeling research, based on previous experiences in proportioning, the mass ratios of fly ash to binder and coal gangue to binder take 2~9 and 4~10 respectively, and the mass concentration is 73%~83%. 30 sets of measured data obtained in the orthogonal test are taken as the samples, of which the first 26 sets are used for model learning, and the other 4 for prediction. See [[#table-1|Table 1]] for details. |
<div class="center" style="font-size: 75%;">'''Table 1'''. Training and inspection samples</div> | <div class="center" style="font-size: 75%;">'''Table 1'''. Training and inspection samples</div> | ||
| − | + | <div id='table-1'></div> | |
| − | {| class="wikitable" style="margin: 1em auto 0.1em auto;border-collapse: collapse;font-size:85%;width: | + | {| class="wikitable" style="margin: 1em auto 0.1em auto;border-collapse: collapse;font-size:85%;width:65%;" |
| − | |- | + | |- |
| − | ! NO !! Coal gangue: binder (%) !! Fly ash : binder (%) !! Mass concentration (%) !! Slump (cm) !! Initial strength (Mpa) !! Later strength (Mpa) | + | ! NO !! Coal gangue: binder (%) !! Fly ash : binder (%) !! Mass concentration (%) !! Slump (cm) !! Initial strength (Mpa) !! Later strength (Mpa) |
|- | |- | ||
| align="center" | 1 || align="center" |7.0 || align="center" |2.0 || align="center" |78 || align="center" |13.5 || align="center" |0.14 || align="center" |3.61 | | align="center" | 1 || align="center" |7.0 || align="center" |2.0 || align="center" |78 || align="center" |13.5 || align="center" |0.14 || align="center" |3.61 | ||
| Line 348: | Line 344: | ||
|} | |} | ||
| − | ===4.3 Analysis of | + | ===4.3 Analysis of application results === |
| − | The problem of paste slurry quality prediction is actually the fitting problem of mapping. The three-layer neural network is chosen for network structure. The value of the number H of hidden layer neurons can be determined by the trial and error method. In other words, a small number of initial hidden layer elements was given firstly to construct a neural network with a small structure for training. If there are many times of training or the convergence condition is not satisfied within the prescribed training times, the number of hidden layer elements is gradually increased to form a new network for retraining until a suitable number of hidden layer elements is found. Through the trial and error method, the number of hidden layer neurons is determined to be 10. As a result, the network topology adopts the form of <math display="inline">3-10-3</math> . | + | The problem of paste slurry quality prediction is actually the fitting problem of mapping. The three-layer neural network is chosen for network structure. The value of the number H of hidden layer neurons can be determined by the trial and error method. In other words, a small number of initial hidden layer elements was given firstly to construct a neural network with a small structure for training. If there are many times of training or the convergence condition is not satisfied within the prescribed training times, the number of hidden layer elements is gradually increased to form a new network for retraining until a suitable number of hidden layer elements is found. Through the trial and error method, the number of hidden layer neurons is determined to be 10. As a result, the network topology adopts the form of <math display="inline">3-10-3</math>. |
| − | + | The Matlab programming is adopted to COBPNN model, and the COBPNN hybrid model is compared with the traditional BPNN model, leading to the results as shown in [[#table-2|Table 2]]. In the design of COBPNN, the activation function of the hidden layer adopts the <math display="inline">S</math> function, the network structure adopts the form <math display="inline">3-10-3</math>, <math display="inline">\epsilon </math> takes <math display="inline">{10}^{-2},{10}^{-3},{10}^{-4}</math> respectively, and the maximum number of iterations is 30000. The time used by cpu during the CO working is expressed by the training time converted into the BPNN algorithm using theCputime function. | |
| − | <div class="center" style=" | + | <div class="center" style="font-size: 75%;">'''Table 2'''. Model precision and interation</div> |
| − | + | <div id='table-2'></div> | |
| − | + | {| class="wikitable" style="margin: 1em auto 0.1em auto;border-collapse: collapse;font-size:85%;width:auto;" | |
| − | {| class="wikitable" style="margin: 1em auto 1em auto;" | + | |
! <math display="inline">\epsilon </math> !! BPNN model !! COBPNN model | ! <math display="inline">\epsilon </math> !! BPNN model !! COBPNN model | ||
|- | |- | ||
| Line 367: | Line 362: | ||
|} | |} | ||
| − | |||
| − | < | + | It can be seen from [[#table-2|Table 2]] that the model proposed herein can converge at a faster rate and have a stronger fitting with the same accuracy. The BP algorithm is prone to a local minimum, and therefore it is impossible to obtain a solution with higher accuracy. For higher network accuracy, the proposed model can obtain appropriate solution, and the convergence speed is significantly faster since the introduction of chaotic mechanism turns the neural network learning process into a chaotic dynamics system and makes numerous ordinary local extremums unstable. In this way, the system can escape from the local minimum in learning process, and finally reach or approximate to global minimum. The randomness, ergodicity and regularity of chaotic motion are adopted to find the optimal value, so as to achieve the global optimum by the neural network learning. |
| − | + | ||
| + | Refer to [[#table-3|Table 3]] for the prediction error of two models with the algorithm accuracy of <math display="inline">\epsilon ={10}^{-3}</math>. According to [[#table-3|Table 3]], when adopting the traditional BP model, the slump error is 11.4%~16.11%, the initial intensity error is 15.02%~21.60%, and the later intensity error is 9.48%~15.49%. When using the COBPNN model, the slump error is 2.39%~7.72%, the initial strength error is 4.39%~8.57%, and the later strength error is 2.77%~6.95%, with a higher prediction accuracy than the model based on BPNN model. | ||
| − | {| class="wikitable" style="margin: 1em auto 1em auto;" | + | <div class="center" style="font-size: 75%;">'''Table 3'''. Prediction error</div> |
| + | <div id='table-3'></div> | ||
| + | {| class="wikitable" style="margin: 1em auto 0.1em auto;border-collapse: collapse;font-size:85%;width:65%;" | ||
! rowspan="2" |NO | ! rowspan="2" |NO | ||
| − | ! colspan="3" |28d strength(MPa) | + | ! colspan="3" |28d strength (MPa) |
| − | ! colspan="3" |8h strength(MPa) | + | ! colspan="3" |8h strength (MPa) |
| − | ! colspan="3" |Slump(mm) | + | ! colspan="3" |Slump (mm) |
|- | |- | ||
! BPNN model !! COBPNN model !! Test !! BPNN model !! COBPNN model !! Test !! BPNN model !! COBPNN model !! Test | ! BPNN model !! COBPNN model !! Test !! BPNN model !! COBPNN model !! Test !! BPNN model !! COBPNN model !! Test | ||
| Line 387: | Line 384: | ||
|- | |- | ||
| align="center" |30 || align="center" |4.511 || align="center" |4.261 || align="center" |4.050 || align="center" |0.299 || align="center" |0.239 || align="center" |0.250 || align="center" |267 || align="center" |227 || align="center" |222 | | align="center" |30 || align="center" |4.511 || align="center" |4.261 || align="center" |4.050 || align="center" |0.299 || align="center" |0.239 || align="center" |0.250 || align="center" |267 || align="center" |227 || align="center" |222 | ||
| − | |} | + | |} |
==5. Field application== | ==5. Field application== | ||
| Line 395: | Line 392: | ||
The concrete blocks and pumping concrete gob-side entry retaining are the commonly application method. Concrete blocks gob-side entry retaining refers to that the cuboid concrete blocks are fabricated on the ground according to the design, after the natural air drying, they are transported underground through the mine transportation system to achieve gob-side entry retaining. This method is characterized as that, the cost is low, and there is no interference with underground production. However, it requirs high demand for mine transportation system and great labor intensity of workers. Pumping paste for gob-side entry retaining is to pump paste into the filling formwork by using a concrete filling pump. It has the characteristics of continuous integral rigid support; The paste wall made of pumped paste has the characteristics of high resistance and early support, so that the roof can be cut and the pressure can be relieved, the maintenance of the roadway can be benefit, and the maintenance cost can be reduced; High degree of mechanization, fast construction speed and large area of one-time entry retaining; Gangue treatment can be realized, which is conducive to the realization of "green" mining of coal mines. Based on the actual situation of 502 working face, it is decided to adopt pumping paste technology to realize gob-side entry retaining. | The concrete blocks and pumping concrete gob-side entry retaining are the commonly application method. Concrete blocks gob-side entry retaining refers to that the cuboid concrete blocks are fabricated on the ground according to the design, after the natural air drying, they are transported underground through the mine transportation system to achieve gob-side entry retaining. This method is characterized as that, the cost is low, and there is no interference with underground production. However, it requirs high demand for mine transportation system and great labor intensity of workers. Pumping paste for gob-side entry retaining is to pump paste into the filling formwork by using a concrete filling pump. It has the characteristics of continuous integral rigid support; The paste wall made of pumped paste has the characteristics of high resistance and early support, so that the roof can be cut and the pressure can be relieved, the maintenance of the roadway can be benefit, and the maintenance cost can be reduced; High degree of mechanization, fast construction speed and large area of one-time entry retaining; Gangue treatment can be realized, which is conducive to the realization of "green" mining of coal mines. Based on the actual situation of 502 working face, it is decided to adopt pumping paste technology to realize gob-side entry retaining. | ||
| − | According to past experience, three paste proportioning schemes are prepared and then predicted according to the established COBPNN model. The prediction results are shown in Table 4. | + | According to past experience, three paste proportioning schemes are prepared and then predicted according to the established COBPNN model. The prediction results are shown in [[#table-4|Table 4]]. |
| − | <div class="center" style=" | + | <div class="center" style="font-size: 75%;">'''Table 4. '''The paste proportioning schemes</div> |
| − | + | <div id='table-4'></div> | |
| − | {| class="wikitable" style="margin: 1em auto 1em auto;" | + | {| class="wikitable" style="margin: 1em auto 0.1em auto;border-collapse: collapse;font-size:85%;width:65%;" |
|- | |- | ||
! NO !! Coal gangue: binder(%) !! Fly ash : binder(%) !! Mass concentration (%) !! Initial strength (Mpa) !! Later strength (Mpa) !! Slump (mm) | ! NO !! Coal gangue: binder(%) !! Fly ash : binder(%) !! Mass concentration (%) !! Initial strength (Mpa) !! Later strength (Mpa) !! Slump (mm) | ||
| Line 411: | Line 408: | ||
|} | |} | ||
| − | ===5.1 Parameter | + | ===5.1 Parameter design of gob-side entry retaining=== |
| − | + | The "Separated Rock Block Method" of Noel Whittaker in U.K. is adopted to calculate the load of paste support body [22]. The theoretical basis of this method is that the weight of separated rock block in a certain range above gob-side roadway and support body constitutes the support body load. Filling body is set along the high wall of the roadway. The establishment of a mechanical model is shown in [[#img-6|Figure 6]]. | |
| + | <div id='img-6'></div> | ||
| + | {| style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: auto;max-width: auto;" | ||
| + | |- | ||
| + | |style="padding:10px;"| [[File:Draft_Lv_342604230-image77-c.jpeg|alt=|centre|450x450px]] | ||
| + | |- style="text-align: center; font-size: 75%;" | ||
| + | | colspan="1" style="padding-bottom:10px;"| '''Figure 6'''. Mechanical model | ||
| + | |} | ||
| − | |||
| − | Where | + | Where <math>q</math> is the filling body load, <math>\alpha </math> is the coal seam angle, taken 19<sup>0</sup>, <math>w</math> is the width of roadway, taken 3.5m, <math>b</math> is the distance from the filling body to the high wall of roadway, which is 0.5m, <math>l</math> is the width of the filling body, taken 1.5m, <math>h</math> is the mining height of working face, taken 1.7m, <math>x</math> is the hanging top distance on the outside of the filling body, which is 0.5m, <math>\gamma </math> is the weight of the direct roof block, taken 30kN/m<sup>3</sup>, <math>\beta </math> is the shear angle, chosen empirically as 26<sup>0</sup> and <math>R</math> is the height of the roof. |
The load calculation of the filling body is shown in Eq. (9): | The load calculation of the filling body is shown in Eq. (9): | ||
| Line 427: | Line 430: | ||
{| style="text-align: left; margin:auto;width: 100%" | {| style="text-align: left; margin:auto;width: 100%" | ||
|- | |- | ||
| − | | style="text-align: center;" | <math>q=\frac{ | + | | style="text-align: center;" | <math>q=\frac{8h tg\theta +2(w+b+l+x)}{l}\times \frac{h(w+b+l+x)\gamma \times \cos\alpha }{w+b+\frac{1}{2}l}</math> |
|} | |} | ||
| style="width: 5px;text-align: right;white-space: nowrap;" | (9) | | style="width: 5px;text-align: right;white-space: nowrap;" | (9) | ||
|} | |} | ||
| − | According to Eq. (9), where <math>\theta </math> , <math>b</math> | + | According to Eq. (9), where <math>\theta </math>, <math>b</math> and <math>\gamma </math> are fixed values, and the factors that affect the load of the filling body mainly include <math>\alpha </math>, <math>l</math>, <math>w</math>, <math>x</math>, <math>h</math>. [[#img-7|Figure 7]] shows the relationship between the influencing factors and the load of filling body. Since there are almost no coal seams with a dip angle of 90<sup>0</sup> and such coal seams cannot theoretically achieve gob-side entry retaining, the angle range of this analysis is 0-80<sup>0</sup>. |
| − | <div | + | <div id='img-6'></div> |
| + | {| style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: auto;max-width: auto;" | ||
| + | |- | ||
| + | |style="padding:10px;"| [[File:Draft_Lv_951343694-image1.png|centre|750x750px|]] | ||
| + | |- style="text-align: center; font-size: 75%;" | ||
| + | | colspan="1" style="padding-bottom:10px;"| '''Figure 7'''. The relationship between the influencing factors and the load of filling body | ||
| + | |} | ||
| − | It can be seen from | + | It can be seen from [[#img-7|Figure 7]] that, with the increase in coal seam angle, the load of filling body decreased continuously. When <math>\alpha <{20}^0</math>, the load did not change largely, and when <math>\alpha >{20}^0</math>, it decreased obviously, and the gap was increasing. When <math>\alpha ={80}^0</math>, the load of filling body fell to only 138.96KPa, which is because with the continuous increase in coal seam angle, the component force of the separated rock decreased towards the vertical direction of the filling body decreased, causing the reduce in the load of support body. The width of filling body is an important parameter in the design of gob-side entry retaining. Its value not only affects the stability of the filling body and the size of the roof controlling area, but also affects the dynamic strength and economic cost of gob-side entry retaining. When the height is fixed, the filling body with too narrow width has poor stability, is easy to lose stability in load-carrying capability and has a small support area for the roof, resulting in serious stress concentration at the filling area and aggravated stress and sinking of the roof; along with the increase in the width of filling body, the roof controlling area of filling body increased gradually, the roof controlling effect was gradually strengthened, and the load of filling body decreased continuously, but the gap was getting smaller and smaller. However, when <math>l>1.5m</math>, with the increase in the width of roadway, the load of filling body increased continuously, but did not change largely, the maximum increase of the load is only 10.2KPa for every increase of 0.2m, which means that the increase in width leads to the increase in the filling cost but has little impact on the filling effect. When the gob-side entry retaining is adopted, the size of the roadway can be designed according to the actual situation of the coal seam, without considering the filling parameters. With the increase of mining height, the movable space of the roof increased accordingly, and the load of filling body was increased obviously. When <math>h=3.3m</math>, the load reached 1960.37KPa, 3.7 times the value when <math>h=1.3m</math>. With the increase in the hanging top distance on the outside of the filling body, the component force of the separated rock to the filling body gradually increased, and the load of filling body kept increasing, basically showing a linear growth trend. |
The calculated load of the filling body is as follows: | The calculated load of the filling body is as follows: | ||
| − | + | <center> | |
<math>\begin{array}{c} | <math>\begin{array}{c} | ||
| − | q=\frac{8\times 1.7\times | + | q=\displaystyle\frac{8\times 1.7\times tg 26\mbox{°}+2\times (3.5+0.5+1.5+0.5)}{1.5}\times \displaystyle\frac{1.7\times (3.5+0.5+1.5+0.5)\times 30\times \cos{19}^0}{\left(3.5+0.5+\displaystyle\frac{1}{2}\times 1.5\right)}=756.5kPa\end{array}</math> |
| + | </center> | ||
| − | The supporting load of filling body per unit length is <math>N_1=504.3kN</math> | + | The supporting load of filling body per unit length is <math>N_1=504.3kN</math>. |
The bearing capacity of the filling body is shown in Eq. (10): | The bearing capacity of the filling body is shown in Eq. (10): | ||
| Line 458: | Line 468: | ||
|} | |} | ||
| − | + | where <math>N_2</math> is the bearing capacity of the filling body, <math>N</math>, <math>\varphi </math> is the stability coefficient of filling body, taken 1.2, <math>f_c</math> is the axial compressive strength of the filling body, N/mm<sup>2</sup> and <math>A</math> is the cross-sectional area of the filling body, mm<sup>2</sup>. | |
| − | The bearing capacity of the filling body is shown in Table 5. | + | The bearing capacity of the filling body is shown in [[#table-5|Table 5]]. |
| − | <div class="center" style=" | + | <div id='table-5'></div> |
| − | + | <div class="center" style="font-size: 75%;">'''Table 5'''. The bearing capacity of the filling body</div> | |
| − | {| class="wikitable" style="margin: 1em auto 1em auto;" | + | {| class="wikitable" style="margin: 1em auto 0.1em auto;border-collapse: collapse;font-size:85%;width:45%;" |
|- | |- | ||
! NO !! <math>N_2</math> ( kN) !! <math>N_2/N_1</math> | ! NO !! <math>N_2</math> ( kN) !! <math>N_2/N_1</math> | ||
| Line 475: | Line 485: | ||
| align="center" |3 || align="center" |2995.7 ||align="center" |5.94 | | align="center" |3 || align="center" |2995.7 ||align="center" |5.94 | ||
|} | |} | ||
| + | |||
Through the above calculation, it is known that the bearing capacity of the roadside filling body of the three schemes is appropriate. In order to save costs and improve liquidity, option 3 is selected as the final option. | Through the above calculation, it is known that the bearing capacity of the roadside filling body of the three schemes is appropriate. In order to save costs and improve liquidity, option 3 is selected as the final option. | ||
| Line 480: | Line 491: | ||
When the filling body is formed, the gangue falling from the goaf will pile up to the side of the filling body, which forms a certain lateral pressure on the filling body. In order to verify the stability of filling body, the lateral pressure of collapsed gangue should be considered. The lateral pressure is the maximum when the gangue is piled up on one side of filling body. | When the filling body is formed, the gangue falling from the goaf will pile up to the side of the filling body, which forms a certain lateral pressure on the filling body. In order to verify the stability of filling body, the lateral pressure of collapsed gangue should be considered. The lateral pressure is the maximum when the gangue is piled up on one side of filling body. | ||
| − | 1) Lateral pressure calculation of gangue | + | ''1) Lateral pressure calculation of gangue'' |
The calculation of the lateral pressure on the filling body is shown in Eq. (11): | The calculation of the lateral pressure on the filling body is shown in Eq. (11): | ||
| Line 489: | Line 500: | ||
{| style="text-align: left; margin:auto;width: 100%" | {| style="text-align: left; margin:auto;width: 100%" | ||
|- | |- | ||
| − | | style="text-align: center;" | <math>E_a=\frac{1}{2}\gamma H^ | + | | style="text-align: center;" | <math>E_a=\frac{1}{2}\gamma H^2\tan^2\left({45}^0-\frac{\varphi }{2}\right)</math> |
|} | |} | ||
| style="width: 5px;text-align: right;white-space: nowrap;" | (11) | | style="width: 5px;text-align: right;white-space: nowrap;" | (11) | ||
|} | |} | ||
| − | Where | + | Where <math>E_a</math> is the lateral pressure formed by collapsed gangue, <math>H</math> is the height of collapsed gangue, taken as 1.7m, <math>\gamma </math> is the unit weight of collapsed gangue, taken 21kN/m<sup>3</sup> and <math>\varphi </math> is the internal friction angle of collapsed gangues, taken 30°. |
The lateral pressure formed by gangue can be obtained as follows by calculation: | The lateral pressure formed by gangue can be obtained as follows by calculation: | ||
| + | <center> | ||
| + | <math>E_a=\displaystyle\frac{1}{2}\times 21\times {1.7}^2\times {\tan}^2\left({45}^{\circ }-\displaystyle\frac{{30}^{\circ }}{2}\right)=10.11\mbox{kN}/\mbox{m}</math> | ||
| + | </center> | ||
| − | + | ''2) Balance verification'' | |
| − | + | ||
| − | 2) Balance verification | + | |
The balance calculation of filling body is shown in Eq. (12): | The balance calculation of filling body is shown in Eq. (12): | ||
| Line 509: | Line 521: | ||
{| style="text-align: left; margin:auto;width: 100%" | {| style="text-align: left; margin:auto;width: 100%" | ||
|- | |- | ||
| − | | style="text-align: center;" | <math>K_t=\frac{G\times a+ | + | | style="text-align: center;" | <math>K_t=\frac{G\times a + E_a \sin\alpha \times c}{E_a \cos\alpha \times z}</math> |
|} | |} | ||
| style="width: 5px;text-align: right;white-space: nowrap;" | (12) | | style="width: 5px;text-align: right;white-space: nowrap;" | (12) | ||
|} | |} | ||
| − | + | where <math>K_t</math> is the balance safety coefficient, <math>G</math> is the weight per meter of filling body, <math>1.5\times 1.7\times 21=53.55kN/m</math>, <math>a</math> is the distance between the filling body gravity center and the instability point, taken 0.75m, <math>z</math> is the distance between the action point of lateral pressure of clasped gangues and the instability point of filling body, taken 1.59m and <math>c</math> is the distance between the lateral pressure of clasped gangue and the instability point of filling body, taken 1.5m. | |
The balance safety coefficient can be obtained as follows by calculation: | The balance safety coefficient can be obtained as follows by calculation: | ||
| + | <center> | ||
| + | <math>K_t=\displaystyle\frac{53.55\times 0.75+10.11\times \sin{19}^{\circ }\times 1.5}{10.11\times \cos{19}^{\circ }\times 1.59}=2.97</math> | ||
| + | </center> | ||
| + | Due to the minimum factor of balance safety coefficient against overturning is 1.5, and the balance safety coefficient of filling body is 2.97, which is greater than the minimum value of 1.5. Therefore, the filling body is safe. | ||
| − | + | ===5.2 Mining pressure observation and entry retaining effect=== | |
| − | + | ====5.2.1 Observation results of surface convergence of surrounding rock of roadway==== | |
| − | + | The cross point method is used to obtain the displacement data of roadway surface. Six measuring points are arranged in 502 roadway to observe the movement of the roof and floor and the two sides. The No. 1 measuring point is arranged at a distance of 5m from the working face. After that, each measuring point is spaced at a distance of 5m and the data are measured once a day. The moving curves of the roof and floor and two sides are shown in [[#img-8|Figure 8]]. The positive and negative signs of the abscissa refer to the front and rear of working face, respectively. | |
| − | = | + | <div id='img-8'></div> |
| − | + | {| style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: auto;max-width: auto;" | |
| + | |- | ||
| + | |style="padding:10px;"| [[File:Draft_Lv_981833112-image2.png|centre|750x750px|]] | ||
| + | |- style="text-align: center; font-size: 75%;" | ||
| + | | colspan="1" style="padding-bottom:10px;"| '''Figure 8'''. The moving curves of the roof and floor and two sides | ||
| + | |} | ||
| − | |||
In the process of working face advancing, the surface displacement of 502 fully mechanized mining face roadway is not large. The maximum amount of roof and floor moving closer is 123mm, and the maximum amount of two sides moving closer is 103mm. The deformation amount of roadway is mainly generated in the mining influence range whether the roof and floor or the two sides of the roadway, i.e. The surrounding rock of the roadway starts to produce obvious deformation within 15m from the working face, and the deformation speed is obviously accelerated within 10m. This shows that the upper and lower ends of the working face are the key points of support control. | In the process of working face advancing, the surface displacement of 502 fully mechanized mining face roadway is not large. The maximum amount of roof and floor moving closer is 123mm, and the maximum amount of two sides moving closer is 103mm. The deformation amount of roadway is mainly generated in the mining influence range whether the roof and floor or the two sides of the roadway, i.e. The surrounding rock of the roadway starts to produce obvious deformation within 15m from the working face, and the deformation speed is obviously accelerated within 10m. This shows that the upper and lower ends of the working face are the key points of support control. | ||
| − | ====5.2.2 Observation | + | ====5.2.2 Observation results of internal load of filling body==== |
| − | The load of the filling body is measured according to the hydraulic pillow embedded in the filling body. | + | The load of the filling body is measured according to the hydraulic pillow embedded in the filling body. [[#img-9|Figure 9]] is the relationship curve between the load of the filling body and the position of the working face. |
| + | |||
| + | <div id='img-8'></div> | ||
| + | |||
| + | {| style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: auto;max-width: 70%;" | ||
| + | |- | ||
| + | |style="padding:10px;"| [[File:Draft_Lv_342604230-image117-c.png|centre|379x379px|]] | ||
| + | |- style="text-align: center; font-size: 75%;" | ||
| + | | colspan="1" style="padding:10px;"| '''Figure 9'''. The relationship curve between the backfilling load and the position of the working face | ||
| + | |} | ||
| − | |||
| − | As can be seen from the | + | As can be seen from the [[#img-9|Figure 9]], the change of the load in the filling body beside the roadway increases rapidly within 10m behind the working face, but the load is relatively small. Within 20m behind the working face, the filling load increases sharply. Within 25~50m behind the working face, the filling body load reaches the maximum, then the load gradually decreases, but the decreasing range is not large, and then the filling body load basically remains stable. |
====5.2.3 Entry retaining effect==== | ====5.2.3 Entry retaining effect==== | ||
| Line 572: | Line 600: | ||
==References== | ==References== | ||
| − | <span style="text-align: center; font-size: 85%;">[1] Zhang | + | <span style="text-align: center; font-size: 85%;">[1] Zhang Q., Zhang J.X., Huang Y.L., Ju F. Backfilling technology and strata behaviors in fully mechanized coal mining working face. Int. J. Min. Sci. Technol., 22:151–157, 2012.</span> |
| − | <span style="text-align: center; font-size: 85%;">[2] Seryakov | + | <span style="text-align: center; font-size: 85%;">[2] Seryakov V.M. Mathematical modeling of stress-strain state in rock mass during mining with backfill. J. Min. Sci., 50:847–854, 2014.</span> |
| − | <span style="text-align: center; font-size: 85%;">[3] Wu | + | <span style="text-align: center; font-size: 85%;">[3] Wu D., Hou, Y., Deng T., Chen Y., Zhao X. Thermal, hydraulic and mechanical performances of cemented coal gangue-fly ash backfill. Int. J. Miner. Process., 162:12–18, 2017.</span> |
| − | <span style="text-align: center; font-size: 85%;">[4] Zhang | + | <span style="text-align: center; font-size: 85%;">[4] Zhang J.X., Li B.Y., Zhou N., Zhang Q. Application of solid backfilling to reduce hard-roof caving and longwall coal face burst potential. Int. J. Rock Mech. Min., 88:197–205, 2016.</span> |
| − | <span style="text-align: center; font-size: 85%;">[5] Al Heib | + | <span style="text-align: center; font-size: 85%;">[5] Al Heib M.M., Didier C., Masrouri F. Improving short- and long-term stability of underground gypsum mine using partial and total backfill. Rock Mech. Rock Eng., 43:447–461, 2010.</span> |
| − | <span style="text-align: center; font-size: 85%;">[6] Wu | + | <span style="text-align: center; font-size: 85%;">[6] Wu D., Cai S.J., Liu Y.C. Effects of binder on suction in cemented gangue backfill. Mag. Concr. Res., 68: 593–603, 2016.</span> |
| − | <span style="text-align: center; font-size: 85%;">[7] Khaldoun | + | <span style="text-align: center; font-size: 85%;">[7] Khaldoun A., Ouadif L., Baba K., Bahi L. Valorization of mining waste and tailings through paste backfilling solution, Imiter operation, Morocco. Int. J. Min. Sci. Tech., 26:511–516, 2016.</span> |
| − | <span style="text-align: center; font-size: 85%;">[8] Zhang | + | <span style="text-align: center; font-size: 85%;">[8] Zhang J.X., Zhang Q., Sun Q., Gao R., Germain D., Abro S. Surface subsidence control theory and application to backfill coal mining technology. Environ. Earth Sci., 74:1439–1448, 2015. </span> |
| − | <span style="text-align: center; font-size: 85%;">[9] Ercikdi | + | <span style="text-align: center; font-size: 85%;">[9] Ercikdi B., Cihangir F., Kesimal A., Deveci H., Alp İ. Utilization of industrial waste products as pozzolanic material in cemented paste backfill of high sulphide mill tailings. J. Hazard. Mater., 168:848–856, 2009.</span> |
| − | <span style="text-align: center; font-size: 85%;">[10] Benzaazoua | + | <span style="text-align: center; font-size: 85%;">[10] Benzaazoua M., Fall M., Belem T. A contribution to understanding the hardening process of cemented pastefill. Miner. Eng., 17:141–152, 2004.</span> |
| − | <span style="text-align: center; font-size: 85%;">[11] Huang | + | <span style="text-align: center; font-size: 85%;">[11] Huang P., Li B.Y., Xiao M., Chen Z.W., Pei Y.L. The design of critical filling ratio in close distance coal seams by upward backfill mining technology. J. Min. Saf. Eng., 4:597–603, 2016.</span> |
| − | <span style="text-align: center; font-size: 85%;">[12] Deng | + | <span style="text-align: center; font-size: 85%;">[12] Deng D., Liu L., Yao Z., Song K.-I., Lao D. A practice of ultra-fine tailings disposal as filling material in a gold mine. J. Environ. Manag., 196:100–109, 2017.</span> |
| − | <span style="text-align: center; font-size: 85%;">[13] Liu | + | <span style="text-align: center; font-size: 85%;">[13] Liu M., Liu X., Wu M., Li L., Xiu L. Integrating spectral indices with environmental parameters for estimating heavy metal concentrations in rice using a dynamic fuzzy neural-network model. Comput. Geosci., 37:1642–1652, 2011.</span> |
| − | <span style="text-align: center; font-size: 85%;">[14] Wang D. | + | <span style="text-align: center; font-size: 85%;">[14] Wang D. Quantitative investment model based on data mining. Rev. Int. Métodos Numér. Cálc. Diseño Ing., 36, (1), 22, 2020.</span> |
| − | <span style="text-align: center; font-size: 85%;">[15] Heo | + | <span style="text-align: center; font-size: 85%;">[15] Heo S., Lee J.H. Fault detection and classification using artificial neural networks. IFAC-Papers Online, 51:470–475, 2018.</span> |
| − | <span style="text-align: center; font-size: 85%;">[16] Ditto | + | <span style="text-align: center; font-size: 85%;">[16] Ditto W., Munakata T. Principles and applications of chaotic systems. Commun. ACM., 38:96–102, 1995.</span> |
| − | <span style="text-align: center; font-size: 85%;">[17] Yang | + | <span style="text-align: center; font-size: 85%;">[17] Yang D., Liu Z., Zhou J. Chaos optimization algorithms based on chaotic maps with different probability distribution and search speed for global optimization. Commun. Nonlinear Sci. Numer. Simul., 19:1229–1246, 2014.</span> |
| − | <span style="text-align: center; font-size: 85%;">[18] Sun | + | <span style="text-align: center; font-size: 85%;">[18] Sun Q., Zhang J., Zhang Q., Yan H. A case study of mining-induced impacts on the stability of multi-tunnels with the backfill mining method and controlling strategies. Environ. Earth Sci., 77:234, 2018.</span> |
| − | <span style="text-align: center; font-size: 85%;">[19] Bharatkumar | + | <span style="text-align: center; font-size: 85%;">[19] Bharatkumar B.H., Narayanan R., Raghuprasad B.K., Ramachandramurthy D.S. Mix proportioning of high performance concrete. Cem. Concr. Compos., 23:71–80, 2001.</span> |
| − | <span style="text-align: center; font-size: 85%;">[20] Yilmaz | + | <span style="text-align: center; font-size: 85%;">[20] Yilmaz T., Ercikdi B., Karaman K., Kulekci G. Assessment of strength properties of cemented paste backfill by ultrasonic pulse velocity test. Ultrasonics., 54:1386–1394, 2014.</span> |
| − | <span style="text-align: center; font-size: 85%;">[21] Tang | + | <span style="text-align: center; font-size: 85%;">[21] Tang W., Zhang X.Y., Li D.P. Chaotic optimization method for neural network's weights. J. Harbin. Inst. Technol., 6:12-14, 2000.</span> |
| − | <span style="text-align: center; font-size: 85%;">[22] Wang | + | <span style="text-align: center; font-size: 85%;">[22] Wang H.S., Zhang D.S., Li S.G., Wang L., Wu L.Z. Rational width of narrow coal pillar based on the fracture line location of key rock B in main roof. J. Min. Saf. Eng., 31:10-16, 2014.</span> |
Latest revision as of 14:58, 1 March 2021
Abstract
With the increasing importance of environmental protection, more and more attention has been paid to backfilling coal mining. The prediction and design of the proportioning of backfill materials are significantly important for paste backfilling coal mining. In this study, the key factors affecting paste slurry mass optimization are identified, including mass concentration, solid-cement ratio, and fly ash-cement ratio. According to the identified factors, a paste slurry mass prediction numerical model is established to effectively predict the paste slurry mass of backfilling mining, based on a hybrid algorithm of the back propagation neural network (BPNN) with chaos optimization (CO). With the adopted model indicators, the orthogonal test data of backfill materials are used as samples for learning, training and testing. The performance of the COBPNN and traditional BPNN models are assessed using experimental results. Finally, a mechanical model of gob-side entry retaining is development, and the surface convergence of surrounding rock of roadway and the internal load of filling body are detected in the tested working face. The results indicate that the proposed model has improved the performance of the traditional BPNN model, in terms of tardy convergence, low convergence precision, proneness to local minimum, enables high fitting accuracy and strong generalization, and more accurate and reliable prediction for the paste slurry mass, thus providing a more effective approach for optimizing the proportioning of paste slurry for backfilling coal mining.
Keywords: Backfilling coal mining, paste slurry, numerical model, mechanical model, BP neural network
1. Introduction
Paste backfill, as a new backfill technology developed in recent years, features low backfill cost, good fluidity of slurry, high strength of backfill body and environmental friendliness [1,2]. The application of backfilling mining with the paste has innovated the coal mining technology and become an effective way for coal mining operation under buildings, railways and water bodies in China [3,4]. Thus it is of great significance to theoretical study and production of mining subsidence reduction. The system of backfilling mining with the paste consists of three components, including backfill material as the core, backfill process and equipment, and mining strata control theory [5,6]. This paper focuses on how to control the slurry mass of paste backfill material. Accurate prediction on the proportioning of backfill materials is of great significance to improving the backfill body support and surface subsidence control as the control effect of surface subsidence caused by backfilling mining with the paste mainly depends on the mass of paste backfill material [7]. The mass of paste backfill consists of the fluidity of the paste slurry and the strength of the paste backfill body, which are influenced by slurry concentration, dosage and composition of the binder, and dosage of aggregate [8,9]. At present, the methods of paste slurry quality predictions are mainly: empirical analogy method, BPNN method, physical simulation method and elastic mechanics analysis method, etc [10,11,12]. However, the factors affecting the quality of paste slurry are complex, some of which can be described quantitatively, but some of which are random, qualitative and fuzzy, and there may be complex nonlinear relationship between paste and these factors. It is difficult to describe them completely and accurately by mathematical or mechanical methods and only a semi-quantitative regular description or a certain range of values are given in macroscopic view. The method of obtaining paste slurry quality by repeatedly mechanics experiment requires not only takes a long experiment cycle, but also needs to consume a lot of manpower, financial resources, and it is difficult to achieve efficient production of coal mine.
BPNN technology has self-organization, self-learning and strong fault-tolerant performance, and has strong nonlinear mapping and data fitting ability, which provides a new idea for solving nonlinear problems and simulating the control process of unknown systems. This algorithm has the advantages of simplicity and plasticity. Therefore, it has been more and more widely used in mining engineering and other fields, providing a reliable theoretical basis for exploring the prediction method of slurry quality of paste. But it is calculated mainly on the basis of gradient method, which has the disadvantages of slow in convergence speed, low in convergence precision and easy to fall into the local minimum [13,14,15]. However, as a new type of global optimization algorithm, CO algorithm does not have high requirements for optimization problems, and does not need to have continuity and differentiability. As long as the mapping relationship between variables is obtained, it is suitable for the optimization problem which is difficult to express accurately by mathematical expression in the actual industrial production process [16,17]. In recent years, this algorithm has received more and more attention, but its application in the prediction of backfilling mining has been less studied. CO belongs to a non-derivative optimization method, which can overcome the shortcoming of high dependence of gradient information on the derivative optimization method. The CO method was introduced into the BPNN algorithm. First, it was converged the local optimal by using the BPNN algorithm, and then the local minimum point of the weight parameter was escaped by using the ergodicity property of chaos, obtaining meaningful results for obtaining a better global network.
Therefore, based on the comprehensive analysis of the factors affecting the proportioning of backfill materials, the strengths of both algorithms mentioned above are adopted to build a COBPNN numerical model for predicting paste slurry mass, and study the paste slurry mass prediction according to the measured data of the orthogonal test.
2. Analysis of factors affecting the mass of paste slurry
The key factors that affect paste slurry mass include slurry mass concentration, type and dosage of binder, dosage of fly ash and coarse aggregate. The mass control objectives consist of workability of the backfill slurry and early strength and later strength of the filling body [18]. In field practice, the values of certain factors sometimes remain relatively constant, such as aggregates, binder type, etc. Therefore, the study on the proportioning of paste backfill material aims to figure out the relationship between the slurry mass concentration, dosage of coal gangue and dosage of fly ash and binder and the slump of the paste slurry and the strength of the filling body. Among them, the dosages of binder, fly ash and coal gangue can be expressed by their mass ratios, i.e. the dosage of binder is taken as 1, the dosages of fly ash and coal gangue can be expressed by their ratios against the dosage of binder.
The physical properties of backfilling materials are measured following the “Standard for test method of performance on ordinary fresh concrete” (GB/T 50080-2002) and the compressive strength is measured using “Standard for test method of mechanical properties on ordinary fresh concrete” (GB/T 50081-2002). The tested samples are prepared with a physical dimension of 150 mm×150 mm×150 mm. The MTS815 rock mechanics testing system is used for the compression test in this study, as shown in Figure 1. The pressurization system is mainly used for testing the mechanical properties of rock specimens, and the seepage system is mainly used for testing the permeability of the specimens.

|
| Figure 1. MTS rock mechanics testing system |
Then, the paste slurry mass is analyzed by the slurry mass concentration, the solid-cement ratio (the ratio of the coal gangue dosage to binder dosage), the fly ash-cement ratio (the ratio of the fly ash dosage to binder dosage). Following previous studies on the formula of paste materials, the mass concentration ranges from 78 to 82, the solid-cement ratio ranges from 6.0 to 10.0, and the fly ash-cement ratio is from 2.0 to 6.0.
2.1 Mass concentration
As the most important factor affecting the pumpability of the paste backfill slurry, the paste mass concentration has decisive influence on the pumpability and strength of the paste backfill slurry.
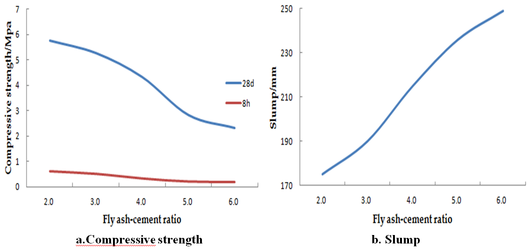
Figure 2 demonstrates the strength (28d,8h) and slump for different paste mass concentration (78%,79%,80%,81%,82%). As shown in Figure 2, with other conditions unchanged, the higher the mass concentration of the paste, the lower its slump, the worse its fluidity, and the higher the compressive strength is. The reason is that the paste viscosity increases with the increase of the mass concentration, while the increased friction resistance among various raw materials reduces the slump. When the paste backfill slurry is subject to full vibration-compacting, the lower the mass concentration, the higher the water consumption is. The excess water forms bubbles or channels in the paste, leaving voids after the paste curing by evaporation, thus lowering the paste strength. Otherwise, the greater the mass concentration, the lower the water consumption, the less the voids and the higher the strength is. The greater strength of the paste provides better support for the surrounding rock. Therefore, the mass concentration of the paste shall be appropriately increased to control the surface subsidence, provided that the paste fluidity is ensured.
| Figure 2. The relationship of the paste mass concentration with slump and strength |
2.2 Solid-cement ratio
Portland cement is a commonly used as the binder for the paste. The effects of the cement on performance characteristics of the paste backfill are mainly reflected by the changes of water-cement ratio due to its micro-aggregate effect and cement content. The solid material used for the paste is the gangue from the coal mine.
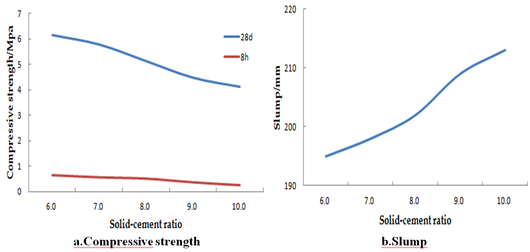
Figure 3 demonstrates the strength (28d,8h) and slump for different solid-cement ratio (6.0,7.0,8.0,9.0,10.0). As shown in Figure 3, with other conditions unchanged, the higher the solid-cement ratio, the greater the slump, the better the fuildity, and the lower the compressive strength is. When the dosage of cement slurry is constant, the cement slurry layer that can be used to bind up the coal gangue aggregate gets thinner and its compressive strength (28d,8h) reduces.
| Figure 3. The relationship of the solid-cement ratio with slump and paste strength |
2.3 Fly ash-cement ratio
The fly ash mainly has the micro-aggregate effect on the pumpability of the paste backfill slurry. It can significantly improve the workability of the paste backfill slurry and fully allow lubricating ball effect of its spherical particles to improve the fluidity of the newly mixed paste, reduce bleeding, and prevent from segregation [19,20].
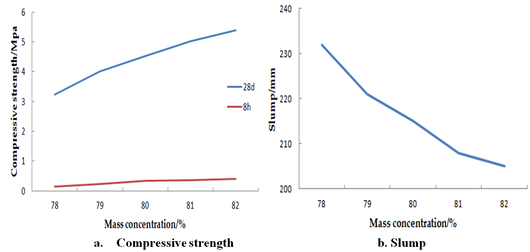
Figure 4 demonstrates the strength (28d,8h) and slump for different fly ash-cement ratio (2.0,3.0,4.0,5.0,6.0). As shown in Figure 4, with other conditions unchanged, the higher the fly ash-cement ratio, the greater the slump, the better the fuildity, and the lower the compressive strength is. The reason is that the fine particles of fly ash evenly distributed in the cement particles has the micro-aggregate effect to prevent adhesive aggregation of the cement particles, and release some of the residual mixing water between the cement particles, thus improving the slump and fluidity of the paste slurry.
| Figure 4. The relationship of the fly ash-cement ratio with slump and paste strength |
3. COBPNN mixed algorithm
3.1 Improved BPNN algorithm
BPNN model, the error back-propagation neural network, is the most widely used neural network model [13]. In terms of structure, it is a typical multilayered network, consisting of three layers, i.e. input layer, hidden layer and output layer, among which the full connection mode is adopted.
The basic principle of BPNN model is to adjust the weights and thresholds using the gradient descent method so as to minimize the mean square error between the actual output value and the expected output value of the network. However, there are some gaps, such as slow convergence of the network and proneness to local optimum. The oscillation often occurs at a higher learning rate. Therefore, an improved BP learning algorithm is adopted to lessen the oscillation trend of the learning process and improve the convergence through introducing the momentum term.
The learning process of BPNN is as follows:
Step 1. Network Initialization.
Step 2. The output of and are as follows:
|
|
(1) |
|
|
(2) |
where is the input of BPNN, is the output of hidden layer, is the number of nodes of input layer, is the threshold value of the hidden layer, is the number of nodes of hidden layer, is the logsig function, , is the output of the output layer, is the connection weights of the hidden and output layer, is the threshold value of the output layer, is the number of nodes of output layer.
Step 3. Modified weight value. Suppose is the learning rate, is the momentum factor
|
|
(3) |
|
|
(4) |
where
|
|
|
|
where , are the network output and expected value of the sample , respectively. is the number of training sample.
Step 4. Modified Threshold value.
|
|
(5) |
Step 5. If meeting the requirements, the iteration ends, otherwise return to Step 2.
3.2 CO algorithm
Chaos is a kind of nonlinear phenomenon that exists widely in nature. It seems random, but it implies delicate internal structure, and has ergodicity, randomness and extreme sensitivity to initial conditions. It can iterate all the states in a certain range according to its own law and optimize searching by using these properties of chaotic motion. The CO method directly uses the chaotic variables to search, and the search process is carried out according to the laws of chaotic motion itself, instead of jumping out of the local optimal solution by accepting the worse solution according to a certain probability as some random optimization methods, so it is more likely to escape from the local minimum point.
Problem Description:
|
|
(6) |
where is the number of elements of the vector and the objective function of the optimization problem.
The most commonly used chaotic mapping in CO algorithm is the Logistic mapping [21]
|
|
(7) |
where , is the parameter, when , the system is in a chaotic state. Taking any initial point, it can get the traversal column of points on . Mapping of Logistic are irreversible mappings on .
In order to improve the efficiency of chaos algorithm, the "multiple carriers" technology is adopted in the search process, and the found approximate optimal solution is used to inspire the search for the global optimal solution. After a period of search, a carrier can quickly find an approximate optimal solution, which is often in the region of the true optimal solution. Then, on the basis of the approximate optimal solution, and the carrier is carried again to reduce the search space, which is equivalent to a fine search in the field of the approximate optimal solution, so that the global optimal solution can be found quickly and the search speed can be greatly improved. This process is repeated, and the optimization ends when the given accuracy of the objective function is reached or the given number of iterations is reached.
The specific steps of CO algorithm are:
Step 1. Initialize, and assign initial values of different smile differences to
Step 2. Assuming that is a chaotic variable, its value range is , the can be carried out to expand its value range to , namely:
|
|
(8) |
where and are the upper and lower limits of the variable value.
According to Eq. (8), the chaotic vector are carried separately to make the mapping as . Take another set of vector , is set to a larger value.
Step 3. The chaotic vectors are iterated by Eq. (7) to obtain vector , and then mapped to according to Eq. (8).
Step 4. Make the following judgment:
|
|
Step 5. If you go through several searches in Step 3 and Step 4 and remain unchanged, skip to the next step.
Step 6. Calculate the new search range, narrow the range to , carry out the secondary carrier according to Eq. (8), assign the on , and carry out the cross-border check after giving the value.
Step 7. Perform the iterative search of steps 3-6 until the value of reaches the allowable network error accuracy or reaches the given number of iterations.
4. COBPNN modeling and evaluation
4.1 Modeling principle
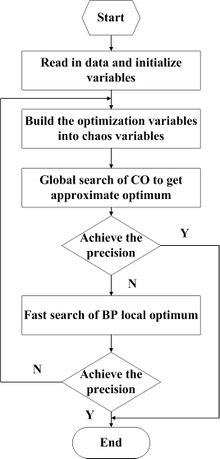
The COBPNN model combines the advantages and disadvantages of the CO and BPNN, and make the best of their strong points to improve the prediction quality of the model. The process is shown in Figure 5.
| Figure 5. Process of the COBPNN Model |
4.2 Selection of model index
A massive volume of measured data and theoretical studies have shown that the factors affecting the mass of paste slurry in backfilling mining with the paste of coal mine include the slurry mass concentration, solid-cement ratio and fly ash-cement ratio. Taking into account both the integrity of relevant factors and adequacy of the data samples, the above three main factors are chosen as the input parameters of the model. Among them, the paste slump refers to the paste workability, i.e. the capability of ensuring normal backfilling, including water retention, fluidity and cohesiveness of the paste. The slump, initial strength (8h) and later strength (28d) are used as outputs of the model.
In the modeling research, based on previous experiences in proportioning, the mass ratios of fly ash to binder and coal gangue to binder take 2~9 and 4~10 respectively, and the mass concentration is 73%~83%. 30 sets of measured data obtained in the orthogonal test are taken as the samples, of which the first 26 sets are used for model learning, and the other 4 for prediction. See Table 1 for details.
| NO | Coal gangue: binder (%) | Fly ash : binder (%) | Mass concentration (%) | Slump (cm) | Initial strength (Mpa) | Later strength (Mpa) |
|---|---|---|---|---|---|---|
| 1 | 7.0 | 2.0 | 78 | 13.5 | 0.14 | 3.61 |
| 2 | 10.0 | 8.0 | 77 | 15.3 | 0.05 | 2.79 |
| 3 | 6.0 | 7.0 | 78 | 23.0 | 0.05 | 2.41 |
| 4 | 6.0 | 2.0 | 76 | 14.1 | 0.20 | 3.85 |
| 5 | 10.0 | 4.0 | 80 | 21.5 | 0.39 | 4.52 |
| 6 | 8.0 | 3.0 | 80 | 20.2 | 0.51 | 5.10 |
| 7 | 4.0 | 3.0 | 79 | 13.6 | 0.13 | 3.72 |
| 8 | 7.0 | 6.0 | 75 | 21.5 | 0.09 | 3.01 |
| 9 | 9.0 | 3.5 | 80 | 22.3 | 0.43 | 4.79 |
| 10 | 4.0 | 2.0 | 73 | 21.3 | 0.13 | 4.87 |
| 11 | 7.0 | 6.0 | 76 | 21.5 | 0.08 | 2.96 |
| 12 | 9.0 | 3.5 | 82 | 20.5 | 0.41 | 5.42 |
| 13 | 8.0 | 3.0 | 73 | 22.0 | 0.07 | 3.56 |
| 14 | 8.0 | 9.0 | 76 | 26.3 | 0.03 | 2.44 |
| 15 | 7.0 | 4.0 | 76 | 20.5 | 0.09 | 2.93 |
| 16 | 9.0 | 6.0 | 79 | 22.9 | 0.05 | 2.06 |
| 17 | 9.0 | 5.0 | 73 | 23.3 | 0.05 | 2.13 |
| 18 | 5.0 | 5.0 | 76 | 18.1 | 0.11 | 3.59 |
| 19 | 8.0 | 3.5 | 81 | 19.9 | 0.39 | 5.02 |
| 20 | 4.0 | 5.0 | 78 | 22.1 | 0.12 | 3.51 |
| 21 | 10.0 | 3.0 | 76 | 19.5 | 0.07 | 3.02 |
| 22 | 8.0 | 8.0 | 74 | 25.5 | 0.02 | 2.32 |
| 23 | 5.0 | 2.0 | 74 | 19.2 | 0.15 | 4.21 |
| 24 | 6.0 | 3.0 | 78 | 20.5 | 0.23 | 3.76 |
| 25 | 5.0 | 2.0 | 83 | 9.0 | 0.85 | 6.32 |
| 26 | 8.0 | 7.0 | 73 | 27.9 | 0.01 | 2.01 |
| 27 | 6.0 | 4.0 | 75 | 23.0 | 0.13 | 2.92 |
| 28 | 8.0 | 4.0 | 78 | 21.2 | 0.18 | 3.43 |
| 29 | 5.0 | 7.0 | 76 | 25.1 | 0.06 | 2.19 |
| 30 | 7.0 | 5.0 | 80 | 22.2 | 0.25 | 4.05 |
4.3 Analysis of application results
The problem of paste slurry quality prediction is actually the fitting problem of mapping. The three-layer neural network is chosen for network structure. The value of the number H of hidden layer neurons can be determined by the trial and error method. In other words, a small number of initial hidden layer elements was given firstly to construct a neural network with a small structure for training. If there are many times of training or the convergence condition is not satisfied within the prescribed training times, the number of hidden layer elements is gradually increased to form a new network for retraining until a suitable number of hidden layer elements is found. Through the trial and error method, the number of hidden layer neurons is determined to be 10. As a result, the network topology adopts the form of .
The Matlab programming is adopted to COBPNN model, and the COBPNN hybrid model is compared with the traditional BPNN model, leading to the results as shown in Table 2. In the design of COBPNN, the activation function of the hidden layer adopts the function, the network structure adopts the form , takes respectively, and the maximum number of iterations is 30000. The time used by cpu during the CO working is expressed by the training time converted into the BPNN algorithm using theCputime function.
| BPNN model | COBPNN model | |
|---|---|---|
| 1367 | 432 | |
| 10623 | 2577 | |
| 16892 |
It can be seen from Table 2 that the model proposed herein can converge at a faster rate and have a stronger fitting with the same accuracy. The BP algorithm is prone to a local minimum, and therefore it is impossible to obtain a solution with higher accuracy. For higher network accuracy, the proposed model can obtain appropriate solution, and the convergence speed is significantly faster since the introduction of chaotic mechanism turns the neural network learning process into a chaotic dynamics system and makes numerous ordinary local extremums unstable. In this way, the system can escape from the local minimum in learning process, and finally reach or approximate to global minimum. The randomness, ergodicity and regularity of chaotic motion are adopted to find the optimal value, so as to achieve the global optimum by the neural network learning.
Refer to Table 3 for the prediction error of two models with the algorithm accuracy of . According to Table 3, when adopting the traditional BP model, the slump error is 11.4%~16.11%, the initial intensity error is 15.02%~21.60%, and the later intensity error is 9.48%~15.49%. When using the COBPNN model, the slump error is 2.39%~7.72%, the initial strength error is 4.39%~8.57%, and the later strength error is 2.77%~6.95%, with a higher prediction accuracy than the model based on BPNN model.
| NO | 28d strength (MPa) | 8h strength (MPa) | Slump (mm) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| BPNN model | COBPNN model | Test | BPNN model | COBPNN model | Test | BPNN model | COBPNN model | Test | |
| 27 | 3.393 | 3.123 | 2.920 | 0.155 | 0.141 | 0.130 | 256 | 238 | 230 |
| 28 | 3.005 | 3.525 | 3.430 | 0.153 | 0.197 | 0.180 | 182 | 229 | 212 |
| 29 | 2.476 | 2.102 | 2.190 | 0.073 | 0.065 | 0.060 | 218 | 239 | 251 |
| 30 | 4.511 | 4.261 | 4.050 | 0.299 | 0.239 | 0.250 | 267 | 227 | 222 |
5. Field application
No. 5 coal seam is being mined in the test mine, which is simple in structure and does not contain gangue. The coal thickness is 1.5~1.9m with an average thickness of 1.7m, and the coal seam inclination angle is 17~210 with an average of 190. The roadway adopts special-shaped section, the height of low wall is 2.0m, the height of high wall is 4.5m, and the width is 3.5m. It is a low-gas mine. The mine has the current situation of less single-sided recoverable reserves and low degree of mechanization. In order to meet the requirements of mine production capacity, multiple coal mining faces and multiple tunneling faces are often used to ensure the production status quo with quantity. Mining replacement tension often occurs, and mining workers and technicians are lost from time to time due to difficult conditions. Therefore, it is very necessary to solve the continuation tension status quo from the technical level. Therefore, after comprehensive comparison, it is decided to implement gob-side entry retaining in 502 working face roadway.
The concrete blocks and pumping concrete gob-side entry retaining are the commonly application method. Concrete blocks gob-side entry retaining refers to that the cuboid concrete blocks are fabricated on the ground according to the design, after the natural air drying, they are transported underground through the mine transportation system to achieve gob-side entry retaining. This method is characterized as that, the cost is low, and there is no interference with underground production. However, it requirs high demand for mine transportation system and great labor intensity of workers. Pumping paste for gob-side entry retaining is to pump paste into the filling formwork by using a concrete filling pump. It has the characteristics of continuous integral rigid support; The paste wall made of pumped paste has the characteristics of high resistance and early support, so that the roof can be cut and the pressure can be relieved, the maintenance of the roadway can be benefit, and the maintenance cost can be reduced; High degree of mechanization, fast construction speed and large area of one-time entry retaining; Gangue treatment can be realized, which is conducive to the realization of "green" mining of coal mines. Based on the actual situation of 502 working face, it is decided to adopt pumping paste technology to realize gob-side entry retaining.
According to past experience, three paste proportioning schemes are prepared and then predicted according to the established COBPNN model. The prediction results are shown in Table 4.
| NO | Coal gangue: binder(%) | Fly ash : binder(%) | Mass concentration (%) | Initial strength (Mpa) | Later strength (Mpa) | Slump (mm) |
|---|---|---|---|---|---|---|
| 1 | 4.0 | 5.0 | 81 | 0.18 | 3.65 | 202 |
| 2 | 7.0 | 3.0 | 82 | 0.33 | 4.56 | 185 |
| 3 | 8.0 | 5.0 | 79 | 0.11 | 2.76 | 221 |
5.1 Parameter design of gob-side entry retaining
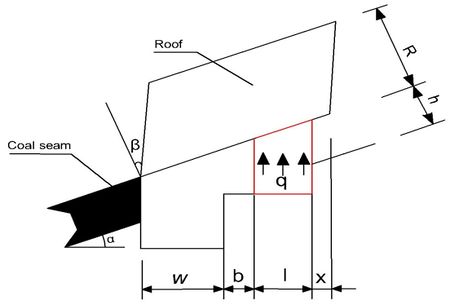
The "Separated Rock Block Method" of Noel Whittaker in U.K. is adopted to calculate the load of paste support body [22]. The theoretical basis of this method is that the weight of separated rock block in a certain range above gob-side roadway and support body constitutes the support body load. Filling body is set along the high wall of the roadway. The establishment of a mechanical model is shown in Figure 6.
| Figure 6. Mechanical model |
Where is the filling body load, is the coal seam angle, taken 190, is the width of roadway, taken 3.5m, is the distance from the filling body to the high wall of roadway, which is 0.5m, is the width of the filling body, taken 1.5m, is the mining height of working face, taken 1.7m, is the hanging top distance on the outside of the filling body, which is 0.5m, is the weight of the direct roof block, taken 30kN/m3, is the shear angle, chosen empirically as 260 and is the height of the roof.
The load calculation of the filling body is shown in Eq. (9):
|
|
(9) |
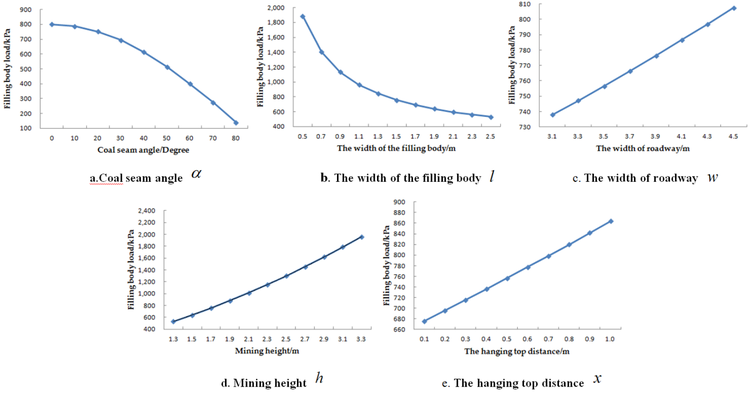
According to Eq. (9), where , and are fixed values, and the factors that affect the load of the filling body mainly include , , , , . Figure 7 shows the relationship between the influencing factors and the load of filling body. Since there are almost no coal seams with a dip angle of 900 and such coal seams cannot theoretically achieve gob-side entry retaining, the angle range of this analysis is 0-800.
| Figure 7. The relationship between the influencing factors and the load of filling body |
It can be seen from Figure 7 that, with the increase in coal seam angle, the load of filling body decreased continuously. When , the load did not change largely, and when , it decreased obviously, and the gap was increasing. When , the load of filling body fell to only 138.96KPa, which is because with the continuous increase in coal seam angle, the component force of the separated rock decreased towards the vertical direction of the filling body decreased, causing the reduce in the load of support body. The width of filling body is an important parameter in the design of gob-side entry retaining. Its value not only affects the stability of the filling body and the size of the roof controlling area, but also affects the dynamic strength and economic cost of gob-side entry retaining. When the height is fixed, the filling body with too narrow width has poor stability, is easy to lose stability in load-carrying capability and has a small support area for the roof, resulting in serious stress concentration at the filling area and aggravated stress and sinking of the roof; along with the increase in the width of filling body, the roof controlling area of filling body increased gradually, the roof controlling effect was gradually strengthened, and the load of filling body decreased continuously, but the gap was getting smaller and smaller. However, when , with the increase in the width of roadway, the load of filling body increased continuously, but did not change largely, the maximum increase of the load is only 10.2KPa for every increase of 0.2m, which means that the increase in width leads to the increase in the filling cost but has little impact on the filling effect. When the gob-side entry retaining is adopted, the size of the roadway can be designed according to the actual situation of the coal seam, without considering the filling parameters. With the increase of mining height, the movable space of the roof increased accordingly, and the load of filling body was increased obviously. When , the load reached 1960.37KPa, 3.7 times the value when . With the increase in the hanging top distance on the outside of the filling body, the component force of the separated rock to the filling body gradually increased, and the load of filling body kept increasing, basically showing a linear growth trend.
The calculated load of the filling body is as follows:
The supporting load of filling body per unit length is .
The bearing capacity of the filling body is shown in Eq. (10):
|
|
(10) |
where is the bearing capacity of the filling body, , is the stability coefficient of filling body, taken 1.2, is the axial compressive strength of the filling body, N/mm2 and is the cross-sectional area of the filling body, mm2.
The bearing capacity of the filling body is shown in Table 5.
| NO | ( kN) | |
|---|---|---|
| 1 | 3961.7 | 7.86 |
| 2 | 4949.4 | 9.81 |
| 3 | 2995.7 | 5.94 |
Through the above calculation, it is known that the bearing capacity of the roadside filling body of the three schemes is appropriate. In order to save costs and improve liquidity, option 3 is selected as the final option.
When the filling body is formed, the gangue falling from the goaf will pile up to the side of the filling body, which forms a certain lateral pressure on the filling body. In order to verify the stability of filling body, the lateral pressure of collapsed gangue should be considered. The lateral pressure is the maximum when the gangue is piled up on one side of filling body.
1) Lateral pressure calculation of gangue
The calculation of the lateral pressure on the filling body is shown in Eq. (11):
|
|
(11) |
Where is the lateral pressure formed by collapsed gangue, is the height of collapsed gangue, taken as 1.7m, is the unit weight of collapsed gangue, taken 21kN/m3 and is the internal friction angle of collapsed gangues, taken 30°.
The lateral pressure formed by gangue can be obtained as follows by calculation:
2) Balance verification
The balance calculation of filling body is shown in Eq. (12):
|
|
(12) |
where is the balance safety coefficient, is the weight per meter of filling body, , is the distance between the filling body gravity center and the instability point, taken 0.75m, is the distance between the action point of lateral pressure of clasped gangues and the instability point of filling body, taken 1.59m and is the distance between the lateral pressure of clasped gangue and the instability point of filling body, taken 1.5m.
The balance safety coefficient can be obtained as follows by calculation:
Due to the minimum factor of balance safety coefficient against overturning is 1.5, and the balance safety coefficient of filling body is 2.97, which is greater than the minimum value of 1.5. Therefore, the filling body is safe.
5.2 Mining pressure observation and entry retaining effect
5.2.1 Observation results of surface convergence of surrounding rock of roadway
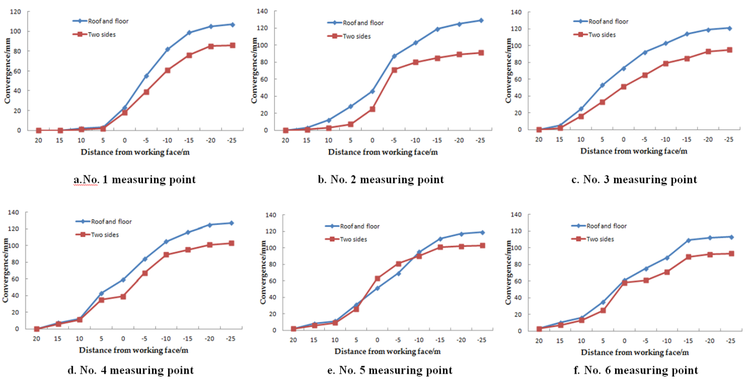
The cross point method is used to obtain the displacement data of roadway surface. Six measuring points are arranged in 502 roadway to observe the movement of the roof and floor and the two sides. The No. 1 measuring point is arranged at a distance of 5m from the working face. After that, each measuring point is spaced at a distance of 5m and the data are measured once a day. The moving curves of the roof and floor and two sides are shown in Figure 8. The positive and negative signs of the abscissa refer to the front and rear of working face, respectively.
| Figure 8. The moving curves of the roof and floor and two sides |
In the process of working face advancing, the surface displacement of 502 fully mechanized mining face roadway is not large. The maximum amount of roof and floor moving closer is 123mm, and the maximum amount of two sides moving closer is 103mm. The deformation amount of roadway is mainly generated in the mining influence range whether the roof and floor or the two sides of the roadway, i.e. The surrounding rock of the roadway starts to produce obvious deformation within 15m from the working face, and the deformation speed is obviously accelerated within 10m. This shows that the upper and lower ends of the working face are the key points of support control.
5.2.2 Observation results of internal load of filling body
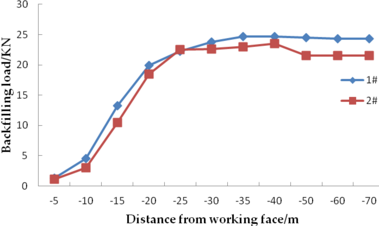
The load of the filling body is measured according to the hydraulic pillow embedded in the filling body. Figure 9 is the relationship curve between the load of the filling body and the position of the working face.
| Figure 9. The relationship curve between the backfilling load and the position of the working face |
As can be seen from the Figure 9, the change of the load in the filling body beside the roadway increases rapidly within 10m behind the working face, but the load is relatively small. Within 20m behind the working face, the filling load increases sharply. Within 25~50m behind the working face, the filling body load reaches the maximum, then the load gradually decreases, but the decreasing range is not large, and then the filling body load basically remains stable.
5.2.3 Entry retaining effect
The gob-side entry retaining construction of 502 fully mechanized mining face in this mine has been successfully completed with a successful entry retaining of 550m. Through observation, when the roof sinks, the filling body can provide timely support resistance to support the roof and slow down the deformation of the roadway. In addition, the failure and deformation degree of the filling body in the process of supporting the roof is small, which meets the bearing requirements. This shows that the strength of the filling body meets the design requirements. Therefore, the pumping paste is used to fill and maintain the roadway, which is in good condition and achieves the expected purpose. Through theoretical analysis, mechanical model calculation and field industrial tests, the newly-built model proves that the technology is feasible, innovative, practical and advanced.
6. Conclusions
The following conclusions can be drawn from this study:
With other conditions unchanged, the higher the mass concentration of the paste, the lower its slump, the worse its fluidity, and the higher the compressive strength is. The higher the solid-cement ratio and fly ash-cement ratio, the greater the slump, the better the fuildity, and the lower the compressive strength is.
The COBPNN hybrid algorithm designed by integrating CO and BPNN algorithms can fill the gaps of the traditional BPNN algorithm, such as tardy convergence, low convergence precision and proneness to local minimum. The COBPNN model for paste slurry mass proposed based on the complementarity between BPNN and CO has not only significantly improved the learning rate and accuracy, but also rendered more reliable prediction results. It also has a higher fitting accuracy and stronger generalization ability. Through theoretical analysis, mechanical model calculation and field industrial tests, the newly-built model proves that the technology is feasible, innovative, practical and advanced.
To accurately and scientifically predict the mass of paste slurry, in addition to the prediction method, it is imminent to make greater efforts in further strengthening the study on paste slurry proportioning optimization mechanism and collection of basic data so as to ensure that the application of the theory has more complete and reliable basic data, and obtain more appropriate proportioning of paste backfill material.
Fundings
This study was financially supported by the National Natural Science Foundation of China (Nos. 51974226), the Natural Science Basic Research Program of Shaanxi (Nos. 2019JM-351) and the Major Science and Technology Innovation Projects in Shandong Province (Nos. 2019JZZY020326).
Acknowledgments
The authors would like to extend their sincere appreciation to the SiChuan Coal Industry Group Co., Ltd for field test and data collection.
Conflicts of Interest
The authors declare no conflict of interest.
Author contributions
W.Y. developed the idea and provided theoretical direction. X.F. and K. designed and analyzed the model and carried out the test work.
References
[1] Zhang Q., Zhang J.X., Huang Y.L., Ju F. Backfilling technology and strata behaviors in fully mechanized coal mining working face. Int. J. Min. Sci. Technol., 22:151–157, 2012.
[2] Seryakov V.M. Mathematical modeling of stress-strain state in rock mass during mining with backfill. J. Min. Sci., 50:847–854, 2014.
[3] Wu D., Hou, Y., Deng T., Chen Y., Zhao X. Thermal, hydraulic and mechanical performances of cemented coal gangue-fly ash backfill. Int. J. Miner. Process., 162:12–18, 2017.
[4] Zhang J.X., Li B.Y., Zhou N., Zhang Q. Application of solid backfilling to reduce hard-roof caving and longwall coal face burst potential. Int. J. Rock Mech. Min., 88:197–205, 2016.
[5] Al Heib M.M., Didier C., Masrouri F. Improving short- and long-term stability of underground gypsum mine using partial and total backfill. Rock Mech. Rock Eng., 43:447–461, 2010.
[6] Wu D., Cai S.J., Liu Y.C. Effects of binder on suction in cemented gangue backfill. Mag. Concr. Res., 68: 593–603, 2016.
[7] Khaldoun A., Ouadif L., Baba K., Bahi L. Valorization of mining waste and tailings through paste backfilling solution, Imiter operation, Morocco. Int. J. Min. Sci. Tech., 26:511–516, 2016.
[8] Zhang J.X., Zhang Q., Sun Q., Gao R., Germain D., Abro S. Surface subsidence control theory and application to backfill coal mining technology. Environ. Earth Sci., 74:1439–1448, 2015.
[9] Ercikdi B., Cihangir F., Kesimal A., Deveci H., Alp İ. Utilization of industrial waste products as pozzolanic material in cemented paste backfill of high sulphide mill tailings. J. Hazard. Mater., 168:848–856, 2009.
[10] Benzaazoua M., Fall M., Belem T. A contribution to understanding the hardening process of cemented pastefill. Miner. Eng., 17:141–152, 2004.
[11] Huang P., Li B.Y., Xiao M., Chen Z.W., Pei Y.L. The design of critical filling ratio in close distance coal seams by upward backfill mining technology. J. Min. Saf. Eng., 4:597–603, 2016.
[12] Deng D., Liu L., Yao Z., Song K.-I., Lao D. A practice of ultra-fine tailings disposal as filling material in a gold mine. J. Environ. Manag., 196:100–109, 2017.
[13] Liu M., Liu X., Wu M., Li L., Xiu L. Integrating spectral indices with environmental parameters for estimating heavy metal concentrations in rice using a dynamic fuzzy neural-network model. Comput. Geosci., 37:1642–1652, 2011.
[14] Wang D. Quantitative investment model based on data mining. Rev. Int. Métodos Numér. Cálc. Diseño Ing., 36, (1), 22, 2020.
[15] Heo S., Lee J.H. Fault detection and classification using artificial neural networks. IFAC-Papers Online, 51:470–475, 2018.
[16] Ditto W., Munakata T. Principles and applications of chaotic systems. Commun. ACM., 38:96–102, 1995.
[17] Yang D., Liu Z., Zhou J. Chaos optimization algorithms based on chaotic maps with different probability distribution and search speed for global optimization. Commun. Nonlinear Sci. Numer. Simul., 19:1229–1246, 2014.
[18] Sun Q., Zhang J., Zhang Q., Yan H. A case study of mining-induced impacts on the stability of multi-tunnels with the backfill mining method and controlling strategies. Environ. Earth Sci., 77:234, 2018.
[19] Bharatkumar B.H., Narayanan R., Raghuprasad B.K., Ramachandramurthy D.S. Mix proportioning of high performance concrete. Cem. Concr. Compos., 23:71–80, 2001.
[20] Yilmaz T., Ercikdi B., Karaman K., Kulekci G. Assessment of strength properties of cemented paste backfill by ultrasonic pulse velocity test. Ultrasonics., 54:1386–1394, 2014.
[21] Tang W., Zhang X.Y., Li D.P. Chaotic optimization method for neural network's weights. J. Harbin. Inst. Technol., 6:12-14, 2000.
[22] Wang H.S., Zhang D.S., Li S.G., Wang L., Wu L.Z. Rational width of narrow coal pillar based on the fracture line location of key rock B in main roof. J. Min. Saf. Eng., 31:10-16, 2014.
Document information
Published on 15/06/20
Accepted on 04/06/20
Submitted on 01/06/20
Volume 36, Issue 2, 2020
DOI: 10.23967/j.rimni.2020.06.003
Licence: CC BY-NC-SA license