| Line 47: | Line 47: | ||
{| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 100%;max-width: 100%;" | {| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 100%;max-width: 100%;" | ||
|- | |- | ||
| − | |[[Image:draft_Jokinen_791615861-Insert_koetulokset.png| | + | |[[Image:draft_Jokinen_791615861-Insert_koetulokset.png|540px|Insert cycle experimental force-displacement curves.]] |
|- style="text-align: center; font-size: 75%;" | |- style="text-align: center; font-size: 75%;" | ||
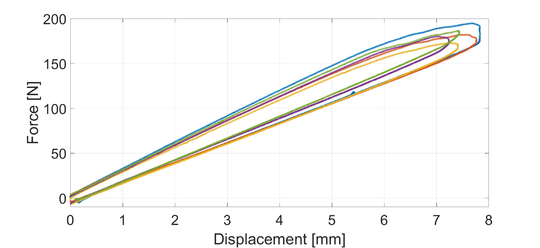
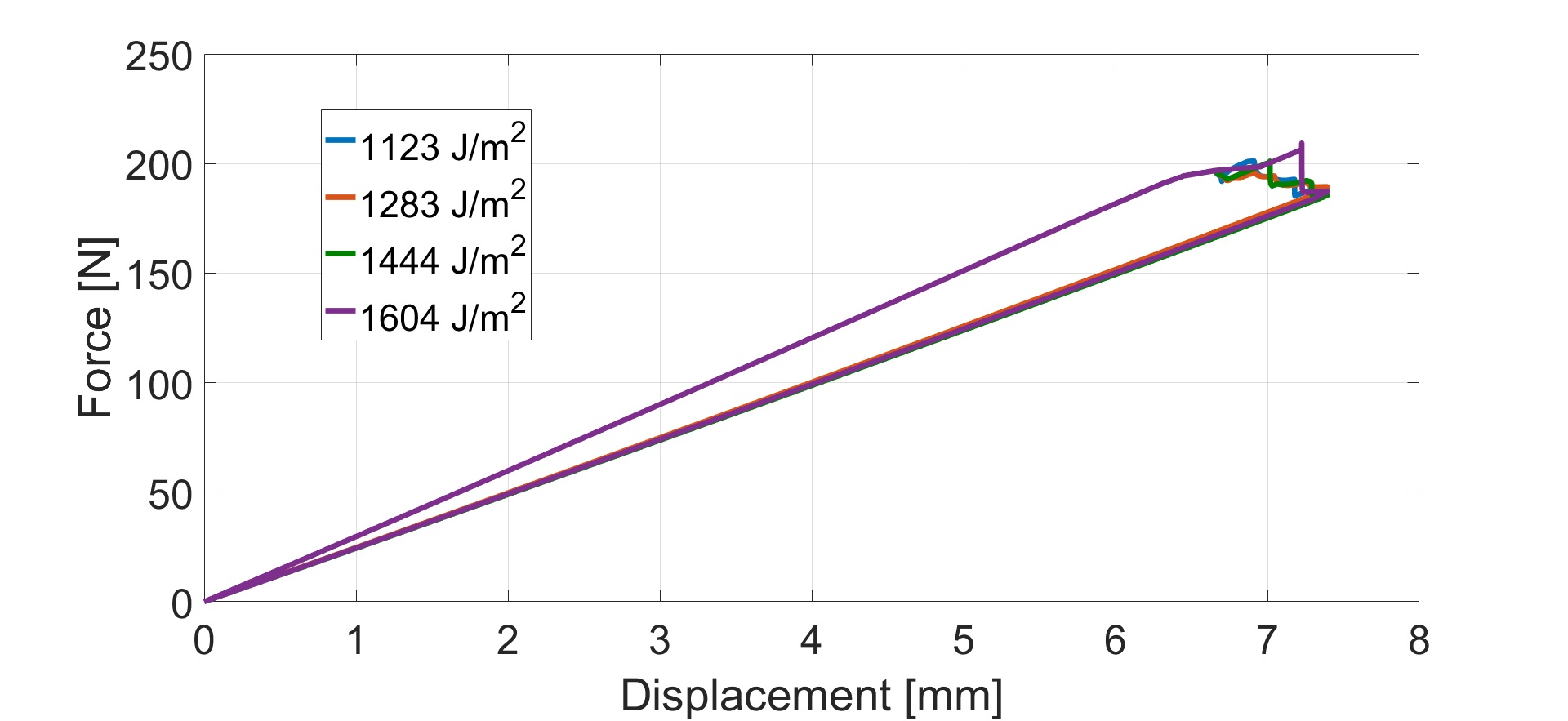
| colspan="1" | '''Figure 1:''' Insert cycle experimental force-displacement curves. | | colspan="1" | '''Figure 1:''' Insert cycle experimental force-displacement curves. | ||
Revision as of 22:53, 28 April 2017
Crack onset analysis of adhesives for the CZM-VCCT method
Jarno Jokinen and Mikko Kanerva
| Department of Materials Science |
| Tampere University of Technology |
| P.O.B 589, FI-33101 Tampere |
| e-mail: jarno.jokinen@tut.fi |
| Department of Materials Science |
| Tampere University of Technology |
| P.O.B 589, FI-33101 Tampere |
| e-mail: mikko.kanerva@tut.fi |
Abstract
For testing and analysing crack propagation under fatigue loading, crack onset precedes any crack growth. In this work, crack onset during the testing of Double Cantilever Beam (DCB) specimens is studied. The insert cycle experiments provide an experimental reference for our analysis using finite element methods. The insert cycle is analysed using three different methods, which are the Virtual Crack Closure Technique (VCCT), Cohesive Zone Modelling (CZM) and a combined method. In the combined method, the crack onset is modelled using CZM and propagation using VCCT. In other words, we strive to model the crack nucleation phenomenon in the adhesive bond of DCB specimen.
keywords Crack onset, virtual crack closure technique, cohesive zone modeling, double cantilever beam
1 INTRODUCTION
An application for polymers is adhesive bonding. Adhesive bonds are prone to debonds during long-term operation and the crack onset plays a major role in the fatigue of the polymer in general. In experimental testing of adhesive bonds, an artificial initial crack is typically prepared into the specimen. For studying the natural crack propagation under variable amplitude loading, an additional load cycle is needed to create a natural crack front.
Double Cantilever Beam (DCB) is a standardized experimental method for defining fracture toughness for adhesive debond in mode I loading. In the DCB experiment, a pre-cracked specimen is loaded while crack propagation is being monitored. DCB test includes two load cycles, which are called the insert cycle and pre-crack cycle. The initial crack is carefully prepared during the manufacture by placing teflon film at the adhesive interface. During the insert cycle, the specimen is loaded until observing crack growth at the specimen side edge for the first time. The target of the insert cycle is to form natural crack front. The specimen is unloaded after the insert cycle and re-loaded until the crack has propagated 60 mm during the pre-crack cycle.
Typically the crack growth during the latter cycle is of interest. That is indeed reasonable when fracture mechanics propagation models are being validated and propagation mechanisms are studied. In this work, our focus is to study the insert cycle and, in detail, the crack nucleation. The target of the work is to model the crack onset behavior. The analysis is performed using the combined method, which use cohesive zone modelling (CZM) for the crack onset and virtual crack closure technique (VCCT) for the crack propagation. To support the analysis, the insert cycle is modelled using both pure VCCT and CZM.
2 Materials and methods
2.1 Reference experiment
The reference experiments applied to this work are based on work by Jokinen et al.[1]. They studied epoxy film adhesive FM-300-2K by Cytec® using Double Cantilever Beam (DCB) [1]; six specimens were tested. The DCB specimens were manufactured using two adhesive film plies. The initial crack was created placing an insert between the adhesive plies. Adherend and loading blocks were manufactured from aluminium alloy 7075-T76. Thickness of aluminium and adhesive parts were 3.1 mm and 0.57 mm, respectively. The width of the specimen is 20.04 mm and length 150 mm. The initial crack length was 55.36 mm. The load was transferred using loading blocks, which cross-section was 14 14 mm.
The insert cycles' force-displacement curves are shown in Figure 1. Force-displacement curves show nonlinear behavior before reaching the maximum force. Fracture toughness can be evaluated when combining the force and displacement data with the crack length. Fracture toughness was evaluated using the Corrected Beam Theory (CBT), which is described in the DCB standard [2]. Fracture toughnesses of 1604 J/m and 1820 J/m for the insert and pre-crack cycle, respectively, were determined [1]. The measured crack growth in the insert cycle was in average 1.3 mm.
|
| Figure 1: Insert cycle experimental force-displacement curves. |
2.2 Finite element model
The finite element model of the DCB was created using Abaqus 6.14. Adhesive, adherend and the loading blocks were modelled as separate parts. These parts were connected to each other using the tie constraint, which allowed us using dissimilar meshes. The usage of the dissimilar meshes was beneficial since it allowed us to limit the analysis size. The finest mesh, 0.1 mm (CPE4I element), was used in the adhesive. In the adherend, the element dimension (CPE4R) was 0.5 mm and in the loading block 1 mm. The finite element model is shown in Figure 2.
The loading of the model was attached at the centre points of the loading blocks. At the lower centre point, both vertical and horizontal displacement were restricted. At the upper centre point, horizontal displacement was restricted. The loading was applied to the upper point. The loading was performed using two analysis steps. In the first step, an opening displacement of 7.395 mm was performed. In the second step, the loading was removed.
The debond analysis was performed at the middle of the adhesive, which refers to the middle plane of the model. The definitions required by the analysis method were located at this plane (VCCT does not require additional elements). The default dimension of applied CZM elements (COH2D4) was 0.1 mm.

|
| Figure 2: The finite element model. |
2.3 Cohesive zone modelling (CZM)
Cohesive zone modelling (CZM) is based on work by Barenblatt [3] and Dugdale [4]. CZM is modelled using a traction-separation law. The most simplest law is the bi-linear law, where cohesive strength defines the maximum force and a fracture toughness value (limit) the final failure. The bi-linear traction-separation law can be extracted in the following form:
|
|
(1) |
where [5]
|
|
(2) |
In the equation, is the cohesive stiffness and is the cohesive strength.
2.4 Virtual crack closure technique (VCCT)
Virtual crack closure technique (VCCT) is a numerical analysis method for a variety of debond analyses. The method is founded on the Irwin's crack closure integral, from which Rybicki and Kanninen [6] developed the method. The idea by Rybicki and Kanninen was to modify the integral to be appropriate for a FE analysis. They used spring elements to define the force and displacement at the crack tip. Later on, the spring has been removed and the evaluation of force and displacement has been separated between adjacent nodal points. The energy release rate using VCCT can be computed by the form:
|
|
(3) |
where is the reaction force, is the nodal separation, and are the element width and length. Krueger [7] has surveyed VCCT equations and applications.
2.5 Combined method
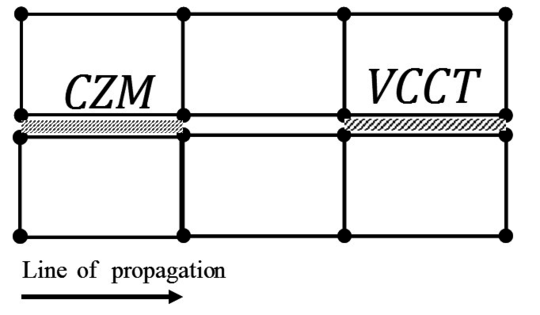
The original target of the combined method was to study the onset and propagation as separate models and to account for the two physical processes [8]. The onset behavior is modelled by CZM, while the propagation phase is modelled using VCCT. The combined model is described in Figure 3.
|
| Figure 3: Combined method. |
3 Results and discussion
3.1 Pure VCCT and CZM modelling
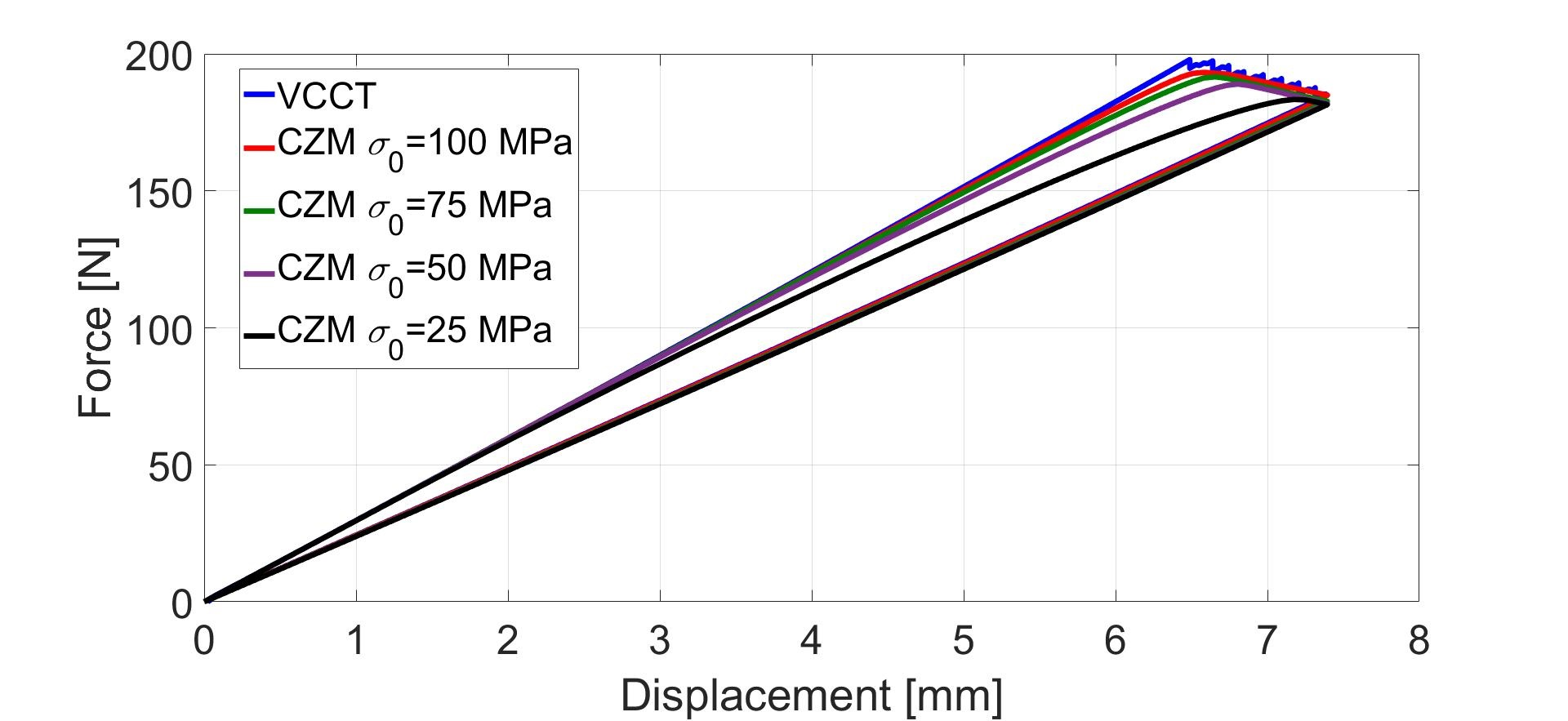
The DCB insert cycle was first analyzed using VCCT and CZM separately. The CZM analysis was performed for a range of cohesive strength values. The results of the VCCT and CZM analyses are shown in Figure 4. The CZM results agree with the VCCT results when the cohesive strength is increased over our anticipated range of values. The VCCT results indicate oscillation, which is caused by the tolerance of the critical fracture toughness level set in for the simulation. The use of tolerance is basically a method to improve VCCT analysis convergence [9]. In detail, either VCCT or CZM alone are not able to provide fully corresponding nonlinear behavior than what is shown by experiments.
|
| Figure 4: VCCT and CZM results. |
3.2 Combined method
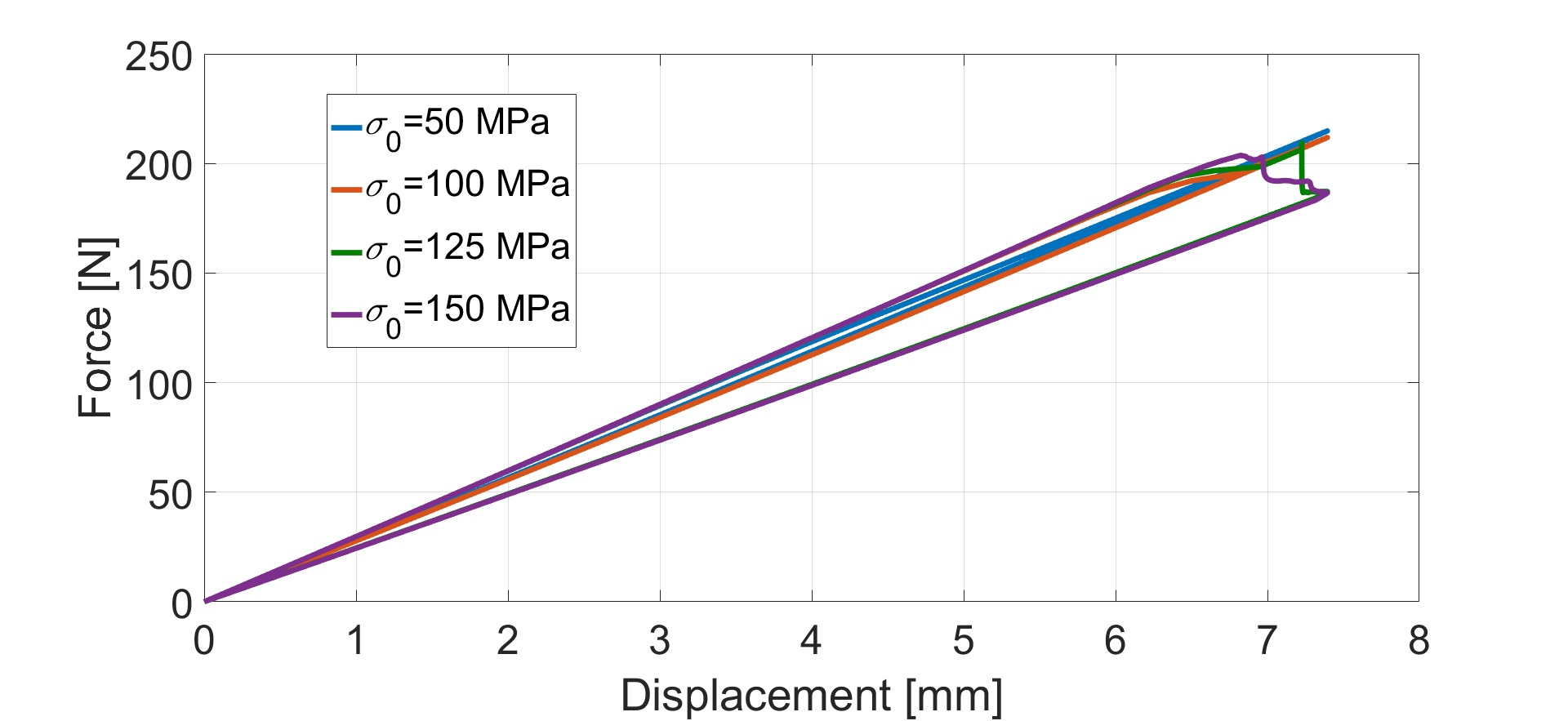
In the combined method analysis, CZM region was limited to the experimentally observed crack onset length (1.3 mm). The fracture toughness value in the CZM was set by the experimental insert cycle, while the cohesive strength still had to be fitted. The combined method analysis using different cohesive strength values is shown in Figure 5. The slope of the loading and unloading curves (50 MPa) has only minor discrepancy, which actually states negligible crack propagation. The use of 150 MPa value provides crack propagation of 3.8 mm, which is almost three times longer than what is observed during real crack propagation. The result can be explained by the nail-shaped crack front where the crack is longer at the centre compared to the edge of the specimen [10]. A comparison between Figures 4 and 5 remarks the VCCT's impact: The VCCT limits the cohesive zone existing beyond the crack tip. This feature virtually forces to modify cohesive strength values (CZM portion) in the combined method.
|
| Figure 5: The combined method when varying (=1604 J/m). |
Furthermore, a force drop existed upon the simulation (125 MPa), which suggests that the crack propagation stopped before reaching the maximum force. This was assumed to be caused by the VCCT region and because no smooth transition between CZM and VCCT does not exist. For solving this problem, the first VCCT node's critical fracture toughness value was set slightly lower. Figure 6 shows the case when the first nodal point's fracture toughness value for VCCT is scaled downwards. For this, already a minor decrease in the fracture toughness leads to the removal of the force drop in the behavior.
|
| Figure 6: The combined method's results when varying the VCCT region's first nodal point's value. |
3.3 Comparison of experiments and simulation using the combined method
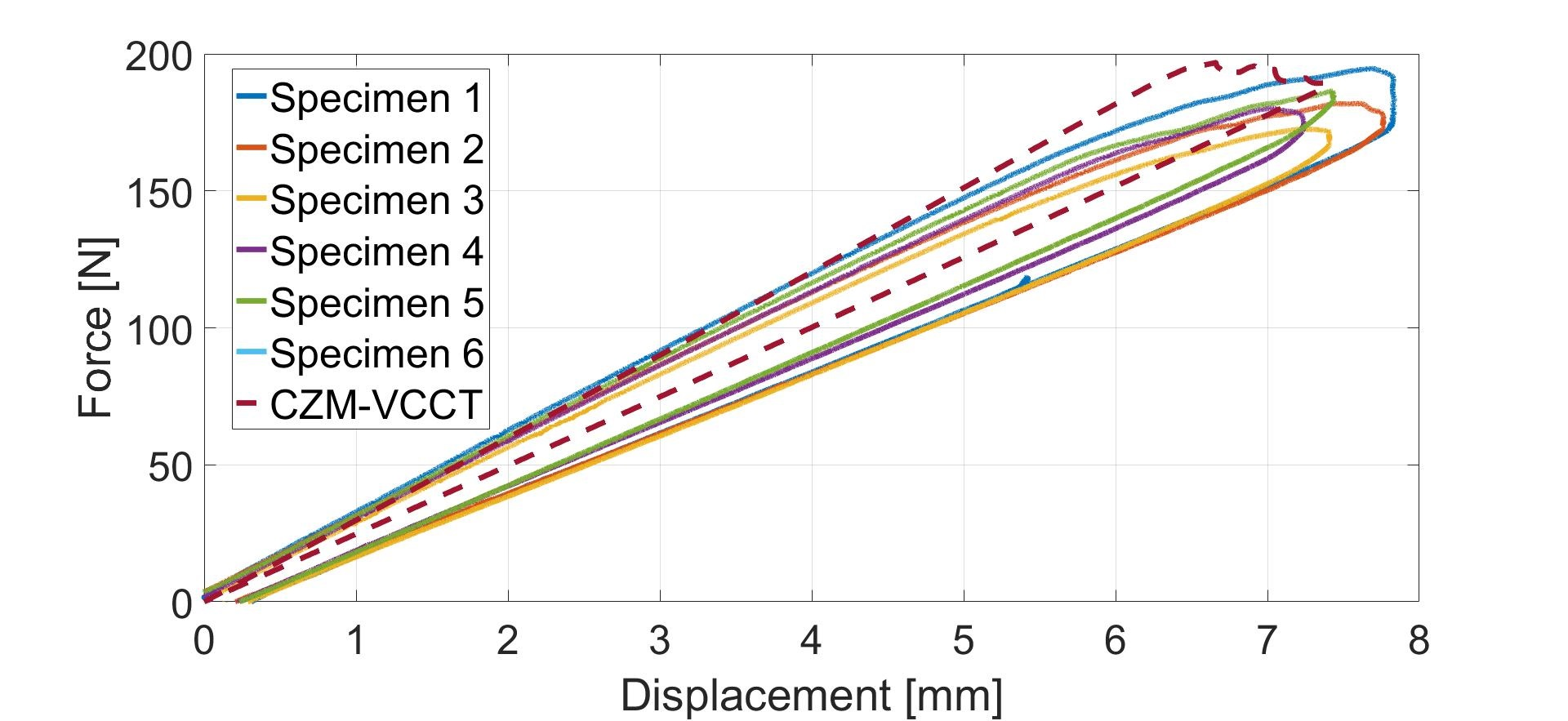
The combined method's results compared to experimental curves are shown in Figure 7. The FE model is evidently stiffer than the experimental reference. The main interest lies at the crack onset and, especially, along the short propagation length and when nonlinear response occurs. The nonlinear region observed from the experiments is still larger compared to what is observed using the combined method analysis. The unloading curve for the combined method also indicates stiffer behavior than for the experiments. This in turn indicates that the effective crack length in the real specimen should be somewhat larger than what is given by the analysis.
|
| Figure 7: The combined method's results compared to experiments. |
4 Conclusion
In this work, the target was to study the crack onset modelling for adhesive debond simulation. Our analysis remarked the sensitivity of the cohesive strength value selection for pure CZM and for the combined method analysis. The nonlinear nucleation behavior found in the experimental force-displacement curve can be controllably simulated by modifying the CZM region's cohesive strength.
Here, the insert cycle of the DCB experiment was analysed. The analyses were performed using three different finite element method based models, which read VCCT, CZM and the combined method. The pure VCCT results did not provide any nonlinearity until the nodal failure. In the pure CZM analysis, nonlinearity was readily observed. The pure CZM analysis performed well when the cohesive strength value was set to 50 MPa. The analysis results, when increasing the cohesive strength in steps, were approaching the pure VCCT simulation results. Finally, rather a good match with the pure VCCT was reached using a cohesive strength value of 100 MPa.
In turn, the use of 50...100 MPa cohesive strength in the combined method led to negligible crack propagation. Finally, a cohesive strength of 150 MPa produced feasibly fitted crack growth. This value, however, is three times higher than what was fitted for the pure CZM model. The application of 125 MPa led to a step-like force drop in the analysis behavior. The reason for the drop was assumed to be caused by the transition between the VCCT and CZM regions. For studying the transition, the first VCCT nodal point's value was decreased. A ten percent decrease smoothened the transition when using a 125 MPa cohesive strength. Clearly, the crack onset model fitting depends on the modelling method and possibly any transition between methods.
BIBLIOGRAPHY
[1] Jokinen, J., Wallin, M. and Saarela, O. Applicability of VCCT in mode I loading of yielding adhesively bonded joints-a case study. Int. J. Adhes. Adhes. (2015) 62:85-91 [2] Adhesives-Determination of the mode 1 adhesive fracture energy of structural adhesive joints using double cantilever beam and tapered double cantilever beam specimens. ISO 25217, International standard, 2009. [3] Barenblatt, G. I. The mathematical theory of equilibrium cracks in brittle fracture. Adv. Appl. Mech. (1962) 7:55-129 [4] Dugdale, D. S. Yielding of steel sheets containing slits. J. Mech. Phys. Solids (1960) 8:100-104 [5] Alfano, G. On the influence of the shape of the interface law on the application of cohesive-zone models. Compos. Sci. Technol. (2006) 66:723-730 [6] Rybicki, E. F. and Kanninen, M. F. A finite element calculation of stress intensity factors by a modified crack closure integral. Eng. Fract. Mech. (1977) 9:931-938 [7] Krueger, R. The virtual crack closure technique: history, approach and applications. Appl. Mech. Rev. (2004) 57:109–143 [8] Kanerva, M. and Jokinen, J. The effect of computational parameters on the performance of a combined CZM-VCCT method, 29th Nordic Seminar on Computational Mechanics, Gothenburg, 26-28 October, 2016 [9] Jokinen, J. and Wallin, M. The Effect of Numerical Parameters on Debond Analyses Using VCCT in Abaqus, Nafems Nordic Seminar: Simulating composite materials and structures, 17th-18th November, Stockholm[10] Jokinen, J., Wallin, M. and Saarela, O. Three-dimensional analysis of DCB specimen energy release rate distributions, 3rd ECCOMAS Thematic Conference on the Mechanical Response of Composites, Hannover, September 21-23, 2011
Document information
Published on 02/05/17
Submitted on 28/04/17
Licence: CC BY-NC-SA license
Share this document
Keywords
claim authorship
Are you one of the authors of this document?