1 Introducción
Los polímeros reforzados con fibras de carbono (CFRP) son cada vez más usados para reemplazar componentes metálicos en aeronaves, gracias a su reducida relación peso-resistencia. Sin embargo, materiales metálicos (como por ejemplo aluminio o titanio) se siguen utilizando, lo cual ha conllevado a la presencia de ensamblajes híbridos CFRP-metal en las alas, fuselajes, empenaje, etc. [1,2]. Usualmente, estos ensamblajes se suelen unir utilizando uniones atornilladas, sobre todo debido a la gran rigidez y resistencia que estas ofrecen, además de su facilidad para desmontarse y repararse [3-4,5]. Durante su uso, una aeronave sufre saltos de temperatura (la diferencia entre la fase de vuelo y la de tierra puede superar los 140 ºC). Dado que los metales y los CFRP tienen coeficientes de dilatación térmicos muy distintos, estos grandes saltos de temperatura causan una distinta expansión térmica entre los componentes de los ensamblajes. Consecuentemente, se producen tensiones térmicas que pueden afectar el comportamiento mecánico y la integridad estructural [6-78].
En las últimas décadas ha aumentado la preocupación por la integridad estructural de tales ensamblajes híbridos en la industria aeronáutica. Un ejemplo típico es el Airbus A380, que utiliza ensamblajes híbridos en las alas. Tras años de servicio, se descubrieron grietas en los pies de las costillas, originadas en la unión entre la costilla (de aluminio) y las pieles (componente de carbono). Además, también se encontraron grietas en la pared de las costillas [2,9,10]. La aparición de estas se atribuyó a altas tensiones producidas por el diferencial de expansión térmico entre los distintos componentes. Desafortunadamente, el comportamiento de las uniones atornilladas híbridas es muy complejo debido a la presencia de fricción y deslizamiento entre componentes, el contacto, la holgura del agujero con el tornillo, y la precarga de los tornillos, entre otros, además de los efectos térmicos [3,7,8,11-,12,13,14]. Por tanto, el análisis y diseño de un ensamblaje atornillado híbrido supone un gran reto y su comportamiento es difícil de anticipar.
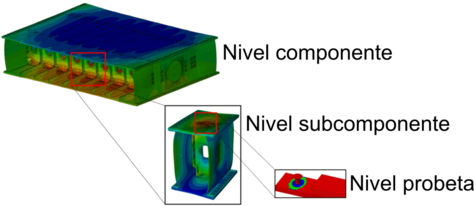
Actualmente, el proceso de diseño en la industria aeronáutica consiste en verificar la resistencia estática y a fatiga a través de ensayos experimentales, siguiendo una estructura piramidal [1,15], véase Figura 1. Desafortunadamente, realizar ensayos en los niveles de subcomponente y componente no es simple, debido a la necesidad de equipamiento complejo y caro, la dificultad de analizar grandes cantidades de datos, los costes de fabricación, la dificultad de conocer previo al ensayo las partes más críticas que deben ser instrumentadas, así como la dificultad de medir con precisión pequeñas deformaciones [8].
De forma complementaria o incluso alternativa a los ensayos experimentales, los ensayos virtuales utilizando modelos numéricos también se suelen llevar a cabo. Los modelos numéricos pueden brindar más información sobre el comportamiento global de grandes estructuras que los ensayos experimentales, aunque estos deben de validarse. Los métodos para simular uniones atornilladas se pueden categorizar en tres grupos [14,27]: métodos analíticos [11,16], métodos de rigidez [14,17] y elementos finitos [2-,3,4,5,8,18-,19,20,21,22,23,24,25,26]. Los métodos analíticos y de rigidez consideran los tornillos y componentes como una sucesión de muelles y masas [23]. Aunque computacionalmente eficientes, estos no pueden capturar con precisión el comportamiento de la unión. Por otro lado, los Modelos de Elementos Finitos (MEF) pueden capturar con precisión el comportamiento de la unión, pero con un alto coste computacional [3,18,20-,21,22,25].
Desafortunadamente, simular una gran estructura atornillada (como por ejemplo un cajón de ala, con centenares de uniones atornilladas) usando un modelo de elementos finitos con un gran nivel de detalle no es factible [14,27]. Por ello, modelos más simples han sido propuestos [8,19,23]. Por un lado, las piezas atornilladas pueden ser simuladas con elementos shell continuos, o elementos shell [8,19]. Por otro lado, el tornillo se puede substituir por elementos viga, un sólido rígido, puede ser eliminado, etc. [8,16,24,27]. Recientemente, Guerrero et al. [27] presentaron un modelo simplificado donde las partes atornilladas se modelan con elementos shell continuos, mientras que los tornillos se modelan con elementos viga y elementos superficie. Esta combinación permite capturar razonablemente bien el comportamiento de la unión, incluso en la dirección fuera del plano, y reducir significativamente el tiempo computacional.
Pese a los grandes avances en la literatura, prácticamente todos los modelos numéricos han sido validados a nivel de probeta. De la misma manera, la mayoría de ensayos se encuentran realizados a esa misma escala. Además, existe una enorme escasez de investigación sobre el comportamiento de uniones atornilladas híbridas bajo cargas térmicas [2,8,27]. Con el objetivo de aumentar el conocimiento en esta temática, en este artículo realizamos ensayos experimentales y simulaciones con elementos finitos de uniones atornilladas híbridas a diferentes escalas, bajo cargas térmicas, representado los típicos ciclos térmicos que se producen en la vida útil de una aeronave. Primero, a escala de probeta, se ensayan probetas (como por ejemplo una unión a solape simple) para comprender la respuesta global de la unión. Tras ello, a nivel subcomponente, se simula y ensaya experimentalmente un subelemento que representa una unidad de un cajón de ala híbrido de una aeronave. Finalmente, se simula y ensaya el cajón de ala híbrido completo (Figura 1). El artículo detalla el plan instrumental para realizar los ensayos, así como los modelos numéricos desarrollados. Nuestros resultados muestran que las cargas térmicas producen tensiones críticas que pueden conducir a la formación y propagación de grietas, sobretodo bajo condiciones de servicio o fatiga. Además, el modelo numérico de elementos finitos reproduce de forma razonable los resultados experimentales.
Este trabajo es parte del proyecto ‘INNOHYBOX’ enmarcado dentro del programa aeronáutico europeo Clean Sky 2, desarrollado con el consorcio de Dassault Aviation, el grupo de investigación AMADE de la Universitat de Girona, el centro tecnológico EURECAT y la empresa SOFITEC, con el objetivo global de analizar un cajón de ala híbrido atornillado sujeto a cargas termo-mecánicas.
2 Metodología experimental
En esta sección se presenta la metodología y ensayos experimentales llevados a cabo en las tres escalas: nivel probeta, nivel subcomponente y nivel componente (Figura 1).
2.1 Nivel probeta
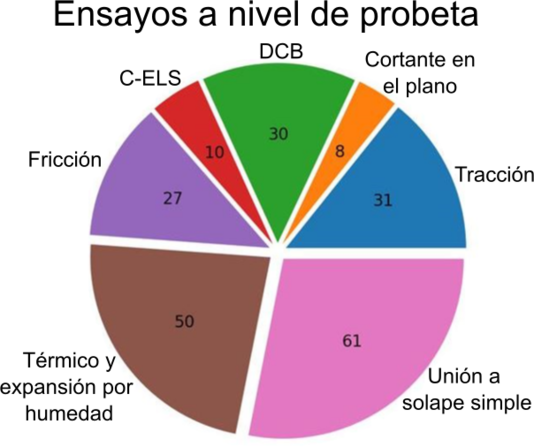
A nivel de probeta se realizaron ensayos de fricción, así como ensayos típicos estandarizados como el End Loaded Split (C-ELS), Double Cantilever Beam (DCB), cortante en el plano, tracción, unión atornillada a solape simple, térmicos y expansión por humedad. La Figura 2 muestra un resumen de los experimentos realizados, así como el número de probetas ensayadas con cada uno. Los ensayos se realizaron siguiendo las normativas correspondientes [28-,29,30].
Los ensayos de uniones a solape simple consistieron en un ensamblaje atornillado híbrido CFRP-aluminio, representativo de una unión de las que se pueden encontrar típicamente en un cajón de ala (véase Figura 1 y Figura 3). Estos cupones se ensayaron bajo cargas térmicas, basadas en los típicos ciclos térmicos que ocurren en aeronaves, para comprender la respuesta termo-mecánica de una unión híbrida a una escala menor. Por otro lado, los demás ensayos experimentales se utilizaron para caracterizar las propiedades mecánicas de los materiales usados en el proyecto (propiedades elásticas y de resistencia, fractura interlaminar, coeficientes de expansión térmicos, coeficientes de fricción, etc.). La Figura 3 muestra fotografías de algunos de los ensayos llevados a cabo a temperaturas criogénicas (-55 ºC).
2.2 Nivel subcomponente
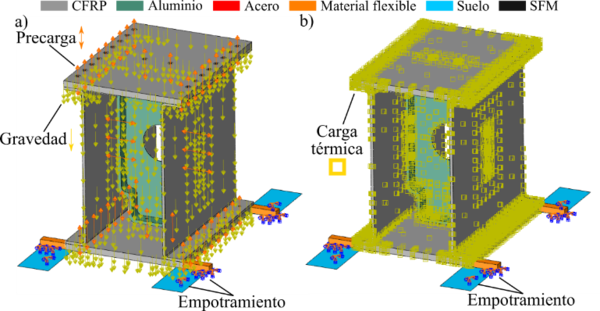
A nivel de subcomponente se ensayó un subelemento, el cual representa una pequeña unidad o sección de un cajón de ala de una aeronave híbrida carbono-aluminio ensamblado con tornillos, véase Figura 1 y Figura 4. El subcomponente consta de dos pieles (superior e inferior, fabricadas de CFRP), dos largueros (izquierdo y derecho), también de CFRP y una costilla en el centro, de aluminio. El ensamblaje está unido por un total de 46 tornillos de acero NAS-1153. Cada piel se une a la costilla con dos tornillos, los largueros se ensamblan con la costilla con 6 tornillos (3 tornillos cada larguero), mientras que las pieles y largueros están unidos con 36 tornillos en total, véase Figura 4. El par de apriete de los tornillos es de 3.4 N·m (aproximadamente equivalente a 6000 N de precarga). El subcomponente sirve, por tanto, como paso previo al estudio del cajón de ala completo, al ser una estructura similar, pero de menor tamaño.
El ensamblaje se ensayó en los laboratorios de AMADE de la Universitat de Girona. Se realizaron dos ensayos distintos bajo cargas térmicas, con el objetivo de reproducir los saltos de temperatura que ocurren típicamente en una aeronave:
- Salto térmico negativo: des de temperatura ambiente (25 ºC) a criogénica (-40 ºC).
- Salto térmico positivo: des de temperatura ambiente (25 ºC) a elevada (80 ºC).
Para realizar cada ensayo, el subelemento se colocó dentro de una cámara climática diseñada y construida durante el proyecto, suficientemente grande para albergar el subcomponente (y posteriormente el cajón de ala completo, véase Figura 5a). La cámara está formada por paneles sándwich de lana de roca y acero de 100 mm. Las esquinas y paredes están aisladas térmicamente mediante espuma. Además, el subcomponente se colocó sobre un marco de aluminio, que estaba aislado de la pared del suelo y la piel inferior del componente, para evitar la transferencia de calor por conducción en los puntos de contacto, véase Figura 5a. El generador se conecta a la cámara a través de dos tuberías de 150 mm, la inferior es la entrada de aire de la cámara mientras que la superior aspira para garantizar la circulación de aire. La temperatura se controla mediante un ordenador PLC SIEMENS.
El salto térmico correspondiente se aplicó muy lentamente para llegar a la temperatura final deseada de forma uniforme. Un total de 16 termopares fueron colocados a lo largo de la estructura para verificar que la temperatura era homogénea durante el ensayo. Además, con el objetivo de obtener la deformación global de la estructura, el subcomponente fue instrumentado con un total de 32 galgas con compensación de temperatura de HBM. La costilla fue instrumentada con galgas para aluminio, mientras que las pieles y largueros fueron instrumentados con galgas de cuarzo (el cual tiene un coeficiente de expansión pequeño, similar al CFRP). Nótese que aplicamos una corrección a las mediciones experimentales obtenidas por las galgas para eliminar errores debido a la expansión térmica propia de las galgas. Esta metodología puede encontrarse en otro artículo [8]. La Figura 5b muestra fotografías justo al finalizar el ensayo térmico a temperatura criogénica (-40 ºC).
2.3 Nivel componente
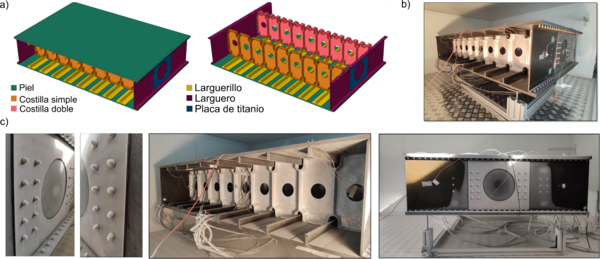
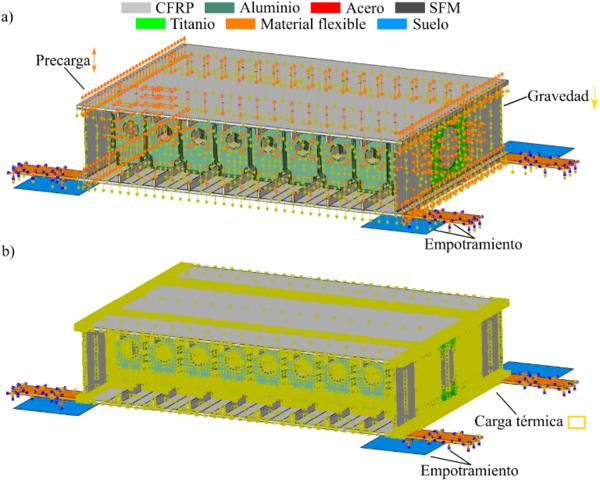
A nivel de componente ensayamos el cajón de ala completo. Todas las partes que lo conforman y sus materiales se presentan en la Figura 6a. El ensamblaje, de dimensiones 1500 x 1000 x 320 mm (longitud x anchura x altura) contiene dos diseños de costillas distintas, una llamada “costilla simple”, y la otra denominada “costilla doble” (Figura 6a). Las costillas están atornilladas con las pieles y con los largueros. Las pieles están atornilladas con los largueros y, además, una placa de titanio se encuentra atornillada con los largueros a cada lado para reforzarlo. Asimismo, las pieles están reforzadas con larguerillos.
Igual que con el subcomponente, realizamos dos ensayos:
- Salto térmico negativo: des de temperatura ambiente (25 ºC) a criogénica (-50 ºC).
- Salto térmico positivo: des de temperatura ambiente (25 ºC) a elevada (80 ºC).
Los ensayos se realizaron en la misma cámara climática usada con el subcomponente, con el cajón de ala reposando nuevamente sobre un marco de aluminio aislado (Figura 6b).
Dado el gran tamaño de la estructura, el salto de temperatura se aplicó gradualmente en un período de 8 horas, para asegurar que esta fuese homogénea a lo largo de todo el ensamblaje. En total, repartimos 16 termopares a lo largo del cajón de ala para corroborar que la temperatura era la deseada. Además, el ensamblaje fue instrumentado con un total de 64 galgas colocadas a lo largo de todo el cajón de ala para extraer la deformación de la estructura durante el ensayo. La Figura 6c muestra fotografías tras el ensayo a temperatura criogénica (-50 ºC).
3 Metodología numérica
En esta sección presentamos los modelos de elementos finitos del subcomponente (nivel subelemento) y del cajón de ala completo (nivel componente). Dado que el enfoque numérico es el mismo en las dos escalas, primero, explicaremos con detalle la modelización de la unión atornillada. Los modelos han sido implementados en Abaqus/Standard, versión 6.14 [31]. El enfoque se encuentra explicado con mayor detalle en Guerrero et al. [27].
3.1 Modelización unión atornillada
Las dos partes unidas por el tornillo se modelan con elementos Continuum Shell (aquí llamados CONTS). Estos elementos parecen como elementos sólidos 3D pero su cinemática y ley constitutiva es más parecida a un elemento placa tipo shell [31].
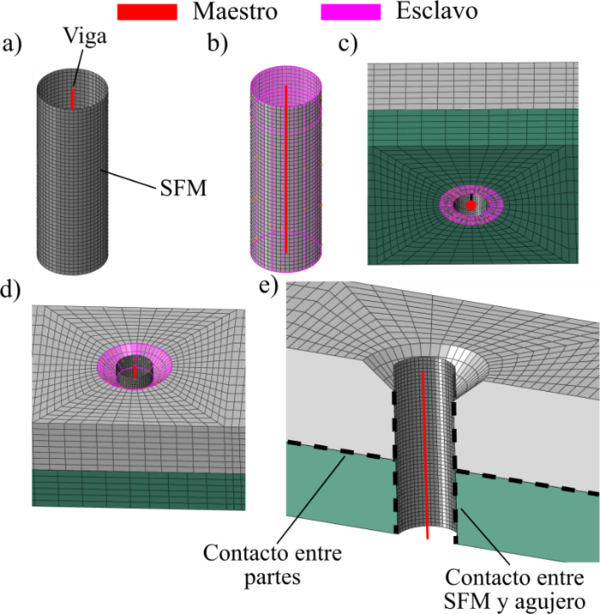
Por otro lado, el tornillo se modela con elementos viga, tomando una sección virtual cilíndrica igual al diámetro nominal del tornillo. Además, para representar físicamente la sección del tornillo y mejorar el contacto, hacemos uso de elementos superficie (SFM), véase Figura 7a. Los elementos viga y el SFM se conectan con una condición de restricción “tie” (Figura 7b). También aplicamos un tie entre el nodo inferior de la viga y la parte inferior del ensamblaje donde la arandela estaría en contacto. Esto permite omitir la arandela y la tuerca (Figura 7c). Similarmente, se aplica un tie entre la parte superior de la viga y el avellanado del agujero, como se muestra en la Figura 7d.
El contacto se modela con el algoritmo “surface-to-surface” de Abaqus, con comportamiento tangencial usando formulación “penalty” incluyendo fricción, mientras que el comportamiento normal viene dado por un contacto tipo “hard” [31]. Los coeficientes de fricción, determinados experimentalmente según los ensayos realizados a nivel de probeta, dependen de la temperatura y de la interfaz de contacto. Estos resultados se mostraran en la sección 4.1. La unión incluye el contacto entre las dos partes unidas, así como entre el SFM (representado la sección física del tornillo) y el agujero, véase Figura 7e.
3.2 Modelo del subcomponente
El modelo del subcomponente representa la misma geometría que el experimental (véase Figura 4). La modelización numérica es la descrita anteriormente en la sección 3.1. Los tornillos son de acero, y juntamente con la costilla de aluminio, se modelan como materiales elásticos e isótropos mientras que el CFRP se toma como un material ortótropo. El coeficiente de expansión térmico (CTE) es isótropo para el acero y aluminio, y ortótropo para el CFRP. El laminado se modela usando la opción “composite layup” de Abaqus, la cual asume teoría de laminados [31]. Las propiedades de los materiales se mostraran en la sección 4.1.
Las condiciones de contorno están basadas en el ensayo experimental. Por tanto, las 4 esquinas del ensamblaje reposan sobre cuatro suelos rígidos, los cuales están empotrados (ver Figura 8). Además, para evitar movimiento rígido del subcomponente, enganchamos 4 vigas flexibles ficticias, de rigidez 0.1 GPa, en las cuatro esquinas de la piel inferior (Figura 8). La mitad de estas está empotrada. Este método permite que la piel inferior se mueva libremente, dado que las vigas flexibles no afectan al movimiento, y a su vez, evitamos movimiento de sólido rígido [8,27].
Siguiendo el experimental, la simulación consiste en dos pasos:
- Paso 1 precarga. Aplicamos una precarga de 6000 N a los 46 tornillos de la estructura, y la temperatura se impone a 25 ºC. Además, aplicamos la gravedad para tener en cuenta el peso, véase Figura 8a.
- Paso 2: salto térmico. Se aplica un salto térmico positivo (de 25 ºC a 80 ºC) o negativo (de 25 ºC a -40 ºC), como en los experimentos, véase Figura 8b.
El tamaño del elemento global es de 1 mm y de 0.75 mm, alrededor del agujero, para el CFRP y aluminio. Además, se usaron cuatro elementos a lo largo del espesor de los componentes. El tornillo usa un tamaño de elemento de 0.3 mm. Estas dimensiones son suficientes para capturar el comportamiento global del ensamblaje.
3.3 Modelo del cajón de ala
Similar al subcomponente, el modelo del cajón de ala representa la misma geometría que el experimental (Figura 6). El modelo es idéntico al del subcomponente, únicamente cambia la geometría y número de tornillos. Además, la simulación también tiene los mismos pasos. Por tanto, siguiendo los experimentos, el salto térmico aplicado es de 25 ºC a -50 ºC (cuando el salto es negativo) y de 25 ºC a 80 ºC cuando es positivo. La Figura 9 muestra el modelo juntamente con los pasos y las condiciones de contorno. Nótese que los laminados de carbono (piel, larguero y larguerillo) incluyen una capa de fibra de vidrio (GFRP) para protegerlos de corrosión galvánica, que también fue incluida en las simulaciones.
4 Resultados y discusión
4.1 Nivel probeta
Los coeficientes de fricción obtenidos experimentalmente se presentan en la Tabla 1, mientras que las constantes de ingeniería obtenidas a partir de los ensayos realizados a nivel de probeta se muestran en la Tabla 2. A partir de estos datos, caracterizamos de forma precisa los materiales e interacciones en los modelos de elementos finitos en las escalas subcomponente (subelemento del cajón de ala) y componente (cajón de ala completo).
| Interfaz de contacto | Temperatura [ºC] | Coeficiente de fricción [-] |
| CFRP-CFRP | -55 | 0.161 |
| 25 | 0.126 | |
| 80 | 0.104 | |
| CFRP-Aluminio | -55 | 0.373 |
| 25 | 0.315 | |
| 80 | 0.273 | |
| Acero-Aluminio y Acero-CFRP | [-25, 80] | 0.315 |
| Material | Propiedad | Fuente | |
| Acero | E [MPa] | 210000 | [32] |
| [-] | 0.3 | ||
| [ m/mºC] | 11 | ||
| [g/ ] | 8 | ||
| Aluminio 7175 | E [MPa] | 73100 | [32] |
| [-] | 0.33 | ||
| [ m/mºC] | 21.0 | ||
| [g/ ] | 2.7 | ||
| Titanio TA6V | E [MPa] | 113800 | [32] |
| [-] | 0.342 | ||
| [ m/mºC] | 8.6 | ||
| [g/ ] | 4.4 | ||
| CFRP (M21 EV / IMA) | [MPa] | 165000 | [33] |
| [MPa] | 9300 | Propia* | |
| [-] | 0.35 | [33] | |
| [-] | 0.487 | Propia * | |
| [MPa] | 5080 | Propia * | |
| [MPa] | 3127.1 | ||
| [ m/mºC] | 0.4±0.2 | Propia * | |
| [ m/mºC] | 27±0.5 | Propia * | |
| [ m/mºC] | 33±2.1 | Propia * | |
| [g/ ] | 1.5 | - | |
| Espesor capa [mm] | 0.192 | - | |
| GFRP | [MPa] | 38750 | - |
| [MPa] | 8470 | ||
| [-] | 0.325 | ||
| [MPa] | 3047 | ||
| [MPa] | 3196.22 | ||
| [ m/mºC] | 36.0 | ||
| [g/ ] | 1.64 | ||
| Espesor capa [mm] | 0.066 | ||
4.2 Nivel subcomponente
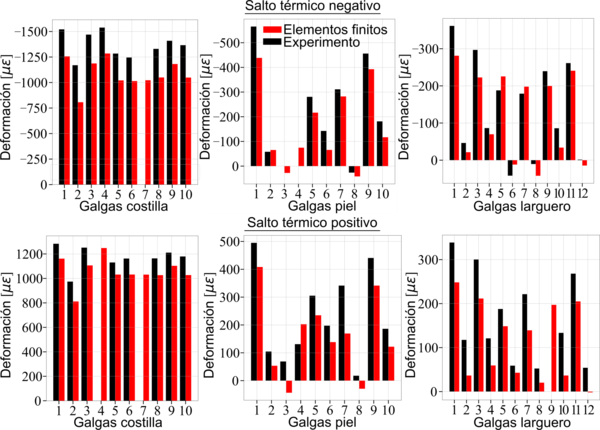
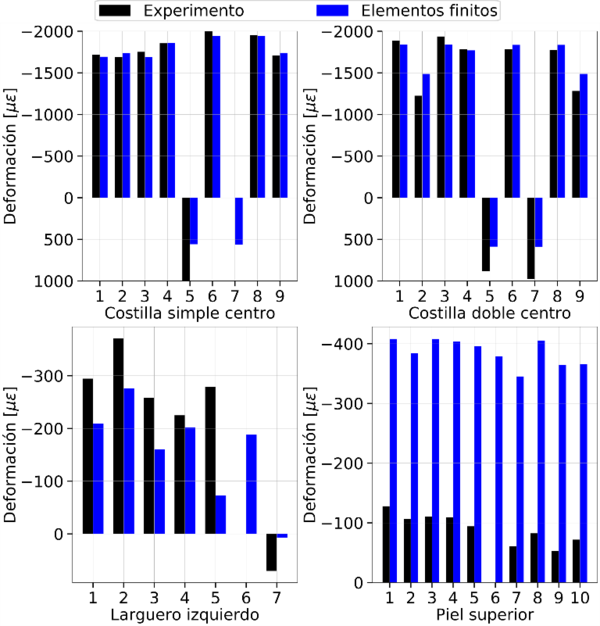
La Figura 10 presenta la predicción numérica de las galgas ubicadas a lo largo de la costilla, piel y larguero, comparadas con los resultados experimentales con un salto térmico positivo (a una temperatura de 80 ºC) y negativo (-40 ºC).
Los resultados muestran que las deformaciones son negativas (y por tanto los componentes se comprimen) para un salto térmico negativo, mientras que son positivas para un salto positivo y, por ende, el ensamblaje se expande. El modelo de elementos finitos predice razonablemente bien las tendencias, la magnitud y el signo de la deformación con todos los componentes. Sin embargo, existe una pequeña subestimación del valor absoluto. Esta diferencia puede venir dada por varias razones [8]:
- Tensiones residuales en los laminados debido al curado, omitidas en el modelo.
- Durante el montaje, se forzó a los componentes para poder atornillarlos debido a las pequeñas tolerancias, causando tensiones residuales las cuales son desconocidas.
- Pequeños gradientes de temperatura a lo largo del ensamblaje en los experimentos (mientras que en el modelo la temperatura es homogénea).
- La deformación en los laminados es muy pequeña y, por tanto, difícil de medir con precisión en el ensayo.
- El coeficiente de expansión en la dirección de la fibra del laminado (Tabla 2) presenta una dispersión considerable que afecta el cálculo del coeficiente equivalente del laminado.
En cualquier caso, la comparativa favorable entre el modelo y los experimentos prueba que el modelo de elementos finitos es suficientemente preciso. Consecuentemente, el uso de elementos viga y superficie para modelar los tornillos es adecuado.
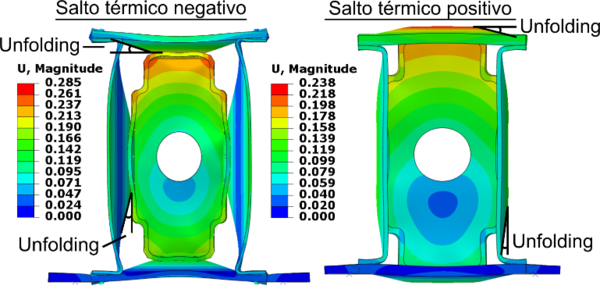
La Figura 11 muestra el desplazamiento del subcomponente al final del salto térmico. La costilla se expande o contrae (según si el salto es positivo o negativo) más que los laminados, por tanto, forzándolos a deformarse a flexión. Nótese, además que, debido a la flexión, el ángulo entre la costilla y la piel, así como entre el larguerillo y la piel (que previo a las cargas era de 90º) ha variado. Este efecto, llamado “unfolding” puede producir cargas indeseadas debido al cambio de forma de la costilla. Este es un aspecto importante a considerar en el diseño de la costilla. Finalmente, destacamos que el tiempo computacional, usando 24 cpus, es aproximadamente de 3
horas, mostrando la eficiencia del modelo. Con el modelo ya validado a nivel subcomponente, procedemos a estudiar el cajón de ala completo.
4.3 Nivel componente: cajón de ala
Las mediciones experimentales de varias galgas en la costilla, piel superior y larguero se comparan con el modelo en la Figura 12 para el salto térmico negativo. Igual que con el subcomponente, la predicción del modelo en las costillas es excelente, tanto en valor como en tendencia. Por otro lado, en los laminados las tendencias están bien predichas por el modelo, aunque los valores absolutos están significativamente subestimados en el larguero y muy sobreestimados en la piel.
Estas diferencias las atribuimos a las mismas razones antes comentadas en la sección 4.2, especialmente, a las tensiones producidas durante el ensamblaje. En cualquier caso, teniendo en cuenta la complejidad de la estructura, el modelo captura razonablemente bien las deformaciones. La comparativa con un salto térmico positivo fue muy similar. A continuación, usamos el modelo para estudiar con más detalle el comportamiento del cajón de ala.
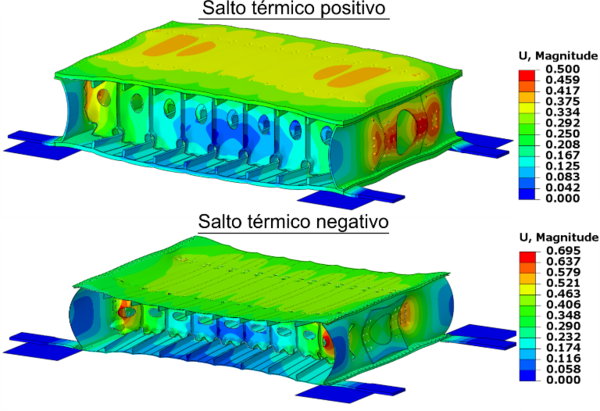
La Figura 13 muestra el desplazamiento del cajón de ala predicho por el modelo al final del salto térmico positivo y negativo. Como con el subcomponente, la costilla se expande o contrae (según el signo del salto de temperatura) más que el resto de componentes, forzándolos a flexionar. La flexión es bastante significativa en el centro del cajón. Todo seguido estudiamos algunas de las áreas más críticas según el modelo: el agujero central de las costillas, el agujero de ratón (el pequeño espacio entre unidades de la costilla) y las cargas en los tornillos. Además, comparamos el diferente comportamiento entre las dos costillas.
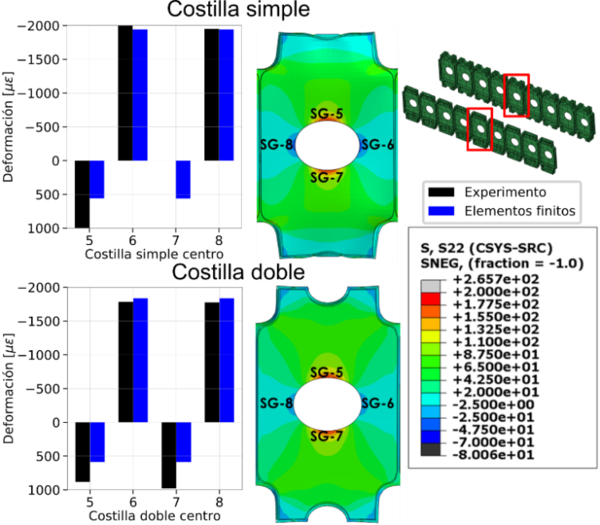
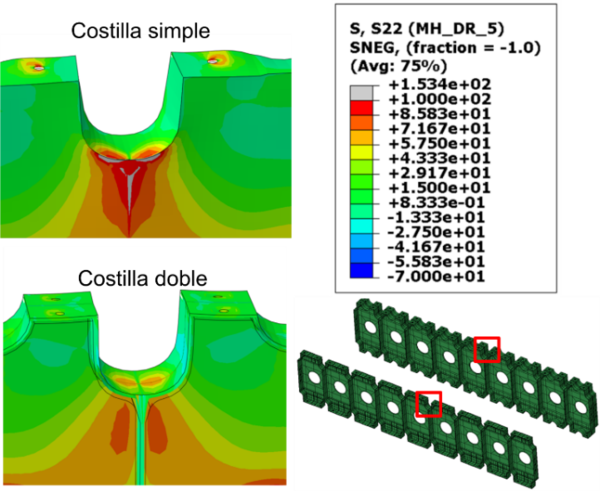
La tensión circunferencial en el agujero central de las dos costillas en la unidad del centro se muestra en la Figura 14 con un salto térmico negativo, dado que es el caso más crítico. Podemos observar tensiones de hasta 200 MPa en la parte superior e inferior del agujero central, siendo el valor ligeramente superior con la costilla simple. Estas tensiones son por tanto muy críticas especialmente bajo condiciones de fatiga térmica. Nótese la deformación del agujero, que pasa a ser elíptico debido a la flexión de las pieles y la compresión de la estructura. Además, las galgas ubicadas alrededor del agujero en los experimentos muestran la misma tendencia que la simulación, validando nuevamente el modelo numérico. Por otro lado, estas tensiones desaparecen en las unidades de las costillas situadas en los extremos, que están unidas con el larguero (véase Figura 15). Esto se produce por el hecho que la flexión vertical es menor en las unidades de las costillas unidas al larguero, que en las unidades centrales. Un detalle importante es que la costilla del subcomponente se comporta similar a estas unidades de la costilla del cajón unidas a los largueros. Consecuentemente, el subcomponente no captura las altas tensiones circunferenciales observadas en las unidades centrales de las costillas del cajón de ala. Por tanto, el subcomponente no es una unidad suficientemente representativa del cajón completo.
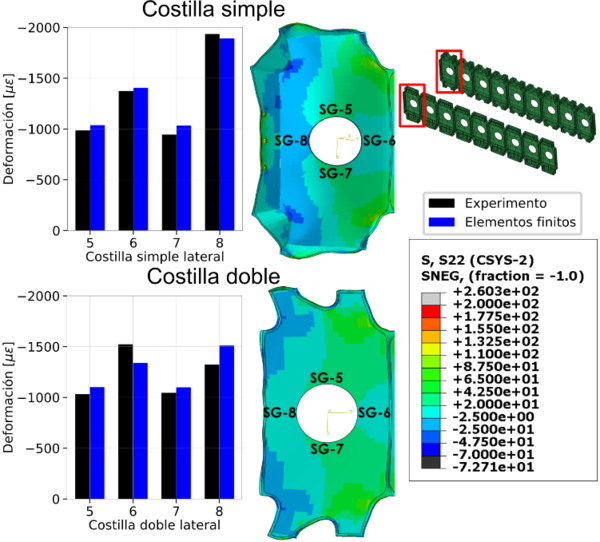
Otro punto importante es la gran diferencia en deformación entre las costillas simple y doble en la unión con el larguero, véase Figura 15. Mientras que la costilla doble casi no se deforma debido a su alta rigidez, la costilla simple no es suficientemente rígida para mantener su forma. Las galgas ubicadas alrededor del agujero en los experimentos muestran nuevamente la misma tendencia que la simulación (Figura 15). En cualquier caso, se produce “unfolding” con el larguerillo y con las pieles. Aunque se intentó medir el unfolding usando galgas en los ensayos, desafortunadamente la ubicación en donde se colocaron las galgas resultó no ser óptima para capturar este fenómeno.
Otro punto crítico, como se ha avanzado anteriormente, es el denominado “agujero de ratón”. Las tensiones circunferenciales en esta región se muestran para las dos costillas en la Figura 16, en las unidades centrales. Nuevamente, aparecen tensiones significativas del orden de 150 MPa, siendo algo inferiores para la costilla doble. Igual que en el agujero central, estas tensiones son críticas en ciclos de fatiga. Viendo el análisis de todas las zonas críticas, podemos concluir que la costilla doble funciona mejor que la simple, sobretodo en la unión con el larguero, sin embargo, esta es más pesada. Por tanto, la opción más eficiente sería un diseño híbrido entre las dos: costilla doble en la unión con los largueros, y costilla simple en el resto de unidades.
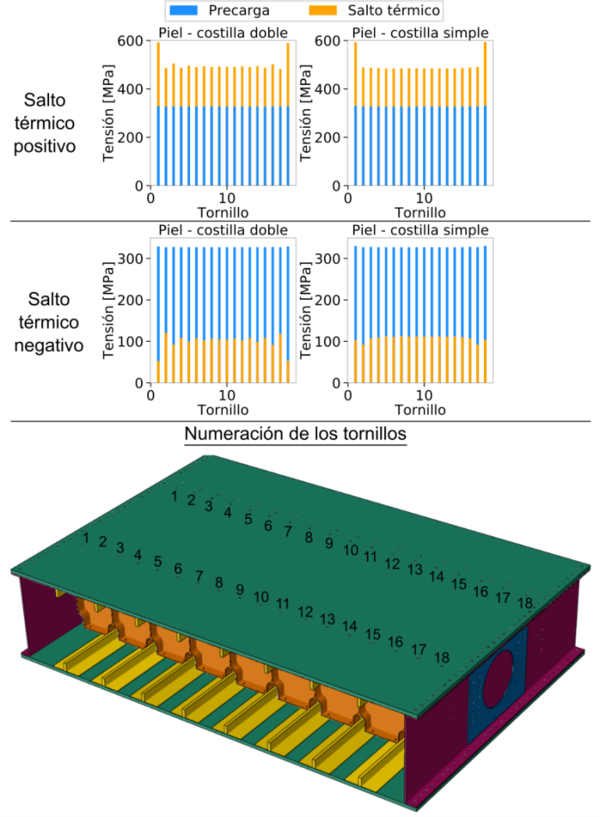
Además, otro punto de importancia es la variación de la tensión soportada por los tornillos debido a los cambios de temperatura. La Figura 17 muestra la tensión longitudinal promedio en los tornillos que unen la piel superior con cada costilla (dado que estos son los más críticos) para ambos saltos de temperatura. Bajo un salto térmico positivo, podemos observar que la tensión aumenta considerablemente en los tornillos, alcanzando los 600 MPa. Esto ocurre debido a que los componentes ensamblados se expanden más que el tornillo, forzándolo a alargarse. Este hecho es importante dado que puede conllevar a la fluencia de los tornillos y poner en peligro la unión. El fenómeno contrario ocurre con un salto negativo, donde la carga de los tornillos se ve hasta casi tres veces reducida. Con saltos térmicos mayores, la carga podría reducirse hasta llegar a la separación de la unión [2,8,27].
Por último, destacamos que el tiempo computacional para simular el cajón completo fue de unas 9 horas usando 24 cpus, mostrando de nuevo la eficiencia del modelo.
En resumen, este trabajo ha permitido obtener el comportamiento experimental y numérico de un subcomponente de un cajón de ala, así como del cajón de ala completo. La simulación de elementos finitos se correlaciona relativamente bien con los resultados experimentales. Consecuentemente, el enfoque numérico presentado en este trabajo se puede usar como substitución o complemento a ensayos experimentales para diseñar y analizar el comportamiento de un cajón de ala. Además, se ha determinado que la costilla es el componente crítico en la respuesta de un cajón de ala sometido a cargas térmicas. Para un correcto diseño, las cargas térmicas deben ser consideradas.
5 Conclusiones
En este artículo hemos presentado una metodología numérica y experimental para predecir el comportamiento de un cajón de ala de una aeronave sometida a cargas térmicas. Siguiendo una estrategia de diseño estructural piramidal, primero realizamos ensayos a nivel de probeta para caracterizar los materiales y comprender el comportamiento de uniones híbridas atornilladas. Tras ello, simulamos y ensayamos un subcomponente representativo de un cajón de ala, y finalmente, ensayamos y simulamos una sección del cajón completo.
La metodología experimental permite obtener la deformación en una gran estructura en función de la temperatura, corrigiendo, además, errores derivados en la lectura de las galgas. Por otro lado, el modelo de elementos finitos se correlaciona razonablemente bien con los resultados experimentales, incluso en el nivel de componente. La metodología numérica permite simular una estructura atornillada con centenas de tornillos, incluyendo contacto, fricción, expansión térmica, precarga, etc., de forma precisa y con un coste computacional relativamente bajo. Por ende, el enfoque numérico puede utilizarse como herramienta para analizar y diseñar este tipo de estructuras, reduciendo los costes experimentales y el tiempo de certificación de estructuras aeronáuticas.
Las discrepancias entre el modelo numérico y los ensayos se pueden atribuir a incertezas en la medida de las galgas, así como a la presencia de tensiones residuales térmicas debido al proceso de curado de la matriz y, sobre todo, tensiones generadas durante el proceso de montaje de los ensamblajes.
Agradecimientos
Este trabajo se ha llevado a cabo en el marco del proyecto EU H2020 Clean Sky 2 INNOHYBOX - Innovative solutions for metallic ribs or fittings introduced in a composite box to optimally deal with thermo-mechanical effects, del programa Clean Sky 2 Joint Undertaking (JU) bajo el acuerdo de subvención No. 785433.
Referencias
[1] Z. Kapidžić, L. Nilsson, H. Ansell, Conceptual studies of a composite–aluminum hybrid wing box demonstrator, Aerospace Science and Technology 32, 1, pág. 42-50 (2014). https://doi.org/10.1016/j.ast.2013.11.002
[2] A. Sasikumar, J.M. Guerrero, A. Quintanas-Corominas, J. Costa, Numerical study to understand thermo-mechanical effects on a composite-aluminium hybrid bolted joint, Composite Structures 275, 114396 (2021).
https://doi.org/10.1016/j.compstruct.2021.114396
[3] C. Stocchi, P. Robinson, S.T. Pinho, A detailed finite element investigation of composite bolted joints with countersunk fasteners, Composites Part A: Applied Science and Manufacturing 52, pág. 143-150 (2013).
https://doi.org/10.1016/j.compositesa.2012.09.013
[4] S. Noroozi, P. Sewell, J. Vinney, Investigation of Bolt Group Configurations on Load Distribution and Joint Failure, Mechanics of Advanced Materials and Structures 21, 4, pág. 422-432 (2014).
https://doi.org/10.1080/15376494.2012.697604
[5] C. Qiu , Z. Guan, S. Du, An improved characteristic length method for predicting the single bolt joint bearing strength considering secondary bending effect, Mechanics of Advanced Materials and Structures 0, 0, pág. 1-13 (2020).
https://doi.org/10.1080/15376494.2020.1821265
[6] N. Hirano, Y. Takao, W. Wang, Effects of Temperature on the Bearing Strength of CF/Epoxy Pinned Joints, Journal of Composite Materials 41, 3, pág. 335-351 (2007).
https://doi.org/10.1177/0021998306063374
[7] C. Coman, D.M. Constantinescu, Temperature effects on joint strength and failure modes of hybrid aluminum–composite countersunk bolted joints, Proceedings of the Institution of Mechanical Engineers, Part L: Journal of Materials: Design and Applications 233, 11, pág. 2204-2218 (2019).
https://doi.org/10.1177/1464420719837299
[8] J.M. Guerrero, A. Sasikumar, J. Llobet, J. Costa, Testing and simulation of a composite-aluminium wingbox subcomponent subjected to thermal loading. En preparación.
[9] EASA, Notification of a proposal to issue an airworthiness directive: Wing rib feet modification.
[10] Airbus A380 wing flaw undetected for a decade, https://www.reuters.com/article/uk-airbus-a380/airbus-a380wing-flaw-undetected-for-a-decade-iduslne84o00j20120525
[11] E. Madenci, S. Shkarayev, B. Sergeev, D. W. Oplinger, P. Shyprykevich, Analysis of composite laminates with multiple fasteners, International Journal of Solids and Structures 35, 15, pág. 1793-1811 (1998).
https://doi.org/10.1016/S0020-7683(97)00152-2
[12] M.A. McCarthy, V.P. Lawlor, W.F. Stanley, C.T. McCarthy, Bolt-hole clearance effects and strength criteria in single-bolt, single-lap, composite bolted joints, Composites Science and Technology 62, 10-11, pág. 1415-1431 (2002).
https://doi.org/10.1016/S0266-3538(02)00088-X
[13] C. Girard, M. L. Dano, A. Picard, G. Gendron, Bearing Behavior of Mechanically Fastened Joints in Composite Laminates--Part I: Strength and Local Strains, Mechanics of Advanced Materials and Structures 10, 1, pág. 1-21 (2003).
https://doi.org/10.1080/15376490306740
[14] L. Zhao, Z. Fang, F. Liu, M. Shan, J. Zhang, A modified stiffness method considering effects of hole tensile deformation on bolt load distribution in multi-bolt composite joints, Composites Part B: Engineering 171, pág. 264-271 (2019).
https://doi.org/10.1016/j.compositesb.2019.05.010
[15] J. Rouchon, Certification of large airplane composite structures, recent progress and new trends in compliance philosophy, 17th ICAS Congress 1, pág. 1439-1447 (1990).
http://www.icas.org/ICAS_ARCHIVE/ICAS1990/ICAS-90-1.8.1
[16] O. Omran, V. D. Nguyen, H. Jaffal, P. Coorevits, Development of a connector element for multi-material bolted-joint under tensile loading, Mechanics of Advanced Materials and Structures 0, 0, pág. 1-12 (2018).
https://doi.org/10.1080/15376494.2018.1452314
[17] J. Xiang, S. Zhao, D. Li, Y. Wu, An improved spring method for calculating the load distribution in multi-bolt composite joints, Composites Part B: Engineering 117, pág. 1-8 (2017).
http://dx.doi.org/10.1016/j.compositesb.2017.02.024
[18] T. Ireman, Three-dimensional stress analysis of bolted single-lap composite joints, Composite Structures 43, 3, pág. 195-216 (1998).
https://doi.org/10.1016/S0263-8223(98)00103-2
[19] M. L. Dano, G. Gendron, A. Picard, Stress and failure analysis of mechanically fastened joints in composite laminates, Composite Structures 50, 3, pág. 287-296 (2000).
https://doi.org/10.1016/S0263-8223(00)00119-7
[20] K.I. Tserpes, G. Labeas, P. Papanikos, Th. Kermanidis, Strength prediction of bolted joints in graphite/epoxy composite laminates, Composites Part B: Engineering 33, 7, pág. 521-529 (2002).
https://doi.org/10.1016/S1359-8368(02)00033-1
[21] M.A. McCarthy, C.T. McCarthy, V.P. Lawlor, W.F. Stanley, Three-dimensional finite element analysis of single-bolt, single-lap composite bolted joints: Part I - Model development and validation, Composite Structures 71, 2, pág. 140-158 (2005).
https://doi.org/10.1016/j.compstruct.2004.09.024
[22] C.T. McCarthy, M.A. McCarthy, Three-dimensional finite element analysis of single-bolt, single-lap composite bolted joints: Part II - Effects of bolt-hole clearance, Composite Structures 71, 2, pág. 159-175 (2005).
https://doi.org/10.1016/j.compstruct.2004.09.023
[23] Johan Ekh, Joakim Schön, Finite element modeling and optimization of load transfer in multi-fastener joints using structural elements, Composite Structures 82, 2, pág. 245-256 (2008).
https://doi.org/10.1016/j.compstruct.2007.01.005
[24] P.J. Gray, C.T. McCarthy, A highly efficient user-defined finite element for load distribution analysis of large-scale bolted composite structures, Composites Science and Technology 71, 12, pág. 1517-1527 (2011).
http://dx.doi.org/10.1016/j.compscitech.2011.06.011
[25] B. Mandal, A. Chakrabarti, Numerical failure assessment of multi-bolt FRP composite joints with varying sizes and preloads of bolts, Composite Structures 187, pág. 169-178 (2018).
https://doi.org/10.1016/j.compstruct.2017.12.048
[26] F. Liu, W. Yao, X. Shi, L. Zhao, J. Zhang, Bearing failure optimization of composite double-lap bolted joints based on a three-step strategy marked by feasible region reduction and model decoupling, Computers, Materials and Continua 62, 2, pág. 977-999 (2020).
doi:10.32604/cmc.2020.07184
[27] J.M. Guerrero, A. Sasikumar, J. Llobet, J. Costa, A computationally efficient methodology to simulate hybrid bolted joints including thermal effects, Aceptado para publicación en Mechanics of Advanced Materials and Structures.
[28] ASTM standard E228-11. Standard Test Method for Linear Thermal Expansion of Solid Materials with a Push-Rod Dilatometer, ASTM International, West Conshohocken, PA (2011).
[29] ASTM D3039 / D3039M-17. Standard Test Method for Tensile Properties of Polymer Matrix Composite Materials, ASTM International, West Conshohocken, PA (2017).
[30] ASTM D3518 / D3518M-18. Standard Test Method for In-Plane Shear Response of Polymer Matrix Composite Materials by Tensile Test of a ±45° Laminate, ASTM International, West Conshohocken, PA (2018).
[31] Dassault Systemes/ SIMULIA, ABAQUS, Inc. ABAQUS version 6.14 Documentation (2014).
[32] MatWeb, 2011. [Online]. URL: http://www.matweb.com/
[33] F. S. Jumbo, I. A. Ashcroft, A. D. Crocombe, M. M. Abdel Wahab, Thermal residual stress analysis of epoxy bi-material laminates and bonded joints, International Journal of Adhesion and Adhesives, 30, 7, pág. 523-538 (2010).
Document information
Published on 22/01/22
Accepted on 23/12/21
Submitted on 23/12/21
Volume 06 - AEMAC en PROYECTOS EUROPEOS (2022), Issue Núm. 1 - Monográfico Proyectos Europeos, 2022
DOI: 10.23967/r.matcomp.2022.01.008
Licence: Other
Share this document
Keywords
claim authorship
Are you one of the authors of this document?