Shinsm2021 (talk | contribs) m (Tag: Visual edit) |
|||
| (28 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
== Abstract == | == Abstract == | ||
| − | Robust design has received a great deal of attention from quality researchers in recent years, and a number of optimization methodologies based on the dual response format have been proposed. The majority of existing bi-objective optimization models concentrate on the trade-offs between the process mean and variability functions without investigating the interactions between control factors and quality characteristics. The primary objective of this research is to integrate the Stackelberg leadership model into the robust design procedure and propose a Stackelberg game-based robust design (SGRD) method to determine appropriate control factor settings by minimizing the values of desired optimization targets based on an analysis of possible combinations of input and output quality parameters. Herein, first, a bi-objective robust design optimization problem is formulated as a dual response model using response surface methodology (RSM). Second, the proposed SGRD model is developed via decomposition into two leader-follower game models. Finally, the mean square error (MSE) criterion is applied to evaluate models | + | Robust design has received a great deal of attention from quality researchers in recent years, and a number of optimization methodologies based on the dual response format have been proposed. The majority of existing bi-objective optimization models concentrate on the trade-offs between the process mean and variability functions without investigating the interactions between control factors and quality characteristics. The primary objective of this research is to integrate the Stackelberg leadership model into the robust design procedure and propose a Stackelberg game-based robust design (SGRD) method to determine appropriate control factor settings by minimizing the values of desired optimization targets based on an analysis of possible combinations of input and output quality parameters. Herein, first, a bi-objective robust design optimization problem is formulated as a dual response model using response surface methodology (RSM). Second, the proposed SGRD model is developed via decomposition into two leader-follower game models. Finally, the mean square error (MSE) criterion is applied to evaluate models and select non-dominated solutions in various situations. Numerical examples are used to demonstrate that the proposed method provides significant solutions in cases containing unidentified priorities between the dual responses and undiscovered correlations among several inputs and outcomes. In addition, according to the case study analysis, the proposed method is more efficient than the conventional dual response approach when dealing with bi-objective robust design optimization problems. |
'''Keywords''': Robust Parameter Design, Bi-objective Optimization, Dual Response Approach, Game Theory, Stackelberg Competition model | '''Keywords''': Robust Parameter Design, Bi-objective Optimization, Dual Response Approach, Game Theory, Stackelberg Competition model | ||
| Line 9: | Line 9: | ||
The subject of quality management and improvement has received widespread and consistent attention from researchers in the last century. Many studies on literature have shown that a high-efficiency and cost-efficient system plays a vital role in realistic production processes. Taguchi <span id="cite-_Ref76149437"></span>[[#_Ref76149437|[1]]] introduced a procedure for experimental design, which is also known as robust design, and that improves the robustness of quality characteristics by minimizing the response to noise factors. The main objective of robust design is to determine the optimal design settings for a product that can minimize the process variability and target deviation. Based on Taguchi's philosophy, subsequent experimental design methods have been developed to identify controlled parameter settings and, thus, improve the robustness of the production process. | The subject of quality management and improvement has received widespread and consistent attention from researchers in the last century. Many studies on literature have shown that a high-efficiency and cost-efficient system plays a vital role in realistic production processes. Taguchi <span id="cite-_Ref76149437"></span>[[#_Ref76149437|[1]]] introduced a procedure for experimental design, which is also known as robust design, and that improves the robustness of quality characteristics by minimizing the response to noise factors. The main objective of robust design is to determine the optimal design settings for a product that can minimize the process variability and target deviation. Based on Taguchi's philosophy, subsequent experimental design methods have been developed to identify controlled parameter settings and, thus, improve the robustness of the production process. | ||
| − | Conventional robust design methods can be preliminarily classified as sequential and simultaneous optimization models. Vining and Myers <span id='cite-_Ref76149715'></span>[[#_Ref76149715|[2]]] investigated the application of a dual response approach to minimize the process variability by assigning the process mean at target with defining the priority criterion to separately optimize the estimated functions for the process mean and the standard deviation response based on RSM. Following the prioritized dual response format, Del Castillo and Montgomery <span id='cite-_Ref76149733'></span>[[#_Ref76149733|[3]]] and Copeland and Nelson <span id='cite-_Ref76149745'></span>[[#_Ref76149745|[4]]] presented improved optimization techniques for the situations in which one objective is achieved in advance (i.e., the process bias or variance is customer-specified). Instead of assigning a specific value to the optimization objective, the bias-specified and variability-specified robust design methods reached the goal of robust design by setting upper bounds for the process mean and standard deviation, respectively <span id='cite-_Ref76149761'></span>[[#_Ref76149761|[5,6]]]. Priority-based methods reduce the complexity of problems by transforming multi-objective models | + | Conventional robust design methods can be preliminarily classified as sequential and simultaneous optimization models. Vining and Myers <span id='cite-_Ref76149715'></span>[[#_Ref76149715|[2]]] investigated the application of a dual response approach to minimize the process variability by assigning the process mean at the target with defining the priority criterion to separately optimize the estimated functions for the process mean and the standard deviation response based on RSM. Following the prioritized dual response format, Del Castillo and Montgomery <span id='cite-_Ref76149733'></span>[[#_Ref76149733|[3]]] and Copeland and Nelson <span id='cite-_Ref76149745'></span>[[#_Ref76149745|[4]]] presented improved optimization techniques for the situations in which one objective is achieved in advance (i.e., the process bias or variance is customer-specified). Instead of assigning a specific value to the optimization objective, the bias-specified and variability-specified robust design methods reached the goal of robust design by setting upper bounds for the process mean and standard deviation, respectively <span id='cite-_Ref76149761'></span>[[#_Ref76149761|[5,6]]]. Priority-based methods reduce the complexity of problems by transforming multi-objective models into constrained single-objective models. However, existing prioritization schemes are limited because the majority of feasible solutions in the solution space are removed once the first prioritized objective has finished optimization. In this case, the reliability of efficient solutions in objective space is significantly decreased. |
| − | The MSE method proposed by Lin and Tu <span id='cite-_Ref76150123'></span>[[#_Ref76150123|[7]]], which is based on the relaxed zero-bias assumption, deals with the dual response problem in a simultaneous mode. In terms of the MSE model and its simultaneous optimization order, the concept of weighted sum model is used by Tang and Xu <span id='cite-_Ref76150372'></span>[[#_Ref76150372|[8]]], Koksoy and Doganaksoy <span id='cite-_Ref76150383'></span>[[#_Ref76150383|[9]]] and Ding et al. <span id='cite-_Ref76150396'></span>[[#_Ref76150396|[10]]] to investigate the trade-offs between process bias and variance on different weights, instead of the default equivalent weight terms used by Lin and Tu <span id='cite-_Ref76150123'></span>[[#_Ref76150123|[7]]]. To find non-dominated solutions and non-convex Pareto frontier, Shin and Cho <span id='cite-_Ref76150480'></span>[[#_Ref76150480|[11]]] introduced the lexicographic weighted Tchebycheff method based on the L-infinity norm. The weight-based simultaneous models show good accuracy and efficiency when used to search for the optimal solutions of a robust design problem. Nevertheless, it is difficult to identify the actual weight terms in simultaneous models by quality operators in practice. | + | The MSE method proposed by Lin and Tu <span id='cite-_Ref76150123'></span>[[#_Ref76150123|[7]]], which is based on the relaxed zero-bias assumption, deals with the dual response problem in a simultaneous mode. In terms of the MSE model and its simultaneous optimization order, the concept of weighted sum model is used by Tang and Xu <span id='cite-_Ref76150372'></span>[[#_Ref76150372|[8]]], Koksoy and Doganaksoy <span id='cite-_Ref76150383'></span>[[#_Ref76150383|[9]]] and,, Ding et al. <span id='cite-_Ref76150396'></span>[[#_Ref76150396|[10]]] to investigate the trade-offs between process bias and variance on different weights, instead of the default equivalent weight terms used by Lin and Tu <span id='cite-_Ref76150123'></span>[[#_Ref76150123|[7]]]. To find non-dominated solutions and non-convex Pareto frontier, Shin and Cho <span id='cite-_Ref76150480'></span>[[#_Ref76150480|[11]]] introduced the lexicographic weighted Tchebycheff method based on the L-infinity norm. The weight-based simultaneous models show good accuracy and efficiency when used to search for the optimal solutions of a robust design problem. Nevertheless, it is difficult to identify the actual weight terms in simultaneous models by quality operators in practice. |
The majority of existing robust design optimization methodologies focus on the trade-offs between process bias and variability. However, the interaction between control variables and quality characteristics has always been ignored. To this end, we incorporate the Stackelberg game theory philosophy into classical sequential optimization methods that can consider the impact of control factors on output performance. In the proposed SGRD model in this paper, one object is optimized in advance as the leader, given the constraint of another object (the follower)'s best response function. The leader's objective function may be adjusted according to the follower's best response function, which is variable due to the presence of various controlled factors. Therefore, it is worth discovering situations with permutations and combinations among controlled factors to analyze the correlations between input factors and quality characteristics. Doing so means that every possible interaction between the preferred objective and non-preferred target are taken into account. In addition, in real-world production procedures, quality engineers are often confronted with scenarios in which the importance between process characteristics may be undiscovered or specified by customers. The numerical examples in Section 4 include two cases; the first has unknown priority for quality characteristics, while the second is based on customer-specified bias-prioritized and variance-prioritized situations. | The majority of existing robust design optimization methodologies focus on the trade-offs between process bias and variability. However, the interaction between control variables and quality characteristics has always been ignored. To this end, we incorporate the Stackelberg game theory philosophy into classical sequential optimization methods that can consider the impact of control factors on output performance. In the proposed SGRD model in this paper, one object is optimized in advance as the leader, given the constraint of another object (the follower)'s best response function. The leader's objective function may be adjusted according to the follower's best response function, which is variable due to the presence of various controlled factors. Therefore, it is worth discovering situations with permutations and combinations among controlled factors to analyze the correlations between input factors and quality characteristics. Doing so means that every possible interaction between the preferred objective and non-preferred target are taken into account. In addition, in real-world production procedures, quality engineers are often confronted with scenarios in which the importance between process characteristics may be undiscovered or specified by customers. The numerical examples in Section 4 include two cases; the first has unknown priority for quality characteristics, while the second is based on customer-specified bias-prioritized and variance-prioritized situations. | ||
| Line 43: | Line 43: | ||
=== 3.1 Extensive-form game model === | === 3.1 Extensive-form game model === | ||
| − | Game theory is widely recognized as an analytical tool to exploit the interactions among several participants; it has been applied to many fields. In terms of the properties of the game, a game can be classified as | + | Game theory is widely recognized as an analytical tool to exploit the interactions among several participants; it has been applied to many fields. In terms of the properties of the game, a game can be classified as cooperative/non-cooperative, simultaneous/sequential, perfect information/imperfect information, symmetric/asymmetric, and zero-sum/non-zero-sum. In this paper, we concentrate mostly on a non-cooperative sequential game model with perfect information. |
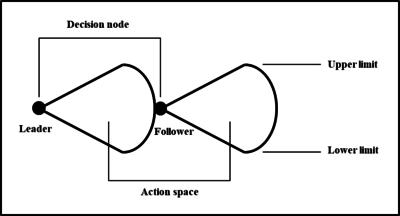
In a general sequential game, which is also known in game theory as an extensive-form game, players take their actions in a specified sequence. Usually, the player who moves first is the front player, and the player who moves later is the rear player. The front player can make his decision in advance according to the anticipation of the rear player's movement. Then, the rear player can move based on the actions of the front player. Similar to a general sequential game, in a Stackelberg game, the player who makes the first decision is called the game leader, and the player who moves after the leader is known as the game follower. A particular extensive-form game with infinite action spaces can be used to represent the Stackelberg competition model, which is illustrated in [[#img-2|Figure 2]]. The potential actions of each player are shown fanning out from the player's decision node. Players can select and make decisions from the action space, which may be constrained by boundaries. | In a general sequential game, which is also known in game theory as an extensive-form game, players take their actions in a specified sequence. Usually, the player who moves first is the front player, and the player who moves later is the rear player. The front player can make his decision in advance according to the anticipation of the rear player's movement. Then, the rear player can move based on the actions of the front player. Similar to a general sequential game, in a Stackelberg game, the player who makes the first decision is called the game leader, and the player who moves after the leader is known as the game follower. A particular extensive-form game with infinite action spaces can be used to represent the Stackelberg competition model, which is illustrated in [[#img-2|Figure 2]]. The potential actions of each player are shown fanning out from the player's decision node. Players can select and make decisions from the action space, which may be constrained by boundaries. | ||
| Line 60: | Line 60: | ||
=== 3.2 The Stackelberg equilibrium: a general formulation === | === 3.2 The Stackelberg equilibrium: a general formulation === | ||
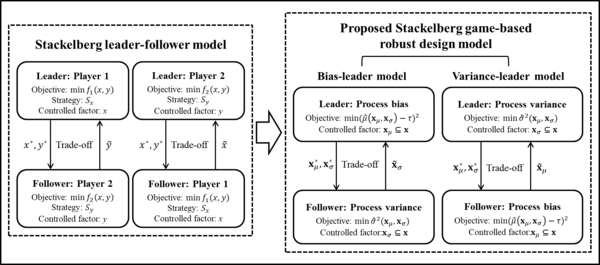
| − | We identify two players in a non-cooperative sequential Stackelberg game that separately control the optimization objectives and control factors. Player 1's objective is to minimize his performance function <math display="inline">{f}_{1}(x,y)</math> and considers only factor <math display="inline">x</math>. Correspondingly, the objective of player 2 is to minimize his performance function <math display="inline">{f}_{2}(x,y)</math> and considers only factor <math display="inline">y</math>. Both functions are based on the factors <math display="inline">x</math> and <math display="inline">y</math>, which means that the strategies of two players | + | We identify two players in a non-cooperative sequential Stackelberg game that separately control the optimization objectives and control factors. Player 1's objective is to minimize his performance function <math display="inline">{f}_{1}(x,y)</math> and considers only factor <math display="inline">x</math>. Correspondingly, the objective of player 2 is to minimize his performance function <math display="inline">{f}_{2}(x,y)</math> and considers only factor <math display="inline">y</math>. Both functions are based on the factors <math display="inline">x</math> and <math display="inline">y</math>, which means that the strategies of two players have interacted. A variable set <math display="inline">(x,y)\in {(S}_{x},\, {S}_{y})</math> refers to a pair of rational strategies played by the two players, where <math display="inline">{S}_{x}</math> and <math display="inline">{S}_{y}</math> are the rational strategies set of the two players, respectively. The game ends when the game leader has optimized his performance function, which also means that an equilibrium is found. The Stackelberg equilibrium point and the associated Stackelberg equilibrium solution are denoted as <math display="inline">\left( {x}^{\ast },{y}^{\ast }\right)</math> and <math display="inline">\lbrace {f}_{1}\left( {x}^{\ast },{y}^{\ast }\right) ,{f}_{2}\left( {x}^{\ast },{y}^{\ast }\right) \rbrace</math> , separately. If player 1 acts as the leader and player 2 acts as the follower, based on the Stackelberg game rules, player 1 optimizes his objective <math display="inline">{f}_{1}(x,y)</math> first, and player 2 optimizes <math display="inline">{f}_{2}(x,y)</math> later. The Stackelberg equilibrium point <math display="inline">({x}^{\ast },{y}^{\ast })</math> can be found in the objective function of player 1 if: |
{| class="formulaSCP" style="width: 100%;border-collapse: collapse;width: 100%;text-align: center;" | {| class="formulaSCP" style="width: 100%;border-collapse: collapse;width: 100%;text-align: center;" | ||
| Line 80: | Line 80: | ||
{| style="text-align: center; margin:auto;width: 100%;" | {| style="text-align: center; margin:auto;width: 100%;" | ||
|- | |- | ||
| − | | style="text-align: center;" | <math>\tilde{y}=\,\mathrm{ | + | | style="text-align: center;" | <math>\tilde{y}=\,\mathrm{argmin}_{y\in {S}_{y}}\,{f}_{2}(x,y)=\frac{\partial {f}_{2}(x,y)}{\partial y}.</math> |
|} | |} | ||
|} | |} | ||
| − | Accordingly, if player 2 is leader and player 1 is the follower, the Stackelberg equilibrium solution can be obtained in the objective function of player 2 if: | + | Accordingly, if player 2 is the leader and player 1 is the follower, the Stackelberg equilibrium solution can be obtained in the objective function of player 2 if: |
{| class="formulaSCP" style="width: 100%;border-collapse: collapse;width: 100%;text-align: center;" | {| class="formulaSCP" style="width: 100%;border-collapse: collapse;width: 100%;text-align: center;" | ||
| Line 103: | Line 103: | ||
{| style="text-align: center; margin:auto;width: 100%;" | {| style="text-align: center; margin:auto;width: 100%;" | ||
|- | |- | ||
| − | | style="text-align: center;" | <math>{\tilde{x}=}\,\mathrm{ | + | | style="text-align: center;" | <math>{\tilde{x}=}\,\mathrm{argmin}_{x\in {S}_{x}}\,{f}_{1}(x,y)=\frac{\partial {f}_{1}(x,y)}{\partial x}.</math> |
|} | |} | ||
|} | |} | ||
| Line 185: | Line 185: | ||
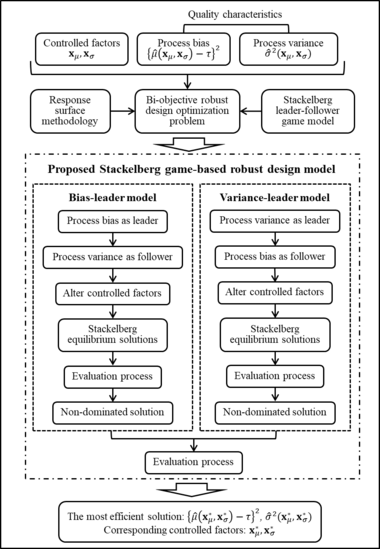
=== 3.4 Proposed SGRD model === | === 3.4 Proposed SGRD model === | ||
| − | The integration procedure of the proposed bi-objective SGRD optimization problem from a Stackelberg game model is shown in | + | The integration procedure of the proposed bi-objective SGRD optimization problem from a Stackelberg game model is shown in [[#img-3|Figure 3]]. The process bias and variance can be identified as the two game players of the proposed SGRD model. Then, the objective functions introduced in the Stackelberg leader-follower model, <math display="inline">{f}_{1}\left( x,y\right)</math> and <math display="inline">{f}_{2}\left( x,y\right)</math> , can be replaced by the estimated functions of process bias <math display="inline">{(\hat{\mu }\left( \boldsymbol\mathrm{x}\right) -\tau )}^{2}</math> and variance <math display="inline">{\hat{\sigma }}^{2}(\boldsymbol\mathrm{x})</math>, respectively. The optimization objectives of the bi-objective optimization problem <math display="inline">\left\{ {(\hat{\mu }\left( \boldsymbol\mathrm{x}\right) -\tau )}^{2},\, {\hat{\sigma }}^{2}(\boldsymbol\mathrm{x})\right\}</math> and the input factors <math display="inline">\boldsymbol\mathrm{x}</math> are separately controlled by the process bias and variance. We can define the input factors that are controlled by the process bias are denoted by <math display="inline">\, {\boldsymbol\mathrm{x}}_{\mu }</math>, and <math display="inline">\, {\boldsymbol\mathrm{x}}_{\mu }\subseteq \boldsymbol\mathrm{x}</math>. Correspondingly,''' '''as the complement of <math display="inline">{\boldsymbol\mathrm{x}}_{\mu }</math>, the input factors that are controlled by the process variance are denoted by <math display="inline">{\boldsymbol\mathrm{\, x}}_{\sigma }</math>,where <math display="inline">{\boldsymbol\mathrm{x}}_{\sigma }=</math><math>{{\boldsymbol\mathrm{x}}_{\mu }}^{c}\subseteq \boldsymbol\mathrm{x}</math>. Similar to the Stackelberg game model, the response functions of process bias and variance are depended on the controlled factors <math display="inline">{\boldsymbol\mathrm{x}}_{\mu }</math> and <math display="inline">{\boldsymbol\mathrm{x}}_{\sigma }</math>. Thus, the objective functions for the process bias and variance can be written as <math display="inline">{(\hat{\mu }\left( {\boldsymbol\mathrm{x}}_{\mu },{\boldsymbol\mathrm{x}}_{\sigma }\right) -\tau )}^{2}</math> and <math display="inline">{\hat{\sigma }}^{2}({\boldsymbol\mathrm{x}}_{\mu },{\boldsymbol\mathrm{x}}_{\sigma })</math>, respectively. Based on the Stackelberg game rules, the target of process bias is to minimize <math display="inline">{(\hat{\mu }\left( {\boldsymbol\mathrm{x}}_{\mu },{\boldsymbol\mathrm{x}}_{\sigma }\right) -\tau )}^{2}</math> and considers only factor <math display="inline">{\boldsymbol\mathrm{x}}_{\mu }</math>. Accordingly, the target of process variance is to minimize <math display="inline">{\hat{\sigma }}^{2}({\boldsymbol\mathrm{x}}_{\mu },{\boldsymbol\mathrm{x}}_{\sigma })</math> and considers only factor <math display="inline">{\boldsymbol\mathrm{x}}_{\sigma }</math>. |
<div id='img-3'></div> | <div id='img-3'></div> | ||
| Line 215: | Line 215: | ||
{| style="text-align: center; margin:auto;width: 100%;" | {| style="text-align: center; margin:auto;width: 100%;" | ||
|- | |- | ||
| − | | style="text-align: center;" | <math>\mathrm{{\tilde{\boldsymbol\mathrm{x}}}_{\sigma }=}\,\mathrm{ | + | | style="text-align: center;" | <math>\mathrm{{\tilde{\boldsymbol\mathrm{x}}}_{\sigma }=}\,\mathrm{argmin}_{{\boldsymbol\mathrm{x}}_{\sigma }\in X}\,{\hat{\sigma }}^{2}({\boldsymbol\mathrm{x}}_{\mu },{\boldsymbol\mathrm{x}}_{\sigma })=\frac{\partial {\hat{\sigma }}^{2}({\boldsymbol\mathrm{x}}_{\mu },{\boldsymbol\mathrm{x}}_{\sigma })}{\partial {\boldsymbol\mathrm{x}}_{\sigma }}</math> |
|} | |} | ||
|} | |} | ||
| Line 240: | Line 240: | ||
{| style="text-align: center; margin:auto;width: 100%;" | {| style="text-align: center; margin:auto;width: 100%;" | ||
|- | |- | ||
| − | | style="text-align: center;" | <math>\mathrm{{\tilde{\boldsymbol\mathrm{x}}}_{\mu }=}\,\mathrm{ | + | | style="text-align: center;" | <math>\mathrm{{\tilde{\boldsymbol\mathrm{x}}}_{\mu }=}\,\mathrm{argmin}_{{\boldsymbol\mathrm{x}}_{\mu }\in X}\,{(\hat{\mu }\left( {\boldsymbol\mathrm{x}}_{\mu },{\boldsymbol\mathrm{x}}_{\sigma }\right) -\tau )}^{2}=\frac{\partial {(\hat{\mu }\left( {\boldsymbol\mathrm{x}}_{\mu },{\boldsymbol\mathrm{x}}_{\sigma }\right) -\tau )}^{2}}{\partial {\boldsymbol\mathrm{x}}_{\mu }}</math> |
|} | |} | ||
|} | |} | ||
| Line 251: | Line 251: | ||
<div id='tab-1'></div> | <div id='tab-1'></div> | ||
| − | {| class="wikitable" style="margin: 1em auto 0.1em auto;border-collapse: collapse;font-size:85%;width: | + | {| class="wikitable" style="margin: 1em auto 0.1em auto;border-collapse: collapse;font-size:85%;width:75%;" |
|-style="text-align:left" | |-style="text-align:left" | ||
| − | | '''Step 1. Input data and assign controlled factors''' | + | | style="padding-top:10px;"| '''Step 1. Input data and assign controlled factors''' |
| − | Separate the input factors <math display="inline">\boldsymbol\mathrm{x}</math> into controlled factors by the process bias <math display="inline">\left( {\boldsymbol\mathrm{x}}_{\mu }\right)</math> and variance <math display="inline">\left( {\boldsymbol\mathrm{x}}_{\sigma }\right)</math> . | + | :Separate the input factors <math display="inline">\boldsymbol\mathrm{x}</math> into controlled factors by the process bias <math display="inline">\left( {\boldsymbol\mathrm{x}}_{\mu }\right)</math> and variance <math display="inline">\left( {\boldsymbol\mathrm{x}}_{\sigma }\right)</math>. |
'''Step 2. Obtain estimated functions of the quality characteristics''' | '''Step 2. Obtain estimated functions of the quality characteristics''' | ||
| − | Use RSM to estimate the response functions of the process mean <math display="inline">\hat{\mu }\left( {\boldsymbol\mathrm{x}}_{\mu },{\boldsymbol\mathrm{x}}_{\sigma }\right)</math> and standard deviation <math display="inline">\hat{\sigma }\left( {\boldsymbol\mathrm{x}}_{\mu },{\boldsymbol\mathrm{x}}_{\sigma }\right)</math> . | + | :Use RSM to estimate the response functions of the process mean <math display="inline">\hat{\mu }\left( {\boldsymbol\mathrm{x}}_{\mu },{\boldsymbol\mathrm{x}}_{\sigma }\right)</math> and standard deviation <math display="inline">\hat{\sigma }\left( {\boldsymbol\mathrm{x}}_{\mu },{\boldsymbol\mathrm{x}}_{\sigma }\right)</math>. |
'''Step 3. Formulate a bi-objective robust design model''' | '''Step 3. Formulate a bi-objective robust design model''' | ||
| − | Formulate the estimated functions of process bias <math display="inline">{(\hat{\mu }\left( {\boldsymbol\mathrm{x}}_{\mu },{\boldsymbol\mathrm{x}}_{\sigma }\right) -\tau )}^{2}</math> and variance <math display="inline">{\hat{\sigma }}^{2}({\boldsymbol\mathrm{x}}_{\mu },{\boldsymbol\mathrm{x}}_{\sigma })</math> as a bi-objective optimization problem: | + | :Formulate the estimated functions of process bias <math display="inline">{(\hat{\mu }\left( {\boldsymbol\mathrm{x}}_{\mu },{\boldsymbol\mathrm{x}}_{\sigma }\right) -\tau )}^{2}</math> and variance <math display="inline">{\hat{\sigma }}^{2}({\boldsymbol\mathrm{x}}_{\mu },{\boldsymbol\mathrm{x}}_{\sigma })</math> as a bi-objective optimization problem: |
| − | <math>\mathrm{min}~{\left[ {(\hat{\mu }\left( {\boldsymbol\mathrm{x}}_{\mu },{\boldsymbol\mathrm{x}}_{\sigma }\right) -\tau )}^{2},\, {\hat{\sigma }}^{2}({\boldsymbol\mathrm{x}}_{\mu },{\boldsymbol\mathrm{x}}_{\sigma })\right] }^{T}.</math> | + | :<math>\mathrm{min}~{\left[ {(\hat{\mu }\left( {\boldsymbol\mathrm{x}}_{\mu },{\boldsymbol\mathrm{x}}_{\sigma }\right) -\tau )}^{2},\, {\hat{\sigma }}^{2}({\boldsymbol\mathrm{x}}_{\mu },{\boldsymbol\mathrm{x}}_{\sigma })\right] }^{T}.</math> |
'''Step 4. Evaluate the bias-leader model of the proposed SGRD model''' | '''Step 4. Evaluate the bias-leader model of the proposed SGRD model''' | ||
| − | Evaluate the bias-leader model: <math display="inline">\left\{ \begin{matrix}\mathrm{{(\hat{\mu }\left( {\boldsymbol\mathrm{x}}_{\mu }^{\ast },{\boldsymbol\mathrm{x}}_{\sigma }^{\ast }\right) -\tau )}^{2}=}\,\mathrm{inf}_{{\boldsymbol\mathrm{x}}_{\mu }\in X}\,{(\hat{\mu }\left( {\boldsymbol\mathrm{x}}_{\mu },{\tilde{\boldsymbol\mathrm{x}}}_{\sigma }\right) -\tau )}^{2}\\\mathrm{{\tilde{\boldsymbol\mathrm{x}}}_{\sigma }=}\,\mathrm{ | + | :Evaluate the bias-leader model: <math display="inline">\left\{ \begin{matrix}\mathrm{{(\hat{\mu }\left( {\boldsymbol\mathrm{x}}_{\mu }^{\ast },{\boldsymbol\mathrm{x}}_{\sigma }^{\ast }\right) -\tau )}^{2}=}\,\mathrm{inf}_{{\boldsymbol\mathrm{x}}_{\mu }\in X}\,{(\hat{\mu }\left( {\boldsymbol\mathrm{x}}_{\mu },{\tilde{\boldsymbol\mathrm{x}}}_{\sigma }\right) -\tau )}^{2}\\\mathrm{{\tilde{\boldsymbol\mathrm{x}}}_{\sigma }=}\,\mathrm{argmin}_{{\boldsymbol\mathrm{x}}_{\sigma }\in X}\,{\hat{\sigma }}^{2}({\boldsymbol\mathrm{x}}_{\mu },{\boldsymbol\mathrm{x}}_{\sigma })=\frac{\partial {\hat{\sigma }}^{2}({\boldsymbol\mathrm{x}}_{\mu },{\boldsymbol\mathrm{x}}_{\sigma })}{\partial {\boldsymbol\mathrm{x}}_{\sigma }}\end{matrix}\right.</math> |
| − | Find the Stackelberg equilibrium solution. | + | :Find the Stackelberg equilibrium solution. |
'''Step 5. Determine the non-dominated solution for the bias-leader model''' | '''Step 5. Determine the non-dominated solution for the bias-leader model''' | ||
| − | Alter possible combinations of <math display="inline">{\boldsymbol\mathrm{x}}_{\sigma }</math> and repeat Step 4. | + | :Alter possible combinations of <math display="inline">{\boldsymbol\mathrm{x}}_{\sigma }</math> and repeat Step 4. |
| − | Determine the non-dominated solution for the bias-leader model based on the MSE criterion, and go to Step 6. | + | :Determine the non-dominated solution for the bias-leader model based on the MSE criterion, and go to Step 6. |
'''Step 6. Evaluate the variance-leader model of the proposed SGRD model''' | '''Step 6. Evaluate the variance-leader model of the proposed SGRD model''' | ||
| − | Evaluate the variance-leader model: <math display="inline">\left\{ \begin{matrix}\mathrm{{\hat{\sigma }}^{2}({\boldsymbol\mathrm{x}}_{\mu }^{\ast },{\boldsymbol\mathrm{x}}_{\sigma }^{\ast })=}\,\mathrm{inf}_{{\boldsymbol\mathrm{x}}_{\sigma }\in X}\,{\hat{\sigma }}^{2}({\tilde{\boldsymbol\mathrm{x}}}_{\mu },{\boldsymbol\mathrm{x}}_{\sigma })\\\mathrm{{\tilde{\boldsymbol\mathrm{x}}}_{\mu }=}\,\mathrm{ | + | :Evaluate the variance-leader model: <math display="inline">\left\{ \begin{matrix}\mathrm{{\hat{\sigma }}^{2}({\boldsymbol\mathrm{x}}_{\mu }^{\ast },{\boldsymbol\mathrm{x}}_{\sigma }^{\ast })=}\,\mathrm{inf}_{{\boldsymbol\mathrm{x}}_{\sigma }\in X}\,{\hat{\sigma }}^{2}({\tilde{\boldsymbol\mathrm{x}}}_{\mu },{\boldsymbol\mathrm{x}}_{\sigma })\\\mathrm{{\tilde{\boldsymbol\mathrm{x}}}_{\mu }=}\,\mathrm{argmin}_{{\boldsymbol\mathrm{x}}_{\mu }\in X}\,{(\hat{\mu }\left( {\boldsymbol\mathrm{x}}_{\mu },{\boldsymbol\mathrm{x}}_{\sigma }\right) -\tau )}^{2}=\frac{\partial {(\hat{\mu }\left( {\boldsymbol\mathrm{x}}_{\mu },{\boldsymbol\mathrm{x}}_{\sigma }\right) -\tau )}^{2}}{\partial {\boldsymbol\mathrm{x}}_{\mu }}\end{matrix}\right.</math> |
| − | Find the Stackelberg equilibrium solution. | + | :Find the Stackelberg equilibrium solution. |
'''Step 7. Determine the non-dominated solution for the bias-leader model''' | '''Step 7. Determine the non-dominated solution for the bias-leader model''' | ||
| − | Alter possible combinations of <math display="inline">{\boldsymbol\mathrm{x}}_{\mu }</math> and repeat Step 6. | + | :Alter possible combinations of <math display="inline">{\boldsymbol\mathrm{x}}_{\mu }</math> and repeat Step 6. |
| − | Determine the non-dominated solution for the variance-leader model based on the MSE criterion, and go to Step 8. | + | :Determine the non-dominated solution for the variance-leader model based on the MSE criterion, and go to Step 8. |
'''Step 8. Determine the most efficient solution for the proposed SGRD model''' | '''Step 8. Determine the most efficient solution for the proposed SGRD model''' | ||
| − | Compare the non-dominated solution of the bias-leader model with that of the variance-leader model based on the MSE criterion. | + | :Compare the non-dominated solution of the bias-leader model with that of the variance-leader model based on the MSE criterion. |
| − | Determine the most efficient solution <math display="inline">\ | + | :Determine the most efficient solution <math display="inline">\left\{ {\left( \hat{\mu }\left( {\boldsymbol\mathrm{x}}_{\mu }^{\ast },{\boldsymbol\mathrm{x}}_{\sigma }^{\ast }\right) -\tau \right) }^{2},{\hat{\sigma }}^{2}\left( {\boldsymbol\mathrm{x}}_{\mu }^{\ast },{\boldsymbol\mathrm{x}}_{\sigma }^{\ast }\right) \right\}</math> of the proposed model with the corresponding controlled factor setting <math display="inline">({\boldsymbol\mathrm{x}}_{\mu }^{\ast },{\boldsymbol\mathrm{x}}_{\sigma }^{\ast })</math> based on the MSE criterion. |
|} | |} | ||
==4. Numerical examples== | ==4. Numerical examples== | ||
| − | === 4.1 | + | === 4.1 Example 1 === |
| − | A printing machine example is discussed in <span id='cite-_Ref76149715'></span>[[#_Ref76149715|[2]]]. The authors investigated how the printer's ability ( <math display="inline">y</math>) to apply colored inks to package labels is affected by speed ( <math display="inline">{x}_{1}</math>), pressure ( <math display="inline">{x}_{2}</math>), and distance ( <math display="inline">{x}_{3}</math>). This is a three-level factorial experimental design with three runs ( <math display="inline">{r}_{i}</math>) at each design point. Detailed experimental data is shown in Table 2, where <math display="inline">\overline{y}</math> and <math display="inline">s</math> represent the process mean and process standard deviation, respectively.< | + | A printing machine example is discussed in <span id='cite-_Ref76149715'></span>[[#_Ref76149715|[2]]]. The authors investigated how the printer's ability (<math display="inline">y</math>) to apply colored inks to package labels is affected by speed (<math display="inline">{x}_{1}</math>), pressure (<math display="inline">{x}_{2}</math>), and distance (<math display="inline">{x}_{3}</math>). This is a three-level factorial experimental design with three runs (<math display="inline">{r}_{i}</math>) at each design point. Detailed experimental data is shown in [[#tab-2|Table 2]], where <math display="inline">\overline{y}</math> and <math display="inline">s</math> represent the process mean and process standard deviation, respectively. |
| − | + | ||
| − | + | ||
| + | <div class="center" style="font-size: 75%;">'''Table 2'''. Printing study data [[#_Ref76149715|[2]]]</div> | ||
| + | |||
| + | <div id='tab-1'></div> | ||
| + | {| class="wikitable" style="margin: 1em auto 0.1em auto;border-collapse: collapse;font-size:85%;width:auto;" | ||
| + | |-style="text-align:center" | ||
| + | ! Run (<math display="inline">{r}_{i}</math>) !! <math>{x}_{1}</math> !! <math>{x}_{2}</math> !! <math>{x}_{3}</math> !! <math>{y}_{1}</math> !! <math>{y}_{2}</math> !! <math>{y}_{3}</math> !! <math>\overline{y}</math> !! <math>s</math> | ||
|- | |- | ||
| − | + | | style="text-align: center;" |1 | |
| − | + | | style="text-align: center;" |- | |
| − | + | | style="text-align: center;" |- | |
| − | + | | style="text-align: center;" |- | |
| − | + | | style="text-align: center;" |34 | |
| − | + | | style="text-align: center;" |10 | |
| − | + | | style="text-align: center;" |28 | |
| − | + | | style="text-align: center;" |24.00 | |
| − | + | | style="text-align: center;" |12.50 | |
| − | |- | + | |
| − | | style=" | + | |
| − | + | ||
| − | | style=" | + | |
| − | + | ||
| − | + | ||
| − | | style=" | + | |
| − | | style=" | + | |
| − | | style=" | + | |
| − | | style=" | + | |
|- | |- | ||
| style="text-align: center;" |2 | | style="text-align: center;" |2 | ||
| Line 575: | Line 571: | ||
| style="text-align: center;" |138.90 | | style="text-align: center;" |138.90 | ||
|- | |- | ||
| − | | style=" | + | | style="text-align: center;" |27 |
| − | | style=" | + | | style="text-align: center;" |+ |
| − | | style=" | + | | style="text-align: center;" |+ |
| − | | style=" | + | | style="text-align: center;" |+ |
| − | | style=" | + | | style="text-align: center;" |878 |
| − | | style=" | + | | style="text-align: center;" |991 |
| − | | style=" | + | | style="text-align: center;" |1 161 |
| − | | style=" | + | | style="text-align: center;" |1 010.00 |
| − | | style=" | + | | style="text-align: center;" |142.50 |
|} | |} | ||
| + | |||
The fitted response surface functions for the process mean and standard deviation in <span id='cite-_Ref76149715'></span>[[#_Ref76149715|[2]]] are: | The fitted response surface functions for the process mean and standard deviation in <span id='cite-_Ref76149715'></span>[[#_Ref76149715|[2]]] are: | ||
| Line 597: | Line 594: | ||
| style="text-align: right;vertical-align: top;width: 5px;text-align: right;white-space: nowrap;"|(9) | | style="text-align: right;vertical-align: top;width: 5px;text-align: right;white-space: nowrap;"|(9) | ||
|} | |} | ||
| − | |||
where | where | ||
| − | + | {| class="formulaSCP" style="width: 100%; text-align: left;" | |
| − | + | |- | |
| + | | | ||
| + | {| style="text-align: center; margin:auto;width: 100%;" | ||
| + | |- | ||
| + | | style="text-align: center;" | <math>\boldsymbol\mathrm{a}=\, \left[ \begin{matrix}177\\109.4\\131.5\end{matrix}\right] \quad</math> and <math display="inline">\quad \boldsymbol\mathrm{A}=</math><math>\, \left[ \begin{matrix}32&66&75.5\\66&-22.4&43.6\\75.5&43.6&-29.1\end{matrix}\right]</math>, | ||
| + | |} | ||
| + | |} | ||
and | and | ||
| Line 615: | Line 617: | ||
| style="text-align: right;vertical-align: top;width: 5px;text-align: right;white-space: nowrap;"|(10) | | style="text-align: right;vertical-align: top;width: 5px;text-align: right;white-space: nowrap;"|(10) | ||
|} | |} | ||
| − | |||
where | where | ||
| − | + | {| class="formulaSCP" style="width: 100%; text-align: left;" | |
| − | + | |- | |
| + | | | ||
| + | {| style="text-align: center; margin:auto;width: 100%;" | ||
| + | |- | ||
| + | | style="text-align: center;" | <math>\boldsymbol\mathrm{b}=\, \left[ \begin{matrix}11.5\\15.3\\29.2\end{matrix}\right] \quad</math> and <math display="inline">\quad \boldsymbol\mathrm{B}=</math><math>\, \left[ \begin{matrix}4.2&7.7&5.1\\7.7&-1.3&14.1\\5.1&14.1&16.8\end{matrix}\right]</math>. | ||
| + | |} | ||
| + | |} | ||
The feasible solution set <math display="inline">X=\left\{ \boldsymbol\mathrm{x}\in {R}^{3}:\, g\left( \boldsymbol\mathrm{x}\right) =\right. </math><math>\left. \left| {x}_{m}\right| -1\leq 0,\, m=1,2,3\right\} .</math> The target value of the process mean is assumed to be 500. The process mean and variance can be considered by “Nominal the best” and “Smaller the better” types of quality characteristics. Generally, it is possible to analyze this bi-objective optimization problem by decomposing the proposed SGRD model into a bias-leader model and a variance-leader model. In addition, we consider different correlations between input variables and quality characteristics to analyze all possible situations and find the follower's best responses in each model. | The feasible solution set <math display="inline">X=\left\{ \boldsymbol\mathrm{x}\in {R}^{3}:\, g\left( \boldsymbol\mathrm{x}\right) =\right. </math><math>\left. \left| {x}_{m}\right| -1\leq 0,\, m=1,2,3\right\} .</math> The target value of the process mean is assumed to be 500. The process mean and variance can be considered by “Nominal the best” and “Smaller the better” types of quality characteristics. Generally, it is possible to analyze this bi-objective optimization problem by decomposing the proposed SGRD model into a bias-leader model and a variance-leader model. In addition, we consider different correlations between input variables and quality characteristics to analyze all possible situations and find the follower's best responses in each model. | ||
| − | ====4.1.1 | + | ====4.1.1 Bias-leader model==== |
| − | First, we consider a situation in which the process bias is optimized first as the leader in a Stackelberg game. In this situation, process variance is the follower. The detailed results using Eq. (7) of the bias-leader model are shown in | + | First, we consider a situation in which the process bias is optimized first as the leader in a Stackelberg game. In this situation, process variance is the follower. The detailed results using Eq. (7) of the bias-leader model are shown in [[#tab-3|Table 3]]. |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | Bias-leader | + | <div class="center" style="font-size: 75%;">'''Table 3'''. Bias-leader Stackelberg game results (example 1)</div> |
| − | + | ||
| − | ! | + | <div id='tab-3'></div> |
| − | ! | + | {| class="wikitable" style="margin: 1em auto 0.1em auto;border-collapse: collapse;font-size:85%;width:auto;" |
| − | ! | + | |-style="text-align:center" |
| − | ! | + | ! SGRD <br> Bias-leader model !! <math>{x}_{1}^{\ast }</math> !! <math>{x}_{2}^{\ast }</math> !! <math>{x}_{3}^{\ast }</math> !! <math>{\left( \hat{\mu }\left( {\boldsymbol\mathrm{x}}^{\ast }\right) -\tau \right) }^{2}</math> !! <math>{\hat{\sigma }}^{2}({\boldsymbol\mathrm{x}}^{\ast })</math> !! MSE |
| − | + | |-style="text-align:left;" | |
| − | + | | style="text-align: left;" | Variance control <math display="inline">{x}_{1}</math> | |
| − | | style=" | + | | style="text-align: center;" |-0.8262 |
| − | | style=" | + | | style="text-align: center;" |-0.5404 |
| − | | style=" | + | | style="text-align: center;" |-0.0783 |
| − | | style=" | + | | style="text-align: center;" |113 390 |
| − | | style=" | + | | style="text-align: center;" |475.21 |
| − | | style=" | + | | style="text-align: center;" |113 865.21 |
| − | | style=" | + | |-style="text-align:left;" |
| − | |- | + | | style="text-align: left;" |Variance control <math display="inline">{x}_{2}</math> |
| − | | style="text-align: | + | |
| style="text-align: center;" |0.1818 | | style="text-align: center;" |0.1818 | ||
| style="text-align: center;" |1 | | style="text-align: center;" |1 | ||
| Line 655: | Line 657: | ||
| style="text-align: center;" |630.14 | | style="text-align: center;" |630.14 | ||
| style="text-align: center;" |67 239.14 | | style="text-align: center;" |67 239.14 | ||
| − | |- | + | |-style="text-align:left;" |
| − | | style="text-align: | + | | style="text-align: left;" |Variance control <math display="inline">{x}_{3}</math> |
| style="text-align: center;" |1 | | style="text-align: center;" |1 | ||
| style="text-align: center;" |-0.0496 | | style="text-align: center;" |-0.0496 | ||
| Line 663: | Line 665: | ||
| style="text-align: center;" |1 066.35 | | style="text-align: center;" |1 066.35 | ||
| style="text-align: center;" |43 543.35 | | style="text-align: center;" |43 543.35 | ||
| − | |- | + | |-style="text-align:left;" |
| − | | style="text-align: | + | | style="text-align: left;" |Variance control <math display="inline">{x}_{1},{x}_{2}</math> |
| style="text-align: center;" |-1 | | style="text-align: center;" |-1 | ||
| style="text-align: center;" |-0.0406 | | style="text-align: center;" |-0.0406 | ||
| Line 671: | Line 673: | ||
| style="text-align: center;" |378.26 | | style="text-align: center;" |378.26 | ||
| style="text-align: center;" |128 208.26 | | style="text-align: center;" |128 208.26 | ||
| − | |- | + | |-style="text-align:left;" |
| − | | style="text-align: | + | | style="text-align: left;" |Variance control <math display="inline">{x}_{1},{x}_{3}</math> |
| style="text-align: center;" |-0.5029 | | style="text-align: center;" |-0.5029 | ||
| style="text-align: center;" |-0.5814 | | style="text-align: center;" |-0.5814 | ||
| Line 679: | Line 681: | ||
| style="text-align: center;" |325.32 | | style="text-align: center;" |325.32 | ||
| style="text-align: center;" |123 795.32 | | style="text-align: center;" |123 795.32 | ||
| − | |- | + | |-style="text-align:left;" |
| − | | style="text-align: | + | |style="text-align: left;" |Variance control <math display="inline">{x}_{2},{x}_{3}</math> |
| style="text-align: center;" |-0.0450 | | style="text-align: center;" |-0.0450 | ||
| style="text-align: center;" |0.3283 | | style="text-align: center;" |0.3283 | ||
| Line 687: | Line 689: | ||
| style="text-align: center;" |500.01 | | style="text-align: center;" |500.01 | ||
| style="text-align: center;" |102 440.01 | | style="text-align: center;" |102 440.01 | ||
| − | |- | + | |-style="text-align:left;" |
| − | + | | style="text-align: left;" |Variance control <math display="inline">{x}_{1},{x}_{2},{x}_{3}</math> | |
| − | | style=" | + | | style="text-align: center;" |-0.8046 |
| − | | style=" | + | | style="text-align: center;" |-0.1676 |
| − | | style=" | + | | style="text-align: center;" |-0.6766 |
| − | | style=" | + | | style="text-align: center;" |129 900 |
| − | | style=" | + | | style="text-align: center;" |365.31 |
| − | | style=" | + | | style="text-align: center;" |130 265.31 |
|} | |} | ||
| + | |||
As shown in the table, if we consider that the process variance is highly correlated to <math display="inline">{x}_{3}</math>, the minimum MSE value (43 543.35) with the related control factor setting <math display="inline">({x}_{1}^{\ast },\, {x}_{2}^{\ast },\, {x}_{3}^{\ast })=(1,\, -0.0496,\, -</math><math>1)</math> is obtained when <math display="inline">{\left( \hat{\mu }\left( {\boldsymbol\mathrm{x}}^{\ast }\right) -\tau \right) }^{2}=</math><math>42\, 477</math> and <math display="inline">{\hat{\sigma }}^{2}\left( {\boldsymbol\mathrm{x}}^{\ast }\right) =</math><math>1\, 066.35</math>. | As shown in the table, if we consider that the process variance is highly correlated to <math display="inline">{x}_{3}</math>, the minimum MSE value (43 543.35) with the related control factor setting <math display="inline">({x}_{1}^{\ast },\, {x}_{2}^{\ast },\, {x}_{3}^{\ast })=(1,\, -0.0496,\, -</math><math>1)</math> is obtained when <math display="inline">{\left( \hat{\mu }\left( {\boldsymbol\mathrm{x}}^{\ast }\right) -\tau \right) }^{2}=</math><math>42\, 477</math> and <math display="inline">{\hat{\sigma }}^{2}\left( {\boldsymbol\mathrm{x}}^{\ast }\right) =</math><math>1\, 066.35</math>. | ||
| − | ====4.1.2 | + | ====4.1.2 Variance-leader model==== |
| − | Next, we consider a situation in which the process variance is prioritized as the Stackelberg game leader. The results, which are derived using Eq. (8) of the variance-leader model, are presented in Table 4. Based on the assumption of process bias controls <math display="inline">{x}_{1}</math> and <math display="inline">{x}_{2}</math>, we obtain the efficient result that <math display="inline">MSE=</math><math>2\, 049.10</math>. The process variance is 2 049.10 in the zero-bias condition, and the corresponding variable setting is <math display="inline">({x}_{1}^{\ast },\, {x}_{2}^{\ast },\, {x}_{3}^{\ast })=(1,\, 0.3229,\, -</math><math>0.3911)</math>. | + | Next, we consider a situation in which the process variance is prioritized as the Stackelberg game leader. The results, which are derived using Eq. (8) of the variance-leader model, are presented in [[#tab-4|Table 4]]. Based on the assumption of process bias controls <math display="inline">{x}_{1}</math> and <math display="inline">{x}_{2}</math>, we obtain the efficient result that <math display="inline">MSE=</math><math>2\, 049.10</math>. The process variance is 2 049.10 in the zero-bias condition, and the corresponding variable setting is <math display="inline">({x}_{1}^{\ast },\, {x}_{2}^{\ast },\, {x}_{3}^{\ast })=(1,\, 0.3229,\, -</math><math>0.3911)</math>. |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | Variance-leader | + | <div class="center" style="font-size: 75%;">'''Table 4.''' Variance-leader Stackelberg game results (example 1)</div> |
| − | + | ||
| − | ! | + | <div id='tab-4'></div> |
| − | ! | + | {| class="wikitable" style="margin: 1em auto 0.1em auto;border-collapse: collapse;font-size:85%;width:auto;" |
| − | ! | + | |-style="text-align:center" |
| − | ! | + | ! SGRD <br> Variance-leader model !! <math>{x}_{1}^{\ast }</math> !! <math>{x}_{2}^{\ast }</math> !! <math>{x}_{3}^{\ast }</math> !! <math>{\left( \hat{\mu }\left( {\boldsymbol\mathrm{x}}^{\ast }\right) -\tau \right) }^{2}</math> !! <math>{\hat{\sigma }}^{2}({\boldsymbol\mathrm{x}}^{\ast })</math> !! MSE |
| − | ! | + | |
|- | |- | ||
| − | | style=" | + | | style="text-align: left;" |Bias control <math display="inline">{x}_{1}</math> |
| − | | style=" | + | | style="text-align: center;" |-1 |
| − | | style=" | + | | style="text-align: center;" |-1 |
| − | | style=" | + | | style="text-align: center;" |-0.6225 |
| − | | style=" | + | | style="text-align: center;" |161 760 |
| − | | style=" | + | | style="text-align: center;" |360.44 |
| − | | style=" | + | | style="text-align: center;" |162 120.44 |
|- | |- | ||
| − | | style="text-align: | + | | style="text-align: left;" |Bias control <math display="inline">{x}_{2}</math> |
| style="text-align: center;" |-0.6593 | | style="text-align: center;" |-0.6593 | ||
| style="text-align: center;" |0.5935 | | style="text-align: center;" |0.5935 | ||
| Line 731: | Line 729: | ||
| style="text-align: center;" |133 238.73 | | style="text-align: center;" |133 238.73 | ||
|- | |- | ||
| − | | style="text-align: | + | | style="text-align: left;" |Bias control <math display="inline">{x}_{3}</math> |
| style="text-align: center;" |-1 | | style="text-align: center;" |-1 | ||
| style="text-align: center;" |-1 | | style="text-align: center;" |-1 | ||
| Line 739: | Line 737: | ||
| style="text-align: center;" |146 296.27 | | style="text-align: center;" |146 296.27 | ||
|- | |- | ||
| − | | style="text-align: | + | | style="text-align: left;" |Bias control <math display="inline">{x}_{1},{x}_{2}</math> |
| style="text-align: center;" |1 | | style="text-align: center;" |1 | ||
| style="text-align: center;" |0.3229 | | style="text-align: center;" |0.3229 | ||
| Line 747: | Line 745: | ||
| style="text-align: center;" |2 049.10 | | style="text-align: center;" |2 049.10 | ||
|- | |- | ||
| − | | style="text-align: | + | | style="text-align: left;" |Bias control <math display="inline">{x}_{1},{x}_{3}</math> |
| style="text-align: center;" |1 | | style="text-align: center;" |1 | ||
| style="text-align: center;" |-0.1030 | | style="text-align: center;" |-0.1030 | ||
| Line 755: | Line 753: | ||
| style="text-align: center;" |2 063.07 | | style="text-align: center;" |2 063.07 | ||
|- | |- | ||
| − | | style="text-align: | + | | style="text-align: left;" |Bias control <math display="inline">{x}_{2},{x}_{3}</math> |
| style="text-align: center;" |1 | | style="text-align: center;" |1 | ||
| style="text-align: center;" |-0.0820 | | style="text-align: center;" |-0.0820 | ||
| Line 763: | Line 761: | ||
| style="text-align: center;" |2 057.15 | | style="text-align: center;" |2 057.15 | ||
|- | |- | ||
| − | | style=" | + | | style="text-align: left;" |Bias control <math display="inline">{x}_{1},{x}_{2},{x}_{3}</math> |
| − | | style=" | + | | style="text-align: center;" |0.9991 |
| − | | style=" | + | | style="text-align: center;" |-0.1369 |
| − | | style=" | + | | style="text-align: center;" |-0.0591 |
| − | | style=" | + | | style="text-align: center;" |0 |
| − | | style=" | + | | style="text-align: center;" |2 075.53 |
| − | | style=" | + | | style="text-align: center;" |2 075.53 |
|} | |} | ||
| − | ====4.1.3 | + | ====4.1.3 Results and discussion==== |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
Comparing the non-dominated results of the bias-leader and variance-leader models in example 1 based on the MSE criterion shows that the variance-leader model provides a more efficient outcome, and it is more appropriate to optimize process variance in advance when the process bias is treated as a restriction. In addition, <math display="inline">{x}_{1}</math> and <math display="inline">{x}_{2}</math> are regarded as the controlled factors for process bias, and the solution set is <math display="inline">\left\{ {\left( \hat{\mu }\left( {\boldsymbol\mathrm{x}}^{\ast }\right) -\tau \right) }^{2},\, {\hat{\sigma }}^{2}\left( {\boldsymbol\mathrm{x}}^{\ast }\right) \right\} =</math><math>(0,\, 2\, 049.10)</math>. | Comparing the non-dominated results of the bias-leader and variance-leader models in example 1 based on the MSE criterion shows that the variance-leader model provides a more efficient outcome, and it is more appropriate to optimize process variance in advance when the process bias is treated as a restriction. In addition, <math display="inline">{x}_{1}</math> and <math display="inline">{x}_{2}</math> are regarded as the controlled factors for process bias, and the solution set is <math display="inline">\left\{ {\left( \hat{\mu }\left( {\boldsymbol\mathrm{x}}^{\ast }\right) -\tau \right) }^{2},\, {\hat{\sigma }}^{2}\left( {\boldsymbol\mathrm{x}}^{\ast }\right) \right\} =</math><math>(0,\, 2\, 049.10)</math>. | ||
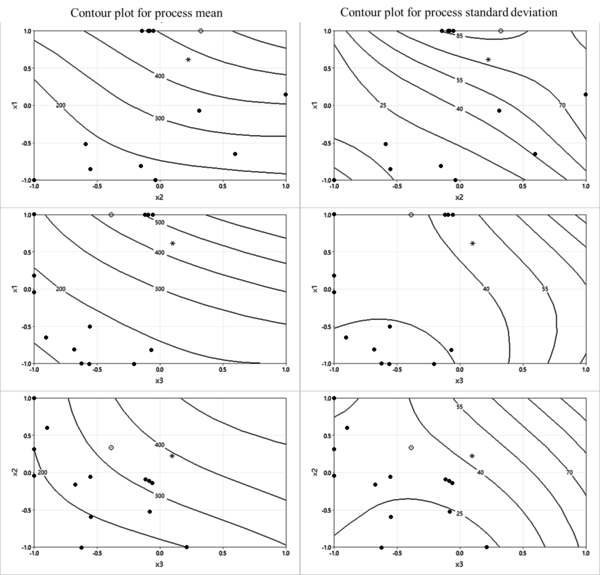
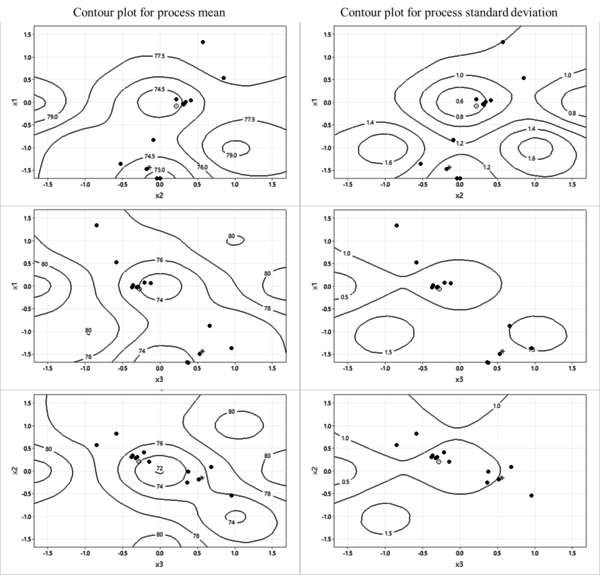
| − | A comparison of the significant results of example 1 between the dual response approach in <span id='cite-_Ref76149715'></span>[[#_Ref76149715|[2]]] and the proposed SGRD model is exhibited in Table 5. As evidenced by the results, the proposed SGRD model is more efficient than the dual response model based on the same zero-bias condition. Since the dual response approach is a pure priority-based optimization method, the comparison also shows the importance of considering the correlations between controlled factors and optimization objectives. The contour plots for the process mean and standard deviation are shown in | + | A comparison of the significant results of example 1 between the dual response approach in <span id='cite-_Ref76149715'></span>[[#_Ref76149715|[2]]] and the proposed SGRD model is exhibited in [[#tab-5|Table 5]]. As evidenced by the results, the proposed SGRD model is more efficient than the dual response model based on the same zero-bias condition. Since the dual response approach is a pure priority-based optimization method, the comparison also shows the importance of considering the correlations between controlled factors and optimization objectives. The contour plots for the process mean and standard deviation are shown in [[#img-4|Figure 4]], where the Stackelberg equilibrium solutions of the bias-leader model and variance-leader model are denoted by dots. The solution obtained by usingthe ual response approach is plotted as a star, and the most efficient solution provided by the proposed SGRD model is marked as a circle. |
| − | + | ||
| − | == | + | <div class="center" style="font-size: 75%;">'''Table 5'''. Comparison of the optimization results (example 1) </div> |
| − | + | ||
| − | { | + | <div id='tab-5'></div> |
| − | + | {| class="wikitable" style="margin: 1em auto 0.1em auto;border-collapse: collapse;font-size:85%;width:auto;" | |
| + | |-style="text-align:center" | ||
| + | ! Method !! <math>{x}_{1}^{\ast }</math> !! <math>{x}_{2}^{\ast }</math> !! <math>{x}_{3}^{\ast }</math> !! <math>{\left( \hat{\mu }\left( {\boldsymbol\mathrm{x}}^{\ast }\right) -\tau \right) }^{2}</math> !! <math>{\hat{\sigma }}^{2}({\boldsymbol\mathrm{x}}^{\ast })</math> !! MSE | ||
|- | |- | ||
| − | + | | style="text-align: center;" |Dual response approach | |
| + | | style="text-align: center;" |0.614 | ||
| + | | style="text-align: center;" |0.228 | ||
| + | | style="text-align: center;" |0.100 | ||
| + | | style="text-align: center;" |0 | ||
| + | | style="text-align: center;" |2 680.96 | ||
| + | | style="text-align: center;" |2 680.96 | ||
| + | |- | ||
| + | | style="text-align: center;" |Proposed SGRD model | ||
| + | | style="text-align: center;" |1 | ||
| + | | style="text-align: center;" |0.3229 | ||
| + | | style="text-align: center;" |-0.3911 | ||
| + | | style="text-align: center;" |0 | ||
| + | | style="text-align: center;" |2 049.10 | ||
| + | | style="text-align: center;" |2 049.10 | ||
| + | |} | ||
| − | + | ||
| − | + | <div id='img-4'></div> | |
| + | {| style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: auto;max-width: auto;" | ||
|- | |- | ||
| − | + | |style="padding:10px;"| [[File:Draft_Shin_703976401-image4.png|centre|600x600px|]] | |
| + | |- style="text-align: center; font-size: 75%;" | ||
| + | | colspan="1" style="padding:10px;"| '''Figure 4'''. Contour plots for process mean and standard deviation (example 1) | ||
| + | |} | ||
| − | + | ===4.2 Example 2=== | |
| − | + | ||
| − | <math>{x}_{ | + | The experimental data in example 2 concerns the bare silicon wafer production process of an injection-molding company for a large motor corporation. The dataset appears in <span id='cite-_Ref76151131'></span>[[#_Ref76151131|[6]]]. Three essential factors <math display="inline">({x}_{i})</math>, mold temperature, injection flow rate, and cooling rate, are considered to affect the coating thickness ( <math display="inline">y</math>) of bare silicon wafers. The coded and uncoded units of control factors are shown in [[#tab-6|Table 6]], and the spherical central composite design is presented in [[#tab-7|Table 7]]. |
| − | + | ||
| − | <math>{x}_{3}</math> | + | <div class="center" style="font-size: 75%;">'''Table 6'''. Uncoded and coded units of three control factors [[#_Ref76151131|[6]]]</div> |
| + | |||
| + | <div id='tab-6'></div> | ||
| + | {| class="wikitable" style="margin: 1em auto 0.1em auto;border-collapse: collapse;font-size:85%;width:auto;" | ||
| + | |-style="text-align:center" | ||
| + | ! rowspan="2" | Levels of coded <br> variables !! colspan="3" |Uncoded or original variables <math display="inline">({x}_{i})</math> | ||
| + | |- | ||
| + | ! Mold temperature (F) <br> <math>{x}_{1}</math> !! Injection flow rate (lbs/sec) <br> <math>{x}_{2}</math> !! Cooling rate (F/sec) <br> <math>{x}_{3}</math> | ||
|- | |- | ||
| − | | style=" | + | | style="text-align: center;" |<math>-\alpha \, (-1.682)</math> |
| − | | style=" | + | | style="text-align: center;" |99.6 |
| − | | style=" | + | | style="text-align: center;" |40 |
| − | | style=" | + | | style="text-align: center;" |4.8 |
|- | |- | ||
| style="text-align: center;" |-1 | | style="text-align: center;" |-1 | ||
| Line 846: | Line 842: | ||
| style="text-align: center;" |45 | | style="text-align: center;" |45 | ||
|- | |- | ||
| − | | style=" | + | | style="text-align: center;" |<math>+\alpha \, (+1.682)</math> |
| − | | style=" | + | | style="text-align: center;" |301.4 |
| − | | style=" | + | | style="text-align: center;" |70 |
| − | | style=" | + | | style="text-align: center;" |55.2 |
|} | |} | ||
| − | < | + | |
| − | + | <div class="center" style="font-size: 75%;">'''Table 7'''. The layout of central composite design [[#_Ref76151131|[6]]]</div> | |
| − | + | ||
| + | <div id='tab-7'></div> | ||
| + | {| class="wikitable" style="margin: 1em auto 0.1em auto;border-collapse: collapse;font-size:85%;width:auto;" | ||
| + | |-style="text-align:center" | ||
| + | ! <math>{x}_{1}</math> !! <math>{x}_{2}</math> !! <math>{x}_{3}</math> !! <math>{y}_{1}</math> !! <math>{y}_{2}</math> !! <math>{y}_{3}</math> !! <math>{y}_{4}</math> !! <math>\overline{y}</math> !! <math>s</math> | ||
|- | |- | ||
| − | + | | style="text-align: center;" |- | |
| − | + | | style="text-align: center;" |- | |
| − | + | | style="text-align: center;" |- | |
| − | + | | style="text-align: center;" |76.30 | |
| − | + | | style="text-align: center;" |80.50 | |
| − | + | | style="text-align: center;" |77.70 | |
| − | + | | style="text-align: center;" |81.10 | |
| − | + | | style="text-align: center;" |78.90 | |
| − | + | | style="text-align: center;" |2.28 | |
| − | |- | + | |
| − | | style=" | + | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | | style=" | + | |
| − | | style=" | + | |
| − | | style=" | + | |
| − | | style=" | + | |
| − | | style=" | + | |
|- | |- | ||
| style="text-align: center;" |+ | | style="text-align: center;" |+ | ||
| Line 1,056: | Line 1,046: | ||
| style="text-align: center;" |0.66 | | style="text-align: center;" |0.66 | ||
|- | |- | ||
| − | | style=" | + | | style="text-align: center;" |0 |
| − | | style=" | + | | style="text-align: center;" |0 |
| − | | style=" | + | | style="text-align: center;" |0 |
| − | | style=" | + | | style="text-align: center;" |71.00 |
| − | | style=" | + | | style="text-align: center;" |70.40 |
| − | | style=" | + | | style="text-align: center;" |70.90 |
| − | | style=" | + | | style="text-align: center;" |69.90 |
| − | | style=" | + | | style="text-align: center;" |70.55 |
| − | | style=" | + | | style="text-align: center;" |0.51 |
|} | |} | ||
| + | |||
The estimated functions for the process mean and standard deviation in <span id="cite-_Ref76151131"></span>[[#_Ref76151131|[6]]] derived using RSM are: | The estimated functions for the process mean and standard deviation in <span id="cite-_Ref76151131"></span>[[#_Ref76151131|[6]]] derived using RSM are: | ||
| Line 1,074: | Line 1,065: | ||
{| style="vertical-align: top;margin:auto;width: 100%;" | {| style="vertical-align: top;margin:auto;width: 100%;" | ||
|- | |- | ||
| − | | <math | + | | <math>\hat{\mu }\left( \boldsymbol\mathrm{x}\right) =\, 72.21+\, {\boldsymbol\mathrm{X}}^{T}\boldsymbol\mathrm{a}+</math><math>{\boldsymbol\mathrm{X}}^{T}\boldsymbol\mathrm{AX}</math>, |
|} | |} | ||
| style="text-align: right;vertical-align: top;width: 5px;text-align: right;white-space: nowrap;" |(11) | | style="text-align: right;vertical-align: top;width: 5px;text-align: right;white-space: nowrap;" |(11) | ||
| Line 1,081: | Line 1,072: | ||
where | where | ||
| − | + | {| class="formulaSCP" style="width: 100%;border-collapse: collapse;width: 100%;text-align: center;" | |
| − | + | |- | |
| + | | | ||
| + | {| style="vertical-align: top;margin:auto;width: 100%;" | ||
| + | |- | ||
| + | | <math>\boldsymbol\mathrm{a}=\, \left[ \begin{matrix}0.59\\-0.35\\-0.01\end{matrix}\right] \quad</math> and <math display="inline">\quad \boldsymbol\mathrm{A}=</math><math>\, \left[ \begin{matrix}0.28&0.09&1.66\\0.09&1.29&1.51\\1.66&1.51&1.85\end{matrix}\right]</math>, | ||
| + | |} | ||
| + | |} | ||
and | and | ||
| Line 1,091: | Line 1,088: | ||
{| style="vertical-align: top;margin:auto;width: 100%;" | {| style="vertical-align: top;margin:auto;width: 100%;" | ||
|- | |- | ||
| − | | <math | + | | <math>\hat{\sigma }\left( \boldsymbol\mathrm{x}\right) =\, 2.55+\, {\boldsymbol\mathrm{X}}^{T}\boldsymbol\mathrm{b}+</math><math>\, {\boldsymbol\mathrm{X}}^{T}\boldsymbol\mathrm{BX}</math>, |
|} | |} | ||
| style="text-align: right;vertical-align: top;width: 5px;text-align: right;white-space: nowrap;"|(12) | | style="text-align: right;vertical-align: top;width: 5px;text-align: right;white-space: nowrap;"|(12) | ||
|} | |} | ||
| − | |||
where | where | ||
| − | + | {| class="formulaSCP" style="width: 100%;border-collapse: collapse;width: 100%;text-align: center;" | |
| − | + | |- | |
| + | | | ||
| + | {| style="vertical-align: top;margin:auto;width: 100%;" | ||
| + | |- | ||
| + | | <math>\boldsymbol\mathrm{b}=\, \left[ \begin{matrix}0.38\\-0.43\\0.56\end{matrix}\right] \quad</math> and <math display="inline">\quad \boldsymbol\mathrm{B}=</math><math>\, \left[ \begin{matrix}0.49&-0.47&0.72\\-0.47&0.61&-0.12\\0.72&-0.12&0.85\end{matrix}\right]</math>, | ||
| + | |} | ||
| + | |} | ||
| − | The feasible solution set <math display="inline">X=\left\{ \boldsymbol\mathrm{x}\in {R}^{3}:\, g\left( \boldsymbol\mathrm{x}\right) =\right. </math><math>\left. \sum _{m=1}^{3}{x}_{m}^{2}-3\leq 0,\, m=1,2,3\right\} .</math> The target coating thickness is specified by the customer and is set at 71.14. The goal of the bi-objective optimization problem is to minimize process bias and variability. Based on the same optimization progress in example 1, the proposed SGRD model can be decomposed into a bias-leader model and variance-leader model, which are stated below. | + | The feasible solution set <math display="inline">X=\left\{ \boldsymbol\mathrm{x}\in {R}^{3}:\, g\left( \boldsymbol\mathrm{x}\right) =\right. </math><math>\left. \sum _{m=1}^{3}{x}_{m}^{2}-3\leq 0,\, m=1,2,3\right\}.</math> The target coating thickness is specified by the customer and is set at 71.14. The goal of the bi-objective optimization problem is to minimize process bias and variability. Based on the same optimization progress in example 1, the proposed SGRD model can be decomposed into a bias-leader model and variance-leader model, which are stated below. |
| − | ====4.2.1 | + | ====4.2.1 Bias-leader model==== |
| − | In the bias-leader model, process variance is imagined as the optimization constraints while optimizing the process bias, and various combinations of the controlled variables have been taken into account. Eq. (7) of the proposed SGRD model is applied, and the experimental outcome is shown in | + | In the bias-leader model, process variance is imagined as the optimization constraints while optimizing the process bias, and various combinations of the controlled variables have been taken into account. Eq. (7) of the proposed SGRD model is applied, and the experimental outcome is shown in [[#tab-8|Table 8]]. |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | Bias-leader | + | <div class="center" style="font-size: 75%;">'''Table 8'''. Bias-leader Stackelberg game results (example 2)</div> |
| − | + | ||
| − | ! | + | <div id='tab-8'></div> |
| − | ! | + | {| class="wikitable" style="margin: 1em auto 0.1em auto;border-collapse: collapse;font-size:85%;width:auto;" |
| − | ! | + | |-style="text-align:center" |
| − | ! | + | ! SGRD <br> Bias-leader model !! <math>{x}_{1}^{\ast }</math> !! <math>{x}_{2}^{\ast }</math> !! <math>{x}_{3}^{\ast }</math> !! <math>{\left( \hat{\mu }\left( {\boldsymbol\mathrm{x}}^{\ast }\right) -\tau \right) }^{2}</math> !! <math>{\hat{\sigma }}^{2}({\boldsymbol\mathrm{x}}^{\ast })</math> !! MSE |
| − | ! | + | |
|- | |- | ||
| − | | style=" | + | | style="text-align: left;" |Variance control <math display="inline">{x}_{1}</math> |
| − | | style=" | + | | style="text-align: center;" |-1.3436 |
| − | | style=" | + | | style="text-align: center;" |-0.5222 |
| − | | style=" | + | | style="text-align: center;" |0.9602 |
| − | | style=" | + | | style="text-align: center;" |0.0316 |
| − | | style=" | + | | style="text-align: center;" |11.8185 |
| − | | style=" | + | | style="text-align: center;" |11.8501 |
|- | |- | ||
| − | | style="text-align: | + | | style="text-align: left;" |Variance control <math display="inline">{x}_{2}</math> |
| style="text-align: center;" |-1.4786 | | style="text-align: center;" |-1.4786 | ||
| style="text-align: center;" |-0.1643 | | style="text-align: center;" |-0.1643 | ||
| Line 1,137: | Line 1,133: | ||
| style="text-align: center;" |9.1059 | | style="text-align: center;" |9.1059 | ||
|- | |- | ||
| − | | style="text-align: | + | | style="text-align: left;" |Variance control <math display="inline">{x}_{3}</math> |
| style="text-align: center;" |-1.6885 | | style="text-align: center;" |-1.6885 | ||
| style="text-align: center;" |0.0014 | | style="text-align: center;" |0.0014 | ||
| Line 1,145: | Line 1,141: | ||
| style="text-align: center;" |10.1125 | | style="text-align: center;" |10.1125 | ||
|- | |- | ||
| − | | style="text-align: | + | | style="text-align: left;" |Variance control <math display="inline">{x}_{1},{x}_{2}</math> |
| style="text-align: center;" |-0.8403 | | style="text-align: center;" |-0.8403 | ||
| style="text-align: center;" |0.0954 | | style="text-align: center;" |0.0954 | ||
| Line 1,153: | Line 1,149: | ||
| style="text-align: center;" |9.1410 | | style="text-align: center;" |9.1410 | ||
|- | |- | ||
| − | | style="text-align: | + | | style="text-align: left;" |Variance control <math display="inline">{x}_{1},{x}_{3}</math> |
| style="text-align: center;" |-0.0778 | | style="text-align: center;" |-0.0778 | ||
| style="text-align: center;" |0.2155 | | style="text-align: center;" |0.2155 | ||
| Line 1,161: | Line 1,157: | ||
| style="text-align: center;" |6.9746 | | style="text-align: center;" |6.9746 | ||
|- | |- | ||
| − | | style="text-align: | + | | style="text-align: left;" |Variance control <math display="inline">{x}_{2},{x}_{3}</math> |
| style="text-align: center;" |-1.6743 | | style="text-align: center;" |-1.6743 | ||
| style="text-align: center;" |-0.2570 | | style="text-align: center;" |-0.2570 | ||
| Line 1,169: | Line 1,165: | ||
| style="text-align: center;" |9.7947 | | style="text-align: center;" |9.7947 | ||
|- | |- | ||
| − | | style=" | + | | style="text-align: left;" |Variance control <math display="inline">{x}_{1},{x}_{2},{x}_{3}</math> |
| − | | style=" | + | | style="text-align: center;" |-0.0146 |
| − | | style=" | + | | style="text-align: center;" |0.3173 |
| − | | style=" | + | | style="text-align: center;" |-0.3008 |
| − | | style=" | + | | style="text-align: center;" |1.2398 |
| − | | style=" | + | | style="text-align: center;" |5.7351 |
| − | | style=" | + | | style="text-align: center;" |6.9749 |
|} | |} | ||
| + | |||
According to the MSE criterion, the solution set <math display="inline">\left\{ {\left( \hat{\mu }\left( {\boldsymbol\mathrm{x}}^{\ast }\right) -\tau \right) }^{2},\, {\hat{\sigma }}^{2}\left( {\boldsymbol\mathrm{x}}^{\ast }\right) \right\} =</math><math>\left( 1.2160,\, 5.7586\right)</math> with input variable setting <math display="inline">({x}_{1}^{\ast },\, {x}_{2}^{\ast },\, {x}_{3}^{\ast })=(-0.0778,\, 0.2155,\, -</math><math>0.2813)</math> has been identified as the non-dominated result in this model, where the MSE value is 6.9746. Moreover, controlled factors <math display="inline">{x}_{1}</math> and <math display="inline">{x}_{3}</math> are assumed to be significantly correlated with the game follower, which is process variance. | According to the MSE criterion, the solution set <math display="inline">\left\{ {\left( \hat{\mu }\left( {\boldsymbol\mathrm{x}}^{\ast }\right) -\tau \right) }^{2},\, {\hat{\sigma }}^{2}\left( {\boldsymbol\mathrm{x}}^{\ast }\right) \right\} =</math><math>\left( 1.2160,\, 5.7586\right)</math> with input variable setting <math display="inline">({x}_{1}^{\ast },\, {x}_{2}^{\ast },\, {x}_{3}^{\ast })=(-0.0778,\, 0.2155,\, -</math><math>0.2813)</math> has been identified as the non-dominated result in this model, where the MSE value is 6.9746. Moreover, controlled factors <math display="inline">{x}_{1}</math> and <math display="inline">{x}_{3}</math> are assumed to be significantly correlated with the game follower, which is process variance. | ||
| − | ====4.2.2 | + | ====4.2.2 Variance-leader model==== |
| − | Using Eq. (8) from the proposed SGRD model yields the results listed in Table 9. The non-dominated solution set of the variance-leader model is <math display="inline">\left\{ {\left( \hat{\mu }\left( {\boldsymbol\mathrm{x}}^{\ast }\right) -\tau \right) }^{2},\, {\hat{\sigma }}^{2}\left( {\boldsymbol\mathrm{x}}^{\ast }\right) \right\} =</math><math>(1.2414,\, 5.7351),</math> with a minimum MSE value of 6.9765. The corresponding control variable setting is <math display="inline">({x}_{1}^{\ast },\, {x}_{2}^{\ast },\, {x}_{3}^{\ast })=(-0.0158,\, 0.3130,\, -</math><math>0.3021)</math>, and the input factor <math display="inline">{x}_{2}</math> is regarded as controlled by the process bias. | + | Using Eq. (8) from the proposed SGRD model yields the results listed in [[#tab-9|Table 9]]. The non-dominated solution set of the variance-leader model is <math display="inline">\left\{ {\left( \hat{\mu }\left( {\boldsymbol\mathrm{x}}^{\ast }\right) -\tau \right) }^{2},\, {\hat{\sigma }}^{2}\left( {\boldsymbol\mathrm{x}}^{\ast }\right) \right\} =</math><math>(1.2414,\, 5.7351),</math> with a minimum MSE value of 6.9765. The corresponding control variable setting is <math display="inline">({x}_{1}^{\ast },\, {x}_{2}^{\ast },\, {x}_{3}^{\ast })=(-0.0158,\, 0.3130,\, -</math><math>0.3021)</math>, and the input factor <math display="inline">{x}_{2}</math> is regarded as controlled by the process bias. |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | Variance-leader | + | <div class="center" style="font-size: 75%;">'''Table 9.''' Variance-leader Stackelberg game results (example 2)</div> |
| − | + | ||
| − | ! | + | <div id='tab-9'></div> |
| − | ! | + | {| class="wikitable" style="margin: 1em auto 0.1em auto;border-collapse: collapse;font-size:85%;width:auto;" |
| − | ! | + | |-style="text-align:center" |
| − | ! | + | ! SGRD <br> Variance-leader model !! <math>{x}_{1}^{\ast }</math> !! <math>{x}_{2}^{\ast }</math> !! <math>{x}_{3}^{\ast }</math> !! <math>{\left( \hat{\mu }\left( {\boldsymbol\mathrm{x}}^{\ast }\right) -\tau \right) }^{2}</math> !! <math>{\hat{\sigma }}^{2}({\boldsymbol\mathrm{x}}^{\ast })</math> !! MSE |
| − | ! | + | |
|- | |- | ||
| − | | style=" | + | | style="text-align: left;" |Bias control <math display="inline">{x}_{1}</math> |
| − | | style=" | + | | style="text-align: center;" |-0.0056 |
| − | | style=" | + | | style="text-align: center;" |0.3090 |
| − | | style=" | + | | style="text-align: center;" |-0.3703 |
| − | | style=" | + | | style="text-align: center;" |1.3680 |
| − | | style=" | + | | style="text-align: center;" |5.7528 |
| − | | style=" | + | | style="text-align: center;" |7.1208 |
|- | |- | ||
| − | | style="text-align: | + | | style="text-align: left;" |Bias control <math display="inline">{x}_{2}</math> |
| style="text-align: center;" |-0.0158 | | style="text-align: center;" |-0.0158 | ||
| style="text-align: center;" |0.3130 | | style="text-align: center;" |0.3130 | ||
| Line 1,213: | Line 1,204: | ||
| style="text-align: center;" |6.9765 | | style="text-align: center;" |6.9765 | ||
|- | |- | ||
| − | | style="text-align: | + | | style="text-align: left;" |Bias control <math display="inline">{x}_{3}</math> |
| style="text-align: center;" |0.0623 | | style="text-align: center;" |0.0623 | ||
| style="text-align: center;" |0.4282 | | style="text-align: center;" |0.4282 | ||
| Line 1,221: | Line 1,212: | ||
| style="text-align: center;" |7.0888 | | style="text-align: center;" |7.0888 | ||
|- | |- | ||
| − | | style="text-align: | + | | style="text-align: left;" |Bias control <math display="inline">{x}_{1},{x}_{2}</math> |
| style="text-align: center;" |0.0124 | | style="text-align: center;" |0.0124 | ||
| style="text-align: center;" |0.3570 | | style="text-align: center;" |0.3570 | ||
| Line 1,229: | Line 1,220: | ||
| style="text-align: center;" |7.1378 | | style="text-align: center;" |7.1378 | ||
|- | |- | ||
| − | | style="text-align: | + | | style="text-align: left;" |Bias control <math display="inline">{x}_{1},{x}_{3}</math> |
| style="text-align: center;" |0.5313 | | style="text-align: center;" |0.5313 | ||
| style="text-align: center;" |0.8449 | | style="text-align: center;" |0.8449 | ||
| Line 1,237: | Line 1,228: | ||
| style="text-align: center;" |8.7640 | | style="text-align: center;" |8.7640 | ||
|- | |- | ||
| − | | style="text-align: | + | | style="text-align: left;" |Bias control <math display="inline">{x}_{2},{x}_{3}</math> |
| style="text-align: center;" |0.0945 | | style="text-align: center;" |0.0945 | ||
| style="text-align: center;" |0.2044 | | style="text-align: center;" |0.2044 | ||
| Line 1,245: | Line 1,236: | ||
| style="text-align: center;" |7.2145 | | style="text-align: center;" |7.2145 | ||
|- | |- | ||
| − | | style=" | + | | style="text-align: left;" |Bias control <math display="inline">{x}_{1},{x}_{2},{x}_{3}</math> |
| − | | style=" | + | | style="text-align: center;" |1.3620 |
| − | | style=" | + | | style="text-align: center;" |0.5836 |
| − | | style=" | + | | style="text-align: center;" |-0.8465 |
| − | | style=" | + | | style="text-align: center;" |1.8876 |
| − | | style=" | + | | style="text-align: center;" |8.5498 |
| − | | style=" | + | | style="text-align: center;" |10.4374 |
|} | |} | ||
| − | ====4.2.3 | + | ====4.2.3 Results and discussion==== |
| − | + | ||
| − | + | A comparison of the non-dominated results of the bias-leader and variance-leader models in example 2 based on the MSE criterion shows that the result of the bias-leader model is slightly better than that of the variance-leader model. | |
| − | + | ||
| + | The bias-leader model of the proposed SGRD method is next compared with the dual response approach; the results are presented in [[#tab-10|Table 10]]. Based on the zero-bias assumption, the process variance and MSE values obtained using the dual response approach are equal to 9.0854. With the more relaxed bias assumption, the proposed SGRD model provides a more efficient solution. [[#img-5|Figure 5]] is the contour plots for the process mean and standard deviation, where the notation dot, star, and circle represent the Stackelberg equilibrium solution, the solution obtained by using dual response approach, and the most efficient solution provided by the proposed SGRD model, respectively. | ||
| + | |||
| + | <div class="center" style="font-size: 75%;">'''Table 10'''. Comparison of the optimization results (example 2) </div> | ||
| + | |||
| + | <div id='tab-10'></div> | ||
| + | {| class="wikitable" style="margin: 1em auto 0.1em auto;border-collapse: collapse;font-size:85%;width:auto;" | ||
| + | |-style="text-align:center" | ||
| + | ! Method !! <math>{x}_{1}^{\ast }</math> !! <math>{x}_{2}^{\ast }</math> !! <math>{x}_{3}^{\ast }</math> !! <math>{\left( \hat{\mu }\left( {\boldsymbol\mathrm{x}}^{\ast }\right) -\tau \right) }^{2}</math> !! <math>{\hat{\sigma }}^{2}({\boldsymbol\mathrm{x}}^{\ast })</math> !! MSE | ||
|- | |- | ||
| − | + | | style="text-align: center;" |Dual response approach | |
| − | + | | style="text-align: center;" |-1.4561 | |
| − | + | | style="text-align: center;" |-0.1456 | |
| − | + | | style="text-align: center;" |0.5596 | |
| − | + | | style="text-align: center;" |0 | |
| − | + | | style="text-align: center;" |9.0854 | |
| − | + | | style="text-align: center;" |9.0854 | |
|- | |- | ||
| − | | style=" | + | | style="text-align: center;" |Proposed SGRD model |
| − | + | | style="text-align: center;" |-0.0778 | |
| − | + | | style="text-align: center;" |0.2155 | |
| − | + | | style="text-align: center;" |-0.2813 | |
| − | + | | style="text-align: center;" |1.2160 | |
| − | + | | style="text-align: center;" |5.7586 | |
| − | + | | style="text-align: center;" |6.9746 | |
| − | + | ||
| − | + | ||
| − | | style=" | + | |
| − | | style=" | + | |
| − | | style=" | + | |
| − | | style=" | + | |
| − | | style=" | + | |
| − | | style=" | + | |
|} | |} | ||
| − | |||
| − | + | <div id='img-5'></div> | |
| − | [[File:Draft_Shin_703976401-image5.png|centre | + | {| style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: auto;max-width: auto;" |
| + | |- | ||
| + | |style="padding:10px;"| [[File:Draft_Shin_703976401-image5.png|centre|600x600px]] | ||
| + | |- style="text-align: center; font-size: 75%;" | ||
| + | | colspan="1" style="padding:10px;"| '''Figure 5'''. Contour plots for the process mean and standard deviation (example 2) | ||
| + | |} | ||
==5. Conclusion== | ==5. Conclusion== | ||
| Line 1,298: | Line 1,293: | ||
==References== | ==References== | ||
| − | <span id='_Ref76149437'></span>[[#cite-_Ref76149437|[1]]] Taguchi | + | <div class="auto" style="text-align: left;width: auto; margin-left: auto; margin-right: auto;font-size: 85%;"> |
| + | |||
| + | <span id='_Ref76149437'></span>[[#cite-_Ref76149437|[1]]] Taguchi G. Introduction to quality engineering. Asian Productivity Organization, UNIPUB, White Plains, NY, 1986. | ||
| − | <span id='_Ref76149715'></span>[[#cite-_Ref76149715|[2]]] Vining | + | <span id='_Ref76149715'></span>[[#cite-_Ref76149715|[2]]] Vining G.G., Myers R.H. Combining Taguchi and response surface philosophies: a dual response approach. Journal of Quality Technology, 22(1):38-45, 1990. |
| − | <span id='_Ref76149733'></span>[[#cite-_Ref76149733|[3]]] Del Castillo | + | <span id='_Ref76149733'></span>[[#cite-_Ref76149733|[3]]] Del Castillo E., Montgomery D.C. A nonlinear programming solution to the dual response problem. Journal of Quality Technology, 25(3):199-204, 1993. |
| − | <span id='_Ref76149745'></span>[[#cite-_Ref76149745|[4]]] Copeland | + | <span id='_Ref76149745'></span>[[#cite-_Ref76149745|[4]]] Copeland K.A., Nelson P.R. Dual response optimization via direct function minimization. Journal of Quality Technology, 28(3):331-336, 1996. |
| − | <span id='_Ref76149761'></span>[[#cite-_Ref76149761|[5]]] Shin | + | <span id='_Ref76149761'></span>[[#cite-_Ref76149761|[5]]] Shin S., Cho B.R. Bias-specified robust design optimization and its analytical solutions. Computers & Industrial Engineering, 48(1):129-140, 2005. |
| − | <span id='_Ref76151131'></span>[[#cite-_Ref76151131|[6]]] Shin | + | <span id='_Ref76151131'></span>[[#cite-_Ref76151131|[6]]] Shin S., Cho B.R. Robust design models for customer-specified bounds on process parameters. Journal of Systems Science and Systems Engineering, 15(1):2-18, 2006. |
| − | <span id='_Ref76150123'></span>[[#cite-_Ref76150123|[7]]] Lin | + | <span id='_Ref76150123'></span>[[#cite-_Ref76150123|[7]]] Lin D.K., Tu W. Dual response surface optimization. Journal of Quality Technology, 27(1):34-39, 1995. |
| − | <span id='_Ref76150372'></span>[[#cite-_Ref76150372|[8]]] Tang | + | <span id='_Ref76150372'></span>[[#cite-_Ref76150372|[8]]] Tang L.C., Xu K. A unified approach for dual response surface optimization. Journal of Quality Technology, 34(4):437-447, 2002. |
| − | <span id='_Ref76150383'></span>[[#cite-_Ref76150383|[9]]] Köksoy | + | <span id='_Ref76150383'></span>[[#cite-_Ref76150383|[9]]] Köksoy O., Doganaksoy N. Joint optimization of mean and standard deviation using response surface methods. Journal of Quality Technology, 35(3):239-252, 2003. |
| − | <span id='_Ref76150396'></span>[[#cite-_Ref76150396|[10]]] Ding | + | <span id='_Ref76150396'></span>[[#cite-_Ref76150396|[10]]] Ding R., Lin D.K., Wei D. Dual-response surface optimization: a weighted MSE approach. Quality Engineering, 16(3):377-385, 2004. |
| − | <span id='_Ref76150480'></span>[[#cite-_Ref76150480|[11]]] Shin | + | <span id='_Ref76150480'></span>[[#cite-_Ref76150480|[11]]] Shin S., Cho B.R. Studies on a biobjective robust design optimization problem. IIE Transactions, 41(11):957-968, 2009. |
| − | <span id='_Ref76150513'></span>[[#cite-_Ref76150513|[12]]] Brewer | + | <span id='_Ref76150513'></span>[[#cite-_Ref76150513|[12]]] Brewer K., Carraway L., Ingram D. Forward selection as a candidate for constructing nonregular robust parameter designs. Technical Report, Arkansas State University, 2010. |
| − | <span id='_Ref76150626'></span>[[#cite-_Ref76150626|[13]]] Cho | + | <span id='_Ref76150626'></span>[[#cite-_Ref76150626|[13]]] Cho B.R., Philips M.D., Kapur K.C. Quality improvement by RSM modeling for robust design. The 5th Industrial Engineering Research Conference, pp. 650-655, May 1996. |
| − | <span id='_Ref76150673'></span>[[#cite-_Ref76150673|[14]]] Kim | + | <span id='_Ref76150673'></span>[[#cite-_Ref76150673|[14]]] Kim K.J., Lin D.K. Dual response surface optimization: a fuzzy modeling approach. Journal of Quality Technology, 30(1):1-10, 1998. |
| − | <span id='_Ref76150750'></span>[[#cite-_Ref76150750|[15]]] Kim | + | <span id='_Ref76150750'></span>[[#cite-_Ref76150750|[15]]] Kim Y.J., Cho B.R. Development of priority-based robust design. Quality Engineering, 14(3):355-363, 2002. |
| − | <span id='_Ref76150810'></span>[[#cite-_Ref76150810|[16]]] Steenackers | + | <span id='_Ref76150810'></span>[[#cite-_Ref76150810|[16]]] Steenackers G., Guillaume P. Bias-specified robust design optimization: A generalized mean squared error approach. Computers & Industrial Engineering, 54(2):259-268, 2008. |
| − | <span id='_Ref76150823'></span>[[#cite-_Ref76150823|[17]]] Kovach | + | <span id='_Ref76150823'></span>[[#cite-_Ref76150823|[17]]] Kovach J., Cho B.R., Antony J. Development of a variance prioritized multiresponse robust design framework for quality improvement. The International Journal of Quality & Reliability Management, 26(4):380, 2009. |
| − | <span id='_Ref76150835'></span>[[#cite-_Ref76150835|[18]]] Myerson | + | <span id='_Ref76150835'></span>[[#cite-_Ref76150835|[18]]] Myerson R.B. Game theory. Harvard University Press, 1997. |
| − | <span id='_Ref76150849'></span>[[#cite-_Ref76150849|[19]]] Chen | + | <span id='_Ref76150849'></span>[[#cite-_Ref76150849|[19]]] Chen C.L., Cruz J. Stackelburg solution for two-person games with biased information patterns. IEEE Transactions on Automatic Control, 17(6):791-798, 1972. |
| − | <span id='_Ref76150858'></span>[[#cite-_Ref76150858|[20]]] Simaan | + | <span id='_Ref76150858'></span>[[#cite-_Ref76150858|[20]]] Simaan M., Cruz J.B. On the Stackelberg strategy in nonzero-sum games. Journal of Optimization Theory and Applications, 11(5):533-555, 1973. |
| − | <span id='_Ref76150867'></span>[[#cite-_Ref76150867|[21]]] Shimizu | + | <span id='_Ref76150867'></span>[[#cite-_Ref76150867|[21]]] Shimizu K., Aiyoshi E. A new computational method for Stackelberg and min-max problems by use of a penalty method. IEEE Transactions on Automatic Control, 26(2):460-466, 1981. |
| − | <span id='_Ref76150876'></span>[[#cite-_Ref76150876|[22]]] Anandalingam | + | <span id='_Ref76150876'></span>[[#cite-_Ref76150876|[22]]] Anandalingam G., White D.J. A solution method for the linear static Stackelberg problem using penalty functions. IEEE Transactions on Automatic Control, 35(10):1170-1173, 1990. |
| − | <span id='_Ref76150902'></span>[[#cite-_Ref76150902|[23]]] Lai | + | <span id='_Ref76150902'></span>[[#cite-_Ref76150902|[23]]] Lai Y.J. Hierarchical optimization: A satisfactory solution. Fuzzy Sets and Systems, 77(3):321-335, 1996. |
| − | <span id='_Ref76150919'></span>[[#cite-_Ref76150919|[24]]] Shih | + | <span id='_Ref76150919'></span>[[#cite-_Ref76150919|[24]]] Shih H.S., Lai Y.J., Lee E.S. Fuzzy approach for multi-level programming problems. Computers & Operations Research, 23(1):73-91, 1996. |
| − | [25] Farahi | + | [25] Farahi M.H., Ansari E. A new approach to solve Multi-objective linear bilevel programming problems. Journal of Mathematics and Computer Science, 1(4):313-320, 2010. |
| − | [26] Roy | + | [26] Roy S.K., Maiti S.K. Stochastic bi level programming with multi-choice for Stackelberg game via fuzzy programming. International Journal of Operational Research, 29(4):508-530, 2017. |
| − | <span id='_Ref76150935'></span>[[#cite-_Ref76150935|[27]]] Liu | + | <span id='_Ref76150935'></span>[[#cite-_Ref76150935|[27]]] Liu B. Stackelberg-Nash equilibrium for multilevel programming with multiple followers using genetic algorithms. Computers & Mathematics with Applications, 36(7):79-89, 1998. |
| − | <span id='_Ref76150943'></span>[[#cite-_Ref76150943|[28]]] D'Amato | + | <span id='_Ref76150943'></span>[[#cite-_Ref76150943|[28]]] D'Amato E., Daniele E., Mallozzi L., Petrone G., Tancredi S. A hierarchical multimodal hybrid Stackelberg–Nash GA for a leader with multiple followers game. Dynamics of Information Systems: Mathematical Foundations, Springer, New York, pp. 267-280, 2012. |
| − | <span id='_Ref76150950'></span>[[#cite-_Ref76150950|[29]]] Hong | + | <span id='_Ref76150950'></span>[[#cite-_Ref76150950|[29]]] Hong Z., Chu C., Zhang L.L., Yu Y. Optimizing an emission trading scheme for local governments: A Stackelberg game model and hybrid algorithm. International Journal of Production Economics, 193:172-182, 2017. |
| − | <span id='_Ref76150957'></span>[[#cite-_Ref76150957|[30]]] He | + | <span id='_Ref76150957'></span>[[#cite-_Ref76150957|[30]]] He X., Prasad A., Sethi S.P., Gutierrez G.J. A survey of Stackelberg differential game models in supply and marketing channels. Journal of Systems Science and Systems Engineering, 16(4):385-413, 2007. |
| + | </div> | ||
Latest revision as of 06:37, 4 May 2022
Abstract
Robust design has received a great deal of attention from quality researchers in recent years, and a number of optimization methodologies based on the dual response format have been proposed. The majority of existing bi-objective optimization models concentrate on the trade-offs between the process mean and variability functions without investigating the interactions between control factors and quality characteristics. The primary objective of this research is to integrate the Stackelberg leadership model into the robust design procedure and propose a Stackelberg game-based robust design (SGRD) method to determine appropriate control factor settings by minimizing the values of desired optimization targets based on an analysis of possible combinations of input and output quality parameters. Herein, first, a bi-objective robust design optimization problem is formulated as a dual response model using response surface methodology (RSM). Second, the proposed SGRD model is developed via decomposition into two leader-follower game models. Finally, the mean square error (MSE) criterion is applied to evaluate models and select non-dominated solutions in various situations. Numerical examples are used to demonstrate that the proposed method provides significant solutions in cases containing unidentified priorities between the dual responses and undiscovered correlations among several inputs and outcomes. In addition, according to the case study analysis, the proposed method is more efficient than the conventional dual response approach when dealing with bi-objective robust design optimization problems.
Keywords: Robust Parameter Design, Bi-objective Optimization, Dual Response Approach, Game Theory, Stackelberg Competition model
1. Introduction
The subject of quality management and improvement has received widespread and consistent attention from researchers in the last century. Many studies on literature have shown that a high-efficiency and cost-efficient system plays a vital role in realistic production processes. Taguchi [1] introduced a procedure for experimental design, which is also known as robust design, and that improves the robustness of quality characteristics by minimizing the response to noise factors. The main objective of robust design is to determine the optimal design settings for a product that can minimize the process variability and target deviation. Based on Taguchi's philosophy, subsequent experimental design methods have been developed to identify controlled parameter settings and, thus, improve the robustness of the production process.
Conventional robust design methods can be preliminarily classified as sequential and simultaneous optimization models. Vining and Myers [2] investigated the application of a dual response approach to minimize the process variability by assigning the process mean at the target with defining the priority criterion to separately optimize the estimated functions for the process mean and the standard deviation response based on RSM. Following the prioritized dual response format, Del Castillo and Montgomery [3] and Copeland and Nelson [4] presented improved optimization techniques for the situations in which one objective is achieved in advance (i.e., the process bias or variance is customer-specified). Instead of assigning a specific value to the optimization objective, the bias-specified and variability-specified robust design methods reached the goal of robust design by setting upper bounds for the process mean and standard deviation, respectively [5,6]. Priority-based methods reduce the complexity of problems by transforming multi-objective models into constrained single-objective models. However, existing prioritization schemes are limited because the majority of feasible solutions in the solution space are removed once the first prioritized objective has finished optimization. In this case, the reliability of efficient solutions in objective space is significantly decreased.
The MSE method proposed by Lin and Tu [7], which is based on the relaxed zero-bias assumption, deals with the dual response problem in a simultaneous mode. In terms of the MSE model and its simultaneous optimization order, the concept of weighted sum model is used by Tang and Xu [8], Koksoy and Doganaksoy [9] and,, Ding et al. [10] to investigate the trade-offs between process bias and variance on different weights, instead of the default equivalent weight terms used by Lin and Tu [7]. To find non-dominated solutions and non-convex Pareto frontier, Shin and Cho [11] introduced the lexicographic weighted Tchebycheff method based on the L-infinity norm. The weight-based simultaneous models show good accuracy and efficiency when used to search for the optimal solutions of a robust design problem. Nevertheless, it is difficult to identify the actual weight terms in simultaneous models by quality operators in practice.
The majority of existing robust design optimization methodologies focus on the trade-offs between process bias and variability. However, the interaction between control variables and quality characteristics has always been ignored. To this end, we incorporate the Stackelberg game theory philosophy into classical sequential optimization methods that can consider the impact of control factors on output performance. In the proposed SGRD model in this paper, one object is optimized in advance as the leader, given the constraint of another object (the follower)'s best response function. The leader's objective function may be adjusted according to the follower's best response function, which is variable due to the presence of various controlled factors. Therefore, it is worth discovering situations with permutations and combinations among controlled factors to analyze the correlations between input factors and quality characteristics. Doing so means that every possible interaction between the preferred objective and non-preferred target are taken into account. In addition, in real-world production procedures, quality engineers are often confronted with scenarios in which the importance between process characteristics may be undiscovered or specified by customers. The numerical examples in Section 4 include two cases; the first has unknown priority for quality characteristics, while the second is based on customer-specified bias-prioritized and variance-prioritized situations.
Section 2 presents a literature review and background information regarding the robust parameter design model and Stackelberg leader-follower model. A description of the proposed SGRD model is given in Section 3. Two numerical examples are discussed and drawn in Section 4. Section 5 includes the conclusion and discussion of this paper. Figure 1 shows an overview of the proposed bi-objective SGRD optimization procedure.
| Figure 1. Optimization procedure of the proposed SGRD model |
2. Literature review
2.1 Robust parameter design
The robust parameter design introduced by Genichi Taguchi is an experimental design technique that investigates the interactions between noise factors and outputs [12]. Taguchi proposed a two-step model using the signal theory that considered both mean and standard deviation of quality characteristics. The goal of this method is to minimize the effects of uncontrolled factors by finding the optimal settings for the controlled factors, process bias, and variance, more accurately. Despite the ongoing debate about the accuracy of the Taguchi method for modeling noise factors, the basic philosophy of robust design has generally been applied in the quality management area.
From the perspective of optimization order, the robust design process can be said to consist of simultaneous and sequential optimization procedures. In simultaneous optimization models, the weight term is considered a crucial criterion on which to evaluate the trade-off among objectives. Lin and Tu [7] integrated the MSE model, which takes both process bias and variance into account simultaneously, to solve the large variance problem in [2]. As illustrated by Lin and Tu [7], the MSE model's estimation is based on the assumption that the two objectives have the same weight. To identify more flexible and appropriate weight terms, Cho et al. [13], Tang and Xu [8], Koksoy and Doganaksoy [9] and Ding et al. [10] suggested using the concept of weighted sum based on the MSE model. In terms of the L-infinity norm, Kim and Lin [14] used fuzzy logic and membership functions to optimize process mean and variance simultaneously. Instead of the weighted sum model, Shin and Cho [11] suggested a lexicographical weighted Tchebycheff method to assign weight terms and find non-dominated solutions for a bi-objective optimization problem.
A sequential optimization procedure is also known as a priority-based performance method. RSM with the priority criterion was used in the first attempt at integration into the dual-response method in [2]. To achieve bi-objective optimization, Vining and Myers [2] assigned the mean value of the dual-response model at a customer-specified target and individually minimized the performance variance. Del Castillo and Montgomery [3] and Copeland and Nelson [4] incorporated the generalized reduced gradient method and Nelder-Mead simplex method into the dual-response model to guarantee a locally optimal solution. Kim and Cho [15] and Tang and Xu [8] improved the dual-response model using the goal programming method with a prioritized model. Shin and Cho [5, 6] introduced bias-specified and variability-specified robust design models using the e-constraint method for customer-specified bias and variance upper bounds. Combined with the bias-specified model, Steenackers and Guillaume [16] used the MSE model to determine the optimal design points. Regarding the variance-preference case, Kovach et al. [17] introduced a variance-prioritized multi-response robust design model that contains multiple quality characteristics via goal programming.
2.2 The Stackelberg leadership model
Game theory is the study of mathematical models of strategic interaction among rational decision-makers [18]. Modern Game Theory is considered to have begun with the 1944 book "Theory of Games and Economics Behavior" by John von Neumann and Oskar Morgenstern. Game Theory was later fleshed out by John Forbes Nash to mathematically represent strategic interactions among rational agents. It has been wildly used in all social science domains, and its applications have been extended to the majority of other fields associated with decision making.
The Stackelberg model is an economic strategy game described by Heinrich Freiherr von Stackelberg in 1934. This leadership game holds that, in a market, a leader firm and follower firm compete for quantity and take actions in sequence. Chen and Cruz [19] and Simaan and Cruz [20] extended the static two-person non-cooperative nonzero-sum Stackelberg game to a dynamic game format with an asymmetric information criterion. Shimizu and Aiyoshi [21] introduced a general bi-level Stackelberg game format and proposed an interior penalty method (i.e., barrier method) to solve the Stackelberg game-based non-linear min-max optimization problem. The penalty method was used in a static linear non-convex Stackelberg game model by Anandalingam and White [22]. In addition, Anandalingam and White [22] introduced and integrated the follower's rational reaction set into the leader's objective function. However, Lai [23] pointed out that the use of the penalty method may restrict the leader's power to make decisions and applied membership functions in extended hierarchical/multi-level Stackelberg game models. A fuzzy approach was combined with the membership function and used for multi-level programming in [24-26]. To search the Stackelberg equilibrium in a multi-level optimization problem, Liu [27], D'Amato et al. [28], and Hong et al. [29] discussed the application of a genetic algorithm. The Stackelberg leader-follower competition model has been extensively applied in the security defense and supply chain domains, as discussed in [30].
3. Models and methods
3.1 Extensive-form game model
Game theory is widely recognized as an analytical tool to exploit the interactions among several participants; it has been applied to many fields. In terms of the properties of the game, a game can be classified as cooperative/non-cooperative, simultaneous/sequential, perfect information/imperfect information, symmetric/asymmetric, and zero-sum/non-zero-sum. In this paper, we concentrate mostly on a non-cooperative sequential game model with perfect information.
In a general sequential game, which is also known in game theory as an extensive-form game, players take their actions in a specified sequence. Usually, the player who moves first is the front player, and the player who moves later is the rear player. The front player can make his decision in advance according to the anticipation of the rear player's movement. Then, the rear player can move based on the actions of the front player. Similar to a general sequential game, in a Stackelberg game, the player who makes the first decision is called the game leader, and the player who moves after the leader is known as the game follower. A particular extensive-form game with infinite action spaces can be used to represent the Stackelberg competition model, which is illustrated in Figure 2. The potential actions of each player are shown fanning out from the player's decision node. Players can select and make decisions from the action space, which may be constrained by boundaries.
| Figure 2. An extensive-form Stackelberg game with infinite action space |
In sequential games, a backward induction methodology is applied to search for the sub-game perfect Nash equilibrium, where the consideration order is reversed so that it flows from the follower to the leader. Concerning the Stackelberg leadership model, a first partial derivative method is applied to analyze the later player's best response functions located in the follower's action space.
3.2 The Stackelberg equilibrium: a general formulation
We identify two players in a non-cooperative sequential Stackelberg game that separately control the optimization objectives and control factors. Player 1's objective is to minimize his performance function and considers only factor . Correspondingly, the objective of player 2 is to minimize his performance function and considers only factor . Both functions are based on the factors and , which means that the strategies of two players have interacted. A variable set refers to a pair of rational strategies played by the two players, where and are the rational strategies set of the two players, respectively. The game ends when the game leader has optimized his performance function, which also means that an equilibrium is found. The Stackelberg equilibrium point and the associated Stackelberg equilibrium solution are denoted as and , separately. If player 1 acts as the leader and player 2 acts as the follower, based on the Stackelberg game rules, player 1 optimizes his objective first, and player 2 optimizes later. The Stackelberg equilibrium point can be found in the objective function of player 1 if:
|
|
(1) |
where represents the objective function of player 1 that considers the best response of player 2 with the related controlled factor , which can be found in the objective function of player 2 by:
|
|
Accordingly, if player 2 is the leader and player 1 is the follower, the Stackelberg equilibrium solution can be obtained in the objective function of player 2 if:
|
|
(2) |
where denotes the objective function of player 2 that takes the best response of player 1 with the corresponding controlled factor into account, which can be found in the objective function of player 1 by:
|
|
3.3 Bi-objective robust design model
In a bi-objective robust design model, the optimization target is to minimize both the process bias and the process variance , where is denoted as the vector of input factors. Then, a bi-objective robust design optimization problem can be integrated and formulated as follows:
|
|
(3) |
where refers to the target value of the process mean. represents the feasible solution set, where , and denotes the mth constraint. One possible solution is claimed that can dominate another solution , if and . An efficient solution (with the corresponding outcomes and ) is called the non-dominated solution if it cannot be dominated by any other solution in the model; it can then be regarded as an efficient trade-off between the objectives.
The conventional RSM is used to model and analyze response functions for estimating the process mean and standard deviation , which are:
|
|
(4) |
where
|
and
|
|
(5) |
where
|
In these two second-order equations, parameters and are the vector and matrix of regression coefficients for the estimated process mean; parameters and are the vector and matrix of regression coefficients for estimated process variance. The ordinary least square method is used to obtain the values of and .
For an intuitive comparison among the Stackelberg solutions based on various situations, an MSE model is introduced as an evaluation criterion to determine the non-dominated solution, which is formulated as:
|
(6) |
3.4 Proposed SGRD model
The integration procedure of the proposed bi-objective SGRD optimization problem from a Stackelberg game model is shown in Figure 3. The process bias and variance can be identified as the two game players of the proposed SGRD model. Then, the objective functions introduced in the Stackelberg leader-follower model, and , can be replaced by the estimated functions of process bias and variance , respectively. The optimization objectives of the bi-objective optimization problem and the input factors are separately controlled by the process bias and variance. We can define the input factors that are controlled by the process bias are denoted by , and . Correspondingly, as the complement of , the input factors that are controlled by the process variance are denoted by ,where . Similar to the Stackelberg game model, the response functions of process bias and variance are depended on the controlled factors and . Thus, the objective functions for the process bias and variance can be written as and , respectively. Based on the Stackelberg game rules, the target of process bias is to minimize and considers only factor . Accordingly, the target of process variance is to minimize and considers only factor .
| Figure 3. Integration procedure from a Stackelberg game model |
The proposed SGRD model can be investigated via decomposition into the bias-leader model and variance-leader model according to the optimization sequence. If the process bias is optimized in advance, the bias-leader model of the proposed SGRD model can be applied, and Eq. (1) of the two-player Stackelberg game model can be transformed into the bias-leader model. The Stackelberg equilibrium solution with the Stackelberg equilibrium point can be determined by the process bias if:
|
|
(7) |
where is the response function of the process bias that considers the best response of the process variance with the related controlled factor , which can be performed in the response function of the process variance by:
|
|
and where is the estimated regression function for the process variability, which is performed using RSM.
Correspondingly, when the process variability is regarded as the game leader, the variance-leader of the proposed SGRD model can be implemented, and Eq. (2) can be transformed into the variance-leader model. Hence, the Stackelberg equilibrium can be determined by the process variance if:
|
|
(8) |
where represents the response function of the process variance that considers the best response of the process bias with the corresponding controlled factor , which can be performed in the response function of process bias by:
|
|
and where is the estimated regression function for the process mean that can be obtained using RSM.
For clarity, the algorithm of the proposed SGRD is presented in a stepwise fashion in Table 1. In this paper, we used the MATLAB software package to perform the proposed methodology and identify the Stackelberg equilibrium for each optimization objective.
Step 1. Input data and assign controlled factors
Step 2. Obtain estimated functions of the quality characteristics
Step 3. Formulate a bi-objective robust design model
Step 4. Evaluate the bias-leader model of the proposed SGRD model
Step 5. Determine the non-dominated solution for the bias-leader model
Step 6. Evaluate the variance-leader model of the proposed SGRD model
Step 7. Determine the non-dominated solution for the bias-leader model
Step 8. Determine the most efficient solution for the proposed SGRD model
|
4. Numerical examples
4.1 Example 1
A printing machine example is discussed in [2]. The authors investigated how the printer's ability () to apply colored inks to package labels is affected by speed (), pressure (), and distance (). This is a three-level factorial experimental design with three runs () at each design point. Detailed experimental data is shown in Table 2, where and represent the process mean and process standard deviation, respectively.
| Run () | ||||||||
|---|---|---|---|---|---|---|---|---|
| 1 | - | - | - | 34 | 10 | 28 | 24.00 | 12.50 |
| 2 | 0 | - | - | 115 | 116 | 130 | 120.30 | 8.40 |
| 3 | + | - | - | 192 | 186 | 263 | 213.70 | 42.80 |
| 4 | - | 0 | - | 82 | 88 | 88 | 86.00 | 3.70 |
| 5 | 0 | 0 | - | 44 | 178 | 188 | 136.70 | 80.40 |
| 6 | + | 0 | - | 322 | 350 | 350 | 340.70 | 16.20 |
| 7 | - | + | - | 141 | 110 | 86 | 112.30 | 27.60 |
| 8 | 0 | + | - | 259 | 251 | 259 | 256.30 | 4.60 |
| 9 | + | + | - | 290 | 280 | 245 | 271.70 | 23.60 |
| 10 | - | - | 0 | 81 | 81 | 81 | 81.00 | 0.00 |
| 11 | 0 | - | 0 | 90 | 122 | 93 | 101.70 | 17.70 |
| 12 | + | - | 0 | 319 | 376 | 376 | 3570 | 32.90 |
| 13 | - | 0 | 0 | 180 | 180 | 154 | 171.30 | 15.00 |
| 14 | 0 | 0 | 0 | 372 | 372 | 372 | 372.00 | 0.00 |
| 15 | + | 0 | 0 | 541 | 658 | 396 | 501.70 | 92.50 |
| 16 | - | + | 0 | 288 | 192 | 312 | 264.00 | 63.50 |
| 17 | 0 | + | 0 | 432 | 336 | 513 | 427.00 | 88.60 |
| 18 | + | + | 0 | 713 | 725 | 754 | 730.70 | 21.10 |
| 19 | - | - | + | 364 | 99 | 199 | 220.70 | 133.80 |
| 20 | 0 | - | + | 232 | 221 | 266 | 239.70 | 23.50 |
| 21 | + | - | + | 408 | 415 | 443 | 422.00 | 18.50 |
| 22 | - | 0 | + | 182 | 233 | 182 | 199.00 | 29.40 |
| 23 | 0 | 0 | + | 507 | 515 | 434 | 485.30 | 44.60 |
| 24 | + | 0 | + | 846 | 535 | 640 | 673.70 | 158.20 |
| 25 | - | + | + | 236 | 126 | 168 | 176.70 | 55.50 |
| 26 | 0 | + | + | 660 | 440 | 403 | 501.00 | 138.90 |
| 27 | + | + | + | 878 | 991 | 1 161 | 1 010.00 | 142.50 |
The fitted response surface functions for the process mean and standard deviation in [2] are:
|
(9) |
where
|
and
|
(10) |
where
|
The feasible solution set The target value of the process mean is assumed to be 500. The process mean and variance can be considered by “Nominal the best” and “Smaller the better” types of quality characteristics. Generally, it is possible to analyze this bi-objective optimization problem by decomposing the proposed SGRD model into a bias-leader model and a variance-leader model. In addition, we consider different correlations between input variables and quality characteristics to analyze all possible situations and find the follower's best responses in each model.
4.1.1 Bias-leader model
First, we consider a situation in which the process bias is optimized first as the leader in a Stackelberg game. In this situation, process variance is the follower. The detailed results using Eq. (7) of the bias-leader model are shown in Table 3.
| SGRD Bias-leader model |
MSE | |||||
|---|---|---|---|---|---|---|
| Variance control | -0.8262 | -0.5404 | -0.0783 | 113 390 | 475.21 | 113 865.21 |
| Variance control | 0.1818 | 1 | -1 | 66 609 | 630.14 | 67 239.14 |
| Variance control | 1 | -0.0496 | -1 | 42 477 | 1 066.35 | 43 543.35 |
| Variance control | -1 | -0.0406 | -0.5465 | 127 830 | 378.26 | 128 208.26 |
| Variance control | -0.5029 | -0.5814 | -0.5487 | 123 470 | 325.32 | 123 795.32 |
| Variance control | -0.0450 | 0.3283 | -1 | 101 940 | 500.01 | 102 440.01 |
| Variance control | -0.8046 | -0.1676 | -0.6766 | 129 900 | 365.31 | 130 265.31 |
As shown in the table, if we consider that the process variance is highly correlated to , the minimum MSE value (43 543.35) with the related control factor setting is obtained when and .
4.1.2 Variance-leader model
Next, we consider a situation in which the process variance is prioritized as the Stackelberg game leader. The results, which are derived using Eq. (8) of the variance-leader model, are presented in Table 4. Based on the assumption of process bias controls and , we obtain the efficient result that . The process variance is 2 049.10 in the zero-bias condition, and the corresponding variable setting is .
| SGRD Variance-leader model |
MSE | |||||
|---|---|---|---|---|---|---|
| Bias control | -1 | -1 | -0.6225 | 161 760 | 360.44 | 162 120.44 |
| Bias control | -0.6593 | 0.5935 | -0.9013 | 132 930 | 308.73 | 133 238.73 |
| Bias control | -1 | -1 | 0.2131 | 145 830 | 466.27 | 146 296.27 |
| Bias control | 1 | 0.3229 | -0.3911 | 0 | 2 049.10 | 2 049.10 |
| Bias control | 1 | -0.1030 | -0.0892 | 0 | 2 063.07 | 2 063.07 |
| Bias control | 1 | -0.0820 | -0.1069 | 0 | 2 057.15 | 2 057.15 |
| Bias control | 0.9991 | -0.1369 | -0.0591 | 0 | 2 075.53 | 2 075.53 |
4.1.3 Results and discussion
Comparing the non-dominated results of the bias-leader and variance-leader models in example 1 based on the MSE criterion shows that the variance-leader model provides a more efficient outcome, and it is more appropriate to optimize process variance in advance when the process bias is treated as a restriction. In addition, and are regarded as the controlled factors for process bias, and the solution set is .
A comparison of the significant results of example 1 between the dual response approach in [2] and the proposed SGRD model is exhibited in Table 5. As evidenced by the results, the proposed SGRD model is more efficient than the dual response model based on the same zero-bias condition. Since the dual response approach is a pure priority-based optimization method, the comparison also shows the importance of considering the correlations between controlled factors and optimization objectives. The contour plots for the process mean and standard deviation are shown in Figure 4, where the Stackelberg equilibrium solutions of the bias-leader model and variance-leader model are denoted by dots. The solution obtained by usingthe ual response approach is plotted as a star, and the most efficient solution provided by the proposed SGRD model is marked as a circle.
| Method | MSE | |||||
|---|---|---|---|---|---|---|
| Dual response approach | 0.614 | 0.228 | 0.100 | 0 | 2 680.96 | 2 680.96 |
| Proposed SGRD model | 1 | 0.3229 | -0.3911 | 0 | 2 049.10 | 2 049.10 |
| Figure 4. Contour plots for process mean and standard deviation (example 1) |
4.2 Example 2
The experimental data in example 2 concerns the bare silicon wafer production process of an injection-molding company for a large motor corporation. The dataset appears in [6]. Three essential factors , mold temperature, injection flow rate, and cooling rate, are considered to affect the coating thickness ( ) of bare silicon wafers. The coded and uncoded units of control factors are shown in Table 6, and the spherical central composite design is presented in Table 7.
| Levels of coded variables |
Uncoded or original variables | ||
|---|---|---|---|
| Mold temperature (F) |
Injection flow rate (lbs/sec) |
Cooling rate (F/sec) | |
| 99.6 | 40 | 4.8 | |
| -1 | 140.5 | 46 | 15 |
| 0 | 200.5 | 55 | 30 |
| +1 | 260.5 | 64 | 45 |
| 301.4 | 70 | 55.2 | |
| - | - | - | 76.30 | 80.50 | 77.70 | 81.10 | 78.90 | 2.28 |
| + | - | - | 79.10 | 81.20 | 78.80 | 79.60 | 79.68 | 1.07 |
| - | + | - | 82.50 | 81.50 | 79.50 | 80.90 | 81.10 | 1.25 |
| + | + | - | 72.30 | 74.30 | 75.70 | 72.70 | 73.75 | 1.56 |
| - | - | + | 70.60 | 72.70 | 69.90 | 71.50 | 71.18 | 1.21 |
| + | - | + | 74.10 | 77.90 | 76.20 | 77.10 | 76.33 | 1.64 |
| - | + | + | 78.50 | 80.00 | 76.20 | 75.30 | 77.50 | 2.14 |
| + | + | + | 84.90 | 83.10 | 83.90 | 83.50 | 83.85 | 0.77 |
| -1.682 | 0 | 0 | 74.10 | 71.80 | 72.50 | 71.90 | 72.58 | 1.06 |
| 1.682 | 0 | 0 | 76.40 | 78.70 | 79.20 | 79.30 | 78.40 | 1.36 |
| 0 | -1.682 | 0 | 79.20 | 80.70 | 81.00 | 82.30 | 80.80 | 1.27 |
| 0 | 1.682 | 0 | 77.90 | 76.40 | 76.90 | 77.40 | 77.15 | 0.65 |
| 0 | 0 | -1.682 | 82.40 | 82.70 | 82.60 | 83.10 | 82.70 | 0.29 |
| 0 | 0 | 1.682 | 79.70 | 82.40 | 81.00 | 81.20 | 81.08 | 1.11 |
| 0 | 0 | 0 | 70.40 | 70.60 | 70.80 | 71.10 | 70.73 | 0.30 |
| 0 | 0 | 0 | 70.90 | 69.70 | 69.00 | 69.90 | 69.88 | 0.78 |
| 0 | 0 | 0 | 70.70 | 71.90 | 71.70 | 71.20 | 71.38 | 0.54 |
| 0 | 0 | 0 | 70.20 | 71.00 | 71.50 | 70.40 | 70.78 | 0.59 |
| 0 | 0 | 0 | 71.50 | 71.10 | 71.20 | 70.00 | 70.95 | 0.66 |
| 0 | 0 | 0 | 71.00 | 70.40 | 70.90 | 69.90 | 70.55 | 0.51 |
The estimated functions for the process mean and standard deviation in [6] derived using RSM are:
|
(11) |
where
|
and
|
(12) |
where
|
The feasible solution set The target coating thickness is specified by the customer and is set at 71.14. The goal of the bi-objective optimization problem is to minimize process bias and variability. Based on the same optimization progress in example 1, the proposed SGRD model can be decomposed into a bias-leader model and variance-leader model, which are stated below.
4.2.1 Bias-leader model
In the bias-leader model, process variance is imagined as the optimization constraints while optimizing the process bias, and various combinations of the controlled variables have been taken into account. Eq. (7) of the proposed SGRD model is applied, and the experimental outcome is shown in Table 8.
| SGRD Bias-leader model |
MSE | |||||
|---|---|---|---|---|---|---|
| Variance control | -1.3436 | -0.5222 | 0.9602 | 0.0316 | 11.8185 | 11.8501 |
| Variance control | -1.4786 | -0.1643 | 0.5381 | 0 | 9.1059 | 9.1059 |
| Variance control | -1.6885 | 0.0014 | 0.3858 | 0.0039 | 10.1086 | 10.1125 |
| Variance control | -0.8403 | 0.0954 | 0.6783 | 0.5461 | 8.5949 | 9.1410 |
| Variance control | -0.0778 | 0.2155 | -0.2813 | 1.2160 | 5.7586 | 6.9746 |
| Variance control | -1.6743 | -0.2570 | 0.3616 | 0.0303 | 9.7644 | 9.7947 |
| Variance control | -0.0146 | 0.3173 | -0.3008 | 1.2398 | 5.7351 | 6.9749 |
According to the MSE criterion, the solution set with input variable setting has been identified as the non-dominated result in this model, where the MSE value is 6.9746. Moreover, controlled factors and are assumed to be significantly correlated with the game follower, which is process variance.
4.2.2 Variance-leader model
Using Eq. (8) from the proposed SGRD model yields the results listed in Table 9. The non-dominated solution set of the variance-leader model is with a minimum MSE value of 6.9765. The corresponding control variable setting is , and the input factor is regarded as controlled by the process bias.
| SGRD Variance-leader model |
MSE | |||||
|---|---|---|---|---|---|---|
| Bias control | -0.0056 | 0.3090 | -0.3703 | 1.3680 | 5.7528 | 7.1208 |
| Bias control | -0.0158 | 0.3130 | -0.3021 | 1.2414 | 5.7351 | 6.9765 |
| Bias control | 0.0623 | 0.4282 | -0.2000 | 1.2609 | 5.8279 | 7.0888 |
| Bias control | 0.0124 | 0.3570 | -0.3789 | 1.3797 | 5.7581 | 7.1378 |
| Bias control | 0.5313 | 0.8449 | -0.5805 | 2.2640 | 6.5000 | 8.7640 |
| Bias control | 0.0945 | 0.2044 | -0.1231 | 1.1757 | 6.0388 | 7.2145 |
| Bias control | 1.3620 | 0.5836 | -0.8465 | 1.8876 | 8.5498 | 10.4374 |
4.2.3 Results and discussion
A comparison of the non-dominated results of the bias-leader and variance-leader models in example 2 based on the MSE criterion shows that the result of the bias-leader model is slightly better than that of the variance-leader model.
The bias-leader model of the proposed SGRD method is next compared with the dual response approach; the results are presented in Table 10. Based on the zero-bias assumption, the process variance and MSE values obtained using the dual response approach are equal to 9.0854. With the more relaxed bias assumption, the proposed SGRD model provides a more efficient solution. Figure 5 is the contour plots for the process mean and standard deviation, where the notation dot, star, and circle represent the Stackelberg equilibrium solution, the solution obtained by using dual response approach, and the most efficient solution provided by the proposed SGRD model, respectively.
| Method | MSE | |||||
|---|---|---|---|---|---|---|
| Dual response approach | -1.4561 | -0.1456 | 0.5596 | 0 | 9.0854 | 9.0854 |
| Proposed SGRD model | -0.0778 | 0.2155 | -0.2813 | 1.2160 | 5.7586 | 6.9746 |
| Figure 5. Contour plots for the process mean and standard deviation (example 2) |
5. Conclusion
Conventional priority-based robust design optimization methodologies are based on the assumption of preset priorities. However, in a real-world production process, the exact priorities and weights among several objectives are always unknown. In order to find a reasonable solution based on that situation, in this paper, we proposed a bi-objective robust design optimization method based on game theory. Furthermore, existing priority-based approaches place an emphasis on investigating the trade-offs among several different optimization objectives, but it is worth considering the interaction relationships among input control factors and quality characteristics. To this end, we introduced the proposed SGRD optimization procedure to integrate the effects of control factors. As shown in the numerical examples, the proposed SGRD model can be used to analyze all scenarios with different optimization sequences and various combinations of control factors. Therefore, it is helpful for quality engineers to determine the most appropriate condition from the perspective of game theory. In this paper, we discussed a bi-objective optimization model based on a single quality response, which can be extended to multi-response robust design optimization models in the future.
Acknowledgment
This work was supported by the National Research Foundation of Korea (NRF) (No. NRF- 2019R1F1A1060067).
References
[1] Taguchi G. Introduction to quality engineering. Asian Productivity Organization, UNIPUB, White Plains, NY, 1986.
[2] Vining G.G., Myers R.H. Combining Taguchi and response surface philosophies: a dual response approach. Journal of Quality Technology, 22(1):38-45, 1990.
[3] Del Castillo E., Montgomery D.C. A nonlinear programming solution to the dual response problem. Journal of Quality Technology, 25(3):199-204, 1993.
[4] Copeland K.A., Nelson P.R. Dual response optimization via direct function minimization. Journal of Quality Technology, 28(3):331-336, 1996.
[5] Shin S., Cho B.R. Bias-specified robust design optimization and its analytical solutions. Computers & Industrial Engineering, 48(1):129-140, 2005.
[6] Shin S., Cho B.R. Robust design models for customer-specified bounds on process parameters. Journal of Systems Science and Systems Engineering, 15(1):2-18, 2006.
[7] Lin D.K., Tu W. Dual response surface optimization. Journal of Quality Technology, 27(1):34-39, 1995.
[8] Tang L.C., Xu K. A unified approach for dual response surface optimization. Journal of Quality Technology, 34(4):437-447, 2002.
[9] Köksoy O., Doganaksoy N. Joint optimization of mean and standard deviation using response surface methods. Journal of Quality Technology, 35(3):239-252, 2003.
[10] Ding R., Lin D.K., Wei D. Dual-response surface optimization: a weighted MSE approach. Quality Engineering, 16(3):377-385, 2004.
[11] Shin S., Cho B.R. Studies on a biobjective robust design optimization problem. IIE Transactions, 41(11):957-968, 2009.
[12] Brewer K., Carraway L., Ingram D. Forward selection as a candidate for constructing nonregular robust parameter designs. Technical Report, Arkansas State University, 2010.
[13] Cho B.R., Philips M.D., Kapur K.C. Quality improvement by RSM modeling for robust design. The 5th Industrial Engineering Research Conference, pp. 650-655, May 1996.
[14] Kim K.J., Lin D.K. Dual response surface optimization: a fuzzy modeling approach. Journal of Quality Technology, 30(1):1-10, 1998.
[15] Kim Y.J., Cho B.R. Development of priority-based robust design. Quality Engineering, 14(3):355-363, 2002.
[16] Steenackers G., Guillaume P. Bias-specified robust design optimization: A generalized mean squared error approach. Computers & Industrial Engineering, 54(2):259-268, 2008.
[17] Kovach J., Cho B.R., Antony J. Development of a variance prioritized multiresponse robust design framework for quality improvement. The International Journal of Quality & Reliability Management, 26(4):380, 2009.
[18] Myerson R.B. Game theory. Harvard University Press, 1997.
[19] Chen C.L., Cruz J. Stackelburg solution for two-person games with biased information patterns. IEEE Transactions on Automatic Control, 17(6):791-798, 1972.
[20] Simaan M., Cruz J.B. On the Stackelberg strategy in nonzero-sum games. Journal of Optimization Theory and Applications, 11(5):533-555, 1973.
[21] Shimizu K., Aiyoshi E. A new computational method for Stackelberg and min-max problems by use of a penalty method. IEEE Transactions on Automatic Control, 26(2):460-466, 1981.
[22] Anandalingam G., White D.J. A solution method for the linear static Stackelberg problem using penalty functions. IEEE Transactions on Automatic Control, 35(10):1170-1173, 1990.
[23] Lai Y.J. Hierarchical optimization: A satisfactory solution. Fuzzy Sets and Systems, 77(3):321-335, 1996.
[24] Shih H.S., Lai Y.J., Lee E.S. Fuzzy approach for multi-level programming problems. Computers & Operations Research, 23(1):73-91, 1996.
[25] Farahi M.H., Ansari E. A new approach to solve Multi-objective linear bilevel programming problems. Journal of Mathematics and Computer Science, 1(4):313-320, 2010.
[26] Roy S.K., Maiti S.K. Stochastic bi level programming with multi-choice for Stackelberg game via fuzzy programming. International Journal of Operational Research, 29(4):508-530, 2017.
[27] Liu B. Stackelberg-Nash equilibrium for multilevel programming with multiple followers using genetic algorithms. Computers & Mathematics with Applications, 36(7):79-89, 1998.
[28] D'Amato E., Daniele E., Mallozzi L., Petrone G., Tancredi S. A hierarchical multimodal hybrid Stackelberg–Nash GA for a leader with multiple followers game. Dynamics of Information Systems: Mathematical Foundations, Springer, New York, pp. 267-280, 2012.
[29] Hong Z., Chu C., Zhang L.L., Yu Y. Optimizing an emission trading scheme for local governments: A Stackelberg game model and hybrid algorithm. International Journal of Production Economics, 193:172-182, 2017.
[30] He X., Prasad A., Sethi S.P., Gutierrez G.J. A survey of Stackelberg differential game models in supply and marketing channels. Journal of Systems Science and Systems Engineering, 16(4):385-413, 2007.
Document information
Published on 08/10/21
Accepted on 24/09/21
Submitted on 27/07/21
Volume 37, Issue 4, 2021
DOI: 10.23967/j.rimni.2021.09.008
Licence: CC BY-NC-SA license
Share this document
Keywords
claim authorship
Are you one of the authors of this document?