| Line 1: | Line 1: | ||
| − | ==On using linear elements in incompressible plane strain problems. | + | ==On using linear elements in incompressible plane strain problems. A simple edge based approach for triangles== |
| − | A simple edge based approach for triangles== | + | |
'''B. Boroomand''', '''B. Khalilian''' | '''B. Boroomand''', '''B. Khalilian''' | ||
| Line 7: | Line 6: | ||
Civil Engineering Department, Isfahan University of Technology, Isfahan, Iran | Civil Engineering Department, Isfahan University of Technology, Isfahan, Iran | ||
| − | ''To express our gratitude to Professor O. C. Zienkiewicz for his numerous contributions to the subject. | + | ''To express our gratitude to Professor O. C. Zienkiewicz for his numerous contributions to the subject. This paper is dedicated to him on occasion of his 83 birthday.'' |
| − | This paper is dedicated to him on occasion of his 83 birthday.'' | + | |
Revision as of 14:37, 14 December 2016
On using linear elements in incompressible plane strain problems. A simple edge based approach for triangles
B. Boroomand, B. Khalilian
Civil Engineering Department, Isfahan University of Technology, Isfahan, Iran
To express our gratitude to Professor O. C. Zienkiewicz for his numerous contributions to the subject. This paper is dedicated to him on occasion of his 83 birthday.
Abstract
In this paper a simple iterative method is presented for finite element solution of incompressible plane strain problems using linear elements. Instead of using a mixed formulation approach, we use an equivalent displacement/velocity approach in an iterative manner. Control volumes are taken for regions where are to exhibit incompressible behavior. For triangular elements the control volume is chosen as the area built on the parts of each pair of elements at the sides of an edge. In this case, elements are let to exchange volume. It is shown that the proposed edge based approach removes the deficiency of the linear triangular elements i.e. locking effect.
Similar edge based approach is applied to the linear quadrilateral elements. However, if the control volume is chosen as the element volume the formulation gives similar results as the discontinuous mixed formulation using one pressure point without exhibiting instability behavior. The formulation is based on decomposition of the displacement/velocity field into deviatoric and volumetric parts. The volumetric part is iteratively eliminated without confronting locking or instability phenomenon. The iterative procedure is very cheap and simple to be implemented in any FEM code. Several examples are given to demonstrate the performance of the procedure.
Keywords: Incompressibility, linear triangular elements, edge based, plane strain, locking, instability.
1. INTRODUCTION
Due to the practical importance, simulation of materials with incompressible behavior has received considerable attention during the past few decades. Numerical solutions of problems with rubber-like materials or problems incorporating large deformation such as metal forming processes are notable examples in solid mechanics context. Also in fluid dynamics context incompressible behavior of liquids is of great importance for simulation.
In simulations using finite element method, linear elements are of special interest because of simplicity and cost effectiveness. However, application of this class of elements, in its standard one field form, faces some restrictions due to excessive number of constraints encountering the solution. Instability and locking effects are commonly seen in solution of plane strain problems, for instance. Similar effect is seen when simulation of materials with fully plastic behavior is of concern especially for materials obeying von-Mises yield criterion or even Mohr-Coulomb materials with non-associative flow rule. This effect is basically due to volumetric constraint induced during the plastic deformation leading to an incompressible behavior of the material. Although numerous efforts have been made to circumvent the locking problem in some non-standard forms, retrieve of the elements in a standard one field solution is still of importance.
An early attempt to formulate the incompressible or nearly incompressible behavior of materials appears to be the work performed by Hermann [1] known as mixed formulation. In such a variational formulation pressure is used as an additional variable. The formulation was further used, in a discontinuous form, by Hughes [2] and Malkus [3] and shown to be equivalent to the use of selective integration technique. Generalization of the selective integration technique and the mixed method to nonlinear problems, especially with elastoplasticity behavior, was performed by Hughes [4] and Simo et al [5] within the framework of Hu-Washizu variational principle.
Since the basis of all above advances is mixed formulation, the Babuška-Brezzi criteria for stability of the solution are met by choosing appropriate number of pressure variables in each element. A simple patch test approach as a necessary but not sufficient condition, as used in [6], may be employed to show the liability of the elements to pass BB criteria. However, it may easily be shown that none of the linear elements can generally pass the patch test (see [6]). This means that the use of linear elements may lead to either instability or locking effect during the solution process.
For linear quadrilateral elements using discontinuous mixed formulation, although both locking and instability are of concern, the instability effect is much more pronounced. The instability modes of the displacement/velocities are known as hourglass patterns especially when the elements are in rectangular shapes. The source of the instability has been studied by Hueck et al in reference 7 where some remedy is given to eliminate the spurious modes at the element level. However, it has been shown by Zienkiewicz et al that a simple iterative scheme can also be employed to remove such spurious modes [8]. The iterative method may be interpreted as an extension of Usawa’s method, proposed for general optimization procedures [9], to the mixed formulation of incompressible problems. In the iterative method, a fictitious compressibility matrix is temporarily used to obtain stable increments of displacements.
In the context of linear rectangular elements the method of using incompatible modes, suggested by Wilson et al [10] for plane elasticity, should be mentioned here. The method was further modified by Taylor et al [11] for general linear quadrilateral elements. The method was proposed for improvement of bending behavior of quadrilateral elements and appeared to be effective for application to problems with nearly incompressible behavior. Another class of approaches known as assumed strain/stress methods should also be considered. The pioneering work due to Nagtegaal et al [12] is the representative of the assumed strain methods and among them are the B-bar methods by Hughes [4] and Simo et al [5]. The formulation introduced by Simo and Rifai [13] for quadrilateral elements also falls in the assumed strain category of approaches and appears to be working well in nearly incompressible cases of elasticity and plasticity problems. Representatives of the assumed stress class of approaches are the formulations introduced by Pian and Sumihara [14] and Puch and Atluri [15] for quadrilateral elements.
For linear triangular elements the use of discontinuous mixed formulation is equivalent to the standard displacement formulation since the stress field is constant. The locking effect is of more concern in this type of element. Such a locking effect, if not controlled, increases the mesh dependency of the solution due to directional behavior of the elements (see reference [16] for instance). It should be mentioned that the directional behavior of linear elements is generally due to both locking effect and poor bending behavior of the elements [17]. But when the locking effect is circumvented the bending behavior is improved, as will be seen in the beam example in this paper, and therefore directional behavior is effectively reduced.
Generally, the locking phenomenon may be evidently observed in plane strain problems since the transverse strain is zero and the volume change can not be compensated by increase of the element thickness as the case for plane stress problems. But it must be noted that even in a plane stress problem, though not explicitly seen, there will be no guarantee for obtaining correct thickness changes. This simple discussion shows that the importance of any remedy for triangular element does not limit to its application to plane strain problems.
Several remedies have been proposed for elements failing to pass the mixed formulation patch tests especially for triangular ones. One immediate remedy, of course, is introduction of bubble function for displacement to increase the number of displacement variables. However, some difficulties arise when the acceleration terms encounter the problem. Other remedies are basically proposed for application in fluid dynamics problems. Although the remedies are basically suggested for convection dominant problems, we mention some of them here since their applications to steady-state Stokes flow problems, as special cases, can be regarded as their use in incompressible linear elasticity problems. Galerkin Least Square (GLS) approach was used by Hughes et al [18] as a mean of stabilizing solutions in flow problems. A series of time integration based approaches for both solid and fluid problems were proposed by Zienkiewicz and Wu [19]. Some more complete algorithms, called Characteristic Based Split (CBS) algorithm, suitable for full fluid equations were also proposed by Zienkiewicz et al in a series of papers [20-22]. The method follows the idea initially introduced by Chorin [23]. The method was also employed for plasticity problems in reference 24. In the context of stabilization of problems with linear triangular elements the work by Oñate and co-workers [25] using finite calculus (FIC) formulation proposed in reference 26 should be mentioned here.
The method proposed in this paper is basically devised for triangular elements and we shall demonstrate its performance through several examples. The method is based on calculation of some consistent unbalanced forces to reduce the volume changes. The force based nature of the method helps to choose edge based control volumes which play the key role for solution of problems with meshes of linear triangular elements. However, if the method is applied to quadrilateral elements using each element as the control volume, it may be interpreted as a special case of the method proposed by Zienkiewicz et al in [8] though the pressure projection part is different.
The layout of the paper will be as follows. In the next section the conventional mixed formulation is revisited. The formulation for our proposal iterative method is given in section three where the step by step algorithm is described and a discussion on its similarities with the mixed formulation is given. The formulation for linear quadrilateral and triangular elements is given in section four. In section five, numerical results are presented for solution of some benchmark problems.
2. FINITE ELEMENT MODEL
The mathematical model of an incompressible elastic problem can be summarized as a system of differential equations in domain of interest, , as
to be solved with boundary conditions on as
and additional side constraint for incompressibility as
Where ,
is the vector of stress components,
is body force vector,
is an operator defining strain vector from displacement components
,
is a matrix containing components of unit normal to the boundary with traction
and
for two dimensional problems. The stress tensor is decomposed into deviatoric and hydrostatic pressure parts which for two dimensional cases, in a vector notation, is written as
The deviatoric part of the stress vector is proportional to the deviatoric part of the strains
in which
Where denotes the shear modulus of the material. The deviatoric stresses can directly be written in terms of total strains
as
In which
The equilibrium equation (1) is written as
The equilibrium state of the system can be obtained using weak formulation or virtual work concept as
| |
(10) |
To employ a finite element formulation, after a domain discretization the displacement field is expressed approximately in terms of shape functions and the nodal values
In that case the strains are evaluated through the following well known relation
This requires that Equation (10) be written in terms of the displacements. It can be seen that in (10) the stress field can partially be written in terms of the displacements through its deviatoric part as Equation (7). However, since for fully incompressible materials pressure is a mechanical quantity, the pressure part of the stress field in (10) may not be written in terms of the displacements. Based on the treatment of the pressure part in the formulation, this class of problems may be branched in to two categories, i.e. fully incompressible or nearly incompressible material behavior modeling. In the next subsection we shall briefly over view the conventional approaches used for such formulations.
2.1 Penalty and Lagrange multiplier approaches – a brief review
Similar to optimization procedures, the main problem, here, is to apply an equality constraint during minimization of a suitable functional, i.e. the deviatoric potential energy. For further use we rewrite Equation (10) in its equivalent form using (4), (7) and (3) as
In the case of using a penalty approach the constraint is enforced by adding its quadratic form to the deviatoric potential energy assuming
. Here
is a penalty factor and plays the role of bulk modulus. Depending on the value chosen for
locking or instability may be seen in the solution. To reduce the locking effect a selective integration scheme may be employed.
In the case that Lagrange multipliers approach is used the equality constrain is added though a suitable multiplier, to the deviatoric potential energy, and minimizing the corresponding functional with respect to both main variables and the multipliers. It is shown that multiplier field is identical to the pressure field and thus the formulation is called mixed
method. The pressure field is expressed in terms of independent variables as
, where
are appropriate shape functions to be chosen for the pressure field. Taking into account the variation of the pressure field in a separate set of equations, the following system of equations (see [6] for more details) are then obtained
| |
In above is a force vector identical to the one in the conventional displacement formulation. In order to avoid ill-condition/instability, Babuška-Brezzi conditions must be checked. Depending on the choice of shape functions employed for the pressure field, the method may be categorized into two forms, i.e. mixed methods with continuous/discontinuous pressure field.
In the continuous mixed formulation a series of hat functions, similar to those used for the displacements, are used and a continuous field of pressure is obtained. But such inevitable choice of shape functions disqualifies some classes of elements, e.g. linear elements. However, some stabilization techniques may be used for such interpolation of displacements/pressure values. The reader may consult to reference 6 for the history of the techniques or to the recent work in [27] for solid mechanics problems which is basically the extension of the approach due to Hughes [28].
In the discontinuous mixed formulation, however, the pressure field is expressed through a series of step functions defined over the elements. A simple patch test shows that for some special patterns of linear quadrilateral elements, instability may happen (see [6] for example).
The system of equations (14) may also be solved iteratively. To explore the main differences between our method and the existing iterative one, we give a brief overview for such a method. The iterative method is in fact the extension of Uzawa’s method to general mixed formulation and the core of it is updating the pressure values during the iterations as (see [8] for more details)
Where is suitable projection matrix usually taken proportional to identity matrix as
, and
is the same matrix as introduced in (14). The nodal displacements are evaluated by exact satisfaction of the first set of equations in (14) assuming that the pressure values are known a priori. The procedure leads to inverse of
which is not available generally. Therefore
is temporarily replaced by
Where is a fictitious bulk modulus. Thus from the first set of equations in (14) we have
The iteration continues until the residual of the second set of equations in (14), i.e. , vanishes or becomes sufficiently small. The procedure has been shown to be convergent and depending on the integration scheme used in
the instability modes may still be seen in the solution. The reader is referred to reference 6 for further information about the limitations and the history. Here one may notice that the iterative procedure just intends to solve Equation (14) and does not suggest any escaping way from mixed formulation limitations, i.e. Babuška-Brezzi conditions.
In all cases mentioned above, the formulations require evaluation of both nodal displacement and pressure values simultaneously. However, a fully displacement based approach may be sought by assuming the material to be nearly incompressible, i.e. instead of
in (13), and thus eliminating the pressure value at the element level. It can easily be shown that such a formulation is equivalent to the penalty method using selective integration scheme and thus possesses the same disadvantages mentioned previously.
In the next section we shall propose a cheap, iterative and displacement based method for solution of fully incompressible problems.
3. A simple iterative method
3.1 Nodal force correction
To illustrate our approach we start from the integral form of equilibrium relations, i.e. Equation (10), which is the result of virtual work principles or equivalent weak formulations as
We can assume that the stress field, , is decomposable into two parts, one of which is the conventional finite element stress field, as;
where is a stress corrector and obviously has no projection on the deviatoric stresses vector. We note that in (19) the
matrix can be an auxiliary material modulus and it may contain any bulk modulus with finite value. Such a correction of stress is in fact a correction to the pressure at the point and in the case that the volumetric modes are removed from the displacement field the corrector part will play the role of pressure at the point. Since in fully incompressible problems the pressure is a mechanical quantity, there will be no explicit relation between pressure and the displacement field. This means that evaluation of stress corrector
from information available at each point is not generally possible. Therefore for using (19) in (18) one can replace
with its associated nodal forces as
in which is nodal force corrector induced by
. It is important to note that replacing equation (19) with equation (20) means that we are seeking for a solution that preserves finite volumes rather than infinitesimal volumes. For quadrilateral elements the finite volumes may be considered as the elements volumes, similar to the case of discontinuous mixed formulations with one pressure point, but for triangular elements appropriate control volumes must be devised to prevent locking phenomenon.
Our problem, thus, converts to finding a correction to the nodal force vector as so that the volumetric displacement modes vanish. This may be accomplished by inserting (20) into (18) as
and relating to the volumetric part of the displacements. This can be performed iteratively. We note that the advantage of using (21) is that no instability occurs since the well known conventional stiffness matrix used in problems with compressible material, with just shear modulus equal to the incompressible material, is employed.
Although Equation (21) is written for the whole domain, it is usually obtained from assembling of the element contributions. Therefore in the following subsections we shall first focus on decomposing the displacement field in an element into volumetric and deviatoric parts and then derive expressions for the nodal force correction.
3.2 Decomposition of displacement/velocity field in an element
Starting from volumetric strain expression,
and replacing displacement vector with the interpolated field, we have
Then the element volume change is written as
(24)
Where
Equation (24) implies that there exists one mode so that the projection of displacements on it results in the total volume change of the element.
Now it is assumed that the displacement field is decomposable into two parts as
where is the nodal displacements inducing volumetric change, which here we call it volumetric part of the nodal displacements, and
is the deviatoric part. Then the volumetric part of the displacements can be written as the volume change times a vector producing unit volume change
Multiplying both sides by , we have
But we notice that the deviatoric part of the displacements produces no volumetric change. Thus
This means that Equation (28), with replacing its left hand side by (24), can be written as
which implies that
Then a possible choice for is as
Therefore the displacement field may be decomposed as follows
and
where
Having found an appropriate displacement field associated with the volume change of the element, the corresponding nodal force vector, to be used in (21), can be calculated as described in the next subsection.
3.3 Nodal forces associate with the volumetric change
To calculate the volumetric nodal forces of an element due to the volumetric part of the displacement field, we assume that the element is just undergoing the volumetric part of the displacement and write the equilibrium equations through minimization of the corresponding potential
with respect to . We note that writing pressure potential
as the first part of the right hand side of (36) inherently means that we are using a pressure field proportional to the volumetric strain. This means that instead of the actual incompressible material we are temporarily using a compressible one. In that case we rewrite (36) as
with being an auxiliary bulk modulus. In practice, for a fully incompressible material, for which a shear modulus is available, one can choose an appropriate Poisson’s ratio,
, and replace the auxiliary bulk modulus with its equivalent in terms of
and
. This helps to use the conventional elasticity matrix, and hence the conventional formulations as used in (21), during the iterative procedure.
Rewriting Equation (37) in term of volumetric displacements leads to:
Where is used to evaluated volumetric strain
from strain vector
. Minimization of
with respect to
results to the relation between the nodal forces and nodal displacements
In which
and
Now with volumetric nodal forces in hand, one may use (21) in an iterative procedure to eliminate the volumetric displacement modes. The outline of the iterative procedure is given in the next subsection.
3.4 Removing the volumetric modes through an iterative procedure
The statement of the problem is to find in (21) so that
To achieve (42) a Newton Raphson iteration may be used
Using (33) in (43) gives
or
Equation (45) suggests that for eliminating volumetric modes from (21) the volumetric part of the displacements, produced in the previous iteration, can be projected back for the next iteration step, i.e. . During such iteration, the forces required for the projection is evaluated from (39).
or
To accelerate the convergence of the iterative procedure one may use a relaxation/accelerator coefficient in the nodal forces calculation, i.e.
We shall give a separate study for appropriate value of the relaxation/accelerator factor .
To present the step by step procedure more clearly, we assume that a fully incompressible problem, with a shear modulus , is to be solved. The iteration steps can be summarized as
- 2. Start from
in (21) and solve the system of equation for
similar to the conventional FEM solution i.e.
A triangular factorization technique may be used instead of direct evaluation of (see [29] for instance). The triangular and diagonal matrices are stored for further use in step 5.
- 3. Use the nodal displacements as an initial guess to compute the volumetric forces at each element.
- 5. Find the increment of the nodal displacements using (21) as
Here is the same coefficient matrix as obtained in the second step.
- 6. Evaluate the total nodal displacements
As demonstrated through the forthcoming numerical results, the procedure exhibits a good convergence. It gives results similar to those of a discontinuous mixed formulation approach using one pressure point. When compared with such a mixed formulation, for linear quadrilateral elements for instance, the main advantage of the present formulation is stability of the results. This is because that the conventional elasticity matrix is employed during the iterations.
It can be seen that the proposed iterative procedure
- is very simple and cheap for application in any available finite element code.
- has capability of dealing with fully incompressible problems.
- does not exhibit locking/instability behavior since the conventional coefficient matrix is used.
- is compatible with the iterations in nonlinear problems.
- results in some unbalanced nodal forces. These unbalanced forces are in fact produced by the pressure distribution induced during the iterative process. The pressure values, indeed, can be calculated from such nodal forces for each element by an inverse method.
Regarding the last two points, the reader will note that the unbalanced forces for correction of the volume change may be added to those obtained from residuals in nonlinear problems, e.g. problems involving plastic deformations, during the Newton-Raphson iteration. In that case the formulation is written in its incremental form ( will be replaced by
and so forth). We note that
and
in (40) are dependent on a fictitious modulus and the geometry of the problem, respectively, and are independent of the history. However, study on the behavior of such a nonlinear procedure for some realistic problems needs further investigations which of course are beyond the scopes of this paper.
Finally, the last point states that the pressure distribution may be determined from the unbalanced forces at nodes, i.e. . This can be accomplished in several ways. If the pressure field is assumed to be constant on an element area then the contribution of each element to the global unbalanced forces may, easily be used to calculate the associated constant pressure. For this, one may use the principle of virtual work and consider components of unbalanced nodal forces separately.
Where is the
th component of the vector of the nodal forces at element level and
Here is an element displacement vector with zero components except for the
th one.
If is taken as a constant value in (49), then the remaining part to be integrated is written as (see Eqn. (24))
Where is the
th component of
. From (49) it follows that
We note that the denominator of (52) may not vanish since is a part of total volume change of the element, pertinent to the movement of
th degree of freedom, except for when the element has just one freedom which of course is not feasible. Since the procedure can be performed for each component of
, one may use their average as the element pressure. Therefore
with being total number of components in
.
Having found the pressure values at each element, a continuous pressure field may be constructed by averaging the values around a vertex node using the shape functions.
It may be noticed that the proposed procedure is somewhat similar to an extension of Usawa’s method described in Section 2.1. The similarity becomes clearer when in expression for the fictitious bulk modulus
is replaced by
, as in (40) and (41). In that case matrix
in (16) will be identical to
in (40) and thus
. However, the main differences between the two procedures lie under the following features:
- In the proposed method the correction of the displacements due to the pressure values is evaluated, in an implicit manner, from corresponding nodal forces rather than projection of the pressure variables. We note that several choices may be suggested for projection of pressure variables in (15) while in our approach a unique form of force evaluation is obtained (viz. Equation (47) ).
- Since we are just dealing with unbalanced nodal forces, the choice of pressure variables is not important. In other words the choices of control volumes are much versatile than the choices for the standard mixed formulation described in Section 2.1. Therefore some inter-elements control volumes may be defined, instead of element volumes, by defining auxiliary nodes inside the elements. In such cases the unbalanced forces at the auxiliary nodes are treated as resultant of external body forces and are transferred to the main nodes, by principle of virtual work for instance, to construct the required unbalanced nodal forces.
The most important advantage of the proposed approach will be discovered when applied to linear triangular elements. This will be shown in the next subsections where we shall apply the formulation to the linear elements and propose a very simple remedy for problems using triangular elements.
4. Application to the linear elements
Although the proposed algorithm is applicable to higher order elements, as we mentioned previously, linear elements are of more interest due to the simplicity of the formulation and less computational cost. In this section we shall focus on using our algorithm in solution of problems with conventional linear elements.
4.1 Quadrilateral elements
Linear quadrilateral elements are commonly used in problems encountering incompressibility. It has been shown that use of simple mixed formulation with one point pressure usually leads to solutions exhibiting instability, e.g. “hourglass” effect for rectangular elements. The so called “hourglass” effect is mainly due to ill-conditioned coefficient matrix. However, on using the proposed iterative method we note that there is no possibility for excitation of instable modes of displacements since the coefficient matrix is that of conventional displacement formulations and of course is not ill-conditioned. In this case the control volumes are taken as element volumes and the procedure follows precisely as stated in steps 1 to 7 in Section 2.2. Through some numerical examples we shall demonstrate that the results are similar to solutions using mixed formulation while no instability is seen.
4.2 Triangular elements
Linear triangular elements are widely used in explicit/implicit formulations because of their simplicity, requiring no complex integration scheme and producing minimum band width. However, when incompressibility encounters, the results will not be reliable since “locking” effect is quite common in solutions using such elements. Mesh dependency is also much pronounced due to the locking effect.
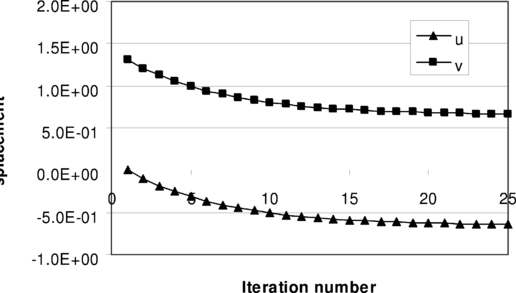
It is well understood that when the control volumes are taken as the element volumes in a mesh of linear triangles the directional behavior of the elements deteriorates the solution accuracy even if the so called locking phenomenon is not completely experienced, i.e. non zero but wrong answers is obtained. An example exhibiting the worst locking effect is given in Figure 1-a. When the material is considered fully incompressible, all deformation components vanish due to the directional behavior of the triangles. It is clear that if a larger mesh is constructed with such a configuration for elements, the locking effect will still resume (see Figure 1-b).
To overcome the deficiency, here, we shall employ a different control volume in the general mesh of triangular elements.
The idea can be explained by recalling from the previous sections that using linear quadrilateral elements, with standard mixed formulation, usually gives unstable results. Combining the instability of linear quadrilateral elements with over stiffness effect of linear triangular elements may lead to a clue for overcoming the locking behavior of triangular meshes. If each pair of triangular elements with a shared edge is considered as a control volume then the possibility of exchanging mass between the pairs of elements may reduce the excessive stiffness of the system. In that case, the pairs of triangles may play the role of quadrilateral elements. The problem of overlapping control volumes may be solved by dividing each element into three sub-elements and then defining each pair of the new neighboring sub-triangles, at two sides of the main edges, as a new control volume. Figure 2 shows a part of general mesh of triangular element divided into sub-triangles. Center points of the elements are chosen as auxiliary nodes.
The iterative procedure is then modified, for triangular elements, as follows;
- As a primary step, the mesh of triangles is sub-divided to smaller triangles using center points of the elements.
- On each edge of the main elements an auxiliary quadrilateral element is constructed as shown in Figure 2.
- The unbalanced volumetric force components associate with the auxiliary nodes are transferred to the main vertex nodes using the linear shape functions of the main triangular elements (since the auxiliary nodes are at the center of the main elements, it is just necessary to add one third of the auxiliary nodal forces to the vertex nodes of the main elements).
- The contributions of auxiliary sub-domains are assembled at main vertex nodes.
- The procedure continuous from the step five as stated previously.
There are two points that must be explained here. First, application of the proposed method is consistent with the implicit formulations involving iterative procedures. However, when application to an explicit formulation is of concern, the new formulation will involve a simple iteration which can use the latest information available. Note that in the module of elasticity
and the Poisson’s ratio
are auxiliary values and
is just dependent on the geometry. Therefore in this regard the combined formulation may be viewed as a semi-explicit formulation but not a fully implicit one.
As the second point, we may notice that in the proposed algorithm for the triangular elements, the volumetric change of each element will not vanish precisely but the volume of the whole domain and the auxiliary sub-domains volumes are preserved.
It also worthwhile to mention that application of the method to three dimensional problems using tetrahedral elements is very simple. The main step is to divide tetrahedral elements into four smaller elements and then combine sub-elements sharing main faces in order to make hexahedral elements. The rest of the procedure is straightforward.
4.3 Balance of pressure and displacement unknowns - simple patch test
A simple explanation for non-locking behavior may be explained by a patch test approach similar to reference 6. A comparison between the number of constraints and main unknowns in a simple patch of triangular elements for a mixed formulation and the proposed method reveals that the test is passed for the latter method. Figure 3 shows a typical patch of elements suitable for schematically testing the method,. It can be seen that when a discontinuous mixed method is followed the number of constraints may exceed the number of main unknown displacement components. For linear triangular elements, such a lack of balance between the unknowns usually leads to locking effect or over stiffness of the system, rather than instability effect. The most simple example of such a situation was discussed and given in Figure 1-a. However, when the proposed method is employed the number of constraints will be less than that of main unknowns. This is because application of an edge based formulation leads to an implicit relation between each two element volumes and thus the number of the effective constraints reduces to one, in Figure 3-b for instance. This clearly removes the over stiffness effect of system and may simply be demonstrated by revisiting the example shown in Figure 1-a. It can be seen that upon application of the proposed method, the locking effect is removed and the displacement components are correctly evaluated. Figure 4 depicts the solution results during the iterations.
Similar patch test may be performed for linear quadrilateral elements and thus similar discussion may be given for comparison of both the mixed and proposed methods if the new approach is applied in an edge based manner. But we note that unlike the case of triangular elements, in this case although the number of pressure and displacement unknowns are not balanced for mixed discontinuous approach, the problem of locking is not much pronounced in large patches. Instead, the dominant effect is instability. This means that edge based form of our approach, though convenient to employ, is not as crucial for application as the case of triangular elements. The most advantage of the proposed method is removal of the instable modes of displacements.
5. NUMERICAL RESULTS
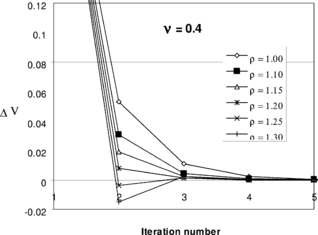
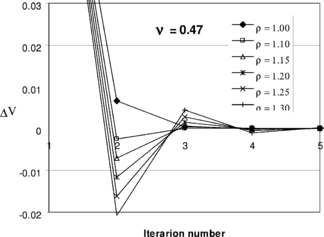
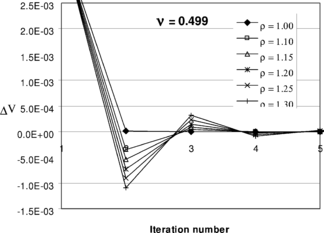
In this section we demonstrate the capabilities of the proposed method through some numerical examples. But before presenting the examples, we suggest a best value for relaxation/acceleration coefficient by examining the convergence of the solution in a sample problem.
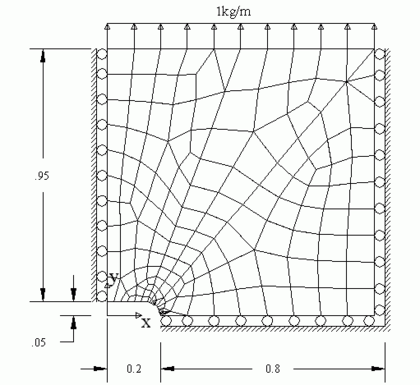
A perforated plane strain rectangular plate under uniform traction, as shown in Figure 5, is considered as a sample problem. Due to the symmetry of the domain, a quarter of the problem is solved. The material is considered to be fully incompressible with . A mesh of quadrilateral elements is employed for finite element solution.
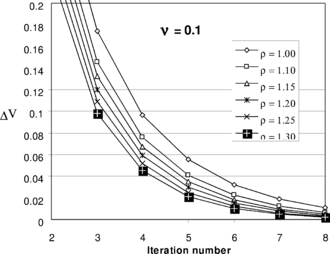
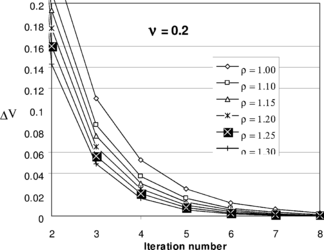
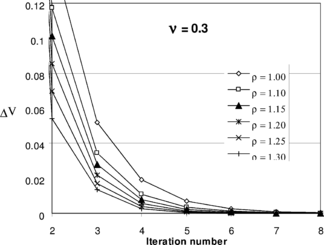
The problem is solved using the proposed iterative method. A series of auxiliary Poisson’s ratios have been selected for evaluation of the equivalent elastic modulus, (see the step by step procedure in section 2.2). For each choice, a series of solutions are performed using different values for
. The volumetric change of the problem, during the iterations, is shown in Figures 6-a to 6-f. The figures clearly show that, firstly, the procedure is convergent and only few steps are needed to obtain a reasonable low volume change. Secondly, for some values of
monotonic rate of convergence is observed. Comparing all figures and determining the ranges of
within which monotonic convergence is obtained, a practical value for the acceleration coefficient may be suggested as
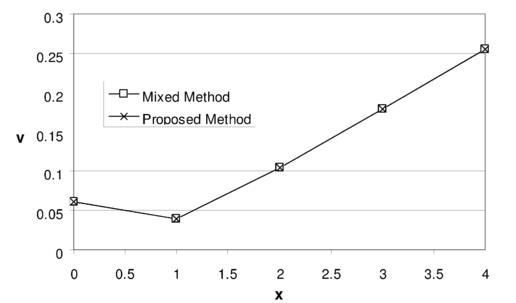
With the aid of such a choice for the acceleration coefficient, the problem is solved once again to examine the performance of the procedure. A discontinuous mixed formulation with one point pressure is also employed to perform a comparison. Figure 7 demonstrates that the results of the proposed method and those of the mixed formulation are matching and no locking/instability is observed in both results.
Now we present some more results for three benchmark problems. The first problem is a tension strip with slot, the second is a driven cavity and the third one is a cantilever beam.
A slotted tension strip
Figure 8 shows a quarter of a slotted strip under uniform tensile traction with unstructured mesh of quadrilateral elements. Here again the material is considered to be fully incompressible with . The problem will be solved for two series of grids, i.e. linear quadrilateral and triangular meshes. We shall first demonstrate the results of both mixed and penalty approaches for one of the quadrilateral based meshes and compare them to those obtained from the proposed method. Figure 9 illustrates normal displacement at the top edge of the domain,
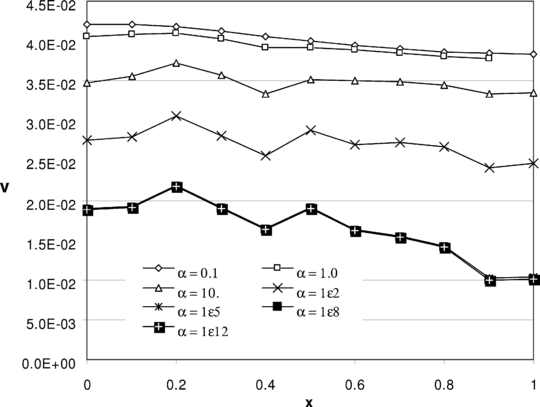
, obtained by application of both discontinuous mixed formulation and the proposed iterative method on a mesh of linear quadrilateral elements. The volume change calculated for mixed formulation is of order 1e-17 which is ideal for a fully incompressible solution. Excellent volume change may be achieved by increasing the number of iterations in the proposed method and no instability/locking effect is seen. Figure 10 demonstrates the convergence and the volume changes during the iterations.
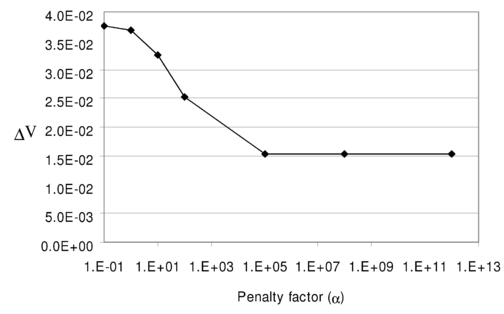
However, when the penalty approach is employed no unique answer is obtained due to ill-conditioning of the coefficient matrix. Figure 11 depicts the non-uniqueness of the solution for different values of penalty factor. The volume change achieved, compared to mixed method, is not satisfactory as shown by Figure 12.
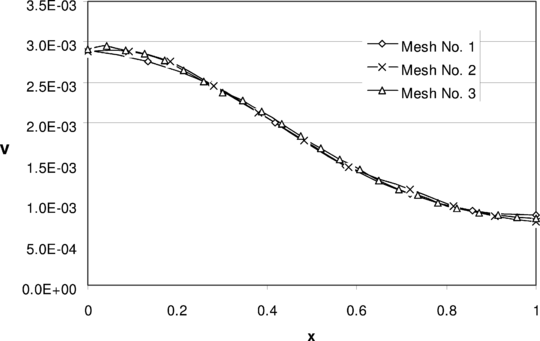
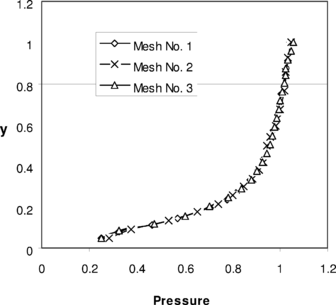
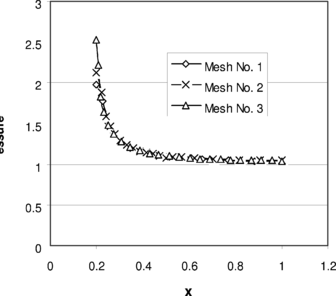
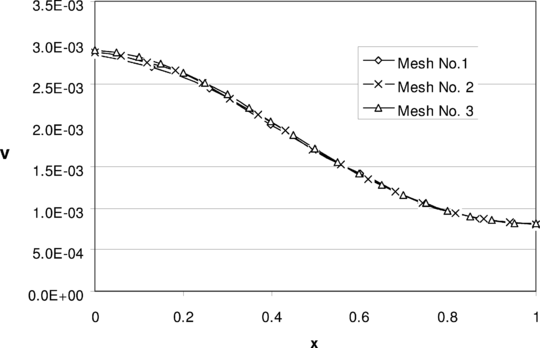
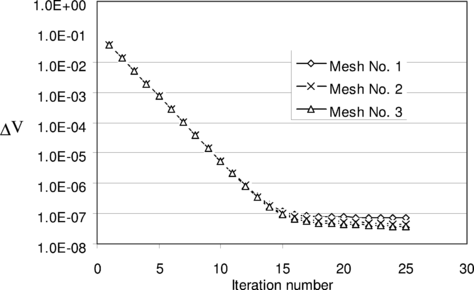
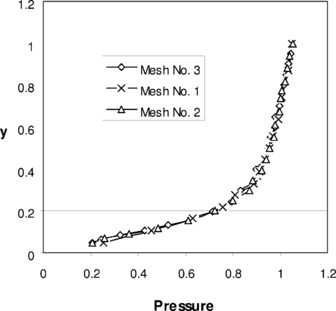
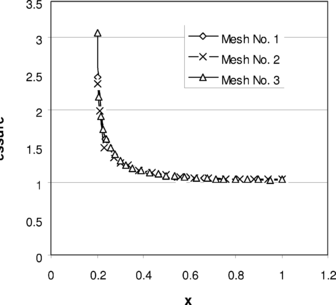
To study the effects of mesh configuration, a series of meshes as shown in Figure 13 are selected and solved. Figures 14 to 16, respectively, demonstrate top edge displacements, pressure distributions along and
, and convergence of the volume changes for the three meshes.
A series of meshes as shown in Figure 17 are chosen to demonstrate the performance of the method on triangular meshes. Figure 18 depicts the vertical displacement at . This figure may be compared to other similar figures 9 and 14. It can be seen that results are almost identical. The convergence of the volume change is shown in Figure 19. The pressure distributions along
and
are given in Figures 20-a & b.
Driven cavity
As another problem, a driven cavity shown in Figure 21 is considered. The system is restrained at three edges for both components of the velocity and set free at the top edge where a prescribed uniform tangential velocity distribution is considered. The viscosity is assumed to be . Although the problem is defined in velocity space and should be solved in its steady state, it can be treated as a conventional plane strain displacement based problem by assuming a unit time interval and also
.
Similar to the previous example, the problem is solved first by a mixed formulation and a penalty approach and then the results are compared to those obtained from the new approach. A regular mesh of linear quadrilateral elements is selected for demonstrating the mixed formulation performance.
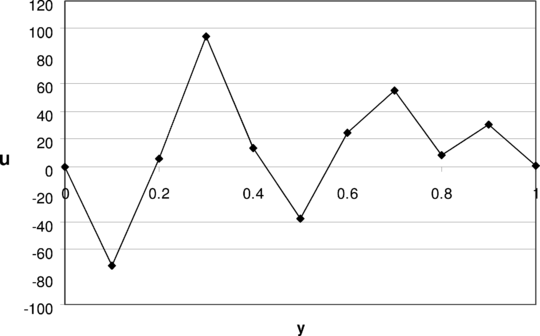
Figure 22 show the variation of the horizontal component of the velocity along obtained from application of mixed formulation with one point pressure. It can be seen that the solution is not stable. This is the case for many problems solved with the regular meshes and mixed formulation. However, when problem is solved by a penalty approach a better result is achieved though there is still lack of solution uniqueness because of several choices for the penalty factor. Figure 23 clearly show the lack of uniqueness of the solutions. This figure also shows that when the penalty factor is chosen as a rather large number, a sort of instable hourglass mode is seen. This effect was predictable since the penalty method with selective integration scheme is in fact equivalent to the mixed method. The velocity distribution, modeled as deformation, is given in Figure 24.
The effects of instability and non uniqueness are completely removed from the solution when the proposed approach is employed. The results for variation of the horizontal velocity component along are given in Figure 23. As mentioned in Section 3-4, although regarding satisfaction of constrains the procedure is similar to discontinuous mixed formulation, no hourglass effect is seen since the coefficient matrix is not ill conditioned.
Series of irregular quadrilateral and triangular meshes are chosen as Figure 25 and 26 to give a view of mesh independency of the solution. Figures 27 and 28 depict the velocity obtained along and pressure distribution along
. It can be seen that the finite element solution is not dependent on the mesh used.
Cantilever beam
As a final example we consider the cantilever beam of Figure 29. Plane strain conditions are assumed and two types of elements are employed in the solution. In order to compare the results with an exact solution we replace the one dimensional problem of Figure 29-a with its equivalent form as a two dimensional problem of Figure 29-b. Considering a fully incompressible material with shear modulus , the exact solution is given as
Where and
are displacements in
and
directions and also
and
are the width and height of the beam. The body force and traction of the problem are found from the exact solution and applied to the meshes shown in Figures 29-c and 29-d. The reader may notice that the body force has just vertical component,
, and has a relation with vertical component of tractions at
as
. The problem is solved using
,
,
and
. The results for vertical displacement of the beam tip, i.e. at
and
, are shown in Table 1 and are normalized with respect to the corresponding exact value. The results are obtained from both conventional displacement approach, with
, and the proposed method for meshes shown in the figure and some finer meshes with similar patterns. It can be clearly seen that the proposed method does not exhibit locking behavior for both linear rectangular and triangular types of elements. To compare the results with compressible cases we have included results obtained from
(the values are normalized with respect to exact solution at fully incompressible limit).
The numerical results of this section clearly reveal that the simple iterative proposed is capable of giving solution to fully incompressible problems using linear elements, especially triangular ones, without exhibiting locking/instability effect.
Table 1. Results for tip displacement of the beam of Fig. 29 obtained from proposed method and conventional displacement method using different meshes. The results are normalized with respect to the exact value obtained at fully incompressible limit.
6. CONCLUSIONS
A simple iterative method has been presented for finite element solution of fully incompressible problems using mesh of linear elements. For linear quadrilateral elements the control volumes are taken as elements volumes and for linear triangular elements the control volumes are built on partial contributions of elements adjacent to edges. In the case that elements are considered as control volumes, the procedure may be interpreted as a special case of general iterative methods available for mixed formulation though the pressure correction part is different. However, the most advantage of the proposed method is its capability to be extended to more general cases of control volumes as described for the case of triangular elements.
The formulation is based on calculation of some unbalanced forces so that the volume constraint is met. The unbalanced forces are then utilized to construct the pressure field at the end of the procedure.
The iteration procedure is very cheap and utilizes the coefficient matrix evaluated at the first step. The convergence and robustness of the method has been shown through solution of several examples. Only few iteration steps are needed to reduce the volume change considerably.
It has been demonstrated that although the formulation is based on displacement/velocity field, the method eliminates the locking/instability effects generally observed in linear elements and the answers obtained are similar to those obtained from mixed formulation. The iteration procedure is consistent with non-linear problems and can be implemented in any finite element code without need of much effort.
Acknowledgment
The authors wish to thank Dr. A.R. Pishevar in Mechanical Engineering Department of Isfahan University of Technology for useful discussions.
REFERENCES
[1] Herrmann, L., “Elasticity equations for incompressible and nearly incompressible materials by a variational theorem”, AIAA J., Vol. 3, pp. 1896-1900, 1965.
[2] Hughes, T.R.J., “Equivalence of finite elements for nearly incompressible elasticity”, J. Appl. Mech. ASME, Vol. 44, pp. 181-183,1977.
[3] Malkus, D.S., “A finite element displacement model valid for any value for incompressibility”, Int. J. Solids Struct., Vol. 12, pp. 731-738, 1976.
[4] Hughes, T.R.J., “ Generalization of selective integration procedures to anisotropic and nonlinear media”, Int. J. Numer. Meth. Engrg., Vol. 15, pp. 1413-1418, 1980.
[5] Simo, J.C., Taylor, R.L. and Pister, K.S., “ Variational and projection methods for the volume constraint in finite deformation elasto-plasticity”, Comput. Methods Appl. Mech. Eng., Vol. 51, pp. 177-208, 1985.
[6] Zienkiewicz, O. C. and Taylor, R. L., “The finite element method”, 5th edition, Vol. I & III, Butterworth-Heineman, 2000.
[7] Hueck, U., Schreyer, H.L., and Wriggers, P., “On the incompressible constraint of the 4-node quadrilateral element”, Int. J. Numer. Meth. Engrg., Vol. 38, pp. 3039-3053, 1995.
[8] Zienkiewicz, O.C., Vilotte, J.P., Toyoshima, S. and Nakazawa, S., “Iterative method for constrained and mixed approximation. An inexpensive improvement of F.E.M. performance”, Comput. Methods Appl. Mech. Eng., Vol. 51, pp. 3-29, 1985.
[9] Arrow, K.J., Hurwicz, L., and Uzawa, H., Studies in Non-Linear Programming, Stanford University Press, Stanford, CA, 1985.
[10] Wilson, E.L., Taylor, R.L., Doherty, W.P., and Ghaboussi, J. “Incompatible displacement models” in Numerical and Computer Models in Structural Mechanics, eds. S.J. Fenves, N, Perrone, A.R. Robinson and W.C. Schnobrich. New York, Academic Press, 1973.
[11] Taylor, R.L., Beresford, P.J., and Wilson, E.L., “A nonconforming element for stress analysis”, Int. J. Numer. Meth. Engrg.,, Vol. 10, pp. 1211-1219, 1976.
[12] Nagtegaal, J.C., Parks, D.M. and Rice, J.R. “On numerically accurate finite element solutions in the fully plastic range”, Comput. Methods Appl. Mech. Eng., Vol. 4, pp. 153-177, 1974.
[13] Simo, J.C. and Rifai, M.S., “A class of mixed assumed strain methods and the method of incompatible modes”, Int. J. Numer. Meth. Engrg., Vol. 29, pp. 1595-1838, 1990.
[14] Pian, T.H.H. and Sumihara, K.’ “Rational approach for assumed stress finite elements”, Int. J. Numer. Meth. Engrg., Vol. 20, pp. 1685-1695, 1985.
[15] Puch, E.F. and Atluri, S.N., “Development and testing of stable, invariant, isoparametric curvilinear 2- and 3-D hybrid-stress elements”, Comput. Methods Appl. Mech. Eng., Vol. 47, pp. 331-356, 1984.
[16] Zienkiewiz, O.C., Huang, M.S. and Pastor, M., “Localization problems in plasticity using finite elements with adaptive remeshing”, Int. J. Numer. Anal. Meth. Geomech., Vol. 19, pp. 127-148, 1995.
[17] Mabssout, M. and Pastor, M., “A Taylor-Galerkin algorithm for shock wave propagation and strain localization failure of viscoplastic continua”, Comput. Methods Appl. Mech. Eng., Vol. 192, pp. 955-971, 2003.
[18] Hughes, T.J.R., Franca, L.P., and Hulbert, G.M., “ A new finite element formulation for computational fluid dynamics: VIII. The Galerkin/least-squares method for advective-diffusive equations”, Comput. Methods Appl. Mech. Eng., Vol. 73, pp. 173-189, 1989.
[19] Zienkiewicz, O.C. and Wu, J., “Incompressibility without tears-How to avoid restrictions of mixed formulation”, Int. J. Numer. Meth. Engrg., Vol. 32, pp. 1189-1203, 1991.
[20] Zienkiewicz, O.C. and Codina, R., “ A general algorithm for compressible and incompressible flow- Part I: The split, characteristic-based scheme”, Int. J. Numer. Meth. Fluids., Vol. 20, pp. 869-885, 1995.
[21] Zienkiewicz, O.C., Morgan, K., Satya Sai, B.V.K., Codina, R. and Vazquez, M., “A general algorithm for compressible and incompressible flow – Part II: Tests on the explicit form” Int. J. Numer. Meth. Fluids., Vol. 20, pp. 887-913, 1995.
[22] Zienkiewicz, O.C., Nithiarasu, P., Codina R., Vazquez, M. and Ortiz, P. “The characteristic-based-split procedure: An efficient and accurate algorithm for fluid problems”, Int. J. Numer. Meth. Fluids., Vol. 31, pp. 359-392, 1999.
[23] Chorin, A.J., “Numerical solution of Navier-Stokes equations”, Math. Comput., Vol. 22, pp. 745-762, 1968.
[24] Zienkiewicz, O.C., Rojek, J., Taylor, R.L. and Pastor, M., “Triangles and tetrahedra in explicit dynamic codes for solids”, Int. J. Numer. Meth. Engrg., Vol. 43, pp. 565-583, 1998.
[25] Oñate, E., Rojek, J., Taylor, R.L and Zienkiewicz, O.C.,” Linear triangular and tetrahedra for incompressible problems using a finite calculus formulation”, European Conference on Computational Mechanics, ECCM-2001, Cracow, Poland, 2001.
[26] Oñate, E., “Derivation of stabilized equations for numerical solution of advective-diffusive transport and fluid flow problems”, Comput. Methods Appl. Mech. Eng., Vol. 151, pp. 233-265, 1998.
[27] Chiumenti, M., Valverde, Q., Agelet de Saracibar, C., and Cervera, M., “A stabilized formulation for incompressible elasticity using linear displacement and pressure interpolations”, Comput. Methods Appl. Mech. Eng., Vol. 191, pp. 5253-5264, 2002.
[28] Hughes, T.J.R., “Multiscale phenomenon: Green’s function Dirichlet-to Neumann formulation, subgrid scale models, bubbles and the origins of stabilized formulations”, Comput. Methods Appl. Mech. Eng., Vol. 127, pp. 387-401, 1995.
[29] Bathe, J.K., “Finite Element Procedures”, Prentice-Hall, Englewood Cliffs, NJ, 1996.
List of Figures
1 Simple assemblies of linear triangular elements for which the displacement approaches
show locking effect. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 26
2 In a mesh of triangular elements control volumes are constructed using smaller elements
from subdivision of main elements adjacent to edges. . . . . . . . . . . . . . . . . . . . . 26
3 Simple patch test for formulation. Nodes in black are restrained ones; (a) Linear
triangles with one point pressure, locking happens when the number of unconstrained
pressure points exceeds the number of displacement variables, (b) Linear triangles using
the edge approach which is equivalent to use one pressure point for the whole patch leading
to removal of the locking effect- the number of pressure point is less than that of
displacement variables. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 26
4 Displacements obtained from application of the proposed iterative method to the problem
of Fig. 1-a (a square domain with unit dimensions and ) for which the conventional
approaches result to zero values. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 27
5 A perforated plated under tensile traction as a sample problem, (a) the whole domain,
(b) a quarter of domain is solved for with boundary conditions representing the symmetry
of the domain. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 27
6 Choosing relaxation factor , in Eqn. (48), suitable for a wide range of auxiliary Poisson’s
ratio values; (a) solution with
, (b) solution with
, (c) solution with
,
(d) solution with , (e) solution with
, (f) solution with
. . . . . . 28
7 Vertical displacement at the top edge of the problem of Fig. 5 obtained from discontinuous
mixed formulation and the proposed iterative method. . . . . . . . . . . . . . . . . . . . . 29
8 A slotted plate under tension. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 29
9 Vertical displacement at the top edge of the slotted plate of Fig. 8 obtained from application
of the discontinuous mixed formulation and the proposed method. . . . . . . . . . . . . . . . 30
10 Volume change obtained from application of the proposed method to the problem of Fig. 8
during the iterations. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .30
11 Vertical displacement at the top edge of the slotted plate of Fig. 8 obtained from application
of the penalty method using various values for the penalty factor . . . . . . . . . . . . . . 31
12 Volume change obtained from application of the penalty approach to the problem of Fig. 8
using various values for the penalty factor. . . . . . . . . . . . . . . . . . . . . . . . . . . 31
13 Three meshes of quadrilateral elements for slotted plate problem of Fig 8. . . . . . . . . . . 32
14 Comparison of the vertical displacements at the top edge of the slotted plate problem
obtained from application of the proposed method to three meshes of Fig 13. . . . . . . . . 32
15 Comparison of the pressure distributions along and
axis of the slotted plate problem
obtained from application of the proposed method to three meshes of Fig 13; (a) pressure
distribution along , (b) pressure distribution along
. . . . . . . . . . . . . . . . . 33
16 Comparison of the convergences for the volume changes of the slotted plate problem
obtained from application of the proposed method to three meshes of Fig 13. . . . . . . . . 34
17 Three meshes of triangular elements for slotted plate problem of Fig 8. . . . . . . . . . . . 34
18 Comparison of the vertical displacements at the top edge of the slotted plate problem
obtained from application of the proposed method to three meshes of triangles in Fig 17. . . . 34
19 Comparison of the convergences for the volume changes of the slotted plate problem
obtained from application of the proposed method to three meshes of triangles in Fig 17. . . . 35
20 Comparison of the pressure distributions along and
axis of the slotted plate problem
obtained from application of the proposed method to three meshes of triangles in Fig 17;
(a) pressure distribution along , (b) pressure distribution along
. . . . . . . . . . 35
21 The problem of driven cavity ( ). . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 36
22 Variation of the horizontal component of the velocity ( ) along
obtained from
application of discontinuous mixed formulation to the problem of driven cavity in Fig. 21. . . 36
23 Variation of the horizontal component of the velocity ( ) along
obtained from
application of the penalty formulation, using various values for the penalty factor, and
the proposed method to the problem of driven cavity in Fig. 21. . . . . . . . . . . . . . . . 37
24 Hourglass modes obtained from application of the penalty method to the problem of driven
cavity; (a) solution with , (b) solution with
. . . . . . . . . . . . . . . . . . . 37
25 Three meshes of quadrilateral elements for the problem of driven cavity in Fig. 21. . . . . . 38
26 Three meshes of triangular elements for the problem of driven cavity in Fig. 21. . . . . . . . 38
27 Comparison of variations of the horizontal velocity ( ) along
obtained from
application of the proposed method to quadrilateral and triangular meshes of
in Figs. 25 and 26. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 38
28 Comparison of the pressure distributions along obtained from application of the
proposed method to quadrilateral and triangular meshes of in Figs. 25 and 26. . . . . . . . . 39
29 The problem of plane strain beam; (a) the geometry of the beam, (b) the replaced two
dimensional problem, (c) the mesh of linear quadrilateral elements (16 elements) and
the boundary conditions used, (d) the mesh of linear triangular elements (32 elements). . . . 39
List of Tables
1 Results for tip displacement of the beam of Fig. 29 obtained from proposed method
and conventional displacement method using different meshes. The results are
normalized with respect to the exact value obtained at fully incompressible limit. . . . . . . . 19

(a) |

(b) |
Figure 1. Simple assemblies of linear triangular elements for which the displacement approaches show locking effect.

|
Figure 2. In a mesh of triangular elements control volumes are constructed using smaller elements from subdivision of main elements adjacent to edges.

|

|
| (a) | (b) |
Figure 3. Simple patch test for formulation. Nodes in black are restrained ones; (a) Linear triangles with one point pressure, locking happens when the number of unconstrained pressure points exceeds the number of displacement variables, (b) Linear triangles using the edge approach which is equivalent to use one pressure point for the whole patch leading to removal of the locking effect- the number of pressure point is less than that of displacement variables.
Figure 4. Displacements obtained from application of the proposed iterative method to the problem of Fig. 1-a (a square domain with unit dimensions and ) for which the conventional approaches result to zero values.

|

|
| (a) | (b) |
Figure 5. A perforated plated under tensile traction as a sample problem, (a) the whole domain, (b) a quarter of domain is solved for with boundary conditions representing the symmetry of the domain.
|
(a) |
(b) |
|
(c) |
(d) |
|
(e) |
(f) |
Figure 6. Choosing relaxation factor , in Eqn. (48), suitable for a wide range of auxiliary Poisson’s ratio
values; (a) solution with
, (b) solution with
, (c) solution with
, (d) solution with
, (e) solution with
, (f) solution with
.
Figure 7. Vertical displacement at the top edge of the problem of Fig. 5 obtained from discontinuous mixed formulation and the proposed iterative method.
Figure 9. Vertical displacement at the top edge of the slotted plate of Fig. 8 obtained from application of the discontinuous mixed formulation and the proposed method.
Figure 10. Volume change obtained from application of the proposed method to the problem of Fig. 8 during the iterations.
Figure 11. Vertical displacement at the top edge of the slotted plate of Fig. 8 obtained from application of the penalty method using various values for the penalty factor .
Figure 12. Volume change obtained from application of the penalty approach to the problem of Fig. 8 using various values for the penalty factor.
Mesh No. 1 Mesh No. 2 Mesh No. 3
| (a) | (b) |
Figure 15. Comparison of the pressure distributions along and
axis of the slotted plate problem obtained from application of the proposed method to three meshes of Fig 13; (a) pressure distribution along
, (b) pressure distribution along
.
Figure 16. Comparison of the convergences for the volume changes of the slotted plate problem obtained from application of the proposed method to three meshes of Fig 13.
Mesh No. 1 Mesh No. 2 Mesh No. 3
Figure 18. Comparison of the vertical displacements at the top edge of the slotted plate problem obtained from application of the proposed method to three meshes of triangles in Fig 17.
Figure 19. Comparison of the convergences for the volume changes of the slotted plate problem obtained from application of the proposed method to three meshes of triangles in Fig 17.
|
| |
| (a) | (b) |
Figure 20. Comparison of the pressure distributions along and
axis of the slotted plate problem obtained from application of the proposed method to three meshes of triangles in Fig 17; (a) pressure distribution along
, (b) pressure distribution along
.
Figure 22. Variation of the horizontal component of the velocity ( ) along
obtained from application of discontinuous mixed formulation to the problem of driven cavity in Fig. 21.
Figure 23. Variation of the horizontal component of the velocity ( ) along
obtained from application of the penalty formulation, using various values for the penalty factor, and the proposed method to the problem of driven cavity in Fig. 21.

|

|
| (a) | (b) |
Figure 24. Hourglass modes obtained from application of the penalty method to the problem of driven cavity; (a) solution with , (b) solution with
.

|
Mesh Q1 Mesh Q2 Mesh Q3
Mesh T1 Mesh T2 Mesh T3
Figure 27. Comparison of variations of the horizontal velocity ( ) along
obtained from application of the proposed method to quadrilateral and triangular meshes of in Figs. 25 and 26.
Figure 28. Comparison of the pressure distributions along obtained from application of the proposed method to quadrilateral and triangular meshes of in Figs. 25 and 26.

|

|
| (a)
|
(b) |

|

|
| (c) | (d) |
Figure 29. The problem of plane strain beam; (a) the geometry of the beam, (b) the replaced two dimensional problem, (c) the mesh of linear quadrilateral elements (16 elements) and the boundary conditions used, (d) the mesh of linear triangular elements (32 elements).
Document information
Published on 13/07/18
Submitted on 13/07/18
Licence: CC BY-NC-SA license
Share this document
Keywords
claim authorship
Are you one of the authors of this document?