Latest revision as of 16:26, 28 February 2017

Resumen

El objeto del presente artículo es presentar una propuesta para comprobar la resistencia a pandeo de las estructuras metálicas de entramados, con la que se completa el método propuesto en la norma EN 1993-1-1. La idea es desarrollar la propuesta de la norma de realizar análisis no-lineales de sistemas imperfectos, en lugar de emplear complejas fórmulas de interacción a nivel barra. En el apartado 5.3.2(11) se define la imperfección geométrica para sistemas susceptibles de pandeo por flexión debido a la compresión, quedando por definir la imperfección en el caso de que el pandeo sea por torsión o flexotorsión a causa de la compresión o de la flexión. A continuación se propone un método para definir la imperfección geométrica para un caso general, demostrándose que la propuesta de la norma es un caso particular.

Abstract

The purpose of this paper is to present a proposal for the design of steel structures sensitive to buckling to fill the gaps in the current Standard EN 1993-1-1, providing guidelines to obtain the magnitude of the imperfection generalizing the procedure given in clause 5.3.2(11) of EN 1993-1-1 for steel structures sensitive to flexural buckling under compression. According to the standard there are still uncertainties about how to obtain the imperfection when the structures are sensitive to torsional or flexural-torsional buckling due to either compression or bending. In this paper a general procedure to obtain the imperfection is provided and it can be proved that the recommendation given in EN 1993-1-1 is a particular case.

Palabras clave

Pandeo ; Torsión ; Flexión ; Diseño ; Acero ; Imperfección geométrica ; No-lineal ; EN 1993-1-1

Keywords

Buckling ; Torsion ; Bending ; Design ; Steel ; Geometric imperfection ; Nonlinear ; EN 1993-1-1

1. Introducción

El diseño de estructuras metálicas con elementos flectados y comprimidos debe tener en consideración los efectos no-lineales y la existencia de imperfecciones geométricas, tensiones residuales, etc. En particular, la norma EN 1993-1-1 [1] los tiene en cuenta de 2 formas:

A- Indirectamente : utilizando fórmulas de interacción a nivel barra Greiner [2] y Boissonade [3] (apartado 6.3; por defecto, en este artículo todos los apartados se refieren a la norma [1] ).

B- Directamente : realizando el análisis no-lineal de la estructura con imperfecciones geométricas.

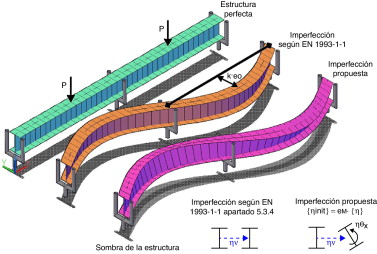
B.1- En sistemas susceptibles de pandeo inducido por compresión: las imperfecciones geométricas se pueden incluir de 2 maneras: la primera de ellas, descrita en los apartados (5.3.2 (1)-(10)), en los que se define una imperfección global y otra local, tiene el inconveniente de que existen muchas posibles combinaciones de imperfecciones globales y locales entre las cuales el proyectista tiene que encontrar la más desfavorable (Agüero [4] , Serna et al. [5] ). La segunda, descrita en el apartado (5.3.2 (11)), permite obtener la imperfección dándole la forma del primer modo de pandeo y la magnitud si el pandeo es por flexión, quedando por definir la magnitud para posibles casos de pandeo por torsión o de flexotorsión. Trabajos con imperfecciones afines al primer modo de pandeo son los de Agüero y Pallarés [6] y Gonçalves y Camotim [7] , y en ninguno de estos se permite abordar el pandeo por torsión.

B.2- En sistemas susceptibles de pandeo inducido por flexión: incluyen imperfecciones geométricas equivalentes. En la norma se hace una referencia a esta imperfección en el apartado 5.3.4 (3). «En el caso de un análisis en segundo orden teniendo en cuenta el pandeo lateral de un elemento flectado, puede adoptarse una imperfección k·e_o , donde e_o es la imperfección inicial en arco según el eje débil del perfil considerado. Generalmente no resulta necesario incluir una imperfección de torsión». Esta imperfección presenta 2 inconvenientes: encontrar la combinación de imperfecciones locales más desfavorable y el hecho de que e_o /L debe depender también de la esbeltez para que la carga de pandeo coincida con la de los resultados experimentales y numéricos con no-linealidad geométrica y mecánica (incluyendo tensiones residuales e imperfecciones geométricas, en las que se basa el coeficiente χ_LT ). Por ello, se va a generalizar la propuesta del apartado 5.3.2 (11) para elementos flectados. Algunos trabajos previos que realizan esta generalización son los de Agüero [4] , para un sistema de barras, o los de Bijlaard et al. [8] y Wieschollek et al. [9] , que simplifican el problema considerando las alas de los perfiles en doble T como elementos comprimidos. En ninguno de los trabajos previos se tiene en cuenta la interacción con las tensiones tangenciales debidas a la torsión de Saint Venant que se incorpora en el presente trabajo.

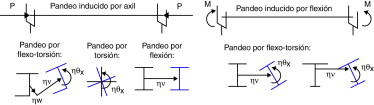
En la figura 1 se muestran las imperfecciones geométricas a considerar para elementos susceptibles de pandeo lateral por flexión con la propuesta de la norma [1] , y la propuesta que se hace en este trabajo utilizando una imperfección cuya forma viene dada por el primer modo de pandeo.

Figura 1. Imperfección según el método propuesto y la norma EN 1993-1-1.

2. Planteamiento del problema

El equilibrio de sistema imperfecto se puede formular imponiendo que la primera variación del potencial total sea nula δV  = 0; el potencial total se puede escribir sumando la energía de deformación al potencial de las fuerzas exteriores V  = U₁  + U₂  + U₃ (Trahair [10] y Chen y Atsuta [11] ); y la resolución del problema se puede realizar con el método de los elementos finitos:

donde (U) es el desplazamiento en la dirección de la directriz del centro de gravedad; (v, w ) son los desplazamientos en las direcciones principales (y) y (z) del centro de esfuerzos cortantes; θ_x es la rotación de torsión; A , el área; I_y , I_z , los momentos de inercia respecto a los ejes y, z; I_t , el módulo torsión; I_w , el módulo de alabeo; y_sc , z_sc , las coordenadas del centro de esfuerzos cortantes; E , el módulo de elasticidad del acero; G , el módulo de rigidez a cortante; y L , la longitud del elemento.

Según Chen y Atsuta [11] , la suma de la primera variación del potencial es:

donde [K_L ] es la matriz de rigidez lineal; [K_G ], la matriz de rigidez geométrica;{d_NL }, el vector de desplazamientos no-lineales; {F_ext }, el vector de fuerzas exteriores; {η_init }, el vector de imperfecciones geométricas equivalentes; NB , el número de elementos; y KB , el número genérico de una barra.

La carga crítica α_cr es el valor que anula el determinante ${\textstyle \left|\left[K_{L}\right]+\right.}$${\displaystyle \left.{\alpha }_{cr}\left[K_{G}\right]\right|=0}$ y el modo de pandeo ({η_cr } según [1] ) es el autovalor asociado ${\textstyle \left(\left[K_{L}\right]+\right.}$${\displaystyle \left.{\alpha }_{cr}\left[K_{G}\right]\right)\left\{{\eta }_{cr}\right\}=}$${\displaystyle 0}$ . En el presente artículo se denotará {η}, esto es,{η_cr } = {η}.

En la figura 2 se muestran algunos modos de pandeo para piezas sometidas a compresión y flexión.

Figura 2. Modos de pandeo.

Los esfuerzos asociados al modo de pandeo se denotan con el subíndice η:

Momento de eje y ${\textstyle M_{y,\eta }=}$${\displaystyle -EI_{y}{\frac {d^{2}{\eta }_{w}}{dx^{2}}}}$ ; momento de eje z ${\textstyle M_{z,\eta }=}$${\displaystyle EI_{z}{\frac {d^{2}{\eta }_{v}}{dx^{2}}}}$ ; bimomento ${\textstyle Bi_{\eta }=}$${\displaystyle EI_{w}{\frac {d^{2}{\eta }_{\theta x}}{dx^{2}}}}$ ; torsor ${\textstyle T_{\eta }=}$${\displaystyle T_{t,\eta }+T_{w,\eta }=GI_{t}{\frac {d{\eta }_{\theta x}}{dx}}-}$${\displaystyle EI_{w}{\frac {d^{3}{\eta }_{\theta x}}{dx^{3}}}}$ ; torsor de Saint Venan ${\textstyle T_{t,\eta }=}$${\displaystyle GI_{t}{\frac {d{\eta }_{\theta x}}{dx}}}$ ; cortante en la dirección (y) y (z): ${\textstyle V_{y,\eta }=}$${\displaystyle EI_{z}{\frac {d^{3}{\eta }_{v}}{dx^{3}}}}$ ; ${\textstyle V_{z,\eta }=}$${\displaystyle EI_{y}{\frac {d^{3}{\eta }_{w}}{dx^{3}}}}$ .

Los esfuerzos que se producen cuando la estructura tiene una imperfección con la forma del primer modo de pandeo son los anteriores escalados por el factor ${\textstyle {\frac {1}{{\alpha }_{cr}-1}}}$[4] . Que para algún elemento susceptible de pandeo la energía de deformación asociada al primer modo de pandeo sea nula ${\textstyle {\left\{\eta \right\}}^{T}\left[K_{L}\right]\left\{\eta \right\}=}$${\displaystyle 0}$ significa que esta imperfección no está teniendo ningún efecto adverso sobre el diseño de este elemento. Esto puede conducir a diseños del lado de la inseguridad, por lo que se debería buscar la imperfección asociada al modo de pandeo {η_j } con menor carga crítica α_j que verifique ${\textstyle {\left\{{\eta }_{j}\right\}}^{T}\left[K_{L}\right]\left\{{\eta }_{j}\right\}>0}$ y α_j  < 25 (esta segunda recomendación se obtiene del apartado 6.3.1.2 (4) de la EN 1993-1-1 [1] ) que se deberá tener en cuenta en el análisis global de la estructura, de forma alternativa.

Cuando existan varias imperfecciones {η_j } asociadas a cargas críticas similares α_j para conocer la dirección de la imperfección que en combinación con las fuerzas exteriores produce un efecto más desfavorable, se recomienda utilizar la imperfección que maximiza la expresión ${\textstyle U=}$${\displaystyle {\frac {{\left\{{\eta }_{d}\right\}}^{T}}{\left\|{\eta }_{d}\right\|}}\left\{F_{EXT}\right\}}$ (trabajo de las fuerzas exteriores cuando se produce un movimiento definido por la imperfección), donde ${\textstyle \left\{{\eta }_{d}\right\}=}$${\displaystyle \sum _{j=1}^{n}c_{j}\left\{{\eta }_{j}\right\},{\mbox{ }}{\left\|{\eta }_{j}\right\|}^{2}=}$${\displaystyle {\left\{{\eta }_{j}\right\}}^{T}\left[K_{L}\right]\left\{{\eta }_{j}\right\}}$ , teniendo que determinar las magnitudes c_j que dan lugar al máximo.

En los apartados 3.1 y 3.2 se obtiene la magnitud de la imperfección para estructuras susceptibles de pandeo debido a compresión y flexión, respectivamente. Con el objeto de ilustrar la aplicación del método se han seleccionado casos sencillos.

3. Imperfecciones en el análisis global

Un punto clave es calibrar la magnitud de la imperfección con la que se opera. En este trabajo aplicamos la cláusula 6.3.4 para obtener la carga de pandeo del sistema estructural susceptible de pandeo por compresión o flexión:

• De un análisis lineal se obtiene la mínima carga que hace que la sección más desfavorable alcance la resistencia característica sin tener en cuenta el pandeo:
• A.1 Para la compresión α_{ult ,k}  = min(A  · f_y /N ).
• A.2 Para la flexión α_{ult ,k}  = min(W_y  · f_y /M_y ).
• La esbeltez se puede obtener de la expresión ${\textstyle {\overline {\lambda }}_{op}=}$${\displaystyle {\sqrt {\frac {{\alpha }_{ult,k}}{{\alpha }_{cr,op}}}}}$ , donde α_{cr ,op} es la carga crítica considerando solo los esfuerzos primarios de compresión o de flexión.
• Se puede obtener el coeficiente de pandeo χ_op y, por tanto, la carga de pandeo de la estructura ${\textstyle {\alpha }_{b}=}$${\displaystyle {\frac {{\alpha }_{ult,k}\cdot {\chi }_{op}}{{\gamma }_{M1}}}}$ .

3.1. Magnitud de la imperfección para estructuras susceptibles de pandeo por compresión

En este apartado se obtiene el factor de escala e_c por el que se debe multiplicar el modo de pandeo (inducido por la compresión) para que la imperfección quede completamente definida ${\textstyle \left\{{\eta }_{init}\right\}=}$${\displaystyle e_{c}\left\{{\eta }_{cr}\right\}=e_{c}\left\{\eta \right\}}$ . Se obtiene imponiendo que la carga de pandeo obtenida aplicando la cláusula 6.3.4 α_b coincida con la que se obtiene con el análisis no-lineal geométrico de la estructura imperfecta:

• En secciones de clase 2 el agotamiento ocurre cuando la sección plastifica (6.2 [1] ).
• En secciones de clase 3, cuando la máxima tensión de von Mises ${\textstyle max\left({\sqrt {{\sigma }^{2}+3\cdot {\tau }^{2}}}\right)=}$${\displaystyle f_{y}/{\gamma }_{M0}}$ alcanza el límite elástico (6.2.1 [1] ).

Nota : para secciones de pared delgada las tensiones tangenciales asociadas al cortante y la torsión alabeada, debidas a la imperfección, son despreciables.

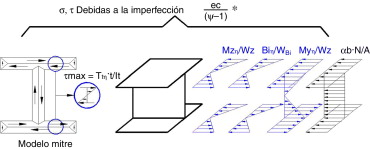
Los esfuerzos que se producen en la estructura imperfecta serán el axil (α_b ·N ) y los asociados a la imperfección que se obtienen escalando {M_y,η , M_z,η , Bi_η , T_η }, por ${\textstyle {\frac {e_{c}}{\psi -1}}}$ , siendo ${\textstyle \psi =}$${\displaystyle {\frac {{\alpha }_{crit}}{{\alpha }_{b}}}}$ .

A continuación se obtiene la expresión del factor de escala e_c considerando o despreciando las tensiones tangenciales τ debidas a la torsión de Saint Venant.

3.1.1. Tensiones tangenciales no despreciables τ ≠ 0

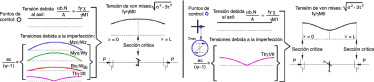
La tensión normal (fig. 3 ) en la estructura imperfecta viene dada por:

siendo W_z , W_y y W_Bi los módulos resistentes a la flexión de eje y, z y al bimomento.

Figura 3. Tensiones en la estructura imperfecta con esfuerzo primario de compresión.

La tensión tangencial para una sección de pared delgada abierta debido al torsor de Saint Venant es:

donde t es el espesor de la chapa, I_t es el módulo de torsión, y ξ varía de cero a uno en función del punto de la sección transversal que se considere.

La magnitud de e_c que hace que la tensión de von Mises sea máxima ${\textstyle {\sqrt {{\sigma }^{2}+3\cdot {\tau }^{2}}}\leq f_{y}/{\gamma }_{M0}}$ se puede obtener de la ecuación:

siendo ${\textstyle {\omega }_{1}=\left({\frac {M_{z,\eta }}{W_{z}}}+\right.}$${\displaystyle \left.{\frac {M_{y,\eta }}{W_{y}}}+{\frac {Bi_{\eta }}{W_{Bi}}}\right)}$ ; ${\textstyle {\omega }_{2}=}$${\displaystyle \left({\frac {{\alpha }_{b}\cdot N\cdot {\gamma }_{M0}}{A\cdot f_{y}}}\right)}$

La expresión se debe calcular en los puntos de control, especialmente en los que se entienda que la tensión de von Mises será máxima.

Para secciones de clase 2 la magnitud de e_c que produce la plastificación de la sección se puede obtener si utilizamos una fórmula de interacción lineal y depreciamos el torsor:

Resultando e_c :

Si no se desprecia la interacción con la torsión de Saint Venant debemos utilizar la ecuación de interacción apropiada para cada tipo de sección.

3.1.2. Tensiones tangenciales despreciables τ ≅ 0

En este caso la magnitud e_c se puede obtener:

Utilizando las relaciones ${\textstyle \psi =}$${\displaystyle {\frac {{\gamma }_{M1}}{{\overline {{\lambda }^{2}}}\chi }}}$ , ${\textstyle {\alpha }_{b}\cdot N=}$${\displaystyle {\frac {A\cdot f_{y}\chi }{{\gamma }_{M1}}}}$ , considerando ${\textstyle {\frac {{\gamma }_{M1}}{{\gamma }_{M0}}}=}$${\displaystyle 1}$ y, si la sección donde se produce α_ult coincide con la sección en la que e_c es mínimo, se puede aplicar la expresión dada en 6.3.1.2 [1] : ${\textstyle {\frac {\left(1-\chi \right)\left(1-{\overline {{\lambda }^{2}}}\chi \right)}{\chi }}=}$${\displaystyle \alpha \left({\overline {\lambda }}-0,2\right)}$ , siendo α el factor de imperfección de la tabla 6.1 la EN 1993-1-1 [1] ,resultando la magnitud de la imperfección e_c :

Esta ecuación se puede escribir en función de los movimientos del modo de pandeo para ver la semejanza con la propuesta por EN 1993-1-1 [1] :

La expresión de la ecuación (5.9) dada en 5.3.2 (11) [1] es un caso particular de la anterior, si el pandeo se produce por flexión:

3.1.3. Ejemplos

En la figura 4 se muestran las tensiones en 2 columnas imperfectas. El ejemplo de la izquierda es un perfil en forma de jota en la que el pandeo por flexión de eje y está acoplado con el de eje z y el de torsión. En este caso el efecto de τ es despreciable al ser la sección crítica la central en la que el torsor es cero. El ejemplo de la derecha tiene la sección en forma de cruz, pandea por torsión y no puede despreciarse el efecto del torsor y la imperfección viene dada por:

Figura 4. Tensiones en las columnas imperfectas.

3.2. Magnitud de la imperfección para estructuras susceptible de pandeo por flexión

En este apartado se obtiene el factor de escala e_M por el que se debe multiplicar el modo de pandeo (inducido por la flexión de eje fuerte) para que la imperfección quede completamente definida ${\textstyle \left\{{\eta }_{init}\right\}=}$${\displaystyle e_{M}\left\{\eta \right\}}$ . Se obtiene imponiendo que la carga de pandeo obtenida α_b con la cláusula 6.3.4 coincida con la que se obtiene con el análisis no-lineal geométrico de la estructura imperfecta:

3.2.1. Tensión tangencial no despreciable τ ≠ 0

Las tensiones normales en la estructura imperfecta son:

Al igual que antes, las tensiones tangenciales vienen dadas por:

La magnitud de e_M para una sección de clase 3 es:

Para secciones de clase 2 la magnitud de e_M que produce la plastificación de la sección se puede obtener utilizando una fórmula de interacción lineal y depreciando el torsor:

Resultando e_M :

Si no se desprecia la interacción con la torsión debemos utilizar la fórmula apropiada para cada tipo de sección.

3.2.2. Tensión tangencial despreciable τ ≅ 0

En este caso la magnitud de e_M es:

Utilizando las relaciones ${\textstyle \psi =}$${\displaystyle {\frac {{\gamma }_{M1}}{{\overline {\lambda }}^{2}{\chi }_{LT}}},{\mbox{ }}{\alpha }_{b}\cdot M_{y}=}$${\displaystyle {\frac {W_{y}\cdot f_{y}{\chi }_{LT}}{{\gamma }_{M1}}}}$ ; considerando ${\textstyle {\frac {{\gamma }_{M1}}{{\gamma }_{M0}}}=}$${\displaystyle 1}$ y, si la sección donde se produce α_ult coincide con la sección en la que e_M es mínimo, se puede aplicar la expresión dada en 6.3.2.2 [1] : ${\textstyle \left\{{\frac {\left(1-{\chi }_{LT}\right)\left(1-{\overline {\lambda }}_{LT}^{2}{\chi }_{LT}\right)}{{\chi }_{LT}}}=\right.}$${\displaystyle \left.{\alpha }_{LT}\left({\overline {\lambda }}_{LT}-\right.\right.}$${\displaystyle \left.\left.0,2\right)\right\}}$ , siendo α_LT el factor de imperfección:

Esta ecuación se puede escribir en función de los movimientos del modo de pandeo para ver la semejanza con la propuesta por EN 1993-1-1 [1] :

3.2.3. Ejemplos

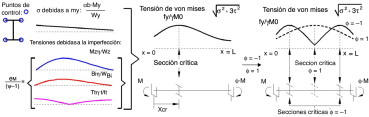
En la figura 5 se muestra la imperfección geométrica según la norma EN 1993-1-1 [1] y la propuesta realizada en este artículo para una viga en doble T (ancho B, canto H) con apoyos de horquilla y con flexión uniforme. La expresión analítica de esta última es:

Figura 5. Imperfección geométrica propuesta y según la norma EN 1993-1-1 [1] .

La figura 6 muestra las tensiones normales, tangenciales y de von Mises en una estructura sometida a momentos en ambos extremos; se puede apreciar que la sección en la que la tensión de von Mises es máxima y, por tanto, se obtiene el valor de e_M , únicamente coincide con la sección en la que se define α_ult (x = 0) para ϕ  = 1. Para un IPE-550 y acero S355 se ha obtenido la posición en la que la tensión de von Mises es máxima para la viga imperfecta: x_cr /L  = 0, 05 · ϕ²  + 0, 17 · ϕ  + 0, 28 válido si ${\textstyle \phi \in \left[-\right.}$${\displaystyle \left.1,1\right]}$ .

Figura 6. Tensiones en estructura imperfecta susceptible de pandeo lateral.

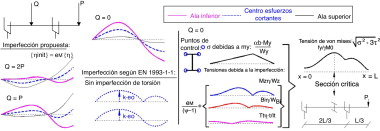
En la zona izquierda de la figura 7 se muestra la imperfección geométrica para distintos casos de carga con la metodología propuesta y la norma EN 1993-1-1 [1] . La máxima imperfección en el centro de esfuerzos cortantes con la metodología propuesta se puede obtener en función de la esbeltez mediante la ecuación ${\textstyle {\frac {L}{e_{max}}}=}$${\displaystyle 320+840{\overline {\lambda }}-910{\overline {\lambda }}^{2}+}$${\displaystyle 330{\overline {\lambda }}^{3}-41{\overline {\lambda }}^{4}}$ , según la norma EN 1993-1-1 [1] con ${\textstyle {\frac {L}{e_{max}}}=}$${\displaystyle 750}$ . En la zona derecha de la misma figura se obtienen las tensiones en el sistema imperfecto de Q = 0.

Figura 7. Estructura imperfecta. Definición de la imperfección y tensiones.

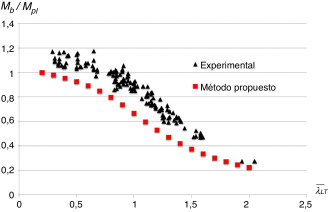
Por último, se comparan los resultados experimentales para perfiles laminados [12] con el método propuesto que utiliza una imperfección geométrica equivalente (fig. 5 para un IPE-550 S355). En la figura 8 se muestra la relación entre el momento de pandeo lateral y el momento de plastificación, al igual que en los trabajos de Bijlaard et al. [8] y Wieschollek et al. [9] se concluye que la metodología conduce a cargas de pandeo lateral seguras comparadas con los resultados experimentales.

Figura 8. Comparación del método propuesto con resultados experimentales.

4. Conclusiones

Se ha presentado un método para generalizar las recomendaciones de la norma EN 1993-1-1 [1] , apartado 5.3.2 (11), definiendo la imperfección geométrica equivalente en estructuras susceptibles de pandeo por flexión y/o torsión inducido por el axil o la flexión.

Con el objeto de ilustrar la aplicación del método se han obtenido, para algunas estructuras sencillas, las imperfecciones y tensiones asociadas.

Bibliografía

1. [1] EN 1993-1-1:2005. Eurocode 3: Design of Steel Structures. Part 1.1: General rules and rules for buildings.
2. [2] R. Greiner, J. Lindner; Interaction formulae for members subjected to bending and axial compression in Eurocode 3—the Method 2 approach; J. Constr. Steel Res., 62 (2006), pp. 757–770
3. [3] N. Boissonade, J.P. Jaspart, J.P. Muzeau, M. Villette; Improvement of the interaction formulae for beam columns in Eurocode 3; Comput. Struct., 21 (80) (2002), pp. 2375–2385
4. [4] A. Agüero; Método aproximado para estimar el estado límite último en entramados metálicos esbeltos; Tesis doctoral, Valencia (Spain): Ed. ByProquest (2004)
5. [5] M. Serna, E. Bayo, J. Ibáñez; Imperfections for global analysis of frames: EC-3 drawbacks and energy based procedure; 7th Euromech Solid Mechanics Conference, Lisbon (2009)
6. [6] A. Agüero, F.J. Pallarés; Proposal to evaluate the ultimate limit state of slender structures. Part 1: Technical aspects; Eng. Struct., 29 (2007), pp. 483–497
7. [7] R. Gonçalves, D. Camotim; On the incorporation of equivalent member imperfections in the in-plane design of steel frames; J. Constr. Steel Res., 61 (2005), pp. 1226–1240
8. [8] F. Bijlaard, M. Feldmann, J. Naumes, G. Sedlacek; The «general method» for assessing the out of plane stability of structural members and frames and the comparison with alternative rules in EN1993–Eurocode 3–Part1-1; Stco., 3 (1) (2010), pp. 19–33
9. [9] M. Wieschollek, N. Schillo, M. Feldmann, G. Sedlacek; Lateral-torsional buckling checks of steel frames using second-order analysis; Stco., 5 (2) (2012), pp. 71–86
10. [10] N. S. Trahair, Flexural–torsional buckling of structures. E&Fn spon; (1993).
11. [11] W.F. Chen, T. Atsuta; Theory of Beam–columns; McGraw-Hill, New York (1977)
12. [12] G. Sedlacek, D. Ungermann, J. Kuck, R. Maquoi, J. Janss, Eurocode 3-Part 1, Background Documentation Chapter 5 Document 5.03 (partim): Evaluation of test results on beams with cross sectional classes 1-3 in order to obtain strength functions and suitable model factors. Eurocode 3 Editorial Group (1984).