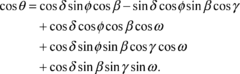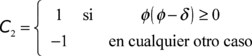RESUMEN
Por experiencia sabemos que la posición del Sol, relativa a un observador situado sobre la superficie de la Tierra, cambia según el día del año y la latitud en la que se encuentra dicho observador. En general, el Sol describe, en la bóveda celeste, una trayectoria diferente para cada día del año que está determinada por los ángulos del azimut y del zenit. El cálculo analítico para determinar la posición angular en cualquier momento (hora solar) resulta ser una tarea abrumadora. En el lenguaje de programación del software Mathematica®, desarrollamos un código que nos permite determinar, con precisión temporal de 60 segundos (1 minuto), y para cualquier latitud, los ángulos del azimut y del zenit que determinan la posición del Sol a lo largo de un año. Con el propósito de presentar resultados de interés en situaciones prácticas, en este trabajo estudiamos resultados de la distribución anual de las posiciones angulares y las horas de luz en la latitud 21 grados (correspondiente a la Ciudad de Mérida). Los resultados muestran que el Sol sigue trayectorias con inclinación hacia el norte para días de más de 12 horas de luz solar, y hacia el sur para días de menos de 12 horas de luz solar. La información que se presenta puede utilizarse en diversas situaciones, por ejemplo, para un aprovechamiento óptimo de las horas de luz de colectores solares, sistemas autónomos de seguimiento solar, ubicación y orientación de paneles solares, así como para el diseño y orientación espacial de casas habitación en las que se desee que la radiación solar incida de manera parcial sobre paredes verticales y aumentar el confort térmico.
I. INTRODUCCIÓN
El Sol, localizado aproximadamente a 150 millones de kilómetros de la Tierra, es por exelencia la fuente primordial de energía para nuestro planeta. El crecimiento y desarrollo de bosques, plantas alimenticias, frutos, semillas, algas marinas, etc., se debe en gran medida al Sol. Es imposible que la vida en nuestro planeta, con todo el conjunto de factores que la favorecen, sea como lo es en nuestros días sin la presencia del Sol. A lo largo de la historia humana, el Sol ha sido venerado por diferentes culturas de todo el mundo, considerándolo, en muchos casos, como una divinidad (Sitler, R. K., 2006, Aveni, A. F., 1992). En particular, en la península de Yucatán, la cultura Maya perfeccionó su calendario en base a observaciones de los ciclos orbitales de la Tierra alrededor del Sol, y del sistema solar en su conjunto en su órbita alrededor de nuestra galaxia, la vía láctea (Kinsella, J., Day Bradley, A. 1934). En nuestros días es indispensable saber en qué posición, en la bóveda celeste se encontrará el Sol en una hora y día paticular, para ello se han implementado algoritmos que aproximan la posición del Sol entre 1950 y 2015 (Michalsky, J. J. 1988). En casos prácticos, los algoritmos de cálculo de la posición solar, son implementados en sistemas de seguimiento solar (Abdallah, S. y Nijmeh S. 2004, Roth, A., Georgiev, A., Boudinov, H., 2005, Chia-Yen Lee, et. al., 2009) y también en algoritmos para determinar la radiación solar (Reda, I. Adreas, A. 2004).
En aplicaciones de paneles solares, para una optimización de la captación de radiación solar, la superficie del panel debe ser normal (perpendicular) a la luz incidente, y por tanto es necesario conocer la posición angular del Sol a nivel local. En algunos casos menos sofisticados, los seguidores solares contienen medidores de radiación, que permiten fijar la posición del panel solar cuando la radiación incidente está un máximo local, en los casos más simples (en la mayoría), los paneles están fijos, con un ángulo de inclinación igual a la latitud de la región de interés. Resulta importante destacar que en la península de Yucatán, siendo una región con un alto índice de radiación solar, donde se tienen registros de temperaturas que han sobrepasado los 40 grados centígrados, y con sensaciones térmicas por encima de los 50 grados, la posición relativa del Sol no sea tomada en cuenta en el diseño de casas habitación, lo que permitiría reducir la radiación incidente sobre las paredes verticales, en ventanas y puertas, logrando un confort mayor en el interior de dichas viviendas.
En este trabajo de investigación presentamos el desarrollo de un código en el lenguaje de programación Mathematica® (el lector interesado puede contactar a los autores y solicitar el código), que permite obtener los ángulos del zenit y del azimut que determinan la posición del Sol (ver Figura 1), con una resolución temporal de 1 minuto, en el intervalo de 12 horas de un día, desde las 6 de la mañana y hasta las 6 de la tarde (del alba al ocaso), y durante los 365 días del año.
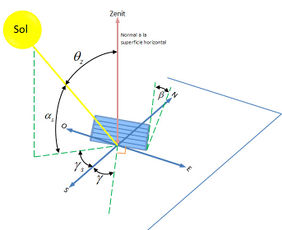
Figura 1. Esquema para determinar la posición del Sol en términos del ángulo zenit (θz) y el ángulo azimtal (Υs). Note que el ángulo de altitud solar (αs) es 90- θz. Se incluye una superficie de incidencia (rectángulo azul) con un ángulo de inclinación β y ángulo azimutal Υ. En la figura, el Sol se encuentra al oeste del sur.
El código está diseñado para su fácil uso y se puede aplicar a cualquier región (en función de la latitud). Como aplicación de nuestro código, nosotros fijamos la latidud a 21 grados (correspondiente a la Ciudad de Mérida), y los datos obtenidos son analizados estadísticamente, y presentados en forma de funciones de densidades de probabilidad (PDF), ya que resultaría impráctico incluir 365 tablas (una para cada día del año), con 720 pares de ángulos (un par por minuto durante 12 horas de cada día). En la siguiente sección mostramos el marco teórico, y posteriormente presentamos la sección de resultados y discusión finalizando con las conclusiones.
II. MARCO TEÓRICO
Las relaciones geométricas entre un plano de cualquier orientación particular relativa a la Tierra, en cualquier momento (ya sea que el plano esté fijo o en movimiento relativo a la Tierra, ver rectángulo azul en la Fig. 1.), y el haz de la radiación solar incidente, esto es, la posición relativa del sol con ese plano, puede ser descrita en términos de varios ángulos (Benford y Bock, 1939). La figura 1 muestra los ángulos que permiten determinar la radiación solar incidente y la posición relativa del Sol. Las definiciones de latitud y declinación, los ángulos horario y de incidencia, así como el conjunto de ángulos para determinar la radiación solar incidente y la posición relativa del Sol, se presentan a continuación:
𝜙(Latitud), la ubicación angular al norte o sur del ecuador, siendo el norte positivo; -90º≤𝜙≤90º.
δ (Declinación), la posición angular del sol al medio día, con respecto al plano del ecuador, siendo el norte positivo -23.45º≤ δ ≤23.45º.
β (Inclinación), el ángulo entre el plano de la superficie en cuestión y la horizontal, 0º≤ β ≤180º. (β > 90º significa que la superficie tiene una componente que mira hacia abajo).
𝛾(Ángulo Azimutal de la superficie), la desviación de la proyección en un plano horizontal de la normal a la superficie del meridiano local, siendo cero el sur, el este negativo y el oeste positivo -180º≤ 𝛾≤180º.
ω (Ángulo horario), el desplazamiento angular del sol al este o al oeste del meridiano local debido a la rotación de la tierra sobre su eje a 15º por hora, siendo por la mañana negativo y positivo por la tarde.
θ (Ángulo de incidencia), el ángulo entre el haz de la radiación incidente en una superficie y la normal a esa superficie.
Se definen a continuación ángulos adicionales que describen la posición del sol en la bóveda celeste:
θz(Ángulo del zenit), el ángulo entre la vertical y una línea con el sol, es decir, el ángulo de incidencia del haz de radiación solar sobre una superficie horizontal.
αs(Ángulo de altitud solar), el ángulo entre la horizontal y una línea con el sol, es decir el complemento del ángulo del zenit.
𝛾s(Ángulo Azimutal solar), el desplazamiento angular desde el sur de la proyección del haz de la radiación en el plano horizontal. Los desplazamientos al este del sur son negativos (valores antes del medio día solar), y los desplazamientos al oeste del sur son positivos (valores después del medio solar).
Los valores de la declinación solar, para cada día del año, pueden hallarse con la fórmula de Cooper (Cooper 1969):
|
(1) |
donde n es el n-ésimo día del año.
Usando la ecuación anterior, en la figura 2 se muestran los valores de la declinación (línea punteada) a lo largo de un año.
Por otra parte, existe un conjunto útil de relaciones entre los ángulos anteriormente definidos. Tales ecuaciones relacionan el ángulo de incidencia del haz de radiación θ sobre una superficie plana con los distintos ángulos (δ,𝜙, β, 𝛾, ω) anteriormente definidos. La primer relación está dada por:
|
(2) |
Como un caso particular, para una superficie horizontal, el ángulo de inclinación es igual a cero, y en dicho caso el ángulo del zenit es igual al ángulo de incidencia, así, de la ecuación anterior tenemos que:
|
(3) |
De la ecuación anterior podemos calcular el valor del ángulo del zenit en términos de la declinación, la latitud y el ángulo horario. La segunda relación importante está dada por:
|
(4) |
El ángulo de Azimut solar 𝛾spuede tomar valores en el rango entre 180º a -180º. Para latitudes norte o sur entre 23.45º y 66.45º, 𝛾sestará entre 90º y -90º para días con menos de 12 horas de duración. Para días con más de 12 horas entre el amanecer y el ocaso, 𝛾sserá menor de -90º o mayor de 90º, en la mañana o en la tarde, respectivamente, cuando el Sol esté al norte de la línea este-oeste en el hemisferio norte, o al sur de la línea este-oeste en el hemisferio sur. Para latitudes tropicales 𝛾spuede tomar cualquier valor cuando (δ-𝜙) es positivo en el hemisferio norte, o negativo en el sur.
Así, para calcular 𝛾snecesitamos saber en qué cuadrante estará el sol. Esto se determina midiendo la relación entre el ángulo horario ω y el ángulo horario ωew, cuando el sol está hacia el este (o el oeste). Una formulación general para 𝛾sestalecida por Braun y Michell (1983), puede escribirse convenientemente en términos de 𝛾s’, definido como un ángulo azimutal solar ficticio, para el primer o cuarto cuadrante. De acuerdo con Braun y Michell (1983), el ángulo azimutal solar está dado por:
|
(5) |
donde,
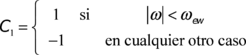
|
si ![]() es mayor que 1, el Sol nunca se dirige hacia el este o el oeste del observador. En este caso haga C1=1, es mejor evitar hacer ð=0.
es mayor que 1, el Sol nunca se dirige hacia el este o el oeste del observador. En este caso haga C1=1, es mejor evitar hacer ð=0.
III. RESULTADOS Y DISCUSIÓN
Con las ecuaciones de la sección II, es posible determinar los ángulos azimutal y zenit, los cuales determinan unívocamente la posición del Sol en la bóveda celeste, para ello es necesario conocer la latitud de la región de interés, y el ángulo horario. En nuestro caso, para la latidud de 21 grados (latitud de la Ciudad de Mérida), programamos las ecuaciones en el lenguage de programación Mathematica® (ver apéndice I para conocer el código desarrollado). Independientemente del valor del ángulo azimutal, el amanecer ocurre cuando el ángulo del zenit es menor o igual a 90º. La figura 3 muestra la hora del amanecer para cada día del año.
Fig. 3. Hora del amanecer. Se observan aproximadamente 80 minutos de diferencia entr los días que más tarde sale el Sol, con respecto a los días que amanece más temprano.
El horario mostrado en el eje vertical de la figura 3 no necesariamente corresponde al horario que cotidianamente usamos en nuestros relojes, mostramos los resultados en términos del horario solar, donde el medio día solar queda definido cuando el ángulo azimutal solar vale cero grados. De la figura 3 podemos notar que hay aproximadamente 90 minutos de diferencia entre el día que más tarde sale el Sol (día 355 del año), con respecto al día que más temprano amanece (día 172 del año). Un cálculo adicional nos permite determinar el número total de horas de luz para cada día del año (ver Fig. 4). De la figura 4 podemos identificar qué días son los más largos y cortos del año, así como los días de más (o menos) horas. Por ejemplo, a partir del día 81 comienzan los días con más de 12 horas de duración, lo que normalmente correspondería al inicio del conocido horario de verano, y el día 263 terminan los días con más de 12 horas de luz (terminaría el horario de verano). Los días 81 y 263 corresponden a los equinoccios. De la misma figura 4 podemos identificar que el día 172 es el de mayor horas de luz (13:16, trece horas con 16 minutos), mientras que el de menor horas de luz es el día 355 (10:43, diez horas con 43 minutos), día cuando ocurre el solsticio de invierno.
Fig. 4. Horas de luz para cada día del año, podemos identificar periodos de menos de 11 horas de luz y de más de 13 horas de luz.
Los valores de los ángulos que determinan la posición del Sol fueron obtenidos para cada uno de los
 365 días del año, y para cada día en intervalos de un minuto, desde el alba hasta el ocaso. El intervalo temporal cuenta con la resolución suficiente para que los datos obtenidos puedan ser utilizados en sistemas autónomos de seguimiento solar. Además, los resultados de este trabajo pueden usarse para estimar la componente directa de la radiación solar en regiones donde no se tengan registros históricos. Si el lector lo requiere puede ponerse en contacto con los autores y solicitar los datos de los resultados de los ángulos.
365 días del año, y para cada día en intervalos de un minuto, desde el alba hasta el ocaso. El intervalo temporal cuenta con la resolución suficiente para que los datos obtenidos puedan ser utilizados en sistemas autónomos de seguimiento solar. Además, los resultados de este trabajo pueden usarse para estimar la componente directa de la radiación solar en regiones donde no se tengan registros históricos. Si el lector lo requiere puede ponerse en contacto con los autores y solicitar los datos de los resultados de los ángulos.
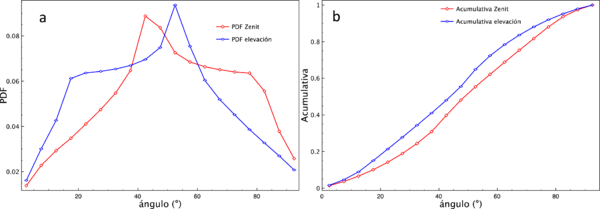
El ángulo de zenit fue obtenido por medio de la ecuación (2). Los resultados correspondientes se muestran como histogramas en la figura 1(a). En dicha figura se observa que los ángulos del zenit de mayor frecuencia están en el intervalo entre 50º y 55º, y se observa una frecuencia con mínima variación en el intervalo de 15º a 40º. Para el caso del ángulo de altitud, la frecuencia es mayor en el intervalo de 35º a 40º, y mínima variación de la frecuencia en el intervalo de 50º a 75º, lo cual es congruente dada la relación entre altitud y zenit. En la figura 1(b) se muestran los valores acumulativos de la gráfica 1(a), que en este caso corresponden a la probabilidad de que el ángulo del zenit o elevación esté dentro de un intervalo particular. Por ejemplo, se tiene una probabilidad de aproximadamente 0.18 de que al medir el ángulo de elevación éste se encuentre dentro del intervalo entre 0º y 20º. Los resultados mostrados en la figura 5 son una representación estadística, pero para fines prácticos, son poco útiles. Más adelante mostraremos resultados con mayor potencial de aplicación.
Con respecto al ángulo azimutal, en la figura 6 mostramos un análisis similar al de la figura 5. Es importante notar que los valores del ángulo azimutal entre -180º y 0º grados corresponden a posiciones del Sol antes del medio día (durante la mañana), y los valores entre 0º y 180º corresponden a (durante la tarde).spu en nuessponden un anacto con los autores y solicitar los datos de los enta con la resoluciamos en nuesposiciones del Sol después del medio día (durante la tarde). La figura 6 muestra 3 regiones, definidas por los intervalos R1(-180º, -90º), R2(-90º, 90º) y R3(90º, 180º). La región R1 indica que el Sol se encuentra, durante el transcurso de la mañana inclinado hacia el norte de la línea este-oeste y, de la misma manera para la región R3 durante la tarde. Mientras que la región R2 indica que el Sol se encuentra hacia el sur de la línea este-oeste, es decir, existen días para los cuales la proyección de nuestra sombra se dirige al sur, cuando el Sol está en la región R1 y R3, y al norte, cuando el Sol está en la región R2. Es interesante mencionar que usualmente los paneles solares se encuentran en una posición fija, y orientados hacia el sur con un ángulo de inclinación
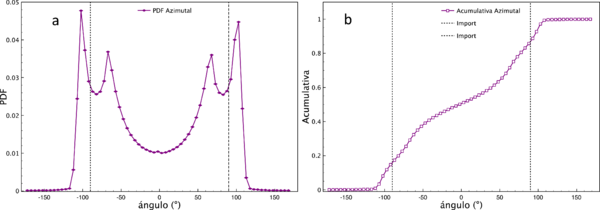 de 21º, de acuerdo con la figura 1, en éste caso ð¾ = 0 y β = 21º. Sin duda este hecho resulta en una disminución de la radiación directa incidente sobre los paneles solares, lo cual afecta su eficiencia. De manera análoga a la figura 5b, de la figura 6b podemos inferir que la probailidad de que por la mañana el Sol se encuentre al norte es aproximadamente 0.2. Con fines de mayor aplicación, es necesario conocer cuáles son los días que el Sol se inclina hacia el norte o hacia el
de 21º, de acuerdo con la figura 1, en éste caso ð¾ = 0 y β = 21º. Sin duda este hecho resulta en una disminución de la radiación directa incidente sobre los paneles solares, lo cual afecta su eficiencia. De manera análoga a la figura 5b, de la figura 6b podemos inferir que la probailidad de que por la mañana el Sol se encuentre al norte es aproximadamente 0.2. Con fines de mayor aplicación, es necesario conocer cuáles son los días que el Sol se inclina hacia el norte o hacia el
sur y qué porcentaje del día permanece en una u otra orientación. La figura 7 muestra que a partir del día 1 del año y hasta el día 81 el Sol sigue una trayectoria siempre inclinado hacia el sur, y a partir del día 82 sigue una trayectoria en la cual comienza a inclinarse hacia el norte, resulta interesante observar que a partir del día 82 comienzan los días con más de 12 horas de luz, finalizando en el día 263, justo cuando el Sol vuelve en su totalidad a la región R2, es decir, siempre haciendo un recorrido inclinado hacia el sur. Es importante notar que del día 146 al 199 el Sol hace su recorrido manteniéndose en su totalidad con una inlinación hacia el norte (regiones R1 y R3) y que el 50% del año el Sol recorre el firmamento siempre inclinado hacia el sur, el 14.5% siempre inclinado hacia el norte, y el resto lo hace en combinación norte-sur. Ahora que conocemos los días que el Sol sigue una trayectoria con inclinación hacia el norte o el sur, resulta importante saber cuál es ángulo del zenit, que nos indicaría qué tan inclinado al norte o sur se encuentra. Dado que el número de datos es enorme, en este estudio nos centramos en los valores cuando la radiación directa debe ser máxima, es decir, al medio día solar. La figura 8 muestra los valores del ángulo zenit justo al medio día solar. De las figuras 7 y 8 podemos inferir que cuando el Sol está en la región R2 (siempre inclinado hacia el sur), el ángulo de zenit, θz, alcanza un valor máximo de 45o grados aproximadamente, es decir, el Sol tiene la mínima altitud. De manera análoga, cuando el Sol inicia su recorrido por la región R1, o finaliza su recorrido por la región R3, el ángulo θz alcanza un valor máximo de aproximadamente 20o (mínima altitud). De la figura 8 notamos que cuando el Sol inicia y termina su trayectoria con una inclinación siempre hacia el norte (días 81 y 263), el ángulo del zenit a medio día es igual a cero, correspondiente al equinoccio. Por otra parte, cuando el Sol transita siempre inclinado hacia el norte (del día 146 al 199), el ángulo θz alcanza ahora 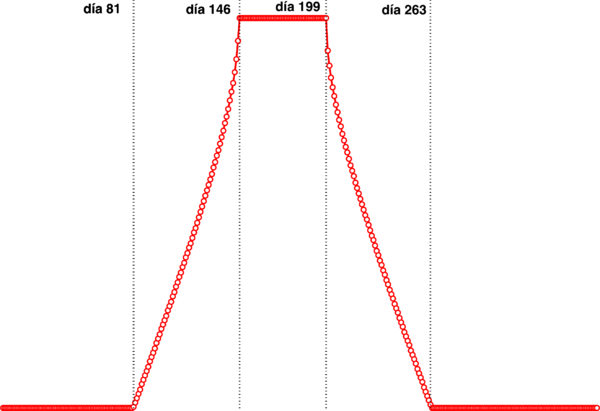 un valor máximo de 5o. Los resultados anteriores pueden ser
un valor máximo de 5o. Los resultados anteriores pueden ser
Figura 7. Porcentaje de tiempo que el Sol se localiza hacia el norte. Desde el día 1 y hasta el 81 el Sol siempre permance inclinado hacia el sur, y a partir del día 82 aumenta el porcentaje de tiempo en los que el Sol se inclina hacia el norte. Del día 146 al 199 el Sol permanece el 100% de tiempo inclinado hacia el norte.
aplicados, por ejemplo, en sistemas de seguimiento solar, en paneles solares y en la industria de casas habitación. Si se desea que la luz del Sol no incida sobre una pared vertical cuando la radiación sea máxima (a medio día solar), es necesario construir terrazas que proyecten sombra sobre la pared vertical. Así, si h es la altura de una pared vertical, entonces la longitud L de la terraza, para garantizar que al medio solar la radiación no incida sobre dicha pared, está dada por: L = hTan(θz). Usando los valores del zenit máximo tenemos que cuando el sol está inclinado hacia el sur L = h, mientras que si el Sol está inclinado hacia el norte, L =0.36h.
IV. CONCLUSIONES
Los ángulos del zenit y del azimut, que determinan la posición del Sol fueron calculadas por medio del modelo matemático propuesto por Braun y Michell (1983). Con el lenguaje de programación del software Mathematica® se obtuvieron dichos ángulos, minuto a minuto, para los 365 días del año en la latitud de 21 grados. Los resultados muestran que el Sol sigue trayectorias con inclinación hacia el norte y hacia el sur, contrastando con la posición fija de los paneles solares por el poco tiempo que la radiación directa incide sobre sus superficies. Presentamos una relación que permite determinar la longitud de terrazas mínima que garanticen que al medio día solar, se proyecte una sombra sobre las paredes verticales, lo cual puede aplicarse en casas habitación para aumentar el confort térmico. Los resultados de la presente investigación pueden implementarse en modelos para cuantificar la radiación solar incidente sobre superficies que siguen al Sol.
V. AGRADECIMIENTOS
Este trabajo se realizó bajo el soporte del proyecto FING-2017-0004 de la Universidad Autónoma de Yucatán.
REFERENCIAS
Sitler R. K. (2006). “The 2016 Phenomenon New Age Appropriation of an Ancient Mayan Calendar”, Nova Religio: The Journal of Alternative and Emergent Religions, Vol. 19 No. 3, pp. 24-38 (DOI: 10.1525/nr.2006.9.3.024)
Aveni, A. F. (1992). “The sky in Mayan literature”, Osxford University Press, New York (USA), 307 p., ISBN 0-19-506844-0.
Kinsella, J., Day Bradley, A. (1934). “The mayan calendar”, The mathematics teacher, Vol. 27, No. 7, pp. 340-343.
Michalsky, J. J. (1988). “The Astronomical Almanac’s algorithm for approximate solar position (1950-2050)”. Solar Energy, Vol. 40 Issue 3, pp. 227-235.
Abdallah, S. y Nijmeh S. (2004). “Two axes sun tracking system with PLC control”, Energy Conversion and Management. Vol. 45, Issue 11-12, pp. 1931-1939.
Roth, A., Georgiev, A., Boudinov, H., (2005). “Cheap two axis sun following device”, Energy Conversion and Management. Vol. 46, Issue 7-8, pp. 1179-1192.
Chia-Yen Lee, et. al., (2009). “Sun Traking Systems: Areview”, Sensors. Vol. 9(05), pp. 3875-3890. (DOI: 10.3390/s90503875).
Reda, I. Adreas, A. (2004). “Solar position algorithm for solar radiation applications”. Solar Energy. Vol. 76, Issue 5, pp. 577-589.
Benford, F., y Bock, J. E., (1939). “A time analisys of Sunshine”, Trans. Of the American Illumination Engineering Soc. Vol. 34 p. 200.
Cooper, P. L. (1969). “The Absortion of Solar Radiation in Solar Stills”, Solar Energy. Vol. 12, p. 3.
Braun, J. E., y Mitchell, J. C. (1983). “Solar Geometry for Fixed and Traking Surfaces”, Solar Energy. Vol 31, p. 439.
Document information
Published on 08/02/19
Accepted on 04/12/18
Submitted on 05/09/17
Volume 35, Issue 1, 2019
DOI: 10.23967/j.rimni.2018.12.003
Licence: CC BY-NC-SA license