Composite slabs micromechanics characterization of the steel-concrete interaction with finite element models

Resumen

El objetivo del presente artículo es la mejora de la caracterización, mediante el uso de modelos avanzados de elementos finitos, del comportamiento de las losas mixtas con perfil de acero conformado y hormigón. El modelado de las geometrías tridimensionales de un perfil comercial de acero a escala real habilita el estudio de su micromecánica. La inclusión en el perfil de acero de las embuticiones, espesores, ángulos de inclinación y separación entre embuticiones elimina la necesidad de las simplificaciones en el complejo contacto que se produce entre ambos materiales. La gran correlación obtenida entre los modelos de elementos finitos y sus respectivos especímenes de laboratorio abre la puerta a una mejor comprensión de las complejas distribuciones de tensiones y a su caracterización. En particular, se introduce la novedosa representación de la tensión longitudinal rasanteτ_u y de una nueva tensión vertical normal σ_u entre el acero y el hormigón que frecuentemente determinan la capacidad resistente de la losa mixta. El estudio se complementa con una representación en los modelos de elementos finitos de resultados experimentales de tensiones y deformaciones obtenidos mediante galgas extensiométricas.

Abstract

This study focuses on the improvement of composite slabs characterization throughout the use of advanced finite elements models. The accurate three-dimensional modelling of a full scale commercial steel sheet and concrete slab geometries enables the analysis of the composite slab micromechanics. The inclusion of the embossments depth and slope, the steel sheet thickness, the tilting angle, the length and width and spacing of embossments, and the profiling angle of the rib shape removes the need of simplifications for the complex phenomenon at the steel – concrete interface. The accuracy observed at the finite element models once compared with the laboratory specimens enables a new approach to describe the complex stress distributions in composite slabs. In particular, this study introduces a novel representation of the longitudinal shear strength τ_u and a newly defined vertical normal stress σ_u between the steel and concrete that frequently define the overall composite slab bearing capacity. Subsequently, this study compares detailed stress diagrams and deformations from the finite elements models with experimental data obtained through piezoelectric gauges at the laboratory specimens.

1. Introducción

Las losas mixtas compuestas por un perfil conformado metálico y hormigón han proliferado abundantemente en las últimas décadas en construcción por su simplicidad de ejecución, ligereza, sencillez de puesta en obra y sus tolerancias controladas en entornos de fabricación. La unión simbiótica entre el perfil de acero con embuticiones y el hormigonado in situ las convierten en un elemento estructural alternativo a la losa maciza convencional para requerimientos moderados de capacidad resistente y luces. Aun así, su difícil caracterización resistente basada en métodos semi-empíricos con costosos ensayos en laboratorio ha condicionado una difusión más amplia. Normativamente, el Eurocódigo 4 [1] propone su estudio en base a dos métodos: el Método m-k y el Método de la Conexión Parcial (MCP) apoyándose para ambos casos en los resultados de una batería de ensayos de laboratorio.

El fallo mecánico en las losas mixtas puede ser causado por flexión, tensión vertical o longitudinal según su localización y relacionado con el grado de interacción entre materiales. El fallo causado por la tensión longitudinal rasante es el más común de los anteriores, proviniendo su resistencia de la adherencia química inicial, la fricción entre hormigón y acero, y la resistencia mecánica de las embuticiones características del perfil de acero. La principal función de éstas últimas es la de habilitar que la tensión longitudinal se transmita entre ambos materiales y por lo tanto evitar que se produzca deslizamiento relativo entre sus respectivas superficies de contacto.

Con el objetivo de mejorar la caracterización de su comportamiento resistente y la influencia de los distintos aspectos que componen las losas mixtas, numerosos autores han optado por la utilización de modelos de elementos finitos (EF). Los modelos de EF crean una plataforma sólida de estudio del comportamiento de las losas mixtas con multitud de posibles configuraciones en base a su calibración inicial con especímenes de laboratorio.

Daniels y Crisinel [2,3] introdujeron el primer modelo de EF de losa mixta para el estudio de un nuevo método de diseño. An [4] creó un modelo de EF bidimensional e introdujo el concepto de muelles para la interface acero – hormigón. Posteriormente, numerosos otros autores (Veljkovic [5], Widjaja [6], Abdullah y Easterling [7]) prosiguieron la senda de modelos de EF más complejos pero aún con la necesidad de mantener distintos grados de simplificaciones para la interface acero-hormigón y con geometrías reducidas. Ferrer et al. [8] realizó estudios paramétricos sobre los valores que más influyen en comportamiento global de la losa mixta modelando la geometría real del perfil de acero, aunque se centró en una única rebanada de un nervio de la losa mixta. Seres y Dunai [9], dividieron sus estudios en dos partes, según si caracterizaban el comportamiento del hormigón o del acero.

Por otro lado, López et al. [10] y Chen y Shi [11] realizaron modelos de EF de toda la geometría de la losa mixta para el ensayo a flexión normativo con el objetivo de determinar la resistencia del conjunto a rasante. López et al. utilizaron modelos con representación de fisuración para el hormigón, centrándose mayoritariamente en un estudio en zonas concretas. Chen y Shi usaron sólidos elásticos y en base a resultados de ensayos previos a escala reducida pull-out, presentaron un modelo de EF tridimensional universal. Estos modelos obviaban la introducción de la geometría real de los elementos y basaba su funcionamiento en la elección de los parámetros de contacto para compensar la no inclusión de elementos geométricos. Para Mistakidis y Dimitriadis [12] ganó relevancia el comportamiento del acero por delante del hormigón mediante la realización de dos tipos de ensayos: uno a tracción y otro a flexión. Los resultados permitieron parametrizar variables como el grueso del perfil de acero y la altura de sus embuticiones.

Los modelos de EF de losas mixtas han requerido de simplificaciones significativas debido a la complejidad inherente del comportamiento diferente de los materiales hormigón y acero y al coste computacional asociado. En particular, las simplificaciones incluyeron representaciones parciales del conjunto como una rebanada, la no inclusión de la geometría detallada de los elementos de la superficie del acero como las embuticiones, o el análisis individual para el perfil de acero y el hormigón de forma separada. Estas simplificaciones condicionaron la capacidad de explorar la micromecánica de las losas mixtas que actualmente es mayoritariamente desconocida. De especial interés es la tensión longitudinal a rasante τ_u que para el método de diseño MCP del Eurocodigo 4 y multitud de estudios como los de Patrick y Bridge [13], Bode et al [14], Johson y Anderson [15], Abdullah y Easterling [7], y Crisinel y Marimon [16] se consideró con un valor constante en la zona de rasante. Como hipótesis, el deslizamiento relativo de la losa de hormigón por encima del perfil de acero genera una tensión de valor constante τ_u que hasta la fecha no se ha podido validar.

Como novedad en este artículo, los modelos de EF desarrollados representan por primera vez el comportamiento de las losas mixtas largas (L=5000 mm) que estipula el ensayo normativo a flexión del Eurocodigo 4 incluyendo los componentes estructurales a escala real con la geometría tridimensional detallada para sus embuticiones. La principal aportación es la observación de la compleja micromecánica existente entre hormigón y acero bajo condiciones de carga. La geometría de las embuticiones fue modelada de forma exacta, así como se habilitó el efecto cuña entre el hormigón y acero que transforma el deslizamiento longitudinal en tensión de sujeción transversal “clamping” en la chapa de acero.

La sección 2 presenta el procedimiento seguido para el ensayo. La sección 3 muestra una visión detallada de los modelos de EF desarrollados. En la sección 4 se resumen los resultados obtenidos para la micromecánica en las losas mixtas, en particular para las tensiones longitudinal rasante τ_u y vertical normal σ_u, y de forma cualitativa las tensiones puntuales obtenidas con galgas extensiométricas. Finalmente, en la sección 5 se presentan las conclusiones.

2. Ensayo experimentales y modelos de elementos finitos

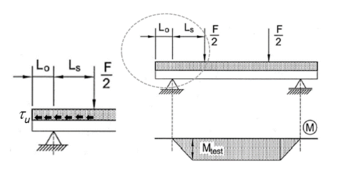
La figura 1 muestra la configuración del ensayo según normativa Eurocódigo 4 que incluyó probetas de un perfil comercial con una longitud de L=5.000 mm [17]. La distribución experimental consideró la aplicación de cargas lineales a un cuarto de la longitud total respecto a cada extremo. Se dispusieron cuatro captadores de desplazamiento, los dos primeros en los extremos y los siguientes en el eje transversal, midiendo el deslizamiento relativo acero-hormigón y la flecha central del conjunto. También se colocaron galgas extensiométricas para capturar el efecto de las tensiones longitudinales y transversales en el perfil de acero como aspecto experimental adicional, aunque no relacionado con los requerimientos de la normativa.

(a)

(b)

Figura 1: Disposición de ensayo a flexión en losas mixtas (a) configuración en laboratorio, adaptación de Eurocódigo 4; (b) fotografía espécimen real

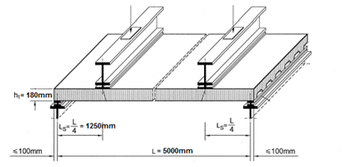
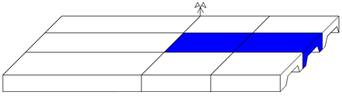
Los modelos de EF propuestos se beneficiaron de las simetrías existentes en los especímenes de laboratorio: una primera especular en el plano central de la chapa reduciendo así su longitud a la mitad; otra cíclica en los nodos pertenecientes al plano inferior de la chapa acoplándolos y forzando un desplazamiento similar; finalmente, una especular a ambos lados del nervio modelado tal como se muestra en la figura 2.

Figura 2: Modelado EF de espécimen de laboratorio

Los modelos de EF se realizaron mediante el software comercial ANSYS y las simulaciones se basaron en el método no-lineal de Newton-Rapson mediante desplazamiento vertical en el punto L_s=L/4. La caracterización del acero se realizó mediante el elemento membrana elasto-plástica SHELL281 con capacidad de endurecimiento basado en el criterio de von Mises, f_yp = 336 N/mm² y E = 210 000 N/mm² para el módulo de elasticidad. El elemento hormigón se realizó mediante SOLID185 que habilita un coste computacional bajo para la simulación del hormigón y f_ck = 25 N /mm². Los elementos TARGE170 y CONTA174 se utilizaron como elementos de contacto para las superficies tridimensionales. El coeficiente de fricción fue introducido considerando el modelo de Coulomb con un coeficiente µ de 0.5 mientras que la adhesión no se consideró. Buernet y Oehlers [18] estudiaron la influencia del parámetro de fricción proponiendo valores entre 0 a 0.6, mientras Tsalkatidis y Avdelas [19] y Chen and Shi [11] utilizaron un valor de 0.3. El mallado de las distintas geometrías se realizó de forma más refinada en los puntos más irregulares para una mejor caracterización de las tensiones y de forma menos intensa en zonas más regulares para reducir el coste computacional. Las diferentes opciones de mallado así como su caracterización final se realizaron mediante un proceso iterativo de optimización de la convergencia de los modelos.

La simulación del ensayo de laboratorio se realizó mediante la creación de dos modelos de EF diferenciados QL60-SI sin inductor de fisura y QL60-FI con inductor de fisura en el punto de aplicación de la carga. Plans et al. [20] propusieron la realización de dos modelos diferenciados para el estudio de losas mixtas debido al comportamiento significativamente diferente que existe en las fases iniciales de carga previas al deslizamiento inicial entre materiales y posteriores cuando existe desplazamiento relativo. La figura 3 muestra la existencia del elemento inductor de fisura en los especímenes de laboratorio.

(a)

(b)

Figura 3: Modelado y influencia del inductor de fisura (a) preparación espécimen laboratorio, (b) influencia en ensayo

3. Análisis modelos elementos finitos

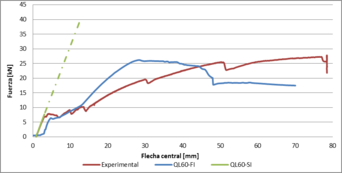
Para la verificación de la solidez de los modelos de EF éstos fueron calibrados con los resultados de los especímenes de laboratorio. La figura 4 muestra la evolución de la flecha vertical en el centro del vano para los especímenes de laboratorio y la de las simulaciones. El modelo sin inductor QL60-SI se comporta de manera muy similar en los primeros momentos de simulación, concretamente entre los 0 i 5 mm de flecha central donde aún no existe ningún deslizamiento longitudinal entre el acero y el hormigón y el comportamiento es lineal. Se puede observar como la gráfica se solapa con la experimental hasta los 7 kN de capacidad resistente.

Figura 4: Evolución flecha central entre espécimen de laboratorio y modelos de EF

El modelo QL60-FI también tiene un comportamiento parecido manteniendo las mismas pendientes hasta los 15 mm de flecha central, dónde se empiezan a producir los primeros deslizamientos entre acero y hormigón. A partir de este punto, a medida que crece la carga y la flecha, también incrementa la diferencia entre las gráficas. En el instante de deformación 50 mm, ambas gráficas sufren una caída de capacidad resistente y ésta empieza a decrecer progresivamente. Esta caída es un patrón común para el perfil comercial del estudio según multitud de ensayos realizados en base a una adherencia química inicial muy elevada [17].

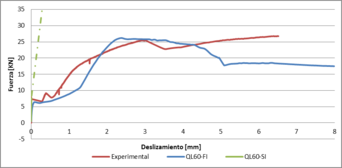
Las gráficas del comportamiento de los modelos de EF y del espécimen de laboratorio para los deslizamientos relativos en el extremo de la losa mixta se muestran en la figura 5. El modelo QL60-SI representa de forma muy fiel los primeros instantes de carga donde no existe deslizamiento entre el hormigón y el acero. Una vez se produce el primer deslizamiento, el modelo QL60-FI pasa a representar el comportamiento del espécimen de laboratorio de forma muy lineal hasta un deslizamiento de 2 mm. Para deslizamientos mayores, las gráficas del espécimen y del modelo de EF muestran patrones y comportamientos parecidos con mínimas desviaciones.

Figura 5: Desplazamiento relativo acero-hormigón en extremo losa entre espécimen de laboratorio y modelos de EF

La tabla 1 muestra la correlación del comportamiento de los dos modelos QL60-SI y QL60-FI con el espécimen de laboratorio para la flecha central y el deslizamiento del acero y el hormigón relativo en el extremo de la losa. La utilización de dos modelos diferenciados de EF habilita una mejor alineación con el comportamiento real, especialmente en etapas iniciales de la simulación donde existe adherencia química difícil de cuantificar. Concretamente, el modelo QL60_SI presenta variaciones menores al 3% respecto a los tests de laboratorio para ambos desplazamientos. Una vez los deslizamientos entre el acero y el hormigón se han iniciado, el modelo QL60-FI representa el patrón de comportamiento del espécimen de laboratorio con desviaciones fluctuantes, pero con un comportamiento general igual al experimental. Concretamente, la simulación presenta variaciones puntuales que oscilan entre el 10% y el 40% con amplios segmentos de correlación. Las discrepancias observadas están en línea con resultados similares en modelado de losas mixtas con EF reportados por otros autores citados en la sección 1, con la diferencia que en este estudio no se utilizan simplificaciones para la interface acero-hormigón.

Tabla 1: Comparativa numérica desplazamientos modelos EF y espécimen de laboratorio

Carga [kN]	Modelo	Experimental		Simulación		Desviación [%]
		Flecha [mm]	Deslizamiento [mm]	Flecha [mm]	Deslizamiento [mm]	Flecha [%]	Deslizamiento [%]
0.50	QL60-SI	0.94	0.00	0.94	0.00	0.0	-
1.00	QL60-SI	1.19		1.19		0.0	-
5.00	QL60-SI	2.31		2.30		0.4	-
7.00	QL60-SI	2.97		2.90		2.3	-
Deslizamiento inicial
7.00	QL60-FI	7.60	0.30	8.05	0.38	5.6	21.0
10.00	QL60-FI	12.41	0.74	12.24	1.20	1.3	38.3
15.00	QL60-FI	20.80	1.04	16.40	1.68	21.1	38.1
20.00	QL60-FI	33.70	1.61	20.40	2.11	39.5	23.7
25.00	QL60-FI	48.50	2.80	25.80	2.51	46.8	10.3
Caida capacidad resistente
25.00	QL60-FI	48.60	4.80	38.60	5.32	18.52	9.7

4. Micromecánica losas mixtas y discusión

4.1 Tensión longitudinal rasante τ_u

La inclusión dentro de los modelos de EF de las geometrías tridimensionales detalladas de los elementos acero y hormigón permiten el análisis de la micromecánica para el conjunto de la losa en cualquiera de los estados de carga simulados. En particular, la tensión longitudinal a rasante τ_u se define según la ecuación (1) y es la base del MCP del Eurocódigo 4 que se apoya en un modelo mecánico. Los especímenes de laboratorio están sujetos a una distribución de esfuerzos que permiten el estudio del grado de interacción entre el acero – hormigón. Conceptualmente, el hormigón desliza sobre el perfil de acero al entrar en carga y la tensión longitudinal rasante τ_u en la superficie de contacto se mantiene constante para la zona a esfuerzo rasante como se muestra en la figura 6. Diversos autores han desarrollado métodos de diseño para losas mixtas basados en esta hipótesis aunque hasta la fecha la visualización de la distribución de las tensiones no había sido posible

${\textstyle \tau _{u}={\frac {\eta Ncf-\mu Vt}{b(Ls+Lo)}}}$(1)

Figura 6: Representación conceptual tensión longitudinal a rasante τ_u'

La figura 7 representa la visualización de la tensión longitudinal τ_u a lo largo de la losa mixta para la carga última F = 26.2 kN en el modelo de EF QL60-FI. Esta distribución se ha obtenido considerando la resultante del esfuerzo rasante para cada rebanada, dividiéndola por la superficie horizontal proyectada del perfil de acero, para posteriormente obtener la tensión τ_u. En la rebanada número 16 se encuentra localizado el inductor de fisura y en la 31 el punto de apoyo para los modelos de EF.

(a)

(b)

(c)

Figura 7: Tensión longitudinal rasante τ_u' (a) representación 1-32 de las rebanadas modelo de EF, (b) representación discreta de tensiones, (c) representación envolvente de conjunto tensiones

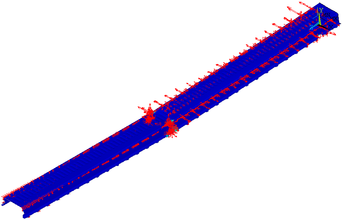
La tensión longitudinal a rasante τ_u es prácticamente nula para las rebanadas anteriores a la 13 donde se encuentra la zona a flexión del modelo observándose un máximo en el inductor de fisura. A partir de la rebanada 16, la tensión disminuye hasta volverse constante en la zona a rasante para posteriormente volver a incrementarse en el punto de apoyo en la rebanada 31 donde se consigue el segundo máximo. Esta representación detallada de la tensión τ_u abre la puerta a nuevas caracterizaciones del comportamiento de las losas mixtas considerando las singularidades observadas en las zonas de apoyo y carga y evitando las simplificaciones pasadas de tensión con valor constante. La figura 8 complementa la visualización de las tensiones a lo largo del modelo de EFs con la introducción de los esfuerzos vectoriales y las deformadas existentes para el estado de carga particular analizado.

Figura 8: Distribución de esfuerzos vectoriales en modelo EF

4.2 Tensión vertical normal σ_u

Se define una nueva tensión vertical normal σ_u como la resultante vertical de los esfuerzos dividida por la superficie horizontal proyectada del perfil de acero en cada rebanada. La figura 9 muestra la evolución a lo largo de la losa mixta para el estado de carga última F = 26.2 kN para el modelo de EF QL60-FI. Como en el caso de la tensión longitudinal a rasante τ_u, se observan concentraciones de tensiones en las zonas de apoyo y aplicación de carga con valores a tracción positivos. Para las zonas de flexión entre las rebanadas 1 a 14 y a rasante entre 17 a 29, se observan valores a compresión. Éstos representan los esfuerzos en el perfil de acero en la interface acero-hormigón para evitar la separación de los dos materiales. El efecto cuña entre el hormigón y acero transforma el deslizamiento longitudinal en tensión de sujeción transversal “clamping” en la chapa de acero.

(a)

(b)

(c)

Figura 9: Tensión vertical normal σ_u' (a)representación 1-32 de las rebanadas modelo de EF, (b) representación discreta de tensiones, (c) representación envolvente de conjunto tensiones

4.3 Tensiones y microdeformaciones locales

La inclusión de lecturas de galgas extensiométricas en los especímenes de laboratorio permite considerar otra novedosa representación para la compleja micromecánica de las losas mixtas mediante los modelos de EF. La figura 10 muestra la colocación de las distintas galgas a lo largo de la longitud del espécimen de laboratorio. Captadores numerados g17 a g32 recogieron las microdeformaciones existentes en la cara extrema vertical del perfil de acero.

Figura 10: Disposición de galgas extensiométricas en el espécimen de laboratorio

En los modelos de EF se tomaron las deformaciones observadas en cada patrón en los mismos puntos donde se habían considerado experimentalmente. La figura 11 muestra las deformaciones observadas en las galgas a lo largo de toda la longitud del espécimen de laboratorio para distintos estados de carga como parte de los resultados analizados por Ortlieb [21]. La figura 12 representa los resultados obtenidos mediante los modelos de EF. Cualitativamente, se observa una buena correlación tanto para los distintos estados de carga que abarcan desde 0 a 29,6 kN analizados, como para los distintos puntos de lectura considerados g17 a g32. El patrón de las curvas de las deformadas, sus valores absolutos y parciales entre ciclos de carga, muestran la gran solidez de los modelos de EF para representar la micromecánica que ocurre en las losas mixtas.

Figura 11: Gráfica lectura galgas extensiométricas g17-g32 para el rango de carga sobre la losa mixta de 0 – 29.6 kN

Figura 12: Gráfica de las deformaciones obtenidas durante la simulación del modelo QL60-FI para el rango de carga sobre la losa mixta de 0 – 29.60 kN

4.4 Resultados cualitativos

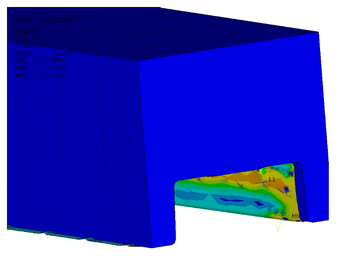
A parte de la obtención de resultados de tensiones y deformadas de forma detallada, los modelos de EF también permiten la verificación de comportamientos globales del conjunto de la losa mixta. Las figuras 13 y 14 muestran distintos aspectos que refuerzan la gran correlación de éstos con los datos experimentales. En particular, el deslizamiento relativo entre acero y hormigón en el extremo de la losa y la abolladura del acero en el punto de aplicación de la carga.

(a)

(b)

Figura 13: Deslizamiento relativo en el extremo de la losa (a) modelo EF, (b) espécimen laboratorio

Figura 14: Representaciones abolladura del alma del perfil de acero

5. Conclusiones

La realización de modelos de EF a escala real de losas mixtas con la inclusión de la geometría detallada de sus elementos acero y hormigón permite la observación de aspectos de su micromecánica. La distribución de las distintas tensiones, la deformación de los materiales como elementos singulares o en su acción mixta habilitan una comprensión mucho más amplia de sus propiedades, derivando a una mejor futura caracterización de su comportamiento resistente. En particular, los análisis realizados en este artículo presentan:

• Novedoso modelado a escala real de espécimen de laboratorio de perfil de acero con una longitud de 5000 mm con inclusión de las geometrías reales de los componentes acero y hormigón. La posibilidad del uso gradualmente de equipos con una mayor potencia de computación habilitan la elaboración de modelos de EF mucho más complejos. En particular, la utilización de dos modelos de EF, QL60-SI sin inductor de fisura para etapas iniciales de simulación y QL60-FI con inductor de fisura para las finales, permite la observación de la totalidad del ensayo normativo a flexión de Eurocódigo 4 para losas mixtas. Previos autores se apoyaron también en los modelos de EF para el estudio de las losas mixtas, aunque estos o bien consideraron elementos parciales, o bien modelos a escala real pero con simplificaciones significativas en los contactos entre el hormigón y el acero.

• Representación de la tensión longitudinal a rasante τ_u en toda la longitud de la losa mixta para el esfuerzo máximo del ensayo a través de los modelos de EF como parte de la micromecánica. En particular, su novedosa visualización permite observar el comportamiento diferenciado en la zona de flexión, zona de apoyo, zona de carga puntual y zona de rasante.

• Definición de una nueva tensión vertical normal σ_u y su representación en toda la longitud de la losa mixta para el esfuerzo máximo del ensayo. La representación habilita la observación del efecto de sujeción “campling” entre el acero y hormigón. Las gráficas de las tensiones τ_u y σ_u, así como la posibilidad de obtener los esfuerzos en cualquier parte del modelo de EF, abren la puerta a una mejor compresión de las complejas distribuciones presentes en las losas mixtas y consecuentemente, a una futura caracterización más detallada de la que propone actualmente el Eurocódigo 4 en sus métodos de diseño.

• Representación cualitativa de tensiones y deformaciones locales durante el ensayo de laboratorio. La correlación de los resultados obtenidos en los especímenes de laboratorio mediante las galgas extensiométricas y la de sus respectivos modelos de EF confirman la solidez de éstos para el estudio de la micromecánica de las losas mixtas.

BIBLIOGRAFIA

[1] EN 1994-1-1. Eurocode 4. Design of composite steel and concrete structures - Part 1-1: General rules and rules for buildings, 2004.

[2] B.J. Daniels, M. Crisinel, Composite slab behavior and strength analysis. Part I: Calculation procedure, Journal of Structural Engineering 119 (1) (1993) 16-35.

[3] B.J. Daniels, M. Crisinel, Composite slab behavior and strength analysis. Part II: Comparisons with test results and parametric analysis, Journal of Structural Engineering 119 (1) (1993) 36-49.

[4] L. An, Load Bearing Capacity and Behaviour of Composite Slabs with Profiled Steel Sheet, PhD tesis, Chalmers University of Technology, 1993

[5] M. Veljkovic, Influence of load arrangement on composite slab behavior and recommendations for design, Journal of Construction Steel Research 45 (2) (1998) 149-178.

[6] R.B. Widjaja, Analysis and Design of Steel Deck-Concrete Composite Slabs. PhD tesis, Virginia Polytechnic Institute, 1997.

[7] R. Abdullah, W. Easterling, New evaluation and modeling procedure for horizontal shear bond in composite slabs. Journal of Constructional Steel Research 65 (4) (2009) 891-899.

[8] M. Ferrer, F. Marimon, M. Crisinel, Designing cold-formed steel sheets for composite slabs: An experimentally validated FEM approach to slip failure mechanics, Thin-Walled Structures 44 (12) (2006) 1261-1271.

[9] N. Seres, L. Dunai, Experimental and numerical studies on concrete encased embossments of steel strips under shear action for composite slabs with profiled steel decking, Steel and Composite Structures 11 (1) (2011) 39-58.

[10] M. López, R. Larrúa, C. Reacrey, Estimación de la resistencia a cortante longitudinal en losas compuestas con lámina metálica colaborante, Revista Ingeniería de Construcción 24 (1) (2009) 95-113.

[11] S. Chen, X. Shi, Shear bond mechanism of composite slabs - A universal FE approach, Journal of Constructional Steel Research 67 (10) (2011) 1475-1484.

[12] E. Mistakidis, K. Dimitriadis, Bending resistance of composite slabs made with thin-walled steel sheeting with indentations or embossments, Thin-Walled Structures Journal 46 (2) (2008) 192-206.

[13] M. Patrick, R.Q. Bridge, Partial shear connection design of composite slabs. Engineering Structures 16 (5) (1994) 348-362.

[14] H. Bode, F. Minas I. Sauerborn, Partial connection design of composite slabs. Structural Engineering International 6 (1) (1996) 53-56.

[15] R.P. Johnson, D. Anderson, Designers' guide to EN-1994-1-1 Eurocode 4: design of composite steel and concrete structures. Part 1.1: General rules and rules for buildings. Thomas Telford, Londres, 2004.

[16] M. Crisinel, F. Marimon, A new simplified method for the design of composite slabs. Journal of Constructional Steel Research, 60 (3-5) (2003) 481-491.

[17] LERMA, Ensayo paramétrico de losas mixtas con el perfil QL-60 de British Robertson S.L., Laboratori d’Elasticitat i Resistència de Materials, Universistat Politècnica de Catalunya, 2004.

[18] M.J. Burnet, D.J. Oehlers, Rib shear connectors in composite profiled slabs. Journal of Constructional Steel Research 57 (12) (2001) 1267–87.

[19] T. Tsalkatidis, A. Avdelas, The unilateral contact problema in composite slabs: experimental study and numerical threatment. Journal Construction Steel Research 66 (3) (2010) 480-486.

[20] A. Plans, A. Gras, M. Ferrer, F. Marimon, A. Andreu, 3D non-linear realistic simulations of composite slabs bending test. In: Proceedings of the 7th European Conference on Steel and Composite Structures Eurosteel, Naples, Italy 2014 523-524.

[21] S. Ortlieb, Etude de la Distribution des efforts tranchants longitudinaux dans la zone de flexion simple d’une dalle mixte, Master tesis, Universitat Politècnica de Catalunya, 2005.