Investigating how to avoid delamination migration in mode I delamination tests with multidirectional specimens

1. Introduction

Improving the efficiency of aerospace structures involves reducing their weight while maintaining safety throughout their life cycle. A deep knowledge of the damage mechanisms in composite materials is crucial to avoid oversizing, and interlaminar fracture is one of the most critical issues. Understanding delamination behavior and characterizing the Interlaminar Fracture Toughness (IFT) of composites is key to designing safe and efficient structures.

Standard tests to quantify IFT are limited to specimens with unidirectional (UD) layups, where delamination propagation is parallel to the direction of the fibers. Thus, IFT can be characterized uniquely by a specific interface under particular conditions. However, structures are often built using multidirectional (MD) laminates, where delamination may appear at any interface and propagate in any direction. In these situations, IFT may differ from that obtained through standard tests. The lack of standards for IFT characterization of non-UD interfaces limits our predictive and design capabilities, leading to oversized and inefficient structures.

One major problem between the IFT in MD laminates is delamination migration, which has been well studied. It has been shown that if the shear stress at the crack tip drives the delamination towards an off-axis layer, migration can occur. However, if it drives it towards a 0º orientation layer, migration does not happen. In pure mode I test, by definition, there should be no shear stress, so ideally, under pure mode I conditions, the crack will progress flat and not be driven towards the upper or lower bounding plies. However, the crack may migrate towards one of the embedding layers, and this could occur. Therefore, in designing MD specimens for delamination testing, there is a competing interest between trying to achieve pure mode I and to avoid delamination migration.

Since migration depends on the state of shear stress at the delamination crack tip, our objective is to find a way to design MD specimens for the mode I test that could avoid migration.

2. Methodology

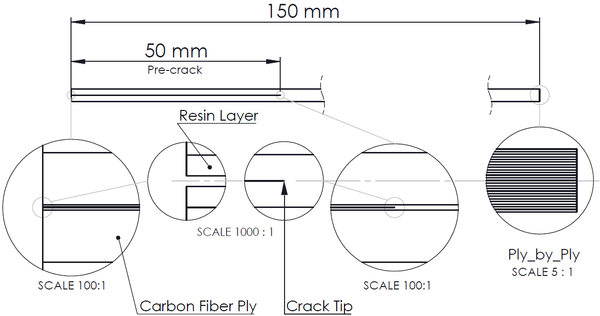
Previous studies have documented both the absence [19], [21] and presence [9], [18], [19] of delamination migration. To understand what makes the difference between successful and unsuccessful previous studies, we built a simple 2D FE model. Our objective is to investigate the shear stress at the delamination tip for different stacking sequence configurations found in the literature and identify potential trends. The 2D model of a Double Cantilever Beam (DCB) specimen includes three parts: an upper arm, a lower arm, and a thin resin layer on the interface where the crack is propagated. The length of the specimen is 150 mm, and the initial delamination length is 50 mm. In the upper and lower arms, a ply-by-ply discretization is adopted, and each ply is assigned material properties according to its orientation. The central resin layer thickness was defined as ten percent of the corresponding carbon fiber ply thickness. The FE model has been created in Abaqus using plane strain elements. Such a simple model is a fast and convenient approach for a preliminary assessment of literature results, to understand if a trend can be identified to distinguish successful studies from unsuccessful ones.

Figure 1. DCB 2D model with Resin Layer.

3. Results and discussion

To validate the behavior of the 2D model, an asymmetric UD specimen (ADCB) was used to obtain shear stresses at the delamination tip. It was confirmed that the shear stress state would drive the crack toward the thinner (thus less stiff) arm.

Figure 2. ${\textstyle \alpha }$ for 2D UD DCB model.

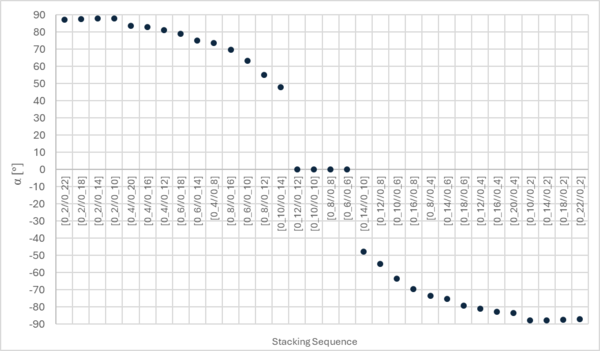
Figure 2 shows the behavior of 28 UD ADCB tests in the fifth node after the crack tip in the mid-plane of the resin layer. Variations in the number of plies in each arm of the specimen result in a change in the position of the interface (//) between them. On the left of the plot are located the specimens with less stiff upper arms, in the middle the symmetric specimens, and on the right those with less stiff lower arms. Each marker represents the value of the angle ${\textstyle \left(\alpha \right)}$ , in degrees, calculated using Equation (1), where the shear stress is normalized with respect to the difference between the normal stress component ${\textstyle {\sigma }_{11}}$ and the average of the in-plane normal stress. The angle is measured at the first ten nodes along the midplane of the resin layer, starting from the crack tip.

$\alpha ={\frac {180{^{\circ }}}{\pi }}\left(Atan\left({\frac {{\tau }_{12}}{{\sigma }_{11}-{\frac {{\sigma }_{11}+{\sigma }_{22}}{2}}}}\right)\right)$

(1)

For those asymmetric specimens with the same number of layers in the arms ( ${\textstyle [{\theta }_{a}//{\theta }_{b}],[{\theta }_{b}//{\theta }_{a}]}$), the magnitude of the angle is the same, but with opposite sign, thus when the angle is positive the less stiff part is the upper arm, and when the angle is negative the thinner part is located in the lower arm. For Symmetric double cantilever beam (SDCB) the shear stress at the interface is equal to zero.

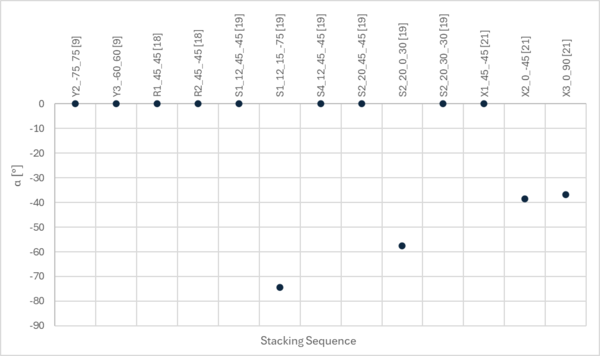
The 2D DCB model tested with UD specimens was used to simulate MD sequences obtained from the literature, Table 1.

600px

Table 1. Stacking Sequences simulated in the 2D DCB model.

Figure 3. ${\textstyle \alpha }$ for 2D MD DCB model.

Figure 3 presents the behavior of the ${\textstyle \alpha }$ angle across the MD specimens summarized in Table 1. For all specimens with interfaces of the form ${\textstyle [\pm \theta //\pm \theta ]}$, the angle ${\textstyle \alpha }$ is zero, indicating that the shear stress is negligible. In contrast, for ${\textstyle [{\theta }_{a}//{\theta }_{b}]\,}$ interfaces, ${\textstyle \alpha }$ assumes nonzero values. As previously discussed, a negative ${\textstyle \alpha }$ value indicates that the less stiff part corresponds to the lower arm.

Although an ${\textstyle \alpha }$ value of zero does not necessarily imply the absence of delamination migration. As reported in [9], migration and propagation of delamination from the pre-cracked plane through the adjacent lower ply occurred for both specimens with ${\textstyle [\pm \theta //\pm \theta ]}$, interfaces.

Additionally, in [18] for the conventional DCB test, ${\textstyle [45//45]}$ and ${\textstyle [45//-}$$45]$ interfaces exhibit highly uneven fracture surfaces with considerable amounts of fiber bridging. The ${\textstyle [45//45]}$ interface specimen, the crack oscillates around the intended interface, mainly contained within the two central plies, only occasionally reaching the interface between a ${\textstyle 0{^{\circ }}}$ ply and a ${\textstyle \pm 45{^{\circ }}}$. In contrast, for specimen with a ${\textstyle [45//-}$$45]$ interface, the crack initially propagated partially along the intended midplane interface and partly into the adjacent plies, forming a dense zone of fiber bridging behind the crack tip.

In [19], different delamination propagation modes in multidirectional laminates under Mode I loading are reported. Interfaces ${\textstyle [\theta //-}$$\theta ]$ with ${\textstyle \alpha }$ =0º generally exhibited smooth propagation. An exception was observed for the 45//-45 interface with a reduced number of plies per arm (S1_12_45_-45, S4_12_45_-45, 12 plies by arm), of which four specimens exhibited stair shape, while another developed double cracking. Interfaces of the form ${\textstyle [{\theta }_{a}//{\theta }_{b}]\,}$ with ${\textstyle \alpha }$ values below -50º demonstrated a strong tendency towards crack jumping and double cracking. Only two specimens showed smooth propagation at the interface ${\textstyle [0{^{\circ }}//30{^{\circ }}]}$, for this configuration, the crack either jumps to ${\textstyle [30{^{\circ }}//-30{^{\circ }}]}$ interface in two specimens or, in one case, a second crack initiates at this interface, spontaneously creating the phenomenon of double cracking.

On the other hand, in [21], for ${\textstyle [0{^{\circ }}//-45{^{\circ }}]}$ interface the fiber bridging occurs in the beginning of crack propagation, as a consequence the crack jumped to the -45º layer side and propagate in it afterwards, for ${\textstyle [45{^{\circ }}//-45{^{\circ }}]}$ and ${\textstyle [0{^{\circ }}//90{^{\circ }}]}$ interfaces, the fiber bridging occurs in the entire propagation process, although, for ${\textstyle [45{^{\circ }}//-45{^{\circ }}]\,}$ interface the crack propagates along the midplane, while for ${\textstyle [0{^{\circ }}//90{^{\circ }}]}$ interface, the crack jumped to the adjacent interface.

4. Conclusions

The 2D model, supported by results from the cited references, identifies that when ${\textstyle \alpha }$ value differs from zero, there is a clear tendency for delamination to migrate in laminates with interfaces of the ${\textstyle [{\theta }_{a}//{\theta }_{b}]}$ type, with propagation of the delamination towards the arm with less stiffness, which can be inferred from the ${\textstyle \alpha }$ sign.

One limitation of the 2D model, which we used and that becomes evident when analyzing some literatures results, is that since it is 2D it cannot capture out-of-plane effects and plies at ${\textstyle \pm \theta }$ considered as equal, so for some specimens with these orientations, our model cannot capture all effects of the stacking sequence.

Due to the limited information obtained from the 2D model, we are now working with a 3D model, which can capture additional effects and will allow us to study these aspects in greater depth.

The objective is to obtain as complete a picture as possible of what we can understand from the literature results and then utilize this information to determine how to design MD specimens that could achieve a mode as close to pure mode I as possible while avoiding migration.

5. References

[1] Adluru, H., Hoos, K., Iarve, E., & Ratcliffe, J. (2019). Delamination initiation and migration modeling in clamped tapered laminated beam specimens under static loading. Composites Part A, 202-212.

[2] Canturri, C., Greenhalgh, E., & Pinho, S. (2014). The relationship between mixed-mode II/III delamination and delamination migration in composite laminates. Composites Science and Technology, 102-109.

[3] Canturri, C., Greenhalgh, E., Pinho, S., & Ankersen, J. (2013). Delamination growth directionality and the subsequent migration processes - The key to damage tolerant design. Composites: Part A, 79-87.

[4] de Morais, A. (2003). Double cantilever beam testing of multidirectional laminates. Composites: Part A, 1135-1142.

[5] de Morais, A., de Moura, M., Marques, A., & de Castro, P. (2002). Mode-I interlaminar fracture of carbon/epoxy cross-ply composites. Composites Science and Technology, 679-686.

[6] Garulli, T., Catapano, A., Fanteria, D., Huang, W., Jumel, J., & Martin, E. (2020). Experimental assessment of Fully-Uncoupled Multi-Directional specimens for mode I delamination test. Composites Science and Technology, 1-31.

[7] Garulli, T., Catapano, A., Fanteria, D., Jumel, J., & Martin, E. (2019). Design and finite element assessment of fully uncoupled multi-directional layups for delamination tests. Journal of Composite Materials, 1-18.

[8] Garulli, T., Catapano, A., Montemurro, M., Jumel, J., & Fanteria, D. (2018). Quasi-trivial stacking sequences for the design of thick laminates. Composite Structures, 614-623.

[9] Gong, Y., Zhang, B., & Hallet, S. (2018). Delamination migration in multidirectional composite laminates under mode I quasi-static and fatigue loading. Composite Structure, 160-176.

[10] Greenhalgh, E., Rogers, C., & Robinson, P. (2009). Fractographic observations on delamination growth and the subsequent migration through the laminate. Composites Science and Technology, 2345-2351.

[11] Herráez, M., Pichler, N., Pappas, G., Blondeau, C., & Botsis, J. (2020). Experiments and numerical modelling on angle-ply laminates under remote mode II loading. Composites Part A, 1-12.

[12] Libin Zhao, Yu Gong, Jianyu Zhang, Yuli Chen, & Binjun Fei. (2014). Simulation of delamination growth in multidirectional laminates under mode I and mixed mode I/II loading using cohesive elements. Composite Structures, 509-522.

[13] Niu, M. C.-Y. (1992). Composite Airframe Structures Practical Design Information and Data. Hong Kong: Conmilit Press LTD.

[14] Pernice, M., De Carvalho, N., Ratcliffe, J., & Hallett, S. (2015). Experimental study on delamination migration in composite laminates. Composites: Part A, 20-34.

[15] Pichler, N., Herráez, M., & Botsis, J. (2020). Mixed-mode fracture response of anti-symmetric laminates: Experiments and modelling. Composite Part B, 1-13.

[16] Ratcliffe, J., & De Carvalho, N. (2014). Investigating Delamination Migration in Composite Tape Laminates. NASA Center for AeroSpace Information.

[17] Ratcliffe, J., Czabaj, M., & O'Brien, T. (2012). Characterizing Delamination Migration in Carbon/Epoxy Tape Laminates. American Society for Composites - Twenty-Seventh Technical Conference.

[18] Robinson, P., & Song, D. (1992). A Modified DCB Specimen for Mode I Testing of Multidirectional Laminates. Journal of Composite Materials, 1554 - 1577.

[19] Sebaey, T., Blanco, N., Costa, J., & Lopes, C. (2012). Characterization of crack propagation in mode I delamination of multidirectional CFRP laminates. Composites Science and Technology, 1251-1256.

[20] Sebaey, T., Blanco, N., Lopes, C., & Costa, J. (2011). Numerical investigation to prevent crack jumping in Doubler Cantilever Beam test of multidirectional composite laminates. Composites Science and Technology, 1587-1592.

[21] Zonghong Xie, Xiang Li, Jian Zhao, Jie Hao, Yanpeng Sun, & Xiaodong Sui. (2013). Study on the Mode I Interlaminar Fracture Toughness of Multi-directional Composite Laminates. Advanced Materials Research, 186-190.