1 Introducción
La aparición de los materiales compuestos y su uso en determinadas áreas de primera importancia industrial, como la areronáutica, conllevó poner atención en la aparición de fenómenos y comportamientos desconocidos en los materiales convencionales, tratados como homogéneos e isótropos.
Uno de estos fenómenos fue lo que se denominó como efecto escala, debido al cual el material no tenía una propiedad identificada sino que ella dependía de la ubicación del material en la estructura, lo que acuñó el término de valores in-situ de las propiedades. En concreto, una de las cuestiones que concitó más atención fue la aparición del primer daño en las láminas de 90 grados de laminados [0,90n]S.
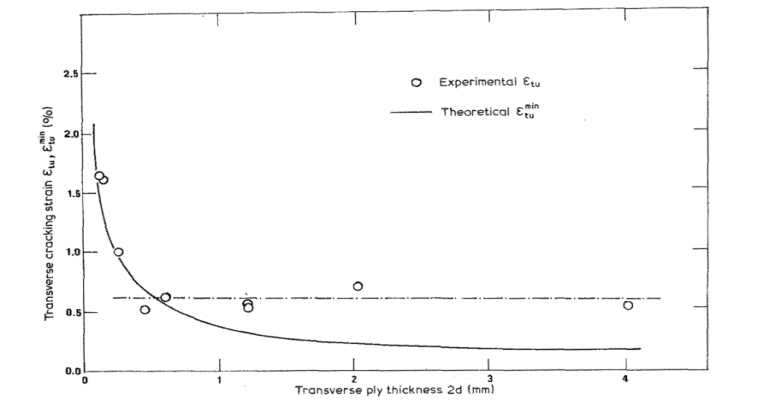
Una referencia obligada es el estudio de Parvizi et al [1] cuyas principales conclusiones se recojen en la figura 1, donde en el eje vertical aparece el valor de la deformación nominal que origina el primer daño, consistente en una grieta transversal en la lámina de 90 grados, en función del espesor de la lámina de 90 grados, recogido a través de n.
El estudio de Parvizi et al se realizó con fibra de vidrio, más fácil de detectar el daño visualmente, pero de forma inmediata se extendíó al uso de fibra de carbono, ver por ejemplo Flaggs y Kural [2], que obtuvieron conclusiones similares desde un punto de vista cualitativo, aumento de la resistencia nominal de la lámina de 90 grados en función de la disminución del espesor de la lámina.
La comprensión de dicho fenómeno ha concitado múltiples explicaciones, siendo de obligada mención el trabajo de Dvorak y Laws [3] y el de Li y Wisnom [4], entre muchos otros. Más recientemente García et al [5] han dado una explicación en base a los conceptos de Mecánica de la Fractura Finita (MFF).
La cuestión bajo consideración se enmarca dentro de un aspecto aún hoy abierto de los materiales compuestos, cual es el de los criterios de fallo de los mismos, cuestión abordada a nivel mundial en los World Wide Failure Exercise (WWFE), ver por ejemplo Kaddour et al [6].
En un estudio sobre la representatividad de los criterios de fallo, París [7] ponía de manifiesto la necesidad de caminar en el sentido de buscar criterios físicamente basados, lo que implica tener que descender a nivel micromecánico, donde los diferentes mecanismos de daño tienen lugar. Esto, evidentemente, no era fácil llevarlo a cabo dadas las complejidades numéricas que una simulación involucrando las fibras y el daño entre ellas o en la matriz, pudiera generar. Por ello en una serie de artículos, París et al fueron aislando problemas básicos del daño entre fibras, a nivel micromecánico, en las láminas más expuestas, correlacionando dicho daño con las predicciones de un modelo numérico [8], estudiando el papel de la tensión paralela al plano de fallo [9], correlacionando la evidencia en el fallo a compresión con las predicciones numéricas [10], dando una explicación al crecimiento del daño en fatiga con ciclos de compresión [11], o explicando el papel de las tensiones de curado en el fallo entre fibras [12], entre muchas otras cuestiones. Todos estos estudios se realizan sobre modelos de una o dos fibras usando el Método de los Elementos de Contorno (MEC), París y Cañas [13].
La aparición de láminas ultradelgadas ha atraído de nuevo el interés sobre esta cuestión, dado que ello puede retrasar significativamente la aparición de daño en las láminas más expuestas.
Saito et al [14, 15] realizaron un estudio experimental y numérico con un modelo básico de representación del daño en base al Método de los Elementos Finitos. Modelos más refinados para intentar explicar el efecto escala en el daño bajo consideración han sido elaborados por Arteiro et al [16] y Herráez et al [17]. Se tratan ambos de modelos basados en el Método de los Elementos Finitos (MEF) en los que el daño de despegue entre fibra y matriz se simula a través de elementos cohesivos y la rotura de matriz a través de comportamiento elastoplástico.
París et al han estudiado el problema con un enfoque diferente a los estudios anteriormente mencionados, manteniendo representaciones simples involucrando un número reducido de fibras, intentando entender los mecanismos básicos de daño y su relación con el efecto escala, ver por ejemplo Velasco et al [18], París et al [19] y Velasco et al [20], entre otros.
El objetivo final de este artículo es sumarizar y presentar el conocimiento alcanzado en aras a explicar la capacidad de los modelos micromecánicos para arrojar luz sobre el efecto escala anteriormente descrito. Es importante poner de manifiesto que este estudio no tiene propósito de predicciones cuantitativas sino de comprender el mecanismo de daño a nivel micromecánico asociado al efecto escala.
2 Predicciones micromecánicas
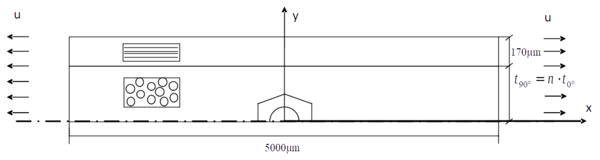
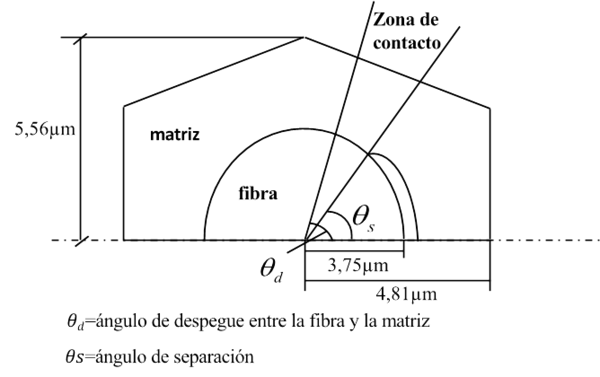
Aunque ya se ha comentado la profusión de estudios realizados por los autores en relación al daño en las láminas de 90 sobre modelos de un número reducido de fibras sobre matriz infinita, tomar en consideración el efecto escala requiere un modelo numérico mucho más complejo dado que es preciso que dicho modelo admita el estudio del efecto del espesor de la lámina de 90 grados, representado por el número de dichas láminas, n. La figura 2 recoge el modelo multiescala desarrollado basado en el MEC. Dicho modelo incluye una célula en la lámina de 90 grados en la que a nivel micromecánico (con una fibra en la célula representada en la figura 2 y con más detalle en la figura 3) se recoge el posible despegue entre fibra y matriz, ver Velasco et al [20] para más detalles de dicho modelo y las dificultades encontradas y solventadas. Las propiedades de los materiales involucrados se recogen en la tabla 1.
| Material | Propiedades |
| Lámina 0˚ (ortótropa) | E11=135GPa, E22=E33=8.75GPa
ν12= ν13=0.3, ν23=0.4, G12=4.75GPa |
| Lámina 90˚ (isótropa) | E(E22=E33)=8.75GPa, ν=0.4 |
| Matriz (epoxy, isótropa) | E=4.2GPa, ν=0.32 |
| Fibra (carbono, isótropa) | E (E22)=15GPa, ν=0.2 |
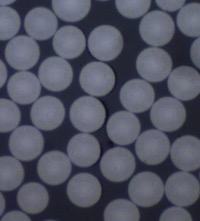
Es evidente que al intentar modelar el daño intralaminar, el comienzo y la propagación del mismo dependerá de las propiedades de los materiales involucrados, fundamentalmente matriz e interfase fibra-matriz. Sin embargo, es también evidente que en general la parte más débil en la consideración del fallo entre fibras es la interfase entre fibra y matriz, habiendo obtenido múltiples pruebas de ello a través de los experimentos llevados a cabo, mostrándose, con propósito ilustrativo, una muestra en la figura 4.
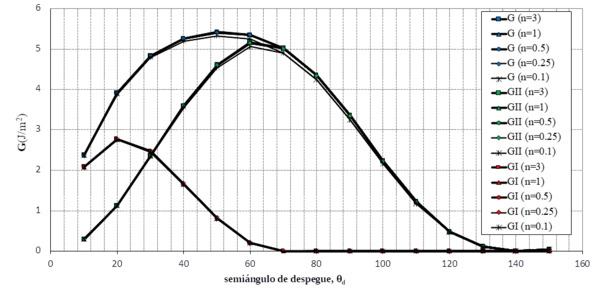
En base a esto parece lógico caracterizar en primer lugar el daño de despegue entre fibra y matriz en el modelo multiescala representado en la figura 2. Así, la figura 5 recoge la evolución del índice de liberación de energía, G, de una grieta de interfase para diferentes ángulos de despegue. Este estudio ya fue realizado con anterioridad para el caso de matriz infinita, París et al [8], siendo la novedad ahora que el cálculo se realiza en un modelo multiescala y se toma en consideración el efecto del espesor de la lámina de 90 grados. Puede observarse que el carácter creciente de G hasta un entorno de un semidespegue de 60 grados y decreciente a partir de él predispondría a encontrar estructuras de daño con esa morfología, ver por ejemplo Correa et al [21].
Lo más significativo en todo caso de la figura 5 es la independencia de la evolución de G con el espesor de la lámina de 90 grados. Esto pone de manifiesto que la aparición de daño de despegue entre fibra y matriz, su progresión y su detención es independiente de lo que hemos llamado efecto escala (espesor de la lámina de 90 grados en el caso estudiado) y por tanto su aparición estará en la práctica controlada por el carácter heterogéneo del material compuesto. Así, los despegues aparecerán por un lado en aquellas fibras peor adheridas a la matriz, y siempre teniendo en cuenta por otro lado aquellos factores (como la orientación y distancia de otras fibras cercanas), ver Sandino et al [22], que alteran, aumentando o disminuyendo, los valores de la energía liberada en el despegue, favoreciendo o retrasando su aparición.
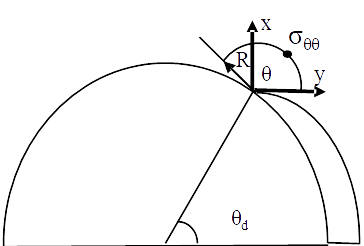
Una vez se ha caracterizado la primera fase del daño, la segunda será el abandono del despegue de la interfase fibra-matriz, para penetrar en la propia matriz. A tal efecto, vamos a estudiar la distribución de tensiones circunferenciales en el entorno del fondo de la grieta de despegue para predecir en base a dicha distribución la dirección más plausible de desvío de la grieta de despegue y penetración en la matriz para continuar el daño.
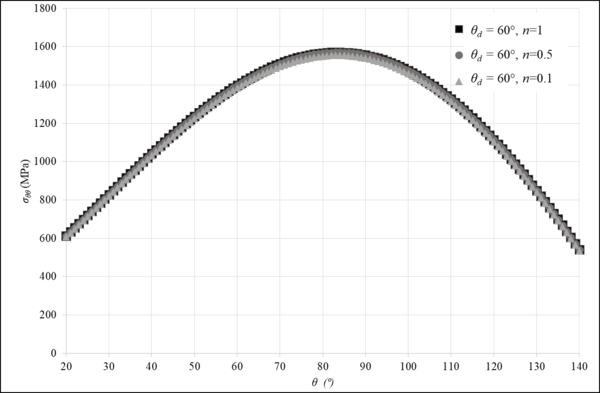
A tal efecto, en la figura 6 se representa la configuración en estudio, donde el ángulo de despegue se ha elegido asociado a la evolución de G encontrada en la figura 5 y se ha tomado θdigual a 60 grados. De nuevo con elementos de contorno se ha estudiado la evolución de σθ con θ, lo que se representa en la figura 7, en función del espesor de la lámina de 90 grados, tomando tres valores de n.
De la evolución de σθ en el entorno del fondo de la grieta de despegue, resulta obvio por un lado que el máximo valor de σθ se da en una orientación, de acuerdo al esquema de la figura 6, para un valor del ángulo de penetración en la matriz de 90 grados, lo que corresponde a una orientación perpendicular a la carga actuante, lo que está lleno de sentido físico. Por otro lado, lo que es el sentido de este estudio, los resultados no se ven afectados por el espesor de la lámina de 90 grados, lo que indica que también en esta fase del daño no hay efecto escala sobre el mismo, produciéndose una predicción de abandono del despegue y penetración de la matriz en la dirección perpendicular a la carga aplicada.
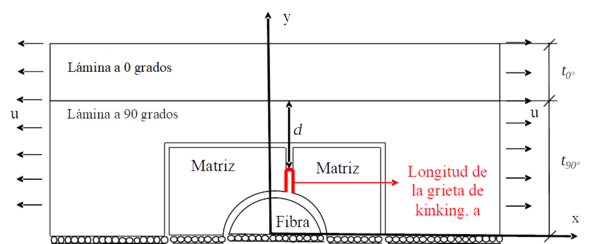
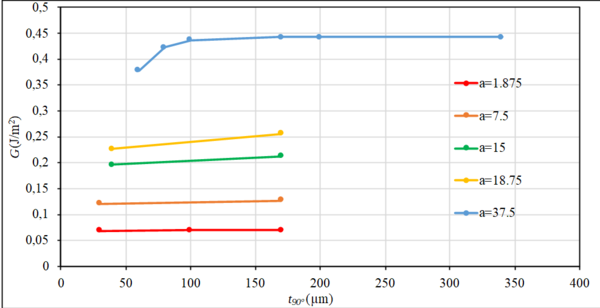
Una vez determinada la dirección en que la grieta de despegue penetra en la matriz, es preciso estudiar la evolución en el laminado de una grieta en la lámina de 90 grados, lo que requiere la elaboración de un nuevo modelo. La figura 8 recoge la presencia de una grieta proveniente de un despegue que ha abandonado la interfase fibra y matriz y comienza a propagarse en la lámina de 90, en dirección a la lámina de 0 grados. El modelo permite jugar con el espesor de la lámina de 90 y con los valores de la longitud de la nueva grieta, a, y la distancia del extremo de esta grieta a la lámina de 0 grados, d. La figura 9 recoge la evolución de G para diferentes longitudes de la grieta transversal en función del espesor de la lámina de 90 grados.
Lo primero que llama la atención de estos resultados es que a medida que la grieta transversal es mayor los valores de G son mayores, lo que es absolutamente obvio en función de la orientación de la grieta (inalterable) con respecto a la orientación de la carga, trabajando la grieta nominalmente en modo I. En relación al objeto de estudio de este trabajo, lo que se estaría buscando es, para una determinada grieta transversal, observar que los valores de G, para una determinada configuración de grieta se ven alterados, o no, por el espesor de la lámina de 90 grados. Si nos fijamos en el caso de la grieta más pequeña, a=1.875 μm, lo que corresponde a una longitud del orden de medio radio de la fibra, el valor de G no se ve alterado. Este hecho parece lógico si contemplamos la posición de la grieta y en particular de la punta de dicha grieta en relación a la configuración completa del laminado, no variando significativamente las variables involucradas (desplazamientos de los labios de la grieta y tensiones en el entorno del fondo de la misma) de un caso a otro.
Si aumentamos el valor de a (a=7.5, 15, 18.75 μm) vemos que la situación es equivalente (solo se representan un par de espesores por simplicidad): no hay efecto apreciable del espesor de la lámina de 90 en los valores de G.
Para conseguir observar predicciones de la evolución de G en el sentido esperado, anteriormente mencionado, habría que llegar a un valor de a=37.5 μm, situación para la cual la punta de grieta se encuentra a una distancia de la lámina de 0 grados, del orden de una o dos fibras.
Aunque a primera vista parece que hay un cierto efecto escala para esta configuración, hay que decir en primer lugar que es muy pequeño (nada parecido a lo que esperamos en base a los resultados experimentales encontrados), y en segundo lugar que el descenso de G en este caso hay que interpretarlo en función de la morfología de la configuración estudiada, dado que para pequeños valores de t90 la punta de la grieta en la lámina de 90 está muy cerca de la interfase con la lámina de 0, mucho más rígida en el sentido de apertura de la grieta transversal en la lámina de 90 trabajando en modo I, poniéndose de manifiesto el efecto Cook-Gordon de detención de una grieta al acercarse a un material más rígido, situación que no se ponía de manifiesto en los casos de valores anteriormente estudiados. De hecho, aunque no se han incluido valores de G correspondientes a espesores más pequeños de t90 por razones numéricas, el valor de G tiende a cero a medida que la punta de la grieta transversal se acerque a la interfase con la lámina de 0.
Es importante hacer notar que todo el estudio anterior corresponde a una visión del problema de progresión del daño en base a la Mecánica de la Fractura convencional de Griffith, estando el crecimiento controlado por los valores de G.
3 Discusión
Es evidente que todos los indicios encontrados apuntarían a que no existe el efecto escala a través de esta visión micromecánica, incluso alguno que pueda creer más en los modelos que en la realidad podría argüir que no existe el efecto escala. Lo que es preciso entender es que los cálculos realizados se corresponden con un determinado modelo de daño, plausible, pero no necesariamente el que aparece durante el ensayo de un laminado y la aparición del primer daño en forma de grieta transversal. En efecto, tal como se ha indicado anteriormente, el cálculo del valor de G para diferentes configuraciones conlleva que estamos encomendando la progresión del daño a una sucesión de aplicaciones de la Mecánica de la Fractura (convencional de Griffith o de grietas de interfase, según que el daño estuviere progresando por la matriz o por la interfase fibra-matriz), lo que implica una visión de expansión del daño de forma progresiva.
Nótese que esto es independiente de la visión micromecánica del daño, pues de hecho la tercera fase del daño se ha hecho sobre grietas en la lámina de 90 con los labios perpendiculares a la dirección de la carga sin tener en cuenta la estructura micromecánica, situación plausible pues dada la estructura heterogénea, hasta bien podría ser esta la configuración del daño, progresando por la matriz.
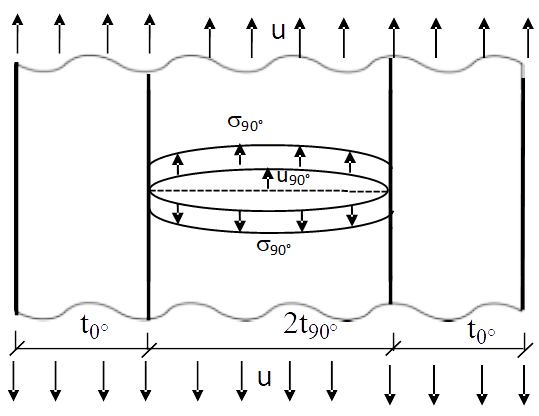
Esta no es la única forma en la que el daño puede producirse, ya que alternativamente puede haber una forma explosiva de generación del mismo en base a un balance de energía global del sistema, de manera que de una situación sin daño (o con daño asociado a despegues aislados motivados por el carácter heterogéneo del material) se pueda pasar a una configuración dañada de forma completa. En este caso, tal y como se muestra en la figura 10, las tensiones nominales σ de la lámina dentro del laminado (σ90) trabajan sobre los desplazamientos finales u de la grieta completa (u90) en la lámina de 90 grados.
El balance de energía para que aparezca el daño se podría representar en la forma:
|
|
(1) |
donde γ representa la energía necesaria para romper los enlaces internos del material por unidad de superficie libre creada.
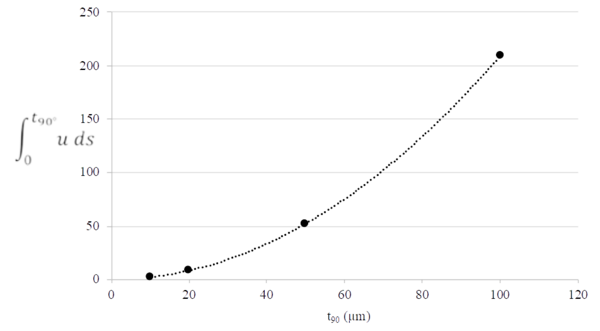
A continuación, en la figura 11, se representa el valor de la integral que aparece en la expresión (1) en función del espesor de la lámina de 90, integral que está obviamente asociada a la capacidad de liberar energía si la grieta completa se produjera.
Para un determinado material con un valor de tenacidad γ, la grieta aparecería si se cumple que:
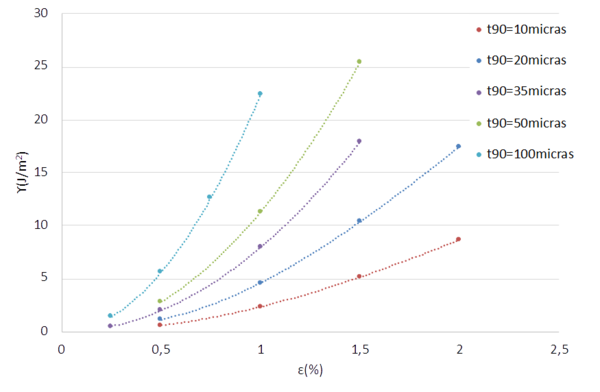
por lo que podemos representar ahora, para diferentes valores de t90, los valores nominales de la deformación longitudinal que habría que aplicar en el laminado para conseguir alcanzar un determinado valor de γ, lo que se representa en la figura 12.
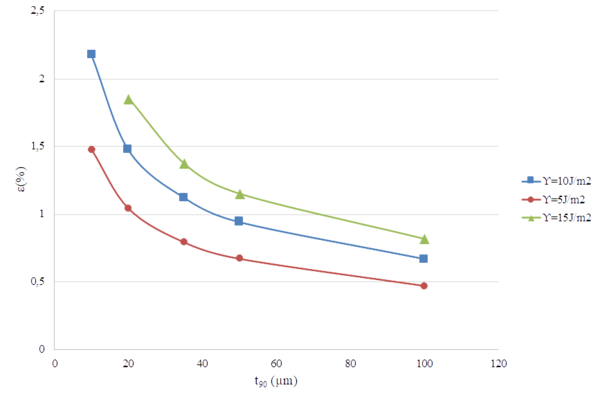
Si consideramos ahora un material con un determinado valor de γ, trazando horizontales en la figura 12 podemos obtener una representación de la evolución de la deformación a aplicar para un determinado material en función del espesor de la lámina de 90 grados, lo que se representa en la Figura 13. En este caso, los valores tomados corresponden con los sugeridos por Saito et al [14, 15] en su estudio del efecto escala en laminados.
Puede ahora perfectamente observarse cómo las predicciones de los valores de la deformación que producen la primera grieta suben de forma significativa al disminuir el espesor de la lámina de 90, poniendo así de manifiesto, ahora sí, la presencia del efecto escala.
4 Conclusiones
Un estudio micromecánico, modelando fibra y matriz, en un modelo multiescala ha puesto de manifiesto que no hay ningún indicio de incidencia del espesor de la lámina de 90 grados en las diferentes etapas de daño que aparecerían de forma lógica en una generación de daño progresivo que comience en la presumiblemente zona más débil de la lámina de 90 grados, la interfase fibra matriz.
Sin embargo, un balance global de energía que lleve a la aparición instantánea del daño explica perfectamente el efecto escala observado experimentalmente en los laminados, requiriéndose más deformación para producir la primera grieta a medida que el espesor de la lámina de 90 grados disminuye.
Aunque el estudio micromecánico no recoge el efecto escala y el balance global, que corresponde a un estudio mesomecánico, sí, sería un error asignar las diferentes conclusiones al nivel de representación del material, por cuanto ambos estudios corresponden en realidad a dos mecanismos de daño diferentes, uno progresivo y otro instantáneo, pudiendo este último hacerse también a nivel micromecánico en el sentido de recoger la morfología del daño teniendo en cuenta la presencia de fibra y matriz.
Agradecimientos
Los autores desean agradecer al Ministerio de Educación, Cultura y Deportes la subvención de este trabajo a través del proyecto MAT2016-80879-P.
Referencias
- [1] Parvizi A., Garret K.V., Bailey J.E. Constrained cracking in glass fibre-reinforced epoxy cross-ply laminates. J of Mat Sci 1978;13:195–201.
- [2] Flaggs D.L., Kural M.H. Experimental Determination of the In Situ Transverse Lamina Strength in Graphite/Epoxy Laminates, J Com Mat 1982;16:103-116.
- [3] Dvorak G.J., Laws, N. Analysis of Progressive Matrix Cracking In Composite Laminates II. First Ply Failure, J Comp Mat 1987; 21, 309–329.
- [4] Li D.S., Wisnom M.R., Evaluating Weibull Parameters for Transverse Cracking in Cross-Ply Laminates, J Comp Mat 1997; 31, 935–951.
- [5] García I.G., Mantič V., Blázquez A., París F. Transverse crack onset and growth in cross-ply [0/90n]s laminates under tension. Application of a coupled stress and energy criterion, Int J Sol Struct 2014; 51, 3844-3856.
- [6] Kaddour A.S., Hinton M.J., Smith P.A., Li S. A comparison between the predictive capability of current matrix cracking, continuum damage and fracture criteria for fibre reinforced composite laminates: Part A of WWFE-III, J Compos Mater, 2013; 47 (20-21), 2749-2779.
- [7] París F., A study of Failure Criteria of Fibrous Composite Materials, NASA/ CR-2001-210661, 2001.
- [8] París F., Correa E., Cañas J. Micromechanical view of failure of the matrix in fibrous composite materials, Compos Sci Tech 2003; 63, 1041-1052.
- [9] París F., Correa E., Mantič V. Kinking of Transversal Interface Cracks Between Fiber and Matrix. J App Mech 2007;74, 703-716.
- [10] Correa E., Mantič V., París F. A micromechanical view of inter-fibre failure of composite materials under compression transverse to the fibres. Compos Sci Tech 2008; 68, 2010-2021.
- [11] Correa E., Gamstedt E.K., París F., Mantič V. Effects of the presence of compression in transverse cyclic loading on fibre–matrix debonding in unidirectional composite plies. Compos Part A 2007; 38, 2260–2269.
- [12] Correa E., Mantič V., París F. Effect of thermal residual stresses on matrix failure under transverse tension at micromechanical level: A numerical and experimental analysis. Compos Sci Tech 2011; 71, 622-629.
- [13] París F., Cañas J. Boundary Element Method. Fundamentals and Applications. Oxford, OUP, 1997.
- [14] Saito H., Takeuchi H., Kimpara, I. Experimental Evaluation of the Damage Growth Restraining in 90° Layer of Thin-ply CFRP Cross-ply Laminates, Adv Comp Mat 2012; 21, 57–66.
- [15] Saito H., Takeuchi H., Kimpara I. A study of crack suppression mechanism of thin-ply carbon-fiber-reinforced polymer laminate with mesoscopic numerical simulation, J Comp Mat 2014: 48, 2085–2096.
- [16] Arteiro A., Catalanotti G., Melro A.R., Linde P., Camanho P.P. Micro-mechanical analysis of the in situ effect in polymer composite laminates, Comp Struct 2014; 116, 827–840.
- [17] Herráez M., Mora D., Naya F., Slopes C.S., González C., LLorca J. Transverse cracking of cross ply laminates: a computational micro mechanics perspective. Comp Sci Tech 2015; 110, 196-204.
- [18] Velasco M.L., París F., Correa E. Estudio Micromecánico del Efecto Escala en Laminados de Material Compuesto, MATCOMP XII, 2017.
- [19] París F., Velasco M.L., Correa E. Micromechanical study on the influence of scale effect in the first stage of damage in composites, Comp Sci Tech 2018; 160, 1-8.
- [20] Velasco M.L., Graciani E., Távara L., Correa E. y París F. BEM multiscale modelling involving micromechanical damage in fibrous composites, Eng Anal Bound Elem 2018; 93, 1-9.
- [21] Correa E., Valverde M.I., Velasco M.L., París F. Microscopical observations of inter-fibre failure under tension, Comp Sci Tech 2018; 155, 213-220.
- [22] Sandino C., Correa E., París F. Numerical analysis of the influence of a nearby fibre on the interface crack growth in composites under transverse tensile load, Eng Fract Mech 2016; 168, 58–75.
Document information
Published on 15/04/21
Accepted on 04/07/19
Submitted on 06/06/19
Volume 05 - Comunicaciones Matcomp19 (2021), Issue Núm. 2 - Caracterización analítica, numérica y experimental de los materiales compuestos. Materiales multifuncionales. Comportamiento de componentes estructurales., 2021
DOI: 10.23967/r.matcomp.2021.04.001
Licence: Other
Share this document
Keywords
claim authorship
Are you one of the authors of this document?