| Line 131: | Line 131: | ||
| style="border: 1pt solid black;text-align: center;"|'''Temperatura [°C]''' | | style="border: 1pt solid black;text-align: center;"|'''Temperatura [°C]''' | ||
| style="border: 1pt solid black;text-align: center;"|<math>Y\, [MPa]</math> | | style="border: 1pt solid black;text-align: center;"|<math>Y\, [MPa]</math> | ||
| − | | style="border: 1pt solid black;text-align: | + | | style="border: 1pt solid black;text-align: center;"|<math>{E}_{2}\, [GPa]</math> |
| style="border: 1pt solid black;text-align: center;"|<math display="inline">{Y}_{\epsilon }</math> [%] | | style="border: 1pt solid black;text-align: center;"|<math display="inline">{Y}_{\epsilon }</math> [%] | ||
| style="border: 1pt solid black;text-align: center;"|<math display="inline">{\nu }_{21}</math> [-] | | style="border: 1pt solid black;text-align: center;"|<math display="inline">{\nu }_{21}</math> [-] | ||
Revision as of 23:24, 4 July 2025
1. Introducción
En las últimas décadas, el creciente interés por reducir la huella ambiental en los procesos industriales ha impulsado la investigación y el desarrollo de materiales compuestos reforzados con fibras naturales. Esta tendencia responde a la necesidad de sustituir las fibras sintéticas, como las de vidrio o carbono, por alternativas más sostenibles que permitan reducir el consumo energético en su fabricación y la emisión de gases contaminantes durante su ciclo de vida [1]. En este contexto, las fibras vegetales han cobrado relevancia en aplicaciones estructurales de bajo y medio requerimiento mecánico debido a su disponibilidad, bajo coste, carácter renovable, biodegradabilidad y menores requerimiento energéticos de los procesos de fabricación [2] y [3].
Entre estas fibras naturales, el lino es una de las alternativas más prometedoras por su elevada relación resistencia-peso, rigidez específica y buen comportamiento a fatiga y corrosión. Diversos estudios han demostrado que los laminados basados en fibras de lino y matrices termoestables, como la resina epoxi, presentan propiedades específicas competitivas frente a materiales compuestos de fibra de vidrio en condiciones de servicio estándar [3-5] No obstante, una limitación crítica de estos materiales naturales es la variabilidad en sus propiedades mecánicas asociada a la variedad de planta de la que se han extraído las fibras, el terreno donde se han cultivado, el régimen de lluvias, la temperatura, etc.
Un aspecto relevante en diversos sectores como el aeronáutico, automotriz, ferroviario o de infraestructuras es la influencia de la temperatura, bien porque la estructura tiene que operar en climas fríos o porque contiene un líquido o gas a baja temperatura [6]. Aunque existen algunos trabajos de la influencia de la temperatura en laminados de fibra de lino [7], el comportamiento mecánico a baja temperatura todavía no está suficientemente conocido.
Consecuentemente, en este trabajo se presenta un estudio experimental del comportamiento mecánico de laminados de tipo sarga de fibra de lino y resina epoxi sometidos a condiciones de baja temperatura, con el objetivo de aportar conocimiento sobre la respuesta de estos materiales ante esfuerzos de tracción y cortadura en el plano a temperaturas que alcanzan hasta -70 °C.
2. Materiales y métodos
2.1 Materiales
El material empleado en este estudio se fabricó a partir de un pre-impregnado de fibra de lino, Evopreg EPC300 AmpliTex™ 5043, con una arquitectura de tejido sarga 2x2 en una resina epoxi. El material presenta un contenido en volumen de fibra del 47 %, una densidad de 1310 kg/m³ y un espesor curado de 0,29 mm por lámina. La masa areal del laminado es de 0,200 kg/m², lo que, junto con el patrón de tejido seleccionado, ofrece un compromiso eficaz entre rigidez en el plano y resistencia mecánica. El laminado fue fabricado en el Área d Materiales Compuestos del Instituto Nacional de Técnica Aeroespacial siguiendo las recomendaciones del fabricante del pre-impregnado. El proceso de curado se llevó a cabo en autoclave, bajo condiciones térmicas y de presión controladas, a una temperatura de 120 °C y una presión de 6 bares durante 60 minutos.
2.2 Procedimiento experimental
Los ensayos estáticos seleccionados para la caracterización mecánica del material fueron realizados conforme a las normas establecidas por la Sociedad Americana para Pruebas y Materiales (ASTM), y comprenden ensayos de tracción en dirección longitudinal y transversal y ensayos de cortadura en el plano del laminado.
Se ensayaron al menos seis probetas por condición experimental, lo que permitió obtener una base estadística sólida para el análisis de resultados. Asimismo, con el fin de mantener la reproducibilidad de las condiciones térmicas, especialmente en los ensayos a baja temperatura, las probetas fueron previamente acondicionadas en un congelador industrial. En el caso de los ensayos a –40 °C y –70 °C, las probetas permanecieron al menos 24 horas en refrigeración a la temperatura seleccionada , herméticamente selladas al vacío, a fin de evitar la absorción de humedad y preservar la integridad del material.
Los ensayos se llevaron a cabo en una máquina universal Zwick/Roell Z010, operando a una velocidad constante de 5 mm/min. La carga aplicada fue registrada mediante una célula de carga de 10 kN, mientras que el desplazamiento vertical se midió utilizando el sensor de posición integrado en el equipo.
La medida de la deformación se realizó mediante la técnica de correlación digital de imágenes (DIC). Las imágenes se grabaron con una frecuencia de 10 fotograma por segundo mediante una cámara Basler acA2440-75um. Se construyeron mapas de deformación, a partir de los cuales se pudo estimar en función del tiempo tanto la deformación longitudinal como la transversal con la técnica de extensometría virtual. Todos los ensayos se realizaron bajo condiciones ambientales controladas, asegurando la reproducibilidad de las mediciones. A partir de las curvas tensión-deformación se estimaron la resistencia mecánica y el módulo de elasticidad en la dirección de la urdimbre y la trama (X, Y, E1 y E2 respectivamente). Además se determinaron los coeficientes de Poisson principal y secundario (ν12 y ν21) a partir del cociente entre la deformación transversal y longitudinal. Los módulos de elasticidad y los coeficiente de Poisson se calcularon en el intervalo comprendido entre 1000 y 3000 με, conforme a lo prescrito por la norma ASTM D3039 [8], con el objetivo de asegurar la comparabilidad de los resultados entre probetas.
Las probetas destinadas al ensayo de cortadura en el plano fueron obtenidas a partir de laminados con configuración de apilamiento [±45]4s, conforme a la norma ASTM D3518 [9]. La geometría de los especímenes fue análoga a la utilizada en los ensayos de tracción, con una longitud total de 228 mm, un ancho de 25 mm y un espesor de 2,6 mm. Para construir la curva de tensión tangencial-deformación angular se utilizó el registro de carga-desplazamiento que proporciona la máquina y las fórmulas propuestas en la norma.
2.3 Método de correlación de imágenes digitales (DIC)
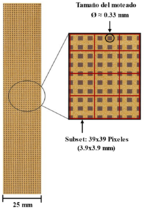
Se empleó la técnica de correlación digital de imágenes bidimensional (2D-DIC) para la medición de las deformaciones longitudinales y transversales durante los ensayos. La dimensión del patrón de moteado se estableció de forma que cada punto abarcara entre 3 y 5 píxeles, garantizando una correlación fiable en el procesamiento de imágenes, como se muestra en la figura 1.
Para ello, se calculó previamente el tamaño de píxel físico , en función del campo de visión vertical y de la resolución de la cámara en ese eje ( ), según la expresión:
|
|
(1) |
Se utilizó una cámara Basler acA2440-75um, con una resolución de 5 MP y un sensor de 8,45 × 7,07 mm, acoplada a un objetivo Edmund Optics 50 mm f/2.0, lo que permitió ajustar adecuadamente el campo de visión al tamaño de las probetas.
El análisis de las imágenes se realizó mediante el software VIC-2D. El tamaño del subconjunto fue definido para incluir entre 3 y 5 moteados, mientras que el tamaño del paso se fijó entre 1/2 y 1/3 del tamaño del subconjunto, con el fin de garantizar una adecuada resolución espacial y precisión en la medición.
Figura 1. Tamaño del subconjunto y patrón de moteado para correlación digital de imágenes.
3. Resultados y discusiones
3.1 Comportamiento a tracción
Los resultados de los ensayos de tracción tanto para la configuración longitudinal como para la transversal se presentan en la Figura 2 y 3, y en las Tablas 1 y 2.
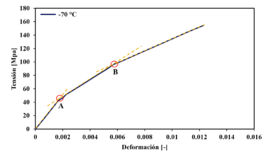
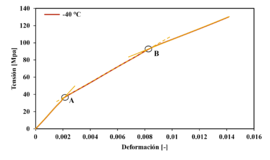
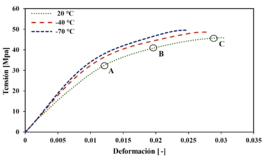
Las curvas tensión-deformación a tracción muestran , tanto en la dirección longitudinal como en la transversal, un comportamiento no lineal a todas las temperaturas ensayadas. En las curvas se pueden definir dos puntos de transición, Figura 2, que permiten modelizar el comportamiento del laminado como un modelo trilinear a partir de tres módulos de elasticidad aparentes asociados a cada tramo. En la tablas 1 y 2 se muestran los valores de deformación en la dirección de la carga para los dos puntos de transición a las tres temperaturas ensayadas. Otros autores, ensayando laminados unidireccionales de lino/epoxi tipo cinta han encontrado únicamente un punto de transición por lo que en los laminados de cinta un modelo bilineal puede ser válido [3] y [5]. Este cambio de pendiente en la curva se atribuye a la redistribución de esfuerzos entre la fibra y la matriz [10]. En el laminado estudiado, que tiene una arquitectura de tejido tipo sarga 2×2, este fenómeno puede verse amplificado por la orientación cruzada de urdimbre y trama y el progresivo alineamiento de los hilos de refuerzo de la trama bajo carga. En particular, se interpreta que el primer cambio de pendiente puede estar asociado a la rotura o degradación progresiva de las fibras de la trama, mientras que el segundo cambio de pendiente correspondería al inicio de fallo en las fibras de la urdimbre responsables de la mayor parte de la carga soportada. Esta transición sugiere una evolución en el mecanismo de transferencia de carga a lo largo del ensayo, particularmente influenciada por la arquitectura textil y la interacción fibra-matriz.
Figura 2. Curvas tensión-deformación en tracción mostrando los puntos de transición: a) en dirección longitudinal, b) en dirección transversal
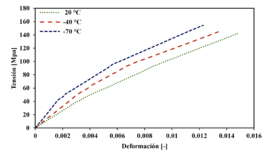
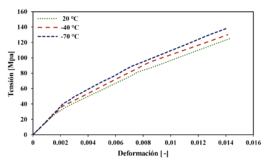
Figura 3. Curvas tensión-deformación representativas de los ensayos de tracción a diferentes temperaturas: a) en dirección longitudinal, b) en dirección transversal .
Los datos obtenidos muestran una influencia apreciable de la temperatura sobre el comportamiento mecánico de los laminados lino/epoxi, tanto en la orientación longitudinal como transversal. En ambas configuraciones se observa un incremento progresivo del módulo elástico al disminuir la temperatura, lo que evidencia una mayor rigidez del compuesto, siendo este efecto más pronunciado en la dirección longitudinal. Esta tendencia se atribuye principalmente a la mayor rigidez de la matriz epoxi a bajas temperaturas, así como a una posible mejora en la transferencia de carga en la interfaz fibra-matriz.
En la dirección longitudinal, el módulo de elasticidad (E1) aumentó un 45% entre 20 °C y –70 °C, con un incremento leve en la resistencia máxima a tracción (X), aumentando un 6%, Tabla 1. En la dirección transversal, se registró una evolución similar en la resistencia transversal (Y) y del módulo de elasticidad (E2), aunque con valores ligeramente inferiores en todos los casos lo que se debe a que las fibras de la trama están onduladas y deben alinearse al aplicar la carga, Tabla 2. Cabe destacar que, si bien la rigidez mejora con el descenso de temperatura, la deformación máxima a rotura (Xε) disminuye, lo que sugiere una pérdida de tenacidad del material atribuible al aumento de la fragilidad de la matriz polimérica. Por otro lado, el coeficiente de Poisson (ν12) mostró una ligera tendencia creciente con el descenso de la temperatura, aunque con cierta dispersión asociada a la sensibilidad de la medición en deformaciones transversales pequeñas.
| Temperatura [°C] | [%] | [-] | [%] | [%] | ||
| 20 | 141,01 ± 4,10 | 15,07 ± 1,30 | 1,39 ± 0,10 | 0,10 ± 0,01 | 0,32 ± 0,03 | 0,86 ± 0,01 |
| - 40 | 148,83 ± 3,95 | 17,12 ± 0,47 | 1,37 ± 0,04 | 0,11 ± 0,02 | 0,29 ± 0,01 | 0,70 ± 0,01 |
| - 70 | 149,16 ± 2,33 | 21,97 ± 2,84 | 1,26 ± 0,13 | 0,13 ± 0,05 | 0,20 ± 0,02 | 0,56 ± 0,02 |
| Temperatura [°C] | [%] | [-] | [%] | [%] | ||
| 20 | 129,99 ± 3,06 | 16,46 ± 1,15 | 1,43 ± 0,05 | 0,09 ± 0,03 | 0,23 ± 0,02 | 0,76 ± 0,09 |
| - 40 | 137,32 ± 2,35 | 17,19 ± 1,38 | 1,42 ± 0,11 | 0,11 ± 0,01 | 0,21 ± 0,01 | 0,82 ± 0,03 |
| - 70 | 138,04 ± 3,01 | 18,46 ± 0,53 | 1,40 ± 0,12 | 0,12 ± 0,02 | 0,20 ± 0,02 | 0,72 ± 0,06 |
3.2 Comportamiento a cortadura en el plano
En los ensayos de cortadura realizados sobre laminados con configuración [±45]₄ₛ, también se observó un aumento de la rigidez con la disminución de la temperatura, Tabla 3. El módulo de cortadura (G₁₂) aumentó un 30% entre 20 °C y –70 °C, mientras que el esfuerzo cortante máximo (S) presenta un ligero aumento de un 7%. Al igual que en tracción, la deformación máxima (Sε) decrece con la temperatura, confirmando una mayor rigidez pero menor capacidad de deformación.
| Temperatura [°C] | S [MPa] | G12 [Gpa] | Sε [%] |
| 20 | 45,10 ± 1,01 | 2,85 ± 0,12 | 3,40 ± 0,35 |
| - 40 | 47,87 ± 2,05 | 3,45 ± 0,17 | 2,72 ± 0,11 |
| - 70 | 48,18 ± 2,00 | 3,73 ± 0,22 | 2,64 ± 0,17 |
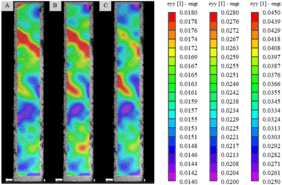
Un análisis complementario se llevó a cabo mediante la técnica de correlación digital de imágenes (DIC) con el objetivo de caracterizar la evolución espacial de las deformaciones durante los ensayos de cortadura. En particular, se seleccionó la muestra a temperatura ambiente como caso representativo, Figura 4, sobre la cual se identificaron tres estados de carga (denominados puntos A, B y C en la curva tensión-deformación) que reflejan distintas fases en la progresión del daño. En el estado A, se observó una localización inicial de la deformación en una de las esquinas de la probeta, con orientación diagonal respecto al eje de carga, lo cual es indicativo del inicio del mecanismo de cortadura en plano. En el estado B, la deformación se había propagado hacia la zona central de la probeta, con un incremento notable en la magnitud y extensión del campo de deformación. Finalmente, en el estado C, correspondiente a la inmediatez del fallo estructural, se registró una concentración máxima de deformación en el centro del área útil, coincidiendo con la ubicación de la fractura.
Este análisis respalda la existencia de un proceso de acumulación progresiva de daño por cortadura [11], coherente con los mecanismos descritos en laminados [±45]nS, y pone de manifiesto la capacidad de la DIC para detectar de forma no invasiva la localización y evolución del daño antes del colapso del material.
4. Resumen y conclusiones
Se investigó el comportamiento mecánico a baja temperatura de laminados de lino/epoxi con arquitectura sarga 2×2, aportando evidencia experimental en un campo aún poco documentado. Se evaluaron propiedades en tracción y cortadura en el plano, en un rango de temperatura de 20 °C a –70 °C, mediante ensayos estáticos normalizados y técnicas de correlación digital de imágenes (DIC).
En tracción, se observó un incremento progresivo del módulo de elasticidad con el descenso térmico, alcanzando valores de hasta 21,97 GPa en la dirección longitudinal. Esta rigidez creciente se atribuye al endurecimiento de la matriz epoxi y a una mejora en la transferencia de carga en la interfaz fibra-matriz. No obstante, esta ganancia se acompaña de una reducción de la deformación a rotura, lo que evidencia un comportamiento más frágil del compuesto. Las curvas tensión-deformación revelaron un comportamiento no lineal, con dos cambios de pendiente atribuidos a la degradación inicial de las fibras a 90° y al posterior fallo progresivo de las fibras a 0°.Esto sugiere que un modelo trilinear puede ser adecuado para reproducir el comportamiento del material.
En cortadura, el módulo G₁₂ aumentó un 31 %, mientras que la deformación γ₁₂ se redujo notablemente. El análisis DIC mostró una evolución clara del daño por cortadura, con concentración de deformaciones que anticipa la fractura en la zona central.
Los resultados obtenidos validan el potencial de estos compuestos sostenibles en condiciones térmicas adversas, y ofrecen una base sólida para futuros modelos predictivos y aplicaciones estructurales en entornos fríos.
5. Bibliografía
- [1] S. V. Joshi, L. T. Drzal, A. K. Mohanty, and S. Arora, “Are natural fiber composites environmentally superior to glass fiber reinforced composites?,” Composites Part A: Applied Science and Manufacturing, vol. 35, no. 3, pp. 371–376, 2004, doi: 10.1016/j.compositesa.2003.09.016.
- [2] K. L. Pickering, M. G. A. Efendy, and T. M. Le, “A review of recent developments in natural fibre composites and their mechanical performance,” Composites Part A: Applied Science and Manufacturing, vol. 83, pp. 98–112, 2016, doi: 10.1016/j.compositesa.2015.08.038.
- [3] S. Liang, P.-B. Gning, and L. Guillaumat, “Quasi-static behaviour and damage assessment of flax/epoxy composites,” Materials & Design, vol. 67, pp. 344–353, 2015, doi: 10.1016/j.matdes.2014.11.034.
- [4] H. N. Dhakal, Z. Y. Zhang, and M. O. W. Richardson, “Effect of water absorption on the mechanical properties of hemp fibre reinforced unsaturated polyester composites,” Composites Science and Technology, vol. 67, no. 7–8, pp. 1674–1683, 2007, doi: 10.1016/j.compscitech.2006.06.019.
- [5] M. Kersani, S. V. Lomov, A. W. Van Vuure, A. Bouabdallah, and I. Verpoest, “Damage in flax/epoxy quasi-unidirectional woven laminates under quasi-static tension,” Journal of Composite Materials, vol. 49, no. 4, pp. 403–413, 2015, doi: 10.1177/0021998314521603.
- [6] L. Yan, B. Kasal, and L. Huang, “A review of recent research on the use of cellulosic fibres, their fibre fabric reinforced cementitious, geo-polymer and polymer composites in civil engineering,” Composites Part B: Engineering, vol. 92, pp. 94–132, 2016, doi: 10.1016/j.compositesb.2016.02.002.
- [7] E. Raponi, C. Sergi, S. Boria, J. Tirillò, F. Sarasini, and A. Calzolari, “Temperature effect on impact response of flax/epoxy laminates: Analytical, numerical and experimental results,” Composite Structures, vol. 274, p. 114316, 2021, doi: 10.1016/j.compstruct.2021.114316.
- [8] ASTM D3039/D3039M-17, Standard Test Method for Tensile Properties of Polymer Matrix Composite Materials, ASTM International, West Conshohocken, PA, 2017.
- [9] ASTM D3518/D3518M-13, Standard Test Method for In-Plane Shear Response of Polymer Matrix Composite Materials by Tensile Test of a ±45° Laminate, ASTM International, West Conshohocken, PA, 2013.
- [10] M. Colamartino, F. Sarasini, M. Tirillò, L. Torre, and J. J. Martinez-Hergueta, “Fatigue and static response of flax fibre reinforced composites: Effect of temperature and frequency,” Composite Structures, vol. 254, 2021, Art. no. 112861, doi: 10.1016/j.compstruct.2020.112861.
- [11] S. Liang, G. F. Fernando, J. S. Lyons, and H. F. Field, “Damage progression in ±45° angle-ply laminated composites: An experimental study using digital image correlation,” Journal of Composite Materials, vol. 49, no. 19, pp. 2335–2347, 2015, doi: 10.1177/0021998314559329.
Agradecimientos
Esta publicación es parte del proyecto de I+D+i PID2021-127174OB-I00, financiado por AEI y FEDER/UE
Document information
Published on 21/01/26
Accepted on 14/07/25
Submitted on 13/04/25
Volume 09 - Comunicaciones MatComp25 (2025), Issue Núm. 3 - Caracterización Experimental, 2026
DOI: 10.23967/r.matcomp.2025.09.23
Licence: Other
Share this document
Keywords
claim authorship
Are you one of the authors of this document?