(Tag: Visual edit) |
|||
| Line 75: | Line 75: | ||
{| style="width: 100%;border-collapse: collapse;" | {| style="width: 100%;border-collapse: collapse;" | ||
|- | |- | ||
| − | | colspan='3' style="border-bottom: 2pt solid black;text-align: center;"|<span id='_Ref482340447'>'''Tabla 2'''. Resistencia obtenida de los ensayos </span> | + | | colspan='3' style="border-bottom: 2pt solid black;text-align: center;"|<span id='_Ref482340447;'style="text-align: center; font-size: 75%;">'''Tabla 2'''. Resistencia obtenida de los ensayos </span> |
|- | |- | ||
| style="border-top: 2pt solid black;border-bottom: 1pt solid black;text-align: right;"| | | style="border-top: 2pt solid black;border-bottom: 1pt solid black;text-align: right;"| | ||
Revision as of 18:34, 20 October 2022
1 Introducción
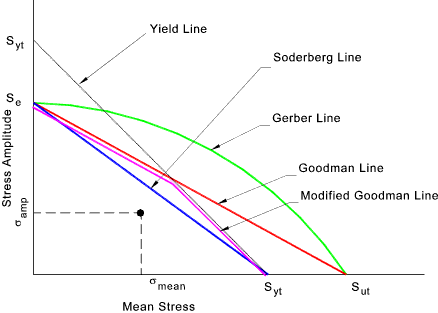
Existen en la bibliografía diferentes métodos para calcular la vida a fatiga de los materiales en función de la tensión alterna a la que están sometidos. En [1] se pueden observar resumidas las teorías clásicas (Gerber, Goodman, Soderberg) y sus diferentes variantes, Figura 1. Estas se fundamentan el cálculo de una tensión equivalente en función de la media y alterna, que es comparada con diferentes criterios teniendo en cuenta las resistencias elásticas y a rotura de los materiales. Otros modelos [2], tienen en cuenta además, la degradación del material con la acumulación de ciclos, y desarrollan en su formulación leyes de evolución de la resistencia y de la rigidez en función de las tensiones medias, alternas y número de ciclos. Modelos más evolucionados [3], desarrollan diferentes correcciones de la tensión media para mejorar la precisión del cálculo.
Sin embargo, en lo que se refiere a los materiales compuestos, el efecto del modo de solicitación de tracción o compresión, y la relación de tensiones máxima y mínima a la que se somete el material, influyen de manera determinante en el cálculo a fatiga. Recientemente, se ha demostrado buena efectividad a la hora de predecir la vida de estos materiales mediante diagramas de vida constante [4], que tienen en cuenta estos factores, aunque para su obtención es necesario un gran número de ensayos, con un consumo de recursos en términos de tiempo muy elevado. Es por ello que se observa la necesidad de desarrollar métodos acelerados de caracterización para el cálculo de vida a fatiga de materiales compuestos.
En este trabajo se aborda la obtención del diagrama de vida constante de un composite de fibra de carbono, con una combinación de métodos de caracterización universales con otros acelerados; todo ello combinado con el uso de métodos estadísticos, con el fin de reducir al máximo el tiempo de obtención de estos diagramas sin comprometer su precisión.
2 Materiales
El material empleado en este trabajo, en un compuesto de fibra de carbono embebido en matriz de resina expoxy de 3,6 mm de espesor formada por 18 láminas con la siguiente orientación [45,0,-45,45,0,45,-45,0,45] 0=0/90 & 45=-45/45. Los datos de resistencia suministrados por el fabricante se muestran en la Tabla 1.
| Tabla 1. Resistencia a rotura. (Datos del fabricante) | ||
| Tipo de solicitación | σu(MPa) | |
| Tracción | 464 | |
| Compresión | 229 | |
3 Metodología
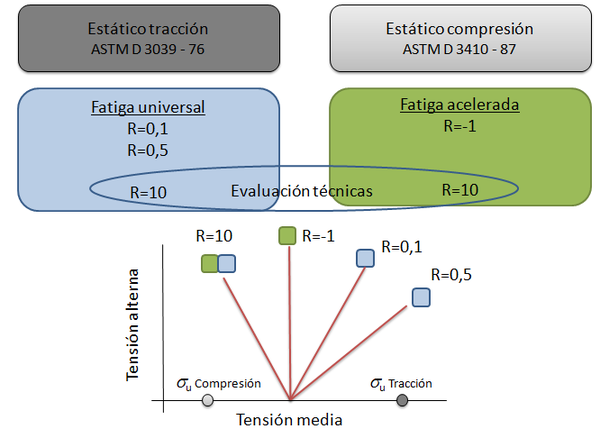
Para la obtención del diagrama de vida constante, se ha seguido la siguiente metodología con los ensayos correspondientes, Figura 2:
1.- Obtención de la tensión de rotura a tracción mediante ensayos en maquina universal. 6 ensayos.
2.- Obtención de la tensión de rotura a compresión mediante ensayos en maquina universal. 6 ensayos.
3.- Obtención de la curva S-N a fatiga correspondiente para diferentes R’s (relación entre tensión mínima y máxima de fatiga). Entre 6 y 8 ensayos para cada R.
4.- Tratamiento de los datos de fatiga para la obtención de tensiones de rotura con probabilidad cero de fallo siguiendo la metodología estadística de cálculo propuesta en [5].
5.- Construcción del diagrama de vida constante uniendo los puntos de iso-vida para las diferentes R`s con las resistencias ultimas de tracción y compresión.
4 Medios de ensayo
Los ensayos de tracción y compresión estáticos han sido realizados en una maquina de ensayos universales Zwick/Rowell con capacidad de carga hasta 300KN. Los ensayos de fatiga universal indicados en la Figura 2, han sido llevados a cabo en una Máquina servo hidráulica SERVOSIS de hasta 160KN.
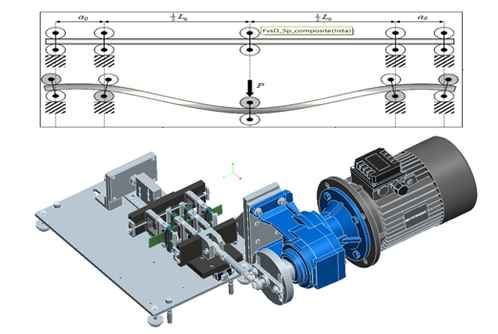
Para los ensayos de fatiga acelerada se empleó un desarrollo propio patentado [6] que se muestra en la Figura 3. La máquina está compuesta por dos partes, la parte dinámica el cual va conectado al sistema de biela manivela y aplica las cargas a las probetas; y la parte estática, el cual compone la estructura de la máquina y donde se encuentran la célula de carga y el sensor de posición. La máquina es capaz de realizar ensayos tanto de F3P como F5P a alta velocidad con un desplazamiento de hasta 25 mm. La frecuencia del ensayo está limitada a 20 Hz, por calentamiento excesivo del material ensayado, aunque su principal ventaja es el gran desplazamiento aplicable a altas frecuencias, aspecto limitado en las máquinas servo-hidráulicas comerciales de fatiga.
5 Resultados
5.1 Ensayos estáticos (tracción/compresión)
Los resultados de resistencia a tracción y compresión, Tabla 2, han sido obtenidos como el resultado de 6 ensayos para cada tipo de solicitación, ajustándose los resultados a una distribución normal tal que, el resultado se indica para 3 desviaciones estándar que corresponde a un intervalo de confianza del 99,7%, y que son muy similares a los ofrecidos por el fabricante, Tabla 1.
| Tabla 2. Resistencia obtenida de los ensayos | ||
| Tipo de solicitación | σu(MPa) Confianza 99,7% | |
| Tracción | 464 | |
| Compresión | 247 | |
Las probetas, de 25 x 250 mm, han sido ensayadas en la maquina indicada en el apartado 4, a una velocidad de deformación dentro del rango estático de 10-3 s-1. Para minimizar la concentración de tensiones en los amarres, se colocaron end-tabs de aluminio de 2 x 50 mm en los extremos adheridos con Araldite 2011; dando lugar, como se observa en la Figura 4, a que la rotura de las probetas se produjera lejos de la zona de amarre. En los ensayos de compresión se redujo la longitud de probeta hasta una longitud libre entre end-tabs de 50 mm, 100 mm menor a las de tracción, para evitar el pandeo.
5.2 Ensayos de fatiga (estándar y acelerados)
Para los ensayos de fatiga tanto acelerada como estándar, se han realizado, por cada relación de R, entre 6 y 8 ensayos a diferentes niveles de tensión. Con los resultados se ha construido una curva S-N por cada R, (ejemplo en la Figura 5) mediante la metodología estadística definida en [5], que permite, mediante el uso de distribuciones de Weibull, la obtención del número de ciclos de vida a fatiga antes de la rotura para cualquier nivel de probabilidad, cero incluido. Las ventajas de esta metodología son varias y enfocadas a la reducción del tiempo y numero de ensayos necesarios. Por una parte, no es necesario realizar repeticiones de ensayos a un mismo nivel de carga, ya que el método ajusta los resultados en todo el rango de tensión y ciclos. Por otra parte, se puede limitar el número máximo de ciclos, y aunque algunos ensayos no lleguen hasta la rotura, la metodología es capaz de extrapolar los resultados de esos ensayos hasta la rotura.
5.3 Diagrama de vida constante
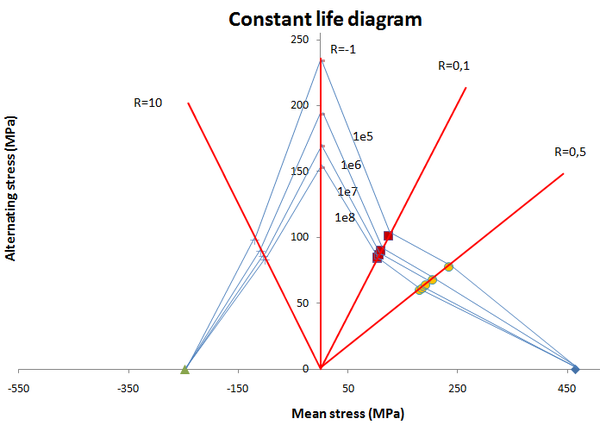
Con los datos de tensión de rotura a tracción y compresión, así como con las 4 curvas S-N obtenidas a fatiga para diferentes R´s, se puede obtener el diagrama de vida constante mostrado en la Figura 6. Este diagrama muestra curvas de iso vida para diferentes números de ciclos para cualquier combinación de tensión media, alterna y nivel de probabilidad de fallo. De esta manera es posible conocer para cualquier carga de fatiga, si se supera el criterio de fallo, y el nivel de daño para aplicar reglas como la de Miner dividiendo en número de ciclos de carga entre el número de ciclos de rotura del diagrama.
5.4 Fatiga acelerada vs Estándar
Los ensayos de fatiga estándar han sido realizados en configuración tracción-tracción en máquina servohidráulica, mientras que los acelerados has sido realizados en configuración F5P en maquinaria propia patentada tal y como se describe en el apartado 4.
La principal ventaja de la metodología acelerada, es la posibilidad de reducir el tiempo de ensayo, ya que se pueden conseguir grandes desplazamientos a altas frecuencias, limitación inherente a los métodos de ensayo servohidráulicos, ya que con la tecnología actual la amplitud de ensayo se reduce al aumentar la frecuencia del mismo, impidiendo así llegar a deformaciones de rotura para altas frecuencias. Mediante la metodología acelerada, es posible alcanzar la combinación de altas frecuencias y grandes desplazamientos muchas veces necesarios en probetas de composite.
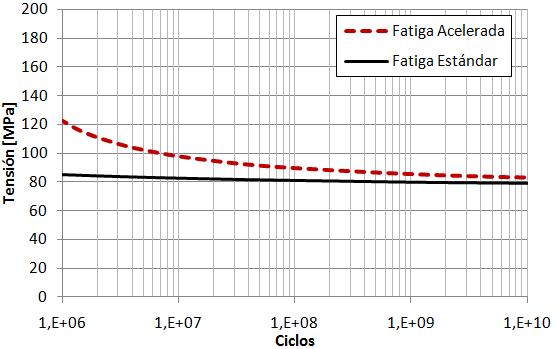
Sin embargo, la configuración de ensayo de ambos métodos no es exactamente la misma, y se observan diferencias, Figura 7, en las tensiones de rotura dependiendo del método. A pesar de ello, ambos métodos obtienen el mismo valor de límite de fatiga, 74,2 MPa para el método estándar y 74,5 para el acelerado. Esta diferencia a menores ciclos, se debe a que en la configuración acelerada la probeta está sometida a flexión, y el cálculo de tensiones recogido en la Figura 7 corresponde a la tensión máxima que es la de la capa más lejana de la fibra neutra. Al avanzar el ensayo, las capas rompen secuencialmente hacia el interior, reduciéndose la tensión real en la probeta por reducirse el momento de inercia de la misma. Es por ello que, para construir diagramas de vida constante con métodos acelerados, deben emplearse valores cercanos al límite a fatiga si se quiere estar por el lado de la seguridad. Por lo tanto, en el diagrama de vida constante de la Figura 6, la curva de iso-vida más alta (108 ciclos), nos permite estar por el lado de la seguridad, mientras que para valores más bajos de vida, la zona de R=-1, (que es la única curva de fatiga acelerada empleada en la construcción del diagrama) puede estar ofreciendo valores sobreestimados en tensión.
De cualquier manera, se observa que, los métodos de fatiga acelerada, permiten construir diagramas de vida constante fiables para el diseño de vida a fatiga a alto número de ciclos, en un tiempo menor que los métodos estándar. Por otra parte también se observa que la utilización de los métodos clásicos de cálculo de fatiga en composites, puede sobreestimar el cálculo de vida sobre todo en relaciones de tensión donde la tensión media y alterna son similares, (R=0,1 y R=10), pudiendo dar origen a fallos de diseño por rotura a fatiga.
6 Conclusiones
- Se ha obtenido el diagrama completo de vida constante a fatiga de un material compuesto de fibra de carbono mediante métodos de caracterización estándar y acelerados.
- Los métodos de caracterización acelerados, son válidos para obtener valores limites de vida a fatiga para cualquier tensión alterna y media, así como cualquier valor de probabilidad de fallo.
- Los métodos de caracterización acelerados, sobreestiman la vida a fatiga para bajos ciclos.
- Los métodos de caracterización acelerada empleados permiten reducir el tiempo de caracterización sin perder fiabilidad.
7 Referencias
[1] Schütz, W. A history of fatigue. Engineering Fracture Mechanics, 54(2):263-300 (1996).
[2] Shokrieh, M.M; Lessard,L.B. Progressive fatigue damage modeling of composite materials Part II: Material characterization and model verification. Journal of Composite Materials 34 (13), 1081-1116. (2000)
[3] Dowling, N.E. Mean stress effects in strain–life fatigue. Fatigue & Fracture of Engineering Materials & Structures, 32: 1004–1019. (2009)
[4] Thawre, M.M., Paretkar, R.K., Peshwe, D.R., Sundaram, R., Manjunatha, C.M. Construction of constant fatigue life diagram for a carbon fiber composite. Transactions of the Indian Institute of Metal, 64, pp. 301-303, (2011).
[5] Castillo,E; Fernandez Cantelli, A.Libro: Metodología estadística unificada para modelar el daño a fatiga. Ed. Real Academia de la Ingeniería. (2009)
[6] Asensio, M.; Perez de Goldarazena, N.; WO2014096467 (A1) 2014-06-26. Support device for specimens subjected to fatigue tests with multiple-point bending, suitable for being fixed to a fatigue test Machine. (2014)
Document information
Published on 14/10/18
Accepted on 14/10/18
Submitted on 14/10/18
Volume 02 - Comunicaciones Matcomp17 (2018), Issue Núm. 4 - Comportamiento en servicio de los materiales compuestos (2), 2018
DOI: 10.23967/r.matcomp.2018.10.018
Licence: Other
Share this document
Keywords
claim authorship
Are you one of the authors of this document?