Revision as of 09:42, 3 September 2020 (view source) Rimni (talk | contribs) (→‎Appendix 1) ← Older edit		Revision as of 09:44, 3 September 2020 (view source) Rimni (talk | contribs) Newer edit →
Line 838:		Line 838:
	!  I – Categorical (3) !! II – Binary(4)		!  I – Categorical (3) !! II – Binary(4)
	|-		|-
−	|  rowspan='12' style="text-align: left;width:210px;"|(1) Legal Status	+	|  rowspan='12' style="text-align: left;width:180px;"|(1) Legal Status
	|  style="text-align: left;"|(1) Limited partnership		|  style="text-align: left;"|(1) Limited partnership
−	|  style="text-align: left;"|1	+	|  style="text-align: center;"|1
	|  style="text-align: center;"|100000000000		|  style="text-align: center;"|100000000000
	|-		|-

---

Revision as of 09:44, 3 September 2020

Abstract

The purpose of this article is to compare the performance of a credit scoring model by applying different Machine Learning techniques for the classification of payers in bank financing of companies (5 432 historical records). Clients were considered “non-default” or “default” depending on their default index, thus, 4 238 were considered “non-default” and 1 194 “default”, including the information related to 10 variables (features) that composed the database. First, a random undersampling technique was applied to solve the unbalanced data problem. The variables were then coded in two ways: Code I (categorical variables) and Code II (binary or dummy variables). This was followed by the feature selection methods to detect the most important variables. Finally, we used three classifier algorithms of Machine Learning (ML), Bayesian Networks (BN), Decision Tree (DT) and Support Vector Machine (SVM) comparatively. All these techniques were implemented in WEKA (Waikato Environment for Knowledge Analysis) software. The best performance was 95.2% using balanced classes, with the attributes coded in a binary way and the SVM machine learning technique. So, in this way, it is possible to automatically classify (“non-default” or “default”) new instances making use of the proposed methodology with high performance.

Keywords: Classifier algorithms, feature selection, unbalanced classes, credit scoring model

1. Introduction

The term “credit”, in the context of banking, is a type of transaction or contract through which a financial institution makes a certain amount of money available to someone (individual or company) with the promise of returning the money later in one or more instalments. This is a complex decision, as this operation involves risk and can lead to serious consequences. Credit operations for companies, when taken together, can amount to significant financial resources. Therefore, risk assessment is very important, since in extreme cases, i.e., default, these operations can lead to the bankruptcy of the financial institution [1].

This issue is so important that the Brazilian Central Bank has set limits on credit operations in accordance with Resolutions 1559 and 1556 of the National Monetary Council (Conselho Monetário Nacional, CMN) of 22 December 1988. Furthermore, financial institutions have to list their credit operations according to the risk they incur, in accordance with CMN Resolution 2682 of 21 December 1999. Thus, credit concessions have to be ranked and dubious prospective borrowers listed by level of risk, the collateral they provide and the kind of operation [2].

Even with these security measurements with regard to risk, the decision on whether to authorize a loan is made by a credit committee, consisting of managers of the institutions, using diverse measurement methods and managerial mechanisms. In general terms, these methods seek to transform a set of data into information to define default and non-default clients.

The economic pressures resulting from the high demand for credit, the fierce competition in the sector and the emergence of new computer technologies have led to the development of sophisticated credit concession models that are objective, rapid and reliable [3,4].

Traditional models, also known as credit scoring, essentially focus on whether to grant credit by evaluating the likelihood of repayment, in other words, whether the individual or company will default, in accordance with overdue payments on loans [5].

Linear Discriminant Analysis (LDA), Linear Regression (LinR) and Decision Trees (DT), as used by Medina and Selva [6], and Linear Programming (LP), may be highlighted as techniques for constructing credit risk models [7]. Methods with a multiple-criteria decision approach have also been used for this purpose [8].

The techniques to aid this decision-making have been constantly improved, mainly by researchers in the field of Artificial Intelligence (AI). Tools such as database analysis, Data Mining (DM) and Machine Learning (ML) are among the new technologies used to increase the quality and efficiency of decisions in banking institutions [9].

The aim of the present article is to propose an efficient and effective methodology for determining whether to grant credit to companies. To this end, the performances of different classifier algorithms of ML (Bayesian Networks, BN; Decision Tree, DT and Support Vector Machine, SVM) will be compared. Prior to using these classifiers, data treatment will be performed: class balancing, coding of features (categorical and binary) and feature selection, with a view to improving the accuracy of those algorithms. To illustrate the methodology better, real data provided by a banking institution will be used.

The article contributes to several aspects of the field, such as defining a client default index (rather than simply defining clients as default or non-default); performing data treatment using techniques generally neglected by researchers and providing a geometric illustration to identify the most important features.

The present study seeks to address the following questions: a) Which classifier algorithms result in better performance of the credit scoring prediction model? b) How does the problem of class unbalancing affect the performance of the model? c) How does the feature selection stage contribute to the credit scoring model? d) What are the practical implications of getting a good defaulter and non-defaulter classification?

The article is organized as follows. Following this introduction, the theoretical framework about credit risk analysis is presented in Section 2. In Section 3, the data collection and organization are explained. The methodology is presented in Section 4, and the results are shown in Section 5. Finally, the conclusions and suggestions for future studies are given in Section 6.

2. Theoretical framework

The theoretical framework is organized into the presentation of types and models of risk assessment and correlated works.

2.1. Types and models of credit risk

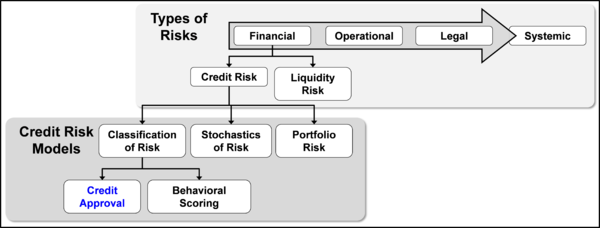
As mentioned above, every granted credit operation, as it involves a future expectation of payment, is open to risks. Frascaroli, Paes and Ramos [10] highlight four kinds of risk: financial risk, operational risk, legal risk and systemic risk, as shown in Figure 1.

Figure 1. Types of risk and classification of credit risk models

Financial risk is credit and liquidity risk. Operational risk is risk resulting from human failure, equipment failure and the failure of operational systems, increasing credit and liquidity risk. Legal risk results from a legal and regulatory base that is not suited to liquidation, an activity that it is intended to monitor and control. In turn, jointly or separately, these risks can lead to systemic risk, which may be defined as the possibility of credit and/or liquidity gaps that can lead to general default by the participants in a financial system [10].

Models that assess and/or measure credit risks can be classified into three groups, in accordance with Silva Brito and Assaf Neto [11]: risk classification models, stochastic credit risk models and portfolio risk models. Risk classification models seek to quantify the risk of a borrower or operation and grade the debtor or loan. Stochastic models are used to determine the stochastic behavior of the credit risk or the variables included in its calculation. Portfolio risk models estimate the distribution of likelihood of loss or the value of a credit portfolio and thus produce estimates of risk.

Risk classification models, i.e., credit scoring, in turn, are divided into two categories: credit approval models and behavioral scoring models. The main difference between the two categories is that in the latter, the financial institution analyzes the behavior of the client in previous operations, whereas in credit approval models, the financial institution relies on companies’ registration data. It should be highlighted that the present study uses risk classification models based on ML models for the concession/approval or refusal of credit (in blue color in Figure 1).

2.2. Some correlated works

Credit risk assessment, since it was introduced in the nineteen fifties, has been widely used, mainly for granting loans [12]. This problem consists of evaluating the risks involved when a financial institution lends money to a company or individual. For this purpose, researchers have used a wide range of techniques to minimize losses for financial institutions. Some works related to this subject will now be briefly described in chronological order since 2012 and comparatively summarized in Table 1. In this table, the techniques that have shown the best performance are in bold.

Authors, year	Techniques	Databases (DB) used
Loterman et al., 2012 [13]	24 techniques: B-OLS; ANN; SVM e statistical techniques	6 DB
Brown and Mues, 2012 [14]	DT; FF; LR; ANN; SVM	5 DB
Wang et al., 2012 [15]	DT; RBF; LR	2 UCI DB
Hens and Tiwari, 2012 [16]	Híbrid (SVM e AG) and RNA	2 DB: Australian and German
Marqués et al., 2012 [17]	7 techniques (DT; ANN; others) with ensemble or without ensemble	UCI DB
Akkoç, 2012 [18]	LDA; LR; ANN; Hybrids	DB from Turkey
Kao et al., 2012 [19]	Proposed method (Bayesian latente variables); LDA; CART; MARS; ANN; SVM	DB from Tawain
Tong et al., 2012 [20]	LR, Cox Regression, Mixed Cure Model	Portfolio of loans in the United Kingdom
García et al., 2012 [21]	SVM, ENN, NCN, CHC	8 DB
Li et al., 2013 [22]	SVM (with and without ensamble)	2 DB
Nikolic et al., 2013 [23]	LR	Company DB
Marqués et al., 2013 [24]	LR, SVM (with and without resampling)	UCI DB
Zhu et al., 2013 [25]	LDA, QDA, DT, LR, SVM	UCI DB
Blanco et al., 2013 [26]	LDA; QDA; ANN; LR	DB from Peru
Cubiles-de-la-Veja et al., 2013 [27]	DT; LDA; QDA; LR; ANN; SVM; bagging; boosting	DB from Peru
Oreski and Oreski, 2014 [28]	Hybrid (GA and ANN)	DB from Croatia
Chih-Fong and Chihli, 2014 [29]	ANN; ANN Ensembles; Hybrid RNA	3 DB: Australian; German; Japanese
Niklis et al., 2014 [30]	SVM, LR	Greek DB
Tong e Li, 2015 [31]	SVM and combinations; RVM	Credit Risk of Chinese companies
Yi e Zhu, 2015 [32]	Different SVM techniques	2 DB: Australian and German
Bravo et al., 2015 [33]	LR; ANN; Clustering	Chilean Public Agency
Koutanaei et al. 2015 [34]	Hybrid (PCA and GA); SVM; ANN with and without ensemble	Iranian Development Bank
Harris, 2015 [35]	LinR; LR; ANN; DT; SVM	2 DB: German and from Barbados
Danenas and Garvas, 2015 [36]	ANN; PSO; SVM	EDGAR DB
Zhao et al., 2015 [37]	ANN (Three different strategies)	German DB
Silva et al., 2015 [38]	ANN	DB 13th. Pacific-Asia KDD and DM Conference
Abedini et al., 2016 [39]	ANN MLP with and without FR, SVM, RL with and without bagging	DB UCI
Zakirov et al., 2016 [40]	SVM with and without application of RF	Real DB
Ozturk et al., 2016 [41]	BN, CART, MLP, SVM	DB with 1 022 observations from 92 countries
Abdou et al., 2016 [42]	LR, CART e ANN	DB of banks from Cameroon
Punniyamoorthy and Sridevi, 2016 [43]	ANN; SVM	DB from the United Kingdom
Ala’raj and Abbod, 2016 [44]	LR; ANN e SVM (with and without RF); DT	5 DB: German; Australian; Japanese; Iranian and Polish
Andric and Kalpic, 2016 [45]	LR; ANN (with and without gradient boosting)	2 DB: German and Japanese
Li, 2016 [46]	SVM with fuzzy logic	Real DB
Guo and Dong, 2017 [47]	DT, BN, PSO, LR, ANN	2 DB: United Kigdom and Germany
Luo et al., 2017 [48]	ANN (deep learning and MLP), LR and SVM	CDS DB
Bequé and Lessmann, 2017 [49]	ANN, ELM	Real DB
Lanzarini, 2017 [50]	PSO Hybrid	Tunisian bank DB
Maldonado et al., 2017 [51]	Different SVM techniques (Fisher-SVM)	DB with 7 309 clients (small and micro businesses)
Assef et al., 2019 [52]	ANN (MLP and RBF), LR	DB with 5 432 clients

Legend: ADL (Linear Discriminant Analysis); ANN (Artificial Neural Networks); BN (Bayesian Networks); B-OLS (Beta Ordinary Least Square); CART (Classification and Regression Trees); CDS (Common Data Service); DT (Decision Trees); ELM (Extreme Learning Machine); ENN (Edited Nearest Neighbor); GA (Genetic Algorithms); LinR (Linear Regression); LR (Logistic Regression); RF (Random Forest); MARS (Multivariate Adaptive Regression Splines); MLP (MultiLayer Perceptron); NCN (Nearest Centroid Neighbors Editing); PCA (Principal Components Analysis); PSO (Particle Swarm Optimization); QDA (Quadratic Discriminant Analysis); RBF (Radial Basis Function); RVM (Relevance Vector Machines); SVM (Support Vector Machines).

Loterman et al. [13] compared 24 techniques used to classify banking credit, including heuristic procedures, Artificial Neural Networks (ANN), the SVM and statistical models, evaluated in six real databases. The ANN and B-OLS techniques had the best performances in more than one database. Brown and Mues [14] also made an extensive comparison of techniques, this time using five real databases. The techniques employed were Logistic Regression (LR), ANN, DT, SVM and Random Forests (RF). In general, RF had the best performance. In Wang et al. [15], the performances of ANN were compared with the Radial Basis Function (RBF), DT and LR in two credit databases of the UCI (UC Irvine Machine Learning Repository). The best results were obtained with LR, with accuracy greater than 88% in every case presented. Hens and Tiwari [16] developed a hybrid of SVM and Genetic Algorithms (GA) and compared this methodology with ANN. The accuracy of the proposed model, although greater, was very close to that of ANN. The rates obtained were 86.76% and 86.71%, respectively.

Marqués et al. [17] presented seven classification techniques, varying in the use (or not) of ensemble techniques. The best results were for tests using ensemble and the best performance was for DT, closely followed by ANN. The poorest results were the BN (Bayesian Networks) classifiers. Akkoç [18] proposed a hybrid for banking credit classification in a Turkish database. Initially, three techniques were analyzed separately: LDA, LR, ANN. These techniques were then hybridized. The resulting hybrid had a better performance than the other techniques, with an average accuracy of 60% in the tests that were conducted. In Kao, Chiu and Chiu [19], a client classification model was proposed based on Bayesian latent variables. The proposed method was compared with techniques such as LDA, ANN, SVM, CART (Classification and Regression Trees) and MARS (Multivariate Adaptive Regression Splines). The model was 92.9% accurate in its classification, followed by CART, with approximately 90%.

Tong et al. [20] compared statistical techniques such as LR, a mixed cure model and Cox regression, with highly similar performances. García et al. [21] analyzed 20 algorithms, using different types of SVM, statistical techniques and heuristics in applications for eight different databases. The best performances were for three heuristic models, Edited Nearest Neighbor (ENN), Nearest Centroid Neighbors Editing (NCN) and finally the CHC evolutionary algorithm. Li, Wei and Hao [22] proposed an ensemble methodology together with the SVM technique and PCA (Principal Component Analysis) in two databases. Not only did the proposed method have the best accuracy (89%) of the tested models, but it was also the most stable. Nikolic et al. [23], using a LR approach, proposed a credit risk assessment model for companies from different databases over five years (2007-2011). Accuracy varied between 50.99% and 53.91% according to the number of variables analyzed. Marqués et al. [24] tested the ability of data resampling methods. LR and the SVM were compared and the authors found that resampling models can improve the performance of the classification techniques.

Zhu et al. [25] tested eight methods, including LDA, QDA (Quadratic Discriminant Analysis), DT, LR and SVM, applied in two UCI databases. For a database of a Peruvian bank, Blanco et al. [26] used ANN, LDA, QDA and LR techniques to predict the likelihood of default of 5 500 clients. The performance of ANN was better than the other techniques. Using different classification methods, Cubiles-de-la-Veja et al. [27] analyzed the credit risk of a Peruvian financial institution, showing that the MLP (Multiple Layer Perceptron) model reduces the costs of classification error by 13.7% in relation to the application of the other methods that were tested. Oreski and Oreski [28] presented a hybrid of GA and ANN in a Croatian database. The proposed algorithm showed a promising classification “ability” for selecting features and classifying risk compared with the other techniques. Chih-Fong and Chihli [29] compared ensembles of ANN and a hybrid of ANN in three databases (Australian, German and Japanese). The results showed that both the hybrid and the ensembles outdid the performance of pure ANN. Niklis et al. [30] compared different types of SVM and LR to evaluate the credit risk of real data from 2005 to 2010. The best results were obtained by one of the SVM techniques (79.6%). Tong and Li [31], again using SVM and possible combinations of this technique, sought to assess the credit risk of Chinese companies. The best result obtained (9% error) was for the technique known as Relevance Vector Machines (RVM), a variant of SVM. Another analysis of different SVM techniques was conducted by Yi and Zhu [32], applied to an Australian database and a German one. The best result for the German database was obtained through RBF together with the SVM, achieving accuracy of 76%. For the Australian database, the greatest accuracy was 84.83% using polynomial functions in the tested SVM.

Bravo et al. [33] proposed a methodology that divides clients into “good payers”, “can’t pays” and “won’t pays”. The authors used a clustering algorithm, LR and Multinomial LR, together with ANN. Dividing clients in this way can mean a significant improvement over the classical division (good payers and bad payers). Koutanaei et al. [34] developed a hybrid model that, in the first stage, pre-processes information using PCA and GA. The parameters obtained are then used as inputs for the SVM and ANN to compare these methods. The results showed that ANN, with the AdaBoost (adaptive boosting) ensemble technique achieved greater accuracy than the others that were tested. Harris [35] investigated LinR and LR, in addition to ANN, DT and the SVM to classify clients in a German database and another from a bank in Barbados. The best accuracy was obtained using the SVM.

Danenas and Garvas [36] presented ANN, PSO (Particle Swarm Optimization) and SVM techniques to classify clients in a database from 1999-2007 known as “EDGAR” (Electronic Data Gathering). The experimental research showed that the SVM had the best performance (over 90%). Zhao et al. [37] proposed an MLP type ANN analysis in an attempt to improve performance using three strategies. The first strategy involved optimizing the distribution of information from the databases using a method known as Average Random Choosing. The second involved comparing the effects of the number of instances of training, test and validation. The third involved finding the best number of neurons for the hidden layer. Using the client base of a German bank, the authors achieved a level of accuracy of 87% for 31 neurons in the hidden layer. Silva et al. [38] also used MLP to explore the idea of generating cases in pattern regions, in which it is more difficult to produce consistent responses. The ratio of defaulters and non-defaulters in the database used by the authors was 80% to 20%, with a greater tendency of information for non-defaulters, lowering the accuracy of the methods tested.

Abedini et al. [39] proposed an approach using an ensemble classification technique with ANN, MLP, SVM, LinR and LR with bagging and MLP using RF. The proposed model performed better than when the techniques were applied on their own. The best accuracy level was 76.67% for the application of MLP with the RF ensemble technique. Zakirov, Bondarev and Momtselidye [40] presented a structure to compare different classification methods, in which the RF methodology was the most accurate. Applying the CART, MLP, SVM and BN, Ozturk et al. [41] examined the forecasting of different AI techniques to analyze bank credit. The results showed that the prediction techniques were over 90% accurate, while conventional statistical models were approximately 70% accurate. Abdou et al. [42] applied three correlation classification methods, LR, CART and ANN, to a database of banks in Cameroon. The best performance was obtained with ANN, with a 97.43% accurate identification of “good payers”. Punniyamoorthy and Sridevi [43] used ANN and compared them with an SVM model to classify bank clients in the United Kingdom. The SVM had better results than the ANN method, with accuracies of 80% and 77%, respectively.

Ala’raj and Abbod [44] presented an approach with six classifiers: LR, ANN, SVM, RF, DT and BN. Five databases were used (German, Australian, Japanese, Iranian and Polish), with RF having the best performance in four of the five bases, followed by ANN, with the highest level of accuracy in the German base. Andric and Kalpic [45] compared three classification algorithms, LR, ANN and gradient boosting. Regarding the first database, the German one, ANN and gradient boosting were both 75% accurate. For the second database, the Japanese one, gradient boosting had the best result, with 91% accuracy.

Li [46] conducted a credit risk analysis using the SVM based on fuzzy logic, for which the rate of accuracy was 77.7%. Guo and Dong [47] proposed a multi-objective PSO model for classifying customers and compared it with BN, LR, sequential minimal optimization, DT and ANN. The accuracy of the proposed model was greater than the other tested models (74.64%) for the first database that was tested. However, for the second, ANN had better performance than the others, with 61.15% accuracy. For the last database that was tested, LR had the best performance, with 76.70% accuracy.

In Luo et al. [48], the performance of credit scoring models was tested, applied to the CDS (Common Data Service) database. Deep learning ANN were used, as well as MLP, LR and the SVM, to compare the tests. The best accuracy was for the deep learning ANN (100%), followed by MLP (87.85%). Bequé and Lessmann [49] compared ANN and other classification methods with the ensemble technique known as extreme learning machines (ELM). Lanzarini et al. [50] presented an alternative model that could generate rules that worked not only with numerical features, but also with nominal ones. The technique was based on LVQ-PSO (Learning Vector Quantization combined with PSO). The highest level of accuracy obtained by the proposed algorithm was 81.05% in the tests that were performed. Maldonado et al. [51] developed two proposals based on the SVM to select features and classify clients with regard to bank credit. Among the tested SVM, the Fisher-SVM was the most accurate (accuracy rate of 70.6%). This algorithm uses a Fisher scoring algorithm to select features according to costs and the SVM is then applied. In Assef et al. [52], compared ANN-MLP, ANN-RBF and LR in a problem with 5 432 data with 15 features, considering three classes: non-default; default and temporarily default; the authors present new insights towards research over Credit Risk Assessment.

It should be highlighted that in this work, compared with those analyzed (Table 1), a default index was determined for every client and, also, in order to get better performance for the classifier algorithms of ML, techniques were applied for the data treatment: random undersampling for class balancing; features were coded as categorical and binary; and, finally, the features were selected using filter techniques (information gain) and wrapper techniques. With these data preprocessed, the Bayesian Networks (BN), Decision Tree (DT) and Support Vector Machine (SVM), were used comparatively. To provide a better illustration of the methodology, real data provided by a banking institution were used.

3. Data organization and collection

The data used in this work were obtained from a large Brazilian financial institution with regard to the concession of credit to companies located in Paraná State (PR). Historical records from January 1996 to June 2017 were used, with over 39000 credit operations involving 5432 companies, chosen by the institution’s specialists (credit managers), in order to get good representations of the general bank client mix.

The data of the operations conducted during the research period were classified concerning the situation of payment as follows, as the institution specialists’ suggestions.

• Class I (paid in full or payable): operations with payments made on time or within the deadline for payment;

• Class II (overdue): operations overdue for up to 180 days;

• Class III (losses): operations overdue for more than 180 days.

Thus, every one of the 5432 companies were classified by the number of operations resulting in each of the aforementioned classes of observation. For this purpose, a function of the default rate was determined, as shown in (1),

${\textstyle Q\left(x\right)=\,{\frac {{n}^{III}(x)}{{n}^{I}(x)\,{+\,n}^{III}(x)}}}$

(1)

where ${\textstyle Q\left(x\right)\,\in [0.1]}$ represents the default rate of each company ${\textstyle x}$; ${\textstyle {n}^{I}}$ represents the number of operations of each company ${\textstyle x}$ belonging to Class I; and ${\textstyle {n}^{III}}$ the number of operations of each company ${\textstyle x}$ in Class III.

Thus, the classification (value of the default rate) of each company actually represents a proportion of the Class III operations in relation to Classes I and III. In other words, they are operations with no expectation of payment in relation to the number of operations that the company had already paid or are within the deadline for payment (Class I). Therefore, when the default rate is closer to “1”, this means that the company has more Class III operations than Class I and is consequently more of a “defaulter”. Using Equation (1), the companies will be “penalized” in proportion to the number of overdue payments.

This must be considered because there may be companies that have a profile of commitment and responsibility regarding the repayment of loans but, for some reason, have not been able to repay some of the instalments of the credit operation. For example, a company with 50 Class I operations and five in Class III will not be considered a “defaulter” because of the five overdue payments. Rather, all the other 45 operations will be considered, resulting in a default rate of 0.09.

Class II operations were not considered in the calculation of the default index because they are on the threshold between default and non-default, as these payments can still be settled and become Class I.

Having said this, the classification feature of the companies regarding repayment, corresponding to the output feature, was defined by a dichotomous variable ${\textstyle Y\left(x\right)}$, assuming the values shown in (2)

${\textstyle Y\left(x\right)=\left\{{\begin{array}{ll}''Defaulter'',&0.5<Q\left(x\right)\leq 1\\''Non-defaulter'',&0<Q(x)\leq 0.5\end{array}}\right.}$

(2)

Therefore, of the total instances (5432 companies), 4238 were considered “non-defaulters” and 1194 “defaulters”. The 10 features selected with the help of a specialist from the banking institution to compose the prediction model were: Legal Status, Gross Annual Revenue, Number of Employees, Company Activity, Date of Incorporation, Time as Client, Market Sector, Risk Assessment, Borrower’s Credit Limit and, finally, Loan Restrictions (weak or impeditive). The feature selection using the expertise tries to avoid a high bias that could lead to a model underfitting.

4. Methodology

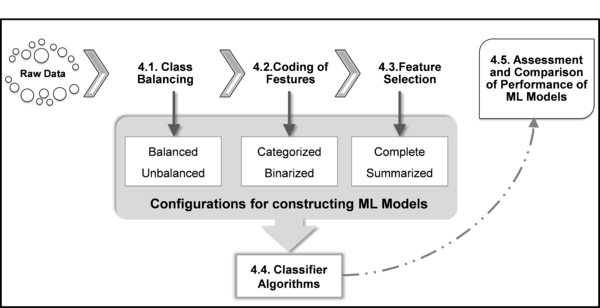
The methodology was defined using in the five following stages: class balancing, coding features (categorical and binary), feature selection, application of machine learning algorithms and evaluation and comparison of their performance. These stages are illustrated in the flowchart in Figure 2 and briefly described in the next subsections.

Figure 2. Proposed methodology

4.1 Class balancing

The evident unbalancing or disproportionate number of instances in each class (4238 were considered “non-defaulters” and 1194 “defaulters”) can make the minority instances (“defaulters”) have “strong” chances of being classified incorrectly [53]. Therefore, the random undersampling technique [54] was applied to solve the problem of unbalancing, which consists of the random elimination of instances in the majority class (“non-defaulters"), so that the two classes have the same number (1194) of instances. This technique was used due to its simplicity and fast computation.

4.2 Coding of features

The raw data (continuous variables) underwent a coding procedure that consisted of categorizing the features and transforming them into dummy (binary) variables [55]. The continuous type features were categorized/binarized due to the significant differences between their values ranges.

The categorization of the features that were originally described by continuous variables consisted of creating four levels of discrete variables that corresponded to the quartiles of the value intervals of the original continuous variable. The “Gross Annual Revenue”, “Number of Employees”, “Date of Incorporation” and “Time as Client” features are included in this case.

The features described with variables that were originally categorical, with many levels, also had some of their levels regrouped to avoid the existence of categories with a small number of instances, which could affect the estimation of the model’s parameters. The features that fit this scenario are “Legal Status”, “Company Activity”, “Market Sector”, Risk Assessment”, “Borrower’s Credit Limit” and “Restrictions”. The variables were then “binarized” using the dummy coding, which is done by attributing the value of “1” when it has a characteristic represented by the level of the feature and a value of “0” otherwise. The use of dummies can help improve the assertiveness of the predictions of the classification models [3,9,56,57]. The number of dummies is equal to the number of levels of each feature. Therefore, in the model in question, there was a total of 74 dummy variables.

4.3. Feature selection

Feature selection techniques were used that can improve the performance of the predictor models, facilitate visualization and understanding of the estimated parameters and prevent problems of overfitting [58].

There are different approaches to feature selection, two of which were used in the present work: a) Filter (Feature Ranking) to establish a ranking of the features based on information gain, independent of the classifier algorithm [59]; and b) Wrapper (Forward Selection) to select a subset of features that results in better “merit” (better assessment performance), depending on the classifier algorithm, using the method WrapperSubsetEval, proposed by Kohavi and John [60].

With the feature selection using the Wrapper method, the models, which before were “complete” (with all the features), became “summarized” models. In other words, they came to include only the predictor variables considered most important for each classifier algorithm.

4.4. Classifier algorithms

A number of ML techniques have been used in classification problems [61,62]. The classifier algorithms selected for the case in question were Bayesian Networks (BN; [63]), Decision Tree (DT; [64]) and the Support Vector Machine (SVM; [65]), as they had the best performances in the correlated works that were analyzed (Table 1).

A BN is a directed acyclic graph that codifies a joint probability distribution on a set of discrete random variables ${\textstyle U\,=\,\lbrace {X}_{1},\,...,\,{X}_{n}\rbrace }$ where each variable X_i can assume values of a finite set [66]. Formally, a BN for ${\textstyle U}$ is a pair ${\textstyle B=\left\langle G,\Theta \right\rangle ,\,}$ where the first component, ${\textstyle G}$, is a directed acyclic graph whose vertices correspond to the random variables and whose edges represent direct dependences between these variables. The second component, ${\textstyle \Theta }$, represents the set of parameters that quantifies the network [67].

A DT is a tree-based method, introduced by Breiman et al. [68]. The initial algorithm has been improved and expanded in several ways over the years, but the general principles remain: given a set of training data, the input variables and their corresponding levels are observed to determine possible division points. Each division point is then evaluated to determine which division is “better”. The process is then repeated with each subgroup until a stop condition is achieved [69].

Finally, the original concept of the SVM [70] was intended to find ideal hyperplanes for linearly separable classes [71], but also has the ability of building nonlinear classifiers [72]. These hyperplanes depend on a subset of the training data, which are known as support vectors [69]. The SVM is widely used in real world problems due to a better generalization ability, including less overfitting problems.

4.5. Evaluation and comparison of the performance of the models

The metrics used to assess the performance of the predictions of classification models, based on the confusion matrix were: a) Accuracy, measured by the Total Accuracy Rate (TAR); and b) Specificity, also called the true negative rate (TNR), measured by the rate of accuracy in “Defaulter” prediction.

The rates TAR and TNR can be calculated using equations (3) and (4), respectively [73]

${\textstyle Accuracy=TAR=({n}_{aa}+{n}_{ii})/{n}_{T}}$

(3)

${\textstyle Specificity=TNR=\,{n}_{ii}/{n}_{i}}$

(4)

where ${\textstyle {n}_{aa}\,}$ represents the number of non-default operations and correctly classified as “non-default” (true positive, TP); ${\textstyle {n}_{ii}}$, the number of default operations correctly classified as “default” (true negative, TN); ${\textstyle {n}_{T}}$, the total instances considered and ${\textstyle {n}_{i}}$, the total number of “Defaulters”.

The accuracy is the proportion of true results, both true positives (“non-default”) and true negatives (“default”), among the total number of 5432 cases examined. The specificity measures the proportion of actual negatives (“default”) that are correctly identified as such defaulters.

Another important evaluation metrics for checking the classification model’s performance is the AUC (Area Under the Curve) ROC (Receiver Operating Characteristics) curve, also written as AUROC (Area Under the Receiver Operating Characteristics). This measurement is obtained through the graphical representation of the pairs ${\textstyle x}$ and ${\textstyle y}$, which correspond the false positive rate against the true positive rate (sensitivity) [74]. The AUROC can be obtained through numerical integration methods [73].

The AUROC measurement is preferable to only using accuracy, specificity or sensitivity, as it has a number of desirable properties [75] and can be interpreted as follows: the closer to “1” the obtained value is, the better the classifier algorithm will be in the task of separating the two classes. Values between 0.8 and 0.9 are considered acceptable, and values over 0.9, excellent.

The models were compared to verify the existence of significant differences between the performance measurements (Accuracy, Specificity and AUROC) in the different classifier algorithms using the ${\textstyle t}$ test for coupled samples, with a level of significance of ${\textstyle \alpha =0.05}$.

5. Obtaining and discussion of results

Following the data balancing, as in Section 4.1, the remaining stages of the methodology were followed.

5.1. Feature coding

Following the procedures described in Section 4.2, the two configurations to be tested were obtained: a) Code I (Categorical Variables): with the 10 features categorized into 74 different alternatives; and b) Code II (Binarized Variables): with the 10 features transformed into 74 dummy variables. Detailed descriptions of the 10 self-explanatory features and Codes I and II are shown in Table A in the Appendix 1.

5.2. Results of the feature selection

Different “complete” and “summarized” models (filter method or information gain; wrapper) were constructed and tested and named as shown in Table 2, depending on whether the classes are balanced and also on the type of feature coding (categorical or binary).

	Complete Models (CM)				Summarized Models (SM)
	CM.A	CM.B	CM.C	CM.D	SM.A	SM.B	SM.C	SM.D
Class Balancing
Unbalanced Classes (5 432 instances)	x	x			x	x
Balanced Classes (2 388 instances)			x	x			x	X
Feature Coding
Code I Features (Categorical)	x		x		x		x
Code II Features (Binary)		x		x		x		x

Therefore, for example, CM.A is complete, the classes are unbalanced and its features are Code I (categorical features). The other models can be interpreted likewise.

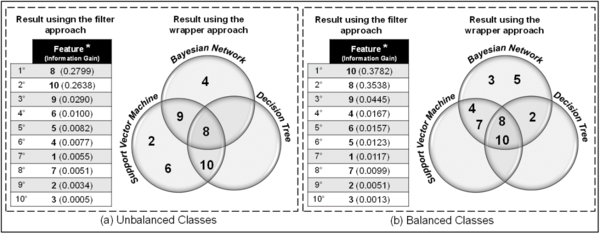
It was now time for the feature selection. The results of this selection are shown in Figure 3, in the format of Code I (categorical), with balanced and unbalanced classes for defining the ranking (obtained using the filter or information gain approach), and for constituting the subset of features for each classifier algorithm (obtained using the wrapper approach).

Figure 3. Ranking of features in Code I (categorical) format and selected subsets for each classifier algorithm Feature’s Legend: (1) Legal Status, (2) Gross Annual Revenue, (3) Number of Employees, (4) Company Activity, (5) Incorporation Data, (6) Time as Client, (7) Market Sector, (8) Risk Assessment, (9) Borrower’s Credit Limit, (10) Loan Restrictions. For more information, see Table A (Appendix 1).

According to the ranking shown in Figure 3, Features 8 and 10, “Risk Assessment” and “Loan Restrictions” are occupying positions 1 and 2 (table at the left in Figure 3), swapping their positions in the balanced classes (table at the right in Figure 3). Thus, these two features are highly relevant to the model, with the information gain higher than 0.26. Features 2 and 3, “Gross Annual Revenue” and “Number of Employees” (positions 9 and 10 in Figure 3) contributed least to the information gain in the model.

Moreover, Feature 8, “Risk Assessment”, was selected for the subset of features that result in greater “merit” (wrapper approach) for all thee classifier algorithms in both cases, Unbalanced and Balanced, as shown in the Venn diagram. This did not occur in the case of Feature 10, “Loan Restrictions”, which was selected in all the algorithms only when the classes were balanced.

Other features were also selected to compose each subset, but the interesting fact was the substantial reduction in their number, which went from 10 to a minimum of two features (8 and 10; DT with unbalanced classes) and a maximum of seven features (2, 3, 4, 5, 7, 8 and 10; BN with balanced classes).

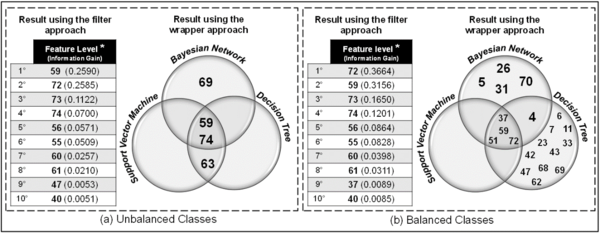
Meanwhile for Code II (binary), with balanced and unbalanced classes, the results of the feature selection are shown in Figure 4. With this coding, not only the features with all their levels were selected, but rather the specific levels of each feature with greater representativeness for the model.

Figure 4. Ranking of features in the Code II (binary) format and selected subset for each classifier algorithm Feature's Legend: (4) Simple partnership, (5) Individual limited company, (6) Individual entrepreneur, (7) Individual firm, (11) Civil association, (23) Industrial machinery, (26) Sales of cosmetics, toiletries and hygiene products, (31) Dental products, (33) Debt recovery and registered information, (37) IT Technical support, maintenance and service, (40) 15/02/1939 a 01/06/1997, (42) 20/02/2004 a 19/02/2009, (43) 26/02/2009 a 02/12/2016, (47) 16/06/2011 a 05/12/2016, (51) Middle-level business, (55) A, (56) B, (59) E, (60) Level 1, (61) Level 2, (62) Level 3, (63) Level 4, (68) Level 9, (69) Level 10, (70) Level 11, (72) Impeditive restriction, (73) No restriction, (74) Weak restriction/information. For more information, see Table A (Appendix 1).

The same features (59 and 72) occupied the first two places in the ranking using the filter approach, reversing positions in the case of unbalanced and balanced classes. These features are actually levels of the “Risk Assessment” and “Loan Restrictions” features, representing “Risk E” and “Impeditive Risk”. In other words, the binary format revealed the specific level of the most important features for the models.

Feature 59, “Risk E”, which appears in the intersection of the Venn diagram, was selected for the subset of features that results in better “merit” (wrapper approach) for all three classifier algorithms in both cases, Unbalanced and Balanced. In the case of the unbalanced classes, there was a radical reduction in the number of features, going from 74 to four in the total for the subset, with three in each classifier algorithm: BN with Features 59, 69 and 74; DT and SVM with Features 59, 74 and 63. With the balanced classes, this reducing effect was less marked, except for the SVM (Features 37, 51, 59 and 72). It remains to be seen whether this reduction in the number of features is advantageous in the sense of better performance of the models.

5.4. Results of the classifier algorithms

The algorithms used (BN, DT and SVM) were implemented in WEKA^® software (Waikato Environment for Knowledge Analysis, available at: http://www.cs.waikato.ac.nz/ml/weka) and the tests were conducted with the option of cross-validation (${\displaystyle k}$-fold), with ${\displaystyle k=10}$ partitions and with a standard configuration in all parameters. More specifically, in the case of BN, the SimpleEstimator method was used with ${\displaystyle \alpha =0.5}$ to determine the values of the conditional probability tables [76] and the K2 method to determine the network structure. For the DT, the depth of the tree was considered unlimited, 100 was the number of iterations to be used and a single random seed was used. For the SVM, the complexity parameter, ${\displaystyle c=1}$, the logistic method was used for calibration, and the Polynomial Kernel to determine the kernel.

The results of the tests with the different classifier algorithms, considering the different constructed models (CM.A to CM.D and SM.A to SM.D), are shown in Table 3. In this table, the metrics for assessing the performance of the models are presented, as well as a comparison to determine whether there is a significant difference between the performances of the complete models.

Assessment Metric	Classifier Algorithm	Complete Models				Summarized Model
		CM.A	CM.B	CM.C	CM.D	SM.A	SM.B	SM.C	SM.D
Accuracy	BN	0.873	0.858	0.856	0.858	0.888	0.890	0.862	0.867
	SVM	0.889+	0.890+	0.861	0.861	0.890	0.890	0.862	0.864
	DT	0.882+	0.879+	0.848	0.856	0.890	0.890	0.863	0.873
Specificity	BN	0.719	0.768	0.886	0.891	0.619	0.620	0.913	0.950
	SVM	0.616-	0.616-	0.946+	0.946+	0.617	0.619	0.947	0.952
	DT	0.681-	0.669-	0.874	0.886	0.619	0.619	0.925	0.946
AUROC	BN	0.931	0.928	0.925	0.923	0.863	0.830	0.925	0.913
	SVM	0.791-	0.791-	0.861-	0.861-	0.792	0.793	0.852	0.864
	DT	0.923-	0.925	0.916-	0.918	0.920	0.830	0.918	0.915

The performances of the complete models for each performance metric are compared by attributing superscript signs, (+) and (-), when there is a greater or lesser significant difference, respectively, always compared with the performance with the BN classifier algorithm. For instance, in Model CM.A, the accuracies of the SVM (0.889) and DT (0.882) algorithms showed significant differences in relation to that of BN (0.873). As this difference is greater, a plus sign (+) was added. Regarding the specificity of this CM.A, there was a significant difference for the SVM (0.616) and DT (0.681) in relation to BN (0.719). However, in this case, the value was lower (-).

It should be highlighted that for each CM, the tests were conducted with an identical model (same features) to apply the three classifier algorithms. Thus, the t test could be used to compare their performances. However, for the Summarized Models (SMs), the Wrapper method has a classifier dependency and it can select different features for each classifier technique, becoming impossible to compare means between these classifiers.

Although this statistical comparison could not be made, the accuracies of all the SMs are greater than or at least equal to those of the CMs. In other words, the feature selection stage, in addition to significantly reducing the number of features, also resulted in greater accuracy in all the models. However, regarding the specificity of the model, improvements were only seen in the models with balanced classes (SM.C and SM.D). With the AUROC, it is not possible to establish a generalization of improvement among the SMs in comparison with the CMs, as each model is unique.

The greatest accuracy achieved by the complete models was 0.890 by the SVM only in CM.B. In the summarized models, the maximum value was also achieved by BN (SM.B), SVM (SM.A and SM.B) and DT (SM.A and SM.B) with this same value (0.890). In other words, with the summarized models, the maximum accuracy was obtained more times.

Although the SVM achieved the highest values for accuracy several times, this algorithm was disappointing in assessments with the AUROC metric, with much lower values in all the models, including the summarized models. Furthermore, as expected, the specificity of the models, complete and summarized, was greater in those with balanced classes.

In general, SM.D had the best accuracy for the SVM technique, with a value of 0.952. Regarding the performance of the AUROC metric, CM.A for the BN technique had the best result, with a value of 0.931.

6. Conclusions

Addressing the application of improved and sophisticated tools to increasingly complex problems, this work achieved its goal, as it adopted an analysis methodology that incorporated various innovative ML techniques to obtain a predictive credit scoring model to minimize losses for banking institutions.

In addition to the differential in the use of these techniques, in this work, an alternative way from those usually employed to classify clients as “defaulters” or “non-defaulters” was presented. In other words, a “default index” was used instead of only checking for overdue operations. Another differential lay in defining the features considered to compose the model, which are not related to the behavior of clients in previous operations so, in this way, new clients (without a historical data) of the institution can also be classified using the methodology.

With the results obtained through the proposed methodology, it was possible to answer the questions outlined at the beginning of the article: a) All the three methods (BN; SVM and DT) presented similar performances for the credit scoring prediction close to 95% (specificity) as can be observed in Table 3, in other words, these models can correctly classify about 95% of clients as “defaulters” or “non-defaulters”. This result reinforces the main intention of a financial institution when using these classifier algorithms (ML): identify as assertively as possible clients who are prone to being “defaulters”, it is preferable to use a technique with greater specificity; (b) Besides, we can say that for the problem approached here, the class unbalancing affect the performance of the model, as we can verify comparing the CM and SM models in Table 3, i.e., it is important that the classes are balanced in order to get better performance results; (c) The feature selection stage contributes to the credit scoring model, showing what are the main features or in which features the specialists must give special attention. In the approached problem, the features “risk assessment” and “loan restrictions” are occupying the main positions, as shown in Figure 3. On the other hand, the features “gross annual revenue” and “number of employees” are less important; (d) As for the practical implications of the present study, it becomes fundamental in a critical scenario of instability of Brazilian companies regarding “default”, since in March 2019 the number of debtors grew by 3.3% (Serviço de Proteção ao Crédito, SPC, or Credit Protection Services). In general, the market is slow to act against these high levels of defaulting companies [77, 78].

Suggestions for future studies include conducting tests with other classifier algorithms, as Random Forest, XGBoost, and others, based on ensemble method, for example, always with a view to improving their performance as much as possible. Another suggestion is related to the random undersampling to solve the unbalanced data problem, which sometimes causes bias results; so, in this way, it would be interesting implement it more than 10 times using the average, standard deviation of accuracy and specificity as the results.

Indeed, some other metrics for assessment other than those used in this article, such as the F-score, could be used. Another suggestion would be construct a specific model from the stratification of a relevant feature such as “Risk”, i.e., constructing, training and testing a model for each class (Risk = A; B; C; D; E). There is also the possibility of using data from the same banking institution for an analysis involving the opinion of a decision maker, such as the credit manager of the institution in question to employ multiple criteria decision techniques.

Acknowledgements

This study was financed in part by PUCPR and the Coordination for the Improvement of Higher Education Personnel – Brazil (CAPES), and by the National Council for Scientific and Technological Development – Brazil.

References

Appendix 1

Features (1)	Levels of features (2)	Types of coding
		I – Categorical (3)	II – Binary(4)
(1) Legal Status	(1) Limited partnership	1	100000000000
	(2) Private company limited by shares	2	010000000000
	(3) Individual micro entrepreneur	3	001000000000
	(4) Simple partnership	4	000100000000
	(5) Individual limited company	5	000010000000
	(6) Individual entrepreneur	6	000001000000
	(7) Individual firm	7	000000100000
	(8) Closed Corporation	8	000000010000
	(9) For-profit organization	9	000000001000
	(10) Collective partnership	10	000000000100
	(11) Civil association	11	000000000010
	(12) State authority	12	000000000001
(2) Gross Annual Revenue	(13) 0 a 536200	1	1000
	(14) 536237,04 a 1372514,63	2	0100
	(15) 1372791,74 a 3156893,44	3	0010
	(16) 3158540,99 a 769665000,00	4	0001
(3) Number of Employees	(17) 0 a 1	1	1000
	(18) 2 a 4	2	0100
	(19) 5 a 11	3	0010
	(20) 12 a 5113	4	0001
(4) Company Activity	(21) Real estate management	1	1000000000000000000
	(22) Hotels	2	0100000000000000000
	(23) Industrial machinery	3	0010000000000000000
	(24) Production of circuses and similar events	4	0001000000000000000
	(25) Public road transport	5	0000100000000000000
	(26) Sales of cosmetics, toiletries and hygiene products	6	0000010000000000000
	(27) Fair and party organization	7	0000001000000000000
	(28) Department stores or shops	8	0000000100000000000
	(29) Customs dispatching	9	0000000010000000000
	(30) Road fright transport	10	0000000001000000000
	(31) Dental products	11	0000000000100000000
	(32) Tatto and piercing services	12	0000000000010000000
	(33) Debt recovery and registered information	13	0000000000001000000
	(34) Retailer of vehicle parts and accessories	14	0000000000000100000
	(35) Repair os electric and eletronic equipamento	15	0000000000000010000
	(36) Retail Jeweler	16	0000000000000001000
	(37) IT Technical support, maintenance and servisse	17	0000000000000000100
	(38) Outpatient medical services	18	0000000000000000010
	(39) Footwear retailer	19	0000000000000000001
(5) Incorporation Data	(40) 15/02/1939 a 01/06/1997	1	1000
	(41) 03/06/1997 a 19/02/2004	2	0100
	(42) 20/02/2004 a 19/02/2009	3	0010
	(43) 26/02/2009 a 02/12/2016	4	0001
(6) Time as Client	(44) 23/06/1975 a 29/10/2003	1	1000
	(45) 30/10/2003 a 26/02/2008	2	0100
	(46) 27/02/2008 a 15/06/2011	3	0010
	(47) 16/06/2011 a 05/12/2016	4	0001
(7) Market Sector	(48) Small Company	1	1000000
	(49) Company	2	0100000
	(50) Micro Business	3	0010000
	(51) Middle-level business	4	0001000
	(52) Company (unclassifiable)	5	0000100
	(53) Corporate	6	0000010
	(54) State	7	0000001
(8) Risk Assessment	(55) A	1	10000
	(56) B	2	01000
	(57) C	3	00100
	(58) D	4	00010
	(59) E	5	00001
(9) Borrower’s Credit Limit (hierarchical decision level)	(60) Level 1	1	100000000000
	(61) Level 2	2	010000000000
	(62) Level 3	3	001000000000
	(63) Level 4	4	000100000000
	(64) Level 5	5	000010000000
	(65) Level 6	6	000001000000
	(66) Level 7	7	000000100000
	(67) Level 8	8	000000010000
	(68) Level 9	9	000000001000
	(69) Level 10	10	000000000100
	(70) Level 11	11	000000000010
	(71) Level 12	12	000000000001
(10) Loan Restrictions	(72) Impeditive restriction	1	100
	(73) No restriction	2	010
	(74) Weak restriction/information	3	001