m (Scipediacontent moved page Review 696322221495 to Draft Trias 212243902 without leaving a redirect) |
Dani trias (talk | contribs) m (Dani trias moved page Draft Trias 212243902 to Review 784880587039) |
(No difference)
| |
Revision as of 11:31, 12 May 2025
1. Introducción
El proyecto SUCCESSBLADE tiene como objeto le evaluación de una pala para aerogenerador pequeño usando un material compuesto que emplea una resina reciclable, de manera que, en el fin de vida de la pala, la resina se pudiera utilizar en la fabricación de otra pala de con las mismas características. En el ámbito del proyecto se considera también el uso, al menos parcial, de fibras naturales.
Es bien sabido que las fibras naturales ofrecen una rigidez y resistencia menor que las fibras de vidrio y de carbono usadas habitualmente en la fabricación de palas para aerogenerador. Sin embargo, pueden ofrecer algunas ventajas como el mayor factor de amortiguamiento que podría conllevar, por ejemplo, una reducción de la amplitud de las vibraciones.
El factor de amortiguamiento (ζ) se define como la relación entre el amortiguamiento real (c) respecto el amortiguamiento crítico (cc):
|
|
(1) |
De manera que 0 supone la absencia de amortiguamiento, valores entre 0 y 1, conducen a una respuesta oscilatoria con distinto grado de amortiguamiento, 1 es el valor de transición denominado amortiguamiento crítico y finalmente valores superiores a 1 corresponden al sobre-amortiguamiento, es decir la absencia de respuesta oscilatoria.
Otra medida posible del amortiguamiento es el índice de decrecimiento logarítmico δ:
|
|
(2) |
Que se puede relacionar con las medidas anteriores mediante:
Los metales ingenieriles tienen valores del factor de amortiguamiento inferiores a 0.05 (5%), la mayoría de ellos inferiores al 0.02, mientras que los materiales compuestos laminados de fibra de vidrio y fibra de carbono se encuentran en el rango, aún inferior de 1.25-3% [1] [2] [3]. Algunos investigadores han mostrado como se puede usar la inserción de capas de fibra de lino en un laminado de fibra de carbono, de manera que la rigidez se obtenga de este segundo material, mientras que la fibra de lino aporte un mayor factor de amortiguamiento [2].
Para la determinación experimental del factor de amortiguamiento se pueden usar métodos basados en martillo de impacto y cámara de alta velocidad [3] o bien un dispositivo de impacto y cámara de alta velocidad [1] . En ambos casos se pretende capturar la curva de decaimiento y a partir de ella deducir el índice de decremento logarítmico δ. Si bien el uso del método de la vibración en voladizo (vibration cantilever beam method) es aparentemente sencillo y rápido, y se presentaba hace unos años como muy prometedor [4], ni los estándares existentes [5] ni las escasas publicaciones científicas que emplean este método experimental detallan los parámetros a utilizar para garantizar tanto la precisión como repetitividad de los resultados.
En el presente trabajo analiza los principales parámetros del mencionado ensayo (tipo de excitación, número de repeticiones de la excitación y método de cálculo de la media, posición del acelerómetro, masa del acelerómetro) que pueden afectar la medición con el fin de proponer una metodología que permita la obtención experimental del factor de amortiguamiento en el citado proyecto.
2. Materiales y métodos
Materiales
Se fabrican paneles para el ensayo de las principales propiedades mecánicas usando fibra unidireccional GF 8092 de 625 g/m2 y un tejido biaxial 45o de fibra de vidrio BXE600 1270 STD. Cada tipo de fibra se combina con dos resinas: un epoxy comercial (sicomin) y la resina reciclable (akelite). De cada panel se cortan las probetas 250mm x 10 mm, para la obtención del factor de amortiguamiento. La Tabla 1 muestra también los laminados, con el módulo de Young en la dirección longitudinal (obtenido mediante norma ASTM D3039), espesor y orientación de las capas de las probetas empleadas.
| Material | E11 [GPa] | Espesor [mm] |
| GF 8092 UD 0o + Sicomin | 45.05 | 1.1 |
| GF 8092 UD 90o + Sicomin | 11.66 | 2 |
| GF 8092 UD 0o +akelite | 43.94 | 1.1 |
| GF 8092 UD 90o +akelite | 10.10 | 2 |
| BXE600 1270 STD BIAX ±45 o+Sicomin | 8.45 | 3.7 |
| BXE600 1270 STD BIAX ±45 o+akelite | 10.35 | 3.7 |
Equipo
El equipo está basado en el vibrador Bruel & Kjaer LDS V406, con 6 insertos M4 más 1 central, diámetro armadura de 38mm y fuerza máxima de 98N. Éste se alimenta mediante el amplificador Bruel & Kjaer LPA100. Se dispone de acelerómetros CCLD miniatura, el modelo B&K 10 mV/g, 0,6 gramos, 10 mV/m·s-2 de 0.6 g y el modelo B&K 4508-1 de 100 mV/m·s de 4.8 g de masa que se adhieren a las muestras mediante cera de abeja.
El módulo de adquisición de 4 canales de entrada y 1canal de salida (generador) hasta 25,6 kHz sirve para adquirir las medidas de los acelerómetros y para controlar el vibrador.
Método
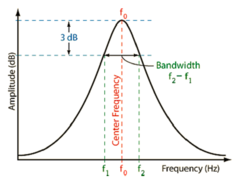
Se utiliza el método del medio ancho de banda (half bandwith) o de “los 3dB”, que se basa en la obtención del ancho de banda (f2-f1) en que el pico de la frecuencia propia se reduce en 3dB, tal como se muestra en la Figura 1 (derecha). Con esto se calcula el factor de amplificación Qi del modo de vibración i como:
|
|
(3) |
A partir de este se puede calcular el factor de amortiguamiento ζi como:
|
|
(4) |
Tal como puede apreciarse por el hecho que las expresiones anteriores dependen del modo de vibración i, el factor de amortiguamiento no es constante.
Por otro lado, como es sabido, para el montaje descrito se pueden calcular analíticamente las frecuencias naturales usando la expresión
|
|
(5) |
Por otro lado, el mismo valor se puede obtener mediante un modelo de elementos finitos. Se calculan
| Proveta | fn según ec. (3) [Hz] | fn según FEM
[Hz] |
| UD + Sicomin 0o | 18.247 | 18.238 |
| UD + Sicomin 90o | 16.878 | 17.413 |
| UD+akelite 0o | 18.021 | 18.021 |
| UD+akelite 90o | 15.709 | 16.968 |
| BIAX ±45 o+Sicomin | 26.581 | 22.188 |
| BIAX ±45 o+akelite | 29.418 | 29.451 |
2. Análisis paramétrico
Excitación
La excitación debe producirse en un rango de frecuencias que incluyan las frecuencias propias en que se desea determinar el factor de amortiguamiento. La opción más inmediata es generar un barrido de frecuencias equidistantes entre un valor mínimo y un máximo, con una tasa de variación prefijada. Por otro lado, el software de control permite la generación de vibraciones aleatorias dentro de un rango predeterminado. Debe tenerse en cuenta que, en situaciones en que las frecuencias naturales muestran picos muy estrechos la excitación puede producir errores de filtración [6].
En todo caso, la excitación se repite un número de veces y la medida se calcula como la media de los resultados. Esta media puede ser lineal (todas las medidas tienen el mismo peso) o bien exponencial, que asigna mayor relevancia a medidas posteriores en el tiempo, contribuyendo a evitar el filtrado, como se ilustra en la
Para poder excitar un rango de frecuencias que incluya el primer modo de vibración se toma un rango con centro en 18 Hz, un ancho de banda de 12.5 Hz y una resolución de 0.125 Hz. Los resultados de los distintos ensayos se muestran en la Tabla 2. Hay que tener en cuenta que corresponden a valores del factor de amortiguamiento en el primer modo de vibración en el que, tal como se menciona en [5], la medida del factor de amortiguamiento se ve afectada por el encastre en mayor medida que en los otros modos.
| Método de excitación | Repeticiones | Tipo de media | Tiempo [s] | fn [Hz] | ζ [%] |
| Periodic Random | 2 | Exponencial | 16 | 22 | 3.92 |
| Burst Random | 2 | Exponencial | 16 | 21.88 | 0.83 |
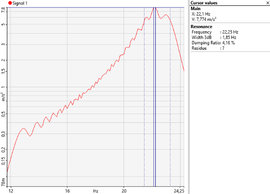
| Periodic Chirp | 10 | Lineal | 80 | 22.25 | 4.16 |
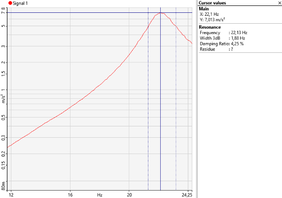
| Periodic Random | 10 | Exponencial | 80 | 22.13 | 4.25 |
| Pseudo Random | 10 | Exponencial | 26.67 | 22.5 | 1.31 |
| Random | 10 | Lineal | 58.67 | 22.5 | - |
| Random | 20 | Lineal | 105.35 | 21.63 | - |
| Random | 50 | Lineal | 138.7 | 21.75 | 3.73 |
| Random | 100 | Lineal | 272 | 22 | 3.96 |
Posición del acelerómetro
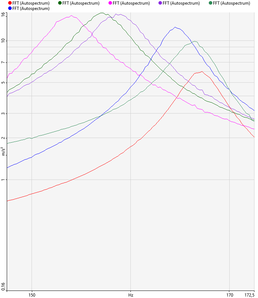
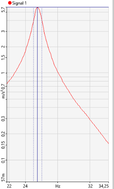
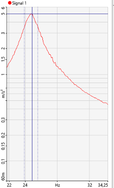
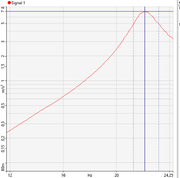
Para este análisis se fija el modo de excitación a periodic Random realizando la media exponencial de 10 repeticiones. Se sitúa el acelerómetro a distintas distancias medidas des del punto de sujeción. La Figura 3 muestra como no solo se obtiene un valor menor de Q sino que se estima también una frecuencia natural mayor. Este efecto se acentúa conforme el acelerómetro se aleja del extremo.
|
|
|
| X = ½ L | X= 2/3 L | X = L |
| fn = 25.5 Hz, Q=2.01% | fn= 24.88 Hz, Q = 3.39% | fn=22.13 Hz, Q=4.25% |
Si se realiza en mismo análisis para el segundo modo de vibración también se produce el desplazamiento de la frecuencia adquirida, pero en este caso el factor de amortiguamiento tiene una variabilidad inferior (1.21 – 1.66%), como se muestra en la Figura 4.
Masa del acelerómetro
Tal como se ha mencionado en la sección anterior se dispone de acelerómetros de con masas distintas. Aunque se da por hecho que el de masa menor (0,6 g) proporcionará un resultado más preciso y, disponiendo de él, carece de sentido considerar otro de una masa mayor (4,8g) se pretende evaluar la diferencia de resultados obtenidos por si en caso de necesidad podría considerarse el uso del segundo. En este caso se obtiene una frecuencia propia de 16.38Hz y un factor de amortiguamiento del 4.24%.
3. Conclusiones
De los resultados se deduce que la excitación Periodic Random ofrece una mayor precisión incluso para un número relativamente pequeño de repeticiones. A pesar de las diferencias en la obtención de Q, todos los métodos permiten estimar la frecuencia natural amortiguada con facilidad.
La posición del acelerómetro condiciona la captura de la frecuencia natural amortiguada y del factor de amortiguamiento.
La masa del acelerómetro afecta la medición de la frecuencia propia, tal como se indica en [6]. Sin embargo, la estimación del factor de amortiguamiento parece alterarse muy poco. Se deberá explorar con más detalles este aspecto.
4. Agradecimientos
Los autores agradecemos el apoyo financiero del Ministerio de Ciencia, Innovación y Universidades de España a través del proyecto coordinado SUCCESS BLADE (TED2021-130201B-C31 y TED2021-130201B-C32), cofinanciado por NextGenerationEU, Unión Europea).
5. Bibliografía
| 1. | MURCINKOVA, Z. et al. Damping properties of fibre composite and conventional materials measured by free damped vibration response. Advances in Mechanical Engineering, v. 11, n. 5, p. 1-11, 2019. |
| 2. | SAEID HOSSEINPOUR DASHATAN, M. S. Z. Z. E. G. J. M. Y. H. H. N. D. Enhanced vibration damping and viscoelastic properties of flax/epoxy. Composites Part A, n. 175, 2023. ISSN 107819. |
| 3. | ZHANG, B. et al. Research on damping performance and strength of the composite laminate. Nature. Scientific Reports, n. 11, 2021. ISSN 18281. |
| 4. | GIBSON, R. F. Modal vibration response measurements for characterization. Composites Science and Technology , v. 60, p. 2769-2780, 2000. |
| 5. | UNE. Plastics. Determination of dynamic mechanical properties. Part 3: Flexural vibration. Resonance curve method. ISO. [S.l.]. 2021. (UNE-EN ISO 6721-3). |
| 6. | BRÜEL & KJAER. Structural Testing. Part 1: Mechanical Mobility Measurements. Brüel & Kjaer. [S.l.]. 1988. |
Document information
Published on 21/01/26
Accepted on 21/07/25
Submitted on 12/05/25
Volume 09 - Comunicaciones MatComp25 (2025), Issue Núm. 3 - Caracterización Experimental, 2026
DOI: 10.23967/r.matcomp.2025.09.33
Licence: Other
Share this document
claim authorship
Are you one of the authors of this document?