Carmemlage (talk | contribs) |
Carmemlage (talk | contribs) |
||
| Line 29: | Line 29: | ||
Perfis tubulares estruturais são aplicados em diversos tipos de sistemas treliçados, tais como treliças planas e espaciais de passarelas de pedestres, pontes, coberturas, estádios, torres, guindastes, plataformas offshore entre outros. Um dos requisitos importantes a ser considerado no projeto desses sistemas treliçados é o cálculo de seções transversais adequadas para as barras, de forma a alcançar um nível de segurança e desempenho estrutural admissíveis. | Perfis tubulares estruturais são aplicados em diversos tipos de sistemas treliçados, tais como treliças planas e espaciais de passarelas de pedestres, pontes, coberturas, estádios, torres, guindastes, plataformas offshore entre outros. Um dos requisitos importantes a ser considerado no projeto desses sistemas treliçados é o cálculo de seções transversais adequadas para as barras, de forma a alcançar um nível de segurança e desempenho estrutural admissíveis. | ||
| − | Na otimização paramétrica, as variáveis | + | Na otimização paramétrica, as variáveis independentes, cujos valores podem ser alterados para melhorar um projeto, são chamadas de variáveis de projeto, que por sua vez geralmente são parâmetros geométricos, como as dimensões das seções transversais das barras. Assim, a otimização paramétrica pode ser utilizada para auxiliar os engenheiros a determinar as melhores dimensões viáveis para as barras desses sistemas sujeitas a um determinado conjunto de restrições de projeto impostos pelas normas ou códigos. Tais soluções, na maioria dos problemas de engenharia, partem da necessidade de obter o custo mínimo possível de fabricação, peso mínimo da estrutura ou o máximo de confiabilidade possível [1]. |
| − | Dentre as técnicas de computação evolucionárias, os algoritmos genéticos (AGs) tem sido utilizados com sucesso para a otimização de sistemas treliçados | + | Dentre as técnicas de computação evolucionárias, os algoritmos genéticos (AGs) tem sido utilizados com sucesso para a otimização de sistemas treliçados [2,3,4,5,6]. Os AGs apresentam uma melhor robustez em relação aos métodos matemáticos tradicionais, ou seja, são capazes de atingir ou ficarem próximos do extremo (ótimo) global da função objetivo, sendo menos propensos a ficarem presos em extremos locais. Os AGs usam métodos estocásticos para gerar de forma aleatória as possíveis soluções do problema de otimização dentro do espaço de projeto [2]. São algoritmos de busca inspirados nos conceitos de seleção natural e genética, baseados na estratégia de sobrevivência do mais apto [7]. |
| − | Alguns problemas de otimização estrutural podem apresentar um grande número de variáveis ou serem de difícil modelagem matemática e geométrica. Além disso, dependendo do tipo de variáveis, a função objetivo também pode ser complexa e difícil de ser definida de maneira explícita. Há no mercado mundial uma ampla disponibilidade de ferramentas comerciais, tanto para a análise quanto para a otimização estrutural, | + | Alguns problemas de otimização estrutural podem apresentar um grande número de variáveis ou serem de difícil modelagem matemática e geométrica. Além disso, dependendo do tipo de variáveis, a função objetivo também pode ser complexa e difícil de ser definida de maneira explícita. Há no mercado mundial uma ampla disponibilidade de ferramentas comerciais, tanto para a análise quanto para a otimização estrutural, conforme descrito em [8], que podem trabalhar de forma autônoma ou integradas e que podem viabilizar a solução desses e de outros problemas de otimização de ordem estrutural. Estudos de otimização envolvendo a integração de programas podem ser encontrados em [9,10,11]. |
| − | Um dos grandes desafios dos problemas de otimização estrutural é lidar com as restrições de projeto, pois a maioria dos problemas tendem a ser não-lineares, o que complica a solução do problema. A fim de obter soluções para problemas de otimização de sistemas treliçados de ordem mais prática é necessário restringir o problema em função dos requisitos normativos, tais como os apresentados | + | Um dos grandes desafios dos problemas de otimização estrutural é lidar com as restrições de projeto, pois a maioria dos problemas tendem a ser não-lineares, o que complica a solução do problema. A fim de obter soluções para problemas de otimização de sistemas treliçados de ordem mais prática é necessário restringir o problema em função dos requisitos normativos, tais como os apresentados em [12,13].Este último trabalho [13] trata mais especificamente do dimensionamento ótimo de estruturas treliçadas tubulares. Em se tratando de estruturas tubulares, há diversas normas e códigos, tais como as apresentadas em [14,15,16], que contemplam seu dimensionamento. |
Nesse contexto, o objetivo deste trabalho é avaliar a confiabilidade e eficiência da metodologia interativa, com base em um algoritmo genético, que seja capaz de otimizar estruturas de ordem prática, com restrições normativas, eliminando assim a necessidade de grande revisão ou adaptação do modelo ótimo. Os resultados serão comparados com os da literatura. | Nesse contexto, o objetivo deste trabalho é avaliar a confiabilidade e eficiência da metodologia interativa, com base em um algoritmo genético, que seja capaz de otimizar estruturas de ordem prática, com restrições normativas, eliminando assim a necessidade de grande revisão ou adaptação do modelo ótimo. Os resultados serão comparados com os da literatura. | ||
| − | Este artigo propõe uma metodologia interativa para a otimização de estruturas, utilizando dois programas comerciais: Ansys® [17] e Matlab® [18]. A metodologia proposta é baseado na integração desses programas, utilizando-se do Método dos Elementos Finitos (MEF) presente no programa Ansys® | + | Este artigo propõe uma metodologia interativa para a otimização de estruturas, utilizando dois programas comerciais: Ansys® [17] e Matlab® [18]. A metodologia proposta é baseado na integração desses programas, utilizando-se do Método dos Elementos Finitos (MEF) presente no programa Ansys® para a análise da estrutura, em conjunto com a Ferramenta de otimização GA de Algoritmos Genéticos do Matlab®, adaptada para o problema em questão. Por outro lado, o modelo estrutural é criado de forma paramétrica por meio da linguagem APDL (''Ansys Parametric Design Language'') via arquivo de texto. O ''script'' de otimização desenvolvido não requer intervenção do usuário até que a solução seja encontrada ou seja atingido um critério de parada. |
| − | A metodologia proposta será aplicada em dois modelos numéricos de treliças, sendo o primeiro um caso clássico da literatura e o segundo de uma das treliças analisadas por Jármai et al. [13], treliça plana formada por perfis tubulares circulares, com restrições de geometria, flambagem e modos de falha prescritos | + | A metodologia proposta será aplicada em dois modelos numéricos de treliças, sendo o primeiro um caso clássico da literatura e o segundo de uma das treliças analisadas por Jármai et al. [13], treliça plana formada por perfis tubulares circulares, com restrições de geometria, flambagem e modos de falha prescritos em [15,16]. No primeiro modelo, o objetivo é obter o menor peso possível da estrutura, variando-se as áreas das seções transversais das barras; enquanto que no segundo modelo, as dimensões das seções transversais (diâmetros e espessuras dos tubos) serão variadas com o objetivo de obter o menor volume possível da estrutura. |
A principal contribuição deste trabalho consiste na proposição de uma metodologia integrada de dois programas, universalmente usados, aplicados como ferramentas de projeto na otimização de estruturas treliçadas tubulares sob um conjunto de restrições normativas, num processo automatizado. | A principal contribuição deste trabalho consiste na proposição de uma metodologia integrada de dois programas, universalmente usados, aplicados como ferramentas de projeto na otimização de estruturas treliçadas tubulares sob um conjunto de restrições normativas, num processo automatizado. | ||
Revision as of 13:43, 28 January 2019
Abstract
Practical size structural optimization problems can involve a large number of variables and constraints that meet regulatory requirements for safety and structural performance. Most optimization problems tend to find the minimum value of the objective function within a feasible set that satisfies the constraints. Among evolutionary computation techniques, genetic algorithms (GAs) have been successfully used for the optimization of structures, including lattice systems. This article proposes an automated interactive methodology for the optimization of structures based on the integration of two commercial programs: Ansys and Matlab. The developed script uses the Finite Element Method for the analysis of the structure, together with the Genetic Algorithms for the optimization. The objective of the article is to evaluate the applicability, precision and efficiency of the proposed methodology. Two numerical examples of trusses were solved with the proposed methodology, classic truss of the literature and truss with normative restrictions. The results show that the methodology is adequate for the solution of size structural optimization problems with a good precision of the results.
Resumo
Problemas de otimização estrutural paramétrica de ordem prática podem envolver um grande número de variáveis e restrições, que atendam aos requisitos normativos de segurança e desempenho estrutural. A maioria dos problemas de otimização tendem a encontrar o valor mínimo da função objetivo dentro de um conjunto viável que satisfaça as restrições. Entre as técnicas de computação evolucionária, os algoritmos genéticos (AGs) tem sido utilizados com sucesso para a otimização de estruturas, incluindo os sistemas treliçados. Esse artigo propõe uma metodologia interativa automatizada para a otimização de estruturas baseado na integração de dois programas comerciais: Ansys e Matlab. O script desenvolvido utiliza-se do MEF para a análise da estrutura, em conjunto com os Algoritmos Genéticos para a otimização. O objetivo do artigo é avaliar a aplicabilidade, precisão e eficiência da metodologia proposta. Foram resolvidos 2 exemplos numéricos de treliças com a metodologia proposta, treliça clássica da literatura e treliça com restrições normativas. Os resultados mostram que a metodologia é adequada para a solução de problemas de otimização estrutural paramétrica com uma boa precisão dos resultados.
Palavras-chave
Otimização paramétrica; treliças tubulares; restrições normativas; algoritmo genético; Integração Ansys e Matlab
1. Introdução
Perfis tubulares estruturais são aplicados em diversos tipos de sistemas treliçados, tais como treliças planas e espaciais de passarelas de pedestres, pontes, coberturas, estádios, torres, guindastes, plataformas offshore entre outros. Um dos requisitos importantes a ser considerado no projeto desses sistemas treliçados é o cálculo de seções transversais adequadas para as barras, de forma a alcançar um nível de segurança e desempenho estrutural admissíveis.
Na otimização paramétrica, as variáveis independentes, cujos valores podem ser alterados para melhorar um projeto, são chamadas de variáveis de projeto, que por sua vez geralmente são parâmetros geométricos, como as dimensões das seções transversais das barras. Assim, a otimização paramétrica pode ser utilizada para auxiliar os engenheiros a determinar as melhores dimensões viáveis para as barras desses sistemas sujeitas a um determinado conjunto de restrições de projeto impostos pelas normas ou códigos. Tais soluções, na maioria dos problemas de engenharia, partem da necessidade de obter o custo mínimo possível de fabricação, peso mínimo da estrutura ou o máximo de confiabilidade possível [1].
Dentre as técnicas de computação evolucionárias, os algoritmos genéticos (AGs) tem sido utilizados com sucesso para a otimização de sistemas treliçados [2,3,4,5,6]. Os AGs apresentam uma melhor robustez em relação aos métodos matemáticos tradicionais, ou seja, são capazes de atingir ou ficarem próximos do extremo (ótimo) global da função objetivo, sendo menos propensos a ficarem presos em extremos locais. Os AGs usam métodos estocásticos para gerar de forma aleatória as possíveis soluções do problema de otimização dentro do espaço de projeto [2]. São algoritmos de busca inspirados nos conceitos de seleção natural e genética, baseados na estratégia de sobrevivência do mais apto [7].
Alguns problemas de otimização estrutural podem apresentar um grande número de variáveis ou serem de difícil modelagem matemática e geométrica. Além disso, dependendo do tipo de variáveis, a função objetivo também pode ser complexa e difícil de ser definida de maneira explícita. Há no mercado mundial uma ampla disponibilidade de ferramentas comerciais, tanto para a análise quanto para a otimização estrutural, conforme descrito em [8], que podem trabalhar de forma autônoma ou integradas e que podem viabilizar a solução desses e de outros problemas de otimização de ordem estrutural. Estudos de otimização envolvendo a integração de programas podem ser encontrados em [9,10,11].
Um dos grandes desafios dos problemas de otimização estrutural é lidar com as restrições de projeto, pois a maioria dos problemas tendem a ser não-lineares, o que complica a solução do problema. A fim de obter soluções para problemas de otimização de sistemas treliçados de ordem mais prática é necessário restringir o problema em função dos requisitos normativos, tais como os apresentados em [12,13].Este último trabalho [13] trata mais especificamente do dimensionamento ótimo de estruturas treliçadas tubulares. Em se tratando de estruturas tubulares, há diversas normas e códigos, tais como as apresentadas em [14,15,16], que contemplam seu dimensionamento.
Nesse contexto, o objetivo deste trabalho é avaliar a confiabilidade e eficiência da metodologia interativa, com base em um algoritmo genético, que seja capaz de otimizar estruturas de ordem prática, com restrições normativas, eliminando assim a necessidade de grande revisão ou adaptação do modelo ótimo. Os resultados serão comparados com os da literatura.
Este artigo propõe uma metodologia interativa para a otimização de estruturas, utilizando dois programas comerciais: Ansys® [17] e Matlab® [18]. A metodologia proposta é baseado na integração desses programas, utilizando-se do Método dos Elementos Finitos (MEF) presente no programa Ansys® para a análise da estrutura, em conjunto com a Ferramenta de otimização GA de Algoritmos Genéticos do Matlab®, adaptada para o problema em questão. Por outro lado, o modelo estrutural é criado de forma paramétrica por meio da linguagem APDL (Ansys Parametric Design Language) via arquivo de texto. O script de otimização desenvolvido não requer intervenção do usuário até que a solução seja encontrada ou seja atingido um critério de parada.
A metodologia proposta será aplicada em dois modelos numéricos de treliças, sendo o primeiro um caso clássico da literatura e o segundo de uma das treliças analisadas por Jármai et al. [13], treliça plana formada por perfis tubulares circulares, com restrições de geometria, flambagem e modos de falha prescritos em [15,16]. No primeiro modelo, o objetivo é obter o menor peso possível da estrutura, variando-se as áreas das seções transversais das barras; enquanto que no segundo modelo, as dimensões das seções transversais (diâmetros e espessuras dos tubos) serão variadas com o objetivo de obter o menor volume possível da estrutura.
A principal contribuição deste trabalho consiste na proposição de uma metodologia integrada de dois programas, universalmente usados, aplicados como ferramentas de projeto na otimização de estruturas treliçadas tubulares sob um conjunto de restrições normativas, num processo automatizado.
2. Perfis tubulares em sistemas estruturais
Os perfis tubulares suportam cargas de compressão maiores que os perfis abertos convencionais, pois apresentam altos valores de raio de giração ao redor do eixo central de inércia. Os perfis de seção circular apresentam a mesma resistência a flambagem em todas as direções e nos retangulares a variação é pequena.
As ligações tubulares planas podem ter as mais variadas configurações dependendo de como são feitas as ligações dos montantes (dispostos perpendicularmente ao banzo) e/ou diagonais (dispostas obliquamente ao banzo) com o banzo. As ligações das diagonais e/ou montantes podem se dar com o banzo por soldagem simples ou por sobreposição. Podem ser identificadas pelas letras do alfabeto, a que se assemelham, gerando dessa forma as ligações uniplanares K, T, KT, N, X e Y.
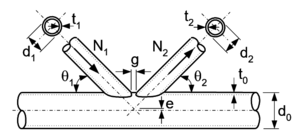
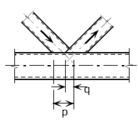
Na Figura 1a é ilustrado algumas das notações normalmente utilizadas numa ligação tubular planar do tipo K, com perfis tubulares circulares. Os números subscritos são utilizados para denotar o tipo de membro estrutural: o subscrito 0 refere-se ao banzo e os subscritos 1 ou 2 referem-se as diagonais. O termo d0, d1 e d2 são o diâmetros exteriores dos perfis circulares; t0, t1 e t2 correspondem as espessuras dos perfis; o termo g (gap) é o vão entre os elementos soldados; o termo e é a excentricidade entre a linha de centro do banzo e o prolongamento da linha central das diagonais/montante; θ1 e θ2 são o ângulo formado entre a diagonal e o banzo e N1 e N2 são as cargas axiais. Quando ocorre a sobreposição entre os elementos soldados, diz-se que a ligação é do tipo overlap ![]() , conforme ilustrado na Figura 1b.
, conforme ilustrado na Figura 1b.
(a) |
(b) |
| Figura 1.
Variáveis geométricas de uma ligação tubular do tipo K: (a) com afastamento; (b) com sobreposição. Fonte: Wardenier et al. [16] | |
3. Otimização estrutural paramétrica
Em geral, a otimização paramétrica envolve a minimização de uma função objetivo das variáveis de projeto sujeitas a um determinado conjunto de restrições. De acordo com Bendse e Sigmund [19], a principal característica de um problema de otimização paramétrica é que o domínio do modelo de projeto e das variáveis de estado é conhecido a priori.
A forma matemática padrão de um problema de otimização estrutural paramétrica pode ser escrita de acordo com as Equações 1, 2, 3 e 4 a seguir:
|
|
|
(1) | ||
|
|
|
(2) | ||
|
|
|
(3) | ||
|
|
|
(4) |
onde x = {x1, x2, ..., xk}T é o vetor das variáveis de projeto, f( x ) é a função objetivo, gi ( x ) são as restrições de desigualdade, hj ( x ) são as restrições de igualdade, e blInf e blSupsão, respectivamente, o limite inferior e o limite superior das variáveis de projeto. Assim, procura-se encontrar o valor mínimo da função objetivo dentro de uma região viável do domínio, que satisfaça as restrições.
4. Algoritmos genéticos
O algoritmo genético é um método heurístico e diferentemente das técnicas matemáticas de programação usuais, utiliza-se de técnicas de busca estocástica para definir soluções aleatórias no espaço de projeto e, então convergi-las para um valor ótimo. Além disso, os AGs são frequentemente utilizados na otimização estrutural, pois além de serem capazes de capturar soluções próximas ao ótimo global, podem operar com variáveis discretas, contínuas, inteiras e reais; além de tratar com espaços de busca convexos e não convexos.
Os AGs são baseados nos princípios da genética e evolução natural das espécies proposta por Charles Darwin e que considera a sobrevivência dos indivíduos mais aptos, Goldberg [7]. Assim, os indivíduos que constituem as possíveis soluções candidatas do problema de otimização são representados por uma cadeia de bits ou caracteres, correspondentes ao genótipo. O genótipo é composto de um ou mais cromossomos.
Os algoritmos evolucionários, tais como os AGs, requerem uma função objetivo e uma função aptidão (fitness), que são fundamentalmente diferentes. De acordo com Coello et al. [20], a função objetivo define a condição de ótimo do AG (e é uma característica do domínio do problema), enquanto a função aptidão avalia o quão boa uma solução particular satisfaz essa condição. Na função aptidão é onde insere-se as restrições do problema. Genericamente, a função aptidão pode ser definida de acordo com a Equação 5:
|
|
|
(5) |
onde f (x) é a função objetivo e fpenal(x) é a função de penalização, onde estão inseridas as restrições do problema. Se todas as restrições são satisfeitas fpenal (x) = 0. Portanto, neste caso, a função aptidão equivale à função objetivo.
O processo de otimização por meio dos AGs normalmente envolve as seguintes etapas: (1) uma população de indivíduos é criada de forma aleatória; (2) eles passam por um processo de evolução simulada que envolve etapas de avaliação e seleção, onde seleciona-se os indivíduos mais aptos; (3) cria-se uma nova população (próxima geração), por meio de operadores genéticos, tais como, crossover (cruzamento) e mutação. O processo anterior se repete até que seja atingido um ponto ótimo (solução candidata viável) ou seja alcançado um critério de parada. Resultados ligeiramente diferentes são produzidos a cada execução do algoritmo genético, em função de sua natureza estocástica e por envolver operadores aleatórios. São necessárias várias execuções para criar confiança na solução obtida.
O tamanho da população inicial e o número de gerações são parâmetros de evolução importantes. Uma população muito grande pode conduzir a um custo computacional alto, enquanto uma população pequena pode convergir a solução prematuramente para um ponto ótimo local. Por outro lado, o número de gerações, normalmente utilizado como um dos critérios de parada, deve cobrir todo o espaço de busca de projeto. No entanto, um valor grande também exigirá um tempo de processamento maior.
5. Metodologia interativa proposta
A metodologia interativa proposta para a análise estrutural e otimização numérica é baseada na integração de dois programas comerciais: Ansys® [17] e Matlab® [18]. Os scripts desenvolvidos para processo de análise e otimização funcionam de forma iterativa e não requer intervenção do usuário até que a solução seja encontrada ou seja atingido um critério de parada.
A análise da estrutura é feita pelo Ansys® [17] via MEF, executando-se em batch mode um script na linguagem de programação APDL, que inicia e sai do programa de EF para cada análise necessária. Tanto a otimização, quanto a interface entre os dois programas são escritos na linguagem de programação do Matlab® [18]. A interface é criada dentro de uma função aptidão e é responsável pelo loop de todo o processo. Nesta interface também são lidos e gravados dados importantes, tais como os valores das variáveis de projeto, que serão usados no programa de EF para análise da estrutura. Os dados resultantes dessas análises (forças axiais, tensões, volume), servirão para cálculo das restrições e para avaliação da função aptidão no código escrito no Matlab® [18].
Há na literatura diferentes tipos de funções de penalidades para lidar com as restrições. Neste trabalho será utilizado uma constante simples para penalizar a função objetivo na região inviável, ou seja, somente quando alguma restrição é violada.
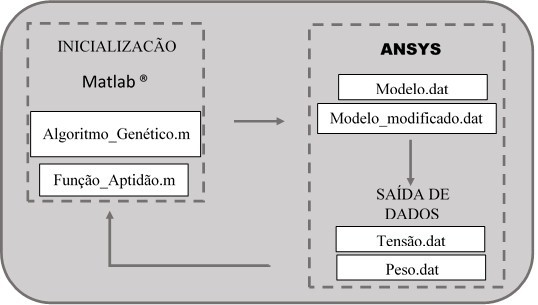
Na Figura 2, apresenta-se o fluxograma que ilustra a implementação computacional da metodologia interativa proposta. O processo inicia-se pelo Matlab® [18] por meio de uma função (Algoritmo_Genético.m) que contém as informações do algoritmo genético. Nesta etapa são definidos: a quantidade de variáveis e seu espaço de busca, com valores inferiores e superiores, as opções do algoritmo: tamanho da população, quantidade de gerações, tolerância da função e critérios de parada, bem como os operadores genéticos (seleção, cruzamento, mutação e substituição). Nessa mesma etapa também é criado um comando, que busca o pacote de ferramentas GA do Matlab® [18] e que executa o algoritmo genético. O script do algoritmo genético é responsável por chamar a função aptidão (Função_Aptidão.m), que avalia o quanto uma solução representada por um indivíduo é boa em relação às outras soluções da população para o problema em questão.
Na APDL (Modelo.dat) os dados da seção transversal das barras, que serão as variáveis de projeto, tais como área, diâmetro ou espessura (dependendo do modelo a ser analisado neste trabalho), são parametrizados partindo de um dado valor inicial. Também são inseridos na APDL os dados do material da estrutura, o tipo de elemento finito, as condições de apoio, as cargas aplicadas na estrutura e o tipo de análise. Os valores das variáveis do modelo são gerados aleatoriamente pelo Matlab® [18] e substituídos na APDL original (Modelo.dat). Para alimentar cada análise no programa de EF, é gerado um novo arquivo com os valores atualizados, chamado Modelo_modificado.dat. Os valores são alterados de acordo com o loop de otimização.
Na sequência, as informações resultantes da análise, tais como tensão e peso, são armazenadas em arquivos de texto (Tensão.dat e Peso.dat), gerados por comandos escritos no programa de EF e que serão utilizados posteriormente pelo Matlab® [18] para avaliar a função aptidão. O loop de otimização é interrompido até que o mínimo da função ou critério de parada seja alcançado.
A Ferramenta GA do Matlab® [18] utiliza quatro critérios diferentes para determinar quando o solver será interrompido. Esses critérios estão relacionados aos seguintes parâmetros: MaxGenerations, MaxStallGenerations (Stall G), MaxStallTime (Stall T) e FunctionTolerance (TolFun). O parâmetro MaxGenerations especifica o número máximo de iterações a serem executadas pelo AG. O parâmetro Stall T interrompe o algoritmo se não houver melhoria no melhor valor da função encontrado para a função aptidão num determinado intervalo de tempo especificado no algoritmo. Por outro lado, o parâmetro TolFun cessa o algoritmo se a alteração relativa média no melhor valor da função aptidão sobre um determinado número de gerações for menor ou igual a tolerância da função. Por último, o parâmetro Stall G tem um comportamento semelhante ao TolFun, e também é utilizado para garantir que um valor mínimo de gerações sejam calculadas independentemente dos demais critérios de convergência adotados.
| Figura 2.
Fluxograma da metodologia utilizada para a otimização das estruturas. |
6. Experimentos numéricos
Apresenta-se a seguir dois experimentos numéricos de treliças planas articuladas, onde a metodologia proposta é aplicada para a análise linear e otimização das estruturas. O primeiro exemplo é um caso clássico da literatura limitado apenas à restrições de tensão. No segundo caso são inseridas todas as restrições normativas. Nos dois casos foram consideradas variáveis contínuas na otimização. O modelo de elementos finitos (EFs) proposto para esses exemplos utiliza elementos de barras uniaxiais definidos por dois nós, com três graus de liberdade em cada nó: translação nas direções x, y e z. É considerado nos EFs apenas esforços de tração e compressão. Nos dois exemplos foi adotado como critério de parada do algoritmo, além do número de gerações, a convergência relacionada ao parâmetro de tolerância TolFun/Stall G do Matlab® [18] para a função objetivo, com um valor igual a 10-6. Neste caso, o algoritmo interrompe o processo caso não ocorra uma melhora dos valores da função objetivo de acordo com essa tolerância, após sucessivas gerações.
6.1. Treliça de 10 barras
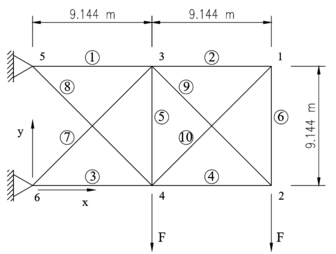
O primeiro experimento analisado corresponde a um problema clássico da literatura, quando se trata de otimização de treliças, estudado por diversos autores, tais como Adeli [21], Haftka e Gürdal [22], Lemonge e Barbosa [23] e Vargas et al. [24]. Trata-se de uma estrutura de treliça uniplanar hiperestática composta por 10 barras e 6 nós. As dimensões das barras e condições de apoio podem ser visualizados na Figura 3. Há duas cargas de 444.82 x 103 N aplicadas nos nós 2 e 4, na direção y (representadas na Figura 3 por F). O Módulo de Young do material (alumínio) e densidade são E = 6.89 x 1011 N/m2 e ρ = 2767.99 kg/m3, respectivamente.
|
| Figura 3.
Treliça de 10 barras. |
Os valores de partida das áreas (variáveis de projeto) das barras, inseridos na APDL, são iguais à 3.22x10-3 m2 para todas as barras, com peso inicial da treliça igual à 951.74 kg. Na Tabela 1 são apresentados os valores de tensões correspondentes à essas áreas iniciais e ao carregamento aplicado.
| Barra | 1 | 2 | 3 | 4 | 5 |
| Tensões (N/m2) | 269.39x106 | 55.33x106 | -282.18x106 | -82.56x106 | 48.93x106 |
| Barra | 6 | 7 | 8 | 9 | 10 |
| Tensões (N/m2) | 55.33x106 | 204.05x106 | -185.97x106 | 116.76x106 | -78.24x106 |
O objetivo é minimizar o peso da estrutura, modificando-se as áreas (variáveis de projeto) das seções transversais das barras, sujeitas a restrições de tensão, limitadas a 172.36 x 106 N/m2 (tração) e -172.36 x 106 N/m2 (compressão), totalizando então 10 variáveis de projeto e 10 restrições. A área mínima permitida para as barras é igual a 6.45 x 10-5 m2. Os resultados encontrados serão comparados com os de Haftka e Gürdal [22], que aplicaram em suas análises o método denominado Fully Stressed Design (FSD).
Na Tabela 2 são apresentados os parâmetros de entrada do AG. A aplicação do algoritmo genético baseou-se numa população inicial constituída por 200 indivíduos (soluções candidatas), geradas de forma aleatória. Considerou-se 1000 gerações, produzindo um total de 200 000 avaliações. Foi utilizado o valor default do Matlab® [18] para os demais parâmetros disponíveis na ferramenta de AG. Foi definido ainda no código do algoritmo, o campo de busca das variáveis de projeto: 6.45 x 10-5 m2 e 5.48 x 10-3 m2, correspondendo aos valores inferiores e superiores das áreas, respectivamente.
| Parâmetro do Matlab® [18] | Significado | Valor adotado |
| PopulationSize
|
Tamanho de população | 200 |
| Generations
|
Número de gerações | 1000 |
| EliteCount
|
Elitismo | 10 |
| TolFun/Stall G
|
Tolerância da função objetivo | 10-6 |
6.2. Treliça de 19 barras com restrições normativas
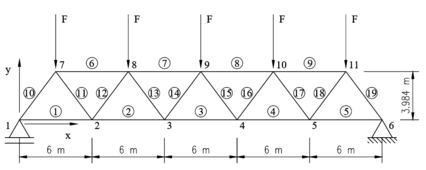
O segundo experimento analisado é a treliça de 19 barras ilustrada na Figura 4a, estudada por Jármai et al. [13]. Trata-se de uma treliça uniplanar simétrica composta de perfis de seção circular, tanto nos banzos quanto diagonais e configuração do tipo Warren, com ligações do tipo K. Considera-se que não há excentricidade na ligação.
Há cinco cargas de 1 x 106 N aplicadas nos nós 7, 8, 9, 10 e 11, na direção do eixo y (representadas na Figura 4a por F). O material (aço Fe-510) tem densidade ρ = 7850 kg/m3, Módulo de Young E = 210 000 MPa, limite de escoamento fy = 355 MPa e limite de resistência à tração fu = 510 MPa.
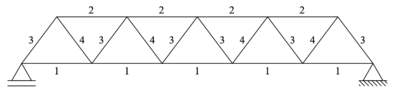
As barras da treliça são divididas em 4 grupos, representados na Figura 4b por: (grupo 1) banzos inferiores, (grupo 2) banzos superiores, (grupos 3) diagonais comprimidas e (grupo 4) diagonais tracionadas. Os membros de cada grupo tem comprimentos e seções transversais idênticas. Cada grupo i, i = 1, 2, 3 e 4 tem duas variáveis de projeto, diâmetro di e espessura ti da seção transversal do perfil, totalizando 8 variáveis de projeto.
|
(a) |
|
(b) |
| Figura 4.
Treliça de 19 barras. |
Na Tabela 3 são apresentados os valores de partida para os diâmetros e espessuras das barras (variáveis de projeto) inseridos na APDL e valores correspondentes de volume total e volume escalonado (razão do volume total por ![]() , onde a0 =3 m é a metade do comprimento entre os nós do banzo inferior).
, onde a0 =3 m é a metade do comprimento entre os nós do banzo inferior).
| Grupo de barras | Diâmetro (m) | Espessura (m) | ||
| 1 | d1 | 0.300 | t1 | 0.022 |
| 2 | d2 | 0.300 | t2 | 0.022 |
| 3 | d3 | 0.250 | t3 | 0.020 |
| 4 | d4 | 0.200 | t4 | 0.020 |
| Volume total (m3) | 1.69 | |||
| Volume escalonado* (m2) | 0.0896 | |||
- volume escalonado é igual à razão do volume por 6π
O objetivo é minimizar o volume da estrutura escalonado por ![]() , conforme Equação (6), modificando-se os diâmetros e espessuras das seções transversais das barras, sujeitas a restrições de flambagem, modos de falha e geometria, prescritos pelo Eurocode 3 [15] e Wardenier et al. [16]. Os resultados encontrados serão comparados com os de Jármai et al. [13], que aplicaram em suas análises o método denominado Leap-frog (LFOPC).
, conforme Equação (6), modificando-se os diâmetros e espessuras das seções transversais das barras, sujeitas a restrições de flambagem, modos de falha e geometria, prescritos pelo Eurocode 3 [15] e Wardenier et al. [16]. Os resultados encontrados serão comparados com os de Jármai et al. [13], que aplicaram em suas análises o método denominado Leap-frog (LFOPC).
|
|
|
(6) |
onde a0 =3 m é a metade do comprimento entre os nós do banzo inferior.
Na Tabela 4 são apresentados os parâmetros de entrada do AG. A aplicação do algoritmo genético baseou-se numa população inicial constituída por 100 indivíduos (soluções candidatas), geradas de forma aleatória. Considerou-se 200 gerações, produzindo um total de 20 000 avaliações. Foi utilizado o valor default do Matlab® [18] para os demais parâmetros disponíveis na ferramenta de AG. Os limites inferior e superior do campo de busca das variáveis de projeto correspondem à 3,2 mm e 25,0 mm para as espessuras e 88,9 mm e 508,0 mm para os diâmetros.
| Parâmetro do Matlab® [18] | Significado | Valor adotado |
| PopulationSize
|
Tamanho de população | 100 |
| Generations
|
Número de gerações | 200 |
| EliteCount
|
Elitismo | 10 |
| TolFun/Stall G
|
Tolerância da função objetivo | 10-6 |
6.2.1. Restrições aplicadas à treliça de 19 barras
São consideradas nesta análise restrições de geometria, flambagem e modos de falha prescritos pelo Eurocode 3 [15] e Wardenier et al. [16]. Todas as restrições são de desigualdade, na forma padrão .
A força resistente de cálculo das ligações soldadas entre perfis tubulares circulares deve ser tomada como o menor valor encontrado entre os seguintes modos de falha: plastificação da face do banzo ou ruptura por punção da parede do banzo, desde que seja atendida a seguinte condição, conforme Equação (7) referente às restrições :
|
|
|
(7) |
onde os termos di e ti referem-se ao diâmetro e espessura das barras do grupo i. Para ligações que não atendam essa condição, deve-se considerar os demais modos de falha prescrito pelo Eurocode 3 [15].
As restrições , refere-se à condição de dimensionamento para barras submetidas à força axial de compressão (barras dos grupos 2 e 3), definidas por:
|
|
|
(8) | ||
|
|
|
(9) | ||
onde é a máxima força axial de compressão solicitante de cálculo e é a força axial de compressão resistente de cálculo, determinada conforme a Equação (10):
|
|
|
(10) |
onde é a área da barra, é o coeficiente de ponderação da resistência e é o fator de redução associado à resistência à compressão, dado por:
|
|
|
(11) |
onde é determinado pela Equação 12a e 12b:
| (12a) | ||
| (12b) |
Sendo o comprimento de flambagem, onde é o comprimento destravado da barra e o coeficiente de flambagem. De acordo com Rondal et al. [25] apud Wardenier et al. [16], K = 0.9 para barras comprimidas do banzo e K = 0.75 para barras comprimidas das diagonais. O termo refere-se ao índice de esbeltez.
As restrições , referem-se à condição de dimensionamento para barras submetidas à força axial de tração (barras dos grupos 1 e 4), definidas por:
|
|
|
(13) | ||
|
|
|
(14) | ||
onde é a máxima força axial de tração solicitante de cálculo e é a força axial de tração resistente de cálculo, determinada conforme a Equação (15):
|
|
|
(15) |
onde é a área da barra e é o coeficiente de ponderação da resistência. As restrições referem-se à uma condição de fabricação, onde os diâmetros das barras diagonais devem ser inferiores aos diâmetros das barras do banzo, de acordo com as Equações (16), (17), (18) e (19):
|
|
|
(16) | ||
|
|
|
(17) | ||
|
|
|
(18) | ||
|
|
|
(19) |
A capacidade resistente de cálculo das ligações entre perfis tubulares referente à plastificação da face do banzo ou de toda a seção transversal do banzo, junto a diagonais ou montantes é restringida por:
|
|
|
(20) | ||
|
|
|
(21) |
onde é a máxima força axial de compressão solicitante de cálculo referente as barras do grupo 3 e é a força axial resistente de cálculo referente à plastificação do banzo, dada por:
|
|
|
(22) |
sendo que é o fator geométrico para ligação com banzo circular, dado por:
|
|
|
(23) |
onde é a relação geométrica entre o diâmetro do banzo e duas vezes a sua espessura. O comprimento do afastamento entre diagonais, , é dado por:
|
|
|
(24) |
Sendo g3 e g4 igual à metade do comprimento do afastamento entre diagonais. As restrições , referente à verificação das ligações entre as barras dos grupos 1 e 4 e barras dos grupos 2 e 4 é calculada com formulação similar às Equações (20) e (21). A capacidade resistente de cálculo das ligações entre perfis tubulares das barras dos grupos 2 e 3 referente à ruptura por punção da parede do banzo na área de contato com diagonais ou montantes é restringida por:
|
|
|
(25) |
onde é a máxima força axial de compressão solicitante de cálculo referente as barras do grupo 3 e é o ângulo formado entre as barras diagonais e as barras dos banzos.
A resistência das soldas nas ligações entre as barras dos banzos e diagonais de acordo com o método direcional dado pelo Eurocode 3 [15], é calculada por:
|
|
|
(26) | ||
sendo que é um fator de correlação (tabelado), que é função das propriedades mecânicas do aço e é um fator parcial de segurança. As tensões devido ao esforço normal transversal, , devido ao cisalhamento transversal, , e devido ao cisalhamento longitudinal, , são dadas por:
|
|
|
(27) | ||
|
|
|
(28) | ||
onde é a máxima força axial de compressão solicitante de cálculo e é a dimensão do filete de solda. Substituindo as Equações (27) e (28) na Equação (26), tem-se as restrições , dadas por:
|
|
|
(29) |
7. Resultados e discussão
7.1. Treliça de 10 barras
Neste item são apresentados os resultados obtidos para o melhor e o pior valor da função aptidão, considerando o caso clássico da literatura da treliça de 10 barras. Em ambos os casos, optou-se por utilizar uma penalidade igual ao valor constante de 4536 kg em todas as execuções do algoritmo. Além disso, foi utilizado como critério de parada o número de gerações e o parâmetro Stall G da Ferramenta GA do Matlab® [18], relacionado à uma tolerância igual à 1x10-6 para a função objetivo.
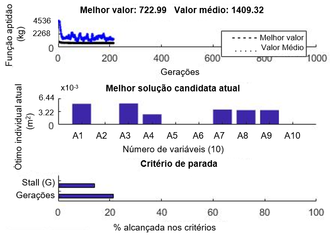
Na Figura 5a, gerada pelo Matlab® [18], pode-se visualizar a evolução da melhor solução encontrada ao longo das gerações, com o Melhor valor e o Valor médio de peso encontrado para a função aptidão. Nesta figura, observa-se que a convergência do problema se deu com 220 gerações, aproximadamente. No entanto, é possível obter um resultado próximo ao da literatura com 100 gerações apenas. A partir desse número, há pouca variação no resultado da função aptidão. Na Figura 5b, são apresentados os valores das 10 variáveis (áreas), correspondentes ao valor da função objetivo. Algumas áreas apresentaram um valor próximo de zero. Isso ocorre em função de que algumas barras são contabilizadas apenas na estabilidade da estrutura. Por último, na Figura 5c, ilustra-se a porcentagem alcançada para os critérios de parada. O critério de parada atingido pelo algoritmo foi o relacionado à tolerância da função objetivo.
|
(a) |
| (b) | |
| (c) | |
| Figura 5.
Resultados encontrados para o melhor valor da função objetivo – treliça de 10 barras | |
Na Tabela 5 são apresentados os resultados obtidos para a melhor solução viável utilizando a metodologia proposta neste estudo e o resultado de Haftka e Gürdal [22]. É possível observar que os resultados obtidos ficaram próximos aos da literatura. Calculando-se a diferença percentual entre os valores de peso obtidos neste estudo e nos estudos de Haftka e Gürdal [22], obtêm-se 0,05%, o que representa uma boa precisão da metodologia proposta.
| Barra | Área (m2) | Presente trabalho/GA | Haftka e Gürdal [22]/ FSD |
| 1 | A1 | 5.10 x 10-3 | 5.12 x 10-3 |
| 2 | A2 | 0.0645 x 10-3 | 0.0645 x 10-3 |
| 3 | A3 | 5.20 x 10-3 | 5.19 x 10-3 |
| 4 | A4 | 2.52 x 10-3 | 2.54 x 10-3 |
| 5 | A5 | 0.0645 x 10-3 | 0.0645 x 10-3 |
| 6 | A6 | 0.0645 x 10-3 | 0.0645 x 10-3 |
| 7 | A7 | 3.71 x 10-3 | 3.70 x 10-3 |
| 8 | A8 | 3.58 x 10-3 | 3.59 x 10-3 |
| 9 | A9 | 3.58 x 10-3 | 3.59 x 10-3 |
| 10 | A10 | 0.0838 x 10-3 | 0.0645 x 10-3 |
| Peso (kg) | 722.99 | 722.66 | |
Na Tabela 6 são apresentados os valores de tensões finais nas barras, obtidos em função da melhor solução candidata apresentada anteriormente na Tabela 5 e diferença percentual em relação ao valores limites de tensões de ± 172.36 x 106 N/m2. É possível inferir que as restrições de tensões referentes às barras 1, 3, 4, 7, 8 e 9 ficaram ativas, ou seja, os valores das restrições ficaram na fronteira do domínio do problema de otimização, alcançando o valor limite de tensão. Por outro lado, a restrição de tensão referente à barra 10 ficou longe da fronteira do domínio, apresentando um valor de tensão bem abaixo do valor limite de 172.36 x 106 N/m2. Conforme comentando anteriormente, algumas barras são menos solicitadas e contribuem apenas para a estabilidade da estrutura.
| Barras | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Tensões finais (N/m2) | 172.36 x 106 | 121.48 x 106 | 172.36 x 106 | 172.36 x 106 | 0.68 | 119.07 x 106 | 172.36 x 106 | 172.36 x 106 | 172.36 x 106 | 138.23 x106 |
| Diferença percentual (%) | 0 | 70.48 | 0 | 0 | 0.39x10-6 | 69.08 | 0 | 0 | 0 | 80.19 |
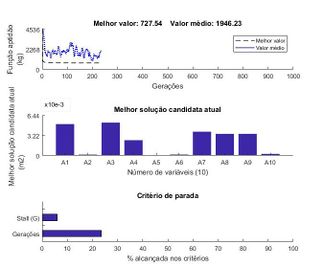
Por outro lado, na Figura 6, apresenta-se o pior valor obtido para a função aptidão. Observa-se pela Figura 6a que convergência do problema se deu aproximadamente com 230 gerações, que corresponde a um número ligeiramente superior ao da melhor solução encontrada para a função aptidão. É possível inferir pela Figura 6b que as barras menos solicitadas da treliça também apresentaram um valor de área (variáveis de projeto) próximo de zero. Por fim, na Figura 6c, ilustra-se a porcentagem alcançada para os critérios de parada. O critério de parada atingido pelo algoritmo neste caso também foi o parâmetro Stall G.
|
(a) |
| (b) | |
| (c) | |
| Figura 6.
Resultados encontrados para o pior valor da função objetivo – treliça de 10 barras | |
Para esse experimento numérico foram realizadas 5 execuções do algoritmo. Na Tabela 7 é apresentado uma análise estatística dos resultados de peso obtidos. É importante destacar que o pior resultado da função aptidão obtido na otimização apresenta uma diferença de menos de 1% em relação à melhor solução encontrada. Apesar do algoritmo genético gerar valores diferentes de função aptidão à cada execução, há uma variação relativamente pequena dos resultados, indicando uma boa robustez do algoritmo ao ficar próximo do ótimo global da função aptidão.
| Melhor Solução
(kg) |
Pior Solução
(kg) |
Média
(kg) |
Mediana
(kg) |
| 722.99 | 727.54 | 724.70 | 724.81 |
7.2. Treliça de 19 barras
Nesta análise também são apresentados os resultados obtidos para o melhor e o pior valor da função aptidão. Adotou-se em todas as execuções uma penalidade igual ao valor constante de 100 000 mm2, além dos seguintes critérios de parada: número de gerações e parâmetro Stall G, relacionado à tolerância da função objetivo igual à 1x10-6.
Na Figura 7a, gerada pelo Matlab® [18], pode-se visualizar a evolução da melhor solução encontrada ao longo das gerações, com o Melhor valor e o Valor médio de peso encontrado para a função aptidão. Nesta figura, observa-se que a convergência do problema se deu com 190 gerações, aproximadamente. Nas primeiras 20 gerações, aproximadamente, os indivíduos não atenderam à todas as restrições do problema e foram penalizados pelo valor constante igual à 100 000. Na Figura 7b, são apresentados os valores das 8 variáveis (diâmetros e espessuras), correspondentes ao valor da função objetivo. Alguns valores de diâmetros e espessuras obtidos representam valores mínimos para atender determinado critério de resistência. Isso será melhor discutido com os resultados obtidos de acordo com a Tabela 9. Na Figura 7c, ilustra-se a porcentagem alcançada para os critérios de parada. O critério atingido pelo algoritmo foi o relacionado à tolerância da função objetivo.
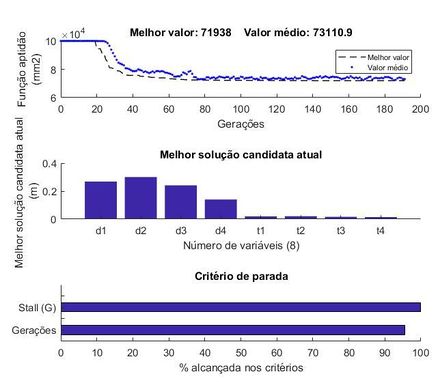
|
(a) |
| (b) | |
| (c) | |
| Figura 7.
Resultados encontrados para o melhor valor da função objetivo – treliça de 19 barras | |
Na Tabela 8 são apresentados os resultados obtidos para a melhor solução viável utilizando a metodologia proposta neste estudo e o resultado de Jármai et al. [13]. É possível observar que os resultados alcançados ficaram próximos aos da literatura. Calculando-se a diferença percentual entre os valores de volume obtidos neste estudo e nos estudos de Jármai et al. [13], obtêm-se 2.22%, o que representa novamente uma boa precisão da metodologia proposta.
| Pesquisador/Metodologia de otimização | Presente trabalho/GA | Jármai et al. [13]/LFOPC | |
| Diâmetro (mm) | d1 | 268.5 | 256.6 |
| d2 | 300.4 | 286.1 | |
| d3 | 241.5 | 211 | |
| d4 | 140.0 | 150.7 | |
| Espessura (mm) | t1 | 19.4 | 20.44 |
| t2 | 20.6 | 20.41 | |
| t3 | 16.6 | 19.22 | |
| t4 | 14.8 | 13.50 | |
| Volume escalonado
(mm2) |
71938 | 70374.3 | |
| Volume escalonado
(m2) |
0.0719 | 0.0703 | |
Na Figura 8 pode-se visualizar a evolução de três das principais forças axiais resistentes ao longo das gerações, referentes às barras mais solicitadas do respectivo grupo. Na Figura 8a são apresentados os valores de força axial de tração no banzo (Ndrt1) referente à restrição g7 (x). Na Figura 8b são apresentados os valores de força axial de compressão no banzo (Ndrc2) referente à restrição g5 (x). Por outro lado na Figura 8c são apresentados os valores de força axial devido à plastificação da face do banzo tracionado com diagonal comprimida (Ndrp1) referente à restrição g13 (x). É possível inferir pelas Figuras 8a, 8b e 8c que houve uma variação muito grande do valor das três forças axiais resistentes até 65 gerações, aproximadamente. Após esse número de gerações, os valores dos esforços axiais resistentes se mantiveram constantes.
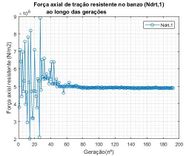
|
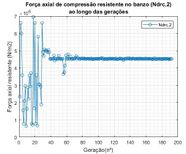
|
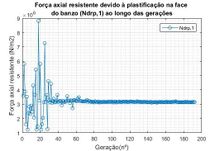
|
| (a) | (b) | (c) |
| Figura 8.
Evolução das forças axiais resistentes ao longo das gerações – treliça de 19 barras | ||
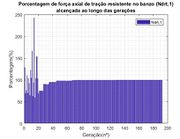
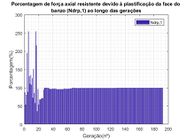
Na Figura 9 são apresentados as porcentagens de forças axiais resistentes alcançadas ao longo das gerações. Na Figura 9a e Figura 9b são apresentados os valores de força axial de tração (Ndrt1) e compressão (Ndrc2) no banzo. Por outro lado, na Figura 9c são apresentados os valores de força axial devido à plastificação da face do banzo tracionado com diagonal comprimida (Ndrp1). É possível inferir que as três restrições ficaram ativas, ou seja, os valores finais de forças axiais resistentes referentes às restrições ficaram na fronteira do domínio do problema de otimização, alcançando o valor limite de resistência (esforço solicitante). Por outro lado, todas as três restrições alcançaram valores superiores à 100% nas vinte primeiras gerações, aproximadamente, ou seja, o valor do esforço resistente foi inferior ao valor do esforço solicitante. Conforme visto anteriormente na Figura 7a, os indivíduos foram penalizados nas primeiras 20 gerações, aproximadamente, porque uma ou mais restrições do problema não foram atendidas, como é o caso dessas três restrições.
|

|
|
| (a) | (b) | (c) |
| Figura 9.
Porcentagem de força axial resistente alcançada ao longo das gerações – treliça de 19 barras | ||
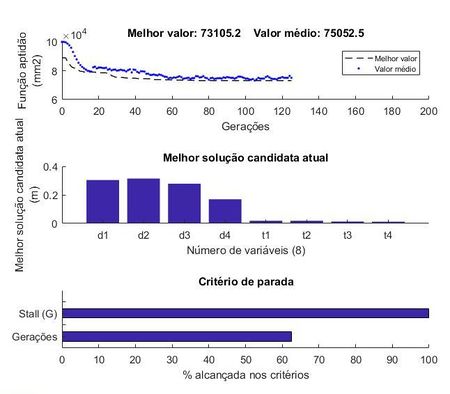
Na Figura 10, apresenta-se o pior valor obtido para a função aptidão. Observa-se pela Figura 8a que convergência do problema se deu aproximadamente com 120 gerações, que corresponde à um número inferior ao da melhor solução encontrada para a função aptidão. Na Figura 8b, o comportamento das variáveis do gráfico foi semelhante ao da melhor solução obtida para a função aptidão. E na Figura 8c, novamente o critério de parada atingido pelo algoritmo foi o parâmetro Stall G.
Para esse experimento numérico foram realizadas 5 execuções do algoritmo. Na Tabela 9 é apresentado uma análise estatística dos resultados de volume escalonado obtidos. É possível inferir pela tabela que assim como no experimento anterior, o pior resultado representa uma diferença de 1,62% em relação à melhor solução encontrada. Além disso, tanto a média quando a mediana apresentaram valores próximos do valor da melhor solução, indicando que há uma baixa discrepância dos resultados e uma tendência do algoritmo em ficar próximo do ótimo global, ainda que com poucas execuções.
|
(a) |
| (b) | |
| (c) | |
| Figura 10.
Resultados encontrados para o pior valor da função objetivo – treliça de 19 barras | |
| Melhor Solução
(mm2) |
Pior Solução
(mm2) |
Média
(mm2) |
Mediana
(mm2) |
| 71938 | 73105.2 | 72744.44 | 72999.1 |
8. Conclusão
Neste trabalho, foi proposta uma metodologia para a otimização das estruturas treliçadas, baseada na integração dos programas Ansys® [17] e Matlab® [18], utilizando-se a Ferramenta de otimização GA de Algoritmos Genéticos do Matlab® [18], e o MEF do Ansys® [17]. Para demonstrar a aplicabilidade e precisão da metodologia proposta, foram resolvidos dois exemplos numéricos de estruturas treliçadas de 10 e 19 barras.
Os resultados obtidos permitem concluir que a metodologia proposta em conjunto com os Algoritmos Genéticos é uma ferramenta eficaz na busca do ótimo global de problemas de otimização. A metodologia proposta não é limitado à sistemas treliçados com EFs de barras. Estudo mais complexos, incluindo modelos com não-linearidades, outros carregamentos e análises locais (ligação soldada, por exemplo) com EFs de casca, podem ser abordados em pesquisas futuras.
Espera-se que este estudo seja uma contribuição no âmbito da otimização de sistemas treliçados com o uso de diferentes ferramentas de trabalho; além de auxiliar no entendimento dos efeitos dos parâmetros normativos das ligações tubulares na otimização das estruturas.
9. Agradecimentos
Os autores agradecem à Universidade Federal de Ouro Preto pelo financiamento para realização deste trabalho.
10. Bibliografia
[1] Deb K. Multi-objective optimization using evolutionary algorithms. 1ed, Chichester, UK, Wiley, 2001.
[2] Coello C. A. C., Christiansen A. Multiobjective optimization of trusses using genetic algorithms. Comput. Struct., 75 (6): 647–660, 2000.
[3] Deb K., Gulati, S. Design of Truss-Structures for Minimum Weight Using Genetic Algorithms. Finite Elements in Analysis and Design, 37 (5): 447-465, 2001.
[4] Kaveh A., Shahrouzi M. Direct index coding for discrete sizing optimization of structures by genetic algorithms. International Journal of Civil Engineering, 3 (3-4): 166–181, 2005.
[5] Sawada K., Matsuo A. and Shimizu H. Randomized line search techniques in combined GA for discrete sizing optimization of truss structures. Struct. Multidisc. Optim., 44: 337-350, 2011.
[6] Tang W., Tong L. and Gu Y. Improved genetic algorithm for design optimization of truss structures with sizing, shape and topology variables. Int. J. Numer. Meth. Engng., 62: 1737-1762, 2005.
[7] Goldberg D.E. Genetic Algorithms in Search, Optimization and Machine Learning. Addison-Wesley Publishing Co., 1989.
[8] Messac A. Optimization in Practice with Matlab: For Engineering students and professionals. Cambridge University Press, New York, 2015.
[9] Carvalho M., Vale J., Pinheiro L. and Neves M. Techniques adopted in integrating structural analysis with numerical optimization; 5th International Conference on Mechanics and Materials in Design, 2006.
[10] Gil L., Andreu A. and Blanco E. Integration methodology of different software tools for constrained optimization of structures. Computers and Structures, 82: 1639-1647, 2004.
[11] Ali N., Behdinan K. and Fawaz Z. Applicability and viability of a GA based finite elemento analysis architecture for structural design optimization. Computers and Structures, 81: 2259-2271, 2003.
[12] Dominguez A., Stiharu I. and Sedaghati R. Practical design optimization of truss structures using the genetic algorithms. Res. Eng. Desing, 17: 73-84, 2006.
[13] Jármai K., Snyman J. and Farkas J. Application of novel constrained optimization algorithms to the minimum volume design of planar chs trusses with parallel chords. Engineering Optimization, 36 (4): 457-471, 2004.
[14] Associação Brasileira de Normas Técnicas – ABNT NBR 16239: Projeto de estruturas de aço e de estruturas mistas de aço e concreto de edificações com perfis tubulares, 2013.
[15] Eurocode 3, EN 1993-1-8. 2005. Design of steel structures. Part 1-8: Design of joints. CEN, European Committee for Standardisation.
[16] Wardenier et al. Design Guide for Circular Hollow Section Joints Under Predominantly Static Loading. TÜV Rheinland, Köln, 1991.
[17] Ansys. Structural analysis guide – release 17.0. In: ANSYS I, editor; 2017.
[18] Mathworks. Matlab – getting started guide. Natick, USA, 2017.
[19] Bendse, M. and Sigmund, O. Topology Optimization: Theory, Methods and Applications. Springer. New York, USA, 2003.
[20] Coello C. A. C., Lamont G. B and Veldhuizen D. A. Van. Evolutionary Algorithms for Solving Multi-Objective Problems. 2nd Edition. Springer, 2007.
[21] Adeli, H. Advances in Design Optimization. Chapman & Hall, 1994.
[22] Haftka R. T., Gürdal Z. Elements of Structural Optimization. Kluwer Academic Publishers, Dordrecht, 1992.
[23] Lemonge A.C.C., Barbosa H.J.C. An adaptive penalty scheme for genetic algorithms in structural optimization. International Journal For Numerical Methods In Engineering, 59 (5): 703–706, 2004.
[24] Vargas D.E.C., Lemonge A.C.C., Barbosa H.J.C. and Bernardino H.S. Um algoritmo baseado em evolução diferencial para problemas de otimização estrutural multiobjetivo com restrições. Rev. int. métodos numér. cálc. diseño ing., 32(2): 91-99, 2016.
[25] Rondal J. et al. Structural Stability of Hollow Sections. TÜV Rheinland, Köln, 1992.
Document information
Published on 18/09/19
Accepted on 15/09/19
Submitted on 09/01/19
Volume 35, Issue 3, 2019
DOI: 10.23967/j.rimni.2019.09.004
Licence: CC BY-NC-SA license
Share this document
Keywords
claim authorship
Are you one of the authors of this document?