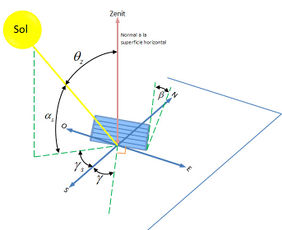
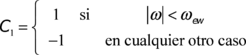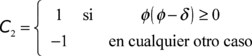| Failed to parse (syntax error): \delta = 23.45\sin \left( {360\frac{{284 + n}}{{365}}} \right)<math> |} | style="width: 5px;text-align: right;white-space: nowrap;" | (1) |} donde ''n'' es el n-ésimo día del año. Usando la ecuación anterior, en la figura 2 se muestran los valores de la declinación (línea punteada) a lo largo de un año. <div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> [[Image:draft_Acosta_858489502-image3.png|282px]] </div> <div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> <span style="text-align: center; font-size: 75%;">Figura 2. Declinación solar.</span></div> Por otra parte, existe un conjunto útil de relaciones entre los ángulos anteriormente definidos. Tales ecuaciones relacionan el ángulo de incidencia del haz de radiación θ sobre una superficie plana con los distintos ángulos (δ,𝜙, β, 𝛾, ω) anteriormente definidos. La primer relación está dada por: {| class="formulaSCP" style="width: 100%; text-align: center;" |- | {| style="text-align: center; margin:auto;" |- | [[Image:draft_Acosta_858489502-image4.png|240px]] |} | style="width: 5px;text-align: right;white-space: nowrap;" | (2) |} Como un caso particular, para una superficie horizontal, el ángulo de inclinación es igual a cero, y en dicho caso el ángulo del zenit es igual al ángulo de incidencia, así, de la ecuación anterior tenemos que: {| class="formulaSCP" style="width: 100%; text-align: center;" |- | {| style="text-align: center; margin:auto;" |- | [[Image:draft_Acosta_858489502-image5.png|228px]] |} | style="width: 5px;text-align: right;white-space: nowrap;" | (3) |} De la ecuación anterior podemos calcular el valor del ángulo del zenit en términos de la declinación, la latitud y el ángulo horario. La segunda relación importante está dada por: {| class="formulaSCP" style="width: 100%; text-align: center;" |- | {| style="text-align: center; margin:auto;" |- | [[Image:draft_Acosta_858489502-image6.png|246px]] |} | style="width: 5px;text-align: right;white-space: nowrap;" | (4) |} El ángulo de Azimut solar 𝛾<sub>s</sub>puede tomar valores en el rango entre 180º a -180º. Para latitudes norte o sur entre 23.45º y 66.45º, 𝛾<sub>s</sub>estará entre 90º y -90º para días con menos de 12 horas de duración. Para días con más de 12 horas entre el amanecer y el ocaso, 𝛾<sub>s</sub>será menor de -90º o mayor de 90º, en la mañana o en la tarde, respectivamente, cuando el Sol esté al norte de la línea este-oeste en el hemisferio norte, o al sur de la línea este-oeste en el hemisferio sur. Para latitudes tropicales 𝛾<sub>s</sub>puede tomar cualquier valor cuando (δ-𝜙) es positivo en el hemisferio norte, o negativo en el sur. Así, para calcular 𝛾<sub>s</sub>necesitamos saber en qué cuadrante estará el sol. Esto se determina midiendo la relación entre el ángulo horario ω y el ángulo horario ω<sub>ew</sub>, cuando el sol está hacia el este (o el oeste). Una formulación general para 𝛾<sub>s</sub>estalecida por Braun y Michell (1983), puede escribirse convenientemente en términos de 𝛾<sub>s</sub>’, definido como un ángulo azimutal solar ficticio, para el primer o cuarto cuadrante. De acuerdo con Braun y Michell (1983), el ángulo azimutal solar está dado por: {| class="formulaSCP" style="width: 100%; text-align: center;" |- | {| style="text-align: center; margin:auto;" |- | [[Image:draft_Acosta_858489502-image7.png|198px]] |} | style="width: 5px;text-align: right;white-space: nowrap;" | (5) |} donde [[Image:draft_Acosta_858489502-image8.png|132px]] o [[Image:draft_Acosta_858489502-image9.png|210px]] donde, <math>\cos {\omega _{ew}} = \frac{{\tan \delta }}{{\tan \phi }}.
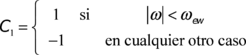
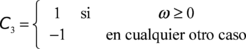
Es importante notar que si es mayor que 1, entonces no es posible determinar si el Sol está hacia el este o el oeste del observador. En tal caso es suficiente con hacer C1 = 1, evitando de esta manera el caso 𝝓 = 0.
III. RESULTADOS Y DISCUSIÓN
Con las ecuaciones de la sección II es posible determinar los ángulos azimutal y zenit para el día n y ángulo horario ω, tales ángulos determinan unívocamente la posición local del Sol en la bóveda celeste, para ello es necesario fijar la latitud de la región de interés. En nuestro caso, para la latidud de 21 grados (latitud de la Ciudad de Mérida, Yucatán México), programamos las ecuaciones en el lenguage de programación mathematica® (ver apéndice I para conocer el código desarrollado). Independientemente del valor del ángulo azimutal, el amanecer ocurre cuando el ángulo del zenit es menor o igual a 90º. La figura 3 muestra la hora del amanecer para cada día del año.
Fig. 3. Hora del amanecer. Se observan aproximadamente 80 minutos de diferencia entr los días que más tarde sale el Sol, con respecto a los días que amanece más temprano.
El horario mostrado en el eje vertical de la figura 3 no necesariamente corresponde al horario que cotidianamente usamos en nuestros relojes, mostramos los resultados en términos del horario solar, donde el medio día solar queda definido cuando el ángulo azimutal solar vale cero grados. De la figura 3 podemos notar que hay aproximadamente 90 minutos de diferencia entre el día que más tarde sale el sol (día 355 del año), con respecto al día que más temprano amanece (día 172 del año). Un calculo adicional nos permite determinar el número total de horas de luz para cada día del año (ver Fig. 4). De la figura 4 podemos identificar qué días son los más largos y cortos del año, así como los días de más (o menos) horas. Por ejemplo, a partir del día 81 comienzan los días con más de 12 horas de duración, lo que normalmente correspondería al inicio del conocido horario de verano en México, y en el día 263 terminan los días con más de 12 horas de luz (terminaría el horario de verano). Los días 81 y 263 corresponden a los equinoccios de la latitud de interés. De la misma figura 4 podemos identificar que el día 172 es el que más horas de luz tiene (13:16, trece horas con 16 minutos), mientras que el de menor horas de luz es el día 355 (10:43, diez horas con 43 minutos), día cuando ocurre el solsticio de invierno.

Fig. 4. Horas de luz para cada día del año, podemos identificar periodos de menos de 11 horas de luz y de más de 13 horas de luz.
Los valores de los ángulos que determinan la posición del Sol fueron obtenidos para cada uno de los 365 días del año, y para cada día en intervalos de un minuto, desde el alba hasta el ocaso. El intervalo temporal cuenta con la resolución suficiente para que los datos obtenidos puedan ser utilizados en sistemas autónomos de seguimiento solar. Además, los resultados de este trabajo pueden usarse para estimar la componente directa de la radiación solar en regiones donde no se tengan registros históricos. Si el lector lo requiere puede ponerse en contacto con los autores y solicitar los datos de los resultados de los ángulos.
 365 días del año, y para cada día en 365 días del año, y para cada día en
Los valores del ángulo de zenit fueron obtenidos por medio de la ecuación (2). Los resultados correspondientes se muestran como histogramas en la figura 5(a). En dicha figura se observa que los ángulos del zenit (curva roja) de mayor frecuencia están en el intervalo entre 50º y 55º, y se observa una frecuencia de valores del zenit con mínima variación en el intervalo de 15º a 40º. Para el caso del ángulo de altitud (curva azul), la frecuencia es mayor en el intervalo de 35º a 40º, y mínima variación de la frecuencia en el intervalo de 50º a 75º, lo cual es congruente dada la relación entre altitud y zenit. En la figura 5(b) se muestran los valores acumulativos de la gráfica 5(a), que en este caso corresponden a la probabilidad de que el ángulo del zenit o elevación esté dentro de un intervalo particular. Por ejemplo, se tiene una probabilidad de aproximadamente 0.18 de que al medir el ángulo de elevación éste se encuentre dentro del intervalo entre 0º y 20º. Los resultados mostrados en la figura 5 son una representación estadística, pero para fines prácticos, son poco útiles. Más adelante mostramos resultados con mayor potencial de aplicación.
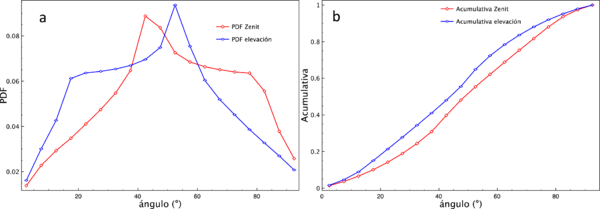
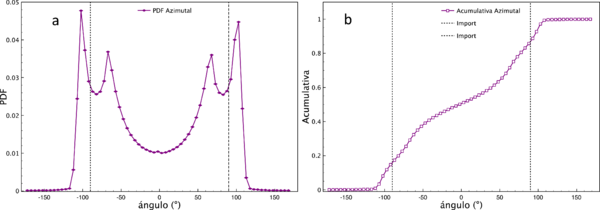
Con respecto al ángulo azimutal, en la figura 6 mostramos un análisis similar al de la figura 5. Es importante notar que los valores del ángulo azimutal entre -180º y 0º grados corresponden a posiciones del Sol antes del medio día (durante la mañana), y los valores entre 0º y 180º corresponden a posiciones del Sol después del medio día (durante la tarde). La figura 6 muestra 3 regiones, definidas por los intervalos R1(-180º, -90º), R2(-90º, 90º) y R3(90º, 180º). La región R1 indica que el Sol se encuentra, durante el transcurso de la mañana inclinado hacia el norte de la línea este-oeste y, de la misma manera para la región R3 durante la tarde. Mientras que la región R2 indica que el sol se encuentra hacia el sur de la línea este-oeste. Es decir, existen días para los cuales la proyección de nuestra sombra se dirige al sur, cuando el Sol está en la región R1 y R3, y al norte, cuando el Sol está en la región R2. Es interesante mencionar que en la latitud de este estudio, usualmente los paneles solares se encuentran en una posición fija, y orientados hacia el sur con un ángulo de inclinación de 21º, de acuerdo con la figura 1, en éste caso 𝛾 = 0 y β = 21º. Sin duda este hecho resulta en una disminución de la radiación directa incidente sobre los paneles solares, lo cual afecta su eficiencia. De manera análoga a la figura 5b, de la figura 6b podemos inferir que la probailidad de que por la mañana el Sol se encuentre al norte es aproximadamente 0.2. Con fines de mayor aplicación, es necesario conocer cuáles son los días en los que el Sol se inclina hacia el norte o hacia el sur y qué porcentaje del día permanece en una u otra orientación. La figura 7 muestra que a partir del día 1 del año y hasta el día 81 el Sol sigue una trayectoria siempre inclinado hacia el sur, y a partir del día 82 sigue una trayectoria en la cual comienza a inclinarse hacia el norte, resulta interesante observar que a partir del día 82 comienzan los días con más de 12 horas de luz, finalizando en el día 263, justo cuando el Sol vuelve en su totalidad a la región R2, es decir, siempre haciendo un recorrido inclinado hacia el sur.
 de 21º, de acuerdo con la figura 1, en de 21º, de acuerdo con la figura 1, en
alcanza ahora  un valor máximo de 5o. Los resultados anteriores pueden ser un valor máximo de 5o. Los resultados anteriores pueden ser
Figura 7. Porcentaje de tiempo que el Sol se localiza hacia el norte. Desde el día 1 y hasta el 81 el Sol siempre permance inclinado hacia el sur, y a partir del día 82 aumenta el porcentaje de tiempo en los que el Sol se inclina hacia el norte. Del día 146 al 199 el Sol permanece el 100% de tiempo inclinado hacia el norte.
También es importante notar que del día 146 al 199 el Sol hace su recorrido manteniéndose en su totalidad con una inlinación hacia el norte (regiones R1 y R3) y que el 50% de los días del año el Sol recorre el firmamento siempre inclinado hacia el sur, el 14.5% siempre inclinado hacia el norte, y el resto lo hace en combinación norte-sur. Ahora que conocemos los días en los que el Sol sigue una trayectoria con inclinación hacia el norte o el sur, resulta importante saber cuál es ángulo del zenit para esas trayectorias, lo cual nos indicaría qué tan inclinado al norte o sur se encuentra. Dado que el número de datos es enorme, en este estudio nos centramos en los valores cuando la radiación directa debe ser máxima, es decir, al medio día solar. La figura 8 muestra los valores del ángulo zenit justo al medio día solar. De las figuras 7 y 8 podemos inferir que cuando el Sol está en la región R2 (siempre inclinado hacia el sur), el ángulo de zenit, θz, alcanza un valor máximo de 45ogrados aproximadamente, es decir, el Sol tiene la mínima altitud. De manera análoga, cuando el Sol inicia su recorrido por la región R1, o finaliza su recorrido por la región R3, el ángulo θzalcanza un valor máximo de aproximadamente 20o(mínima altitud). De la figura 8 notamos que cuando el Sol inicia y termina su trayectoria con una inclinación siempre hacia el norte (días 81 y 263), el ángulo del zenit a medio día es igual a cero, correspondiente al equinoccio. Por otra parte, cuando el sol transita siempre inclinado hacia el norte (del día 146 al 199), el ángulo θzalcanza ahora un valor máximo de 5o. Los resultados anteriores pueden ser aplicados, por ejemplo, en sistemas de seguimiento solar, en paneles solares y en la industria de casas habitación. Si se desea que la luz del Sol no incida sobre una pared vertical cuando la radiación sea máxima (a medio día solar), es necesario construir terrazas para que proyecten sombra sobre la pared vertical. Así, si h es la altura de una pared vertical, entonces la longitud L de la terraza, para garantizar que al medio solar la radiación no incida sobre dicha pared, está dada por: L = hTan(θz). Usando los valores del zenit máximo tenemos que cuando el sol está inclinado hacia el sur L = h, mientras que si el Sol está inclinado hacia el norte, L =0.36h.
IV. CONCLUSIONES
Los ángulos del zenit y del azimut, que determinan la posición del Sol fueron calculadas por medio del modelo matemático propuesto por Braun y Michell (1983). Con el software Mathematica® se obtuvieron dichos ángulos, minuto a minuto, para los 365 días del año en la latitud de 21 grados (Ciudad de Mérida, Yucatán México). Los resultados muestran que el Sol sigue trayectorias con inclinación hacia el norte y hacia el sur, contrastando con la posición fija de los paneles solares por el poco tiempo que la radiación directa incide sobre sus superficies. Presentamos una relación que permite determinar la longitud de terrazas mínima que garanticen que al medio día solar, se proyecte una sombra sobre las paredes verticales, lo cual puede aplicarse en casas habitación para aumentar el confort térmico. Los resultados de la presente investigación pueden implemenanterse en modelos para cuantificar la radiación solar incidente sobre superficies que siguen al Sol.
V. AGRADECIMIENTOS
Este trabajo se realizó bajo el soporte del proyecto FING-2017-0004 de la Universidad Autónoma de Yucatán.
REFERENCIAS
Sitler R. K. (2006). “The 2016 Phenomenon New Age Appropriation of an Ancient Mayan Calendar”, Nova Religio: The Journal of Alternative and Emergent Religions, Vol. 19 No. 3, pp. 24-38 (DOI: 10.1525/nr.2006.9.3.024)
Aveni, A. F. (1992). “The sky in Mayan literature”, Osxford University Press, New York (USA), 307 p., ISBN 0-19-506844-0.
Kinsella, J., Day Bradley, A. (1934). “The mayan calendar”, The mathematics teacher, Vol. 27, No. 7, pp. 340-343.
Michalsky, J. J. (1988). “The Astronomical Almanac’s algorithm for approximate solar position (1950-2050)”. Solar Energy, Vol. 40 Issue 3, pp. 227-235.
Abdallah, S. y Nijmeh S. (2004). “Two axes sun tracking system with PLC control”, Energy Conversion and Management. Vol. 45, Issue 11-12, pp. 1931-1939.
Roth, A., Georgiev, A., Boudinov, H., (2005). “Cheap two axis sun following device”, Energy Conversion and Management. Vol. 46, Issue 7-8, pp. 1179-1192.
Chia-Yen Lee, et. al., (2009). “Sun Traking Systems: Areview”, Sensors. Vol. 9(05), pp. 3875-3890. (DOI: 10.3390/s90503875).
Reda, I. Adreas, A. (2004). “Solar position algorithm for solar radiation applications”. Solar Energy. Vol. 76, Issue 5, pp. 577-589.
Benford, F., y Bock, J. E., (1939). “A time analisys of Sunshine”, Trans. Of the American Illumination Engineering Soc. Vol. 34 p. 200.
Cooper, P. L. (1969). “The Absortion of Solar Radiation in Solar Stills”, Solar Energy. Vol. 12, p. 3.
Braun, J. E., y Mitchell, J. C. (1983). “Solar Geometry for Fixed and Traking Surfaces”, Solar Energy. Vol 31, p. 439.
APÉNDICE I
(*Comenzamos con la lectura del archivo de inicio (al final del apéndice ejemplificamos el archive init_file.dat), el cual es importado desde la misma carpeta en la que se encuentra el archivo Seguidor_diario_anual-ok.nb El usuario solo debe modifcar los datos numéricos, dejando el texto inalterado*)
directory=ToString[NotebookDirectory[]<>"init_file.dat"]; archivoinicio=Import[directory];
(*Se leen los datos de inicio para comenzar a ejecutar el programa*)
LATITUD=archivoinicio1,3; diainteres=archivoinicio2,3; mesinteres=archivoinicio3,3;
(*El siguiente conjunto de algoritmos genera los valores de la declinación, la hora del amanecer, la duración de horas de luz solar, en función de la latitud y el día que se quieran ver los datos, al final se viusualizan las gráficas*)
(*tablafechas, es para correlacionar la fecha en que se quiere conocer específicamente la posición del Sol*)
tablafechas=List[0,31,59,90,120,151,181,212,243,274,304 ,334];
(*Datos para iniciar el algoritmo, day es el día en particular en que queramos visualizar los gráficos, es calculado a partir de los datos del archivo init_file.dat*)
radian=Pi/180; day=diainteres+tablafechasmesinteres;
(*Cálculo de la declinación solar, el "bamboleo de la tierra mientras rota"*)
DECLINACION=23.45Sin[radian*360(284+n)/365]; DECLINACIONANIO=Table[{n,DECLINACION},{n,1,365}]; declinaciongraf=ListLinePlot[DECLINACIONANIO, PlotStyle->Green, AxesLabel- >{{dia},{declinación}}, ImageSize->500];
(*hora del amanecer en hora ángulo, 90o corresponden a las 6 am hora solar, 75o a las 7 am hora solar, .....*)
HORAAMANECERANIO=Table[{j,(180/Pi)ArcCos[- Tan[radian*LATITUD]Tan[(radian)DECLINACIONANIOj,2]]},{j,1,365}]; horaamanecergraf=ListLinePlot[Table[{dia,IntegerPart[12- HORAAMANECERANIOdia,2/15]+IntegerPart[(12-HORAAMANECERANIOdia,2/15- IntegerPart[12-HORAAMANECERANIOdia,2/15])*60]/100.0},{dia,1,365}],PlotRange- >{{1,365},{5,7}}, PlotStyle->Cyan, AxesLabel->{{dia},{hora_amancecer}},ImageSize->500];
HORAAMANECERANIOexport=Table[{dia,IntegerPart[12- HORAAMANECERANIOdia,2/15]+IntegerPart[(12-HORAAMANECERANIOdia,2/15- IntegerPart[12-HORAAMANECERANIOdia,2/15])*60]/100.0},{dia,1,365}];
(*horas totales de luz solar, desde el amanecer hasta la puesta de sol, son horas ángulo, y el día de mayor duración de luz solar, el mas largo y el mas corto*)
HORASLUZANIO=Table[{j,(2/15)*(180/Pi)ArcCos[- Tan[radian*LATITUD]Tan[(radian)DECLINACIONANIOj,2]]},{j,1,365}]; horasluzgraf=ListLinePlot[HORASLUZANIO,PlotRange->{{1,365},{0,14}}, PlotStyle- >Magenta,AxesLabel->{{dia},{horas_de _luz}},ImageSize->500];
(*Dependiendo de la latitud se obtiene el día más largo del año, veamos en largeday*)
largeday=Flatten[Position[Flatten[Table[HORASLUZANIOdia,2,{dia,1,365}]],Max[Flatten[Table [HORASLUZANIOdia,2,{dia,1,365}]]]]]
{172}
(*De la misma manera, se puede conocer cuál es día más corto del año*)
minday=Flatten[Position[Flatten[Table[HORASLUZANIOdia,2,{dia,1,365}]],Min[Flatten[Table[ HORASLUZANIOdia,2,{dia,1,365}]]]]]
{355}
(*Las horas de luz de sol del día más largo del año*)
horasluzmax=HORASLUZANIO[[largeday1]] {172,13.278}
(*Las horas de luz del día más corto del año*)
horasluzmin=HORASLUZANIO[[minday1]] {355,10.722}
(*La diferencia de horas de luz entre el día más largo y el más corto*)
diferenciahorasluz=horasluzmax2-horasluzmin2 2.55597
(*ángulo del zenith, calculado a partir de las 6 am hora solar, y medido cada minuto, si es mayor que 90 significa que el sol aún no ha salido, y con respecto al áungulo de elevación solar (el complemento del zenit), si es menor que cero significa que el sol aún no ha salido*)
thetaZdiario=Table [Table [ArcCos[Cos[radian*LATITUD]Cos[radian*DECLINACIONANIOdia,2]Cos[-radian(90- k*(15/60))]+Sin[radian*LATITUD]Sin[radian*DECLINACIONANIOdia,2]](180/Pi),{k,0,720}],{dia, 1,365}];
angulozenithgraf=Table[ListLinePlot[Table[{6+k/60,thetaZdiariodays,k},{k,1,Length[thetaZdia riodays]}],PlotStyle->Blue,AxesLabel->{{hora_solar},{ángulo_zenit}},ImageSize- >500],{days,1,365}];
altitudsolargraf=Table[ListLinePlot[Table[{6+k/60,90- thetaZdiariodays,k},{k,1,Length[thetaZdiariodays]}],PlotStyle->{Blue,Dashed},AxesLabel- >{{hora_solar},{ángulo_altitud}},ImageSize->500],{days,1,365}]; angulozenithvalues=Table[Table[{6+k/60.0,thetaZdiariodays,k},{k,1,Length[thetaZdiarioday s]}],{days,1,365}];
altitudsolarvalues=Table[Table[{6+k/60.0,90- thetaZdiariodays,k},{k,1,Length[thetaZdiariodays]}],{days,1,365}];
(*Acá creamos una carpeta: Angulo_Zenit, donde vamos a exportar los datos del ángulo de zenit para cada uno de los 365 días*)
dir1=CreateDirectory[NotebookDirectory[]<>"Angulo_Zenit"]; For[dia=1,dia<=Length[angulozenithvalues],dia++,f[time_]:=Export[ToFileName[dir1,ToString[ti me<>DayZenit]<>".dat"],angulozenithvaluesdia];
f[dia]]
(*Acá creamos una carpeta: Angulo_elevation, donde vamos a exportar los datos del ángulo de elevación para cada uno de los 365 días*)
dir2=CreateDirectory[NotebookDirectory[]<>"Angulo_elevation"]; For[dia=1,dia<=Length[angulozenithvalues],dia++,f[time_]:=Export[ToFileName[dir2,ToString[ti me<>DayElevation]<>".dat"],altitudsolarvaluesdia];
f[dia]]
(*Lo siguiente es para calcular al áungulo azimutal solar*)
PSEUDOGAMAS= Table[Table[ArcSin[Sin[radian*((k-1)*(15/60)- 90)]*Cos[radian*DECLINACIONANIOdia,2]/Sin[radian*thetaZdiariodia,k]],{k,1,Length[thet aZdiariodia]}],{dia,1,365}];
(*Si Tan[declination]/Tan[Latitud] > 1, entonces se debe hacer C1=1, lo que ocurre cuando Wew es imaginario*)
Wew= Table[ArcCos[Tan[radian*DECLINACIONANIOdia,2]/Tan[radian*LATITUD]],{dia,1,365}];
(*algoritmo para calcular el valor C1, iniciando con CC, CC0 y al final con C1*)
CC=Table[Table[(Abs[radian*(90-W*(15/60))]-Wewdia),{W,0,720}],{dia,1,365}]; CC0=Table[Table[If[Im[CCdia,W]!=0,- Abs[Re[CCdia,W]],CCdia,W],{W,1,Length[CCdia]}],{dia,1,365}]; C1=Table[Table[If[CC0dia,W<0,1,-1],{W,1,Length[CC0dia]}],{dia,1,365}];
(*algoritmo para calcular el valor de C2*)
CC2=Table[LATITUD(LATITUD-DECLINACIONANIOdia,2),{dia,1,365}]; C2=Table[If[CC2dia>=0,1,-1],{dia,1,365}];
(*algoritmo para calcular el valor de C3*)
C3=Table[((15/60)*k-89.99)/Abs[(15/60)*k-89.99],{k,0,720}];
(*azimutalsolar es el valor del ángulo azimutal solar para cada hora angular solar y cada día del año*)
azimutalsolar=Table[Table[C1dia,W*C2dia*PSEUDOGAMASdia,W+(C3W*((1- C1dia,W*C2dia)/2)*180)*radian,{W,1,Length[PSEUDOGAMASdia]}],{dia,1,365}]; azimutalsolargraf=Table[ListLinePlot[Table[{6+k/60,azimutalsolardays,k/radian},{k,1,720}], PlotStyle->{Red, Dashed,Thick},AxesLabel->{{hora_solar},{ángulo_azimutal}},ImageSize- >500],{days,1,365}]; azimutalsolarvalues=Table[Table[{6+k/60.0,azimutalsolardays,k/radian},{k,1,720}],{days,1,36 5}];
(*Acá creamos una carpeta: Angulo_Azimutal, donde vamos a exportar los datos del ángulo de azimutal para cada uno de los 365 días*)
dir3=CreateDirectory[NotebookDirectory[]<>"Angulo_Azimutal"]; For[dia=1,dia<=Length[azimutalsolarvalues],dia++,f[time_]:=Export[ToFileName[dir3,ToString[ti me<>DayAzimutal]<>".dat"],azimutalsolarvaluesdia];
f[dia]]
(*Finalmente, aca se muestrarán todos los datos graficados*)
DeclinacionGraf=declinaciongraf
DeclinaGrafdisk=Table[{DECLINACIONANIOk,Show[DeclinacionGraf,Graphics[{Red,Disk[DECLI NACIONANIOk,1]}]]},{k,1,Length[DECLINACIONANIO]}]
(*Exportación de los datos para realizar gráficos externos de la declinación*) Export[ToString[NotebookDirectory[]<>"Declinación_anual.dat"],DECLINACIONANIO];
(*Gráfica para visualizar la hora solar a la que amanece, cuando sale el Sol*) HoraSalidaSolGraf=horaamanecergraf
(*Algunos datos relevantes, número de días con más de 12 horas de luz solar: numlargday; día donde comienzan los días con más de 12 horas de luz: numlargadayinit; número de día donde terminan los días con más de 12 horas de luz: numlargedayfin*)
largedays=Cases[Table[If[HORAAMANECERANIOexportday,2<6,HORAAMANECERANIOexport day],{day,1,365}],Except[Null]];
numlargeday=Length[largedays] 182 numlargedayinit=largedays1 {82,5.59} numlargedayfin=largedays-1 {263,5.59}
(*Exportación de los datos para realizar gráficos externos de la hora de salida del Sol, para cada día del año*)
Export[ToString[NotebookDirectory[]<>"Hrs_salida_Sol.dat"],HORAAMANECERANIOexport]
(*Exportación de los datos para realizar gráficos externos de las horas de luz para cada día del año*)
HrsLuzexport=Table[{d,(HORASLUZANIOd,2- IntegerPart[HORASLUZANIOd,2])*0.6+IntegerPart[HORASLUZANIOd,2]},{d,1,365}];
Export[ToString[NotebookDirectory[]<>"Hrs_luz_de_dia.dat"],HrsLuzexport] HorasLuzSolarGraf=horasluzgraf
(*finalmente, conjuntamos un archivo con algunos datos de interés, como días mas largo y corto, horas de luz del día más largo, etc., y lo exportamos*)
resumen=List[{"dia mas largo","=",largeday1},{"horas luz dia mas largo","=",horasluzmax2},{"dia mas corto","=",minday1},{"horas luz dia mas corto","=", horasluzmin2}, {"diferencia horas luz","=",diferenciahorasluz}]
Contenido del archivo: init_file.dat
Latitud grados 21 dia interes 29 mes interes 1
|