m (Arac moved page Review 340049356361 to Review 576619708258) |
m (Gstinoco moved page Review 432319853501 to Aranda 2025a) |
||
| (12 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
| + | ==1 Introducción== | ||
| − | + | La complejidad que presenta la estimación de las conexiones neuronales en el cerebro humano ha impulsado el desarrollo de diversas herramientas para su adquisición y estudio. Entre ellas, la tractografía cerebral, basada en imágenes por resonancia magnética de difusión (dMRI), se ha convertido en un método clave para estimar estas conexiones estructurales. Esta técnica permite estimar las trayectorias de las fibras axonales que conectan distintas regiones cerebrales, proporcionando información importante sobre la organización y la integridad del conectoma humano <span id='citeF-1'></span>[[#cite-1|[1]]]. Sin embargo, a pesar de los avances en esta técnica, persisten desafíos importantes que limitan su precisión, como la alta incidencia de trayectorias erróneas (falsos positivos) y la incapacidad de resolver de manera adecuada la complejidad estructural en zonas donde las fibras se cruzan o bifurcan <span id='citeF-2'></span><span id='citeF-3'></span><span id='citeF-4'></span>[[#cite-2|[2,3,4]]]. En este contexto, la presente investigación propone abordar dichas limitaciones mediante la implementación de un enfoque de optimización convexa basado en microestructura, inspirado en el algoritmo ''Convex Optimization Modeling for Microstructure Informed Tractography'' (COMMIT) <span id='citeF-5'></span>[[#cite-5|[5]]]. Esta propuesta integra información microestructural detallada en el proceso de la estimación de trayectorias de haces axonales, reduciendo tanto los falsos positivos como las incertidumbres en áreas de complejidad anatómica. | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | La complejidad que presenta la estimación de las conexiones neuronales en el cerebro humano | + | |
La relevancia de esta investigación es significativa, ya que un avance en la precisión de la tractografía cerebral no solo aportaría un mayor entendimiento sobre la conectividad estructural en individuos sanos, sino que también abriría nuevas posibilidades en el estudio de enfermedades neurológicas, donde el análisis detallado de las vías neuronales es crucial para la comprensión de los mecanismos patológicos <span id='citeF-6'></span>[[#cite-6|[6]]]. Además, este desarrollo podría impactar directamente en áreas como la planificación quirúrgica y la medicina personalizada, donde la exactitud en la reconstrucción de los tractos neuronales es esencial para evitar errores clínicos <span id='citeF-7'></span><span id='citeF-8'></span>[[#cite-7|[7,8]]]. | La relevancia de esta investigación es significativa, ya que un avance en la precisión de la tractografía cerebral no solo aportaría un mayor entendimiento sobre la conectividad estructural en individuos sanos, sino que también abriría nuevas posibilidades en el estudio de enfermedades neurológicas, donde el análisis detallado de las vías neuronales es crucial para la comprensión de los mecanismos patológicos <span id='citeF-6'></span>[[#cite-6|[6]]]. Además, este desarrollo podría impactar directamente en áreas como la planificación quirúrgica y la medicina personalizada, donde la exactitud en la reconstrucción de los tractos neuronales es esencial para evitar errores clínicos <span id='citeF-7'></span><span id='citeF-8'></span>[[#cite-7|[7,8]]]. | ||
| − | + | Este trabajo se enfoca en las limitaciones actuales de los métodos de tractografía para mejorar la reconstrucción de las conexiones cerebrales integrando información microestructural mediante optimización convexa, ofreciendo un marco más robusto para futuras aplicaciones clínicas y de investigación. | |
| − | == | + | ==2 Trabajos relacionados== |
| − | La tractografía es un enfoque que | + | La tractografía es un enfoque que permite estimar las trayectorias de haces de axones mediante curvas tridimensionales (3D), a partir de las orientaciones derivadas de las dMRI <span id='citeF-9'></span>[[#cite-9|[9]]]. En general, la construcción de una trayectoria comienza con la selección de un punto inicial, denominado semilla. A partir de este punto, la trayectoria se propaga utilizando la información proporcionada por las dMRI, generando así una curva que representa el recorrido estimado de las fibras axonales. El movimiento de la trayectoria puede describirse mediante la siguiente ecuación de actualización: |
{| class="formulaSCP" style="width: 100%; text-align: left;" | {| class="formulaSCP" style="width: 100%; text-align: left;" | ||
| Line 32: | Line 21: | ||
|} | |} | ||
| − | donde <math display="inline">y_t</math> | + | donde <math display="inline">y_t</math> representa la posición tridimensional (3D) de la partícula en el tiempo <math display="inline">t</math>, <math display="inline">d_t</math> corresponde a la dirección de propagación y <math display="inline">\Delta </math> es el tamaño de paso. Así, una trayectoria, <math display="inline">s</math>, está formada por <math display="inline">s = \{ y_1,y_2,\ldots ,y_m\} </math>. En términos generales, la principal diferencia entre los distintos métodos de tractografía radica en la manera en que se estima la dirección <math display="inline">d_t</math> en cada paso de la trayectoria <span id='citeF-10'></span><span id='citeF-11'></span>[[#cite-10|[10,11]]]. |
| − | Una clase de métodos que han demostrado un gran desempeño son | + | Una clase de métodos que han demostrado un gran desempeño son aquellos que logran integrar información de vecindades para estimar <math display="inline">d_t</math> <span id='citeF-6'></span>[[#cite-6|[6]]]. Entre estos métodos se encuentran: la Tractografía basada en Comportamiento Colectivo (TCC) <span id='citeF-12'></span>[[#cite-12|[12]]], la Tractografía por Filtro de Partículas (TFP) <span id='citeF-13'></span>[[#cite-13|[13]]] y la Tractografía por Transporte Paralelo (TTP) <span id='citeF-14'></span>[[#cite-14|[14]]]. |
| − | + | TCC modela la propagación de las trayectorias inspirándose en el comportamiento colectivo de bandadas (''flocking''). Cada trayectoria sigue reglas locales de alineamiento, cohesión y separación, lo que permite que las trayectorias se ajusten mutuamente mientras avanzan. Esto genera un comportamiento colaborativo que reduce rutas aisladas y guía a las fibras hacia patrones anatómicamente plausibles. El método incorpora información de vecindades del conjunto de trayectorias, y no únicamente del punto local de difusión. Como resultado, produce tractogramas más coherentes y con menos falsos positivos. | |
| − | + | ||
| − | + | ||
| − | + | TFP tiene como objetivo reducir la cantidad de trayectorias que terminan prematuramente dentro de la materia blanca o en el líquido cefalorraquídeo. La idea central de este método es realizar un retroceso en los tiempos <math display="inline">t-i</math> en aquellas trayectorias que han experimentado una terminación anticipada. De esta manera, se aplica una corrección a la trayectoria estimada, permitiendo que alcance adecuadamente un punto de terminación válido. | |
| − | = | + | Finalmente, TTP es un método que define un marco ortonormal a lo largo de cada trayectoria para evitar rotaciones arbitrarias en la orientación de las fibras. Utiliza el concepto geométrico de ''transporte paralelo'' <span id='citeF-15'></span>[[#cite-15|[15]]] para actualizar las direcciones locales de manera suave y consistente. Esto permite que la dirección de propagación se adapte fielmente a los cambios en la estructura de la materia blanca. A diferencia de los métodos clásicos, evita giros abruptos y mantiene la coherencia direccional. Como resultado, se obtiene una tractografía más estable, precisa y menos afectada por artefactos de orientación. |
| − | + | Al igual que los métodos previamente descritos, en este trabajo también proponemos la integración de vecindades de información; sin embargo, incorporamos información microestructural mediante el algoritmo COMMIT <span id='citeF-5'></span>[[#cite-5|[5]]] directamente durante el proceso de generación de la tractografía. Esta integración se realiza de forma local, aplicando COMMIT a pequeñas vecidades alrededor del punto <math display="inline">y_t</math>. Con ello, no solo se optimiza la selección de las trayectorias más plausibles, sino que además se posibilita la recuperación de falsos negativos, mejorando la precisión de las conexiones anatómicas estimadas. | |
| − | == | + | ==3 Algoritmo propuesto== |
| − | + | Nuestra contribución principal radica en la integración del algoritmo COMMIT <span id='citeF-5'></span>[[#cite-5|[5]]] en el proceso de generación de tractografías, aplicándolo a pequeñas vecindades durante la estimación de las trayectorias, lo cual nos permite calcular <math display="inline">d_t</math>. A diferencia de las implementaciones tradicionales de COMMIT, que se aplican de manera posterior a la generación de las tractografías, nuestra propuesta explora su aplicación en tiempo real, reduciendo la dependencia de ajustes posteriores y preservando una mayor cantidad de información durante el proceso de reconstrucción. | |
| − | + | ===3.1 COMMIT=== | |
| + | |||
| + | Para abordar la problemática de la presencia de falsos positivos en las reconstrucciones de las tractografías, Daducci et al. (2015) <span id='citeF-5'></span>[[#cite-5|[5]]] propusieron el algoritmo COMMIT, el cual utiliza un marco de optimización convexa para refinar tractografías mediante la eliminación de trayectorias inconsistentes con los datos de difusión. A diferencia de otros métodos de posprocesamiento, COMMIT incorpora información microestructural del tejido cerebral, ajustando la contribución de cada fibra en la señal medida y filtrando aquellas que no se justifican a partir del modelo físico subyacente. | ||
| + | |||
| + | Dado un tractograma, el modelo matemático de COMMIT se basa en la siguiente ecuación lineal: | ||
{| class="formulaSCP" style="width: 100%; text-align: left;" | {| class="formulaSCP" style="width: 100%; text-align: left;" | ||
| Line 57: | Line 48: | ||
{| style="text-align: left; margin:auto;width: 100%;" | {| style="text-align: left; margin:auto;width: 100%;" | ||
|- | |- | ||
| − | | style="text-align: center;" | <math>\mathbf{y} = \mathbf{A} \mathbf{x} + \eta , | + | | style="text-align: center;" | <math>\mathbf{y} = \mathbf{A}\mathbf{x} + \eta , </math> |
|} | |} | ||
| style="width: 5px;text-align: right;white-space: nowrap;" | (2) | | style="width: 5px;text-align: right;white-space: nowrap;" | (2) | ||
|} | |} | ||
| − | donde | + | donde <math display="inline">\mathbf{y} \in \mathbb{R}^M</math> representa la señal de difusión medida en cada vóxel, <math display="inline">\mathbf{A} \in \mathbb{R}^{M \times N}</math> es la matriz de diseño que describe la contribución de cada trayectoria a la señal medida, <math display="inline">\mathbf{x} \in \mathbb{R}^N</math> es el vector de pesos asociado a cada trayectoria candidata y <math display="inline">\eta \in \mathbb{R}^M</math> corresponde al ruido de medición. |
| − | + | El objetivo de COMMIT es encontrar el vector <math display="inline">\mathbf{x}</math> que mejor explica la señal <math display="inline">\mathbf{y}</math>, imponiendo restricciones de no negatividad y promoviendo la dispersión en <math display="inline">\mathbf{x}</math> para eliminar trayectorias irrelevantes. Esto se logra mediante la siguiente formulación de optimización convexa: | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | El objetivo de COMMIT es encontrar el vector <math display="inline">\mathbf{x}</math> que mejor explica la señal <math display="inline">\mathbf{y}</math>, imponiendo restricciones de no negatividad y promoviendo la dispersión en <math display="inline">\mathbf{x}</math> para eliminar | + | |
<span id="eq-3"></span> | <span id="eq-3"></span> | ||
| Line 77: | Line 63: | ||
{| style="text-align: left; margin:auto;width: 100%;" | {| style="text-align: left; margin:auto;width: 100%;" | ||
|- | |- | ||
| − | | style="text-align: center;" | <math>\min _{\mathbf{x} \geq 0} \| \mathbf{A} \mathbf{x} - \mathbf{y}\| _2^2 + \lambda \| \mathbf{x}\| _1, | + | | style="text-align: center;" | <math>\min _{\mathbf{x} \geq 0} \| \mathbf{A}\mathbf{x} - \mathbf{y}\| _2^2 + \lambda \| \mathbf{x}\| _1, </math> |
|} | |} | ||
| style="width: 5px;text-align: right;white-space: nowrap;" | (3) | | style="width: 5px;text-align: right;white-space: nowrap;" | (3) | ||
| Line 84: | Line 70: | ||
donde el primer término minimiza el error de reconstrucción de la señal, mientras que el término de regularización <math display="inline">\| \mathbf{x}\| _1</math> promueve la selección de un subconjunto reducido de fibras, eliminando aquellas que no contribuyen significativamente a la señal observada. El parámetro <math display="inline">\lambda </math> controla el grado de regularización <span id='citeF-5'></span>[[#cite-5|[5]]]. | donde el primer término minimiza el error de reconstrucción de la señal, mientras que el término de regularización <math display="inline">\| \mathbf{x}\| _1</math> promueve la selección de un subconjunto reducido de fibras, eliminando aquellas que no contribuyen significativamente a la señal observada. El parámetro <math display="inline">\lambda </math> controla el grado de regularización <span id='citeF-5'></span>[[#cite-5|[5]]]. | ||
| − | COMMIT incorpora modelos de microestructura basados en principios biológicos, como | + | COMMIT incorpora modelos de microestructura basados en principios biológicos, como el modelo Stick–Tensor <span id='citeF-16'></span>[[#cite-16|[16]]] (que representa axones como cilindros delgados con difusión restringida ) y el modelo de compartimentos mixtos <span id='citeF-5'></span>[[#cite-5|[5]]] (que considera la presencia de múltiples tipos de tejidos, como fibras y espacio extracelular). Estos modelos, codificados en la matriz <math display="inline">\mathbf{A}</math>, permiten ajustar la contribución de cada trayectoria de acuerdo con su compatibilidad con la estructura neuronal, lo que ayuda a eliminar conexiones falsas <span id='citeF-17'></span>[[#cite-17|[17]]]. |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | Estos modelos, codificados en la | + | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | Este proceso permite mejorar la especificidad de la tractografía y reducir significativamente la cantidad de falsos positivos, | + | Tras la resolución del problema de optimización presentado en la ecuación [[#eq-3|(3)]] (donde la matriz <math display="inline">\mathbf{A}</math> es de una escala muy grande), se obtiene un conjunto refinado de fibras, en el cual muchas de las trayectorias originales han sido eliminadas debido a su baja contribución a la señal medida. El criterio de eliminación se basa en el valor de <math display="inline">\mathbf{x}</math> obtenido para cada fibra. Si <math display="inline">x_i \approx 0</math>, la trayectoria <math display="inline">i</math> se considera inconsistente con la señal de difusión y es eliminada. De lo contrario, si <math display="inline">x_i > 0</math>, la trayectoria <math display="inline">i</math> es retenida en la tractografía final. Este proceso permite mejorar la especificidad de la tractografía y reducir significativamente la cantidad de falsos positivos, dando lugar a estimaciones de conectividad más precisas <span id='citeF-5'></span><span id='citeF-18'></span>[[#cite-5|[5,18]]]. |
| − | === | + | ===3.2 Tractografía basada en COMMIT=== |
| − | Dado un tractograma base, calculado con cualquier algoritmo de tractografía, con <math display="inline">S = \{ s_1, s_2, \ldots , | + | Dado un tractograma base, calculado con cualquier algoritmo de tractografía, con <math display="inline">S = \{ s_1, s_2, \ldots , s_K\} </math>, en cada paso del proceso de generación de las estimaciones de los haces de axones se obtienen trayectorias candidatas aplicando criterios de filtrado basados en un cono direccional (vecindad) alrededor de la trayectoria central estimada. Sea <math display="inline">\hat{s}_i</math> el segmento de la trayectoria <math display="inline">s_i</math> contenido dentro del cono. Formalmente, si <math display="inline">\mathbf{c}</math> denota la dirección del cono y <math display="inline">\mathbf{u}_{\hat{s}_i,j}</math> representa la dirección del segmento <math display="inline">j</math> de la trayectoria <math display="inline">\hat{s}_i</math>, dicho segmento se considera válido si todos sus subsegmentos satisfacen un umbral angular máximo <math display="inline">\theta _{\mathrm{tol}}</math>: |
{| class="formulaSCP" style="width: 100%; text-align: left;" | {| class="formulaSCP" style="width: 100%; text-align: left;" | ||
| Line 116: | Line 88: | ||
|} | |} | ||
| − | o equivalentemente en términos del producto escalar, | + | o equivalentemente en términos del producto escalar, |
| − | + | ||
| − | + | ||
{| class="formulaSCP" style="width: 100%; text-align: left;" | {| class="formulaSCP" style="width: 100%; text-align: left;" | ||
| Line 125: | Line 95: | ||
{| style="text-align: left; margin:auto;width: 100%;" | {| style="text-align: left; margin:auto;width: 100%;" | ||
|- | |- | ||
| − | | style="text-align: center;" | <math>\mathbf{ | + | | style="text-align: center;" | <math>\frac{| \mathbf{u}_{\hat{s}_i,j}\cdot \mathbf{c}|}{\| \mathbf{u}_{\hat{s}_i,j}\| \| \mathbf{c}\| }\ge \cos (\theta _{\mathrm{tol}}), </math> |
|} | |} | ||
| style="width: 5px;text-align: right;white-space: nowrap;" | (5) | | style="width: 5px;text-align: right;white-space: nowrap;" | (5) | ||
|} | |} | ||
| − | + | para todo segmento. Este criterio garantiza que las trayectorias en el cono no se alejen demasiado de la dirección predominante en la vencindad del cono. | |
| + | |||
| + | Para cada trayectoria <math display="inline">\hat{s}_i</math> en el cono, se calcula la dirección promedio de todos sus segmentos. Si la trayectoria <math display="inline">\hat{s}_i</math> tiene <math display="inline">N_{\hat{s}_i}</math> segmentos con vectores de dirección <math display="inline">\mathbf{u}_{\hat{s}_i,j}</math>, su dirección promedio se define como | ||
{| class="formulaSCP" style="width: 100%; text-align: left;" | {| class="formulaSCP" style="width: 100%; text-align: left;" | ||
| Line 137: | Line 109: | ||
{| style="text-align: left; margin:auto;width: 100%;" | {| style="text-align: left; margin:auto;width: 100%;" | ||
|- | |- | ||
| − | | style="text-align: center;" | <math> | + | | style="text-align: center;" | <math>\mathbf{d}_{\hat{s}_i} = \frac{1}{N_{\hat{s}_i}}\sum _{j=1}^{N_{\hat{s}_i}}\mathbf{u}_{\hat{s}_i,j}. </math> |
|} | |} | ||
| style="width: 5px;text-align: right;white-space: nowrap;" | (6) | | style="width: 5px;text-align: right;white-space: nowrap;" | (6) | ||
|} | |} | ||
| − | + | A continuación se normaliza este vector promedio para obtener la dirección unitaria: | |
| − | + | ||
| − | + | ||
| + | <span id="eq-7"></span> | ||
{| class="formulaSCP" style="width: 100%; text-align: left;" | {| class="formulaSCP" style="width: 100%; text-align: left;" | ||
|- | |- | ||
| Line 151: | Line 122: | ||
{| style="text-align: left; margin:auto;width: 100%;" | {| style="text-align: left; margin:auto;width: 100%;" | ||
|- | |- | ||
| − | | style="text-align: center;" | <math>\ | + | | style="text-align: center;" | <math>\hat{\mathbf{d}}_{\hat{s}_i} = \frac{\mathbf{d}_{\hat{s}_i}}{\| \mathbf{d}_{\hat{s}_i}\| }. </math> |
|} | |} | ||
| style="width: 5px;text-align: right;white-space: nowrap;" | (7) | | style="width: 5px;text-align: right;white-space: nowrap;" | (7) | ||
|} | |} | ||
| − | + | De esta manera cada trayectoria válida queda representada por su dirección promedio unitaria <math display="inline">\hat{\mathbf{d}}_{\hat{s}_i}</math>, lo cual facilita la comparación entre fibras. | |
| − | + | La similitud direccional entre dos trayectorias se cuantifica mediante el coseno del ángulo entre sus direcciones promedio. Para dos vectores unitarios <math display="inline">\hat{\mathbf{d}}_{\hat{s}_i}</math> y <math display="inline">\mathbf{d}_t</math>, la métrica de similitud direccional se define como su producto escalar: | |
{| class="formulaSCP" style="width: 100%; text-align: left;" | {| class="formulaSCP" style="width: 100%; text-align: left;" | ||
| Line 165: | Line 136: | ||
{| style="text-align: left; margin:auto;width: 100%;" | {| style="text-align: left; margin:auto;width: 100%;" | ||
|- | |- | ||
| − | | style="text-align: center;" | <math>\ | + | | style="text-align: center;" | <math>\sigma _i(\hat{s}_i,t) = \bigl|\hat{\mathbf{d}}_{\hat{s}_i} \cdot \mathbf{d}_t\bigr| = \cos \bigl(\angle (\hat{\mathbf{d}}_{\hat{s}_i},\mathbf{d}_t)\bigr). </math> |
|} | |} | ||
| style="width: 5px;text-align: right;white-space: nowrap;" | (8) | | style="width: 5px;text-align: right;white-space: nowrap;" | (8) | ||
|} | |} | ||
| − | + | Este valor se encuentra en el rango <math display="inline">[0,1]</math> y mide cuán alineadas están las direcciones de dos trayectorias. En particular, la similitud de cada trayectoria <math display="inline">s</math> puede evaluarse respecto a la dirección predominante o frente a otras fibras candidatas, penalizando aquellas que desvían significativamente su orientación. | |
| + | |||
| + | Finalmente, cada trayectoria candidata se puntúa con una función compuesta que pondera su peso dado por COMMIT y su similitud direccional. Si <math display="inline">x_{\hat{s}_i}</math> es el peso asignado por COMMIT al segmento de trayectoria <math display="inline">\hat{s}_i</math>, se puede definir el peso normalizado como <math display="inline">\tilde{x}_{\hat{s}_i} = x_{\hat{s}_i} \big/\sum _{k} x_k</math>, donde <math display="inline">x_k</math> son los pesos de todos los segmentos en el cono. Con un parámetro <math display="inline">\lambda \in [0,1]</math> que regula la importancia relativa, se define la puntuación compuesta: | ||
{| class="formulaSCP" style="width: 100%; text-align: left;" | {| class="formulaSCP" style="width: 100%; text-align: left;" | ||
| Line 177: | Line 150: | ||
{| style="text-align: left; margin:auto;width: 100%;" | {| style="text-align: left; margin:auto;width: 100%;" | ||
|- | |- | ||
| − | | style="text-align: center;" | <math>\hat{s} | + | | style="text-align: center;" | <math>\kappa _{\hat{s}_i} = (1 - \lambda )\,\tilde{x}_{\hat{s}_i} \;+\; \lambda \,\sigma _i(\hat{s}_i,t). </math> |
|} | |} | ||
| style="width: 5px;text-align: right;white-space: nowrap;" | (9) | | style="width: 5px;text-align: right;white-space: nowrap;" | (9) | ||
|} | |} | ||
| − | + | De esta forma, si <math display="inline">\lambda = 0</math> se toma en cuenta solo el criterio COMMIT y si <math display="inline">\lambda = 1</math> solo la similitud direccional. Finalmente, se selecciona la trayectoria <math display="inline">\hat{s}^*</math> con la mayor puntuación compuesta: | |
| − | == | + | {| class="formulaSCP" style="width: 100%; text-align: left;" |
| + | |- | ||
| + | | | ||
| + | {| style="text-align: left; margin:auto;width: 100%;" | ||
| + | |- | ||
| + | | style="text-align: center;" | <math>\hat{s}^* \;=\; \arg \max _{\hat{s}_i} \,\kappa _{\hat{s}_i}. </math> | ||
| + | |} | ||
| + | | style="width: 5px;text-align: right;white-space: nowrap;" | (10) | ||
| + | |} | ||
| − | + | Posteriormente, podemos usar <math display="inline">\hat{s}^*</math> para calcular <math display="inline">d_{t+1}</math> usando ecuación ([[#eq-7|7]]). | |
| − | + | ==4 Experimentos y resultados== | |
| − | + | Con el objetivo de evaluar el desempeño del método propuesto de tractografía informada por microestructura mediante optimización convexa, esta sección detalla los experimentos y resultados. | |
| − | + | Se emplean dos conjuntos de datos sintéticos ampliamente usados en la comunidad científica: el ISMRM Tractography Challenge 2015 (actualización 2023) <span id='citeF-19'></span>[[#cite-19|[19]]] y DiSCo (Diffusion-Simulated Connectivity) <span id='citeF-6'></span>[[#cite-6|[6]]]. El primero se usará para análisis espaciales y estructurales. El segundo, para evaluación cuantitativa de conectividad. Su uso complementario ofrece un marco sólido para validar el nuevo método de tractografía propuesto. | |
| − | < | + | En ambos casos se generarán tractografías con el algoritmo propuesto y con métodos tradicionales ampliamente utilizados. Posteriormente se aplicarán métricas de evaluación adecuadas al tipo de datos: para el primer conjunto se emplea la técnica Linear Fascicle Evaluation (LiFE) <span id='citeF-20'></span>[[#cite-20|[20]]] para estimar la contribución predictiva de cada trayectoria. Para el segundo se usan métricas de correlación, exactitud y área bajo la curva ROC (AUC), tal como lo establece el protocolo de evaluación del DiSCo Challenge <span id='citeF-6'></span>[[#cite-6|[6]]]. |
| − | + | Para la validación anatómica cualitativa y cuantitativa basada en trayectorias con el conjunto ISMRM, primero se seleccionará una semilla en el cuerpo calloso, una región con conectividad interhemisférica bien definida que resulta ideal para evaluar la coherencia geométrica de las tractografías generadas. A partir de esta semilla se obtendrán tractografías mediante algoritmos determinísticos convencionales (como FACT, TEND, SD-Stream o iFOD2) y mediante el algoritmo propuesto, que integra restricciones microestructurales mediante COMMIT durante la generación de las trayectorias. Cada tractografía se evaluará con el algoritmo LiFE, que estima la contribución predictiva de cada trayectoria sobre la señal dMRI original, permitiendo filtrar trayectorias no justificadas y evaluar el ajuste global de cada modelo. Finalmente se comparará el rendimiento del algoritmo propuesto con el de los métodos convencionales considerando su coherencia anatómica respecto de las fibras de referencia, la puntuación de predicción bajo el modelo LiFE y el número de líneas filtradas por LiFE como no justificadas. | |
| − | + | ||
| − | + | La validación cuantitativa de conectividad estructural entre regiones cerebrales utilizará el conjunto de datos del DiSCo Challenge. En este caso se evaluará solo el desempeño del algoritmo propuesto para contrastar sus resultados con los obtenidos por otros métodos participantes del challenge original. Se usará el subconjunto de alta resolución del DiSCo1, en sus versiones con ruido Rician a niveles de Relación señal-ruido (SNR por sus siglas en inglés) de 10, 20, 30 y 50. A partir de las tractografías generadas, se estimarán matrices de conectividad ponderadas entre las 16 regiones de interés (ROIs) definidas en el conjunto de datos. Las conexiones se cuantificarán según el número de trayectorias entre cada par de ROIs y, cuando corresponda, según el peso estimado en función de la microestructura. La calidad de estas matrices se evaluará mediante las métricas del DiSCo Challenge: correlación de Pearson con la matriz de referencia (peso continuo), área bajo la curva ROC (comparando con la matriz binaria de referencia) y exactitud de clasificación (pares correctamente identificados como conectados o no conectados). Finalmente, se analizará el comportamiento del algoritmo frente a diferentes niveles de ruido para evaluar su robustez y sensibilidad a condiciones adversas. | |
| − | + | ||
| − | + | ||
| − | + | ===4.1 Resultados=== | |
| − | + | ||
| − | + | La Figura [[#img-1|1]] muestra una comparación visual de tres tractografías generadas a partir de una misma semilla localizada en el cuerpo calloso, utilizando diferentes algoritmos. Todas las tractografías fueron generadas con la misma cantidad de trayectorias, lo que permite una observación cualitativa más equitativa entre métodos. | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | A partir de esta visualización inicial pueden identificarse algunas diferencias notables entre las tres reconstrucciones. El algoritmo iFOD2 (Figura [[#img-1|1]]a) presenta una mayor dispersión de trayectorias hacia regiones laterales, algo que puede relacionarse con su naturaleza probabilística, propensa a explorar recorridos menos restringidos. SD-Stream (Figura [[#img-1|1]]b) exhibe una estructura más centralizada y simétrica en la región del cuerpo calloso; las trayectorias aparecen más alineadas, aunque ello podría limitar la cobertura en zonas periféricas. El algoritmo propuesto (Figura [[#img-1|1]]c) parece mantener un equilibrio entre coherencia espacial y extensión: las trayectorias se distribuyen dentro de un rango anatómicamente plausible y sin una dispersión excesiva. Estos resultados corresponden únicamente a una inspección visual preliminar. | |
| − | + | Aunque el comportamiento del algoritmo propuesto resulta alentador, es necesario complementar este análisis con métricas cuantitativas en las siguientes secciones para validar su desempeño de forma objetiva. Para complementar el análisis visual anterior se aplicó el modelo LiFE a cada una de las tractografías generadas. Esta herramienta filtra las fibras que no contribuyen de manera significativa a explicar la señal de difusión y, de este modo, ofrece un estimador indirecto de la fidelidad anatómica de las trayectorias reconstruidas. | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
<div id='img-1'></div> | <div id='img-1'></div> | ||
{| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 100%;max-width: 100%;" | {| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 100%;max-width: 100%;" | ||
|- | |- | ||
| − | |[[Image: | + | |[[Image:Review_432319853501-resultados.png|600px|Comparación visual de tractografías generadas desde una semilla en el cuerpo calloso: a) iFOD2, b) SD-Stream, c) Algoritmo propuesto.]] |
|- style="text-align: center; font-size: 75%;" | |- style="text-align: center; font-size: 75%;" | ||
| colspan="1" | '''Figura 1:''' Comparación visual de tractografías generadas desde una semilla en el cuerpo calloso: a) iFOD2, b) SD-Stream, c) Algoritmo propuesto. | | colspan="1" | '''Figura 1:''' Comparación visual de tractografías generadas desde una semilla en el cuerpo calloso: a) iFOD2, b) SD-Stream, c) Algoritmo propuesto. | ||
|} | |} | ||
| − | |||
| − | |||
| Line 282: | Line 219: | ||
|} | |} | ||
| − | + | La Tabla [[#table-1|1]] muestra los resultados obtenidos al aplicar LiFE. Aunque todos los métodos partieron del mismo número total de fibras (780), se observa una diferencia en la cantidad de trayectorias que LiFE considera significativas. En particular, la tractografía generada con el algoritmo propuesto retuvo una mayor proporción de fibras, lo cual podría indicar una mejor coherencia con los datos de difusión. | |
| − | + | Adicionalmente, se calcularon métricas cuantitativas para evaluar la similitud entre las matrices de conectividad estimadas y la matriz de referencia proporcionada por el DiSCo Challenge. Las métricas consideradas incluyen la correlación de Pearson (<math display="inline">r</math>), el AUC y la exactitud, esta última evaluada considerando un umbral de conectividad del 5% | |
| Line 317: | Line 254: | ||
|} | |} | ||
| − | Los resultados | + | Los resultados en la Tabla [[#table-2|2]] muestran una correlación positiva significativa en todos los niveles de ruido, con valores de <math display="inline">r</math> superiores a 0.83, lo cual indica una correspondencia estructural consistente entre las matrices estimadas y la matriz de referencia. Asimismo, los valores de AUC cercanos a 0.95 en todos los casos sugieren una buena capacidad del algoritmo para discriminar entre conexiones presentes y ausentes. En cuanto a la exactitud, los valores absolutos son moderados. |
| − | Un aspecto central en la evaluación del algoritmo propuesto es determinar su comportamiento frente a distintas condiciones de ruido y la sensibilidad respecto a los parámetros de construcción de fibras, en particular el tamaño del cono ( | + | Un aspecto central en la evaluación del algoritmo propuesto es determinar su comportamiento frente a distintas condiciones de ruido y la sensibilidad respecto a los parámetros de construcción de fibras, en particular el tamaño del cono (cone_size) y el ángulo de apertura (<math display="inline">\theta _{tol}</math>). La Tabla [[#table-3|3]] resume los valores de las métricas de desempeño en función de dichos parámetros, considerando diferentes niveles de SNR. Los resultados muestran que, de manera general, tanto la correlación <math display="inline">r</math> como el AUC presentan valores más altos para configuraciones intermedias de parámetros, mientras que valores extremos tienden a deteriorar el rendimiento. |
{| class="floating_tableSCP wikitable" style="text-align: right; margin: 1em auto;min-width:50%;" | {| class="floating_tableSCP wikitable" style="text-align: right; margin: 1em auto;min-width:50%;" | ||
| − | |+ style="font-size: 75%;" |<span id='table-3'></span>Tabla. 3 Sensibilidad del algoritmo según parámetros de construcción ( | + | |+ style="font-size: 75%;" |<span id='table-3'></span>Tabla. 3 Sensibilidad del algoritmo propuesto según parámetros de construcción (cone_size y <math>\theta _{tol}</math>) en diferentes niveles de SNR. Se muestran los valores de correlación <math>r</math>, AUC y exactitud. |
|- style="border-top: 2px solid;" | |- style="border-top: 2px solid;" | ||
| rowspan='2' style="text-align: left;" | Métrica | | rowspan='2' style="text-align: left;" | Métrica | ||
| Line 464: | Line 401: | ||
| 0.972 | | 0.972 | ||
|- style="border-top: 2px solid;" | |- style="border-top: 2px solid;" | ||
| − | | style="text-align: left;" | | + | | style="text-align: left;" | exactitud |
| style="text-align: left;" | 10 | | style="text-align: left;" | 10 | ||
| 0.333 | | 0.333 | ||
| Line 479: | Line 416: | ||
| 0.467 | | 0.467 | ||
|- | |- | ||
| − | | style="text-align: left;" | | + | | style="text-align: left;" | exactitud |
| style="text-align: left;" | 20 | | style="text-align: left;" | 20 | ||
| 0.358 | | 0.358 | ||
| Line 494: | Line 431: | ||
| 0.483 | | 0.483 | ||
|- | |- | ||
| − | | style="text-align: left;" | | + | | style="text-align: left;" | exactitud |
| style="text-align: left;" | 30 | | style="text-align: left;" | 30 | ||
| 0.325 | | 0.325 | ||
| Line 509: | Line 446: | ||
| 0.492 | | 0.492 | ||
|- style="border-bottom: 2px solid;" | |- style="border-bottom: 2px solid;" | ||
| − | | style="text-align: left;" | | + | | style="text-align: left;" | exactitud |
| style="text-align: left;" | 50 | | style="text-align: left;" | 50 | ||
| 0.383 | | 0.383 | ||
| Line 526: | Line 463: | ||
|} | |} | ||
| − | == | + | ==5 Conclusiones== |
| − | El presente trabajo se centró en el desarrollo y la evaluación preliminar de un algoritmo de tractografía cerebral que integra el marco de optimización convexa COMMIT de manera temprana en la construcción de fibras. El objetivo principal fue explorar si esta estrategia permite reducir falsos positivos y recuperar falsos negativos desde la fase inicial de la generación de | + | El presente trabajo se centró en el desarrollo y la evaluación preliminar de un algoritmo de tractografía cerebral que integra el marco de optimización convexa COMMIT de manera temprana en la construcción de fibras. El objetivo principal fue explorar si esta estrategia permite reducir falsos positivos y recuperar falsos negativos desde la fase inicial de la generación de trayectorias, en lugar de aplicar la validación únicamente como un paso posterior. Los resultados presentados demuestran el potencial del enfoque planteado. Si bien el desempeño aún no alcanza niveles competitivos, especialmente en términos de exactitud, las mejoras observadas en correlación y AUC respaldan la hipótesis de que la validación temprana con COMMIT puede convertirse en una herramienta prometedora para incrementar la precisión de las tractografías. |
| − | El método propuesto | + | El método propuesto presenta como principal limitación su dependencia de una tractografía inicial, lo cual puede afectar directamente el desempeño global. No obstante, los hallazgos obtenidos sientan las bases para futuras líneas de investigación orientadas a refinar el método, optimizar su implementación y ampliar su validación en escenarios más cercanos a la práctica clínica. |
===BIBLIOGRAFÍA=== | ===BIBLIOGRAFÍA=== | ||
| Line 577: | Line 514: | ||
<div id="cite-15"></div> | <div id="cite-15"></div> | ||
| − | '''[[#citeF-15|[15]]]''' | + | '''[[#citeF-15|[15]]]''' Bishop, Richard L. (1975) "There Is More than One Way to Frame a Curve", Volume 82. The American Mathematical Monthly 3 246–251 |
<div id="cite-16"></div> | <div id="cite-16"></div> | ||
| − | '''[[#citeF-16|[16]]]''' | + | '''[[#citeF-16|[16]]]''' Zhang, Hui and Schneider, Torben and Wheeler-Kingshott, Claudia A. and Alexander, Daniel C. (2012) "NODDI: practical in vivo neurite orientation dispersion and density imaging of the human brain", Volume 61. Elsevier. NeuroImage 4 1000–1016 |
<div id="cite-17"></div> | <div id="cite-17"></div> | ||
| − | '''[[#citeF-17|[17]]]''' | + | '''[[#citeF-17|[17]]]''' Behrens, Timothy E. and Berg, Hauke J. and Jbabdi, Saad and Rushworth, Matthew F. and Woolrich, Mark W. (2007) "Probabilistic diffusion tractography with multiple fibre orientations: What can we gain?", Volume 34. Elsevier. Neuroimage 1 144–155 |
<div id="cite-18"></div> | <div id="cite-18"></div> | ||
| − | '''[[#citeF-18|[18]]]''' | + | '''[[#citeF-18|[18]]]''' Smith, Robert E and Tournier, Jacques-Donald and Calamante, Fernando and Connelly, Alan. (2013) "SIFT: Spherical-deconvolution informed filtering of tractograms", Volume 67. Elsevier. Neuroimage 298–312 |
<div id="cite-19"></div> | <div id="cite-19"></div> | ||
| − | '''[[#citeF-19|[19]]]''' Pestilli, Franco and Yeatman, Jason D and Rokem, Ariel and Kay, Kendrick N and Wandell, Brian A. (2014) "Evaluation and statistical inference for human connectomes", Volume 11. Nature Publishing Group. Nature Methods 10 1058–1063 | + | '''[[#citeF-19|[19]]]''' Renauld, E. and Théberge, A. and Petit, L. and others. (2023) "Validate your white matter tractography algorithms with a reappraised ISMRM 2015 Tractography Challenge scoring system", Volume 13. Nature Publishing Group. Scientific Reports 2347 |
| + | |||
| + | <div id="cite-20"></div> | ||
| + | '''[[#citeF-20|[20]]]''' Pestilli, Franco and Yeatman, Jason D and Rokem, Ariel and Kay, Kendrick N and Wandell, Brian A. (2014) "Evaluation and statistical inference for human connectomes", Volume 11. Nature Publishing Group. Nature Methods 10 1058–1063 | ||
Latest revision as of 22:41, 27 December 2025
1 Introducción
La complejidad que presenta la estimación de las conexiones neuronales en el cerebro humano ha impulsado el desarrollo de diversas herramientas para su adquisición y estudio. Entre ellas, la tractografía cerebral, basada en imágenes por resonancia magnética de difusión (dMRI), se ha convertido en un método clave para estimar estas conexiones estructurales. Esta técnica permite estimar las trayectorias de las fibras axonales que conectan distintas regiones cerebrales, proporcionando información importante sobre la organización y la integridad del conectoma humano [1]. Sin embargo, a pesar de los avances en esta técnica, persisten desafíos importantes que limitan su precisión, como la alta incidencia de trayectorias erróneas (falsos positivos) y la incapacidad de resolver de manera adecuada la complejidad estructural en zonas donde las fibras se cruzan o bifurcan [2,3,4]. En este contexto, la presente investigación propone abordar dichas limitaciones mediante la implementación de un enfoque de optimización convexa basado en microestructura, inspirado en el algoritmo Convex Optimization Modeling for Microstructure Informed Tractography (COMMIT) [5]. Esta propuesta integra información microestructural detallada en el proceso de la estimación de trayectorias de haces axonales, reduciendo tanto los falsos positivos como las incertidumbres en áreas de complejidad anatómica.
La relevancia de esta investigación es significativa, ya que un avance en la precisión de la tractografía cerebral no solo aportaría un mayor entendimiento sobre la conectividad estructural en individuos sanos, sino que también abriría nuevas posibilidades en el estudio de enfermedades neurológicas, donde el análisis detallado de las vías neuronales es crucial para la comprensión de los mecanismos patológicos [6]. Además, este desarrollo podría impactar directamente en áreas como la planificación quirúrgica y la medicina personalizada, donde la exactitud en la reconstrucción de los tractos neuronales es esencial para evitar errores clínicos [7,8].
Este trabajo se enfoca en las limitaciones actuales de los métodos de tractografía para mejorar la reconstrucción de las conexiones cerebrales integrando información microestructural mediante optimización convexa, ofreciendo un marco más robusto para futuras aplicaciones clínicas y de investigación.
2 Trabajos relacionados
La tractografía es un enfoque que permite estimar las trayectorias de haces de axones mediante curvas tridimensionales (3D), a partir de las orientaciones derivadas de las dMRI [9]. En general, la construcción de una trayectoria comienza con la selección de un punto inicial, denominado semilla. A partir de este punto, la trayectoria se propaga utilizando la información proporcionada por las dMRI, generando así una curva que representa el recorrido estimado de las fibras axonales. El movimiento de la trayectoria puede describirse mediante la siguiente ecuación de actualización:
|
|
(1) |
donde representa la posición tridimensional (3D) de la partícula en el tiempo , corresponde a la dirección de propagación y es el tamaño de paso. Así, una trayectoria, , está formada por . En términos generales, la principal diferencia entre los distintos métodos de tractografía radica en la manera en que se estima la dirección en cada paso de la trayectoria [10,11].
Una clase de métodos que han demostrado un gran desempeño son aquellos que logran integrar información de vecindades para estimar [6]. Entre estos métodos se encuentran: la Tractografía basada en Comportamiento Colectivo (TCC) [12], la Tractografía por Filtro de Partículas (TFP) [13] y la Tractografía por Transporte Paralelo (TTP) [14].
TCC modela la propagación de las trayectorias inspirándose en el comportamiento colectivo de bandadas (flocking). Cada trayectoria sigue reglas locales de alineamiento, cohesión y separación, lo que permite que las trayectorias se ajusten mutuamente mientras avanzan. Esto genera un comportamiento colaborativo que reduce rutas aisladas y guía a las fibras hacia patrones anatómicamente plausibles. El método incorpora información de vecindades del conjunto de trayectorias, y no únicamente del punto local de difusión. Como resultado, produce tractogramas más coherentes y con menos falsos positivos.
TFP tiene como objetivo reducir la cantidad de trayectorias que terminan prematuramente dentro de la materia blanca o en el líquido cefalorraquídeo. La idea central de este método es realizar un retroceso en los tiempos en aquellas trayectorias que han experimentado una terminación anticipada. De esta manera, se aplica una corrección a la trayectoria estimada, permitiendo que alcance adecuadamente un punto de terminación válido.
Finalmente, TTP es un método que define un marco ortonormal a lo largo de cada trayectoria para evitar rotaciones arbitrarias en la orientación de las fibras. Utiliza el concepto geométrico de transporte paralelo [15] para actualizar las direcciones locales de manera suave y consistente. Esto permite que la dirección de propagación se adapte fielmente a los cambios en la estructura de la materia blanca. A diferencia de los métodos clásicos, evita giros abruptos y mantiene la coherencia direccional. Como resultado, se obtiene una tractografía más estable, precisa y menos afectada por artefactos de orientación.
Al igual que los métodos previamente descritos, en este trabajo también proponemos la integración de vecindades de información; sin embargo, incorporamos información microestructural mediante el algoritmo COMMIT [5] directamente durante el proceso de generación de la tractografía. Esta integración se realiza de forma local, aplicando COMMIT a pequeñas vecidades alrededor del punto . Con ello, no solo se optimiza la selección de las trayectorias más plausibles, sino que además se posibilita la recuperación de falsos negativos, mejorando la precisión de las conexiones anatómicas estimadas.
3 Algoritmo propuesto
Nuestra contribución principal radica en la integración del algoritmo COMMIT [5] en el proceso de generación de tractografías, aplicándolo a pequeñas vecindades durante la estimación de las trayectorias, lo cual nos permite calcular . A diferencia de las implementaciones tradicionales de COMMIT, que se aplican de manera posterior a la generación de las tractografías, nuestra propuesta explora su aplicación en tiempo real, reduciendo la dependencia de ajustes posteriores y preservando una mayor cantidad de información durante el proceso de reconstrucción.
3.1 COMMIT
Para abordar la problemática de la presencia de falsos positivos en las reconstrucciones de las tractografías, Daducci et al. (2015) [5] propusieron el algoritmo COMMIT, el cual utiliza un marco de optimización convexa para refinar tractografías mediante la eliminación de trayectorias inconsistentes con los datos de difusión. A diferencia de otros métodos de posprocesamiento, COMMIT incorpora información microestructural del tejido cerebral, ajustando la contribución de cada fibra en la señal medida y filtrando aquellas que no se justifican a partir del modelo físico subyacente.
Dado un tractograma, el modelo matemático de COMMIT se basa en la siguiente ecuación lineal:
|
|
(2) |
donde representa la señal de difusión medida en cada vóxel, es la matriz de diseño que describe la contribución de cada trayectoria a la señal medida, es el vector de pesos asociado a cada trayectoria candidata y corresponde al ruido de medición.
El objetivo de COMMIT es encontrar el vector que mejor explica la señal , imponiendo restricciones de no negatividad y promoviendo la dispersión en para eliminar trayectorias irrelevantes. Esto se logra mediante la siguiente formulación de optimización convexa:
|
|
(3) |
donde el primer término minimiza el error de reconstrucción de la señal, mientras que el término de regularización promueve la selección de un subconjunto reducido de fibras, eliminando aquellas que no contribuyen significativamente a la señal observada. El parámetro controla el grado de regularización [5].
COMMIT incorpora modelos de microestructura basados en principios biológicos, como el modelo Stick–Tensor [16] (que representa axones como cilindros delgados con difusión restringida ) y el modelo de compartimentos mixtos [5] (que considera la presencia de múltiples tipos de tejidos, como fibras y espacio extracelular). Estos modelos, codificados en la matriz , permiten ajustar la contribución de cada trayectoria de acuerdo con su compatibilidad con la estructura neuronal, lo que ayuda a eliminar conexiones falsas [17].
Tras la resolución del problema de optimización presentado en la ecuación (3) (donde la matriz es de una escala muy grande), se obtiene un conjunto refinado de fibras, en el cual muchas de las trayectorias originales han sido eliminadas debido a su baja contribución a la señal medida. El criterio de eliminación se basa en el valor de obtenido para cada fibra. Si , la trayectoria se considera inconsistente con la señal de difusión y es eliminada. De lo contrario, si , la trayectoria es retenida en la tractografía final. Este proceso permite mejorar la especificidad de la tractografía y reducir significativamente la cantidad de falsos positivos, dando lugar a estimaciones de conectividad más precisas [5,18].
3.2 Tractografía basada en COMMIT
Dado un tractograma base, calculado con cualquier algoritmo de tractografía, con , en cada paso del proceso de generación de las estimaciones de los haces de axones se obtienen trayectorias candidatas aplicando criterios de filtrado basados en un cono direccional (vecindad) alrededor de la trayectoria central estimada. Sea el segmento de la trayectoria contenido dentro del cono. Formalmente, si denota la dirección del cono y representa la dirección del segmento de la trayectoria , dicho segmento se considera válido si todos sus subsegmentos satisfacen un umbral angular máximo :
|
|
(4) |
o equivalentemente en términos del producto escalar,
|
|
(5) |
para todo segmento. Este criterio garantiza que las trayectorias en el cono no se alejen demasiado de la dirección predominante en la vencindad del cono.
Para cada trayectoria en el cono, se calcula la dirección promedio de todos sus segmentos. Si la trayectoria tiene segmentos con vectores de dirección , su dirección promedio se define como
|
|
(6) |
A continuación se normaliza este vector promedio para obtener la dirección unitaria:
|
|
(7) |
De esta manera cada trayectoria válida queda representada por su dirección promedio unitaria , lo cual facilita la comparación entre fibras.
La similitud direccional entre dos trayectorias se cuantifica mediante el coseno del ángulo entre sus direcciones promedio. Para dos vectores unitarios y , la métrica de similitud direccional se define como su producto escalar:
|
|
(8) |
Este valor se encuentra en el rango y mide cuán alineadas están las direcciones de dos trayectorias. En particular, la similitud de cada trayectoria puede evaluarse respecto a la dirección predominante o frente a otras fibras candidatas, penalizando aquellas que desvían significativamente su orientación.
Finalmente, cada trayectoria candidata se puntúa con una función compuesta que pondera su peso dado por COMMIT y su similitud direccional. Si es el peso asignado por COMMIT al segmento de trayectoria , se puede definir el peso normalizado como , donde son los pesos de todos los segmentos en el cono. Con un parámetro que regula la importancia relativa, se define la puntuación compuesta:
|
|
(9) |
De esta forma, si se toma en cuenta solo el criterio COMMIT y si solo la similitud direccional. Finalmente, se selecciona la trayectoria con la mayor puntuación compuesta:
|
|
(10) |
Posteriormente, podemos usar para calcular usando ecuación (7).
4 Experimentos y resultados
Con el objetivo de evaluar el desempeño del método propuesto de tractografía informada por microestructura mediante optimización convexa, esta sección detalla los experimentos y resultados.
Se emplean dos conjuntos de datos sintéticos ampliamente usados en la comunidad científica: el ISMRM Tractography Challenge 2015 (actualización 2023) [19] y DiSCo (Diffusion-Simulated Connectivity) [6]. El primero se usará para análisis espaciales y estructurales. El segundo, para evaluación cuantitativa de conectividad. Su uso complementario ofrece un marco sólido para validar el nuevo método de tractografía propuesto.
En ambos casos se generarán tractografías con el algoritmo propuesto y con métodos tradicionales ampliamente utilizados. Posteriormente se aplicarán métricas de evaluación adecuadas al tipo de datos: para el primer conjunto se emplea la técnica Linear Fascicle Evaluation (LiFE) [20] para estimar la contribución predictiva de cada trayectoria. Para el segundo se usan métricas de correlación, exactitud y área bajo la curva ROC (AUC), tal como lo establece el protocolo de evaluación del DiSCo Challenge [6].
Para la validación anatómica cualitativa y cuantitativa basada en trayectorias con el conjunto ISMRM, primero se seleccionará una semilla en el cuerpo calloso, una región con conectividad interhemisférica bien definida que resulta ideal para evaluar la coherencia geométrica de las tractografías generadas. A partir de esta semilla se obtendrán tractografías mediante algoritmos determinísticos convencionales (como FACT, TEND, SD-Stream o iFOD2) y mediante el algoritmo propuesto, que integra restricciones microestructurales mediante COMMIT durante la generación de las trayectorias. Cada tractografía se evaluará con el algoritmo LiFE, que estima la contribución predictiva de cada trayectoria sobre la señal dMRI original, permitiendo filtrar trayectorias no justificadas y evaluar el ajuste global de cada modelo. Finalmente se comparará el rendimiento del algoritmo propuesto con el de los métodos convencionales considerando su coherencia anatómica respecto de las fibras de referencia, la puntuación de predicción bajo el modelo LiFE y el número de líneas filtradas por LiFE como no justificadas.
La validación cuantitativa de conectividad estructural entre regiones cerebrales utilizará el conjunto de datos del DiSCo Challenge. En este caso se evaluará solo el desempeño del algoritmo propuesto para contrastar sus resultados con los obtenidos por otros métodos participantes del challenge original. Se usará el subconjunto de alta resolución del DiSCo1, en sus versiones con ruido Rician a niveles de Relación señal-ruido (SNR por sus siglas en inglés) de 10, 20, 30 y 50. A partir de las tractografías generadas, se estimarán matrices de conectividad ponderadas entre las 16 regiones de interés (ROIs) definidas en el conjunto de datos. Las conexiones se cuantificarán según el número de trayectorias entre cada par de ROIs y, cuando corresponda, según el peso estimado en función de la microestructura. La calidad de estas matrices se evaluará mediante las métricas del DiSCo Challenge: correlación de Pearson con la matriz de referencia (peso continuo), área bajo la curva ROC (comparando con la matriz binaria de referencia) y exactitud de clasificación (pares correctamente identificados como conectados o no conectados). Finalmente, se analizará el comportamiento del algoritmo frente a diferentes niveles de ruido para evaluar su robustez y sensibilidad a condiciones adversas.
4.1 Resultados
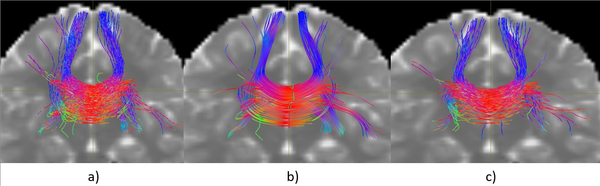
La Figura 1 muestra una comparación visual de tres tractografías generadas a partir de una misma semilla localizada en el cuerpo calloso, utilizando diferentes algoritmos. Todas las tractografías fueron generadas con la misma cantidad de trayectorias, lo que permite una observación cualitativa más equitativa entre métodos.
A partir de esta visualización inicial pueden identificarse algunas diferencias notables entre las tres reconstrucciones. El algoritmo iFOD2 (Figura 1a) presenta una mayor dispersión de trayectorias hacia regiones laterales, algo que puede relacionarse con su naturaleza probabilística, propensa a explorar recorridos menos restringidos. SD-Stream (Figura 1b) exhibe una estructura más centralizada y simétrica en la región del cuerpo calloso; las trayectorias aparecen más alineadas, aunque ello podría limitar la cobertura en zonas periféricas. El algoritmo propuesto (Figura 1c) parece mantener un equilibrio entre coherencia espacial y extensión: las trayectorias se distribuyen dentro de un rango anatómicamente plausible y sin una dispersión excesiva. Estos resultados corresponden únicamente a una inspección visual preliminar.
Aunque el comportamiento del algoritmo propuesto resulta alentador, es necesario complementar este análisis con métricas cuantitativas en las siguientes secciones para validar su desempeño de forma objetiva. Para complementar el análisis visual anterior se aplicó el modelo LiFE a cada una de las tractografías generadas. Esta herramienta filtra las fibras que no contribuyen de manera significativa a explicar la señal de difusión y, de este modo, ofrece un estimador indirecto de la fidelidad anatómica de las trayectorias reconstruidas.
|
| Figura 1: Comparación visual de tractografías generadas desde una semilla en el cuerpo calloso: a) iFOD2, b) SD-Stream, c) Algoritmo propuesto. |
| Método | Fibras | Fibras retenidas |
| iFOD2 | 780 | 597 |
| SD-Stream | 780 | 571 |
| Propuesto | 780 | 642 |
La Tabla 1 muestra los resultados obtenidos al aplicar LiFE. Aunque todos los métodos partieron del mismo número total de fibras (780), se observa una diferencia en la cantidad de trayectorias que LiFE considera significativas. En particular, la tractografía generada con el algoritmo propuesto retuvo una mayor proporción de fibras, lo cual podría indicar una mejor coherencia con los datos de difusión.
Adicionalmente, se calcularon métricas cuantitativas para evaluar la similitud entre las matrices de conectividad estimadas y la matriz de referencia proporcionada por el DiSCo Challenge. Las métricas consideradas incluyen la correlación de Pearson (), el AUC y la exactitud, esta última evaluada considerando un umbral de conectividad del 5%
| SNR | Correlación de Pearson () | AUC | Exactitud (umbral 5%) |
| 10 | 0.8460 | 0.9505 | 0.2833 |
| 20 | 0.8325 | 0.9406 | 0.2917 |
| 30 | 0.8715 | 0.9499 | 0.2833 |
| 50 | 0.8819 | 0.9543 | 0.3160 |
Los resultados en la Tabla 2 muestran una correlación positiva significativa en todos los niveles de ruido, con valores de superiores a 0.83, lo cual indica una correspondencia estructural consistente entre las matrices estimadas y la matriz de referencia. Asimismo, los valores de AUC cercanos a 0.95 en todos los casos sugieren una buena capacidad del algoritmo para discriminar entre conexiones presentes y ausentes. En cuanto a la exactitud, los valores absolutos son moderados.
Un aspecto central en la evaluación del algoritmo propuesto es determinar su comportamiento frente a distintas condiciones de ruido y la sensibilidad respecto a los parámetros de construcción de fibras, en particular el tamaño del cono (cone_size) y el ángulo de apertura (). La Tabla 3 resume los valores de las métricas de desempeño en función de dichos parámetros, considerando diferentes niveles de SNR. Los resultados muestran que, de manera general, tanto la correlación como el AUC presentan valores más altos para configuraciones intermedias de parámetros, mientras que valores extremos tienden a deteriorar el rendimiento.
| Métrica | SNR | cone_size = 5 | cone_size = 7 | cone_size = 10 | |||||||||
| 90° | 120° | 150° | 170° | 90° | 120° | 150° | 170° | 90° | 120° | 150° | 170° | ||
| 10 | 0.854 | 0.853 | 0.840 | 0.847 | 0.865 | 0.834 | 0.817 | 0.808 | 0.834 | 0.827 | 0.759 | 0.777 | |
| 20 | 0.844 | 0.834 | 0.820 | 0.811 | 0.850 | 0.816 | 0.790 | 0.798 | 0.833 | 0.806 | 0.758 | 0.762 | |
| 30 | 0.885 | 0.881 | 0.867 | 0.868 | 0.866 | 0.881 | 0.858 | 0.847 | 0.870 | 0.872 | 0.862 | 0.853 | |
| 50 | 0.901 | 0.893 | 0.887 | 0.888 | 0.893 | 0.900 | 0.902 | 0.892 | 0.887 | 0.894 | 0.886 | 0.880 | |
| AUC | 10 | 0.959 | 0.951 | 0.948 | 0.947 | 0.968 | 0.967 | 0.944 | 0.929 | 0.952 | 0.944 | 0.905 | 0.912 |
| AUC | 20 | 0.964 | 0.975 | 0.978 | 0.970 | 0.977 | 0.972 | 0.972 | 0.976 | 0.959 | 0.950 | 0.961 | 0.952 |
| AUC | 30 | 0.946 | 0.947 | 0.936 | 0.938 | 0.946 | 0.948 | 0.941 | 0.936 | 0.946 | 0.939 | 0.946 | 0.935 |
| AUC | 50 | 0.968 | 0.967 | 0.965 | 0.966 | 0.967 | 0.967 | 0.976 | 0.974 | 0.969 | 0.971 | 0.979 | 0.972 |
| exactitud | 10 | 0.333 | 0.342 | 0.350 | 0.333 | 0.350 | 0.383 | 0.383 | 0.392 | 0.383 | 0.417 | 0.442 | 0.467 |
| exactitud | 20 | 0.358 | 0.383 | 0.375 | 0.375 | 0.358 | 0.408 | 0.383 | 0.400 | 0.408 | 0.442 | 0.450 | 0.483 |
| exactitud | 30 | 0.325 | 0.342 | 0.342 | 0.342 | 0.325 | 0.350 | 0.417 | 0.408 | 0.400 | 0.408 | 0.442 | 0.492 |
| exactitud | 50 | 0.383 | 0.383 | 0.400 | 0.400 | 0.417 | 0.417 | 0.417 | 0.433 | 0.375 | 0.425 | 0.475 | 0.492 |
5 Conclusiones
El presente trabajo se centró en el desarrollo y la evaluación preliminar de un algoritmo de tractografía cerebral que integra el marco de optimización convexa COMMIT de manera temprana en la construcción de fibras. El objetivo principal fue explorar si esta estrategia permite reducir falsos positivos y recuperar falsos negativos desde la fase inicial de la generación de trayectorias, en lugar de aplicar la validación únicamente como un paso posterior. Los resultados presentados demuestran el potencial del enfoque planteado. Si bien el desempeño aún no alcanza niveles competitivos, especialmente en términos de exactitud, las mejoras observadas en correlación y AUC respaldan la hipótesis de que la validación temprana con COMMIT puede convertirse en una herramienta prometedora para incrementar la precisión de las tractografías.
El método propuesto presenta como principal limitación su dependencia de una tractografía inicial, lo cual puede afectar directamente el desempeño global. No obstante, los hallazgos obtenidos sientan las bases para futuras líneas de investigación orientadas a refinar el método, optimizar su implementación y ampliar su validación en escenarios más cercanos a la práctica clínica.
BIBLIOGRAFÍA
[1] Shapey, J. and Vos, S.B. and Vercauteren, T. and Bradford, R. and Saeed, S.R. and Bisdas, S. and Ourselin, S. (2019) "Clinical Applications for Diffusion MRI and Tractography of Cranial Nerves Within the Posterior Fossa: A Systematic Review", Volume 13. Frontiers in Neuroscience 23
[2] Derek K. Jones and Thomas R. Knösche and Robert Turner. (2013) "White matter integrity, fiber count, and other fallacies: The do's and don'ts of diffusion MRI", Volume 73. NeuroImage 239-254
[3] Boudreau, Mathieu and Karakuzu, Agah and Cohen-Adad, Julien and Bozkurt, Ecem and Carr, Madeline and Castellaro, Marco and Concha, Luis and Doneva, Mariya and Dual, Seraina A. and Ensworth, Alex and Foias, Alexandru and Fortier, Véronique and Gabr, Refaat E. and Gilbert, Guillaume and Glide-Hurst, Carri K. and Grech-Sollars, Matthew and Hu, Siyuan and Jalnefjord, Oscar and Jovicich, Jorge and Keskin, Kübra and Koken, Peter and Kolokotronis, Anastasia and Kukran, Simran and Lee, Nam G. and Levesque, Ives R. and Li, Bochao and Ma, Dan and Mädler, Burkhard and Maforo, Nyasha G. and Near, Jamie and Pasaye, Erick and Ramirez-Manzanares, Alonso and Statton, Ben and Stehning, Christian and Tambalo, Stefano and Tian, Ye and Wang, Chenyang and Weiss, Kilian and Zakariaei, Niloufar and Zhang, Shuo and Zhao, Ziwei and Stikov, Nikola and the ISMRM Reproducible Research Study Group and the ISMRM Quantitative MR Study Group. (2024) "Repeat it without me: Crowdsourcing the T1 mapping common ground via the ISMRM reproducibility challenge", Volume 92. Magnetic Resonance in Medicine 3 1115-1127
[4] Kurt G. Schilling and François Rheault and Laurent Petit and Colin B. Hansen and Vishwesh Nath and Fang-Cheng Yeh and Gabriel Girard and Muhamed Barakovic and Jonathan Rafael-Patino and Thomas Yu and Elda Fischi-Gomez and Marco Pizzolato and Mario Ocampo-Pineda and Simona Schiavi and Erick J. Canales-Rodríguez and Alessandro Daducci and Cristina Granziera and Giorgio Innocenti and Jean-Philippe Thiran and Laura Mancini and Stephen Wastling and Sirio Cocozza and Maria Petracca and Giuseppe Pontillo and Matteo Mancini and Sjoerd B. Vos and Vejay N. Vakharia and John S. Duncan and Helena Melero and Lidia Manzanedo and Emilio Sanz-Morales and Ángel Peña-Melián and Fernando Calamante and Arnaud Attyé and Ryan P. Cabeen and Laura Korobova and Arthur W. Toga and Anupa Ambili Vijayakumari and Drew Parker and Ragini Verma and Ahmed Radwan and Stefan Sunaert and Louise Emsell and Alberto De Luca and Alexander Leemans and Claude J. Bajada and Hamied Haroon and Hojjatollah Azadbakht and Maxime Chamberland and Sila Genc and Chantal M.W. Tax and Ping-Hong Yeh and Rujirutana Srikanchana and Colin D. Mcknight and Joseph Yuan-Mou Yang and Jian Chen and Claire E. Kelly and Chun-Hung Yeh and Jerome Cochereau and Jerome J. Maller and Thomas Welton and Fabien Almairac and Kiran K Seunarine and Chris A. Clark and Fan Zhang and Nikos Makris and Alexandra Golby and Yogesh Rathi and Lauren J. O'Donnell and Yihao Xia and Dogu Baran Aydogan and Yonggang Shi and Francisco Guerreiro Fernandes and Mathijs Raemaekers and Shaun Warrington and Stijn Michielse and Alonso Ramírez-Manzanares and Luis Concha and Ramón Aranda and Mariano Rivera Meraz and Garikoitz Lerma-Usabiaga and Lucas Roitman and Lucius S. Fekonja and Navona Calarco and Michael Joseph and Hajer Nakua and Aristotle N. Voineskos and Philippe Karan and Gabrielle Grenier and Jon Haitz Legarreta and Nagesh Adluru and Veena A. Nair and Vivek Prabhakaran and Andrew L. Alexander and Koji Kamagata and Yuya Saito and Wataru Uchida and Christina Andica and Masahiro Abe and Roza G. Bayrak and Claudia A.M. Gandini Wheeler-Kingshott and Egidio D'Angelo and Fulvia Palesi and Giovanni Savini and Nicolò Rolandi and Pamela Guevara and Josselin Houenou and Narciso López-López and Jean-François Mangin and Cyril Poupon and Claudio Román and Andrea Vázquez and Chiara Maffei and Mavilde Arantes and José Paulo Andrade and Susana Maria Silva and Vince D. Calhoun and Eduardo Caverzasi and Simone Sacco and Michael Lauricella and Franco Pestilli and Daniel Bullock and Yang Zhan and Edith Brignoni-Perez and Catherine Lebel and Jess E Reynolds and Igor Nestrasil and René Labounek and Christophe Lenglet and Amy Paulson and Stefania Aulicka and Sarah R. Heilbronner and Katja Heuer and Bramsh Qamar Chandio and Javier Guaje and Wei Tang and Eleftherios Garyfallidis and Rajikha Raja and Adam W. Anderson and Bennett A. Landman and Maxime Descoteaux. (2021) "Tractography dissection variability: What happens when 42 groups dissect 14 white matter bundles on the same dataset?", Volume 243. NeuroImage 118502
[5] Daducci, Alessandro and Dal Palu, Alessandro and Lemkaddem, Alia and Thiran, Jean-Philippe. (2015) "COMMIT: Convex optimization modeling for microstructure informed tractography", Volume 34. IEEE. IEEE Transactions on Medical Imaging 1 246–257
[6] Girard, Gabriel and Rafael-Patiño, Jonathan and Truffet, Raphaël and Aydogan, Dogu Baran and Adluru, Nagesh and et al. (2023) "Tractography passes the test: Results from the diffusion-simulated connectivity (disco) challenge", Volume 277. Elsevier. NeuroImage 120231
[7] Fernández-Miranda, Juan C. and Pathak, Sudhir and Engh, Johnathan and Jarbo, Kevin and Verstynen, Timothy and Sí, Fang-Cheng and Wang, Yibao and Mintz, Arlan and Boada, Fernando and Schneider, Walter and Friedlander, Robert. (2012) "Tractografía de fibra de alta definición del cerebro humano: Validación neuroanatómica y aplicaciones neuroquirúrgicas", Volume 71. Neurocirugía 2 430–453
[8] Lee B. Reid and Marcela I. Cespedes and Kerstin Pannek. (2020) "How many streamlines are required for reliable probabilistic tractography? Solutions for microstructural measurements and neurosurgical planning", Volume 211. NeuroImage 116646
[9] Dell'Acqua, Flavio and Descoteaux, Maxime and Leemans, Alexander. (2024) "Handbook of Diffusion MR Tractography: Imaging Methods, Biophysical Models, Algorithms and Applications". Elsevier, Academic Press
[10] Alexander Leemans and Flavio Dell’Acqua and Maxime Descoteaux. (2025) "Chapter 13 - Deterministic fiber tractography". Handbook of Diffusion MR Tractography. Academic Press 241-255
[11] Gabriel Girard and Dogu Baran Aydogan and Flavio Dell’Acqua and Alexander Leemans and Maxime Descoteaux and Stamatios N. Sotiropoulos. (2025) "Chapter 14 - Probabilistic tractography". Handbook of Diffusion MR Tractography. Academic Press 257-274
[12] Ramon Aranda and Mariano Rivera and Alonso Ramirez-Manzanares. (2014) "A flocking based method for brain tractography", Volume 18. Medical Image Analysis 3 515-530
[13] Girard, Gabriel and Whittingstall, Kevin and Deriche, Rachid and Descoteaux, Maxime. (2014) "Towards quantitative connectivity analysis: Reducing tractography biases", Volume 98. NeuroImage 266–278
[14] Aydogan, Dogu Baran and Shi, Yonggang. (2021) "Parallel Transport Tractography", Volume 40. IEEE Transactions on Medical Imaging 2 635–647
[15] Bishop, Richard L. (1975) "There Is More than One Way to Frame a Curve", Volume 82. The American Mathematical Monthly 3 246–251
[16] Zhang, Hui and Schneider, Torben and Wheeler-Kingshott, Claudia A. and Alexander, Daniel C. (2012) "NODDI: practical in vivo neurite orientation dispersion and density imaging of the human brain", Volume 61. Elsevier. NeuroImage 4 1000–1016
[17] Behrens, Timothy E. and Berg, Hauke J. and Jbabdi, Saad and Rushworth, Matthew F. and Woolrich, Mark W. (2007) "Probabilistic diffusion tractography with multiple fibre orientations: What can we gain?", Volume 34. Elsevier. Neuroimage 1 144–155
[18] Smith, Robert E and Tournier, Jacques-Donald and Calamante, Fernando and Connelly, Alan. (2013) "SIFT: Spherical-deconvolution informed filtering of tractograms", Volume 67. Elsevier. Neuroimage 298–312
[19] Renauld, E. and Théberge, A. and Petit, L. and others. (2023) "Validate your white matter tractography algorithms with a reappraised ISMRM 2015 Tractography Challenge scoring system", Volume 13. Nature Publishing Group. Scientific Reports 2347
[20] Pestilli, Franco and Yeatman, Jason D and Rokem, Ariel and Kay, Kendrick N and Wandell, Brian A. (2014) "Evaluation and statistical inference for human connectomes", Volume 11. Nature Publishing Group. Nature Methods 10 1058–1063
Document information
Published on 27/12/25
Submitted on 09/12/25
Licence: CC BY-NC-SA license
Share this document
Keywords
claim authorship
Are you one of the authors of this document?