| (One intermediate revision by the same user not shown) | |||
| Line 2: | Line 2: | ||
| − | < | + | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> |
| + | <big>'''Quantum dynamics of dissipative Chern insulator'''</big></div> | ||
| − | + | <div id="OLE_LINK26" class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | |
| − | + | Jilian Zhonga<sup> *</sup>, Xiaoyue Li<sup>a</sup></div> | |
| − | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | + | |
| − | < | + | |
| + | ''<sup>a</sup> Department of Physics, Jiangsu University, Zhenjiang 212013, People’s Republic of China'' | ||
| + | <span id='OLE_LINK28'></span>''<sup>*</sup>Corresponding address: [mailto:zhongjilian0505@163.com zhongjilian0505@163.com]'' | ||
-->==Abstract== | -->==Abstract== | ||
| − | + | This research is aimed at Laser processing of micro holes there are recast layer and microcracks, analyzed the laser processing of recast layer formation mechanism and surface geometry features not, and for the laser processing of the formation of the recast layer in the process of analog simulation, for electrochemical finishing processing to remove the recast layer to provide a theoretical basis. The laser-electrolysis asynchronous composite processing experimental system was developed, and the electrolytic removal of recast layer on the wall of laser perforated holes and the process research of aperture trimming were carried out, which mainly analyzed the effects of electrolysis voltage, electrolyte and pulse electrolysis parameters on the rate of electrolysis and the effect of the removal of the recast layer. The cathode lifting method is also proposed to lift the tool cathode for orifice shaping after effective removal of the recast layer. The experimental results show that: when the current density is greater than 10.09 A/cm<sup>2</sup>, the electrolysis rate is proportional to the voltage; when the constant voltage electrolysis, the mixed solution of NaNO<sub>3</sub> and NaCl enhances the effect of the recast layer removal significantly, and relative to the single solution with the same electrical conductivity, the value of the change in the surface roughness of the workpiece before and after the finishing process is enhanced more significantly, and there is no significant difference in the processing efficiency; the low-frequency wide pulse and high-frequency narrow pulse in the pulse electrolysis processing is favorable for the removal of recast layer. Pulse, high-frequency narrow pulse is conducive to the improvement of electrolysis rate, and the frequency of 1 kHz, the duty cycle of 40% to 60% of the electrolysis rate is the largest; at the same time, the use of cathodic enhancement method of aperture trimming processing, the use of the truncation effect, through the appropriate electrolytic processing parameters, to achieve the complete removal of the laser hole hole wall recast layer at the same time to complete the aperture trimming processing, to meet the demand for the use of performance of the small holes to further enhance the processing efficiency and small holes, and to improve the processing efficiency of the laser hole. Enhance the processing efficiency and functionality of small holes. | |
| − | '''Keywords''': | + | '''Keywords''': Laser processing, recast layer simulation, electrochemical finishing, cathodic lift |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
==1. Introduction== | ==1. Introduction== | ||
| − | + | In the field of modern machinery and equipment, the application of microporous in enhancing the use of equipment performance and reliability and other aspects of the value is increasingly apparent. For example, in the key high-temperature components of aircraft engines, the application of microporous promotes the development of air film cooling technology, and effectively make up for the limitations of high-temperature-resistant materials to enhance the reliability and durability of the engine; in the field of internal combustion engines, the application of microporous design of injector nozzles not only significantly improves the effect of fuel atomization, but also plays an important role in improving combustion efficiency and effectively reducing harmful emissions. Therefore, the application of microporous not only promotes the development of greening technology, but also promotes the innovation of microporous machining technology and process, which makes the special machining technology such as electric discharge technology (EDM) [1], electrochemical machining (ECM) [2], and laser machining (LM) [3] become the mainstream microporous machining methods. | |
| − | + | However, micro-hole machining technology based on special machining methods such as EDM, laser machining and electron beam is also facing some technical challenges. Due to the existence of the recast layer, the changes in its composition, structure, hardness and strength affect the performance of micro-holes in use, so scholars at home and abroad have carried out a wide range of white research in the removal of the recast layer and its effects. On the one hand, some scholars have deeply studied the formation mechanism of the recast layer, and while revealing the physical and chemical processes of the formation of the recast layer, they have also proposed the introduction of new processing media (e.g., nano-fluid, carnauba oil, etc.) [4,5] to adjust the processing environment [6,7] (e.g., temperature, pressure, etc.) and the development of new machining tools [8,9] and other means, which have effectively reduced the thickness of the recast layer; on the other hand, some scholars have reduced the formation and thickness of the recast layer by optimizing the process parameters [10,11] (e.g., current, voltage, and processing speed, etc.); in addition, some scholars have utilized post-processing techniques (e.g., chemical etching [12], ion-beam polishing [13], and electron-beam evaporation [14], as well as femtosecond laser technology, etc.) to achieve efficient removal of the recast layer and improve the microporosity. efficient removal and improved processing quality of micro-holes. | |
| − | + | Despite this, some major problems remain. The formation of recast layers involves complex physical and chemical processes, including melting, solidification, and phase transformation of the material. These processes are influenced by a variety of factors, such as processing temperature, pressure, material composition etc. Their complexity makes it difficult in controlling the formation of recast layers. During micro-hole machining, the optimization of machining parameters is crucial to reduce the recast layer. However, finding the best combination of parameters is a challenging task due to the diversity of machining parameters and the coupling of interactions. In addition, the optimal parameters may be different for different materials and machining conditions, which further increases the difficulty of parameter optimization. Limitations of post-processing technologies: chemical etching may introduce new surface defects or contaminants, while ion and electron beams may be limited by equipment cost and operability, resulting in restricted form geometry of the processed object. The problem of the balance between processing efficiency and quality. In the process of micro-hole machining, there is a certain contradiction between improving the processing efficiency and guaranteeing the processing quality, in order to reduce the formation of recast layer, it may be necessary to reduce the processing speed or processing steps, but this will sacrifice the processing efficiency. Therefore, based on the characteristics of electrochemical light finishing processing, this paper proposes the concept of using electrochemical anodic dissolution to remove the recast layer, and the process method of electrochemical removal of recast layer is studied. Finally, a two-step lifting process method is proposed to complete the micro-hole orifice trimming processing on the basis of satisfying the high quality removal of the recast layer, so that it can meet the specific use performance requirements. | |
| − | + | ==2. Experimental programming== | |
| − | + | ===2.1 Formation mechanism and simulation of recast layer and its surface geometric characteristics=== | |
| − | + | ====2.1.1 Formation mechanism and simulation of recast layer==== | |
| − | + | Laser processing is the result of the superposition of multiple single molten pools, so the recast layer formed by laser processing is inextricably linked to the formation of the single molten pool recast layer, the basic process of which is shown in [[Draft Seryazdan 514767809#img-1|Figure 1]](a). The material under a single pulsed laser irradiation is rapidly heated to the melting and boiling points, and melting and vaporization occur, forming a solid, liquid, and vapor three-phase coexistence. The melt flows along the walls of the processed area under a combination of vaporizing pressure and thermal influences, resulting in the formation of a concave contour of the melt pool that resembles a replica of the laser energy distribution curve. At the end of a single laser pulse, the vaporized metal in the center of the melt pool releases a large amount of thermal energy, which causes the melt attached to the walls of the melt pool and the curved melt at the bottom to be subjected to the recoil pressure of the metal vapor jet directly, which leads to the splashing of melt in the melt pool. Among them, part of the melt splashes out of the melt pool to form melt spatter, and accumulates at the edge of the melt pool to form a flying edge or burr, the simulation results are shown in [[Draft Seryazdan 514767809#img-1|Figure 1]](b); the other part of the melt will be deposited and attached to the surface of the inner wall of the melt pool,, and under the action of the combined coupling force, the melt will flow downward along the wall surface and reach a static equilibrium to form a smooth and excessive linear melt. After rapid cooling, the surface of the single molten pool forms a recast layer covered by a fused cladding after being subjected to a pressure gradient and a temperature gradient. The final laser process consists of the superposition of individual melt pools in the axial direction of the processing area and the formation of a recast layer with a periodic stream-like distribution on the surface of the hole wall.<div id="img-1"></div> | |
| − | + | {| class="wikitable" style="margin: 0em auto 0.1em auto;border-collapse: collapse;width:auto;" | |
| − | + | |- style="background:white;" | |
| − | {| class=" | + | | style="text-align: center;padding:10px;" | [[Image:Draft_Seryazdan_636830651-image1.png|486px|link=https://www.scipedia.com/public/File:Draft_Seryazdan_636830651-image1.png]] |
| − | |- | + | |
| − | + | ||
| − | + | ||
|- | |- | ||
| − | | | + | | style="background:#efefef;text-align:left;padding:10px;font-size: 85%;" | '''Figure 1'''. Schematic diagram of the simulation of recast layer formation |
|} | |} | ||
| − | + | ====2.1.2 Surface geometry of the recast layer==== | |
| − | + | As shown in [[Draft Seryazdan 514767809#img-2|Figure 2]](a), at the surface of the initial melt pool, due to the large temperature gradient, the overflowed melt is mainly subject to Marangoni force, surface tension and gravity. The Marangoni force affects the flow of the melt, thus forming the shape of a domed dome; the surface tension and gravity in turn cause the overflowed melt to shrink outside the hole to form a ring-shaped accumulation. | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | | | + | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | As can be seen in [[Draft Seryazdan 514767809#img-2|Figure 2]](b) below, in the upper part of the inner wall of the micro-hole, the recast layer has a smooth surface and relatively low thickness but is unevenly distributed along the periphery of the hole. Because the steam action is the strongest here, the melt pool is shallow, the metal vapor expansion rate is unevenly distributed, and a large amount of molten metal is randomly discharged, but under the action of the Marangoni force, it shows a smooth and excessive gully shape. In the 1/3 position from the top of the orifice, the recast layer surface formed a turbulent ripple-like undulation, randomly distributed in the circumferential direction, the thickness of a relative increase in the molten metal was a localized layer accumulation. Because with the non-stop stacking of the molten pool, the pressure gradient and the molten liquid velocity increase, so that the molten liquid layer of the explosion, the small size of the fast particles and the large size of the liquid particles with small velocity successively excluded by spattering, the vapor flow still has a high recoil force but weakened in relation to the orifice. In the middle and lower part of the micro-hole, the flow on the surface of the recast layer tends to stabilize, and the flow direction is more consistent, but the thickness reaches the maximum; at the same time, the layer spacing decreases, and a large number of overlapping melts blown down by the gas stream appear in the cross-section. Because here the melt pool flow rate has been lower, the melt by gravity and surface tension to reach equilibrium, the formation of a large number of droplets of solute accumulation, and at the same time because of the convection of the melt pool so that the melt can not be quickly discharged and thus re-melting and condensation to form a thicker recast layer. At the bottom of the micro-hole, the surface of the recast layer shows an obvious insufficient flow, because the steam effect here is weakened, and the melt sputtering becomes the main mode of discharge to increase the viscosity of the melt, which leads to the formation of localized agglomerates. Overall, the surface geometry of the laser-processed recast layer shows a stable and continuous periodic stripe distribution, which is characterized by an orderly wave-like microstructure on the macroscopic level and a spherical dome distribution of "peaks and valleys" on the microscopic level.<div id="img-2"></div> | |
| − | {| class=" | + | {| class="wikitable" style="margin: 0em auto 0.1em auto;border-collapse: collapse;width:auto;" |
| + | |- style="background:white;" | ||
| + | | style="text-align: center;padding:10px;" | [[Image:Draft_Seryazdan_636830651-image2.png|600px|link=https://www.scipedia.com/public/File:Draft_Seryazdan_636830651-image2.png]] | ||
|- | |- | ||
| − | + | | style="background:#efefef;text-align:left;padding:10px;font-size: 85%;" | '''Figure 2'''. Simulation of surface geometric features of recast layer with SEM | |
| − | + | ||
| − | | | + | |
| − | + | ||
|} | |} | ||
| − | + | ====2.2 Design of experimental platforms==== | |
| − | + | Experimentally used electrolytic combination processing device shown in [[Draft Seryazdan 514767809#img-3|Figure 3]], the device has electrochemical processing module and three-coordinate displacement platform, the platform is equipped with <math display="inline"> X, Y, Z</math> three axes, three-axis linkage can be realized. <math display="inline"> z </math>-axis is equipped with electrochemical machining device, <math display="inline"> XY </math> motion platform is equipped with a work box, electrochemical removal processing in the work box. The working box is made of plexiglass and resin materials, which not only realizes the electrical insulation from the machine tool, but also facilitates the observation of the experimental process.<div id="img-3"></div> | |
| − | {| class=" | + | {| class="wikitable" style="margin: 0em auto 0.1em auto;border-collapse: collapse;width:auto;" |
| + | |- style="background:white;" | ||
| + | | style="text-align: center;padding:10px;" | [[Image:Draft_Seryazdan_636830651-picture- 1.svg|center|600px|link=https://www.scipedia.com/public/File:Draft_Seryazdan_636830651-picture-_1.svg]] | ||
|- | |- | ||
| − | + | | style="background:#efefef;text-align:left;padding:10px;font-size: 85%;" | '''Figure 3'''. Electrochemical light finishing processing experimental platform | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | | | + | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
|} | |} | ||
| − | + | ===2.3 Design of experimental methodology=== | |
| − | + | ====2.3.1 Experimental flow design and preparation of samples==== | |
| − | == | + | The basic idea of the experiment, the laser was first used to process the prefabricated holes in the 2 mm thick metal plate, and then electrochemical processing was used to remove the recast layer on the hole wall, the specific process is shown in [[Draft Seryazdan 514767809#img-4|Figure 4]]. Laser parameters for the optimized parameters: pulse width of 0.2ms, peak power of 16kW, repetition frequency of 70Hz, drilling process along the laser head sprayed 0.6MPa argon to accelerate the exclusion of molten material, to reduce the burr, melt spattering and residual in the hole wall of the recast layer. Electrochemical processing, the use of motion control systems to insert the electrode wire centered in the pre-fabricated holes, detect whether the short circuit and set the pulse power parameters. First turn on the electrolyte pump, wait for the electrolyte to flow evenly through the hole and see a clear and stable liquid column at the exit, turn on the pulse power supply to start electrolysis, observe the experimental phenomena and power supply parameter changes, and turn off the power supply according to the set electrolysis time. The electrolyte is a neutral solution configured with pure water, and the dynamic liquid flushing method is used. In the experiment, considering the experimental error, 3 holes were processed under each parameter, and after the completion of the processing, the samples were cleaned, polished and metallurgically corroded, and the micro-hole morphology was observed with a scanning electron microscope, and the pore diameter was observed and measured with an optical microscope, and the average value of the 3 holes' diameters was finally taken under the same parameter. The micro-hole morphology of the sample is shown in [[Draft Seryazdan 514767809#img-5|Figure 5]].<div id="img-4"></div> |
| − | + | {| class="wikitable" style="margin: 0em auto 0.1em auto;border-collapse: collapse;width:auto;" | |
| − | {| class="wikitable" style="margin: 0em auto 0.1em auto;border-collapse: collapse;width: | + | |
|- style="background:white;" | |- style="background:white;" | ||
| − | | style="text-align: center;padding:10px;" | [[Image: | + | | style="text-align: center;padding:10px;" | [[Image:Draft_Seryazdan_636830651-image5-c.png|504px|link=https://www.scipedia.com/public/File:Draft_Seryazdan_636830651-image5-c.png]] |
|- | |- | ||
| − | | style="background:#efefef;text-align: | + | | style="background:#efefef;text-align:left;padding:10px;font-size: 85%;" | '''Figure 4'''. Micro-hole machining process flowchart |
| − | |} | + | |}<div id="img-5"></div> |
| − | {| class="wikitable" style="margin: 0em auto 0.1em auto;border-collapse: collapse;width: | + | {| class="wikitable" style="margin: 0em auto 0.1em auto;border-collapse: collapse;width:auto;" |
|- style="background:white;" | |- style="background:white;" | ||
| − | | style="text-align: center;padding:10px;" | [[Image: | + | | style="text-align: center;padding:10px;" | [[Image:Draft_Seryazdan_636830651-image6.png|600px|link=https://www.scipedia.com/public/File:Draft_Seryazdan_636830651-image6.png]] |
|- | |- | ||
| − | | style="background:#efefef;text-align: | + | | style="background:#efefef;text-align:left;padding:10px;font-size: 85%;" | '''Figure 5'''. Laser processing sample drawing |
| − | + | |} | |
| − | {| class="wikitable" style="margin: 0em auto 0.1em auto;border-collapse: collapse;width: | + | ====2.3.2 Determination of electrochemical processing method==== |
| + | In the electrochemical machining process, generally keep the processing current or processing voltage constant, with the increase of workpiece aperture, the electrolyte resistance increases gradually. When the current is constant, the voltage increases with the increase of the electrolyte resistance, and the current density decreases with the increase of the processed surface area when; when the voltage is constant, the current decreases with the increase of the electrolyte resistance, and the current density decreases rapidly with the decrease of the current and the increase of the processed surface area. In summary, it can be found that, when the voltage is constant, the decreasing trend of current density is greater than that of constant current, which is conducive to ensuring the processing efficiency in the early stage while ensuring the surface quality in the later stage of processing, so this paper adopts constant voltage for electrolytic processing. | ||
| + | ====2.3.3 Selection of electrolyte in electrochemical processing==== | ||
| + | Electrolytic processing, the electrode potential applied at the interface between the workpiece and the solution is different, the workpiece processing surface is in a different state, NaNO<sub>3</sub> solution is a passive electrolyte, the polarization curve of the anode of the workpiece into a non-linear distribution, passivation area of the metal surface to form an adsorbed oxygen layer or an oxide layer, i.e., passivation film; and precipitation of the oxygen area of the workpiece and the interface of the solution at the OH- ions easy to oxidize, precipitation of oxygen, precipitation of O<sub>2</sub> easy to oxidation Metal surface, so that the workpiece processing surface at the passivation film becomes thicker. The passivation film is less conductive, which in turn reduces the processing current density and lowers the dissolution rate of the metal. The NaCl solution is an active electrolyte, and the polarization curve of the anode of the workpiece is linearly distributed. The activation capacity of Cl- in the solution is very strong, the anode surface in a variety of conditions are in the active state of low-value dissolution, does not produce passivation and its side reactions, so the metal dissolution rate is higher, but at the same time there is a serious stray corrosion, which seriously affects the machining accuracy. In order to improve the nonlinear dissolution characteristics of the electrolyte, improve the current efficiency, soften the passivation salt film, this paper adopts a certain concentration of NaNO<sub>3</sub> solution mixed with a certain proportion of NaCl solution, in order to improve the machining efficiency at the same time easier to achieve the uneven dissolution or uneven super-passivation of the dissolution state, so as to improve the machining quality of the workpiece. | ||
| + | ==3. Results and analysis of removal of recast layer and orifice reshaping based on electrochemical light leveling== | ||
| + | ===3.1 Effect of electrolysis parameters on the removal of recast layers=== | ||
| + | When constant voltage electrolysis is used, the appropriate voltage should be selected. Theoretically, when the electrolysis voltage increases, the amount of electricity passing through the surface increases and the electrolysis rate increases. The electrolysis products and heat in the processing gap also increase, increasing the flow resistance in the gap, resulting in a decrease in the flow of electrolyte, so that the ability to exclude electrolysis products and heat is reduced. When there is a serious imbalance between the two, abnormal phenomena such as evaporation, boiling, and cavitation will occur in the processing gap, leading to serious failures such as short circuits and scarring, resulting in the interruption of processing. In addition, with the increase in current density, the electric field strength around the electrode wire increases, the stray corrosion around the orifice is enhanced, and the orifice is not rounded after electrolysis. Therefore, the voltage increase should not destroy the above balance as a prerequisite for the given electrolytic processing conditions, need to choose a suitable voltage value. Take the electrolysis time of 30s, the electrolyte is the conductivity of 100.4ms/cm NaNO<sub>3</sub> and NaCl mixed solution solution, respectively, with a voltage of 3-18V (interval 3V) for the recast layer removal experiment. | ||
| + | |||
| + | After the completion of the experiment, the experimental results are processed: take the amount of hole expansion after processing and surface roughness change value as the reference amount; different voltage electrolysis, the expansion of the hole diameter is different, take the median value of the hole diameter in the process of electrolysis (with the minimum voltage electrolysis hole median value) as the benchmark, and take the change in the quality of the processing before and after the processing as an auxiliary reference for processing rate. | ||
| + | |||
| + | From the [[Draft Seryazdan 514767809#img-6|Figure 6]], it can be seen that after the same time of electrolysis, the pore radius and electrolysis rate increased with the increase of electrolysis voltage. When the voltage is 15V, the recast layer is completely removed. At this time, the electrolysis current is 0.5 A. Calculation gives a minimum current density of 10.09 A/cm<sup>2</sup>. The mass change and pore radius change shown in [[Draft Seryazdan 514767809#img-6|Figure 6]] reflect that the electrolysis rate is approximately proportional to the voltage. When electrolysis removes the recast layer, the volume electrochemical equivalent <math>\omega</math> of the material is a constant value, and the oxidation reaction of Ni, Fe, Cr, and other elements in the material occurs, in which Ni, Fe, and Cr will be oxidized with multiple valences according to the current density, and when the current density is greater than, all three elements are oxidized to the cation with the highest valence, i.e., the current efficiency <math>\eta</math> is constant. When the electrolysis voltage is 6 V, the extension of the fitted primary curve can be found that the electrolysis rate is larger at this time. This is because when the current density is small, Ni, Fe, Cr elements are partially oxidized to low valence cations, at this time the current efficiency <math>\eta</math> is larger, and the proportion of high valence oxidation of these three elements increases with the increase of current density, that is, the current efficiency decreases with the increase of current density.<div id="img-6"></div> | ||
| + | {| class="wikitable" style="margin: 0em auto 0.1em auto;border-collapse: collapse;width:auto;" | ||
|- style="background:white;" | |- style="background:white;" | ||
| − | | style="text-align: center;padding:10px;" | [[Image: | + | | style="text-align: center;padding:10px;" | [[Image:Draft_Seryazdan_636830651-image9.png|400px|link=https://www.scipedia.com/public/File:Draft_Seryazdan_636830651-image9.png]] |
|- | |- | ||
| − | | style="background:#efefef;text-align: | + | | style="background:#efefef;text-align:left;padding:10px;font-size: 85%;" | '''Figure 6'''. Plot of the effect of voltage parameters on the removal of recast layer processing |
| − | + | |}[[Draft Seryazdan 514767809#img-7|Figure 7]] shows the SEM and metallographic images of the control holes and after removal of the recast layer by light-needle processing, from which it can be seen that the holes are rounded after light-finishing processing, and the recast layer is completely removed and the hole wall is smooth. When the constant pressure finishing process, the higher the voltage, the higher the current density, the higher the electrolysis rate. But at the same time as the voltage increases due to the hole entrance surface near the tool cathode, the electric field effect than other parts of the General Assembly serious stray corrosion, and because the entrance surface to increase the auxiliary anode, and by providing a potential difference to change the direction of the electric field of the anode entrance surface to reduce the entrance of the stray corrosion, effective control of electrochemical reaction of the hole entrance near the upper surface of the hole inlet, practical electrolytic machining, generally according to the cut-off In actual electrolytic processing, the voltage is generally determined according to the cut-off voltage and the electrolytic processing area. Under the condition of ensuring the processing surface quality, the electrolytic voltage can be increased in order to obtain a higher electrolytic rate, and the electrolyte flow rate can be increased at the same time in order to meet the exclusion of electrolytic processing products and heat.<div id="img-7"></div> | |
| − | {| class="wikitable" style="margin: 0em auto 0.1em auto;border-collapse: collapse;width: | + | {| class="wikitable" style="margin: 0em auto 0.1em auto;border-collapse: collapse;width:auto;" |
|- style="background:white;" | |- style="background:white;" | ||
| − | | style="text-align: center;padding:10px;" | [[Image: | + | | style="text-align: center;padding:10px;" | [[Image:Draft_Seryazdan_636830651-image10.png|600px|link=https://www.scipedia.com/public/File:Draft_Seryazdan_636830651-image10.png]] |
|- | |- | ||
| − | | style="background:#efefef;text-align: | + | | style="background:#efefef;text-align:left;padding:10px;font-size: 85%;" | '''Figure 7'''. SEM and metallographic images after removal of the recast layer |
|} | |} | ||
| − | == | + | ===3.2 Effect of pulsed power supply on the removal of recast layers=== |
| − | + | The traditional DC electrolytic machining has a strong ability to scatter etching and a weak ability to centralized etching, which affects the accuracy of electrolytic machining, the general three-dimensional surface molding accuracy of 0.2 to 0.5 mm, and the hole machining molding accuracy of 0.025 to 0.05 mm. High-frequency, narrow pulse electrolytic machining can achieve high precision (dimensional accuracy less than 5<math>\mu</math>m, surface roughness less than 0.03mm), small gap (10 to 50<math>\mu</math>m) machining, machining quality is greatly improved. The principle of pulse electrolytic processing is to replace the continuous DC power supply with periodic intermittent power supply, and the anode undergoes periodic intermittent dissolution in the electrolyte. It uses the intermittent depolarization of the pulse gap with power failure to dissipate heat from the workpiece, and the electrochemical properties, flow field, and electric field of the machining gap are restored to the starting state. Pulse current electrolysis, the gap produces hydrogen pressure wave synchronized with the pulse current, the frequency and intensity with the increase of pulse frequency and enhancement, which strengthens the stirring effect on the electrolyte, so that the flow field distribution in the gap tends to be uniform, and to improve the heat dissipation conditions in the gap, so as to make the minimum stable machining gap is greatly reduced, and thus to enhance the fixed-domain nature of electrolytic machining. Therefore, this paper compares the difference between the processing quality of pulse power supply and DC power supply, and finally chooses the processing method of pulse current electrolysis to get a higher electrolysis rate under the premise that the processing quality can be guaranteed. | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | As can be seen from [[Draft Seryazdan 514767809#img-8|Figure 8]](a), the surface quality obtained after processing with DC as the processing power source is relatively rough, the recast layer is not completely removed, and the electrochemical dissolution effect is small, and because of the DC electrolytic processing scattering corrosion ability is strong, so that the stray corrosion area is larger and the corrosion effect is more obvious, and at the same time, due to the fact that by-products can't be eliminated in time during the DC processing and electrolytic solution can't be renewed in time, which makes the local resistance increase, resulting in the inner wall of the small holes in part of the recast layer was not removed. As can be seen from [[Draft Seryazdan 514767809#img-8|Figure 8]](b), the use of pulsed current as the power supply processing after the surface is more smooth, the recast layer is completely removed and the processing quality is relatively stable, effectively solving the problems arising from the DC power supply, and further improving the quality and stability of the processing of electrolytic removal of the recast layer.<div id="img-8"></div> | |
| − | + | {| class="wikitable" style="margin: 0em auto 0.1em auto;border-collapse: collapse;width:auto;" | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | {| class="wikitable" style="margin: 0em auto 0.1em auto;border-collapse: collapse;width: | + | |
|- style="background:white;" | |- style="background:white;" | ||
| − | | style="text-align: center;padding:10px;" | [[Image: | + | | style="text-align: center;padding:10px;" | [[Image:Draft_Seryazdan_636830651-image11.png|600px|link=https://www.scipedia.com/public/File:Draft_Seryazdan_636830651-image11.png]] |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
|- | |- | ||
| − | | | + | | style="background:#efefef;text-align:left;padding:10px;font-size: 85%;" | '''Figure 8'''. Comparison chart of AC power supply and DC power supply |
|} | |} | ||
| − | + | ===3.3 Influence of cathodic lifting method on orifice reshaping=== | |
| − | + | In order to further improve the machining effect of micro small hole workpieces, a staged combination of processing methods is proposed, based on the electrolytic removal of the recast layer, in the same station to further complete the small hole electrolytic repair of the machining method, i.e., cathode lifting method. The method is as follows: in the first stage, the surface quality of the workpiece is rapidly improved and the surface roughness is reduced by relatively large voltage processing to ensure the rapid removal of the recast layer; in the second stage, after the completion of the removal of the recast layer, the electric field distribution is influenced by changing the electrode position and the relatively small voltage is used for the trimming process to obtain a better surface quality and to realize the goal of the trimming of the micro-hole aperture. Due to the use of hybrid electrolyte, as mentioned above, the electrolyte has the characteristic of cutting the gap, when using small voltage processing, this time the inner wall of the hole although the current through, but the anode does not dissolve, the current efficiency is 0, which has been processed to protect the wall of the hole at the same time as the hole inlet trimming the shape of the hole to make the micro-hole has a better to meet the demand for the performance of the use of the micro-hole. Based on the above research, the experimental process parameters are as follows: the electrolyte used is a mixed solution of NaNO<sub>3</sub> and NaCl with a conductivity of 100.4ms/cm, the electrolysis voltage is 4v, and the electrolysis time is 20s. | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | From the [[Draft Seryazdan 514767809#img-9|Figure 9]](a) can be seen, without improving the processing method workpiece due to the over-processing phase of the surface obtained on the more rough and micro-hole expansion obvious, poor machining locality, taper relative to the [[Draft Seryazdan 514767809#img-9|Figure 9]](b) is greater, at the same time, the effect of repairing the shape of the micro-hole can not meet the demand for the use of the performance of the micro-hole is not obvious; from the [[Draft Seryazdan 514767809#img-9|Figure 9]](b) can be seen, after the elevation of the method of low-pressure combination of machining, the inner wall of the hole in the cut off gap characteristics of the end of the end of the protection of the dissolution occurred, the machining of locality Higher, the height of the surface bulge is reduced, the surface of the workpiece becomes relatively flat, the taper relative to the [[Draft Seryazdan 514767809#img-9|Figure 9]](a) has obvious improvement, while the effect of the repair effect is good, can meet the functional requirements of the micro-hole.<div id="img-9"></div> | |
| − | + | {| class="wikitable" style="margin: 0em auto 0.1em auto;border-collapse: collapse;width:auto;" | |
| − | + | ||
| − | {| class="wikitable" style="margin: 0em auto 0.1em auto;border-collapse: collapse;width: | + | |
|- style="background:white;" | |- style="background:white;" | ||
| − | | style="text-align: center;padding:10px;" | [[Image: | + | | style="text-align: center;padding:10px;" | [[Image:Draft_Seryazdan_636830651-image12.png|600px|link=https://www.scipedia.com/public/File:Draft_Seryazdan_636830651-image12.png]] |
|- | |- | ||
| − | | style="background:#efefef;text-align: | + | | style="background:#efefef;text-align:left;padding:10px;font-size: 85%;" | '''Figure 9'''. Comparison of the results of the cathodic lift method |
|} | |} | ||
| − | == | + | ==4. Conclusions== |
| − | In | + | In this paper, the use of electrochemical finishing processing method to remove the heavy casting layer left on the hole wall by laser processing and at the same time complete the orifice trimming processing can better meet the demand of micro-hole performance. Theoretical analysis and simulation of the formation mechanism of the recast layer and the surface geometrical features during laser processing were carried out, and experiments were carried out for the removal of the recast layer and orifice shaping, and small holes with the recast layer completely removed and the orifice rounded were obtained. Based on the experimental results, the following conclusions were obtained: |
| − | + | ||
| − | + | ||
| − | + | 1. Laser processing is made by a single molten pool superimposed in the axial direction of the processing area, the molten material remaining in the molten pool in the combined force coupling role in the formation of a smooth excess of linear melt, and in the rapid cooling of the single molten pool surface in the pressure gradient and the temperature gradient, the formation of a recast layer covered by the fusion layer. The surface geometry of the laser-processed recast layer shows a stable and continuous periodic stripe distribution, which is characterized by an ordered wave-like microstructure on the macro level and a spherical dome distribution of "peaks and valleys" on the micro level. | |
| − | + | 2. Current density is an important parameter affecting the electrolysis rate. When using mixed solution finishing processing recast layer, the current density is greater than 10.09A/cm<sup>2</sup>, the current efficiency remains unchanged, and the electrolysis rate is proportional to the electrolysis voltage. When the actual processing, the current density is too large easily lead to processing area scarring, short circuit and other quality defects. Therefore, according to the current density greater than 10.09A/cm<sup>2</sup> and electrolytic processing area to determine the current voltage, according to the electrolyte flow rate to increase the voltage to obtain a higher efficiency of finishing processing. | |
| − | + | 3. When the electrolyte with the same conductivity is used under constant pressure processing conditions, the surface quality of the surface processed with the mixed electrolyte of NaNO<sub>3</sub> and NaCl is good, and the recast layer is completely removed; while the surface processed with the electrolyte of NaCl is seriously corroded by stray corrosion, and the recast layer is not completely removed. | |
| − | + | 4. The pulse effect in pulse finishing, the passivation of the anode of the workpiece, the stirring effect of the hydrogen pressure wave and the maintenance of the stability of the flow and electric fields during the power-off gap play a key role in enhancing the surface quality of the finish after the removal of the recast layer by the finishing process. | |
| − | + | 5. When the cathodic lifting method is used to process the micro-hole, the truncation effect is utilized so that the inner wall surface of the micro-hole will not be processed twice while the orifice is trimmed to achieve the shape of the process, and ultimately the inner wall is smooth and the orifice is rounded to obtain a micro-hole with better usability. | |
| − | + | ==Acknowledgements== | |
| − | + | This work was supported by Application of corrosion protection and online monitoring technology based on chlor-alkali industry (ZYYD2023B03). | |
| − | + | ==References== | |
| − | + | <div class="auto" style="text-align: left;width: auto; margin-left: auto; margin-right: auto;font-size: 85%;"> | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | [ | + | [1] Han L., Sartin M.M., Tian Z.-Q., Zhan D., Tian Z.-W. Electrochemical nanomachining. Curr. Opin. Electrochem., 22:80–86, 2020. |
| − | [ | + | [2] Sisodiya M.S., Shukla S., Bajpai V. Feasibility analysis of novel Maglev EDM by comparing with conventional micro EDM. Sci. Rep., 12, 2613, 2022. |
| − | [ | + | [3] Schmidt M., et al. Advances in macro-scale laser processing. CIRP Ann., 67:719–742, 2018. |
| − | [ | + | [4] Wang X., et al. Nanofluids application in machining: a comprehensive review. Int. J. Adv. Manuf. Technol., 131:3113–3164, 2024. |
| − | [ | + | [5] Kozak J., Rozenek M., Dabrowski L. Study of electrical discharge machining using powder-suspended working media. Proceedings of the Institution of Mechanical Engineers, Part B: Journal of Engineering Manufacture, 217:1597-1602, 2003. |
| − | [ | + | [6] Chen C., Xiao Z., Zhang W., Wang Y., Zhu H. Effect of laser jump speed on temperature distribution and thermal stress in laser powder bed fusion. Opt. Laser Technol., 142, 107275, 2021. |
| − | [ | + | [7] Maity K.P., Choubey M. A review on vibration-assisted EDM, micro-EDM and WEDM. Surf. Rev. Lett., 26(5), 1830008, 2019. |
| − | [ | + | [8] Singh P., Singh L., Singh S. A review on magnetically assisted abrasive flow machining and abrasive material type. Proc. Inst. Mech. Eng. Part E J. Process Mech. Eng., 236:2765–2781, 2022. |
| − | [ | + | [9] Zhou J., et al. Study on the mechanism of ultrasonic-assisted water confined laser micromachining of silicon. Opt. Lasers Eng., 132, 106118, 2020. |
| − | [ | + | [10] Sun C., et al. Study on the effect of electrolytes on processing efficiency and accuracy of titanium alloy utilizing laser and shaped tube electrochemical machining. Materials, 17(3):689, 2024. |
| − | [ | + | [11] Garcia S.M., Ramos J., Lamikiz A., Figueras J. Influence of process parameters in laser piercing. Appl. Sci., 9(16), 3231, 2019. |
| − | [ | + | [12] Lu D., Liu Z., Wei X., Chen C., Wang D. Effect of post-processing methods on the surface quality of Ti6Al4V fabricated by laser powder bed fusion. Front. Mater., 10, 1126749, 2023. |
| − | [ | + | [13] Deng T., Li J., Zheng Z., Tian W., Li G. Influence of plasma beam polishing process parameters on surface roughness of AISI 304 stainless steel. Appl. Surf. Sci., 585, 152741, 2022. |
| − | [ | + | [14] Zhong T., et al. Fabrication and characterization of silicon-based antimonene thin film via electron beam evaporation. Materials, 17(5), 1090, 2024. |
| − | + | ||
Latest revision as of 04:39, 10 November 2025
Abstract
This research is aimed at Laser processing of micro holes there are recast layer and microcracks, analyzed the laser processing of recast layer formation mechanism and surface geometry features not, and for the laser processing of the formation of the recast layer in the process of analog simulation, for electrochemical finishing processing to remove the recast layer to provide a theoretical basis. The laser-electrolysis asynchronous composite processing experimental system was developed, and the electrolytic removal of recast layer on the wall of laser perforated holes and the process research of aperture trimming were carried out, which mainly analyzed the effects of electrolysis voltage, electrolyte and pulse electrolysis parameters on the rate of electrolysis and the effect of the removal of the recast layer. The cathode lifting method is also proposed to lift the tool cathode for orifice shaping after effective removal of the recast layer. The experimental results show that: when the current density is greater than 10.09 A/cm2, the electrolysis rate is proportional to the voltage; when the constant voltage electrolysis, the mixed solution of NaNO3 and NaCl enhances the effect of the recast layer removal significantly, and relative to the single solution with the same electrical conductivity, the value of the change in the surface roughness of the workpiece before and after the finishing process is enhanced more significantly, and there is no significant difference in the processing efficiency; the low-frequency wide pulse and high-frequency narrow pulse in the pulse electrolysis processing is favorable for the removal of recast layer. Pulse, high-frequency narrow pulse is conducive to the improvement of electrolysis rate, and the frequency of 1 kHz, the duty cycle of 40% to 60% of the electrolysis rate is the largest; at the same time, the use of cathodic enhancement method of aperture trimming processing, the use of the truncation effect, through the appropriate electrolytic processing parameters, to achieve the complete removal of the laser hole hole wall recast layer at the same time to complete the aperture trimming processing, to meet the demand for the use of performance of the small holes to further enhance the processing efficiency and small holes, and to improve the processing efficiency of the laser hole. Enhance the processing efficiency and functionality of small holes.
Keywords: Laser processing, recast layer simulation, electrochemical finishing, cathodic lift
1. Introduction
In the field of modern machinery and equipment, the application of microporous in enhancing the use of equipment performance and reliability and other aspects of the value is increasingly apparent. For example, in the key high-temperature components of aircraft engines, the application of microporous promotes the development of air film cooling technology, and effectively make up for the limitations of high-temperature-resistant materials to enhance the reliability and durability of the engine; in the field of internal combustion engines, the application of microporous design of injector nozzles not only significantly improves the effect of fuel atomization, but also plays an important role in improving combustion efficiency and effectively reducing harmful emissions. Therefore, the application of microporous not only promotes the development of greening technology, but also promotes the innovation of microporous machining technology and process, which makes the special machining technology such as electric discharge technology (EDM) [1], electrochemical machining (ECM) [2], and laser machining (LM) [3] become the mainstream microporous machining methods.
However, micro-hole machining technology based on special machining methods such as EDM, laser machining and electron beam is also facing some technical challenges. Due to the existence of the recast layer, the changes in its composition, structure, hardness and strength affect the performance of micro-holes in use, so scholars at home and abroad have carried out a wide range of white research in the removal of the recast layer and its effects. On the one hand, some scholars have deeply studied the formation mechanism of the recast layer, and while revealing the physical and chemical processes of the formation of the recast layer, they have also proposed the introduction of new processing media (e.g., nano-fluid, carnauba oil, etc.) [4,5] to adjust the processing environment [6,7] (e.g., temperature, pressure, etc.) and the development of new machining tools [8,9] and other means, which have effectively reduced the thickness of the recast layer; on the other hand, some scholars have reduced the formation and thickness of the recast layer by optimizing the process parameters [10,11] (e.g., current, voltage, and processing speed, etc.); in addition, some scholars have utilized post-processing techniques (e.g., chemical etching [12], ion-beam polishing [13], and electron-beam evaporation [14], as well as femtosecond laser technology, etc.) to achieve efficient removal of the recast layer and improve the microporosity. efficient removal and improved processing quality of micro-holes.
Despite this, some major problems remain. The formation of recast layers involves complex physical and chemical processes, including melting, solidification, and phase transformation of the material. These processes are influenced by a variety of factors, such as processing temperature, pressure, material composition etc. Their complexity makes it difficult in controlling the formation of recast layers. During micro-hole machining, the optimization of machining parameters is crucial to reduce the recast layer. However, finding the best combination of parameters is a challenging task due to the diversity of machining parameters and the coupling of interactions. In addition, the optimal parameters may be different for different materials and machining conditions, which further increases the difficulty of parameter optimization. Limitations of post-processing technologies: chemical etching may introduce new surface defects or contaminants, while ion and electron beams may be limited by equipment cost and operability, resulting in restricted form geometry of the processed object. The problem of the balance between processing efficiency and quality. In the process of micro-hole machining, there is a certain contradiction between improving the processing efficiency and guaranteeing the processing quality, in order to reduce the formation of recast layer, it may be necessary to reduce the processing speed or processing steps, but this will sacrifice the processing efficiency. Therefore, based on the characteristics of electrochemical light finishing processing, this paper proposes the concept of using electrochemical anodic dissolution to remove the recast layer, and the process method of electrochemical removal of recast layer is studied. Finally, a two-step lifting process method is proposed to complete the micro-hole orifice trimming processing on the basis of satisfying the high quality removal of the recast layer, so that it can meet the specific use performance requirements.
2. Experimental programming
2.1 Formation mechanism and simulation of recast layer and its surface geometric characteristics
2.1.1 Formation mechanism and simulation of recast layer
Laser processing is the result of the superposition of multiple single molten pools, so the recast layer formed by laser processing is inextricably linked to the formation of the single molten pool recast layer, the basic process of which is shown in Figure 1(a). The material under a single pulsed laser irradiation is rapidly heated to the melting and boiling points, and melting and vaporization occur, forming a solid, liquid, and vapor three-phase coexistence. The melt flows along the walls of the processed area under a combination of vaporizing pressure and thermal influences, resulting in the formation of a concave contour of the melt pool that resembles a replica of the laser energy distribution curve. At the end of a single laser pulse, the vaporized metal in the center of the melt pool releases a large amount of thermal energy, which causes the melt attached to the walls of the melt pool and the curved melt at the bottom to be subjected to the recoil pressure of the metal vapor jet directly, which leads to the splashing of melt in the melt pool. Among them, part of the melt splashes out of the melt pool to form melt spatter, and accumulates at the edge of the melt pool to form a flying edge or burr, the simulation results are shown in Figure 1(b); the other part of the melt will be deposited and attached to the surface of the inner wall of the melt pool,, and under the action of the combined coupling force, the melt will flow downward along the wall surface and reach a static equilibrium to form a smooth and excessive linear melt. After rapid cooling, the surface of the single molten pool forms a recast layer covered by a fused cladding after being subjected to a pressure gradient and a temperature gradient. The final laser process consists of the superposition of individual melt pools in the axial direction of the processing area and the formation of a recast layer with a periodic stream-like distribution on the surface of the hole wall. 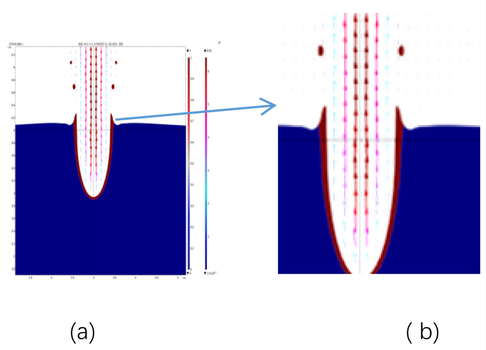
|
| Figure 1. Schematic diagram of the simulation of recast layer formation |
2.1.2 Surface geometry of the recast layer
As shown in Figure 2(a), at the surface of the initial melt pool, due to the large temperature gradient, the overflowed melt is mainly subject to Marangoni force, surface tension and gravity. The Marangoni force affects the flow of the melt, thus forming the shape of a domed dome; the surface tension and gravity in turn cause the overflowed melt to shrink outside the hole to form a ring-shaped accumulation.
As can be seen in Figure 2(b) below, in the upper part of the inner wall of the micro-hole, the recast layer has a smooth surface and relatively low thickness but is unevenly distributed along the periphery of the hole. Because the steam action is the strongest here, the melt pool is shallow, the metal vapor expansion rate is unevenly distributed, and a large amount of molten metal is randomly discharged, but under the action of the Marangoni force, it shows a smooth and excessive gully shape. In the 1/3 position from the top of the orifice, the recast layer surface formed a turbulent ripple-like undulation, randomly distributed in the circumferential direction, the thickness of a relative increase in the molten metal was a localized layer accumulation. Because with the non-stop stacking of the molten pool, the pressure gradient and the molten liquid velocity increase, so that the molten liquid layer of the explosion, the small size of the fast particles and the large size of the liquid particles with small velocity successively excluded by spattering, the vapor flow still has a high recoil force but weakened in relation to the orifice. In the middle and lower part of the micro-hole, the flow on the surface of the recast layer tends to stabilize, and the flow direction is more consistent, but the thickness reaches the maximum; at the same time, the layer spacing decreases, and a large number of overlapping melts blown down by the gas stream appear in the cross-section. Because here the melt pool flow rate has been lower, the melt by gravity and surface tension to reach equilibrium, the formation of a large number of droplets of solute accumulation, and at the same time because of the convection of the melt pool so that the melt can not be quickly discharged and thus re-melting and condensation to form a thicker recast layer. At the bottom of the micro-hole, the surface of the recast layer shows an obvious insufficient flow, because the steam effect here is weakened, and the melt sputtering becomes the main mode of discharge to increase the viscosity of the melt, which leads to the formation of localized agglomerates. Overall, the surface geometry of the laser-processed recast layer shows a stable and continuous periodic stripe distribution, which is characterized by an orderly wave-like microstructure on the macroscopic level and a spherical dome distribution of "peaks and valleys" on the microscopic level. 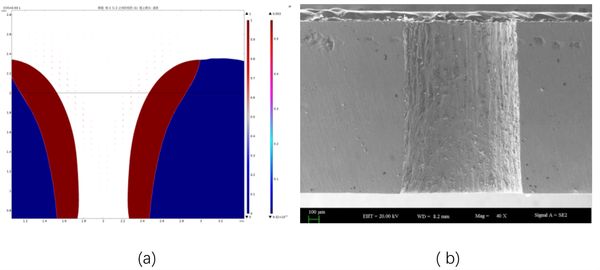
|
| Figure 2. Simulation of surface geometric features of recast layer with SEM |
2.2 Design of experimental platforms
Experimentally used electrolytic combination processing device shown in Figure 3, the device has electrochemical processing module and three-coordinate displacement platform, the platform is equipped with three axes, three-axis linkage can be realized. -axis is equipped with electrochemical machining device, motion platform is equipped with a work box, electrochemical removal processing in the work box. The working box is made of plexiglass and resin materials, which not only realizes the electrical insulation from the machine tool, but also facilitates the observation of the experimental process.| Figure 3. Electrochemical light finishing processing experimental platform |
2.3 Design of experimental methodology
2.3.1 Experimental flow design and preparation of samples
The basic idea of the experiment, the laser was first used to process the prefabricated holes in the 2 mm thick metal plate, and then electrochemical processing was used to remove the recast layer on the hole wall, the specific process is shown in Figure 4. Laser parameters for the optimized parameters: pulse width of 0.2ms, peak power of 16kW, repetition frequency of 70Hz, drilling process along the laser head sprayed 0.6MPa argon to accelerate the exclusion of molten material, to reduce the burr, melt spattering and residual in the hole wall of the recast layer. Electrochemical processing, the use of motion control systems to insert the electrode wire centered in the pre-fabricated holes, detect whether the short circuit and set the pulse power parameters. First turn on the electrolyte pump, wait for the electrolyte to flow evenly through the hole and see a clear and stable liquid column at the exit, turn on the pulse power supply to start electrolysis, observe the experimental phenomena and power supply parameter changes, and turn off the power supply according to the set electrolysis time. The electrolyte is a neutral solution configured with pure water, and the dynamic liquid flushing method is used. In the experiment, considering the experimental error, 3 holes were processed under each parameter, and after the completion of the processing, the samples were cleaned, polished and metallurgically corroded, and the micro-hole morphology was observed with a scanning electron microscope, and the pore diameter was observed and measured with an optical microscope, and the average value of the 3 holes' diameters was finally taken under the same parameter. The micro-hole morphology of the sample is shown in Figure 5. 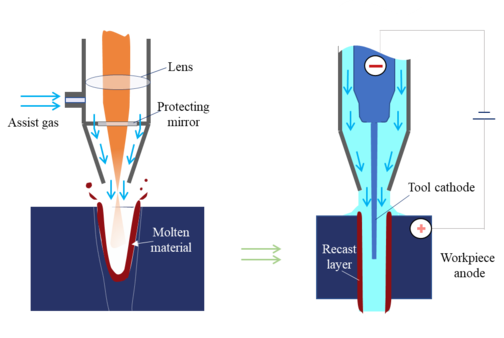
|
| Figure 4. Micro-hole machining process flowchart |

|
| Figure 5. Laser processing sample drawing |
2.3.2 Determination of electrochemical processing method
In the electrochemical machining process, generally keep the processing current or processing voltage constant, with the increase of workpiece aperture, the electrolyte resistance increases gradually. When the current is constant, the voltage increases with the increase of the electrolyte resistance, and the current density decreases with the increase of the processed surface area when; when the voltage is constant, the current decreases with the increase of the electrolyte resistance, and the current density decreases rapidly with the decrease of the current and the increase of the processed surface area. In summary, it can be found that, when the voltage is constant, the decreasing trend of current density is greater than that of constant current, which is conducive to ensuring the processing efficiency in the early stage while ensuring the surface quality in the later stage of processing, so this paper adopts constant voltage for electrolytic processing.
2.3.3 Selection of electrolyte in electrochemical processing
Electrolytic processing, the electrode potential applied at the interface between the workpiece and the solution is different, the workpiece processing surface is in a different state, NaNO3 solution is a passive electrolyte, the polarization curve of the anode of the workpiece into a non-linear distribution, passivation area of the metal surface to form an adsorbed oxygen layer or an oxide layer, i.e., passivation film; and precipitation of the oxygen area of the workpiece and the interface of the solution at the OH- ions easy to oxidize, precipitation of oxygen, precipitation of O2 easy to oxidation Metal surface, so that the workpiece processing surface at the passivation film becomes thicker. The passivation film is less conductive, which in turn reduces the processing current density and lowers the dissolution rate of the metal. The NaCl solution is an active electrolyte, and the polarization curve of the anode of the workpiece is linearly distributed. The activation capacity of Cl- in the solution is very strong, the anode surface in a variety of conditions are in the active state of low-value dissolution, does not produce passivation and its side reactions, so the metal dissolution rate is higher, but at the same time there is a serious stray corrosion, which seriously affects the machining accuracy. In order to improve the nonlinear dissolution characteristics of the electrolyte, improve the current efficiency, soften the passivation salt film, this paper adopts a certain concentration of NaNO3 solution mixed with a certain proportion of NaCl solution, in order to improve the machining efficiency at the same time easier to achieve the uneven dissolution or uneven super-passivation of the dissolution state, so as to improve the machining quality of the workpiece.
3. Results and analysis of removal of recast layer and orifice reshaping based on electrochemical light leveling
3.1 Effect of electrolysis parameters on the removal of recast layers
When constant voltage electrolysis is used, the appropriate voltage should be selected. Theoretically, when the electrolysis voltage increases, the amount of electricity passing through the surface increases and the electrolysis rate increases. The electrolysis products and heat in the processing gap also increase, increasing the flow resistance in the gap, resulting in a decrease in the flow of electrolyte, so that the ability to exclude electrolysis products and heat is reduced. When there is a serious imbalance between the two, abnormal phenomena such as evaporation, boiling, and cavitation will occur in the processing gap, leading to serious failures such as short circuits and scarring, resulting in the interruption of processing. In addition, with the increase in current density, the electric field strength around the electrode wire increases, the stray corrosion around the orifice is enhanced, and the orifice is not rounded after electrolysis. Therefore, the voltage increase should not destroy the above balance as a prerequisite for the given electrolytic processing conditions, need to choose a suitable voltage value. Take the electrolysis time of 30s, the electrolyte is the conductivity of 100.4ms/cm NaNO3 and NaCl mixed solution solution, respectively, with a voltage of 3-18V (interval 3V) for the recast layer removal experiment.
After the completion of the experiment, the experimental results are processed: take the amount of hole expansion after processing and surface roughness change value as the reference amount; different voltage electrolysis, the expansion of the hole diameter is different, take the median value of the hole diameter in the process of electrolysis (with the minimum voltage electrolysis hole median value) as the benchmark, and take the change in the quality of the processing before and after the processing as an auxiliary reference for processing rate.
From the Figure 6, it can be seen that after the same time of electrolysis, the pore radius and electrolysis rate increased with the increase of electrolysis voltage. When the voltage is 15V, the recast layer is completely removed. At this time, the electrolysis current is 0.5 A. Calculation gives a minimum current density of 10.09 A/cm2. The mass change and pore radius change shown in Figure 6 reflect that the electrolysis rate is approximately proportional to the voltage. When electrolysis removes the recast layer, the volume electrochemical equivalent of the material is a constant value, and the oxidation reaction of Ni, Fe, Cr, and other elements in the material occurs, in which Ni, Fe, and Cr will be oxidized with multiple valences according to the current density, and when the current density is greater than, all three elements are oxidized to the cation with the highest valence, i.e., the current efficiency is constant. When the electrolysis voltage is 6 V, the extension of the fitted primary curve can be found that the electrolysis rate is larger at this time. This is because when the current density is small, Ni, Fe, Cr elements are partially oxidized to low valence cations, at this time the current efficiency is larger, and the proportion of high valence oxidation of these three elements increases with the increase of current density, that is, the current efficiency decreases with the increase of current density. 
|
| Figure 6. Plot of the effect of voltage parameters on the removal of recast layer processing |

|
| Figure 7. SEM and metallographic images after removal of the recast layer |
3.2 Effect of pulsed power supply on the removal of recast layers
The traditional DC electrolytic machining has a strong ability to scatter etching and a weak ability to centralized etching, which affects the accuracy of electrolytic machining, the general three-dimensional surface molding accuracy of 0.2 to 0.5 mm, and the hole machining molding accuracy of 0.025 to 0.05 mm. High-frequency, narrow pulse electrolytic machining can achieve high precision (dimensional accuracy less than 5m, surface roughness less than 0.03mm), small gap (10 to 50m) machining, machining quality is greatly improved. The principle of pulse electrolytic processing is to replace the continuous DC power supply with periodic intermittent power supply, and the anode undergoes periodic intermittent dissolution in the electrolyte. It uses the intermittent depolarization of the pulse gap with power failure to dissipate heat from the workpiece, and the electrochemical properties, flow field, and electric field of the machining gap are restored to the starting state. Pulse current electrolysis, the gap produces hydrogen pressure wave synchronized with the pulse current, the frequency and intensity with the increase of pulse frequency and enhancement, which strengthens the stirring effect on the electrolyte, so that the flow field distribution in the gap tends to be uniform, and to improve the heat dissipation conditions in the gap, so as to make the minimum stable machining gap is greatly reduced, and thus to enhance the fixed-domain nature of electrolytic machining. Therefore, this paper compares the difference between the processing quality of pulse power supply and DC power supply, and finally chooses the processing method of pulse current electrolysis to get a higher electrolysis rate under the premise that the processing quality can be guaranteed.
As can be seen from Figure 8(a), the surface quality obtained after processing with DC as the processing power source is relatively rough, the recast layer is not completely removed, and the electrochemical dissolution effect is small, and because of the DC electrolytic processing scattering corrosion ability is strong, so that the stray corrosion area is larger and the corrosion effect is more obvious, and at the same time, due to the fact that by-products can't be eliminated in time during the DC processing and electrolytic solution can't be renewed in time, which makes the local resistance increase, resulting in the inner wall of the small holes in part of the recast layer was not removed. As can be seen from Figure 8(b), the use of pulsed current as the power supply processing after the surface is more smooth, the recast layer is completely removed and the processing quality is relatively stable, effectively solving the problems arising from the DC power supply, and further improving the quality and stability of the processing of electrolytic removal of the recast layer. 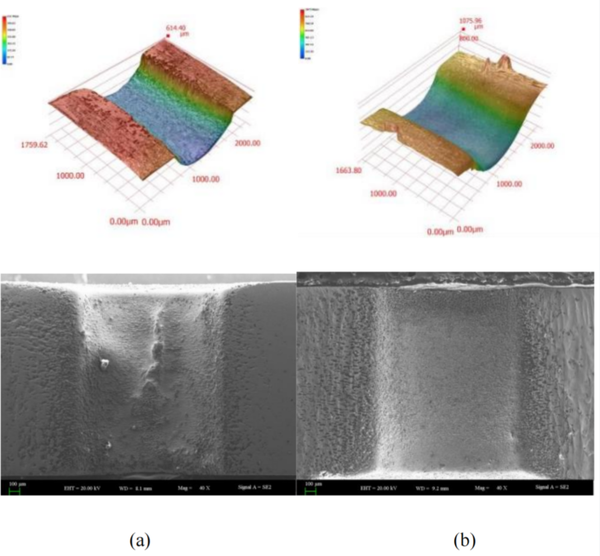
|
| Figure 8. Comparison chart of AC power supply and DC power supply |
3.3 Influence of cathodic lifting method on orifice reshaping
In order to further improve the machining effect of micro small hole workpieces, a staged combination of processing methods is proposed, based on the electrolytic removal of the recast layer, in the same station to further complete the small hole electrolytic repair of the machining method, i.e., cathode lifting method. The method is as follows: in the first stage, the surface quality of the workpiece is rapidly improved and the surface roughness is reduced by relatively large voltage processing to ensure the rapid removal of the recast layer; in the second stage, after the completion of the removal of the recast layer, the electric field distribution is influenced by changing the electrode position and the relatively small voltage is used for the trimming process to obtain a better surface quality and to realize the goal of the trimming of the micro-hole aperture. Due to the use of hybrid electrolyte, as mentioned above, the electrolyte has the characteristic of cutting the gap, when using small voltage processing, this time the inner wall of the hole although the current through, but the anode does not dissolve, the current efficiency is 0, which has been processed to protect the wall of the hole at the same time as the hole inlet trimming the shape of the hole to make the micro-hole has a better to meet the demand for the performance of the use of the micro-hole. Based on the above research, the experimental process parameters are as follows: the electrolyte used is a mixed solution of NaNO3 and NaCl with a conductivity of 100.4ms/cm, the electrolysis voltage is 4v, and the electrolysis time is 20s.
From the Figure 9(a) can be seen, without improving the processing method workpiece due to the over-processing phase of the surface obtained on the more rough and micro-hole expansion obvious, poor machining locality, taper relative to the Figure 9(b) is greater, at the same time, the effect of repairing the shape of the micro-hole can not meet the demand for the use of the performance of the micro-hole is not obvious; from the Figure 9(b) can be seen, after the elevation of the method of low-pressure combination of machining, the inner wall of the hole in the cut off gap characteristics of the end of the end of the protection of the dissolution occurred, the machining of locality Higher, the height of the surface bulge is reduced, the surface of the workpiece becomes relatively flat, the taper relative to the Figure 9(a) has obvious improvement, while the effect of the repair effect is good, can meet the functional requirements of the micro-hole. 
|
| Figure 9. Comparison of the results of the cathodic lift method |
4. Conclusions
In this paper, the use of electrochemical finishing processing method to remove the heavy casting layer left on the hole wall by laser processing and at the same time complete the orifice trimming processing can better meet the demand of micro-hole performance. Theoretical analysis and simulation of the formation mechanism of the recast layer and the surface geometrical features during laser processing were carried out, and experiments were carried out for the removal of the recast layer and orifice shaping, and small holes with the recast layer completely removed and the orifice rounded were obtained. Based on the experimental results, the following conclusions were obtained:
1. Laser processing is made by a single molten pool superimposed in the axial direction of the processing area, the molten material remaining in the molten pool in the combined force coupling role in the formation of a smooth excess of linear melt, and in the rapid cooling of the single molten pool surface in the pressure gradient and the temperature gradient, the formation of a recast layer covered by the fusion layer. The surface geometry of the laser-processed recast layer shows a stable and continuous periodic stripe distribution, which is characterized by an ordered wave-like microstructure on the macro level and a spherical dome distribution of "peaks and valleys" on the micro level.
2. Current density is an important parameter affecting the electrolysis rate. When using mixed solution finishing processing recast layer, the current density is greater than 10.09A/cm2, the current efficiency remains unchanged, and the electrolysis rate is proportional to the electrolysis voltage. When the actual processing, the current density is too large easily lead to processing area scarring, short circuit and other quality defects. Therefore, according to the current density greater than 10.09A/cm2 and electrolytic processing area to determine the current voltage, according to the electrolyte flow rate to increase the voltage to obtain a higher efficiency of finishing processing.
3. When the electrolyte with the same conductivity is used under constant pressure processing conditions, the surface quality of the surface processed with the mixed electrolyte of NaNO3 and NaCl is good, and the recast layer is completely removed; while the surface processed with the electrolyte of NaCl is seriously corroded by stray corrosion, and the recast layer is not completely removed.
4. The pulse effect in pulse finishing, the passivation of the anode of the workpiece, the stirring effect of the hydrogen pressure wave and the maintenance of the stability of the flow and electric fields during the power-off gap play a key role in enhancing the surface quality of the finish after the removal of the recast layer by the finishing process.
5. When the cathodic lifting method is used to process the micro-hole, the truncation effect is utilized so that the inner wall surface of the micro-hole will not be processed twice while the orifice is trimmed to achieve the shape of the process, and ultimately the inner wall is smooth and the orifice is rounded to obtain a micro-hole with better usability.
Acknowledgements
This work was supported by Application of corrosion protection and online monitoring technology based on chlor-alkali industry (ZYYD2023B03).
References
[1] Han L., Sartin M.M., Tian Z.-Q., Zhan D., Tian Z.-W. Electrochemical nanomachining. Curr. Opin. Electrochem., 22:80–86, 2020.
[2] Sisodiya M.S., Shukla S., Bajpai V. Feasibility analysis of novel Maglev EDM by comparing with conventional micro EDM. Sci. Rep., 12, 2613, 2022.
[3] Schmidt M., et al. Advances in macro-scale laser processing. CIRP Ann., 67:719–742, 2018.
[4] Wang X., et al. Nanofluids application in machining: a comprehensive review. Int. J. Adv. Manuf. Technol., 131:3113–3164, 2024.
[5] Kozak J., Rozenek M., Dabrowski L. Study of electrical discharge machining using powder-suspended working media. Proceedings of the Institution of Mechanical Engineers, Part B: Journal of Engineering Manufacture, 217:1597-1602, 2003.
[6] Chen C., Xiao Z., Zhang W., Wang Y., Zhu H. Effect of laser jump speed on temperature distribution and thermal stress in laser powder bed fusion. Opt. Laser Technol., 142, 107275, 2021.
[7] Maity K.P., Choubey M. A review on vibration-assisted EDM, micro-EDM and WEDM. Surf. Rev. Lett., 26(5), 1830008, 2019.
[8] Singh P., Singh L., Singh S. A review on magnetically assisted abrasive flow machining and abrasive material type. Proc. Inst. Mech. Eng. Part E J. Process Mech. Eng., 236:2765–2781, 2022.
[9] Zhou J., et al. Study on the mechanism of ultrasonic-assisted water confined laser micromachining of silicon. Opt. Lasers Eng., 132, 106118, 2020.
[10] Sun C., et al. Study on the effect of electrolytes on processing efficiency and accuracy of titanium alloy utilizing laser and shaped tube electrochemical machining. Materials, 17(3):689, 2024.
[11] Garcia S.M., Ramos J., Lamikiz A., Figueras J. Influence of process parameters in laser piercing. Appl. Sci., 9(16), 3231, 2019.
[12] Lu D., Liu Z., Wei X., Chen C., Wang D. Effect of post-processing methods on the surface quality of Ti6Al4V fabricated by laser powder bed fusion. Front. Mater., 10, 1126749, 2023.
[13] Deng T., Li J., Zheng Z., Tian W., Li G. Influence of plasma beam polishing process parameters on surface roughness of AISI 304 stainless steel. Appl. Surf. Sci., 585, 152741, 2022.
[14] Zhong T., et al. Fabrication and characterization of silicon-based antimonene thin film via electron beam evaporation. Materials, 17(5), 1090, 2024.Document information
Published on 04/06/24
Accepted on 20/05/24
Submitted on 04/05/24
Volume 40, Issue 2, 2024
DOI: 10.23967/j.rimni.2024.05.008
Licence: CC BY-NC-SA license
Share this document
claim authorship
Are you one of the authors of this document?
