m (Marherna moved page Review 244593342486 to Zaidi et al 2025a) |
|||
| (7 intermediate revisions by one other user not shown) | |||
| Line 125: | Line 125: | ||
| − | [[ | + | [[File:Draft_Farjas_373606442_4402_Figura2.png]] |
<span id='_Ref193274074'></span>Figura 2. (a) Medidas isotermas DSC. (b) representación del logaritmo del tiempo de inicio de la reacción respecto el reciproco de la temperatura. | <span id='_Ref193274074'></span>Figura 2. (a) Medidas isotermas DSC. (b) representación del logaritmo del tiempo de inicio de la reacción respecto el reciproco de la temperatura. | ||
| Line 148: | Line 148: | ||
donde ''m<sub>i</sub>'' y ''m<sub>f</sub>'' son las masas inicial y final, respectivamente. | donde ''m<sub>i</sub>'' y ''m<sub>f</sub>'' son las masas inicial y final, respectivamente. | ||
| − | [[ | + | [[File:Draft_Farjas_373606442_7407_Figura3.png]] |
<span id='_Ref193280385'></span>Figura 3. (a) Líneas continuas: ritmo de degradación, <math display="inline">d\alpha /dt</math>, y grado de degradación, <math display="inline">\alpha</math> , en función de la temperatura obtenido a partir de las medidas TGA. Símbolos: predicción isoconversional obtenida a partir de la ecuación <span id='cite-_Ref193215384'></span>[[#_Ref193215384|(4)]]. (b) Energía de activación de la reacción de degradado determinada mediante el análisis isoconversional de Friedman (eje de la izquierda), junto con el coeficiente de correlación del ajuste lineal (eje de la derecha). | <span id='_Ref193280385'></span>Figura 3. (a) Líneas continuas: ritmo de degradación, <math display="inline">d\alpha /dt</math>, y grado de degradación, <math display="inline">\alpha</math> , en función de la temperatura obtenido a partir de las medidas TGA. Símbolos: predicción isoconversional obtenida a partir de la ecuación <span id='cite-_Ref193215384'></span>[[#_Ref193215384|(4)]]. (b) Energía de activación de la reacción de degradado determinada mediante el análisis isoconversional de Friedman (eje de la izquierda), junto con el coeficiente de correlación del ajuste lineal (eje de la derecha). | ||
| Line 154: | Line 154: | ||
En la <span id='cite-_Ref193280385'></span>[[#_Ref193280385|Figura 3]] hemos representado la evolución de la degradación para diferentes velocidades de calentamiento juntamente con el análisis isoconversional de Friedman. En este caso obtenemos un buen ajuste en un rango amplio ( <math display="inline">\alpha >0,06)</math>. De hecho, las predicciones obtenidas a partir de la ecuación <span id='cite-_Ref193215384'></span>[[#_Ref193215384|(4)]] se ajustan perfectamente a las evoluciones medidas, con lo cual a partir del análisis isoconversional es posible predecir la evolución de la degradación. | En la <span id='cite-_Ref193280385'></span>[[#_Ref193280385|Figura 3]] hemos representado la evolución de la degradación para diferentes velocidades de calentamiento juntamente con el análisis isoconversional de Friedman. En este caso obtenemos un buen ajuste en un rango amplio ( <math display="inline">\alpha >0,06)</math>. De hecho, las predicciones obtenidas a partir de la ecuación <span id='cite-_Ref193215384'></span>[[#_Ref193215384|(4)]] se ajustan perfectamente a las evoluciones medidas, con lo cual a partir del análisis isoconversional es posible predecir la evolución de la degradación. | ||
| − | A partir del análisis cinético hemos construido un diagrama tiempo-temperatura de transformación (TTT) del proceso de degradación. Para ello y con la ayuda de la ecuación <span id='cite-_Ref193215384'></span>[[#_Ref193215384|(4)]] determinaremos el tiempo necesario para que la muestra llegue a un determinado grado de degradación. El resultado se presenta en la | + | A partir del análisis cinético hemos construido un diagrama tiempo-temperatura de transformación (TTT) del proceso de degradación. Para ello y con la ayuda de la ecuación <span id='cite-_Ref193215384'></span>[[#_Ref193215384|(4)]] determinaremos el tiempo necesario para que la muestra llegue a un determinado grado de degradación. El resultado se presenta en la [[#_Ref193297864|Figura 4]]. |
<div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | ||
| − | + | [[File:Draft_Farjas_373606442_5701_Figura4.png|366px]] | |
| + | </div> | ||
| − | + | <span id='_Ref193297859'></span>Figura 4. Mapa de procesado de la resina Akelite. | |
<div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | ||
| − | + | [[File:Draft_Farjas_373606442_9473_Figura5.png|366px]] | |
| + | </div> | ||
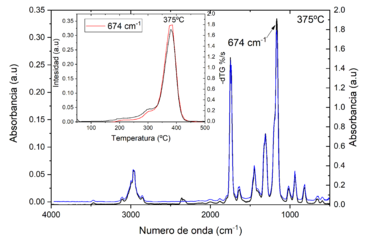
<span id='_Ref193294182'></span>Figura 5. Línea negra: Espectro de infrarrojo de los volátiles obtenido a la temperatura de 375 °C cuando la muestra se calienta a 20 °C/min, línea azul espectro del MMA [19]. Recuadro interior: la línea roja es la evolución de la intensidad del pico de absorción principal del MMA y la línea negra es la evolución de la pérdida de la masa. | <span id='_Ref193294182'></span>Figura 5. Línea negra: Espectro de infrarrojo de los volátiles obtenido a la temperatura de 375 °C cuando la muestra se calienta a 20 °C/min, línea azul espectro del MMA [19]. Recuadro interior: la línea roja es la evolución de la intensidad del pico de absorción principal del MMA y la línea negra es la evolución de la pérdida de la masa. | ||
| + | |||
Finalmente, hemos analizado la composición de los gases durante la degradación y el principal volátil es el monómero, el metacrilato de metilo (MMA). En la <span id='cite-_Ref193294182'></span>[[#_Ref193294182|Figura 5]] hemos superpuesto el espectro del MMA (línea azul) con el espectro registrado a la temperatura a la cual la velocidad de degradación es máxima, y los dos espectros son virtualmente idénticos. Además, hemos representado en el recuadro interior la velocidad de pérdida de masa y la intensidad el pico de absorción principal del MMA, podemos ver que ambas evoluciones son idénticas, lo que confirma que durante todo el proceso de degradación el principal volátil es el MMA. | Finalmente, hemos analizado la composición de los gases durante la degradación y el principal volátil es el monómero, el metacrilato de metilo (MMA). En la <span id='cite-_Ref193294182'></span>[[#_Ref193294182|Figura 5]] hemos superpuesto el espectro del MMA (línea azul) con el espectro registrado a la temperatura a la cual la velocidad de degradación es máxima, y los dos espectros son virtualmente idénticos. Además, hemos representado en el recuadro interior la velocidad de pérdida de masa y la intensidad el pico de absorción principal del MMA, podemos ver que ambas evoluciones son idénticas, lo que confirma que durante todo el proceso de degradación el principal volátil es el MMA. | ||
| Line 217: | Line 220: | ||
[19] W. Wallace, Infrared spectra, in: P.J. Linstrom, W.G. Mallard (Eds.), NIST Chem. WebBook, NIST Stand. Ref. Database, Institute of Standards and Technology, Gaithersburg MD, 2019: p. 20899. [https://doi.org/10.18434/T4D303. https://doi.org/10.18434/T4D303.] | [19] W. Wallace, Infrared spectra, in: P.J. Linstrom, W.G. Mallard (Eds.), NIST Chem. WebBook, NIST Stand. Ref. Database, Institute of Standards and Technology, Gaithersburg MD, 2019: p. 20899. [https://doi.org/10.18434/T4D303. https://doi.org/10.18434/T4D303.] | ||
| − | |||
| − | |||
Latest revision as of 21:33, 2 July 2025
1. Introducción
La energía eólica se considera una tecnología crucial para alcanzar los objetivos climáticos europeos de 2030 y la neutralidad de carbono en 2050 [1]. Sin embargo, las palas eólicas reforzadas con fibra no pueden reciclarse y en su mayoría se depositan en vertederos. La generación de aerogeneradores instalados en la década de 2000 llegará al final de su vida útil entre 2020 y 2030. En 2050, se acumularán 43 millones de toneladas de residuos de palas en todo el mundo, el 25% de ellos en Europa. Por tanto, urge desarrollar materiales reciclables para las palas eólicas [2].
En esta contribución, analizamos la cinética de polimerización y la degradación de una nueva resina termoplástica desarrollada por el Instituto de Ciencia y Tecnología de Polímeros (ICTP-CSIC) y 100% reciclable, Akelite [3]. Akelite es una resina acrílica liquida de baja viscosidad, lo que la hace idónea para la fabricación de piezas de materiales compuestos a base de fibra y matriz polimérica; no es necesario aplicar temperatura para impregnar las fibras lo que permite utilizar las técnicas convencionales desarrolladas para la fabricación de materiales compuestos de fibra y matriz termoestable de resinas epoxi. Además, la resina tiene una estabilidad superior a los seis meses cuando se conserva a temperatura ambiente. Además, la resina Akelite ha mostrado excelentes propiedades mecánicas, lo que la convierte en una candidata potencialmente ecológica para la fabricación de piezas estructurales en aerogeneradores [4]. Para ello, caracterizaremos tanto la cinética de polimerización como la de degradación. A partir de la caracterización crearemos el mapa de procesado. Ello permitirá determinar las condiciones de fabricación de piezas de material compuesto evitando la degradación térmica. Los resultados ayudarán a las empresas fabricantes de palas de aerogeneradores a evaluar la capacidad de los materiales reciclables desarrollados como sustitutos de los materiales que utilizan actualmente.
2. Materiales y métodos
2.1 Materiales.
La muestra objeto de estudio es una resina termoplástica, Akelite [3] suministrada por el ICTP-CSIC. El monómero mayoritario de la resina es el metacrilato de metilo (MMA) y se utiliza una iniciación térmica con peróxido para producir la polimerización en masa del monómero. La temperatura de transición vítrea máxima de esta resina está en torno a los 125 °C. La viscosidad de la resina se puede controlar durante su síntesis adaptándola a valores próximos a los 150 cP a temperatura ambiente.
Para estudiar el proceso de curado, se mezcla el monómero con un 3% en peso del iniciador. Para conseguir una mezcla homogénea esta se realiza en un baño de ultrasonidos. A continuación, se deposita la mezcla en crisoles herméticos de aluminio de 40 μL de capacidad fabricados por TA instruments. El uso de crisoles herméticos permite evitar la pérdida por evaporación del monómero. Típicamente, la masa de las muestras es de 0,5 a 1 mg a fin de evitar sobrecalentamientos y asegurar la termalización de la muestra durante los experimentos de análisis térmico [5].
2.2 Calorimetría diferencial de barrido.
La reacción de curado se monitorizó mediante un calorímetro diferencial de barrido (DSC) Q2000 de TA Instruments. Para ello, se han llevado a cabo experimentos a distintas velocidades de calentamiento en el rango de 1,25 a 20 °C/min y experimentos isotermos en el rango de 90 a 120 °C. Las muestras no curadas se han analizado en una atmósfera inerte, mantenida por un flujo constante de 50 mL/min de nitrógeno de alta pureza. Se ha utilizado como referencia un crisol similar al de la muestra.
En los experimentos isotermos se ha determinado la temperatura de transición vítrea, Tg, con el fin de establecer si la muestra se había curado totalmente. Para ello, después de la medida isoterma, la muestra se somete a un segundo ensayo en la que se calienta desde 0ºC hasta 200ºC a 20ºC/min. De acuerdo con la metodología estándar, la Tg se determinó a partir del punto medio de las temperaturas de transición inicial y final extrapoladas.
2.3 Análisis termogravimétrico.
Se ha utilizado una termobalanza de la casa Mettler Toledo (modelo TGA/DSC1) para analizar la degradación térmica de la resina curada mediante termogravimetría (TGA). Se han realizado una serie de experimentos a diferentes velocidades de calentamiento, desde 1,25 hasta 20 °C/min, bajo un flujo de gas de 60 mL/min de nitrógeno de alta pureza, utilizando muestras de aproximadamente 6 mg y crisoles de Al2O3 de 150 μL de volumen. Además, se realizaron mediciones simultáneas TGA/FTIR para identificar los principales gases volátiles desprendidos durante la descomposición. Para ello, la salida del horno TGA se conectó a una celda de gases de un espectrómetro de infrarrojos (IR) de la casa Bruker (modelo ALPHA) a través de un tubo de acero de 40 cm de longitud que se calentó a 200 °C para evitar la condensación de volátiles. Los espectros IR se obtuvieron tras promediar 24 barridos consecutivos en un rango de números de onda entre 500 y 4000 cm-1 en modo de transmisión.
2.4 Análisis cinético.
Los parámetros cinéticos de curado y la degradación, incluyendo la energía de activación aparente de la reacción y el factor preexponencial, se calcularon mediante el método isoconversional de Friedman [6,7]. Los métodos isoconversionales se basan en la hipótesis de que, para un determinado grado de conversión α, la tasa de conversión es sólo función de la temperatura [8,9]:
|
|
(1) |
Donde es el grado de curado ( ), T es la temperatura, R la constante universal de los gases y es la energía de activación para un grado de transformación dado. En la mayoría de los procesos reales activados térmicamente, las barreras energéticas microscópicas permanecen casi constantes a medida que avanza la transformación [10]. En el caso de transformaciones complejas, la dependencia de respecto a α es el resultado de la participación de diferentes procesos, cada uno asociado a una energía de activación particular, o de la participación de procesos que no obedecen a la dependencia Arrhenius de la constante de velocidad respecto a la temperatura [11–13]. Por lo tanto, en general, debe interpretarse como una energía de activación aparente más que como una energía de activación real.
La evolución del ritmo de curado se obtiene a partir de la integración de la ecuación (1):
|
|
(2) |
Para un grado de curado dado, la velocidad de curado solo depende de dos parámetros: la energía de activación aparente Eα y el producto . El objetivo de los métodos isoconversionales es, por tanto, determinar estos dos parámetros en función del grado de conversión. Para ello, el grado de transformación se discretiza en intervalos pequeños y constantes; . Así, el objetivo es determinar el conjunto discreto de valores Ej and . Para ello, hay que realizar varios experimentos [14,15] a diferentes velocidades de calentamiento, (no isotérmicas) o temperaturas fijas (isotérmicas). Por ejemplo, el método isoconversional diferencial de Friedman se basa directamente en la ecuación (2):
|
|
(3) |
donde el subíndice i representa un experimento concreto, , y el subíndice j representa un grado de curado dado . Más concretamente, para cada velocidad de calentamiento y para un dado determinamos el grado de transformación, , y la temperatura asociada, . Según la ecuación (3), la representación del frente al recíproco de la temperatura debería dar una línea recta. El parámetro y el producto se obtienen a partir de la pendiente y la intersección con el eje vertical, respectivamente.
Una vez conocidos y , y a partir de la integración de la ecuación (2), podemos hacer fácilmente predicciones de la evolución del curado para un programa de temperatura determinado:
|
|
(4) |
3. Caracterización de la cinética de curado
Para determinar la evolución del grado de curado con la temperatura, suponemos que el flujo de calor desprendido por la muestra es proporcional al ritmo de curado, de esta forma la velocidad de curado, , se obtiene directamente de la señal DSC normalizado a la entalpia total del proceso, el cual se obtiene de la integración de la curva DSC [16]:
|
|
(5) |
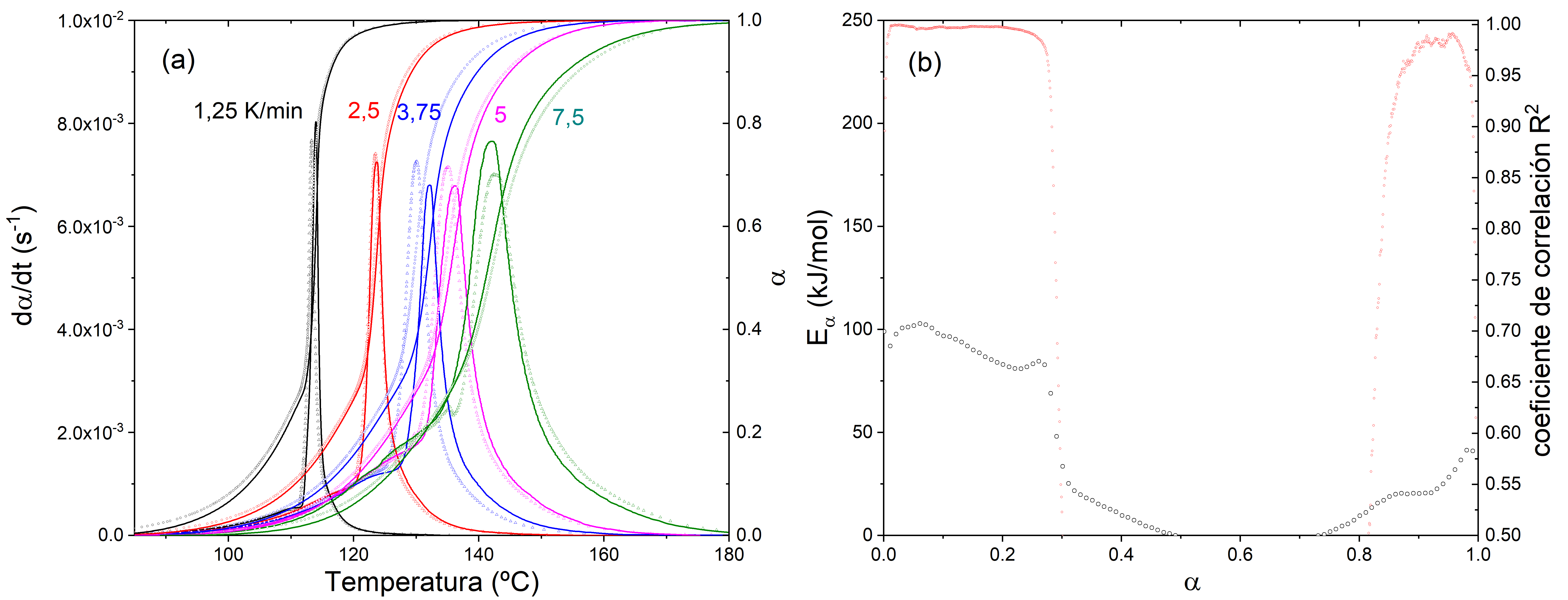
Donde es la entalpia total del proceso y es el flujo de calor medido por el DSC. En la Figura 1.a se representa la evolución del ritmo y grado de curado obtenido a partir de medidas DSC realizadas cuando la muestra se calienta a un ritmo constante, concretamente se han analizado cinco velocidades de calentamiento diferentes: 1,25, 2,5, 3,75, 5 y 7,5 °C/min.
Figura 1. (a) Líneas continuas: ritmo de transformación, , y grado de curado, , en función de la temperatura obtenido a partir de la integración de los termogramas DSC. Símbolos: predicción isoconversional obtenida a partir de la ecuación (4). (b) Energía de activación de la reacción de curado determinada mediante el análisis isoconversional de Friedman (eje de la izquierda), junto con el coeficiente de correlación del ajuste lineal (eje de la derecha).
El resultado del análisis isoconversional de Friedman, ecuación (3), se presenta en la Figura 1.b. A partir de un grado de curado del 30% ( ) la energía de activación se anula y el coeficiente de correlación indica que los puntos no están alineados. Ello es indicativo de que a partir de este grado de curado la reacción ya no está activada térmicamente.
Como test de autoconsistencia del ajuste isoconversional, utilizamos la ecuación (4) para simular la evolución en las mismas condiciones que se han obtenido las curvas. El resultado se muestra como símbolos en la Figura 1.a. A pesar de que el ajuste no es fiable a partir de se obtiene una buena reproducción de los resultados experimentales, por lo que es posible predecir la evolución de la polimerización para experimentos no-isotermos en el rango explorado, esto es para velocidades comprendidas entre 1,25 y 7,5 °C/min.
La presencia de un peróxido indica que se está promoviendo la polimerización por radicales libres. El papel de este compuesto es actuar como iniciador de una reacción en cadena. La descomposición térmica de esta molécula hace que el enlace O-O se rompa homolíticamente. Los dos radicales que se forman se transfieren a dos monómeros presentes, que a su vez los transfieren a otros monómeros en una etapa de propagación en la que el polímero aumenta la longitud de su cadena. No obstante, es conocido que la descomposición del peróxido es lenta. Además, la reacción del radical hidroperoxilo con un radical hidroxilo puede ralentizar la polimerización dando como resultado un largo período de inducción previo a la reacción en cadena [17].
En la evolución de la velocidad de curado, Figura 1.a, se distinguen claramente dos etapas, una primera etapa en la que la evolución es suave seguida de un cambio abrupto en el que la velocidad de curado se dispara. Este comportamiento se puede describir como el efecto del período de inducción [18]; inicialmente la reacción de polimerización progresa lentamente, pero cuando la descomposición del peróxido es suficientemente rápida provoca la reacción en cadena de la polimerización. Como resultado, la velocidad de curado aumenta de forma notoria y el proceso deja de estar activado térmicamente.
Por lo tanto, para caracterizar la cinética es necesario determinar la dependencia del período de inducción con la temperatura. Típicamente este período de inducción también está activado térmicamente:
|
|
(6) |
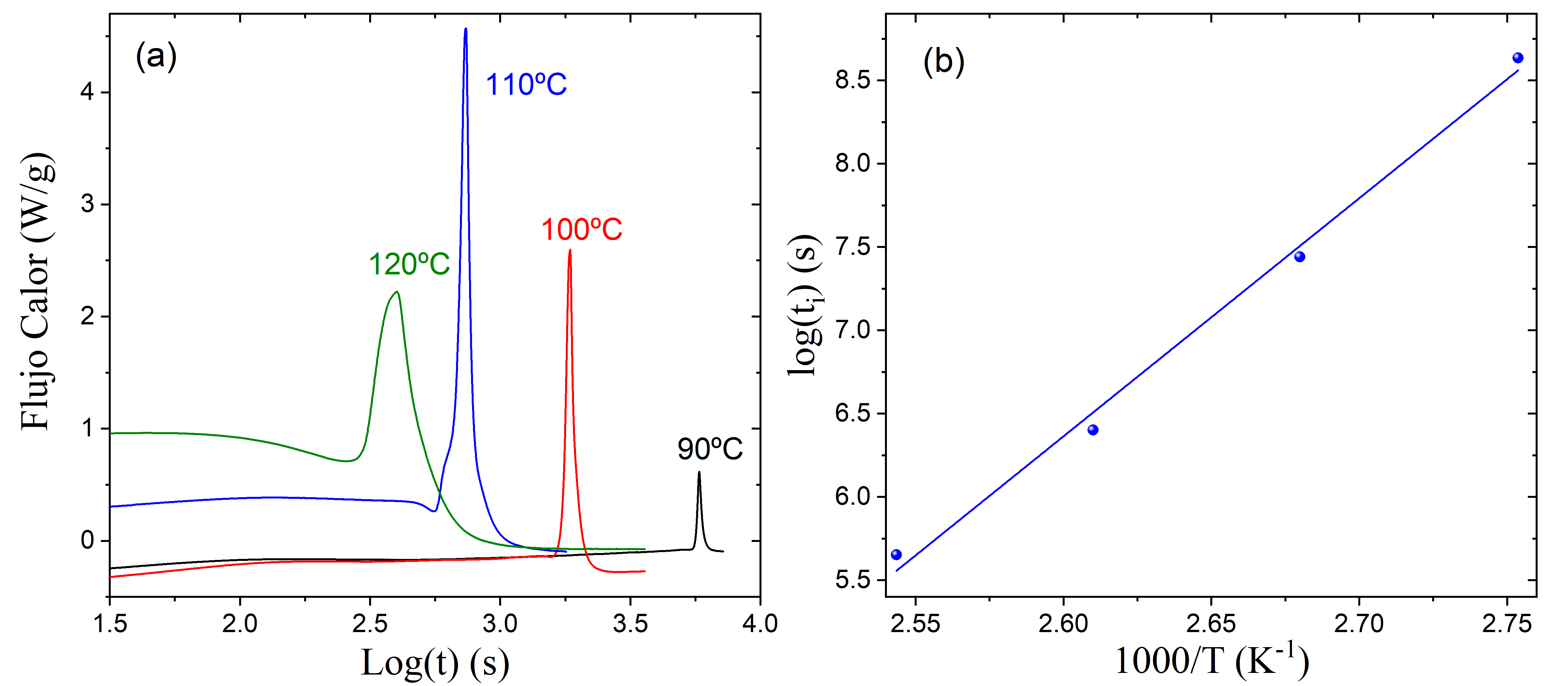
Figura 2. (a) Medidas isotermas DSC. (b) representación del logaritmo del tiempo de inicio de la reacción respecto el reciproco de la temperatura.
Para caracterizar el período de inhibición hemos realizado una serie de experimentos isotermos, Figura 2.a. Según la ecuación (6) la representación del logaritmo del tiempo de inicio de la reacción respecto el reciproco de la temperatura es una recta. A partir del ajuste lineal es posible determinar la energía de activación i el termino pre-exponencial. El ajuste se muestra en la Figura 2.b y obtenemos una energía de activación kJ/mol, el termino pre-exponencial es s y el coeficiente de correlación R2 es 0,991.
4. Caracterización de la degradación térmica
La TGA también es especialmente adecuada para caracterizar la cinética de degradación porque controla la evolución de la masa. En este caso, se suele suponer que el grado de degradación depende linealmente de la masa:
|
|
(7) |
donde mi y mf son las masas inicial y final, respectivamente.
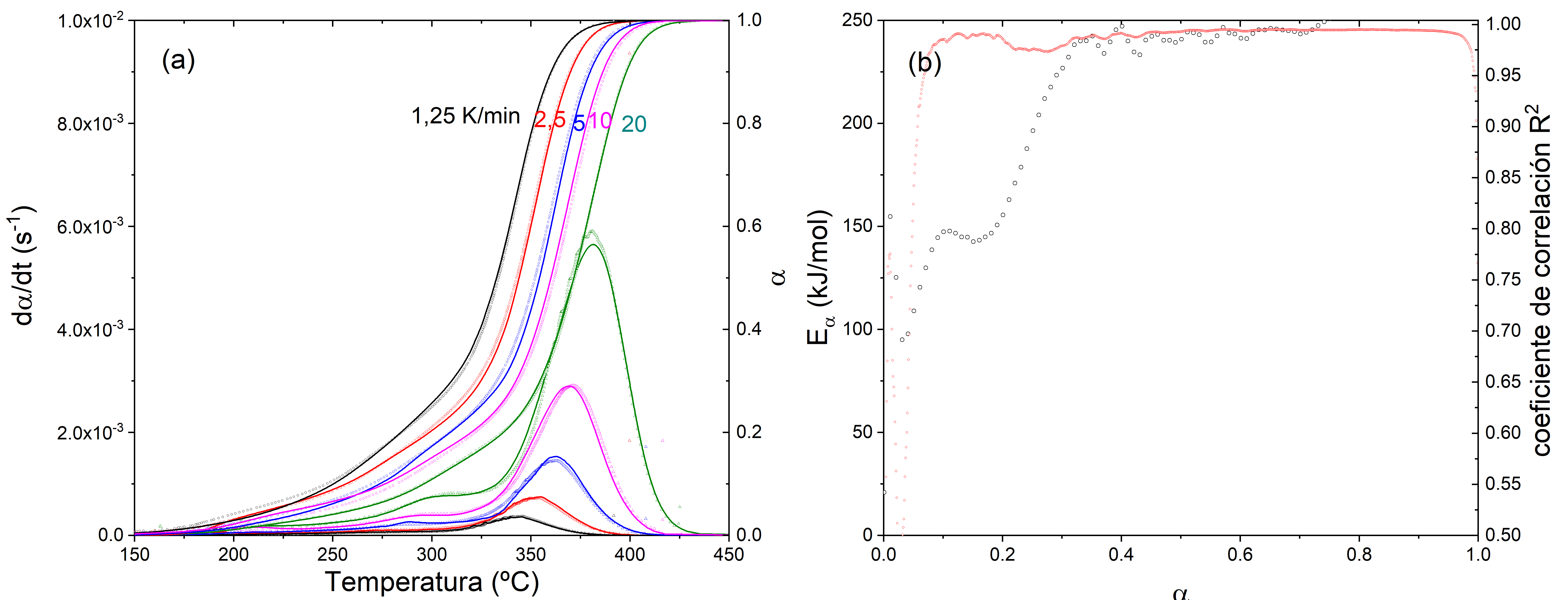
Figura 3. (a) Líneas continuas: ritmo de degradación, , y grado de degradación, , en función de la temperatura obtenido a partir de las medidas TGA. Símbolos: predicción isoconversional obtenida a partir de la ecuación (4). (b) Energía de activación de la reacción de degradado determinada mediante el análisis isoconversional de Friedman (eje de la izquierda), junto con el coeficiente de correlación del ajuste lineal (eje de la derecha).
En la Figura 3 hemos representado la evolución de la degradación para diferentes velocidades de calentamiento juntamente con el análisis isoconversional de Friedman. En este caso obtenemos un buen ajuste en un rango amplio ( . De hecho, las predicciones obtenidas a partir de la ecuación (4) se ajustan perfectamente a las evoluciones medidas, con lo cual a partir del análisis isoconversional es posible predecir la evolución de la degradación.
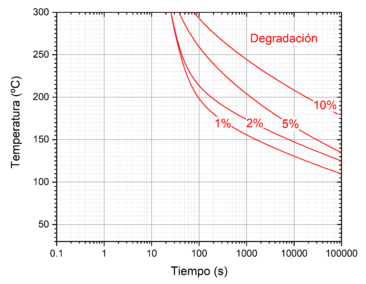
A partir del análisis cinético hemos construido un diagrama tiempo-temperatura de transformación (TTT) del proceso de degradación. Para ello y con la ayuda de la ecuación (4) determinaremos el tiempo necesario para que la muestra llegue a un determinado grado de degradación. El resultado se presenta en la Figura 4.
Figura 4. Mapa de procesado de la resina Akelite.
Figura 5. Línea negra: Espectro de infrarrojo de los volátiles obtenido a la temperatura de 375 °C cuando la muestra se calienta a 20 °C/min, línea azul espectro del MMA [19]. Recuadro interior: la línea roja es la evolución de la intensidad del pico de absorción principal del MMA y la línea negra es la evolución de la pérdida de la masa.
Finalmente, hemos analizado la composición de los gases durante la degradación y el principal volátil es el monómero, el metacrilato de metilo (MMA). En la Figura 5 hemos superpuesto el espectro del MMA (línea azul) con el espectro registrado a la temperatura a la cual la velocidad de degradación es máxima, y los dos espectros son virtualmente idénticos. Además, hemos representado en el recuadro interior la velocidad de pérdida de masa y la intensidad el pico de absorción principal del MMA, podemos ver que ambas evoluciones son idénticas, lo que confirma que durante todo el proceso de degradación el principal volátil es el MMA.
5. Conclusiones
En este trabajo se ha analizado la cinética de curado y degradación de la resina Akelite. Se ha observado que la presencia de un iniciador resulta en la existencia de un período de inducción que controla la cinética del proceso. A partir del análisis isotermo se ha podido caracterizar la dependencia del periodo de inducción en función de la temperatura.
A través del análisis isoconversional de la degradación se ha caracterizado el proceso y construido un diagrama TTT de la degradación. Este mapa indica que existe un amplio rango de parámetros en el cual es posible fabricar paneles sin riesgo a que la matriz se degrade térmicamente
6. Agradecimientos
Los autores agradecemos el apoyo financiero del Ministerio de Ciencia, Innovación y Universidades de España a través del proyecto coordinado SUCCESS BLADE (TED2021-130201B-C31 y TED2021-130201B-C32), cofinanciado por NextGenerationEU, Unión Europea).
7. Bibliografía
[1] European Commission: Directorate-General for Communication, What is the European Green Deal?, Publications Office, 2019. https://doi.org/doi/10.2775/275924.
[2] P.D. Jensen, P. Purnell, A.P.M. Velenturf, Highlighting the need to embed circular economy in low carbon infrastructure decommissioning: The case of offshore wind, Sustain Prod Consum 24 (2020) 266–280. https://doi.org/10.1016/j.spc.2020.07.012.
[3] R. VERDEJO MÁRQUEZ, M.Á. LÓPEZ MANCHADO, A. SANTIAGO BETHENCOURT, Polímeros reforzados con fibras basados en matrices termoplásticas, PCT/ES2021/070751, 2021.
[4] R. Carnicero, L. Cano, I. Cruz, M.A. Lopez-Manchado, R. Verdejo, Analysis of a small recyclable wind turbine blade, IOP Conf Ser Mater Sci Eng 1293 (2023) 012008. https://doi.org/10.1088/1757-899X/1293/1/012008.
[5] D. Sánchez-Rodríguez, H. Eloussifi, J. Farjas Silva, P. Roura, M. Dammak, Thermal gradients in thermal analysis experiments: Criterions to prevent inaccuracies when determining sample temperature and kinetic parameters, Thermochim Acta 589 (2014) 37–46. https://doi.org/10.1016/j.tca.2014.05.001.
[6] M.H. Friedman, A generalized thermal explosion criterion—Exposition and illustrative applications, Combust Flame 11 (1967) 239–246. https://doi.org/10.1016/0010-2180(67)90051-X.
[7] J. Farjas, P. Roura, Isoconversional analysis of solid state transformations. A critical review. Part I. Single step transformations with constant activation energy, J Therm Anal Calorim 105 (2011) 757–766. https://doi.org/10.1007/s10973-011-1446-4.
[8] S. Vyazovkin, Thermal Analysis, Anal Chem 82 (2010) 4936–4949. https://doi.org/10.1021/ac100859s.
[9] S. Vyazovkin, C.A. Wight, Isothermal and Nonisothermal Reaction Kinetics in Solids: In Search of Ways toward Consensus, J Phys Chem A 101 (1997) 8279–8284. https://doi.org/10.1021/jp971889h.
[10] J. Farjas, P. Roura, Isoconversional analysis of solid state transformations: A critical review. Part II. Complex transformations, J Therm Anal Calorim 105 (2011) 767–773. https://doi.org/10.1007/s10973-011-1447-3.
[11] S. Vyazovkin, Activation energies and temperature dependencies of the rates of crystallization and melting of polymers, Polymers (Basel) 12 (2020). https://doi.org/10.3390/POLYM12051070.
[12] S. Vyazovkin, D. Achilias, X. Fernandez-Francos, A. Galukhin, N. Sbirrazzuoli, ICTAC Kinetics Committee recommendations for analysis of thermal polymerization kinetics, Thermochim Acta 714 (2022) 179243. https://doi.org/https://doi.org/10.1016/j.tca.2022.179243.
[13] S. Vyazovkin, A.K. Burnham, L. Favergeon, N. Koga, E. Moukhina, L.A. Pérez-Maqueda, N. Sbirrazzuoli, ICTAC Kinetics Committee recommendations for analysis of multi-step kinetics, Thermochim Acta 689 (2020) 178597. https://doi.org/https://doi.org/10.1016/j.tca.2020.178597.
[14] S. Vyazovkin, A.K. Burnham, J.M. Criado, L.A. Pérez-Maqueda, C. Popescu, N. Sbirrazzuoli, ICTAC Kinetics Committee recommendations for performing kinetic computations on thermal analysis data, Thermochim Acta 520 (2011) 1–19. https://doi.org/https://doi.org/10.1016/j.tca.2011.03.034.
[15] S. Vyazovkin, Comments on multiple publications reporting single heating rate kinetics, Appl Organomet Chem 37 (2023) e6929. https://doi.org/https://doi.org/10.1002/aoc.6929.
[16] M. Joseph D., P. R. Bruce, eds., Thermal Analysis of Polymers, John Wiley & Sons, Hoboken, NJ, USA, 2009. https://doi.org/10.1002/9780470423837.
[17] S.C. Ng, The kinetics of hydrogen peroxide initiated polymerisation of methacrylamide, Eur Polym J 18 (1982) 917–919. https://doi.org/10.1016/0014-3057(82)90028-3.
[18] B. Likozar, M. Krajnc, Simulation of chemical kinetics of elastomer crosslinking by organic peroxides, Polym Eng Sci 49 (2009) 60–72. https://doi.org/10.1002/pen.21218.
[19] W. Wallace, Infrared spectra, in: P.J. Linstrom, W.G. Mallard (Eds.), NIST Chem. WebBook, NIST Stand. Ref. Database, Institute of Standards and Technology, Gaithersburg MD, 2019: p. 20899. https://doi.org/10.18434/T4D303.
Document information
Published on 21/01/26
Accepted on 02/07/25
Submitted on 08/04/25
Volume 09 - Comunicaciones MatComp25 (2025), Issue Núm. 3 - Caracterización Experimental, 2026
DOI: 10.23967/r.matcomp.2025.09.28
Licence: Other
Share this document
Keywords
claim authorship
Are you one of the authors of this document?