Sergio.horta (talk | contribs) m (Errores en la numeración y referencias a figuras) (Tag: Visual edit) |
Ferminotero (talk | contribs) m (Ferminotero moved page Review 789234476536 to Horta Munoz Serna Moreno 2025a) |
||
| (4 intermediate revisions by one other user not shown) | |||
| Line 33: | Line 33: | ||
| style="text-align: center;width: 5px;text-align: right;white-space: nowrap;"|(1) | | style="text-align: center;width: 5px;text-align: right;white-space: nowrap;"|(1) | ||
|} | |} | ||
| − | |||
donde <math display="inline">{u}_{j}</math> representa el desplazamiento en el grado de libertad <math display="inline">j</math>, <math display="inline">i+</math> e <math display="inline">i-</math> indican las caras opuestas del RVE normales al eje <math display="inline">i</math>, <math display="inline">{\epsilon }_{ij}^{H}</math> es la componente <math display="inline">ij</math> de deformación homogeneizada, y <math display="inline">{L}_{i}</math> es la dimensión del RVE en dicha dirección. Esta formulación permite que el contorno del RVE se deforme de manera coherente con el campo de deformaciones impuesto, como se ilustra en la Figura 1. | donde <math display="inline">{u}_{j}</math> representa el desplazamiento en el grado de libertad <math display="inline">j</math>, <math display="inline">i+</math> e <math display="inline">i-</math> indican las caras opuestas del RVE normales al eje <math display="inline">i</math>, <math display="inline">{\epsilon }_{ij}^{H}</math> es la componente <math display="inline">ij</math> de deformación homogeneizada, y <math display="inline">{L}_{i}</math> es la dimensión del RVE en dicha dirección. Esta formulación permite que el contorno del RVE se deforme de manera coherente con el campo de deformaciones impuesto, como se ilustra en la Figura 1. | ||
<div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | ||
| − | + | [[File:Review_789234476536_8053_RVEs_PBCs.svg]] </div> | |
| − | + | ||
<div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | ||
| − | Figura 1. Representación gráfica de un RVE sometido a PBC, en el cual se esquematiza los desplazamientos y deformaciones debidos a una tracción uniaxial horizontal [19].</div> | + | Figura 1. Representación gráfica de un RVE sometido a PBC, en el cual se esquematiza los desplazamientos y deformaciones debidos a una tracción uniaxial horizontal. Reproducción basada en [19].</div> |
El tensor de tensiones efectivo a mesoescala se obtiene mediante una homogeneización del campo de tensiones dentro del volumen del RVE: | El tensor de tensiones efectivo a mesoescala se obtiene mediante una homogeneización del campo de tensiones dentro del volumen del RVE: | ||
Latest revision as of 15:08, 23 June 2025
1. Introducción
Los materiales compuestos de matriz polimérica reforzados con fibras (FRP) se han consolidado como una solución clave en aplicaciones estructurales de alta exigencia mecánica, debido a su excelente relación rigidez/peso y a la posibilidad de diseñar propiedades direccionales mediante el apilado de capas con fibras unidireccionales (UD). Sin embargo, su comportamiento está fuertemente influido por su microestructura heterogénea y anisótropa, así como por la multiplicidad de mecanismos de daño, lo que dificulta la predicción precisa de su respuesta en servicio [1-2].
Cuando estos materiales se someten a carga, pueden presentar grietas en la matriz, delaminaciones entre capas o despegue fibra-matriz, los cuales pueden conducir al fallo localizado o global del laminado. Comprender y modelar estos mecanismos de fallo es esencial para garantizar la seguridad estructural y optimizar procedimientos de inspección y reparación. Por ello, la caracterización experimental y el desarrollo de herramientas numéricas capaces de simular la evolución del daño constituyen un pilar fundamental del diseño con FRP.
En sectores como el aeroespacial o el de las energías renovables, muchas estructuras de material compuesto están sometidas a estados de carga multiaxial o, al menos, biaxial, que en muchos casos pueden aproximarse a un estado de tensión plana. En este contexto, el estudio del comportamiento bajo combinaciones de tensiones normales y de cortadura resulta prioritario para un diseño estructural eficiente.
Las láminas UD presentan un comportamiento ortótropo lineal-elástico, frágil en sus direcciones principales, pero altamente deformable ante esfuerzos de cortadura. Este comportamiento se ha asociado con la pseudo-ductilidad observada en laminados angle-ply, particularmente en configuraciones [±45]nS, que permiten alcanzar grandes deformaciones antes del fallo gracias a la rotación progresiva de las fibras y a la deformación no lineal de la matriz [3-10].
Estudios recientes [3–9] han caracterizado este fenómeno en tracción y compresión uniaxial, destacando su relevancia en la respuesta cíclica de laminados [±45]2S. En particular, Serna Moreno y Horta Muñoz [9] analizaron las distintas fases de la respuesta pseudo-dúctil, relacionando la pérdida de rigidez con la energía disipada y propusieron un modelo de daño apoyado en mediciones experimentales mediante correlación digital de imagen. No obstante, para representar adecuadamente las etapas finales del fallo es necesario recurrir a modelos micromecánicos que incorporen explícitamente los mecanismos de daño a escala local, como sugieren también Chevalier et al. [1] y Sui et al. [2].
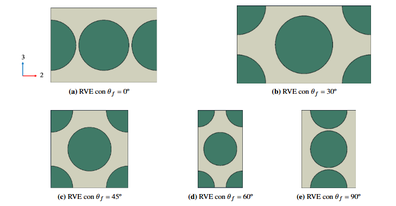
En este trabajo se propone un enfoque de modelado micromecánico, basado en elementos representativos de volumen (RVE), que permite simular la iniciación y evolución del daño bajo diferentes estados de tensión (o deformación) plana. Para ello, se consideran diferentes configuraciones geométricas a microescala, variando los ángulos y distancias relativas entre fibras, y se incorporan superficies cohesivas en las interfaces fibra-matriz, junto con la técnica XFEM para modelar la propagación de grietas. Este planteamiento se apoya en estudios previos sobre distribución aleatoria de fibras [10-16], así como en el uso combinado de técnicas numéricas avanzadas para modelar el fallo a nivel de interfaz y de matriz [17–19]. Además, permite estimar la rigidez y resistencia residuales a través de procesos de homogeneización, contribuyendo a una mejor comprensión y predicción del comportamiento multiaxial de los laminados angle-ply.
2. Metodología numérica
Para analizar el comportamiento mecánico no lineal de laminados angle-ply bajo estados de carga multiaxial, se emplea un enfoque numérico de micromecánica basado en el Método de los Elementos Finitos (FEM). Este enfoque se apoya en el uso de un Elemento Representativo de Volumen (RVE), que reproduce explícitamente la microestructura de una lámina, diferenciando las fases de fibra, matriz e interfaz.
El RVE se define como un volumen mínimo que encapsula las características estadísticas y geométricas necesarias para describir el comportamiento de un material heterogéneo. Debe ser lo suficientemente grande como para incluir un número representativo de heterogeneidades (fibras, matriz e interfaces), pero suficientemente pequeño como para considerarse homogéneo a escala macroscópica. En este trabajo, se considera un RVE periódico con fibras distribuidas regularmente o con pequeñas variaciones controladas, con el fin de representar una microestructura realista manteniendo condiciones computacionalmente manejables.
La formulación numérica se implementa en ABAQUS/Standard 2024, donde se aplican condiciones de contorno periódicas (PBCs) sobre las superficies del RVE para garantizar una deformación homogénea. Estas condiciones se formulan según la ecuación 1.
|
|
(1) |
donde representa el desplazamiento en el grado de libertad , e indican las caras opuestas del RVE normales al eje , es la componente de deformación homogeneizada, y es la dimensión del RVE en dicha dirección. Esta formulación permite que el contorno del RVE se deforme de manera coherente con el campo de deformaciones impuesto, como se ilustra en la Figura 1.
El tensor de tensiones efectivo a mesoescala se obtiene mediante una homogeneización del campo de tensiones dentro del volumen del RVE:
|
|
(2) |
Siendo el volumen total del RVE, el volumen de cada elemento del mallado, su tensión local y la tensión equivalente en la mesoescala. Este procedimiento permite estimar propiedades efectivas del material a partir de su comportamiento microscópico, y utilizar dichas propiedades para analizar estados de carga plana en el plano del laminado, incluyendo configuraciones de tensiones/deformaciones transversales y de cortadura.
El modelo incorpora comportamiento lineal elástico isótropo en la matriz y ortotrópo en las fibras, para dar paso a una iniciación de distintos mecanismos de daño representativos de la evolución de la microestructura bajo carga.
El daño en la matriz polimérica se implementa mediante la técnica XFEM (eXtended Finite Element Method), restringida a la matriz dado que esta es más susceptible a iniciar grietas antes que la fibra. El criterio de inicio de daño se basa en la tensión principal máxima, produciéndose una evolución controlada mediante la tasa de liberación de energía ( ).
Para la interfaz fibra-matriz, se utiliza una formulación de elementos cohesivos con un criterio de iniciación de daño por tensión máxima (modos desacoplados) y evolución según el modelo mixto de Benzeggagh-Kenane. Este modelo requiere definir las tasas de liberación de energía , y , asociadas a los modos puro normal y tangenciales.
En paralelo, se definen dos parámetros característicos para cuantificar la evolución del daño, que se esquematizan en la Figura 2. Por un lado, el ángulo relativo entre fibras ( ), que mide la orientación relativa entre fibras vecinas respecto a la horizontal. Por otro lado, el ángulo de apertura de la interfaz fibra-matriz ( ), que indica el avance de la separación cohesiva.
Con el objetivo de comprender la influencia de la geometría y distribución de fibras sobre las propiedades efectivas, se desarrollan estudios paramétricos mediante ABAQUS Scripting. Estos estudios permitirán evaluar el impacto del ángulo relativo entre fibras (Figura 3), la fracción volumétrica de las mismas, o la relación de aspecto del RVE, en términos de la resistencia y la acumulación de daño en la interfaz y grietas en la matriz.
2.1. Script para medición geométrica de daños
Como complemento al análisis numérico, se ha desarrollado un script en MATLAB capaz de procesar automáticamente secuencias de imágenes obtenidas de simulaciones en ABAQUS. Este código permite analizar la evolución de grietas en la matriz, especialmente aquellas originadas en la interfaz fibra-matriz, evaluando su propagación en función de la deformación aplicada.
El script identifica de forma autónoma las fibras presentes en el RVE, asigna las grietas detectadas a su fibra más próxima, y calcula parámetros clave como el punto de iniciación, el ángulo de apertura respecto al centro de la fibra y la evolución temporal de su longitud. Estos resultados se presentan tanto en formato numérico como mediante gráficas que facilitan su interpretación.
El código ha sido validado con éxito en distintos tipos de RVE, incluyendo configuraciones con diferentes relaciones de aspecto, densidades de fibras y número de grietas, siempre que estas sean distinguibles y no se crucen entre sí. Además, su estructura permite adaptar fácilmente los parámetros de entrada y aplicar el análisis a nuevas geometrías o condiciones de contorno sin necesidad de modificar el núcleo del algoritmo.
Este sistema automatizado resulta especialmente útil para el estudio de la cohesión en la interfaz fibra-matriz, proporcionando una herramienta robusta para correlacionar de forma cuantitativa los resultados de simulación con la evolución del daño observado a microescala.
3. Resultados
Las simulaciones realizadas permiten analizar un abanico amplio de parámetros microestructurales y mecánicos. En esta sección se presentan únicamente los resultados más representativos, centrándose en dos aspectos principales: (i) la comparación de las curvas de fallo para diferentes configuraciones de posición relativa entre fibras (es decir, distintas relaciones de aspecto del RVE), y (ii) el comportamiento bajo estados combinados de tensión transversal y tangencial, evaluado en distintos escenarios geométricos.
En primer lugar, al analizar la curva de tensión de fallo obtenida numéricamente (Figura 4), se observa que presenta una distribución coherente con la de curvas de las teorías de fallo disponibles en la literatura. Este resultado valida el modelo propuesto, que logra capturar el comportamiento del material compuesto bajo estados de tensión plana con un nivel de precisión satisfactorio.
En cuanto a las configuraciones geométricas analizadas, se constata que la disposición con un ángulo relativo entre fibras de 45° es la que mejor desempeño mecánico presenta, registrando los valores más altos tanto de tensión tangencial ( ) como de tensión transversal ( ) antes del inicio del fallo. Este comportamiento ya se había identificado en simulaciones previas restringidas a esfuerzos puros de cortadura, y se confirma además con la incorporación del componente transversal. La explicación de este resultado radica en una redistribución más eficiente de las tensiones a través de la matriz, reduciendo la concentración de esfuerzos en zonas críticas.
Por el contrario, la configuración de 60° se identifica como la más desfavorable, ya que el inicio del fallo se produce a valores notablemente inferiores respecto al resto de configuraciones. Este resultado se atribuye a una disposición menos eficiente para la transferencia de cargas y a un comportamiento más frágil de la interfaz fibra-matriz bajo este ángulo específico.
En el caso de las configuraciones de 30° y 90°, los resultados muestran que la disposición de 30º proporciona una mejor resistencia estructural, superando en todos los casos a la configuración ortogonal (90°). Esto indica que, dentro de los ángulos analizados, aquellos intermedios tienden a ofrecer un compromiso más favorable entre rigidez, resistencia y ductilidad aparente.
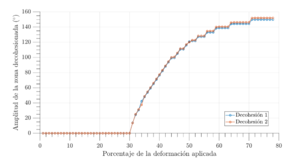
Posteriormente, se ha analizado de forma localizada la evolución del daño en la microestructura. En la Figura 5 se representa la progresión de la longitud de las grietas en distintas interfaces fibra-matriz, así como el ángulo de inicio de decohesión () a lo largo del incremento de deformación aplicado. Estos resultados se han extraído automáticamente a partir del postprocesado de imágenes generado por las simulaciones mediante el código desarrollado en MATLAB.
Dicha herramienta permite identificar y rastrear cada grieta visible en los fotogramas, asociándola a su fibra más cercana y extrayendo información clave sobre el punto y el ángulo de iniciación, así como su evolución temporal. Esta capacidad automatizada ha permitido observar cómo el desarrollo del daño depende fuertemente de la distribución local de fibras y del tipo de carga aplicada, ofreciendo una vía muy potente para correlacionar la microestructura con la respuesta global del material.
En conjunto, estos resultados sientan las bases para futuras investigaciones orientadas a estudiar en profundidad el efecto de la densidad y distribución local de fibras, así como el modo de carga aplicado, sobre la propagación del daño. La combinación del modelado micromecánico, técnicas de homogeneización y herramientas avanzadas de análisis post-simulacional proporciona un marco robusto para la optimización de diseños microestructurales en materiales compuestos estructurales.
4. Conclusiones
El presente trabajo ha permitido establecer un marco de simulación numérica robusto para el análisis del comportamiento micromecánico de materiales compuestos, en particular de láminas reforzadas con fibras sometidas a estados de tensión plana. A través del uso de modelos de Elementos Finitos aplicados sobre elementos de volumen representativo (RVE), y mediante la aplicación de condiciones de contorno periódicas, se ha podido capturar con notable precisión la respuesta mecánica tanto en términos globales (curvas de fallo en tensión aparente) como locales (evolución de grietas y daño en la interfaz).
Una de las principales aportaciones del estudio ha sido la identificación del ángulo relativo entre fibras como un parámetro clave en la resistencia del material. Se ha demostrado que configuraciones de 45° entre fibras optimizan la respuesta ante estados combinados de tensión tangencial y transversal, retrasando el inicio del fallo y aumentando los niveles de tensión admisibles. Por el contrario, disposiciones como la de 60° conducen a un comportamiento significativamente más frágil, incluso cuando la densidad de fibras se mantiene constante.
Además, se ha desarrollado una herramienta automatizada de postprocesado en MATLAB, capaz de analizar fotogramas generados por las simulaciones y extraer información cuantitativa sobre la nucleación y evolución de las grietas. Este código no solo permite identificar la localización y longitud de cada grieta, sino también calcular su ángulo de inicio respecto a la fibra más próxima, lo que aporta una visión detallada del mecanismo de daño en la microescala. Su aplicación ha permitido observar cómo el daño tiende a iniciarse en zonas específicas de la matriz, especialmente entre fibras cercanas, y cómo evoluciona en función de la orientación relativa y del tipo de carga aplicada.
En conjunto, los resultados obtenidos no solo confirman tendencias identificadas previamente en la literatura, sino que ofrecen nuevas herramientas y enfoques para el estudio detallado del daño en materiales compuestos. Este enfoque microescala se presenta como una base sólida para futuras investigaciones centradas en el diseño de materiales con arquitecturas optimizadas frente a estados de carga multiaxial, con especial interés en los dominados por cortadura debido a su comportamiento mecánico aparente altamente no-lineal.
5. Agradecimientos
Este trabajo se engloba en el marco de los proyectos DPI2016-77715-R, PDC2021-121154-I00, PID2022-137387OB-I00 y SBPLY/23/180225/000114 financiados por MICIU/AEI/10.13039/501100011033, "FEDER Una manera de hacer Europa" y "Unión Europea Next Generation/PRTR" y la Junta de Comunidades de Castilla-La Mancha.
6. Bibliografía
[1] J. Chevalier, P.P. Camanho, F. Lani y T. Pardoen, «Multi-scale characterization and modelling of the transverse compression response of unidirectional carbon fiber reinforced epoxy,» Composite Structures, vol. 209, págs. 160–176 (2018).
[2] X.M. Sui, M. Tiwari, I. Greenfeld, R.L. Khalfin, H. Meeuw, B. Fiedler y H.D. Wagner, «Extreme scale-dependent tensile properties of epoxy fibers,» eXPRESS Polymer Letters vol. 13, nº 11, págs. 993-1003, 2019.
[3] W. Van Paepegem, I. De Baere, J. Degrieck. «Modelling the nonlinear shear stress–strain response of glass fibre-reinforced composites. Part I: Experimental results,» Composites Science and Technology, vol. 66, nº 10, págs. 1455–1464, 2006.
[4] J.D. Fuller, M. R. Wisnom, «Pseudo-ductility and damage suppression in thin ply CFRP angle-ply laminates,» Composites Part A, vol. 69, págs. 64–71, 2015.
[5] H. Cui, D. Thomson, A. Pellegrino, J. Wiegand, N. Petrinic, «Effect of strain rate and fibre rotation on the in-plane shear response of ±45º laminates in tension and compression tests,» Composites Science and Technology, vol. 135, págs. 106–115, 2016.
[6] F. Sket, A. Enfedaque, C. Díaz López, C. González, J. Molina-Aldareguía y J. LLorca, «X-ray computed tomography analysis of damage evolution in open hole carbon fiber-reinforced laminates subjected to in-plane shear,» Composites Science and Technology, vol. 133, págs. 40–50, 2016.
[7] S. Horta Muñoz, «Complexity of the structural response of fibre reinforced polymer matrix composites,» Tesis Doctoral, Universidad de Castilla-La Mancha, 2020.
[8] M.C. Serna Moreno, S. Horta Muñoz, «Pseudo-ductile effects in ±45° angle-ply CFRP laminates under uniaxial loading: compression and cyclic tensile test,» Composites Part B, vol. 233, 109631, 2022.
[9] S. Horta Muñoz, M.C. Serna Moreno, «Tension–compression biaxial test with ±45° symmetric angle ply laminates for determining the pure shear response in principal material directions of a lamina,» Composites Part B: Engineering, vol. 261, 110792, 2023.
[10] A. Arteiro, G. Catalanotti, A.R. Melro, P. Linde y P.P. Camanho, «Micro-mechanical analysis of the in situ effect in polymer composite laminates,» Composite Structures, vol. 116, págs. 827-840, 2014.
[11] A. Arteiro, G. Catalanotti, A.R. Melro, P. Linde, P.P. Camanho, «Micro-mechanical analysis of the effect of ply thickness on the transverse compressive strength of polymer composites,» Composites Part A, vol. 79, págs. 127-137, 2015.
[12] W. Wang, Y. Dai, C. Zhang, X. Gao y M. Zhao, «Micromechanical Modeling of Fiber-Reinforced Composites with Statistically Equivalent Random Fiber Distribution,» Materials, vol. 9, nº 8, 624 2016.
[13] D. Garoz, F.A. Gilabert, R.D.B. Sevenois, S.W.F. Spronk y W. Van Paepegem, «Material parameter identification of the elementary ply damage mesomodel using virtual micromechanical tests of a carbon fiber epoxy system,» Composite Structures, vol. 1, págs. 181391–404, 2017.
[14] D. Garoz, F.A. Gilabert, R.D.B. Sevenois, S.W.F. Spronky W. Van Paepegem, «Consistent application of periodic boundary conditions in implicit and explicit finite element simulations of damage in composites,» Composites Part B, vol. 168, págs. 254–266, 2019.
[15] F. Naya, C. González, C.S. Lopes, S. Van der Veen y F. Pons, «Computational micromechanics of the transverse and shear behavior of unidirectional fiber reinforced polymers including environmental effects,» Composites Part A, vol. 92, págs 146-157, 2017.
[16] S.-M. Park, J. H. Lim, M. T. Seong y D. Sohn, «Efficient generator of random fiber distribution with diverse volume fractions by random fiber removal,» Composites Part B, vol. 16, págs. 302-316, 2019.
[17] M. Kästner, S. Müller y V. Ulbricht, «XFEM Modelling of Inelastic Material Behaviour and Interface Failure in Textile-Reinforced Composites,» Procedia Materials Science, vol. 2, págs. 43-51, 2013.
[18] F. Gilabert, D. Garoz y W. Van Paepegem, «Macro- and micro-modeling of crack propagation in encapsulation-based self-healing materials: Application of XFEM and cohesive surface techniques,» Materials & Design, vol. 130, págs. 459-478, 2017.
[19] M. Naghdinasab, A. Farrokhabadi y H. Madadi, «A numerical method to evaluate the material properties degradation in composite RVEs due to fiber-matrix debonding and induced matrix cracking,» Finite Elements in Analysis and Design, vol. 146, págs. 84-95, 2018.
[15] E. Totry, J. M. Molina-Aldareguía, C. González, J. LLorca, «Effect of fiber, matrix and interface properties on the in-plane shear deformation of carbon-fiber reinforced composites,» Composites Science and Technology, vol. 70 (6), 970-980 (2010).
[16] F. Naya, C. González, C.S. Lopes, S. Van der Veen, F. Pons. «Computational micromechanics of the transverse and shear behavior of unidirectional fiber reinforced polymers including environmental effects,» Composites Part A, vol. 92, págs. 146–157, 2017.
[17] W. Tan, F. Naya, L. Yang, T. Chang, B.G. Falzon, L. Zhan, J.M. Molina-Aldareguía, C. González, J. Llorca. «The role of interfacial properties on the intralaminar and interlaminar damage behaviour of unidirectional composite laminates: Experimental characterization and multiscale modelling,» Composites Part B, vol. 138, págs. 206–221, 2017.
[18] F. Danzi, D. Fanteria, E. Panettieri, M. Palermo, «A numerical micro-mechanical study of the influence of fiber-matrix interphase failure on carbon/epoxy material properties,» Composite Structures, vol. 159, 625–635, 2017.
[19] A.G. Reisinger «Modeling and Validation of Multiscale Lamellar Bone Elasticity,» Tesis Doctoral, Technische Universität Wien, 2011.