(→2. Mechanical model) |
|||
| (41 intermediate revisions by 2 users not shown) | |||
| Line 10: | Line 10: | ||
==Abstract== | ==Abstract== | ||
| − | The granular-media-based push-bending process has been developed to manufacture thin-wall elbow tube with t/ | + | The granular-media-based push-bending process has been developed to manufacture thin-wall elbow tube with t/D<math>\le 0.01</math> (the ratio of wall thickness to outer diameter) and R/D<math>\le 1.5</math> (the ratio of bending radius to outer diameter). In the process, a tubular blank is filled with granular media and then pushed into a die to form an elbow shape. To investigate the process, a FEM-DEM coupling model has been developed, in which FEM is used to simulate bending deformation of tubular blank, and DEM is used to calculate contact forces between spherical particles in granular media. In this work, an improved numerical formulation is proposed in order to reach mechanical equilibrium quickly and accelerate the convergence of DEM simulation, when the new contacts are no longer created and the old contacts are no longer deleted in granular media. Using the proposed numerical formulation, the improved FEM-DEM coupling simulation for granular-media-based thin-wall elbow tube push-bending process is less time-consuming than before under the same simulation condition. |
'''Keywords:''' Elbow tube, granular-media-based, push bending, energetic formulation, FEM-DEM coupling | '''Keywords:''' Elbow tube, granular-media-based, push bending, energetic formulation, FEM-DEM coupling | ||
| Line 16: | Line 16: | ||
==1. Introduction== | ==1. Introduction== | ||
| − | The thin-wall elbow tubes with t/D≤0.01 and R/ | + | The thin-wall elbow tubes with t/D≤0.01 and R/D<math>\le 1.5</math> (where t is wall thickness, D is outer diameter, and R is bending radius) are widely used in rocket engine pipelines [1-3]. In the bending process of elbow tube with quite small t/D and R/D, the forming defects such as wrinkling and fracture is difficult to be avoided, and the dimensional precision is difficult to satisfy the requirements due to the springback and cross-sectional ovalization. Push-bending process is demonstrated to be applicable for manufacturing elbow tubes with small R/D [4-5]. The recently developed granular-media-based push-bending process can be used to manufacture the thin-wall elbow tube with t/D<math>\le 0.01</math> and R/D<math>\le 1.5</math> as required [6]. The granular-media-based thin-wall elbow push-bending process involves filling a tube with spherical granular media and pushing the tube into a die to bend a tubular blank into an elbow shape. The spherical granular media introduced as filler has great potential for its flexibility [7], resistance to high forming temperature [8-9], and characteristics of pressure-transmission [10-11]. In addition, the spherical granular media is controllable and predictable because of its regular shape. |
To investigate the granular-media-based thin-wall elbow push-bending process, a 3D FEM-DEM coupling model is developed [12]. In the coupling model, FEM is used to simulate bending deformation of tubular blank (continuum), and DEM is used to calculate contact forces between spherical particles in granular media (discrete media). DEM is a dynamic method, and damping is applied to the equations of motion in order to absorb vibration energy and reach mechanical equilibrium. The biggest time overhead in the coupling model is absorbing vibration energy in DEM simulation to reach mechanical equilibrium. To accelerate the convergence of DEM simulation, a static energetic method is proposed in the present paper. | To investigate the granular-media-based thin-wall elbow push-bending process, a 3D FEM-DEM coupling model is developed [12]. In the coupling model, FEM is used to simulate bending deformation of tubular blank (continuum), and DEM is used to calculate contact forces between spherical particles in granular media (discrete media). DEM is a dynamic method, and damping is applied to the equations of motion in order to absorb vibration energy and reach mechanical equilibrium. The biggest time overhead in the coupling model is absorbing vibration energy in DEM simulation to reach mechanical equilibrium. To accelerate the convergence of DEM simulation, a static energetic method is proposed in the present paper. | ||
| Line 27: | Line 27: | ||
<div id='img-1'></div> | <div id='img-1'></div> | ||
| − | {| class="wikitable" style="margin: 0em auto 0.1em auto;border-collapse: collapse;width: | + | {| class="wikitable" style="margin: 0em auto 0.1em auto;border-collapse: collapse;width:60%;" |
|-style="background:white;" | |-style="background:white;" | ||
|style="text-align: center;padding:10px;"| [[Image:Review_294821678474-image1-c.png|378px]] | |style="text-align: center;padding:10px;"| [[Image:Review_294821678474-image1-c.png|378px]] | ||
| Line 43: | Line 43: | ||
{| style="text-align: center; margin:auto;" | {| style="text-align: center; margin:auto;" | ||
|- | |- | ||
| − | | <math>{x}_{i}={\left[ \begin{matrix}{x}_{i1}&{x}_{i2}&{x}_{i3}\end{matrix}\right] }^{T}</math> | + | | <math>{\bf x}_{i}={\left[ \begin{matrix}{x}_{i1}&{x}_{i2}&{x}_{i3}\end{matrix}\right] }^{T}</math> |
|} | |} | ||
| style="width: 5px;text-align: right;white-space: nowrap;" | (1) | | style="width: 5px;text-align: right;white-space: nowrap;" | (1) | ||
| Line 57: | Line 57: | ||
{| style="text-align: center; margin:auto;" | {| style="text-align: center; margin:auto;" | ||
|- | |- | ||
| − | | <math>\begin{matrix}{v}_{i}={\left[ \begin{matrix}{v}_{i1}&{v}_{i2}&{v}_{i3}\end{matrix}\right] }^{T}\\\, {w}_{i}={\left[ \begin{matrix}{w}_{i1}&{w}_{i2}&{w}_{i3}\end{matrix}\right] }^{T}\end{matrix}\,</math> | + | | <math>\begin{matrix}{\bf v}_{i}={\left[ \begin{matrix}{v}_{i1}&{v}_{i2}&{v}_{i3}\end{matrix}\right] }^{T}\\\, {\bf w}_{i}={\left[ \begin{matrix}{w}_{i1}&{w}_{i2}&{w}_{i3}\end{matrix}\right] }^{T}\end{matrix}\,</math> |
|} | |} | ||
| style="width: 5px;text-align: right;white-space: nowrap;" | (2) | | style="width: 5px;text-align: right;white-space: nowrap;" | (2) | ||
| Line 64: | Line 64: | ||
where <math>v_{il}</math> denotes the <math>l</math>-th displacement component of the <math>i</math>-th particle, and <math>w_{il}</math> denotes the <math>l</math>-th rotation component of the <math>i</math>-th particle. | where <math>v_{il}</math> denotes the <math>l</math>-th displacement component of the <math>i</math>-th particle, and <math>w_{il}</math> denotes the <math>l</math>-th rotation component of the <math>i</math>-th particle. | ||
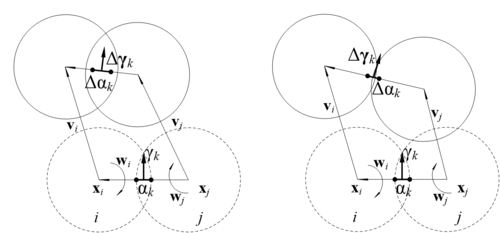
| − | The contact <math>k_c</math> formed by the particle <math>i</math> and the particle <math>j</math>, | + | The contact <math>k_c</math> formed by the particle <math>i</math> and the particle <math>j</math>, as shown in [[#img-2|Figure 2]]. |
<div id='img-2'></div> | <div id='img-2'></div> | ||
| − | {| class="wikitable" style="margin: 0em auto 0.1em auto;border-collapse: collapse;width: | + | {| class="wikitable" style="margin: 0em auto 0.1em auto;border-collapse: collapse;width:60%;" |
|-style="background:white;" | |-style="background:white;" | ||
| − | |style="text-align: center;padding:10px;"| [[Image:Review_294821678474-image2.png| | + | |style="text-align: center;padding:10px;"| [[Image:Review_294821678474-image2.png|500px]] |
|- | |- | ||
| style="background:#efefef;text-align:left;padding:10px;font-size: 85%;"| '''Figure 2'''. Relation between normal overlap and displacements of a pair of spherical particles in contact. The dashed circles denote the initial positions and the solid circles denote the positions after loading | | style="background:#efefef;text-align:left;padding:10px;font-size: 85%;"| '''Figure 2'''. Relation between normal overlap and displacements of a pair of spherical particles in contact. The dashed circles denote the initial positions and the solid circles denote the positions after loading | ||
| Line 75: | Line 75: | ||
| − | Assuming that elastic deformations are localized in very small neighborhoods of the contact points, so that, the relative displacement between the rigid part of the two particles near the contact point <math display="inline">{x}^{{(k}_{c})}</math> is: | + | Assuming that elastic deformations are localized in very small neighborhoods of the contact points, so that, the relative displacement between the rigid part of the two particles near the contact point <math display="inline">{\bf x}^{{(k}_{c})}</math> is: |
{| class="formulaSCP" style="width: 100%; text-align: center;" | {| class="formulaSCP" style="width: 100%; text-align: center;" | ||
| Line 82: | Line 82: | ||
{| style="text-align: center; margin:auto;" | {| style="text-align: center; margin:auto;" | ||
|- | |- | ||
| − | | <math | + | | <math>\Delta \boldsymbol{\delta }_{{k}_{c}}=\left( {\bf v}_{j}-{\bf v}_{i}\right) +</math><math>R{\tilde{\bf n}}_{{k}_{c}}\left( {\bf w}_{j}+{\bf w}_{i}\right)</math> |
|} | |} | ||
| style="width: 5px;text-align: right;white-space: nowrap;" | (3) | | style="width: 5px;text-align: right;white-space: nowrap;" | (3) | ||
|} | |} | ||
| − | + | where <math display="inline">R</math> denotes the particle radius, <math display="inline">{\tilde{\bf n}}_{{k}_{c}}</math> denotes the antisymmetric matrix formed by the components of the unit normal vector <math display="inline">{\bf n}_{{k}_{c}}</math> | |
| − | where | + | |
{| class="formulaSCP" style="width: 100%; text-align: center;" | {| class="formulaSCP" style="width: 100%; text-align: center;" | ||
| Line 95: | Line 94: | ||
{| style="text-align: center; margin:auto;" | {| style="text-align: center; margin:auto;" | ||
|- | |- | ||
| − | | <math | + | | <math>{\tilde{\bf n}}_{{k}_{c}}=\left[ \begin{matrix}0&{n}_{{k}_{c}3}&-{n}_{{k}_{c}2}\\-{n}_{{k}_{c}3}&0&{n}_{{k}_{c}1}\\{n}_{{k}_{c}2}&-{n}_{{k}_{c}1}&0\end{matrix}\right]</math> |
|} | |} | ||
| style="width: 5px;text-align: right;white-space: nowrap;" | (4) | | style="width: 5px;text-align: right;white-space: nowrap;" | (4) | ||
| Line 101: | Line 100: | ||
| − | If the contact point <math display="inline">{x}^{{(k}_{c})}</math> is formed by the particles | + | If the contact point <math display="inline">{\bf x}^{{(k}_{c})}</math> is formed by the particles <math>i</math> and <math>j</math>, we have: |
{| class="formulaSCP" style="width: 100%; text-align: center;" | {| class="formulaSCP" style="width: 100%; text-align: center;" | ||
| Line 108: | Line 107: | ||
{| style="text-align: center; margin:auto;" | {| style="text-align: center; margin:auto;" | ||
|- | |- | ||
| − | | <math | + | | <math>{\bf n}_{{k}_{c}}=\frac{\left( {\bf x}_{j}-{\bf x}_{i}\right) }{\left| {\bf x}_{j}-{\bf x}_{i}\right| }\quad \quad \quad \, {k}_{c}=</math><math>1,2,\ldots ,{M}_{c}</math> |
|} | |} | ||
| style="width: 5px;text-align: right;white-space: nowrap;" | (5) | | style="width: 5px;text-align: right;white-space: nowrap;" | (5) | ||
| Line 114: | Line 113: | ||
| − | If the contact point <math display="inline">{x}^{{(k}_{c})}</math> is formed by the particles | + | If the contact point <math display="inline">{\bf x}^{{(k}_{c})}</math> is formed by the particles <math>i</math> and the boundary wall, we have: |
{| class="formulaSCP" style="width: 100%; text-align: center;" | {| class="formulaSCP" style="width: 100%; text-align: center;" | ||
| Line 121: | Line 120: | ||
{| style="text-align: center; margin:auto;" | {| style="text-align: center; margin:auto;" | ||
|- | |- | ||
| − | | <math | + | | <math>{\bf n}_{{k}_{c}}=\frac{\left( {\bf x}_{B{k}_{c}}-{\bf x}_{i}\right) }{\left| {\bf x}_{B{k}_{c}}-{\bf x}_{i}\right| }\quad \quad \, {k}_{c}=</math><math>1,2,\ldots ,{M}_{b}</math> |
|} | |} | ||
| style="width: 5px;text-align: right;white-space: nowrap;" | (6) | | style="width: 5px;text-align: right;white-space: nowrap;" | (6) | ||
|} | |} | ||
| + | where <math display="inline">{\bf x}_{B{k}_{c}}</math> denotes the contact point of index <math>k_c</math> between the particle <math>i</math> and the boundary wall. | ||
| − | + | Assuming that the relative displacement <math display="inline">{\Delta \boldsymbol{\delta} }_{{k}_{c}}</math> is small, the change of distance between the two neighbor particles’ centers can be determined as the normal component of their relative displacement, which is set equal to an incremental normal overlap: | |
| − | + | ||
| − | Assuming that the relative displacement <math display="inline">{\Delta \delta }_{{k}_{c}}</math> is small, the change of distance between the two neighbor particles’ centers can be determined as the normal component of their relative displacement, which is set equal to an incremental normal overlap: | + | |
{| class="formulaSCP" style="width: 100%; text-align: center;" | {| class="formulaSCP" style="width: 100%; text-align: center;" | ||
| Line 136: | Line 134: | ||
{| style="text-align: center; margin:auto;" | {| style="text-align: center; margin:auto;" | ||
|- | |- | ||
| − | | <math | + | | <math>\begin{matrix}-\Delta {\alpha }_{{k}_{c}}={\bf n}_{{k}_{c}}^{T}{\Delta \boldsymbol{\delta} }_{{k}_{c}}={\bf n}_{{k}_{c}}^{T}\left[ \left( {\bf v}_{j}-{\bf v}_{i}\right) +R{\tilde{\bf n}}_{{k}_{c}}\left( {\bf w}_{j}+{\bf w}_{i}\right) \right] ={\bf n}_{{k}_{c}}^{T}\left( {\bf v}_{j}-{\bf v}_{i}\right) \\\, \Delta {\alpha }_{{k}_{c}}=-{\alpha }_{{k}_{c}}\, ,\, \, if\, \, \Delta {\alpha }_{{k}_{c}}<-{\alpha }_{{k}_{c}}\, \\\, \, {k}_{c}=1,2,\ldots ,{M}_{c}\end{matrix}</math> |
|} | |} | ||
| style="width: 5px;text-align: right;white-space: nowrap;" | (7) | | style="width: 5px;text-align: right;white-space: nowrap;" | (7) | ||
|} | |} | ||
| − | + | where <math display="inline">\Delta {\alpha }_{{k}_{c}}</math> is positive if the distance between the two centers decreases, while <math display="inline">\Delta {\alpha }_{{k}_{c}}</math> is negative if the distance between the two centers increases. When <math display="inline">\Delta {\alpha }_{{k}_{c}}</math> is negative, <math display="inline">\Delta {\alpha }_{{k}_{c}}</math> can not be smaller than the initial normal overlap <math display="inline">{\alpha }_{{k}_{c}}</math>. <math>M_c</math> is the total number of contacts in the granular media. | |
| − | where <math display="inline">\Delta {\alpha }_{{k}_{c}}</math> is positive if the distance between the two centers decreases, while <math display="inline">\Delta {\alpha }_{{k}_{c}}</math> is negative if the distance between the two centers increases. When <math display="inline">\Delta {\alpha }_{{k}_{c}}</math> is negative, <math display="inline">\Delta {\alpha }_{{k}_{c}}</math> can not be smaller than the initial normal overlap <math display="inline">{\alpha }_{{k}_{c}}</math>. | + | |
In a similar way, the incremental tangential relative displacement due to the elastic deformations of particles can be written as: | In a similar way, the incremental tangential relative displacement due to the elastic deformations of particles can be written as: | ||
| Line 151: | Line 148: | ||
{| style="text-align: center; margin:auto;" | {| style="text-align: center; margin:auto;" | ||
|- | |- | ||
| − | | <math | + | | <math>\begin{align}{\Delta \boldsymbol{\gamma }}_{{k}_{c}} & =\left( {\bf I}-{\bf n}_{{k}_{c}}{\bf n}_{{k}_{c}}^{T}\right) {\Delta \boldsymbol{\delta} }_{{k}_{c}}\\\, |
| + | & =\left( {\bf I}-{\bf n}_{{k}_{c}}{\bf n}_{{k}_{c}}^{T}\right) \left[ \left( {\bf v}_{j}-{\bf v}_{i}\right) +R{\tilde{\bf n}}_{{k}_{c}}\left( {\bf w}_{j}+{\bf w}_{i}\right) \right] \\\, | ||
| + | & =\left( {\bf I}-{\bf n}_{{k}_{c}}{\bf n}_{{k}_{c}}^{T}\right) \left( {\bf v}_{j}-{\bf v}_{i}\right) +R{\tilde{\bf n}}_{{k}_{c}}\left( {\bf w}_{j}+{\bf w}_{i}\right) \quad \quad \quad \, {k}_{c}=1,2,\ldots ,{M}_{c}\end{align}</math> | ||
|} | |} | ||
| style="width: 5px;text-align: right;white-space: nowrap;" | (8) | | style="width: 5px;text-align: right;white-space: nowrap;" | (8) | ||
| Line 157: | Line 156: | ||
| − | Further, | + | Further, Eq.(8) can be rewritten as: |
{| class="formulaSCP" style="width: 100%; text-align: center;" | {| class="formulaSCP" style="width: 100%; text-align: center;" | ||
| Line 164: | Line 163: | ||
{| style="text-align: center; margin:auto;" | {| style="text-align: center; margin:auto;" | ||
|- | |- | ||
| − | | <math | + | | <math>{\Delta \boldsymbol{\gamma }}_{{k}_{c}}={\tilde{\boldsymbol{\gamma }}}_{{k}_{c}}\Delta {\alpha }_{{k}_{c}}</math> |
|} | |} | ||
| style="width: 5px;text-align: right;white-space: nowrap;" | (9) | | style="width: 5px;text-align: right;white-space: nowrap;" | (9) | ||
|} | |} | ||
| + | where <math display="inline">{\tilde{\boldsymbol{\gamma }}}_{{k}_{c}}</math> denotes the slope vector with respect the unit normal vector <math display="inline">{\bf n}_{{k}_{c}}</math> of the contact elastic relative displacement <math display="inline">{\Delta \boldsymbol{\delta}}_{{k}_{c}}</math>. | ||
| − | + | In the same way, when the particle <math>i</math> is in contact with the boundary wall, we have: | |
| − | + | ||
| − | + | ||
{| class="formulaSCP" style="width: 100%; text-align: center;" | {| class="formulaSCP" style="width: 100%; text-align: center;" | ||
| Line 179: | Line 177: | ||
{| style="text-align: center; margin:auto;" | {| style="text-align: center; margin:auto;" | ||
|- | |- | ||
| − | | <math | + | | <math>\begin{matrix}-\Delta \boldsymbol{\alpha }_{{k}_{c}}={\bf n}_{{k}_{c}}^{T}\left( {\overline{\bf v}}_{B{k}_{c}}-{\bf v}_{i}\right) \\\, {\Delta \boldsymbol{\gamma }}_{{k}_{c}}=\, \left( {\bf I}-{\bf n}_{{k}_{c}}{\bf n}_{{k}_{c}}^{T}\right) \left[ {\overline{\bf v}}_{B{k}_{c}}-{\bf v}_{i}+R{\tilde{\bf n}}_{{k}_{c}}{\bf w}_{i}\right] ={\tilde{\boldsymbol{\gamma }}}_{{k}_{c}}\Delta {\alpha }_{{k}_{c}}\quad \, \, {k}_{c}=1,2,\ldots ,{M}_{b}\end{matrix}</math> |
|} | |} | ||
| style="width: 5px;text-align: right;white-space: nowrap;" | (10) | | style="width: 5px;text-align: right;white-space: nowrap;" | (10) | ||
| Line 185: | Line 183: | ||
| − | The unknown displacements and rotations of the particles are collected in the | + | The unknown displacements and rotations of the particles are collected in the <math>6N\times 1</math> column matrix <math>\bf U</math>: |
{| class="formulaSCP" style="width: 100%; text-align: center;" | {| class="formulaSCP" style="width: 100%; text-align: center;" | ||
| Line 192: | Line 190: | ||
{| style="text-align: center; margin:auto;" | {| style="text-align: center; margin:auto;" | ||
|- | |- | ||
| − | | <math | + | | <math>\begin{align}{\bf U}^{T} & =\left[ \begin{matrix}{\bf V}^{T}&{\bf W}^{T}\end{matrix}\right] \\\, {\bf V}^{T} & ={\left[ {v}_{11}\, \, {v}_{12}\, \, {v}_{13}\, \ldots \, \, {v}_{i1}\, \, {v}_{i2}\, \, {v}_{i3}\, \ldots \quad {v}_{N1}\, \, {v}_{N2}\, \, {v}_{N3}\right] }^{T}\\\, {\bf W}^{T} & ={\left[ {w}_{11}\, \, {w}_{12}\, \, {w}_{13}\, \ldots \, \, {w}_{i1}\, \, {w}_{i2}\, \, {w}_{i3}\, \ldots \quad {w}_{N1}\, \, {w}_{N2}\, \, {w}_{N3}\right] }^{T}\end{align}</math> |
|} | |} | ||
| style="width: 5px;text-align: right;white-space: nowrap;" | (11) | | style="width: 5px;text-align: right;white-space: nowrap;" | (11) | ||
|} | |} | ||
| − | + | The incremental normal overlaps of contacts between spherical particles are collected in the <math display="inline">M_c \times 1</math> column matrixes <math>\Delta \boldsymbol{\alpha }_C</math>. The incremental tangential relative displacements are collected in the <math display="inline">3M_c \times 1</math> column matrixes <math>\Delta \boldsymbol{\gamma }_C</math>. In the same way, the incremental relative displacements of the contacts between spherical particles and the boundary wall are collected in the <math display="inline">M_b \times 1</math> column matrixes <math>\Delta \boldsymbol{\alpha }_B</math> and in the <math display="inline">3M_b \times 1</math> column matrixes <math>\Delta \boldsymbol{\gamma }_B</math>. Then, Eqs. (3) to (10) can be summarized as: | |
| − | The incremental normal overlaps of contacts between spherical particles are collected in the | + | |
{| class="formulaSCP" style="width: 100%; text-align: center;" | {| class="formulaSCP" style="width: 100%; text-align: center;" | ||
| Line 205: | Line 202: | ||
{| style="text-align: center; margin:auto;" | {| style="text-align: center; margin:auto;" | ||
|- | |- | ||
| − | | <math | + | | <math>\left\{ \begin{align}\Delta \boldsymbol{\delta} & =\left[ \begin{matrix}-\Delta \boldsymbol{\alpha} \\\Delta \boldsymbol{\gamma} \end{matrix}\right] ={\bf A}^{T}\Delta U\\\, \Delta \boldsymbol{\gamma } & =\tilde{\Upsilon }\Delta \boldsymbol{\alpha } \\\, \left[ \tilde{\Upsilon }\right] & =\left[ {\tilde{\boldsymbol{\gamma }}}_{1}\quad {\tilde{\boldsymbol{\gamma }}}_{2}\, \, \ldots \, \, \ldots \quad {\tilde{\boldsymbol{\gamma }}}_{{M}_{c}+{M}_{b}}\right] \end{align}\right.</math> |
|} | |} | ||
| style="width: 5px;text-align: right;white-space: nowrap;" | (12) | | style="width: 5px;text-align: right;white-space: nowrap;" | (12) | ||
|} | |} | ||
| + | where <math display="inline">{\bf A}^{T}=\left[ \begin{matrix}{\bf n}^{T}&{\bf 0}\\\left( {\bf I}-{\bf nn}^{T}\right) &{\bf R}\tilde{\mathit{\boldsymbol{n}}}\end{matrix}\right]</math> is a (<math>4M_c + 4M_b)\times 6N</math> matrix composed by unit normal vectors <math display="inline">{\bf n}_{{k}_{c}}</math>. | ||
| − | + | ===2.2 Statics=== | |
| − | + | ||
| − | + | ||
Due to the deformations of particles, the compressive normal forces and tangential forces are developed. The equilibrium equations of the particles can be written as: | Due to the deformations of particles, the compressive normal forces and tangential forces are developed. The equilibrium equations of the particles can be written as: | ||
| Line 222: | Line 218: | ||
{| style="text-align: center; margin:auto;" | {| style="text-align: center; margin:auto;" | ||
|- | |- | ||
| − | | <math | + | | <math>\begin{align}{\bf AF}&={\bf A}_{C}{\bf F}_{C}+{\bf A}_{B}{\bf F}_{B}={\bf T}\\\, {\bf F}_{\bf C}^{T}&=\left[ {\bf N}_{C}^{T}\quad \quad {\bf V}_{C}^{T}\right] \\\, {\bf F}_{B}^{T}&=\left[ {\bf N}_{B}^{T}\quad \quad {\bf V}_{B}^{T}\right] \end{align}</math> |
|} | |} | ||
| style="width: 5px;text-align: right;white-space: nowrap;" | (13) | | style="width: 5px;text-align: right;white-space: nowrap;" | (13) | ||
|} | |} | ||
| + | where <math>{\bf N}_B</math> is the <math display="inline">M_b \times 1</math> column matrix of the normal compressive contact forces and <math>{\bf V}_B</math> is the <math display="inline">3M_b \times 1</math> column matrix of the tangential contact forces exerted on the boundary wall; <math>{\bf N}_C</math> is the <math display="inline">M_c \times 1</math> column matrix of the normal compressive contact forces exerted in the contacts between spherical particles and <math>{\bf V}_C</math> is the <math display="inline">3M_c \times 1</math> column matrix of the tangential contact forces; <math>{\bf T}</math> is the <math display="inline">6N\times 1</math> column matrix of the external forces (such as gravity, boundary forces). | ||
| − | + | ===2.3 Contact-stiffness model=== | |
| − | + | ||
| − | + | ||
After the equilibrium and kinematic relations are established, a contact force-relative displacement law must be introduced. The DEM simulation in this work is performed using PFC<sup>3D</sup> solver. PFC<sup>3D</sup> provides two stiffness models: a linear model and a simplified Hertz-Mindlin model. In the linear model, the forces and relative displacements are linearly related by the constant contact stiffness. Here, the linear contact model is adopted, which can be written as: | After the equilibrium and kinematic relations are established, a contact force-relative displacement law must be introduced. The DEM simulation in this work is performed using PFC<sup>3D</sup> solver. PFC<sup>3D</sup> provides two stiffness models: a linear model and a simplified Hertz-Mindlin model. In the linear model, the forces and relative displacements are linearly related by the constant contact stiffness. Here, the linear contact model is adopted, which can be written as: | ||
| Line 239: | Line 234: | ||
{| style="text-align: center; margin:auto;" | {| style="text-align: center; margin:auto;" | ||
|- | |- | ||
| − | | <math | + | | <math>\left\{ \begin{matrix}{N}_{{k}_{c}}={k}^{n}{\alpha }_{{k}_{c}}\\\, \Delta {\bf V}_{{k}_{c}}={k}^{s}{\Delta \boldsymbol{\gamma }}_{{k}_{c}}\end{matrix}\right.</math> |
|} | |} | ||
| style="width: 5px;text-align: right;white-space: nowrap;" | (14) | | style="width: 5px;text-align: right;white-space: nowrap;" | (14) | ||
|} | |} | ||
| − | + | where <math>k^n</math> and <math>k^s</math> are the normal and shear-contact stiffnesses. | |
| − | where | + | |
The above relation (14) can be summarized in the form of matrix as follows: | The above relation (14) can be summarized in the form of matrix as follows: | ||
| Line 254: | Line 248: | ||
{| style="text-align: center; margin:auto;" | {| style="text-align: center; margin:auto;" | ||
|- | |- | ||
| − | | <math | + | | <math>\left\{ \begin{matrix}{\bf N} ={\bf K}^{n}\boldsymbol{\alpha} \\\, \Delta {\bf V}={\bf K}^{s}\Delta \boldsymbol{\gamma }\end{matrix}\right.</math> |
|} | |} | ||
| style="width: 5px;text-align: right;white-space: nowrap;" | (15) | | style="width: 5px;text-align: right;white-space: nowrap;" | (15) | ||
|} | |} | ||
| + | ===2.4 Incremental work=== | ||
| − | + | We assume that in a given equilibrium state the elastic displacement vector is <math display="inline">\overline{\mathit{\boldsymbol{\delta }}}=</math><math>\left( \overline{\mathit{\boldsymbol{\alpha }}}\, ,\, \overline{\mathit{\boldsymbol{\gamma }}}\right)</math> and that a small incremental elastic displacement vector <math display="inline">\Delta \boldsymbol{\delta }=</math><math>\left( \Delta \mathit{\boldsymbol{\alpha }}\, ,\, \Delta \mathit{\boldsymbol{\gamma }}\right)</math> is further applied. Then the incremental work done by the contact forces can be written as: | |
| − | + | ||
| − | We assume that in a given equilibrium state the elastic displacement vector is <math display="inline">\overline{\mathit{\boldsymbol{\delta }}}=</math><math>\left( \overline{\mathit{\boldsymbol{\alpha }}}\, ,\, \overline{\mathit{\boldsymbol{\gamma }}}\right)</math> and that a small incremental elastic displacement vector <math display="inline">\Delta \delta =</math><math>\left( \Delta \mathit{\boldsymbol{\alpha }}\, ,\, \Delta \mathit{\boldsymbol{\gamma }}\right)</math> is further applied. Then the incremental work done by the contact forces can be written as: | + | |
{| class="formulaSCP" style="width: 100%; text-align: center;" | {| class="formulaSCP" style="width: 100%; text-align: center;" | ||
| Line 269: | Line 262: | ||
{| style="text-align: center; margin:auto;" | {| style="text-align: center; margin:auto;" | ||
|- | |- | ||
| − | | <math | + | | <math>\int_{\overline{\mathit{\boldsymbol{\delta }}}}^{\overline{\mathit{\boldsymbol{\delta }}}+\Delta \delta }{{\bf F}\left( \boldsymbol{\delta } \right) }^{T}d\boldsymbol{\delta } =</math><math>{\overline{\bf F}}^{T}\Delta \boldsymbol{\delta } +\frac{1}{2}\Delta {\bf F}^{T}\Delta \boldsymbol{\delta }</math> |
|} | |} | ||
| style="width: 5px;text-align: right;white-space: nowrap;" | (16) | | style="width: 5px;text-align: right;white-space: nowrap;" | (16) | ||
|} | |} | ||
| − | |||
In the same way, the incremental work done by the external forces can be written as: | In the same way, the incremental work done by the external forces can be written as: | ||
| Line 282: | Line 274: | ||
{| style="text-align: center; margin:auto;" | {| style="text-align: center; margin:auto;" | ||
|- | |- | ||
| − | | <math | + | | <math>\int_{\overline{U}}^{\overline{U}+\Delta U}{\bf T}^{T}d{\bf U}={\overline{\bf T}}^{T}\Delta {\bf U}+</math><math>\frac{1}{2}\Delta {\bf T}^{T}\Delta {\bf U}</math> |
|} | |} | ||
| style="width: 5px;text-align: right;white-space: nowrap;" | (17) | | style="width: 5px;text-align: right;white-space: nowrap;" | (17) | ||
| Line 288: | Line 280: | ||
| − | In view of (12) and (13), | + | In view of Eqs. (12) and (13), Eq. (17) can be rewritten as: |
{| class="formulaSCP" style="width: 100%; text-align: center;" | {| class="formulaSCP" style="width: 100%; text-align: center;" | ||
| Line 295: | Line 287: | ||
{| style="text-align: center; margin:auto;" | {| style="text-align: center; margin:auto;" | ||
|- | |- | ||
| − | | <math | + | | <math>\int_{\overline{U}}^{\overline{U}+\Delta U}{\bf T}^{T}d{\bf U}={\overline{\boldsymbol{F}}}^{T}{\bf A}^{\mathit{\boldsymbol{T}}}\Delta {\bf U}+</math><math>\frac{1}{2}\Delta {\bf T}^{T}\Delta {\bf U}={\overline{\boldsymbol{F}}}^{T}\Delta \boldsymbol{\delta} +</math><math>\frac{1}{2}\Delta {\bf T}^{T}\Delta {\bf U}</math> |
|} | |} | ||
| style="width: 5px;text-align: right;white-space: nowrap;" | (18) | | style="width: 5px;text-align: right;white-space: nowrap;" | (18) | ||
| Line 308: | Line 300: | ||
{| style="text-align: center; margin:auto;" | {| style="text-align: center; margin:auto;" | ||
|- | |- | ||
| − | | <math | + | | <math>\Psi \left( \Delta {\bf U}\right) =\int_{\overline{\mathit{\boldsymbol{\delta }}}}^{\overline{\mathit{\boldsymbol{\delta }}}+\Delta \delta }{\bf F}\left( \boldsymbol{\delta } \right)^{T}d\boldsymbol{\delta } -</math><math>\int_{\overline{U}}^{\overline{U}+\Delta U}{\bf T}^{T}d{\bf U}=\frac{1}{2}\Delta {\bf F}^{T}\Delta \boldsymbol{\delta } -</math><math>\frac{1}{2}\Delta {\bf T}^{T}\Delta {\bf U}</math> |
|} | |} | ||
| style="width: 5px;text-align: right;white-space: nowrap;" | (19) | | style="width: 5px;text-align: right;white-space: nowrap;" | (19) | ||
|} | |} | ||
| + | ===2.5 Minimum principle for incremental total energy=== | ||
| − | + | In the following, we will assign a superscript * both to any kinematically admissible system of incremental displacements and to any mechanical quantity associated to it by means of Eq. (12) to (19). Then we have: | |
| − | + | ||
| − | In the following, we will assign a superscript * both to any kinematically admissible system of incremental displacements and to any mechanical quantity associated to it by means of | + | |
{| class="formulaSCP" style="width: 100%; text-align: center;" | {| class="formulaSCP" style="width: 100%; text-align: center;" | ||
| Line 323: | Line 314: | ||
{| style="text-align: center; margin:auto;" | {| style="text-align: center; margin:auto;" | ||
|- | |- | ||
| − | | <math | + | | <math>\Psi \left( {\Delta {\bf U}}^{\ast }\right) -</math><math>\Psi \left( \Delta {\bf U}\right) =\frac{1}{2}\left( {\Delta {\bf F}}^{\ast T}{\Delta \boldsymbol{\delta } }^{\ast }-\right. </math><math>\left. \Delta {\bf F}^{T}{\Delta \boldsymbol{\delta } }^{\ast }\right) +\frac{1}{2}\Delta {\bf T}^{T}\left( \Delta {\bf U}-\right. </math><math>\left. {\Delta {\bf U}}^{\ast }\right)</math> |
|} | |} | ||
| style="width: 5px;text-align: right;white-space: nowrap;" | (20) | | style="width: 5px;text-align: right;white-space: nowrap;" | (20) | ||
| Line 329: | Line 320: | ||
| − | In view of (12) and (13), | + | In view of Eqs. (12) and (13), Eq. (20) can be rewritten as: |
{| class="formulaSCP" style="width: 100%; text-align: center;" | {| class="formulaSCP" style="width: 100%; text-align: center;" | ||
| Line 336: | Line 327: | ||
{| style="text-align: center; margin:auto;" | {| style="text-align: center; margin:auto;" | ||
|- | |- | ||
| − | | <math | + | | <math>\begin{align}\Psi \left( {\Delta {\bf U}}^{\ast }\right) -\Psi \left( \Delta {\bf U}\right) & =\frac{1}{2}\left( {\Delta {\bf F}}^{\ast T} \Delta \boldsymbol{\delta}^{\ast } - \Delta {\bf F}^{T}\Delta \boldsymbol{\delta}^{\ast}\right) + \frac{1}{2}{\Delta {\bf F}}^{T}{\bf A}^{\mathit{\boldsymbol{T}}}\left( \Delta {\bf U} - {\Delta {\bf U}}^{\ast }\right) \\\, & =\frac{1}{2}\left( {\Delta {\bf F}}^{\ast T} - \Delta {\bf F}^{T}\right) {\Delta \boldsymbol{\delta } }^{\ast } + \frac{1}{2}{\Delta {\bf F}}^{T}\left( \Delta \boldsymbol{\delta } - {\Delta \boldsymbol{\delta } }^{\ast }\right) \\\, & =\frac{1}{2}{\left( {\Delta \boldsymbol{\delta } }^{\ast }- \Delta \boldsymbol{\delta } \right) }^{\mathit{\boldsymbol{T}}}{\bf K}\left( {\Delta \boldsymbol{\delta } }^{\ast } - \Delta \boldsymbol{\delta } \right) \end{align}</math> |
|} | |} | ||
| style="width: 5px;text-align: right;white-space: nowrap;" | (21) | | style="width: 5px;text-align: right;white-space: nowrap;" | (21) | ||
| Line 342: | Line 333: | ||
| − | where <math display="inline">K=\left[ \begin{matrix}{K}^{n}&0\\0&{K}^{s}\end{matrix}\right]</math> is the stiffness matrix, which is diagonal and definite positive. it can be noted that, | + | where <math display="inline">{\bf K}=\left[ \begin{matrix}{\bf K}^{n}&{\bf 0}\\{\bf 0}&{\bf K}^{s}\end{matrix}\right]</math> is the stiffness matrix, which is diagonal and definite positive. it can be noted that, <math display="inline">\Psi \left( {\Delta {\bf U}}^{\ast }\right) -</math><math>\Psi \left( \Delta {\bf U}\right)</math> is always positive. So it can be concluded that, The incremental total energy <math display="inline">\Psi \left( {\Delta {\bf U}}^{\ast }\right)</math> attains its minimum if the kinematically admissible system of incremental displacements is such to satisfy the equilibrium equations (13). |
| − | =3 Numerical model= | + | ==3. Numerical model== |
| − | The minimum principle for incremental total energy <math display="inline">\Psi \left( {\Delta U}^{\ast }\right)</math> proposed in the section 2, can be used to accelerate the convergence of DEM simulation. The numerical form of the minimum principle can be written as: | + | The minimum principle for incremental total energy <math display="inline">\Psi \left( {\Delta {\bf U}}^{\ast }\right)</math> proposed in the section 2, can be used to accelerate the convergence of DEM simulation. The numerical form of the minimum principle can be written as: |
{| class="formulaSCP" style="width: 100%; text-align: center;" | {| class="formulaSCP" style="width: 100%; text-align: center;" | ||
| Line 353: | Line 344: | ||
{| style="text-align: center; margin:auto;" | {| style="text-align: center; margin:auto;" | ||
|- | |- | ||
| − | | <math | + | | <math>\begin{align}& \min\quad \frac{1}{2}{\Delta {\bf U}^{\mathit{\boldsymbol{\ast }}}}^{T}\mathit{\boldsymbol{\cdot }}{\bf AK}{\bf A}^{T}\cdot \Delta {\bf U}^{\mathit{\boldsymbol{\ast }}}-\frac{1}{2}\Delta {\bf T}^{T}\Delta {\bf U}^{\mathit{\boldsymbol{\ast }}}\quad \\ |
| + | & \, s.t.\, \, \left\{ \begin{align} & {\bf K} {\bf A}_{\mathit{\boldsymbol{B}}}^{\mathit{\boldsymbol{T}}} \Delta {\bf U}^{\mathit{\boldsymbol{\ast }}}=\Delta {\bf F}_{\mathit{\boldsymbol{B}}}\\ | ||
| + | & \, {\bf A}^{T}\mathit{\boldsymbol{=}}\left[ \begin{matrix}{\bf n}^{T}&{\bf 0}\\\left( {\bf I}-{\bf nn}^{T}\right) &{\bf R}\tilde{\mathit{\boldsymbol{\bf n}}}\end{matrix}\right] \\ | ||
| + | & \, {\bf K} =\left[ \begin{matrix}{\bf K}^{n}&{\bf 0}\\{\bf 0}&{\bf K}^{s}\end{matrix}\right] \end{align}\right. \\\, \end{align}</math> | ||
|} | |} | ||
| style="width: 5px;text-align: right;white-space: nowrap;" | (22) | | style="width: 5px;text-align: right;white-space: nowrap;" | (22) | ||
|} | |} | ||
| + | where <math>{\bf F}_B</math> denotes the contact forces exerted on the boundary wall, which is equal to the external boundary force. | ||
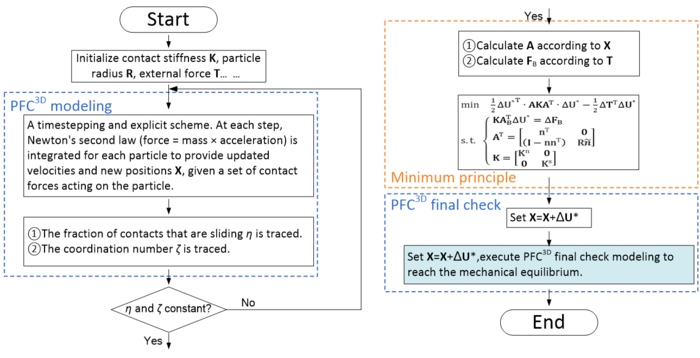
| − | + | In this work, the movement and interaction of spherical particles is modeled by PFC<sup>3D</sup>. In the later stage of PFC<sup>3D</sup> modeling, when the new contacts are no longer detected and created, and the old contacts are no longer broken and deleted, Eq. (22) is introduced in order to reach mechanical equilibrium quickly. The improved DEM formulation is shown in [[#img-3|Figure 3]]. | |
| − | + | <div id='img-3'></div> | |
| − | + | {| class="wikitable" style="margin: 0em auto 0.1em auto;border-collapse: collapse;width:auto;" | |
| − | + | |-style="background:white;" | |
| − | + | |style="text-align: center;padding:10px;"| [[Image:Review_294821678474-image3.png|700px]] | |
| + | |- | ||
| + | | style="background:#efefef;text-align:left;padding:10px;font-size: 85%;"| '''Figure 3'''. Improved DEM formulation based on the minimum principle for incremental total energy | ||
| + | |} | ||
| − | |||
| − | + | Generally the tangential contact force is smaller or much smaller than the corresponding normal contact forces. Especially in the later stage of DEM simulation, the particles are unbalanced mainly subject to the normal contact forces. In order to require modest sizes of computer memory, considering the incremental work is mainly done by the normal contact forces, the numerical srategy can be rewritten as: | |
{| class="formulaSCP" style="width: 100%; text-align: center;" | {| class="formulaSCP" style="width: 100%; text-align: center;" | ||
| Line 375: | Line 372: | ||
{| style="text-align: center; margin:auto;" | {| style="text-align: center; margin:auto;" | ||
|- | |- | ||
| − | | <math | + | | <math>\begin{align}& \min\quad \frac{1}{2}{\Delta {\bf V}^{\mathit{\boldsymbol{\ast }}}}^{T}\mathit{\boldsymbol{\cdot }}{\bf AK}^{n}{\bf A}^{T}\cdot \Delta {\bf V}^{\mathit{\boldsymbol{\ast }}}-\frac{1}{2}\Delta {\bf T}^{T}\Delta {\bf V}^{\mathit{\boldsymbol{\ast }}}\quad \\ |
| + | & \, s.t.\, \, \left\{ \begin{align}& {\bf A}^{T}={\bf n}^{T}\\ | ||
| + | & \, {\bf K}^{n}{\bf A}_{\mathit{\boldsymbol{B}}}^{\mathit{\boldsymbol{T}}}\Delta {\bf V}^{\mathit{\boldsymbol{\ast }}}=\Delta {\bf F}_{\mathit{\boldsymbol{B}}}\end{align}\right. \\\, \end{align}</math> | ||
|} | |} | ||
| style="width: 5px;text-align: right;white-space: nowrap;" | (23) | | style="width: 5px;text-align: right;white-space: nowrap;" | (23) | ||
| Line 381: | Line 380: | ||
| − | + | Eq. (23) is also introduced into the improved DEM formulation shown in [[#img-3|Figure 3]] to observe the computational efficiency. | |
| − | + | The numerical calculation of the minimum principle is performed on MATLAB. The MATLAB provides a solver “quadprog” for quadratic objective functions with linear constraints. The solver “quadprog” finds a minimum for a problem specified by: | |
{| class="formulaSCP" style="width: 100%; text-align: center;" | {| class="formulaSCP" style="width: 100%; text-align: center;" | ||
| Line 390: | Line 389: | ||
{| style="text-align: center; margin:auto;" | {| style="text-align: center; margin:auto;" | ||
|- | |- | ||
| − | | <math | + | | <math>\begin{matrix}\mathrm{\underbrace{min}_{x}}\,\frac{1}{2}{x}^{T}Hx+{f}^{T}x\quad \\\, s.t.\, \, \left\{ \begin{matrix}A\cdot x\leq b\\Aeq\cdot x=beq\\lb\leq x\leq ub\end{matrix}\right. \\\, \end{matrix}</math> |
|} | |} | ||
| style="width: 5px;text-align: right;white-space: nowrap;" | (24) | | style="width: 5px;text-align: right;white-space: nowrap;" | (24) | ||
|} | |} | ||
| + | where <math>H</math>, <math>A</math>, and <math>Aeq</math> are matrices, and <math>f</math>, <math>b</math>, <math>beq</math>, <math>lb</math>, <math>ub</math>, and <math>x</math> are vectors. The solver “quadprog” in MATLAB can be used to solve Eq. (22) or (23). | ||
| − | < | + | The improved DEM formulation completed after a PFC<sup>3D</sup> final check, because of the FEM-DEM coupling settings and the introduction of Eq. (23) that the tangential contact force is neglected. |
| − | + | ==4. Examination of the numerical model== | |
| − | + | The improved DEM formulation is examined numerically using the 3D FEM-DEM coupling model reported by Liu et al. [12]. The units of length/mm, force/N, time/s, stress/MPa are used in the coupling model. | |
| − | < | + | In the FEM model, an elbow tube of stainless steel (1Cr18Ni9Ti) with wall thickness <math>t=0.3</math>mm, outer diameter <math>D=30</math>mm, bending radius <math>R=90</math>mm, is formed. The material parameters of 1Cr18Ni9Ti stainless steel are listed in [[#tab-1|Table 1]], and the stress-strain curve is shown in [[#img-4|Figure 4]]. |
| − | < | + | <div class="center" style="font-size: 75%;">'''Table 1'''. Room temperature mechanical properties of 1Cr18Ni9Ti </div> |
| − | <div class=" | + | <div id='tab-1'></div> |
| − | + | {| class="wikitable" style="margin: 1em auto 0.1em auto;border-collapse: collapse;font-size:85%;width:auto;" | |
| + | |-style="text-align:center" | ||
| + | ! Young's modulus (GPa) !! Poisson ratio !! Density (kg/m<sup>3</sup>) !! Yield strength (MPa)!! Tensile strength (MPa)!! Elongation (%) | ||
| + | |-style="text-align:center" | ||
| + | | 202 | ||
| + | | 0.29 | ||
| + | | 7850 | ||
| + | | 219 | ||
| + | | 755 | ||
| + | | 48 | ||
| + | |} | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | <div id='img-4'></div> | |
| + | {| class="wikitable" style="margin: 0em auto 0.1em auto;border-collapse: collapse;width:auto;" | ||
| + | |-style="background:white;" | ||
| + | |style="text-align: center;padding:10px;"| [[Image:Review_294821678474-image4-c.jpeg|336px]] | ||
|- | |- | ||
| − | | | + | | style="background:#efefef;text-align:left;padding:10px;font-size: 85%;"| '''Figure 4'''. Stress-strain curve of 1Cr18Ni9Ti |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
|} | |} | ||
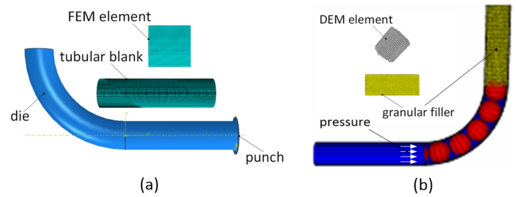
| − | + | The FEM model of ABAQUS [13] shown in [[#img-5|Figure 5]](a), considers nonlinear geometry through a large-strain description of elbow tube, and material is considered both elastic and elastic-plastic (1Cr18Ni9Ti stainless steel). The FEM model is three-dimensional, and four-node reduced-integration shell elements (S4R) are employed for modeling of the thin-wall elbow tube. Contact forces between particles and tube are imposed on the four nodes nearby the particle-tube contact points in the form of concentrated force. Regarding the number of elements in the longitudinal direction, at least 5 elements per particle size are employed in the tube. Friction coefficient between die and tube is set 0.05. | |
| − | + | ||
| − | <div class=" | + | <div id='img-5'></div> |
| − | + | {| class="wikitable" style="margin: 0em auto 0.1em auto;border-collapse: collapse;width:auto;" | |
| + | |-style="background:white;" | ||
| + | |style="text-align: center;padding:10px;"| [[Image:Review_294821678474-image5.png|516px]] | ||
| + | |- | ||
| + | | style="background:#efefef;text-align:left;padding:10px;font-size: 85%;"| '''Figure 5'''. FEM-DEM coupling model of the elbow tube push-bending. (a) FEM model. (b) DEM model | ||
| + | |} | ||
| − | |||
| − | + | It is shown in [[#img-5|Figure 5]](b) that, the cast iron granular media with particle diameter 1.58mm is modeled as filler by DEM. The granulometric distribution of granular media is uniform (monodisperse). Wall boundary is created according to the tube shape determined in FEM. The linear model with constant stiffness is employed to model the particle-wall and inter-particle contacts. The friction coefficients of both particle-wall and inter-particle are set 0.05. The properties of cast iron granular media are listed in [[#tab-2|Table 2]]. | |
| − | + | ||
| − | <div | + | <div class="center" style="font-size: 75%;">'''Table 2'''. Mechanical properties of cast iron granular media</div> |
| − | + | ||
| − | < | + | <div id='tab-1'></div> |
| − | + | {| class="wikitable" style="margin: 1em auto 0.1em auto;border-collapse: collapse;font-size:85%;width:auto;" | |
| − | + | |-style="text-align:center" | |
| − | + | ! Young's modulus (GPa) !! Shear modulus (GPa) !! Poisson's ratio !! Density (kg/m<sup>3</sup>) | |
| − | + | ||
| − | + | ||
|- | |- | ||
| − | | style=" | + | | style="text-align: center;"|150 |
| − | + | | style="text-align: center;"|58 | |
| − | + | | style="text-align: center;"|0.3 | |
| − | + | | style="text-align: center;"|7300 | |
| − | + | ||
| − | + | ||
| − | | style=" | + | |
| − | | style=" | + | |
| − | | style=" | + | |
|} | |} | ||
| − | In the FEM-DEM coupling program, at the | + | In the FEM-DEM coupling program, at the <math display="inline"> i </math>-th increment, the shape of tube is calculated in FEM under the force boundary conditions (contact forces between particles and tube) determined at the (<math display="inline">i-1</math>)th increment in DEM. The contact forces distribution in granular media is calculated in DEM under the displacement boundary conditions (tube shape) determined at the (<math display="inline">i-1</math>)th increment in FEM. |
| − | + | The PFC<sup>3D</sup>, ABAQUS and MATLAB use different default computational accuracy to complete the simulation or optimization. The default computational accuracy of the solver “quadprog” in MATLAB (tolerance <math display="inline">\le 10^{-6}</math>) is much smaller than that of PFC<sup>3D </sup>(the maximum unbalanced force <math display="inline">\le 10^{-2}</math>). For comparison, the completed condition of PFC<sup>3D</sup> simulation is set to “the maximum unbalanced force <math display="inline">\le 10^{-6}</math>”. | |
| − | The time-consuming results of the different FEM-DEM coupling models with no minimum principle, with | + | The time-consuming results of the different FEM-DEM coupling models with no minimum principle, with Eq. (22) and with Eq. (23) under the same simulation condition, are listed in [[#tab-3|Table 3]]. |
| − | <div class="center" style=" | + | <div class="center" style="font-size: 75%;">'''Table 3'''. The time-consuming results of the different FEM-DEM coupling models</div> |
| − | Table 3. The time-consuming results of the different FEM-DEM coupling models</div> | + | |
| − | {| style=" | + | <div id='tab-1'></div> |
| + | {| class="wikitable" style="margin: 1em auto 0.1em auto;border-collapse: collapse;font-size:85%;width:auto;" | ||
| + | |-style="text-align:center" | ||
| + | ! [[Image:Review_294821678474-image6.png|122px]] !! Not using the minimum principle !! Using Eq. (22) !! Using Eq. (23) | ||
|- | |- | ||
| − | | style=" | + | | style="text-align: center;"|Time consuming (hour) |
| − | + | | style="text-align: center;"|≈210 | |
| − | + | | style="text-align: center;"|≈170 | |
| − | + | | style="text-align: center;"|≈120 | |
| − | + | ||
| − | + | ||
| − | | style=" | + | |
| − | | style=" | + | |
| − | | style=" | + | |
|} | |} | ||
| − | It is shown in Table 3 that, the improved FEM-DEM coupling simulation using the minimum principle | + | It is shown in [[#tab-3|Table 3]] that, the improved FEM-DEM coupling simulation using the minimum principle Eq. (22) or Eq. (23) is less time-consuming than the previous coupling model. |
| − | + | ==5. Conclusions== | |
Considering the new contacts are no longer created and the old contacts are no longer deleted in the later stage of DEM simulation, an improved numerical formulation is proposed in order to reach mechanical equilibrium quickly and accelerate the convergence of DEM simulation. The improved numerical formulation is based on the minimum principle for incremental total energy in granular media. The improved DEM formulation is examined numerically using the 3D FEM-DEM coupling model of the granular-media-based thin-wall elbow tube push-bending process. It is demonstrated that the improved FEM-DEM coupling model is less time-consuming than the previous under the same simulation condition. | Considering the new contacts are no longer created and the old contacts are no longer deleted in the later stage of DEM simulation, an improved numerical formulation is proposed in order to reach mechanical equilibrium quickly and accelerate the convergence of DEM simulation. The improved numerical formulation is based on the minimum principle for incremental total energy in granular media. The improved DEM formulation is examined numerically using the 3D FEM-DEM coupling model of the granular-media-based thin-wall elbow tube push-bending process. It is demonstrated that the improved FEM-DEM coupling model is less time-consuming than the previous under the same simulation condition. | ||
| Line 497: | Line 488: | ||
==References== | ==References== | ||
| − | [1] H. | + | <div class="auto" style="text-align: left;width: auto; margin-left: auto; margin-right: auto;font-size: 85%;"> |
| + | |||
| + | [1] Yang H., Li H., Zhang Z.Y., Zhan M., Liu J., Li G. Advances and trends on tube bending forming technologies. Chinese J. Aeronaut., 25(1):1–12, 2012. | ||
| − | [2] B.G. | + | [2] Teng B.G., Hu L., Liu G., Yuan S.J. Wrinkling behavior of hydro bending of carbon steel Al alloy bilayered tubes. Trans. Nonferrous Met. Soc. China, 22:560−565, 2012. |
| − | [3] | + | [3] Xu X.F., Fan Y.B., Wu Y.W., Wu K.W., Xiao J. A novel differential lubrication method for push-bending of L-shaped thin-walled tube with 1D bending radius. International Journal of Material Forming, 14:691–701, 2021. |
| − | [4] Y. | + | [4] Zeng Y., Li Z. Experimental research on the tube push-bending process. Journal of Materials Processing Technology, 122(2-3):237–240, 2002. |
| − | [5] Oh I Y, Han S W, Woo Y Y, | + | [5] Oh I.Y., Han S.W., Woo Y.Y., Ra J.H., Moon Y.H. Tubular blank design to fabricate an elbow tube by a push-bending process. Journal of Materials Processing Technology, 260:112–122, 2018. |
| − | [6] H. | + | [6] Liu H., Zhang S.H., Ding Y.P., Shi G.L., Geng Z. A simplified formulation for predicting wrinkling of thin-wall elbow tube in granular media–based push-bending process. International Journal of Advanced Manufacturing Technology, 115:541–549, 2021. |
| − | [7] B. | + | [7] Du B., Zhao C.C., Dong G.J., Bi J. FEM-DEM coupling analysis for solid granule medium forming new technology. J. Mater. Process. Technol., 249:108–117, 2017. |
| − | [8] H. | + | [8] Chen H., Güner A., Khalifa N.B., Tekkaya A.E. Granular media-based tube press hardening. J. Mater. Process. Technol., 228:145–159, 2016. |
| − | [9] H. | + | [9] Chen H., Hess S., Haeberle J., Pitikaris S., Born P., Güner A., Sperl M., Tekkaya A.E. Enhanced granular medium-based tube and hollow profile press hardening. CIRP Ann.-Manuf. Technol., 65:273–276, 2016. |
| − | [10] G.J. | + | [10] Dong G.J., Zhao C.C., Peng Y.X., Li Y. Hot granules medium pressure forming process of AA7075 conical parts. Chin. J. Mech. Eng., 28:580–591, 2015. |
| − | [11] G.J. | + | [11] Dong G.J., Bi J., Du B., Zhao C.C. Research on AA6061 tubular components prepared by combined technology of heat treatment and internal high pressure forming. J. Mater. Process. Technol., 242:126–138, 2017. |
| − | [12] H. | + | [12] Liu H., Zhang S.H., Song H.W., Shi G.L., Cheng M. 3D FEM-DEM coupling analysis for ranular-media-based thin-wall elbow tube push-bending process. International Journal of Material Forming, 12:985-994, 2019. |
| − | [13] H.D. | + | [13] Hibbit H.D., Karlsson B.I., Sorensen P. Theory Manual, ABAQUS, Version 6.7. Providence, RI, USA, 2007. |
| + | <!-- | ||
---- | ---- | ||
E-mail address: hliu[mailto:@ @]<span style="text-align: center; font-size: 75%;">alum.imr.ac.cn</span> | E-mail address: hliu[mailto:@ @]<span style="text-align: center; font-size: 75%;">alum.imr.ac.cn</span> | ||
Latest revision as of 14:06, 30 May 2023
Abstract
The granular-media-based push-bending process has been developed to manufacture thin-wall elbow tube with t/D (the ratio of wall thickness to outer diameter) and R/D (the ratio of bending radius to outer diameter). In the process, a tubular blank is filled with granular media and then pushed into a die to form an elbow shape. To investigate the process, a FEM-DEM coupling model has been developed, in which FEM is used to simulate bending deformation of tubular blank, and DEM is used to calculate contact forces between spherical particles in granular media. In this work, an improved numerical formulation is proposed in order to reach mechanical equilibrium quickly and accelerate the convergence of DEM simulation, when the new contacts are no longer created and the old contacts are no longer deleted in granular media. Using the proposed numerical formulation, the improved FEM-DEM coupling simulation for granular-media-based thin-wall elbow tube push-bending process is less time-consuming than before under the same simulation condition.
Keywords: Elbow tube, granular-media-based, push bending, energetic formulation, FEM-DEM coupling
1. Introduction
The thin-wall elbow tubes with t/D≤0.01 and R/D (where t is wall thickness, D is outer diameter, and R is bending radius) are widely used in rocket engine pipelines [1-3]. In the bending process of elbow tube with quite small t/D and R/D, the forming defects such as wrinkling and fracture is difficult to be avoided, and the dimensional precision is difficult to satisfy the requirements due to the springback and cross-sectional ovalization. Push-bending process is demonstrated to be applicable for manufacturing elbow tubes with small R/D [4-5]. The recently developed granular-media-based push-bending process can be used to manufacture the thin-wall elbow tube with t/D and R/D as required [6]. The granular-media-based thin-wall elbow push-bending process involves filling a tube with spherical granular media and pushing the tube into a die to bend a tubular blank into an elbow shape. The spherical granular media introduced as filler has great potential for its flexibility [7], resistance to high forming temperature [8-9], and characteristics of pressure-transmission [10-11]. In addition, the spherical granular media is controllable and predictable because of its regular shape.
To investigate the granular-media-based thin-wall elbow push-bending process, a 3D FEM-DEM coupling model is developed [12]. In the coupling model, FEM is used to simulate bending deformation of tubular blank (continuum), and DEM is used to calculate contact forces between spherical particles in granular media (discrete media). DEM is a dynamic method, and damping is applied to the equations of motion in order to absorb vibration energy and reach mechanical equilibrium. The biggest time overhead in the coupling model is absorbing vibration energy in DEM simulation to reach mechanical equilibrium. To accelerate the convergence of DEM simulation, a static energetic method is proposed in the present paper.
Generally in the earlier stage of DEM simulation, some new contacts between pairs of particles are detected and created, and some old contacts are broken and deleted. But in the later stage of DEM simulation, the new contacts are no longer detected and created, the old contacts are no longer broken and deleted, and a static energetic formulation can be used to determine mechanical equilibrium.
2. Mechanical model
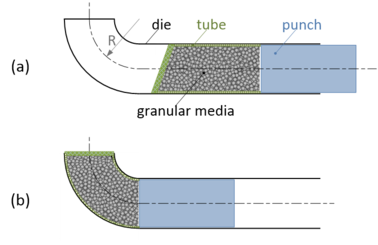
The granular-media-based push-bending process is illustrated in Figure 1. A tubular blank with predetermined dimensions and filled with granular media is inserted into the die and then deformed according to the shape of the die. The tubular blank is bended under the forming force of punch, constraint force of die, and interaction of granular filler. The forming force of punch and constraint force of die is simulated with FEM. The contact forces between neighbor particles in granular media is simulated with DEM.
|
| Figure 1. Illustration of the granular-media-based thin-wall elbow push-bending process. (a) Before bending. (b) Bending |
2.1 Kinematics
In the DEM simulation, when the new contacts are no longer created and the old contacts are no longer deleted in granular media, the positions of the spherical particles are collected in the column matrixes:
|
|
(1) |
where denotes the -th position component of the -th particle. The spherical particles in the granular media are labeled by the indexes . The symbol denotes the transpose of a matrix.
In the same way, the centroid displacements and the rotation components of particles are collected in the column matrixes:
|
|
(2) |
where denotes the -th displacement component of the -th particle, and denotes the -th rotation component of the -th particle.
The contact formed by the particle and the particle , as shown in Figure 2.
Assuming that elastic deformations are localized in very small neighborhoods of the contact points, so that, the relative displacement between the rigid part of the two particles near the contact point is:
|
|
(3) |
where denotes the particle radius, denotes the antisymmetric matrix formed by the components of the unit normal vector
|
|
(4) |
If the contact point is formed by the particles and , we have:
|
|
(5) |
If the contact point is formed by the particles and the boundary wall, we have:
|
|
(6) |
where denotes the contact point of index between the particle and the boundary wall.
Assuming that the relative displacement is small, the change of distance between the two neighbor particles’ centers can be determined as the normal component of their relative displacement, which is set equal to an incremental normal overlap:
|
|
(7) |
where is positive if the distance between the two centers decreases, while is negative if the distance between the two centers increases. When is negative, can not be smaller than the initial normal overlap . is the total number of contacts in the granular media.
In a similar way, the incremental tangential relative displacement due to the elastic deformations of particles can be written as:
|
|
(8) |
Further, Eq.(8) can be rewritten as:
|
|
(9) |
where denotes the slope vector with respect the unit normal vector of the contact elastic relative displacement .
In the same way, when the particle is in contact with the boundary wall, we have:
|
|
(10) |
The unknown displacements and rotations of the particles are collected in the column matrix :
|
|
(11) |
The incremental normal overlaps of contacts between spherical particles are collected in the column matrixes . The incremental tangential relative displacements are collected in the column matrixes . In the same way, the incremental relative displacements of the contacts between spherical particles and the boundary wall are collected in the column matrixes and in the column matrixes . Then, Eqs. (3) to (10) can be summarized as:
|
|
(12) |
where is a ( matrix composed by unit normal vectors .
2.2 Statics
Due to the deformations of particles, the compressive normal forces and tangential forces are developed. The equilibrium equations of the particles can be written as:
|
|
(13) |
where is the column matrix of the normal compressive contact forces and is the column matrix of the tangential contact forces exerted on the boundary wall; is the column matrix of the normal compressive contact forces exerted in the contacts between spherical particles and is the column matrix of the tangential contact forces; is the column matrix of the external forces (such as gravity, boundary forces).
2.3 Contact-stiffness model
After the equilibrium and kinematic relations are established, a contact force-relative displacement law must be introduced. The DEM simulation in this work is performed using PFC3D solver. PFC3D provides two stiffness models: a linear model and a simplified Hertz-Mindlin model. In the linear model, the forces and relative displacements are linearly related by the constant contact stiffness. Here, the linear contact model is adopted, which can be written as:
|
|
(14) |
where and are the normal and shear-contact stiffnesses.
The above relation (14) can be summarized in the form of matrix as follows:
|
|
(15) |
2.4 Incremental work
We assume that in a given equilibrium state the elastic displacement vector is and that a small incremental elastic displacement vector is further applied. Then the incremental work done by the contact forces can be written as:
|
|
(16) |
In the same way, the incremental work done by the external forces can be written as:
|
|
(17) |
In view of Eqs. (12) and (13), Eq. (17) can be rewritten as:
|
|
(18) |
An incremental total energy is defined as:
|
|
(19) |
2.5 Minimum principle for incremental total energy
In the following, we will assign a superscript * both to any kinematically admissible system of incremental displacements and to any mechanical quantity associated to it by means of Eq. (12) to (19). Then we have:
|
|
(20) |
In view of Eqs. (12) and (13), Eq. (20) can be rewritten as:
|
|
(21) |
where is the stiffness matrix, which is diagonal and definite positive. it can be noted that, is always positive. So it can be concluded that, The incremental total energy attains its minimum if the kinematically admissible system of incremental displacements is such to satisfy the equilibrium equations (13).
3. Numerical model
The minimum principle for incremental total energy proposed in the section 2, can be used to accelerate the convergence of DEM simulation. The numerical form of the minimum principle can be written as:
|
|
(22) |
where denotes the contact forces exerted on the boundary wall, which is equal to the external boundary force.
In this work, the movement and interaction of spherical particles is modeled by PFC3D. In the later stage of PFC3D modeling, when the new contacts are no longer detected and created, and the old contacts are no longer broken and deleted, Eq. (22) is introduced in order to reach mechanical equilibrium quickly. The improved DEM formulation is shown in Figure 3.
|
| Figure 3. Improved DEM formulation based on the minimum principle for incremental total energy |
Generally the tangential contact force is smaller or much smaller than the corresponding normal contact forces. Especially in the later stage of DEM simulation, the particles are unbalanced mainly subject to the normal contact forces. In order to require modest sizes of computer memory, considering the incremental work is mainly done by the normal contact forces, the numerical srategy can be rewritten as:
|
|
(23) |
Eq. (23) is also introduced into the improved DEM formulation shown in Figure 3 to observe the computational efficiency.
The numerical calculation of the minimum principle is performed on MATLAB. The MATLAB provides a solver “quadprog” for quadratic objective functions with linear constraints. The solver “quadprog” finds a minimum for a problem specified by:
|
|
(24) |
where , , and are matrices, and , , , , , and are vectors. The solver “quadprog” in MATLAB can be used to solve Eq. (22) or (23).
The improved DEM formulation completed after a PFC3D final check, because of the FEM-DEM coupling settings and the introduction of Eq. (23) that the tangential contact force is neglected.
4. Examination of the numerical model
The improved DEM formulation is examined numerically using the 3D FEM-DEM coupling model reported by Liu et al. [12]. The units of length/mm, force/N, time/s, stress/MPa are used in the coupling model.
In the FEM model, an elbow tube of stainless steel (1Cr18Ni9Ti) with wall thickness mm, outer diameter mm, bending radius mm, is formed. The material parameters of 1Cr18Ni9Ti stainless steel are listed in Table 1, and the stress-strain curve is shown in Figure 4.
| Young's modulus (GPa) | Poisson ratio | Density (kg/m3) | Yield strength (MPa) | Tensile strength (MPa) | Elongation (%) |
|---|---|---|---|---|---|
| 202 | 0.29 | 7850 | 219 | 755 | 48 |

|
| Figure 4. Stress-strain curve of 1Cr18Ni9Ti |
The FEM model of ABAQUS [13] shown in Figure 5(a), considers nonlinear geometry through a large-strain description of elbow tube, and material is considered both elastic and elastic-plastic (1Cr18Ni9Ti stainless steel). The FEM model is three-dimensional, and four-node reduced-integration shell elements (S4R) are employed for modeling of the thin-wall elbow tube. Contact forces between particles and tube are imposed on the four nodes nearby the particle-tube contact points in the form of concentrated force. Regarding the number of elements in the longitudinal direction, at least 5 elements per particle size are employed in the tube. Friction coefficient between die and tube is set 0.05.
|
| Figure 5. FEM-DEM coupling model of the elbow tube push-bending. (a) FEM model. (b) DEM model |
It is shown in Figure 5(b) that, the cast iron granular media with particle diameter 1.58mm is modeled as filler by DEM. The granulometric distribution of granular media is uniform (monodisperse). Wall boundary is created according to the tube shape determined in FEM. The linear model with constant stiffness is employed to model the particle-wall and inter-particle contacts. The friction coefficients of both particle-wall and inter-particle are set 0.05. The properties of cast iron granular media are listed in Table 2.
| Young's modulus (GPa) | Shear modulus (GPa) | Poisson's ratio | Density (kg/m3) |
|---|---|---|---|
| 150 | 58 | 0.3 | 7300 |
In the FEM-DEM coupling program, at the -th increment, the shape of tube is calculated in FEM under the force boundary conditions (contact forces between particles and tube) determined at the ()th increment in DEM. The contact forces distribution in granular media is calculated in DEM under the displacement boundary conditions (tube shape) determined at the ()th increment in FEM.
The PFC3D, ABAQUS and MATLAB use different default computational accuracy to complete the simulation or optimization. The default computational accuracy of the solver “quadprog” in MATLAB (tolerance ) is much smaller than that of PFC3D (the maximum unbalanced force ). For comparison, the completed condition of PFC3D simulation is set to “the maximum unbalanced force ”.
The time-consuming results of the different FEM-DEM coupling models with no minimum principle, with Eq. (22) and with Eq. (23) under the same simulation condition, are listed in Table 3.
 |
Not using the minimum principle | Using Eq. (22) | Using Eq. (23) |
|---|---|---|---|
| Time consuming (hour) | ≈210 | ≈170 | ≈120 |
It is shown in Table 3 that, the improved FEM-DEM coupling simulation using the minimum principle Eq. (22) or Eq. (23) is less time-consuming than the previous coupling model.
5. Conclusions
Considering the new contacts are no longer created and the old contacts are no longer deleted in the later stage of DEM simulation, an improved numerical formulation is proposed in order to reach mechanical equilibrium quickly and accelerate the convergence of DEM simulation. The improved numerical formulation is based on the minimum principle for incremental total energy in granular media. The improved DEM formulation is examined numerically using the 3D FEM-DEM coupling model of the granular-media-based thin-wall elbow tube push-bending process. It is demonstrated that the improved FEM-DEM coupling model is less time-consuming than the previous under the same simulation condition.
Funding Information
The present work is funded by the Scientific Research Foundation of SIIT (2022kyqd001), Natural Science Research General Project of Universities in Jiangsu Province (no.21KJB430006).
References
[1] Yang H., Li H., Zhang Z.Y., Zhan M., Liu J., Li G. Advances and trends on tube bending forming technologies. Chinese J. Aeronaut., 25(1):1–12, 2012.
[2] Teng B.G., Hu L., Liu G., Yuan S.J. Wrinkling behavior of hydro bending of carbon steel Al alloy bilayered tubes. Trans. Nonferrous Met. Soc. China, 22:560−565, 2012.
[3] Xu X.F., Fan Y.B., Wu Y.W., Wu K.W., Xiao J. A novel differential lubrication method for push-bending of L-shaped thin-walled tube with 1D bending radius. International Journal of Material Forming, 14:691–701, 2021.
[4] Zeng Y., Li Z. Experimental research on the tube push-bending process. Journal of Materials Processing Technology, 122(2-3):237–240, 2002.
[5] Oh I.Y., Han S.W., Woo Y.Y., Ra J.H., Moon Y.H. Tubular blank design to fabricate an elbow tube by a push-bending process. Journal of Materials Processing Technology, 260:112–122, 2018.
[6] Liu H., Zhang S.H., Ding Y.P., Shi G.L., Geng Z. A simplified formulation for predicting wrinkling of thin-wall elbow tube in granular media–based push-bending process. International Journal of Advanced Manufacturing Technology, 115:541–549, 2021.
[7] Du B., Zhao C.C., Dong G.J., Bi J. FEM-DEM coupling analysis for solid granule medium forming new technology. J. Mater. Process. Technol., 249:108–117, 2017.
[8] Chen H., Güner A., Khalifa N.B., Tekkaya A.E. Granular media-based tube press hardening. J. Mater. Process. Technol., 228:145–159, 2016.
[9] Chen H., Hess S., Haeberle J., Pitikaris S., Born P., Güner A., Sperl M., Tekkaya A.E. Enhanced granular medium-based tube and hollow profile press hardening. CIRP Ann.-Manuf. Technol., 65:273–276, 2016.
[10] Dong G.J., Zhao C.C., Peng Y.X., Li Y. Hot granules medium pressure forming process of AA7075 conical parts. Chin. J. Mech. Eng., 28:580–591, 2015.
[11] Dong G.J., Bi J., Du B., Zhao C.C. Research on AA6061 tubular components prepared by combined technology of heat treatment and internal high pressure forming. J. Mater. Process. Technol., 242:126–138, 2017.
[12] Liu H., Zhang S.H., Song H.W., Shi G.L., Cheng M. 3D FEM-DEM coupling analysis for ranular-media-based thin-wall elbow tube push-bending process. International Journal of Material Forming, 12:985-994, 2019.
[13] Hibbit H.D., Karlsson B.I., Sorensen P. Theory Manual, ABAQUS, Version 6.7. Providence, RI, USA, 2007.
Document information
Published on 30/05/23
Accepted on 19/05/23
Submitted on 08/05/23
Volume 39, Issue 2, 2023
DOI: 10.23967/j.rimni.2023.05.005
Licence: CC BY-NC-SA license
Share this document
claim authorship
Are you one of the authors of this document?