| Line 13: | Line 13: | ||
--> | --> | ||
| − | '''Abstract: '''In this study, IGA is introduced into the performance analysis of the expansion water seal for an exact representation of its complex geometrical shape. Firstly, the incremental equilibrium equations used in the large deformation analysis are derived for the IGA discretization model based on the updated Lagrangian formulation. The contact forces are | + | '''Abstract: '''In this study, IGA is introduced into the performance analysis of the expansion water seal for an exact representation of its complex geometrical shape. Firstly, the incremental equilibrium equations used in the large deformation analysis are derived for the IGA discretization model based on the updated Lagrangian formulation. The unknown contact forces are directly involved in the equilibrium equations, which results in a simple expression. Then, through the investigation of the contact conditions, the normal and tangential contact forces are verified to be the solutions of two box-constrained variational inequalities representing the normal and tangential contact conditions, respectively. Furthermore, the incremental equilibrium equations for all components of the water seal system and the variational inequalities for all contacts between the components are assembled together and reformulated as a global variational inequality, which is resolved by using the Extra-gradient method. Ultimately, the new method is applied in the performance comparison of two optional expansion water seals, in which the capability and precision of the proposed method are investigated. Results verify that the proposed method is effective in the numerical simulation of the expansion water seal and has a higher precision than the traditional FEM under the same conditions. |
'''Key words:''' expansion water seal; performance analysis; isogeometric analysis; frictional contact; variational inequality | '''Key words:''' expansion water seal; performance analysis; isogeometric analysis; frictional contact; variational inequality | ||
| Line 23: | Line 23: | ||
Both model tests and numerical simulations were employed in the researches on the expansion water seal. To pursue a high reliability in terms of working performance of the expansion water seal, model tests were conducted for the hydraulic steel gate design in some large hydropower stations, e.g., Pubugou, Longtan and Laxiwa[2]. Although model tests have resolved the performance evaluation for these stations successfully, they are costly and time-consuming. Moreover, the results of a special model test may be wrong when the conditions change. Therefore, numerical simulations become more popular in performance analysis of expansion water seal recently. | Both model tests and numerical simulations were employed in the researches on the expansion water seal. To pursue a high reliability in terms of working performance of the expansion water seal, model tests were conducted for the hydraulic steel gate design in some large hydropower stations, e.g., Pubugou, Longtan and Laxiwa[2]. Although model tests have resolved the performance evaluation for these stations successfully, they are costly and time-consuming. Moreover, the results of a special model test may be wrong when the conditions change. Therefore, numerical simulations become more popular in performance analysis of expansion water seal recently. | ||
| − | Reasonability and reliability of numerical simulation come from the thorough knowledge on the mechanical properties of water seal material and the fundamental theories of numerical methods adopted. Expansion water seal is made of rubber, a typical hyperelastic material, which is marked by large deformation and incompressibility. An accurate constitutive model denoting the relation between the strain and stress in the expansion water seal is important to promise the precision of numerical results, which attracted many scholars’ devotion. Based on the test results of rubber material in laboratory, Mooney-Rivlin model[3] and Ogden model[4] were suggested for nonlinear analysis on expansion water seal, and the applicability of the two models were further investigated by Tan[5]. Considering that Mooney-Rivlin model is reliable to describe the stress-strain relation of rubber material, if the strain is no more than 1.50[6], it gains more popularity than Ogden model in previous researches[7, 8] due to its simple expression. When Mooney-Rivlin model is employed, increasing the number of parameters in the model will enhance the precision of stress-strain relation adopted, but damage the computational efficiency. The optimal number of parameters in model is investigated by Hu [9] to reach a balance between the precision and the computational efficiency, and Mooney-Rivlin model with three parameters is recommended ultimately. Generally speaking, scholars have profound acquaintance with the mechanical properties of water seal materials after abundant explorations. | + | Reasonability and reliability of numerical simulation come from the thorough knowledge on the mechanical properties of water seal material and the fundamental theories of numerical methods adopted. Expansion water seal is made of rubber, a typical hyperelastic material, which is marked by large deformation and incompressibility. An accurate constitutive model denoting the relation between the strain and stress in the expansion water seal is important to promise the precision of numerical results, which attracted many scholars’ devotion. Based on the test results of rubber material in laboratory, Mooney-Rivlin model[3]and Ogden model[4] were suggested for nonlinear analysis on expansion water seal, and the applicability of the two models were further investigated by Tan[5]. Considering that Mooney-Rivlin model is reliable to describe the stress-strain relation of rubber material, if the strain is no more than 1.50[6], it gains more popularity than Ogden model in previous researches[7, 8] due to its simple expression. When Mooney-Rivlin model is employed, increasing the number of parameters in the model will enhance the precision of stress-strain relation adopted, but damage the computational efficiency. The optimal number of parameters in model is investigated by Hu[9] to reach a balance between the precision and the computational efficiency, and Mooney-Rivlin model with three parameters is recommended ultimately. Generally speaking, scholars have profound acquaintance with the mechanical properties of water seal materials after abundant explorations. |
Up to now, the finite element method (FEM) is commonly used in the existing numerical simulation of water seal, for the commercial FEM software is matured in simulating the material nonlinearity caused by the constitutive model of rubber material, the geometric nonlinearity caused by large deformation, and the nonlinear boundary conditions due to the contact between water seal and the steel plates[10]. However, the structure complexity of the expansion water seal leads the modeling to be complicated and time-consuming when using traditional FEM. More importantly, the geometry difference between FEM model and the actual water seal undoubtedly affects the accuracy of the results, albeit it is subtle. Therefore, a numerical method with more reliability and high efficiency is expected to replace the traditional FEM for a better analysis on the performance of water seal. | Up to now, the finite element method (FEM) is commonly used in the existing numerical simulation of water seal, for the commercial FEM software is matured in simulating the material nonlinearity caused by the constitutive model of rubber material, the geometric nonlinearity caused by large deformation, and the nonlinear boundary conditions due to the contact between water seal and the steel plates[10]. However, the structure complexity of the expansion water seal leads the modeling to be complicated and time-consuming when using traditional FEM. More importantly, the geometry difference between FEM model and the actual water seal undoubtedly affects the accuracy of the results, albeit it is subtle. Therefore, a numerical method with more reliability and high efficiency is expected to replace the traditional FEM for a better analysis on the performance of water seal. | ||
| Line 29: | Line 29: | ||
Isogeometric analysis (IGA), a novel numerical method proposed by Hughes et al.[11], originally aimed to bridge the gap between computer aided design (CAD) and finite element analysis (FEA). Because the nonuniform rational B-splines, which are widely used in most CAD tools, are adopted as basis functions, IGA is capable of representing the exact geometry of engineering structures. Moreover, the conventional FEM uses Lagrange polynomials feature ''C''<sup>0</sup> continuity at nodes regardless of their order, while IGA with spline functions of order ''p'' has the ability to provide ''C''<sup>p−1</sup> continuity at all non-multiple knots. This means that IGA shows better robustness and accuracy compared to the conventional FEM for the same amount of degrees of freedom[12]. Owing to these significant advantages, IGA served as a hot topic in engineering analysis since its birth and were adopted in the resolution of diverse problems in structural mechanics, solid mechanics, and fluid mechanics. Developments of IGA theory and the related computer implementation until 2015 were reviewed by Nguyen et al.[13]. Meanwhile, numerous enhancements have been made to improve the ability of IGA to optimize the engineering structure, the progresses of which were reviewed by Wang et al.[14] in 2018 and Gao et al.[15] in 2020. IGA could play an important role in the performance analysis of water seal. On the one hand, the complex shape of the water seal can be represented exactly in IGA. On the other hand, the capacity of IGA to treat the incompressibility in case of large deformation had been fully developed[16]. Thus, IGA is employed in this article to investigate the performance of expansion water seal in diverse conditions. | Isogeometric analysis (IGA), a novel numerical method proposed by Hughes et al.[11], originally aimed to bridge the gap between computer aided design (CAD) and finite element analysis (FEA). Because the nonuniform rational B-splines, which are widely used in most CAD tools, are adopted as basis functions, IGA is capable of representing the exact geometry of engineering structures. Moreover, the conventional FEM uses Lagrange polynomials feature ''C''<sup>0</sup> continuity at nodes regardless of their order, while IGA with spline functions of order ''p'' has the ability to provide ''C''<sup>p−1</sup> continuity at all non-multiple knots. This means that IGA shows better robustness and accuracy compared to the conventional FEM for the same amount of degrees of freedom[12]. Owing to these significant advantages, IGA served as a hot topic in engineering analysis since its birth and were adopted in the resolution of diverse problems in structural mechanics, solid mechanics, and fluid mechanics. Developments of IGA theory and the related computer implementation until 2015 were reviewed by Nguyen et al.[13]. Meanwhile, numerous enhancements have been made to improve the ability of IGA to optimize the engineering structure, the progresses of which were reviewed by Wang et al.[14] in 2018 and Gao et al.[15] in 2020. IGA could play an important role in the performance analysis of water seal. On the one hand, the complex shape of the water seal can be represented exactly in IGA. On the other hand, the capacity of IGA to treat the incompressibility in case of large deformation had been fully developed[16]. Thus, IGA is employed in this article to investigate the performance of expansion water seal in diverse conditions. | ||
| − | However, as mentioned above, the contact between the water seal and the steel plates should be taken into account carefully when simulating the mechanical behavior of the water seal. A number of approaches, such as the interior method[17] and surface potentials method[18], had been proposed to model contact in IGA. These methods fall into two categories. The first type of method utilizes the classical penalty method to impose the contact conditions. In this case, the value of the penalty parameter is vital in the analyses but hard to be determined. While, the second type of method always adds the contact potential to the total potential analysis based on some assumptions, e.g., surface potentials and the third medium[19], in which the rationality of those assumptions should be further investigated. To avoid the demerit of the existing approaches, variational inequality (VI) theory[20] is introduced to formulate the contact conditions as variational inequalities, and the extra-gradient method[21] is used to solve the equations derived in the study. Considering that VI theory has been successfully used in the resolution of contact for a system of discrete bodies[22], the new approach is theoretical feasible to improve the ability of IGA in contact simulation. | + | However, as mentioned above, the contact between the water seal and the steel plates should be taken into account carefully when simulating the mechanical behavior of the water seal. A number of approaches, such as the interior method[17] and surface potentials method[18], had been proposed to model contact in IGA. These methods fall into two categories. The first type of method utilizes the classical penalty method to impose the contact conditions. In this case, the value of the penalty parameter is vital in the analyses but hard to be determined. While, the second type of method always adds the contact potential to the total potential analysis based on some assumptions, e.g., surface potentials and the third medium[19], in which the rationality of those assumptions should be further investigated. To avoid the demerit of the existing approaches, variational inequality (VI) theory[20] is introduced to formulate the contact conditions as variational inequalities, and the extra-gradient method[21]is used to solve the equations derived in the study. Considering that VI theory has been successfully used in the resolution of contact for a system of discrete bodies[22], the new approach is theoretical feasible to improve the ability of IGA in contact simulation. |
| − | The remainder of this study is organized as follows. Section 2 briefly explains how the expansion water seal works and presents the constitutive model of the expansion water seal. In Section 3, the basic theory of IGA is provided, and formulations for larger deformation problem are illustrated. In Section 4, VI theory is briefly given firstly, and then, the conditions regarding to the contacts between the expansion water seal and the steel plates are investigated, inducing two variational inequalities equivalent to the normal and tangential contact conditions, respectively. Section 5 presents how the proposed | + | The remainder of this study is organized as follows. Section 2 briefly explains how the expansion water seal works and presents the constitutive model of the expansion water seal. In Section 3, the basic theory of IGA is provided, and formulations for larger deformation problem are illustrated. In Section 4, VI theory is briefly given firstly, and then, the conditions regarding to the contacts between the expansion water seal and the steel plates are investigated, inducing two variational inequalities equivalent to the normal and tangential contact conditions, respectively. Section 5 presents how the proposed formulation to be resolved. In Section 6, an engineering example is simulated by using the proposed method, including a comprehensive analysis on all focused properties and a comparative analysis for two optional shapes of the water seal head. Section 7 concludes the paper. |
=2 A brief description of the expansion water seal and its constitutive model = | =2 A brief description of the expansion water seal and its constitutive model = | ||
| Line 37: | Line 37: | ||
==2.1 Introduction of the expansion water seal== | ==2.1 Introduction of the expansion water seal== | ||
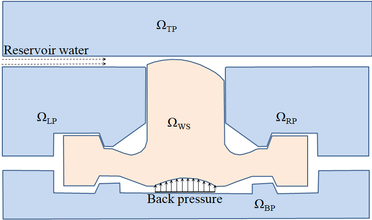
| − | In the case that the expansion water seal is employed, the water seal system in the hydraulic steel gate is typically consisted of | + | In the case that the expansion water seal is employed, the water seal system in the hydraulic steel gate is typically consisted of water stop panel, left pressing plate, right pressing plate, bed plate and the expansion water seal, as shown in Fig. 1. Domains of water stop panel, left pressing plate, right pressing plate, bed plate and the expansion water seal are denoted as Ω<sub>TP</sub>, Ω<sub>LP</sub>, Ω<sub>RP</sub>, Ω<sub>BP</sub> and Ω<sub>WS</sub>, respectively. It is noticed that the gaps between the components are enlarged in Fig.1 for a clear demonstration. Water stop panel, pressing plates and bed plate are made of steel, while the water seal is usually made of rubber. Through regulating the magnitude of back pressure, the deformation of the expansion water seal and the contact between the water seal and water stop panel are adjusted to seal up the reservoir water. When the hydraulic steel gate is to be closed, the back pressure is exerted on the expansion water seal by using a specialized water or air pressure installation, and then the expansion water seal deforms and moves upward. Back pressure will increase until the water seal contacts the water stop panel with the expected length and stress, which stuffs up the gap between the water stop panel and the pressing plate. Finally, the reservoir water is sealed up. Conversely, if the hydraulic steel gate is to be open, the back pressure is discharged gradually and the expansion water seal backtracks. The gap emerges and the reservoir water flows in the gap freely, which means that the force offered by the hoisting device to open the gate can be small. |
<div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | ||
| − | [[Image: | + | [[Image:Review_990962974820-image1.png|372px]] </div> |
<div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | ||
| − | '''Figure 1,''' A schematic diagram for the expansion water seal | + | <span style="text-align: center; font-size: 75%;">'''Figure 1,''' A schematic diagram for the expansion water seal</span></div> |
The performance of the expansion water seal is always evaluated from the following aspects. At First, the back cavity formed by the expansion water seal and the bed plate is one critical section, the leakproofness of which directly impacts the operation of imposing a prescribed back pressure. Once the water seal system has been assembled, the stress magnitudes with regard to the contacts between the two water seal wings and the pressing plates and the bed plate are the key variables to estimate whether the leakproofness of the back cavity is satisfactory. Next, the stress magnitudes regarding to the contact between the water seal head and the water stop panel are the variables of the greatest importance to assess the effectiveness of the water seal to seal up the reservoir water, which varies with the width of the gap, the back pressure as well as the reservoir water pressure. Finally, the offset of the water seal head appears due to the singularity of the reservoir water flowing, which is always investigated for a better understanding on the wear of the water seal head. In summary, an expansion water seal should meet the specified requirements in case of prescribed back pressure and reservoir water pressure. | The performance of the expansion water seal is always evaluated from the following aspects. At First, the back cavity formed by the expansion water seal and the bed plate is one critical section, the leakproofness of which directly impacts the operation of imposing a prescribed back pressure. Once the water seal system has been assembled, the stress magnitudes with regard to the contacts between the two water seal wings and the pressing plates and the bed plate are the key variables to estimate whether the leakproofness of the back cavity is satisfactory. Next, the stress magnitudes regarding to the contact between the water seal head and the water stop panel are the variables of the greatest importance to assess the effectiveness of the water seal to seal up the reservoir water, which varies with the width of the gap, the back pressure as well as the reservoir water pressure. Finally, the offset of the water seal head appears due to the singularity of the reservoir water flowing, which is always investigated for a better understanding on the wear of the water seal head. In summary, an expansion water seal should meet the specified requirements in case of prescribed back pressure and reservoir water pressure. | ||
| Line 92: | Line 92: | ||
| − | where ''n'' is the order of polynomials, and ''C<sub>ij</sub>'' is the material parameters. A different ''n'' adopted in Eq. (3) indicates a different polynomial. | + | where ''n'' is the order of polynomials, and ''C<sub>ij</sub>'' is the material parameters. A different ''n'' adopted in Eq. (3) indicates a different polynomial. Mooney-Rivlin models with two parameters, three parameters, five parameters and nine parameters were employed by Hu[9] in the numerical simulation of the expansion water seal, and the precisions of the results and the computational costs were compared. It was verified that Mooney-Rivlin model with three parameters had an accuracy close to that with five and nine parameters, while its computational cost was apparently lower. Thus, Mooney-Rivlin model with three parameters is used in this study, which actually sets ''n'' in Eq. (3) as one and has the formulation as follows. |
{| class="formulaSCP" style="width: 100%; text-align: center;" | {| class="formulaSCP" style="width: 100%; text-align: center;" | ||
| Line 155: | Line 155: | ||
| − | It is noticed that a knot in Ξ is permitted to repeat by augmenting Eq. (6) and (7) with a definition | + | It is noticed that a knot in Ξ is permitted to repeat by augmenting Eq. (6) and Eq. (7) with a definition |
{| class="formulaSCP" style="width: 100%; text-align: center;" | {| class="formulaSCP" style="width: 100%; text-align: center;" | ||
| Line 168: | Line 168: | ||
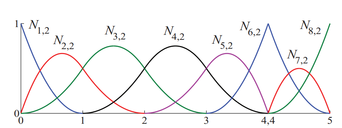
| − | Denoting the multiplicity of the knots as ''k'', the continuity of the B-spline basis functions between knot spans is ''C<sup>p</sup>''<sup>−</sup>''<sup>k</sup>''. For a better understanding, a quadratic example is presented in | + | Denoting the multiplicity of the knots as ''k'', the continuity of the B-spline basis functions between knot spans is ''C<sup>p</sup>''<sup>−</sup>''<sup>k</sup>''. For a better understanding, a quadratic example is presented in Fig. 2 for the knot vector Ξ'' ''= {''ξ''<sub>1</sub>, ''ξ''<sub>2</sub>, ''ξ''<sub>3</sub>, ''ξ''<sub>4</sub>, ''ξ''<sub>5</sub>, ''ξ''<sub>6</sub>, ''ξ''<sub>7</sub>, ''ξ''<sub>8</sub>, ''ξ''<sub>9</sub>, ''ξ''<sub>10</sub>, ''ξ''<sub>11</sub>} = {0, 0, 0, 1, 2, 3, 4, 4, 5, 5, 5}. |
<div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | ||
| − | [[Image: | + | [[Image:Review_990962974820-image10.png|342px]] </div> |
<div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | ||
| − | '''Figure 2,''' A quadratic example for the B-spline basis function</div> | + | <span style="text-align: center; font-size: 75%;">'''Figure 2,''' A quadratic example for the B-spline basis function</span></div> |
With the basis functions in hand, a B-spline curve can be constructed as their linear combination: | With the basis functions in hand, a B-spline curve can be constructed as their linear combination: | ||
| Line 189: | Line 189: | ||
| − | in which ''P'' <sub>i</sub>''∈R''<sup>d</sup>'', ''i ''= 1, 2, …, ''m'', are called as control points, and ''d'' is the dimension of the physical space. | + | in which '''P''' ''<sub>i</sub>''∈R''<sup>d</sup>'', ''i ''= 1, 2, …, ''m'', are called as control points, and ''d'' is the dimension of the physical space. |
B-spline surfaces and solids are the tensor product of univariate B-splines. Given a control net '''P''' ''<sub>i</sub>''<sub>, </sub>''<sub>j</sub>''∈R''<sup>d</sup>'', ''i ''= 1, 2, …, ''m'', ''j ''= 1, 2, …, ''n'', polynomial orders ''p'' and ''q'', and knot vectors Ξ'' ''={''ξ''<sub>1</sub>, ''ξ''<sub>2</sub>, …, ''ξ<sub>m</sub>''<sub>+</sub>''<sub>p</sub>''<sub>+1</sub>}, and Θ'' ''={''η''<sub>1</sub>, ''η''<sub>2</sub>, …, ''η<sub>n</sub>''<sub>+</sub>''<sub>q</sub>''<sub>+1</sub>}, a tensor product B-spline surface is generated by | B-spline surfaces and solids are the tensor product of univariate B-splines. Given a control net '''P''' ''<sub>i</sub>''<sub>, </sub>''<sub>j</sub>''∈R''<sup>d</sup>'', ''i ''= 1, 2, …, ''m'', ''j ''= 1, 2, …, ''n'', polynomial orders ''p'' and ''q'', and knot vectors Ξ'' ''={''ξ''<sub>1</sub>, ''ξ''<sub>2</sub>, …, ''ξ<sub>m</sub>''<sub>+</sub>''<sub>p</sub>''<sub>+1</sub>}, and Θ'' ''={''η''<sub>1</sub>, ''η''<sub>2</sub>, …, ''η<sub>n</sub>''<sub>+</sub>''<sub>q</sub>''<sub>+1</sub>}, a tensor product B-spline surface is generated by | ||
| Line 258: | Line 258: | ||
| − | Finally, the extension of Eq. (13) and (14) to the 3D situation induces a NURBS solid. It is noticed that B-splines can be considered as a special case of NURBS where the weights are all equal. | + | Finally, the extension of Eq. (13) and Eq. (14) to the 3D situation induces a NURBS solid. It is noticed that B-splines can be considered as a special case of NURBS where the weights are all equal. |
A series of important properties of NURBS basis functions (likewise for B-spines) is illustrated by taking ''R<sub>ij,pq</sub>''(''ξ, η'') as an example. Firstly, throughout the patch [''ξ''<sub>1</sub>, ''ξ<sub>m</sub>''<sub>+</sub>''<sub>p</sub>''<sub>+1</sub>)× [''η''<sub>1</sub>, ''η<sub>n</sub>''<sub>+</sub>''<sub>q</sub>''<sub>+1</sub>),'' R<sub>ij,pq</sub>''(''ξ, η'') is nonnegative. The second is the partition of unity all over the patch. The third is the local support, which means that ''R<sub>ij,pq</sub>''(''ξ, η'') = 0 if (''ξ, η'')''' '''is outside the span domain of [''ξ<sub>i</sub>'', ''ξ<sub>i</sub>''<sub>+</sub>''<sub>p</sub>''<sub>+1</sub>)× [''η<sub>j</sub>'', ''η<sub>j</sub>''<sub>+</sub>''<sub>q</sub>''<sub>+1</sub>). The last one is the continuity that the interior of the knot span domain is continuous up to C<sup>∞</sup>, while the continuity between knot spans are ''C<sup>p</sup>''<sup>−</sup>''<sup>k</sup>'' and ''C<sup>q</sup>''<sup>−</sup>''<sup>l</sup>''in which ''k'' and ''l'' denote the multiplicity along two directions, respectively. | A series of important properties of NURBS basis functions (likewise for B-spines) is illustrated by taking ''R<sub>ij,pq</sub>''(''ξ, η'') as an example. Firstly, throughout the patch [''ξ''<sub>1</sub>, ''ξ<sub>m</sub>''<sub>+</sub>''<sub>p</sub>''<sub>+1</sub>)× [''η''<sub>1</sub>, ''η<sub>n</sub>''<sub>+</sub>''<sub>q</sub>''<sub>+1</sub>),'' R<sub>ij,pq</sub>''(''ξ, η'') is nonnegative. The second is the partition of unity all over the patch. The third is the local support, which means that ''R<sub>ij,pq</sub>''(''ξ, η'') = 0 if (''ξ, η'')''' '''is outside the span domain of [''ξ<sub>i</sub>'', ''ξ<sub>i</sub>''<sub>+</sub>''<sub>p</sub>''<sub>+1</sub>)× [''η<sub>j</sub>'', ''η<sub>j</sub>''<sub>+</sub>''<sub>q</sub>''<sub>+1</sub>). The last one is the continuity that the interior of the knot span domain is continuous up to C<sup>∞</sup>, while the continuity between knot spans are ''C<sup>p</sup>''<sup>−</sup>''<sup>k</sup>'' and ''C<sup>q</sup>''<sup>−</sup>''<sup>l</sup>''in which ''k'' and ''l'' denote the multiplicity along two directions, respectively. | ||
| Line 264: | Line 264: | ||
==3.2 Large deformation analysis using IGA with updated Lagrangian formulation== | ==3.2 Large deformation analysis using IGA with updated Lagrangian formulation== | ||
| − | + | In this section, the formulations regarding to the expansion water seal is derived in the first place. Under the back pressure and the reservoir water pressure, the large deformation of the expansion water seal usually happens. In the conventional FEM, Total Lagrangian formulation and updated Lagrangian formulation were provided for large deformation analysis. Considering that the updated Lagrangian (U.L.) formulation is more applicable to the situation that the external loads vary with the body deformation, U.L. formulation is used for numerical analysis on the expansion water seal in this study. Thus, a large deformation analysis using IGA with U.L. formulation is demonstrated in this section. For a simple expression, the tensor notation is utilized in this section. | |
The incremental analysis is essential for the large deformation problems, which means that all physical quantities at time ''t'' are assumed to be known, and the quantities at time ''t''+Δ''t'' are required to be solved. A pre-superscript is introduced to indicate the time when the physical quantities are measured, e.g., ''<sup>t</sup>u<sub>k</sub>'' is the displacement measured at time ''t''. The principle of virtual displacement equivalent to the equilibrium condition required for the body at time ''t''+Δ''t'' is formulated for the U.L. formulation as | The incremental analysis is essential for the large deformation problems, which means that all physical quantities at time ''t'' are assumed to be known, and the quantities at time ''t''+Δ''t'' are required to be solved. A pre-superscript is introduced to indicate the time when the physical quantities are measured, e.g., ''<sup>t</sup>u<sub>k</sub>'' is the displacement measured at time ''t''. The principle of virtual displacement equivalent to the equilibrium condition required for the body at time ''t''+Δ''t'' is formulated for the U.L. formulation as | ||
| Line 273: | Line 273: | ||
{| style="text-align: center; margin:auto;" | {| style="text-align: center; margin:auto;" | ||
|- | |- | ||
| − | | <math>{\int | + | | <math>\mbox{ }\int S_{}{}_{ij}\delta {\epsilon }_{}{}_{ij}\mbox{d}\Omega =</math><math>Q_{}</math> |
|} | |} | ||
| style="width: 5px;text-align: right;white-space: nowrap;" | (15) | | style="width: 5px;text-align: right;white-space: nowrap;" | (15) | ||
| Line 286: | Line 286: | ||
{| style="text-align: center; margin:auto;" | {| style="text-align: center; margin:auto;" | ||
|- | |- | ||
| − | | <math>Q_{}\mbox{=} | + | | <math>Q_{}\mbox{=}\int t_{}{}_k\delta u_{}{}_k\mbox{d}{\Gamma }_t+</math><math>\int p_{}{}_k\delta u_{}{}_k\mbox{d}{\Gamma }_c+\int f_{}{}_k\delta u_{}{}_k\mbox{d}\Omega </math> |
|} | |} | ||
| style="width: 5px;text-align: right;white-space: nowrap;" | (16) | | style="width: 5px;text-align: right;white-space: nowrap;" | (16) | ||
| Line 292: | Line 292: | ||
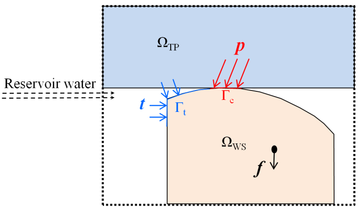
| − | in which '' | + | in which Γ<sub>t</sub> and Γ<sub>c</sub> represent the part of the boundary where the water seal doesn’t contact the adjacent steel plates and the part of the boundary where the contact happens, respectively. ''f<sub>k</sub>'' denotes the known body force of the expansion water seal. ''t<sub>k</sub>'' is the known tractions on Γ<sub>t</sub>, which is resulted by the back pressure or the reservoir water pressure. ''p<sub>k</sub>'' is the unknown contact forces on Γ<sub>c</sub>, which comes from by the compression and the friction between the expansion water seal and the steel plates. Taking the water seal head in Fig. 3 as an example, the reservoir water pressure induces ''t<sub>k</sub>'' where no contact between the expansion water seal and the top plate happens, but the forces on the water seal are unknown at the boundary where the water seal contacts the top plate. Since the unknown contact forces are directly involved in Eq. (16), some additional formulations have to be augmented for the determining of ''p<sub>k</sub>'', which will be illustrated in the next section. |
| + | |||
| + | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | ||
| + | [[Image:Review_990962974820-image19.png|360px]] </div> | ||
| + | |||
| + | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | ||
| + | <span style="text-align: center; font-size: 75%;">'''Figure 3,''' Known tractions and unknown contact forces at the boundary of the water seal head</span></div> | ||
The updated Kirchhoff stress''<sup> t</sup>''<sup>Δ</sup>''<sup>t</sup>S<sub>ij</sub>'' is the summation of and the updated Kirchhoff stress increment Δ''S<sub>ij</sub>'' and the known Cauchy stress ''<sup>t</sup>τ<sub>ij</sub>'', that is | The updated Kirchhoff stress''<sup> t</sup>''<sup>Δ</sup>''<sup>t</sup>S<sub>ij</sub>'' is the summation of and the updated Kirchhoff stress increment Δ''S<sub>ij</sub>'' and the known Cauchy stress ''<sup>t</sup>τ<sub>ij</sub>'', that is | ||
| Line 320: | Line 326: | ||
| − | in which Δ''u<sub>k</sub>'' represents the incremental displacement during the time interval Δ''t''. Substituting Eq. (17) and (18) into Eq. (15), we have | + | in which Δ''u<sub>k</sub>'' represents the incremental displacement during the time interval Δ''t''. Substituting Eq. (17) and Eq. (18) into Eq. (15), we have |
{| class="formulaSCP" style="width: 100%; text-align: center;" | {| class="formulaSCP" style="width: 100%; text-align: center;" | ||
| Line 327: | Line 333: | ||
{| style="text-align: center; margin:auto;" | {| style="text-align: center; margin:auto;" | ||
|- | |- | ||
| − | | <math> | + | | <math>\int \Delta S_{ij}\delta \left(\Delta {\epsilon }_{ij}\right)\mbox{d}\Omega \mbox{+}\int {\tau }_{}{}_{ij}\delta \left(\Delta {\epsilon }_{ij}{}^N\right)\mbox{d}\Omega =</math><math>Q_{}-\int {\tau }_{}{}_{ij}\delta \left(\Delta {\epsilon }_{ij}{}^L\right)\mbox{d}\Omega </math> |
|} | |} | ||
| style="width: 5px;text-align: right;white-space: nowrap;" | (19) | | style="width: 5px;text-align: right;white-space: nowrap;" | (19) | ||
| Line 353: | Line 359: | ||
{| style="text-align: center; margin:auto;" | {| style="text-align: center; margin:auto;" | ||
|- | |- | ||
| − | | <math> | + | | <math>\int D_{ijkl}\left(\Delta {\epsilon }_{kl}{}^L\right)\delta \left(\Delta {\epsilon }_{ij}{}^L\right)\mbox{d}\Omega \mbox{+}\int {\tau }_{}{}_{ij}\delta \left(\Delta {\epsilon }_{ij}{}^N\right)\mbox{d}\Omega =</math><math>Q_{}-\int {\tau }_{}{}_{ij}\delta \left(\Delta {\epsilon }_{ij}{}^L\right)\mbox{d}\Omega </math> |
|} | |} | ||
| style="width: 5px;text-align: right;white-space: nowrap;" | (21) | | style="width: 5px;text-align: right;white-space: nowrap;" | (21) | ||
| Line 359: | Line 365: | ||
| − | The domain of the expansion water seal | + | The domain of the expansion water seal Ω<sub>ws</sub>R<sup>2</sup> can be discretized into a set of elements, that is, Ω<sub>ws</sub> =∪Ω<sup>e</sup>. NURBS functions in Eq. (13) are used for the approximation of the displacement field ''<sup>t</sup>'' '''u''' ''<sup>e</sup>'', the displacement increment Δ'''u''' ''<sup>e</sup>'', and the coordinates '''x''' ''<sup>e</sup>'' within each element as |
{| class="formulaSCP" style="width: 100%; text-align: center;" | {| class="formulaSCP" style="width: 100%; text-align: center;" | ||
| Line 374: | Line 380: | ||
in which, ''<sup>t</sup>'' '''u''' ''<sup>e</sup>'' and ''<sup>t</sup>'' '''x''' ''<sup>e</sup>'' are the arrays containing the displacements and the coordinates of ''n<sup>e</sup>'' number of control points in an element at time ''t'',Δ'''u''' ''<sup>e</sup>'' is the array containing the displacement incremental of control points in an element within the time interval Δ''t''. '''R'''(''ξ'', ''η'') = [''R''<sub>1</sub>(''ξ'', ''η'')'''I''', ''R''<sub>2</sub>(''ξ'', ''η'')'''I''', …, ''R<sub>ne</sub>''(''ξ'', ''η'')'''I'''] is a matrix of size 2 × 2''n<sup>e</sup>'' with identity matrix '''I''' in R<sup>2</sup>. Here, ''R'' (''ξ'', ''η'') is a simplified notation of ''R<sub>ij,pq</sub>''(''ξ, η'') in Eq. (13), and ''n<sup>e</sup>'' denotes the total number of control points whose ''R'' (''ξ'', ''η'') has local support in an element Ω<sup>e</sup>. | in which, ''<sup>t</sup>'' '''u''' ''<sup>e</sup>'' and ''<sup>t</sup>'' '''x''' ''<sup>e</sup>'' are the arrays containing the displacements and the coordinates of ''n<sup>e</sup>'' number of control points in an element at time ''t'',Δ'''u''' ''<sup>e</sup>'' is the array containing the displacement incremental of control points in an element within the time interval Δ''t''. '''R'''(''ξ'', ''η'') = [''R''<sub>1</sub>(''ξ'', ''η'')'''I''', ''R''<sub>2</sub>(''ξ'', ''η'')'''I''', …, ''R<sub>ne</sub>''(''ξ'', ''η'')'''I'''] is a matrix of size 2 × 2''n<sup>e</sup>'' with identity matrix '''I''' in R<sup>2</sup>. Here, ''R'' (''ξ'', ''η'') is a simplified notation of ''R<sub>ij,pq</sub>''(''ξ, η'') in Eq. (13), and ''n<sup>e</sup>'' denotes the total number of control points whose ''R'' (''ξ'', ''η'') has local support in an element Ω<sup>e</sup>. | ||
| − | Combined Eq. (21) and (22), a matrix expression of the equilibrium equation can be obtained for an element Ω<sup>e</sup> as the following formulation. | + | Combined Eq. (21) and Eq. (22), a matrix expression of the equilibrium equation can be obtained for an element Ω<sup>e</sup> as the following formulation. |
{| class="formulaSCP" style="width: 100%; text-align: center;" | {| class="formulaSCP" style="width: 100%; text-align: center;" | ||
| Line 381: | Line 387: | ||
{| style="text-align: center; margin:auto;" | {| style="text-align: center; margin:auto;" | ||
|- | |- | ||
| − | | <math>\left(\boldsymbol{K}_L+\boldsymbol{K}_{NL}\right)\Delta u=</math><math>\boldsymbol{Q}-\boldsymbol{F}</math> | + | | <math>\left(\boldsymbol{K}_L^e+\boldsymbol{K}_{NL}^e\right)\Delta u^e=</math><math>\boldsymbol{Q}^e-\boldsymbol{F}^e</math> |
|} | |} | ||
| style="width: 5px;text-align: right;white-space: nowrap;" | (23) | | style="width: 5px;text-align: right;white-space: nowrap;" | (23) | ||
| Line 387: | Line 393: | ||
| − | + | Here the superscript ''e'' represents the quantity being defined for an element Ω<sup>e</sup>. In Eq. (23), | |
{| class="formulaSCP" style="width: 100%; text-align: center;" | {| class="formulaSCP" style="width: 100%; text-align: center;" | ||
| Line 394: | Line 400: | ||
{| style="text-align: center; margin:auto;" | {| style="text-align: center; margin:auto;" | ||
|- | |- | ||
| − | | <math>\boldsymbol{K}_L\mbox{=} | + | | <math>\boldsymbol{K}_L^e\mbox{=}\int \boldsymbol{B}_L^T\boldsymbol{D}\boldsymbol{B}_L\mbox{d}{\Omega }^e</math> |
|} | |} | ||
| style="width: 5px;text-align: right;white-space: nowrap;" | (24) | | style="width: 5px;text-align: right;white-space: nowrap;" | (24) | ||
| Line 404: | Line 410: | ||
{| style="text-align: center; margin:auto;" | {| style="text-align: center; margin:auto;" | ||
|- | |- | ||
| − | | <math>\boldsymbol{K}_{NL}\mbox{=} | + | | <math>\boldsymbol{K}_{NL}^e\mbox{=}\int \boldsymbol{B}_{NL}^T\boldsymbol{\tau }\boldsymbol{B}_{NL}\mbox{d}{\Omega }^e</math> |
|} | |} | ||
| style="width: 5px;text-align: right;white-space: nowrap;" | (25) | | style="width: 5px;text-align: right;white-space: nowrap;" | (25) | ||
| Line 414: | Line 420: | ||
{| style="text-align: center; margin:auto;" | {| style="text-align: center; margin:auto;" | ||
|- | |- | ||
| − | | <math>\boldsymbol{F}\mbox{=} | + | | <math>\boldsymbol{F}^e\mbox{=}\int \boldsymbol{B}_L^T\boldsymbol{{\tau }^{{'}}}\mbox{d}{\Omega }^e</math> |
|} | |} | ||
| style="width: 5px;text-align: right;white-space: nowrap;" | (26) | | style="width: 5px;text-align: right;white-space: nowrap;" | (26) | ||
| Line 427: | Line 433: | ||
{| style="text-align: center; margin:auto;" | {| style="text-align: center; margin:auto;" | ||
|- | |- | ||
| − | | | + | | [[Image:Review_990962974820-image30.png|348px]] |
| − | + | ||
| − | + | ||
| − | + | ||
|} | |} | ||
| style="width: 5px;text-align: right;white-space: nowrap;" | (27) | | style="width: 5px;text-align: right;white-space: nowrap;" | (27) | ||
| Line 481: | Line 484: | ||
| − | Finally, | + | Finally, |
{| class="formulaSCP" style="width: 100%; text-align: center;" | {| class="formulaSCP" style="width: 100%; text-align: center;" | ||
| Line 488: | Line 491: | ||
{| style="text-align: center; margin:auto;" | {| style="text-align: center; margin:auto;" | ||
|- | |- | ||
| − | | <math>\boldsymbol{Q}\mbox{ | + | | <math>\boldsymbol{Q}^\mbox{e}\mbox{=}\int \boldsymbol{R}{\left(\boldsymbol{\xi }\right)}^T\boldsymbol{t}\mbox{d}{\Gamma }_t^e+</math><math>\int \boldsymbol{R}{\left(\boldsymbol{\xi }\right)}^T\boldsymbol{p}\mbox{d}{\Gamma }_c^e\mbox{+}\int \boldsymbol{R}{\left(\boldsymbol{\xi }\right)}^T\boldsymbol{f}\mbox{d}{\Omega }^e</math> |
|} | |} | ||
| style="width: 5px;text-align: right;white-space: nowrap;" | (31) | | style="width: 5px;text-align: right;white-space: nowrap;" | (31) | ||
| Line 494: | Line 497: | ||
| − | + | here, '''t''' = (''t<sub>x</sub>'', ''t<sub>y</sub>'')''<sup>T</sup>'',''' p''' = (''p<sub>x</sub>'', ''p<sub>y</sub>'')''<sup>T</sup>'' and '''f''' = (''f<sub>x</sub>'', ''f<sub>y</sub>'')''<sup>T</sup>'' are the vector expressions for ''t<sub>k</sub>'', ''p<sub>k</sub>'' and ''f<sub>k</sub>'', respectively. There is no barrier to obtain the value of the body force '''f'''. However, the value of the contact force '''p''' is temporarily unknown. Furthermore, the boundaries Γ<sub>t</sub>'' ''and'' ''Γ<sub>c</sub> are uncertain, so the contribution of the known tractions to ''Q''<sup>e</sup> is also an issue. The issues will be settled by introducing VI theory, which is demonstrated in the next section. | |
| − | Besides the expansion water seal, the entire water seal system comprises the water stop panel, the left and right pressing plate as well as the bed plate. These components are made of steel and their deformation is usually restrained in the elastic stage. | + | Besides the expansion water seal, the entire water seal system comprises the water stop panel, the left and right pressing plate as well as the bed plate. These components are made of steel and their deformation is usually restrained in the elastic stage. Elastic analysis is a fundamental application of IGA[12], so the detailed derivation of the formulations and matrix equations in terms of elastic analysis of the steel plates are left out in this study. The equilibrium equation for an element Ω<sup>e</sup> in the steel plates can be expressed as the following matrix formulation after the IGA discretization. |
{| class="formulaSCP" style="width: 100%; text-align: center;" | {| class="formulaSCP" style="width: 100%; text-align: center;" | ||
| Line 503: | Line 506: | ||
{| style="text-align: center; margin:auto;" | {| style="text-align: center; margin:auto;" | ||
|- | |- | ||
| − | | <math>\boldsymbol{K}^\mbox{ | + | | <math>\boldsymbol{K}^\mbox{p}\Delta u^\mbox{p}=\boldsymbol{Q}^\mbox{p}-</math><math>\boldsymbol{F}^\mbox{p}\mbox{ for }{\Omega }^\mbox{e}\in {\Omega }_{\mbox{TP}}\mbox{, }{\Omega }_{\mbox{LP}},\mbox{ }{\Omega }_{\mbox{RP}},\mbox{ }{\Omega }_{\mbox{BP}}</math> |
|} | |} | ||
| style="width: 5px;text-align: right;white-space: nowrap;" | (32) | | style="width: 5px;text-align: right;white-space: nowrap;" | (32) | ||
| Line 509: | Line 512: | ||
| − | in which '''K'''<sup> | + | in which '''K'''<sup>p</sup> is the element stiffness matrix to be calculated as '''K''' ''<sub>L</sub>'' in Eq. (24), Δ'''u'''<sup>p</sup> is the array containing the displacement incremental of control points for the steel plates, '''Q'''<sup>p</sup> is the load vector and '''F'''<sup>p</sup> is the vector denoting the contribution of the existing stress to the equation. '''F'''<sup>p</sup> and '''Q'''<sup>p</sup> can be calculated based on Eq. (26) and Eq. (31). By assembling Eq. (23) for the expansion water seal and Eq. (32) for the steel plates, the global equilibrium equation of the whole water seal device will be obtained. |
| − | It is noticed that the contact forces acting on | + | It is noticed that the contact forces acting on the steel plates are also uncertain in the resolution of Eq. (32). Therefore, the positions and forces regarded to the contacts between the expansion water seal and these steel plates are the critical quantities to be determined in the numerical simulation for the performance of the water seal system. |
=4 Variational inequalities for estimating the traction on the expansion water seal= | =4 Variational inequalities for estimating the traction on the expansion water seal= | ||
| Line 570: | Line 573: | ||
==4.2 VI for normal contact conditions== | ==4.2 VI for normal contact conditions== | ||
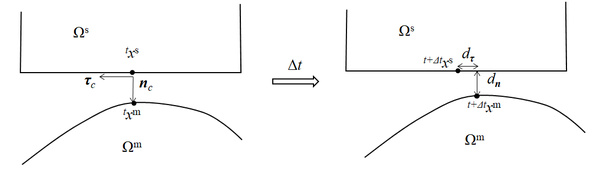
| − | + | Fig. 4 plots two elastic bodies coming into contact and undergoing deformation, one of which is called as the slave body Ω<sup>s</sup>, and another one is called as Ω<sup>m</sup>, referring to the monograph[27] by Wriggers. Compared with the expansion water seal, the deformation of the steel plate is small. Therefore, the water seal is directly assigned as the master body, while the steel plate is assigned as the slave body. ''<sup>t</sup>'' '''x'''<sup>m</sup> represents the coordinates of a knot point located on the boundary of the expansion water seal at time ''t'', and its projection point ''<sup>t</sup>'' '''x'''<sup>s</sup> is determined based on the minimum distance criterion[28]. The two points constitute a typical contact pair. Then, a framework ('''n'''<sub>c</sub>, '''τ'''<sub>c</sub>) to identify the normal and tangential directions regarding to the contact pair is defined, where '''n'''<sub>c</sub> is specified as the inner normal direction of the expansion water seal boundary at ''<sup>t</sup>'' '''x'''<sup>m</sup>. | |
<div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | ||
| − | [[ | + | [[Image:Review_990962974820-image40.png|600px]] </div> |
| − | + | ||
| − | + | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | |
| − | + | <span style="text-align: center; font-size: 75%;">'''Figure 4,''' A schematic illustration of the contact restraints for a typical contact pair</span></div> | |
Within a small time interval Δ''t'', both the master and slave bodies deform, which induces a change in the configuration of the contact pair at the end of this time step. The normal distance ''d'' '''<sub>n</sub>''' and the tangential relative displacement ''d'' '''<sub>τ</sub>''' can be calculated for given Δ'''u''' ''<sup>m</sup> ''and Δ'''u''' ''<sup>s</sup>''. Here, Δ'''u''' ''<sup>m</sup> ''and Δ'''u''' ''<sup>s</sup>'' are the increment displacements of the master and slave bodies within the time interval, respectively. Then, the tractions on ''<sup>t+</sup>''<sup>Δ</sup>''<sup>t</sup>'' '''x'''<sup>m</sup> and ''<sup>t+</sup>''<sup>Δ</sup>''<sup>t</sup>'' '''x'''<sup>s</sup> can be estimated based on VI theory, which finally induces two ''VI''s as important augments to the equilibrium equations for both the master and slave bodies. | Within a small time interval Δ''t'', both the master and slave bodies deform, which induces a change in the configuration of the contact pair at the end of this time step. The normal distance ''d'' '''<sub>n</sub>''' and the tangential relative displacement ''d'' '''<sub>τ</sub>''' can be calculated for given Δ'''u''' ''<sup>m</sup> ''and Δ'''u''' ''<sup>s</sup>''. Here, Δ'''u''' ''<sup>m</sup> ''and Δ'''u''' ''<sup>s</sup>'' are the increment displacements of the master and slave bodies within the time interval, respectively. Then, the tractions on ''<sup>t+</sup>''<sup>Δ</sup>''<sup>t</sup>'' '''x'''<sup>m</sup> and ''<sup>t+</sup>''<sup>Δ</sup>''<sup>t</sup>'' '''x'''<sup>s</sup> can be estimated based on VI theory, which finally induces two ''VI''s as important augments to the equilibrium equations for both the master and slave bodies. | ||
| Line 593: | Line 596: | ||
| − | The normal contact force ''p'' '''<sub>n</sub> '''is directly related to the normal distance ''d'' '''<sub>n</sub>'''. The expansion water seal suffers the back pressure on the back and the reservoir water pressure on the head, which both have specified | + | The normal contact force ''p'' '''<sub>n</sub> '''is directly related to the normal distance ''d'' '''<sub>n</sub>'''. The expansion water seal suffers the back pressure on the back and the reservoir water pressure on the head, which both have specified values. If the expansion water seal contacts the steel plate tightly, in other words, ''d'' '''<sub>n</sub>'''=0, ''p'' '''<sub>n</sub>''' must be greater than the normal force induced by the back pressure or the water pressure. The normal force resulted by the back pressure and the water pressure can be calculated as ('''n<sub>c</sub>''')<sup>T</sup>''' t''', which is actually the modulus of '''t''' because both the back pressure and the water pressure act on the expansion water seal boundary along the inner normal direction. Moreover, if ''d'' '''<sub>n</sub>'''>0, the normal force applied to ''<sup>t+</sup>''<sup>Δ</sup>''<sup>t</sup>'' '''x'''<sup>m</sup> is ('''n<sub>c</sub>)'''<sup>T</sup>''' t'''. The above conditions can be expressed as |
{| class="formulaSCP" style="width: 100%; text-align: center;" | {| class="formulaSCP" style="width: 100%; text-align: center;" | ||
| Line 601: | Line 604: | ||
|- | |- | ||
| <math>\begin{array}{c} | | <math>\begin{array}{c} | ||
| − | p_\boldsymbol{n}={ | + | p_\boldsymbol{n}={\left(\boldsymbol{n}_c\right)}^T\boldsymbol{t}\Rightarrow d_\boldsymbol{n}>0\mbox{ }\\ |
| − | p_\boldsymbol{n}>{ | + | p_\boldsymbol{n}>{\left(\boldsymbol{n}_c\right)}^T\boldsymbol{t}\Rightarrow d_\boldsymbol{n}\mbox{=}0\mbox{ } |
\end{array}</math> | \end{array}</math> | ||
|} | |} | ||
| Line 609: | Line 612: | ||
| − | Comparing Eq. (37) with (35), (37) is equivalent to a box-constrained variational inequality with ''a<sub>i</sub>'' = '' | + | Comparing Eq. (37) with Eq. (35), Eq. (37) is equivalent to a box-constrained variational inequality with ''a<sub>i</sub>'' =('''n<sub>c</sub>''')<sup>T</sup>''' t''' and ''b<sub>i</sub>'' = +∞; thus, the normal contact force must be the solution of the following ''VI'' |
{| class="formulaSCP" style="width: 100%; text-align: center;" | {| class="formulaSCP" style="width: 100%; text-align: center;" | ||
| Line 616: | Line 619: | ||
{| style="text-align: center; margin:auto;" | {| style="text-align: center; margin:auto;" | ||
|- | |- | ||
| − | | <math>VI\left(K^\boldsymbol{n},\boldsymbol{F}^\boldsymbol{n}\right),\mbox{ with }K^\boldsymbol{n}=</math><math>\left[{ | + | | <math>VI\left(K^\boldsymbol{n},\boldsymbol{F}^\boldsymbol{n}\right),\mbox{ with }K^\boldsymbol{n}=</math><math>\left[{\left(\boldsymbol{n}_c\right)}^T\boldsymbol{t},+\right. </math><math>\left. \infty \right),\mbox{ and }\boldsymbol{F}^\boldsymbol{n}=</math><math>d_\boldsymbol{n}</math> |
|} | |} | ||
| style="width: 5px;text-align: right;white-space: nowrap;" | (38) | | style="width: 5px;text-align: right;white-space: nowrap;" | (38) | ||
|} | |} | ||
| + | |||
| + | |||
| + | It is noticed that the boundaries Γ<sub>t</sub>'' ''and'' ''Γ<sub>c</sub> is determined when the normal contact conditions are formulated as Eq. (37). if ''d'' '''<sub>n</sub>'''>0, the point '''x'''<sup>m</sup> is situated at the boundary Γ<sub>t</sub> of Ω<sup>m</sup>, and the point '''x'''<sup>s</sup> is situated at the boundary Γ<sub>t</sub> of Ω<sup>s</sup>. At this point the normal forces applied to the two points are the known tractions. if ''d'' '''<sub>n</sub>'''=0, the point '''x'''<sup>m</sup> is situated at the boundary Γ<sub>c</sub> of Ω<sup>m</sup>, and the point '''x'''<sup>s</sup> is situated at the boundary Γ<sub>c</sub> of Ω<sup>s</sup>. At this moment the normal forces applied to the two points are uncertain. Because the two cases are uniformly involved in Eq. (37), it is unnecessary to determine the boundaries Γ<sub>t</sub>'' ''and'' ''Γ<sub>c</sub> in advance. | ||
==4.3 VI for tangential contact conditions== | ==4.3 VI for tangential contact conditions== | ||
| − | As shown in Fig. | + | As shown in Fig. 4, if ''d'' '''<sub>n</sub>'''>0 the normal contact force is ('''n<sub>c</sub>)'''<sup>T</sup>''' t''', and the tangential force must be zero considering that the properties of water pressure and air pressure. However, if ''d'' '''<sub>n</sub>'''=0, the expansion water seal contacts the steel plate tightly, the tangential contact force must be taken into account. In this case, a contact pair might be in one of two contact states: the sticky state and the sliding state. The tangential relative displacement ''d'' '''<sub>τ</sub>''' can be computed as |
{| class="formulaSCP" style="width: 100%; text-align: center;" | {| class="formulaSCP" style="width: 100%; text-align: center;" | ||
| Line 669: | Line 675: | ||
| − | Comparing Eq. (40) and (41) with Eq. (35), the two conditions can be considered as another box-constrained variational inequality with ''a<sub>i</sub>'' =-''μp'' '''<sub>n</sub>''' and ''b<sub>i</sub>'' = ''μp'' '''<sub>n</sub>'''; therefore, ''p'' '''<sub>τ </sub>'''must be the solution of the following ''VI'' | + | Comparing Eq. (40) and Eq. (41) with Eq. (35), the two conditions can be considered as another box-constrained variational inequality with ''a<sub>i</sub>'' =-''μp'' '''<sub>n</sub>''' and ''b<sub>i</sub>'' = ''μp'' '''<sub>n</sub>'''; therefore, ''p'' '''<sub>τ </sub>'''must be the solution of the following ''VI'' |
{| class="formulaSCP" style="width: 100%; text-align: center;" | {| class="formulaSCP" style="width: 100%; text-align: center;" | ||
| Line 682: | Line 688: | ||
| − | For each | + | For each knot point located on the boundary of the expansion water seal at time ''t+''Δ''t'', the normal and tangential contact forces must be the solutions of Eq. (38) and Eq. (42), which are the supplement equations for Eq. (23) and Eq. (32) to estimate the traction on the expansion water seal. |
=5 Solution Strategy= | =5 Solution Strategy= | ||
| − | Up to now, a set of formulations, including Eq. (23), (32), (38), and (42), are derived to simulate the entire water seal system, which can be resolved by various approaches. Actually, | + | Up to now, a set of formulations, including Eq. (23), Eq. (32), Eq. (38), and Eq. (42), are derived to simulate the entire water seal system, which can be resolved by various approaches. Actually, an arbitrary equation can be considered as a degenerated ''VI'' in the framework of VI theory. Thus, gathering the formulations together will induce a total ''VI'', and then, Path Newton Method based on the merit function[22] can be employed to solve it. However, this way may be inefficient because it doesn’t take full advantage of the structural features of the formulations. The structural feature is analyzed as follows. |
| − | To begin with, | + | To begin with, once the unknown contact forces are given, there is no difficulty to solve Eq. (23) and Eq. (32) based on the classical FEM theory. And then, the normal distance ''d'' '''<sub>n</sub>''' and the tangential relative displacement ''d'' '''<sub>τ</sub>''' can be regarded as functions of the unknown contact forces. Finally, the relations between the unknown contact forces and ''d'' '''<sub>n</sub>''' and ''d'' '''<sub>τ</sub>''' are expressed as Eq. (38) and Eq. (42). Therefore, selecting the unknown contact forces as the unknown quantity may be an advisable choice, which means that the increment displacements of all components of the water seal system are considered as the intermediate variables. |
| − | Assuming the number of contact pairs is ''m''<sub>c</sub> during the current time step, the normal contact force ''p'' '''<sub>n</sub>''' and the tangential contact force ''p'' '''<sub>τ </sub>'''in terms of ''m''<sub>c</sub> contact pairs constitute two arrays '''p<sub>n</sub>''' and '''p<sub>τ</sub>''', respectively. The normal distance ''d'' '''<sup>n</sup>''' and the tangential relative displacement ''d'' '''<sup>τ</sup>''' constitute two arrays '''d<sup>n</sup>''' and '''d<sup>τ</sup>''', respectively. Then, the formulations including Eq. (23), (32), (38), and (42) can be expressed as the following ''VI''. Let the subset '''K'''<sup>G</sup>=''' K<sup>n</sup>'''×'''K<sup>τ</sup>''', the mapping | + | Assuming the number of contact pairs is ''m''<sub>c</sub> during the current time step, the normal contact force ''p'' '''<sub>n</sub>''' and the tangential contact force ''p'' '''<sub>τ </sub>'''in terms of ''m''<sub>c</sub> contact pairs constitute two arrays '''p<sub>n</sub>''' and '''p<sub>τ</sub>''', respectively. The normal distance ''d'' '''<sup>n</sup>''' and the tangential relative displacement ''d'' '''<sup>τ</sup>''' constitute two arrays '''d<sup>n</sup>''' and '''d<sup>τ</sup>''', respectively. Then, the formulations including Eq. (23), Eq. (32), Eq. (38), and Eq. (42) can be expressed as the following ''VI''. Let the subset '''K'''<sup>G</sup>=''' K<sup>n</sup>'''×'''K<sup>τ</sup>''', the mapping |
{| class="formulaSCP" style="width: 100%; text-align: center;" | {| class="formulaSCP" style="width: 100%; text-align: center;" | ||
| Line 706: | Line 712: | ||
| − | then ('''p<sub>n</sub>''', '''p<sub>τ</sub>''') is the solution of ''VI''('''K'''<sup>G</sup>, '''F'''<sup>G</sup>). '''K<sup>n</sup>''' and '''K<sup>τ</sup>''' is composed of ''K'' '''<sup>n</sup>''' in Eq. (37) and ''K'' '''<sup>τ</sup>''' in Eq. (41) regarding to ''m''<sub>c</sub> contact pairs, respectively. | + | then ('''p<sub>n</sub>''', '''p<sub>τ</sub>''') is the solution of ''VI''('''K'''<sup>G</sup>, '''F'''<sup>G</sup>). '''K<sup>n</sup>''' and '''K<sup>τ</sup>''' is composed of ''K'' '''<sup>n</sup>''' in Eq. (37) and ''K'' '''<sup>τ</sup>''' in Eq. (41) regarding to ''m''<sub>c</sub> contact pairs, respectively. The mapping '''F'''<sup>G</sup> represents the calculation of '''d<sup>n</sup>''' and −'''d<sup>τ</sup>''' for a given ('''p<sub>n</sub>''', '''p<sub>τ</sub>'''). Once the value of ('''p<sub>n</sub>''', '''p<sub>τ</sub>''') is given, the increment displacements of all components of the water seal system can be resolved based on Eq. (23) and Eq. (32), and then '''d<sup>n</sup>''' and −'''d<sup>τ </sup>'''can be calculated based on Eq. (36) and Eq. (39). |
| + | |||
| + | Eq. (43) is called as the global variational inequality for the problem, which is resolved by using the Extra-gradient method. For a better understanding of the Extra-gradient method, an important definition and a proposition in VI theory are introduced as follows. | ||
| + | |||
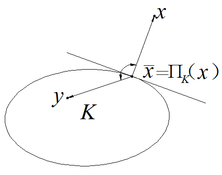
| + | '''Definition 3 (Euclidean projector) '''Let''' ''' ''K'' be''' '''a convex subset of ''R<sup>n</sup>''. It is well known from convex analysis that for every vector '''x'''∈''R''<sup>n</sup> there is a unique vector <math>\boldsymbol{\overline{x}}\in K</math> that is closet to '''x''' in the Euclidean norm, as shown in Fig. 5. This closet vector <math>\boldsymbol{\overline{x}}</math> is called the Euclidean projector of '''x''' onto ''K'' and denoted by <math>{\Pi }_K\left(\boldsymbol{x}\right)</math> . The mapping <math>{\Pi }_K�\boldsymbol{x}\mapsto {\Pi }_K\left(\boldsymbol{x}\right)</math> is called the Euclidean projector onto'' K''. | ||
| + | |||
| + | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | ||
| + | [[Image:Review_990962974820-image53.png|222px]] </div> | ||
| + | |||
| + | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | ||
| + | <span style="text-align: center; font-size: 75%;">'''Figure 5,''' The projection of a point onto a closed convex</span></div> | ||
| + | |||
| + | '''Proposition 1. '''Let <math>K\subset R^n</math> ''' '''be a closed convex and <math>\boldsymbol{F}:K\rightarrow R^n</math> be arbitrary. A point '''x'''∈''K'' is a solution of <math>VI\left(K,\boldsymbol{F}\right)</math> if and only if | ||
| + | |||
| + | {| class="formulaSCP" style="width: 100%; text-align: center;" | ||
| + | |- | ||
| + | | | ||
| + | {| style="text-align: center; margin:auto;" | ||
| + | |- | ||
| + | | ''' ''' <math>\boldsymbol{F}_K^{nat}\left(\boldsymbol{x}\right)=</math><math>\boldsymbol{x}-{\Pi }_K\left(\boldsymbol{x}-\boldsymbol{F}\left(\boldsymbol{x}\right)\right)=</math><math>0</math> ''' ''' | ||
| + | |} | ||
| + | | style="width: 5px;text-align: right;white-space: nowrap;" | (44) | ||
| + | |} | ||
| + | |||
| + | |||
| + | where <math>\boldsymbol{F}_K^{nat}\left(\boldsymbol{x}\right)</math> is called the natural map associated with ''K''; <math>{\Pi }_K\left(\boldsymbol{x}\right)</math> is the Euclidean projector. | ||
| + | |||
| + | In the resolution of ''VI'', various projection methods have been proposed based on Proposition 1, in which the Extra-gradient method is most widely acceptable[20]. The whole computation process of the Extra-gradient method is described below. | ||
| + | |||
| + | ==Algorithm Extra-Gradient Method== | ||
| + | |||
| + | Step 0. Set <math>{\beta }_0\mbox{=}1.0</math> , <math>{\eta }_1,{\eta }_2\in \left(0,1\right)</math> and <math>{\eta }_1<{\eta }_2</math> , <math>x^0\in K</math> , ''k'' = 0, error limit ''ε'' | ||
| + | |||
| + | Step 1. <math>{\boldsymbol{\tilde{x}}}^k={\Pi }_K\left(\boldsymbol{x}^k-\right. </math><math>\left. {\beta }_k\boldsymbol{F}\left(\boldsymbol{x}^k\right)\right)</math> , if <math>{\Vert \boldsymbol{x}^k-{\boldsymbol{\tilde{x}}}^k\Vert }_{\infty }\geq \epsilon </math> , go to step 2. | ||
| + | |||
| + | Step 2. <math>r^k=\frac{{\beta }_k\Vert \boldsymbol{F}\left(\boldsymbol{x}^k\right)-\boldsymbol{F}\left({\boldsymbol{\tilde{x}}}^k\right)\Vert }{\Vert \boldsymbol{x}^k-{\boldsymbol{\tilde{x}}}^k\Vert }</math> | ||
| + | |||
| + | while <math>r^k>{\eta }_2</math> , <math>{\beta }_k\mbox{=}{\beta }_k\times 0.5</math> | ||
| + | |||
| + | <math>{\boldsymbol{\tilde{x}}}^k={\Pi }_K\left(\boldsymbol{x}^k-\right. </math><math>\left. {\beta }_k\boldsymbol{F}\left(\boldsymbol{x}^k\right)\right)</math> , <math>r^k=\frac{{\beta }_k\Vert \boldsymbol{F}\left(\boldsymbol{x}^k\right)-\boldsymbol{F}\left({\boldsymbol{\tilde{x}}}^k\right)\Vert }{\Vert \boldsymbol{x}^k-{\boldsymbol{\tilde{x}}}^k\Vert }</math> | ||
| + | |||
| + | end (while) | ||
| + | |||
| + | if <math>r^k<{\eta }_1</math> , <math>{\beta }_k\mbox{=}{\beta }_k\times 1.5</math> . | ||
| + | |||
| + | Step 3. <math>\boldsymbol{x}^{k+1}={\boldsymbol{\tilde{x}}}^k</math> , <math>{\beta }_{k+1}={\beta }_k</math> , and <math>k=k+1</math> , go to Step 1. | ||
| + | |||
| + | In this study, the parameters in the Extra-Gradient Method algorithm are set as ''ε''=0.00001, ''η''<sub>1</sub>=0.4 and ''η''<sub>2</sub>=0.9. More details of the Extra-gradient method can be referred to the monograph[20] by Facchinei and Pang and the article[21] by Jiang et al. | ||
=6 Performance analysis for the expansion water seal using the proposed method= | =6 Performance analysis for the expansion water seal using the proposed method= | ||
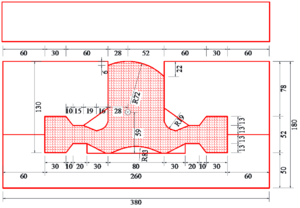
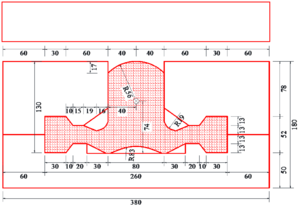
| − | According to the requirements of the steel gate design for a planned hydropower station located in the downstream of the Jinsha River in southwest China, the performance analysis is implemented for two optional expansion water seals | + | According to the requirements of the steel gate design for a planned hydropower station located in the downstream of the Jinsha River in southwest China, the performance analysis is implemented for two optional expansion water seals, the geometries of which are illustrated in Fig. 6. It can be observed that the main difference between the two options is the shape of their seal heads. |
| + | |||
| + | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | ||
| + | |||
| + | {| | ||
| + | |- | ||
| + | | [[Image:Review_990962974820-image76.png|300px]] | ||
| + | | [[Image:Review_990962974820-image77.png|center|300px]] | ||
| + | |} | ||
| + | </div> | ||
| + | |||
| + | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | ||
| + | <span style="text-align: center; font-size: 75%;">(a) Option A (b) Option B </span></div> | ||
| + | |||
| + | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | ||
| + | <span style="text-align: center; font-size: 75%;">'''Figure 6,''' The geometries of two optional expansion water seals (unit: mm)</span></div> | ||
| + | |||
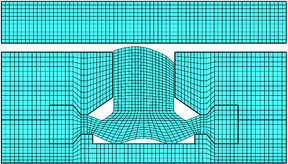
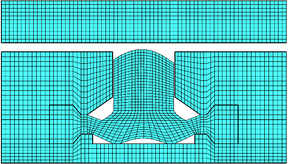
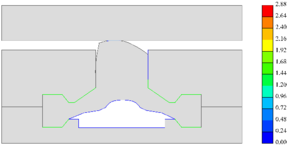
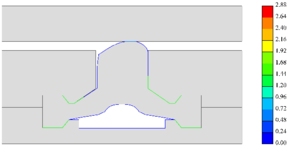
| + | The proposed method is employed in the simulation of the deformation of the two options. And their IGA discretization models are plotted in Fig.7. Performance comparison is executed in terms of the leakproofness of the back cavity, the contact between the seal head and the stop panel as well as the offset of the seal head. Finally, a better option is recommended after a comprehensive consideration. | ||
<div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | ||
| Line 716: | Line 786: | ||
{| | {| | ||
|- | |- | ||
| − | | [[Image: | + | | [[Image:Review_990962974820-image78-c.png|288px]] |
| − | | [[Image: | + | | [[Image:Review_990962974820-image79-c.png|center|288px]] |
|} | |} | ||
</div> | </div> | ||
<div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | ||
| − | (a) Option A, (b) Option B</div> | + | <span style="text-align: center; font-size: 75%;">(a) Option A, (b) Option B</span></div> |
<div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | ||
| − | '''Figure | + | <span style="text-align: center; font-size: 75%;">'''Figure 7,''' The IGA discretization models for two optional expansion water seals</span></div> |
The two options are both made of LD-19 rubber, which is commonly used for the expansion water seal in hydraulic power stations such as Three Gorges Project. Their values of ''C''<sub>10</sub>, ''C''<sub>01</sub>, and ''C''<sub>11</sub> in Eq. (4) have been measured by Liu et al.[3], which are 1.1505, -0.3286 and 0.0816, respectively. The steel plates have physical properties: Young’s modulus ''E'' = 2.07×10<sup>5</sup> MPa, Poisson’s ratio ν = 0.3. Referring to the design code, the friction coefficient ''μ'' is taken as 0.60 for the contact between the water seal and the steel plate. | The two options are both made of LD-19 rubber, which is commonly used for the expansion water seal in hydraulic power stations such as Three Gorges Project. Their values of ''C''<sub>10</sub>, ''C''<sub>01</sub>, and ''C''<sub>11</sub> in Eq. (4) have been measured by Liu et al.[3], which are 1.1505, -0.3286 and 0.0816, respectively. The steel plates have physical properties: Young’s modulus ''E'' = 2.07×10<sup>5</sup> MPa, Poisson’s ratio ν = 0.3. Referring to the design code, the friction coefficient ''μ'' is taken as 0.60 for the contact between the water seal and the steel plate. | ||
| Line 731: | Line 801: | ||
==6.1 The free expansion of the water seal head== | ==6.1 The free expansion of the water seal head== | ||
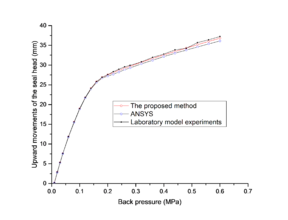
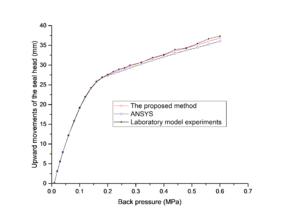
| − | The free expansion of the water seal head, that is, the upward movement of the seal head without the effect of the water stop panel and the reservoir water pressure, is an important reference value in determining the width of the gap between the pressing plate and the water stop panel. By using the proposed method, the deformations of the two optional expansion water seals only suffered, when the back pressures are investigated, and the upward movements of the water seal head are measured. To verify the validity of the proposed method, the resulted movements are compared with the results of the laboratory model experiments[7] and the results of traditional FEM. The traditional FEM analysis is accomplished by ANSYS, and the established model in ANSYS has an equal number of elements to the IGA model in Fig. | + | The free expansion of the water seal head, that is, the upward movement of the seal head without the effect of the water stop panel and the reservoir water pressure, is an important reference value in determining the width of the gap between the pressing plate and the water stop panel. By using the proposed method, the deformations of the two optional expansion water seals only suffered, when the back pressures are investigated, and the upward movements of the water seal head are measured. To verify the validity of the proposed method, the resulted movements are compared with the results of the laboratory model experiments[7] and the results of traditional FEM. The traditional FEM analysis is accomplished by ANSYS, and the established model in ANSYS has an equal number of elements to the IGA model in Fig.7 for an objective comparison. The upward movements of the water seal head resulted by the proposed method, ANSYS, and the laboratory model experiments are all plotted in Fig.8. |
<div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | ||
| Line 737: | Line 807: | ||
{| | {| | ||
|- | |- | ||
| − | | [[Image: | + | | [[Image:Review_990962974820-image80-c.png|288px]] |
| − | | [[Image: | + | | [[Image:Review_990962974820-image81-c.png|center|288px]] |
|} | |} | ||
</div> | </div> | ||
| Line 746: | Line 816: | ||
<div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | ||
| − | <span style="text-align: center; font-size: 75%;">'''Figure | + | <span style="text-align: center; font-size: 75%;">'''Figure 8,''' Free expansion results for two optional expansion water seals</span></div> |
| − | As Fig. | + | As Fig.8 shows, the variation tendencies of the upward movements on the back pressure resulted by the proposed method and ANSYS are consistent with the results of the model experiments. The gap between the experiment results and the numerical simulation results becomes larger with the back pressure increasing. However, the result of the proposed method are more close to the experiment results than that of ANSYS. The peak value of the difference between the experiment results and the results of the proposed method is smaller than 0.50 mm, while the peak value of the difference between the experiment results and the results of ANSYS exceeds 1.0 mm. Therefore, the new method proposed in this study is effective in the numerical simulation of the expansion water seal and has a higher precision than the traditional FEM. |
When the two options are suffering the same back pressure, a little difference between their results appears, indicating that the shape of the water seal head imposes no influence on the free expansion of the water seal head. Upward movement of the water seal head increases with an increasing back pressure, which apparently presents a nonlinear feature and can be described as the following four stages. In the first stage, the back pressure is less than 0.01 MPa and the upward movements are near zero. In the second stage, the back pressure rises from 0.02 MPa to 0.14 MPa and the upward movements appear to be increased dramatically. The upward movements at the end of the second stage arrive at 65.60% and 65.36% of the total upward movements for Option A and Option B, respectively. In the third stage, the back pressure rises from 0.15 MPa to 0.18 MPa and the slopes of the upward movement curves are becoming smaller, which can be considered as a transition stage. In the fourth stage, the back pressure is greater than 0.18 MPa and the upward movements present a linear increase with a gentle slope. | When the two options are suffering the same back pressure, a little difference between their results appears, indicating that the shape of the water seal head imposes no influence on the free expansion of the water seal head. Upward movement of the water seal head increases with an increasing back pressure, which apparently presents a nonlinear feature and can be described as the following four stages. In the first stage, the back pressure is less than 0.01 MPa and the upward movements are near zero. In the second stage, the back pressure rises from 0.02 MPa to 0.14 MPa and the upward movements appear to be increased dramatically. The upward movements at the end of the second stage arrive at 65.60% and 65.36% of the total upward movements for Option A and Option B, respectively. In the third stage, the back pressure rises from 0.15 MPa to 0.18 MPa and the slopes of the upward movement curves are becoming smaller, which can be considered as a transition stage. In the fourth stage, the back pressure is greater than 0.18 MPa and the upward movements present a linear increase with a gentle slope. | ||
| Line 756: | Line 826: | ||
==6.2 The leakproofness of the back cavity== | ==6.2 The leakproofness of the back cavity== | ||
| − | After the assembly of the water seal system, the leakproofness of the back cavity is dominated by the contacts between the two water seal wings and the pressing plates and the bed plate. If the contact stress is greater than the back pressure, the back cavity is considered to have a satisfactory leakproofness. According to the engineering design scheme, the reservoir water pressure acting on the expansion water seal is 0.2 MPa, which means that the steel gate suffers the hydraulic head of 20 m. The working back pressure is 0.4 MPa. The width of gap between the pressing plate and the water stop panel has been set as 25 mm. The deformations of two optional expansion water seals under the above conditions are investigated by using the proposed method, and the results of deformations and stresses are plotted in Fig. | + | After the assembly of the water seal system, the leakproofness of the back cavity is dominated by the contacts between the two water seal wings and the pressing plates and the bed plate. If the contact stress is greater than the back pressure, the back cavity is considered to have a satisfactory leakproofness. According to the engineering design scheme, the reservoir water pressure acting on the expansion water seal is 0.2 MPa, which means that the steel gate suffers the hydraulic head of 20 m. The working back pressure is 0.4 MPa. The width of gap between the pressing plate and the water stop panel has been set as 25 mm. The deformations of two optional expansion water seals under the above conditions are investigated by using the proposed method, and the results of deformations and stresses are plotted in Fig.9. |
<div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | ||
| Line 762: | Line 832: | ||
{| | {| | ||
|- | |- | ||
| − | | [[Image: | + | | [[Image:Review_990962974820-image82-c.png|288px]] |
| − | | [[Image: | + | | [[Image:Review_990962974820-image83-c.png|center|288px]] |
|} | |} | ||
</div> | </div> | ||
| Line 774: | Line 844: | ||
{| | {| | ||
|- | |- | ||
| − | | [[Image: | + | | [[Image:Review_990962974820-image84-c.png|288px]] |
| − | | [[Image: | + | | [[Image:Review_990962974820-image85-c.png|center|288px]] |
|} | |} | ||
</div> | </div> | ||
| Line 783: | Line 853: | ||
<div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | ||
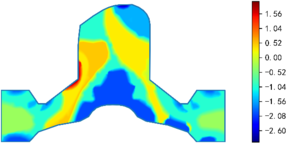
| − | <span style="text-align: center; font-size: 75%;">'''Figure | + | <span style="text-align: center; font-size: 75%;">'''Figure 9,''' Results of deformations and stresses for two optional expansion water seals</span></div> |
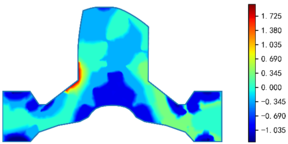
Option A is investigated in the first place. Under the prescribed working conditions, the peak value of the principal stress ''σ''<sub>1</sub> is 1.73 MPa, far less than LD-19 rubber’s break strength 7.64 MPa. Regarding the contact between the water seal wings and the adjacent plates, the peak value of the stress is 2.03 MPa, and the average value is about 1.08 MPa, which is far more than the working back pressure 0.40 MPa. Thus, the leakproofness of the back cavity is satisfied by Option A. | Option A is investigated in the first place. Under the prescribed working conditions, the peak value of the principal stress ''σ''<sub>1</sub> is 1.73 MPa, far less than LD-19 rubber’s break strength 7.64 MPa. Regarding the contact between the water seal wings and the adjacent plates, the peak value of the stress is 2.03 MPa, and the average value is about 1.08 MPa, which is far more than the working back pressure 0.40 MPa. Thus, the leakproofness of the back cavity is satisfied by Option A. | ||
| Line 789: | Line 859: | ||
Then, Option B is investigated. The peak value of the principal stress ''σ''<sub>1</sub> is 1.56 MPa in the water seal under the same working conditions. The peak value of the contact stress is 2.01 MPa, and the mean value is about 1.09 MPa. In this case, the expansion water seal will not be broken and the leakproofness of the back cavity is also satisfied. | Then, Option B is investigated. The peak value of the principal stress ''σ''<sub>1</sub> is 1.56 MPa in the water seal under the same working conditions. The peak value of the contact stress is 2.01 MPa, and the mean value is about 1.09 MPa. In this case, the expansion water seal will not be broken and the leakproofness of the back cavity is also satisfied. | ||
| − | + | In short, both Option A and Option B can satisfy the leakproofness of the back cavity. Moreover, there is a little difference in stresses regarding to the contacts between their wings and the adjacent plates, which can be attributed to the fact that the water seal wings of the two options are identical. | |
==6.3 The effectiveness to seal up the reservoir water== | ==6.3 The effectiveness to seal up the reservoir water== | ||
| Line 795: | Line 865: | ||
The stress in terms of the contact between the water seal head and the water stop panel is a critical quantity to assess the effectiveness of the water seal to seal up the reservoir water. In general, the back pressure required for successfully sealing up the reservoir water should be determined under an assumed gap width. | The stress in terms of the contact between the water seal head and the water stop panel is a critical quantity to assess the effectiveness of the water seal to seal up the reservoir water. In general, the back pressure required for successfully sealing up the reservoir water should be determined under an assumed gap width. | ||
| − | First of all, taking the back pressure and the reservoir water into account, the contact between the seal head and the stop panel is investigated for a given gap width. To reveal the variation law of the contact stress and width, it is assumed that the back pressure varies from 0.10 MPa to 0.60 MPa, and the water pressure varies from 0.05 MPa to 0.30 MPa. The deformation of the expansion water seal is simulated, and the stress and width of contact between the seal head and the stop panel are recorded. Take Option A with a 10 mm gap width as an example, the mean value of contact stress and the contact width vary as Fig. | + | First of all, taking the back pressure and the reservoir water into account, the contact between the seal head and the stop panel is investigated for a given gap width. To reveal the variation law of the contact stress and width, it is assumed that the back pressure varies from 0.10 MPa to 0.60 MPa, and the water pressure varies from 0.05 MPa to 0.30 MPa. The deformation of the expansion water seal is simulated, and the stress and width of contact between the seal head and the stop panel are recorded. Take Option A with a 10 mm gap width as an example, the mean value of contact stress and the contact width vary as Fig.10 shows. |
<div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | ||
| Line 801: | Line 871: | ||
{| | {| | ||
|- | |- | ||
| − | | [[Image: | + | | [[Image:Review_990962974820-image86-c.png|288px]] |
| − | | [[Image: | + | | [[Image:Review_990962974820-image87-c.png|center|288px]] |
|} | |} | ||
</span></div> | </span></div> | ||
| Line 810: | Line 880: | ||
<div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | ||
| − | <span style="text-align: center; font-size: 75%;">'''Figure | + | <span style="text-align: center; font-size: 75%;">'''Figure 10,''' The variation of the contact stress and width with the back pressure and the reservoir water pressure</span></div> |
Both the mean value of contact stress and the contact width rise with an increasing back pressure when the reservoir water pressure is fixed. While, they both decrease with an increasing reservoir water pressure, when the back pressure remains unchanged. In case that the water seal head contacts the water stop panel, the results comparison verifies that the back pressure has a more significant effect on the contact stress and the contact width than the reservoir water pressure. | Both the mean value of contact stress and the contact width rise with an increasing back pressure when the reservoir water pressure is fixed. While, they both decrease with an increasing reservoir water pressure, when the back pressure remains unchanged. In case that the water seal head contacts the water stop panel, the results comparison verifies that the back pressure has a more significant effect on the contact stress and the contact width than the reservoir water pressure. | ||
| Line 816: | Line 886: | ||
Although the effect of the reservoir water pressure on the stress and width of contact is relatively small, the reservoir water pressure is a key quantity in determining the threshold value required for the back pressure. If the reservoir water pressure increases, a larger threshold value is required for the back pressure to seal up the reservoir water. Once the water seal head contacts the stop panel, the contact stress will be greater than the reservoir water pressure and be mainly dominated by the back pressure. Therefore, the threshold value required for the back pressure should be determined based on the reservoir water pressure. | Although the effect of the reservoir water pressure on the stress and width of contact is relatively small, the reservoir water pressure is a key quantity in determining the threshold value required for the back pressure. If the reservoir water pressure increases, a larger threshold value is required for the back pressure to seal up the reservoir water. Once the water seal head contacts the stop panel, the contact stress will be greater than the reservoir water pressure and be mainly dominated by the back pressure. Therefore, the threshold value required for the back pressure should be determined based on the reservoir water pressure. | ||
| − | A general criterion that the contact between the water seal head and the water stop panel results in the contact stress greater than the reservoir water pressure is used to determine the threshold value required for the back pressure. Through numerical simulation, the threshold values required for the back pressure are acquired for different combinations of gap width and reservoir water pressure, which are plotted in Fig. | + | A general criterion that the contact between the water seal head and the water stop panel results in the contact stress greater than the reservoir water pressure is used to determine the threshold value required for the back pressure. Through numerical simulation, the threshold values required for the back pressure are acquired for different combinations of gap width and reservoir water pressure, which are plotted in Fig. 11. |
<div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | ||
| − | [[Image: | + | [[Image:Review_990962974820-image88-c.png|372px]] </div> |
<div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | ||
| − | <span style="text-align: center; font-size: 75%;">'''Figure | + | <span style="text-align: center; font-size: 75%;">'''Figure 11,''' Threshold values of the back pressure required for the two options </span></div> |
Results show that the threshold values of the back pressure required for the two options are almost indistinguishable under the same reservoir water pressure and gap width. Both the increase of the reservoir water pressure and the gap width result in a rising threshold value of the required back pressure. However, when the gap width arrives at 30 mm, the threshold value of the back pressure will be greater than the prescribed working back pressure 0.40 MPa. Under a gap width of 25 mm, the threshold value of the back pressure are less than the prescribed working back pressure, even if the reservoir water pressure increases to 0.30 MPa. Thus, it is reasonable to prescribe the gap width as 25 mm. In conclusion, there is little difference between the two optional expansion water seals in their ability to seal up the reservoir water, and both of them can work efficiently by using the prescribed gap width. | Results show that the threshold values of the back pressure required for the two options are almost indistinguishable under the same reservoir water pressure and gap width. Both the increase of the reservoir water pressure and the gap width result in a rising threshold value of the required back pressure. However, when the gap width arrives at 30 mm, the threshold value of the back pressure will be greater than the prescribed working back pressure 0.40 MPa. Under a gap width of 25 mm, the threshold value of the back pressure are less than the prescribed working back pressure, even if the reservoir water pressure increases to 0.30 MPa. Thus, it is reasonable to prescribe the gap width as 25 mm. In conclusion, there is little difference between the two optional expansion water seals in their ability to seal up the reservoir water, and both of them can work efficiently by using the prescribed gap width. | ||
| Line 831: | Line 901: | ||
<div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | ||
| − | [[Image: | + | [[Image:Review_990962974820-image89-c.png|372px]] </div> |
<div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | ||
| − | <span style="text-align: center; font-size: 75%;">'''Figure | + | <span style="text-align: center; font-size: 75%;">'''Figure 12,''' Horizontal displacement of the water seal head for the two options</span></div> |
| − | The horizontal displacements at the reference point are recorded for the two options and plotted in Fig. | + | The horizontal displacements at the reference point are recorded for the two options and plotted in Fig. 12 in case that the gap width takes the prescribed value 25 mm. To reveal the variation of the offset, the reservoir water pressure is assumed to vary from 0.20 MPa to 0.30 MPa, and the back pressure varies from the corresponding threshold value to the prescribed working back pressure 0.40 MPa. Increasing reservoir water pressure induces a larger horizontal displacement, while the increase of the back pressure results in a smaller horizontal displacement. In case of the same back pressure and the same reservoir water pressure, the horizontal displacement at the reference point of Option A are about 1 mm less than that of Option B. Considering that the maximum value of the horizontal displacement in Fig. 12 is about 7 mm, the difference is considerable. Thus, a conclusion can be drawn that Option A is better than Option B in terms of the deformation recovery capacity and working life. |
==6.5 The recommended option== | ==6.5 The recommended option== | ||
| Line 862: | Line 932: | ||
==Authors’ Contributions== | ==Authors’ Contributions== | ||
| − | Conceptualization, Zhou Yida; Formal analysis, Hu | + | Conceptualization, Zhou Yida; Formal analysis, Hu Jianke; Methodology, Hu Taoyong; Resources, Shi Shoujin; Software, Han Yifeng; Validation, Wang Jinkun; Visualization, Lou Yidan; Writing – original draft, Hou Tao. |
==This research received no funding.== | ==This research received no funding.== | ||
| Line 870: | Line 940: | ||
1.Li, C.H. Numerical analysis of water seal in gate under high pressure and its application in engineering [D]. Msc Thesis, School of Civil Engineering & Architectural Engineering, Wuhan University, Wuhan, Hubei, P. R. China, '''2005'''. | 1.Li, C.H. Numerical analysis of water seal in gate under high pressure and its application in engineering [D]. Msc Thesis, School of Civil Engineering & Architectural Engineering, Wuhan University, Wuhan, Hubei, P. R. China, '''2005'''. | ||
| − | 2.Chen, W.Y.; Ou, Z.G.; Liu, L.H.; Wang, D. Research on the hermetic capability and water-stop criterion [J]''. Journal of Hydroelectric Engineering''. '''2010''', 05, 232-236. | + | 2.Chen, W.Y.; Ou, Z.G.; Liu, L.H.; Wang, D. Research on the hermetic capability and water-stop criterion [J]''. Journal of Hydroelectric Engineering''. '''2010''', 05, 232-236. |
3.Liu, L.H.; Wang, D.; Fang, H.M.; Sun, D.X.; Wei, X.B.; Ou, Z.G. Nonlinear calculation of the preload pressure of gate water seal with Rivlin model[J]''. Journal of Hydroelectric Engineering''. '''2011''', 05, 170-174. | 3.Liu, L.H.; Wang, D.; Fang, H.M.; Sun, D.X.; Wei, X.B.; Ou, Z.G. Nonlinear calculation of the preload pressure of gate water seal with Rivlin model[J]''. Journal of Hydroelectric Engineering''. '''2011''', 05, 170-174. | ||
| − | 4.Liu, L.H.; Wang, D.; Ou, Z.G.; Wei, X.B. Nonlinear calculation on the pressure-filled telescopic water seal based on the Ogden formula[J]''. Chinese Journal of Solid Mechanics''. '''2011''', 01, 102-107. | + | 4.Liu, L.H.; Wang, D.; Ou, Z.G.; Wei, X.B. Nonlinear calculation on the pressure-filled telescopic water seal based on the Ogden formula[J]''. Chinese Journal of Solid Mechanics''. '''2011''', 01, 102-107. |
5.Tan, X.W.; Wang, Z.Z.; Yu, X.K.; Liang, L.J.; Liu, Q.H. Hyperelasticity and viscoelasticity of rubber water stop material[J]''. Journal of Vibration and Shock''. '''2014''', 19, 97-103. | 5.Tan, X.W.; Wang, Z.Z.; Yu, X.K.; Liang, L.J.; Liu, Q.H. Hyperelasticity and viscoelasticity of rubber water stop material[J]''. Journal of Vibration and Shock''. '''2014''', 19, 97-103. | ||
| Line 880: | Line 950: | ||
6.Ding, Z.P.; Zeng, J.X.; Lin, S.; Huang, Y.J. Structure strength analysis and parameter optimization of rubber spring[J]''. Journal of Vibration and Shock''. '''2019''', 12, 246-251. | 6.Ding, Z.P.; Zeng, J.X.; Lin, S.; Huang, Y.J. Structure strength analysis and parameter optimization of rubber spring[J]''. Journal of Vibration and Shock''. '''2019''', 12, 246-251. | ||
| − | 7.Yang, B. Deformation calculation theory and application research of rubber water seal [D]. Ph.D. Thesis, School of Civil Engineering & Architectural Engineering, Wuhan University, Wuhan, Hubei, P.R.China, '''2014'''. | + | 7.Yang, B. Deformation calculation theory and application research of rubber water seal [D]. Ph.D. Thesis, School of Civil Engineering & Architectural Engineering, Wuhan University, Wuhan, Hubei, P.R.China, '''2014'''. |
| − | 8.Xiong, W.; Liu, L.H. Nonlinear simulation analysis of seal component of high press gate [J]''. Engineering Journal of Wuhan University''. '''2011''', 01, 66-68. | + | 8.Xiong, W.; Liu, L.H. Nonlinear simulation analysis of seal component of high press gate [J]''. Engineering Journal of Wuhan University''. '''2011''', 01, 66-68. |
9.Hu, J.K.; Chen, J.F.; Wang, Z.N.; Hu, B.W.; Wang, J.; Hao, N.N.; Cai, K.; Hu, M.X. Nonlinear simulation of high head expansion water seal based on the mooney-rivlin model[J]''. China Rural Water and Hydropower''. '''2022''', 04, 215-220. | 9.Hu, J.K.; Chen, J.F.; Wang, Z.N.; Hu, B.W.; Wang, J.; Hao, N.N.; Cai, K.; Hu, M.X. Nonlinear simulation of high head expansion water seal based on the mooney-rivlin model[J]''. China Rural Water and Hydropower''. '''2022''', 04, 215-220. | ||
| − | 10.Xue, X.X.; Wu Y.H.; Li Z.C.; Cao Y.N.; Zhang D. Study on deformation and sealing performance of p-type water seal for high-head plane gate[J]. ''Journal of Hydroelectric Engineering''. '''2012''', 01, 56-61. | + | 10.Xue, X.X.; Wu Y.H.; Li Z.C.; Cao Y.N.; Zhang D. Study on deformation and sealing performance of p-type water seal for high-head plane gate[J]. ''Journal of Hydroelectric Engineering''. '''2012''', 01, 56-61. |
11.Hughes, T.; Cottrell J.A.; Bazilevs Y. Isogeometric analysis: cad, finite elements, NURBS, exact geometry and mesh refinement [J]. ''Computer Methods in Applied Mechanics & Engineering''. '''2005''', 39-41, 4135-4195. | 11.Hughes, T.; Cottrell J.A.; Bazilevs Y. Isogeometric analysis: cad, finite elements, NURBS, exact geometry and mesh refinement [J]. ''Computer Methods in Applied Mechanics & Engineering''. '''2005''', 39-41, 4135-4195. | ||
| Line 922: | Line 992: | ||
27.Wriggers P. Computational Contact Mechanics [M]. ''Wiley & Sons'': Chichester, West Sussex, United Kingdom, | 27.Wriggers P. Computational Contact Mechanics [M]. ''Wiley & Sons'': Chichester, West Sussex, United Kingdom, | ||
| − | 28.Agrawal V.; Gautam S. S. Varying-order NURBS discretization: an accurate and efficient method for isogeometric analysis of large deformation contact problems [J]. ''Computer Methods in Applied Mechanics & Engineering''. '''2020,''' 367, 113125. | + | <span id='_GoBack'></span>28.Agrawal V.; Gautam S. S. Varying-order NURBS discretization: an accurate and efficient method for isogeometric analysis of large deformation contact problems [J]. ''Computer Methods in Applied Mechanics & Engineering''. '''2020,''' 367, 113125. |
Revision as of 05:18, 16 November 2022
Abstract: In this study, IGA is introduced into the performance analysis of the expansion water seal for an exact representation of its complex geometrical shape. Firstly, the incremental equilibrium equations used in the large deformation analysis are derived for the IGA discretization model based on the updated Lagrangian formulation. The unknown contact forces are directly involved in the equilibrium equations, which results in a simple expression. Then, through the investigation of the contact conditions, the normal and tangential contact forces are verified to be the solutions of two box-constrained variational inequalities representing the normal and tangential contact conditions, respectively. Furthermore, the incremental equilibrium equations for all components of the water seal system and the variational inequalities for all contacts between the components are assembled together and reformulated as a global variational inequality, which is resolved by using the Extra-gradient method. Ultimately, the new method is applied in the performance comparison of two optional expansion water seals, in which the capability and precision of the proposed method are investigated. Results verify that the proposed method is effective in the numerical simulation of the expansion water seal and has a higher precision than the traditional FEM under the same conditions.
Key words: expansion water seal; performance analysis; isogeometric analysis; frictional contact; variational inequality
1 Introduction
Developing clean energy plays an important role in pollution reduction and has been placed at the core of the environmental protection policy in a lot of countries. As a traditional clean energy, hydropower development has a long history, especially in China. The hydraulic steel gate is a key component in the hydropower station. Because the performance of the water seal directly determines the sealing effectiveness of the gate, reasonable and accurate evaluations of the performance of the water seal are essential in the hydraulic steel gate design. In the last two decades, a series of large hydropower stations, such as Wudongde, Baihetan, Xiluodu, and Xiajiaba projects, have been constructed in the downstream of the Jinsha River in China, which are typically featured with high pressure and large capacity. In this situation, the expansion water seal is verified to be more applicable than the conventional pre-compression water seal[1], thus it is extensively used in the gate now. As a consequence, the performance analysis of expansion water seal gained more attention in recent years.
Both model tests and numerical simulations were employed in the researches on the expansion water seal. To pursue a high reliability in terms of working performance of the expansion water seal, model tests were conducted for the hydraulic steel gate design in some large hydropower stations, e.g., Pubugou, Longtan and Laxiwa[2]. Although model tests have resolved the performance evaluation for these stations successfully, they are costly and time-consuming. Moreover, the results of a special model test may be wrong when the conditions change. Therefore, numerical simulations become more popular in performance analysis of expansion water seal recently.
Reasonability and reliability of numerical simulation come from the thorough knowledge on the mechanical properties of water seal material and the fundamental theories of numerical methods adopted. Expansion water seal is made of rubber, a typical hyperelastic material, which is marked by large deformation and incompressibility. An accurate constitutive model denoting the relation between the strain and stress in the expansion water seal is important to promise the precision of numerical results, which attracted many scholars’ devotion. Based on the test results of rubber material in laboratory, Mooney-Rivlin model[3]and Ogden model[4] were suggested for nonlinear analysis on expansion water seal, and the applicability of the two models were further investigated by Tan[5]. Considering that Mooney-Rivlin model is reliable to describe the stress-strain relation of rubber material, if the strain is no more than 1.50[6], it gains more popularity than Ogden model in previous researches[7, 8] due to its simple expression. When Mooney-Rivlin model is employed, increasing the number of parameters in the model will enhance the precision of stress-strain relation adopted, but damage the computational efficiency. The optimal number of parameters in model is investigated by Hu[9] to reach a balance between the precision and the computational efficiency, and Mooney-Rivlin model with three parameters is recommended ultimately. Generally speaking, scholars have profound acquaintance with the mechanical properties of water seal materials after abundant explorations.
Up to now, the finite element method (FEM) is commonly used in the existing numerical simulation of water seal, for the commercial FEM software is matured in simulating the material nonlinearity caused by the constitutive model of rubber material, the geometric nonlinearity caused by large deformation, and the nonlinear boundary conditions due to the contact between water seal and the steel plates[10]. However, the structure complexity of the expansion water seal leads the modeling to be complicated and time-consuming when using traditional FEM. More importantly, the geometry difference between FEM model and the actual water seal undoubtedly affects the accuracy of the results, albeit it is subtle. Therefore, a numerical method with more reliability and high efficiency is expected to replace the traditional FEM for a better analysis on the performance of water seal.
Isogeometric analysis (IGA), a novel numerical method proposed by Hughes et al.[11], originally aimed to bridge the gap between computer aided design (CAD) and finite element analysis (FEA). Because the nonuniform rational B-splines, which are widely used in most CAD tools, are adopted as basis functions, IGA is capable of representing the exact geometry of engineering structures. Moreover, the conventional FEM uses Lagrange polynomials feature C0 continuity at nodes regardless of their order, while IGA with spline functions of order p has the ability to provide Cp−1 continuity at all non-multiple knots. This means that IGA shows better robustness and accuracy compared to the conventional FEM for the same amount of degrees of freedom[12]. Owing to these significant advantages, IGA served as a hot topic in engineering analysis since its birth and were adopted in the resolution of diverse problems in structural mechanics, solid mechanics, and fluid mechanics. Developments of IGA theory and the related computer implementation until 2015 were reviewed by Nguyen et al.[13]. Meanwhile, numerous enhancements have been made to improve the ability of IGA to optimize the engineering structure, the progresses of which were reviewed by Wang et al.[14] in 2018 and Gao et al.[15] in 2020. IGA could play an important role in the performance analysis of water seal. On the one hand, the complex shape of the water seal can be represented exactly in IGA. On the other hand, the capacity of IGA to treat the incompressibility in case of large deformation had been fully developed[16]. Thus, IGA is employed in this article to investigate the performance of expansion water seal in diverse conditions.
However, as mentioned above, the contact between the water seal and the steel plates should be taken into account carefully when simulating the mechanical behavior of the water seal. A number of approaches, such as the interior method[17] and surface potentials method[18], had been proposed to model contact in IGA. These methods fall into two categories. The first type of method utilizes the classical penalty method to impose the contact conditions. In this case, the value of the penalty parameter is vital in the analyses but hard to be determined. While, the second type of method always adds the contact potential to the total potential analysis based on some assumptions, e.g., surface potentials and the third medium[19], in which the rationality of those assumptions should be further investigated. To avoid the demerit of the existing approaches, variational inequality (VI) theory[20] is introduced to formulate the contact conditions as variational inequalities, and the extra-gradient method[21]is used to solve the equations derived in the study. Considering that VI theory has been successfully used in the resolution of contact for a system of discrete bodies[22], the new approach is theoretical feasible to improve the ability of IGA in contact simulation.
The remainder of this study is organized as follows. Section 2 briefly explains how the expansion water seal works and presents the constitutive model of the expansion water seal. In Section 3, the basic theory of IGA is provided, and formulations for larger deformation problem are illustrated. In Section 4, VI theory is briefly given firstly, and then, the conditions regarding to the contacts between the expansion water seal and the steel plates are investigated, inducing two variational inequalities equivalent to the normal and tangential contact conditions, respectively. Section 5 presents how the proposed formulation to be resolved. In Section 6, an engineering example is simulated by using the proposed method, including a comprehensive analysis on all focused properties and a comparative analysis for two optional shapes of the water seal head. Section 7 concludes the paper.
2 A brief description of the expansion water seal and its constitutive model
2.1 Introduction of the expansion water seal
In the case that the expansion water seal is employed, the water seal system in the hydraulic steel gate is typically consisted of water stop panel, left pressing plate, right pressing plate, bed plate and the expansion water seal, as shown in Fig. 1. Domains of water stop panel, left pressing plate, right pressing plate, bed plate and the expansion water seal are denoted as ΩTP, ΩLP, ΩRP, ΩBP and ΩWS, respectively. It is noticed that the gaps between the components are enlarged in Fig.1 for a clear demonstration. Water stop panel, pressing plates and bed plate are made of steel, while the water seal is usually made of rubber. Through regulating the magnitude of back pressure, the deformation of the expansion water seal and the contact between the water seal and water stop panel are adjusted to seal up the reservoir water. When the hydraulic steel gate is to be closed, the back pressure is exerted on the expansion water seal by using a specialized water or air pressure installation, and then the expansion water seal deforms and moves upward. Back pressure will increase until the water seal contacts the water stop panel with the expected length and stress, which stuffs up the gap between the water stop panel and the pressing plate. Finally, the reservoir water is sealed up. Conversely, if the hydraulic steel gate is to be open, the back pressure is discharged gradually and the expansion water seal backtracks. The gap emerges and the reservoir water flows in the gap freely, which means that the force offered by the hoisting device to open the gate can be small.
The performance of the expansion water seal is always evaluated from the following aspects. At First, the back cavity formed by the expansion water seal and the bed plate is one critical section, the leakproofness of which directly impacts the operation of imposing a prescribed back pressure. Once the water seal system has been assembled, the stress magnitudes with regard to the contacts between the two water seal wings and the pressing plates and the bed plate are the key variables to estimate whether the leakproofness of the back cavity is satisfactory. Next, the stress magnitudes regarding to the contact between the water seal head and the water stop panel are the variables of the greatest importance to assess the effectiveness of the water seal to seal up the reservoir water, which varies with the width of the gap, the back pressure as well as the reservoir water pressure. Finally, the offset of the water seal head appears due to the singularity of the reservoir water flowing, which is always investigated for a better understanding on the wear of the water seal head. In summary, an expansion water seal should meet the specified requirements in case of prescribed back pressure and reservoir water pressure.
The expansion water seal has a much greater magnitude in the axis direction than on the cross section. Meanwhile, it suffers external loads having their directions parallel to its cross section and remaining unchanged in the axis direction. These mechanical features induce that the expansion water seal can be treated as a plane stress problem in numerical simulation.
2.2 The constitutive model for the expansion water seal
To simulate the performance of the expansion water seal reasonably, the constitutive model for the components of the water seal system should be determined in advance, in which the model for the water seal is a key point. Because the material of expansion water seal is rubber, Mooney-Rivlin model[23] gained more popularity in existing researches, which is retained in this study. Based on the assumption of phenomenological theory of continuum mechanics, the mechanical behavior of rubber is denoted by the strain energy per unit volume, due to its hyperelasticity and isotropy. And then, the derivations of the strain energy in terms of the strain components are the corresponding stress components. Here some fundamental formulations and notations are introduced briefly.
The strain energy W is always evaluated through Green strain invariants, I1, I2 and I3. Green strain invariants are defined as.
|
|
(1) |
In Eq. (1), λ1, λ2 and λ3 denote the elongation of a volume element along the three principle axes, respectively. It is noticed that I3 identically equals to one for the incompressible material. Therefore, W is only calculated by using I1 and I2, that is
|
|
(2) |
Then, based on the definitions in Eq. (1), Eq. (2) can be reformulated as the following polynomial by using the power series expansion method.
|
|
(3) |
where n is the order of polynomials, and Cij is the material parameters. A different n adopted in Eq. (3) indicates a different polynomial. Mooney-Rivlin models with two parameters, three parameters, five parameters and nine parameters were employed by Hu[9] in the numerical simulation of the expansion water seal, and the precisions of the results and the computational costs were compared. It was verified that Mooney-Rivlin model with three parameters had an accuracy close to that with five and nine parameters, while its computational cost was apparently lower. Thus, Mooney-Rivlin model with three parameters is used in this study, which actually sets n in Eq. (3) as one and has the formulation as follows.
|
|
(4) |
Furthermore, a hyperelastic constitutive model representing the nonlinear stress-strain relationship of the expansion water seal can be expressed by using the following incremental formulation
|
|
(5) |
in which Sij is the Kirchhoff stress tensor, εijis the Green strain tensor.
Last but not least, the material parameters Cijin Eq. (3) are usually determined by regression analysis on the experiment data of the uniaxial stress state test and pure shear test.
3 IGA for the large deformation problem
3.1 B-spline and NURBS basis functions
Although a series of new spline technologies[24-26] have been introduced into IGA, B-splines and nonuniform rational B-splines (NURBS) are still the most prevalent spline technologies in IGA at present. In B-splines, a knot vector Ξ ={ξ1, ξ2, …, ξm+p+1} is a sequence of nondecreasing real numbers in the parametric space, where m is the number of control points and p is the order of the spline curve. The interval [ξ1, ξm+p+1) is denoted as a patch, and the interval [ξi, ξi+1) is denoted as a span. Once a knot vector is available, B-spline basis functions can be recursively defined as
|
|
(6) |
and
|
|
(7) |
It is noticed that a knot in Ξ is permitted to repeat by augmenting Eq. (6) and Eq. (7) with a definition
|
|
(8) |
Denoting the multiplicity of the knots as k, the continuity of the B-spline basis functions between knot spans is Cp−k. For a better understanding, a quadratic example is presented in Fig. 2 for the knot vector Ξ = {ξ1, ξ2, ξ3, ξ4, ξ5, ξ6, ξ7, ξ8, ξ9, ξ10, ξ11} = {0, 0, 0, 1, 2, 3, 4, 4, 5, 5, 5}.
With the basis functions in hand, a B-spline curve can be constructed as their linear combination:
|
|
(9) |
in which P i∈Rd, i = 1, 2, …, m, are called as control points, and d is the dimension of the physical space.
B-spline surfaces and solids are the tensor product of univariate B-splines. Given a control net P i, j∈Rd, i = 1, 2, …, m, j = 1, 2, …, n, polynomial orders p and q, and knot vectors Ξ ={ξ1, ξ2, …, ξm+p+1}, and Θ ={η1, η2, …, ηn+q+1}, a tensor product B-spline surface is generated by
|
|
(10) |
where Ni, p(ξ) and Mj, q(η) are univariate B-spline basis functions of order p and q, corresponding to the knot vectors Ξ and Θ, respectively. Similar to B-spline surfaces, a tensor product B-spline solid can be defined if a control lattice P i, j, k, three polynomial orders, and three knot vectors are given.
Based on univariate B-spline basis functions, univariate NURBS basis functions can be defined by pairing a positive weight wiwith each basis function
|
|
(11) |
And a NURBS curve can be constructed as
|
|
(12) |
Then, the bivariate NURBS basis functions are obtained as
|
|
(13) |
And a NURBS surface results from
|
|
(14) |
Finally, the extension of Eq. (13) and Eq. (14) to the 3D situation induces a NURBS solid. It is noticed that B-splines can be considered as a special case of NURBS where the weights are all equal.
A series of important properties of NURBS basis functions (likewise for B-spines) is illustrated by taking Rij,pq(ξ, η) as an example. Firstly, throughout the patch [ξ1, ξm+p+1)× [η1, ηn+q+1), Rij,pq(ξ, η) is nonnegative. The second is the partition of unity all over the patch. The third is the local support, which means that Rij,pq(ξ, η) = 0 if (ξ, η) is outside the span domain of [ξi, ξi+p+1)× [ηj, ηj+q+1). The last one is the continuity that the interior of the knot span domain is continuous up to C∞, while the continuity between knot spans are Cp−k and Cq−lin which k and l denote the multiplicity along two directions, respectively.
3.2 Large deformation analysis using IGA with updated Lagrangian formulation
In this section, the formulations regarding to the expansion water seal is derived in the first place. Under the back pressure and the reservoir water pressure, the large deformation of the expansion water seal usually happens. In the conventional FEM, Total Lagrangian formulation and updated Lagrangian formulation were provided for large deformation analysis. Considering that the updated Lagrangian (U.L.) formulation is more applicable to the situation that the external loads vary with the body deformation, U.L. formulation is used for numerical analysis on the expansion water seal in this study. Thus, a large deformation analysis using IGA with U.L. formulation is demonstrated in this section. For a simple expression, the tensor notation is utilized in this section.
The incremental analysis is essential for the large deformation problems, which means that all physical quantities at time t are assumed to be known, and the quantities at time t+Δt are required to be solved. A pre-superscript is introduced to indicate the time when the physical quantities are measured, e.g., tuk is the displacement measured at time t. The principle of virtual displacement equivalent to the equilibrium condition required for the body at time t+Δt is formulated for the U.L. formulation as
|
|
(15) |
where tΔtSij and tΔtεij are the updated Kirchhoff stress tensor and the updated Green strain tensor, which are both defined referring to the configuration at time t. tΔtQ is the virtual work resulted by the external loads, which is calculated by
|
|
(16) |
in which Γt and Γc represent the part of the boundary where the water seal doesn’t contact the adjacent steel plates and the part of the boundary where the contact happens, respectively. fk denotes the known body force of the expansion water seal. tk is the known tractions on Γt, which is resulted by the back pressure or the reservoir water pressure. pk is the unknown contact forces on Γc, which comes from by the compression and the friction between the expansion water seal and the steel plates. Taking the water seal head in Fig. 3 as an example, the reservoir water pressure induces tk where no contact between the expansion water seal and the top plate happens, but the forces on the water seal are unknown at the boundary where the water seal contacts the top plate. Since the unknown contact forces are directly involved in Eq. (16), some additional formulations have to be augmented for the determining of pk, which will be illustrated in the next section.
The updated Kirchhoff stress tΔtSij is the summation of and the updated Kirchhoff stress increment ΔSij and the known Cauchy stress tτij, that is
|
|
(17) |
Considering that tεij is known, δtΔtεij is only determined by the updated Green stain increment Δεij. Δεij is the sum of the linear part ΔεijL and the nonlinear part ΔεijN, which can be computed as
|
|
(18) |
in which Δuk represents the incremental displacement during the time interval Δt. Substituting Eq. (17) and Eq. (18) into Eq. (15), we have
|
|
(19) |
Based on Eq. (5), the incremental stress-strain relation is written as
|
(20) |
in which Dijkl is the tensor denoting the constitutive relation. By ignoring the contribution of high-order terms, Eq. (19) can be further expressed as
|
|
(21) |
The domain of the expansion water seal ΩwsR2 can be discretized into a set of elements, that is, Ωws =∪Ωe. NURBS functions in Eq. (13) are used for the approximation of the displacement field t u e, the displacement increment Δu e, and the coordinates x e within each element as
|
|
(22) |
in which, t u e and t x e are the arrays containing the displacements and the coordinates of ne number of control points in an element at time t,Δu e is the array containing the displacement incremental of control points in an element within the time interval Δt. R(ξ, η) = [R1(ξ, η)I, R2(ξ, η)I, …, Rne(ξ, η)I] is a matrix of size 2 × 2ne with identity matrix I in R2. Here, R (ξ, η) is a simplified notation of Rij,pq(ξ, η) in Eq. (13), and ne denotes the total number of control points whose R (ξ, η) has local support in an element Ωe.
Combined Eq. (21) and Eq. (22), a matrix expression of the equilibrium equation can be obtained for an element Ωe as the following formulation.
|
|
(23) |
Here the superscript e represents the quantity being defined for an element Ωe. In Eq. (23),
|
|
(24) |
|
|
(25) |
|
|
(26) |
B L and B NL are given by
|
(27) |
|
|
(28) |
Matrices τ and τ′ associated with the Cauchy stress tensor t τ ij are given by
|
|
(29) |
|
|
(30) |
Finally,
|
|
(31) |
here, t = (tx, ty)T, p = (px, py)T and f = (fx, fy)T are the vector expressions for tk, pk and fk, respectively. There is no barrier to obtain the value of the body force f. However, the value of the contact force p is temporarily unknown. Furthermore, the boundaries Γt and Γc are uncertain, so the contribution of the known tractions to Qe is also an issue. The issues will be settled by introducing VI theory, which is demonstrated in the next section.
Besides the expansion water seal, the entire water seal system comprises the water stop panel, the left and right pressing plate as well as the bed plate. These components are made of steel and their deformation is usually restrained in the elastic stage. Elastic analysis is a fundamental application of IGA[12], so the detailed derivation of the formulations and matrix equations in terms of elastic analysis of the steel plates are left out in this study. The equilibrium equation for an element Ωe in the steel plates can be expressed as the following matrix formulation after the IGA discretization.
|
|
(32) |
in which Kp is the element stiffness matrix to be calculated as K L in Eq. (24), Δup is the array containing the displacement incremental of control points for the steel plates, Qp is the load vector and Fp is the vector denoting the contribution of the existing stress to the equation. Fp and Qp can be calculated based on Eq. (26) and Eq. (31). By assembling Eq. (23) for the expansion water seal and Eq. (32) for the steel plates, the global equilibrium equation of the whole water seal device will be obtained.
It is noticed that the contact forces acting on the steel plates are also uncertain in the resolution of Eq. (32). Therefore, the positions and forces regarded to the contacts between the expansion water seal and these steel plates are the critical quantities to be determined in the numerical simulation for the performance of the water seal system.
4 Variational inequalities for estimating the traction on the expansion water seal
4.1 Basic conception of VI theory
For convenience, a brief introduction to VI theory is given in this section; the details can be found in the monograph[20] by Facchinei and Pang. A variational inequality is formally defined below.
Definition 1 (VI) Given a subset K of the n-dimensional Euclidean space Rn and a mapping F: K→Rn, the variational inequality, denoted by VI(K, F), is to find a vector x∈K such that
|
|
(33) |
Here, means “for any” and ∈ “belonging to”.
Definition 2 (Box constrained VI), The box constrained VI(K, F) is such that the set K is a closed rectangle given by
|
|
(34) |
Here, ai and bi are possibly infinite scalars satisfying .
Box constrained VI(K, F) is an important linearly constrained variational inequality and has some familiar degenerate forms. A point x∈K is a solution to the box constrained VI(K, F) if and only if for every i,
|
|
(35) |
In the subsequent analysis, Eq. (35) is used to transform the contact conditions into VI.
4.2 VI for normal contact conditions
Fig. 4 plots two elastic bodies coming into contact and undergoing deformation, one of which is called as the slave body Ωs, and another one is called as Ωm, referring to the monograph[27] by Wriggers. Compared with the expansion water seal, the deformation of the steel plate is small. Therefore, the water seal is directly assigned as the master body, while the steel plate is assigned as the slave body. t xm represents the coordinates of a knot point located on the boundary of the expansion water seal at time t, and its projection point t xs is determined based on the minimum distance criterion[28]. The two points constitute a typical contact pair. Then, a framework (nc, τc) to identify the normal and tangential directions regarding to the contact pair is defined, where nc is specified as the inner normal direction of the expansion water seal boundary at t xm.
Within a small time interval Δt, both the master and slave bodies deform, which induces a change in the configuration of the contact pair at the end of this time step. The normal distance d n and the tangential relative displacement d τ can be calculated for given Δu m and Δu s. Here, Δu m and Δu s are the increment displacements of the master and slave bodies within the time interval, respectively. Then, the tractions on t+Δt xm and t+Δt xs can be estimated based on VI theory, which finally induces two VIs as important augments to the equilibrium equations for both the master and slave bodies.
The normal direction is investigated in the first place. Because the master and slave bodies cannot be penetrated into each other, the normal distance d n should be nonnegative, that is,
|
|
(36) |
The normal contact force p n is directly related to the normal distance d n. The expansion water seal suffers the back pressure on the back and the reservoir water pressure on the head, which both have specified values. If the expansion water seal contacts the steel plate tightly, in other words, d n=0, p n must be greater than the normal force induced by the back pressure or the water pressure. The normal force resulted by the back pressure and the water pressure can be calculated as (nc)T t, which is actually the modulus of t because both the back pressure and the water pressure act on the expansion water seal boundary along the inner normal direction. Moreover, if d n>0, the normal force applied to t+Δt xm is (nc)T t. The above conditions can be expressed as
|
|
(37) |
Comparing Eq. (37) with Eq. (35), Eq. (37) is equivalent to a box-constrained variational inequality with ai =(nc)T t and bi = +∞; thus, the normal contact force must be the solution of the following VI
|
|
(38) |
It is noticed that the boundaries Γt and Γc is determined when the normal contact conditions are formulated as Eq. (37). if d n>0, the point xm is situated at the boundary Γt of Ωm, and the point xs is situated at the boundary Γt of Ωs. At this point the normal forces applied to the two points are the known tractions. if d n=0, the point xm is situated at the boundary Γc of Ωm, and the point xs is situated at the boundary Γc of Ωs. At this moment the normal forces applied to the two points are uncertain. Because the two cases are uniformly involved in Eq. (37), it is unnecessary to determine the boundaries Γt and Γc in advance.
4.3 VI for tangential contact conditions
As shown in Fig. 4, if d n>0 the normal contact force is (nc)T t, and the tangential force must be zero considering that the properties of water pressure and air pressure. However, if d n=0, the expansion water seal contacts the steel plate tightly, the tangential contact force must be taken into account. In this case, a contact pair might be in one of two contact states: the sticky state and the sliding state. The tangential relative displacement d τ can be computed as
|
|
(39) |
The relative tangential movement in terms of a contact pair is dominated by the Coulomb friction law. Considering that the direction of the friction acting on the slave body Ωs is in agreement with the tangential relative movement, it is denoted as p τ. If a relative displacement happens, that is, d τ≠0, the magnitude of p τ will arrive at the maximum value μp n allowed by the Coulomb friction law, in which μ denotes the Coulomb friction coefficient. Otherwise, if d τ=0, the magnitude of p τ is certainly smaller than μp n, but its direction is undetermined.
Based on the above analysis, for the sticky state, we have
|
|
(40) |
The conditions about the tangential relative movement in Eq. (40) are written as a formulation of d τ with the opposite sign, which aims to provide an intuitive form for the subsequent analysis.
For the sliding state, we have
|
|
(41) |
Comparing Eq. (40) and Eq. (41) with Eq. (35), the two conditions can be considered as another box-constrained variational inequality with ai =-μp n and bi = μp n; therefore, p τ must be the solution of the following VI
|
|
(42) |
For each knot point located on the boundary of the expansion water seal at time t+Δt, the normal and tangential contact forces must be the solutions of Eq. (38) and Eq. (42), which are the supplement equations for Eq. (23) and Eq. (32) to estimate the traction on the expansion water seal.
5 Solution Strategy
Up to now, a set of formulations, including Eq. (23), Eq. (32), Eq. (38), and Eq. (42), are derived to simulate the entire water seal system, which can be resolved by various approaches. Actually, an arbitrary equation can be considered as a degenerated VI in the framework of VI theory. Thus, gathering the formulations together will induce a total VI, and then, Path Newton Method based on the merit function[22] can be employed to solve it. However, this way may be inefficient because it doesn’t take full advantage of the structural features of the formulations. The structural feature is analyzed as follows.
To begin with, once the unknown contact forces are given, there is no difficulty to solve Eq. (23) and Eq. (32) based on the classical FEM theory. And then, the normal distance d n and the tangential relative displacement d τ can be regarded as functions of the unknown contact forces. Finally, the relations between the unknown contact forces and d n and d τ are expressed as Eq. (38) and Eq. (42). Therefore, selecting the unknown contact forces as the unknown quantity may be an advisable choice, which means that the increment displacements of all components of the water seal system are considered as the intermediate variables.
Assuming the number of contact pairs is mc during the current time step, the normal contact force p n and the tangential contact force p τ in terms of mc contact pairs constitute two arrays pn and pτ, respectively. The normal distance d n and the tangential relative displacement d τ constitute two arrays dn and dτ, respectively. Then, the formulations including Eq. (23), Eq. (32), Eq. (38), and Eq. (42) can be expressed as the following VI. Let the subset KG= Kn×Kτ, the mapping
|
|
(43) |
then (pn, pτ) is the solution of VI(KG, FG). Kn and Kτ is composed of K n in Eq. (37) and K τ in Eq. (41) regarding to mc contact pairs, respectively. The mapping FG represents the calculation of dn and −dτ for a given (pn, pτ). Once the value of (pn, pτ) is given, the increment displacements of all components of the water seal system can be resolved based on Eq. (23) and Eq. (32), and then dn and −dτ can be calculated based on Eq. (36) and Eq. (39).
Eq. (43) is called as the global variational inequality for the problem, which is resolved by using the Extra-gradient method. For a better understanding of the Extra-gradient method, an important definition and a proposition in VI theory are introduced as follows.
Definition 3 (Euclidean projector) Let K be a convex subset of Rn. It is well known from convex analysis that for every vector x∈Rn there is a unique vector that is closet to x in the Euclidean norm, as shown in Fig. 5. This closet vector is called the Euclidean projector of x onto K and denoted by . The mapping Failed to parse (syntax error): {\Pi }_K�\boldsymbol{x}\mapsto {\Pi }_K\left(\boldsymbol{x}\right)
is called the Euclidean projector onto K.
Proposition 1. Let be a closed convex and be arbitrary. A point x∈K is a solution of if and only if
|
|
(44) |
where is called the natural map associated with K; is the Euclidean projector.
In the resolution of VI, various projection methods have been proposed based on Proposition 1, in which the Extra-gradient method is most widely acceptable[20]. The whole computation process of the Extra-gradient method is described below.
Algorithm Extra-Gradient Method
Step 0. Set , and , , k = 0, error limit ε
Step 1. , if , go to step 2.
Step 2.
while ,
,
end (while)
if , .
Step 3. , , and , go to Step 1.
In this study, the parameters in the Extra-Gradient Method algorithm are set as ε=0.00001, η1=0.4 and η2=0.9. More details of the Extra-gradient method can be referred to the monograph[20] by Facchinei and Pang and the article[21] by Jiang et al.
6 Performance analysis for the expansion water seal using the proposed method
According to the requirements of the steel gate design for a planned hydropower station located in the downstream of the Jinsha River in southwest China, the performance analysis is implemented for two optional expansion water seals, the geometries of which are illustrated in Fig. 6. It can be observed that the main difference between the two options is the shape of their seal heads.
The proposed method is employed in the simulation of the deformation of the two options. And their IGA discretization models are plotted in Fig.7. Performance comparison is executed in terms of the leakproofness of the back cavity, the contact between the seal head and the stop panel as well as the offset of the seal head. Finally, a better option is recommended after a comprehensive consideration.
The two options are both made of LD-19 rubber, which is commonly used for the expansion water seal in hydraulic power stations such as Three Gorges Project. Their values of C10, C01, and C11 in Eq. (4) have been measured by Liu et al.[3], which are 1.1505, -0.3286 and 0.0816, respectively. The steel plates have physical properties: Young’s modulus E = 2.07×105 MPa, Poisson’s ratio ν = 0.3. Referring to the design code, the friction coefficient μ is taken as 0.60 for the contact between the water seal and the steel plate.
6.1 The free expansion of the water seal head
The free expansion of the water seal head, that is, the upward movement of the seal head without the effect of the water stop panel and the reservoir water pressure, is an important reference value in determining the width of the gap between the pressing plate and the water stop panel. By using the proposed method, the deformations of the two optional expansion water seals only suffered, when the back pressures are investigated, and the upward movements of the water seal head are measured. To verify the validity of the proposed method, the resulted movements are compared with the results of the laboratory model experiments[7] and the results of traditional FEM. The traditional FEM analysis is accomplished by ANSYS, and the established model in ANSYS has an equal number of elements to the IGA model in Fig.7 for an objective comparison. The upward movements of the water seal head resulted by the proposed method, ANSYS, and the laboratory model experiments are all plotted in Fig.8.
As Fig.8 shows, the variation tendencies of the upward movements on the back pressure resulted by the proposed method and ANSYS are consistent with the results of the model experiments. The gap between the experiment results and the numerical simulation results becomes larger with the back pressure increasing. However, the result of the proposed method are more close to the experiment results than that of ANSYS. The peak value of the difference between the experiment results and the results of the proposed method is smaller than 0.50 mm, while the peak value of the difference between the experiment results and the results of ANSYS exceeds 1.0 mm. Therefore, the new method proposed in this study is effective in the numerical simulation of the expansion water seal and has a higher precision than the traditional FEM.
When the two options are suffering the same back pressure, a little difference between their results appears, indicating that the shape of the water seal head imposes no influence on the free expansion of the water seal head. Upward movement of the water seal head increases with an increasing back pressure, which apparently presents a nonlinear feature and can be described as the following four stages. In the first stage, the back pressure is less than 0.01 MPa and the upward movements are near zero. In the second stage, the back pressure rises from 0.02 MPa to 0.14 MPa and the upward movements appear to be increased dramatically. The upward movements at the end of the second stage arrive at 65.60% and 65.36% of the total upward movements for Option A and Option B, respectively. In the third stage, the back pressure rises from 0.15 MPa to 0.18 MPa and the slopes of the upward movement curves are becoming smaller, which can be considered as a transition stage. In the fourth stage, the back pressure is greater than 0.18 MPa and the upward movements present a linear increase with a gentle slope.
Additionally, the upward movement where the third stage begins is always treated as a reference to determine the width of the gap between the pressing plate and the water stop panel. According to the upward movement curves, the gap width is temporarily assumed to be 25 mm for both optional expansion water seals.
6.2 The leakproofness of the back cavity
After the assembly of the water seal system, the leakproofness of the back cavity is dominated by the contacts between the two water seal wings and the pressing plates and the bed plate. If the contact stress is greater than the back pressure, the back cavity is considered to have a satisfactory leakproofness. According to the engineering design scheme, the reservoir water pressure acting on the expansion water seal is 0.2 MPa, which means that the steel gate suffers the hydraulic head of 20 m. The working back pressure is 0.4 MPa. The width of gap between the pressing plate and the water stop panel has been set as 25 mm. The deformations of two optional expansion water seals under the above conditions are investigated by using the proposed method, and the results of deformations and stresses are plotted in Fig.9.
Option A is investigated in the first place. Under the prescribed working conditions, the peak value of the principal stress σ1 is 1.73 MPa, far less than LD-19 rubber’s break strength 7.64 MPa. Regarding the contact between the water seal wings and the adjacent plates, the peak value of the stress is 2.03 MPa, and the average value is about 1.08 MPa, which is far more than the working back pressure 0.40 MPa. Thus, the leakproofness of the back cavity is satisfied by Option A.
Then, Option B is investigated. The peak value of the principal stress σ1 is 1.56 MPa in the water seal under the same working conditions. The peak value of the contact stress is 2.01 MPa, and the mean value is about 1.09 MPa. In this case, the expansion water seal will not be broken and the leakproofness of the back cavity is also satisfied.
In short, both Option A and Option B can satisfy the leakproofness of the back cavity. Moreover, there is a little difference in stresses regarding to the contacts between their wings and the adjacent plates, which can be attributed to the fact that the water seal wings of the two options are identical.
6.3 The effectiveness to seal up the reservoir water
The stress in terms of the contact between the water seal head and the water stop panel is a critical quantity to assess the effectiveness of the water seal to seal up the reservoir water. In general, the back pressure required for successfully sealing up the reservoir water should be determined under an assumed gap width.
First of all, taking the back pressure and the reservoir water into account, the contact between the seal head and the stop panel is investigated for a given gap width. To reveal the variation law of the contact stress and width, it is assumed that the back pressure varies from 0.10 MPa to 0.60 MPa, and the water pressure varies from 0.05 MPa to 0.30 MPa. The deformation of the expansion water seal is simulated, and the stress and width of contact between the seal head and the stop panel are recorded. Take Option A with a 10 mm gap width as an example, the mean value of contact stress and the contact width vary as Fig.10 shows.
Both the mean value of contact stress and the contact width rise with an increasing back pressure when the reservoir water pressure is fixed. While, they both decrease with an increasing reservoir water pressure, when the back pressure remains unchanged. In case that the water seal head contacts the water stop panel, the results comparison verifies that the back pressure has a more significant effect on the contact stress and the contact width than the reservoir water pressure.
Although the effect of the reservoir water pressure on the stress and width of contact is relatively small, the reservoir water pressure is a key quantity in determining the threshold value required for the back pressure. If the reservoir water pressure increases, a larger threshold value is required for the back pressure to seal up the reservoir water. Once the water seal head contacts the stop panel, the contact stress will be greater than the reservoir water pressure and be mainly dominated by the back pressure. Therefore, the threshold value required for the back pressure should be determined based on the reservoir water pressure.
A general criterion that the contact between the water seal head and the water stop panel results in the contact stress greater than the reservoir water pressure is used to determine the threshold value required for the back pressure. Through numerical simulation, the threshold values required for the back pressure are acquired for different combinations of gap width and reservoir water pressure, which are plotted in Fig. 11.
Results show that the threshold values of the back pressure required for the two options are almost indistinguishable under the same reservoir water pressure and gap width. Both the increase of the reservoir water pressure and the gap width result in a rising threshold value of the required back pressure. However, when the gap width arrives at 30 mm, the threshold value of the back pressure will be greater than the prescribed working back pressure 0.40 MPa. Under a gap width of 25 mm, the threshold value of the back pressure are less than the prescribed working back pressure, even if the reservoir water pressure increases to 0.30 MPa. Thus, it is reasonable to prescribe the gap width as 25 mm. In conclusion, there is little difference between the two optional expansion water seals in their ability to seal up the reservoir water, and both of them can work efficiently by using the prescribed gap width.
6.4 The offset of the water seal head
Due to the singularity of the reservoir water flowing, the offset of the water seal head is inevitable. In case of an excessive offset, the deformation recovery of the water seal head maybe difficult at the time that the back pressure is cancelled, and then the working life will be shortened. Therefore, the offset should be inspected for estimating the deformation recovery capacity and the working life of the expansion water seal. In this study, the horizontal displacement of the water seal head at the highest point of the upper curved boundary is taken as a reference value for the offset.
The horizontal displacements at the reference point are recorded for the two options and plotted in Fig. 12 in case that the gap width takes the prescribed value 25 mm. To reveal the variation of the offset, the reservoir water pressure is assumed to vary from 0.20 MPa to 0.30 MPa, and the back pressure varies from the corresponding threshold value to the prescribed working back pressure 0.40 MPa. Increasing reservoir water pressure induces a larger horizontal displacement, while the increase of the back pressure results in a smaller horizontal displacement. In case of the same back pressure and the same reservoir water pressure, the horizontal displacement at the reference point of Option A are about 1 mm less than that of Option B. Considering that the maximum value of the horizontal displacement in Fig. 12 is about 7 mm, the difference is considerable. Thus, a conclusion can be drawn that Option A is better than Option B in terms of the deformation recovery capacity and working life.
6.5 The recommended option
Up to now, the back cavity leakproofness, the effectiveness on sealing up the reservoir water, and the seal head offset have been comprehensively investigated for the two optional expansion water seals. Both options are capable to satisfy the back cavity leakproofness and are effective in sealing up the reservoir water by using the prescribed gap width and the prescribed working back pressure. The main difference between the two options is the offset of the seal head. Under the same conditions, the seal head offset of Option A is smaller than Option B, indicating that Option A may have a better deformation recovery capacity and a longer working life than Option B. Thus, Option A is recommended for the hydraulic steel gate design finally.
7 Conclusions
The work presented in this article aims at developing an effective and accurate method based on IGA analysis to investigate the performance of the expansion water seal in the hydraulic steel gate. The proposed method has the following advantages:
(1) The complex geometrical shape of the expansion water seal can be represented more exactly by using IGA analysis than by the traditional FEM method.
(2) The estimation of the contact force is accomplished by solving the variational inequality in terms of the contact conditions, which avoids the demerits of the existing approaches and simplifies the incremental equilibrium equations.
(3) The proposed method is effective in the numerical simulation of the expansion water seal and has a higher precision than the traditional FEM under the same conditions.
Data Availability
The data used to support the findings of this study are available from the corresponding author upon request.
Conflicts of Interest
The authors declare that there are no conflicts of interest regarding the publication of this article.
Authors’ Contributions
Conceptualization, Zhou Yida; Formal analysis, Hu Jianke; Methodology, Hu Taoyong; Resources, Shi Shoujin; Software, Han Yifeng; Validation, Wang Jinkun; Visualization, Lou Yidan; Writing – original draft, Hou Tao.
This research received no funding.
References
1.Li, C.H. Numerical analysis of water seal in gate under high pressure and its application in engineering [D]. Msc Thesis, School of Civil Engineering & Architectural Engineering, Wuhan University, Wuhan, Hubei, P. R. China, 2005.
2.Chen, W.Y.; Ou, Z.G.; Liu, L.H.; Wang, D. Research on the hermetic capability and water-stop criterion [J]. Journal of Hydroelectric Engineering. 2010, 05, 232-236.
3.Liu, L.H.; Wang, D.; Fang, H.M.; Sun, D.X.; Wei, X.B.; Ou, Z.G. Nonlinear calculation of the preload pressure of gate water seal with Rivlin model[J]. Journal of Hydroelectric Engineering. 2011, 05, 170-174.
4.Liu, L.H.; Wang, D.; Ou, Z.G.; Wei, X.B. Nonlinear calculation on the pressure-filled telescopic water seal based on the Ogden formula[J]. Chinese Journal of Solid Mechanics. 2011, 01, 102-107.
5.Tan, X.W.; Wang, Z.Z.; Yu, X.K.; Liang, L.J.; Liu, Q.H. Hyperelasticity and viscoelasticity of rubber water stop material[J]. Journal of Vibration and Shock. 2014, 19, 97-103.
6.Ding, Z.P.; Zeng, J.X.; Lin, S.; Huang, Y.J. Structure strength analysis and parameter optimization of rubber spring[J]. Journal of Vibration and Shock. 2019, 12, 246-251.
7.Yang, B. Deformation calculation theory and application research of rubber water seal [D]. Ph.D. Thesis, School of Civil Engineering & Architectural Engineering, Wuhan University, Wuhan, Hubei, P.R.China, 2014.
8.Xiong, W.; Liu, L.H. Nonlinear simulation analysis of seal component of high press gate [J]. Engineering Journal of Wuhan University. 2011, 01, 66-68.
9.Hu, J.K.; Chen, J.F.; Wang, Z.N.; Hu, B.W.; Wang, J.; Hao, N.N.; Cai, K.; Hu, M.X. Nonlinear simulation of high head expansion water seal based on the mooney-rivlin model[J]. China Rural Water and Hydropower. 2022, 04, 215-220.
10.Xue, X.X.; Wu Y.H.; Li Z.C.; Cao Y.N.; Zhang D. Study on deformation and sealing performance of p-type water seal for high-head plane gate[J]. Journal of Hydroelectric Engineering. 2012, 01, 56-61.
11.Hughes, T.; Cottrell J.A.; Bazilevs Y. Isogeometric analysis: cad, finite elements, NURBS, exact geometry and mesh refinement [J]. Computer Methods in Applied Mechanics & Engineering. 2005, 39-41, 4135-4195.
12.Cottrell, A.J.; Hughes T.; Bazilevs Y. Isogeometric analysis: toward integration of cad and FEA [M]. Wiley & Sons: Chichester, West Sussex, United Kingdom, 2009.
13.Nguyen, V.P.; Anitescu C.; Bordas S.P.A.; Rabczuk T. Isogeometric analysis: an overview and computer implementation aspects [J]. Mathematics & Computers in Simulation. 2015, 11, 89-116.
14.Wang, Y.; Wang Z.; Xia Z.; Poh L.H. Structural design optimization using Isogeometric analysis: a comprehensive review [J]. Computer Modeling in Engineering & Sciences. 2018, 12, 53.
15.Gao, J.; Xiao M.; Zhang Y.; Gao L. A comprehensive review of Isogeometric topology optimization: methods, applications and prospects [J]. Chinese Journal of Mechanical Engineering. 2020, 1, 87.
16.Elguedj, T.; Bazilevs Y.; Calo V.M.; Hughes T.J.R. F-bar projection method for finite deformation elasticity and plasticity using NURBS based Isogeometric analysis[J]. International Journal of Material Forming. 2008, 1, 1091-1094.
17.Temizer; Abdalla M.M.; Gürdal Z. An interior point method for Isogeometric contact [J]. Computer Methods in Applied Mechanics and Engineering. 2014, 276, 589-611.
18.Thang, X.D.; Roger A.S. A concise frictional contact formulation based on surface potentials and Isogeometric discretization [J]. Computational Mechanics. 2019, 4, 951-907.
19.Kruse R.; Nguyen-Thanh N.; Wriggers P.; De Lorenzis L. isogeometric frictionless contact analysis with the third medium method [J]. Computational Mechanics. 2018, 62, 1009-1021.
20.Facchinei F.; Pang J. S. Finite-dimensional variational inequalities and complementary problems [M]. New York, Springer, 2003
21.Jiang W.; Zheng H.; Sun G. H.; Chen W.; Song P. C. 3D DDA Based on Variational Inequality Theory and Its Solution Scheme [J]. Int J Comput Methods. 2018, 15:1510081
22.Jiang W, Zheng H. Discontinuous deformation analysis based on variational inequality theory. Int J Comput Methods. 2011, 8:193-208
23.Mooney, M. A. Theory of large elastic deformation [J]. Journal of Applied Physics. 1940, 9, 582-592.
24.Bazilevs, Y.; Calo, V.M.; Cottrell, J.A.; Evans, J.A.; Hughes, T.J.P. Isogeometric analysis using T-splines[J]. Computer Methods in Applied Mechanics and Engineering. 2015, 5-8 229-263.
25.Speleers, H.; Manni, C.; Pelosi, F.; Sampoli, M.L. Isogeometric analysis with powell-sabin splines for advection-diffusion-reaction problems[J]. Computer Methods in Applied Mechanics & Engineering, 2012, 221, 132-148.
26.Wu, Z.J.; Huang Z.D.; Liu Q.H.; Zuo B.Q. A local solution approach for adaptive hierarchical refinement in Isogeometric analysis[J]. Computer Methods in Applied Mechanics & Engineering. 2015, 283, 1467-1492.
27.Wriggers P. Computational Contact Mechanics [M]. Wiley & Sons: Chichester, West Sussex, United Kingdom,
28.Agrawal V.; Gautam S. S. Varying-order NURBS discretization: an accurate and efficient method for isogeometric analysis of large deformation contact problems [J]. Computer Methods in Applied Mechanics & Engineering. 2020, 367, 113125.
Document information
Published on 25/11/22
Accepted on 22/11/22
Submitted on 26/10/22
Volume 38, Issue 4, 2022
DOI: 10.23967/j.rimni.2022.11.003
Licence: CC BY-NC-SA license
Share this document
Keywords
claim authorship
Are you one of the authors of this document?