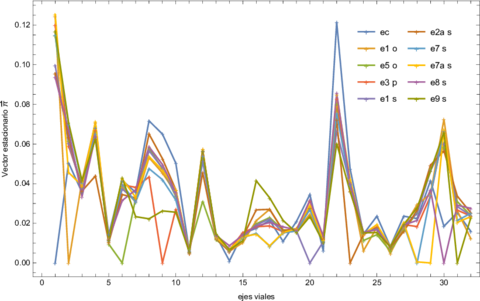m (Move page script moved page Review 635848621558 to Olivares-Quiroz Pereda 2021a) |
|||
| (12 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
| − | = | + | =1 Introducción= |
| − | + | El tráfico vehicular es uno de los problemas más importantes que enfrentan actualmente las grandes urbes en función del número creciente de vehículos que circulan y del limitado espacio existente <span id='citeF-1'></span>[[#cite-1|[1]]]. Los efectos producidos por el incremento del flujo vehicular van más allá del impacto económico, alcanzando la esfera social, el medio ambiente y la calidad de vida de los habitantes en sí misma <span id='citeF-2'></span>[[#cite-2|[2]]]. Por tanto, cada vez es más necesario contar con herramientas formales y cuantitativas que permitan el diseño de redes de flujo vehicular (avenidas, ciclovías, sistemas de transporte público) que permitan una comunicación más eficiente y efectiva entre los distintos puntos de una ciudad <span id='citeF-3'></span>[[#cite-3|[3]]]. Ésta no es una preocupación reciente. Los primeros estudios sobre el tráfico vehicular se remontan a la década de 1930-1940 con los trabajos de B D Greenshield, quien aplicó por primera vez métodos fotográficos y matemáticos para la medición de diferentes variables relacionadas con el tráfico vehicular y la descripción de su comportamiento <span id='citeF-4'></span>[[#cite-4|[4]]]. | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | El tráfico vehicular es uno de los problemas más importantes que enfrentan actualmente las grandes urbes en función del número creciente de vehículos que circulan y del limitado espacio existente <span id='citeF-1'></span>[[#cite-1|[1]]]. Los efectos producidos por el incremento del flujo vehicular van más | + | |
Diferentes modelos matemáticos se han aplicado para analizar el problema del transporte eficiente y del flujo vehicular en redes urbanas. Dependiendo del nivel de detalle, los modelos de tráfico vehicular generalmente se clasifican como microscópicos, mesoscópicos y macroscópicos <span id='citeF-5'></span>[[#cite-5|[5]]]. Existen modelos matemáticos basados en ecuaciones diferenciales parciales (EDP) <span id='citeF-6'></span>[[#cite-6|[6]]], autómatas celulares (AC) <span id='citeF-7'></span>[[#cite-7|[7]]], modelos basados en agentes <span id='citeF-8'></span>[[#cite-8|[8]]], ecuaciones diferenciales estocásticas, entre otros. En este trabajo abordaremos el análisis del flujo vehicular mediante el formalismo de los procesos estocásticos en tiempo discreto. Más específicamente, definiremos una cadena de Markov discreta ( CMD) sobre un grafo dual <math display="inline">\mathcal{G}</math> el cual representará la dinámica del flujo vehicular a tiempo discreto sobre un conjunto de nodos <math display="inline">\{ n_j \} </math> y enlaces <math display="inline">\{ e_j \} </math> los cuales representan a los ejes viales y sus intersecciones. Basaremos este análisis en el trabajo de Crisostomi ''et al'' <span id='citeF-9'></span>[[#cite-9|[9]]], en donde se discute ampliamente las ventajas del enfoque Markoviano para este tipo de análisis. Tal como mostraremos en este trabajo, el enfoque estocástico mediante CMD nos permitirá extraer información relevante de conectividad y flujo dentro de la red <span id='citeF-10'></span>[[#cite-10|[10]]] <span id='citeF-11'></span>[[#cite-11|[11]]]. | Diferentes modelos matemáticos se han aplicado para analizar el problema del transporte eficiente y del flujo vehicular en redes urbanas. Dependiendo del nivel de detalle, los modelos de tráfico vehicular generalmente se clasifican como microscópicos, mesoscópicos y macroscópicos <span id='citeF-5'></span>[[#cite-5|[5]]]. Existen modelos matemáticos basados en ecuaciones diferenciales parciales (EDP) <span id='citeF-6'></span>[[#cite-6|[6]]], autómatas celulares (AC) <span id='citeF-7'></span>[[#cite-7|[7]]], modelos basados en agentes <span id='citeF-8'></span>[[#cite-8|[8]]], ecuaciones diferenciales estocásticas, entre otros. En este trabajo abordaremos el análisis del flujo vehicular mediante el formalismo de los procesos estocásticos en tiempo discreto. Más específicamente, definiremos una cadena de Markov discreta ( CMD) sobre un grafo dual <math display="inline">\mathcal{G}</math> el cual representará la dinámica del flujo vehicular a tiempo discreto sobre un conjunto de nodos <math display="inline">\{ n_j \} </math> y enlaces <math display="inline">\{ e_j \} </math> los cuales representan a los ejes viales y sus intersecciones. Basaremos este análisis en el trabajo de Crisostomi ''et al'' <span id='citeF-9'></span>[[#cite-9|[9]]], en donde se discute ampliamente las ventajas del enfoque Markoviano para este tipo de análisis. Tal como mostraremos en este trabajo, el enfoque estocástico mediante CMD nos permitirá extraer información relevante de conectividad y flujo dentro de la red <span id='citeF-10'></span>[[#cite-10|[10]]] <span id='citeF-11'></span>[[#cite-11|[11]]]. | ||
| Line 41: | Line 19: | ||
es decir, sólo depende del valor de la variable estocástica en el paso inmediato anterior. Tal proceso se denomina proceso de Markov o cadena de Markov discreta (CMD) y fue propuesto por Andrei Markov . | es decir, sólo depende del valor de la variable estocástica en el paso inmediato anterior. Tal proceso se denomina proceso de Markov o cadena de Markov discreta (CMD) y fue propuesto por Andrei Markov . | ||
| − | Este trabajo se presenta de la siguiente manera. En la Sección II discutiremos los elementos básicos de la teoría de los procesos de Markov discretos. A continuación presentaremos la aplicación de estos resultados a la red de 32 ejes viales principales de la Ciudad de México. Posteriormente efectuaremos un análisis cuantitativo detallado de las cantidades mencionadas previamente y analizaremos el impacto del cierre de un eje vial dado a la circulación mediante el uso del bloqueo de un eje vial <math display="inline">n^{\dagger }</math> dentro de la red y el cálculo de este efecto en las cantidades | + | Este trabajo se presenta de la siguiente manera. En la Sección II discutiremos los elementos básicos de la teoría de los procesos de Markov discretos. A continuación presentaremos la aplicación de estos resultados a la red de 32 ejes viales principales de la Ciudad de México. Posteriormente efectuaremos un análisis cuantitativo detallado de las cantidades mencionadas previamente y analizaremos el impacto del cierre de un eje vial dado a la circulación mediante el uso del bloqueo de un eje vial <math display="inline">n^{\dagger }</math> dentro de la red y el cálculo de este efecto en las cantidades anteriormente descritas. Finalmente presentaremos un conjunto de conclusiones y perspectivas que pueden considerarse en un análisis posterior a futuro de este trabajo. |
| − | + | =2 Cadenas de Markov discretas. Un proceso estocástico clásico = | |
En este trabajo representaremos la conectividad de los ejes viales bajo consideración y el tráfico vehicular dentro de la Ciudad de México mediante una cadena de Markov discreta (CMD). Una CMD representa un proceso estocástico discreto definido por un conjunto de estados <math display="inline"> \{ S_i \} </math>, para los cuales existe una probabilidad de transición <math display="inline">p _{ij}</math> de pasar del estado <math display="inline">S _{i}</math> al estado <math display="inline">S _{j}</math>. Esta probabilidad <math display="inline">p_{ij}</math> cumple la propiedad de Markov la cual establece que si el estado <math display="inline">S_n</math> al tiempo <math display="inline">n</math> y el conjunto de estados discretos a tiempos previos <math display="inline">S _{1}, ..., S _{n-1}</math> son conocidos, la probabilidad del estado futuro <math display="inline">S _{n+1}</math> no depende de los estados anteriores <math display="inline">S _{1}, ..., S _{n-1}</math>, sino solo depende del estado actual <math display="inline">S _{n}</math>. Esto es, <span id='citeF-15'></span>[[#cite-15|[15]]]: | En este trabajo representaremos la conectividad de los ejes viales bajo consideración y el tráfico vehicular dentro de la Ciudad de México mediante una cadena de Markov discreta (CMD). Una CMD representa un proceso estocástico discreto definido por un conjunto de estados <math display="inline"> \{ S_i \} </math>, para los cuales existe una probabilidad de transición <math display="inline">p _{ij}</math> de pasar del estado <math display="inline">S _{i}</math> al estado <math display="inline">S _{j}</math>. Esta probabilidad <math display="inline">p_{ij}</math> cumple la propiedad de Markov la cual establece que si el estado <math display="inline">S_n</math> al tiempo <math display="inline">n</math> y el conjunto de estados discretos a tiempos previos <math display="inline">S _{1}, ..., S _{n-1}</math> son conocidos, la probabilidad del estado futuro <math display="inline">S _{n+1}</math> no depende de los estados anteriores <math display="inline">S _{1}, ..., S _{n-1}</math>, sino solo depende del estado actual <math display="inline">S _{n}</math>. Esto es, <span id='citeF-15'></span>[[#cite-15|[15]]]: | ||
| Line 67: | Line 45: | ||
|} | |} | ||
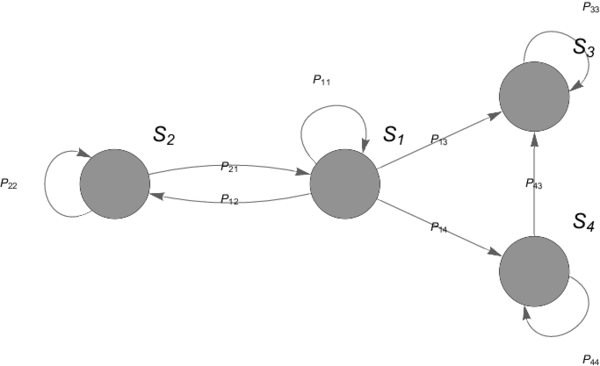
| − | la Figura [[#img-1|(1)]] muestra una representación de una cadena de Markov discreta con un | + | la Figura [[#img-1|(1)]] muestra una representación de una cadena de Markov discreta con un conjunto de estados dado por el conjunto <math display="inline">\{ S_1, S_2, S_3, S_4\} </math> con probabilidades de transición <math display="inline">p_{ij}</math> determinadas. Una CMD está por tanto determinada por una matriz de tamaño <math display="inline">N \times N</math> llamada matriz de probabilidades de transición <math display="inline">\bold{P}</math> cuyas entradas <math display="inline">p_{ij} </math> denotan la probabilidad de pasar del estado <math display="inline"> S_i </math> al estado <math display="inline"> S_j </math> en una unidad de tiempo dada. Esto es, |
<div id='img-1'></div> | <div id='img-1'></div> | ||
{| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 100%;max-width: 100%;" | {| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 100%;max-width: 100%;" | ||
|- | |- | ||
| − | |[[Image:Review_635848621558-Ejemplocadena.png|600px|Representación de una cadena de Markov con espacio de estados S₁, S₂, S₃ y S₄ para los cuales existe una | + | |[[Image:Review_635848621558-Ejemplocadena.png|600px|Representación de una cadena de Markov con espacio de estados S₁, S₂, S₃ y S₄ para los cuales existe una probabilidad de transición probabilidad p <sub>ij</sub> de que el estado S<sub>i</sub> pueda pasar al estado S <sub>j</sub>. Adicionalmente, dentro de una cadena de Markov pueden existir ''loops'' en los cuales puede existir una probabilidad de transición p<sub>ii</sub> \neq 0, tal como se muestra en la representación. ]] |
|- style="text-align: center; font-size: 75%;" | |- style="text-align: center; font-size: 75%;" | ||
| − | | colspan="1" | '''Figura 1:''' Representación de una cadena de Markov con espacio de estados <math>S_1, S_2, S_3</math> y <math>S_4</math> para los cuales existe una | + | | colspan="1" | '''Figura 1:''' Representación de una cadena de Markov con espacio de estados <math>S_1, S_2, S_3</math> y <math>S_4</math> para los cuales existe una probabilidad de transición probabilidad <math>p _{ij}</math> de que el estado <math>S_i</math> pueda pasar al estado <math>S _{j}</math>. Adicionalmente, dentro de una cadena de Markov pueden existir ''loops'' en los cuales puede existir una probabilidad de transición <math>p_{ii} \neq 0</math>, tal como se muestra en la representación. |
|} | |} | ||
| Line 172: | Line 150: | ||
donde la suma inicia en el índice <math display="inline">j=2</math>. La ecuación [[#eq-9|(9)]] enfatiza el hecho de que <math display="inline"> K </math> solo depende en realidad de <math display="inline">\bold{P}</math> y que aumenta si uno o más valores propios de <math display="inline">\bold{P}</math> es real y cercano a 1. <span id='citeF-22'></span>[[#cite-22|[22]]]. | donde la suma inicia en el índice <math display="inline">j=2</math>. La ecuación [[#eq-9|(9)]] enfatiza el hecho de que <math display="inline"> K </math> solo depende en realidad de <math display="inline">\bold{P}</math> y que aumenta si uno o más valores propios de <math display="inline">\bold{P}</math> es real y cercano a 1. <span id='citeF-22'></span>[[#cite-22|[22]]]. | ||
| − | + | =3 Aplicaciones a redes de transporte. Caso de la Ciudad de México= | |
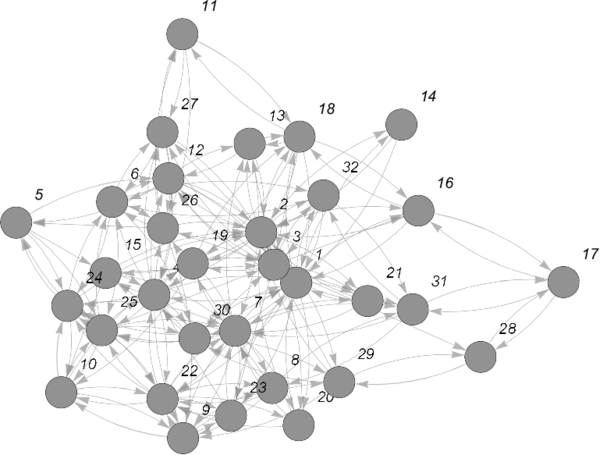
Con base en las herramientas anteriores, definiremos una cadena de Markov discreta (CMD) para analizar cuantitativamente las propiedades del flujo de tráfico dentro de un conjunto de ejes viales de la Ciudad de México. Para ello, seleccionaremos un conjunto de avenidas o ejes viales principales y sus respectivos puntos de cruce como los elementos del grafo <math display="inline">G</math>. En esta representación <math display="inline">G</math>, a la cual definimos como ''grafo primario'', las intersecciones son los nodos de la red y los enlaces son los ejes viales mismos. Para este grafo <math display="inline">G</math> se define el grafo dual <math display="inline">\mathcal{G}</math> como aquel en el cual los nodos serán ahora los ejes viales y las intersecciones de los ejes viales corresponden a los enlaces del grafo <math display="inline">\mathcal{G}</math>. Esto es, los enlaces <math display="inline">e_j</math> y los nodos <math display="inline">n_j</math> intercambian su papel <span id='citeF-23'></span>[[#cite-23|[23]]]. La Figura [[#img-2|(2)]] muestra la red de ejes viales de la Ciudad de México que analizaremos en este trabajo, la cual consta de los 32 principales ejes viales de la Ciudad de México <span id='citeF-24'></span>[[#cite-24|[24]]]. | Con base en las herramientas anteriores, definiremos una cadena de Markov discreta (CMD) para analizar cuantitativamente las propiedades del flujo de tráfico dentro de un conjunto de ejes viales de la Ciudad de México. Para ello, seleccionaremos un conjunto de avenidas o ejes viales principales y sus respectivos puntos de cruce como los elementos del grafo <math display="inline">G</math>. En esta representación <math display="inline">G</math>, a la cual definimos como ''grafo primario'', las intersecciones son los nodos de la red y los enlaces son los ejes viales mismos. Para este grafo <math display="inline">G</math> se define el grafo dual <math display="inline">\mathcal{G}</math> como aquel en el cual los nodos serán ahora los ejes viales y las intersecciones de los ejes viales corresponden a los enlaces del grafo <math display="inline">\mathcal{G}</math>. Esto es, los enlaces <math display="inline">e_j</math> y los nodos <math display="inline">n_j</math> intercambian su papel <span id='citeF-23'></span>[[#cite-23|[23]]]. La Figura [[#img-2|(2)]] muestra la red de ejes viales de la Ciudad de México que analizaremos en este trabajo, la cual consta de los 32 principales ejes viales de la Ciudad de México <span id='citeF-24'></span>[[#cite-24|[24]]]. | ||
| Line 184: | Line 162: | ||
|} | |} | ||
| − | El flujo vehicular, es decir, el número de vehículos que circulan en los ejes principales es información no fácilmente accesible. Sin embargo, es factible conocer datos estadísticos a partir de la información en las bases de datos del INEGI (Instituto Nacional de Estadística, Geografía e Informática) <span id='citeF-25'></span>[[#cite-25|[25]]]. Para determinar la matriz <math display="inline">\bold{P}</math> se requiere conocer el número total de viajes <math display="inline">V_{ij}</math> que parten del eje vial <math display="inline">E_i</math> y se dirigen al eje vial <math display="inline">E_j</math>. Esto es una cantidad compleja de determinar, sin embargo, se considerará la información disponible para una ventana de tiempo y espacio restringido. En este caso, consideraremos inicialmente un día en particular de la semana durante un lapso de tiempo de 2 horas, | + | El flujo vehicular, es decir, el número de vehículos que circulan en los ejes principales es información no fácilmente accesible. Sin embargo, es factible conocer datos estadísticos a partir de la información en las bases de datos del INEGI (Instituto Nacional de Estadística, Geografía e Informática) <span id='citeF-25'></span>[[#cite-25|[25]]]. Para determinar la matriz <math display="inline">\bold{P}</math> se requiere conocer el número total de viajes <math display="inline">V_{ij}</math> que parten del eje vial <math display="inline">E_i</math> y se dirigen al eje vial <math display="inline">E_j</math>. Esto es una cantidad compleja de determinar, sin embargo, se considerará la información disponible para una ventana de tiempo y espacio restringido. En este caso, consideraremos inicialmente un día en particular de la semana durante un lapso de tiempo de 2 horas, específicamente consideramos una ventana temporal entre 8 y 10 horas de la mañana. Por tanto entonces, la probabilidad <math display="inline">p_{ij}</math> se determina por |
<span id="eq-10"></span> | <span id="eq-10"></span> | ||
| Line 223: | Line 201: | ||
|} | |} | ||
| − | Uno de los objetivos centrales de este trabajo es determinar la matriz de primer visita promedio, (''mean first passage time'') <math display="inline">\bold{M}= \{ M_{ij} \} </math> la cual nos indica, en promedio, el número de pasos requerido para pasar de un nodo <math display="inline">n_i</math> a un nodo <math display="inline">n_j</math> dentro de la red. En este caso, dado que el conjunto de nodos <math display="inline">{ n_k}</math> se refiere a los ejes viales en cuestión, el elemento <math display="inline">M_{ij}</math> se refiere al tiempo promedio, considerando todas las rutas posibles, en el cual partiendo del eje vial <math display="inline">i</math> se alcanza el eje vial <math display="inline">j</math> por ''primera vez''. Es fundamental considerar que este tiempo (o número de pasos) se refiere a la primera vez que se alcanza el nodo <math display="inline">n_j</math> dentro de la red. En principio es perfectamente posible construir trayectorias que lleguen a <math display="inline">n_j</math> muchas más de una vez, pero no son las que se consideran en el proceso estocástico aquí descrito | + | Uno de los objetivos centrales de este trabajo es determinar la matriz de primer visita promedio, (''mean first passage time'') <math display="inline">\bold{M}= \{ M_{ij} \} </math> la cual nos indica, en promedio, el número de pasos requerido para pasar de un nodo <math display="inline">n_i</math> a un nodo <math display="inline">n_j</math> dentro de la red. En este caso, dado que el conjunto de nodos <math display="inline">{ n_k}</math> se refiere a los ejes viales en cuestión, el elemento <math display="inline">M_{ij}</math> se refiere al tiempo promedio, considerando todas las rutas posibles, en el cual partiendo del eje vial <math display="inline">i</math> se alcanza el eje vial <math display="inline">j</math> por ''primera vez''. Es fundamental considerar que este tiempo (o número de pasos) se refiere a la primera vez que se alcanza el nodo <math display="inline">n_j</math> dentro de la red. En principio es perfectamente posible construir trayectorias que lleguen a <math display="inline">n_j</math> muchas más de una vez, pero no son las que se consideran en el proceso estocástico aquí descrito. |
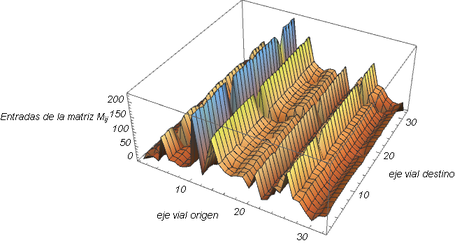
| − | + | La figura [[#img-5|(5)]] muestra una representación tridimensional de <math display="inline">\bold{M}</math>, en donde los ejes <math display="inline">x</math> e <math display="inline">y</math> representan los ejes viales de origen y destino, mientras que el eje <math display="inline">z</math> se refiere al valor correspondiente de <math display="inline">M_{ij}</math>. Los valores más grandes de las entradas <math display="inline">M_{ij}</math> representan los tiempos ''promedio'' más grandes de recorrido entre dos ejes viales determinados. | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
<div id='img-5'></div> | <div id='img-5'></div> | ||
| Line 1,299: | Line 215: | ||
Finalmente, se ha determinado también la llamada constante de Kemeny <math display="inline">K</math>, la cual en teoría de grafos corresponde al número de pasos promedio requeridos para alcanzar cualquier nodo <math display="inline">n_j</math> dentro de la red a partir de un nodo inicial <math display="inline">n_i</math>. Interesantemente y como ha sido demostrado, el valor de la constante de Kemeny no depende de que nodo <math display="inline">n_i</math> se elija <span id='citeF-19'></span>[[#cite-19|[19]]] <span id='citeF-20'></span>[[#cite-20|[20]]]. En la literatura se ha utilizado como una medida de la eficacia de la red, pues redes caracterizadas por pequeños valores en la constante de Kemeny generalmente tienen un mayor grado de eficiencia <span id='citeF-19'></span>[[#cite-19|[19]]]. Para nuestro caso, el valor calculado es <math display="inline">K = 34.4376</math>, el cual es un indicador de desempeño vial de la red en general. Para comprender mejor el significado de <math display="inline">K</math> considere un conductor al azar que se mueve dentro de la red de acuerdo a las probabilidades de transición <math display="inline">p_{ij}</math> dadas de la matriz <math display="inline">\bold{P}</math>. En algún momento, nuestro conductor está perdido y no sabe el estado (eje vial) en que se encuentra y hacia dónde se dirige. En este contexto, la constante de Kemeny puede interpretarse como el número promedio de pasos que seguirá el conductor al azar antes de llegar a su destino <span id='citeF-26'></span>[[#cite-26|[26]]]. | Finalmente, se ha determinado también la llamada constante de Kemeny <math display="inline">K</math>, la cual en teoría de grafos corresponde al número de pasos promedio requeridos para alcanzar cualquier nodo <math display="inline">n_j</math> dentro de la red a partir de un nodo inicial <math display="inline">n_i</math>. Interesantemente y como ha sido demostrado, el valor de la constante de Kemeny no depende de que nodo <math display="inline">n_i</math> se elija <span id='citeF-19'></span>[[#cite-19|[19]]] <span id='citeF-20'></span>[[#cite-20|[20]]]. En la literatura se ha utilizado como una medida de la eficacia de la red, pues redes caracterizadas por pequeños valores en la constante de Kemeny generalmente tienen un mayor grado de eficiencia <span id='citeF-19'></span>[[#cite-19|[19]]]. Para nuestro caso, el valor calculado es <math display="inline">K = 34.4376</math>, el cual es un indicador de desempeño vial de la red en general. Para comprender mejor el significado de <math display="inline">K</math> considere un conductor al azar que se mueve dentro de la red de acuerdo a las probabilidades de transición <math display="inline">p_{ij}</math> dadas de la matriz <math display="inline">\bold{P}</math>. En algún momento, nuestro conductor está perdido y no sabe el estado (eje vial) en que se encuentra y hacia dónde se dirige. En este contexto, la constante de Kemeny puede interpretarse como el número promedio de pasos que seguirá el conductor al azar antes de llegar a su destino <span id='citeF-26'></span>[[#cite-26|[26]]]. | ||
| − | + | ==3.1 Identificación de ejes viales importantes== | |
Una pregunta interesante en el diseño de redes viales es, qué le sucede a la red con respecto a las ocupaciones de los ejes viales y el tiempo promedio dentro de ella <span id='citeF-27'></span>[[#cite-27|[27]]]. En particular, un tema central que discutiremos aquí es tratar de estimar que sucede cuando uno de los ejes viales se cierra o es bloqueado al flujo vehicular, debido a desastres naturales, obras viales, manifestaciones, entre otras posibilidades. Para realizar esta estimación, consideraremos la red descrita anterior y llamaremos <math display="inline">n^{\dagger }</math> al nodo asociado al eje vial que se encuentra bloqueado o inaccesible al flujo vehicular en función de las razones descritas. Para analizar el efecto de la inaccesibilidad del nodo <math display="inline">n^{\dagger }</math> para el flujo de vehicular dentro de la red, realizaremos lo siguiente. Para el nodo <math display="inline">n^{\dagger }</math> sustituiremos por ceros los valores de la columna de la matriz <math display="inline">\bold{P}</math> asociada al nodo <math display="inline">n^{\dagger }</math>. Esto indicará que eje vial <math display="inline">\dagger </math> no está disponible para poder circular y así sucesivamente. Es decir, se construyen 32 redes diferentes en donde se considera el cierre de cada nodo, la información de las nuevas entradas de cada matriz de transición se obtiene de acuerdo a la ecuación [[#eq-10|(10)]], como estamos considerando que <math display="inline">V_{ij}</math> el número total de viajes que parten del eje vial <math display="inline">E_{i}</math> y se dirigen al eje vial <math display="inline">E_{j}</math> y el eje vial <math display="inline">E_{j}</math> permanece cerrado (denotado como <math display="inline">n^{\dagger }</math>), entonces su valor será 0, es decir no se van a considerar los viajes a ese destino aunque existan, este cambio o restricción hace que en la parte del denominador de la ecuación [[#eq-10|(10)]] se considere un viaje menos del total que parten del eje vial <math display="inline">E_{i}</math> y así se vuelven a distribuir las probabilidades para que las filas sumen 1. | Una pregunta interesante en el diseño de redes viales es, qué le sucede a la red con respecto a las ocupaciones de los ejes viales y el tiempo promedio dentro de ella <span id='citeF-27'></span>[[#cite-27|[27]]]. En particular, un tema central que discutiremos aquí es tratar de estimar que sucede cuando uno de los ejes viales se cierra o es bloqueado al flujo vehicular, debido a desastres naturales, obras viales, manifestaciones, entre otras posibilidades. Para realizar esta estimación, consideraremos la red descrita anterior y llamaremos <math display="inline">n^{\dagger }</math> al nodo asociado al eje vial que se encuentra bloqueado o inaccesible al flujo vehicular en función de las razones descritas. Para analizar el efecto de la inaccesibilidad del nodo <math display="inline">n^{\dagger }</math> para el flujo de vehicular dentro de la red, realizaremos lo siguiente. Para el nodo <math display="inline">n^{\dagger }</math> sustituiremos por ceros los valores de la columna de la matriz <math display="inline">\bold{P}</math> asociada al nodo <math display="inline">n^{\dagger }</math>. Esto indicará que eje vial <math display="inline">\dagger </math> no está disponible para poder circular y así sucesivamente. Es decir, se construyen 32 redes diferentes en donde se considera el cierre de cada nodo, la información de las nuevas entradas de cada matriz de transición se obtiene de acuerdo a la ecuación [[#eq-10|(10)]], como estamos considerando que <math display="inline">V_{ij}</math> el número total de viajes que parten del eje vial <math display="inline">E_{i}</math> y se dirigen al eje vial <math display="inline">E_{j}</math> y el eje vial <math display="inline">E_{j}</math> permanece cerrado (denotado como <math display="inline">n^{\dagger }</math>), entonces su valor será 0, es decir no se van a considerar los viajes a ese destino aunque existan, este cambio o restricción hace que en la parte del denominador de la ecuación [[#eq-10|(10)]] se considere un viaje menos del total que parten del eje vial <math display="inline">E_{i}</math> y así se vuelven a distribuir las probabilidades para que las filas sumen 1. | ||
| Line 1,331: | Line 247: | ||
|} | |} | ||
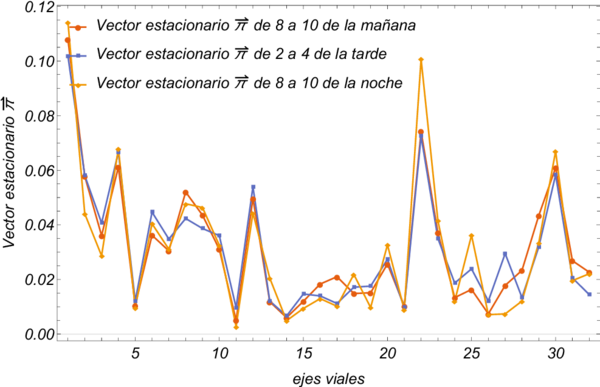
| − | Tal como se mencionó anteriormente,la determinación de la matriz de probabilidad <math display="inline">\bold{P}</math> y la matriz <math display="inline">\bold{M}</math> se realizaron para un horario específico. Se extendió este cálculo considerando la información de las bases de datos del INEGI correspondientes a tres horarios diferentes <span id='citeF-25'></span>[[#cite-25|[25]]]. Con base en la información de las matrices origen-destino (OD) correspondientes a tres horarios diferentes se calcularon las matrices de probabilidad de transición <math display="inline">\bold{P}</math> y la matriz de primer visita promedio <math display="inline">\bold{M}</math> en los tres casos. La Figura [[#img-8|(8)]] muestra una comparación del vector de distribución de probabilidad estacionaria <math display="inline">\vec{\pi }</math> en cada caso, correspondientes a 3 diferentes horarios para un día entre semana, de 8 a 10 | + | Tal como se mencionó anteriormente,la determinación de la matriz de probabilidad <math display="inline">\bold{P}</math> y la matriz <math display="inline">\bold{M}</math> se realizaron para un horario específico. Se extendió este cálculo considerando la información de las bases de datos del INEGI correspondientes a tres horarios diferentes <span id='citeF-25'></span>[[#cite-25|[25]]]. Con base en la información de las matrices origen-destino (OD) correspondientes a tres horarios diferentes se calcularon las matrices de probabilidad de transición <math display="inline">\bold{P}</math> y la matriz de primer visita promedio <math display="inline">\bold{M}</math> en los tres casos. La Figura [[#img-8|(8)]] muestra una comparación del vector de distribución de probabilidad estacionaria <math display="inline">\vec{\pi }</math> en cada caso, correspondientes a 3 diferentes horarios para un día entre semana, de 8 a 10 Hrs. de la mañana, 2 a 4 Hrs. de la tarde y 8 a 10 Hrs. de la noche. Se observa que esencialmente los tres vectores de distribución de probabilidad estacionaria tienen esencialmente el mismo comportamiento. Éste resultado es interesante, dado que en principio, se podría pensar que cada horario podría tener un vector de distribución de probabilidad estacionaria <math display="inline">\vec{\pi }</math> completamente diferente. Sin embargo éste no es el caso. |
<div id='img-8'></div> | <div id='img-8'></div> | ||
| Line 1,341: | Line 257: | ||
|} | |} | ||
| − | Finalmente, se realizó el cálculo de las constantes de Kemeny con la red completa y funcional para cada uno de los horarios descritos. Tal como se ha mencionado, la constante de Kemeny es una estimación cuantitativa del tiempo promedio de flujo o tránsito dentro de la red. Los cálculos mostrados en la Tabla [[#table- | + | Finalmente, se realizó el cálculo de las constantes de Kemeny con la red completa y funcional para cada uno de los horarios descritos. Tal como se ha mencionado, la constante de Kemeny es una estimación cuantitativa del tiempo promedio de flujo o tránsito dentro de la red. Los cálculos mostrados en la Tabla [[#table-1|1]] muestran que <math display="inline">K</math> sí tiene una variación dependiendo del horario. Es decir, en tanto que el vector de distribución de probabilidad estacionaria <math display="inline">\vec{\pi }</math> es esencialmente constante, el valor de <math display="inline">K</math> sí depende del horario. El valor mayor de <math display="inline">K</math> corresponde al horario matutino, posteriormente el horario de la tarde y finalmente el horario nocturno. Así, el flujo dentro de la red es mucho más lento por la mañana que la tarde o noche. |
{| class="floating_tableSCP wikitable" style="text-align: center; margin: 1em auto;min-width:50%;" | {| class="floating_tableSCP wikitable" style="text-align: center; margin: 1em auto;min-width:50%;" | ||
| − | |+ style="font-size: 75%;" |<span id='table- | + | |+ style="font-size: 75%;" |<span id='table-1'></span>Tabla. 1 Comparación de las variaciones del valor de la Constante de Kemeny donde, todos los ejes viales están disponibles para poder circular, la constante de Kemeny contiene información acerca del tiempo promedio dentro de la red en 3 diferentes horarios, de 8 a 10 de la mañana, 2 a 4 horas de la tarde y de 8 a 10 de la noche, estimada por Wolfram Mathematica mediante la ecuación [[#eq-8|(8)]] donde, <math>K=\sum _{j=1}^{n} \bold{M}_{ij}\vec{\pi } _{j}</math>. |
|- style="border-top: 2px solid;" | |- style="border-top: 2px solid;" | ||
| style="border-left: 2px solid;border-right: 2px solid;" | Horario | | style="border-left: 2px solid;border-right: 2px solid;" | Horario | ||
| Line 1,361: | Line 277: | ||
|} | |} | ||
| − | + | Los valores de las constantes de Kemeny obtenidas son bastantes cercanas, por lo que no hay un aumento significativo en el tiempo promedio de viaje de un eje vial arbitrario a un destino elegido al azar de acuerdo con la distribución estacionaria en estos horarios. Los tiempos de viaje son constantes para todas los ejes viales en los tres horarios (por lo tanto, no hay tráfico, o al menos se distribuye uniformemente). En cuanto a la eficiencia de la red, la red vial correspondiente al horario de 8 a 10 Hrs. de la noche tiene el menor valor de constante de Kemeny, y redes caracterizadas por valores pequeños de la constante de Kemeny deberían ser más eficientes en términos de flujo de tráfico. | |
| − | + | =4 Conclusiones= | |
En este trabajo se propuso un modelo de cadena de Markov discreta (CMD) para analizar el flujo de tráfico dentro de la red de treinta y dos ejes viales principales de la Ciudad de México. La red de los 32 principales ejes viales de la Ciudad de México y sus intersecciones se definieron mediante un grafo dual <math display="inline">\mathcal{G}</math> en donde los nodos <math display="inline">n_j</math> corresponden a los ejes viales y los enlaces a sus intersecciones. Sobre esta red, se define una cadena de Markov discreta (CMD) con matriz de probabilidades de transición <math display="inline">\bold{P}= \{ p_{ij} \} </math> la cual se obtiene a partir de las matrices de origen-destino (OD) de las bases de datos del INEGI. A partir del cómputo de <math display="inline">\bold{P}</math> es posible determinar otros cuantificadores como el vector de distribución de probabilidad estacionario <math display="inline">\vec{\pi }</math>, la matriz de primer visita promedio <math display="inline">\bold{M}</math> y la constante de Kemeny. | En este trabajo se propuso un modelo de cadena de Markov discreta (CMD) para analizar el flujo de tráfico dentro de la red de treinta y dos ejes viales principales de la Ciudad de México. La red de los 32 principales ejes viales de la Ciudad de México y sus intersecciones se definieron mediante un grafo dual <math display="inline">\mathcal{G}</math> en donde los nodos <math display="inline">n_j</math> corresponden a los ejes viales y los enlaces a sus intersecciones. Sobre esta red, se define una cadena de Markov discreta (CMD) con matriz de probabilidades de transición <math display="inline">\bold{P}= \{ p_{ij} \} </math> la cual se obtiene a partir de las matrices de origen-destino (OD) de las bases de datos del INEGI. A partir del cómputo de <math display="inline">\bold{P}</math> es posible determinar otros cuantificadores como el vector de distribución de probabilidad estacionario <math display="inline">\vec{\pi }</math>, la matriz de primer visita promedio <math display="inline">\bold{M}</math> y la constante de Kemeny. | ||
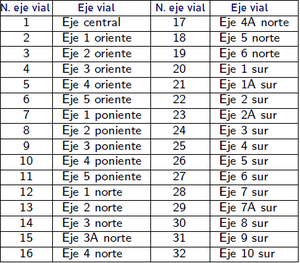
| − | A partir de los cuantificadores anteriores, se calculó el vector de distribución de probabilidad estacionaria <math display="inline">\vec{\pi }</math> para la red de ejes viales en completa funcional, observándose que existe algunos ejes con mayor probabilidad de ocupación en el horario considerado inicialmente de 8 a 10 Hrs AM, que son los ejes viales 1, 22, 4, 30 y | + | A partir de los cuantificadores anteriores, se calculó el vector de distribución de probabilidad estacionaria <math display="inline">\vec{\pi }</math> para la red de ejes viales en completa funcional, observándose que existe algunos ejes con mayor probabilidad de ocupación en el horario considerado inicialmente de 8 a 10 Hrs AM, que son los ejes viales 1, 22, 4, 30 y 2, correspondientes al eje Central, eje 2 sur, eje 3 oriente, eje 8 sur y eje 1 oriente. Uno de los resultados centrales de este trabajo es que al considerar tres diferentes horarios de flujo vehicular, de 8 a 10 Hrs am, de 14 a 16 Hrs y de 20 a 22 Hrs no se observa una diferencia sustancial para el vector de distribución de probabilidad estacionaria <math display="inline">\vec{\pi }</math>. Existen diferencias muy pequeñas, pero que en realidad no son significativas, indicando entonces que en promedio los tres horarios considerados tienen una probabilidad extremadamente similar de ocupación. Posteriormente se analizó la influencia del bloqueo de un eje vial particular <math display="inline">n^{\dagger }</math> dentro de la red para evaluar la relevancia de este nodo para el flujo de tráfico vehicular. Para hacer esta valoración, se generaron 32 redes viales diferentes en cada una de las cuales se bloqueó uno de los ejes viales. Se calculó cada uno de los vectores de distribución de probabilidad estacionaria para cada una de estas redes y se observa que dado el cierre de un eje vial en particular tiene como consecuencia el aumento de la ocupación de los demás, de igual forma se aprecia que en algunos casos, el grado de ocupación de algunos ejes viales disminuye cuando alguno otro se cierra implicando entonces una mejora en la circulación. |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
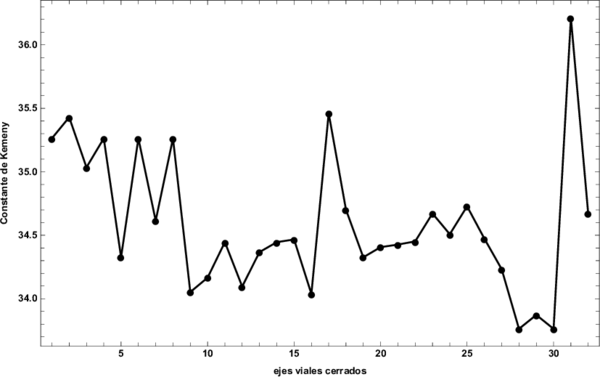
| − | < | + | En una segunda fase de este trabajo se evalúo la constante de Kemeny <math display="inline">K</math> tanto para la red vial inicial completa y funcional, como para cada una de sus 32 variantes en donde existía un eje bloqueado <math display="inline">n^{\dagger }</math>. El valor de <math display="inline">K</math> para la red vial inicial es de <math display="inline">K=34.43</math> el cual es nuestro valor de referencia. Se observa que al generar diferentes bloqueos en distintos nodos <math display="inline">n^{\dagger }</math> de la red la constante de Kemeny <math display="inline">k^{\dagger }</math> puede incrementarse o disminuir su valor, incluso por debajo del valor de referencia. Éste es el caso por ejemplo que ocurre en el bloqueo de los ejes que tienen un valor de <math display="inline">K</math> menor que el de referencia, que son el 28, 29 y 30 que corresponden a los ejes viales 7 sur, 7A sur y 8 sur. En forma contraintuitiva, el bloqueo de estos ejes viales reduce los tiempos promedios de viaje dentro de la red dado que el flujo vehicular se distribuirá en ejes de mayor capacidad. En general, el fenómeno que se observa es que la intuición indicaría. El bloqueo de un eje vial <math display="inline">n^{\dagger }</math> induce un incremento en la constante de Kemeny correspondiente. En general, esto sucede en todos los casos, pero es particularmente notorio en el caso de los ejes viales 31, 17 y 2 correspondientes a los ejes viales 9 sur, 4A norte y 1 oriente |
| − | + | ||
| − | + | Como nota final consideramos que este análisis cuantitativo puede contribuir a la generación de políticas públicas relevantes en el mantenimiento de los ejes viales actuales de la Ciudad de México en función de su relevancia dentro de la red vehicular, pero también en el diseño de nuevas rutas estratégicas que puedan mejorar la conectividad de esta gran urbe que es la Ciudad de México. | |
| − | + | ||
| − | + | ==BIBLIOGRAFÍA== | |
<div id="cite-1"></div> | <div id="cite-1"></div> | ||
Latest revision as of 16:37, 23 December 2021
1 Introducción
El tráfico vehicular es uno de los problemas más importantes que enfrentan actualmente las grandes urbes en función del número creciente de vehículos que circulan y del limitado espacio existente [1]. Los efectos producidos por el incremento del flujo vehicular van más allá del impacto económico, alcanzando la esfera social, el medio ambiente y la calidad de vida de los habitantes en sí misma [2]. Por tanto, cada vez es más necesario contar con herramientas formales y cuantitativas que permitan el diseño de redes de flujo vehicular (avenidas, ciclovías, sistemas de transporte público) que permitan una comunicación más eficiente y efectiva entre los distintos puntos de una ciudad [3]. Ésta no es una preocupación reciente. Los primeros estudios sobre el tráfico vehicular se remontan a la década de 1930-1940 con los trabajos de B D Greenshield, quien aplicó por primera vez métodos fotográficos y matemáticos para la medición de diferentes variables relacionadas con el tráfico vehicular y la descripción de su comportamiento [4].
Diferentes modelos matemáticos se han aplicado para analizar el problema del transporte eficiente y del flujo vehicular en redes urbanas. Dependiendo del nivel de detalle, los modelos de tráfico vehicular generalmente se clasifican como microscópicos, mesoscópicos y macroscópicos [5]. Existen modelos matemáticos basados en ecuaciones diferenciales parciales (EDP) [6], autómatas celulares (AC) [7], modelos basados en agentes [8], ecuaciones diferenciales estocásticas, entre otros. En este trabajo abordaremos el análisis del flujo vehicular mediante el formalismo de los procesos estocásticos en tiempo discreto. Más específicamente, definiremos una cadena de Markov discreta ( CMD) sobre un grafo dual el cual representará la dinámica del flujo vehicular a tiempo discreto sobre un conjunto de nodos y enlaces los cuales representan a los ejes viales y sus intersecciones. Basaremos este análisis en el trabajo de Crisostomi et al [9], en donde se discute ampliamente las ventajas del enfoque Markoviano para este tipo de análisis. Tal como mostraremos en este trabajo, el enfoque estocástico mediante CMD nos permitirá extraer información relevante de conectividad y flujo dentro de la red [10] [11].
En este trabajo se analizará el conjunto de 32 ejes viales principales de la Ciudad de México, el cual en conjunto con sus intersecciones conforma un grafo dual . A partir de este grafo dual, definimos un proceso estocástico de tipo cadena de Markov a tiempo discreto con matriz de probabilidad . Para determinar los elementos de la matriz utilizaremos información estadística obtenida a partir de las matrices origen destino (OD) del INEGI y la Secretaría de Movilidad de la Ciudad de México [12]. Con esta información evaluaremos tanto el vector de distribución de probabilidad estacionaria de la cadena de Markov como la matriz de primer visita promedio y la constante de Kemeny . Las cadenas de Markov constituyen uno de los formalismos estocásticos más utilizados en la modelación de un proceso probabilístico[13]. En esencia, este tipo de procesos estocásticos establece que el estado actual del proceso sólo depende del resultado inmediato anterior y no del conjunto de estados previos [14]. La propiedad de Markov menciona que la distribución de probabilidad del valor futuro de una variable aleatoria depende únicamente de su valor presente, siendo independiente de la historia de dicha variable, por lo que podemos expresarla como:
|
|
(1) |
es decir, sólo depende del valor de la variable estocástica en el paso inmediato anterior. Tal proceso se denomina proceso de Markov o cadena de Markov discreta (CMD) y fue propuesto por Andrei Markov .
Este trabajo se presenta de la siguiente manera. En la Sección II discutiremos los elementos básicos de la teoría de los procesos de Markov discretos. A continuación presentaremos la aplicación de estos resultados a la red de 32 ejes viales principales de la Ciudad de México. Posteriormente efectuaremos un análisis cuantitativo detallado de las cantidades mencionadas previamente y analizaremos el impacto del cierre de un eje vial dado a la circulación mediante el uso del bloqueo de un eje vial dentro de la red y el cálculo de este efecto en las cantidades anteriormente descritas. Finalmente presentaremos un conjunto de conclusiones y perspectivas que pueden considerarse en un análisis posterior a futuro de este trabajo.
2 Cadenas de Markov discretas. Un proceso estocástico clásico
En este trabajo representaremos la conectividad de los ejes viales bajo consideración y el tráfico vehicular dentro de la Ciudad de México mediante una cadena de Markov discreta (CMD). Una CMD representa un proceso estocástico discreto definido por un conjunto de estados , para los cuales existe una probabilidad de transición de pasar del estado al estado . Esta probabilidad cumple la propiedad de Markov la cual establece que si el estado al tiempo y el conjunto de estados discretos a tiempos previos son conocidos, la probabilidad del estado futuro no depende de los estados anteriores , sino solo depende del estado actual . Esto es, [15]:
|
|
(2) |
|
|
la Figura (1) muestra una representación de una cadena de Markov discreta con un conjunto de estados dado por el conjunto con probabilidades de transición determinadas. Una CMD está por tanto determinada por una matriz de tamaño llamada matriz de probabilidades de transición cuyas entradas denotan la probabilidad de pasar del estado al estado en una unidad de tiempo dada. Esto es,
|
|
(3) |
Los elementos satisfacen que y . Es decir, las filas de la matriz suman la unidad.
Dada la matriz de probabilidades estacionarias determinaremos el vector de distribución de probabilidad estacionaria, el cual es una distribución de probabilidad invariante para una cadena de Markov con matriz de probabilidades de transición si cumple que [16]:
|
|
(4) |
Lo anterior es equivalente a y significa que si una variable aleatoria inicial tiene una distribución entonces la distribución de también es , es decir, esta distribución no cambia con el paso del tiempo [17]. Para CMD ergódicas, i.e, aquellas en las que es posible alcanzar cualquier estado en un número finito de pasos, determinamos la matriz y la matriz fundamental dadas por
|
|
(5) |
donde es una matriz con todas sus filas idénticas al vector de distribución de probabilidad estacionaria discutido anteriormente. La matriz fundamental de esta CMD ergódica está dada por [18]
|
|
(6) |
donde es la matriz identidad, la matriz de probabilidades de transición y la matriz discutida anteriormente. Es importante mencionar que la matriz fundamental para cadenas ergódicas desempeña un papel muy importante, pues puede usarse para identificar un conjunto de parámetros relevantes, como la matriz de primer visita promedio (mean first passage time matrix, en inglés) [20], la cual nos será fundamental en este trabajo como una cantidad relevante para calcular la relevancia de los distintos ejes viales de la Ciudad de México.
La matriz de primer visita promedio, en inglés (MFPT) denotada como , es el número promedio de pasos para llegar por primera vez al estado partiendo de . Se puede calcular de acuerdo con la siguiente expresión:
|
|
(7) |
donde la diagonal con de acuerdo a la definición dada. Sin embargo, es posible extender esta definición para incluir los elementos diagonales de . Con esa generalización, los elementos diagonales son inversamente proporcionales a los tiempos de recurrencia . Esto es, [21]. Finalmente, en este trabajo calcularemos también la constante de Kemeny, la cual nos permite cuantificar la eficiencia de flujo de información dentro de la red, de acuerdo a [22]:
|
|
(8) |
donde hemos tomando la convención de , la constante es la suma de las entradas del vector de tamaño que resulta del producto de la matriz por el vector de distribución de probabilidad estacionaria . La constante de Kemeny proporciona una cantidad interesante para las cadenas finitas de Markov ergódicas, que es independiente del estado inicial de la cadena de Markov como se puede ver en [22]. Por lo tanto, la constante de Kemeny es una medida intrínseca para este proceso estocástico, y si la matriz de transición tiene valores propios entonces otra forma de calcular es:
|
|
(9) |
donde la suma inicia en el índice . La ecuación (9) enfatiza el hecho de que solo depende en realidad de y que aumenta si uno o más valores propios de es real y cercano a 1. [22].
3 Aplicaciones a redes de transporte. Caso de la Ciudad de México
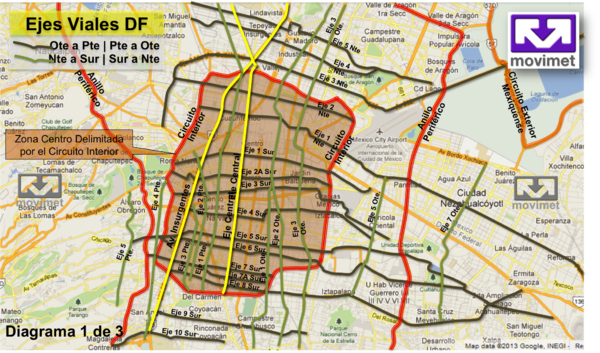
Con base en las herramientas anteriores, definiremos una cadena de Markov discreta (CMD) para analizar cuantitativamente las propiedades del flujo de tráfico dentro de un conjunto de ejes viales de la Ciudad de México. Para ello, seleccionaremos un conjunto de avenidas o ejes viales principales y sus respectivos puntos de cruce como los elementos del grafo . En esta representación , a la cual definimos como grafo primario, las intersecciones son los nodos de la red y los enlaces son los ejes viales mismos. Para este grafo se define el grafo dual como aquel en el cual los nodos serán ahora los ejes viales y las intersecciones de los ejes viales corresponden a los enlaces del grafo . Esto es, los enlaces y los nodos intercambian su papel [23]. La Figura (2) muestra la red de ejes viales de la Ciudad de México que analizaremos en este trabajo, la cual consta de los 32 principales ejes viales de la Ciudad de México [24].
|
| Figura 2: Mapa vial de la Ciudad de México en donde se muestra los 32 principales ejes viales de la ciudad. |
El flujo vehicular, es decir, el número de vehículos que circulan en los ejes principales es información no fácilmente accesible. Sin embargo, es factible conocer datos estadísticos a partir de la información en las bases de datos del INEGI (Instituto Nacional de Estadística, Geografía e Informática) [25]. Para determinar la matriz se requiere conocer el número total de viajes que parten del eje vial y se dirigen al eje vial . Esto es una cantidad compleja de determinar, sin embargo, se considerará la información disponible para una ventana de tiempo y espacio restringido. En este caso, consideraremos inicialmente un día en particular de la semana durante un lapso de tiempo de 2 horas, específicamente consideramos una ventana temporal entre 8 y 10 horas de la mañana. Por tanto entonces, la probabilidad se determina por
|
|
(10) |
donde son las entradas de la matriz de probabilidad de transición. Con esta información es posible determinar y el grafo correspondiente, el cual se muestra en la Figura (3).
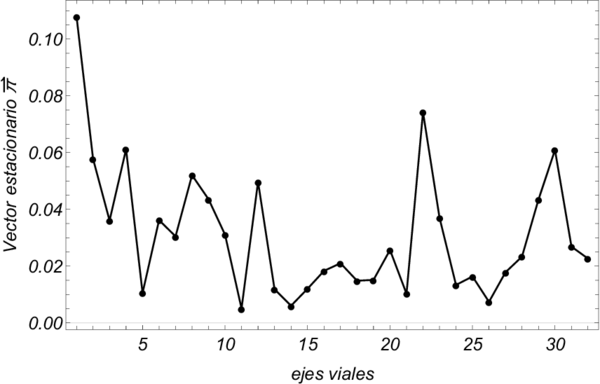
A partir de esta información, determinamos el vector de distribución de probabilidad estacionaria , el cual nos indica el estado de equilibrio de la cadena de Markov definida sobre la red. La figura (4) muestra el vector de distribución de probabilidad estacionaria en función del nodo, es decir, de los ejes viales considerados. El vector de distribución de probabilidad estacionaria indica aquellos ejes viales con mayor probabilidad de ocupación para un día particular de la semana, en un horario de 8 a 10 horas de la mañana. Los ejes viales que muestran una mayor probabilidad de ocupación, a tiempos largos de evolución de la CMD son los correspondientes a los ejes viales 1, 22, 4, 30 y 2, correspondientes al eje Central, eje 2 sur, eje 3 oriente, eje 8 sur y eje 1 oriente.
|
| Figura 4: Vector de distribución de probabilidad estacionaria correspondiente de la red de ejes viales de la CDMX calculada mediante la ecuación (4) en donde , contiene información de la probabilidad de ocupación de cada eje vial. |
Uno de los objetivos centrales de este trabajo es determinar la matriz de primer visita promedio, (mean first passage time) la cual nos indica, en promedio, el número de pasos requerido para pasar de un nodo a un nodo dentro de la red. En este caso, dado que el conjunto de nodos se refiere a los ejes viales en cuestión, el elemento se refiere al tiempo promedio, considerando todas las rutas posibles, en el cual partiendo del eje vial se alcanza el eje vial por primera vez. Es fundamental considerar que este tiempo (o número de pasos) se refiere a la primera vez que se alcanza el nodo dentro de la red. En principio es perfectamente posible construir trayectorias que lleguen a muchas más de una vez, pero no son las que se consideran en el proceso estocástico aquí descrito.
La figura (5) muestra una representación tridimensional de , en donde los ejes e representan los ejes viales de origen y destino, mientras que el eje se refiere al valor correspondiente de . Los valores más grandes de las entradas representan los tiempos promedio más grandes de recorrido entre dos ejes viales determinados.
Finalmente, se ha determinado también la llamada constante de Kemeny , la cual en teoría de grafos corresponde al número de pasos promedio requeridos para alcanzar cualquier nodo dentro de la red a partir de un nodo inicial . Interesantemente y como ha sido demostrado, el valor de la constante de Kemeny no depende de que nodo se elija [19] [20]. En la literatura se ha utilizado como una medida de la eficacia de la red, pues redes caracterizadas por pequeños valores en la constante de Kemeny generalmente tienen un mayor grado de eficiencia [19]. Para nuestro caso, el valor calculado es , el cual es un indicador de desempeño vial de la red en general. Para comprender mejor el significado de considere un conductor al azar que se mueve dentro de la red de acuerdo a las probabilidades de transición dadas de la matriz . En algún momento, nuestro conductor está perdido y no sabe el estado (eje vial) en que se encuentra y hacia dónde se dirige. En este contexto, la constante de Kemeny puede interpretarse como el número promedio de pasos que seguirá el conductor al azar antes de llegar a su destino [26].
3.1 Identificación de ejes viales importantes
Una pregunta interesante en el diseño de redes viales es, qué le sucede a la red con respecto a las ocupaciones de los ejes viales y el tiempo promedio dentro de ella [27]. En particular, un tema central que discutiremos aquí es tratar de estimar que sucede cuando uno de los ejes viales se cierra o es bloqueado al flujo vehicular, debido a desastres naturales, obras viales, manifestaciones, entre otras posibilidades. Para realizar esta estimación, consideraremos la red descrita anterior y llamaremos al nodo asociado al eje vial que se encuentra bloqueado o inaccesible al flujo vehicular en función de las razones descritas. Para analizar el efecto de la inaccesibilidad del nodo para el flujo de vehicular dentro de la red, realizaremos lo siguiente. Para el nodo sustituiremos por ceros los valores de la columna de la matriz asociada al nodo . Esto indicará que eje vial no está disponible para poder circular y así sucesivamente. Es decir, se construyen 32 redes diferentes en donde se considera el cierre de cada nodo, la información de las nuevas entradas de cada matriz de transición se obtiene de acuerdo a la ecuación (10), como estamos considerando que el número total de viajes que parten del eje vial y se dirigen al eje vial y el eje vial permanece cerrado (denotado como ), entonces su valor será 0, es decir no se van a considerar los viajes a ese destino aunque existan, este cambio o restricción hace que en la parte del denominador de la ecuación (10) se considere un viaje menos del total que parten del eje vial y así se vuelven a distribuir las probabilidades para que las filas sumen 1.
Posteriormente calculamos el nuevo vector de distribución de probabilidad estacionaria para cada una de las redes. Cada nueva red se refiere al bloque del eje vial asociado al nodo , el cual recorre todos los índices de la red.
Para cada valor del vector de distribución de probabilidad estacionaria , el cual en este caso recorrerá todos los nodos de los ejes viales de la CDMX, se calculará el vector de distribución de probabilidad estacionaria de acuerdo a la prescripción anterior. A partir de estos resultados se han calculado las constantes de Kemeny para cada caso. La Figura (6) muestra el vector de distribución de probabilidad estacionaria , el cual indica el valor más probable de la distribución estacionaria de ocupación de cada eje vial , una vez que se ha bloqueado un eje particular, en cada caso se bloquea el el nodo asociado al eje vial que se encuentra bloqueado o inaccesible al flujo vehicular. Uno de los resultados más interesantes de este análisis es que el cierre de un eje vial en particular tiene como consecuencia el aumento de la ocupación de los demás. Asimismo se puede observar que en algunos casos, el grado de ocupación de algunos ejes viales disminuye cuando algún otro se cierra implicando entonces una mejora en la circulación.
La relevancia de un eje vial dado dentro de una red de comunicación puede definirse de acuerdo a diferentes criterios, pero en este trabajo consideraremos que un eje vial posee un alto grado de relevancia si el tiempo promedio de viaje dentro de la red aumentan cuando se cierra este eje vial. Así, entonces diremos que es un eje vial crítico dentro de la red si se cumple que la constante de Kemeny es mayor que la constante de Kemeny de la red sin perturbación. Para determinar aquellos ejes viales cuya relevancia es mayor dentro de la red, calcularemos las constantes de Kemeny asociadas al bloqueo de cada uno de los ejes viales, tal como se realizó anteriormente. La Figura (7) muestra los valores de en función del bloqueo del nodo . El cálculo de muestra que existen al menos dos ejes viales para los cuales el tiempo promedio de recorrido dentro de la red se incrementa sustancialmente. Éstos son y los cuales corresponden a los ejes 5 norte y 10 sur. Por otro lado, se observa que es posible se presente el fenómeno inverso. Es decir, que el bloqueo de un eje determinado pueda disminuir sustancialmente el flujo de la red. Es importante mencionar que estamos discutiendo fenómenos dentro de la red en un proceso estocástico. De forma que de un cierto conjunto de realizaciones del proceso estocástico, en promedio se observan estas características. No siempre se observará esta disminución o aumento de la constante de Kemeny pero resulta un indicador de la estructura de conectividad de la red. Los valores más grandes del conjunto se obtienen si se cierran los ejes viales 31, 17 y 2, correspondientes a eje 9 sur, eje 4A norte, eje 1 oriente; estos ejes viales pueden considerarse las más críticas de la red. En tanto que los menos críticos son los ejes viales 28, 30 y 29, correspondientes a eje 7 sur, eje 8 sur y eje 7A sur, como se muestra en la Figura (7), en donde a medida que se cierra algún eje vial, las demás son afectadas o beneficiadas.
Tal como se mencionó anteriormente,la determinación de la matriz de probabilidad y la matriz se realizaron para un horario específico. Se extendió este cálculo considerando la información de las bases de datos del INEGI correspondientes a tres horarios diferentes [25]. Con base en la información de las matrices origen-destino (OD) correspondientes a tres horarios diferentes se calcularon las matrices de probabilidad de transición y la matriz de primer visita promedio en los tres casos. La Figura (8) muestra una comparación del vector de distribución de probabilidad estacionaria en cada caso, correspondientes a 3 diferentes horarios para un día entre semana, de 8 a 10 Hrs. de la mañana, 2 a 4 Hrs. de la tarde y 8 a 10 Hrs. de la noche. Se observa que esencialmente los tres vectores de distribución de probabilidad estacionaria tienen esencialmente el mismo comportamiento. Éste resultado es interesante, dado que en principio, se podría pensar que cada horario podría tener un vector de distribución de probabilidad estacionaria completamente diferente. Sin embargo éste no es el caso.
Finalmente, se realizó el cálculo de las constantes de Kemeny con la red completa y funcional para cada uno de los horarios descritos. Tal como se ha mencionado, la constante de Kemeny es una estimación cuantitativa del tiempo promedio de flujo o tránsito dentro de la red. Los cálculos mostrados en la Tabla 1 muestran que sí tiene una variación dependiendo del horario. Es decir, en tanto que el vector de distribución de probabilidad estacionaria es esencialmente constante, el valor de sí depende del horario. El valor mayor de corresponde al horario matutino, posteriormente el horario de la tarde y finalmente el horario nocturno. Así, el flujo dentro de la red es mucho más lento por la mañana que la tarde o noche.
| Horario | Constante de Kemeny |
| 8 a 10 hrs. de la mañana | 34.4376 |
| 2 a 4 hrs. de la tarde | 34.2413 |
| 8 a 10 hrs. de la noche | 34.1795 |
Los valores de las constantes de Kemeny obtenidas son bastantes cercanas, por lo que no hay un aumento significativo en el tiempo promedio de viaje de un eje vial arbitrario a un destino elegido al azar de acuerdo con la distribución estacionaria en estos horarios. Los tiempos de viaje son constantes para todas los ejes viales en los tres horarios (por lo tanto, no hay tráfico, o al menos se distribuye uniformemente). En cuanto a la eficiencia de la red, la red vial correspondiente al horario de 8 a 10 Hrs. de la noche tiene el menor valor de constante de Kemeny, y redes caracterizadas por valores pequeños de la constante de Kemeny deberían ser más eficientes en términos de flujo de tráfico.
4 Conclusiones
En este trabajo se propuso un modelo de cadena de Markov discreta (CMD) para analizar el flujo de tráfico dentro de la red de treinta y dos ejes viales principales de la Ciudad de México. La red de los 32 principales ejes viales de la Ciudad de México y sus intersecciones se definieron mediante un grafo dual en donde los nodos corresponden a los ejes viales y los enlaces a sus intersecciones. Sobre esta red, se define una cadena de Markov discreta (CMD) con matriz de probabilidades de transición la cual se obtiene a partir de las matrices de origen-destino (OD) de las bases de datos del INEGI. A partir del cómputo de es posible determinar otros cuantificadores como el vector de distribución de probabilidad estacionario , la matriz de primer visita promedio y la constante de Kemeny.
A partir de los cuantificadores anteriores, se calculó el vector de distribución de probabilidad estacionaria para la red de ejes viales en completa funcional, observándose que existe algunos ejes con mayor probabilidad de ocupación en el horario considerado inicialmente de 8 a 10 Hrs AM, que son los ejes viales 1, 22, 4, 30 y 2, correspondientes al eje Central, eje 2 sur, eje 3 oriente, eje 8 sur y eje 1 oriente. Uno de los resultados centrales de este trabajo es que al considerar tres diferentes horarios de flujo vehicular, de 8 a 10 Hrs am, de 14 a 16 Hrs y de 20 a 22 Hrs no se observa una diferencia sustancial para el vector de distribución de probabilidad estacionaria . Existen diferencias muy pequeñas, pero que en realidad no son significativas, indicando entonces que en promedio los tres horarios considerados tienen una probabilidad extremadamente similar de ocupación. Posteriormente se analizó la influencia del bloqueo de un eje vial particular dentro de la red para evaluar la relevancia de este nodo para el flujo de tráfico vehicular. Para hacer esta valoración, se generaron 32 redes viales diferentes en cada una de las cuales se bloqueó uno de los ejes viales. Se calculó cada uno de los vectores de distribución de probabilidad estacionaria para cada una de estas redes y se observa que dado el cierre de un eje vial en particular tiene como consecuencia el aumento de la ocupación de los demás, de igual forma se aprecia que en algunos casos, el grado de ocupación de algunos ejes viales disminuye cuando alguno otro se cierra implicando entonces una mejora en la circulación.
En una segunda fase de este trabajo se evalúo la constante de Kemeny tanto para la red vial inicial completa y funcional, como para cada una de sus 32 variantes en donde existía un eje bloqueado . El valor de para la red vial inicial es de el cual es nuestro valor de referencia. Se observa que al generar diferentes bloqueos en distintos nodos de la red la constante de Kemeny puede incrementarse o disminuir su valor, incluso por debajo del valor de referencia. Éste es el caso por ejemplo que ocurre en el bloqueo de los ejes que tienen un valor de menor que el de referencia, que son el 28, 29 y 30 que corresponden a los ejes viales 7 sur, 7A sur y 8 sur. En forma contraintuitiva, el bloqueo de estos ejes viales reduce los tiempos promedios de viaje dentro de la red dado que el flujo vehicular se distribuirá en ejes de mayor capacidad. En general, el fenómeno que se observa es que la intuición indicaría. El bloqueo de un eje vial induce un incremento en la constante de Kemeny correspondiente. En general, esto sucede en todos los casos, pero es particularmente notorio en el caso de los ejes viales 31, 17 y 2 correspondientes a los ejes viales 9 sur, 4A norte y 1 oriente
Como nota final consideramos que este análisis cuantitativo puede contribuir a la generación de políticas públicas relevantes en el mantenimiento de los ejes viales actuales de la Ciudad de México en función de su relevancia dentro de la red vehicular, pero también en el diseño de nuevas rutas estratégicas que puedan mejorar la conectividad de esta gran urbe que es la Ciudad de México.
BIBLIOGRAFÍA
[1] JEROME HARRI, FETHI FILALI Y CHRISTIAN BONNET (2009) Mobility Models for Vehicular Ad Hoc Networks: A Survey and Taxonomy. IEEE commnications surveys and tutorials, fourth quarter, Vol. 11.
[2] CAL y MAYOR, R (2007) Ingeniería de Tránsito Fundamentos y aplicaciones, 8ª Edición, Alfa Omega Grupo Editor, S.A. de CV., México D.F.
[3] KÜHNE, R. D. (2011) Greenshields’ legacy: Highway traffic, Transportation Research E-Circular, págs. E-C149.
[4] GREENSHIELDS, B., CHANNING, W., MILLER, H. (1935) A study of traffic capacity. In Highway research board proceedings,volume 1935, National Research Council (USA), Highway Research Board.
[5] TAYLOR H. M. y KARLIN S. (1994) An introduction to stochastic modeling, Academic Press.
[6] SERDAR COLAK, ANTONIO LIMA, MARTA C. GONZA (2016) Understanding congested travel in urban areas, Nature Communications.
[7] En línea. http://lancis.ecologia.unam.mx/iai/modelacion/agentes
[8] J. DELGADO, P. SAAVEDRA, R.M. VELASCO (2012) Modelación matemática del flujo vehicular, Publicaciones C.B.I. UAM.
[9] CRISOSTOMI E, KIRKLAND S, SHORTEN R (2011) A Google-like model of road network dynamics and its application to regulation and control, International Journal of Control, accepted for publication.
[10] S.M. ROSS (1996) Stochastic Processes, John Wiley y Sons, New York, NY, 2nd edition.
[11] REITER, J.G. (2015) Application of a Markov Chain Traffic Model to the Greater Philadelphia Region, pág. 38.
[12] En línea. https://www.semovi.cdmx.gob.mx/
[13] MAGNANTI, T.L., WONG, R.T. (1984) Network design and transportation planning: Models and algorithms, Transportation science 18, págs. 1–55.
[14] CABALLERO M. E. (2004) Cadenas de Markov: un enfoque elemental, Aportaciones Matemáticas, Serie Textos 29, Sociedad Matemática Mexicana.
[15] RINCÓN, LUIS (2012) Introducción a los procesos estocásticos,Departamento de Matemáticas, Facultad de Ciencias UNAM, México DF, págs. 27–93.
[16] CHO GE, MEYER CD , (2001) Comparison of perturbation bounds for the stationary distribution of a Markov chain, Linear Algebra and its Applications, págs. 137–150.
[17] KIRKLAND, S. (1988–1996) Fastest Expected Time to Mixing for a Markov Chain on a Directed Graph, Linear Algebra and its Applications , pág.433.
[18] A. A. MARKOV (1913) An Example of Statistical Analysis of the Text of Eugene Onegin Illustrating the Association of Trials into a Chain, Bulletin de l'Acadamie Imperiale des Sciences de St. Petersburg, serie 6, vol. 7, págs. 153–162.
[19] PETER G. DOYLE (2009) The Kemeny constant of a Markov chain,GNU Free Documentation License. https://arxiv.org/pdf/0909.2636.pdf
[20] NORRIS J. (1997) Markov chains, Cambridge University Press.
[21] S. REDNER (2001) A guide to first-passage processes, Cambridge University Press, Cambridge. https://g.co/kgs/2q2CQQ
[22] KEMENY, J.G. y SNELL, J.L. (1960) Finite Markov Chains, Princeton: Van Nostrand.
[23] RÉKA A, BARABÁSI A (2002) Statistical Mechanics of Complex Networks, Reviews of Modern Physics.
[24] En línea. http://maps.google.com/
[25] En línea. http://gaia.inegi.org.mx/mdm6/?v
[26] LEVENE, MARK y LOIZOU, G. (2002) Kemeny Constant and the Random Surfer,American Mathematical Monthly 109, págs.741–745.
[27] SALMAN, S., ALASWAD, S. (2017) Urban Road Network Crisis Response Management, Proceedings of the 2017 Industrial and Systems Engineering Conference.
Document information
Published on 18/12/21
Submitted on 05/11/21
Licence: CC BY-NC-SA license