Experimental and numerical analysis of the response of a carbon fiber composite material to an explosion.

1. Introducción

El uso de materiales compuestos sigue aumentando de manera progresiva desde que se empezaron a emplear en los años 70. En un principio, su alto coste de fabricación limitaba su uso a piezas muy concretas del sector aeroespacial. Sin embargo, los avances que se han ido realizando en los métodos de fabricación y la reducción de costes han permitido que su uso se extienda a otros sectores. En contraposición con sus excepcionales propiedades en el plano, una de sus principales desventajas es su debilidad ante cargas fuera del plano Existen numerosos estudios que tratan estos materiales en escenarios típicos de la ingeniería aeronáutica ante este tipo de cargas, principalmente ante impacto. Impactos de alta o baja velocidad de proyectiles rígidos, o impactos de alta velocidad de proyectiles dúctiles. Sin embargo, dado que se pretende seguir aumentando el uso de estos materiales, es necesario conocer y entender el comportamiento de estos materiales ante otro tipo de cargas fuera del plano como son las cargas impulsivas, como las que se producen en explosiones.

En la literatura apenas se pueden encontrar estudios que investiguen la respuesta de estos materiales ante cargas dinámicas como el impacto de una onda de choque, como la derivada de una explosión [1], [2]. Además, estos autores han empleado cargas explosivas reales, lo que supone un alto riesgo. Para evitar este riesgo, la manera más controlada de someter estructuras a este tipo de cargas es mediante el empleo de un tubo de choque (o Shock tube, en inglés). Éstos se emplean para emular el comportamiento que tienen las ondas de presión de una explosión, sin necesidad de explosivos. En la literatura, se han encontrado solo un par de artículos que aporten ensayos relacionados [3], [4] y ninguno de ellos realiza un análisis numérico del mismo.

Con este trabajo se pretende estudiar el fenómeno de las cargas impulsivas en laminados de fibras de carbono (CFRP) empleando técnicas experimentales de vanguardia complementando el estudio realizado mediante el uso de simulaciones numéricas.

2. Materiales y ensayo

2.1. Material

El material empleado en este trabajo son laminados de tejido de carbono/epoxi fabricados por el método conocido como RTM (por sus siglas en inglés ‘Resin Transfer Moulding’ ), cuyas fibras se denominan comercialmente como TENAX E HTA 40 E13 6K, y van siguiendo una secuencia de trenzado 5H Satin. En cuanto a la matriz epoxi, se ha empleado una resina RTM6, certificada para usos aeronáuticos. La secuencia de apilamiento sigue un patrón simétrico de láminas a 0/90^o y ±45^o, quedando de la siguiente forma: [((±45)/(0/90))₃]_s. Las dimensiones de las placas que se van a ensayar son 300 mm x 300 mm y tienen un espesor aproximado de 4.4 mm, con un espesor aproximado de 0.363 por lámina.

2.2. Procedimiento de ensayo: Impacto de onda de choque

Para el estudio experimental de la carga impulsiva ello se emplea un cañón de gas capaz de reproducir un estado similar al impuesto por las ondas de presión derivadas de una emplosión. Los estudios se han realizado empleado el tubo de choque del laboratorio del departamento de Ingeniería Estructural, en la Universidad Noruega de Ciencia y Tecnología (NTNU). El mismo procedimiento que se va a emplear en este trabajo ha sido validado por otros estudios [5]–[7]

El dispositivo experimental que aquí se emplea y que se puede visualizar en la Figura 1 consta de tres partes principales: el depósito que acumulará aire antes del ensayo (Driver), el tubo por el que viajará instantes previos al impacto (Driven) y que mide 16,2 m de largo, y el tanque (Tank), donde se localizará la probeta. Previo al impacto, el Driver que se encuentra en la parte delantera acumula aire a muy alta presión. Para mantener dicha presión, en la cara contigua al tubo del cañón se emplean varias membranas, entre las cuales se establecen distintos pasos de presión para reducir progresivamente la diferencia entre ambas secciones. Para desencadenar el impacto, se vacía rápidamente la presión de uno de los pasos, y es la sobrepresión que tiene el depósito la que rompe las membranas. Entonces, el fluido comprimido empieza a fluir por el tubo hasta alcanzar la probeta.

Poco antes de llegar a la probeta, dos sensores piezoeléctricos miden la presión en ese punto, de tal modo que se conoce exactamente la presión que impacta al material. Para una información más detallada sobre este ensayo, el lector puede referirse a trabajos previos tales como [5], [8].

Además de esto, para sujetar la probeta al final del tubo se emplean dos partes de acero de 200 mm de espesor, entre las cuales queda apretada la placa, dejando una superficie interna libre de 280 mm x 280 mm. También, para garantizar su correcta alineación, se emplea otra parte metálica del mismo espesor que la placa y que a su vez encaja con las dos primeras.

Figura 1: Esquema del tubo de choque (o Shock Tube, en inglés) empleado durante los ensayos experimentales

Además de los sistemas de medida acoplados al cañón, se emplean dos cámaras de alta velocidad (Phantmon v2511), dispuestas según lo que se ve en la Figura 1 y en la Figura 2, las cuales graban el ensayo a 37 000 imágenes por segundo. El objetivo de estas cámaras es, mediante la técnica de correlación de imágenes, obtener los campos de desplazamientos durante el ensayo. Para eso, es necesario pintar un patrón de puntos aleatorios como el que se ve en la Figura 2.

Figura 2: a) Sistemas de medida acoplados al cañón; b) Patrón de puntos aleatorios

Para esta campaña experimental se ensayan cuatro presiones diferentes, desde una sobrepresión de 15 bares en el depósito (P = 15 bar) hasta una máxima de 60 bares (P = 60 bar). Comentar que la distribución de ensayos no es uniforme, ya que las presiones intermedias se sitúan en P = 25 bar y P = 35 bar. Esto es porque la presión que alcanza a la probeta no es lineal con la presión del depósito, si no que sigue una distribución logarítmica.

3. Simulación numérica

Para desarrollar un modelo numérico del ensayo experimental citado anteriormente, se ha empleado un método de elementos finitos en el software comercial Abaqus.

En primer lugar, se ha empleado una subrutina de usuario para representar el comportamiento del material compuesto. De esta forma, se logra implementar un modelo de daño continuo. Dicha subrutina, denominada ‘ABQ_PLY_Fabric’, se encuentra disponible en el software empleado, y ha sido desarrollada especialmente para reproducir el comportamiento de este tipo de materiales compuestos tipo tejido. Con ella, el material se comporta como elástico lineal ortótropo hasta el inicio del daño. Para una explicación detallada de la subrutina, el lector se puede referir a la documentación del software

Como criterios de inicio de daño en dirección de las fibras, se emplean cuatro ecuaciones diferentes resumidas en (1), en las cuales intervienen la resistencia del material según la orientación ( ${\textstyle {X}_{\alpha }}$), donde α representa los estados de carga de tracción o compresión, y las dos orientaciones de fibras (1,2): α = 1(+/-), 2(+/-). Se considera el daño en cualquiera de las direcciones cuando ${\textstyle {F}_{I}\geq 1}$.

${F}_{I}={\frac {{\sigma }_{\alpha }}{{X}_{\alpha }}}$

(1)

Para la propagación del daño en dirección de las fibras, se emplean las variables d_α, cuya evolución sigue la tendencia de una exponencial inversa y que se calculan de la siguiente forma:

${d}_{\alpha }=1-\mathrm {exp} \,(-{C}_{\alpha })$

(2)

Donde ${\textstyle {C}_{\alpha }\,}$ es un valor que se calcula en función del módulo de Young, la energía de fractura, la longitud característica del elemento y el daño . Nótese que d_α = 0 implica que no existe el daño y d_α = 1 que se ha alcanzado el límite.

Por último, el comportamiento a cortadura del material se modela siguiendo una ley de endurecimiento seguida de un inicio del daño idéntica a la anterior y su correspondiente propagación, que en este caso sigue una evolución logarítmica.

Por otro lado, se describe el comportamiento interlaminar que tendrá el material, el cual se representa mediante una interacción de superficie cohesiva, también incluida en el software empleado, que considera un comportamiento en modo mixto, con comportamiento elástico hasta el inicio del daño. Este inicio de daño viene marcado por un criterio de tensiones cuadrático y una evolución lineal según los desplazamientos efectivos. Para más información, el autor se puede referir a la documentación del software [9].

Para representar el laminado, se han creado doce partes diferentes, una para cada una de las láminas, unidas por las interacciones cohesivas antes mencionadas. El mallado de cada una de las partes es homogéneo y con un tamaño de elemento de 2 mm.

Las principales propiedades asignadas al laminado siguen lo indicado en la Tabla 1.

Tabla 1: Propiedades del material compuesto empleado en las simulaciones

Propiedades elásticas	Propiedades resistentes	Energías de fractura
${E}_{1+}=59\,GPa$	${X}_{1+}=804\,MPa$	${G}_{1+}=60\,mJ/m{m}^{2}$
${E}_{2+}=55\,GPa$	${X}_{2+}=773\,MPa$	${G}_{2+}=60\,mJ/m{m}^{2}$
${E}_{1-}=47\,GPa$	${X}_{1-}=743\,MPa$	${G}_{1-}=30\,mJ/m{m}^{2}$
${E}_{2-}=45\,GPa$	${X}_{2-}=747\,MPa$	${G}_{2-}=30\,mJ/m{m}^{2}$
${G}_{12}=6.4\,GPa$	$S=81\,MPa$
${\vartheta }_{12}=0.035$

Se han representado además las otras tres partes metálicas que sirven para fijar la placa. Éstas se han representado con materiales perfectamente elásticos y lineales, con un módulo de Young de 210 GPa, coeficiente de poisson de 0.3 y densidad de 7850 kg/m³.

4. Resultados

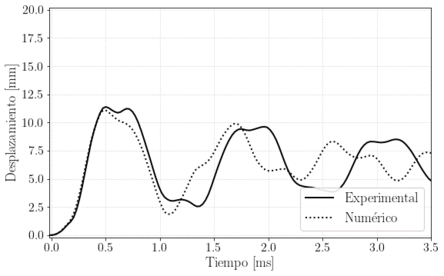
Los resultados que se pueden extraer tanto de los ensayos experimentales como de las simulaciones numéricas se dividen en dos partes. Por un lado, gracias a la técnica de 3D-DIC se tienen los campos de desplazamientos de la placa durante el ensayo. Así se puede extraer el desplazamiento en cualquier punto del laminado. Si se representa el desplazamiento del punto central de la placa con respecto al tiempo (ya que es el punto que experimenta mayores desplazamientos), se obtiene una gráfica como la que se muestra en la Figura 3, la cual se corresponde con una presión en el tanque de 15 bares. En dicha figura se puede ver cómo crece el desplazamiento poco después de ser alcanzado por la onda de choque, alcanzando un máximo local en t = 0.5 ms. Tras esto, el desplazamiento se reduce hasta alcanzar el mínimo local en t = 1.4 ms. Posteriormente, se pueden identificar varias oscilaciones del desplazamiento con el tiempo en las cuales la amplitud va disminuyendo progresivamente. Finalmente, se podrá concluir que la placa recupera el estado inicial.

Figura 3: Tiempo frente a desplazamiento del punto central de una placa ensayada a P = 15 bar

En la misma figura se muestra también el desplazamiento obtenido con el método de elementos finitos. Aunque se pueden apreciar pequeñas diferencias en la forma de la curva como es el alcance de máximos y mínimos locales, se ha logrado reproducir numéricamente la tendencia que sigue el laminado cuando es sometido a este tipo de ensayos.

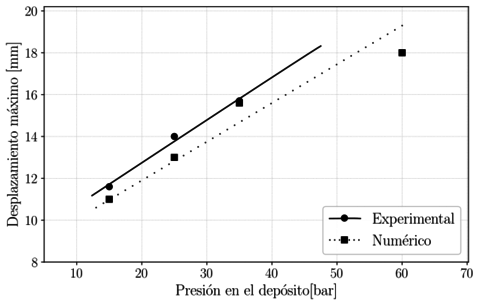
Si se comparan los desplazamientos máximos registrados por las curvas de desplazamiento, tanto experimentales como numéricos (Figura 4), para todas las presiones consideradas, se observa una tendencia lineal creciente. Se observa además que dicha tendencia queda registrada también por las simulaciones numéricas, lo que indica que se está reproduciendo correctamente el ensayo. Hay que tener en cuenta que el desplazamiento numérico máximo es siempre ligeramente inferior al experimental, lo que indica una mayor rigidez del conjunto. La mayor diferencia encontrada sucede para la máxima presión ensayada, que equivale a P = 60 bar. En este caso concreto, la carga ejercida es tal que conlleva el fallo total de la placa. Sin embargo, este efecto no se reproduce adecuadamente con la simulación, la cual no rompe de la misma manera, y sigue mostrando un máximo local.

Figura 4: Recopilación de desplazamientos máximos, experimentales y numéricos, en función de la presión en el depósito

Por otro lado, de los ensayos experimentales y simulaciones numéricas se pueden obtener resultados de daño una vez finalizado el estado de carga. En lo que a ensayos experimentales se refiere, las probetas fueron sometidas a una inspección no destructiva por ultrasonidos. De este modo, se analiza y cuantifica la extensión de los daños internos. En cuanto a los resultados numéricos, se pueden analizar fácilmente las distintas variables del daño para cada una de las láminas. Destacar que únicamente el ensayo realizado a P = 35 bar tiene un daño significativo para ser comparado con las simulaciones numéricas.

Para estudiar estos resultados, la Figura 5 a) muestra el daño interno obtenido mediante ultrasonidos y la Figura 5 b) muestra la variable de daño interlaminar, ambas a P = 35 bar. Si se analizan los daños, se puede comprobar que están localizados en torno a las condiciones de contorno. Esto se puede explicar por la forma en la que una onda de choque actúa contra la placa plana. Al aplicar una presión uniforme en toda la placa, el punto que más desplazamiento encuentra es el punto que se encuentra en medio de la placa. Sin embargo, considerando los gradientes de deformación y las tensiones, se encuentran en la zona de encastrado. Por tanto, antes de producirse el fallo en la zona central se producirá en la parte fija. Observando ambas figuras, se observa una diferencia en la forma del fallo. Mientras que el ensayo experimental muestra el daño hacia el interior de la placa, el daño numérico se corresponde con el límite del marco y se expande hacia el centro de la probeta. Por último, analizando las imágenes obtenidas durante el ensayo experimental a P = 60 bar, se puede observar cómo la rotura de la placa se inicia en las condiciones de contorno y se propaga alrededor de éstas.

Figura 5. Daño resultante tras un ensayo a P= 35 bar. a) Experimental; b) Numérico.

5. Conclusiones

Las principales conclusiones de este trabajo se resumen en los siguientes puntos:

• Se ha podido realizar un ensayo experimental de manera controlada que emule el impacto de una onda de choque sobre una placa de material compuesto. Además, los dispositivos utilizados como las cámaras de alta velocidad permiten un análisis más profundo de los campos de desplazamientos.

• El modelo numérico es capaz de reproducir las tendencias en términos de desplazamiento de la simulación. Se reproduce tanto la amplitud como las oscilaciones que tiene la placa durante el ensayo. También los daños obtenidos se asemejan a los resultantes de los ensayos realizados.

• A máxima presión (P = 60 bar) los datos difieren notablemente, lo que indica que se requiere de un modelo de daño continuo más específico para reproducir el comportamiento del material en dichas situaciones.

Bibliografía

[1] A. Gargano, K. Pingkarawat, V. L. Pickerd, M. E. Ibrahim, y A. P. Mouritz, «Effect of fibre-matrix interfacial strength on the explosive blast resistance of carbon fibre laminates», Compos. Sci. Technol., vol. 138, pp. 68-79, ene. 2017, doi: 10.1016/j.compscitech.2016.11.009.

[2] M. Yazid Yahya, W. J. Cantwell, G. S. Langdon, y G. N. Nurick, «The blast resistance of a woven carbon fiber-reinforced epoxy composite», J. Compos. Mater., vol. 45, n.^o 7, pp. 789-801, abr. 2011, doi: 10.1177/0021998310376103.

[3] P. Kumar, D. S. Stargel, y A. Shukla, «Effect of plate curvature on blast response of carbon composite panels», Compos. Struct., vol. 99, pp. 19-30, may 2013, doi: 10.1016/j.compstruct.2012.11.036.

[4] J. LeBlanc, A. Shukla, C. Rousseau, y A. Bogdanovich, «Shock loading of three-dimensional woven composite materials», Compos. Struct., vol. 79, n.^o 3, pp. 344-355, jul. 2007, doi: 10.1016/j.compstruct.2006.01.014.

[5] V. Aune, G. Valsamos, F. Casadei, M. Langseth, y T. Børvik, «On the dynamic response of blast-loaded steel plates with and without pre-formed holes», Int. J. Impact Eng., vol. 108, pp. 27-46, oct. 2017, doi: 10.1016/j.ijimpeng.2017.04.001.

[6] V. Aune, G. Valsamos, F. Casadei, M. Langseth, y T. Børvik, «Fluid-structure interaction effects during the dynamic response of clamped thin steel plates exposed to blast loading», Int. J. Mech. Sci., vol. 195, p. 106263, abr. 2021, doi: 10.1016/j.ijmecsci.2020.106263.

[7] M. Kristoffersen, J. E. Pettersen, V. Aune, y T. Børvik, «Experimental and numerical studies on the structural response of normal strength concrete slabs subjected to blast loading», Eng. Struct., vol. 174, pp. 242-255, nov. 2018, doi: 10.1016/j.engstruct.2018.07.022.

[8] V. Aune, E. Fagerholt, M. Langseth, y T. Børvik, «A shock tube facility to generate blast loading on structures», Int. J. Prot. Struct., vol. 7, n.^o 3, pp. 340-366, sep. 2016, doi: 10.1177/2041419616666236.

[9] «ABAQUS Analysis User’s Manual (v6.6)». https://classes.engineering.wustl.edu/2009/spring/mase5513/abaqus/docs/v6.6/books/usb/default.htm?startat=pt06ch26s05alm40.html (accedido 18 de mayo de 2023).