(Created page with "==Resumen== Dentro de los artefactos explosivos improvisados se encuentran aquellos que generan proyectiles formados por explosión, penetradores de blindajes y sistemas acor...") |
m (Scipediacontent moved page Draft Content 641131776 to Yenes et al. 2015a) |
(No difference)
| |
Latest revision as of 16:37, 13 October 2016
Resumen
Dentro de los artefactos explosivos improvisados se encuentran aquellos que generan proyectiles formados por explosión, penetradores de blindajes y sistemas acorazados, como los utilizados por grupos insurgentes contra las fuerzas aliadas en zona de operaciones. El objeto de este estudio es reproducir y entender el comportamiento de dichos artefactos explosivos improvisados capaces de generar proyectiles de alta velocidad y gran capacidad de penetración. La comprensión de su comportamiento permitirá mejorar el conocimiento sobre ellos, y por ende, combatirlos de forma más eficaz. Para ello se han realizado los ensayos correspondientes, obteniéndose las primeras caracterizaciones de proyectiles formados por explosión construidos de manera artesanal, tal y como haría un terrorista. Además, se han creado los modelos numéricos correspondientes a cada ensayo, que simulan todo el evento desde su inicio hasta el impacto en el objetivo, recorriendo todos los pasos intermedios. Se han ensayado 3 configuraciones y posteriormente se han simulado, usando el software de análisis por elementos finitos, LS-DYNA® , con una configuración 2 D axisimétrica, con mallados lagrangianos. Los resultados obtenidos por el modelo han alcanzado un alto grado de precisión con relación a los datos experimentales. A partir de aquí se puede concluir que los artefactos explosivos improvisados-proyectiles formados por explosión son una seria amenaza, y que los modelos generados permitirán conocer y ahorrar costes en la lucha contra esta amenaza, y por ende contra el terrorismo, al disponer de un enfoque holístico de la amenaza, y finalmente reducir los costes de la experimentación.
Abstract
Within the category of improvised explosive devices are those that form explosively formed projectiles which penetrate armor and armored systems, such as those used by insurgents against allied forces in operational areas. The purpose of this study is to reproduce and understand the behavior of these improvised explosive devices capable of generating high-velocity, high penetration projectiles. Understanding their behavior will allow for improved knowledge about them, and thus will allow us to more effectively combat them. Thus, the corresponding tests were carried out and the results were obtained from the first characterizations of explosively formed projectiles built using traditional methods, just as a terrorist would have built them. Along with this, numerical models were created for each test simulating the entire event from beginning to impact on the target, including all the intermediate steps. There were three configurations tested and simulated using the software of finite element analysis, LS-DYNA® , a 2-D asymmetric configuration with Lagrangian meshes. The results obtained by the model were compared with data obtained in the experimental tests, yielding a high precision between simulated and tested data. With the data obtained in this study it can be concluded that the improvised explosive devices -explosively formed projectiles is a serious threat. Generated models will allow us to know more about these weapons, to reduce costs in the fight against the threat of improvised explosive devices-explosively formed projectiles and therefore against terrorism with explosively formed projectiles, and to have a holistic approach to the threat and to reduce the cost of experimentation. Minimize the experimental expense.
Palabras clave
LS-DYNA® ; Proyectiles formados por explosión ; Artefactos explosivos improvisados ; Simulación lagrangiana ; Elementos finitos
Keywords
LS-DYNA® ; Explosively formed projectiles ; Improvised explosive devices ; Lagrangian simulation ; Finite elements
1. Introducción
En los últimos años, los artefactos explosivos improvisados (cuyas siglas en inglés son IED) se han convertido en la principal causa de pérdida de vidas humanas por ataques terroristas contra las fuerzas en misión de paz en áreas de conflicto. En la mayoría de estos ataques se utilizaron los denominados proyectiles formados por explosión (conocidos como EFP por sus siglas en inglés), cuya potencia destructiva es tal que la supervivencia de los ocupantes de los vehículos acorazados se ve seriamente comprometida cuando son atacados con estos artefactos. Un EFP es un dispositivo simple compuesto de una carcasa y un disco cóncavo o liner, que se rellena de explosivo y al que se le introduce un detonador que inicia y transmite el tren de fuego al explosivo. Este tipo de artefactos pertenecen a la familia de las cargas conformadas, que han sido estudiadas ampliamente [1] , [2] , [3] , [4] and [5] , ya que son las más usadas en la lucha contra los sistemas acorazados.
El proceso de formación de un EFP es un fenómeno complejo de altas presiones y temperaturas, en el que numerosos factores pueden condicionar la correcta detonación de la carga explosiva así como la formación del proyectil. La mayor parte de los trabajos de investigación realizados con EFP resaltan que la capacidad de penetración de los mismos depende principalmente de su forma, de las características de vuelo y de la velocidad en el momento del impacto [1] , [6] , [7] and [8] . Además, en el caso de IED hay que añadir una variable difícil de controlar, la habilidad de la persona que construye el artefacto.
Hasta ahora las investigaciones realizadas y los trabajos publicados se han centrado en los proyectiles formados por explosión conformados de manera industrial y no artesanal, tal y cómo haría por norma general un grupo terrorista [8] , [9] , [10] and [11] . Además, en la fabricación de IED, los grupos terroristas o insurgentes suelen usar diferentes materiales metálicos y explosivos comunes para cada región, por lo que los IED pueden tener formas, materiales y tamaños muy diversos lo que dificulta su estudio y modelización [12] . Por tanto, está claro que existe un vacío que se trata de cubrir en este estudio, ya que en los ensayos realizados los EFP se han desvinculado de los procesos industriales de fabricación y se han creado conformes a las directrices que se pueden encontrar en los manuales de los grupos terroristas e insurgentes disponibles. Asimismo la recuperación de EFP en buenas condiciones para su análisis científico no es un ejercicio trivial [8] . Hay que pensar que los EFP pueden llegar a pesar 0,5 kg, tener velocidades de más de 1.000 m/s y llegar a penetrar unos 10 cm de blindaje. Para ello se ha diseñado y fabricado un sistema de recuperación de proyectiles, compuesto con diferentes materiales, que ha permitido detener dichos proyectiles evitando su fuga y manteniendo su geometría, para su posterior análisis y comparación con el modelo. El trabajo con IED-EFP supone un gran reto a la hora de su enfoque científico ya que el control de las variables afecta al resultado final, pero es necesario debido a la mencionada falta de información técnica a este respecto.
Para el análisis y estudio del proceso de formación de los EFP y los factores que lo condicionan está muy extendido el uso de los modelos de simulación numérica basados en elementos finitos con diversos software como LS-DYNA® o ABAQUS® . Coexisten diversas corrientes para modelizar proyectiles (o EFP) donde desde un punto de vista geométrico aparecen los modelados 3 D [11] , [13] and [14] y los 2 D axisimétricos [3] , [8] and [15] ; y desde un punto de vista de la técnica de resolución existen el método lagrangiano [7] , [16] and [17] o la técnica lagrangiana euleriana arbitraria [ALE] [9] , [10] and [11] . Sin embargo, solo algunos trabajos tratan las características del vuelo y la capacidad de penetración de manera sistemática para EFP. De estos trabajos, algunos son más teóricos centrados en la comparación entre diversas soluciones numéricas para los problemas de proyectiles-impactos y su grado de correlación, sin tener ensayos reales con los que validar dichos resultados [7] , [17] and [18] . Unos tratan de identificar las características de generación y vuelo de los proyectiles, conformados con diferentes materiales, y comparándolas con los resultados numéricos, pero sin preocuparse de las características de los impactos producidos [11] , [19] and [20] ; mientras que otros se centran en el estudio de la capacidad de penetración de proyectiles sobre diferentes soluciones constructivas en el objetivo [14] . Finalmente un pequeño número de trabajos trata este problema de manera conjunta y con una gran batería de ensayos [8] , [9] and [21] ; y como se ha mencionado, esta escasez se acentúa cuando hablamos de artefactos improvisados creados tal y cómo haría un terrorista [22] .
Desde el punto de vista de la técnica de resolución, en el modelo lagrangiano la malla requiere ser fijada o ligada sobre un elemento material dentro de todo el proceso de cálculo, y así la malla se mueve junto con los elementos materiales. Por el contrario, la técnica ALE permite que los nodos de la malla computacional se muevan siguiendo a los puntos materiales del continuo como ocurre en una formulación lagrangiana, que se mantengan fijos como en el método euleriano, o que se puedan mover de forma arbitraria adoptando posiciones intermedias entre las 2 anteriores. Ambas técnicas tienen sus pros y sus contras que se detallan en la tabla 1 . En este trabajo se ha utilizado un modelo 2 D axisimétrico con mallado lagrangiano y elementos tipo shell debido a la alta precisión que aportan con cortos tiempos de cálculo, la posibilidad de realizar las simulaciones del modelo a tamaño real sin escalamiento y la claridad en los contactos entre materiales/elementos [13] and [23] . El problema podría presentarse en la deformación de la malla, pero diversos autores como Du Bois y Schwer [24] limitan el uso del modelo lagrangiano para velocidades a partir de unos 2 o 2,5 km/s que es aproximadamente el límite máximo que un IED-EFP puede alcanzar.
| Lagrangiano | ALE |
|---|---|
| Pros | |
| Precisión | No hay que definir contactos |
| Velocidad | No hay que introducir erosión |
| Mayor disponibilidad de materiales | Calidad de los elementos |
| Facilidad en el tratamiento de datos | |
| Contras | |
| Posible distorsión del mallado | Tamaño del modelo |
| Definición de contactos | Tiempos de cálculo |
| Posible necesidad de erosión | Contactos difusos entre materiales |
| Complejidad en el tratamiento de datos | |
Este trabajo se centra en la modelización matemática y su validación a través de numerosos datos experimentales, de la detonación, conformación, vuelo y penetración-impacto de un EFP sobre una placa de acero con espesores iguales a los usados en los blindajes empleados en los sistemas acorazados. Para ello, se explica qué es un EFP y sus principales características, se describen los ensayos realizados y a continuación se detallan los modelos numéricos creados. Finalmente, se presentan los resultados obtenidos en la modelización y su comparación con los datos medidos en los ensayos, resultando en un importante avance en la comprensión de los IED-EFP.
2. Antecedentes-cargas conformadas. Parámetros de configuración de los artefactos explosivos improvisados-proyectiles formados por explosión
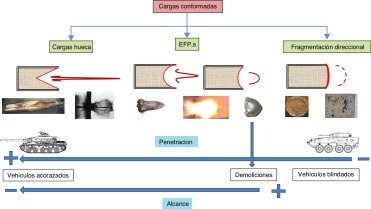
Los EFP pertenecen a la familia de las cargas conformadas (fig. 1 ), que son aquellas que tienen la particularidad de concentrar o focalizar su energía hacia el eje central de la carga [12] . Este efecto se consigue gracias a la distribución y geometría del explosivo dentro del artefacto. Las cargas conformadas se clasifican según su geometría en cargas huecas (discos cónicos con ángulos agudos), EFP (discos cónicos con ángulos obtusos o discos cóncavos) y en cargas de fragmentación direccional (discos convexos). En función de estas, se producen diferentes efectos sobre su capacidad de penetración y la distancia efectiva de daño. En cuanto a la capacidad de penetración, las cargas huecas son capaces de perforar vehículos acorazados de espesores hasta 8 veces más gruesos que el diámetro del disco (usados para el combate con los blindajes más robustos, por ejemplo el Leopardo 2 E), mientras que los EFP penetran menores blindajes de hasta 0,8 veces el diámetro del disco, por tanto, se emplean más contra vehículos blindados (usados para transporte de tropas con menor blindaje que los acorazados, por ejemplo el Iveco LMV Lince). En cuanto a la distancia efectiva de daño, las cargas huecas para ser eficaces solo se pueden separar unas decenas de centímetros del objetivo, mientras que los EFP pueden alcanzar objetivos a varias decenas de metros. Finalmente, con una capacidad de penetración limitada, así como una distancia efectiva de daño, tenemos las cargas de fragmentación direccional que concentran un porcentaje elevado de metralla formada por la fragmentación del disco en una zona o dirección determinada (fig. 1 ).
|
|
|
Figura 1. Clasificación de las cargas conformadas, capacidad de penetración y distancia de daño efectiva. |
Dentro de los IED-EFP existen diversos factores que influyen en su diseño y posterior formación:
- Confinamiento del explosivo : tanto el material empleado como el espesor del mismo será clave a la hora de obtener un mejor confinamiento. A mayor confinamiento, mayor energía se transmite en la dirección deseada. Sin embargo, un confinamiento escaso o deficiente producirá una mayor disipación de energía antes de tiempo, lo que disminuirá las probabilidades de una correcta formación del proyectil. Con un buen confinamiento se puede reducir la cantidad de explosivo necesaria para obtener un proyectil bien formado.
- Disco cóncavo o liner: es el componente más importante en el diseño del IED-EFP ( fig. 2 ). Se trata de un disco que después de la detonación se va a transformar en un proyectil a alta velocidad y con gran capacidad de penetración, también conocido como slug. La efectividad del proyectil vendrá marcada por el material empleado y la geometría (forma, concavidad del disco, diámetro o espesor) dada en su diseño inicial. El material empleado en el disco debe tener un alto punto de fusión, alta densidad, una estructura cristalina cerrada y una gran elasticidad. A nivel industrial se diseñan geometrías para el liner de tipo hemisférico, hiperbólico, cónico, disco balístico, etc. mientras que en el caso de los IED-EFP por sencillez se centran en los cónicos y cóncavos. Los primeros se parecen más a las cargas huecas o JET (fig. 1 ), mientras que los segundos tienden a generar proyectiles o slugs con mayores superficies de contacto. Con altas concavidades, próximas a geometrías cónicas, la velocidad del proyectil será mayor pero penalizará la formación del proyectil, por contra, con una concavidad menor se obtendrá una mejor formación del proyectil a costa de reducir su velocidad. En cuanto al diámetro, a mayores diámetros mejores penetraciones, pero con un coste infinitamente más elevado. La selección del espesor dependerá de la geometría, de las propiedades del material, del método de fabricación y las propiedades requeridas para el EFP. En la industria armamentística los espesores van del 1 al 4% del diámetro del disco aunque, dependiendo del uso, este puede llegar hasta un 8% del diámetro [8] and [12] . Como norma general, un disco con menor espesor da una formación mejor de proyectil y mayores velocidades que otro con mayor espesor.
|
|
|
Figura 2. A) EFP realizado como parte de los ensayos preliminares. B) Esquema de la conformación del proyectil. C) Imágenes de la cámara de alta velocidad de un proyectil de cobre. D) Orificio generado por un proyectil de 13,6 mm en una plancha de acero de 30 mm de espesor. |
- Altura de la carga: se entiende como la distancia entre el disco y el punto de inicio de la detonación de la carga explosiva, que condicionará la forma del frente de onda en el momento de incidir sobre el disco. A mayor distancia se tiene un frente plano que proporciona una presión uniforme sobre el disco, mientras que a menor distancia se tiene un frente hemisférico con una presión no uniforme que podrá penalizar la correcta formación y velocidad final del proyectil. Existe un límite para este parámetro, superado el cual no se produce mejora alguna en la formación, velocidad y penetración del proyectil, siendo dicho valor aproximadamente 1,5 veces el diámetro del disco.
- Carga explosiva: la forma en la que el explosivo es introducido en el interior del artefacto es una variable que dependerá de la habilidad del individuo que realiza el trabajo. La carga debe estar distribuida uniformemente y no debe haber espacio entre la carga y el disco, generando en caso contrario cierto factores asimétricos que disminuyen las habilidades del EFP.
- Método de disparo o iniciación: el método de disparo puede ser muy amplio en el caso de los IED y de su elección dependerá la correcta trasmisión del tren de fuego desde el detonador a la carga principal. Los métodos de un solo punto de detonación generarán menores velocidades pero tienen menos posibilidades de fragmentar el disco y, por tanto, romper el slug disminuyendo su capacidad destructiva [8] .
3. Descripción de los ensayos
Como se ha mencionado en la sección 1, un EFP o penetrador de formación explosiva es un tipo especial de carga conformada diseñada para penetrar con eficacia el blindaje de vehículos a grandes distancias. Como el nombre sugiere, es la detonación de la carga explosiva la que produce una deformación en el disco cóncavo metálico transformándolo en un proyectil (tipo bala) que es acelerado a velocidades superiores a los 1.000 m/s hacia un blanco que puede o no ser penetrado (fig. 2 ). Este tipo de artefactos fueron descubiertos a finales del siglo xix y principios del siglo xx aunque su desarrollo y uso generalizado ocurrió durante la Segunda Guerra Mundial.
Las fases iniciales de este estudio se centraron en la búsqueda de un IED-EFP con una configuración óptima (fig. 2 A), con el fin de alcanzar un artefacto con las mejores prestaciones y consumiendo el menor número de recursos, a lo que se debe sumar la reducción o minoración de variables propias del «bombmaker». Esta fase de análisis teórico y ensayo de las diferentes configuraciones se realizó en el Centro de Excelencia Contra Artefactos Explosivos Improvisados (CIED-COE) de la OTAN en Hoyo de Manzanares, Madrid (España) durante el primer trimestre de 2013.
Una vez determinadas las características técnicas de los EFP mencionadas en la sección 2, se llevaron a cabo los ensayos en el Instituto Tecnológico Militar (ITM) de «La Marañosa» en San Martín de la Vega, Madrid (España) en las instalaciones de la Unidad de Balística de Efectos, con los medios y personal técnico adecuado. Debido a que los EFP que se ensayaron estaban realizados de manera casera (por tanto son IED), tal y como haría un terrorista, en una primera fase los trabajos del personal cualificado se centraron en el aprendizaje del relleno óptimo y la distribución homogénea del explosivo dentro del artefacto. Este paso es crucial pues, como se ha mencionado, es una fuente de numerosos problemas si no se evitan las variaciones de densidad o la aparición de vacíos en el interior del explosivo. Una vez completados estos trabajos, se realizaron 2 baterías de ensayos, el primero de una semana de duración en el mes de mayo de 2013, y un segundo de 2 semanas de duración en el mes de noviembre de 2013. Durante estos ensayos, se obtuvieron datos clave para comprender los IED-EFP, que además han ayudado a realizar las simulaciones de manera realista. Los datos principales extraídos fueron las velocidades de vuelo del proyectil a diferentes distancias (fig. 2 C), las velocidades de impacto, las geometrías de los proyectiles antes del impacto (necesidad de un recuperador), y el tamaño y características de los impactos producidos (fig. 2 D).
3.1. Construcción de los artefactos explosivos improvisados-proyectiles formados por explosión
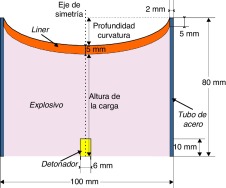
Los IED-EFP fueron construidos con una carcasa o tubo de acero, rellenos de un explosivo plástico y coronados por unos discos de cobre con diferentes curvaturas y profundidades variables para cada ensayo (fig. 3 ). La carcasa es fundamental pues produce un confinamiento del explosivo, y por consiguiente de los gases de expansión de la detonación, aumentando la presión y por ende la energía transmitida al disco o liner. Para los ensayos se utilizó un tubo de acero del tipo S-275 de 2 mm de espesor. El explosivo utilizado fue PG-2, explosivo de uso militar y comercializado por la empresa española Expal. Dicho explosivo está formado en un 85% por RDX y un 15% de aglutinante, la densidad es de 1.450 kg/m3 y la velocidad de detonación es ± 8.000 m/s [25] . La decisión de usar un explosivo plástico de uso comercial y no un explosivo casero, tipo ANFO, viene determinada por las condiciones de seguridad en el manejo de sustancias explosivas. El PG-2 presenta unas excelentes propiedades adhesivas, no es tóxico y permite moldearlo para adaptarse a la geometría requerida, en este caso superficies curvas con pequeñas irregularidades. Para conseguir una correcta detonación de la carga principal se optó por utilizar detonadores de uso militar que se introdujeron 1 cm en el explosivo (fig. 3 ). Mención aparte merece el liner, que fue construido de manera cóncava y de cobre debido a que reúne las características indicadas en el apartado 2, además de ser uno de los materiales más empleados por las células terroristas ya que es un material común, relativamente asequible y fácilmente moldeable. Como se puede deducir de la figura 3 , el diámetro del disco o liner era de 96 mm, el espesor siempre constante e igual a 5 mm, pero sin embargo 3 configuraciones diferentes fueron ensayadas con relación a la curvatura y profundidad máxima del mismo: 6,2 mm; 13,6 mm y finalmente 16,6 mm. Estas 3 profundidades de curvatura fueron elegidas durante la fase inicial de estudio antes mencionada en el CIED-COE, debido a que son diámetros suficientes para producir un daño significativo y además no conducen a la fragmentación del proyectil o slug [10] . Por último, otro parámetro importante a considerar es la altura de la carga. Dicha altura guarda una relación aproximadamente igual a 0,8 veces el valor del diámetro, y por tanto, el frente de onda incidirá en el disco de manera óptima o lo que es lo mismo casi plana (ver sección 2).
|
|
|
Figura 3. Esquema y dimensiones generales de los IED-EFP ensayados. |
3.2. Velocidades de vuelo e impacto
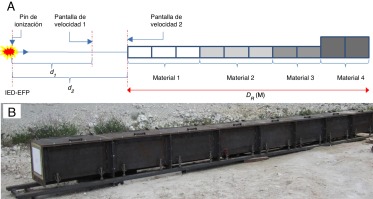
Las velocidades de vuelo y las velocidades antes del impacto se obtuvieron por 2 medios diferentes: grabación con cámaras de alta velocidad y medición por láminas de cortocircuito o «velocity screens» . Son láminas con un circuito impreso que emiten una señal cuando son atravesadas por un proyectil; la diferencia entre 2 señales, conocida la distancia, nos da la velocidad entre placas. La primera velocidad de vuelo fue medida con la lámina de cortocircuito a unos 3,5 m de distancia d1 (pantalla de velocidad 1 en figura 4 ), siendo el tiempo cero el de la detonación del EFP. Para medir la velocidad antes del impacto se colocó otra lámina de cortocircuito a la entrada del recuperador que se encontraba a una distancia de unos 5,0 m (d2 ), y que es la misma distancia donde se colocó la placa de acero para los ensayos de impacto (pantalla de velocidad 2 en figura 4 ). Con el fin de obtener una trazabilidad en los resultados experimentales, estos ensayos se repitieron 3 veces por cada configuración de los IED-EFP (6,2 mm; 13,6 mm; y 16,6 mm) dando un total de 9 ensayos (tabla 2 ). La masa del explosivo media, con la que se puede deducir la densidad, para cada una de las configuraciones también se detalla en la tabla referenciada anteriormente. Los valores de velocidad de vuelo para la distancia de impacto d2 oscilan entre 1.184 m/s para el EFP de 16,6 mm, y 1.404 m/s para el EFP de 6,2 mm. Esto da una idea de la dificultad que plantea el poder detener dichos proyectiles sin que presenten deformación alguna por impacto, a unas velocidades entre 3 y 4 veces superiores a la del sonido.
|
|
|
Figura 4. A) Sistema de recuperación de proyectiles y ubicación de las pantallas de medición de velocidad. B) Foto del sistema de recuperación empleado en los ensayos. |
| EFP | N.o ensayo | Carga de explosivo | Distancia 1.a placa d1 | Velocidad 1.a placa | Distancia 2.a placa d2 | Velocidad 2.a placa |
|---|---|---|---|---|---|---|
| kg | m | m/s | m | m/s | ||
| 6,2mm | 1 | 0,738 | 3,93 | 1.312 | 5,43 | 1.301 |
| 2 | – | – | – | – | ||
| 3 | 3,87 | 1.416 | 5,39 | 1.404 | ||
| 13,6mm | 4 | 0,712 | – | – | – | – |
| 5 | 3,63 | 1.289 | 5,16 | 1.243 | ||
| 6 | 3,56 | 1.250 | 5,07 | 1.243 | ||
| 16,6mm | 7 | 0,696 | 3,74 | 1.358 | 5,26 | 1.354 |
| 8 | 3,78 | 1.249 | 5,35 | 1.245 | ||
| 9 | 3,76 | 1.211 | 5,34 | 1.184 |
3.3. Geometrías preimpacto e impactos producidos
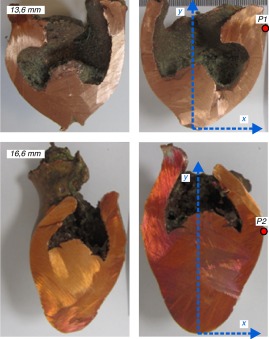
Para conseguir una total validación de las geometrías obtenidas en la simulación es crucial la recuperación de proyectiles preimpacto sin deformación. Para ello se desarrolló un sistema de recuperación de proyectiles, creado con 4 materiales diferentes con diversos tamaños y longitudes, capaz de detenerlos en un espacio inferior a los 10 m (DR ), evitando su fuga al exterior y manteniendo intacta la geometría preimpacto del proyectil (fig. 4 ). En los ensayos realizados con los discos de 13,6 mm y 16,6 mm, todos los proyectiles se recuperaron sin deformación. Sin embargo, los proyectiles en los ensayos con discos de 6,2 mm no pudieron recuperarse por no impactar dentro del sistema. Con el fin de obtener sus medidas se realizó un corte por el eje central de simetría para cada proyectil (fig. 5 ). El punto de control de las geometrías de los proyectiles serán los puntos más anchos de los mismos y marcados como P1 y P2 en la figura 5 . En ella se detallan los ejes de cálculo locales x e y , sobre los que se han calculado el ancho máximo de cada proyectil y su altura correspondiente desde la punta del mismo. Para el EFP de 13,6 mm las coordenadas de P1 son x = 33 mm e y = 24,9 mm; mientras que para el EFP de 16,6 mm las coordenadas de P2 son x = 32 mm e y = 17,4 mm.
|
|
|
Figura 5. Cortes de los IED-EFP recuperados. Detalle de los ejes de cálculo locales para cada proyectil. Las fotos de arriba corresponden al EFP de 13,6 mm y punto P1 , mientras que las fotos de abajo corresponden al EFP de 16,6 mm y punto P2 . |
Como se ha mencionado en el apartado 3.2, la placa de acero de 30 mm de espesor y de 600 × 600 mm de lado, y que simula el blindaje que puede llevar un vehículo común utilizado en las zonas de conflicto, se colocó en los ensayos a una distancia aproximada de unos 5 m en la cabecera del recuperador. Con el fin de obtener el mayor número de datos posibles para caracterizar la capacidad de penetración de los IED-EFP se han realizado 3 ensayos para el de 6,2 mm, 2 para el de 13,6 mm y otros 3 para el de 16,6 mm, resultando en un total de 8 ensayos detallados en la tabla 3 .
| EFP | N.o ensayo | Carga de explosivo | Penetración | Distancia a objetivo | Diámetro de entrada | Diámetro de salida |
|---|---|---|---|---|---|---|
| kg | m | mm | mm | |||
| 6,2mm | 10 | 0,738 | No | 5,432 | 88,8±14,4 | – |
| 11 | No | 5,394 | 95±4,1 | – | ||
| 12 | No | 5,401 | 81,3±6,3 | – | ||
| 13,6mm | 13 | 0,712 | Sí | 5,113 | 73,8±4,8 | 63,8±4,8 |
| 14 | Sí | 5,094 | 76,3±4,8 | 71,3±7,5 | ||
| 16,6mm | 15 | 0,696 | Sí | 5,305 | 72,5±2,9 | 63,8±4,8 |
| 16 | Sí | 5,321 | 56,3±2,5 | 57,5±2,9 | ||
| 17 | sí | 5,317 | 67,5±2,9 | 77,5±6,5 |
4. Descripción del modelo
El siguiente paso en el trabajo fue la modelización con LS-DYNA® de los IED-EFP, según las configuraciones iniciales de los artefactos y los materiales empleados en ellos. En este trabajo se ha utilizado un modelo 2 D axisimétrico con una formulación de elementos lagrangiana. Se ha elegido esta configuración debido a las características geométricas de los IED-EFP (simetría) y por la gran precisión de este tipo de formulación para tiempos muy cortos de computación. El cálculo completo de formación del proyectil, vuelo hasta impacto (unos 5 m) e impacto sobre el objetivo, tarda por regla general menos de un minuto en un procesador i7-3610QM a 2,30 GHz y 6 GB de RAM, mientras que el uso de la formulación ALE nos obligaría a escalar el vuelo hasta un máximo de 0,3 o 0,5 m [8] y con el mismo procesador las simulaciones se irían hasta los 40 o 45 min. En el mallado realizado para cada una de las partes que componen el IED-EFP, tubo de acero, explosivo y liner, se han utilizado elementos de 4 nodos básicamente cuadrados con un tamaño de los mismos de 1 × 1 mm. Este mallado fino es fundamental para poder reproducir lo más fielmente posible el comportamiento del disco en su proceso de formación en proyectil y su posterior impacto en el objetivo. Siguiendo la misma idea y tamaño de malla, se ha mallado la plancha de acero donde impactará el proyectil.
Para la definición del material del tubo de acero se ha empleado el modelo Piecewise Linear Plasticity o modelo material número 24 de LS-DYNA®[26] . Este material se viene utilizando en la modelización de cubiertas de balas [13] and [14] o el interior de otro tipo de proyectiles [16] . En la bibliografía encontrada, el tubo de acero no suele ser incluido en el modelo, dado que aumenta el número de componentes del mismo, y por tanto, su complejidad y dificultad [2] , [4] , [8] , [9] and [11] . Sin embargo esto puede conducir a errores, ya que se ha demostrado que el confinamiento que produce el tubo sobre el explosivo es crucial en la formación del proyectil [12] . Este material representa a la perfección el comportamiento de la carcasa de acero con una pequeña deformación plástica, seguida de la erosión del material, una vez superado el límite plástico. Además, este modelo tiene 2 grandes ventajas; la primera, que no requiere de ecuación de estado para su aplicación [26] , y la segunda, que el número de datos a emplear para definir el material son pocos y fácilmente accesibles. Las propiedades que se han de utilizar en el modelo para la definición del acero S-275 [27] , [28] and [29] son la densidad (ρs ) 7.850 kg/m3 ; el módulo de Young (Es ) 210 × 109 Pa; el coeficiente de Poisson (ν ) 0,3; el límite elástico (σy ) 275 × 106 Pa; el módulo tangente (ET ) 1,042 × 109 Pa y el alargamiento en rotura (ɛR ) 0,15.
El explosivo utilizado fue el PG-2 y se ha modelizado con el material tipo High Explosive Burn o modelo material número 8 de LS-DYNA®[26] . Los datos necesarios para definir este modelo son la densidad, la velocidad de detonación y la presión de detonación o presión en el estado Chapman-Jouguet más conocido como el estado CJ. La densidad del explosivo para cada EFP, de curvaturas 6,2; 13,6; y 16,6 mm que condicionan el volumen de carga disponible, dependerá de la masa cargada por el «bombmaker» en cada caso. Una vez conocida la masa cargada y el volumen para cada EFP, se calcula su densidad. La presión CJ y velocidad de detonación se han evaluado con el código termodinámico, W-Detcom [30] , el cual permite el cálculo de estados de detonación y combustión, así como la expansión posterior de los gases, en función de la composición y densidad del explosivo. Para ello se ha utilizado una densidad tipo para el PG-2 igual a 1.400 kg/m3 , para la cual se obtuvo una velocidad de detonación de 8.100 m/s, así como una presión CJ de 21,8618 × 109 Pa [25] . Este material debe ir acompañado de una ecuación de estado (EOS) que defina el comportamiento de la detonación y expansión del explosivo en relación con su presión-volumen-energía. Para ello se tomará la conocida JWL o Jones-Wilkins-Lee [8] , [9] , [10] , [11] , [16] and [31] que regirá el comportamiento de la presión de los gases de detonación como función del volumen relativo (V ) y la energía interna (E ):
|
|
( 1) |
donde A , B , R1 , R2 y ω son constantes a determinar de manera experimental, siendo la metodología más común el ensayo del cilindro [30] . Mientras que V = ρ /ρ0 que es el ratio entre la densidad actual y la inicial. Finalmente E es la energía interna por unidad de volumen calculada a través de la energía de Gurney y la energía total disponible (E0 ). En la actualidad no existe un conjunto de valores determinados para la JWL del PG-2 debido a su uso regional casi exclusivo para España y al alto coste de la experimentación (ensayos de cilindro) necesaria para ello. Para solventar esta dificultad, se puede trabajar en 2 vías: la primera calcular el equivalente TNT del PG-2 y usar su JWL o la segunda que consiste en utilizar la JWL de un explosivo de similares características a las PG-2, en cuanto a la detonación y productos generados durante la misma. En este trabajo se ha optado por la segunda vía, utilizando los parámetros de la ecuación de estado JWL del C-4 (tabla 4 ), explosivo plástico de similar composición aunque con valores algo mayores de densidad (1.601 kg/m3 ), velocidad detonación (8.190 m/s) y presión CJ (25 × 109 Pa) extraídos de Wang [32] y Børvik et al. [33] .
| A Pa | B Pa | R1- | R2- | W - | E0 J/m3 |
|---|---|---|---|---|---|
| 610×109 | 12,95×109 | 4,5 | 1,4 | 0,25 | 9×109 |
En cuanto al disco de cobre o liner se ha incorporado en el modelo con el material Johnson-Cook (JC) o material número 15 de LS-DYNA®[26] . Este modelo material es idóneo para representar el comportamiento de materiales metálicos sometidos a grandes deformaciones, a altas velocidades de deformación y altas temperaturas [15] and [34] . La ecuación que rige el comportamiento del material JC es una expresión empírica que relaciona la tensión efectiva o tensión de von Mises (σ ) con la deformación plástica efectiva ( ):
|
|
( 2) |
donde AJC , BJC , C , N , y M son las constantes empíricas que determinan el comportamiento del material. Siendo la velocidad de deformación plástica efectiva (s−1 ), y la velocidad de deformación de referencia definida en el test cuasiestático usado para determinar los parámetros AJC , BJC y N del modelo JC (depende de las unidades en las que estemos trabajando, en este caso = s−1 - [26] and [34] ). El valor de la constante AJC (Pa) representa el límite elástico a una temperatura ambiente de 20 °C, mientras que BJC (Pa) es el módulo de endurecimiento, C es un coeficiente relativo a la sensibilidad a la deformación plástica, N coeficiente de acritud, mientras que M es el coeficiente de ablandamiento térmico. El primer grupo de la ecuación 2 corresponde al término elástico-plástico, el segundo corresponde a la componente de viscosidad debido a la velocidad de deformación y el tercer grupo de la ecuación 2 corresponde al efecto de la temperatura. Mientras que finalmente TH es la variable temperatura adimensionalizada mediante la ecuación:
|
|
( 3) |
Los valores de las constantes utilizadas en estas expresiones fueron determinadas de manera empírica con el valor medio de diferentes test sobre cobre para un amplio rango de temperaturas y velocidades de deformación. Los datos utilizados en el modelo se han extraído de la bibliografía original de Johnson y Cook [34] y se encuentran en la tabla 5 .
| ρ kg/m3 | G GPa | AJC MPa | BJC MPa | C'- | N'- | M'- | Tfusión K | Tambiente K | Cp J/(kgK) |
|---|---|---|---|---|---|---|---|---|---|
| 8.960 | 46 | 90 | 292 | 0,025 | 0,31 | 1,09 | 1356 | 293 | 383 |
Sin embargo, este modelo requiere de la utilización de una EOS que sirva para definir los cambios de presión que tienen lugar en el material con respecto al volumen especifico y la energía interna, siendo la más común la EOS Gruneisen [6] , [10] , [13] , [15] and [33] . Los parámetros de ajuste de la ecuación de choque Hugoniot en función de la velocidad de choque y velocidad de partículas para el cobre introducidos son C0 = 3.910 m/s y S = 1,51[35] ; el coeficiente de Gruneisen es Γ = 2,02 + 0,47 V para un rango de presión que va desde 17 GPa hasta 144 GPa que coincide con los valores presentes en este estudio [36] .
Por último se han de definir los materiales que describan el comportamiento de la plancha de acero objetivo de impacto del proyectil y en caso necesario su correspondiente EOS. Para ello es importante entender que las variables que caracterizan la respuesta de una estructura ante una carga impulsiva dependen en su mayoría de la velocidad de impacto. Como norma general puede decirse que a medida que aumenta la velocidad de impacto el comportamiento de la geometría de la estructura se hace secundario frente al comportamiento del material [37] . Cuando la velocidad de impacto supera los 300 m/s las propiedades mecánicas del material, límite elástico, resistencia a compresión, resistencia a tracción, controlan la respuesta del sólido. Si el impacto tiene velocidades muy elevadas, mayores de 1.000 m/s como es este caso, nos encontramos en el régimen que se conoce como hipervelocidad [37] , en el cual se puede considerar que los materiales se comportan como un fluido sometido a presiones enormes.
Para la descripción del acero estructural S-275 empleado en la plancha objetivo se han usado 2 tipos de modelos de material en la simulación numérica en LS-DYNA® : Plastic-Kinematic o PK [8] and [32] y JC [15] , [33] and [38] . Ambos modelos se han venido utilizando ampliamente en los últimos años con este mismo objetivo pues cada uno tiene sus ventajas e inconvenientes. El primero de ellos es una definición de material que presenta un endurecimiento elastoplástico dependiente de la velocidad de deformación. Dicha velocidad depende del modelo de Cowper y Symonds que escala la tensión efectiva según un factor que varía según la deformación plástica y unos parámetros C y D de dicho modelo [39] . Además, no requiere de EOS, y también, los datos a introducir son pocos y fácilmente accesibles, siendo los mismos que los introducidos en el Piecewise Linear Plasticity descrito anteriormente. Sin embargo, diversos autores han encontrado que la deformación que se produce con este material tras el impacto de un proyectil no es del todo realista [8] and [40] . El segundo modelo empleado es el JC y ha sido explicado en detalle con anterioridad. En este caso, los parámetros empleados han sido los del acero A-36 de EE. UU. que es el equivalente al acero S-275 Español, pues como se ha dicho este modelo es empírico y nadie ha obtenido aún los parámetros de dicho acero (tabla 6 ). Los parámetros de ecuación de choque Hugoniot utilizados para el cálculo de la EOS Gruneisen para el acero S-275 son C0 = 4569 m/s y S = 1,49[35] ; siendo el coeficiente gamma de Γ = 2,17 para el rango de presión trabajado [15] .
| P kg/m3 | G GPa | ACJ MPa | BCJ MPa | C'- | N'- | M'- | Tfusión K | Tambiente K | Cp J/(kgK) |
|---|---|---|---|---|---|---|---|---|---|
| 7.850 | 76,9 | 250 | 477 | 0,18 | 0,012 | 1 | 1.773 | 293 | 486 |
Por otra parte, en un modelo lagrangiano como se ha mencionado en la sección 1, los contactos entre materiales en la mayoría de los casos tienen que definirse explícitamente. En este caso, para el contacto entre el liner y el tubo de acero se ha utilizado el módulo 2D-Automatic-Surface-To-Surface [8] and [26] de LS-DYNA® . Los contactos entre tubo de acero-explosivo y entre explosivo-liner no hace falta definirlos ya que los nodos de contacto son coincidentes. Además, se han de definir los contactos entre el liner (una vez conformado el proyectil) y la plancha de acero. En este caso se definen, nuevamente, como 2D-Automatic-Surface-To-Surface al igual que hacen otros autores [3] , [8] and [26] , dado que las posibilidades de definición de contactos en 2 D no son muy abundantes. Por otra parte, se han definido unos criterios de erosión extra con el fin de ayudar al modelo material a eliminar elementos, y así ajustar el modelo, pero solo en el caso del material JC. Se ha utilizado el criterio de la deformación máxima a cortante (EPSSH) de valor límite igual a 0,8 [17] and [24] .
5. Análisis y discusión de resultados
Para realizar la pertinente calibración y verificar la fiabilidad de los modelos numéricos generados, los resultados obtenidos se han comparado con los medidos en los ensayos de campo. Los modelos generados fueron los correspondientes a las 3 geometrías presentes en los ensayos: 6,2 mm; 13,6 mm y finalmente 16,6 mm.
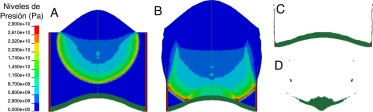
Con una sola línea de iniciación, 3 puntos que se corresponden con las coordenadas de la línea del detonador (fig. 3 ) insertado 1 cm, la onda de choque generada incide sobre el disco de cobre de manera aproximadamente plana, tal y como debe ocurrir en la realidad. Dicha onda de choque, al incidir sobre el disco de cobre y por efecto de las elevadas presiones generadas, provoca la deformación plástica del cobre en un fenómeno similar a la extrusión, transformándolo en un proyectil. Las presiones generadas pueden alcanzar unos picos del orden de 2,6 × 1010 Pa; este valor está en consonancia y dentro del rango de valores de presión PCJ del explosivo (presión que no se puede superar en ningún caso durante la expansión) que oscilan entre los 2,1 × 1010 Pa y los 2,8 × 1010 Pa (fig. 6 A). El proyectil que se genera es acelerado en cuestión de microsegundos a velocidades superiores a los 1.000 m/s, dotándolo de una gran capacidad de penetración. Dichas presiones también afectan a la carcasa de acero que confina el explosivo, produciendo su destrucción e incluso pudiendo llegar a su total desintegración. En el modelo generado la carcasa desaparece completamente (figs. 6 B-D), reproduciendo el comportamiento observado en los test donde no se recuperaron fragmentos significativos de acero. La ausencia del explosivo en las figuras 6 C-D se debe a que la malla del explosivo tiene una alta deformación y no permite una buena visión de los demás materiales. Además, para evitar errores numéricos, el explosivo se elimina una vez que ha aportado toda su energía al proyectil.
|
|
|
Figura 6. Modelo del IED-EFP de 13,6 mm de curvatura, el azul (o parte interior deformada donde viaja la onda de choque) corresponde al explosivo, el rojo (o parte de los extremos vertical y delgada) al tubo de acero y el verde (o parte convexa del artefacto) al liner de cobre. A) Onda de choque de la detonación expresada en función de la presión. B) La misma onda una vez impacta contra el liner y el tubo de acero. C) «Despegue» del liner o inicio de la formación del proyectil. D) Erosión casi completa del tubo de acero y formación del proyectil e inicio del vuelo. |
5.1. Resultados de la velocidad del proyectil durante el vuelo y preimpacto
Se puede observar cómo el valor simulado de la velocidad de vuelo obtenido en la distancia d1 (tabla 7 ), en la configuración de 6,2 mm, cae directamente en el rango de valores medidos en los ensayos (tabla 2 ). Lo mismo sucede para los valores simulados a una distancia d2 . En este caso, se puede afirmar que los datos de la simulación se corresponden con los datos experimentales, y por tanto, se puede confiar en esta configuración para la posterior simulación del impacto sobre el objetivo.
| EFP | Distancia 1.a placa d1 | Velocidad 1.a placa | Distancia 2.a placa d2 | Velocidad 2.a placa |
|---|---|---|---|---|
| m | m/s | m | m/s | |
| 6,2mm | 3,9 | 1.317 | 5,4 | 1.315 |
| 13,6mm | 3,6 | 1.136 | 5,1 | 1.130 |
| 16,6mm | 3,7 | 1.164 | 5,3 | 1.162 |
Para la configuración de 13,6 mm, el valor simulado de la velocidad de vuelo obtenido en la distancia d1 (tabla 7 ) difiere con el medido en campo (tabla 2 ) en 114 m/s (aproximadamente un 9%). Se observa la misma tendencia para los valores simulados a una distancia d2 , manteniéndose ese 9% de diferencia. En ambos casos no se supera el 10% que se suele considerar de confianza en ingeniería dado el número de variables y condicionantes que forman parte del proceso de simulación y de la toma de datos reales. Por tanto, los datos aportados por el modelo numérico siguen siendo de relativa confianza.
Por último, para la configuración de 16,6 mm, el valor simulado de la velocidad de vuelo obtenido en la distancia d1 (tabla 7 ) difiere en menos de un 4% con respecto al valor inferior medido en campo (tabla 2 ). En cuanto a los valores obtenidos a la distancia d2 , el porcentaje baja situándose por debajo incluso del 2% para el límite inferior del rango de medidas. Esto indica que aunque el valor de la velocidad simulada es inferior al medido en los ensayos, la precisión es bastante buena en términos ingenieriles.
Sin embargo, conviene destacar que al haber empleado un modelo de tipo lagrangiano, donde el aire que existe entre el EFP y la plancha objetivo no ha sido incluido en el modelo, los valores de velocidades entre d1 y d2 deberían ser los mismos, pues no existe el efecto de frenado por rozamiento del aire que se podría haber simulado de usar un modelo tipo ALE [8] ; efecto que puede intuirse por los valores obtenidos de manera real (tabla 3 ) en las velocidades entre d1 y d2 . Por tanto, los pequeños cambios en la velocidad que se producen en la simulación son única y exclusivamente achacables a los cálculos numéricos en cada una de las iteraciones [7] and [24] .
5.2. Geometría preimpacto e impactos simulados
En general, los resultados del modelo en cuanto a la geometría final del proyectil proporcionan unos datos plenamente satisfactorios, ya que la geometría de los proyectiles simulados tiene una gran coincidencia con los proyectiles reales, dentro de un margen de confianza.
En el caso del disco de 6,2 mm los proyectiles generados impactaron fuera del sistema de recuperación, por lo que sufrieron grandes deformaciones lo que imposibilitó su comparación con los resultados del modelo. Debido a esta dificultad, para el disco de 6,2 mm la única comparativa posible es el tamaño del impacto sobre la placa. En ningún caso estos proyectiles llegaron a penetrar la plancha de acero en su totalidad, por lo que no se dispone de orificio de salida. Los resultados obtenidos por el modelo simulado con el material JC (tabla 8 ) se ajustan bastante bien a lo ensayado (tabla 3 ). El tamaño del orificio de entrada simulado concuerda con el valor medio ± desviación típica en 2 de los 3 casos, y por tanto y desde un punto de vista estadístico, no se puede decir que el valor del diámetro del orificio de entrada simulado sea diferente a los valores medidos en los ensayos. Además, el proyectil simulado no llega a penetrar la plancha de acero como ocurre en la realidad. Sin embargo, en el modelo de material PK el valor obtenido es bastante inferior, y aunque dentro del rango óptimo, subestima la penetración producida. Asimismo, se puede observar que la deformación producida por el modelo de material PK no guarda tanta similitudes con la deformación que se produce en la realidad (fig. 2 ) como sí lo hace el modelo JC (fig. 7 ).
| Modelo material Johnson-Cook | Modelo material Plastic-Kinematic | ||||
|---|---|---|---|---|---|
| EFP | Distancia a objetivo m | Diámetro de entrada mm | Diámetro de salida mm | Diámetro de entrada mm | Diámetro de salida mm |
| 6,2mm | 5,4 | 99,0 | - | 79,6 | - |
| 13,6mm | 5,1 | 75,6 | 71,2 | 50 | 60 |
| 16,6mm | 5,3 | 50,8 | 64,8 | 36 | 56,4 |
|
|
|
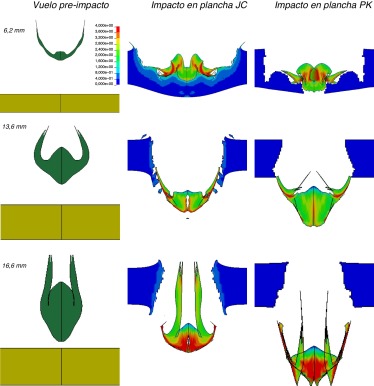
Figura 7. Proyectiles preimpacto y postimpacto en función del material usado para definir la plancha. Por filas se muestran los diferentes IED-EFP según su curvatura; por columnas antes de impacto, el impacto en una plancha definida con el modelo de material Johnson-Cook y finalmente una plancha definida con el modelo de material Plastic-Kinematic. La leyenda corresponde a la deformación plástica. Las imágenes extraídas de LS-DYNA® no están a escala. |
En el caso de la configuración de 13,6 mm, sí se pudieron recuperar proyectiles preimpacto. El punto de mayor diámetro del proyectil simulado (equivalente al P1 ) se encuentra a una altura de 33 mm con respecto a la cabeza del proyectil (utilizando las mismas coordenadas locales que en la figura 5 ), obteniéndose un valor de anchura máxima de 23,8 mm, mientras que el real es de 24,9 mm (fig. 5 ). Así, la desviación en el radio es del 4,4% y por tanto, seguimos en un rango de valores más que aceptable. Para la simulación realizada con el modelo de material JC, tanto los diámetros de entrada como los de salida, obtenidos en la simulación (tabla 8 ) se encuentran en el rango de valores obtenidos en los ensayos realizados (tabla 3 ). Esto sin duda confirma que el modelo generado para este tipo de IED-EFP está dentro del rango de la realidad observada en los test. Los datos obtenidos para el orificio de entrada en el modelo PK son bastante inferiores a los reales, de al menos un 32%. En cuanto a los orificios de salida, el PK se ajusta algo mejor a los datos reales pero siempre en el rango inferior de los mismos ( Tabla 3 and Tabla 8 ). Al igual que pasaba en la configuración de 6,2 mm, es posible observar que la deformación producida por el modelo de material PK (digamos la rebaba que se genera por el efecto de la penetración) no guarda tanta similitudes con la deformación real (fig. 2 ), como sí lo hace el modelo JC (fig. 7 ).
Por último, para la configuración de 16,6 mm también se recuperaron proyectiles preimpacto. El punto de mayor diámetro del proyectil simulado se encuentra a una altura de 32 mm con respecto a la cabeza del proyectil (utilizando las mismas coordenadas locales que en la figura 5 ), obteniéndose un valor de su radio de 17,45 mm, mientras que el real (fig. 5 ) es de 17,4 mm, lográndose un resultado extremadamente preciso. Los resultados simulados con el modelo de material JC para la configuración de 16,6 mm presentan en la plancha de acero unos orificios de entrada, con un diámetro inferior al medido en los test, en al menos un 9%. En cambio, los diámetros de salida simulados (tabla 8 ) concuerdan de una manera bastante aproximada con los datos experimentales (tabla 3 ). El valor de simulación obtenido con el modelo de material PK presenta una diferencia con respecto a los valores medidos en los test de al menos un 36%. Sin embargo, el valor del orificio de salida obtenido en las simulaciones (tabla 8 ) no se puede decir que sea diferente desde un punto de vista estadístico del menor valor obtenido en los ensayos (segundo dato del EFP de 16,6 mm en la tabla 3 ). Al igual que pasaba en la configuración de 6,2 mm y de 13,6 mm, es posible observar que la deformación producida por el modelo PK no guarda tanta similitudes con la deformación real (fig. 2 ), como sí lo hace el modelo JC (fig. 7 ).
Los resultados obtenidos no hacen otra cosa que corroborar los que Trana [40] pone de manifiesto para el modelado, mediante los mismos modelos de material, del ensayo conocido como barra de Taylor. En ellos los valores obtenidos mediante JC nunca difieren de los resultados experimentales más del 5%, mientras que los suministrados por el PK presentan desviaciones con respecto a los resultados experimentales que superan con creces dicho límite. Una explicación razonable a la diferencia de comportamiento puede deberse a que JC recoge el comportamiento anisótropo triaxial en función de la velocidad de deformación [41] , mientras que el PK carece de dicha posibilidad.
5.3. Influencia de la configuración del proyectil formado por explosión en su comportamiento
A la luz de los resultados obtenidos tanto en los ensayos como en la simulación, podemos concluir que los proyectiles generados con EFP cuyas curvaturas son pequeñas, unos 6,2 mm, no producen penetración en blindajes de 30 mm. Esta capacidad de penetración va asociada al tamaño y características del proyectil, así como a la velocidad a la que se mueve el mismo. Las velocidades registradas en todos los test son similares, siendo, si cabe, un poco mayores en los proyectiles generados con los EFP de menor curvatura de 6,2 mm, de lo que se deduce que para estos materiales y tamaños la velocidad no será el hecho diferenciador en sus características como armas. Sin embargo, los de 13,6 y 16,6 mm sí que producen la penetración total de dichos blindajes. Por otra parte, los diámetros de entrada son mayores para los proyectiles generados en los EFP de 6,2 mm, aunque también se observa que según aumenta la curvatura los diámetros de las penetraciones disminuyen. También, el diámetro de los proyectiles disminuye según la curvatura del liner aumenta, y por ende, los diámetros de los impactos producidos. Este fenómeno se debe a que, aparentemente, los proyectiles conformados de EFP con mayores curvaturas se compactan más en el centro del mismo (fig. 5 ), aportándoles una mayor capacidad de penetración al disminuir su deformación por impacto.
6. Conclusiones
En función de los resultados obtenidos en las simulaciones numéricas y los ensayos de vuelo, recuperación y penetración de los 3 tipos de IED-EFP, las conclusiones que podemos extraer son las siguientes:
- Se presenta por primera vez una batería de ensayos y simulaciones de artefactos explosivos improvisados creados de manera artesanal según a manuales terroristas.
- En los test se ha logrado reproducir el comportamiento de los IED-EFP existentes en las zonas de conflicto, y que como se ha visto en los ensayos pueden llegar a perforar blindajes de, al menos, 30 mm.
- Se ha comprobado experimentalmente que los IED-EFP con mayores curvaturas 13,6 y 16,6 mm, producen impactos con penetración total a unas velocidades en torno a los 1.200 m/s. Sin embargo, menores curvaturas no llegan a producir dichas penetraciones a pesar de que los proyectiles generados tienen algo más de velocidad y diámetro.
- Aunque es difícil de simular el proceso completo de formación, vuelo y penetración de un IED-EFP, en este trabajo se han conseguido reproducir los valores experimentales de 8 ensayos. Aunque las velocidades simuladas en el punto de control a unos 3,5 m de distancia han sido un poco bajas con respecto a las experimentales, las velocidades preimpacto están todas en un rango menor al 10% de error. Las geometrías de los proyectiles, así como los impactos obtenidos mediante simulación, tienen todos ellos una desviación con respecto a los valores experimentales pequeña en algunos casos menor del milímetro.
- Se ha demostrado, de acuerdo a otros artículos [8] and [40] , cómo el modelo de material PK no presenta tan buenos resultados como el modelo de material JC, para deformaciones producidas por impactos de proyectiles a alta velocidad.
- En este caso, además, se ha simulado el proceso completo con la carcasa o tubo de acero que conforma el IED-EFP, por tanto dichas simulaciones son, si cabe, más realistas.
A la luz de estos resultados, se puede establecer un punto de partida para posteriores simulaciones de los efectos que puedan tener los IED-EFP sobre vehículos acorazados o cualquier otro tipo de estructura susceptible de ser atacada por este tipo de artefactos. Además el uso de modelos como los aquí desarrollados son muy importantes para optimizar costes y reducir tiempo en investigación y desarrollo de soluciones, para la neutralización y mitigación de los efectos de estas amenazas, que puedan salvar muchas vidas en zonas de conflicto. Sería interesante completar este estudio con la recuperación de proyectiles de 6,2 mm de curvatura, el posible efecto del ángulo de ataque del proyectil sobre la plancha de acero, así como, la medición de las velocidades de salida postimpacto.
Agradecimientos
Este trabajo se encuentra financiado por el Centro de Excelencia Contra Artefactos Explosivos Improvisados (C-IED COE) y la Organización del Tratado del Atlántico Norte (OTAN). Además, se ha contado con la colaboración del Grupo de Explosivos de la E.T.S.I . Minas y Energía de la Universidad Politécnica de Madrid. Los ensayos se han realizado en el Instituto Tecnológico Militar (ITM) y su ayuda siempre será reconocida. Las opiniones vertidas por los autores no tienen porqué representar la opinión oficial de las instituciones involucradas.
Bibliografía
- [1] C. Yu, Y.J. Tong, C.L. Yan, F.B. Li, Y.L. Gui, M. Zhang, et al.; Applied research of shaped charge; Int. J. Impact. Eng., 23 (1 Pt 2) (1999), pp. 981–988
- [2] S. Pappu, L.E. Murr; Hydrocode microstructural analysis of explosively formed penetrators; J. Mater. Sci., 37 (2) (2002), pp. 233–248
- [3] C. Wang, S.R. Yun, F.L. Huang; Numerical simulation on jet formation by wide angle shaped charge and penetration into multilayer targets; Explo. Shock Wave, 23 (4) (2003), pp. 349–354
- [4] C. Yu, Q.D. Dong, C.W. Sun; The experimental studies of explosively formed projectile with star shaped tail; Explo. Shock Wave, 23 (6) (2003), pp. 561–564
- [5] G. Scholtes, P. Hooijmeijer, R. Verbeek; An EFP Impact in Comparison With the IM Fragment Impact Test; TNO, Rijswijk, The Netherlands (2011)
- [6] K. Weimann, Flight stability of EFP with star shaped tail, en: Proceedings of 14th International Symposium on Ballistics, Quebec, Canada, 1993, pp. 755-763
- [7] G.R. Johnson, R.A. Stryk; Some considerations for 3 D EFP computations; Int. J. Impact. Eng., 32 (10) (2006), pp. 1621–1634
- [8] J. Wu, J. Liu, Y. Du; Experimental and numerical study on the flight and penetration properties of explosively-formed projectile; Int. J. Impact. Eng., 34 (7) (2007), pp. 1147–1162
- [9] W. Li, X. Wang, W. Li; The effect of annular multi-point initiation on the formation and penetration of an explosively formed penetrator; Int. J. Impact. Eng., 37 (4) (2010), pp. 414–424
- [10] W. Li, X. Wang, W. Li, Y. Zheng; Research on the optimum length–diameter ratio of the charge of a multimode warhead; Shock Waves, 22 (3) (2012), pp. 265–274
- [11] G. Hussain, A. Hameed, J.G. Hetherington, A.Q. Malik, K. Sanaullah; Analytical performance study of explosively formed projectiles; J. Appl. Mech. Tech. Phys., 54 (1) (2013), pp. 10–20
- [12] OTAN, Allied Joint Doctrine for Countering Improvised Explosive Devices (C-IED). AJP 3.15, 2 nd ed. NATO, Bruselas, 2012.
- [13] A. Deb, M. Raguraman, N.K. Gupta, V. Madhu; Numerical simulation of projectile impact on mild steel armour plates using LS-DYNA® : Part I: Validation ; Defence Sci. J., 58 (3) (2008), pp. 422–432
- [14] M. Raguraman, A. Deb, N.K. Gupta; CAE-based prediction of projectile residual velocity for impact on single and multi-layered metallic armour plates; Lat. Am. J. Solids Stru., 6 (3) (2009), pp. 247–263
- [15] T. Elshenawy, Q.M. Li; Influences of target strength and confinement on the penetration depth of an oil well perforator; Int. J. Impact Eng., 54 (2013), pp. 130–137
- [16] K. Krishnan, S. Sockalingam, S. Bansal, S.D. Rajan; Numerical simulation of ceramic composite armor subjected to ballistic impact; Comp. Part BEng, 41 (8) (2010), pp. 583–593
- [17] G.R. Johnson; Numerical algorithms and material models for high-velocity impact computations; Int. J. Impact Eng., 38 (6) (2011), pp. 456–472
- [18] G. Hussain, A. Hameed, P. Barton, A.Q. Malik, M.B. Khan, A. Hussain; Liner materials output characteristics of explosively formed projectiles (EFPs); Key Eng Mat., 510 (2012), pp. 148–155
- [19] Y. Zheng, S.D. Li, X.M. Wang, W.B. Li, W.B. Li; Numerical approach in predicting the formation process of tandem explosively formed projectile; Adv. Mat. Res., 148 (2011), pp. 653–658
- [20] J.Q. Liu, W.B. Gu, M. Lu, H.M. Xu, S.Z. Wu; Formation of explosively formed penetrator with fins and its flight characteristics; Defence Tech., 10 (2014), pp. 119–123
- [21] J.P. Fu, Z.G. Chen, X.C. Hou, S.Q. Li, S.C. Li, J.W. Wang; Simulation and experimental investigation of jetting penetrator charge at large stand-off distance; Defence Tech., 9 (2) (2013), pp. 91–97
- [22] M. Voort; IED. effects research at TNO Defence Security and Safety; En: 13th International Symposium of the Interaction of the Effects of Munitions with Structures (2009) 1-18
- [23] T. Belytschko, W.K. Liu, B. Moran, K. Elkhodary; Nonlinear Finite elements for continua And Structures; (2 nd ed.)John Wiley & Sons, New York (2014)
- [24] P. Du Bois, L. Schwer, LS-DYNA® homeland security course: blast and penetration applications [obtenido Sep 2013}. Disponible en: http://www.duboisschwertraining.com/
- [25] A. Terradillos Sánchez, Determinación de la velocidad de detonación mediante diferentes métodos de medida. Proyecto fin de carrera dirigido por L. López, E.T.S.I. Minas y Energía (UPM), Madrid, 2012.
- [26] J.O. Hallquist; LS-DYNA® Keyword Users Manual, Version 971 R6.1.0 ; Livermore Software Technology Corporation, Livermore, Ca. (2012)
- [27] UNE, EN. 1994. 10025: Hot rolled products of non-alloy steels technical delivery conditions, AENOR, 1994
- [28] UNE, EN. 10025: Hot rolled products of structural steels-Part 2: Technical delivery conditions for non-alloy structural steels, AENOR, 2006.
- [29] J. M. Lleonart, Estructuras metálicas para la edificación: adaptado al CTE, Ed. Universidad Politécnica de Valencia, Valencia, 2006.
- [30] J.A. Sanchidrián, L.M. López; Calculation of the energy of explosives with a partial reaction model. Comparison with Cylinder Test Data. Propellants; Explos. Pyrotech., 31 (1) (2006), pp. 25–32
- [31] E.L. Lee, H.C. Hornig, J.W. Kury; Adiabatic Expansion of High Explosive Detonation Products; University of California, Lawrence Radiation Laboratory, Report UCRL-50422, Livermore (1968)
- [32] J. Wang; Simulation of Landmine Explosion Using LS-DYNA® 3D Software: Benchmark Work of Simulation of Explosion in Soil And Air (No. DSTO-TR-1168) ; Defense Science and Technology Organization, Canberra (Australia) (2001)
- [33] T. Børvik, L. Olovsson, A.G. Hanssen, K.P. Dharmasena, H. Hansson, H.N.H. Wadley; A discrete particle approach to simulate the combined effect of blast and sand impact loading of steel plates; J. Mech. Phys. Solids, 59 (5) (2011), pp. 940–958
- [34] G. Johnson, W. Cook; A constitutive model and data for metals subjected to large strains, high strain rates and high temperatures; Proceedings of the seventh international symposium on ballistics, Hague, Netherlands, 19-21 April (1983)
- [35] S.P. Marsh; LASL shock Hugoniot data (Vol. 5); University of California Press, Berkley, CA (1980)
- [36] R. Vignjevic, J.C. Campbell, N.K. Bourne, N. Djordjevic; Modeling shock waves in orthotropic elastic materials; J. Appl. Phys., 104 (4) (2008), p. 044904
- [37] A. Bhatnagar; Lightweight Ballistic Composites: Military and Law-Enforcement Applications; (1 st. ed)Woodhead Pub Ltd on behalf of The Institute of Materials, Minerals & Mining, Cambridge, UK (2006)
- [38] G. Hussain, A. Hameed, J.G. Hetherington, P.C. Barton, A.Q. Malik; Hydrocode simulation with modified Johnson-Cook model and experimental analysis of explosively formed projectiles; J. Energ. Mater., 31 (2) (2013), pp. 143–155
- [39] J.T. Wang, W.L. Yu, T. Wang; Flying posture of tandem warhead influences its penetrating and following performance; J. Eng. Sci. Technol. Rev., 7 (1) (2014), pp. 76–81
- [40] E. Trana, Plastic-Kinematic vs Johnson-Cook model in FEM Taylor test simulation, en: 11th International Research/Expert Conference Trends in the Development of Machinary and Associated Technology, Hammamet, Tunisia, 05-09 September, 2007.
- [41] H. Ebelsheiser, M. Feucht, F. Neukamm; On Calibrating Advanced Damage Models Using Sheet Metal Coupon Tests; Proceedings of the 7 th LS-DYNA® Forum, Bamberg, Germany (2008)
Document information
Published on 01/03/16
Accepted on 24/11/14
Submitted on 27/06/14
Volume 32, Issue 1, 2016
DOI: 10.1016/j.rimni.2014.11.003
Licence: Other
Share this document
Keywords
claim authorship
Are you one of the authors of this document?