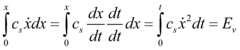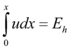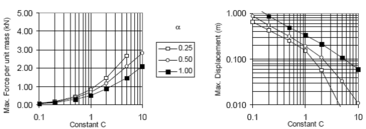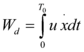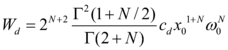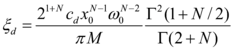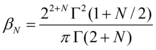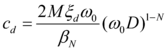m (Cinmemj moved page Draft Samper 432909089 to Valdebenito et al 2018a) |
|||
| (13 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
| − | == | + | ==Acknowledgments== |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
The authors wish to thank to the Department of Geotechnical Engineering and Geosciences and the Department of Construction Engineering at Technical University of Catalonia for their help and support during the doctorate years of Mr. Galo Valdebenito. This work is inspired in the basic result of that investigation. Likewise, thank to the Faculty of Engineering Sciences and the Department of Research and Development ''(DID)'' at Universidad Austral de Chile for their help and support in this publication. | The authors wish to thank to the Department of Geotechnical Engineering and Geosciences and the Department of Construction Engineering at Technical University of Catalonia for their help and support during the doctorate years of Mr. Galo Valdebenito. This work is inspired in the basic result of that investigation. Likewise, thank to the Faculty of Engineering Sciences and the Department of Research and Development ''(DID)'' at Universidad Austral de Chile for their help and support in this publication. | ||
| − | + | ==Preface== | |
| − | + | ||
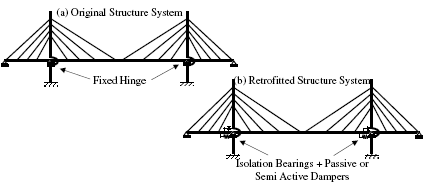
Earthquakes can be really destructive. There is no doubt. Recent seismic events have demonstrated the important effects on structures, and especially on bridges. In this sense, cable-stayed bridges are not an exception, although their seismic performance during recent events has been satisfactory. Their inherent condition as part of life-lines makes the seismic design and retrofitting of such structures be seriously considered. | Earthquakes can be really destructive. There is no doubt. Recent seismic events have demonstrated the important effects on structures, and especially on bridges. In this sense, cable-stayed bridges are not an exception, although their seismic performance during recent events has been satisfactory. Their inherent condition as part of life-lines makes the seismic design and retrofitting of such structures be seriously considered. | ||
| Line 43: | Line 24: | ||
<big>Llavaneras (Barcelona), October 2009.</big></div> | <big>Llavaneras (Barcelona), October 2009.</big></div> | ||
| + | <!-- | ||
<div style="text-align: right; direction: ltr; margin-left: 1em;"> | <div style="text-align: right; direction: ltr; margin-left: 1em;"> | ||
<big>'''Contents'''</big></div> | <big>'''Contents'''</big></div> | ||
| − | [[Image:draft_Samper_432909089-picture-Lienzo 2.svg|center|600px]] | + | [[Image:draft_Samper_432909089-monograph-picture-Lienzo 2.svg|center|600px]] |
| − | + | {| style="width: 100%;border-collapse: collapse;" | |
| − | {| style="width: 100%;border-collapse: | + | |
|- | |- | ||
| style="vertical-align: top;"|<big>'''Chapter 1. Introduction'''</big> | | style="vertical-align: top;"|<big>'''Chapter 1. Introduction'''</big> | ||
| Line 347: | Line 328: | ||
--> | --> | ||
| − | + | ==Chapter 1. Introduction== | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
:<big>1.1 Cable-Stayed Bridges and Seismic Protection </big> | :<big>1.1 Cable-Stayed Bridges and Seismic Protection </big> | ||
| Line 362: | Line 339: | ||
<div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | ||
| − | [[Image:draft_Samper_432909089-image1-c.png|516px]] </div> | + | [[Image:draft_Samper_432909089-monograph-image1-c.png|516px]] </div> |
<div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | ||
| Line 368: | Line 345: | ||
<div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | ||
| − | [[Image:draft_Samper_432909089-image2-c.png|516px]] </div> | + | [[Image:draft_Samper_432909089-monograph-image2-c.png|516px]] </div> |
<div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | ||
| Line 430: | Line 407: | ||
{| style="width: 100%;" | {| style="width: 100%;" | ||
|- | |- | ||
| − | | style="vertical-align: top;width: | + | | style="vertical-align: top;width: 63%;"|[[Image:draft_Samper_432909089-monograph-image3-c.jpeg|384px]] |
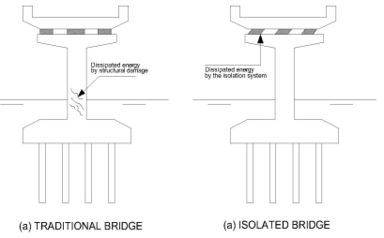
'''Fig. 1.2''' (a) Energy Dissipation of a Traditional Bridge, (b) Energy Dissipation of a Seismic Isolated Bridge [Adapted from Jara and Casas, 2002] | '''Fig. 1.2''' (a) Energy Dissipation of a Traditional Bridge, (b) Energy Dissipation of a Seismic Isolated Bridge [Adapted from Jara and Casas, 2002] | ||
| Line 443: | Line 420: | ||
{| style="width: 100%;" | {| style="width: 100%;" | ||
|- | |- | ||
| − | | style="text-align: center;vertical-align: top;width: | + | | style="text-align: center;vertical-align: top;width: 52%;"|[[Image:draft_Samper_432909089-monograph-image4.png|312px]] |
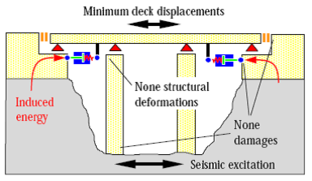
'''Fig. 1.3''' Minimized Seismic Energy Penetration by Seismic Isolation and Energy Dissipation | '''Fig. 1.3''' Minimized Seismic Energy Penetration by Seismic Isolation and Energy Dissipation | ||
| Line 453: | Line 430: | ||
<div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | ||
| − | [[Image:draft_Samper_432909089-image5.jpeg|372px]] </div> | + | [[Image:draft_Samper_432909089-monograph-image5.jpeg|372px]] </div> |
<div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | ||
| Line 466: | Line 443: | ||
{| style="width: 100%;" | {| style="width: 100%;" | ||
|- | |- | ||
| − | | style="vertical-align: top;"|<big>''' [[Image:draft_Samper_432909089-image6.png|336px]] '''</big> | + | | style="vertical-align: top;"|<big>''' [[Image:draft_Samper_432909089-monograph-image6.png|336px]] '''</big> |
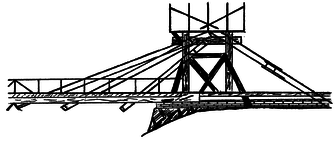
'''Fig. 1.5 '''Löscher-type Timber Bridge [Courtesy of the British Constructional Steelwork Association, Ltd] | '''Fig. 1.5 '''Löscher-type Timber Bridge [Courtesy of the British Constructional Steelwork Association, Ltd] | ||
| Line 483: | Line 460: | ||
{| style="width: 100%;" | {| style="width: 100%;" | ||
|- | |- | ||
| − | | style="vertical-align: top;width: | + | | style="vertical-align: top;width: 53%;"|[[Image:draft_Samper_432909089-monograph-image7.jpeg|288px]] |
'''Fig. 1.6 '''Niagara Falls Bridge [Courtesy of the Niagara Falls Bridge Commission] | '''Fig. 1.6 '''Niagara Falls Bridge [Courtesy of the Niagara Falls Bridge Commission] | ||
| − | | style="vertical-align: top;"|<span style="text-align: center; font-size: 75%;"> [[Image:draft_Samper_432909089-image8.jpeg|270px]] </span> | + | | style="vertical-align: top;"|<span style="text-align: center; font-size: 75%;"> [[Image:draft_Samper_432909089-monograph-image8.jpeg|270px]] </span> |
'''Fig. 1.7 '''Brooklyn Bridge [from [http://www.elclubdigital.com] www.elclubdigital.com]] | '''Fig. 1.7 '''Brooklyn Bridge [from [http://www.elclubdigital.com] www.elclubdigital.com]] | ||
| Line 498: | Line 475: | ||
{| style="width: 100%;border-collapse: collapse;" | {| style="width: 100%;border-collapse: collapse;" | ||
|- | |- | ||
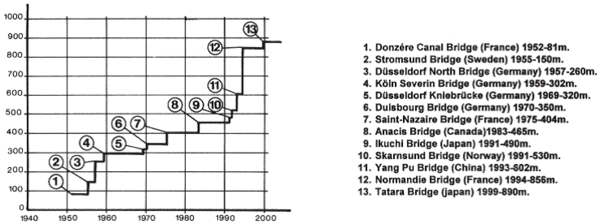
| − | | style="vertical-align: top;width: | + | | style="vertical-align: top;width: 50%;"|[[Image:draft_Samper_432909089-monograph-image9.jpeg|294px]] |
'''Fig. 1.8''' The Bridge over the Donzère Canal, France [photo: J. Kerisel] | '''Fig. 1.8''' The Bridge over the Donzère Canal, France [photo: J. Kerisel] | ||
| Line 505: | Line 482: | ||
However, the real development came from Germany with papers published by Franz Dischinger and with the famous series of steel bridges crossing the river Rhine, as the Oberkassel Bridge, in Düsseldorf, Germany (Fig. 1.9). | However, the real development came from Germany with papers published by Franz Dischinger and with the famous series of steel bridges crossing the river Rhine, as the Oberkassel Bridge, in Düsseldorf, Germany (Fig. 1.9). | ||
|- | |- | ||
| − | | style="vertical-align: top;"|<span style="text-align: center; font-size: 75%;"> [[Image:draft_Samper_432909089-image10.jpeg|288px]] </span> | + | | style="vertical-align: top;"|<span style="text-align: center; font-size: 75%;"> [[Image:draft_Samper_432909089-monograph-image10.jpeg|288px]] </span> |
'''Fig. 1.9 '''Oberkassel Bridge, Düsseldorf, Germany | '''Fig. 1.9 '''Oberkassel Bridge, Düsseldorf, Germany | ||
| − | | style="vertical-align: top;"|<span style="text-align: center; font-size: 75%;"> [[Image:draft_Samper_432909089-image11.jpeg|282px]] </span> | + | | style="vertical-align: top;"|<span style="text-align: center; font-size: 75%;"> [[Image:draft_Samper_432909089-monograph-image11.jpeg|282px]] </span> |
'''Fig. 1.10''' Maracaibo Bridge, Venezuela [from en.structurae.de] | '''Fig. 1.10''' Maracaibo Bridge, Venezuela [from en.structurae.de] | ||
| Line 522: | Line 499: | ||
{| style="width: 100%;" | {| style="width: 100%;" | ||
|- | |- | ||
| − | | style="text-align: center;vertical-align: top;"|<span style="text-align: center; font-size: 75%;"> [[Image:draft_Samper_432909089-image12.jpeg|300px]] </span> | + | | style="text-align: center;vertical-align: top;"|<span style="text-align: center; font-size: 75%;"> [[Image:draft_Samper_432909089-monograph-image12.jpeg|300px]] </span> |
'''Fig. 1.11 '''Barrios de Luna Bridge, Spain [from en.structurae.de] | '''Fig. 1.11 '''Barrios de Luna Bridge, Spain [from en.structurae.de] | ||
| − | | style="text-align: center;vertical-align: top;width: | + | | style="text-align: center;vertical-align: top;width: 46%;"|[[Image:draft_Samper_432909089-monograph-image13.png|180px]] |
'''Fig. 1.12''' Yang Pu Bridge, China [photo: M. Virlogeux] | '''Fig. 1.12''' Yang Pu Bridge, China [photo: M. Virlogeux] | ||
|- | |- | ||
| − | | style="text-align: center;vertical-align: top;"|<span style="text-align: center; font-size: 75%;"> [[Image:draft_Samper_432909089-image14.jpeg|228px]] </span> | + | | style="text-align: center;vertical-align: top;"|<span style="text-align: center; font-size: 75%;"> [[Image:draft_Samper_432909089-monograph-image14.jpeg|228px]] </span> |
'''Fig. 1.13''' Normandie Bridge, France [from fr.structurae.de] | '''Fig. 1.13''' Normandie Bridge, France [from fr.structurae.de] | ||
| − | | style="text-align: center;vertical-align: top;width: | + | | style="text-align: center;vertical-align: top;width: 46%;"|[[Image:draft_Samper_432909089-monograph-image15.jpeg|288px]] |
'''Fig. 1.14''' Tatara Bridge, Japan [from [http://www.answers.com] www.answers.com]] | '''Fig. 1.14''' Tatara Bridge, Japan [from [http://www.answers.com] www.answers.com]] | ||
| Line 541: | Line 518: | ||
<div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | ||
| − | [[Image:draft_Samper_432909089-image16.png|600px]] </div> | + | [[Image:draft_Samper_432909089-monograph-image16.png|600px]] </div> |
<div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | ||
| Line 548: | Line 525: | ||
{| style="width: 100%;" | {| style="width: 100%;" | ||
|- | |- | ||
| − | | style="text-align: center;vertical-align: top;width: 50%;"| [[Image:draft_Samper_432909089-image17.png|192px]] | + | | style="text-align: center;vertical-align: top;width: 50%;"|[[Image:draft_Samper_432909089-monograph-image17.png|192px]] |
'''Fig. 1.16 '''Millau Bridge, France | '''Fig. 1.16 '''Millau Bridge, France | ||
| − | | | + | | style="vertical-align: top;width: 50%;"|[[Image:Draft_Samper_432909089_8898_monograph-image18.png|312px]] |
'''Fig. 1.17''' Sutong Bridge, Nantong, China | '''Fig. 1.17''' Sutong Bridge, Nantong, China | ||
| Line 561: | Line 538: | ||
{| style="width: 100%;" | {| style="width: 100%;" | ||
|- | |- | ||
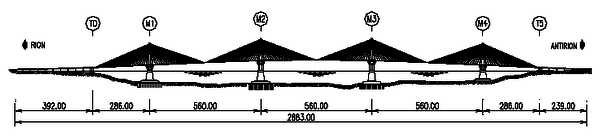
| − | | style="vertical-align: top;width: | + | | style="vertical-align: top;width: 54%;"|[[Image:draft_Samper_432909089-monograph-image19-c.png|336px]] |
'''Fig. 1.18''' Rion-Antirion Viscous Dampers [Courtesy of ''FIP'' Industriale, Italy] | '''Fig. 1.18''' Rion-Antirion Viscous Dampers [Courtesy of ''FIP'' Industriale, Italy] | ||
| Line 572: | Line 549: | ||
{| style="width: 100%;" | {| style="width: 100%;" | ||
|- | |- | ||
| − | | style="text-align: center;vertical-align: top;width: | + | | style="text-align: center;vertical-align: top;width: 55%;"|[[Image:draft_Samper_432909089-monograph-image20.png|384px]] |
'''Fig. 1.19''' Dongting Lake Bridge, China | '''Fig. 1.19''' Dongting Lake Bridge, China | ||
| Line 580: | Line 557: | ||
|} | |} | ||
| + | ==Chapter 2. Fluid Viscous Damping Technology== | ||
| − | + | :<big>2.1 General Overview </big> | |
| − | <big> | + | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
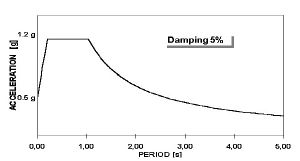
Structures situated on seismic areas must be designed to resist earthquake ground motions. A fundamental rule regarding the seismic design of structures, express that higher damping implies lower induced seismic forces. For conventional constructions, the induced earthquake energy is dissipated by the structural components of the system designed to resist gravity loads. It is well known that damping level during the elastic seismic behaviour is generally very low, which implies not much dissipated energy. During strong ground motion, energy dissipation can be reached through damage of important structural elements, and considering only the resulting response forces within the structure due to an earthquake leads to massive structural dimensions, stiff structures with enormous local energy accumulation and plastic hinges. This strengthening method combined with usual bearing arrangements permits plastic deformations by way of leading to yield stress and cracks. In this sense, structural repair after an important seismic event is generally very expensive, the structure is set temporarily out of service and sometimes a lot of damaged structures must be demolished [Alvarez, 2004]. | Structures situated on seismic areas must be designed to resist earthquake ground motions. A fundamental rule regarding the seismic design of structures, express that higher damping implies lower induced seismic forces. For conventional constructions, the induced earthquake energy is dissipated by the structural components of the system designed to resist gravity loads. It is well known that damping level during the elastic seismic behaviour is generally very low, which implies not much dissipated energy. During strong ground motion, energy dissipation can be reached through damage of important structural elements, and considering only the resulting response forces within the structure due to an earthquake leads to massive structural dimensions, stiff structures with enormous local energy accumulation and plastic hinges. This strengthening method combined with usual bearing arrangements permits plastic deformations by way of leading to yield stress and cracks. In this sense, structural repair after an important seismic event is generally very expensive, the structure is set temporarily out of service and sometimes a lot of damaged structures must be demolished [Alvarez, 2004]. | ||
| Line 597: | Line 569: | ||
{| style="width: 100%;" | {| style="width: 100%;" | ||
|- | |- | ||
| − | | style="vertical-align: top;width: | + | | style="vertical-align: top;width: 55%;"|[[Image:draft_Samper_432909089-monograph-image21-c.png|318px]] |
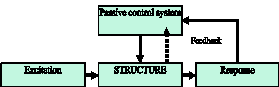
'''Fig. 2.1 '''Block Diagram of Passive Control System [Symans and Constantinou, 1999] | '''Fig. 2.1 '''Block Diagram of Passive Control System [Symans and Constantinou, 1999] | ||
| Line 614: | Line 586: | ||
The new tendencies regarding the seismic analysis and design of fluid viscous dampers capture the frequency dependence of such devices [Singh ''et al'', 2003]; the earthquake response of non-linear fluid viscous dampers [Peckan ''et al'', 1999; Lin and Chopra, 2002]; the seismic performance and behaviour of these devices during near-field ground motion [Tan ''et al'', 2005; Xu ''et al'', 2007] and the performance-based design of viscous dampers [Kim ''et al'', 2003; Li and Liang, 2007]. A state-of-the-art review can be found in the works of Lee and Taylor (2001) and Symans ''et al'' (2008). | The new tendencies regarding the seismic analysis and design of fluid viscous dampers capture the frequency dependence of such devices [Singh ''et al'', 2003]; the earthquake response of non-linear fluid viscous dampers [Peckan ''et al'', 1999; Lin and Chopra, 2002]; the seismic performance and behaviour of these devices during near-field ground motion [Tan ''et al'', 2005; Xu ''et al'', 2007] and the performance-based design of viscous dampers [Kim ''et al'', 2003; Li and Liang, 2007]. A state-of-the-art review can be found in the works of Lee and Taylor (2001) and Symans ''et al'' (2008). | ||
| − | :<big> | + | :<big>2.2 Technological Aspects</big> |
| − | :<big> | + | :<big>2.2.1 Historical Background</big> |
As with many other types of engineered components, the requirements, needs and available funds from the military allowed rapid design evolution of fluid dampers to satisfy the needs of armed forces. Early fluid damping devices operated by viscous effects, where the operating medium was sheared by vanes or plates within the damper. Designs of this type were mere laboratory curiosities, since the maximum pressure available from shearing a fluid is limited by the onset of cavitation, which generally occurs at between 0.06 N/mm<sup>2</sup> and 0.1 N/mm<sup>2</sup>, depending on the viscosity of the fluid. This operating pressure was so low that for any given output level, a viscous damper was much larger and more costly than other types [Taylor, 1996]. | As with many other types of engineered components, the requirements, needs and available funds from the military allowed rapid design evolution of fluid dampers to satisfy the needs of armed forces. Early fluid damping devices operated by viscous effects, where the operating medium was sheared by vanes or plates within the damper. Designs of this type were mere laboratory curiosities, since the maximum pressure available from shearing a fluid is limited by the onset of cavitation, which generally occurs at between 0.06 N/mm<sup>2</sup> and 0.1 N/mm<sup>2</sup>, depending on the viscosity of the fluid. This operating pressure was so low that for any given output level, a viscous damper was much larger and more costly than other types [Taylor, 1996]. | ||
| Line 626: | Line 598: | ||
With the end of the Cold War in the late 80`s, much of this fully developed defence technology became available for civilian applications. In this context, demonstration of the benefits of damping technology on structures could take place immediately, using existing dampers and the seismic test facilities available at U.S. university research centres. In this sense, application of fluid viscous dampers as part of seismic energy dissipation systems was experimentally and analytically studied, being validated by extensive testing on one-sixth to one-half scale building and bridge models in the period 1990 – 1993 at the Multidisciplinary Centre for Earthquake Engineering Research (MCEER), located on the campus of the State University of New York at Buffalo in USA. Thus, implementation of fluid viscous damping technology began relatively swiftly, with wind protection usage beginning in 1993, and seismic protection usage beginning in 1995 [Taylor and Duflot, 2002]. | With the end of the Cold War in the late 80`s, much of this fully developed defence technology became available for civilian applications. In this context, demonstration of the benefits of damping technology on structures could take place immediately, using existing dampers and the seismic test facilities available at U.S. university research centres. In this sense, application of fluid viscous dampers as part of seismic energy dissipation systems was experimentally and analytically studied, being validated by extensive testing on one-sixth to one-half scale building and bridge models in the period 1990 – 1993 at the Multidisciplinary Centre for Earthquake Engineering Research (MCEER), located on the campus of the State University of New York at Buffalo in USA. Thus, implementation of fluid viscous damping technology began relatively swiftly, with wind protection usage beginning in 1993, and seismic protection usage beginning in 1995 [Taylor and Duflot, 2002]. | ||
| − | :<big> | + | :<big>2.2.2 General Behaviour</big> |
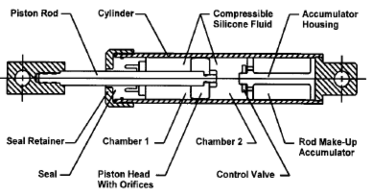
Fluid viscous dampers operate on the principle of fluid flow through orifices. A stainless steel piston travels through chambers that are filled with silicone oil. The silicone oil is inert, non flammable, non toxic and stable for extremely long periods of time. The pressure difference between the two chambers cause silicone oil to flow through an orifice in the piston head and seismic energy is transformed into heat, which dissipates into the atmosphere. This associated temperature increase can be significant, particularly when the damper is subjected to long-duration or large-amplitude motions [Makris 1998; Makris ''et al'', 1998]. Mechanisms are available to compensate for the temperature rise such that the influence on the damper behaviour is relatively minor [Soong and Dargush, 1997]. However, the increase in temperature may be of concern due to the potential for heat-induced damage to the damper seals. In this case, the temperature rise can be reduced by reducing the pressure differential across the piston head (e.g., by employing a damper with a larger piston head) [Makris ''et al'', 1998]. Interestingly, although the damper is called a ''fluid viscous damper'', the fluid typically has a relatively low viscosity (e.g., silicone oil with a kinematic viscosity on the order of 0.001 m<sup>2</sup> /s at 20°C). The term ''fluid viscous damper ''is associated with the macroscopic behaviour of the damper which is essentially the same as that of an ideal linear or nonlinear viscous dashpot (i.e., the resisting force is directly related to the velocity). Generally, the fluid damper includes a double-ended piston rod (i.e., the piston rod projects outward from both sides of the piston head and exits the damper at both ends of the main cylinder). Such configurations are useful for minimizing the development of restoring forces (stiffness) due to fluid compression [Symans ''et al'', 2008]. The force/velocity relationship for this kind of damper can be characterized as ''F = C.V<sup>α</sup>'' where ''F'' is the output force, ''V'' the relative velocity across the damper; ''C'' is the damping coefficient and ''α'' is a constant exponent which is usually a value between 0.1 and 1.0 for earthquake protection, although at the present time some manufactures begin to apply dampers with very low damping coefficients, typically in the order of 0.02. Fluid viscous dampers can operate over temperature fluctuations ranging from –40°C to +70°C, and they have the unique ability to simultaneously reduce both stress and deflection within a structure subjected to a transient. This is because a fluid viscous damper varies its force only with velocity, which provides a response that is inherently out-of-phase with stresses due to flexing of the structure [Taylor and Duflot, 2002]. | Fluid viscous dampers operate on the principle of fluid flow through orifices. A stainless steel piston travels through chambers that are filled with silicone oil. The silicone oil is inert, non flammable, non toxic and stable for extremely long periods of time. The pressure difference between the two chambers cause silicone oil to flow through an orifice in the piston head and seismic energy is transformed into heat, which dissipates into the atmosphere. This associated temperature increase can be significant, particularly when the damper is subjected to long-duration or large-amplitude motions [Makris 1998; Makris ''et al'', 1998]. Mechanisms are available to compensate for the temperature rise such that the influence on the damper behaviour is relatively minor [Soong and Dargush, 1997]. However, the increase in temperature may be of concern due to the potential for heat-induced damage to the damper seals. In this case, the temperature rise can be reduced by reducing the pressure differential across the piston head (e.g., by employing a damper with a larger piston head) [Makris ''et al'', 1998]. Interestingly, although the damper is called a ''fluid viscous damper'', the fluid typically has a relatively low viscosity (e.g., silicone oil with a kinematic viscosity on the order of 0.001 m<sup>2</sup> /s at 20°C). The term ''fluid viscous damper ''is associated with the macroscopic behaviour of the damper which is essentially the same as that of an ideal linear or nonlinear viscous dashpot (i.e., the resisting force is directly related to the velocity). Generally, the fluid damper includes a double-ended piston rod (i.e., the piston rod projects outward from both sides of the piston head and exits the damper at both ends of the main cylinder). Such configurations are useful for minimizing the development of restoring forces (stiffness) due to fluid compression [Symans ''et al'', 2008]. The force/velocity relationship for this kind of damper can be characterized as ''F = C.V<sup>α</sup>'' where ''F'' is the output force, ''V'' the relative velocity across the damper; ''C'' is the damping coefficient and ''α'' is a constant exponent which is usually a value between 0.1 and 1.0 for earthquake protection, although at the present time some manufactures begin to apply dampers with very low damping coefficients, typically in the order of 0.02. Fluid viscous dampers can operate over temperature fluctuations ranging from –40°C to +70°C, and they have the unique ability to simultaneously reduce both stress and deflection within a structure subjected to a transient. This is because a fluid viscous damper varies its force only with velocity, which provides a response that is inherently out-of-phase with stresses due to flexing of the structure [Taylor and Duflot, 2002]. | ||
| Line 634: | Line 606: | ||
{| style="width: 100%;" | {| style="width: 100%;" | ||
|- | |- | ||
| − | | style="text-align: center;vertical-align: top;width: 50%;"| [[Image:draft_Samper_432909089-image22.png|282px]] | + | | style="text-align: center;vertical-align: top;width: 50%;"|[[Image:draft_Samper_432909089-monograph-image22.png|282px]] |
'''Fig 2.2 '''General view of a Fluid Viscous Damper [Courtesy of ''FIP ''Industriale s.P.a., Italy] | '''Fig 2.2 '''General view of a Fluid Viscous Damper [Courtesy of ''FIP ''Industriale s.P.a., Italy] | ||
| − | | style="text-align: center;vertical-align: top;width: 50%;"| [[Image:draft_Samper_432909089-image23.jpeg|252px]] | + | | style="text-align: center;vertical-align: top;width: 50%;"|[[Image:draft_Samper_432909089-monograph-image23.jpeg|252px]] |
'''Fig. 2.3 '''Fluid Viscous Dampers for De Las Piedras-High Speed Railway Bridge, Spain [Courtesy of ''Maurer Sönhe'', Germany] | '''Fig. 2.3 '''Fluid Viscous Dampers for De Las Piedras-High Speed Railway Bridge, Spain [Courtesy of ''Maurer Sönhe'', Germany] | ||
| Line 647: | Line 619: | ||
{| style="width: 100%;" | {| style="width: 100%;" | ||
|- | |- | ||
| − | | style="text-align: center;vertical-align: top;width: | + | | style="text-align: center;vertical-align: top;width: 59%;"|[[Image:draft_Samper_432909089-monograph-image24.png|372px]] |
'''Fig. 2.4''' Typical Viscous Damper [Lee and Taylor, 2001] | '''Fig. 2.4''' Typical Viscous Damper [Lee and Taylor, 2001] | ||
| Line 668: | Line 640: | ||
{| style="width: 100%;" | {| style="width: 100%;" | ||
|- | |- | ||
| − | | style="text-align: center;vertical-align: top;width: 50%;"| [[Image:draft_Samper_432909089-image25.png|264px]] | + | | style="text-align: center;vertical-align: top;width: 50%;"|[[Image:draft_Samper_432909089-monograph-image25.png|264px]] |
'''Fig. 2.5''' Typical Plot of Base Shear Against Interstorey Drift [Lee and Taylor, 2001] | '''Fig. 2.5''' Typical Plot of Base Shear Against Interstorey Drift [Lee and Taylor, 2001] | ||
| − | | style="text-align: center;vertical-align: top;width: 50%;"| [[Image:draft_Samper_432909089-image26.png|240px]] | + | | style="text-align: center;vertical-align: top;width: 50%;"|[[Image:draft_Samper_432909089-monograph-image26.png|240px]] |
'''Fig. 2.6''' Base Shear Against Interstorey Drift with Added Dampers [Lee and Taylor, 2001] | '''Fig. 2.6''' Base Shear Against Interstorey Drift with Added Dampers [Lee and Taylor, 2001] | ||
| Line 710: | Line 682: | ||
| style="vertical-align: top;"|In terms of the efficiency, the damping coefficient ξ relates to the efficiency η according to: | | style="vertical-align: top;"|In terms of the efficiency, the damping coefficient ξ relates to the efficiency η according to: | ||
| − | + | ||
| − | + | [[Image:draft_Samper_432909089-monograph-image27.png|54px]] [Eq. 2.1] | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
This ends up in a maximum efficiency ''η = 96% ''for fluid viscous dampers. | This ends up in a maximum efficiency ''η = 96% ''for fluid viscous dampers. | ||
|} | |} | ||
| Line 743: | Line 709: | ||
:* Non-toxic, not inflammable and not ageing fluids are applied. | :* Non-toxic, not inflammable and not ageing fluids are applied. | ||
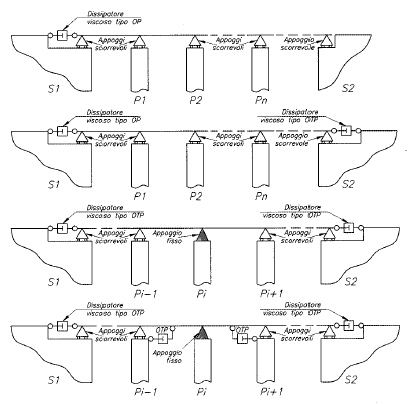
| − | :<big> | + | :<big>2.2.3 Application to Bridges</big> |
Decks for viaducts and long-span bridges require adequate expansion joints for large displacements under service conditions to absorb the effects of creep and thermal expansion. A common structural layout used in Europe, consists of continuous deck supported by ''POT'' devices [Priestley ''et al'', 1996]. By this way, the idea of employing devices with an insignificant response under long-period displacements and at the same time, capable of dissipating much induced seismic energy, was developed. | Decks for viaducts and long-span bridges require adequate expansion joints for large displacements under service conditions to absorb the effects of creep and thermal expansion. A common structural layout used in Europe, consists of continuous deck supported by ''POT'' devices [Priestley ''et al'', 1996]. By this way, the idea of employing devices with an insignificant response under long-period displacements and at the same time, capable of dissipating much induced seismic energy, was developed. | ||
| Line 754: | Line 720: | ||
<div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | ||
| − | <big>''' [[Image:draft_Samper_432909089-image28-c.png|432px]] '''</big></div> | + | <big>''' [[Image:draft_Samper_432909089-monograph-image28-c.png|432px]] '''</big></div> |
<div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | ||
| Line 761: | Line 727: | ||
{| style="width: 100%;" | {| style="width: 100%;" | ||
|- | |- | ||
| − | | style="vertical-align: top;width: 50%;"| [[Image:draft_Samper_432909089-image29.jpeg|276px]] | + | | style="vertical-align: top;width: 50%;"|[[Image:draft_Samper_432909089-monograph-image29.jpeg|276px]] |
'''Fig. 2.8''' Fluid Viscous Dampers at G4-Egnatia Motorway Bridge, Greece [Courtesy of ''Maurer Sönhe,'' Germany] | '''Fig. 2.8''' Fluid Viscous Dampers at G4-Egnatia Motorway Bridge, Greece [Courtesy of ''Maurer Sönhe,'' Germany] | ||
| − | | style="vertical-align: top;width: 50%;"| [[Image:draft_Samper_432909089-image30.png|228px]] | + | | style="vertical-align: top;width: 50%;"|[[Image:draft_Samper_432909089-monograph-image30.png|228px]] |
'''Fig. 2.9''' 850 kN Capacity Damper for the Chun-Su Bridge, South Korea [Courtesy of ''FIP ''Industriale s.P.a., Italy] | '''Fig. 2.9''' 850 kN Capacity Damper for the Chun-Su Bridge, South Korea [Courtesy of ''FIP ''Industriale s.P.a., Italy] | ||
| Line 770: | Line 736: | ||
| − | :<big> | + | :<big>2.3 Mechanical Behaviour</big> |
| − | :<big> | + | :<big>2.3.1 Energy Approach</big> |
An earthquake is an energy phenomenon and therefore this energy character should be considered to achieve the best possible seismic protection for the structure. Without seismic protection system, the seismic energy is entering the structure very concentrated at the fixed axis. By means of shock transmission units the entering energy is distributed to several spots within the structure. In this case the energy input into the structure is still in same magnitude like without those devices, but now the energy is spread over the entire structure in more portions. By implementing additional energy dissipation capability, less energy is entering the structure, with the consequent response mitigation. | An earthquake is an energy phenomenon and therefore this energy character should be considered to achieve the best possible seismic protection for the structure. Without seismic protection system, the seismic energy is entering the structure very concentrated at the fixed axis. By means of shock transmission units the entering energy is distributed to several spots within the structure. In this case the energy input into the structure is still in same magnitude like without those devices, but now the energy is spread over the entire structure in more portions. By implementing additional energy dissipation capability, less energy is entering the structure, with the consequent response mitigation. | ||
| Line 778: | Line 744: | ||
The principles of physics that govern the effects of dissipation on the control of dynamic phenomena were studied more than two centuries ago [D`Alembert, Traité de Dynamique, 1743]. Nonetheless, their practical application has come about much later and within a much different time-frame in several sectors of engineering. As was previously exposed, the sector that was the first to adopt such damping technology was the military [France, 1897], followed by the automobile industry. In 1956 Housner already suggested an energy-based design of structures. Kato and Akiyama (1975) and Uang and Bertero (1990) made a valuable contribution to the development of the aspects of an energy-based approach, which presently meets with great concensus. | The principles of physics that govern the effects of dissipation on the control of dynamic phenomena were studied more than two centuries ago [D`Alembert, Traité de Dynamique, 1743]. Nonetheless, their practical application has come about much later and within a much different time-frame in several sectors of engineering. As was previously exposed, the sector that was the first to adopt such damping technology was the military [France, 1897], followed by the automobile industry. In 1956 Housner already suggested an energy-based design of structures. Kato and Akiyama (1975) and Uang and Bertero (1990) made a valuable contribution to the development of the aspects of an energy-based approach, which presently meets with great concensus. | ||
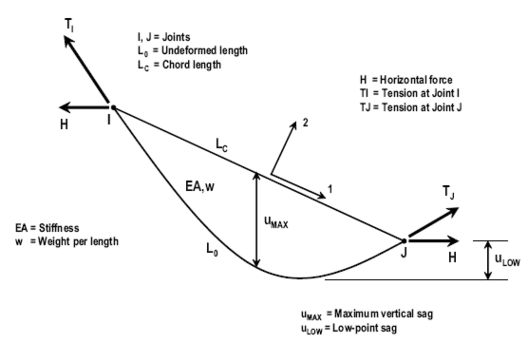
| − | The dynamic equation of a single-degree-of-freedom structure with mass ''m<sub>s</sub>'' damping coefficient ''c<sub>s</sub>'', stiffness ''k<sub>s</sub> ''and control force ''u'', subject to ground acceleration '' [[Image:draft_Samper_432909089-image31.png|36px]] ''is: | + | The dynamic equation of a single-degree-of-freedom structure with mass ''m<sub>s</sub>'' damping coefficient ''c<sub>s</sub>'', stiffness ''k<sub>s</sub> ''and control force ''u'', subject to ground acceleration '' [[Image:draft_Samper_432909089-monograph-image31.png|36px]] ''is: |
| − | + | ||
| − | + | [[Image:draft_Samper_432909089-monograph-image32.png|234px]] [Eq. 2.2] | |
| − | + | ||
| − | + | where [[Image:draft_Samper_432909089-monograph-image33.png|30px]] , [[Image:draft_Samper_432909089-monograph-image34.png|30px]] and [[Image:draft_Samper_432909089-monograph-image35.png|30px]] are the displacement, velocity and acceleration responses respectively. The involved parameters are clearly explained in Fig. 2.10, which shows a simplified scheme for a single-degree-of-freedom system. Of course, each term in Eq. 2.2 is a force. | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | where | + | |
{| style="width: 100%;" | {| style="width: 100%;" | ||
|- | |- | ||
| − | | style="text-align: center;vertical-align: top;width: | + | | style="text-align: center;vertical-align: top;width: 44%;"|[[Image:draft_Samper_432909089-monograph-image36.png|228px]] |
'''Fig. 2.10''' Complex Bridge Structure Explained with a Simplified Single Oscillation Mass | '''Fig. 2.10''' Complex Bridge Structure Explained with a Simplified Single Oscillation Mass | ||
| style="vertical-align: top;"|Integrating Eq. 2.2 with respect to ''x:'' | | style="vertical-align: top;"|Integrating Eq. 2.2 with respect to ''x:'' | ||
| − | + | [[Image:draft_Samper_432909089-monograph-image37.png|354px]] | |
where each term is now an energy component. Thus, we can define: | where each term is now an energy component. Thus, we can define: | ||
| − | + | ||
| − | + | [[Image:draft_Samper_432909089-monograph-image38.png|276px]] [Eq. 2.3] | |
| − | + | ||
| − | + | [[Image:draft_Samper_432909089-monograph-image39.png|240px]] [Eq. 2.4] | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | | | + | |
| − | + | ||
|} | |} | ||
| − | + | ||
| − | + | [[Image:draft_Samper_432909089-monograph-image40.png|138px]] [Eq. 2.5] | |
| − | + | ||
| − | + | [[Image:draft_Samper_432909089-monograph-image41.png|72px]] [Eq. 2.6] | |
| − | + | ||
| − | + | [[Image:draft_Samper_432909089-monograph-image42.png|102px]] [Eq. 2.7] | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
An energy balance equation can be proposed in terms of the above defined: | An energy balance equation can be proposed in terms of the above defined: | ||
| − | + | ||
| − | + | [[Image:draft_Samper_432909089-monograph-image43.png|240px]] [Eq. 2.8] | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
where: | where: | ||
| Line 857: | Line 793: | ||
{| style="width: 100%;border-collapse: collapse;" | {| style="width: 100%;border-collapse: collapse;" | ||
|- | |- | ||
| − | | style="vertical-align: top;width: | + | | style="vertical-align: top;width: 40%;"|[[Image:draft_Samper_432909089-monograph-image44.png|228px]] |
| style="vertical-align: top;"|'''Fig. 2.11 '''Concept of Energy Approach Considering the Energy Exchange Between Structure and Environment | | style="vertical-align: top;"|'''Fig. 2.11 '''Concept of Energy Approach Considering the Energy Exchange Between Structure and Environment | ||
|} | |} | ||
| − | + | [[Image:draft_Samper_432909089-monograph-image45.png|84px]] : Stored energy within structure | |
| − | + | [[Image:draft_Samper_432909089-monograph-image46.png|90px]] : Dissipated energy within structure | |
Thus: | Thus: | ||
| − | + | ||
| − | + | [[Image:draft_Samper_432909089-monograph-image47.png|84px]] [Eq. 2.9] | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
The control force ''u'' by non-linear viscous dampers with damping coefficient ''c<sub>d</sub>'' is expressed as | The control force ''u'' by non-linear viscous dampers with damping coefficient ''c<sub>d</sub>'' is expressed as | ||
| − | <div style="text-align: | + | <div style="text-align: left; direction: ltr; margin-left: 1em;"> |
| − | [[Image:draft_Samper_432909089-image48.png|120px]] [Eq. 2.10]</div> | + | [[Image:draft_Samper_432909089-monograph-image48.png|120px]] [Eq. 2.10]</div> |
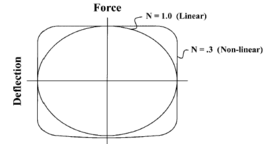
In Eq. 2.10, the exponent ''N'' controls the damper nonlinearity and has typical values in the range of 0.10 to 1.0 for seismic applications. For the special case of ''N = 1'', Eq. 2.10 represents the force applied by linear viscous dampers. In the case of ''N = 0, ''Eq. 2.10 changes to a friction damper as follows: | In Eq. 2.10, the exponent ''N'' controls the damper nonlinearity and has typical values in the range of 0.10 to 1.0 for seismic applications. For the special case of ''N = 1'', Eq. 2.10 represents the force applied by linear viscous dampers. In the case of ''N = 0, ''Eq. 2.10 changes to a friction damper as follows: | ||
| − | <div style="text-align: | + | <div style="text-align: left; direction: ltr; margin-left: 1em;"> |
| − | [[Image:draft_Samper_432909089-image49.png|90px]] [Eq. 2.11]</div> | + | [[Image:draft_Samper_432909089-monograph-image49.png|90px]] [Eq. 2.11]</div> |
{| style="width: 100%;" | {| style="width: 100%;" | ||
|- | |- | ||
| − | | style="text-align: center;vertical-align: top;width: | + | | style="text-align: center;vertical-align: top;width: 55%;"|[[Image:draft_Samper_432909089-monograph-image50-c.png|312px]] |
'''Fig. 2.12''' Plot of Force Against Velocity for Several Values of Damping Exponent ''N'' | '''Fig. 2.12''' Plot of Force Against Velocity for Several Values of Damping Exponent ''N'' | ||
| Line 898: | Line 828: | ||
Applying the force – velocity relationship expressed in Eq. 2.10 to Eq. 2.6 results: | Applying the force – velocity relationship expressed in Eq. 2.10 to Eq. 2.6 results: | ||
| − | + | ||
| − | + | [[Image:draft_Samper_432909089-monograph-image51.png|168px]] [Eq. 2.12] | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
which represents the dissipated energy for a non-linear fluid viscous damper. The hysteretic behaviour of fluid viscous dampers can be plotted and shown in Fig. 2.13. | which represents the dissipated energy for a non-linear fluid viscous damper. The hysteretic behaviour of fluid viscous dampers can be plotted and shown in Fig. 2.13. | ||
{| style="width: 100%;" | {| style="width: 100%;" | ||
|- | |- | ||
| − | | style="text-align: center;vertical-align: top;width: | + | | style="text-align: center;vertical-align: top;width: 65%;"|[[Image:draft_Samper_432909089-monograph-image52.png|264px]] |
'''Fig. 2.13''' Hysteresis Loops for Linear and Non-linear Fluid Viscous Dampers [Lee and Taylor, 2001] | '''Fig. 2.13''' Hysteresis Loops for Linear and Non-linear Fluid Viscous Dampers [Lee and Taylor, 2001] | ||
| Line 921: | Line 845: | ||
<div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | ||
| − | <big>''' [[Image:draft_Samper_432909089-image53.png|486px]] '''</big></div> | + | <big>''' [[Image:draft_Samper_432909089-monograph-image53.png|486px]] '''</big></div> |
<div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | ||
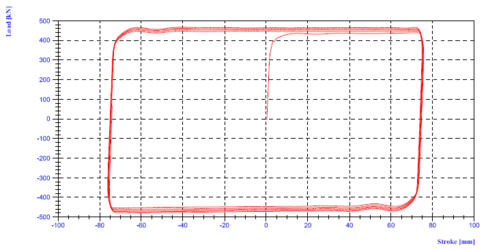
'''Fig. 2.14''' Force – Displacement Hysteretic Diagram of a Viscous Damper, ''N = 0.15'' [Courtesy of ''FIP ''Industriale, s.P.a., Italy]</div> | '''Fig. 2.14''' Force – Displacement Hysteretic Diagram of a Viscous Damper, ''N = 0.15'' [Courtesy of ''FIP ''Industriale, s.P.a., Italy]</div> | ||
| − | :<big> | + | :<big>2.3.2 Effect of the Damper Parameters</big> |
| − | :'' | + | :''2.3.2.1 Damping coefficient c<sub>d</sub>'' |
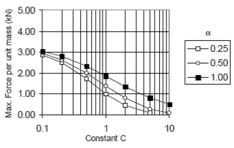
In general terms, for viscous dampers, ''c<sub>d</sub>'' does not affect the shape of the hysteretic force – displacement cycle; however, an increase of the value of this parameter increases the energy dissipation capacity and the maximum force in the device [Guerreiro, 2006]. In this sense, the work carried out by Virtuoso ''et al ''(2000) studies the modelling of the seismic behaviour of bridges with added viscous dampers, analyzing the effects of the constant ''c<sub>d</sub>'' (here called ''C'')''.'' To allow an analysis on the influence of that parameter on the structural response, values of the constant ''C ''between 0.10 and 10 were considered, since those values, together with the values considered for the parameter ''N ''(here called ''α''), will cover forces corresponding to seismic coefficient varying from 1% to 50% of the weight. In this study a set of five artificial accelerograms compatible with the response spectrum defined in Eurocode 8 – Part 2 [CEN, 1998b] with a peak ground acceleration of 0.30g, type B soil and 30 sec total duration of the series, were used. Two extreme cases were considered: a solution without elastic stiffness (deck totally free over the piers) and a solution with elastic stiffness (low stiffness elastic connection between the piers and the deck). Also, in this research the configurations of the force – velocity relation curves were presented for different values of ''α'', corresponding to the linear branch, which, were defined by the origin and the point corresponding to 10% of the maximum velocity and force corresponding to the defined seismic action and obtained without the consideration of the linear branch. Figs. 2.15 and 2.16 show maximum forces and displacements in the viscous damper without and with elastic stiffness respectively. They show that solution involving a higher displacement control always lead to higher force levels in the device. It is also possible to observe that the more efficient solutions, with better displacement control for the same force level, generally corresponds to low ''α'' values. Likewise, for device solutions with low values of the constant ''C'', the elastic stiffness of the structure has an important contribution on the displacement control. It is important to notice that the contribution of the elastic force is out of phase with the one transmitted by the devices, what means that, in a solution of this type there is always a force restraining the movement of the deck. The problem is that the forces transmitted to the structure must be controlled to limit the contribution of the piers to values lower than their elastic limit. | In general terms, for viscous dampers, ''c<sub>d</sub>'' does not affect the shape of the hysteretic force – displacement cycle; however, an increase of the value of this parameter increases the energy dissipation capacity and the maximum force in the device [Guerreiro, 2006]. In this sense, the work carried out by Virtuoso ''et al ''(2000) studies the modelling of the seismic behaviour of bridges with added viscous dampers, analyzing the effects of the constant ''c<sub>d</sub>'' (here called ''C'')''.'' To allow an analysis on the influence of that parameter on the structural response, values of the constant ''C ''between 0.10 and 10 were considered, since those values, together with the values considered for the parameter ''N ''(here called ''α''), will cover forces corresponding to seismic coefficient varying from 1% to 50% of the weight. In this study a set of five artificial accelerograms compatible with the response spectrum defined in Eurocode 8 – Part 2 [CEN, 1998b] with a peak ground acceleration of 0.30g, type B soil and 30 sec total duration of the series, were used. Two extreme cases were considered: a solution without elastic stiffness (deck totally free over the piers) and a solution with elastic stiffness (low stiffness elastic connection between the piers and the deck). Also, in this research the configurations of the force – velocity relation curves were presented for different values of ''α'', corresponding to the linear branch, which, were defined by the origin and the point corresponding to 10% of the maximum velocity and force corresponding to the defined seismic action and obtained without the consideration of the linear branch. Figs. 2.15 and 2.16 show maximum forces and displacements in the viscous damper without and with elastic stiffness respectively. They show that solution involving a higher displacement control always lead to higher force levels in the device. It is also possible to observe that the more efficient solutions, with better displacement control for the same force level, generally corresponds to low ''α'' values. Likewise, for device solutions with low values of the constant ''C'', the elastic stiffness of the structure has an important contribution on the displacement control. It is important to notice that the contribution of the elastic force is out of phase with the one transmitted by the devices, what means that, in a solution of this type there is always a force restraining the movement of the deck. The problem is that the forces transmitted to the structure must be controlled to limit the contribution of the piers to values lower than their elastic limit. | ||
<div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | ||
| − | [[Image:draft_Samper_432909089-image54.png|366px]] </div> | + | [[Image:draft_Samper_432909089-monograph-image54.png|366px]] </div> |
<div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | ||
| Line 939: | Line 863: | ||
<div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | ||
| − | [[Image:draft_Samper_432909089-image55.png|366px]] </div> | + | [[Image:draft_Samper_432909089-monograph-image55.png|366px]] </div> |
<div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | ||
| Line 950: | Line 874: | ||
{| style="width: 100%;" | {| style="width: 100%;" | ||
|- | |- | ||
| − | | style="vertical-align: top;width: | + | | style="vertical-align: top;width: 61%;"|[[Image:draft_Samper_432909089-monograph-image56.png|234px]] |
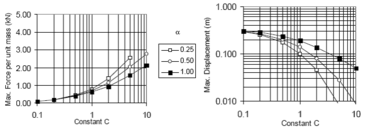
'''Fig. 2.17 '''Maximum Forces in the Structure – Solution with Dampers and Elastic Stiffness [Virtuoso ''et al'', 2000] | '''Fig. 2.17 '''Maximum Forces in the Structure – Solution with Dampers and Elastic Stiffness [Virtuoso ''et al'', 2000] | ||
| Line 959: | Line 883: | ||
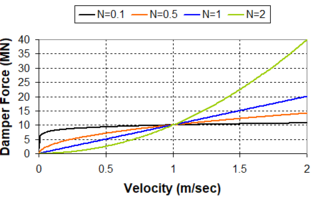
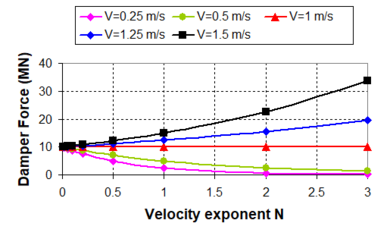
| − | :'' | + | :''2.3.2.2 Velocity exponent N'' |
The damping exponent ''N'' represents the essence of the non-linear behaviour of fluid viscous dampers. On the contrary of the damping coefficient ''c<sub>d</sub>'', this parameter does not affect the size of the hysteretic force-displacement cycle and for that reason incidence of this parameter on the seismic response is not decisive as occurs with the damping coefficient, aspect enlarged in 2.3.2.1. Changes in the ''N-''exponent imply changes in the shape of the hysteretic force-displacement cycle, as was explained in Fig. 2.13. Low damping exponents tend to expose rectangular force-displacement hysteresis, as well as linear behaviour implies more elliptical force-displacement hysteresis cycles. The more practical incidence of the ''N-''exponent relates with the damper forces, depending on the relative velocities. | The damping exponent ''N'' represents the essence of the non-linear behaviour of fluid viscous dampers. On the contrary of the damping coefficient ''c<sub>d</sub>'', this parameter does not affect the size of the hysteretic force-displacement cycle and for that reason incidence of this parameter on the seismic response is not decisive as occurs with the damping coefficient, aspect enlarged in 2.3.2.1. Changes in the ''N-''exponent imply changes in the shape of the hysteretic force-displacement cycle, as was explained in Fig. 2.13. Low damping exponents tend to expose rectangular force-displacement hysteresis, as well as linear behaviour implies more elliptical force-displacement hysteresis cycles. The more practical incidence of the ''N-''exponent relates with the damper forces, depending on the relative velocities. | ||
| Line 965: | Line 889: | ||
If we consider the force at the dampers ''F'' as a function of the exponent ''N'', we can write | If we consider the force at the dampers ''F'' as a function of the exponent ''N'', we can write | ||
| − | + | [[Image:draft_Samper_432909089-monograph-image57.png|90px]] where ''c<sub>d</sub>'' is a constant. | |
| − | If ''c<sub>d</sub>'' is constant, ''F'' is maximum if '' | + | If ''c<sub>d</sub>'' is constant, ''F'' is maximum if '' [[Image:draft_Samper_432909089-monograph-image58.png|18px]] ''is maximum. |
| − | Let | + | Let [[Image:draft_Samper_432909089-monograph-image59.png|78px]] .Maximizing ''f'': |
| − | + | [[Image:draft_Samper_432909089-monograph-image60.png|144px]] if and only if | |
{| | {| | ||
|- | |- | ||
| − | | | + | | [[Image:draft_Samper_432909089-monograph-image61.png|126px]] |
| − | | | + | | [[Image:draft_Samper_432909089-monograph-image62.png|center|150px]] |
|} | |} | ||
| − | + | [[Image:draft_Samper_432909089-monograph-image63.png|60px]] if and only if [[Image:draft_Samper_432909089-monograph-image64.png|36px]] which implies a constant force ''F = c<sub>d</sub>'' | |
Analyzing ''f'' in its domain: | Analyzing ''f'' in its domain: | ||
| − | :(1) If | + | :(1) If [[Image:draft_Samper_432909089-monograph-image65.png|36px]] then ''f'' is maximum if ''N'' is maximum, that is to say, if [[Image:draft_Samper_432909089-monograph-image66.png|54px]] |
| − | :(2) If | + | :(2) If [[Image:draft_Samper_432909089-monograph-image67.png|60px]] then [[Image:draft_Samper_432909089-monograph-image68.png|78px]] can be written as [[Image:draft_Samper_432909089-monograph-image69.png|192px]] . |
| − | Then, ''f'' is maximum if | + | Then, ''f'' is maximum if [[Image:draft_Samper_432909089-monograph-image70.png|24px]] is little, which implies [[Image:draft_Samper_432909089-monograph-image71.png|48px]] . |
| − | This analytical approach shows that the critical point is | + | This analytical approach shows that the critical point is [[Image:draft_Samper_432909089-monograph-image72.png|36px]] . Being the damper velocities larger than 1, the maximum damper forces are obtained for high values of the damping exponent, on the contrary of the case where the damper velocities are lower than 1, in which the maximum damper forces are obtained when ''N'' is close to zero, that is to say, for non-linear dampers. Graphically, the above-mentioned can be clearly exposed in Fig. 2.18. Fig. 2.18 exposes variations of the dampers forces with the velocity exponent ''N'' for some common damper velocities. From these results, it is necessary to be cautious if velocity pulses are considered in the presence of linear dampers or dampers with ''N'' > 1. Likewise, similar considerations are necessary to take into account if non-linear dampers are considered in the presence of low velocities. |
{| style="width: 100%;" | {| style="width: 100%;" | ||
|- | |- | ||
| − | | style="text-align: center;vertical-align: top;width: | + | | style="text-align: center;vertical-align: top;width: 61%;"|[[Image:draft_Samper_432909089-monograph-image73.png|390px]] |
'''Fig. 2.18''' Plot of Damper Forces as Function of the ''N''-exponent for Several Velocities and ''c<sub>d</sub>'' = 10 MN/(m/s)<sup>N</sup> | '''Fig. 2.18''' Plot of Damper Forces as Function of the ''N''-exponent for Several Velocities and ''c<sub>d</sub>'' = 10 MN/(m/s)<sup>N</sup> | ||
| Line 1,128: | Line 1,052: | ||
{| style="width: 100%;" | {| style="width: 100%;" | ||
|- | |- | ||
| − | | style="text-align: center;vertical-align: top;width: 47%;"| [[Image:draft_Samper_432909089-image74-c.png|240px]] | + | | style="text-align: center;vertical-align: top;width: 47%;"|[[Image:draft_Samper_432909089-monograph-image74-c.png|240px]] |
'''Fig. 2.19''' Extra-low Damping for Viscous Damper with ''N''=0.015 | '''Fig. 2.19''' Extra-low Damping for Viscous Damper with ''N''=0.015 | ||
| Line 1,137: | Line 1,061: | ||
| − | :<big> | + | :<big>2.3.3 Non-linear Viscous Dampers</big> |
| − | :'' | + | :''2.3.3.1 Earthquake response'' |
Numerous experimental and analytical investigations have focused on linear fluid viscous dampers, because they can be modelled simply by a linear dashpot. While being effective in reducing seismic demands on the structure, linear viscous dampers may develop excessive damper forces in applications where large structural velocities can occur, as for example in long period structures subjected to intense ground shaking, especially in the near-fault region. Recently, some researchers and earthquake engineering professionals have begun to focus on fluid viscous dampers exhibiting non-linear Force-Velocity relationship because of their ability to limit the peak damper force at large structural velocities while still providing sufficient supplemental damping [Lin and Chopra, 2002; Symans ''et al'', 2008]. | Numerous experimental and analytical investigations have focused on linear fluid viscous dampers, because they can be modelled simply by a linear dashpot. While being effective in reducing seismic demands on the structure, linear viscous dampers may develop excessive damper forces in applications where large structural velocities can occur, as for example in long period structures subjected to intense ground shaking, especially in the near-fault region. Recently, some researchers and earthquake engineering professionals have begun to focus on fluid viscous dampers exhibiting non-linear Force-Velocity relationship because of their ability to limit the peak damper force at large structural velocities while still providing sufficient supplemental damping [Lin and Chopra, 2002; Symans ''et al'', 2008]. | ||
| Line 1,148: | Line 1,072: | ||
<div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | ||
| − | <sub> [[Image:draft_Samper_432909089-image75.png|600px]] </sub></div> | + | <sub> [[Image:draft_Samper_432909089-monograph-image75.png|600px]] </sub></div> |
<div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | ||
| Line 1,157: | Line 1,081: | ||
{| style="width: 100%;" | {| style="width: 100%;" | ||
|- | |- | ||
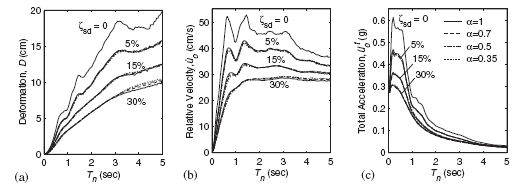
| − | | style="vertical-align: top;width: | + | | style="vertical-align: top;width: 57%;"|[[Image:draft_Samper_432909089-monograph-image76.png|336px]] |
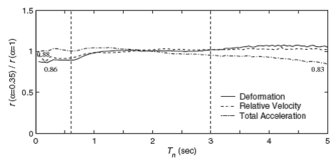
'''Fig. 2.21''' Influence of Damper Non-linearity on Mean Peak Responses, ''r'': Deformation, Relative Velocity, and Total Acceleration for Systems with ''ξ<sub>d</sub> = 30%'' [Lin and Chopra, 2002]. | '''Fig. 2.21''' Influence of Damper Non-linearity on Mean Peak Responses, ''r'': Deformation, Relative Velocity, and Total Acceleration for Systems with ''ξ<sub>d</sub> = 30%'' [Lin and Chopra, 2002]. | ||
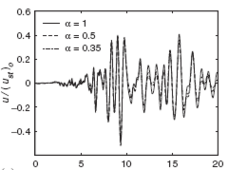
| − | | style="vertical-align: top;width: | + | | style="vertical-align: top;width: 42%;"|[[Image:draft_Samper_432909089-monograph-image77.png|228px]] |
'''Fig. 2.22 '''Response History for Deformation of a SDF System (''T<sub>n</sub> = 1 sec, ξ = 5%'') with ''ξ<sub>d</sub> = 15%'' [Lin and Chopra, 2002]. | '''Fig. 2.22 '''Response History for Deformation of a SDF System (''T<sub>n</sub> = 1 sec, ξ = 5%'') with ''ξ<sub>d</sub> = 15%'' [Lin and Chopra, 2002]. | ||
| Line 1,167: | Line 1,091: | ||
It is important to say that for a given force and displacement amplitude, the energy dissipated per cycle for a nonlinear fluid damper is larger, by a factor λ/π (where λ is a parameter whose value depends exclusively on the velocity exponent), than that for the linear case and increases monotonically with reducing velocity exponent (up to a theoretical limit of 4/π=1.27 which corresponds to a velocity exponent of zero); however, the additional energy dissipation afforded by the nonlinear dampers is minimal. For a given frequency of motion, ''ω'', and displacement amplitude, ''x<sub>0</sub>'', to dissipate the same amount of energy per cycle, the damping coefficient of the nonlinear damper, ''c<sub>dNL</sub>'', must be larger than that of the linear damper, ''c<sub>dL</sub>'', as given by | It is important to say that for a given force and displacement amplitude, the energy dissipated per cycle for a nonlinear fluid damper is larger, by a factor λ/π (where λ is a parameter whose value depends exclusively on the velocity exponent), than that for the linear case and increases monotonically with reducing velocity exponent (up to a theoretical limit of 4/π=1.27 which corresponds to a velocity exponent of zero); however, the additional energy dissipation afforded by the nonlinear dampers is minimal. For a given frequency of motion, ''ω'', and displacement amplitude, ''x<sub>0</sub>'', to dissipate the same amount of energy per cycle, the damping coefficient of the nonlinear damper, ''c<sub>dNL</sub>'', must be larger than that of the linear damper, ''c<sub>dL</sub>'', as given by | ||
| − | + | ||
| − | + | [[Image:draft_Samper_432909089-monograph-image78.png|138px]] [Eq. 2.13] | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
As an example, for a frequency of 1.0 Hz and displacement amplitude of 5 cm, the damping coefficient of a nonlinear damper with velocity exponent of 0.5 must be approximately three times larger than that of a linear damper to dissipate the same amount of energy per cycle. Conversely, if nonlinear dampers are used to limit the damper force, a reduction in energy dissipation capacity as compared to the case of linear dampers would be accepted [Symans ''et al'', 2008]. | As an example, for a frequency of 1.0 Hz and displacement amplitude of 5 cm, the damping coefficient of a nonlinear damper with velocity exponent of 0.5 must be approximately three times larger than that of a linear damper to dissipate the same amount of energy per cycle. Conversely, if nonlinear dampers are used to limit the damper force, a reduction in energy dissipation capacity as compared to the case of linear dampers would be accepted [Symans ''et al'', 2008]. | ||
A last aspect to consider regarding the earthquake response of non-linear fluid viscous dampers, is that the earthquake-induced force in a non-linear viscous damper can be estimated from the damper force in a corresponding system with linear viscous damping, its peak deformation, and peak relative velocity; however, the relative velocity should not be approximated by the pseudo-velocity as this approximation introduces a large error in the damper force. In fact, if spectral pseudo-velocities are used, they are based on design displacements ''(S<sub>v</sub> = ω<sub>0</sub>S<sub>d</sub>)''. It is well known that effectiveness of non-linear viscous dampers is highly dependent on operating velocities, being necessary to have reliable estimates of the true velocity in the device [Pekcan ''et al'', 1999; Lin and Chopra, 2002]. | A last aspect to consider regarding the earthquake response of non-linear fluid viscous dampers, is that the earthquake-induced force in a non-linear viscous damper can be estimated from the damper force in a corresponding system with linear viscous damping, its peak deformation, and peak relative velocity; however, the relative velocity should not be approximated by the pseudo-velocity as this approximation introduces a large error in the damper force. In fact, if spectral pseudo-velocities are used, they are based on design displacements ''(S<sub>v</sub> = ω<sub>0</sub>S<sub>d</sub>)''. It is well known that effectiveness of non-linear viscous dampers is highly dependent on operating velocities, being necessary to have reliable estimates of the true velocity in the device [Pekcan ''et al'', 1999; Lin and Chopra, 2002]. | ||
| − | :'' | + | :''2.3.3.2 Equivalent linear viscous damping'' |
The energy dissipation capacity of a fluid viscous damper can be characterized by the supplemental damping ratio'' ξ<sub>d</sub>'' and its non-linearity by the parameter ''N; ''and it is found that the structural response is most effectively investigated in terms of these parameters because they are dimensionless and independent, and the structural response varies linearly with the excitation intensity [Lin and Chopra, 2002]. In this sense, a system with non-linear dampers is usually replaced by an equivalent linear system, with its properties determined using different methods: equalling the energy dissipated in the two systems [Jacobsen, 1930; Fabunmi, 1985]; equalling power consumption in the two systems [Pekcan ''et al'', 1999]; replacing the non-linear viscous damping by an array of frequency and amplitude-dependent linear viscous model [Rakheja and Sankar, 1986]; random vibration theory [Caughey, 1963; Roberts, 1976], and more recently, applying closed-form formulas based on probabilistic concept to obtain fundamental modal damping ratio without carrying out structural analysis [Lee ''et al'', 2004]. | The energy dissipation capacity of a fluid viscous damper can be characterized by the supplemental damping ratio'' ξ<sub>d</sub>'' and its non-linearity by the parameter ''N; ''and it is found that the structural response is most effectively investigated in terms of these parameters because they are dimensionless and independent, and the structural response varies linearly with the excitation intensity [Lin and Chopra, 2002]. In this sense, a system with non-linear dampers is usually replaced by an equivalent linear system, with its properties determined using different methods: equalling the energy dissipated in the two systems [Jacobsen, 1930; Fabunmi, 1985]; equalling power consumption in the two systems [Pekcan ''et al'', 1999]; replacing the non-linear viscous damping by an array of frequency and amplitude-dependent linear viscous model [Rakheja and Sankar, 1986]; random vibration theory [Caughey, 1963; Roberts, 1976], and more recently, applying closed-form formulas based on probabilistic concept to obtain fundamental modal damping ratio without carrying out structural analysis [Lee ''et al'', 2004]. | ||
| Line 1,186: | Line 1,104: | ||
Thus, equalling the energy dissipated in a vibration cycle of the non-linear system to that of equivalent viscous system [Pekcan ''et al'', 1999] and considering equation 2.10: | Thus, equalling the energy dissipated in a vibration cycle of the non-linear system to that of equivalent viscous system [Pekcan ''et al'', 1999] and considering equation 2.10: | ||
| − | + | [[Image:draft_Samper_432909089-monograph-image48.png|120px]] | |
Soong and Constantinou (1994) have shown that the work done (dissipated energy) in one cycle of sinusoidal loading can be written as | Soong and Constantinou (1994) have shown that the work done (dissipated energy) in one cycle of sinusoidal loading can be written as | ||
| − | + | ||
| − | + | <div style="text-align: left; direction: ltr; margin-left: 1em;"> | |
| − | + | [[Image:draft_Samper_432909089-monograph-image79.png|84px]] [Eq. 2.14]</div> | |
| − | + | ||
| − | + | that is basically the same equation as 2.6. Here, ''T<sub>0</sub> = 2π/ω<sub>0</sub>, ''where ''ω<sub>0</sub>'' is the circular frequency of the system and'' [[Image:draft_Samper_432909089-monograph-image80.png|90px]] .'' | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | that is basically the same equation as 2.6. Here, ''T<sub>0</sub> = 2π/ω<sub>0</sub>, ''where ''ω<sub>0</sub>'' is the circular frequency of the system and'' | + | |
Equation 2.14 can be integrated to give | Equation 2.14 can be integrated to give | ||
| − | + | ||
| − | + | <div style="text-align: left; direction: ltr; margin-left: 1em;"> | |
| − | + | [[Image:draft_Samper_432909089-monograph-image81.png|228px]] [Eq. 2.15]</div> | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
where ''Г( ) ''is the gamma function. | where ''Г( ) ''is the gamma function. | ||
The equivalent (added) damping is calculated by equating equation 2.15 and the energy dissipated in equivalent viscous damping: | The equivalent (added) damping is calculated by equating equation 2.15 and the energy dissipated in equivalent viscous damping: | ||
| − | <div style="text-align: | + | <div style="text-align: left; direction: ltr; margin-left: 1em;"> |
| − | ''4πξ<sub>d</sub>ω<sub>0</sub>E<sub>s</sub> = W<sub>d</sub>'' [Eq. 2.16]</div> | + | '''4πξ<sub>d</sub>ω<sub>0</sub>E<sub>s</sub> = W<sub>d</sub>''' [Eq. 2.16]</div> |
| + | |||
in which strain energy ''E<sub>s</sub> = kx<sub>0</sub><sup>2</sup>/2. ''Solving Eq. 2.16 for equivalent damping ratio: | in which strain energy ''E<sub>s</sub> = kx<sub>0</sub><sup>2</sup>/2. ''Solving Eq. 2.16 for equivalent damping ratio: | ||
| − | + | ||
| − | + | <div style="text-align: left; direction: ltr; margin-left: 1em;"> | |
| − | + | [[Image:draft_Samper_432909089-monograph-image82.png|234px]] [Eq. 2.17]</div> | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
where ''M'' is the mass of the system, and ''x<sub>0</sub>'' the amplitude of harmonic motion at the undamped natural frequency ''ω<sub>0</sub>.'' | where ''M'' is the mass of the system, and ''x<sub>0</sub>'' the amplitude of harmonic motion at the undamped natural frequency ''ω<sub>0</sub>.'' | ||
Of course, the additional damping that the passive system introduces to the structure can be obtained by its energy dissipation capacity in each hysteretic cycle. This dissipated energy for each cycle, can be obtained calculating the area of the cycle in the force – displacement relationship of the viscous damper. Thus, for a selected cycle, it is possible to assess the equivalent damping ratio as follows: | Of course, the additional damping that the passive system introduces to the structure can be obtained by its energy dissipation capacity in each hysteretic cycle. This dissipated energy for each cycle, can be obtained calculating the area of the cycle in the force – displacement relationship of the viscous damper. Thus, for a selected cycle, it is possible to assess the equivalent damping ratio as follows: | ||
| − | + | ||
| − | + | [[Image:draft_Samper_432909089-monograph-image83.png|114px]] [Eq. 2.18] | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
where ''u<sub>max</sub> ''and ''x<sub>max</sub>'' are the maximum force and maximum displacement at the damper respectively. | where ''u<sub>max</sub> ''and ''x<sub>max</sub>'' are the maximum force and maximum displacement at the damper respectively. | ||
Pekcan ''et al ''(1999), proposed a simple method for making the transformation from the non-linear damper behaviour to equivalent viscous damping. They explain that for velocity-dependent systems such as viscous dampers, consideration of the ''rate'' of energy dissipation – that is power (rather than energy) – becomes more important in seeking the equivalent linear properties for these systems. The proposed equivalent damping is | Pekcan ''et al ''(1999), proposed a simple method for making the transformation from the non-linear damper behaviour to equivalent viscous damping. They explain that for velocity-dependent systems such as viscous dampers, consideration of the ''rate'' of energy dissipation – that is power (rather than energy) – becomes more important in seeking the equivalent linear properties for these systems. The proposed equivalent damping is | ||
| − | + | ||
| − | + | <div style="text-align: left; direction: ltr; margin-left: 1em;"> | |
| − | + | [[Image:draft_Samper_432909089-monograph-image84.png|126px]] [Eq. 2.19]</div> | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
Given the customary definition of damping ratio (''ξ'') obtained from ''c = 2ξω<sub>0</sub>M'', equation 2.19 can be expressed as follows: | Given the customary definition of damping ratio (''ξ'') obtained from ''c = 2ξω<sub>0</sub>M'', equation 2.19 can be expressed as follows: | ||
| − | + | ||
| − | + | <div style="text-align: left; direction: ltr; margin-left: 1em;"> | |
| − | + | [[Image:draft_Samper_432909089-monograph-image85.png|156px]] [Eq. 2.20]</div> | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
This formulation, also called ''power equivalent approach'', predicts higher damping values compared with energy based method (Eq. 2.17). This difference is greater for low values of ''N'', and for that reason it is necessary to be cautious using any of the above formulations for small ''N'' powers (''N<0.1''), since the mechanism of the devices changes from viscous (velocity dependent) to Coulomb friction type (when ''N'' tends to zero). | This formulation, also called ''power equivalent approach'', predicts higher damping values compared with energy based method (Eq. 2.17). This difference is greater for low values of ''N'', and for that reason it is necessary to be cautious using any of the above formulations for small ''N'' powers (''N<0.1''), since the mechanism of the devices changes from viscous (velocity dependent) to Coulomb friction type (when ''N'' tends to zero). | ||
| − | :<big> | + | :<big>2.3.4 Performance of Viscous Dampers During Near-field Ground Motions</big> |
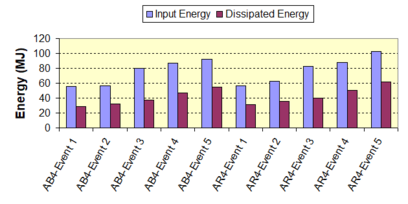
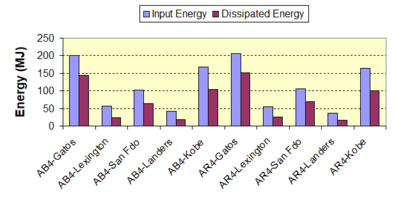
Near-field earthquakes are characterized by short duration pulses of long period with large peak ground velocities and accelerations. It has been observed from recent earthquake records that motions in the fault-normal direction contain destructive long-period pulses with high peak ground velocities, aspect that negatively affects long-period structures such as cable-stayed bridges. A lot of approaches to model these pulses have been recently proposed [Makris, 1997; He, 2003; Mavroeidis ''et al'', 2004]. | Near-field earthquakes are characterized by short duration pulses of long period with large peak ground velocities and accelerations. It has been observed from recent earthquake records that motions in the fault-normal direction contain destructive long-period pulses with high peak ground velocities, aspect that negatively affects long-period structures such as cable-stayed bridges. A lot of approaches to model these pulses have been recently proposed [Makris, 1997; He, 2003; Mavroeidis ''et al'', 2004]. | ||
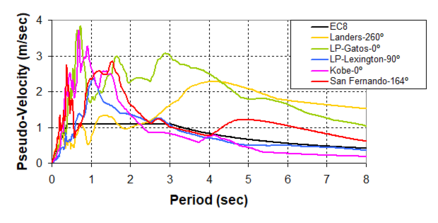
| Line 1,273: | Line 1,161: | ||
Although the damper non-linearity does not significantly influence the displacement response (As was demonstrated in the research by Lin and Chopra, 2002), in general terms non-linear viscous dampers are more advantageous than linear dampers in reducing peak structural displacements and peak input energies when a structure is subjected to pulse-type excitation with pulse period longer than the natural period of the structure. | Although the damper non-linearity does not significantly influence the displacement response (As was demonstrated in the research by Lin and Chopra, 2002), in general terms non-linear viscous dampers are more advantageous than linear dampers in reducing peak structural displacements and peak input energies when a structure is subjected to pulse-type excitation with pulse period longer than the natural period of the structure. | ||
| − | :<big> | + | :<big>2.4 Analysis and Design Issues</big> |
| − | :<big> | + | :<big>2.4.1 Structural Analysis Including Viscous Dampers</big> |
The first step in the analysis is to find out how added damping affects the structure. This is generally done with a simple stick model with one node for each storey. Adding global damping to the stick model provides a good indication of how damping elements can benefit the structure. The analyst will then construct a simple two-dimensional model of the structure. In this model the dampers are entered as discrete elements. At this point there are a number of variables to play with: force capacity of the dampers, location and number of dampers, damper coefficient and damper exponent. The analyst has the task of finding the best solution. This is generally a trial-and-error process but there are some general guidelines. It is always best to minimize the number of dampers and the number of bays that use dampers. Also, it is known from experience that approximately 20%–30% of critical damping is a desirable range, and that 5% of this can be structural, leaving 15%–25% for viscous damping. So the first objective of the analyst is to determine the smallest possible number of dampers to provide approximately 20% critical damping without overloading either the beams or the columns. Also, it is always best to start with linear dampers and then find out what happens with nonlinear dampers after the locations, number and characteristics of the dampers have been fairly well determined [Lee and Taylor, 2001]. | The first step in the analysis is to find out how added damping affects the structure. This is generally done with a simple stick model with one node for each storey. Adding global damping to the stick model provides a good indication of how damping elements can benefit the structure. The analyst will then construct a simple two-dimensional model of the structure. In this model the dampers are entered as discrete elements. At this point there are a number of variables to play with: force capacity of the dampers, location and number of dampers, damper coefficient and damper exponent. The analyst has the task of finding the best solution. This is generally a trial-and-error process but there are some general guidelines. It is always best to minimize the number of dampers and the number of bays that use dampers. Also, it is known from experience that approximately 20%–30% of critical damping is a desirable range, and that 5% of this can be structural, leaving 15%–25% for viscous damping. So the first objective of the analyst is to determine the smallest possible number of dampers to provide approximately 20% critical damping without overloading either the beams or the columns. Also, it is always best to start with linear dampers and then find out what happens with nonlinear dampers after the locations, number and characteristics of the dampers have been fairly well determined [Lee and Taylor, 2001]. | ||
| Line 1,283: | Line 1,171: | ||
Finally, it can be important to say that in the present days exist good and powerful computing tools that permit to solve non-linear structures equipped with linear/non-linear energy dissipation devices such as fluid viscous dampers. Commercial computing codes such as ''ANSYS ''[Ansys Inc, 2005] or ''SAP2000'' [Computers & Structures, 2007] include the option of applying non-linear energy dissipation devices. However, modelling of some damping elements (e.g. dampers with temperature-dependent or frequency-dependent) can be more challenging or, in some cases, not possible with a given program. When the modelling of such behaviour is not possible, the expected response may be bounded by analyzing the structure over a range of behaviours. Fortunately, for majority of fluid viscous dampers actually manufactured, properties are largely independent with respect to frequency and temperature [Symans ''et al'', 2008]. | Finally, it can be important to say that in the present days exist good and powerful computing tools that permit to solve non-linear structures equipped with linear/non-linear energy dissipation devices such as fluid viscous dampers. Commercial computing codes such as ''ANSYS ''[Ansys Inc, 2005] or ''SAP2000'' [Computers & Structures, 2007] include the option of applying non-linear energy dissipation devices. However, modelling of some damping elements (e.g. dampers with temperature-dependent or frequency-dependent) can be more challenging or, in some cases, not possible with a given program. When the modelling of such behaviour is not possible, the expected response may be bounded by analyzing the structure over a range of behaviours. Fortunately, for majority of fluid viscous dampers actually manufactured, properties are largely independent with respect to frequency and temperature [Symans ''et al'', 2008]. | ||
| − | :<big> | + | :<big>2.4.2 Design Issues for Viscous Dampers</big> |
The peak force ''f<sub>D0</sub>(N)'' in the non-linear fluid viscous damper with known non-linear parameter ''N ''can be expressed as | The peak force ''f<sub>D0</sub>(N)'' in the non-linear fluid viscous damper with known non-linear parameter ''N ''can be expressed as | ||
| − | <div style="text-align: | + | <div style="text-align: left; direction: ltr; margin-left: 1em;"> |
| − | [[Image:draft_Samper_432909089-image86.png|168px]] [Eq. 2.21]</div> | + | [[Image:draft_Samper_432909089-monograph-image86.png|168px]] [Eq. 2.21]</div> |
where ''V = ω<sub>0</sub>x<sub>0</sub>'' is the spectral pseudo-velocity for the SDF system; ''c<sub>1</sub>'' is the damping coefficient of the linear system and ''β<sub>N </sub>''is a constant defined as | where ''V = ω<sub>0</sub>x<sub>0</sub>'' is the spectral pseudo-velocity for the SDF system; ''c<sub>1</sub>'' is the damping coefficient of the linear system and ''β<sub>N </sub>''is a constant defined as | ||
| − | <div style="text-align: | + | <div style="text-align: left; direction: ltr; margin-left: 1em;"> |
| − | [[Image:draft_Samper_432909089-image87.png|156px]] [Eq. 2.22]</div> | + | [[Image:draft_Samper_432909089-monograph-image87.png|156px]] [Eq. 2.22]</div> |
| + | |||
| + | The non-linear damper force can be computed from Eq. 2.21 if ''x<sub>0</sub>'' and '' [[Image:draft_Samper_432909089-monograph-image88.png|18px]] ''are known. They can be estimated as the peak values of deformation and relative velocity of the corresponding linear system. Equation 2.21 is almost exact in the velocity-sensitive region of the spectrum, overestimates the damper force in the acceleration-sensitive region (by at most 15%); and underestimates in the displacement-sensitive region (by at most 7%). Moreover, the accuracy of Eq. 2.21 deteriorates slightly with the increase of the equivalent damping ''ξ<sub>d</sub>. ''However, the actual velocity '' [[Image:draft_Samper_432909089-monograph-image88.png|12px]] ''of the corresponding linear system required in Eq. 2.21 and to compute ''f<sub>D0 </sub>(N=1) = c<sub>1</sub> [[Image:draft_Samper_432909089-monograph-image88.png|12px]] ''is not readily available, because the velocity spectrum is not plotted routinely. If the velocity '' [[Image:draft_Samper_432909089-monograph-image88.png|18px]] ''is replaced by the pseudo-velocity, Eq. 2.21 changes to | ||
| + | |||
| + | <div style="text-align: left; direction: ltr; margin-left: 1em;"> | ||
| + | [[Image:draft_Samper_432909089-monograph-image89.png|186px]] [Eq. 2.23]</div> | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
The resulting estimate of the damper force is not accurate, which increase with the system’s period, damper non-linearity and supplemental damping ratio. Thus, velocity should not be approximated by the pseudo-velocity [Lin and Chopra, 2002]. | The resulting estimate of the damper force is not accurate, which increase with the system’s period, damper non-linearity and supplemental damping ratio. Thus, velocity should not be approximated by the pseudo-velocity [Lin and Chopra, 2002]. | ||
Another important point regarding the design of non-linear fluid viscous dampers is how to select the properties ''c<sub>d</sub>'' and ''N'' to satisfy a design requirement. As was previously explained, the structural deformation is essentially unaffected by the damper non-linearity parameter ''N'' and it is essentially the same as that for the corresponding linear system. The total damping capacity that must be provided in the system to limit the deformation of a linear system to a design value can be determined directly from the design spectrum. Subtracting the inherent damping in the structure from the total damping required gives ''ξ<sub>d</sub>'', the necessary supplemental damping. Many different non-linear fluid viscous dampers can be chosen to provide the required supplemental damping ratio ''ξ<sub>d</sub>''. Thus, for a selected value of ''N:'' | Another important point regarding the design of non-linear fluid viscous dampers is how to select the properties ''c<sub>d</sub>'' and ''N'' to satisfy a design requirement. As was previously explained, the structural deformation is essentially unaffected by the damper non-linearity parameter ''N'' and it is essentially the same as that for the corresponding linear system. The total damping capacity that must be provided in the system to limit the deformation of a linear system to a design value can be determined directly from the design spectrum. Subtracting the inherent damping in the structure from the total damping required gives ''ξ<sub>d</sub>'', the necessary supplemental damping. Many different non-linear fluid viscous dampers can be chosen to provide the required supplemental damping ratio ''ξ<sub>d</sub>''. Thus, for a selected value of ''N:'' | ||
| − | + | ||
| − | + | <div style="text-align: left; direction: ltr; margin-left: 1em;"> | |
| − | + | [[Image:draft_Samper_432909089-monograph-image90.png|168px]] [Eq. 2.24]</div> | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
where ''M ''is the mass of the system and ''D'' is the allowable deformation. | where ''M ''is the mass of the system and ''D'' is the allowable deformation. | ||
Fig. 2.21 suggests that the selected damper defined by Eq. 2.24 should satisfy the design constraint reasonably well. Also, the structural deformation should be very close to the allowable value in the velocity-sensitive region, less than the allowable value in the acceleration–sensitive spectral region, but exceed slightly the allowable value in the displacement-sensitive spectral region [Lin and Chopra, 2002]. | Fig. 2.21 suggests that the selected damper defined by Eq. 2.24 should satisfy the design constraint reasonably well. Also, the structural deformation should be very close to the allowable value in the velocity-sensitive region, less than the allowable value in the acceleration–sensitive spectral region, but exceed slightly the allowable value in the displacement-sensitive spectral region [Lin and Chopra, 2002]. | ||
| − | :<big> | + | :<big>2.5 Practical Applications</big> |
| − | :<big> | + | :<big>2.5.1 Study Case 1: Rion-Antirion Bridge, Greece</big> |
Amongst long-span cable-stayed bridges that incorporate additional passive seismic protection, the recently inaugurated Rion – Antirion Bridge in the Gulf of Corinth, Greece, is one of the most interesting bridges located in a high seismicity zone generated by active local faults. | Amongst long-span cable-stayed bridges that incorporate additional passive seismic protection, the recently inaugurated Rion – Antirion Bridge in the Gulf of Corinth, Greece, is one of the most interesting bridges located in a high seismicity zone generated by active local faults. | ||
| Line 1,332: | Line 1,210: | ||
<div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | ||
| − | [[Image:draft_Samper_432909089-image91.jpeg|372px]] </div> | + | [[Image:draft_Samper_432909089-monograph-image91.jpeg|372px]] </div> |
<div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | ||
| Line 1,338: | Line 1,216: | ||
<div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | ||
| − | [[Image:draft_Samper_432909089-image92.png|600px]] </div> | + | [[Image:draft_Samper_432909089-monograph-image92.png|600px]] </div> |
<div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | ||
| Line 1,346: | Line 1,224: | ||
|- | |- | ||
| style="vertical-align: top;"|The damping system consisted in fuses and viscous dampers acting in parallel, connecting the deck with the pylons in the transverse direction. The fuses were designed to work as rigid connections to resist low-to-moderate intensity earthquakes as well as high wind loads. For the design earthquake, the fuses were calculated to fail allowing energy dissipation through the fluid viscous dampers. | | style="vertical-align: top;"|The damping system consisted in fuses and viscous dampers acting in parallel, connecting the deck with the pylons in the transverse direction. The fuses were designed to work as rigid connections to resist low-to-moderate intensity earthquakes as well as high wind loads. For the design earthquake, the fuses were calculated to fail allowing energy dissipation through the fluid viscous dampers. | ||
| − | | style="text-align: center;vertical-align: top;width: | + | | style="text-align: center;vertical-align: top;width: 50%;"|[[Image:draft_Samper_432909089-monograph-image93.jpeg|300px]] |
'''Fig. 2.25''' Response Design Spectrum [Combault ''et al,'' 2000] | '''Fig. 2.25''' Response Design Spectrum [Combault ''et al,'' 2000] | ||
| Line 1,370: | Line 1,248: | ||
{| style="width: 100%;" | {| style="width: 100%;" | ||
|- | |- | ||
| − | | style="vertical-align: top;width: | + | | style="vertical-align: top;width: 46%;"|[[Image:draft_Samper_432909089-monograph-image94.jpeg|198px]] |
'''Fig. 2.26''' Isolation System in the Antirion Approach Viaduct [Infanti ''et al'', 2004] | '''Fig. 2.26''' Isolation System in the Antirion Approach Viaduct [Infanti ''et al'', 2004] | ||
| − | | style="text-align: center;vertical-align: top;width: | + | | style="text-align: center;vertical-align: top;width: 53%;"|[[Image:draft_Samper_432909089-monograph-image95-c.png|282px]] |
'''Fig. 2.27''' Fuse Restraint [Infanti ''et al,'' 2003] | '''Fig. 2.27''' Fuse Restraint [Infanti ''et al,'' 2003] | ||
| Line 1,387: | Line 1,265: | ||
{| style="width: 100%;" | {| style="width: 100%;" | ||
|- | |- | ||
| − | | style="text-align: center;vertical-align: top;width: | + | | style="text-align: center;vertical-align: top;width: 54%;"|[[Image:draft_Samper_432909089-monograph-image96.jpeg|228px]] |
'''Fig. 2.28''' Full-Scale Viscous Damper Prototype Testing [Infanti ''et al, ''2004] | '''Fig. 2.28''' Full-Scale Viscous Damper Prototype Testing [Infanti ''et al, ''2004] | ||
| − | | style="text-align: center;vertical-align: top;width: | + | | style="text-align: center;vertical-align: top;width: 45%;"|[[Image:draft_Samper_432909089-monograph-image97.jpeg|138px]] |
'''Fig. 2.29''' Fuse Element During Fatigue Test [Infanti'' et al,'' 2004] | '''Fig. 2.29''' Fuse Element During Fatigue Test [Infanti'' et al,'' 2004] | ||
| Line 1,398: | Line 1,276: | ||
{| style="width: 100%;" | {| style="width: 100%;" | ||
|- | |- | ||
| − | | style="text-align: center;vertical-align: top;width: 50%;"| [[Image:draft_Samper_432909089-image98.jpeg|156px]] | + | | style="text-align: center;vertical-align: top;width: 50%;"|[[Image:draft_Samper_432909089-monograph-image98.jpeg|156px]] |
'''Fig. 2.30 '''Internal Hydraulic Damper [Lecinq ''et al,'' 2003] | '''Fig. 2.30 '''Internal Hydraulic Damper [Lecinq ''et al,'' 2003] | ||
| − | | style="text-align: center;vertical-align: top;width: 50%;"| [[Image:draft_Samper_432909089-image99.jpeg|126px]] | + | | style="text-align: center;vertical-align: top;width: 50%;"|[[Image:draft_Samper_432909089-monograph-image99.jpeg|126px]] |
'''Fig. 2.31''' External Hydraulic Damper on Normandy Bridge [Lecinq ''et al,'' 2003] | '''Fig. 2.31''' External Hydraulic Damper on Normandy Bridge [Lecinq ''et al,'' 2003] | ||
| Line 1,409: | Line 1,287: | ||
In his MSc Thesis, Morgenthal (1999) carries out a detailed research on the seismic behaviour of the Rion-Antirion Bridge. He describes the bridge and exposes analytical modelling using finite elements to study the seismic control strategies incorporating different seismic protection devices, such as structural fuses, hydraulic dampers, seismic connectors and elasto-plastic isolators. Finally, a parametric analysis of the seismic behaviour of different deck isolation devices is exposed. | In his MSc Thesis, Morgenthal (1999) carries out a detailed research on the seismic behaviour of the Rion-Antirion Bridge. He describes the bridge and exposes analytical modelling using finite elements to study the seismic control strategies incorporating different seismic protection devices, such as structural fuses, hydraulic dampers, seismic connectors and elasto-plastic isolators. Finally, a parametric analysis of the seismic behaviour of different deck isolation devices is exposed. | ||
| − | :<big> | + | :<big>2.5.2 Study Case 2: Tempozan Bridge, Japan</big> |
Due to severe damage to bridges caused by the Hyogo-ken-Nanbu earthquake in 1995, very high ground motion was required according to the bridge design specifications set in 1996 [Japan Road Association, 1996], in addition to the relatively frequent earthquake motion specifications by which old structures were designed and constructed. Hence, seismic safety of cable-stayed bridges that were built prior to that specification was reviewed, and seismic retrofit was performed. In order to study the effectiveness of passive control to the seismic retrofit of a cable-stayed bridge, a numerical analysis on a model of a cable-stayed bridge was carried out. An existing cable-stayed bridge with fixed-hinge connections between deck and towers was modelled and its connections were replaced by isolation bearings and dampers. The isolation bearings were assumed to be of the elastic and hysteretic type. The dampers were linear and variable. The objective was to increase the damping ratio of the bridge by using passive control technologies. The chosen bridge model was the Tempozan Bridge, located in Osaka, Japan. | Due to severe damage to bridges caused by the Hyogo-ken-Nanbu earthquake in 1995, very high ground motion was required according to the bridge design specifications set in 1996 [Japan Road Association, 1996], in addition to the relatively frequent earthquake motion specifications by which old structures were designed and constructed. Hence, seismic safety of cable-stayed bridges that were built prior to that specification was reviewed, and seismic retrofit was performed. In order to study the effectiveness of passive control to the seismic retrofit of a cable-stayed bridge, a numerical analysis on a model of a cable-stayed bridge was carried out. An existing cable-stayed bridge with fixed-hinge connections between deck and towers was modelled and its connections were replaced by isolation bearings and dampers. The isolation bearings were assumed to be of the elastic and hysteretic type. The dampers were linear and variable. The objective was to increase the damping ratio of the bridge by using passive control technologies. The chosen bridge model was the Tempozan Bridge, located in Osaka, Japan. | ||
| Line 1,417: | Line 1,295: | ||
{| style="width: 100%;" | {| style="width: 100%;" | ||
|- | |- | ||
| − | | style="vertical-align: top;"|<span style="text-align: center; font-size: 75%;"> [[Image:draft_Samper_432909089-image100.jpeg|228px]] </span> | + | | style="vertical-align: top;"|<span style="text-align: center; font-size: 75%;"> [[Image:draft_Samper_432909089-monograph-image100.jpeg|228px]] </span> |
'''Fig. 2.32''' Tempozan Bridge [from en.structurae.de] | '''Fig. 2.32''' Tempozan Bridge [from en.structurae.de] | ||
| − | | style="vertical-align: top;width: | + | | style="vertical-align: top;width: 61%;"|[[Image:draft_Samper_432909089-monograph-image101.png|384px]] |
'''Fig. 2.33''' Side View of the Tempozan Bridge [Iemura and Pradono, 2003] | '''Fig. 2.33''' Side View of the Tempozan Bridge [Iemura and Pradono, 2003] | ||
| Line 1,433: | Line 1,311: | ||
<div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | ||
| − | [[Image:draft_Samper_432909089-image102.png|432px]] </div> | + | [[Image:draft_Samper_432909089-monograph-image102.png|432px]] </div> |
<div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | ||
| Line 1,443: | Line 1,321: | ||
<div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | ||
| − | [[Image:draft_Samper_432909089-image103.png|324px]] </div> | + | [[Image:draft_Samper_432909089-monograph-image103.png|324px]] </div> |
<div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | ||
| Line 1,526: | Line 1,404: | ||
As a conclusion remark, it is clear that additional viscous damping to control the seismic response of cable-stayed bridges is beneficial, reducing the seismic forces on members as well as their displacements by increasing the structural damping. | As a conclusion remark, it is clear that additional viscous damping to control the seismic response of cable-stayed bridges is beneficial, reducing the seismic forces on members as well as their displacements by increasing the structural damping. | ||
| − | + | ==Chapter 3. Seismic Response. Parametric Analysis== | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | :<big> | + | :<big>3.1 Introduction</big> |
As a starting point, the seismic analysis without the incorporation of additional damping devices is presented. In order to compare the analysis results of the bridge models considering the incorporation of additional passive devices, this part is essential, and must be employed as basic configuration (reference structures). | As a starting point, the seismic analysis without the incorporation of additional damping devices is presented. In order to compare the analysis results of the bridge models considering the incorporation of additional passive devices, this part is essential, and must be employed as basic configuration (reference structures). | ||
| Line 1,542: | Line 1,416: | ||
The last point of this chapter corresponds to the seismic response of the selected bridges considering far-fault and near-fault ground motions respectively. In this part, nonlinear time history analysis is conducted taking into account the geometric and material nonlinearities of the structures and the cable vibration effects. The input ground motions are acceleration time histories: five artificial three-orthogonal component acceleration records for far-fault analysis and five real three-orthogonal component acceleration records for near-fault analysis. The seismic response of the bridges considers the displacement, velocity and acceleration time histories and the response of the deck, cables and towers. Because of the complex nature of the nonlinear time history analysis and according to the recommendations of Eurocode 8 Part 2 [CEN, 1998b], the average of the maximum response parameters in the assessment of the structural response for the record selection is considered. | The last point of this chapter corresponds to the seismic response of the selected bridges considering far-fault and near-fault ground motions respectively. In this part, nonlinear time history analysis is conducted taking into account the geometric and material nonlinearities of the structures and the cable vibration effects. The input ground motions are acceleration time histories: five artificial three-orthogonal component acceleration records for far-fault analysis and five real three-orthogonal component acceleration records for near-fault analysis. The seismic response of the bridges considers the displacement, velocity and acceleration time histories and the response of the deck, cables and towers. Because of the complex nature of the nonlinear time history analysis and according to the recommendations of Eurocode 8 Part 2 [CEN, 1998b], the average of the maximum response parameters in the assessment of the structural response for the record selection is considered. | ||
| − | :<big> | + | |
| + | :<big>3.2 Structural Modelling</big> | ||
The seismic response analysis of the concrete cable-stayed bridges takes into consideration eight ''3-D'' symmetric bridge models for an adequate study. The chosen bridges were taken from the specialized literature, and specifically, from Walter’s Bridges [Walter, 1999] including the recommendations of Aparicio and Casas (2000) and Priestley ''at al'' (1996). The examination is based on a symmetric multi-stay reference cable-stayed bridge, having two pylons, double-plane cable layout and a main span length of about 200 m. Two stay cable layouts were selected: fan-type and harp-type. The semi-harp pattern was rejected because this typology is an intermediate pattern, and both harp and fan patterns are enough for an adequate analysis. The main span lengths of the bridges are 217 m and 204.60 m, depending on the stay spacing. In this sense, long-span cable-stayed bridges have experienced adequate performance during recent earthquake events, and it is expected that short-to-medium spans bridges show a worse seismic performance, mainly if near-source effects are considered. That is the main reason to select the proposed span lengths. Moreover, the deck pattern considers two cases: a slab-type deck and a hollow-box type deck. The first one, due to its inherent flexibility, considers a stay spacing of 6.20 m. In the second case, 12.40 m - stay spacing is considered. The selected tower, for all cases, is a concrete frame-type tower, with deck levels of 30 and 60 m from bottom. The height of the towers is 81 m and 111 m respectively. All these dimensions were taken from Walter’s recommendations. | The seismic response analysis of the concrete cable-stayed bridges takes into consideration eight ''3-D'' symmetric bridge models for an adequate study. The chosen bridges were taken from the specialized literature, and specifically, from Walter’s Bridges [Walter, 1999] including the recommendations of Aparicio and Casas (2000) and Priestley ''at al'' (1996). The examination is based on a symmetric multi-stay reference cable-stayed bridge, having two pylons, double-plane cable layout and a main span length of about 200 m. Two stay cable layouts were selected: fan-type and harp-type. The semi-harp pattern was rejected because this typology is an intermediate pattern, and both harp and fan patterns are enough for an adequate analysis. The main span lengths of the bridges are 217 m and 204.60 m, depending on the stay spacing. In this sense, long-span cable-stayed bridges have experienced adequate performance during recent earthquake events, and it is expected that short-to-medium spans bridges show a worse seismic performance, mainly if near-source effects are considered. That is the main reason to select the proposed span lengths. Moreover, the deck pattern considers two cases: a slab-type deck and a hollow-box type deck. The first one, due to its inherent flexibility, considers a stay spacing of 6.20 m. In the second case, 12.40 m - stay spacing is considered. The selected tower, for all cases, is a concrete frame-type tower, with deck levels of 30 and 60 m from bottom. The height of the towers is 81 m and 111 m respectively. All these dimensions were taken from Walter’s recommendations. | ||
| Line 1,550: | Line 1,425: | ||
Regarding the bridge modelling, the analysis is carried out considering the use of beam and cable elements for all the bridges. The deck is modelled using a single spine to avoid the use of shell elements, with the incorporation of transverse rigid-links to simulate the anchor of cables. In fact, the use of beam elements can be more useful to assess forces on members, with clear graphical results and a considerable decrease of the computing time, especially when non-linear time history analysis is applied. Moreover, the non-linear analysis takes into consideration the geometric non-linearities that are present in almost all cable-stayed bridges. These non-linearities due to high compressions in the deck and pylons are considered by the axial – bending interaction. Non-linear behaviour of cables is considered by a multi-element cable formulation (''tension-only'' elements), in order to take into account the spatial vibrations of them. Likewise, non-linearities due to large displacements in the overall geometry are considered too. Spatial variability is not considered because of the main span length of the bridges (of about 200 m), that not recommends this effect according to Eurocode 8. | Regarding the bridge modelling, the analysis is carried out considering the use of beam and cable elements for all the bridges. The deck is modelled using a single spine to avoid the use of shell elements, with the incorporation of transverse rigid-links to simulate the anchor of cables. In fact, the use of beam elements can be more useful to assess forces on members, with clear graphical results and a considerable decrease of the computing time, especially when non-linear time history analysis is applied. Moreover, the non-linear analysis takes into consideration the geometric non-linearities that are present in almost all cable-stayed bridges. These non-linearities due to high compressions in the deck and pylons are considered by the axial – bending interaction. Non-linear behaviour of cables is considered by a multi-element cable formulation (''tension-only'' elements), in order to take into account the spatial vibrations of them. Likewise, non-linearities due to large displacements in the overall geometry are considered too. Spatial variability is not considered because of the main span length of the bridges (of about 200 m), that not recommends this effect according to Eurocode 8. | ||
| − | :<big> | + | |
| + | :<big>3.2.1 Geometric Layout</big> | ||
The longitudinal layout of the cable stays is one of the fundamental items in the design of cable-stayed bridges. It influences, in fact, not only the structural performance of the bridge, but also the method of erection and the economics. | The longitudinal layout of the cable stays is one of the fundamental items in the design of cable-stayed bridges. It influences, in fact, not only the structural performance of the bridge, but also the method of erection and the economics. | ||
| Line 1,566: | Line 1,442: | ||
{| style="width: 100%;border-collapse: collapse;" | {| style="width: 100%;border-collapse: collapse;" | ||
|- | |- | ||
| − | | style="border: 1pt solid black;text-align: center;vertical-align: top;width: 50%;"| [[Image:draft_Samper_432909089-image104.jpeg|204px]] | + | | style="border: 1pt solid black;text-align: center;vertical-align: top;width: 50%;"|[[Image:draft_Samper_432909089-monograph-image104.jpeg|204px]] |
| − | | style="border: 1pt solid black;text-align: center;vertical-align: top;width: 50%;"| [[Image:draft_Samper_432909089-image105.jpeg|192px]] | + | | style="border: 1pt solid black;text-align: center;vertical-align: top;width: 50%;"|[[Image:draft_Samper_432909089-monograph-image105.jpeg|192px]] |
|- | |- | ||
| − | | style="border: 1pt solid black;text-align: center;vertical-align: top;width: 50%;"| [[Image:draft_Samper_432909089-image106.jpeg|210px]] | + | | style="border: 1pt solid black;text-align: center;vertical-align: top;width: 50%;"|[[Image:draft_Samper_432909089-monograph-image106.jpeg|210px]] |
| − | | style="border: 1pt solid black;text-align: center;vertical-align: top;width: 50%;"| [[Image:draft_Samper_432909089-image107.jpeg|192px]] | + | | style="border: 1pt solid black;text-align: center;vertical-align: top;width: 50%;"|[[Image:draft_Samper_432909089-monograph-image107.jpeg|192px]] |
|} | |} | ||
| − | + | '''Fig. 3.1'' Longitudinal Layouts for Fan Pattern (dimensions in metres) | |
{| style="width: 100%;border-collapse: collapse;" | {| style="width: 100%;border-collapse: collapse;" | ||
|- | |- | ||
| − | | style="border: 1pt solid black;text-align: center;vertical-align: top;width: 50%;"| [[Image:draft_Samper_432909089-image108.jpeg|192px]] | + | | style="border: 1pt solid black;text-align: center;vertical-align: top;width: 50%;"|[[Image:draft_Samper_432909089-monograph-image108.jpeg|192px]] |
| − | | style="border: 1pt solid black;text-align: center;vertical-align: top;width: 50%;"| [[Image:draft_Samper_432909089-image109.jpeg|186px]] | + | | style="border: 1pt solid black;text-align: center;vertical-align: top;width: 50%;"|[[Image:draft_Samper_432909089-monograph-image109.jpeg|186px]] |
|- | |- | ||
| − | | style="border: 1pt solid black;text-align: center;vertical-align: top;width: 50%;"| [[Image:draft_Samper_432909089-image110.jpeg|198px]] | + | | style="border: 1pt solid black;text-align: center;vertical-align: top;width: 50%;"|[[Image:draft_Samper_432909089-monograph-image110.jpeg|198px]] |
| − | | style="border: 1pt solid black;text-align: center;vertical-align: top;width: 50%;"| [[Image:draft_Samper_432909089-image111.jpeg|198px]] | + | | style="border: 1pt solid black;text-align: center;vertical-align: top;width: 50%;"|[[Image:draft_Samper_432909089-monograph-image111.jpeg|198px]] |
|} | |} | ||
| − | + | '''Fig. 3.2''' Longitudinal Layouts for Harp Pattern (dimensions in metres) | |
In the transverse direction, the majority of existing structures consist of two planes of cables, generally on the edge of the structure. However, several bridges have been successfully built recently with only one central plane of cables. In principle, it is quite possible to envisage solutions using three or more planes, with the aim of reducing the cross-sectional forces when the deck is very wide, but this possibility has been rarely exploited [Walter, 1999]. | In the transverse direction, the majority of existing structures consist of two planes of cables, generally on the edge of the structure. However, several bridges have been successfully built recently with only one central plane of cables. In principle, it is quite possible to envisage solutions using three or more planes, with the aim of reducing the cross-sectional forces when the deck is very wide, but this possibility has been rarely exploited [Walter, 1999]. | ||
| Line 1,591: | Line 1,467: | ||
{| style="width: 100%;" | {| style="width: 100%;" | ||
|- | |- | ||
| − | | style="vertical-align: top;"|''' [[Image:draft_Samper_432909089-image112.png|174px]] ''' | + | | style="vertical-align: top;"|''' [[Image:draft_Samper_432909089-monograph-image112.png|174px]] ''' |
'''Fig. 3.3''' Transverse Configuration | '''Fig. 3.3''' Transverse Configuration | ||
| Line 1,606: | Line 1,482: | ||
{| style="width: 100%;" | {| style="width: 100%;" | ||
|- | |- | ||
| − | | style="text-align: center;vertical-align: top;width: 50%;"| [[Image:draft_Samper_432909089-image113-c.png|234px]] | + | | style="text-align: center;vertical-align: top;width: 50%;"|[[Image:draft_Samper_432909089-monograph-image113-c.png|234px]] |
<span style="text-align: center; font-size: 75%;">'''(a)''' A-type Pylon</span> | <span style="text-align: center; font-size: 75%;">'''(a)''' A-type Pylon</span> | ||
| − | | style="vertical-align: top;"|<span style="text-align: center; font-size: 75%;">''' [[Image:draft_Samper_432909089-image114-c.png|234px]] '''</span> | + | | style="vertical-align: top;"|<span style="text-align: center; font-size: 75%;">''' [[Image:draft_Samper_432909089-monograph-image114-c.png|234px]] '''</span> |
<span style="text-align: center; font-size: 75%;">'''(b)''' B-type Pylon</span> | <span style="text-align: center; font-size: 75%;">'''(b)''' B-type Pylon</span> | ||
| Line 1,624: | Line 1,500: | ||
{| style="width: 100%;" | {| style="width: 100%;" | ||
|- | |- | ||
| − | | style="vertical-align: top;"|''' [[Image:draft_Samper_432909089-image115-c.jpeg|312px]] ''' | + | | style="vertical-align: top;"|''' [[Image:draft_Samper_432909089-monograph-image115-c.jpeg|312px]] ''' |
<span style="text-align: center; font-size: 75%;">'''(a)''' Slab-Type Deck</span> | <span style="text-align: center; font-size: 75%;">'''(a)''' Slab-Type Deck</span> | ||
| − | | style="vertical-align: top;"|<span style="text-align: center; font-size: 75%;">''' [[Image:draft_Samper_432909089-image116.jpeg|288px]] '''</span> | + | | style="vertical-align: top;"|<span style="text-align: center; font-size: 75%;">''' [[Image:draft_Samper_432909089-monograph-image116.jpeg|288px]] '''</span> |
<span style="text-align: center; font-size: 75%;">'''(b)''' Hollow-box Type Deck</span> | <span style="text-align: center; font-size: 75%;">'''(b)''' Hollow-box Type Deck</span> | ||
|} | |} | ||
| − | + | '''Fig. 3.5''' Proposed Decks for the Analysis (dimensions in metres) | |
| − | + | ||
<div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | ||
| Line 1,671: | Line 1,546: | ||
The cross-section areas for the slab-type and the hollow-box type are the same, which implies the same weight. This point is very important, because the main difference between both typologies is the inertia. The slab-type deck considers a very low inertia. The slenderness ratio in this case is ''h/L = 0.40/217 = 1/543 ''for the fan pattern, and ''h/L = 0.40/204.6 = 1/512'' for the harp pattern, which implies a very slender deck. Of course, in this case bending moments are expected to be low. The hollow-box type deck shows a high inertia. The slenderness ratio is ''h/L =2.25/217=1/96 ''for the fan pattern, and ''h/L = 2.25/204.6 = 1/91'' for the harp pattern, which implies a rigid deck. These differences involve the use of 6.2 m stay-spacing for the flexible deck (slab-type), and 12.4 m stay-spacing for the rigid deck (hollow-box type). | The cross-section areas for the slab-type and the hollow-box type are the same, which implies the same weight. This point is very important, because the main difference between both typologies is the inertia. The slab-type deck considers a very low inertia. The slenderness ratio in this case is ''h/L = 0.40/217 = 1/543 ''for the fan pattern, and ''h/L = 0.40/204.6 = 1/512'' for the harp pattern, which implies a very slender deck. Of course, in this case bending moments are expected to be low. The hollow-box type deck shows a high inertia. The slenderness ratio is ''h/L =2.25/217=1/96 ''for the fan pattern, and ''h/L = 2.25/204.6 = 1/91'' for the harp pattern, which implies a rigid deck. These differences involve the use of 6.2 m stay-spacing for the flexible deck (slab-type), and 12.4 m stay-spacing for the rigid deck (hollow-box type). | ||
| − | :<big> | + | |
| + | :<big>3.2.2 Basis of Design and Actions</big> | ||
Materials and their mechanical properties have been chosen according to the general specifications and regulations for bridge design, taking into account seismic considerations [Priestley ''et al'', 1996; Walter, 1999; Ministerio de Fomento, 2000; Aparicio and Casas, 2000]. | Materials and their mechanical properties have been chosen according to the general specifications and regulations for bridge design, taking into account seismic considerations [Priestley ''et al'', 1996; Walter, 1999; Ministerio de Fomento, 2000; Aparicio and Casas, 2000]. | ||
| Line 1,743: | Line 1,619: | ||
{| style="width: 100%;border-collapse: collapse;" | {| style="width: 100%;border-collapse: collapse;" | ||
|- | |- | ||
| − | | style="text-align: center;vertical-align: top;"|<big>''' [[Image:draft_Samper_432909089-image117.png|270px]] '''</big> | + | | style="text-align: center;vertical-align: top;"|<big>''' [[Image:draft_Samper_432909089-monograph-image117.png|270px]] '''</big> |
'''Fig. 3.6''' Parallel-Strand Cables | '''Fig. 3.6''' Parallel-Strand Cables | ||
| Line 1,791: | Line 1,667: | ||
For the above mentioned, to combine the loads on the bridge models, it is necessary to add each action: ''q<sub>PL</sub> + q<sub>SPL</sub> + q<sub>E</sub>.'' | For the above mentioned, to combine the loads on the bridge models, it is necessary to add each action: ''q<sub>PL</sub> + q<sub>SPL</sub> + q<sub>E</sub>.'' | ||
| − | :<big> | + | |
| + | :<big>3.2.3 Nonlinearities</big> | ||
Nonlinearities can be broadly divided into geometric and material nonlinearities. Material nonlinearities depend on the specific structure (materials used, loads acting, design assumptions). Although it is certain that the elastic-plastic effect tends to reduce the seismic response of long-span cable-stayed bridges [Ren and Obata, 1999], material nonlinearities depend highly on the characteristics of the input earthquake records. In general terms, cable-stayed bridges experience very long periods, and for that reason formation of plastic hinges at the supports can be difficult. In fact, EC8 – 2 [CEN, 1998b] recommends for a well-designed cable-stayed bridge a behaviour factor ''q = 1'', that is to say, an elastic seismic behaviour. Moreover, because of the high axial forces on the pylons, ductility of them can be questionable, and due to the importance of such structures, it is preferable an elastic behaviour of the materials, without formation of plastic hinges at the pylons. That is the main reason why the inelastic behaviour is not considered in this research. In this sense, dimensions and some special considerations for the selected bridge typologies take into account an elastic seismic behaviour of the materials. However, material nonlinearities due to the presence of additional viscous dampers as well as the ''tension-only'' nonlinear effect of the cables are considered. | Nonlinearities can be broadly divided into geometric and material nonlinearities. Material nonlinearities depend on the specific structure (materials used, loads acting, design assumptions). Although it is certain that the elastic-plastic effect tends to reduce the seismic response of long-span cable-stayed bridges [Ren and Obata, 1999], material nonlinearities depend highly on the characteristics of the input earthquake records. In general terms, cable-stayed bridges experience very long periods, and for that reason formation of plastic hinges at the supports can be difficult. In fact, EC8 – 2 [CEN, 1998b] recommends for a well-designed cable-stayed bridge a behaviour factor ''q = 1'', that is to say, an elastic seismic behaviour. Moreover, because of the high axial forces on the pylons, ductility of them can be questionable, and due to the importance of such structures, it is preferable an elastic behaviour of the materials, without formation of plastic hinges at the pylons. That is the main reason why the inelastic behaviour is not considered in this research. In this sense, dimensions and some special considerations for the selected bridge typologies take into account an elastic seismic behaviour of the materials. However, material nonlinearities due to the presence of additional viscous dampers as well as the ''tension-only'' nonlinear effect of the cables are considered. | ||
| Line 1,805: | Line 1,682: | ||
Those nonlinearities are especially considered in this research, because in some sense they govern the behaviour of this kind of structures, as was explained before. Geometric nonlinearity can be considered on a step-by-step basis in nonlinear static and direct integration time history analysis, and incorporated in the stiffness matrix for linear analysis. | Those nonlinearities are especially considered in this research, because in some sense they govern the behaviour of this kind of structures, as was explained before. Geometric nonlinearity can be considered on a step-by-step basis in nonlinear static and direct integration time history analysis, and incorporated in the stiffness matrix for linear analysis. | ||
| − | |||
| − | :'' | + | :<big>3.2.4 Modelling</big> |
| + | |||
| + | :''3.2.4.1 Tower modelling '' | ||
{| style="width: 100%;" | {| style="width: 100%;" | ||
|- | |- | ||
| − | | style="text-align: center;vertical-align: top;width: | + | | style="text-align: center;vertical-align: top;width: 40%;"|[[Image:draft_Samper_432909089-monograph-image118-c.png|246px]] |
'''Fig. 3.7 '''Modelling of the Towers | '''Fig. 3.7 '''Modelling of the Towers | ||
| Line 1,824: | Line 1,702: | ||
For the adequate consideration of the vibrational characteristics of the towers, the distribution of lumped masses shown in Fig. 3.7 was considered. The masses were obtained from the elements using the mass density of the materials and the volume of the elements. These uncoupled masses are equal for each of the three translational degrees-of-freedom. In the case of the code RAM Advanse, these masses need to be explicitly added in the selected joints. In SAP2000, these masses are automatically added at the end joints of the elements. However, it was necessary to place additional masses to take into account an adequate distribution of lumped masses in order to have a more accurate dynamic model. The lumped masses involves no mass coupling between degrees of freedom at a joint or between different joints | For the adequate consideration of the vibrational characteristics of the towers, the distribution of lumped masses shown in Fig. 3.7 was considered. The masses were obtained from the elements using the mass density of the materials and the volume of the elements. These uncoupled masses are equal for each of the three translational degrees-of-freedom. In the case of the code RAM Advanse, these masses need to be explicitly added in the selected joints. In SAP2000, these masses are automatically added at the end joints of the elements. However, it was necessary to place additional masses to take into account an adequate distribution of lumped masses in order to have a more accurate dynamic model. The lumped masses involves no mass coupling between degrees of freedom at a joint or between different joints | ||
| − | :'' | + | :''3.2.4.2 Deck Modelling'' |
As was previously mentioned, the decks of the bridges are of two kinds: a slab-type deck for a stay spacing of 6.2 m and a hollow box-type deck for a stay spacing of 12.40 m. To simplify the computing process, the decks were modelled using a single spine passing through the centroid of the cross-sections, and applying linear beam elements. To simulate the exact stiffness and masses of the decks, an accurate definition of the geometry of the cross sections was developed with the computational code RAM Advanse and also exported to SAP2000. That was possible modifying the internal code in RAM Advanse, in order to generate the desired sections. A ''3-D ''rendering of the deck models can be seen in Fig. 3.8. | As was previously mentioned, the decks of the bridges are of two kinds: a slab-type deck for a stay spacing of 6.2 m and a hollow box-type deck for a stay spacing of 12.40 m. To simplify the computing process, the decks were modelled using a single spine passing through the centroid of the cross-sections, and applying linear beam elements. To simulate the exact stiffness and masses of the decks, an accurate definition of the geometry of the cross sections was developed with the computational code RAM Advanse and also exported to SAP2000. That was possible modifying the internal code in RAM Advanse, in order to generate the desired sections. A ''3-D ''rendering of the deck models can be seen in Fig. 3.8. | ||
| Line 1,830: | Line 1,708: | ||
{| style="width: 100%;" | {| style="width: 100%;" | ||
|- | |- | ||
| − | | style="text-align: center;vertical-align: top;width: 50%;"| [[Image:draft_Samper_432909089-image119.png|174px]] | + | | style="text-align: center;vertical-align: top;width: 50%;"|[[Image:draft_Samper_432909089-monograph-image119.png|174px]] |
<span style="text-align: center; font-size: 75%;">'''(a)''' Slab-type deck</span> | <span style="text-align: center; font-size: 75%;">'''(a)''' Slab-type deck</span> | ||
| − | | style="text-align: center;vertical-align: top;width: 50%;"| [[Image:draft_Samper_432909089-image120.png|198px]] | + | | style="text-align: center;vertical-align: top;width: 50%;"|[[Image:draft_Samper_432909089-monograph-image120.png|198px]] |
<span style="text-align: center; font-size: 75%;">'''(b)''' Hollow-box type deck</span> | <span style="text-align: center; font-size: 75%;">'''(b)''' Hollow-box type deck</span> | ||
| Line 1,846: | Line 1,724: | ||
{| style="width: 100%;" | {| style="width: 100%;" | ||
|- | |- | ||
| − | | style="vertical-align: top;width: | + | | style="vertical-align: top;width: 38%;"|[[Image:draft_Samper_432909089-monograph-image121-c.png|222px]] |
'''Fig. 3.9''' Deck Modelling | '''Fig. 3.9''' Deck Modelling | ||
| Line 1,855: | Line 1,733: | ||
As for the non-structural components, such as parapets and beacons, their contribution to the structural rigidity is expected to be quite insignificant and therefore is ignored in the modelling. Likewise, since the cross sections of the deck are rigid (especially the hollow-box type deck), the corresponding warping constants are very large. Consequently, no cross-sectional warping is anticipated. | As for the non-structural components, such as parapets and beacons, their contribution to the structural rigidity is expected to be quite insignificant and therefore is ignored in the modelling. Likewise, since the cross sections of the deck are rigid (especially the hollow-box type deck), the corresponding warping constants are very large. Consequently, no cross-sectional warping is anticipated. | ||
| − | :'' | + | :''3.2.4.3 Stay cable model'' |
In a first stage, truss-elements for the cables were applied to compute the prestressing forces on the stays. The strategy of modelling stay cables using truss-elements has been widely used, in which the nonlinear behaviour of the cables is accounted by linearizing the cable stiffness using the concept of an equivalent modulus of elasticity [Ernst, 1965]. However, prediction of the tri-dimensional vibration of the cables is not possible, aspect that can be important for an accurate dynamic analysis, especially if the cable-deck interaction plays an important role. For that reason, this strategy was only considered for the evaluation of the cable forces, through the nonlinear static analysis applying the code RAM Advanse. | In a first stage, truss-elements for the cables were applied to compute the prestressing forces on the stays. The strategy of modelling stay cables using truss-elements has been widely used, in which the nonlinear behaviour of the cables is accounted by linearizing the cable stiffness using the concept of an equivalent modulus of elasticity [Ernst, 1965]. However, prediction of the tri-dimensional vibration of the cables is not possible, aspect that can be important for an accurate dynamic analysis, especially if the cable-deck interaction plays an important role. For that reason, this strategy was only considered for the evaluation of the cable forces, through the nonlinear static analysis applying the code RAM Advanse. | ||
| Line 1,868: | Line 1,746: | ||
<div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | ||
| − | [[Image:draft_Samper_432909089-image122.png|528px]] </div> | + | [[Image:draft_Samper_432909089-monograph-image122.png|528px]] </div> |
<div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | ||
| Line 1,948: | Line 1,826: | ||
{| style="width: 100%;" | {| style="width: 100%;" | ||
|- | |- | ||
| − | | style="vertical-align: top;"|'''Table 3.7''' Nominal Diameters of the Stays | + | | style="vertical-align: top;width: 40%;"|'''Table 3.7''' Nominal Diameters of the Stays |
| − | + | [[Image:draft_Samper_432909089-monograph-image123-c.png|294px]] | |
| − | | style="vertical-align: top;"|A last aspect in the stay cable design is the fact that cables on each bridge were designed uniformly, that is to say, for the worse stress condition. Table 3.7 shows the pre-design of the stays for each bridge model | + | | style="vertical-align: top;width: 60%;"|A last aspect in the stay cable design is the fact that cables on each bridge were designed uniformly, that is to say, for the worse stress condition. Table 3.7 shows the pre-design of the stays for each bridge model |
|} | |} | ||
| − | :'' | + | :''3.2.4.4 Connections and boundary conditions'' |
If the deck is connected with very flexible bearings to the towers, the induced seismic forces will be kept to minimum values but the deck may have a large displacement response. On the other hand, a very stiff connection between the deck and the towers will result in lower deck displacement response but will attract much higher seismic forces during an earthquake [Iemura and Pradono, 2003]. The influence of different support conditions on the mode distribution has been investigated by Ali and Abdel-Ghaffar (1995) and Tuladhar and Dilger (1999). Movable supports lead to a more flexible structure, and of course, the decision upon the support conditions of the deck is usually governed by serviceability as well as earthquake considerations. A restrained deck will avoid excessive movements due to traffic and wind loading, however, in the case of an earthquake a restrained deck will generate high axial forces which are applied to the pier-pylon system. Elastic supports for the deck at the towers give very low deck displacements and deck bending moments compared to pinned or fixed connections. Roller supports also cause the bridge have very low first longitudinal direction mode frequency, indicating that the bridge is very flexible in that direction. | If the deck is connected with very flexible bearings to the towers, the induced seismic forces will be kept to minimum values but the deck may have a large displacement response. On the other hand, a very stiff connection between the deck and the towers will result in lower deck displacement response but will attract much higher seismic forces during an earthquake [Iemura and Pradono, 2003]. The influence of different support conditions on the mode distribution has been investigated by Ali and Abdel-Ghaffar (1995) and Tuladhar and Dilger (1999). Movable supports lead to a more flexible structure, and of course, the decision upon the support conditions of the deck is usually governed by serviceability as well as earthquake considerations. A restrained deck will avoid excessive movements due to traffic and wind loading, however, in the case of an earthquake a restrained deck will generate high axial forces which are applied to the pier-pylon system. Elastic supports for the deck at the towers give very low deck displacements and deck bending moments compared to pinned or fixed connections. Roller supports also cause the bridge have very low first longitudinal direction mode frequency, indicating that the bridge is very flexible in that direction. | ||
| Line 1,961: | Line 1,839: | ||
{| style="width: 100%;" | {| style="width: 100%;" | ||
|- | |- | ||
| − | | style="text-align: center;vertical-align: top;"|''' [[Image:draft_Samper_432909089-image124-c.png|246px]] ''' | + | | style="text-align: center;vertical-align: top;width: 40%"|''' [[Image:draft_Samper_432909089-monograph-image124-c.png|246px]] ''' |
'''Fig. 3.11''' Modelling of the Tower-deck Connection | '''Fig. 3.11''' Modelling of the Tower-deck Connection | ||
| − | | style="vertical-align: top;"|In the present investigation, connection between deck and towers is supported by the lower strut through vertical rigid links with pinned bearings at the end-joints, in the connection with the deck (Fig. 3.11). These rigid links were idealized using linear massless springs with all the directional degrees-of-freedom fixed. For the abutment-to-deck connection, sliding bearings were used, in order to permit free longitudinal displacements of the structure due to normal expansions, and free rotations about the transverse axes (Fig. 3.12). | + | | style="vertical-align: top;width: 60%"|In the present investigation, connection between deck and towers is supported by the lower strut through vertical rigid links with pinned bearings at the end-joints, in the connection with the deck (Fig. 3.11). These rigid links were idealized using linear massless springs with all the directional degrees-of-freedom fixed. For the abutment-to-deck connection, sliding bearings were used, in order to permit free longitudinal displacements of the structure due to normal expansions, and free rotations about the transverse axes (Fig. 3.12). |
|} | |} | ||
| Line 1,973: | Line 1,851: | ||
<div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | ||
| − | ''' [[Image:draft_Samper_432909089-image125-c.png|390px]] '''</div> | + | ''' [[Image:draft_Samper_432909089-monograph-image125-c.png|390px]] '''</div> |
<div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | ||
| Line 1,980: | Line 1,858: | ||
{| style="width: 100%;" | {| style="width: 100%;" | ||
|- | |- | ||
| − | | style="text-align: center;vertical-align: top;width: 45%;"| [[Image:draft_Samper_432909089-image126-c.png|282px]] | + | | style="text-align: center;vertical-align: top;width: 45%;"|[[Image:draft_Samper_432909089-monograph-image126-c.png|282px]] |
<span style="text-align: center; font-size: 75%;">'''(a) ''' ''AB1'' pattern</span> | <span style="text-align: center; font-size: 75%;">'''(a) ''' ''AB1'' pattern</span> | ||
| − | | style="text-align: center;vertical-align: top;width: | + | | style="text-align: center;vertical-align: top;width: 54%;"|[[Image:draft_Samper_432909089-monograph-image127-c.png|264px]] |
<span style="text-align: center; font-size: 75%;">'''(b) ''' ''AB4 ''pattern</span> | <span style="text-align: center; font-size: 75%;">'''(b) ''' ''AB4 ''pattern</span> | ||
|- | |- | ||
| − | | style="text-align: center;vertical-align: top;width: 45%;"| [[Image:draft_Samper_432909089-image128.png|270px]] | + | | style="text-align: center;vertical-align: top;width: 45%;"|[[Image:draft_Samper_432909089-monograph-image128.png|270px]] |
<span style="text-align: center; font-size: 75%;">'''(c) ''' ''AR1 ''pattern</span> | <span style="text-align: center; font-size: 75%;">'''(c) ''' ''AR1 ''pattern</span> | ||
| − | | style="text-align: center;vertical-align: top;width: | + | | style="text-align: center;vertical-align: top;width: 54%;"|[[Image:draft_Samper_432909089-monograph-image129.png|246px]] |
<span style="text-align: center; font-size: 75%;">'''(d) ''' ''AR4'' Pattern</span> | <span style="text-align: center; font-size: 75%;">'''(d) ''' ''AR4'' Pattern</span> | ||
| Line 2,001: | Line 1,879: | ||
'''Fig. 3.13''' Complete ''3-D'' Finite Element Models of Some Bridges</div> | '''Fig. 3.13''' Complete ''3-D'' Finite Element Models of Some Bridges</div> | ||
| − | :<big> | + | |
| + | :<big>3.3 Nonlinear Static Analysis under Service Loads</big> | ||
As a first step of the nonlinear seismic analysis, a nonlinear static analysis under gravity loads and stay prestressing forces was carried out. Nonlinearities in this stage include the stay cable sag effect, axial force-bending moment interaction, large displacements effect and the material nonlinearity due to the ''tension only'' formulation of the cable elements. Of course, the nonlinear static analysis was performed for each bridge model, considering the actualized data of the stay prestressing forces. | As a first step of the nonlinear seismic analysis, a nonlinear static analysis under gravity loads and stay prestressing forces was carried out. Nonlinearities in this stage include the stay cable sag effect, axial force-bending moment interaction, large displacements effect and the material nonlinearity due to the ''tension only'' formulation of the cable elements. Of course, the nonlinear static analysis was performed for each bridge model, considering the actualized data of the stay prestressing forces. | ||
| Line 2,011: | Line 1,890: | ||
{| style="width: 100%;" | {| style="width: 100%;" | ||
|- | |- | ||
| − | | style="vertical-align: top;"|''' [[Image:draft_Samper_432909089-image130-c.png|246px]] ''' | + | | style="vertical-align: top;width: 40%"|''' [[Image:draft_Samper_432909089-monograph-image130-c.png|246px]] ''' |
'''Fig. 3.14''' Location of Measured Displacements | '''Fig. 3.14''' Location of Measured Displacements | ||
| − | | style="vertical-align: top;"|Fig. 3.14 shows the location of the measured displacements on the bridges. ''∆<sub>1-L</sub>'' corresponds to the longitudinal displacement of the tower-top, and ''∆<sub>1-T</sub>''corresponds to the transverse displacement of the same point. ''∆<sub>3-V</sub>'' is the vertical displacement of the deck at the mid-span, and finally, ''∆<sub>4-L</sub>''corresponds to the longitudinal displacement of the deck-ends. | + | | style="vertical-align: top;width: 60%"|Fig. 3.14 shows the location of the measured displacements on the bridges. ''∆<sub>1-L</sub>'' corresponds to the longitudinal displacement of the tower-top, and ''∆<sub>1-T</sub>''corresponds to the transverse displacement of the same point. ''∆<sub>3-V</sub>'' is the vertical displacement of the deck at the mid-span, and finally, ''∆<sub>4-L</sub>''corresponds to the longitudinal displacement of the deck-ends. |
|} | |} | ||
| Line 2,085: | Line 1,964: | ||
<span style="text-align: center; font-size: 75%;"><sup>a</sup> Positive value implies a displacement toward the mid-span</span> | <span style="text-align: center; font-size: 75%;"><sup>a</sup> Positive value implies a displacement toward the mid-span</span> | ||
| − | <sup>b</sup> Negative value implies a descending | + | <span style="text-align: center; font-size: 75%;"><sup>b</sup> Negative value implies a descending</span> |
<div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | ||
| Line 2,177: | Line 2,056: | ||
<span style="text-align: center; font-size: 75%;"><sup>a</sup> At the tower base <sup>c</sup> In the bridge plane <sup>e</sup> Out-of-plane</span> | <span style="text-align: center; font-size: 75%;"><sup>a</sup> At the tower base <sup>c</sup> In the bridge plane <sup>e</sup> Out-of-plane</span> | ||
| − | <sup>b</sup> At the tower-deck level <sup>d </sup>At the upper strut level - Implies compression | + | <span style="text-align: center; font-size: 75%;"><sup>b</sup> At the tower-deck level <sup>d </sup>At the upper strut level - Implies compression</span> |
Values of displacements and forces shown in Tables 3.8 and 3.9 are in accordance with the structures. Although a static parametric analysis is not the aim of this investigation, it can be interesting to observe that maximum displacements at the deck-ends are associated with the harp pattern. Because of the loads and geometric symmetry of the structures, transverse deflections at the tower-deck level as well as the longitudinal and transverse deflections of the decks at the mid-span are zero. | Values of displacements and forces shown in Tables 3.8 and 3.9 are in accordance with the structures. Although a static parametric analysis is not the aim of this investigation, it can be interesting to observe that maximum displacements at the deck-ends are associated with the harp pattern. Because of the loads and geometric symmetry of the structures, transverse deflections at the tower-deck level as well as the longitudinal and transverse deflections of the decks at the mid-span are zero. | ||
| Line 2,187: | Line 2,066: | ||
{| style="width: 100%;" | {| style="width: 100%;" | ||
|- | |- | ||
| − | | style="text-align: center;vertical-align: top;width: 48%;"| [[Image:draft_Samper_432909089-image131-c.png|324px]] | + | | style="text-align: center;vertical-align: top;width: 48%;"|[[Image:draft_Samper_432909089-monograph-image131-c.png|324px]] |
<span style="text-align: center; font-size: 75%;">(a) In-plane bending moments of the deck</span> | <span style="text-align: center; font-size: 75%;">(a) In-plane bending moments of the deck</span> | ||
| − | | style="text-align: center;vertical-align: top;width: | + | | style="text-align: center;vertical-align: top;width: 51%;"|[[Image:draft_Samper_432909089-monograph-image132.png|258px]] |
<span style="text-align: center; font-size: 75%;">(b) Axial forces of the deck</span> | <span style="text-align: center; font-size: 75%;">(b) Axial forces of the deck</span> | ||
|- | |- | ||
| − | | style="text-align: center;vertical-align: top;width: 48%;"| [[Image:draft_Samper_432909089-image133.png|246px]] | + | | style="text-align: center;vertical-align: top;width: 48%;"|[[Image:draft_Samper_432909089-monograph-image133.png|246px]] |
<span style="text-align: center; font-size: 75%;">(c) In-plane bending moments of the pylon</span> | <span style="text-align: center; font-size: 75%;">(c) In-plane bending moments of the pylon</span> | ||
| − | | style="text-align: center;vertical-align: top;width: | + | | style="text-align: center;vertical-align: top;width: 51%;"|[[Image:draft_Samper_432909089-monograph-image134.png|264px]] |
<span style="text-align: center; font-size: 75%;">(d) Axial forces of the pylon</span> | <span style="text-align: center; font-size: 75%;">(d) Axial forces of the pylon</span> | ||
| Line 2,208: | Line 2,087: | ||
{| style="width: 100%;" | {| style="width: 100%;" | ||
|- | |- | ||
| − | | style="text-align: center;vertical-align: top;"|<big>''' [[Image:draft_Samper_432909089-image135.png|258px]] '''</big> | + | | style="text-align: center;vertical-align: top;"|<big>''' [[Image:draft_Samper_432909089-monograph-image135.png|258px]] '''</big> |
<span style="text-align: center; font-size: 75%;">(a) In-plane bending moments of the deck</span> | <span style="text-align: center; font-size: 75%;">(a) In-plane bending moments of the deck</span> | ||
| − | | style="text-align: center;vertical-align: top;"|<big>''' [[Image:draft_Samper_432909089-image136.png|258px]] '''</big> | + | | style="text-align: center;vertical-align: top;"|<big>''' [[Image:draft_Samper_432909089-monograph-image136.png|258px]] '''</big> |
<span style="text-align: center; font-size: 75%;">(b) Axial forces of the deck</span> | <span style="text-align: center; font-size: 75%;">(b) Axial forces of the deck</span> | ||
|- | |- | ||
| − | | style="text-align: center;vertical-align: top;"|<big>''' [[Image:draft_Samper_432909089-image137.png|234px]] '''</big> | + | | style="text-align: center;vertical-align: top;"|<big>''' [[Image:draft_Samper_432909089-monograph-image137.png|234px]] '''</big> |
<span style="text-align: center; font-size: 75%;">(c) In-plane bending moments of the pylon</span> | <span style="text-align: center; font-size: 75%;">(c) In-plane bending moments of the pylon</span> | ||
| − | | style="text-align: center;vertical-align: top;"|<big>''' [[Image:draft_Samper_432909089-image138.png|246px]] '''</big> | + | | style="text-align: center;vertical-align: top;"|<big>''' [[Image:draft_Samper_432909089-monograph-image138.png|246px]] '''</big> |
<span style="text-align: center; font-size: 75%;">(d) Axial forces of the pylon</span> | <span style="text-align: center; font-size: 75%;">(d) Axial forces of the pylon</span> | ||
| Line 2,270: | Line 2,149: | ||
From Table 3.10, it is clear that in this case ''P-Δ'' and large-displacement effects are not very significant on the longitudinal deck displacements. More important differences can be found for the bending moments of the deck, with differences up to 30% comparing the case of only cable sag effect and the case including all the geometric nonlinearities. Differences for the axial force of the towers, axial force of the deck and axial force of the cables are less sensitive, which implies that ''P-Δ'' and large-displacement effects are not very important in such cases. However, it can be supposed that those differences could be more important on longer bridges, and of course, in the nonlinear dynamic analyses. For that reason it is important to consider all those nonlinearities in the static case as starting point for the nonlinear seismic analyses [Abdel-Ghaffar, 1991; Morgenthal, 1999]. | From Table 3.10, it is clear that in this case ''P-Δ'' and large-displacement effects are not very significant on the longitudinal deck displacements. More important differences can be found for the bending moments of the deck, with differences up to 30% comparing the case of only cable sag effect and the case including all the geometric nonlinearities. Differences for the axial force of the towers, axial force of the deck and axial force of the cables are less sensitive, which implies that ''P-Δ'' and large-displacement effects are not very important in such cases. However, it can be supposed that those differences could be more important on longer bridges, and of course, in the nonlinear dynamic analyses. For that reason it is important to consider all those nonlinearities in the static case as starting point for the nonlinear seismic analyses [Abdel-Ghaffar, 1991; Morgenthal, 1999]. | ||
| − | |||
| − | :<big> | + | :<big>3.4 Modal Analysis</big> |
| + | |||
| + | :<big>3.4.1 Natural Frequencies and Modal Shapes</big> | ||
The dynamic response of a structure can be well characterized by a modal analysis. Because of the complex nature of these structures and their seismic response, a two-dimensional analysis is not adequate to capture the three-dimensionality of the system, and for that reason, a ''3D'' analysis is always recommended for the nonlinear static/dynamic analysis of cable-stayed bridges, and of course, for a modal analysis. | The dynamic response of a structure can be well characterized by a modal analysis. Because of the complex nature of these structures and their seismic response, a two-dimensional analysis is not adequate to capture the three-dimensionality of the system, and for that reason, a ''3D'' analysis is always recommended for the nonlinear static/dynamic analysis of cable-stayed bridges, and of course, for a modal analysis. | ||
| Line 2,278: | Line 2,158: | ||
As first approach of the seismic response of these structures, a characterization of natural frequencies, modal shapes, modal participation factors as well as damping mechanism is highly recommended, as was explained in the state-of-the-art review. In order to obtain the modified stiffness matrix considering all nonlinearities available, a nonlinear static analysis was performed first using the proposed finite element modelling. The dynamic free vibration analysis is then performed based on the deformed configuration, and considering as previous stage the nonlinear static analysis. As a consequence, the modal analysis can be used as the basis for modal superposition in the response-spectrum analysis. | As first approach of the seismic response of these structures, a characterization of natural frequencies, modal shapes, modal participation factors as well as damping mechanism is highly recommended, as was explained in the state-of-the-art review. In order to obtain the modified stiffness matrix considering all nonlinearities available, a nonlinear static analysis was performed first using the proposed finite element modelling. The dynamic free vibration analysis is then performed based on the deformed configuration, and considering as previous stage the nonlinear static analysis. As a consequence, the modal analysis can be used as the basis for modal superposition in the response-spectrum analysis. | ||
| − | A lot of strategies to find the natural frequencies have been proposed. The Eigenvector analysis determines the undamped free-vibration mode shapes and frequencies of the system, solving the generalized eigenvalue problem | + | A lot of strategies to find the natural frequencies have been proposed. The Eigenvector analysis determines the undamped free-vibration mode shapes and frequencies of the system, solving the generalized eigenvalue problem [[Image:draft_Samper_432909089-monograph-image139.png|120px]] , where M is the diagonal mass matrix, K is the stiffness matrix, ω<sup>2 </sup>is the diagonal matrix of eigenvalues, and Φ is the matrix of the corresponding eigenvectors (modal shapes). This problem can be solved using the classical tools of linear algebra, or applying approximate strategies to speed-up the solution, as for example the Stodola-Vianella method. |
The Ritz-vector analysis is another strategy to solve this problem, in which the analysis seeks to find modes that are excited by a particular loading. In this sense, it has been demonstrated [Wilson et al, 1982] that dynamic analyses based on a special set of load-dependent Ritz vectors yield more accurate results than the use of the same number of natural mode shapes. The reason why the Ritz vectors yield good results is that they are generated by taking into account the spatial distribution of the dynamic loading, whereas the direct use of the natural mode shapes neglects this very important information. In addition, the Ritz-vector algorithm automatically includes the advantages of the proven numerical techniques of static condensation, Guyan reduction and static correction due to higher-mode truncation. The spatial distribution of the dynamic load vector serves as a starting load vector to initiate the procedure. The first Ritz vector is the static displacement vector corresponding to the starting load vector. The remaining vectors are generated from a recurrence relationship in which the mass matrix is multiplied by the previously obtained Ritz vector and used as the load vector for the next static solution. | The Ritz-vector analysis is another strategy to solve this problem, in which the analysis seeks to find modes that are excited by a particular loading. In this sense, it has been demonstrated [Wilson et al, 1982] that dynamic analyses based on a special set of load-dependent Ritz vectors yield more accurate results than the use of the same number of natural mode shapes. The reason why the Ritz vectors yield good results is that they are generated by taking into account the spatial distribution of the dynamic loading, whereas the direct use of the natural mode shapes neglects this very important information. In addition, the Ritz-vector algorithm automatically includes the advantages of the proven numerical techniques of static condensation, Guyan reduction and static correction due to higher-mode truncation. The spatial distribution of the dynamic load vector serves as a starting load vector to initiate the procedure. The first Ritz vector is the static displacement vector corresponding to the starting load vector. The remaining vectors are generated from a recurrence relationship in which the mass matrix is multiplied by the previously obtained Ritz vector and used as the load vector for the next static solution. | ||
| Line 2,286: | Line 2,166: | ||
{| style="width: 100%;border-collapse: collapse;" | {| style="width: 100%;border-collapse: collapse;" | ||
|- | |- | ||
| − | | style="vertical-align: top;"|'''Table 3.11''' Natural Periods for the Longest Cables | + | | style="vertical-align: top;width: 60%;"|'''Table 3.11''' Natural Periods for the Longest Cables |
{| style="width: 55%;border-collapse: collapse;" | {| style="width: 55%;border-collapse: collapse;" | ||
| Line 2,328: | Line 2,208: | ||
| − | | style="vertical-align: top;"|Table 3.11 shows predominant periods for the longest cables of the bridges that depend on the tension forces (''T''), the angle of the cable sag with regard to the horizontal plane (''α<sub>0</sub>''), the unitary mass of the cables (''m'') and the horizontal projection of the cables (''L).'' | + | | style="vertical-align: top;width: 40%;"|Table 3.11 shows predominant periods for the longest cables of the bridges that depend on the tension forces (''T''), the angle of the cable sag with regard to the horizontal plane (''α<sub>0</sub>''), the unitary mass of the cables (''m'') and the horizontal projection of the cables (''L).'' |
|} | |} | ||
| Line 2,703: | Line 2,583: | ||
|- | |- | ||
| style="border-top: 1pt solid black;border-right: 1pt solid black;text-align: center;"|<span style="text-align: center; font-size: 75%;">'''AB1'''</span> | | style="border-top: 1pt solid black;border-right: 1pt solid black;text-align: center;"|<span style="text-align: center; font-size: 75%;">'''AB1'''</span> | ||
| − | | style="border-top: 1pt solid black;border-left: 1pt solid black;border-right: 1pt solid black;text-align: center;width: 0%;"| [[Image:draft_Samper_432909089-image140.png|162px]] | + | | style="border-top: 1pt solid black;border-left: 1pt solid black;border-right: 1pt solid black;text-align: center;width: 0%;"|[[Image:draft_Samper_432909089-monograph-image140.png|162px]] |
<span style="text-align: center; font-size: 75%;">T = 1.806 sec</span> | <span style="text-align: center; font-size: 75%;">T = 1.806 sec</span> | ||
| − | | style="border-top: 1pt solid black;border-left: 1pt solid black;border-right: 1pt solid black;text-align: center;width: 0%;"| [[Image:draft_Samper_432909089-image141.png|162px]] | + | | style="border-top: 1pt solid black;border-left: 1pt solid black;border-right: 1pt solid black;text-align: center;width: 0%;"|[[Image:draft_Samper_432909089-monograph-image141.png|162px]] |
<span style="text-align: center; font-size: 75%;">T = 1.663 sec</span> | <span style="text-align: center; font-size: 75%;">T = 1.663 sec</span> | ||
| − | | style="border-top: 1pt solid black;border-left: 1pt solid black;text-align: center;width: 0%;"| [[Image:draft_Samper_432909089-image142.png|168px]] | + | | style="border-top: 1pt solid black;border-left: 1pt solid black;text-align: center;width: 0%;"|[[Image:draft_Samper_432909089-monograph-image142.png|168px]] |
<span style="text-align: center; font-size: 75%;">T = 1.585sec</span> | <span style="text-align: center; font-size: 75%;">T = 1.585sec</span> | ||
|- | |- | ||
| style="border-right: 1pt solid black;text-align: center;"|<span style="text-align: center; font-size: 75%;">'''AB2'''</span> | | style="border-right: 1pt solid black;text-align: center;"|<span style="text-align: center; font-size: 75%;">'''AB2'''</span> | ||
| − | | style="border-left: 1pt solid black;border-right: 1pt solid black;text-align: center;width: 0%;"| [[Image:draft_Samper_432909089-image143.png|162px]] | + | | style="border-left: 1pt solid black;border-right: 1pt solid black;text-align: center;width: 0%;"|[[Image:draft_Samper_432909089-monograph-image143.png|162px]] |
<span style="text-align: center; font-size: 75%;">T = 2.694 sec</span> | <span style="text-align: center; font-size: 75%;">T = 2.694 sec</span> | ||
| − | | style="border-left: 1pt solid black;border-right: 1pt solid black;text-align: center;width: 0%;"| [[Image:draft_Samper_432909089-image144.png|180px]] | + | | style="border-left: 1pt solid black;border-right: 1pt solid black;text-align: center;width: 0%;"|[[Image:draft_Samper_432909089-monograph-image144.png|180px]] |
<span style="text-align: center; font-size: 75%;">T = 2.539 sec</span> | <span style="text-align: center; font-size: 75%;">T = 2.539 sec</span> | ||
| − | | style="border-left: 1pt solid black;text-align: center;width: 0%;"| [[Image:draft_Samper_432909089-image145.png|186px]] | + | | style="border-left: 1pt solid black;text-align: center;width: 0%;"|[[Image:draft_Samper_432909089-monograph-image145.png|186px]] |
<span style="text-align: center; font-size: 75%;">T = 2.064 sec</span> | <span style="text-align: center; font-size: 75%;">T = 2.064 sec</span> | ||
|- | |- | ||
| style="border-right: 1pt solid black;text-align: center;"|<span style="text-align: center; font-size: 75%;">'''AB3'''</span> | | style="border-right: 1pt solid black;text-align: center;"|<span style="text-align: center; font-size: 75%;">'''AB3'''</span> | ||
| − | | style="border-left: 1pt solid black;border-right: 1pt solid black;text-align: center;width: 0%;"| [[Image:draft_Samper_432909089-image146.png|162px]] | + | | style="border-left: 1pt solid black;border-right: 1pt solid black;text-align: center;width: 0%;"|[[Image:draft_Samper_432909089-monograph-image146.png|162px]] |
<span style="text-align: center; font-size: 75%;">T = 1.801 sec</span> | <span style="text-align: center; font-size: 75%;">T = 1.801 sec</span> | ||
| − | | style="border-left: 1pt solid black;border-right: 1pt solid black;text-align: center;width: 0%;"| [[Image:draft_Samper_432909089-image147.png|162px]] | + | | style="border-left: 1pt solid black;border-right: 1pt solid black;text-align: center;width: 0%;"|[[Image:draft_Samper_432909089-monograph-image147.png|162px]] |
<span style="text-align: center; font-size: 75%;">T = 1.798 sec</span> | <span style="text-align: center; font-size: 75%;">T = 1.798 sec</span> | ||
| − | | style="border-left: 1pt solid black;text-align: center;width: 0%;"| [[Image:draft_Samper_432909089-image148.png|186px]] | + | | style="border-left: 1pt solid black;text-align: center;width: 0%;"|[[Image:draft_Samper_432909089-monograph-image148.png|186px]] |
<span style="text-align: center; font-size: 75%;">T = 1.689 sec</span> | <span style="text-align: center; font-size: 75%;">T = 1.689 sec</span> | ||
|- | |- | ||
| style="border-right: 1pt solid black;text-align: center;"|<span style="text-align: center; font-size: 75%;">'''AB4'''</span> | | style="border-right: 1pt solid black;text-align: center;"|<span style="text-align: center; font-size: 75%;">'''AB4'''</span> | ||
| − | | style="border-left: 1pt solid black;border-right: 1pt solid black;text-align: center;width: 0%;"| [[Image:draft_Samper_432909089-image149.png|162px]] | + | | style="border-left: 1pt solid black;border-right: 1pt solid black;text-align: center;width: 0%;"|[[Image:draft_Samper_432909089-monograph-image149.png|162px]] |
<span style="text-align: center; font-size: 75%;">T = 2.804 sec</span> | <span style="text-align: center; font-size: 75%;">T = 2.804 sec</span> | ||
| − | | style="border-left: 1pt solid black;border-right: 1pt solid black;text-align: center;width: 0%;"| [[Image:draft_Samper_432909089-image150.png|180px]] | + | | style="border-left: 1pt solid black;border-right: 1pt solid black;text-align: center;width: 0%;"|[[Image:draft_Samper_432909089-monograph-image150.png|180px]] |
<span style="text-align: center; font-size: 75%;">T = 2.662 sec</span> | <span style="text-align: center; font-size: 75%;">T = 2.662 sec</span> | ||
| − | | style="border-left: 1pt solid black;text-align: center;width: 0%;"| [[Image:draft_Samper_432909089-image151.png|186px]] | + | | style="border-left: 1pt solid black;text-align: center;width: 0%;"|[[Image:draft_Samper_432909089-monograph-image151.png|186px]] |
<span style="text-align: center; font-size: 75%;">T = 2.156 sec</span> | <span style="text-align: center; font-size: 75%;">T = 2.156 sec</span> | ||
|- | |- | ||
| style="border-right: 1pt solid black;text-align: center;"|<span style="text-align: center; font-size: 75%;">'''AR1'''</span> | | style="border-right: 1pt solid black;text-align: center;"|<span style="text-align: center; font-size: 75%;">'''AR1'''</span> | ||
| − | | style="border-left: 1pt solid black;border-right: 1pt solid black;text-align: center;width: 0%;"| [[Image:draft_Samper_432909089-image152.png|162px]] | + | | style="border-left: 1pt solid black;border-right: 1pt solid black;text-align: center;width: 0%;"|[[Image:draft_Samper_432909089-monograph-image152.png|162px]] |
<span style="text-align: center; font-size: 75%;">T = 1.992 sec</span> | <span style="text-align: center; font-size: 75%;">T = 1.992 sec</span> | ||
| − | | style="border-left: 1pt solid black;border-right: 1pt solid black;text-align: center;width: 0%;"| [[Image:draft_Samper_432909089-image153.png|180px]] | + | | style="border-left: 1pt solid black;border-right: 1pt solid black;text-align: center;width: 0%;"|[[Image:draft_Samper_432909089-monograph-image153.png|180px]] |
<span style="text-align: center; font-size: 75%;">T = 1.900 sec</span> | <span style="text-align: center; font-size: 75%;">T = 1.900 sec</span> | ||
| − | | style="border-left: 1pt solid black;text-align: center;width: 0%;"| [[Image:draft_Samper_432909089-image154.png|186px]] | + | | style="border-left: 1pt solid black;text-align: center;width: 0%;"|[[Image:draft_Samper_432909089-monograph-image154.png|186px]] |
<span style="text-align: center; font-size: 75%;">T = 1.733 sec</span> | <span style="text-align: center; font-size: 75%;">T = 1.733 sec</span> | ||
|- | |- | ||
| style="border-right: 1pt solid black;text-align: center;"|<span style="text-align: center; font-size: 75%;">'''AR2'''</span> | | style="border-right: 1pt solid black;text-align: center;"|<span style="text-align: center; font-size: 75%;">'''AR2'''</span> | ||
| − | | style="border-left: 1pt solid black;border-right: 1pt solid black;text-align: center;width: 0%;"| [[Image:draft_Samper_432909089-image155.png|162px]] | + | | style="border-left: 1pt solid black;border-right: 1pt solid black;text-align: center;width: 0%;"|[[Image:draft_Samper_432909089-monograph-image155.png|162px]] |
<span style="text-align: center; font-size: 75%;">T = 2.938 sec</span> | <span style="text-align: center; font-size: 75%;">T = 2.938 sec</span> | ||
| − | | style="border-left: 1pt solid black;border-right: 1pt solid black;text-align: center;width: 0%;"| [[Image:draft_Samper_432909089-image156.png|168px]] | + | | style="border-left: 1pt solid black;border-right: 1pt solid black;text-align: center;width: 0%;"|[[Image:draft_Samper_432909089-monograph-image156.png|168px]] |
<span style="text-align: center; font-size: 75%;">T = 2.568 sec</span> | <span style="text-align: center; font-size: 75%;">T = 2.568 sec</span> | ||
| − | | style="border-left: 1pt solid black;text-align: center;width: 0%;"| [[Image:draft_Samper_432909089-image157.png|186px]] | + | | style="border-left: 1pt solid black;text-align: center;width: 0%;"|[[Image:draft_Samper_432909089-monograph-image157.png|186px]] |
<span style="text-align: center; font-size: 75%;">T = 2.130 sec</span> | <span style="text-align: center; font-size: 75%;">T = 2.130 sec</span> | ||
|- | |- | ||
| style="border-right: 1pt solid black;text-align: center;"|<span style="text-align: center; font-size: 75%;">'''AR3'''</span> | | style="border-right: 1pt solid black;text-align: center;"|<span style="text-align: center; font-size: 75%;">'''AR3'''</span> | ||
| − | | style="border-left: 1pt solid black;border-right: 1pt solid black;text-align: center;width: 0%;"| [[Image:draft_Samper_432909089-image158.png|162px]] | + | | style="border-left: 1pt solid black;border-right: 1pt solid black;text-align: center;width: 0%;"|[[Image:draft_Samper_432909089-monograph-image158.png|162px]] |
<span style="text-align: center; font-size: 75%;">T = 2.020 sec</span> | <span style="text-align: center; font-size: 75%;">T = 2.020 sec</span> | ||
| − | | style="border-left: 1pt solid black;border-right: 1pt solid black;text-align: center;width: 0%;"| [[Image:draft_Samper_432909089-image159.png|162px]] | + | | style="border-left: 1pt solid black;border-right: 1pt solid black;text-align: center;width: 0%;"|[[Image:draft_Samper_432909089-monograph-image159.png|162px]] |
<span style="text-align: center; font-size: 75%;">T = 1.795 sec</span> | <span style="text-align: center; font-size: 75%;">T = 1.795 sec</span> | ||
| − | | style="border-left: 1pt solid black;text-align: center;width: 0%;"| [[Image:draft_Samper_432909089-image160.png|186px]] | + | | style="border-left: 1pt solid black;text-align: center;width: 0%;"|[[Image:draft_Samper_432909089-monograph-image160.png|186px]] |
<span style="text-align: center; font-size: 75%;">T = 1.772 sec</span> | <span style="text-align: center; font-size: 75%;">T = 1.772 sec</span> | ||
|- | |- | ||
| style="border-bottom: 2pt solid black;border-right: 1pt solid black;text-align: center;"|<span style="text-align: center; font-size: 75%;">'''AR4'''</span> | | style="border-bottom: 2pt solid black;border-right: 1pt solid black;text-align: center;"|<span style="text-align: center; font-size: 75%;">'''AR4'''</span> | ||
| − | | style="border-left: 1pt solid black;border-bottom: 2pt solid black;border-right: 1pt solid black;text-align: center;width: 0%;"| [[Image:draft_Samper_432909089-image161.png|162px]] | + | | style="border-left: 1pt solid black;border-bottom: 2pt solid black;border-right: 1pt solid black;text-align: center;width: 0%;"|[[Image:draft_Samper_432909089-monograph-image161.png|162px]] |
<span style="text-align: center; font-size: 75%;">T = 2.845 sec</span> | <span style="text-align: center; font-size: 75%;">T = 2.845 sec</span> | ||
| − | | style="border-left: 1pt solid black;border-bottom: 2pt solid black;border-right: 1pt solid black;text-align: center;width: 0%;"| [[Image:draft_Samper_432909089-image162.png|180px]] | + | | style="border-left: 1pt solid black;border-bottom: 2pt solid black;border-right: 1pt solid black;text-align: center;width: 0%;"|[[Image:draft_Samper_432909089-monograph-image162.png|180px]] |
<span style="text-align: center; font-size: 75%;">T = 2.535 sec</span> | <span style="text-align: center; font-size: 75%;">T = 2.535 sec</span> | ||
| − | | style="border-left: 1pt solid black;border-bottom: 2pt solid black;text-align: center;width: 0%;"| [[Image:draft_Samper_432909089-image163.png|186px]] | + | | style="border-left: 1pt solid black;border-bottom: 2pt solid black;text-align: center;width: 0%;"|[[Image:draft_Samper_432909089-monograph-image163.png|186px]] |
<span style="text-align: center; font-size: 75%;">T = 2.080 sec</span> | <span style="text-align: center; font-size: 75%;">T = 2.080 sec</span> | ||
| Line 3,264: | Line 3,144: | ||
| − | :<big> | + | :<big>3.4.2 Damping</big> |
Damping on cable-stayed bridges is low, of about 2%, according to Morgenthal (1999). Kawashima and Unjoh (1991) found that critical damping ratio was dependent with the excitation amplitude and modal shape, aspect that makes the damping estimation very complex. Of course, this approach is not by the side of this research, and constant values for the damping ratio are suggested for each bridge, depending on the modal shape. In this sense, the approximation by Kawashima and Unjoh (1991), in which the critical damping ratio for the main modes is correlated with the natural frequencies of the bridges, can be applied here. Table 3.17 shows results of this formulation. Here, ξ<sup>BV</sup>, ξ<sup>BH</sup> and ξ<sup>T</sup> are the critical damping ratios for vertical bending oscillations, transverse bending oscillations and torsional oscillations, respectively. | Damping on cable-stayed bridges is low, of about 2%, according to Morgenthal (1999). Kawashima and Unjoh (1991) found that critical damping ratio was dependent with the excitation amplitude and modal shape, aspect that makes the damping estimation very complex. Of course, this approach is not by the side of this research, and constant values for the damping ratio are suggested for each bridge, depending on the modal shape. In this sense, the approximation by Kawashima and Unjoh (1991), in which the critical damping ratio for the main modes is correlated with the natural frequencies of the bridges, can be applied here. Table 3.17 shows results of this formulation. Here, ξ<sup>BV</sup>, ξ<sup>BH</sup> and ξ<sup>T</sup> are the critical damping ratios for vertical bending oscillations, transverse bending oscillations and torsional oscillations, respectively. | ||
| Line 3,321: | Line 3,201: | ||
Finally, it is important to say that results of the damping analysis are in accordance with real measures on bridges, as can be seen in the works of Garevski and Savern (1992, 1993); Yamaguchi and Manabu (1997) and Atkins and Wilson (2000). | Finally, it is important to say that results of the damping analysis are in accordance with real measures on bridges, as can be seen in the works of Garevski and Savern (1992, 1993); Yamaguchi and Manabu (1997) and Atkins and Wilson (2000). | ||
| − | :<big> | + | |
| + | :<big>3.5 Seismic Response Analysis Applying the Response Spectrum Method</big> | ||
The response spectrum method for the seismic analysis of structures is a useful and powerful tool, well implemented in the current seismic regulations. This methodology computes the maximum seismic response of a structure using modal superposition, on the basis of a modal analysis previously performed, and applying an elastic design response spectrum as seismic input. Although this strategy is questionable in the case of structures with nonlinear seismic behaviour, it can be applicable as first approach for the seismic analysis, in order to compare the maximum seismic responses with those obtained from the nonlinear time history analysis considering similar conditions of soil and effective ground acceleration. | The response spectrum method for the seismic analysis of structures is a useful and powerful tool, well implemented in the current seismic regulations. This methodology computes the maximum seismic response of a structure using modal superposition, on the basis of a modal analysis previously performed, and applying an elastic design response spectrum as seismic input. Although this strategy is questionable in the case of structures with nonlinear seismic behaviour, it can be applicable as first approach for the seismic analysis, in order to compare the maximum seismic responses with those obtained from the nonlinear time history analysis considering similar conditions of soil and effective ground acceleration. | ||
| Line 3,401: | Line 3,282: | ||
{| style="width: 100%;" | {| style="width: 100%;" | ||
|- | |- | ||
| − | | ''' [[Image:draft_Samper_432909089-image164-c.png|294px]] ''' | + | | ''' [[Image:draft_Samper_432909089-monograph-image164-c.png|294px]] ''' |
'''Fig. 3.17''' Design Acceleration Response Spectra | '''Fig. 3.17''' Design Acceleration Response Spectra | ||
| − | | style="text-align: center;"|''' [[Image:draft_Samper_432909089-image165-c.png|276px]] ''' | + | | style="text-align: center;"|''' [[Image:draft_Samper_432909089-monograph-image165-c.png|276px]] ''' |
'''Fig. 3.18''' Design Velocity Response Spectra | '''Fig. 3.18''' Design Velocity Response Spectra | ||
| Line 3,416: | Line 3,297: | ||
{| style="width: 100%;" | {| style="width: 100%;" | ||
|- | |- | ||
| − | | style="text-align: center;vertical-align: top;width: 50%;"| [[Image:draft_Samper_432909089-image166.png|204px]] | + | | style="text-align: center;vertical-align: top;width: 50%;"|[[Image:draft_Samper_432909089-monograph-image166.png|204px]] |
'''Fig. 3.19 '''Maximum Seismic Longitudinal Displacements for 81 m - height Towers | '''Fig. 3.19 '''Maximum Seismic Longitudinal Displacements for 81 m - height Towers | ||
| − | | style="text-align: center;vertical-align: top;width: 50%;"| [[Image:draft_Samper_432909089-image167.png|198px]] | + | | style="text-align: center;vertical-align: top;width: 50%;"|[[Image:draft_Samper_432909089-monograph-image167.png|198px]] |
'''Fig. 3.20 '''Maximum Seismic Longitudinal Displacements for 111 m - height Towers | '''Fig. 3.20 '''Maximum Seismic Longitudinal Displacements for 111 m - height Towers | ||
| Line 3,427: | Line 3,308: | ||
{| style="width: 100%;" | {| style="width: 100%;" | ||
|- | |- | ||
| − | | style="vertical-align: top;"|''' [[Image:draft_Samper_432909089-image168.png|204px]] ''' | + | | style="vertical-align: top;"|''' [[Image:draft_Samper_432909089-monograph-image168.png|204px]] ''' |
'''Fig. 3.21''' Maximum Tower Longitudinal Displacements for ''AB1'' Bridge | '''Fig. 3.21''' Maximum Tower Longitudinal Displacements for ''AB1'' Bridge | ||
| − | | style="text-align: center;vertical-align: top;width: 50%;"| [[Image:draft_Samper_432909089-image169.png|204px]] | + | | style="text-align: center;vertical-align: top;width: 50%;"|[[Image:draft_Samper_432909089-monograph-image169.png|204px]] |
'''Fig. 3.22''' Maximum Tower Longitudinal Displacements for ''AR4'' Bridge | '''Fig. 3.22''' Maximum Tower Longitudinal Displacements for ''AR4'' Bridge | ||
| Line 3,442: | Line 3,323: | ||
{| style="width: 100%;" | {| style="width: 100%;" | ||
|- | |- | ||
| − | | style="text-align: center;vertical-align: top;width: | + | | style="text-align: center;vertical-align: top;width: 50%;"|[[Image:draft_Samper_432909089-monograph-image170.png|288px]] |
'''Fig. 3.23''' Maximum Vertical Seismic Displacements – Slab-type Deck | '''Fig. 3.23''' Maximum Vertical Seismic Displacements – Slab-type Deck | ||
| − | | style="text-align: center;vertical-align: top;width: | + | | style="text-align: center;vertical-align: top;width: 49%;"|[[Image:draft_Samper_432909089-monograph-image171.png|282px]] |
'''Fig. 3.24''' Maximum Vertical Seismic Displacements – Hollow box-type Deck | '''Fig. 3.24''' Maximum Vertical Seismic Displacements – Hollow box-type Deck | ||
| Line 3,453: | Line 3,334: | ||
{| style="width: 100%;" | {| style="width: 100%;" | ||
|- | |- | ||
| − | | style="text-align: center;vertical-align: top;width: | + | | style="text-align: center;vertical-align: top;width: 50%;"|[[Image:draft_Samper_432909089-monograph-image172.png|288px]] |
'''Fig. 3.25''' Maximum Vertical Deck Displacements for ''AB1'' Bridge | '''Fig. 3.25''' Maximum Vertical Deck Displacements for ''AB1'' Bridge | ||
| − | | style="text-align: center;vertical-align: top;width: | + | | style="text-align: center;vertical-align: top;width: 49%;"|[[Image:draft_Samper_432909089-monograph-image173.png|282px]] |
'''Fig. 3.26''' Maximum Vertical Deck Displacements for ''AR4'' Bridge | '''Fig. 3.26''' Maximum Vertical Deck Displacements for ''AR4'' Bridge | ||
| Line 3,468: | Line 3,349: | ||
{| style="width: 100%;" | {| style="width: 100%;" | ||
|- | |- | ||
| − | | style="text-align: center;vertical-align: top;width: 49%;"| [[Image:draft_Samper_432909089-image174-c.png|210px]] | + | | style="text-align: center;vertical-align: top;width: 49%;"|[[Image:draft_Samper_432909089-monograph-image174-c.png|210px]] |
'''Fig. 3.27''' Envelope of Maximum Seismic Compressive Forces for 81 m-Height Towers | '''Fig. 3.27''' Envelope of Maximum Seismic Compressive Forces for 81 m-Height Towers | ||
| − | | style="text-align: center;vertical-align: top;width: 50%;"| [[Image:draft_Samper_432909089-image175-c.png|204px]] | + | | style="text-align: center;vertical-align: top;width: 50%;"|[[Image:draft_Samper_432909089-monograph-image175-c.png|204px]] |
'''Fig. 3.28''' Envelope of Maximum Seismic Compressive Forces for 111 m-Height Towers | '''Fig. 3.28''' Envelope of Maximum Seismic Compressive Forces for 111 m-Height Towers | ||
| Line 3,483: | Line 3,364: | ||
{| style="width: 100%;" | {| style="width: 100%;" | ||
|- | |- | ||
| − | | style="text-align: center;vertical-align: top;width: 50%;"| [[Image:draft_Samper_432909089-image176-c.png|186px]] | + | | style="text-align: center;vertical-align: top;width: 50%;"|[[Image:draft_Samper_432909089-monograph-image176-c.png|186px]] |
'''Fig. 3.29''' Envelope of Maximum Tower Axial Forces for ''AB1'' Bridge | '''Fig. 3.29''' Envelope of Maximum Tower Axial Forces for ''AB1'' Bridge | ||
| − | | style="text-align: center;vertical-align: top;width: 50%;"| [[Image:draft_Samper_432909089-image177-c.png|192px]] | + | | style="text-align: center;vertical-align: top;width: 50%;"|[[Image:draft_Samper_432909089-monograph-image177-c.png|192px]] |
'''Fig. 3.30''' Envelope of Maximum Tower Axial Forces for ''AR4'' Bridge | '''Fig. 3.30''' Envelope of Maximum Tower Axial Forces for ''AR4'' Bridge | ||
| Line 3,494: | Line 3,375: | ||
{| style="width: 100%;" | {| style="width: 100%;" | ||
|- | |- | ||
| − | | style="text-align: center;vertical-align: top;width: | + | | style="text-align: center;vertical-align: top;width: 50%;"|[[Image:draft_Samper_432909089-monograph-image178-c.png|294px]] |
'''Fig. 3.31 '''Envelope of Seismic Axial Forces for Decks – 81 m Tower-Height | '''Fig. 3.31 '''Envelope of Seismic Axial Forces for Decks – 81 m Tower-Height | ||
| − | | style="text-align: center;vertical-align: top;width: | + | | style="text-align: center;vertical-align: top;width: 49%;"|[[Image:draft_Samper_432909089-monograph-image179-c.png|288px]] |
'''Fig. 3.32 '''Envelope of Seismic Axial Forces for Decks – 111 m Tower-Height | '''Fig. 3.32 '''Envelope of Seismic Axial Forces for Decks – 111 m Tower-Height | ||
| Line 3,509: | Line 3,390: | ||
{| style="width: 100%;" | {| style="width: 100%;" | ||
|- | |- | ||
| − | | style="text-align: center;vertical-align: top;width: | + | | style="text-align: center;vertical-align: top;width: 50%;"|[[Image:draft_Samper_432909089-monograph-image180-c.png|300px]] |
'''Fig. 3.33''' Response Comparison for Axial Forces – Deck of ''AB1'' Bridge | '''Fig. 3.33''' Response Comparison for Axial Forces – Deck of ''AB1'' Bridge | ||
| − | | style="text-align: center;vertical-align: top;width: | + | | style="text-align: center;vertical-align: top;width: 49%;"|[[Image:draft_Samper_432909089-monograph-image181-c.png|294px]] |
'''Fig. 3.34''' Response Comparison for Axial Forces – Deck of ''AR4'' Bridge | '''Fig. 3.34''' Response Comparison for Axial Forces – Deck of ''AR4'' Bridge | ||
| Line 3,524: | Line 3,405: | ||
{| style="width: 100%;" | {| style="width: 100%;" | ||
|- | |- | ||
| − | | style="text-align: center;vertical-align: top;width: | + | | style="text-align: center;vertical-align: top;width: 52%;"|[[Image:draft_Samper_432909089-monograph-image182.png|264px]] |
<span style="text-align: center; font-size: 75%;">'''(a)''' Tower moments of ''AB1'' bridge</span> | <span style="text-align: center; font-size: 75%;">'''(a)''' Tower moments of ''AB1'' bridge</span> | ||
| − | | style="text-align: center;vertical-align: top;width: 47%;"| [[Image:draft_Samper_432909089-image183-c.png|276px]] | + | | style="text-align: center;vertical-align: top;width: 47%;"|[[Image:draft_Samper_432909089-monograph-image183-c.png|276px]] |
<span style="text-align: center; font-size: 75%;">'''(b)''' Deck moments of ''AB1'' bridge</span> | <span style="text-align: center; font-size: 75%;">'''(b)''' Deck moments of ''AB1'' bridge</span> | ||
|- | |- | ||
| − | | style="vertical-align: top;width: | + | | style="vertical-align: top;width: 52%;"|[[Image:draft_Samper_432909089-monograph-image184.png|294px]] |
<span style="text-align: center; font-size: 75%;">'''(c)''' Tower moments of ''AB3'' bridge</span> | <span style="text-align: center; font-size: 75%;">'''(c)''' Tower moments of ''AB3'' bridge</span> | ||
| − | | style="vertical-align: top;width: 47%;"| [[Image:draft_Samper_432909089-image185.png|264px]] | + | | style="vertical-align: top;width: 47%;"|[[Image:draft_Samper_432909089-monograph-image185.png|264px]] |
<span style="text-align: center; font-size: 75%;">'''(d)''' Deck moments of ''AB3'' bridge</span> | <span style="text-align: center; font-size: 75%;">'''(d)''' Deck moments of ''AB3'' bridge</span> | ||
|- | |- | ||
| − | | style="vertical-align: top;width: | + | | style="vertical-align: top;width: 52%;"|[[Image:draft_Samper_432909089-monograph-image186.jpeg|288px]] |
<span style="text-align: center; font-size: 75%;">'''(e)''' Tower moments of ''AR1'' bridge</span> | <span style="text-align: center; font-size: 75%;">'''(e)''' Tower moments of ''AR1'' bridge</span> | ||
| − | | style="vertical-align: top;width: 47%;"| [[Image:draft_Samper_432909089-image187.jpeg|264px]] | + | | style="vertical-align: top;width: 47%;"|[[Image:draft_Samper_432909089-monograph-image187.jpeg|264px]] |
<span style="text-align: center; font-size: 75%;">'''(f)''' Deck moments of ''AR1'' bridge</span> | <span style="text-align: center; font-size: 75%;">'''(f)''' Deck moments of ''AR1'' bridge</span> | ||
|- | |- | ||
| − | | style="vertical-align: top;width: | + | | style="vertical-align: top;width: 52%;"|[[Image:draft_Samper_432909089-monograph-image188.jpeg|294px]] |
<span style="text-align: center; font-size: 75%;">'''(g)''' Tower moments of ''AR3'' bridge</span> | <span style="text-align: center; font-size: 75%;">'''(g)''' Tower moments of ''AR3'' bridge</span> | ||
| − | | style="vertical-align: top;width: 47%;"| [[Image:draft_Samper_432909089-image189.jpeg|264px]] | + | | style="vertical-align: top;width: 47%;"|[[Image:draft_Samper_432909089-monograph-image189.jpeg|264px]] |
<span style="text-align: center; font-size: 75%;">'''(h)''' Deck moments of ''AR3'' bridge</span> | <span style="text-align: center; font-size: 75%;">'''(h)''' Deck moments of ''AR3'' bridge</span> | ||
| Line 3,565: | Line 3,446: | ||
{| style="width: 100%;" | {| style="width: 100%;" | ||
|- | |- | ||
| − | | style="text-align: center;vertical-align: top;width: 49%;"| [[Image:draft_Samper_432909089-image190.png|276px]] | + | | style="text-align: center;vertical-align: top;width: 49%;"|[[Image:draft_Samper_432909089-monograph-image190.png|276px]] |
<span style="text-align: center; font-size: 75%;">'''(a)''' Tower moments of ''AB2'' bridge</span> | <span style="text-align: center; font-size: 75%;">'''(a)''' Tower moments of ''AB2'' bridge</span> | ||
| − | | style="vertical-align: top;width: | + | | style="vertical-align: top;width: 50%;"|[[Image:draft_Samper_432909089-monograph-image191.png|282px]] |
<span style="text-align: center; font-size: 75%;">'''(b)''' Deck moments of ''AB2'' bridge</span> | <span style="text-align: center; font-size: 75%;">'''(b)''' Deck moments of ''AB2'' bridge</span> | ||
|- | |- | ||
| − | | style="vertical-align: top;width: 49%;"| [[Image:draft_Samper_432909089-image192.jpeg|282px]] | + | | style="vertical-align: top;width: 49%;"|[[Image:draft_Samper_432909089-monograph-image192.jpeg|282px]] |
<span style="text-align: center; font-size: 75%;">'''(c)''' Tower moments of ''AB4'' bridge</span> | <span style="text-align: center; font-size: 75%;">'''(c)''' Tower moments of ''AB4'' bridge</span> | ||
| − | | style="vertical-align: top;width: | + | | style="vertical-align: top;width: 50%;"|[[Image:draft_Samper_432909089-monograph-image193.jpeg|288px]] |
<span style="text-align: center; font-size: 75%;">'''(d)''' Deck moments of ''AB4'' bridge</span> | <span style="text-align: center; font-size: 75%;">'''(d)''' Deck moments of ''AB4'' bridge</span> | ||
| Line 3,583: | Line 3,464: | ||
|- | |- | ||
| − | | style="vertical-align: top;width: 49%;"| [[Image:draft_Samper_432909089-image194.jpeg|282px]] | + | | style="vertical-align: top;width: 49%;"|[[Image:draft_Samper_432909089-monograph-image194.jpeg|282px]] |
<span style="text-align: center; font-size: 75%;">'''(e)''' Tower moments of ''AR2'' bridge</span> | <span style="text-align: center; font-size: 75%;">'''(e)''' Tower moments of ''AR2'' bridge</span> | ||
| − | | style="vertical-align: top;width: | + | | style="vertical-align: top;width: 50%;"|[[Image:draft_Samper_432909089-monograph-image195.jpeg|294px]] |
<span style="text-align: center; font-size: 75%;">'''(f)''' Deck moments of ''AR2'' bridge</span> | <span style="text-align: center; font-size: 75%;">'''(f)''' Deck moments of ''AR2'' bridge</span> | ||
| Line 3,594: | Line 3,475: | ||
|- | |- | ||
| − | | style="vertical-align: top;width: 49%;"| [[Image:draft_Samper_432909089-image196.png|282px]] | + | | style="vertical-align: top;width: 49%;"|[[Image:draft_Samper_432909089-monograph-image196.png|282px]] |
<span style="text-align: center; font-size: 75%;">'''(g)''' Tower moments of ''AR4'' bridge</span> | <span style="text-align: center; font-size: 75%;">'''(g)''' Tower moments of ''AR4'' bridge</span> | ||
| − | | style="vertical-align: top;width: | + | | style="vertical-align: top;width: 50%;"|[[Image:draft_Samper_432909089-monograph-image197.png|288px]] |
<span style="text-align: center; font-size: 75%;">'''(h)''' Deck moments of ''AR4'' bridge</span> | <span style="text-align: center; font-size: 75%;">'''(h)''' Deck moments of ''AR4'' bridge</span> | ||
| Line 3,894: | Line 3,775: | ||
<span style="text-align: center; font-size: 75%;"><sup>a</sup> At the tower base <sup>c</sup> Near the mid-span <sup>e</sup> Out-of-plane</span> | <span style="text-align: center; font-size: 75%;"><sup>a</sup> At the tower base <sup>c</sup> Near the mid-span <sup>e</sup> Out-of-plane</span> | ||
| − | <sup>b</sup> At the tower-deck connection <sup>d</sup> In the bridge plane <sup>f</sup> At the upper strut level | + | <span style="text-align: center; font-size: 75%;"><sup>b</sup> At the tower-deck connection <sup>d</sup> In the bridge plane <sup>f</sup> At the upper strut level</span> |
- Implies compression | - Implies compression | ||
| Line 4,004: | Line 3,885: | ||
| − | :<big> | + | :<big>3.6 Effect of Variation of the Stay Prestressing Forces on the Seismic Response of Cable-Stayed Bridges</big> |
In order to investigate if static variations of the stay prestressing forces of cable-stayed bridges are important regarding their seismic response, two bridge models were considered to simulate this effect. ''AB1'' and ''AR4 ''bridges were employed in this study, because they are representative of extreme cases of all the analyzed bridges in this work. | In order to investigate if static variations of the stay prestressing forces of cable-stayed bridges are important regarding their seismic response, two bridge models were considered to simulate this effect. ''AB1'' and ''AR4 ''bridges were employed in this study, because they are representative of extreme cases of all the analyzed bridges in this work. | ||
| Line 4,020: | Line 3,901: | ||
| colspan='9' style="border-top: 2pt solid black;border-left: 1pt solid black;border-bottom: 1pt solid black;border-right: 1pt solid black;text-align: center;"|<span style="text-align: center; font-size: 75%;">'''Stay Prestressing Forces [kN].'''</span> | | colspan='9' style="border-top: 2pt solid black;border-left: 1pt solid black;border-bottom: 1pt solid black;border-right: 1pt solid black;text-align: center;"|<span style="text-align: center; font-size: 75%;">'''Stay Prestressing Forces [kN].'''</span> | ||
|- | |- | ||
| − | | rowspan='8' style="border-top: 1pt solid black;border-left: 1pt solid black;border-right: 1pt solid black;text-align: center;vertical-align: top;"|<span style="text-align: center; font-size: 75%;">''' [[Image:draft_Samper_432909089-image198.png|216px]] '''</span> | + | | rowspan='8' style="border-top: 1pt solid black;border-left: 1pt solid black;border-right: 1pt solid black;text-align: center;vertical-align: top;"|<span style="text-align: center; font-size: 75%;">''' [[Image:draft_Samper_432909089-monograph-image198.png|216px]] '''</span> |
<span style="text-align: center; font-size: 75%;">'''(a) ''' ''AB1''- Original Load Condition</span> | <span style="text-align: center; font-size: 75%;">'''(a) ''' ''AB1''- Original Load Condition</span> | ||
| Line 4,103: | Line 3,984: | ||
| style="border-left: 1pt solid black;border-bottom: 1pt solid black;border-right: 1pt solid black;text-align: center;vertical-align: top;"| | | style="border-left: 1pt solid black;border-bottom: 1pt solid black;border-right: 1pt solid black;text-align: center;vertical-align: top;"| | ||
|- | |- | ||
| − | | rowspan='8' style="border-top: 1pt solid black;border-left: 1pt solid black;border-right: 1pt solid black;text-align: center;vertical-align: top;"|<span style="text-align: center; font-size: 75%;">''' [[Image:draft_Samper_432909089-image198.png|216px]] '''</span> | + | | rowspan='8' style="border-top: 1pt solid black;border-left: 1pt solid black;border-right: 1pt solid black;text-align: center;vertical-align: top;"|<span style="text-align: center; font-size: 75%;">''' [[Image:draft_Samper_432909089-monograph-image198.png|216px]] '''</span> |
<span style="text-align: center; font-size: 75%;">'''(b)''' ''AB1'' – Optimal Load Condition</span> | <span style="text-align: center; font-size: 75%;">'''(b)''' ''AB1'' – Optimal Load Condition</span> | ||
| Line 4,186: | Line 4,067: | ||
| style="border-left: 1pt solid black;border-bottom: 1pt solid black;border-right: 1pt solid black;text-align: center;vertical-align: top;"| | | style="border-left: 1pt solid black;border-bottom: 1pt solid black;border-right: 1pt solid black;text-align: center;vertical-align: top;"| | ||
|- | |- | ||
| − | | rowspan='8' style="border-top: 1pt solid black;border-left: 1pt solid black;border-right: 1pt solid black;text-align: center;vertical-align: top;"|''' [[Image:draft_Samper_432909089-image199.png|210px]] ''' | + | | rowspan='8' style="border-top: 1pt solid black;border-left: 1pt solid black;border-right: 1pt solid black;text-align: center;vertical-align: top;"|''' [[Image:draft_Samper_432909089-monograph-image199.png|210px]] ''' |
<span style="text-align: center; font-size: 75%;">'''(c)''' '' AR4'' – Original Load Conditio'''n'''</span> | <span style="text-align: center; font-size: 75%;">'''(c)''' '' AR4'' – Original Load Conditio'''n'''</span> | ||
| Line 4,269: | Line 4,150: | ||
| style="border-left: 1pt solid black;border-bottom: 1pt solid black;border-right: 1pt solid black;text-align: center;vertical-align: top;"| | | style="border-left: 1pt solid black;border-bottom: 1pt solid black;border-right: 1pt solid black;text-align: center;vertical-align: top;"| | ||
|- | |- | ||
| − | | rowspan='8' style="border-top: 1pt solid black;border-left: 1pt solid black;border-right: 1pt solid black;text-align: center;vertical-align: top;"|''' [[Image:draft_Samper_432909089-image199.png|210px]] ''' | + | | rowspan='8' style="border-top: 1pt solid black;border-left: 1pt solid black;border-right: 1pt solid black;text-align: center;vertical-align: top;"|''' [[Image:draft_Samper_432909089-monograph-image199.png|210px]] ''' |
<span style="text-align: center; font-size: 75%;">'''(d)''' '' AR4'' – Optimal Load Condition</span> | <span style="text-align: center; font-size: 75%;">'''(d)''' '' AR4'' – Optimal Load Condition</span> | ||
| Line 4,362: | Line 4,243: | ||
{| style="width: 100%;margin: 1em auto 0.1em auto;" | {| style="width: 100%;margin: 1em auto 0.1em auto;" | ||
|- | |- | ||
| − | | style="text-align: center;vertical-align: top;"|<span style="text-align: center; font-size: 75%;">''' [[Image:draft_Samper_432909089-image200.png|192px]] '''</span> | + | | style="text-align: center;vertical-align: top;"|<span style="text-align: center; font-size: 75%;">''' [[Image:draft_Samper_432909089-monograph-image200.png|192px]] '''</span> |
'''Fig. 3.37''' Longitudinal displacements of the tower –''AB1'' Bridge | '''Fig. 3.37''' Longitudinal displacements of the tower –''AB1'' Bridge | ||
| − | | style="text-align: center;vertical-align: top;width: | + | | style="text-align: center;vertical-align: top;width: 51%;"|[[Image:draft_Samper_432909089-monograph-image201.png|198px]] |
'''Fig. 3.38 '''Longitudinal displacements of the tower –''AR4'' Bridge | '''Fig. 3.38 '''Longitudinal displacements of the tower –''AR4'' Bridge | ||
| Line 4,373: | Line 4,254: | ||
{| style="width: 100%;margin: 1em auto 0.1em auto;" | {| style="width: 100%;margin: 1em auto 0.1em auto;" | ||
|- | |- | ||
| − | | style="text-align: center;vertical-align: top;width: | + | | style="text-align: center;vertical-align: top;width: 48%;"|[[Image:draft_Samper_432909089-monograph-image202.png|288px]] |
'''Fig. 3.39''' Vertical displacements of the deck –''AB1'' Bridge | '''Fig. 3.39''' Vertical displacements of the deck –''AB1'' Bridge | ||
| − | | style="text-align: center;vertical-align: top;"|<span style="text-align: center; font-size: 75%;">''' [[Image:draft_Samper_432909089-image203.png|306px]] '''</span> | + | | style="text-align: center;vertical-align: top;"|<span style="text-align: center; font-size: 75%;">''' [[Image:draft_Samper_432909089-monograph-image203.png|306px]] '''</span> |
'''Fig. 3.40''' Vertical displacements of the deck –''AR4'' Bridge | '''Fig. 3.40''' Vertical displacements of the deck –''AR4'' Bridge | ||
| Line 4,390: | Line 4,271: | ||
{| style="width: 100%;margin: 1em auto 0.1em auto;" | {| style="width: 100%;margin: 1em auto 0.1em auto;" | ||
|- | |- | ||
| − | | style="text-align: center;vertical-align: top;width: | + | | style="text-align: center;vertical-align: top;width: 49%;"|[[Image:draft_Samper_432909089-monograph-image204.png|192px]] |
'''Fig. 3.41''' Compressive forces of the tower –''AB1'' Bridge | '''Fig. 3.41''' Compressive forces of the tower –''AB1'' Bridge | ||
| − | | colspan='2' style="text-align: center;vertical-align: top;width: | + | | colspan='2' style="text-align: center;vertical-align: top;width: 50%;"|[[Image:draft_Samper_432909089-monograph-image205-c.png|192px]] |
'''Fig. 3.42''' Compressive forces of the tower –''AR4'' Bridge | '''Fig. 3.42''' Compressive forces of the tower –''AR4'' Bridge | ||
|- | |- | ||
| − | | colspan='2' style="text-align: center;vertical-align: top;width: | + | | colspan='2' style="text-align: center;vertical-align: top;width: 50%;"|[[Image:draft_Samper_432909089-monograph-image206-c.png|300px]] |
'''Fig. 3.43''' Axial forces of the deck –''AB1'' Bridge | '''Fig. 3.43''' Axial forces of the deck –''AB1'' Bridge | ||
| − | | style="text-align: center;vertical-align: top;width: | + | | style="text-align: center;vertical-align: top;width: 49%;"|[[Image:draft_Samper_432909089-monograph-image207.png|300px]] |
'''Fig. 3.44''' Axial forces of the deck –''AR4'' Bridge | '''Fig. 3.44''' Axial forces of the deck –''AR4'' Bridge | ||
| Line 4,410: | Line 4,291: | ||
{| style="width: 100%;" | {| style="width: 100%;" | ||
|- | |- | ||
| − | | style="text-align: center;vertical-align: top;width: | + | | style="text-align: center;vertical-align: top;width: 48%;"|[[Image:draft_Samper_432909089-monograph-image208-c.png|288px]] |
<span style="text-align: center; font-size: 75%;">'''(a)''' Bending moments of the towers – original load condition</span> | <span style="text-align: center; font-size: 75%;">'''(a)''' Bending moments of the towers – original load condition</span> | ||
| − | | style="text-align: center;vertical-align: top;width: | + | | style="text-align: center;vertical-align: top;width: 51%;"|[[Image:draft_Samper_432909089-monograph-image209.png|294px]] |
<span style="text-align: center; font-size: 75%;">'''(b) '''Bending moments of the towers – optimal load condition</span> | <span style="text-align: center; font-size: 75%;">'''(b) '''Bending moments of the towers – optimal load condition</span> | ||
|- | |- | ||
| − | | style="text-align: center;vertical-align: top;width: | + | | style="text-align: center;vertical-align: top;width: 48%;"|[[Image:draft_Samper_432909089-monograph-image210.png|306px]] |
<span style="text-align: center; font-size: 75%;">'''(c)''' Deck bending moments – original load cond.</span> | <span style="text-align: center; font-size: 75%;">'''(c)''' Deck bending moments – original load cond.</span> | ||
| − | | style="text-align: center;vertical-align: top;width: | + | | style="text-align: center;vertical-align: top;width: 51%;"|[[Image:draft_Samper_432909089-monograph-image211-c.png|300px]] |
<span style="text-align: center; font-size: 75%;">'''(d)''' Deck bending moments – optimal load cond.</span> | <span style="text-align: center; font-size: 75%;">'''(d)''' Deck bending moments – optimal load cond.</span> | ||
| Line 4,433: | Line 4,314: | ||
{| style="width: 100%;" | {| style="width: 100%;" | ||
|- | |- | ||
| − | | style="text-align: center;vertical-align: top;width: | + | | style="text-align: center;vertical-align: top;width: 48%;"|[[Image:draft_Samper_432909089-monograph-image212.png|306px]] |
<span style="text-align: center; font-size: 75%;">'''(a)''' Tower bending moments – original load cond.</span> | <span style="text-align: center; font-size: 75%;">'''(a)''' Tower bending moments – original load cond.</span> | ||
| − | | style="text-align: center;vertical-align: top;width: | + | | style="text-align: center;vertical-align: top;width: 51%;"|[[Image:draft_Samper_432909089-monograph-image213.png|288px]] |
<span style="text-align: center; font-size: 75%;">'''(b)''' Tower bending moments – optimal load cond.</span> | <span style="text-align: center; font-size: 75%;">'''(b)''' Tower bending moments – optimal load cond.</span> | ||
|- | |- | ||
| − | | style="text-align: center;vertical-align: top;width: | + | | style="text-align: center;vertical-align: top;width: 48%;"|[[Image:draft_Samper_432909089-monograph-image214.png|306px]] |
<span style="text-align: center; font-size: 75%;">'''(c)''' Deck bending moments – original load cond.</span> | <span style="text-align: center; font-size: 75%;">'''(c)''' Deck bending moments – original load cond.</span> | ||
| − | | style="text-align: center;vertical-align: top;width: | + | | style="text-align: center;vertical-align: top;width: 51%;"|[[Image:draft_Samper_432909089-monograph-image215.png|288px]] |
<span style="text-align: center; font-size: 75%;">'''(d)''' Deck bending moments – optimal load cond.</span> | <span style="text-align: center; font-size: 75%;">'''(d)''' Deck bending moments – optimal load cond.</span> | ||
| Line 4,588: | Line 4,469: | ||
{| style="width: 100%;" | {| style="width: 100%;" | ||
|- | |- | ||
| − | | style="text-align: center;vertical-align: top;width: | + | | style="text-align: center;vertical-align: top;width: 58%;"|[[Image:draft_Samper_432909089-monograph-image216.png|336px]] |
'''Fig. 3.47''' Average Variation of the Seismic Response | '''Fig. 3.47''' Average Variation of the Seismic Response | ||
| Line 4,599: | Line 4,480: | ||
As a conclusion, this study shows that low-to-moderate variations of the stay prestressing forces on cable-stayed bridges imply low variations of the seismic response. These variations of the seismic response are not very different if the stay cable layout, stay spacing or deck level is changed, and only specific differences regarding the shape of the internal forces or displacements can be found, and specially for the deck. The main variations of the seismic response come from the vertical deflections and internal forces of the deck, as long as variations for the seismic response of the towers are less sensitive, especially the longitudinal displacements and axial forces. | As a conclusion, this study shows that low-to-moderate variations of the stay prestressing forces on cable-stayed bridges imply low variations of the seismic response. These variations of the seismic response are not very different if the stay cable layout, stay spacing or deck level is changed, and only specific differences regarding the shape of the internal forces or displacements can be found, and specially for the deck. The main variations of the seismic response come from the vertical deflections and internal forces of the deck, as long as variations for the seismic response of the towers are less sensitive, especially the longitudinal displacements and axial forces. | ||
| − | |||
| − | :<big> | + | :<big>3.7 Seismic Response Applying Nonlinear Direct Integration Time History Analysis</big> |
| + | |||
| + | :<big>3.7.1 General Considerations and Selected Models</big> | ||
All the subsequent analyses consider the application of step-by-step strategies to solve the cable-stayed bridge models of this work, considering that nonlinear direct integration time history analysis is the best alternative to accurately represent the complex nature of such structures. The structures are solved using the code SAP2000 [Computers & Structures, 2007], considering all the nonlinearities available and previously explained. In spite of the tremendous computational effort involved, this methodology is the best suitable, and application of the Hilber-Hughes-Taylor-α integration procedure seems to be more adequate [Hilber ''et al'', 1977], according to the explanations of Appendix A. | All the subsequent analyses consider the application of step-by-step strategies to solve the cable-stayed bridge models of this work, considering that nonlinear direct integration time history analysis is the best alternative to accurately represent the complex nature of such structures. The structures are solved using the code SAP2000 [Computers & Structures, 2007], considering all the nonlinearities available and previously explained. In spite of the tremendous computational effort involved, this methodology is the best suitable, and application of the Hilber-Hughes-Taylor-α integration procedure seems to be more adequate [Hilber ''et al'', 1977], according to the explanations of Appendix A. | ||
| Line 4,607: | Line 4,489: | ||
Response spectrum analysis of the bridge models left clear that the largest displacements are obtained with the highest deck level, and the worse condition for the internal forces is obtained with the fan pattern bridges. Although the modal analysis of the bridges showed that higher order modes can be important especially on bridges with low deck level, structures with high deck level may experience important geometric nonlinear effects, especially large nonlinear axial force – bending moment interaction for the tower and longitudinal girder elements as well as large nonlinear behaviour due to the geometric change caused by the large displacements on the whole structure. On the other hand, the deck level is generally conditioned by functional aspects, constituting a geometric parameter that cannot be modified. For those reasons, the worse condition occurs with bridges with high deck level, and only those structures are considered in the subsequent analyses. Even through the effect of the stay spacing can be important, the response spectrum analysis gave a good idea about the incidence of this parameter on the seismic response of the bridge models, and it is not necessary to consider its variation during the nonlinear time history analysis. Thus, according to the above explained and in order to avoid the large information generated and the excessive computer effort due to the application of the nonlinear time history analysis if all cases are considered, only two models are studied: bridges ''AB4 ''and ''AR4'', that is to say, fan and harp pattern bridges with 12.4 m-stay spacing (hollow box type deck) and 60 m-deck level. Those structures are considered as critical, especially the ''AB4 ''model. Although ''AR4'' bridge seems to be not very critical, its consideration permits an adequate analysis between fan and harp pattern layouts. Moreover, those structures contain less joints and elements than the other models, reducing the computer time that can be crucial in a nonlinear time history analysis. In some sense, influence of the bridge configuration on the seismic response was analyzed applying the response spectrum method. Thus, the next pages are focused on the nonlinear seismic response of the bridges for different input ground motion typologies, and taking into account the stay cable layout, with and without the incorporation of additional energy dissipation devices. | Response spectrum analysis of the bridge models left clear that the largest displacements are obtained with the highest deck level, and the worse condition for the internal forces is obtained with the fan pattern bridges. Although the modal analysis of the bridges showed that higher order modes can be important especially on bridges with low deck level, structures with high deck level may experience important geometric nonlinear effects, especially large nonlinear axial force – bending moment interaction for the tower and longitudinal girder elements as well as large nonlinear behaviour due to the geometric change caused by the large displacements on the whole structure. On the other hand, the deck level is generally conditioned by functional aspects, constituting a geometric parameter that cannot be modified. For those reasons, the worse condition occurs with bridges with high deck level, and only those structures are considered in the subsequent analyses. Even through the effect of the stay spacing can be important, the response spectrum analysis gave a good idea about the incidence of this parameter on the seismic response of the bridge models, and it is not necessary to consider its variation during the nonlinear time history analysis. Thus, according to the above explained and in order to avoid the large information generated and the excessive computer effort due to the application of the nonlinear time history analysis if all cases are considered, only two models are studied: bridges ''AB4 ''and ''AR4'', that is to say, fan and harp pattern bridges with 12.4 m-stay spacing (hollow box type deck) and 60 m-deck level. Those structures are considered as critical, especially the ''AB4 ''model. Although ''AR4'' bridge seems to be not very critical, its consideration permits an adequate analysis between fan and harp pattern layouts. Moreover, those structures contain less joints and elements than the other models, reducing the computer time that can be crucial in a nonlinear time history analysis. In some sense, influence of the bridge configuration on the seismic response was analyzed applying the response spectrum method. Thus, the next pages are focused on the nonlinear seismic response of the bridges for different input ground motion typologies, and taking into account the stay cable layout, with and without the incorporation of additional energy dissipation devices. | ||
| − | The geometry, structural modelling, mechanical properties, material data as well as the loads and analysis cases were well explained. Now, the seismic input is considered by use of acceleration time histories and taking into account the largest spectral velocity of each event in the period range of interest, applied to the principal direction of the structures as measure of the seismic hazard, in order to consider the velocity-sensitivity of the bridge models. The complex damping mechanism is simplified here and considered as only dependent on the modal shapes, according to Kawashima and Unjoh (1991). In this sense, proportional damping to stiffness and mass is considered in the direct integration analysis (Rayleigh’s damping), that is to say, | + | The geometry, structural modelling, mechanical properties, material data as well as the loads and analysis cases were well explained. Now, the seismic input is considered by use of acceleration time histories and taking into account the largest spectral velocity of each event in the period range of interest, applied to the principal direction of the structures as measure of the seismic hazard, in order to consider the velocity-sensitivity of the bridge models. The complex damping mechanism is simplified here and considered as only dependent on the modal shapes, according to Kawashima and Unjoh (1991). In this sense, proportional damping to stiffness and mass is considered in the direct integration analysis (Rayleigh’s damping), that is to say, [[Image:draft_Samper_432909089-monograph-image217.png|102px]] , in which ''C'' is the damping matrix, ''M'' is the mass matrix'', K'' is the stiffness matrix, ''α'' is the mass proportional coefficient, and ''β'' is the stiffness proportional coefficient. For the selected bridges, ''α'' = 0.0734 and ''β'' = 0.000513 values were used. |
For the step-by-step integration of equations of motion, 20 analysis cases involving more than 13 hours of computer time for the far-fault analysis, and more than 48 hours of computer time for the near-fault analysis were required. An estimation of more than 120 hours of computer time including trial-and-error tests, parameter adjusts and convergence trials were necessary for successful and accurate results. Although the Hilber-Hughes-Taylor-α method is unconditionally stable for linear analysis, in the case of the selected models sometimes the convergence was difficult, and a lot of error-and-trial tests were necessary to reach an adequate convergence. In this sense, the far-fault analysis was easier, with the exception of some analysis cases for ''AR4'' bridge''. ''For the case of the near-fault analysis, the convergence is more complicated, aspect that is reflected in the enormous computer time required, because of the modifications necessary in the convergence parameters. Those experiences reflect the highly nonlinear behaviour of the models and the strong incidence of the long-period velocity-pulses of the near-fault ground motions, aspect enlarged in Appendix A. In a recent publication, Chen and Ricles (2008b) expose the stability conditions of direct integration algorithms for nonlinear analysis. | For the step-by-step integration of equations of motion, 20 analysis cases involving more than 13 hours of computer time for the far-fault analysis, and more than 48 hours of computer time for the near-fault analysis were required. An estimation of more than 120 hours of computer time including trial-and-error tests, parameter adjusts and convergence trials were necessary for successful and accurate results. Although the Hilber-Hughes-Taylor-α method is unconditionally stable for linear analysis, in the case of the selected models sometimes the convergence was difficult, and a lot of error-and-trial tests were necessary to reach an adequate convergence. In this sense, the far-fault analysis was easier, with the exception of some analysis cases for ''AR4'' bridge''. ''For the case of the near-fault analysis, the convergence is more complicated, aspect that is reflected in the enormous computer time required, because of the modifications necessary in the convergence parameters. Those experiences reflect the highly nonlinear behaviour of the models and the strong incidence of the long-period velocity-pulses of the near-fault ground motions, aspect enlarged in Appendix A. In a recent publication, Chen and Ricles (2008b) expose the stability conditions of direct integration algorithms for nonlinear analysis. | ||
| Line 4,613: | Line 4,495: | ||
In order to control the convergence of the models, several time integration parameters were taken into account. The ''numerical damping'' of the Hilber-Hughes-Taylor-α method was selected as -0.2 for all the analysis cases. This value adequately controls the instability due to the high frequency content, with an acceptable accuracy. To control the iteration and sub-stepping process, some important parameters were considered. The ''maximum sub-step size'' reflects the upper limit on the step size used for integration. The ''minimum sub-step size'' limits the smallest sub-step size, in order to stop the analysis bellow this limit indicating that convergence has failed. The ''maximum iterations per sub-step'' controls the number of iterations allowed in a step before the use of smaller sub-steps, a number usually higher for the analysis of cable structures. The ''iteration convergence tolerance'' compares the magnitude of force error with the magnitude of the force acting on the structure to guarantee that equilibrium is achieved at each step of the analysis, a value that usually decreases when large-displacement effects are considered. Anyway, for all the analysis cases in this work, time-step size of 0.02 sec was employed. | In order to control the convergence of the models, several time integration parameters were taken into account. The ''numerical damping'' of the Hilber-Hughes-Taylor-α method was selected as -0.2 for all the analysis cases. This value adequately controls the instability due to the high frequency content, with an acceptable accuracy. To control the iteration and sub-stepping process, some important parameters were considered. The ''maximum sub-step size'' reflects the upper limit on the step size used for integration. The ''minimum sub-step size'' limits the smallest sub-step size, in order to stop the analysis bellow this limit indicating that convergence has failed. The ''maximum iterations per sub-step'' controls the number of iterations allowed in a step before the use of smaller sub-steps, a number usually higher for the analysis of cable structures. The ''iteration convergence tolerance'' compares the magnitude of force error with the magnitude of the force acting on the structure to guarantee that equilibrium is achieved at each step of the analysis, a value that usually decreases when large-displacement effects are considered. Anyway, for all the analysis cases in this work, time-step size of 0.02 sec was employed. | ||
| − | :<big> | + | |
| + | :<big>3.7.2 Input Ground Motions</big> | ||
In order to consider different characteristics of the input ground motions in this research, earthquake records were divided into far-fault and near-fault ground motions depending on the source distance. For the analysis, a collection of 10 earthquake records was selected as input ground motion considering three components for each one. The number of earthquake events was selected to take into consideration the average of the response parameter in the assessment of the structural response, and according to Eurocode 8, Part 1, a minimum of 5 accelerograms is necessary for each case. Because of the structures are founded on bedrock, time histories need to be recorded on rock or hard soil, and for that reason, soil-structure interaction is not considered here. Regarding the record selection and according to the previously exposed, a collection of 5 artificial accelerograms compatible with response spectra defined by Eurocode 8 Part 2, were generated in order to analyze the far-fault effects. For near-fault ground motions, it is preferable to employ real acceleration records, because in this case that option may reflect in a better way the basic aspects of the complex nature of the near-source effects, including the incidence of forward rupture directivity (velocity pulse-type earthquakes). In fact, near-fault effects cannot be adequately described by uniform scaling of a fixed response spectral shape; the shape of the spectrum must become richer at long periods as the level of the spectrum increases [Somerville, 1997]. Although there are some investigations about the formulation and application of near-fault design spectra, this strategy is not clearly defined for bridges, and a lot of uncertainties are involved. In this sense, the works of Li and Zhu (2003) and Akkar and Gülkan (2003) propose and explain the procedure for implementation of near-fault design spectra on building design codes. In this research, the record selection for near-fault ground motions was made choosing the current practice to carefully select records that reflect the expected magnitude, distance and other characteristics of the source of the events that are in some sense most likely to threaten the structure. | In order to consider different characteristics of the input ground motions in this research, earthquake records were divided into far-fault and near-fault ground motions depending on the source distance. For the analysis, a collection of 10 earthquake records was selected as input ground motion considering three components for each one. The number of earthquake events was selected to take into consideration the average of the response parameter in the assessment of the structural response, and according to Eurocode 8, Part 1, a minimum of 5 accelerograms is necessary for each case. Because of the structures are founded on bedrock, time histories need to be recorded on rock or hard soil, and for that reason, soil-structure interaction is not considered here. Regarding the record selection and according to the previously exposed, a collection of 5 artificial accelerograms compatible with response spectra defined by Eurocode 8 Part 2, were generated in order to analyze the far-fault effects. For near-fault ground motions, it is preferable to employ real acceleration records, because in this case that option may reflect in a better way the basic aspects of the complex nature of the near-source effects, including the incidence of forward rupture directivity (velocity pulse-type earthquakes). In fact, near-fault effects cannot be adequately described by uniform scaling of a fixed response spectral shape; the shape of the spectrum must become richer at long periods as the level of the spectrum increases [Somerville, 1997]. Although there are some investigations about the formulation and application of near-fault design spectra, this strategy is not clearly defined for bridges, and a lot of uncertainties are involved. In this sense, the works of Li and Zhu (2003) and Akkar and Gülkan (2003) propose and explain the procedure for implementation of near-fault design spectra on building design codes. In this research, the record selection for near-fault ground motions was made choosing the current practice to carefully select records that reflect the expected magnitude, distance and other characteristics of the source of the events that are in some sense most likely to threaten the structure. | ||
| Line 4,627: | Line 4,510: | ||
{| style="width: 100%;border-collapse: collapse;" | {| style="width: 100%;border-collapse: collapse;" | ||
|- | |- | ||
| − | | style="vertical-align: top;"|'''Table 3.25''' Ground Motion Parameters for Far-Fault Events | + | | style="vertical-align: top;width: 40%;"|'''Table 3.25''' Ground Motion Parameters for Far-Fault Events |
{| style="width: 64%;margin: 1em auto 0.1em auto;border-collapse: collapse;" | {| style="width: 64%;margin: 1em auto 0.1em auto;border-collapse: collapse;" | ||
| Line 4,778: | Line 4,661: | ||
| − | | style="vertical-align: top;"|''R<sub>e</sub>'' is the closest distance to the fault rupture surface; ''t<sub>e</sub>'' is the effective duration of the strong motion (obtained using the Arias Intensity of the earthquake events) and ''PGA, PGV'' and ''PGD'' are the peak ground acceleration, velocity and displacement respectively. All these ground motion parameters were obtained using the code SeismoSignal [Seismosoft, 2006]. | + | | style="vertical-align: top;width: 60%;"|''R<sub>e</sub>'' is the closest distance to the fault rupture surface; ''t<sub>e</sub>'' is the effective duration of the strong motion (obtained using the Arias Intensity of the earthquake events) and ''PGA, PGV'' and ''PGD'' are the peak ground acceleration, velocity and displacement respectively. All these ground motion parameters were obtained using the code SeismoSignal [Seismosoft, 2006]. |
|} | |} | ||
| Line 4,956: | Line 4,839: | ||
<div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | ||
| − | [[Image:draft_Samper_432909089-image218.png|438px]] </div> | + | [[Image:draft_Samper_432909089-monograph-image218.png|438px]] </div> |
<div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | ||
| Line 4,964: | Line 4,847: | ||
<div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | ||
| − | [[Image:draft_Samper_432909089-image219.png|438px]] </div> | + | [[Image:draft_Samper_432909089-monograph-image219.png|438px]] </div> |
<div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | ||
'''Fig. 3.49''' Comparison of Horizontal Elastic Pseudo-velocity Response Spectra for Near-Fault Ground Motions</div> | '''Fig. 3.49''' Comparison of Horizontal Elastic Pseudo-velocity Response Spectra for Near-Fault Ground Motions</div> | ||
| − | :<big> | + | |
| + | :<big>3.7.3 Importance of Velocity Spectra on the Seismic Response of Long-Period Structures</big> | ||
Traditionally, the employ of the ''PGA'' or the effective ground acceleration as measure of the seismic hazard has been widely applied in the seismic analysis of structures, and worldwide implemented in the current seismic regulations. It is known that this approximation is inaccurate because additional parameters such as the frequency content, strong motion duration of the earthquake input and some additional parameters involved with the source can be important. The approximation of the ''PGA'' as measure of the seismic hazard sometimes works good mainly on short-period structures. However, in the case of long-period structures this approximation can be wrong, and structures could be more affected by velocities or even displacements. | Traditionally, the employ of the ''PGA'' or the effective ground acceleration as measure of the seismic hazard has been widely applied in the seismic analysis of structures, and worldwide implemented in the current seismic regulations. It is known that this approximation is inaccurate because additional parameters such as the frequency content, strong motion duration of the earthquake input and some additional parameters involved with the source can be important. The approximation of the ''PGA'' as measure of the seismic hazard sometimes works good mainly on short-period structures. However, in the case of long-period structures this approximation can be wrong, and structures could be more affected by velocities or even displacements. | ||
| Line 4,981: | Line 4,865: | ||
{| style="width: 100%;margin: 1em auto 0.1em auto;" | {| style="width: 100%;margin: 1em auto 0.1em auto;" | ||
|- | |- | ||
| − | | style="text-align: center;vertical-align: top;"|<span style="text-align: center; font-size: 75%;">''' [[Image:draft_Samper_432909089-image220.png|312px]] '''</span> | + | | style="text-align: center;vertical-align: top;"|<span style="text-align: center; font-size: 75%;">''' [[Image:draft_Samper_432909089-monograph-image220.png|312px]] '''</span> |
<span style="text-align: center; font-size: 75%;">'''(a)''' Pseudo-acceleration </span> | <span style="text-align: center; font-size: 75%;">'''(a)''' Pseudo-acceleration </span> | ||
| − | | style="text-align: center;vertical-align: top;width: | + | | style="text-align: center;vertical-align: top;width: 51%;"|[[Image:draft_Samper_432909089-monograph-image221.png|312px]] |
<span style="text-align: center; font-size: 75%;">'''(b)''' Pseudo-velocity </span> | <span style="text-align: center; font-size: 75%;">'''(b)''' Pseudo-velocity </span> | ||
| Line 4,995: | Line 4,879: | ||
{| style="width: 100%;margin: 1em auto 0.1em auto;" | {| style="width: 100%;margin: 1em auto 0.1em auto;" | ||
|- | |- | ||
| − | | style="text-align: center;vertical-align: top;"|<big>''' [[Image:draft_Samper_432909089-image222.png|312px]] '''</big> | + | | style="text-align: center;vertical-align: top;"|<big>''' [[Image:draft_Samper_432909089-monograph-image222.png|312px]] '''</big> |
<span style="text-align: center; font-size: 75%;">'''(a)''' Pseudo-acceleration</span> | <span style="text-align: center; font-size: 75%;">'''(a)''' Pseudo-acceleration</span> | ||
| − | | style="text-align: center;vertical-align: top;"|<span style="text-align: center; font-size: 75%;">''' [[Image:draft_Samper_432909089-image223.png|312px]] '''</span> | + | | style="text-align: center;vertical-align: top;"|<span style="text-align: center; font-size: 75%;">''' [[Image:draft_Samper_432909089-monograph-image223.png|312px]] '''</span> |
<span style="text-align: center; font-size: 75%;">'''(b)''' Pseudo-velocity</span> | <span style="text-align: center; font-size: 75%;">'''(b)''' Pseudo-velocity</span> | ||
| Line 5,086: | Line 4,970: | ||
<span style="text-align: center; font-size: 75%;">Mw: Moment magnitude; Re: Closest distance to the fault rupture; t: Duration of the event</span> | <span style="text-align: center; font-size: 75%;">Mw: Moment magnitude; Re: Closest distance to the fault rupture; t: Duration of the event</span> | ||
| − | te: Effective duration of the strong-motion; PGA: Peak ground accel. PGV: Peak ground vel. | + | <span style="text-align: center; font-size: 75%;">te: Effective duration of the strong-motion; PGA: Peak ground accel. PGV: Peak ground vel.</span> |
Table 3.27 shows that both stations were very close to the fault rupture, with short effective durations of the strong motion (obtained here using the Arias intensity of the earthquake components). Important ground accelerations for all the components are appreciated, and especially for San Fernando event, with ground accelerations higher than ''1.0g'' for the horizontal components. Important ground velocities are observed for the horizontal components, especially the components 260º (Landers) and 164º (San Fernando), coincidently with the components for which the maximum spectral velocities were observed. Those components experience ground velocities higher than 1 m/sec. | Table 3.27 shows that both stations were very close to the fault rupture, with short effective durations of the strong motion (obtained here using the Arias intensity of the earthquake components). Important ground accelerations for all the components are appreciated, and especially for San Fernando event, with ground accelerations higher than ''1.0g'' for the horizontal components. Important ground velocities are observed for the horizontal components, especially the components 260º (Landers) and 164º (San Fernando), coincidently with the components for which the maximum spectral velocities were observed. Those components experience ground velocities higher than 1 m/sec. | ||
| Line 5,094: | Line 4,978: | ||
{| style="width: 100%;margin: 1em auto 0.1em auto;" | {| style="width: 100%;margin: 1em auto 0.1em auto;" | ||
|- | |- | ||
| − | | style="text-align: center;vertical-align: top;width: | + | | style="text-align: center;vertical-align: top;width: 50%;"|[[Image:draft_Samper_432909089-monograph-image224.png|300px]] |
<span style="text-align: center; font-size: 75%;">'''(a)''' Landers, Lucerne station</span> | <span style="text-align: center; font-size: 75%;">'''(a)''' Landers, Lucerne station</span> | ||
| − | | style="text-align: center;vertical-align: top;width: | + | | style="text-align: center;vertical-align: top;width: 50%;"|[[Image:draft_Samper_432909089-monograph-image225.png|300px]] |
<span style="text-align: center; font-size: 75%;">'''(b)''' San Fernando, Pacoima Dam Abut. station</span> | <span style="text-align: center; font-size: 75%;">'''(b)''' San Fernando, Pacoima Dam Abut. station</span> | ||
| Line 5,108: | Line 4,992: | ||
{| style="width: 100%;margin: 1em auto 0.1em auto;" | {| style="width: 100%;margin: 1em auto 0.1em auto;" | ||
|- | |- | ||
| − | | style="text-align: center;vertical-align: top;width: | + | | style="text-align: center;vertical-align: top;width: 51%;"|[[Image:draft_Samper_432909089-monograph-image226.png|300px]] |
<span style="text-align: center; font-size: 75%;">'''(a)''' Landers, Lucerne station</span> | <span style="text-align: center; font-size: 75%;">'''(a)''' Landers, Lucerne station</span> | ||
| − | | style="text-align: center;vertical-align: top;width: | + | | style="text-align: center;vertical-align: top;width: 48%;"|[[Image:draft_Samper_432909089-monograph-image227.png|300px]] |
<span style="text-align: center; font-size: 75%;">'''(b)''' San Fernando, Pacoima Dam Abut. station</span> | <span style="text-align: center; font-size: 75%;">'''(b)''' San Fernando, Pacoima Dam Abut. station</span> | ||
| Line 5,122: | Line 5,006: | ||
{| style="width: 100%;margin: 1em auto 0.1em auto;" | {| style="width: 100%;margin: 1em auto 0.1em auto;" | ||
|- | |- | ||
| − | | style="text-align: center;vertical-align: top;width: | + | | style="text-align: center;vertical-align: top;width: 50%;"|[[Image:draft_Samper_432909089-monograph-image228.png|300px]] |
<span style="text-align: center; font-size: 75%;">'''(a)''' Landers, Lucerne station</span> | <span style="text-align: center; font-size: 75%;">'''(a)''' Landers, Lucerne station</span> | ||
| − | | style="text-align: center;vertical-align: top;width: | + | | style="text-align: center;vertical-align: top;width: 50%;"|[[Image:draft_Samper_432909089-monograph-image229.png|300px]] |
<span style="text-align: center; font-size: 75%;">'''(b)''' San Fernando, Pacoima Dam Abut. station</span> | <span style="text-align: center; font-size: 75%;">'''(b)''' San Fernando, Pacoima Dam Abut. station</span> | ||
| Line 5,140: | Line 5,024: | ||
Investigations regarding these matters have been focused on the need of having seismic design spectra for long-periods. It is known that velocity or displacement spectra obtained from direct conversion of acceleration spectra in most codes are unrealistic in both shape and amplitude, and for that reason, velocity or even displacement design spectra not obtained from acceleration spectra for long-periods have been proposed since the middle of the 90´s. The works of Trifunac (1995), Tolis (1999), Bommer (1999), Bommer ''et al'' (2000), Hu and Yu (2000) and Faccioli ''et al'' (2004) are some proposals of spectra for long-period structures. | Investigations regarding these matters have been focused on the need of having seismic design spectra for long-periods. It is known that velocity or displacement spectra obtained from direct conversion of acceleration spectra in most codes are unrealistic in both shape and amplitude, and for that reason, velocity or even displacement design spectra not obtained from acceleration spectra for long-periods have been proposed since the middle of the 90´s. The works of Trifunac (1995), Tolis (1999), Bommer (1999), Bommer ''et al'' (2000), Hu and Yu (2000) and Faccioli ''et al'' (2004) are some proposals of spectra for long-period structures. | ||
| − | :<big> | + | |
| + | :<big>3.7.4 Seismic Response Considering Far-fault Ground Motions</big> | ||
In the analysis of the bridge models considering far-fault ground motions, each orthogonal three-component event was applied with a time-step size of 0.02 sec. The time integration parameters to control the convergence were chosen in order to guarantee the stability conditions of the nonlinear analysis with an adequate accuracy. In this sense, the maximum and minimum sub-step size employed was zero, the maximum iterations per sub-step were 60 (for which an adequate accuracy using cable formulation was obtained in the nonlinear static analysis), and the iteration convergence tolerance was 1x10<sup>-4</sup>, for which adequate results were obtained in the large-displacement analyses. In general terms the convergence was easy to obtain in these cases, with the exception of some cases for the ''AR4'' model. | In the analysis of the bridge models considering far-fault ground motions, each orthogonal three-component event was applied with a time-step size of 0.02 sec. The time integration parameters to control the convergence were chosen in order to guarantee the stability conditions of the nonlinear analysis with an adequate accuracy. In this sense, the maximum and minimum sub-step size employed was zero, the maximum iterations per sub-step were 60 (for which an adequate accuracy using cable formulation was obtained in the nonlinear static analysis), and the iteration convergence tolerance was 1x10<sup>-4</sup>, for which adequate results were obtained in the large-displacement analyses. In general terms the convergence was easy to obtain in these cases, with the exception of some cases for the ''AR4'' model. | ||
| Line 5,150: | Line 5,035: | ||
{| style="width: 100%;margin: 1em auto 0.1em auto;" | {| style="width: 100%;margin: 1em auto 0.1em auto;" | ||
|- | |- | ||
| − | | style="text-align: center;vertical-align: top;width: 50%;"| [[Image:draft_Samper_432909089-image230.png|312px]] | + | | style="text-align: center;vertical-align: top;width: 50%;"|[[Image:draft_Samper_432909089-monograph-image230.png|312px]] |
<span style="text-align: center; font-size: 75%;">'''(a)''' ''AB4'' bridge</span> | <span style="text-align: center; font-size: 75%;">'''(a)''' ''AB4'' bridge</span> | ||
| − | | style="text-align: center;vertical-align: top;width: 50%;"| [[Image:draft_Samper_432909089-image231.png|312px]] | + | | style="text-align: center;vertical-align: top;width: 50%;"|[[Image:draft_Samper_432909089-monograph-image231.png|312px]] |
<span style="text-align: center; font-size: 75%;">'''(b)''' ''AR4'' bridge</span> | <span style="text-align: center; font-size: 75%;">'''(b)''' ''AR4'' bridge</span> | ||
| Line 5,164: | Line 5,049: | ||
{| style="width: 100%;margin: 1em auto 0.1em auto;" | {| style="width: 100%;margin: 1em auto 0.1em auto;" | ||
|- | |- | ||
| − | | style="text-align: center;vertical-align: top;width: | + | | style="text-align: center;vertical-align: top;width: 50%;"|[[Image:draft_Samper_432909089-monograph-image232.png|312px]] |
<span style="text-align: center; font-size: 75%;">'''(a)''' ''AB4'' bridge</span> | <span style="text-align: center; font-size: 75%;">'''(a)''' ''AB4'' bridge</span> | ||
| − | | style="text-align: center;vertical-align: top;width: | + | | style="text-align: center;vertical-align: top;width: 50%;"|[[Image:draft_Samper_432909089-monograph-image233.png|312px]] |
<span style="text-align: center; font-size: 75%;">'''(b)''' ''AR4'' bridge</span> | <span style="text-align: center; font-size: 75%;">'''(b)''' ''AR4'' bridge</span> | ||
| Line 5,178: | Line 5,063: | ||
{| style="width: 100%;margin: 1em auto 0.1em auto;" | {| style="width: 100%;margin: 1em auto 0.1em auto;" | ||
|- | |- | ||
| − | | style="text-align: center;vertical-align: top;width: | + | | style="text-align: center;vertical-align: top;width: 50%;"|[[Image:draft_Samper_432909089-monograph-image234.png|312px]] |
<span style="text-align: center; font-size: 75%;">'''(a)''' ''AB4'' bridge</span> | <span style="text-align: center; font-size: 75%;">'''(a)''' ''AB4'' bridge</span> | ||
| − | | style="text-align: center;vertical-align: top;width: | + | | style="text-align: center;vertical-align: top;width: 50%;"|[[Image:draft_Samper_432909089-monograph-image235.png|312px]] |
<span style="text-align: center; font-size: 75%;">'''(b)''' ''AR4'' bridge</span> | <span style="text-align: center; font-size: 75%;">'''(b)''' ''AR4'' bridge</span> | ||
| Line 5,194: | Line 5,079: | ||
{| style="width: 100%;margin: 1em auto 0.1em auto;" | {| style="width: 100%;margin: 1em auto 0.1em auto;" | ||
|- | |- | ||
| − | | style="text-align: center;vertical-align: top;width: | + | | style="text-align: center;vertical-align: top;width: 50%;"|[[Image:draft_Samper_432909089-monograph-image236.png|312px]] |
<span style="text-align: center; font-size: 75%;">'''(a)''' ''AB4'' bridge</span> | <span style="text-align: center; font-size: 75%;">'''(a)''' ''AB4'' bridge</span> | ||
| − | | style="text-align: center;vertical-align: top;width: | + | | style="text-align: center;vertical-align: top;width: 50%;"|[[Image:draft_Samper_432909089-monograph-image237.png|312px]] |
<span style="text-align: center; font-size: 75%;">'''(b)''' ''AR4'' bridge</span> | <span style="text-align: center; font-size: 75%;">'''(b)''' ''AR4'' bridge</span> | ||
| Line 5,208: | Line 5,093: | ||
{| style="width: 100%;margin: 1em auto 0.1em auto;" | {| style="width: 100%;margin: 1em auto 0.1em auto;" | ||
|- | |- | ||
| − | | style="text-align: center;vertical-align: top;width: | + | | style="text-align: center;vertical-align: top;width: 50%;"|[[Image:draft_Samper_432909089-monograph-image238.png|312px]] |
<span style="text-align: center; font-size: 75%;">'''(a)''' ''AB4'' bridge</span> | <span style="text-align: center; font-size: 75%;">'''(a)''' ''AB4'' bridge</span> | ||
| − | | style="text-align: center;vertical-align: top;width: | + | | style="text-align: center;vertical-align: top;width: 50%;"|[[Image:draft_Samper_432909089-monograph-image239.png|312px]] |
<span style="text-align: center; font-size: 75%;">'''(b)''' ''AR4'' bridge</span> | <span style="text-align: center; font-size: 75%;">'''(b)''' ''AR4'' bridge</span> | ||
| Line 5,226: | Line 5,111: | ||
{| style="width: 100%;margin: 1em auto 0.1em auto;" | {| style="width: 100%;margin: 1em auto 0.1em auto;" | ||
|- | |- | ||
| − | | style="text-align: center;vertical-align: top;width: | + | | style="text-align: center;vertical-align: top;width: 50%;"|[[Image:draft_Samper_432909089-monograph-image240.png|312px]] |
<span style="text-align: center; font-size: 75%;">'''(a)''' ''AB4'' bridge</span> | <span style="text-align: center; font-size: 75%;">'''(a)''' ''AB4'' bridge</span> | ||
| − | | style="text-align: center;vertical-align: top;width: | + | | style="text-align: center;vertical-align: top;width: 50%;"|[[Image:draft_Samper_432909089-monograph-image241.png|312px]] |
<span style="text-align: center; font-size: 75%;">'''(b)''' ''AR4'' bridge</span> | <span style="text-align: center; font-size: 75%;">'''(b)''' ''AR4'' bridge</span> | ||
| Line 5,242: | Line 5,127: | ||
{| style="width: 100%;margin: 1em auto 0.1em auto;" | {| style="width: 100%;margin: 1em auto 0.1em auto;" | ||
|- | |- | ||
| − | | style="text-align: center;vertical-align: top;width: | + | | style="text-align: center;vertical-align: top;width: 50%;"|[[Image:draft_Samper_432909089-monograph-image242.png|312px]] |
<span style="text-align: center; font-size: 75%;">'''(a)''' ''AB4'' bridge</span> | <span style="text-align: center; font-size: 75%;">'''(a)''' ''AB4'' bridge</span> | ||
| − | | style="text-align: center;vertical-align: top;width: | + | | style="text-align: center;vertical-align: top;width: 50%;"|[[Image:draft_Samper_432909089-monograph-image243.png|312px]] |
<span style="text-align: center; font-size: 75%;">'''(b)''' ''AR4'' bridge</span> | <span style="text-align: center; font-size: 75%;">'''(b)''' ''AR4'' bridge</span> | ||
| Line 5,256: | Line 5,141: | ||
{| style="width: 100%;margin: 1em auto 0.1em auto;" | {| style="width: 100%;margin: 1em auto 0.1em auto;" | ||
|- | |- | ||
| − | | style="text-align: center;vertical-align: top;width: | + | | style="text-align: center;vertical-align: top;width: 50%;"|[[Image:draft_Samper_432909089-monograph-image244.png|312px]] |
<span style="text-align: center; font-size: 75%;">'''(a)''' ''AB4'' bridge</span> | <span style="text-align: center; font-size: 75%;">'''(a)''' ''AB4'' bridge</span> | ||
| − | | style="text-align: center;vertical-align: top;width: | + | | style="text-align: center;vertical-align: top;width: 50%;"|[[Image:draft_Samper_432909089-monograph-image245.png|312px]] |
<span style="text-align: center; font-size: 75%;">'''(b)''' ''AR4'' bridge</span> | <span style="text-align: center; font-size: 75%;">'''(b)''' ''AR4'' bridge</span> | ||
| Line 5,272: | Line 5,157: | ||
{| style="width: 100%;margin: 1em auto 0.1em auto;" | {| style="width: 100%;margin: 1em auto 0.1em auto;" | ||
|- | |- | ||
| − | | style="text-align: center;vertical-align: top;width: | + | | style="text-align: center;vertical-align: top;width: 50%;"|[[Image:draft_Samper_432909089-monograph-image246.png|312px]] |
<span style="text-align: center; font-size: 75%;">'''(a)''' ''AB4'' bridge</span> | <span style="text-align: center; font-size: 75%;">'''(a)''' ''AB4'' bridge</span> | ||
| − | | style="text-align: center;vertical-align: top;width: | + | | style="text-align: center;vertical-align: top;width: 50%;"|[[Image:draft_Samper_432909089-monograph-image247.png|312px]] |
<span style="text-align: center; font-size: 75%;">'''(b)''' ''AR4'' bridge</span> | <span style="text-align: center; font-size: 75%;">'''(b)''' ''AR4'' bridge</span> | ||
| Line 5,286: | Line 5,171: | ||
{| style="width: 100%;margin: 1em auto 0.1em auto;" | {| style="width: 100%;margin: 1em auto 0.1em auto;" | ||
|- | |- | ||
| − | | style="text-align: center;vertical-align: top;width: | + | | style="text-align: center;vertical-align: top;width: 50%;"|[[Image:draft_Samper_432909089-monograph-image248.png|312px]] |
<span style="text-align: center; font-size: 75%;">'''(a)''' ''AB4'' bridge</span> | <span style="text-align: center; font-size: 75%;">'''(a)''' ''AB4'' bridge</span> | ||
| − | | style="text-align: center;vertical-align: top;width: | + | | style="text-align: center;vertical-align: top;width: 50%;"|[[Image:draft_Samper_432909089-monograph-image249.png|312px]] |
<span style="text-align: center; font-size: 75%;">'''(b)''' ''AR4'' bridge</span> | <span style="text-align: center; font-size: 75%;">'''(b)''' ''AR4'' bridge</span> | ||
| Line 5,664: | Line 5,549: | ||
<span style="text-align: center; font-size: 75%;"><sup>a</sup> At the tower base <sup>c</sup> In-plane</span> | <span style="text-align: center; font-size: 75%;"><sup>a</sup> At the tower base <sup>c</sup> In-plane</span> | ||
| − | <sup>b</sup> At the tower-deck connection <sup>d</sup> Out-of-plane | + | <span style="text-align: center; font-size: 75%;"><sup>b</sup> At the tower-deck connection <sup>d</sup> Out-of-plane</span> |
| + | |||
| − | :<big> | + | :<big>3.7.5 Seismic Response Considering Near-Fault Ground Motions</big> |
Basically, the same considerations were used in the near-fault analysis for the models, including the time-step size, damping characterization and zero-time conditions among other things. Because of the inherent highly nonlinear behaviour involved in the near-source ground motion, some convergence troubles were experienced as was previously explained. In this sense, sometimes the integration parameters were strongly modified in order to reach the desired stability with the required accuracy. Numerical damping of -0.2 was enough to guarantee that the solution was invariant, with an adequate control of the high frequency content. Maximum sub-step size between 0 – 0.02 was employed, and a minimum sub-step size of zero was selected for all the bridge models. With regard to the maximum iterations per sub-step, different values were necessary to apply depending on the event and model. In the case of far-fault analysis, 60 iterations were enough; however, for near-fault ground motions, 120 iterations were a normal value, and sometimes up to 180 iterations were necessary (Landers event), with the obvious increment of computer time. To guarantee an adequate tolerance of the iterations, especially when large-displacement effects are considered, 1x10<sup>-3</sup> value was used. | Basically, the same considerations were used in the near-fault analysis for the models, including the time-step size, damping characterization and zero-time conditions among other things. Because of the inherent highly nonlinear behaviour involved in the near-source ground motion, some convergence troubles were experienced as was previously explained. In this sense, sometimes the integration parameters were strongly modified in order to reach the desired stability with the required accuracy. Numerical damping of -0.2 was enough to guarantee that the solution was invariant, with an adequate control of the high frequency content. Maximum sub-step size between 0 – 0.02 was employed, and a minimum sub-step size of zero was selected for all the bridge models. With regard to the maximum iterations per sub-step, different values were necessary to apply depending on the event and model. In the case of far-fault analysis, 60 iterations were enough; however, for near-fault ground motions, 120 iterations were a normal value, and sometimes up to 180 iterations were necessary (Landers event), with the obvious increment of computer time. To guarantee an adequate tolerance of the iterations, especially when large-displacement effects are considered, 1x10<sup>-3</sup> value was used. | ||
| Line 5,676: | Line 5,562: | ||
{| style="width: 100%;margin: 1em auto 0.1em auto;" | {| style="width: 100%;margin: 1em auto 0.1em auto;" | ||
|- | |- | ||
| − | | style="text-align: center;vertical-align: top;width: | + | | style="text-align: center;vertical-align: top;width: 50%;"|[[Image:draft_Samper_432909089-monograph-image250.png|312px]] |
<span style="text-align: center; font-size: 75%;">'''(a)''' ''AB4'' bridge</span> | <span style="text-align: center; font-size: 75%;">'''(a)''' ''AB4'' bridge</span> | ||
| − | | style="text-align: center;vertical-align: top;width: | + | | style="text-align: center;vertical-align: top;width: 50%;"|[[Image:draft_Samper_432909089-monograph-image251.png|312px]] |
<span style="text-align: center; font-size: 75%;">'''(b)''' ''AR4'' bridge</span> | <span style="text-align: center; font-size: 75%;">'''(b)''' ''AR4'' bridge</span> | ||
| Line 5,690: | Line 5,576: | ||
{| style="width: 100%;margin: 1em auto 0.1em auto;" | {| style="width: 100%;margin: 1em auto 0.1em auto;" | ||
|- | |- | ||
| − | | style="text-align: center;vertical-align: top;width: | + | | style="text-align: center;vertical-align: top;width: 50%;"|[[Image:draft_Samper_432909089-monograph-image252.png|312px]] |
<span style="text-align: center; font-size: 75%;">'''(a)''' ''AB4'' bridge</span> | <span style="text-align: center; font-size: 75%;">'''(a)''' ''AB4'' bridge</span> | ||
| − | | style="text-align: center;vertical-align: top;width: | + | | style="text-align: center;vertical-align: top;width: 50%;"|[[Image:draft_Samper_432909089-monograph-image253.png|312px]] |
<span style="text-align: center; font-size: 75%;">'''(b)''' ''AR4'' bridge</span> | <span style="text-align: center; font-size: 75%;">'''(b)''' ''AR4'' bridge</span> | ||
| Line 5,706: | Line 5,592: | ||
{| style="width: 100%;margin: 1em auto 0.1em auto;" | {| style="width: 100%;margin: 1em auto 0.1em auto;" | ||
|- | |- | ||
| − | | style="text-align: center;vertical-align: top;width: | + | | style="text-align: center;vertical-align: top;width: 50%;"|[[Image:draft_Samper_432909089-monograph-image254.png|312px]] |
<span style="text-align: center; font-size: 75%;">'''(a)''' ''AB4'' bridge</span> | <span style="text-align: center; font-size: 75%;">'''(a)''' ''AB4'' bridge</span> | ||
| − | | style="text-align: center;vertical-align: top;width: | + | | style="text-align: center;vertical-align: top;width: 50%;"|[[Image:draft_Samper_432909089-monograph-image255.png|312px]] |
<span style="text-align: center; font-size: 75%;">'''(b)''' ''AR4'' bridge</span> | <span style="text-align: center; font-size: 75%;">'''(b)''' ''AR4'' bridge</span> | ||
| Line 5,722: | Line 5,608: | ||
{| style="width: 100%;margin: 1em auto 0.1em auto;" | {| style="width: 100%;margin: 1em auto 0.1em auto;" | ||
|- | |- | ||
| − | | style="text-align: center;vertical-align: top;width: | + | | style="text-align: center;vertical-align: top;width: 50%;"|[[Image:draft_Samper_432909089-monograph-image256.png|312px]] |
<span style="text-align: center; font-size: 75%;">'''(a)''' ''AB4'' bridge</span> | <span style="text-align: center; font-size: 75%;">'''(a)''' ''AB4'' bridge</span> | ||
| − | | style="text-align: center;vertical-align: top;width: | + | | style="text-align: center;vertical-align: top;width: 50%;"|[[Image:draft_Samper_432909089-monograph-image257.png|312px]] |
<span style="text-align: center; font-size: 75%;">'''(b)''' ''AR4'' bridge</span> | <span style="text-align: center; font-size: 75%;">'''(b)''' ''AR4'' bridge</span> | ||
| Line 5,736: | Line 5,622: | ||
{| style="width: 100%;margin: 1em auto 0.1em auto;" | {| style="width: 100%;margin: 1em auto 0.1em auto;" | ||
|- | |- | ||
| − | | style="text-align: center;vertical-align: top;width: | + | | style="text-align: center;vertical-align: top;width: 50%;"|[[Image:draft_Samper_432909089-monograph-image258.png|312px]] |
<span style="text-align: center; font-size: 75%;">'''(a)''' ''AB4'' bridge</span> | <span style="text-align: center; font-size: 75%;">'''(a)''' ''AB4'' bridge</span> | ||
| − | | style="text-align: center;vertical-align: top;width: | + | | style="text-align: center;vertical-align: top;width: 50%;"|[[Image:draft_Samper_432909089-monograph-image259.png|312px]] |
<span style="text-align: center; font-size: 75%;">'''(b)''' ''AR4'' bridge</span> | <span style="text-align: center; font-size: 75%;">'''(b)''' ''AR4'' bridge</span> | ||
| Line 5,756: | Line 5,642: | ||
{| style="width: 100%;margin: 1em auto 0.1em auto;" | {| style="width: 100%;margin: 1em auto 0.1em auto;" | ||
|- | |- | ||
| − | | style="text-align: center;vertical-align: top;width: | + | | style="text-align: center;vertical-align: top;width: 50%;"|[[Image:draft_Samper_432909089-monograph-image260.png|312px]] |
<span style="text-align: center; font-size: 75%;">'''(a)''' ''AB4'' bridge</span> | <span style="text-align: center; font-size: 75%;">'''(a)''' ''AB4'' bridge</span> | ||
| − | | style="text-align: center;vertical-align: top;width: | + | | style="text-align: center;vertical-align: top;width: 50%;"|[[Image:draft_Samper_432909089-monograph-image261.png|312px]] |
<span style="text-align: center; font-size: 75%;">'''(b)''' ''AR4'' bridge</span> | <span style="text-align: center; font-size: 75%;">'''(b)''' ''AR4'' bridge</span> | ||
| Line 5,772: | Line 5,658: | ||
{| style="width: 100%;margin: 1em auto 0.1em auto;" | {| style="width: 100%;margin: 1em auto 0.1em auto;" | ||
|- | |- | ||
| − | | style="text-align: center;vertical-align: top;width: | + | | style="text-align: center;vertical-align: top;width: 50%;"|[[Image:draft_Samper_432909089-monograph-image262.png|312px]] |
<span style="text-align: center; font-size: 75%;">'''(a)''' ''AB4'' bridge</span> | <span style="text-align: center; font-size: 75%;">'''(a)''' ''AB4'' bridge</span> | ||
| − | | style="text-align: center;vertical-align: top;width: | + | | style="text-align: center;vertical-align: top;width: 50%;"|[[Image:draft_Samper_432909089-monograph-image263.png|312px]] |
<span style="text-align: center; font-size: 75%;">'''(b)''' ''AR4'' bridge</span> | <span style="text-align: center; font-size: 75%;">'''(b)''' ''AR4'' bridge</span> | ||
| Line 5,786: | Line 5,672: | ||
{| style="width: 100%;margin: 1em auto 0.1em auto;" | {| style="width: 100%;margin: 1em auto 0.1em auto;" | ||
|- | |- | ||
| − | | style="text-align: center;vertical-align: top;width: | + | | style="text-align: center;vertical-align: top;width: 50%;"|[[Image:draft_Samper_432909089-monograph-image264.png|312px]] |
<span style="text-align: center; font-size: 75%;">'''(a)''' ''AB4'' bridge</span> | <span style="text-align: center; font-size: 75%;">'''(a)''' ''AB4'' bridge</span> | ||
| − | | style="text-align: center;vertical-align: top;width: | + | | style="text-align: center;vertical-align: top;width: 50%;"|[[Image:draft_Samper_432909089-monograph-image265.png|312px]] |
<span style="text-align: center; font-size: 75%;">'''(b)''' ''AR4'' bridge</span> | <span style="text-align: center; font-size: 75%;">'''(b)''' ''AR4'' bridge</span> | ||
| Line 5,802: | Line 5,688: | ||
{| style="width: 100%;margin: 1em auto 0.1em auto;" | {| style="width: 100%;margin: 1em auto 0.1em auto;" | ||
|- | |- | ||
| − | | style="text-align: center;vertical-align: top;width: | + | | style="text-align: center;vertical-align: top;width: 50%;"|[[Image:draft_Samper_432909089-monograph-image266.png|312px]] |
<span style="text-align: center; font-size: 75%;">'''(a)''' ''AB4'' bridge</span> | <span style="text-align: center; font-size: 75%;">'''(a)''' ''AB4'' bridge</span> | ||
| − | | style="text-align: center;vertical-align: top;width: | + | | style="text-align: center;vertical-align: top;width: 50%;"|[[Image:draft_Samper_432909089-monograph-image267.png|312px]] |
<span style="text-align: center; font-size: 75%;">'''(b)''' ''AR4'' bridge</span> | <span style="text-align: center; font-size: 75%;">'''(b)''' ''AR4'' bridge</span> | ||
| Line 5,816: | Line 5,702: | ||
{| style="width: 100%;margin: 1em auto 0.1em auto;" | {| style="width: 100%;margin: 1em auto 0.1em auto;" | ||
|- | |- | ||
| − | | style="text-align: center;vertical-align: top;width: | + | | style="text-align: center;vertical-align: top;width: 50%;"|[[Image:draft_Samper_432909089-monograph-image268.png|312px]] |
<span style="text-align: center; font-size: 75%;">'''(a)''' ''AB4'' bridge</span> | <span style="text-align: center; font-size: 75%;">'''(a)''' ''AB4'' bridge</span> | ||
| − | | style="text-align: center;vertical-align: top;width: | + | | style="text-align: center;vertical-align: top;width: 50%;"|[[Image:draft_Samper_432909089-monograph-image269.png|312px]] |
<span style="text-align: center; font-size: 75%;">'''(b)''' ''AR4'' bridge</span> | <span style="text-align: center; font-size: 75%;">'''(b)''' ''AR4'' bridge</span> | ||
| Line 6,194: | Line 6,080: | ||
<span style="text-align: center; font-size: 75%;"><sup>a</sup> At the tower base <sup>c</sup> In-plane</span> | <span style="text-align: center; font-size: 75%;"><sup>a</sup> At the tower base <sup>c</sup> In-plane</span> | ||
| − | <sup>b</sup> At the tower-deck connection <sup>d</sup> Out-of-plane | + | <span style="text-align: center; font-size: 75%;"><sup>b</sup> At the tower-deck connection <sup>d</sup> Out-of-plane</span> |
| − | :<big> | + | |
| + | :<big>3.8 Comparative Results</big> | ||
The last point of this chapter exposes some comparisons between the obtained responses applying far-fault ground motions and near-fault ground motions. Moreover, in addition of the seismic responses obtained with the nonlinear time history analysis, maximum responses obtained with the response spectrum analysis are considered in order to compare results. | The last point of this chapter exposes some comparisons between the obtained responses applying far-fault ground motions and near-fault ground motions. Moreover, in addition of the seismic responses obtained with the nonlinear time history analysis, maximum responses obtained with the response spectrum analysis are considered in order to compare results. | ||
| Line 6,212: | Line 6,099: | ||
{| style="width: 100%;margin: 1em auto 0.1em auto;" | {| style="width: 100%;margin: 1em auto 0.1em auto;" | ||
|- | |- | ||
| − | | style="text-align: center;vertical-align: top;width: | + | | style="text-align: center;vertical-align: top;width: 50%;"|[[Image:draft_Samper_432909089-monograph-image270.png|258px]] |
<span style="text-align: center; font-size: 75%;">'''(a)''' Longitudinal displacement of the deck</span> | <span style="text-align: center; font-size: 75%;">'''(a)''' Longitudinal displacement of the deck</span> | ||
| − | | style="text-align: center;vertical-align: top;width: | + | | style="text-align: center;vertical-align: top;width: 50%;"|[[Image:draft_Samper_432909089-monograph-image271.png|258px]] |
<span style="text-align: center; font-size: 75%;">'''(b) '''Vertical deflection of the deck at the mid-span</span> | <span style="text-align: center; font-size: 75%;">'''(b) '''Vertical deflection of the deck at the mid-span</span> | ||
|- | |- | ||
| − | | style="text-align: center;vertical-align: top;width: | + | | style="text-align: center;vertical-align: top;width: 50%;"|[[Image:draft_Samper_432909089-monograph-image272.png|258px]] |
<span style="text-align: center; font-size: 75%;">'''(c)''' Transverse displacement of the deck at the mid-span</span> | <span style="text-align: center; font-size: 75%;">'''(c)''' Transverse displacement of the deck at the mid-span</span> | ||
| − | | style="text-align: center;vertical-align: top;width: | + | | style="text-align: center;vertical-align: top;width: 50%;"|[[Image:draft_Samper_432909089-monograph-image273.png|258px]] |
<span style="text-align: center; font-size: 75%;">'''(d)''' Longitudinal displacement of the tower-top</span> | <span style="text-align: center; font-size: 75%;">'''(d)''' Longitudinal displacement of the tower-top</span> | ||
| Line 6,239: | Line 6,126: | ||
{| style="width: 100%;margin: 1em auto 0.1em auto;" | {| style="width: 100%;margin: 1em auto 0.1em auto;" | ||
|- | |- | ||
| − | | style="text-align: center;vertical-align: top;width: 50%;"| [[Image:draft_Samper_432909089-image274.png|258px]] | + | | style="text-align: center;vertical-align: top;width: 50%;"|[[Image:draft_Samper_432909089-monograph-image274.png|258px]] |
<span style="text-align: center; font-size: 75%;">'''(a)''' Compressive forces at the tower base</span> | <span style="text-align: center; font-size: 75%;">'''(a)''' Compressive forces at the tower base</span> | ||
| − | | style="text-align: center;vertical-align: top;width: 50%;"| [[Image:draft_Samper_432909089-image275.png|258px]] | + | | style="text-align: center;vertical-align: top;width: 50%;"|[[Image:draft_Samper_432909089-monograph-image275.png|258px]] |
<span style="text-align: center; font-size: 75%;">'''(b)''' Compressive forces of the deck at the tower-deck connection</span> | <span style="text-align: center; font-size: 75%;">'''(b)''' Compressive forces of the deck at the tower-deck connection</span> | ||
| Line 6,249: | Line 6,136: | ||
<div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | ||
| − | [[Image:draft_Samper_432909089-image276.png|258px]] </div> | + | [[Image:draft_Samper_432909089-monograph-image276.png|258px]] </div> |
<div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | ||
| Line 6,259: | Line 6,146: | ||
{| style="width: 100%;margin: 1em auto 0.1em auto;" | {| style="width: 100%;margin: 1em auto 0.1em auto;" | ||
|- | |- | ||
| − | | style="text-align: center;vertical-align: top;"|<big>''' [[Image:draft_Samper_432909089-image277.png|258px]] '''</big> | + | | style="text-align: center;vertical-align: top;"|<big>''' [[Image:draft_Samper_432909089-monograph-image277.png|258px]] '''</big> |
<span style="text-align: center; font-size: 75%;">'''(a)''' In-plane bending moments at the tower base</span> | <span style="text-align: center; font-size: 75%;">'''(a)''' In-plane bending moments at the tower base</span> | ||
| − | | style="text-align: center;vertical-align: top;"|<big>''' [[Image:draft_Samper_432909089-image278.png|258px]] '''</big> | + | | style="text-align: center;vertical-align: top;"|<big>''' [[Image:draft_Samper_432909089-monograph-image278.png|258px]] '''</big> |
<span style="text-align: center; font-size: 75%;">'''(b) '''Out-of-plane bending moments at the tower base</span> | <span style="text-align: center; font-size: 75%;">'''(b) '''Out-of-plane bending moments at the tower base</span> | ||
| Line 6,269: | Line 6,156: | ||
<div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | ||
| − | <big>''' [[Image:draft_Samper_432909089-image279.png|258px]] '''</big></div> | + | <big>''' [[Image:draft_Samper_432909089-monograph-image279.png|258px]] '''</big></div> |
<div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | ||
| Line 6,277: | Line 6,164: | ||
'''Fig. 3.77''' Average of the Maximum Bending Moments for ''AR4 ''Bridge</div> | '''Fig. 3.77''' Average of the Maximum Bending Moments for ''AR4 ''Bridge</div> | ||
| − | + | ==Chapter 4. Seismic Protection. Application of Fluid Viscous Dampers== | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | :<big> | + | :<big>4.1 General Considerations</big> |
Fluid viscous dampers constitute an attractive methodology to protect structures against earthquakes. Application of those strategies on buildings and bridges has been widely used, but their incorporation on cable-stayed bridges has been slow. For that reason, this study is focused on the implementation of nonlinear viscous dampers as additional energy dissipation devices on such structures, with the purpose of analyze their seismic response in the presence of both far-fault and near-fault ground motions. In order to simplify this analysis and to consider the same nonlinear time history analyses cases previously discussed, ''AB4'' and ''AR4'' bridge models are studied. With this selection, the incidence of the stay cable layout on the seismic response and an adequate comparison with the undamped cases is possible. | Fluid viscous dampers constitute an attractive methodology to protect structures against earthquakes. Application of those strategies on buildings and bridges has been widely used, but their incorporation on cable-stayed bridges has been slow. For that reason, this study is focused on the implementation of nonlinear viscous dampers as additional energy dissipation devices on such structures, with the purpose of analyze their seismic response in the presence of both far-fault and near-fault ground motions. In order to simplify this analysis and to consider the same nonlinear time history analyses cases previously discussed, ''AB4'' and ''AR4'' bridge models are studied. With this selection, the incidence of the stay cable layout on the seismic response and an adequate comparison with the undamped cases is possible. | ||
| Line 6,293: | Line 6,176: | ||
The Chapter begins with the definition of the structural modelling of the viscous dampers, and the considered parameters. With the aim to select the optimal arrange of the dampers, five different damper layouts are studied, considering the worse conditions for both far-fault and near-fault ground motions. With this analysis, the definitive structural layout for the study of the bridges including additional viscous dampers is achieved, and the new dynamic characterization of the bridges is exposed, including evaluation of natural periods, modal shapes and modal damping. In order to select the optimal damper parameters, a parametric study is conducted with one of the bridge models and considering again the worse conditions for both far-fault and near-fault ground motions. After that, the influence of the velocity exponent of the dampers is analyzed. The nonlinear time history analysis applying the optimal damper parameters for both structures is then performed, considering all the analysis cases for both far-fault and near-fault ground motions. Finally, comparative studies between the optimal solutions, with and without the incorporation of additional dampers, are performed. Comparisons between far-fault and near-fault ground motions considering the effects of the stay cable layout are included, as well as an energy characterization of the problem. | The Chapter begins with the definition of the structural modelling of the viscous dampers, and the considered parameters. With the aim to select the optimal arrange of the dampers, five different damper layouts are studied, considering the worse conditions for both far-fault and near-fault ground motions. With this analysis, the definitive structural layout for the study of the bridges including additional viscous dampers is achieved, and the new dynamic characterization of the bridges is exposed, including evaluation of natural periods, modal shapes and modal damping. In order to select the optimal damper parameters, a parametric study is conducted with one of the bridge models and considering again the worse conditions for both far-fault and near-fault ground motions. After that, the influence of the velocity exponent of the dampers is analyzed. The nonlinear time history analysis applying the optimal damper parameters for both structures is then performed, considering all the analysis cases for both far-fault and near-fault ground motions. Finally, comparative studies between the optimal solutions, with and without the incorporation of additional dampers, are performed. Comparisons between far-fault and near-fault ground motions considering the effects of the stay cable layout are included, as well as an energy characterization of the problem. | ||
| − | :<big> | + | :<big>4.2 Modelling of Nonlinear Fluid Viscous Dampers</big> |
Modelling of nonlinear fluid viscous dampers considers the use of nonlinear ''link ''elements according to the structural code SAP2000. Because of the inherent nonlinear behaviour of the dampers, during the analysis, the nonlinear force-deformation relationships are used at all degrees-of-freedom for which nonlinear properties were specified, and for that reason, linear effective stiffness and linear effective damping is not used for any nonlinear analysis. In this sense, nonlinear time-history analysis is absolutely necessary when nonlinear additional energy dissipation devices are added. This is the correct way to determine the effect of added dampers, since nonlinear time-history analysis does not use the effective damping values, and the energy dissipation in the elements is directly accounted for, as well as the effects of modal cross-coupling [Computers & Structures, 2007]. | Modelling of nonlinear fluid viscous dampers considers the use of nonlinear ''link ''elements according to the structural code SAP2000. Because of the inherent nonlinear behaviour of the dampers, during the analysis, the nonlinear force-deformation relationships are used at all degrees-of-freedom for which nonlinear properties were specified, and for that reason, linear effective stiffness and linear effective damping is not used for any nonlinear analysis. In this sense, nonlinear time-history analysis is absolutely necessary when nonlinear additional energy dissipation devices are added. This is the correct way to determine the effect of added dampers, since nonlinear time-history analysis does not use the effective damping values, and the energy dissipation in the elements is directly accounted for, as well as the effects of modal cross-coupling [Computers & Structures, 2007]. | ||
| Line 6,299: | Line 6,182: | ||
{| style="width: 100%;" | {| style="width: 100%;" | ||
|- | |- | ||
| − | | style="vertical-align: top;width: 30%;"| [[Image:draft_Samper_432909089-image280.png|102px]] | + | | style="vertical-align: top;width: 30%;"|[[Image:draft_Samper_432909089-monograph-image280.png|102px]] |
'''Fig. 4.1''' Maxwell Viscoelasticity Model for Nonlinear Dampers | '''Fig. 4.1''' Maxwell Viscoelasticity Model for Nonlinear Dampers | ||
| Line 6,306: | Line 6,189: | ||
The nonlinear force-deformation relationship is given by: | The nonlinear force-deformation relationship is given by: | ||
| − | + | [[Image:draft_Samper_432909089-monograph-image281.png|12px]] [[Image:draft_Samper_432909089-monograph-image282.png|102px]] [Eq. 4.1] | |
| − | where ''k'' is the spring constant, ''c'' is the damping coefficient, ''N'' is the velocity exponent of the damper, ''d<sub>k</sub>'' is the deformation across the spring, and | + | where ''k'' is the spring constant, ''c'' is the damping coefficient, ''N'' is the velocity exponent of the damper, ''d<sub>k</sub>'' is the deformation across the spring, and [[Image:draft_Samper_432909089-monograph-image283.png|18px]] is the deformation rate of the damper. |
|} | |} | ||
| Line 6,320: | Line 6,203: | ||
Finally, it is important to say that, on the contrary of the viscoelastic dampers, frequency and temperature dependency is minimum [Symans ''et al'', 2008], which simplifies the mathematical modelling of the viscous dampers. | Finally, it is important to say that, on the contrary of the viscoelastic dampers, frequency and temperature dependency is minimum [Symans ''et al'', 2008], which simplifies the mathematical modelling of the viscous dampers. | ||
| − | :<big> | + | :<big>4.3 Optimal Arrange of the Dampers</big> |
One of the questions that designers need to respond is the best configuration of the dampers into the structure. The dampers are external devices, normally not affected by direct permanent loads, and located at places where the replacement or inspection is easy. In buildings, this task sometimes can be complicated, because of the numerous possibilities in which the dampers can be located; and for that reason, optimization procedures can be an excellent tool that can help designers in those decisions. In the case of bridges, possibilities for the location of the external devices are much more limited, and normally the dampers need to be installed at the deck-ends (abutment-deck connection) and/or at the pylon/tower-deck connection. | One of the questions that designers need to respond is the best configuration of the dampers into the structure. The dampers are external devices, normally not affected by direct permanent loads, and located at places where the replacement or inspection is easy. In buildings, this task sometimes can be complicated, because of the numerous possibilities in which the dampers can be located; and for that reason, optimization procedures can be an excellent tool that can help designers in those decisions. In the case of bridges, possibilities for the location of the external devices are much more limited, and normally the dampers need to be installed at the deck-ends (abutment-deck connection) and/or at the pylon/tower-deck connection. | ||
| Line 6,326: | Line 6,209: | ||
In order to investigate the best locations of the damper devices for this research, a brief study was conducted considering five analysis cases, all applied to the ''AB4'' model. The first case considered locations of the dampers at the deck-ends only, in the longitudinal direction. Case 2 considered longitudinal dampers at the deck-ends and at the tower-deck connections, in which the fixed-hinge of the tower-deck connections was changed by roller supports plus the dampers. Case 3 considered dampers at the deck-ends plus longitudinal damper in one of the tower-deck connections, and the replacement of the associated tower-deck connection by roller supports. Case 4 considered dampers at the deck-ends and transverse dampers plus roller supports at the tower-deck connections. Finally, case 5 considered dampers at the deck-ends and at the tower-deck connections for both directions, plus the corresponding replacement of the tower-deck connections by roller supports. It is obvious that cases 4 and 5 are an attempt of exploring the tri-dimensional response of the bridges in the presence of additional damping devices selected to control the longitudinal and transverse responses. Table 4.1 summarizes the five analysis cases. | In order to investigate the best locations of the damper devices for this research, a brief study was conducted considering five analysis cases, all applied to the ''AB4'' model. The first case considered locations of the dampers at the deck-ends only, in the longitudinal direction. Case 2 considered longitudinal dampers at the deck-ends and at the tower-deck connections, in which the fixed-hinge of the tower-deck connections was changed by roller supports plus the dampers. Case 3 considered dampers at the deck-ends plus longitudinal damper in one of the tower-deck connections, and the replacement of the associated tower-deck connection by roller supports. Case 4 considered dampers at the deck-ends and transverse dampers plus roller supports at the tower-deck connections. Finally, case 5 considered dampers at the deck-ends and at the tower-deck connections for both directions, plus the corresponding replacement of the tower-deck connections by roller supports. It is obvious that cases 4 and 5 are an attempt of exploring the tri-dimensional response of the bridges in the presence of additional damping devices selected to control the longitudinal and transverse responses. Table 4.1 summarizes the five analysis cases. | ||
| − | + | '''Table 4.1''' Layout of the Tower-Deck Connections and Dampers for the Analysis Cases | |
{| style="width: 100%;margin: 1em auto 0.1em auto;border-collapse: collapse;" | {| style="width: 100%;margin: 1em auto 0.1em auto;border-collapse: collapse;" | ||
| Line 6,429: | Line 6,312: | ||
{| style="width: 100%;margin: 1em auto 0.1em auto;" | {| style="width: 100%;margin: 1em auto 0.1em auto;" | ||
|- | |- | ||
| − | | style="text-align: center;vertical-align: top;"|<span style="text-align: center; font-size: 75%;">''' [[Image:draft_Samper_432909089-image284.png|312px]] '''</span> | + | | style="text-align: center;vertical-align: top;"|<span style="text-align: center; font-size: 75%;">''' [[Image:draft_Samper_432909089-monograph-image284.png|312px]] '''</span> |
<span style="text-align: center; font-size: 75%;">'''(a) '''Far-fault ground motion</span> | <span style="text-align: center; font-size: 75%;">'''(a) '''Far-fault ground motion</span> | ||
| − | | style="text-align: center;vertical-align: top;"|<span style="text-align: center; font-size: 75%;">''' [[Image:draft_Samper_432909089-image285.png|312px]] '''</span> | + | | style="text-align: center;vertical-align: top;"|<span style="text-align: center; font-size: 75%;">''' [[Image:draft_Samper_432909089-monograph-image285.png|312px]] '''</span> |
<span style="text-align: center; font-size: 75%;">'''(b) '''Near-fault ground motion</span> | <span style="text-align: center; font-size: 75%;">'''(b) '''Near-fault ground motion</span> | ||
| Line 6,438: | Line 6,321: | ||
| − | + | '''Fig. 4.2''' Longitudinal Displacement of the Deck | |
{| style="width: 100%;margin: 1em auto 0.1em auto;" | {| style="width: 100%;margin: 1em auto 0.1em auto;" | ||
|- | |- | ||
| − | | style="text-align: right;vertical-align: top;"|<span style="text-align: center; font-size: 75%;">''' [[Image:draft_Samper_432909089-image286.png|312px]] '''</span> | + | | style="text-align: right;vertical-align: top;"|<span style="text-align: center; font-size: 75%;">''' [[Image:draft_Samper_432909089-monograph-image286.png|312px]] '''</span> |
<span style="text-align: center; font-size: 75%;">'''(a) '''Far-fault ground motion</span> | <span style="text-align: center; font-size: 75%;">'''(a) '''Far-fault ground motion</span> | ||
| − | | style="text-align: center;vertical-align: top;"|<span style="text-align: center; font-size: 75%;">''' [[Image:draft_Samper_432909089-image287.png|312px]] '''</span> | + | | style="text-align: center;vertical-align: top;"|<span style="text-align: center; font-size: 75%;">''' [[Image:draft_Samper_432909089-monograph-image287.png|312px]] '''</span> |
<span style="text-align: center; font-size: 75%;">'''(b) '''Near-fault ground motion</span> | <span style="text-align: center; font-size: 75%;">'''(b) '''Near-fault ground motion</span> | ||
| Line 6,451: | Line 6,334: | ||
| − | + | '''Fig. 4.3''' Transverse Displacement of the Deck at the Mid-Span | |
{| style="width: 100%;margin: 1em auto 0.1em auto;" | {| style="width: 100%;margin: 1em auto 0.1em auto;" | ||
|- | |- | ||
| − | | style="text-align: center;vertical-align: top;"|<span style="text-align: center; font-size: 75%;">''' [[Image:draft_Samper_432909089-image288.png|312px]] '''</span> | + | | style="text-align: center;vertical-align: top;"|<span style="text-align: center; font-size: 75%;">''' [[Image:draft_Samper_432909089-monograph-image288.png|312px]] '''</span> |
<span style="text-align: center; font-size: 75%;">'''(a) '''Far-fault ground motion</span> | <span style="text-align: center; font-size: 75%;">'''(a) '''Far-fault ground motion</span> | ||
| − | | style="text-align: center;vertical-align: top;"|<span style="text-align: center; font-size: 75%;">''' [[Image:draft_Samper_432909089-image289.png|312px]] '''</span> | + | | style="text-align: center;vertical-align: top;"|<span style="text-align: center; font-size: 75%;">''' [[Image:draft_Samper_432909089-monograph-image289.png|312px]] '''</span> |
<span style="text-align: center; font-size: 75%;">'''(b) '''Near-fault ground motion</span> | <span style="text-align: center; font-size: 75%;">'''(b) '''Near-fault ground motion</span> | ||
| Line 6,464: | Line 6,347: | ||
| − | + | '''Fig. 4.4'''Axial Force at the Tower Base | |
An exhaustive comparison between different damper layouts shows that the worse conditions for both far-fault and near fault ground motions are obtained with case 3 followed close by cases 1 and 4. Best cases for an adequate control of the longitudinal and transverse displacements of the deck are obtained with cases 2 and 5. Similarly, axial forces of the tower and deck are better controlled with cases 2 and 5. | An exhaustive comparison between different damper layouts shows that the worse conditions for both far-fault and near fault ground motions are obtained with case 3 followed close by cases 1 and 4. Best cases for an adequate control of the longitudinal and transverse displacements of the deck are obtained with cases 2 and 5. Similarly, axial forces of the tower and deck are better controlled with cases 2 and 5. | ||
| Line 6,470: | Line 6,353: | ||
{| style="width: 100%;margin: 1em auto 0.1em auto;" | {| style="width: 100%;margin: 1em auto 0.1em auto;" | ||
|- | |- | ||
| − | | style="text-align: center;vertical-align: top;"|<span style="text-align: center; font-size: 75%;">''' [[Image:draft_Samper_432909089-image290.png|312px]] '''</span> | + | | style="text-align: center;vertical-align: top;"|<span style="text-align: center; font-size: 75%;">''' [[Image:draft_Samper_432909089-monograph-image290.png|312px]] '''</span> |
<span style="text-align: center; font-size: 75%;">'''(a) '''Far-fault ground motion</span> | <span style="text-align: center; font-size: 75%;">'''(a) '''Far-fault ground motion</span> | ||
| − | | style="text-align: center;vertical-align: top;"|<span style="text-align: center; font-size: 75%;">''' [[Image:draft_Samper_432909089-image291.png|312px]] '''</span> | + | | style="text-align: center;vertical-align: top;"|<span style="text-align: center; font-size: 75%;">''' [[Image:draft_Samper_432909089-monograph-image291.png|312px]] '''</span> |
<span style="text-align: center; font-size: 75%;">'''(b) '''Near-fault ground motion</span> | <span style="text-align: center; font-size: 75%;">'''(b) '''Near-fault ground motion</span> | ||
| Line 6,479: | Line 6,362: | ||
| − | + | '''Fig. 4.5''' Axial Force of the Deck at the Tower-Deck Connection | |
{| style="width: 100%;margin: 1em auto 0.1em auto;" | {| style="width: 100%;margin: 1em auto 0.1em auto;" | ||
|- | |- | ||
| − | | style="text-align: center;vertical-align: top;"|<span style="text-align: center; font-size: 75%;">''' [[Image:draft_Samper_432909089-image292.png|312px]] '''</span> | + | | style="text-align: center;vertical-align: top;"|<span style="text-align: center; font-size: 75%;">''' [[Image:draft_Samper_432909089-monograph-image292.png|312px]] '''</span> |
<span style="text-align: center; font-size: 75%;">'''(a) '''Far-fault ground motion</span> | <span style="text-align: center; font-size: 75%;">'''(a) '''Far-fault ground motion</span> | ||
| − | | style="text-align: center;vertical-align: top;"|<span style="text-align: center; font-size: 75%;">''' [[Image:draft_Samper_432909089-image293.png|312px]] '''</span> | + | | style="text-align: center;vertical-align: top;"|<span style="text-align: center; font-size: 75%;">''' [[Image:draft_Samper_432909089-monograph-image293.png|312px]] '''</span> |
<span style="text-align: center; font-size: 75%;">'''(b) '''Near-fault ground motion</span> | <span style="text-align: center; font-size: 75%;">'''(b) '''Near-fault ground motion</span> | ||
| Line 6,492: | Line 6,375: | ||
| − | + | '''Fig. 4.6''' Deck-end Damper Forces | |
{| style="width: 100%;margin: 1em auto 0.1em auto;" | {| style="width: 100%;margin: 1em auto 0.1em auto;" | ||
|- | |- | ||
| − | | style="text-align: center;vertical-align: top;"|<span style="text-align: center; font-size: 75%;">''' [[Image:draft_Samper_432909089-image294.png|312px]] '''</span> | + | | style="text-align: center;vertical-align: top;"|<span style="text-align: center; font-size: 75%;">''' [[Image:draft_Samper_432909089-monograph-image294.png|312px]] '''</span> |
<span style="text-align: center; font-size: 75%;">'''(a) '''Far-fault ground motion</span> | <span style="text-align: center; font-size: 75%;">'''(a) '''Far-fault ground motion</span> | ||
| − | | style="text-align: center;vertical-align: top;"|<span style="text-align: center; font-size: 75%;">''' [[Image:draft_Samper_432909089-image295.png|312px]] '''</span> | + | | style="text-align: center;vertical-align: top;"|<span style="text-align: center; font-size: 75%;">''' [[Image:draft_Samper_432909089-monograph-image295.png|312px]] '''</span> |
<span style="text-align: center; font-size: 75%;">'''(b) '''Near-fault ground motion</span> | <span style="text-align: center; font-size: 75%;">'''(b) '''Near-fault ground motion</span> | ||
| Line 6,505: | Line 6,388: | ||
| − | + | '''Fig. 4.7''' Longitudinal Damper Forces at the Tower-Deck Connection | |
{| style="width: 100%;margin: 1em auto 0.1em auto;" | {| style="width: 100%;margin: 1em auto 0.1em auto;" | ||
|- | |- | ||
| − | | style="text-align: center;vertical-align: top;"|<span style="text-align: center; font-size: 75%;">''' [[Image:draft_Samper_432909089-image296.png|312px]] '''</span> | + | | style="text-align: center;vertical-align: top;"|<span style="text-align: center; font-size: 75%;">''' [[Image:draft_Samper_432909089-monograph-image296.png|312px]] '''</span> |
<span style="text-align: center; font-size: 75%;">'''(a) '''Far-fault ground motion</span> | <span style="text-align: center; font-size: 75%;">'''(a) '''Far-fault ground motion</span> | ||
| − | | style="text-align: center;vertical-align: top;"|<span style="text-align: center; font-size: 75%;">''' [[Image:draft_Samper_432909089-image297.png|312px]] '''</span> | + | | style="text-align: center;vertical-align: top;"|<span style="text-align: center; font-size: 75%;">''' [[Image:draft_Samper_432909089-monograph-image297.png|312px]] '''</span> |
<span style="text-align: center; font-size: 75%;">'''(b) '''Near-fault ground motion</span> | <span style="text-align: center; font-size: 75%;">'''(b) '''Near-fault ground motion</span> | ||
| Line 6,518: | Line 6,401: | ||
| − | + | '''Fig. 4.8''' Transverse Damper Forces at the Tower-Deck Connection | |
The analysis of the damper forces shows that for far-fault ground motion case 2 controls efficiently deck-end damper forces and longitudinal damper forces at the tower-deck connection. For near-fault ground motion, cases 2 and 5 adequately control deck-end damper forces, but for the longitudinal damper forces at the tower-deck connection, case 5 is the best choice and case 2 seems to be an unfavourable layout. Regarding the transverse damper forces at the tower-deck connection, time-history plots show that for both far-fault and near-fault ground motions, cases 4 and 5 are practically superimposed, experiencing the same behaviour. This implies that both cases are the same in terms of the control of the transverse damper forces. | The analysis of the damper forces shows that for far-fault ground motion case 2 controls efficiently deck-end damper forces and longitudinal damper forces at the tower-deck connection. For near-fault ground motion, cases 2 and 5 adequately control deck-end damper forces, but for the longitudinal damper forces at the tower-deck connection, case 5 is the best choice and case 2 seems to be an unfavourable layout. Regarding the transverse damper forces at the tower-deck connection, time-history plots show that for both far-fault and near-fault ground motions, cases 4 and 5 are practically superimposed, experiencing the same behaviour. This implies that both cases are the same in terms of the control of the transverse damper forces. | ||
| Line 6,526: | Line 6,409: | ||
As a complement of the time-history plots, Tables 4.2 to 4.5 show a summary of the maximum main responses for the five cases in terms of displacements, velocities, internal forces, damper forces and damper velocities respectively. ''Δ<sub>1-L</sub>'' is the maximum displacement of the tower-top in the longitudinal direction; ''Δ<sub>3-V</sub>'' is the maximum vertical displacement of the deck at the mid-span; ''Δ<sub>3-T</sub>'' is the maximum transverse displacement of the deck at the mid-span; and ''Δ<sub>4-L</sub>'' is the maximum longitudinal displacement of the deck. Analogously, velocities ''V'' at the same points for the control of displacements were defined, according to the nomenclature for the seismic responses applied in Chapter 3. Displacements and velocities are shown as absolute values for simplicity. Likewise, maximum internal forces on the structure are shown as absolute values for bending moments. Nomenclature for internal forces is the same considered in Chapter 3. In Table 4.5, maximum damper velocities (''V<sub>max</sub>'') and forces (''F<sub>max</sub>'') are shown for deck-end dampers, longitudinal tower dampers and transverse tower dampers respectively. Response of the dampers is shown in absolute values. | As a complement of the time-history plots, Tables 4.2 to 4.5 show a summary of the maximum main responses for the five cases in terms of displacements, velocities, internal forces, damper forces and damper velocities respectively. ''Δ<sub>1-L</sub>'' is the maximum displacement of the tower-top in the longitudinal direction; ''Δ<sub>3-V</sub>'' is the maximum vertical displacement of the deck at the mid-span; ''Δ<sub>3-T</sub>'' is the maximum transverse displacement of the deck at the mid-span; and ''Δ<sub>4-L</sub>'' is the maximum longitudinal displacement of the deck. Analogously, velocities ''V'' at the same points for the control of displacements were defined, according to the nomenclature for the seismic responses applied in Chapter 3. Displacements and velocities are shown as absolute values for simplicity. Likewise, maximum internal forces on the structure are shown as absolute values for bending moments. Nomenclature for internal forces is the same considered in Chapter 3. In Table 4.5, maximum damper velocities (''V<sub>max</sub>'') and forces (''F<sub>max</sub>'') are shown for deck-end dampers, longitudinal tower dampers and transverse tower dampers respectively. Response of the dampers is shown in absolute values. | ||
| − | + | '''Table 4.2''' Maximum Relative Displacements [cm] and Velocities [m/sec] in the Structure | |
{| style="width: 100%;border-collapse: collapse;" | {| style="width: 100%;border-collapse: collapse;" | ||
| Line 6,645: | Line 6,528: | ||
According to Table 4.2, similar results are obtained for the displacements in the presence of far-fault ground motion, for each measured response. Maximum differences are obtained for the longitudinal displacements of the deck (43%), with maximum value for case 3. Similar differences are obtained comparing velocities between the analyzed cases. For near-fault ground motion, more important differences are obtained, and especially for the vertical and transverse displacements of the deck. Analogue differences are obtained for velocities. Furthermore, for both near-fault and far-fault ground motions, maximum displacements and velocities are obtained for the transverse displacements of the deck, independent on the damper layout. Likewise, it is confirmed that the worse condition is obtained for case 3, and the best results are obtained for cases 1, 2 and 5, for both far-fault and near-fault earthquakes. In this sense, comparing cases 2 and 5, it is obvious that practically the same maximum responses are obtained in both situations | According to Table 4.2, similar results are obtained for the displacements in the presence of far-fault ground motion, for each measured response. Maximum differences are obtained for the longitudinal displacements of the deck (43%), with maximum value for case 3. Similar differences are obtained comparing velocities between the analyzed cases. For near-fault ground motion, more important differences are obtained, and especially for the vertical and transverse displacements of the deck. Analogue differences are obtained for velocities. Furthermore, for both near-fault and far-fault ground motions, maximum displacements and velocities are obtained for the transverse displacements of the deck, independent on the damper layout. Likewise, it is confirmed that the worse condition is obtained for case 3, and the best results are obtained for cases 1, 2 and 5, for both far-fault and near-fault earthquakes. In this sense, comparing cases 2 and 5, it is obvious that practically the same maximum responses are obtained in both situations | ||
| − | + | '''Table 4.3''' Maximum Main Forces on the Structure – Far-Fault Ground Motion | |
{| style="width: 100%;margin: 1em auto 0.1em auto;border-collapse: collapse;" | {| style="width: 100%;margin: 1em auto 0.1em auto;border-collapse: collapse;" | ||
| Line 6,699: | Line 6,582: | ||
| − | + | '''Table 4.4''' Maximum Main Forces on the Structure – Near-Fault Ground Motion | |
{| style="width: 100%;margin: 1em auto 0.1em auto;border-collapse: collapse;" | {| style="width: 100%;margin: 1em auto 0.1em auto;border-collapse: collapse;" | ||
| Line 6,759: | Line 6,642: | ||
The analysis of the internal forces shows again the worse condition obtained with case 3. For far-fault ground motion, the best results are obtained with case 1, on the contrary of the near-fault ground motion, in which minimum responses are obtained with cases 2 and 4. Likewise, the analysis of the maximum internal forces shows more important differences than the analysis of displacements and velocities. On the other hand, comparing far-fault with near-fault ground motions, it is interesting to observe that maximum bending moments of the towers are obtained at the base in the longitudinal direction (in-plane) for the near-fault condition; on the contrary of the case of the far-fault condition, in which maximum bending moments are obtained in the transverse direction (out-of-plane). This implies that the selected dampers are more effective in reducing the in-plane bending moments of the towers for far-fault ground motion, independent on the damper layout, because according to the undamped analysis of the bridge models, for both far-fault and near-fault ground motions, maximum moments of the towers were always obtained in the longitudinal direction (in-plane). Likewise, as happens with the previous results, maximum responses are always obtained for near-fault ground motion. | The analysis of the internal forces shows again the worse condition obtained with case 3. For far-fault ground motion, the best results are obtained with case 1, on the contrary of the near-fault ground motion, in which minimum responses are obtained with cases 2 and 4. Likewise, the analysis of the maximum internal forces shows more important differences than the analysis of displacements and velocities. On the other hand, comparing far-fault with near-fault ground motions, it is interesting to observe that maximum bending moments of the towers are obtained at the base in the longitudinal direction (in-plane) for the near-fault condition; on the contrary of the case of the far-fault condition, in which maximum bending moments are obtained in the transverse direction (out-of-plane). This implies that the selected dampers are more effective in reducing the in-plane bending moments of the towers for far-fault ground motion, independent on the damper layout, because according to the undamped analysis of the bridge models, for both far-fault and near-fault ground motions, maximum moments of the towers were always obtained in the longitudinal direction (in-plane). Likewise, as happens with the previous results, maximum responses are always obtained for near-fault ground motion. | ||
| − | + | '''Table 4.5''' Maximum Damper Forces [kN] and Velocities [m/sec] | |
{| style="width: 100%;margin: 1em auto 0.1em auto;border-collapse: collapse;" | {| style="width: 100%;margin: 1em auto 0.1em auto;border-collapse: collapse;" | ||
| Line 6,879: | Line 6,762: | ||
{| style="width: 100%;margin: 1em auto 0.1em auto;" | {| style="width: 100%;margin: 1em auto 0.1em auto;" | ||
|- | |- | ||
| − | | style="text-align: center;vertical-align: top;width: 50%;"| [[Image:draft_Samper_432909089-image298.png|276px]] | + | | style="text-align: center;vertical-align: top;width: 50%;"|[[Image:draft_Samper_432909089-monograph-image298.png|276px]] |
<span style="text-align: center; font-size: 75%;">'''(a)''' Maximum displacements of the deck</span> | <span style="text-align: center; font-size: 75%;">'''(a)''' Maximum displacements of the deck</span> | ||
| − | | style="text-align: center;vertical-align: top;width: 50%;"| [[Image:draft_Samper_432909089-image299.png|276px]] | + | | style="text-align: center;vertical-align: top;width: 50%;"|[[Image:draft_Samper_432909089-monograph-image299.png|276px]] |
<span style="text-align: center; font-size: 75%;">'''(b)''' Maximum bending moments at the tower base</span> | <span style="text-align: center; font-size: 75%;">'''(b)''' Maximum bending moments at the tower base</span> | ||
| Line 6,888: | Line 6,771: | ||
| − | + | '''Fig. 4.9''' Comparison of Maximum Responses for Damped and Undamped Cases – AB4 Model | |
The analysis was performed for ''AB4'' model, considering the event Gatos as input ground motion. For the damped analysis, layout of case 5 was applied, that is to say, both longitudinal and transverse protection of the bridge with fluid viscous dampers, according to Table 4.1. | The analysis was performed for ''AB4'' model, considering the event Gatos as input ground motion. For the damped analysis, layout of case 5 was applied, that is to say, both longitudinal and transverse protection of the bridge with fluid viscous dampers, according to Table 4.1. | ||
| Line 6,899: | Line 6,782: | ||
<div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | ||
| − | [[Image:draft_Samper_432909089-image300-c.png|600px]] </div> | + | [[Image:draft_Samper_432909089-monograph-image300-c.png|600px]] </div> |
<div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | ||
| − | :<span style="text-align: center; font-size: 75%;">(1) Longitudinal layout of supports and dampers</span></div> | + | :<span style="text-align: center; font-size: 75%;">'''(1)''' Longitudinal layout of supports and dampers</span></div> |
{| style="width: 100%;margin: 1em auto 0.1em auto;" | {| style="width: 100%;margin: 1em auto 0.1em auto;" | ||
|- | |- | ||
| − | | style="text-align: center;vertical-align: top;"|<span style="text-align: center; font-size: 75%;"> [[Image:draft_Samper_432909089-image301-c.png|204px]] </span> | + | | style="text-align: center;vertical-align: top;"|<span style="text-align: center; font-size: 75%;"> [[Image:draft_Samper_432909089-monograph-image301-c.png|204px]] </span> |
<span style="text-align: center; font-size: 75%;">'''(b) '''Detail A</span> | <span style="text-align: center; font-size: 75%;">'''(b) '''Detail A</span> | ||
| − | | style="text-align: center;vertical-align: top;"|<span style="text-align: center; font-size: 75%;"> [[Image:draft_Samper_432909089-image302-c.png|228px]] </span> | + | | style="text-align: center;vertical-align: top;"|<span style="text-align: center; font-size: 75%;"> [[Image:draft_Samper_432909089-monograph-image302-c.png|228px]] </span> |
<span style="text-align: center; font-size: 75%;">'''(c) '''Detail B</span> | <span style="text-align: center; font-size: 75%;">'''(c) '''Detail B</span> | ||
| Line 6,915: | Line 6,798: | ||
| − | + | '''Fig. 4.10''' Optimal Layout of the Dampers | |
Position of the damper at the tower-deck connection considers an oblique location. Of course, it is possible to locate those devices considering other proposals; however this layout is simple for repairing or maintenance. This configuration needs to be considered only as basic or schematic solution, because definitive position and the main details must be materialized according to the definitive design, manufacturer’s specifications and constructive issues. | Position of the damper at the tower-deck connection considers an oblique location. Of course, it is possible to locate those devices considering other proposals; however this layout is simple for repairing or maintenance. This configuration needs to be considered only as basic or schematic solution, because definitive position and the main details must be materialized according to the definitive design, manufacturer’s specifications and constructive issues. | ||
| Line 6,921: | Line 6,804: | ||
The exposed analysis represents the general tendency of cable-stayed bridges considering different layouts of supports and dampers. The analysis was performed using the worse conditions for both far-fault and near-fault ground motions according to the selected earthquake database, and of course, some variations may be experienced if different conditions are considered. Regarding the bridge models, similar conclusions may be obtained if ''AR4 ''bridge is analyzed, according to the results of Chapter 3. | The exposed analysis represents the general tendency of cable-stayed bridges considering different layouts of supports and dampers. The analysis was performed using the worse conditions for both far-fault and near-fault ground motions according to the selected earthquake database, and of course, some variations may be experienced if different conditions are considered. Regarding the bridge models, similar conclusions may be obtained if ''AR4 ''bridge is analyzed, according to the results of Chapter 3. | ||
| − | :<big> | + | :<big>4.4 Modal Analysis Considering the Optimal Arrange of the Dampers</big> |
An exhaustive modal analysis was performed for the undamped bridge models in Chapter 3. That study left clear the importance of an adequate modal analysis as first step in the nonlinear seismic analysis of cable-stayed bridges. | An exhaustive modal analysis was performed for the undamped bridge models in Chapter 3. That study left clear the importance of an adequate modal analysis as first step in the nonlinear seismic analysis of cable-stayed bridges. | ||
| Line 6,931: | Line 6,814: | ||
Table 4.6 shows natural periods and nature of the modal shapes for the first 15 modes, in which some changes on the natural periods for both bridge models compared with the undamped cases are obtained. As was explained, those changes are in accordance with the change of the support conditions at the tower-deck connection, which enlarges the fundamental period for both structures. It is observed a higher fundamental period for ''AB4'' bridge (6.0 sec) compared with ''AR4'' bridge (3.24 sec). This implies for these new conditions, that ''AR4'' model is longitudinally stiffer than ''AB4'' model, aspect that can be explained because of the intrinsic additional stiffness provided by the shortest cables of the harp pattern in the presence of roller supports at the tower-deck connection. For fixed-hinge connections, as happens with the undamped cases, this additional stiffness is not obvious, as can be seen in Chapter 3. In this sense, it was demonstrated that the stay spacing was not decisive on the determination of the fundamental periods of cable-stayed bridges, with higher periods obtained for the harp pattern, if fixed-hinge connections at the tower-deck level are employed. In other words, a flexibility increase implies more incidence of the longitudinal stiffness provided by the stay cable layout. | Table 4.6 shows natural periods and nature of the modal shapes for the first 15 modes, in which some changes on the natural periods for both bridge models compared with the undamped cases are obtained. As was explained, those changes are in accordance with the change of the support conditions at the tower-deck connection, which enlarges the fundamental period for both structures. It is observed a higher fundamental period for ''AB4'' bridge (6.0 sec) compared with ''AR4'' bridge (3.24 sec). This implies for these new conditions, that ''AR4'' model is longitudinally stiffer than ''AB4'' model, aspect that can be explained because of the intrinsic additional stiffness provided by the shortest cables of the harp pattern in the presence of roller supports at the tower-deck connection. For fixed-hinge connections, as happens with the undamped cases, this additional stiffness is not obvious, as can be seen in Chapter 3. In this sense, it was demonstrated that the stay spacing was not decisive on the determination of the fundamental periods of cable-stayed bridges, with higher periods obtained for the harp pattern, if fixed-hinge connections at the tower-deck level are employed. In other words, a flexibility increase implies more incidence of the longitudinal stiffness provided by the stay cable layout. | ||
| − | + | '''Table 4.6''' Natural Periods and Modal Shapes for Damped Models | |
{| style="width: 88%;margin: 1em auto 0.1em auto;border-collapse: collapse;" | {| style="width: 88%;margin: 1em auto 0.1em auto;border-collapse: collapse;" | ||
| Line 7,044: | Line 6,927: | ||
{| style="width: 100%;border-collapse: collapse;" | {| style="width: 100%;border-collapse: collapse;" | ||
|- | |- | ||
| − | | style="vertical-align: top;"|'''Table 4.7 '''Critical Damping Ratios – Damped Cases | + | | style="vertical-align: top;width: 40%;"|'''Table 4.7 '''Critical Damping Ratios – Damped Cases |
{| style="width: 50%;margin: 1em auto 0.1em auto;border-collapse: collapse;" | {| style="width: 50%;margin: 1em auto 0.1em auto;border-collapse: collapse;" | ||
| Line 7,069: | Line 6,952: | ||
| − | | style="vertical-align: top;"|Modal damping exposed in Table 4.7 was obtained applying the empirical formulation by Kawashima ''et al'' (1993). In general terms, critical damping ratios for the damped cases are different compared with the undamped cases, with the exception of damping associated with transverse bending vibrations. | + | | style="vertical-align: top;width: 60%;"|Modal damping exposed in Table 4.7 was obtained applying the empirical formulation by Kawashima ''et al'' (1993). In general terms, critical damping ratios for the damped cases are different compared with the undamped cases, with the exception of damping associated with transverse bending vibrations. |
|} | |} | ||
| Line 7,075: | Line 6,958: | ||
Damping associated to vertical bending vibrations for the damped models is lower than that obtained with the undamped cases, and especially ''AB4'' model. An opposite situation occurs with damping associated to torsional oscillations, in which damping for the undamped models are almost 50% the damping of the damped cases. | Damping associated to vertical bending vibrations for the damped models is lower than that obtained with the undamped cases, and especially ''AB4'' model. An opposite situation occurs with damping associated to torsional oscillations, in which damping for the undamped models are almost 50% the damping of the damped cases. | ||
| − | |||
| − | :<big> | + | :<big>4.5 Optimal Damper Parameters</big> |
Point 4.3 demonstrated that the best damper layout corresponds to longitudinal dampers located at the deck-ends and at the tower-deck connection. However, the best option necessarily includes selection of the optimal damper parameters, considering that capacity of damping devices depends on the specific damping coefficient ''C'' and velocity exponent ''N''. An adequate selection of those parameters is not trivial, and for that reason the aim of this part is to select the best combination of ''C'' and ''N'' that minimize the seismic response of the structures as well as the response of the dampers for both far-fault and near-fault ground motions. It is known that high control of the seismic forces into the structure implies higher damper forces, which necessarily requires higher damper capacities. As a result, an adequate selection of the damper parameters is essential to avoid wrong designs with the subsequent uncertainty about the seismic behaviour. | Point 4.3 demonstrated that the best damper layout corresponds to longitudinal dampers located at the deck-ends and at the tower-deck connection. However, the best option necessarily includes selection of the optimal damper parameters, considering that capacity of damping devices depends on the specific damping coefficient ''C'' and velocity exponent ''N''. An adequate selection of those parameters is not trivial, and for that reason the aim of this part is to select the best combination of ''C'' and ''N'' that minimize the seismic response of the structures as well as the response of the dampers for both far-fault and near-fault ground motions. It is known that high control of the seismic forces into the structure implies higher damper forces, which necessarily requires higher damper capacities. As a result, an adequate selection of the damper parameters is essential to avoid wrong designs with the subsequent uncertainty about the seismic behaviour. | ||
| Line 7,085: | Line 6,967: | ||
The analyses are performed using ''AB4'' model, and considering that the seismic response of ''AR4 ''model is similar, according to Chapter 3. The optimal damper layout previously analyzed is considered here, taking into account the same specifications for all the dampers. The geometry, structural modelling, loads and combinations, materials and analysis hypotheses are the same considered before. All the analyses are performed using the code SAP2000, and considering all available nonlinearities. As seismic input, the worse conditions for both far-fault and near-fault ground motions are applied, meaning that the orthogonal three-component earthquakes of Event 5 (far-fault) and Gatos (near-fault) are used again. Nonlinear direct integration time history analysis is applied for all the analyses, using the Hilber-Hughes-Taylor-α step-by-step integration method to solve the equations of motion. Time integration parameters considered to reach an accurate convergence are 0.02 sec time-step size, -0.2 numerical damping, 0.02 sec maximum sub-step size, 0 sec minimum sub-step size, 70 and 140 maximum iterations per sub-step for far-fault and near-fault ground motions respectively, and 1x10<sup>-4</sup> and 1x10<sup>-3</sup> iteration convergence tolerance for far-fault and near-fault ground motions respectively. Damping mechanism is considered as Rayleigh’s type, according to the modal damping previously obtained. | The analyses are performed using ''AB4'' model, and considering that the seismic response of ''AR4 ''model is similar, according to Chapter 3. The optimal damper layout previously analyzed is considered here, taking into account the same specifications for all the dampers. The geometry, structural modelling, loads and combinations, materials and analysis hypotheses are the same considered before. All the analyses are performed using the code SAP2000, and considering all available nonlinearities. As seismic input, the worse conditions for both far-fault and near-fault ground motions are applied, meaning that the orthogonal three-component earthquakes of Event 5 (far-fault) and Gatos (near-fault) are used again. Nonlinear direct integration time history analysis is applied for all the analyses, using the Hilber-Hughes-Taylor-α step-by-step integration method to solve the equations of motion. Time integration parameters considered to reach an accurate convergence are 0.02 sec time-step size, -0.2 numerical damping, 0.02 sec maximum sub-step size, 0 sec minimum sub-step size, 70 and 140 maximum iterations per sub-step for far-fault and near-fault ground motions respectively, and 1x10<sup>-4</sup> and 1x10<sup>-3</sup> iteration convergence tolerance for far-fault and near-fault ground motions respectively. Damping mechanism is considered as Rayleigh’s type, according to the modal damping previously obtained. | ||
| − | :<big> | + | :<big>4.5.1 Parametric Analysis</big> |
In order to consider representative possibilities of linear and nonlinear viscous damping, damping coefficients between 5 and 50 MN/(m/sec)<sup>N</sup>, and velocity exponents between 0.015 and 1.0 are studied, implying commercial alternatives for the dampers, currently available according to some manufacturers. Those velocity exponents cover a wide-range, from linear to highly nonlinear dampers. More than 40 nonlinear analyses were performed, implying more than 120 hours of computer time. | In order to consider representative possibilities of linear and nonlinear viscous damping, damping coefficients between 5 and 50 MN/(m/sec)<sup>N</sup>, and velocity exponents between 0.015 and 1.0 are studied, implying commercial alternatives for the dampers, currently available according to some manufacturers. Those velocity exponents cover a wide-range, from linear to highly nonlinear dampers. More than 40 nonlinear analyses were performed, implying more than 120 hours of computer time. | ||
| Line 7,093: | Line 6,975: | ||
{| style="width: 100%;margin: 1em auto 0.1em auto;" | {| style="width: 100%;margin: 1em auto 0.1em auto;" | ||
|- | |- | ||
| − | | style="text-align: center;vertical-align: top;width: 50%;"| [[Image:draft_Samper_432909089-image303.png|312px]] | + | | style="text-align: center;vertical-align: top;width: 50%;"|[[Image:draft_Samper_432909089-monograph-image303.png|312px]] |
<span style="text-align: center; font-size: 75%;">'''(a) '''Far-fault ground motion</span> | <span style="text-align: center; font-size: 75%;">'''(a) '''Far-fault ground motion</span> | ||
| − | | style="text-align: center;vertical-align: top;width: 50%;"| [[Image:draft_Samper_432909089-image304.png|312px]] | + | | style="text-align: center;vertical-align: top;width: 50%;"|[[Image:draft_Samper_432909089-monograph-image304.png|312px]] |
<span style="text-align: center; font-size: 75%;">'''(b) '''Near-fault ground motion</span> | <span style="text-align: center; font-size: 75%;">'''(b) '''Near-fault ground motion</span> | ||
| Line 7,107: | Line 6,989: | ||
{| style="width: 100%;margin: 1em auto 0.1em auto;" | {| style="width: 100%;margin: 1em auto 0.1em auto;" | ||
|- | |- | ||
| − | | style="text-align: center;vertical-align: top;width: 50%;"| [[Image:draft_Samper_432909089-image305.png|312px]] | + | | style="text-align: center;vertical-align: top;width: 50%;"|[[Image:draft_Samper_432909089-monograph-image305.png|312px]] |
<span style="text-align: center; font-size: 75%;">'''(a) '''Far-fault ground motion</span> | <span style="text-align: center; font-size: 75%;">'''(a) '''Far-fault ground motion</span> | ||
| − | | style="text-align: center;vertical-align: top;width: 50%;"| [[Image:draft_Samper_432909089-image306.png|312px]] | + | | style="text-align: center;vertical-align: top;width: 50%;"|[[Image:draft_Samper_432909089-monograph-image306.png|312px]] |
<span style="text-align: center; font-size: 75%;">'''(b) '''Near-fault ground motion</span> | <span style="text-align: center; font-size: 75%;">'''(b) '''Near-fault ground motion</span> | ||
| Line 7,116: | Line 6,998: | ||
| − | + | '''Fig. 4.12''' Maximum Vertical Displacements of the Deck at the Mid-Span | |
{| style="width: 100%;margin: 1em auto 0.1em auto;" | {| style="width: 100%;margin: 1em auto 0.1em auto;" | ||
|- | |- | ||
| − | | style="text-align: center;vertical-align: top;width: | + | | style="text-align: center;vertical-align: top;width: 50%;"|[[Image:draft_Samper_432909089-monograph-image307.png|312px]] |
<span style="text-align: center; font-size: 75%;">'''(a) '''Far-fault ground motion</span> | <span style="text-align: center; font-size: 75%;">'''(a) '''Far-fault ground motion</span> | ||
| − | | style="text-align: center;vertical-align: top;width: | + | | style="text-align: center;vertical-align: top;width: 50%;"|[[Image:draft_Samper_432909089-monograph-image308.png|312px]] |
<span style="text-align: center; font-size: 75%;">'''(b) '''Near-fault ground motion</span> | <span style="text-align: center; font-size: 75%;">'''(b) '''Near-fault ground motion</span> | ||
| Line 7,129: | Line 7,011: | ||
| − | + | '''Fig. 4.13''' Maximum Axial Forces at the Tower Base | |
{| style="width: 100%;margin: 1em auto 0.1em auto;" | {| style="width: 100%;margin: 1em auto 0.1em auto;" | ||
|- | |- | ||
| − | | style="text-align: center;vertical-align: top;width: | + | | style="text-align: center;vertical-align: top;width: 50%;"|[[Image:draft_Samper_432909089-monograph-image309.png|312px]] |
<span style="text-align: center; font-size: 75%;">'''(a) '''Far-fault ground motion</span> | <span style="text-align: center; font-size: 75%;">'''(a) '''Far-fault ground motion</span> | ||
| − | | style="text-align: center;vertical-align: top;width: | + | | style="text-align: center;vertical-align: top;width: 50%;"|[[Image:draft_Samper_432909089-monograph-image310.png|312px]] |
<span style="text-align: center; font-size: 75%;">'''(b) '''Near-fault ground motion</span> | <span style="text-align: center; font-size: 75%;">'''(b) '''Near-fault ground motion</span> | ||
| Line 7,142: | Line 7,024: | ||
| − | + | '''Fig. 4.14''' Maximum In-Plane Bending Moments at the Tower Base | |
Longitudinal displacements of the deck decrease as damping coefficient increases. For ''C'' > 30 MN/(m/sec)<sup>N </sup>displacements become independent on the damping coefficient, for both, far-fault and near-fault ground motion, which implies that control of longitudinal displacements of the deck cannot increase for damping coefficients higher than 30 MN/(m/sec)<sup>N</sup>. For far-fault ground motion, maximum displacements tend to 10 cm for high damping coefficients. In the case of near-fault ground motion, maximum displacements of the deck tend to 20 cm for high damping coefficients, independent on the velocity exponent ''N'', as happens with the far-fault condition. The analysis of the velocity exponent ''N'' shows a general tendency in which lower deck displacements are achieved with lower velocity exponents for far-fault ground motion. An opposite behaviour occurs with near-fault ground motion, especially for ''C'' ''' '''< 20 MN/(m/sec)<sup>N</sup>. This behaviour can be explained in the fact that velocities near to 1 m/sec are demanding the dampers for the near-fault condition, which implies that higher forces are demanding the dampers for high velocity exponents, implying lower deck response; on the contrary of the case of the far-fault ground motion. | Longitudinal displacements of the deck decrease as damping coefficient increases. For ''C'' > 30 MN/(m/sec)<sup>N </sup>displacements become independent on the damping coefficient, for both, far-fault and near-fault ground motion, which implies that control of longitudinal displacements of the deck cannot increase for damping coefficients higher than 30 MN/(m/sec)<sup>N</sup>. For far-fault ground motion, maximum displacements tend to 10 cm for high damping coefficients. In the case of near-fault ground motion, maximum displacements of the deck tend to 20 cm for high damping coefficients, independent on the velocity exponent ''N'', as happens with the far-fault condition. The analysis of the velocity exponent ''N'' shows a general tendency in which lower deck displacements are achieved with lower velocity exponents for far-fault ground motion. An opposite behaviour occurs with near-fault ground motion, especially for ''C'' ''' '''< 20 MN/(m/sec)<sup>N</sup>. This behaviour can be explained in the fact that velocities near to 1 m/sec are demanding the dampers for the near-fault condition, which implies that higher forces are demanding the dampers for high velocity exponents, implying lower deck response; on the contrary of the case of the far-fault ground motion. | ||
| Line 7,158: | Line 7,040: | ||
{| style="width: 100%;margin: 1em auto 0.1em auto;" | {| style="width: 100%;margin: 1em auto 0.1em auto;" | ||
|- | |- | ||
| − | | style="text-align: center;vertical-align: top;width: | + | | style="text-align: center;vertical-align: top;width: 50%;"|[[Image:draft_Samper_432909089-monograph-image311.png|312px]] |
<span style="text-align: center; font-size: 75%;">'''(a) '''Far-fault ground motion</span> | <span style="text-align: center; font-size: 75%;">'''(a) '''Far-fault ground motion</span> | ||
| − | | style="text-align: center;vertical-align: top;width: | + | | style="text-align: center;vertical-align: top;width: 50%;"|[[Image:draft_Samper_432909089-monograph-image312.png|312px]] |
<span style="text-align: center; font-size: 75%;">'''(b) '''Near-fault ground motion</span> | <span style="text-align: center; font-size: 75%;">'''(b) '''Near-fault ground motion</span> | ||
| Line 7,167: | Line 7,049: | ||
| − | + | '''Fig. 4.15''' Maximum Deck-End Damper Forces | |
{| style="width: 100%;margin: 1em auto 0.1em auto;" | {| style="width: 100%;margin: 1em auto 0.1em auto;" | ||
|- | |- | ||
| − | | style="text-align: center;vertical-align: top;width: | + | | style="text-align: center;vertical-align: top;width: 50%;"|[[Image:draft_Samper_432909089-monograph-image313.png|312px]] |
<span style="text-align: center; font-size: 75%;">'''(a) '''Far-fault ground motion</span> | <span style="text-align: center; font-size: 75%;">'''(a) '''Far-fault ground motion</span> | ||
| − | | style="text-align: center;vertical-align: top;width: | + | | style="text-align: center;vertical-align: top;width: 50%;"|[[Image:draft_Samper_432909089-monograph-image314.png|312px]] |
<span style="text-align: center; font-size: 75%;">'''(b) '''Near-fault ground motion</span> | <span style="text-align: center; font-size: 75%;">'''(b) '''Near-fault ground motion</span> | ||
| Line 7,180: | Line 7,062: | ||
| − | + | '''Fig. 4.16''' Maximum Damper Forces at the Tower-Deck Connection | |
The analysis of the damper velocities (Figs. 4.17 and 4.18) shows an opposite situation compared with the damper forces, that is to say, minimum velocities obtained for highly nonlinear dampers. In other words, minimum velocity responses imply maximum damper forces. Velocities tend to decrease as the damping coefficient increases, although for ''C'' > 30 MN/(m/sec)<sup>N</sup>, velocities are independent on the damping coefficient for both far-fault and near-fault ground motion. Likewise, it is clear that maximum damper velocities can be obtained for the near-fault condition. | The analysis of the damper velocities (Figs. 4.17 and 4.18) shows an opposite situation compared with the damper forces, that is to say, minimum velocities obtained for highly nonlinear dampers. In other words, minimum velocity responses imply maximum damper forces. Velocities tend to decrease as the damping coefficient increases, although for ''C'' > 30 MN/(m/sec)<sup>N</sup>, velocities are independent on the damping coefficient for both far-fault and near-fault ground motion. Likewise, it is clear that maximum damper velocities can be obtained for the near-fault condition. | ||
| Line 7,188: | Line 7,070: | ||
{| style="width: 100%;margin: 1em auto 0.1em auto;" | {| style="width: 100%;margin: 1em auto 0.1em auto;" | ||
|- | |- | ||
| − | | style="text-align: center;vertical-align: top;width: | + | | style="text-align: center;vertical-align: top;width: 50%;"|[[Image:draft_Samper_432909089-monograph-image315.png|312px]] |
<span style="text-align: center; font-size: 75%;">'''(a) '''Far-fault ground motion</span> | <span style="text-align: center; font-size: 75%;">'''(a) '''Far-fault ground motion</span> | ||
| − | | style="text-align: center;vertical-align: top;width: | + | | style="text-align: center;vertical-align: top;width: 50%;"|[[Image:draft_Samper_432909089-monograph-image316.png|312px]] |
<span style="text-align: center; font-size: 75%;">'''(b) '''Near-fault ground motion</span> | <span style="text-align: center; font-size: 75%;">'''(b) '''Near-fault ground motion</span> | ||
| Line 7,197: | Line 7,079: | ||
| − | + | '''Fig. 4.17''' Maximum Deck-End Damper Velocities | |
{| style="width: 100%;margin: 1em auto 0.1em auto;" | {| style="width: 100%;margin: 1em auto 0.1em auto;" | ||
|- | |- | ||
| − | | style="text-align: center;vertical-align: top;width: | + | | style="text-align: center;vertical-align: top;width: 50%;"|[[Image:draft_Samper_432909089-monograph-image317.png|312px]] |
<span style="text-align: center; font-size: 75%;">'''(a) '''Far-fault ground motion</span> | <span style="text-align: center; font-size: 75%;">'''(a) '''Far-fault ground motion</span> | ||
| − | | style="text-align: center;vertical-align: top;width: | + | | style="text-align: center;vertical-align: top;width: 50%;"|[[Image:draft_Samper_432909089-monograph-image318.png|312px]] |
<span style="text-align: center; font-size: 75%;">'''(b) '''Near-fault ground motion</span> | <span style="text-align: center; font-size: 75%;">'''(b) '''Near-fault ground motion</span> | ||
| Line 7,210: | Line 7,092: | ||
| − | + | '''Fig. 4.18''' Maximum Damper Velocities at the Tower-Deck Connection | |
| − | :<big> | + | :<big>4.5.2 Selection of the Damper Parameters</big> |
Selection of the optimal damper parameters necessarily consists in obtaining an efficient control of both the structural response and the damper response. In this sense, optimization techniques can be employed in this task. It seems to be that a reasonable approximation is to minimize the maximum longitudinal displacements of the deck as characteristic measure of the structural response, and to minimize the maximum damper forces as characteristic measure of the damper response; considering those maximum responses as absolute values for simplicity. By this way, we can define the longitudinal deck displacement matrix ''A'', in which ''a<sub>ij</sub>'' represents the maximum absolute longitudinal displacement of the deck [cm] for damping coefficient ''i'' and velocity exponent ''j''. Similarly, it is possible to define the damper force matrix ''B'', in which ''b<sub>ij</sub>'' represents the maximum absolute damper force [kN] associated to the damping coefficient ''i'' and velocity exponent ''j. ''Thus, defining matrix ''F = AB'', the task is to seek the minimum values of ''F''. This simple procedure can be applied separately for deck-end dampers as well as the dampers located at the tower-deck connection, for far-fault and near-fault ground motions. | Selection of the optimal damper parameters necessarily consists in obtaining an efficient control of both the structural response and the damper response. In this sense, optimization techniques can be employed in this task. It seems to be that a reasonable approximation is to minimize the maximum longitudinal displacements of the deck as characteristic measure of the structural response, and to minimize the maximum damper forces as characteristic measure of the damper response; considering those maximum responses as absolute values for simplicity. By this way, we can define the longitudinal deck displacement matrix ''A'', in which ''a<sub>ij</sub>'' represents the maximum absolute longitudinal displacement of the deck [cm] for damping coefficient ''i'' and velocity exponent ''j''. Similarly, it is possible to define the damper force matrix ''B'', in which ''b<sub>ij</sub>'' represents the maximum absolute damper force [kN] associated to the damping coefficient ''i'' and velocity exponent ''j. ''Thus, defining matrix ''F = AB'', the task is to seek the minimum values of ''F''. This simple procedure can be applied separately for deck-end dampers as well as the dampers located at the tower-deck connection, for far-fault and near-fault ground motions. | ||
| Line 7,218: | Line 7,100: | ||
Of course, this simplified approximation considers that the main parameters that affect both the seismic response of the structure and the seismic response of the dampers are conditioned by displacements of the deck and forces on the dampers. Approximations considering more sophisticated optimization techniques can also be applied, as well as energy approaches; however, for simplicity, the procedure here explained was used. | Of course, this simplified approximation considers that the main parameters that affect both the seismic response of the structure and the seismic response of the dampers are conditioned by displacements of the deck and forces on the dampers. Approximations considering more sophisticated optimization techniques can also be applied, as well as energy approaches; however, for simplicity, the procedure here explained was used. | ||
| − | : | + | :4.5.2.1 Far-fault ground motion |
:''(1) Deck-end dampers:'' | :''(1) Deck-end dampers:'' | ||
| Line 7,226: | Line 7,108: | ||
{| | {| | ||
|- | |- | ||
| − | | | + | | [[Image:draft_Samper_432909089-monograph-image319.png|12px]] |
| − | | [[Image:draft_Samper_432909089-image320.png|center|600px]] | + | | [[Image:draft_Samper_432909089-monograph-image320.png|center|600px]] |
|} | |} | ||
| − | + | [[Image:draft_Samper_432909089-monograph-image321.png|12px]] </div> | |
{| style="width: 68%;margin: 1em auto 0.1em auto;border-collapse: collapse;" | {| style="width: 68%;margin: 1em auto 0.1em auto;border-collapse: collapse;" | ||
| Line 7,284: | Line 7,166: | ||
<div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | ||
| − | [[Image:draft_Samper_432909089-image322.png|270px]] </div> | + | [[Image:draft_Samper_432909089-monograph-image322.png|270px]] </div> |
| − | + | [[Image:draft_Samper_432909089-monograph-image323.png|12px]] | |
{| style="width: 77%;margin: 1em auto 0.1em auto;border-collapse: collapse;" | {| style="width: 77%;margin: 1em auto 0.1em auto;border-collapse: collapse;" | ||
| Line 7,334: | Line 7,216: | ||
| − | + | In those analyses, units of C are [MN/(m/sec)<sup>N</sup>]. | |
Values signed in green represent good candidates that minimize both maximum longitudinal displacements of the deck and maximum damper forces. ''C = 5 ''is not recommended because of the small energy dissipation associated. This implies that the optimal solution, for all damper locations, seems to be ''C = 10 ''or ''C = ''20. It is interesting to observe that the linear solution (''N = 1'') is not an optimal value, and for that reason, the best candidates for the velocity exponent are ''N = 0.1'' and ''N = 0.5.'' It is clear that ''C = 10''; ''N = 0.1'' is the same as ''C = 20; N = 0.5'' for both deck-end dampers and dampers located at the tower-deck connection. If we consider more structural response parameters, it is possible to achieve the desired optimal solution. Thus, employing results obtained from the parametric analysis, it is clear that the best option to control the vertical displacements of the deck is ''N = 0.5'' and ''C ≤ 30.'' For the tower moments, the best option is ''N = 0.5'' or ''N = 0.1'' and 10 ''≤ C ≤ 30.'' For deck-end damper forces, ''N = 0.5'' and ''C ≤ 30'' is a good solution. For deck-end damper velocities, an adequate control occurs if ''N = 0.1'' and ''10 ≤ C ≤ 50''; or ''N = 0.5 ''and ''C ≥ 20. ''The best solution for the damper forces at the tower-deck connection is ''N = 0.5 ''and ''C ≤ 30''. In the case of the damper velocities at the tower-deck connection'', N = 0.1'' and ''C ≥ 20'' is a good option. As a result, the best option involving all the considered aspects is to choose ''C = 20'' and ''N = 0.5.'' | Values signed in green represent good candidates that minimize both maximum longitudinal displacements of the deck and maximum damper forces. ''C = 5 ''is not recommended because of the small energy dissipation associated. This implies that the optimal solution, for all damper locations, seems to be ''C = 10 ''or ''C = ''20. It is interesting to observe that the linear solution (''N = 1'') is not an optimal value, and for that reason, the best candidates for the velocity exponent are ''N = 0.1'' and ''N = 0.5.'' It is clear that ''C = 10''; ''N = 0.1'' is the same as ''C = 20; N = 0.5'' for both deck-end dampers and dampers located at the tower-deck connection. If we consider more structural response parameters, it is possible to achieve the desired optimal solution. Thus, employing results obtained from the parametric analysis, it is clear that the best option to control the vertical displacements of the deck is ''N = 0.5'' and ''C ≤ 30.'' For the tower moments, the best option is ''N = 0.5'' or ''N = 0.1'' and 10 ''≤ C ≤ 30.'' For deck-end damper forces, ''N = 0.5'' and ''C ≤ 30'' is a good solution. For deck-end damper velocities, an adequate control occurs if ''N = 0.1'' and ''10 ≤ C ≤ 50''; or ''N = 0.5 ''and ''C ≥ 20. ''The best solution for the damper forces at the tower-deck connection is ''N = 0.5 ''and ''C ≤ 30''. In the case of the damper velocities at the tower-deck connection'', N = 0.1'' and ''C ≥ 20'' is a good option. As a result, the best option involving all the considered aspects is to choose ''C = 20'' and ''N = 0.5.'' | ||
| − | : | + | :4.5.2.2 Near-fault ground motion |
| − | + | The analysis of the near-fault condition is analogue to the far-fault analysis. | |
:''(1) Deck-end dampers:'' | :''(1) Deck-end dampers:'' | ||
<div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | ||
| − | + | [[Image:draft_Samper_432909089-monograph-image324.png|600px]] </div> | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
{| style="width: 63%;margin: 1em auto 0.1em auto;border-collapse: collapse;" | {| style="width: 63%;margin: 1em auto 0.1em auto;border-collapse: collapse;" | ||
| Line 7,410: | Line 7,278: | ||
<div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | ||
| − | + | [[Image:draft_Samper_432909089-monograph-image325.png|276px]] </div> | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
{| style="width: 64%;margin: 1em auto 0.1em auto;border-collapse: collapse;" | {| style="width: 64%;margin: 1em auto 0.1em auto;border-collapse: collapse;" | ||
| Line 7,469: | Line 7,330: | ||
Summarizing, ''C = 20'' and ''N = 0.5'' is selected for far-fault ground motion; and ''C = 30'' and ''N = 0.015'' is applied for near-fault ground motion. Those values are used independent on the damper location. | Summarizing, ''C = 20'' and ''N = 0.5'' is selected for far-fault ground motion; and ''C = 30'' and ''N = 0.015'' is applied for near-fault ground motion. Those values are used independent on the damper location. | ||
| − | :<big> | + | :<big>4.5.3 Influence of the Velocity Exponent and Damping Coefficient</big> |
The analyses have shown the important incidence of the damper parameters on the seismic response of the structure and dampers. The velocity exponent of the dampers plays an important role on the seismic response of the dampers, in which linear dampers tend to minimize the damper forces although important damper velocities can be experienced mainly for low damping coefficients. However, it was demonstrated that the optimal solution, as a whole, involves the employ of nonlinear dampers, and especially in the presence of near-fault ground motions. | The analyses have shown the important incidence of the damper parameters on the seismic response of the structure and dampers. The velocity exponent of the dampers plays an important role on the seismic response of the dampers, in which linear dampers tend to minimize the damper forces although important damper velocities can be experienced mainly for low damping coefficients. However, it was demonstrated that the optimal solution, as a whole, involves the employ of nonlinear dampers, and especially in the presence of near-fault ground motions. | ||
| Line 7,477: | Line 7,338: | ||
{| style="width: 100%;margin: 1em auto 0.1em auto;" | {| style="width: 100%;margin: 1em auto 0.1em auto;" | ||
|- | |- | ||
| − | | style="text-align: center;vertical-align: top;width: 50%;"| [[Image:draft_Samper_432909089-image326.png|312px]] | + | | style="text-align: center;vertical-align: top;width: 50%;"|[[Image:draft_Samper_432909089-monograph-image326.png|312px]] |
<span style="text-align: center; font-size: 75%;">'''(a) ''' ''C = 10 ''MN/(m/sec)<sup>N</sup></span> | <span style="text-align: center; font-size: 75%;">'''(a) ''' ''C = 10 ''MN/(m/sec)<sup>N</sup></span> | ||
| − | | style="text-align: center;vertical-align: top;width: 50%;"| [[Image:draft_Samper_432909089-image327.png|312px]] | + | | style="text-align: center;vertical-align: top;width: 50%;"|[[Image:draft_Samper_432909089-monograph-image327.png|312px]] |
<span style="text-align: center; font-size: 75%;">'''(b) ''' ''C = 50 ''MN/(m/sec)<sup>N</sup></span> | <span style="text-align: center; font-size: 75%;">'''(b) ''' ''C = 50 ''MN/(m/sec)<sup>N</sup></span> | ||
| Line 7,495: | Line 7,356: | ||
{| style="width: 100%;margin: 1em auto 0.1em auto;" | {| style="width: 100%;margin: 1em auto 0.1em auto;" | ||
|- | |- | ||
| − | | style="text-align: center;vertical-align: top;width: 50%;"| [[Image:draft_Samper_432909089-image328.png|312px]] | + | | style="text-align: center;vertical-align: top;width: 50%;"|[[Image:draft_Samper_432909089-monograph-image328.png|312px]] |
<span style="text-align: center; font-size: 75%;">'''(a) ''' ''C = 10 ''MN/(m/sec)<sup>N</sup></span> | <span style="text-align: center; font-size: 75%;">'''(a) ''' ''C = 10 ''MN/(m/sec)<sup>N</sup></span> | ||
| − | | style="text-align: center;vertical-align: top;width: 50%;"| [[Image:draft_Samper_432909089-image329.png|312px]] | + | | style="text-align: center;vertical-align: top;width: 50%;"|[[Image:draft_Samper_432909089-monograph-image329.png|312px]] |
<span style="text-align: center; font-size: 75%;">'''(b) ''' ''C = 50 ''MN/(m/sec)<sup>N</sup></span> | <span style="text-align: center; font-size: 75%;">'''(b) ''' ''C = 50 ''MN/(m/sec)<sup>N</sup></span> | ||
| Line 7,513: | Line 7,374: | ||
As a summary, an important effect of the velocity exponent of the dampers is observed on the damper forces, as well as a not important effect on the structural response. The damping coefficient notably affects both the structural response and the damper response, with an increase of the structural response when the damping coefficient decreases, on the contrary of the damper response, in which an increase of the damping coefficient increases the damper forces. | As a summary, an important effect of the velocity exponent of the dampers is observed on the damper forces, as well as a not important effect on the structural response. The damping coefficient notably affects both the structural response and the damper response, with an increase of the structural response when the damping coefficient decreases, on the contrary of the damper response, in which an increase of the damping coefficient increases the damper forces. | ||
| − | : | + | :4.6 <big>Nonlinear Time-History Analysis </big> |
The previous analyses were focused on the search of the optimal damper layout, optimal damper parameters and the importance of the damping coefficient and velocity exponent. This part analyzes the seismic response of both ''AB4'' and ''AR4 ''bridge models considering all the far-fault and near-fault events described in Chapter 3. The aim of this study is to obtain the nonlinear seismic response for the damped systems considering the optimal conditions before mentioned, in order to compare the responses between both structures, and with the undamped cases, considering the far-fault and near-fault conditions. | The previous analyses were focused on the search of the optimal damper layout, optimal damper parameters and the importance of the damping coefficient and velocity exponent. This part analyzes the seismic response of both ''AB4'' and ''AR4 ''bridge models considering all the far-fault and near-fault events described in Chapter 3. The aim of this study is to obtain the nonlinear seismic response for the damped systems considering the optimal conditions before mentioned, in order to compare the responses between both structures, and with the undamped cases, considering the far-fault and near-fault conditions. | ||
| Line 7,521: | Line 7,382: | ||
The study is divided into far-fault and near-fault ground motions, in which time histories and maximum responses are exposed for the structures and dampers. As occurs with the undamped cases, shear forces were not included in this analysis because the response of cable-stayed bridges (internal forces) is basically controlled by axial forces, bending moments and their interaction. | The study is divided into far-fault and near-fault ground motions, in which time histories and maximum responses are exposed for the structures and dampers. As occurs with the undamped cases, shear forces were not included in this analysis because the response of cable-stayed bridges (internal forces) is basically controlled by axial forces, bending moments and their interaction. | ||
| − | :<big> | + | :<big>4.6.1 Far-Fault Ground Motion</big> |
For the far-fault ground motion analysis, the same artificially generated earthquake events before employed are used here. Likewise, the same general considerations explained in Chapter 3 are valid here. In this sense, time-history plots shown in the following figures expose the response for the zone associated to the strong motion duration, obtained from the Arias Intensity of each event. Furthermore, at time equal to zero, the response is generally non-zero because it is obtained at the end of the nonlinear static analysis, and considered as starting point of the nonlinear direct integration time history analysis. | For the far-fault ground motion analysis, the same artificially generated earthquake events before employed are used here. Likewise, the same general considerations explained in Chapter 3 are valid here. In this sense, time-history plots shown in the following figures expose the response for the zone associated to the strong motion duration, obtained from the Arias Intensity of each event. Furthermore, at time equal to zero, the response is generally non-zero because it is obtained at the end of the nonlinear static analysis, and considered as starting point of the nonlinear direct integration time history analysis. | ||
| Line 7,529: | Line 7,390: | ||
{| style="width: 100%;margin: 1em auto 0.1em auto;" | {| style="width: 100%;margin: 1em auto 0.1em auto;" | ||
|- | |- | ||
| − | | style="text-align: center;vertical-align: top;width: 50%;"| [[Image:draft_Samper_432909089-image330.png|312px]] | + | | style="text-align: center;vertical-align: top;width: 50%;"|[[Image:draft_Samper_432909089-monograph-image330.png|312px]] |
<span style="text-align: center; font-size: 75%;">'''(a)''' ''AB4'' bridge</span> | <span style="text-align: center; font-size: 75%;">'''(a)''' ''AB4'' bridge</span> | ||
| − | | style="text-align: center;vertical-align: top;width: 50%;"| [[Image:draft_Samper_432909089-image331.png|312px]] | + | | style="text-align: center;vertical-align: top;width: 50%;"|[[Image:draft_Samper_432909089-monograph-image331.png|312px]] |
<span style="text-align: center; font-size: 75%;">'''(b)''' ''AR4'' bridge</span> | <span style="text-align: center; font-size: 75%;">'''(b)''' ''AR4'' bridge</span> | ||
| Line 7,543: | Line 7,404: | ||
{| style="width: 100%;margin: 1em auto 0.1em auto;" | {| style="width: 100%;margin: 1em auto 0.1em auto;" | ||
|- | |- | ||
| − | | style="text-align: center;vertical-align: top;width: | + | | style="text-align: center;vertical-align: top;width: 50%;"|[[Image:draft_Samper_432909089-monograph-image332.png|312px]] |
<span style="text-align: center; font-size: 75%;">'''(a)''' ''AB4'' bridge</span> | <span style="text-align: center; font-size: 75%;">'''(a)''' ''AB4'' bridge</span> | ||
| − | | style="text-align: center;vertical-align: top;width: | + | | style="text-align: center;vertical-align: top;width: 50%;"|[[Image:draft_Samper_432909089-monograph-image333.png|312px]] |
<span style="text-align: center; font-size: 75%;">'''(b)''' ''AR4'' bridge</span> | <span style="text-align: center; font-size: 75%;">'''(b)''' ''AR4'' bridge</span> | ||
| Line 7,559: | Line 7,420: | ||
{| style="width: 100%;margin: 1em auto 0.1em auto;" | {| style="width: 100%;margin: 1em auto 0.1em auto;" | ||
|- | |- | ||
| − | | style="text-align: center;vertical-align: top;width: 50%;"| [[Image:draft_Samper_432909089-image334.png|312px]] | + | | style="text-align: center;vertical-align: top;width: 50%;"|[[Image:draft_Samper_432909089-monograph-image334.png|312px]] |
<span style="text-align: center; font-size: 75%;">'''(a)''' ''AB4'' bridge</span> | <span style="text-align: center; font-size: 75%;">'''(a)''' ''AB4'' bridge</span> | ||
| − | | style="text-align: center;vertical-align: top;width: 50%;"| [[Image:draft_Samper_432909089-image335.png|312px]] | + | | style="text-align: center;vertical-align: top;width: 50%;"|[[Image:draft_Samper_432909089-monograph-image335.png|312px]] |
<span style="text-align: center; font-size: 75%;">'''(b)''' ''AR4'' bridge</span> | <span style="text-align: center; font-size: 75%;">'''(b)''' ''AR4'' bridge</span> | ||
| Line 7,577: | Line 7,438: | ||
{| style="width: 100%;margin: 1em auto 0.1em auto;" | {| style="width: 100%;margin: 1em auto 0.1em auto;" | ||
|- | |- | ||
| − | | style="text-align: center;vertical-align: top;width: 50%;"| [[Image:draft_Samper_432909089-image336.png|312px]] | + | | style="text-align: center;vertical-align: top;width: 50%;"|[[Image:draft_Samper_432909089-monograph-image336.png|312px]] |
<span style="text-align: center; font-size: 75%;">'''(a)''' ''AB4'' bridge</span> | <span style="text-align: center; font-size: 75%;">'''(a)''' ''AB4'' bridge</span> | ||
| − | | style="text-align: center;vertical-align: top;width: 50%;"| [[Image:draft_Samper_432909089-image337.png|312px]] | + | | style="text-align: center;vertical-align: top;width: 50%;"|[[Image:draft_Samper_432909089-monograph-image337.png|312px]] |
<span style="text-align: center; font-size: 75%;">'''(b)''' ''AR4'' bridge</span> | <span style="text-align: center; font-size: 75%;">'''(b)''' ''AR4'' bridge</span> | ||
| Line 7,593: | Line 7,454: | ||
{| style="width: 100%;margin: 1em auto 0.1em auto;" | {| style="width: 100%;margin: 1em auto 0.1em auto;" | ||
|- | |- | ||
| − | | style="text-align: center;vertical-align: top;width: 50%;"| [[Image:draft_Samper_432909089-image338.png|312px]] | + | | style="text-align: center;vertical-align: top;width: 50%;"|[[Image:draft_Samper_432909089-monograph-image338.png|312px]] |
<span style="text-align: center; font-size: 75%;">'''(a)''' ''AB4'' bridge</span> | <span style="text-align: center; font-size: 75%;">'''(a)''' ''AB4'' bridge</span> | ||
| − | | style="text-align: center;vertical-align: top;width: 50%;"| [[Image:draft_Samper_432909089-image339.png|312px]] | + | | style="text-align: center;vertical-align: top;width: 50%;"|[[Image:draft_Samper_432909089-monograph-image339.png|312px]] |
<span style="text-align: center; font-size: 75%;">'''(b)''' ''AR4'' bridge</span> | <span style="text-align: center; font-size: 75%;">'''(b)''' ''AR4'' bridge</span> | ||
| Line 7,607: | Line 7,468: | ||
{| style="width: 100%;margin: 1em auto 0.1em auto;" | {| style="width: 100%;margin: 1em auto 0.1em auto;" | ||
|- | |- | ||
| − | | style="text-align: center;vertical-align: top;width: | + | | style="text-align: center;vertical-align: top;width: 50%;"|[[Image:draft_Samper_432909089-monograph-image340.png|312px]] |
<span style="text-align: center; font-size: 75%;">'''(a)''' ''AB4'' bridge</span> | <span style="text-align: center; font-size: 75%;">'''(a)''' ''AB4'' bridge</span> | ||
| − | | style="text-align: center;vertical-align: top;width: | + | | style="text-align: center;vertical-align: top;width: 50%;"|[[Image:draft_Samper_432909089-monograph-image341.png|312px]] |
<span style="text-align: center; font-size: 75%;">'''(b)''' ''AR4'' bridge</span> | <span style="text-align: center; font-size: 75%;">'''(b)''' ''AR4'' bridge</span> | ||
| Line 7,623: | Line 7,484: | ||
{| style="width: 100%;margin: 1em auto 0.1em auto;" | {| style="width: 100%;margin: 1em auto 0.1em auto;" | ||
|- | |- | ||
| − | | style="text-align: center;vertical-align: top;width: | + | | style="text-align: center;vertical-align: top;width: 50%;"|[[Image:draft_Samper_432909089-monograph-image342.png|312px]] |
<span style="text-align: center; font-size: 75%;">'''(a)''' ''AB4'' bridge</span> | <span style="text-align: center; font-size: 75%;">'''(a)''' ''AB4'' bridge</span> | ||
| − | | style="text-align: center;vertical-align: top;width: | + | | style="text-align: center;vertical-align: top;width: 50%;"|[[Image:draft_Samper_432909089-monograph-image343.png|312px]] |
<span style="text-align: center; font-size: 75%;">'''(b)''' ''AR4'' bridge</span> | <span style="text-align: center; font-size: 75%;">'''(b)''' ''AR4'' bridge</span> | ||
| Line 7,637: | Line 7,498: | ||
{| style="width: 100%;margin: 1em auto 0.1em auto;" | {| style="width: 100%;margin: 1em auto 0.1em auto;" | ||
|- | |- | ||
| − | | style="text-align: center;vertical-align: top;width: | + | | style="text-align: center;vertical-align: top;width: 50%;"|[[Image:draft_Samper_432909089-monograph-image344.png|312px]] |
<span style="text-align: center; font-size: 75%;">'''(a)''' ''AB4'' bridge</span> | <span style="text-align: center; font-size: 75%;">'''(a)''' ''AB4'' bridge</span> | ||
| − | | style="text-align: center;vertical-align: top;width: | + | | style="text-align: center;vertical-align: top;width: 50%;"|[[Image:draft_Samper_432909089-monograph-image345.png|312px]] |
<span style="text-align: center; font-size: 75%;">'''(b)''' ''AR4'' bridge</span> | <span style="text-align: center; font-size: 75%;">'''(b)''' ''AR4'' bridge</span> | ||
| Line 7,655: | Line 7,516: | ||
{| style="width: 100%;margin: 1em auto 0.1em auto;" | {| style="width: 100%;margin: 1em auto 0.1em auto;" | ||
|- | |- | ||
| − | | style="text-align: center;vertical-align: top;width: | + | | style="text-align: center;vertical-align: top;width: 50%;"|[[Image:draft_Samper_432909089-monograph-image346.png|312px]] |
<span style="text-align: center; font-size: 75%;">'''(a)''' ''AB4'' bridge</span> | <span style="text-align: center; font-size: 75%;">'''(a)''' ''AB4'' bridge</span> | ||
| − | | style="text-align: center;vertical-align: top;width: | + | | style="text-align: center;vertical-align: top;width: 50%;"|[[Image:draft_Samper_432909089-monograph-image347.png|312px]] |
<span style="text-align: center; font-size: 75%;">'''(b)''' ''AR4'' bridge</span> | <span style="text-align: center; font-size: 75%;">'''(b)''' ''AR4'' bridge</span> | ||
| Line 7,671: | Line 7,532: | ||
{| style="width: 100%;margin: 1em auto 0.1em auto;" | {| style="width: 100%;margin: 1em auto 0.1em auto;" | ||
|- | |- | ||
| − | | style="text-align: center;vertical-align: top;width: | + | | style="text-align: center;vertical-align: top;width: 50%;"|[[Image:draft_Samper_432909089-monograph-image348.png|312px]] |
<span style="text-align: center; font-size: 75%;">'''(a)''' ''AB4'' bridge</span> | <span style="text-align: center; font-size: 75%;">'''(a)''' ''AB4'' bridge</span> | ||
| − | | style="text-align: center;vertical-align: top;width: | + | | style="text-align: center;vertical-align: top;width: 50%;"|[[Image:draft_Samper_432909089-monograph-image349.png|312px]] |
<span style="text-align: center; font-size: 75%;">'''(b)''' ''AR4'' bridge</span> | <span style="text-align: center; font-size: 75%;">'''(b)''' ''AR4'' bridge</span> | ||
| Line 7,963: | Line 7,824: | ||
<span style="text-align: center; font-size: 75%;"><sup>a</sup> At the tower base <sup>c</sup> In-plane</span> | <span style="text-align: center; font-size: 75%;"><sup>a</sup> At the tower base <sup>c</sup> In-plane</span> | ||
| − | <sup>b</sup> At the tower-deck connection <sup>d</sup> Out-of-plane | + | <span style="text-align: center; font-size: 75%;"><sup>b</sup> At the tower-deck connection <sup>d</sup> Out-of-plane</span> |
The analysis of the maximum forces and velocities of the dampers can be appreciated in Table 4.11. For simplicity, response of the dampers is exposed in absolute values again. Almost the same results are observed for both structures, with insignificant differences between the seismic events. Important differences are observed comparing deck-end damper response with the tower damper response, in which average velocities of about 0.30 m/sec and 0.18 m/sec are obtained respectively. With regard to the average maximum damper forces, differences of about 20% are evaluated between both damper locations. Of course, maximum damper forces are obtained at the deck-ends, implying higher energy dissipation than that associated to the tower-deck connection. | The analysis of the maximum forces and velocities of the dampers can be appreciated in Table 4.11. For simplicity, response of the dampers is exposed in absolute values again. Almost the same results are observed for both structures, with insignificant differences between the seismic events. Important differences are observed comparing deck-end damper response with the tower damper response, in which average velocities of about 0.30 m/sec and 0.18 m/sec are obtained respectively. With regard to the average maximum damper forces, differences of about 20% are evaluated between both damper locations. Of course, maximum damper forces are obtained at the deck-ends, implying higher energy dissipation than that associated to the tower-deck connection. | ||
| Line 8,052: | Line 7,913: | ||
| − | :<big> | + | :<big>4.6.2 Near-Fault Ground Motion</big> |
Addition of long-period velocity pulses on the seismic records involves a very different behaviour compared with results recently exposed. Of course, the main differences come from the real nature of the seismic events that now are analyzed, with evident lower frequency content, as can be seen in Chapter 3. Velocity pulses are the basic characteristic of the near-source effects, and the presence of those phenomena on long-period structures can be dramatic, with important response increases, as was demonstrated with the undamped bridges. Time histories are very different compared with those obtained during the far-fault analysis, and results show important variations from one event to another. Likewise, maximum responses are very different depending on the considered event; however, general tendencies and important observations can be proposed. The main observation is the important decrease of the seismic response when additional dampers are included, and especially the longitudinal response, as occurs with the far-fault analysis. | Addition of long-period velocity pulses on the seismic records involves a very different behaviour compared with results recently exposed. Of course, the main differences come from the real nature of the seismic events that now are analyzed, with evident lower frequency content, as can be seen in Chapter 3. Velocity pulses are the basic characteristic of the near-source effects, and the presence of those phenomena on long-period structures can be dramatic, with important response increases, as was demonstrated with the undamped bridges. Time histories are very different compared with those obtained during the far-fault analysis, and results show important variations from one event to another. Likewise, maximum responses are very different depending on the considered event; however, general tendencies and important observations can be proposed. The main observation is the important decrease of the seismic response when additional dampers are included, and especially the longitudinal response, as occurs with the far-fault analysis. | ||
| Line 8,062: | Line 7,923: | ||
{| style="width: 100%;margin: 1em auto 0.1em auto;" | {| style="width: 100%;margin: 1em auto 0.1em auto;" | ||
|- | |- | ||
| − | | style="text-align: center;vertical-align: top;width: | + | | style="text-align: center;vertical-align: top;width: 50%;"|[[Image:draft_Samper_432909089-monograph-image350.png|312px]] |
<span style="text-align: center; font-size: 75%;">'''(a)''' ''AB4'' bridge</span> | <span style="text-align: center; font-size: 75%;">'''(a)''' ''AB4'' bridge</span> | ||
| − | | style="text-align: center;vertical-align: top;width: | + | | style="text-align: center;vertical-align: top;width: 50%;"|[[Image:draft_Samper_432909089-monograph-image351.png|312px]] |
<span style="text-align: center; font-size: 75%;">'''(b)''' ''AR4'' bridge</span> | <span style="text-align: center; font-size: 75%;">'''(b)''' ''AR4'' bridge</span> | ||
| Line 8,076: | Line 7,937: | ||
{| style="width: 100%;margin: 1em auto 0.1em auto;" | {| style="width: 100%;margin: 1em auto 0.1em auto;" | ||
|- | |- | ||
| − | | style="text-align: center;vertical-align: top;width: | + | | style="text-align: center;vertical-align: top;width: 50%;"|[[Image:draft_Samper_432909089-monograph-image352.png|312px]] |
<span style="text-align: center; font-size: 75%;">'''(a)''' ''AB4'' bridge</span> | <span style="text-align: center; font-size: 75%;">'''(a)''' ''AB4'' bridge</span> | ||
| − | | style="text-align: center;vertical-align: top;width: | + | | style="text-align: center;vertical-align: top;width: 50%;"|[[Image:draft_Samper_432909089-monograph-image353.png|312px]] |
<span style="text-align: center; font-size: 75%;">'''(b)''' ''AR4'' bridge</span> | <span style="text-align: center; font-size: 75%;">'''(b)''' ''AR4'' bridge</span> | ||
| Line 8,096: | Line 7,957: | ||
{| style="width: 100%;margin: 1em auto 0.1em auto;" | {| style="width: 100%;margin: 1em auto 0.1em auto;" | ||
|- | |- | ||
| − | | style="text-align: center;vertical-align: top;width: | + | | style="text-align: center;vertical-align: top;width: 50%;"|[[Image:draft_Samper_432909089-monograph-image354.png|312px]] |
<span style="text-align: center; font-size: 75%;">'''(a)''' ''AB4'' bridge</span> | <span style="text-align: center; font-size: 75%;">'''(a)''' ''AB4'' bridge</span> | ||
| − | | style="text-align: center;vertical-align: top;width: | + | | style="text-align: center;vertical-align: top;width: 50%;"|[[Image:draft_Samper_432909089-monograph-image355.png|312px]] |
<span style="text-align: center; font-size: 75%;">'''(b)''' ''AR4'' bridge</span> | <span style="text-align: center; font-size: 75%;">'''(b)''' ''AR4'' bridge</span> | ||
| Line 8,110: | Line 7,971: | ||
{| style="width: 100%;margin: 1em auto 0.1em auto;" | {| style="width: 100%;margin: 1em auto 0.1em auto;" | ||
|- | |- | ||
| − | | style="text-align: center;vertical-align: top;width: | + | | style="text-align: center;vertical-align: top;width: 50%;"|[[Image:draft_Samper_432909089-monograph-image356.png|312px]] |
<span style="text-align: center; font-size: 75%;">'''(a)''' ''AB4'' bridge</span> | <span style="text-align: center; font-size: 75%;">'''(a)''' ''AB4'' bridge</span> | ||
| − | | style="text-align: center;vertical-align: top;width: | + | | style="text-align: center;vertical-align: top;width: 50%;"|[[Image:draft_Samper_432909089-monograph-image357.png|312px]] |
<span style="text-align: center; font-size: 75%;">'''(b)''' ''AR4'' bridge</span> | <span style="text-align: center; font-size: 75%;">'''(b)''' ''AR4'' bridge</span> | ||
| Line 8,124: | Line 7,985: | ||
{| style="width: 100%;margin: 1em auto 0.1em auto;" | {| style="width: 100%;margin: 1em auto 0.1em auto;" | ||
|- | |- | ||
| − | | style="text-align: center;vertical-align: top;width: | + | | style="text-align: center;vertical-align: top;width: 50%;"|[[Image:draft_Samper_432909089-monograph-image358.png|312px]] |
<span style="text-align: center; font-size: 75%;">'''(a)''' ''AB4'' bridge</span> | <span style="text-align: center; font-size: 75%;">'''(a)''' ''AB4'' bridge</span> | ||
| − | | style="text-align: center;vertical-align: top;width: | + | | style="text-align: center;vertical-align: top;width: 50%;"|[[Image:draft_Samper_432909089-monograph-image359.png|312px]] |
<span style="text-align: center; font-size: 75%;">'''(b)''' ''AR4'' bridge</span> | <span style="text-align: center; font-size: 75%;">'''(b)''' ''AR4'' bridge</span> | ||
| Line 8,138: | Line 7,999: | ||
{| style="width: 100%;margin: 1em auto 0.1em auto;" | {| style="width: 100%;margin: 1em auto 0.1em auto;" | ||
|- | |- | ||
| − | | style="text-align: center;vertical-align: top;width: | + | | style="text-align: center;vertical-align: top;width: 50%;"|[[Image:draft_Samper_432909089-monograph-image360.png|312px]] |
<span style="text-align: center; font-size: 75%;">'''(a)''' ''AB4'' bridge</span> | <span style="text-align: center; font-size: 75%;">'''(a)''' ''AB4'' bridge</span> | ||
| − | | style="text-align: center;vertical-align: top;width: | + | | style="text-align: center;vertical-align: top;width: 50%;"|[[Image:draft_Samper_432909089-monograph-image361.png|312px]] |
<span style="text-align: center; font-size: 75%;">'''(b)''' ''AR4'' bridge</span> | <span style="text-align: center; font-size: 75%;">'''(b)''' ''AR4'' bridge</span> | ||
| Line 8,152: | Line 8,013: | ||
{| style="width: 100%;margin: 1em auto 0.1em auto;" | {| style="width: 100%;margin: 1em auto 0.1em auto;" | ||
|- | |- | ||
| − | | style="text-align: center;vertical-align: top;width: | + | | style="text-align: center;vertical-align: top;width: 50%;"|[[Image:draft_Samper_432909089-monograph-image362.png|312px]] |
<span style="text-align: center; font-size: 75%;">'''(a)''' ''AB4'' bridge</span> | <span style="text-align: center; font-size: 75%;">'''(a)''' ''AB4'' bridge</span> | ||
| − | | style="text-align: center;vertical-align: top;width: | + | | style="text-align: center;vertical-align: top;width: 50%;"|[[Image:draft_Samper_432909089-monograph-image363.png|312px]] |
<span style="text-align: center; font-size: 75%;">'''(b)''' ''AR4'' bridge</span> | <span style="text-align: center; font-size: 75%;">'''(b)''' ''AR4'' bridge</span> | ||
| Line 8,170: | Line 8,031: | ||
{| style="width: 100%;margin: 1em auto 0.1em auto;" | {| style="width: 100%;margin: 1em auto 0.1em auto;" | ||
|- | |- | ||
| − | | style="text-align: center;vertical-align: top;width: | + | | style="text-align: center;vertical-align: top;width: 50%;"|[[Image:draft_Samper_432909089-monograph-image364.png|312px]] |
<span style="text-align: center; font-size: 75%;">'''(a)''' ''AB4'' bridge</span> | <span style="text-align: center; font-size: 75%;">'''(a)''' ''AB4'' bridge</span> | ||
| − | | style="text-align: center;vertical-align: top;width: | + | | style="text-align: center;vertical-align: top;width: 50%;"|[[Image:draft_Samper_432909089-monograph-image365.png|312px]] |
<span style="text-align: center; font-size: 75%;">'''(b)''' ''AR4'' bridge</span> | <span style="text-align: center; font-size: 75%;">'''(b)''' ''AR4'' bridge</span> | ||
| Line 8,186: | Line 8,047: | ||
{| style="width: 100%;margin: 1em auto 0.1em auto;" | {| style="width: 100%;margin: 1em auto 0.1em auto;" | ||
|- | |- | ||
| − | | style="text-align: center;vertical-align: top;width: | + | | style="text-align: center;vertical-align: top;width: 50%;"|[[Image:draft_Samper_432909089-monograph-image366.png|312px]] |
<span style="text-align: center; font-size: 75%;">'''(a)''' ''AB4'' bridge</span> | <span style="text-align: center; font-size: 75%;">'''(a)''' ''AB4'' bridge</span> | ||
| − | | style="text-align: center;vertical-align: top;width: | + | | style="text-align: center;vertical-align: top;width: 50%;"|[[Image:draft_Samper_432909089-monograph-image367.png|312px]] |
<span style="text-align: center; font-size: 75%;">'''(b)''' ''AR4'' bridge</span> | <span style="text-align: center; font-size: 75%;">'''(b)''' ''AR4'' bridge</span> | ||
| Line 8,200: | Line 8,061: | ||
{| style="width: 100%;margin: 1em auto 0.1em auto;" | {| style="width: 100%;margin: 1em auto 0.1em auto;" | ||
|- | |- | ||
| − | | style="text-align: center;vertical-align: top;width: | + | | style="text-align: center;vertical-align: top;width: 50%;"|[[Image:draft_Samper_432909089-monograph-image368.png|312px]] |
<span style="text-align: center; font-size: 75%;">'''(a)''' ''AB4'' bridge</span> | <span style="text-align: center; font-size: 75%;">'''(a)''' ''AB4'' bridge</span> | ||
| − | | style="text-align: center;vertical-align: top;width: | + | | style="text-align: center;vertical-align: top;width: 50%;"|[[Image:draft_Samper_432909089-monograph-image369.png|312px]] |
<span style="text-align: center; font-size: 75%;">'''(b)''' ''AR4'' bridge</span> | <span style="text-align: center; font-size: 75%;">'''(b)''' ''AR4'' bridge</span> | ||
| Line 8,496: | Line 8,357: | ||
<span style="text-align: center; font-size: 75%;"><sup>a</sup> At the tower base <sup>c</sup> In-plane</span> | <span style="text-align: center; font-size: 75%;"><sup>a</sup> At the tower base <sup>c</sup> In-plane</span> | ||
| − | <sup>b</sup> At the tower-deck connection <sup>d</sup> Out-of-plane | + | <span style="text-align: center; font-size: 75%;"><sup>b</sup> At the tower-deck connection <sup>d</sup> Out-of-plane</span> |
.Summarizing, the analysis considering near-fault ground motions shows that the largest seismic responses are obtained with events Gatos and Kobe. A similar situation occurs for the undamped bridges. Responses obtained for ''AB4 ''and ''AR4 ''models are similar, mainly for displacements and velocities. Most important differences are observed with the deck response for internal forces and cable forces, as long as the tower response is less sensitive. This behaviour is independent on the earthquake nature (far-fault – near-fault) or the damped or undamped condition of the bridges. As was concluded for the undamped condition, it is difficult to select the best stay cable layout in terms of the seismic response. There are not clear tendencies, and application of time-history analysis can be confused for this purpose. | .Summarizing, the analysis considering near-fault ground motions shows that the largest seismic responses are obtained with events Gatos and Kobe. A similar situation occurs for the undamped bridges. Responses obtained for ''AB4 ''and ''AR4 ''models are similar, mainly for displacements and velocities. Most important differences are observed with the deck response for internal forces and cable forces, as long as the tower response is less sensitive. This behaviour is independent on the earthquake nature (far-fault – near-fault) or the damped or undamped condition of the bridges. As was concluded for the undamped condition, it is difficult to select the best stay cable layout in terms of the seismic response. There are not clear tendencies, and application of time-history analysis can be confused for this purpose. | ||
| Line 8,585: | Line 8,446: | ||
| − | :<big> | + | :<big>4.6.3 Specifications of the Dampers</big> |
Nonlinear time-history analysis of the bridge models considering the optimal dampers permits the specifications required for the dampers. This selection can be made in terms of the earthquake nature and locations of the dampers. Because of the same damper responses for both bridge models, the same dampers are specified. Table 4.15 summarizes the main damper specifications. The number of dampers corresponds to those required for each single damper location. Requirements for the dampers here exposed satisfy seismic requirements, and of course, additional damper parameters should be defined by the manufacturer, according to the design specifications. | Nonlinear time-history analysis of the bridge models considering the optimal dampers permits the specifications required for the dampers. This selection can be made in terms of the earthquake nature and locations of the dampers. Because of the same damper responses for both bridge models, the same dampers are specified. Table 4.15 summarizes the main damper specifications. The number of dampers corresponds to those required for each single damper location. Requirements for the dampers here exposed satisfy seismic requirements, and of course, additional damper parameters should be defined by the manufacturer, according to the design specifications. | ||
| Line 8,635: | Line 8,496: | ||
| − | :<big> | + | :<big>4.7 Comparative Results and Discussion</big> |
Results of the nonlinear time history analysis have demonstrated the direct incidence of the fluid viscous dampers on the seismic response of the bridge models. In Chapter 3, the dynamic characterization of cable-stayed bridges was obtained by means of the modal analysis. The response spectrum analysis gave a first approach of the seismic response of the bridge models, a general seismic characterization, and allowed the selection of the bridge models for the nonlinear time-history analysis. Time-history analysis gave an accurate seismic description for the considered bridge models, in which the responses where obtained and characterized in terms of stay cable layout and earthquake nature. Chapter 4 introduces the effect of viscous dampers as passive energy dissipation devices, in which selection of the damper layout, selection of the optimal damper parameters as well as the definitive seismic responses are obtained for both models in the presence of far-fault and near-fault ground motions. | Results of the nonlinear time history analysis have demonstrated the direct incidence of the fluid viscous dampers on the seismic response of the bridge models. In Chapter 3, the dynamic characterization of cable-stayed bridges was obtained by means of the modal analysis. The response spectrum analysis gave a first approach of the seismic response of the bridge models, a general seismic characterization, and allowed the selection of the bridge models for the nonlinear time-history analysis. Time-history analysis gave an accurate seismic description for the considered bridge models, in which the responses where obtained and characterized in terms of stay cable layout and earthquake nature. Chapter 4 introduces the effect of viscous dampers as passive energy dissipation devices, in which selection of the damper layout, selection of the optimal damper parameters as well as the definitive seismic responses are obtained for both models in the presence of far-fault and near-fault ground motions. | ||
| Line 8,641: | Line 8,502: | ||
The last part of this chapter compares the seismic responses in terms of the damped Vs undamped time histories for both bridge models and taking into account the earthquake nature. Comparative results on the average of the maximum responses are analyzed, and finally, results of the energy approach are exposed and discussed. | The last part of this chapter compares the seismic responses in terms of the damped Vs undamped time histories for both bridge models and taking into account the earthquake nature. Comparative results on the average of the maximum responses are analyzed, and finally, results of the energy approach are exposed and discussed. | ||
| − | :<big> | + | :<big>4.7.1 Seismic Response Comparison</big> |
With comparative purposes, Figs. 4.41 to 4.46 show average responses of longitudinal displacements of the deck, vertical displacements of the deck at the mid-span, in-plane bending moments at the tower base, in-plane bending moments of the deck at the mid-span, axial forces at the tower base and out-of-plane bending moments at the tower base respectively. Those average responses were obtained for each time step, considering all the analyzed events for both far-fault and near-fault ground motions; and selecting ''AB4'' bridge as the analyzed model. As was explained before, it is expected a similar response for ''AR4 ''bridge, and for that reason it is not considered here. The aim of this response comparison is to show the main differences between damped Vs undamped cases. | With comparative purposes, Figs. 4.41 to 4.46 show average responses of longitudinal displacements of the deck, vertical displacements of the deck at the mid-span, in-plane bending moments at the tower base, in-plane bending moments of the deck at the mid-span, axial forces at the tower base and out-of-plane bending moments at the tower base respectively. Those average responses were obtained for each time step, considering all the analyzed events for both far-fault and near-fault ground motions; and selecting ''AB4'' bridge as the analyzed model. As was explained before, it is expected a similar response for ''AR4 ''bridge, and for that reason it is not considered here. The aim of this response comparison is to show the main differences between damped Vs undamped cases. | ||
| Line 8,649: | Line 8,510: | ||
{| style="width: 100%;margin: 1em auto 0.1em auto;" | {| style="width: 100%;margin: 1em auto 0.1em auto;" | ||
|- | |- | ||
| − | | style="text-align: center;vertical-align: top;width: | + | | style="text-align: center;vertical-align: top;width: 50%;"|[[Image:draft_Samper_432909089-monograph-image370.png|312px]] |
<span style="text-align: center; font-size: 75%;">'''(a)''' Far-fault ground motion</span> | <span style="text-align: center; font-size: 75%;">'''(a)''' Far-fault ground motion</span> | ||
| − | | style="text-align: center;vertical-align: top;width: | + | | style="text-align: center;vertical-align: top;width: 50%;"|[[Image:draft_Samper_432909089-monograph-image371.png|312px]] |
<span style="text-align: center; font-size: 75%;">'''(b)''' Near-fault ground motion</span> | <span style="text-align: center; font-size: 75%;">'''(b)''' Near-fault ground motion</span> | ||
| Line 8,665: | Line 8,526: | ||
{| style="width: 100%;margin: 1em auto 0.1em auto;" | {| style="width: 100%;margin: 1em auto 0.1em auto;" | ||
|- | |- | ||
| − | | style="text-align: center;vertical-align: top;width: | + | | style="text-align: center;vertical-align: top;width: 50%;"|[[Image:draft_Samper_432909089-monograph-image372.png|312px]] |
<span style="text-align: center; font-size: 75%;">'''(a)''' Far-fault ground motion</span> | <span style="text-align: center; font-size: 75%;">'''(a)''' Far-fault ground motion</span> | ||
| − | | style="text-align: center;vertical-align: top;width: | + | | style="text-align: center;vertical-align: top;width: 50%;"|[[Image:draft_Samper_432909089-monograph-image373.png|312px]] |
<span style="text-align: center; font-size: 75%;">'''(b)''' Near-fault ground motion</span> | <span style="text-align: center; font-size: 75%;">'''(b)''' Near-fault ground motion</span> | ||
| Line 8,679: | Line 8,540: | ||
{| style="width: 100%;margin: 1em auto 0.1em auto;" | {| style="width: 100%;margin: 1em auto 0.1em auto;" | ||
|- | |- | ||
| − | | style="text-align: center;vertical-align: top;width: | + | | style="text-align: center;vertical-align: top;width: 50%;"|[[Image:draft_Samper_432909089-monograph-image374.png|312px]] |
<span style="text-align: center; font-size: 75%;">'''(a)''' Far-fault ground motion</span> | <span style="text-align: center; font-size: 75%;">'''(a)''' Far-fault ground motion</span> | ||
| − | | style="text-align: center;vertical-align: top;width: | + | | style="text-align: center;vertical-align: top;width: 50%;"|[[Image:draft_Samper_432909089-monograph-image375.png|312px]] |
<span style="text-align: center; font-size: 75%;">'''(b)''' Near-fault ground motion</span> | <span style="text-align: center; font-size: 75%;">'''(b)''' Near-fault ground motion</span> | ||
| Line 8,695: | Line 8,556: | ||
{| style="width: 100%;margin: 1em auto 0.1em auto;" | {| style="width: 100%;margin: 1em auto 0.1em auto;" | ||
|- | |- | ||
| − | | style="text-align: center;vertical-align: top;width: | + | | style="text-align: center;vertical-align: top;width: 50%;"|[[Image:draft_Samper_432909089-monograph-image376.png|312px]] |
<span style="text-align: center; font-size: 75%;">'''(a)''' Far-fault ground motion</span> | <span style="text-align: center; font-size: 75%;">'''(a)''' Far-fault ground motion</span> | ||
| − | | style="text-align: center;vertical-align: top;width: | + | | style="text-align: center;vertical-align: top;width: 50%;"|[[Image:draft_Samper_432909089-monograph-image377.png|312px]] |
<span style="text-align: center; font-size: 75%;">'''(b)''' Near-fault ground motion</span> | <span style="text-align: center; font-size: 75%;">'''(b)''' Near-fault ground motion</span> | ||
| Line 8,709: | Line 8,570: | ||
{| style="width: 100%;margin: 1em auto 0.1em auto;" | {| style="width: 100%;margin: 1em auto 0.1em auto;" | ||
|- | |- | ||
| − | | style="text-align: center;vertical-align: top;width: | + | | style="text-align: center;vertical-align: top;width: 50%;"|[[Image:draft_Samper_432909089-monograph-image378.png|312px]] |
<span style="text-align: center; font-size: 75%;">'''(a)''' Far-fault ground motion</span> | <span style="text-align: center; font-size: 75%;">'''(a)''' Far-fault ground motion</span> | ||
| − | | style="text-align: center;vertical-align: top;width: | + | | style="text-align: center;vertical-align: top;width: 50%;"|[[Image:draft_Samper_432909089-monograph-image379.png|312px]] |
<span style="text-align: center; font-size: 75%;">'''(b)''' Near-fault ground motion</span> | <span style="text-align: center; font-size: 75%;">'''(b)''' Near-fault ground motion</span> | ||
| Line 8,723: | Line 8,584: | ||
{| style="width: 100%;margin: 1em auto 0.1em auto;" | {| style="width: 100%;margin: 1em auto 0.1em auto;" | ||
|- | |- | ||
| − | | style="text-align: center;vertical-align: top;width: | + | | style="text-align: center;vertical-align: top;width: 50%;"|[[Image:draft_Samper_432909089-monograph-image380.png|312px]] |
<span style="text-align: center; font-size: 75%;">'''(a)''' Far-fault ground motion</span> | <span style="text-align: center; font-size: 75%;">'''(a)''' Far-fault ground motion</span> | ||
| − | | style="text-align: center;vertical-align: top;width: | + | | style="text-align: center;vertical-align: top;width: 50%;"|[[Image:draft_Samper_432909089-monograph-image381.png|312px]] |
<span style="text-align: center; font-size: 75%;">'''(b)''' Near-fault ground motion</span> | <span style="text-align: center; font-size: 75%;">'''(b)''' Near-fault ground motion</span> | ||
| Line 8,741: | Line 8,602: | ||
{| style="width: 100%;margin: 1em auto 0.1em auto;" | {| style="width: 100%;margin: 1em auto 0.1em auto;" | ||
|- | |- | ||
| − | | style="text-align: center;vertical-align: top;"|''' [[Image:draft_Samper_432909089-image382.png|312px]] ''' | + | | style="text-align: center;vertical-align: top;"|''' [[Image:draft_Samper_432909089-monograph-image382.png|312px]] ''' |
'''Fig. 4.47''' Average of the Maximum Longitudinal Displacements of the Deck | '''Fig. 4.47''' Average of the Maximum Longitudinal Displacements of the Deck | ||
| − | | style="text-align: center;vertical-align: top;width: | + | | style="text-align: center;vertical-align: top;width: 50%;"|[[Image:draft_Samper_432909089-monograph-image383.png|312px]] |
'''Fig. 4.48''' Average of the Maximum Vertical Displacements of the Deck at the Mid-Span | '''Fig. 4.48''' Average of the Maximum Vertical Displacements of the Deck at the Mid-Span | ||
| Line 8,752: | Line 8,613: | ||
|- | |- | ||
| − | | style="text-align: center;vertical-align: top;"|''' [[Image:draft_Samper_432909089-image384.png|312px]] ''' | + | | style="text-align: center;vertical-align: top;"|''' [[Image:draft_Samper_432909089-monograph-image384.png|312px]] ''' |
'''Fig. 4.49''' Average of the Maximum Transverse Displacements of the Deck at the Mid-Span | '''Fig. 4.49''' Average of the Maximum Transverse Displacements of the Deck at the Mid-Span | ||
| − | | style="text-align: center;vertical-align: top;width: | + | | style="text-align: center;vertical-align: top;width: 50%;"|[[Image:draft_Samper_432909089-monograph-image385.png|312px]] |
'''Fig. 4.50''' Average of the Maximum Longitudinal Displacements at the Tower-Top | '''Fig. 4.50''' Average of the Maximum Longitudinal Displacements at the Tower-Top | ||
| Line 8,763: | Line 8,624: | ||
|- | |- | ||
| − | | style="text-align: center;vertical-align: top;width: | + | | style="text-align: center;vertical-align: top;width: 49%;"|[[Image:draft_Samper_432909089-monograph-image386.png|312px]] |
'''Fig. 4.51''' Average of the Maximum Transverse Displacements of the Tower-Top | '''Fig. 4.51''' Average of the Maximum Transverse Displacements of the Tower-Top | ||
| Line 8,776: | Line 8,637: | ||
{| style="width: 100%;margin: 1em auto 0.1em auto;" | {| style="width: 100%;margin: 1em auto 0.1em auto;" | ||
|- | |- | ||
| − | | style="text-align: center;vertical-align: top;width: | + | | style="text-align: center;vertical-align: top;width: 50%;"|[[Image:draft_Samper_432909089-monograph-image387.png|312px]] |
'''Fig. 4.52 '''Average Compressive Forces at the Tower Base | '''Fig. 4.52 '''Average Compressive Forces at the Tower Base | ||
| − | | style="text-align: center;vertical-align: top;width: | + | | style="text-align: center;vertical-align: top;width: 50%;"|[[Image:draft_Samper_432909089-monograph-image388.png|312px]] |
'''Fig. 4.53 '''Average Compressive Forces of the Deck at the Tower-Deck Connection | '''Fig. 4.53 '''Average Compressive Forces of the Deck at the Tower-Deck Connection | ||
| Line 8,787: | Line 8,648: | ||
{| style="width: 100%;margin: 1em auto 0.1em auto;" | {| style="width: 100%;margin: 1em auto 0.1em auto;" | ||
|- | |- | ||
| − | | style="text-align: center;vertical-align: top;"|''' [[Image:draft_Samper_432909089-image389.png|312px]] ''' | + | | style="text-align: center;vertical-align: top;"|''' [[Image:draft_Samper_432909089-monograph-image389.png|312px]] ''' |
'''Fig. 4.54 '''Average Tension Forces of the Most Loaded Cables | '''Fig. 4.54 '''Average Tension Forces of the Most Loaded Cables | ||
| − | | style="vertical-align: top;"|''' [[Image:draft_Samper_432909089-image390.png|312px]] ''' | + | | style="vertical-align: top;"|''' [[Image:draft_Samper_432909089-monograph-image390.png|312px]] ''' |
'''Fig. 4.55 '''Average In-Plane Moments at the Tower Base | '''Fig. 4.55 '''Average In-Plane Moments at the Tower Base | ||
| Line 8,798: | Line 8,659: | ||
{| style="width: 100%;margin: 1em auto 0.1em auto;" | {| style="width: 100%;margin: 1em auto 0.1em auto;" | ||
|- | |- | ||
| − | | style="text-align: center;vertical-align: top;"|''' [[Image:draft_Samper_432909089-image391.png|312px]] ''' | + | | style="text-align: center;vertical-align: top;"|''' [[Image:draft_Samper_432909089-monograph-image391.png|312px]] ''' |
'''Fig. 4.56 '''Average Out-of-Plane Moments at the Tower Base | '''Fig. 4.56 '''Average Out-of-Plane Moments at the Tower Base | ||
| − | | style="vertical-align: top;"|''' [[Image:draft_Samper_432909089-image392.png|312px]] ''' | + | | style="vertical-align: top;"|''' [[Image:draft_Samper_432909089-monograph-image392.png|312px]] ''' |
'''Fig. 4.57 '''Average Moments of the Deck at the Mid-Span | '''Fig. 4.57 '''Average Moments of the Deck at the Mid-Span | ||
| Line 8,809: | Line 8,670: | ||
The analysis of the internal forces shows very similar results for the average axial forces of the towers (Fig. 4.52), independent on the bridge model, far-fault or near-fault condition and damped or undamped situation, as was observed with time-histories. This behaviour confirms the null effect of the viscous dampers on the axial forces of the towers. The effect of the additional dampers on the seismic response reduction is especially evident for compressive forces of the deck, tension forces of the cables, in-plane bending moments of the towers and moments of the deck, with average response reductions of 13%, 37%, 69% and 45% for far-fault ground motions respectively. For near-fault ground motions, average reductions of 12%, 35%, 54% and 32% are obtained respectively. This analysis demonstrates that additional viscous dampers are extremely efficient on the seismic response control of in-plane moments of the towers and deck. By this way, taking into account results obtained from this analysis and considering the displacement response comparison, it is possible to observe that the largest response reductions are generally obtained for the far-fault ground motions, although differences with the near-fault condition can be not very interesting. On the other hand, as happens with displacements, the comparison between far-fault and near-fault ground motions shows that the largest averages of the maximum responses are obtained for the near-fault condition, basically for in-plane responses, independent on the damped or undamped situation and bridge model. Likewise, comparing ''AB4'' with ''AR4'' model, for the damped and undamped conditions, it is confirmed that basically the same response of the towers is obtained, and important differences can be appreciated for the deck and cable responses. Surprisingly, average out-of-plane moments at the tower base expose an analogue behaviour compared with the transverse response of displacements before studied, confirming the negligible effect of the viscous dampers on the transverse response. | The analysis of the internal forces shows very similar results for the average axial forces of the towers (Fig. 4.52), independent on the bridge model, far-fault or near-fault condition and damped or undamped situation, as was observed with time-histories. This behaviour confirms the null effect of the viscous dampers on the axial forces of the towers. The effect of the additional dampers on the seismic response reduction is especially evident for compressive forces of the deck, tension forces of the cables, in-plane bending moments of the towers and moments of the deck, with average response reductions of 13%, 37%, 69% and 45% for far-fault ground motions respectively. For near-fault ground motions, average reductions of 12%, 35%, 54% and 32% are obtained respectively. This analysis demonstrates that additional viscous dampers are extremely efficient on the seismic response control of in-plane moments of the towers and deck. By this way, taking into account results obtained from this analysis and considering the displacement response comparison, it is possible to observe that the largest response reductions are generally obtained for the far-fault ground motions, although differences with the near-fault condition can be not very interesting. On the other hand, as happens with displacements, the comparison between far-fault and near-fault ground motions shows that the largest averages of the maximum responses are obtained for the near-fault condition, basically for in-plane responses, independent on the damped or undamped situation and bridge model. Likewise, comparing ''AB4'' with ''AR4'' model, for the damped and undamped conditions, it is confirmed that basically the same response of the towers is obtained, and important differences can be appreciated for the deck and cable responses. Surprisingly, average out-of-plane moments at the tower base expose an analogue behaviour compared with the transverse response of displacements before studied, confirming the negligible effect of the viscous dampers on the transverse response. | ||
| − | :<big> | + | :<big>4.7.2 Energy Analysis</big> |
An adequate study of the energies involved is fundamental to understand the seismic response of the bridge models. In this stage, we are basically interested in the input energy provided by the ground motion to the structures, and the dissipated energy by additional viscous damping. A comparison between both energies gives an idea about the performance of the structures in terms of the absorbed and dissipated energy; and the efficiency of the additional viscous damping system. | An adequate study of the energies involved is fundamental to understand the seismic response of the bridge models. In this stage, we are basically interested in the input energy provided by the ground motion to the structures, and the dissipated energy by additional viscous damping. A comparison between both energies gives an idea about the performance of the structures in terms of the absorbed and dissipated energy; and the efficiency of the additional viscous damping system. | ||
| − | The input energy depends on the mass ''m<sub>s</sub>'' of the system, the input ground acceleration | + | The input energy depends on the mass ''m<sub>s</sub>'' of the system, the input ground acceleration [[Image:draft_Samper_432909089-monograph-image393.png|18px]] and the relative velocity of the system [[Image:draft_Samper_432909089-monograph-image394.png|12px]] . On the other hand, the dissipated energy by additional viscous damping depends on the damping coefficient ''c<sub>d</sub>'', the velocity exponent ''N'', and the velocity of the system [[Image:draft_Samper_432909089-monograph-image395.png|12px]] . However, in practical terms, the dissipated energy is strongly influenced by the damping coefficient, as was previously demonstrated (see Chapter 2). As example, Fig. 4.58 exposes the input energy and the dissipated energy by additional viscous damping considering events 5 and Kobe as input ground motions, applied to ''AR4 ''bridge. Both input records are characterized by the same duration. |
Distribution of both input energy and dissipated energy are quite different comparing the seismic events. Event 5 represents a typical far-fault ground motion, in which both energies linearly vary with time. The input energy is gradually introduced, but also dissipated for all the event duration. The total input energy achieved is 100 MJ, and the total dissipated energy is 60 MJ. Kobe earthquake, JMA Station, is a near-fault ground motion, in which all the input energy is introduced in brief time (≈ 13 sec), and practically all the dissipated energy is achieved in 15 sec, taking into account that both input and dissipated energies start at time equal to 7 – 8 sec. For time over 20 sec, no additional input or dissipated energy is experienced. The total input energy introduced is 160 MJ, and the total dissipated energy is 100 MJ; higher than those obtained for Event 5. | Distribution of both input energy and dissipated energy are quite different comparing the seismic events. Event 5 represents a typical far-fault ground motion, in which both energies linearly vary with time. The input energy is gradually introduced, but also dissipated for all the event duration. The total input energy achieved is 100 MJ, and the total dissipated energy is 60 MJ. Kobe earthquake, JMA Station, is a near-fault ground motion, in which all the input energy is introduced in brief time (≈ 13 sec), and practically all the dissipated energy is achieved in 15 sec, taking into account that both input and dissipated energies start at time equal to 7 – 8 sec. For time over 20 sec, no additional input or dissipated energy is experienced. The total input energy introduced is 160 MJ, and the total dissipated energy is 100 MJ; higher than those obtained for Event 5. | ||
| Line 8,821: | Line 8,682: | ||
{| style="width: 100%;margin: 1em auto 0.1em auto;" | {| style="width: 100%;margin: 1em auto 0.1em auto;" | ||
|- | |- | ||
| − | | style="text-align: center;vertical-align: top;"|''' [[Image:draft_Samper_432909089-image396.png|312px]] ''' | + | | style="text-align: center;vertical-align: top;"|''' [[Image:draft_Samper_432909089-monograph-image396.png|312px]] ''' |
<span style="text-align: center; font-size: 75%;">'''(a) '''Event 5 </span> | <span style="text-align: center; font-size: 75%;">'''(a) '''Event 5 </span> | ||
| − | | style="vertical-align: top;"|''' [[Image:draft_Samper_432909089-image397.png|312px]] ''' | + | | style="vertical-align: top;"|''' [[Image:draft_Samper_432909089-monograph-image397.png|312px]] ''' |
<span style="text-align: center; font-size: 75%;">'''(b) '''Kobe Earthquake, JMA Station</span> | <span style="text-align: center; font-size: 75%;">'''(b) '''Kobe Earthquake, JMA Station</span> | ||
| Line 8,834: | Line 8,695: | ||
<div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | ||
| − | <big>''' [[Image:draft_Samper_432909089-image398.png|408px]] '''</big></div> | + | <big>''' [[Image:draft_Samper_432909089-monograph-image398.png|408px]] '''</big></div> |
<div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | ||
| Line 8,840: | Line 8,701: | ||
<div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | ||
| − | [[Image:draft_Samper_432909089-image399.png|396px]] </div> | + | [[Image:draft_Samper_432909089-monograph-image399.png|396px]] </div> |
<div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | ||
| Line 8,853: | Line 8,714: | ||
{| style="width: 100%;margin: 1em auto 0.1em auto;" | {| style="width: 100%;margin: 1em auto 0.1em auto;" | ||
|- | |- | ||
| − | | style="text-align: center;vertical-align: top;"|''' [[Image:draft_Samper_432909089-image400.png|318px]] ''' | + | | style="text-align: center;vertical-align: top;"|''' [[Image:draft_Samper_432909089-monograph-image400.png|318px]] ''' |
<span style="text-align: center; font-size: 75%;">'''(a) '''Far-fault ground motion </span> | <span style="text-align: center; font-size: 75%;">'''(a) '''Far-fault ground motion </span> | ||
| − | | style="vertical-align: top;"|'''4 [[Image:draft_Samper_432909089-image401.png|312px]] ''' | + | | style="vertical-align: top;"|'''4 [[Image:draft_Samper_432909089-monograph-image401.png|312px]] ''' |
<span style="text-align: center; font-size: 75%;">'''(b) '''Near-fault ground motion</span> | <span style="text-align: center; font-size: 75%;">'''(b) '''Near-fault ground motion</span> | ||
| Line 8,869: | Line 8,730: | ||
As a general conclusion, very high energy dissipation rates are obtained, which confirms the important incidence of the addition of fluid viscous dampers as passive energy dissipation devices to reduce the seismic response of cable-stayed bridges. | As a general conclusion, very high energy dissipation rates are obtained, which confirms the important incidence of the addition of fluid viscous dampers as passive energy dissipation devices to reduce the seismic response of cable-stayed bridges. | ||
| − | + | ==Appendix A. Step-by-Step Nonlinear Time History Analysis== | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
<big>A.1 General Considerations</big> | <big>A.1 General Considerations</big> | ||
| Line 8,896: | Line 8,753: | ||
The α-method uses the Newmark method to solve the following modified equations of motion: | The α-method uses the Newmark method to solve the following modified equations of motion: | ||
| − | + | ||
| − | + | [[Image:draft_Samper_432909089-monograph-image402.png|456px]] [Eq. A.1] | |
| − | + | ||
| − | + | where ''M'' is the mass matrix, ''C'' is the viscous damping matrix, ''K'' is the stiffness matrix, ''F<sub>t</sub> ''is the vector of forces that depends on the time ''t'', α is the numerical damping parameter and ''u, [[Image:draft_Samper_432909089-monograph-image403.png|12px]] ''and [[Image:draft_Samper_432909089-monograph-image404.png|12px]] are the respective vectors of displacements, velocities and accelerations. | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | where ''M'' is the mass matrix, ''C'' is the viscous damping matrix, ''K'' is the stiffness matrix, ''F<sub>t</sub> ''is the vector of forces that depends on the time ''t'', α is the numerical damping parameter and ''u, | + | |
Equation A.1 can be expressed as: | Equation A.1 can be expressed as: | ||
| − | + | ||
| − | + | [[Image:draft_Samper_432909089-monograph-image405.png|222px]] [Eq. A.2] | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
that represents the equilibrium equation for the instant ''t<sub>n+1</sub>'' expressed in generalized coordinates ''q''. | that represents the equilibrium equation for the instant ''t<sub>n+1</sub>'' expressed in generalized coordinates ''q''. | ||
The following formulas are applied: | The following formulas are applied: | ||
| − | + | ||
| − | + | [[Image:draft_Samper_432909089-monograph-image406.png|366px]] [Eqs. A.3] | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
where ''q'' is the vector of generalized coordinates, ''Δt'' is the time-step size and ''F<sup>q</sup>'' is part of the vector of forces only depending on the generalized coordinates and their derivatives. | where ''q'' is the vector of generalized coordinates, ''Δt'' is the time-step size and ''F<sup>q</sup>'' is part of the vector of forces only depending on the generalized coordinates and their derivatives. | ||
| Line 8,938: | Line 8,773: | ||
<div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | ||
| − | + | [[Image:draft_Samper_432909089-monograph-image407.png|300px]] </div> | |
In the case of α=0, the method reduces to the Newmark`s constant or average acceleration method (trapezoid rule). Using α=0 offers the highest accuracy of the available methods, but may permit excessive vibrations in the higher frequency modes, i.e., those modes with periods of the same order as or less than the time-step size. For more negative values of alpha, the higher frequency modes are more severely damped. This is not physical damping, since it decreases as smaller time-steps are used. However, it is often necessary to use a negative value of alpha to encourage a nonlinear solution to converge. For best results, it is recommended the use of the smallest time-step practical, and select α as close to zero as possible, and trying with different values of α and time-step size to be sure that the solution is not too dependent upon these parameters [Computers & Structures, 2007]. For α=-1/3, maximum numerical dissipation is reached, aspect that can be dangerous because much high frequency content could be severely damped. | In the case of α=0, the method reduces to the Newmark`s constant or average acceleration method (trapezoid rule). Using α=0 offers the highest accuracy of the available methods, but may permit excessive vibrations in the higher frequency modes, i.e., those modes with periods of the same order as or less than the time-step size. For more negative values of alpha, the higher frequency modes are more severely damped. This is not physical damping, since it decreases as smaller time-steps are used. However, it is often necessary to use a negative value of alpha to encourage a nonlinear solution to converge. For best results, it is recommended the use of the smallest time-step practical, and select α as close to zero as possible, and trying with different values of α and time-step size to be sure that the solution is not too dependent upon these parameters [Computers & Structures, 2007]. For α=-1/3, maximum numerical dissipation is reached, aspect that can be dangerous because much high frequency content could be severely damped. | ||
| Line 8,950: | Line 8,785: | ||
{| style="width: 100%;border-collapse: collapse;" | {| style="width: 100%;border-collapse: collapse;" | ||
|- | |- | ||
| − | | style="text-align: center;vertical-align: top;width: | + | | style="text-align: center;vertical-align: top;width: 53%;"|[[Image:draft_Samper_432909089-monograph-image408-c.png|306px]] |
'''Fig. A.1 '''Examples of Structures with Lumped Nonlinear Elements [Wilson, 2002] | '''Fig. A.1 '''Examples of Structures with Lumped Nonlinear Elements [Wilson, 2002] | ||
| Line 8,956: | Line 8,791: | ||
In this methodology, the dynamic equilibrium equations of a linear elastic structure with predefined nonlinear elements subjected to an arbitrary load can be written as: | In this methodology, the dynamic equilibrium equations of a linear elastic structure with predefined nonlinear elements subjected to an arbitrary load can be written as: | ||
| − | + | ||
| − | + | [[Image:draft_Samper_432909089-monograph-image409.png|252px]] [Eq. A.4] | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
|} | |} | ||
| − | | | + | where ''M'' is the diagonal mass matrix, ''C'' is the proportional damping matrix, ''K<sub>L</sub>'' is the stiffness matrix for the linear elastic elements (all elements except those with nonlinear behaviour), ''r<sub>N</sub>'' is the vector of forces from the nonlinear degrees-of-freedom in the link elements, ''r'' is the vector of applied loads and ''u, [[Image:draft_Samper_432909089-monograph-image410.png|12px]] ''and [[Image:draft_Samper_432909089-monograph-image411.png|12px]] are the respective displacement, velocity and acceleration vectors. |
| + | If the computer model is unstable without the nonlinear elements, it is possible to add ''effective elastic elements'' (at the location of the nonlinear elements) of arbitrary stiffness. If these effective forces, ''K<sub>e</sub>u(t)'', are added to both sides of Eq. A.1, the exact equilibrium equations can be written as: | ||
| − | + | [[Image:draft_Samper_432909089-monograph-image412.png|264px]] [Eq. A.5] | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
where ''K<sub>e</sub>'' is the effective stiffness of arbitrary value. Therefore, the ''exact'' dynamic equilibrium equations for the nonlinear model can be written as: | where ''K<sub>e</sub>'' is the effective stiffness of arbitrary value. Therefore, the ''exact'' dynamic equilibrium equations for the nonlinear model can be written as: | ||
| − | + | ||
| − | + | [[Image:draft_Samper_432909089-monograph-image413.png|126px]] [Eq. A.6] | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
where | where | ||
| − | + | ||
{| | {| | ||
|- | |- | ||
| − | | | + | | [[Image:draft_Samper_432909089-monograph-image414.png|222px]] |
| − | | | + | | [[Image:draft_Samper_432909089-monograph-image415.png|center|18px]] |
|} | |} | ||
| − | is known, and the effective external load | + | is known, and the effective external load [[Image:draft_Samper_432909089-monograph-image416.png|12px]] must be evaluated by iteration. If a good estimate of the effective elastic stiffness can be made, the rate of convergence may be accelerated because the unknown term [[Image:draft_Samper_432909089-monograph-image417.png|72px]] will be small [Wilson, 2002]. |
The solution for this integration methodology involves the application of the stiffness and mass orthogonal Load Dependent Ritz Vectors of the elastic structural system to reduce the size of the nonlinear system to be solved. For that reason, this methodology is also called ''Nonlinear Modal Time History Analysis, ''because in some sense, this is a hybrid between time history analysis and modal analysis''.'' The forces in the nonlinear elements are calculated by iteration at the end of each time or load step, and the uncoupled modal equations are solved exactly for each time increment. By iteration within each time-step, equilibrium, compatibility and all element force-deformation equations within each nonlinear element are identically satisfied. | The solution for this integration methodology involves the application of the stiffness and mass orthogonal Load Dependent Ritz Vectors of the elastic structural system to reduce the size of the nonlinear system to be solved. For that reason, this methodology is also called ''Nonlinear Modal Time History Analysis, ''because in some sense, this is a hybrid between time history analysis and modal analysis''.'' The forces in the nonlinear elements are calculated by iteration at the end of each time or load step, and the uncoupled modal equations are solved exactly for each time increment. By iteration within each time-step, equilibrium, compatibility and all element force-deformation equations within each nonlinear element are identically satisfied. | ||
| Line 9,213: | Line 9,026: | ||
For analysis of large structural systems, it is not possible to store all information within high-speed storage. If data needs to be obtained from low-speed disk storage, the effective speed of a computer can be reduced significantly. For that reason, it is recommended the use of computer codes with the transfer data to and from disk storage conducted in large blocks to minimize disk access time, also called ''paging operating systems''. | For analysis of large structural systems, it is not possible to store all information within high-speed storage. If data needs to be obtained from low-speed disk storage, the effective speed of a computer can be reduced significantly. For that reason, it is recommended the use of computer codes with the transfer data to and from disk storage conducted in large blocks to minimize disk access time, also called ''paging operating systems''. | ||
| − | + | ==References== | |
| − | + | ||
Abdel – Ghaffar, A.M. (1991), “Cable-Stayed Bridges under Seismic Action”, ''Proceedings of the Seminar Cable – Stayed Bridges: Recent Development and their Future'', Yokohama, Japan. | Abdel – Ghaffar, A.M. (1991), “Cable-Stayed Bridges under Seismic Action”, ''Proceedings of the Seminar Cable – Stayed Bridges: Recent Development and their Future'', Yokohama, Japan. | ||
Latest revision as of 15:05, 29 May 2018
Acknowledgments
The authors wish to thank to the Department of Geotechnical Engineering and Geosciences and the Department of Construction Engineering at Technical University of Catalonia for their help and support during the doctorate years of Mr. Galo Valdebenito. This work is inspired in the basic result of that investigation. Likewise, thank to the Faculty of Engineering Sciences and the Department of Research and Development (DID) at Universidad Austral de Chile for their help and support in this publication.
Preface
Earthquakes can be really destructive. There is no doubt. Recent seismic events have demonstrated the important effects on structures, and especially on bridges. In this sense, cable-stayed bridges are not an exception, although their seismic performance during recent events has been satisfactory. Their inherent condition as part of life-lines makes the seismic design and retrofitting of such structures be seriously considered.
Traditionally, seismic protection strategies have been based on provide enough strength and ductility. In the case of buildings or bridges with adequate supports and degrees of redundancy, that approach can be satisfactory, however, in the case of structures with few degrees of redundancy, or questionable ductility, that scheme could be inadequate, and worse, dangerous, as usually happens with cable-stayed bridges. All traditional modern strategies to design seismic structures are focused on the adequate comprehension of the mechanisms involved, in which ductility can be provided by some elements specially designed for these purposes. In these sense, strategies such as performed-based design or displacement-based design consider that well-designed structures need to dissipate enough energy by hysteresis in order to obtain economic and safe structures.
The incorporation of additional energy dissipation and isolation devices, by means of passive, active, semi-active and hybrid strategies, constitutes without doubt efficient schemes to protect structures controlling or avoiding damage, in which the energy dissipation is guaranteed through the action of external elements specially designed for those purposes. By this way, now it is possible to provide enough strength and energy dissipation capacity at the same time, avoiding damage on important structural elements, with the subsequent guaranty of the functionality, very important on life-lines, even during strong ground motions.
The present work constitutes an approach to the seismic protection of cable-stayed bridges including the incorporation of fluid viscous dampers as additional energy dissipation devices. The idea of the authors is to provide an up-to-date vision of the problem taking into account that long-period structures such as those proposed here, need to be adequately protected against strong motions, and considering that, because of their importance, an elastic behaviour is desirable. Chapter 1 describes the object to study in general terms. Chapter 2 constitutes a state-of-the-art review regarding the seismic behaviour and performance of fluid viscous dampers as external energy dissipation devices. The mechanical behaviour and technological aspects are now introduced with an energetic point of view, in which some practical applications are exposed and discussed. Chapter 3 describes the seismic response of cable-stayed bridges without external seismic protection, considering a parametric analysis in order to study the effects of the stay cable layout, stay spacing and deck level. A complete modal characterization is exposed, followed by a response spectrum analysis for comparative purposes. The effect of variations of the stay forces is analyzed, and finally, a nonlinear step-by-step analysis is performed for the critical structures, considering the velocity dependence of such bridges and the effects of far-fault and near-fault ground motions. The last Chapter exposes the seismic analysis of the selected structures including the incorporation of fluid viscous dampers as passive additional energy dissipation devices. Because of the inherent nonlinear behaviour of the structures and external devices, a mandatory nonlinear direct integration time-history analysis is performed for all the cases, in which parametric analyses are carried out in order to select the best damper parameters, and for the case of both far-fault and near-fault ground motions. In this part, comparative results are exposed with the aim to propose some practical recommendations.
Chapter 1. Introduction
- 1.1 Cable-Stayed Bridges and Seismic Protection
Bridges are without a doubt attractive civil engineering works from a structural point of view. But they are not only exciting as a structure: the project, construction, maintenance, operation as well as functional, aesthetic, economic and political aspects make them extremely interesting constituting a great social event [Maldonado et al, 1998].
Suspension bridges are very interesting and useful structures because they can be used for long-spans, solving many practical problems for which is necessary to cross large distances without intermediate supports. These kinds of structures are a challenge from all points of view, due to the constant increase of the main span length demand, constituting most of the times a human whim or that competitive and insatiable desire to break goals at any price. Cable supported bridges can be divided into suspended and cable-stayed bridges, as can be appreciated in Fig. 1.1.
From a structural point of view, both types of bridges are completely different, since contrary to suspended bridges, in cable-stayed bridges the cables are prestressed. Keeping in mind functional and economical aspects, suspension bridges permit longer spans with more economical results than cable-stayed bridges [Podolny and Scalzi, 1986]. Actually, the longer main spans in cable-stayed bridges reach 900 m, although recent investigations show the feasibility and possibility of building bridges of this kind with main spans exceeding 1000 m. These studies are based on the current high standard technologies and the lightness of superstructures that use orthotropic slabs [Aschrafi, 1998; Nagai et al, 1998].
In spite of the relative simplicity of bridges, the recent earthquake events of San Fernando (1971), Loma Prieta (1989), Northridge (1994), Kobe (1995) and Taiwan (1999) have shown that these systems are very vulnerable, mainly those of reinforced concrete. For that reason, is a high-priority to improve the comprehension of this phenomenon, learning from the recent earthquake lessons [Priestley et al, 1996]. These structural systems expose a few degrees of redundancy, and the collapse mechanisms should be known in detail to reach an appropriate performance. Some aspects that should be considered are: degree of redundancy of the system, soil-structure interaction, spatial variability effects, near source effects, geological faults and geotechnical aspects, bridge length effects, vertical component of motion and damping [Valdebenito, 2005]. All these aspects are explained in the references of Ghasemi (1999), Kawashima (2000); Cheung et al (2000) and Calvi (2004).
The structural analysis of a bridge depends undoubtedly on the structural modelling. Therefore, a well-done modelling is reflected in the degree of accuracy of the results. The vertiginous development of high-performance computers permits to solve more complex and large structures, testing a lot of conditions in a relatively short time. Thus, computing time will depend on the modelling used and the required accuracy for the results. Because of almost all the seismic isolators or energy dissipators experience non-linear behaviour, consideration of non-linear aspects in the analysis of the bridge – energy dissipation system is advisable. In spite of the current computer capacity and better non-linear structural analysis software, it is clear that the time and knowledge level of the designer are two serious limitations of the extensive application of these methodologies [Jara and Casas, 2002]. In fact, sometimes is preferable the use of simplified methods that show sufficiently accurate results in short time. In the case of long-span cable-stayed bridges, the problem is more complex, maybe due to the high non-linear behaviour of those structures, and hence, non-linear analysis becomes an indispensable condition, leaving aside the classical response spectrum analysis or the equivalent static analysis. Thus, a relatively complex structure can be solved by the iterative definition of the stiffness and equivalent damping.
Traditional seismic control strategies are based on the modification of stiffness, mass or geometric properties of the structure, reducing inertial forces and displacements caused by an earthquake. Thus, in the current design is necessary to permit controlled structural damage by the ductility provided, with the aim of avoiding too conservative designs and expensive costs. In other words, in the current philosophy, a structure with energy dissipation capacity is required, more than a resistant structure against all events. Although it is certain that traditional strategies for the seismic protection of bridges have progressed in the last years, for appropriate bridge strength and to assure a satisfactory behaviour for different intensity levels, development of special vibration control devices has given origin to a new path in seismic engineering. In general terms, instead of provide more strength, is more attractive to reduce internal forces and displacements through special isolation systems or energy dissipation devices. This energy distribution means that the seismic energy proceeding from the subsoil is distributed to different structural components and thus significant energy accumulation is avoided.
Amongst the existent control systems on bridges, passive strategies are well accepted because of their low comparative price, simple installation and maintenance as well as their great reliability and better theoretical and technological development [Jara and Casas, 2002]. Active, semi-active and hybrid systems seems to be an excellent strategy for the seismic control of structures, however, a lack of regulations and uncertainty regarding their real performance under strong ground motions are important limitations for their application. Without a doubt, there is a very promising future, mainly with semi-active and hybrid systems because of their incomparable advantages, although now their use is very limited, not been properly tested on real structures with real earthquakes. Thus, the general approach reducing the seismic demand of structures, more than trying to increase their strength or deformation capacity with appropriate criteria, is without a doubt an advantageous seismic protection system. These new seismic control strategies are conceived for the reduction of the seismic demand, and the appropriate application of this approach leads to systems that behave elastically during great earthquakes, on the contrary of a traditional design, where high energy dissipation capacity by controlled damage is needed. Passive control systems convert the kinetic energy of the system into heat, transferring it among different vibration modes. They do not require additional external energy for their operation, constituting their main advantage. In general terms, these systems operate elastically during great earthquakes, permitting structural functionality conditions after the event. Because of their low cost, high efficiency and low maintenance, they are additional seismic protection systems widely used in the world. Passive control systems can be classified as follows (Table 1.1):
| Base Isolation | Energy Dissipators | Seismic Connectors | Resonant Dampers |
| 1. Rubber Bearings (RB) | 1. Metallic Yield Dampers (MD) | 1. Shock transmission Units TU) | 1. Tuned Mass dampers (TMD) |
| 2. High Damping Rubber Bearings (HDR) | 2. Friction Dampers (FD) | 2. Displacement Control Devices (DCD) | 2. Tuned Liquid Dampers (TLD) |
| 3. Lead Rubber Bearings (LRB) | 3. Viscoelastic Dampers (VE) | 3. Rigid Connection Devices (RCD) | |
| 4. Rubber Bearings with Additional Energy Dissipation | 4. Fluid Viscous Dampers (VF) | ||
| 5. Sliding Bearings (SB) | 5. Lead Extrusion Dampers (LED) | ||
| 6. Shape Memory Alloy (SMA) |
Base isolation and dissipation result in decreasing the energy applied to the system and the transformation from energy to heat. This is also designated as energy approach, which especially takes into account the energy character of the seismic event. In the seismic isolation, the structure is separated from the subsoil, automatically limiting the energy that affects the structure, which is considerably reduced. As a result, the natural period is increased, which causes a considerable reduction of the structural acceleration during seismic events. Depending on the installed type of isolator, they do not only guarantee the vertical load transmission but also the restoring capacity during and after a seismic event.
Base isolation systems and seismic connectors applied to bridges have been properly tested and used for more than 20 years, and there is a lot of documentation and experience regarding to this. In relation to energy dissipation systems, the use of fluid viscous dampers can be the future for the application to large structures such as long-span cable-stayed bridges, mainly due to their high capacity, robustness, and good results of recent investigations.
In the case of cable-stayed bridges, their seismic behaviour has been, in general terms, very satisfactory, maybe due to their great flexibility. In spite of the above-mentioned, comprehension of their behaviour is very complex being appropriate and promising to consider special systems of additional seismic protection. On those structures, these additional systems have been applied basically to control vibrations on cables due to the effect of the wind and rain (rain - wind vibration), to solve aerodynamic problems on unstable and complex structures and for the seismic retrofit of existing bridges. Now, application of these devices for the control of seismic actions begins to be used with more frequency; not only on the cables to mitigate the cable-deck interaction [Macdonald and Georgakis, 2002] but also to isolate the superstructure, as can be appreciated in the recently inaugurated Rion-Antirion Bridge (Fig. 1.4), in the Gulf of Corinthian, Greece [Infanti et al, 2004].
Design of almost all cable-stayed bridges located at moderate-to-high seismicity zones is more complex than design of conventional bridges. Bridge design regulations and modern previsions have been developed in general terms and for standard bridges, in order to provide safe and economical structures. As general design philosophy, it is accepted the important request of having structural damage but permitting emergency communications for a not frequent severe earthquake. For the new cable-stayed bridges, code previsions cannot be applicable, being necessary the urgent improvement of regulations and general recommendations for the seismic design of these bridges, based on numeric, experimental or full-scale testing investigations. Also, the lack of information about the real performance of these bridges during strong earthquakes increases the uncertainty in terms of an appropriate design [Abdel-Ghaffar, 1991]. In fact, according to Eurocode 8 Part 2 [CEN, 1998b], cable-stayed bridges are classified as special bridges, aspect that implies that these regulations need to be considered only as general recommendations. At the moment, existent regulations with regard to passive systems are limited to seismic isolation and energy dissipation devices, without the incorporation of hybrid, active or semi-active systems. Design specifications for bridges with LRB systems, published by the New Zealand Ministry of Works and Development in 1983, were the first regulations about bridges with special seismic protection based on isolation and energy dissipation systems. Later, in the 90s, official recommendations for the first time in USA [1991, 2000], Italy (1991), Japan (1996), and Europe through Eurocode 8 [CEN, 1998a, 1998b] were published.
- 1.2 Historical Background
The early stayed bridges used chains or bars for the stays. The advent of various types of structural cables, with their inherent high carrying capacity and ease of installation, led engineers and contractors to replace the chains and bars [Podolny and Scalzi, 1986].
Cable-stayed bridges might have become a conventional form of construction had it not been for the bad publicity that followed the collapses of two bridges: the 79 m pedestrian bridge crossing the Tweed River near Dryburgh-Abbey (England) in 1818; and the 78 m long bridge over the Saale River near Nienburg, Germany, in 1824 [Podolny and Scalzi, 1986]. The famous French engineer, Navier, discussed these failures with his colleagues, and his adverse comments are assumed to have condemned the stay-bridge concept to relative obscurity. Whatever the reason, engineers turned to the suspension bridge, which was also emerging, as the preferred type of bridge for river crossings.
The principle of using stays to support a bridge superstructure returned with the works of John Roebling. The Niagara Falls Bridge (Fig. 1.6), the Old St. Clair Bridge in Pittsburgh (USA), the Cincinnati Bridge over the Ohio River (USA) and the Brooklyn Bridge (Fig. 1.7) in New York (USA) are good examples.

Fig. 1.6 Niagara Falls Bridge [Courtesy of the Niagara Falls Bridge Commission] |

Fig. 1.7 Brooklyn Bridge [from [2] www.elclubdigital.com]] |
It should be noted that the stays used by Roebling in his suspension bridges were used as an addition to the classical suspension bridge with the main catenary cable and its suspenders. During Roebling’s time the suspension bridge concept was suffering with failures resulting from wind forces. He knew that by incorporating the diagonal stays he could minimize the susceptibility of his structures to adverse wind loading. However, it is not clear whether he used the two suspension systems compositely.
Towards the end of the 19th century, the success of these hybrid structures – part suspension, part stayed – resulted in a slowing down of the use of structures supported exclusively by inclined rods. However, it was not until 1899 that the French engineer A. Gislard further advanced the development of stayed bridges by the introduction of a new system of hangers, at the same time economic and sufficiently rigid [Walter, 1999]. The system was characterized by the addition of cables intended to take up the horizontal components of the forces set up by the stays. This arrangement cancels out any compressive forces in the deck and thus avoids deck instability.
The increasing popularity of this new type of structure with German engineers slowly extended to other countries. Thus, the Italian architect R. Morandi designed several cable-stayed bridges in reinforced and prestressed concrete. His most outstanding work is the bridge on Lake Maracaibo, Venezuela, built in 1962 (Fig. 1.10).
The international development of this bridge type began in the 1970s, but a very big step forward took place in the 1990s, when cable-stayed bridges entered the domain of very long spans which was previously reserved for suspension bridges. As examples, the Barrios de Luna Bridge – also called the Fernandez Casado Bridge – in Spain (430 m, 1983, Fig. 1.11); the Yang Pu Bridge in Shangai, China (602 m, 1993, Fig. 1.12); the Normandie Bridge in Le Havre, France (856 m, 1994, Fig. 1.13) and the Tatara Bridge in Japan (890 m, 1998, Fig. 1.14). It is extremely interesting to analyse the progress in the world record for cable-stayed bridges, since it provides keys to understand the evolution of their design (Fig. 1.15).
The recently inaugurated Millau Bridge in the Tarn Valley, France, is one of the world’s famous multi-span cable-stayed bridge, with 342 m main span length and 343 m height for the highest pylon. This also called “bridge over the clouds” is one of the more interesting French engineering works at the present (Fig. 1.16). In the same way, the new Sutong Bridge, in Nantong, China (inaugurated in 2008), is considered the longest cable-stayed bridge of the world, with a main span length of 1088 m, and surpassing the Japanese record reached with the Tatara Bridge (Fig. 1.17).

Fig. 1.11 Barrios de Luna Bridge, Spain [from en.structurae.de] |

Fig. 1.12 Yang Pu Bridge, China [photo: M. Virlogeux] |

Fig. 1.13 Normandie Bridge, France [from fr.structurae.de] |

Fig. 1.14 Tatara Bridge, Japan [from [3] www.answers.com]]
|

Fig. 1.16 Millau Bridge, France |

Fig. 1.17 Sutong Bridge, Nantong, China |
Although the use of energy dissipation devices began as an attempt to control the cable vibration on cable-stayed and suspension bridges, very common on those structures due to the inherent low damping of the cable system, the inclusion of additional seismic protection, with the introduction of passive and active energy dissipation devices, has just begun. In this sense, the use of fluid viscous dampers in the recently inaugurated Rion-Antirion Bridge (Greece) is an exceptional opportunity to test in situ, with a real structure in a high-seismicity zone, those devices (Fig. 1.18). The deck of this multi-span cable-stayed bridge is continuous and fully suspended from four pylons (total length of 2252 meters). Its approach viaducts comprise 228m of concrete deck on the Antirion side and 986m of steel composite deck on the Rion side. The Main Bridge seismic protection system comprises fuse restraints and viscous dampers of dimensions heretofore never built. The same act in parallel, connecting the deck to the pylons. The restrainers of the Rion Antirion Bridge were designed as a rigid link intended to withstand high wind loads up to a pre-determined force. Under the reaction of the design earthquake, fuse restrainers will fail and leave the dampers free to dissipate the earthquake-induced energy acting upon the structure. The Approach Viaducts were seismically isolated utilizing elastomeric isolators and viscous dampers [Infanti et al, 2004].
The recent application of active (i.e. hybrid, semi-active) systems on cable-stayed bridges is very limited. Actually, a benchmark structural problem for cable-stayed bridges was defined in order to provide a test bed for the development of strategies for the seismic control of those structures. The problem is based on the new cable-stayed bridge that spans the Mississippi River: the Bill Emerson Memorial Bridge, in Cape Girardeau, Missouri, USA. [Dyke et al, 2002].
Chapter 2. Fluid Viscous Damping Technology
- 2.1 General Overview
Structures situated on seismic areas must be designed to resist earthquake ground motions. A fundamental rule regarding the seismic design of structures, express that higher damping implies lower induced seismic forces. For conventional constructions, the induced earthquake energy is dissipated by the structural components of the system designed to resist gravity loads. It is well known that damping level during the elastic seismic behaviour is generally very low, which implies not much dissipated energy. During strong ground motion, energy dissipation can be reached through damage of important structural elements, and considering only the resulting response forces within the structure due to an earthquake leads to massive structural dimensions, stiff structures with enormous local energy accumulation and plastic hinges. This strengthening method combined with usual bearing arrangements permits plastic deformations by way of leading to yield stress and cracks. In this sense, structural repair after an important seismic event is generally very expensive, the structure is set temporarily out of service and sometimes a lot of damaged structures must be demolished [Alvarez, 2004].
General concepts for appropriate protection of structures against earthquakes do not exist, as every structure is quite unique and requires individual considerations. Earthquakes are often interpreted in terms of deformations and acting forces induced upon the structure. As a consequence, there is a tendency to think only about increasing the strength of the structure. Actually, forces and displacements are nothing but a mere manifestation of seismic attacks and do not in fact represent their very essence. An earthquake is actually an energy phenomenon and the forces causing stresses in the structure are the final effect of that event.
In recent years, other strategies have been developed to reduce the seismic response of the structures using additional passive devices. A passive control system may be defined as a system which does not require an external power source for operation and utilizes the motion of the structure to develop the control forces, as a function of the response of the structure at the location of the passive control system, according to Fig. 2.1.
Passive supplemental damping strategies, including base isolation systems, viscoelastic dampers and tuned mass dampers are well understood and are widely accepted by the engineering community as a means for mitigating the effects of dynamic loading on structures. In this sense, energy dissipation systems can be considered as an important passive strategy in which the objective of these devices is to absorb a significant amount of the seismic input energy, thus reducing the demand on the structure by means of the relative motion within the passive devices which, in turn, dissipate energy. In general terms, these devices are not part of the structural system that resists gravity loads, constituting an external system that can be easily replaced after a strong earthquake. Of course, in this case the structural functionality is not affected as well as the stability of the structure, with a low replacement cost of such devices compared with repair or service interruption costs.
Additional damping devices dissipate energy by means of yielding, friction, Viscoelastic action or fluid flow through orifices [Soong and Dargush, 1997; Constantinou, 2003]. In this sense, fluid viscous dampers constitutes one of the well accepted energy dissipation systems by the scientific and engineering community, being considered as additional damping system in this work, as was previously explained and justified. These systems are capable of dissipate an important amount of energy during strong ground motions as well as to control long period displacements. These dampers are basically comprised of a cylinder filled with silicone fluid (oil or paste) and a piston that divides it into two chambers and is free to move in both directions. In case of sudden movements, due to earthquakes or other dynamic actions like braking, wind, etc., lamination of silicone fluid occur through an appropriate hydraulic circuit and leads to energy dissipation. In case of slow displacements, due to structure thermal expansion, such flow is obstructed, so that during normal service the behaviour is substantially rigid, acting like a shock absorber. Because of those advantages, utilization of this technology permits to take full advantage of the strength of structural elements, because it is possible to maximize energy dissipation reaching the maximum level of force that the structure can sustain, without exceeding it. As a consequence, structural elements remain in the elastic field also during high intensity earthquakes.
Actually, manufacture of fluid viscous dampers permits to design such devices for a wide range of specific requirements of velocity and force, constituting a good choice for implementation on new and existing facilities. Those devices are properly tested at specific laboratories, especially when they are applied on important structures or they are required for special conditions. In this sense, manufacturers such as Alga s.P.a. (Milano, Italy); FIP Industriale s.P.a. (Selvazzano, Italy), Taylor Devices, Inc. (New York, USA), Maurer Söhne (München, Germany), Mageba (Bülach, Switzerland) or Nanjing Damper Technology Engineering Co. Ltd (Nanjing, China) design and manufacture a wide variety of such systems.
Today an increasing number of applications of energy dissipation devices on bridges for the control of seismic displacements and energy dissipation is taking place. The more common solution is, probably, the use of linear / non-linear viscous dampers, permitting an adequate control of the displacements avoiding an increase of the structural internal forces and the increase of stiffness for piers and abutments [Jerónimo and Guerreiro, 2002].
The new tendencies regarding the seismic analysis and design of fluid viscous dampers capture the frequency dependence of such devices [Singh et al, 2003]; the earthquake response of non-linear fluid viscous dampers [Peckan et al, 1999; Lin and Chopra, 2002]; the seismic performance and behaviour of these devices during near-field ground motion [Tan et al, 2005; Xu et al, 2007] and the performance-based design of viscous dampers [Kim et al, 2003; Li and Liang, 2007]. A state-of-the-art review can be found in the works of Lee and Taylor (2001) and Symans et al (2008).
- 2.2 Technological Aspects
- 2.2.1 Historical Background
As with many other types of engineered components, the requirements, needs and available funds from the military allowed rapid design evolution of fluid dampers to satisfy the needs of armed forces. Early fluid damping devices operated by viscous effects, where the operating medium was sheared by vanes or plates within the damper. Designs of this type were mere laboratory curiosities, since the maximum pressure available from shearing a fluid is limited by the onset of cavitation, which generally occurs at between 0.06 N/mm2 and 0.1 N/mm2, depending on the viscosity of the fluid. This operating pressure was so low that for any given output level, a viscous damper was much larger and more costly than other types [Taylor, 1996].
In the late 1800`s, applications for dampers arose in the field of artillery, where a high performance device was needed to attenuate the recoil of large cannons. After extensive experimentation, the French Army incorporated a unique (and “top-secret”) fluid damper into the design of their 75 mm gun. These first fluid damper designs used inertial flows, where oil was forced through small orifices at high speeds, in turn generating high damping forces. This allowed the damper to operate at relatively high operating pressures, in the 20 N/mm2 range. The output of those devices was not affected by viscosity changes of the fluid, but rather by the specific mass of the fluid, which changes only slightly with temperature. Thus, the technology of fluid inertial dampers became widespread within the armies and navies of most countries in the 1900 – 1945 period.
During the World War II, the emergence of radar and similar electronic systems required the development of specialized shock isolation techniques. During the Cold War period, the guided missile became the weapon of choice for the military, and the fluid inertial damper was again turned to by the military as the most cost effective way of protecting missiles against both conventional and nuclear weapon detonation. In these cases, transient shock from a miss near weapons detonation can contain free field velocities of 3 to 12 m/s, displacements of up to 2000 mm, and accelerations up to 1000 times gravity. For that reason, extremely high damping forces were needed to attenuate these transient pulses on large structures, and fluid inertial dampers became a preferred solution to these problems [Taylor, 1996].
With the end of the Cold War in the late 80`s, much of this fully developed defence technology became available for civilian applications. In this context, demonstration of the benefits of damping technology on structures could take place immediately, using existing dampers and the seismic test facilities available at U.S. university research centres. In this sense, application of fluid viscous dampers as part of seismic energy dissipation systems was experimentally and analytically studied, being validated by extensive testing on one-sixth to one-half scale building and bridge models in the period 1990 – 1993 at the Multidisciplinary Centre for Earthquake Engineering Research (MCEER), located on the campus of the State University of New York at Buffalo in USA. Thus, implementation of fluid viscous damping technology began relatively swiftly, with wind protection usage beginning in 1993, and seismic protection usage beginning in 1995 [Taylor and Duflot, 2002].
- 2.2.2 General Behaviour
Fluid viscous dampers operate on the principle of fluid flow through orifices. A stainless steel piston travels through chambers that are filled with silicone oil. The silicone oil is inert, non flammable, non toxic and stable for extremely long periods of time. The pressure difference between the two chambers cause silicone oil to flow through an orifice in the piston head and seismic energy is transformed into heat, which dissipates into the atmosphere. This associated temperature increase can be significant, particularly when the damper is subjected to long-duration or large-amplitude motions [Makris 1998; Makris et al, 1998]. Mechanisms are available to compensate for the temperature rise such that the influence on the damper behaviour is relatively minor [Soong and Dargush, 1997]. However, the increase in temperature may be of concern due to the potential for heat-induced damage to the damper seals. In this case, the temperature rise can be reduced by reducing the pressure differential across the piston head (e.g., by employing a damper with a larger piston head) [Makris et al, 1998]. Interestingly, although the damper is called a fluid viscous damper, the fluid typically has a relatively low viscosity (e.g., silicone oil with a kinematic viscosity on the order of 0.001 m2 /s at 20°C). The term fluid viscous damper is associated with the macroscopic behaviour of the damper which is essentially the same as that of an ideal linear or nonlinear viscous dashpot (i.e., the resisting force is directly related to the velocity). Generally, the fluid damper includes a double-ended piston rod (i.e., the piston rod projects outward from both sides of the piston head and exits the damper at both ends of the main cylinder). Such configurations are useful for minimizing the development of restoring forces (stiffness) due to fluid compression [Symans et al, 2008]. The force/velocity relationship for this kind of damper can be characterized as F = C.Vα where F is the output force, V the relative velocity across the damper; C is the damping coefficient and α is a constant exponent which is usually a value between 0.1 and 1.0 for earthquake protection, although at the present time some manufactures begin to apply dampers with very low damping coefficients, typically in the order of 0.02. Fluid viscous dampers can operate over temperature fluctuations ranging from –40°C to +70°C, and they have the unique ability to simultaneously reduce both stress and deflection within a structure subjected to a transient. This is because a fluid viscous damper varies its force only with velocity, which provides a response that is inherently out-of-phase with stresses due to flexing of the structure [Taylor and Duflot, 2002].
Fluid velocity is very high in the piston head so the upstream pressure energy converts almost entirely to kinetic energy. When the fluid subsequently expands into the full volume on the other side of the piston head it slows down and loses its kinetic energy into turbulence. There is very little pressure on the downstream side of the piston head compared with the full pressure on the upstream side of the piston head. This difference in pressures produces a large force that resists the motion of the damper. Viscous dampers, when correctly designed and fabricated, have zero leakage and require no accumulator or external liquid storage device to keep them full of fluid. They have nearly perfect sealing. In a correctly designed and fabricated viscous damper there is nothing to wear out or deteriorate over time so there is no practical limit on expected life. Warranty periods of 35 years are common [Lee and Taylor, 2001]. Fig. 2.2 shows a general view of a fluid viscous damper, and Fig. 2.3 shows fluid viscous dampers for a high-speed railway bridge in Spain.
Fig. 2.4 exposes a schematic of a typical fluid viscous damper showing its elements, which are described next.
The cylinder contains the working fluid and must withstand the pressure loading when the damper operates. Cylinders are usually made from seamless steel tubing and are sometimes machined from steel bars. Proof pressure is generally 1 - 5 times expected internal pressure for the maximum credible seismic event.
Structural applications require a fluid that is fire-resistant, non-toxic, thermally stable and that will not degrade with age. Under current OSHA (Occupational Safety & Health) guidelines this means a flash point of at least 200°F. Silicone fluid is often used as it has a flash point over 650°F and is cosmetically inert, completely non-toxic and one of the most thermally stable fluids available.
The seal must provide a service life of at least 35 years without replacement. As dampers often sit for long periods without use, the seal must not exhibit long-term sticking or allow fluid seepage. The dynamic seal is made from high-strength structural polymer to eliminate sticking or compression set during long periods of inactivity. Acceptable materials include Teflon®, stabilized nylon and members of the acetyl resin family. Dynamic seals made from structural polymers do not age, degrade or cold flow over time.
The piston head attaches to the piston rod and effectively divides the cylinder into two separate pressure chambers. This space between the outside diameter of the piston and in the inside diameter of the cylinder forms the orifice. Very often the piston head is made from a different material than the cylinder to provide thermal compensation. As the temperature rises the annulus between the piston head and the cylinder shrinks to compensate for thinning of the fluid.
The damper shown in Fig. 2.4 uses an internal accumulator to make up for the change in volume as the rod strokes. This accumulator is either a block of closed-cell plastic foam or a movable pressurized piston, or a rubber bladder. The accumulator also accommodates thermal expansion of the silicone fluid.
Viscous dampers add energy dissipation to a structure, which significantly reduces response to earthquakes, blasts, wind gusts and other shock and vibration inputs. A value of 30% of the critical damping ratio is a practical upper limit for combined viscous and structural damping. Around 25% of this is viscous damping and the remaining 5% is structural damping [Lee and Taylor, 2001]. This provides a 50% reduction in structural response compared with the same structure without viscous dampers. Note that the addition of viscous dampers does not change the period of the structure. This is because viscous damping is 90 degrees out of phase with the structural forces. Fig. 2.5 shows a typical plot of base shear against interstorey drift, taken from a laboratory test, according to Lee and Taylor (2001).
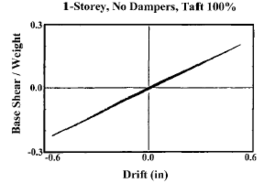
Fig. 2.5 Typical Plot of Base Shear Against Interstorey Drift [Lee and Taylor, 2001] |
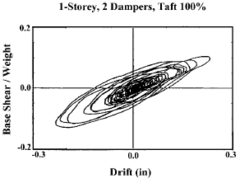
Fig. 2.6 Base Shear Against Interstorey Drift with Added Dampers [Lee and Taylor, 2001] |
Note that the hysteresis loop is very flat and thin as there is only 5% damping. Figure 2.6 shows a plot of the same structure with the same input only this time with added viscous damping. Note that interstorey drift is 50% less and that the hysteresis curve is much fuller. In this case, 20% of added linear damping to the structure increased its earthquake resistance compared to that of the same structure without added damping. The area inside the hysteresis loop is the same as in Fig. 2.5. It is theoretically possible to provide enough viscous damping to completely prevent plastic hinging. This provides a totally linear structure. Economically, it is best to retain some plastic hinging as this results in the least overall cost. Viscous dampers still limit interstorey drift sufficiently to provide immediate occupancy after a worst-case event. They also limit and control the degree of plastic hinging and greatly reduce base shear and interstorey shear [Lee and Taylor, 2001]. Only as comparative purpose Table 2.1 shows equivalent damping coefficients for different structures and components. It is clear that an enormous amount of energy can be dissipated with the implementation of seismic dampers, reaching the largest values of dissipated energy. Of course, with those quantities, structural damping in the case of cable-stayed bridges may represent no more than 3% of the additional damping provided by the dampers, that is to say, a negligible amount.
Table 2.1 Comparison of Equivalent Damping Coefficients ξ of Different Structures and Components [Courtesy of Maurer Sönhe, Germany]
|
In terms of the efficiency, the damping coefficient ξ relates to the efficiency η according to:
This ends up in a maximum efficiency η = 96% for fluid viscous dampers. |
As a summary, the overall characteristics of fluid viscous dampers include:
- During service conditions the device is not pre-tensioned and the fluid is under insignificant pressure
- An extra-low damping exponent, such as those proposed from some manufacturers, provides maximum and well-defined force to a certain limit. No structural damages due to higher damping forces occur even in case the vibration frequency exceeds the expected value.
- With the current technology, velocity ranges from 0.1 mm/sec to 1500 mm/sec or even more can be reached for fluid viscous dampers, which implies wide-variety of applications.
- Maximum response force is given within tenths of second, so structural displacements and vibrations can be more effectively minimized.
- Automatic volume compensation of the fluid caused by temperature changes without pressure increase inside the devices. Any compensation containers are located inside.
- No maintenance works necessarily. Visual inspection can be recommended during the period bridge inspections. Depending on the accumulated displacements and displacement velocities the service life can be reach up to 40 years.
- With the current development, the devices are not prone to leaking
- Range of operating temperatures varies from -40ºC to +70ºC.
- Non-toxic, not inflammable and not ageing fluids are applied.
- 2.2.3 Application to Bridges
Decks for viaducts and long-span bridges require adequate expansion joints for large displacements under service conditions to absorb the effects of creep and thermal expansion. A common structural layout used in Europe, consists of continuous deck supported by POT devices [Priestley et al, 1996]. By this way, the idea of employing devices with an insignificant response under long-period displacements and at the same time, capable of dissipating much induced seismic energy, was developed.
Some manufacturers differentiate the type of damper according to the motion of the device in the presence of slow displacements. In this case, as for example when thermal expansion occurs, in the OTP type the fluid flows from one chamber to the other with minimum opposition (normally smaller than 10% of the maximum force), while in the OP type such a flow is obstructed, so that during normal service the behaviour is substantially rigid [see the scheme of the typical application of viscous dampers on bridges in Fig. 2.7].
Application of fluid viscous dampers to bridges have been used since middle 90`s. Although these devices may be applied to any kind of structures, their application is easier and more effective in bridges. One of the problems in the use of such devices is that the analysis of the dynamic behaviour becomes more elaborated and difficult than the analysis of a bridge with its seismic resistance based on the ductile capacity of the piers [Virtuoso et al, 2000]. Figs. 2.8 and 2.9 show some examples of application of fluid viscous dampers to bridges.
An important aspect to consider is that, if there is some available stiffness and resistance in the connection between the deck and the piers/towers or abutments, it is possible to obtain optimised solutions without inducing significant forces in the structure. That stiffness as the advantage of guaranteeing recentering capability after an earthquake can be used to improve the structure behaviour under other actions [Virtuoso et al, 2000].
- 2.3 Mechanical Behaviour
- 2.3.1 Energy Approach
An earthquake is an energy phenomenon and therefore this energy character should be considered to achieve the best possible seismic protection for the structure. Without seismic protection system, the seismic energy is entering the structure very concentrated at the fixed axis. By means of shock transmission units the entering energy is distributed to several spots within the structure. In this case the energy input into the structure is still in same magnitude like without those devices, but now the energy is spread over the entire structure in more portions. By implementing additional energy dissipation capability, less energy is entering the structure, with the consequent response mitigation.
The principles of physics that govern the effects of dissipation on the control of dynamic phenomena were studied more than two centuries ago [D`Alembert, Traité de Dynamique, 1743]. Nonetheless, their practical application has come about much later and within a much different time-frame in several sectors of engineering. As was previously exposed, the sector that was the first to adopt such damping technology was the military [France, 1897], followed by the automobile industry. In 1956 Housner already suggested an energy-based design of structures. Kato and Akiyama (1975) and Uang and Bertero (1990) made a valuable contribution to the development of the aspects of an energy-based approach, which presently meets with great concensus.
The dynamic equation of a single-degree-of-freedom structure with mass ms damping coefficient cs, stiffness ks and control force u, subject to ground acceleration ![]() is:
is:
where ![]() ,
, ![]() and
and ![]() are the displacement, velocity and acceleration responses respectively. The involved parameters are clearly explained in Fig. 2.10, which shows a simplified scheme for a single-degree-of-freedom system. Of course, each term in Eq. 2.2 is a force.
are the displacement, velocity and acceleration responses respectively. The involved parameters are clearly explained in Fig. 2.10, which shows a simplified scheme for a single-degree-of-freedom system. Of course, each term in Eq. 2.2 is a force.
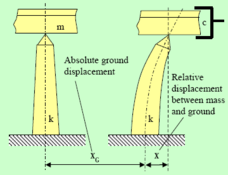
Fig. 2.10 Complex Bridge Structure Explained with a Simplified Single Oscillation Mass |
Integrating Eq. 2.2 with respect to x:
where each term is now an energy component. Thus, we can define: |
An energy balance equation can be proposed in terms of the above defined:
where:
Ek: Kinetic energy
Ev: Dissipated energy by inherent damping
Ee: Elastic strain energy
Eh: Dissipated energy by additional damping devices
Ei: Induced energy in the structure.
The concept of energy approach (Fig. 2.11) easily explains the energy terms involved in Eq. 2.8. The amount of structural stored energy (Es) has to be as low as possible to avoid damages. Therefore the value of the dissipated energy (Ed) must be great. In the term Eh energy dissipated by hysteretic or plastic deformation may be included; however this part must be kept low, as this way of energy dissipation causes structural yielding and cracks. For that reason, the drastic increase of the value of the energy of additional damping devices is the final opportunity to control the energy balance of the structure.

|
Fig. 2.11 Concept of Energy Approach Considering the Energy Exchange Between Structure and Environment |
![]() : Stored energy within structure
: Stored energy within structure
![]() : Dissipated energy within structure
: Dissipated energy within structure
Thus:
The control force u by non-linear viscous dampers with damping coefficient cd is expressed as
In Eq. 2.10, the exponent N controls the damper nonlinearity and has typical values in the range of 0.10 to 1.0 for seismic applications. For the special case of N = 1, Eq. 2.10 represents the force applied by linear viscous dampers. In the case of N = 0, Eq. 2.10 changes to a friction damper as follows:
Linear damping is easy to analyze and can be handled by most software packages. Also, linear damping is unlike to excite higher modes in a structure. Another advantage of linear damping is that there is very little interaction between damping forces and structural forces. Structural forces peak when damping forces are zero as well as damping forces peak when structural forces are zero. Between these points there is a gradual transfer of force [Lee and Taylor, 2001].
Applying the force – velocity relationship expressed in Eq. 2.10 to Eq. 2.6 results:
which represents the dissipated energy for a non-linear fluid viscous damper. The hysteretic behaviour of fluid viscous dampers can be plotted and shown in Fig. 2.13.
In the case of a linear damper, the hysteresis loop is a pure ellipse. In this case it is clear that the dissipated energy is lower than the case of a non-linear damper for similar conditions. As example, Fig. 2.14 shows typical Force – Displacement hysteretic curves of a non-linear viscous damper according to prototype tests carried out by FIP Industriale Laboratories (Italy).
- 2.3.2 Effect of the Damper Parameters
- 2.3.2.1 Damping coefficient cd
In general terms, for viscous dampers, cd does not affect the shape of the hysteretic force – displacement cycle; however, an increase of the value of this parameter increases the energy dissipation capacity and the maximum force in the device [Guerreiro, 2006]. In this sense, the work carried out by Virtuoso et al (2000) studies the modelling of the seismic behaviour of bridges with added viscous dampers, analyzing the effects of the constant cd (here called C). To allow an analysis on the influence of that parameter on the structural response, values of the constant C between 0.10 and 10 were considered, since those values, together with the values considered for the parameter N (here called α), will cover forces corresponding to seismic coefficient varying from 1% to 50% of the weight. In this study a set of five artificial accelerograms compatible with the response spectrum defined in Eurocode 8 – Part 2 [CEN, 1998b] with a peak ground acceleration of 0.30g, type B soil and 30 sec total duration of the series, were used. Two extreme cases were considered: a solution without elastic stiffness (deck totally free over the piers) and a solution with elastic stiffness (low stiffness elastic connection between the piers and the deck). Also, in this research the configurations of the force – velocity relation curves were presented for different values of α, corresponding to the linear branch, which, were defined by the origin and the point corresponding to 10% of the maximum velocity and force corresponding to the defined seismic action and obtained without the consideration of the linear branch. Figs. 2.15 and 2.16 show maximum forces and displacements in the viscous damper without and with elastic stiffness respectively. They show that solution involving a higher displacement control always lead to higher force levels in the device. It is also possible to observe that the more efficient solutions, with better displacement control for the same force level, generally corresponds to low α values. Likewise, for device solutions with low values of the constant C, the elastic stiffness of the structure has an important contribution on the displacement control. It is important to notice that the contribution of the elastic force is out of phase with the one transmitted by the devices, what means that, in a solution of this type there is always a force restraining the movement of the deck. The problem is that the forces transmitted to the structure must be controlled to limit the contribution of the piers to values lower than their elastic limit.
Fig. 2.17 presents the forces in the structure corresponding to the device solutions considered in the study and whose results, in terms of devices response, were represented in Fig. 2.16. The results show that, for low C values the forces transmitted to the structure are important and higher than the corresponding forces in the devices. For C values higher than 1 a significant reduction on the displacements is verified. For the device solutions in this range there is no influence of the elastic stiffness in the device forces. From these results, it can be concluded that the best solutions corresponds to devices with C values higher than 1.
The contribution of the elastic spring is irrelevant for the forces in the device and conducts to some negligible reduction in the displacements when C > 1. From these results, consideration of the elastic stiffness of the structure is not important for the displacement control of the deck.
- 2.3.2.2 Velocity exponent N
The damping exponent N represents the essence of the non-linear behaviour of fluid viscous dampers. On the contrary of the damping coefficient cd, this parameter does not affect the size of the hysteretic force-displacement cycle and for that reason incidence of this parameter on the seismic response is not decisive as occurs with the damping coefficient, aspect enlarged in 2.3.2.1. Changes in the N-exponent imply changes in the shape of the hysteretic force-displacement cycle, as was explained in Fig. 2.13. Low damping exponents tend to expose rectangular force-displacement hysteresis, as well as linear behaviour implies more elliptical force-displacement hysteresis cycles. The more practical incidence of the N-exponent relates with the damper forces, depending on the relative velocities.
If we consider the force at the dampers F as a function of the exponent N, we can write
If cd is constant, F is maximum if ![]() is maximum.
is maximum.
| |
![]() if and only if
if and only if ![]() which implies a constant force F = cd
which implies a constant force F = cd
Analyzing f in its domain:
Then, f is maximum if ![]() is little, which implies
is little, which implies ![]() .
.
This analytical approach shows that the critical point is ![]() . Being the damper velocities larger than 1, the maximum damper forces are obtained for high values of the damping exponent, on the contrary of the case where the damper velocities are lower than 1, in which the maximum damper forces are obtained when N is close to zero, that is to say, for non-linear dampers. Graphically, the above-mentioned can be clearly exposed in Fig. 2.18. Fig. 2.18 exposes variations of the dampers forces with the velocity exponent N for some common damper velocities. From these results, it is necessary to be cautious if velocity pulses are considered in the presence of linear dampers or dampers with N > 1. Likewise, similar considerations are necessary to take into account if non-linear dampers are considered in the presence of low velocities.
. Being the damper velocities larger than 1, the maximum damper forces are obtained for high values of the damping exponent, on the contrary of the case where the damper velocities are lower than 1, in which the maximum damper forces are obtained when N is close to zero, that is to say, for non-linear dampers. Graphically, the above-mentioned can be clearly exposed in Fig. 2.18. Fig. 2.18 exposes variations of the dampers forces with the velocity exponent N for some common damper velocities. From these results, it is necessary to be cautious if velocity pulses are considered in the presence of linear dampers or dampers with N > 1. Likewise, similar considerations are necessary to take into account if non-linear dampers are considered in the presence of low velocities.
The consideration of the damper parameters must be taken carefully, because sometimes interpretation of the results could be confused. In this sense, tables 2.2 and 2.3 show similar conditions of the damper parameters. Table 2.2 exposes the forces for a damper with cd = 2015 kN/(mm/sec)N, and design velocity of 300 mm/sec for three different values of N. The obtained forces increase when N increases. On the right, in Table 2.3, the same situation is represented; however, the units have been changed. Because of the units for the damping coefficient cd depend on the value of N it is necessary to be cautious with the change of units. This transformation implies a change of the values for the damping coefficients. Now, cd increases as a result of this change, which implies that the damper forces obviously increase. Notice that in Table 2.2 damper velocities are higher than 1.0, which implies that for a constant value of cd damper forces increase as the damper exponent increases, as was previously explained. In Table 2.3, damper forces increase because the damping coefficient increases, regardless the damper exponent increases and the damper velocity is lowers than 1.0.
Table 2.2 Damper Forces for Three Different Damper Exponents and cd in kN/(mm/sec)N
|
Table 2.3 Damper Forces for Three Different Damper Exponents and cd in kN/(m/sec)N
|
A similar situation is exposed in tables 2.4 and 2.5. Table 2.4 shows the damper forces considering the same damper exponents, a constant value of 2235 kN/(m/sec)N for cd, and 0.3 m/sec for the damper velocity. In this case, the damper forces decrease as the damper exponent increases. This situation is in agreement with results shown in Fig. 2.18 because now the damper velocity is lower than 1. In Table 2.5, the same situation is represented, but now the units have been changed to [kN/(mm/sec)N] for cd. This change implies that the values of the damping coefficient decrease, which implies that the damper forces decrease regardless the damper velocity is higher than 1. Results of this analysis show that influence of the damper exponent N on the damper forces is in relation with relative velocities of the dampers, being one the critical value. It is not possible to formulate valid conclusions only considering the damper exponent and the damper velocity, as some manufacturers propose. It is necessary to take into account the damping coefficient cd and its units, which depends in some sense on the damping exponent.
Table 2.4 Damper Forces for Three Different Damper Exponents and cd in kN/(m/sec)N
|
Table 2.5 Damper Forces for Three Different Damper Exponents and cd in kN/(mm/sec)N
|
Commonly, use of fluid viscous dampers limits the damping exponent N between 0.1 and 1.0 for seismic applications. Recently, some manufacturers propose the application of extra-low damping exponents, using values in the order of 0.02 or lower. As was previously explained, using damping exponents close to zero implies an almost constant response force for the damper, aspect that can be useful for situations involving high damper velocities or velocity pulses, as usually happens in the presence of near-fault ground motions. Fig. 2.19 shows the Damper Force – Velocity relation for an extra-low damping exponent damper. In this case, 0.015 damping exponent was selected according to practical applications of some manufacturers. For damper velocities higher than 0.7-1.0 m/sec, the damper responses with an almost constant force, well defined to a certain limit. This special characteristic can be very positive to control peak responses when high velocities are demanding the damper, however, this selection cannot be an efficient solution for earthquakes inducing low-to-moderate velocities.
- 2.3.3 Non-linear Viscous Dampers
- 2.3.3.1 Earthquake response
Numerous experimental and analytical investigations have focused on linear fluid viscous dampers, because they can be modelled simply by a linear dashpot. While being effective in reducing seismic demands on the structure, linear viscous dampers may develop excessive damper forces in applications where large structural velocities can occur, as for example in long period structures subjected to intense ground shaking, especially in the near-fault region. Recently, some researchers and earthquake engineering professionals have begun to focus on fluid viscous dampers exhibiting non-linear Force-Velocity relationship because of their ability to limit the peak damper force at large structural velocities while still providing sufficient supplemental damping [Lin and Chopra, 2002; Symans et al, 2008].
In the last years, some analytical and experimental investigations have been conducted regarding the dynamic response of fluid viscous dampers, and especially, with non-linear dampers. In order to verify the behaviour and constitutive laws, prototype viscous dampers have been tested at National Center for Earthquake Engineering Research in Buffalo, USA [Seleemah and Constantinou, 1997]; University of Florence [Terenzi, 1999] and University of California at Berkeley [Infanti et al, 2003].
Although the mean response spectra for deformation, relative velocity, and total acceleration are affected very little by damper non-linearity, the influence increases at longer periods and for smaller values of the non-linearity parameter (here called α). Fig. 2.20 shows as example, the mean response spectra for deformation, relative velocity and total acceleration for elastic single-degree-of-freedom systems and considering 20 ground motions. If the ratio of responses r for α=0.35 and 1 are plotted for three response quantities, as shown in Fig. 2.21, clearly, then damper non-linearity has essentially no influence on system response in the velocity-sensitive spectral region (0.6 ≤ Tn ≤ 3 sec) and small influence in the displacement (Tn ≥ 3 sec) and acceleration (Tn ≤ 0.6 sec) sensitive regions. These aspects has the useful implication for design applications that, for a given supplemental damping ratio ξd, the response of systems with non-linear fluid viscous dampers can be estimated to a sufficient degree of accuracy by analysing the corresponding linear viscous system (α = 1). Likewise, damper non-linearity has very little influence on the deformation, velocity and acceleration time histories of the system (Fig. 2.22), but affects the damper force significantly, primarily near the response peaks, as was previously explained.
Regarding the influence of supplemental damping, as expected, it reduces the structural response, with greater reduction achieved by the addition of more damping (Fig. 2.20). As Tn→0, supplemental damping does not affect response because the structure moves rigidly with the ground. And as Tn→∞, supplemental damping again does not affect the response because the structural mass stays still while the ground underneath moves. The response reduction is significant over the range of periods considered. Moreover, the reduction in responses is essentially unaffected by damper non-linearity in the velocity-sensitive region and only weakly dependent in the acceleration and displacement sensitive regions (Fig. 2.21).
It is important to say that for a given force and displacement amplitude, the energy dissipated per cycle for a nonlinear fluid damper is larger, by a factor λ/π (where λ is a parameter whose value depends exclusively on the velocity exponent), than that for the linear case and increases monotonically with reducing velocity exponent (up to a theoretical limit of 4/π=1.27 which corresponds to a velocity exponent of zero); however, the additional energy dissipation afforded by the nonlinear dampers is minimal. For a given frequency of motion, ω, and displacement amplitude, x0, to dissipate the same amount of energy per cycle, the damping coefficient of the nonlinear damper, cdNL, must be larger than that of the linear damper, cdL, as given by
As an example, for a frequency of 1.0 Hz and displacement amplitude of 5 cm, the damping coefficient of a nonlinear damper with velocity exponent of 0.5 must be approximately three times larger than that of a linear damper to dissipate the same amount of energy per cycle. Conversely, if nonlinear dampers are used to limit the damper force, a reduction in energy dissipation capacity as compared to the case of linear dampers would be accepted [Symans et al, 2008].
A last aspect to consider regarding the earthquake response of non-linear fluid viscous dampers, is that the earthquake-induced force in a non-linear viscous damper can be estimated from the damper force in a corresponding system with linear viscous damping, its peak deformation, and peak relative velocity; however, the relative velocity should not be approximated by the pseudo-velocity as this approximation introduces a large error in the damper force. In fact, if spectral pseudo-velocities are used, they are based on design displacements (Sv = ω0Sd). It is well known that effectiveness of non-linear viscous dampers is highly dependent on operating velocities, being necessary to have reliable estimates of the true velocity in the device [Pekcan et al, 1999; Lin and Chopra, 2002].
- 2.3.3.2 Equivalent linear viscous damping
The energy dissipation capacity of a fluid viscous damper can be characterized by the supplemental damping ratio ξd and its non-linearity by the parameter N; and it is found that the structural response is most effectively investigated in terms of these parameters because they are dimensionless and independent, and the structural response varies linearly with the excitation intensity [Lin and Chopra, 2002]. In this sense, a system with non-linear dampers is usually replaced by an equivalent linear system, with its properties determined using different methods: equalling the energy dissipated in the two systems [Jacobsen, 1930; Fabunmi, 1985]; equalling power consumption in the two systems [Pekcan et al, 1999]; replacing the non-linear viscous damping by an array of frequency and amplitude-dependent linear viscous model [Rakheja and Sankar, 1986]; random vibration theory [Caughey, 1963; Roberts, 1976], and more recently, applying closed-form formulas based on probabilistic concept to obtain fundamental modal damping ratio without carrying out structural analysis [Lee et al, 2004].
Thus, equalling the energy dissipated in a vibration cycle of the non-linear system to that of equivalent viscous system [Pekcan et al, 1999] and considering equation 2.10:
Soong and Constantinou (1994) have shown that the work done (dissipated energy) in one cycle of sinusoidal loading can be written as
that is basically the same equation as 2.6. Here, T0 = 2π/ω0, where ω0 is the circular frequency of the system and ![]() .
.
Equation 2.14 can be integrated to give
where Г( ) is the gamma function.
The equivalent (added) damping is calculated by equating equation 2.15 and the energy dissipated in equivalent viscous damping:
in which strain energy Es = kx02/2. Solving Eq. 2.16 for equivalent damping ratio:
where M is the mass of the system, and x0 the amplitude of harmonic motion at the undamped natural frequency ω0.
Of course, the additional damping that the passive system introduces to the structure can be obtained by its energy dissipation capacity in each hysteretic cycle. This dissipated energy for each cycle, can be obtained calculating the area of the cycle in the force – displacement relationship of the viscous damper. Thus, for a selected cycle, it is possible to assess the equivalent damping ratio as follows:
where umax and xmax are the maximum force and maximum displacement at the damper respectively.
Pekcan et al (1999), proposed a simple method for making the transformation from the non-linear damper behaviour to equivalent viscous damping. They explain that for velocity-dependent systems such as viscous dampers, consideration of the rate of energy dissipation – that is power (rather than energy) – becomes more important in seeking the equivalent linear properties for these systems. The proposed equivalent damping is
Given the customary definition of damping ratio (ξ) obtained from c = 2ξω0M, equation 2.19 can be expressed as follows:
This formulation, also called power equivalent approach, predicts higher damping values compared with energy based method (Eq. 2.17). This difference is greater for low values of N, and for that reason it is necessary to be cautious using any of the above formulations for small N powers (N<0.1), since the mechanism of the devices changes from viscous (velocity dependent) to Coulomb friction type (when N tends to zero).
- 2.3.4 Performance of Viscous Dampers During Near-field Ground Motions
Near-field earthquakes are characterized by short duration pulses of long period with large peak ground velocities and accelerations. It has been observed from recent earthquake records that motions in the fault-normal direction contain destructive long-period pulses with high peak ground velocities, aspect that negatively affects long-period structures such as cable-stayed bridges. A lot of approaches to model these pulses have been recently proposed [Makris, 1997; He, 2003; Mavroeidis et al, 2004].
Linear viscous dampers have been found to perform well during mild to moderate earthquakes. However, the force demand on linear dampers during pulse-type excitations may be excessive, leading to device capacity saturation and larger force demands on structural components. Non-linear viscous dampers may be more suitable in such situations because of their inherent force saturation capability at high velocities.
The recent investigation by Xu et al (2007) on the performance of passive energy dissipation systems during near-field ground motions, shows that both linear and non-linear viscous dampers with 25% supplemental damping ratio are effective in achieving more than 40% displacement reduction when 3/5 < Tn/Tp < 5/3, Tn and Tp being structural and excitation periods, respectively. Non-linear viscous dampers can yield additional 10% reductions in displacement and input energy over those by linear dampers when Tp > 4/5Tn and they achieve less displacement reduction when Tp < 4/5Tn. Likewise, performance of viscous dampers depends on their absorbability of instantaneous input energy. If a damper cannot dissipate the input energy instantaneously, even through it may have an excellent ability to dissipate the total input energy, the structure may still undergo damage due to instantaneous accumulation of input energy during an earthquake.
Although the damper non-linearity does not significantly influence the displacement response (As was demonstrated in the research by Lin and Chopra, 2002), in general terms non-linear viscous dampers are more advantageous than linear dampers in reducing peak structural displacements and peak input energies when a structure is subjected to pulse-type excitation with pulse period longer than the natural period of the structure.
- 2.4 Analysis and Design Issues
- 2.4.1 Structural Analysis Including Viscous Dampers
The first step in the analysis is to find out how added damping affects the structure. This is generally done with a simple stick model with one node for each storey. Adding global damping to the stick model provides a good indication of how damping elements can benefit the structure. The analyst will then construct a simple two-dimensional model of the structure. In this model the dampers are entered as discrete elements. At this point there are a number of variables to play with: force capacity of the dampers, location and number of dampers, damper coefficient and damper exponent. The analyst has the task of finding the best solution. This is generally a trial-and-error process but there are some general guidelines. It is always best to minimize the number of dampers and the number of bays that use dampers. Also, it is known from experience that approximately 20%–30% of critical damping is a desirable range, and that 5% of this can be structural, leaving 15%–25% for viscous damping. So the first objective of the analyst is to determine the smallest possible number of dampers to provide approximately 20% critical damping without overloading either the beams or the columns. Also, it is always best to start with linear dampers and then find out what happens with nonlinear dampers after the locations, number and characteristics of the dampers have been fairly well determined [Lee and Taylor, 2001].
Note that analysis of a structure with dampers always involves a step-by-step time-history simulation. Sometimes a time-history is not available for a particular location but a shock spectrum is. In this case, a time-history can be arrived at by going through a library of time histories, comparing their shock spectra with the specified shock spectrum at the site and selecting the one that fits best. Likewise, with the current computer capability, a detailed non-linear time history analysis to satisfy individual requirements can be applied. Some advantages of a non-linear time history analysis include: more exact determination of structural displacements, more accurate assessment of the seismic response forces acting onto the device and structure, exact evaluation of real structural safety factors and possible economical benefits due to savings in design.
Finally, it can be important to say that in the present days exist good and powerful computing tools that permit to solve non-linear structures equipped with linear/non-linear energy dissipation devices such as fluid viscous dampers. Commercial computing codes such as ANSYS [Ansys Inc, 2005] or SAP2000 [Computers & Structures, 2007] include the option of applying non-linear energy dissipation devices. However, modelling of some damping elements (e.g. dampers with temperature-dependent or frequency-dependent) can be more challenging or, in some cases, not possible with a given program. When the modelling of such behaviour is not possible, the expected response may be bounded by analyzing the structure over a range of behaviours. Fortunately, for majority of fluid viscous dampers actually manufactured, properties are largely independent with respect to frequency and temperature [Symans et al, 2008].
- 2.4.2 Design Issues for Viscous Dampers
The peak force fD0(N) in the non-linear fluid viscous damper with known non-linear parameter N can be expressed as
where V = ω0x0 is the spectral pseudo-velocity for the SDF system; c1 is the damping coefficient of the linear system and βN is a constant defined as
The non-linear damper force can be computed from Eq. 2.21 if x0 and ![]() are known. They can be estimated as the peak values of deformation and relative velocity of the corresponding linear system. Equation 2.21 is almost exact in the velocity-sensitive region of the spectrum, overestimates the damper force in the acceleration-sensitive region (by at most 15%); and underestimates in the displacement-sensitive region (by at most 7%). Moreover, the accuracy of Eq. 2.21 deteriorates slightly with the increase of the equivalent damping ξd. However, the actual velocity
are known. They can be estimated as the peak values of deformation and relative velocity of the corresponding linear system. Equation 2.21 is almost exact in the velocity-sensitive region of the spectrum, overestimates the damper force in the acceleration-sensitive region (by at most 15%); and underestimates in the displacement-sensitive region (by at most 7%). Moreover, the accuracy of Eq. 2.21 deteriorates slightly with the increase of the equivalent damping ξd. However, the actual velocity ![]() of the corresponding linear system required in Eq. 2.21 and to compute fD0 (N=1) = c1
of the corresponding linear system required in Eq. 2.21 and to compute fD0 (N=1) = c1 ![]() is not readily available, because the velocity spectrum is not plotted routinely. If the velocity
is not readily available, because the velocity spectrum is not plotted routinely. If the velocity ![]() is replaced by the pseudo-velocity, Eq. 2.21 changes to
is replaced by the pseudo-velocity, Eq. 2.21 changes to
The resulting estimate of the damper force is not accurate, which increase with the system’s period, damper non-linearity and supplemental damping ratio. Thus, velocity should not be approximated by the pseudo-velocity [Lin and Chopra, 2002].
Another important point regarding the design of non-linear fluid viscous dampers is how to select the properties cd and N to satisfy a design requirement. As was previously explained, the structural deformation is essentially unaffected by the damper non-linearity parameter N and it is essentially the same as that for the corresponding linear system. The total damping capacity that must be provided in the system to limit the deformation of a linear system to a design value can be determined directly from the design spectrum. Subtracting the inherent damping in the structure from the total damping required gives ξd, the necessary supplemental damping. Many different non-linear fluid viscous dampers can be chosen to provide the required supplemental damping ratio ξd. Thus, for a selected value of N:
where M is the mass of the system and D is the allowable deformation.
Fig. 2.21 suggests that the selected damper defined by Eq. 2.24 should satisfy the design constraint reasonably well. Also, the structural deformation should be very close to the allowable value in the velocity-sensitive region, less than the allowable value in the acceleration–sensitive spectral region, but exceed slightly the allowable value in the displacement-sensitive spectral region [Lin and Chopra, 2002].
- 2.5 Practical Applications
- 2.5.1 Study Case 1: Rion-Antirion Bridge, Greece
Amongst long-span cable-stayed bridges that incorporate additional passive seismic protection, the recently inaugurated Rion – Antirion Bridge in the Gulf of Corinth, Greece, is one of the most interesting bridges located in a high seismicity zone generated by active local faults.
The structure is a concrete multi-span double-plane semi-harp type cable-stayed bridge, with a continuous floating deck, as can be appreciated in Fig. 2.23. The 2252 m-long bridge is divided into three spans of 560 m and two of 286 m (Fig. 2.24). A general description of the structure and the basic aspects regarding the design and construction can be found in the works of Combault et al (2000), Teyssandier (2002) and Teyssandier et al (2003).
The bridge was designed to resist seismic events of 0.48g – peak ground acceleration, and tectonic motion for two consecutive pylons up to 2 m at any direction. That was possible by using an energy dissipation system, connecting the deck with each pylon, which limited their motion during the occurrence of a strong earthquake, while it dissipated energy. The basic aspects of the seismic design of the bridge include a response design spectrum that corresponds to a 2000 years return period (Fig. 2.25) with a peak spectral acceleration equal to 1.20g.
For the dynamic analysis, a 3D-finite element model was used for the whole structure, taking into consideration important aspects, such as [Combault et al, 2000]:
- Non-linear hysteretic behaviour of the reinforced soil
- Possible sliding of the pylon bases on the gravel beds precisely adjusted to the accompanying vertical force
- Non-linear behaviour of the reinforced concrete of the pylon legs (including cracking and stiffening of concrete due to confinement)
- Non-linear behaviour of the cable-stays
- Non-linear behaviour of the composite deck (including yielding of steel and cracking of the reinforced concrete slab)
- Second order effects
Fig. 2.26 shows the isolation system in the Antirion approach viaduct and Fig. 2.27 shows the fuse restraint general configuration.

Fig. 2.26 Isolation System in the Antirion Approach Viaduct [Infanti et al, 2004] |
Fig. 2.27 Fuse Restraint [Infanti et al, 2003] |
On each pylon, four viscous dampers of 3500 kN - reaction capacity each and damping constant C = 3000 kN/(m/s)0.15 were installed. The fuses consider a reaction capacity of 10500 kN. For the transition pylons, the same previous dampers were used, but in conjunction with structural fuses of 3400 kN - reaction capacity each.
The seismic performance and the energy dissipation requirements were evaluated applying non-linear time history analysis of a 3D model of the structure. However, the seismic design hypotheses and the real behaviour of the devices could be verified with a full-scale testing. Fluid Viscous Damper Prototype tests were performed at the laboratory of the University of California – San Diego (USA), and the Fuse Restraints were tested at the FIP Industriale Testing Laboratory (Italy). The full-scale testing of the seismic devices is explained by Infanti et al (2003, 2004). In their works, they show the methodology, implementation and results of the full-scale testing. Figs. 2.28 and 2.29 show the full-scale damper testing and a view of the Fuse Restraint Testing during fatigue test respectively.
Another interesting aspect included in the Rion-Antirion Bridge, is the addition of anti-seismic deviators that work as dampers for the stay-cable vibration mitigation. Although hydraulic dampers are also used on cable-stayed and suspended bridges to reduce rain-wind vibration, they have a clear anti-seismic purpose as was commented in the previous pages. Under certain circumstances, cable vibrations can modify the global seismic response of the bridge, introducing energy in higher order vibration modes. In this sense, Lecinq et al (2003) gives a description of the alternatives to increase the damping on stay-cables, and explain the anti-seismic deviators employed in the Rion-Antirion Bridge. Fig. 2.30 shows a render view of an internal hydraulic damper used for cable vibration mitigation of cable-stayed bridges. Fig. 2.31 shows an external damper for cable vibration used in the Normandy Bridge (France).

Fig. 2.28 Full-Scale Viscous Damper Prototype Testing [Infanti et al, 2004] |

Fig. 2.29 Fuse Element During Fatigue Test [Infanti et al, 2004] |

Fig. 2.30 Internal Hydraulic Damper [Lecinq et al, 2003] |

Fig. 2.31 External Hydraulic Damper on Normandy Bridge [Lecinq et al, 2003] |
In his MSc Thesis, Morgenthal (1999) carries out a detailed research on the seismic behaviour of the Rion-Antirion Bridge. He describes the bridge and exposes analytical modelling using finite elements to study the seismic control strategies incorporating different seismic protection devices, such as structural fuses, hydraulic dampers, seismic connectors and elasto-plastic isolators. Finally, a parametric analysis of the seismic behaviour of different deck isolation devices is exposed.
- 2.5.2 Study Case 2: Tempozan Bridge, Japan
Due to severe damage to bridges caused by the Hyogo-ken-Nanbu earthquake in 1995, very high ground motion was required according to the bridge design specifications set in 1996 [Japan Road Association, 1996], in addition to the relatively frequent earthquake motion specifications by which old structures were designed and constructed. Hence, seismic safety of cable-stayed bridges that were built prior to that specification was reviewed, and seismic retrofit was performed. In order to study the effectiveness of passive control to the seismic retrofit of a cable-stayed bridge, a numerical analysis on a model of a cable-stayed bridge was carried out. An existing cable-stayed bridge with fixed-hinge connections between deck and towers was modelled and its connections were replaced by isolation bearings and dampers. The isolation bearings were assumed to be of the elastic and hysteretic type. The dampers were linear and variable. The objective was to increase the damping ratio of the bridge by using passive control technologies. The chosen bridge model was the Tempozan Bridge, located in Osaka, Japan.
The Tempozan Bridge, built in 1988, is a three-span, continuous steel, cable-stayed bridge situated on reclaimed land. It crosses the mouth of the Aji River in Osaka, Japan. The total length of the bridge is 640 m with a centre span of 350 m, while the lengths of side spans are 170 and 120 m (Figs. 2.32 and 2.33).

Fig. 2.32 Tempozan Bridge [from en.structurae.de] |
Fig. 2.33 Side View of the Tempozan Bridge [Iemura and Pradono, 2003] |
The main towers are A-shaped to improve the torsional rigidity. The cable in the superstructure is a two-plane, fan pattern, multicable system with nine stay cables in each plane. The bridge is supported on a 35-m-thick soft soil layer and the foundation consists of cast-in-place reinforced concrete piles of 2-m diameter. The main deck is fixed at both towers to resist horizontal seismic forces. The bridge is relatively flexible with a predominant period of 3.7 sec. As to the seismic design in transverse direction, the main deck is fixed at the towers and the end piers [Iemura and Pradono, 2003].
If the deck is connected with very flexible bearings to the towers, the induced seismic forces will be kept to minimum values but the deck may have a large displacement response. On the other hand, a very stiff connection between the deck and the towers will result in lower deck displacement response but will attract much higher seismic forces during an earthquake, which is the case of the original bridge structure. Therefore, it is important to replace the existing fixed-hinge bearings with special bearings or devices at the deck-tower connection to reduce seismic forces, absorb large seismic energy, and reduce the response amplitudes. Additionally, energy-absorbing devices may also be put between the deck-ends and piers. However, because doing so will attract a relatively large lateral force to the piers, this is avoided for this bridge at present.
The original structure system has fixed-hinge connections between the towers and the deck and roller connections between the deck-ends and piers, so that the deck longitudinal movement is constrained by the towers (Fig. 2.34a). For the retrofitted bridge, isolation bearings and dampers connect the deck to the towers (Fig. 2.34b). The cables were modelled by truss elements, the towers and deck were modelled by beam elements, and the isolation bearings were modelled by spring elements. The moment–curvature relationship of the members was calculated based on sectional properties of members and material used.
The first modes of the structures are interesting because these modes have the largest contribution to the longitudinal motion of the bridge. The first mode shape of the original structure is shown in Fig. 2.35a. The natural period (T) of this mode is 3.75 sec, which is close to the design value for the bridge (3.7 sec). This first mode has effective modal mass as a fraction of total mass of 84%. For the retrofitted structure, the stiffness of bearings was an important issue as large stiffness produces large bearing force and makes any energy-absorbing device work ineffectively in these connections (Fig. 2.35b). However, very flexible connections produce large displacement response. Therefore, based on a study on a simplified model of the bridge under seismic motions, a bearing stiffness that produced a retrofitted main period (T) 1.7 times the original main period was chosen. This bearing stiffness makes the energy-absorbing devices work well in reducing seismic-induced force and displacement. The main natural period of the retrofitted bridge (T′) then becomes 6.31 sec and the effective modal mass as a fraction of total mass is 92%. It is clear from the figures that smaller curvatures were found at the towers and the decks of the retrofitted structure than were found in those of the original structure.
The models were analyzed by a commercial finite element program [Prakash and Powell, 1993] which produces a piecewise dynamic time history using Newmark’s constant average acceleration (β= 1/4) integration of the equations of motion, governing the response of a nonlinear structure to a chosen base excitation. The input earthquake motions were artificial acceleration data used in Japan for design for soft soil condition, according to the 1996 Seismic Design Specifications of Highway Bridges [Japan Road Association, 1996]. The data are intended as Type I (inter-plate type). Table 2.6 shows the seismic response effects due to different kinds of bearings and dampers: fixed-hinge bearings for the original bridge model, elastic bearings, elastic bearings plus viscous dampers, and hysteretic bearings for the retrofitted bridge model.
From the table, if only elastic bearings are used for seismic retrofit, the sectional forces can be reduced to about 40% of the original ones; however, the displacement response increases to 176% of the original one. By adding viscous dampers to the elastic bearings, the sectional forces can be reduced to about 25% of the original ones and the displacement response is reduced to 63% of the original one. So the viscous dampers plus bearings work to reduce the seismic response of the retrofitted bridge. The structural damping ratio is calculated as 35%. If hysteretic bearings are used for seismic retrofit, the sectional forces are reduced to about 29% of the original ones and the displacement response is reduced to 67% of the original one. Equivalent structural damping ratio is calculated as 13.1% by using pushover analysis to obtain a hysteretic loop at the main mode. The hysteretic bearings are modelled by bilinear model and the second stiffness of the hysteretic bearings is 0.03 times the initial stiffness and produces a first mode natural period of 6.31 sec.
| Retrofitted Structure | ||||
| Items | Original Structure | Elastic Bearings | Elastic Bearings + Viscous Dampers | Hysteretic Bearings |
| Deck displacement | 2.37 m | 4.17 m | 1.50 m | 1.58 m |
| Tower moment a | 3100 MN.m | 2000 MN.m | 900 MN.m | 900 MN.m |
| Tower axial force a | 48000 kN | 15000 kN | 15000 kN | 21000 kN |
| Cable force | 24000 kN | 3440 kN | 4000 kN | 5000 kN |
| Bearing force b | 94000 kN | 44000 kN | 17000 kN | 25000 kN |
| Deck moment | 370 MN.m | 95 MN.m | 75 MN.m | 95 MN.m |
| Deck axial force | 56000 kN | 21000 kN | 11000 kN | 15000 kN |
| Damping ratio | 2% | 2% | 35% | 13.1% |
| Natural period | 3.75 s | 6.31 s | 6.73 s | 3.86 and 6.31 s c |
As a conclusion remark, it is clear that additional viscous damping to control the seismic response of cable-stayed bridges is beneficial, reducing the seismic forces on members as well as their displacements by increasing the structural damping.
Chapter 3. Seismic Response. Parametric Analysis
- 3.1 Introduction
As a starting point, the seismic analysis without the incorporation of additional damping devices is presented. In order to compare the analysis results of the bridge models considering the incorporation of additional passive devices, this part is essential, and must be employed as basic configuration (reference structures).
The structural analysis begins with the nonlinear static analysis under service loading. This analysis is very important, because the assessment of some geometric nonlinearities involved with the overall change in the bridge geometry is based on the deformed shape of the structures under this static condition, being the starting point of the nonlinear time history analysis. In other words, these initial stresses and strains, including all nonlinearities available, are considered as starting point for the subsequent analyses.
Secondly, the assessment of the natural frequencies, modal shapes and damping properties in order to obtain a general dynamic characterization of the bridge models, is exposed. After that, and only as first approach, the seismic response of the cable-stayed bridges applying the response spectrum method is obtained. This analysis gives an idea about the seismic response of the structures, of course, considering a linear behaviour. Because of the inherent nonlinear behaviour of the bridges, this analysis permits a comparison of the maximum values of the structural responses for a linear condition with regard to the nonlinear time history analysis, with the aim to recommend the best structural configurations for those bridges. With this analysis, the critical bridges to be analyzed applying the direct integration nonlinear time history analysis are selected. Because of the tremendous computational effort involved in the step-by-step analysis, two comparable structures are selected for the subsequent analyses.
The last point of this chapter corresponds to the seismic response of the selected bridges considering far-fault and near-fault ground motions respectively. In this part, nonlinear time history analysis is conducted taking into account the geometric and material nonlinearities of the structures and the cable vibration effects. The input ground motions are acceleration time histories: five artificial three-orthogonal component acceleration records for far-fault analysis and five real three-orthogonal component acceleration records for near-fault analysis. The seismic response of the bridges considers the displacement, velocity and acceleration time histories and the response of the deck, cables and towers. Because of the complex nature of the nonlinear time history analysis and according to the recommendations of Eurocode 8 Part 2 [CEN, 1998b], the average of the maximum response parameters in the assessment of the structural response for the record selection is considered.
- 3.2 Structural Modelling
The seismic response analysis of the concrete cable-stayed bridges takes into consideration eight 3-D symmetric bridge models for an adequate study. The chosen bridges were taken from the specialized literature, and specifically, from Walter’s Bridges [Walter, 1999] including the recommendations of Aparicio and Casas (2000) and Priestley at al (1996). The examination is based on a symmetric multi-stay reference cable-stayed bridge, having two pylons, double-plane cable layout and a main span length of about 200 m. Two stay cable layouts were selected: fan-type and harp-type. The semi-harp pattern was rejected because this typology is an intermediate pattern, and both harp and fan patterns are enough for an adequate analysis. The main span lengths of the bridges are 217 m and 204.60 m, depending on the stay spacing. In this sense, long-span cable-stayed bridges have experienced adequate performance during recent earthquake events, and it is expected that short-to-medium spans bridges show a worse seismic performance, mainly if near-source effects are considered. That is the main reason to select the proposed span lengths. Moreover, the deck pattern considers two cases: a slab-type deck and a hollow-box type deck. The first one, due to its inherent flexibility, considers a stay spacing of 6.20 m. In the second case, 12.40 m - stay spacing is considered. The selected tower, for all cases, is a concrete frame-type tower, with deck levels of 30 and 60 m from bottom. The height of the towers is 81 m and 111 m respectively. All these dimensions were taken from Walter’s recommendations.
The structural analysis considers the application of two codes: RAM Advanse [RAM International, 2003] and SAP2000 [Computers & Structures, 2007]. The first software is employed to generate the whole geometry of the bridges, the 3-D meshing, the structural modelling and to carry out the static analysis. Also, this tool is employed to obtain the general dynamic characterization, such as natural frequencies and modal shapes, and the seismic analysis applying the design response spectrum method. This structural analysis package is very easy to use, with an excellent graphical interface. Some specific characteristics in relation to the structural modelling and analysis such as intuitive member selection, advanced automatic data generation, realistic rendering of 3-D structures, rigid links, tension – only elements (cable elements), P – Δ effects, eccentricity due to offset columns and beams, automatic self-weigh calculation and dynamic analysis using response spectra are considered by this software. The second tool is employed for the non-linear time history analysis of the critical bridges previously selected. To use this software, all available data is exported from RAM ADVANSE using [. DXF] extension files. This software can be used for the nonlinear seismic analysis of the bridges considering cable element modelling, incorporation of nonlinear fluid viscous dampers as link elements and the incorporation of all material and geometric nonlinearities available. Also, some specific bridge analysis tools are incorporated in the last version of this software.
Regarding the bridge modelling, the analysis is carried out considering the use of beam and cable elements for all the bridges. The deck is modelled using a single spine to avoid the use of shell elements, with the incorporation of transverse rigid-links to simulate the anchor of cables. In fact, the use of beam elements can be more useful to assess forces on members, with clear graphical results and a considerable decrease of the computing time, especially when non-linear time history analysis is applied. Moreover, the non-linear analysis takes into consideration the geometric non-linearities that are present in almost all cable-stayed bridges. These non-linearities due to high compressions in the deck and pylons are considered by the axial – bending interaction. Non-linear behaviour of cables is considered by a multi-element cable formulation (tension-only elements), in order to take into account the spatial vibrations of them. Likewise, non-linearities due to large displacements in the overall geometry are considered too. Spatial variability is not considered because of the main span length of the bridges (of about 200 m), that not recommends this effect according to Eurocode 8.
- 3.2.1 Geometric Layout
The longitudinal layout of the cable stays is one of the fundamental items in the design of cable-stayed bridges. It influences, in fact, not only the structural performance of the bridge, but also the method of erection and the economics.
The main longitudinal layouts are the harp pattern, semi-harp pattern and fan pattern. Whilst the harp pattern is not the best from the static or economic point of view, it is attractive because of its undeniable aesthetics advantages [Walter, 1999]. Also, this structural configuration can be very interesting from a dynamic point of view. The fan pattern brings all the stays together to the top of the pylons, being used in several recent structures. Some important advantages, according to Walter (1999) are: the total weight of the cables needed is substantially below that for a harp pattern; horizontal force introduced by the cable in the deck is less; longitudinal bending moments of the pylons remains moderate; movements of the deck due to changes in temperature can be absorbed by conventional expansion joints placed across the abutments, if the horizontal connection between the pylons and the deck is freed; flexibility of the structure is favourable where horizontal movements of the deck take place and increases the stability against seismic activity. However, the Achilles` heel of the fan pattern solution lies in the design and construction of the heads of the pylon, which are heavily stressed.
Regarding the stay spacing, it can be said that the use of wide spacing between the stays may still be imposed today. The multiple-stay has numerous advantages: the large number of elastic supports leads to moderate longitudinal bending in the deck; the individual cables are smaller than in a structure with concentrated staying, which simplifies their installation and anchoring; replacement of stays is relatively simple, which is an important aspect to consider mainly when structural damage occurs after an important earthquake for example. Of course, when it is a matter of major bridges, with spans of some hundred metres, the multiple-stay is the only possible solution. The maximum spacing of the stays depends of several parameters, in particular on the width and stiffness of the deck. In fact, as general rule, spacings between 6 m and 25 m are adopted for concrete decks [Walter, 1999].
For this study, eight cases were considered for the chosen typologies. Fig. 3.1 (a) shows the case of a fan pattern with stay spacing of 6.2 m, 30 m – deck level and 81 m – tower height. Fig. 3.1 (b) is similar to Fig. 3.1 (a), but it considers a tower height of 111 m and 60 m – deck level. Figs. 3.1 (c) and (d) are similar to Figs. 3.1 (a) and (b) respectively, but the stay spacing is 12.4 m. The main span length is 217 m for all cases, with 93 m span length at the approximation spans. The relationship (l/L) = 0.43 implies rigid pylons in this case. Moreover, the relationship (H/L) = 0.23 implies a good selection for the deck level and the towers in conjunction with the whole geometry, according to the design recommendations [Aparicio and Casas, 2000].
The geometry for the harp pattern can be seen in Figs. 3.2 (a), (b), (c) and (d). In the first case, 6.2 m stay spacing, 30 m – deck level and 81 m – tower height are considered. The second case is similar to the previous one, but with 60 m – deck level and 111 m – tower height. Figs. 3.2 (c) and (d) show similar conditions to the previous cases, with 12.4 m – stay spacing. In these cases the relationship (l/L) = 0.48 implies rigid pylons, and (H/L) = 0.25 is adequate according to the design recommendations [Aparicio and Casas, 2000]. The main span length for this configuration is 204.6 m.
The extreme spacings of 6.2 m and 12.4 m were selected according to the deck type. In fact, 6.2 m – stay spacing is adequate for flexible decks, as long as 12.4 m –stay spacing is a good length for rigid decks, as the hollow-box type.
|
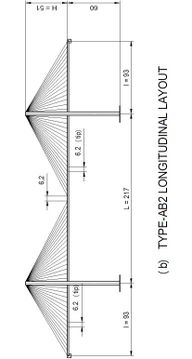
|
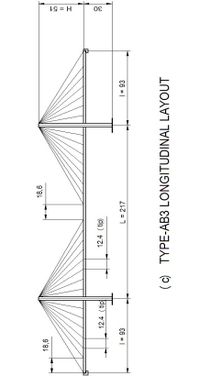
|
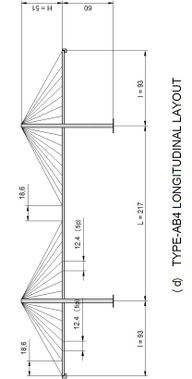
|
'Fig. 3.1 Longitudinal Layouts for Fan Pattern (dimensions in metres)

|
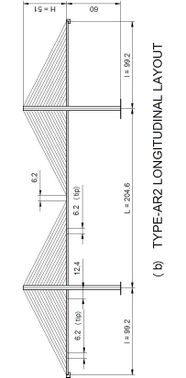
|
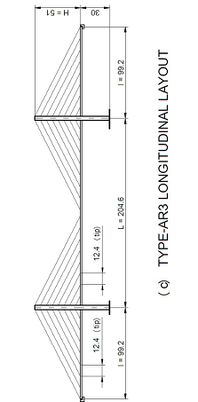
|
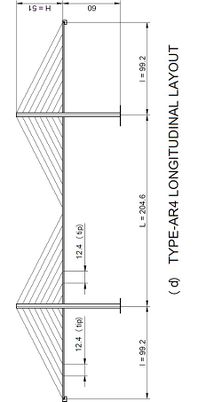
|
Fig. 3.2 Longitudinal Layouts for Harp Pattern (dimensions in metres)
In the transverse direction, the majority of existing structures consist of two planes of cables, generally on the edge of the structure. However, several bridges have been successfully built recently with only one central plane of cables. In principle, it is quite possible to envisage solutions using three or more planes, with the aim of reducing the cross-sectional forces when the deck is very wide, but this possibility has been rarely exploited [Walter, 1999].
In the case of cable-stayed bridges with vertical lateral suspension, the stays ensure a rigid connection between the pylons and deck. The vertical suspension does not give rise to any clearance problem above the deck. The width of the deck depends on the minimum distance required for the arms of the pylons. Of course, it is possible to reduce this one by placing these arms outside the deck, as occurs in this research (Fig. 3.3). On the other hand, the vertical lateral suspension seems to be an advantage from a seismic point of view, maybe due to its better stability, mainly when the earthquake occurs in the transverse direction. Although the stiffness and stability of the structure can be further improved by the use of A-frame pylons, the inclined suspension can give rise to certain clearance problems in the transverse direction. Also, the erection of A-frame pylons is generally more complicated than that of vertical pylons. Lateral suspension with this kind of pylons is particular suited for bridges of very large spans, where aerodynamic stability becomes all-important [Walter, 1999]. As can be appreciated in Fig. 3.4, and taking into account the above mentioned, a frame- type pylon with lateral suspension was selected. Its geometric simplicity and better comprehension of the structural and non-linear seismic characteristics is one of the main reasons to consider this typology in this study. T
Two deck levels were chosen for this study: 30 m and 60 m. The first height was selected as general rule. The second one was selected to take into consideration free height below the deck for navigation. Of course, those deck levels are a different structural and seismic condition for the bridges. In fact, in the second case due to its inherent flexibility, natural periods will be larger than the first case. This can be a special condition for the supports, and for that reason, a fixed hinge support between the deck and the pylons is selected for the bridges.
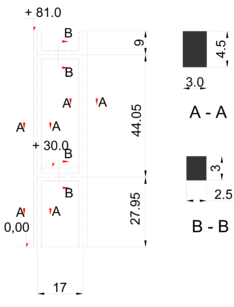
(a) A-type Pylon |
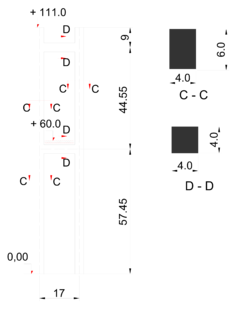
(b) B-type Pylon |
The main dimensions for the towers were selected according to the recommendations of Walter [1999] and Aparicio and Casas (2000). Special seismic considerations according to the recommendations of Priestley et al (1996) were applied too, considering an elastic seismic behaviour of the structures according to the general guidelines of Eurocode 8 Part 2 [CEN, 1998b] for this special kind of bridges. For the A-type pylon, the critical mechanical slenderness is λ = 124.7, which is a reasonable value for the arms. The dimensions of the cross-beams are enough, and are in relation with the whole geometry of the structure. For the B-type pylon, the critical mechanical slenderness is λ = 128, so the geometric dimensions of the arms are enough to guarantee an adequate geometric stability. Likewise, dimensions of the cross-beams are adequate. Nevertheless, the whole dimensions of the pylons (pre-design) were checked for service loads.
Regarding the decks, two 13 m - width concrete decks are proposed: slab-type and hollow-box type, as can be appreciated in Figs. 3.5 (a) and (b). The main geometric characteristics (height, area A, shear areas AV, torsion constant JT and inertias I) can be seen in Table 3.1. Y and Z are the horizontal and vertical axis respectively.

(a) Slab-Type Deck |
(b) Hollow-box Type Deck |
Fig. 3.5 Proposed Decks for the Analysis (dimensions in metres)
| Deck type | Height (m) | A (m2) | AVy (m2) | AVz (m2) | JT (m4) | Iy (m4) | Iz (m4) |
| Slab | 0.40 | 5.20 | 4.33 | 4.33 | 0.272 | 0.0693 | 73.23 |
| Hollow-box | 2.25 | 5.20 | 3.20 | 1.06 | 9.735 | 3.710 | 63.489 |
The cross-section areas for the slab-type and the hollow-box type are the same, which implies the same weight. This point is very important, because the main difference between both typologies is the inertia. The slab-type deck considers a very low inertia. The slenderness ratio in this case is h/L = 0.40/217 = 1/543 for the fan pattern, and h/L = 0.40/204.6 = 1/512 for the harp pattern, which implies a very slender deck. Of course, in this case bending moments are expected to be low. The hollow-box type deck shows a high inertia. The slenderness ratio is h/L =2.25/217=1/96 for the fan pattern, and h/L = 2.25/204.6 = 1/91 for the harp pattern, which implies a rigid deck. These differences involve the use of 6.2 m stay-spacing for the flexible deck (slab-type), and 12.4 m stay-spacing for the rigid deck (hollow-box type).
- 3.2.2 Basis of Design and Actions
Materials and their mechanical properties have been chosen according to the general specifications and regulations for bridge design, taking into account seismic considerations [Priestley et al, 1996; Walter, 1999; Ministerio de Fomento, 2000; Aparicio and Casas, 2000].
For the seismic design, high strength concrete is employed, with strengths between 22.5 Mpa and 45Mpa, avoiding higher strengths because of their less ductility. For decks and pylons on all the bridges, a prestressed concrete HP-40 (Table 3.2) is employed according to the Spanish regulation EHE [Ministerio de Fomento, 2000]. Regarding the steel for reinforced concrete, welding steel B-400-SD with special characteristics for ductility is employed according to Ministerio de Fomento (2000). Its mechanical properties are shown in Table 3.3.
|
Table 3.3 Properties of Steel for Reinforced Concrete
|
The stays have been considered applying parallel-strand cables (Fig. 3.6). The employed steel is Y 1860 S7 according to the EHE instruction [Ministerio de Fomento, 2000]. For the non-linear analysis, the mechanical properties of the stays were considered taking into account a multi-cable formulation, with the incorporation of tension - only elements. The main properties of the stays (Table 3.4) have been obtained from the reference of Walter (1999).
Regarding the design of the stays, consideration of strength and fatigue factors according to the recommendations of Aparicio and Casas (2000) were applied in order to satisfy strength requirements as well as fatigue design criteria.
For definition of the actions in this research, the criteria of the Dirección General de Carreteras de España [Ministerio de Fomento, 1998] and the specific regulations of Eurocode 8 - Part 2 [CEN, 1998b] regarding the seismic action on bridges, were considered. The main objective of this research is to study the seismic response of cable-stayed bridges, and that is the reason why some actions are not considered. In fact, some prestressing forces, rheological, thermic or brake loads are not considered. It means that these actions are less important with regard to dead loads, live loads and of course the seismic action.
In this investigation, the bridges were considered with a medium importance and normal design traffic. These considerations involve a seismic importance factor γI = 1.00 according to Eurocode 8 Part 2 [CEN, 1998b], and a live load factor ψ21 = 0, according to Eurocode 1 Part 3 [CEN, 1998c]. By this way, to study the seismic response of the bridges, the only considered actions are the permanent loads (qPL), the stay prestressing forces (qSPL) and the seismic action of course (qE). These considerations are reasonable because the permanent loads of a cable-stayed bridge may contribute 80 – 90% to total bridge loads [Ren and Obata, 1999].
For the above mentioned, to combine the loads on the bridge models, it is necessary to add each action: qPL + qSPL + qE.
- 3.2.3 Nonlinearities
Nonlinearities can be broadly divided into geometric and material nonlinearities. Material nonlinearities depend on the specific structure (materials used, loads acting, design assumptions). Although it is certain that the elastic-plastic effect tends to reduce the seismic response of long-span cable-stayed bridges [Ren and Obata, 1999], material nonlinearities depend highly on the characteristics of the input earthquake records. In general terms, cable-stayed bridges experience very long periods, and for that reason formation of plastic hinges at the supports can be difficult. In fact, EC8 – 2 [CEN, 1998b] recommends for a well-designed cable-stayed bridge a behaviour factor q = 1, that is to say, an elastic seismic behaviour. Moreover, because of the high axial forces on the pylons, ductility of them can be questionable, and due to the importance of such structures, it is preferable an elastic behaviour of the materials, without formation of plastic hinges at the pylons. That is the main reason why the inelastic behaviour is not considered in this research. In this sense, dimensions and some special considerations for the selected bridge typologies take into account an elastic seismic behaviour of the materials. However, material nonlinearities due to the presence of additional viscous dampers as well as the tension-only nonlinear effect of the cables are considered.
Moreover, geometric nonlinearities are present in any cable-stayed bridge, and they originate from [Nazmy and Abdel-Ghaffar, 1990; Morgenthal, 1999]:
- The non-linear cable sag effect due to the inclined cable stays which governs axial elongation and the axial tension;
- The non-linear axial force and bending moment interaction for the tower and longitudinal girder elements;
- The non-linear behaviour due to the geometry change caused by the large displacements on the whole structure.
Those nonlinearities are especially considered in this research, because in some sense they govern the behaviour of this kind of structures, as was explained before. Geometric nonlinearity can be considered on a step-by-step basis in nonlinear static and direct integration time history analysis, and incorporated in the stiffness matrix for linear analysis.
- 3.2.4 Modelling
- 3.2.4.1 Tower modelling
Fig. 3.7 Modelling of the Towers
|
The bridge towers are represented by three-dimensional portal frames, as shown in Fig. 3.7. The tower legs and struts were modelled using linear elastic beam elements based on gross cross-section properties. Inertia factors Ief/Ig equal to 0.70 for the legs and 0.50 for the struts, where Ief is the effective moment of inertia and Ig is the moment of inertia of the gross cross-section, were considered to take into account a modified stiffness of the frames, according to recommendations of Priestley et al (1996). Moreover, because of the finite cross-sectional dimensions of the members and the significant length of the overlaps of the connecting elements, rigid links for the strut – leg connection were considered. This approximation allows an adequate modelling of the encasement of the struts into the tower legs. |
The stiffening effect of the rigid links for the modelling of the leg-strut connection (also called End Offsets) is accounted by specification of rigid-end factors, which give the fraction of each end offset that is assumed to be rigid for bending and shear deformation. In the case of the portal frames used for the towers, a value of 0.5 for the rigid-end factor was used.
For the adequate consideration of the vibrational characteristics of the towers, the distribution of lumped masses shown in Fig. 3.7 was considered. The masses were obtained from the elements using the mass density of the materials and the volume of the elements. These uncoupled masses are equal for each of the three translational degrees-of-freedom. In the case of the code RAM Advanse, these masses need to be explicitly added in the selected joints. In SAP2000, these masses are automatically added at the end joints of the elements. However, it was necessary to place additional masses to take into account an adequate distribution of lumped masses in order to have a more accurate dynamic model. The lumped masses involves no mass coupling between degrees of freedom at a joint or between different joints
- 3.2.4.2 Deck Modelling
As was previously mentioned, the decks of the bridges are of two kinds: a slab-type deck for a stay spacing of 6.2 m and a hollow box-type deck for a stay spacing of 12.40 m. To simplify the computing process, the decks were modelled using a single spine passing through the centroid of the cross-sections, and applying linear beam elements. To simulate the exact stiffness and masses of the decks, an accurate definition of the geometry of the cross sections was developed with the computational code RAM Advanse and also exported to SAP2000. That was possible modifying the internal code in RAM Advanse, in order to generate the desired sections. A 3-D rendering of the deck models can be seen in Fig. 3.8.

(a) Slab-type deck |

(b) Hollow-box type deck |
Most of the nodes were arranged corresponding to the anchor locations of the cables. The cable anchorages and the deck spine were connected by massless rigid links placed horizontally at 90o to the spine (Fig. 3.9). These rigid links were idealized by linear springs, with all the degrees-of-freedom fixed.
Fig. 3.9 Deck Modelling |
Also, translational and rotational lumped masses were considered in the centroid of the cross-sections, with the same spacing of the anchorages (Fig. 3.9). Specifically, rotational lumped masses were added to take into account the torsional modes due to eccentricity of the cross-section of the hollow box type deck. Translational masses consider the action of the permanent load including the effect of the dead load. Moreover, because of the decks are made of prestressed concrete, an inertia factor equal to 1.0 was considered. |
As for the non-structural components, such as parapets and beacons, their contribution to the structural rigidity is expected to be quite insignificant and therefore is ignored in the modelling. Likewise, since the cross sections of the deck are rigid (especially the hollow-box type deck), the corresponding warping constants are very large. Consequently, no cross-sectional warping is anticipated.
- 3.2.4.3 Stay cable model
In a first stage, truss-elements for the cables were applied to compute the prestressing forces on the stays. The strategy of modelling stay cables using truss-elements has been widely used, in which the nonlinear behaviour of the cables is accounted by linearizing the cable stiffness using the concept of an equivalent modulus of elasticity [Ernst, 1965]. However, prediction of the tri-dimensional vibration of the cables is not possible, aspect that can be important for an accurate dynamic analysis, especially if the cable-deck interaction plays an important role. For that reason, this strategy was only considered for the evaluation of the cable forces, through the nonlinear static analysis applying the code RAM Advanse.
For all the subsequent analyses, cables were modelled using a multi-element cable formulation (tension-only elements), employing 5-node isoparametric cable elements [Ali and Abdel-Ghaffar, 1995; Förars et al, 2000], formulation that is considered in the structural codes applied.
For an inclined cable, the force-deformation relation is expected to be non-linear due to cable tension and cable sagging. The cable element uses an elastic catenary formulation to represent the behaviour of a slender cable under its own self-weight, temperature and strain loading. This highly nonlinear behaviour inherently includes tension-stiffening and large-deflection effects, that is to say, slack and taut behaviour. Although it is possible to model the cable as a series of straight elements to consider material nonlinearity or complicated loadings, the catenary formulation is better suited to most applications. In the case of the formulation here employed, it was necessary to determine the undeformed length of the cable, using a shape calculator. This point is very important, because the relationship between the undeformed length and the cord length (the distance between the two end joints) is extremely critical in determining the behaviour of the cable; although recently some researchers have proposed the use of cable models applying iterative numerical techniques using the finite difference method, in which the initial cable geometry is not required, being internally computed [Girija Vallabhan, 2008]. In simple terms, when the undeformed length is longer than the chord length, the cable is slack and has significant sag. When the undeformed length is shorter than the chord length, the cable is taut and carries significant tension with little sag (Fig. 3.10).
If the undeformed length of the cable is shorter than the chord length at the beginning of a nonlinear analysis, tension will immediately exist in the cable and iteration may be required to bring the structure into equilibrium before any load is applied, as always happens with cable-stayed bridges. With regard to the initial geometry of the cables, a lot of ways to calculate it are available, as for example: specifying the undeformed length, either absolute or relative to the chord length; specifying the maximum vertical sag, measured from the chord to the cable; specifying the tension at either end of the cable, etc. In the case of cable-stayed bridges, because of the high stay prestressing forces, it is advisable to specify the undeformed length as the initial geometry of the cables, as was applied in this work. Of course, the shape calculated here may not actually occur during any analysis case, because only the cable length is determined. The deformed shape of the cable and the tensions it carries will depend upon the loads applied and the behaviour of the structure during analysis.
With regard to the modelling of the cable forces applied in SAP2000, the prestress of the stays was considered applying negative axial deformation loads, which cause a decrease of the undeformed length of the cables, implying an internal tension. This axial deformation was calculated for each cable of the bridge models, according to the specified cable tensions, the elasticity modulus, the undeformed length and the area of the cables. In the case of the code RAM Advanse, the prestressing forces of the stays were directly applied. The self-weight load was automatically included with the previous data of mass density and cable geometry.
For the mass distribution along the cables, it was necessary a discretization of the cable elements in order to obtain lumped masses to provide accurate results from the dynamic analyses including the spatial vibration of the cables. Of course, the mass contributed by the cable element is lumped at the end joints, with no inertial effects considered within the element itself. For that reason, discretization in multi-cable elements was mandatory to capture full dynamics of the cable itself. To decide the number of segments necessary for this purpose, a preliminary modal analysis was conducted for the models AB4 and AR4. Those structures were selected because they consider the same deck type, deck level and stay spacing, being differentiated in the stay cable layout. The cables for each bridge were divided into 4 and 12 segments, and a modal analysis using eigenvectors was performed. Tables 3.5 and 3.6 show the first periods obtained for the cables considering both discretizations.
Table 3.5 Cable Periods for AB4 Bridge
|
Table 3.6 Cable Periods for AR4 Bridge
| ||||||||||||||||||||||||||||||||||||
Results of this analysis showed that differences for both bridges are very similar. In both cases, the lowest periods were obtained for a discretization with 12 segments of the cables. Likewise, differences up to 2.3% were obtained for the first periods of the cables and the same magnitude of the differences were obtained for higher order modes of the cables. This implies that a minimum of four segments is adequate to capture full cable behaviour, although more segments imply more accurate results. For that reason, 12 segments were employed in this research.
The influence of the stay cable vibration on the response of the bridge is either ignored or considered by approximate procedures. The transverse vibration of the stay cables, which can be significant in some cases, is usually neglected. The common practice of modelling the cables by a single truss element is inadequate for seismic response calculations because it essentially precludes the lateral cable vibration modes. In fact, cable vibration effects are found to be significant for seismic response calculations, particularly when the cable fundamental frequencies are overlapping with the first few frequencies of the bridge. In this case, the equivalent modulus method cannot in any way account for the cable vibration effects [Tuladhar et al, 1995]. Only if the mass distribution along the cable is modelled and associated with extra degrees of freedom, the vibrational response of the cables can be obtained. The investigations of Förars et al (2000) and Cheng and Lau (2002) are a good approach regarding the cable vibration effects on the seismic response of cable-stayed bridges.
Another aspect that is interesting is the convergence conditions using cable elements. Models with cable elements will usually converge better if a large number of iterations in the analyses are allowed. In the case of SAP2000, at least 25 iterations are recommended [Computers & Structures, 2007]. Convergence behaviour is generally improved by using fewer elements in the cable object, and by applying larger load increments. In this research, accurate results and convergence were reached with 60 iterations for the static nonlinear analyses. For the nonlinear direct integration time history analyses, up to 180 iterations were necessary depending on the bridge model and the input record, aspect enlarged in Chapter 4.
The stay cable design considers the employ of parallel strand cables. Nominal diameters were obtained with the described multi-cable formulation. This preliminary design work considered the bridges in their operational status, and the inclusion of the permanent loads and the prestressing forces of the stays. Design of the stays took into account the strength criteria and recommendations for the dimensioning on a fatigue basis [Walter, 1999; Aparicio and Casas, 2000]. A safety factor γ1 = 1.30 and a behaviour factor γ2 = 1.25 were considered, that is to say, an allowable stress σu = 0.45 fu, where fu is the ultimate tensile strength of the stays.
| Table 3.7 Nominal Diameters of the Stays | A last aspect in the stay cable design is the fact that cables on each bridge were designed uniformly, that is to say, for the worse stress condition. Table 3.7 shows the pre-design of the stays for each bridge model |
- 3.2.4.4 Connections and boundary conditions
If the deck is connected with very flexible bearings to the towers, the induced seismic forces will be kept to minimum values but the deck may have a large displacement response. On the other hand, a very stiff connection between the deck and the towers will result in lower deck displacement response but will attract much higher seismic forces during an earthquake [Iemura and Pradono, 2003]. The influence of different support conditions on the mode distribution has been investigated by Ali and Abdel-Ghaffar (1995) and Tuladhar and Dilger (1999). Movable supports lead to a more flexible structure, and of course, the decision upon the support conditions of the deck is usually governed by serviceability as well as earthquake considerations. A restrained deck will avoid excessive movements due to traffic and wind loading, however, in the case of an earthquake a restrained deck will generate high axial forces which are applied to the pier-pylon system. Elastic supports for the deck at the towers give very low deck displacements and deck bending moments compared to pinned or fixed connections. Roller supports also cause the bridge have very low first longitudinal direction mode frequency, indicating that the bridge is very flexible in that direction.
Fig. 3.11 Modelling of the Tower-deck Connection |
In the present investigation, connection between deck and towers is supported by the lower strut through vertical rigid links with pinned bearings at the end-joints, in the connection with the deck (Fig. 3.11). These rigid links were idealized using linear massless springs with all the directional degrees-of-freedom fixed. For the abutment-to-deck connection, sliding bearings were used, in order to permit free longitudinal displacements of the structure due to normal expansions, and free rotations about the transverse axes (Fig. 3.12). |
The towers were founded to bedrock and their bases were treated as being fixed in all degrees-of-freedom at the piers, as usually happens on cable-stayed bridges. This affirmation implies that soil-structure interaction is not considered here, as was previously explained. For situations involving large amplitude–large force response, such as during an earthquake, it may be appropriate to reconsider the realistic nature of these boundary conditions as well as the permissible degrees-of-freedom of the deck-tower bearings [Wilson and Gravelle, 1991].
For the incorporation of viscous dampers, it is important to replace the existing pinned bearings by roller supports plus these special devices at the deck-tower connection to reduce seismic forces, absorb large seismic energy, and reduce the response amplitudes considering pure viscous damping. Additionally, energy-absorbing devices may also be put between the deck-ends and the abutments. In order to show some of the complete 3-D finite element models of the bridges, Fig. 3.13 exposes a general structural view of the bridges AB1, AB4, AR1 and AR4.
(a) AB1 pattern
|
(b) AB4 pattern |
(c) AR1 pattern |
(d) AR4 Pattern |
- 3.3 Nonlinear Static Analysis under Service Loads
As a first step of the nonlinear seismic analysis, a nonlinear static analysis under gravity loads and stay prestressing forces was carried out. Nonlinearities in this stage include the stay cable sag effect, axial force-bending moment interaction, large displacements effect and the material nonlinearity due to the tension only formulation of the cable elements. Of course, the nonlinear static analysis was performed for each bridge model, considering the actualized data of the stay prestressing forces.
Mathematically, nonlinear static analysis does not always guarantee a unique solution. Inertial forces in dynamic analysis and in the real world limit the path a structure can follow. But this is not true for static analysis, particularly in unstable cases where strength is lost due to material or geometrical nonlinearity. In this sense, small changes in properties or loading can cause large changes in nonlinear response [Computers & Structures, 2007].
With regard to the nonlinear solution control, the specified combination of loads is applied incrementally, with as many steps as necessary to satisfy equilibrium. The nonlinear equations are solved iteratively in each step, requiring re-forming and re-solving the stiffness matrix, until the solution converges. The parameters to control the iterations include the maximum total steps, which are the maximum number of steps allowed in the analysis, including saved and intermediate sub-steps. This parameter permits to control over how long the analysis will run, considering that the length of time it takes to run a nonlinear static analysis is approximately proportional to the number of steps. For all the bridge models in this research, the maximum total steps per stage were 200. The maximum null steps occur when iteration does not converge and a smaller step size is required. An excessive number of null steps indicate that the solution is stalled due to catastrophic failure or numerical sensitivity. In this investigation, the maximum null steps were 50. The number of iterations allowed in a step before the use of smaller sub-steps (maximum iterations per step) depends on the nature of the employed elements in the analysis. In the case of frame elements, normally 10 iterations is enough, however in the case of cable structures, more iterations are necessary. In the static analysis presented here, the convergence was guaranteed selecting 60 maximum iterations per step. With regard to the iteration convergence tolerance (a comparison of the magnitude force error acting on the structure), accurate results were obtained using a value of 1x10-6. In this sense, it is necessary to explain that the smaller values of this parameter are necessary when large-displacement problems are solved, how occurs in this investigation.
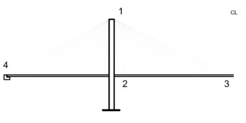
Fig. 3.14 Location of Measured Displacements |
Fig. 3.14 shows the location of the measured displacements on the bridges. ∆1-L corresponds to the longitudinal displacement of the tower-top, and ∆1-Tcorresponds to the transverse displacement of the same point. ∆3-V is the vertical displacement of the deck at the mid-span, and finally, ∆4-Lcorresponds to the longitudinal displacement of the deck-ends. |
Mmax-tower corresponds to the maximum bending moments of the towers; Mmax-deck2is the maximum in-plane bending moment of the deck at the tower-deck connection; Mmax-deck3 is the maximum in-plane bending moment of the deck at the mid-span; Nmax-tower corresponds to the maximum compressive force of the tower legs; Nmax-deck corresponds to the maximum compressive force of the deck and Nmax-cable is the maximum axial force of the cables.
Table 3.8 summarizes the maximum main displacements and Table 3.9 summarizes the maximum main forces for each bridge.
| BRIDGE | ∆1-La | ∆1-T | ∆3-Vb | ∆4-La |
| AB1 | 0.38 | 0..40 | -1.55 | 1.83 |
| AB2 | 0.30 | 0.16 | -1.51 | 1.88 |
| AB3 | 0.05 | 0.35 | -1.41 | 1.57 |
| AB4 | 0.03 | 0.14 | -1.55 | 1.59 |
| AR1 | 0.00 | 0.02 | -0.45 | 2.11 |
| AR2 | 0.52 | 0.03 | -1.59 | 2.13 |
| AR3 | 0.13 | 0.01 | -0.11 | 1.92 |
| AR4 | 0.02 | 0.04 | -0.28 | 1.97 |
a Positive value implies a displacement toward the mid-span
b Negative value implies a descending
| BRIDGE | Mmax-towera, c [MN.m] | Mmax-towerd, e [MN.m] | Mmax-deck3c [MN.m] | Mmax-deck2c [MN.m] | Nmax-towera [kN] | Nmax-deckb[kN] | Nmax-cable [kN] |
| AB1 | 18.0 | 8.15 | 0.48 | 1.58 | -57200 | -25200 | 4800 |
| AB2 | 21.2 | 10.81 | 0.48 | 1.38 | -101200 | -25500 | 4950 |
| AB3 | 15.7 | 7.50 | 7.59 | 13.3 | -52900 | -22100 | 5630 |
| AB4 | 18.3 | 9.09 | 7.60 | 12.9 | -97000 | -22400 | 5770 |
| AR1 | 11.0 | 6.55 | 0.77 | 3.94 | -52900 | -36400 | 1560 |
| AR2 | 23.0 | 9.72 | 0.71 | 3.81 | -97000 | -36900 | 1790 |
| AR3 | 19.5 | 6.36 | 6.24 | 22.9 | -51300 | -32000 | 2700 |
| AR4 | 23.5 | 8.67 | 6.06 | 22.2 | -95300 | -32500 | 2820 |
a At the tower base c In the bridge plane e Out-of-plane
b At the tower-deck level d At the upper strut level - Implies compression
Values of displacements and forces shown in Tables 3.8 and 3.9 are in accordance with the structures. Although a static parametric analysis is not the aim of this investigation, it can be interesting to observe that maximum displacements at the deck-ends are associated with the harp pattern. Because of the loads and geometric symmetry of the structures, transverse deflections at the tower-deck level as well as the longitudinal and transverse deflections of the decks at the mid-span are zero.
Regarding the internal forces, it can be observed in general terms that maximum bending moments of the towers occur for the tallest structures (for both in-plane and out-of-plane directions). Likewise, because of the longer dimensions of the towers, maximum compressive forces of the tower legs occur for the bridges AB2, AB4, AR2 and AR4. Of course, maximum in-plane bending moments and axial forces of the towers occur at their base. With regard to the internal forces of the decks, it can be appreciated that maximum in-plane bending moments are associated with the longest stay spacing, aspect that is obvious because the stays work as elastic supports. In the same way, maximum bending moments take place for the harp pattern with the longest stay spacing at the tower-deck connection, and maximum axial forces of the decks occur for the harp pattern with the shortest stay spacing at the tower-deck connection. In general terms, an increase of the stay spacing increases the bending moments of the deck, but decreases the compressive forces. The maximum compressive forces and bending moments of the decks take place in the vicinity of the tower-deck connection, because of the presence of the fixed hinges. This issue can be very important in a seismic analysis, and it can be a sign for the location of additional energy dissipation devices in order to mitigate excessive axial forces. With regard to the cable forces, maximum values occur for the longest back stays. It is interesting to observe that the highest cable forces are associated with the fan pattern, and it is clear that longer stay spacing involves higher cable forces. In other words, the worse cable condition occurs for the back stays in the presence of fan pattern with the longest stay spacing. A detailed static parametric analysis can be found in the reference of Walter (1999).
As example, Figs. 3.15 and 3.16 show some results of the static analysis under service loads for the bridges AB1 and AR4. These bridges were chosen because they can be considered as extreme cases. Because of the loads and geometric symmetry of the structures, only one-half is shown.

(a) In-plane bending moments of the deck |

(b) Axial forces of the deck |

(c) In-plane bending moments of the pylon |

(d) Axial forces of the pylon |

(a) In-plane bending moments of the deck |

(b) Axial forces of the deck |

(c) In-plane bending moments of the pylon |
(d) Axial forces of the pylon |
Nonlinearities associated to large-displacements and axial force-bending moment interaction involved in the static analysis, are less important than those nonlinearities in the dynamic analysis. Because of the rapid change of the forces during an earthquake, those geometric nonlinearities can be very important in this situation. In this sense, Table 3.10 shows a brief comparison of the static response for AB4 bridge, considering only cable-sag effect, cable sag plus P-Δ effects and cable sag plus P-Δ plus large-displacement effects. Displacements are shown in [cm], forces in [kN] and moments in [MN.m].
| Measured response | Nonlinearities considered | ||
| Cable sag | Cable sag + P-Δ | Cable sag + P-Δ+large displ. | |
| Δ4-L | 1.57 | 1.57 | 1.59 |
| Mmax-deck2 | 9.00 | 9.07 | 12.9 |
| Nmax-tower | 94300 | 94300 | 97000 |
| Nmax-dexk | 22100 | 22200 | 22400 |
| Nmax-cable | 5720 | 5730 | 5770 |
From Table 3.10, it is clear that in this case P-Δ and large-displacement effects are not very significant on the longitudinal deck displacements. More important differences can be found for the bending moments of the deck, with differences up to 30% comparing the case of only cable sag effect and the case including all the geometric nonlinearities. Differences for the axial force of the towers, axial force of the deck and axial force of the cables are less sensitive, which implies that P-Δ and large-displacement effects are not very important in such cases. However, it can be supposed that those differences could be more important on longer bridges, and of course, in the nonlinear dynamic analyses. For that reason it is important to consider all those nonlinearities in the static case as starting point for the nonlinear seismic analyses [Abdel-Ghaffar, 1991; Morgenthal, 1999].
- 3.4 Modal Analysis
- 3.4.1 Natural Frequencies and Modal Shapes
The dynamic response of a structure can be well characterized by a modal analysis. Because of the complex nature of these structures and their seismic response, a two-dimensional analysis is not adequate to capture the three-dimensionality of the system, and for that reason, a 3D analysis is always recommended for the nonlinear static/dynamic analysis of cable-stayed bridges, and of course, for a modal analysis.
As first approach of the seismic response of these structures, a characterization of natural frequencies, modal shapes, modal participation factors as well as damping mechanism is highly recommended, as was explained in the state-of-the-art review. In order to obtain the modified stiffness matrix considering all nonlinearities available, a nonlinear static analysis was performed first using the proposed finite element modelling. The dynamic free vibration analysis is then performed based on the deformed configuration, and considering as previous stage the nonlinear static analysis. As a consequence, the modal analysis can be used as the basis for modal superposition in the response-spectrum analysis.
A lot of strategies to find the natural frequencies have been proposed. The Eigenvector analysis determines the undamped free-vibration mode shapes and frequencies of the system, solving the generalized eigenvalue problem ![]() , where M is the diagonal mass matrix, K is the stiffness matrix, ω2 is the diagonal matrix of eigenvalues, and Φ is the matrix of the corresponding eigenvectors (modal shapes). This problem can be solved using the classical tools of linear algebra, or applying approximate strategies to speed-up the solution, as for example the Stodola-Vianella method.
, where M is the diagonal mass matrix, K is the stiffness matrix, ω2 is the diagonal matrix of eigenvalues, and Φ is the matrix of the corresponding eigenvectors (modal shapes). This problem can be solved using the classical tools of linear algebra, or applying approximate strategies to speed-up the solution, as for example the Stodola-Vianella method.
The Ritz-vector analysis is another strategy to solve this problem, in which the analysis seeks to find modes that are excited by a particular loading. In this sense, it has been demonstrated [Wilson et al, 1982] that dynamic analyses based on a special set of load-dependent Ritz vectors yield more accurate results than the use of the same number of natural mode shapes. The reason why the Ritz vectors yield good results is that they are generated by taking into account the spatial distribution of the dynamic loading, whereas the direct use of the natural mode shapes neglects this very important information. In addition, the Ritz-vector algorithm automatically includes the advantages of the proven numerical techniques of static condensation, Guyan reduction and static correction due to higher-mode truncation. The spatial distribution of the dynamic load vector serves as a starting load vector to initiate the procedure. The first Ritz vector is the static displacement vector corresponding to the starting load vector. The remaining vectors are generated from a recurrence relationship in which the mass matrix is multiplied by the previously obtained Ritz vector and used as the load vector for the next static solution.
In this research, it was found that differences regarding the application of eigenvectors or Ritz-vector analysis were absolutely negligible, with differences of about 0.5%. In spite of the low differences, the modal analysis was performed applying the Ritz-vector Analysis, according to the algorithm detailed in Wilson (1985). The total number of modes was selected to reach at least 90% of the effective translational mass, in which more than 300 modes were necessary, although a total of 30 natural periods for each bridge were obtained that range between 0.237 and 2.938 sec. Depending on the relative amplitudes of the modal shapes, these modes were classified into the following groups: vertical modes (V), transverse modes (Tr), longitudinal modes (L) and torsional modes (Tor) for the deck and towers. All the dynamic properties were obtained applying the structural code RAM Advanse [RAM International, 2003]. For all the analyses, the predominant period of a structure corresponds to the natural period associated with the highest translational mass, sometimes different from the fundamental period, usually associated with the first natural frequency.
Table 3.11 Natural Periods for the Longest Cables
|
Table 3.11 shows predominant periods for the longest cables of the bridges that depend on the tension forces (T), the angle of the cable sag with regard to the horizontal plane (α0), the unitary mass of the cables (m) and the horizontal projection of the cables (L). |
Longest periods for the cables can be observed in the bridges AB1 and AB2 (2.51 sec) as well as the shortest periods correspond to the bridges AR3 and AR4 (1.12 sec). The main differences on the determination of the predominant periods of the cables come from the mass m and the prestressing forces T.
Tables 3.12 and 3.13 show natural periods and nature of the modal shapes for the first 15 modes considering the fan and harp pattern respectively. Table 3.14 shows modal shapes of the bridges for the first three modes, as well as Tables 3.15 and 3.16 show modal participation factors for the fan and harp pattern respectively. The longest fundamental periods correspond to the bridges AR2, AR4, AB4 and AB2 with values of 2.938, 2.845, 2.804 and 2.694 sec respectively. Those results are obvious because they are the tallest bridges, that is to say, the more flexible structures. For those cases, longitudinal/vertical motion of the deck governs; with the highest periods for the harp pattern; and modal participation factors for the fundamental periods over 70%. For the smallest bridges, fundamental periods of 2.020, 1.992, 1.806 and 1.801 sec, associated to bridges AR3, AR1, AB1 and AB3 were obtained respectively. In this case, modal shapes are governed by longitudinal/vertical oscillations of the deck, for the harp pattern; as long as transverse oscillations govern the modal shapes of the fan pattern bridges. Regarding the modal participation factors associated with the fundamental periods for the smallest bridges, values over 55% were observed. Comparing fundamental periods for tall and small bridges, it is easy to see that the highest periods were obtained with the harp pattern bridges. In other words, for these support conditions, harp pattern structures are more flexible than the fan pattern bridges. Analyzing the incidence of the stay spacing, fundamental period of AB1 bridge is slightly longer than period of AB3 bridge; and fundamental period of AB4 bridge is longer than period of AB2 bridge. For the harp pattern, fundamental period of AR3 bridge is longer than period of AR1 bridge; as long as fundamental period of AR2 bridge is longer than period of AR4 bridge. As a result, an increase of the longitudinal stiffness if the stay spacing decreases is not evident and significant.
If the regression analysis provided by Kawashima et al (1993), is applied here, an average predominant period of 1.76 sec is obtained. This value, associated with vertical bending vibrations, is relatively close to the average fundamental period computed with the modal analysis for the smallest bridges (T = 1.90 sec), which implies 7.4% difference.
From Tables 3.12 and 3.13 it is evident that the close spacing of the natural periods is a vibrational characteristic of these bridges, in accordance with the observations of Abdel-Ghaffar (1991). In this sense, some modal participation factors (Tables 3.15 and 3.16) are very close, indicating strong modal coupling, a very important characteristic of the dynamic behaviour of cable-stayed bridges.
It is interesting to observe that the first ten modes for all bridges are associated with periods that range between 0.4 and 2.94 sec, that is to say, those structures can be more affected by velocity than acceleration or displacements according to Eurocode 8 [CEN, 1998a]. In fact, this code explains that velocity-sensitive region corresponds to periods in the range between 0.4<T<3 sec. On the other hand, for structures equipped with additional damping devices, the reduction in responses is essentially unaffected by damper nonlinearity in the velocity-sensitive region. For that reason, cable-stayed bridge models of this work can be more affected by velocity, with no incidence of the damper nonlinearity on the seismic response. These aspects are necessary to be taken into account in the analysis of the bridges.
| Mode | AB1 | AB2 | AB3 | AB4 | ||||
| Period (sec) | Nature of modal shape | Period (sec) | Nature of modal shape | Period (sec) | Nature of modal shape | Period (sec) | Nature of modal shape | |
| 1 | 1.806 | Deck Tr | 2.694 | Deck L | 1.801 | Deck Tr | 2.804 | Deck L |
| 2 | 1.663 | Deck Lon | 2.539 | Deck Tr | 1.798 | Deck V | 2.662 | Deck Tr |
| 3 | 1.585 | Deck V | 2.064 | Tower Tr | 1.689 | Deck L | 2.156 | Tower Tr |
| 4 | 1.532 | Tower Tr | 1.567 | Deck V | 1.528 | Tower Tr | 1.737 | Deck V |
| 5 | 1.340 | Deck + Tower Tr | 1.320 | Deck Tr | 1.341 | Deck Tr+Tower Tr | 1.348 | Deck Tr |
| 6 | 1.027 | Deck V | 1.065 | Deck V | 0.983 | Deck V | 1.021 | Deck V |
| 7 | 0.768 | Deck Tor+Tower L | 0.858 | Deck Tor+Tower L | 0.850 | Deck Tor+Tower L | 0.932 | Deck Tor+Tower L |
| 8 | 0.766 | Deck Tor+Tower L | 0.845 | Deck Tor+Tower L | 0.773 | Deck Tor+Tower L | 0.879 | Deck Tor+Tower L |
| 9 | 0.655 | Tower L+deck Tr | 0.701 | Tower Tr | 0.679 | Deck V | 0.720 | Tower Tr |
| 10 | 0.549 | Tower Tr+Deck Tr | 0.660 | Tower Tr | 0.663 | Tower Tr | 0.705 | Deck V |
| 11 | 0.490 | Deck V + Tower L | 0.526 | Deck V | 0.582 | Deck V | 0.671 | Tower Tr |
| 12 | 0.479 | Deck V | 0.509 | Deck Tr | 0.550 | Tower Tr | 0.584 | Deck Tr+Tower L |
| 13 | 0.449 | Tower Tr+Deck Tr | 0.479 | Deck V | 0.532 | Deck V | 0.525 | Deck V |
| 14 | 0.439 | Deck V | 0.440 | Deck V | 0.460 | Tower Tr+Deck Tr | 0.567 | Deck V |
| 15 | 0.406 | Deck V | 0.402 | Deck V | 0.488 | Deck V | 0.495 | Deck V |
| Mode | AR1 | AR2 | AR3 | AR4 | ||||
| Period (sec) | Nature of mode shape | Period (sec) | Nature of mode shape | Period (sec) | Nature of mode shape | Period (sec) | Nature of mode shape | |
| 1 | 1.992 | Deck L | 2.938 | Deck L | 2.020 | Deck V | 2.845 | Deck L |
| 2 | 1.900 | Deck V | 2.568 | Deck Tr | 1.795 | Deck L | 2.535 | Deck Tr |
| 3 | 1.733 | Deck Tr | 2.130 | Tower Tr | 1.772 | Deck Tr | 2.080 | Tower Tr |
| 4 | 1.532 | Tower Tr | 1.772 | Deck V | 1.528 | Tower Tr | 1.886 | Deck V |
| 5 | 1.287 | Deck Tr | 1.269 | Deck Tr+Deck Tor | 1.323 | Deck Tr | 1.312 | Deck Tr |
| 6 | 1.049 | Deck V | 1.164 | Deck V | 1.058 | Deck V | 1.110 | Deck V |
| 7 | 0.877 | Deck Tor+Tower L | 0.950 | Deck Tor+Tower L | 0.955 | Deck V | 0.932 | Deck V |
| 8 | 0.867 | Deck Tor+Tower L | 0.928 | Deck Tor+Tower L | 0.864 | Deck Tor+Tower L | 0.918 | Deck Tor+Tower L |
| 9 | 0.747 | Deck V | 0.700 | Tower Tr | 0.832 | Deck V | 0.854 | Deck Tor+Tower L |
| 10 | 0.681 | Deck V | 0.662 | Tower Tr | 0.750 | Deck Tor+Tower L | 0.832 | Deck V |
| 11 | 0.636 | Tower Tr | 0.658 | Deck V | 0.681 | Deck V | 0.690 | Tower Tr |
| 12 | 0.635 | Deck V | 0.626 | Deck V | 0.639 | Tower Tr | 0.680 | Deck V |
| 13 | 0.622 | Tower Tr | 0.625 | Deck V | 0.556 | Tower Tr | 0.656 | Tower Tr |
| 14 | 0.564 | Deck V | 0.580 | Deck V | 0.510 | Tower Tr | 0.611 | Deck V |
| 15 | 0.551 | Deck V | 0.493 | Deck Tr | 0.508 | Deck V | 0.504 | Deck V |
From Tables 3.12, 3.13 and 3.14 it is clear, for all bridges, that first modes are associated with the deck. They are followed by tower or cable modes, depending on the bridge configuration. In this sense, some cable modes are overlapped with the deck modes, especially on bridges AB1, AB2 and AR1, aspect that can imply some incidence of the cable vibrations on the seismic response of the bridges, according to Tuladhar et al (1995).
From Tables 3.15 and 3.16, it is clear that some important higher order modes are present, especially on bridges AB1, AB3, AR1 and AR3, that is to say, the smallest structures. Because of the relatively low vertical modal participation factors, importance of the vertical motion on the seismic response seems to be not very significant, although some important vertical effects can occur in the presence of near-source earthquakes.
Another interesting observation can be proposed with regard to the modal shapes related to the deck torsion. The deck torsion is coupled with the longitudinal motion of the tower legs, with no evidence of pure torsion for the first 15 modes and independently on the deck type, stay spacing, stay cable layout and deck level. This implies that torsion generated by the eccentricity of the cross-section of the hollow-box type deck can be ignored.
| Mode 1 | Mode 2 | Mode 3 | |
| AB1 | T = 1.806 sec |
T = 1.663 sec |
T = 1.585sec |
| AB2 | 
T = 2.694 sec |
T = 2.539 sec |
T = 2.064 sec |
| AB3 | T = 1.801 sec |
T = 1.798 sec |

T = 1.689 sec |
| AB4 | 
T = 2.804 sec |
T = 2.662 sec |
T = 2.156 sec |
| AR1 | T = 1.992 sec |
T = 1.900 sec |
T = 1.733 sec |
| AR2 | T = 2.938 sec |
T = 2.568 sec |
T = 2.130 sec |
| AR3 | T = 2.020 sec |
T = 1.795 sec |
T = 1.772 sec |
| AR4 | T = 2.845 sec |
T = 2.535 sec |
T = 2.080 sec |
| MODE | AB1 | AB2 | AB3 | AB4 | ||||||||
| long | vert | transv | long | vert | transv | long | vert | transv | long | vert | transv | |
| 1 | 0.00 | 0.00 | 61.21 | 76.08 | 0.00 | 0.00 | 0.00 | 0.12 | 59.54 | 75.88 | 0.00 | 0.00 |
| 2 | 63.56 | 0.00 | 0.00 | 0.00 | 0.00 | 73.94 | 0.00 | 3.59 | 1.98 | 0.00 | 0.00 | 73.04 |
| 3 | 0.00 | 1.40 | 0.00 | 0.00 | 0.00 | 0.00 | 66.35 | 0.00 | 0.00 | 0.00 | 0.00 | 1.88 |
| 4 | 0.00 | 0.00 | 0.00 | 0.00 | 0.67 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 1.70 | 0.00 |
| 5 | 0.00 | 0.00 | 7.17 | 0.00 | 0.00 | 6.98 | 23.42 | 0.00 | 0.00 | 0.00 | 0.00 | 5.77 |
| 6 | 27.32 | 0.00 | 0.00 | 9.25 | 0.00 | 0.00 | 0.00 | 0.00 | 7.79 | 8.54 | 0.00 | 0.00 |
| 7 | 0.00 | 0.00 | 0.5 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.50 | 0.00 | 0.00 | 0.15 |
| 8 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.18 | 0.00 | 10.38 | 0.00 | 0.00 | 0.00 | 0.04 |
| 9 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.43 |
| 10 | 0.00 | 0.00 | 20.82 | 0.00 | 0.00 | 6.02 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 6.54 |
| 11 | 0.00 | 2.51 | 0.00 | 0.00 | 0.00 | 0.00 | 0.2 | 0.00 | 0.00 | 0.00 | 5.01 | 0.00 |
| 12 | 0.00 | 2.42 | 0.00 | 0.00 | 0.73 | 0.00 | 0.00 | 0.00 | 21.48 | 0.01 | 2.53 | 0.00 |
| 13 | 0.00 | 0.00 | 0.00 | 0.00 | 1.66 | 0.00 | 0.00 | 7.14 | 0.00 | 0.00 | 0.00 | 0.00 |
| 14 | 0.08 | 0.00 | 0.00 | 0.17 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.21 | 0.00 | 0.00 |
| 15 | 0.00 | 9.86 | 0.00 | 0.00 | 5.74 | 0.00 | 0.00 | 8.09 | 0.00 | 0.00 | 6.69 | 0.00 |
| MODE | AR1 | AR2 | AR3 | AR4 | ||||||||
| long | vert | transv | long | vert | transv | long | vert | transv | long | vert | transv | |
| 1 | 58.10 | 0.00 | 0.00 | 70.06 | 0.00 | 0.00 | 0.00 | 3.13 | 0.00 | 74.7 | 0.00 | 0.00 |
| 2 | 0.00 | 0.24 | 0.00 | 0.00 | 0.00 | 75.85 | 54.66 | 0.00 | 0.00 | 0.00 | 0.00 | 75.12 |
| 3 | 0.00 | 0.00 | 44.05 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 62.92 | 0.00 | 0.00 | 0.00 |
| 4 | 33.41 | 0.00 | 0.00 | 0.00 | 0.19 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 1.73 | 0.00 |
| 5 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 4.85 | 0.00 | 0.00 | 5.55 | 0.00 | 0.00 | 5.89 |
| 6 | 0.00 | 0.00 | 22.37 | 15.32 | 0.00 | 0.00 | 35.62 | 0.00 | 0.00 | 9.10 | 0.00 | 0.00 |
| 7 | 0.00 | 0.00 | 0.12 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.50 | 0.00 | 0.00 | 0.14 |
| 8 | 0.00 | 0.82 | 0.00 | 0.00 | 0.00 | 0.08 | 0.00 | 18.78 | 0.00 | 0.00 | 10.83 | 0.00 |
| 9 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.02 | 0.00 | 0.00 | 0.01 | 0.00 | 0.00 |
| 10 | 1.44 | 0.00 | 0.00 | 0.00 | 0.00 | 6.18 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 11 | 0.00 | 0.00 | 0.00 | 0.00 | 6.38 | 0.00 | 0.00 | 8.83 | 0.00 | 0.00 | 3.24 | 0.00 |
| 12 | 0.00 | 15.92 | 0.00 | 0.00 | 3.38 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.97 | 0.00 |
| 13 | 0.00 | 4.36 | 0.00 | 0.01 | 0.18 | 0.00 | 0.00 | 0.00 | 21.66 | 0.00 | 0.00 | 6.06 |
| 14 | 0.01 | 0.00 | 0.00 | 0.17 | 0.00 | 0.00 | 0.00 | 0.23 | 0.00 | 0.00 | 0.00 | 0.00 |
| 15 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.05 | 0.00 | 0.00 | 0.72 | 0.00 | 0.00 |
- 3.4.2 Damping
Damping on cable-stayed bridges is low, of about 2%, according to Morgenthal (1999). Kawashima and Unjoh (1991) found that critical damping ratio was dependent with the excitation amplitude and modal shape, aspect that makes the damping estimation very complex. Of course, this approach is not by the side of this research, and constant values for the damping ratio are suggested for each bridge, depending on the modal shape. In this sense, the approximation by Kawashima and Unjoh (1991), in which the critical damping ratio for the main modes is correlated with the natural frequencies of the bridges, can be applied here. Table 3.17 shows results of this formulation. Here, ξBV, ξBH and ξT are the critical damping ratios for vertical bending oscillations, transverse bending oscillations and torsional oscillations, respectively.
As can be seen, critical damping ratios are similar for all bridges and strongly dependent on the considered mode. Lowest values of the critical damping ratio correspond to torsional oscillations (≈ 0.50%). They are followed by vertical bending oscillations (≈ 0.80%). The highest values of the critical damping ratio correspond to transverse bending oscillations, with an average value of 1.70%. Anyway, all the damping values are very low, and very different from the classical 5% of the critical damping adopted in the design codes. Likewise, it can be observed that damping associated with vertical bending, transverse bending and torsional oscillations depend on the deck level, that is to say, the bridge flexibility. In this sense, the lowest damping ratios are experienced with the tallest structures.
| Modal shape | Bridge | |||||||
| AB1 | AB2 | AB3 | AB4 | AR1 | AR2 | AR3 | AR4 | |
| Vertical bending | 0.89 | 0.75 | 0.86 | 0.74 | 0.83 | 0.73 | 0.83 | 0.74 |
| Transverse bending | 1.73 | 1.67 | 1.73 | 1.67 | 1.74 | 1.70 | 1.73 | 1.67 |
| Torsional | 0.58 | 0.50 | 0.51 | 0.45 | 0.49 | 0.42 | 0.50 | 0.46 |
Finally, it is important to say that results of the damping analysis are in accordance with real measures on bridges, as can be seen in the works of Garevski and Savern (1992, 1993); Yamaguchi and Manabu (1997) and Atkins and Wilson (2000).
- 3.5 Seismic Response Analysis Applying the Response Spectrum Method
The response spectrum method for the seismic analysis of structures is a useful and powerful tool, well implemented in the current seismic regulations. This methodology computes the maximum seismic response of a structure using modal superposition, on the basis of a modal analysis previously performed, and applying an elastic design response spectrum as seismic input. Although this strategy is questionable in the case of structures with nonlinear seismic behaviour, it can be applicable as first approach for the seismic analysis, in order to compare the maximum seismic responses with those obtained from the nonlinear time history analysis considering similar conditions of soil and effective ground acceleration.
Design response spectra considered in this research were obtained from Eurocode 8 [CEN, 1998a, 1998b]. This code was selected because it considers specific recommendations and the definition of the response spectra for bridges. The structural parameters involved with the definition of the response spectra consider a medium importance for the bridges and an elastic seismic behaviour (behaviour factor q equal to 1.0). The structures are founded on bedrock, and the considered maximum effective ground acceleration is 0.5g for the horizontal component, and 0.35g for the vertical component, where g is the gravity acceleration. These values are representative for structures located in high seismicity areas founded on bedrock, as usually happens in the subduction zone of the Mexican coast (Pacific ocean) [CFE, 1993]; several areas of the California coast [AASHTO, 1994, section 3.10]; and some areas of Japan [Japan Road Association, 1996, section 6.3]. The vertical component was assessed as a function of the horizontal one, according to Eurocode 8. Critical damping ratio of 1.7% was selected according to the modal analysis of the bridges previously exposed. The damping correction factor η, for values different from the classical 5%-critical damping ratio, was applied in this case. Table 3.18 summarizes the definition of the considered parameters. Thus, the design acceleration response spectra, for both horizontal and vertical components, were obtained according to Fig. 3.17. Likewise, Fig. 3.18 shows the design velocity response spectra, which is of interest in the formulation of the artificial accelerograms.
| DESCRIPTION | PARAMETER | VALUE | |
| Structural importance | Medium | γ | 1.00 |
| Structural behaviour | Elastic | q | 1.00 |
| Soil | A (Rock) | S | 1.00 |
| Tb | 0.10 | ||
| Tc | 0.40 | ||
| Td | 3.00 | ||
| β0 | 2.50 | ||
| k1 | 1.00 | ||
| k2 | 2.00 | ||
| Maximum effective ground acceleration | horizontal | ag | 0.5g |
| Critical damping ratio | ξ | 1.70% | |
| Damping correction | η | 1.38 |
Fig. 3.17 Design Acceleration Response Spectra |
Fig. 3.18 Design Velocity Response Spectra |
With regard to the modal superposition, CQC modal combination rule was applied because of the strong modal coupling that cable-stayed bridges experience. The bridge models were analyzed for each load condition, in which the seismic components were combined applying the 30% rule according to Eurocode 8. All the analyses were performed applying the structural code RAM Advanse [RAM International, 2003].
The analysis results show some differences regarding the longitudinal displacements of the shortest towers (bridges AB1, AB3, AR1 and AR3), aspect that is not obvious for the case of the tallest bridges. In fact, for the shortest towers, maximum displacements can be obtained for the bridges AR1 and AB3. In the same way, longitudinal displacements of the tower of AB1 bridge are larger than longitudinal displacements of the tower of AR3 bridge; however, not very interesting conclusions can be formulated according to the above mentioned, as can be seen in Figs. 3.19 and 3.20. In the case of the 111 m height-towers, differences regarding the longitudinal displacements of the towers are negligible (Fig. 3.19). Of course, maximum longitudinal displacements of the towers are obtained for the tallest bridges, with maximum values at the tower-top of about 40 cm for the tallest towers, and 30 cm for the shortest ones. Likewise, it can be appreciated that maximum longitudinal displacements at the tower-top for AB3 bridge are larger than maximum longitudinal displacements at the tower-top of AB1 bridge. In the case of AB4 bridge, maximum top displacements are larger than displacements of AB2 bridge. A similar situation can be observed with the maximum longitudinal displacements at the tower-top of the bridges AR3, AR1, AR4 and AR2; concluding that bridges with longer stay spacing experience an increase of the longitudinal displacements of the tower-top. Following with the longitudinal displacements of the towers, a brief comparison between the analysis under service loads and the seismic displacements can be observed in Figs. 3.21 and 3.22 (plots of longitudinal displacements using logarithmic scale), in this case, for the extreme cases AB1 and AR4. In both situations is clear the tremendous difference between the static and seismic longitudinal displacements of the towers, with seismic displacements more than 78 times the static displacements (AB1 bridge) and 50 times for the AR4 bridge. Of course, similar conditions can be found with the rest of the cases. It is interesting to note that maximum longitudinal seismic displacements occur at the tower-top, aspect that is not always certain for the static condition under service loads.
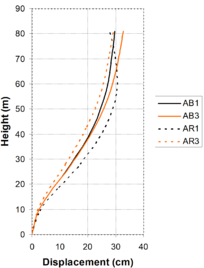
Fig. 3.19 Maximum Seismic Longitudinal Displacements for 81 m - height Towers |
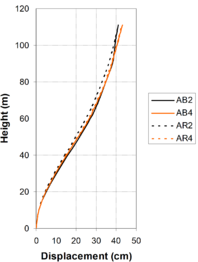
Fig. 3.20 Maximum Seismic Longitudinal Displacements for 111 m - height Towers |
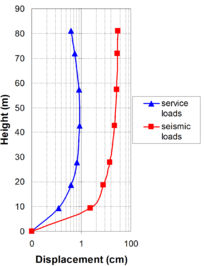
Fig. 3.21 Maximum Tower Longitudinal Displacements for AB1 Bridge |
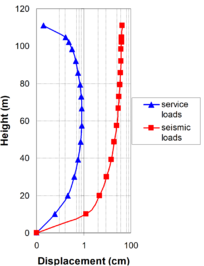
Fig. 3.22 Maximum Tower Longitudinal Displacements for AR4 Bridge |
With regard to the maximum vertical seismic displacements of the decks, more interesting observations can be formulated. Because of the differences with the flexural stiffness of the decks, the analysis was carried out considering the slab-type deck (bridges AB1, AB2, AR1 and AR2) and the hollow-box type deck (bridges AB3, AB4, AR3 and AR4) separately. In the first case, maximum vertical displacements are concentrated in the extreme spans (in the first third-length) and the vicinity of the main-span centre (see Fig. 3.23), distribution that can be very different from the static condition (Fig. 3.25). Maximum values of the vertical displacements vary from 33 to 40 cm, depending on the bridge model. It is clear that maximum vertical displacements are obtained for the AR1 model, followed by the bridges AR2, AB1 and AB2 respectively. Fig. 3.25 exposes a comparison between the seismic and service loading condition (in this case, the extreme condition AB1), with differences in the seismic condition up to 35 times the service condition, as can be appreciated.
In the case of the hollow box-type deck (stay spacing of 12.4 m), the displacement distribution is very different from the slab-type deck, with maximum values concentrated in the half-length of the extreme spans, and the third-length of the main span, as can be seen in Fig. 3.24. Maximum displacements vary from 23 to 33 cm, depending on the bridge model. Likewise, maximum values of deck displacements are obtained for AR3 bridge followed by the bridges AR4, AB3 and AB4 respectively (see Fig. 3.24). Fig. 3.26 exposes a comparison between the seismic and static deck displacements under service loads, for the extreme condition AR4, showing differences for the seismic condition more than 20 times the service displacements.
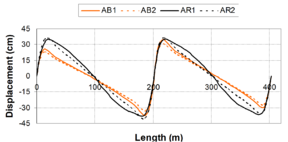
Fig. 3.23 Maximum Vertical Seismic Displacements – Slab-type Deck |
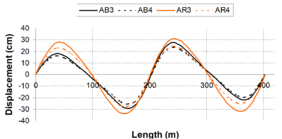
Fig. 3.24 Maximum Vertical Seismic Displacements – Hollow box-type Deck |
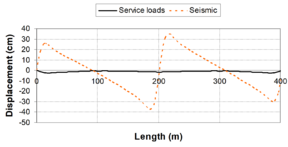
Fig. 3.25 Maximum Vertical Deck Displacements for AB1 Bridge |
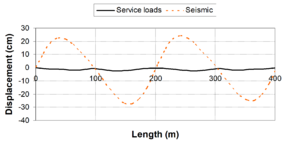
Fig. 3.26 Maximum Vertical Deck Displacements for AR4 Bridge |
Of course, a comparison between vertical displacements of the slab-type deck and the hollow box-type deck is not possible because they involve different stay spacing; however, it is clear that maximum values and maximum differences between the seismic and static condition under service loads are obtained with the slab-type deck because of the low flexural stiffness. In this sense, it seems to be that the deck displacement distribution can be more affected by the stay spacing than the deck type. Regarding the influence of the stay cable layout, it is evident that vertical deck displacements for the harp pattern are higher than displacements for the fan pattern, with some influence of the deck level; showing that bridges with the shortest deck level experience larger deck displacements than bridges with the highest deck level.
The comparison of internal forces shows interesting conclusions. The analysis of the compressive forces of the tower legs exposes variations for the maximum values (base) of the shortest towers with differences no greater than 5%. The results (Fig. 3.27) show important differences of the maximum values over the deck level (30 m), and increasing with the altitude. In fact, at the tower-top, differences up to 95% can be found. Also, Fig. 3.27 exposes that maximum compressive forces are obtained for AB1 bridge, followed by AR1 bridge (below the deck level) and AB3 (above the deck level). The lowest compressive forces are obtained for AR3 bridge. In a similar situation, the analysis of the compressive forces of the tower legs for the tallest bridges shows variations of the maximum values with negligible differences below the deck level (see Fig. 3.28), and more important variations above the deck level (60 m). In this case, differences up to 93% can be found at the tower-top. Below the deck level, maximum compressive forces are obtained for AB2 bridge, and minimum compressive force for AB4 bridge, on the contrary above the deck level, for which the maximum compressive forces are obtained for AB4 bridge, and the minimum values for AR4 bridge. The above mentioned implies that distribution of the seismic compressive forces depends on the deck level, with more important differences above that level. In this sense, axial forces on AB1 bridge are higher than axial forces on AR1 bridge; axial forces on AB3 bridge are higher than forces on AR3 bridge; axial forces on AB2 bridge are higher than that of AR2 bridge; and axial forces on AB4 bridge are higher than that of AR4 bridge above the deck level. As a conclusion, in general terms bridges with fan pattern show an increase of the seismic axial forces of the towers compared with the harp pattern. On the other hand, not important conclusions can be formulated with regard to the influence of the stay spacing on the compressive forces of the towers.
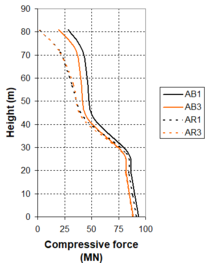
Fig. 3.27 Envelope of Maximum Seismic Compressive Forces for 81 m-Height Towers |
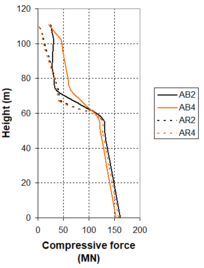
Fig. 3.28 Envelope of Maximum Seismic Compressive Forces for 111 m-Height Towers |
Of course, maximum compressive forces of the towers are obtained at their bases, with maximum average values of 90 MN and 158 MN for the 81 m-height towers and 111 m-height towers respectively. Figs. 3.29 and 3.30 show a comparison for compressive forces between the service loading condition and the seismic condition for the extreme cases AB1 and AR4. In these plots, it is clear the influence of the vertical component of the seismic motion on the axial forces of the tower legs, below the deck level, and mainly on AR4 bridge. In both situations, an increase of the maximum compressive forces of about 40% can be obtained, comparing the seismic and service loading cases.
The seismic analysis of the decks shows a similar distribution of the axial forces regarding the analysis under service loads. In fact, in both situations maximum compressive forces occur at the tower-deck connection, as can be appreciated in Figs. 3.31 to 3.34. Fig. 3.31 exposes the envelope of axial forces of the decks associated to bridges AB1, AB3, AR1 and AR3 (bridges with the shortest towers), as well as Fig. 3.32 exposes the envelope of axial forces of the decks for the rest of the cases.
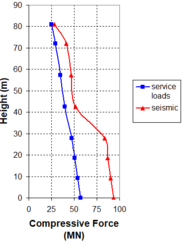
Fig. 3.29 Envelope of Maximum Tower Axial Forces for AB1 Bridge |
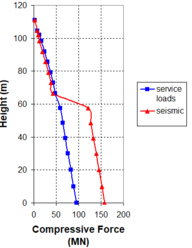
Fig. 3.30 Envelope of Maximum Tower Axial Forces for AR4 Bridge |
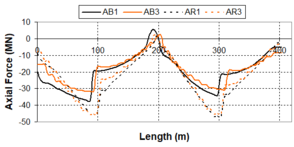
Fig. 3.31 Envelope of Seismic Axial Forces for Decks – 81 m Tower-Height |
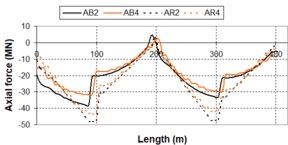
Fig. 3.32 Envelope of Seismic Axial Forces for Decks – 111 m Tower-Height |
Maximum values of the compressive forces on the decks vary from 32 MN (AB3 bridge) to 48 MN (AR2 bridge), that is to say, with a difference of 33%. Those values are very high due to the fixed hinge condition of the tower-deck connection, and they are in accordance with the explanations given before, constituting a potential point for the location of additional energy dissipation devices. Likewise, for all cases, a tension-zone at the mid-span of the decks can be appreciated, with values lower than 6 MN.
Some interesting appreciations can be formulated comparing the stay cable layout and the stay spacing with regard to the axial forces of the decks, according to Figs. 3.31 and 3.32. In general terms, axial forces on AR1bridge are higher than deck axial forces of AB1bridge; and axial forces of AR3 bridge are higher than axial forces of AB3 bridge. For bridges with 60 m-deck level, axial forces of AR2 bridge are higher than axial forces of AB2 bridge; and axial forces of AR4 bridge are higher than axial forces of AB4 bridge. This analysis implies that seismic axial forces of decks associated to bridges with harp pattern are higher than axial forces of decks for the fan pattern. In the same way, comparing the effect of the stay spacing, deck axial forces of AB1 bridge are higher than axial forces of AB3 bridge; axial forces of AR1 bridge are higher than axial forces of AR3 bridge; axial forces of AB2 bridge are higher than that of AB4 bridge; and finally, axial forces of AR2 bridge are higher than that of AR4 bridge, which implies that bridges with longer stay spacing show lower seismic axial forces for their decks. This situation is similar to the one observed for the static condition under service loads, and of course, this comparisons are only approaches, exposing a general tendency, as can be seen in Figs. 3.31 and 3.32. The highest axial forces for the decks are obtained for bridges AR1 and AR2, and the lowest axial forces correspond to bridges AB3 and AB4; that is to say, the worse condition for the axial forces of the decks are obtained with the harp pattern and the shortest stay spacing. As a comparison, Figs. 3.33 and 3.34 expose the envelope of axial forces taking into account the seismic and service loading cases, for two extreme conditions: bridges AB1 and AR4. It is easy to see that very important differences between both loading conditions can be observed, with differences in their maximum values up to 33% (AB1 bridge) and 28% (AR4 bridge). In this sense, and comparing with axial forces of the towers, more important differences on the determination of the maximum seismic axial forces are obtained for the tower legs.
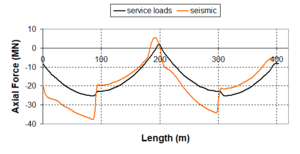
Fig. 3.33 Response Comparison for Axial Forces – Deck of AB1 Bridge |
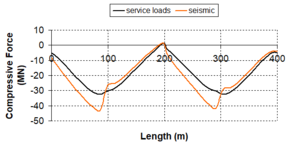
Fig. 3.34 Response Comparison for Axial Forces – Deck of AR4 Bridge |
Plots of bending moments are more complex and it can be not very clear to superimpose those diagrams. For that reason, in-plane bending moments of decks and towers for each bridge were represented separately, as can be seen in Figs. 3.35 and 3.36. The analysis of bending moments for the towers shows a similar behaviour for all cases. As usually happens, maximum bending moments were obtained at the base of the tallest towers, with maximum moments varying from 403 to 496 MN.m (AR4 bridge), which means a difference of 19%. For the case of 81 m-tower height, maximum bending moments of the towers vary from 178 MN.m (AR1 bridge) to 337.6 MN.m (AB1 bridge), which implies a difference of 48%. Comparing the effect of the stay cable layout on the bending moments of the towers, maximum tower moments of AB1 bridge are higher than maximum tower moments of AR1 bridge; maximum moments of AB3 bridge are higher than moments of AR3 bridge; maximum moments of AB2 bridge are higher than that of AR2 bridge; however, maximum moments of AB4 bridge are lower than that of AR4 bridge. According to the previous ideas, it seems to be that maximum tower bending moments for bridges with fan pattern are higher than maximum tower bending moments for bridges with harp pattern.
Regarding the influence of the stay spacing on the tower bending moments, it is easy to see that maximum tower moments of AB1 bridge are higher than maximum tower moments of AB3 bridge; maximum moments of AB2 bridge are higher than maximum moments of AB4 bridge; however, maximum moments of AR1 bridge are lower than that of AR3 bridge; and maximum moments of AR2 bridge are lower than that of AR4 bridge. This behaviour implies that for fan pattern bridges, an increase of the stay spacing decreases the maximum tower bending moments, on the contrary of the harp pattern, for which an increase of the stay spacing implies an increase of the maximum bending moments of the towers.

(a) Tower moments of AB1 bridge |

(b) Deck moments of AB1 bridge |

(c) Tower moments of AB3 bridge |

(d) Deck moments of AB3 bridge |
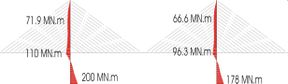
(e) Tower moments of AR1 bridge |
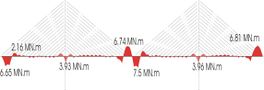
(f) Deck moments of AR1 bridge |
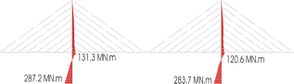
(g) Tower moments of AR3 bridge
|
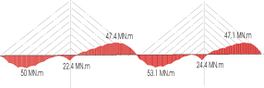
(h) Deck moments of AR3 bridge |
The analysis of in-plane deck bending moments shows a comparable behaviour depending on the stay spacing. Because of the longer stay spacing of bridges with hollow box-type deck, higher deck moments are obtained in this situation. In the seismic case, maximum deck bending moments occur in the central area of the main span, with an important modification of the curvature that makes significant variations of the moments. They are followed close by very high moments near the deck-ends, on the contrary of the static condition under service loads, for which maximum deck moments occur at the tower-deck connection.
The seismic response for decks with the longest stay spacing shows a more uniform distribution of the deck moments compared with bridges with the shortest stay spacing, for which maximum moments near the mid-span and near the deck-ends are very concentrated. For the longest stay spacing, maximum deck moments vary from 45.6 MN.m (AR4 bridge) to 62.2 MN.m (AB3 bridge), which implies a difference of 27%. For the shortest stay spacing, maximum deck moments vary from 7.5 MN.m (AR1 bridge) to 10.8 MN.m (AB1 bridge), which implies a difference of 30%, that is to say, the same magnitude order for moment difference can be obtained. The influence of the stay cable layout on the seismic response of the decks, shows for 6.2 m stay spacing, that maximum deck moment of AB1 bridge is higher than maximum deck moment of AR1 bridge; and maximum deck moment of AB2 bridge is higher than that of AR2 bridge. For 12.4 m stay spacing, maximum deck moment of AB3 bridge is higher than that of AR3 bridge; and maximum deck moment of AB4 bridge is higher than moment of AR4 bridge.

(a) Tower moments of AB2 bridge |

(b) Deck moments of AB2 bridge |
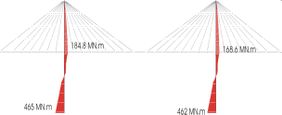
(c) Tower moments of AB4 bridge
|
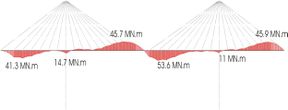
(d) Deck moments of AB4 bridge
|
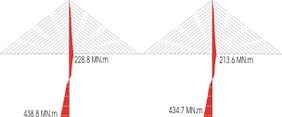
(e) Tower moments of AR2 bridge
|
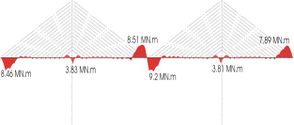
(f) Deck moments of AR2 bridge
|

(g) Tower moments of AR4 bridge
|

(h) Deck moments of AR4 bridge
|
As a conclusion, maximum deck moments for the fan pattern are higher than maximum deck moments for bridges with harp pattern. Comparing the influence of the deck level on the seismic moments of the decks, maximum deck moment of AB1 bridge is higher than that of AB2 bridge; maximum deck moment of AB3 bridge is higher than moment of AB4 bridge; maximum deck moment of AR3 bridge is higher than that of AR4 bridge; however maximum deck moment of AR1 bridge is lower than maximum moment of AR2 bridge. It seems to be that bridges with the lowest deck level show higher maximum bending moments of the decks.
As a summary, Tables 3.19 and 3.20 expose maximum static (service loads) and seismic displacements as well as maximum main forces for each bridge respectively. Location of the control points for displacements is represented in Fig. 3.14, with the same parameters of Table 3.8, plus Δ3-T (maximum transverse displacement at the mid-span). The explanations of the parameters of the maximum main forces are the same considered in Table 3.9.
| BRIDGE | ∆1-La | ∆1-T | ∆3-Vb | ∆3-T | ∆4-La | |||||
| Stat | Seis | Stat | Seis | Stat | Seis | Stat | Seis | Stat | Seis | |
| AB1 | 0.38 | 29.7 | 0.40 | 28.9 | -1.55 | -15.8 | 0.00 | 51.2 | 1.83 | 17.5 |
| AB2 | 0.30 | 40.9 | 0.16 | 32.3 | -1.51 | -14.1 | 0.00 | 62.9 | 1.88 | 28.3 |
| AB3 | 0.05 | 32.7 | 0.35 | 28.7 | -1.41 | -13.2 | 0.00 | 51.5 | 1.57 | 17.2 |
| AB4 | 0.03 | 43.0 | 0.14 | 27.6 | -1.55 | -12.0 | 0.00 | 59.1 | 1.59 | 27.5 |
| AR1 | 0.00 | 27.8 | 0.02 | 21.3 | -0.45 | -12.1 | 0.00 | 44.0 | 2.11 | 20.4 |
| AR2 | 0.52 | 41.2 | 0.03 | 33.9 | -1.59 | -15.0 | 0.00 | 57.9 | 2.13 | 26.0 |
| AR3 | 0.13 | 28.6 | 0.01 | 29.7 | -0.11 | -18.0 | 0.00 | 48.0 | 1.92 | 16.7 |
| AR4 | 0.02 | 42.6 | 0.04 | 33.1 | -0.28 | -15.5 | 0.00 | 59.4 | 1.97 | 27.1 |
a Positive value implies a displacement toward the mid-span
b Negative value implies a descending
From Table 3.19, it is interesting to observe that maximum seismic displacements correspond to transverse deflections of the deck at the mid-span, with values that range between 44 and 63 cm. Of course, those maximum transverse displacements are associated with the highest deck level, and are difficult to control due to the flexibility of the bridges in that direction. The deflection analysis of the towers shows values of the maximum displacements in the same magnitude order for the longitudinal and transverse direction. Those displacements are slightly minor in the transverse direction. Regarding the longitudinal seismic displacements at the deck-ends, maximum value corresponds to AB2 bridge (28.3 cm); and the minimum displacement corresponds to AR3 bridge (16.7 cm), which implies a difference of 41%. Seismic displacements are 12 times the static displacements (average), which can be adequately controlled with the addition of fluid viscous dampers. Likewise, in general terms, maximum longitudinal displacements at the deck-ends for the fan pattern are longer than that of the harp pattern.
From Table 3.20, maximum in-plane tower bending moments were obtained considering the earthquake acting in the longitudinal direction, and of course, in-plane bending moments are lower when the earthquake acts in the transverse direction. In this sense, analysis of out-of-plane tower seismic moments shows that tower moments when the earthquake acts in the transverse direction are lower than in-plane tower moments when the earthquake acts in the longitudinal direction, which implies that the worse analysis condition corresponds to the earthquake acting in the longitudinal direction. Maximum out-of-plane tower moments were obtained for bridges AB4 and AR2 (347.8 MN.m and 347.9 MN.m respectively); and minimum out-of-plane moments were obtained for AR1 bridge (186 MN.m). Comparing in-plane and out-of-plane tower moments, it is easy to see that in-plane bending moments are larger than out-of-plane moments; and differences between in-plane and out-of-plane tower moments vary from 7% (AR1 bridge) to 35% (AB3 bridge) . These conclusions implies that seismic design of the structural elements are governed by in-plane internal forces, and for that reason, only longitudinal seismic effects are considered in this part of the investigation.
| BRIDGE | Nmax-towera [kN | Nmax-deckb[kN] | Nmax-cable [kN] | Mmax-towera, d [MN.m] | Mmax-towere [MN.m] | Mmax-deckd [MN.m] | Base Shear (kN) | ||||||
| Stat | Seis | Stat | Seis | Stat | Seis | Stat | Seis | Statf | Seisa | Statb | Seisc | ||
| AB1 | -57200 | -93500 | -25200 | -37400 | 4800 | 11600 | 18.0 | 337.6 | 8.15 | 197.3 | 1.58 | 10.8 | 57600 |
| AB2 | -101200 | -161500 | -25500 | -38000 | 4950 | 11500 | 21.2 | 491.0 | 10.81 | 332.6 | 1.38 | 9.33 | 52250 |
| AB3 | -52900 | -88600 | -22100 | -31800 | 5630 | 9090 | 15.7 | 301.5 | 7.50 | 195.9 | 13.3 | 62.2 | 56970 |
| AB4 | -97000 | -153600 | -22400 | -31700 | 5770 | 9100 | 18.3 | 465.0 | 9.09 | 347.8 | 12.9 | 53.6 | 48360 |
| AR1 | -52900 | -91400 | -36400 | -46700 | 1560 | 5260 | 11.0 | 200.0 | 6.55 | 186.0 | 3.94 | 7.50 | 40000 |
| AR2 | -97000 | -158000 | -36900 | -47900 | 1790 | 6370 | 23.0 | 438.8 | 9.72 | 347.9 | 3.81 | 9.20 | 53670 |
| AR3 | -51300 | -88300 | -32000 | -45500 | 2700 | 4660 | 19.5 | 287.2 | 6.36 | 204.2 | 22.9 | 53.1 | 59560 |
| AR4 | -95300 | -158200 | -32500 | -43200 | 2820 | 5000 | 23.5 | 496.0 | 8.67 | 340.8 | 22.2 | 45.6 | 52140 |
a At the tower base c Near the mid-span e Out-of-plane
b At the tower-deck connection d In the bridge plane f At the upper strut level
- Implies compression
The analysis of cable forces in Table 3.20 shows that maximum tension forces correspond to bridges with fan pattern (for both loading conditions). Likewise, comparing bridges AB1 with AB3, AB2 with AB4, AR1 with AR3 and AR2 with AR4, it is easy to see, for the seismic condition of the maximum cable forces, that an increase of the stay spacing involves a decrease of the maximum cable forces. An opposite and intuitive situation occurs for the static condition under service loads, for which an increase of the stay spacing involves an increase of the maximum cable forces. The above mentioned implies that the worse seismic condition for the maximum stay cable forces, occurs on bridges with fan pattern and short stay spacing. Moreover, it is interesting to observe the tremendous difference between the maximum bending moments of the towers for both loading conditions. Those differences can be more than 23 times the static condition under service loads, especially for the tallest towers.
The information previous exposed can be confused in order to make a decision regarding the best geometric parameters or the best configurations that minimize the seismic response of the bridge models. The influence of the analyzed parameters can be summarized in Table 3.21, which shows the best configurations of the cable-stayed bridges only taking into account the seismic response of such structures applying the response spectrum method under strong ground motion. The most decisive response parameters include maximum displacements of the towers and decks; maximum axial forces of towers, decks and cables and maximum bending moments of towers and decks. As a result, Table 3.21 shows that reduction of vertical displacements of the deck can be better controlled by using bridges with fan pattern, and especially with high deck level. Longitudinal displacements of the towers are lower by using bridges with the shortest towers and the shortest stay spacing; and the longitudinal displacements of the deck are better controlled by using bridges with low deck level. In general terms, the bridge with the fan pattern cable layout, lowest deck level and shortest stay spacing (AB1 bridge) is a good choice to reduce displacements; however it is not a good selection to control the internal forces.
Regarding the reduction of internal forces, it is clear that the best option is the harp pattern, with the exception of the deck axial forces, for which fan pattern bridges with the longest stay spacing seems to be more adequate. Tower and deck bending moments are better controlled by using the harp pattern with the shortest stay spacing; and the cable forces are lower using the harp pattern with the longest stay spacing. A good choice to reduce both internal forces and displacements is the AR1 bridge, that is to say, a harp pattern bridge, with the shortest stay spacing and deck level. According to this simplified analysis, the worse conditions are obtained with the fan pattern bridges, and especially the AB2 and AB4 bridges, which consider the highest deck level. Of course, because of the complex nature of the seismic phenomena, it is very difficult to reduce displacements and internal forces at the same time, and for that reason, these recommendations are only general guidelines. An only optimal solution does not exist, and this selection necessarily depends on the specific requirements of the bridge prototype. For this reason, the aim of this comparative analysis is to show some results regarding the incidence of some parameters associated with the geometric configuration of the structures on the seismic response of the bridges.
| BRIDGE | Displacements | Internal Forces | ||||||
| ∆3-V | ∆1-L | ∆4-L | Nmax-tower | Nmax-deck | Nmax-cable | Mmax-tower | Mmax-deck | |
| AB1 | good | good | good | good | ||||
| AB2 | very good | good | ||||||
| AB3 | good | good | very good | |||||
| AB4 | very good | very good | ||||||
| AR1 | good | good | good | good | Very good | very good | ||
| AR2 | good | good | good | Very good | very good | |||
| AR3 | good | good | very good | good | good | |||
| AR4 | good | good | very good | good | good | |||
- 3.6 Effect of Variation of the Stay Prestressing Forces on the Seismic Response of Cable-Stayed Bridges
In order to investigate if static variations of the stay prestressing forces of cable-stayed bridges are important regarding their seismic response, two bridge models were considered to simulate this effect. AB1 and AR4 bridges were employed in this study, because they are representative of extreme cases of all the analyzed bridges in this work.
For the static variation of the stay prestressing forces, two extreme conditions were considered: an original load condition, where the cable forces were directly obtained from the nonlinear static analysis under service loads; and the second condition, here called optimal load condition, where a rectification of the back stay forces was introduced to minimize values of longitudinal displacements of the tower-top, and the vertical displacements of the deck at the mid-span. This correction was carried out applying an iterative procedure in which the cable forces were gradually increased, controlling the displacements of the structures. As a result, an increase of 20% for the back stay forces of the cables C1, C2 and C3 (AB1 bridge), and an increase of 12% for all the back stay forces of AR4 bridge were applied. Table 3.22 summarizes this idea.
The input ground motion is characterized by use of the response spectrum method defined by Eurocode 8 [CEN, 1998a, 1998b]. Although this procedure, on the basis of a performed modal analysis, can be questionable due to the supposed linearity involved in this strategy, here, with the aim to compare results of the static and dynamic structural analysis and to obtain maximum values for the seismic response of the structures, it is adequate to employ this method. In fact, in this case, conclusions taken from a time history analysis can be difficult to obtain, and strongly dependent on the considered earthquake database, being confused in the present analysis. Likewise, as a consequence of the elastic response of those structures this strategy is preferable.
| Bridge | Stay Prestressing Forces [kN]. | ||||||||
(a) AB1- Original Load Condition |
C1 | C2 | C3 | C4 | C5 | C6 | C7 | C8 | C9 |
| 4635 | 1460 | 1330 | 1220 | 1160 | 1100 | 1000 | 960 | 900 | |
| C10 | C11 | C12 | C13 | C14 | C15 | C16 | C17 | C18 | |
| 850 | 800 | 760 | 710 | 780 | 490 | 490 | 780 | 710 | |
| C19 | C20 | C21 | C22 | C23 | C24 | C25 | C26 | C27 | |
| 760 | 800 | 850 | 900 | 960 | 1020 | 1090 | 1160 | 1240 | |
| C28 | C29 | C30 | C31 | C32 | |||||
| 1300 | 1400 | 1470 | 1600 | 1600 | |||||

(b) AB1 – Optimal Load Condition |
C1 | C2 | C3 | C4 | C5 | C6 | C7 | C8 | C9 |
| 5560 | 1750 | 1600 | 1220 | 1160 | 1100 | 1000 | 960 | 900 | |
| C10 | C11 | C12 | C13 | C14 | C15 | C16 | C17 | C18 | |
| 850 | 800 | 760 | 710 | 780 | 490 | 490 | 780 | 710 | |
| C19 | C20 | C21 | C22 | C23 | C24 | C25 | C26 | C27 | |
| 760 | 800 | 850 | 900 | 960 | 1020 | 1090 | 1160 | 1240 | |
| C28 | C29 | C30 | C31 | C32 | |||||
| 1300 | 1400 | 1470 | 1600 | 1600 | |||||
(c) AR4 – Original Load Condition |
C1 | C2 | C3 | C4 | C5 | C6 | C7 | C8 | C9 |
| 2570 | 1970 | 2790 | 2930 | 2850 | 2630 | 2000 | 760 | 890 | |
| C10 | C11 | C12 | C13 | C14 | C15 | C16 | |||
| 2000 | 2580 | 2760 | 2800 | 2700 | 2600 | 2300 | |||

(d) AR4 – Optimal Load Condition |
C1 | C2 | C3 | C4 | C5 | C6 | C7 | C8 | C9 |
| 3080 | 2200 | 3120 | 3280 | 3190 | 2950 | 2240 | 850 | 890 | |
| C10 | C11 | C12 | C13 | C14 | C15 | C16 | |||
| 2000 | 2580 | 2760 | 2800 | 2700 | 2600 | 2300 | |||
The models were analyzed for each load condition, in which the components of the seismic action were combined with the permanent loading applying the directional combination according to Eurocode 8 (30% rule), that is to say, to add the earthquake input, 100% of one component was added to 30% of the other components of the seismic action and considering all possibilities. The modelling and the static and dynamic analyses were carried out applying the code RAM advanse [RAM International, 2003] considering the required modes to reach over 90% of the effective translational mass. The modal analyses were performed applying the Ritz Vector Analysis; and due to the strong modal coupling that cable-stayed bridges experience, CQC modal combination rule was applied.
Results of the analyses showed that longitudinal displacements of the towers are similar for both conditions, with the maximum at the top for the original load condition. [Figs. 3.37 and 3.38]. Of course, maximum longitudinal displacements for the towers occur for the tallest bridge (AR4 bridge). With regard to the vertical displacements of the decks, the deformed shape is quite different if we compare AB1 bridge with AR4 bridge. For AB1 bridge, maximum vertical deflection occurs near the mid span, as long as for AR4 bridge maximum vertical deflection occurs of about ¾ of the mid span [Figs. 3.39 and 3.40]. These differences come from the incidence of the stay cable layout and from differences in the stay spacing.
Considering the internal forces, plots for axial forces and bending moments were obtained from the dynamic analyses considering the original and optimal load conditions. Figs. 3.41 to 3.44 show a comparison for the compressive forces of the towers and axial forces of the decks. Because of the differences in the variation of the stay prestressing forces for bridges AB1 and AR4, it is not possible to compare differences for displacements and internal forces between those structures. However, it is easy to see that for both bridges, differences regarding the longitudinal displacements and axial forces of the towers are negligible, and more important differences can be found for vertical displacements and axial forces of the decks. For both bridges and for both load conditions, maximum axial forces on the decks (compression) occur in the vicinity of the tower-deck connection, with very high values, as usually happens on cable-stayed bridges with fixed hinge connection between the deck and the tower.
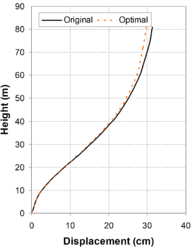
Fig. 3.37 Longitudinal displacements of the tower –AB1 Bridge |
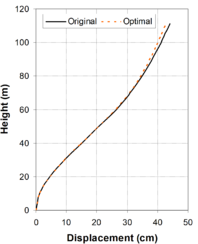
Fig. 3.38 Longitudinal displacements of the tower –AR4 Bridge |
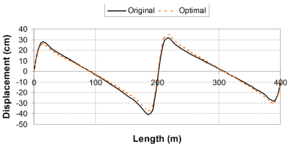
Fig. 3.39 Vertical displacements of the deck –AB1 Bridge |
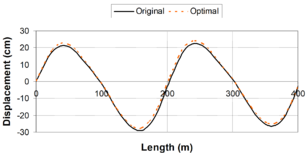
Fig. 3.40 Vertical displacements of the deck –AR4 Bridge |
For bending moments, because of the complexity of such plots, it is preferable to show them separately, that is to say, for each load condition and for each bridge, as can be seen in Figs. 3.45 and 3.46. Differences for the maximum values of the tower moments are negligible for both bridges [Figs. 3.45(a) and 3.45(b); Figs. 3.46(a) and 3.46(b)].
The shape of the plot for the bending moments of the deck is very different between AB1 bridge and AR4 bridge. In both situations, maximum values occur near the mid span or near the deck-ends, with very high values for AR4 bridge [Figs. 3.45(c) and 3.45(d); Figs. 3.46(c) and 3.46(d)]. These differences mainly come from differences in the stay spacing. Likewise, not very important differences are obtained comparing the maximum bending moments for both load conditions.
As a summary, for both structures, maximum differences of the measured displacements were obtained for the vertical deflections of the deck, and the maximum differences of the measured internal forces were obtained for the axial forces of the deck, followed by maximum bending moments of deck and towers.
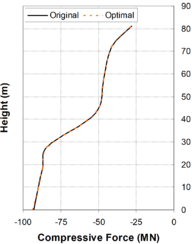
Fig. 3.41 Compressive forces of the tower –AB1 Bridge
|
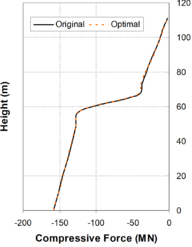
Fig. 3.42 Compressive forces of the tower –AR4 Bridge | |
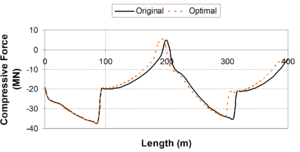
Fig. 3.43 Axial forces of the deck –AB1 Bridge |
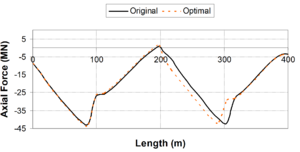
Fig. 3.44 Axial forces of the deck –AR4 Bridge | |

(a) Bending moments of the towers – original load condition |

(b) Bending moments of the towers – optimal load condition |

(c) Deck bending moments – original load cond. |

(d) Deck bending moments – optimal load cond. |
The maximum seismic response of the bridges for the original and optimal load conditions is summarized in Tables 3.23 and 3.24. Mmax1 corresponds to the maximum in-plane bending moments of the deck at the mid span; Mmax2 are the maximum in-plane bending moments at the deck-ends; Mmax3 are the maximum in-plane bending moments of the tower legs in the longitudinal direction (that occurs at the base level); Nmax1 corresponds to the maximum compressive force of the deck (that occurs in the tower-deck connection) and Nmax2 is the maximum compressive force of the tower legs (that occurs at the base level). In the same way, Δ1corresponds to the vertical displacement of the deck at the mid span; Δ2is the longitudinal displacement of the deck at the mid span; Δ3 is the transverse displacement of the deck at the mid span; Δ4 corresponds to the longitudinal displacement at the deck-ends; Δ5 is the longitudinal displacement of the tower-top and Δ6 is the transverse displacement of the tower-top.

(a) Tower bending moments – original load cond. |
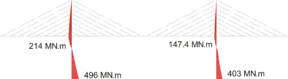
(b) Tower bending moments – optimal load cond. |

(c) Deck bending moments – original load cond. |

(d) Deck bending moments – optimal load cond. |
| Original Load Condition | Mmax1 | Mmax2 | Mmax3 | Nmax1 | Nmax2 | Base Shear |
| 10.7 | 10.5 | 336 | 37.1 | 93.4 | 57.6 | |
| Δ1 | Δ2 | Δ3 | Δ4 | Δ5 | Δ6 | |
| 19.3 | 15.5 | 51.2 | 17.5 | 31.4 | 28.9 | |
| Optimal Load Condition | Mmax1 | Mmax2 | Mmax3 | Nmax1 | Nmax2 | Base Shear |
| 10.8 | 10 | 337.6 | 37.4 | 93.5 | 57.6 | |
| Δ1 | Δ2 | Δ3 | Δ4 | Δ5 | Δ6 | |
| 15.8 | 15.5 | 51.2 | 17.5 | 29.7 | 28.9 |
| Original Load Condition | Mmax1 | Mmax2 | Mmax3 | Nmax1 | Nmax2 | Base Shear |
| 44.8 | 43 | 490 | 42.4 | 158.2 | 54 | |
| Δ1 | Δ2 | Δ3 | Δ4 | Δ5 | Δ6 | |
| 5.7 | 25.1 | 61.1 | 27.1 | 44.0 | 32.6 | |
| Optimal Load Condition | Mmax1 | Mmax2 | Mmax3 | Nmax1 | Nmax2 | Base Shear |
| 45.6 | 40.3 | 496 | 43 | 158.2 | 54 | |
| Δ1 | Δ2 | Δ3 | Δ4 | Δ5 | Δ6 | |
| 3.5 | 25.1 | 61.1 | 27.1 | 42.7 | 32.6 |
Displacements in cm; forces in MN; moments in MN.m
If the average variation of the seismic response is now computed for the bridges AB1 and AR4, the graphs plotted in Fig. 3.47 are obtained.
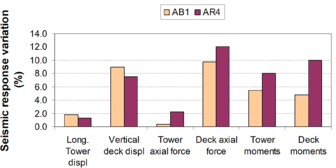
Fig. 3.47 Average Variation of the Seismic Response |
According to Fig. 3.47, average variations of the axial forces in the order of 0.3% (tower legs of AB1 bridge); 9.7% (deck of AB1 bridge); 2.2% (tower legs of AR4 bridge) and 12% (deck of AR4 bridge) can be found. Average variations of the bending moments on AB1 bridge are in the order of 5.5% for the towers, and 4.8% for the deck. A similar condition can be found for AR4 bridge, with main differences for bending moments of about 8% (towers), and 10% (deck). |
For the displacements, average differences in the order of 1.8% (tower legs of AB1 bridge); 9% (deck of AB1 bridge); 1.3% (tower legs of AR4 bridge) and 7.5% (deck of AR4 bridge) are obtained.
As a conclusion, this study shows that low-to-moderate variations of the stay prestressing forces on cable-stayed bridges imply low variations of the seismic response. These variations of the seismic response are not very different if the stay cable layout, stay spacing or deck level is changed, and only specific differences regarding the shape of the internal forces or displacements can be found, and specially for the deck. The main variations of the seismic response come from the vertical deflections and internal forces of the deck, as long as variations for the seismic response of the towers are less sensitive, especially the longitudinal displacements and axial forces.
- 3.7 Seismic Response Applying Nonlinear Direct Integration Time History Analysis
- 3.7.1 General Considerations and Selected Models
All the subsequent analyses consider the application of step-by-step strategies to solve the cable-stayed bridge models of this work, considering that nonlinear direct integration time history analysis is the best alternative to accurately represent the complex nature of such structures. The structures are solved using the code SAP2000 [Computers & Structures, 2007], considering all the nonlinearities available and previously explained. In spite of the tremendous computational effort involved, this methodology is the best suitable, and application of the Hilber-Hughes-Taylor-α integration procedure seems to be more adequate [Hilber et al, 1977], according to the explanations of Appendix A.
Response spectrum analysis of the bridge models left clear that the largest displacements are obtained with the highest deck level, and the worse condition for the internal forces is obtained with the fan pattern bridges. Although the modal analysis of the bridges showed that higher order modes can be important especially on bridges with low deck level, structures with high deck level may experience important geometric nonlinear effects, especially large nonlinear axial force – bending moment interaction for the tower and longitudinal girder elements as well as large nonlinear behaviour due to the geometric change caused by the large displacements on the whole structure. On the other hand, the deck level is generally conditioned by functional aspects, constituting a geometric parameter that cannot be modified. For those reasons, the worse condition occurs with bridges with high deck level, and only those structures are considered in the subsequent analyses. Even through the effect of the stay spacing can be important, the response spectrum analysis gave a good idea about the incidence of this parameter on the seismic response of the bridge models, and it is not necessary to consider its variation during the nonlinear time history analysis. Thus, according to the above explained and in order to avoid the large information generated and the excessive computer effort due to the application of the nonlinear time history analysis if all cases are considered, only two models are studied: bridges AB4 and AR4, that is to say, fan and harp pattern bridges with 12.4 m-stay spacing (hollow box type deck) and 60 m-deck level. Those structures are considered as critical, especially the AB4 model. Although AR4 bridge seems to be not very critical, its consideration permits an adequate analysis between fan and harp pattern layouts. Moreover, those structures contain less joints and elements than the other models, reducing the computer time that can be crucial in a nonlinear time history analysis. In some sense, influence of the bridge configuration on the seismic response was analyzed applying the response spectrum method. Thus, the next pages are focused on the nonlinear seismic response of the bridges for different input ground motion typologies, and taking into account the stay cable layout, with and without the incorporation of additional energy dissipation devices.
The geometry, structural modelling, mechanical properties, material data as well as the loads and analysis cases were well explained. Now, the seismic input is considered by use of acceleration time histories and taking into account the largest spectral velocity of each event in the period range of interest, applied to the principal direction of the structures as measure of the seismic hazard, in order to consider the velocity-sensitivity of the bridge models. The complex damping mechanism is simplified here and considered as only dependent on the modal shapes, according to Kawashima and Unjoh (1991). In this sense, proportional damping to stiffness and mass is considered in the direct integration analysis (Rayleigh’s damping), that is to say, ![]() , in which C is the damping matrix, M is the mass matrix, K is the stiffness matrix, α is the mass proportional coefficient, and β is the stiffness proportional coefficient. For the selected bridges, α = 0.0734 and β = 0.000513 values were used.
, in which C is the damping matrix, M is the mass matrix, K is the stiffness matrix, α is the mass proportional coefficient, and β is the stiffness proportional coefficient. For the selected bridges, α = 0.0734 and β = 0.000513 values were used.
For the step-by-step integration of equations of motion, 20 analysis cases involving more than 13 hours of computer time for the far-fault analysis, and more than 48 hours of computer time for the near-fault analysis were required. An estimation of more than 120 hours of computer time including trial-and-error tests, parameter adjusts and convergence trials were necessary for successful and accurate results. Although the Hilber-Hughes-Taylor-α method is unconditionally stable for linear analysis, in the case of the selected models sometimes the convergence was difficult, and a lot of error-and-trial tests were necessary to reach an adequate convergence. In this sense, the far-fault analysis was easier, with the exception of some analysis cases for AR4 bridge. For the case of the near-fault analysis, the convergence is more complicated, aspect that is reflected in the enormous computer time required, because of the modifications necessary in the convergence parameters. Those experiences reflect the highly nonlinear behaviour of the models and the strong incidence of the long-period velocity-pulses of the near-fault ground motions, aspect enlarged in Appendix A. In a recent publication, Chen and Ricles (2008b) expose the stability conditions of direct integration algorithms for nonlinear analysis.
In order to control the convergence of the models, several time integration parameters were taken into account. The numerical damping of the Hilber-Hughes-Taylor-α method was selected as -0.2 for all the analysis cases. This value adequately controls the instability due to the high frequency content, with an acceptable accuracy. To control the iteration and sub-stepping process, some important parameters were considered. The maximum sub-step size reflects the upper limit on the step size used for integration. The minimum sub-step size limits the smallest sub-step size, in order to stop the analysis bellow this limit indicating that convergence has failed. The maximum iterations per sub-step controls the number of iterations allowed in a step before the use of smaller sub-steps, a number usually higher for the analysis of cable structures. The iteration convergence tolerance compares the magnitude of force error with the magnitude of the force acting on the structure to guarantee that equilibrium is achieved at each step of the analysis, a value that usually decreases when large-displacement effects are considered. Anyway, for all the analysis cases in this work, time-step size of 0.02 sec was employed.
- 3.7.2 Input Ground Motions
In order to consider different characteristics of the input ground motions in this research, earthquake records were divided into far-fault and near-fault ground motions depending on the source distance. For the analysis, a collection of 10 earthquake records was selected as input ground motion considering three components for each one. The number of earthquake events was selected to take into consideration the average of the response parameter in the assessment of the structural response, and according to Eurocode 8, Part 1, a minimum of 5 accelerograms is necessary for each case. Because of the structures are founded on bedrock, time histories need to be recorded on rock or hard soil, and for that reason, soil-structure interaction is not considered here. Regarding the record selection and according to the previously exposed, a collection of 5 artificial accelerograms compatible with response spectra defined by Eurocode 8 Part 2, were generated in order to analyze the far-fault effects. For near-fault ground motions, it is preferable to employ real acceleration records, because in this case that option may reflect in a better way the basic aspects of the complex nature of the near-source effects, including the incidence of forward rupture directivity (velocity pulse-type earthquakes). In fact, near-fault effects cannot be adequately described by uniform scaling of a fixed response spectral shape; the shape of the spectrum must become richer at long periods as the level of the spectrum increases [Somerville, 1997]. Although there are some investigations about the formulation and application of near-fault design spectra, this strategy is not clearly defined for bridges, and a lot of uncertainties are involved. In this sense, the works of Li and Zhu (2003) and Akkar and Gülkan (2003) propose and explain the procedure for implementation of near-fault design spectra on building design codes. In this research, the record selection for near-fault ground motions was made choosing the current practice to carefully select records that reflect the expected magnitude, distance and other characteristics of the source of the events that are in some sense most likely to threaten the structure.
For far-fault earthquakes, five collections of artificially generated accelerograms compatible with response spectra defined by Eurocode 8 [CEN, 1998a, 1998b] were considered. For an adequate 3-D analysis both horizontal and vertical response spectra were generated considering the structures founded on bedrock, with effective ground accelerations of 0.5g (horizontal) and 0.35g (vertical), characteristic of strong ground motions. As a second stage, synthetic accelerograms compatible with those response spectra were generated applying the code SIMQKE1 [Gasparini and Vanmarcke, 1976]. This software computes a power spectral density function from a specified smooth response spectrum and generates artificial acceleration time histories which match a specified response spectrum and it refines the spectral match through an iterative procedure based on the fact that any periodic function can be represented by sinusoidal waves, in which the obtained records are non-stationary in intensity but stationary in frequency spectrum. All the generated time histories consider a magnitude MS = 7.0, 1.7% critical damping ratio and 0.02 sec time-step size. This value of magnitude is representative for strong earthquakes, as long as the chosen value for the critical damping ratio was taken from the modal analysis of the bridges, in which the longitudinal and transverse bending of the decks of the bridges govern. Taking into account that the seismic hazard for long-period structures, such as those proposed here, can be better represented by the spectral velocity in addition to the magnitude and effective duration (obtained from Arias Intensity of the time histories), different conditions were proposed, in which the considered closest distance to the fault rupture were 30, 45, 60, 90 and 120 km, and taking into account that an increase of the source distance implies an increase of the effective duration of the strong motion. Of course, from one target horizontal response spectrum, two artificial earthquakes were obtained, for each horizontal component. By this way, different horizontal time histories were obtained, and the corresponding vertical components were obtained considering the same parameters and the respective vertical response spectrum, in order to generate for each earthquake event, two horizontal components and the respective vertical one.
For all cases, a trapezoidal intensity envelope was used, in which the earthquake level time of the intensity envelope was associated with the effective duration, pre-defined using empirical formulation, and then checked with the values of the Arias Intensity of the records. When synthetic accelerograms are obtained, a baseline correction is performed for each record, applying a linear polynomial formulation using the code SeismoSignal V.3.2.0 [Seismosoft, 2006].
For near-source ground motions, three-component real acceleration time histories were selected. Selection criteria of the earthquakes considered strong ground motions recorded on rock or hard soil with source distances up to 10 km and Mw > 6.0. In order to take into account time histories with the inclusion of forward rupture directivity pulse effects, recommendations of Somerville (1997, 2002 and 2003), Cox and Ashford (2002) and Akkar and Gülkan (2003) were considered. In this sense, it is important to select time histories which appropriately include rupture directivity effects, because this aspect is very important if near-source earthquakes are considered. In fact, earthquake events with less than 15 km source distances not necessarily include velocity pulses, that is to say, forward rupture directivity pulse effects; and for that reason it is important to select an appropriate proportion of time histories that include these effects if time histories represent the response spectrum. Because of the most important limitation is the relatively limited amount of seismic recordings including long-period velocity-pulses, selection of time histories considering near-fault effects is restricted. While seismographs and seismic recordings have been in place for many years, the development of strong motion seismographs is a relatively recent event, with instruments able to accurately record ground accelerations approaching or surpassing the acceleration of gravity. Because of the high cost of large instalment of these instruments, the inability to predict time, location and rupture zone as well as difficulties with maintenance, recorded events considering near-fault effects is scarce [Cox and Ashford, 2002]. In the present research, all the near-source events contain velocity pulses, and their selection was taken from catalogues of near-fault earthquakes from Cox and Ashford (2002), Somerville (2003) and Akkar and Gülkan (2003). The selected earthquakes are: Landers, Lucerne station (06/28/1992, Mw = 7.3); Loma Prieta, Los Gatos Pres. Center station (10/18/1989, Mw = 6.9); Loma Prieta, Lexington Dam station (10/18/1989, Mw = 6.9); Kobe, JMA station (01/16/1995, Mw = 6.9) and San Fernando, Pacoima Dam Abut. station (02/09/1971, Mw = 6.6). All the acceleration records were obtained in the form of [.txt] files from Pacific Earthquake Engineering Research Center (2005). The acceleration time histories were adjusted to 0.02 sec time-step size and then typically filtered using highpass, lowpass or bandpass Butterworth-type filters, depending on the specific record. To do that, the free software SeismoSignal [Seismosoft, 2006] was applied. Likewise, acceleration time histories were corrected by baseline using linear polynomial-type correction. It is important to say, as was previously explained, that near-fault acceleration time histories were not scaled to some common level in order to avoid some uncertainties involved with this procedure [Somerville, 1997]. Because of the near-source effects imply velocity pulses at specific frequency bands, it is not recommendable to scale acceleration time histories. That is the best way to reproduce the complex nature of the near-source effects. After the correction of the acceleration records, velocity and displacement time histories were obtained.
As a brief summary, Tables 3.25 and 3.26 expose the main ground motion parameters of the considered events for both far-fault and near-fault earthquakes. MS and MW are the surface wave magnitude and moment magnitude respectively.
Table 3.25 Ground Motion Parameters for Far-Fault Events
|
Re is the closest distance to the fault rupture surface; te is the effective duration of the strong motion (obtained using the Arias Intensity of the earthquake events) and PGA, PGV and PGD are the peak ground acceleration, velocity and displacement respectively. All these ground motion parameters were obtained using the code SeismoSignal [Seismosoft, 2006]. |
Analyzing the far-fault ground motion parameters, it is easy to see that the effective duration increases as the closest distance to the fault rupture increases. PGV values are similar from one event to another, with more important differences for PGD values. Average values for PGV are in the order of 0.46 m/sec and 0.22 m/sec for horizontal and vertical components respectively. Likewise, average values for PGD of 0.27 m and 0.15 m, associated with horizontal and vertical components are obtained respectively.
| EVENT | Station | Mw | Re (Km) | Component | te (sec) | PGA (g) | PGV (m/sec) | PGD (m) |
| 260º | 13.10 | 0.67 | 0.95 | 0.67 | ||||
| Landers 06/28/1992 | Lucerne | 7.3 | 2.2 | 345º | 13.80 | 0.78 | 0.31 | 0.16 |
| Up | 13.00 | 0.71 | 0.37 | 0.16 | ||||
| 0º | 10.10 | 0.57 | 1.21 | 0.49 | ||||
| Loma Prieta 10/18/1989 | Los Gatos Pres. Center | 6.9 | 3.9 | 90º | 7.80 | 0.52 | 0.54 | 0.19 |
| Up | 7.10 | 0.60 | 0.45 | 0.46 | ||||
| 0º | 4.20 | 0.40 | 0.59 | 0.16 | ||||
| Loma Prieta 10/18/1989 | Lexington Dam | 6.9 | 5 | 90º | 4.00 | 0.50 | 0.72 | 0.22 |
| Up | 7.60 | 0.15 | 0.19 | 0.11 | ||||
| 0º | 8.30 | 0.76 | 0.85 | 0.16 | ||||
| Kobe 01/16/1995 | JMA | 6.9 | 0.96 | 90º | 9.50 | 0.56 | 0.82 | 0.16 |
| Up | 9.60 | 0.34 | 0.37 | 0.10 | ||||
| 164º | 7.00 | 1.06 | 0.92 | 0.31 | ||||
| San Fernando 02/09/1971 | Pacoima Dam Abut. | 6.6 | 1.8 | 254º | 7.30 | 1.14 | 0.53 | 0.10 |
| Dwn | 6.90 | 0.68 | 0.42 | 0.17 |
Regarding the near-fault ground motions, it is not certain that the effective duration increases as the closest distance to the fault rupture increases, as usually happens with far-fault motions. Maximum values for PGA were obtained for San Fernando earthquake, with peaks larger than 1g for both horizontal components. In general terms, all the PGA peaks are larger than 0.4g for the horizontal components. Likewise, the vertical components are important, with values that can be larger than the horizontal components, as can be seen for the earthquakes of Landers and Loma Prieta, LGPC station. With regard to the PGV values, all pulses are larger than 0.7 m/sec, with maximum of 1.21 m/sec (Gatos). Peak ground displacements strongly depend on the earthquake event and component, with maximum value for the component 260º, Landers (0.67 m).
With comparative purposes, Figs. 3.48 and 3.49 expose horizontal elastic pseudo-velocity response spectra associated to the strongest direction of each earthquake event. These components were selected applying the criterion of the largest spectral velocity component because, as was previously explained, for the period range of interest in this research, the structures can be more affected by velocity than acceleration; and the traditional application of the earthquake component with the highest PGA is not advisable. As can be checked, all these selected components of the earthquake events were applied to the longitudinal direction of the bridge models. Fig. 3.48 shows pseudo-velocity response spectra for far-fault earthquake events (artificially generated) including the pseudo-velocity response spectrum corresponding to Eurocode 8, with 0.5g-effective ground acceleration and critical damping ratio of 1.7%. Because of the artificial earthquakes were generated from the elastic acceleration response spectrum corresponding to Eurocode 8, an excellent co-relation can be appreciated. In fact, for the period range of interest in this investigation, the pseudo-velocity response spectrum of Eurocode 8 corresponds to the average pseudo-velocity response spectra of the horizontal earthquake events. For periods larger than 4.5 sec, the pseudo-velocity response spectra for all the earthquake events exceed the response spectrum of Eurocode 8.
In the same way, Fig. 3.49 shows a comparison between the horizontal elastic pseudo-velocity response spectrum corresponding to Eurocode 8 (considering the same previously defined parameters) and the pseudo-velocity response spectra associated to the selected near-fault ground motions. Near-fault pseudo-velocity response spectra are associated to the horizontal strongest component of each earthquake event (largest spectral velocity in the period range of interest), as occurs for far-fault ground motions. It is easy to see that for periods lower than 2 sec, all the spectral velocities exceed the spectral velocity of Eurocode 8, with the relative exception of Landers earthquake. For the period range of interest in this research (periods larger than 2-3 sec), some spectra exceed the response spectrum of Eurocode 8 (Loma Prieta – Gatos, Landers and San Fernando) and some spectra are below the response spectrum of Eurocode 8 (Kobe, Loma Prieta - Lexington); however, these last response spectra are the closest to the response spectrum of Eurocode 8. The event Loma Prieta – LGPC – 0º experiences the largest pseudo-velocity response spectrum in the period range of interest and for that reason is considered the critical event.
- 3.7.3 Importance of Velocity Spectra on the Seismic Response of Long-Period Structures
Traditionally, the employ of the PGA or the effective ground acceleration as measure of the seismic hazard has been widely applied in the seismic analysis of structures, and worldwide implemented in the current seismic regulations. It is known that this approximation is inaccurate because additional parameters such as the frequency content, strong motion duration of the earthquake input and some additional parameters involved with the source can be important. The approximation of the PGA as measure of the seismic hazard sometimes works good mainly on short-period structures. However, in the case of long-period structures this approximation can be wrong, and structures could be more affected by velocities or even displacements.
In order to expose the great differences that can occur if the PGA is applied as measure of the seismic hazard for long-period structures, a brief comparison was performed. To do that, AB4 model was selected as long-period reference structure. Two near-fault events containing long-period velocity-pulses were selected: San Fernando, Pacoima Dam Abut. Station (02/09/1971) and Landers, Lucerne Station (06/28/1992). The nonlinear analyses were performed applying step-by-step strategies as was previously explained. Figs. 3.50 and 3.51 show pseudo-acceleration and pseudo-velocity response spectra of the selected earthquake events, and Table 3.27 contains a summary of the main parameters of the earthquake inputs.
San Fernando earthquake shows important spectral accelerations in the period range of 0.2 – 0.5 sec, with the highest value for the component 164º. For periods longer than 1 sec, an important decrease of the spectral accelerations is experienced for all the components. With regard to the spectral velocities, important amplifications are experienced in the period range 0.4 – 2 sec for both horizontal components, and especially the component 164º.
The response spectra of Landers Earthquake (Fig. 3.51) show important amplifications of the acceleration spectra in the period range 0.1 – 0.2 sec, and an abrupt decrease of the spectral components for periods longer than 0.3 sec. The vertical component shows a very high peak (almost 5g), higher than the horizontal components, a characteristic that usually happens in the short-period range when near-fault earthquakes are considered [Button et al, 2002]. Velocity spectra show a very different behaviour, because important amplifications are present for periods longer than 3 sec, and especially the component 260º. As a summary, in the period range of interest for AB4 model (fundamental period of 2.8 sec), the horizontal components 164º (San Fernando) and 260º (Landers) of the velocity response spectra are interesting, showing the highest amplifications.
(a) Pseudo-acceleration |
(b) Pseudo-velocity |
(a) Pseudo-acceleration |
(b) Pseudo-velocity |
| EVENT | Station | Mw | Re (Km) | Component | t (sec) | te (sec) | PGA (g) | PGV (m/sec) |
| 260º | 13.10 | 0.63 | 1.37 | |||||
| Landers 06/28/1992 | Lucerne | 7.3 | 2.2 | 345º | 48 | 13.90 | 0.79 | 0.30 |
| Up | 13.00 | 0.71 | 0.41 | |||||
| 164º | 7.00 | 1.06 | 1.12 | |||||
| San Fernando 02/09/1971 | Pacoima Dam Abut. | 6.6 | 1.8 | 254º | 42 | 7.30 | 1.16 | 0.54 |
| Dwn | 6.90 | 0.67 | 0.55 |
Mw: Moment magnitude; Re: Closest distance to the fault rupture; t: Duration of the event
te: Effective duration of the strong-motion; PGA: Peak ground accel. PGV: Peak ground vel.
Table 3.27 shows that both stations were very close to the fault rupture, with short effective durations of the strong motion (obtained here using the Arias intensity of the earthquake components). Important ground accelerations for all the components are appreciated, and especially for San Fernando event, with ground accelerations higher than 1.0g for the horizontal components. Important ground velocities are observed for the horizontal components, especially the components 260º (Landers) and 164º (San Fernando), coincidently with the components for which the maximum spectral velocities were observed. Those components experience ground velocities higher than 1 m/sec.
If the maximum horizontal PGA component is applied to the principal direction of the bridge, as traditionally happens in the current regulations, components 345º and 254º should be applied for the Landers and San Fernando events respectively, on the contrary of the case when the maximum spectral velocity components in the period range of interest are applied, resulting in different earthquake components to be applied to the principal direction of the bridge (components 260º and 164º for Landers and San Fernando events respectively). Figs. 3.52, 3.53 and 3.54 show comparative results for maximum responses of displacements, axial forces and moments respectively, and considering PGA and spectral velocities as measure of the seismic hazard. Results of this analysis are very clear. For both events, displacements obtained using the PGA are always lower than the case of the application of the spectral velocity, with differences that can be more than 3 times those obtained with the application of the PGA.
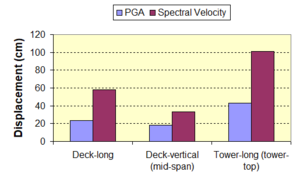
(a) Landers, Lucerne station |
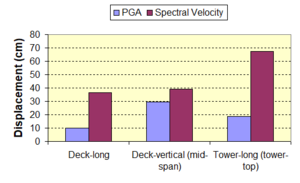
(b) San Fernando, Pacoima Dam Abut. station |
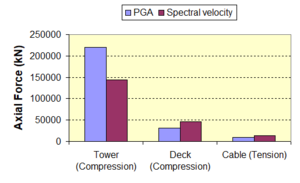
(a) Landers, Lucerne station |
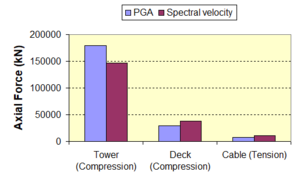
(b) San Fernando, Pacoima Dam Abut. station |
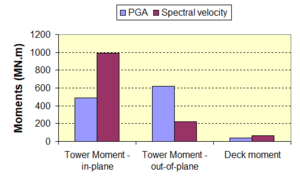
(a) Landers, Lucerne station |
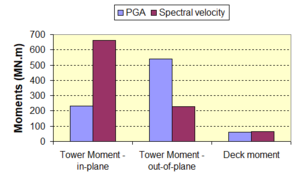
(b) San Fernando, Pacoima Dam Abut. station |
With regard to the axial forces, differences between the application of the PGA and the spectral velocity are less evident than the case of the displacements. Response values obtained with the application of the PGA as measure of the seismic hazard are lower than the case of the application of the velocity spectra, with the exception of the compressive forces of the towers, because of the incidence of the vertical component of the seismic action. A similar condition is observed with the bending moments, with the exception of the maximum out-of-plane bending moments of the towers. On the other hand, comparing results between Landers and San Fernando events, many obtained responses are lower in the case of the San Fernando event despite the higher PGA values observed (Table 3.27), which confirms that PGA is not a good parameter for velocity-sensitive structures.
By this way, these results show the importance of considering the spectral velocity as parameter of the seismic hazard, more than the application of the widely applied PGA value for long-period structures. Application of the seismic components associated with the maximum horizontal spectral velocity in the period range of interest, can induce larger seismic responses than application of the maximum PGA, and for that reason those systems need to be considered as velocity-sensitive, aspect that is taken into account in the subsequent analyses.
Investigations regarding these matters have been focused on the need of having seismic design spectra for long-periods. It is known that velocity or displacement spectra obtained from direct conversion of acceleration spectra in most codes are unrealistic in both shape and amplitude, and for that reason, velocity or even displacement design spectra not obtained from acceleration spectra for long-periods have been proposed since the middle of the 90´s. The works of Trifunac (1995), Tolis (1999), Bommer (1999), Bommer et al (2000), Hu and Yu (2000) and Faccioli et al (2004) are some proposals of spectra for long-period structures.
- 3.7.4 Seismic Response Considering Far-fault Ground Motions
In the analysis of the bridge models considering far-fault ground motions, each orthogonal three-component event was applied with a time-step size of 0.02 sec. The time integration parameters to control the convergence were chosen in order to guarantee the stability conditions of the nonlinear analysis with an adequate accuracy. In this sense, the maximum and minimum sub-step size employed was zero, the maximum iterations per sub-step were 60 (for which an adequate accuracy using cable formulation was obtained in the nonlinear static analysis), and the iteration convergence tolerance was 1x10-4, for which adequate results were obtained in the large-displacement analyses. In general terms the convergence was easy to obtain in these cases, with the exception of some cases for the AR4 model.
The time-history plots shown in the following figures expose the response for the zone associated to the strong motion duration of each ground motion, obtained from the Arias Intensity of each event. Because of the far-fault events were generated from the same origin (elastic acceleration response spectra from Eurocode 8), and considering for each event the same basic parameters that define the response spectra, the responses obtained were very similar. The main parameter that changed in this stage was the source distance, implying an increase of the duration of the event as the source distance increases. However, some differences in the seismic responses can be observed comparing each event, as can be appreciated next. At time equal to zero, the response is generally non-zero because it is obtained at the end of the nonlinear static analysis, and considered as starting point of the nonlinear direct integration time history analysis.
The main time histories of relative displacements for both bridge models can be observed in Figs. 3.55 to 3.59.
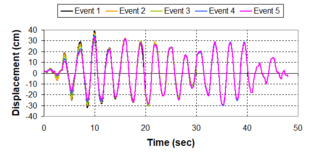
(a) AB4 bridge |
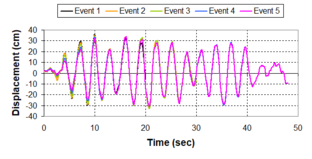
(b) AR4 bridge |
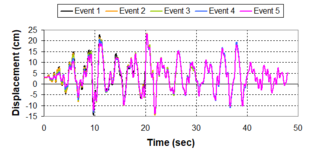
(a) AB4 bridge |
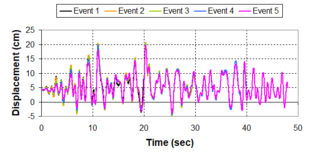
(b) AR4 bridge |
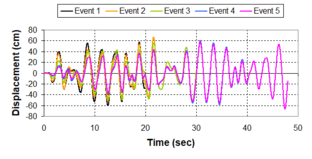
(a) AB4 bridge |
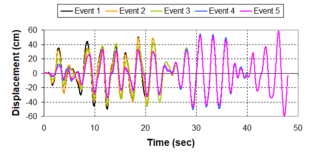
(b) AR4 bridge |
Longitudinal displacements of the deck are very similar for both structures, with maximum values lower than 40 cm (Fig. 3.55). Because of the rich frequency content of the artificial far-fault earthquakes, response time-histories are very regular, with similar peak displacements obtained a lot of times. A comparison between time histories of the vertical displacements at the mid-span (Fig. 3.56) shows slight differences between both bridges. It is clear that maximum values are obtained for the AB4 model, with a peak vertical displacement lower than 25 cm. On the other hand, Fig. 3.57 shows response time histories for the transverse displacements of the deck at the mid-span. In this case, more important differences between both structures are experienced, with maximum values for the AB4 bridge, obtained with Event 5.
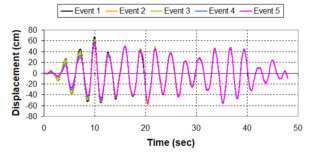
(a) AB4 bridge |
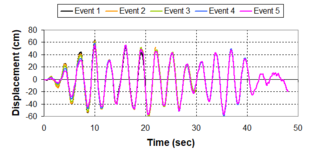
(b) AR4 bridge |
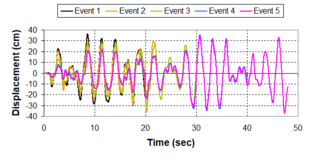
(a) AB4 bridge |
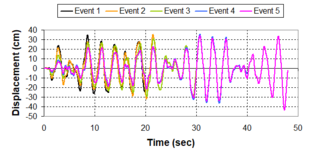
(b) AR4 bridge |
A comparison between the longitudinal displacements of the tower-top (Fig. 3.58), shows a very regular behaviour for both structures, with peak responses in the order of 60 cm. With regard to the transverse displacements of the tower-top, maximum values are very similar for both models, with a comparable response for all the analysis time. Maximum values are obtained for Event 5, of about 40 cm, as can be appreciated in Fig. 3.59. This analysis shows that maximum displacements for both bridges are obtained for the longitudinal displacement of the tower-top and the transverse displacement of the deck at the mid-span, with very similar results. The main differences on the displacement response between both bridges are observed for the vertical and transverse displacements of the deck at the mid-span.
With comparative purposes, Fig. 3.60 exposes the relative longitudinal velocity response of the deck for both structures. Results show a similar response, with maximum velocities in the order of 1 m/sec, about two times the peak ground velocity of those events. All the events experience more or less the same velocity response, repeating during the time interval of the analysis. Those velocity responses can be adequately controlled by additional energy dissipation devices.
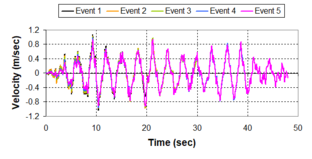
(a) AB4 bridge |
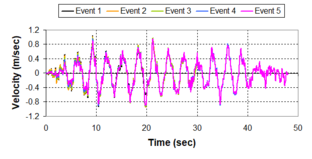
(b) AR4 bridge |
Regarding the main internal forces, a comparison for both bridges can be observed in Figs. 3.61 to 3.64, in which axial forces and bending moments for the main elements are represented as time histories. Shear forces were not included in this analysis because the response of those structures is basically controlled by axial forces, bending moments and their interaction.
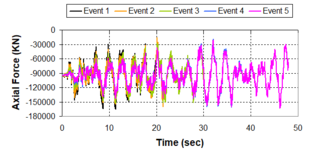
(a) AB4 bridge |
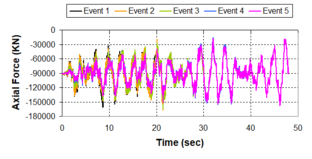
(b) AR4 bridge |
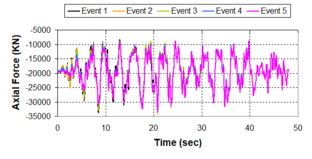
(a) AB4 bridge |
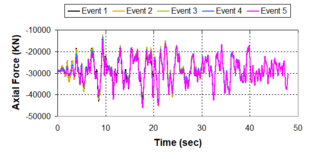
(b) AR4 bridge |
The axial forces of the tower legs (Fig. 3.61) show a comparable average response for both structures, very regular, with maximum compressive forces of about 160000 kN. In this case, time histories show for both bridges that the towers remain in compression during all the time for all the events, with peak compressive forces more than 1.8 times the static forces. The axial forces of the deck at the tower-deck connection showed in Fig. 3.62 represent the point in which maximum axial forces of the deck are experienced. Maximum values obtained are different for both bridges, being higher on AR4 bridge, with a peak response of 45000 kN (compression). Likewise, during all the analysis time, and for all the events, the decks of both bridges are in compression, showing a very regular behaviour of the response. Bending moments shown in Fig. 3.63 are very similar for all the events, with maximum values for both structures in the order of 630 MN.m. In this sense, the static moments at the end of the nonlinear static analysis are almost negligible compared with the tremendous nonlinear dynamic moments, and for that reason they appear showing a value near to zero at time zero of the time histories, according to the used scale. Considering the response spectrum analysis, maximum bending moments of the deck are obtained at the mid-span, and for that reason this point was selected for the analysis of the time histories of the deck moments. It is clear from Fig. 3.64 that maximum moments of the deck are obtained on AB4 bridge, with a peak value of 56 MN.m, 30% higher than the maximum deck moment on AR4 bridge.
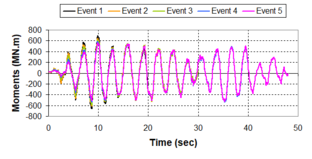
(a) AB4 bridge |
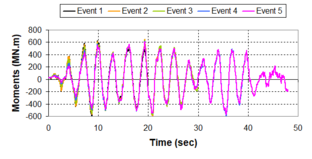
(b) AR4 bridge |
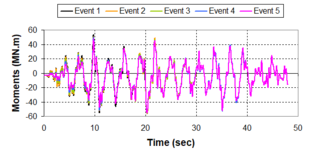
(a) AB4 bridge |
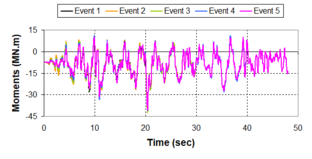
(b) AR4 bridge |
Maximum responses of the relative displacements and velocities for the models AB4 and AR4 are summarized in Tables 3.28 and 3.29. The used nomenclature is basically the same considered before, plus Δ3-T (transverse displacement of the deck at the mid-span); V1-L (longitudinal velocity of the tower-top); V1-T (transverse velocity of the tower-top); V3-V (vertical velocity of the deck at the mid-span); V3-T (transverse velocity of the deck at the mid-span); and V4-L (longitudinal velocity of the deck). In order to expose more clear results, displacement and velocity responses are showed in absolute values, because the sign is not important at this stage. In general terms, the maximum seismic responses for displacements and velocities are similar from one event to another, although some small differences can be appreciated as was previously explained. The average of the maximum responses shows similar results comparing model AB4 with model AR4, with slight differences for vertical displacements of the deck at the mid-span, longitudinal displacements of the deck and the vertical velocities of the deck at the mid-span. More important differences were obtained for the transverse displacements and velocities of the deck at the mid-span. The more important velocities can be appreciated for the longitudinal response of the tower-top and the transverse velocity of the deck at the mid-span, with values higher than 1.5 m/sec. As a result, comparing responses of displacements and velocities between both bridge models, it is clear that the best behaviour is observed on AR4 bridge, that is to say, the harp pattern layout.
| Event | AB4 bridge | AR4 bridge | ||||||||
| Δ1-L | Δ1-T | Δ3-V | Δ3-T | Δ4-L | Δ1-L | Δ1-T | Δ3-V | Δ3-T | Δ4-L | |
| 1 | 66.8 | 36.2 | 22.8 | 60.7 | 39.1 | 63.2 | 34.8 | 18.7 | 50.1 | 35.7 |
| 2 | 62.8 | 35.6 | 23.5 | 66.8 | 37.0 | 62.4 | 35.1 | 20.7 | 49.1 | 35.1 |
| 3 | 60.7 | 31.7 | 23.4 | 56.6 | 35.8 | 60.6 | 30.8 | 20.2 | 46.5 | 34.0 |
| 4 | 58.6 | 35.5 | 23.1 | 60.2 | 34.9 | 59.8 | 36.3 | 19.7 | 54.2 | 33.5 |
| 5 | 56.0 | 37.3 | 23.4 | 66.8 | 33.1 | 57.8 | 43.6 | 19.6 | 59.6 | 33.8 |
| Average | 61.0 | 35.3 | 23.2 | 62.2 | 36.0 | 60.8 | 36.1 | 19.8 | 51.9 | 34.4 |
| Event | AB4 bridge | AR4 bridge | ||||||||
| V1-L | V1-T | V3-V | V3-T | V4-L | V1-L | V1-T | V3-V | V3-T | V4-L | |
| 1 | 1.86 | 1.07 | 0.91 | 1.93 | 1.08 | 1.70 | 1.01 | 0.67 | 1.52 | 1.04 |
| 2 | 1.72 | 0.99 | 0.97 | 1.90 | 1.03 | 1.65 | 0.99 | 0.76 | 1.41 | 1.02 |
| 3 | 1.68 | 1.00 | 0.97 | 1.87 | 1.01 | 1.64 | 1.00 | 0.74 | 1.44 | 0.99 |
| 4 | 1.62 | 1.04 | 0.94 | 1.71 | 0.98 | 1.60 | 1.09 | 0.73 | 1.43 | 0.96 |
| 5 | 1.53 | 1.00 | 0.95 | 1.67 | 0.94 | 1.58 | 1.05 | 0.67 | 1.60 | 0.94 |
| Average | 1.68 | 1.02 | 0.95 | 1.82 | 1.01 | 1.63 | 1.03 | 0.71 | 1.48 | 0.99 |
Tables 3.30 and 3.31 show comparisons of the selected maximum internal forces for both bridge models. Negative values for axial forces imply compression and absolute values for bending moments were used here.
The examination of the internal forces shows more disparities between models AB4 and AR4, and it is difficult to conclude about the best structural typology based on the internal forces only, on the contrary of the displacements and velocities for which differences are clearer. Anyway, it seems to be that AB4 bridge shows a good behaviour. Differences from one event to another are small in general terms, and maximum differences are experienced for maximum in-plane bending moments at the tower base for AB4 bridge (18% difference between event 1 and event 5). For the rest of the internal forces, differences are no greater than 10% from one event to another, and for that reason, the average of the maximum response parameter is a good measure of the response. Maximum axial forces and bending moments at the tower base are similar for both structures, with in-plane moments more than 1.8 times the out-of-plane moments of the towers. Those results are in accordance with the modal analysis and the response spectrum analysis, demonstrating that the principal direction correspond to the longitudinal direction of the bridges. The maximum bending moments of the deck are obtained at the mid-span for both bridges, as was proved with the response spectrum analysis.
As a summary, nonlinear time history analysis for far-fault ground motions shows comparable results for both bridges. AR4 Bridge is recommended for a better control of displacements and velocities, and AB4 bridge seems to be the best choice for a better control of the internal forces, although those differences can be questionable.
| Event | Nmax-towera
[kN] |
Nmax-deckb
[kN] |
Nmax-cable
[kN] |
Mmax-towera, c
[MN.m] |
Mmax-towera, d
[MN.m] |
Mmax-deck2c
[MN.m] |
Mmax-deck3c
[MN.m] |
| 1 | -165000 | -34000 | 10700 | 694.3 | 324.8 | 15.3 | 55.2 |
| 2 | -159500 | -34260 | 10400 | 653.0 | 347.6 | 16.2 | 56.8 |
| 3 | -153000 | -33800 | 10280 | 620.0 | 339.2 | 16.6 | 56.4 |
| 4 | -161000 | -32900 | 10080 | 595.6 | 351.1 | 16.1 | 55.7 |
| 5 | -163000 | -33580 | 9860 | 568.0 | 342.4 | 15.9 | 55.8 |
| Average | -160300 | -33708 | 10264 | 626.2 | 341.0 | 16.0 | 56.0 |
| Event | Nmax-towera
[kN] |
Nmax-deckb
[kN] |
Nmax-cable
[kN] |
Mmax-towera, c
[MN.m] |
Mmax-towera, d
[MN.m] |
Mmax-deck2c
[MN.m] |
Mmax-deck3c
[MN.m] |
| 1 | -160600 | -42900 | 6260 | 625.3 | 314.7 | 22.2 | 36.0 |
| 2 | -168000 | -45300 | 6260 | 652.0 | 348.0 | 23.6 | 42.5 |
| 3 | -164700 | -45300 | 6160 | 638.5 | 334.3 | 23.6 | 34.7 |
| 4 | -155600 | -45000 | 6020 | 617.5 | 356.4 | 23.4 | 41.1 |
| 5 | -157000 | -46100 | 5800 | 614.4 | 400.8 | 22.7 | 40.7 |
| Average | -161180 | -44920 | 6100 | 629.5 | 350.8 | 23.1 | 39.0 |
a At the tower base c In-plane
b At the tower-deck connection d Out-of-plane
- 3.7.5 Seismic Response Considering Near-Fault Ground Motions
Basically, the same considerations were used in the near-fault analysis for the models, including the time-step size, damping characterization and zero-time conditions among other things. Because of the inherent highly nonlinear behaviour involved in the near-source ground motion, some convergence troubles were experienced as was previously explained. In this sense, sometimes the integration parameters were strongly modified in order to reach the desired stability with the required accuracy. Numerical damping of -0.2 was enough to guarantee that the solution was invariant, with an adequate control of the high frequency content. Maximum sub-step size between 0 – 0.02 was employed, and a minimum sub-step size of zero was selected for all the bridge models. With regard to the maximum iterations per sub-step, different values were necessary to apply depending on the event and model. In the case of far-fault analysis, 60 iterations were enough; however, for near-fault ground motions, 120 iterations were a normal value, and sometimes up to 180 iterations were necessary (Landers event), with the obvious increment of computer time. To guarantee an adequate tolerance of the iterations, especially when large-displacement effects are considered, 1x10-3 value was used.
The plots of time histories shown in the following pages are very different from results obtained with the far-fault analysis, mainly because of the nature of the events (real earthquakes) and the long-period velocity pulses observed in the velocity records.
Figs. 3.65 to 3.69 show time histories for displacement responses considering AB4 and AR4 bridges, and applying the five analyzed earthquake events.
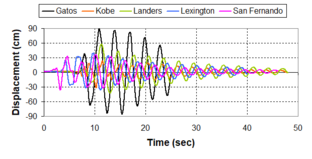
(a) AB4 bridge |
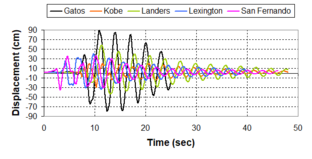
(b) AR4 bridge |
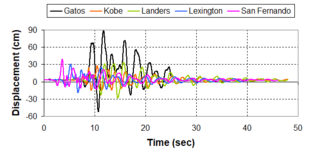
(a) AB4 bridge |
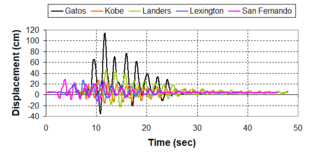
(b) AR4 bridge |
From Fig. 3.65, it is easy to observe that maximum longitudinal deck displacements are obtained with the event Gatos, showing maximum displacements of about 90 cm, for both bridge models. Those maximum displacements are followed by results obtained with event Landers (less than 60 cm maximum displacement). For the rest of the earthquake events, results are similar. It is interesting to observe that both bridges experience basically the same seismic response for longitudinal displacements of the deck.
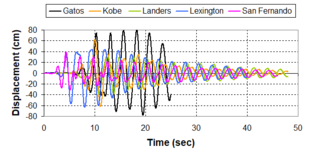
(a) AB4 bridge |
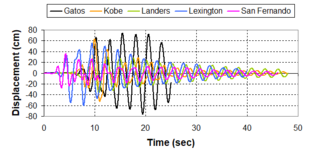
(b) AR4 bridge |
Fig. 3.66 shows time histories for vertical displacements of the deck at the mid-span. Maximum displacements are observed for event Gatos (114 cm for AR4 bridge, 89 cm for AB4 bridge), followed by displacements obtained with event San Fernando (39 cm, AB4 bridge) and event Landers (45 cm, AR4 bridge). On the contrary of the case of the longitudinal displacements of the deck, the vertical displacements are quite different comparing both bridge models, especially with events Gatos, Landers and San Fernando. For both structures, all the vertical displacements are completely damped for times over 30 sec.
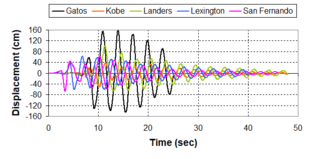
(a) AB4 bridge |
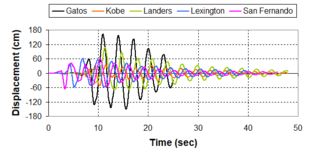
(b) AR4 bridge |
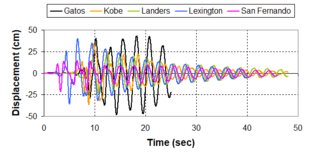
(a) AB4 bridge |
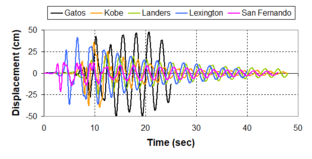
(b) AR4 bridge |
Similar comparisons to the previous formulated can be proposed for the transverse displacements of the deck at the mid-span (Fig. 3.67), longitudinal displacements of the tower-top (Fig. 3.68) and transverse displacements of the tower-top (Fig. 3.69). All of them experience similar responses comparing both models, which implies that incidence of the stay cable layout is not very important regarding the nonlinear seismic response of the displacements obtained. For all the earthquake events, the maximum responses are obtained with event Gatos followed by event Kobe (transverse displacement of the deck), Landers (longitudinal displacement of the tower-top) and Lexington (transverse displacement of the tower-top). In these sense, maximum responses are observed for the longitudinal displacements of the tower-top and vertical displacements of the deck. This pulse-type vertical motion of the deck at the mid-span is especially large for AR4 bridge, a common feature of the near-source effects.
Velocity response of the deck in the longitudinal direction is especially important in order to study the response behaviour at the possible location zones for fluid viscous dampers (energy dissipation devices), aspect enlarged in the next chapter. Plots observed in Fig. 3.70 show that maximum response is obtained, again, for event Gatos, which experiences very high velocities, larger than 2 m/sec. The rest of the earthquakes impose velocities no larger than 1.2 m/sec, as happens with the far-fault ground motions. Velocity responses are very similar comparing both models, showing again that the incidence of the stay cable layout on the seismic response is negligible in this case. These responses are damped for times over 40 sec.
With regard to the selected internal forces of this analysis, Figs. 3.71 to 3.74 show responses for axial forces and bending moments on the towers and decks. Similarly to the far-fault analysis, shear forces were not included in this analysis because the response of those structures is basically controlled by axial forces, bending moments and their interaction.
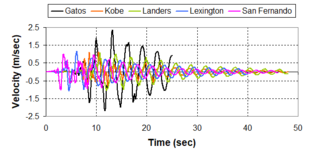
(a) AB4 bridge |
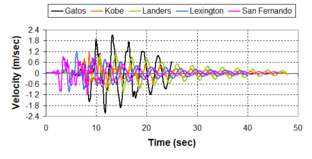
(b) AR4 bridge |
In general terms, plots of the responses for internal forces for both models are similar, and only specific differences of the peak values can be observed. Although this appreciation can be used to conclude that the effect of the stay cable layout on the seismic response is not very important, in the case of the internal forces, those differences are more significant, especially comparing the average responses between both bridges. As happens with the displacements and velocities, maximum responses for the internal forces are obtained with the earthquake event Gatos, followed very close by the event Kobe, in the case of the axial forces at the tower base.
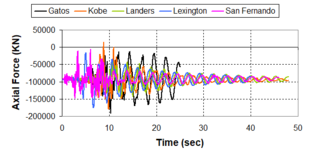
(a) AB4 bridge |
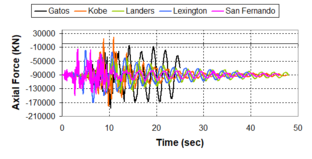
(b) AR4 bridge |
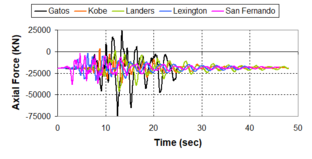
(a) AB4 bridge |
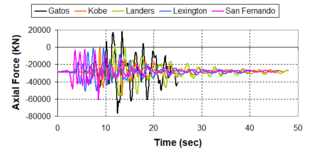
(b) AR4 bridge |
From Figs. 3.71 and 3.72, it is interesting to observe that tower and deck are basically entirely compressed (negative values), during all the time of the duration of the events, although tension forces can be appreciated at the tower base with the event Kobe; and more evidently at the deck, with the events Landers, Kobe and Gatos. The response for axial force of the deck obtained with the event Gatos strongly overpasses the zero-limit at specific times, with peak tension values of about 25000 kN (AB4 bridge) and 20000 kN (AR4 bridge). Of course, if tensions on the towers are obtained during the nonlinear time history analysis, special considerations must be taken with the design of such elements, and mainly with the foundations. The situation involving specific peak tension forces on tower and deck for both bridges was not observed during the far-fault analysis.
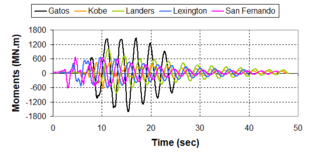
(a) AB4 bridge |
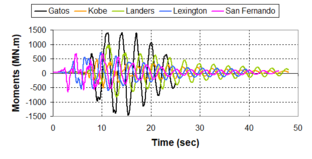
(b) AR4 bridge |
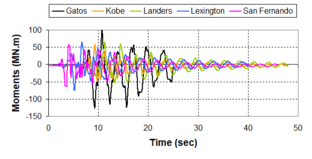
(a) AB4 bridge |
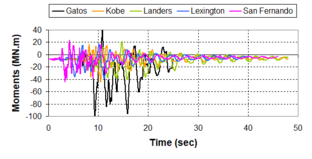
(b) AR4 bridge |
The analysis of bending moments show that very high values were obtained at the tower base, mainly with the event Gatos, followed by the event Landers (Fig. 3.73). For that reason, in order to adjust an adequate scale to represent the obtained values, bending moments at zero-time for both structures seem to be zero, although the initial values were the obtained from the nonlinear static analysis. The peak responses for in-plane bending moments at the tower base are in the order of 1600 MN.m for AB4 bridge, and 1450 MN.m for AR4 bridge, obtained with the event Gatos. Moments at the tower base obtained with the events Kobe, Lexington and San Fernando are comparable, with maximum responses of 660 MN.m. Bending moments of the deck at the mid-span are very high mainly with the event Gatos. In this case, responses for both structures are clearly different, on the contrary of the displacements or axial forces, as can be appreciated in Fig. 3.74.
A summary of the maximum relative displacements and velocities obtained with the nonlinear direct integration time history analysis for both bridges can be appreciated in Tables 7.32 and 7.33. In the same way, Tables 7.34 and 7.35 expose a summary of the selected maximum internal forces according to the near-fault analysis. For simplicity, absolute values of displacements, velocities and bending moments are showed. Negative values of axial forces imply compression. The nomenclature here applied is the same considered before.
Table 7.32 shows that maximum displacements at selected joints are obtained with the event Gatos, with maximum values for the longitudinal displacements at the tower-top (162.3 cm for AR4 bridge and 158.8 cm for AB4 bridge). More interesting observations can be formulated comparing the average of the maximum responses, in which the maximum values are obtained, in both models, for the longitudinal displacements of the tower-top (88.22 cm for AB4 bridge, 90.06 cm for AR4 bridge) and the transverse displacements of the deck at the mid-span (56.80 cm for AB4 bridge, 54.48 cm for AR4 bridge). An analogue situation was observed with the average displacements obtained with the far-fault ground motions. A comparison between both structures for the average of the maximum displacements show that similar results are obtained, with main differences experienced for the vertical displacements of the deck (10%). Velocities observed in Table 7.33 show very high values obtained with the event Gatos, and specifically, for the longitudinal velocities at the tower-top (3.94 m/sec for AR4 bridge, 3.41 m/sec for AB4 bridge). A comparison of the average responses show maximum values obtained, for both structures, with the longitudinal velocities of the tower-top and the transverse velocities of the deck at the mid-span, an analogue situation compared to the average maximum displacements. Likewise, differences on the velocity responses between both bridges are negligible, with values no greater than 5%. In this sense, as happens with the displacement response, it is difficult to formulate recommendations regarding the best stay cable layout in order to minimize the velocity response.
| Event | AB4 bridge | AR4 bridge | ||||||||
| Δ1-L | Δ1-T | Δ3-V | Δ3-T | Δ4-L | Δ1-L | Δ1-T | Δ3-V | Δ3-T | Δ4-L | |
| Gatos | 158.80 | 48.50 | 88.70 | 80.00 | 89.60 | 162.30 | 50.80 | 114.30 | 76.00 | 89.20 |
| Kobe | 50.80 | 36.50 | 27.70 | 62.50 | 31.70 | 52.50 | 39.60 | 27.00 | 63.60 | 29.50 |
| Landers | 101.20 | 24.40 | 33.50 | 38.90 | 58.30 | 107.40 | 24.60 | 45.60 | 36.10 | 58.70 |
| Lexington | 63.00 | 39.90 | 30.60 | 63.60 | 39.70 | 61.60 | 41.50 | 28.80 | 60.30 | 40.30 |
| San Fernando | 67.30 | 21.60 | 39.00 | 39.00 | 36.60 | 66.50 | 21.30 | 28.70 | 36.40 | 36.00 |
| Average | 88.22 | 34.18 | 43.90 | 56.80 | 51.18 | 90.06 | 35.56 | 48.88 | 54.48 | 50.74 |
| Event | AB4 bridge | AR4 bridge | ||||||||
| V1-L | V1-T | V3-V | V3-T | V4-L | V1-L | V1-T | V3-V | V3-T | V4-L | |
| Gatos | 3.41 | 1.42 | 2.23 | 2.10 | 2.36 | 3.94 | 1.28 | 2.84 | 2.15 | 2.22 |
| Kobe | 1.45 | 1.56 | 1.35 | 2.22 | 1.11 | 1.62 | 1.76 | 1.24 | 1.90 | 1.17 |
| Landers | 1.77 | 0.68 | 1.50 | 0.99 | 1.08 | 1.90 | 0.68 | 1.20 | 0.86 | 1.08 |
| Lexington | 1.82 | 1.66 | 1.13 | 1.90 | 1.16 | 1.63 | 1.69 | 0.96 | 2.07 | 1.21 |
| San Fernando | 1.93 | 1.01 | 1.37 | 1.39 | 1.02 | 1.76 | 0.96 | 1.13 | 1.28 | 1.21 |
| Average | 2.08 | 1.27 | 1.52 | 1.72 | 1.35 | 2.17 | 1.27 | 1.47 | 1.65 | 1.38 |
The analysis of the average maximum internal forces illustrated in Tables 7.34 and 7.35, shows more important differences between both bridge models, as occurs with the far-fault analysis. The main differences come from the maximum axial forces of the deck (23.8%), maximum cable forces (38.2%) and bending moments of the deck at the mid-span (31.1%). However, as happens with the displacements and velocities, it is difficult to propose the best cable layout to minimize the seismic response of the internal forces, and for that reason, it is not possible to propose conclusions in these matters. It seems to be that conclusions regarding the best proposal for the stay cable layout can be better formulated applying the far-fault analysis (because of the artificially generated earthquake events are very regular) or the response spectrum analysis, as was previously exposed. Anyway, as happens with the other seismic responses, maximum internal forces are obtained for the event Gatos, which shows very high values for some specific responses, as for example the in-plane bending moments at the tower base, the axial forces of the deck, the cable forces and the bending moments of the deck at the mid-span. As happens with the far-fault analysis, no important differences are appreciated with the maximum axial forces at the tower base; and regarding the maximum bending moments, values of in-plane moments are more than 2.78 and 2.64 times the out-of-plane moments for the models AB4 and AR4 respectively. These differences are more important in the near-fault analysis, which confirms that the longitudinal direction is critical. Regarding the bending moments of the deck, as happens with the far-fault analysis, maximum moments are obtained at the mid-span, with an average difference of the maximum responses of about 30% between both bridges.
| Event | Nmax-towera
[kN] |
Nmax-deckb
[kN] |
Nmax-cable
[kN] |
Mmax-towera, c
[MN.m] |
Mmax-towera, d
[MN.m] |
Mmax-deck2c
[MN.m] |
Mmax-deck3c
[MN.m] |
| Gatos | -191000 | -74400 | 18700 | 1616.3 | 449.8 | 37.9 | 125.9 |
| Kobe | -180000 | -36800 | 9270 | 647.8 | 397.1 | 20.7 | 57.8 |
| Landers | -144100 | -46300 | 13440 | 994.5 | 219.5 | 18.0 | 65.9 |
| Lexington | -176000 | -33600 | 11600 | 660.7 | 352.3 | 15.6 | 75.9 |
| San Fernando | -147100 | -38200 | 10700 | 660.6 | 227.1 | 30.3 | 64.4 |
| Average | -167640 | -45860 | 12742 | 916.0 | 329.2 | 24.5 | 78.0 |
| Event | Nmax-towera
[kN] |
Nmax-deckb
[kN] |
Nmax-cable
[kN] |
Mmax-towera, c
[MN.m] |
Mmax-towera, d
[MN.m] |
Mmax-deck2c
[MN.m] |
Mmax-deck3c
[MN.m] |
| Gatos | -186000 | -76500 | 11640 | 1466.7 | 467.3 | 36.1 | 100.8 |
| Kobe | -180400 | -56200 | 6020 | 519.8 | 396.7 | 36.4 | 44.5 |
| Landers | -141900 | -55900 | 8650 | 975.3 | 214.6 | 28.9 | 40.5 |
| Lexington | -170000 | -50900 | 7000 | 726.6 | 364.2 | 21.7 | 38.8 |
| San Fernando | -150000 | -61500 | 6070 | 691.2 | 210.7 | 32.1 | 44.2 |
| Average | -165660 | -60200 | 7876 | 875.9 | 330.7 | 31.0 | 53.8 |
a At the tower base c In-plane
b At the tower-deck connection d Out-of-plane
- 3.8 Comparative Results
The last point of this chapter exposes some comparisons between the obtained responses applying far-fault ground motions and near-fault ground motions. Moreover, in addition of the seismic responses obtained with the nonlinear time history analysis, maximum responses obtained with the response spectrum analysis are considered in order to compare results.
The comparative analysis takes into consideration the average of the absolute maximum responses because this parameter reflects in a better way the worse average condition for the selected seismic events. In fact, if the maximum of the average response is considered, different values are obtained, in which the average response is computed step-by-step, not by the security side. If the average of the absolute maximum responses is considered, higher average responses are obtained, independent on the time.
The nonlinear time-history analysis proved that the incidence of the stay cable layout was not very important on the seismic response of cable-stayed bridges, and only some specific internal forces of the deck were more affected. For that reason, it is not necessary to compare both structures again in this comparative analysis, and consequently, AR4 is taken as bridge model.
As starting point, some significant displacements are compared. Fig. 3.75 shows a comparison between average displacements considering the response spectrum method and the nonlinear time history analysis, in which both far-fault and near-fault ground motions are considered. In this case, longitudinal displacements of the deck, vertical displacements of the deck at the mid-span (where the vertical deflection of the deck is maximum), transverse displacements of the deck at the mid-span, and longitudinal displacements of the tower-top (where the peak displacements of the tower are obtained) are considered.
In general terms, results obtained with the far-fault analysis are higher than results obtained with the response spectrum analysis, and results obtained with the near-fault analysis are higher than that of the far-fault ground motions. An exception can be observed for the case of the transverse displacements of the deck (Fig. 3.75c), in which the maximum response is obtained applying the response spectrum method. Anyway, in this case the near-fault analysis gives higher average results of the displacements compared with the far-fault analysis. Specifically, differences between results obtained with far-fault and the response spectrum analysis are of 21.2%, 21.7%, 12.6% and 30% for longitudinal displacements of the deck, vertical deflections of the deck, transverse deflections of the deck and longitudinal deflections of the tower-top respectively. Differences between results obtained with far-fault and near-fault analysis are of 32.1%, 59.5%, 4.8% and 32.5% for longitudinal displacements of the deck, vertical deflections of the deck, transverse deflections of the deck and longitudinal deflections of the tower-top respectively. Obviously, more important differences are obtained comparing far-fault with near-fault ground motions, which indicates the importance of an adequate analysis in such situations. Of course, differences between near-fault analysis and the response spectrum analysis are much greater. It is interesting to observe that the analysis of the transverse deflections of the deck shows the same magnitude order for the obtained displacements, with no evident incidence of the ground motion type, even if the response spectrum analysis is applied. The analysis of the average maximum velocities shows similar results than the displacements analysis, and for that reason was not considered here.
Fig. 3.76 shows comparative results for the compressive forces at the tower base, compressive forces of the deck at the tower-deck connection (where the axial forces of the deck are maxima) and the tension forces of the most unfavourable cables respectively. With no exception, average axial forces of the far-fault condition are higher than axial forces obtained with the response spectrum analysis; and the axial forces obtained with near-fault ground motions are higher than that of the far-fault analysis. Specific differences for the axial forces between the far-fault condition and the response spectrum analysis are of 1.9%, 3.8% and 18% for the compressive forces at the tower base, compressive forces of the deck and tension forces of the cables respectively. Comparing near-fault with far-fault ground motions, differences are of 2.7%, 25.4% and 22.6% for the same internal forces. Those results prove again that maximum differences are obtained between near-fault and far-fault ground motions, and lower differences can be appreciated comparing far-fault condition with the response spectrum analysis. Also, analysis of the compressive forces at the tower base show similar results for all the cases, with no important differences.
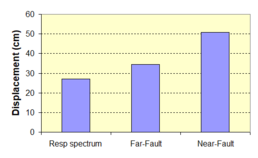
(a) Longitudinal displacement of the deck |
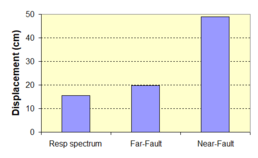
(b) Vertical deflection of the deck at the mid-span |
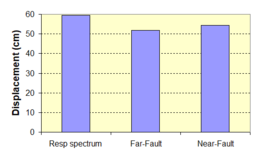
(c) Transverse displacement of the deck at the mid-span |
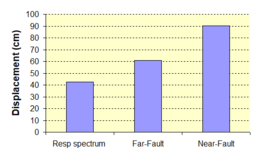
(d) Longitudinal displacement of the tower-top |
The analysis of the bending moments (Fig. 3.77) shows again that the average of the maximum responses for the far-fault condition is higher than the average obtained with the response spectrum analysis, with the exception of the bending moments of the deck at the mid-span. Similarly, average of the maximum responses obtained with the near-fault condition is higher than that obtained with the far-fault analysis, with the exception of the out-of-plane bending moments at the tower base. Specific differences on the average responses between the far-fault condition and the response spectrum analysis are of 21.2%, 2.8% and 14.5% for in-plane bending moments at the tower base, out-of-plane moments at the tower base and bending moments of the deck at the mid-span respectively. Differences on the average responses between far-fault and near-fault conditions are of 28.1%, 5.7% and 27.5% for in-plane bending moments at the tower base, out-of-plane moments at the tower base and bending moments of the deck at the mid-span respectively. Observing Fig. 3.77b and the specific differences obtained, it is easy to see that no important differences on the average response are associated to out-of-plane bending moments at the tower base.
Summarizing, it is observed that the average of the absolute maximum responses associated to the far-fault ground motions are higher than the responses associated to the response spectrum analysis, and similarly, average of the absolute maximum responses associated to the near-fault ground motion are higher than the obtained with the far-fault motions. In this sense, the greatest differences are obtained comparing near-fault with far-fault ground motions. This implies that application of the response spectrum method for the seismic design of cable-stayed bridges is not recommended, and worse, unsecure.
On the other hand, comparing responses obtained with the near-fault ground motions, it is clear that the worse condition is observed with Gatos event. In this sense, San Fernando earthquake experiences the highest PGA, much higher than that observed with Gatos event; however, maximum responses were obtained with Gatos earthquake, which experiences higher spectral velocities than San Fernando earthquake. This confirms that the analyzed structures are more sensitive to velocities than accelerations. A similar situation occurs comparing the events of Landers and San Fernando.
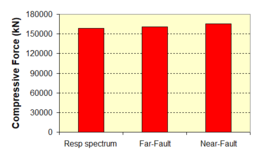
(a) Compressive forces at the tower base |
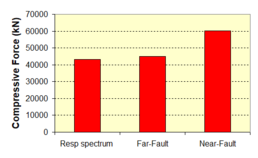
(b) Compressive forces of the deck at the tower-deck connection |
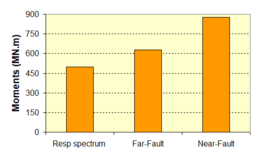
(a) In-plane bending moments at the tower base |
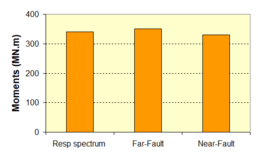
(b) Out-of-plane bending moments at the tower base |
Chapter 4. Seismic Protection. Application of Fluid Viscous Dampers
- 4.1 General Considerations
Fluid viscous dampers constitute an attractive methodology to protect structures against earthquakes. Application of those strategies on buildings and bridges has been widely used, but their incorporation on cable-stayed bridges has been slow. For that reason, this study is focused on the implementation of nonlinear viscous dampers as additional energy dissipation devices on such structures, with the purpose of analyze their seismic response in the presence of both far-fault and near-fault ground motions. In order to simplify this analysis and to consider the same nonlinear time history analyses cases previously discussed, AB4 and AR4 bridge models are studied. With this selection, the incidence of the stay cable layout on the seismic response and an adequate comparison with the undamped cases is possible.
This part of the research considers the analysis of the bridge models applying nonlinear direct integration time history analysis, by using the Hilber-Hughes-Taylor-α method [Hilber et al, 1977], aspect enlarged in Appendix A. All the analyses are performed using the code SAP2000 [Computers & Structures, 2007], with the geometric definition, structural modelling, material data, mechanical properties and loads considered in Chapter 3. Because of the highly nonlinear and complex nature of the fluid viscous dampers, response spectrum analysis is not possible, and only time history analysis cases are applied using both far-fault and near-fault orthogonal three-component recordings processed before, and taking into account the velocity-sensitivity of the structures. The damping characteristics are empirically calculated according to Kawashima and Unjoh (1991), considering that the complex damping mechanism of cable-stayed bridges is only dependent on the modal shapes. The excitation amplitude dependency of the damping is not considered here, and for that reason, Rayleigh’s proportional damping is proposed for the time history analyses. With regard to the stay prestressing forces of the bridges, because of the low variations of the seismic response in the presence of low-to-moderate variations of the static cable forces according to Chapter 3, no additional static modifications of the cable forces are introduced here.
The incorporation of nonlinear fluid viscous dampers makes the analysis very complex because of the highly nonlinear behaviour of the whole structure, and a lot of trial-and-error tests were necessary to guarantee an accurate convergence. As explained in Appendix A, stability conditions are difficult to guarantee when nonlinear behaviour is experienced, and preliminary tests are absolutely necessary to calibrate the parameters of the analysis. In this sense, to control de convergence of the models, the same time integration parameters used in the analysis without additional damping were applied here: 0.02 sec time-step size, maximum and minimum sub-step size, maximum iterations per sub-step and the iteration convergence tolerance. The numerical damping applied to control the instability due to the high frequency content is selected as -0.2, guaranteeing that the response is not dependent on this parameter. As a summary, more than 80 analyses implying more than 280 hours of computer full-time were necessary.
The Chapter begins with the definition of the structural modelling of the viscous dampers, and the considered parameters. With the aim to select the optimal arrange of the dampers, five different damper layouts are studied, considering the worse conditions for both far-fault and near-fault ground motions. With this analysis, the definitive structural layout for the study of the bridges including additional viscous dampers is achieved, and the new dynamic characterization of the bridges is exposed, including evaluation of natural periods, modal shapes and modal damping. In order to select the optimal damper parameters, a parametric study is conducted with one of the bridge models and considering again the worse conditions for both far-fault and near-fault ground motions. After that, the influence of the velocity exponent of the dampers is analyzed. The nonlinear time history analysis applying the optimal damper parameters for both structures is then performed, considering all the analysis cases for both far-fault and near-fault ground motions. Finally, comparative studies between the optimal solutions, with and without the incorporation of additional dampers, are performed. Comparisons between far-fault and near-fault ground motions considering the effects of the stay cable layout are included, as well as an energy characterization of the problem.
- 4.2 Modelling of Nonlinear Fluid Viscous Dampers
Modelling of nonlinear fluid viscous dampers considers the use of nonlinear link elements according to the structural code SAP2000. Because of the inherent nonlinear behaviour of the dampers, during the analysis, the nonlinear force-deformation relationships are used at all degrees-of-freedom for which nonlinear properties were specified, and for that reason, linear effective stiffness and linear effective damping is not used for any nonlinear analysis. In this sense, nonlinear time-history analysis is absolutely necessary when nonlinear additional energy dissipation devices are added. This is the correct way to determine the effect of added dampers, since nonlinear time-history analysis does not use the effective damping values, and the energy dissipation in the elements is directly accounted for, as well as the effects of modal cross-coupling [Computers & Structures, 2007].
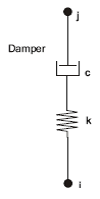
Fig. 4.1 Maxwell Viscoelasticity Model for Nonlinear Dampers |
In the structural modelling of nonlinear fluid viscous dampers, only axial nonlinear properties were defined (axial deformational degree-of-freedom). The damping properties are based on the Maxwell model of viscoelasticity [Malvern, 1969] having a nonlinear damper in series with a spring, according to Fig. 4.1.
The nonlinear force-deformation relationship is given by: where k is the spring constant, c is the damping coefficient, N is the velocity exponent of the damper, dk is the deformation across the spring, and |
The spring and damping deformations sum to the total internal deformation d = dk + dc.
The series spring is very important for capturing realistic behaviour of nonlinear dampers, especially those with fractional exponents. It represents the elastic flexibility of the damping device, including the fluid column and the connecting mechanism, preventing the damping term from producing unrealistic large viscous forces at small velocities. However, with the purpose of obtaining pure viscous damping, the spring deformation was limited introducing large stiffness value of k, typically of about 102 times as large as the corresponding stiffness in any connected elements. It was proved in this work that larger values of k cause numerical difficulties during solution, implying that convergence can be strongly affected. Of course, consideration of pure damping can affect the response of the structures in terms of the permanent displacements after the event, especially in presence of strong ground motions; however, in the practical engineering, incorporation of structural fuses may reduce or limit to zero the permanent displacements under service loads and low-to-moderate earthquakes (aftershock displacements). In this theoretical analysis, this issue is not very important, because the pure damping mechanism is analyzed, that is to say, the energy dissipation capacity of the devices considering pure additional damping, which implies that structural fuses or any other additional mechanism to provide an initial stiffness, have failed. The failure of the additional devices to provide an initial stiffness is absolutely necessary when strong ground motion happens, allowing the desired performance of the dampers. Likewise, the inherent low stiffness of the dampers has minimal influence on the fundamental natural frequency [Symans et al, 2008]. For that reason, in this investigation, the minimal restoring force of the dampers may induce permanent displacements after some earthquake events.
The correct definition of the additional damping devices requires the specification of the nonlinear properties used for nonlinear analysis: stiffness, damping coefficient and velocity exponent. Those specific values are the key of the design of the dampers, and they are specified according to the procedure explained in the point 4.1 of this chapter, starting from initial values taken from practical recommendations, as can be seen next. With regard to the mass and area properties of the dampers, elements with zero-mass and zero-weight were defined because those properties do not longer affect the response of the structures. Similarly, zero-rotational inertias were defined for the same reasons.
Finally, it is important to say that, on the contrary of the viscoelastic dampers, frequency and temperature dependency is minimum [Symans et al, 2008], which simplifies the mathematical modelling of the viscous dampers.
- 4.3 Optimal Arrange of the Dampers
One of the questions that designers need to respond is the best configuration of the dampers into the structure. The dampers are external devices, normally not affected by direct permanent loads, and located at places where the replacement or inspection is easy. In buildings, this task sometimes can be complicated, because of the numerous possibilities in which the dampers can be located; and for that reason, optimization procedures can be an excellent tool that can help designers in those decisions. In the case of bridges, possibilities for the location of the external devices are much more limited, and normally the dampers need to be installed at the deck-ends (abutment-deck connection) and/or at the pylon/tower-deck connection.
In order to investigate the best locations of the damper devices for this research, a brief study was conducted considering five analysis cases, all applied to the AB4 model. The first case considered locations of the dampers at the deck-ends only, in the longitudinal direction. Case 2 considered longitudinal dampers at the deck-ends and at the tower-deck connections, in which the fixed-hinge of the tower-deck connections was changed by roller supports plus the dampers. Case 3 considered dampers at the deck-ends plus longitudinal damper in one of the tower-deck connections, and the replacement of the associated tower-deck connection by roller supports. Case 4 considered dampers at the deck-ends and transverse dampers plus roller supports at the tower-deck connections. Finally, case 5 considered dampers at the deck-ends and at the tower-deck connections for both directions, plus the corresponding replacement of the tower-deck connections by roller supports. It is obvious that cases 4 and 5 are an attempt of exploring the tri-dimensional response of the bridges in the presence of additional damping devices selected to control the longitudinal and transverse responses. Table 4.1 summarizes the five analysis cases.
Table 4.1 Layout of the Tower-Deck Connections and Dampers for the Analysis Cases
| CASE | Deck-ends | Tower 1 | Tower 2 | |||||||
| Support | Damper | Longitudinal Dir | Transverse Dir | Longitudinal Dir | Transverse Dir | |||||
| connection | damper | connection | damper | connection | damper | connection | damper | |||
| 1 | roller | yes | fixed-hinge | no | fixed-hinge | no | fixed-hinge | no | fixed-hinge | no |
| 2 | roller | yes | roller | yes | fixed-hinge | no | roller | yes | fixed-hinge | no |
| 3 | roller | yes | roller | yes | fixed-hinge | no | fixed-hinge | no | fixed-hinge | no |
| 4 | roller | yes | fixed-hinge | no | roller | yes | fixed-hinge | no | roller | yes |
| 5 | roller | yes | roller | yes | roller | yes | roller | yes | roller | yes |
According to Table 4.1, replacement of fixed-hinges by roller connections is selected when dampers are added, allowing the free displacements of them, with the subsequent energy dissipation. The vertical seismic protection with damping devices was not included because of the low incidence of the vertical motion on the overall response of the models according to the Modal Analysis explained in Chapter 3. Although the vertical motion can be especially important in the presence of near-source earthquakes, this analysis is not the aim of this work, and can be proposed as further research.
In order to study the effects of both far-fault and near-fault ground motions for the analysis cases, the worse seismic conditions were selected according to Chapter 3. The orthogonal three-component seismic inputs of Event 5 (far-fault) and Gatos (near-fault) were applied here.
The modelling of AB4 bridge is basically the same previously considered, with the replacement of some tower-deck connections and the addition of the dampers. The roller connection between the lower strut of the tower and the deck was idealized using massless linear rigid-links of zero-length, in which the non operative degrees-of-freedom were fixed, allowing free rotations and displacements according to the allowable degrees-of-freedom. These rotations and relative displacements were permitted by using zero-stiffness associated to the activated degrees-of-freedom of the rigid-links. Modelling of the dampers was conducted using the code SAP2000, according to the specifications of point 4.2, and considering that all the dampers were initially identical, independent on the location or action direction. This assumption is very important because involves the same damping conditions for all the cases, allowing adequate comparisons. In this sense, recommendations of Alvarez (2004) were applied here to select the nonlinear damper properties; considering a provided damping of 25%, damping coefficient C equal to 30 MN/(m/sec)0.5, and velocity exponent N of 0.5.
The analysis of all the nonlinear cases was performed using the code SAP2000, applying the Hilber-Hughes-Taylor-α step-by-step integration method. The stability conditions with accurate results were guaranteed considering 0.02 sec time-step size, -0.2 numerical damping, maximum sub-step size of 0.02 sec, minimum sub-step size equal to zero, 70 and 140 maximum iterations per sub-step for far-fault and near-fault ground motions respectively, and 0.0001 or 0.001 iteration convergence tolerance for far-fault and near-fault ground motions respectively. As was previously explained, the damping mechanism was selected as Rayleigh’s type, applying 0.074 mass proportional coefficient and 5.13x10-4 stiffness proportional coefficient according to the modal damping exposed in Chapter 3.
Time histories shown in Figs. 4.2 to 4.8 represent the seismic response of the AB4 model for both far-fault and near-fault conditions, and considering that those plots give a good idea about the whole response of the structure when subjected to strong ground motion in the presence of additional damping devices. The presence of additional dampers basically permits an adequate control of the deck motion and the subsequent control of the internal forces of the structure. Consequently, longitudinal displacements of the deck, transverse displacements of the deck at the mid-span, axial forces at the tower base and axial forces of the deck at the tower-deck connection are represented in Figs. 4.2 to 4.5. Figs. 4.6, 4.7 and 4.8 show the obtained forces into the dampers at the deck-ends and at the tower-deck connection in the longitudinal and transverse directions respectively. Similarly to Chapter 3, time-history plots associated to the strong motion duration of far-fault ground motion are shown. Positive values of axial forces imply tension, and negative axial forces imply compression. Similarly, negative forces at the dampers imply compression of the silicone fluid.
As happens with the undamped cases, time histories begin with non-zero initial conditions (with the exception of the transverse displacements of the deck) because of the results of the nonlinear static analysis are considered as starting point of the nonlinear time history analysis.
In general terms, a comparable behaviour of the seismic response is observed, independent on the analyzed case, that is to say, similar plots of the seismic responses are obtained for each measured response, with no important differences between the damper layouts. For that reason, the best layout is obviously the case implying few dampers controlling the best possible and imposing the lowest damper forces. Plots of displacements and axial forces show the highest values of the seismic response for the near-fault condition. A similar situation is observed with the damper forces. With regard to the axial forces, compressions at the tower base are observed for all the cases; however, for the axial forces of the deck, tension peaks can be appreciated with cases 3 and 4.
(a) Far-fault ground motion |
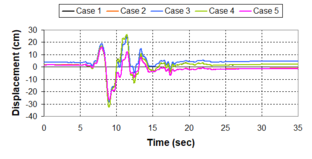
(b) Near-fault ground motion |
Fig. 4.2 Longitudinal Displacement of the Deck
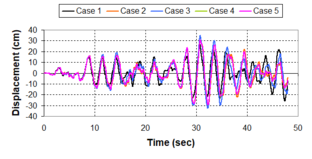
(a) Far-fault ground motion |
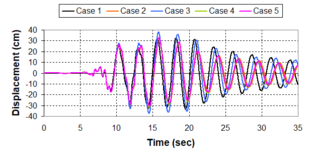
(b) Near-fault ground motion |
Fig. 4.3 Transverse Displacement of the Deck at the Mid-Span
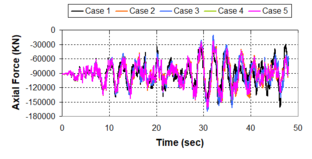
(a) Far-fault ground motion |
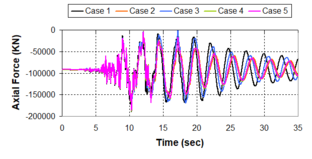
(b) Near-fault ground motion |
Fig. 4.4Axial Force at the Tower Base
An exhaustive comparison between different damper layouts shows that the worse conditions for both far-fault and near fault ground motions are obtained with case 3 followed close by cases 1 and 4. Best cases for an adequate control of the longitudinal and transverse displacements of the deck are obtained with cases 2 and 5. Similarly, axial forces of the tower and deck are better controlled with cases 2 and 5.
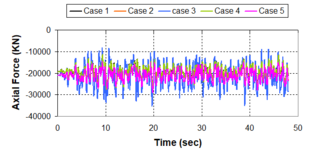
(a) Far-fault ground motion |
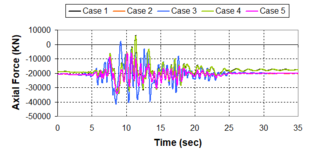
(b) Near-fault ground motion |
Fig. 4.5 Axial Force of the Deck at the Tower-Deck Connection
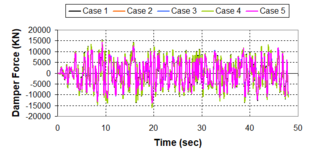
(a) Far-fault ground motion |
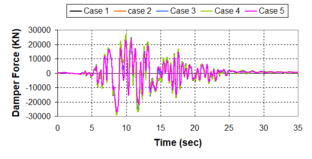
(b) Near-fault ground motion |
Fig. 4.6 Deck-end Damper Forces
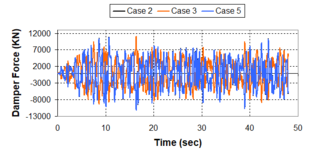
(a) Far-fault ground motion |
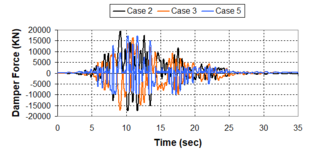
(b) Near-fault ground motion |
Fig. 4.7 Longitudinal Damper Forces at the Tower-Deck Connection
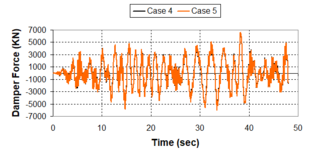
(a) Far-fault ground motion |
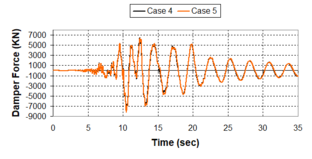
(b) Near-fault ground motion |
Fig. 4.8 Transverse Damper Forces at the Tower-Deck Connection
The analysis of the damper forces shows that for far-fault ground motion case 2 controls efficiently deck-end damper forces and longitudinal damper forces at the tower-deck connection. For near-fault ground motion, cases 2 and 5 adequately control deck-end damper forces, but for the longitudinal damper forces at the tower-deck connection, case 5 is the best choice and case 2 seems to be an unfavourable layout. Regarding the transverse damper forces at the tower-deck connection, time-history plots show that for both far-fault and near-fault ground motions, cases 4 and 5 are practically superimposed, experiencing the same behaviour. This implies that both cases are the same in terms of the control of the transverse damper forces.
As a conclusion of the analysis of the time-history plots, case 3 is definitively rejected, and cases 2 and 5 seem to be good candidates, although not very important differences can be appreciated in some cases.
As a complement of the time-history plots, Tables 4.2 to 4.5 show a summary of the maximum main responses for the five cases in terms of displacements, velocities, internal forces, damper forces and damper velocities respectively. Δ1-L is the maximum displacement of the tower-top in the longitudinal direction; Δ3-V is the maximum vertical displacement of the deck at the mid-span; Δ3-T is the maximum transverse displacement of the deck at the mid-span; and Δ4-L is the maximum longitudinal displacement of the deck. Analogously, velocities V at the same points for the control of displacements were defined, according to the nomenclature for the seismic responses applied in Chapter 3. Displacements and velocities are shown as absolute values for simplicity. Likewise, maximum internal forces on the structure are shown as absolute values for bending moments. Nomenclature for internal forces is the same considered in Chapter 3. In Table 4.5, maximum damper velocities (Vmax) and forces (Fmax) are shown for deck-end dampers, longitudinal tower dampers and transverse tower dampers respectively. Response of the dampers is shown in absolute values.
Table 4.2 Maximum Relative Displacements [cm] and Velocities [m/sec] in the Structure
| CASE | Far-Fault Ground Motion | Near-Fault Ground Motion | ||||||||||||||
| Δ1-L | Δ3-V | Δ3-T | Δ4-L | V1-L | V3-V | V3-T | V4-L | Δ1-L | Δ3-V | Δ3-T | Δ4-L | V1-L | V3-V | V3-T | V4-L | |
| 1 | 12.1 | 13.8 | 66.7 | 8.7 | 0.51 | 0.71 | 1.66 | 0.31 | 59.2 | 26.2 | 84.5 | 32.4 | 1.55 | 0.97 | 1.92 | 0.99 |
| 2 | 13.4 | 15.1 | 70.9 | 5.5 | 0.49 | 0.7 | 1.72 | 0.25 | 59.3 | 33.2 | 78.2 | 26.6 | 1.52 | 0.82 | 1.91 | 0.87 |
| 3 | 12.7 | 17.7 | 67.6 | 9.5 | 0.56 | 0.72 | 1.65 | 0.27 | 66.6 | 45.8 | 78.7 | 28.6 | 1.67 | 1.36 | 2.05 | 0.96 |
| 4 | 13.5 | 13.9 | 69.8 | 8.7 | 0.5 | 0.75 | 1.75 | 0.3 | 59.1 | 25.9 | 70.8 | 32.5 | 1.55 | 0.96 | 1.84 | 0.99 |
| 5 | 13.5 | 15.4 | 70 | 5.4 | 0.49 | 0.72 | 1.76 | 0.25 | 59.4 | 32.6 | 71.6 | 26.6 | 1.52 | 0.83 | 1.83 | 0.87 |
According to Table 4.2, similar results are obtained for the displacements in the presence of far-fault ground motion, for each measured response. Maximum differences are obtained for the longitudinal displacements of the deck (43%), with maximum value for case 3. Similar differences are obtained comparing velocities between the analyzed cases. For near-fault ground motion, more important differences are obtained, and especially for the vertical and transverse displacements of the deck. Analogue differences are obtained for velocities. Furthermore, for both near-fault and far-fault ground motions, maximum displacements and velocities are obtained for the transverse displacements of the deck, independent on the damper layout. Likewise, it is confirmed that the worse condition is obtained for case 3, and the best results are obtained for cases 1, 2 and 5, for both far-fault and near-fault earthquakes. In this sense, comparing cases 2 and 5, it is obvious that practically the same maximum responses are obtained in both situations
Table 4.3 Maximum Main Forces on the Structure – Far-Fault Ground Motion
| CASE | Mmax-towera, c [MN.m] | Mmax-towera, d [MN.m] | Mmax-deck3e [MN.m] | Nmax-towera [kN] | Nmax-deckb[kN] | Nmax-cable [kN] |
| 1 | 189.9 | 341.5 | 31.0 | -161400 | -27900 | 6970 |
| 2 | 187.2 | 414.2 | 33.1 | -163400 | -29100 | 6800 |
| 3 | 177.0 | 428.2 | 33.4 | -169400 | -35300 | 6800 |
| 4 | 204.7 | 403.2 | 31.7 | -163000 | -28800 | 7070 |
| 5 | 187.4 | 405.5 | 33.6 | -163000 | -29000 | 6830 |
Table 4.4 Maximum Main Forces on the Structure – Near-Fault Ground Motion
| CASE | Mmax-towera, c [MN.m] | Mmax-towera, d [MN.m] | Mmax-deck3e [MN.m] | Nmax-towera [kN] | Nmax-deckb[kN] | Nmax-cable [kN] |
| 1 | 536.2 | 435.9 | 63.2 | -189400 | -34000 | 8400 |
| 2 | 581.1 | 419.3 | 70.0 | -184000 | -34500 | 8600 |
| 3 | 606.4 | 485.5 | 73.5 | -189000 | -41600 | 8300 |
| 4 | 518.2 | 418.4 | 62.7 | -188200 | -33800 | 8270 |
| 5 | 580.2 | 421.1 | 70.3 | -186000 | -34300 | 8620 |
a At the tower base c In the bridge plane d Out-of-plane
b At the tower-deck level - Implies compression e At the mid-span
The analysis of the internal forces shows again the worse condition obtained with case 3. For far-fault ground motion, the best results are obtained with case 1, on the contrary of the near-fault ground motion, in which minimum responses are obtained with cases 2 and 4. Likewise, the analysis of the maximum internal forces shows more important differences than the analysis of displacements and velocities. On the other hand, comparing far-fault with near-fault ground motions, it is interesting to observe that maximum bending moments of the towers are obtained at the base in the longitudinal direction (in-plane) for the near-fault condition; on the contrary of the case of the far-fault condition, in which maximum bending moments are obtained in the transverse direction (out-of-plane). This implies that the selected dampers are more effective in reducing the in-plane bending moments of the towers for far-fault ground motion, independent on the damper layout, because according to the undamped analysis of the bridge models, for both far-fault and near-fault ground motions, maximum moments of the towers were always obtained in the longitudinal direction (in-plane). Likewise, as happens with the previous results, maximum responses are always obtained for near-fault ground motion.
Table 4.5 Maximum Damper Forces [kN] and Velocities [m/sec]
| CASE | Far-fault ground motion | Near-fault ground motion | ||||||||||
| Deck-end
damper |
Long tower
damper |
Transv tower
damper |
Deck-end
damper |
Long tower
damper |
Transv tower
damper | |||||||
| Vmax | Fmax | Vmax | Fmax | Vmax | Fmax | Vmax | Fmax | Vmax | Fmax | Vmax | Fmax | |
| 1 | 0.28 | 16000 | --- | --- | --- | --- | 0.94 | 29100 | --- | --- | --- | --- |
| 2 | 0.23 | 14400 | 0.14 | 11100 | --- | --- | 0.83 | 27300 | 0.43 | 19600 | --- | --- |
| 3 | 0.26 | 15300 | 0.14 | 11100 | --- | --- | 0.91 | 28700 | 0.33 | 17300 | --- | --- |
| 4 | 0.28 | 16000 | --- | --- | 0.047 | 6500 | 0.94 | 29100 | --- | --- | 0.072 | 8070 |
| 5 | 0.23 | 14500 | 0.14 | 11100 | 0.048 | 6600 | 0.82 | 27200 | 0.42 | 19500 | 0.075 | 8200 |
Results observed in Table 4.5, show again maximum damper forces and velocities obtained for near-fault ground motion. The highest velocities are obtained for deck-end dampers, independent on the damper layout case, with values up to 2.75 times the velocity of the longitudinal tower dampers (case 3, near-fault ground motion). The lowest damper velocities are obtained for transverse dampers at the tower-deck connection, with differences up to 5.6 times compared with longitudinal velocities (case 5, near-fault ground motion). Of course, an analogue situation is experienced with the damper forces, with peak values obtained for deck-end dampers, followed by longitudinal dampers at the tower-deck connection and transverse dampers respectively. Comparing the analyzed cases, it is easy to see that the best results are obtained, for far-fault and near-fault ground motions, with cases 2 and 5. It is important to say that damper forces are a condition that cannot be forgotten, because the price of the dampers are directly related with their capacity, and for that reason we are interested in the lowest damper forces.
As a conclusion of the analysis of time histories and maximum responses obtained, cases 2 and 5 are the best options that minimize the response of the structure and dampers, for both far-fault and near-fault ground motions. Differences on the maximum responses between these cases are absolutely negligible, and considering that the minimum number of dampers (involving a lower price) is the optimal solution; it is evident that case 2 is the best choice.
The chosen damper layout means a solution implying in-plane location of the dampers, that is to say, a negligible effect of the transverse protection that was the proposal of case 5. As example, Fig. 4.9(a) shows a comparison of the damped and undamped maximum displacements of the deck for both longitudinal and transverse directions; and Fig. 4.9(b) shows bending moments at the tower base for both in-plane and out-of-plane directions respectively.
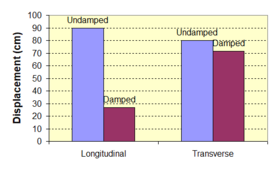
(a) Maximum displacements of the deck |
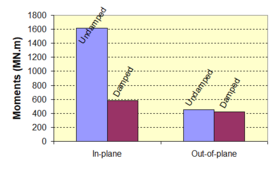
(b) Maximum bending moments at the tower base |
Fig. 4.9 Comparison of Maximum Responses for Damped and Undamped Cases – AB4 Model
The analysis was performed for AB4 model, considering the event Gatos as input ground motion. For the damped analysis, layout of case 5 was applied, that is to say, both longitudinal and transverse protection of the bridge with fluid viscous dampers, according to Table 4.1.
Results of this comparison are evident. In the case of maximum displacements of the deck, 70% reduction between the undamped and damped longitudinal displacements is obtained. For the transverse displacements of the deck at the mid-span, reduction of 10.5% is obtained. Observing Fig. 4.9(b), 64% reduction of in-plane bending moments at the tower base is obtained; and 6.4% reduction for out-of-plane bending moments. Similar results are obtained if far-fault ground motions are considered. In other words, really important reductions of the seismic response are experienced in the longitudinal direction, as long as reductions in the transverse direction are very little, even if special dampers are located in the transverse direction. Those results are confirmed with the analysis of the damper forces (Table 4.5), in which maximum velocities and damper forces were obtained for the longitudinally located dampers, implying lower seismic response. As a conclusion, transverse dampers are not efficient in this case, and only in-plane layout is enough for an adequate protection.
The reason why transverse dampers are not very efficient can be explained in the fact that those devices are located at the tower-deck connection, that is to say, as part of the structure. This means that motion of transverse dampers, as rigid body, is governed by motion of the tower at that level, as well as the deck motion; and for that reason, energy dissipation is controlled by relative displacements between the lower strut of the tower and the deck. In other words, tower, deck and dampers move jointly during seismic events, and energy dissipation occurs when relative displacements between those elements happen. A similar situation occurs with longitudinal dampers located at the tower-deck connection. However, in this case, more important velocities and damper forces are reached, with the subsequent higher energy dissipation compared with the transverse dampers. The highest velocities and damper forces are reached for deck-end dampers, and of course, higher energy dissipation is experienced, aspect that can be confirmed with the important seismic response control appreciated in Tables 4.2 to 4.4. In this case, longitudinal dampers are located between the deck-ends and the abutments, that is to say, those devices cannot be considered as part of the structure, with higher relative displacements and the subsequent higher energy dissipation. In other words, deck-end dampers imply one fixed-end and one movable-end. Tower dampers in both longitudinal and transverse directions imply movable-ends. As a conclusion, longitudinal dampers at the deck-ends are the most efficient devices, dissipating the largest amount of energy. Longitudinal dampers at the tower-deck connection increase the seismic response control basically reducing displacements of the deck.
Summarizing, damper layout considering devices located in the longitudinal direction, on towers and deck-ends, permits an efficient seismic response control, being the optimal solution. Fig. 4.10 shows the layout of the supports and damper devices at the deck-ends and at the tower-deck connection.
- (1) Longitudinal layout of supports and dampers
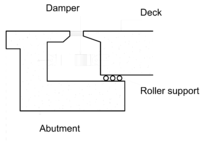
(b) Detail A |
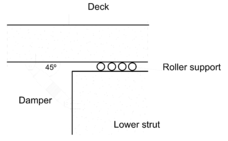
(c) Detail B |
Fig. 4.10 Optimal Layout of the Dampers
Position of the damper at the tower-deck connection considers an oblique location. Of course, it is possible to locate those devices considering other proposals; however this layout is simple for repairing or maintenance. This configuration needs to be considered only as basic or schematic solution, because definitive position and the main details must be materialized according to the definitive design, manufacturer’s specifications and constructive issues.
The exposed analysis represents the general tendency of cable-stayed bridges considering different layouts of supports and dampers. The analysis was performed using the worse conditions for both far-fault and near-fault ground motions according to the selected earthquake database, and of course, some variations may be experienced if different conditions are considered. Regarding the bridge models, similar conclusions may be obtained if AR4 bridge is analyzed, according to the results of Chapter 3.
- 4.4 Modal Analysis Considering the Optimal Arrange of the Dampers
An exhaustive modal analysis was performed for the undamped bridge models in Chapter 3. That study left clear the importance of an adequate modal analysis as first step in the nonlinear seismic analysis of cable-stayed bridges.
Incorporation of additional damping devices, and specifically fluid viscous dampers, does not change the structural period because of viscous damping is 90º out-of-phase with respect to the structural forces [Lee and Taylor, 2001]. However, modification of the support conditions at the tower-deck connection by roller supports inherently includes modal changes. For that reason, considering the optimal damper layout for both AB4 and AR4 bridge models, a modal analysis is performed. The aim of this study is to show results of natural periods, modal shapes and modal damping for those structures. Because of the same general conclusions of the modal analysis for the undamped cases are valid in this case, a brief summary of the main results is exposed.
Due to its accuracy and information regarding the spatial distribution of the dynamic loads, Ritz-vector analysis is applied considering the stiffness at the end of the nonlinear static analysis. The analysis took into account the necessary starting load vectors, including loads applied on elements, links and dampers. Modelling, loads, materials and general properties are the same considered before.
Table 4.6 shows natural periods and nature of the modal shapes for the first 15 modes, in which some changes on the natural periods for both bridge models compared with the undamped cases are obtained. As was explained, those changes are in accordance with the change of the support conditions at the tower-deck connection, which enlarges the fundamental period for both structures. It is observed a higher fundamental period for AB4 bridge (6.0 sec) compared with AR4 bridge (3.24 sec). This implies for these new conditions, that AR4 model is longitudinally stiffer than AB4 model, aspect that can be explained because of the intrinsic additional stiffness provided by the shortest cables of the harp pattern in the presence of roller supports at the tower-deck connection. For fixed-hinge connections, as happens with the undamped cases, this additional stiffness is not obvious, as can be seen in Chapter 3. In this sense, it was demonstrated that the stay spacing was not decisive on the determination of the fundamental periods of cable-stayed bridges, with higher periods obtained for the harp pattern, if fixed-hinge connections at the tower-deck level are employed. In other words, a flexibility increase implies more incidence of the longitudinal stiffness provided by the stay cable layout.
Table 4.6 Natural Periods and Modal Shapes for Damped Models
| Mode | AB4 Bridge | AR4 Bridge | ||
| Period (sec) | Nature of modal shape | Period (sec) | Nature of modal shape | |
| 1 | 6.00 | Deck Long | 3.24 | Deck long |
| 2 | 2.78 | Deck Tr | 2.74 | Deck Tr |
| 3 | 2.33 | Tower Tr | 2.32 | Tower Tr |
| 4 | 2.11 | Deck Vert | 2.14 | Deck Vert |
| 5 | 1.39 | Deck Tr + Cable Tr | 1.33 | Deck Vert + Cable Long |
| 6 | 1.33 | Cable Tr | 1.27 | Deck Tr + Cable Tr |
| 7 | 1.33 | Cable Tr | 1.22 | Cable Tr |
| 8 | 1.33 | Cable Tr | 1.22 | Cable Tr |
| 9 | 1.33 | Cable Tr | 1.22 | Cable Tr |
| 10 | 1.29 | Cable Long + Cable Tr | 1.21 | Cable Tr |
| 11 | 1.29 | Cable Tr | 1.19 | Cable Long |
| 12 | 1.29 | Cable Tr | 1.19 | Cable Long |
| 13 | 1.29 | Cable Tr | 1.19 | Cable Long |
| 14 | 1.29 | Cable Tr | 1.18 | Cable Long |
| 15 | 1.27 | Cable Long | 1.16 | Cable Tr |
Long: Longitudinal Tr: Transverse Vert: Vertical
Modes 2, 3 and 4 are very similar on both bridges; with more important differences for the natural periods of the cables. Those cable periods are very close-spacing, a vibrational characteristic of cable-stayed bridges. For both models, it is observed that modes higher than 5 represent cable modes.
The modal analysis takes into account the modified stiffness matrix, that is to say, the stiffness matrix at the end of the nonlinear static analysis. This point is very important, because if not, important differences can be obtained. The modal analysis is linear, and if it starts from zero initial conditions, the important geometric nonlinearities that cable-stayed bridges experience are not considered, and especially nonlinearities due to cable behaviour, with the imprecision involved.
Table 4.7 Critical Damping Ratios – Damped Cases
|
Modal damping exposed in Table 4.7 was obtained applying the empirical formulation by Kawashima et al (1993). In general terms, critical damping ratios for the damped cases are different compared with the undamped cases, with the exception of damping associated with transverse bending vibrations. | ||||||||||||||
Damping associated to vertical bending vibrations for the damped models is lower than that obtained with the undamped cases, and especially AB4 model. An opposite situation occurs with damping associated to torsional oscillations, in which damping for the undamped models are almost 50% the damping of the damped cases.
- 4.5 Optimal Damper Parameters
Point 4.3 demonstrated that the best damper layout corresponds to longitudinal dampers located at the deck-ends and at the tower-deck connection. However, the best option necessarily includes selection of the optimal damper parameters, considering that capacity of damping devices depends on the specific damping coefficient C and velocity exponent N. An adequate selection of those parameters is not trivial, and for that reason the aim of this part is to select the best combination of C and N that minimize the seismic response of the structures as well as the response of the dampers for both far-fault and near-fault ground motions. It is known that high control of the seismic forces into the structure implies higher damper forces, which necessarily requires higher damper capacities. As a result, an adequate selection of the damper parameters is essential to avoid wrong designs with the subsequent uncertainty about the seismic behaviour.
To select the best damper parameters, a parametric analysis is conducted, in which maximum responses of the structure and dampers are analyzed by means of variation of the desired response as function of the damping coefficient C for different velocity exponents N, including the linear case and the extra-low velocity exponent. An optimization procedure is then applied to select the available options that are compared in order to choose the optimal parameters. Also, influence of the velocity exponent on the seismic response is especially analyzed.
The analyses are performed using AB4 model, and considering that the seismic response of AR4 model is similar, according to Chapter 3. The optimal damper layout previously analyzed is considered here, taking into account the same specifications for all the dampers. The geometry, structural modelling, loads and combinations, materials and analysis hypotheses are the same considered before. All the analyses are performed using the code SAP2000, and considering all available nonlinearities. As seismic input, the worse conditions for both far-fault and near-fault ground motions are applied, meaning that the orthogonal three-component earthquakes of Event 5 (far-fault) and Gatos (near-fault) are used again. Nonlinear direct integration time history analysis is applied for all the analyses, using the Hilber-Hughes-Taylor-α step-by-step integration method to solve the equations of motion. Time integration parameters considered to reach an accurate convergence are 0.02 sec time-step size, -0.2 numerical damping, 0.02 sec maximum sub-step size, 0 sec minimum sub-step size, 70 and 140 maximum iterations per sub-step for far-fault and near-fault ground motions respectively, and 1x10-4 and 1x10-3 iteration convergence tolerance for far-fault and near-fault ground motions respectively. Damping mechanism is considered as Rayleigh’s type, according to the modal damping previously obtained.
- 4.5.1 Parametric Analysis
In order to consider representative possibilities of linear and nonlinear viscous damping, damping coefficients between 5 and 50 MN/(m/sec)N, and velocity exponents between 0.015 and 1.0 are studied, implying commercial alternatives for the dampers, currently available according to some manufacturers. Those velocity exponents cover a wide-range, from linear to highly nonlinear dampers. More than 40 nonlinear analyses were performed, implying more than 120 hours of computer time.
Figs. 4.11 to 4.14 show results of the analyses for the maximum responses of the structure, considering those maxima as absolute values, in terms of longitudinal and vertical displacements of the deck, as well as in-plane bending moments and axial forces of the towers. Those results are representative of the seismic response of the model.
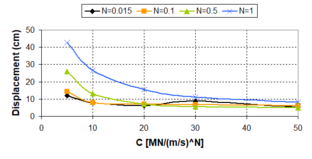
(a) Far-fault ground motion |
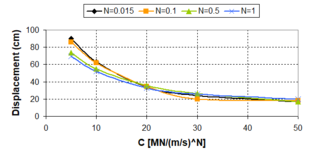
(b) Near-fault ground motion |
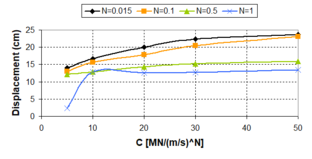
(a) Far-fault ground motion |
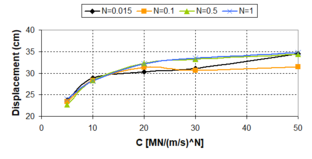
(b) Near-fault ground motion |
Fig. 4.12 Maximum Vertical Displacements of the Deck at the Mid-Span
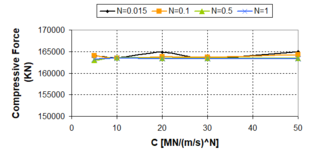
(a) Far-fault ground motion |
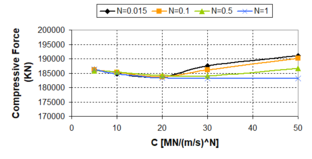
(b) Near-fault ground motion |
Fig. 4.13 Maximum Axial Forces at the Tower Base
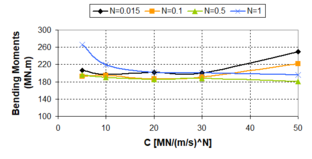
(a) Far-fault ground motion |
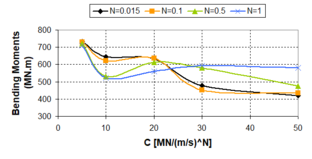
(b) Near-fault ground motion |
Fig. 4.14 Maximum In-Plane Bending Moments at the Tower Base
Longitudinal displacements of the deck decrease as damping coefficient increases. For C > 30 MN/(m/sec)N displacements become independent on the damping coefficient, for both, far-fault and near-fault ground motion, which implies that control of longitudinal displacements of the deck cannot increase for damping coefficients higher than 30 MN/(m/sec)N. For far-fault ground motion, maximum displacements tend to 10 cm for high damping coefficients. In the case of near-fault ground motion, maximum displacements of the deck tend to 20 cm for high damping coefficients, independent on the velocity exponent N, as happens with the far-fault condition. The analysis of the velocity exponent N shows a general tendency in which lower deck displacements are achieved with lower velocity exponents for far-fault ground motion. An opposite behaviour occurs with near-fault ground motion, especially for C < 20 MN/(m/sec)N. This behaviour can be explained in the fact that velocities near to 1 m/sec are demanding the dampers for the near-fault condition, which implies that higher forces are demanding the dampers for high velocity exponents, implying lower deck response; on the contrary of the case of the far-fault ground motion.
Maximum vertical displacements of the deck tend to increase as the damping coefficient increases. This is true up to damping coefficient of 30 MN/(m/sec)N , and constant values of the maximum vertical displacements are experienced for higher values of C, for both far-fault and near-fault ground motions. In general terms, for the far-fault condition, lower vertical displacements occur if linear exponents are used, on the contrary of the case of the near-fault condition, in which lower vertical displacements are obtained with highly nonlinear exponents. This behaviour is especially evident for far-fault ground motion, and represents an opposite situation compared to the longitudinal deck displacements. As a conclusion, it seems to be that high control of the longitudinal deck displacements implies low control of the vertical deck displacements, which explains the seismic behaviour of the deck.
The analysis of the maximum compressive forces of the deck shows a characteristic behaviour in which maximum tower forces are independent on the damping coefficient and velocity exponent, especially for far-fault ground motion. For near-fault ground motion, this is true for C < 20 MN/(m/sec)N. For higher damping coefficients, compressive forces are independent on the damping coefficient, but dependent on the velocity exponent. In fact, if C > 20 MN/(m/sec)N , lower compressive forces are obtained for more linear velocity exponents.
Maximum in-plane bending moments at the tower base show more irregular behaviour, especially for near-fault ground motion. For far-fault ground motion, tower moments are independent on the damping coefficient for N = 0.5. For N = 1, tower moments are independent on the damping coefficient if C > 15 MN/(m/sec)N. For highly nonlinear exponents of N (0.1, 0.015), tower moments are independent on the damping coefficient if C < 30 MN/(m/sec)N. In spite of the complex behaviour of the tower moments as function of the damping coefficient and velocity exponent, it seems to be that lower tower moments are obtained for linear damper behaviour if the presence of high amount of damping; on the contrary of the case of near-fault ground motion, in which lower tower moments are obtained for highly nonlinear damper behaviour and C > 30 MN/(m/sec)N.
Figs. 4.15 to 4.18 expose the seismic response of the dampers, in terms of maximum damper forces and velocities as function of the damping coefficient for different velocity exponents. The analysis is performed for both deck-end dampers and those located at the tower-deck connection. For simplicity, maximum damper forces and velocities are signed as absolute values. As happens with the maximum responses of the structure, both far-fault and near-fault ground motions are analyzed, considering Event 5 and Gatos respectively. Damping coefficients vary from zero to 50 MN/(m/sec)N, and the same velocity exponents considered before have been applied here.
Results of the analysis of the damper forces (Figs. 4.15 and 4.16) show a similar behaviour for all the dampers. The linear response of the damper forces with C is obvious since the constitutive equation that governs the response of the dampers with velocity. Of course, maximum damper forces are obtained for the highest damping coefficient. Likewise, it is observed an important effect of the velocity exponent on the damper forces. In fact, lowest damper forces are obtained for linear dampers, as long as highest damper forces are observed for extra-low velocity exponent for both, far-fault and near-fault ground motion. This implies less than 1 m/sec operating velocities inside the dampers according to results exposed in Chapter 2, even for near-fault ground motion. According to this, if only the damper forces are considered, the linear solution for the dampers is the best option. A comparison between far-fault and near-fault conditions shows similar responses for highly nonlinear dampers, and more important differences for higher velocity exponents, in which the maximum responses are achieved for the near-fault condition.
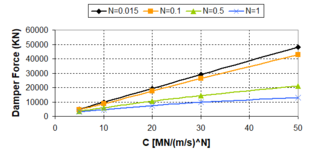
(a) Far-fault ground motion |
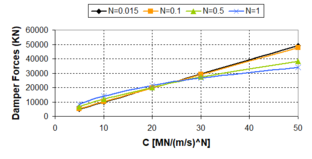
(b) Near-fault ground motion |
Fig. 4.15 Maximum Deck-End Damper Forces
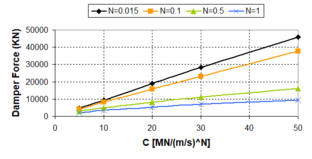
(a) Far-fault ground motion |
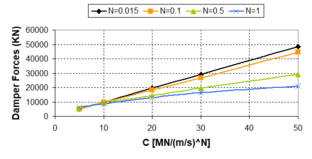
(b) Near-fault ground motion |
Fig. 4.16 Maximum Damper Forces at the Tower-Deck Connection
The analysis of the damper velocities (Figs. 4.17 and 4.18) shows an opposite situation compared with the damper forces, that is to say, minimum velocities obtained for highly nonlinear dampers. In other words, minimum velocity responses imply maximum damper forces. Velocities tend to decrease as the damping coefficient increases, although for C > 30 MN/(m/sec)N, velocities are independent on the damping coefficient for both far-fault and near-fault ground motion. Likewise, it is clear that maximum damper velocities can be obtained for the near-fault condition.
As a summary, higher damping coefficients permit a better structural control, mainly with longitudinal displacements of the deck, but also an increase of the damper forces and a decrease of the damper velocities. The effect of the velocity exponent on the seismic response is more complicated; although it seems to be that an efficient control of the damper forces can be achieved selecting adequate velocity exponents.
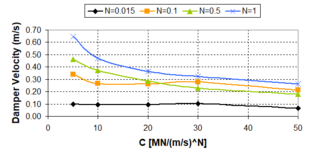
(a) Far-fault ground motion |
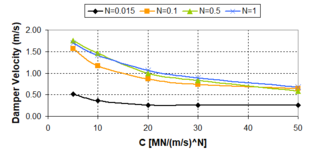
(b) Near-fault ground motion |
Fig. 4.17 Maximum Deck-End Damper Velocities
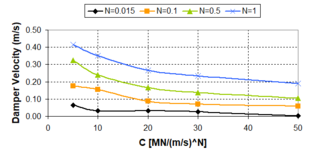
(a) Far-fault ground motion |
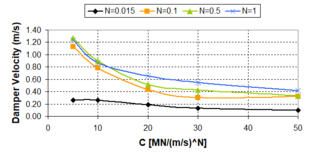
(b) Near-fault ground motion |
Fig. 4.18 Maximum Damper Velocities at the Tower-Deck Connection
- 4.5.2 Selection of the Damper Parameters
Selection of the optimal damper parameters necessarily consists in obtaining an efficient control of both the structural response and the damper response. In this sense, optimization techniques can be employed in this task. It seems to be that a reasonable approximation is to minimize the maximum longitudinal displacements of the deck as characteristic measure of the structural response, and to minimize the maximum damper forces as characteristic measure of the damper response; considering those maximum responses as absolute values for simplicity. By this way, we can define the longitudinal deck displacement matrix A, in which aij represents the maximum absolute longitudinal displacement of the deck [cm] for damping coefficient i and velocity exponent j. Similarly, it is possible to define the damper force matrix B, in which bij represents the maximum absolute damper force [kN] associated to the damping coefficient i and velocity exponent j. Thus, defining matrix F = AB, the task is to seek the minimum values of F. This simple procedure can be applied separately for deck-end dampers as well as the dampers located at the tower-deck connection, for far-fault and near-fault ground motions.
Of course, this simplified approximation considers that the main parameters that affect both the seismic response of the structure and the seismic response of the dampers are conditioned by displacements of the deck and forces on the dampers. Approximations considering more sophisticated optimization techniques can also be applied, as well as energy approaches; however, for simplicity, the procedure here explained was used.
- 4.5.2.1 Far-fault ground motion
- (1) Deck-end dampers:
| C | N =0.015 | N =0.1 | N =0.5 | N =1.0 | |
| 5 | 58443 | 64656 | 88740 | 138305 | |
| 10 | 76235 | 70080 | 80520 | 124550 | |
| F = | 20 | 117730 | 122500 | 73830 | 112420 |
| 30 | 255200 | 179520 | 79200 | 109312 | |
| 50 | 259200 | 265360 | 103880 | 106110 |
- (2) Dampers at the tower-deck connection:
Here, we can use the same values of matrix A, considering that the same longitudinal displacements are obtained for the deck at the tower-deck connection.
Thus,
| C | N =0.015 | N =0.1 | N =0.5 | N =1.0 | |
| 5 | 58080 | 60480 | 74385 | 88389 | |
| 10 | 75050 | 66400 | 64680 | 92750 | |
| F = | 20 | 115900 | 109900 | 56304 | 81620 |
| 30 | 249920 | 156400 | 61050 | 78400 | |
| 50 | 248400 | 233740 | 79380 | 76950 |
In those analyses, units of C are [MN/(m/sec)N].
Values signed in green represent good candidates that minimize both maximum longitudinal displacements of the deck and maximum damper forces. C = 5 is not recommended because of the small energy dissipation associated. This implies that the optimal solution, for all damper locations, seems to be C = 10 or C = 20. It is interesting to observe that the linear solution (N = 1) is not an optimal value, and for that reason, the best candidates for the velocity exponent are N = 0.1 and N = 0.5. It is clear that C = 10; N = 0.1 is the same as C = 20; N = 0.5 for both deck-end dampers and dampers located at the tower-deck connection. If we consider more structural response parameters, it is possible to achieve the desired optimal solution. Thus, employing results obtained from the parametric analysis, it is clear that the best option to control the vertical displacements of the deck is N = 0.5 and C ≤ 30. For the tower moments, the best option is N = 0.5 or N = 0.1 and 10 ≤ C ≤ 30. For deck-end damper forces, N = 0.5 and C ≤ 30 is a good solution. For deck-end damper velocities, an adequate control occurs if N = 0.1 and 10 ≤ C ≤ 50; or N = 0.5 and C ≥ 20. The best solution for the damper forces at the tower-deck connection is N = 0.5 and C ≤ 30. In the case of the damper velocities at the tower-deck connection, N = 0.1 and C ≥ 20 is a good option. As a result, the best option involving all the considered aspects is to choose C = 20 and N = 0.5.
- 4.5.2.2 Near-fault ground motion
The analysis of the near-fault condition is analogue to the far-fault analysis.
- (1) Deck-end dampers:
| C | N =0.015 | N =0.1 | N =0.5 | N =1.0 | |
| 5 | 445500 | 450303 | 489957 | 587818 | |
| 10 | 622520 | 631952 | 666710 | 735560 | |
| F = | 20 | 662480 | 681620 | 712000 | 700770 |
| 30 | 699720 | 584910 | 726180 | 681050 | |
| 50 | 833000 | 874740 | 649400 | 670320 |
- (2) Dampers at the tower-deck connection
| C | N =0.015 | N =0.1 | N =0.5 | N =1.0 | |
| 5 | 441000 | 435666 | 416796 | 428892 | |
| 10 | 619360 | 607072 | 523450 | 450660 | |
| F = | 20 | 659100 | 636640 | 512640 | 430990 |
| 30 | 692580 | 534660 | 521360 | 421480 | |
| 50 | 821100 | 816180 | 493000 | 409640 |
It is clear that selection of the optimal damper parameters for the near-fault condition seems to be more complicated, and it is absolutely necessary to consider results obtained from the parametric analysis. Not considering C = 5 for the same reasons previously explained, a good candidate seems to be C = 30 and N = 0.1. A more exhaustive review of the parametric analysis shows that an adequate control of the longitudinal displacements of the deck is obtained with C ≥ 30, for all values of N. The vertical displacements of the deck are good controlled using C ≤ 30 for all values of N. For the tower moments, C ≥ 30 and N = 0.015 or N = 0.1 is a good solution. An adequate control of deck-end damper forces is achieved with C ≤ 30 for all values of N. Velocities of the dampers at the deck-ends are controlled using C ≥ 10 and N = 0.015 or C ≥ 20 and N = 0.1. For the damper forces at the tower-deck connection, best results are obtained if C ≤ 30 and N = 1 or N = 0.5. The control of the damper velocities at the tower-deck connection is achieved with C ≥ 10 and N = 0.015 or C ≥ 30 and N = 0.1. From these results, it is clear that C = 30 is the best option; however, selection of the velocity exponent could be N = 0.1 or N = 0.015, with practically the same results. Extra-low velocity exponents permits a better control of the peak damper forces, in which those responses are not dependent on the damper velocity according to results exposed here; aspect that can be very important in the near-source region, when long-period velocity pulses affect long-period structures. For that reason, N = 0.015 is selected as velocity exponent in this case.
Summarizing, C = 20 and N = 0.5 is selected for far-fault ground motion; and C = 30 and N = 0.015 is applied for near-fault ground motion. Those values are used independent on the damper location.
- 4.5.3 Influence of the Velocity Exponent and Damping Coefficient
The analyses have shown the important incidence of the damper parameters on the seismic response of the structure and dampers. The velocity exponent of the dampers plays an important role on the seismic response of the dampers, in which linear dampers tend to minimize the damper forces although important damper velocities can be experienced mainly for low damping coefficients. However, it was demonstrated that the optimal solution, as a whole, involves the employ of nonlinear dampers, and especially in the presence of near-fault ground motions.
If response time histories are plotted for AB4 bridge model and considering the near-fault event Gatos as input earthquake, results of Fig. 4.19 are obtained. Here, time histories of longitudinal displacements of the deck are considered as characteristic parameter of the seismic response of the bridge, for different velocity exponents and damping coefficients C = 10 MN/(m/sec)N and C = 50 MN/(m/sec)N. Results show the enormous influence of the damping coefficient C, in which a great response control of the structure is achieved for high damping coefficients, because of the higher energy dissipation capacity. Variations of the velocity exponent are not very important on the response of the deck, and especially for the lowest values of N (0.015 and 0.1).
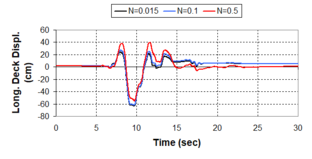
(a) C = 10 MN/(m/sec)N |
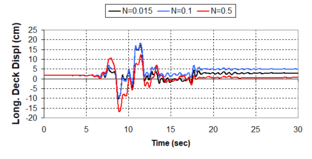
(b) C = 50 MN/(m/sec)N |
The shape of the time histories depends on the damping coefficient; however, it is clear that for a specific damping coefficient, velocity exponent of the dampers is not decisive on the seismic response of the structure, which confirms the studies of Lin and Chopra (2002). They proposed that reductions in responses were essentially unaffected by damper nonlinearity in the velocity-sensitive region and only weakly dependent in the acceleration and displacement sensitive regions, as occurs in this study.
On the other hand, if the response of the dampers is analyzed in terms of the influence of the velocity exponent, more important differences are obtained. Fig. 4.20 shows deck-end damper forces for AB4 model in the presence of the same earthquake input (Gatos), considering C = 10 and C = 50 MN/(m/sec)N.
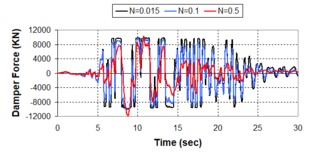
(a) C = 10 MN/(m/sec)N |
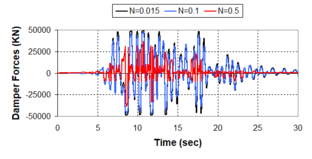
(b) C = 50 MN/(m/sec)N |
Results show that maximum damper forces are obtained with the lowest velocity exponents, that is to say, a better control of the dampers is achieved with linear dampers, as was obtained during the parametric study. This implies low-to-moderate operating velocities, because it is known an opposite behaviour when higher velocities are experienced. It is clear that the main advantage of using extra-low velocity exponents is the control of the peak damper responses, as can be appreciated for both damping coefficients. Extra-low velocity exponent imposes a maximum damper response in terms of forces, where the damper forces are independent on the damper velocity for high velocities, aspect that is especially important when long-period velocity pulses are experienced, as usually happens during near-source events. In this case, the control of the peak responses of the dampers is observed with the upper and lower “roof” that limits higher damper responses.
Regarding the damping coefficient, as happens with the structural response, C notably affects the damper forces, and contrarily to the structural forces, an increase of the damping coefficient implies an important increase of the damper forces.
As a summary, an important effect of the velocity exponent of the dampers is observed on the damper forces, as well as a not important effect on the structural response. The damping coefficient notably affects both the structural response and the damper response, with an increase of the structural response when the damping coefficient decreases, on the contrary of the damper response, in which an increase of the damping coefficient increases the damper forces.
- 4.6 Nonlinear Time-History Analysis
The previous analyses were focused on the search of the optimal damper layout, optimal damper parameters and the importance of the damping coefficient and velocity exponent. This part analyzes the seismic response of both AB4 and AR4 bridge models considering all the far-fault and near-fault events described in Chapter 3. The aim of this study is to obtain the nonlinear seismic response for the damped systems considering the optimal conditions before mentioned, in order to compare the responses between both structures, and with the undamped cases, considering the far-fault and near-fault conditions.
The geometry, structural modelling, loads, material data and analysis hypothesis are the same considered before. All the analyses were performed using the code SAP2000, applying the Hilber-Hughes-Taylor-α step-by-step time integration procedure for the computations of the nonlinear direct integration time history analyses. Convergence conditions with accurate results were obtained using 0.02 sec time-step size, -0.2 numerical damping, 0.02 sec maximum sub-step size and zero sec minimum sub-step size. For the maximum iterations per sub-step, for far-fault ground motions, values of 70 and 100 were used for AB4 and AR4 models respectively. For near-fault ground motions, maximum iterations were 140 and 180 for AB4 model, and 180 for AR4 model. The iteration convergence tolerance was 1x10-4 and 1x10-3 for AB4 model considering far-fault and near-fault ground motions respectively; and 1x10-3 for both far-fault and near-fault ground motions on AR4 model. The analyses were performed applying Rayleigh’s damping, according to the modal damping previously exposed in this chapter. All the analyses required more than 100 hours of computational effort to achieve the desired results, in which the employed time for calibration of the parameters is not considered.
The study is divided into far-fault and near-fault ground motions, in which time histories and maximum responses are exposed for the structures and dampers. As occurs with the undamped cases, shear forces were not included in this analysis because the response of cable-stayed bridges (internal forces) is basically controlled by axial forces, bending moments and their interaction.
- 4.6.1 Far-Fault Ground Motion
For the far-fault ground motion analysis, the same artificially generated earthquake events before employed are used here. Likewise, the same general considerations explained in Chapter 3 are valid here. In this sense, time-history plots shown in the following figures expose the response for the zone associated to the strong motion duration, obtained from the Arias Intensity of each event. Furthermore, at time equal to zero, the response is generally non-zero because it is obtained at the end of the nonlinear static analysis, and considered as starting point of the nonlinear direct integration time history analysis.
Figs. 4.21, 4.22 and 4.23 show time histories for longitudinal displacements of the deck, vertical displacements of the deck at the mid-span and longitudinal displacements of the tower-top respectively.
(a) AB4 bridge |
(b) AR4 bridge |
(a) AB4 bridge |
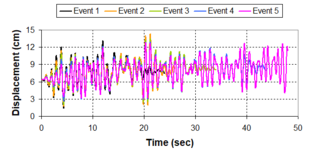
(b) AR4 bridge |
Time-history plots of longitudinal and vertical displacements of the deck show a similar response comparing AB4 model with AR4 model. Likewise, for each bridge, similar responses are obtained with each earthquake event for the same reasons explained in Chapter 3. Of course, very different responses are obtained for the damped analysis compared with the undamped analysis, and especially for longitudinal displacements of the deck. The presence of longitudinal viscous dampers is clear in the time history plots of longitudinal deck displacements. Maximum longitudinal displacements are obtained with AR4 model, although differences with the other model are negligible, as happens with the vertical deck displacements. A similar situation to the previous exposed occurs with longitudinal displacements of the tower-top (Fig. 4.23), in which negligible differences can be appreciated. It seems to be that the general response and peak values for displacements are very similar for both structures, in spite of the higher longitudinal stiffness provided by the stay cable layout of AR4 bridge.
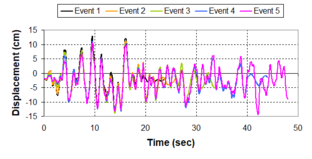
(a) AB4 bridge |
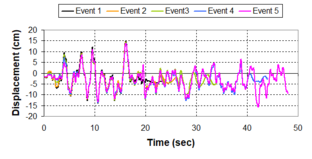
(b) AR4 bridge |
As occurs with the displacements, a comparable response of longitudinal velocities of the deck is observed for both structures, according to Fig. 4.24. Peak velocities of about 0.3 m/sec are observed, lower than those obtained with the undamped cases, in which peak values of 1 m/sec were obtained, that is to say, more than three times. Likewise, it is appreciated an almost perfect coincidence for all the events, and a higher frequency content compared with the undamped cases, as happens with the vertical displacements of the deck.
Figs. 4.25 to 4.28 expose time histories of axial forces at the tower base, axial forces of the deck at the tower-deck connection, in-plane bending moments at the tower base, and bending moments of the deck at the mid-span respectively. As happens with the undamped cases, those internal forces were selected because they are representative of the seismic response of the bridge models, and the specific locations where time histories are shown, were chosen because maximum values are experienced, according to the response spectrum analysis results obtained in Chapter 3.
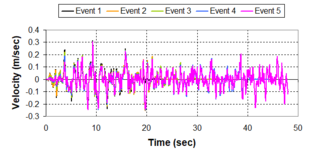
(a) AB4 bridge |
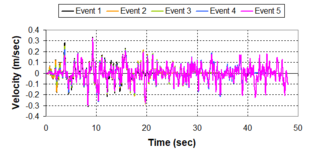
(b) AR4 bridge |
Axial forces at the tower base (Fig. 4.25) are very similar for both bridge models. Maximum compressions are practically the same, with peak values obtained, in both cases, with events 1 and 5. Similar responses were obtained with the undamped cases, demonstrating the null effect of the viscous dampers on the axial forces of the towers. Axial forces of the deck at the tower-deck connection (Fig. 4.26) show more important differences between both bridges, with higher compressions experienced on AR4 bridge. In both structures, insignificant differences are appreciated comparing the seismic events.
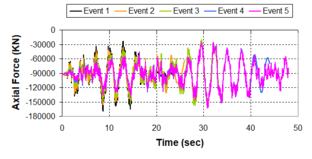
(a) AB4 bridge |
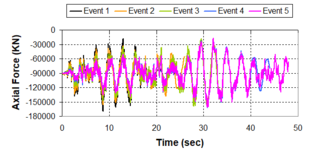
(b) AR4 bridge |
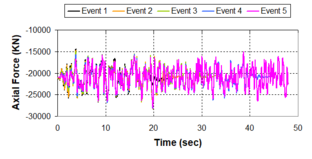
(a) AB4 bridge |
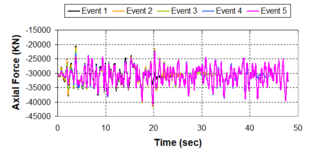
(b) AR4 bridge |
The analysis of in-plane bending moments at the tower base (Fig. 4.27) show similar results for both bridges. Time histories are very similar, with peak responses of about 200 MN.m. Comparing with the undamped cases, higher frequency content is experienced with the damped cases, and of course, significant lower moments. Bending moments of the deck at the mid-span (Fig. 4.28) show more important differences, with maximum responses obtained with AB4 model. Higher frequency content compared with the undamped models is experienced again, as well as lower moments.
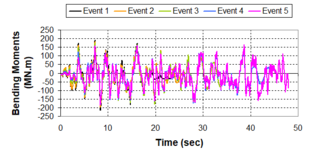
(a) AB4 bridge |
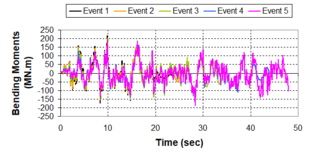
(b) AR4 bridge |
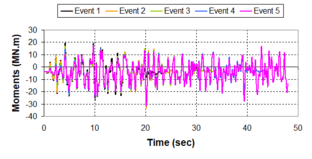
(a) AB4 bridge |
(b) AR4 bridge |
As a summary, main differences of the seismic response between both structures are obtained with the internal forces of the deck, as long as differences with the tower response seem to be negligible. Likewise, displacements and velocities are very similar between both bridges, as happens with the undamped cases.
Figs. 4.29 and 4.30 show damper forces at the deck-ends and at the tower-deck connection.
(a) AB4 bridge |
(b) AR4 bridge |
A comparison between AB4 and AR4 models show that damper responses are very similar, independent on the seismic event, as happens with the previous results. Peak damper forces of about 10500 kN and 8200 kN are obtained for deck-end damper forces and tower damper forces respectively. Higher damper forces for the deck-ends are a normal behaviour, because those dampers are not part of the structure, that is to say, larger relative motions are experienced, with the subsequent higher energy dissipation, as was explained before. It is interesting to observe that both structures experience basically the same damper response, considering that AR4 model is longitudinally stiffer than AB4 bridge, because of the stay cable layout. This implies that the analysis of the dampers is independent on the stay cable layout.
(a) AB4 bridge |
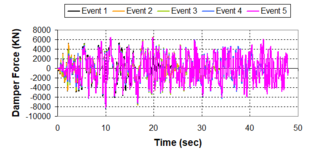
(b) AR4 bridge |
A summary of the maximum main displacements and velocities for both bridge models is exposed in Table 4.8. As used before, Δ1-L is the maximum longitudinal displacement of the tower-top; Δ1-T is the maximum transverse displacement of the tower-top; Δ4-L is the maximum longitudinal displacement of the deck; Δ3-V is the maximum vertical displacement of the deck at the mid-span; Δ3-T is the maximum transverse displacement of the deck at the mid-span; V1-L is the maximum longitudinal velocity of the tower-top; and V4-L is the maximum longitudinal velocity of the deck. Due to simplicity reasons, absolute values of maximum responses are exposed.
| Event | AB4 Bridge | AR4 Bridge | ||||||||||||
| Δ1-L | Δ1-T | Δ4-L | Δ3-V | Δ3-T | V1-L | V4-L | Δ1-L | Δ1-T | Δ4-L | Δ3-V | Δ3-T | V1-L | V4-L | |
| 1 | 13.5 | 45.8 | 8.0 | 11.9 | 69.5 | 0.61 | 0.32 | 14.8 | 46.4 | 10.3 | 13.2 | 65.0 | 0.63 | 0.34 |
| 2 | 13.3 | 37.3 | 7.4 | 14.8 | 55.8 | 0.56 | 0.30 | 14.5 | 37.8 | 10.3 | 14.3 | 52.1 | 0.60 | 0.32 |
| 3 | 13.9 | 49.9 | 6.9 | 14.4 | 76.7 | 0.55 | 0.30 | 14.4 | 50.8 | 9.9 | 13.4 | 71.3 | 0.59 | 0.31 |
| 4 | 13.3 | 45.6 | 7.0 | 14.3 | 70.4 | 0.56 | 0.31 | 14.0 | 47.6 | 9.8 | 12.9 | 65.2 | 0.60 | 0.33 |
| 5 | 14.4 | 46.0 | 6.9 | 14.3 | 70.9 | 0.55 | 0.30 | 15.8 | 47.5 | 9.8 | 12.8 | 65.0 | 0.59 | 0.32 |
| Average | 13.7 | 44.9 | 7.2 | 13.9 | 68.7 | 0.57 | 0.31 | 14.7 | 46.0 | 10.0 | 13.3 | 63.7 | 0.60 | 0.32 |
As happens with the maximum displacements and velocities for the undamped cases, very similar results are obtained for all the events, and especially, with velocities. For that reason, the average of the maximum responses is an excellent response parameter for far-fault ground motions. Maximum displacements are obtained for the transverse movements of the deck at the mid-span, followed by transverse displacements of the tower-top. Comparing with the undamped cases, it is interesting to observe that a great control of the longitudinal displacements is achieved with incorporation of viscous dampers, and for that reason, now transverse displacements are larger. Comparisons between both structures show similar average responses, with main differences for the maximum longitudinal displacements of the deck (28%). It is difficult to propose the best stay cable layout from results of the average of the maximum responses. In fact, although higher responses are obtained basically with the harp pattern, those differences are negligible, and an efficient comparison is not possible. Tables 4.9 and 4.10 expose maximum main internal forces for both bridge models. The nomenclature here applied is the same considered before. Negative values of axial forces imply compression and absolute values for bending moments are considered for simplicity.
Compared with the analysis of displacements, the examination of the internal forces shows more disparities between the seismic events, mainly for bending moments of the towers. Maximum compressions of the towers, for both structures, are very similar; and basically the same average response is obtained compared with the undamped cases, which confirms that the addition of fluid viscous dampers does not affect the seismic compressions of the towers. Main differences on the average of the maximum responses between both bridges are observed for compressions of the deck (32%), cable forces (48%), and bending moments of the deck at the mid-span (31%). From these results, main differences come from the seismic response of the deck and cables, as was discussed using time histories. It is interesting to check the tremendous decrease of in-plane tower moments compared with the undamped cases. In fact, for the damped bridges, now transverse moments of the towers are larger than in-plane tower moments, on the contrary of the undamped bridges. As a consequence and taking into account the large transverse displacements obtained, this implies that the transverse response of the bridge can become a weakness of the system, and an important aspect to solve during further research. However, the application of transverse dampers at the tower-deck connection is not an efficient solution as was demonstrated before, and schemes using external dampers for the towers to mitigate the transverse response can be the answer. The best stay cable layout in terms of the internal forces for the damped bridges is not easy to obtain, because both structures show advantages. The best alternative to compare the stay cable layouts is the use of the response spectrum method.
| Event | Nmax-towera
[kN] |
Nmax-deckb
[kN] |
Nmax-cable
[kN] |
Mmax-towera, c
[MN.m] |
Mmax-towera, d
[MN.m] |
Mmax-deck3c
[MN.m] |
| 1 | -169000 | -26700 | 7000 | 216.0 | 403.9 | 27.7 |
| 2 | -156200 | -28360 | 6900 | 198.2 | 329.7 | 33.3 |
| 3 | -157400 | -28180 | 6900 | 186.7 | 420.2 | 32.1 |
| 4 | -163300 | -28200 | 6820 | 179.2 | 420.1 | 31.9 |
| 5 | -163300 | -28070 | 6820 | 185.3 | 414.9 | 31.7 |
| Average | -161840 | -27902 | 6888 | 193.1 | 397.8 | 31.3 |
| Event | Nmax-towera
[kN] |
Nmax-deckb
[kN] |
Nmax-cable
[kN] |
Mmax-towera, c
[MN.m] |
Mmax-towera, d
[MN.m] |
Mmax-deck3c
[MN.m] |
| 1 | -169000 | -39100 | 3600 | 216.4 | 410.4 | 21.4 |
| 2 | -156000 | -41900 | 3570 | 200.8 | 331.7 | 21.7 |
| 3 | -159000 | -41400 | 3590 | 187.5 | 436.9 | 21.6 |
| 4 | -162000 | -41200 | 3560 | 189.7 | 420.3 | 21.5 |
| 5 | -161400 | -41100 | 3540 | 186.7 | 409.5 | 21.3 |
| Average | -161480 | -40940 | 3572 | 196.2 | 401.8 | 21.5 |
a At the tower base c In-plane
b At the tower-deck connection d Out-of-plane
The analysis of the maximum forces and velocities of the dampers can be appreciated in Table 4.11. For simplicity, response of the dampers is exposed in absolute values again. Almost the same results are observed for both structures, with insignificant differences between the seismic events. Important differences are observed comparing deck-end damper response with the tower damper response, in which average velocities of about 0.30 m/sec and 0.18 m/sec are obtained respectively. With regard to the average maximum damper forces, differences of about 20% are evaluated between both damper locations. Of course, maximum damper forces are obtained at the deck-ends, implying higher energy dissipation than that associated to the tower-deck connection.
| EVENT | AB4 Bridge | AR4 Bridge | ||||||
| Deck-end damper | Tower Damper | Deck-end damper | Tower Damper | |||||
| Vmax [m/s] | Fmax [kN] | Vmax [m/s] | Fmax [kN] | Vmax [m/s] | Fmax [kN] | Vmax [m/s] | Fmax [kN] | |
| 1 | 0.29 | 10800 | 0.19 | 8770 | 0.31 | 11100 | 0.18 | 8400 |
| 2 | 0.28 | 10600 | 0.18 | 8440 | 0.30 | 10900 | 0.17 | 8300 |
| 3 | 0.28 | 10600 | 0.18 | 8450 | 0.29 | 10800 | 0.17 | 8200 |
| 4 | 0.29 | 10700 | 0.18 | 8460 | 0.30 | 11000 | 0.17 | 8300 |
| 5 | 0.29 | 10700 | 0.17 | 8160 | 0.30 | 10900 | 0.17 | 8200 |
| Average | 0.29 | 10680 | 0.18 | 8456 | 0.30 | 10940 | 0.17 | 8280 |
- 4.6.2 Near-Fault Ground Motion
Addition of long-period velocity pulses on the seismic records involves a very different behaviour compared with results recently exposed. Of course, the main differences come from the real nature of the seismic events that now are analyzed, with evident lower frequency content, as can be seen in Chapter 3. Velocity pulses are the basic characteristic of the near-source effects, and the presence of those phenomena on long-period structures can be dramatic, with important response increases, as was demonstrated with the undamped bridges. Time histories are very different compared with those obtained during the far-fault analysis, and results show important variations from one event to another. Likewise, maximum responses are very different depending on the considered event; however, general tendencies and important observations can be proposed. The main observation is the important decrease of the seismic response when additional dampers are included, and especially the longitudinal response, as occurs with the far-fault analysis.
Figs. 4.31, 4.32 and 4.33 show longitudinal displacements of the deck, vertical displacements of the deck at the mid-span and longitudinal displacements of the tower-top respectively.
Displacement response show important peak values because of the presence of velocity pulses that characterizes near-fault earthquakes, which is especially evident with longitudinal displacements of the deck (Fig. 4.31). Maximum peak responses for longitudinal displacements of the deck are observed for events Kobe and Gatos. For vertical displacements of the deck, maximum responses are obtained with events Kobe and San Fernando; as long as important peak responses for longitudinal displacements of the tower-top are observed for all the seismic events. An important characteristic of the displacement response is the presence of permanent displacements after an earthquake, for both structures, and especially evident with the longitudinal displacements of the deck. 6-to-10 cm maximum permanent displacements are experienced, depending on the considered event, although all the events show permanent displacements. It is interesting to observe that permanent displacements were not detected during the far-fault analysis, which supposes that the effect of velocity pulses is affecting the seismic behaviour. To avoid those permanent displacements, and to provide an adequate capability of self-centring, addition of elastic supports at the tower-deck connection can be a good idea. As was previously explained, the presence of elastic supports is not important for the displacement control of the deck; and the seismic response can be adequately studied with the dampers and supports provided here [Virtuoso et al, 2000]. The presence of the elastic force transmitted by the towers can be important to recover the initial position of the deck after an earthquake and to provide a minimum stiffness for deck slow movements. Another interesting observation is the significant damping capability of the added dampers, which is especially evident with the rapid amplitude decrease of the longitudinal displacements of the deck, a characteristic that is not observed with the rest of the studied responses. A comparison between AB4 and AR4 bridges shows similar responses between both bridges, although differences are more explicit than the far-fault analysis.
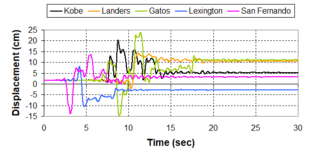
(a) AB4 bridge |
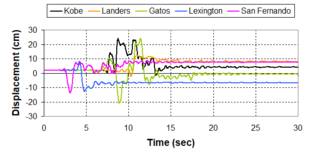
(b) AR4 bridge |
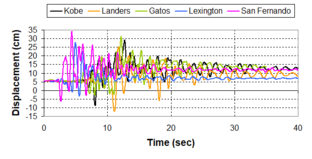
(a) AB4 bridge |
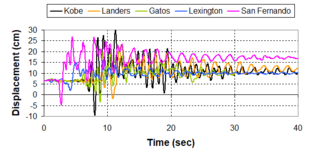
(b) AR4 bridge |
Fig. 4.34 show longitudinal velocities of the deck for both bridges. Maximum responses are obtained with events Gatos and Kobe for AB4 and AR4 bridges respectively. Peak responses of about 1 m/sec are observed, higher than those obtained with the undamped cases. An important damping of peak velocities is appreciated for time over 15sec.
Figs. 4.35 to 4.38 show responses of axial forces at the tower base, axial forces of the deck at the tower-deck connection, in-plane bending moments at the tower base and bending moments of the deck at the mid-span, that is to say, where maximum internal forces occur.
Tower axial force time-histories are very comparable for both bridge models (Fig. 4.35). Peak responses are practically the same, with maximum values experienced with Gatos event for both models. A comparison with the undamped cases shows differences no greater than 3%, in which maximum axial forces are observed for the undamped cases. As occurs with the far-fault analysis, these negligible differences imply the inefficiency of the viscous dampers in reducing the axial forces of the towers. Moreover, peak tension forces at the tower base are checked for both bridges with Kobe earthquake. The same situation occurs with the undamped cases.
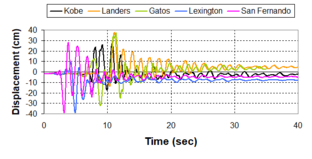
(a) AB4 bridge |
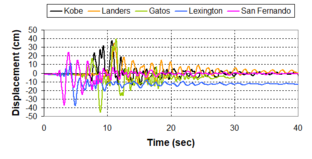
(b) AR4 bridge |
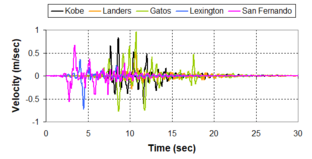
(a) AB4 bridge |
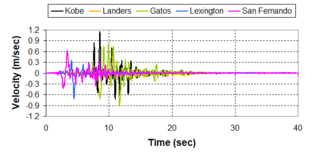
(b) AR4 bridge |
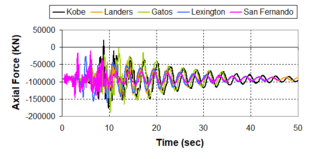
(a) AB4 bridge |
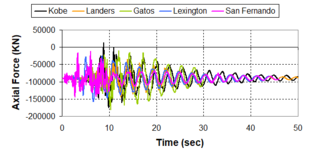
(b) AR4 bridge |
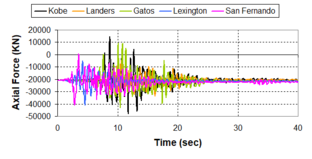
(a) AB4 bridge |
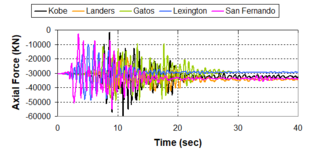
(b) AR4 bridge |
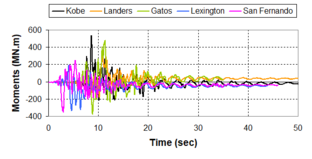
(a) AB4 bridge |
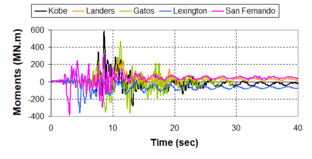
(b) AR4 bridge |
With regard to the axial forces of the deck at the tower-deck connection (Fig. 4.36), more important differences are experienced between both models. In fact, peak tension forces are observed with events Kobe and Gatos for AB4 model, as long as no evidence of tension forces on the deck is observed with AR4 model, on the contrary of the undamped analysis, in which important tension forces were obtained for both models. For AB4 and AR4 bridges, highest compressive forces of the deck are obtained with Kobe event, in which maximum values correspond to the harp pattern. In-plane bending moments at the tower base (Fig. 4.37) are similar for both models, although some differences can be observed, mainly with responses obtained from San Fernando Earthquake. Largest moments of the towers are obtained with Kobe and Gatos events for both bridges, with peak responses absolutely lower than the undamped cases. As occurs with the undamped models, in-plane bending moments of the deck at the mid-span (Fig. 4.38) show more important differences if both bridges are compared. Peak responses are obtained with San Fernando and Lexington events for AB4 bridge, and with Kobe and Gatos events for AR4 model. These maximum deck moments are lower than those obtained with the undamped bridges, which confirm the important effect of the added dampers on the moment response of towers and decks.
Figs. 4.39 and 4.40 show damper responses for AB4 and AR4 bridges in terms of damper force time histories for devices located at the deck-ends, and located at the tower-deck connection respectively.
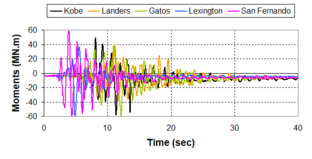
(a) AB4 bridge |
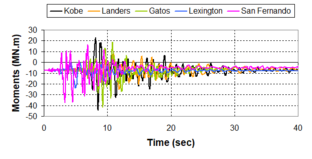
(b) AR4 bridge |
Damper responses are similar for both bridges and for both locations of the devices. Peak responses of about 30000 kN are obtained for all the dampers, independent of the seismic event and location of the devices. Higher responses are not possible to obtain because of the “roof” imposed by the extra-low damping exponent employed with the dampers for the near-fault analysis. This behaviour is very important, because higher peak responses are not possible to obtain, even if higher peak velocities are experienced, a common feature of near-source events, as occurs with these results. When far-fault events were analyzed, maximum responses of about 10000 kN were obtained, lower than the maximum peak response imposed by the velocity exponent. Basically, the same maximum response is obtained for all the dampers, independent on their locations; a different situation when far-fault ground motions are analyzed, in which maximum damper forces are obtained for those located at the deck-ends. This implies maximum capacity work for near-fault dampers.
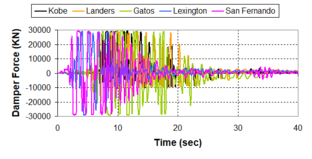
(a) AB4 bridge |
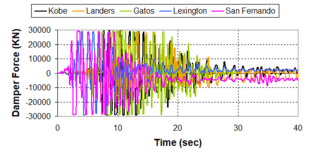
(b) AR4 bridge |
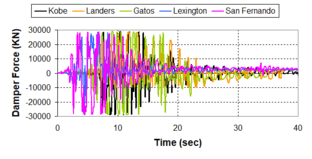
(a) AB4 bridge |
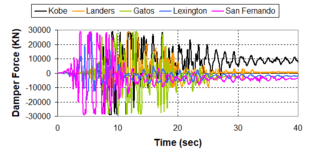
(b) AR4 bridge |
Another interesting observation is the apparent permanent forces on the devices, obtained for AR4 bridge, mainly with San Fernando and Kobe events. The explanation of this behaviour comes from the remnant forces into the devices, as a consequence of the non-zero velocities. As was explained in Chapter 2, when extra-low velocity exponents are used, small velocity variations can induce large variations on the damper forces for low velocities, and as happens here, low remnant velocities impose non-zero damper forces. Those forces can be appreciated with damper response time histories, and tend to zero when time is long, that is to say, when velocities are zero. As a conclusion, is important to take into account that remnant damper forces can appear after an earthquake, for long time, when dampers with extra-low velocity exponent are employed.
Table 4.11 summarizes the maximum relative displacements and velocities at selected joints considering near-fault ground motions. The same nomenclature and considerations employed with the far-fault analysis are considered here. A comparison between both bridges confirms that average of the maximum responses is very similar. Main differences are obtained with the vertical displacements of the deck (20%), as long as differences for velocities are less sensitive. Moreover, as happens with the far-fault analysis, selection of the best stay cable layout in terms of the maximum relative displacements and velocities is not possible considering the obtained results.
Tables 4.12 and 4.13 summarize the main internal forces for both bridges respectively. Again, nomenclature here applied is the same considered before, in which absolute values for bending moments are considered due to simplicity reasons; and positive values for axial forces imply tension.
| Event | AB4 Bridge | AR4 Bridge | ||||||||||||
| Δ1-L | Δ1-T | Δ4-L | Δ3-V | Δ3-T | V1-L | V4-L | Δ1-L | Δ1-T | Δ4-L | Δ3-V | Δ3-T | V1-L | V4-L | |
| Kobe | 26.9 | 42.0 | 20.2 | 29.1 | 65.4 | 1.31 | 0.84 | 37.5 | 41.7 | 24.0 | 30.2 | 61.9 | 1.51 | 1.15 |
| Gatos | 37.1 | 47.5 | 23.9 | 31.1 | 65.1 | 1.28 | 0.96 | 45.1 | 50.1 | 24.1 | 23.1 | 67.9 | 1.78 | 0.92 |
| Landers | 37.5 | 28.9 | 14.2 | 25.2 | 43.8 | 1.12 | 0.53 | 34.6 | 28.8 | 12.1 | 21.3 | 38.4 | 0.93 | 0.44 |
| Lexington | 38.8 | 39.2 | 10.6 | 27.6 | 61.6 | 1.16 | 0.72 | 37.9 | 40.2 | 12.7 | 16.5 | 57.9 | 1.07 | 0.72 |
| San Fernando | 39.2 | 21.4 | 13.7 | 34.0 | 32.2 | 1.59 | 0.66 | 37.0 | 21.1 | 13.8 | 26.8 | 31.2 | 1.56 | 0.63 |
| Average | 35.9 | 35.8 | 16.5 | 29.4 | 53.6 | 1.29 | 0.74 | 38.4 | 36.4 | 17.3 | 23.6 | 51.5 | 1.37 | 0.77 |
A comparison of the average of the maximum internal forces between both models shows differences of 2% for compressive forces of the tower, 20% for axial forces of the deck, 46% for cable forces, 3% for in-plane bending moments of the towers, 4.5% for out-of-plane bending moments of the towers and 35.5% for in-plane bending moments of the deck at the mid-span. From these results, maximum differences are obtained with the tension forces of the cables, followed by the response of the deck. Likewise, it is not possible to select the best stay cable layout in terms of the internal forces here considered. It is interesting to observe that in-plane average bending moments of the towers are larger than out-of-plane average bending moments, for both bridges, on the contrary of the far-fault condition. In this sense, almost the same average out-of-plane tower moments are obtained for the damped and undamped cases, which demonstrate that additional damping devices are not efficient in the transverse direction.
| Event | Nmax-towera
[kN] |
Nmax-deckb
[kN] |
Nmax-cable
[kN] |
Mmax-towera, c
[MN.m] |
Mmax-towera, d
[MN.m] |
Mmax-deck3c
[MN.m] |
| Kobe | -176700 | -48070 | 8300 | 536.0 | 430.9 | 57.6 |
| Gatos | -187600 | -42900 | 8330 | 478.0 | 421.1 | 60.1 |
| Landers | -148000 | -33950 | 10000 | 324.7 | 246.3 | 39.6 |
| Lexington | -160200 | -40800 | 8000 | 336.1 | 347.4 | 61.5 |
| San Fernando | -145500 | -40800 | 9570 | 354.5 | 188.3 | 60.6 |
| Average | -163600 | -41304 | 8840 | 405.9 | 326.8 | 55.9 |
Table 4.14 exposes the maximum response of the dampers, in terms of velocities and forces, for both bridge models. Results show great differences for the maximum velocities, for both bridges and for both locations of the dampers; however negligible differences for the damper forces are appreciated. In fact, average of the maximum damper forces is very similar from one bridge to another, as well as comparing both damper locations. Those results confirm the important effect of extra-low velocity exponent of the dampers when near-fault ground motions are considered. Even if important velocities are experienced, peak damper responses are guaranteed to maximum values
| Event | Nmax-towera
[kN] |
Nmax-deckb
[kN] |
Nmax-cable
[kN] |
Mmax-towera, c
[MN.m] |
Mmax-towera, d
[MN.m] |
Mmax-deck3c
[MN.m] |
| Kobe | -174400 | -60400 | 4730 | 590.2 | 446.5 | 44.4 |
| Gatos | -181200 | -49200 | 4840 | 471.0 | 443.4 | 41.8 |
| Landers | -144000 | -44300 | 5600 | 285.3 | 249.0 | 25.1 |
| Lexington | -157200 | -48800 | 3550 | 358.5 | 364.6 | 23.6 |
| San Fernando | -145000 | -55000 | 5160 | 388.9 | 207.2 | 37.3 |
| Average | -160360 | -51540 | 4776 | 418.8 | 342.1 | 34.4 |
a At the tower base c In-plane
b At the tower-deck connection d Out-of-plane
.Summarizing, the analysis considering near-fault ground motions shows that the largest seismic responses are obtained with events Gatos and Kobe. A similar situation occurs for the undamped bridges. Responses obtained for AB4 and AR4 models are similar, mainly for displacements and velocities. Most important differences are observed with the deck response for internal forces and cable forces, as long as the tower response is less sensitive. This behaviour is independent on the earthquake nature (far-fault – near-fault) or the damped or undamped condition of the bridges. As was concluded for the undamped condition, it is difficult to select the best stay cable layout in terms of the seismic response. There are not clear tendencies, and application of time-history analysis can be confused for this purpose.
| EVENT | AB4 Bridge | AR4 Bridge | ||||||
| Deck-end damper | Tower Damper | Deck-end damper | Tower Damper | |||||
| Vmax [m/s] | Fmax [kN] | Vmax [m/s] | Fmax [kN] | Vmax [m/s] | Fmax [kN] | Vmax [m/s] | Fmax [kN] | |
| Kobe | 0.80 | 29900 | 0.33 | 29500 | 0.33 | 29500 | 0.10 | 29000 |
| Gatos | 1.00 | 30000 | 0.41 | 29600 | 0.26 | 29400 | 0.10 | 29000 |
| Landers | 0.13 | 29100 | 0.05 | 28700 | 0.08 | 28900 | 0.05 | 28650 |
| Lexington | 0.21 | 29300 | 0.03 | 28500 | 0.21 | 29300 | 0.05 | 28700 |
| San Fernando | 0.16 | 29200 | 0.07 | 28800 | 0.16 | 29200 | 0.10 | 29000 |
| Average | 0.46 | 29500 | 0.18 | 29020 | 0.21 | 29260 | 0.08 | 28870 |
- 4.6.3 Specifications of the Dampers
Nonlinear time-history analysis of the bridge models considering the optimal dampers permits the specifications required for the dampers. This selection can be made in terms of the earthquake nature and locations of the dampers. Because of the same damper responses for both bridge models, the same dampers are specified. Table 4.15 summarizes the main damper specifications. The number of dampers corresponds to those required for each single damper location. Requirements for the dampers here exposed satisfy seismic requirements, and of course, additional damper parameters should be defined by the manufacturer, according to the design specifications.
| Damper location | Far-fault ground motion | Near-fault ground motion | ||||||||
| Number of dampers | Capacity [kN] | Max. Stroke [mm] | Damping coefficient [MN/(m/sec)N] | Velocity exponent | Number of dampers | Capacity [kN] | Max. Stroke [mm] | Damping coefficient [MN/(m/sec)N] | Velocity exponent | |
| Deck-end | 4 | 3000 | 150 | 20 | 0.5 | 6 | 5000 | 200 | 30 | 0.015 |
| Tower | 3 | 3000 | 150 | 20 | 0.5 | 6 | 5000 | 200 | 30 | 0.015 |
- 4.7 Comparative Results and Discussion
Results of the nonlinear time history analysis have demonstrated the direct incidence of the fluid viscous dampers on the seismic response of the bridge models. In Chapter 3, the dynamic characterization of cable-stayed bridges was obtained by means of the modal analysis. The response spectrum analysis gave a first approach of the seismic response of the bridge models, a general seismic characterization, and allowed the selection of the bridge models for the nonlinear time-history analysis. Time-history analysis gave an accurate seismic description for the considered bridge models, in which the responses where obtained and characterized in terms of stay cable layout and earthquake nature. Chapter 4 introduces the effect of viscous dampers as passive energy dissipation devices, in which selection of the damper layout, selection of the optimal damper parameters as well as the definitive seismic responses are obtained for both models in the presence of far-fault and near-fault ground motions.
The last part of this chapter compares the seismic responses in terms of the damped Vs undamped time histories for both bridge models and taking into account the earthquake nature. Comparative results on the average of the maximum responses are analyzed, and finally, results of the energy approach are exposed and discussed.
- 4.7.1 Seismic Response Comparison
With comparative purposes, Figs. 4.41 to 4.46 show average responses of longitudinal displacements of the deck, vertical displacements of the deck at the mid-span, in-plane bending moments at the tower base, in-plane bending moments of the deck at the mid-span, axial forces at the tower base and out-of-plane bending moments at the tower base respectively. Those average responses were obtained for each time step, considering all the analyzed events for both far-fault and near-fault ground motions; and selecting AB4 bridge as the analyzed model. As was explained before, it is expected a similar response for AR4 bridge, and for that reason it is not considered here. The aim of this response comparison is to show the main differences between damped Vs undamped cases.
The analysis of the average responses shows evident results. Very important reductions of displacements and internal forces are obtained when additional damping devices are included, for both far-fault and near-fault ground motions. Important reductions are obtained especially for longitudinal displacements of the deck and in-plane bending moments of the towers, aspect that can be appreciated for far-fault and near-fault ground motions. With regard to near-fault earthquakes, it can be observed the average permanent displacements experienced with the damped cases, that are evident if longitudinal and vertical displacements of the deck are analyzed, aspect that was previously discussed.
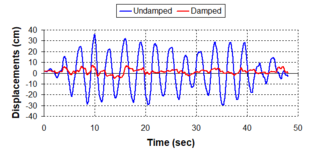
(a) Far-fault ground motion |
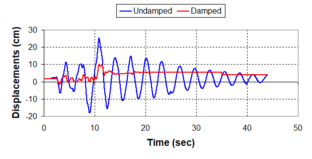
(b) Near-fault ground motion |
On the other hand, the analysis of the average axial forces of the towers shows very similar responses, for both kinds of earthquakes, if damped and undamped cases are compared, which confirms that the effect of additional damping devices is negligible for the seismic control of the axial forces of the towers. An analogue situation is observed if out-of-plane bending moments at the tower base are analyzed. As a conclusion, this implies that the addition of damping devices is extremely efficient for in-plane response control of cable-stayed bridges; however the transverse control is not very effective, even if transverse dampers are added at the tower-deck connection as was demonstrated before.
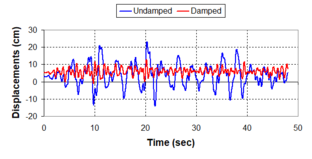
(a) Far-fault ground motion |
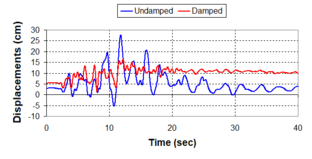
(b) Near-fault ground motion |
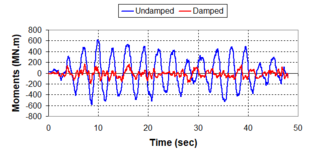
(a) Far-fault ground motion |
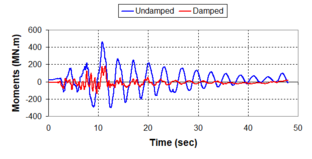
(b) Near-fault ground motion |
If the average responses for far-fault and near-fault ground motions are compared, maximum responses are obtained for the far-fault condition without exception. This apparent contradiction regarding the results obtained before can be explained if average of the absolute maximum responses is considered (as was taken into account in the previous analyses). The point is that the average response is obtained point-to-point, for each time step, in which positive and negative values are pondered; on the contrary of the average of the absolute maximum responses, in which absolute maximum values of each event are pondered independent on the time. In other words, the presence of long-period velocity pulses contained in the near-fault records, imply that average of the absolute maximum responses is higher than the maximum of the average response. These results are very important for design implications, because if time-histories are employed in the analysis, the worse response condition is obtained with the average of the maximum responses. In this sense, if near-fault earthquakes are considered, it is important to apply the average of the maximum responses, because if not, the pulse-type characteristics of the near-source ground motions may be underestimated.
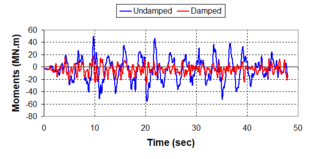
(a) Far-fault ground motion |
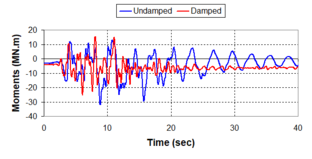
(b) Near-fault ground motion |
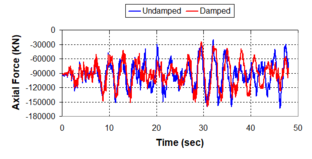
(a) Far-fault ground motion |
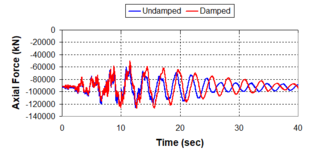
(b) Near-fault ground motion |
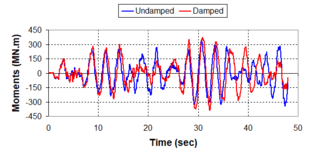
(a) Far-fault ground motion |
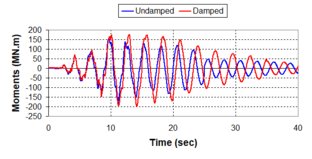
(b) Near-fault ground motion |
Figs. 4.47 to 4.51 show a comparison of the average of the absolute maximum displacements of deck and towers, for both bridge models and considering far-fault and near-fault ground motions. Over the bars, maximum values are signed.
From theses graphics, the effect of the additional damping devices is unquestionable, and especially for longitudinal displacements of deck and towers. Important reductions of longitudinal displacements of the deck, vertical displacements of the deck at the mid-span and longitudinal displacements at the tower-top are obtained for the damped cases, for both structures and for both far-fault and near-fault ground motions. Average reductions of 75%, 37% and 77% are obtained with longitudinal displacements of the deck, vertical displacements of the deck at the mid-span and longitudinal displacements of the tower-top for the far-fault condition respectively. Analogously, for the near-fault condition, those average reductions are 67%, 42% and 58% respectively. In those cases it is observed very similar responses comparing both bridges, in which the maximum average responses are always obtained for the near-fault ground motions, for both damped and undamped cases. It is important to notice that those responses are obtained considering the average of the absolute maximum responses, before explained.
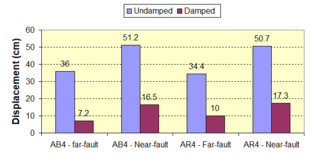
Fig. 4.47 Average of the Maximum Longitudinal Displacements of the Deck
|
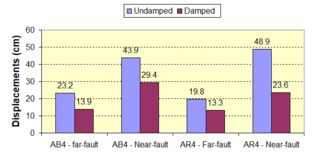
Fig. 4.48 Average of the Maximum Vertical Displacements of the Deck at the Mid-Span
|
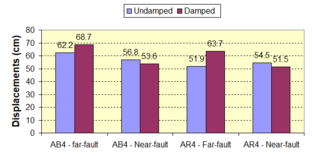
Fig. 4.49 Average of the Maximum Transverse Displacements of the Deck at the Mid-Span
|
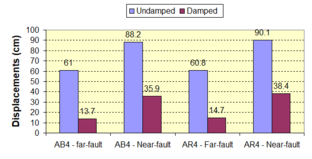
Fig. 4.50 Average of the Maximum Longitudinal Displacements at the Tower-Top
|
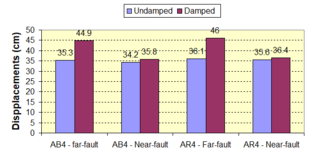
Fig. 4.51 Average of the Maximum Transverse Displacements of the Tower-Top |
An opposite situation is observed with transverse displacements of the deck and tower-top (Figs. 4.49 and 4.51 respectively). In those cases, very similar results are obtained comparing both bridges; however, average responses for the damped cases can be higher than those obtained with the undamped cases, especially for transverse displacements of the tower-top. |
Differences between damped and undamped cases are less important, which implies that additional damping devices are not effective in reducing the transverse response, as was demonstrated with time-histories. Likewise, not important differences on the seismic responses are observed between the far-fault and near-fault ground motions, and especially with the undamped cases.
Comparison of the internal forces can be observed in Figs. 4.52 to 4.57, in which compressive forces at the tower base, compressive forces of the deck at the tower-deck connection, tension forces of the cables, in-plane moments at the tower base, out-of-plane moments at the tower base and in-plane moments of the deck at the mid-span are exposed respectively. Those average responses were obtained again considering the average of the absolute maximum responses of each event, and considering the damped and undamped cases, for both bridges and for far-fault and near-fault ground motions.
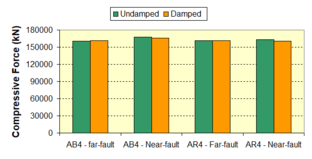
Fig. 4.52 Average Compressive Forces at the Tower Base |
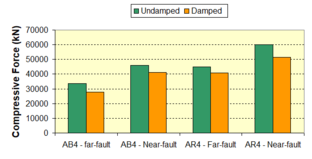
Fig. 4.53 Average Compressive Forces of the Deck at the Tower-Deck Connection |
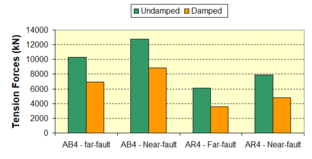
Fig. 4.54 Average Tension Forces of the Most Loaded Cables |
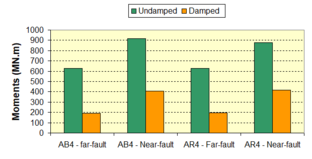
Fig. 4.55 Average In-Plane Moments at the Tower Base |
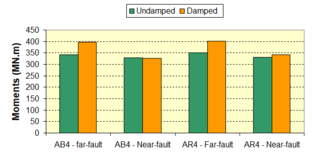
Fig. 4.56 Average Out-of-Plane Moments at the Tower Base |
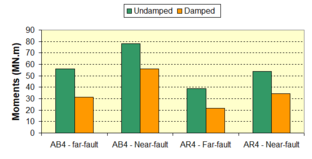
Fig. 4.57 Average Moments of the Deck at the Mid-Span |
The analysis of the internal forces shows very similar results for the average axial forces of the towers (Fig. 4.52), independent on the bridge model, far-fault or near-fault condition and damped or undamped situation, as was observed with time-histories. This behaviour confirms the null effect of the viscous dampers on the axial forces of the towers. The effect of the additional dampers on the seismic response reduction is especially evident for compressive forces of the deck, tension forces of the cables, in-plane bending moments of the towers and moments of the deck, with average response reductions of 13%, 37%, 69% and 45% for far-fault ground motions respectively. For near-fault ground motions, average reductions of 12%, 35%, 54% and 32% are obtained respectively. This analysis demonstrates that additional viscous dampers are extremely efficient on the seismic response control of in-plane moments of the towers and deck. By this way, taking into account results obtained from this analysis and considering the displacement response comparison, it is possible to observe that the largest response reductions are generally obtained for the far-fault ground motions, although differences with the near-fault condition can be not very interesting. On the other hand, as happens with displacements, the comparison between far-fault and near-fault ground motions shows that the largest averages of the maximum responses are obtained for the near-fault condition, basically for in-plane responses, independent on the damped or undamped situation and bridge model. Likewise, comparing AB4 with AR4 model, for the damped and undamped conditions, it is confirmed that basically the same response of the towers is obtained, and important differences can be appreciated for the deck and cable responses. Surprisingly, average out-of-plane moments at the tower base expose an analogue behaviour compared with the transverse response of displacements before studied, confirming the negligible effect of the viscous dampers on the transverse response.
- 4.7.2 Energy Analysis
An adequate study of the energies involved is fundamental to understand the seismic response of the bridge models. In this stage, we are basically interested in the input energy provided by the ground motion to the structures, and the dissipated energy by additional viscous damping. A comparison between both energies gives an idea about the performance of the structures in terms of the absorbed and dissipated energy; and the efficiency of the additional viscous damping system.
The input energy depends on the mass ms of the system, the input ground acceleration ![]() and the relative velocity of the system
and the relative velocity of the system ![]() . On the other hand, the dissipated energy by additional viscous damping depends on the damping coefficient cd, the velocity exponent N, and the velocity of the system
. On the other hand, the dissipated energy by additional viscous damping depends on the damping coefficient cd, the velocity exponent N, and the velocity of the system ![]() . However, in practical terms, the dissipated energy is strongly influenced by the damping coefficient, as was previously demonstrated (see Chapter 2). As example, Fig. 4.58 exposes the input energy and the dissipated energy by additional viscous damping considering events 5 and Kobe as input ground motions, applied to AR4 bridge. Both input records are characterized by the same duration.
. However, in practical terms, the dissipated energy is strongly influenced by the damping coefficient, as was previously demonstrated (see Chapter 2). As example, Fig. 4.58 exposes the input energy and the dissipated energy by additional viscous damping considering events 5 and Kobe as input ground motions, applied to AR4 bridge. Both input records are characterized by the same duration.
Distribution of both input energy and dissipated energy are quite different comparing the seismic events. Event 5 represents a typical far-fault ground motion, in which both energies linearly vary with time. The input energy is gradually introduced, but also dissipated for all the event duration. The total input energy achieved is 100 MJ, and the total dissipated energy is 60 MJ. Kobe earthquake, JMA Station, is a near-fault ground motion, in which all the input energy is introduced in brief time (≈ 13 sec), and practically all the dissipated energy is achieved in 15 sec, taking into account that both input and dissipated energies start at time equal to 7 – 8 sec. For time over 20 sec, no additional input or dissipated energy is experienced. The total input energy introduced is 160 MJ, and the total dissipated energy is 100 MJ; higher than those obtained for Event 5.
As a summary, Figs. 7.59 and 4.60 show a comparison of both input and dissipated total energies, for AB4 and AR4 bridge models, and considering far-fault and near-fault ground motions respectively. These energies were obtained from the analyses considering the optimal damper parameters.
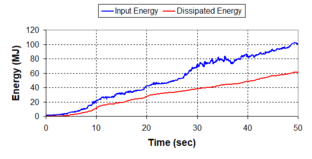
(a) Event 5 |
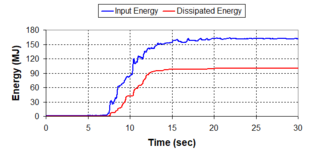
(b) Kobe Earthquake, JMA Station |
The analysis for far-fault ground motions (Fig. 4.59) shows an increasing input energy as well as dissipated energy by additional viscous damping as the duration of the events increase. Because far-fault events were artificially generated, rich frequency content is implicitly considered; and as was previously explained, all those events are very similar because they are originated from the same seed. The main differences come from the source distance, which implies longer durations for the longest source distances (event 5). For that reason, minimum input energy is observed for the shortest event (event 1), and gradually increased as the source distance increases. A similar behaviour is observed for the dissipated energy. No evident differences are observed between AB4 and AR4 models, that is to say, basically the same input and dissipated energies are experienced for both structures.
The analysis considering near-fault ground motions is quite different. These real earthquakes are arranged from the shortest duration (Gatos event) to the longest duration (Kobe event). Because of the different frequency content of the events and the considerable amounts of energy introduced by some velocity pulses (a characteristic of near-source earthquakes), different behaviour is obtained compared with the far-fault analysis. Now, input energies are not in accordance with the duration, which means that some earthquakes are more energetic than others, independent on the duration. Important amounts of input and dissipated energy are observed for events Gatos and Kobe, precisely in accordance with the largest responses previously obtained with those specific events. As happens with the far-fault condition, no important differences are obtained between AB4 and AR4 bridges.
Comparing near-fault with far-fault ground motions, it is clear the important differences, in which higher input energy is observed for near-fault earthquakes. A similar situation occurs with the dissipated energy. In fact, average input energies of 76.3 MJ and 113.5 MJ are obtained for far-fault and near-fault conditions respectively. Likewise, average dissipated energies of 41.8 MJ and 71.5 MJ are obtained for the same conditions respectively. Those differences imply that near-source earthquakes are more energetic than far-fault earthquakes. However, to capture the dissipated energy in terms of the input energy, it is better to analyze the energy dissipation rates, as can be appreciated in Fig. 4.61.
(a) Far-fault ground motion |
4 
(b) Near-fault ground motion |
Results of the energy dissipation rates show a more uniform behaviour for the far-fault condition. In this case, 55% average of the input energy is dissipated by additional viscous damping, as long as 57% average of the input energy is dissipated for the near-fault condition when additional dampers are added. Those similar values imply basically the same average energy dissipation rate, for both kinds of earthquakes, as was observed when seismic responses where compared in terms of the damped Vs undamped conditions. In terms of the efficiency of the dampers, for the far-fault conditions, the dampers are basically equally efficient for all the seismic events. For the near-fault condition, additional viscous dampers are more efficient with events Gatos, San Fernando and Kobe, that is to say, the more energetic events. This feature is a very important aspect to take into account, and can be explained because of the increase of the damping and the decrease of the natural frequencies of the structures [Moroni and Sarrazin, 2005]. Regarding the bridge models, as expected, not important differences are observed for the energy dissipation rates if the stay cable layout is changed.
As a general conclusion, very high energy dissipation rates are obtained, which confirms the important incidence of the addition of fluid viscous dampers as passive energy dissipation devices to reduce the seismic response of cable-stayed bridges.
Appendix A. Step-by-Step Nonlinear Time History Analysis
A.1 General Considerations
Step-by-step time integration algorithms have been widely used to solve structural dynamic problems. However, much experience is required to choose the right algorithm and tweak the parameters for their efficient application. These methodologies involve the attempt to satisfy dynamic equilibrium at discrete points in time after the solution has been defined at time zero. Most methods use equal time intervals at Δt, 2Δt, 3Δt…..NΔt; involving a solution of the complete set of equilibrium equations at each time increment. All these approaches can fundamentally be classified as either explicit or implicit integration methods.
An integration algorithm is classified as explicit if the displacements for the next time step can be determined from the accelerations, velocities and displacements at the current and previous time step. They do not involve the solution of a set of linear equations at each step. For most real structures, which contain stiff elements, a very small time step is required to obtain stable solution. Therefore, all explicit methods are conditionally stable with respect to the size of the time step.
Implicit methods attempt to satisfy the differential equation at time “t” after the solution at time “t-Δt” has been found. Those methods require the solution of a set of linear equations at each time step; however, larger time steps may be used. Most implicit strategies are unconditionally stable, defining an integration algorithm as stable if the numerical solution of a free-vibration structure will not grow without bound from any arbitrary set of initial conditions. In this sense, the conditional stable algorithms usually have a time step size restriction imposed by stability, which is associated with the highest natural frequency of vibration of the system. When the total number of degrees-of-freedom of the system become large, resulting in high natural frequencies, the required time step size can become extremely small as a result [Chen and Ricles, 2008a].
A large number of different incremental solution methods have been proposed since the Newmark family methods at the end of the 50s [Newmark, 1959]. Wilson θ method [Wilson, 1968], Hilber-Hughes-Taylor-α method [Hilber et al, 1977], Collocation method [Hilber and Hughes, 1978], Wood-Bossak-Zienkiewics-α method [Wood et al, 1981], Hoff-Pahl-θ1 method [Hoff and Pahl, 1988a, 1988b], Chung-Hulbert-α method [Chung and Hulbert, 1993] and CH-SSH method [Chung and Hulbert, 1994] are good examples of single-step (i.e. the solution of an equation of motion at a current time step depends only on the solution at the previous time step), implicit, second-order accurate and unconditionally stable methodologies for step-by-step time history analysis. Various methods have been used to develop integration algorithms, including Taylor series expansions, weighted residual methods, Hamilton`s principle and least-square methods [Wood, 1990]. In the reference of Wilson (2002), a brief description and stability conditions for the most used time history integration methodologies is found.
In the case of non-linear analysis, it may be necessary to reform the incremental stiffness matrix for the complete structural system at each time step, with the obvious computing time increment. In other words, the non-linear nature of the system is accounted by re-evaluating the structural properties at the end of the time-step, to be appropriate to the current deformed state at that time. Iterations are then made to achieve the state of dynamic equilibrium at the end of this time step and the computed velocities and displacements are then used as initial conditions for the next interval; thus the process may be continued step-by-step from the initiation of loading to any desired time [Nazmy and Abdel-Ghaffar, 1990]. Many different numerical tricks, including element-by-element methods, have been developed to minimize the computational requirements. In addition, artificial or numerical damping (numerical dissipation) must be added to most incremental solution methods to dissipate spurious high-frequency response due to the spatial domain discretized by a standard finite element method, obtaining stable solutions [KaiPing, 2008]. The exact solution of many nonlinear structures requires that the acceleration, the second derivative of the displacements, are not smooth functions. This discontinuity of the acceleration is caused by the nonlinear hysteresis of most structural materials, contact between parts of the structure, and bucking of elements [Wilson, 2002].
With regard to the stability conditions of the integration algorithms, studies involving the stability under nonlinear structural behaviour are limited. Hughes (1976) discussed the stability of the Newmark method with constant acceleration under structural nonlinearity. Numerical examples for different types of nonlinearity showed that the Newmark method with constant acceleration remains stable for nonlinear structural behaviour when using the proper iteration tolerance to limit the amount of unbalanced loads from being carried over to the next time step. Because the stiffness varies in a structure with nonlinear response during the analysis, it is difficult to determine the stability of a direct integration algorithm. Therefore, a small time-step is often used by researchers to obtain a stable solution using an integration algorithm for nonlinear structural dynamics. In a recent publication, Chen and Ricles (2008b) utilized Discrete Control Theory to investigate the stability of direct integration algorithms for nonlinear structural dynamics. They studied the Newmark family of integration algorithms, the Hilber-Hughes-Taylor-α method and a newly developed integration algorithm, referred to as the CR integration algorithm. They showed that the stability of an integration algorithm under nonlinear structural behaviour is dependent on the poles and zeros of its open-loop discrete transfer function. Also, they proved that an unconditionally stable integration algorithm for linear elastic structures not always remain stable under nonlinear structural behaviour.
All the previous ideas imply that selection of step-by-step integration strategies is not trivial. It is apparent that a large number of different direct numerical integration methods are possible by specifying different integration parameters. For single-degree-of-freedom systems, the Newmark`s method of central difference (γ=1/2; β=0; δ=0) is more accurate and the Newmark`s method of linear acceleration (γ=1/2; β=1/6; δ=0) is more accurate than the average acceleration method (γ=1/2; β=1/4; δ=0). However, if only single-degree-of-freedom systems are to be integrated, the piece-wise exact method previously presented should not be used because there is no need to use an approximate method. In the case of general structural systems, it appears that the Newmark´s modified average acceleration method (γ=1/2; β=1/4; δ=ΔT/π), with a minimum addition of stiffness proportional damping, is a good selection that damp out periods shorter than the time-step introducing a minimum error in long-period responses. According to Wilson (2002), Newmark`s constant acceleration method, with the addition of very small amounts of numerical damping, is recommended for dynamic analysis of nonlinear structures. However, for all methods of direct integration, great care should be taken to make certain that the numerical damping does not eliminate important high-frequency response.
A.2 The Hilber-Hughes-Taylor-α Method
This strategy for direct integration time history analysis is an implicit method that has been successfully used in the field of classical mechanical simulation and structural dynamics, originally proposed by Hilber et al (1977). This methodology introduces an α-factor that represents a controlled numerical damping (for that reason this method is also called α-method), keeping a quadratic convergence. This characteristic makes this strategy very robust for the integration of highly nonlinear systems. That was the reason why this method was selected as integration procedure in this work.
The α-method uses the Newmark method to solve the following modified equations of motion:
where M is the mass matrix, C is the viscous damping matrix, K is the stiffness matrix, Ft is the vector of forces that depends on the time t, α is the numerical damping parameter and u, ![]() and
and ![]() are the respective vectors of displacements, velocities and accelerations.
are the respective vectors of displacements, velocities and accelerations.
Equation A.1 can be expressed as:
that represents the equilibrium equation for the instant tn+1 expressed in generalized coordinates q.
The following formulas are applied:
where q is the vector of generalized coordinates, Δt is the time-step size and Fq is part of the vector of forces only depending on the generalized coordinates and their derivatives.
For linear systems it can be demonstrated that the method is unconditionally stable if the parameters α, β and γ are in accordance with:
In the case of α=0, the method reduces to the Newmark`s constant or average acceleration method (trapezoid rule). Using α=0 offers the highest accuracy of the available methods, but may permit excessive vibrations in the higher frequency modes, i.e., those modes with periods of the same order as or less than the time-step size. For more negative values of alpha, the higher frequency modes are more severely damped. This is not physical damping, since it decreases as smaller time-steps are used. However, it is often necessary to use a negative value of alpha to encourage a nonlinear solution to converge. For best results, it is recommended the use of the smallest time-step practical, and select α as close to zero as possible, and trying with different values of α and time-step size to be sure that the solution is not too dependent upon these parameters [Computers & Structures, 2007]. For α=-1/3, maximum numerical dissipation is reached, aspect that can be dangerous because much high frequency content could be severely damped.
The stability conditions of the α-method are guaranteed for linear structural systems. In case of nonlinear systems, stability conditions are very hard to find. Chen and Ricles (2008b) have proposed that the Newmark method with constant acceleration and the α-method remain unconditionally stable for both stiffening and softening behaviour.
A.3 Fast Nonlinear Analysis
The response of real structures when subjected to a large dynamic input often involves significant nonlinear behaviour. In general, nonlinear behaviour includes the effects of large displacements and/or nonlinear material properties. The more complicated problem associated with large displacements, which cause large strains in all members of the structure, requires tremendous amount of computational effort and computer time to obtain a solution. Certain types of large strains, such as those in rubber bearings, base isolators and gap elements can be treated as lumped nonlinear elements. In this sense, a large number of very practical structures have a limited number of points or members in which nonlinear behaviour takes place when subjected to static or dynamic loading. Local buckling, uplifting of foundations, contact phenomena, and yielding of few elements are examples of structures with local nonlinear behaviour, as can be seen in Fig. A.1.
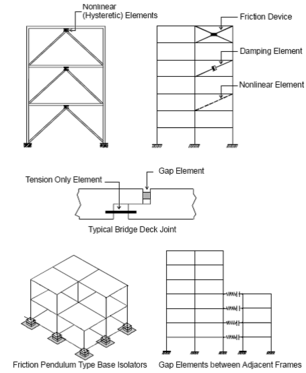
Fig. A.1 Examples of Structures with Lumped Nonlinear Elements [Wilson, 2002] |
At the end of the 80´s, a new strategy for both static and dynamic analysis of structures which are primarily linear elastic with a limited number of predefined nonlinear elements was developed by Ibrahimbegovic and Wilson (1989) and Wilson (1993). The method, called Fast Nonlinear Analysis (FNA), is extremely efficient and accurate for structural systems with lumped nonlinear elements, and it is incorporated in structural codes such as SAP2000, in which all nonlinearities are restricted to link/support elements.
In this methodology, the dynamic equilibrium equations of a linear elastic structure with predefined nonlinear elements subjected to an arbitrary load can be written as: |
where M is the diagonal mass matrix, C is the proportional damping matrix, KL is the stiffness matrix for the linear elastic elements (all elements except those with nonlinear behaviour), rN is the vector of forces from the nonlinear degrees-of-freedom in the link elements, r is the vector of applied loads and u, ![]() and
and ![]() are the respective displacement, velocity and acceleration vectors.
are the respective displacement, velocity and acceleration vectors.
If the computer model is unstable without the nonlinear elements, it is possible to add effective elastic elements (at the location of the nonlinear elements) of arbitrary stiffness. If these effective forces, Keu(t), are added to both sides of Eq. A.1, the exact equilibrium equations can be written as:
where Ke is the effective stiffness of arbitrary value. Therefore, the exact dynamic equilibrium equations for the nonlinear model can be written as:
where
| |
is known, and the effective external load ![]() must be evaluated by iteration. If a good estimate of the effective elastic stiffness can be made, the rate of convergence may be accelerated because the unknown term
must be evaluated by iteration. If a good estimate of the effective elastic stiffness can be made, the rate of convergence may be accelerated because the unknown term ![]() will be small [Wilson, 2002].
will be small [Wilson, 2002].
The solution for this integration methodology involves the application of the stiffness and mass orthogonal Load Dependent Ritz Vectors of the elastic structural system to reduce the size of the nonlinear system to be solved. For that reason, this methodology is also called Nonlinear Modal Time History Analysis, because in some sense, this is a hybrid between time history analysis and modal analysis. The forces in the nonlinear elements are calculated by iteration at the end of each time or load step, and the uncoupled modal equations are solved exactly for each time increment. By iteration within each time-step, equilibrium, compatibility and all element force-deformation equations within each nonlinear element are identically satisfied.
Structures subjected to static loads can also be solved using this strategy. It is only necessary to apply the loads slowly to a constant value and add large modal damping values. Therefore, the final converged solution will be in static equilibrium and will not contain inertial forces. This procedure can also be applied to add static loads in a dynamic problem.
The main advantage of this methodology is the tremendous computational time economy. With a small number of nonlinear elements, a small percentage of the required time in a nonlinear direct integration time history analysis is needed for the same structure. As example, to solve a structure with 92 nodes, 103 elastic frames, 56 nonlinear elements and 600 time-steps at 0.02 sec for a nonlinear direct integration time history analysis using a well-known computer program in which stiffness matrix for the complete structure was recalculated for each time-step, 4320 minutes (3 days!) were required using an Intel 486 processor. Using the supercomputer Cray XMP-1, the final time to solve the same structure with the same nonlinear direct integration strategy was reduced to 3 hours. Applying the Fast Nonlinear Analysis method, with the Intel 486 processor, the final time required to solve the structure was less than 3 minutes [Wilson, 2002].
It is necessary to emphasize that the Fast Nonlinear Analysis can be very fast and accurate for structures with nonlinearities lumped in some joints or elements, however for highly nonlinear structures, cable structures or structures in which the nonlinearity is mainly of geometric type, this strategy can be inaccurate. As example, the AB4 cable-stayed bridge model of this work was selected to compare results applying the Fast Nonlinear Analysis with the nonlinear direct integration time history analysis (in this case the Hilber-Hughes-Taylor-α method). Event 1 was selected as input ground motion (1000 time steps at 0.02 sec). Results of this comparison are shown in Table A.1.
Results of this comparison showed that the main differences for the earthquake response are associated with the internal forces on members. Main differences come from the towers, with up to 23% for bending moments and 21% for the compressive forces. Maximum differences for the deck compression are in the order of 11%. For the maximum cable forces, differences are less sensitive. With regard to the displacements, maximum differences were obtained for the maximum longitudinal displacements of the deck (17%).
| Response Measured | Analysis strategy | |
| Fast nonlinear analysis | Direct integration | |
| Max. long. Tower displ. [cm] | 73.5 | 67.0 |
| Max. vertical deck displ. [cm] | 23.2 | 23.0 |
| Max. long. Deck displ [cm] | 47.0 | 39.0 |
| Max. tower moment [MN.m] | 917 | 710 |
| Max. tower compression [kN] | 210000 | 165000 |
| Max. deck compression [kN] | 44800 | 39800 |
| Max. cable force [kN] | 11000 | 10900 |
For all cases, the seismic responses obtained with the application of the direct integration algorithm were lower than the responses obtained with the fast nonlinear analysis. As a conclusion, it seems to be that accuracy of the Fast Nonlinear Analysis can be questionable when apply to highly nonlinear structures such as cable-stayed bridges. This implies that the analysis of nonlinear cable structures such as those proposed in this research necessarily need to be solved applying nonlinear direct integration algorithms, with the great computational effort involved. A good choice could be the application of the Hilber-Hughes-Taylor-α method.
A.4 Recent Integration Algorithms
Integration algorithms are often used to solve the temporally discretized equations of motion of structures at selected time steps. The first strategies began with the investigations of Newmark [Newmark, 1959], and since those first studies, numerous time integration algorithms have been proposed.
In a recent publication, Chen and Ricles (2008a) have developed a new explicit integration algorithm, called the CR Algorithm. A discrete transfer function was used to study the properties of integration algorithms, and a pole mapping rule from control theory in conjunction with this transfer function was used to develop the algorithm. The properties of the algorithm were investigated and compared with other well established methods such as the Newmark family of integration. By assigning proper stable poles to the discrete transfer function, the authors demonstrated that the new explicit method was unconditionally stable, with the same accuracy of the Newmark method with constant acceleration. The CR algorithm is based on expressions for displacements and velocity that are both explicit in form, making it an appealing integration algorithm.
KaiPing (2008) presented a new family of generalized-α time integration algorithms without overshoot for structural dynamics. The incorporation of seven free parameters into the single-step three-stage formulation, proved through finite difference analysis that these algorithms were unconditionally stable, second-order accurate and numerical dissipation controllable. Comparisons with the commonly used α-methods showed that the newly developed algorithms have the advantage of eliminating the overshooting characteristics exhibited by the commonly used algorithms, while their property of dissipation is preserved.
A.5 Current Speed of Personal Computers for Nonlinear Analysis
Although new and faster simplified methodologies have appeared to solve complex structural systems in the time domain, the application of direct integration time history analysis strategies is an inevitable procedure to solve highly nonlinear structures, with the computational effort involved. In this sense, with the appearance of the new Multi-Core processors and the 64-bit multi-processing/multi-threading algorithms, computer time to solve large, complex and highly nonlinear structures can be drastically reduced, in a way that now those systems can be easily analyzed with personal computers in a few hours, task exclusively made by clusters a few years ago.
With the aim to compare results of the computing time to solve highly nonlinear structures, a brief analysis was conducted. To do that, the AR4 bridge model was selected. This structure is a harp pattern, double-plane cable layout concrete cable-stayed bridge with the geometric, material and loading specifications enlarged in Chapter 3. The three-dimensional model considered the use of 109 nonlinear beam elements, 68 linear link elements and 64 cable elements joined by 172 joints modelled by the structural code SAP2000 [Computers & Structures, 2007]. Nonlinearities involved in this analysis took into account the axial force-bending moment interaction, cable-sag effect, large displacements and the material nonlinearity of the tension-only formulation of the cables. The input data of the earthquake records were obtained from Chapter 3 of this work, considering the artificially generated events 1 and 4 for far-fault ground motions. For near-fault records, the real earthquakes of Loma Prieta-Gatos and Kobe-JMA were used. These events were applied considering the three components of each one, according to the explanations given before.
The analyses were performed applying the Hilber-Hughes-Taylor-α method for direct integration of the equations of motion. These nonlinear equations were solved iteratively in each time step. This required re-forming and re-solving the stiffness and damping matrices, in which, for each iteration, a line-search was used to determine the optimum displacement increment to apply. Firstly, constant-stiffness iteration was tried, followed by Newton-Raphson iteration if that failed. If convergence still cannot achieved, the algorithm automatically divided the time-step into a smaller sub-step, trying again. The basic parameters to control the solution and convergence of the nonlinear static analysis considered the maximum total steps per stage, maximum null steps per stage, the maximum iterations per step and the iteration convergence tolerance. The basic parameters for the nonlinear direct integration time history analysis considered the numerical damping of the integration method, the maximum sub-step size, the maximum iterations per sub-step and the iteration convergence tolerance. Table A.2 exposes the basic nonlinear parameters considered to control the solution and convergence for both nonlinear static and nonlinear dynamic analyses.
| Event | Convergence parameters | |||||||
| Nonlinear static | Nonlinear direct integration | |||||||
| Max total steps | Max null steps | Max iterations per step | Iteration tolerance | Numerical damping | Max sub-step | Max iterations per sub-step | Iteration tolerance | |
| 1 | 200 | 50 | 60 | 1x10-6 | -0.2 | 0.02 | 60 | 1x10-4 |
| 4 | 200 | 50 | 60 | 1x10-6 | -0.2 | 0.02 | 60 | 1x10-4 |
| Gatos | 200 | 50 | 60 | 1x10-6 | -0.2 | 0.02 | 120 | 1x10-3 |
| JMA | 200 | 50 | 60 | 1x10-6 | -0.2 | 0.02 | 120 | 1x10-3 |
The same nonlinear static convergence parameters were used for all the events; however it was necessary to apply more iterations per sub-step to reach the convergence in the case of near-fault ground motions for the nonlinear direct integration. Likewise, to guarantee the convergence with an accurate response, the iteration convergence tolerance was limited to lower values than the static case. The numerical damping selected did not affect the response behaviour of the structures, and limited efficiently the very high frequency content.
Regarding the damping matrix, it was considered by using the Rayleigh’s uncoupled formulation, that is to say, damping proportional to stiffness and mass. The mass proportional coefficient was 0.0729 and the stiffness proportional coefficient was 0.000513.
For the analyses, three 32-bit computers were employed to compare results of different configurations and earthquake inputs. Computer 1 used an Intel Pentium Centrino Processor of 1.86 GHz and 1 GB RAM memory; Computer 2 used an Intel Core 2 Duo Processor of 2.13 GHz and 2 GB RAM memory; and Computer 3 used an Intel Core 2 Quad Processor of 2.4 GHz and 2 GB RAM memory. Table A.3 shows results of the computer time to obtain the complete responses of each event, which can be evaluated adding the employed time for the nonlinear static analysis to the time for the nonlinear direct integration time history analysis.
| Event | Total time steps | Time step size (sec) | Computer time (sec) | |||||
| Computer 1 | Computer 2 | Computer 3 | ||||||
| Nonlinear static | Nonlinear time history | Nonlinear static | Nonlinear time history | Nonlinear static | Nonlinear time history | |||
| 1 | 1000 | 0.02 | 12 | 3330 | 9 | 3000 | 8 | 1937 |
| 4 | 2000 | 0.02 | 11 | 6430 | 9 | 5900 | 8 | 3850 |
| Gatos | 1250 | 0.02 | 11 | 13724 | 9 | 11840 | 8 | 9815 |
| JMA | 2500 | 0.02 | 11 | 25973 | 9 | 23990 | 8 | 20650 |
Results of the analyses showed that the employed time for the nonlinear static analysis is absolutely negligible compared with the required time for the nonlinear direct integration time history analysis. Likewise, because of the same control parameters were employed for all the nonlinear static analyses, the same computer time is obtained in this stage.
The main differences in the computer time were obtained with the nonlinear time history analysis. It is clear the tremendous difference when the computer is changed. The improvements in the computer capabilities notably increase the speed of the analyses, and especially if multi-processors are added (Computers 2 and 3). The maximum speed was obtained with Computer 3, which used 4 processors; however, this computer was not 4 times faster than Computer 1. In this sense, results showed that computer 3 was 1.72 times faster than computer 1 for Event 1; 1.67 times faster for Event 2; 1.40 times faster for the event Gatos and 1.26 times faster for the event JMA. From these results, it seems to be that the efficiency not only depends on the hardware specifications or the methodology chosen, but also on the characteristics of the seismic input.
Comparing Event 1 with Event 4, the required time for the analysis of Event 4 was approximately twice time of Event 1, for all the computers. The same situation was observed comparing events Gatos and JMA. This approximation comes from the total integration time, and of course, it is expected that the total time for the analysis of an event two times longer will be approximately two times slower, although some differences can be experienced because of the different characteristics of the input records. However, a linear behaviour was experienced.
Comparing the required time for the analysis of far-fault and near-fault ground motions, more important differences were obtained. The more problematic convergence was observed with the near-fault earthquakes, because of the long-period velocity pulses contained in the records which originated highly nonlinear behaviour of the structure, with the consequent difficulties of the convergence. For that reason, it was necessary to modify some integration parameters, and specifically the maximum number of iterations per sub-step. For far-fault ground motions, 60 iterations max. were accepted, but for near-fault earthquakes, convergence was reached with 120 iterations max, which implied a notable increase of the computer time for the analyses. In fact, although event Gatos is 1.25 times longer than Event 1, the required time to solve the event Gatos was 4.12 times longer than Event 1 with Computer 1, 3.95 times longer with Computer 2 and 5 times longer with Computer 3. Similar results were obtained comparing Event 4 with event JMA, which demonstrates that the analysis of near-fault earthquakes sometimes experience some convergence difficulties, implying more computational effort.
For analysis of large structural systems, it is not possible to store all information within high-speed storage. If data needs to be obtained from low-speed disk storage, the effective speed of a computer can be reduced significantly. For that reason, it is recommended the use of computer codes with the transfer data to and from disk storage conducted in large blocks to minimize disk access time, also called paging operating systems.
References
Abdel – Ghaffar, A.M. (1991), “Cable-Stayed Bridges under Seismic Action”, Proceedings of the Seminar Cable – Stayed Bridges: Recent Development and their Future, Yokohama, Japan.
Akkar, S., Gülkan, P. (2003), “A Near-Fault Spectrum and its Drift Limits”, Proceedings of the 4th International Conference on Earthquake Engineering and Seismology, Tehran, Iran.
Ali, H-E., Abdel Ghaffar, A.M. (1991a), “Passive Seismic Control of Cable-Stayed Bridges”, Proceedings of the First U.S. – Japan Workshop on Earthquake Protective Systems for Bridges, National Center for Earthquake Engineering Research, Buffalo, USA, pp 543 – 556.
Ali, H-E., Abdel Ghaffar, A.M. (1991b), “Seismic Energy Dissipation for Cable-Stayed Bridges using Passive Devices”, Earthquake Engineering and Structural Dynamics, Vol. 23, pp 877 – 893.
Ali, H-E., Abdel-Ghaffar, A.M. (1995), “Modelling the Nonlinear Seismic Behaviour of Cable-Stayed Bridges with Passive Control Bearings”, Computers & Structures, Vol. 54, No. 3, pp 461 – 492.
Álvarez, J. (2004), “Respuesta Sísmica de Puentes Arco Empleando Amortiguamiento Viscoso Suplementario”, Tesis Doctoral, Departamento de Ingeniería del Terreno, Cartográfica y Geofísica, ETSECCPB, Universidad Politécnica de Catalunya, Barcelona, España.
American Association of State Highway and Transportation Officials (AASHTO) (1994), “LRFD Bridge Design Specifications”, 1st Edition, Washington, DC, USA.
American Association of State Highway and Transportation Officials (AASHTO) (2000), “Guide Specifications for Seismic Isolation Design”, 2nd edition, Washington, D.C., USA.
ANSYS Inc (2005), “ANSYS V. 7.0”, Canonsburg, Pa, USA.
Aparicio, A.C., Casas, J.R. (2000), “Ponts. Apunts de Ponts”, Department d`Enginyeria de la Construcció, ETSECCPB, Universitat Politècnica de Catalunya, Barcelona.
Aschrafi, M. (1998), “Comparative Investigations of Suspension Bridges and Cable-Stayed Bridges for Spans Exceeding 1000 m”, Proceedings of the IABSE Symposium Japan 1998 Long – Span and High Rise Structures, Kobe, Japan, pp 447 – 452.
Atkins, J.C., Wilson, J. (2000), “Analysis of Damping in Earthquake Response of Cable-Stayed Bridges”, Proceedings of the 12th World Conference on Earthquake Engineering, Auckland, NZ, Paper no. 1468.
Bommer, J.J. (1999), “Displacement Spectra for Seismic Design”, Journal of Earthquake Engineering, Vol. 3, No. 1, pp 1 – 32..
Bommer, J.J., Elnashai, A.S., Weir, A.G. (2000), “Compatible Acceleration and Displacement Spectra for Seismic Design Codes”, Proceedings of the 12th World Conference on Earthquake Engineering, Auckland, New Zealand, Paper No. 0207.
Button, M.R., Cronin, C.J., Mayes, R.L. (2002), “Effect of Vertical Motions on Seismic Response of Highway Bridges”, Journal of Structural Engineering, Vol. 128, No. 12, pp 1551 – 1564.
Calvi, G.M. (2004), “Recent Experience and Innovative Approaches in Design and Assessment of Bridges”, Proceedings of the 13th World Conference on Earthquake Engineering, Vancouver, Canada, Paper No. 5009.
Caughey, T.K. (1963), “Equivalent Linearization Techniques”, Journal of the Acoustical Society of America, Vol. 35, pp 1706 – 1711.
Chen, Ch., Ricles, J.M. (2008a), “Development of Direct Integration Algorithms for Structural Dynamics Using Discrete Control Theory”, Journal of Engineering Mechanics, Vol. 134, No. 8, pp 676 – 683.
Chen, Ch., Ricles, J,M, (2008b), “Stability Analysis of Direct Integration Algorithms Applied to Nonlinear Structural Dynamics”, Journal of Engineering Mechanics, Vol. 134, No. 9, pp 703 – 711.
Chen, Z.Q., Wang, X.Y., Ko, J.M., Ni, Y.Q., Spencer, B.F., Yang, G. (2003), “MR Damping System on Dongting Lake Cable-Stayed Bridge”, Proceedings of the Conference: Smart Structures and Materials 2003: Smart Systems and Non-destructive Evaluation for Civil Infrastructures, San Diego, USA.
Cheng, S.H., Lau, D.T. (2002), “Modelling of Cable Vibration Effects of Cable-Stayed Bridges”, Journal of Earthquake Engineering and Engineering Vibration, Vol.1, No.1.
Cheung, M.S., Lau, D.T., Li, W.C. (2000), “Recent Development on Computer Bridge Analysis and Design”, Progress in Structural Engineering and Materials, Vol. 2, No. 3, pp. 376 – 385.
Chung, J., Hulbert, G.M. (1993), “A Time Integration Algorithm for Structural Dynamics with Improved Numerical Dissipation: The Generalized-α Method”, Journal of Applied Mechanics (ASME), Vol. 60, pp 371 – 375.
Chung, J., Hulbert, G.M. (1994), “A Family of Single-Step Houbolt Time Integration Algorithms for Structural Dynamics“, Computer Methods in Applied Mechanics and Engineering, Vol. 118, pp 1 – 11.
Combault, J., Morand, P., Pecker, A. (2000), “Structural Response of the Rion-Antirion Bridge”, Proceedings of the 12th World Conference on Earthquake Engineering, Auckland, New Zealand, Paper No. 1609.
Comisión Federal de Electricidad (CFE) (1993), “Manual de Diseño de Obras Civiles. Diseño por Sismo. Acciones”, Instituto de Investigaciones Eléctricas, México.
Comité Europeo de Normalización (CEN) (1998a), “Eurocódigo 8: Disposiciones Para el Proyecto de Estructuras Sismorresistentes. Parte 1 – 1: Reglas Generales. Acciones Sísmicas y Requisitos Generales de las Estructuras”, Asociación Española de Normalización y Certificación, Madrid, España.
Comité Europeo de Normalización (CEN) (1998b), “Eurocódigo 8: Disposiciones Para el Proyecto de Estructuras Sismorresistentes. Parte 2: Puentes”, Asociación Española de Normalización y Certificación, Madrid, España.
Comité Europeo de Normalización (CEN) (1998c), “Eurocódigo 1: Bases de Proyecto y Acciones en Estructuras. Parte 3: Acciones del Tráfico en Puentes”, Asociación Española de Normalización y Certificación, Madrid, España.
Computers & Structures (2007), “SAP2000 V. 11.0 – Integrated Software for Structural Analysis & Design”, Berkeley, CA, USA.
Constantinou, M.C. (2003), “Damping Systems for New and Retrofit Construction”, Proceedings of the FIB Symposium: Concrete Structures in Seismic Regions, Athens, Greece.
Cox, K.E, Ashford, S.A. (2002), “Characterization of Large Velocity Pulses for Laboratory Testing”, Final Report on Research, Pacific Earthquake Engineering Research Center, College of Engineering, University of California, Berkeley, USA.
Dyke, S.J., Caicedo, J.M., Turan, G., Bergman, L.A., Hague, S. (2002), “Introducing Phase I of the Benchmark Problem on the Seismic Response Control of Cable-Stayed Bridges”, Proceedings of the 7th US National Conference on Earthquake Engineering, Boston, MA, USA.
Ernst, H.J. (1965), “Der E-Modul von Seilen unter Berücksichtigung des Durchhängens”, Bauingenieur, Vol. 40, pp 52 – 55.
Fabunmi, J.A. (1985), “Extended Damping Models for Vibration Data Analysis”, Journal of Sound and Vibration, Vol. 101, No. 2, pp 181 – 192.
Faccioli, E., Paolucci, R., Rey, J. (2004), “Displacement Spectra for Long Periods”, Earthquake Spectra, Vol. 20, No. 2, pp 347 – 376.
Förars, K., Brownjohn, J.M.W., Warnitchai, P. (2000), “Effects of Cable Dynamics on the Seismic Performance of Cable – Stayed Bridges”, Proceedings of the International Conference on Advances in Structural Dynamics, Hong Kong, Peoples Rep. China.
Garevski, M.A., Severn, R.T. (1992), “Dynamic Analysis of Cable-Stayed Bridges by Means of 3D Analytical and Physical Modelling”, Proceedings of the 10th World Conference on Earthquake Engineering, Madrid, Spain, pp 4809 – 4814.
Garevski, M.A., Severn, R.T. (1993), “Damping and Response Measurement on a Small – Scale Model of a Cable-Stayed Bridge”, Earthquake Engineering and Structural Dynamics, Vol. 22, pp 13 – 29.
Gasparini, D.A., Vanmarcke, E.H. (1976), “SIMQKE: A Program for Artificial Motion Generation”, Department of Civil Engineering, Massachusetts Institute of Technology, Cambridge, Massachusetts, USA.
Ghasemi, H. (1999), “Seismic Protection of Bridges”, Public Roads, Mar/Apr 1999, ProQuest Science Journals.
Girija Vallabhan, C.V. (2008), “Two-Dimensional Nonlinear Analysis of Long Cables”, Journal of Engineering Mechanics, Vol. 134, No. 8, pp 694 – 697.
Guerreiro, L. (2006), “Sistemas de Dissipação de Energia”, Apuntes de Dinâmica e Engenharia Sismica, Mestrado en Engenharia de Estruturas, Instituto Superior Tecnico, Universidade Tecnica de Lisboa.
Hancock, J., Bommer, J.J., Stafford, P.J. (2008), “Number of Scaled and Matched Accelerograms Required for Inelastic Dynamic Analyses”, Earthquake Engineering and Structural Dynamics, Vol. 37, No. 13, pp. 1585 – 1607.
He, W.L. (2003), “Smart Energy Dissipation Systems for Protection of Civil Infrastructures from Near-Field Earthquakes”, PhD Dissertation, The City University of New York, USA.
Hernández, J.J., López, O.A. (2002), “Response to Three-Component Seismic Motion of Arbitrary Direction”, Earthquake Engineering and Structural Dynamics, Vol. 31, pp 55 – 77.
Hilber, H.M., Hughes, T.J.R. (1978), “Collocation Dissipation and “Overshoot” for Time Integration Schemes in Structural Dynamics”, Earthquake Engineering and Structural Dynamics, Vol. 6, pp 99 – 118.
Hilber, H.M., Hughes, T.J.R., Taylor, R.L.T. (1977), “Improved Numerical Dissipation for Time Integration Algorithms in Structural Dynamics”, Earthquake Engineering and Structural Dynamics, Vol. 5, pp 283 – 292.
Hoff, C., Pahl, P.J. (1988a), “Development of an Implicit Method with Numerical Dissipation from Generalized Single-Step Algorithm for Structural Dynamics”, Computer Methods in Applied Mechanics and Engineering, Vol. 67, pp 367 – 385.
Hoff, C., Pahl, P.J. (1988b), “Practical Performance of the θ1 Method and Comparison with Other Dissipation Algorithm in Structural Dynamics”, Computer Methods in Applied Mechanics and Engineering, Vol. 67, pp 87 - 110.
Housner, G.W. (1956), “Limit Design of Structures to Resist Earthquakes”, Proceedings of the First World Conference on Earthquake Engineering, Vol. 5, Berkeley, USA.
Hu, Y., Yu, Y-X. (2000), “A Combine Approach of Evaluation of Long-Period Design Spectrum”, Proceedings of the 12th World Conference on Earthquake Engineering, Auckland, New Zealand, Paper No. 0860.
Hughes, T.J.R. (1976), “Stability, Convergence and Grow and Decay of Energy of the Average Acceleration Method in Nonlinear Structural Dynamics”, Computers & Structures, Vol. 6, pp 313 – 324.
Ibrahimbegovic, A., Wilson, E.L. (1989), “Simple Numerical Algorithms for the Mode Superposition Analysis of Linear Structural Systems with Nonproportional Damping”, Computers and Structures, Vol. 33, No. 2, pp 523 – 531.
Iemura, H., Pradono, M.H. (2003), Chapter 19, Structural Control, Earthquake Engineering Handbook, Editors: Chen, W-F, Scawthorn, Ch., CRC Press, USA.
Iervolino, I., Cornell, C.A. (2005), “Record Selection for Nonlinear Seismic Analysis of Structures”, Earthquake Spectra, Vol. 21, No. 3, pp 685 – 713.
Infanti, S., Papanikolas, P., Benzoni, G., Castellano, M.G. (2004), “Rion – Antirion Bridge: Design and Full – Scale Testing of the Seismic Protection Devices”, Proceedings of the 13th World Conference on Earthquake Engineering, Vancouver, Canada, Paper No. 2174.
Infanti, S., Papanikolas, P., Theodossopoulos, G. (2003), “Rion-Antirion Bridge: Full-Scale Testing of Seismic Devices”, Proceedings of the FIB Symposium: Concrete Structures in Seismic Regions, Athens, Greece.
Jacobsen, L.S. (1930), “Steady Forced Vibration as Influenced by Damping”, Transactions of the American Society of Mechanical Engineers, Vol. 52, pp 169 – 181.
Japan Road Association (1996), “1996 Seismic Design Specifications for Highway Bridges”, Tokyo, Japan
Japan Road Association (2002), “2002 Seismic Design Specifications for Highway Bridges”, Tokyo, Japan
Jara, M., Casas, J.R. (2002a), “Control de Vibraciones en Puentes. Un Estado del Arte y de la Práctica”, Monografía CIMNE IS – 48, Centro Internacional de Métodos Numéricos en Ingeniería, Barcelona, España.
Jara, M., Casas, J.R. (2002b), “Criterios de Diseño de Puentes con Aisladores y Disipadores de Energía”, Monografía CIMNE IS – 49, Centro Internacional de Métodos Numéricos en Ingeniería, Barcelona, España.
Jerónimo, E., Guerreiro, L. (2002), “Seismic Displacement Analysis of Bridges With Viscous Dampers”, Proceedings of the 12th European Conference on Earthquake Engineering, London, U.K., Paper No. 373.
Jia, J.F., Ou, J.P. (2008), “Seismic Analysis of Long-Span Cable-Stayed Bridges Subjected to Near-Fault Pulse-Type Ground Motions”, Proceedings of the 14 World Conference on Earthquake Engineering, Beijing, China.
KaiPing, Y. (2008), “A New Family of Generalized-α Time Integration Algorithms without Overshoot for Structural Dynamics”, Earthquake Engineering and Structural Dynamics, Vol. 37, pp 1389 – 1409.
Kato, B., Akiyama, H. (1975), “Energy Input and Damage in Structures Subjected to Severe Earthquakes”, Journal of Structural and Construction Engineering. Transactions of AIJ, Vol. 235, pp 9 – 18.
Kawashima, K. (2000), “Seismic Design and Retrofit of Bridges”, Proceedings of the 12th World Conference on Earthquake Engineering, Auckland, NZ, Paper No. 2828.
Kawashima, K., Unjoh, S. (1989), “Damping Characteristics of Cable-Stayed Bridges Associated with Energy Dissipation at Movable Supports”, Structural Engineering/Earthquake Engineering, Vol.6, No.1, pp 123 – 130.
Kawashima, K., Unjoh, S. (1991), “Seismic Behaviour of Cable-Stayed Bridges”, Proceedings of the Seminar Cable – Stayed Bridges: Recent Development and their Future, Yokohama, Japan.
Kawashima, K., Unjoh, S. (1992), “Damping Characteristics of Cable-Stayed Bridges”, Proceedings of the 10th World Conference on Earthquake Engineering, Madrid, Spain, pp 4803 – 4808.
Kawashima, K., Unjoh, S., Azuta, I. (1988), “Damping Characteristics of Cable-Stayed Bridges”, Proceedings of the 9th World Conference on Earthquake Engineering, Tokyo, Japan, pp 471 – 476.
Kawashima, K., Unjoh, S., Azuta, I. (1990), “Analysis of Damping Characteristics of a Cable-Stayed Bridge Based on Strong Motion Records”, Structural Engineering/Earthquake Engineering, Vol.7, No.1, pp 169 – 178
Kawashima, K., Unjoh, S., Tsunomono, M. (1993), “Estimation of Damping Ratio of Cable-Stayed Bridges for Seismic Design”, Journal of Structural Engineering, Vol. 119, No. 4, pp 1015 – 1031.
Kim, J., Choi, H., Min, K.W. (2003), “Performance-Based Design of Added Viscous Dampers using Capacity Spectrum Method”, Journal of Earthquake Engineering, Vol. 7, No. 1, pp 1 – 24.
Lai, G., Chen, Ch-Ch., Hsu, M.Ch. (2004), “Cable – Stayed Bridge Retrofit using Isolation System”, Proceedings of the 13th World Conference on Earthquake Engineering, Vancouver, Canada, Paper No. 3253.
Lecinq, B., Messein, J.P., Boutillon, L. (2003), “The Rion-Antirion Bridge Stay Cables: A Seismic Approach”, Proceedings of the FIB Symposium: Concrete Structures in Seismic Regions, Athens, Greece.
Lee, D., Taylor, D.P. (2001), “Viscous Damper Development and Future Trends”, The Structural Design of Tall Buildings, Vol. 10, No. 5, pp 311 – 320.
Lee, S-H, Min, K-W, Hwang, J-S, Kim, J. (2004), “Evaluation of Equivalent Damping Ratio of a Structure with Added Dampers”, Engineering Structures, Vol. 26, No. 3, pp 335 – 346.
Lestuzzi, P., Schwab, P., Koller, M., Lacave, C. (2004), “How to Choose Earthquake Recordings for Non-Linear Seismic Analysis of Structures”, Proceedings of the 13th World Conference on Earthquake Engineering, Vancouver, Canada, Paper No. 1241.
Li, B., Liang, X-W (2007), “Design of Supplemental Viscous Dampers in Inelastic SDOF System Based on Improved Capacity Spectrum Method”, Structural Engineering and Mechanics, Vol. 27, No. 5, pp 541 – 554.
Li, X., Zhu, X. (2003), “Study on Near-Fault Design Spectra of Seismic Design Code”, Proceedings of the 3rd International Conference on Earthquake Engineering, Nanjing, China.
Lin, W-H., Chopra, A.K. (2002), “Earthquake Response of Elastic SDF Systems with Non-Linear Fluid Viscous Dampers”, Earthquake Engineering and Structural Dynamics, Vol. 31, No. 9, pp 1623 – 1642.
Macdonald, J.H.G., Georgakis, C.T. (2002), “The Influence of Cable – Deck Interaction on the Seismic Response of Cable – Stayed Bridges”, Proceedings of the 12th European Conference on Earthquake Engineering, London, UK, Paper No. 441.
Makris, N. (1997), “Rigidity – Plasticity – Viscosity: Can Electrorheological Dampers Protect Base-Isolated Structures from Near-Source Ground Motions?”, Earthquake Engineering and Structural Dynamics, Vol. 26, pp 571 – 591.
Makris, N. (1998), “Viscous Heating of Fluid Dampers. I: Small-Amplitude Motions”, Journal of Engineering Mechanics, Vol. 124, No. 11, pp 1210 – 1216.
Makris, N., Roussos, Y., Whittaker, A.S., Kelly, J.M. (1998), “Viscous Heating of Fluid Dampers. II: Large-Amplitude Motions”, Journal of Engineering Mechanics, Vol. 124, No. 11, pp 1217 – 1223.
Málaga-Chuquitaype, C., Bommer, J.J., Pinho, R., Stafford, P.J. (2008), “Selection and Scaling of Ground-Motion Records for Nonlinear Response-History Analyses Based on Equivalent SDOF Systems”, Proceedings of the 14th World Conference on Earthquake Engineering, Beijing, China, Paper No 05-01-0064.
Maldonado, E., Canas, J.A., Casas, J.R., Pujades, L.G. (1998), “Respuesta de Puentes Frente a Acciones Sísmicas”, Monografía CIMNE IS – 27, Centro Internacional de Métodos Numéricos en Ingeniería, Barcelona, España.
Malvern, L. E. (1969), “Introduction to the Mechanics of a Continuous Medium”, Prentice-Hall, Englewood Cliffs, N.J.
Mavroeidis, G.P., Dong, G., Papageorgiou, A.S. (2004), “Near-fault Ground Motions and the Response of Elastic and Inelastic Single-Degree-of-Freedom (SDOF) Systems”, Earthquake Engineering and Structural Dynamics, Vol. 33, No. 9, pp 1023 – 1049.
Ministerio de Fomento (2000), “EHE, Instrucción de Hormigón Estructural”, Comisión Permanente del Hormigón, Madrid, España.
Morgenthal, G. (1999), “Cable-Stayed Bridges – Earthquake Response and Passive Control”, Msc Dissertation, Civil Engineering Department, Imperial College of Science, Technology and Medicine, London, UK.
Moroni, M.O., Sarrazin, M. (2005), “Respuesta Sísmica de Puentes con Sistemas de Protección Sísmica”, Actas del Congreso Chileno de Sismología e Ingeniería Antisísmica - IX Jornadas, Concepción, Chile, Paper No. A13-11.
Nagai, M., Xie, X., Yamaguchi, H., Fujino, Y. (1998), “Economical Comparison Between Cable-Stayed and Suspension Systems with a Span Exceeding 1000 meters”, Journal of Constructional Steel Research, Vol. 46, Nos. 1 – 3, pp 59.
Nazmy, A.S., Abdel – Ghaffar, A.M. (1990a), “Non-Linear Earthquake Response Analysis of Long-Span Cable-Stayed Bridges: Theory”, Earthquake Engineering and Structural Dynamics, Vol. 19, pp 45 – 62.
Nazmy, A.S., Abdel – Ghaffar, A.M., (1990b), “Non-Linear Earthquake Response Analysis of Long-Span Cable-Stayed Bridges: Applications”, Earthquake Engineering and Structural Dynamics, Vol. 19, pp 63 – 76.
New Zealand Ministry of Works and Development (1983), “Design of Lead-Rubber Bridge Bearings”, Civil Division Publication 818/A, Wellington, New Zealand.
Newmark, N.M. (1959), “A Method of Computation for Structural Dynamics”, Journal of Engineering Mechanics Division, Vol. 85, No. 3, pp 67 – 94.
Pacific Earthquake Engineering Research Center (2005), “PEER Strong Motion Database”, URL: [http://peer.berkeley.edu/nga/], University of California, Berkeley, California.
Pekcan, G., Mander, J.B., Chen, S.S. (1999), “Fundamental Considerations for the Design of Non-Linear Viscous Dampers”, Earthquake Engineering and Structural Dynamics, Vol. 28, No. 11, pp 1405 – 1425.
Podolny, W., Scalzi, J.B. (1986), “Construction and Design of Cable – Stayed Bridges”, 2nd Edition, John Wiley & Sons, Inc, New York.
Prakash, V., Powell, G.H. (1993), “Drain-2DX, Drain-3DX and Drain Building: Base Program Design Documentation”, Report No. UCB/SEMM – 93/16, University of California, Berkeley, USA.
Priestley, M.J.N., Seible, F., Calvi, G.M. (1996), “Seismic Design and Retrofit of Bridges”, John Wiley & Sons, Inc., New York.
Rakheja, S., Sankar, S. (1986), “Local Equivalent Constant Representation of Non-linear Damping Mechanisms”, Engineering and Computers, Vol. 3, pp 11 – 17.
RAM International (2003), “RAM ADVANSE V. 5.0 - Structural Analysis and Design Software”, Carlsbad, CA, USA.
Ren, W.X., Obata, M. (1999), “Elastic-Plastic Seismic Behaviour of Long-Span Cable-Stayed Bridges”, Journal of Bridge Engineering, Vol.4, No.3, pp 194 – 203.
Roberts, J.B. (1976), “Stationary Response of Oscillators with Non-linear Damping to Random Excitations”, Journal of Sound and Vibration, Vol. 50, pp 145 – 156.
Seleemah, A.A., Constantinou, M.C. (1997), “Investigation of Seismic Response of Buildings with Linear and Nonlinear Fluid Viscous Dampers”, Technical Report NCEER- 97- 0004, National Center for Earthquake Engineering Research, Buffalo, USA.
Seismosoft (2006), “SeismoSignal V. 3.2.0”, Package for the Processing of Strong-Motion Data, University of Pavia, Italy.
Singh, M.P., Verma, N.P., Moreschi, L.M. (2003), “Seismic Analysis and Design with Maxwell Dampers”, Journal of Engineering Mechanics, Vol. 129, No. 3, pp 273 – 282.
Somerville, P. (1997), “The Characteristics and Quantification of Near Fault Ground Motion” Proceedings of the FHWA/NCEER Workshop on the National Representation of Seismic Ground Motion for New and Existing Highway Facilities, Burlingame, California, pp 293 – 318.
Somerville, P. (2002), “Characterizing Near Fault Ground Motion for the Design and Evaluation of Bridges”, Proceedings of the Third National Seismic Conference & Workshop on Bridges & Highways, Portland, Oregon, USA.
Somerville, P. (2003), “Magnitude Scaling of the Forward Rupture Directivity Pulse in Near-Fault Ground Motions”, Final Report on Research, URS Group, Inc, Pasadena, California.
Soong, T.T., Constantinou, M.C. (1994), “Passive and Active Structural Vibration Control in Civil Engineering”, Springer, New York.
Soong, T.T., Dargush, G.F. (1997), “Passive Energy Dissipation Systems in Structural Engineering”, John Wiley & Sons, Inc, New York.
Symans, M.D., Charney, F.A., Whittaker, M., Constantinou, M.C., Kircher, C.A., Johnson, M.W., McNamara, R.J. (2008), “Energy Dissipation Systems for Seismic Applications: Current Practice and Recent Developments”, Journal of Structural Engineering, Vol. 134, No. 1, pp 3 – 21.
Symans, M.D., Constantinou, M.C. (1999), “Semi-active Control Systems for Seismic Protection of Structures: A State-of-the-Art Review”, Engineering Structures, Vol. 21, pp 469 – 487.
Tan, P., Agrawal, A.K., Pan, Y. (2005), “Near-field Effects on Seismically Excited Highway Bridge Equipped with Nonlinear Viscous Dampers”, Bridge Structures: Assessment, Design and Construction, Vol. 1, No. 3, pp 307 – 318.
Taylor, D.P. (1996), “Fluid Dampers for Applications of Seismic Energy Dissipation and Seismic Isolation”, Proceedings of the 11th World Conference on Earthquake Engineering, Acapulco, México.
Taylor, D., Duflot, P. (2002), “Fluid Viscous Dampers used for Seismic Energy Dissipation in Structures”, Proceedings of the 12th European Conference on Earthquake Engineering, London, U.K., Paper No. 093.
Terenzi, G. (1999), “Dynamics of SDOF Systems with Nonlinear Viscous Damping”, Journal of Engineering Mechanics, Vol. 125, No. 8, pp 956 - 963
Teyssandier, J.P. (2002), “Corinthian Crossing”, Civil Engineering, Oct. 2002, ProQuest Science Journals.
Teyssandier, J.P., Maublanc, G., Morand, P., Papanikolas, P. (2003), “The Rion-Antirion Bridge”, Proceedings of the Symposium: Concrete Structures in Seismic Regions, Athens, Greece.
Tolis, S.V. (1999), “Displacement Design Spectra”, Journal of Earthquake Engineering, Vol. 3, No. 1, pp 107 – 125.
Trifunac, M.D. (1995), “Pseudo Relative Velocity Spectra of Earthquake Ground Motion at Long Periods”, Soil Dynamics and Earthquake Engineering, Vol. 14, pp 331 – 346.
Tuladhar, R., Dilger, W. (1999), “Effect of Support Conditions on Seismic Response of Cable – Stayed Bridges”, Canadian Journal of Civil Engineering, Vol. 26, No.5, pp 631 – 645.
Tuladhar, R., Dilger, W.H., Elbadry, M.M. (1995), “Influence of Cable Vibration on Seismic Response of Cable-Stayed Bridges”, Canadian Journal of Civil Engineering, Vol. 22, No. 5, pp 1001 – 1020.
Uang, C.M., Bertero, B.B. (1990), “Evaluation of Seismic Energy in Structures”, Earthquake Engineering and Structural Dynamics, Vol. 19, pp 77 - 90
Valdebenito, G. (2005), “Comportamiento Sísmico de Puentes”, Apuntes de Clases del Curso de Master en Ingeniería Sísmica y Dinámica Estructural, Departamento de Ingeniería del Terreno, Cartográfica y Geofísica, Universidad Politécnica de Catalunya, Barcelona, España.
Valdebenito, G., Aparicio, A. (2005), “Comportamiento Sísmico de Puentes Atirantados y Disipación de Energía Adicional: Un Estado del Conocimiento”, Monografía CIMNE IS – 54, Centro Internacional de Métodos Numéricos en Ingeniería, Barcelona, España.
Virtuoso, F., Guerreiro, L., Azevedo, J. (2000), “Modelling the Seismic Behaviour of Bridges with Viscous Dampers”, Proceedings of the 12th World Conference on Earthquake Engineering, Auckland, New Zealand, Paper No. 0782.
Walter, R. (1999), “Cable – Stayed Bridges”, 2nd Edition, Thomas Telford Ltd., London, UK.
Wilson, E.L. (1968), “A Computer Program for the Dynamic Stress Analysis of Underground Structures”, SESM Rep. No. 68-1, Division of Structural Engineering and Structural Mechanics, Univ. of California, Berkeley, Calif.
Wilson, E.L. (1985), “A New Method of Dynamic Analysis for Linear and Nonlinear Systems”, Finite Elements in Analysis and Design, Vol. 1, pp 21 – 23.
Wilson, E.L. (1993), “An Efficient Computational Method for the Base Isolation and Energy Dissipation Analysis of Structural Systems”, Proceedings of the Seminar on Seismic Isolation, Passive Energy Dissipation and Active Control, Applied Technology Council, Redwood City, Calif.
Wilson, E.L. (2002), “Three-Dimensional Static and Dynamic Analysis of Structures”, 3rd Edition, Computers and Structures, Inc; Berkeley, California, USA.
Wilson, E.L., Der Kiureghian, A., Bayo, E.P. (1981), “A Replacement for the SRSS Method in Seismic Analysis“, Earthquake Engineering and Structural Dynamics, Vol. 9.
Wilson, J.C., Gravelle, W. (1991), “Modelling of a Cable-Stayed Bridge for Dynamic Analysis”, Earthquake Engineering and Structural Dynamics, Vol. 20, pp 707 – 721.
Wilson, E.L., Yuan, M.W., Dickens, J.M. (1982), “Dynamic Analysis by Direct Superposition of Ritz Vectors”, Earthquake Engineering and Structural Dynamics, Vol. 10, pp 813 – 823.
Wood, W.L. (1990), “Practical Time-Stepping Schemes”, Clarendon, Oxford, U.K.
Wood, W.L., Bossak, M., Zienkiewicz, O.C. (1981), “An Alpha Modification of Newmark´s Method”, International Journal for Numerical Methods in Engineering, Vol. 15, pp 1562 – 1566.
Xu, Z., Agrawal, A.K., He, W.-L., Tan, P. (2007), “Performance of Passive Energy Dissipation Systems during Near-field Ground Motion Type Pulses”, Engineering Structures, Vol. 29. pp 224 – 236.
Yamaguchi, H., Manabu, I. (1997), “Mode – Dependence of Structural Damping in Cable-Stayed Bridges”, Journal of Wind Engineering and Industrial Aerodynamics, Vol. 72, No. pp 289 - 300.
Zhai, C-H., Xie, L-L. (2007), “A New Approach of Selecting Real Input Ground Motions for Seismic Design: The Most Unfavourable Real Seismic Design Ground Motions”, Earthquake Engineering and Structural Dynamics, Vol. 36, No. 8, pp 1009 – 1027.
Document information
Published on 01/01/2010
Licence: CC BY-NC-SA license
Share this document
Keywords
claim authorship
Are you one of the authors of this document?