1 Introduction
In spite of its very long history, bottle manufacturing remains a challenging process and requires further improvements. The continuously growing competition calls for the optimization of the existing processes, diminishing the risks of producing deficient bottles. Thus, such optimization must be based upon a detailed knowledge of the process variables (such as the final topology, wall thickness, stress and temperature distribution) and their dependence upon the input parameters (inlet pressure, cooling conditions, etc). The typical questions that need to be answered are: How can the container weight be reduced without compromising on its strength? What are the optimal operation conditions (air pressure, mould temperature) and duration of the different forming stages? Up-to-date the answers to these and similar questions are predominantly based upon the experience and craftsmanship rather than scientific knowledge.
Numerical modeling and simulation can serve as an efficient tool for answering many questions arising when facing unexpected effects in the real products. Apart from being considerably cheaper than conducting expensive and time-consuming trial-and-error procedures common to factories, only numerical simulation can provide such (otherwise impossible or difficult to obtain) results as: stress distributions within the solidifying melt and temperature distribution.
Up-to-date, there exist several computational tools used by industries for bottle manufacturing simulation. Usually these software model the glass manufacturing process using axis-symmetric formulations. This approximation greatly reduces the associated computational costs. However, it over-simplifies the process: even though many bottle molds are purely axis-symmetric, nearly all containers produced do have non-symmetrical thickness distributions. Additionally, axisymmetric formulations cannot be applied to modeling bottles with non-circular cross-sections, such as e.g. fragrance containers. Thus, 3D simulations appear to be obligatory for obtaining reliable predictions. However, 3D simulations are typically characterized by excessive computational times.
Generally, two classes of methods can be applied to the problem at hand: the fixed mesh (Eulerian) and the mesh-moving (Lagrangian or Arbitrary Lagrangian Eulerian (ALE)) ones. Eulerian formulations require excessively fine meshes for the correct representation of the domain evolution and typically introduce errors in mass conservation (whenever the Level Set method is used for representing the glass-air interface evolution). On the other hand, Lagrangian approaches lead to strongly non-linear systems of equations and large mesh deformations. Thus, a robust and computationally efficient 3D model still presents a major challenge.
In the present work a 3D viscous incompressible fluid formulation using an updated Lagrangian framework is proposed, where the current configuration is the reference one. It adopts the basic features of the Particle Finite Element Method (PFEM) [1]. The key idea of the PFEM is that the variables of interest are stored at the nodes instead of the Gauss points. This results in a hybrid between a standard FE and a mesh-free method. A finite element mesh is created at every time step of the transient problem and the solution is then stored at the nodes. At every time step the governing equations are solved in the standard Finite Element (FE) fashion. The discrete operators are updated at every non-linear iteration step according to the newly obtained domain configuration, ensuring excellent convergence of the iterative procedure. The nodes obtain their new positions and the mesh is re-generated using an unconstrained Delaunay technique. The approach is adapted to the problem at hand introducing a simple but efficient contact algorithm, boundary tracking and a re-meshing strategy. In terms of the method for solving the governing equations, we use a modified fractional step approach, combining the classical technique with a quasi-incompressible prediction [2], [3]. The approach on the one hand allows for a highly computationally efficient solution and, on the other hand, leads to an accurate mass conservation, which is essential for the problems of interest.
The paper concludes with two numerical examples. The first one is used for the validation of the model. The second one shows the potential of the method. Moreover, it can be used as a reference for the comparison and validation of the future models for the bottle forming simulation. Even though several glass forming simulation results are published in literature ([4], [5], [6], [7]), there exist no well-established benchmark up-to-date. The example we propose focuses on the modeling of the final blow stage of a glass manufacturing process. The material and geometrical data as well as all the boundary conditions necessary for reproducing the example are specified.
2 Glass forming
2.1 Industrial process
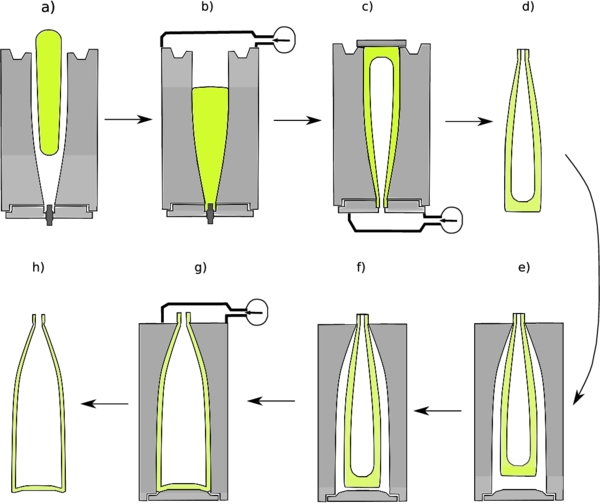
Prior to presenting the model for the glass (in particular, bottle) forming, let us review the industrial process and introduce the corresponding terminology. The standard bottle manufacturing process is sketched on Fig. 1.
|
| Figure 1: Different stages of bottle manufacturing process |
Typically, high speed machines are fed a stream of molten glass1 that is cut with a shearing blade into “gobs” of predetermined weight. These gobs fall into the first blank mold as shown in Fig. 1 a), where the temperature drops to the so-called “working temperature range” (some 1150C for soda-lime glasses). At the base of the mold a cylindrical plunger for shaping the bottle neck is inserted. Air pressure or a plunger is applied in order to push the gob to the bottom of the mold (Fig. 1 b)). Afterwards, air compressed to 0,15 MPa is blown from the bottom of the mold forcing the gob to rise and take the shape of the mold (Fig. 1 c)). This stage is known as a counter-blow process, suggesting that the “blow” is performed against gravity. The intermediate product of the counter-blow is known as “parison”.
Afterwards, the parison is removed from the first mold, turned upside down (Fig. 1 d)) and transferred into the second mold, where it is hung in order to stretch due to gravity (Fig. 1 e)), usually until the contact with the mold bottom is established. Finally, air pressure (slightly lower than the one used in the counter blow mold) is applied leading to the final shape of the bottle (Fig. 1 f)). This stage is known as final blow process. The bottle is then removed from the mold and is transferred to the annealing oven where it is reheated to remove the residual stresses produced during forming and finally it is cooled to the ambient temperature. The forming process, from the time when the gob is dropped into the first mold until the final product is removed from the second mold takes around 6 seconds.
(1) The most prevalent glass used for glass containers is soda-lime glass.
2.2 Material properties
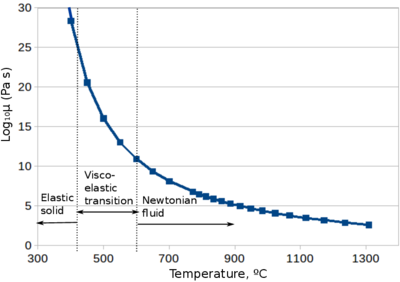
Glass is a visco-elastic material. At low temperatures (roughly, below 400 C) elastic effects dominate, while above 550 C elastic effects are negligible. One can also consider the transition zone where both effects are important (see (Fig. fig:glass_viscosity_a). In the following we shall consider the temperature dependent properties of a typical soda-lime glass.
Mechanical properties: viscosity and density
The viscosity is the most important property in the glass forming process. For example, in a typical temperature range encountered in glass forming processes (between approximately 700 and 1200C) glass viscosity varies from Pa s at 700C to some 400 Pa s. The dependence of glass viscosity upon temperature is typically given by Fulcher expression [8]:
|
|
(1) |
where , A and B are constants from experiments. In the present work, the following parameter values are considered (except for example 2): =220C, B=4700, A=-2.8. The glass viscosity as a function of temperature is shown in a logarithmic scale on Fig. 2a. Due to very large variations of viscosity during the forming process it is mandatory to include thermo-mechanical coupling in the model in order to obtain realistic predictions.
|
![Viscosity-temperature curve of soda-lime glass used for beverage containers [8].](/wd/images/thumb/a/a5/Draft_Garc%C3%ADa-Espinosa_370675429-visc_partial.png/400px-Draft_Garc%C3%ADa-Espinosa_370675429-visc_partial.png)
|
| Figure 2: Viscosity-temperature curve of soda-lime glass used for beverage containers [8]. | |
The temperature distribution in the glass is non-uniform at any stage of the glass manufacturing process. Thus, the viscosity is also non-homogeneous both in space and time. In the context of numerical modeling, Lagrangian formulations are very advantageous when dealing with non-constant properties: the property (for example, viscosity) is automatically transported being “attached” to the moving nodes. In the Eulerian framework, the representation of each non-constant property evolution would require solving the corresponding transport equation.
Glass density does not undergo considerable changes (2438 kg/m3 at 700C and 2367 kg/m3 at 1100 C), thus constant density is an acceptable approximation.
Thermal properties
Heat transfer in the glass is governed not exclusively by conduction, but also by the radiation, which may even be predominant. For strongly absorbing semi-transparent materials this radiation can be modeled as a diffusion process, thus an effective conductivity taking into account both processes is often defined [4]. Real radiation models are complex and computationally expensive. In the scope of this work they are not discussed.
Variation of the specific heat in the temperature range of interest is negligible (1400-1420 J/kg*K between 700 and 1200C). The value of the diffusivity changes from 0.0000015 /s at 700C to 0.0000065 /s at 1100 C.
3 Numerical model
The numerical model for the complex phenomenon of glass forming developed here consists of a mechanical and thermal modules. These models are coupled in order to take into account the temperature-dependent material properties' evolution.
Kinematic framework
Lagrangian description for modeling the glass forming processes appears attractive as it allows to track the evolution of the deforming domain naturally. The position of the evolving domain coincides with the position of the mesh nodes, defined by the solution of the flow problem. An accurate interface capturing using Eulerian approaches would require much higher mesh resolution to achieve similar precision. The additional cost associated to the Lagrangian description is due to the necessity of re-meshing the computational domain in order to avoid excessive element distortion.
The Particle Finite Element Method (PFEM) applied in the present work for modeling the glass forming process is based on the updated Lagrangian description of the governing equations. The key idea of the PFEM is that the variables of interest are stored at the nodes instead of the Gauss points. A finite element mesh is created at every time step of the transient problem and the solution is then stored at the nodes [1]. The nodes are generally maintained (unless adaptive refinement or erasal is performed), thus the mesh re-generation consists in reconnecting the existing nodes. The nodes move to their new position according to their velocity and then the finite element mesh is re-generated using an unconstrained Delaunay triangulation/tesselation [9].
In the following the governing equations for the glass are specified. Air is neglected, thus the glass-air interface becomes simply the glass domain boundary. The fully sticking contact with the mold is considered. In Section 3.2 the issues related to the boundary identification and contact treatment are explained in detail.
3.1 Mechanical model
At forming temperatures, elastic effects in the glass are negligible and the behavior is nearly iscochoric. Thus, hot glass can be modeled as a viscous incompressible fluid. The total stress tensor can be decomposed into hydrostatic and viscous parts and, therefore, the motion of the hot glass can be described by the Navier-Stokes equations for viscous incompressible fluid. These can be written for the glass domain in Cartesian coordiantes as
|
|
(2) |
|
|
(3) |
where is the velocity vector, the pressure, - time, is the material derivative, the gravity, the density, the dynamic viscosity and - the deviatoric strain rate.
Boundary conditions. At the mold walls and other fixed domain parts (e.g. bottle neck during the gravity stretching), homogeneous Dirichlet boundary conditions are prescribed, i.e.
|
|
(4) |
Two type of Neumann boundary conditions will be distinguished. The first one is the so-called “free-surface” condition that can be approximated for vanishing velocity gradients as: at . This condition will be prescribed at the evolving outer surface of the glass prior to the contact with the mold and at the inner surface prior to the application of the compressed air. A Neumann boundary condition will be used in order to account for the air pressure at :
|
|
(5) |
This condition is prescribed at the inner surface of the glass.
3.1.1 Finite Element formulation
An equal order linear interpolations for the velocity and pressure variables over 4-noded tetrahedra (3D) is used here for the space discretization of the governing equations Eqs. (2), (3). We use Backward Euler time discretization scheme exclusively for the sake of simplicity. All the arguments presented in the paper are valid for any implicit time integration scheme. Being standard, the space and time discretization are not discussed here (see e.g. [10], [Lohner]). A pressure stabilization term is added due to the use of the equal order velocity-pressure interpolation (see e.g. [11] or [12]).
Given and at , the time discrete problem consists in finding and at as the solution of
|
|
(6) |
|
|
(7) |
where is the mass matrix, is the Laplacian matrix, is the gradient matrix, and are the velocity and pressure respectively and is the body force vector. Note the absence of the convective term due to Lagrangian kinematic framework.
The matrices and vectors are assembled from the element contributions defined as
|
|
(8) |
|
|
(9) |
|
|
(10) |
|
|
(11) |
|
|
(12) |
|
|
(13) |
stands for standard linear FE shape functions vector, is the element integration domain, is an algorithmic stabilization coefficient defined as , where is the element size [11]. Note also that the discrete operators given by Eqs. 8-13 correspond to the unknown current configuration according to the updated Lagrangian approach [1], [13]. Thus, the system is non-linear and must be solved in an iterative manner by updating the discrete operators at every non-linear iteration.
3.1.1.1 Modified fractional step technique for the efficient solution of governing equations
Solving the governing equation system monolithically (i.e. for velocities and pressure simultaneously) has a considerable computational cost [14]. Pressure segregation or fractional step methods are known for their high computational efficiency, however they often lead to mass conservation problems [15]. We propose to use the modified version of the fractional step approach presented in [2] and further developed in [3]. On the one hand, it inherits the high computational efficiency of the original fractional step procedure ( [16], [17], [18]) due to the decoupling of the velocity and the pressure. On the other hand, it has much better mass conservation properties.
The fractional step split is applied here at purely algebraic level to the governing equations system defined by Eqs. (6)-(7). The momentum equation is split into two parts by introducing the intermediate velocity and the original monolithic system is replaced by
|
|
(14) |
|
|
(15) |
|
|
(16) |
where is an auxiliary vector, representing the intermediate or “fractional” nodal velocities and is the guess of the end-of-step nodal pressure vector. Eq. (14) is known as “fractional momentum” and Eq. (15) as “end-of-step momentum” equations. The novelty of [2] in contrast to the classical fractional step approach consists in using instead of in the fractional momentum equation.
The pressure Poisson's equation is obtained by enforcing the incompressibility condition (Eq. (16)) with the end-of-step momentum equation (Eq. (15)), leading to
|
|
(17) |
Using the typical approximation , we arrive at the final system of discretized equations to be solved:
|
|
(18) |
|
|
(19) |
|
|
(20) |
3.1.1.2 Fractional momentum equation solution and pressure prediction
The momentum equation (Eq. (18)) is non-linear due to the dependence of the discrete operators on the unknown current configuration . Thus, it must be solved iteratively. For this reason, let us define the residual of the fractional momentum equation as
|
|
(21) |
The modified fractional step method proposed in [2] consists in considering the pressure variation in the fractional momentum equation. Thus, cannot be considered constant in the residual expression. In order to obtain the fractional momentum equation dependent on the velocity exclusively (and thus maintain the decoupling of the velocities and the pressure), a prediction for the pressure can be computed using an assumption of slight compressibility. Following this assumption the current-step pressure is obtained by adding the term proportional to the divergence of velocity to the pressure of the previous step (see [13], [2] for details):
|
|
(22) |
where is the compressibility parameter of the fluid. The discrete form of Eq. (22) using linear velocity-pressure finite elements reads
|
|
(23) |
where is the pressure mass matrix.
In order to avoid matrix inversion for obtaining the current step pressure, the pressure mass matrix will be taken in the lumped form. Performing the integration, Eq. (23) can be re-written as
|
|
(24) |
Expressing the pressure in terms of velocity according to Eq. (24) allows to define the iterative solution of the non-linear equation (with defined by Eq. (21)) exclusively in terms of the nodal velocities:
|
|
(25) |
|
|
(26) |
|
|
(27) |
where “i” stands for the non-linear iteration index at time and is the tangent matrix defined as
|
|
(28) |
As the non-constant pressure term is now included in the residual, it must be accounted for in the linearization.
According to [3] the dynamic tangent matrix can be approximated as:
|
|
(29) |
where the operator and the volumetric constitutive matrix are defined (in 2D) as
|
|
(30) |
|
|
(31) |
Elimination of the unknown pressure variables from the left-hand-side of the modified fractional momentum equation enables us to solve it for the velocities only (as it is done in the standard fractional step), thereby preserving the decoupling of the nodal velocities and pressures. However at every non-linear iteration the nodal pressure needs to be updated using Eq. (24).
3.1.1.3 Pressure Poisson's equation and the correction step
The next step to be carried out is the correction of the pressure, i.e. obtaining the end-of-step incompressible pressure field using Eq. (19). Solution of Eq. (19) requires to impose the pressure boundary conditions due to the presence of the Laplacian . According to the methodology presented in [2], can be used as an essential boundary condition for the pressure necessary for solving the Poisson's equation for the pressure. The quality of this approximation is related exclusively to the value of the compressibility constant used in the prediction step. Having the pressure fixed to the predicted value at the free surface, the pressure Poisson's equation is solved elsewhere in the domain to yield the end-of-step pressure vector .
This step can be thus viewed as a correction of the predicted pressure to the correct end-of-step one everywhere except for the free surface, where the “slightly compressible” pressure is maintained. Consequently, the projection step is carried out according to Eq. (20) and returns the end-of-step divergence-free velocity everywhere in the domain except for the pressure boundary, where the divergence-free velocity is approximated.
The implementation of the modified fractional step scheme is very similar to that of the classical fractional step method. It is summarized next.
- Solve the fractional momentum, Eq. (18)
- Update the nodal pressure vector according to Eq. (24) and add it to the fractional momentum residual
- Update the discrete operators according to the new nodal positions
- Repeat two previous steps until convergence for the velocity field is achieved
- Solve the pressure Poisson's Eq. (19), using the predicted pressure as the boundary condition
- Solve the end-of-step momentum equation (Eq. (20))
3.2 Contact modeling and boundary mesh
3.2.1 Contact modeling
Accurate modeling of contact between the glass and the wall of the mold is essential for predicting the wall thickness of the glass object correctly. Literature exhibits a large number of numerical methods. In Eulerian non-matching grid formulations a large variety of methods has been proposed ranging from penalty approaches ([19], [20]) to augmented Lagrange multipliers [21]. For the matching grid methods the contact modeling is usually done using simple geometric considerations [4]. In this study we assume that the mold is a rigid body and the glass sticks to the mold. This is a reasonable and commonly accepted approximation (see e.g. [6], [4]).
We propose here a simple algorithm that allows preserving the overall strategy of the PFEM, but at the same time does not lead to the incorrect prediction of the wall thickness. For the sake of minimizing the computational cost associated with re-meshing, PFEM utilizes unconstrained Delaunay triangulation/tetrahedrization ([tetgen]) equipped with the alpha-shape technique for detecting boundaries.
3.2.2 Modified PFEM contact algorithm
Considering that the nodes follow a variable distribution , which is the minimum distance between two nodes, the alpha-shape technique (see [22], [1]) applied to the unconstrained Delaunay mesh allows to distinguish whether an element defined by the four nodes must be created or not. The radius of a sphere defined by the examined nodes is compared to the corresponding size (average size of the inter-nodal distances). If the ratio , where is the alpha-shape parameter typically taken as 1.5 in 3D, the element is not created and the nodes are marked as belonging to the boundary (for details on the alpha-shape techniques one can see [1]). For the correct contact representation we propose to combine the alpha-shape technique with the boundary markers.
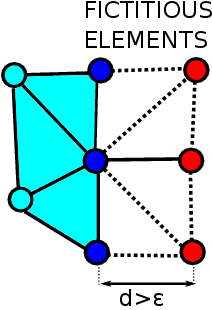
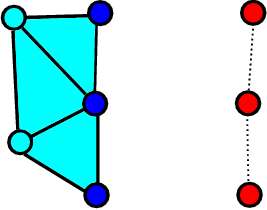
Let us distinguish the outer boundary of the glass domain and the mold wall with an interface and wall flags, respectively. As the interface nodes approach the wall nodes, the distance between them diminishes and an element is created. According to the standard PFEM algorithm such an element immediately obtains the properties of the fluid, thus bringiung the fluid and the solid into contact (see Fig. 3).
|
|
| (a) Glass and wall are separated | (b) Fluid element is created |
| Figure 3: Schematic representation of the standard PFEM contact algorithm | |
However, this newly created element (see Fig. 3a) defines a “premature” contact (both mechanical and thermal) between the glass and the wall, as the distance between the original fluid boundary nodes and the wall are still of order . This implies introducing an error of order in the determination of the thickness of the fluid layer (glass wall in our case). In this work we propose a simple change in the contact algorithm that leads to a considerable improvement in the accuracy of thickness determination.
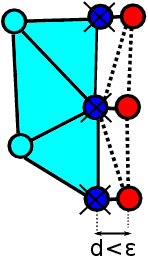
We propose to consider such the newly created contact element a purely geometrical entity, that does not contribute to the governing equation system and thus does not result in any resistance to the fluid motion. This can be formally described as: if the mesher creates an element that contains both interface and wall nodes, mark it as a fictitious element and multiply its contribution (residual and tangent matrix) by zero during the finite element assembly process. Nevertheless, fictitious elements can be used for tracking the distance between the interface nodes and the wall. Moreover, creating fictitious elements as geometric entities enables maintaining the original PFEM unconstrained meshing strategy.
The distance between the interface node and the wall is computed within each fictitious element. As long as is larger than a given tolerance , the fictitious element is maintained and no actual contact between the fluid and the solid is established. As soon as reached a value lower than a given tolerance , the interface node is erased, thus the glass domain gets connected to the wall via a real element in a fully sticking contact (see Fig. 4 c) and d)). This way, the error in the determination of the thickness of the bottle becomes controlled by the user-defined tolerance . In the simulations used in the present work, was taken as 10 of the element size.
3.2.3 Preserving the boundary mesh quality
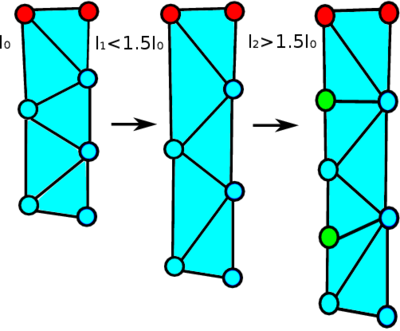
The domain deformation occurring in a glass forming process can be viewed as a stretch in different directions. This leads to the danger of decreasing the mesh resolution and possibility of creating non-physical “holes” at the glass domain boundary due to alpha-shape (see stretching of a domain fragment fixed at the top on Fig. fig:mesh_ref_a). In order to preserve the mesh quality and avoid the creation of holes, an adaptive refinement of glass domain boundary is used. A new node is introduced at the center of the boundary elements edge as the corresponding length reaches of 1.5 times the original value (see Fig. fig:mesh_ref_b).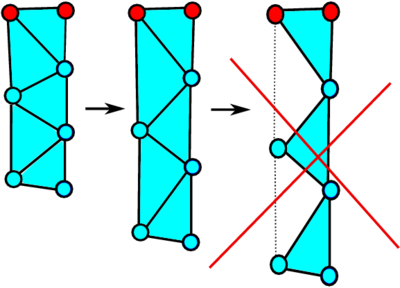
|
|
| (a) Mesh deterioration | (b) Mesh-preserving refinement |
| Figure 5: Mesh refinement at the boundary | |
3.3 Thermal model
During glass forming process the temperature distribution within the glass is highly non-uniform. First of all, the temperature varies in the thickness direction of the glass domain due to cooling of the free surfaces. Second, when the glass reaches the mold wall a local rapid cooling occurs, resulting in a strong increment of viscosity, thus altering the shape evolution: zones with the higher temperature will undergo stronger stretching and thinning [23]. Thus, inclusion of the heat equation is mandatory and purely mechanical models ignoring the heat transfer must be discarded when modeling the problem of interest.
Assuming that the conduction obeys the Fourier law which relates the heat flux with the temperature and the thermal conductivity, the heat transfer equation can be written in the Lagrangian reference frame as:
|
|
(32) |
where is the specific heat, is the temperature, is the thermal conductivity and is the internally generated heat flux. Using linear temperature finite elements and the Backward Euler scheme for space and time discretization, respectively, leads to the following equation:
|
|
(33) |
where and are the mass and Laplacian matrices and . Note the absence of the convective term in the Lagrangian framework. Heat convection is automatic in the Lagrangian model, as the heat is convected by the moving Lagrangian grid “attached to the material”.
The problem must be equipped with the Dirichlet boundary conditions (fixed temperature at mold in the locations to be specified) and Neumann boundary condition (adiabatic condition will be considered in this work. Heat conduction prior to the contact with the mold (occurring due to convection of the air in contact with the glass) will not be considered here. Once the contact with the mold has taken place, the direct heat conduction between the glass and the mold takes place. Temperature field obtained as a solution of Eq. (33) is used for computing the viscosity distribution (Eq. (1)) for the mechanical model. More details on the thermo-mechanical coupling can be found in [24], [25].
3.4 Overall solution algorithm
To this end all the “ingredients” of the thermo-mechanical model are defined. The overall solution algorithm for the bottle forming process is presented next.
- Discretize the glass domain with a finite element mesh.
- Identify the external boundaries for the fluid and glass-mold wall contact elements (using the alpha-shape technique + boundary markers)
- Solve the Lagrangian equations for the glass. Obtain nodal velocities, pressure and displacements.
- Move the mesh nodes to a new position (according to the computed displacements).
- Solve the heat transfer equation. Obtain the temperature distribution of the glass.
- Update viscosity according to the obtained temperature distribution using Eq. 1
- Re-generate the mesh for the glass domain (nodes are generally maintained)
- Go back to the next time step. Start the solution from Step 2
4 Examples
In this section two numerical examples are solved. We mentioned previously that there exist practically no established benchmark for the glass forming models. In the majority of literature on the numerical modeling of the glass manufacturing process the data provided is insufficient for reproducing the tests. Thus, in this section we first validate the proposed formulation by solving one of the very few examples suitable for the validation of the glass forming simulation model on a simple rectangular geometry. Next we propose a numerical test dealing with the bottle-forming that could serve as a reference in the future. The main aim is to accurately define all the data necessery for reporducibility of this example.
4.1 TV panel pressing
This example reported by Berndhauser in [26] models the manufacturing of a TV glass panel. Even though it does not deal explicitly with the bottle manufacturing process, the characteristics of the example are very similar (pressing the glass gob into a mold, accounting for thermo-mechanical nature of the process). Moreover, it provides simple nearly rectangular geometry which facilitates the validation. A portion of molten glass in the shape of cylindrical gob, is pressed into the mold by the plunger (see Fig 6). The plunger is moving downwards with a prescribed time-dependent velocity. During pressing, the glass is flowing while it cools down because of the contact with the colder mold and plunger. The problem settings and material properties presented below are taken from [26].
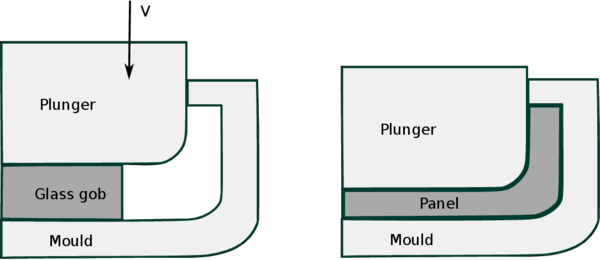
|
| Figure 6: Cross section of the glass pressing process: initial and final states |
The problem to be simulated accounts for the thermo-mechanical process involving the plunger, the glass and the mold. The mold and the plunger are considered to be rigid. The overall time of 3 seconds is simulated. The plunger descends with the vertical velocity m/s for 0.0s t 1.5 s. For 1.5s t 3.0s it remains still. The no-slip condition at the glass-wall interface is considered.
The thermal conditions are as follows: the initial glass temperature C. The initial temperature of the plunger and the mold is =500 C. Dirichlet boundary condition for the temperature is prescribed at the outer surface of the mold and the outer surface of the plunger. The rest of the mold and the plunger surfaces are considered to be adiabatic (heat flux ).
The geometry of the model is shown in Fig. 7. Geometrical details can be found in Fig. 8. The initial distance between the mold and the plunger cm is equal to the original height of the glass gob. The gob has a cylindrical shape with a radius of cm.
Material properties of the plunger, the mold and the glass are summarized in Table 3. Gravity of 9.8 is considered.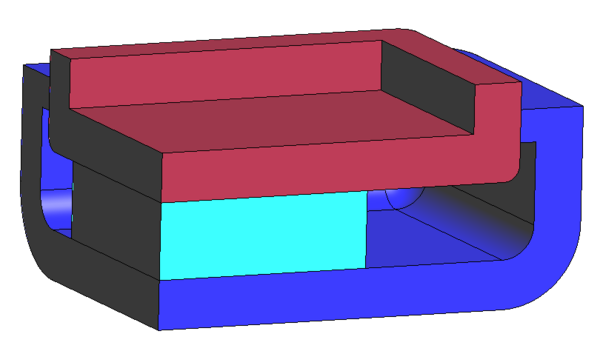
|
| Figure 7: TV screen forming set-up (one quarter): mold, gob and plunger |

| |
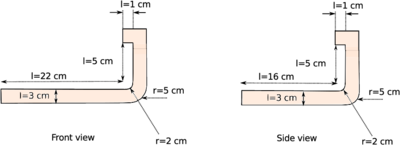
| |
| Figure 8: Dimensions of the mould and the plunger. | |
| Glass | |
| Viscosity | Pa s |
| Conductivity | 5 W/m K |
| Specific heat | 1400 J/kg K |
| Density | 2500 kg/ |
| Plunger and mold | |
| Conductivity | 20 W/m K |
| Specific heat | 500 J/kg K |
| Density | 8000 kg/ |
4.1.1 Results
According to the benchmark proposal, the temperature, pressure and the glass front evolution are analyzed. The values of the variables of interest are inspected at several locations indicated in Fig. 9. “Sensor” lines are located at four corners of the plain part of the mold bottom as L1: x=0, y=0; L2: x=0.22 m y=0; L3: x=0, y=0.16 m; L4: x=0.22, y=0.16 m.![Location of the inspection lines (“sensors”) [26]](/wd/images/thumb/f/f7/Draft_Garc%C3%ADa-Espinosa_370675429-Monitor_Lines_Pavel.png/600px-Draft_Garc%C3%ADa-Espinosa_370675429-Monitor_Lines_Pavel.png)
|
| Figure 9: Location of the inspection lines (“sensors”) [26] |
Fig. 10 displays the evolution of the temperature at L1 reported in [26]. One can see the compressing gob due to the plunger descend. In the beginning the temperature field exhibits a sharp discontinuity at the glass/mold and the glass/plunger interface. As time evolves, the transition region appears. At t=1.5 s the plunger stops and the process is governed by diffusion only.
![Temperature evolution at L1 according to [26]](/wd/images/thumb/3/33/Draft_Garc%C3%ADa-Espinosa_370675429-reference_res_clean_temperature.png/600px-Draft_Garc%C3%ADa-Espinosa_370675429-reference_res_clean_temperature.png)
|
| Figure 10: Temperature evolution at L1 according to [26] |
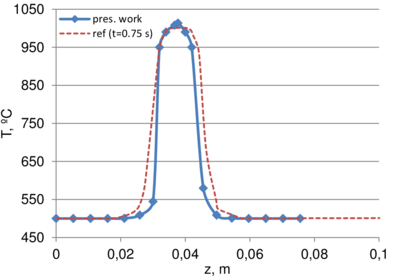
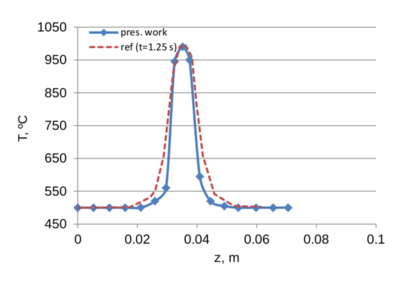
A comparison of the results obtained in the present work with the reference data is displayed in Fig. 11. One can see a good agreement between the compared values. In the beginning the temperature is distributed almost uniformly across the glass thickness (z-direction). Around 0.75 s the maximum temperature concentrates in the middle plain of the gob. At the end of the simulation the maximum temperature in the middle of the glass thickness reduces from 1000 C to some 950 C.
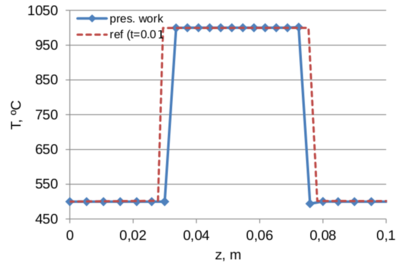
|
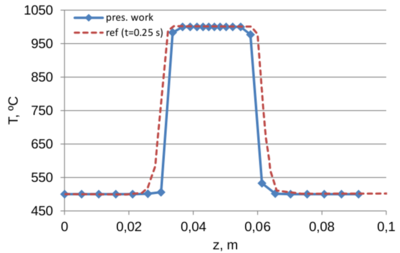
|
| (a) t=0.01 s | (b) t=0.25 s |
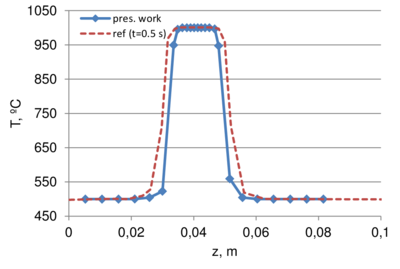
|
|
| (c) t=0.50 s | (d) t=0.55 s |
|
![Temperature along L1 at different time steps. Comparison with [26]](/wd/images/thumb/5/5c/Draft_Garc%C3%ADa-Espinosa_370675429-temper_comparison_3s.png/400px-Draft_Garc%C3%ADa-Espinosa_370675429-temper_comparison_3s.png)
|
| (e) t=1.25 s | (f) t=3.00 s |
| Figure 11: Temperature along L1 at different time steps. Comparison with [26] | |
The slightly smaller temperature observed at t=0.01 s in the lowest edge of the moving plunger (z=0.075) is a spurious “overshoot”, likely to occur due to the steep temperature gradient (this phenomenon is addressed, for example, [27]). Steep temperature gradient is present at both contact interfaces, namely at z=0.03 and z=0.075. However, since mold and the adjacent glass at the bottom (z=0.03) are not moving, no convection occurs there and thus the overshoot is observed only at the contact above (z=0.075), where glass is in contact with the moving plunger. We note that the overshoot is only of some 3 ºC (which is less than 1 of the temperature difference between the mold and the glass).
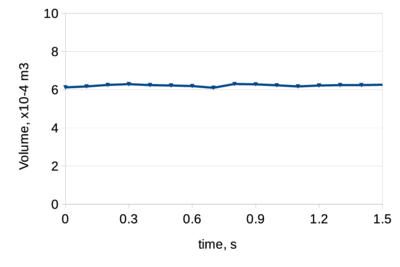
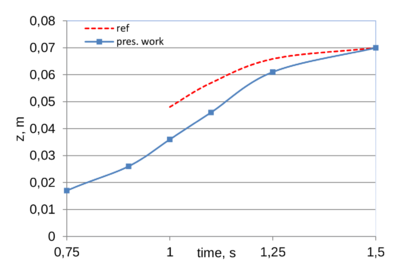
Evolution of glass front in the vertical direction of the xz-cross section (long side, x=0.23 m, y=0) is shown in Fig. 13. In the reference [26] the location of the glass front is reported only for t1 s. We included the results spanning over the total simulation time. Since the plunger reaches zero velocity at t=1.5 s, the glass front position remains constant afterwards. One can see good agreement between the results of the present work and the ones obtained in [26]. Slightly slower increment in height may be attributed to either different mesh resolutions or presence of the gravity in the present work (gravity was neglected in [26]). One other factor that may influence this result is the volume conservation of the method. Spurious volume gain would lead to the faster domain evolution, while volume losses would lead to a slower growth. In order to exclude this source of inaccuracy of our method, the glass volume evolution had been recorded throughout the simulation (see Fig. 12). One can see excellent volume conservation features of the present method. Maximum volume variation observed was below 4 . Volume conservation features of the method are further analyzed in the next example.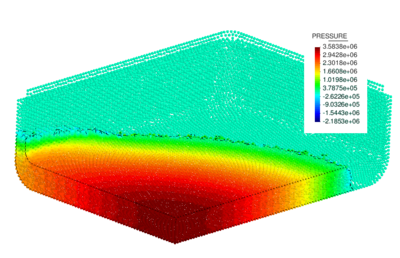
|
|
| Figure 12: TV screen pressing: pressure and volume data. | |
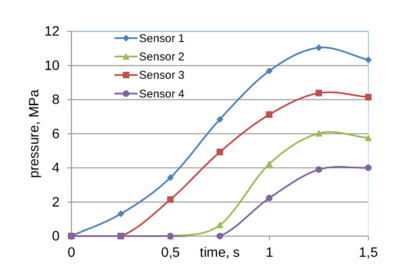
The pressure evolution at four inspection lines is shown in Fig. fig:pressure_sensors. It is important to note that pressure varies insignificantly in the thickness direction. Thus a single value is representative. Originally, glass does not reach the position of sensors L2, L3 and L4 (thus, zero values are observed). First, the glass front reaches L2, then L3 and, finally, the further most corner L4. The maximum pressure of appx. 1.1 MPa is reached at L1 (t=1.25 s). An example of the pressure distribution at t=0.50 s is shown in Fig. fig:pressure_example.
|
|
| (a) Pressure evolution | (b) Glass front evolution |
| Figure 13: Pressure and glass front evolution in the gob | |
4.2 Bottle manufacturing: final blow process
In this example we concentrate our attention on the second stage of the bottle manufacturing process, namely the gravity stretching and the final blow. The objective of this example is to test the capability of the presented numerical approach to solving this challenging problem. Moreover, we strive to establish an example that may be used as a first approximation to a benchmark for the thermo-mechanical simulations of the bottle forming process. In order to facilitate the modeling and reduce computational time, the mold is modeled merely as a set of nodes discretizing its inner wall providing Dirichlet boundary for both the mechanical and the thermal problem. The thermal problem is modeled considering convective and diffusive heat transfer modes (radiation is neglected). We note again that adopting the Lagrangian framework, convection in the glass phase is automatically solved due to the mesh motion. No convection condition at the glass domain boundary is prescribed.
The initial geometry consists of the mold wall and the parison. The geometry data is shown in Fig. fig:final_blow_bench_model_c.
| Viscosity | Pa s |
| Conductivity | 1.5 W/m K |
| Specific heat | 1409 J/kg K |
| Density | 2400 kg/ |
.

|

|

|
| |||
| (a) Contour | (b) Points | (c) 3D model | (d) Initial temperature | |||
| Figure 14: Model for the final blow simulation | ||||||
| Points | x | y | z |
| A | |||
| B | |||
| C | |||
| D | |||
| E | |||
| F | |||
| G | |||
| H | |||
| I | |||
| J | |||
| K | |||
| L | |||
| M | |||
| N | |||
| O | |||
| P | |||
| Q | |||
| R | |||
| S | |||
| T |
.
The 3D model can be obtained by applying rotation to the surface (representing the parison) and the curve (mold wall) around the vertical axis (see Fig. fig:final_blow_bench_model_a). The location of the points necessary for reproducing the geometry is shown in Fig. fig:final_blow_bench_model_b and the corresponding coordinates are summarized in Table 5. The mold and the glass domain share the point . The bottle neck and the mold are fixed. The domain boundaries are defined as follows: Dirichlet boundary comprises of the bottle neck and the mold wall. The mold wall becomes part of the computationally domain only once the contact with the glass is established (see Section 3.2 for details). The mold wall, the glass domain as well as Dirichlet and Neumann boundaries are shown in Fig. 15.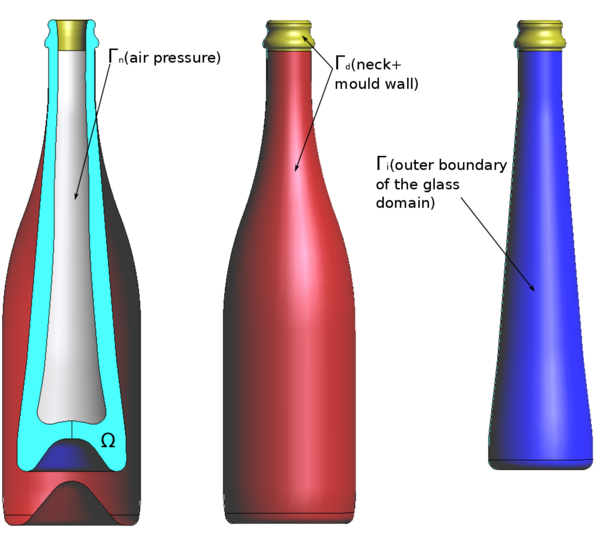
|
| Figure 15: The initial domain and the location of Dirichlet and Neumann boundaries in the final blow mold. |
We shall also distinguish the free outer boundary of the glass domain . Note, that as soon as the glass node belonging to touches the wall, it becomes a part of .
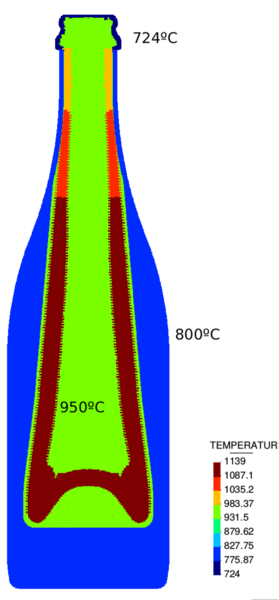
The temperature at mold walls is fixed to 800 C. At the bottle neck the temperature is fixed to 724 C. At the inner and outer surfaces of the glass the initial temperature is set to 950 C. Elsewhere in the glass domain, the initial temperature distribution is prescribed according to , where is the vertical coordinate of the given node, and are the minimum and maximum vertical coordinates of the parison. The initial temperature distribution is shown in Fig. 14a. During first two seconds the parison is exposed to gravity exclusively. At t=2 s air pressure of 0.14 MPa is applied at the inner cavity. At t=2.6 the process is completed. The glass density is 2400 . The viscosity is computed from the temperature field according to: . The industrial partner (see Acknowledgements) has provided the authors directly with the viscosity values for a number of temperatures, rather than the values of Fulcher constants. Thus, simple exponential fitting to find a function approximating this data was used.
4.2.1 Results
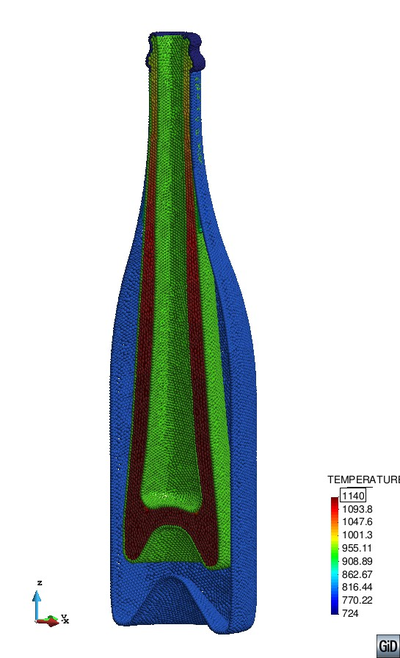
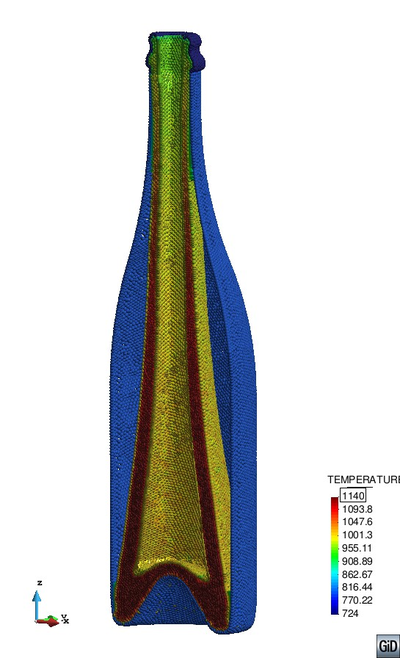
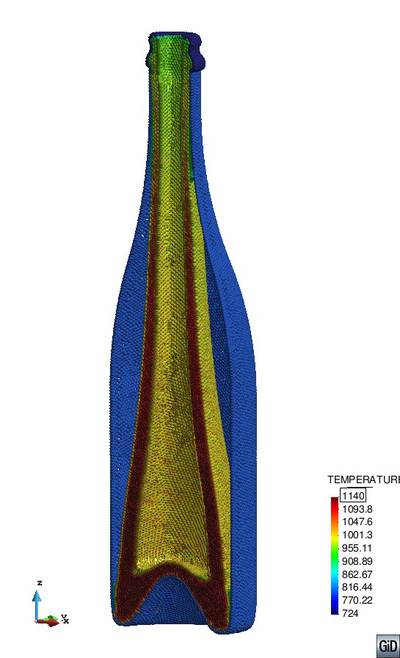
Fig. 16 shows the evolution of the glass object. One can see that around 0.3 seconds glass reaches the mold and accommodates there until the air pressure is applied. It takes less than 0.5 seconds to press the glass into the mold.
|

|

|
|
| (a) 0.0 s | (b) 0.3 s | (c) 1.0 s | (d) 2.0 s |
|

|

|

|
| (e) 2.01 s | (f) 2.02 s | (g) 2.03 s | (h) 2.5 s |
| Figure 16: Gravity stretching and final blow | |||
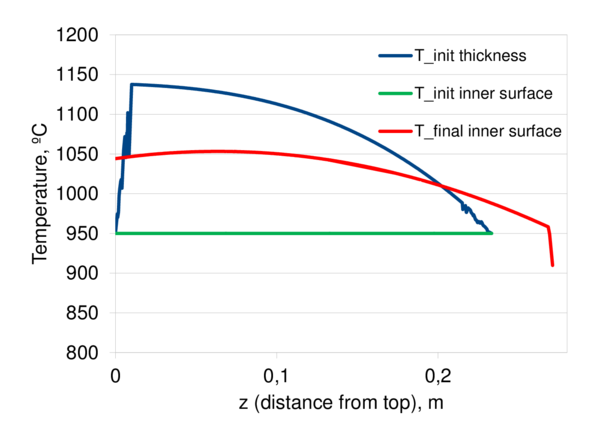
Fig. 17 shows the temperature distribution along the vertical coordinate at the inner bottle surface. In the beginning of the simulation temperature of 950C is set at inner (and outer) surfaces (green line). The initial temperature distribution in the middle of the wall (thickness) is shown in blue. The temperature (and, consequently, viscosity) at the surface of the glass evolves due to convection and diffusion leading to the final temperature distribution at the inner surface (shown in red).
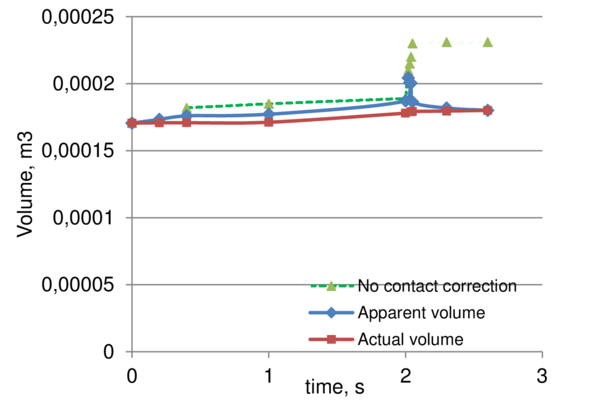
Fig. 18 displays the evolution of the glass volume. In case of using the standard PFEM algorithm (not using the fictitious contact elements approach) the total volume increases by as much as 35 . One can distinguish two stages: the one corresponding to the gravity stretch (the contact between the parison on the mold becomes established at around 0.3 seconds) and the one of the air pressure application. Since the contact area during the gravity stretch is mainly restricted to the bottom of the bottle, the overall volume growth due to contact is minor. On the other hand, air presses the entire outer surface of the bottle towards the mold wall. This process starts at t=2 seconds and at around t=2.3 seconds the entire outer surface of the glass is in contact with the wall. A major spurious volume increment is observed at this stage. From this point onwards no considerable volume change takes place.
|
| Figure 17: Temperature distribution along the bottle height |
|
| Figure 18: Temporal evolution of glass volume |
|
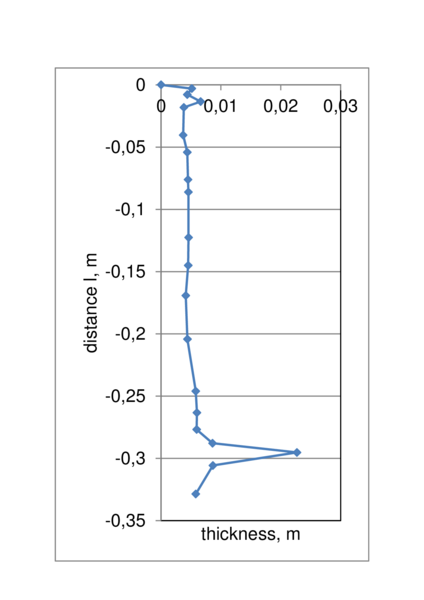
|
| Figure 19: Wall thickness distribution along the bottle height | |
On the other hand, if the fictitious contact elements algorithm is used, the volume conservation considerably improves. One can observe the line corresponding to the apparent volume (actual volume of the glass + volume of the fictitious contact elements): the apparent volume increases when the contact elements are created, but since these elements provide no resistance it reduces to the actual one when these contract and finally vanish. Thus the apparent and the actual glass volumes coincide at the end of the simulations (and, practically coincide at the end of each sub-stage: the gravity stretch and the air blow). In case of using the proposed contact algorithm, volume gain reduces to 5 .
Fig. 19 shows the wall thickness distribution at t=2.6 s (vertical axis being the distance from the top measured along the wall coordinate L). This distribution can be used as the main reference data for the future comparisons.
4.2.2 Summary and conclusions
In this paper we have presented a 3D Lagrangian thermo-mechanical model for glass forming simulation. The model follows the PFEM philosophy combining the features of a classical FEM and a Lagrangian mesh-free method. A modified fractional step methodology has been introduced for obtaining a computationally efficient solution without compromising on the mass conservation.
The model was validated using a TV-panel pressing example, a test characterized by features similar to bottle forming but with a simpler geometry. A numerical example dealing with the gravity stretch and final blow stage of the bottle manufacturing process has been proposed. We intended to create an example that would fulfill the need of a standardized reference lacking up-to-date in the field of bottle manufacturing simulation. All the data necessary for reproducing this test (geometry, material's properties, boundary conditions) has provided. Even though several strong approximations are introduced in this example (such as simplified thermal contact, initial temperature distribution), the example defines a first approximation to a benchmark in the field.
The final blow process was simulated in a reasonable computational time (around 1 hour using a quad-core I7 PC) on a computational mesh containing around 300 000 four-noded tetrahedra elements. The facility of the free-surface evolution tracking together with the automatic transfer of the non-homogeneous and temperature-dependent material properties proves that Lagrangian approaches are more advantageous for the problem at hand than Eulerian ones. Thermal contact did not require any special technique, being an intrinsic feature of a matching-mesh method. The proposed mechanical contact methodology is promising, allowing the user to control the error in the thickness direction. In the present work the geometrical contact tolerance (i.e. the critical distance leading to erasal of the interface node of a fictitious element) was set to 10 of the element size. The simulations carried out have proven that the method possesses excellent mass conservation features ( 5 of volume variation for the given contact tolerance).
Keeping in mind all the advantages of the formulation, it is important to note that it also has some limitations. For optimal functionality of the method the mesh size distribution must be as uniform as possible. Thus only the mesh quality can be easily controlled. Moreover, the time step size was restricted due to the danger of element inversion. Using a novel Jacobian-independent Lagrangian explicit stream-line temporal integration [28] is a promising option that must be investigated further. While keeping the overall architecture of the approach proposed here, this alternative Lagrangian formulation may lead to considerable advantages in computational efficiency removing the time step restrictions faced by the present method. It is important to note that bottle forming simulations deal with a problem involving very large changes in viscosity due to temperature variation. Thus, purely mechanical simulations are meaningless for the practical purposes. Even though the heat equation was included in the present model and viscosity was computed according to the changing temperature field, the present model did not account for radiative heat transfer. It is essential to include this feature in the next development step of this numerical method.
Acknowledgements
This work was supported under the auspices of the FPDI-2013-18471 grant of the Spanish Ministerio de Economia y Competitividad. It was also partially funded by the NUMEXAS project of the European Comission (FP7) and the COMETAD project of the National RTD Plan (ref. MAT2014-60435-C2-1-R) of the Spanish Ministerio de Economia y Competitividad. The authors of this work express their gratitude to Dr. J. Jimenez from Vidrio&Engineering COMM. V. for the consultations regarding the bottle forming technology and, in particualr, the data provided for Example 2.
BIBLIOGRAPHY
[1] Oñate, E. and Idelsohn, S. and Del Pin, F. and Aubry, R.. The Particle Finite Element Method: an overview., Volume 1. International Journal of Computational Methods 267-307, 2004
[2] Ryzhakov, P. and Oñate, E. and Rossi, R. and Idelsohn, S.. Improving mass conservation in simulation of incompressible flows, Volume 90/12. Int. Jour. for Num. Methds. in Eng. 1435-1451, 2012
[3] Ryzhakov, P.. A modified fractional step method for fluid-structure interaction problems. Revista Intern. Met. Num. Ing. (RIMNI), 2016
[4] Cesar de Sa, J.M.A.. Numerical modelling of glass forming processes, Volume 3. Eng. Comput. 266–275, 1986
[5] Matthew, H.. Numerical simulation of glass forming and conditioning, Volume 85. Wiley Online Library. Journal of the American Ceramic Society 5 1047–1056, 2002
[6] Feulvarch, E. and Moulin, N. and Saillard, P. and Lornage, T. and Bergheau, J-M. 3D simulation of glass forming process, Volume 164. Elsevier. Journal of materials processing technology 1197–1203, 2005
[7] Giannopapa, C.G. and Groot, J.. Modeling the blow-blow forming process in glass container manufacturing: a comparison between computations and experiments, Volume 133. American Society of Mechanical Engineers. Journal of Fluids Engineering 2 021103, 2011
[8] Fulcher, G.S.. Analysis of recent measurements of the viscosity of glasses, Volume 8. Wiley Online Library. Journal of the American Ceramic Society 6 339–355, 1925
[9] Delaunay, B.. Sur la sphere vide, Volume 7. Izvestia Akademii Nauk SSSR, Otdelenie Matematicheskikh i Estestvennykh Nauk 793-800, 1934
[10] Donea, J. and Huerta, A.. Finite element method for flow problems, J. Wiley Edition, 2003
[11] Codina, R.. A stabilized finite element method for generalized stationary incompressible flows, Volume 190. Computer Methods in Applied Mechanics and Engineering 20-21 2681 - 2706, 2001
[12] Oñate E.. A stabilized finite element method for incompressible viscous flows using a finite increment calculus formulation., Volume 182. Computer Methods in Applied Mechanics and Engineering 355-370, 2000
[13] Ryzhakov, P. and Rossi, R. and Idelsohn, S. and Oñate, E. . A monolithic Lagrangian approach for fluid-structure interaction problems, Volume 46/6. Journal of Computational Mechanics 883-399, 2010
[14] Ryzhakov, P. and Cotela, J. and Rossi, R. and Oñate, E.. A two-step monolithic method for the efficient simulation of incompressible flows, Volume 74. Wiley Online Library. International Journal for Numerical Methods in Fluids 12 919–934, 2014
[15] Idelsohn, S. and Oñate, E. . The challenge of mass conservation in the solution of free-surface flows with the fractional-step method: problems and solutions, Volume 26. International Journal for Numerical Methods in Biomedical Engineering 1313-1330, 2010
[16] Chorin, A.J.. A numerical method for solving incompressible viscous problems, Volume 2. Journal of Computational Physics 12-26, 1967
[17] Temam, R.. Sur l’approximation de la solution des equations de Navier-Stokes par la methode des pase fractionaires, Volume 32. Archives for Rational Mechanics and Analysis 135-153, 1969
[18] Codina, R.. Pressure stability in fractional step finite element method for incompressible flows, Volume 170. Journal of Computational Physics 112-140, 2001
[19] Peri, D. and Owen, D.. Computational model for 3-D contact problems with friction based on the penalty method, Volume 35. Wiley Online Library. International journal for numerical methods in engineering 6 1289–1309, 1992
[20] Papadopoulos, P. and Taylor, R.. A simple algorithm for three-dimensional finite element analysis of contact problems, Volume 46. Elsevier. Computers & Structures 6 1107–1118, 1993
[21] Simo, J. and Laursen, T.. An augmented Lagrangian treatment of contact problems involving friction, Volume 42. Elsevier. Computers & Structures 1 97–116, 1992
[22] Akkiraju, N. and Edelsbrunner, H. and Facello, M. and Fu P. and Mucke, E. P. and Varela C. Alpha shapes: definition and software. Proceedings of International Computational Geometry Software Workshop, 1995
[23] Grégoire, S. and Cesar de Sá, J. and Moreau, P. and Lochegnies, D.. Modelling of heat transfer at glass/mould interface in press and blow forming processes, Volume 85. Elsevier. Computers & structures 15 1194–1205, 2007
[24] Codina R. and Vazquez M. and Zienkiewizc O.C.. A general algorithm for compressible and incompressible flows, Volume 27. International Journal for Numerical Methods in Fluids 13-32, 1998
[25] Ryzhakov, Pavel and Rossi, Riccardo and Oñate, Eugenio. An algorithm for the simulation of thermally coupled low speed flow problems, Volume 70. Wiley Online Library. International Journal for Numerical Methods in Fluids 1 1–19, 2012
[26] Berndhauser, C.. TC25 - Modelling of glass forming processes Short review of activities 2000 - 2009. International Comission on Glass, 2013
[27] Augustin M. and Caiazzo A. and Fiebach, A. and Fuhrmann, J. and Volker J. and Linke A. and Umla R.. An assessment of discretizations for convection-dominated convection–diffusion equations, Volume 200. Elsevier. Computer Methods in Applied Mechanics and Engineering 47 3395–3409, 2011
[28] Idelsohn, S.R. and Nigro, N. and Gimenez, J. and Rossi, R. and Marti, J. A fast and accurate method to solve the incompressible Navier-Stokes equations, Volume 30. Emerald Group Publishing Limited. Engineering Computations 2 197–222, 2013
Document information
Published on 01/01/2016
DOI: 10.1016/j.compstruc.2016.09.007
Licence: CC BY-NC-SA license