Numerical, theoretical and experimental validation of the material point method to solve geotechnical engineering problems

Validación numérica, teórica y experimental del método del punto material para resolver problemas geotécnicos

Numerical, theoretical and experimental validation of the material point method to solve geotechnical engineering problems

M.A. Llano-Serna^, , M.M. Farias

• Facultad de Ingeniería Civil y Ambiental, Universidad de Brasilia, Brasilia, Brasil

Under a Creative Commons license

Resumen

Este trabajo investiga la posibilidad de utilizar el método del punto material (MPM) para resolver problemas geotécnicos cuasiestáticos de pequeñas deformaciones y problemas dinámicos que presentan grandes distorsiones. Métodos tradicionales como el método de los elementos finitos (MEF) tienen muchas dificultades para resolver los problemas de las grandes deformaciones. Por este motivo, herramientas como el MPM han adquirido importancia en los últimos años. Como cualquier herramienta nueva, es conveniente verificar su eficacia en la simulación de problemas propios de la ingeniería geotécnica. Primero se describe de forma breve la formulación matemática del MPM, y a continuación se presentan algunas simulaciones realizadas con el MPM de una cimentación superficial, un ensayo de compresión no confinada y deformaciones en un talud. A tal efecto, se ha utilizado un software de código abierto y los resultados obtenidos se han comparado con modelos de MEF, soluciones analíticas y ensayos de laboratorio reales. Los resultados muestran una concordancia cualitativa y cuantitativa, y un mejor desempeño en la simulación de las tensiones que en la de las deformaciones. El conjunto de los modelos evaluados demuestra que el MPM es una herramienta válida y útil para simular problemas propios de geotecnia de pequeñas y grandes deformaciones, aunque el MEF tradicional sigue siendo computacionalmente más eficiente para resolver problemas cuasiestáticos.

Abstract

This paper investigates the possibility of using the material point method (MPM) to solve small strains quasi-static problems and dynamic problems related to large distortions. Traditional methods such as the finite element method (FEM) face difficulties when large strains are involved. Therefore, tools such as the MPM have become more important in recent years. As a new tool, the MPM needs to prove its functionality for geotechnical engineering problems. In first place the MPM mathematical formulation is shortly described. Next, numerical simulations of a shallow foundation, an unconfined compression test and a slope problem are performed in an open source MPM code. The results are compared with FEM simulations, analytical solutions and real laboratory tests. The study shows qualitative and quantitative agreement when compared; a better performance of MPM for solving stresses better than strains is detected. The set of simulations validates the MPM to solve geotechnical engineering problems when dealing with small and large strains. However, the traditional FEM showed a better performance for quasi-static cases.

Palabras clave

Método del punto material; Grandes deformaciones; Compresión no confinada de arcillas; Cimentación superficial sobre suelos blandos; Deformaciones en taludes de suelos cohesivos

Keywords

Material point method; Large strains; Unconfined compression of clay; Shallow foundations in soft soil; Slope deformations in cohesive soils

1. Introducción

Debido al comportamiento complejo de los suelos, los ingenieros de hoy en día se ven en la necesidad de utilizar metodologías prácticas para diseñar obras cada vez más complejas al servicio de la sociedad. En las últimas décadas se han desarrollado muchas herramientas numéricas basadas en el método de los elementos finitos (MEF), debido a su versatilidad [1]. En la literatura pueden encontrarse aplicaciones diversas en el campo de la ingeniería geotécnica.

A pesar del uso extendido del MEF, presenta algunas limitaciones evidentes al intentar resolver problemas de grandes deformaciones. Para extender el uso de este método a la simulación de grandes deformaciones, manteniendo su enfoque tradicional, es necesario utilizar tensores de grandes deformaciones y actualizar la configuración del objeto de análisis. Si la malla utilizada para discretizar el medio experimenta una gran distorsión, tiene que ser actualizada, lo cual genera imprecisiones numéricas a consecuencia de la pérdida de información cuando tiene que mapearse una variable de estado al nuevo esquema de discretización [2].

Por ello, las investigaciones más recientes se han centrado en mejorar la simulación de los problemas que implican una gran distorsión. Este tipo de problemas son muy relevantes cuando intervienen fenómenos de impacto, penetración, fragmentación e interacción entre diferentes materiales [3].

Entre las nuevas técnicas para resolver grandes deformaciones, destaca el método del punto material (MPM), por las posibilidades que ofrece. El MPM es una extensión del método particle in cell (PIC), muy utilizado en mecánica computacional de fluidos. Este método puede describirse como la unión de 2 esquemas de discretización: una formulación lagrangiana para representar el cuerpo continuo como un conjunto de puntos materiales y una formulación euleriana para resolver las ecuaciones de campo mediante una malla de cálculo.

2. Antecedentes del método del punto material

Según Beuth et al. [4], el MPM surgió en la década de 1960 en el Laboratorio Nacional de Los Álamos durante el proceso de búsqueda de una solución a problemas complejos de mecánica de fluidos, mediante una representación de puntos o partículas que se movían a través de una malla fija [5].

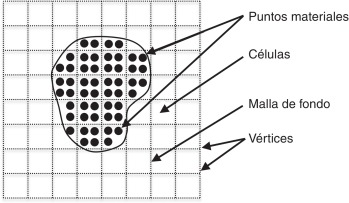
La trayectoria de este conjunto de partículas o puntos materiales (PM) que componen el volumen de análisis normalmente queda registrada. Los PM almacenan toda la información relevante: velocidades, deformaciones, tensiones, etc. La información de los PM es extrapolada o transferida periódicamente a la malla de fondo (similar a una malla de MEF). Las ecuaciones de movimiento (conservación de momento linear) se resuelven de manera explícita, para un intervalo de tiempo finito, utilizando el método de las diferencias finitas (MDF). Una vez resuelto el sistema, las velocidades en la malla de fondo se interpolan de nuevo a los PM para así poder determinar su posición final.

Por último, se calculan las deformaciones en los PM y se actualizan las tensiones mediante una relación constitutiva. En la figura 1 se ilustra el esquema de discretización. Una vez transferida la información a los PM, se descartan los valores de la malla de fondo y el proceso se repite para un nuevo intervalo de tiempo; de esta forma, la solución evoluciona en el tiempo hasta lograr una estabilización total o llegar al punto de análisis deseado. Durante este proceso, los PM pueden circular a través de diferentes células de la malla de fondo. Se observó la presencia de ruido numérico en el MPM cuando los PM cruzaban las fronteras de las células que los contenían, situación que fue resuelta utilizando funciones de interpolación suavizadas [6].

Figura 1. Discretización utilizada en el MPM.

En la literatura existen algunos estudios que tratan de la validación y la aplicación del MPM en la geotecnia, referidos a modelos simples, como vigas en voladizo [4] and [7]; a aspectos relacionados con la consolidación [4] and [8]; a asentamientos en taludes [9] and [10]; a cimentaciones superficiales [1], [11] and [12]; a problemas de penetración [12] and [13]; a empujes activos y pasivos [1], [7], [10], [11], [14] and [15]; a discontinuidades, fisuras y grietas [16] and [17]; a asentamientos en terraplenes [18]; a la estabilidad de los taludes y las laderas [19], [20] and [21]; a cimentaciones sobre suelos blandos [8], y a problemas de penetración [14] and [22]. Sin embargo, cabe destacar que no abundan las validaciones rigurosas sobre los resultados obtenidos.

3. El método del punto material

Es posible encontrar en la literatura numerosas formulaciones que describen el MPM. En este trabajo, nos remitimos a la formulación presentada por Buzzi et al. [23]. La notación tensorial adoptada es la siguiente: el tensor es representado por una letra y su orden es marcado por el número de virgulillas (∼) bajo la letra; un punto en negrita (·) simboliza una contracción simple; los dos puntos (:) significan una contracción doble, y el símbolo (⊗) es el producto diádico o tensorial.

3.1. Formulación

La ecuación de campo que describe el movimiento dinámico de puntos en un medio continuo ha de satisfacer las condiciones de equilibrio, las cuales pueden ser representadas mediante notación tensorial de la manera siguiente:

${\frac {d{\underset {\sim }{\underset {\sim }{\sigma }}}}{d{\underset {\sim }{x}}}}:{\underset {\sim }{\underset {\sim }{I}}}+\rho {\underset {\sim }{b}}=\rho {\underset {\sim }{a}}$

(1)

donde ${\textstyle {\underset {\sim }{\underset {\sim }{\sigma }}}}$ es el tensor de tensiones de segundo orden; ${\textstyle {\underset {\sim }{x}}}$ representa el vector de posición de un punto, ${\textstyle {\underset {\sim }{\underset {\sim }{I}}}}$ expresa el tensor de identidad de segundo orden; ρ   simboliza el campo de densidad escalar; ${\textstyle {\underset {\sim }{b}}}$ son las fuerzas de cuerpo y externas que actúan en un punto, y ${\textstyle {\underset {\sim }{a}}}$ es el vector de aceleración en un punto. La ecuación (1) es simplemente la representación de la segunda ley de Newton para los puntos de un medio continuo.

La forma discreta débil de la ecuación (1) sobre las células de la malla con volumen (V  ) se obtiene utilizando el método de los residuos ponderados, mediante funciones de peso ${\textstyle {\underset {\sim }{w}}\left({\underset {\sim }{x}}\right)}$ similar al MEF, que toma la forma siguiente, después de aplicar el teorema de la divergencia:

$\int _{A}{\underset {\sim }{w}}\cdot {\underset {\sim }{t}}dA+\int _{V}\rho {\underset {\sim }{w}}\cdot {\underset {\sim }{b}}dV-\int _{V}{\frac {d{\underset {\sim }{w}}}{d{\underset {\sim }{x}}}}:{\underset {\sim }{\underset {\sim }{\sigma }}}dV=\int _{V}\rho {\underset {\sim }{w}}\cdot {\underset {\sim }{a}}dV$

(2)

donde ${\textstyle {\underset {\sim }{t}}}$ representa las fuerzas de tracción en la superficie en una región A.

Los PM ocupan solo una fracción del volumen de la célula, normalmente entre 1/4 y 1/9 del volumen total de la célula (V  ), y los PM pueden moverse libremente entre las células, por lo cual su dominio debe registrarse. Esto se logra mediante una función característica en la partícula ${\textstyle \chi _{p}\left({\underset {\sim }{x}}\right)}$ que toma el valor de 1 cuando se encuentra dentro del dominio del punto material y de 0 cuando se halla fuera de sus límites. Utilizando este artificio matemático, y tras realizar algunas manipulaciones matemáticas, la ecuación (2) puede transformarse en:

${\underset {{\underset {\sim }{f}}_{n}^{ext}}{\underbrace {\int _{A}S_{n}{\underset {\sim }{t}}dA+\sum _{p}m_{p}{\underset {\sim }{b}}{\bar {S}}_{np}} }}-{\underset {{\underset {\sim }{f}}_{n}^{int}}{\underbrace {\sum _{p}V_{p}{\underset {\sim }{\underset {\sim }{\sigma }}}_{p}\cdot {\underset {\sim }{\bar {G}}}_{np}} }}={\underset {{\underset {\sim }{\dot {q}}}_{n}}{\underbrace {\sum _{p}{\dot {\underset {\sim }{q}}}_{p}{\bar {S}}_{np}} }}$

(3)

La ecuación (3) establece que la tasa de cambio del momento lineal en los vértices de la malla ${\textstyle {\underset {\sim }{\dot {q}}}_{n}}$ es igual a la resultante de la sumatoria de las fuerzas externas e internas, es decir, se cumple la ley de conservación del momento lineal.

Las fuerzas externas en los vértices de la malla ${\textstyle {\underset {\sim }{f}}_{n}^{ext}}$ reciben las contribuciones de las tracciones en la superficie ${\textstyle \left({\underset {\sim }{t}}\right)}$ y de las fuerzas de cuerpo ${\textstyle \left({\underset {\sim }{b}}\right)}$ aplicadas en el medio continuo. De forma similar al MEF, las tracciones en la superficie son transferidas directamente a los vértices, multiplicándolas por las funciones de forma S_n e integrándolas sobre el área de la superficie, lo cual se representa por el primer término de la ecuación (3).

Las fuerzas de cuerpo también han de transponerse de los PM internos de las células a los vértices de la malla, lo cual se logra mediante las funciones de forma y posterior integración sobre el dominio:

${\bar {S}}_{np}({\underset {\sim }{x}})={\frac {1}{V_{p}}}\int _{V\ast }S_{n}({\underset {\sim }{x}})\chi _{p}({\underset {\sim }{x}})dV$

(4)

Por otro lado, la transferencia de tensiones se logra multiplicándolas por el gradiente de la función de forma ${\textstyle {\underset {\sim }{G}}_{n}=dS_{n}({\underset {\sim }{x}})/d{\underset {\sim }{x}}}$, que solo deberá calcularse dentro del dominio del PM dado por la función ${\textstyle \chi _{p}\left({\underset {\sim }{x}}\right)}$. De esta manera, la extrapolación se obtiene del ${\textstyle {\underset {\sim }{\bar {G}}}_{np}}$, calculado de la manera siguiente:

${\underset {\sim }{\bar {G}}}_{np}({\underset {\sim }{x}})={\frac {1}{V_{p}}}\int _{V\ast }{\frac {dS_{n}({\underset {\sim }{x}})}{d{\underset {\sim }{x}}}}\chi _{p}({\underset {\sim }{x}})dV$

(5)

Las integrales de las ecuaciones (4) y (5) pueden calcularse analíticamente, puesto que su forma es sencilla y, por tanto, no es necesario utilizar un esquema de integración numérica. En el trabajo de Bardenhagen y Kober [6] pueden encontrarse expresiones explícitas para estas matrices, y el ciclo completo de la solución es descrito en detalle por Buzzi et al. [23].

4. Simulaciones numéricas

Las simulaciones presentadas fueron ejecutadas en condiciones bidimensionales, en estado plano de tensiones y utilizando el código abierto NairnMPM 8.1.0 [24]. Este código ha sido verificado para algunos problemas de madera. Debido al uso extendido del MEF, es natural comparar los resultados obtenidos en este trabajo con este método, como también es válido el uso de ensayos de laboratorio y soluciones analíticas. Para las simulaciones con el MEF, se utilizó el código comercial Plaxis.

4.1. Ensayo de compresión no confinada

Uno de los problemas que permite evaluar, de forma sencilla y efectiva, la eficacia del MPM para grandes deformaciones es el ensayo de compresión no confinada o compresión simple [25]. El material utilizado para ejecutar el ensayo fue caolín manufacturado. Con el objetivo de alcanzar una gran distorsión, la muestra de suelo fue llevada hasta una deformación del 35 %, midiendo la tensión principal y la deformación en el eje vertical.

Una vez ejecutado el ensayo, se seleccionó un modelo de ruptura simple del tipo Von Mises, dado que el ensayo de compresión no confinada solo supone la medición de las tensiones totales y la muestra de suelo fue sometida a condiciones saturadas no drenadas (carga rápida). Además, se supuso un comportamiento elástico en la primera etapa de la carga, asumiendo que el suelo tiene 2 tipos de comportamiento: primero perfectamente elástico y, una vez lograda la ruptura, perfectamente plástico.

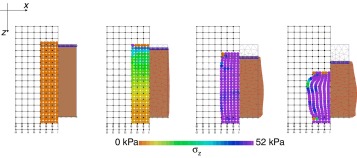
El módulo de elasticidad secante calculado suponiendo un 3% de deformación fue E = 405 kPa; la tensión de plastificación, σ_y = 52 kPa, y la densidad, γ = 18 kN/m³. Y debido a que la muestra se encontraba en condiciones saturadas, se asumió ν = 0,5. En la figura 2 se presentan las etapas de deformación simuladas hasta alcanzar una deformación de un 35% con el MPM (lado izquierdo de cada etapa). En el caso del MEF (lado derecho), el problema solo se consiguió simular hasta una deformación máxima del 23% —las diferencias se acentúan en la última etapa del esquema. Es importante señalar que la simulación con el MPM puede reproducir mayores distorsiones y que la simulación que aquí se presenta se detuvo expresamente una vez superada la frontera establecida por el MEF (Plaxis).

Figura 2. Etapas de deformación en la simulación del ensayo de compresión no confinada utilizando MPM.

En la tabla 1 se enumeran a título comparativo las características geométricas y numéricas de las simulaciones realizadas con ambos métodos numéricos. También se indica el tiempo computacional que invirtió cada uno de los modelos: el MPM tardó un 30% más tiempo en lograr el mismo nivel de deformación que el MEF y 151 s en total en alcanzar la máxima deformación registrada.

Tabla 1. Características generales de la simulación del ensayo de compresión no confinada

	MPM	MEF
Elementos	238 cuadrados	226 triangulares (15 nodos)
Discretización	324 puntos materiales	2.711 puntos de Gauss
Tiempo computacional (s)	113	88

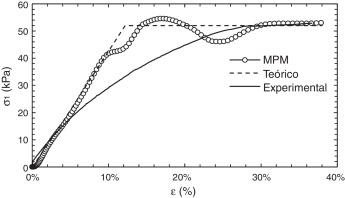
En la figura 3 se indican los resultados de las curvas obtenidas en el laboratorio, la idealización teórica y el modelo numérico en el MPM. Es posible ver que, en el intervalo de deformaciones elásticas hasta alcanzar una deformación del 10%, los resultados de la simulación tienen una tendencia muy similar a la teórica. Sin embargo, a partir de este punto se observa que la solución numérica experimenta oscilaciones hasta alcanzar la tensión de plastificación, fenómeno conocido como kinematic locking[26]. No obstante, los resultados de la simulación alcanzan la tensión de ruptura con una diferencia del 3% con respecto al ensayo real.

Figura 3. Comparación de las curvas tensión vertical-deformación del ensayo de compresión no confinada.

Al comparar la simulación con los datos experimentales puede observarse que el ensayo en el laboratorio presenta una transición más suave ya que, de hecho, muestra un comportamiento elastoplástico desde el inicio de la deformación. A pesar de las diferencias en la transición elastoplástica, las simulaciones numéricas presentaron un excelente desempeño en el tramo inicial (intervalo elástico) y el tramo final (intervalo plástico). Coetzee [1] y Konagai y Johansson [27] obtuvieron unos resultados similares.

4.2. Cimentación superficial sobre un estrato de suelo finito

Uno de los problemas clásicos de la ingeniería geotécnica son las cimentaciones superficiales, las cuales se pueden representar como una carga distribuida uniforme sobre un estrato de suelo finito. Los resultados de las simulaciones utilizando el MPM se compararon con soluciones analíticas y modelos numéricos utilizando el MEF con el programa Plaxis.

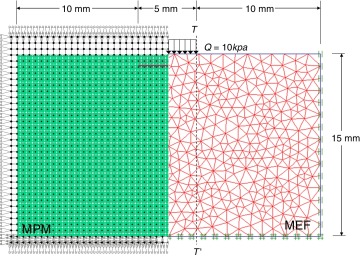
La solución analítica a las tensiones considerando una interfaz rugosa entre el estrato de suelo y la base rígida es proporcionada por Poulos y Davis [28]. Para las simulaciones numéricas se utilizaron modelos constitutivos elásticos lineales, con las propiedades medidas en el ensayo de compresión no confinada. La geometría del modelo cuasiestático se representa en la figura 4, donde se resalta la sección de análisis (T-T’). Debido a que las estrategias de discretización inherentes al método son diferentes, se intentó realizar una división similar del dominio.

Figura 4. Modelo geométrico de la discretización realizada en MPM y MEF.

En la tabla 2 se establecen las características geométricas y numéricas de los modelos numéricos de cimentación superficial; la más importante de ellas, y que es preciso resaltar, es el tiempo de cómputo. En este sentido, el MEF es claramente mucho más eficiente, pues reduce 100 veces el tiempo de cálculo.

Tabla 2. Características generales de la simulación de una cimentación superficial

	MPM	MEF
Elementos/tipo	1.768 cuadrados	1.139 triangulares (15 nodos)
Discretización	6.000 puntos materiales	9.275 puntos de Gauss
Tiempo computacional (s)	193	2

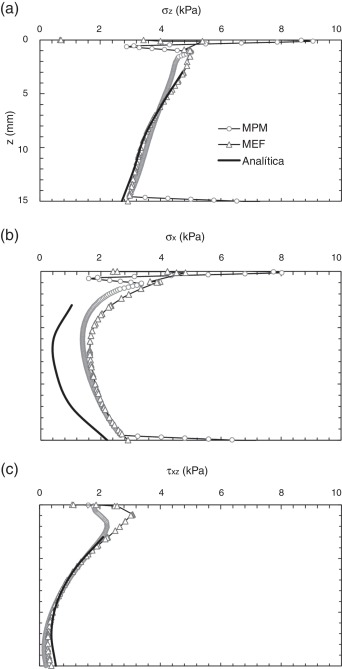
En la figura 5 se indican las tensiones a lo largo del eje de análisis. En el primer milímetro de profundidad (20% del ancho de la carga) ambos métodos numéricos presentan tensiones muy divergentes. Estos problemas en la frontera de análisis se deben a las condiciones de contorno aplicadas en el MPM y a las extrapolaciones calculadas en los puntos de Gauss para la superficie, en el caso del MEF. Además, este es un punto singular para la solución teórica, pues la sección de análisis se encuentra en el límite entre la carga y el tramo libre.

Figura 5. Tensiones en la masa de suelo a lo largo del eje T-T’: a) tensión vertical; b) tensión horizontal; c) tensión cortante.

En el caso de la tensión vertical, el primer tramo de la curva calculada con el MEF se ajusta mejor al de la solución teórica, mientras que el MPM la subestima. Después del primer tercio, en cambio, las 3 aproximaciones arrojan prácticamente el mismo valor. Las tensiones horizontales calculadas numéricamente presentan una mayor concordancia entre ellas y conservan la misma tendencia cualitativa con la solución analítica, pero sobreestimando su valor al compararla a la solución analítica.

También se observa una cierta divergencia superficial en el caso de las tensiones cizallantes, debido a las condiciones de contorno de las soluciones. Sin embargo, un 20% por debajo de la profundidad de análisis, los resultados numéricos y teóricos coinciden.

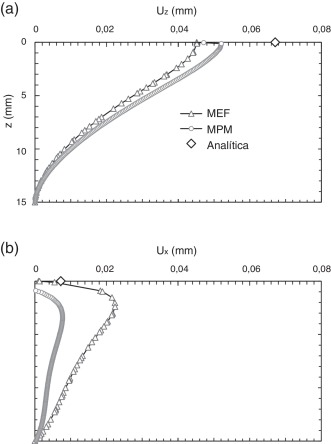
En la figura 6 se han grafiado los desplazamientos. Los desplazamientos verticales máximos calculados con el MPM son un 25% mayores que los calculados con el MEF. Además, el error estimado con el MPM es del 26%, mientras que el del MEF fue del 36%, comparado con la solución analítica. En el caso de los desplazamientos horizontales, cabe notar que ambas tendencias numéricas son similares y que el valor máximo de la solución del MPM es mucho más preciso que el obtenido aplicando el MEF.

Figura 6. Desplazamientos en la masa de suelo a lo largo del eje T-T’: a) desplazamiento vertical; b) desplazamiento horizontal.

4.3. Deformación de un talud artificial

Por último, se comparan los resultados de los cálculos obtenidos utilizando el MEF y el MPM de una serie de taludes artificiales. Ambos modelos utilizaron las mismas condiciones de contorno (desplazamientos verticales y rotaciones restringidas en la base y restricción de los desplazamientos horizontales y rotaciones en el segmento vertical opuesto al talud). El material de referencia para todos los taludes correspondía a la muestra de caolín descrita anteriormente y se asumía una resistencia no drenada de s_u = 0,5 σ_y. Para las simulaciones se utilizó un modelo elástico lineal perfectamente plástico, con un criterio de falla Von Mises en el modelo del MPM y Mohr-Coulomb (ϕ ≈ 0) en el modelo del MEF.

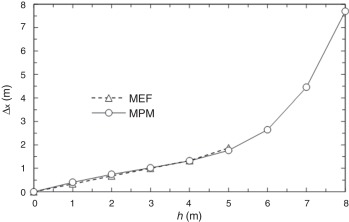
Se eligió arbitrariamente una inclinación de 45° y una altura variable de entre 1 y 8 m. De acuerdo con el ábaco de estabilidad de Taylor revisado por Steward et al. [29] en suelos puramente cohesivos, el factor de seguridad del talud a una altura de 8 m estaría muy cerca de la unidad (colapso). En la figura 7 se muestra la variación del desplazamiento horizontal del borde superior del talud como producto de las deformaciones ocasionadas por el propio peso de la masa de suelo ante la variación de altura del mismo. Pueden encontrarse resultados similares en la literatura [9] and [10].

Figura 7. Relación entre el desplazamiento horizontal en la corona del talud y la altura para diferentes taludes.

En la figura 7 se comparan las curvas de desplazamiento calculadas con el MPM con los resultados del programa Plaxis. Puede observarse que, aunque los esquemas de discretización utilizados son diferentes, el resultado entre ambos métodos numéricos es prácticamente el mismo. Sin embargo, destaca que, a partir de 5 m, el exceso de deformaciones impide obtener una respuesta mediante el MEF, mientras que el MPM calcula sin problemas las deformaciones hasta la altura de la falla del talud. Además, cabe señalar que, puesto que el MPM es un método explícito en el tiempo, es necesario utilizar amortiguamiento numérico para obtener una solución comparable con el MEF; de lo contrario se obtendrán valores de desplazamiento superiores en un 30%, debido al impacto generado por la carga gravitacional.

El amortiguamiento numérico es necesario ya que se pretende simular un problema cuasiestático por medio de una formulación dinámica. Para tal fin, la ecuación (3) debe amortiguarse a través del llamado amortiguamiento local viscoso, buscando un equilibrio para no sobreamortiguar el modelo. Su estimación tuvo como base el primer período de oscilación de un estrato uniforme de suelo [24].

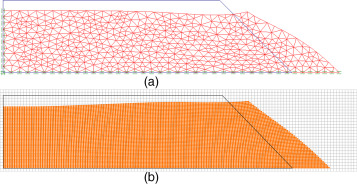
La figura 8 muestra el esquema de discretización típico adoptado por cada método, así como el estado final de deformación a escala real para la máxima altura comparable del talud (5 m de altura). En la tabla 3 se comparan los detalles numéricos entre ambos modelos y se observa nuevamente que, a pesar de que el MPM está preparado para resolver el problema de las grandes deformaciones, el MEF es más veloz.

Figura 8. Discretización numérica y estado de deformación final de un talud sintético de 5 m de alto y 45° de inclinación por medio de métodos numéricos: a) MEF; b) MPM.

Tabla 3. Características generales de la simulación de un talud artificial

	MPM	MEF
Elementos/tipo	3.416 cuadrados	1.010 triangulares (15 nodos)
Discretización	8.775 puntos materiales	12.120 puntos de Gauss
Tiempo computacional (s)	134	30

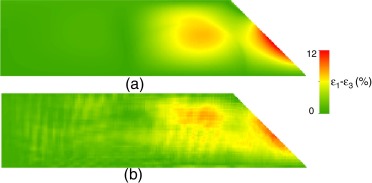
Finalmente, la figura 9 muestra la deformación de desviación (ɛ₁ − ɛ₃) calculada en la masa de suelo. En este caso destaca la similitud entre la magnitud de los valores calculados y la forma general en que las deformaciones están distribuidas, sin olvidar que el fenómeno de kinematic locking puede observarse nuevamente en los resultados del MPM. En ambos gráficos también puede verse que las deformaciones de desviación se concentran en la cara del talud, lo cual da una idea del inicio de la superficie de falla.

Figura 9. Deformación desviadora en la masa de suelo de un talud sintético utilizando métodos numéricos: a) MEF; b) MPM.

5. Conclusiones

Tanto el MPM como el software de código abierto NairnMPM se han utilizado con éxito en la simulación de problemas clásicos de la ingeniería geotécnica. Y se han obtenido con éxito soluciones cuasiestáticas como una cimentación superficial y un talud, además de resolver un problema explícito en el tiempo con solución dinámica, como la compresión no confinada.

Los resultados obtenidos han sido positivos, desde el punto de vista cualitativo y cuantitativo, y son comparables en precisión a las soluciones obtenidas con un método numérico conocido y ampliamente utilizado como es el MEF. Sin embargo, cabe señalar que, pese a que el MPM es utilizado cada vez con más frecuencia, los resultados disponibles en la literatura no siempre están acompañados de evaluaciones rigurosas de los mismos.

La limitación principal del MPM sigue siendo el tiempo de cómputo: en el caso de la solución cuasiestática, el MEF es mucho más veloz. No obstante, el MPM sigue siendo una herramienta atractiva para simular problemas de grandes deformaciones, como ha quedado demostrado y validado en el caso del ensayo de compresión no confinada y de las deformaciones en un talud.

Debido al mayor tiempo de cálculo del MPM con respecto al MEF, los dominios numéricos voluminosos deben analizarse con precisión, buscando un nivel óptimo de refinamiento de la malla entre el nivel de detalle que se requiere y el tiempo de procesamiento. Mallas muy refinadas y problemas tridimensionales pueden hacer inviable la simulación numérica utilizando los computadores convencionales.

Agradecimientos

Los autores desear expresar su agradecimiento a la Coordinación de Perfeccionamiento del Personal de Nivel Superior (CAPES) y al Consejo Nacional de Investigación (CNPq) del Gobierno brasileño por el apoyo económico recibido para la ejecución de este trabajo.

Bibliografía

1. [1] C.J. Coetzee; The Modelling of Granular Flow Using the Particle-in-Cell Method [tesis doctoral]; Universidad de Stellenbosch (2004)
2. [2] I.K.J. Al-Kafaji; Formulation of a Dynamic Material Point Method (MPM) for Geomechanical Problems [tesis doctoral]; Universidad de Stuttgart (2013)
3. [3] Z. Chen, R. Brannon; An Evaluation of the Material Point Method; Sandia National Laboratories, Albuquerque and Livermore (2002)
4. [4] L. Beuth, T. Benz, P.A. Vermeer, Z. Wieckowsi, C.J. Coetzee; Large deformation analysis using a quasi-static Material Point Method; Comput. Meth. Mech. (2007), pp. 1–6
5. [5] F.H. Harlow; The particle-in-cell computing method for fluid dynamics; Meth. Comput. Phys., 3 (1964), pp. 319–343
6. [6] S.G. Bardenhagen, E.M. Kober; The generalized interpolation material point method; Tech. Sci. Press, 5 (6) (2004), pp. 477–495
7. [7] L. Beuth, Z. Wieckowski, P.A. Vermeer; Solution of quasi-static large-strain problems by the material point method; Int. J. Numer. Anal. Meth. Geomech., 35 (2011), pp. 1451–1465
8. [8] F. Zabala; Modelacion de problemas geotécnicos hidromecánicos utilizando el método del punto material [tesis doctoral]; Universitat Politècnica de Catalunya (2010)
9. [9] L. Beuth, T. Benz, P.A. Vermeer; Large deformation analysis using a quasi-static material point method; J. Theor. Appl. Mech., 38 (1-2) (2008), pp. 45–60
10. [10] P.A. Vermeer, L. Beuth, T. Benz; A Quasi-Static Method for Large Deformation Problems in Geomechanics; 12th International Conference on Computer Methods and Advances in Geomechanics, Goa (2008), pp. 55–63
11. [11] D.Z. Zhang, X. Ma, P. Giguere; Computation of multi-material interactions using material point method; Int. Conf. Particle Based. Meth. Barcelona (2009), pp. 1–8
12. [12] J. Ma; Multiscale Simulation Using the Generalized Interpolation Material Point Method, Discrete Dislocations and Molecular Dynamics [tesis doctoral]; Oklahoma State University (2002)
13. [13] R.K. Raghav; Three Dimensional Generalized Interpolation Material Point (GIMP) Simulations in Samrai Environment [disertación de Maestría]; Oklahoma State University (2005)
14. [14] Z. Wieckowski; The material point method in soil mechanics problems; 21st International Congress of Theoretical and Applied Mechanics, Warsaw, Polonia (2004), pp. 3–4
15. [15] Z. Wieckowski; Application of dynamic relaxation in material point method; Comput. Meth. Mech (CMM-2011), Warsaw, Polonia (2011), pp. 1–2
16. [16] Y.J. Guo, J.A. Nairn; Three-dimensional dynamic fracture analysis using the material point method; Tech Sci. Press, 1 (1) (2006), pp. 11–25
17. [17] N.P. Daphalapurkar, H. Lu, D. Coker, R. Komanduri; Simulation of dynamic crack growth using the generalized interpolation material point (GIMP) method; Int. J. Fract., 143 (2007), pp. 79–102
18. [18] S. Zhou, J. Stormont, Z. Chen; Simulation of geomembrane response to settlement in landfills by using the material point method; Int. J. Numer. Methods Geomech., 23 (1999), pp. 1977–1994
19. [19] M. Numada, K. Konagai, H. Ito, J. Johansson; Material point method for run-out analysis of earthquake-induced long-traveling soil flows; JSCE J. Earthq. Eng., 27 (2003), pp. 1–4
20. [20] W. Shin, G.R. Miller, P. Arduino, P. Mackenzie-Helnwein; Dynamic meshing for material point method computations; Eng. Technol., 48 (9) (2010), pp. 84–92
21. [21] S. Andersen, L. Andersen; Modelling of landslides with the material-point method; Comput. Geosci., 14 (1) (2010), pp. 137–147
22. [22] M.A. Llano-Serna; Aplicação do Método do Ponto Material (MPM) a problemas geotécnicos [disertación de Maestria]; Universidad de Brasilia (2012)
23. [23] O. Buzzi, D.M. Pedroso, A. Giacomini; Caveats on the implementation of the generalized material point method; Tech. Sci. Press., 31 (2) (2008), pp. 85–106
24. [24] J. A. Nairn, Software para MPM y FEA de código abierto — NairnMPM y NairnFEA [consultado 2014]. Disponible en: http://osupdocs.forestry.oregonstate.edu/index.php/Main_Page
25. [25] ASTM D 2216, Standard test method for laboratory determination of water (moisture) content of soil and rock by mass; Am. Soc. Test. Mater. (2010), pp. 1–5
26. [26] C.M. Mast, P. Mackenzie-Helnwein, P. Arduino, G.R. Miller, W. Shin; Mitigating kinematic locking in the material point method; J. Comput. Phys., 231 (16) (2012), pp. 5351–5373
27. [27] K. Konagai, J. Johansson; Two dimensional lagrangian particle finite difference method for modeling large soil deformations; Struct. Eng. Eng., 18 (2) (2001), pp. 105–110
28. [28] H.G. Poulos, E.H. Davis; Elastic Solutions for Soil and Rock Mechanics; John Wiley, New York (1974)
29. [29] T. Steward, N. Sivakugan, S.K. Shukla, B.M. Das; Taylor's Slope Stability Charts revisited; Int. J. Geomech. (2011), pp. 348–352