(Created page with "==Summary== The effect of waterproof membrane and steel reinforcement protection on the concrete bridge deck is modeled. The attention is paid to the durability prediction re...") |
m (Scipediacontent moved page Draft Content 123404731 to Konecny Lehner 2015a) |
(No difference)
| |
Latest revision as of 14:56, 5 October 2016
Summary
The effect of waterproof membrane and steel reinforcement protection on the concrete bridge deck is modeled. The attention is paid to the durability prediction related to steel reinforcement corrosion initiation based on the chloride penetration. Thus 2-D finite element chloride ingress model is applied. The transient finite element model serves to solve Ficks second diffusion law using the computer tool compatible with the Matlab environment. The model focuses on the transport of chloride ions through a reinforced concrete bridge deck with and without the effect of waterproof membrane and on an estimate of the concentration of chlorides at the reinforcement level or in places with damage to the epoxide coating of the reinforcement. The model allows the incorporation of damage to the waterproof insulation under the asphalt coating. The time to chloride induced onset of corrosion is predicted and results are compared. The effect of water proof membrane reinforcement protection strategy typical for Central Europe and epoxy-coating protection widely used in North-Western United States is evaluated.
Keywords
Concrete ; Finite element analysis ; Durability assessment ; Chloride ingress ; Aging ; Corrosion ; Reinforcement ; Initiation ; Propagation ; Chlorides
Introduction
The reliability of reinforced concrete bridge structures is, in many cases, predetermined by durability. Many structures require premature repairs, rehabilitation or replacement as a result of defects caused by e.g. the effect of environment as well as the long-term actions of loads including chemical actions. Shortened lifespan leading to increased costs over the life cycle of the structure contributes indirectly to high costs to public budgets. The production of more durable construction systems may contribute to reduction of the overall costs of the structure. These can be better proposed with knowledge of the progress of the degradation process brought on by the long-term actions of environment and structural loading.
The models capable of chloride related corrosion process evaluation are being developed worldwide (see e.g. Stewart and Rosowsky, 1998 , Tikalsky et al., 2005 , Benz and Thomas, 2001 , Konečný et al., 2007 , Novák et al., 2014 , Konečný et al., 2011 and Vořechovská et al., 2015 ). From the above mentioned, the 1-D ideal bridge deck probabilistic models (Stewart and Rosowsky, 1998 and Tikalsky et al., 2005 ) are based on the analytical formulation of chloride ingress (Collepardi et al., 1972 ). The work (Stewart and Rosowsky, 1998 ) represents comprehensive analysis ranging from corrosion initiation to ultimate flexural resistance, where corrosion current is input parameter. The other probabilistic analysis is limited to corrosion initiation only (Tikalsky et al., 2005 ). Whereas, Tikalsky et al. (2005) is based on the extensive data from filed study by Sohangpurwala and Scannell (1998) . It is focused on initiation only. Konečný et al. (2007) model extends the work (Tikalsky et al., 2005 ) by the evaluation of epoxy-coated reinforcement and concrete bridge deck cracking effect. The effect of crack width on the penetration of chlorides into concrete is discussed in ACI 222 (2001) . There are works supporting the relationship between cracks and the capability of concrete to facilitate the passage of chlorides which leads to a more rapid propagation of corrosion include (Djerbi et al., 2008 and Bentz et al., 2013 ). In the introduction to the work (Djerbi et al., 2008 ) with reference to Francois et al. (2005) it is stated that the concentration of chlorides in a crack wider than 205 μm is equal to the concentration of chlorides at the surface. Djerbi et al. (2008) carry out an analysis of the effect of the width of cracks on the penetration of chlorides with the use of a modified accelerated test of the penetration of chlorides. (AASHTO T277, 1993 ). These tests determine the capability of concrete to resist the penetration of chlorides. Through the passage of an electric charge it can also determine the diffusion coefficient describing its capability to prevent the penetration of chlorides into concrete (Andrade, 1993 ).
Concrete is prone to cracking thus considering the crack effect on the chloride ion penetration shall be paid attention. The 2-D interaction of crack in the bridge deck with steel reinforcement durability was modeled by Konečný et al. (2007) . Comparison of 2D experiments and numerical analysis was conducted by Marsavina et al. (2009) and Bentz et al. (2013) . Marsavina et al. (2009) and Konečný et al. (2007) applied boundary conditions of a concentration of chlorides directly in crack. In contrast Bentz et al. (2013) model the effects of cracks in the form of changes in the material parameters in the area of the crack. The crack width effect important for the chloride ion penetration into concrete is discussed by Djerbi et al. (2008) .
This incorporation of crack effect into chloride ion penetration allows for the corrosion initiation assessment of bridge deck with crack; however, modification of the model is necessary in order to address the effect of waterproof barrier bellow asphalt overlay.
Motivation
The aim of the author herein is to briefly introduce tool for comparison of the directly exposed bridge deck with the bridge deck protected by water proof insulation under an asphalt overlay. The work aims in particular on the preparation of possibilities to compare variants of directly exposed bridge decks and bridge decks protected by waterproof insulation. An innovation is the preparation of the model of a reinforced concrete bridge deck from ordinary Portland concrete with steel reinforcement protected by waterproof insulation under an asphalt overlay.
Modeling the durability of reinforced concrete bridge decks
The paper discusses the durability assessment of reinforced concrete bridge decks considering the actions of chlorides. The durability of reinforced concrete bridge decks can be affected by many factors, such as alkalinity, acids, repeated changes of humidity, cyclical temperature changes, carbonation, the action of chlorides, UV radiation, sulphides, fatigue and other influences including cracks. The action of de-icing agents is generally most detrimental for bridged decks. Chlorides penetrate through the surface to the steel reinforcement, causing corrosion of the reinforcement. It is one of the most important factors lowering the life span of bridge decks both in Central Europe and also in the North East of the USA. The typical solutions are epoxy-coating on the reinforcement or waterproof membrane above concrete bridge deck. The protection strategies are given in Fig. 1 .
|
|
|
Figure 1. The RC bridge deck scheme with epoxide protection of reinforcement typical for the North East of USA (left) and waterproof insulation typical for Central Europe (right). |
It is possible to use analytical or numerical models to model the durability of reinforced concrete bridge decks from the point of view of chloride action, which describe the risk of reinforcement corrosion occurring and thus the risk of the occurrence of degradation processes. If corrosion caused by the penetration of chlorides to the steel reinforcement is regarded as the dominant parameter affecting its durability then its lifespan can be recorded according to Tutti (1982) as:
|
|
( 1) |
where the time to the occurrence of corrosion is tinitiation and tpropagation which corresponds to the time in reaching an unacceptable level of corrosion in reinforced concrete reinforcement.
The corrosion of steel reinforcement is primarily controlled by the diffusion of chlorides. The effect of hydraulic pressure and capillary sorption is not considered in the model described as in most cases it can be ignored. Diffusion is thus the most common way in which chloride ions are brought into contact with the reinforcement of reinforced concrete bridges decks. Diffusion occurs as a result of concentration gradients. See e.g. Collepardi et al. (1972) and Hooton et al. (2001) .
Whether the analytical or numerical model is used to determine the concentration of chlorides at the level of reinforcement or at the point of damage to the epoxide covering, the output is the concentration of chlorides Cx ,t . Through a comparison of the chloride threshold Cth with the actual concentration at a given time it is possible to calculate whether the corrosion has begun or not. The durability of bridge decks describable by the reliability function RFt is expressed as a time dependent crossing of the corrosion threshold Cth , by the concentration of chlorides Cxy ,t which is locally dependent on the parameters of the cover of the reinforcement. The function of reliability characterizing the above described limit state is expressed as:
|
|
( 2) |
Durability can be related to the initiation of corrosion which corresponds to relationship (2) or the decrease in the area of reinforcement or the occurrence of cracks caused by corrosion due to chlorides. The period to the start of corrosion ti can be determined from the balance of concentrations of chlorides and the chloride threshold or from the reliability function RFt in Eq. (2) .
If there is a crack in the concrete then this crack allows the simpler passage of aggressive substances to the reinforcement. Simplified modeling of the effects on cracks by placing a concentration of chlorides at the point of the crack in concrete was considered in a probabilistic 2D analysis of the durability of RC bridge decks (Konečný et al., 2007 ). A similar method of applying marginal conditions of a concentration of chlorides directly in a crack is used by Marsavina et al. (2009) for instance. In contrast Bentz et al. (2013) model the effects of cracks in the form of changes in the material parameters in the area of the crack.
The improvement of the model (Konečný et al., 2007 ) is done via implementation of the crack effect by increasing the diffusion coefficient in respective nodes. Description of diffusion reduction is prepared experimental results (Djerbi et al., 2008 ). For details see Konečný (2015) .
2D FEA diffusion model taking into account the effects of cracks
The applied 2D FEA model (Lehner et al., 2014 ) serves to solve Ficks second diffusion law using the computer tool compatible with the Matlab environment. The model focusses on the transport of chloride ions through a reinforced concrete bridge deck with a transverse crack and on an estimate of the concentration of chlorides at the reinforcement level or in places with damage to the epoxide coating of the reinforcement. The model allows the inclusion of cracks in the concrete and also damage to the waterproof insulation under the asphalt coating. The numerical model is the extension of Tikalsky et al. (2005) , Konečný et al. (2007) , and Lehner et al. (2014) . Model details and introduced assumptions and simplifications are given in detail in Konečný (2015) . A crack can be introduced in the form of a boundary condition of surface concentration to a nodes corresponding to the assumed positioning of the crack as introduced in models (Konečný et al., 2007 and Marsavina et al., 2009 ). A more advanced approach following on from the work of Bentz et al. (2013) is the second possible method of introducing a reduced diffusion coefficient taking into account the size of cracks and the modification of the FEA mesh.
Sample bridge deck durability analysis
There is shown solution for a concrete bridge deck with crack and steel reinforcement. The analogy between heat and diffusion problems is used for the solution of both heat and diffusion tasks. Four-node is oparametric finite elements are used. A slab of 0.23 m is vertically divided into 46 right triangular elements with dimensions of 10 × 10 mm2 . The time step of the time related analysis (transient analysis) is controlled automatically on the basis of the size of the element and the diffusion coefficient.
An analysis with a crack in a reinforced concrete bridge deck using ordinary concrete
In the model with cracks and ordinary concrete (alternative P1B), the referential diffusion coefficient Dc,28 within 28 days of concreting is considered as 5.59 × 10−12 m2 /s for ordinary concrete, which corresponds to the average value of the 100TII mix (Ghosh and Tran, 2014 ). The aging factor is considered as m = 0.26. The initial concentration on the concrete surface (marginal conditions at relevant junctions) C0 is chosen as 0.6 percent (weight of material with cement properties) of soluble chloride ions (Tikalsky et al., 2005 ). The value of the concentration at which the initiation of corrosion Cth occurs is 0.2 ( Tikalsky et al., 2005 and ACI Manual 222R-01, 2001 ). The clear cover of concrete reinforcement above the upper layer of reinforcement is 0.05 m. The steel reinforcement is unprotected. A crack is positioned at the halfway point of the width of the model which has a value of 1 m. The depth of the crack is chosen as 0.025 m and its width is 0.3 mm. Due to the modeled width of the crack of 3 mm (300 μm) the diffusion coefficient in the crack is introduced as Dc,crack = 14 × 10−10 m2 /s.
The action of cracks allowing the movement of the chloride ions both in the vertical and the horizontal direction is illustrated in graphical output from the FEA analysis (see Fig. 2 ). Chlorides can travel to the reinforcement faster in an area with cracks. The progress of the development of chloride concentrations in time are for even decades given in addendum. In relation to the 2D analysis of the chloride concentration in time, information is obtained for the alternative with unprotected reinforcement about the highest concentration of chlorides at reinforcement level.
|
|
|
Figure 2. The concentration of chloride ions in a concrete bridge deck with a crack made from ordinary concrete without taking into account the effect of the curing of the concrete. Deterministic solution for an exposure period t = 20 years (top) shows the FEA meshed elements and concentration in the form of contours. |
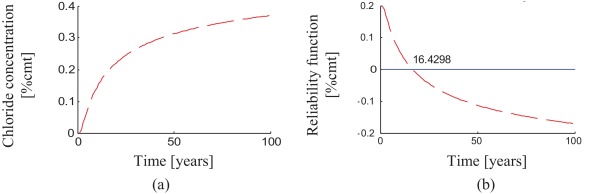
After deducting the time progress of the chloride concentration at the reinforcement level at the point with the greatest concentration Cz ,t and after comparing with the value of the chloride threshold Cth the period to the initiation of corrosion ti = 16.4 years is computed for ordinary reinforcement. See Fig. 3 (b).
|
|
|
Figure 3. Durability analysis at the level of the reinforcement of a concrete bridge deck with a crack in ordinary concrete taking into account the concrete maturing. The unprotected steel reinforcement is considered (marked as P1B). (a) The concentration of chlorides, (b) function of reliability for the analysis of durability. |
Evaluation of durability with epoxide protection of steel reinforcement
A model of the epoxide coating is incorporated into the analysis in the form of the identification of defects in reinforcement (alternative P1E). The difference when compared with unprotected reinforcement on the directly exposed bridge deck (alternative P1B) is thus in the definition of the places where the concentration of chlorides at the level of the reinforcement is evaluated. For illustration a starting defect in the epoxide coating 5 cm from the left edge of the model is selected and other defects repeat every 20 cm. The durability is extended to ti = 24.1 years.
Analysis with a defect in the waterproof insulation and a crack in a reinforced concrete bridge deck
If we add to the previous solution of the bridge deck with a crack and ordinary concrete (P1EB) asphalt overlay and waterproof insulation with a defect 40 cm from the left hand margin we obtain a model corresponding to the traditional solution in central Europe. It is assumed that the area of the defect in the barrier will grow by 1 cm per year. The below mentioned output is for 20 and 40 years: the size of the defect in the waterproof insulation here corresponds to an unmeasured age and is 20 cm for 20 years or 40 cm for a 40 year age. In the concentrations of chlorides it is clear that the surface concentration representing a defect in the waterproof insulation is localized to the area of the defect and the area of the defect grows in time. Fig. 4 shows the chloride concentration plot for bridge deck with asphalt overlay.
|
|
|
Figure 4. The concentration of chloride ions in the concrete bridge deck covered in an asphalt covering with a crack in the middle of the bridge deck and a defect in the waterproof insulation 40 cm from the left edge of the model. The output shown is for ordinary concrete when considering the effect of concrete curing. Deterministic solution – alternative P2EB for an exposure period of t = 20 years shows the FEA meshed elements and concentration in the form of contours. |
Through an analysis of the reliability function it was calculated that the initiation of corrosion begins for unprotected reinforcement after 44.0 year, whereas for reinforcement with an epoxide protection it will be 46.9 years. If the effect of epoxide protection is significant up to an age of 25 years, then the area of damage to the waterproof insulation is so extensive that it corresponds to the decomposition defect on the epoxide coating. The advantage of epoxide protection is then lost.
Discussion and summary of the deterministic solution
In the results there is a clear difference in the lifespan when considering the concrete mix design. It is also clear that there is a significant difference between the alternatives with waterproof insulation and with a directly exposed bridge deck with a crack.
As expected the unprotected directly exposed bridge deck without reinforcement protection (P1B) fares the worst when considering the epoxide protection (P1E) a doubling occurs in the period to the initiation of corrosion. If the bridge deck is also protected with waterproof insulation an extension of 6 times the lifespan of the steel reinforcement occurs compared to the alternative (P1B). The epoxide coating also extends lifespan but the difference compared to unprotected reinforcement is not that significant.
Conclusions
The paper focuses on analysis of the durability of reinforced concrete bridge decks from the point of view of the chloride induced initiation of corrosion. There are presented examples of deterministic assessments of the initiation of corrosion for selected alternatives of reinforced concrete bridge decks.
The 2D chloride ingress is considered. Two main alternatives with waterproof insulation and a directly exposed bridge deck made from ordinary Portland cement concrete were discussed. The implementation of a new model of cracks is introduced in the form of introducing a highly permeable area representing the crack area is introduced. This approach also allows crack effect modeling via change of diffusion coefficient on respective elements. The crack effect is related to their size. An approach with a change of value of the diffusion coefficient is selected because the effect of cracks in concrete on the introduction of a concentration of chlorides at a node corresponds to a crack under the waterproof insulation cannot be included if the defect in the waterproof insulation is in a different position to the crack in the concrete.
Due to the fact that the development of methods for the analysis of the durability of reinforced concrete structures continues, there is a plan for extending the program by further modules for following the durability of reinforced concrete bridge decks in the area of corrosion propagation.
Conflict of interest
The authors declare that there is no conflict of interest.
Acknowledgements
The financial support of the Ministry of Education, Youth and Sports of the Czech Republic through the VSB – Technical University of Ostrava, Ostrava, Czech Republic is highly acknowledged. The project registration number is SGS SP2015/131.
References
- AASHTO T277-93, 1993 AASHTO T277-93; Electrical Indication of Concretes Ability to Resist Chloride; American Association of State and Highway Transportation Officials, Washington, DC [USA] (1993)
- ACI Manual 222R-01, 2001 ACI Manual 222R-01; Protection of Metals in Concrete Against Corrosion; American Concrete Institute, Farmington Hills, MI [USA] (2001)
- Andrade, 1993 C. Andrade; Calculation of chloride diffusion coefficients in concrete from ionic migration measurements; Cement Concrete Res., 23 (3) (1993), pp. 724–742 http://dx.doi.org/10.1016/0008-8846(93)90023-3
- Bentz et al., 2013 D.P. Bentz, E.J. Garboczi, Y. Lu, N. Martys, A.R. Sakulich, J.W. Weiss; Modeling of the influence of transverse cracking on chloride penetration into concrete; Cement Concrete Compos., 38 (April) (2013), pp. 65–74 http://dx.doi.org/10.1016/j.cemconcomp.2013.03.003
- Benz and Thomas, 2001 E. Benz, M.D.A. Thomas; Life-365 Service Life Prediction Model: Computer Program for Predicting the Service Life and Life-Cycle Costs of Reinforced Concrete Exposed to Chlorides; (2001) Available from: http://www.life-365.org
- Djerbi et al., 2008 A. Djerbi, S. Bonnet, A. Khelidj, V. Baroghel-Bouny; Influence of traversing crack on chloride diffusion into concrete; Cement Concrete Res., 38 (6) (2008), pp. 877–883 http://dx.doi.org/10.1016/j.cemconres.2007.10.007g
- Collepardi et al., 1972 M. Collepardi, A. Marcialis, R. Turrizuani; Penetration of chloride ions into cement pastes and concretes; J. Am. Ceramic Res. Soc., 55 (10) (1972), pp. 534–535
- Francois et al., 2005 R. Francois, A. Toumi, M. Ismail, A. Castel, T. Vidal; Effect of cracks on local diffusion of chloride and long-term corrosion behavior of reinforced concrete members; International Workshop on Durability of Reinforced Concrete Under Combined Mechanical and Climatic Loads, Qingdao Technological University, Qingdao [China] (2005), pp. 113–122
- Ghosh and Tran, 2014 P. Ghosh, Q. Tran; Correlation between bulk and surface resistivity of concrete; Int. J. Concrete Struct. Mater., 9 (1) (2014), pp. 119–132 http://dx.doi.org/10.1007/s40069-014-0094-z
- Hooton et al., 2001 R.D. Hooton, M.D.A. Thomas, K. Standish; Testing the chloride penetration resistance of concrete: a literature review: FHWA Contract DTFH61-97-R-00022 Prediction of Chloride Penetration in Concrete; Federal Highway Administration, Washington, DC [USA] (2001) 405 p
- Konečný et al., 2007 P. Konečný, P.J. Tikalsky, D.G. Tepke; Performance evaluation of concrete bridge deck affected by chloride ingress: simulation-based reliability assessment and finite element modeling; Transport. Res. Record, 2007 (2028) (2007), pp. 3–8 http://dx.doi.org/10.3141/2028-01
- Konečný et al., 2011 P. Konečný, J. Brožovský, P. Ghosh; Evaluation of chloride influence on the cracking in reinforced concrete using Korozeeneck software; Transactions of the VŠB – Technical University of Ostrava, Civil Engineering Series, 11 (1) (2011), pp. 1–7 http://dx.doi.org/10.2478/v10160-011-0006-y
- Konečný, 2015 P. Konečný; Probabilistic Evaluation of the Durability of Reinforced Concrete Bridge Decks Exposed to the Actions of Chlorides; Faculty of Civil Engineering VŠB – Technical University of Ostrava, Ostrava, Czech Republic (2015) Available from: http://fast10.vsb.cz/konecny/files/Konecny_SI-2015.pdf (accessed 21.07.15)
- Lehner et al., 2014 P. Lehner, P. Konečný, P. Ghosh, Q. TRAN; Numerical analysis of chloride diffusion considering time-dependent diffusion coefficient; Int. J. Math. Comput. Simulat., 8 (1) (2014), pp. 103–106 ISSN: 1998-0159
- Marsavina et al., 2009 L. Marsavina, K. Audenaert, G. De Schutter, N. Faur, D. Marsavina; Experimental and numerical determination of the chloride penetration in cracked concrete; Construct. Build. Mater., 23 (1) (2009), pp. 264–274 http://dx.doi.org/10.1016/j.conbuildmat.2009.12.015 ISSN 0950-0618
- Novák et al., 2014 D. Novák, M. Vořechovský, B. Teplý; FReET: Software for the statistical and reliability analysis of engineering problems and FReET-D: Degradation module; Adv. Eng. Softw., 72 (June) (2014), pp. 179–192
- Sohangpurwala and Scannell, 1998 A. Sohangpurwala, W.T. Scannell; Verification of Effectiveness of Epoxy-Coated Rebars. Final Report to Pennsylvania Department of Transportation, Project No. 94-05; ConCorr, Ashburn, VA, USA (1998)
- Stewart and Rosowsky, 1998 M.G. Stewart, D.V. Rosowsky; Time-dependent reliability of deteriorating reinforced concrete bridge decks; Struct. Safety, 20 (1) (1998), pp. 91–109 http://dx.doi.org/10.1016/S0167-4730(97)00021-0 19 p
- Tikalsky et al., 2005 P.J. Tikalsky, D. Pustka, P.P. Marek; Statistical variations in chloride diffusion in concrete bridges; ACI Struct. J., 102 (3) (2005), pp. 481–486
- Tutti, 1982 K. Tutti; Corrosion of steel in concrete. CBI Research Report 4:82; Swedish Cement and Concrete Research Institute, Stockholm, Sweden. (1982)
- Vořechovská et al., 2015 D. Vořechovská, B. Teplý, M. Šomodíková, D. Lehký; Modelling of service life of concrete structures under combined mechanical and environmental actions; Modelling in Mechanics 2015, Ostrava, Czech Republic. CD-ROM (2015) 13 p
Document information
Published on 05/10/16
Licence: Other
Share this document
Keywords
claim authorship
Are you one of the authors of this document?