Revision as of 16:19, 28 February 2017 (view source) Scipediacontent (talk | contribs) (Created page with "==Resumen== En este trabajo se ha utilizado la formulación estabilizada de elementos finitos ''Unusual Stabilized Finite Element Method'' (USFEM) asociada al método de Rot...")	Latest revision as of 16:27, 28 February 2017 (view source) Scipediacontent (talk | contribs) m (Scipediacontent moved page Draft Content 486883310 to Alvarez-H. Coutinho 2013a)
(No difference)

---

Latest revision as of 16:27, 28 February 2017

Resumen

En este trabajo se ha utilizado la formulación estabilizada de elementos finitos Unusual Stabilized Finite Element Method (USFEM) asociada al método de Rothe para resolver el problema del redistanciamiento en el método de Funciones de Nivel. Se ha utilizado el método de Rothe primero para el avance de la solución en el pseudotiempo y la formulación USFEM para la solución del problema advectivo–reactivo en estado estacionario, para cada paso de tiempo resultante. Se han hecho ejemplos en 2D y se han comparado sus resultados con el esquema de estabilización SUPG, incrementado con un operador de captura de discontinuidades no lineal.

Abstract

In this work we use the Unusual Stabilized Finite Element Method (USFEM) associated to Rothes method for solving the redistancing problem in the Level Set Method . Rothes method is used first for advancing the solution in (pseudo)time and USFEM for solving the resulting steady advective–reaction problem in each time step. Several 2D problems are solved and results compared with SUPG scheme supplemented with a nonlinear discontinuity–capturing operator.

Palabras clave

Método de funciones de nivel ; Método de Rothe ; Formulación estabilizada de elementos finitos

Keywords

Level sets ; Rothes method ; Unusual finite element method

1. Introducción

Los problemas de la hidrodinámica que involucran el fenómeno de flujo en superficie libre suscitan un gran interés en científicos de diversas áreas: oceanografía, ambiental, recursos hídricos, aeroespacial, entre otras. La trayectoria seguida por el agua después de la rotura de una presa, la agitación de un líquido dentro de un tanque o el rompimiento de las olas sobre las estructuras costeras o marítimas son fenómenos que han motivado el surgimiento de muchos métodos numéricos en el intento por describir adecuadamente el movimiento de la interfase entre una parte líquida de mayor densidad (p. ej., agua, petróleo) y una parte gaseosa de menor densidad (p. ej., aire, gas).

En particular, para el flujo en superficie libre se desarrollaron varios métodos numéricos con el propósito de describir el fenómeno apropiadamente. Dichos métodos pueden agruparse en 2 grandes familias: los que hacen un seguimiento de la interfase (Interface–Tracking) y los que capturan la interfase propiamente (Interface–capturing)[1] , [2] , [3]  and [4] . En este trabajo se hace referencia exclusivamente a los últimos.

Los métodos que capturan la interfase emplean una malla fija que abarca los dominios de las fases presentes, no solo la que es de interés de estudio (la fase líquida en la mayoría de las veces) sino también la fase gaseosa. Los métodos denominados Volumen de Fluido (Volume of Fluid en inglés, o simplemente VOF) [5] , [6]  and [7] y Función de Nivel (Level Set en inglés, o simplemente LS) [8] , [9]  and [10] son los que se utilizan con más frecuencia. En Xia et al. [11] se puede encontrar una revisión de las aplicaciones de LS en CFD para la industria aeroespacial.

Los métodos LS son técnicas numéricas que se emplean para calcular la posición de frentes que se propagan [2]  and [3] . Se basan principalmente en la advección de una función que determina una curva o superficie, definida en todo el dominio y que abarca las fases de los fluidos involucrados (generalmente 2), cuyo valor de la función es cero en la interfase entre ambos. Una de las principales ventajas de usar LS es su capacidad de tratar eficientemente los cambios de topología y/o discontinuidades presentes en la curva o superficie [8] .

La solución de la ecuación de transporte dependiente de un (pseudo)tiempo, que advecta la función de la interfase, se hizo por el esquema de Rothe [12] que establece que primero se realiza la discretización temporal y luego la discretización espacial, empleando alguno de los esquemas de estabilización presentes en la literatura. En este trabajo se empleó la formulación de elementos finitos estabilizados USFEM [13] .

El trabajo está dividido en las siguientes secciones: en la sección 2 se presenta la formulación matemática y numérica del problema de captura de interfase usando el método de las funciones de nivel (LS), la descripción de la discretización temporal empleando el método de Rothe, la descripción del esquema estabilizado de elementos finitos USFEM empleado en la discretización espacial, y por último, la descripción de la formulación estabilizada de elementos finitos clásica SUPG [14] con operador de captura de discontinuidades CAU [15] . En la sección 3 se presenta una serie de experimentos numéricos que permitieron demostrar el buen desempeño de la formulación USFEM propuesta, comparando los resultados con el esquema SUPG incrementado con el operador de captura de discontinuidades no lineal CAU. Finalmente, la sección 4 presenta las conclusiones de este trabajo y los futuros retos que deben ser abordados.

2. Formulación matemática y numérica del problema de transporte advectivo

2.1. Formulación del problema

El problema de evolución de la interfase se puede escribir como una ecuación de transporte advectivo dependiente de un (pseudo)tiempo t[16] :

${\displaystyle {\frac {\partial \phi }{\partial t}}+{\boldsymbol {\beta }}\cdot \nabla \phi =}$${\displaystyle sign({\phi }_{0})}$

( 1)

${\displaystyle {\boldsymbol {\beta }}={\frac {\nabla \phi }{\left|\nabla \phi \right|}}sign({\phi }_{0})}$

( 2)

${\displaystyle \phi (x,t=0)={\phi }_{0}({\boldsymbol {\mbox{x}}},t)}$

( 3)

Donde β es el campo de velocidades conocido, solenoidal (∇ · β  = 0), que indica la condición de incompresibilidad; ϕ es una función de nivel (o Level Set ) suave, definida en todo el dominio espacial Ω, que incluye las 2 fases de los fluidos involucrados (líquida y gaseosa) que debe ser determinada para cada instante de tiempo t  ∈ [0, T ] y definida así:

${\displaystyle \phi ({\boldsymbol {\mbox{x}}},t)={\begin{array}{lll}>0&si&{\boldsymbol {\mbox{x}}}\in {\Omega }_{l}\\=0&si&{\boldsymbol {\mbox{x}}}\in {\Gamma }_{I}\\<0&si&{\boldsymbol {\mbox{x}}}\in {\Omega }_{g}\end{array}}}$

( 4)

x indica la posición espacial donde la función es evaluada, Ω = Ω_l  ∪ Ω_g , Ω_g  = Ω ∖ Ω_l , los subíndices l y g   se refieren a las fases líquida y gaseosa respectivamente y su interfase es definida como: ${\textstyle {\Gamma }_{I}=}$${\displaystyle \left\{{\boldsymbol {\mbox{x}}}\vert \phi ({\boldsymbol {\mbox{x}}},t)=\right.}$${\displaystyle \left.0\right\}}$ ; sign (ϕ ) es la función signo , dada por:

${\displaystyle sign(\phi )=2(H_{\epsilon }(\phi )-1/2)}$

( 5)

donde H_ϵ (ϕ ) es una función tipo Heaviside , definida así:

${\displaystyle H_{\epsilon }(\phi )={\begin{array}{lll}0&si&\phi <-\epsilon \\{\frac {1}{2}}\left[1+{\frac {\phi }{\epsilon }}+{\frac {1}{\pi }}sin\left({\frac {\pi \phi }{\epsilon }}\right)\right]&si&\left|\phi \right|\leq \epsilon \\1&si&\phi >\epsilon \end{array}}}$

( 6)

${\textstyle \epsilon \in R^{+}}$ es un valor pequeño que está directamente relacionado con el espesor de la interfase, que es aproximadamente ${\textstyle 2\epsilon /\left|\phi \right|}$[4] . La función Heaviside se usa para proporcionar una variación suave de la variable ϕ   para que cuando ${\textstyle \left|\phi \right|\leq \epsilon }$ entonces ${\textstyle \left|\nabla \phi \right|=}$${\displaystyle 1}$ y garantizar un espesor de la interfase igual a 2ϵ , por lo que la selección del valor de ϵ debe estar ajustada al tamaño de los elementos cercanos a la interfase. En este trabajo el valor de ϵ   está dado por ${\textstyle \epsilon =}$${\displaystyle {\frac {1}{2}}min\left\{h_{e}\right\}}$ , donde h_e es el tamaño característico del elemento.

2.2. Discretización temporal

El método de Rothe [12] consiste en discretizar primero en el tiempo y luego en el espacio. Discretizamos la ecuación diferencial (1) mediante el método de la regla trapezoidal generalizada en términos de ϕ_n (x ) y ${\textstyle {\dot {\phi }}_{n}({\boldsymbol {\mbox{x}}})}$ , como se mostró en Henao et al. [17] y se resume a continuación:

${\displaystyle {\dot {\phi }}_{n+1}+{\boldsymbol {\beta }}\cdot \nabla {\phi }_{n+1}=}$${\displaystyle sign({\phi }_{0})}$

( 7)

${\displaystyle {\phi }_{n+1}={\tilde {\phi }}_{n+1}+\gamma \Delta t{\dot {\phi }}_{n+1}}$

( 8)

${\displaystyle {\tilde {\phi }}_{n+1}={\phi }_{n}+(1-\gamma )\Delta t{\dot {\phi }}_{n}}$

( 9)

Sustituyendo la ecuación (8) en la (7) y reorganizando términos:

${\displaystyle {\dot {\phi }}_{n+1}+\beta \cdot \nabla ({\tilde {\phi }}_{n+1}+}$${\displaystyle \gamma \Delta t{\dot {\phi }}_{n+1})=sign({\phi }_{0})}$

( 10)

${\displaystyle {\dot {\phi }}_{n+1}+\beta \cdot \nabla {\tilde {\phi }}_{n+1}+}$${\displaystyle \gamma \Delta t\beta \cdot \nabla {\dot {\phi }}_{n+1}=}$${\displaystyle sign({\phi }_{0})}$

( 11)

${\displaystyle {\dot {\phi }}_{n+1}+{\overset {\mbox{ˆ}}{\boldsymbol {\beta }}}\cdot \nabla {\dot {\phi }}_{n+1}=}$${\displaystyle {\overset {\mbox{ˆ}}{f}}_{n+1}}$

( 12)

donde

${\displaystyle {\overset {\mbox{ˆ}}{\boldsymbol {\beta }}}=\gamma \Delta t\beta }$

( 13)

${\displaystyle {\overset {\mbox{ˆ}}{f}}_{n+1}=sign({\phi }_{0})-\beta \cdot \nabla {\tilde {\phi }}_{n+1}}$

( 14)

En la ecuación (2) el campo de velocidades, dado por el vector β , depende del gradiente de la solución transformando la ecuación (1) en una ecuación no lineal. Si usamos pequeños pasos de tiempo en el esquema de avance en el tiempo, podemos transformar la ecuación (1) en una ecuación pseudo–lineal, «linealizando»dicha ecuación al usar el valor de la solución del paso de tiempo inmediatamente anterior; esto se logra tomando los valores en ${\textstyle {\overset {\mbox{ˆ}}{f}}_{n}}$ .

2.3. Discretización espacial

La ecuación (12) puede interpretarse como una ecuación de convección–reacción en estado estacionario para la variable ${\textstyle {\dot {\phi }}}$ . Reescribiendo:

${\displaystyle {\overset {\mbox{ˆ}}{\boldsymbol {\beta }}}\cdot \nabla {\dot {\phi }}_{n+1}-}$${\displaystyle {\overset {\mbox{ˆ}}{\sigma }}{\dot {\phi }}_{n+1}={\overset {\mbox{ˆ}}{f}}_{n}}$

( 15)

donde el parámetro ${\textstyle {\overset {\mbox{ˆ}}{\sigma }}=}$${\displaystyle -1}$ .

Hay que hacer énfasis en esta idea, ya que realmente no existe como tal un parámetro de reacción dentro de la ecuación sino que, al desarrollarse algebraicamente el esquema de Rothe, el término dependiente del tiempo se asemeja al término reactivo. Por lo tanto, el valor ${\textstyle {\overset {\mbox{ˆ}}{\sigma }}=}$${\displaystyle -1}$ no significa que haya absorción o disipación.

Ahora podemos reescribir el método de Galerkin en su forma débil:

${\displaystyle {\overset {\mbox{ˆ}}{a}}({\omega }^{h},{\dot {\phi }}_{n+1}^{h})=}$${\displaystyle ({\omega }^{h},{\overset {\mbox{ˆ}}{f}}(t_{n}))}$

( 16)

donde

${\displaystyle {\overset {\mbox{ˆ}}{a}}({\omega }^{h},{\dot {\phi }}_{n+1}^{h})=}$${\displaystyle ({\omega }^{h},{\overset {\mbox{ˆ}}{\boldsymbol {\beta }}}\cdot \nabla {\dot {\phi }}_{n+1})-}$${\displaystyle ({\omega }^{h},{\overset {\mbox{ˆ}}{\sigma }}{\dot {\phi }}_{n+1})}$

( 17)

${\displaystyle ({\omega }^{h},{\overset {\mbox{ˆ}}{f}}(t_{n+1}))=({\omega }^{h},sign({\phi }_{0}))-}$${\displaystyle a({\omega }^{h},{\tilde {\phi }}_{n+1}^{h})}$

( 18)

${\displaystyle a({\omega }^{h},{\tilde {\phi }}_{n+1}^{h})=({\omega }^{h},{\boldsymbol {\beta }}\cdot \nabla {\tilde {\phi }}_{n+1})}$

( 19)

Como es sabido, la ecuación (15) presenta problemas de estabilidad numérica que deben ser corregidos mediante la aplicación de algún esquema de estabilización adecuado. Aplicando el esquema USFEM [13] a la ecuación (16) tenemos:

${\displaystyle {\overset {\mbox{ˆ}}{a}}({\omega }^{h},{\dot {\phi }}_{n+1}^{h})-}$${\displaystyle {\tau }_{USFEM}(L^{\ast }{\omega }^{h},{\overset {\mbox{ˆ}}{L}}{\dot {\phi }}_{n+1}^{h}-}$${\displaystyle {\overset {\mbox{ˆ}}{f}}(t_{n}))=({\omega }^{h},{\overset {\mbox{ˆ}}{f}}(t_{n}))}$

( 20)

donde

${\displaystyle L^{\ast }{\omega }^{h}=-{\overset {\mbox{ˆ}}{\boldsymbol {\beta }}}\cdot \nabla {\omega }^{h}-}$${\displaystyle {\overset {\mbox{ˆ}}{\sigma }}{\omega }^{h}}$

( 21)

${\displaystyle {\overset {\mbox{ˆ}}{L}}{\omega }^{h}={\overset {\mbox{ˆ}}{\boldsymbol {\beta }}}\cdot \nabla {\omega }^{h}-}$${\displaystyle {\overset {\mbox{ˆ}}{\sigma }}{\omega }^{h}}$

( 22)

${\textstyle L^{\ast }}$ es el adjunto del operador lineal. El parámetro de estabilización τ_USFEM es presentado en Franca y Valentin [18] :

${\displaystyle {\tau }_{USFEM}={\frac {h_{e}^{2}}{-{\overset {\mbox{ˆ}}{\sigma }}h_{e}^{2}\xi ({Pe}_{k}^{\left(1\right)}({\tilde {x}}))+{\frac {2{\overset {\mbox{ˆ}}{\kappa }}}{m_{k}}}\xi ({Pe}_{k}^{\left(2\right)}({\tilde {x}}))}}}$

( 23)

${\displaystyle {Pe}_{k}^{\left(1\right)}({\tilde {x}})={\frac {2{\overset {\mbox{ˆ}}{\kappa }}}{m_{k}(-{\overset {\mbox{ˆ}}{\sigma }})h_{e}^{2}}}}$

( 24)

${\displaystyle {Pe}_{k}^{\left(2\right)}({\tilde {x}})={\frac {m_{k}{\left|{\overset {\mbox{ˆ}}{\boldsymbol {\beta }}}\right|}_{p}h_{e}}{\overset {\mbox{ˆ}}{\kappa }}}}$

( 25)

${\displaystyle \xi (x)={\begin{array}{lll}1&si&0\leq x<1\\x&si&x\geq 1\end{array}}}$

( 26)

${\displaystyle {\left|{\overset {\mbox{ˆ}}{\boldsymbol {\beta }}}\right|}_{p}=}$${\displaystyle {\left(\sum _{i=1}^{N}{\left|{\overset {\mbox{ˆ}}{\boldsymbol {\beta }}}_{i}({\tilde {x}})\right|}^{p}\right)}^{\frac {1}{p}};1\leq p<\infty }$

( 27)

${\displaystyle m_{k}=min(1/3,C_{k})}$

( 28)

${\displaystyle C_{k}\sum _{k}^{}h^{2}{\left\|\Delta v\right\|}_{0,k}^{2}\leq {\left\|\Delta v\right\|}_{0}^{2};\forall v\in V_{h}}$

( 29)

Comentario: Nótese que como ${\textstyle {\overset {\mbox{ˆ}}{\kappa }}=}$${\displaystyle 0}$ (problema sin difusión) ${\textstyle {Pe}_{k}^{\left(1\right)}=}$${\displaystyle 0}$ , entonces, ${\textstyle \xi ({Pe}_{k}^{\left(1\right)}({\tilde {x}}))=}$${\displaystyle 1}$ y ${\textstyle {Pe}_{k}^{\left(2\right)}\rightarrow \infty }$ , por lo tanto, ${\textstyle \xi ({Pe}_{k}^{\left(2\right)}({\tilde {x}}))\rightarrow {Pe}_{k}^{\left(2\right)}}$ . Reemplazando estos valores en (23) y obteniendo el límite para cuando ${\textstyle {\overset {\mbox{ˆ}}{\kappa }}\rightarrow 0}$ (empleando la regla de L’Hôpital para evitar la indeterminación que se presenta), se obtiene que:

${\displaystyle {\tau }_{USFEM}={\frac {h_{e}}{h_{e}+2{\left|{\overset {\mbox{ˆ}}{\boldsymbol {\beta }}}\right|}_{p}}}}$

( 30)

recordando que ${\textstyle {\overset {\mbox{ˆ}}{\boldsymbol {\beta }}}=}$${\displaystyle \gamma \Delta t\beta }$ , entonces cuando Δt  → 0 τ_USFEM  → 1.

Empleando las funciones de interpolación estándares de elementos finitos:

${\displaystyle u^{h}=\sum _{i=1}^{nnodos}N_{i}u_{i}}$

( 31)

donde nnodos es el número de nodos de cada elemento de la malla y N una matriz que contiene las funciones de interpolación. Sustituyendo la ecuación (31) junto con su derivada en la ecuación (20) , se obtiene un sistema de ecuaciones ordinarias lineales en estado estacionario de la forma:

${\displaystyle {\boldsymbol {\mbox{K}}}{\dot {\boldsymbol {\mbox{d}}}}={\boldsymbol {\mbox{F}}}}$

( 32)

donde K es la matriz de rigidez, en analogía a la mecánica de sólidos, e involucra los coeficientes de la parte advectiva y reactiva de Galerkin y de la formulación USFEM, ${\textstyle {\dot {\boldsymbol {\mbox{d}}}}}$ es un vector que contiene los valores de la derivada temporal de d , y F un vector con los términos fuente.

El avance en el tiempo del sistema de ecuaciones ordinarias (32) se hace empleando un algoritmo implícito predictor corrector [19] de la familia de la regla trapezoidal generalizada, con parámetro θ  = 1/2. En este sistema de ecuaciones resulta una matriz de coeficientes no simétrica, que se resuelve empleando el algoritmo generalizado de mínimos cuadrados, o GMRES [20] por sus siglas en inglés, con precondicionamiento diagonal, generando 10 vectores en la base de los sub–espacios de Krylov. La tolerancia para el método iterativo GMRES es de 1.0E⁻³ en todos los ejemplos .

2.4. Formulación estabilizada SUPG+CAU

La formulación estabilizada SUPG+CAU [14]  and [15] está dada por:

${\displaystyle a\left({\omega }^{h},{\phi }_{n+1}^{h}\right)+{\tau }_{SUPG}\left(L^{adv}{\omega }^{h},L{\phi }_{n+1}^{h}\right)+}$${\displaystyle {\delta }_{OCD}\left(\nabla {\omega }^{h},\nabla {\phi }_{n+1}^{h}\right)=}$${\displaystyle ({\omega }^{h},f(t_{n+1}))}$

( 33)

En la ecuación (33) , el primer término corresponde a la formulación de Galerkin, el segundo corresponde a la estabilización lineal SUPG y el tercero a la estabilización no lineal del operador de captura de discontinuidades. ${\textstyle L^{adv}}$ corresponde a la parte advectiva del operador lineal:

${\displaystyle L\left({\phi }^{h}\right)={\frac {\partial {\phi }^{h}}{\partial t}}+}$${\displaystyle {\boldsymbol {\beta }}\cdot \nabla {\phi }^{h}-f}$

( 34)

En la literatura revisada se han encontrado varias formas de calcular el valor del parámetro de estabilización τ_SUPG[14] , [21] , [22]  and [23] . Escoger una u otra forma de calcular τ_SUPG es un tema muy controversial y depende más del tipo de fenómeno que se está estudiando. En este trabajo se escogió el propuesto por Codina [22] por su fácil implementación y sus resultados aceptables, y se calcula así:

${\displaystyle {\tau }_{SUPG}={\frac {1}{{\frac {4\kappa }{h_{e}^{2}}}+{\frac {2\left\|\beta \right\|}{h_{e}}}+\sigma }}}$

( 35)

El tipo de problema que debe ser resuelto por el esquema SUPG+CAU [ver ecuación (33) ] es puramente advectivo, por lo que κ  = 0 y σ  = 0; entonces, el parámetro de estabilización τ_SUPG se reduce a:

${\displaystyle {\tau }_{SUPG}={\frac {h_{e}}{2\left\|\beta \right\|}}}$

( 36)

Igual que sucede con la determinación del parámetro de estabilización τ_SUPG , la determinación del parámetro de estabilización no lineal, también llamado operador de captura de discontinuidades, es un tema abierto al estudio. Se encuentran diferentes propuestas para su determinación en la literatura revisada [15] , [24] , [25] , [26]  and [27] . En este trabajo se escogió el operador CAU [15] , en donde la estabilidad en la solución se obtiene modificando las funciones peso de la formulación SUPG, que pasan a actuar en la dirección del gradiente aproximado. Este término introduce de manera consistente una difusión artificial que es proporcional al residuo de la solución aproximada. El resultado es una formulación que consigue suavizar las oscilaciones presentes en la solución. El parámetro del operador de captura de discontinuidades CAU, δ_CAU , está dado por:

${\displaystyle {\delta }_{CAU}={\frac {1}{2}}{\alpha }_{c}h_{e}{\frac {\left|L\left({\phi }^{h}\right)\right|}{\left\|\nabla {\phi }^{h}\right\|}}}$

( 37)

donde

${\displaystyle {\alpha }_{c}=min\left({\frac {1}{4}}{Pe}_{\parallel }^{e},1\right)}$

( 38)

${\displaystyle {Pe}_{\parallel }^{e}={\frac {1}{2}}h_{e}{\frac {{\left\|{\beta }_{\parallel }^{e}\right\|}^{3}}{{\left({\beta }_{\parallel }^{e}\right)}^{T}{\boldsymbol {\mbox{D}}}{\beta }_{\parallel }^{e}}}}$

( 39)

${\displaystyle {\beta }_{\parallel }^{e}={\frac {\beta \nabla \phi }{\left\|\nabla \phi \right\|}}\nabla \phi }$

( 40)

${\textstyle {\beta }_{\parallel }^{e}}$ es la velocidad en el elemento en la dirección paralela al gradiente de la solución, ${\textstyle {Pe}_{\parallel }^{e}}$ es el número de Péclet correspondiente a la velocidad paralela, ${\textstyle \left|L\left({\phi }^{h}\right)\right|}$ es el módulo del residuo en el interior del elemento y D es un tensor de segundo orden que contiene los coeficientes de difusión del material, que en este tipo de problema tratado D  = 0 entonces ${\textstyle {Pe}_{\parallel }^{e}\rightarrow \infty }$ . Pueden encontrarse estudios comparativos de este y otros parámetros de estabilización no lineal en Henao [28] y en John y Knobloch [29]  and [30] .

Haciendo uso de las funciones de interpolación de elementos finitos [ver ecuación (31) ], la ecuación (33) se transforma en un sistema de ecuaciones ordinarias no lineales de la forma:

${\displaystyle {\boldsymbol {\mbox{M}}}{\dot {\boldsymbol {\mbox{d}}}}+{\boldsymbol {\mbox{K}}}({\boldsymbol {\mbox{d}}}){\boldsymbol {\mbox{d}}}=}$${\displaystyle {\boldsymbol {\mbox{F}}}}$

( 41)

donde M es la matriz de masa, K (d ) es la matriz de rigidez, que involucra los coeficientes de la parte advectiva de Galerkin, Petrov–Galerkin y del operador de captura de discontinuidades no lineal, d es el vector solución que contiene los valores escalares, ${\textstyle {\dot {\boldsymbol {\mbox{d}}}}}$ es un vector que contiene los valores de la derivada temporal de d , y F un vector con los términos fuente.

Similar a lo realizado para la formulación USFEM, el avance en el tiempo del sistema de ecuaciones ordinarias no lineal (41) se hace empleando un algoritmo implícito predictor multicorrector [19] de la familia de la regla trapezoidal generalizada, con parámetro θ  = 1/2. La cantidad de veces que el algoritmo realiza el proceso multicorrector en cada paso de tiempo se ha fijado en 4 para todos los ejemplos. En este sistema de ecuaciones también resulta una matriz de coeficientes no simétrica, que se resuelve empleando el algoritmo GMRES con precondicionamiento diagonal y generando 10 vectores en la base de los sub–espacios de Krylov. La tolerancia para el método iterativo GMRES es de 1.0E⁻³ en todos los ejemplos.

3. Experimentos numéricos

Se han realizado varios experimentos numéricos empleando la formulación estabilizada de elementos finitos USFEM/Rothe propuesta, y se compararon los resultados con los obtenidos mediante el uso del esquema estabilizado SUPG incrementado con el operador de captura de discontinuidades CAU [15] . Se presentan diferentes tipos de mallas en 2D, estructuradas y no estructuradas, compuestas de triángulos lineales de 3 nodos. Para todos los experimentos numéricos se utilizó un paso de tiempo Δt = 0,01 y un tiempo máximo de ejecución variable, hasta alcanzar el estado estacionario (donde la solución no cambiaba) en cada uno de los casos. Como criterio para determinar el momento en que se ha alcanzado el estado estacionario, se ha empleado el error relativo de la solución calculada entre 2 pasos de tiempo consecutivos:

${\displaystyle E_{ss}={\frac {\left\|s_{n+1}-s_{n}\right\|}{\left\|s_{n}\right\|}}}$

( 42)

donde E_ss es el error relativo, s_n y s_{n +1} son las soluciones encontradas en los pasos de tiempo n y n  + 1. Para todos los ejemplos, se considera que se ha alcanzado el estado estacionario cuando se cumple la condición E_ss  ≤ 1.0E⁻¹² .

Como caso general, para los tipos de malla empleados en los ejemplos, un tamaño de paso de tiempo mayor que el propuesto resultaría en una condición CFL  > 1.0 y daría lugar a una pérdida de precisión en la solución de todos los ejemplos.

3.1. Problema de advección pura: disco de Zalesak en movimiento rotacional

El primer experimento numérico es la advección de un disco tipo Zalesak en movimiento rotacional [31] sin términos fuente, f  = 0, ampliamente empleado para evaluar la precisión en los resultados de los solucionadores de problemas advectivos en el contexto de la formulación Level Set[3]  and [32] . El problema consiste en un disco ranurado centrado en (50,75) de radio 15. La ranura tiene un ancho de 5 y longitud de 25. El campo de velocidad rotacional constante está dado por:

${\displaystyle {\beta }_{x}={\frac {\pi }{314}}(50-y)}$

( 43)

${\displaystyle {\beta }_{y}={\frac {\pi }{314}}(x-50)}$

( 44)

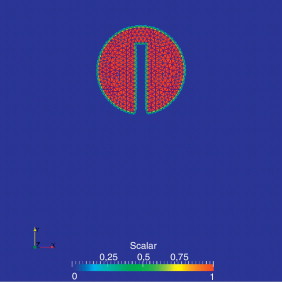
el disco completa una revolución cada 628 unidades de tiempo. En la figura 1 se muestra la malla no estructurada de elementos finitos con 5.287 nodos y 10.304 elementos triangulares lineales de 3 nodos.

Figura 1. Advección pura – Disco de Zalesak – Malla de elementos finitos y condición inicial.

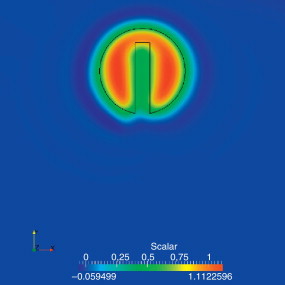
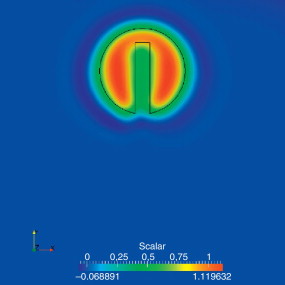
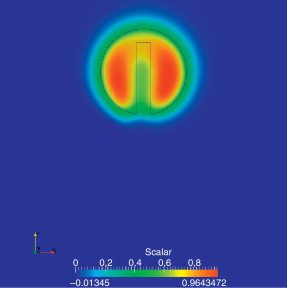
En las figuras Figura 2 , Figura 3  and Figura 4 se presentan los resultados para el último instante de tiempo obtenidos con las formulaciones estabilizadas USFEM/Rothe, SUPG y SUPG+CAU para un paso de tiempo Δt  = 0.01. Se observa que las soluciones con las formulaciones linearizadas USFEM/Rothe y SUPG son muy parecidas, aunque la formulación USFEM/Rothe presenta una solución levemente mejor comparada con el esquema lineal SUPG. El esquema no lineal SUPG+CAU resultó ser difusivo, tal como se esperaba de la teoría expuesta.

Figura 2. USFEM – Advección pura – Disco de Zalesak – Condición inicial vs último paso de tiempo.

Figura 3. SUPG – Advección pura – Disco de Zalesak – Condición inicial vs último paso de tiempo.

Figura 4. SUPG+CAU – Advección pura – Disco de Zalesak – Condición inicial vs último paso de tiempo.

3.2. Cálculo de la función distancia para un cuadrado

El segundo experimento es un cuadrado centrado en (0,5, 0,5) en una malla estructurada de elementos finitos, compuesta de 3.200 elementos triangulares lineales y 1.681 nodos. El dominio tiene dimensiones [1,0 × 1,0] y el cuadrado interno es de [0,25 × 0,25]. La parte interna del cuadrado presenta el valor ϕ  = −1, la parte externa el valor ϕ  = +1 y la interfase el valor de ϕ  = 0. La solución exacta para la distancia en cualquier punto es fácil de obtener mediante relaciones geométricas simples.

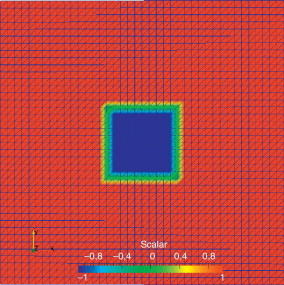
En las figuras Figura 5 , Figura 6  and Figura 7 se presentan la malla de elementos finitos, algunas de las funciones de nivel (LS) y una sección transversal hecha en un eje A–B con coordenadas: A(0, 0,5) y B(1, 0,5).

Figura 5. Cuadrado - Malla de elementos finitos.

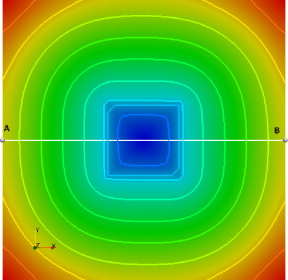
Figura 6. Cuadrado - USFEM/Rothe LevelSet.

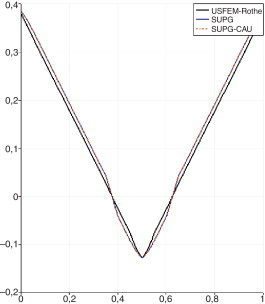
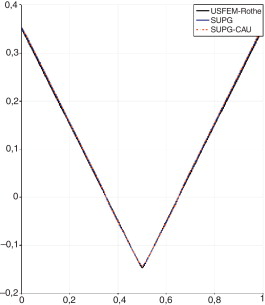
Figura 7. Cuadrado - USFEM/Rothe vs SUPG y SUPG+CAU.

En la figura 6 , para la formulación USFEM/Rothe, se observa la transición suave entre las curvas de nivel cuadradas hacia casi circulares a medida que se alejan del centro.

En la figura 7 se comparan los resultados obtenidos con las formulaciones USFEM/Rothe y SUPG (esquemas linealizados) y SUPG+CAU (esquema no lineal). Se aprecia que el cono de distancia formado por la formulación USFEM/Rothe es más uniforme que el presentado por las formulaciones SUPG y SUPG+CAU. La única diferencia entre estas 2 últimas radica en que el esquema no lineal SUPG+CAU alcanza el estado estacionario en una menor cantidad de pasos de tiempo. Mediante relaciones geométricas simples se puede comprobar que la respuesta exacta para el valor de la distancia máxima sería de 0,375 y la mínima de 0,125. Los valores extremos obtenidos con la formulación USFEM/Rothe son de 0,368 para el máximo y 0,128 para el mínimo, con un error relativo del 5,1% para el máximo y 2,4% para el mínimo en esta sección transversal seleccionada. Se obtienen resultados muy similares para cualquier otra sección transversal arbitraria.

3.3. Cálculo de la función distancia para un círculo

En el último experimento presentamos un círculo centrado en (0,50, 0,75) y de radio 0,15, en una malla no estructurada de elementos finitos con 45.667 nodos y 90.532 elementos triangulares lineales. El domino es un cuadrado de [1,0 x 1,0] y al igual que en el anterior ejemplo, la parte interna del círculo tiene valor de ϕ  = −1, la parte externa el valor ϕ  = +1 y la interfase el valor de ϕ  = 0.

En las figuras 8 –9 se presentan el dominio computacional, algunas de las funciones de nivel (LS) y una sección transversal hecha en un eje A–B con coordenadas: A(0, 0,75) y B(1, 0,75). No se muestra la malla de elementos finitos debido a la gran densidad de elementos, perdiéndose la resolución de los triángulos.

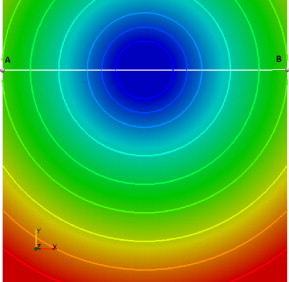
Figura 8. Círculo - USFEM/Rothe LevelSet.

Figura 9. Círculo - USFEM/Rothe vs SUPG+CAU.

En la figura 8 , para la formulación USFEM/Rothe, se observan las curvas de nivel perfectamente circulares alejándose del centro.

En la figura 9 se muestra nuevamente una comparación de la formación del cono de distancia al nivel cero para las formulaciones empleadas. En las 3 formulaciones se observan resultados muy similares, teniendo en cuenta que los esquemas USFEM/Rothe y SUPG son linealizados y el esquema SUPG+CAU es no lineal. Al igual que en el caso del ejemplo del cuadrado, a través de relaciones geométricas sencillas se puede constatar que la respuesta exacta para el valor máximo sería de 0,350 y el mínimo de 0,150, y para todas las formulaciones estudiadas se tiene como valores extremos 0,350 para el máximo y 0,148 para el mínimo, obteniéndose un error relativo del 0% para el máximo y 1,3% para el mínimo en esta sección transversal seleccionada. Para cualquier otra sección transversal arbitraria, se obtienen resultados similares.

4. Conclusiones

El buen rendimiento obtenido mediante la formulación estabilizada USFEM/Rothe se demostró gracias a una serie de ejemplos, tanto con bordes suaves como con bordes angulosos. En ellos observamos que la formulación propuesta es completamente viable para tratar este tipo de problemas, más aún si se aprovecha la propiedad del parámetro de estabilización τ  → 1 cuando Δt  → 0, maximizándose la cantidad de estabilización requerida para suavizar las inestabilidades numéricas que pueden presentarse. Se demostró que la formulación USFEM/Rothe, aun siendo linealizada, presentaba mejor rendimiento que la formulación clásica SUPG+CAU, que es no lineal.

La idea de realizar primero la discretización temporal y luego la espacial, resultando en una serie de ecuaciones diferenciales en estado estacionario, se mostró adecuada en la resolución de este tipo de problemas de cálculo de la función distancia para el esquema LS. El siguiente paso es involucrar este procedimiento al de renormalización de la función de nivel, también empleando el esquema USFEM/Rothe en la discretización espacio–temporal.

Agradecimientos

Los autores agradecen a la Agencia Brasilera de Petróleos, ANP, por la financiación del proyecto. También expresamos nuestra gratitud al profesor L.P. Franca por la fructífera discusión durante la preparación de este trabajo.

References

1. [1] J.A. Sethian; Fast Marching Methods; SIAM Review, 41 (2) (1999), pp. 199–235
2. [2] R.N. Elias, M.A.D. Martins, Coutinho ALGA; Simple finite element-based computation of distance functions in unstructured grids; Int. J. Numer. Methods Engrg., 72 (9) (2007), pp. 1095–1110
3. [3] R.N. Elias, Coutinho ALGA; Stabilized edge-based finite element simulation of free-surface flows; Int. J. Numer. Meth. Fluids, 54 (2007), pp. 965–993
4. [4] L. Battaglia, M.A. Storti, J. D’Elía; Bounded renormalization with continuous penalization for level set interface-capturing methods; Int. J. Numer. Methods Engrg., 84 (7) (2010), pp. 830–848
5. [5] C.W. Hirt, B.D. Nichols; Volume of fluid (VOF) method for the dynamics of free boundaries; J. Comput. Phys., 39 (1) (1981), pp. 201–225
6. [6] W.J. Rider, D.B. Kothe; Reconstructing volume tracking; J. Comput. Phys., 141 (1998), pp. 112–152
7. [7] D.J. Benson; Volume of fluid interface reconstruction methods for multi-material problems; Appl. Mech. Rev., 55 (2002), pp. 151–165
8. [8] S. Osher, J.A. Sethian; Fronts propagating with curvature-dependent speed: Algorithms based on Hamilton-Jacobi formulations; J. Comput. Phys., 79 (1) (1988), pp. 12–49
9. [9] J.A. Sethian; A fast marching level set method for monotonically advancing fronts; Proc. Natl. Acad. Sci., 93 (1996), pp. 1591–1595
10. [10] J.A. Sethian, P. Smereka; Level set methods for fluid interfaces; Annual Review of Fluid Mechanics, 35 (2003), pp. 341–372
11. [11] H. Xia, P.G. Tucker, W.N. Dawes; Level sets for CFD in aerospace engineering Prog. Aerosp. Sci., 46 (2010), pp. 274–283
12. [12] E. Rothe; Zweidimensionale parabolische Randwertaufgaben als Grenzfall eindimensionaler Randwertaufgaben; Mathematishe Annalen, 102 (1930), pp. 650–670
13. [13] L.P. Franca, C. Farhat; Bubble functions prompt unusual stabilized finite element methods; Comput. Methods Appl. Mech. Engrg., 123 (1995), pp. 299–308
14. [14] A.N. Brooks, T.J.R. Hughes; Streamline-Upwind/Petrov-Galerkin formulations for convection dominated flows with particular emphasis on the incompressible Navier-Stokes equation; Comput. Methods Appl. Mech. Engrg., 32 (1982), pp. 199–259
15. [15] A.C. Galeão, E.G. Do Carmo; A consistent approximate Upwind Petrov-Galerkin method for convection-dominated Problems; Comput. Methods Appl. Mech. Engrg., 68 (1988), pp. 83–95
16. [16] M. Sussman, E. Fatemi, P. Smereka, S. Osher; An improved Level Set method for incompressible two-phase flows; Comput. Fluids, 27 (5-6) (1998), pp. 663–680
17. [17] C.A.A. Henao, A.L.G.A. Coutinho, L.P. Franca; A stabilized method for transient transport equations; Comput. Mech., 46 (2010), pp. 199–204
18. [18] L.P. Franca, F. Valentin; On an improved unusual stabilized finite element method for the advective-reactive-diffusive equation; Comput. Methods Appl. Mech. Engrg., 190 (2000), pp. 1785–1800
19. [19] T.J.R. Hughes; The Finite Element Method - Linear Static and Dynamic Finite Element Analysis; Englewood Cliffs, NJ, Prentice-Hall (1987)
20. [20] Y. Saad, M.H. Schultz; GMRES: Generalized Minimal Residual Algorithm for Solving Non-Symmetric Systems; SIAM Journal of Scientific and Statistical Computing, 7 (1996), pp. 856–869
21. [21] Shakib F. (1989) Finite element analysis of the compressible Euler and Navier-Stokes equation. Ph.D Thesis, Division of Applied Mechanics. Stanford University, USA.
22. [22] R. Codina; Comparison of some finite element methods for solving the diffusion-convection-reaction equation; Comput. Methods Appl. Mech. Engrg., 156 (1998), pp. 185–210
23. [23] E.T. Tezduyar, Y. Osawa; Finite element stabilization parameters computed from element matrices and vectors; Comput. Methods Appl. Mech. Engrg., 190 (2000), pp. 411–430
24. [24] R. Codina; A discontinuity-capturing crosswind-dissipation for the finite element solution of the convection-diffusion equation; Comput. Methods Appl. Mech. Engrg., 110 (1993), pp. 325–342
25. [25] P.A.B. Sampaio, A.L.G.A. Coutinho; A natural derivation of discontinuity capturing operator for convection-difusion problems; Comput. Methods Appl. Mech. Engrg., 190 (2001), pp. 6291–6308
26. [26] Juanes R, Patzek TW. (2001) Multiple-scale stabilized finite elements for the simulation of tracer injections and waterflood SPE/DOE 13th Symposium on Improved Oil Recovery, Tulsa, Oklahoma, SPE Journal 75231.
27. [27] E.T. Tezduyar, M. Senga; SUPG finite element computation of inviscid supersonic flows with YZβ shock-Capturing  ; Comput. Fluids, 36 (2007), pp. 147–159
28. [28] Henao CAA. (2004) Um estudo sobre operadores de captura de descontinuidades para problemas de transporte advectivos. MSc. Tesis, COPPE/UFRJ Engenharia Civil. Rio de Janeiro, RJ - Brasil.
29. [29] V. John, P. Knobloch; On spurious oscillations at layers diminishing (SOLD) methods for convection-diffusion equations: Part I - A review; Comput. Methods Appl. Mech. Engrg., 196 (2007), pp. 2197–2215
30. [30] V. John, P. Knobloch; On spurious oscillations at layers diminishing (SOLD) methods for convection-diffusion equations: Part II - Analysis for P1 and Q1 finite elements; Comput. Methods Appl. Mech. Engrg., 197 (2008), pp. 1997–2014
31. [31] S.T. Zalesak; Fully multidimensional flux-corrected transport algorithms for fluids; J. Comput. Phys., 31 (1979), pp. 335–362
32. [32] D. Enright, R. Fedkiw, J. Ferziger, I. Mitchell; A hybrid level set method for improved interface capturing; J. Comput. Phys., 183 (2002), pp. 83–116