Simulation of moving loads on structures using a moving finite element mesh

Resumen

En este artículo se presenta una metodología para analizar la respuesta dinámica de estructuras sometidas a cargas móviles. Para ello se ha desarrollado un algoritmo de mallado adaptativo de elementos finitos que se mueve de forma solidaria a la carga móvil que actúa sobre la estructura. El algoritmo de mallado móvil se ha validado con la solución analítica de una carga móvil que recorre una viga simplemente apoyada.

Abstract

This paper presents a methodology to analyze the dynamic behavior of structures under moving loads. A finite element moving mesh algorithm has been developed in order to integrally move a part of the mesh following a moving load. This algorithm has been validated with the analytical solution of a moving load applied on a simply supported beam.

Palabras clave

Dinámica de estructuras ; Carga móvil ; Análisis no lineal ; Malla móvil

Keywords

Dynamic of structures ; Moving load ; Non-linear analysis ; Moving mesh

1. Introducción

La simulación de cargas dinámicas móviles suscita gran interés en diversas aplicaciones ingenieriles como por ejemplo el estudio de la interacción dinámica catenaria-pantógrafo, el comportamiento de viaductos al paso de vehículos, las máquinas de mecanizado por alta velocidad, etc. Focalizando la atención en la analogía del fenómeno teórico de cargas móviles en la interacción vehículo-plataforma destaca Olsson [1] , trabajo en el que el autor sugiere la reducción del modelo de un tren sobre un viaducto a un modelo masa-muelle desplazándose a velocidad constante sobre una viga, desarrollando la formulación teórica de su modelo y analizando la sensibilidad de los diferentes parámetros del modelo masa-muelle del tren en comparación con un modelo de fuerzas móviles. En la misma línea, en Visweswara [2] se presenta un estudio de la respuesta dinámica de un modelo de fuerzas móviles sobre vigas simplemente apoyadas. Entre otros trabajos destacan: Katz et al. [3] sobre la inestabilidad producida por una secuencia de cargas móviles, Akin and Mofid [4] presentando un método numérico para estudiar la respuesta de una carga móvil sobre una viga bajo diferentes condiciones de contorno y, más recientemente, Bruno et al. [5] estudia el efecto de cargas móviles sobre largos vanos de puentes suspendidos.

Son escasos los estudios esencialmente analíticos de la respuesta de un sistema elástico no lineal a una carga móvil; no obstante, destacan el estudio clásico de Yen y Sing [6] y más actualmente el de Metrikine [7] . Sin embargo, aunque los métodos analíticos proporcionan soluciones exactas, su alcance se ve limitado a geometrías simples alejadas de los problemas asociados a las aplicaciones prácticas, lo cual les hace perder competitividad frente a métodos numéricos. Esto, unido a los avances en las posibilidades de computación, hace que los métodos numéricos se hayan convertido en una de las herramientas más empleadas en el análisis de los problemas de cargas móviles. En [1]  and [8] se presentan los fundamentos de un método basado en descomposición modal para el estudio de cargas móviles en la interacción dinámica entre vehículo y raíl. Empleando la descomposición de Helmholtz y la transformada rápida de Fourier, en [9] se investiga la transmisión de las vibraciones debidas a una carga armónica y en [10] se emplean tanto elementos finitos como de contorno para problemas bidimensionales con cargas dinámicas.

Entre los trabajos más relevantes en este campo durante la última década, cabe citar el método numérico de elementos móviles propuesto en Koh et al. [11] que aborda el problema de la interacción vehículo-raíl modelando el raíl como una viga discretizada en elementos que fluyen con el vehículo. Posteriormente en [12] se extiende el concepto de elementos móviles a elementos bidimensionales. También son reseñables las publicaciones sobre el cálculo de estructuras con coordenadas móviles: en Nguyen y Duhamel [13] se aplica el procedimiento a una carga axial móvil sobre una barra infinita y en [14] a cargas armónicas sobre una viga infinita. Este tipo de sistemas excitados por una carga móvil pueden entrar en resonancia a determinadas velocidades, lo cual es bien conocido; ver por ejemplo Fryba [15] o algunos trabajos recientes relacionados con el control de la respuesta de la estructura, como es el de Qian y Tang [16] .

Cuando la fidelidad con el fenómeno físico modelado y la precisión en los cálculos son factores clave, la calidad del mallado es importante en la medida que determina el error de simulación; ver por ejemplo Babuška y Aziz [17] . Hay que considerar 2 aspectos, por una parte que el número de elementos es relevante por el elevado coste computacional asociado a elevadas densidades de malla, y por otra parte, que el tamaño de los elementos influye en la definición del paso de tiempo a emplear para garantizar la estabilidad dinámica.

El problema de encontrar una malla óptima de elementos finitos para cálculo estructural ha sido estudiado por numerosos autores durante las últimas décadas considerando distintos enfoques, incluyendo métodos basados en la minimización de energía como el propuesto por Fellipa en [18] , u otros basados en meras consideraciones geométricas como sugiere Cheng en [19] . Asimismo, la literatura científica también presenta diferentes técnicas de remallado basadas tanto en las estrategias de refinado-h[19] , donde nuevos nodos son añadidos localmente, como de refinado-r descrito en Zhu y Zienkiewicz [20] , donde un número fijo de nodos es redistribuido en el dominio. También otros tipos de estrategias adaptativas han sido desarrolladas en este campo, e.g. las de refinado-p que permiten la modificación del orden de los elementos finitos obteniendo mayor precisión en los resultados, como la que presenta Babuška en [21] .

En este artículo se propone un modelo de elementos finitos con una malla gruesa para todo el continuo sobre la que se superpone una malla móvil fina. El propósito de esta malla móvil es refinar dinámicamente la estructura de contacto en torno al punto de aplicación de la carga móvil. La principal aportación de este artículo es precisamente el desarrollo de una metodología para simular el contacto entre un continuo unidimensional sobre el que actúa un contacto móvil. De hecho, a lo largo del artículo se emplean indistintamente los conceptos carga móvil o contacto móvil. Dentro de esta metodología, la consecución de un contacto nodo-nodo de forma permanente con el movimiento de una malla móvil solidaria a la carga es beneficioso en la simulación de estructuras que presentan no linealidad geométrica, como pueden ser las estructuras de cables. Las ventajas que aporta esta metodología general son: (i) que contempla de forma natural las principales no linealidades presentes en el problema del contacto, (ii) proporciona un nivel de precisión muy notable y, sobre todo, (iii) permite obtener soluciones en tiempos de simulación muy razonables.

El presente artículo está estructurado de la siguiente forma. En primer lugar se presenta en la sección 2 la propuesta de discretización dinámica enfocada al tratamiento de problemas de carga móvil sobre estructuras. Para ello se define el entorno del dominio local de la malla móvil, se muestra el acoplamiento de la malla móvil con la malla global del continuo completo y se acaba realizando la validación de la metodología propuesta en la sección 3 mediante la comparación de los resultados obtenidos con los correspondientes a la solución analítica del problema de una carga móvil desplazándose sobre una viga simplemente apoyada. Finalmente, en la sección 4 se presentan las principales conclusiones que se pueden extraer del método propuesto.

2. Discretización dinámica para problemas de carga móvil

El análisis de la respuesta dinámica de una estructura sobre la que actúa una carga móvil puede requerir una gran capacidad de cálculo en caso de que esta presente, además de las no linealidades asociadas a la interacción entre la propia carga y el punto de contacto, no linealidades materiales y geométricas, ver Moller and Rubinstein [22] , así como la aparición de ondas y sus efectos sobre la estructura. Para mejorar el modelado del fenómeno tanto desde el punto de vista de la precisión como de las actuaciones del método numérico se ha desarrollado una técnica de remallado móvil que representa una novedad en el modelado de este tipo de sistemas. Esta técnica de remallado móvil conserva el número de grados de libertad del problema al igual que el remallado de refinado-r , sin embargo, el concepto es esencialmente diferente a la mayoría de otros remallados, ya que en cada instante de la simulación dinámica el método aquí propuesto aumenta la densidad de elementos del mallado en la zona del contacto. El continuo sobre el que actúa la carga móvil y más concretamente la zona de contacto entre la carga y la estructura es el entorno donde se concentra la malla móvil, lo cual permite concentrar la mayor parte del esfuerzo computacional en el subdominio del modelo con mayor predominancia de no linealidad permitiendo obtener la precisión deseada y limitando el coste computacional. Hay que destacar 2 aspectos complementarios e igualmente relevantes en la implementación de la malla móvil: en primer lugar la configuración y distribución de nodos en el subdominio de malla móvil y, en segundo lugar, su ensamblado y seguimiento del contacto sobre el mallado grueso original.

2.1. Definición del subdominio de malla móvil

Partiendo de la hipótesis según la cual el número de elementos permanece invariable, es preciso especificar en qué partes del dominio se concentran más nodos y en qué otras se toman esos nodos durante el proceso de cálculo tal como se apunta en Huerta et al. [23] . Para ello, se define el subdominio de refinamiento-r   , Ω, en el cual el número de los elementos será constante, como el intervalo ${\textstyle \Omega =\left[x_{t}-x_{ri},x_{t}+x_{rs}\right]}$ , donde x_t representa el punto de contacto entre la estructura y la carga móvil, así como x_ri y x_rs los límites inferior y superior del intervalo de refinamiento, fuera del cual la longitud, l , de los elementos es constante. La distribución nodal de dicho subdominio, considerando así la malla fina de forma independiente, se ha basado en el indicador de redistribución definido en Pijaudier-Cabot et al. [24] , según

${\begin{array}{l}\displaystyle R_{i}l_{i}=Constante\\\displaystyle \int _{l_{i}}R(x)dx=Constante\forall i:\sum _{i=1}^{n}l_{i}=\Omega \end{array}}$

( 1)

donde se refleja la relación constante entre el indicador de redistribución de la posición de los nodos en torno al punto móvil, denotado por ${\textstyle R}$ , y la longitud l para cada elemento i , aumentando el valor del indicador de redistribución allí donde se precisen elementos más pequeños y viceversa.

La redistribución nodal debe ser independiente del sistema de coordenadas espaciales, el cual permanece fijo durante el proceso de simulación, como se indica en Huerta y Liu [25] , [26] y [24] . Por tanto, la ecuación (1) se escribe en forma diferencial como

${\frac {\partial }{\partial \Psi }}\left(R(x){\frac {\partial x}{\partial \Psi }}\right)=0,$

( 2)

donde el sistema de coordenadas Ψ denota la referencia respecto a la cual se lleva a cabo la redistribución nodal.

Considerando que el sistema Ψ se desplaza de forma solidaria a la carga móvil, y referenciando la distribución de nodos al origen de coordenadas móviles, el indicador de redistribución ${\textstyle R}$ puede definirse como la inversa del tamaño deseado para cada elemento, según

$R={\frac {1}{s\left(\Omega ,n,\xi _{i},c\right)}},$

( 3)

de esta forma la separación ${\textstyle s\left(\Omega ,n,\xi _{i},c\right)}$ entre los nodos de la malla fina viene determinada por el propio intervalo Ω, la localización horizontal ξ_i de los n nodos distribuidos en la malla fina del subdominio de refinamiento y por el parámetro de concentración nodal c .

En este trabajo se ha optado por una distribución exponencial de los nodos, que permite concentrar más nodos en las proximidades de la zona de contacto y menos en los extremos del subdominio de remallado. El algoritmo implementado parte de la hipótesis de que existe igual número de nodos a uno y otro lado del punto de contacto, lo cual no implica una distribución simétrica ya que los límites inferior, ξ_ri , y superior, ξ_rs , del intervalo Ω no son necesariamente simétricos. Sin embargo el algoritmo sí conlleva un número impar de nodos en el subdominio de remallado para conseguir un contacto nodo-nodo, es decir, siempre existirá un nodo siguiendo el contacto móvil, distribuyéndose n_s nodos a ambos lados del contacto de forma que:

$n_{s}=\left\{{\begin{array}{cc}(n-1)/2&si\quad n\quad es{\mbox{   }}impar\\n/2-1&si\quad n\quad es{\mbox{   }}par\end{array}}\right.$

La distribución nodal exponencial implementada define la localización ξ_k de los nodos, respecto del sistema móvil, según

$\xi _{k}=\left\{{\begin{array}{cc}exp\left(1/c\right)-exp\left(1/c\right)exp\left(A(\xi _{ri})\right)&\forall \quad \xi _{k}\in \left[\xi _{ri},0\right){\mbox{   }}:{\mbox{   }}k\leq n_{s}\in \mathbb {N} ,\\exp\left(1/c\right)exp\left(A(\xi _{rs})\right)-exp\left(1/c\right)&\forall \quad \xi _{k}\in \left(0,\xi _{rs}\right]{\mbox{   }}:{\mbox{   }}k\leq n_{s}\in \mathbb {N} ,\end{array}}\right.$

( 4)

donde A (ξ ) es

$A(\xi )={\frac {k\left(c\quad ln\left(\xi +exp\left(1/c\right)\right)-1\right)}{c\quad n_{s}}}.$

Finalmente es posible definir la función ${\textstyle s\left(\Omega ,n,\xi _{i},c\right)}$ del tamaño de los elementos de la malla móvil como una simple diferencia entre los nodos que componen el elemento que ocupa la posición ξ_i , es decir el tamaño del mismo, s , queda definido como

$s\left(\Omega ,n,\xi _{i},c\right)=\xi _{ki^{+}}-\xi _{ki^{-}},$

( 5)

siendo ${\textstyle \xi _{ki^{-}}}$ y ${\textstyle \xi _{ki^{+}}}$ las localizaciones horizontales de los nodos izquierdo y derecho que definen el elemento i , respectivamente.

2.2. Acoplamiento de la malla móvil con la malla global

A continuación y una vez que se ha descrito la distribución de la malla fina móvil en el subdominio de remallado, es necesario definir su acoplamiento con la malla gruesa fija presente en todo el continuo. Desde un punto de vista algorítmico es preciso hacer notar que en cada paso de tiempo se lleva a cabo un nuevo remallado. El hecho de que el proceso de remallado no sea demasiado costoso computacionalmente en comparación con un posible mallado fino del sistema completo permite plantear la ejecución de este procedimiento paso a paso sin incurrir en tiempos de cálculo inaceptables. No obstante, los argumentos no son solo de tiempo de ejecución sino también de precisión de cálculo. En este sentido son 2 los aspectos que pueden resultar claves en la simulación y que justifican el remallado móvil: el tamaño de los elementos en la zona de contacto y la dinámica relativa a este. Respecto al tamaño de los elementos, la posible no linealidad del continuo requiere una discretización espacial muy fina en la región de contacto, no siendo tan necesaria en las regiones adyacentes. Si bien esto justifica la definición del subdominio de remallado Ω, no es motivo suficiente para que se tenga que remallar en cada instante, ya que podría emplearse un remallado útil para ciertos pasos de tiempo. Sin embargo el segundo aspecto, la dinámica del contacto, sí justifica en casos de no linealidad geométrica como las estructuras de cables el procedimiento tal y como se presenta en este trabajo. Además, la dinámica propia de este tipo de estructuras es sensible a efectos de alta frecuencia, resultando determinante en la obtención de una determinada precisión tanto la conveniente elección del integrador temporal como del método de contacto.

El ensamblado de la malla completa se lleva a cabo a 2 niveles. Por una parte se redefinen las nuevas conectividades entre los nodos de la malla primitiva y la nueva posición de la malla fina creando los pertinente elementos nuevos. Y por otra parte, y a efectos de convergencia en el cálculo, se estiman las condiciones iniciales para los nodos de la malla fina en cada paso de tiempo de la simulación dinámica. En la figura 1 se muestra esquemáticamente: una malla fina en contraposición a una malla gruesa, ambas en la parte superior de la figura y que representarían un mallado clásico; y a continuación, en la parte inferior, se presenta el seguimiento de una carga móvil por una malla fina que se superpone a una malla gruesa durante 6 instantes de tiempo. En cada instante se definen no solo los correspondientes nuevos elementos que aparecen entre la malla fina y la gruesa sino también las condiciones iniciales de cada nodo de la nueva malla fina.

Figura 1. Acoplamiento entre malla local y global para varios instantes de tiempo en los que la carga móvil se traslada.

Para la definición de las funciones de forma además de las condiciones esenciales y naturales de los elementos móviles se considerarán únicamente los nodos de la malla primitiva adyacentes al nodo de la malla fina cuyos desplazamientos se desean estimar. Así, para una estructura de, por ejemplo, elementos tipo viga Bernouilli como los descritos en referencias clásicas del método de elementos finitos Zienkiewicz y Taylor [27] , se emplean los conocidos polinomios de interpolación cúbica con continuidad C¹ de Hermite para los desplazamientos en dirección transversal a la directriz del elemento y los giros, y de interpolación lineal para los desplazamientos en dirección axial, siendo estas últimas funciones con continuidad C⁰ . Tanto para el instante inicial como para el resto de pasos de tiempo de la simulación dinámica, las posiciones, Φ_Ω (x_i ), velocidades, ${\textstyle {\dot {\Phi }}_{\Omega }(x_{i})}$ , y aceleraciones, ${\textstyle {\ddot {\Phi }}_{\Omega }(x_{i})}$ , de los nodos de la malla fina, x_i , se obtienen a partir de la interpolación de los correspondientes valores de los nodos de la malla gruesa, según

$\Phi _{\Omega }(x_{i})=N\Phi ,\quad {\dot {\Phi }}_{\Omega }(x_{i})=N{\dot {\Phi ,}}\quad {\ddot {\Phi }}_{\Omega }(x_{i})=N{\ddot {\Phi ,}}$

( 6)

donde ${\textstyle \Phi =\left[\Phi _{1}^{u},\Phi _{1}^{w},\Phi _{1}^{\theta },\Phi _{2}^{u},\Phi _{2}^{w},\Phi _{2}^{\theta }\right]^{t}}$ es el vector de los grados de libertad asociados al desplazamiento en dirección axial Φ^u , transversal ${\textstyle \Phi ^{w}}$ y el giro Φ^θ en los nodos 1 y 2 del elemento de la malla gruesa en el que se sitúa el correspondiente nodo de la malla fina, x_i , y N la matriz de las funciones de forma

$N^{t}=\left[{\begin{array}{ccc}1-x/l&0&0\\0&1-3\left(x/l\right)^{2}+2\left(x/l\right)^{3}&6\quad x/l^{2}+6x^{2}/l^{3}\\0&x\left(1-2x/l+\left(x/l\right)^{2}\right)&1-4x/l+2\left(x/l\right)^{2}\\x/l&0&0\\0&\left(x/l\right)^{2}\left(3-2x/l\right)&6\quad x\left(1-x/l\right)/l^{2}\\0&x^{2}\left(x/l-1\right)/l&x\left(3x/l-2\right)/l\end{array}}\right].$

( 7)

Así, para cada paso de tiempo los vectores globales de desplazamientos, velocidades y aceleraciones (ecuación 6 ) se construyen a partir de la interpolación de los polinomios de Hermite (ecuación 7 ), ${\textstyle H(x_{ini},s\left(\Omega ,n,\xi _{i},c\right))}$ , y los parámetros de la malla móvil.

Una vez que se establece la malla gruesa se construyen las matrices globales de masa, amortiguamiento y rigidez tangente, así como las fuerzas internas y externas. El algoritmo de reensamblado se caracteriza por 3 aspectos. En primer lugar la malla fina introduce un aumento de las dimensiones de las matrices globales. En segundo lugar es el responsable de añadir las nuevas contribuciones a las correspondientes matrices y vectores globales del sistema a partir de las nuevas interconectividades creadas en la construcción de los nuevos elementos. En tercer lugar, el algoritmo de reensamblado modifica en cada paso de tiempo las contribuciones a las matrices y vectores globales correspondientes a los nuevos elementos en su movimiento. Finalmente, en el proceso de reensamblado, las distintas discretizaciones originales y el mismo integrador temporal resultan opacos para la formación de las matrices y vectores globales.

2.3. Implementación del algoritmo en un método de elementos finitos

La formulación clásica de una estructura flexible no lineal por medio de elementos finitos puede escribirse de la forma

$M\cdot {\ddot {u}}+q\left({\dot {u}},u\right)=f$

( 8)

donde M es la matriz de masa, f y q los vectores de fuerzas externas y fuerzas internas y ${\textstyle {\ddot {u}}}$ y ${\textstyle {\dot {u}}}$ representan los vectores aceleración y velocidad nodales. Como es bien sabido, la resolución de este problema no lineal implica, además de la necesidad de un algoritmo de integración temporal, el cálculo de la matriz de rigidez tangente, definida esta como la derivada de las fuerzas internas con respecto a los desplazamientos, K_t  = ∂q /∂u , y de la matriz de amortiguamiento tangente ${\textstyle C_{t}=\partial q/\partial {\dot {u}}}$ .

En la tabla 1 se explicitan los pasos necesarios para la implementación de la metodología propuesta en un método de elementos finitos no lineal y con un algoritmo de integración tipo β -Newmark. Este algoritmo que rige el proceso de remallado móvil comprende el cálculo de equilibrio inicial del sistema con una discretización inicial, partiendo de una malla gruesa equidistribuida de elementos de longitud l sobre la parte de la estructura donde actúa la carga o contacto móvil, estando la estructura flexible únicamente sometida a su propio peso. Esto implica el cálculo de las posiciones nodales u₀ , fuerzas internas q₀ y fuerzas externas f₀ y, para el instante inicial, así como la estimación de las velocidades, ${\textstyle {\dot {u}}_{0}}$ , y aceleraciones, ${\textstyle {\ddot {u}}_{0}}$ , nodales del mallado primitivo según requiere la ecuación general de equilibrio. Posteriormente, se trata el proceso dinámico del movimiento del contacto entre la carga y la estructura. Para ello, se procede al remallado mediante la superposición dinámica de la malla móvil sobre la malla gruesa inicial y la integración temporal del fenómeno de interacción entre la carga o contacto móvil y la estructura.

Tabla 1. Algoritmo de remallado adaptativo

Discretización espacial: xini

tn+1=tn+Δt

Cálculo de la configuración de equilibrio inicial

for n=0⟶ número de pasos de tiempo

tn+1=tn+Δt

Remallado móvil en el contacto

Reensamblado de: Kt, M, Ct, qn+10 y fn+10

Predicción inicial

Evaluación del residuo: Newton-Raphson

end

3. Validación del modelo propuesto

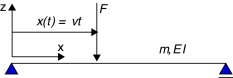
A continuación se presenta una comparación de los resultados analíticos del clásico problema de la respuesta de una viga cuando es recorrida por una carga a velocidad constante, ${\textstyle v}$ , tal y como se ilustra en la figura 2 con los resultados obtenidos para la misma situación empleando la metodología propuesta en este artículo. Despreciando los fenómenos de amortiguamiento interno, la ecuación del desplazamiento transversal, u_z (x , t ), de una viga de longitud L con propiedades uniformes para 0 ≤ x  ≤ L   y ${\textstyle 0\leq t\leq L/v}$ cuando una carga móvil, F , se desplaza sobre ésta, puede expresarse según

$m{\frac {\partial ^{2}u_{z}}{\partial t^{2}}}+EI{\frac {\partial ^{4}u_{z}}{\partial x^{4}}}=\delta (x-vt)F,$

( 9)

donde m es la masa por unidad de longitud, EI es la rigidez a flexión de la viga y δ es la función delta de Dirac. Por otra parte han de considerarse las condiciones de contorno

${\begin{array}{ccc}\left.u_{z}\right|_{x=0}&=0&\quad \left.u_{z}\right|_{x=L}=0,\\\left.{\frac {\partial ^{2}u_{z}}{\partial x^{2}}}\right|_{x=0}&=0&\quad \left.{\frac {\partial ^{2}u_{z}}{\partial x^{2}}}\right|_{x=L}=0,\end{array}}$

así como las condiciones iniciales

${\begin{array}{ccc}\left.u_{z}\right|_{t=0}=0&\quad &\left.{\frac {\partial u_{z}}{\partial t}}\right|_{t=0}=0.\end{array}}$

Figura 2. Fuerza móvil sobre viga simplemente apoyada.

3.1. Solución analítica

La solución analítica de este problema es conocida y puede encontrarse, por ejemplo, en Fryba [15] . Así, definiendo el cociente ${\textstyle \beta _{n}={\overline {\omega }}_{n}/\omega _{n}}$ siendo

$\omega _{n}^{2}={\frac {n^{4}\pi ^{4}EI}{mL^{4}}},$

( 10)

y ${\textstyle {\overline {\omega }}_{n}=n\pi v/L}$ , es posible escribir la solución al problema como

$u_{z}(x,t)=\left\{{\begin{array}{cc}{\frac {96}{\pi ^{4}}}u_{st}(L/2)\sum _{n=1}^{\infty }\Upsilon _{n}(x,t)&\quad si{\mbox{   }}\alpha \not =n,\\&\\{\frac {96}{\pi ^{4}}}u_{st}(L/2)\left(\Upsilon _{\alpha }(x,t)+\sum _{\begin{array}{c}n=1\\n\not =\alpha \end{array}}^{\infty }\Upsilon _{n}(x,t)\right)&\quad si{\mbox{   }}\alpha =n,\end{array}}\right.$

( 11)

donde u_st (L /2) es el desplazamiento estático del punto medio del vano cuando una fuerza F   actúa en dicho punto, es decir, ${\textstyle u_{st}\left(L/2\right)=F\quad L^{3}/(48\quad EI)}$ , siendo ϒ_n (x , t ) y ϒ_α (x , t ) funciones que se expresan según

$\Upsilon _{n}={\frac {1}{n^{2}(n^{2}-\alpha ^{2})}}\left[sin\left(n\pi {\frac {t}{\tau }}\right)-{\frac {\alpha }{n}}sin\left({\frac {n^{2}\pi t}{\alpha \tau }}\right)\right]sin\left(n\pi {\frac {x}{L}}\right),$

( 12)

$\Upsilon _{\alpha }={\frac {1}{2\alpha ^{4}}}\left[sin\left(\alpha \pi {\frac {t}{\tau }}\right)-{\frac {\alpha \pi t}{\tau }}cos\left(\alpha \pi {\frac {t}{\tau }}\right)\right]sin\left(\alpha \pi {\frac {x}{L}}\right),$

( 13)

donde τ   es el tiempo que tarda la carga en recorrer la viga, ${\textstyle \tau =L/v}$ , y α un parámetro adimensional definido según

$\alpha =n\beta _{n}={\frac {\pi v}{\omega _{1}L}}$

( 14)

3.2. Comparación del método propuesto con la solución analítica

De cara a comparar la solución analítica (11) con el modelo propuesto se ha discretizado una viga de 10 m de longitud con únicamente 2 elementos, sobre la que se ha superpuesto una malla móvil de 24 elementos distribuidos en un dominio de 6 m de longitud, un índice de concentración nodal c  = 3, estando la malla móvil centrada en el punto de contacto donde actúa una fuerza F de 800 N. Las características mecánicas de la viga analizada se recogen en la tabla 2 .

Tabla 2. Características mecánicas de la viga empleada en la validación

Propiedad	Valor	Unidades
Módulo de Young	2,0×1011	N/m2
Momento de inercia	1,0×10−5	m4
Masa por unidad de longitud	390	kg/m

Dado que α es una velocidad adimensional, la variación de este parámetro supone en realidad un análisis de sensibilidad de la velocidad de la carga. La tabla 3 recoge los valores de τ   y ${\textstyle v}$ obtenidos directamente, conocidas las expresiones (10) , (14) y que ${\textstyle \tau =L/v}$ , para los valores de α de 0, 25, 0, 5 y 0, 75.

Tabla 3. Valores de τ   y ${\textstyle v}$ en función de α empleados en la validación

Parámetro	α  = 0,25	α  = 0,5	α  = 0,75
τ [s]	1,78	0,89	0,59
v [m/s]	5,61	11,25	16,86

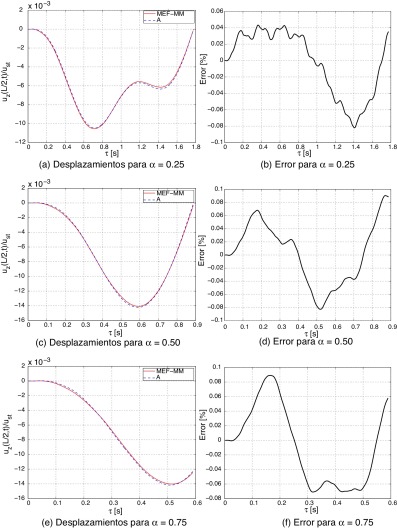
En la figura 3 se muestra la relación entre el desplazamiento dinámico en el centro de la viga u_z (L /2, t ) obtenido mediante la solución analítica deducida en (11) y el modelo propuesto basado en la malla móvil, con respecto al desplazamiento estático en el centro de la viga u_st . En las figuras 3 (a), 3 (c) y 3 (e) se muestran los resultados para velocidades adimensionales α  = 0,25, α  = 0,5 y α  = 0,75, respectivamente. Las gráficas precedentes evidencian gran semejanza entre los resultados obtenidos analítica y numéricamente, lo cual es refrendado por los valores del error absoluto que se muestra en la figura 3 (b,d,f) como función del tiempo y para distintos valores del parámetro α . En la tabla 4 se muestran los valores máximos del error para cada caso y se puede observar que son inferiores al 0, 1%.

Figura 3. Comparación de desplazamientos y errores absolutos entre el modelo de elementos finitos con malla móvil (MEF-MM) y la solución analítica (A).

Tabla 4. Valores estadísticos del error en función de α

	α  = 0,25	α  = 0,5	α  = 0,75
Máxima diferencia por defecto [%]	0,082	0,083	0,071
Máxima diferencia por exceso [%]	0,043	0,091	0,089

4. Conclusiones

En este artículo se ha presentado una metodología para el análisis de la respuesta dinámica de un continuo unidimensional bajo la acción de una carga puntual móvil. La metodología está basada en el acoplamiento de una malla móvil situada en torno al punto de contacto entre la carga móvil y el continuo unidimensional. Mientras que la malla móvil presenta una elevada densidad de elementos en torno al punto de contacto, el resto del continuo presenta una malla con una menor densidad de elementos.

Las principales diferencias que presenta la metodología propuesta con respecto a otros enfoques son: (i) el movimiento de la malla, creando y destruyendo los nodos correspondientes en cada paso de tiempo alrededor de la carga móvil; (ii) la relación del contacto con la la malla móvil, consiguiendo un contacto nodo a nodo en todo instante, y (iii) la integración de la metodología en un esquema suficientemente flexible como para abordar la simulación dinámica de estructuras flexibles, por ejemplo estructuras de cables.

La metodología propuesta se ha validado con respecto la solución analítica de una carga móvil actuando sobre una viga bi-apoyada, cuyos resultados presentan errores con respecto la solución analítica inferiores al 0, 1%. En este trabajo no se ha cuantificado la reducción del coste computacional del método propuesto frente a otros modelos de elementos finitos clásicos, ya que la validación exigiría abordar aplicaciones más complejas y que escapan al alcance de este artículo.

Agradecimientos

Los resultados aquí presentados han sido obtenidos en el desarrollo de diversos proyectos financiados parcialmente por el Colegio Nacional de Ingenieros del ICAI, Cosemel Ingeniería y el Ministerio de Ciencia y Tecnología a través de los proyectos de Plan Nacional TRAN2009-13912-C02-02/TREN y TRA2012-37940.

References

1. [1] M. Olsson; Finite element, modal co-ordinate analysis of structures subjected to moving loads; J. Sound Vibr., 99 (1985), pp. 1–12
2. [2] G. Visweswara; Linear dynamics of an elasctic beam under moving loads; J. Vib. Acoust., 122 (2000), pp. 281–289
3. [3] R. Katz, C.W. Lee, A.G. Ulsoy, R.A. Scott; Dynamic stability and response of a beam subject to a deflection dependent moving load; J. Vib. Acoust. Stress. Reliab. Des., 109 (1987), pp. 361–365
4. [4] J.E. Akin, M. Mofid; Numerical solution for response of beams with moving mass; J. Struct. Eng., 115 (1989), pp. 120–131
5. [5] D. Bruno, F. Greco, P. Lonetti; Dynamic impact analysis of long span cable-stayed bridges under moving loads; Eng. Struct., 30 (2008), pp. 1160–1177
6. [6] D.H.Y. Yen, C.T. Sing; On the non-linear response of an elastic string to a moving load; Int. J. Non-Linear Mech., 5 (1970), pp. 465–474
7. [7] A.V. Metrikine; Stationary waves in a nonlinear elastic system interacting with a moving load; Acoust. Phys., 40 (1994), pp. 573–576
8. [8] M. Olsson; On the fundamental moving load problem; J. Sound Vibr., 145 (2) (1991), pp. 299–307
9. [9] G. Lefeuve-Mesgouez, D. le Houedec, A.T. Peplow; Ground vibration in the vicinity of a high-speed moving harmonic strip load; J. Sound Vibr., 231 (5) (2000), pp. 1289–1309
10. [10] M. Adam, G. Pflanz, G. Schmid; Two- and three- dimensional modelling of half space and train-track embankment under dynamics loading; Soil. Dyn. Earthq. Eng., 19 (2000), pp. 559–573
11. [11] C.G. Koh, J.S.Y. Ong, D.K.H. Chua, J. Feng; Moving element method for train-track dynamics; Int. J. Numer. Meth. Eng., 56 (2003), pp. 1549–1567
12. [12] C.G. Koh, G.H. Chiew, C.C. Lim; A numerical method for moving load on continuum; J. Sound Vibr., 300 (2007), pp. 126–138
13. [13] V.H. Nguyen, D. Duhamel; Finite element procedures for nonlinear structures in moving coordinates. part I: Infinite bar under moving axial loads; Comput. Struct., 84 (2006), pp. 1368–1380
14. [14] V.H. Nguyen, D. Duhamel; Finite element procedures for nonlinear structures in moving coordinates. part II: Infinite beam under moving harmonic loads; Comput. Struct., 86 (2008), pp. 2056–2063
15. [15] L. Fryba; Vibrations of Solids and Structures Under Moving Loads; Noordhoff International Publishing, Groningen (1999)
16. [16] C.Z. Qian, J.S. Tang; A time delay control for a nonlinear dynamic beam under moving load; J. Sound Vibr., 309 (2008), pp. 1–8
17. [17] I. Babuška, K. Aziz; On the angle condition in the finite element method; SINUM, 13 (1976), pp. 214–226
18. [18] C.A. Fellipa; Optimization of finite element grids by direct energy search; App. Math. Modelling, 1 (1976), pp. 93–96
19. [19] J.H. Cheng; Adaptive grid optimization for structural analysis – geometry-based approach; CMAME, 107 (1993), pp. 1–22
20. [20] J.Z. Zhu, O.C. Zienkiewicz; Adaptive techniques in the finite element method; Appl. Num. Methods, 4 (1988), pp. 197–204
21. [21] I. Babuška, B. Szabe, I.N. Katz; The p-version of the finite element method; SINUM, 18 (1981), pp. 515–545
22. [22] O. Moller, M. Rubinstein; Análisis dinámico no lineal físico y geométrico de barras: discusión del campo de aplicación de teorías aproximadas; Rev. Int. Metod. Numer. Calc. Dise., 11 (2) (1995), pp. 151–182
23. [23] A. Huerta, A. Rodriguez-Ferran, P. Diez, J. Sarrate; Adaptive finite element strategies based on error assessment; Int. J. Numer. Meth. Eng., 46 (1999), pp. 1803–1818
24. [24] G. Pijaudier-Cabot, L. Bode, A. Huerta; Arbitrary Lagrangian-Eulerian finite element analysis of strain localization in transient problems; Int. J. Numer. Meth. Eng., 38 (1995), pp. 4171–4191
25. [25] A. Huerta, F. Casadei; New ALE applications in non-linear fast-transient solid dynamics; Eng. Comput., 11 (1994), pp. 317–345
26. [26] A. Huerta, W.K. Liu; Viscous flow with large free surface motion; CMAME, 69 (1988), pp. 277–324
27. [27] O.C. Zienkiewicz, R.L. Taylor; The Finite Element Method; McGraw-Hill, New York (1991)