Aplicación de los métodos iterativos a la solución de sistemas de ecuaciones lineales para el control de columnas de destilación con integración de energía.

Resumen

La destilación es la técnica de separación más común para mezclas líquidas con dos o más componentes. Mediante el uso de etapas en serie se logran separaciones de alta pureza que no son viables por otros medios. El principal inconveniente de la destilación tradicional es su enorme consumo de energía, para reducirlo se han empleado diversas metodologías de integración energética (IE), que en esencia buscan usar las corrientes calientes de salida (que queremos enfriar) para calentar los materiales fríos que entran al proceso o para generar vapor y energía eléctrica en equipos de cogeneració n, para así reducir el consumo de energía y servicios de enfriamiento. El modelo dinámico de una columna de destilación, para los casos tradicional e integrado, se puede describir como un sistema de ecuaciones diferenciales ordinarias de primer orden que incluye los balances de materia y energía de cada etapa, cuando este modelo se lleva al estado estable, se transforma en un sistema de ecuaciones algebraicas no lineales. En este trabajo se aplican diversos métodos de solución al sistema de ecuaciones no lineales, mostrando sus ventajas y desventajas, as í como algunos problemas de convergencia que se presentan durante su solución numérica.

Palabras Clave. Control,sistemas de ecuaciones, integración de energía.

Iterative methods applied to the solution of linear equation systems found in heat integrated distillation column control

Distillation is the most common separation technique for liquid mixtures containing two or more components. High purity separations, unachievable with other techniques, can be obtained using multiple distillation stages in series. Traditional distillation's main drawback is its intensive energy demand. Several energy integration technologies have been developed to cope with it. Essentially integration uses hot currents in need of cooling to heat incoming cold currents, to generate steam or electric power in cogeneration equipment. Traditional and heat integrated distillation column dynamic mathematical models are described by first order ordinary linear differential equation systems, including equilibrium relationships, mass and energy balances for each stage. The steady state for the same model is represented by non linear algebraic equations. In this paper several iterative methods are used to solve those systems, showing their relative advantages. System structure lends itself to convergence problems that are also studied

keywords. Control, nonlinear equations systems, energy  integration.    

1 Introducción

La destilación es el proceso de separación dominante en las industrias de refinación, procesos químicos y bioquímica, en parte porque permite purificar con relativa facilidad mezclas fluidas de dos o más componentes, los principios en los que se basa son bien conocidos y sobre todo, porque su costo es menor que el de otras técnicas capaces de lograr un resultado equivalente.

Las columnas de destilación (CD) son una parte importante de cualquier industria de procesos, su función típica es dividir una mezcla l íquida, aplicando calentamiento para generar dos corrientes, de composición diferente a la original, con el componente más volá til concentrándose en la parte superior (ligeros) y el menos volátil por la parte baja (pesados, residuo o fondos). Debido a la multitud de usos que se le han dado, hay casi tantas técnicas de destilación como aplicaciones y se pueden dividir en continua o por lotes; simple, por etapas o extractiva; binaria o multicomponente; reactiva; atmosférica, a vac ío, presión positiva y de alta presión; por arrastre de vapor, con inyección de vapor y muchas más.[1]

1.1 Volatilidad y equilibrio termodinámico.

Todas estas variantes aprovechan la diferencia de volatilidad entre los componentes de la mezcla alimentada para lograr la separación diferenciada en líquido y vapor; aplicando el concepto de etapa de equilibrio para estimar las composiciones de las dos fases generadas y es una idealización que permite estimar las composiciones del líquido y el vapor saliendo de la etapa si se conoce la presión y temperatura dentro de ella y en conjunto con los balances de materia y energía pertinentes permiten diseñar el equipo y su sistema de control sin necesidad de conocer de antemano los patrones de flujo y las velocidades de transferencia de calor dentro de él.

El estado de equilibrio termodinámico es una condición estática donde las propiedades macroscópicas de un sistema aislado de sus alrededores no cambian con el tiempo

Para un sistema cerrado con una mezcla líquido-vapor en equilibrio no hay tendencia al cambio entre las fases: La temperatura y presión se han igualado y las composiciones de cada fase se mantienen fijas. Aún as í, a nivel molecular las condiciones nunca son estáticas. Muchas mol éculas de cruzan la interfase y se integran a la otra pero la velocidad de transferencia en las dos direcciones será la misma y el transporte total entre fases es nulo[2]. En un sistema abierto análogo las masas de líquido y vapor en el plato (o la sección equivalente en una columna empacada) con sus composiciones a las condiciones locales de presi ón y temperatura constituyen una etapa de equilibrio.

En la descripción previa, se menciona la composición, que en destilación es una variable de importancia :las formas más comunes de expresar la composición son la fracción masa, fracción mol y concentración molar.

La fracción masa y fracción mol se definen como la relación entre la masa o el número de moles de un componente en una mezcla o solución sobre la masa total o los moles totales en la mezcla o soluci ón.

Si el subíndice ${\textstyle i}$ denota a un cierto componente de la mezcla, sus fracciones masa y mol son: ${\textstyle w_{i}={\frac {m_{i}}{m}}}$ y ${\textstyle x_{i}={\frac {n_{i}}{n}}}$

Donde el número de moles de una sustancia se obtiene dividiendo su masa entre su peso molecular, ambos expresados en gramos ${\textstyle n_{i}={\frac {m_{i}}{PM_{i}}}}$.

La suma de las fracciones de todos los componentes de la mezcla, tanto masa como mol es igual a uno ${\textstyle \sum _{i}w_{i}=1}$, ${\textstyle \sum _{i}x_{i}=1}$.

1.2 Destilación simple

A pesar de la multitud de variantes, para entender los aspectos principales de la destilación basta con analizar la destilación simple por etapas, pues sus principios son los mismos que en columnas complejas.

La mezcla a separar se alimenta como líquido o mezcla lí quido-vapor en algún punto cerca del centro de la torre y en el plato respectivo se mezcla con el líquido y vapor provenientes de otras etapas, la fracción no vaporizada de la alimentación cae con el l íquido del plato.

En el fondo de la columna se encuentra el rehervidor - también llamado reboiler - que es donde se suministra la energía necesaria para lograr la separación. El vapor generado fluye hacia arriba y en cada etapa va ganando un poco más de los componentes ligeros. El vapor abandona la columna por la parte superior y se condensa en su totalidad. El líquido obtenido se separa en producto destilado y reflujo de destilado a la torre.

El líquido cae hacia el fondo de la columna ganando pequeñas fracciones de componentes pesados y cediendo ligeros en cada etapa. El l íquido que sale de la columna se divide en el producto pesado que se extrae del sistema y el resto es la fracción a vaporizar que se manda al rehervidor.

1.3 Integración de Procesos

El principal inconveniente de la destilación es su demanda intensiva de energía, con sus problemas asociados de inversión en equipo, combustibles e impacto ambiental significativo. Para reducirlo se ha generado multitud de diseños[3] y una rama completa de termodinámica aplicada, que es la Integración de Procesos. Hay varias escuelas de an álisis y aplicación de la integración, pero en esencia buscan usar las corrientes calientes de salida (que queremos enfriar) para calentar los materiales fríos que entran al proceso o para generar vapor y energ ía eléctrica en equipos de cogeneración para así reducir el consumo total de energía y servicios de enfriamiento. Su aplicaci ón representa beneficios en varios niveles: ahorro de combustibles y servicios de calentamiento innecesarios, costo de bombeo y tratamiento de agua de enfriamiento; reducción de emisiones contaminantes y del impacto ambiental general al bajar la contaminación térmica descargada a la atmósfera en las torres de enfriamiento, entre otras cosas. En una de sus primeras aplicaciones -en Imperial Chemical Industries, 1980- se lograron ahorros de energía del 30% respecto al diseño tradicional, con resultados similares en varios proyectos que le siguieron; con lo que se validó de inmediato la aplicación práctica del concepto teórico [4]. La integración también presenta inconvenientes, como el riesgo de inestabilidad implícito en el cruce corrientes de distintas áreas de operación, pues un problema menor en un punto puede extenderse por todo el sistema hasta detener la operaci ón. Aún en los casos menos serios se introducen lazos de control anidados que no siempre se pueden desacoplar, y se hace difícil mantener estables la operación y además de la interacción entre corrientes calientes y frías, la mayor parte del equipo de intercambio tiene comportamiento no lineal [5], igual que los modelos de predicción de propiedades termodinámicas y los de estimación del equilibrio de fases [6].

2 Metodología

2.1 Modelo matemático

Durante la operación, la columna debe cumplir con los objetivos de proceso en presencia de perturbaciones externas. Esos objetivos suelen ser la fracción de recuperación de un componente clave -destilado o de fondos- o cierta composición mínima de un componente en esas mismas corrientes. Para entender como interactúan las variables de proceso, describir su comportamiento en conjunto y tal vez estimarlo, se necesita una estructura que haga uso de las variables, funciones y reglas de asociació n descritas y entregue resultados análogos a los del sistema analizado, que en este caso es su modelo termodinámico.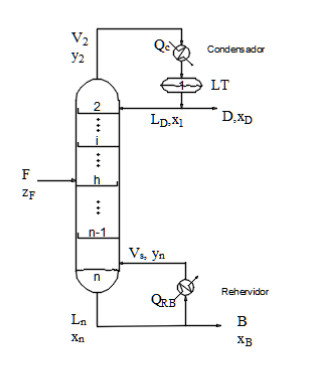

Figura 1: Columna tradicional con n etapas

Para una columna tradicional -como la mostrada en la figura 1- el modelo matemático suele incluir las ecuaciones de balance de masa y energí a -generales y por etapa-, las ecuaciones de equilibrio entre fases, la relación de retorno de pesados en el fondo y el reflujo de destilado, entre otras. En el caso de simulación y control, deben aplicarse las ecuaciones de balance en función del tiempo, considerando términos de acumulación de masa y energía. A estos se les conoce como balances dinámicos del sistema y al modelo resultante como modelo din ámico. Para describir el estado estable basta un sistema de ecuaciones algebraicas pues al tomar condiciones promediadas en el tiempo los té rminos de acumulación - derivadas respecto al tiempo- son cero; mientras que para describir ese mismo sistema con referencia al tiempo, es necesario emplear ecuaciones diferenciales ordinarias, y si se toman en cuenta gradientes de composición, temperatura, presión o velocidad de flujo por sección podrá necesitar de ecuaciones diferenciales parciales para desarrollar las ecuaciones de balance en estado inestable, además de las algebraicas correspondientes.

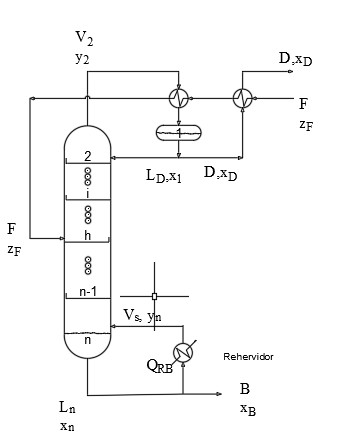
Figura 2: Columna intregrada n platos

Para fines de exposición se supone que las etapas están formadas por charolas de platos perforados que permiten el paso del vapor y con rebosadero para la salida de líquido.

La columna consta de n etapas numeradas desde el condensador -etapa 1- hasta el rehervidor parcial -etapa n- y la de alimentación es la etapa h.

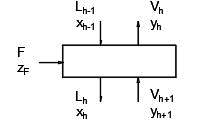
Figura 3: Etapa de alimentacion

Si la alimentación tiene ${\textstyle nc}$ componentes el balance de masa global para la etapa de alimentación es:

${\frac {dm_{f}}{dt}}=L_{h-1}+V_{h+1}+F-L_{h}+V_{h}$ (1)

El balance por componente para cada ${\textstyle j}$ entre ${\textstyle j=1}$ y ${\textstyle nc-1}$:

${\frac {dx_{f,j}m_{f}}{dt}}=L_{h-1}x_{h-1,j}+V_{h+1}y_{h+1,j}+Fz_{F,j}-L_{h}x_{h,j}+V_{h}y_{h,j}$ (2)

El balance de energía para la etapa:

${\frac {d(m_{F}h_{F})}{dt}}=L_{h-1}h_{h-1}+V_{h+1}h_{h+1}+Fh_{F}-L_{h}h_{h}+V_{h}h_{h}$ (3)

Donde ${\textstyle m_{f}}$ es la masa retenida en la etapa y la derivada representa su variación respecto al tiempo.

El flujo molar de vapor y líquido se denotan con ${\textstyle v}$ y ${\textstyle l}$ . Los sub índices ${\textstyle h-1,h}$ y ${\textstyle h+1}$se refieren a la etapa de donde sale la corriente; ${\textstyle x_{k,,j}}$es la fracción mol de componente ${\textstyle j}$en el lí quido saliendo de la etapa ${\textstyle k.}$

Si se tratara de una mezcla de cincuenta hidrocarburos estaríamos viendo, solo en la alimentación, cincuenta y una ecuaciones de balance y cincuenta relaciones de equilibrio entre las composiciones en el lí quido y vapor. Para hacer manejable el análisis se hace necesario introducir algunas suposiciones y simplificaciones:

• Se considera destilación binaria. Como la suma de fracciones mol es igual a uno, los balance se expresarán en términos del componente ligero y la fracción del componente pesado (componente 2) se obtiene por diferencia.

• Suponiendo que la alimentación entra a la columna en lo que se conoce como plato de alimentación (h) con dos componentes, al ingresar a la charola entra en contacto con el vapor y líquido que se encuentran ah í. Si el mezclado es adecuado se puede seguir con la hipótesis de que el líquido que cae y el vapor que sale de esa etapa está en equilibrio, pero considerando la aportación de la corriente alimentada a la composición de la mezcla en el plato.

• Si el calor latente de vaporización de los dos componentes es similar se puede considerar que el componete pesado que condensa en cada etapa produce la evaporación de una cantidad igual del componente ligero.

• No hay retención de vapor en ninguna etapa.

• El volumen de líquido en cada etapa es el mismo.

• Si la columna está bien aislada, se alimenta energía al sistema solo en el rehervidor y se retira solo en el condensador se pueden obviar los balances de energía por etapa.. El calor retirado en el condensador lleva al destilado a líquido saturado, sin subenfriar.

• Como se están definiendo las ecuaciones de balance en el condensador y rehervidor en términos de material condensado y vaporizado, el sistema es directamente aplicable a columnas con integraci ón de energía. En cada caso se hace necesario encontrar la relaci ón fundional ${\textstyle F=f(V_{S},L_{D})}$

• El volumen de líquido en el tanque de destilado es constante.

• No hay acumulación de líquido en el rehervidor.

• El estado de fase de la alimentación se define con la calidad de la alimentación: ${\textstyle q_{F}}$ que varía de 1 para el líquido saturado a 0 para el vapor saturado

La etapa de alimentación h divide efectivamente la destilacion en dos secciones bien diferenciadas: encima de la alimentación está la zona de rectificación o enriquecimiento, por debajo de ella está la zona de agotamiento.

Debido a las condiciones de no retención de vapor en ninguna etapa y al no haber acumulación de líquido en ellas, el flujo de vapor y l íquido en las secciones de rectificación y agotamiento es constante de una etapa a otra, salvo en la propia etapa de alimentación. Para cualquier etapa ${\textstyle i}$

$V_{i}=V_{i+1}=V_{i-1}$ (4)

$L_{i}=L_{i+1}=L_{i-1}$ (5)

Alimentación

El flujo molar de vapor que sale de esta etapa es:

$V_{h}=V_{h+1}+F(1-q_{F})$

(6)

y el flujo de líquido saliendo de ella:

$L_{h}=L_{h-1}+Fq_{F}$

(7)

Condensador

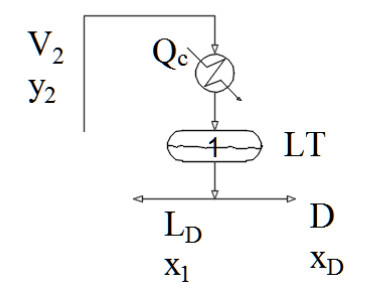
Figura 4: Condensador

$L_{D}+D=L_{2}$

(8)

Rehervidor

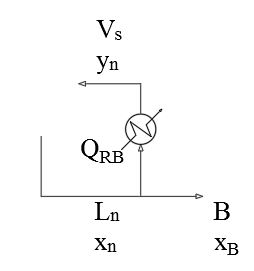
Figura 5: Rehervidor

$B=L_{n-1}-V_{s}$

(9)

Zona de rectificación

$L_{i}=L_{R}=L_{D}$

(10)

$V_{s}=V_{RB}+F(1-q_{F})$

Zona de agotamiento

$L_{i}=L_{S}=L_{R}+Fq_{F}$

(11)

$V_{R}=V_{RB}$

(12)

Los subíndices S, R y RB se refieren a flujos molares en la zona de enriquecimiento, agotamiento y en el rehervidor, respectivamente.

2.2 Modelo dinámico simplificado

Las ecuaciones el balance de componente ligero en cada sección son:

Condensador-Tanque de destilado (etapa 1)

$m_{1}{\frac {dx_{1}}{dt}}=V_{R}(y_{2}-x_{1})$

(13)

Zona de rectificación (etapas ${\textstyle \mathbf {i=2} }$ a ${\textstyle \mathbf {h-1} }$):

$m_{i}{\frac {dxi}{dt}}=L_{R}(x_{i-1}-x_{i})+V_{R}(y_{i+1}-y_{i})$

(14)

Alimentación

$m_{h}{\frac {dx_{h}}{dt}}=L_{R}x_{h-1}-L_{S}x_{h}+V_{S}y_{h+1}-V_{R}y_{h}+Fz_{F}$

(15)

Agotamiento (etapas ${\textstyle \mathbf {i=h+1} }$ a ${\textstyle \mathbf {n-1} }$ ):

$m_{i}{\frac {dxi}{dt}}=L_{S}(x_{i-1}-x_{i})+V_{S}(y_{i+1}-y_{i})$

(16)

Rehervidor

$m_{RB}{\frac {dxi}{dt}}=L_{S}x_{n-1}-Bx_{n})+V_{S}y_{n}$

(17)

Una de las formas más sencillas de expresar la relación entre la fracción mol en el vapor y la del líquido en equilibrio es:

$y_{i}={\frac {\alpha x_{i}}{1+(\alpha -1)x_{i}}}$

(18)

Donde ${\textstyle \alpha }$ es la volatilidad relativa entre los dos componentes, esta relación solo es constante para soluciones ideales donde ambos componentes tienen el mismo calor latente de vaporización

2.3 Modelo en estado estable simplificado

Las ecuaciones el balance de componente ligero en cada sección son:

Condensador-Tanque de destilado (etapa 1)

$V_{R}(y_{2}-x_{1})=0$

(19)

Zona de rectificación (etapas ${\textstyle \mathbf {i=2} }$ a ${\textstyle \mathbf {h-1} }$):

$L_{R}(x_{i-1}-x_{i})+V_{R}(y_{i+1}-y_{i})=0$

(20)

Alimentación

$L_{R}x_{h-1}-L_{S}x_{h}+V_{S}y_{h+1}-V_{R}y_{h}+Fz_{F}=0$

(21)

Agotamiento (etapas ${\textstyle \mathbf {i=h+1} }$ a ${\textstyle \mathbf {n-1} }$ ):

$L_{S}(x_{i-1}-x_{i})+V_{S}(y_{i+1}-y_{i})=0$

(22)

Rehervidor

$L_{S}x_{n-1}-Bx_{n}+V_{S}y_{n}$

(23)

Relación entre la fracción mol en el vapor y la del líquido en equilibrio :

$y_{i}={\frac {\alpha x_{i}}{1+(\alpha -1)x_{i}}}$

(24)

A primera vista parece un sistema de ecuaciones lineales, pero no es así , pues ${\textstyle y}$ es no lineal en la variable de estado y aparece en todas las ecuaciones, haciendo el sistema no lineal incluso cuando ${\textstyle \alpha }$ es constante.

3 RESULTADOS

Muchos paquetes de software contienen rutinas para resolver sistemas de ecuaciones no lineales, normalmente basados en un método quasi-Newton. Estas rutinas suelen ser confiables dentro de su zona de aplicación, pero cuando falla el algoritmo, las indicaciones para encontrar el problema origen son limitadas. Para el estado estable en columnas de destilación (integradas o tradicionales) el sistema obtenido presenta peculiaridades que en ocasiones generan esas fallas.

Para entenderlo mejor se desarrolla a continuación un problema clá sico tomado de la literatura [7]: Se debe encontrar la composición del l íquido en cada etapa dados los siguientes datos.- ${\textstyle F=}$ ${\textstyle 1}$ mol/min ${\textstyle z_{F}=0.5}$, ${\textstyle \alpha =1.5}$ ,${\textstyle L_{D}=2.706}$ mol/min, ${\textstyle D=0.5}$ mol/min y ${\textstyle q_{F}=1.0}$ en una columna de cinco etapas.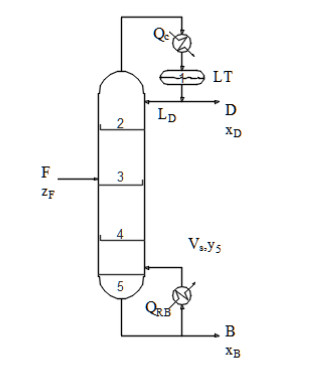

Figura 6: Columna estandar cinco etapas

El sistema simplificado queda:

$f_{1}=-x_{1}+y_{2}=0$ (25) $f_{2}=L_{R}x_{1}-L_{R}x_{2}-V_{R}y_{2}+V_{R}y_{3}=0$ $f_{3}=0+L_{R}x_{2}-L_{S}x_{3}-V_{R}y_{3}+V_{S}y_{4}+Fz_{F}=0$ $f_{4}=0+0+L_{S}x_{3}-L_{S}x_{4}-V_{S}y_{4}+V_{S}y_{5}=0$ $f_{5}=0+0+0+L_{S}x_{4}-Bx_{5}-V_{S}y_{5}=0$ $y_{i}={\frac {\alpha x_{i}}{1+(\alpha -1)x_{i}}}$ (26)

Que es prácticamente un sistema tridiagonal con términos no lineales sobre la diagonal principal y un término constante fuera del esquema. Estos suelen resolverse mediante el método de Newton multivariable donde se busca un vector de valores de ${\textstyle \mathbf {x} }$ que cumpla la condición:

$\mathbf {f} (\mathbf {x} )=\mathbf {0}$

(27)

mediante el algoritmo

$\mathbf {x} _{k+1}=\mathbf {x} _{k}-\mathbf {J} _{k}^{-1}\mathbf {f} (\mathbf {x} _{k})$

(28)

con el Jacobiano definido por:

$\mathbf {J} =\left[{\begin{array}{cccc}{\frac {\partial f_{1}}{\partial x_{1}}}&{\frac {\partial f_{1}}{\partial x_{2}}}&\bullet &{\frac {\partial f_{1}}{\partial x_{n}}}\\{\frac {\partial f_{2}}{\partial x_{1}}}&{\frac {\partial f_{2}}{\partial x_{2}}}&\bullet &{\frac {\partial f_{2}}{\partial x_{n}}}\\\bullet &\bullet &\bullet &\bullet \\{\frac {\partial f_{n}}{\partial x_{1}}}&\bullet &\bullet &{\frac {\partial f_{n}}{\partial x_{n}}}\end{array}}\right]$

(29)

en (30) ${\textstyle x_{k}}$ es el vector de valores de composición del líquido en la iteración previa.

Casi cualquier paquete de software matemático tiene una función est ándar para resolver sistemas no lineales con este método, pero para el modelo específico que se trata, se encontraron zonas donde no hay convergencia y la paquetería no da información acerca de la causa de falla, que para un sistema de control puede ser fatal.

Al no poder resolver el sistema consistentemente por ese camino, se atacó el problema usando una variante del mismo método de Newton multivariable con el algoritmo

$\mathbf {f} (\mathbf {x} _{k})+\mathbf {J} _{k}(\mathbf {x} _{k+1}-\mathbf {x} _{k})=\mathbf {0}$

(30)

Con lo que se transforma en un sistema de ecuaciones lineales, donde para cada iteración se conocen los valores de ${\textstyle \mathbf {x} _{k}}$, ${\textstyle \mathbf {f} (\mathbf {x} _{k})}$ y ${\textstyle \mathbf {J} _{k}}$ que se puede resolver usando los mé todos de Gauss simple, Gauss Jordan, Gauss Seidel, Jacobi, sobre relajamiento, etc.

Para el sistema de ecuaciones de la columna de cinco etapas:

$J_{k}=\left[{\begin{array}{ccccc}{\frac {\partial f_{1}}{\partial x_{1}}}&{\frac {\partial f_{1}}{\partial x_{2}}}&{\frac {\partial f_{1}}{\partial x_{3}}}&{\frac {\partial f_{1}}{\partial x_{4}}}&{\frac {\partial f_{1}}{\partial x_{5}}}\\{\frac {\partial f_{2}}{\partial x_{1}}}&{\frac {\partial f_{2}}{\partial x_{2}}}&{\frac {\partial f_{2}}{\partial x_{3}}}&{\frac {\partial f_{2}}{\partial x_{4}}}&{\frac {\partial f_{2}}{\partial x_{5}}}\\{\frac {\partial f_{3}}{\partial x_{1}}}&{\frac {\partial f_{3}}{\partial x_{2}}}&{\frac {\partial f_{3}}{\partial x_{3}}}&{\frac {\partial f_{3}}{\partial x_{4}}}&{\frac {\partial f_{3}}{\partial x_{5}}}\\{\frac {\partial f_{4}}{\partial x_{1}}}&{\frac {\partial f_{4}}{\partial x_{2}}}&{\frac {\partial f_{4}}{\partial x_{3}}}&{\frac {\partial f_{4}}{\partial x_{4}}}&{\frac {\partial f_{4}}{\partial x_{5}}}\\{\frac {\partial f_{5}}{\partial x_{1}}}&{\frac {\partial f_{5}}{\partial x_{2}}}&{\frac {\partial f_{5}}{\partial x_{3}}}&{\frac {\partial f_{5}}{\partial x_{4}}}&{\frac {\partial f_{5}}{\partial x_{5}}}\end{array}}\right]_{k}$

(31)

Si se obtienen las derivadas parciales del primer renglón:

${\frac {\partial f_{1}}{\partial x_{1}}}=-1$

${\frac {\partial f_{1}}{\partial x_{2}}}=0+{\frac {\partial y_{2}}{\partial x_{2}}}={\frac {\alpha }{\left[1+(\alpha -1)x_{2}\right]^{2}}}$

sustituyendo en el Jacobiano de la iteración ${\textstyle k}$, este queda

$\mathbf {J} _{k}=\left[{\begin{array}{ccccc}-1&\zeta _{2}&0&0&0\\L_{R}&-L_{R}-V_{R}\zeta _{2}&V_{R}\zeta _{3}&0&0\\0&L_{R}&-L_{s}-V_{R}\zeta _{3}&V_{S}\zeta _{4}&0\\0&0&L_{s}&-L_{s}-V_{S}\zeta _{4}&V_{S}\zeta _{5}\\0&0&0&L_{s}&-B-V_{S}\zeta _{5}\end{array}}\right]_{k}$

(32)

donde ${\textstyle \zeta _{i}}$ se define mediante

$\zeta _{i}={\frac {\partial y_{i}}{\partial x_{i}}}{\hbox{ y }}{\frac {\partial y_{i}}{\partial x_{i}}}={\frac {\alpha }{\left[1+(\alpha -1)x_{i}\right]^{2}}}$

Para el caso de la literatura ${\textstyle \alpha =1.5}$ ,${\textstyle L_{R}=2.706}$, ${\textstyle V_{R}=3.206}$, ${\textstyle L_{S}=2.706}$, ${\textstyle V_{S}=3.206}$ y ${\textstyle B=0.5}$ que sustituidos en (25) queda:

$f_{1}=-x_{1}+y_{2}$ (33) $f_{2}=2.706x_{1}-2.706x_{2}-3.206y_{2}+3.206y_{3}$ $f_{3}=2.706x_{2}-3.706x_{3}-3.206y_{3}+3.206y_{4}+0.5$ $f_{4}=3.706x_{3}-3.706x_{4}-3.206y_{4}+3.206y_{5}$ $f_{5}=3.706x_{4}-0.5x_{5}-3.206y_{5}$

El vector de valores iniciales ${\textstyle \mathbf {x} _{0}}$ son las composiciones supuestas del componente ligero en la fase líquida para cada una de las etapas. Como la fracción de este es máxima en el condensador, mí nima en el rehervidor y sus valores están acotados entre cero y uno, se genera el vector inicial asignando un valor ligeramente mayor de cero a la fracción de ligero en la corriente de fondos, ligeramente menor a uno a la fracción en el destilado e interpolando linealmente para los valores de las etapas intermedias. Para las cinco etapas el vector sería:

$\mathbf {x} _{0}=\left[{\begin{array}{c}0.990\\0.745\\0.500\\0.255\\0.010\end{array}}\right]$

(34)

Para resolver el sistema generado en (30) se usaron los métodos clásicos ya mencionados y se alcanza la convergencia cuando:

$\mathbf {x} =\left[{\begin{array}{c}0.6693\\0.5743\\0.4887\\0.4129\\0.3307\end{array}}\right]$

(35)

4 CONCLUSIONES

El modelo que se obtiene del planteamiento de los balances en términos de composiciones y flujos por etapa en el estado estable genera un sistema de ecuaciones no lineales con arreglo en banda parcial. La convergencia del sistema es altamente dependiente de los valores relativos de la alimentaci ón, los flujos internos ${\textstyle L_{S},L_{R},V_{R},V_{S}}$ y la volatilidad relativa ${\textstyle \alpha }$. Al aplicar el modelo a la determinación de la fracci ón mol de componente ligero en el producto destilado y de fondos con los valores proporcionados en el ejemplo se encontró que hay funciones de paquetería estándar que abortan el proceso y reportan que la configuración no es correcta, mientras que otras la resuelven cambiando de rutina interna, pero al hacer variar el reflujo (${\textstyle L_{D})}$ se encontraron intervalos donde los métodos internos del software no convergen. Al aplicar en los mismos casos el método de Newton en términos de ecuaciones lineales se encuentra que no hay ningún método que garantice la solución de todos los casos, pero el más robusto en t érminos generales fue el de Gauss Seidel.

Los problemas de convergencia al parecer están relacionados con la ausencia de diagonal dominante en el sistema y problemas de mal condicionamiento al variar los valores de los parámetros del mismo.

Una ventaja notable del uso de los sistemas de ecuaciones simultáneas es que al presentarse fallas se puede establecer con cierta facilidad un á rbol de decisiones con selección secuencial de métodos para resolver cada caso.

5 REFERENCIAS

[1] Roper, Keith D.; Seader, J.D.; Henley, E. J. (2010). Separation Process Principles. (3rd, Ed.). John Wiley & Sons, Inc.

[2] Sandler, S. I. (2006). Chemical Biochemical And Engineering Thermodynamics. John Wiley & Sons, Inc. (Fourth). John Wiley & Sons, Inc.

[3] Mustafa, M. F., Ibrahim, N., Fazli, N. A., Samad, A., Ibrahim, K. A., Kamaruddin, M., & Hamid, A. B. D. (2014). Design of Energy Efficient Distillation Columns for Separation of Oxygenates Process. In ISIGMA 2014 (Vol. 1, pp. 1–8).

[4] Kemp, I. C; Linnhoff, B. (2007). Pinch Analysis and Process Integration. Pinch Analysis and Process Integration (Second). Butterworth-Heinemann.

[5] Rubio-Maya, C., Pacheco-Ibarra, J. J., Gutiérrez Sanchez, H. C., Mendoza-Covarrubias, C., Martinez Patiño, J., & Picón Nuñez, M. (2009). Aproximaciones de la diferencia media logarítmica de temperatura (DMLT) en problemas de optimización matemática, aplicaci ón al problema CGAM. 1. Memorias Del XV Congreso Internacional Anual de La SOMIM, 1024–1030.

[6] Gundersen, T. (1982). Numerical aspects of the implementation of cubic equations of state in flash calculation routines. Computers and Chemical Engineering, 6(3), 245–255. http://doi.org/10.1016/0098-1354(82)80015-X

[7]Bequette, B. W. (1998). Process dynamics. Modeling, Analysis and Simulation. Prentice Hall PTR Prentice-Hall.